有限元钢架结构分析~手算+matlab+ansys模拟
钢架模型ansys计算
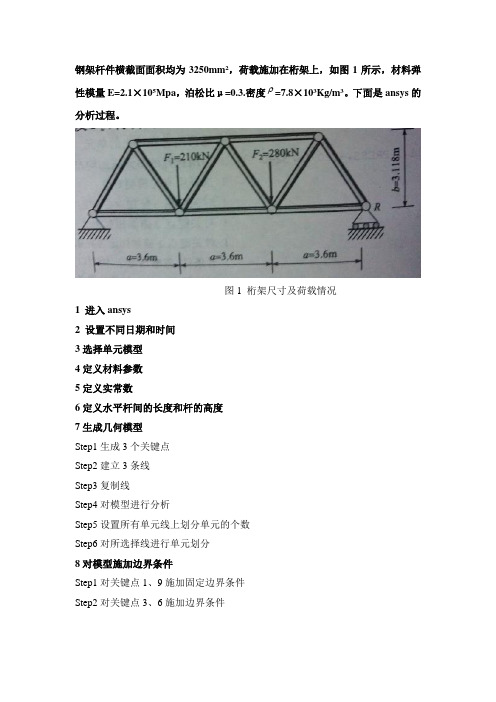
钢架杆件横截面面积均为3250mm2,荷载施加在桁架上,如图1所示,材料弹性模量E=2.1×105Mpa,泊松比μ=0.3.密度 =7.8×103Kg/m3。
下面是ansys的分析过程。
图1 桁架尺寸及荷载情况1 进入ansys2 设置不同日期和时间3选择单元模型4定义材料参数5定义实常数6定义水平杆间的长度和杆的高度7生成几何模型Step1生成3个关键点Step2建立3条线Step3复制线Step4对模型进行分析Step5设置所有单元线上划分单元的个数Step6对所选择线进行单元划分8对模型施加边界条件Step1对关键点1、9施加固定边界条件Step2对关键点3、6施加边界条件图2 模型形状9分析计算10结果的一般显示(1)图3 变形位移显示(2)图4对线形单元按实体效果进行显示(以3倍比例)(3)图5 Y方向的位移云图11 线性单元内力结果显示Step1 定义线性单元I、J节点的轴力Step2 画出单元的受力图图6 轴力情况图轴力结果如下(2)单元计算结果单元轴向力:LOAD STEP= 1 SUBSTEP= 1 TIME= 1.0000 LOAD CASE= 0ELEM SMIS11 -0.26942E+062 0.13470E+063 0.26942E+064 -26942.5 0.28287E+066 26942.7 0.29637E+068 0.14817E+069 -0.29637E+0610 -0.26940E+0611 -0.29634E+06MINIMUM V ALUESELEM 9V ALUE -0.29637E+06MAXIMUM V ALUESELEM 7V ALUE 0.29637E+06单元支反力结果:LOAD STEP= 1 SUBSTEP= 1TIME= 1.0000 LOAD CASE= 0THE FOLLOWING X,Y,Z SOLUTIONS ARE IN THE GLOBAL COORDINATE SYSTEMNODE FX FY1 0.20373E-09 0.23333E+067 0.25667E+06TOTAL V ALUESV ALUE 0.20373E-09 0.49000E+06获取支撑节点1处的y方向支反力,赋给Ry 1:获取支撑节点7处的Y方向支反力,赋值给Ry7计算结果如下:ABBREVIATION STATUS-ABBREV STRINGSA VE_DB SA VERESUM_DB RESUMEQUIT Fnc_/EXITPOWRGRPH Fnc_/GRAPHICSPARAMETER STATUS- ( 25 PARAMETERS DEFINED)(INCLUDING 19 INTERNAL PARAMETERS)NAME V ALUE TYPE DIMENSIONSA 3.60000000 SCALARB 3.11800000 SCALARI 1.00000000 SCALARMAXLAYER 0.00000000 SCALARRY1 233300.000 SCALARRY7 256700.000 SCALAR12 退出系统下面是Log文件/BATCH/COM,ANSYS RELEASE 11.0 UP20070125 18:53:36 11/03/2012 /input,menust,tmp,'',,,,,,,,,,,,,,,,1/GRA,POWER/GST,ON/PLO,INFO,3/GRO,CURL,ON/CPLANE,1/REPLOT,RESIZEWPSTYLE,,,,,,,,0/PLOPTS,INFO,3/PLOPTS,LEG1,1/PLOPTS,LEG2,1/PLOPTS,LEG3,1/PLOPTS,FRAME,1/PLOPTS,TITLE,1/PLOPTS,MINM,1/PLOPTS,FILE,0/PLOPTS,LOGO,1/PLOPTS,WINS,1/PLOPTS,WP,0/PLOPTS,DATE,0/TRIAD,ORIG/REPLOT!*/PREP7!*ET,1,MASS21!*SA VE!* MPTEMP,,,,,,,,MPTEMP,1,0MPDATA,EX,1,,2100000000000 MPDATA,PRXY,1,,0.3 MPTEMP,,,,,,,,MPTEMP,1,0MPDE,EX,1MPDE,PRXY,1MPDATA,EX,1,,210000000000 MPDATA,PRXY,1,,0.3 MPTEMP,,,,,,,,MPTEMP,1,0MPDATA,DENS,1,,7800!*!*ETDEL,1!*ET,1,LINK1!*!*SA VER,1,0.00325, ,!*SA VE*SET,a,3.6*SET,b,3.118SA VEK,1,0,0,0,K,2,a/2,B,0,RESUME/COM,ANSYS RELEASE 11.0 UP20070125 18:59:52 11/03/2012 /AUTO,1/REP,FAST/PNUM,KP,1/PNUM,LINE,1/PNUM,AREA,0/PNUM,VOLU,0/PNUM,NODE,0/PNUM,TABN,0/PNUM,SV AL,0/NUMBER,0!*/PNUM,ELEM,0/REPLOT!*K,1,0,0,0,K,2,a/2,B,0,K,3,a,0,0,SA VELSTR, 1, 2LSTR, 1, 3LSTR, 2, 3SA VEFLST,3,3,4,ORDE,2FITEM,3,1FITEM,3,-3LGEN,3,P51X, , ,a, , , ,0FLST,3,2,4,ORDE,2 FITEM,3,2FITEM,3,5LGEN,2,P51X, , ,a/2,b, , ,0 SA VENUMMRG,ALL, , , ,LOW !*LESIZE,ALL, , ,1, ,1, , ,1, FLST,2,11,4,ORDE,2 FITEM,2,1FITEM,2,-11LMESH,P51XFINISH/SOLFLST,2,1,3,ORDE,1 FITEM,2,1!*/GODK,P51X, , , ,0,ALL, , , , , , FLST,2,1,3,ORDE,1 FITEM,2,9!*/GODK,P51X, , , ,0,UY, , , , , , SA VE/DIST,1,0.924021086472,1 /REP,FASTSA VEFLST,2,1,3,ORDE,1 FITEM,2,3!*/GOFK,P51X,FY,-210e3 FLST,2,1,3,ORDE,1 FITEM,2,6!*/GOFK,P51X,FY,-280000SA VE/STATUS,SOLUSOLVEFINISH/POST1PLDISP,1/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,0.924021086472,1 /REP,FAST/DIST,1,0.924021086472,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,1.08222638492,1/REP,FAST/DIST,1,0.924021086472,1/REP,FAST/DIST,1,0.924021086472,1/REP,FAST/DIST,1,0.924021086472,1/REP,FAST/DIST,1,1.08222638492,1/REP,FAST/DIST,1,1.08222638492,1/REP,FAST/DIST,1,0.924021086472,1/REP,FAST/DIST,1,0.924021086472,1/REP,FAST/DIST,1,1.08222638492,1/REP,FAST/USER, 1/FOC, 1, 6.32209400502 , 0.584690326081 , 0.00000000000 /REPLO/DIST,1,1.08222638492,1/REP,FAST/DIST,1,0.924021086472,1/REP,FAST!*/SHRINK,0/ESHAPE,3/EFACET,1/RATIO,1,1,1/CFORMAT,32,0/REPLOT!*!*/EFACET,1PLNSOL, U,Y, 0,1.0/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,0.924021086472,1 /REP,FAST/DIST,1,0.924021086472,1 /REP,FAST/DIST,1,0.924021086472,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,0.924021086472,1 /REP,FAST/DIST,1,0.924021086472,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,0.924021086472,1/REP,FAST/DIST,1,0.924021086472,1/REP,FAST/DIST,1,1.08222638492,1/REP,FAST/DIST,1,1.08222638492,1/REP,FAST/DIST,1,1.08222638492,1/REP,FAST/REPLOT,RESIZE/REPLOT,RESIZE/REPLOT,RESIZE/REPLOT,RESIZESA VEA VPRIN,0, ,ETABLE,bridge_I,SMISC, 1!*A VPRIN,0, ,ETABLE,bridge_J,SMISC, 1!*A VPRIN,0, ,ETABLE, ,U,X!*ETABLE,,ERASE,3PLLS,BRIDGE_I,BRIDGE_J,0.5,0 /REPLOT,RESIZE/DIST,1,0.924021086472,1/REP,FAST/DIST,1,1.08222638492,1/REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST/DIST,1,0.924021086472,1 /REP,FAST/DIST,1,1.08222638492,1 /REP,FAST!*PRESOL,SMISC,1!*PRRSOL,PRRSOL,FY*SET,Ry1,233300 PRRSOL,FY*SET,Ry7,256700*STATFINISH! /EXIT,ALL。
012 基于MATLAB和ANSYS的有限元分析-二维truss单元理论

基于MATLAB和ANSYS的有限元分析二维桁架truss单元-理论12.二维桁架单元:关键公式12.1坐标系12.2.转换矩阵12.3.刚度矩阵12.4.应变和应力12.4.概述12.1.坐标系3❑局部坐标系统:(r1,s1);(r2,s2). 它们与truss配置相连.❑全局坐标系统:(x,y). 这些坐标是固定的和唯一的。
它通常被选为笛卡尔坐标系O xy❑在全局坐标系中获得最终求解结果 (以位移为单位:u,v)u r 1(1)u r 1(2)=T 1u 1v 1u (2)v (2)T 1=cosθ1sinθ10000cosθ1sinθ1T 2=cosθ2sinθ20000cosθ2sinθ2u r 1(1)u r 1(2)=cosθ1sinθ10000cosθ1sinθ1u 1v 1u (2)v (2)u r 2(2)u r 2(3)=T 2u 2v 2u (3)v (3)xyr 1s 1r 2s 2θ1θ212u (1)v (1)u r 1(2)u (2)v(2)u r 1(1)=u (1)cosθ1+v (1)sinθ1u (2)=u (2)cosθ+v (2)sinθu (1)v (1)u r 1(1)u r 1(1)θ1=v (1)θ1AB C u r 1(1)=AB +BC12.2.变换矩阵T 1,T 2称为单元的变换矩阵类似的:其中:其中:K =i=1NT (i)T k (i)eT (i)T (i)=cosθsinθ0000cosθsinθθr ik (i)e =A i න−11BiT C(B (i))detJdξwheredetJ =L i 2,C =E i ,B (i)=1detJ ðN 1ðξðN 2ðξ=1L i −11N 1ξ=121−ξ;N 2ξ=12(1+ξ)k (i)e =න−11E i A i 2L i 1−1−11dξ12.3. 局部刚度矩阵:k e局部坐标系中的公式N 1,N 2,B ,k e 将和1D T russ 单元一致终点x起点KU=R⇒U=K−1RT(i)=cosθsinθ0000 cosθsinθStrain: e(i)=B(i)u ri,start node u ri,end nodeStress: σi=E i e ixθr iu ri(start node) u ri(end node)=T(i)u(start node)v(start node)u(end node)v(end node)12.4. 应变和应力求解平衡方程得到全局坐标系中的位移场:需要获得局部坐标系中的位移字段:应变和应力:终点起点Strain: e (i)=B (i)u r i ,start node u r i ,end nodeu r i (start node)u r i (end node)=T (i)u (start node)v (start node)u (end node)K =i=1NT (i)T k (i)eT (i)T (i)=cosθsinθ0000cosθsinθxθ起点终点r ik (i)e =A i න−11BiT C(B (i))detJdξwheredetJ =L i 2,C =E i ,B (i)=1detJ ðN 1ðξðN 2ðξ=1L i −11N 1ξ=121−ξ;N 2ξ=12(1+ξ)k (i)e =න−11E i A i 2L i 1−1−11dξ总结局部坐标系中的公式N 1,N 2,B ,k e 将和1DTruss 单元一致。
有限元分析ANSYS理论与应用(第4版).例3.1_MATLAB理论求解

有限元分析ANSYS理论与应⽤(第4版).例3.1_MATLAB理论求解相关帖⼦:有限元分析 ANSYS理论与应⽤(第4版).例3.1_ANSYS.Workbench求解题⽬描述:如图所⽰阳台桁架及其尺⼨。
假设所有杆件均为⽊质材料(道格拉斯红杉),弹性模量E=1.9×106lb/in2,且且⾯积为8in2。
确定每个接头的挠度,以及每个杆件的平均应⼒。
下⾯将MATLAB求解这个问题。
1、将问题结构离散为节点和单元:桁架的每个杆件作为单元,每个杆件的连接点作为节点。
因此,给定的桁架可以⽤5个节点和6个单元进⾏建模。
其中:1ft=12in.Element Node i Node j Length(in.)A(in2)E(lb/in2)θ(°)11236.08 1.9E+06022350.98 1.9E+0613533436.08 1.9E+06042436.08 1.9E+069052550.98 1.9E+064564536.08 1.9E+0602、计算各个单元的刚度矩阵,建⽴整体矩阵,边界条件处理,刚度⽅程及未知位移求解,求解⽀反⼒%% 定义输⼊条件A = 8; %杆件截⾯积E = 1.9E6; % 杆件材料弹性模量L1 = 36; % 1、3、4、6号杆件的长度L2 = 50.9; % 2、5号杆件的长度%% 计算单元刚度矩阵k1 = Bar2D2Node_Stiffness(E, A, L1, 0); %计算单元1刚度矩阵k2 = Bar2D2Node_Stiffness(E, A, L2, 135); %计算单元1刚度矩阵k3 = Bar2D2Node_Stiffness(E, A, L1, 0); %计算单元1刚度矩阵k4 = Bar2D2Node_Stiffness(E, A, L1, 90); %计算单元1刚度矩阵k5 = Bar2D2Node_Stiffness(E, A, L2, 45); %计算单元1刚度矩阵k6 = Bar2D2Node_Stiffness(E, A, L1, 0); %计算单元1刚度矩阵%% 建⽴整体刚度矩阵kk = zeros(10, 10);kk = Bar2D2Node_Assembly(kk, k1, 1, 2);kk = Bar2D2Node_Assembly(kk, k2, 2, 3);kk = Bar2D2Node_Assembly(kk, k3, 3, 4);kk = Bar2D2Node_Assembly(kk, k4, 2, 4);kk = Bar2D2Node_Assembly(kk, k5, 2, 5);kk = Bar2D2Node_Assembly(kk, k6, 4, 5) % 输出整体刚度矩阵%% 边界条件处理k = kk([3478910], [3478910]);%添加位移约束。
用ansys对房屋钢框架结构计算及模态分析

用ansys对房屋钢框架结构计算及模态分析
ANSYS结构分析
题目:房屋钢框架结构计算及模态分析
一.原始数据:
房屋钢框架总尺寸12m x10m x 8.75m
材料质量密度为7.85E-9
压杆面积641mm2,水平拉索面积314mm2
屋顶承受雪荷载为3000KN/M2
立面风荷载为3000KN/M2
材料:杆单元LINCK8,LINCK10,梁单元Beam188
计算模型如图所示
二.操作命令
1.选择单元类型,设置单元实常数,Type1 LINK8,Type2LINK10,实常数为2,3,输入各截面面积。
2.设置杆梁单元Beam188截面数据,圆管,工字形如图
3.设置材料性能数据EX=2E5 泊松比=0.3 密度=7.85E-9
4.通过创建关键点(0,2.2,0),(0,4.4,0),(0,6.6,0)
连线,复制点,线,建立几何模型如图
5.给几何模型附属性,进行网格划分。
6,加载雪荷载,风荷载,重力如图
7.求解及后处理:变形图
Y方向应力图
Z方向应力图
三.模态分析
观察四阶阵型如图第一阶
第二阶阵型
第三阶阵型
第四阶阵型
四.结论
通过观察,该框架在荷载和重力的作用下,X,Y方向的最大变形发生在鱼腹锁,Z方向最大变形在主立柱,其值为-7.73mm。
最大应力发生在主立柱,其值为141.684MPa。
从计算结果看,最大变形和最大应力都不高,均能满足设计要求。
模态分析前四阶阵型无明显变化,在震动作用下,该房屋钢框架较安全。
基于ANSYS软件的支架强度有限元分析报告

基于ANSYS软件的支架强度有限元分析报告一、概述本次大作业主要利用ANSYS软件对支架的应力和应变进行分析,计算出支架的最大应力和应变。
然后与实际情况进行比较,证明分析的正确性,从而为支架的优化分析提供了充分的理论依据,并且通过对ANSYS软件的实际操作深刻体会有限元分析方法的基本思想,对有限元分析方法的实际应用有一个大致的认识。
二、问题分析如图1所示的支架由3mm钢板折弯而成。
该支架的h2一侧为固定支撑,顶部平面承受书本重物载荷,重物重量为500N。
材料的杨氏模量为2E11Pa,泊松比为0.3,密度7850kg/m3。
图1 支架a b h1 h2 w数据80 40 15 40 15三、有限元建模支架由钢板折弯而成,厚度尺寸相对长度和宽度尺寸来说很小,所以在ansys中采用面体单元进行模拟,在Workbench中的单元设置为shell181,材料即为结构钢材料,其弹性模量为2.1e11Pa,泊松比为0.3,密度为7850kg/m^3图2 材料属性双击Geometry进入几何模型建立模块,首先设置单位为mm。
以XY平面为为基准建立如下草绘面。
图3 草绘面1再以此草绘面生成面体,通过概念建模的方式实现。
图4 生成面体对上面面体的长边进行拉伸,拉伸方向为垂直向外,拉伸15mm图5 拉伸成面体对相交区域进行倒角,倒角半径为3图6 最终几何模型双击model进行分析界面进行网格划分,首先定义面体厚度为1mm图7 面体厚度随后进行网格划分,设置网格尺寸为5mm,采用全四边形网格划分方法,同时在倒角位置采用Mapped Face sizing功能映射网格,保证网格过度平滑。
图8 有限元网格模型检查网格质量,Workbench中网格质量柱状分布图如下所示,最差的都大于0.6,网格质量平均值为0.84,可见网格质量很好,满足计算精度图9 网格质量检查添加载荷,如10所示支架h2一侧为固定支撑,采用Fix Support固定方式实现,顶部平面承受500N的均布力,采用Force实现,如下图所示图10 载荷加载四、有限元计算结果(1)位移变化,如图12所示,结果最大变形为0.17mm,发生在左侧边角区域,刚好为载荷加载边缘处,也为结构刚度最为薄弱区域图12 位移云图(2)等效应力计算结果,如图3所示,最大等效应力为213MPa,发生在右侧倒角区域,该处为约束边缘处,由于约束会引起较大的应力集中,所以在实际情况下应该加大此处的倒角过度,减缓应力集中现象。
刚架的有限元分析

刚架的有限元分析有限元分析(Finite Element Analysis,FEA)是一种数值模拟方法,用于解决物体结构、材料、流体等的力学问题。
它将复杂的结构分解成小的、简单的单元,并在每个单元上建立适当的数学模型,最终求解全局问题。
有限元分析的步骤包括:前处理、求解和后处理。
前处理阶段主要包括几何建模、网格划分和单元属性定义等;求解阶段则是通过建立合适的方程组并求解,得到所需的物理量;后处理阶段则是对求解结果进行可视化和分析。
在进行有限元分析时,首先需要对结构进行几何建模。
几何建模的目的是准确描述结构的形状和尺寸。
可以使用CAD软件对结构进行建模,也可以简单地使用几何参数描述结构。
在建模过程中,需要考虑结构的实际工作状态、边界条件和加载情况等。
接下来,需要对结构进行网格划分。
网格划分是将结构分解成小的、简单的单元,以便进行数学建模和计算。
常用的单元包括三角形单元、四边形单元和六面体单元等。
网格划分的精度和密度会影响到最终的求解精度和计算时间。
每个单元都需要定义适当的属性,如材料特性、边界条件和加载情况等。
材料特性包括弹性模量、杨氏模量、泊松比等,它们决定了材料在受力时的变形特性。
边界条件包括约束边界和加载边界,它们描述了结构的边界条件和约束情况。
建立了合适的数学模型后,就可以求解得到所需的物理量了。
通常,求解的过程是通过建立合适的方程组来实现的。
方程组的形式取决于问题的类型和边界条件。
可以使用有限元法、有限差分法或其他数值方法来求解方程组。
求解过程通常需要借助计算机进行,计算时间与问题的复杂度和求解精度有关。
最后,需要对求解结果进行后处理,包括结果的可视化和分析。
常用的后处理工具包括绘图软件和数据分析软件。
可视化结果可以帮助理解结构的行为和变形情况,进而优化设计。
数据分析则可以帮助提取结构的关键参数和性能指标,为结构的工作提供参考依据。
总结起来,有限元分析是一种强大的工程技术手段,可以帮助工程师解决复杂的结构和材料力学问题。
ANSYS软件分析钢结构

两端铰接横向荷载下压弯构件分析
• 建立模型
• 为计算分析方便,在此选用之前所建模型的数据,即 b=0.03m,h=0.05m,l=3m.所以,该构件的欧拉临界力为25.9077KN。由教 材P78~P80可知,
Q y sec(kl /挠度,以
非线性分析的命令流
• • • • • • • • • • • • • • • Finish$/clear$/prep7 b=0.03$h=0.05$l=3$e=2.1e11$et,1,beam189 mp,ex,1,e$mp,prxy,1,0.3 sectype,1,beam,rect$secdata,b,h k,1$k,2,,l$k,10,0,l/2,l/2$l,1,2 latt,1,,1,,10,,1$lesize,all,,,20$lmesh,all finish$/solu$dk,1,ux,,,,uy,uz,roty$dk,2,ux,,,,uz,roty fk,2,fy,-27000$f,10,fx,50$pstres,on solve$finish$/solu$antype,static$nlgeom,on outres,all,all$nsubst,50$autots,on$lnsrch,on solve$finish$/post26$/gropt,divy,10$/color,axes,8 /color,curve,2$/axlab,x,deflection$/axlab,y,force rforce,3,1,f,y$nsol,4,10,u,x$xvar,4$plvar,3 /axlab,x,force$/axlab,y,displacement3 rforce,5,1,f,y$nsol,6,2,u,y$xvar,5$plvar,6
门式钢架轻型钢结构静力有限元分析--ANSYS命令流

R,5,1.9187E-2,8.16667E-4,2.9443E-3,0.48335,0.175,
RMODIF,5,7,1.9853E-2,8.16667E-4,3.428E-3,0.51665,0.175,
RMODIF,1,7,1.7187E-2,8.16667E-4,1.74344E-3,0.38335,0.175
R,2,1.7187E-2,8.16667E-4,1.74344E-3,0.38335,0.175,
RMODIF,2,7,1.7853E-2,8.16667E-4,2.10287E-3,0.41665,0.175,
*SET,H1,10 !设定代表下檐高的变量H1=10m
*SET,B,32 !设定代表横距的变量B=32m
*SET,L,64 !设定代表纵跨距的变量L=64m
!材料参数设定
*SET,E_LZ,2.1E11 !设定梁柱弹性模量
*SET,U_LZ,0.3 !设定梁柱泊松比
CYL4,0.14,0.125,0.09,-180 !生成左下半个圆
CYL4,0.14,0.175,0.09,180 !生成左上半个圆
CYL4,0.36,0.125,0.09,-180 !生成右下半个圆
CYL4,0.36,0.175,0.09,180 !生成右上半个圆
LSEL,ALL
LSEL,S,TYPE,,3
LESIZE,ALL,,,1
LMESH,ALL
/REPLOT
!建立全模型
ALLSEL
LSYMM,X,ALL
ANSYS结构有限元分析流程

ANSYS结构有限元分析流程下面将介绍ANSYS结构有限元分析的流程,包括前处理、求解和后处理三个主要步骤。
1. 前处理(Preprocessing):首先,需要将结构的几何形状导入到ANSYS中,并对其进行几何建模和网格划分。
几何建模可以使用ANSYS自带的几何建模工具,也可以导入CAD套件的几何模型。
然后,对结构进行网格划分,将其划分为有限元网格。
ANSYS提供了多种不同类型的有限元单元,可以根据具体情况选择合适的单元类型,并进行适当的划分。
在划分网格之后,还需要定义边界条件和加载条件。
边界条件包括约束和支撑条件,用于限制结构的自由度。
加载条件包括施加在结构上的载荷和其它外部作用,如压力、温度等。
这些边界条件和加载条件可以通过ANSYS界面设置或者通过命令的方式输入。
2. 求解(Solving):在设置好边界条件和加载条件之后,可以进行求解。
ANSYS使用有限元法将结构离散成许多小的有限元素,并通过求解线性或非线性方程组来预测结构的响应。
求解过程中需要选择求解方法、步长等参数,并可以通过迭代求解来稳定计算过程。
在求解过程中,可以观察结构的应力、应变、变形、位移等结果,并进行后处理分析。
ANSYS提供的针对不同目的的分析工具,如静力学分析、动力学分析、热力学分析等,可以根据需要选择相应的分析类型。
3. 后处理(Postprocessing):求解完成后,可以对计算结果进行后处理和分析。
ANSYS提供了多种后处理工具,用于可视化计算结果、绘制结构的应力、应变、变形等图形,并进行数据分析等。
可以根据需要导出计算结果,用于生成工程报告、论文等。
此外,在分析过程中还可以根据需要进行参数化分析、优化设计等。
参数化分析可以通过改变结构的几何形状、材料性质等参数,来研究这些参数对结构响应的影响。
优化设计可以根据指定的优化目标和约束条件,通过反复分析和优化,得到满足要求的最优结构。
总的来说,ANSYS结构有限元分析流程包括前处理、求解和后处理三个主要步骤。
几款仿真软件的分析

几款地质仿真软件的简介本文将对ANSYS、ADINA、ABAQUS、MSC、FEPG、Femlab(Comsol)、Flac、PETREL进行简短的介绍。
有限元分析是对于结构力学分析迅速发展起来的一种现代计算方法。
有限元分析软件目前流行的有:ANSYS、ADINA、ABAQUS、Femlab(Comsol)、MSC、FEPG等。
ANSYS软件在致力于线性分析的用户中具有很好的声誉,它在计算机资源的利用,用户界面开发等方面也做出了较大的贡献。
ABAQUS软件则致力于更复杂和深入的工程问题,其强大的非线性分析功能在设计和研究的高端用户群中得到了广泛的认可。
而ADINA软件除了求解非线性问题外,其在多物理场的流固耦合求解功能也是全球唯一的专利技术。
COMSOL公司是全球多物理场建模与仿真解决方案的提倡者和领导者,其旗舰产品COMSOL Multiphysics,使所有的物理现象可以在计算机上完美重现。
MSC是比较老的一款软件目前更新速度比较慢。
FEPG是一款国产有限元分析软件。
一、ANSYS、ADINA、ABAQUS、MSC四者的比较由于ANSYS产品进入中国市场早于ABAQUS,并且在五年前ANSYS 的界面是当时最好的界面之一,所以在中国,ANSYS软件在用户数量和市场推广度方面要高于ABAQUS。
ANSYS软件注重应用领域的拓展,目前已覆盖流体、电磁场和多物理场耦合等十分广泛的研究领域。
ABAQUS 则集中于结构力学和相关领域研究,致力于解决该领域的深层次实际问题。
而ADINA软件和ANSYS软件一样都包括结构、温度、流体及流固耦合的功能,因此其应用领域也是相当广泛。
对于常规的结构线性问题,三种软件都可以较好的解决,在模型规模限制、计算流程、计算时间等方面都较为接近。
ABAQUS软件和ADINA软件在求解非线性问题时具有非常明显的优势;而ANSYS软件和ADINA软件则在流体和多物理场耦合功能方面具有无可比拟的优势。
有限元ANSYS MATLAB 应用

有限元在ANSYS和MATLAB中的应用工程学院摘要: 文章简述了有限元分析的基本理论及其求解问题的基本步骤, 介绍了ANSYS 软件的应用,介绍了Matlab 语言特点,给出了Matlab 环境下实现有限元的步骤。
说明如何使用Matlab 进行有限元分析,使用该方法进行分析具有精度高、简便、快速及可视化等诸多优点,具有较强的使用价值。
关键词: 有限元分析; ANSYS 软件; 用Matlab 进行有限元分析的优点1 有限元分析基本理论有限元分析的基本概念是用较简单的问题代替复杂问题后再求解。
它将求解域看成是由许多称为有限元的小的互连子域组成, 对每一单元假定一个合适的近似解,然后推导求解这个域的满足条件, 从而得到问题的解。
这个解不是准确解,而是近似解, 因为实际问题被较简单的问题所代替。
由于大多数实际问题难以得到准确解,而有限元不仅计算精度高, 而且能适应各种复杂形状, 因而成为行之有效的工程分析手段。
有限元是那些集合在一起能够表示实际连续域的离散单元[1]。
有限元的概念早在几个世纪前就已产生并得到了应用, 例如用多边形逼近圆来求得圆的周长, 但作为一种方法而被提出, 则是最近的事。
有限元法最初被称为矩阵近似方法, 应用于航空器的结构强度计算, 并由于其方便性、实用性和有效性而引起从事力学研究的科学家的浓厚兴趣。
经过短短数十年的努力, 随着计算机技术的快速发展和普及, 有限元方法迅速从结构工程强度分析计算扩展到几乎所有的科学技术领域, 成为一种丰富多彩、应用广泛并且实用高效的数值分析方法。
有限元方法与其他求解边值问题近似方法的根本区别在于它的近似性仅限于相对小的子域中。
1.1有限元求解问题的分析过程第一步, 问题及求解域定义: 根据实际问题近似确定求解域的物理性质和几何区域。
第二步, 求解域离散化: 将求解域近似为具有不同有限大小和形状且彼此相连的有限个单元组成的离散域, 习惯上称为有限元网络划分。
基于ANSYS的车架有限元分析

基于ANSYS的车架有限元分析车架有限元分析是一种用于评估车架结构的强度、刚度和振动特性的工程分析方法。
在这种方法中,通过将车架模型转化为一个离散的有限元网格,然后应用力学理论和数值方法,可以对车架在各种工况下的行为进行分析和预测。
ANSYS是一种常用的有限元分析软件,具有强大的建模和分析功能,因此在车架有限元分析中得到广泛应用。
在进行车架有限元分析之前,首先需要进行几何建模。
这通常可以通过CAD软件来完成,然后将几何模型导入到ANSYS中。
在导入模型后,需要对车架进行网格划分。
网格划分是将车架模型划分为多个小单元(或称为网格元素)的过程,这些小单元可以是三角形、四边形、六边形等。
划分网格的目的是为了将车架模型离散化,使得它可以由有限个离散点、面和体来表示。
建立网格后,下一步是定义车架的材料性质。
车架通常由金属或复合材料制成,因此需要将其材料性质输入到ANSYS中。
这些性质包括杨氏模量、泊松比、密度等。
在车架有限元分析中,通常假设材料是各向同性的。
完成了几何建模和材料定义后,接下来可以定义分析类型。
车架有限元分析通常涉及到静态应力分析、模态分析和疲劳分析等。
静态应力分析用于评估车架在静态荷载下的强度和刚度。
模态分析用于确定车架在自由振动下的固有频率和振型。
疲劳分析用于评估车架在长期运行中的疲劳寿命。
对于静态应力分析,需要定义边界条件和加载情况。
边界条件包括固支条件和约束条件,用于限制车架在一些方向上的位移。
加载情况可以是外部力或者预定义的位移。
在进行静态应力分析时,可以计算车架结构的最大应力、最大位移和变形等,用于评估车架的结构强度和刚度。
对于模态分析,需要定义边界条件,用于确定车架的固有频率和振型。
在车架的自由振动中,可以确定车架的主要振型,从而评估其在各个振型下的刚度和振动特性。
对于疲劳分析,需要定义加载循环和载荷幅值。
加载循环可以是振动循环或者工况循环,载荷幅值决定了车架在每个加载循环中的受力情况。
用ANSYS对一桁架结构进行有限元计算

用ANSYS对一桁架结构进行有限元计算有限元分析是一种常用的结构力学计算方法,其可以有效地分析并预测复杂结构的力学行为。
ANSYS是一款广泛使用的有限元分析软件,其提供了强大的功能和工具,可以对各种类型的结构进行有限元计算。
一桁架结构是一种常见的工程结构,其由一根主梁和多个次梁构成。
这种结构广泛应用于桥梁、建筑物和机械设备等领域。
下面将介绍在ANSYS中对一桁架结构进行有限元计算的步骤和方法。
首先,在ANSYS中创建一个新的工程,并选择适当的工作空间和单位。
然后,使用ANSYS的几何建模工具,如DesignModeler或SpaceClaim,创建一桁架结构的三维模型。
可以通过绘制线段、矩形和圆弧等基本几何形状来构建结构。
此外,还可以导入外部CAD文件或使用ANSYS提供的几何建模功能创建结构。
创建完模型后,需要定义结构的材料属性。
根据具体情况,在ANSYS的材料库中选择适当的材料,并将其属性分配给结构中的各个部分。
可以指定材料的弹性模量、泊松比、密度和屈服强度等参数。
接下来,定义结构的约束条件和加载情况。
可以在结构的关键节点上固定约束或施加位移约束,以模拟实际工况中的支撑条件。
此外,在适当的位置上施加集中载荷、分布载荷或压力等加载,以模拟外部力的作用。
在定义好约束条件和加载情况后,需要进行网格划分。
ANSYS提供了多种网格划分算法和工具,如Tetrahedral、Hexahedral和Prism等。
根据模型的复杂程度和预期计算结果的准确性,可以选择适当的网格划分方法。
完成网格划分后,可以开始进行有限元计算。
在ANSYS中,可以选择适当的有限元求解器,并设定求解器的参数。
然后,进行计算并等待计算结果。
在计算完成后,可以对结果进行后处理。
ANSYS提供了丰富的后处理工具和功能,如显示变形、应力云图、位移云图、剖面图等用于分析和解释计算结果。
可以通过这些后处理工具来评估结构的强度和刚度,并与设计要求进行对比。
基于ANSYSWorkbench的支架的有限元分析

基于ANSYSWorkbench的⽀架的有限元分析江苏⼤学《⼯程有限元分析》⼤作业基于ANSYS Workbench的⽀架的有限元分析姓名:学号:专业:机械设计及理论班级:农⼯院11级2012年3⽉31⽇基于ANSYS Workbench的⽀架的有限元分析摘要:为进⼀步改进⽀架的结构设计, 实现⽀架的CAE标准化⽣产, 本⽂采⽤⼤型有限元分析软件ANSYS 对发动机⽀架的应⼒分布进⾏了计算和仿真分析,得出了该构件的应⼒和应变分布云图, 从⽽为⽀架的强度分析研究提供了⽐较实⽤的有限元分析⽅法。
关键词:⽀架,ANSYS,仿真分析Abstract:In order to further improve the structural design and realize the CAE standardization of the support, we adopt finite element software ANSYS to calculate and simulate the stress distribution, and draw out the stress and strain distribution maps in the paper. It has offered the finite element analysis methods for the strength analysis of the support.Key words: support,ANSYS,simulation analysis1 问题描述与分析⽀架是现代化机械⼯程中进⾏⾼效⽣产和安全⽣产最为关键的构件之⼀。
由于⽀架重量过⼤会给运输、安装、搬家带来很多困难, 且材料消耗费⽤也是⽀架成本的主要构成部分, 所以选择其重量以及强度分析具有很实际的意义。
已知某⽀架,在两孔内做约束,在顶⾯上施加1000KN/m2的压强,然后,对⽀架进⾏强度校核,并分析⽀架的最⼤变形以及⽀架的等效应⼒。
各大仿真软件介绍

各大仿真软件介绍目前市面上有许多大型的仿真软件,以下是其中几个比较知名的仿真软件以及它们的算法和原理介绍。
1. AnsysAnsys是一款主要用于结构分析、流体分析和电磁分析的大型有限元分析软件。
它采用有限元方法进行建模和求解,通过将连续物体划分为有限数量的离散元素,将复杂的物理问题离散化为一系列简单的线性代数问题。
Ansys具有强大的分析功能和广泛的应用领域,在工程仿真领域得到了广泛的应用。
2. SimulinkSimulink是一款强大的数据流程仿真环境,用于建模、仿真和分析各种动态系统。
它基于数据流图的模型,可以方便地建立输入和输出之间的关系,使用图形化的方式进行仿真。
Simulink内置了许多常用的算法和模型,可以快速建立各种系统的仿真模型,例如控制系统、通信系统等。
3. solidThinkingsolidThinking是一个由浅入深的全能CAE软件,内含结构、流体、模态、温度分析器和拓扑优化系统。
它采用有限元法进行建模和求解,可以进行多物理场耦合分析。
通过拓扑优化系统,solidThinking可以对结构进行优化设计,实现结构材料的最优分布,减少结构重量和材料成本。
4. MatlabMatlab是一种用于科学计算、数据分析和可视化的高级编程语言和环境。
它提供了各种各样的数学和工程计算函数,可以用于解决各种复杂的数学和工程问题。
Matlab中的仿真工具箱提供了许多专门用于仿真的函数和工具,可以进行各种仿真实验和数据分析。
5. COMSOL MultiphysicsCOMSOL Multiphysics是一款基于有限元方法的多物理场仿真软件。
它可以进行多物理场耦合的仿真分析,如结构力学、电磁场、流体力学、传热和化学反应等。
COMSOL Multiphysics提供了丰富的物理模型和数值求解器,可以进行各种复杂的仿真分析。
总之,这些大型仿真软件都是借助各种数学算法和物理模型来模拟和分析各种复杂的工程和科学问题。
有限元刚架结构matlab程序

有限元刚架结构matlab程序clcclearformat compactformat shortGjd=input('请输⼊节点数:');dy=input('请输⼊单元数:');E=input('请输⼊杨⽒模量E:');I=input('请输⼊惯性矩I:');L=input('请输⼊单元长度L:');A=input('请输⼊单元截⾯积:');FAI=input('请输⼊单元相对旋转⾓度:');%输⼊对应关系时,⼩节点放前⾯[单元节点1 节点2]dy_jd=input('请输⼊单元与节点对应关系:');%输⼊⼒与扭矩约束[值作⽤节点作⽤类型](转矩为3 x⽅向为1 y⽅向为2)lys=input('⼒与转矩约束矩阵:');%输⼊结构约束[作⽤节点作⽤类型](转⾓为3 x⽅向为1 y⽅向为2)wys=input('结构约束矩阵:');%原始数据% L=1;% E=3*10^10;% P=1000;% A=0.05;% dy=2;jd=3;LL=[L 2*L];I=20*A;% dy_jd=[1 1 2;2 2 3];% FAI=[pi/2 0];% q=P/L;M=P*L/10;% lys=[44/125*P 1 1;-12*P*L/125 1 3;81/125*P 2 1;-P 2 2;-67/750*P*L 2 3;-P 3 2;P*L/3 3 3]; % wys=[1 1;1 2;1 3;3 1;3 2;3 3];%对⼒约束与位移约束式⼦分别进⾏编号处理wys(:,3)=(wys(:,1)-1)*3+wys(:,2);lys(:,4)=(lys(:,2)-1)*3+lys(:,3);%对⼒约束与位移约束式⼦进⾏排序lys=sortrows(lys,4);wys=sortrows(wys,3);%单元刚度矩阵syms fai e a i l realk=[e*a/l 0 0 -e*a/l 0 0;0 12*e*i/l^3 6*e*i/l^2 0 -12*e*i/l^3 6*e*i/l^2;0 6*e*i/l^2 4*e*i/l 0 -6*e*i/l^2 2*e*i/l;-e*a/l 0 0 e*a/l 0 0;0 -12*e*i/l^3 -6*e*i/l^2 0 12*e*i/l^3 -6*e*i/l^2;0 6*e*i/l^2 2*e*i/l 0 -6*e*i/l^2 4*e*i/l];t=[ cos(fai), sin(fai), 0;-sin(fai), cos(fai), 0;0, 0, 1];%坐标变换矩阵T=blkdiag(t,t);%总体坐标系下的单元刚度矩阵K=T'*k*T;%带⼊每个单元的数,⽣成单元刚度矩阵kk,其每⼀页对应相应页数的单元的刚度矩阵for j=1:dy; e=E;i=I;l=LL(j);a=A;fai=FAI(j);kk(:,:,j)=eval(K);end%⽣成总体刚度矩阵KK%采⽤元胞数组的⽅式对各项进⾏保存%⽣成空元胞数组,元胞数组的⾏列⼤⼩与节点数相同for j=1:jd;for jj=1:jd;ling1{j,jj}=zeros(3);endendling2=ling1;%将对单元刚度矩阵部分分成4分加⼊元胞数组中for j=1:dy;kk1=kk(1:3,1:3,j);kk2=kk(1:3,4:6,j);kk3=kk(4:6,1:3,j);kk4=kk(4:6,4:6,j);ling2{dy_jd(j,2),dy_jd(j,2)}=kk1+ling2{dy_jd(j,2),dy_jd(j,2)}; ling2{dy_jd(j,2),dy_jd(j,3)}=kk2+ling2{dy_jd(j,2),dy_jd(j,3)}; ling2{dy_jd(j,3),dy_jd(j,2)}=kk3+ling2{dy_jd(j,3),dy_jd(j,2)}; ling2{dy_jd(j,3),dy_jd(j,3)}=kk4+ling2{dy_jd(j,3),dy_jd(j,3)}; end %将元胞数组进⾏拼接,形成总体刚度矩阵for j=1:jd;ling3(:,:,j)=cat(2,ling2{j,:});endKK=ling3(:,:,1);for j=2:jd;KK=[KK;ling3(:,:,j)];end%消去有已知位移的⾏与列b=KK;b(:,wys(:,3))=[];b(wys(:,3),:)=[];kjiejuzhen=inv(b);%提取对应外⼒lyss=lys;for j=1:size(wys,1);for jj=1:size(lys,1);if lyss(jj,4)==wys(j,3);lyss(jj,:)=0;endif jj==size(lyss,1);breakendendendlyss(all(lyss==0,2),:)=[];%求解weiyijie=[作⽤值作⽤节点作⽤类型(转⾓为3 x⽅向为1 y⽅向为2)序列] weiyijie=kjiejuzhen*lyss(:,1);weiyijie(:,1)=weiyijie;weiyijie(:,2)=lyss(:,2);weiyijie(:,3)=lyss(:,3);weiyijie(:,4)=lyss(:,4);%计算不计作⽤在约束⽅向上时的⽀反⼒lysjiee=[作⽤值作⽤节点作⽤类型(转⾓为3 x⽅向为1 y⽅向为2)序列] lysjie(:,1)=KK(wys(:,3),lyss(:,4))*weiyijie(:,1);lysjie(:,2:4)=wys(:,1:3);%将作⽤在约束⽅向上时的⽀反⼒加在上⾯的求解结果上for j=1:size(lysjie,1)for jj=1:size(lys,1);if lysjie(j,4)==lys(jj,4);lysjie(j,1)=lysjie(j,1)-lys(jj,1);endendend%答案weiyijielysjie。
有限元钢架结构分析手算matlabansys模拟

有限元大作业——钢架结构分析选题人:日期:2016年6月2日目录:第一章:问题重述 ...................................................................................................................... 错误!未定义书签。
一、题目内容: .................................................................................................................. 错误!未定义书签。
二、题目要求: .................................................................................................................. 错误!未定义书签。
第二章:有限元法手工求解 ...................................................................................................... 错误!未定义书签。
一、平面两单元离散化 ...................................................................................................... 错误!未定义书签。
二、单元分析 ...................................................................................................................... 错误!未定义书签。
有限元钢架结构分析_手算matlabansys模拟

有限元大作业——钢架结构分析选题人:日期:2016年6月2日目录:第一章:问题重述 (1)一、题目内容: (1)二、题目要求: (1)第二章:有限元法手工求解 (2)一、平面两单元离散化 (2)二、单元分析 (2)三、单元组装 (5)四、边界条件引入及组装总体方程 (5)五、求解整体刚度方程,计算节点2的位移和转角 (6)六、求节点1、3支撑反力 (6)七、设定数据,求解结果 (6)八、绘制轴力图、弯矩图、剪力图 (7)第三章、matlab编程求解: (8)一、总体流程图绘制: (9)二、输入数据: (9)三、计算单元刚度矩阵: (10)四、建立总体刚度矩阵: (10)五、计算未约束点位移: (10)六、计算支反力: (10)七、输出数据: (10)八、编程: (10)第四章有限元求解 (10)一、预处理 (11)二、模型建立: (12)二、分析计算 (14)三、求解结果 (15)四、绘制图像 (16)第五章结果比较 (19)第六章心得体会 (19)一、王小灿: .......................................................... 错误!未定义书签。
二、孙明哲: .......................................................... 错误!未定义书签。
三、张国威 ............................................................ 错误!未定义书签。
第七章附录 (20)一、matlab程序 (21)第一章:问题重述一、题目内容:图示平面钢架结构图1.1 题目内容二、题目要求:(1)采用平面梁单元进行有限元法手工求解,要求写出完整的求解步骤,包括:a)离散化:单元编号、节点编号;b)单元分析:单元刚度矩阵,单元节点等效载荷向量;c)单元组长:总体刚度矩阵,总体位移向量,总体节点等效载荷;d)边界条件的引入及总体刚度方程的求解;e)B点的位移,A、C处支撑反力,并绘制该结构的弯矩图、剪力图和轴力图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元大作业——钢架结构分析选题人:日期:2016年6月2日目录:第一章:问题重述 (1)一、题目内容: (1)二、题目要求: (1)第二章:有限元法手工求解 (2)一、平面两单元离散化 (2)二、单元分析 (2)三、单元组装 (5)四、边界条件引入及组装总体方程 (5)五、求解整体刚度方程,计算节点2的位移和转角 (6)六、求节点1、3支撑反力 (6)七、设定数据,求解结果 (7)八、绘制轴力图、弯矩图、剪力图 (8)第三章、matlab编程求解: (9)一、总体流程图绘制: (9)二、输入数据: (10)三、计算单元刚度矩阵: (10)四、建立总体刚度矩阵: (11)五、计算未约束点位移: (11)六、计算支反力: (11)七、输出数据: (11)八、编程: (11)第四章有限元求解 (11)一、预处理 (11)二、模型建立: (13)二、分析计算 (15)三、求解结果 (16)四、绘制图像 (17)第五章结果比较 (20)第六章心得体会 (20)一、王小灿: .......................................................... 错误!未定义书签。
二、孙明哲: .......................................................... 错误!未定义书签。
三、张国威 ............................................................ 错误!未定义书签。
第七章附录 (21)一、matlab程序 (22)第一章:问题重述一、题目内容:图示平面钢架结构图1.1 题目内容二、题目要求:(1)采用平面梁单元进行有限元法手工求解,要求写出完整的求解步骤,包括:a)离散化:单元编号、节点编号;b)单元分析:单元刚度矩阵,单元节点等效载荷向量;c)单元组长:总体刚度矩阵,总体位移向量,总体节点等效载荷;d)边界条件的引入及总体刚度方程的求解;e)B点的位移,A、C处支撑反力,并绘制该结构的弯矩图、剪力图和轴力图。
(2)编制通用平面钢架分析有限元Matlab程序,并计算盖提,与手工结果进行比较;(3)利用Ansys求解,表格列出B点的位移,A、C处支反力,绘制弯矩图、剪力图和轴力图,并与手算和Matlab程序计算结果比较。
(4)攥写报告,利用A4纸打印;(5)心得体会,并简要说明各成员主要负责完成的工作。
第二章:有限元法手工求解一、平面两单元离散化将平面梁离散为两个单元,单元编号分别为①和②,节点号分别为1、2、3; 如图2-1所示:图2-1 单元离散化示意图二、单元分析首先建立整体坐标系与局部坐标系如图所示; 1、求单元刚度矩阵对于单元①,求局部坐标系的单元刚度矩阵:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------=l EI lEI lEI l EI l EI l EI l EI l EI l EA lEAl EI l EI l EI l EI l EI l EI l EIl EI l EA lEAK 46026061206120000026046061206120000222323222323'1由于单元①局部坐标系与整体坐标系的夹角为:90=ϕ,则单元①的局部坐标变换矩阵为:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--=10000000100001000000010000000100001010000000000000000100000000001ϕϕϕϕϕϕϕϕcos sin sin cos cos sin sin cos eT可以得到在总体坐标系下的单元①的刚度矩阵:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------=⋅⋅=l EI l EI lEI lEI l EA l EA l EI l EI l EI l EI l EI l EI l EI lEIl EA l EA l EI l EI l EI l EI T K TK e T e 4063060000601260123064060000601260122223232223231'111 对于单元②,求局部坐标系的单元刚度矩阵:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------=l EI lEI lEI l EI l EI l EI l EI l EI l EA lEAl EI l EI l EI l EI l EI l EI l EIl EI l EA lEAK 2230230232302323000200223022302323023230002002222323222323'2由于单元②局部坐标系与整体坐标系的夹角为0=ϕ,则'22K K =。
2、求单元节点等效载荷向量将P 等效在单元①两侧节点1,2上:01211==x x F F()1254433211pLb a Fb F y -=+-= ()1258133212p L b a Fa Fy -=+-=125122211plLFab M -=-=125182212pl Lb Fa M ==将均布载荷等效在单元②两侧的节点2,3上:02322==x x F FP plF F y y =-==22322 31221211PlPl M M -=-=-=与作用在节点上的力叠加为整体坐标系下的节点载荷:12544'1p F x =0'1=y F 12512'1plM -= 12581'2pF x = P F y -='2750673110112518'2Pl Pl M -=⎪⎭⎫ ⎝⎛-+= 0'3=x FP F y -='1 3'3pl M =三、单元组装将两个整体坐标系下的单元刚度矩阵组装为整体刚度矩阵:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-+-+------=l EI lEI lEI l EI l EI l EI l EI l EI l EA l EA l EI l EI l EI l EI l EI l EI l EI l EI l EI l EI l EI l EA l EA l EA l EI lEAl EI l EI l EI l EI l EI l EI l EI l EA l EA l EI l EI l EI l EI K 223-0230023-23023-23-0000002002-00023-062362062323-02323000002-6021260120003064060000000060126012222323222223232323222323 四、边界条件引入及组装总体方程由于节点1、3为固定约束,所以节点1和3的x 、y 方向的位移以及转角均为0,节点2无位移约束,不存在支反力,所以力约束即为外力约束。
⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡===-==-=====⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡======⋅0007506712581000000333'22'22'22111333222111θθθθV U Pl M M P F Q p F Q M Q Q V U V U V U K y y x x y x五、求解整体刚度方程,计算节点2的位移和转角提取节点2位移的相关要素:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-==-=====⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡++750671258162362323060212'22'22'22222222323Pl M M P F Q p F Q V U l EI l EI l EI l EI l EIl EA l EI l EA l EI y y x x θ求得:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡++-+-+++-+++--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡)()()()()()(224222422224223224223222721058112531680128311347210583754080419772105837527331614l I AIl l A EI I AIl l A P l I AIl l A E I Al P l I AIl l A E I Al P V U θ六、求节点1、3支撑反力根据总体方程,提取求解节点1支撑反力所需方程:⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡+++++++++++-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡)()()()()()('''2242224222422222422242111222223111721058112511703265529827210583754080419772105837513500206433942306006012I AIl l A I AIl l A Pl I AIl l A I Al P Al I AIl l A I AIl l A P M F F V U l EI l EI lEA l EI l EIM Q Q y x y x θ根据总体方程,提取求解节点2支撑反力所需方程:⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡++++-+++++++-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡)()()()()()('''22422242224222422242223332222233337210582250247680130809626872105837554000501903067721058375273316723023230002I AIl l A I AIl l A Pl I AIl l A I AIl l A P I AIl l A I Al P Al M F F V U l EI l EI l EI l EI l EA M Q Q y x y x θ七、设定数据,求解结果设定各个数据:杨氏模量:Pa E 10103⨯= 泊松比:3.0=μ 力:KN P 1=截面面积:205.0m A = 惯性矩:41m I = 将数据代入结果。
节点2的位移和转角:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⨯=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡++-+-+++-+++--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡0.1190 0.33020.0414101721058112531680128311347210583754080419772105837527331614l 7-224222422224223224223222)()()()()()(I AIl l A EI I AIl l A P l I AIl l A E I Al P l I AIl l A E I Al P V U θ节点1支撑反力:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡+++++++++++-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡564549110037210581125117032655298272105837540804197721058375135002064339422242224222422222422242111...)()()()()()(I AIl l A I AIl l A Pl I AIl l A I Al P Al I AIl l A I AIl l A P M Q Q y x 节点3支撑反力:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡++++-+++++++-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡3.14625.19501.3721058225024768013080962687210583755400050190306772105837527331672242224222422242224222333)()()()()()(I AIl l A I AIl l A Pl I AIl l A I AIl l A P I AIl l A I Al P Al M Q Q y x八、绘制轴力图、弯矩图、剪力图应用材料力学的分析方法,对梁单元进行分析。
