2011海淀高三二模数学(理科)
2011年高考数学北京卷(理科)含答案

2011年高考数学——北京卷(理科)一.选择题1.已知集合 EMBED Equation.DSMT4 , EMBED Equation.DSMT4 .若 EMBED Equation.DSMT4 ,则 EMBED Equation.DSMT4 的取值范围是 ( )A . EMBED Equation.DSMT4B . EMBED Equation.DSMT4C . EMBED Equation.DSMT4 D . EMBED Equation.DSMT42.复数 EMBED Equation.DSMT4( )A . EMBED Equation.DSMT4B . EMBED Equation.DSMT4C . EMBED Equation.DSMT4 D . EMBED Equation.DSMT43.在极坐标系中,圆的圆心的极坐标是 ( ) A . EMBED Equation.DSMT4 B . EMBED Equation.DSMT4C . EMBED Equation.DSMT4 D . EMBED Equation.DSMT44.执行如图所示的程序框图,输出的 EMBED Equation.DSMT4 值为( ) A . EMBED Equation.DSMT4 B . EMBEDEquation.DSMT4 C . EMBED Equation.DSMT4D . EMBED Equation.DSMT45.如图, EMBED Equation.DSMT4 , EMBED Equation.DSMT4, EMBED Equation.DSMT4 分别与圆 EMBED Equation.DSMT4切于点 EMBED Equation.DSMT4 , EMBED Equation.DSMT4 , EMBED Equation.DSMT4 ,延长 EMBED Equation.DSMT4与圆 EMBED Equation.DSMT4 交于另一点 EMBEDEquation.DSMT4 .给出下列三个结论: ① EMBED Equation.DSMT4 ;② EMBED Equation.DSMT4 ;③ EMBED Equation.DSMT4 . 其中正确结论的序号是 ( )A .①②B .②③C .①③D .①②③6.根据统计,一名工人组装第 EMBED Equation.DSMT4 件某产品所用的时间(单位:11s s s -=+0,2i s ==4i <1i i =+s 输出开始结束第4题 CF O EG分钟)为 EMBED Equation.DSMT4( EMBED Equation.DSMT4 , EMBEDEquation.DSMT4 为常数),已知工人组装第4件产品用时30分钟,组装第 EMBED Equation.DSMT4 件产品用时15分钟, 那么 EMBED Equation.DSMT4 和 EMBED Equation.DSMT4 的值分别是( )A .75, 25B .75, 16C .60, 25D .60,167.某四面体的三视图如图所示,该四面体四个面的面积中最大的是( )A .8B . EMBED Equation.DSMT4C .10D . EMBED Equation.DSMT48.设 EMBED Equation.DSMT4 , EMBED Equation.DSMT4 , EMBED Equation.DSMT4 , EMBED Equation.DSMT4 ( EMBED Equation.DSMT4 ).记 EMBED Equation.DSMT4为平行四边形 EMBED Equation.DSMT4 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数 EMBED Equation.DSMT4 的值域为 ( )A . EMBED Equation.DSMT4B . EMBED Equation.DSMT4C . EMBED Equation.DSMT4 D . EMBED Equation.DSMT4二.填空题9.在 EMBED Equation.DSMT4 中,若 EMBED Equation.DSMT4 , EMBED Equation.DSMT4, EMBED Equation.DSMT4 ,则 EMBED Equation.DSMT4_________; EMBED Equation.DSMT4 ________.10.已知向量 EMBED Equation.DSMT4 , EMBED Equation.DSMT4 , EMBED Equation.DSMT4 .若 EMBED Equation.DSMT4 与 EMBED Equation.DSMT4 共线,则 EMBED Equation.DSMT4 ______.11.在等比数列 EMBED Equation.DSMT4 中,若 EMBED Equation.DSMT4 , EMBED Equation.DSMT4,则公比 EMBED Equation.DSMT4 ; EMBED Equation.DSMT4. 12.用数字2,3组成四位数,且数字2,3 至少都出现一次,这样的四位数共有 个(用数字作答).13.已知函数 EMBED Equation.DSMT4若关于 EMBED Equation.DSMT4 的方程 EMBED Equation.DSMT4 有两个不同的实根,则实数 EMBED Equation.DSMT4 的取值范围是 .14.曲线 EMBED Equation.DSMT4 是平面内与两个定点 EMBED Equation.DSMT4 和 EMBED Equation.DSMT4的距离的积等于常数 EMBED Equation.DSMT4 ( EMBED Equation.DSMT4 )的点的轨迹,给出下列三个结论:①曲线 EMBED Equation.DSMT4 过坐标原点;②曲线 EMBED Equation.DSMT4 关于坐标原点对称;③若点 EMBED Equation.DSMT4 在曲线 EMBED Equation.DSMT4 上,则 EMBED Equation.DSMT4 的面积不大于 EMBED Equation.DSMT4. 其中,所有正确结论的序号是 .三.解答题15.(13分)已知函数 EMBED Equation.DSMT4.(1)求 EMBED Equation.DSMT4 的最小正周期;(2)求 EMBED Equation.DSMT4 在区间 EMBED Equation.DSMT4上的最大值和最小值.16.(14分)如图,在四棱锥 EMBED Equation.DSMT4 中, EMBED Equation.DSMT4 平面 EMBED Equation.DSMT4 ,底面EMBED Equation.DSMT4 是菱形, EMBED Equation.DSMT4 , EMBED Equation.DSMT4.(1)求证 EMBED Equation.DSMT4 平面EMBED Equation.DSMT4 ;(2)若 EMBED Equation.DSMT4 ,求 EMBEDEquation.DSMT4 与 EMBED Equation.DSMT4 所成角的余弦值;(3)当平面 EMBED Equation.DSMT4 与平面 EMBED Equation.DSMT4 垂直时,求 EMBEDEquation.DSMT4 的长.17.(13分)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以 EMBED Equation.DSMT4 表示.999X 008甲组乙组 C A B DP(1)如果 EMBED Equation.DSMT4 ,求乙组同学植树棵数的平均数和方差;(2)如果 EMBED Equation.DSMT4 ,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数 EMBED Equation.DSMT4 的分布列和数学期望.18.(13分)已知函数 EMBED Equation.DSMT4 .(1)求 EMBED Equation.DSMT4 的单调区间;(2)若对于任意的 EMBED Equation.DSMT4 ,都有 EMBED Equation.DSMT4,求 EMBED Equation.DSMT4 的取值范围.19.(14分)已知椭圆 EMBED Equation.DSMT4,过点 EMBED Equation.DSMT4作圆 EMBED Equation.DSMT4的切线 EMBED Equation.DSMT4 交椭圆 EMBED Equation.DSMT4 于 EMBED Equation.DSMT4 , EMBED Equation.DSMT4 两点.(1)求椭圆 EMBED Equation.DSMT4 的焦点坐标和离心率;(2)将 EMBED Equation.DSMT4 表示为 EMBED Equation.DSMT4 的函数,并求 EMBED Equation.DSMT4 的最大值.20.(13分)若数列 EMBED Equation.DSMT4 : EMBED Equation.DSMT4 ( EMBED Equation.DSMT4 )满足 EMBED Equation.DSMT4( EMBED Equation.DSMT4 ),则称 EMBED Equation.DSMT4为 EMBED Equation.DSMT4 数列.记 EMBED Equation.DSMT4. (1)写出一个满足 EMBED Equation.DSMT4 ,且 EMBED Equation.DSMT4 的 EMBED Equation.DSMT4 数列 EMBED Equation.DSMT4; (2)若 EMBED Equation.DSMT4, EMBED Equation.DSMT4 .证明: EMBED Equation.DSMT4 数列 EMBED Equation.DSMT4是递增数列的充要条件是 EMBED Equation.DSMT4; (3)对任意给定的整数 EMBED Equation.DSMT4 ( EMBED Equation.DSMT4),是否存在首项为0的 EMBED Equation.DSMT4 数列 EMBED Equation.DSMT4 ,使得 EMBED Equation.DSMT4?若果存在,写出一个满足条件的 EMBED Equation.DSMT4 数列 EMBED Equation.DSMT4;如果不存在,说明理由.HYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76eca 3d71bb8" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca3d71bb8&690" \*MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780ta53e66861fc5" \t "_blank" INCLUDEPICTURE"/middle/4dd45780ta53e66861fc5&690" \*MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76eca 3e4c1a6" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca3e4c1a6&690" \*MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780ta53e672feab7" \t "_blank" INCLUDEPICTURE"/middle/4dd45780ta53e672feab7&690" \*MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76ec a3f73edb" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca3f73edb&690" \*MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780ta53e 67c8b2da" \t "_blank" INCLUDEPICTURE"/middle/4dd45780ta53e67c8b2da&690" \* MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76ec a400870c" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca400870c&690" \* MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76ec a3c042eb" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca3c042eb&690" \* MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780t76ec a3cc5f9e" \t "_blank" INCLUDEPICTURE"/middle/4dd45780t76eca3cc5f9e&690" \* MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780ta53e6 60df7c8" \t "_blank" INCLUDEPICTURE"/middle/4dd45780ta53e660df7c8&690" \* MERGEFORMATINETHYPERLINK "/showpic.html" \l"blogid=4dd457800100to0p&url=/orignal/4dd45780ta53e 64a5792a" \t "_blank" INCLUDEPICTURE"/middle/4dd45780ta53e64a5792a&690" \* MERGEFORMATINET。
北京市海淀区2011年高考一模数学(理)试题及答案
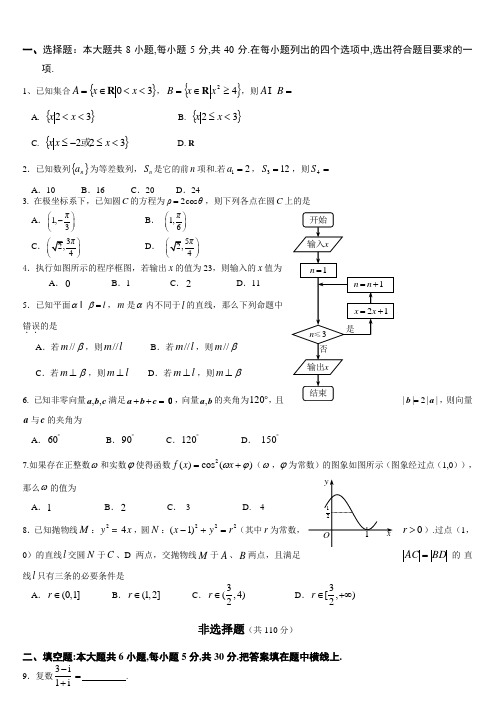
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1、已知集合{}30<<∈=x x A R ,{}42≥∈=x x B R ,则=B AA. {}32<<x xB. {}32<≤x x C. {}322<≤-≤x x x 或 D. R2.已知数列{}n a 为等差数列,n S 是它的前n 项和.若21=a ,123=S ,则=4S A .10 B .16 C .20 D .243. 在极坐标系下,已知圆C 的方程为2cos ρθ=,则下列各点在圆C 上的是 A .1,3π⎛⎫- ⎪⎝⎭B . 1,6π⎛⎫⎪⎝⎭C .32,4π⎛⎫ ⎪⎝⎭D . 52,4π⎛⎫ ⎪⎝⎭4.执行如图所示的程序框图,若输出x 的值为23,则输入的x 值为A .0B .1C .2D .11 5.已知平面l = αβ,m 是α内不同于l 的直线,那么下列命题中 错误..的是 A .若β//m ,则l m // B .若l m //,则β//m C .若β⊥m ,则l m ⊥ D .若l m ⊥,则β⊥m 6. 已知非零向量,,a b c 满足++=a b c 0,向量,a b 的夹角为120,且||2||=b a ,则向量a 与c 的夹角为A .︒60B .︒90C .︒120D . ︒1507.如果存在正整数ω和实数ϕ使得函数)(cos )(2ϕω+=x x f (ω,ϕ为常数)的图象如图所示(图象经过点(1,0)),那么ω的值为A .1B .2C . 3 D. 48.已知抛物线M :24y x =,圆N :222)1(r y x =+-(其中r 为常数,0>r ).过点(1,BD AC =的直0)的直线l 交圆N 于C 、D 两点,交抛物线M 于A 、B 两点,且满足线l 只有三条的必要条件是A .(0,1]r ∈B .(1,2]r ∈C .3(,4)2r ∈D .3[,)2r ∈+∞非选择题(共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.复数3i1i-+= . 21x x =+是否3n ≤1n n =+x输入开始1n =x 输出结束112yOx10.为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为1s ,2s ,3s ,则它们的大小关系为 . (用“>”连接)11.如图,A ,B ,C 是⊙O 上的三点,BE 切⊙O 于点B , D 是CE 与⊙O的交点.若︒=∠70BAC ,则=∠CBE ______;若2=BE ,4=CE ,则=CD .12.已知平面区域}11,11|),{(≤≤-≤≤-=y x y x D ,在区域D 内任取一点,则取到的点位于直线y kx =(k R ∈)下方的概率为____________ .13.若直线l 被圆22:2C x y +=所截的弦长不小于2,则在下列曲线中:①22-=x y ② 22(1)1x y -+= ③ 2212x y += ④ 221x y -=与直线l 一定有公共点的曲线的序号是 . (写出你认为正确的所有序号)14.如图,线段AB =8,点C 在线段AB 上,且AC =2,P 为线段CB 上一动点,点A 绕点C 旋转后与点B 绕点P 旋转后重合于点D .设CP =x ,△CPD 的面积为()f x .则()f x 的定义域为 ;'()f x 的零点是 .三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15. (本小题共13分)在ABC ∆中,内角A 、B 、C 所对的边分别为,,a b c ,已知1tan 2B =,1tan 3C =,且1c =. (Ⅰ)求tan A ;(Ⅱ)求ABC ∆的面积.ACBOD EA C P BDO 元频率组距0.00020.00040.00080.0006乙100015002000250030003500O 元频率组距0.00020.00040.00080.0006丙100015002000250030003500O 元频率组距0.00020.00040.00080.0006甲10001500200025003000350016. (本小题共14分)在如图的多面体中,EF ⊥平面AEB ,AE EB ⊥,//AD EF ,//EF BC , 24BC AD ==,3EF =,2AE BE ==, G 是BC 的中点. (Ⅰ) 求证://AB 平面DEG ; (Ⅱ) 求证:BD EG ⊥;(Ⅲ) 求二面角C DF E --的余弦值.17. (本小题共13分)某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为23.现有10件产品,其中6件是一等品,4件是二等品. (Ⅰ) 随机选取1件产品,求能够通过检测的概率;(Ⅱ)随机选取3件产品,其中一等品的件数记为X ,求X 的分布列; (Ⅲ) 随机选取3件产品,求这三件产品都不能通过检测的概率.18. (本小题共13分)已知函数()ln f x x a x =-,1(), (R).ag x a x+=-∈ (Ⅰ)若1a =,求函数()f x 的极值;(Ⅱ)设函数()()()h x f x g x =-,求函数()h x 的单调区间;(Ⅲ)若在[]1,e (e 2.718...=)上存在一点0x ,使得0()f x <0()g x 成立,求a 的取值范围.19. (本小题共14分)已知椭圆2222:1x y C a b += (0)a b >>经过点3(1,),2M 其离心率为12.(Ⅰ)求椭圆C 的方程;(Ⅱ)设直线1:(||)2l y kx m k =+≤与椭圆C 相交于A 、B 两点,以线段,OA OB 为邻边作平行四边形OAPB ,其中顶点P 在椭圆C 上,O 为坐标原点.求OP 的取值范围.20. (本小题共13分)已知每项均是正整数的数列A :123,,,,n a a a a ,其中等于i 的项有i k 个(1,2,3)i =⋅⋅⋅, 设j j k k k b +++= 21 (1,2,3)j = ,12()m g m b b b nm =+++- (1,2,3)m =⋅⋅⋅.(Ⅰ)设数列:1,2,1,4A ,求(1),(2),(3),(4),(5)g g g g g ;(Ⅱ)若数列A 满足12100n a a a n +++-= ,求函数)(m g 的最小值.A DFEB G C一、选择题(本大题共8小题,每小题5分,共40分) 题号 1 2 3 4 5 6 7 8 答案BCACDBBD非选择题 (共110分)二、填空题(本大题共6小题,每小题5分. 共30分.有两空的题目,第一空3分,第二空2分)9.12i - 10. s 1>s 2>s 3 11. 70 ; 3 12.1213. ① ③ 14. (2,4); 3 三、解答题(本大题共6小题,共80分) 15.(共13分) 解:(I )因为1tan 2B =,1tan 3C =,tan tan tan()1tan tan B C B C B C ++=-, …………………1分代入得到,1123tan()111123B C ++==-⨯ . …………………3分因为180A B C =-- , …………………4分 所以tan tan(180())tan()1A B C B C =-+=-+=-. …………………5分 (II )因为0180A << ,由(I )结论可得:135A = . …………………7分 因为11tan tan 023B C =>=>,所以090C B <<< . …………8分 所以5sin ,5B =10sin 10C =. …………9分由sin sin a cA C=得5a =, …………………11分 所以ABC ∆的面积为:11sin 22ac B =. ………………13分16. (共14分)解:(Ⅰ)证明:∵//,//AD EF EF BC , ∴//AD BC .又∵2BC AD =,G 是BC 的中点, ∴//AD BG ,∴四边形ADGB 是平行四边形,∴ //AB DG . ……………2分 ∵AB ⊄平面DEG ,DG ⊂平面DEG ,∴//AB 平面DEG . …………………4分HADFEB G C(Ⅱ) 解法1证明:∵EF ⊥平面AEB ,AE ⊂平面AEB ,∴EF AE ⊥, 又,AE EB EB EF E ⊥= ,,EB EF ⊂平面BCFE ,∴AE ⊥平面BCFE . ………………………5分过D 作//DH AE 交EF 于H ,则DH ⊥平面BCFE .∵EG ⊂平面BCFE , ∴DH EG ⊥. ………………………6分∵//,//AD EF DH AE ,∴四边形AEHD 平行四边形, ∴2EH AD ==,∴2EH BG ==,又//,EH BG EH BE ⊥,∴四边形BGHE 为正方形,∴BH EG ⊥, ………………………7分又,BH DH H BH =⊂ 平面BHD ,DH ⊂平面BHD ,∴EG ⊥平面BHD . ………………………8分 ∵BD ⊂平面BHD ,∴BD EG ⊥. ………………………9分 解法2∵EF ⊥平面AEB ,AE ⊂平面AEB ,BE ⊂平面AEB ,∴EF AE ⊥,EF BE ⊥, 又AE EB ⊥, ∴,,EB EF EA 两两垂直. ……………………5分 以点E 为坐标原点,,,EB EF EA 分别为,,x y z 轴建立如图的空间直角坐标系.由已知得,A (0,0,2),B (2,0,0), C (2,4,0),F (0,3,0),D (0,2,2), G (2,2,0). …………………………6分∴(2,2,0)EG = ,(2,2,2)BD =-,………7分∴22220BD EG ⋅=-⨯+⨯=, ………8分∴BD EG ⊥. …………………………9分(Ⅲ)由已知得(2,0,0)EB =是平面EFDA 的法向量. …………………………10分 设平面DCF 的法向量为(,,)x y z =n ,∵(0,1,2),(2,1,0)FD FC =-=,∴00FD n FC n ⎧⋅=⎪⎨⋅=⎪⎩ ,即2020y z x y -+=⎧⎨+=⎩,令1z =,得(1,2,1)=-n . …………………………12分 设二面角C DF E --的大小为θ,则26cos cos ,626EB -=<>==-θn , …………………………13分 ∴二面角C DF E --的余弦值为6.6-…………………………14分 x zyA D F EBG C17. (共13分)解:(Ⅰ)设随机选取一件产品,能够通过检测的事件为A …………………………1分事件A 等于事件 “选取一等品都通过检测或者是选取二等品通过检测” ……………2分151332104106)(=⨯+=A p …………………………4分 (Ⅱ) 由题可知X 可能取值为0,1,2,3.30463101(0)30C C P X C ===,21463103(1)10C C P X C ===, 12463101(2)2C C P X C ===,03463101(3)6C C P X C ===. ………………8分… ……………9分(Ⅲ)设随机选取3件产品都不能通过检测的事件为B ……………10分 事件B 等于事件“随机选取3件产品都是二等品且都不能通过检测” 所以,3111()()303810P B =⋅=. ……………13分18. (共13分)解:(Ⅰ)()f x 的定义域为(0,)+∞, ………………………1分 当1a =时,()ln f x x x =-,11()1x f x x x-'=-=, ………………………2分………………………3分所以()f x 在1x =处取得极小值1. ………………………4分(Ⅱ)1()ln ah x x a x x+=+-, 22221(1)(1)[(1)]()1a a x ax a x x a h x x x x x +--++-+'=--==………………………6分 ①当10a +>时,即1a >-时,在(0,1)a +上()0h x '<,在(1,)a ++∞上()0h x '>, 所以()h x 在(0,1)a +上单调递减,在(1,)a ++∞上单调递增; ………………………7分 ②当10a +≤,即1a ≤-时,在(0,)+∞上()0h x '>,所以,函数()h x 在(0,)+∞上单调递增. ………………………8分X 0 1 2 3P301103 21 61 x(0,1)1 (1,)+∞()f x ' — 0 + ()f x极小(III )在[]1,e 上存在一点0x ,使得0()f x <0()g x 成立,即 在[]1,e 上存在一点0x ,使得0()0h x <,即 函数1()ln ah x x a x x+=+-在[]1,e 上的最小值小于零. ………………………9分 由(Ⅱ)可知①即1e a +≥,即e 1a ≥-时, ()h x 在[]1,e 上单调递减,所以()h x 的最小值为(e)h ,由1(e)e 0eah a +=+-<可得2e 1e 1a +>-, 因为2e 1e 1e 1+>--,所以2e 1e 1a +>-; ………………………10分 ②当11a +≤,即0a ≤时, ()h x 在[]1,e 上单调递增,所以()h x 最小值为(1)h ,由(1)110h a =++<可得2a <-; ………………………11分 ③当11e a <+<,即0e 1a <<-时, 可得()h x 最小值为(1)h a +, 因为0ln(1)1a <+<,所以,0ln(1)a a a <+< 故(1)2ln(1)2h a a a a +=+-+>此时,(1)0h a +<不成立. ………………………12分 综上讨论可得所求a 的范围是:2e 1e 1a +>-或2a <-. ………………………13分19. (共14分)解:(Ⅰ)由已知可得222214a b e a -==,所以2234a b = ① ……………1分 又点3(1,)2M 在椭圆C 上,所以221914a b += ② ……………2分 由①②解之,得224,3a b ==.故椭圆C 的方程为22143x y +=. ……………5分 (Ⅱ) 当0k =时,(0,2)P m 在椭圆C 上,解得32m =±,所以||3OP =. ……6分 当0k ≠时,则由22,1.43y kx m x y=+⎧⎪⎨+=⎪⎩ 消y 化简整理得:222(34)84120k x kmx m +++-=,222222644(34)(412)48(34)0k m k m k m ∆=-+-=+-> ③ ……………8分设,,A B P 点的坐标分别为112200(,)(,)(,)x y x y x y 、、,则 012012122286,()23434km mx x x y y y k x x m k k=+=-=+=++=++. ……………9分 由于点P 在椭圆C 上,所以 2200143x y +=. ……………10分从而222222216121(34)(34)k m m k k +=++,化简得22434m k =+,经检验满足③式. ………11分 又22222022226436||(34)(34)k m m OP x y k k =+=+++2222224(169)169(34)43m k k k k ++==++234.43k =-+ ………………………12分因为102k <≤,得23434k <+≤,有2331443k ≤<+, 故1332OP <≤. ………………………13分 综上,所求OP 的取值范围是13[3,]2. ………………………14分 (Ⅱ)另解:设,,A B P 点的坐标分别为112200(,)(,)(,)x y x y x y 、、, 由,A B 在椭圆上,可得2211222234123412x y x y ⎧+=⎨+=⎩①②………………………6分 ①—②整理得121212123()()4()()0x x x x y y y y -++-+=③ ………………………7分由已知可得OP OA OB =+ ,所以120120x x x y y y +=⎧⎨+=⎩④⑤……………………8分由已知当1212y y k x x -=- ,即1212()y y k x x -=- ⑥ ………………………9分把④⑤⑥代入③整理得0034x ky =- ………………………10分与22003412x y +=联立消0x 整理得202943y k =+ ……………………11分 由22003412x y +=得2200443x y =-, 所以222222000002413||4443343OP x y y y y k =+=-+=-=-+ ……………………12分 因为12k ≤,得23434k ≤+≤,有2331443k ≤≤+,故1332OP ≤≤. ………………………13分 所求OP 的取值范围是13[3,]2. ………………………14分 20. (共13分)解:(1)根据题设中有关字母的定义,12342,1,0,1,0(5,6,7)j k k k k k j ======12342,213,2103,4,4(5,6,7,)m b b b b b m ==+==++====112123123412345(1)412(2)423,(3)434,(4)444,(5)45 4.g b g b b g b b b g b b b b g b b b b b =-⨯=-=+-⨯=-=++-⨯=-=+++-⨯=-=++++-⨯=-(2)一方面,1(1)()m g m g m b n ++-=-,根据“数列A 含有n 项”及j b 的含义知1m b n +≤, 故0)()1(≤-+m g m g ,即)1()(+≥m g m g ① …………………7分 另一方面,设整数{}12max ,,,n M a a a = ,则当m M ≥时必有m b n =, 所以(1)(2)(1)()(1)g g g M g M g M ≥≥≥-==+=所以()g m 的最小值为(1)g M -. …………………9分 下面计算(1)g M -的值:1231(1)(1)M g M b b b b n M --=++++--1231()()()()M b n b n b n b n -=-+-+-++-233445()()()()M M M M k k k k k k k k k k =----+----+----++- 23[2(1)]M k k M k =-+++-12312(23)()M M k k k Mk k k k =-++++++++ 123()n M a a a a b =-+++++ 123()n a a a a n=-+++++…………………12分∵123100n a a a a n ++++-= , ∴(1)100,g M -=-∴()g m 最小值为100-. …………………13分。
2011年高考北京数学试题(理科)及参考答案详解

2011年高考数学——北京理科卷详解高考前,我们分别在1月底和4月底帮学生作过预测。
2011年高考与2010年相比:(1)新增知识点将增加出题量。
新增知识不会综合。
(2) 三角函数题变化不大,以函数为主。
(3)立体题考查基本图形中的变化,建系是工具 。
(4)概率大题 突出对数据的认识,图、表、直方图、茎叶图。
如果使用排列组合题目将简单。
(5)导数大题,眼下的题让人猜的透透的,将会有变化。
(6)解析大题,“解析几何首先是几何”“代数是手段”“解析几何的本质是把问题代数化。
(7)数列压轴。
沿用等差等比数列的研究方法研究新定义数列。
一.选择题1.已知集合2{|1}P x x =≤,{}M a =.若P M P = ,则a 的取值范围是( ) A .(,1]-∞- B .[1,)+∞ C .[1,1]- D .(,1][1,)-∞-+∞ 1、答案:C解:数轴法可知1a 1≤≤-2.复数212i i-=+ ( ) A .i B .i - C .4355i -- D . 4355i -+2、答案:A 。
解:i 41)2i 1)(2i (2i 12i z =+--=+-=3.在极坐标系中,圆的圆心的极坐标是 ( ) A .(1,)2πB .(1,)2π- C .(1,0)D .(1,)π 3、答案:B解:θρρsin 22-=,2y y x 22-=+,1)1y (x 22=++, 圆心)1,0(-。
改写为极坐标(1,2π-)4.执行如图所示的程序框图,输出的s 值为 ( ) A .3- B .12- C .13D .24、答案:D 。
解:0<4,i=1,31s =;…,,43<i=4,2s =11s s s -=+0,2i s ==4i <1i i =+s输出开始结束第4题5.如图,AD ,AE ,BC 分别与圆O 切于点D ,E ,F ,延长AF 与圆O 交于另一点G .给出下列三个结论:①AD AE AB BC CA +=++; ②AF AG AD AE ⋅=⋅; ③AFB ADG △△∽.其中正确结论的序号是 ( )A .①②B .②③C .①③D .①②③5、答案:A.解:综合运用切线长定理,圆幂定理。
年北京市海淀区二模理科数学试卷含答案

海淀区高三年级第二学期期末练习数学(理科) 2009.05一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. (1)已知集合{}12A x y x==-,集合{}1B xx = ,则A B 等于( )(A )112x x 禳镲镲#睚镲镲铪 (B ){}1x x ?(C )112x x 禳镲镲-#睚镲镲铪(D ){}1x x ³ (2)某行业主管部门所属的企业有800家,按企业固定资产规模分为大型企业﹑中型企业﹑小型企业. 大﹑中﹑小型企业分别有80家,320家和400家,该行业主管部门要对所属企业的第一季度生产状况进行分层抽样调查,共抽查100家企业. 其中大型企业中应抽查 ( )(A )20家 (B )16家 (C )10家 (D )8家 (3)若102a b <<<,则 ( )(A )22aba> (B )22abb> (C )2log ()1ab >- (D )2log ()2ab <-(4)在ABC ∆中,,,A B C 行 所对的边长分别为,,a b c ,如果cos cos a B b A =,那么ABC∆一定是()(A )锐角三角形 (B )钝角三角形 (C )直角三角形 (D )等腰三角形(5)若直线()1:4l y k x =-与直线2l 关于点)1,2(对称,则直线2l 恒过定点 ( )(A )()0,4 (B )()0,2 (C )()2,4- (D )()4,2-(6)某班班会准备从甲、乙等7名学生中选派4名学生发言,要求甲、乙两名同学至少有一人参加,且若甲乙同时参加,则他们发言时不能相邻.那么不同的发言顺序种数为 ( )(A )360 (B )520 (C )600 (D )720(7)在棱长均为2的正四棱锥P ABCD -中,点E 为PC 的中点,则下列命题正确的是 ( )(A )BE ∥平面PAD ,且BE 到平面PAD 3(B )BE ∥平面PAD ,且BE 到平面PAD 26(C )BE 与平面PAD 不平行,且BE 与平面PAD 所成的角大于30︒(D )BE 与平面PAD 不平行,且BE 与平面PAD 所成的角小于30︒(8)已知点M 是矩形ABC D 所在平面内任意一点,则下列结论中正确的是( )(A )MB MD MA MC -=-(B )()()0MB MD MA MC -?(C )MB MDMA MC ?(D )MA MD MB MC 壮二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.(9)已知等比数列{}n a 中,12a =,26S =,那么5S 的值为 .(10)已知函数()120,0x x f x x a x +ìï>ï=íï+ ïî 是连续函数,则实数a 的值是 .(11)已知tan =2α,则3cos 22πα⎛⎫+⎪⎝⎭的值等于______ _ . (12)已知函数()()sin (0,)2f x x πωφωφ=+><的导函数()'y f x =的部分图象如图所示,且导函数()'f x 有最小值2-,则ω= ,E DCBAPO yxπ6-2-1()'y f x =φ= .(13)以双曲线的一个顶点为圆心的圆经过该双曲线的一个焦点,且与该双曲线的一条准线相切,则该双曲线的离心率为 . (14)下图展示了一个由区间(0,1)到实数集R 的映射过程:区间()0,1中的实数m 对应数轴上的点M ,如图1;将线段AB 围成一个圆,使两端点A 、B 恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在y 轴上,点A 的坐标为()0,1,如图3.图3中直线AM 与x 轴交于点(),0N n ,则m 的象就是n ,记作()f m n =.(ⅰ)方程()0f x =的解是x = ;(ⅱ)下列说法中正确命题的序号是 .(填出所有正确命题的序号) ①114f ⎛⎫=⎪⎝⎭; ②()f x 是奇函数; ③()f x 在定义域上单调递增; ④()f x 的图象关于点1,02⎛⎫ ⎪⎝⎭对称.1NMM AB A xyO 图1 图2 图3三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程. (15)(本小题共13分)已知数列{}n a 的前n 项和为n S ,11a =, 21(1)n n nS n S n cn +-+=+(c ∈R ,1,2,3,...n =).且1S ,22S ,33S 成等差数列. (Ⅰ)求c 的值;(Ⅱ)求数列{}n a 的通项公式.(16)(本小题共13分)检测部门决定对某市学校教室的空气质量进行检测,空气质量分为A、B、C三级.每间教室的检测方式如下:分别在同一天的上、下午各进行一次检测,若两次检测中有C级或两次都是B级,则该教室的空气质量不合格. 设各教室的空气质量相互独立,且每次检测的结果也相互独立. 根据多次抽检结果,一间教室一次检测空气质量为A、B、C三级的频率依次为311 488,,.(Ⅰ)在该市的教室中任取一间,估计该间教室的空气质量合格的概率;(Ⅱ)如果对该市某中学的4间教室进行检测,记在上午检测空气质量为A级的教室间数为ξ,并以空气质量为A级的频率作为空气质量为A级的概率,求ξ的分布列及期望.如图,斜三棱柱111ABC A B C -的底面是直角三角形,90ACB ∠=︒,点1B 在底面ABC 上的射影恰好是BC 的中点,且1BC CA AA ==.(Ⅰ)求证:平面11ACC A ⊥平面11B C CB ; (Ⅱ)求证:1BC 1AB ⊥;(Ⅲ)求二面角11B AB C --的大小.B 1C 1A 1CBA已知:函数()xe f x x a=-(其中常数0a <).(Ⅰ)求函数()f x 的定义域及单调区间; (Ⅱ)若存在实数(],0x a ∈,使得不等式()12f x ≤成立,求a 的取值范围.已知抛物线C :2y x =,过定点()0,0A x 01()8x ≥,作直线l 交抛物线于,P Q (点P 在第一象限).(Ⅰ)当点A 是抛物线C 的焦点,且弦长2PQ =时,求直线l 的方程;(Ⅱ)设点Q 关于x 轴的对称点为M ,直线PM 交x 轴于点B ,且BQ BP ⊥.求证:点B 的坐标是0(,0)x -并求点B 到直线l 的距离d 的取值范围.已知)(x f 定义域为R ,满足:①)1(1)1(->=f f ;②对任意实数y x ,,有)1()1()()()1(--+=+-y f x f y f x f x y f . (Ⅰ)求)0(f ,(3)f 的值; (Ⅱ)求21(16)(3)2f x f x -+的值; (Ⅲ)是否存在常数B A ,,使得不等式2|)2()(|≤++-+B Ax x f x f 对一切实数x 成立.如果存在,求出常数B A ,的值;如果不存在,请说明理由.海淀区高三年级第二学期期末练习数学(理科) 参考答案及评分标准2009.05一、选择题(本大题共8小题,每小题5分,共40分)ACDDB CDC二、填空题(本大题共6小题,每小题5分.有两空的小题,第一空3分,第二空2分,共30分)(9)62 (10)2 (11)45 (12)2,π3(1321 (14)12,③④ 三、解答题(本大题共6小题,共80分) (15)(本小题共13分)解:(Ⅰ)∵21(1)n n nS n S n cn +-+=+(1,2,3,...n =), ∴()2111n n S S n cnn n n n ++-=++(1,2,3,...n =). ………………………………………1分∵1S ,22S ,33S 成等差数列, ∴32122132S S S S -=-. ………………………………………3分 ∴14226c c++=. ………………………………………5分 ∴1c =. ………………………………………6分(Ⅱ)由(Ⅰ)得111n nS S n n+-=+(1,2,3,...n =). ∴数列{}n Sn为首项是11S ,公差为1的等差数列. ………………………………………8分∴1(1)11n S S n n n =+-⋅=. ∴2n S n =. ………………………………………10分 当2n ≥时,221(1)21n n n a S S n n n -=-=--=-. ………………………………………12分当1n =时,上式也成立. ………………………………………13分∴21n a n =-(1,2,3,...n =).(16)(本小题共13分)解:(Ⅰ)该间教室两次检测中,空气质量均为A 级的概率为3394416?.………………………………2分 该间教室两次检测中,空气质量一次为A 级,另一次为B 级的概率为31324816创=. …………………………………4分设“该间教室的空气质量合格”为事件E .则 …………………………………5分()33313244484P E =?创=. …………………………………6分答:估计该间教室的空气质量合格的概率为34. (Ⅱ)由题意可知,ξ的取值为0,1,2,3,4. …………………………………7分()443C )4i ii P i ξ-==3()(1-4()0,1,2,3,4i =. 随机变量ξ的分布列为:ξ0 1 2 3 4P1256 364 27128 2764 81256…………………………………12分解法一: ∴132********+3432566412864256E ξ=??创+?. …………………………………13分解法二: 344B ξ~(,), ∴3434E ξ=?. …………………………………13分(17)(本小题共14分)(Ⅰ)证明:设BC 的中点为M .在斜三棱柱111ABC A B C -中,点1B 在底面ABC 上的射影恰好是BC 的中点, 1B M ∴⊥平面ABC. ……………………1分AC Ì平面ABC ,1B M AC ∴⊥. ……………………2分90ACB ∠=︒, ∴BC AC ⊥. 1B M BC M = ,∴AC ⊥平面11B C CB . ……………………4分AC ⊂平面11ACC A ,∴平面11ACC A ⊥平面11B C CB . ………………………………………5分解法一:(Ⅱ)连接1B C , AC ⊥平面11B C CB ,1B C∴是直线1AB 在平面11B C CB上的射影. ………………………………………5分1BC CC =,∴四边形11B C CB 是菱形.11B C BC ∴⊥. ………………………………………7分11AB BC ∴⊥. …………………………MB 1C 1A 1CB A……………9分(Ⅲ)过点B 作1BH AB ⊥交1AB 于点H ,连接1C H .11AB BC ⊥ ,1AB ∴⊥平面1BHC . 11AB C H ∴⊥.1BHC ∴∠是二面角11B ABC --的平面角. ………………………………………11分设2BC =,则12,BC CA AA === 1,B M BC BM MC ⊥=,112B C B B ∴==. 112BB B C BC ∴===.160.B BC ∴∠=︒ 1120BCC ∴∠=︒. 123BC ∴=.AC ⊥ 平面1BC ,1B C Ì平面1BC , 1AC B C ∴⊥. 122B A ∴=.在1BB A ∆中,可求142BH =∵11111,B B B C B H B H ==,∴111Rt Rt BB H C B H ∆≅∆. ∴1142C H BH ==. 1141412544cos 71414222BHC +-∴∠==-⨯⨯. ………………………………………13分MHB 1C 1A 1CBA15arccos 7BHC π∴∠=-.∴二面角11B ABC --的大小为5arccos 7π-. ………………………………………14分解法二:(Ⅱ)因为点1B 在底面ABC 上的射影是BC 的中点,设BC 的中点为O ,则1B M ⊥平面ABC.以O 为原点,过O 平行于CA 的直线为x 轴,BC 所在直线为y 轴,1OB 所在直线为z 轴,建立如图所示的空间直角坐标系. 设11BC CA AA ===,由题意可知,11131(0,,0),(0,,0),(0,0,(1,,0)2222B C B A --.设1(,,)C x y z ,由11BC B C = ,得13(0,1,2C - ………………………………………7分133(0,,22BC ∴=- .又113(1,,22AB =- . 11133310022AB BC ⎛⎫∴⋅=-⨯+⨯-+= ⎪⎝⎭ .11AB BC ∴⊥. ………………………………………9分(Ⅲ)设平面1ABB 的法向量为111(,,1)x y =n .则1110,0.BA BB ⎧⋅=⎪⎨⋅=⎪⎩n n∴1110,130.22x y y -=⎧⎪⎨-+=⎪⎩ 1(3,3,1)∴=n .z yxOB 1C 11BA设平面11AB C 的法向量为222(,,1)x y =n .则21210,0.AB AC ⎧⋅=⎪⎨⋅=⎪⎩n n∴2222130,2130.22x y x y ⎧-+=⎪⎪⎨⎪--+=⎪⎩ 23(2∴=n . ………………………………………12分1212125cos ,7⋅∴<>==n n n n n n . ………………………………………13分∴二面角11B AB C --的大小为5arccos 7π-. ………………………………………14分(18)(本小题共13分) 解:(Ⅰ)函数()f x 的定义域为{}x x a≠. ………………………………………1分 ()()()()()2211x x x e x a e x a e f x x a x a -+⎡⎤--⋅⎣⎦'==--. ………………………………………3分由()0f x '>,解得1x a >+.由()0f x '<,解得1x a <+且x a ≠.∴()f x 的单调递增区间为()1,a ++∞,单调递减区间为(),a -∞,(),1a a +.………………………………………6分(Ⅱ)由题意可知,0a <,且()x e f x x a =-在(],0a 上的最小值小于等于12时,存在实数(],0x a ∈,使得不等式()12f x ≤成立. ………………………………………7分 若10a +<即1a <-时,x(),1a a +a +1 ()1,0a +()f x ' - 0 + ()f x↘极小值↗∴()f x 在(],0a 上的最小值为()11a f a e ++=.则112a e +≤,得1ln 12a ≤-. ………………………………………10分 若10a +≥即1a ≥-时,()f x 在(],0a 上单调递减,则()f x 在(],0a 上的最小值为()10f a=-.由112a -≤得2a ≤-(舍). ………………………………………12分综上所述,1ln12a ≤-. ………………………………………13分 (19)(本小题共13分)解:(Ⅰ)由抛物线C :2y x =得抛物线的焦点坐标为1(,0)4,设直线l 的方程为:14x ny =+,()()1122,,,P x y Q x y . ………………………………………1分由2,14y x x ny ìï=ïïíï=+ïïî得2104y ny --=. 所以210n ∆=+>,12y y n+=.因为112211,44x ny x ny =+=+, …………………………………3分 所以()12121211112442PQ x x x x n y y =+++=++=++=.所以21n =.即1n = . 所以直线l的方程为:104x y --=或104x y +-=. ………………………………………5分 (Ⅱ)设0:(0)l x my x m =+≠,1122(,),(,)P x y Q x y ,则22(,)M x y -.由02,x my x y x=+⎧⎨=⎩得200y my x --=.因为018x ≥,所以2040m x ∆=+>,12120,y y m y y x +==-. ……………………………………7分 (ⅰ)设(,0)B B x ,则2211(,),(,)B B BM x x y BP x x y =--=-.由题意知:BM ∥BP,211122B B x y y x x y x y ∴-=-+.即2212122112211212()()B y y x x y x y y y y y y y y y +=+=+=+. 显然10,By y += ………………………………………9分(ⅱ)由题意知:BMQ ∆为等腰直角三角形,1PB k ∴=,即12121y y x x +=-,即1222121y y y y +=-. 2212121201. ()4 1. 41y y y y y y m x ∴-=∴+-=∴+=. 20140m x ∴=->.014x ∴<.018x ≥,01184x ∴≤<. ………………………………………11分 002220002261[)2241111()2()(1)1d x m x x x ∴====-+---. 即d的取值范围是61)2. ………………………………………13分 (20)(本小题共14分)解:(Ⅰ)取1==y x ,得(111)(1)(1)(11)(f f f f f -+=?-?,即22(1)(1)(0)f f f =+.因为(f =,所以(0)0f =. ………………………………………1分取0==y x ,得21(1)(1)f f ==-.因为)1(1)1(->=f f ,所以(1)1f -=-. 取2,0==y x ,得(3)(0)(2)(1)(1)f f f f f =?- ,所以(3)1f =-.………………………………………3分(Ⅱ)在)1()1()()()1(--+=+-y f x f y f x f x y f 中取1=y 得)()2(x f x f =-.所以(1)(1)f x f x +=-. 在)1()1()()()1(--+=+-y f x f y f x f x y f 中取xy =,得1)1()(22=-+x f x f .在)1()1()()()1(--+=+-y f x f y f x f x y f 中取0x =, 得(1)(0)()(1)(1)(1)f y f f y f f y f y +=+--=--. 所以(2)0f -=.在)1()1()()()1(--+=+-y f x f y f x f x y f 中取1y =-, 得()()(1)(1)(2)f x f x f f x f -=-+--. 所以()()f x f x -=-.在)1()1()()()1(--+=+-y f x f y f x f x y f 中取y x =-, 得()()()()()1211f x f x f x f x f x -=-+---()()()211f x f x f x =---+()()()()()()222211112f x f x f x f x f x f x =----=-+-=-.所以211(12)()22f x f x -+=对任意实数x 均成立. 所以211(16)(3)22f x f x -+=. ………………………………………9分(Ⅲ)由(Ⅱ)知)()2(x f x f =-,2|)2()(|≤++-+∴B Ax x f x f 2|)(2|≤++⇔B Ax x f在2|)(2|≤++B Ax x f 中,取1-=x ,得222≤+--≤-B A ,即222A B -?- ① 取1=x ,得222≤++≤-B A ②取3=x ,得2322≤++-≤-B A ,即2232A B -?- ③②+①得0≤A ,②+③得0≥A . ∴0=A .将0=A 代入①得0≥B . 将0=A 代入②得0≤B . ∴0=B .由(Ⅱ)知1)1()(22=-+x f x f ,所以|()|1f x £对一切实数x 成立. 故当0==B A 时,2|)(2|≤++B Ax x f 对一切实数x 成立.∴存在常数0==B A ,使得不等式2|)2()(|≤++-+B Ax x f x f 对一切实数x 成立,且0==B A 为满足题设的唯一一组值. ………………………………………14分说明:其它正确解法按相应步骤给分.。
2011-2012学年北京市海淀区高三(上)期末数学试卷(理科)(解析版)

2011-2012学年北京市海淀区高三(上)期末数学试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 复数52+i( )A.2−iB.25+15iC.10−5iD.103−53i2. 如图,正方形中,点E 是DC 的中点,点F 是BC 的一个三等分点.那么EF →=( )A.12AB →−13AD →B.14AB →−12AD →C.13AB →+12DA →D.12AB →−23AD →3. 若数列{a n }满足:a 1=19,a n+1=a n −3(n ∈N ∗),而数列{a n }的前n 项和最大时,n 的值为( ) A.6 B.7C.8D.94. 已知平面α,β,直线l ,若α⊥β,α∩β=l ,则( ) A.垂直于平面β的平面一定平行于平面α B.垂直于直线l 的直线一定垂直于平面α C.垂直于平面β的平面一定平行于直线l D.垂直于直线l 的平面一定与平面α,β都垂直5. 函数f(x)=A sin (2x +φ)(A, φ∈R)的部分图象如图所示,那么f(0)=( )A.−12B.−√32C.−1D.−√36. 执行如图所示的程序框图,输出的i 值为( )A.5B.6C.7D.87. 已知函数f(x)=cos 2x +sin x ,那么下列命题中假命题是( ) A.f(x)既不是奇函数也不是偶函数 B.f(x)在[−π, 0]上恰有一个零点 C.f(x)是周期函数 D.f(x)在(π2,5π6)上是增函数8. 点P 到图形C 上每一个点的距离的最小值称为点P 到图形C 的距离,那么平面内到定圆C 的距离与到定点A 的距离相等的点的轨迹不可能是( ) A.圆 B.椭圆C.双曲线的一支D.直线二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上.(√x +1)5的展开式中x 2的系数是________.(用数字作答)若实数x ,y 满足{x +y −4≤0y −1≥02x +y −5≥0则z =x +2y 的最大值为________.抛物线x2=ay过点A(1,14),则点A到此抛物线的焦点的距离为________.甲和乙两个城市去年上半年每月的平均气温(单位:∘C)用茎叶图记录如下,根据茎叶图可知,两城市中平均温度较高的城市是________,气温波动较大的城市是________.知圆C:(x−1)2+y2=2,过点A(−1, 0)的直线l将圆C分成弧长之比为1:3的两段圆弧,则直线l的方程为________.已知正三棱柱ABC−A′B′C′的正(主)视图和侧(左)视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,射线OA旋转所成的角为x弧度(x可以取到任意一个实数),对应的俯视图的面积为S(x),则函数S(x)的最大值为________;最小正周期为________.说明:“三棱柱绕直线OO′旋转”包括逆时针方向和顺时针方向,逆时针方向旋转时,OA旋转所成的角为正角,顺时针方向旋转时,OA旋转所成的角为负角.三、解答题(共6小题,满分80分)在△ABC中,角A,B,C所对的边分别为a,b,c,A=2B,sin B=√33.(1)求cos A及sin C的值;(2)若b=2,求△ABC的面积.为加强大学生实践、创新能力和团队精神的培养,促进高等教育教学改革,教育部门主办了全国大学生智能汽车竞赛.该竞赛分为预赛和决赛两个阶段,参加决赛的队伍按照抽签方式决定出场顺序.通过预赛,选拔出甲、乙等五支队伍参加决赛.(1)求决赛中甲、乙两支队伍恰好排在前两位的概率;(2)若决赛中甲队和乙队之间间隔的队伍数记为X,求X的分布列和数学期望.在四棱锥P−ABCD中,底面ABCD是直角梯形,AB // CD,∠ABC=90∘,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD.(1)求证:AB⊥平面PBC;(2)求平面PAD和平面BCP所成二面角(小于90∘)的大小;(3)在棱PB上是否存在点M使得CM // 平面PAD?若存在,求PMPB的值;若不存在,请说明理由.已知函数f(x)=e x(x2+ax−a),其中a是常数.(1)当a=1时,求曲线y=f(x)在点(1, f(1))处的切线方程;(2)若存在实数k,使得关于x的方程f(x)=k在[0, +∞)上有两个不相等的实数根,求k的取值范围.已知焦点在x轴上的椭圆C过点(0, 1),且离心率为√32,Q为椭圆C的左顶点.(1)求椭圆C的标准方程;(2)已知过点(−65,0)的直线l与椭圆C交于A,B两点.(I)若直线l垂直于x轴,求∠AQB的大小;(II)若直线l与x轴不垂直,是否存在直线l使得△QAB为等腰三角形?如果存在,求出直线l的方程;如果不存在,请说明理由.已知集合M={1, 2, 3, ..., n}(n∈N∗),若集合A={a1,a2,a3,⋯,a m}(m∈N∗),且对任意的b∈M,存在a i,a j∈A(1≤i≤j≤m),使得b=λ1a i+λ2a j(其中λ1,λ2∈{−1, 0, 1}),则称集合A为集合M的一个m元基底.(Ⅰ)分别判断下列集合A是否为集合M的一个二元基底,并说明理由;①A={1, 5}M={1, 2, 3, 4, 5};②A={2, 3},M={1, 2, 3, 4, 5, 6}.(Ⅱ)若集合A是集合M的一个m元基底,证明:m(m+1)≥n;(Ⅲ)若集合A为集合M={1, 2, 3, ..., 19}的一个m元基底,求出m的最小可能值,并写出当m取最小值时M的一个基底A.参考答案与试题解析2011-2012学年北京市海淀区高三(上)期末数学试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分。
北京海淀2011高三二模考试理综扫描版

海淀区高三年级第二学期期末练习物理参考答案 2011.5选择题,每小题6分,共48分。
选对的得6分,选错或不答的得0分。
非选择题,共72分。
21.(18分) (1)①甲;(2分) ②EDBA ;(2分)③111.10±0.05;(2分)6.4(±0.2)×10-7 m (2分)(2)①ACE ;(2分)②C ;(2分)③m 1·OP = m 1·OM + m 2·ON ;(2分) m 1·OP 2 = m 1·OM 2 + m 2·ON 2;(2分)④321121l m l m l m +=(2分)22.(16分) 解:(1)cd 边进入磁场时产生的感应电动势为BLv E = (2分)整个回路的电阻 R 总=6R (1分) 回路中的电流RBLvR E I 6==总 (2分) ab 边两端电压的大小为BLv IR U 61ab == (2分) (2)为维持线框匀速运动,外力应始终等于安培力,即:F =F 安 (2分) 线框所受安培力为RvL B BIL F 622==安水平拉力 RvL B F F 622==安 (2分)(3)整个线框通过磁场的过程中所经历的时间为 vL v x t 4==(2分) 整个过程中bc 段金属导线上产生的电热为RvL B t R I Q 922322bc =⋅⋅= (3分)用其他方法计算正确的同样给分。
23.(18分) 解:(1)运动员从D 点跃起后在空中做竖直上抛运动,设运动员上升的时间为t 1,根据运动学公式 v D =gt 1运动员在空中完成动作的时间 gv t t D122=='=1.6s (5分) (2)运动员从B 点到C 点,做匀变速直线运动,运动过程的平均速度2C B BC v v t s v +==解得运动员到达C 点时的速度 B C 2v tsv -==15.8m/s (3分) 运动员从C 点到D 点的过程中,克服摩擦力和重力做功,根据动能定理 2C 2D f 2121mv mv mgR W -=-- (3分) 得运动员克服摩擦力做功mgR mv mv W --=2D 2C f 2121代入数值解得 W f =2891J (3分)(3)不可能。
北京市海淀区高三数学理科二模试卷及答案(WORD版)

北京市海淀区2012高三二模数 学(理科)2012.05一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若sin cos 0θθ<,则角θ是 (A )第一或第二象限角 (B )第二或第三象限角 (C )第三或第四象限角 (D )第二或第四象限角 (2)已知命题p :0x ∃∈R ,021x =.则p ⌝是 (A )0x ∀∈R ,021x ≠ (B )0x ∀∉R ,021x ≠ (C )0x ∃∈R ,021x ≠(D )0x ∃∉R ,021x ≠(3)直线11x ty t =+⎧⎨=-⎩(t 为参数)的倾斜角的大小为(A )4-π (B )4π (C )2π(D )34π(4)若整数,x y 满足1,1,3,2x y x y y ìïïï-?ïïï+?íïïïï£ïïî则2x y +的最大值是 (A )1(B )5(C )2 (D )3(5)已知点12,F F 是椭圆2222x y +=的两个焦点,点P 是该椭圆上的一个动点,那么12PF PF +u u u r u u u u r的最小值是(A )0 (B )1 (C )2 (D)(6)为了得到函数2log y =2log y x =的图象上所有的点的(A )纵坐标缩短到原来的12倍,横坐标不变,再向右平移1个单位长度 (B )纵坐标缩短到原来的12倍,横坐标不变,再向左平移1个单位长度(C )横坐标伸长到原来的2倍,纵坐标不变,再向左平移1个单位长度(D )横坐标伸长到原来的2倍,纵坐标不变,再向右平移1个单位长度俯视图主视图(7)某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是(A )203(B )43(C )6 (D )4(8)点(,)P x y 是曲线1:(0)C y x x=>上的一个动点,曲线C 在点P 处的切线与x 轴、y 轴分别交于,A B 两点,点O 是坐标原点. 给出三个命题:①PA PB =;②OAB ∆的周长有最小值4+;③曲线C 上存在两点,M N ,使得OMN ∆为等腰直角三角形.其中真命题的个数是(A )1 (B )2 (C )3 (D )0二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上. (9)在面积为1的正方形ABCD 内部随机取一点P ,则PAB ∆的面积大于等于14的概率是_________. (10)已知1021012311(1)x a a x a x a x +=++++L . 若数列123,,,,(111,)k a a a a k k #?Z L 是一个单调递增数列,则k 的最大值是 . (11)在ABC ∆中,若120A ??,5c =,ABC ∆的面积为,则a = .(12)如图,O e 的直径AB 与弦CD 交于点P ,7, 5, 15CP PD AP ===,则DCB Ð=______.(13)某同学为研究函数()1)f x x =#的性质,构造了如图所示的两个边长为1的正方形ABCD 和BEFC ,点P 是边BC 上的一个动点,设CP x =,则()AP PF f x +=. 请你参考这些信息,推知函数()f x 的图象的对称轴是 ;函数()4()9g x f x =-的零点的个数是 .(14)曲线C 是平面内到定点(1,0)A 的距离与到定直线1x =-的距离之和为3的动点P 的轨迹. 则曲线C 与y 轴交点的坐标是 ;又已知点(,1)B a (a 为常数),那么BEFAB C DPPB PA +的最小值()d a = .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知公差不为0的等差数列{}n a 的前n 项和为n S ,346S a =+,且1413,,a a a 成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列1{}nS 的前n 项和公式. (16)(本小题满分14分)如图所示,PA ^平面ABC ,点C 在以AB 为直径的⊙O 上,30CBA??,2PA AB ==,点E 为线段PB 的中点,点M 在»AB 上,且OM ∥AC . (Ⅰ)求证:平面MOE ∥平面P AC ;(Ⅱ)求证:平面P AC ^平面PCB ;(Ⅲ)设二面角M BP C --的大小为θ,求cos θ的值.(17)(本小题满分13分)某公司准备将100万元资金投入代理销售业务,现有A ,B 两个项目可供选择:且X 1的数学期望E (X 1)=12;(2)投资B 项目一年后获得的利润X 2(万元)与B 项目产品价格的调整有关, B 项目产品价格根据销售情况在4月和8月决定是否需要调整,两次调整相互独立且在4月和8月进行价格调整的概率分别为p (0< p <1)和1-p . 经专家测算评估:B 项目产品价格一年内调整次数X (次)与X 2的关系如下表所示:(Ⅱ)求X 2的分布列;(Ⅲ)若E (X 1)< E (X 2),则选择投资B 项目,求此时 p 的取值范围.(18)(本小题满分13分)已知椭圆C :22221(0)x y a b a b+=>>的右焦点为(1,0)F ,且点(1,2-在椭圆C 上. (Ⅰ)求椭圆C 的标准方程;ME BOCAP(Ⅱ)已知动直线l 过点F ,且与椭圆C 交于A ,B 两点.试问x 轴上是否存在定点Q ,使得716QA QB ⋅=-u u u r u u u r 恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由.(19)(本小题满分14分)已知函数21()ln()(0)2f x a x a x x a =--+<. (Ⅰ)求()f x 的单调区间;(Ⅱ)若12(ln 21)a -<<-,求证:函数()f x 只有一个零点0x ,且012a x a +<<+; (Ⅲ)当45a =-时,记函数()f x 的零点为0x ,若对任意120,[0,]x x x ∈且211,x x -=都有21()()f x f x m -≥成立,求实数m 的最大值.(本题可参考数据:99ln 20.7,ln 0.8,ln 0.5945≈≈≈)(20)(本小题满分13分)将一个正整数n 表示为12(*)p a a a p +++?N L 的形式,其中*i a ÎN ,1,2,,i p =L ,且p a a a ≤≤≤Λ21,记所有这样的表示法的种数为)(n f (如4=4,4=1+3,4=2+2,4=1+1+2,4=1+1+1+1,故5)4(=f ).(Ⅰ)写出)5(),3(f f 的值,并说明理由;(Ⅱ)对任意正整数n ,比较)1(+n f 与)]2()([21++n f n f 的大小,并给出证明; (Ⅲ)当正整数6≥n 时,求证:134)(-≥n n f .海淀区高三年级第二学期期末练习数 学(理科)参考答案及评分标准 2012.05一. 选择题:本大题共8小题,每小题5分,共40分.二.填空题:本大题共6小题,每小题5分,共30分.(9)12(10)6 (11(12)45° (13)12x =;2 (14)(0,±; 1.41,4, 1.41,2, 1 1.a a a a a a ìï??ïïï+-<?íïï--<<ïïïî或注:(13)、(14)题第一空3分;第二空2分.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)解:(Ⅰ)设等差数列{}n a 的公差为0d ¹.因为346S a =+, 所以11323362da a d 创+=++. ① ……………………………………3分 因为1413,,a a a 成等比数列,所以2111(12)(3)a a d a d +=+. ② ……………………………………5分由①,②可得:13,2a d ==. ……………………………………6分 所以21n a n =+. ……………………………………7分 (Ⅱ)由21n a n =+可知:2(321)22n n nS n n ++?==+.……………………………………9分所以11111()(2)22n S n n n n ==-++. ……………………………………11分 所以123111111n nS S S S S -+++++L 11111111111()2132435112n n n n =-+-+-++-+--++L 21111135()212124(1)(2)n n n n n n +=+--=++++.所以数列1{}nS 的前n 项和为2354(1)(2)n n n n +++.……………………………………13分(16)(本小题满分14分)(Ⅰ)证明:因为点E 为线段PB 的中点,点O 为线段AB 的中点,所以 OE ∥PA . ……………………………………1分 因为 PA Ì平面PAC ,OE Ë平面PAC ,所以 OE ∥平面P AC . ……………………………………2分因为 OM ∥AC , 因为 AC Ì平面PAC ,OM Ë平面PAC ,所以 OM ∥平面P AC . ……………………………………3分因为 OE Ì平面MOE ,OM Ì平面MOE ,OE OM O =I ,所以 平面MOE ∥平面P AC . ………………………………………5分(Ⅱ)证明:因为 点C 在以AB 为直径的⊙O 上,所以 90ACB??,即BC AC ⊥.因为 PA ^平面ABC ,BC Ì平面ABC , 所以PA BC ⊥. ……………………………………7分因为 AC Ì平面PAC ,PA Ì平面PAC ,PA AC A =I ,所以 BC ^平面PAC . 因为 BC Ì平面PBC ,所以 平面P AC ^平面PCB . ……………………………………9分(Ⅲ)解:如图,以C 为原点,CA 所在的直线为x 轴,CB 所在的直线为y 轴,建立空间直角坐标系C xyz -. 因为 30CBA??,2PA AB ==,所以2cos30CB =?1AC =.延长MO 交CB 于点D . 因为 OM ∥AC ,所以131, 1,222MD CB MD CD CB ^=+===. 所以 (1,0,2)P ,(0,0,0)C,B,3(2M . 所以 (1,0,2)CP =u u u r,CB =u u u r.设平面PCB 的法向量(,,)=x y z m .因为 0,0.CP CBìï?ïíï?ïîu u u r u u u r m m所以(,,)(1,0,2)0,(,,)0,x y z x y z ì?ïïíï?ïî即20,0.x z ì+=ïïíï=ïî 令1z =,则2,0x y =-=.所以 (2,0,1)=-m . ……………………………………12分 同理可求平面PMB 的一个法向量n ()=.……………………………………13分 所以 1cos ,5⋅==-⋅m n m n m n . 所以 1cos 5θ=. ………………………………………14分 (17)(本小题满分13分) 解:(Ⅰ)由题意得:0.41,11120.41712.a b a b ++=⎧⎨+⨯+=⎩解得:0.5,0.1a b ==. ……………………………………3分 (Ⅱ)X 2 的可能取值为4.12,11.76,20.40.()[]2 4.12(1)1(1)(1)P X p p p p ==---=-,()[]22211.761(1)(1)(1)(1)P X p p p p p p ==--+--=+-,()220.40(1)P X p p ==-.所以X 2的分布列为:(Ⅲ)由(Ⅱ)可得:()2224.12(1)11.76(1)20.40(1)E Xp p p p p p ⎡⎤=-++-+-⎣⎦211.76p p =-++. ……………………………………11分因为E (X 1)< E (X 2),所以21211.76p p<-++. 所以0.40.6p <<.当选择投资B 项目时,p 的取值范围是()0.4,0.6.……………………………………13分(18)(本小题满分13分) 解:(Ⅰ)由题意知:1c =. 根据椭圆的定义得:22a =,即a =……………………………………3分 所以 2211b =-=.所以 椭圆C 的标准方程为2212x y +=. ……………………………………4分 (Ⅱ)假设在x 轴上存在点(,0)Q m ,使得716QA QB ⋅=-u u u r u u u r恒成立. 当直线l 的斜率为0时,(A B .则7,0)(,0)16m m ?=-. 解得 54m =?. ……………………………………6分 当直线l的斜率不存在时,(1,(1,22A B -.由于557(1,(1,424216+?-?,所以54m ?. 下面证明54m =时,716QA QB ⋅=-u u u r u u u r 恒成立.……………………………………8分显然 直线l 的斜率为0时,716QA QB ⋅=-u u u r u u u r .当直线l 的斜率不为0时,设直线l 的方程为:1x ty =+,()()1122,,,A x y B x y .由221,21x y x ty ìïï+=ïíïï=+ïî可得:22(2)210t y ty ++-=. 显然0∆>.1221222,21.2t y y t y y t ìïï+=-ïï+ïíïï=-ïï+ïî……………………………………10分 因为 111x ty =+,221x ty =+,所以 112212125511(,)(,)()()4444x y x y ty ty y y -?=--+ 2121211(1)()416t y y t y y =+-++2221121(1)24216t t t t t =-+++++ 22222172(2)1616t t t --+=+=-+.综上所述:在x 轴上存在点5(,0)4Q ,使得716QA QB ⋅=-u u u r u u u r 恒成立.……………………………………13分(19)(本小题满分14分)(Ⅰ)解:()f x 的定义域为(,)a +∞.2(1)'()1a x a xf x x x a x a-++=-+=--. ……………………………………1分令'()0f x =,0x =或+1x a =.当10a -<<时,+10a >,函数()f x 与'()f x 随x 的变化情况如下表:所以,函数()f x 的单调递增区间是(0,1)a +,单调递减区间是(,0)a 和(1,)a ++?.……………………………………3分当1a =-时,2'()01x f x x -=≤+. 所以,函数()f x 的单调递减区间是(1,)-+?. ……………………………………4分 当1a <-时,+10a <,函数()f x 与'()f x 随x 的变化情况如下表:所以,函数()f x 的单调递增区间是(1,0)a +,单调递减区间是(,1)a a +和(0,)+?.……………………………………5分(Ⅱ)证明:当12(ln21)0a -<<-<时,由(Ⅰ)知,()f x 的极小值为(0)f ,极大值为(1)f a +.因为(0)ln()0f a a =->,2211(1)(1)(1)(1)022f a a a a +=-+++=->,且()f x 在(1,)a ++?上是减函数,所以()f x 至多有一个零点. ……………………………………7分 又因为211(2)ln 2[2(ln 21)]022f a a a a a a +=--=---<, 所以 函数()f x 只有一个零点0x ,且012a x a +<<+.……………………………………9分(Ⅲ)解:因为412(ln 21)5-<-<-, 所以 对任意120,[0,]x x x ∈且211,x x -=由(Ⅱ)可知:1[0,1)x a ∈+,20(1,]x a x ∈+,且21x ≥. ……………………………………10分因为 函数()f x 在[0,1)a +上是增函数,在(1,)a ++?上是减函数,所以 1()f x (0)f ≥,2()f x (1)f ≤. ……………………………………11分 所以 12()()(0)(1)f x f x f f -?.当45a =-时,1(0)(1)ln()12a f f a a -=--=491ln 542->0. 所以 12()()(0)(1)0f x f x f f -?>. ……………………………………13分所以 21()()f x f x -的最小值为491(0)(1)ln 542f f -=-. 所以 使得21()()f x f x m -≥恒成立的m 的最大值为491ln 542-.……………………………………14分(20)(本小题满分13分)(Ⅰ)解:因为3=3,3=1+2,3=1+1+1,所以3)3(=f .因为5=5,5=2+3,5=1+4,5=1+1+3,5=1+2+2,5=1+1+1+2,5=1+1+1+1+1, 所以7)5(=f . ……………………………………3分 (Ⅱ)结论是)1(+n f )]2()([21++≤n f n f . 证明如下:由结论知,只需证).1()2()()1(+-+≤-+n f n f n f n f因为21≥+n ,把1+n 的一个表示法中11a =的1a 去掉,就可得到一个n 的表示法;反之,在n 的一个表示法前面添加一个“1+”,就得到一个1n +的表示法,即1+n 的表示法中11a =的表示法种数等于n 的表示法种数,所以)()1(n f n f -+表示的是1+n 的表示法中11a ¹的表示法数,)1()2(+-+n f n f 是2n +的表示法中11a ¹的表示法数.同样,把一个11a ¹的1+n 的表示法中的p a 加上1, 就可得到一个11a ¹的2n +的表示法,这样就构造了从11a ¹的1+n 的表示法到11a ¹的2+n 的表示法的一个对应.所以有).1()2()()1(+-+≤-+n f n f n f n f ……………………………………9分(Ⅲ)由第(Ⅱ)问可知:当正整数6m ³时,()(1)(1)(2)(6)(5)f m f m f m f m f f --?--吵-L. 又,7)5(,11)6(==f f 所以 ()(1)4f m f m --?. *对于*式,分别取m 为n ,,7,6Λ,将所得等式相加得)5(4)5()(-≥-n f n f .即134)(-≥n n f . ……………………………………13分。
北京市海淀区高三二模数学理科含答案[1]
![北京市海淀区高三二模数学理科含答案[1]](https://img.taocdn.com/s3/m/703ad658bd64783e08122b0c.png)
海淀区高三年级第二学期期末练习数 学 (理科) 2013.5本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上 作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.集合{}|(1)(2)0A x x x =-+≤,B ={}0x x <,则A B = A .(,0]-∞ B .(,1]-∞ C .[1,2] D .[1,)+∞2.已知数列{}n a 是公比为q 的等比数列,且134a a ⋅=,48a =,则1a q +的值为 A .3 B .2 C .3或2- D .3或3-3. 如图,在边长为a 的正方形内有不规则图形Ω. 向正方形内随机撒豆子,若 撒在图形Ω内和正方形内的豆子数分别为,m n ,则图形Ω面积的估计值为A.ma nB.na mC. 2ma nD. 2na m4.某空间几何体的三视图如右图所示,则该几何体的表面积为 A.180 B.240 C.276 D.3005.在四边形ABCD 中,“λ∃∈R ,使得,AB DC AD BC λλ==”是“四边形ABCD 为平行四边形”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件6.用数字1,2,3,4,5组成没有重复数字的五位数,且5不排在百位,2,4都不排在个位和万位,则这样的五位数个数为 A.32 B. 36 C. 42 D.487.双曲线C 的左右焦点分别为12,F F ,且2F 恰为抛物线24y x =的焦点,设双曲线C 与该抛物线的一个交点为A ,若12AF F ∆是以1AF 为底边的等腰三角形,则双曲线C 的离心率为B.112俯视图8. 若数列{}n a 满足:存在正整数T ,对于任意正整数n 都有n T n a a +=成立,则称数列{}n a 为周期数列,周期为T . 已知数列{}n a 满足1(0)a m m =>,11, 1=1, 0 1.n n n n na a a a a +->⎧⎪⎨<≤⎪⎩,则下列结论中错误..的是 A. 若34a =,则m 可以取3个不同的值 B.若m ={}n a 是周期为3的数列C.T ∀∈*N 且2T ≥,存在1m >,{}n a 是周期为T 的数列D.Q m ∃∈且2m ≥,数列{}n a 是周期数列二、填空题:本大题共6小题,每小题5分,共30分.9.在极坐标系中,极点到直线cos 2ρθ=的距离为_______.10.已知1211ln ,sin ,222a b c -===,则,,a b c 按照从.大到小...排列为______. 11.直线1l 过点(2,0)-且倾斜角为30,直线2l 过点(2,0)且与直线1l 垂直,则直线1l 与直线2l 的交点坐标为____.12.在ABC ∆中,30,45,2A B a ∠=∠==,则_____;b =C _____.AB S ∆=13.正方体1111ABCD A B C D -的棱长为1,若动点P 在线段1BD 上运动,则DC AP ⋅的取值范围是______________.14.在平面直角坐标系中,动点(,)P x y 到两条坐标轴的距离之和等于它到点(1,1)的距离,记点P 的轨迹为曲线W . (I) 给出下列三个结论: ①曲线W 关于原点对称; ②曲线W 关于直线y x =对称;③曲线W 与x 轴非负半轴,y 轴非负半轴围成的封闭图形的面积小于12; 其中,所有正确结论的序号是_____; (Ⅱ)曲线W 上的点到原点距离的最小值为______.三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15.(本小题满分13分)已知函数cos2()1π)4x f x x =--.(Ⅰ)求函数()f x 的定义域; (Ⅱ) 求函数()f x 的单调递增区间.16.(本小题满分13分)福彩中心发行彩票的目的是为了获取资金资助福利事业,现在福彩中心准备发行一种面值为5元的福利彩票刮刮卡,设计方案如下:(1)该福利彩票中奖率为50%;(2)每张中奖彩票的中奖奖金有5元,50元和150元三种;(3)顾客购买一张彩票获得150元奖金的概率为p ,获得50元奖金的概率为2%.(I)假设某顾客一次性花10元购买两张彩票,求其至少有一张彩票中奖的概率; (II )为了能够筹得资金资助福利事业, 求p 的取值范围.17. (本小题满分14分)如图1,在直角梯形ABCD 中,90ABC DAB ∠=∠=,30CAB ∠=,2BC =,4AD =. 把DAC ∆沿对角线AC 折起到PAC ∆的位置,如图2所示,使得点P 在平面ABC上的正投影H 恰好落在线段AC 上,连接PB ,点,E F 分别为线段,PA AB 的中点. (I) 求证:平面//EFH 平面PBC ; (II)求直线HE 与平面PHB 所成角的正弦值;(III)在棱PA 上是否存在一点M ,使得M 到点,,,P H A F 四点的距离相等?请说明理由.CDBA图1H E CPBAF图218.(本小题满分13分)已知函数()e x f x =,点(,0)A a 为一定点,直线()x t t a =≠分别与函数()f x 的图象和x 轴交于点M ,N ,记AMN ∆的面积为()S t . (I )当0a =时,求函数()S t 的单调区间;(II )当2a >时, 若0[0,2]t ∃∈,使得0()e S t ≥, 求实数a 的取值范围.19. (本小题满分14分)已知椭圆:M 22221(0)x y a b a b+=>>的四个顶点恰好是一边长为2,一内角为60的菱形的四个顶点.(I )求椭圆M 的方程;(II )直线l 与椭圆M 交于A ,B 两点,且线段AB 的垂直平分线经过点1(0,)2-,求A O B ∆(O 为原点)面积的最大值.20.(本小题满分13分)设A 是由m n ⨯个实数组成的m 行n 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”. (Ⅰ) 数表A 如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);表1(Ⅱ) 数表A 如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数..a 的所有可能值;(Ⅲ)对由m n ⨯个实数组成的m 行n 列的任意一个数表A , 能否经过有限次“操作”以后,使得到的数表每行的各数之表2和与每列的各数之和均为非负整数?请说明理由.22221212a a a a a a a a ------海淀区高三年级第二学期期末练习数 学 (理科)参考答案及评分标准2013.5一、选择题(本大题共8小题,每小题5分,共40分)二、填空题(本大题共6小题,每小题5分, 有两空的小题,第一空3分,第二空2分, 共30分)三、解答题(本大题共6小题,共80分) 15.(本小题满分13分) 解:(I )因为πsin()04x -≠所以ππ,4x k -≠Z k ∈……………………2分 所以函数的定义域为π{|π+,4x x k ≠Z}k ∈……………………4分(II )因为22cos sin ()1sin cos x xf x x x -=--……………………6分= 1(cos sin )x x ++1sin cos x x =++π= 1)4x +……………………8分又sin yx =的单调递增区间为 ππ(2π,2π)22k k -+ ,Z k ∈令πππ2π2π242k x k -<+<+解得 3ππ2π2π44k x k -<<+……………………11分 又注意到ππ+,4x k ≠9. 2 10.c b a >> 11.12. 13.[0,1]14.②③;2所以()f x 的单调递增区间为3ππ(2π,2π)44k k -+, Z k ∈…………………13分16. 解:(I )设至少一张中奖为事件A则2()10.50.75P A =-=…………………4分(II) 设福彩中心卖出一张彩票可能获得的资金为ξ 则ξ可以取5,0,45,145--…………………6分ξ的分布列为…………………8分所以ξ的期望为550%0(50%2%)(45)2%(145)E p p ξ=⨯+⨯--+-⨯+-⨯2.590%145p =--…………………11分所以当 1.61450p ->时,即8725p <…………………12分 所以当80725p <<时,福彩中心可以获取资金资助福利事业…………………13分17.解:(I )因为点P 在平面ABC 上的正投影H 恰好落在线段AC 上 所以PH ⊥平面ABC ,所以PH ⊥AC …………………1分因为在直角梯形ABCD 中,90ABC DAB ∠=∠=,30CAB ∠=,2BC =,4AD =所以4AC =,60CAB ∠=,所以ADC ∆是等边三角形,所以H 是AC 中点, …………………2分所以//HE PC …………………3分 同理可证//EF PB 又,HEEF E CP PB P ==所以平面//EFH 平面PBC …………………5分 (II )在平面ABC 内过H 作AC 的垂线如图建立空间直角坐标系,则(0,2,0)A -,P ,B …………………6分因为(0,E -,(0,HE =- 设平面PHB 的法向量为(,,)n x y z = 因为(3,1,0)HB =,HP =所以有00HB n HP n ⎧⋅=⎪⎨⋅=⎪⎩,即00y z +==⎪⎩,令x =则3,y =-所以(3,3,0)n =-…………………8分cos ,||||22n HE n HEn HE ⋅<>===⋅⋅10分所以直线HE 与平面PHB …………………11分 (III)存在,事实上记点E 为M 即可 …………………12分因为在直角三角形PHA 中,122EH PE EA PA ====,…………………13分 在直角三角形PHB 中,点4,PB =122EF PB == 所以点E 到四个点,,,P O C F 的距离相等…………………14分 18.解: (I) 因为1()||e 2t S t t a =-,其中t a ≠…………………2分 当0a =,1()||e 2t S t t =,其中0t ≠ 当0t >时,1()e 2t S t t =,1'()(1)e 2t S t t =+,所以'()0S t >,所以()S t 在(0,)+∞上递增,…………………4分 当0t <时,1()e 2t S t t =-,1'()(1)e 2t S t t =-+,令1'()(1)e 02t S t t =-+>,解得1t <-,所以()S t 在(,1)-∞-上递增 令1'()(1)e 02t S t t =-+<,解得1t >-,所以()S t 在(1,0)-上递减……………7分综上,()S t 的单调递增区间为(0,)+∞,(,1)-∞-()S t 的单调递增区间为(1,0)-(II )因为1()||e 2t S t t a =-,其中t a ≠ 当2a >,[0,2]t ∈时,1()()e 2t S t a t =-因为0[0,2]t ∃∈,使得0()e S t ≥,所以()S t 在[0,2]上的最大值一定大于等于e1'()[(1)]e 2t S t t a =---,令'()0S t =,得1t a =-…………………8分当12a -≥时,即3a ≥时1'()[(1)]e 02t S t t a =--->对(0,2)t ∈成立,()S t 单调递增所以当2t =时,()S t 取得最大值21(2)(2)e 2S a =-令21(2)e e 2a -≥,解得22ea ≥+, 所以3a ≥…………………10分 当12a -<时,即3a <时1'()[(1)]e 02t S t t a =--->对(0,1)t a ∈-成立,()S t 单调递增1'()[(1)]e 02t S t t a =---<对(1,2)t a ∈-成立,()S t 单调递减所以当1t a =-时,()S t 取得最大值11(1)e 2a S a --=令11(1)e e 2a S a --=≥,解得ln22a ≥+所以ln223a +≤<…………………12分 综上所述,ln22a +≤…………………13分19.解:(I)因为椭圆:M 22221(0)x y a b a b+=>>的四个顶点恰好是一边长为2,一内角为60的菱形的四个顶点,所以1a b ==,椭圆M 的方程为2213x y +=…………………4分(II)设1122(,),(,),A x y B x y 因为AB 的垂直平分线通过点1(0,)2-, 显然直线AB 有斜率,当直线AB 的斜率为0时,则AB 的垂直平分线为y 轴,则1212,x x y y =-=所以111111=|2||||||||2AOB S x y x y x ∆====2211(3)322x x +-≤=,所以AOB S ∆≤1||x =时,AOB S ∆………………7分 当直线AB 的斜率不为0时,则设AB 的方程为y kx t =+所以2213y kx t x y =+⎧⎪⎨+=⎪⎩,代入得到222(31)6330k x ktx t +++-= 当224(933)0k t ∆=+->, 即2231k t +>①方程有两个不同的解又122631kt x x k -+=+,1223231x x ktk +-=+…………………8分 所以122231y y tk +=+, 又1212112202y y x x k ++=-+-,化简得到2314k t +=② 代入①,得到04t <<…………………10分又原点到直线的距离为d =12|||AB x x =-=所以1=||||2AOB S AB d ∆=化简得到AOB S ∆12分 因为04t <<,所以当2t =时,即k =时,AOB S ∆综上,AOB ∆…………………14分 20.(I )解:法1:42123712371237210121012101-−−−−−→−−−−−→----改变第列改变第行法2:14123712371237210121012101----−−−−−→−−−−−→--改变第列改变第列…………………3分(II) 每一列所有数之和分别为2,0,2-,0,每一行所有数之和分别为1-,1; ①如果首先操作第三列,则22221212a a a a a a a a -----则第一行之和为21a -,第二行之和为52a -, 这两个数中,必须有一个为负数,另外一个为非负数, 所以12a ≤或52a ≥ 当12a ≤时,则接下来只能操作第一行, 22221212a a a a a a a a ------此时每列之和分别为2222,22,22,2a a a a --- 必有2220a -≥,解得0,1a =- 当52a ≥时,则接下来操作第二行 22221212a a a a a a a a ------此时第4列和为负,不符合题意. …………………6分 ②如果首先操作第一行22221212a a a a a a a a -----则每一列之和分别为22a -,222a -,22a -,22a当1a =时,每列各数之和已经非负,不需要进行第二次操作,舍掉 当1a ≠时,22a -,22a -至少有一个为负数,所以此时必须有2220a -≥,即11a -≤≤,所以0a =或1a =- 经检验,0a =或1a =-符合要求 综上:0,1a =-…………………9分(III )能经过有限次操作以后,使得得到的数表所有的行和与所有的列和均为非负实数。
2011年北京市高考数学试卷(理科)答案与解析

2011年北京市高考数学试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题5分,满分40分)1.(5分)(2011•北京)已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范围是()A.(﹣∞,﹣1]B.[1,+∞)C.[﹣1,1]D.(﹣∞,﹣1]∪[1,+∞)【考点】集合关系中的参数取值问题.【专题】集合.【分析】通过解不等式化简集合P;利用P∪M=P⇔M⊆P;求出a的范围.【解答】解:∵P={x|x2≤1},∴P={x|﹣1≤x≤1}∵P∪M=P∴M⊆P∴a∈P﹣1≤a≤1故选:C.【点评】本题考查不等式的解法、考查集合的包含关系:根据条件P∪M=P⇔M⊆P是解题关键.2.(5分)(2011•北京)复数=()A.i B.﹣i C.D.【考点】复数代数形式的混合运算.【专题】数系的扩充和复数.【分析】将分子、分母同乘以1﹣2i,再按多项式的乘法法则展开,将i2用﹣1代替即可.【解答】解:==i故选A【点评】本题考查复数的除法运算法则:分子、分母同乘以分母的共轭复数;再按多项式的乘法法则展开即可.3.(5分)(2011•北京)在极坐标系中,圆ρ=﹣2sinθ的圆心的极坐标系是()A.B.C.(1,0)D.(1,π)【考点】简单曲线的极坐标方程.【专题】直线与圆;坐标系和参数方程.【分析】先在极坐标方程ρ=﹣2sinθ的两边同乘以ρ,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得直角坐标系,再利用直角坐标方程求解即可.【解答】解:将方程ρ=﹣2sinθ两边都乘以p得:ρ2=﹣2ρsinθ,化成直角坐标方程为x2+y2+2y=0.圆心的坐标(0,﹣1).∴圆心的极坐标故选B.【点评】本题考查点的极坐标和直角坐标的互化,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互,能在极坐标系中用极坐标刻画点的位置.4.(5分)(2011•北京)执行如图所示的程序框图,输出的s值为()A.﹣3 B.﹣C.D.2【考点】循环结构.【专题】算法和程序框图.【分析】i=0,满足条件i<4,执行循环体,依此类推,当i=4,s=2,此时不满足条件i<4,退出循环体,从而得到所求.【解答】解:i=0,满足条件i<4,执行循环体,i=1,s=满足条件i<4,执行循环体,i=2,s=﹣满足条件i<4,执行循环体,i=3,s=﹣3满足条件i<4,执行循环体,i=4,s=2不满足条件i<4,退出循环体,此时s=2故选:D【点评】根据流程图计算运行结果是算法这一模块的重要题型,处理的步骤一般为:分析流程图,从流程图中即要分析出计算的类型,又要分析出参与计算的数据建立数学模型,根据第一步分析的结果,选择恰当的数学模型解模.算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.5.(5分)(2011•北京)如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论:①AD+AE=AB+BC+CA;②AF•AG=AD•AE③△AFB~△ADG其中正确结论的序号是()A.①② B.②③ C.①③ D.①②③【考点】与圆有关的比例线段.【专题】直线与圆.【分析】根据从圆外一点引圆的两条切线,切线长相等,得到第一个说法是正确的,根据切割线定理知道第二个说法是正确的,根据切割线定理知,两个三角形△ADF~△ADG,得到第三个说法错误.【解答】解:根据从圆外一点引圆的两条切线,切线长相等,有CE=CF,BF=BD,∴AD+AE=AB+BC+CA,故①正确,∵AD=AE,AE2=AF•AG,∴AF•AG=AD•AE,故②正确,根据切割线定理知△ADF~△ADG故③不正确,综上所述①②两个说法是正确的,故选A.【点评】本题考查与圆有关的比例线段,考查圆的切线长定理,考查圆的切割线定理,考查切割线构成的两个相似的三角形,本题是一个综合题目.6.(5分)(2011•北京)根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为(A,C为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是()A.75,25 B.75,16 C.60,25 D.60,16【考点】函数解析式的求解及常用方法.【专题】函数的性质及应用.【分析】首先,x=A的函数值可由表达式直接得出,再根据x=4与x=A的函数值不相等,说明求f(4)要用x <A对应的表达式,将方程组联解,可以求出C、A的值.【解答】解:由题意可得:f(A)==15,所以c=15而f(4)==30,可得出=30故=4,可得A=16从而c=15=60故答案为D【点评】分段函数是函数的一种常见类型,解决的关键是寻找不同自变量所对应的范围,在相应区间内运用表达式加以解决.7.(5分)(2011•北京)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是()A.8 B. C.10 D.【考点】由三视图求面积、体积.【专题】立体几何.【分析】三视图复原的几何体是一个三棱锥,根据三视图的图形特征,判断三棱锥的形状,三视图的数据,求出四面体四个面的面积中,最大的值.【解答】解:三视图复原的几何体是一个三棱锥,如图,四个面的面积分别为:8,6,,10,显然面积的最大值,10.故选C.【点评】本题是基础题,考查三视图复原几何体的知识,考查几何体的面积,空间想象能力,计算能力,常考题型.8.(5分)(2011•北京)设A(0,0),B(4,0),C(t+4,4),D(t,4)(t∈R).记N(t)为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数N(t)的值域为()A.{9,10,11} B.{9,10,12} C.{9,11,12} D.{10,11,12}【考点】集合的含义.【专题】集合.【分析】分别由t=0,1,2求出N(t),排除错误选项A,B,D,从而得到正确选项.【解答】解:当t=0时,▱ABCD的四个顶点是A(0,0),B(4,0),C(4,4),D(0,4),符合条件的点有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共九个,N(t)=9,故选项D不正确.当t=1时,▱ABCD的四个顶点是A(0,0),B(4,0),C(5,4),D(1,4),同理知N(t)=12,故选项A不正确.当t=2时,▱ABCD的四个顶点是A(0,0),B(4,0),C(6,4),D(2,4),同理知N(t)=11,故选项B不正确.故选C.【点评】本题考查集合的性质和应用,解题时要注意排除法的合理运用.本题中取整点是个难点,常用的方法是,先定横(或纵)坐标,在定纵(横)坐标,以确定点的个数,如果从图形上看,就是看直线x=r(r是整数)上有几个整点在四边形内.二、填空题(共6小题,每小题5分,满分30分)9.(5分)(2011•北京)在△ABC中.若b=5,,tanA=2,则sinA= ;a= 2.【考点】正弦定理;同角三角函数间的基本关系.【专题】解三角形.【分析】由tanA的值,利用同角三角函数间的基本关系求出cosA的平方,然后由A的范围,再利用同角三角函数的基本关系求出sinA的值,然后再利用正弦定理,由sinA,sinB及b的值即可求出a的值.【解答】解:由tanA=2,得到cos2A==,由A∈(0,π),得到sinA==,根据正弦定理得:=,得到a===2.故答案为:;2【点评】此题考查学生灵活运用同角三角函数间的基本关系以及正弦定理化简求值,是一道中档题.10.(5分)(2011•北京)已知向量=(,1),=(0,﹣1),=(k,).若与共线,则k= 1 .【考点】平面向量共线(平行)的坐标表示.【专题】平面向量及应用.【分析】利用向量的坐标运算求出的坐标;利用向量共线的坐标形式的充要条件列出方程,求出k的值.【解答】解:∵与共线,∴解得k=1.故答案为1.【点评】本题考查向量的坐标运算、考查向量共线的坐标形式的充要条件:坐标交叉相乘相等.11.(5分)(2011•北京)在等比数列{a n}中,a1=,a4=﹣4,则公比q= ﹣2 ;|a1|+|a2|+…+|a n|=.【考点】等比数列的性质;等比数列的前n项和.【专题】等差数列与等比数列.【分析】先利用等比数列的通项公式求得公比;|a n|是以a1为首项,|q|为公比,进而利用等比数列的求和公式求解.【解答】解:q===﹣2,|a1|+|a2|+…+|a n|==故答案为:﹣2,【点评】本题主要考查了等比数列的性质.考查了对等比数列的通项公式和求和公式的灵活运用.12.(5分)(2011•北京)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有14 个.(用数字作答)【考点】计数原理的应用.【专题】算法和程序框图.【分析】本题是一个分类计数问题,首先确定数字中2和3 的个数,当数字中有1个2,3个3时,当数字中有2个2,2个3时,当数字中有3个2,1个3时,写出每种情况的结果数,最后相加.【解答】解:由题意知本题是一个分类计数问题,首先确定数字中2和3 的个数,当数字中有1个2,3个3时,共有C41=4种结果,当数字中有2个2,2个3时,共有C42=6种结果,当数字中有3个2,1个3时,共有有C41=4种结果,根据分类加法原理知共有4+6+4=14种结果,故答案为:14【点评】本题考查分类计数原理,是一个数字问题,这种问题一般容易出错,注意分类时要做到不重不漏,本题是一个基础题,也是一个易错题,易错点在数字中重复出现的数字不好处理.13.(5分)(2011•北京)已知函数若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是(0,1).【考点】根的存在性及根的个数判断.【专题】函数的性质及应用.【分析】要求程f(x)=k有两个不同的实根是数k的取值范围,根据方程的根与对应函数零点的关系,我们可以转化为求函数y=f(x)与函数y=k交点的个数,我们画出函数的图象,数形结合即可求出答案.【解答】解:函数的图象如下图所示:由函数图象可得当k∈(0,1)时方程f(x)=k有两个不同的实根,故答案为:(0,1)【点评】本题考查的知识点是根的存在性及根的个数判断,其中根据方程的根与对应函数零点的关系,将方程问题转化为函数问题是解答的关键.14.(5分)(2011•北京)曲线C是平面内与两个定点F1(﹣1,0)和F2(1,0)的距离的积等于常数a2(a >1)的点的轨迹.给出下列三个结论:①曲线C过坐标原点;②曲线C关于坐标原点对称;③若点P在曲线C上,则△F1PF2的面积不大于a2.其中,所有正确结论的序号是②③.【考点】轨迹方程.【专题】圆锥曲线的定义、性质与方程.【分析】由题意曲线C是平面内与两个定点F1(﹣1,0)和F2(1,0)的距离的积等于常数a2(a>1),利用直接法,设动点坐标为(x,y),及可得到动点的轨迹方程,然后由方程特点即可加以判断.【解答】解:对于①,由题意设动点坐标为(x,y),则利用题意及两点间的距离公式的得:⇔[(x+1)2+y2]•[(x﹣1)2+y2]=a4(1)将原点代入验证,此方程不过原点,所以①错;对于②,把方程中的x被﹣x代换,y被﹣y 代换,方程不变,故此曲线关于原点对称.②正确;对于③,由题意知点P在曲线C上,则△F1PF2的面积=a2sin∠F1PF2,≤a2,所以③正确.故答案为:②③.【点评】此题重点考查了利用直接法求出动点的轨迹方程,并化简,利用方程判断曲线的对称性及利用解析式选择换元法求出值域.三、解答题(共6小题,满分80分)15.(13分)(2011•北京)已知函数.(Ⅰ)求f(x)的最小正周期:(Ⅱ)求f(x)在区间上的最大值和最小值.【考点】三角函数的周期性及其求法;两角和与差的余弦函数;三角函数的最值.【专题】三角函数的图像与性质.【分析】(Ⅰ)利用两角和公式和二倍角公式对函数的解析式进行化简整理后,利用正弦函数的性质求得函数的最小正周期.(Ⅱ)利用x的范围确定2x+的范围,进而利用正弦函数的单调性求得函数的最大和最小值.【解答】解:(Ⅰ)∵,=4cosx()﹣1=sin2x+2cos2x﹣1=sin2x+cos2x=2sin(2x+),所以函数的最小正周期为π;(Ⅱ)∵﹣≤x≤,∴﹣≤2x+≤,∴当2x+=,即x=时,f(x)取最大值2,当2x+=﹣时,即x=﹣时,f(x)取得最小值﹣1.【点评】本题主要考查了三角函数的周期性及其求法,三角函数的最值.解题的关键是对函数解析式的化简整理.16.(14分)(2011•北京)如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.(Ⅰ)求证:B D⊥平面PAC;(Ⅱ)若PA=AB,求PB与AC所成角的余弦值;(Ⅲ)当平面PBC与平面PDC垂直时,求PA的长.【考点】直线与平面垂直的判定;点、线、面间的距离计算;用空间向量求直线间的夹角、距离.【专题】空间位置关系与距离.【分析】(I)由已知条件可得ACBD,PABD,根据直线与平面垂直的判定定理可证(II)结合已知条件,设AC与BD的交点为O,则OB⊥OC,故考虑分别以OB,OC为x轴、y轴,以过O且垂直于平面ABCD的直线为z轴,建立空间直角坐标系,设PB与AC所成的角为θ,则,代入公式可求(III)分别求平面PBC的法向量,平面PDC的法向量由平面PBC⊥平面PDC可得从而可求t即PA【解答】解:(I)证明:因为四边形ABCD是菱形,所以AC⊥BD,又因为PA⊥平面ABCD,所以PA⊥BD,PA∩AC=A所以BD⊥平面PAC(II)设AC∩BD=O,因为∠BAD=60°,PA=AB=2,所以BO=1,AO=OC=,以O为坐标原点,分别以OB,OC为x轴、y轴,以过O且垂直于平面ABCD的直线为z轴,建立空间直角坐标系O﹣xyz,则P(0,﹣,2),A(0,﹣,0),B(1,0,0),C(0,,0)所以=(1,,﹣2),设PB与AC所成的角为θ,则cosθ=|(III)由(II)知,设,则设平面PBC的法向量=(x,y,z)则=0,所以令,平面PBC的法向量所以,同理平面PDC的法向量,因为平面PBC⊥平面PDC,所以=0,即﹣6+=0,解得t=,所以PA=.【点评】本小题主要考查空间线面关系的垂直关系的判断、异面直线所成的角、用空间向量的方法求解直线的夹角、距离等问题,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力17.(13分)(2011•北京)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.(Ⅰ)如果X=8,求乙组同学植树棵数的平均数和方差;(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和数学期望.(注:方差,其中为x1,x2,…x n的平均数)【考点】茎叶图;众数、中位数、平均数;极差、方差与标准差;离散型随机变量的期望与方差.【专题】概率与统计.【分析】(Ⅰ)根据所给的数据,把所有数据相加再除以4写出这组数据的平均数,再利用所给的方差的公式,做出这组数据的方差.(Ⅱ)根据所给的变量写出随机变量可能的取值,结合变量对应的事件写出变量的概率,写出分布列,做出期望值.【解答】解:(Ⅰ)当X=8,乙组同学植树棵数是8,8,9,10,平均数是=,方差为+=;(Ⅱ)当X=9时,甲组同学的植树棵数是9,9,11,11;乙组同学的植树棵数是9,8,9,10,分别从甲和乙两组中随机取一名同学,共有4×4=16种结果,这两名同学植树的总棵数Y可能是17,18,19,20,21,事件Y=17,表示甲组选出的同学植树9棵,乙组选出的同学植树8棵,∴P(Y=17)=P(Y=18)=P(Y=19)=P(Y=20)=,P(Y=21)=∴随机变量的期望是EY==19.【点评】本题考查一组数据的平均数和方差,考查离散型随机变量的分布列和期望值,考查等可能事件的概率,本题是一个概率与统计的综合题目.18.(13分)(2011•北京)已知函数.(Ⅰ)求f(x)的单调区间;(Ⅱ)若对于任意的x∈(0,+∞),都有f(x )≤,求k的取值范围.【考点】利用导数研究函数的单调性;导数在最大值、最小值问题中的应用.【专题】函数的性质及应用;导数的概念及应用.【分析】(I)求导,令导数等于零,解方程,跟据f′(x),f(x)随x的变化情况即可求出函数的单调区间;(Ⅱ)根据若对于任意的x∈(0,+∞),都有f(x )≤,利用导数求函数f(x)在区间(0,+∞)的最大值,即可求出k的取值范围.【解答】解:(Ⅰ)=,令f′(x)=0,得x=±k当k>0时,f′(x)f(x)随x的变化情况如下:所以,f(x)的单调递增区间是(﹣∞,﹣k),和(k,+∞),单调递减区间是(﹣k,k);当k<0时,f′(x)f(x)随x的变化情况如下:所以,f(x)的单调递减区间是(﹣∞,k),和(﹣k,+∞),单调递增区间是(k,﹣k);(Ⅱ)当k>0时,有f(k+1)=,不合题意,当k<0时,由(I)知f(x)在(0,+∞)上的最大值是f(﹣k)=,∴任意的x∈(0,+∞),f(x)≤,⇔f(﹣k)=≤,解得﹣,故对于任意的x∈(0,+∞),都有f(x)≤,k的取值范围是﹣.【点评】此题是个难题.考查利用导数研究函数的单调性和在闭区间上的最值问题,对方程f'(x)=0根大小进行讨论,体现了分类讨论的思想方法,特别是(II)的设置,有关恒成立问题一般转化为求函数的最值问题,体现了转化的思想,增加了题目的难度.19.(14分)(2011•北京)已知椭圆.过点(m,0)作圆x2+y2=1的切线I交椭圆G于A,B 两点.(Ⅰ)求椭圆G的焦点坐标和离心率;(Ⅱ)将|AB|表示为m的函数,并求|AB|的最大值.【考点】圆与圆锥曲线的综合.【专题】圆锥曲线的定义、性质与方程;圆锥曲线中的最值与范围问题.【分析】(I)由题意及椭圆和圆的标准方程,利用椭圆离心率的定义和点到直线的距离公式即可求解;(II)由题意即m得取值范围分m=1时,m=﹣1及当m≠±1三大类求出|AB|的长度,利用直线方程与椭圆方程进行联立,利用根与系数的关系得到k与m之间关系等式,利用直线与圆相切的条件即可.【解答】解:(I)由题意得a=2,b=1,所以c=∴椭圆G的焦点坐标离心率e=.(II)由题意知:|m|≥1,当m=1时,切线l的方程为x=1,点A(1,)点B(1,﹣)此时|AB|=;当m=﹣1时,同理可得|AB|=;当|m|>1时,设切线l的方程为:y=k(x﹣m),由⇒(1+4k2)x2﹣8k2mx+4k2m2﹣4=0,设A(x1,y1),B(x2,y2)则x1+x2=又由l与圆x2+y2=1相切∴圆心到直线l的距离等于圆的半径即=1⇒m2=,所以|AB|==]=,由于当m=±1时,|AB|=,当m≠±1时,|AB|=,此时m∈(﹣∞,﹣1]∪[1,+∞)又|AB|=≤2(当且仅当m=±时,|AB|=2),所以,|AB|的最大值为2.故|AB|的最大值为2.【点评】此题重点考查了椭圆及圆的标准方程,还考查了点到直线的距离公式,对于第二问,重点考查了利用m 的范围分裂进行讨论,联立直线与椭圆的方程利用整体代换的思想建立m与k的关系等式,还考查两点间的距离公式及又m的范围解出|AB|的最值.20.(13分)(2011•北京)若数列A n=a1,a2,…,a n(n≥2)满足|a k+1﹣a k|=1(k=1,2,…,n﹣1),数列A n为E数列,记S(A n)=a1+a2+…+a n.(Ⅰ)写出一个满足a1=a s=0,且S(A s)>0的E数列A n;(Ⅱ)若a1=12,n=2000,证明:E数列A n是递增数列的充要条件是a n=2011;(Ⅲ)对任意给定的整数n(n≥2),是否存在首项为0的E数列A n,使得S(A n)=0?如果存在,写出一个满足条件的E数列A n;如果不存在,说明理由.【考点】数列的应用.【专题】等差数列与等比数列;点列、递归数列与数学归纳法.【分析】(Ⅰ)根据题意,a2=±1,a4=±1,再根据|a k+1﹣a k|=1给出a5的值,可以得出符合题的E数列A5;(Ⅱ)从必要性入手,由单调性可以去掉绝对值符号,可得是A n公差为1的等差数列,再证充分性,由绝对值的性质得出不等式,再利用同向不等式的累加,可得a k+1﹣a k=1>0,A n是递增数列;(Ⅲ)根据定义构造数列,再用等差数列求和公式求出S(A n),最后通过讨论得出符合条件的S(A n).【解答】解:(Ⅰ)0,1,0,1,0是一个满足条件的E数列A5(Ⅱ)必要性:因为E数列A n是递增数列所以a k+1﹣a k=1(k=1,2, (1999)所以A n是首项为12,公差为1的等差数列.所以a2000=12+(2000﹣1)×1=2011充分性:由于a2000﹣a1999≤1a1999﹣a1998≤1…a2﹣a1≤1,所以a2000﹣a1≤1999,即a2000≤a1+1999又因为a1=12,a2000=2011所以a2000=a1+1999故a k+1﹣a k=1>0(k=1,2,…,1999),即A n是递增数列.综上所述,结论成立.(Ⅲ)设c k=a k+1﹣a k(k=1,2,…,n﹣1),则c k=±1因为a2=a1+c1a3=a1+c1+c2…a n=a1+c1+c2+…+c n﹣1所以S(A n)=na1+(n﹣1)c1+(n﹣2)c2+(n﹣3)c3+…+c n﹣1=(n﹣1)+(n﹣2)+…+1﹣[(1﹣c1)(n﹣1)+(1﹣c2)(n﹣2)+…+(1﹣c n﹣1)]=因为c k=±1,所以1﹣c k为偶数(k=1,2,…,n﹣1))所以(1﹣c1)(n﹣1)+(1﹣c2)(n﹣2)+…+(1﹣c n﹣1)为偶数所以要使S(A n)=0,必须=使为偶数即4整除n(n﹣1),亦即n=4m或n=4m+1(m∈N*)当n=4m(m∈N*)时,E数列A n的项满足a4k+1=a4k﹣1=0,a4k﹣2=﹣1,a4k=1(k=1,2,…,n﹣1))此时,有a1=0且S(A n)=0成立当n=4m+1(m∈N*)时,E数列A n的项满足a4k+1=a4k﹣1=0a4k﹣2=﹣1a4k=1(k=1,2,…,n﹣1))a4m+1=0时,亦有a1=0且S(A n)=0成立当n=4m+2或n=4m+3(m∈N*)(m∈N*)时,n(n﹣1)不能被4整除,此时不存在数列数列A n,使得a1=0且S(A n)=0成立【点评】本题以数列为载体,考查了不等式的运用技巧,属于难题,第三小问注意去绝对值,分类讨论思想的运用.。
2011海淀区高三二模理综试题及答案

2011年北京高考二模理综模拟试题(海淀区)l 3.下列说法中正确的是( )A .在关于物质波的表达式E=hv 和λρh=中,波长A 、频率v 都是描述物质波动性的物理量B .光的偏振现象说州光是纵波C .光的干涉和衍射现象说明光具有粒子性D .光电效应既显示了光的粒子性,又显示了光的波动性 14.下列说法中正确的是 ( )A .天然放射现象的发现,揭示了原子的核式结构B .γ射线是波长很短的电磁波,它的穿透能力比β射线要弱C .若能测出小核反应过程中的质量亏损,就能根据2mc E ∆=∆计算出核反应中释放的核能D .一个氘核(21H )与一个氚核(31H )聚变生成一一个氦核(42He )的同时放出一个电子15.有以下物理现象:在平直公路上行驶的汽车制动后滑行一段距离,最后停下;流星在夜空中坠落并发出明亮的光;降落伞在空中匀速下降;条形磁铁在下落过程中穿过闭合线圈,线圈中产生感应电流。
托这些现象所包含的物理过程中,这些运动的物体具有的相同特征是 ( ) A .都有重力做功 B .物体都要克服阻力做功 C .都有动能转化为其他形式的能 D .都有势能转化为其他形式的能16.图4是一列简谐波在t=0时的波形图,介质中的质点P 沿Y 轴方向做简谐运动的表达式为y=10sin5πt cm 。
关于这列简谐波,下列说法中正确的是 A .这列简谐波的振幅为20cm B .这列简谐波的周期为5.0s C .这列简谐波存该介质中的传播速度为25cm /s D .这列简谐波沿x 轴正向传播17.在如图5所示的电路中,E 为电源,其内阻为r ,L 为小灯泡(其灯丝电阻呵视为不变),R 1、R 2为定值电阻,R 3为光敏电阻,其阻值:犬小随所受照射光强度的增大而减小,○V 为理想电压表。
若将照射R 3的光的强度减弱,则 A .电压表的示数变大 B .小灯泡消耗的功率变小 C .通过R 2的电流变小 D .电源阳极问的电压变小18.如图6所示,水平光滑地而上停放着一辆质最为M 的小车,小车左端靠在竖直墙壁上,其左侧半径为R 的四分之一圆弧轨道AB 是光滑的,轨道最低点B 与水平轨道BC 相切,整个轨道处于同一竖直平面内。
2011年海淀区高三二模数学(理)试题及答案

海淀区高三年级第二学期期末练习选择题(共40分)、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选 出符合题目要求的一项.—― 1.复数1-在复平面上对应的点的坐标是i根据上图,对这两名运动员的成绩进行比较,下列四个结论中,不正确 A. 甲运动员得分的极差大于乙运动员得分的极差B. 甲运动员得分的的中位数大于乙运动员得分的的中位数C. 甲运动员的得分平均值大于乙运动员的得分平均值数 学(理科)2011.5A. (1,1)B. ( 1,1)C.(1, 1) D. (1, 1)2.已知全集U R, 集合 A 1,2,3,4,5 {x R |x 2},下图中阴影部分所表示的集合为A {1}B. {0,1}C. {1,2}D. {0,1,2}3.函数f (x)1A - (0,2). 1 ,,log 2X 一的零点所在区间x(2」)B. C. (1,2)D. (2,3)4.若直线l 的参数方程为3t ..............(t 为参数),则直线l 倾斜角的余弦值4 A.-B.55.某赛季甲、乙两名篮球运动员各C.3 D*5513场比赛得分情况用茎叶图表示如9 6 537 甲乙8 1 7 7 9 9 0 2 2 5 6 7 03 0234的是8 1 29 9D.甲运动员的成绩比乙运动员的成绩稳定6.一个锥体的主视图和左视图如图所示,下面选项中,不A 2一 x7.右椭圆C 〔: 一2的焦点相同且a 1 a 2 .给出如下四个结论:① 椭圆C 1和椭圆C 2一定没有公共点;令 22 2 2a a1 a 2b10)C和椭圆2 x-2a 2a 1D —a 2b 〔 b 2 a 2b i 1 (a 2 b 2 0)b 2.其中,所有正确结论的序号是A.②③④B.①③④C.①②④D.①②③8.在一个正方体ABCD A 1B 1C 1D 1中,P 为正方形A 1B 1C 1D 1四边上的动点,O 为底面正方形 ABCD 的中心, M , N 分别为AB, BC 中点,点Q 为平面 uuun段D 1Q 与OP 互相平分,贝U 满足有A. 0个B. 1个C. 2个D. 3个非选择题(共110分)、填空题:本大题共6小题,每小题5分,共30分.y 9.点2x,x,表示的平面区域内,贝U z 2x y 的最大值为可能是该锥体的俯视图的是y b?ABCD 内一点,线uuuuMN 的实数的值(2)满足f (―) f (— —)的正整数n 的最小值为^666三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程15. (本小题共13分)已知函数f(x) cos 2 x J3sin xcos x (0)的最小正周期为,、一2 、…(I)求f (—)的值;3(n)求函数f (x)的单调区间及其图象的对称轴方程16. (本小题共13分)某商场一号电梯从1层出发后可以在2、3、4层停靠.已知该电梯在1层载有4位乘客, 假设每位乘客在2、3、4层下电梯是等可能的.(I )求这4位乘客中至少有一名乘客在第2层下电梯的概率;10. 运行如图所示的程序框图,若输入 n 4,则输出S 的值为、42 3 4 511 .若 x(1 mx)a i x a 2x a 3x a 4x a 5x其中a 2 6 ,则实数m 的值为________ ;ai a 2 a 3 84 85 的值为.12.如图,已知eO 的弦AB 交半径OC 于点D,若AD 3, BD 2,且D为13.已知数列 a n 满足 a 〔t, , a n 1 a n 2 0 (t一 .* …*N ,n N ),记数列 a n 的前n 项和的最大值为f (t),则f (t)sin x14.已知函数f (x) ---------x①f (x)是偶函数;②f(x) 1 ;③当x其中真命题有3 2时, f (x)取得极小值.(n )用X表示4名乘客在第4层下电梯的人数,求X的分布列和数学期望.17.(本小题共14分)如图,四棱锥P ABCD 的底面是直角梯形, AB// CD , AB AD , PAB 和 PAD 是两个边长为2的正三角形,DC 4 , O 为BD 的中点,E 为PA 的中点.(I)当a 0时,求曲线y f(x)在(e, f (e))处的切线方程(e 2.718...);(II )求函数f(x)的单调区间19. (本小题共13分)在平面直角坐标系 xOy 中,设点P(x, y), M(x, 4),以线段PM 为直径的圆经过原 点O .(I)求动点 P 的轨迹W 的方程;(n)过点E(0, 4)的直线l 与轨迹 W 交于两点A, B ,点A 关于y 轴的对称点为 A',试判 断直线A'B 是否恒过一定点,并证明你的结论.20. (本小题共13分)对于数列A :礼a ?,L , a ”,若满足司 0,1 (i 1,2,3, ,n),则称数列A 为“0-1数 列”.定义变换T , T 将“0-1数列” A 中原有的每个1都变成0, 1,原有的每个0都变成1, 0.例如 A :1,0,1,则T(A):0,1,1,0,0,1.设 A 。
2010—2011海淀区高三数学(理)期末考试题(带答案)

2010—2011海淀区高三数学(理)期末考试题(带答案)D海淀区高三年级第一学期期末练习数 学(理)答案及评分参考 2011.1第Ⅰ卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分)题号 12345678答案B D DC A BD C第Ⅱ卷(非选择题 共110分)二、填空题(本大题共6小题,每小题5分, 共30分.有两空的题目,第一空3分,第二空2分) 9. 222x y x += (1,0) 10. 180 11. 512.M P Ne e e << 13.① ④ 14. 432 (1)2 3 (01)k k k k ⎧+≥⎪⎨⎪+<<⎩三、解答题(本大题共6小题,共80分) 15.(共12分) 解:(I )xx x f 2cos )32cos()(--=πxx x 2cos 3sin2sin 3cos2cos -+=ππ.......................................2分x x 2cos 212sin 23-=)62sin(π-=x . .......................................4分)2,0(π∈x , )65,6(62πππ-∈-∴x , .......................................5分 ]1,21()62sin(-∈-∴πx , 即)(x f 在(0,2π)的值域为]1,21(- . .......................................6分 (II )由(I )可知,)62sin()(π-=A A f , 1)62sin(=-∴πA , ......................................7分 π<<A 0 , 611626πππ<-<-∴A , .....................................8分 3,262πππ==-∴A A . ....................................9分 Abc c b a cos 2222-+= , .....................................10分把73a b ==,代入,得到2320cc -+=, ..................................11分1=∴c 或2=c . ....................................12分 16.(共13分) 解:(I )方法一设选手甲在A 区投两次篮的进球数为X ,则)109,2(~B X , 故591092)(=⨯=X E , ....................................... 2分 则选手甲在A 区投篮得分的期望为6.3592=⨯ . ....................................... 3分设选手甲在B 区投篮的进球数为Y ,则)31,3(~B Y , 故1313)(=⨯=Y E , ....................................... 5分 则选手甲在B 区投篮得分的期望为313=⨯ . ....................................... 6分 36.3> ,∴选手甲应该选择A 区投篮. .......................................7分方法二:(I )设选手甲在A 区投篮的得分为ξ,则ξ的可能取值为0,2,4,212291(0)(1)101009918(2)(1)1010100981(4)().10100P P C P ξξξ==-===⋅-====;;所以ξ的分布列为 ξ 0 2 4 p 1100 18100 81100.......................................2分6.3=∴ξE .......................................3分 同理,设选手甲在B 区投篮的得分为η,则η的可能取值为0,3,6,9,3123223318(0)(1);327114(3)(1);339112(6)()(1);33911(9)().327P P C P C P ηηηη==-===⋅-===-====所以η的分布列为:η0 3 6 9p 827 49 29127.......................................5分3E η∴=, .......................................6分 ηξE E > ,∴选手甲应该选择A 区投篮. .......................................7分(Ⅱ)设选手甲在A 区投篮得分高于在B 区投篮得分为事件C ,甲在A 区投篮得2分在B 区投篮得0分为事件1C ,甲在A 区投篮得4分在B 区投篮得0分为事件2C ,甲在A 区投篮得4分在B 区投篮得3分为事件3C ,则123C C C C =,其中123,,C C C 为互斥事件. .......................................9分则: 123123188******** ()()= ()()()1002710027100975P C P C C C P C P C P C =++=⨯+⨯+⨯=故选手甲在A 区投篮得分高于在B 区投篮得分的概率为4975 ..................................13分17. (共14分)解:(I ) 棱柱ABCD —1111A B C D 的所有棱长都为2, ∴四边形ABCD 为菱形,AC BD ⊥ . .......................................1分 又1A O ⊥平面ABCD, BD ⊂平面ABCD , 1AO BD ∴⊥ . .......................................2分又1AC AO O =,1,AC AO ⊂平面11ACC A , ⊥∴BD 平面11ACC A , .......................................3分 ⊂1AA 平面11ACC A , ∴ BD ⊥1AA . .......................................4分(Ⅱ)连结1BC四边形ABCD 为菱形,AC BD O =O ∴是BD 的中点. ....................................... 5分 又 点F 为1DC 的中点, ∴在1DBC ∆中,1//BC OF , .......................................6分 ⊄OF 平面11BCC B ,⊂1BC 平面11BCC B ∴//OF 平面11BCC B .......................................8分 (III )以O 为坐标系的原点,分别以1,,OA OB OA 所在直线为,,x y z 轴建立空间直角坐标系. 侧棱1AA 与底面ABCD 的所成角为60°,1A O ⊥平面ABCD . 601=∠∴AO A ,在AO A Rt 1∆中,可得11,3,AO AO ==在Rt AOB ∆中,22413OB AB AO =--A BC1B 1C 1AD F1D O得1(1,0,0),3),(0,3,0),3,0)A A D B - ...............................10分 设平面D AA 1的法向量为),,(1111z y x n= ⎪⎩⎪⎨⎧=⋅=⋅∴00111AD n AA n)0,3,1(),3,0,1(1--=-= 11113030x z x ⎧-=⎪∴⎨-=⎪⎩ 可设)1,1,3(1-=n .......................................11分 又 BD ⊥平面11ACC A所以,平面11A ACC 的法向量为23,0)n OB == .......................................12分 55353,cos 212121-=⋅-=⋅>=<∴n n n n , 二面角D —1AA —C 为锐角,故二面角D —1AA —C 的余弦值是55 . ....................................14分18. (共13分) 解:2211(21)()1(1)(1)a x ax a f x a x x x --+-'=--=+++,1x >-, .......................................2分(I )由题意可得13(1)24a f -'==-,解得3a =, ....................................3分因为(1)ln 24f =-,此时在点(1,(1))f 处的切线方程为(ln24)2(1)y x --=--,即2ln22y x =-+-,与直线:21l y x =-+平行,故所求a 的值为3. ....................4分(II ) 令()0f x '=,得到1212,0x x a =-= ,由12a ≥可知120a -≤ ,即10x ≤. ................................5分 ① 即12a =时,12120x x a =-==. 所以,2'2()0,(1,)2(1)x f x x x =-≤∈-+∞+, ................................6分故()f x 的单调递减区间为(1,)-+∞ . ................................7分② 当112a <<时,1120a -<-<,即1210x x -<<=, 所以,在区间1(1,2)a --和(0,)+∞上,'()0f x <; ...............................8分 在区间1(2,0)a -上,'()0f x >. .................................9分 故 ()f x 的单调递减区间是1(1,2)a --和(0,)+∞,单调递增区间是1(2,0)a-. .........10分 ③当1a ≥时,1121x a=-≤-, 所以,在区间(1,0)-上()0f x '>; ................................11分在区间(0,)+∞上()0f x '< , ...............................12分故()f x 的单调递增区间是(1,0)-,单调递减区间是(0,)+∞. ............................13分 综上讨论可得: 当12a =时,函数()f x 的单调递减区间是(1,)-+∞; 当112a <<时,函数()f x 的单调递减区间是1(1,2)a --和(0,)+∞,单调递增区间是1(2,0)a-; 当1a ≥时,函数()f x 的单调递增区间是(1,0)-,单调递减区间是(0,)+∞.19. (共14分)解:(Ⅰ)抛物线22y px = (0)p >的准线为2p x =-, .....................................1分 由抛物线定义和已知条件可知||1()1222p p MF =--=+=, 解得2p =,故所求抛物线方程为24y x =. ......................................3分(Ⅱ)联立2124y x b y x ⎧=-+⎪⎨⎪=⎩,消x 并化简整理得2880y y b +-=.依题意应有64320b ∆=+>,解得2b >-. ..............................................4分 设1122(,),(,)A x y B x y ,则12128,8y y y y b +=-=-, .............................................5分设圆心00(,)Q x y ,则应有121200,422x x y y x y ++===-.因为以AB 为直径的圆与x 轴相切,得到圆半径为0||4r y ==, ........................6分 又22221212121212||()()(14)()5[()4]5(6432)AB x x y y y y y y y y b =-+-+-+-=+.所以 ||25(6432)8AB r b =+, .........................................7分 解得85b =-. .........................................8分 所以12124822224165x x b y b y b +=-+-=+=,所以圆心为24(,4)5-. 故所求圆的方程为2224()(4)165x y -++=. ............................................9分方法二: 联立2124y x b y x ⎧=-+⎪⎨⎪=⎩,消掉y 并化简整理得22(416)40xb x b -++=, 依题意应有2216(4)160b b ∆=+->,解得2b >-. ............................................4分 设1122(,),(,)A x y B x y ,则21212416,4x x b x x b +=+= . .............................................5分设圆心00(,)Q x y ,则应有121200,422x x y y x y ++===-,因为以AB 为直径的圆与x 轴相切,得到圆半径为0||4r y ==. .....................................6分 又2222121212121215||()()(1)()[()4]5(6432)44AB x x y y x x x x x x b =-+-+-+-+, 又||28AB r ==5(6432)8b +, .............................................7分解得85b =-, ..............................................8分 所以12485x x +=,所以圆心为24(,4)5-. 故所求圆的方程为2224()(4)165x y -++=. .............................................9分(Ⅲ)因为直线l 与y 轴负半轴相交,所以0b <,又l 与抛物线交于两点,由(Ⅱ)知2b >-,所以20b -<<,...........................................10分 直线l :12y x b =-+整理得220x y b +-=, 点O 到直线l 的距离55d , .................................................11分 所以321||4224222AOB SAB d b b b b ∆==-++ ..................................................12分 令32()2g b bb =+,20b -<<, 24()343()3g b b b b b '=+=+, b 4(2,)3-- 43- 4(,0)3-()g b ' +0 - ()g b 极大由上表可得()g b 最大值为432()327g -= . ...............................................13分 所以当43b =-时,AOB ∆323. ...............................................14分20.(共14分)解:(Ⅰ)当10n =时,集合{}1,2,3,,19,20A =,{}{}910,11,12,,19,20B x A x =∈>=不具有性质P . ...................................1分 因为对任意不大于10的正整数m ,都可以找到该集合中两个元素110b =与210b m =+,使得12b b m -=成立................2分 集合{}*31,C x A x k k N =∈=-∈具有性质P . ................................................3分 因为可取110m =<,对于该集合中任意一对元素112231,31c k c k =-=-,*12,k k N ∈ 都有121231c c k k -=-≠. .....................................................................4分(Ⅱ)当1000n =时,则{}1,2,3,,1999,2000A =①若集合S 具有性质P ,那么集合{}2001T x x S =-∈一定具有性质P ....................5分 首先因为{}2001T x x S =-∈,任取02001,t x T =-∈ 其中0x S ∈, 因为S A ⊆,所以0{1,2,3,...,2000}x ∈, 从而0120012000x ≤-≤,即,t A ∈所以T A ⊆. ...........................6分由S 具有性质P ,可知存在不大于1000的正整数m , 使得对S 中的任意一对元素12,s s ,都有12s s m -≠.对于上述正整数m , 从集合{}2001T x x S =-∈中任取一对元素11222001,2001t x t x =-=-,其中12,x x S ∈, 则有1212t t x x m -=-≠, 所以集合{}2001T x x S =-∈具有性质P . .............................8分 ②设集合S 有k 个元素.由第①问知,若集合S 具有性质P ,那么集合{}2001T x x S =-∈一定具有性质P . 任给x S ∈,12000x ≤≤,则x 与2001x -中必有一个不超过1000, 所以集合S 与T 中必有一个集合中至少存在一半元素不超过1000,不妨设S 中有t 2k t ⎛⎫≥ ⎪⎝⎭个元素12,,,t b b b 不超过1000.由集合S 具有性质P ,可知存在正整数1000m ≤, 使得对S 中任意两个元素12,s s ,都有12s s m -≠, 所以一定有12,,,t b m b m b m S +++∉.又100010002000i b m +≤+=,故12,,,t b m b m b m A +++∈,即集合A 中至少有t 个元素不在子集S 中, 因此2kk +≤2000k t +≤,所以20002kk +≤,得1333k ≤,当{}1,2,,665,666,1334,,1999,2000S =时,取667m =,则易知对集合S 中任意两个元素12,y y , 都有12||667y y -≠,即集合S 具有性质P ,而此时集合S中有1333个元素.因此集合S 元素个数的最大值是1333. .....................................14分说明:其它正确解法按相应步骤给分.。
北京市海淀区2011高三年级第二学期期中练习数学理科及答案.doc

海淀区高三年级第二学期期中练习数 学 (理科) 2011.4一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1、已知集合{}30<<∈=x x A R ,{}42≥∈=x x B R ,则=B AA. {}32<<x xB. {}32<≤x xC. {}322<≤-≤x x x 或 D. R 2.已知数列{}n a 为等差数列,n S 是它的前n 项和.若21=a ,123=S ,则=4S A .10 B .16 C .20 D .243. 在极坐标系下,已知圆C 的方程为2cos ρθ=,则下列各点在圆C 上的是 A .1,3π⎛⎫- ⎪⎝⎭ B . 1,6π⎛⎫ ⎪⎝⎭C.34π⎫⎪⎭ D .54π⎫⎪⎭4.执行如图所示的程序框图,若输出x 的值为23,则输入的x 值为A .0B .1C .2D .11 5.已知平面l =αβ,m 是α内不同于l 的直线,那么下列命题中错误..的是 A .若β//m ,则l m // B .若l m //,则β//m C .若β⊥m ,则l m ⊥ D .若l m ⊥,则β⊥m6. 已知非零向量,,a b c 满足++=a b c 0,向量,a b 的夹角为120,且||2||=b a , 则向量a 与c 的夹角为A .︒60B .︒90C .︒120D . ︒1507.如果存在正整数ω和实数ϕ使得函数)(cos )(2ϕω+=x x f (ω,ϕ为常数)的图象如图所示(图象经过点(1,0)),那么ω的值为A .1B .2C . 3 D. 48.已知抛物线M :24y x =,圆N :222)1(r y x =+-(其中r 为常数,0>r ).过点(1,0)的直线l 交圆N 于C 、D 两点,交抛物线M 于A 、B 两点,且满足BD AC =的直线l 只有三条的必要条件是A .(0,1]r ∈B .(1,2]r ∈C .3(,4)2r ∈D .3[,)2r ∈+∞二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.复数3i1i-+= .10.为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为1s ,2s ,3s ,则它们的大小关系为 . (用“>”连接)11.如图,A ,B ,C 是⊙O 上的三点,BE 切⊙O 于点B , D 是CE 与⊙O 的交点.若︒=∠70BAC ,则=∠CBE ______;若2=BE ,4=CE , 则=CD .12.已知平面区域}11,11|),{(≤≤-≤≤-=y x y x D ,在区域D 内任取一点, 则取到的点位于直线y kx =(k R ∈)下方的概率为____________ .13.若直线l 被圆22:2C x y +=所截的弦长不小于2,则在下列曲线中:①22-=x y ② 22(1)1x y -+= ③ 2212x y += ④ 221x y -=与直线l 一定有公共点的曲线的序号是 . (写出你认为正确的所有序号) 14.如图,线段AB =8,点C 在线段AB 上,且AC =2,P 为线段CB 上 一动点,点A 绕点C 旋转后与点B 绕点P 旋转后重合于点D .设CP =x , △CPD 的面积为()f x .则()f x 的定义域为 ;'()f x 的零点是 .三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15. (本小题共13分)在ABC ∆中,内角A 、B 、C 所对的边分别为,,a b c ,已知1tan 2B =,1tan 3C =,且1c =. (Ⅰ)求tan A ; (Ⅱ)求ABC ∆的面积. CBD 乙丙甲16. (本小题共14分)在如图的多面体中,EF ⊥平面AEB ,AE EB ⊥,//AD EF ,//EF BC ,24BC AD ==,3EF =,2AE BE ==,G 是BC 的中点.(Ⅰ) 求证://AB 平面DEG ; (Ⅱ) 求证:BD EG ⊥;(Ⅲ) 求二面角C DF E --的余弦值.17. (本小题共13分) 某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为23.现有10件产品,其中6件是一等品,4件是二等品. (Ⅰ) 随机选取1件产品,求能够通过检测的概率;(Ⅱ)随机选取3件产品,其中一等品的件数记为X ,求X 的分布列; (Ⅲ) 随机选取3件产品,求这三件产品都不能通过检测的概率.18. (本小题共13分)已知函数()ln f x x a x =-,1(), (R).ag x a x+=-∈ (Ⅰ)若1a =,求函数()f x 的极值;(Ⅱ)设函数()()()h x f x g x =-,求函数()h x 的单调区间;(Ⅲ)若在[]1,e (e 2.718...=)上存在一点0x ,使得0()f x <0()g x 成立,求a 的取值范围.19. (本小题共14分)已知椭圆2222:1x y C a b += (0)a b >>经过点3(1,),2M 其离心率为12.(Ⅰ)求椭圆C 的方程;(Ⅱ)设直线1:(||)2l y kx m k =+≤与椭圆C 相交于A 、B 两点,以线段,OA OB 为邻边作平行四边形OAPB ,其中顶点P 在椭圆C 上,O 为坐标原点.求OP 的取值范围.20. (本小题共13分)已知每项均是正整数的数列A :123,,,,n a a a a ,其中等于i 的项有i k 个(1,2,3)i =⋅⋅⋅,设j j k k k b +++= 21 (1,2,3)j =,12()m g m b b b nm =+++-(1,2,3)m =⋅⋅⋅.(Ⅰ)设数列:1,2,1,4A ,求(1),(2),(3),(4),(5)g g g g g ; (Ⅱ)若数列A 满足100a a a n +++-=,求函数)(m g 的最小值.ADF EBG C海淀区高三年级第二学期期中练习 数 学(理)2011.4参考答案一、选择题(本大题共8小题,每小题5分,共40分)二、填空题(本大题共6小题,每小题5分. 共30分.有两空的题目,第一空3分,第二空2分) 9.12i - 10. s 1>s 2>s 3 11. 70; 3 12.1213. ① ③ 14. (2,4); 3 三、解答题(本大题共6小题,共80分) 15.(共13分) 解:(I )因为1tan 2B =,1tan 3C =,tan tan tan()1tan tan B CB C B C ++=-, …………………1分代入得到,1123tan()111123B C ++==-⨯ . …………………3分 因为180A B C =-- , …………………4分 所以tan tan(180())tan()1A B C B C =-+=-+=-.…………………5分 (II )因为0180A <<,由(I )结论可得:135A = . …………………7分 因为11tan tan 023B C =>=>,所以090C B <<< . …………8分 所以sin ,5B =sin 10C =. …………9分由sin sin a cA C=得a =, …………………11分 所以ABC ∆的面积为:11sin 22ac B =. ………………13分 16. (共14分)解:(Ⅰ)证明:∵//,//AD EF EF BC ,∴//AD BC . A D∴四边形ADGB 是平行四边形,∴ //AB DG . ……………2分∵AB ⊄平面DEG ,DG ⊂平面DEG ,∴//AB 平面DEG . …………………4分 (Ⅱ) 解法1证明:∵EF ⊥平面AEB ,AE ⊂平面AEB ,∴EF AE ⊥,又,AE EB EBEF E ⊥=,,EB EF ⊂平面BCFE , ∴AE ⊥平面BCFE .……………5分过D 作//DH AE 交EF 于H ,则DH ⊥平面BCFE .∵EG ⊂平面BCFE , ∴DH EG ⊥. ………………………6分 ∵//,//AD EF DH AE ,∴四边形AEHD 平行四边形,∴2EH AD ==, ∴2EH BG ==,又//,EH BG EH BE ⊥,∴四边形BGHE 为正方形,∴BH EG ⊥, ………………………7分 又,BHDH H BH =⊂平面BHD ,DH ⊂平面BHD ,∴EG ⊥平面BHD . ………………………8分 ∵BD ⊂平面BHD ,∴BD EG ⊥. ………………………9分 解法2∵EF ⊥平面AEB ,AE ⊂平面AEB ,BE ⊂平面AEB ,∴EF AE ⊥,EF BE ⊥, 又AE EB ⊥,∴,,EB EF EA 两两垂直. ……………………5分以点E 为坐标原点,,,EB EF EA 分别为,,x y z 轴建立如图的空间直角坐标系. 由已知得,A (0,0,2),B (2,0,0),C (2,4,0),F (0,3,0),D (0,2,2), G (2,2,0). …………………………6分 ∴(2,2,0)EG =,(2,2,2)BD =-,………7分∴22220BD EG ⋅=-⨯+⨯=, ………8分 ∴BD EG ⊥. …………………………9分(Ⅲ)由已知得(2,0,0)EB =是平面EFDA 的法向量. …………………………10分 设平面DCF 的法向量为(,,)x y z =n ,∵(0,1,2),(2,1,0)FD FC =-=,∴00FD n FC n ⎧⋅=⎪⎨⋅=⎪⎩,即2020y z x y -+=⎧⎨+=⎩,令1z =,得(1,2,1)=-n . …………………………12分设二面角C DF E --的大小为θ,则cos cos ,EB =<=θn 13分 ∴二面角C DF E --的余弦值为 …………………………14分 17. (共13分)新 课标 第 一网事件A 等于事件 “选取一等品都通过检测或者是选取二等品通过检测” ……………2分151332104106)(=⨯+=A p …………………………4分 (Ⅱ) 由题可知X 可能取值为0,1,2,3.30463101(0)30C C P X C ===,21463103(1)10C C P X C ===, 12463101(2)2C C P X C ===,03463101(3)6C C P X C ===. ………………8分……………9分(Ⅲ)设随机选取3件产品都不能通过检测的事件为B ……………10分 事件B 等于事件“随机选取3件产品都是二等品且都不能通过检测” 所以,3111()()303810P B =⋅=. ……………13分18. (共13分)解:(Ⅰ)()f x 的定义域为(0,)+∞, ………………………1分 当1a =时,()ln f x xx =-,11()1x f x -'=-=, ………………………2分………………………3分所以()f x 在1x =处取得极小值1. ………………………4分(Ⅱ)1()ln ah x x a x x+=+-, 22221(1)(1)[(1)]()1a a x ax a x x a h x x x x x +--++-+'=--==………………………6分 ①当10a +>时,即1a >-时,在(0,1)a +上()0h x '<,在(1,)a ++∞上()0h x '>, 所以()h x 在(0,1)a +上单调递减,在(1,)a ++∞上单调递增; ………………………7分 ②当10a +≤,即1a ≤-时,在(0,)+∞上()0h x '>,所以,函数()h x 在(0,)+∞上单调递增. ………………………8分 (III )在[]1,e 上存在一点x ,使得()f x <()g x 成立,即在[]1,e 上存在一点0x ,使得0()0h x <,即函数1()ln ah x x a x x+=+-在[]1,e 上的最小值小于零. ………………………9分 由(Ⅱ)可知 ①即1e a +≥,即e 1a ≥-时, ()h x 在[]1,e 上单调递减,所以()h x 的最小值为(e)h ,由1(e)e 0eah a +=+-<可得2e 1e 1a +>-, 因为2e 1e 1e 1+>--,所以2e 1e 1a +>-; ………………………10分 ②当11a +≤,即0a ≤时, ()h x 在[]1,e 上单调递增,所以()h x 最小值为(1)h ,由(1)110h a =++<可得2a <-; ………………………11分 ③当11e a <+<,即0e 1a <<-时, 可得()h x 最小值为(1)h a +,因为0ln(1)1a <+<,所以,0ln(1)a a a <+< 故(1)2ln(1)2h a a a a +=+-+> 此时,(1)0h a +<不成立. ………………………12分综上讨论可得所求a 的范围是:2e 1e 1a +>-或2a <-. ………………………13分19. (共14分)解:(Ⅰ)由已知可得222214a b e a -==,所以2234a b = ① ……………1分 又点3(1,)2M 在椭圆C 上,所以221914a b += ② ……………2分 由①②解之,得224,3a b ==. 故椭圆C 的方程为22143x y +=. ……………5分 (Ⅱ) 当0k =时,(0,2)P m 在椭圆C上,解得m =,所以||OP =……6分 当0k ≠时,则由22,1.43y kx m x y=+⎧⎪⎨+=⎪⎩ 消y 化简整理得:222(34)84120k x kmx m +++-=, 222222644(34)(412)48(34)0k m k m k m ∆=-+-=+-> ③ ……………8分 设,,A B P 点的坐标分别为112200(,)(,)(,)x y x y x y 、、,则 012012122286,()23434km m x x x y y y k x x m k k=+=-=+=++=++. ……………9分由于点P 在椭圆C 上,所以 2200143x y +=. ……………10分 从而222222216121(34)(34)k m m k k +=++,化简得22434m k =+,经检验满足③式. ………11分又||OP ===== ………………………12分因为102k <≤,得23434k <+≤,有2331443k ≤<+OP <≤………13分 综上,所求OP的取值范围是2. ………………………14分 (Ⅱ)另解:设,,A B P 点的坐标分别为112200(,)(,)(,)x y x y x y 、、, 由,A B 在椭圆上,可得2211222234123412x y x y ⎧+=⎨+=⎩①② ………………………6分 ①—②整理得121212123()()4()()0x x x x y y y y -++-+=③ ………………………7分 由已知可得OP OA OB =+,所以120120x x x y y y +=⎧⎨+=⎩④⑤ ……………………8分由已知当1212y y k x x -=- ,即1212()y y k x x -=- ⑥ ………………………9分把④⑤⑥代入③整理得0034x ky =- ………………………10分与22003412x y +=联立消0x 整理得202943y k =+ ……………………11分由22003412x y +=得2200443x y =-, 所以222222000002413||4443343OP x y y y y k =+=-+=-=-+ ……………………12分 因为12k ≤,得23434k ≤+≤,有2331443k ≤≤+OP ≤≤. ……13分 所求OP的取值范围是. ………………………14分 20. (共13分)12342,1,0,1,0(5,6,7)j k k k k k j ======12342,213,2103,4,4(5,6,7,)m b b b b b m ==+==++====112123123412345(1)412(2)423,(3)434,(4)444,(5)45 4.g b g b b g b b b g b b b b g b b b b b =-⨯=-=+-⨯=-=++-⨯=-=+++-⨯=-=++++-⨯=-(2)一方面,1(1)()m g m g m b n ++-=-,根据“数列A 含有n 项”及j b 的含义知1m b n +≤, 故0)()1(≤-+m g m g ,即)1()(+≥m g m g ① …………………7分 另一方面,设整数{}12max ,,,n M a a a =,则当m M ≥时必有m b n =,所以(1)(2)(1)()(1)g g g M g M g M ≥≥≥-==+=所以()g m 的最小值为(1)g M -. …………………9分 下面计算(1)g M -的值:1231(1)(1)M g M b b b b n M --=++++--1231()()()()M b n b n b n b n -=-+-+-++-233445()()()()M M M M k k k k k k k k k k =----+----+----++-23[2(1)]M k k M k =-+++-12312(23)()M M k k k Mk k k k =-++++++++123()n M a a a a b =-+++++ 123()n a a a a n=-+++++…………………12分∵123100n a a a a n ++++-= , ∴(1)100,g M -=-∴()g m 最小值为100-. …………………13分说明:其它正确解法按相应步骤给分.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海淀区高三年级第二学期期末练习数 学 (理科) 2011.5选择题 (共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1. 复数11i+在复平面上对应的点的坐标是A .(1,1) B. (1,1)- C. (1,1)-- D. (1,1)-2. 已知全集R ,U = 集合{}1,2,3,4,5A =,{|2}B x x =∈≥R ,下图中阴影部分所表示的集合为 A {1} B. {0,1} C. {1,2} D. {0,1,2} 3.函数21()log f x x x=-的零点所在区间A .1(0,)2B. 1(,1)2C. (1,2)D. (2,3)4.若直线l 的参数方程为13()24x t t y t =+⎧⎨=-⎩为参数,则直线l 倾斜角的余弦值为A .45-B . 35- C . 35D . 455. 某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下: 甲 乙 9 8 8 1 7 7 9 961225679 95 3 2 0 3 0 2 37 1 0 4根据上图,对这两名运动员的成绩进行比较,下列四个结论中,不正确...的是 A .甲运动员得分的极差大于乙运动员得分的极差B .甲运动员得分的的中位数大于乙运动员得分的的中位数C .甲运动员的得分平均值大于乙运动员的得分平均值D .甲运动员的成绩比乙运动员的成绩稳定6.一个锥体的主视图和左视图如图所示,下面选项中,不.可能是...该锥体的俯视图的是7.若椭圆1C :1212212=+b y a x(011>>b a )和椭圆2C :1222222=+b y a x(022>>b a )的焦点相同且12a a >.给出如下四个结论:① 椭圆1C 和椭圆2C 一定没有公共点; ②1122a b a b >;③ 22212221b b a a -=-; ④1212a a b b -<-.其中,所有正确结论的序号是A .②③④ B. ①③④ C .①②④ D. ①②③8. 在一个正方体1111ABC D A B C D -中,P 为正方形1111A B C D 四,AB BC中边上的动点,O 为底面正方形A B C D 的中心,,M N 分别为点,点Q 为平面A B C D 内一点,线段1D Q 与O P 互相平分,则满足M Q Mλ=的实数λ的值有 A. 0个 B. 1个 C. 2个 D. 3个非选择题(共110分)二、填空题:本大题共6小题,每小题5分,共30分.9.点(,)P x y 在不等式组2,,2y x y x x ≤⎧⎪≥-⎨⎪≤⎩表示的平面区域内,则z x y =+的最大值为_______.10.运行如图所示的程序框图,若输入4n =,则输出S 的值为 .11.若4234512345(1)x m x a x a x a x a x a x -=++++,主视图左视图B ACDA 1D 1A 1C 1B DC BOPNMQ其中26a =-,则实数m 的值为;1234a a a a a ++++的值为 .12.如图,已知O 的弦AB 交半径O C 于点D ,若3A D =,2B D =,且D 为O C 的中点,则C D 的长为 .13.已知数列{}n a 满足1,a t =,120n n a a +-+= (,)t n ∈∈**N N ,记数列{}n a 的前n 项和的最大值为()f t ,则()f t = .14. 已知函数sin ()xf x x=(1)判断下列三个命题的真假:①()f x 是偶函数;②()1f x < ;③当32x π=时,()f x 取得极小值. 其中真命题有____________________;(写出所有真命题的序号)(2)满足()()666n n f f πππ<+的正整数n 的最小值为___________.三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程. 15. (本小题共13分)已知函数2()cos cos f x x x x ωωω=+(0)ω>的最小正周期为π.(Ⅰ)求2()3f π的值;(Ⅱ)求函数()f x 的单调区间及其图象的对称轴方程.16.(本小题共13分)某商场一号电梯从1层出发后可以在2、3、4层停靠.已知该电梯在1层载有4位乘客,假设每位乘客在2、3、4层下电梯是等可能的.(Ⅰ) 求这4位乘客中至少有一名乘客在第2层下电梯的概率;(Ⅱ) 用X 表示4名乘客在第4层下电梯的人数,求X 的分布列和数学期望.17.(本小题共14分)如图,四棱锥P ABC D -的底面是直角梯形,//AB C D ,AB AD ⊥,P A B ∆和PAD ∆是两个边长为2的正三角形,4D C =,O 为BD 的中点,E 为P A 的中点.(Ⅰ)求证:PO ⊥平面A B C D ; (Ⅱ)求证://O E 平面P D C ;(Ⅲ)求直线C B 与平面P D C 所成角的正弦值.18. (本小题共14分)已知函数221()()ln 2f x ax x x ax x =--+.()a ∈R .(I )当0a =时,求曲线()y f x =在(e,(e))f 处的切线方程(e 2.718...=); (II )求函数()f x 的单调区间.19.(本小题共13分)在平面直角坐标系xOy 中,设点(,),(,4)P x y M x -,以线段PM 为直径的圆经过原点O .(Ⅰ)求动点P 的轨迹W 的方程;(Ⅱ)过点(0,4)E -的直线l 与轨迹W 交于两点,A B ,点A 关于y 轴的对称点为'A ,试判断直线'A B 是否恒过一定点,并证明你的结论.20. (本小题共13分)对于数列12n A a a a :,,,,若满足{}0,1(1,2,3,,)i a i n ∈=⋅⋅⋅,则称数列A 为“0-1数列”.定义变换T ,T 将“0-1数列”A 中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如A :1,0,1,则():0,1,1,0,0,1.T A 设0A 是“0-1数列”,令1(),k k A T A -= 12k = ,,3,.(Ⅰ) 若数列2A :1,0,0,1,0,1,1,0,1,0,0,1. 求数列10,A A ;(Ⅱ) 若数列0A 共有10项,则数列2A 中连续两项相等的数对至少有多少对?请说明理由;(Ⅲ)若0A 为0,1,记数列k A 中连续两项都是0的数对个数为k l ,1,2,3,k =⋅⋅⋅.求k l 关于k 的表达式.海淀区高三年级第二学期期末练习数 学(理)答案及评分参考 2011.5选择题 (共40分)AD OCPBE一、选择题(本大题共8小题,每小题5分,共40分)非选择题(共110分)二、填空题(本大题共6小题,每小题5分. 共30分.有两空的题目,第一空3分,第二空2分)9. 6 10. 11 11.32,11613.222, (4(1), (4t tttt⎧+⎪⎪⎨+⎪⎪⎩为偶数)为奇数)14. ①②, 9三、解答题(本大题共6小题,共80分)15. (共13分)解:(Ⅰ)1()(1cos2)222f x x x=++ωω………………2分1sin(2)26x=++πω, …………………3分因为()f x最小正周期为π,所以22ππω=,解得1ω=, …………………………4分所以1()sin(2)62πf x x=++, …………………… 5分所以21()32πf=-. ………………………6分(Ⅱ)分别由222,()262k x k k Zπππππ-≤+≤+∈,3222,()262k x k k Zπππππ+≤+≤+∈可得,()36k x k k Zππππ-≤≤+∈,2,().63k x k k Zππππ+≤≤+∈………………8分所以,函数()f x的单调增区间为[,],()36k k k Zππππ-+∈;()f x的单调减区间为2[,],().63k k k Zππππ++∈………………10分由2,(62ππx k πk Z +=+∈)得,()26k πx πk Z =+∈. 所以,()f x 图象的对称轴方程为 ()26kπx πk Z =+∈. ………………13分16.(共13分)解:(Ⅰ) 设4位乘客中至少有一名乘客在第2层下电梯的事件为A , …………………1分 由题意可得每位乘客在第2层下电梯的概率都是13, …………………………3分则4265()1()1381P A P A ⎛⎫=-=-= ⎪⎝⎭ .…………………………6分(Ⅱ) X 的可能取值为0,1,2,3,4, …………………………7分 由题意可得每个人在第4层下电梯的概率均为13,且每个人下电梯互不影响,所以,1(4,)3X B . ………………………9分………………………11分 14()433E X =⨯=.…………………………13分17.(共14分)(Ⅰ)证明:设F 为D C 的中点,连接BF ,则D F AB = ∵AB AD ⊥,AB AD=,//A B D C , ∴四边形ABFD 为正方形, ∵O 为BD 的中点,∴O 为,AF BD 的交点, ∵2PD PB ==,∴P O B D ⊥, ………………………………..2分 ∵BD ==∴PO ==12AO BD ==,在三角形P A O 中,2224PO AO PA +==,∴P O A O ⊥,……………………………4分ADOCPBEF∵AO BD O = ,∴P O ⊥平面A B C D ; ……………………………5分 (Ⅱ)方法1:连接PF ,∵O 为A F 的中点,E 为P A 中点, ∴//O E P F ,∵O E ⊄平面P D C ,P F ⊂平面P D C ,∴//O E 平面P D C . ……………………………9分方法2:由(Ⅰ)知P O ⊥平面A B C D ,又AB AD ⊥,所以过O 分别做,AD AB 的平行线,以它们做,x y 轴,以O P 为z 轴建立如图所示的空间直角坐标系, 由已知得: (1,1,0)A --,(1,1,0)B -,(1,1,0)D - (1,1,0)F ,(1,3,0)C,(0,P ,11(,222E --,则11(,,)222O E =--,(1,1,PF =,(1,1,PD =-,(1,3,P C = .∴12O E P F =-∴//O E P F∵O E ⊄平面P D C ,P F ⊂平面P D C ,∴//O E 平面P D C ; …………………………………9分 (Ⅲ) 设平面P D C 的法向量为111(,,)n x y z =,直线C B 与平面P D C 所成角θ,则00n P C n P D ⎧⋅=⎪⎨⋅=⎪⎩,即11111130x y x y ⎧+-=⎪⎨--=⎪⎩,解得1110y x =⎧⎪⎨=⎪⎩,令11z =,则平面P D C的一个法向量为0,1)n = ,又(2,2,0)C B =--则sin cos ,3θn C B =<>==,∴直线C B 与平面P D C3. ………………………………………14分18. (共14分)解:(I )当0a =时,()ln f x x x x =-,'()ln f x x =-, ………………………2分 所以()0f e =,'()1f e =-, ………………………4分所以曲线()y f x =在(e,(e))f 处的切线方程为y x e =-+.………………………5分 (II )函数()f x 的定义域为(0,)+∞21'()()(21)ln 1(21)ln f x ax x ax x ax ax x x=-+--+=-,…………………………6分①当0a ≤时,210ax -<,在(0,1)上'()0f x >,在(1,)+∞上'()0f x <所以()f x 在(0,1)上单调递增,在(1,)+∞上递减; ……………………………………………8分 ②当102a <<时,在(0,1)和1(,)2a+∞上'()0f x >,在1(1,)2a上'()0f x <所以()f x 在(0,1)和1(,)2a+∞上单调递增,在1(1,)2a上递减;………………………10分③当12a =时,在(0,)+∞上'()0f x ≥且仅有'(1)0f =,所以()f x 在(0,)+∞上单调递增; ……………………………………………12分 ④当12a >时,在1(0,)2a和(1,)+∞上'()0f x >,在1(,1)2a上'()0f x <所以()f x 在1(0,)2a和(1,)+∞上单调递增,在1(,1)2a上递减……………………………14分19.(共13分)解:(I )由题意可得O P O M ⊥, ……………………………2分所以0OP OM ⋅=,即(,)(,4)0x y x -= ………………………………4分 即240x y -=,即动点P 的轨迹W 的方程为24x y = ……………5分 (II )设直线l 的方程为4y kx =-,1122(,),(,)A x y B x y ,则11'(,)A x y -.由244y kx x y=-⎧⎨=⎩消y 整理得24160x kx -+=, ………………………………6分 则216640k ∆=->,即||2k >. ………………………………7分12124,16x x k x x +==. …………………………………9分直线212221':()y y A B y y x x x x --=-+212221222212212222121222112()1()4()41444y 44y y y x x y x x x x y x x x x x x x x x x y x x x x x x x -∴=-++-∴=-++--∴=-+-∴=+……………………………………12分即2144x x y x -=+所以,直线'A B 恒过定点(0,4). ……………………………………13分20. (共13分)解:(Ⅰ)由变换T 的定义可得1:0,1,1,0,0,1A …………………………………2分0:1,0,1A …………………………………4分(Ⅱ) 数列0A 中连续两项相等的数对至少有10对 …………………………………5分证明:对于任意一个“0-1数列”0A ,0A 中每一个1在2A 中对应连续四项1,0,0,1,在0A 中每一个0在2A 中对应的连续四项为0,1,1,0,因此,共有10项的“0-1数列”0A 中的每一个项在2A 中都会对应一个连续相等的数对,所以2A 中至少有10对连续相等的数对. …………………………………………………………8分 (Ⅲ) 设k A 中有k b 个01数对,1k A +中的00数对只能由k A 中的01数对得到,所以1k k l b +=,1k A +中的01数对有两个产生途径:①由k A 中的1得到; ②由k A 中00得到,由变换T 的定义及0:0,1A 可得k A 中0和1的个数总相等,且共有12k +个,所以12kk k b l +=+,所以22kk k l l +=+,由0:0,1A 可得1:1,0,0,1A ,2:0,1,1,0,1,0,0,1A 所以121,1l l ==,当3k ≥时,若k 为偶数,222k k k l l --=+ 4242k k k l l ---=+ 2422l l =+上述各式相加可得122421(14)11222(21)143k k kk l ---=++++==-- ,经检验,2k =时,也满足1(21)3k k l =-若k 为奇数,222k k k l l --=+ 4242k k k l l ---=+ 312l l =+上述各式相加可得12322(14)112221(21)143k k kk l ---=++++=+=+- ,经检验,1k =时,也满足1(21)3k k l =+所以1(21),31(21),3kk k k l k ⎧+⎪⎪=⎨⎪-⎪⎩为奇数为偶数…………………………………………………………………………………..13分说明:其它正确解法按相应步骤给分.。
