导体杆模型归类解析
高三物理总复习:电磁感应中的“杆+导轨”类问题(3大模型)解题技巧归类例析
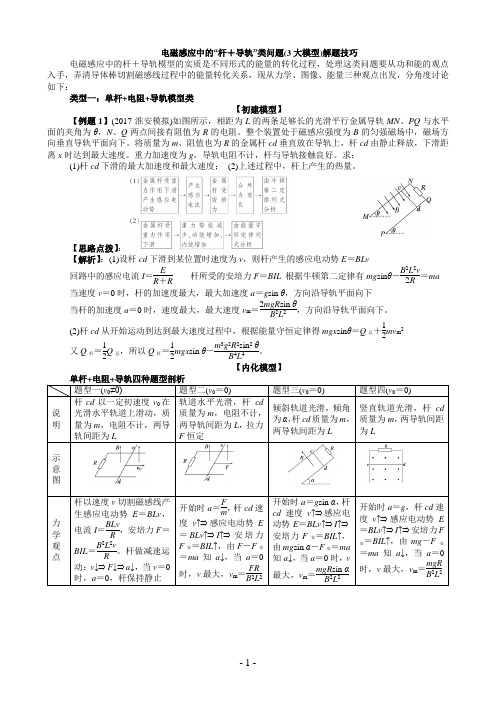
电磁感应中的“杆+导轨”类问题(3大模型)解题技巧电磁感应中的杆+导轨模型的实质是不同形式的能量的转化过程,处理这类问题要从功和能的观点入手,弄清导体棒切割磁感线过程中的能量转化关系,现从力学、图像、能量三种观点出发,分角度讨论如下:类型一:单杆+电阻+导轨模型类【初建模型】【例题1】(2017·淮安模拟)如图所示,相距为L 的两条足够长的光滑平行金属导轨MN 、PQ 与水平面的夹角为θ,N 、Q 两点间接有阻值为R 的电阻。
整个装置处于磁感应强度为B 的匀强磁场中,磁场方向垂直导轨平面向下。
将质量为m 、阻值也为R 的金属杆cd 垂直放在导轨上,杆cd 由静止释放,下滑距离x 时达到最大速度。
重力加速度为g ,导轨电阻不计,杆与导轨接触良好。
求:(1)杆cd 下滑的最大加速度和最大速度; (2)上述过程中,杆上产生的热量。
【思路点拨】: 【解析】:(1)设杆cd 下滑到某位置时速度为v ,则杆产生的感应电动势E =BLv回路中的感应电流I =E R +R杆所受的安培力F =BIL 根据牛顿第二定律有mg sin θ-B 2L 2v2R =ma当速度v =0时,杆的加速度最大,最大加速度a =g sin θ,方向沿导轨平面向下当杆的加速度a =0时,速度最大,最大速度v m =2mgR sin θB 2L 2,方向沿导轨平面向下。
(2)杆cd 从开始运动到达到最大速度过程中,根据能量守恒定律得mgx sin θ=Q 总+12mv m 2又Q 杆=12Q 总,所以Q 杆=12mgx sin θ-m 3g 2R 2sin 2θB 4L 4。
【内化模型】题型一(v 0≠0) 题型二(v 0=0) 题型三(v 0=0) 题型四(v 0=0) 说明 杆cd 以一定初速度v 0在光滑水平轨道上滑动,质量为m ,电阻不计,两导轨间距为L 轨道水平光滑,杆cd质量为m ,电阻不计,两导轨间距为L ,拉力F 恒定倾斜轨道光滑,倾角为α,杆cd 质量为m ,两导轨间距为L 竖直轨道光滑,杆cd质量为m ,两导轨间距为L示意图力学观点 杆以速度v 切割磁感线产生感应电动势E =BLv ,电流I =BLvR ,安培力F =BIL =B 2L 2v R 。
高中物理电磁学中导体棒模型分析

������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
的2倍
分 析:通电 后,弹 体 棒 受 到 向 右 的 安 培 力,加 速 向 右 弹
出.电流I 为原来的2倍,磁 感 应 强 度 B 变 为 原 来 的 2 倍,
F安 变为原来的4倍,加速度变为原来的4倍,由v2=2aL 得
其速度变为原来的2倍.若轨道长度 L 为原来的4倍,速度
变为原来的2倍,所以 B、D 正确.
高中物理电磁学中导体棒模型分析
王 毅
摘 要:导体棒问题是高中物理电磁学中最典型的模 型,涉 及 力、运 动、动 量、能 量、电 路、磁 场、电 磁 感 应 等 多 方 面 知 识,其 特 点 是 过 程 复 杂 ,变 式 多 ,是 高 考 考 查 的 重 点 、热 点 ,能 对 学 生 的 综 合 能 力 进 行 有 效 考 查 .
( )
A.2.5 m/s 1 W B.5 m/s 1 W C.7.5 m/s 9 W D.15 m/s 9 W 分析:(1)棒受 力 如 图,由 平 衡 条 件 得 F安 +μmg cos37° =mg sin37° 有 F安 =mg(sin37°-μcos37°)=0.4N 由 F安 =BIL 得I=1A,P=I2RMN =1 W, E=I(R灯 +RMN )=2V, 导体棒的速度v=E/(BL)=5 m/s,选 B. 解题策略:建立“动→电→动”的思 维 程 序:(1)找 准 主 动 运动者;(2)画等效电路图;(3)分析 导 体 棒 的 速 度、加 速 度 的 变 化 情 况 及 棒 的 最 终 状 态 ;(4)列 平 衡 方 程 求 解 . (三 )两 个 模 型 的 综 合 应 用
电磁感应中的“杆+导轨”模型

电磁感应中的“杆+导轨”模型电磁感应中的“杆+导轨”模型一、单棒模型阻尼式:在单棒模型中,导体棒相当于电源,根据洛伦兹力的公式,可以得到安培力的特点为阻力,并随速度减小而减小,加速度随速度减小而减小,最终状态为静止。
根据能量关系、动量关系和瞬时加速度,可以得到公式B2l2v R rF和q mv/Bl,其中q表示流过导体棒的电荷量。
需要注意的是,当有摩擦或者磁场方向不沿竖直方向时,模型的变化会受到影响。
举例来说,如果在电阻不计的光滑平行金属导轨固定在水平面上,间距为L、导轨左端连接一阻值为R的电阻,整个导轨平面处于竖直向下的磁感应强度大小为B的匀强磁场中,一质量为m的导体棒垂直于导轨放置,a、b之间的导体棒阻值为2R,零时刻沿导轨方向给导体棒一个初速度v,一段时间后导体棒静止,则零时刻导体棒的加速度为0,零时刻导体棒ab两端的电压为BLv,全过程中流过电阻R的电荷量为mv/Bl,全过程中导体棒上产生的焦耳热为0.二、发电式在发电式中,导体棒同样相当于电源,当速度为v时,电动势E=Blv。
根据安培力的特点,可以得到公式22Blv/l=Blv/(R+r)。
加速度随速度增大而减小,最终特征为匀速运动。
在稳定后的能量转化规律中,F-BIl-μmg=m*a,根据公式可以得到a=-(F-μmg)/m、v=0时,有最大加速度,a=0时,有最大速度。
需要注意的是,当电路中产生的焦耳热为mgh时,电阻R中产生的焦耳热也为mgh。
1.如图所示,相距为L的两条足够长的光滑平行金属导轨MN、PQ与水平面的夹角为θ,N、Q两点间接有阻值为R的电阻。
整个装置处于磁感应强度为B的匀强磁场中,磁场方向垂直导轨平面向下。
将质量为m、阻值也为R的金属杆cd垂直放在导轨上,杆cd由静止释放,下滑距离x时达到最大速度。
重力加速度为g,导轨电阻不计,杆与导轨接触良好。
求:1)杆cd下滑的最大加速度和最大速度;2)上述过程中,杆上产生的热量。
专题36+电磁感应中的:杆+导轨模型-2017-2018学年高二物理专题提升之电学+Word版含解析

一:专题概述1.模型构建“杆+导轨”模型是电磁感应问题高考命题的“基本道具”,也是高考的热点,考查的知识点多,题目的综合性强,物理情景变化空间大.“杆+导轨”模型又分为“单杆”型和“双杆”型(重点考查“单杆”型);导轨放置方式可分为水平、竖直和倾斜;杆的运动状态可分为匀速、匀变速、非匀变速运动等.2.模型分类及特点(1) 单杆水平式磁感应强度为拉力恒为(2) 单杆倾斜式感应电动势↑电流安培加速度二:典例精讲典例1:如图所示,两根足够长、电阻不计的平行光滑金属导轨相距为L ,导轨平面与水平面成θ角,质量均为m 、阻值均为R 的金属棒a 、b 紧挨着放在两导轨上,整个装置处于垂直于导轨平面的匀强磁场中,磁感应强度大小为B ,以一平行于导轨平面向上的恒力F =2mg sin θ拉a 棒,同时由静止释放b 棒,直至b 棒刚好匀速时,在此过程中通过棒的电量为q ,棒与导轨始终垂直并保持良好接触,重力加速度为g 。
求:(1)b 棒刚好匀速时,a 、b 棒间的距离s ; (2)b 棒最终的速度大小v b ; (3)此过程中a 棒产生的热量Q 。
【答案】(1)2qR BL ;(2)mgR sin θB 2L 2;(3)mgqR sin θBL -m 3g 2R 2sin 2θ2B 4L 4【解析】(1)根据法拉第电磁感应定律有E =ΔΦΔt① 根据闭合电路欧姆定律有I =E 2R②又q =I Δt ③得q =ΔΦ2R =B ΔS 2R =BLs 2R ,解得s =2qRBL④ (2)b 棒匀速时有 BIL =mg sin θ ⑤ E =BL (v a +v b ) ⑥I=E2R⑦对a棒向上加速的任一时刻由牛顿第二定律得F-BIL-mg sin θ=ma1,即mg sin θ-BIL=ma1⑧对b棒向下加速的任一时刻由牛顿第二定律得mg sin θ-BIL=ma2⑨由⑧⑨式可得a1=a2,故a、b棒运动规律相似,速度同时达到最大,且最终v a=v b⑩由⑤⑥⑦⑩式可得v b=mgR sinθB2L2⑪典例2:如图甲所示,MN、PQ两条平行的光滑金属轨道与水平面成θ=30°角固定,N、Q之间接电阻箱R,导轨所在空间存在匀强磁场,磁场方向垂直于轨道平面向上,磁感应强度为B=0.5T.质量为m的金属杆ab水平放置在轨道上,其接入电路的电阻值为r.现从静止释放杆ab,测得最大速度为v m.改变电阻箱的阻值R,得到v m与R 之间的关系如图乙所示.已知导轨间距为L=2 m,重力加速度取g=10m/s2,轨道足够长且电阻不计.求:甲乙(1) 当R=0时,杆ab匀速下滑过程中产生感应电动势E的大小及杆中的电流方向.(2) 金属杆的质量m及阻值r.(3) 当R=4Ω时,回路瞬时电功率每增加1W的过程中合外力对杆做的功W.【答案】(1) 3V b→a(2) 0.2kg3Ω(3) 0.7J【解析】(1) 由图乙可知,当R=0时,杆以最终速度3 m/s匀速运动,产生电动势为E=BLv,代入数据得E=3 V,杆中电流方向为b→a.从图象可知:斜率为m/(s·Ω)=1 m/(s·Ω),截距为v0=3 m/s,得到0,代入数据得m=0.2 kg,r=3Ω.(3) 由题意知E=BLv,得所以Δ由动能定理得得P,代入数据得W=0.7J.典例3:如图所示,两根足够长的平行金属导轨固定在倾角θ=30°的斜面上,导轨电阻不计,间距L=0.4 m。
电磁感应中的杆和导轨问题

电磁感应中的杆+导轨问题“杆+导轨”模型是电磁感应问题高考命题的“基本道具”,也是各种考试的热点,考查的知识点多,题目的综合性强,物理情景富于变化,是我们学习中的重点和难点。
导轨放置方式可分为水平、竖直和倾斜;轨道可能光滑,也可能粗糙;杆可能有电阻也可能没有电阻;杆的运动状态可分为匀速运动、匀变速运动、非匀变速运动或转动等;磁场的状态可分为恒定不变、均匀变化和非均匀变化等等,多种情景组合复杂,题目形式多变。
下面是几种最基本的模型及分析,有兴趣(无兴趣可以无视)的同学可以学习、体会、研究。
需要注意的是:模型中的结论是基于表中所述的基本模型而言,不一定有普遍性,物理情景有变化,结论可能不同,但分析的方法是相同的、有普遍性的。
1.单杆水平式物理模型匀强磁场与导轨垂直,磁感应强度为B,棒ab长为L,质量为m,初速度为零,拉力恒为F,水平导轨光滑,除电阻R外,其他电阻不计动态分析设运动过程中某时测得的速度为v,由牛顿第二定律知棒ab的加速度为a=Fm -=B2L2vmR,a、v同向,随速度的增加,棒的加速度a减小,当a=0时,v最大,电流I=BLv mR不再变化收尾状态运动形式匀速直线运动力学特征受力平衡,a=0 电学特征I不再变化2.单杆倾斜式物理模型匀强磁场与导轨垂直,磁感应强度为B,导轨间距为L,导体棒质量为m,电阻为R,导轨光滑,电阻不计动态分析棒ab刚释放时a=g sin α,棒ab的速度v↑→感应电动势E=BLv↑→电流I=ER↑→安培力F =BIL↑→加速度a↓,当安培力F=mg sin α时,a=0,速度达到最大v m=mgR sin αB2L2收运动形式匀速直线运动尾状态力学特征 受力平衡,a =0电学特征I 不再变化3、有初速度的单杆物理模型杆cd 以一定初速度v 0在光滑水平轨道上滑动,质量为m ,电阻不计,两导轨间距为L动态分析杆以速度v 切割磁感线产生感应电动势E =BLv ,电流I =BLv R ,安培力F =BIL =B 2L 2vR.杆做减速运动:v ↓?F ↓?a ↓,当v =0时,a =0,杆保持静止能量转化情况动能全部转化为内能:Q =12mv 24、含有电容器的单杆物理模型轨道水平光滑,单杆ab 质量为m ,电阻不计,两导轨间距为L ,拉力F 恒定动态分析开始时a=Fm,杆ab速度v?感应电动势E=BLv,经过时间Δt速度为v+Δv,此时感应电动势E′=BL(v+Δv),Δt时间内流入电容器的电荷量Δq=CE′-C E=CBLΔv电流I=ΔqΔt=CBLΔvΔt=CBLa (所以电流的大小恒定)安培力F安=BLI=CB2L2a(所以安培力的大小恒定)F-F安=ma,a=Fm+B2L2C,所以杆以恒定的加速度匀加速运动能量转化情况F做的功使其它形式的能E其它一部分转化为动能,一部分转化为电场能E电场能:W F=E其它=12mv2+E电场能5、含有电源时的单杆物理模型轨道水平光滑,单杆ab质量为m,电阻不计,两导轨间距为L。
电磁感应中的双导体棒和线框模型(解析版)-2024届新课标高中物理模型与方法

2024版新课标高中物理模型与方法电磁感应中的双导体棒和线框模型目录一.无外力等距双导体棒模型二.有外力等距双导体棒模型三.不等距导轨双导体棒模型四.线框模型一.无外力等距双导体棒模型【模型如图】1.电路特点棒2相当于电源;棒1受安培力而加速起动,运动后产生反电动势.2.电流特点:I =Blv 2−BLv 1R 1+R 2=Bl (v 2−v 1)R 1+R 2随着棒2的减速、棒1的加速,两棒的相对速度v 2−v 1变小,回路中电流也变小。
v 1=0时:电流最大,I =Blv 0R 1+R 2。
v 1=v 2时:电流 I =03.两棒的运动情况安培力大小:F 安=BIl =B 2L 2(v 2−v 1)R 1+R 2两棒的相对速度变小,感应电流变小,安培力变小.棒1做加速度变小的加速运动,棒2做加速度变小的减速运动,最终两棒具有共同速度。
4.两个规律(1)动量规律:两棒受到安培力大小相等方向相反,系统合外力为零,系统动量守恒.m 2v 0=(m 1+m 2)v 共(2)能量转化规律:系统机械能的减小量等于内能的增加量.(类似于完全非弹性碰撞)Q =12m 2v 20−12(m 1+m 2)v 2共两棒产生焦耳热之比:Q 1Q 2=R 1R 2;Q =Q 1+Q 25.几种变化:(1)初速度的提供方式不同(2)磁场方向与导轨不垂直(3)两棒都有初速度(两棒动量守恒吗?)(4)两棒位于不同磁场中(两棒动量守恒吗?)1(2023春·江西赣州·高三兴国平川中学校联考阶段练习)如图所示,MN 、PQ 是相距为0.5m 的两平行光滑金属轨道,倾斜轨道MC 、PD 分别与足够长的水平直轨道CN 、DQ 平滑相接。
水平轨道CN 、DQ 处于方向竖直向下、磁感应强度大小为B =1T 的匀强磁场中。
质量m =0.1kg 、电阻R =1Ω、长度L =0.5m 的导体棒a 静置在水平轨道上,与a 完全相同的导体棒b 从距水平轨道高度h =0.2m 的倾斜轨道上由静止释放,最后恰好不与a 相撞,运动过程中导体棒a 、b 始终与导轨垂直且接触良好,导轨电阻不计,重力加速度g 取10m/s 2。
电磁感应现象中的双杆模型归类与剖析

电磁感应现象中的双杆模型归类与剖析作者:郑行军来源:《物理教学探讨》2016年第01期摘要:电磁感应现象的知识应用历来都是高考的重点,其中有关杆切割磁感线的问题是典型的综合题之一,其综合性强、能力要求高,是高考命题的热点。
利用模型化的思想构建出可能会出现的双导体杆切割问题,引导学生快速找到此类问题的解题方向,有助于培养学生的逻辑推理能力和分析问题、解决问题的能力。
关键词:双导体杆;动力学关系;功能关系;交替切割;稳态中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2016)1-0075-3在电磁感应问题中,常遇到杆在匀强磁场中切割磁感线运动的问题,这类题目的共同特征是导体杆沿互相平行的轨道做切割磁感线运动,简称为“杆+导轨”模型。
其中,有关双导体杆的切割磁感线问题是此类模型的难点,这类问题的特点是研究对象多、运动情况复杂、知识和能力的综合性强,不仅要用到电磁学中的有关规律,还要涉及到力学中的有关规律。
本文就双导体杆切割磁感线问题归纳可能构建的题型及相应的解题策略。
1.两导体杆均处于磁场内,其中一杆切割磁感线,另一杆处于静止。
例1 如图1甲所示,固定在水平桌边上的L双轨型平行金属导轨足够长,倾角θ=53 °,间距L=2 m,电阻不计。
导轨上两根金属棒a、b的阻值分别为R1=25 Ω,R2=4 Ω。
a棒的质量m1=5.0 kg,b棒质量m2=1.0 kg。
a棒与导轨间的动摩擦因数μ1=2/15,b棒与导轨间的动摩擦因数μ2=0.5。
设最大静摩擦力等于滑动摩擦力,整个导轨置于磁感应强度B=5 T、方向垂直倾斜导轨平面向上的匀强磁场中。
现将a棒从导轨上离桌面某一高度处由静止释放,当它刚要滑出导轨时,b棒也恰好开始滑动,且a棒下滑阶段,通过a棒的电荷量为q=2 C,g取l0m/s2。
(1)求在a棒整个下滑阶段,b棒中产生的热量;(2)若a棒无论从多高的位置释放,b棒都不动,求a棒的质量满足的条件。
9-07-物理建模:电磁感应中的“杆+导轨”模型

2017版高三一轮物理教学实用课件
第3页
返回目录
结束放映
二、模型分类及特点 Ⅰ.单杆水平式
物理 模型
F 设运动过程中某时刻棒的速度为 v,加速度为 a=m- B2L2v mR ,a、v 同向,随 v 的增加,a 减小,当 a=0 时,v BLv 最大,I= R 恒定
动态 分析
运动形式 收尾 状态 力学特征 电学特征
2017版高三一轮物理教学实用课件
第20页
转解析
返回目录 结束放映
5.真题演练
2017版高三一轮物理教学实用课件
第22页
返回目录
结束放映
【真题】 (2012· 山东卷· 20)如图示,相距为L的两条足够长的光滑 平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场 垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放, 当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向 下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运 动.导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电 阻,重力加速度为g.下列选项正确的是( ). A.P=2mgvsin θ B.P=3mgvsin θ C.当导体棒速度达到时加速 度大小为sin θ D.在速度达到2v以后匀速运 动的过程中,R上产生的焦耳 热等于拉力所做的功
2017版高三一轮物理教学实用课件
第4页
匀速直线运动
a= 0 v 最大 vm= FR B2L2
I 恒定
返回目录 结束放映
Ⅱ.单杆倾斜式
物理 模型 棒 释 放 后 下 滑 , 此 时 a = gsin α, 速 度 v↑→E = E BLv↑→I = R ↑→F = BIL↑→a↓, 当 安 培 力 F = mgsin α 时,a=0,v 最大 运动形式 匀速直线运动 mgRsin α 力学特征 a=0 v 最大 vm= B2L2 电学特征 I 恒定
电磁感应中的单导体棒模型(解析版)--2024届新课标高中物理模型与方法

2024版新课标高中物理模型与方法电磁感应中的单导体棒模型目录一.阻尼式单导体棒模型二.发电式单导体棒模型三.无外力充电式单导体棒模型四.无外力放电式单导体棒模型五.有外力充电式单导体棒模型六.含“源”电动式模型一.阻尼式单导体棒模型【模型如图】1.电路特点:导体棒相当于电源。
当速度为v 时,电动势E =BLv2.安培力的特点:安培力为阻力,并随速度减小而减小:F 安=BIL =B 2L 2v R +r∝v3.加速度特点:加速度随速度减小而减小,a =B 2L 2vm (R +r )+μg4.运动特点:速度如图所示。
a 减小的减速运动5.最终状态:静止6.四个规律(1)全过程能量关系:−μmgx −Q =0−12mv 20 , 速度为v 时的能量关系−μmgx −Q =12mv 2-12mv 20电阻产生的焦耳热Q R Q=RR +r (2)瞬时加速度:a =B 2L 2vm (R +r )+μg ,(3)电荷量q =I Δt =ER +r Δt =ΔφΔt (R +r )Δt =ΔφR +r (4)动量关系:μmg Δt −BIL Δt =μmg Δt -BqL =0−mv 0(安培力的冲量F Δt =BIL Δt =BqL )安培力的冲量公式是μmg Δt −BIL Δt =0−mv 0①闭合电路欧姆定律I =ER +r ②平均感应电动势:E =BLv③位移:x =vt ④①②③④得μmg Δt +B 2L 2xR +r=mv 01(2023春·山西晋城·高三校联考期末)舰载机利用电磁阻尼减速的原理可看作如图所示的过程,在磁感应强度大小为B 、方向竖直向下的匀强磁场中,有间距为L 的水平平行金属导轨ab 、cd ,ac 间连接一电阻R ,质量为m 、电阻为r 的粗细均匀的金属杆MN 垂直于金属导轨放置,现给金属杆MN 一水平向右的初速度v 0,滑行时间t 后停下,已知金属杆MN 与平行金属导轨间的动摩擦因数为μ,MN 长为2L ,重力加速度为g ,下列说法中正确的是()A.当MN 速度为v 1时,MN 两端的电势差为U MN =2BLv 1B.当MN 速度为v 1时,MN 的加速度大小为a =μg +2B 2L 2v 1m 2R +r C.当MN 速度为v 1时,MN 的加速度大小为a =2μg +2B 2L 2v 1m R +rD.MN 在平行金属导轨上滑动的最大距离为s =mv 0-μmgt 2R +r2B 2L 2【答案】BD【详解】A .根据题意可知,MN 速度为v 1时,MN 单独切割产生的电势差2BLv 1,但由于MN 中间当电源,所以MN 两端的电势差小于感应电动势,故A 错误;BC .MN 速度为v 1时,水平方向受摩擦力、安培力,由牛顿第二定律有μmg +B 2L 2v 1R +r 2=ma解得a =μg +2B 2L 2v 1m 2R +r故B 正确,C 错误;D .MN 在平行金属导轨上滑动时,由动量定理有-μmgt -∑BIL Δt =0-mv 0又有∑I Δt =q =ΔΦR +r 2=2BLs2R +r 联立解得s =mv 0-μmgt 2R +r2B 2L 2故D 正确。
电磁感应拓展延伸(各种单双棒模型汇总)

电磁感应中的导体棒专题掌握基本模型:1、光滑导轨宽为L ,导体棒受向右的恒力F 从静止开始向右运动,定值电阻为R ,其它电阻不计。
磁感应强度为B ,分析导体棒的运动情况并判断最终状态。
2、光滑导轨宽为L ,导体棒以初速度v 0向右开始运动,定值电阻为R ,其它电阻不计。
磁感应强度为B 。
分析导体棒的运动情况并判断最终状态。
3、光滑导轨宽为L ,质量为m 的导体棒以初速度v 0向右开始运动,电容为C ,磁感应强度为B 。
分析导体棒的运动情况并判断最终状态。
4、光滑导轨宽为L ,质量为m 的导体棒受向右的恒力F 从静止开始向右运动,电容为C ,磁感应强度为B ,分析导体棒的运动情况并判断最终状态。
5、光滑导轨宽为L ,质量为m 、电阻为R 的导体棒由静止开始向右开始运动,磁感应强度为B ,电源电动势为E ,内阻为r,分析导体棒的运动情况并判断最终状态。
6、导体棒1以初速度v 0向右开始运动,两棒电阻分别为R 1和R 2,质量分别为m 1和m 2,其它电阻不计。
磁感应强度为B 。
分析导体棒的运动情况并判断最终状态。
7、导体棒1受恒力F 从静止开始向右运动,两棒电阻分别为R 1和R 2,质量分别为m 1和m 2,其它电阻不计。
磁感应强度为B 。
分析导体棒的运动情况并判断最终状态。
强化练习:1、如图所示,在光滑的水平面上,有一垂直向下的匀强磁场分布在宽为L 的区域内,有一个边长为a (a<L )的正方形闭合线圈以初速v0垂直磁场边界滑过磁场后速度变为v (v<v0)那么( ) A. 完全进入磁场中时线圈的速度大于(v0+v )/2 B. 安全进入磁场中时线圈的速度等于(v0+v )/2 C. 完全进入磁场中时线圈的速度小于(v0+v )/2 D. 以上情况A 、B 均有可能,而C 是不可能的R2、两根相距d=0.20m的平行金属长导轨固定在同一水平面内,并处于竖直方向的匀强磁场中,磁场的磁感应强度B=0.2T,导轨上面横放着两条金属细杆,构成矩形回路,每条金属细杆的电阻为r=0.25Ω,回路中其余部分的电阻可不计。
物理杆模型总结归纳

物理杆模型总结归纳物理杆模型是物理学中常用的一种模型,用来描述和解决与杆、杠杆、旋转等相关的物理问题。
通过对物理杆模型的总结和归纳,我们可以更好地理解和应用这一模型。
一、物理杆模型的基本概念和特点物理杆是指一个具有质量、长度和能够绕其中一点转动的刚体。
在物理杆模型中,一般有以下几个基本概念和特点:1. 杆的长度:杆的长度是指杆的实际长度,相对于其他物体来说,杆可以是短的,也可以是长的。
2. 杆的质量:杆的质量是指杆所具有的质量,它可以影响杆的惯性和稳定性。
3. 杆的转动轴:杆的转动轴是指杆固定或支撑的点,它可以是杆的一端,也可以是杆的中点或其他位置。
4. 杆的转动惯量:杆的转动惯量是指杆围绕转动轴旋转时的惯性量度,它与杆的质量和形状有关。
二、物理杆模型的应用物理杆模型在解决各种与杆、杠杆、旋转有关的物理问题中具有广泛的应用。
以下是几个常见的应用例子:1. 杠杆平衡问题:杆可以用来解决平衡问题,例如天平的平衡、杠杆的平衡等。
通过对力的平衡条件的分析,可以推导出物体在杆上的力的大小和方向。
2. 转动力矩计算:杆的转动惯量和力矩的概念密切相关。
在物理杆模型中,利用杆的转动惯量和力矩的概念可以计算物体的转动力矩,进而解决与杆的转动有关的问题。
3. 杆的振动问题:杆不仅可以进行转动,还可以进行振动。
通过对杆的自由振动进行分析,可以求解杆的固有频率和振动模态。
三、物理杆模型的分析方法在使用物理杆模型解决问题时,可以采用以下几种分析方法:1. 力的平衡条件:根据杆的平衡状态和力的平衡条件,可以列出力的方程式,并解出未知力的大小和方向。
2. 动量守恒:对于杆的碰撞或其他动态问题,可以利用动量守恒定律,结合杆的特性,求解出问题中的未知量。
3. 转动惯量的计算:根据杆的形状和质量分布,可以计算出杆的转动惯量,从而得到杆的特性参数。
四、物理杆模型的局限性虽然物理杆模型具有广泛的应用,但也存在一定的局限性。
1. 实际情况的假设:在使用物理杆模型解决问题时,常常需要进行一些假设,例如忽略空气阻力、摩擦力等。
杆模型知识点总结

杆模型知识点总结一、概念杆模型是指在力学中用于研究棒状物体受力情况的一种模型。
在杆模型中,棒状物体通常被视为无质量、无弹性的理想化对象,用来分析棒状物体在受外力作用下的受力情况和运动规律。
杆模型是力学学科中的一个重要概念,广泛应用于工程技术、物理学、工业设计、建筑等领域。
二、杆模型的基本属性1. 无质量在杆模型中,棒状物体通常被假设为无质量的对象。
这是为了简化问题的分析,将物体的质量对力学分析的影响忽略掉。
由于棒状物体的质量与受力情况并无直接的关系,因此可以将棒状物体视为无质量的理想化对象。
2. 刚性杆模型中的物体通常被视为刚体,即在受力情况下不发生形变的物体。
这是为了使问题的分析更加简化,忽略掉物体的变形对受力情况的影响。
在杆模型中,通常假设棒状物体是刚性的,使得分析更为方便。
3. 无弹性在杆模型中,棒状物体通常被假设为无弹性的。
这意味着在受到外力作用后,棒状物体不会发生形变或者变形极小,忽略掉物体的变形对受力情况的影响。
这样假设可以使问题的分析更加简化,减少了变形引起的复杂计算。
三、杆模型的应用1. 物体受力分析杆模型广泛应用于物体受力分析的问题中。
通过建立杆模型,可以便于分析物体受力的情况,包括受到的外力和支持反力等。
利用杆模型,可以清晰地了解物体受力的方向和大小,从而进行有效的受力分析。
2. 结构设计在工程技术和建筑领域中,杆模型常常用于结构设计中。
通过建立杆模型,可以对结构的受力情况进行分析和计算,以确保结构在受力情况下能够满足设计要求,保证结构的稳定和安全。
3. 力的传递杆模型在力的传递问题中也有着重要的应用。
通过建立杆模型,可以分析和计算力的传递过程,包括力的大小、方向和传递路径等。
通过杆模型的分析,可以有效地设计和优化力的传递系统。
四、杆模型的基本原理1. 受力分析杆模型的基本原理之一是受力分析。
通过建立杆模型,可以清晰地了解物体受力的情况,包括受到的外力和支持反力等。
在受力分析过程中,可以利用受力平衡的原理,确定物体受力的方向和大小,实现对受力情况的全面分析。
高中物理电磁学中导体棒模型解析

高中物理电磁学中导体棒模型解析作者:周健来源:《中学课程辅导·教学研究(下)》 2019年第12期周健摘要:高中物理课是高中阶段学生的一门必修课,对学生的高考和未来的工作与生活有着一定的影响,这就要求广大教师一定要最大限度地提高物理教学的教育质量。
但是,由于物理课程电磁学中讲授的导体棒模型比较抽象也比较晦涩难懂,这就给物理课程的学习带来了困难,同时也造成了学生物理学习能力很难得到提升等问题,在一定程度上影响了物理教学的效果。
那么怎样才能从根本上改变这些现象,提高学生的物理成绩呢?本文通过以下几个方面进行了总结和分析。
关键词:电磁学;导体棒模型;问题对策中图分类号:G633.7 文献标识码:A 文章编号:1992-7711(2019)12-0116高中物理学科具有自然特性,合理的教学方法和教学策略是影响高中物理课程教学能否取得有效发展的关键性因素。
就目前高中物理学科的实际情况而言,由于目前很多学校的高中物理教学依然采用旧的教学模式,造成物理教学效率低下,这样的教学已经无法满足学生的需求。
这就要求物理教师必须不断探索和实践,不断改变自己的观念和思维方式,通过对自己的观念和思维方式的调整,探索出一套有效的学习策略,促进中学物理教育教学工作的发展。
一、高中物理教学存在的主要问题1. 学生的物理学习中缺少“眼见为实”高中学生年龄和心理还处于成长的初期,因此在学习过程中,对抽象的物理知识缺乏直观的感受,以至于在学习过程中对物理知识难以理解甚至是曲解其意。
其次,部分学生依然采用死记硬背的学习方法,严重阻碍了学生思维能力的发展,也使教师难以达成教学目标。
2. 学生在解决物理问题时容易“化实为虚”高中学生虽然在一定程度上已经掌握了基本的物理常识,但由于对这些知识的理解不够深入和透彻,因此在应用过程中经常无从下手,更谈不上将知识应用于生活实际中去解决实际问题。
因此,当前物理教学并没有提高学生解决实际问题的能力。
电磁感应中的导棒运动模型归类分析

电磁感应中的导棒运动模型归类分析作者:古焕标来源:《中学物理·高中》2017年第11期摘要:导棒运动模型是电磁感应问题命题的“基本道具”,也是高考的热点,考查的知识点多,题目的综合性强,物理情境变化空间大,是高考复习中的难点.导棒运动模型可分为单杆、双杆模型;导轨放置方式又分为水平、倾斜和竖直,所以受命题者青睐.关键词:电磁感应;导棒运动;归类分析1考纲要求与命题特点导棒运动模型是高中物理电磁学中的典型模型,常涉及动力学、功能关系、动量的观点和电磁学等问题,可综合多个高中物理的主干知识(如牛顿运动定律、功能关系等).此类问题在《考试大纲》中作为电磁感应的综合问题,是高中物理的重点内容之一,同时也是高考命题的重点、热点内容;从高考的命题形式看,此类问题既有单独考查的选择题,也有综合考查的计算题,且综合命题的频率高,难度大.2导棒运动模型的分类与解题思路对于电磁感应中的导棒运动模型,可分为单杆、双杆模型,每一种模型按导棒运动的轨道平面来分类,又可分为水平轨道面、倾斜轨道面、竖直轨道面的导棒运动.我们可以从导棒在不同的运动轨道平面入手分析导棒的受力和运动情况,建立导棒运动的物理模型,运用动力学知识、功能关系、动量观点和电磁学等知识来综合解题.求解导棒问题的一般思路如图1所示.3导棒运动模型的实例分析31水平轨道面的导棒运动例1如图2所示,在水平面内固定着U形光滑金属导轨,轨道间距为50cm,金属导体棒ab质量为01kg,电阻为02Ω,横放在导轨上,电阻R的阻值是08Ω(导轨其余部分电阻不计).现加上竖直向下的磁感应强度为02T的匀强磁场.用水平向右的恒力F=01N拉动ab,使其从静止开始运动,则A.导体棒ab开始运动后,电阻R中的电流方向是从P流向MB.导体棒ab运动的最大速度为10m/sC.导体棒ab开始运动后,a、b两点的电势差逐渐增加到1V后保持不变D.导体棒ab开始运动后任一时刻,F的功率总等于导体棒ab和电阻R的发热功率之和解析由右手定则可判断电阻R中的感应电流方向是从M流向P,A错;当金属导体棒受力平衡时,其速度将达到最大值,由F=BIL,I=EmR总=BLvmR总可得F=B2L2vmR总,代入数据解得vm=10m/s,B对;感应电动势的最大值Em=1V,a、b两点的电势差为路端电压,最大值小于1V,C错;在达到最大速度以前,F所做的功一部分转化为内能,另一部分转化为导体棒的动能,D错.例2如图3所示,两根相距为d=020m的平行金属长导轨固定在同一水平面内,并处于竖直方向的匀强磁场中,磁场的磁感应强度B=020T.导轨上面横放着两条金属细杆,构成矩形回路.每条金属细杆的电阻r=025Ω.回路中其余部分的电阻可不计.已知两金属细杆在平行于导轨的拉力作用下沿导轨朝相反的方向匀速平移,速度大小都是v=50m/s,不计导轨的摩擦.(1)求作用于每条细杆的拉力的大小;(2)求两金属细杆在间距增加040m的滑动过程中共产生的热量.解析(1)无论磁场方向是竖直向上还是竖直向下,当两金属细杆都以速度v朝相反方向滑动时,两金属细杆产生大小相同方向一致的感应电动势.E1=E2=Bdv由闭合电路欧姆定律,回路中的电流I=E1+E22r因拉力与安培力平衡,作用于每根金属杆的拉力大小为F1=F2=BdI解得:F1=F2=B2d2vr=32×10-2N.(2)设金属杆之间增加的距离为ΔL,则两金属杆共产生的热量Q=I2·2r·ΔL2v,代入数据得Q=128×10-2J.32倾斜轨道面的导棒运动例3如图4所示,两根足够长的平行金属导轨与水平面的夹角为θ,两导轨间距为L,上端接有阻值为R的电阻.一根质量为m的均匀直导体棒ab放在两导轨上,并与导轨垂直.整套装置处于竖直向上的匀强磁场中,磁场的磁感应强度为B,导轨和导体棒的电阻可忽略.让导体棒沿导轨由静止开始下滑,导轨和导体棒接触良好,不计它们之间的摩擦.重力加速度为g.下列选项正确的是A.导体棒下滑时的最大加速度为gsinθB.导体棒匀速运动时所受的安培力为mgsinθC.导体棒匀速运动时产生的电动势为mgtanθBLRD.导体棒匀速运动时的速度为mgRsinθB2L2cos2θ解析导体棒刚开始下滑时所受合外力最大,为mgsi nθ,所以产生的加速度最大,为gsinθ,A正确;当导体棒匀速运动时,由受力分析知,安培力F=mgtanθ,所以B错误;由F=BIL得I=FBL=mgtanθBL,所以电动势E=IR=mgtanθBLR,C正确;由E=BLvcosθ,得v=mgRsinθB2L2cos2θ,所以D正确.例4如图5所示,两根足够长的平行金属导轨固定在倾角θ=30°的斜面上,导轨电阻不计,间距L=04m.导轨所在空间被分成区域Ⅰ和Ⅱ,两区域的边界与斜面的交线为MN,Ⅰ中的匀强磁场方向垂直斜面向下,Ⅱ中的匀强磁场方向垂直斜面向上,两磁场的磁感应强度大小均为B=05T.在区域Ⅰ中,将质量m1=01kg,电阻R1=01Ω的金属条ab放在导轨上,ab刚好不下滑.然后,在区域Ⅱ中将质量m2=04kg,电阻R2=01Ω的光滑导体棒cd置于导轨上,由静止开始下滑.cd在滑动过程中始终处于区域Ⅱ的磁场中,ab、cd始终与导轨垂直且两端与导轨保持良好接触,取g=10m/s2,问:(1) cd下滑的过程中,ab中的电流方向;(2) ab刚要向上滑动时,cd的速度v多大;(3)从cd开始下滑到ab刚要向上滑动的过程中,cd滑动的距离x=38m,此过程中ab上产生的热量Q是多少.解析(1)根据右手定则判知cd中电流方向由d流向c,故ab中电流方向由a流向b.(2)开始放置ab刚好不下滑时,ab所受摩擦力为最大摩擦力,设其为Fmax,有Fmax=m1gsinθ设ab刚好要上滑时,cd棒的感应电动势为E,由法拉第电磁感应定律有E=BLv设电路中的感应电流为I,由闭合电路欧姆定律有I=ER1+R2设ab所受安培力为F安,有F安=BIL此时ab受到的最大摩擦力方向沿斜面向下,由平衡条件有F安=m1gsinθ+Fmax解得:v=5m/s.(3)设cd棒的运动过程中电路中产生的总热量为Q总,由能量守恒定律,有m2gxsinθ=Q总+12m2v2由串联电路规律有Q=R1R1+R2Q总联立解得:Q=13J.33竖直轨道面的导棒运动例5如图6所示,竖直平面内有一足够长的宽度为L的金属导轨,质量为m的金属导体棒ab可在导轨上无摩擦地上下滑动,且导体棒ab与金属导轨接触良好,ab电阻为R,其他电阻不计.导体棒ab由静止开始下落,过一段时间后闭合开关S,发现导体棒ab仍然做变速运动,则在以后导体棒ab的运动过程中,下列说法中正确的是A.导体棒ab做变速运动期间加速度一定减小B.单位时间内克服安培力做的功全部转化为电能,电能又转化为内能C.导体棒减少的机械能转化为闭合电路中的电能和电热之和,符合能的转化和守恒定律D.导体棒ab最后做匀速运动时,速度大小为v=mgRB2L2解析导体棒由静止下落,在竖直向下的重力作用下做加速运动.开关闭合时,由右手定则判定,导体中产生的电流方向为逆时针方向,再由左手定则,可判定导体棒受到的安培力方向向上,F=BIL=BBLvRL,导体棒受到的重力和安培力的合力变小,加速度变小,物体做加速度越来越小的运动,A正确;最后合力为零,加速度为零,做匀速运动,由F-mg=0得,BBLvRL=mg,v=mgRB2L2,D正确;导体棒克服安培力做功,减少的机械能转化为电能,由于电流的热效应,电能又转化为内能,B正确.例6相距L=15m、足够长的金属导轨竖直放置,质量m1=1kg的金属棒ab和质量m2=027kg的金属棒cd,均通过自身两端的套环水平地套在金属导轨上,如图7甲所示,虚线上方磁场的方向垂直纸面向里,虚线下方磁场的方向竖直向下,两处磁场的磁感应强度大小相同.ab棒光滑,cd棒与导轨间的动摩擦因数μ=075,两棒总电阻为18Ω ,导轨电阻不计.ab棒在方向竖直向上、大小按图7乙所示规律变化的外力F作用下,从静止开始沿导轨匀加速运动,同时cd棒也由静止释放.(g取10m/s2)(1)求ab棒加速度的大小和磁感应强度B的大小;(2)已知在2s内外力F做了268J的功,求这一过程中两金属棒产生的总焦耳热;(3)求出cd棒达到最大速度所需的时间t0,并在图7丙中定性画出cd棒所受摩擦力fcd 随时间变化的图线.解析(1)对ab,由牛顿第二定律得F-m1g-FA=m1a其中FA=BIL=BBLvRL=B2L2atR所以F=m1g+m1a+B2L2atR由图7乙的截距可知,m1g+m1a=11N,解得a=1m/s2由图7乙的斜率可知:B2L2aR=146-112-0,解得B=12T.(2)v=at=2m/sh=12at2=2m对ab棒有WF+WG1+WA=12m1v2-0,代入数据,解得WA=-48J,Q热=-WA=48J.(3) cd棒达到最大速度时,m2g=fcd,fcd=μN=μFA=μB2L2at0R,m2g=μB2L2at0R,解得t0=2s.cd棒所受摩擦力fcd随时间变化的图线如图8所示.参考文献:[1]刘树田电磁感应导轨类问题解题思路的优化[J].物理教学,2014(1):48-51.[2]王珍惠《电磁感应》2011高考试题分类赏析[J].中学物理,2011,29(11):31-33.。
导轨杆模型的几种类型型
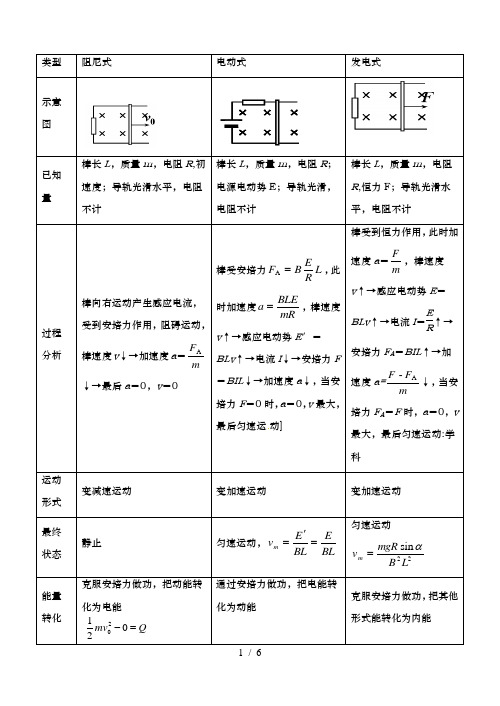
类型阻尼式电动式发电式示意图已知量棒长L,质量m,电阻R,初速度;导轨光滑水平,电阻不计棒长L,质量m,电阻R;电源电动势E;导轨光滑,电阻不计棒长L,质量m,电阻R,恒力F;导轨光滑水平,电阻不计过程分析棒向右运动产生感应电流,受到安培力作用,阻碍运动,棒速度v↓→加速度a=mFA↓→最后a=0,v=0棒受安培力LREBF=A,此时加速度mRBLEa=,棒速度v↑→感应电动势E′=BLv↑→电流I↓→安培力F=BIL↓→加速度a↓,当安培力F=0时,a=0,v最大,最后匀速运动]棒受到恒力作用,此时加速度a=mF,棒速度v↑→感应电动势E=BLv↑→电流I=ER↑→安培力F A=BIL↑→加速度a=mFFA-↓,当安培力F A=F时,a=0,v最大,最后匀速运动:学科运动形式变减速运动变加速运动变加速运动最终状态静止匀速运动,BLEBLEvm='=匀速运动22sinLBmgRvmα=能量转化克服安培力做功,把动能转化为电能通过安培力做功,把电能转化为动能克服安培力做功,把其他形式能转化为内能212mv Q-=1. 阻尼式单棒:(1)电路特点:导体棒相当于电源。
(2)安培力的特点:安培力为阻力,并随速度减小而减小。
(3)加速度特点:加速度随速度减小而减小 (4)运动特点:a 减小的减速运动 (5)最终状态:静止 (6)三个规律:①能量关系: ②动量关系: ③瞬时加速度: 2. 电动式单棒(1)电路特点:导体为电动边,运动后产生反电动势。
(2)安培力的特点:安培力为运动动力,并随速度减小而减小。
(3)加速度特点:加速度随速度增大而减小22B B l vF BIl R r==+22()B F B l v a m m R r ==+20102mv Q -=RrQ RQ r=00BIl t mv -⋅∆=-0mv q Bl=Bl s q n R r R rφ∆⋅∆==++22()B F B l v a m m R r ==+B F BIl =(E E B l R r-=+反)(B E lv B l R r -+)=B F mga mμ-=(B ()E lv B l g m R r μ--+)=(4)运动特点:a 减小的加速运动 (5)最终特征:匀速运动 (6)两个极值:①最大加速度:v=0时,E 反=0,电流、加速度最大②最大速度:稳定时,速度最大,电流最小(7)稳定后的能量转化规律:3. 发电式单棒(1)电路特点: 导体棒相当于电源,当速度为v 时,电动势E =Blv (2)安培力的特点:安培力为阻力,并随速度增大而增大 (3)加速度特点:加速度随速度增大而减小m E I R r=+,m m F BI l =m m F mga mμ-=min,m E Blv I R r-=+minmin mg F BI l μ===l rR Blv E Bm+-22)(l B r R mg Bl E v m +-=μmin min ()2min mI E I E I R r mgv μ=+++反B F BIl =Blv Bl R r=+22B l vR r +=B F F mg a mμ--=22=--+()F B l vg m m R r μ(4)运动特点:a 减小的加速运动 (5)最终特征:匀速运动 (6)两个极值:①v=0时,有最大加速度:②a=0时,有最大速度:③瞬时加速度:4. 电容放电式单棒(1)电路特点:电容器放电,电容器相当于电源;导体棒受安培力而运动。
高考物理二轮复习课件:电磁感应中的“导体杆”模型

(2)v-t图象如图所示。
WA2=模型(x2一-x1):=0.单杆与电源构成闭合回路
8 m 处时撤去外力F,此后棒ab将继续运动,最终返回至x=0处。
(2)抓住杆的稳定状态,一般杆的稳定状态为匀速直线运动或匀加速直线运动,此时闭合回路中的电流为0或恒定。
从t=0时刻起,棒ab在沿x轴正方向的外力F作用下从x=0处由静止开始沿斜面向上运动,其速度与位移x满足v=kx(可导出a=kv),k=5 s-1。
(2)v-t图象如图所示。
(3)稳定状态。
导体杆最终做匀加速直线运动,回路中的电流I为定值。
(4)稳定时导体杆ab、cd具有相同的加速度:F=(mab+mcd)a,稳定时导体杆ab、cd
的速度差满足:vcd-vab= (5)模型变式。
(Rab Rcd)mabF B2L2(mab mcd)
。
①导轨倾斜放置提供外力;②导体杆ab、cd均受到外力作用;③导轨间距不相
等。
3.应用技巧: (1)做好受力分析和运动过程分析,注意各物理量间的相互制约关系:导体棒运 动→感应电动势→感应电流→安培力→合外力→加速度→速度。 (2)抓住杆的稳定状态,一般杆的稳定状态为匀速直线运动或匀加速直线运动, 此时闭合回路中的电流为0或恒定。 (3)做好动量分析和能量转化分析。
【典例】(2019·浙江4月选考真题)如图所示,倾角θ=37°、间距l=0.1 m的足 够长金属导轨底端接有阻值R=0.1 Ω 的电阻,质量m=0.1 kg的金属棒ab垂直 导轨放置,与导轨间的动摩擦因数μ=0.45。建立原点位于底端、方向沿导轨 向上的坐标轴x。在0.2 m≤x≤0.8 m 区间有垂直导轨平面向上的匀强磁场。 从t=0时刻起,棒ab在沿x轴正方向的外力F作用下从x=0处由静止开始沿斜面向 上运动,其速度与位移x满足v=kx(可导出a=kv),k=5 s-1。当棒ab运动至x1= 0.2 m 处时,电阻R消耗的电功率P=0.12 W,运动至x2=0.8 m 处时撤去外力F,此 后棒ab将继续运动,最终返回至x=0处。棒ab始终保持与导轨垂直,不计其他电 阻,求:(提示:可以用F-x图象下的“面积”代表力F做的功)
电磁感应知识点总结导体棒

电磁感应现象中的“杆+导轨”模型问题解决电磁感应电路问题的关键就是借鉴或利用相似原型来启发理解和变换物理模型,即把电磁感应的问题等效转换成稳恒直流电路,把产生感应电动势的那部分导体等效为内电路.感应电动势的大小相当于电源电动势.其余部分相当于外电路,并画出等效电路图.此时,处理问题的方法与闭合电路求解基本一致,惟一要注意的是电磁感应现象中,有时导体两端有电压,但没有电流流过,这类似电源两端有电势差但没有接入电路时,电流为零。
变换物理模型,是将陌生的物理模型与熟悉的物理模型相比较,分析异同并从中挖掘其内在联系,从而建立起熟悉模型与未知现象之间相互关系的一种特殊解题方法.巧妙地运用“类同”变换,“类似”变换,“类异”变换,可使复杂、陌生、抽象的问题变成简单、熟悉、具体的题型,从而使问题大为简化.电磁感应现象部分的知识历来是高考的重点、热点,出题时可将力学、电磁学等知识溶于一体,能很好地考查学生的理解、推理、分析综合及应用数学处理物理问题的能力.通过近年高考题的研究,此部分每年都有“杆+导轨”模型的高考题出现。
一、命题演变“杆+导轨”模型类试题命题的“基本道具”:导轨、金属棒、磁场,其变化点有: 1.导轨(1)导轨的形状:常见导轨的形状为U 形,还可以为圆形、三角形、三角函数图形等; (2)导轨的闭合性:导轨本身可以不闭合,也可闭合; (3)导轨电阻:不计、均匀分布或部分有电阻、串上外电阻; (4)导轨的放置:水平、竖直、倾斜放置等等.[例1](2003·上海·22)如图1所示,OACO 为置于水平面内的光滑闭合金属导轨,O 、C 处分别接有短电阻丝(图中粗线表法),R 1= 4Ω、R 2=8Ω(导轨其它部分电阻不计).导轨OAC 的形状满足方程y =2sin (3x )(单位:m ).磁感强度B=0.2T 的匀强磁场方向垂直于导轨平面.一足够长的金属棒在水平外力F 作用下,以恒定的速率v=5.0m/s 水平向右在导轨上从O 点滑动到C 点,棒与导轨接触良好且始终保持与OC 导轨垂直,不计棒的电阻.求:(1)外力F 的最大值;(2)金属棒在导轨上运动时电阻丝R 1上消耗的最大功率; (3)在滑动过程中通过金属棒的电流I 与时间t 的关系.解析:本题难点在于导轨呈三角函数图形形状,金属棒的有效长度随时间而变化,但第(1)(2)问均求的是某一状态所对应的物理量,降低了一定的难度.解第(3)问时可根据条件推导出外力F 的表达式及电流I 与时间t 的关系式,由三角函数和其他条件求出需要的量即可.(1)金属棒匀速运动F 外=F 安 ,当安培力为最大值时,外力有最大值. 又∵E=BLv 总R E I =∴F 安=BIL=总R v L B 22即当L 取最大值时,安培力有最大值∵L max =22sin π=2(m )38R 2121=+=R R R R 总(Ω)∴总R v L B F 2max 2max =代入数据得F max =0.3(N )(2)R 1、R 2相并联,由电阻丝R 1上的功率121R EP =,可知当max L L =时P 1有最大功率,即14.522.0222122max 212max max =⨯⨯===R vL B R E P (W )(3)金属棒与导轨接触点间的长度随时间变化 L =2sin (3πx )(m )且x=vt ,E=BLv∴ I=总总R BLv R E == 43sin (35πt )(A )2.金属棒(1)金属棒的受力情况:受安培力以外的拉力、阻力或仅受安培力; (2)金属棒的初始状态:静止或运动;(3)金属棒的运动状态:匀速、匀变速、非匀变速直线运动,转动;图1(4)金属棒割磁感线状况:整体切割磁感线或部分切割磁感线;(5)金属棒与导轨的连接:金属棒可整体或部分接入电路,即金属棒的有效长度问题. 3.磁场(1)磁场的状态:磁场可以是稳定不变的,也可以均匀变化或非均匀变化. (2)磁场的分布:有界或无界. 二、模型转换电磁感应现象考查的知识重点是法拉第电磁感应定律,根据法拉第电磁感应定律的表达式tBS ntnE ∆∆=∆∆Φ=)(,有下列四个模型转换:1.B 变化,S 不变 (1)B 均匀变化 ①B 随时间均匀变化如果B 随时间均匀变化,则可以写出B 关于时间t 的表达式,再用法拉第电磁感应定律解题,如例2第(1)问.②B 随位置均匀变化B 随位置均匀变化的解题方法类似于B 随时间均匀变化的情形. (2)B 非均匀变化B 非均匀变化的情况在高中并不多见,如例2第(3)问.如果题目给出了B 非均匀变化的表达式,也可用后面给出的求导法求解.[例2](2000·上海·23)如图2所示,固定于水平桌面上的金属框架cdef ,处在竖直向下的匀强磁场中,金属棒ab 搁在框架上,可无摩擦滑动.此时abed 构成一个边长为l 的正方形,棒的电阻为r ,其余部分电阻不计.开始磁感强度为B 0.(1)若从t =0时刻起,磁感强度均匀增加,每秒增量为k ,同时棒保持静止.求棒中的感应电流.在图上标出感应电流的方向;(2)在上述(1)情况中,始终保持棒静止,当t =t 1末时需加的垂直于棒的水平拉力为多大?(3)若t =0时刻起,磁感强度逐渐减小,当棒以恒定速度v 向右做匀速运动时,可使棒中不产生感应电流,则磁感强度应怎样随时间变化(写出B 与t 的关系式)?解析:将加速度的定义式和电磁感应定律的表达式类比,弄清k 的物理意义,写出可与dat v v t +=0相对照的B 的表达式kt B B +=0;第(3)问中B 、S 均在变化,要能抓住产生感应电流的条件(①回路闭合;②回路中有磁通量的变化)解题.(1)磁感强度均匀增加,每秒增量为k ,得k tB =∆∆∵感应电动势2S kl tB tE =∆∆=∆∆Φ=∴感应电流rkl rE I 2==由楞次定律可判定感应电流方向为逆时针,棒ab 上的电流方向为b →a . (2)t=t 1时,B=B 0+kt 1 又∵F=BIl ∴rkl kt B F 310)(+=(3)∵棒中不产生感应电流 ∴回路中总磁通量不变 ∴Bl (l+vt )=B 0l 2 得vtl l B B +=02.B 不变,S 变化(1)金属棒运动导致S 变化金属棒在匀强磁场中做切割磁感线的运动时,其感应电动势的常用计算公式为BLv E =,此类题型较常见,如例3.[例3](2002·上海·22)如图3所示,两条互相平行的光滑金属导轨位于水平面内,距离为l =0.2m ,在导轨的一端接有阻值为R =0.5Ω的电阻,在x ≥0处有一与水平面垂直的均匀磁场,磁感强度B =0.5T .一质量为m =0.1kg 的金属直杆垂直放置在导轨上,并以v 0=2m/s 的初速度进入磁场,在安培力和一垂直于杆的水平外力F 的共同作用下做匀变速直线运动,加速度大小为a =2m/s 2、方向与初速度方向相反.设导轨和金属杆的电阻都可以忽略,且接触良好.求:(1)电流为零时金属杆所处的位置;(2)电流为最大值的一半时施加在金属杆上外力F 的大小和方向;(3)保持其他条件不变,而初速度v 0取不同值,求开始时F 的方向与初速度v 0取值的关系.解析:杆在水平外力F 和安培力的共同作用下做匀变速直线运动,加速度a 方向向左.杆的运动过程:向右匀减速运动→速度为零→向左匀加速运动;外力F 方向的判断方法:先假设,再根据结果的正负号判断.(1)感应电动势E=Blv ,感应电流I=RBlv RE =∴I=0时v=0 ∴x =av 22=1(m )(2)当杆的速度取最大速度v 0时,杆上有最大电流I m =RBlv 0RBlv I I m 22'0==安培力F 安=BI ’l=Rv l B 2022=0.02(N )向右运动时F+F 安=ma ,得F=ma- F 安=0.18(N ),方向与x 轴相反 向左运动时F- F 安=ma ,得F=ma+F 安=0.22(N ),方向与x 轴相反 (3)开始时v=v 0,F 安=BI m l=R v l B 022F+F 安=ma ,F=ma- F 安=ma-Rv l B 022∴当v 0< 22lB maR =10m/s 时,F >0,方向与x 轴相反当v 0>22lB maR =10m/s 时,F <0,方向与x 轴相同(2)导轨变形导致S 变化常常根据法拉第电磁感应定律解题,如例4.[例4] (2001·上海·22)如图4所示,半径为a 的圆形区图4域内有均匀磁场,磁感强度为B =0.2T ,磁场方向垂直纸面向里,半径为b 的金属圆环与磁场同心地放置,磁场与环面垂直,其中a =0.4m ,b =0.6m ,金属环上分别接有灯L 1、L 2,两灯的电阻均为R 0=2Ω,一金属棒MN 与金属环接触良好,棒与环的电阻均忽略不计(1)若棒以v 0=5m/s 的速率在环上向右匀速滑动,求棒滑过圆环直径OO ’的瞬时(如图所示),MN 中的电动势和流过灯L 1的电流.(2)撤去中间的金属棒MN 将右面的半圆环OL 2O ’以OO ’为轴向上翻转90º,若此时磁场随时间均匀变化,其变化率为π4=∆∆tB (T/s ),求L 1的功率.解析:(1)当棒滑过圆环直径OO ’的瞬时,棒的有效长度为2a ,灯L 1、L 2是并联的. E 1=B 2av =0.2×0.8×5 =0.8(V )4.028.011===R E I (A )(2)将右面的半圆环OL 2O ’以OO ’为轴向上翻转90º后,圆环的有效面积为半圆.其中B 随时间是均匀变化的,注意此时灯L 1、L 2是串联的.32.0222=⨯∆∆=∆∆Φ=a tB t E π (V )R E P 221)2(==1.28×102(W )另外还可在S 不规则变化上做文章,如金属棒旋转、导轨呈三角形等等. 3. “双杆+导轨”模型[例5]足够长的光滑金属导轨E F ,P Q 水平放置,质量为m 电阻为R 的相同金属棒ab ,cd 与导轨垂直且接触良好,磁感强度为B 的匀强磁场垂直导轨平面向里如图5所示。
圆周运动中绳模型和杆模型的一般解析

圆周运动中绳模型和杆模型的一般解析一:绳模型:若已不可伸长的绳子长L ,其一端栓有一质量m 的小球(可看成质点)。
现使绳子拉着小球绕一点O 做匀速圆周运动,则(1)小球恰好通过最高点的速度v 。
(2)当能通过最高点时,绳子拉F 。
解:(1)小球恰能通过最高点的临界条件是绳子没有拉力, 则对小球研究,其只受重力mg 作用,故,由其做圆周运动得:L v m mg 2= 故 gL v =(2)由分析得,当小球到最高点时速度gL v v =>'时,则,mg Lmv F -=2' 而,当gL v v =<'时,那么小球重力mg 大于其所需向心力,因此小球做向心运动。
二:杆模型:若一硬质轻杆长L ,其一端有一质量m的小球(可看成质点)。
现使杆和小球绕一点O 做匀速圆周运动, 则 (1)小球恰好通过最高点的速度v 。
(2)当能通过最高点时,杆对小球的作用力F 。
解:(1)因为杆具有不可弯曲不可伸长的性质,所以小球在最高点,当速度为0时,恰好能通过。
(2)①由绳模型可知,当小球通过最高点速度gL v =时,恰好有绳子拉力为0,则同理可知,当杆拉小球到最高点时, 若小球速度gL v =时,小球所需向心力恰好等于重力mg , 故,此时杆对小球没有作用力。
②当小球通过最高点时速度gL v >时,则小球所需向心力比重力mg 大,所以此时杆对小球表现为拉力,使小球不至于做离心运动故对小球有, L mv mg F 2=+③同理,当小球通过最高点时速度gL v <时,则小球所需向心力小于重力mg ,所以此时小球对杆有压力作用,有牛顿第三定律得,杆对小球表现为支持力作用,故对小球有, L mv F mg 2=-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的总电动 则应一 势 为E、 两者: 合 j }
( 正负极依次相连则相加、 之则相 反 减) l 如果当 体棒不动时; 路中不 导 回 产生电动孝 这就说明回路磁通量的 变化也是由于导体棒 的运动而产生 的 回路磁通量 的变化产生感应电动 势和切 割磁感线 产生电动势是一回
法, 一定要避免重复计算
() 2如
( ) 甲
导体 棒 刚滑 动 的临界
条 件 回路 磁通 量变 化 产 生 感 应 电 动
势
: z回 2 路电流为,墨 、 一 .
At At R n
双棒 模 型
1 .建 立
又 : 以, BoO2 t B B= + .0
联 立解 得 t1 。 05A. 向沿 = 3sI . 方 =
一
() 2 电学 角 度 : 割 磁 感 线 的 导 体 切
根 质 量 为 m- .0k 的 均 匀 金 属 导 体 - 5 g O
堡 5 壹 兰 监 墼 犟7 塑 生圭
T瑟
棒 静 止 在 导 轨 上 且 接 触 良 好 .
n l恰好 围 成 一 个 正 方 形 。 该 导 轨 6 P
擦 因数 为 ,受 到 的滑 动摩 擦力 为
tm go X
便有变化而产生感应电 招 导体
棒运动还产生一个电动势 , 回路中
应 强度胁= - 。 棒 的 电 阻 为R= 0 0T 4
01 . 他 各 部 分 电 阻 均 不 计 。 . 0Q 其
() 1 由图2 乙) ( 可知 :
平 行轨 道分 为水 平放 置 和倾斜 放 置 磁
过程 . 当外 力 克 服 安 培 力 做 功 时 . 有 就 其他 形 式 的能转 化 为 电能 : 当安培 力做 正功 时 . 能转化 为其 他形 式 的能 。 电
3 .解 题策 略 抓 住 力 是 改变 物体 运 动状 态 的原 因 , 过分 析 受力 , 合 运动 过程 , 通 结 知道
割 的有效 速度 、 回路 总电 阻。 为
结论 2 单 棒 单 电源 模 型 中单 棒 的
2 .特 点
安 培 力 冲量IB q 曰 匀 强 磁场 的磁感 = l.为
( ) 电角 度 : 1力 与单 棒 组 成 的 闭合
回路 中磁 通 量 发 生 变 化一 导 体 棒 产 生
应 强度 、为 通过 回路横 截 面 的电荷 量 、 q f 为垂 直切 割磁 感线 的长 度 。
r—— —
感 应 电 动势 一 感 应 电 流一 导 体棒 受 安
培 力一 合 外 力 变 化一 加 速 度 变 化一 速 度变 化一 感应 电 动势变 化一 ……
如 图2 甲) ( 所示 , 个足 够 一
长 的 “ 形 金 属 导 轨 N Q固 定 在 水 平 U” MP 面 内 , 两 导 轨 间距 离 为 /05 MN、 = .0m。
6斗 — 0
两 根 导体 棒 垂 直 切 割 磁 感线 运
动 双 棒在运 动过 程 中切 割磁 感线产
生感 应 电动势 , 当于两个 电源 。当 相
( ) 过时 间t 3经 金属 导体棒 运动 位
移 为s-q a’ 得s . o- t 解 - , 庐1 5m 2
t5s 受 到 的 外 力 为 多 大 ? = 时
化产生 的感应电动势的判定方法: 如 果导体棒≥ 运动 F 闭合 回路的磁通 量 自
解析 设 导体 棒与轨 道 间 的动摩
平 面处在 竖直 向上 的 匀强磁 场 中. 磁
感 应 强 度 大 小 可 以 调 节 . 始 时 磁 感 开
场 分 为 磁 感 应 强 度 不 变 的匀 强 磁 场 和 随时 间均匀 变 化 的匀强 磁 场 . 者 为切 前 割磁感 线 的单 电 源 ( 单棒 单 电 源模 型 ) ,
后 者 为 切 割 磁 感 线 与磁 场 变 化 引 起 的
双 电源 ( 棒双 电 源模 型 ) 单 。
加速 度 和速 度 的关 系 ,结合 动量 定 理 、 能量 守恒 定律 求解 。
磁 感线 运 动 . 常是 在垂 直 于匀 强磁 场 通
的导轨 上做 垂 直切 割磁 感 线 运动 . 图 如 1 所示 .简 言 之 即是 导体 棒垂 直 切 割磁
图一 应 用 串并 联 电路 特 点 和 闭合 电路 欧姆 定律 求解
( ) 能角 度 : 3力 功是 能 量 转 化 的量
当f0 , 2N, f ma = 时 =  ̄-=
当£ s ,  ̄ 时 F- N, - 6
FB 2。 - 警 f -
又根 据速 度公式 联立 以上各 式得 : 户07 a 25 /  ̄= .5 .5 N、= . s e01 m
事 这只是计算感应电动势的两乖方 }
T璧
导体杆模型归类解析
◇ 河北省 安 国 中学 杜 占英
单棒 模 型 :
1 .建 立
棒 为 电源一 根据 E
求感 应 电动 势 大
小一 利 用右 手定 则 或 楞 次 定 律 判 断 电 流 方 向一 分 析 电路 结 构一 画 等效 电路
导体 棒 在 磁 场 中 的导 轨 上 做 切 割
度 .外 力 通 过 安 培 力 做 功 实现 能 量 转 化 。 电磁 感应 现 象 中 , 安培 力 做功 是其
他 形 式 的 能 和 回路 电能 转 化 的 手段 和
感 线运 动 单 棒在 运动 过程 中切割 磁感 线 产生 感应 电动势 . 因此 单棒 在 电路 中 相 当 于 电源 , 与轨 道 构成 一 个 回路 。轨 道 有 圆形 轨道 、三角轨 道 和 平行 轨 道 ,
] × — × × × 、+ B 0 — ×
× x × × × ×
4 .重 要 结 论
结论 1 单 棒 单 电 源模 型 中单 棒 受 到 的安 培 力 为 F = , 磁 感 应 强 曰为
×
× Biblioteka × × ×
×
图1
度、 Z 为单棒 垂 直切 割 的长 度 、为垂 直切
