高中数学 三角函数学第一章单元测试题 新人教B版必修4
高中数学数学必修四第一章三角函数单元测试题--经典

高中数学必修 四第一章三角函数、选择题(60 分)1.将—300o 化为弧度为( 4 二 3c.D.2•如果点P (sinvcosH2cosv )位于第三象限,那么角 二所在象限是(C.第三象限 A .第一象限 B.第二象限 3. 下列选项中叙述正确的是A .三角形的内角是第一象限角或第二象限角B .锐角是第一象限的角C .第二象限的角比第一象限的角大D .终边不同的角同一三角函数值不相等 4. 下列函数中为偶函数的是( ) A . y 二 sin | x | B . y 二 sin 2x D.第四象限C. y - -sin x5已知函数y = As in (• ‘x •「厂B 的一部分图象如右图所示,如果 A. A = 4 C.6函数八Ssgx 石)的单调递减区间( 5 二D. y 二 sin x 1A. IHA k , k 「: _12 12k ,k (k Z) - 3 6三匕:三( 12 12D . k 二二k 二兰(k Z ) - 632(k Z) B.k Z) C.已知〉是三角形的一个内角,且sin " cos,则这个三角形(3C .A .锐角三角形B .钝角三角形1 -2sin (二 2)cos (二 2)等于 A . sin2 — cos2 若角:' 的终边落在直线 不等腰的直角三角形 D •等腰直角三角形B. B . cos2 — sin2 y=2x 上,则 sin :2屆C. 5 C . 的值为± (sin2 —cos2): )D. -12sin 2+cos210.函数 2y=cos x-3cosx+2 的最小值是 11.如果:-在第三象限,则 a —必定在 2 A.第一或第二象限 B.第一或第三象限 C.第三或第四象限 D. 第二或第四象12 .已知函数y 二Asin ( x 在同一周期内 ,当x时有最大值2,当x=0时有最小值-2,那么函数的解析3式为B. y =2sin(3x) C. y =2sin(3x ' ) D • y =」sin3x2 2 2二.填空题(20分)三.计算题(70 分)JIcos(— + a )sin (—兀-a )17. (15分)已知角〉终边上一点P (-4, 3),求2的值cos()sin()2 218(20分).已知函数y=Asin ( w x+ $ )+b (A>0,| $ |< n ,b 为常数)的一段图象(如图)所示. ①求函数的解析式;3219.已知 tan,求 2 sin hcosv - cos 二 的值。
高中数学必修四《第一章三角函数》单元测试题新人教版必修4

1 13. (0, ) 14. sin 2x cosx 15. 16.
3
2
2
17.原式 ( 3) 2 1 1 ( 3 )2 1 1
2
2 22
18. tan
3,且
3
2
D 12.D
sin
3 cos
sin
sin 0,cos 0,由
得
sin2
cos2
1
cos
3
2 sin cos 1 3
1
2
2
19.设需 x 秒上升 100cm . 则 x 60
第一章三角函数单元测试
一、选择题:共 12 小题,在每小题给出的四个选项中,只有一项是符合题目要求的.(
48
分)
1、已知 A={第一象限角 } , B={锐角 } , C={小于 90°的角 } ,那么 A、 B、 C 关系是( )
A. B=A∩ C
B . B∪ C=C
C. A C
D.A=B=C
2、将分针拨慢 5 分钟,则分钟转过的弧度数是
20。– 2tan α
42
50 100, x 15 (秒)
21. y tan2 x 2atan x 5 (tan x a)2 a2 5
x [ , ] tan x [1, ] 42
当 a 1时, y a2 5 ,此时 tan x a
当 a 1 时, y a2 5 ,此时 tan x 1
22.④②或②⑥
4
4
8
8
位
7、如图,曲线对应的函数是
()
A. y=|sin x|
B. y=sin| x|
C. y=- sin| x|
D. y=- |sin x|
(好题)高中数学必修四第一章《三角函数》测试题(有答案解析)

一、选择题1.已知函数()sin()f x A x ωϕ=+(0A >,0>ω,2πϕ<)的部分图像如图所示,则()f x 的解析式为( )A .()2sin 26f x x π⎛⎫=- ⎪⎝⎭B .()2sin 26f x x π⎛⎫=+ ⎪⎝⎭C .()3sin 26f x x π⎛⎫=-⎪⎝⎭D .1()3sin 26f x x π⎛⎫=-⎪⎝⎭ 2.函数()2cos 3⎛⎫=+ ⎪⎝⎭πf x x 在[]0,π的单调递增区间是( ) A .20,3π⎡⎤⎢⎥⎣⎦B .2,33ππ⎡⎤⎢⎥⎣⎦C .,3ππ⎡⎤⎢⎥⎣⎦D .2π,π33.将函数sin()y x ϕ=+的图像上所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得图像向左平移12π个单位后得到的函数图像关于原点中心对称,则sin 2ϕ=( )A .12-B .12C .3D 34.已知函数()f x 是定义在R 上的增函数,()0,1A -,()3,1B 是其图象上的两点,那么|(2sin 1)|1f x +≤ 的解集为( ) A .,33x k x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣ B .722,66x k x k k ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭Z ∣ C .,63xk x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣ D .722,66xk x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣5.如图,一半径为4.8m 的筒车按逆时针方向转动,已知筒车圆心O 距离水面2.4m ,筒车每60s 转动一圈,如果当筒车上点P 从水中浮现时(图中点0P )开始计时,则( )A .点P 第一次到达最高点需要10sB .点P 距离水面的高度h (单位:m )与时间t (单位:s )的函数解析式为4.8sin 2.4306h t ππ⎛⎫=-+ ⎪⎝⎭ C .在筒车转动的一圈内,点P 距离水面的高度不低于4.8m 共有10s 的时间 D .当筒车转动50s 时,点P 在水面下方,距离水面1.2m 6.设函数()3cos22sin cos f x x x x =+,给出下列结论: ①()f x 的最小正周期为π ②()y f x =的图像关于直线12x π=对称③()f x 在2,63ππ⎡⎤⎢⎥⎣⎦单调递减 ④把函数2cos2y x =的图象上所有点向右平移12π个单位长度,可得到函数()y f x =的图象.其中所有正确结论的编号是( ). A .①④B .②④C .①②④D .①②③7.已知函数()sin 0,2y x πωϕωϕ⎛⎫=+><⎪⎝⎭的部分图象如图所示,则( )A .1ω=,6π=ϕ B .1ω=,6πϕ=-C .2ω=,6π=ϕ D .2ω=,6πϕ=-8.《九章算术》中《方田》章有弧田面积计算问题,术日:以弦乘矢,矢又自乘,并之,二而一.其大意是弧田面积计算公式为:弧田面积12=(弦×矢+矢×矢).弧田是由圆弧(弧田弧)及圆弧两端点的弦(弧田弦)围成的平面图形,公式中的“弦”指的是弧田弦的长,“矢”指的是弧田所在圆的半径与圆心到孤田弦的距离之差,现有一弧田,其矢长等于8米,若用上述弧田面积计算公式算得该弧田的面积为128平方米,则其弧田弧所对圆心角的正弦值为( ) A .60169B .120169C .119169D .591699.已知函数()[][]sin cos cos sin f x x x =+,其中[]x 表示不超过实数x 的最大整数,则( )A .()f x 是奇函数B .π2π33f f ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭C .()f x 的一个周期是πD .()f x 的最小值小于010.已知函数()sin cos f x x x =+,则下列说法正确的是( ) A .()f x 的最小值为0 B .()f x 的最大值为2 C .()()2f x f x π-=D .1()2f x =在0,2π⎡⎤⎢⎥⎣⎦上有解11.若函数)22()sin 2cos sin f x x x x =-的图像为E ,则下列结论正确的是( ) A .()f x 的最小正周期为2π B .对任意的x ∈R ,都有()()3f x f x π=-C .()f x 在7(,)1212ππ上是减函数 D .由2sin 2y x =的图像向左平移3π个单位长度可以得到图像E 12.函数22y cos x sinx =- 的最大值与最小值分别为( ) A .3,-1 B .3,-2 C .2,-1D .2,-2二、填空题13.关于1()sin sin f x x x=-,有如下四个结论: ①()f x 是奇函数. ②()f x 图像关于y 轴对称.③2x π=是()f x 的一条对称轴.④()f x 有最大值和最小值. 其中说法正确的序号是________. 14.对任意0,4πϕ⎡⎤∈⎢⎥⎣⎦,函数()sin()f x x ωϕ=+在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递增,则实数ω的取值范围是________.15.若函数π()sin()cos()3f x x x ωω=++的一个周期是π,则常数ω的一个取值可以为__________.16.如图,以正方形的各边为底可向外作四个腰长为1的等腰三角形,则阴影部分面积的最大值是___________.17.sin 75=______.18.已知函数()()()sin 0,πf x x ωϕωϕ=+><的图像如图所示,则ϕ=__________.19.关于函数()()4sin 23f x x x R π⎛⎫=+∈ ⎪⎝⎭,有下列命题: ①函数()y f x =的表达式可以改写为4cos 26y x π⎛⎫=- ⎪⎝⎭; ②函数()y f x =是以2π为最小正周期的周期函数; ③函数()y f x =的图象关于点,06π⎛⎫-⎪⎝⎭对称; ④函数()y f x =的图象关于直线6x π=-对称.其中正确的序号是______.20.如图是函数()2sin(),(0,)2f x x πωφωφ=+><的图象上的一段,则ω=_________φ =____三、解答题21.已知()442sin cos cossin f x x x x x ωωωω=+-(其中ω>0).(1)若()f x 的最小正周期是π,求ω的值及此时()f x 的对称中心; (2)若将()y f x =的图像向左平移4π个单位,再将所得的图像纵坐标不变,横坐标缩小为原来的12,得到()g x 的图像,若yg x 在0,8π⎡⎤⎢⎥⎣⎦上单调递减,求ω的取值范围.22.在①()f x 的图象关于直线3x π=对称,②()f x 的图象关于点,06π⎛⎫-⎪⎝⎭对称,③()f x 的图象上最高点中,有一个点的横坐标为6π这三个条件中任选一个,补充在下面问题中,并解答.问题:已知函数()()sin 0,0,02f x A x A πωϕωϕ⎛⎫=+>><<⎪⎝⎭的振幅为2,初相为3π,最小正周期不小于...π,且______. (1)求()f x 的解析式;(2)求()f x 在区间[],0π-上的最大值和最小值以及取得最大值和最小值时自变量x 的值.注:如果选择多个条件分别解答,按第一个解答计分. 23.已知函数()12sin 26x f x π⎛⎫=+⎪⎝⎭,x ∈R . (1)用“五点法”画出函数()f x 一个周期内的图象; (2)求函数()f x 在[],ππ-内的值域; (3)若将函数()f x 的图象向右平移6π个单位长度,得到函数()g x 的图象,求函数()g x 在[],ππ-内的单调增区间.24.已知函数()()sin f x A x ωϕ=+(0A >,0>ω,02πϕ<<)的部分图象如图所示,其中最高点以及与x 轴的一个交点的坐标分别为,16π⎛⎫⎪⎝⎭,5,012π⎛⎫ ⎪⎝⎭.(1)求()f x 的解析式;(2)设M ,N 为函数y t =的图象与()f x 的图象的两个交点(点M 在点N 左侧),且3MN π=,求t 的值.25.已知函数()2sin(2)(0)6f x x πωω=+>.(1)若点5(,0)8π是函数()f x 图像的一个对称中心,且(0,1)ω∈,求函数()f x 在3[0,]4π上的值域; (2)若函数()f x 在(,)33π2π上单调递增,求实数ω的取值范围.26.海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表: 时刻 0:00 1:00 2:00 3:00 4:00 5:00 水深 5.000 6.250 7.165 7.500 7.165 6.250 时刻 6:00 7:00 8:00 9:00 10:00 11:00 水深 5.000 3.754 2.835 2.500 2.835 3.754 时刻 12:00 13:00 14:00 15:00 16:00 17:00 水深 5.000 6.250 7.165 7.500 7.165 6.250 时刻 18:00 19:00 20:00 21:00 22:00 23:00 水深5.0003.7542.8352.5002.8353.754(1)这个港口的水深与时间的关系可用函数(,)近似描述,试求出这个函数解析式;(2)一条货船的吃水深度(船底与水面的距离)为5米,安全条例规定至少要有1.25米的安全间隙(船底与洋底的距离),利用(1)中的函数计算,该船何时能进入港口?在港口最多能呆多久?【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】 本题首先可根据33π44T 求出ω,然后根据当43x π=时函数()f x 取最大值求出ϕ,最后代入30,2⎛⎫- ⎪⎝⎭,即可求出A 的值. 【详解】因为4π7π3π3124,所以33π44T ,T π=,因为2T πω=,所以2ω=,()sin(2)f x A x ϕ=+,因为当43x π=时函数()sin(2)f x A x ϕ=+取最大值, 所以()42232k k Z ππϕπ⨯+=+∈,()26k k Z πϕπ=-+∈,因为2πϕ<,所以6πϕ=-,()sin 26f x A x π⎛⎫=-⎪⎝⎭, 代入30,2⎛⎫- ⎪⎝⎭,3sin 26A π⎛⎫-=- ⎪⎝⎭,解得3A =,()3sin 26f x x π⎛⎫=- ⎪⎝⎭, 故选:C. 【点睛】关键点点睛:本题考查根据函数图像求函数解析式,对于()sin()f x A x ωϕ=+,可通过周期求出ω,通过最值求出A ,通过代入点坐标求出ϕ,考查数形结合思想,是中档题.2.C解析:C 【分析】先求出函数的单调增区间,再给k 取值即得解.【详解】令22223+<+<+ππk πx πk π(k ∈Z ) ∴42233+<<+ππk πx k π(k ∈Z ), 所以函数的单调递增区间为4[2,2]33ππk πk π++(k ∈Z ), 当1k =-时,5233ππx -<<- 当0k =时,433x ππ<<又∵[]0,x π∈, 故选:C 【点睛】方法点睛:求三角函数()cos()f x A wx ϕ=+的单调区间,一般利用复合函数的单调性原理解答:首先是对复合函数进行分解,接着是根据复合函数的单调性原理分析出分解出的函数的单调性,最后根据分解函数的单调性求出复合函数的单调区间.3.C解析:C 【分析】先根据条件写出图像变换后的函数解析式,然后根据图像关于原点中心对称可知函数为奇函数,由此得到ϕ的表示并计算出sin 2ϕ的结果. 【详解】因为变换平移后得到函数sin 26y x πϕ⎛⎫=++ ⎪⎝⎭,由条件可知sin 26y x πϕ⎛⎫=++ ⎪⎝⎭为奇函数,所以6k πϕπ+=,sin 2sin 2sin 33k ππϕπ⎛⎫⎛⎫=-=-= ⎪ ⎪⎝⎭⎝⎭故选C . 【点睛】本题考查三角函数的图像变换以及根据函数奇偶性判断参数值,难度一般.正弦型函数()()sin f x A x =+ωϕ为奇函数时,k k Z ϕπ=∈,为偶函数时,2k k Z πϕπ=+∈.4.D解析:D 【分析】由题意可得()01f =-,()31f =,所要解的不等式等价于()()0(2sin 1)3f f x f ≤+≤,再利用单调性脱掉f ,可得02sin 13x ≤+≤,再结合正弦函数的图象即可求解. 【详解】由|(2sin 1)|1f x +≤可得1(2sin 1)1f x -≤+≤, 因为()0,1A -,()3,1B 是函数()f x 图象上的两点,所以()01f =-,()31f =,所以()()0(2sin 1)3f f x f ≤+≤, 因为()f x 是定义在R 上的增函数, 可得02sin 13x ≤+≤,解得:1sin 12x -≤≤, 由正弦函数的性质可得722,66k x k k Z ππππ-+≤≤+∈, 所以原不等式的解集为722,66xk x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣, 故选:D 【点睛】关键点点睛:本题解题的关键点是将要解得不等式转化为()()0(2sin 1)3f f x f ≤+≤利用单调性可得02sin 13x ≤+≤.5.B解析:B 【分析】先建立坐标系,从点0P 开始计时,建立三角函数模型()0sin h A t b ωϕ=++,通过题中条件求出参数0,,,A b ωϕ,再利用函数解析式对选项依次判断正误即可. 【详解】以水面所在直线为t 轴,过O 作OO t '⊥轴,建立坐标系如图:设点P 距离水面的高度h (单位:m )与时间t (单位:s )的函数解析式为()0sin h A t b ωϕ=++.依题意可知, 2.4OO '=, 2.41sin 4.82OPO '∠==,6OPO π'∠=. 高度h 最大值为2.4 4.87.2+=,最小值为2.4 4.8 2.4-=-,故()()7.2 2.47.2 2.44.8, 2.422A b --+-====,周期60T =s ,则230T ππω==, 0t =时,06πϕ=-,故函数解析式为 4.8sin 2.4306h t ππ⎛⎫=-+⎪⎝⎭,故B 正确;点P 到达最高点时 4.8sin 2.47.2306h t ππ⎛⎫=-+= ⎪⎝⎭,即sin 1306t ππ⎛⎫-= ⎪⎝⎭,故2,3062t k k Z ππππ-=+∈,即2060,t k k Z =+∈,又0t ≥,故第一次到达最高点时,0,20k t ==s ,故A 错误;在筒车转动的一圈内,点P 距离水面的高度不低于4.8m ,即4.8sin 2.4 4.8306h t ππ⎛⎫=-+≥ ⎪⎝⎭,得1sin 3062t ππ⎛⎫-≥ ⎪⎝⎭,故563066t ππππ≤-≤,解得1030t ≤≤,故共有20 s 时间,C 错误;当筒车转动50s 时,即50t =代入 4.8sin 2.4306h t ππ⎛⎫=-+⎪⎝⎭得,34.8sin 50 2.4 4.8sin 2.4 2.43062h πππ⎛⎫=⨯-+=+=- ⎪⎝⎭,故点P 在水面下方,距离水面2.4m ,故D 错误. 故选:B. 【点睛】 关键点点睛:本题解题关键在于按照题意,建立三角函数模型()0sin h A t b ωϕ=++,并解出解析式,才能解决选项中的实际问题,突破难点.6.C解析:C 【分析】根据题意,利用辅助角公式和两角和的正弦公式化简得()2sin(2)3f x x π=+,根据2T ωπ=求出最小正周期即可判断①;利用整体代入法求出()y f x =的对称轴,即可判断②;利用整体代入法求出()y f x =的单调减区间,从而可得在区间2,63ππ⎡⎤⎢⎥⎣⎦上先减后增,即可判断③;根据三角函数的平移伸缩的性质和诱导公式化简,即可求出平移后函数,从而可判断④. 【详解】解:函数()2sin cos sin 22sin(2)3f x x x x x x x π++=+,即:()2sin(2)3f x x π=+,所以()f x 的最小正周期为222T πππω===,故①正确; 令2,32πππ+=+∈x k k Z ,解得:,122k x k Z ππ=+∈, 当0k =时,则直线12x π=为()y f x =的对称轴,故②正确; 令3222,232k x k k Z πππππ+≤+≤+∈,解得:7,1212ππππ+≤≤+∈k x k k Z , 所以()f x 的单调递减区间为:7,,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦, 当0k =时,()f x 的一个单调递减区间为7,1212ππ⎡⎤⎢⎥⎣⎦, 则区间7,612ππ⎡⎤⎢⎥⎣⎦上单调递减,故在区间2121,3228,6ππππ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦上先减后增,故③错误; 把函数2cos2y x =的图象上所有点向右平移12π个单位长度, 得到s 2)2cos 22co 22cos 2126332sin(2y x x x x πππππ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=-=-=+-= ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎦⎣⎦+⎝⎭⎣ 即平移后得到函数()y f x =的图象,故④正确.所以所有正确结论的编号是:①②④.故选:C.【点睛】关键点点睛:本题考查三角函数的图象和性质,熟练掌握正弦型函数的周期、对称轴、单调区间的求法,以及三角函数的平移伸缩是解题的关键,还考查辅助角公式、两角和的正弦公式以及诱导公式的应用,考查学生化简运算能力.7.D解析:D【分析】根据函数的图象求出函数的周期,然后可以求出ω,通过函数经过的最大值点求出ϕ值,即可得到结果.【详解】由函数的图象可知:74123T πππ⎛⎫=-⨯=⎪⎝⎭,22T πω∴==. 当3x π=,函数取得最大值1,所以sin 213πϕ⎛⎫⨯+= ⎪⎝⎭,2232k k Z ππϕπ+=+∈,,||,02k πϕ<∴=,6πϕ∴=-, 故选:D.【点睛】 本题主要考查了由三角函数的图象求解析式,通过周期求ω的值,通过最值点求ϕ的值是解题的关键,属于基础题.8.B解析:B【分析】求出弦长,再求出圆的半径,然后利用三角形面积求解.【详解】如图,由题意8CD =,弓琖ACB 的面积为128,1(8)81282AB ⨯+⨯=,24AB =, 设所在圆半径为R ,即OA OB R ==,则22224(8)2R R ⎛⎫=-+ ⎪⎝⎭,解得13R =, 5OD =,由211sin 22AB OD OA AOB ⨯=∠得 2245120sin 13169AOB ⨯∠==. 故选:B .【点睛】关键点点睛:本题考查扇形与弓形的的有关计算问题,解题关键是读懂题意,在读懂题意基础上求出弦长AB ,然后求得半径R ,从而可解决扇形中的所有问题.9.D解析:D【分析】利用奇函数的性质判断A ,分别求3f π⎛⎫ ⎪⎝⎭和23f π⎛⎫ ⎪⎝⎭判断大小,取特殊值验证的方法判断C ,分区间计算一个周期内的最小值,判断选项D 。
高中数学(人教,必修4)第一章《三角函数》测试题B卷.docx

高中数学学习材料鼎尚图文*整理制作高中数学必修4第一章 《三角函数》测试题B 卷考试时间:100分钟,满分:150分一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).1.sin(-103π)的值等于 ( )A.12 B .-12 C.32 D .-322.若点(a,9)在函数y =3x 的图象上,则tan a π6的值为 ( )A .0 B.33C .1 D. 33.函数y =sin(2x +π3)图象的对称轴方程可能是 ( )A .x =-π6B .x =-π12C .x =π6D .x =π124.已知f (sin x )=x ,且x ∈[0,π2],则f (12)的值等于( )A .sin 12 B.12 C .-π6 D.π65.已知sin(α+π2)=13,α∈(-π2,0),则tan α等于 ( )A .-2 2B .22C .-24 D.246.如果sin α+cos α=34,那么|sin 3α-cos 3α|的值为 ( )A.2512823 B .-2512823 C.2512823或-2512823 D .以上全错7.若sin θ+cos θsin θ-cos θ=2,则sin θcos 3θ+cos θsin 3θ的值为 ( )A .-81727 B.81727 C.82027D .-820278.若sin α是5x 2-7x -6=0的根,则sin (-α-3π2)sin (3π2-α)tan 2(2π-α)cos (π2-α)cos (π2+α)sin (π+α)= ( )A.35B.53C.45D.549.若函数y =f (x )的图象上各点的纵坐标保持不变,横坐标伸长到原来的2倍,然后再将整个图象沿x 轴向左平移π2个单位,沿y 轴向下平移1个单位,得到的曲线与y =12sin x 的图象相同,则y =f (x )是( ) A .y =12sin ⎝⎛⎭⎫2x +π2+1 B .y =12sin ⎝⎛⎭⎫2x -π2+1 C .y =12sin ⎝⎛⎭⎫2x -π4+1 D .y =12sin ⎝⎛⎭⎫2x +π4+1 10.已知某帆船中心比赛场馆区的海面上每天海浪高度y (米)可看作是时间t (0≤t ≤24,单位:小时)的函数,记作y =f (t ),经长期观测,y =f (t )的曲线可近似地看成是函数y =A cos ωt +b ,下表是某日各时的浪高数据:t /时 0 3 6 9 12 15 18 21 24 y /米2321322320.99322则最能近似地表示表中数据间对应关系的函数是( )A .y =12cos π6t +1B .y =12cos π6t +32C .y =2cos π6t +32D .y =12cos6πt +32二、填空题(每小题6分,共计24分).11.已知tan θ=2,则sin θsin 3θ-cos 3θ=________.12.已知函数f (x )=3sin(ωx -π6)(ω>0)和g (x )=2cos(2x +φ)+1的图象的对称轴完全相同.若x ∈[0,π2],则f (x )的取值范围是____________.13.据市场调查,某种商品每件的售价按月呈f (x )=A sin(ωx +φ)+B (A >0,ω>0,|φ|<π2)的模型波动(x 为月份),已知3月份达到最高价8千元,7月份价格最低为4千元,则f (x )=________. 14.关于函数f (x )=4sin(2x +π3)(x ∈R ),有下列命题:①函数y =f (x )的表达式可改写为y =4cos(2x -π6);②函数y =f (x )是以2π为最小正周期的周期函数; ③函数y =f (x )的图象关于点(-π6,0)对称;④函数y =f (x )的图象关于直线x =-π6对称.其中,正确的是________.(填上你认为正确命题的序号) 三、解答题(共76分).15.(本题满分12分)已知:f (x )=2010x +2011sin 3x +1,且f (5)=7,求f (-5).16.(本题满分12分)已知α是第三象限的角,且f (α)=sin (π-α)cos (2π-α)tan (-α+32π)·tan (-α-π)sin (-α-π),(1)化简f (α);(2)若cos(α-32π)=15,求f (α);(3)若α=-313π,求f (α).17.(本题满分12分)设函数f (x )=sin(2x +φ)(-π<φ<0),y =f (x )图象的一个对称中心是(π8,0).(1)求φ;(2)求函数y =f (x )的单调增区间.18.(本题满分12分)已知函数f (x )=3sin ⎝⎛⎭⎫12x +π4-1,x ∈R . 求:(1)函数f (x )的最小值及此时自变量x 的取值集合;(2)函数y =sin x 的图象经过怎样的变换得到函数f (x )=3sin ⎝⎛⎭⎫12x +π4-1的图象?19.(本题满分14分)如图,某市拟在长为8 km 的道路OP 的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM ,该曲线段为函数y =A sin ωx (A >0,ω>0),x ∈[0,4]的图象,且图象的最高点为S (3,23);赛道的后一部分为折线段MNP .试求A 、ω的值和M 、P 两点间的距离.20.(本题满分14分)已知函数f (x )=A sin(ωx +φ)+B (A >0,ω>0)的一系列对应值如下表:x -π6 π3 5π6 4π3 11π6 7π3 17π6 y-1131-113(1)根据表格提供的数据求函数f (x )的一个解析式;(2)根据(1)的结果,若函数y =f (kx )(k >0)的周期为2π3,当x ∈[0,π3]时,方程f (kx )=m 恰有两个不同的解,求实数m 的取值范围.高中数学必修4第一章 《三角函数》测试题B 卷参考答案一、选择题1.【答案】C.【解析】 sin(-103π)=sin(-4π+2π3) =sin 2π3=sin(π-π3)=sin π3=32.2. 【答案】D.【解析】∵点(a,9)在函数y =3x 的图象上,∴9=3a ,∴a =2,∴tan a π6=tan π3= 3.3. 【答案】D.【解析】 y =sin(2x +π3)的对称轴方程为2x +π3=k π+π2(k ∈Z ).∴x =k ·π2+π12(k ∈Z ),令k =0即得.4. 【答案】D.【解析】∵f (sin x )=x ,且x ∈[0,π2], ∴求f (12),即解sin x =12,且x ∈[0,π2],∴x =π6,故选D.5.【答案】A.【解析】sin(α+π2)=cos α=13. ∵α∈(-π2,0),∴sin α=-1-cos 2α=-223,∴tan α=sin αcos α=-2 2.6. 【答案】 C【解析】 由已知,两边平方得sin αcos α=-732. ∴|sin 3α-cos 3α|=|(sin α-cos α)(sin 2α+cos 2α+sin αcos α)|=1-2sin αcos α·|1+sin αcos α|=2523128.∴sin 3α-cos 3α=±2523128. 7. 【答案】 C【解析】 ∵sin θ+cos θsin θ-cos θ=2,∴sin θ=3cos θ , ∴sin θcos 3θ+cos θsin 3θ=3cos 2θ+127cos 2θ=8227cos 2θ 由⎩⎪⎨⎪⎧sin θ=3cos θsin 2θ+cos 2θ=1得cos 2θ=110, ∴sin θcos 3θ+cos θsin 3θ=82027. 8. 【答案】 B【解析】方程5x 2-7x -6=0的两根为x 1=-35,x 2=2.则sin α=-35 , 原式=cos α(-cos α)tan 2αsin α(-sin α)(-sin α)=-1sin α=53.9.【答案】B【解析】逆向法解决,将y =12sin x 的图象沿y 轴向上平移1个单位,得函数y =12sin x +1的图象;再将函数y =12sin x +1的图象向右平移π2个单位,得函数y =12sin ⎝⎛⎭⎫x -π2+1的图象;再将函数y =12sin ⎝⎛⎭⎫x -π2+1图象上各点的纵坐标保持不变,横坐标缩短到原来的12,得函数y =12sin ⎝⎛⎭⎫2x -π2+1. 10. 【答案】 B【解析】 ∵T =12-0=12,∴ω=2πT =2π12=π6. 又最大值为2,最小值为1,则⎩⎪⎨⎪⎧A +b =2,-A +b =1,解得A =12,b =32,∴y =12cos π6t +32.二、填空题11.【答案】107【解析】sin θsin 3θ-cos 3θ=sin θ(sin 2θ+cos 2θ)sin 3θ-cos 3θ =sin 3θ+sin θcos 2θsin 3θ-cos 3θ =tan 3θ+tan θtan 3θ-1 =23+223-1=107.12. 【答案】[-32,3]【解析】由对称轴完全相同知两函数周期相同,∴ω=2,∴f (x )=3sin(2x -π6).由x ∈[0,π2],得-π6≤2x -π6≤56π,∴-32≤f (x )≤3.13.【答案】 2sin ⎝⎛⎭⎫π4x -π4+6【解析】 由题意得⎩⎪⎨⎪⎧A +B =8,-A +B =4,解得A =2,B =6. 周期T =2(7-3)=8,∴ω=2πT =π4.∴f (x )=2sin ⎝⎛⎭⎫π4x +φ+6. 又当x =3时,y =8,∴8=2sin ⎝⎛⎭⎫3π4+φ+6. ∴sin ⎝⎛⎭⎫3π4+φ=1,取φ=-π4. ∴f (x )=2sin ⎝⎛⎭⎫π4x -π4+6. 14. 【答案】 ①③【解析】①f (x )=4sin(2x +π3)=4cos(π2-2x -π3)=4cos(-2x +π6)=4cos(2x -π6).②T =2π2=π,最小正周期为π.③∵2x +π3=k π,当k =0时,x =-π6,函数f (x )关于点(-π6,0)对称.④2x+π3=π2+k π,当x =-π6时,k =-12,与k ∈Z 矛盾.∴①③正确. 二、解答题15. 解:法一:f (-x )-1=-2010x -2011sin 3x =-[f (x )-1], ∴f (x )-1为奇函数.∴f (-5)-1=-[f (5)-1]=-(7-1)=-6.∴f (-5)=1-6=-5,即f (-5)=-5即为所求.法二:⎭⎪⎬⎪⎫f (5)=2010×5+2011·sin 35+1=7f (-5)=-2010×5-2011·sin 35+1二式相加,得:f (-5)+7=2,∴f (-5)=2-7=-5.16. 解:(1)f (α)=sin (π-α)cos (2π-α)tan[π+(π2-α)]tan[-(α+π)]sin[-(π+α)]=sin α·cos α·tan (π2-α)[-tan (π+α)][-sin (π+α)]=sin αcos α·cot α(-tan α)sin α=-cos α.(2)由cos(α-32π)=15得:cos[-2π+(α+π2)]=cos(π2+α)=-sin α=15.∴sin α=-15.∵α是第三象限的角,∴cos α<0.∴f (α)=-cos α=1-sin 2α=1-125=265. (3)若α=-313π,∵-313π=-5×2π-π3,∴cos(-313π)=cos(-5×2π-π3)=cos(-π3)=cos π3=12.∴此时,f (α)=-cos(-313π)=-12.17. 解:(1)∵(π8,0)是函数y =f (x )的图象的对称中心,∴sin(2×π8+φ)=0,∴π4+φ=k π(k ∈Z ),∴φ=k π-π4(k ∈Z ).∵-π<φ<0,∴φ=-π4.(2)由(1)知φ=-π4,因此y =sin(2x -π4),由题意得:2k π-π2≤2x -π4≤2k π+π2,k ∈Z ,即:k π-π8≤x ≤k π+3π8,k ∈Z ,所以函数y =sin(2x -π4)的单调增区间为:[k π-π8,k π+3π8],k ∈Z .18. 解: (1)函数f (x )的最小值是3×(-1)-1=-4,此时有12x +π4=2k π-π2,解得x =4k π-3π2(k ∈Z ), 即函数f (x )的最小值是-4,此时自变量x 的取值集合是⎩⎨⎧⎭⎬⎫x ⎪⎪x =4k π-3π2,k ∈Z . (2)步骤是:①将函数y =sin x 的图象向左平移π4个单位长度,得到函数y =sin ⎝⎛⎭⎫x +π4的图象; ②将函数y =sin ⎝⎛⎭⎫x +π4的图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数y =sin ⎝⎛⎭⎫12x +π4的图象;③将函数y =sin ⎝⎛⎭⎫12x +π4的图象上所有点的纵坐标伸长为原来的3倍(横坐标不变),得到函数y =3sin ⎝⎛⎭⎫12x +π4的图象;④将函数y =3sin ⎝⎛⎭⎫12x +π4的图象向下平移1个单位长度,得函数y =3sin ⎝⎛⎭⎫12x +π4-1的图象. 19. 解: ∵函数y =A sin ωx (A >0,ω>0)图象的最高点为S (3,23), ∴A =2 3.由图象,得T4=3,∴T =12.又T =2πω,∴ω=π6,即y =23sin π6x .当x =4时,y =23sin 2π3=3. ∴M (4,3).又P (8,0). ∴|MP |=42+32=5, 即MP 的长是5.20. 解: (1)设f (x )的最小正周期为T ,则T =11π6-(-π6)=2π,由T =2πω,得ω=1,又⎩⎪⎨⎪⎧B +A =3,B -A =-1,解得⎩⎪⎨⎪⎧A =2B =1,令ω·5π6+φ=π2,即5π6+φ=π2, 解得φ=-π3,∴f (x )=2sin(x -π3)+1.(2)∵函数y =f (kx )=2sin(kx -π3)+1的周期为2π3,又k >0,∴k =3,令t =3x -π3,∵x ∈[0,π3],∴t ∈[-π3,2π3],如图,sin t =s 在[-π3,2π3]上有两个不同的解,则s ∈[32,1],∴方程 f (kx )=m 在x ∈[0,π3]时恰好有两个不同的解,则m ∈[3+1,3],即实数m 的取值范围是[3+1,3].。
高中数学北师大版必修4《第一章三角函数》单元测试卷含试卷分析详解

所示,则当t =1100s 时,电流强度是( )A .-5 AB .5 AC .5 3 AD .10 A 答案:A解析:由图像知A =10,T 2=4300-1300=1100,∴T =150,∴ω=2πT=100π,∴I =10sin(100πt+φ).又⎝⎛⎭⎫1300,10在图像上,∴100π×1300+φ=π2+2k π,k ∈Z .又0<φ<π2,∴φ=π6 .∴I =10sin ⎝⎛⎭⎫100πt +π6,当t =1100 s 时,l =-5 A ,故选A. 7.下列四个命题:①函数y =tan x 在定义域内是增函数;②函数y =tan(2x +1)的最小正周期是π;③函数y =tan x 的图像关于点(π,0)成中心对称;④函数y =tan x 的图像关于点⎝⎛⎭⎫-π2,0成中心对称.其中正确命题的个数是( ) A .0 B .1 C .2 D .3 答案:C解析:对于①,函数y =tan x 仅在区间⎝⎛⎭⎫k π-π2,k π+π2(k ∈Z )内递增,如π4<5π4,但tan π4=tan 5π4,所以①不正确;对于②,其最小正周期是π2,所以②也不正确;观察正切曲线可知命题③④都正确.8.要得到函数y =sin2x 的图像,只需将函数y =cos(2x -π4)的图像( )A .向左平移π8个单位B .向右平移π8个单位C .向左平移π4个单位D .向右平移π4个单位答案:B解析:将函数y =cos(2x -π4)向右平移π8个单位,得到y =cos ⎝⎛⎭⎫2⎝⎛⎭⎫x -π8-π4=cos ⎝⎛⎭⎫2x -π2=sin2x ,故选B.9.在△ABC 中,若sin A sin B cos C <0,则△ABC 是( ) A .锐角三角形 B .直角三角形 C .钝角三角形D .锐角或钝角三角形 答案:C解析:正弦函数在区间(0,π)的函数值都为正,故cos C <0,角C 为钝角.10.已知定义在区间⎣⎡⎦⎤0,3π2上的函数y =f (x )的图像关于直线x =3π4对称,当x ≥3π4时,。
必修四第一章三角函数测试题(含答案)

图象有 7 个交点,所以方程有 7 个解.
13、答案 0
π
2π
解析 方法一 由图可知,Error!T=Error!- =π,即 T= 4
,∴ω= =3。∴y=2sin T
(3x+φ),
将(Error!,0)代入上式 sin(Error!+φ)=0。
6
必修四第一章三角函数测试题(含答案)(word 版可编辑修改)
( )
A.1
B.2
C.Error!
D.Error!
5.函数 f(x)=cos(3x+φ)的图象关于原点成中心对称,则 φ 等于
( )
A.-
B.2kπ-Error!(k∈Z) C.kπ(k∈Z)
sin θ+c 的值是
sin θ-cos θ
A.-
B.
C.±Error!
2π 得 = ,即 T=π,∴ω=Error!= =2.
π
由点 M (3),-2)在图象上得 2sin(2π,3)+φf)=-2,
即 sin =-1,故 +φ=2kπ- (k∈Z), ∴φ=2kπ- (k∈Z). 又 φ∈Error!,∴φ= ,故 f(x)=2sinError!。 (2)∵x∈ ,∴2x+ ∈[]),
5π
19π
所以 cos(4x0- 6 )=Error!,且 ≤4x0- ≤ 6 ,
11π
5π
从而得 4x0- = 6 ,或 4x0- 6 = ,即 x0= ,或 x0= 。
9
π 由题意得 2kπ- ≤2x- ≤2kπ+ ,k∈Z.
2 ∴函数 y=sin 的单调增区间为Error!,k∈Z。
(3)由 y=sin())),知
x
0
Error!
(典型题)高中数学必修四第一章《三角函数》检测卷(包含答案解析)(1)
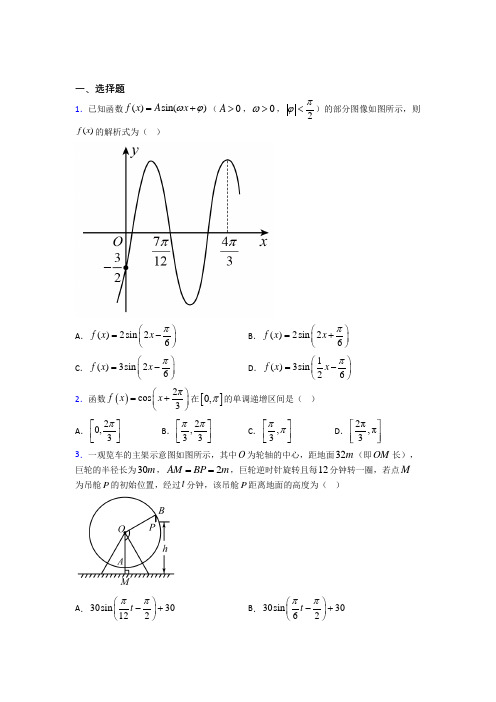
一、选择题1.已知函数()sin()f x A x ωϕ=+(0A >,0>ω,2πϕ<)的部分图像如图所示,则()f x 的解析式为( )A .()2sin 26f x x π⎛⎫=- ⎪⎝⎭B .()2sin 26f x x π⎛⎫=+ ⎪⎝⎭C .()3sin 26f x x π⎛⎫=-⎪⎝⎭D .1()3sin 26f x x π⎛⎫=-⎪⎝⎭ 2.函数()2cos 3⎛⎫=+ ⎪⎝⎭πf x x 在[]0,π的单调递增区间是( ) A .20,3π⎡⎤⎢⎥⎣⎦B .2,33ππ⎡⎤⎢⎥⎣⎦C .,3ππ⎡⎤⎢⎥⎣⎦D .2π,π33.一观览车的主架示意图如图所示,其中O 为轮轴的中心,距地面32m (即OM 长),巨轮的半径长为30m ,2AM BP m ==,巨轮逆时针旋转且每12分钟转一圈,若点M 为吊舱P 的初始位置,经过t 分钟,该吊舱P 距离地面的高度为( )A .30sin 30122t ππ⎛⎫-+⎪⎝⎭B .30sin 3062t ππ⎛⎫-+⎪⎝⎭C .30sin 3262t ππ⎛⎫-+⎪⎝⎭D .30sin 62t ππ⎛⎫-⎪⎝⎭ 4.已知函数()sin 26f x x π⎛⎫=-⎪⎝⎭,若方程()35f x =的解为1x ,2x (120x x π<<<),则()12sin x x -=( )A .35B .45-C .D .5.将函数()sin 25f x x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度后得到函数()y g x =的图象,对于函数()y g x =有以下四个判断: ①该函数的解析式为2sin 210y x π⎛⎫=+ ⎪⎝⎭; ②该函数图象关于点,02π⎛⎫⎪⎝⎭对称; ③该函数在区间,44ππ⎡⎤-⎢⎥⎣⎦上单调递增; ④该函数在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增. 其中,正确判断的序号是( ) A .②③B .①②C .②④D .③④6.已知函数()()cos f x x ωϕ=+(0>ω,0πϕ-<<)的图象关于点,08π⎛⎫⎪⎝⎭对称,且其相邻对称轴间的距离为23π,将函数()f x 的图象向左平移3π个单位长度后,得到函数()g x 的图象,则下列说法中正确的是( )A .()f x 的最小正周期23T π= B .58πϕ=-C .()317cos 248πx g x ⎛⎫=- ⎪⎝⎭D .()g x 在0,2π⎡⎤⎢⎥⎣⎦上的单调递减区间为,82ππ⎡⎤⎢⎥⎣⎦7.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用.假设在水流量稳定的情况下,简车上的每一个盛水筒都做逆时针匀速圆周运动.现将筒车抽象为一个几何图形,如图所示,圆O 的半径为4米,盛水筒M 从点0P 处开始运动,0OP 与水平面的所成角为30,且每分钟恰好转动1圈,则盛水筒M 距离水面的高度H (单位;m )与时间t (单位:s )之间的函数关系式的图象可能是( )A .B .C .D .8.下列结论正确的是( ) A .sin1cos1< B .2317cos cos 54ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭C .()()tan 52tan 47->-D .sin sin 1810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭9.使函数()3)cos(2)f x x x θθ=+++是偶函数,且在0,4⎡⎤⎢⎥⎣⎦π上是减函数的θ的一个值是( ) A .6π B .3π C .23π D .56π 10.已知函数()[][]sin cos cos sin f x x x =+,其中[]x 表示不超过实数x 的最大整数,则( )A .()f x 是奇函数B .π2π33f f ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭C .()f x 的一个周期是πD .()f x 的最小值小于011.如图,摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距离地面高度为120m ,转盘直径为110m 设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要20min .游客甲坐上摩天轮的座舱,开始转动t min 后距离地面的高度为H m ,则在转动一周的过程中,高度H 关于时间t 的函数解析式是( )A .()55cos 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭B .()55sin 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭C .()55cos 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭D .()55sin 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭12.已知函数()()()3cos 0g x x ωϕω=+>在7,6ππ⎛⎫ ⎪⎝⎭上具有单调性,且满足04g π⎛⎫= ⎪⎝⎭,()3g π=,则ω的取值共有( ) A .6个B .5个C .4个D .3个二、填空题13.已知3()tan 1f x a x x =+(a ,b 为实数),且3(lg log 10)5f =,则(lglg3)f =____________.14.已知定义在R 上的函数()f x 满足:()()2f x f x π+=,且当[]0,x π∈时,()sin f x x =.若对任意的(],x m ∈-∞,都有()2f x ≤,则实数m 的取值范围是______. 15.如图,某公园要在一块圆心角为3π,半径为20m 的扇形草坪OAB 中修建一个内接矩形文化景观区域CDEF ,若//EF AB ,则文化景观区域面积的最大值为______2m .16.若函数f (x )=2sin(ωx +φ)(ω>0,0<φ<π)的图象经过点,26π⎛⎫⎪⎝⎭,且相邻两条对称轴间的距离为2π,则4f π⎛⎫⎪⎝⎭的值为________. 17.设函数()y f x =的定义域为D ,若对任意的1x ∈D ,总存在2x ∈D ,使得()()121f x f x ⋅=,则称函数()f x 具有性质M .下列结论:①函数3y x x =-具有性质M ; ②函数35x x y =+具有性质M ;③若函数()[]8log 2,0,y x x t =+∈具有性质M ,则510t =; ④若3sin y x a =+具有性质M ,则5a =. 其中正确结论的序号是____________.18.函数251612()sin (0)236x x f x x x x ππ-+⎛⎫=--> ⎪⎝⎭的最小值为_______. 19.关于函数()4sin(2)(),3f x x x R π=+∈有下列命题:①由12()()0f x f x ==可得12x x -必是π的整数倍;②()y f x =的图象关于点(,0)6π-对称;③()y f x =的表达式可改写为4cos(2);6y x π=-④()y f x =的图象关于直线6x π=-对称.其中正确命题的序号是_________.20.将函数()sin (0)f x x ωω=>的图象向右平移6π个单位长度,得到函数()y g x =的图像,若()y g x =是偶函数,则ω的最小值为________.三、解答题21.已知函数()12sin 26x f x π⎛⎫=+⎪⎝⎭,x ∈R .(1)用“五点法”画出函数()f x 一个周期内的图象; (2)求函数()f x 在[],ππ-内的值域; (3)若将函数()f x 的图象向右平移6π个单位长度,得到函数()g x 的图象,求函数()g x 在[],ππ-内的单调增区间.22.函数()sin()f x A x ωϕ=+(0,0,[0,2))A ωϕπ>>∈的图象如图所示:(1)求()f x 的解析式; (2)()f x 向左平移12π个单位后得到函数()g x ,求()g x 的单调递减区间;(3)若,2x ππ⎡⎤∈-⎢⎥⎣⎦且()32f x ≥,求x 的取值范围.23.已知向量a =(cosωx -sinωx ,sinωx),b =(-cosωx -sinωx,2cosωx).设函数f(x)=a b ⋅+λ(x ∈R)的图象关于直线x =π对称,其中ω,λ为常数,且ω∈1,12⎛⎫⎪⎝⎭.(1)求函数f(x)的最小正周期; (2)若y =f(x)的图象经过点,04π⎛⎫⎪⎝⎭,求函数f(x)在区间30,5π⎡⎤⎢⎥⎣⎦上的取值范围 24.已知函数()()()f x g x h x =,其()22g x x =,()h x =_____. (1)写出函数()f x 的一个周期(不用说明理由); (2)当,44x ππ⎡⎤∈-⎢⎥⎣⎦时,求函数()f x 的最大值和最小值. 从①cos 4x π⎛⎫+⎪⎝⎭,②2sin 24x π⎛⎫- ⎪⎝⎭这两个条件中任选一个,补充在上面问题中并作答, 注:如果选择多个条件分别解答.按第一个解答计分. 25.已知sin(3)(),cos x f x x R xπ-=∈(1)若α为第三象限角,且3sin 5α=-,求()f α的值. (2)若,34x ππ⎡⎤∈-⎢⎥⎣⎦,且21()2()1cos g x f x x =++,求函数()g x 的最小值,并求出此时对应的x 的值.26.函数()cos()(0)f x x ωφω=+>的部分图像如图所示.(1)求()f x 的表达式; (2)若[1,2]x ∈,求()f x 的值域;(3)将()f x 的图像向右平移112个单位后,再将所得图像横坐标伸长到原来的2倍,纵坐标不变,得到函数()y g x =的图像,求()g x 的单调递减区间.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】 本题首先可根据33π44T 求出ω,然后根据当43x π=时函数()f x 取最大值求出ϕ,最后代入30,2⎛⎫- ⎪⎝⎭,即可求出A 的值. 【详解】因为4π7π3π3124,所以33π44T ,T π=,因为2T πω=,所以2ω=,()sin(2)f x A x ϕ=+,因为当43x π=时函数()sin(2)f x A x ϕ=+取最大值,所以()42232k k Z ππϕπ⨯+=+∈,()26k k Z πϕπ=-+∈,因为2πϕ<,所以6πϕ=-,()sin 26f x A x π⎛⎫=- ⎪⎝⎭,代入30,2⎛⎫- ⎪⎝⎭,3sin 26A π⎛⎫-=- ⎪⎝⎭,解得3A =,()3sin 26f x x π⎛⎫=- ⎪⎝⎭, 故选:C. 【点睛】关键点点睛:本题考查根据函数图像求函数解析式,对于()sin()f x A x ωϕ=+,可通过周期求出ω,通过最值求出A ,通过代入点坐标求出ϕ,考查数形结合思想,是中档题.2.C解析:C 【分析】先求出函数的单调增区间,再给k 取值即得解. 【详解】 令22223+<+<+ππk πx πk π(k ∈Z ) ∴42233+<<+ππk πx k π(k ∈Z ), 所以函数的单调递增区间为4[2,2]33ππk πk π++(k ∈Z ), 当1k =-时,5233ππx -<<- 当0k =时,433x ππ<<又∵[]0,x π∈, 故选:C 【点睛】方法点睛:求三角函数()cos()f x A wx ϕ=+的单调区间,一般利用复合函数的单调性原理解答:首先是对复合函数进行分解,接着是根据复合函数的单调性原理分析出分解出的函数的单调性,最后根据分解函数的单调性求出复合函数的单调区间.3.B解析:B 【分析】先通过计算得出转动的角速度,然后利用三角函数模型表示在转动的过程中点B 的纵坐标满足的关系式,则吊舱到底面的距离为点B 的纵坐标减2. 【详解】如图所示,以点M 为坐标原点,以水平方向为x 轴,以OM 所在直线为y 轴建立平面直角坐标系.因为巨轮逆时针旋转且每12分钟转一圈,则转动的角速度为6π每分钟, 经过t 分钟之后,转过的角度为6BOA t π∠=,所以,在转动的过程中,点B 的纵坐标满足:3230sin 30sin 322662y t t ππππ⎛⎫⎛⎫=--=-+ ⎪ ⎪⎝⎭⎝⎭则吊舱距离地面的距离30sin 32230sin 306262h t t ππππ⎛⎫⎛⎫=-+-=-+ ⎪ ⎪⎝⎭⎝⎭. 故选:B . 【点睛】建立三角函数模型解决实际问题的一般步骤: (1)审题:审清楚题目条件、要求、理解数学关系; (2)建模:分析题目变化趋势,选择合适的三角函数模型; (3)求解:对所建立的数学模型进行分析研究,从而得到结论.4.B解析:B 【分析】求出函数()f x 在(0,)π上的对称轴,然后由正弦函数性质得1223x x π+=,这样12sin()x x -化为2222sin(2)sin 2cos(2)336x x x πππ⎛⎫-=+=- ⎪⎝⎭,而已知条件为23sin(2)65x π-=,再由正弦函数性质确定226x π-的范围,从而由平方关系求得结论.【详解】函数()sin 26f x x π⎛⎫=-⎪⎝⎭的对称轴满足:()262x k k Z πππ-=+∈,即()23k x k Z ππ=+∈,令0k =可得函数在区间()0,π上的一条对称轴为3x π=,结合三角函数的对称性可知1223x x π+=,则:1223x x π=-,()122222sin sin 2sin 2cos 2336x x x x x πππ⎛⎫⎛⎫⎛⎫-=-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,由题意:0πx <<,则112666x πππ-<-<,23sin 265x π⎛⎫-= ⎪⎝⎭,120x x π<<<,则2226x πππ<-<,由同角三角函数基本关系可知:24cos 265x π⎛⎫-=- ⎪⎝⎭, 故选:B . 【点睛】关键点点睛:本题考查正弦函数的性质,考查平方关系.解题时根据自变量的范围求得此范围内函数的对称轴,从而得出两个变量12,x x 的关系,可化双变量为单变量,再根据函数值及函数性质确定出单变量的范围,从而求得结论.注意其中诱导公式的应用,目的是把求值式与已知条件中的角化为一致.5.A解析:A 【分析】根据函数平移变换得sin 2y x =,再根据正弦函数的性质依次讨论即可得答案. 【详解】解:由函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象平移变换的性质可知: 将sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后 解析式为sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,选项①错误; 令2x k =π,k Z ∈,求得2k x =π,k Z ∈, 故函数的图象关于点,02k ⎛⎫⎪⎝⎭π对称, 令1k =,故函数的图象关于点,02π⎛⎫⎪⎝⎭对称,选项②正确; 则函数的单调递增区间满足:222()22k x k k Z ππππ-≤≤+∈,即()44k x k k Z ππππ-≤≤+∈,令0k =可得函数的一个单调递增区间为,44ππ⎡⎤-⎢⎥⎣⎦,选项③正确,④错误.故选:A. 【点睛】本题考查三角函数平移变换,正弦型函数的单调区间,对称中心等,考查运算求解能力,解题的易错点在于平移变换时,当1ω≠时,须将ω提出,平移只针对x 进行平移,具体的在本题中,sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后得sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,而不是sin 2sin 251010y x x πππ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,是中档题. 6.D解析:D 【分析】首先根据三角函数的性质,可知相邻对称轴间的距离是半个周期,判断A ;再求函数的解析式,判断B ;根据平移规律得到函数()g x ,判断C ;最后根据函数()g x 的解析式,利用整体代入的方法求函数的单调递减区间. 【详解】相邻对称轴间的距离是半个周期,所以周期是43π,故A 不正确; 243T ππω==,解得:32ω=,()f x 的图象关于点,08π⎛⎫⎪⎝⎭对称,3,282k k Z ππϕπ∴⨯+=+∈,解得:5,16k k Z πϕπ=+∈ 0πϕ-<<, 1116πϕ∴=-,故B 不正确; ()311cos 216f x x π⎛⎫=- ⎪⎝⎭,向左平移3π个单位长度后得()31133cos cos 2316216g x x x πππ⎡⎤⎛⎫⎛⎫=+-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 故C 不正确; 当02x π≤≤时,3339,2161616x πππ⎡⎤-∈-⎢⎥⎣⎦,当3390,21616x ππ⎡⎤-∈⎢⎥⎣⎦时,函数单调递减,即 ,82x ππ⎡⎤∈⎢⎥⎣⎦,故D 正确. 故选:D 【点睛】关键点点睛:本题的关键是根据三角函数的性质求得函数()f x 的解析式,第四个选项是关键,需根据整体代入的方法,先求33216x π-的范围,再确定函数的单调递减区间. 7.D解析:D 【分析】先根据题意建立坐标系,写出盛水筒M 距离水面的高度H 与时间t 之间的函数关系式,再根据关系式即可判断. 【详解】解:以O 为圆心,过点O 的水平直线为x 轴,建立如图所示的平面直角坐标系:0306xOP π∠==,OP ∴在()t s 内转过的角为:26030t t ππ=, ∴以x 轴正半轴为始边,以OP 为终边的角为:306t ππ-,P ∴点的纵坐标为:4sin 306t ππ⎛⎫-⎪⎝⎭, H ∴与t 之间的函数关系式为:4sin 2306H t ππ⎛⎫=-+⎪⎝⎭, 当sin 1306t ππ⎛⎫-= ⎪⎝⎭时,max 426H =+=, 当sin 1306t ππ⎛⎫-=-⎪⎝⎭时,max 422H =-+=-, 对A ,B ,由图像易知max min H H =-,故A ,B 错误; 对C ,max min H H <-,故C 错误; 对D ,max min H H >-,故D 正确. 故选:D. 【点睛】关键点点睛:本题解题的关键是理解题意,根据题意写出H 与t 之间的函数关系式.8.D解析:D 【分析】利用正弦函数的单调性可判断AD 选项的正误;利用正切函数的单调性可判断C 选项的正误;利用余弦函数的单调性可判断B 选项的正误. 【详解】对于A 选项,因为正弦函数sin y x =在0,2π⎛⎫⎪⎝⎭上单调递增, 且01122ππ<-<<,则sin1sin 1cos12π⎛⎫>-=⎪⎝⎭,A 选项错误; 对于B 选项,因为余弦函数cos y x =在()0,π上为减函数,23233cos cos cos 555πππ⎛⎫-== ⎪⎝⎭,1717cos cos cos 444πππ⎛⎫-== ⎪⎝⎭, 3045πππ<<<,则3cos cos 54ππ<,即2317cos cos 54ππ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭,B 选项错误; 对于C 选项,当900x -<<时,正切函数tan y x =单调递增, 因为9052470-<-<-<,所以,()()tan 52tan 47-<-,C 选项错误;对于D 选项,因为正弦函数sin y x =在,02π⎛⎫- ⎪⎝⎭上单调递增,因为021018πππ-<-<-<,所以,sin sin 1810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭,D 选项正确. 故选:D. 【点睛】思路点睛:解答比较函数值大小问题,常见的思路有两个: (1)判断各个数值所在的区间; (2)利用函数的单调性直接解答.9.B解析:B 【解析】1())cos(2))cos(2))2sin(2)26f x x x x x x πθθθθθ=+++=+++=++,由于()f x 为偶函数,则(0)2sin()26f πθ=+=±,sin()1,662k πππθθπ+=±+=+,3k πθπ=+,当0k =时,3πθ=,()2sin(2)2sin(2)362f x x x πππ=++=+2cos2x =,当[0,]4x π∈时,2[0,]2x π∈,()2cos2f x x =为减函数,符合题意,所以选B.10.D解析:D 【分析】利用奇函数的性质判断A ,分别求3f π⎛⎫⎪⎝⎭和23f π⎛⎫⎪⎝⎭判断大小,取特殊值验证的方法判断C ,分区间计算一个周期内的最小值,判断选项D 。
人教版 必修4第一章三角函数测试题

高一数学必修4第一章《三角函数》测试题一、选择题(本大题共12小题,每小题5分,共60分) 1.下列命题正确的是( ).A.终边相同的角都相等B.钝角比第三象限角小C.第一象限角都是锐角D.锐角都是第一象限角 2.若角︒600的终边上有一点()a ,4-,则a 的值是( ). A.34- B.34± C.3 D.34). A.3cos5π B.3cos5π-C.3cos5π± D.2cos 5π 4.下列函数中,最小正周期为π,且图象关于直线3x π=对称的是( ).A.)62sin(+=x yB.sin()26x y π=+C.sin(2)6y x π=-D.sin(2)y x π=-5.函数)sin(ϕω+=x y 的部分图象如右图,则ω,ϕA.,24ωϕππ== B.,36ωϕππ==C.5,44ωϕππ==D.,44ωϕππ== 6.要得到3sin(2)4y x π=+的图象,只需将x y 2sin 3=的图象( ).A.向左平移4π个单位B.向右平移4π个单位C.向左平移8π个单位D.向右平移8π个单位7.设tan()2απ+=,则sin()cos()sin()cos()αααα-π+π-=π+-π+( ).A.3B.13C.1D.1- 8.A 为三角形ABC 的一个内角,若12sin cos 25A A +=,则这个三角形的形状为( ).A. 锐角三角形B. 钝角三角形C. 等腰直角三角形D. 等腰三角形 9.定义在R 上的函数)(x f 既是偶函数又是周期函数,若)(x f 的最小正周期是π,且当[0,]2x π∈时,x x f sin )(=,则5()3f π的值为( ).A.21-B.23 C.23-D.2110.函数y =( ).A.2,2()33k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦ B.2,2()66k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦C.22,2()33k k k Z ππππ++∈⎡⎤⎢⎥⎣⎦D.222,2()33k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦11.函数2sin(2)6y x π=-([0,]x ∈π)的单调递增区间是( ). A.[0,]3π B.7[,]1212ππ C.5[,]36ππ D.5[,]6ππ 12. 函数x x y sin sin -=的值域是 ( )A .0B .[]1,1-C .[]1,0D .[]0,2-二、填空题(本大题共4小题,每小题5分,共20分.)13.在扇形中,已知半径为8,弧长为12,则圆心角是 弧度,扇形面积是 . 14.函数xxy cos 2cos 2-+=的最大值为________.15.方程x x lg sin =的解的个数为__________.16.设()sin()cos()f x a x b x αβ=π++π+,其中βα,,,b a 为非零常数.若1)2009(-=f ,则=)2010(f . 三、解答题(本大题共6小题,共70分.)17.(本小题满分10分)已知α是第三角限角,化简ααααsin 1sin 1sin 1sin 1+---+.18.(本小题满分12分)已知角α的终边在直线x y 2=上,求角α的正弦、余弦和正切值.19.(本小题满分12分)(1)当3tan =α,求αααcos sin 3cos 2-的值;(2)设3222cos sin (2)sin()32()22cos ()cos()f θθθθθθπ+π-++-=+π++-,求()3f π的值.20.(本小题满分12分)已知函数())4f x x π=-,x ∈R .(1)求函数()f x 的最小正周期和单调递增区间;(2)求函数()f x 在区间[]82ππ-,上的最小值和最大值,并求出取得最值时x 的值.21.(本小题满分12分)已知()2sin(2)26f x a x a b π=-+++,3[,]44x ππ∈,是否存在常数Q b a ∈,,使得)(x f 的值域为}133|{-≤≤-y y ?若存在,求出b a ,的值;若不存在,说明理由.22.(本小题满分12分)已知函数()()()sin 0,0f x A x B A ωϕω=++>>的一系列对应值如下表:(1)根据表格提供的数据求函数()f x 的一个解析式; (2)根据(1)的结果,若函数()()0y f kx k =>周期为23π,当[0,]3x π∈时,方程()f kx m =恰有两个不同的解,求实数m 的取值范围.参考答案一、选择题1.D 由任意角和象限角的定义易得只有D 正确.2.A 因为360tan )60540tan(4600tan =︒=︒+︒=-=︒a,故34-=a .3.B33|cos |cos 55ππ===-. 4.C ∵最小正周期为π,∴2ω=,又∵图象关于直线3x π=对称,∴()13f π=±,故只有C 符合.5.D ∵2134=-=T ,∴8=T ,4ωπ=,又由142ϕππ⨯+=得4ϕπ=.6.C ∵3sin 2()3sin(2)84y x x ππ=+=+,故选C.7.A 由tan()2απ+=,得tan 2α=, 故sin()cos()sin cos sin cos tan 13sin()cos()sin (cos )sin cos tan 1αααααααααααααα-π+π---++====π+-π+-----.8.B 将52cos sin =+A A 两边平方,得254cos cos sin 2sin 22=++A A A A , ∴025211254cos sin 2<-=-=A A , 又∵0A <<π, ∴A 为钝角.9.B 5()(2)()()sin 33333f f f f πππππ=π-=-===10.D 由01cos 2≥+x 得21cos -≥x ,∴222233k x k πππ-≤≤π+,Z k ∈. 11.C 由3222262k x k πππ+π≤-≤+π得236k x k ππ-+π≤≤-+π(Z k ∈),又∵[0,]x ∈π, ∴单调递增区间为5[,]36ππ.12.D ∵π20≤≤x , ∴1sin 1≤≤-x , ∴1sin ≤x ∴0sin sin 2≤-≤-x x∴函数x x y sin sin -=的值域是 []0,2- 二、填空题 13.23,48 圆心角23812===r l α,扇形面积488122121=⨯⨯==lr S . 14.3 22221(2c o s )2c o s ,c o s 11,3113y y y x x x y y y ---=+=⇒-≤≤≤≤++.15.3 画出函数x y sin =和x y lg =的图象,结合图象易知这两个函数的图象有3交点.16.1 (2009)s i n (2009)c o s (2009f a b αβ=π++π+=-, (2010)s i n (2010)c o s (20f a bαπβ=π+++ sin[(2009)]cos[(2009)]a b αβ=π+π++π+π+ [sin(2009)cos(2009)]1a b αβ=-π++π+=.三、解答题17.解:∵α是第三角限角, ∴0sin 1>+α,0sin 1>-α,0cos <α,∴)sin 1)(sin 1()sin 1()sin 1)(sin 1()sin 1(sin 1sin 1sin 1sin 122αααααααααα-+-++-+=+---+αααααααα22222222cos )sin 1(cos )sin 1(sin 1)sin 1(sin 1)sin 1(--+=----+= ααααααααc o s s i n 1c o s s i n 1|c o s s i n 1||c o s s i n 1|-++-=--+=αααtan 2cos sin 2-=-=. 18. 解:设角α终边上任一点)2,(k k P (0≠k ),则k x =,k y 2=,||5k r =.当0>k 时,k r 5=,α是第一象限角, 55252s i n ===k k r y α,555cos ===kk r x α,22tan ===k k x y α; 当0<k 时,k r 5-=,α是第三象限角, 55252s i n -=-==k k r y α,555cos -=-==k k r x α,22tan ===k k x y α. 综上,角α的正弦、余弦和正切值分别为552,55,2或552-,55-,2. 19.解:(1)因为1tan tan 31cos sin cos sin 3cos cos sin 3cos 22222+-=+-=-αααααααααα, 且3tan =α, 所以,原式=+⨯-=13331254-.(2)θθθθθθθπθπθπθθcos cos 223cos sin cos 2)cos()(cos 223)2sin()2(sin cos 2)(223223++-++=-+++-++-+=fθθθθθθθθθθθθcos cos 22)1(cos cos )1cos )(cos 1(cos 2cos cos 222cos cos cos 222223++--++-=++-+-=1cos 2cos cos 2)2cos cos 2)(1(cos 22-=++++-=θθθθθθ,∴1()cos1332f ππ=-=-. 20.解:(1)因为())4f x x π=-,所以函数()f x 的最小正周期为22T π==π,由2224k x k π-π+π≤-≤π,得388k x k ππ-+π≤≤+π,故函数)(x f 的递调递增区间为3[,]88k k ππ-+π+π(Z k ∈); (2)因为())4f x x π=-在区间[]88ππ-,上为增函数,在区间[]82ππ,上为减函数,又()08f π-=,()8f π=π())1244f ππ=π-==-,故函数()f x 在区间[]82ππ-,8x π=;最小值为1-,此时2x π=.21.解:存在1-=a ,1=b 满足要求.∵344x ππ≤≤, ∴252363x πππ≤+≤,∴1sin(2)6x π-≤+≤, 若存在这样的有理b a ,,则(1)当0>a 时,⎪⎩⎪⎨⎧-=++-=++-,1322,323b a a b a a 无解;(2)当0<a 时,⎩⎨⎧-=++--=++,1323,322b a a b a a 解得1-=a ,1=b ,即存在1-=a ,1=b 满足要求. 22. 解:(1)设()f x 的最小正周期为T ,得11()266T ππ=--=π, 由2T ωπ=,得1ω=,又31B A B A +=⎧⎨-=-⎩,解得21A B =⎧⎨=⎩令562ωϕππ⋅+=,即562ϕππ+=,解得3ϕπ=-, ∴()2sin 13f x x π⎛⎫=-+ ⎪⎝⎭. (2)∵函数()2sin 13y f kx kx π⎛⎫==-+ ⎪⎝⎭的周期为23π,又0k >, ∴3k =, 令33t x π=-,∵0,3x π⎡⎤∈⎢⎥⎣⎦, ∴2[,]33t ππ∈-, 如图,s t =sin 在2[,]33ππ-上有两个不同的解,则)1,23[∈s ,∴方程()f kx m =在[0,]3x π∈时恰好有两个不同的解,则)1,3m ∈,即实数m 的取值范围是)1,3。
(必考题)高中数学必修四第一章《三角函数》测试(有答案解析)

一、选择题1.已知函数()sin()f x A x ωϕ=+(0A >,0>ω,2πϕ<)的部分图像如图所示,则()f x 的解析式为( )A .()2sin 26f x x π⎛⎫=- ⎪⎝⎭B .()2sin 26f x x π⎛⎫=+ ⎪⎝⎭C .()3sin 26f x x π⎛⎫=-⎪⎝⎭D .1()3sin 26f x x π⎛⎫=-⎪⎝⎭ 2.已知关于x 的方程2cos ||2sin ||20(0)+-+=≠a x x a a 在(2,2)x ππ∈-有四个不同的实数解,则实数a 的取值范围为( ) A .(,0)(2,)-∞+∞B .(4,)+∞C .(0,2)D .(0,4)3.已知角α顶点在坐标原点,始边与x 轴非负半轴重合,终边过点()3,4P -,将α的终边逆时针旋转180︒,这时终边所对应的角是β,则cos β=( ) A .45-B .35C .35D .454.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积12=(弦⨯矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有弧AB 长为83π,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )3 1.73≈)A .6平方米B .9平方米C .12平方米D .15平方米5.函数1sin3y x =-的图像与直线3x π=,53x π=及x 轴所围成的图形的面积是( ) A .23π B .πC .43π D .53π 6.已知奇函数()f x 满足()(2)f x f x =+,当(0,1)x ∈时,函数()2x f x =,则12log 23f ⎛⎫= ⎪⎝⎭( ) A .1623-B .2316-C .1623D .23167.《九章算术》中《方田》章有弧田面积计算问题,术日:以弦乘矢,矢又自乘,并之,二而一.其大意是弧田面积计算公式为:弧田面积12=(弦×矢+矢×矢).弧田是由圆弧(弧田弧)及圆弧两端点的弦(弧田弦)围成的平面图形,公式中的“弦”指的是弧田弦的长,“矢”指的是弧田所在圆的半径与圆心到孤田弦的距离之差,现有一弧田,其矢长等于8米,若用上述弧田面积计算公式算得该弧田的面积为128平方米,则其弧田弧所对圆心角的正弦值为( ) A .60169B .120169C .119169D .591698.已知函数()[][]sin cos cos sin f x x x =+,其中[]x 表示不超过实数x 的最大整数,则( )A .()f x 是奇函数B .π2π33f f ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭C .()f x 的一个周期是πD .()f x 的最小值小于09.下列函数中,既是偶函数,又在(),0-∞上是增函数的是( ) A .()22xxf x -=- B .()23f x x =-C .()2ln =-f x xD .()cos3=f x x x10.现有四个函数:①y =x |sin x |,②y =x 2cos x ,③y =x ·e x ;④1y x x=+的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )A .①②③④B .①③②④C .②①③④D .③②①④11.若函数()22()sin 23cos sin f x x x x =+-的图像为E ,则下列结论正确的是( ) A .()f x 的最小正周期为2π B .对任意的x ∈R ,都有()()3f x f x π=-C .()f x 在7(,)1212ππ上是减函数D .由2sin 2y x =的图像向左平移3π个单位长度可以得到图像E 12.函数22y cos x sinx =- 的最大值与最小值分别为( ) A .3,-1 B .3,-2 C .2,-1D .2,-2二、填空题13.下列判断正确的是___________(将你认为所有正确的情况的代号填入横线上). ①函数1tan 21tan 2xy x+=-的最小正周期为π;②若函数()lg f x x =,且()()f a f b =,则1ab =; ③若22tan 3tan 2αβ=+,则223sin sin 2αβ-=;④若函数()2221sin 41x xy x ++=+的最大值为M ,最小值为N ,则2M N +=.14.函数()()sin f x x ωϕ=+的部分图象如图所示,则()f x 的单调递增区间为___________.15.sin 75=______.16.如图,从气球A 上测得正前方的B ,C 两点的俯角分别为75︒,30,此时气球的高是60m ,则BC 的距离等于__________m .17.如图,游乐场所的摩天轮匀速旋转,每转一周需要l2min ,其中心O 离地面45米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请问:当你第六次距离地面65米时,用了________分钟?18.函数251612()sin (0)236x x f x x x x ππ-+⎛⎫=--> ⎪⎝⎭的最小值为_______. 19.关于函数()4sin(2)(),3f x x x R π=+∈有下列命题:①由12()()0f x f x ==可得12x x -必是π的整数倍;②()y f x =的图象关于点(,0)6π-对称;③()y f x =的表达式可改写为4cos(2);6y x π=-④()y f x =的图象关于直线6x π=-对称.其中正确命题的序号是_________. 20.给出下列命题: ①函数()4cos 23f x x π⎛⎫=+⎪⎝⎭的一个对称中心为5,012π⎛⎫-⎪⎝⎭; ②若α,β为第一象限角,且αβ>,则tan tan αβ>;③在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,若40a =,20b =,25B =︒,则ABC ∆必有两解.④函数sin 2y x =的图象向左平移4π个单位长度,得到sin 24y x π⎛⎫=+ ⎪⎝⎭的图象.其中正确命题的序号是 _________(把你认为正确的序号都填上).三、解答题21.已知函数()()1sin 226f x x x R π⎛⎫=+∈ ⎪⎝⎭. (1)填写下表,并用“五点法”画出()f x 在[0,]π上的图象;26x π+6π 136πxπ ()f x(2)将()y f x =的图象向上平移1个单位,横坐标缩短为原来的2,再将得到的图象上所有点向右平移4π个单位后,得到()g x 的图象,求()g x 的对称轴方程. 22.现给出以下三个条件:①()f x 的图象与x 轴的交点中,相邻两个交点之间的距离为2π;②()f x 的图象上的一个最低点为2,23A π⎛⎫- ⎪⎝⎭; ③()01f =.请从上述三个条件中任选两个,补充到下面试题中的横线上,并解答该试题. 已知函数()()2sin 05,02f x x πωϕωϕ⎛⎫=+<<<< ⎪⎝⎭,满足________,________. (1)根据你所选的条件,求()f x 的解析式; (2)将()f x 的图象向左平移6π个单位长度,得到()g x 的图象求函数()()1y f x g x =-的单调递增区间.23.函数()cos()0,02f x x πωϕωϕ⎛⎫=+><<⎪⎝⎭的部分图象如图所示.(1)写出()f x 的解析式; (2)将函数()f x 的图象向右平移12π个单位后得到函数()g x 的图象,讨论关于x 的方程()3()0f x g x m -=(11)m -<≤在区间,2ππ⎡⎤-⎢⎥⎣⎦上的实数解的个数.24.已知函数π()3sin 26f x x ⎛⎫=+⎪⎝⎭. (1)用“五点法”画出函数()y f x =在一个周期内的简图;(2)说明函数()y f x =的图像可以通过sin y x =的图像经过怎样的变换得到?(3)若003()[2π3π]2f x x =∈,,,写出0x 的值. 25.已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭,,28M π⎛⎫⎪⎝⎭、5,28N π⎛⎫- ⎪⎝⎭分别为其图象上相邻的最高点、最低点. (1)求函数()f x 的解析式; (2)求函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的单调区间和值域. 26.已知函数()2sin(2)(0)6f x x πωω=+>.(1)若点5(,0)8π是函数()f x 图像的一个对称中心,且(0,1)ω∈,求函数()f x 在3[0,]4π上的值域; (2)若函数()f x 在(,)33π2π上单调递增,求实数ω的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C解析:C 【分析】 本题首先可根据33π44T 求出ω,然后根据当43x π=时函数()f x 取最大值求出ϕ,最后代入30,2⎛⎫- ⎪⎝⎭,即可求出A 的值. 【详解】因为4π7π3π3124,所以33π44T ,T π=,因为2T πω=,所以2ω=,()sin(2)f x A x ϕ=+,因为当43x π=时函数()sin(2)f x A x ϕ=+取最大值, 所以()42232k k Z ππϕπ⨯+=+∈,()26k k Z πϕπ=-+∈,因为2πϕ<,所以6πϕ=-,()sin 26f x A x π⎛⎫=-⎪⎝⎭, 代入30,2⎛⎫- ⎪⎝⎭,3sin 26A π⎛⎫-=- ⎪⎝⎭,解得3A =,()3sin 26f x x π⎛⎫=- ⎪⎝⎭, 故选:C. 【点睛】关键点点睛:本题考查根据函数图像求函数解析式,对于()sin()f x A x ωϕ=+,可通过周期求出ω,通过最值求出A ,通过代入点坐标求出ϕ,考查数形结合思想,是中档题.2.D解析:D 【分析】令2()cos ||2sin ||2(0)=+-+≠f x a x x a a ,易知函数()f x 是偶函数,将问题转化为研究当(0,2)x π∈时,2()cos 2sin 2=+-+f x a x x a 有两个零点,令sin t x =,则转化为2()22(0)=--≠h t at t a 有一个根(1,1)t ∈-求解.【详解】当(2,2)x ππ∈-,2()cos ||2sin ||2(0)=+-+≠f x a x x a a ,则()()f x f x -=,函数()f x 是偶函数,由偶函数的对称性,只需研究当(0,2)x π∈时,2()cos 2sin 2=+-+f x a x x a 有两个零点,设sin t x =,则2()22(0)=--≠h t at t a 有一个根(1,1)t ∈- ①当0a <时,2()22=--h t at t 是开口向下,对称轴为10t a=<的二次函数,(0)20h =-<则(1)0->=h a ,这与0a <矛盾,舍去;②当0a >时,2()22=--h t at t 是开口向上,对称轴为10t a=>的二次函数, 因为(0)20h =-<,(1)220-=+->=h a a , 则存在(1,0)t ∈-,只需(1)220=--<h a ,解得4a <, 所以04a <<.综上,非零实数a 的取值范围为04a <<. 故选:D . 【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法: (1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解3.B解析:B 【分析】先根据已知条件求解出cos α的值,然后根据,αβ之间的关系结合诱导公式求解出cos β的值. 【详解】 因为3cos 5α==,且180βα=+︒, 所以()3cos cos 180cos 5βαα=+︒=-=-, 故选:B. 【点睛】结论点睛:三角函数定义有如下推广:设点(),P x y 为角α终边上任意一点且不与原点重合,r OP =,则()sin ,cos ,tan 0y x yx r r xααα===≠. 4.B解析:B 【分析】根据已知求出矢2=,弦2AD ==. 【详解】由题意可得:823=43AOB ππ∠=,4OA =,在Rt AOD 中,可得:3AOD π∠=,6DAO π∠=,114222OD AO ==⨯=, 可得:矢422=-=, 由3sin4233AD AO π==⨯=, 可得:弦243AD ==, 所以:弧田面积12=(弦⨯矢+矢221)(4322)43292=⨯+=+≈平方米.故选:B 【点睛】方法点睛:有关扇形的计算,一般是利用弧长公式l r α=、扇形面积公式12S lr =及直角三角函数求解.5.C解析:C 【分析】作出函数1sin3y x =-的图像,利用割补法,补成长方形,计算面积即可. 【详解】作出函数1sin3y x =-的图象,如图所示,利用割补法,将23π到π部分的图象与x 轴围成的图形补到图中3π到23π处阴影部分,凑成一个长为3π,宽为2的长方形,后面π到53π,同理;∴1sin3y x =-的图象与直线3x π=,53x π=及x 轴所围成的面积为24233ππ⨯=,故选:C. 【点睛】用“五点法”作()sin y A ωx φ=+的简图,主要是通过变量代换,设z x ωϕ=+,由z 取0,2π,π,32π,2π来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图象. 6.B解析:B【分析】由已知得到(2)()f x f x +=,即得函数的周期是2,把12(log 23)f 进行变形得到223()16f log -, 由223(0,1)16log ∈满足()2x f x =,求出即可. 【详解】(2)()f x f x +=,所以函数的周期是2.根据对数函数的图象可知12log 230<,且122log 23log 23=-;奇函数()f x 满足(2)()f x f x +=和()()f x f x -=-则2312222223(log 23)(log )(log 23)(log 234)()16f f f f f log =-=-=--=-, 因为223(0,1)16log ∈ 2231622323()21616log f log ∴-=-=-,故选:B . 【点睛】考查学生应用函数奇偶性的能力,函数的周期性的掌握能力,以及运用对数的运算性质能力.7.B解析:B 【分析】求出弦长,再求出圆的半径,然后利用三角形面积求解. 【详解】如图,由题意8CD =,弓琖ACB 的面积为128,1(8)81282AB ⨯+⨯=,24AB =, 设所在圆半径为R ,即OA OB R ==,则22224(8)2R R ⎛⎫=-+ ⎪⎝⎭,解得13R =, 5OD =,由211sin 22AB OD OA AOB ⨯=∠得 2245120sin 13169AOB ⨯∠==. 故选:B .【点睛】关键点点睛:本题考查扇形与弓形的的有关计算问题,解题关键是读懂题意,在读懂题意基础上求出弦长AB ,然后求得半径R ,从而可解决扇形中的所有问题.8.D解析:D 【分析】利用奇函数的性质判断A ,分别求3f π⎛⎫⎪⎝⎭和23f π⎛⎫⎪⎝⎭判断大小,取特殊值验证的方法判断C ,分区间计算一个周期内的最小值,判断选项D 。
高中数学数学必修四第一章三角函数单元测试题__北师大版

高中数学必修四第一章三角函数一、选择题(60分)1.将-300o化为弧度为( ) A .-43π;B .-53π;C .-76π;D .-74π; 2.如果点)cos 2,cos (sin θθθP 位于第三象限,那么角θ所在象限是( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3.下列选项中叙述正确的是 ( )A .三角形的内角是第一象限角或第二象限角B .锐角是第一象限的角C .第二象限的角比第一象限的角大D .终边不同的角同一三角函数值不相等 4.下列函数中为偶函数的是( )A .sin ||y x =B .2sin y x =C .sin y x =-D .sin 1y x =+ 5已知函数sin()y A x B ωϕ=++的一部分图象如右图所示,如果0,0,||2A πωϕ>><,则( )C.6πϕ=A.4=AB.1ω=6.函数3sin(2)6y x π=+的单调递减区间( )A5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦()k Z ∈B .511,1212k k ππππ⎡⎤++⎢⎥⎣⎦()k Z ∈C .,36k k ππππ⎡⎤-+⎢⎥⎣⎦()k Z ∈D .2,63k k ππππ⎡⎤++⎢⎥⎣⎦()k Z ∈7.已知α是三角形的一个内角,且32cos sin =+αα,则这个三角形( ) A .锐角三角形 B .钝角三角形C .不等腰的直角三角形D .等腰直角三角形8.)2cos()2sin(21++-ππ等于 ( )A .sin2-cos2B .cos2-sin2C .±(sin2-cos2)D .sin2+cos2 9.若角α的终边落在直线y =2x 上,则sin α的值为( ) A. 15±B. 55±C. 255± D. 12± 10.函数y=cos 2x –3cosx+2的最小值是 () A .2B .0C .41D .611.如果α在第三象限,则2α必定在()A .第一或第二象限B .第一或第三象限C .第三或第四象限D .第二或第四象 12.已知函数)sin(φϖ+=x A y 在同一周期内,当3π=x 时有最大值2,当x=0时有最小值-2,那么函数的解析式为( )A .x y 23sin2= B .)23sin(2π+=x y C .)23sin(2π-=x y D .x y 3sin 21=二.填空题(20分)14、已知角α的终边经过点P(3,3),则与α终边相同的角的集合是______ 13.1tan 、2tan 、3tan 的大小顺序是14.函数()lg 1tan y x =-的定义域是 .16.函数sin(2)6y x π=-+的单调递减区间是 。
人教版高一数学必修四测试题(含详细答案)

高一数学试题(必修4)(特别适合按14523顺序的省份)必修4 第一章三角函数(1)一、选择题:1.已知A={第一象限角},B={锐角},C={小于90°的角},那么A、B、C关系是()A.B=A∩C B.B∪C=C C.AC D.A=B=C2 等于()A B C D3.已知的值为()A.-2 B.2 C.D.-4.下列函数中,最小正周期为π的偶函数是()A.y=sin2xB.y=cos C .sin2x+cos2x D. y=5 若角的终边上有一点,则的值是()A B C D6.要得到函数y=cos()的图象,只需将y=sin的图象()A.向左平移个单位 B.同右平移个单位C.向左平移个单位 D.向右平移个单位7.若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向左平移个单位,沿y轴向下平移1个单位,得到函数y=sinx的图象则y=f(x)是()A.y= B.y=C.y=D.8. 函数y=sin(2x+)的图像的一条对轴方程是()A.x=-B. x=- C .x=D.x=9.若,则下列结论中一定成立的是()A. B. C. D.10.函数的图象()A.关于原点对称 B.关于点(-,0)对称 C.关于y轴对称 D.关于直线x=对称11.函数是()A.上是增函数 B.上是减函数C.上是减函数D.上是减函数12.函数的定义域是()A.B.C. D.二、填空题:13. 函数的最小值是 .14 与终边相同的最小正角是_______________15. 已知则 .16 若集合,,则=_______________________________________三、解答题:17.已知,且.a)求sinx、cosx、tanx的值.b)求sin3x – cos3x的值.18 已知,(1)求的值(2)求的值19. 已知α是第三角限的角,化简20.已知曲线上最高点为(2,),由此最高点到相邻的最低点间曲线与x轴交于一点(6,0),求函数解析式,并求函数取最小值x的值及单调区间必修4 第一章三角函数(2)一、选择题:1.已知,则化简的结果为()A. B. C. D. 以上都不对2.若角的终边过点(-3,-2),则( )A.sin tan>0 B.cos tan>0C.sin cos>0 D.sin cot>03 已知,,那么的值是()A B C D4.函数的图象的一条对称轴方程是()A. B. C. D.5.已知,,则tan2x= ( ) A. B. C. D.6.已知,则的值为()A. B. 1 C. D. 2 7.函数的最小正周期为()A.1 B. C. D.8.函数的单调递增区间是()A. B.C. D.9.函数,的最大值为()A.1 B. 2 C. D.10.要得到的图象只需将y=3sin2x的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位 D.向右平移个单位11.已知sin(+α)=,则sin(-α)值为()A. B. — C. D. —12.若,则()A. B. C. D.二、填空题13.函数的定义域是14.的振幅为初相为15.求值:=_______________16.把函数先向右平移个单位,然后向下平移2个单位后所得的函数解析式为________________________________三、解答题17 已知是关于的方程的两个实根,且,求的值18.已知函数,求:(1)函数y的最大值,最小值及最小正周期;(2)函数y的单调递增区间19.已知是方程的两根,且,求的值20.如下图为函数图像的一部分(1)求此函数的周期及最大值和最小值(2)求与这个函数图像关于直线对称的函数解析式必修4 第三章三角恒等变换(1)一、选择题:1.的值为 ( )A 0BC D2.,,,是第三象限角,则()A B C D3.设则的值是( )A B C D4. 已知,则的值为()A B C D5.都是锐角,且,,则的值是()A B C D6. 且则cos2x的值是()A B C D7.在中,的取值域范围是 ( )A B C D8. 已知等腰三角形顶角的余弦值等于,则这个三角形底角的正弦值为()A B C D9.要得到函数的图像,只需将的图像()A、向右平移个单位B、向右平移个单位C、向左平移个单位D、向左平移个单位10. 函数的图像的一条对称轴方程是()A、 B、 C、 D、11.若是一个三角形的最小内角,则函数的值域是( )A B C D12.在中,,则等于 ( )A B C D二、填空题:13.若是方程的两根,且则等于14. .在中,已知tanA ,tanB是方程的两个实根,则15. 已知,则的值为16. 关于函数,下列命题:①若存在,有时,成立;②在区间上是单调递增;③函数的图像关于点成中心对称图像;④将函数的图像向左平移个单位后将与的图像重合.其中正确的命题序号(注:把你认为正确的序号都填上)三、解答题:17. 化简18. 求的值.19. 已知α为第二象限角,且sinα=求的值.20.已知函数,求(1)函数的最小值及此时的的集合。
(压轴题)高中数学必修四第一章《三角函数》检测卷(包含答案解析)

一、选择题1.已知角α顶点在坐标原点,始边与x 轴非负半轴重合,终边过点()3,4P -,将α的终边逆时针旋转180︒,这时终边所对应的角是β,则cos β=( ) A .45-B .35C .35D .452.已知函数f (x )=2sinxsin (x+3φ)是奇函数,其中(0,)2πϕ∈ ,则函数g (x )=cos (2x-φ)的图象( ) A .关于点(,0)12π对称 B .关于轴512x π=-对称 C .可由函数f (x )的图象向右平移6π个单位得到 D .可由函数f (x )的图象向左平移3π个单位得到 3.函数()()12cos 20211f x x x π=++⎡⎤⎣⎦-在区间[]3,5-上所有零点的和等于( ) A .2B .4C .6D .84.如果一个函数在给定的区间上的零点个数恰好为8,则称该函数为“比心8中函数”.若函数()2sin()1f x x ωπ=-,(0)>ω是区间[0,1]上的“比心8中函数”,则ω的取值范围是( )A .4149,66⎡⎫⎪⎢⎣⎭B .4953,66⎡⎫⎪⎢⎣⎭C .3741,66⎡⎫⎪⎢⎣⎭D .[8,9)5.已知函数()()πsin 0,2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭图象相邻两条对称轴之间的距离为π2,将函数()y f x =的图象向左平移π6个单位后,得到的图象关于y 轴对称,那么函数()y f x =的图象( ) A .关于点π,012⎛⎫⎪⎝⎭对称 B .关于点π,012⎛⎫-⎪⎝⎭对称 C .关于直线π12x =对称 D .关于直线π12x =-对称6.使函数())cos(2)f x x x θθ=+++是偶函数,且在0,4⎡⎤⎢⎥⎣⎦π上是减函数的θ的一个值是( ) A .6π B .3π C .23π D .56π7.平面直角坐标系xOy 中,点()00,P x y 在单位圆O 上,设xOP α∠=,若5,36ππα⎛⎫∈ ⎪⎝⎭,且3sin 65πα⎛⎫+= ⎪⎝⎭,则0x 的值为A B C D 8.已知曲线1C :sin y x =,2C :cos 23y x π⎛⎫=- ⎪⎝⎭,则下面结论正确的是( )A .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CB .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移23π个单位长度,得到曲线2CC .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移12π个单位长度,得到曲线2CD .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移12π个单位长度,得到曲线2C9.已知1sin 34x π⎛⎫+= ⎪⎝⎭,则22sin sin 36x x ππ⎛⎫⎛⎫-+-=⎪ ⎪⎝⎭⎝⎭( )A .1B C .1916D .3410.已知函数()[][]sin cos cos sin f x x x =+,其中[]x 表示不超过实数x 的最大整数,则( )A .()f x 是奇函数B .π2π33f f ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭C .()f x 的一个周期是πD .()f x 的最小值小于011.675︒用弧度制表示为( ) A .114π B .134π C .154π D .174π 12.已知函数()sin()f x A x ωϕ=+(0A >,0>ω,0ϕπ≤≤)的部分图象如图所示,则()f x 的解析式是( )A .()2sin 6f x x π⎛⎫=+⎪⎝⎭B .()2sin 3f x x π⎛⎫=+⎪⎝⎭C .()2sin 26f x x π⎛⎫=+⎪⎝⎭D .2n 2)3(si f x x π⎛⎫=+⎪⎝⎭二、填空题13.将函数()sin (0)f x x ωω=>的图象向右平移12π个单位长度得到函数()y g x =的图象,若函数()g x 在区间0,2π⎡⎤⎢⎥⎣⎦上是单调递增函数,则实数ω的取值范围是__________.14.若函数()f x 为定义在R 上的偶函数,且在(0,)+∞内是增函数,又()20f =,则不等式sin ()0x f x ⋅>,[,]x ππ∈-的解集为_________.15.已知定义在R 上的奇函数()f x 满足()()20f x f x -+=,且当(]0,1x ∈时,()21log f x x=,若函数()()()sin F x f x x π=-在区间[]1,m -上有且仅有10个零点,则实数m 的取值范围是__________. 16.已知3cos 6απ⎛⎫-= ⎪⎝⎭,则54cos sin 63ππαα⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭的值为_____.17.如图,某公园要在一块圆心角为3π,半径为20m 的扇形草坪OAB 中修建一个内接矩形文化景观区域CDEF ,若//EF AB ,则文化景观区域面积的最大值为______2m .18.函数()3sin 23f x x π⎛⎫=- ⎪⎝⎭的图象为C ,以下结论中正确的是______(写出所有正确结论的编号).①图象C 关于直线1112π=x 对称; ②图象C 关于点2,03π⎛⎫⎪⎝⎭对称; ③函数()f x 在区间5,1212ππ⎛⎫- ⎪⎝⎭内是增函数;④由3sin 2y x =的图象向右平移3π个单位长度可以得到图象C . 19.已知函数f (x ),任意x 1,x 2∈,22ππ⎛⎫- ⎪⎝⎭(x 1≠x 2),给出下列结论:①f (x +π)=f (x );②f (-x )=f (x );③f (0)=1;④1212()()f x f x x x -->0;⑤1212()()22x x f x f x f ++⎛⎫> ⎪⎝⎭.当()tan f x x =时,正确结论的序号为________.20.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数()()cos[6]1,2,...,126y A x B x π=-+=来表示.已知6月份的平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温为______℃. 三、解答题21.已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>><⎪⎝⎭的部分图象如图所示.(1)求()f x 的解析式;(2)将()y f x =图象上所有点的横坐标缩小到原来的12倍(纵坐标不变),再将图象上所有点的纵坐标扩大到原来的2倍(横坐标不变),最后向下平移2个单位得到()y g x =图象,求函数()y g x =的解析式及在R 上的对称中心坐标. 22.已知函数()2sin()0,02f x x πωϕωϕ⎛⎫=+><< ⎪⎝⎭的图象与直线2y =的相邻两个交点间的距离为2π,且________.在①函数6f x π⎛⎫+⎪⎝⎭为偶函数;②33f π⎛⎫=⎪⎝⎭③x R ∀∈,()6f x f π⎛⎫≤⎪⎝⎭;这三个条件中任选一个,补充在上面问题中,并解答. (1)求函数()f x 的解析式;(2)求函数()f x 在[]0,π上的单调递增区间. 23.已知()442sin cos cossin f x x x x x ωωωω=+-(其中ω>0).(1)若()f x 的最小正周期是π,求ω的值及此时()f x 的对称中心; (2)若将()y f x =的图像向左平移4π个单位,再将所得的图像纵坐标不变,横坐标缩小为原来的12,得到()g x 的图像,若y g x 在0,8π⎡⎤⎢⎥⎣⎦上单调递减,求ω的取值范围.24.已知函数1()sin 2126f x x a π⎛⎫=+++ ⎪⎝⎭(其中a 为常数). (1)求()f x 的单调减区间; (2)若0,2x π⎡⎤∈⎢⎥⎣⎦时,()f x 的最小值为2,求a 的值.25.已知函数2()22cos 1f x x x =+-.(I )求函数()f x 的最小正周期; (II )求函数()f x 的单调增区间; (III )当0,2x π⎡⎤∈⎢⎥⎣⎦时,求函数()f x 的最小值. 26.已知函数()2sin 213f x x π⎛⎫=++ ⎪⎝⎭,x ∈R . (Ⅰ)求函数()f x 的单调递增区间;(Ⅱ)求()f x 在区间06,π⎡⎤⎢⎥⎣⎦上的最大值与最小值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】先根据已知条件求解出cos α的值,然后根据,αβ之间的关系结合诱导公式求解出cos β的值.【详解】 因为3cos 5α==,且180βα=+︒, 所以()3cos cos 180cos 5βαα=+︒=-=-, 故选:B. 【点睛】结论点睛:三角函数定义有如下推广:设点(),P x y 为角α终边上任意一点且不与原点重合,r OP =,则()sin ,cos ,tan 0y x yx r r xααα===≠. 2.B解析:B 【分析】利用三角函数的奇偶性求得φ,再利用三角函数的图象对称性、函数y=Asin (ωx+φ)的图象变换规律,判断各个选项是否正确,从而得出结论. 【详解】函数f (x )=2sinxsin (x+3φ)是奇函数,其中0,2πϕ⎛⎫∈ ⎪⎝⎭, ∴y=2sinxsin (x+3φ)是奇函数,∴3φ=2π,φ=6π,则函数g (x )=cos (2x ﹣φ)=cos (2x ﹣6π). 当12x π=时,206x π-=,112g π⎛⎫= ⎪⎝⎭,则函数不关于点,012π⎛⎫⎪⎝⎭对称,选项A 错误; 当512x π=-时,26x ππ-=-,则函数关于直线512x π=-对称,选项B 正确;函数()2sin sin 2sin cos sin 22f x x x x x x π⎛⎫=+== ⎪⎝⎭, 其图像向右平移6π个单位的解析式为sin 2sin 2sin 263y x x x ππ⎡⎤⎛⎫⎛⎫==-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项C 错误; 其图像向左平移3π个单位的解析式为2sin 2sin 2sin 233y x x x ππ⎡⎤⎛⎫⎛⎫==+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项D 错误; 故选B. 【点睛】本题主要考查三角函数的奇偶性、对称性,函数y=Asin (ωx+φ)的图象变换规律,属于中档题.函数()sin y A x ωϕ=+(A >0,ω>0)的性质:(1)奇偶性:=k ϕπ ,k Z ∈时,函数()sin y A x ωϕ=+为奇函数;=2k πϕπ+,k Z ∈时,函数()sin y A x ωϕ=+为偶函数.;(2)周期性:()sin y A x ωϕ=+存在周期性,其最小正周期为T =2πω;(3)单调性:根据y =sin t 和t =x ωϕ+的单调性来研究,由+22,22k x k k Z πππωϕπ-≤+≤+∈得单调增区间;由3+22,22k x k k Z πππωϕπ≤+≤+∈得单调减区间;(4)对称性:利用y =sin x 的对称中心为()(),0k k Z π∈求解,令()x k k ωϕπ+=∈Z ,求得x ;利用y =sin x 的对称轴为()2x k k Z ππ=+∈求解,令()+2x k k πωϕπ+=∈Z ,得其对称轴.3.D解析:D 【分析】由图可得函数的零点就是11y x =-和2cos y x π=交点的横坐标,画出函数图象,可得出()f x 在[]3,5-有8个零点,且关于1x =对称,即可求出.【详解】()()112cos 20212cos 11f x x x x x ππ=++=-⎡⎤⎣⎦--, 令()0f x =,则12cos 1x x π=-, 则函数的零点就是11y x =-和2cos y x π=交点的横坐标, 可得11y x =-和2cos y x π=的函数图象都关于1x =对称,则交点也关于1x =对称, 画出两个函数的图象,观察图象可知,11y x =-和2cos y x π=在[]3,5-有8个交点, 即()f x 有8个零点,且关于1x =对称,故所有零点的和为428⨯=. 故选:D. 【点睛】本题考查求函数的零点之和,解题的关键是将题目化为找11y x =-和2cos y x π=交点的横坐标,从而通过函数图象求解.4.A解析:A 【分析】根据题意问题转化为方程1sin()2x ωπ=在区间[0,1]上有8个解,根据正弦函数的图像与性质可求得1sin()2x ωπ=在区间[0,1]上取第8个解为416x ω=、第9个解为496x ω=,则4149166ωω≤<,解不等式即可. 【详解】根据题意,函数()2sin()1f x x ωπ=-,(0)>ω是区间[0,1]上零点个数为8,即方程1sin()2x ωπ=在区间[0,1]上有8个解, ∴26x k πωππ=+或52,6x k k Z πωππ=+∈, 当0k =时,1sin()2x ωπ=在区间[0,1]上取第1个解16x ω=,取第2个解56x ω=; 当1k =时,1sin()2x ωπ=在区间[0,1]上取第3个解136x ω=,取第4个解176x ω=; 当3k =时,1sin()2x ωπ=在区间[0,1]上取第7个解376x ω=,取第8个解416x ω=;当4k =时,1sin()2x ωπ=在区间[0,1]上取第9个解496x ω=. 则4149166ωω≤<,解得414966ω≤<. 故选:A5.B解析:B 【分析】由相邻两条对称轴之间的距离为2π,可知22T π=,从而可求出2ω=,再由()y f x =的图像向左平移6π个单位后,得到的图象关于y 轴对称,可得sin 13πϕ⎛⎫+=± ⎪⎝⎭,从而可求出ϕ的值,然后逐个分析各个选项即可 【详解】因为相邻两条对称轴的距离为2π,故22T π=,T π=,从而2ω=. 设将()f x 的图像向左平移6π单位后,所得图像对应的解析式为()g x , 则()sin 23g x x πϕ⎛⎫=++ ⎪⎝⎭,因()g x 的图像关于y 轴对称,故(0)1g =±, 所以sin 13πϕ⎛⎫+=± ⎪⎝⎭,,32k k Z ππϕπ+=+∈,所以,6k k Z πϕπ=+∈, 因||2ϕπ<,所以6π=ϕ. 又()sin 26f x x π⎛⎫=+ ⎪⎝⎭,令2,62x k k Z πππ+=+∈,故对称轴为直线,26k x k Z ππ=+∈,所以C ,D 错误; 令2,6x k k ππ+=∈Z ,故,212k x k Z ππ=-∈,所以对称中心为,0,212k k Z ππ⎛⎫-∈ ⎪⎝⎭,所以A 错误,B 正确. 故选:B 【点睛】此题考查了三角函数的图像变换和三角函数的图像和性质,属于基础题.6.B解析:B 【解析】1())cos(2)2()cos(2))2sin(2)226f x x x x x x πθθθθθ=+++=+++=++,由于()f x 为偶函数,则(0)2sin()26f πθ=+=±,sin()1,662k πππθθπ+=±+=+,3k πθπ=+,当0k =时,3πθ=,()2sin(2)2sin(2)362f x x x πππ=++=+2cos2x =,当[0,]4x π∈时,2[0,]2x π∈,()2cos2f x x =为减函数,符合题意,所以选B.7.A解析:A 【分析】由题意根据三角函数定义可知0x cos α=,先根据角α的取值范围求出6πα⎛⎫+ ⎪⎝⎭的取值范围继而求出4cos 65πα⎛⎫+=- ⎪⎝⎭,再通过凑角求cos α. 【详解】5,36ππα⎛⎫∈ ⎪⎝⎭,则26ππαπ<+<,则由3sin 65πα⎛⎫+= ⎪⎝⎭,得4cos 65πα⎛⎫+=- ⎪⎝⎭.由点()00,P x y 在单位圆O 上,设xOP α∠=,则0x cos α=. 又cos αcos 66ππα⎡⎤⎛⎫=+-⎪⎢⎥⎝⎭⎣⎦cos sin 6666cos sin ππππαα⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭431552=-+⨯=故0x =.选A. 【点睛】本题考查三角函数定义及三角恒等变换的简单应用.解题中注意所求角的取值范围.由配凑法根据已知角构造所求角进行求解是三角恒等变换中常用的解题技巧.8.C解析:C 【分析】由题意利用诱导公式得1sin cos :2C y x x π⎛⎫==- ⎪⎝⎭,根据函数()cos y A x ωϕ=+的图象变换规律,得出结论. 【详解】已知曲线1sin cos :2C y x x π⎛⎫==-⎪⎝⎭,2cos 23:C y x π⎛⎫=-⎪⎝⎭, ∴把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,可得cos 22y x π⎛⎫=- ⎪⎝⎭的图象,再把得到的曲线向左平移 12π个单位长度,得到曲线2cos 2cos 263:2C x x πππ⎛⎫⎛⎫+-=- ⎪ ⎪⎝⎭⎝⎭的图象,故选C .【点睛】本题主要考查函数()cos y A x ωϕ=+的图象变换规律,属于基础题.9.C解析:C 【分析】由诱导公式求得cos 6x π⎛⎫- ⎪⎝⎭,然后再由平方关系和诱导公式计算. 【详解】 由已知1cos cos sin 62334x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 222115sin 1cos 166416x x ππ⎛⎫⎛⎫⎛⎫-=--=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,21sin sin cos 32664x x x ππππ⎛⎫⎛⎫⎛⎫-=+-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以2211519sin sin 3641616x x ππ⎛⎫⎛⎫-+-=+= ⎪ ⎪⎝⎭⎝⎭. 故选:C . 【点睛】关键点点睛:本题考查三角函数的求值.解题关键是确定“已知角”和“未知角”的关系,选用适当的公式进行变形求值.本题中首先利用诱导公式得出cos 6x π⎛⎫- ⎪⎝⎭,然后再用诱导公式得出2sin 3x π⎛⎫-⎪⎝⎭,用平方关系得出2sin 6x π⎛⎫- ⎪⎝⎭,这样求解比较方便.10.D解析:D 【分析】利用奇函数的性质判断A ,分别求3f π⎛⎫ ⎪⎝⎭和23f π⎛⎫ ⎪⎝⎭判断大小,取特殊值验证的方法判断C ,分区间计算一个周期内的最小值,判断选项D 。
完整版)高中三角函数测试题及答案

完整版)高中三角函数测试题及答案高一数学必修4第一章三角函数单元测试班级:__________ 姓名:__________ 座号:__________评分:__________一、选择题:共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
(48分)1、已知$A=\{\text{第一象限角}\}$,$B=\{\text{锐角}\}$,$C=\{\text{小于90°的角}\}$,那么$A$、$B$、$C$ 关系是()A.$B=A\cap C$B.$B\cup C=C$C.$A\cap D$D.$A=B=C$2、将分针拨慢5分钟,则分钟转过的弧度数是A。
$\frac{\pi}{3}\sin\alpha-\frac{2}{3}\cos\alpha$ B。
$-\frac{\pi}{3}$C。
$\frac{\pi}{6}$D。
$-\frac{\pi}{6}$3、已知 $\tan\alpha=-5$,那么 $\tan\alpha$ 的值为A。
2B。
$\frac{1}{6164}$C。
$-\frac{1}{6164}$D。
$-\frac{2}{3}$4、已知角 $\alpha$ 的余弦线是单位长度的有向线段,那么角 $\alpha$ 的终边()A。
在 $x$ 轴上B。
在直线 $y=x$ 上C。
在 $y$ 轴上D。
在直线 $y=x$ 或 $y=-x$ 上5、若 $f(\cos x)=\cos 2x$,则 $f(\sin 15^\circ)$ 等于()A。
$-\frac{2}{3}$B。
$\frac{3}{2}$C。
$\frac{1}{2}$D。
$-\frac{1}{2}$6、要得到 $y=3\sin(2x+\frac{\pi}{4})$ 的图象只需将$y=3\sin 2x$ 的图象A。
向左平移 $\frac{\pi}{4}$ 个单位B。
向右平移 $\frac{\pi}{4}$ 个单位C。
必修4第一章三角函数单元基础测试题及答案

1
A. 5
1
B. 4
13
C. 18
13
D. 22
11.sin1,cos1,tan1 的大小关系是(
)
A.tan1>sin1>cos1
B.tan1>cos1>sin1
C。cos1>sin1>tan1
D.sin1〉cos1>tan1
12.已知函数 f (x)=f (x),且当 x( , ) 时,f (x)=x+sinx,设 a=f (1),b=f
4 3
3、已知 cosθ=cos30°,则θ等于( )
A. 30°
B. k·360°+30°(k∈Z)
C。 k·360°±30°(k∈Z)
D. k·180°+30°(k∈Z)
4、若 cos 0,且sin 2 0,则角 的终边所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限( )
18.解、∵ tan 3 ∴ cos 0
(4sin 2 cos ) 1∴Fra bibliotek式=cos
(5cos 3sin ) 1
cos
= 4 tan 2
5 3 tan
= 432
5 33
=5
7
19. 解: f (x) 2 cos x(sin x cos x) 1 sin 2x cos 2x 2 sin(2x )
5、函数
的递增区间是(
)
y 5sin(2x )
6、函数
6 图象的一条对称轴方程是( )
( A)
x
12
;
(B) x 0;
(C)
x
6
;
(D)
x
完整版必修4第一章三角函数单元基础测试题及答案

三角函数数学试卷?600sin的值是(、)一、选择题13311;?;;?;)D((CA))B)((2222 3??cos),P(3y???tan5(终边上一点,)2 、为,则3344???(A)(B)(C)(D)3344θθ等于(°,则)、已知cos =cos303A.kk∈Z) °(·360°+3030°B.kkkk∈(Z)°+·180360°±30°(30∈Z) D. C. °·???则角0sin2,cos??0,且的终边所在象限是、若4( )A.第一象限 B.第二象限 C.第三象限 D.第四象限()( )5、函数的递增区间是?)?sin(2xy?56、函数6)图象的一条对称轴方程是(???;?;x?x?;x?))(A()D(C(B);0x?36127、函数的图象向左平移个单位,再将图象上各点的横坐标压缩为原来的,那么所得图象的函数表达式为( )f(x)?|tanx|的周期为、函数( )8????224 D. C. B. A. 31???????sincos?sincos????cos(?)??44( 9、锐角),,则满足,115115??816168 B. D. C.A.??3242254β-α+))=), 那么10、已知tan(α+βtan()=的值是(,tan(131311 224518. D B CA...).sin1,cos1,tan1的大小关系是(11A.tan1>sin1>cos1B.tan1>cos1>sin1C.cos1>sin1>tan1D.sin1>cos1>tan1??f f bf f xxxxaf x=(??时,),且当=(,)=设12.已知函数+sin((1),)=)(??,x 22f c(3),则( (2),)=c<a<b a<b<cc<b<a b<c<a D. C.A. B.二、填空题??171300, 。
(好题)高中数学必修四第一章《三角函数》测试卷(包含答案解析)(1)

一、选择题1.若函数()sin 2f x x =与()2cos g x x =都在区间(),a b 上单调递减,则b a -的最大值是( ) A .π4B .π3C .π2D .2π32.已知函数f (x )=2sinxsin (x+3φ)是奇函数,其中(0,)2πϕ∈ ,则函数g (x )=cos (2x-φ)的图象( ) A .关于点(,0)12π对称 B .关于轴512x π=-对称 C .可由函数f (x )的图象向右平移6π个单位得到 D .可由函数f (x )的图象向左平移3π个单位得到 3.将函数()sin 25f x x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度后得到函数()y g x =的图象,对于函数()y g x =有以下四个判断: ①该函数的解析式为2sin 210y x π⎛⎫=+ ⎪⎝⎭; ②该函数图象关于点,02π⎛⎫⎪⎝⎭对称; ③该函数在区间,44ππ⎡⎤-⎢⎥⎣⎦上单调递增;④该函数在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增.其中,正确判断的序号是( ) A .②③B .①②C .②④D .③④4.将函数sin()y x ϕ=+的图像上所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得图像向左平移12π个单位后得到的函数图像关于原点中心对称,则sin 2ϕ=( )A .12-B .12C .D .25.已知函数()cos2sin 2f x x x =-,将()y f x =的图象向左平移a (0a >)个单位长度可以得到一个奇函数的图象,将()y f x =的图象向右平移b (0b >)个单位长度可以得到一个偶函数的图象,则a b -的最小值等于( )A .0B .8π C .4π D .2π 6.声音是由物体振动产生的声波.我们听到的每个音都是由纯音合成的,纯音的数学模型是函数sin y A wt =.音有四要素:音调、响度、音长和音色,它们都与函数sin y A wt =中的参数有关,比如:响度与振幅有关,振幅越大响度越大,振幅越小响度越小;音调与频率有关,频率低的声音低沉,频率高的声音尖利.像我们平时听到乐音不只是一个音在响,而是许多音的结合,称为复合音.我们听到的声音函数是111sin sin 2sin 3sin 4234y x x x x =++++.结合上述材料及所学知识,你认为下列说法中正确的有( ).A .函数1111sin sin 2sin3sin 4sin100234100y x x x x x =+++++不具有奇偶性; B .函数111()sin sin 2sin3sin 4234f x x x x x =+++在区间,1616ππ⎡⎤-⎢⎥⎣⎦上单调递增; C .若某声音甲对应函数近似为111()sin sin 2sin3sin 4234f x x x x x =+++,则声音甲的响度一定比纯音1()sin 22h x x =响度大; D .若某声音甲对应函数近似为1()sin sin 22g x x x =+,则声音甲一定比纯音1()sin33h x x =更低沉.7.下列函数中,既是偶函数,又在(),0-∞上是增函数的是( ) A .()22xxf x -=- B .()23f x x =-C .()2ln =-f x xD .()cos3=f x x x8.设函数()()sin 16f x x N πωω*⎛⎫=-+∈ ⎪⎝⎭在55,126ππ⎡⎤⎢⎥⎣⎦上单调递减,则下述结论: ①()f x 关于,012π⎛⎫⎪⎝⎭中心对称;②()f x 关于直线23x π=轴对称;③()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的值域为30,2⎡⎤⎢⎥⎣⎦;④方程()1f x =在[]0,2π有4个不相同的根. 其中正确结论的编号是( ) A .①②B .②③C .②④D .③④9.已知函数()sin()f x x ωϕ=+,具有以下性质:(1)对任意的x ∈R ,都有()()12()f x f x f x ≤≤,且12x x -的最小值为2π; (2)6f x π⎛⎫+⎪⎝⎭为奇函数;(3)任取12,0,4x x π⎡⎤∈⎢⎥⎣⎦,当12x x ≠时,都有()()()()11222112x f x x f x x f x x f x +>+. 同时满足上述性质的一个函数可以是( ) A .4sin 23y x π⎛⎫=- ⎪⎝⎭ B .sin 23y x π⎛⎫=- ⎪⎝⎭C .2sin 23y x π⎛⎫=+⎪⎝⎭D .sin 26y x π⎛⎫=+⎪⎝⎭10.已知函数()tan()0,2f x x πωϕωϕ⎛⎫=+≠< ⎪⎝⎭,点2,03π⎛⎫⎪⎝⎭和7,06π⎛⎫⎪⎝⎭是其相邻的两个对称中心,且在区间54,63ππ⎛⎫⎪⎝⎭内单调递减,则ϕ=( ) A .6π B .6π-C .3π D .3π-11.函数()sin ln ||f x x x =⋅的部分图象大致为( )A .B .C .D .12.函数22y cos x sinx =- 的最大值与最小值分别为( ) A .3,-1 B .3,-2 C .2,-1D .2,-2二、填空题13.对任意0,4πϕ⎡⎤∈⎢⎥⎣⎦,函数()sin()f x x ωϕ=+在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递增,则实数ω的取值范围是________.14.已知函数()sin()0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,关于函数()y f x =有下列结论:①图象关于点,03π⎛⎫⎪⎝⎭对称; ②单调递减区间为2,,63k k k ππππ⎛⎫++∈ ⎪⎝⎭Z ; ③若()f x a =,则cos 32a x πω⎛⎫-= ⎪⎝⎭; ④2()()log g x f x x =-有4个零点. 则其中结论正确的有____________(填上所有正确结论的序号)15.2020年是苏颂诞辰1000周年,苏颂发明的水运仪象台被誉为世界上最早的天文钟.水运仪象台的原动轮叫枢轮,是一个直径约3.4米的水轮,它转一圈需要30分钟.如图,当点P 从枢轮最高处随枢轮开始转动时,退水壶内水面位于枢轮中心下方1.19米处.此时打开退水壶出水口,壶内水位以每分钟0.017米的速度下降,将枢轮转动视为匀速圆周运动,则点P 至少经过______分钟(结果取整数)进入水中.(参考数据:cos0.9815π≈,2cos0.9115π≈,cos 0.815π≈)16.函数()2sin(2),0,32f x x x ππ⎡⎤=-∈⎢⎥⎣⎦的单调减区间___________ 17.已知()()sin 03f x x πωϕω⎛⎫=++> ⎪⎝⎭同时满足下列三个条件:①T π=;②3y f x π⎛⎫=-⎪⎝⎭是奇函数;③()06f f π⎛⎫<⎪⎝⎭.若()f x 在[)0,t 上没有最小值,则实数t 的取值范围是___________.18.某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60和30,第一排和最后一排的距离为106米(如图所示),旗杆底部与第一排在一个水平面上,若国歌长度约为50秒,升旗手应以__________(米 /秒)的速度匀速升旗.19.已知函数()2sin()(0)f x x ωϕω=+>满足()24f π=,()0f π=,且()f x 在区间(,)43ππ上单调,则ω的值有_________个.20.关于函数()4sin(2)(),3f x x x R π=+∈有下列命题:①由12()()0f x f x ==可得12x x -必是π的整数倍;②()y f x =的图象关于点(,0)6π-对称;③()y f x =的表达式可改写为4cos(2);6y x π=-④()y f x =的图象关于直线6x π=-对称.其中正确命题的序号是_________.三、解答题21.在①将函数f (x )图象向右平移12π个单位所得图象关于y 轴对称:②函数6y f x π⎛⎫=+ ⎪⎝⎭是奇函数;③当712x π=时,函数6y f x π⎛⎫=- ⎪⎝⎭取得最大值.三个中任选一个,补充在题干中的横线处,然后解答问题.题干:已知函数()2sin()f x x ωϕ=+,其中0,||2πωϕ><,其图象相邻的对称中心之间的距离为2π,___________. (1)求函数y =f (x )的解析式;(2)求函数y =f (x )在,22ππ⎡⎤-⎢⎥⎣⎦上的最小值,并写出取得最小值时x 的值. 注:如果选择多个条件分别解答,按第一个解答计分.22.如图,在矩形OABC 中,22OA OC ==,将矩形OABC 绕着顶点O 逆时针旋转,得到矩形OA B C ''',记旋转的角度为θ,0,2πθ⎛⎫∈ ⎪⎝⎭旋转前后两个矩形公共部分的面积为()S θ.(1)求3S π⎛⎫⎪⎝⎭; (2)若()728S θ=,求sin θ. 23.为整治校园环境,设计如图所示的平行四边形绿地ABCD ,在绿地中种植两块相同的扇形花卉景观,两扇形的边(圆心分别为A 和C )均落在平行四边形ABCD 的边上,圆弧均与BD 相切,其中扇形的圆心角为120°,扇形的半径为12米.(1)求两块花卉景观扇形的面积;(2)记BDA θ∠=,求平行四边形绿地ABCD 占地面积S 关于θ的函数解析式,并求面积S 的最小值.24.下图是函数()()sin()0,0f x x ωϕωϕπ=+><<的部分图象.(1)求ϕ的值及()f x 单调递增区间.(2)若()f x 的图象横坐标不变,纵坐标扩大为原来的2倍,然后再将所得图象向右平移3π个单位,最后向上平移1个单位,得到函数()g x 的图象,若()g x 在[0,](0)b b >上恰有10个零点,求b 的取值范围.25.长春某日气温()C y ︒是时间t (024t ≤≤,单位:小时)的函数,下面是某天不同时间的气温预报数据: t (时)3 6 9 12 15 18 21 24 ()C y ︒ 15.714.015.720.024.226.024.220.015.7cos()y A t b ωϕ=++的图象.(1)根据以上数据,试求cos()y A t b ωϕ=++(0A >,0>ω,0ϕπ<<)的表达式; (2)大数据统计显示,某种特殊商品在室外销售可获3倍于室内销售的利润,但对室外温度要求是气温不能低于23C ︒.根据(1)中所得模型,一个24小时营业的商家想获得最大利润,应在什么时间段(用区间表示)将该种商品放在室外销售,单日室外销售时间最长不能超过多长时间?(忽略商品搬运时间及其它非主要因素,理想状态下哦,奥力给!)26.如图,在平面直角坐标系xOy 中,31,22A ⎛⎫⎪ ⎪⎝⎭为单位圆上一点,射线OA 绕点O 按逆时针方向旋转θ后交单位圆于点B ,点B 的纵坐标y 关于θ的函数为()y fθ=.(1)求函数()y f θ=的解析式,并求223f f ππ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭; (2)若1()3f θ=,求7cos sin 36ππθθ⎛⎫⎛⎫--+⎪ ⎪⎝⎭⎝⎭的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】根据题意求出(),()f x g x 原点附近的单调递减区间,根据递减区间分析可得max 3π4b =,min π4a =,相减即可. 【详解】 解:由题意函数()sin 2f x x =在π3π,44⎛⎫⎪⎝⎭上单调递减,函数()2cos g x x =在()0,π上单调递减, 所以则max 3π4b =,min π4a =,所以b a -的最大值为3πππ442-=. 故选:C. 【点睛】求三角函数单调区间的2种方法:(1)代换法:就是将比较复杂的三角函数处理后的整体当作一个角u (或t ),利用基本三角函数的单调性来求所要求的三角函数的单调区间;(2)图象法:函数的单调性表现在图象上是从左到右,图象上升趋势的区间为单调递增区间,图象下降趋势的区间为单调递减区间,画出三角函数的图象,结合图象易求它的单调区间.2.B解析:B 【分析】利用三角函数的奇偶性求得φ,再利用三角函数的图象对称性、函数y=Asin (ωx+φ)的图象变换规律,判断各个选项是否正确,从而得出结论. 【详解】函数f (x )=2sinxsin (x+3φ)是奇函数,其中0,2πϕ⎛⎫∈ ⎪⎝⎭, ∴y=2sinxsin (x+3φ)是奇函数,∴3φ=2π,φ=6π,则函数g (x )=cos (2x ﹣φ)=cos (2x ﹣6π). 当12x π=时,206x π-=,112g π⎛⎫= ⎪⎝⎭,则函数不关于点,012π⎛⎫ ⎪⎝⎭对称,选项A 错误;当512x π=-时,26x ππ-=-,则函数关于直线512x π=-对称,选项B 正确;函数()2sin sin 2sin cos sin 22f x x x x x x π⎛⎫=+== ⎪⎝⎭, 其图像向右平移6π个单位的解析式为sin 2sin 2sin 263y x x x ππ⎡⎤⎛⎫⎛⎫==-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项C 错误; 其图像向左平移3π个单位的解析式为2sin 2sin 2sin 233y x x x ππ⎡⎤⎛⎫⎛⎫==+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项D 错误; 故选B. 【点睛】本题主要考查三角函数的奇偶性、对称性,函数y=Asin (ωx+φ)的图象变换规律,属于中档题.函数()sin y A x ωϕ=+(A >0,ω>0)的性质:(1)奇偶性:=k ϕπ ,k Z ∈时,函数()sin y A x ωϕ=+为奇函数;=2k πϕπ+,k Z ∈时,函数()sin y A x ωϕ=+为偶函数.;(2)周期性:()sin y A x ωϕ=+存在周期性,其最小正周期为T =2πω;(3)单调性:根据y =sin t 和t =x ωϕ+的单调性来研究,由+22,22k x k k Z πππωϕπ-≤+≤+∈得单调增区间;由3+22,22k x k k Z πππωϕπ≤+≤+∈得单调减区间;(4)对称性:利用y =sin x 的对称中心为()(),0k k Z π∈求解,令()x k k ωϕπ+=∈Z ,求得x ;利用y =sin x 的对称轴为()2x k k Z ππ=+∈求解,令()+2x k k πωϕπ+=∈Z ,得其对称轴.3.A解析:A 【分析】根据函数平移变换得sin 2y x =,再根据正弦函数的性质依次讨论即可得答案. 【详解】解:由函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象平移变换的性质可知:将sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后 解析式为sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,选项①错误; 令2x k =π,k Z ∈,求得2k x =π,k Z ∈, 故函数的图象关于点,02k ⎛⎫⎪⎝⎭π对称, 令1k =,故函数的图象关于点,02π⎛⎫⎪⎝⎭对称,选项②正确; 则函数的单调递增区间满足:222()22k x k k Z ππππ-≤≤+∈,即()44k x k k Z ππππ-≤≤+∈,令0k =可得函数的一个单调递增区间为,44ππ⎡⎤-⎢⎥⎣⎦,选项③正确,④错误. 故选:A. 【点睛】本题考查三角函数平移变换,正弦型函数的单调区间,对称中心等,考查运算求解能力,解题的易错点在于平移变换时,当1ω≠时,须将ω提出,平移只针对x 进行平移,具体的在本题中,sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后得sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,而不是sin 2sin 251010y x x πππ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,是中档题. 4.C解析:C 【分析】先根据条件写出图像变换后的函数解析式,然后根据图像关于原点中心对称可知函数为奇函数,由此得到ϕ的表示并计算出sin 2ϕ的结果. 【详解】因为变换平移后得到函数sin 26y x πϕ⎛⎫=++ ⎪⎝⎭,由条件可知sin 26y x πϕ⎛⎫=++ ⎪⎝⎭为奇函数,所以6k πϕπ+=,sin 2sin 2sin 332k ππϕπ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭故选C . 【点睛】本题考查三角函数的图像变换以及根据函数奇偶性判断参数值,难度一般.正弦型函数()()sin f x A x =+ωϕ为奇函数时,k k Z ϕπ=∈,为偶函数时,2k k Z πϕπ=+∈.5.A解析:A 【分析】先整理函数,再根据平移后函数的奇偶性得到a ,b 的值,即可得结果. 【详解】解:函数()cos 2sin 224f x x x x π⎛⎫=-=+ ⎪⎝⎭,函数()24f x x π⎛⎫=+ ⎪⎝⎭的图象向左平移a 个单位得到()224g x x a π⎛⎫=++ ⎪⎝⎭,又因为函数为奇函数,则242a k πππ+=+(k Z ∈),整理得28k a ππ=+(k Z ∈);函数()24f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移b 个单位得到()224h x x b π⎛⎫=-+ ⎪⎝⎭,由于得到的函数的图象为偶函数,2=4b k ππ-+-,=,()82k b k Z ππ+∈;当0k =时,min 0a b -= 故选:A. 【点睛】本题考查了三角函数的平移变换和奇偶性,属于中档题.6.B解析:B 【分析】A.结合奇偶性的定义判断即可B.用正弦型函数的单调性作出判断 CD 可取特值说明 【详解】A. ()1111sin sin 2sin 3sin 4sin100234100f x x x x x x =+++++ ()()()()()()()1111sin sin 2sin 3sin 4sin 100234100f x x x x x x f x -=-+-+-+-++-=-,()f x 为奇函数B. ,1616x ππ⎡⎤∈-⎢⎥⎣⎦时,2,88x ππ⎡⎤∈-⎢⎥⎣⎦,333,1616x ππ⎡⎤∈-⎢⎥⎣⎦,4,44x ππ⎡⎤∈-⎢⎥⎣⎦,故sin ,sin 2,sin 3,sin 4x x x x 在,1616ππ⎡⎤-⎢⎥⎣⎦上均为增函数故111()sin sin 2sin3sin 4234f x x x x x =+++在区间,1616ππ⎡⎤-⎢⎥⎣⎦上单调递增. C. ()()11()sin sin 3sin 434g x f x h x x x x =-=++()()11()sin sin 3sin 434g x f x h x x x x =-=++()()11()sin sin 3sin 4034g f h ππππππ=-=++=故声音甲的响度不一定比纯音1()sin 22h x x =响度大 D. ()11()()sin sin 2sin 323h x g x h x x x x =-=+- ()11()()sin sin 2sin 3023h g h ππππππ=-=+-=甲不一定比纯音1()sin33h x x =更低沉 故选:B 【点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变才是制胜法宝.7.C解析:C 【分析】利用奇偶性的定义判断函数奇偶性,判断AD 错误,结合常见基本初等函数的单调性判断B 错误,C 正确即可. 【详解】选项A 中,()22xxf x -=-,定义域R ,()()()2222xx x x f x f x ---=-=--=-,则()f x 是奇函数,不符合题意;选项D 中,()cos3=f x x x ,定义域R ,()()()cos 3cos3f x x x x x f x -=--=-=-,则()f x 是奇函数,不符合题意;选项B 中,()23f x x =-,定义域R ,()()()2233x x f x f x -=--=-=,则()f x 是偶函数,但二次函数()23f x x =-在在(),0-∞上是减函数,在()0,∞+上是增函数,故不符合题意;选项C 中,()2ln =-f x x ,定义域为(),0-∞()0,+∞,()()2ln 2ln f x x x f x -=--=-=,则()f x 是偶函数.当()0,x ∈+∞时,()2ln f x x =-是减函数,所以由偶函数图象关于y 轴对称可知,()f x 在(),0-∞上是增函数,故符合题意. 故选:C. 【点睛】 方法点睛:定义法判断函数()f x 奇偶性的方法: (1)确定定义域关于原点对称; (2)计算()f x -;(3)判断()f x -与()f x 的关系,若()()f x f x -=,则()f x 是偶函数;若()()f x f x -=-,则()f x 是奇函数;若两者均不成立,则()f x 是非奇非偶函数.8.D解析:D 【分析】利用题干中的已知条件求得2ω=,可得出()sin 216f x x π⎛⎫=-+ ⎪⎝⎭,利用正弦型函数的对称性可判断①②的正误,利用正弦型函数的值域可判断③的正误,求出方程()1f x =在[]0,2π上的解,可判断④的正误. 【详解】N ω*∈,由55,126x ππ⎡⎤∈⎢⎥⎣⎦可得55126666x πωπππωπω-≤-≤-, 由于函数()()sin 16f x x N πωω*⎛⎫=-+∈ ⎪⎝⎭在55,126ππ⎡⎤⎢⎥⎣⎦上单调递减, 所以,()553,2,21266622k k k Z πωππωπππππ⎡⎤⎡⎤--⊆++∈⎢⎥⎢⎥⎣⎦⎣⎦,所以,521262532662k k ωππππωππππ⎧-≥+⎪⎪⎨⎪-≤+⎪⎩,解得()248121055k k k Z ω++≤≤∈,由248121055k k ++≤,解得16k ≤,N ω*∈且k Z ∈,0k ∴=,可得825ω≤≤,2ω∴=,则()sin 216f x x π⎛⎫=-+ ⎪⎝⎭.对于①,sin 2sin 00126ππ⎛⎫⨯-== ⎪⎝⎭,所以,112f π⎛⎫= ⎪⎝⎭, 所以,函数()f x 的图象关于点,112π⎛⎫⎪⎝⎭成中心对称,①错误; 对于②,271sin 2sin 13662πππ⎛⎫⨯-==-≠± ⎪⎝⎭,②错误;对于③,当,2x ππ⎡⎤∈⎢⎥⎣⎦时,5112,666x πππ⎡⎤-∈⎢⎥⎣⎦,则11sin 262x π⎛⎫-≤-≤ ⎪⎝⎭, 所以,()302f x ≤≤,即()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的值域为30,2⎡⎤⎢⎥⎣⎦,③正确; 对于④,当[]0,2x π∈时,232,666x πππ⎡⎤-∈-⎢⎥⎣⎦, 令()1f x =,可得sin 206x π⎛⎫-= ⎪⎝⎭,206x π∴-=或26x ππ-=或226x ππ-=或236x ππ-=.所以,方程()1f x =在[]0,2π有4个不相同的根,④正确. 故选:D. 【点睛】方法点睛:求函数()()sin f x A x =+ωϕ在区间[],a b 上值域的一般步骤: 第一步:三角函数式的化简,一般化成形如()sin y A x k ωϕ=++的形式或()cos y A x k ωϕ=++的形式;第二步:由x 的取值范围确定x ωϕ+的取值范围,再确定()sin x ωϕ+(或()cos x ωϕ+)的取值范围;第三步:求出所求函数的值域(或最值).9.B解析:B 【分析】根据题设的条件可得正弦型函数的周期、对称中心以及函数在0,4⎡⎤⎢⎥⎣⎦π上的单调性,再逐项检验各选项中的函数是否满足即可得到正确的选项. 【详解】因为对任意的x ∈R ,都有()()12()f x f x f x ≤≤,且12x x -的最小值为2π, 故()f x 的半周期为2π即周期为π,此时A B C D 各选项中的函数均满足. 因为6f x π⎛⎫+⎪⎝⎭为奇函数,故()f x 图象的对称中心为,06π⎛⎫⎪⎝⎭, 对于D 中的函数,因为sin 2166ππ⎛⎫⨯+= ⎪⎝⎭,故,06π⎛⎫⎪⎝⎭不是sin 26y x π⎛⎫=+ ⎪⎝⎭图象的对称中心,故排除D . 因为()()()()11222112x f x x f x x f x x f x +>+等价于()()()12120x x f x f x -->⎡⎤⎣⎦, 故()f x 在0,4⎡⎤⎢⎥⎣⎦π上为增函数, 当0,4x π⎡⎤∈⎢⎥⎣⎦时,4452336x πππ-≤-≤-,而sin y u =在45,36ππ⎡⎤--⎢⎥⎣⎦为减函数, 故4sin 23y x π⎛⎫=-⎪⎝⎭在0,4⎡⎤⎢⎥⎣⎦π为减函数,不合题意,舍; 当0,4x π⎡⎤∈⎢⎥⎣⎦时,2336x πππ-≤-≤,而sin y u =在,36ππ⎡⎤-⎢⎥⎣⎦为增函数, 故sin 23y x π⎛⎫=- ⎪⎝⎭在0,4⎡⎤⎢⎥⎣⎦π为增函数,符合; 当0,4x π⎡⎤∈⎢⎥⎣⎦时,2272336x πππ≤+≤,而sin y u =在27,36ππ⎡⎤⎢⎥⎣⎦为减函数,故2sin 23y x π⎛⎫=+ ⎪⎝⎭在0,4⎡⎤⎢⎥⎣⎦π为减函数,不合题意,舍; 故选:B . 【点睛】方法点睛:已知检验给定的点是否正弦型函数的对称中心,可以用代入检验法,而单调性的研究则需结合“同增异减”的原则来判断.10.A解析:A 【分析】由正切函数的图象性质,得出相邻两个对称中心之间的距离为半个周期,可求出T ,然后由T πω=求出ω,然后再代点讨论满足题意的ϕ,即可得出答案. 【详解】由正切函数图象的性质可知相邻两个对称中心的距离为2T ,得72263T πππ⎛⎫=-= ⎪⎝⎭. 则由1T πω==得1ω=,即得1ω=±. 由2πϕ<,且在区间54,63ππ⎛⎫⎪⎝⎭内单调递减,则可得1ω=-, ∴()()()tan tan f x x x ϕϕ=-+=--. 由2,32k k Z ππϕ-=∈得2,32k k Z ππϕ=-∈,因2πϕ<,可得6π=ϕ或3π-,当3πϕ=-时,()tan +3f x x π⎛⎫=- ⎪⎝⎭,由+,232k x k k Z πππππ-<<+∈,得5,66k x k k Z ππππ-<<+∈, 则函数()f x 的单调减区间为5,,66k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭, 令1k =,由54,63ππ⎛⎫ ⎪⎝⎭7,66ππ⎛⎫ ⎪⎝⎭⊄,得函数()f x 在54,63ππ⎛⎫⎪⎝⎭上不是单调递减, 所以3πϕ=-不满足题意;当6π=ϕ时,()tan 6f x x π⎛⎫=-- ⎪⎝⎭,由,262k x k k Z πππππ-<-<+∈,得2,33k x k k Z ππππ-<<+∈,则函数()f x 的单调减区间为2,,33k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭, 令1k =,由25,3354,63ππππ⎛⎫⊂⎛⎫ ⎪⎝ ⎪⎝⎭⎭,得函数()f x 在54,63ππ⎛⎫⎪⎝⎭上单调递减, 所以6π=ϕ满足题意; 综上可得:6π=ϕ满足题意. 故选:A.【点睛】关键点睛:正切型函数的对称中心和单调性的问题,通常采用代入检验法,注意正切函数的对称中心为0,2k k Z π⎛⎫∈⎪⎝⎭,. 11.D解析:D 【分析】先根据函数的奇偶性,可排除A ,C ,根据当01x <<时,()0f x <即可排除B .得出答案. 【详解】因为()sin ln ||(0)f x x x x =⋅≠,所以()sin()ln ||sin ln ||()f x x x x x f x -=-⋅-=-=-,所以()f x 为奇函数,故排除A ,C .当01x <<时,sin 0x >,ln ||0x <,则()0f x <,故排除B , 故选:D .【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.12.D解析:D 【解析】分析:将2cos x 化为21sin x -,令()sin 11x t t =-≤≤,可得关于t 的二次函数,根据t 的取值范围,求二次函数的最值即可.详解:利用同角三角函数关系化简,22cos 2sin sin 2sin 1y x x x x =-=--+ 设()sin 11x t t =-≤≤,则()()22211211y t t t t =--+=-++-≤≤,根据二次函数性质当1t =-时,y 取最大值2,当1t =时,y 取最小值2-.故选D.点睛:本题考查三角函数有关的最值问题,此类问题一般分为两类,一种是解析式化为2sin sin y A x B x C =++的形式,用换元法求解;另一种是将解析式化为()sin y A x k ωϕ=++的形式,根据角的范围求解.二、填空题13.【分析】根据题意可得从而可得讨论或再求出的单调递增区间只需是单调递增区间的子集即可求解【详解】由正弦函数的性质的每个增区间的长度为其中函数的最小正周期为函数在区间上单调地藏可得即①当时此时单调递增当解析:130,42⎛⎤⎧⎫⋃-⎨⎬ ⎥⎝⎦⎩⎭【分析】 根据题意可得22T π≥,从而可得2ω≤,讨论0>ω,0ω=或0ω<,再求出()sin()f x x ωϕ=+的单调递增区间,只需,2ππ⎡⎤⎢⎥⎣⎦是单调递增区间的子集即可求解.【详解】()()sin f x x ωϕ=+,0,4πϕ⎡⎤∈⎢⎥⎣⎦,由正弦函数的性质,()f x 的每个增区间的长度为2T,其中函数()f x 的最小正周期为2T ωπ=.函数()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调地藏,可得22T π≥,即2ω≤.①当0>ω时,此时02ω<≤,x ωϕ+单调递增,当2,2,22x k k k Z ππωϕππ⎡⎤+∈-+∈⎢⎥⎣⎦,()f x 单调递增, 解得112,2,22x k k k Z πππϕπϕωω⎡⎤⎛⎫⎛⎫∈--+-∈ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 只需11,2,2,222k k k Z πππππϕπϕωω⎡⎤⎡⎤⎛⎫⎛⎫⊆--+-∈ ⎪ ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎝⎭⎣⎦, 从而可得1222,122k k Z k πππϕωπππϕω⎧⎛⎫≥-- ⎪⎪⎪⎝⎭∈⎨⎛⎫⎪≤+- ⎪⎪⎝⎭⎩,解得2141,2,2k k k Z ϕϕωππ⎡⎤∈--+-∈⎢⎥⎣⎦对0,4πϕ⎡⎤∀∈⎢⎥⎣⎦成立, 则21410214k k πωππ--⨯≤≤+-⨯,即141,2,4k k k Z ω⎡⎤∈-+∈⎢⎥⎣⎦,由124141204k k k ⎧+>-⎪⎪⎨⎪+>⎪⎩,解得1588k -<<,k Z ∈,0k ∴=.所以,10,4ω⎛⎤∈ ⎥⎝⎦;②当0ω=时,函数()sin f x ϕ=为常函数,不合乎题意; ③当0ω<时,20ω-≤<,x ωϕ+单调递减, 由322,22k x k k Z πππωϕπ+≤+≤+∈, 解得13122,22k x k k Z πππϕπϕωω⎛⎫⎛⎫+-≤≤+-∈ ⎪ ⎪⎝⎭⎝⎭对0,4πϕ⎡⎤∀∈⎢⎥⎣⎦成立, 可得13222,122k k Z k πππϕωπππϕω⎧⎛⎫≥+- ⎪⎪⎪⎝⎭∈⎨⎛⎫⎪≤+- ⎪⎪⎝⎭⎩,解得122,43,2k k k Z ϕϕωππ⎡⎤∈+-+-∈⎢⎥⎣⎦对0,4πϕ⎡⎤∀∈⎢⎥⎣⎦成立,于是12210434k k πωππ+-⨯≤≤+-⋅,即521,4,2k k k Z ω⎡⎤∈++∈⎢⎥⎣⎦,由5142225402k k k ⎧+≥+⎪⎪⎨⎪+<⎪⎩,解得518k -≤<-,由k Z ∈,1k =-,此时,32ω=-.综上所述,实数ω的取值范围是130,42⎛⎤⎧⎫⋃-⎨⎬ ⎥⎝⎦⎩⎭.故答案为:130,42⎛⎤⎧⎫⋃-⎨⎬ ⎥⎝⎦⎩⎭.【点睛】关键点点睛:本题考查了三角函数的性质,解题的关键是求出函数的单调递增区间,使,2ππ⎡⎤⎢⎥⎣⎦是单调递增区间的子集,考查了分类讨论的思想. 14.②③【分析】先根据图象结合已知条件限制求出的解析式再利用代入验证法判断①错误;利用整体代入法求单调区间判断②正确;解方程并结合诱导公式判断③正确;将函数零点问题转化成函数交点问题数形结合判断④错误即解析:②③ 【分析】先根据图象,结合已知条件限制求出()y f x =的解析式,再利用代入验证法判断①错误;利用整体代入法求单调区间判断②正确;解方程并结合诱导公式判断③正确;将函数零点问题转化成函数交点问题,数形结合判断④错误即可. 【详解】由图象可知,2A =,(0)2sin 1f ϕ==,故1sin 2ϕ=,又2πϕ<,故6π=ϕ,故()2sin 6f x x πω⎛⎫=+ ⎪⎝⎭,又由11112sin 012126f πππω⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭得,112,126k k Z ππωπ+=∈,即224,1111kk Z ω=-+∈, 由题意0>ω,由图知1112T π>,即22411T πω=<,故1k =时2ω=.故()2sin 26f x x π⎛⎫=+ ⎪⎝⎭. ①因为252sin 2sin 103366f ππππ⎛⎫⎛⎫=+==≠⎪ ⎪⎝⎭⎝⎭,故点,03π⎛⎫ ⎪⎝⎭不是()y f x =图象的对称中心,故错误; ②令322,2,622x k k k Z πππππ⎛⎫+∈++∈ ⎪⎝⎭, 解得单调递减区间为2,,63k k k ππππ⎛⎫++∈⎪⎝⎭Z ,故正确;③若()2sin 26f x x a π⎛⎫=+= ⎪⎝⎭,则sin 262a x π⎛⎫+= ⎪⎝⎭,则cos cos 2sin 2sin 2332362a x x x x πππππω⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=-=+-=+= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,故正确; ④令2()()log 0g x f x x =-=,得方程2()log f x x =的根的问题, 即函数()2sin 26y f x x π⎛⎫==+⎪⎝⎭与函数2log y x =的交点个数问题,如图,令22,62x k k Z πππ+=+∈,则,6x k k Z ππ=+∈时()y f x =取得最大值2.如图,6x π=时,2()log f x x >;76x π=时,746π<,227log log 426π<=2()2log f x x =>;当136x π=时,1346π>,2213log log 426π>=,2()2log f x x =<. 故函数()2sin 26y f x x π⎛⎫==+ ⎪⎝⎭与函数2log y x =有3个交点,即2()()log g x f x x =-有3个零点.故错误. 故答案为:②③. 【点睛】方法点睛:判断函数零点个数的方法(1)直接法:令()0f x =,如果能求出解,那么有几个不同的解就有几个零点; (2)利用函数的零点存在性定理:利用函数的零点存在性定理时,不仅要求函数的图象在区间[],a b 上是连续不断的曲线,并且()()0f a f b ⋅<,还必须结合函数的图象与性质,(如单调性、奇偶性)才能确定函数有多少个零点;(3)图象法:画出函数()f x 的图象,函数()f x 的图象与x 轴交点的个数就是函数()f x 的零点个数;将函数()f x 拆成两个函数,()h x 和()g x 的形式,根据()0f x =等价于()()h x g x =,则函数()f x 的零点个数就是函数()y h x =和()y g x =的图象交点个数;(4)利用函数的性质:若能确定函数的单调性,则其零点个数不难得到,若所考查的函数是周期函数,则需要求出在一个周期内的零点个数,根据周期性则可以得出函数的零点个数.15.【分析】根据题意作出示意图结合枢纽中心到初始水平面的高度水面下降的高度刚进入水面时枢纽中心到水面的高度这三者间的关系列出关于运动时间的方程结合所给数据分析的取值即可【详解】设至少经过分钟进入水中如下 解析:13【分析】根据题意作出示意图,结合枢纽中心到初始水平面的高度、水面下降的高度、P 刚进入水面时枢纽中心到水面的高度这三者间的关系,列出关于运动时间x 的方程,结合所给数据分析x 的取值即可. 【详解】设至少经过x 分钟,P 进入水中,如下图P '为刚好进入水中的位置,由条件可知: 1.7, 1.19OP OA '==,P 转过的角度为23015x x ππ⋅=,所以15xP OB ππ'∠=-,因为OA AB OB +=,所以1.170.017 1.7cos 15x x ππ⎛⎫+=-⎪⎝⎭,所以70100cos 15x x ππ⎛⎫+=- ⎪⎝⎭(*),根据所给数据可知:当12x =时,(*)的左边82=,右边81=,此时左边>右边,说明P 还未进入水中,当13x =时,(*)的左边83=,右边91=,此时左边<右边,说明P 已经进入水中, 当14x =时,(*)的左边84=,右边98=,此时左边<右边,说明P 已经进入水中, 由上可知:x 的取值介于12和13之间,又因为x 的结果取整数,所以13x =, 故答案为:13. 【点睛】关键点点睛:解答本题的关键是通过示意图寻找到枢纽中心到水面的高度与水面下降高度之间的等量关系,通过所给的数据去分析方程的解也是很重要的一步.16.【解析】当时由得所以减区间为解析:5,122ππ⎡⎤⎢⎥⎣⎦【解析】当[0,]2x π∈时,ππ2π2[,]333x -∈-,由22233x πππ≤-≤,得5122x ππ≤≤,所以减区间为5[,]122ππ. 17.【分析】由周期公式可得由三角函数的中心对称可得结合即可得为奇数即可得由可得进而可得即可得解【详解】由可得由是奇函数可得函数的图象关于中心对称所以即又所以所以为奇数由可得因为在上没有最小值所以即故答案解析:511,612ππ⎛⎤⎥⎝⎦【分析】由周期公式可得ω,由三角函数的中心对称可得,3k k Z πϕπ=+∈,结合()06f f π⎛⎫< ⎪⎝⎭即可得k 为奇数,即可得()sin 23πf x x ⎛⎫=- ⎪⎝⎭,由[)0,x t ∈可得2,2333x t πππ⎡⎫-∈--⎪⎢⎣⎭,进而可得432332t πππ<-≤,即可得解. 【详解】由T π=可得22T πω==,()sin 23f x x πϕ⎛⎫=++ ⎪⎝⎭由3y f x π⎛⎫=- ⎪⎝⎭是奇函数可得函数()f x 的图象关于,03π⎛-⎫⎪⎝⎭中心对称, 所以2,33k k Z ππϕπ⎛⎫⨯-++=∈ ⎪⎝⎭,即,3k k Z πϕπ=+∈, 又()06f f π⎛⎫< ⎪⎝⎭,所以2sin sin 33ππϕϕ⎛⎫⎛⎫+<+ ⎪ ⎪⎝⎭⎝⎭, 所以,3k k πϕπ=+为奇数,()sin 2sin 2333f x x k x ππππ⎛⎫⎛⎫=+++=- ⎪ ⎪⎝⎭⎝⎭,由[)0,x t ∈可得2,2333x t πππ⎡⎫-∈--⎪⎢⎣⎭, 因为()f x 在[)0,t 上没有最小值,所以432332t πππ<-≤即511,612t ππ⎛⎤∈⎥⎝⎦. 故答案为:511,612ππ⎛⎤⎥⎝⎦. 【点睛】本题考查了三角函数图象与性质的应用,考查了运算求解能力,牢记知识点是解题关键,属于中档题.18.6【分析】根据题意可求得然后利用正弦定理求得最后在中利用求得答案【详解】在中由正弦定理得;在中(米)所以升旗速度(米/秒)故答案为06【点睛】本题主要考查了解三角形的实际应用此类问题的解决关键是建立解析:6 【分析】根据题意可求得,45BDC ∠=︒,30CBD ∠=︒,CD =BC ,最后在Rt ABC 中利用sin60AB BC =︒求得答案. 【详解】在BCD 中,45BDC ∠=︒,30CBD ∠=︒,CD =由正弦定理,得sin 45sin 30CD BC ︒==︒在Rt ABC 中,sin?6030AB BC =︒==(米). 所以升旗速度300.650t AB v ===(米/秒). 故答案为0.6. 【点睛】本题主要考查了解三角形的实际应用.此类问题的解决关键是建立数学模型,把实际问题转化成数学问题,利用所学知识解决,属于中档题.19.9【分析】由在区间上单调可得故进一步求出范围即可【详解】由知故;又在区间上单调故即18符合条件的的值有9个故答案为:9【点睛】本题考查三角函数的图象与性质考查转化与化归思想考查逻辑推理能力运算求解能解析:9 【分析】 由()f x 在区间(,)43ππ上单调,可得342T ππ-,故6T π,进一步求出ω范围即可. 【详解】由()24f π=,()0f π=知,34244T kT πππ+=-=,k ∈N , 故312T k π=+,2(12)3k ω+=,k ∈N ; 又()f x 在区间(,)43ππ上单调,∴342T ππ-,故6T π,∴212T πω=,即2(12)123k +, ∴172k,k ∈N , 0k ∴=,1,2⋯,8符合条件的ω的值有9个. 故答案为:9. 【点睛】本题考查三角函数的图象与性质,考查转化与化归思想,考查逻辑推理能力、运算求解能力,属中档题.20.②③【分析】根据三角函数的零点性质三角函数对称和三角函数诱导公式依次判断每个选项得到答案【详解】①中是的两个零点即是的整数倍①错误;②中②正确;故④错误;③中③正确;所以正确命题序号是②③故答案为:解析:②③ 【分析】根据三角函数的零点性质,三角函数对称和三角函数诱导公式依次判断每个选项得到答案. 【详解】①中12,x x 是()f x 的两个零点,即12x x -是2π的整数倍,①错误; ②中06f π⎛⎫-= ⎪⎝⎭,②正确;故④错误; ③中4sin 24cos 2cos 23236y x x x ππππ⎛⎫⎛⎫⎛⎫=+=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,③正确; 所以正确命题序号是②③. 故答案为:②③. 【点睛】本题考查了三角函数的对称,零点,诱导公式,意在考查学生对于三角函数知识的综合应用.三、解答题21.条件选择见解析;(1)()2sin 23f x x π⎛⎫=- ⎪⎝⎭;(2)12x π=-时,函数f (x )取得最小值,最小值为2-. 【分析】(1)由相邻中心距离得周期,从而可得ω,选择①,写出平移后解析式,由对称性得新函数为偶函数,结合诱导公式求得ϕ,选择②,求出6y f x π⎛⎫=+ ⎪⎝⎭,由函数为奇函数,结合诱导公式求得ϕ,选择③,求出()6y f x π=-,代入712x π=,结合正弦函数最大值可得ω, 从而得函数解析式; (2)()2sin 23f x x π⎛⎫=- ⎪⎝⎭由,求得23x π-的范围,然后由正弦函数性质得最小值.【详解】(1)因为函数f (x )=2sin(ωx +φ)的图象相邻的对称中心之间的距离为2π, 所以周期22T π=,即T =π,所以22T πω==.若选择①,因为函数f (x )图象向右平移12π个单位所得图象关于y 轴对称,所以()2sin 22sin 2126g x x x ππϕϕ⎡⎤⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图象关于y 轴对称,所以62k ππϕπ-=+,k Z ∈,因为||2ϕπ<,所以3πϕ=-.所以函数y =f (x )的解析式为()2sin 23f x x π⎛⎫=- ⎪⎝⎭.若选择②,因为2sin 22sin 2663y f x x x πππϕϕ⎡⎤⎛⎫⎛⎫⎛⎫=+=++=++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦是奇函数,所以3k πϕπ+=,k Z ∈,因为||2ϕπ<,所以3πϕ=-.所以函数y =f (x )的解析式为()2sin 23f x x π⎛⎫=- ⎪⎝⎭.若选择③,2sin 22sin 2663y f x x x πππϕϕ⎡⎤⎛⎫⎛⎫⎛⎫=-=⨯-+=-+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,由题设,当712x π=时,函数6y f x π⎛⎫=- ⎪⎝⎭取得最大值,所以当722()1232k k Z πππϕπ⨯-+=+∈,即2()3k k Z πϕπ=-∈, 因为||2ϕπ<,所以3πϕ=-.所以函数y =f (x )的解析式为()2sin 23f x x π⎛⎫=- ⎪⎝⎭.(2)因为()2sin 23f x x π⎛⎫=-⎪⎝⎭,,22x ππ⎡⎤∈-⎢⎥⎣⎦,所以422,333x πππ⎡⎤-∈-⎢⎥⎣⎦,所以当232x ππ-=-,即12x π=-时,函数f (x )取得最小值,最小值为2-.【点睛】关键点点睛:本题考查由三角函数的图象与性质求解析式,解题关键是掌握正弦函数的图象与性质,解题时注意“五点法”和整体思想的应用.对于奇偶性问题注意诱导公式的应用,由此计算比较方便. 22.(1)336S π⎛⎫= ⎪⎝⎭;(2)1sin 3θ=. 【分析】(1)作出图形,可知公共部分区域为直角三角形,计算出两直角边的长,由此可求得该直角三角形的面积; (2)分6πθ=、06πθ<<、62ππθ<<三种情况讨论,求出()S θ的表达式,结合()72S θ=可求得sin θ的值. 【详解】 (1)当3πθ=时,A '点在矩形OABC 外部,公共部分形状为三角形,设A O BC D '⋂=,则6COD π∠=,3tan6CD CO π==, 则11331322S CD CO π⎛⎫=⨯⨯=⨯⨯=⎪⎝⎭;(2)①当6πθ=时,点A '在线段BC 上,此时,223A C A O OC ''-=11313622S OC A C π⎛⎫'=⨯=⨯=⎪⎝⎭; ②当06πθ<<时,公共部分为四边形,A '点在矩形OABC 内部,过点A '作线段AB 的平行线,分别交线段AO 、BC 于点E 、。
(完整word版)高中数学数学必修四第一章三角函数单元测试题(word文档良心出品)

1•将—300°化为弧度为( )B. C. 7 6 D. 7 4 2.如果点P (sinvcos )2cosv )位于第三象限,那么角 二所在象限是( A .第一象限 B.第二象限 C.第三象限 D.第四象限 3 .下列选项中叙述正确的是 A. 三角形的内角是第一象限角或第二象限角 B. 锐角是第一象限的角 C. 第二象限的角比第一象限的角大 D.终边不同的角同一三角函数值不相等4 .下列函数中为偶函数的是( ) A . y =sin | x | B . y = sin 2x C y = _sin x D 5已知函数y = As in (• ‘x W ) • B 的一部分图象如右图所示,如果 B. ,=1 C.6 函数y =3si n ( 2x •—)的单调递减区间( 6 5 二 .| nA k , kr : 一12聖,匚竺(k Z )12 12.k 二二k 二三(k Z )-632 C . k ,kr : -3 (k Z) B . 12 (k Z) D 6」 已知「是三角形的一个内角,且sin 爲^cos ,则这个三角形()3不等腰的直角三角形A .锐角三角形B .钝角三角形 C. D .等腰直角三角形1 -2sin (二 2)cos (二 2)等于 A . sin2 — cos2 B .cos2 — sin2 C. 土 (sin2 — cos2)9 .若角:-的终边落在直线 y =2x 上,贝U sin :- 的值为( )人 丄1 .2苗1 A. B. C. D. + — 5 5 52 10.函数 2 [ i .y=cos x - 3cosx+2的最小值是 ( ) A . 2 B . 0 C. 1D. 6 4 a11 .如二在第三象限,则 一必定在( ) ()8. D . sin2+cos2A .第一或第二象限B .第一或第三象限C .第三或第四象限 D.第二或第四象 12.已知函数y =Asin ( )在同一周期内,当 x时有最大值2,当x=0时有最小值-2,那么函数的解析3式为A . y =2sin —x B- y =2sin (3x) C - y =2sin (3x ) D y =」sin3x2 2 2 2二.填空题(20分)14、已知角a 的终边经过点P (3 , 7—),则与a 终边相同的角的集合是 __________ 13. tan i 、tan 2、tan 3的大小顺序是 ____________________________ 14.函数y =lg 1「tanx 的定义域是 _______________ .16. _____________________________________________________________ 函数 y _si n ( _2x 亠')的单调递减区间是 __________________________________________________ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
爱心专心 1
三角函数单元测试题(2)
一、选择题(30分)
1、若
13
sin()=,-)
22
A A
ππ
+-则cos(的值是()
A、
1
2
- B、
1
2
C、、-
2、要得到sin(2)
3
y x
π
=-的图象,只要将sin2
y x
=的图象()
A、向左平移
3
π
B、向右平移
3
π
C、向左平移
6
π
D、向右平移
6
π
3、已知函数[]
3cos02
y xπ
=在,的图象和直线3
y=围成一个封闭的平面图形,这个封闭图形的面积是( )
A、4π
B、6π
C、9
D、6
4、函数()sin()(0)
3
f x x
π
ωω
=+>的最小正周期为π,则该函数的图象()
A、关于点0
3
π
(,)对称 B、关于点0
4
π
(,)对称
C、关于直线
3
x
π
=对称 D、关于直线
4
x
π
=对称
5、函数
13
cos(2)
22
y x
π
=+的单调减区间是(选项中k是整数)()
A、(,
44
k k
ππ
ππ
-+) B、
3
(+,
24
k k
ππ
ππ+)
C、
3
(+,
44
k k
ππ
ππ+) D、(+,
4
k k
π
πππ
+)
6.设sin123°=a,则tan123°=( )
A.
1-a2
a
B.
a
1-a2
C.
1-a2
1-a2
D.
a1-a2
a2-1
二、填空题(10分)
7、函数
3
3sin(2),,
334
y x x
πππ
⎡⎤
=-∈⎢⎥
⎣⎦
的值域是
8、22
1
sin cos,sin cos
2
x x x x
-=-=
则
用心 爱心 专心 2
姓名:
7.
8. 三、解答题(30分)
9、已知2222
3sin ()2cos ()+sin(2)cos()
tan()2,12sin +cos παπαπαπαπααα
----+-=+求的值 10分)
10、已知cos 2 (0)y a b x b =->的最大值是
32,最小值是12-,求函数4sin(3)3
y a bx π
=-+的周期、最大值及取得最大值时x 的值的集合。
(10分)
11、设函数()sin(2) (0),f x x ϕπϕ=+-<<()y f x =的一条对称轴是直线8
x π
=。
(1)求ϕ得值; (2)求()y f x =得单调增区间。
(10分)。
