第一部分专题14
高考政治二轮总复习第1部分专题过关突破过关微专题14家庭婚姻与就业创业核心考点2就业与创业

第1部分过关微专题14 核心考点2一、选择题1.(2022·山东威海二模)2022年2月9日,被告人小强(15岁,化名)因犯盗窃罪,被北京市平谷区法院判处有期徒刑8个月。
法院认为,小强的父母对小强缺乏必要的家庭教育,向小强父母发出北京法院首份《家庭教育令》,以法的形式督促父母“把爱带回家”。
该判决( A )①旨在规范家庭教育主体正确履行监护职责②说明受教育权是未成年人享有的最基础权利③为增强父母的家庭教育意识提供法治引导④通过法律强制性发挥道德在家庭教育中的作用A.①③B.①④C.②③D.②④【解析】法院向小强父母发出北京法院首份《家庭教育令》,以法的形式督促父母“把爱带回家”。
该判决为增强父母的家庭教育意识提供法治引导,旨在规范家庭教育主体正确履行监护职责,①③符合题意;生命健康权是未成年人享有的最基础权利,②错误;通过法律强制性发挥法律在家庭教育中的作用,④错误。
2.(2022·北京东城区二模)某班同学以“常回家看看为什么要立法”为议题开展讨论。
对同学们的观点评析正确的是( B )①甲的观点具有合理性,老年人的精神需求应当得到关切②乙的观点也有道理,技术手段可以实现法律的功能③丙的观点是正确的,法律规范道德,道德才有力量④丁的观点具有合理性,真正的“孝”是内心的自觉A.①③B.①④C.②③D.②④【解析】有关常回家看看为什么要立法的议题,甲认为父母年龄大了渴望团圆,应加强这方面的立法,其观点具有合理性,老年人的精神需求应当得到关切,①正确;乙认为利用通信就可以与父母沟通,没必要立法,其观点只看到技术手段解决的通信便利,没有看到父母年龄大了渴望团圆的切身感受,且技术手段并不能实现法律的功能,②不合理;“法律规范道德,道德才有力量”该选项的说法太绝对,③排除;法律能够规定探望父母的次数,但是不能确保“孝”的效果,丁的观点具有合理性,真正的“孝”是内心的自觉,④正确。
3.(2022·天津市河西区三模)2018年6月10日,老王立下一份遗嘱,将大部分财产留给儿子,少部分的存款留给女儿。
专题14:文言翻译(教师版)

第六章文言文阅读文言翻译文言文翻译题的综合性较强,涉及文言知识点多,是检查考生文言文阅读能力的重要手段,属必考题。
文言文翻译集中考查实词、虚词、特殊句式、古代文化常识等多方面的知识,考查考生文言文阅读的综合能力,是高考文言文阅读的重点和难点。
一、文言文翻译“三大赋分点”文言文翻译和很多题目一样,也是按得分点赋分的。
文言文翻译语句的赋分点主要体现在实词、虚词、特殊句式上,找准了这三点,也就抓住了翻译题的命题点和基本的得分点。
赋分点一重要实词所谓重要实词,从词性上看,以动词居多,其次是形容词和名词。
把重要实词翻译到位,就是把句中的通假字、古今异义词、偏义复词、活用词语(名词用作状语、形容词用作动词、意动用法、使动用法等)和借助语境推断词义的多义词准确理解,并且在译文中正确地体现出来。
赋分点二关键虚词虚词主要指文言语句中的副词、连词、介词、助词等。
虚词的翻译要注意两点:①有些虚词必须译出。
有实词义项的,如作代词的“之”“其”等;现代汉语中有与之相对应的虚词进行互换的,如“之”“而”“以”“于”等。
这两类需要译出。
②有些虚词不必译出。
在句中起语法作用的“之”、发语词及句末语气助词等,此类一般不必译出。
总之,我们在翻译虚词时,要仔细辨明词性及意义,能译则译,不需要译出的切不可强行译出。
赋分点三文言句式文言句式在翻译题目中是重要的得分点,翻译时审出译句中的特殊句式是关键。
审出译句中的特殊句式后,考生要灵活运用学过的文言句式的判断方法和翻译格式,重点把握容易忽略的省略句、宾语前置句和固定句式等。
要掌握各种句式的翻译格式。
①判断句:必须加上“是”“就是”等词语。
②被动句:必须加上“被”字。
③倒装句:必须用“调”的方法将译句按现代汉语的语法习惯调整过来。
如:状语后置句,译时要将状语调到动词前;定语后置句和宾语前置句,译时要将定语和宾语恢复原位。
④省略句:必须用“补”的方法补出省略的成分,确保句意通顺。
⑤固定句式(结构):千万不要生硬地翻译,它有固定的译法,须在平时掌握好。
小学数学专题讲座

小学数学专题讲座
辅导老师:封剑飞
第一部分数与代数
专题一:数的认识
1.整数的认识
2.分数的认识
3.小数的认识
4.百分数的认识与小数、分数、百分数的互化
5.负数的认识
专题二:数的运算
6.整数的四则运算
7.分数的四则运算
8.小数的四则运算
9.计算方法与计算工具
专题三:常见的量
专题四:式与方程
10.用字母表示数
11.简易方程
专题五:比和比例
12.比
13.比例
专题六:探索规律
第二部分空间与图形
专题一:基本图形
14.线
15.角
16.线与角的测量
专题二:平面图形
17.平行四边形、长方形和正方形
18.三角形
19.梯形
20.圆和圆形、扇形
21.平面图形的测量
专题三:立体图形
22.长方体和立方体
23.圆柱、圆锥和球
24.立体图形的测量
专题四:图形与位置
专题五:图形与变换
第三部分统计与概率
专题一:统计
专题二:可能性
第四部分实践与综合应用
专题一:一般复合实际问题
专题二:典型实际问题
专题三:分数、百分数的实际问题
专题四:比和比例的实际问题
专题五:解决问题的策略
专题六:列方程解应用题
专题七:综合应用
以上专题,家长、学生可以参考自身的情况选择学习。
上海市高中地理第一学习练习册答案

专题1地球在宇宙中的位置一、填空1、恒星、星云2、矮行星、彗星(流行群)3、木星、水星;水星、海王星;金星、火星,金星二、选择1、A 2、D 3、B 4、A 5、?6、C 7、C、D 8、B、C三、连线略四、读图分析1、(1)A、C、B、D (2)D、B、C、A2、略3、(1)日冕、色球、光球(2)、太阳黑子→光球太阳风→日冕耀斑→色球(3)光球→六千多K 色球→四五千至几万K 日冕→几百万K (4)A、C五、简答1、恒星能自己发光;星云与恒星比,具有质量大、体积小和密度小的特点。
2、行星由固体物质组成;彗星由冰物质组成,质量很小。
专题2地球的伙伴——月球一、选择1、C 2、D 3、A、C、D 4、A、B二、读图分析1、新月、上弦月、满月、下弦月2、A、C 3、大三、判断(每句话都有不当之处:轰鸣、凛冽的寒风、沉重的、艰难跋涉、一点星光也没有、电闪雷鸣、照亮、飞扬的等)专题3人类对太空的探索一、填空1、1957;1981 2、地月、太阳、银河3、空间资源、太阳能资源、矿产资源、环境资源二、选择1、D 2、A 3、C 4、A、B、C三、读图分析C、B、E、D、A专题4地球的运动一、填空1、赤道,两极2、西十二,东十二3、减一天4、1,快;7,慢5、黄赤交角,23°26′6、23°26′,北回归线,南回归线7、春分,秋分, 0°8、23°26′S,0° 9、最长、最短,昼,极昼;极夜10、黄赤交角,太阳直射点,正午太阳高度、昼夜长短,四季更替二、选择1、B 2、D 3、C 4、A 5、B 6、D 7、D 8、B 9、A 10、C 11、C三、读图分析1(1)__南__、__北__。
(2)A.__30°S__,__45°E__;B.__30°N__,__135°W__。
(3)__东南<SE>__,__正西<W>__。
专题14

选修模块3-5
二、应用动量守恒定律解题的步骤 (1)选取研究系统和研究过程. (2)分析系统的受力情况,判断系统动量是否守恒. (3)规定正方向,确定系统初末状态的动量. (4)根据动量守恒定律列方程求解.
第37页
新课标高三大二轮复习·物理
模块十四
选修模块3-5
冲关必试 1. 某同学用如图所示的装置“验证动量守恒定律”,其操 作步骤如下:
第12页
新课标高三大二轮复习·物理
模块十四
选修模块3-5
(4)普适性:它不仅适用于两个物体所组成的系统,也适用 于多个物体组成的系统;不仅适用于宏观物体组成的系统,也 适用于微观粒子组成的系统.
第13页
新课标高三大二轮复习·物理
模块十四
选修模块3-5
4.碰撞的种类 分类标准 能量是 种类 弹性碰撞 特点 动量守恒,机械能守恒 动量守恒,机械能有损失 动量守恒,机械能损失最大 碰撞前后速度共线 碰撞前后速度不共线
新课标高三大二轮复习·物理
模块十四
选修模块3-5
2. 人工转变 (1)质子的发现:14N+4He→17O+1H 7 2 8 1 (2)中子的发现:9Be+4He→12C+1n 4 2 6 0
1 (3)重核裂变:235U+1n→136Xe+90Sr+100n 92 0 54 38 235 1 U+1n→141Ba+92Kr+30n 92 0 56 36 2 4 (4)轻核聚变:1H+3H→2He+1n 1 0
第二部分
专题知识大突破
第1页
新课标高三大二轮复习·物理
第二部分
专题知识大突破
专题十四
选修模块3-5
第2页
新课标高三大二轮复习·物理
模块十四
数学中考一轮复习专题14一次函数的应用课件

知识点梳理
知识点1:一次函数解析式的确定
1.确定一次函数解析式的方法: (1)待定系数法; (2)根据题意中等量关系直接列出解析式; (3)通过几何变换(通常为平移)前后的解析式特征(自变量“左加右减”, 函数值“上加下减”)确定新函数解析式.
知识点1:一次函数解析式的确定
知识点梳理
2.用待定系数法求一次函数表达式的一般步骤:
7k b b 4
3
,
解得
k
1 7
,
b 4
∴直线BD的解析式为 y 1 x 4 . 7
故选:A.
知识点2:一次函数的几何应用
典型例题
【例6】(3分)(202X•呼伦贝尔•兴安盟17/26)如图,点B1在直线l:y
1 2
x
上,
点B1的横坐标为1,过点B1作B1A1⊥x轴,垂足为A1,以A1B1为边向右作正方形
典型例题
知识点1:一次函数解析式的确定
【解答】解:(1)把点P的横坐标为2代入得,y=-2+5=3,
∴点P(2,3),
∴
S△AOP
1 2
43
(2)当S=4时,即
6 1
; 4
y
4
,
2
∴y=2,
当y=2时,即2=-x+5,
解得x=3,
∴点P(3,2);
典型例题
知识点1:一次函数解析式的确定
(3)由题意得, S 1 OA y 2y 2(x 5) 2x 10 ,
(2)把x=﹣2代入 y= 1 x 1 ,求得y=﹣2, 2
∴函数y=mx(m≠0)与一次函数 y= 1 x 1 的交点 2
为(﹣2,﹣2),
把点(﹣2,﹣2)代入y=mx,求得m=1,
中考一轮复习 数学专题14 圆与正多边形(学生版)
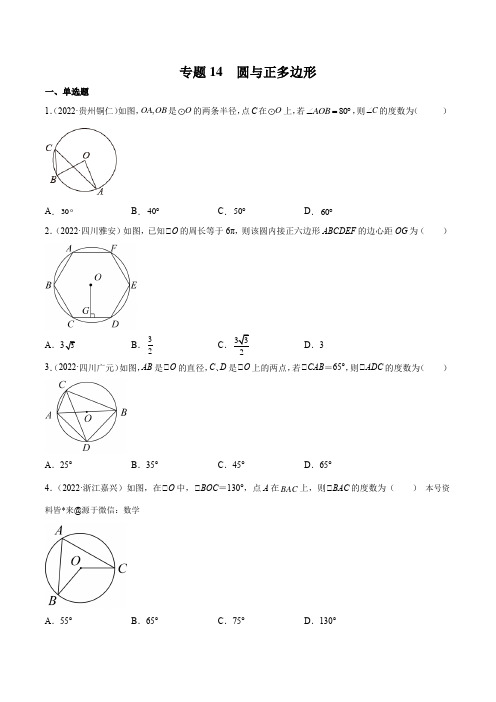
专题14 圆与正多边形一、单选题1.(2022·贵州铜仁)如图,,OA OB 是O 的两条半径,点C 在O 上,若80AOB ∠=︒,则C ∠的度数为( )A .30B .40︒C .50︒D .60︒2.(2022·四川雅安)如图,已知⊙O 的周长等于6π,则该圆内接正六边形ABCDEF 的边心距OG 为( )A .B .32CD .33.(2022·四川广元)如图,AB 是⊙O 的直径,C 、D 是⊙O 上的两点,若⊙CAB =65°,则⊙ADC 的度数为( )A .25°B .35°C .45°D .65°4.(2022·浙江嘉兴)如图,在⊙O 中,⊙BOC =130°,点A 在BAC 上,则⊙BAC 的度数为( ) 本号资料皆*来@源于微信:数学A .55°B .65°C .75°D .130°5.(2022·浙江宁波)已知圆锥的底面半径为4cm,母线长为6cm,则圆锥的侧面积为()A.236πcm B.224πcm C.216πcm D.212πcm6.(2021·广西桂林)如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,BC,则⊙C的度数是()A.60°B.90°C.120°D.150°7.(2021·内蒙古呼伦贝尔)一个正多边形的中心角为30,这个正多边形的边数是()A.8B.12C.3D.68.(2021·吉林)如图,四边形ABCD内接于O,点P为边AD上任意一点(点P不与点A,D重合)连接CP.若120B∠=︒,则APC∠的度数可能为()A.30B.45︒C.50︒D.65︒9.(2021·广西贺州)如图,在边长为2的等边ABC中,D是BC边上的中点,以点A为圆心,AD为半径作圆与AB,AC分别交于E,F两点,则图中阴影部分的面积为()A.π6B.π3C.π2D.2π310.(2021·吉林长春)如图,AB 是O 的直径,BC 是O 的切线,若35BAC ∠=︒,则ACB ∠的大小为( )A .35︒B .45︒C .55︒D .65︒11.(2021·湖南长沙)如图,点A ,B ,C 在⊙O 上,54BAC ∠=︒,则BOC ∠的度数为( )A .27︒B .108︒C .116︒D .128︒12.(2020·广西)如图,AB 是⊙O 的弦,AC 与⊙O 相切于点A ,连接OA ,OB ,若⊙O =130°,则⊙BAC 的度数是( )A .60°B .65°C .70°D .75°13.(2020·重庆)如图,AB 是O 的切线,A 切点,连接OA ,OB ,若20B ∠=︒,则AOB ∠的度数为( )A .40°B .50°C .60°D .70°14.(2020·四川巴中)如图,在O 中,点、、A B C 在圆上,45,ACB AB ︒∠==O 的半径OA 的长是( )AB .2C .D .315.(2020·四川广安)如图,点A ,B ,C ,D 四点均在圆O 上,⊙AOD =68°,AO //DC ,则⊙B 的度数为( )A .40°B .60°C .56°D .68°16.(2020·广西柳州)如图,点A 、B 、C 在⊙O 上,若⊙BOC =70°,则⊙A 的度数为( )A .35°B .40°C .55°D .70°17.(2020·辽宁鞍山)如图,⊙O 是∆ABC 的外接圆,半径为2cm ,若2cm BC =,则A ∠的度数为( )A .30°B .25°C .15°D .10°18.(2020·江苏镇江)如图,AB 是半圆的直径,C 、D 是半圆上的两点,⊙ADC =106°,则⊙CAB 等于( )A .10°B .14°C .16°D .26°19.(2020·四川雅安)如图,ABC 内接于圆,90ACB ∠=︒,过点C 的切线交AB 的延长线于点28P P ∠=︒,.则∠=CAB ( )A .62︒B .31︒C .28︒D .56︒20.(2020·山东淄博)如图,放置在直线l 上的扇形OAB .由图⊙滚动(无滑动)到图⊙,再由图⊙滚动到图⊙.若半径OA =2,⊙AOB =45°,则点O 所经过的最短路径的长是( )A .2π+2B .3πC .52πD .52π+221.(2021·贵州黔西)图1是一把扇形书法纸扇,图2是其完全打开后的示意图,外侧两竹条OA 和OB 的夹角为150︒,OA 的长为30cm ,贴纸部分的宽AC 为18cm ,则CD 的长为( )A .5πcmB .10πcmC .20πcmD .25πcm22.(2021·山东青岛)如图,AB 是O 的直径,点E ,C 在O 上,点A 是EC 的中点,过点A 画O 的切线,交BC 的延长线于点D ,连接EC .若58.5ADB ∠=︒,则ACE ∠的度数为( )A .29.5︒B .31.5︒C .58.5︒D .63︒23.(2021·四川内江)如图,O 是ABC ∆的外接圆,60BAC ∠=︒,若O 的半径OC 为2,则弦BC 的长为( )A .4B .C .3 D24.(2021·山东滨州)如图,O 是ABC 的外接圆,CD 是O 的直径.若10CD =,弦6AC =,则cos ABC ∠的值为( )A .45B .35C .43D .3425.(2021·辽宁鞍山)如图,AB 为O 的直径,C ,D 为O 上的两点,若54ABD ∠︒=,则C ∠的度数为( )A .34︒B .36︒C .46︒D .54︒26.(2021·江苏镇江)如图,⊙BAC =36°,点O 在边AB 上,⊙O 与边AC 相切于点D ,交边AB 于点E ,F ,连接FD ,则⊙AFD 等于( )A .27°B .29°C .35°D .37°27.(2021·湖南湘潭)如图,BC 为⊙O 的直径,弦AD BC ⊥于点E ,直线l 切⊙O 于点C ,延长OD 交l 于点F ,若2AE =,22.5ABC ∠=︒,则CF 的长度为( )A .2B .C .D .428.(2022·广西贺州)某餐厅为了追求时间效率,推出一种液体“沙漏”免单方案(即点单完成后,开始倒转“沙漏”, “沙漏”漏完前,客人所点的菜需全部上桌,否则该桌免费用餐).“沙漏”是由一个圆锥体和一个圆柱体相通连接而成.某次计时前如图(1)所示,已知圆锥体底面半径是6cm ,高是6cm ;圆柱体底面半径是3cm ,液体高是7cm .计时结束后如图(2)所示,求此时“沙漏”中液体的高度为( )A .2cmB .3cmC .4cmD .5cm29.(2022·广西河池)如图,AB 是⊙O 的直径,P A 与⊙O 相切于点A ,⊙ABC =25°,OC 的延长线交P A 于点P ,则⊙P 的度数是( )A .25°B .35°C .40°D .50°30.(2022·内蒙古包头)如图,,AB CD 是O 的两条直径,E 是劣弧BC 的中点,连接BC ,DE .若22ABC ∠=︒,则CDE ∠的度数为( )A .22︒B .32︒C .34︒D .44︒31.(2022·辽宁锦州)如图,线段AB 是半圆O 的直径。
【创新设计 简易通】(江苏专用)高考英语二轮复习 第一部分 知识运用专题专练 专题14 情景交际体验高考

第一部分英语知识运用第一节单项填空专题十四情景交际1.(2013·山东,23)—How far can you run without stopping?— .I've never tried.A.Don't mention it B.That's all rightC.I have no idea D.Go ahead解析考查情景交际。
根据题意,你可以不间断地跑多远?然后回答是“我从来没有尝试过”,因此要选C“我也不知道”。
A别提了;B没关系;别客气;D继续;加油。
答案 C2.(2013·浙江,1)—Hey,can I ask you a favor?—Sure,A.here you are. B.just as I thought.C.how is it going?D.what can I do for you?解析考查交际用语。
句意:——你能帮我个忙吗?——当然,我能为你做些什么?A 项意为“给你”;B项意为“和我刚才想的一样”;C项意为“进展如何?”,都不符合上下文逻辑。
故答案为D项。
答案 D3.(2013·江苏,22)—The Tshirt I received is not the same as is shown online.—?But I promise you we'll look into it right away.A.Who says B.How comeC.What for D.Why worry解析考查交际用语。
句意:——我收到的T恤衫与网上展示的不一样。
——怎么会这样呢?但我向你承诺,我们马上进行调查。
A“谁说的”,B“怎么会这样呢”,what for“为什么”,why worry“为何烦恼”。
答案 B4.(2013·福建,33)—Would you mind answering some questions on shopping habits?— .A.Yes,with great pleasureB.No,I am afraid I can't make itC.Yes,it is worth the timeD.No,as long as it doesn't take long解析问句句意:你介意回答关于购物习惯的一些问题吗?A项意为“介意,非常高兴”,前后矛盾;B项意为“不介意,我害怕不能成功”;C项意为“介意,它是值得花时间的”;D项意为“不介意,只要不花很长时间”。
18第一部分 板块三 专题十四 中国特色社会主义建设道路与思想和科教文艺

考点一20世纪50—70年代中国社会主义建设道路的曲折探索1.社会主义制度和计划经济体制的确立(1949—1956年底)(1)国民经济恢复——奠基1949—1952年,新中国仅用三年时间,就完成了国民经济的恢复工作,为国家开展有计划的经济建设创造了条件。
(2)“一五”计划——建设①特点:发展生产力与改造生产关系相结合,优先发展重工业。
②成果:初步建立了独立的工业体系,初步形成了合理的工业布局。
(3)社会主义三大改造——确立①性质:生产资料私有制变为社会主义公有制。
②意义:社会主义经济体系在中国基本建立起来。
2.社会主义经济建设的曲折发展(1956—1976年)(1)中共八大——成功探索①内容:主要矛盾是人民对于建立先进的工业国的要求同落后的农业国的现实之间的矛盾;人民对于经济文化迅速发展的需要同当前经济文化不能满足人民需要的状况之间的矛盾;主要任务是集中力量把我国尽快地从落后的农业国变为先进的工业国。
②评价:是对社会主义建设的一次成功探索,但在实践中未能坚持下来。
(2)“左”倾泛滥——严重失误①表现:1958年开始的总路线、“大跃进”和人民公社化运动。
②原因:急于求成,改变落后局面的心情迫切;没有经济建设经验;毛泽东等中央领导人“左”倾冒进,夸大了人的主观能动性。
③结果:经济比例失调,环境破坏,农民的积极性受挫,是造成三年经济困难的主要原因。
(3)“八字”方针——调整恢复1960年冬,提出“调整、巩固、充实、提高”的“八字”方针;1962年底,经济形势好转。
(4)“文化大革命”——严重破坏①实质:“左”倾错误发展成以阶级斗争为纲的恶果。
②影响:国民经济基本瘫痪,面临崩溃;人民生活水平长期在低水平徘徊。
[重点深化]三大改造的完成标志着我国社会主义制度的建立(1)从革命性质来看,三大改造前是过渡时期,由新民主主义社会向社会主义社会过渡;三大改造完成后,我国基本上完成了社会主义革命的任务。
(2)从经济基础来看,三大改造前,以公有制经济为主体,多种所有制形式并存;三大改造后,生产资料私有制变为社会主义公有制。
2023年中考数学总复习专题14二次函数与线段数量关系最值定值问题(学生版)

(全国通用)专题14二次函数与线段数量关系最值定值问题图形运动的过程中,求两条线段之间的函数关系,是中考数学的热点问题.产生两条线段间的函数关系,常见的情况有两种,一是勾股定理,二是比例关系.还有一种不常见的,就是线段全长等于部分线段之和.由比例线段产生的函数关系问题,在两种类型的题目中比较常用.一是由平行线产生的对于线段成比例,二是相似三角形的对应边成比例.一般步骤是先说理产生比例关系,再代入数值或表示数的字母,最后整理、变形,根据要求写出定义域.关键是寻找比例关系,难点是有的整理、变形比较繁琐,容易出错.【例1】(2022•武汉模拟)抛物线y=x2﹣2x+m的顶点A在x轴上,与y轴交于点B.(1)求抛物线的解析式;(2)如图1,直线CD∥AB交抛物线于C,D两点,若,求△COD的面积;(3)如图2,P为抛物线对称轴上顶点下方的一点,过点P作直线交抛物线于点E,F,交x轴于点M,求的值.【例2】(2022•黄石)如图,抛物线y=﹣x2+x+4与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.(1)A,B,C三点的坐标为,,.(2)连接AP,交线段BC于点D,①当CP与x轴平行时,求的值;②当CP与x轴不平行时,求的最大值;(3)连接CP,是否存在点P,使得∠BCO+2∠PCB=90°,若存在,求m的值,若不存在,请说明理由.【例3】(2022•河南三模)如图,抛物线y=ax2+bx﹣4交x轴于A,B两点,交y轴于点C,OB=2OC=4OA,连接AC,BC.(1)求抛物线的解析式;(2)点D是抛物线y=ax2+bx﹣4的图象上在第四象限内的一动点,DE⊥x轴于点E,交BC于点F.设点D的横坐标为m.①请用含m的代数式表示线段DF的长;②已知DG∥AC,交BC于点G,请直接写出当时点D的坐标.【例4】(2021•大庆)如图,抛物线y=ax2+bx+c与x轴交于原点O和点A,且其顶点B关于x轴的对称点坐标为(2,1).(1)求抛物线的函数表达式;(2)抛物线的对称轴上存在定点F,使得抛物线y=ax2+bx+c上的任意一点G到定点F的距离与点G到直线y=﹣2的距离总相等.①证明上述结论并求出点F的坐标;②过点F的直线l与抛物线y=ax2+bx+c交于M,N两点.证明:当直线l绕点F旋转时,+是定值,并求出该定值;(3)点C(3,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQBC周长最小,直接写出P,Q的坐标.1.(2020•道里区二模)已知:在平面直角坐标系中,点O为坐标原点,抛物线y=﹣+bx+3交x轴于A、B两点(点B在点A的右边)交y轴于点C,OB=3OC.(1)如图1,求抛物线的解析式;(2)如图2,点E是第一象限抛物线上的点,连接BE,过点E作ED⊥OB于点D,tan∠EBD=,求△BDE的面积;(3)如图3,在(2)的条件下,连接BC交DE于点Q,点K是第四象限抛物线上的点,连接EK交BC于点M,交x轴于点N,∠EMC=45°,过点K作直线KT⊥x轴于点T,过点E作EL∥x轴,交直线KT于点L,点F是抛物线对称轴右侧第一象限抛物线上的点,连接ET、LF,LF的延长线交ET于点P,连接DP并延长交EL于点S,SE=2SL,求点F的坐标.2.(2020•三明二模)如图,抛物线y=x2+mx(m<0)交x轴于O,A两点,顶点为点B.(Ⅰ)求△AOB的面积(用含m的代数式表示);(Ⅱ)直线y=kx+b(k>0)过点B,且与抛物线交于另一点D(点D与点A不重合),交y轴于点C.过点C作CE∥AB交x轴于点E.(ⅰ)若∠OBA=90°,2<<3,求k的取值范围;(ⅱ)求证:DE∥y轴.3.(2022•杜尔伯特县一模)如图,已知抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(m,0)两点,与y轴相交于点C(0,﹣3),抛物线的顶点为D.(1)求抛物线的解析式;(2)若点E在x轴上,且∠ECB=∠CBD,求点E的坐标.(3)若P是直线BC下方抛物线上任意一点,过点P作PH⊥x轴于点H,与BC交于点M.①求线段PM长度的最大值.②在①的条件下,若F为y轴上一动点,求PH+HF+CF的最小值.4.(2020•江岸区校级一模)已知:抛物线y=x2+x+m交x轴于A,B两点,交y轴于点C,其中点B在点A的右侧,且AB=7.(1)如图1,求抛物线的解析式;(2)如图2,点D在第一象限内抛物线上,连接CD,AD,AD交y轴于点E.设点D的横坐标为d,△CDE的面积为S,求S与d之间的函数关系式(不要求写出自变量d的取值范围);(3)如图3,在(2)的条件下,过点D作DH⊥CE于点H,点P在DH上,连接CP,若∠OCP=2∠DAB,且HE:CP=3:5,求点D的坐标及相应S的值.5.(2020•涡阳县一模)如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).(1)求抛物线的解析式.(2)点P是直线上方的抛物线上的一个动点,求△ABP的面积最大时的P点坐标.(3)若点P是抛物线上的一个动点(不与点A点B重合),过点P作直线PD⊥x轴于点D,交直线AB 于点E.当PE=2ED时,求P点坐标;(4)设抛物线与y轴交于点F,在抛物线的第一象限内,是否存在一点M,使得AM被FC平分?若存在,请求出点M的坐标;若不存在,说明理由.6.(2021•桂林)如图,已知抛物线y=a(x﹣3)(x+6)过点A(﹣1,5)和点B(﹣5,m),与x轴的正半轴交于点C.(1)求a,m的值和点C的坐标;(2)若点P是x轴上的点,连接PB,P A,当=时,求点P的坐标;(3)在抛物线上是否存在点M,使A,B两点到直线MC的距离相等?若存在,求出满足条件的点M的横坐标;若不存在,请说明理由.7.(2021•甘肃)如图,在平面直角坐标系中,抛物线y=x2+bx+c与坐标轴交于A(0,﹣2),B(4,0)两点,直线BC:y=﹣2x+8交y轴于点C.点D为直线AB下方抛物线上一动点,过点D作x轴的垂线,垂足为G,DG分别交直线BC,AB于点E,F.(1)求抛物线y=x2+bx+c的表达式;(2)当GF=时,连接BD,求△BDF的面积;(3)①H是y轴上一点,当四边形BEHF是矩形时,求点H的坐标;②在①的条件下,第一象限有一动点P,满足PH=PC+2,求△PHB周长的最小值.8.(2021•丽水)如图,已知抛物线L:y=x2+bx+c经过点A(0,﹣5),B(5,0).(1)求b,c的值;(2)连结AB,交抛物线L的对称轴于点M.①求点M的坐标;②将抛物线L向左平移m(m>0)个单位得到抛物线L1.过点M作MN∥y轴,交抛物线L1于点N.P是抛物线L1上一点,横坐标为﹣1,过点P作PE∥x轴,交抛物线L于点E,点E在抛物线L对称轴的右侧.若PE+MN=10,求m的值.9.(2020•陕西)已知抛物线L:y=﹣x2+bx+c过点(﹣3,3)和(1,﹣5),与x轴的交点为A,B(点A 在点B的左侧).(1)求抛物线L的表达式;(2)若点P在抛物线L上,点E、F在抛物线L的对称轴上,D是抛物线L的顶点,要使△PEF∽△DAB (P的对应点是D),且PE:DA=1:4,求满足条件的点P的坐标.10.(2020•盘锦)如图1,直线y=x﹣4与x轴交于点B,与y轴交于点A,抛物线y=﹣x2+bx+c经过点B和点C(0,4),△ABO沿射线AB方向以每秒个单位长度的速度平移,平移后的三角形记为△DEF (点A,B,O的对应点分别为点D,E,F),平移时间为t(0<t<4)秒,射线DF交x轴于点G,交抛物线于点M,连接ME.(1)求抛物线的解析式;(2)当tan∠EMF=时,请直接写出t的值;(3)如图2,点N在抛物线上,点N的横坐标是点M的横坐标的,连接OM,NF,OM与NF相交于点P,当NP=FP时,求t的值.11.(2022•深圳三模)如图1,抛物线y=ax2+bx经过点A(﹣5,0),点B(﹣1,﹣2).(1)求抛物线解析式;(2)如图2,点P为抛物线上第三象限内一动点,过点Q(﹣4,0)作y轴的平行线,交直线AP于点M,交直线OP于点N,当点P运动时,4QM+QN的值是否变化?若变化,说明变化规律,若不变,求(3)如图3,长度为的线段CD(点C在点D的左边)在射线AB上移动(点C在线段AB上),连接OD,过点C作CE∥OD交抛物线于点E,线段CD在移动的过程中,直线CE经过一定点F,直接写出定点F的坐标与的最小值.12.(2022•阿克苏地区一模)如图1.抛物线与x轴交于A、B两点,与y轴交于点C,连接BC,已知点B(4,0).(1)若C(0,3),求抛物线的解析式.(2)在(1)的条件下,P(﹣2,m)为该抛物线上一点,Q是x轴上一点求的最小值,并求此时点Q的坐标.(3)如图2.过点A作BC的平行线,交y轴与点D,交抛物线于另一点E.若DE=7AD,求c的值.13.(2022•松江区二模)如图,在平面直角坐标系中,已知直线y=2x+8与x轴交于点A、与y轴交于点B,抛物线y=﹣x2+bx+c经过点A、B.(1)求抛物线的表达式;(2)P是抛物线上一点,且位于直线AB上方,过点P作PM∥y轴、PN∥x轴,分别交直线AB于点M、①当MN=AB时,求点P的坐标;②联结OP交AB于点C,当点C是MN的中点时,求的值.14.(2022•游仙区模拟)如图,抛物线与坐标轴分别交于A(﹣1,0),B(3,0),C(0,3).(1)求抛物线的解析式;(2)抛物线上是否存在点P,使得∠CBP=∠ACO,若存在,求出点P的坐标;若不存在,说明理由;(3)如图2,Q是△ABC内任意一点,求++的值.15.(2022•龙岩模拟)抛物线y=ax2+bx+c经过A(﹣1,0),B(3,4)两点,与y轴交于点C.(1)求抛物线的解析式(用含a的式子表示);(2)当a>0时,连接AB,BC,若tan∠ABC=,求a的值;(3)直线y=﹣x+m与线段AB交于点P,与抛物线交于M,N两点(点M在点N的左侧),若PM•PN =6,求m的值.16.(2022•雷州市模拟)如图(1),抛物线y=ax2+bx+6与x轴交于点A(﹣6,0)、B(2,0),与y轴交于点C,抛物线对称轴交抛物线于点M,交x轴于点N.点P是抛物线上的动点,且位于x轴上方.(1)求抛物线的解析式.(2)如图(2),点D与点C关于直线MN对称,若∠CAD=∠CAP,求点P的坐标.(3)直线BP交y轴于点E,交直线MN于点F,猜想线段OE、FM、MN三者之间存在的数量关系,并证明.17.(2022•马鞍山二模)如图,抛物线y=ax2+bx﹣3交x轴于点A(﹣1,0)、B(3,0),与y轴交于C点,直线y=kx(k<0)交线段BC下方抛物线于D点,交BC于E点(1)分别求出a、b的值;(2)求出线段BC的函数关系式,并写出自变量取值范围;(3)探究是否有最大值,若存在,请求出此时k值,若不存在,请说明理由.18.(2022•南岗区校级二模)如图1,在平面直角坐标系中,O为坐标原点,抛物线y=﹣ax2+6ax+6与y 轴交于点B,交x轴的负半轴于点A,交x轴的正半轴于点C,且S△ABC=30.(1)求抛物线的解析式;(2)如图2,点P为第一象限抛物线上一点,其横坐标为t,PD⊥x轴于点D,设tan∠P AD等于m,求m与t之间的函数关系式;(3)如图3,在(2)的条件下,当m=时,过点B作BN⊥AB交∠P AC的平分线于点N,点K在线段AB上,点M在线段AN上,连接KM、KN,∠MKN=2∠BNK,作MT⊥KN于点T,延长MT交BN 于点H,若NH=4BH,求直线KN的解析式.19.(2022•江汉区校级模拟)如图1,已知抛物线y=ax2+bx+c(a>0)与x轴交于A(﹣1,0),B(3,0),与y轴交于点C.(1)若C(0,﹣3),求抛物线的解析式;(2)在(1)的条件下,E是线段BC上一动点,AE交抛物线于F点,求的最大值;(3)如图2,点N为y轴上一点,AN、BN交抛物线于E、F两点,求•的值.20.(2022•成都模拟)如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y 轴交于点C.(1)求点A,B,C的坐标及抛物线的对称轴;(2)如图1,点P(1,m),Q(1,m﹣2)是两动点,分别连接PC,QB,请求出|PC﹣QB|的最大值,并求出m的值;(3)如图2,∠BAC的角平分线交y轴于点D,过D点的直线l与射线AB,AC分别于E,F,当直线l 绕点D旋转时,是否为定值,若是,请求出该定值;若不是,请说明理由.21.(2022•沈阳模拟)如图,在平面直角坐标系中,抛物线y=﹣x2+x+2与x轴交于A,B两点(点A 在点B左侧),与y轴交于点C,直线l:y=kx+b经过点B,点C,点P是抛物线上一动点,连接OP交直线BC于点D.(1)求直线l的解析式;(2)当=时,求点P的坐标;(3)在(2)的条件下,点N是直线BC上一动点,连接ON,过点D作DF⊥ON于点F,点F在线段ON上,当OD=DF时,请直接写出点N的坐标.22.(2022•沈阳模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣过点A(3,2)和点B (,0),与x轴的另一个交点为点C.(1)求抛物线的函数表达式.(2)判断△ABC的形状,并说明理由.(3)点D在线段BC上,连接AD,作DE⊥AD,且DE=AD,连接AE交x轴于点F.点F不与点C 重合,射线DP⊥AE,交AE于点P,交AC于点Q.①当AD=AF时,请直接写出∠CAE的度数;②当=时,请直接写出CQ的长.。
中考语文第一部分古诗文阅读专题一文言文阅读第14篇《马说》作业(含答案)

第14篇马说一、[原创新题]请阅读下面的文字,完成1~4题。
(16分)马说韩愈世有伯乐,然后有千里马。
千里马常有,而伯乐不常有。
故虽有名马,祗辱于奴隶人之手,骈死于槽枥之间,不以千里称也。
马之千里者,一食或尽粟一石。
食马者不知其能千里而食也。
是马也,虽有千里之能,食不饱,力不足,才美不外见,且欲与常马等不可得,安求其能千里也?策之不以其道,食之不能尽其材,鸣之而不能通其意,执策而临之,曰:“天下无马!”呜呼!其真无马邪?其真不知马也!马诗二十三首(其四)李贺此马非凡马,房星【注】本是星。
向前敲瘦骨,犹自带铜声。
【注】房星:星宿名,这里指马。
《晋书·天文志》载,“房四星,亦曰天驷,为天马,主车驾。
房星明,则王者明”。
1.请解释下列加点词在文中的意思。
(4分)(1)才美不外见.见:(2)策.之不以其道策:(3)执策而临.之临:(4)犹.自带铜声犹:2.请把下面的句子翻译成现代汉语。
(4分)(1)祗辱于奴隶人之手,骈死于槽枥之间,不以千里称也。
(2)马之千里者,一食或尽粟一石。
3.《马说》中,千里马“才美不外见”的根本原因是“”;《马诗二十三首》(其四)中,瘦马“犹自带铜声”的根本原因是“”。
(用原文语句填空)(2分)4.《马说》和《马诗二十三首》(其四)分别采用了什么表现手法?各自表达了作者怎样的思想感情?(6分)二、[2021合肥包河区二模]请阅读下面的文字,完成1~4题。
(16分)【甲】世有伯乐,然后有千里马。
千里马常有,而伯乐不常有。
故虽有名马,祗辱于奴隶人之手,骈死于槽枥之间,不以千里称也。
马之千里者,一食或尽粟一石。
食马者不知其能千里而食也。
是马也,虽有千里之能,食不饱,力不足,才美不外见,且欲与常马等不可得,安求其能千里也?策之不以其道,食之不能尽其材,鸣之而不能通其意,执策而临之,曰:“天下无马!”呜呼!其真无马邪?其真不知马也!(韩愈《马说》)【乙】齐桓深知宁戚①,将任之以政,群臣争谗之,曰:“宁戚卫人,去齐不远,君可使人问之。
专题14 近代经济、社会生活与教育文化事业的发展(第01期)(解析版)

专题14 近代经济、社会生活与教育文化事业的发展一、选择题1.(2021·江苏南京市·中考真题)20世纪初,清政府统一全国学制,“仍以忠君和尊孔为……大幅度增加西方教育中的自然科学与社会科学内容”。
当时中国教育A.开始出现新式学校B.呈现出新旧并存特点C.掀起尊孔复古思潮D.举起民主、科学旗帜【答案】B【详解】依据所学知识可知,1905年清政府废除科举考试,与此同时,清政府还通令兴办学堂,颁布各级学堂章程,统一全国学制,中国近代新式教育逐渐发展起来,但在教学内容上“仍以忠君和尊孔为……大幅度增加西方教育中的自然科学与社会科学内容”,因此20世纪初,中国教育呈现出新旧并存特点,故B正确;洋务运动时期,洋务派先后兴办了同文馆、福州船政学堂等一批新式学校,故A错误;袁世凯窃取辛亥革命胜利果实后,掀起尊孔复古思潮,故C错误;新文化运动举起民主、科学旗帜,故D错误。
综上答案B。
2.(2021·山东东营市·中考真题)近代中国人创办的第一个也是规模最大的文化出版机构是A.新华书店B.开明书店C.中华书局D.商务印书馆【答案】D【详解】1897年在上海创办的商务印书馆,是近代中国历史最长、规模最大的文化出版机构,当时使用的课本和字典很多都是由它出版的。
商务印书馆是近代中国人创办的第一个规模最大的文化出版机构,故选D;ABC不符合题意,排除。
3.(2021·陕西中考真题)第一次世界大战期间,中国民族工业获得了迅速发展的良机,出现了“短暂的春天”。
出现这种状况的主要原因是()A.有识之士发出“实业救国”的呼声B.开始引进西方先进科学技术C.国民党官僚资本的建立和扩张D.西方列强忙于欧洲战事,暂时放松对中国的经济侵略【答案】D【详解】试卷第1页,总8页根据所学知识可知,第一次世界大战期间,西方列强忙于欧洲战事,暂时放松了对中国经济侵略,中国民族工业获得了迅速发展的良机,出现了“短暂的春天”,所以D项符合题意;清末状元张謇等有识之士发出“实业救国”的呼声,所以A项不符合题意;洋务运动开始引进西方先进科学技术,所以B项不符合题意;国民党官僚资本的建立和扩张,使民族工业发展艰难,所以C项不符合题意。
【备战2013】高考化学 考前30天冲刺押题系列 第一部分 专题14 化学计算

考前30天之备战2013高考化学冲刺押题系列第一部分 专题14化学计算【2013高考考纲】题型示例1 有关溶液pH 的简单计算【样题1】已知在100℃的温度下(本题涉及的溶液温度均为100℃),水的离子积K W = 1×10-12。
下列说法正确的是A .0.05 mol/L 的H 2SO 4溶液pH =1B .0.001 mol/L 的NaOH 溶液pH =11C .0.005 mol/L 的H 2SO 4溶液与0.01 mol/L 的NaOH 溶液等体积混合,混合溶液pH 为6,溶液显酸性D .完全中和pH =3的H 2SO 4溶液50 mL ,需要pH =11的NaOH 溶液50 mL题型示例2 与电化学有关计算【样题1】500 mL KNO 3和Cu(NO 3)2的混合溶液中c (NO 3-)=6.0 mol·L -1,用石墨作电极电解此溶液,当通电一段时间后,两极均收集到22.4 L 气体(标准状况),假定电解后溶液体积仍为500 mL ,下列说法正确的是A .原混合溶液中c (K +)为4 mol·L -1B .上述电解过程中共转移4 mol 电子C .电解得到的Cu 的物质的量为0.5 molD .电解后溶液中c (H +)为2 mol·L -1【解题指导】选B 。
惰性电极电解混合溶液时,根据离子放电顺序,阴极先发生:Cu 2++2e -=Cu 后发生:2H ++2e -=H 2↑ 阳极:4OH --4e -=O 2↑+2H 2O 。
两极都收集1mol 气体,由阳极转移电子为4mol ,又知阴极生成1molH 2转移电子2mol ,根据电子得失守恒可得:n (Cu2+)=1mol 。
再根据电荷守恒,在500 mL KNO 3和Cu(NO 3)2的混合溶液中存在关系:2c (Cu 2+)+c (K +)=c (NO 3-),可以求出c (K +)=2 mol·L -1 。
无锡新领航教育特供:【三维设计】(江苏专版)2013高中数学二轮专题 第一部分 专题14配套专题检

小升初 中高考 高二会考 艺考生文化课 一对一辅导/wxxlhjy QQ:157171090无锡新领航教育特供:【三维设计】(江苏专版)2013高中数学二轮专题 第一部分 专题14配套专题检测1.(2012²上海春招)抛物线y 2=8x 的焦点坐标为________.解析:由p =4得焦点坐标为(2,0).答案:(2,0)2.已知方程x 2m -1+y 22-m =1表示焦点在y 轴上的椭圆,则m 的取值范围是________;若该方程表示双曲线,则m 的取值范围是________.解析:若方程表示焦点在y 轴上的椭圆,则⎩⎪⎨⎪⎧ m -1>0,2-m >0,2-m >m -1,解得1<m <32;若方程表示双曲线,则(m -1)(2-m )<0,解得m <1或m >2. 答案:⎝ ⎛⎭⎪⎫1,32 (-∞,1)∪(2,+∞) 3.点P 为椭圆x 2a 2+y 2b2=1(a >b >0)上一点,F 1,F 2为椭圆的焦点,如果∠PF 1F 2=75°,∠PF 2F 1=15°,则椭圆的离心率为________.解析:由题意得∠F 1PF 2=90°,PF 1=2c cos 75°,PF 2=2c sin 75°,所以2c (sin 75°+cos 75°)=2a ,e =1sin 75°+cos 75°=63. 答案:634.已知抛物线y 2=2px (p >0),过其焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为________.解析:直线AB 的方程为y =x -p 2,即x =y +p 2,代入y 2=2px 得,y 2-2py -p 2=0. 则y A +y B =2p =4,p =2,准线方程为x =-1.答案:x =-1 5.(2011²天津高考)已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的一条渐近线方程是y =3x ,它的一个焦点在抛物线y 2=24x 的准线上,则双曲线的方程为________.解析:由题设可得双曲线方程满足3x 2-y 2=λ(λ>0),即x 2λ3-y 2λ=1.于是c 2=λ3+λ。
专题14二次函数解答压轴题-2021年中考数学真题分项汇编(原卷版)【全国通用】(第01期)

2021年中考数学真题分项汇编【全国通用】(第01期)专题14二次函数解答压轴题(共32题)姓名:__________________ 班级:______________ 得分:_________________一、解答题1.(2021·北京中考真题)在平面直角坐标系xOy 中,点()1,m 和点()3n ,在抛物线()20y ax bx a =+>上. (1)若3,15m n ==,求该抛物线的对称轴;(2)已知点()()()1231,,2,,4,y y y -在该抛物线上.若0mn <,比较123,,y y y 的大小,并说明理由.2.(2021·江苏南京市·中考真题)已知二次函数2y ax bx c =++的图像经过()()2,1,2,3--两点.(1)求b 的值.(2)当1c >-时,该函数的图像的顶点的纵坐标的最小值是________.(3)设()0m ,是该函数的图像与x 轴的一个公共点,当13m -<<时,结合函数的图像,直接写出a 的取值范围.3.(2021·安徽中考真题)已知抛物线221(0)y ax x a =-+≠的对称轴为直线1x =.(1)求a 的值;(2)若点M (x 1,y 1),N (x 2,y 2)都在此抛物线上,且110x -<<,212x <<.比较y 1与y 2的大小,并说明理由;(3)设直线(0)y m m =>与抛物线221y ax x =-+交于点A 、B ,与抛物线23(1)y x =-交于点C ,D ,求线段AB 与线段CD 的长度之比.4.(2021·浙江绍兴市·中考真题)小聪设计奖杯,从抛物线形状上获得灵感,在平面直角坐标系中画出截面示意图,如图1,杯体ACB 是抛物线的一部分,抛物线的顶点C 在y 轴上,杯口直径4AB =,且点A ,B 关于y 轴对称,杯脚高4CO =,杯高8DO =,杯底MN 在x 轴上.(1)求杯体ACB 所在抛物线的函数表达式(不必写出x 的取值范围).(2)为使奖杯更加美观,小敏提出了改进方案,如图2,杯体A CB ''所在抛物线形状不变,杯口直径//A B AB '',杯脚高CO 不变,杯深CD '与杯高OD '之比为0.6,求A B ''的长.5.(2021·湖北恩施土家族苗族自治州·中考真题)如图,在平面直角坐标系中,四边形ABCD 为正方形,点A ,B 在x 轴上,抛物线2y x bx c =++经过点B ,()4,5D -两点,且与直线DC 交于另一点E .(1)求抛物线的解析式;(2)F 为抛物线对称轴上一点,Q 为平面直角坐标系中的一点,是否存在以点Q ,F ,E ,B 为顶点的四边形是以BE 为边的菱形.若存在,请求出点F 的坐标;若不存在,请说明理由;(3)P 为y 轴上一点,过点P 作抛物线对称轴的垂线,垂足为M ,连接ME ,BP .探究EM MP PB ++是否存在最小值.若存在,请求出这个最小值及点M 的坐标;若不存在,请说明理由.6.(2021·四川南充市·中考真题)如图,已知抛物线2()40y ax bx a =++≠与x 轴交于点A (1,0)和B ,与y 轴交于点C ,对称轴为52x =.(1)求抛物线的解析式;(2)如图1,若点P 是线段BC 上的一个动点(不与点B ,C 重合),过点P 作y 轴的平行线交抛物线于点Q ,连接OQ .当线段PQ 长度最大时,判断四边形OCPQ 的形状并说明理由.(3)如图2,在(2)的条件下,D 是OC 的中点,过点Q 的直线与抛物线交于点E ,且2DQE ODQ ∠=∠.在y 轴上是否存在点F ,使得BEF 为等腰三角形?若存在,求点F 的坐标;若不存在,请说明理由.7.(2021·四川广元市·中考真题)如图1,在平面直角坐标系xOy 中,抛物线2y ax bx c =++与x 轴分别相交于A 、B 两点,与y 轴相交于点C ,下表给出了这条抛物线上部分点(,)x y 的坐标值:x … 1- 0 1 2 3 …y 03 4 3 0 … (1)求出这条抛物线的解析式及顶点M 的坐标;(2)PQ 是抛物线对称轴上长为1的一条动线段(点P 在点Q 上方),求AQ QP PC ++的最小值; (3)如图2,点D 是第四象限内抛物线上一动点,过点D 作DF x ⊥轴,垂足为F ,ABD △的外接圆与DF 相交于点E .试问:线段EF 的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.8.(2021·湖北荆州市·中考真题)已知:直线1y x =-+与x 轴、y 轴分别交于A 、B 两点,点C 为直线AB 上一动点,连接OC ,AOC ∠为锐角,在OC 上方以OC 为边作正方形OCDE ,连接BE ,设BE t =. (1)如图1,当点C 在线段AB 上时,判断BE 与AB 的位置关系,并说明理由;(2)真接写出点E 的坐标(用含t 的式子表示);(3)若tan AOC k ∠=,经过点A 的抛物线()20y ax bx c a =++>顶点为P ,且有6320a b c ++=,POA 的面积为12k .当22t =时,求抛物线的解析式.9.(2021·四川资阳市·中考真题)抛物线2y x bx c =-++与x 轴交于A 、B 两点,与y 轴交于点C ,且()()1,0,0,3B C -.(1)求抛物线的解析式;(2)如图1,点P 是抛物线上位于直线AC 上方的一点,BP 与AC 相交于点E ,当:1:2PE BE =时,求点P 的坐标;(3)如图2,点D 是抛物线的顶点,将抛物线沿CD 方向平移,使点D 落在点D 处,且2DD CD '=,点M 是平移后所得抛物线上位于D 左侧的一点,//MN y 轴交直线OD '于点N ,连结CN .当55D N CN '+的值最小时,求MN 的长.10.(2021·四川南充市·中考真题)超市购进某种苹果,如果进价增加2元/千克要用300元;如果进价减少2元/千克,同样数量的苹果只用200元.(1)求苹果的进价.(2)如果购进这种苹果不超过100千克,就按原价购进;如果购进苹果超过100千克,超过部分购进价格减少2元/千克.写出购进苹果的支出y (元)与购进数量x (千克)之间的函数关系式.(3)超市一天购进苹果数量不超过300千克,且购进苹果当天全部销售完.据统计,销售单价z (元/千克)与一天销售数量x (千克)的关系为112100z x =-+.在(2)的条件下,要使超市销售苹果利润w (元)最大,求一天购进苹果数量.(利润=销售收入-购进支出) 11.(2021·湖北十堰市·中考真题)已知抛物线25y ax bx =+-与x 轴交于点()1,0A -和()5,0B -,与y 轴交于点C ,顶点为P ,点N 在抛物线对称轴上且位于x 轴下方,连AN 交抛物线于M ,连AC 、CM .(1)求抛物线的解析式;(2)如图1,当tan 2ACM ∠=时,求M 点的横坐标;(3)如图2,过点P 作x 轴的平行线l ,过M 作MD l ⊥于D ,若3MD MN =,求N 点的坐标. 12.(2021·湖北十堰市·中考真题)某商贸公司购进某种商品的成本为20元/kg ,经过市场调研发现,这种商品在未来40天的销售单价y (元/kg )与时间x (天)之间的函数关系式为:0.2530(120)35(2040)x x y x +≤≤⎧=⎨<≤⎩且x 为整数,且日销量()kg m 与时间x (天)之间的变化规律符合一次函数关系,如下表: 时间x (天) 1 3 6 10 …日销量()kg m 142 138 132 124 …填空:(1)m 与x 的函数关系为___________;(2)哪一天的销售利润最大?最大日销售利润是多少?(3)在实际销售的前20天中,公司决定每销售1kg 商品就捐赠n 元利润(4n <)给当地福利院,后发现:在前20天中,每天扣除捐赠后的日销售利润随时间x 的增大而增大,求n 的取值范围.13.(2021·四川达州市·中考真题)渠县是全国优质黄花主产地,某加工厂加工黄花的成本为30元/千克,根据市场调查发现,批发价定为48元/千克时,每天可销售500千克.为增大市场占有率,在保证盈利的情况下,工厂采取降价措施.批发价每千克降低1元,每天销量可增加50千克.(1)写出工厂每天的利润W 元与降价x 元之间的函数关系.当降价2元时,工厂每天的利润为多少元? (2)当降价多少元时,工厂每天的利润最大,最大为多少元?(3)若工厂每天的利润要达到9750元,并让利于民,则定价应为多少元?14.(2021·湖南怀化市·中考真题)某超市从厂家购进A 、B 两种型号的水杯,两次购进水杯的情况如下表: 进货批次 A 型水杯(个) B 型水杯(个) 总费用(元)一100 200 8000 二 200 300 13000(1)求A 、B 两种型号的水杯进价各是多少元?(2)在销售过程中,A 型水杯因为物美价廉而更受消费者喜欢.为了增大B 型水杯的销售量,超市决定对B 型水杯进行降价销售,当销售价为44元时,每天可以售出20个,每降价1元,每天将多售出5个,请问超市应将B 型水杯降价多少元时,每天售出B 型水杯的利润达到最大?最大利润是多少?(3)第三次进货用10000元钱购进这两种水杯,如果每销售出一个A 型水杯可获利10元,售出一个B 型水杯可获利9元,超市决定每售出一个A 型水杯就为当地“新冠疫情防控”捐b 元用于购买防控物资.若A 、B 两种型号的水杯在全部售出的情况下,捐款后所得的利润始终不变,此时b 为多少?利润为多少?15.(2021·湖北黄冈市·中考真题)已知抛物线23y ax bx =+-与x 轴相交于(1,0)A -,(3,0)B 两点,与y轴交于点C ,点(,0)N n 是x 轴上的动点.(1)求抛物线的解析式;(2)如图1,若3n <,过点N 作x 轴的垂线交抛物线于点P ,交直线BC 于点G .过点P 作PD BC ⊥于点D ,当n 为何值时,PDG BNG ≌;(3)如图2,将直线BC 绕点B 顺时针旋转,使它恰好经过线段OC 的中点,然后将它向上平移32个单位长度,得到直线1OB .①1tan BOB ∠=______;①当点N 关于直线1OB 的对称点1N 落在抛物线上时,求点N 的坐标.16.(2021·湖北黄冈市·中考真题)红星公司销售一种成本为40元/件的产品,若月销售单价不高于50元/件.一个月可售出5万件;月销售单价每涨价1元,月销售量就减少0.1万件.其中月销售单价不低于成本.设月销售单价为x (单位:元/件),月销售量为y (单位:万件).(1)直接写出y 与x 之间的函数关系式,并写出自变量x 的取值范围;(2)当月销售单价是多少元/件时,月销售利润最大,最大利润是多少万元?(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款a 元.已知该公司捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元,求a 的值.17.(2021·新疆中考真题)已知抛物线223(0)y ax ax a =-+≠. (1)求抛物线的对称轴;(2)把抛物线沿y 轴向下平移3a 个单位,若抛物线的顶点落在x 轴上,求a 的值;(3)设点()1,P a y ,()22,Q y 在抛物线上,若12y y >,求a 的取值范围.18.(2021·湖南长沙市·中考真题)我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两点关于y 轴对称,则把该函数称之为“T 函数”,其图象上关于y 轴对称的不同两点叫做一对“T 点”.根据该约定,完成下列各题.(1)若点()1,A r 与点(),4B s 是关于x 的“T 函数”()()240,0,0,.x x y tx x t t ⎧-<⎪=⎨⎪≥≠⎩是常数的图象上的一对“T 点”,则r =______,s =______,t =______(将正确答案填在相应的横线上);(2)关于x 的函数y kx p =+(k ,p 是常数)是“T 函数”吗?如果是,指出它有多少对“T 点”;如果不是,请说明理由;(3)若关于x 的“T 函数”2y ax bx c =++(0a >,且a ,b ,c 是常数)经过坐标原点O ,且与直线:l y mx n =+(0m ≠,0n >,且m ,n 是常数)交于()11,M x y ,()22,N x y 两点,当1x ,2x 满足()11211x x --+=时,直线l 是否总经过某一定点?若经过某一定点,求出该定点的坐标;否则,请说明理由. 19.(2021·四川广安市·中考真题)如图,在平面直角坐标系中,抛物线2y x bx c =-++的图象与坐标轴相交于A 、B 、C 三点,其中A 点坐标为()3,0,B 点坐标为()1,0-,连接AC 、BC .动点P 从点A 出发,在线段AC C 做匀速运动;同时,动点Q 从点B 出发,在线段BA 上以每秒1个单位长度向点A 做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接PQ ,设运动时间为t 秒.(1)求b 、c 的值;(2)在P 、Q 运动的过程中,当t 为何值时,四边形BCPQ 的面积最小,最小值为多少?(3)在线段AC 上方的抛物线上是否存在点M ,使MPQ 是以点P 为直角顶点的等腰直角三角形?若存在,请求出点M 的坐标;若不存在,请说明理由.20.(2021·陕西中考真题)已知抛物线228y x x =-++与x 轴交于点A 、B (其中A 在点B 的左侧),与y轴交于点C .(1)求点B 、C 的坐标;(2)设点C '与点C 关于该抛物线的对称轴对称在y 轴上是否存在点P ,使PCC '△与POB 相似且PC 与PO 是对应边?若存在,求点P 的坐标;若不存在,请说明理由.21.(2021·浙江杭州市·中考真题)在直角坐标系中,设函数21y ax bx =++(a ,b 是常数,0a ≠).(1)若该函数的图象经过()1,0和()2,1两点,求函数的表达式,并写出函数图象的顶点坐标.(2)写出一组a ,b 的值,使函数21y ax bx =++的图象与x 轴有两个不同的交点,并说明理由.(3)已知1a b ==,当,x p q =(p ,q 是实数,p q ≠)时,该函数对应的函数值分别为P ,Q .若2p q +=,求证6P Q +>.22.(2021·重庆中考真题)如图,在平面直角坐标系中,抛物线24(0)y ax bx a =+-≠与x 轴交于点()1,0A -,()4,0B ,与y 轴交于点C .(1)求该抛物线的解析式;(2)直线l 为该抛物线的对称轴,点D 与点C 关于直线l 对称,点P 为直线AD 下方抛物线上一动点,连接P A ,PD ,求PAD △面积的最大值;(3)在(2)的条件下,将抛物线24(0)y ax bx a =+-≠沿射线AD 平移42得到新的抛物线1y ,点E 为点P 的对应点,点F 为1y 的对称轴上任意一点,在1y 上确定一点G ,使得以点D ,E ,F ,G 为顶点的四边形是平行四边形,写出所有符合条件的点G 的坐标,并任选其中一个点的坐标,写出求解过程. 23.(2021·四川遂宁市·中考真题)如图,已知二次函数的图象与x 轴交于A 和B (-3,0)两点,与y 轴交于C (0,-3),对称轴为直线1x =-,直线y =-2x +m 经过点A ,且与y 轴交于点D ,与抛物线交于点E ,与对称轴交于点F . (1)求抛物线的解析式和m 的值;(2)在y 轴上是否存在点P ,使得以D 、E 、P 为顶点的三角形与①AOD 相似,若存在,求出点P 的坐标;若不存在,试说明理由;(3)直线y =1上有M 、N 两点(M 在N 的左侧),且MN =2,若将线段MN 在直线y =1上平移,当它移动到某一位置时,四边形MEFN 的周长会达到最小,请求出周长的最小值(结果保留根号).24.(2021·四川泸州市·中考真题)如图,在平面直角坐标系xOy 中,抛物线213442y x x =-++与两坐标轴分别相交于A ,B ,C 三点 (1)求证:①ACB =90°(2)点D 是第一象限内该抛物线上的动点,过点D 作x 轴的垂线交BC 于点E ,交x 轴于点F . ①求DE +BF 的最大值;①点G 是AC 的中点,若以点C ,D ,E 为顶点的三角形与AOG 相似,求点D 的坐标.25.(2021·云南中考真题)已知抛物线22y x bxc 经过点()0,2-,当4x <-时,y 随x 的增大而增大,当4x >-时,y 随x 的增大而减小.设r 是抛物线22y x bxc 与x 轴的交点(交点也称公共点)的横坐标,97539521601r r r r r m r r +-++-=+-. (1)求b 、c 的值:(2)求证:2242160r r r -+=;(3)以下结论:1,1,1m m m <=>,你认为哪个正确?请证明你认为正确的那个结论.26.(2021·山东泰安市·中考真题)二次函数2()40y ax bx a =++≠的图象经过点(4,0)A -,(1,0)B ,与y 轴交于点C ,点P 为第二象限内抛物线上一点,连接BP 、AC ,交于点Q ,过点P 作PD x ⊥轴于点D .(1)求二次函数的表达式;(2)连接BC ,当2DPB BCO ∠=∠时,求直线BP 的表达式; (3)请判断:PQQB是否有最大值,如有请求出有最大值时点P 的坐标,如没有请说明理由. 27.(2021·江苏连云港市·中考真题)如图,抛物线()223(69)y mx m x m =++-+与x 轴交于点A 、B ,与y 轴交于点C ,已知(3,0)B .(1)求m 的值和直线BC 对应的函数表达式;(2)P 为抛物线上一点,若PBC ABC S S =△△,请直接写出点P 的坐标; (3)Q 为抛物线上一点,若45ACQ ∠=︒,求点Q 的坐标.28.(2021·重庆中考真题)如图,在平面直角坐标系中,抛物线2y x bx c =++经过A (0,﹣1),B (4,1).直线AB 交x 轴于点C ,P 是直线AB 下方抛物线上的一个动点.过点P 作PD ①AB ,垂足为D ,PE ①x 轴,交AB 于点E .(1)求抛物线的函数表达式;(2)当①PDE 的周长取得最大值时,求点P 的坐标和①PDE 周长的最大值;(3)把抛物线2y x bx c =++平移,使得新抛物线的顶点为(2)中求得的点P .M 是新抛物线上一点,N 是新抛物线对称轴上一点,直接写出所有使得以点A ,B ,M ,N 为顶点的四边形是平行四边形的点M 的坐标,并把求其中一个点M 的坐标的过程写出来.29.(2021·浙江中考真题)今年以来,我市接待的游客人数逐月增加,据统计,游玩某景区的游客人数三月份为4万人,五月份为5.76万人.(1)求四月和五月这两个月中,该景区游客人数平均每月增长百分之几; (2)若该景区仅有,A B 两个景点,售票处出示的三种购票方式如表所示:据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万.并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票.①若丙种门票价格下降10元,求景区六月份的门票总收入;①问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?30.(2021·湖北武汉市·中考真题)在“乡村振兴”行动中,某村办企业以A ,B 两种农作物为原料开发了一种有机产品,A 原料的单价是B 原料单价的1.5倍,若用900元收购A 原料会比用900元收购B 原料少100kg .生产该产品每盒需要A 原料2kg 和B 原料4kg ,每盒还需其他成本9元.市场调查发现:该产品每盒的售价是60元时,每天可以销售500盒;每涨价1元,每天少销售10盒. (1)求每盒产品的成本(成本=原料费+其他成本);(2)设每盒产品的售价是x 元(x 是整数),每天的利润是w 元,求w 关于x 的函数解析式(不需要写出自变量的取值范围);(3)若每盒产品的售价不超过a 元(a 是大于60的常数,且是整数),直接写出每天的最大利润.31.(2021·四川乐山市·中考真题)已知二次函数2y ax bx c =++的图象开口向上,且经过点30,2A ⎛⎫ ⎪⎝⎭,12,2B ⎛⎫- ⎪⎝⎭.(1)求b 的值(用含a 的代数式表示);(2)若二次函数2y ax bx c =++在13x ≤≤时,y 的最大值为1,求a 的值;(3)将线段AB 向右平移2个单位得到线段A B ''.若线段A B ''与抛物线241y ax bx c a =+++-仅有一个交点,求a 的取值范围.32.(2021·四川自贡市·中考真题)如图,抛物线(1)()y x x a =+-(其中1a >)与x 轴交于A 、B 两点,交y 轴于点C .(1)直接写出OCA ∠的度数和线段AB 的长(用a 表示);(2)若点D 为ABC 的外心,且BCD △与ACO △104,求此抛物线的解析式; (3)在(2)的前提下,试探究抛物线(1)()y x x a =+-上是否存在一点P ,使得CAP DBA ∠=∠?若存在,求出点P 的坐标;若不存在,请说明理由.。
易错专题14 侯氏制碱法生产纯碱-2024-2025学年高一化学易错题典例精讲与习题精练(人教版20

易错专题14 侯氏制碱法生产纯碱 典例精讲易错点一 不清楚侯氏制碱法的原料和反应原理【易错典例】例1 (2022秋·广东广州·高一广州市第七中学校考期中)实验室利用下列反应装置模拟侯氏制碱法制备3NaHCO ,反应原理为:32234NH CO H O NaCl NaHCO NH Cl +++=↓+,下列说法错误..的是A .通过活塞K 可控制2CO 的流速B .装置b 、d 依次盛装饱和23Na CO 溶液、稀硫酸C .装置c 中含氨的饱和食盐水提高了2CO 吸收效率D .反应后将装置c 中的锥形瓶浸入冷水充分冷却,过滤得到3NaHCO 晶体【答案】B【解析】A .关闭活塞K 时,气体可将球形容器内的液体压入漏斗内,从而使碳酸钙脱离液面,反应停止,所以通过调节活塞K 可控制CO 2的流速,A 正确;B .装置b 的作用是除去二氧化碳中混有的氯化氢,故装置b 内应盛装饱和NaHCO 3溶液,B 错误;C .装置c 中含氨的饱和食盐水呈碱性,CO 2的溶解度增大,C 正确;D .反应后将装置c 中的锥形瓶浸入冷水,NaHCO 3降温结晶,过滤得NaHCO 3晶体,D 正确; 故选B 。
【解题必备】1.原料:食盐、氨、二氧化碳等2.化学反应原理:(1)生产碳酸氢铵和氯化铵:NH 3+CO 2+H 2O=NH 4HCO 3、NH 4HCO 3+NaCl=NaHCO 3↓+NH 3Cl(在反应中NaHCO 3沉淀,所以这里有沉淀符号)总反应方程式:NaCl+CO2+H2O+NH3=NaHCO3↓+NH4Cl(2)制取碳酸钠:2NaHCO3Na2CO3+H2O+CO2↑(CO2循环使用)【变式突破】1.某探究活动小组根据侯德榜制碱原理,按下面设计的方案制备碳酸氢钠。
实验装置如图所示(图中夹持、固定用的仪器未画出)。
下列说法正确的是A.乙装置中盛放的是NaOH 溶液,以便除去HCl 气体B.丙装置中的溶液变浑浊,因为有碳酸氢钠晶体析出C.丁装置中倒扣的漏斗主要作用是防止污染性空气逸出D.实验结束后,分离碳酸氢钠的操作是蒸发结晶【答案】B【解析】甲装置为CO2的制取装置,乙装置为除去CO2中混有HCl的装置,丙装置为制取NaHCO3的装置,丁装置为尾气处理装置。
新教材高中地理微专题14地方性分异规律新人教版选择性必修1(含答案)

幼儿园陶艺探索:手工艺术教育案例分析一、引言在当前社会,随着人们对教育理念不断深入的探讨和对个性化教育需求的增加,手工艺术教育逐渐成为了备受关注的教育领域。
而在幼儿教育中,陶艺教育作为一种特殊的手工艺术教育形式,更是备受家长和教育者的青睐。
本文将通过对幼儿园陶艺探索的案例分析,深入探讨幼儿园陶艺教育的意义、方法和效果,以及对幼儿发展的影响。
二、幼儿园陶艺教育的意义1. 创造力和想象力的培养幼儿园陶艺教育是一个能够促进幼儿创造力和想象力发展的重要途径。
通过陶艺创作,幼儿能够尽情发挥自己的想象力,创造出各种有趣的作品。
2. 手眼协调能力的培养在陶艺过程中,幼儿需要通过动手操作来完成作品的塑造和设计。
这种过程需要极强的手眼协调能力,能够帮助幼儿提高动手能力和专注力。
3. 情感与审美的培养陶艺作为一门艺术,不仅仅是一种手工技能,更是一种审美情感的表达方式。
通过陶艺创作,幼儿可以表达自己的情感,培养审美情感,增强对美的感知和认知。
三、幼儿园陶艺教育的方法1. 提供丰富的原材料和工具在进行陶艺教育时,幼儿园需要准备丰富多样的原材料和工具,如黏土、彩绘工具等,以满足幼儿在创作过程中的需求。
2. 鼓励自由创作和表达在陶艺教育中,教师应该给予幼儿充分的自由,鼓励他们按照自己的想法去创作和表达,而不是过多地进行干预和指导。
3. 注重过程的体验和感悟在陶艺教育中,重点不在于作品的成品,而在于创作的过程和幼儿在创作过程中的体验、感悟和发现。
教师需要注重引导幼儿去体验、感悟和发现。
四、幼儿园陶艺教育的效果1. 提高幼儿艺术修养通过陶艺教育,幼儿能够接触并了解艺术创作,提高自己的艺术修养,培养对艺术的兴趣和热爱。
2. 促进幼儿综合发展陶艺教育不仅可以促进幼儿的艺术发展,还能够促进幼儿的智力、情感、社交、动手能力等多方面的综合发展。
3. 塑造积极的人生态度通过陶艺教育,幼儿可以学会耐心、细心和坚持,这些品质将对他们的人生态度产生积极影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
] 命题形式上看,选择题和非选择题均有涉及。 2015年高考,
要重视结合抗震救灾精神、载人航天精神等新时期民族精 神的体现,考查中华民族精神的内涵、特征,以及培育民 族精神的意义。
常考点1
中华民族精神的基本内涵和核心
化由中华各民族文化构成,且融入了佛教、伊斯兰教、
基督教等外来宗教文化,体现了中华文化具有包容性的
特征,故D项符合题意,可以入选。
A、B、C三项在材料中并未体现出来,故不能入选。
答案 D
2.自 20世纪 90年代以来,各种“中国威胁论 ” 不绝于耳。2013
年7月9日,日本内阁通过了一年一度的《防卫白皮书》,这
C.面向世界,博采众长
B.独树一帜,独领风骚
D.薪火相传,越燃越旺
解析
我国幅员辽阔,各地自然条件千差万别,经济社会发
展程度不同,受历史、地理等因素的影响,各地区的文化带 有明显的区域特征。题中吉祥物阿福、阿仙,身穿福建民间
服饰,衣服上的浪花纹样代表福建海洋环境和传统海洋文化,
体现了文化的地域性特征,答案A正确;
灿烂的中华文化 中华民族精神
热 点 探 究
栏目索引
考点一
灿烂的中华文化
易错点排查
)
1.中华文化源远流长的见证是文字与史学典籍。(
提示
错误。是汉字,不是文字。文字的发明,使人类文明
得以传承,标志着人类进入文明时代。汉字是中华文明的重 要标志。 2.各具特色的地域文化长期相互借鉴而日趋同一。 ( 提示 )
物质文化遗产名录。珠算是我国1 800多年前的重大发明,今 天依然有顽强的生命力。它以简便的计算工具和独特的数理 内涵,被誉为“世界上最古老的计算机”。珠算的历史及内涵 体现了中华文化( ) B.薪火相传,永久繁荣 D.独树一帜,兼收并蓄
A.源远流长,博大精深 C.一脉相承,世界通用
常考点1
解析
中华文化的基本特征
济的发展和综合国力的提高。
考点二
中华民族精神
易错点排查
)
5.弘扬和培育民族精神就必须抵制外来文化的影响。( 提示
错误。两者并不矛盾,但要正确对待外来思想文化的影响,
既要注意借鉴世界各国人民创造的先进文明成果,汲取世界各民
族的长处,又要警惕外来腐朽文化的影响。
考点二
中华民族精神
常考点突破
中华民族精神是中华文化的结晶,弘扬和培育民族精神是
错误。中华文化具有区域性特征,不同地区的文化相互
交流、借鉴、吸收,既渐趋融合,又保持着各自的特色。
考点一
灿烂的中华文化
易错点排查
)
3.中华文化源远流长得益于汉字和史学典籍的延续。( 提示 即求同存异和兼收并蓄。
错误。中华文化源远流长还得益于它所特有的包容性,
4.中华文化呈现多种民族文化的丰富色彩,民族不同,民族文化
华民族精神是中华民族共同的价值追求,故③当选。材料体现了
中华民族精神砥砺我们奋力前行,这对中华民族生存发展起到精
神支柱作用,故④当选。故选D。
答案
D
2. 历史表明,中华民族近代以来的复兴,不仅需要雄厚的经济实 力和强大的科技实力作支撑,而且需要有生生不息的伟大中华民 族精神来推动,正是这种伟大的民族精神,引领一个民族穿越“千 年未有之变局”,战胜“千年未有之强敌”,把命运牢牢掌握在自己 手中,开启了建设自己国家的伟大进程。在新的征程上,无论面 对什么样的困难,植根于优秀传统文化之中的中华民族精神,始
灿烂的中华文化
常考点突破
本考点是高考的常考点,主要考查中华文化的源远流长和 博大精深、中华文化的包容性,以选择题为主,也有非选 择题。2015年高考,要重视结合中外文化交流活动、各地 继承和发展传统文化的活动考查中华文化的基本特征、中 华文化的包容性。
常考点1
中华文化的基本特征
1.2013年12月4日,珠算正式被联合国教科文组织列入人类非
B、C、D不符合题意。
答案 A
迁移整合
1.正确把握源远流长和博大精深
源远流长 博大精深
角 从中华文化历史悠久(纵向) 从中华文化的内涵丰富、厚 度 侧 的角度来说的 重(横向)的角度来说的
侧重从动态上,即中华文化 侧重从静态上,即中华文化 发展的轨迹上说明中华文化 的内涵上说明中华文化的特 的特征,表明中华文化历史 征,表明中华文化的内容丰 悠久 富、独特
重
点
独树一帜,独领风骚(独特 见证或 汉字和史书典籍是中华 性);一方水土,一方文化( 表现 文化源远流长的见证 地域性);中华之瑰宝,民 族之骄傲(民族性)
2.中华文化与中华各民族文化的关系
(2)中华各民族文化都是中华文化宝库中的瑰宝,都是中华民族的
(1)中华各民族文化,既有中华文化的共性,又有各自的民族特性。
本题考查中华文化源远流长、博大精深。 “ 珠算是我
国1 800多年前的重大发明,今天依然有顽强的生命力”体现 了中华文化从古至今,一脉相承,源远流长;珠算以简便的 计算工具和独特的数理内涵,被誉为 “ 世界上最古老的计算 机 ” 体现了在古代,中国的科学技术长期处于世界的前列, 反映了中华文化的内容极为丰富,说明中华文化博大精深。 答案 A
考点二
中华民族精神
易错点排查
)
1.极具传统特色的“中国元素”是中华民族精神的核心。 ( 提示 错误。爱国主义是中华民族精神的核心。
2.中华民族精神,深深植根于绵延数千年的优秀传统文化之中,
所以,中华民族精神是不变的。( 提示 )
错误。民族精神的形成与发展是长期历史积淀的过程,
会随着时代变化而不断丰富。
的色彩也就不同。(
提示
)
错误。中华各民族的文化,既有各自的民族特性,又有
中华文化的共性,各民族文化相互交融、相互促进,各族人民
对共同拥有的中华文化有认同感和归属感。
考点一
灿烂的中华文化
易错点排查
)
5.文学艺术是一个民族文明程度的重要标志之一。(
提示
错误。科学技术是一个民族文明程度的重要标志之一。
考点一
(1)中华民族精神作为中华文化的精髓,具有凝聚和动员民
族力量、展示民族形象的功能。中华民族精神集中体现了 中华民族的整体风貌和精神特征,体现了中华民族共同的 价值追求,是中华民族永远的精神火炬。 (2)中华文化的力量集中表现为民族精神的力量,中华民族 精神深深植根于优秀传统文化之中。 (3)中华文化的力量深深熔铸在民族的生命力、创造力和凝 聚力之中。
勤劳勇敢、自强不息。
5.中华民族精神是维系中华各族人民共同生活的精神纽带,
支撑中华民族生存、发展的精神支柱,推动中华民族走向繁
荣、强大的精神动力,是中华民族之魂。
6.弘扬和培育中华民族精神,是提高全民族综合素质的必然 要求,是不断增强我国国际竞争力的要求,是坚持社会主义 道路的需要。
考点一 考点二
③蕴涵着中华民族共同的价值追求 B.①④ C.②③ D.③④
民族生存发展的精神支柱
常考点2
解析
弘扬和培育民族精神
本题考查中华民族精神。材料涉及的时间是在同一历史时
期,显示了民族精神相同的内容,故①不选。材料中没有表明中
华民族精神兼收并蓄的特质,故②不选。从材料中生命至上的国
家理念、万众一心的民族情怀和百折不挠的坚韧品格,都说明中
B.①③④ D.①②③
常考点1
解析
中华民族精神的基本内涵和核心
由 “ 为仁由己 ”“ 君子求诸己 ”“ 得天下者,先自得也 ”
可知引文体现的是自强不息的民族精神。 答案 A
2.民族精神是一个民族赖以生存和发展的精神支柱。下列各选项 体现中华民族精神的有( ①“天下兴亡,匹夫有责”
B)
②“好雨知时节,当春乃发生” ④ “人不为己,天
考点二
中华民族精神
)
易错点排查
3.弘扬民族精神就是爱社会主义。(
提示
错误。弘扬民族精神在不同的历史时期有不同的具体内涵。
在当代中国,爱国与爱社会主义本质上是一致的。
4.经济建设是我国当前所有工作的中心,一切活动都要围绕 经济建设展开,弘扬民族精神会影响经济建设。( )
提示
错误。弘扬民族精神不会影响经济建设,反而有利于经
B.①③
C.②③
解析
ቤተ መጻሕፍቲ ባይዱ
本题考查了爱好和平的知识。中华文化具有求同存
异的优秀品质、爱好和平是中华民族精神的基本内涵之一
都能够充分说明中国自古以来就是热爱和平的国家,能够
充分说明中国威胁论的错误,故 ①② 正确; ③④ 不能说明
中国威胁论的错误,故排除。答案选A。
答案 A
迁移整合
深入理解中华文化的包容性
份白皮书颠倒黑白,矛头直指中国,妄称中国的海上行动对
日本的安全和地区稳定 “ 构成威胁 ” 。下列观点能充分说明
“中国威胁论”错误的是( 民族精神的基本内涵之一
动力
)
② 爱好和平是中华
① 中华文化具有求同存异的优秀品质
③ 自强不息是中华民族的内在 D.③④
④中华文化是激励人们努力奋斗的力量之源
A.①②
常考点2
弘扬和培育民族精神
1.中华民族历经苦难而又生生不息。从汶川到玉树、再到芦 山,那生命至上的国家理念,那万众一心的民族情怀,那百 折不挠的坚韧品格,定格为无数震撼心灵的画面,砥砺我们 奋力前行。这表明,中华民族精神( )
①在不同历史时期具有不同的内容
并蓄的特质 A.①②
②具有博大精深和兼收
④是中华
专 题 14
网络构建
中华文化与民族精神
主干速记
1.中华文化源远流长。汉字与史书典籍是源远流长的见证。
