08年数学解题能力展示四年级试题
2008学年第二学期数学能力测试卷

2008学年第二学期数学能力测试卷一、基础知识(一)填空1、木星离太阳的距离是778330000千米,改写成亿作单位的数是()。
2、一个数有3个十,5个十分之一,3个千分之一组成,这个数是()。
3、A+B+C=A+(B+C)这里运用了()。
4、3400公顷=()平方千米 9.02吨=()吨()千克50克=()千克 5.3平方米=()平方米()平方分米5、晓明家在学校的西偏南的方向上,那么学校在()偏()的方向上。
6、一个正方形方阵,最外层每边排着12位同学,那么最外层共排着()位同学。
7、东灵路全长1000米,在它的一侧每隔50米放一个垃圾桶(两头都放),共需()个垃圾桶。
8、小华在用乘法分配律计算10×(△-4)时,它等于10×△-4,那么所得的结果与正确的答案相差()。
9、一个等腰三角形的一个底角是45°,它的顶角是()度,按角分类是一个()三角形。
10、一个两位小数,取近似数后是8.5,这个两位数最大是(),最小是()。
(二)判断题11、25×4÷25×4=1 ()12、任何一个三角形中,至少有两个锐角。
()13、两个面积相等的梯形,一定能拼成一个平行四边形。
()14、用长度为3厘米、4厘米、8厘米的三根小棒,头尾相连,一定能摆出一个三角形。
()15、锯一根10米长的木头,每锯一段要5分钟,分三段要15分钟。
()(三)选择题16、大于4.9而小于5.1的小数有()。
A、 1个B、9个C、无数个17、把120.065的小数点先向右移动两位,再向左移动三位,则原数变为()A、 1.20065B、 12.0065C、 120.06518、用两个三角板不可能拼出的角是()。
A、105B、 180C、145D、12019、在5.804中,0所在数位的计数单位是()。
A、0B、十分之一C、0.0120、正五边形的四周共放了20盆花,每边最多可以放()盆花。
2013解题能力展示初赛四年级(Word解析)

2013“数学解题能力展示”读者评选活动笔试试题小学四年级(2012年12月22日)一、填空题(每小题8分,共24分)1.1+3+5++1407+19+20+22+_________.+=2.爸爸生日是5月1日,而春春生日是7月1日,从2012年12月26日算起(第1天),直到第2013天,爸爸和春春总共过了_________个生日.3.笼子里有30只蛐蛐和30只蝈蝈.红毛魔术师每变一次,会把其中的4只蝈蝈变成1只蛐蛐;绿毛魔术师每变一次会把其中的5只蛐蛐变成2只蝈蝈.两个魔术师一共变了18次后,笼子里只有蝈蝈没有蛐蛐了.这时蝈蝈有_________只.二、填空题(每小题12分,共36分)4.从1,2,3,4,5,6,7中选择若干个不同的数(所选数不计顺序),使得其中偶数之和等于奇数之和,则符合条件的选法共有_________种.5.从4、5、6、7、8、9这六个数字钟选出互不相同的5个填入右面方格内,使得等式成立.有_________种不同的填法.6.A、B、C三人在猜一个1~99中的自然数.A:“它是偶数,比6小.”B:“它比7小,是个两位数.”C:“A的前半句是对的,A的后半句是错的.”如果这3人当中有1人两句都为真话,有1人两句都为假话,有1人两句话一真一假.那么,这个数是_________.三、填空题(每小题15分,共60分)7.如图,有两个小正方形和一个大正方形,大正方形的边长是小正方形边长的2倍,阴影部分三角形面积为240,请问三个正方形的面积和是_________.8.小张早晨8点整从甲地出发去乙地,速度是每小时60千米.早晨9点整小王从乙地出发去甲地.小张到达乙地后立即沿原路返回,恰好在12点整与小王同时到达甲地.那么两人相遇时距离甲地_________千米.9.下图是由9个22的小网格组成的一个正方形大网格并要求相邻两个小网格内的相邻数字完全相同(这些小网格可以旋转,但不能翻转).现在大网格中已放好一个小网格,请你将剩余8个网格按要求放好.右下角的格内的数是_________.10.狼堡的狼欺羊太甚,终于导致羊群造反.接到攻打狼堡的通知后,小羊们陆续出发7点时小灰灰登高一望,发现有5只羊到狼堡的距离恰好是一个公差为20(单位:米)的等差数列,从前到后,这5只羊分别为A、B、C、D、E;8点时,小灰灰登高一望,发现这5只羊到狼堡的距离仍然是一个公差为30(单位:米)的等差数列,但从前到后的顺序变成了B、E、C、A、D.这5只羊中跑的最快的羊比跑得最慢的羊,每小时多跑_________米.2013“数学解题能力展示”读者评选活动笔试试题小学四年级参考答案1 2 3 4 5430 11 6 7 126 7 8 9 108 360 96 3 140部分解析一、填空题(每小题8分,共24分)1.1+3+5++1407+19+20+22+_________.+=【考点】计算【难度】☆☆【答案】430【解析】用等差数列求和公式,分两部分.也可以用奇数等差数列和偶数等差数列求和公式,13571719++++⋯++奇数等差数列求和,共10项,和为210=100,20+22++40=(20+40)112=330⨯÷,100+330=430.2.爸爸生日是5月1日,而春春生日是7月1日,从2012年12月26日算起(第1天),直到第2013天,爸爸和春春总共过了_________个生日.【考点】周期问题【难度】☆☆☆【答案】11【解析】从2012.12.26到2012.12.31共6天,剩余2007天,20073655182÷=,五年内必有一个闰年,所以应该余181,五年内两人共过10个生日,那么181天正好是6.30,爸爸又过了一个,但春春没过,所以共过了11个生日.3.笼子里有30只蛐蛐和30只蝈蝈.红毛魔术师每变一次,会把其中的4只蝈蝈变成1只蛐蛐;绿毛魔术师每变一次会把其中的5只蛐蛐变成2只蝈蝈.两个魔术师一共变了18次后,笼子里只有蝈蝈没有蛐蛐了.这时蝈蝈有_________只.【考点】应用题【难度】☆☆☆【答案】6【解析】41=52=3--,不管是谁变,每变一次总和少3,那么共变了18次.60-18×3=6,最后只剩下蝈蝈有6只.二、填空题(每小题12分,共36分)4.从1,2,3,4,5,6,7中选择若干个不同的数(所选数不计顺序),使得其中偶数之和等于奇数之和,则符合条件的选法共有_________种.【考点】计数【难度】☆☆☆【答案】7【解析】偶数之和只能为2、4、6、8、10、12,奇数之和最少是两数之和,否则凑不成偶数,最小和为4一种情况,和为6偶数有2种,奇数1种.和为8偶数有1种,奇数有2种,和为10偶数有1种,奇数有1种,和为12偶数有1种,奇数有1种,那么选法共有1+2+2+1+1=7种.5.从4、5、6、7、8、9这六个数字钟选出互不相同的5个填入右面方格内,使得等式成立.有_________种不同的填法.【考点】算式谜【难度】☆☆☆【答案】12【解析】观察题目必须有借位的发生,否则不能得到一位数,十位必须相差1.用尾数来分析,最后得4只能是95,排除结果得5,□4-□9可选7469-,2种-、8479结果得6,□4-□8,4、6、8已用无相差1的数填十位,□5-□9可选8579-,1种结果得7,□5-□8排除,□6-□9有5649-可选,2种-、8679结果得8,□4-□6排除,□5-□7排除,□6-□8排除,□7-□9,5749-,2种-、6759结果得9,□4-□5,7465-、6758-,共5-,□7-□8,5748-、8475-,□5-□6,8576种.一共12种.6.A、B、C三人在猜一个1~99中的自然数.A:“它是偶数,比6小.”B:“它比7小,是个两位数.”C:“A的前半句是对的,A的后半句是错的.”如果这3人当中有1人两句都为真话,有1人两句都为假话,有1人两句话一真一假.那么,这个数是_________.【考点】逻辑推理【难度】☆☆【答案】8【解析】假设A为真话,那么B一假一真,C也一假一真,不符合题意,假设B为真话,那么前后相矛盾那C为真话,A前半句为真话,后半句为假话,B全为假话,A的话表示首先这个数是偶数且比6大,B全为假话,那么它比7大,且是一位数,只有8符合.这个数是8.三、填空题(每小题15分,共60分)7.如图,有两个小正方形和一个大正方形,大正方形的边长是小正方形边长的2倍,阴影部分三角形面积为240,请问三个正方形的面积和是_________.【考点】几何 【难度】☆☆☆ 【答案】360【解析】连接AD 、BC 、EF ,POF EDCB A那么在梯形ABCD 中△COD 的面积等于AOB ∆的面积,梯形AFED 中DPE ∆的面积,那么阴影的面积等于大正方形的面积为240,小正方形面积为大正方形的14.24042240360÷⨯+=.8.小张早晨8点整从甲地出发去乙地,速度是每小时60千米.早晨9点整小王从乙地出发去甲地.小张到达乙地后立即沿原路返回,恰好在12点整与小王同时到达甲地.那么两人相遇时距离甲地_________千米. 【考点】行程问题 【难度】☆☆☆☆ 【答案】96【解析】小张8:00-12:00共走完两个全程,那么全程=(4×60)÷2=120千米,那么小王的速度为120÷3=40千米/小时.俩人的相遇时间(120-60)÷(60+40)=0.6小时.相遇时距甲地距离为:60+60×0.6=96千米.9.下图是由9个22⨯的小网格组成的一个正方形大网格并要求相邻两个小网格内的相邻数字完全相同(这些小网格可以旋转,但不能翻转).现在大网格中已放好一个小网格,请你将剩余8个网格按要求放好.右下角的格内的数是_________.【考点】游戏策略 【难度】☆☆☆☆ 【答案】3【解析】从最小可能入手,1、2相邻的只有2号符合条件,同时有两个2出现的只有6号方格符合条件,放的时候必须把3放在右侧否则无其它方格可以与两个2相邻, 接下来只能填一个有2、3,2、4的方格,只有4号方格符合,同时有两个4在一侧的有5号方格和7号方格,但7号方格中的两个1是要放在最上方的,那么右下角填入5号方格,右下角为3.4444413332222222111110.狼堡的狼欺羊太甚,终于导致羊群造反.接到攻打狼堡的通知后,小羊们陆续出发7点时小灰灰登高一望,发现有5只羊到狼堡的距离恰好是一个公差为20(单位:米)的等差数列,从前到后,这5只羊分别为A 、B 、C 、D 、E ;8点时,小灰灰登高一望,发现这5只羊到狼堡的距离仍然是一个公差为30(单位:米)的等差数列,但从前到后的顺序变成了B 、E 、C 、A 、D .这5只羊中跑的最快的羊比跑得最慢的羊,每小时多跑_________米.【考点】行程问题 【难度】☆☆☆☆ 【答案】140【解析】首先确定E 跑的最快,从离B 60米到30米,且追上了之前所有的羊,A 最慢,E 7点时距A 80米,8点时,E 领先A 60米.那么80+60=140也就是E 每小时比A 多跑的距离140米.。
2008年“数学解题能力展示”读者评选活动三年级组初赛试卷及详解答案

2008“数学解题能力展示”读者评选活动(三年级)三年级组初赛试题(测评时间:2007年12月2日11:00—12:00;满分150)一、填空题Ⅰ(每题10分,共60分)1. 计算:24+63+52+17+49+81+74+38+95=________。
2.计算:53×57-47×43=_____________。
3. 星期天小明、小强和小佳一起去采摘。
小强说:“我摘的苹果最多了,比你们俩摘的苹果总和还多1个。
”小明回答说:“是啊。
你比我多摘了10个,但我比小佳多摘了10个。
”那么他们三人共摘了_____________个苹果。
4. 用火柴棍拼成的数字和符号如下图所示,那么用火柴棍拼成一个减法等式最少要用_____________根火柴。
5. 将1~9这9个数字分别填入下图的方框中,每个数字恰好用一次,使等式成立;现已将8填入,则最左边的两个方框中所填的两位数是________。
6. 一个文具店中橡皮的售价为每块5角,圆珠笔的售价为每支1元,签字笔的售价为每支2元5角。
小明要在该店花5元5角购买其中两种文具,他有___________种不同的选择。
二、填空题Ⅱ(每题15分,共90分)1. 一个书架上有数学、语文、英语、历史4种书共27本,且每种书的数量互不相同。
其中数学书和英语书共有12本,语文书和英语书共有13本。
有一种书恰好有7本,是_____________书。
2. 下面两个算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,那么A+B+C+D +E+F+G=_____________。
3. 小名、小亮两人玩扑克牌,他们手里各有点数为1、2、3、4、5、6、7、8、9、10的纸牌各一张,两人每轮各出一张牌,点数大的为胜,并将两张牌的点数差(大减小),做为获胜一方的分数,另一方不得分,10轮牌出完之后,两人总分之和最大是_____________。
4. 有125个同样大小的正方体木块,木块的每个面的面积均为1平方厘米,其中63个表面涂上白色,还有62个表面涂上蓝色。
2008学年度下学期四年级数学思维竞赛题

2008学年度下学期数学思维竞赛题成绩:一、填空题。
(每小题4分,10小题,共40分)1、1米8分米=()米1米8分米=()分米2、一个三角形里最多有()个锐角。
一个三角形里最多有()条边相等。
3、左图中有()个长方形,左图中有()个正方形。
4、小数点向左移动一位,这个数就缩小到原来的()。
小数点向右移动两位,这个数就扩大到原来的()倍。
5、0.89×5.2+0.89×4.8能运用()律,进行简便运算。
0.4×0.75×0.25能运用()律,进行简便运算。
6、在○里填上“<”“>”“=”。
0.3×0.8○0.3 0.3×1.1○0.37、最接近100的两位小数是()。
最接近0的两位小数是()。
8、按规律填数。
(1)3.5、 5.5、7.5、。
(2)23.5、17.5、11.5、。
9、0.4和0.6之间的一位小数有()个。
0.4和0.6之间的两位小数有()个。
10、把除数化为整数。
8.54÷0.6=()÷()1、下面三根小棒()不可以摆成三角形。
A、6cm、5cm、4cmB、6cm、2cm、3cmC、6cm、7cm、4cmD、6cm、6cm、6cm2、三角形有两个锐角分别为45度、55度,这个三角形是()。
A、直角三角形B、锐角三角形C、等边三角形D、等腰三角形3、50.624中的“4”表示()。
A、4个110B、4个1100C、4个11000D、4个0.014、用一张平行四边形纸能剪出()个平行四边形。
A、1个B、2个C、3个D、无数个5、梯形有()对边平行。
A、最多两组B、可能有两组C、可能没有D、只有一组三、判断题。
(每小题2分,5小题,共10分)1、小数都比整数小。
()2、0.4和0.5之间没有其它小数。
()3、小数的末尾加上两个零,这个小数的大小没有改变。
()4、一个三角形的三个角都是60度,它一定是等边三角形。
数学解题能力展示四年级真题汇编0730

三、填空题(每小题 15 分,共 60 分)
7.如图,有两个小正方形和一个大正方形,大正方形的边长是小正方形边长的 2 倍,阴影部分三角形面积为 240,请问三个正方形的面积和是________。
-3-
指南针小升初
8.小张早晨 8 点整从甲地出发去乙地,速度是每小时 60 千米。早晨 9 点整小王从 乙地出发去甲地。小张到达乙地后立即沿原路返回,恰好在 12 点整与小王同时 到达甲地。那么两人相遇时距离甲地________千米。 9.下图是由 9 个 2×2 的小网格组成的一个正方形大网格并要求相邻两个小网格内 的相邻数字完全相同(这些小网格可以旋转,但不能翻转)。现在大网格中已放 好一个小网格, 请你将剩余 8 个网格按要求放好。右下角格内的数是 ________。
三、填空题(每小题 15 分,共 30 分)
9.如图,一个周长为 24 厘米的小正方形和 4 个周长为 32 厘米的相同长方形拼成一 个大正方形,那么一个长方形的面积是_____对爸爸说:“我特别期待 2013 年的到来。”爸爸 问:“为什么呢?”小杰说:“你看,2013 的 4 个数字互不相同,我长这么 大,头一次过这样的年份呢。”爸爸笑道:“是呀,我们可以把这种各个数字 都不相同的年份叫做‘幸运年’,这样算来,明年爸爸就过第 13 个‘幸运年’ 了。”小杰想了想说:“当我像您这么大的时候,我刚好也过第 13 个‘幸运 年’。”那么,小杰明年________岁。
11.若三位数 abc (其中a,b,c都是非零数字)满足 ab bc ca ,则称该三位数为 “龙腾数”,那么共________个“龙腾数”。 12.在边缘的每个空白格内都填入一个箭头,方格中的数字表示指向该数字的箭头 个数,箭头的方向可以是上、下、左、右、左上、左下、右上、右下,但每个 箭头至少指向一个数字,例如,图2的填法是图1的答案.请按照此规则在图3中 填入箭头,那么指向右下方向的箭头共有________个。
2008年“数学解题能力展示”复试读者评选活动中年级组题(B版)
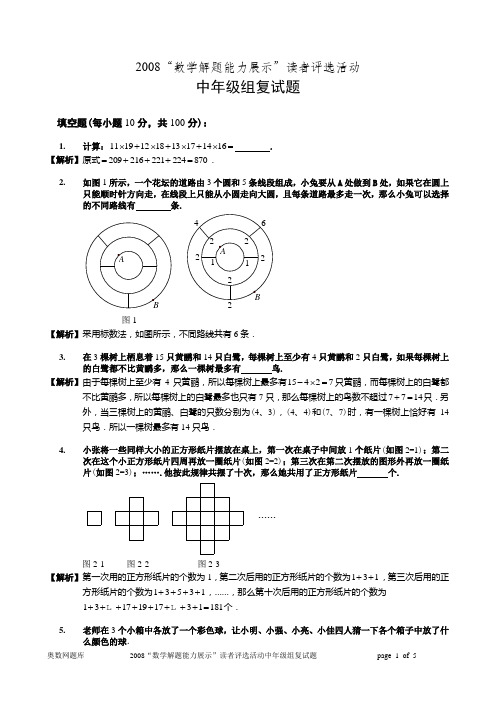
2008“数学解题能力展示”读者评选活动中年级组复试题填空题(每小题10分,共100分):1. 计算:1119121813171416⨯+⨯+⨯+⨯= .【解析】 原式209216221224870=+++=.2. 如图1所示,一个花坛的道路由3个圆和5条线段组成,小兔要从A 处做到B 处,如果它在圆上只能顺时针方向走,在线段上只能从小圆走向大圆,且每条道路最多走一次,那么小兔可以选择的不同路线有 条.图1【解析】 采用标数法,如图所示,不同路线共有6条.3. 在3棵树上栖息着15只黄鹂和14只白鹭,每棵树上至少有4只黄鹂和2只白鹭,如果每棵树上的白鹭都不比黄鹂多,那么一棵树最多有 鸟.【解析】 由于每棵树上至少有4只黄鹂,所以每棵树上最多有15427-⨯=只黄鹂,而每棵树上的白鹭都不比黄鹂多,所以每棵树上的白鹭最多也只有7只,那么每棵树上的鸟数不超过7714+=只.另外,当三棵树上的黄鹂、白鹭的只数分别为(4、3),(4、4)和(7、7)时,有一棵树上恰好有14只鸟.所以一棵树最多有14只鸟.4. 小张将一些同样大小的正方形纸片摆放在桌上,第一次在桌子中间放1个纸片(如图2-1);第二次在这个小正方形纸片四周再放一圈纸片(如图2-2);第三次在第二次摆放的图形外再放一圈纸片(如图2-3);…….他按此规律共摆了十次,那么她共用了正方形纸片个. ……图2-1 图2-2 图2-3【解析】 第一次用的正方形纸片的个数为1,第二次后用的正方形纸片的个数为131++,第三次后用的正方形纸片的个数为13531++++,……,那么第十次后用的正方形纸片的个数为1317191731181++++++++= 个.5. 老师在3个小箱中各放了一个彩色球,让小明、小强、小亮、小佳四人猜一下各个箱子中放了什么颜色的球.小明说:“1号箱子中放的是黄色的,2号箱子中放的是黑色的,3号箱子中放的是红色的.” 小亮说:“1号箱子中放的是橙色的,2号箱子中放的是黑色的,3号箱子中放的是绿色的.” 小强说:“1号箱子中放的是紫色的,2号箱子中放的是黄色的,3号箱子中放的是蓝色的.”小佳说:“1号箱子中放的是橙色的,2号箱子中放的是绿色的,3号箱子中放的是紫色的.” 老师说:“你们中有一个人恰好猜对了两个,其余三人都只猜对了一个.”那么3号箱子中放的是 色的球.【解析】 观察可知,小明、小强、小佳三人所猜的每一个箱中的颜色都各不相同,如果他们三人中有一个人猜中了两个,那么另外两个人猜中的都是这个人猜错的那个箱子的颜色,但是这另外的两个人猜的颜色也不相同,矛盾.所以他们三人中没有人猜中两个,而是各猜中一个,猜中两个的是小亮.由于小亮猜的1号箱子颜色与小佳猜的相同,2号箱子颜色与小明相同,所以小亮猜中了1、2号箱子,小佳猜中1号箱子,小明猜中2号箱子,那么小强猜中3号箱子,故3号箱子中放的是蓝色的球.6. 在下面两个算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,那么四位数ABCD为 .2008A B C DE F G H- 2424A E F G E F G H -【解析】 如果8D H -=,那么将有0C G -=,即C G =,与题意不符,所以108D H +-=,即2D H +=.类似分析可知1100C G -+-=,即9C G +=,故0C =,9G =.由9G =知4G H -=,故5H =,3D =.由102F G +-=得1F =,由10B F --=得2B =,由14E F --=得6E =,由2A E -=得8A =,故四位数ABCD 为8203.7. 如图3所示,一个长方形广场的正中央有一个长方形的水池,水池长8米、宽3米,水池周围用边长为1米的方砖一圈一圈的向外铺.恰好铺了若干圈,共用了152块方砖,那么共铺了 圈.图3【解析】 由于水池的四周均铺上方砖,那么铺上方砖后得到的大长方形的长与宽之差等于水池的长与宽之差,为835-=.如果水池中也铺上方砖,需要8324⨯=块,那么整个大长方形需要15224176+=块,而1761611=⨯,16与11的差恰好为5,所以大长方形的长为16米,共铺了(168)24-÷=圈.8. 现有5段铁链,每段上有4个封闭的铁环.现在要打开一些铁环,把这20个铁环焊接成一个一环套一环的圆圈.如果每打开一个铁环要2分钟,焊接上一个铁环要3分钟,那么焊成这个圆圈,最少需要 分钟.图4【解析】 要焊成这个圆圈必须得打开若干个铁环,每打开一个铁环最后就得将它焊上,每一个铁环上花的时间为235+=分钟,为使用的时间最少,应打开最少的铁环.如果只打开3个铁环,那么还剩下5段铁链(尽管有可能有1段铁链只剩1个圈),用3个铁环无法将5段铁链连起来,所以只打开3个铁环无法焊成圆圈.如果打开4个铁环,可以将原来的某段铁链的4个铁环全打开,这样还剩下4段铁链,用打开的4个铁环可以将它们连成一个圆圈,所以最少需打开4个铁环,那么用的时间最少为5420⨯=分钟.9.在下面的表1中,一条直线穿过其中若干个方格,穿过的方格中各数之和为1513105649++++=。
四年级奥数真题收集版

目录试题部分1.2008年第八届“春蕾杯”小学数学邀请赛初赛四年级试题 (1)2.2008年第八届“春蕾杯”小学数学邀请赛决赛四年级试题 (2)3.第六届小学“希望杯”全国数学邀请赛四年级1试试题 (3)4.第六届小学“希望杯”全国数学邀请赛四年级2试试题 (5)5.2008年第六届“走进美妙的数学花园”中国青年数学论坛趣味数学解题技能展示大赛初赛四年级试题 (6)6.2008年第六届“走进美妙的数学花园”中国青年数学论坛趣味数学解题技能展示大赛决赛四年级试题 (7)7.第九届“中环杯”小学生思维能力训练活动初赛四年级试题 (9)8.第九届“中环杯”小学生思维能力训练活动决赛四年级试题 (10)9.第七届“小机灵杯”数学竞赛复赛四年级试题 (12)10.第七届“聪明小机灵”小学数学邀请赛决赛四年级试题 (14)11.2008年第一届“学而思杯”综合素质测评四年级数学试题(A卷) (15)参考答案12.2008年第八届“春蕾杯”小学数学邀请赛初赛四年级试题答案 (17)13.2008年第八届“春蕾杯”小学数学邀请赛决赛四年级试题答案 (18)14.第六届小学“希望杯”全国数学邀请赛四年级1试试题答案 (18)目录15.第六届小学“希望杯”全国数学邀请赛四年级2试试题答案 (19)16.2008年第六届“走进美妙的数学花园”中国青年数学论坛趣味数学解题技能展示大赛初赛四年级试题答案 (20)17.2008年第六届“走进美妙的数学花园”中国青年数学论坛趣味数学解题技能展示大赛决赛四年级试题答案 (21)18.第九届“中环杯”小学生思维能力训练活动初赛四年级试题答案 (21)19.第九届“中环杯”小学生思维能力训练活动决赛四年级试题答案 (22)20.第七届“小机灵杯”数学竞赛复赛四年级试题答案 (22)21.第七届“聪明小机灵”小学数学邀请赛决赛四年级试题答案 (23)22.2008年第一届“学而思杯”综合素质测评四年级数学试题(A卷)答案 (23)2008年第八届“春蕾杯”小学数学邀请赛初赛四年级1. 找规律填数:(1) 2、7、12、17、22、 、32、37。
2012年“迎春杯”数学解题能力展示初赛试卷(四年级)-含答案解析

2021年“迎春杯〞数学解题能力展示初赛试卷〔四年级〕一、填空题1.〔8分〕计算:12+34×56+7+89=.2.〔8分〕骆驼有两种,背上只有一个驼峰的单峰骆驼和背上有两个驼峰的双峰骆驼,单峰骆驼比拟高大,四肢较长,在沙漠中可走可跑;双峰骆驼四肢短粗,适合在沙漠和雪地中行走.有一群骆驼有23个驼峰,60只脚,这些骆驼有只.3.〔8分〕在如图的每个方框中填入一个数字,使得乘法竖式成立.那么,这个算式的乘积是.4.〔8分〕A、B、C三人采西瓜.A与B所采西瓜的个数之和比C少6个;B与C所采西瓜的个数之和比A多16个;C与A所采西瓜的个数之和比B多8个;请问他们共采西瓜个.二、填空题5.〔10分〕30名同学按身高由低到高排成一队,相邻两个同学的身高差相同.前10名同学的身高和是12.5米,前20名同学的身高和是26.5米,那么这30名同学的身高和是米.6.〔10分〕正方形ABCD与长方形BEFG如图放置,AG=CE=2厘米,那么正方形ABCD 的面积比长方形BEFG的面积大平方厘米.7.〔10分〕红、黄、蓝3种颜色的球分别有11、12、17个,每次操作可以将2个不同颜色的球换成2个第三种颜色的球,那么在操作过程中,红色球至多有个.8.〔10分〕宁宁、蕾蕾和凡凡三人合租一辆轿车从学校回家〔如图〕,他们约定:共同乘坐的局部所产生的车费由乘坐者平均分摊;单独乘坐的局部所产生的车费,由乘坐者单独承当.结果,三人承当的车费分别为10元、25元、85元,宁宁家距离学校12公里,凡凡家距离学校公里.三、填空题9.〔12分〕甲乙二人相距30米面对面站好,两人玩“石头、剪子、布〞.胜者向前走3米,负者向后退2米,平局两人各向前走1米,玩了15局后,甲距出发点17米,乙距出发点2米.甲胜了次.10.〔12分〕在羊羊运动会上,喜羊羊、沸羊羊、懒羊羊、暖羊羊和灰太郎进行了400米赛跑,赛完结束后,五人谈论比赛结果.第一名说:“喜羊羊跑得比懒羊羊快.〞第二名说:“我比暖羊羊跑得快.〞第三名说:“我比灰太郎跑得快.〞第四名说:“喜羊羊比沸羊羊跑得快.〞第五名说:“暖羊羊比灰太郎跑得快.〞如果五人中只有灰太郎说了假话,那么喜羊羊得了第名.11.〔12分〕假设三位数〔其中a、b、c都是非零数字〕满足>>,那么称该三位数为“龙腾数〞,那么共有个“龙腾数〞.12.〔12分〕在边缘的每个空白格内都填入一个箭头,方格中的数字表示指向该数字的箭头个数,箭头的方向可以是上、下、左、右、左上、左下、右上、右下,但每个箭头必须指向一个数字,例如,图2的填法是图1的答案,请按照此规律在图3中填入箭头,那么指向右下方向的箭头共有个.2021年“迎春杯〞数学解题能力展示初赛试卷〔四年级〕参考答案与试题解析一、填空题1.〔8分〕计算:12+34×56+7+89=2021.【解答】解:12+34×56+7+89=12+1904+7+89=1916+7+89=1923+89=2021;故答案为:2021.2.〔8分〕骆驼有两种,背上只有一个驼峰的单峰骆驼和背上有两个驼峰的双峰骆驼,单峰骆驼比拟高大,四肢较长,在沙漠中可走可跑;双峰骆驼四肢短粗,适合在沙漠和雪地中行走.有一群骆驼有23个驼峰,60只脚,这些骆驼有15只.【解答】解:60÷4=15〔只〕,答:一共有15只.故答案为:15.3.〔8分〕在如图的每个方框中填入一个数字,使得乘法竖式成立.那么,这个算式的乘积是837.【解答】解:依题意可知:根据结果的尾数是7,推理出第一个乘数的个位是7,再根据乘积的结果首位是2.可推理出第一个乘数是27;再根据27乘以一个数字尾数是1同时是2位数,那么只能是27×3=81;所以27×31=837.故答案为:8374.〔8分〕A、B、C三人采西瓜.A与B所采西瓜的个数之和比C少6个;B与C所采西瓜的个数之和比A多16个;C与A所采西瓜的个数之和比B多8个;请问他们共采西瓜18个.【解答】解:根据分析,第一句可知,C﹣〔A+B〕=6;第二句可知,B+C﹣A=16;第三句可知,C+A﹣B=8;将三个等式加起来得:〔A+B﹣C〕+〔B+C﹣A〕+〔C+A﹣B〕=﹣6+16+8⇒2〔A+B+C〕﹣〔A+B+C〕=A+B+C=18∴他们共采西瓜18故答案是:18.二、填空题5.〔10分〕30名同学按身高由低到高排成一队,相邻两个同学的身高差相同.前10名同学的身高和是12.5米,前20名同学的身高和是26.5米,那么这30名同学的身高和是42米.【解答】解:根据分析,30名同学的身高是一个等差数列,设第n名同学的身高为a n,前n名同学的身高和为S n,那么S10=12.5米,S20=26.5米,根据等差数列的性质,S10=a1+a2+…a10;S20﹣S10=a11+a12+…+a20;S30﹣S20=a21+a22+…+a30.易知,S10;S20﹣S10;S30﹣S20是等差数列,得S20﹣S10﹣12.5=14米;S30﹣S20=S10+2×〔14﹣12.5〕=12.5+3=15.5米;⇒S30=S20+15.5=26.5+15.5=42米.∴这30名同学的身高和是42米.故答案是:42米.6.〔10分〕正方形ABCD与长方形BEFG如图放置,AG=CE=2厘米,那么正方形ABCD 的面积比长方形BEFG的面积大4平方厘米.【解答】解:根据分析,图中公共局部为长方形GHCB,故:正方形ABCD的面积﹣长方形BEFG的面积=长方形ADHG的面积﹣长方形EFHC的面积=AG×AD﹣CE×CH=2×AD﹣2×CH=2×〔AD﹣CH〕=2×〔CD﹣CH〕=2×DH=2×2=4〔平方厘米〕.故答案是:4.47.〔10分〕红、黄、蓝3种颜色的球分别有11、12、17个,每次操作可以将2个不同颜色的球换成2个第三种颜色的球,那么在操作过程中,红色球至多有39个.【解答】解:三种球的个数除以3的余数分别为2.0、2,任意操作一次后,除以3的余数均加2,因此黄色球和蓝色球除以3的余数不可能相同,即不能出现0个黄色球和0个蓝色球的情况,所以红色球的个数不可能有40个.经验证.前两次将红色球和蓝色球换成黄色球,球数变为9、16、15;再把黄色球和蓝色球换成红色球,球数变为39、1、0.所以操作过程中,红色球至多有39个.答:红色球至多有39个.故答案为:39.8.〔10分〕宁宁、蕾蕾和凡凡三人合租一辆轿车从学校回家〔如图〕,他们约定:共同乘坐的局部所产生的车费由乘坐者平均分摊;单独乘坐的局部所产生的车费,由乘坐者单独承当.结果,三人承当的车费分别为10元、25元、85元,宁宁家距离学校12公里,凡凡家距离学校48公里.【解答】解:[〔25﹣10〕×2+〔85﹣25〕]÷〔10×3÷12〕+12=[30+60]÷2.5+12=90÷2.5+12=36+12=48〔公里〕答:凡凡家距离学校48公里.三、填空题9.〔12分〕甲乙二人相距30米面对面站好,两人玩“石头、剪子、布〞.胜者向前走3米,负者向后退2米,平局两人各向前走1米,玩了15局后,甲距出发点17米,乙距出发点2米.甲胜了7次.【解答】解:依题意可知:那么如果有胜负那么前进1米,如果平局前进2米.他们共同15次前进19米.那么15局如果都是胜负局故有15米的距离.所以是有4局平局.11局胜负局.17﹣4=13〔米〕.根据11局胜负可前进13米.如果全部是赢需要进33米.数量差是33﹣13=20〔米〕每一局差5分,共是4局差20分.故甲是7胜4负.7×3﹣4×2=13〔米〕.故答案为:710.〔12分〕在羊羊运动会上,喜羊羊、沸羊羊、懒羊羊、暖羊羊和灰太郎进行了400米赛跑,赛完结束后,五人谈论比赛结果.第一名说:“喜羊羊跑得比懒羊羊快.〞第二名说:“我比暖羊羊跑得快.〞第三名说:“我比灰太郎跑得快.〞第四名说:“喜羊羊比沸羊羊跑得快.〞第五名说:“暖羊羊比灰太郎跑得快.〞如果五人中只有灰太郎说了假话,那么喜羊羊得了第二名.【解答】解:假设第三名为灰太狼,那么其他人说的都是真话.即暖羊羊比灰太狼快,第二名比暖羊羊快,而灰太狼就是第三名,此时暖羊羊介于第二名和第三名之间,矛盾.同理假设灰太狼是第五名,根据表达可知,也是矛盾的.所以,所以灰太狼一定是第四名.其他人说的都是正确的,接下来就有:喜羊羊比懒羊羊快、第二名比暖羊羊快、第三名比灰太狼快、沸羊羊比喜羊羊快、暖羊羊比太狼快.所以,沸羊羊是第一名、喜羊羊是第二名、暖羊羊是第三名、懒羊羊是第五名.、11.〔12分〕假设三位数〔其中a、b、c都是非零数字〕满足>>,那么称该三位数为“龙腾数〞,那么共有120个“龙腾数〞.【解答】解:根据分析,>>,那么a≥b≥c,分三种情况:①a=b>c时,有=36个;②a>b=c时,由>可知,c>a与题意矛盾,故不成立;③a>b>c时,a、b、c可以取1~9之间不相等的数,有=84个.综上,共有:36+84=120个“龙腾数〞.故答案是:120.12.〔12分〕在边缘的每个空白格内都填入一个箭头,方格中的数字表示指向该数字的箭头个数,箭头的方向可以是上、下、左、右、左上、左下、右上、右下,但每个箭头必须指向一个数字,例如,图2的填法是图1的答案,请按照此规律在图3中填入箭头,那么指向右下方向的箭头共有2个.【解答】解:根据题干分析可得:图3中填入箭头如下:那么指向右下方向的箭头共有2个.故答案为:2.。
2008年“数学解题能力展示”读者评选活动四年级组初赛试卷详解

2008年“数学解题能力展示”读者评选活动四年级组初赛试题一、填空题I(每题l0分,共60分)(2008年“数学解题能力展示”读者评选活动四年级组初赛试题)1. 计算:l2345×2345+2469×38275=。
分析:首先注意到:12345=5×2469所以如果将后一项中的其中的乘数2469乘一个5,那么就可以利用乘法分配律了.可以从38275借.于是12345×2345+2469×38275=12345×2345+(2469×5)×38275÷5=12345×2345+12345×7655=12345×(2345+7655)=12345×10000=123450000(2008年“数学解题能力展示”读者评选活动四年级组初赛试题)2. 2008年奥运会在北京举行。
“奥”、“运”、“会”、“北”、“京”这五个汉字代表五个连续的自然数,将其分别填在五环图案的五个环内,满足“奥”+“运”+“会”=“北”+“京”。
这五个自然数的和最大是。
分析:不妨设最小一个数是x,那么这5个数是x,x+1,x+2,x+3,x+4.但无法将它们对应,但无论怎么样,列出的方程一定是这个形式的:(x+a)+(x+b)+(x+c)=(x+d)+(x+e)其中a、b、c、d、e分别是0、1、2、3、4.方程解得:x=(d+e)-(a+b+c)如果连续5个自然数最大,那么最小的那个自然数也必须取得最大,显然减号前是3、4,减号后0、1、2时,x取得最大值4,所以这5个数是4、5、6、7、8,和为30(2008年“数学解题能力展示”读者评选活动四年级组初赛试题)3.电子数字O~9如图l所示,图2是由电子数字组成的乘法算式,但有一些模糊不清,请将图2的电子数字恢复,并将它写成横式形式:。
分析:1、显然乘积的百位只能是2,2、被乘数的十位和乘数只能是0、2、6、8,才有可能形如,0首先排除3、如果被乘数十位是6或8,那么乘数无论是2、6或8,都不可能乘出百位是2的三位数. 所以被乘数十位是2,相应得乘数是8.4、被乘数大于25,通过尝试得到符合条件的答案:28×8=224.(2008年“数学解题能力展示”读者评选活动四年级组初赛试题)4.如图.4 4方格被分成了五块;请你在每格中填入l、2、3、4中的一个,使得每行、每列的四个数各不相同,且每块上所填数的和都相等。
2013年数学解题能力展示网络评选活动四年级组初试试卷(解析)

2013“数学解题能力展示”网络评选活动 四年级组初试试卷解析一.填空题(每小题 8 分,共 24 分)1.1 3 5 17 19 20 22 40 _________.【考点】等差数列求和 【难度】☆☆ 【答案】 430 【分析】分成两组等差数列,一个奇数数列(连续奇数的和,10 个奇数,直接就是 102 100 ) ,一个 偶数数列(偶数个数要能数对,11 个) ,原式=(1 19) 10 (20 40) 11 430 . 2 22.爸爸生日是 5 月 1 日, 而春春生日是 7 月 1 日. 从 2012 年 12 月 26 日算起 (第 1 天) , 直到第 2013 天,爸爸和春春总共过了_________个生日.【考点】日历周期问题(注意闰年) 【难度】☆☆☆ 【答案】11 【分析】 2013 365 5188 ,直接用下面的算式表示 2013:2013 6 365 365 365 366 365 31 28 31 30 31 30 ,(注意 2016 年是闰年,12 月 26 是第一天,第 7 天才是 1 月 1 日) ,所以第 2014 天才是 7 月 1 日 (所以春春没有过第 6 个生日) ,所以爸爸过了 6 个生日,春春过了 5 个生日,一共 6 5 11 个 生日.3.笼子里有 30 只蛐蛐和 30 只蝈蝈.红毛魔术师每变一次,会把其中的 4 只蝈蝈变成 1 只蛐蛐;绿 毛魔术师每变一次,会把其中的 5 只蛐蛐变成 2 只蝈蝈.两个魔术师一共变了 18 次后,笼子里只 有蝈蝈没有蛐蛐了.这时蝈蝈有_________只.【考点】操作问题 【难度】☆☆☆ 【答案】6 【分析】不管红毛魔术师还是绿毛魔术师,每次操作都减少 3 个动物,那么共操作 18 次,一共减少了18 3 54 个动物,所以还剩 30 30 54 6 个蝈蝈.二.填空题(每小题 12 分,共 36 分)4. 定义 A @ B B B A A ,则 1@ 2 3@ 4 5@ 6 99@100 .【考点】定义新运算、平方差公式 【难度】☆☆☆ 【答案】 5050 【分析】 A @ B B 2 A2 ( B A)( B A) ,1@ 2 3@ 4 5@ 6 99@100 (2 1) (1 2) (4 3) (3 4)+ (100 99) (99 100) 1 2 3 100 50505.从 1、2、3、4、5、6、7 中选择若干个不同的数,使得其中偶数之和等于奇数之和,则符合条件 的选法共有_________种.【考点】枚举计数 【难度】☆☆☆ 【答案】7 【分析】偶数:2、4、6;奇数 1、3、5、7;偶数少,所以看偶数和; 偶数和有:4、6、8、10、12;所以有:4 1 3 ;1 组 6 2 4 1 5 ;2 组 8 2 6 1 7 3 5 ;2 组 10 4 6 3 7 ;1 组 12 2 4 6 5 7 ;1 组所以 1 2 2 1 1 7 组.6.A、B、C 三人在猜一个 1~99 中的自然数.A:“它是偶数,比 6 小.”B:“它比 7 小,是个两位 数.”C:“A 的前半句是对的,A 的后半句是错的.”如果这 3 人当中有 1 人两句都为真话,有 1 人两句都为假话,有 1 人两句话一真一假.那么,这个数是_________.【考点】逻辑推理 【难度】☆☆☆ 【答案】8【分析】假设法;A 与 C 说法有联系,假设 C 是两句话是真话;由下表: 前句 A B C 对 错 对 后句 错 错 对这样就满足的题目要求,得该数比 6 大,比 7 大,并且是一位数,而且是偶数,只有 8 满足要求.三.填空题(每小题 15 分,共 60 分)如图,有两个小正方形和一个大正方形,大正方形的边长是小正方形边长的 2 倍,阴影三角形面 积为 240,那么,三个正方形的面积和是_________.7.【考点】正方形面积、勾股定理; 【难度】☆☆☆ 【答案】3601 2 【分析】由下图该补的补出来,发现 AD BC c ,并且直接可以得到 c 240 (见附的正方形面积): 2所以得到 c 2 480 ,由勾股定理可以得到 c 2 b 2 b 2 ,所以大正方形的面积 b 2 240 ,而小正方 形的边长 2a b ,所以 b2 (2a) 2 4a 2 ,所以 a 2 60 . 可以得到三个正方形的面积是:240 60 60 360 .A Cbc Da B1 2 2 注释: S正 =b c 2bcb8.小张早晨 8 点整从甲地出发去乙地, 速度是每小时 60 千米. 小王早晨 9 点整从乙地出发去甲地. 小 张到达乙地后立即沿原路返回,恰好在 12 点整与小王同时到达甲地.那么两人相遇时距离甲地 _________千米.【考点】行程、相遇问题; 【难度】☆☆☆ 【答案】96 【分析】题意的示意图如下:A 甲CB 乙小张 4 个小时(8 点到 12 点)走了两个全程,所以全程是 4 60 2 120 千米; 小王的速度是每小时 120 (12 9) 40 千米, 小张 1 个小时(8 点到 9 点)走到 C 点: 601 60 千米,当小张和小王相遇时小张又走了60 (60 40) 60 36 千米,此时距甲地 60 36 96 千米.9.将数字 1~9 填入下图竖式的 9 个方格中,每个数字只能用一次,那么和的最小值为_________.2 0 + 3【考点】数字谜; 【难度】☆☆☆ 【答案】 3135 【分析】题目求和的最小值,由弃 9 法得数字和 51,上下两个和除以 9 的余数应该相等,所以都应该 是除以 9 余 3.1b a c d数字和45+6=51由弃九法知道,上面的数字和为 39,下面的最小数字和为 12,进一位数字和少 9,39 12 27 3 9 ,所以进了 3 位;由高位分析,知道 a 2 ,此时最小的和应为 313 的数字和为 3135. 具体的填写过程由下: 1) a 2 ,得 b 9、c 1 ,要想和最小, c 3 ,此时如下: ,因为下面的数字和最小为 12,所以最小4 9 2 1 3 e 6 2 8 7 1 3 5 92)此时没有填写的数字为:4、5、6、7、8, e 5 ,其他就可以填,如上面右图.10. 狼堡的狼欺羊太甚,终于导致羊群造反.接到攻打狼堡的通知后,小羊们陆续出发.7 点时小灰灰 登高一望,发现有 5 只羊到狼堡的距离恰好是一个公差为 20(单位:米)的等差数列,从前到后, 这 5 只羊分别为 A、B、C、D、E;8 点时,小灰灰登高一望,发现这 5 只羊到狼堡的距离仍然是 一个公差为 30(单位:米)的等差数列,但从前到后的顺序变成了 B、E、C、A、D.这 5 只羊 中跑得最快的羊比跑得最慢的羊每小时多跑_________米. 【考点】行程; 【难度】☆☆☆ 【答案】140 【分析】题目如下图表示:7点 E20 D20 C20 B20 A8点 D比较可得,跑的最快的羊是 E,跑的最慢的羊 A.30 A30 C30 E30 B由图比较可得,E 比 A 在 1 个小时多走了 20 4 30 2=140 米.。
2008年数学试题参考答案

2008年数学试题参考答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 答案 DBBCAACBDC二、选择题 11.70; 12,1; 13.5-; 14.27;15.9分(或9);16.20; 17.2; 18.76.三、解答题 19.解:原式21(1)x x xx -=⨯-11x =-.当2x =-时,原式13=-.20.解:(1)500; (2)如图1;(3)A 型号发芽率为90%,B 型号发芽率为92.5%, D 型号发芽率为94%,C 型号发芽率为95%.∴应选C 型号的种子进行推广. (4)3701(B )6303703804705P ==+++取到型号发芽种子. 21.解:(1)由33y x =-+,令0y =,得330x -+=.1x ∴=.(10)D ∴,. (2)设直线2l 的解析表达式为y kx b =+,由图象知:4x =,0y =;3x =,32y =-.4033.2k b k b +=⎧⎪∴⎨+=-⎪⎩,326.k b ⎧=⎪∴⎨⎪=-⎩,∴直线2l 的解析表达式为362y x =-. (3)由3336.2y x y x =-+⎧⎪⎨=-⎪⎩,解得23.x y =⎧⎨=-⎩,(23)C ∴-,. 3A D = ,193322A D C S ∴=⨯⨯-=△.(4)(63)P ,.22.解:(1)B -,C -; (2)过点C 作C D O A ⊥于点D ,如图2,则C D =.图1/km在R t AC D △中,30ACD ∠=,C D =,cos 302C D C A∴==.200C A ∴=.20020630-=,5611+=,∴台风从生成到最初侵袭该城要经过11小时.23.观察计算 (1)2a +; (2探索归纳(1)①<;②>;(2)222212(2)420d d a a -=+-=-.①当4200a ->,即5a >时,22120d d ->,120d d ∴->.12d d ∴>;②当4200a -=,即5a =时,22120d d -=,120d d ∴-=.12d d ∴=;③当4200a -<,即5a <时,22120d d -<,120d d ∴-<.12d d ∴<.综上可知:当5a >时,选方案二; 当5a =时,选方案一或方案二;当15a <<(缺1a >不扣分)时,选方案一. 24.解:(1)A B A P =;AB AP ⊥. (2)BQ AP =;BQ AP ⊥.证明:①由已知,得EF FP =,EF FP ⊥,45EPF ∴∠=.又A C B C ⊥ ,45C Q P C PQ ∴∠=∠=.CQ CP ∴=.在Rt BCQ △和R t A C P △中,B C A C =,90BCQ ACP ∠=∠= ,CQ CP =,Rt Rt BCQ ACP ∴△≌△,BQ AP ∴=.②如图3,延长BQ 交A P 于点M .Rt Rt BCQ ACP △≌△,12∴∠=∠.在Rt BCQ △中,1390∠+∠=,又34∠=∠,lAB FC Q 图3M1234EP241390∴∠+∠=∠+∠=.90Q M A ∴∠=.BQ AP ∴⊥.(3)成立.证明:①如图4,45EPF ∠= ,45C PQ ∴∠= . 又A C B C ⊥ ,45C Q P C PQ ∴∠=∠= .CQ CP ∴=. 在Rt BCQ △和R t A C P △中,B C A C =,90BCQ ACP ∠=∠= ,CQ CP =,Rt Rt BCQ ACP ∴△≌△.BQ AP ∴=.②如图4,延长QB 交A P 于点N ,则PBN CBQ ∠=∠.Rt Rt BCQ ACP △≌△,BQC APC ∴∠=∠.在Rt BCQ △中,90BQC CBQ ∠+∠= ,90APC PBN ∴∠+∠=.90PNB ∴∠=. QB AP ∴⊥.25.解:(1)甲地当年的年销售额为211420x x ⎛⎫-+ ⎪⎝⎭万元; 2399020w x x =-+-甲.(2)在乙地区生产并销售时, 年利润222111590(5)9010105w x nx x x x n x ⎛⎫=-+-++=-+-- ⎪⎝⎭乙. 由214(90)(5)535145n ⎛⎫⨯-⨯--- ⎪⎝⎭=⎛⎫⨯- ⎪⎝⎭,解得15n =或5-. 经检验,5n =-不合题意,舍去,15n ∴=. (3)在乙地区生产并销售时,年利润2110905w x x =-+-乙,将18x =代入上式,得25.2w =乙(万元);将18x =代入2399020w x x =-+-甲,lABQP EF图4N C得23.4w =甲(万元).w w > 乙甲,∴应选乙地. 26.解:(1)25. (2)能.如图5,连结D F ,过点F 作FH AB ⊥于点H , 由四边形C D E F 为矩形,可知Q K 过D F 的中点O 时,Q K 把矩形C D E F 分为面积相等的两部分(注:可利用全等三角形借助割补法或用中心对称等方法说明),此时12.5QH OF ==.由20B F =,H B F C B A △∽△,得16H B =. 故12.5161748t +==.(3)①当点P 在E F 上6(25)7t ≤≤时,如图6.4QB t =,7D E EP t +=,由PQE BCA △∽△,得7202545030t t --=.21441t ∴=.②当点P 在F C 上6(57)7t ≤≤时,如图7.已知4QB t =,从而5P B t =,由735P F t =-,20B F =,得573520t t =-+. 解得172t =.(4)如图8,213t =;如图9,39743t =.(注:判断P G A B ∥可分为以下几种情形:当6027t <≤时,点P 下行,点G 上行,可知其中存在P G A B ∥的时刻,如图8;此后,点G 继续上行到点F 时,4t =,而点P 却在下行到点E 再沿E F 上行,发现点P 在E F 上运动时不存在P G A B ∥;当6577t ≤≤时,点P G ,均在F C 上,也不存在P G A B ∥;由于点P 比点G 先到达点C 并继续沿C D 下行,所以在6787t <<中存在P G A B ∥的时刻,如图9;当810t ≤≤时,点P G ,均在C D 上,不存在P G A B ∥)E B图5B图6E B图7B图8E B图92009年数学试题参考答案一、选择题二、填空题13.>; 14.1.2 × 107; 15.36.4; 16.1; 17.3; 18.20. 三、解答题 19.解:原式=()()1()a b a b a a a b +-+⋅-=1a b ++. 当a = 2,1-=b 时, 原式 = 2.【注:本题若直接代入求值,结果正确也相应给分】 20.解:(1)∵OE ⊥CD 于点E ,CD =24,∴ED =12C D =12.在Rt △DOE 中,∵sin ∠DOE =ED O D=1213,∴OD =13(m ).(2)OE 5.∴将水排干需:5÷0.5=10(小时).21.解:(1)30%; (2)如图1; (3)8021203=;(4)由于月销量的平均水平相同,从折线的走势看,A 品牌的月销量呈下降趋势,而B 品牌的月销量呈上升趋势. 所以该商店应经销B 品牌电视机.时间/月图1第一 第二 第三 第四 电视机月销量折线统计图22.解:(1)-3.t =-6.(2)分别将(-4,0)和(-3,-3)代入2y ax bx =+,得0164,393.a b a b =-⎧⎨-=-⎩解得 1,4.a b =⎧⎨=⎩向上.(3)-1(答案不唯一).【注:写出t >-3且t ≠0或其中任意一个数均给分】 23.解:实践应用(1)2;lc .16;13.(2)54.拓展联想(1)∵△ABC 的周长为l ,∴⊙O 在三边上自转了lc 周.又∵三角形的外角和是360°, ∴在三个顶点处,⊙O 自转了3601360=(周).∴⊙O 共自转了(lc+1)周.(2)lc+1.24.(1)证明:∵四边形BCGF 和CDHN 都是正方形,又∵点N 与点G 重合,点M 与点C 重合,∴FB = BM = MG = MD = DH ,∠FBM =∠MDH = 90°. ∴△FBM ≌ △MDH . ∴FM = MH .∵∠FMB =∠DMH = 45°,∴∠FMH = 90°.∴FM ⊥HM .(2)证明:连接MB 、MD ,如图2,设FM 与AC 交于点P . ∵B 、D 、M 分别是AC 、CE 、AE 的中点, ∴MD ∥BC ,且MD = BC = BF ;MB ∥CD , 且MB =CD =DH .∴四边形BCDM 是平行四边形. ∴ ∠CBM =∠CDM .又∵∠FBP =∠HDC ,∴∠FBM =∠MDH . ∴△FBM ≌ △MDH .图2AHCDEBFG NMP∴FM = MH , 且∠MFB =∠HMD .∴∠FMH =∠FMD -∠HMD =∠APM -∠MFB =∠FBP = 90°. ∴△FMH 是等腰直角三角形. (3)是.25.解:(1)0 ,3.(2)由题意,得2240x y +=, ∴11202y x =-.23180x z +=,∴2603z x =-.(3)由题意,得 121206023Q x y z x x x=++=+-+-.整理,得 11806Q x=-.由题意,得112022603x x ⎧-⎪⎪⎨⎪-⎪⎩解得 x ≤90.【注:事实上,0≤x ≤90 且x 是6的整数倍】由一次函数的性质可知,当x =90时,Q 最小. 此时按三种裁法分别裁90张、75张、0张.26.解:(1)1,85;(2)作QF ⊥AC 于点F ,如图3, AQ = CP = t ,∴3AP t=-.由△AQF ∽△ABC,4BC ==, 得45Q F t =.∴45Q Ft=.∴14(3)25S t t=-⋅,即22655St t=-+.(3)能. ①当DE ∥QB 时,如图4.∵DE ⊥PQ ,∴PQ ⊥QB ,四边形QBED 是直角梯形.P图4P图3F此时∠AQP =90°. 由△APQ ∽△ABC ,得AQ AP ACAB=,即335t t -=. 解得98t=.②如图5,当PQ ∥BC 时,DE ⊥BC ,四边形QBED 是直角梯形. 此时∠APQ =90°. 由△AQP ∽△ABC ,得 AQ AP ABAC=,即353t t -=. 解得158t =.(4)52t=或4514t=.【注:①点P 由C 向A 运动,DE 经过点C . 方法一、连接QC ,作QG ⊥BC 于点G ,如图6.PC t=,222QC QG CG =+2234[(5)][4(5)]55t t =-+--.由22PCQC=,得22234[(5)][4(5)]55tt t =-+--,解得52t =.方法二、由C QC P A Q==,得Q A C Q C A∠=∠,进而可得B BC Q∠=∠,得C QB Q=,∴52AQBQ ==.∴52t =.②点P 由A 向C 运动,DE 经过点C ,如图7.22234(6)[(5)][4(5)]55t t t -=-+--,4514t =】P图52010年河北省初中毕业生升学文化课考试数学试题参考答案一、选择题二、填空题13.5 14.5 15.41 16.1 17.36 π 18. =三、解答题19.解:)1(21-=+x x , 3=x .经检验知,3=x 是原方程的解.20.解:(1)如图1; 【注:若学生作图没用圆规,所画路线光滑且基本准确即给4分】(2)∵90π346π180⨯⨯=,∴点P 经过的路径总长为6 π. 21.解:(1)144;(2)如图2;)甲校的平均分为8.3分,中位数为7分;由于两校平均分相等,乙校成绩的中位数大于甲 校的中位数,所以从平均分和中位数角度上判断, 乙校的成绩较好. )因为选8名学生参加市级口语团体赛,甲校得10分的有8人,而乙校得10分的只有5人,所以应选甲校.22.解:(1)设直线DE 的解析式为b kx y +=,∵点D ,E 的坐标为(0,3)、(6,0),∴ ⎩⎨⎧+==.60,3b k b解得 ⎪⎩⎪⎨⎧=-=.3,21b k ∴ 321+-=x y .∵ 点M 在AB 边上,B (4,2),而四边形OABC 是矩形, ∴ 点M 的纵坐标为2. 又 ∵ 点M 在直线321+-=x y 上,∴ 2 = 321+-x .∴ x = 2.∴ M (2,2).(2)∵xm y =(x >0)经过点M (2,2),∴ 4=m .∴xy 4=.又 ∵ 点N 在BC 边上,B (4,2),∴点N 的横坐标为4.图1乙校成绩条形统计图8分 9分 分数10分 图27分∵ 点N 在直线321+-=x y 上, ∴ 1=y .∴ N (4,1). ∵ 当4=x 时,y =4x= 1,∴点N 在函数 xy 4= 的图象上. (3)4≤ m ≤8.23.解:(1)4 5 6;(2)不对.∵OP = 2,PQ = 3,OQ = 4,且42≠32 + 22,即OQ 2≠PQ 2 + OP 2, ∴OP 与PQ 不垂直.∴PQ 与⊙O 不相切. (3)① 3;②由①知,在⊙O 上存在点P ,P '到l 的距离为3,此时,OP 将不能再向下转动,如图3.OP 在绕点O 左右摆动过程中所扫过的最大扇形就是P 'OP .连结P 'P ,交OH 于点D . ∵PQ ,P 'Q '均与l 垂直,且PQ =P '3Q '=,∴四边形PQ Q 'P '是矩形.∴OH ⊥P P ',PD =P 'D . 由OP = 2,OD = OH -HD = 1,得∠DOP = 60°. ∴∠PO P ' = 120°.∴ 所求最大圆心角的度数为120°.24.解:(1)AO = BD ,AO ⊥BD ;(2)证明:如图4,过点B 作BE ∥CA 交DO 于E ,∴∠ACO = ∠BEO .又∵AO = OB ,∠AOC = ∠BOE , ∴△AOC ≌ △BOE .∴AC = BE .又∵∠1 = 45°,∴∠ACO = ∠BEO = 135°.∴∠DEB = 45°.∵∠2 = 45°,∴BE = BD ,∠EBD = 90°.∴AC = BD . 延长AC 交DB 的延长线于F ,如图4.∵BE ∥AC ,∴∠AFD = 90°.∴AC ⊥BD .(3)如图5,过点B 作BE ∥CA 交DO 于E ,∴∠BEO = ∠ACO .又∵∠BOE = ∠AOC , ∴△BOE ∽ △AOC . ∴AOBO ACBE =.又∵OB = kAO ,图4A D OB C21 MNEFA OBC1D 2图5M NEl图3由(2)的方法易得 BE = BD .∴k AC BD =.25.解:(1)y = 2t ;(2)当BP = 1时,有两种情形:①如图6,若点P 从点M 向点B 运动,有 MB = BC 21= 4,MP = MQ = 3, ∴PQ = 6.连接EM ,∵△EPQ 是等边三角形,∴EM ⊥PQ .∴33=EM . ∵AB = 33,∴点E 在AD 上.∴△EPQ 与梯形ABCD 重叠部分就是△EPQ ,其面 积为39.②若点P 从点B 向点M 运动,由题意得 5=t . PQ = BM + M Q -BP = 8,PC = 7.设PE 与AD 交于点F ,QE 与AD 或AD 的延长线交于点G ,过点P 作PH ⊥AD 于点H ,则 HP = 33,AH = 1.在Rt △HPF 中,∠HPF = 30°, ∴HF = 3,PF = 6.∴FG = FE = 2.又∵FD = 2, ∴点G 与点D 重合,如图7.此时△EPQ 与梯形ABCD 的重叠部分就是梯形FPCG ,其面积为3227. (3)能.4≤t ≤5.26.解:(1)140 57500;(2)w 内 = x (y -20)- 62500 = 1001-x 2+130 x 62500-,w 外 = 1001-x 2+(150a -)x . (3)当x = )1001(2130-⨯-= 6500时,w 内最大;分 由题意得 2214()(62500)1300(150)100114()4()100100a ⨯-⨯----=⨯-⨯-, 解得a 1 = 30,a 2 = 270(不合题意,舍去).所以 a = 30.(4)当x = 5000时,w 内 = 337500, w 外 =5000500000a -+.若w 内 < w 外,则a <32.5;C P M图6若w内= w外,则a = 32.5;若w内>w外,则a>32.5.所以,当10≤a <32.5时,选择在国外销售;当a = 32.5时,在国外和国内销售都一样;当32.5<a ≤40时,选择在国内销售.图7。
2007-2008下期四年级数学期末试题

得 分
评分人
六、解决问题你最行!(4+4+6+5+5+6=30分)
1、一条路第一天修了18.5千米,比第二天少修7.5千米。两天一共修了多少千米?
2、学校要买45套桌椅。已知每张桌子160元,每把椅子70元,一共要花多少钱?
3、东方红社区住户拥有计算机情况如下表。
年 份
2000
2001
2002
2003
拥有计算机(台)
9
15
26
40
(1)根据表中的数据,制成折线统计图。(2分)
(2)根据折线统计图,你获得了什么信息?(1分)
(3)请你提出两个数学问题并解答出来。(3分)
4、“金实百货”商店上午卖出童鞋18双,下午又卖出23双。下午比上午多收入425元。全天卖童鞋多少元?
A、900B、1800C、3600
2、下面各数中,所有的0都可以去掉且大小不变的数是( )。
A、100.30B、0.700 C、6.400D、4000
3、李磊和王强进行60米赛跑,李磊用了13.08秒,王强用了10.11秒。两人的速度( )。
A、王强快B、李磊快C、一样快 D、无法比较
4、被除数是除数的3倍,除数是商的3倍,没有余数。已知商是最大的两位数,那么被除数、除数、商三个数的和是( )。
号
考
名
姓
级
班
校
学
东区第二片区2007~2008学年度(下期)期末练习卷
四年级数学
(满分97分,卷面3分,90分钟完卷)
题号
一
二
三
四
五
六
总分 分
总 分 人
迎春杯初赛四年级年级题库

模块一、计算(一)、凑整【例 1】(2007年数学解题能力展示中年级初赛 1题)计算:98 +197 + 2996 + 39995 + 499994 + 5999993 + 69999992 + 799999991 = .(二)、提取公因数【例 2】(2008 年“数学解题能力展示”读者评选活动四年级组初赛 1 题)计算:l2345×2345 + 2469×38275 = 。
【例 3】(2009“数学解题能力展示"读者评选活动四年级初赛1 题)计算:2009 ÷ 37 + 300 ÷ (37 ×3) = .(三)、多位数计算【例 4】(2007年数学解题能力展示中年级初赛 2题)有一个2007位的整数,其每个数位上的数字都是9,这个数与它自身相乘,所得的积的各个数位上的数字的和是.(四)、公式法【例 5】(2010 年数学解题能力展示四年级初试1 题)计算:64×46 + 73× 37 + 82×28 + 91×19 = .【例 6】(2009“数学解题能力展示"读者评选活动四年级初赛10 题)老师在黑板上写了三个不同的整数,小明每次先擦掉第一个数,然后在最后写上另两个数的平均数,如此做了7 次,这时黑板上三个数的和为159.如果开始时老师在黑板上写的三个数之和为2008,且所有写过的数都是整数.那么开始时老师在黑板上写的第一个数是.(五)、等差数列【例 7】(2010 年数学解题能力展示四年级初试2 题)2010 个连续自然数由小到大排成一排,排在奇数个上的各数的平均数是2345,那么,排在偶数个上各数的平均数是.模块二、几何(一)一笔画问题【例 8】(2009“数学解题能力展示"读者评选活动四年级初赛 6 题)如图所示,某小区花园的道路为一个长480 米,宽200 米的长方形;一个边长为260 米的菱形和十字交叉的两条道路组成.一天,王大爷A 处进入花园,走遍花园的所有道路并从A 处离开.如果他每分钟走60 米,那么他从进入花园到走出花园最少要用分.(二)平面几何——等积变换【例 9】(2007年数学解题能力展示中年级初赛 7题)如图2,六边形ABCDEF 为正六边形,P为对角线CF 上一点,若PBC、PEF 的面积为3与4 ,则正六边形ABCDEF 的面积是.C DB P EF2(三)平面几何——周长与面积【例 10】(2008 年“数学解题能力展示”读者评选活动四年级组初赛12 题)如图,一个长方形被分成A、B、C三块,其中B 和C 都是长方形,A 的八条边的边长分别是l、2、3、4、5、6、7、8 厘米。
2008-2009四年级数学期末试题

一、填一填。
(20分)1、“鸟巢”是2008年北京奥运会的主体育场,建筑面积有260000平方米,读()平方米,改写成以“万”作单位的数是()平方米2、为了成功举办奥运会,北京市在改善城市交通方面的总投资达到九百零一亿三千二百万元,写作()元,省略“亿”后面的尾数约是()元。
3、把60800、60080、68000按从小到大的顺序排列()<()<()。
4、括号里最大能填几?()×40<372 46×()<217 ()×70<592 81×()<432 5、两个数相除,商是20。
如果被除数不变,除数除以4,商是()6、一个锅里一次可以煮3个蛋,煮熟一个蛋需5分钟,煮熟6个蛋需()分钟。
7、如下图已知∠1=∠2=60o,则∠3=∠4=()8、钟面上是3时整,时针和分针呈()角。
()时整,时针与分针够成平角。
9、在一个除法算式里,商是15,除数是23,余数最大能是(),这时被除数是()。
10、根据规律填写数字:5×5=25 95×95=9025 995×995=990025 9995×9995=99900025 99995×99995=()999995×999995=()二、辨一辩(对的打“√”,错的打“×”)(5分)1、我国人约有13亿人,写作1300000000人。
()2、一个因数扩大8倍,积也一定随着扩大8倍。
()3、梯形的高与上、下底都垂直。
()4、两位数乘以三位数,积一定是五位数。
()5、长方形是特殊的平行四边形。
()三、选一选。
(将正确答案的序号填在括号里)(5分)1、下面的数一个零也不读的是()A、560056450B、908900005C、10007650D、600006002、7000÷300=23……()A、1B、10C、100D、10003、与600÷50的商相等的算式是()A、(600+2)÷(50+2)B、(600×2)÷(50÷2)C、(600-2)÷(50-2)D、(600×2)÷(50×2)4、两组对边分别平行,有四个直角且四条边也相等的是()A、正方形B、长方形C、平行四边形D、梯形5、平面上有甲、乙、丙三条直线,它们相互平行,甲、乙之间距离是3厘米,甲、丙之间距离是2厘米,那么乙、丙之间距离是()厘米。
四年级第二学期解题能力比赛试题(含答案)

四年级解题能力竞赛试卷 一、填空题。
(每空2分,共40分) 1.( )是现代计算机技术中广泛采用的一种计数方法,它的进位规则是( ),如2写成这样的数是( )。
2.钟面上从9:45到10:15,分针转动了( )°。
3.从0、9、6、4这四张数字卡片中,挑选三张排成一个三位数。
能排出( )个不同的三位数,其中大约700的数是( )。
4.马虎虎把45×(□-4)错算成45×□-4,他算出的结果与正确的结果相差( )。
5.爸爸今年47岁,儿子今年21岁,( )年前,爸爸的年龄是儿子的3倍。
6.用1、2、4、7、9 这五个数字组成一个两位数和一个三位数,要使乘积最大,算式应是( ),要使乘积最小,算式应是( )。
7. 一个直角梯形,上底3厘米,一腰长10厘米,如果把它的上底增加5厘米,就变成一个正方形,这个梯形的周长是( )厘米。
8.将一张长方形纸折起来(如图),如果∠2=72°,∠1=( )° 9.一个三角形两条边长分别是5cm 和9cm ,第三条边的长度一定大于( )cm ,同时小于( )cm 。
10. 三块钢板共重1026千克,第一块的重量是第二块的4倍,第三块的重量和第一块的一样重,第三块钢板重( )千克。
11. 六边形的内角和是( )°,( )边形的内角和是1800°。
12.一个等腰三角形的相邻两条边的长度分别是5cm 和10cm ,这个三角形的周长是( )cm 。
13. 甲乙两人今年的平均年龄是20岁,三年后甲比乙大8岁。
今年甲( )岁,乙( )岁。
二、简便计算。
(每题5分,共15分) 120×75+750×88 111×37+999×7 99×98+198 三、实践题。
(10分) 1.先数一数,再填一填,你能发现什么规律?1 2 学校_________________班级_____________姓名_______________…………………………………………………………………密封线内不得答题……………………………………………………………………………………三角形个数 1 2 3 4 5 6 …小棒根数 3 5 …②有159根小棒,能摆出多少个这样的三角形?三、解决问题。
2008年第一届四年级A卷

四年级 数学试题(A 卷)1. 计算:123456789876543219⨯= 。
2.3782除以某个整数后所得的商恰好是余数的21倍,那么除数最小可能是 。
3. 如图,从正方形ABCD 的四个角上各切掉一个等腰直角三角形后,剩下一个八边形,已知4EF =,7GH =,8IJ =,那么LK = 。
4. 将1到8这8个自然数分别填入如图数阵中的8个圆圈,使得数阵中各条直线上的三个数之和都相等,那么A 和B 两个圆圈中所填的数之差(大数减小数)是 。
5. 把自然数从1开始,排列成如图的三角阵:第1列为1;第2列为2,3,4;第3列为5,6,7,8,9,…,每一列比前一列多排两个数,依次排下去,“以1开头的行”是这个三角阵的对称轴。
在以1开头的行中,如果我们把13视为“第1项”,则“第2009项”的数除以7的余数是 。
6. 将10、16以及另外4个不同的自然数填入下面六个□,使这6个自然数从左到右构成等差数列,一共有 种不同的填法。
□□□□□□7. 将32个相同的小正方体拼成一个体积为32立方厘米的长方体,将表面涂上红漆,然后分开,其中有2个面涂红的小正方体有24个,则有1个面涂红的小正方体有 个。
8. 甲、乙两人同时A 地出发,在A 、B 两地之间匀速往返行走,甲的速度大于乙的速度,甲每次到达A 地、B 地或遇到乙都会调头往回走,除此以外,两人在AB 之间行走方向不会改变,已知两人第一次相遇的地点距离B 地1800米,第三次的相遇点距离B 地800米,那么第二次相遇的地点距离B 地 。
9. 甲班有56人,已知其中:(1)有人会计算机;(2)有人不会计算机;(3)班长小王不会计算机。
如果上述三句仅一句为真,问:甲班究竟有( )会计算机。
第3题L KJIH G FE DCBA第4题B A第5题 10511261213713481491516A.55人会,仅小王不会。
B.只有小王会,其余人都不会。
C.至少有一人不会。
2014数学解题能力展示读者评选活动试题四年级组

2014“数学解题能力展示”读者评选活动试题四年级组一.选择题(每小题8 分,共32 分)1. 下面计算结果等于9 的是()(A)3×3÷3+3(B)3÷3+3×3(C)3×3-3+3(D)3÷3+3÷3【考点】计算【难度】☆☆【答案】C【分析】经计算,答案为C.3. 亮亮早上8:00 从甲地出发去乙地,速度是每小时8 千米.他在中间休息了1 小时,结果中午12:00到达乙地.那么,甲、乙两地之间的距离是()千米.(A)16 (B)24 (C)32 (D)40【考点】行程【难度】☆☆【答案】B【分析】共用时间为12 8 1 3小时.那么距离为8 3 24千米.【考点】组合【难度】☆☆☆【答案】D【分析】第一个人看别的房间,开灯的9 间,关灯的10 间,所以会关灯.第二个人看别的房间关灯的至少10 间,开灯的至多9 间,所以会关灯.第三个人看别的房间,关灯的至少10 间,所以会关灯.第四个人看别的房间,关灯的至少10 间,所以也会关灯.……所以最后所有房间均为关灯11. 你能根据以下的线索找出百宝箱的密码吗?(1)密码是一个八位数;(2)密码既是3 的倍数又是25 的倍数;(3)这个密码在20000000 到30000000 之间;(4)百万位与十万位上的数字相同;(5)百位数字比万位数字小2;(6)十万位、万位、千位上数字组成的三位数除以千万位、百万位上数字组成的两位数,商是25.依据上面的条件,推理出这个密码应该是().(A)(B)(C)(D)(A)25526250 (B)26650350 (C)27775250 (D)28870350【考点】组合,逻辑推理【难度】☆☆☆【答案】B【分析】将ABCD 逐一代入检验.只有B 满足(1)(2)(3)(4)(5)13. 老师在黑板上将从1 开始的计数连续地写下去:1,3,5,7,9,11……写好后,擦去了其中的两个数,将这些奇数隔成了3 段,如果前两段的和分别是961 和1001,那么,老师擦去的两个奇数之和是().(A)154 (B)156 (C)158 (D)160【考点】计算,等差数列【难度】☆☆☆【答案】A14. 甲乙两人合作打一份材料. 开始甲每分钟打100 个字,乙每分钟打200 个字. 合作到完成总量的一半时,甲速度变为原来的 3 倍,而乙休息了 5 分钟后继续按原速度打字. 最后当材料完成时,甲、乙打字数相等. 那么,这份材料共()个字.(A)3000 (B)6000 (C)12000 (D)18000 【考点】应用题【难度】☆☆☆【答案】D【分析】前一半时乙的工作量是甲的 2 倍,所以后一半甲应是乙的 2 倍. 把后一半工作量分为6 份,甲应为4 份,乙应为2 份,说明乙休息时甲打了1 份,这一份的量是100 3 5 1500字,故总工作量是1500 6 2 18000字.(扫一扫,关注八人教育,可预约真题讲解)。
