The multi-time correlation functions, free white noise, and the generalized Poisson statist
amber动力学常用参数说明

amber动力学常用参数说明个人日记2009-05-08 19:32:18 阅读130 评论1 字号:大中小订阅IMIN Flag to run minimization=0 No minimization (only do molecular dynamics;default)= 1 Perform minimization (and no molecular dynamics)=5 Read in a trajectory for analysis.NTX Option to read the initial coordinates, velocities and box size from the "inpcrd" file. The options 1-2 must be used when one is starting from minimized or model-built coordinates. If an MD restrt file is used as inpcrd, thenoptions 4-7 may be used.= 1 X is read formatted with no initial velocity information (default)= 2 X is read unformatted with no initial velocity information= 4 X and V are read unformatted.= 5 X and V are read formatted; box information will be read if ntb>0. The velocity information will only be used if irest=1.= 6 X, V and BOX(1..3) are read unformatted; in other respects, this is the same as option "5".=7 Same as option "5"; only included for backward compatibility with earlier versions of Amber. IREST Flag to restart the run.= 0 Noeffect (default)= 1 restart calculation. Requires velocities in coordinate input file, so you also may need to reset NTX if restarting MD.NTRX Format of the Cartesian coordinates for restraint from file "refc". Note: the program expects file "refc" to contain coordinates for all the atoms in the system. A subset for the actual restraints is selected by restraintmask in the controlnamelist.= 0 Unformatted (binary) form= 1 Formatted (ascii, default) formNTPR Every NTPR steps energy information will be printed in human-readable form to files "mdout" and "mdinfo". "mdinfo" is closed and reopened each time, so it always contains the most recent energy and temperature. Default 50.NTWR Every NTWR steps during dynamics, the "restrt" file will be written, ensuring that recovery from a crash will not be so painful. In any case, restrt is written ev ery NSTLIM steps for both dynamics and minimization calculations. If NTWR<0, a unique copy of the file, restrt_nstep, is written every abs(NTWR) steps. This option is useful if for example one wants to run free energy perturbations from multiple starting points or save a series of restrt files for minimization. Default 500.NTF Force evaluation. Note: If SHAKE is used (see NTC), it is not necessary to calculate forces for the constrained bonds.= 1 complete interaction is calculated (default)= 2 bond interactions involving H-atoms omitted (use with NTC=2)= 3 all the bond interactions are omitted (use with NTC=3)= 4 angle involving H-atoms and all bonds are omitted= 5 all bond and angle interactions are omitted= 6 dihedrals involving H-atoms and all bonds and all angle interactions are omitted= 7 all bond, angle and dihedral interactions are omitted= 8 all bond, angle, dihedral and non-bonded interactions are omittedNTB Periodic boundary. If NTB .EQ. 0 then a boundary is NOT applied regardless of any boundary condition information in the topology file. The value of NTB specifies whether constant volume or constant pressure dynamics will be used. Options for constant pressure are described in a separate section below.= 0 no periodicity is applied and PME is off= 1 constant volume (default)= 2 constant pressureIf NTB .NE. 0, there must be a periodic boundary in the topology file. Constant pressure is not used in minimization (IMIN=1, above). For a periodic system, constant pressure is the only way to equilibrate densityif the starting state is not correct. For example, the solvent packing scheme used in LEaP can result in a net void when solvent molecules are subtracted which can aggregate into "vacuum bubbles" in a constant volume run. Another potential problem are small gaps at the edges of the box. The upshot is that almost every system needs to be equilibrated at constant pressure (ntb=2, ntp>0) to get to a proper density. But be sure to equilibrate first (at constant volume) to something close to the final temperature, before turning on constant pressure.CUT This is used to specify the nonbonded cutoff, in Angstroms. For PME, the cutoff is used to limit direct space sum, and the default value of 8.0is usually a good value. When igb>0, the cutoff is used to truncate nonbonded pairs (on an atom-by-atom basis); here a larger value than the default is generally required. A separate parameter (RGBMAX) controls the maximum distance between atom pairs that will be considered in carrying out the pairwise summation involved in calculating the effective Born radii, see the generalized Born section below.IBELLY Flag for belly type dynamics.= 0 No belly run (default).= 1 Belly run. A subset of the atoms in the system will be allowed to move, and the coordinates of the rest will be frozen. The moving atoms are specified bellymask. This option is not available when igb>0. Note also that this option does not provide any significant speed advantage, and is maintained primarily for backwards compatibilitywith older version of Amber. Most applications should use the ntr variable instead to restrain parts of the system to stay close to some initial configuration.NTR Flag for restraining specified atoms in Cartesian space using a harmonic potential. The restrained atoms are determined by the restraintmask string. The force constant is given by restraint_wt. The coordinates are read in "restrt" format from the "refc" file (see NTRX, above). = 0 No position restraints (default) = 1 MD with restraint of specified atomsMAXCYC The maximum number of cycles of minimization. Default 1.NCYC If NTMIN is 1 then the method of minimization will be switched from steepest descent to conjugate gradient after NCYC cycles. Default 10.NSTLIM Number of MD-steps to be performed. Default 1.TEMP0Reference temperature at which the system is to be kept, if ntt > 0. Note that for temperatures above 300K, the step size should be reduced since increased distance traveled between evaluations can lead to SHAKE and other problems. Default 300.TEMPI Initial temperature. For the initial dynamics run, (NTX .lt. 3) the velocities are assignedfrom a Maxwellian distribution at TEMPI K. If TEMPI = 0.0, the velocities will be calculated from the forces instead. TEMPI has no effect if NTX .gt. 3. Default 0.0.NTT Switch for temperature scaling. Note that setting ntt=0 corresponds to the microcanonical (NVE) ensemble (which should approach the canonical one for large numbers of degrees of freedom). Some aspects of the "weak-coupling ensemble" (ntt=1) have been examined, and roughly interpolate between the microcanonical and canonical ensembles [63]. The ntt=2 and 3 options correspond to the canonical (constant T) ensemble. The ntt=4 option is included for historical reasons, but does not correspond to any of the traditionalensembles.= 0 Constant total energy classical dynamics (assuming that ntb<2, as should probably always be the case when ntt=0).= 1 Constant temperature, using the weak-coupling algorithm [64]. A single scaling factor is used for all atoms. Note that this algorithm just ensures that the total kinetic energy is appropriate for the desired temperature; it does nothing to ensure that the temperature is even over all parts of the molecule. Atomic collisions should serve to ensure an even temperature distribution, but this is not guaranteed, and can be a particular problem for generalized Born simulations, where there are no collisions with solvent. Other temperature coupling options (especially ntt=3) should probably be used for generalized Born simulations.= 2 Andersen temperature coupling scheme [65], in which imaginary "collisions" randomize the velocities to a distribution corresponding to temp0 every vrand steps. Note that in between these "massive collisions",the dynamics is Newtonian. Hence, time correlation functions (etc.) can be computed in these sections, and the results averaged over an initial canonical distribution. Note also that too high a collision rate (too small a value of vrand) will slow down the speed at which the molecules explore configuration space, whereas too low a rate means that the canonical distribution of energies will be sampled slowly. A discussion of this rate is given by Andersen [66].= 3 Use Langevin dynamics with the collision frequency γ given by gamma_ln, discussed below. Note that when γ has its default value of zero, this is the same as setting ntt = 0.GAMMA_LN The collision frequency γ , in ps-1, when ntt = 3. A simple Leapfrog integrator is used to propagate the dynamics, with the kinetic energy adjusted to be correct for the harmonic oscillator case [67,68]. Note that it is not necessary that γ approximate the physical collision frequency. In fact, it is often advantageous, in terms of sampling or stability of integration, to use much smaller values. Default is 0NTP Flag for constant pressure dynamics. This option should be set to 1 or 2 when Constant Pressure periodic boundary conditions are used (NTB = 2).= 0 Used with NTB not = 2 (default); no pressure scaling= 1 md with isotropic position scaling= 2 md with anisotropic (x-,y-,z-) pressure scaling: this should only be used with orthogonal boxes (i.e. with all angles set to 90). Anisotropic scaling is primarily intended for non-isotropic systems, such as membrane simulations, where the surface tensions are different in different directions; it is generally not appropriate for solutes dissolved in water.NTC Flag for SHAKE to perform bond length constraints [70]. (See also NTF in the Potential function section. In particular, typically NTF = NTC.) The SHAKE option should be used for most MD calculations. The size of the MDtimestep is determined by the fastest motions in the system. SHAKE removes the bond stretching freedom, which is the fastest motion, and consequently allows a larger timestep to be used. For water models, a special "three-point" algorithm is used [71]. Consequently, to employ TIP3P set NTF = NTC = 2. Since SHAKE is an algorithm based on dynamics, the minimizer is not aware of what SHAKE is doing; for this reason, minimizations generally should be carried out without SHAKE. One exception is short minimizations whose purpose is to remove bad contacts before dynamics can begin.= 1 SHAKE is not performed (default)= 2 bonds involving hydrogen are constrained= 3 all bonds are constrained (not available for parallel runs in sander)。
外文翻译--智能断路器电路的预报和预警系统的研究

Intelligent circuit breaker forecastingand rewarding system researchAbstractThis paper describes an intelligent circuit breaker software and hardware design, real-time multi-task alarm system will be introduced into circuit breaker monitoring and control, to the timely opening and timely alarm. According to the different impact parameters, the different alarm information was given, increasing the protection and alerts function of the circuit.1 IntroductionIn recent years, the IEEE Sub-committee of power system reliability had made an investigation on the reliability of low-voltage circuit breakers, the investigation report only pointed out that the main failure mode of circuit breaker is debugging inaccurate of short-circuit protection, but not proposing the solutions. And the reliability of circuit breaker operation is very prominent. In 1986, the IEEE switching equipment technical committee had set up a new reliability working group of circuit breaker, which pointed out that operation failure (mechanical failure) was the main reason for a circuit breaker failure. Thus increasing prediction design is very necessary in the circuit breaker virtual designed.The using number of circuit breakers increasing year by year, the market capacity of online monitoring products is also expanding. Although such equipment in the installation, commissioning, equipment reliability and so on, there are still many problems, but these problems can be improved and solved through technology. According to market research analysis, the prices of domestic on-line monitoring products are in the following 200,000. In 2002, statistical data shows that the potential market capacity of currently on-line monitoring is 500 million Yuan, the actual market capacity only 0.10 million. In these circumstances, the on-line monitoring market capacities of the circuit breaker are relatively larger in the current development.China's industrial Ethernet overall level is not high, low-voltage distribution industries need to do a lot of research and development work in intelligence and network, in order to raise the intelligent level of domestic low-voltage electrical, to learn the world's most advanced industrial Ethernet technology, and solve the real problem. In order to improve reliability, the warning systems of circuit breaker are proposed, before the electrical equipment failures, predicting to users. The subject are completed equipment research and development by using embedded systems, followed MODBUS / TCP industrial Ethernet protocol, and the basic function is areal-time scanning and alarm, error-correcting functions, and hung activated, self-diagnosis, e.g. Additional functions: to realize protocol conversion between Ethernet network and industrial on-line bus.2 Forecasting and Early Warning System2.1 System Architecture DesignAlthough the circuit breaker itself cost than the cost of other equipment is much lower, such as generators, transformers, but the event of an accident, resulting the loss is much larger than the circuit breaker itself value, so the reliability of their work must be take notice.On the current development state, the majority of domestic substation electrical equipment still accorded to the requiring of electrical equipment preventive test order, periodically going on preventive tests. The test project and cycle of circuit breakers oil and SF6 gas were strict requirement, more test projects, the need for a relatively long period of stop power, affecting the users normal electricity; Moreover, the preventive tests that imposed on the test voltage are relatively low, and the difference between the actual operation is large, and difficult to reflect the real operation process of circuit breaker.Accordance with circuit breaker need to provide electrical power system protection, prediction and real-time multi-tasking system are put forward, the system can analysis, monitoring and alarm to the operation of the circuit breaker. System architecture is seen as Fig.1.2.2 Real-time multi-tasking operating systemμC/OS- is a small core of embedded real-time operating system, the entire code can be divided into core layer and transplantation layer, thus easier to transplant. It uses Preemptive scheduling strategy to ensure the real-time task; be able to manage up to 64 tasks; provide mail, message queues, semaphores, memory management, time management, and other system services. At the same time, it is an open-source generation code, which makes the system upgrades and future maintenance are very convenient. μC/OS - core using standard C language code to prepare, the code can be easy to transplant to a variety of microprocessor.After the operating system ported to the device, in combination with the device achieved functions, the above functions will be distributed to the four works to achieve, namely to protect mission, communications tasks, mission control and display tasks. The applications procedure establish various tasks in the operating system, allocating each task different priority level, the operating system dynamic schedule tasks according to the priority and achieve all the functionality of devices. For all tasks, in a moment, there is only one running task. Tasks of the four kinds of state converse based on certain conditions. The state conversion is seen as Fig.2.In the system, the various functions can be divided into different priority task, through real-time operating system to achieve the regulation management of all tasks, in the single task, solving difficult to deal with and real-time poor problems, that also can enhance system reliability.3 System hardware and software designIn electrical intelligent: real-time performance is the key point, using the high-speed 32-bit ARM 7 TDMI microprocessor as the CPU system, the larger expansion of FLASH program storage space, the high-speed SDRAM as running space, while embedded source code open μCDOS-II unified management application process, and allocation tasks priority, so that high-speed data communication network have no congestion.3.1 Condition monitoring and alarmCondition monitoring refers to understand and master the operational status of equipment, including the use of test, measurement, monitoring, analysis and discrimination, with the system's history and current situation, and consideration environmental factors that assess the operation state of switching equipment, judgments its in normal or non-normal conditions, and displaying and recording the status, alarming the unusual circumstances, which operating personnel can be dealt with promptly, and switching equipment failure analysis, performance assessment, the reasonably using of provision information and preparing basis data.Switching equipment state usually can be divided into hardware fault and software fault. Software fault is that the software itself may be problem, but also may be caused by improper operation or may be caused by system mistakes. Hardware failures are caused by the circuit breaker itself. According to the switching equipment the severity of the fault condition, hardware failures are divided into the minor hardware failure and serious hardware failures. The slight hardware failures are the general fault that the circuit breaker state signal will definitely be changes and equipment performance has been deterioration, but can still barely able to maintain operation. Serious hardware failures are the unexpected emergencies that circuit breakers can not run down; leading to the devastating disaster fault, as well as the moment breakdown for some reason.Its basic principle is the circuit breaker in functioning condition, using all kinds of the measurement tool to monitor its working current, voltage, and other parameters. Adoption sensors will be measured signals, extracted electric and non-electric signals, and converted into the standard form signals that measuring devices can detect signal, inputting digital signal acquisition devices, through the A / D converter, then the corresponding data analysis and feature extraction can be executed.According to the detection the fault state of system, diagnosing circuit breaker what should be done. When the monitoring is the software failure, the software changes. When the monitoring is a slight hardware failure, according to the need, circuit breakers can be continued to use, or opening the standby circuit. When the monitoring is a serious hardware failure, which directly open the standby circuit breaker and repair or replacement the circuit. According to the monitoring hardware failure type, the different alarm measure can be used, the indicator light means light-hardware failure, when a serious hardware failure, the ringing form can be used. Hardware failure alarm circuit is seen as Fig.3.When the monitoring that is slight hardware failure, BG2, BG3 works and bright lights. When the monitoring that is a serious hardware failure, BG2, BG3 stops working, BG4 work, alarm and bell.3.2 Self-diagnosis task scheduling algorithmRegular monitoring the circuit breaker, and the need of considering the following major impact parameters.(1) Monitoring circuit breaker current and voltage of open and break.(2) Monitoring the distance and speed of contact characteristic.(3) Monitoring circuit breaker open and break time, temperature index, and arcing time, e.g. this volume indirectly reflects the operation state of the circuit breaker.(4) Monitoring the transformation state of circuit breaker.(5) Monitoring the movement state of circuit breaker, understanding the action situation and the working condition is good.(6) Monitoring Closing bouncing and rebound. That is, monitoring circuit breaker the mechanical vibration situation.According to the different role of the circuit breaker impact parameters, priority order grow from small to large by impact parameters. Minimum priority 1 is the monitoring circuit breaker open and breaks current and voltage, the biggest priority 6 is the monitoring circuit breaker open and breaks time. Priority data is small, the priority is higher. The monitoring parameters priority of Real-time multi-tasking system shown is seen as Tab.1.Because of different priorities, the algorithm time complexity changes from O (nk) to O (kn), k is the number of circuit breakers impact parameter, that is, k is 6. Reducing time complexity shows that introduction priority setting circuit breaker impact parameters is effective.4. ConclusionsIn sum, low-voltage circuit breaker on-line monitoring system assess and diagnosethe running Circuit Breaker, provided targeted maintenance recommendations, preventing accidents occurred, and optimizing operation of circuit breakers, improving their life. From a technical perspective, it is extremely necessary for ensuring the reliability of the power system and the promoting scientific and technological progress of electrical equipment industry that have a significant role, and having a broad application prospects.This research was sponsored by the National Natural Science Foundation of Hebei Province under the Grants No. E2006001037.智能断路器电路的预报和预警系统的研究摘要本文介绍的智能断路器的软件和硬件设计,实时多任务报警系统就会被引入断路器电路的监测和控制,及时开放和及时报警。
copula模拟

求助:谁能帮我详细解读一下,理解了两阶段极大似然估计的方法,却看不懂这个?R> loglik.marg <- function(b, x) sum(dgamma(x, shape = b[1], scale = b[2],+ log = TRUE))R> ctrl <- list(fnscale = -1)R> b1hat <- optim(b1.0, fn = loglik.marg, x = dat[, 1], control = ctrl)$parR> b2hat <- optim(b2.0, fn = loglik.marg, x = dat[, 2], control = ctrl)$parR> udat <- cbind(pgamma(dat[, 1], shape = b1hat[1], scale = b1hat[2]),+ pgamma(dat[, 2], shape = b2hat[1], scale = b2hat[2]))R> fit.ifl <- fitCopula(udat, myMvd@copula, start = a.0)fitCopula {copula} R DocumentationEstimation of the Parameters in Copula ModelsDescriptionFits a copula model to multivariate data belonging to the unit hypercube. The data can be pseudo-observations constructed from empirical or parametric marginal distribution functions, or true observations from the copula.UsageloglikCopula(param, x, copula, hideWarnings)fitCopula(copula, data, method = c("mpl", "ml", "itau", "irho"),start = NULL, lower = NULL, upper = NULL,optim.method = "BFGS", optim.control = list(maxit=1000),estimate.variance = NA, hideWarnings = TRUE)Argumentsparam a vector of parameter values.x, data n x d-matrix of (pseudo-)observations (for "mpl" and "ml" with valuesnecessarily in [0,1]) from the copula to be estimated,where n denotes the sample size and d the dimension. Considerapplying the function pobs() first in order to obtain values in [0,1]. method a character string specifying the method; can be either "ml" (maximum likelihood), "mpl" (maximumpseudo-likelihood), "itau" (inversion of Kendall's tau),and "irho" (inversion of Spearman's rho). The last three methodsassume that the data are pseudo-observations (scaled ranks),while the first method assumes that the data are observationsfrom the unknown copula. The default is "mpl".start a vector of starting values for param.lower, upper bounds on the variables for the "Brent" or "L-BFGS-B" method. optim.control a list of control parameters to be passed to optim(*, control=optim.control).optim.method the method for optim().estimate.variance logical; if true (as by default, if the optimization converges), the asymptotic variance is estimated.loglikCopula() returns the log likelihood evaluated at the given value of "param". The return value of fitCopula() is an object of class "fitCopula" (see there), containing slots (among others!)estimate the estimate of the parameters.var.est large-sample (i.e., asymptotic) variance estimate of the parameter estimator (filled with NA if estimate.variance = FALSE).copula the fitted copula.The summary() method for "fitCopula" objects returns a S3 “class” "summary.fitCopula", simply a list with components method, loglik, and convergence, all three from corresponding slots of the "fitCopula" objects, and coefficients a matrix of estimated coefficients, standard errors, t values and p-values. NoteIn the multiparameter elliptical case and when the estimation is based on Kendall's tau or Spearman's rho, the estimated correlation matrix may not always be positive-definite. If it is not, the correction proposed by Rousseeuw and Molenberghs (1993) is applied and a warning message given.If method "mpl" in fitCopula() is used and if start is not assigned a value, estimates obtained from method "itau" are used as initial values in the optimization.If methods "itau" or "itau" are used in fitCopula(), an estimate of the asymptotic variance (if available for the copula under consideration) will be correctly computed only if the argument data consists of pseudo-observations (see pobs()).For the t copula with df.fixed=FALSE (see ellipCopula()), the methods "itau" and "irho" cannot be used in fitCopula(). For the methods "ml" and "mpl", when start is not specified, the starting value for df is set to copula@df, typically 4. Also, the asymptotic variance cannot (yet) be estimated for method "mpl".To implement the “inference functions for margins” method (see, e.g., Joe 2005), the data need to be pseudo-observations obtained from fitted parametric marginal distribution functions and method needs to be set to "ml". The returned large-sample variance will then underestimate the true variance.Finally, note that the fitting functions generate error messages because invalid parameter values are tried during the optimization process (see optim()). When the number of parameters is one and the parameter space is bounded, using optim.method="Brent" is likely to give less warnings. Furthermore, from experience,optim.method="Nelder-Mead" is sometimes a more robust alternative to optim.method="BFGS".ReferencesGenest, C. (1987). Frank's family of bivariate distributions. Biometrika 74, 549–555. Genest, C. and Rivest, L.-P. (1993). Statistical inference procedures for bivariateArchimedean copulas. Journal of the American Statistical Association 88, 1034–1043. Rousseeuw, P. and Molenberghs, G. (1993). Transformation of nonpositive semidefinite correlation matrices. Communications in Statistics: Theory and Methods 22, 965–984.Genest, C., Ghoudi, K., and Rivest, L.-P. (1995). A semiparametric estimation procedure of dependence parameters in multivariate families of distributions. Biometrika82, 543–552.Joe, H. (2005). Asymptotic efficiency of the two-stage estimation method for copula-based models. Journal of Multivariate Analysis 94, 401–419.Demarta, S. and McNeil, A. J. (2005). The t copula and related copulas. International Statistical Review 73, 111–129.Genest, C. and Favre, A.-C. (2007). Everything you always wanted to know about copula modeling but were afraid to ask. Journal of Hydrologic Engineering 12, 347–368.Kojadinovic, I. and Yan, J. (2010). Comparison of three semiparametric methods for estimating dependence parameters in copula models. Insurance: Mathematics and Economics 47, 52–63.See AlsoCopula, mvdc for fitting multivariate distributions including the margins aka “meta copula”s;gofCopula.For maximum likelihood of (nested) archimedean copulas: emle, etc.Examplesgumbel.cop <- gumbelCopula(3, dim=2)(Xtras <- copula:::doExtras())n <- if(Xtras) 200 else 64set.seed(7) # for reproducibilityx <- rCopula(n, gumbel.cop)## "true" observationsu <- pobs(x) ## pseudo-observations## inverting Kendall's taufit.tau <- fitCopula(gumbel.cop, u, method="itau")fit.taucoef(fit.tau)# named vector## inverting Spearman's rhofit.rho <- fitCopula(gumbel.cop, u, method="irho")fit.rho## maximum pseudo-likelihoodfit.mpl <- fitCopula(gumbel.cop, u, method="mpl")fit.mpl## maximum likelihoodfit.ml <- fitCopula(gumbel.cop, x, method="ml")fit.ml # print()ing works via summary() ...## and of that, what's the log likelihood (in two different ways):(ll. <- logLik(fit.ml))stopifnot(all.equal(as.numeric(ll.),loglikCopula(coef(fit.ml), x=x, copula=gumbel.cop)))## a multiparameter exampleset.seed(6)normal.cop <- normalCopula(c(0.6,0.36, 0.6),dim=3,dispstr="un") x <- rCopula(n, normal.cop) ## "true" observationsu <- pobs(x) ## pseudo-observations## inverting Kendall's taufit.tau <- fitCopula(normal.cop, u, method="itau")fit.tau## inverting Spearman's rhofit.rho <- fitCopula(normal.cop, u, method="irho")fit.rho## maximum pseudo-likelihoodfit.mpl <- fitCopula(normal.cop, u, method="mpl")fit.mplcoef(fit.mpl) # named vectorstr(sf.mpl <- summary(fit.mpl))coef(sf.mpl)# the matrix, with SE, t-value, ...## maximum likelihoodfit.ml <- fitCopula(normal.cop, x, method="ml")fit.ml## with dispstr="toep"normal.cop.toep <- normalCopula(c(0, 0), dim=3, dispstr="toep") ## inverting Kendall's taufit.tau <- fitCopula(normal.cop.toep, u, method="itau")fit.tau## inverting Spearman's rhofit.rho <- fitCopula(normal.cop.toep, u, method="irho")fit.rho## maximum pseudo-likelihoodfit.mpl <- fitCopula(normal.cop.toep, u, method="mpl")fit.mpl## maximum likelihoodfit.ml <- fitCopula(normal.cop.toep, x, method="ml")fit.ml## with dispstr="ar1"normal.cop.ar1 <- normalCopula(c(0), dim=3, dispstr="ar1")## inverting Kendall's taufit.tau <- fitCopula(normal.cop.ar1, u, method="itau")fit.tau## inverting Spearman's rhofit.rho <- fitCopula(normal.cop.ar1, u, method="irho")fit.rho## maximum pseudo-likelihoodfit.mpl <- fitCopula(normal.cop.ar1, u, method="mpl")fit.mpl## maximum likelihoodfit.ml <- fitCopula(normal.cop.ar1, x, method="ml")fit.ml## a t copula with variable df (df.fixed=FALSE):(tCop <- tCopula(c(0.2,0.4,0.6), dim=3, dispstr="un", df=5))set.seed(101)x <- rCopula(n, tCop) ## "true" observationsu <- pobs(x) ## pseudo-observations## maximum likelihood; start := (rho[1:3], df)(tc.ml <- fitCopula(tCop, x, method="ml", start=c(0,0,0, 10)))(tc.ml. <- fitCopula(tCop, x, method="ml")) # without 'start'## maximum pseudo-likelihood; the asymptotic variance cannot be estimated (tc.mpl <- fitCopula(tCop, u, method="mpl", estimate.variance=FALSE,start= c(0,0,0,10)))if(Xtras) { ##---- typically not run with CRAN checking: ---## without start:(tc.mp. <- fitCopula(tCop, u, method="mpl", estimate.variance=FALSE))all.eqCop <- function(x,y, ...) {x@fitting.stats$counts <- y@fitting.stats$counts <- NULLall.equal(x,y, ...) }stopifnot(all.eqCop(tc.ml , tc.ml., tolerance= .005),all.eqCop(tc.mpl, tc.mp., tolerance= .005))## same t copula but with df.fixed=TRUE (--> use same data!)(tC.f <- tCopula(c(0.2,0.4,0.6), dim=3, dispstr="un", df=5, df.fixed=TRUE))## maximum likelihood; start := rho[1:3] -------------(tcF.ml <- fitCopula(tC.f, x, method="ml", start=c(0,0,0)))(tcF.ml. <- fitCopula(tC.f, x, method="ml"))# without 'start'stopifnot(all.eqCop(tcF.ml,tcF.ml., tolerance= 4e-4))## the (estimated, asymptotic) var-cov matrix:vcov(tcF.ml)## maximum pseudo-likelihood; the asymptotic variance cannot be estimated (tcF.mpl <- fitCopula(tC.f, u, method="mpl", estimate.variance=FALSE,start=c(0,0,0)))(tcF.mp. <- fitCopula(tC.f, u, method="mpl", estimate.variance=FALSE)) stopifnot(all.eqCop(tcF.mpl,tcF.mp., tolerance= 1e-5))}## end{typically not run ...}。
通信工程专业Code-division-multiple-access码分多址大学毕业论文外文文献翻译及原文

毕业设计(论文)外文文献翻译文献、资料中文题目:码分多址文献、资料英文题目:Code division multiple access文献、资料来源:文献、资料发表(出版)日期:院(部):专业:班级:姓名:学号:指导教师:翻译日期:2017.02.14外文原文Code division multiple accessCode division multiple access (CDMA) is a channel access method used by various radio communication technologies. It should not be confused with the mobile phone standards called cdmaOne, CDMA2000 (the 3G evolution of cdmaOne) and WCDMA (the 3G standard used by GSM carriers), which are often referred to as simply CDMA, and use CDMA as an underlying channel access method.One of the concepts in data communication is the idea of allowing several transmitters to send information simultaneously over a single communication channel. This allows several users to share a band of frequencies (see bandwidth). This concept is called multiple access. CDMA employs spread-spectrum technology and a special coding scheme (where each transmitter is assigned a code) to allow multiple users to be multiplexed over the same physical channel. By contrast, time division multiple access (TDMA) divides access by time, while frequency-division multiple access (FDMA) divides it by frequency. CDMA is a form of spread-spectrum signalling, since the modulated coded signal has a much higher data bandwidth than the data being communicated.Steps in CDMA ModulationEach user in a CDMA system uses a different code to modulate their signal. Choosing the codes used to modulate the signal is very important in the performance of CDMA systems. The best performance will occur when there is good separation between the signal of a desired user and the signals of other users. The separation of the signals is made by correlating the received signal with the locally generated code of the desired user. If the signal matches the desired user's code then the correlation function will be high and the system can extract that signal. If the desired user's code has nothing in common with the signal the correlation should be as close to zero aspossible (thus eliminating the signal); this is referred to as cross correlation. If the code is correlated with the signal at any time offset other than zero, the correlation should be as close to zero as possible. This is referred to as auto-correlation and is used to reject multi-path interference.In general, CDMA belongs to two basic categories: synchronous (orthogonal codes) and asynchronous (pseudorandom codes).Code division multiplexing (Synchronous CDMA)Synchronous CDMA exploits mathematical properties of orthogonality between vectors representing the data strings. For example, binary string 1011 is represented by the vector (1, 0, 1, 1). Vectors can be multiplied by taking their dot product, by summing the products of their respective components (for example, if u = (a, b) and v = (c, d), then their dot product u·v = ac + bd). If the dot product is zero, the two vectors are said to be orthogonal to each other. Some properties of the dot product aid understanding of how W-CDMA works.Each user in synchronous CDMA uses a code orthogonal to the others' codes to modulate their signal. An example of four mutually orthogonal digital signals is shown in the figure. Orthogonal codes have a cross-correlation equal to zero; in other words, they do not interfere with each other. In the case of IS-95 64 bit Walsh codes are used to encode the signal to separate different users. Since each of the 64 Walsh codes are orthogonal to one another, the signals are channelized into 64 orthogonal signals. The following example demonstrates how each user's signal can be encoded and decoded.Asynchronous CDMAWhen mobile-to-base links cannot be precisely coordinated, particularly due to the mobility of the handsets, a different approach is required. Since it is not mathematically possible to create signature sequences that are both orthogonal forarbitrarily random starting points and which make full use of the code space, unique "pseudo-random" or "pseudo-noise" (PN) sequences are used in asynchronous CDMA systems. A PN code is a binary sequence that appears random but can be reproduced in a deterministic manner by intended receivers. These PN codes are used to encode and decode a user's signal in Asynchronous CDMA in the same manner as the orthogonal codes in synchronous CDMA (shown in the example above). These PN sequences are statistically uncorrelated, and the sum of a large number of PN sequences results in multiple access interference (MAI) that is approximated by a Gaussian noise process (following the central limit theorem in statistics). Gold codes are an example of a PN suitable for this purpose, as there is low correlation between the codes. If all of the users are received with the same power level, then the variance (e.g., the noise power) of the MAI increases in direct proportion to the number of users. In other words, unlike synchronous CDMA, the signals of other users will appear as noise to the signal of interest and interfere slightly with the desired signal in proportion to number of users.All forms of CDMA use spread spectrum process gain to allow receivers to partially discriminate against unwanted signals. Signals encoded with the specified PN sequence (code) are received, while signals with different codes (or the same code but a different timing offset) appear as wideband noise reduced by the process gain.Since each user generates MAI, controlling the signal strength is an important issue with CDMA transmitters. A CDM (synchronous CDMA), TDMA, or FDMA receiver can in theory completely reject arbitrarily strong signals using different codes, time slots or frequency channels due to the orthogonality of these systems. This is not true for Asynchronous CDMA; rejection of unwanted signals is only partial. If any or all of the unwanted signals are much stronger than the desired signal, they will overwhelm it. This leads to a general requirement in any asynchronous CDMA system to approximately match the various signal power levels as seen at the receiver.In CDMA cellular, the base station uses a fast closed-loop power control scheme to tightly control each mobile's transmit power.[edit] Efficient Practical utilization of Fixed Frequency SpectrumIn theory, CDMA, TDMA and FDMA have exactly the same spectral efficiency but practically, each has its own challenges – power control in the case of CDMA, timing in the case of TDMA, and frequency generation/filtering in the case of FDMA.TDMA systems must carefully synchronize the transmission times of all the users to ensure that they are received in the correct time slot and do not cause interference. Since this cannot be perfectly controlled in a mobile environment, each time slot must have a guard-time, which reduces the probability that users will interfere, but decreases the spectral efficiency. Similarly, FDMA systems must use a guard-band between adjacent channels, due to the unpredictable doppler shift of the signal spectrum because of user mobility. The guard-bands will reduce the probability that adjacent channels will interfere, but decrease the utilization of the spectrum.Flexible Allocation of ResourcesAsynchronous CDMA offers a key advantage in the flexible allocation of resources i.e. allocation of a PN codes to active users. In the case of CDM (synchronous CDMA), TDMA, and FDMA the number of simultaneous orthogonal codes, time slots and frequency slots respectively is fixed hence the capacity in terms of number of simultaneous users is limited. There are a fixed number of orthogonal codes, time slots or frequency bands that can be allocated for CDM, TDMA, and FDMA systems, which remain underutilized due to the bursty nature of telephony and packetized data transmissions. There is no strict limit to the number of users that can be supported in an asynchronous CDMA system, only a practical limit governed by the desired bit error probability, since the SIR (Signal to Interference Ratio) varies inversely with the number of users. In a bursty traffic environment like mobile telephony, the advantage afforded by asynchronous CDMA is that the performance(bit error rate) is allowed to fluctuate randomly, with an average value determined by the number of users times the percentage of utilization. Suppose there are 2N users that only talk half of the time, then 2N users can be accommodated with the same average bit error probability as N users that talk all of the time. The key difference here is that the bit error probability for N users talking all of the time is constant, whereas it is a random quantity (with the same mean) for 2N users talking half of the time.In other words, asynchronous CDMA is ideally suited to a mobile network where large numbers of transmitters each generate a relatively small amount of traffic at irregular intervals. CDM (synchronous CDMA), TDMA, and FDMA systems cannot recover the underutilized resources inherent to bursty traffic due to the fixed number of orthogonal codes, time slots or frequency channels that can be assigned to individual transmitters. For instance, if there are N time slots in a TDMA system and 2N users that talk half of the time, then half of the time there will be more than N users needing to use more than N time slots. Furthermore, it would require significant overhead to continually allocate and deallocate the orthogonal code, time slot or frequency channel resources. By comparison, asynchronous CDMA transmitters simply send when they have something to say, and go off the air when they don't, keeping the same PN signature sequence as long as they are connected to the system.Spread-spectrum characteristics of CDMAMost modulation schemes try to minimize the bandwidth of this signal since bandwidth is a limited resource. However, spread spectrum techniques use a transmission bandwidth that is several orders of magnitude greater than the minimum required signal bandwidth. One of the initial reasons for doing this was military applications including guidance and communication systems. These systems were designed using spread spectrum because of its security and resistance to jamming. Asynchronous CDMA has some level of privacy built in because the signal is spread using a pseudo-random code; this code makes the spread spectrum signals appearrandom or have noise-like properties. A receiver cannot demodulate this transmission without knowledge of the pseudo-random sequence used to encode the data. CDMA is also resistant to jamming. A jamming signal only has a finite amount of power available to jam the signal. The jammer can either spread its energy over the entire bandwidth of the signal or jam only part of the entire signal.CDMA can also effectively reject narrow band interference. Since narrow band interference affects only a small portion of the spread spectrum signal, it can easily be removed through notch filtering without much loss of information. Convolution encoding and interleaving can be used to assist in recovering this lost data. CDMA signals are also resistant to multipath fading. Since the spread spectrum signal occupies a large bandwidth only a small portion of this will undergo fading due to multipath at any given time. Like the narrow band interference this will result in only a small loss of data and can be overcome.Another reason CDMA is resistant to multipath interference is because the delayed versions of the transmitted pseudo-random codes will have poor correlation with the original pseudo-random code, and will thus appear as another user, which is ignored at the receiver. In other words, as long as the multipath channel induces at least one chip of delay, the multipath signals will arrive at the receiver such that they are shifted in time by at least one chip from the intended signal. The correlation properties of the pseudo-random codes are such that this slight delay causes the multipath to appear uncorrelated with the intended signal, and it is thus ignored.Some CDMA devices use a rake receiver, which exploits multipath delay components to improve the performance of the system. A rake receiver combines the information from several correlators, each one tuned to a different path delay, producing a stronger version of the signal than a simple receiver with a single correlation tuned to the path delay of the strongest signal.Frequency reuse is the ability to reuse the same radio channel frequency at other cell sites within a cellular system. In the FDMA and TDMA systems frequency planning is an important consideration. The frequencies used in different cells must be planned carefully to ensure signals from different cells do not interfere with each other. In a CDMA system, the same frequency can be used in every cell, because channelization is done using the pseudo-random codes. Reusing the same frequency in every cell eliminates the need for frequency planning in a CDMA system; however, planning of the different pseudo-random sequences must be done to ensure that the received signal from one cell does not correlate with the signal from a nearby cell.Since adjacent cells use the same frequencies, CDMA systems have the ability to perform soft hand offs. Soft hand offs allow the mobile telephone to communicate simultaneously with two or more cells. The best signal quality is selected until the hand off is complete. This is different from hard hand offs utilized in other cellular systems. In a hard hand off situation, as the mobile telephone approaches a hand off, signal strength may vary abruptly. In contrast, CDMA systems use the soft hand off, which is undetectable and provides a more reliable and higher quality signal.Collaborative CDMAIn a recent study, a novel collaborative multi-user transmission and detection scheme called Collaborative CDMA[12] has been investigated for the uplink that exploits the differences between users’ fading channel signatures to increase the user capacity well beyond the spreading length in multiple access interference (MAI) limited environment. The authors show that it is possible to achieve this increase at a low complexity and high bit error rate performance in flat fading channels, which is a major research challenge for overloaded CDMA systems. In this approach, instead of using one sequence per user as in conventional CDMA, the authors group a small number of users to share the same spreading sequence and enable group spreading and despreading operations. The new collaborative multi-user receiver consists of two stages: group multi-user detection (MUD) stage to suppress the MAI between thegroups and a low complexity maximum-likelihood detection stage to recover jointly the co-spread users’ data using minimum Euclidean distance measure and users’ channel gain coefficients. In CDM signal security is high.。
数字信号处理英语词汇

数字信号处理英语词汇AAbsolutely integrable 绝对可积Absolutely integrable impulse response 绝对可积冲激响应Absolutely summable 绝对可和Absolutely summable impulse response 绝对可和冲激响应Accumulator 累加器Acoustic 声学Adder 加法器Additivity property 可加性Aliasing 混叠现象All-pass systems 全通系统AM (Amplitude modulation ) 幅度调制Amplifier 放大器Amplitude modulation (AM)幅度调制Amplitude-scaling factor 幅度放大因子Analog-to-digital (A-to-D) converter 模数转换器Analysis equation 分析公式(方程) Angel (phase) of complex number 复数的角度(相位)Angle criterion 角判据Angle modulation 角度调制Anticausality 反因果Aperiodic 非周期Aperiodic convolution 非周期卷积Aperiodic signal 非周期信号Asynchronous 异步的Audio systems 音频(声音)系统Autocorrelation functions 自相关函数Automobile suspension system 汽车减震系统Averaging system 平滑系统BBand-limited 带(宽)限的Band-limited input signals 带限输入信号Band-limited interpolation 带限内插Bandpass filters 带通滤波器Bandpass signal 带通信号Bandpass-sampling techniques 带通采样技术Bandwidth 带宽Bartlett (triangular) window 巴特利特(三角形)窗Bilateral Laplace transform 双边拉普拉斯变换Bilinear 双线性的Bilinear transformation 双线性变换Bit (二进制)位,比特Block diagrams 方框图Bode plots 波特图Bounded 有界限的Break frequency 折转频率Butterworth filters 巴特沃斯滤波器C“Chirp” transform algorithm “鸟声”变换算法Capacitor 电容器 Carrier 载波Carrier frequency 载波频率Carrier signal 载波信号Cartesian (rectangular) form 直角坐标形式Cascade (series) interconnection 串联,级联Cascade-form 串联形式Causal LTI system 因果的线性时不变系统Channel 信道,频道Channel equalization 信道均衡Chopper amplifier 斩波器放大器Closed-loop 闭环Closed-loop poles 闭环极点Closed-loop system 闭环系统Closed-loop system function 闭环系统函数Coefficient multiplier 系数乘法器Coefficients 系数Communications systems 通信系统Commutative property 交换性(交换律)Compensation for nonideal elements 非理想元件的补偿Complex conjugate 复数共轭Complex exponential carrier 复指数载波Complex exponential signals 复指数信号Complex exponential(s) 复指数Complex numbers 复数Conditionally stable systems 条件稳定系统Conjugate symmetry 共轭对称Conjugation property 共轭性质Continuous-time delay 连续时间延迟Continuous-time filter 连续时间滤波器Continuous-time Fourier series 连续时间傅立叶级数Continuous-time Fourier transform 连续时间傅立叶变换Continuous-time signals 连续时间信号Continuous-time systems 连续时间系统Continuous-to-discrete-time conversion 连续时间到离散时间转换Convergence 收敛Convolution 卷积Convolution integral 卷积积分Convolution property 卷积性质Convolution sum 卷积和Correlation function 相关函数Critically damped systems 临界阻尼系统Crosss-correlation functions 互相关函数Cutoff frequencies 截至频率DDamped sinusoids 阻尼正弦振荡Damping ratio 阻尼系数Dc offset 直流偏移Dc sequence 直流序列Deadbeat feedback systems 临界阻尼反馈系统Decibels (dB) 分贝Decimation 抽取Decimation and interpolation 抽取和内插Degenerative (negative) feedback 负反馈Delay 延迟Delay time 延迟时间Demodulation 解调Difference equations 差分方程Differencing property 差分性质Differential equations 微分方程Differentiating filters 微分滤波器Differentiation property 微分性质Differentiator 微分器Digital-to-analog (D-to-A) converter 数模转换器Direct Form I realization 直接I 型实现Direct form II realization 直接II型实现Direct-form 直接型Dirichlet conditions 狄里赫利条件Dirichlet, P.L. 狄里赫利Discontinuities 间断点,不连续Discrete-time filters 离散时间滤波器Discrete-time Fourier series 离散时间傅立叶级数Discrete-time Fourier series pair 离散时间傅立叶级数对Discrete-time Fourier transform (DFT) 离散时间傅立叶变换Discrete-time LTI filters 离散时间线性时不变滤波器Discrete-time modulation 离散时间调制Discrete-time nonrecursivefilters 离散时间非递归滤波器Discrete-time signals 离散时间信号Discrete-time systems 离散时间系统Discrete-time to continuous-time conversion 离散时间到连续时间转换Dispersion 弥撒(现象)Distortion 扭曲,失真Distribution theory(property) 分配律Dominant time constant 主时间常数Double-sideband modulation (DSB) 双边带调制Downsampling 减采样Duality 对偶性EEcho 回波Eigenfunctions 特征函数Eigenvalue 特征值Elliptic filters 椭圆滤波器Encirclement property 围线性质End points 终点 Energy of signals 信号的能量Energy-density spectrum 能量密度谱Envelope detector 包络检波器Envelope function 包络函数Equalization 均衡化Equalizer circuits 均衡器电路Equation for closed-loop poles 闭环极点方程Euler, L. 欧拉Euler’s relation 欧拉关系(公式) Even signals 偶信号Exponential signals 指数信号Exponentials 指数FFast Fourier transform (FFT) 快速傅立叶变换Feedback 反馈Feedback interconnection 反馈联结Feedback path 反馈路径Filter(s) 滤波器Final-value theorem 终值定理Finite impulse response (FIR) 有限长脉冲响应Finite impulse response (FIR) filters 有限长脉冲响应滤波器Finite sum formula 有限项和公式Finite-duration signals 有限长信号First difference 一阶差分First harmonic components 基波分量 (一次谐波分量)First-order continuous-time systems 一阶连续时间系统First-order discrete-time systems 一阶离散时间系统First-order recursive discrete-time filters 一阶递归离散时间滤波器 First-order systems 一阶系统Forced response 受迫响应Forward path 正向通路Fourier series 傅立叶级数Fourier transform 傅立叶变换Fourier transform pairs 傅立叶变换对Fourier, Jean Baptiste Joseph 傅立叶(法国数学家,物理学家) Frequency response 频率响应Frequency response of LTI systems 线性时不变系统的频率响应Frequency scaling of continuous-time Fourier transform 连续时间傅立叶变化的频率尺度(变换性质) Frequency shift keying (FSK) 频移键控Frequency shifting property 频移性质Frequency-division multiplexing (FDM) 频分多路复用Frequency-domain characterization 频域特征Frequency-selective filter 频率选择滤波器Frequency-shaping filters 频率成型滤波器Fundamental components 基波分量Fundamental frequency 基波频率Fundamental period 基波周期GGain 增益Gain and phase margin 增益和相位裕度General complex exponentials 一般复指数信号Generalized functions 广义函数Gibbs phenomenon 吉伯斯现象Group delay 群延迟HHalf-sample delay 半采样间隔时延Hanning window 汉宁窗Harmonic analyzer 谐波分析议Harmonic components 谐波分量Harmonically related 谐波关系Heat propagation and diffusion 热传播和扩散现象Higher order holds 高阶保持Highpass filter 高通滤波器Highpass-to-lowpass transformations 高通到低通变换Hilbert transform 希尔波特滤波器Homogeneity (scaling) property 齐次性(比例性)IIdeal 理想的Ideal bandstop characteristic 理想带阻特征Ideal frequency-selective filter 理想频率选择滤波器Idealization 理想化Identity system 恒等系统Imaginary part 虚部Impulse response 冲激响应Impulse train 冲激串Incrementally linear systems 增量线性系统Independent variable 独立变量Infinite impulse response (IIR) 无限长脉冲响应Infinite impulse response (IIR) filters 无限长脉冲响应滤波器Infinite sum formula 无限项和公式Infinite taylor series 无限项泰勒级数Initial-value theorem 初值定理Inpulse-train sampling 冲激串采样Instantaneous 瞬时的Instantaneous frequency 瞬时频率Integration in time-domain 时域积分Integration property 积分性质Integrator 积分器Interconnection 互联Intermediate-frequency (IF) stage 中频级Intersymbol interference (ISI) 码间干扰Inverse Fourier transform 傅立叶反变换Inverse Laplace transform 拉普拉斯反变换Inverse LTI system 逆线性时不变系统Inverse system design 逆系统设计Inverse z-transform z反变换Inverted pendulum 倒立摆Invertibility of LTI systems 线性时不变系统的可逆性Invertible systems 逆系统LLag network 滞后网络Lagrange, J.L. 拉格朗日(法国数学家,力学家)Laplace transform 拉普拉斯变换Laplace, P.S. de 拉普拉斯(法国天文学家,数学家)lead network 超前网络left-half plane 左半平面left-sided signal 左边信号Linear 线性Linear constant-coefficient difference equations 线性常系数差分方程 Linear constant-coefficient differential equations 线性常系数微分方程Linear feedback systems 线性反馈系统Linear interpolation 线性插值Linearity 线性性Log magnitude-phase diagram 对数幅,相图Log-magnitude plots 对数模图Lossless coding 无损失码Lowpass filters 低通滤波器Lowpass-to-highpass transformation 低通到高通的转换LTI system response 线性时不变系统响应LTI systems analysis 线性时不变系统分析MMagnitude and phase 幅度和相位Matched filter 匹配滤波器Measuring devices 测量仪器Memory 记忆Memoryless systems 无记忆系统Modulating signal 调制信号Modulation 调制Modulation index 调制指数Modulation property 调制性质Moving-average filters 移动平均滤波器Multiplexing 多路技术Multiplication property 相乘性质Multiplicities 多样性NNarrowband 窄带Narrowband frequency modulation 窄带频率调制Natural frequency 自然响应频率Natural response 自然响应Negative (degenerative) feedback 负反馈Nonanticipatibe system 不超前系统Noncausal averaging system 非因果平滑系统Nonideal 非理想的 Nonidealfilters 非理想滤波器Nonmalized functions 归一化函数Nonrecursive 非递归Nonrecursive filters 非递归滤波器Nonrecursive linear constant-coefficient difference 非递归线性常系数差分方程 equations Nyquist frequency 奈奎斯特频率Nyquist rate 奈奎斯特率Nyquist stability criterion 奈奎斯特稳定性判据OOdd harmonic 奇次谐波Odd signal 奇信号Open-loop 开环Open-loop frequency response 开环频率响应Open-loop system 开环系统Operational amplifier 运算放大器Orthogonal functions 正交函数Orthogonal signals 正交信号Oscilloscope 示波器Overdamped system 过阻尼系统Oversampling 过采样 Overshoot 超量PParallel interconnection 并联Parallel-form block diagrams 并联型框图Parity check 奇偶校验检查Parseval’s rela tion 帕斯伐尔关系(定理)Partial-fraction expansion 部分分式展开Particular and homogeneous solution 特解和齐次解Passband 通频带Passband edge 通带边缘Passband frequency 通带频率Passband ripple 通带起伏(或波纹) Pendulum 钟摆Percent modulation 调制百分数Periodic 周期的Periodic complex exponentials 周期复指数Periodic convolution 周期卷积Periodic signals 周期信号Periodic square wave 周期方波Periodic square-wave modulating signal 周期方波调制信号Periodic train of impulses 周期冲激串Phase (angle) of complex number 复数相位(角度)Phase lag 相位滞后Phase lead 相位超前Phase margin 相位裕度Phase shift 相移Phase-reversal 相位倒置Phase modulation 相位调制Plant 工厂 Polar form 极坐标形式Poles 极点Pole-zero plot(s) 零极点图Polynomials 多项式Positive (regenerative) feedback 正(再生)反馈Power of signals 信号功率Power-series expansion method 幂级数展开的方法Principal-phase function 主值相位函数Proportional (P) control 比例控制Proportional feedback system 比例反馈系统Proportional-plus-derivative 比例加积分Proportional-plus-derivative feedback 比例加积分反馈Proportional-plus-integral-plus-differential (PID) control 比例,积分,微分控制Pulse-amplitude modulation 脉冲幅度调制Pulse-code modulation 脉冲编码调制Pulse-train carrier 冲激串载波QQuadrature distortion 正交失真Quadrature multiplexing 正交多路复用Quality of circuit 电路品质(因数) RRaised consine frequency response 升余弦频率响应Rational frequency responses 有理型频率响应Rational transform 有理变换RC highpass filter RC 高阶滤波器RC lowpass filter RC 低阶滤波器Real 实数Real exponential signals 实指数信号Real part 实部Rectangular (Cartesian) form 直角(卡笛儿)坐标形式Rectangular pulse 矩形脉冲Rectangular pulse signal 矩形脉冲信号Rectangular window 矩形窗口Recursive (infinite impulse response) filters 递归(无时限脉冲响应)滤波器 Recursive linear constant-coefficient difference equations 递归的线性常系数差分方程Regenerative (positive) feedback 再生(正)反馈Region of comvergence 收敛域right-sided signal 右边信号Rise time 上升时间Root-locus analysis 根轨迹分析(方法) Running sum 动求和SS domain S域Sampled-data feedback systems 采样数据反馈系统Sampled-data systems 采样数据系统Sampling 采样Sampling frequency 采样频率Sampling function 采样函数Sampling oscilloscope 采样示波器Sampling period 采样周期Sampling theorem 采样定理Scaling (homogeneity) property 比例性(齐次性)性质Scaling in z domain z域尺度变换Scrambler 扰频器Second harmonic components 二次谐波分量Second-order 二阶Second-order continuous-time system 二阶连续时间系统Second-order discrete-time system 二阶离散时间系统Second-order systems 二阶系统sequence 序列Series (cascade) interconnection 级联(串联)Sifting property 筛选性质Sinc functions sinc函数Single-sideband 单边带Single-sideband sinusoidal amplitude modulation 单边带正弦幅度调制 Singularity functions 奇异函数Sinusoidal 正弦(信号)Sinusoidal amplitude modulation 正弦幅度调制Sinusoidal carrier 正弦载波Sinusoidal frequency modulation 正弦频率调制Sliding 滑动 Spectral coefficient 频谱系数Spectrum 频谱Speech scrambler 语音加密器S-plane S平面Square wave 方波Stability 稳定性Stabilization of unstable systems 不稳定系统的稳定性(度)Step response 阶跃响应Step-invariant transformation 阶跃响应不定的变换Stopband 阻带 Stopband edge 阻带边缘Stopband frequency 阻带频率Stopband ripple 阻带起伏(或波纹) Stroboscopic effect 频闪响应Summer 加法器Superposition integral 叠加积分Superposition property 叠加性质Superposition sum 叠加和Suspension system 减震系统Symmetric periodic 周期对称Symmetry 对称性Synchronous 同步的Synthesis equation 综合方程System function(s) 系统方程TTable of properties 性质列表Taylor series 泰勒级数Time 时间,时域Time advance property of unilateral z-transform 单边z变换的时间超前性质 Time constants 时间常数Time delay property of unilateral z-transform 单边z变换的时间延迟性质 Time expansion property 时间扩展性质Time invariance 时间变量Time reversal property 时间反转(反褶)性Time scaling property 时间尺度变换性Time shifting property 时移性质Time window 时间窗口Time-division multiplexing (TDM) 时分复用Time-domain 时域Time-domain properties 时域性质Tracking system (s) 跟踪系统Transfer function 转移函数transform pairs 变换对Transformation 变换(变形) Transition band 过渡带Transmodulation (transmultiplexing) 交叉调制Triangular (Barlett) window 三角型(巴特利特)窗口Trigonometric series 三角级数Two-sided signal 双边信号Type l feedback system l 型反馈系统UUint impulse response 单位冲激响应Uint ramp function 单位斜坡函数Undamped natural frequency 无阻尼自然相应Undamped system 无阻尼系统Underdamped systems 欠阻尼系统Undersampling 欠采样Unilateral 单边的Unilateral Laplace transform 单边拉普拉斯变换Unilateral z-transform 单边z变换Unit circle 单位圆Unit delay 单位延迟Unit doublets 单位冲激偶Unit impulse 单位冲激Unit step functions 单位阶跃函数Unit step response 单位阶跃响应Unstable systems 不稳定系统Unwrapped phase 展开的相位特性Upsampling 增采样V Variable 变量WWalsh functions 沃尔什函数Wave 波形 Wavelengths 波长Weighted average 加权平均Wideband 宽带Wideband frequency modulation 宽带频率调制Windowing 加窗zZ domain z域Zero force equalizer 置零均衡器Zero-Input response 零输入响应Zero-Order hold 零阶保持Zeros of Laplace transform 拉普拉斯变换的零点Zero-state response 零状态响应z-transform z变换z-transform pairs z变换对。
尼康 NIS-Elements 显微镜软件 digital cameras说明书

MicroscopesSoftwareDigital CamerasNikon offers total software solution covering image capture, archiving, and analysisWhy NIS-Elements?NIS-Elements is an integrated software imaging platform developed by Nikon to achieve comprehensive microscope control, image capture,documentation, data management and analysis.NIS-Elements handles multidimensional imaging tasks flawlessly with support for capture, display, peripheral device control, and datamanagement & analysis of images of up to six dimensions. The system also contributes to experiment efficiency with a database building feature developed to handle archiving, searching, and analysis of large numbers of multidimensional image files.Unified control of the entire imaging system offers significant benefits to users for cutting-edge research, such as live cell imaging.The most sophisticated of the three packages, NIS-Elements AR is optimized for advanced research applications. It features fully automated acquisition and device control through full 6D (X, Y, Z, Lambda (Wavelength), Time,Multipoint) image acquisition and analysis.NIS-Elements BR is suited for standard research applications,such as analysis and photodocumentation of fluorescent imaging. It features acquisition and device control through 4D (up to four dimensions can be selected from X, Y, Z,Lambda (Wavelength), Time, Multipoint) acquisition.NIS-Elements D supports color documentation requirements in bioresearch, clinical and industrial applications, with basic measuring and reporting capabilities.•Highest Quality Optical PerformanceThe world-renowned Nikon CFI60 infinity optical system effectively set a new standard for optical quality by providing longer working distances, higher numerical apertures, and the widest magnification range and documentation field sizes.As a leader in digital imaging technology, Nikon recognized the importance of adapting its optics to optimize the digital image. Nikon’s new objectives and accessories are specifically engineered for digital imaging, with exclusive features, such as the Hi S/N System, which eliminates stray light and provides unprecedented signal-to-noise ratios.Because what you see depends greatly on the quality of your microscope, we strive to power our microscope systems with optical technologies that are nothing but state-of-the-art.•Diverse Line of Powerful Digital CamerasImage capture has become a high priority in microscopy and the demand for products that deliver high quality and versatile functionality has grown considerably in recent years. In accordance, Nikon offers a full line of digital cameras, addressing the varied needs of microscopists in multiple disciplines. Each Nikon digital camera is designed to work seamlessly with Nikon microscopes, peripherals, and software. With Nikon Digital Sight (DS) series cameras, even novice users can take beautiful and accurate microscopic images. For the advanced researcher, hi-resolution image capture and versatile camera control is fast and simple. Together with Nikon’s new software solutions, image processing and analysis have reached new levels of ease-of-use and sophistication.•Intelligent Software SolutionsDesigned to serve the needs of advanced bioresearch, clinical, industrial and documentation professionals, NIS-Elements provides a totally integrated solution for users of Nikon and other manufacturers’ accessories by delivering automated intelligence to microscopes, cameras, and peripheral components. The software optimizes the imaging process and workflow and provides the critical element of information management for system based microscopy.AnnotationsBinary ColorThe NIS-Elements suite is available in three packages scaled to address specific application requirements.Total Imaging SolutionIn designing and bringing to market the mosttechnologically advanced optical systems, Nikon has worked very hard to provide a “total imagingsolution” that meets the ever-evolving demands of the microscope user.As a leading microscope manufacturer, Nikon realizes the importance of providing its customers with system-based solutions to free the user to focus on the work and not the complexities of the microscope. NIS-Elements was designed with this in mind. Never before has a software package achieved such comprehensive control of microscope image capturing and document data management.Optical ConfigurationMicroscope parameters, such as fluorescence filter and shutter combinations, can be saved and displayed as icons in the tool bar,allowing one-click setup. Setting up a CCD camera, applying shading compensation to each objective lens, and saving calibration data is also possible.Multichannel ImageImages using defined filters can be captured to view in various light wavelengths. Simply define the color of channels and the opticalconfiguration that is to be used for capturing the set of images.Z-seriesImages at different Z-axis planes can be captured with a motorized Z-Focus control. NIS-Elements supports two methods of Z-axis capture: Absolute Positioning and Relative Positioning.View SynchronizerThe View Synchronizer allows for the comparison of two or more multidimensional image documents. It automatically synchronizes the views of all documents added.Confocal Image ImportImages acquired with Nikon confocal microscopes C1si and C1plus can be imported.ProcessVarious image views can be selected to study captured data.Time LapseThe sophisticated but user-friendly time-lapse process enables the staggering of image capture simply by defining interval, duration, and frequency of capture.Large Image StitchingThis tool allows composition of large-area images with high magnification. Ultra high-resolution images can be stitched automatically from multiple frames through use of a motorized stage. NIS-Elements uses special algorithms to assure maximal accuracy during stitching. The user can also capture and stitch frames by moving the microscope stage manually.Multipoint ExperimentsWith the motorized stage installed, it is possible to automatically capture images at different XY and Z locations.ViewnD Viewer (Multidimensional image display)Easy-to-use parameters for multidimensional image operation are located on the frame of the screen.T: Time LapseXY: MultipointZ: Z-series (slices)Wavelength: MultichannelVolume renderingMultidimensional image 0 sec.15 sec.30 sec.Image acquisition screenOrthogonal imageRealizing a smooth flow fromimage capture to process and measurementImage AcquisitionDiverse Dimensional Acquisition12312341234Report GeneratorReport Generator enables the user to create customized reports containing images, database descriptions, measured data, user texts, and graphics. PDF files can be created directly from NIS-Elements.Time MeasurementTime Measurement records the average pixel intensities within defined probes during a time interval and can be performed on live or captured data sets. Time measurement also allows for real-time ratios between two channels.Interactive MeasurementNIS-Elements offers all necessary measurement parameters, such as taxonomy, counts, length, semiaxes, area and angle profile.Measurements can be made by drawing the objects directly on the image. All output results can be exported to any spreadsheet editor.Automatic MeasurementNIS-Elements enables automatic measurement by creating a binary image. It can automatically measure length, area, density and colorimetry parameters sets, etc. About 90different object and field features can be measured automatically.ProfileFive possible interactive line profile measurements provide consecutive intensity of a sourced image along an arbitrary path (free line, two-point line, horizontal line, vertical line and polyline).ClassifierClassifier allows segmentation of the image pixels according todifferent user-defined classes, and is based on different pixel features such as intensity values, RGB values, HSI values, or RGB valuesignoring intensity. The classifier enables data to be saved in separatefiles.RAM CapturingRAM Capturing enables the recording of very quick sequences to capture the most rapid biological events by streaming datadirectly to the computer’s video memory.MeasurementImage ProcessingColor Adjustmentcontrast/background subtraction/component mixNIS-Elements is suitable for hue adjustment, independently for each color, and converts the color image to an RGB or HSI component.Filterssmoothing/sharpness/edge detectionNIS-Elements contains intelligent masking filters for image smoothing,sharpness, edge detection, etc. These filters not only filter noise, but also are effective in retaining the image’s sharpness and detail.MorphologyNIS-Elements offers a rich spectrum of mathematical morphology filters for object classification. Morphology filters can be used to segment binary and grayscale images for measurement analysis purposes. Various morphometric parameters mean image processing is easier than ever.•Basic morphology (erosion, dilatation, open, close)•Homotopic transformations (clean, fill holes, contour, smooth)•Skeleton functions (medial axis, skeletonize, pruning) •Morphologic separation and othersMerge ChannelsMultiple single channel images (captured with different optical filters or under different camera settings) can be merged together simply by dragging from one image to another. In addition, the combined images can be stored to a file while maintaining their original bit depths or, optionally, can be converted into an RGB image.Image ArithmeticA+B/A-B/Max/MinNIS-Elements performs arithmetic operations on color images.OriginalBefore using the edge detection filter After using the edge detection filterContourThresholdZones of Influence + SourceThe real-time 2D deconvolution module (from AutoQuant ®) allows the user to observe live specimens with less out-of-focus blur. It allows faint biological processes to be observed that mayotherwise be missed and increases observed signal-to-noise ratio.NIS-Elements can combine X, Y, Z, Lambda (wavelength), Time and Multi-Stage points within one integrated platform formultidimensional imaging. All combinations of multidimensional images can be combined together in one ND2 file sequence using an efficient workflow and intuitive GUI. The user can easily choose the proper parameters for each dimension and the software and hardware will work seamlessly together to provide high quality results. Results may be exported into other supported image and video file formats.The haze and blur of the image that can occur when capturing a thick specimen or a fluorescence image can be eliminated from thecaptured 3D image. Images acquired with Nikon confocal microscopes C1si and C1plus can be imported to NIS-Elements.2D Real-time DeconvolutionMultidimensional Acquisition (4D/6D)3D DeconvolutionNIS-Elements has a powerful image database module that supports image and meta data. Various databases & tables can easily be created and images can be saved to the database via one simple mouse-click. Filtering, sorting and multiple grouping are also available according to the database field given for each image.DatabaseVirtual 3D imageFocused image created from a sequence of Z-stack imagesStereovision image T, XY, Z, λsimultaneous acquisitionConvert sequential images to ND2 fileND documentation exportationMultidimensional image croppingAVI generationBefore deconvolutionAfter deconvolutionVarious convenient plug-ins for advanced imaging and analysis capabilitiesEDF: Extended Depth of FocusExtended Depth of Focus (EDF) is an additional software plug-in for NIS-Elements. Thanks to the EDF function, images that have been captured in a different Z-axis can be combined to create an all-in-focus image. Also, it is possible to create stereovision image & 3D surface image for a virtual 3D image.System Configuration Examples123123123EnFeaturesNIS-Elements AR NIS-Elements BR NIS-Elements DCapture RAM Capture ●Time Lapse ●●●Z-stack●●●Multichannel Fluorescence ●●Multi-position ●●●4D ●6D●Display and process GUI Multi-Window Multi-Window S ingle-WindowAnnotation ●●●Reference ●●●ND Viewer ●●●Filter, Morphology●●Capture, display and multifunction Large Image ●●●EDF●●●3D Deconvolution ●2D RT Deconvolution ●Live Compare ●●●Macro Macro●●●Advanced Interpreter ●●●Measurement Segmentation ●●Time Measurement ●●Auto Measurement ●●●(Available from version 2.3)Report Report Generator ●●●Management Database ●●●Vector Layer●●●Multidimensional File Format●●●Printed in Japan (0605-10.5)T Code No. 2CE-MRPH-2This brochure is printed on recycled paper made from 40% used material.Specifications and equipment are subject to change without any notice or obligation on the part of the manufacturer. May 2006©2006 NIKON CORPORATION* Monitor images are simulated.Company names and product names appearing in this brochure are their registered trademarks or trademarks.NIS-Elements Supported DevicesNikon Devices & CamerasMicroscopes and Accessories Eclipse TE2000-ETE2000-PFS (Perfect Focus System) Eclipse 90iDIH-M/E Digital Imaging Head Eclipse LV100AMotorized Universal Epi-illuminator & Motorized Nosepiece Nikon Motorized Z-Focus Accessory (RFA): optional CamerasDigital Sight 5M/2M Series DS-1QM DQC-FSDXM1200 SeriesOther Cameras & DevicesCamerasRoper cameras: CoolSnap Series, Cascade Series PixelLink camerasHamamatsu ORCA series camerasOptionalPrior (Stage): ProScan, OptiScan Prior Filter wheelsUniblitz (Shutter/Filter wheel) : Uniblitz Shutter Through TE2000-E Hub Sutter Lambda 10-2, 10-3, DG4/5 Z-Focus module: Nikon RFA, Prior Piezo PI E-665Camera Emission Splitter: Optical Insights Dual View and Quad View EXFO (Fiber Illuminator): EXFO X-Cite 120 seriesOperating EnvironmentMinimum PC Requirements: CPU Pentium IV 3.2 GHz or higher RAM 1GB or higher OS Windows XP Professional SP2 English Version Hard Disk 600MB or more required for installation Video 1280X1024 dots, True Color mode●yes ●optionalNIKON INSTRUMENTS (SHANGHAI) CO., LTD.CHINA phone: +86-21-5836-0050 fax: +86-21-5836-0030(Beijing office)phone: +86-10-5869-2255 fax: +86-10-5869-2277(Guangzhou office)phone: +86-20-3882-0552 fax: +86-20-3882-0580NIKON SINGAPORE PTE LTDSINGAPORE phone: +65-6559-3618 fax: +65-6559-3668NIKON MALAYSIA SDN. BHD.MALAYSIA phone: +60-3-78763887 fax: +60-3-78763387NIKON INSTRUMENTS KOREA CO., LTD.KOREA phone: +82-2-2186-8400 fax: +82-2-555-4415NIKON INSTRUMENTS EUROPE B.V.P.O. Box 222, 1170 AE Badhoevedorp, The Netherlands phone: +31-20-44-96-222 fax: +31-20-44-96-298/NIKON FRANCE S.A.S.FRANCE phone: +33-1-45-16-45-16 fax: +33-1-45-16-00-33NIKON GMBHGERMANY phone: +49-211-9414-0 fax: +49-211-9414-322NIKON INSTRUMENTS S.p.A.ITALY phone: + 39-55-3009601 fax: + 39-55-300993NIKON AGSWITZERLAND phone: +41-43-277-2860 fax: +41-43-277-2861NIKON UK LTD.UNITED KINGDOM phone: +44-20-8541-4440 fax: +44-20-8541-4584NIKON INSTRUMENTS INC.1300 Walt Whitman Road, Melville, N.Y. 11747-3064, U.S.A.phone: +1-631-547-8500; +1-800-52-NIKON (within the U.S.A.only) fax: +1-631-547-0306/NIKON CANADA INC.CANADA phone: +1-905-625-9910 fax: +1-905-625-0103NIKON CORPORATIONParale Mitsui Bldg.,8, Higashida-cho, Kawasaki-ku,Kawasaki, Kanagawa 210-0005, Japanphone: +81-44-223-2167 fax: +81-44-223-2182 http://www.nikon-instruments.jp/eng/NIS-Elements is compatible with all common file formats, such as JP2, JPG, TIFF, BMP, GIF, PNG, ND2, JFF, JTF, AVI, ICS/IDS. ND2 is a special format for NIS-Elements.ND2 allows storing sequences of images acquired during nD experiments. It contains information about the hardware settings and the experiment conditions and settings.。
新世纪大学英语综合教程4课后答案(unit1-unit8)

9) a multilateral trade negotiation 10) multiform technological cooperation
2) If it were not for the expense involved, we would go there by plane.
3) If we were to miss the train, we would have to wait another four hours.
4) If we pooled all our resources, we would have enough money to buy the equipment.
However, oddly enough, many people do not feel happier than they used to be. It can be seen that there is no close correlation between people’s income and their happiness. Happiness cannot, after all, be bought with money.
2) The latest survey shows / showed that the majority of the citizens support / supported the government’s plan to build a new library.
3) The two countries could reach agreement successfully on scientific and technological cooperation because several factors favorable to their cooperation had been at work.
数字信号专业英语翻译

电子与通信专业英语Digital Signal Processing (英文翻译)姓名:赵豪班级:信工 122学号:2012020217Digital Signal Processing1、IntroductionDigital signal processing (DSP) is concerned with the representation of th e signals by a sequence of numbers or symbols and the processing of these s ignals. Digital signal processing and analog signal processing are subfields of signal processing. DSP includes subfields like audio and speech signal proce ssing, sonar and radar signal processing, sensor array processing, spectral es timation, statistical signal processing, digital image processing, signal process ing for communications, biomedical signal processing, seismic data processin g, etc.Since the goal of DSP is usually to measure or filter continuous real-world analog signals, the first step is usually to convert the signal from an analog to a digital form, by using an analog to digital converter. Often, the required outp ut signal is another analog output signal, which requires a digital to analog co nverter. Even if this process is more complex than analog processing and has a discrete value range, the stability of digital signal processing thanks to error detection and correction and being less vulnerable to noise makes it advanta geous over analog signal processing for many, though not all, applications.DSP algorithms have long been run on standard computers, on specializ ed processors called digital signal processors (DSP)s, or on purpose-built har dware such as application-specific integrated circuit (ASICs). Today there areadditional technologies used for digital signal processing including more powe rful general purpose microprocessors, field-programmable gate arrays (FPGA s), digital signal controllers (mostly for industrial applications such as motor co ntrol), and stream processors, among others.In DSP, engineers usually study digital signals in one of the following do mains: time domain (one-dimensional signals), spatial domain (multidimensio nal signals), frequency domain, autocorrelation domain, and wavelet domains. They choose the domain in which to process a signal by making an informed guess (or by trying different possibilities) as to which domain best represents t he essential characteristics of the signal. A sequence of samples from a meas uring device produces a time or spatial domain representation, whereas a disc rete Fourier transform produces the frequency domain information that is the f requency spectrum. Autocorrelation is defined as the cross-correlation of the s ignal with itself over varying intervals of time or space.2、Signal SamplingWith the increasing use of computers the usage of and need for digital si gnal processing has increased. In order to use an analog signal on a compute r it must be digitized with an analog to digital converter (ADC). Sampling is us ually carried out in two stages, discretization and quantization. In the discretiz ation stage, the space of signals is partitioned into equivalence classes and q uantization is carried out by replace the signal with representative signal value s are approximated by values from a finite set.The Nyquist-Shannon sampling theorem states that a signal can be exact ly reconstructed from its samples if the samples if the sampling frequency is g reater than twice the highest frequency of the signal. In practice, the sampling frequency is often significantly more than twice the required bandwidth.A digital to analog converter (DAC) is used to convert the digital signal ba ck to analog signal.The use of a digital computer is a key ingredient in digital control systems .3、Time and Space DomainsThe most common processing approach in the time or space domain is e nhancement of the input signal through a method called filtering. Filtering gen erally consists of some transformation of a number of surrounding samples ar ound the current sample of the input or output signal. There are various ways to characterize filters, for example: A“linear” filter is a linear transformation of i nput samples; other filters are “non-linear.” Linear filters satisfy the superpositi on condition, i.e. if an input is a weighted linear combination of different signal s, the output is an equally weighted linear combination of the corresponding o utput signals.A “causal” filter uses only previous samples of the input or output signals; while a “non-causal” filter uses future input samples. A non-causal filter can u sually be changed into a causal filter by adding a delay to it.A“time-invariant” filter has constant properties over time; other filters suchas adaptive filters change in time.Some filters are “stable”, others are “unstable”. A stable filter produces an output that converges to a constant value with time, or remains bounded withi n a finite interval. An converges to a constant value with time, or remains bou nded within a finite interval. An unstable filter can produce an output that grow s without bounds, with bounded or even zero input.A“Finite Impulse Response” (FIR) filter uses only the input signal, while a n “Infinite Impulse Response” filter (IIR) uses both the input signal and previou s samples of the output signal. FIR filters are always stable, while IIR filters m ay be unstable.Most filters can be described in Z-domain (a superset of the frequency do main) by their transfer functions. A filter may also be described as a difference equation, a collection of zeroes and poles or, if it is an FIR filter, an impulse r esponse or step response. The output of an FIR filter to any given input may b e calculated by convolving the input signal with the impulse response. Filters c an also be represented by block diagrams which can then be used to derive a sample processing algorithm to implement the filter using hardware instruction s.4、Frequency DomainSignals are converted from time or space domain to the frequency domai n usually through the Fourier transform. The Fourier transform converts the si gnal information to a magnitude and phase component of each frequency. Often the Fourier transform is converted to the power spectrum, which is the mag nitude of each frequency component squared.The most common purpose for analysis of signals in the frequency domai n is analysis of signal properties. The engineer can study the spectrum to dete rmine which frequencies are present in the input signal and which are missing .Filtering, particularly in non real-time work can also be achieved by conve rting to the frequency domain, applying the filter and then converting back to t he time domain. This is a fast, O (nlogn) operation, and can give essentially a ny filter shape including excellent approximations to brickwall filters.There are some commonly used frequency domain transformations. For example, the cepstrum converts a signal to the frequency domain Fourier tran sform, takes the logarithm, then applies another Fourier transform. This emph asizes the frequency components with smaller magnitude while retaining the o rder of magnitudes of frequency components.Frequency domain analysis is al so called spectrum or spectral analysis.5、signal processing,Signal usually need in different ways.For example, from a sensor output signal may be contaminated the redundant electrical "noise".Electrode is connected to a patient's chest, electrocardiogram (ecg) is measured by the heart and other muscles activity caused by small voltage variation.Due to the strong effect electrical interference from the power supply, signal picked up the"main" is usually adopted.Processing signal filter circuit can eliminate or at least reduce unwanted part of the signal.Now, more and more, is by the DSP technology to extract the signal filter to improve the quality of signal or important information, rather than the analog electronic technology.6、the development of DSPThe development of digital signal processing (DSP) in the 1960 s to large Numbers of digital computing applications using fast Fourier transform (FFT), which allows the frequency spectrum of a signal can be quicklycalculated.These techniques have not been widely used at the time, because suitable computing equipment is usually only in university and other research institutions can be used.7、the digital signal processor (DSP)In the late 1970 s and early 1980 s the introduction of microprocessor makes DSP technology is used in the wider range.General microprocessor, such as Intel x86 family, however, is not suitable for the calculation of DSP intensive demand, with the increase of DSP importance in the 1980 s led to several major electronics manufacturers (such as Texas instruments, analog devices and MOTOROLA) to develop a digital signal processor chip, microprocessor, specifically designed for use in the operation of the digital signal processing requirements type of architecture.(note that abbreviation DSP digital signal processing (DSP) of different meanings, this word is used in digital signal processing, a variety of technical or digital signal processor, aspecial type of microprocessor chips).As a common microprocessors, DSP is one kind has its own local instruction code of programmable devices.DSP chip is able to millions of floating point operations per second, as they are of the same type more famous universal device, faster and more powerful versions are introduced.DSP can also be embedded in a complex "system chip" devices, usually includes analog and digital circuit.8、the application of digital signal processorsDSP technology is widespread in mobile phones, multimedia computers, video recorders, CD players, hard disk drives and controller of the modem equipment, and will soon replace analog circuits in TV and telephone service.DSP is an important application of signal compression and decompression.Signal compression is used for digital cellular phone, in every place of the "unit" let more phone is processed at the same time.DSP signal compression technology not only makes people can talk to each other, and can be installed on the computer by using the small camera make people through the monitor to see each other, and these together is the only needs to be a traditional phone line.In audio CD system, DSP technology to perform complex error detection and correction of raw data, because it is read from CD.Although some of the underlying mathematical theory of DSP technology, such as Fourier transform and Hilbert transform, the design of digital filter and signal compression, can be quite complex, and the actual implementation of these technologies needed for numerical computation is very simple, mainlyincluding operations can be in a cheap four function calculator.A kind of structure design of the DSP chip to operate very fast, deal with the sample of the hundreds of millions of every second, and provide real-time performance: that is, to a real-time signal processing, because it is sample, and then the output signal processing, such as speakers or video display.All of the DSP applications mentioned above instance, such as hard disk drives and mobile phone, for real-time operation.Major electronics manufacturers have invested heavily in DSP technology.Because they now find application in mass-market products, DSP chip electronic device occupies very large proportion in the world market.Sales of billions of dollars a year, and may continue to grow rapidly.DSP is mainly used of audio signal processing, audio compression, digital image processing, video compression, speech processing, speech recognition, digital communication, radar, sonar, earthquake, and biologicalmedicine.Concrete example is in digital mobile telephone voice compression and transmission, space balanced stereo matching, amplification area, good weather forecasts, economic forecasts, seismic data processing, and analysis of industrial process control, computer generated animation film, medical image such as CAT scans and magnetic resonance imaging (MRI),MP3compression, image processing, hi-fi speaker divider and equilibrium, and compared with electric guitar amplifier using audio effect.9、the experiment of digital signal processingDigital signal processing is often use special microprocessor, such as dsp56000 TMS320, or SHARC.These often processing data using the fixed point operation, although some versions can use floating-point arithmetic and more powerful.Faster application of FPGA can flow from a slow start the emergence of application processor Freescale company, traditional slower processors, such as single chip may be appropriate.数字信号处理1、介绍数字信号处理(DSP)的关心表示信号序列的数字或符号和处理这些信号。
交换相关泛函 英语

Exchange-Related Functionals in QuantumMechanicsIn the realm of quantum mechanics, exchange-related functionals play a pivotal role in understanding the interactions and properties of particles. These functionals describe the behavior of particles when they are interchanged or swapped within a given system. The exchange effect is particularly significant in areas such as electron exchange in chemistry, spin exchange in condensed matter physics, and particle exchange in quantum field theory.In the context of chemistry, the exchange-related functionals are often associated with the Pauli exclusion principle, which states that no two electrons can occupy the same quantum state simultaneously. This principle gives rise to the electron exchange interaction, which is responsible for the stability of multi-electron systems and the formation of chemical bonds. The exchange-correlation energy, which is a component of the total energy of a system, accounts for the interactions between electronsthat arise due to their mutual exclusion.In condensed matter physics, spin exchange functionals describe the interactions between magnetic moments or spins of particles. These interactions are crucial in determining the magnetic properties of materials, such as ferromagnetism, antiferromagnetism, and spin glasses. The exchange interaction is also responsible for the emergence of quantum spin liquids, which exhibit exotic magnetic behaviors due to strong spin correlations.In quantum field theory, particle exchange functionals are key in understanding the dynamics of particles andtheir interactions. These functionals describe the probabilities of particles being created, annihilated, or exchanged between different states. They play a fundamental role in quantum field theories such as the Standard Model, which describes the fundamental forces and particles in nature.The study of exchange-related functionals requires advanced mathematical techniques and computational methods. These functionals are often expressed as integrals over space and time, involving complex wavefunctions and operators. The development of accurate and efficientmethods for evaluating these functionals is crucial for making predictions and understanding the behavior of quantum systems.In conclusion, exchange-related functionals are essential in quantum mechanics, providing insights into the interactions and properties of particles. They underlie various phenomena in chemistry, physics, and quantum field theory, and their study requires advanced mathematical and computational techniques. The continuous development of methods for evaluating these functionals holds the promise of deeper understanding and new discoveries in the quantum realm.**交换相关泛函在量子力学中的应用**在量子力学领域,交换相关泛函对于理解粒子间的相互作用和性质起着至关重要的作用。
地震属性的含义
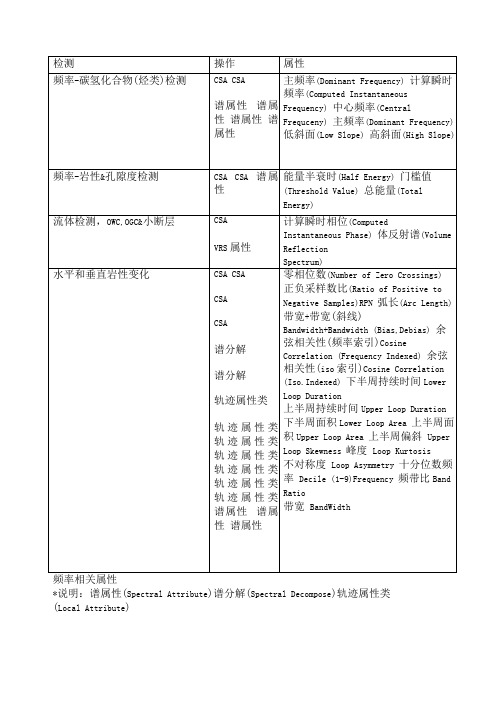
频率相关属性*说明:谱属性(Spectral Attribute)谱分解(Spectral Decompose)轨迹属性类(Local Attribute)振幅相关属性* 说明:层间属性(Interval Attribute )瞬时频率(Inst Frequency):定义为瞬时相位对时间的导数,用Hz表示。
经常用来估计地震振幅的衰减,往往油气的存在引起高频成分的衰减,可用这一属性检测油气。
瞬时相位(Inst Phase):表示在所选样点上各道的相位值,以度或弧度表示。
主要用于增强油藏内弱同相轴,对噪音也有放大作用,最终成图的彩色色标应考虑到结果的周期性,即:由于油气的存在经常引起相位的局部变化,所以这一属性常和其它属性一起用作油气检测的指标之一,也可用于测定薄层的相位特征,其横向变化与流体含量变化及薄层组合有关。
0 +180180 II °Powe反射强度(Reflection Magnitudes):反映了岩性差异、地层连续、地层空间、孔隙度的变化。
反(负)二阶微商变换(Negative of Second Derivative):显著地提升了连续性, 有助于更快、更准确的层位解释。
道积分(Integrated Seismic Trace):能起到伪波阻抗剖面的作用.并不是说用它替代反演,它可以起到快速指示孔隙度变化的作用.谱分解技术(Spectral Decomposition) ------- 分频:用于揭示薄层岩性横向的变化,指示可能的含烃地层圈闭。
最后分频属性和井砂岩厚度结合作出目标层段的砂岩厚度图。
由于不同频率段所看到的东西是有区别的,所以分频还可以观察到河道的形状更清晰,河道内的岩性细节变化。
砂岩厚度图流程图:Find the Power Spectrum usingSYNTHETICSRun Spectral Decomposition SATKExtract Tuning FrequencySATKNet Thickness DeterminationCorrelate using LPM等频体(Iso Frequency):结果是一个某一特定频率的相关数据体。
5_共振荧光

2
假设场在稳态下是统计稳定的,即场的关联函数不 依赖初始时间,而仅仅依赖于时间差τ。
场的双时关联函数可由单时关联函数通过量子回归 定理求得。
2020/8/11
36
量子回归定理描述系统算符和库之间相互作用的运动。 假定所考虑的系统是马尔科夫系统,则该定理可描述为:
如果 M 是系统一系列完备的马尔科夫算符 M 的线性组 合,那么算符 M 随时间的演化可以写为:
确解可求得:
t ei t a1 a2 t eit
a3 t eit a4 z t 1 / 2
z t 1 / 2 b1 b2 t eit b3 t eit b4 z t 1 / 2
2020/8/11
31
其中,
2020/8/11
10
(3)若 g(2)(τ)>1,则意味着先在t时刻测量光子, 延迟一小段时刻τ再测量时,测到光子数的几率更大 了。这说明这种光的光子有着成群结队出现的趋势, 称为聚束效应。
(4)若 g(2)(τ)<1 则相反,即先在t时刻测量光子数, 再在(t+τ)时刻测量时,测到光子数的几率更小了, 即这种光的光子互相排斥,这种现象称为反聚束效应。
2020/8/11
14
因Q的不同,将光子分布区分为泊松分布、 超泊松分布及亚泊松分布:
0, Q 0,
0,
超泊松分布 泊松分布 亚泊松分布
2020/8/11
15
有时也利用Fano因子
n2 n2 n 2
Fn n
n
1, Fn 1,
1,
超泊松分布 泊松分布
亚泊松分布
容易看出 Q Fn 1
2020/8/11
26
二能级原子的共振荧光光谱
数字信号处理英语词汇

AAbsolutely integrable绝对可积Absolutely integrable impulse response绝对可积冲激响应Absolutely summable绝对可和Absolutely summable impulse response绝对可和冲激响应Accumulator累加器Acoustic 声学Adder加法器Additivity property可加性Aliasing混叠现象All-pass systems全通系统AM (Amplitude modulation )幅度调制Amplifier放大器Amplitude modulation (AM)幅度调制Amplitude-scaling factor幅度放大因子Analog-to-digital (A-to-D) converter模数转换器Analysis equation分析公式(方程)Angel (phase) of complex number复数的角度(相位)Angle criterion角判据Angle modulation角度调制Anticausality反因果Aperiodic非周期Aperiodic convolution非周期卷积Aperiodic signal非周期信号Asynchronous异步的Audio systems音频(声音)系统Autocorrelation functions自相关函数Automobile suspension system汽车减震系统Averaging system平滑系统BBand-limited带(宽)限的Band-limited input signals带限输入信号Band-limited interpolation带限内插Bandpass filters带通滤波器Bandpass signal带通信号Bandpass-sampling techniques带通采样技术Bandwidth带宽Bartlett (triangular) window巴特利特(三角形)窗Bilateral Laplace transform双边拉普拉斯变换Bilinear双线性的Bilinear transformation双线性变换Bit(二进制)位,比特Block diagrams方框图Bode plots波特图Bounded有界限的Break frequency折转频率Butterworth filters巴特沃斯滤波器C“Chirp” transform algorithm“鸟声”变换算法Capacitor电容器Carrier载波Carrier frequency载波频率Carrier signal载波信号Cartesian (rectangular) form 直角坐标形式Cascade (series) interconnection串联,级联Cascade-form串联形式Causal LTI system因果的线性时不变系统Channel信道,频道Channel equalization信道均衡Chopper amplifier斩波器放大器Closed-loop闭环Closed-loop poles闭环极点Closed-loop system闭环系统Closed-loop system function闭环系统函数Coefficient multiplier系数乘法器Coefficients系数Communications systems通信系统Commutative property交换性(交换律)Compensation for nonideal elements非理想元件的补偿Complex conjugate复数共轭Complex exponential carrier复指数载波Complex exponential signals复指数信号Complex exponential(s)复指数Complex numbers 复数Conditionally stable systems条件稳定系统Conjugate symmetry共轭对称Conjugation property共轭性质Continuous-time delay连续时间延迟Continuous-time filter连续时间滤波器Continuous-time Fourier series连续时间傅立叶级数Continuous-time Fourier transform连续时间傅立叶变换Continuous-time signals连续时间信号Continuous-time systems连续时间系统Continuous-to-discrete-time conversion连续时间到离散时间转换Convergence 收敛Convolution卷积Convolution integral卷积积分Convolution property卷积性质Convolution sum卷积和Correlation function相关函数Critically damped systems临界阻尼系统Crosss-correlation functions互相关函数Cutoff frequencies截至频率DDamped sinusoids阻尼正弦振荡Damping ratio阻尼系数Dc offset直流偏移Dc sequence直流序列Deadbeat feedback systems临界阻尼反馈系统Decibels (dB) 分贝Decimation抽取Decimation and interpolation抽取和内插Degenerative (negative) feedback负反馈Delay延迟Delay time延迟时间Demodulation解调Difference equations差分方程Differencing property差分性质Differential equations微分方程Differentiating filters微分滤波器Differentiation property微分性质Differentiator微分器Digital-to-analog (D-to-A) converter数模转换器Direct Form I realization直接I型实现Direct form II realization直接II型实现Direct-form直接型Dirichlet conditions狄里赫利条件Dirichlet, P.L.狄里赫利Discontinuities间断点,不连续Discrete-time filters 离散时间滤波器Discrete-time Fourier series离散时间傅立叶级数Discrete-time Fourier series pair离散时间傅立叶级数对Discrete-time Fourier transform (DFT)离散时间傅立叶变换Discrete-time LTI filters离散时间线性时不变滤波器Discrete-time modulation离散时间调制Discrete-time nonrecursive filters离散时间非递归滤波器Discrete-time signals离散时间信号Discrete-time systems离散时间系统Discrete-time to continuous-time conversion离散时间到连续时间转换Dispersion弥撒(现象)Distortion扭曲,失真Distribution theory(property)分配律Dominant time constant主时间常数Double-sideband modulation (DSB)双边带调制Downsampling减采样Duality对偶性EEcho回波Eigenfunctions特征函数Eigenvalue特征值Elliptic filters椭圆滤波器Encirclement property围线性质End points终点Energy of signals信号的能量Energy-density spectrum能量密度谱Envelope detector包络检波器Envelope function包络函数Equalization均衡化Equalizer circuits均衡器电路Equation for closed-loop poles闭环极点方程Euler, L.欧拉Euler’s relation欧拉关系(公式)Even signals偶信号Exponential signals指数信号Exponentials指数FFast Fourier transform (FFT)快速傅立叶变换Feedback反馈Feedback interconnection反馈联结Feedback path反馈路径Filter(s)滤波器Final-value theorem终值定理Finite impulse response (FIR)有限长脉冲响应Finite impulse response (FIR) filters有限长脉冲响应滤波器Finite sum formula有限项和公式Finite-duration signals有限长信号First difference一阶差分First harmonic components基波分量(一次谐波分量)First-order continuous-time systems一阶连续时间系统First-order discrete-time systems一阶离散时间系统First-order recursive discrete-time filters一阶递归离散时间滤波器First-order systems一阶系统Forced response受迫响应Forward path正向通路Fourier series傅立叶级数Fourier transform傅立叶变换Fourier transform pairs傅立叶变换对Fourier, Jean Baptiste Joseph傅立叶(法国数学家,物理学家)Frequency response频率响应Frequency response of LTI systems线性时不变系统的频率响应Frequency scaling of continuous-time Fourier transform 连续时间傅立叶变化的频率尺度(变换性质)Frequency shift keying (FSK)频移键控Frequency shifting property频移性质Frequency-division multiplexing (FDM)频分多路复用Frequency-domain characterization频域特征Frequency-selective filter频率选择滤波器Frequency-shaping filters频率成型滤波器Fundamental components基波分量Fundamental frequency基波频率Fundamental period基波周期GGain增益Gain and phase margin增益和相位裕度General complex exponentials一般复指数信号Generalized functions广义函数Gibbs phenomenon吉伯斯现象Group delay群延迟HHalf-sample delay半采样间隔时延Hanning window汉宁窗Harmonic analyzer谐波分析议Harmonic components谐波分量Harmonically related谐波关系Heat propagation and diffusion热传播和扩散现象Higher order holds高阶保持Highpass filter高通滤波器Highpass-to-lowpass transformations高通到低通变换Hilbert transform希尔波特滤波器Homogeneity (scaling) property齐次性(比例性)IIdeal理想的Ideal bandstop characteristic理想带阻特征Ideal frequency-selective filter理想频率选择滤波器Idealization理想化Identity system恒等系统Imaginary part虚部Impulse response 冲激响应Impulse train冲激串Incrementally linear systems增量线性系统Independent variable独立变量Infinite impulse response (IIR)无限长脉冲响应Infinite impulse response (IIR) filters无限长脉冲响应滤波器Infinite sum formula无限项和公式Infinite taylor series无限项泰勒级数Initial-value theorem初值定理Inpulse-train sampling冲激串采样Instantaneous瞬时的Instantaneous frequency瞬时频率Integration in time-domain时域积分Integration property积分性质Integrator积分器Interconnection互联Intermediate-frequency (IF) stage中频级Intersymbol interference (ISI)码间干扰Inverse Fourier transform傅立叶反变换Inverse Laplace transform拉普拉斯反变换Inverse LTI system逆线性时不变系统Inverse system design逆系统设计Inverse z-transform z反变换Inverted pendulum倒立摆Invertibility of LTI systems线性时不变系统的可逆性Invertible systems逆系统LLag network滞后网络Lagrange, J.L.拉格朗日(法国数学家,力学家)Laplace transform拉普拉斯变换Laplace, P.S. de拉普拉斯(法国天文学家,数学家)lead network超前网络left-half plane左半平面left-sided signal左边信号Linear线性Linear constant-coefficient difference线性常系数差分方程equationsLinear constant-coefficient differential线性常系数微分方程equationsLinear feedback systems线性反馈系统Linear interpolation线性插值Linearity线性性Log magnitude-phase diagram对数幅-相图Log-magnitude plots对数模图Lossless coding无损失码Lowpass filters低通滤波器Lowpass-to-highpass transformation低通到高通的转换LTI system response线性时不变系统响应LTI systems analysis线性时不变系统分析MMagnitude and phase幅度和相位Matched filter匹配滤波器Measuring devices测量仪器Memory记忆Memoryless systems无记忆系统Modulating signal调制信号Modulation调制Modulation index调制指数Modulation property调制性质Moving-average filters移动平均滤波器Multiplexing多路技术Multiplication property相乘性质Multiplicities多样性NNarrowband窄带Narrowband frequency modulation窄带频率调制Natural frequency自然响应频率Natural response自然响应Negative (degenerative) feedback负反馈Nonanticipatibe system不超前系统Noncausal averaging system非因果平滑系统Nonideal非理想的Nonideal filters非理想滤波器Nonmalized functions归一化函数Nonrecursive非递归Nonrecursive filters非递归滤波器Nonrecursive linear constant-coefficient非递归线性常系数差分方程difference equationsNyquist frequency奈奎斯特频率Nyquist rate奈奎斯特率Nyquist stability criterion奈奎斯特稳定性判据OOdd harmonic 奇次谐波Odd signal奇信号Open-loop开环Open-loop frequency response开环频率响应Open-loop system开环系统Operational amplifier运算放大器Orthogonal functions正交函数Orthogonal signals正交信号Oscilloscope示波器Overdamped system过阻尼系统Oversampling过采样Overshoot超量PParallel interconnection并联Parallel-form block diagrams并联型框图Parity check奇偶校验检查Parseval’s relation帕斯伐尔关系(定理)Partial-fraction expansion部分分式展开Particular and homogeneous solution特解和齐次解Passband通频带Passband edge通带边缘Passband frequency通带频率Passband ripple通带起伏(或波纹)Pendulum钟摆Percent modulation调制百分数Periodic周期的Periodic complex exponentials周期复指数Periodic convolution周期卷积Periodic signals周期信号Periodic square wave周期方波Periodic square-wave modulating signal周期方波调制信号Periodic train of impulses周期冲激串Phase (angle) of complex number复数相位(角度)Phase lag相位滞后Phase lead相位超前Phase margin相位裕度Phase shift相移Phase-reversal相位倒置Phase modulation相位调制Plant工厂Polar form极坐标形式Poles极点Pole-zero plot(s)零极点图Polynomials 多项式Positive (regenerative) feedback正(再生)反馈Power of signals信号功率Power-series expansion method幂级数展开的方法Principal-phase function主值相位函数Proportional (P) control比例控制Proportional feedback system比例反馈系统Proportional-plus-derivative比例加积分Proportional-plus-derivative feedback比例加积分反馈Proportional-plus-integral-plus-different比例-积分-微分控制ial (PID) controlPulse-amplitude modulation脉冲幅度调制Pulse-code modulation脉冲编码调制Pulse-train carrier冲激串载波QQuadrature distortion正交失真Quadrature multiplexing正交多路复用Quality of circuit电路品质(因数)RRaised consine frequency response升余弦频率响应Rational frequency responses有理型频率响应Rational transform有理变换RC highpass filter RC 高阶滤波器RC lowpass filter RC 低阶滤波器Real实数Real exponential signals实指数信号Real part实部Rectangular (Cartesian) form 直角(卡笛儿)坐标形式Rectangular pulse矩形脉冲Rectangular pulse signal矩形脉冲信号Rectangular window矩形窗口Recursive (infinite impulse response)递归(无时限脉冲响应)滤波器filtersRecursive linear constant-coefficient 递归的线性常系数差分方程difference equationsRegenerative (positive) feedback再生(正)反馈Region of comvergence收敛域right-sided signal右边信号Rise time上升时间Root-locus analysis根轨迹分析(方法)Running sum动求和SS domain S域Sampled-data feedback systems采样数据反馈系统Sampled-data systems采样数据系统Sampling采样Sampling frequency采样频率Sampling function采样函数Sampling oscilloscope采样示波器Sampling period采样周期Sampling theorem采样定理Scaling (homogeneity) property比例性(齐次性)性质Scaling in z domain z域尺度变换Scrambler扰频器Second harmonic components二次谐波分量Second-order二阶Second-order continuous-time system二阶连续时间系统Second-order discrete-time system二阶离散时间系统Second-order systems二阶系统sequence序列Series (cascade) interconnection级联(串联)Sifting property筛选性质Sinc functions sinc函数Single-sideband单边带Single-sideband sinusoidal amplitude单边带正弦幅度调制modulationSingularity functions奇异函数Sinusoidal正弦(信号)Sinusoidal amplitude modulation正弦幅度调制Sinusoidal carrier正弦载波Sinusoidal frequency modulation正弦频率调制Sliding滑动Spectral coefficient频谱系数Spectrum频谱Speech scrambler语音加密器S-plane S平面Square wave方波Stability稳定性Stabilization of unstable systems不稳定系统的稳定性(度)Step response阶跃响应Step-invariant transformation阶跃响应不定的变换Stopband阻带Stopband edge阻带边缘Stopband frequency阻带频率Stopband ripple 阻带起伏(或波纹)Stroboscopic effect频闪响应Summer加法器Superposition integral叠加积分Superposition property叠加性质Superposition sum叠加和Suspension system减震系统Symmetric periodic 周期对称Symmetry对称性Synchronous同步的Synthesis equation综合方程System function(s)系统方程TTable of properties 性质列表Taylor series泰勒级数Time时间,时域Time advance property of unilateral单边z变换的时间超前性质z-transformTime constants时间常数Time delay property of unilateral单边z变换的时间延迟性质z-transformTime expansion property时间扩展性质Time invariance时间变量Time reversal property时间反转(反褶)性Time scaling property时间尺度变换性Time shifting property时移性质Time window时间窗口Time-division multiplexing (TDM)时分复用Time-domain时域Time-domain properties时域性质Tracking system (s)跟踪系统Transfer function转移函数transform pairs变换对Transformation变换(变形)Transition band过渡带Transmodulation (transmultiplexing) 交叉调制Triangular (Barlett) window三角型(巴特利特)窗口Trigonometric series三角级数Two-sided signal双边信号Type l feedback system l 型反馈系统UUint impulse response单位冲激响应Uint ramp function单位斜坡函数Undamped natural frequency无阻尼自然相应Undamped system无阻尼系统Underdamped systems欠阻尼系统Undersampling欠采样Unilateral单边的Unilateral Laplace transform单边拉普拉斯变换Unilateral z-transform单边z变换Unit circle单位圆Unit delay单位延迟Unit doublets单位冲激偶Unit impulse单位冲激Unit step functions单位阶跃函数Unit step response 单位阶跃响应Unstable systems不稳定系统Unwrapped phase展开的相位特性Upsampling增采样VVariable变量WWalsh functions沃尔什函数Wave波形Wavelengths波长Weighted average加权平均Wideband宽带Wideband frequency modulation宽带频率调制Windowing加窗zZ domain z域Zero force equalizer置零均衡器Zero-Input response零输入响应Zero-Order hold零阶保持Zeros of Laplace transform拉普拉斯变换的零点Zero-state response零状态响应z-transform z变换z-transform pairs z变换对。
面向密闭空间内外温度的时序预测模型

装备环境工程第20卷第11期·166·EQUIPMENT ENVIRONMENTAL ENGINEERING2023年11月面向密闭空间内外温度的时序预测模型周俊炎1,王竟成1,舒畅1,黄伦1,张志豪1,张凯2(1.西南技术工程研究所,重庆 400039;2.甘肃敦煌大气环境材料腐蚀国家野外科学观测研究站,甘肃 敦煌 736202)摘要:目的研究密闭空间条件下已知外部温度时间序列对内部实时温度的预测推理问题。
方法选取密闭空间内外温度时序预测典型场景,抽象为多变量时间序列预测问题,分析变量间的关联性和依赖性。
借鉴特征融合、注意力机制、多任务模型等思路,结合物理机制与数据特征,基于长短期记忆网络基本网络单元,构建密闭空间内外温度时序预测模型,并在万宁、敦煌、漠河对某型密闭空间进行数据采样,基于三地数据集进行不同模型试验。
结果多变量模型比单变量模型具有更好性能,注意力机制对该场景没有显著性能提升,结合物理机制的模型结构设计充分考虑了变量之间的关联性和依赖性,能显著提升预测精度,双输入双输出的多变量时序预测模型具有相对最高的精度和最稳定的鲁棒性,是面向密闭空间内外温度时序预测的相对最优模型。
结论研究结论可指导密闭空间其他环境特征建模,研究思路可为其他多变量时序建模问题中变量之间的关联性、依赖性分析提供参考。
关键词:密闭空间;内外温度;时序预测;物理机制;多变量时间序列;长短期记忆网络中图分类号:TP391 文献标识码:A 文章编号:1672-9242(2023)11-0166-11DOI:10.7643/ issn.1672-9242.2023.11.021Time Series Prediction Model for Internal and ExternalTemperature of Confined SpaceZHOU Jun-yan1, WANG Jing-cheng1, SHU Chang1, HUANG Lun1, ZHANG Zhi-hao1, ZHANG Kai2(1. Southwest Institute of Technology and Engineering, Chongqing 400039, China; 2. Dunhuang Atmospheric MaterialCorrosion Field National Observation and Research Station, Gansu Dunhuang 736202, China)ABSTRACT: Research on the prediction and inference problem of known external temperature time series for internal real-time temperature under confined space conditions. Typical scenarios of internal and external temperature time series prediction in confined spacewere selected, which was abstracted as a multi-variable time series prediction problem, and the correlation and dependence analysis among variables were the key difficulties. By referring to the ideas of feature fusion, attention mechanism and multi-task model, combined with the physical mechanism and data characteristics, and based on the basic network unit of long and short term memory network, the internal and external temperature time series prediction model of confined space was constructed. The data of a certain type of confined space was collected in Wanning, Dunhuang and Mohe, and different model experiments were carried out based on the data sets of the three places. The multi-variable model had better performance than the univariable model, and the attention mechanism did not significantly improve the performance of this scenario. The model structure design combined with the physical mechanism fully considered the correlation and dependence between variables,收稿日期:2023-02-15;修订日期:2023-05-10Received:2023-02-15;Revised:2023-05-10引文格式:周俊炎, 王竟成, 舒畅, 等. 面向密闭空间内外温度的时序预测模型[J]. 装备环境工程, 2023, 20(11): 166-176.ZHOU Jun-yan, WANG Jing-cheng, SHU Chang, et al. Time Series Prediction Model for Internal and External Temperature of Confined Space[J]. Equipment Environmental Engineering, 2023, 20(11): 166-176.第20卷第11期周俊炎,等:面向密闭空间内外温度的时序预测模型·167·which could significantly improve the prediction accuracy. The multi-variable time series prediction model with double input and double output had the highest accuracy and the most stable robustness. It was a relatively optimal model for the prediction of internal and external temperature time series in confined space. The research conclusions can guide the modeling of other en-vironmental characteristics in confined space, and the research ideas can provide references for the correlation and dependency analysis among variables in other multi-variable sequential modeling problems.KEY WORDS: confined space; internal and external temperature; time series prediction; physical mechanism; multi-variable time series; long and short term memory network工业、军事领域中存在大量密闭空间,密闭空间是指与外界相对隔离,进出口受限,自然通风不良,密封式或半密封式的空间。
Stock_Price_Forecasting_Based_on_the_MDT-CNN-CBAM-

Theory and Practice of Science and Technology2022, VOL. 3, NO. 6, 81-90DOI: 10.47297/taposatWSP2633-456914.20220306Stock Price Forecasting Based on the MDT-CNN-CBAM-GRU Model: An Empirical StudyYangwenyuan DengBusiness School, University of New South Wales, Sydney 1466, AustraliaABSTRACTRecently, more researchers have utilized artificial neural network topredict stock price which has the characteristic of time series. This paperproposes the MDT-CNN-CBAM-GRU to forecast the close price of theshares. Meanwhile, three models are set as comparing experiment. CSI300 index and MA 5 are added as new price factors. The daily historicaldata of China Ping An from 1994 to 2020 is utilized to train, validate andtest models. The results of the experiment prove MDT-CNN-CBAM-GRU isthe optimal and GRU has better performance than LSTM. Thus, MDT-CNN-CBAM-GRU can effectively predict the closing price of one stock whichcould be a reference for investing decision.KEYWORDSStock price; Deep learning; Gated Recurrent Unit (GRU); Multi-directionalDelayed Embedding (MDT); Convolutional Block Attention Module(CBAM)1 IntroductionWith the development of Chinese stock market, investors realize the great significance in stock price prediction [1]. Due to the volatility and complexity of stock market, shares prediction contains multi-dimensional variables and massive time-series data [2]. Traditional methods have several shortages such as inefficiency, subjectivity, and poor integrity of inventory content information. To resolve these shortages, artificial intelligence have been introduced to this area. Machine learning such as deep learning, decision trees and logistic regression have emerged in financial data research [3-5].Deep learning is a new branch of machine learning which transfer the low-level feature to high-level feature to simplify learning task [6]. The CNN-LSTM model is a classic model of the deep learning. It has been widely used in different area due to its better performance and prediction accuracy compared with single models [7-8]. Zhao and Xue prove the CBAM module could improve the performance of CNN-LSTM [9]. Cao et al. innovatively applied the multi-directional delayed embedding (MDT) to transform price factor which contributes to the generalization and time-sensitization of forecasting results [10].Based on the CNN-LSTM model, this paper proposes MDT-CNN-CBAM-GRU model. In this experiment, Jupyter notebook is the program platform, and Keras of TensorFlow is used as the neural framework to build model. The experimental data includes the share price factors of ChinaYangwenyuan Deng 82Ping An 1. This experiment will verify the effectiveness of CBAM module and MDT module. Meanwhile, the performance of GRU is compared with LSTM include the time efficiency and prediction errors. Three evaluation indexes are used to present the prediction results.2 Related WorkRecently, machine learning has become a hot spot in financial areas [11]. Artificial neural network (ANN) has been proved as a feasible tool to forecast complex nonlinear statistics while the time efficiency of neural networks is low [12]. In addition, gradient vanishing and local optimal solution affect the further development of ANN model. Based on ANN, recurrent neural network (RNN) was proposed which would memorize short part information of previous stage [13]. In 2014, gated recurrent unit (GRU) is proposed by Cho et al. as a variant of LSTM [14-15]. LSTM and GRU could address the gradient vanishing issue of RNN.Lecun et al. propose the Convolutional Neural Network in 1988 which is a feedforward neural network to solve time series issues [16-17]. CNN-LSTM is widely used in time financial area and further research have been taken to improve it.The first method to improve model is building more complex models. Wang et al. state the CNN-BiSLSTM model has better forecasting accuracy than CNN-LSTM [18]. Kim T and Kim HY prove that CNN-LSTM model combined with stock price features is more effective [19]. Dai et al. proposed a Dual-path attention mechanism with VT-LSTM which improve the model accuracy [20].Price factors selection and pre-processing is another direction to improve models. Zhang et al. add industry factor as model inputs which contributes to better prediction results [21]. The research of Kang et al. proves the self-attention input contributes smaller prediction error [22]. Yu et al. verified that the amount of training samples affects the effectiveness and accuracy of deep learning models [23].3 MDTThe traditional data processing method for the deep learning is the sliding window method [24]. It divides a time series into multiple consecutive subsequences of length along the time step. The two-dimensional time series matrix will be divided it into multiple fixed-size sub-matrices as the inputs of deep learning.The sliding windows fails to consider the correlations of multidimensional time series. To solve this issue, this paper introduces the multi-directional delayed embedding (MDT) tensor processing technology. Shi et al. combine the MDT method and ARIMA model to prove MDT will improve the accuracy of model [25].MDT method will transform daily stock factor vector x=(x1,x2,…,x n),T∈R n into a Hankel matrix M(x) shown in Figure 1:τ1 China Ping An Insurance (Group) Co., Ltd. (hereinafter referred to as "Ping An",) was born in Shekou, Shenzhen in 1988. It is the first joint-stock insurance enterprise in China, and has developed into an integrated, close and diversified comprehensive financial service group integrating financial insurance, banking, investment and other financial businesses.Theory and Practice of Science and Technology The MDT operation can be represented by following formula:M τ(x )=fold (n ,τ)(Cx )Function fold (n ,τ):R τ×(n -τ+1)→R τ×(n -τ+1)is a folding operator that converts vectors into a matrix. Set the Hankel matrix M τ(x )=(v 1,v 2,…v n -τ+1), where v i represents the number i column vector of the Hankel matrix:vi =(xi ,xi +1,…xτ)T 4 CNN-CBAM-GRU(1) CNNCNN is widely used in time series data prediction because of its good performance and time saving. CNN includes pooling layers which transform the data to reduce the feature dimension:l t =tanh (x t *k t +b t )Where l t represent the output of after convolution neural network, x t represents the input vector, k t represents the weight of the convolution kernel, b t is the convolution kernel bias, and tanh is the activation function.(2) CBAMSanghyun et al. introduce the Convolutional Block Attention Module in 2018 which is a simple and effective module which has been widely used in CNN model [26]. The overview of CBAM is presented in Figure 2:The technological process can be concluded as:F 1=Mc (F )⊗F ,F 2=Ms (F 1)⊗F 1,F represents the input which is intermediate feature map F ∈R C ×H ×W . Mc ∈R C ×1×1is a 1D channel attention map and Ms ∈R 1×H ×W is a 2D spatial attention map. ⊗ is the element-wise multiplication which broadcasts the attention values.Channel attention module compress the spatial feature dimension of the input by utilizing the Figure 1 The transformed Hankel matrixFigure 2 The schematic diagram of CBAM 83Yangwenyuan Deng Avg Pooling and Max Pooling at the same time:Mc (F )=σ(MLP (AvgPool (F ))+MLP (MaxPool (F )))=σ(W 1(W 0(F c avg )))+W 1(W 0(F ))Where W 0∈R cr ×c ,W 1∈r cr ×c . the Spatial Attention Module address the issue of where the efficient information area is by aggregating two pooling operations to generate two 2D maps:Mc (F )=σ(f 7×7([AvgPool (F )]))MLP (MaxPool (F ))=σ(f 7×7[F s avg ,F s max ])(3) GRUGRU merge input gate and forget gat into an update gate to improve the efficiency of training while maintain the model accuracy [27]. GRU has two gate structure which respectively are update gate and reset gate. The overview of GRU is presented in Figure 3:1) r t represent the reset gate which controls the amount of the information needed to be forgotten in previous hidden layer h t -1.2) The update gate Z t control the extent to which the information of previous status is brought into current status h ~t .3) W is the weight matrix, b is the bias vector, [h t -1,x t ] represents the connection of the two vectors. σ and tanh are the sigmoid or hyperbolic tangent functions.The process of GRU could be summarized as follow:Z t =σ(W z ⋅h t -1+W z ⋅x t ),rt =σ(W r ⋅ht -1+W r ⋅x t ),h ~t =tanh (W h ~⋅(r t ⊙h t -1)+W h ~⋅x t ),h t =(1-Z t )⊙h t -1+Z t ⊙h t Where ⋅ represents matrix multiplication, and ⊙ represents matrix corresponding elementmultiplication.Figure 3 Gated Recurrent Unit 84Theory and Practice of Science and Technology (4) CNN-CBAM-GRU training and prediction process1) Standardized inputs: Before the MDT process, data of each column have been processed with Z-score normalization:z i =x i -μσ2) Where μ is the mean, σ is the standard deviation. Then, the normalized data will be transferred to Hankel matrices by MDT.3) Network Initialization: initialize the weights and biases of CNN-CBAM-GRU layers.4) CNN layers: through CNN layers, the key features of Hankel matrices are drawn as the input for later layers.5) CBAM module: The CBAM module will further process the features.6) GRU layers: the processed data are used by GRU to predict the close price.7) Output layer: full connection layers utilize the outputs of GRU to calculate the weight of model.8) Prediction result test and circulation: Judge whether the validation loss reduce after training. Return to step 3 until finish all epochs.9) Saving the best model: If validation loss of this epoch is smaller than the previous stored one, save current model as the best model in the experiment folder.10) Load the best model: load the model structure and weight.11) Prediction and denormalization: utilize the weight of best model to predict the test set close price. The prediction result will be denormalized and compared with true value.12) Experiment result: visualize the result and present the evaluation index results.5 Experiments(1) Experimental EnvironmentA notebook computer, equipped with NVIDIA GeForce GTX 1060 6G and Intel 8750H, implements all experiments. Python 3.9 is the programming language. Anaconda with Jupyter notebook is used as the program platform and Keras built in TensorFlow package construct the neuralnetworkFigure 4 The process of model 85Yangwenyuan Deng structure.(2) Experimental DataChina Ping An price factors is used as experimental data and the close price is the forecasting target. The experimental data contain 6000-day price data from 1994 to 2020 downloaded from the Baostock. Total data is divided into 3 parts: 80% for train set and 10% for both validation set and test set. This paper innovatively takes the CSI 300 index and moving average 5 as price factors. There is total 11 parameters to forecast the close price which is presented in Table 1:(3) Model ImplementationEvery model will independently run for 15 times to find the optimal weights. This paper chooses three evaluation indexes, respectively root mean square error (RMSE), mean absolute error (MAE), and R-square (R2) to evaluate the performance of different models. The formulas of them are calculated as follows:MAE =1n i =1n ||||||y ^i-y i ,RMSE =R 2=1-(∑i =1n (y ^i -y i )2)/n (∑i =1n ()y ^i -y i 2)/n ,Where y ^i represent the prediction value of models and y i is the true value. The closer value of MAE and RMSE to 0 indicates the better performance of model. The close value of R 2 to 1 represent the higher accuracy of model.(4) Implementation of MDT-CNN-CBAM-GRUThe pre-setting parameters of MDT-CNN-CBAM-GRU model are listed in Table 2.6 ResultsThe visual results are presented in Figure 5 to Figure 8. Where the orange line with * represent the prediction value of close price and the blue line represent the true value of close price.The evaluation index results of models are presented in Table 3:The average time for each step training is shown in Table 4:Table 1 Stock price factorsDate94-07Amount 1.165176e+07Volume 1385000Turn 0.51547Index 3.84893Open 0.41541PeTTM 12.58321PbMRQ 2.855036PctChg 3.026634Ma50.410159High 0.422353Low 0.42185886Theory and Practice of Science and TechnologyTable 2 Model parametersParametersConvolution layer filters Convolution layer kernel_size Convolution layer activation function MaxPooling2D pool_sizePooling layer paddingPooling layer activation function Dropout layersCBAM_attention reduce axisGRU layerskernel_regularizerNumber of hidden units in GRU layer 1 Number of hidden units in GRU layer 2 GRU layer activation function Dense layers kernel_initializer Dropout layers 2Learning rateTime_stepLoss functionBatch_sizeOptimizerEpochsValue643Relu2SameRelu0.232L2(0.01)12864Relu Random normal0.250.0011Mean square error64Adam200Figure 5 The prediction of CNN-LSTM8788Yangwenyuan Deng ArrayThe prediction of MDT-CNN-GRUFigure 6 The prediction of MDT-CNN-LSTMFigure 7 Theory and Practice of Science and Technology 7 ConclusionThe MDT-CNN-CBAM-GRU proposed has the optimal forecasting accuracy and satisfied time efficiency, which could provide reference for investors investing in share market.Compared with LSTM, GRU has better prediction accuracy and faster speed. However, here are some details to be improved in further research:(1) If time is enough, 30-time independent training for each model will be a better choice.(2) In further research, more experiment of GRU need to be conducted as the GRU has better performance compared with LSTM.(3) The generalization of models needs to be tested in future research by predicting different financial product such as funds, options and other stocks.About the AuthorYangwenyuan Deng, Master of Commerce in Finance of University of New South Wales, and his research field is Finance & Machine Learning.References[1] Meng, S., Fang, H. & Yu, D. (2020). Fractal characteristics, multiple bubbles, and jump anomalies in the Chinese stock market. Complexity, 2020: 7176598.[2] ABU-MOSTAFA, YS. & ATIYA, AF. (1996). Introduction to financial forecasting. Applied intelligence, 6: 205-213.[3] Huang, QP ., Zhou, X., Wei, Y & Gan, JY. (2015). Application of SVM and neural network model in the stock prediction research. Microcomputer and Application, 34: 88-90.[4] Chen, S., Goo, YJ. & Shen, ZD. (2014). A Hybrid Approach of Stepwise Regression, Logistic Regression, Support Vector Machine, and Decision Tree for Forecasting Fraudulent Financial Statements. The Scientific World Journal, 2014: 968712.[5] Fang, X., Cao, HY. & Li, XD. (2019). Stock trend prediction based on improved random forest algorithm. Journal of Hangzhou Dianzi University, 39: 25-30.[6] Zhang, QY., Yang, DM. & Hang, JT. (2021). Research on Stock Price Prediction Combined with Deep Learning and Decomposition Algorithm. Computer Engineering and Applications, 57: 56-64.[7] Luo, X. & Zhang, JL. (2020). Stock price forecasting based on multi time scale compound depth neural network. Wuhan Finance, 2020: 32-40.[8] Lu, W., Li, J., Li, Y., Sun, A. & Wang, J. (2020). A CNN-LSTM-Based Model to Forecast Stock Prices. Complexity, 2020: 6622927.[9] Zhao, HR. & Xue, L. (2021). Research on Stock Forecasting Based on LSTM-CNN-CBAM Model. Computer EngineeringTable 3 Evaluation index values of different modelsModelCNN-GRUMDT-CNN-LSTMMDT-CNN-GRUMDT-CNN-CBAM-GRU RMSE 0.32200.15980.09100.0890MAE 0.22680.13200.07940.0639R 20.94180.98660.99590.9959Table 4 Average training timeModelCNN-GRUMDT-CNN-GRUMDT-CNN-LSTMMDT-CNN-CBAM-GRU Time 2s 11ms / step 1s 9ms/ step 2s 10ms/ step 2s 10ms/ step 89Yangwenyuan Deng 90and Applications, 57: 203-207.[10] Cao, CF., Luo, ZN., Xie, JX. & Li, L. (2022). Stock Price Prediction Based on MDT-CNN-LSTM Model. ComputerEngineering and Applications, 58: 280-286.[11] Li, J., Pan, S., Huang, L. & Zhu, X. (2019). A machine learning based method for customer behavior prediction.Tehnicki Vjesnik Technical Gazette, 26: 1670-1676.[12] L¨angkvist, M., Karlsson, L. & Loutfi, A. (2014). A review of unsupervised feature learning and deep learning for time-series modeling. Pattern Recognition Letters, 42: 11-24.[13] Sherstinsky, A. (2020). Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM)network. Physica D: Nonlinear Phenomena, 404: 132306.[14] Hochreiter, S. & Schmidhuber, J. (1997). Long short-term memory. Neural Computation, 9: 1735–1780.[15] Cho, K., Van Merrienboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H. & Bengio, Y. (2014). Learningphrase representations using RNN encoder-decoder for statistical machine translation. arXiv, 1406: 1078.[16] Lecun, Y., Bottou, L., Bengio, Y. & Haffner, P. (1998). Gradient based learning applied to document recognition.Proceedings of the IEEE, 86: 2278-2324.[17] Hu, Y. (2018). Stock market timing model based on convolutional neural network – a case study of Shanghaicomposite index. Finance& Economy, 4: 71-74.[18] Wang, HY., Wang, JX., Cao, LH., Sun, Q. & Wang, JY. (2021). A Stock Closing Price Prediction Model Based on CNN-BiSLSTM. Complexity, 2021: 5360828.[19] Kim, T. & Kim, HY. (2019). Forecasting stock prices with a feature fusion LSTM-CNN model using differentrepresentations of the same data. PLOS ONE, 14: 0212320.[20] Dai, YR., An, JX. & Tao, QH. (2022). Financial Time-Series Prediction by Fusing Dual-Pathway Attention with VT-LSTM.Computer Engineering and Applications. 6:10.[21] Zhang, YF., Wang, J. Wu, ZH. & L, YF. (2022). Stock movement prediction with dynamic and hierarchical macroinformation of market. Journal of Computer Applications, 6:7.[22] Kang, RX., Niu, BN., Li, X. & Miao, YX. (2021). Predicting Stock Prices Using LSTM with the Self-attention Mechanismand Multi-source Data. Journal of Chinese Computer Systems,12: 9.[23] Yu, SS., Chu, SW., Chan, YK. & Wang, CM. (2019). Share Price Trend Prediction Using CRNN with LSTM Structure.Smart Science, 7: 189-197.[24] Li, XF., Liang, X. & Zhou, XP. (2016). An Empirical Study on Manifold Learning of Sliding Window of Stock Price TimeSeries. Chinese Journal of Management Science, 24: 495-503.[25] SHI, Q., YIN, J. & CAI, J. (2020). Block Hankel tensor ARIMA for multiple short time series forecasting. Proceedings ofthe AAAI Conference on Artificial Intelligence, 34: 5758-5766.[26] Woo, S., Park, J., Lee, JY. & Kweon, S. (2018). CBAM:convolutional block attention module. Proceedings of theEuropean Conference on Computer Vision (ECCV), 2018: 3-19.[27] Dang, JW. & Cong, XQ. (2021). Research on hybrid stock index forecasting model based on CNN and GRU.Computer Engineering and Applications, 57: 167-174.。
Fluent流体数值模拟软件中英对照

Aabort 异常中断, 中途失败, 夭折, 流产, 发育不全,中止计划[任务] accidentally 偶然地, 意外地accretion 增长activation energy 活化能active center 活性中心addition 增加adjacent 相邻的aerosol浮质(气体中的悬浮微粒,如烟,雾等), [化]气溶胶, 气雾剂, 烟雾剂Air flow circuits 气流循环ambient 周围的, 周围环境amines 胺amplitude 广阔, 丰富, 振幅, 物理学名词annular 环流的algebraic stress model(ASM) 代数应力模型algorithm 算法align 排列,使结盟, 使成一行alternately 轮流地analogy 模拟,效仿analytical solution 解析解anisotropic 各向异性的anthracite 无烟煤apparent 显然的, 外观上的,近似的approximation 近似arsenic 砷酸盐assembly 装配associate 联合,联系assume 假设assumption 假设atomization 雾化axial 轴向的Axisymmetry 轴对称的BBaffle 挡流板battlement 城垛式biography 经历bituminous coal 烟煤blow-off water 排污水blowing devices 鼓风(吹风)装置body force 体积力boiler plant 锅炉装置(车间)Boiling 沸腾Boltzmann 玻耳兹曼Bounded central differencing:有界中心差分格式Brownian rotation 布朗转动bulk 庞大的bulk density 堆积密度burner assembly 燃烧器组件burnout 燃尽Ccapability 性能,(实际)能力,容量,接受力carbon monoxide COcarbonate 碳酸盐carry-over loss 飞灰损失Cartesian 迪卡尔坐标的casing 箱,壳,套catalisis 催化channeled 有沟的,有缝的char 焦炭、炭circulation circuit 循环回路circumferential velocity 圆周速度clinkering 熔渣clipped 截尾的clipped Gaussian distribution 截尾高斯分布closure (模型的)封闭cloud of particles 颗粒云close proximity 距离很近cluster 颗粒团coal off-gas 煤的挥发气体coarse 粗糙的coarse grid 疏网格,粗网格Coatingcoaxial 同轴的coefficient of restitution 回弹系数;恢复系数coke 碳collision 碰撞competence 能力competing process 同时发生影响的competing-reactions submodel 平行反应子模型component 部分分量composition 成分computational expense 计算成本cone shape 圆锥体形状configuration 布置,构造confined flames 有界燃烧confirmation 证实, 确认, 批准Configuration 构造,外形conservation 守恒不灭conservation equation 守恒方程conserved scalars 守恒标量considerably 相当地consume 消耗contact angle 接触角contamination 污染contingency 偶然, 可能性, 意外事故, 可能发生的附带事件continuum 连续体Convection 对流converged 收敛的conveyer 输运机convolve 卷cooling duct 冷却管cooling wall 水冷壁coordinate transformation 坐标转换correlation 关联(式)correlation function 相关函数corrosion 腐蚀,锈coupling 联结, 接合, 耦合Cp:等压比热crack 裂缝,裂纹creep up (水)渗上来,蠕升critical 临界critically 精密地cross-correlation 互关联cumulative 累积的curtain wall 护墙,幕墙curve 曲线custom 习惯, 风俗, <动词单用>海关, (封建制度下)定期服劳役, 缴纳租税, 自定义, <偶用作>关税v.定制, 承接定做活的Cyan青色cyano 氰(基),深蓝,青色cyclone 旋风子,旋风,旋风筒cyclone separator 旋风分离器[除尘器]cylindrical 柱坐标的cylindrical coordinate 柱坐标Ddead zones 死区decompose 分解decouple 解藕的defy 使成为不可能Deforming:变形demography 统计Density:密度deposition 沉积derivative with respect to 对…的导数derivation 引出, 来历, 出处, (语言)语源, 词源design cycle 设计流程desposit 积灰,结垢deterministic approach 确定轨道模型deterministic 宿命的deviation 偏差devoid 缺乏devolatilization 析出挥发分,液化作用diffusion 扩散diffusivity 扩散系数digonal 二角(的), 对角的,二维的dilute 稀的diminish 减少direct numerical simulation 直接数值模拟discharge 释放discrete 离散的discrete phase 分散相, 不连续相discretization [数]离散化deselect 取消选定dispersion 弥散dissector 扩流锥dissociate thermally 热分解dissociation 分裂dissipation 消散, 分散, 挥霍, 浪费, 消遣, 放荡, 狂饮distribution of air 布风divide 除以dot line 虚线drag coefficient 牵引系数,阻力系数drag and drop 拖放drag force 曳力drift velocity 漂移速度driving force 驱[传, 主]动力droplet 液滴drum 锅筒dry-bottom-furnace 固态排渣炉dry-bottom 冷灰斗,固态排渣duct 管dump 渣坑dust-air mixture 一次风EEBU---Eddy break up 漩涡破碎模型eddy 涡旋effluent 废气,流出物elastic 弹性的electro-staic precipitators 静电除尘器emanate 散发, 发出, 发源,[罕]发散, 放射embrasure 喷口,枪眼emissivity [物]发射率empirical 经验的endothermic reaction 吸热反应enhance 增,涨enlarge 扩大ensemble 组,群,全体enthalpy 焓entity 实体entrain 携带,夹带entrained-bed 携带床Equation 方程equilibrate 保持平衡equilibrium 化学平衡ESCIMO-----Engulfment(卷吞)Stretching(拉伸)Coherence(粘附)Interdiffusion-interaction(相互扩散和化学反应)Moving-observer(运动观察者)exhaust 用尽, 耗尽, 抽完, 使精疲力尽排气排气装置用不完的, 不会枯竭的exit 出口,排气管exothermic reaction 放热反应expenditure 支出,经费expertise 经验explicitly 明白地, 明确地extinction 熄灭的extract 抽出,提取evaluation 评价,估计,赋值evaporation 蒸发(作用)Eulerian approach 欧拉法Ffacilitate 推动,促进factor 把…分解fast chemistry 快速化学反应fate 天数, 命运, 运气,注定, 送命,最终结果feasible 可行的,可能的feed pump 给水泵feedstock 填料Filling 倒水fine grid 密网格,细网格finite difference approximation 有限差分法flamelet 小火焰单元flame stability 火焰稳定性flow pattern 流型fluctuating velocity 脉动速度fluctuation 脉动,波动flue 烟道(气)flue duck 烟道fluoride 氟化物fold 夹层块forced-and-induced draft fan 鼓引风机forestall 防止Formulation:公式,函数fouling 沾污fraction 碎片部分,百分比fragmentation 破碎fuel-lean flamefuel-rich regions 富燃料区,浓燃料区fuse 熔化,熔融Ggas duct 烟道gas-tight 烟气密封gasification 气化(作用)gasifier 气化器Gauge 厚度,直径,测量仪表,估测。
基于摩擦纳米发电机的柔性可穿戴多功能压力传感器

摘要随着社会的日益进步,医疗水平不断提高,互联网技术快速发展,健康和信息安全成为人们最为关注的焦点。
目前医疗资源的短缺和屡见不鲜的个人信息泄露事件,越来越成为人们的心头之患。
在健康方面,社会老龄化进一步加剧,各类慢性疾病的数量逐年增长,人们越来越意识到医院治疗已不能满足自身健康的需求,日常生活中更需要仪器设备实现自身健康状态长期持续的监测。
在信息安全方面,虽然人们采用密码、U盾及密保等方式保护个人信息,但个人信息依旧被窃取,泄漏在互联网等媒介之上。
如果日常生活中对人们的健康状态进行持续监测,并使用一种独一无二的身份识别方式,将大大减少各类慢性疾病的数量及个人信息泄露的问题。
目前部分可穿戴设备可用于人体生理信号的测量,实现对人体健康状态的检测。
每个人的生物特征是独一无二的,将生物特征用于身份识别,信息将很难被窃取。
但是目前存在的可穿戴设备无法实现健康状态监测和身份识别双重功能。
为此,本文做了以下研究:①本文研究了基于摩擦纳米发电机的柔性可穿戴多功能压力传感器。
该传感器以人耳鼓膜结构进行仿生,结合单电极式摩擦纳米发电机工作模式,采用PTFE 薄膜、Nylon薄膜、ITO薄膜以及PET衬底制作而成。
结合薄膜的振动特性从理论上分析了传感器的振动模态,采用单电极摩擦纳米发电机的工作原理分析传感器的电学输出特性,采用COMSOL Multiphysics对传感器的振动特性和开路电压进行了仿真,验证了设计的传感器具有较宽的工作频带范围,高低频特性较好。
②对传感器测得信号中的噪声进行了分析及处理。
对传感器输出信号中的工频干扰、肌电漂移、运动伪迹和基线漂移噪声进行处理。
采用模拟滤波和数字滤波相结合的方式,对传感器输出信号进行处理。
结合传感器输出信号频谱中信号频率分布,采用10Hz Butterworth低通滤波器和45Hz~1500Hz Butterworth带通滤波器对测量的信号进行了分解,分别得到脉搏波信号和喉咙声信号。
On the asymptotic expansion of the solutions of the separated nonlinear Schroedinger equati

a r X i v :n l i n /0012025v 3 [n l i n .S I ] 10 M a y 2001On the Asymptotic Expansion of the Solutions of the Separated Nonlinear Schr¨o dinger EquationA.A.Kapaev,St Petersburg Department of Steklov Mathematical Institute,Fontanka 27,St Petersburg 191011,Russia,V.E.Korepin,C.N.Yang Institute for Theoretical Physics,State University of New York at Stony Brook,Stony Brook,NY 11794-3840,USAAbstractNonlinear Schr¨o dinger equation with the Schwarzian initial data is important in nonlinear optics,Bose condensation and in the theory of strongly correlated electrons.The asymptotic solutions in the region x/t =O (1),t →∞,can be represented as a double series in t −1and ln t .Our current purpose is the description of the asymptotics of the coefficients of the series.MSC 35A20,35C20,35G20Keywords:integrable PDE,long time asymptotics,asymptotic expansion1IntroductionA coupled nonlinear dispersive partial differential equation in (1+1)dimension for the functions g +and g −,−i∂t g +=12∂2x g −+4g 2−g +,(1)called the separated Nonlinear Schr¨o dinger equation (sNLS),contains the con-ventional NLS equation in both the focusing and defocusing forms as g +=¯g −or g +=−¯g −,respectively.For certain physical applications,e.g.in nonlin-ear optics,Bose condensation,theory of strongly correlated electrons,see [1]–[9],the detailed information on the long time asymptotics of solutions with initial conditions rapidly decaying as x →±∞is quite useful for qualitative explanation of the experimental phenomena.Our interest to the long time asymptotics for the sNLS equation is inspired by its application to the Hubbard model for one-dimensional gas of strongly correlated electrons.The model explains a remarkable effect of charge and spin separation,discovered experimentally by C.Kim,Z.-X.M.Shen,N.Motoyama,H.Eisaki,hida,T.Tohyama and S.Maekawa [19].Theoretical justification1of the charge and spin separation include the study of temperature dependent correlation functions in the Hubbard model.In the papers[1]–[3],it was proven that time and temperature dependent correlations in Hubbard model can be described by the sNLS equation(1).For the systems completely integrable in the sense of the Lax representa-tion[10,11],the necessary asymptotic information can be extracted from the Riemann-Hilbert problem analysis[12].Often,the fact of integrability implies the existence of a long time expansion of the generic solution in a formal series, the successive terms of which satisfy some recurrence relation,and the leading order coefficients can be expressed in terms of the spectral data for the associ-ated linear system.For equation(1),the Lax pair was discovered in[13],while the formulation of the Riemann-Hilbert problem can be found in[8].As t→∞for x/t bounded,system(1)admits the formal solution given byg+=e i x22+iν)ln4t u0+∞ n=12n k=0(ln4t)k2t −(1t nv nk ,(2)where the quantitiesν,u0,v0,u nk and v nk are some functions ofλ0=−x/2t.For the NLS equation(g+=±¯g−),the asymptotic expansion was suggested by M.Ablowitz and H.Segur[6].For the defocusing NLS(g+=−¯g−),the existence of the asymptotic series(2)is proven by P.Deift and X.Zhou[9] using the Riemann-Hilbert problem analysis,and there is no principal obstacle to extend their approach for the case of the separated NLS equation.Thus we refer to(2)as the Ablowitz-Segur-Deift-Zhou expansion.Expressions for the leading coefficients for the asymptotic expansion of the conventional NLS equation in terms of the spectral data were found by S.Manakov,V.Zakharov, H.Segur and M.Ablowitz,see[14]–[16].The general sNLS case was studied by A.Its,A.Izergin,V.Korepin and G.Varzugin[17],who have expressed the leading order coefficients u0,v0andν=−u0v0in(2)in terms of the spectral data.The generic solution of the focusing NLS equation contains solitons and radiation.The interaction of the single soliton with the radiation was described by Segur[18].It can be shown that,for the generic Schwarzian initial data and generic bounded ratio x/t,|c−xthese coefficients as well as for u n,2n−1,v n,2n−1,wefind simple exact formulaeu n,2n=u0i n(ν′)2n8n n!,(3)and(20)below.We describe coefficients at other powers of ln t using the gener-ating functions which can be reduced to a system of polynomials satisfying the recursion relations,see(24),(23).As a by-product,we modify the Ablowitz-Segur-Deift-Zhou expansion(2),g+=exp i x22+iν)ln4t+i(ν′)2ln24t2] k=0(ln4t)k2t −(18t∞n=02n−[n+1t n˜v n,k.(4)2Recurrence relations and generating functions Substituting(2)into(1),and equating coefficients of t−1,wefindν=−u0v0.(5) In the order t−n,n≥2,equating coefficients of ln j4t,0≤j≤2n,we obtain the recursion−i(j+1)u n,j+1+inu n,j=νu n,j−iν′′8u n−1,j−2−−iν′8u′′n−1,j+nl,k,m=0l+k+m=nα=0, (2)β=0, (2)γ=0, (2)α+β+γ=ju l,αu k,βv m,γ,(6) i(j+1)v n,j+1−inv n,j=νv n,j+iν′′8v n−1,j−2++iν′8v′′n−1,j+nl,k,m=0l+k+m=nα=0, (2)β=0, (2)γ=0, (2)α+β+γ=ju l,αv k,βv m,γ,(7)where the prime means differentiation with respect toλ0=−x/(2t).Master generating functions F(z,ζ),G(z,ζ)for the coefficients u n,k,v n,k are defined by the formal seriesF(z,ζ)= n,k u n,k z nζk,G(z,ζ)= n,k v n,k z nζk,(8)3where the coefficients u n,k,v n,k vanish for n<0,k<0and k>2n.It is straightforward to check that the master generating functions satisfy the nonstationary separated Nonlinear Schr¨o dinger equation in(1+2)dimensions,−iFζ+izF z= ν−iν′′8zζ2 F−iν′8zF′′+F2G,iGζ−izG z= ν+iν′′8zζ2 G+iν′8zG′′+F G2.(9) We also consider the sectional generating functions f j(z),g j(z),j≥0,f j(z)=∞n=0u n,2n−j z n,g j(z)=∞n=0v n,2n−j z n.(10)Note,f j(z)≡g j(z)≡0for j<0because u n,k=v n,k=0for k>2n.The master generating functions F,G and the sectional generating functions f j,g j are related by the equationsF(zζ−2,ζ)=∞j=0ζ−j f j(z),G(zζ−2,ζ)=∞j=0ζ−j g j(z).(11)Using(11)in(9)and equating coefficients ofζ−j,we obtain the differential system for the sectional generating functions f j(z),g j(z),−2iz∂z f j−1+i(j−1)f j−1+iz∂z f j==νf j−z iν′′8f j−ziν′8f′′j−2+jk,l,m=0k+l+m=jf k f lg m,2iz∂z g j−1−i(j−1)g j−1−iz∂z g j=(12)=νg j+z iν′′8g j+ziν′8g′′j−2+jk,l,m=0k+l+m=jf kg l g m.Thus,the generating functions f0(z),g0(z)for u n,2n,v n,2n solve the systemiz∂z f0=νf0−z (ν′)28g0+f0g20.(13)The system implies that the product f0(z)g0(z)≡const.Since f0(0)=u0and g0(0)=v0,we obtain the identityf0g0(z)=−ν.(14) Using(14)in(13),we easilyfindf0(z)=u0e i(ν′)28n n!z n,4g0(z)=v0e−i(ν′)28n n!z n,(15)which yield the explicit expressions(3)for the coefficients u n,2n,v n,2n.Generating functions f1(z),g1(z)for u n,2n−1,v n,2n−1,satisfy the differential system−2iz∂z f0+iz∂z f1=νf1−z iν′′8f1−ziν′8g0−z(ν′)24g′0+f1g20+2f0g0g1.(16)We will show that the differential system(16)for f1(z)and g1(z)is solvable in terms of elementary functions.First,let us introduce the auxiliary functionsp1(z)=f1(z)g0(z).These functions satisfy the non-homogeneous system of linear ODEs∂z p1=iν4−ν′′4f′0z(p1+q1)−i(ν′)28−ν′g0,(17)so that∂z(q1+p1)=−(ν2)′′8z,p1(z)= −iνν′′8−ν′u′032z2,g1(z)=q1(z)g0(z),g0(z)=v0e−i(ν′)24−ν′′4v0 z+i(ν′)2ν′′4−ν′′4u0 ,v1,1=v0 iνν′′8−ν′v′0u n,2n −1=−2u 0i n −1(ν′)2(n −1)n −1ν′′u 0,n ≥2,v n,2n −1=−2v 0(−i )n −1(ν′)2(n −1)n −1ν′′v 0,n ≥2.Generating functions f j (z ),g j (z )for u n,2n −j ,v n,2n −j ,j ≥2,satisfy the differential system (12).Similarly to the case j =1above,let us introduce the auxiliary functions p j and q j ,p j =f jg 0.(21)In the terms of these functions,the system (12)reads,∂z p j =iνz(p j +q j )+b j ,(22)wherea j =2∂z p j −1+i (ν′)28−j −14(p j −1f 0)′8f 0+iν4−ν′′zq j −1−−ν′g 0+i(q j −2g 0)′′zj −1 k,l,m =0k +l +m =jp k q l q m .(23)With the initial condition p j (0)=q j (0)=0,the system is easily integrated and uniquely determines the functions p j (z ),q j (z ),p j (z )= z 0a j (ζ)dζ+iνzdζζζdξ(a j (ξ)+b j (ξ)).(24)These equations with expressions (23)together establish the recursion relationfor the functions p j (z ),q j (z ).In terms of p j (z )and q j (z ),expansion (2)readsg +=ei x22+iν)ln 4t +i(ν′)2ln 24tt2t−(18tv 0∞ j =0q j ln 24tln j 4t.(25)6Let a j (z )and b j (z )be polynomials of degree M with the zero z =0of multiplicity m ,a j (z )=M k =ma jk z k,b j (z )=Mk =mb jk z k .Then the functions p j (z )and q j (z )(24)arepolynomials of degree M +1witha zero at z =0of multiplicity m +1,p j (z )=M +1k =m +11k(a j,k −1+b j,k −1)z k ,q j (z )=M +1k =m +11k(a j,k −1+b j,k −1) z k.(26)On the other hand,a j (z )and b j (z )are described in (23)as the actions of the differential operators applied to the functions p j ′,q j ′with j ′<j .Because p 0(z )=q 0(z )≡1and p 1(z ),q 1(z )are polynomials of the second degree and a single zero at z =0,cf.(19),it easy to check that a 2(z )and b 2(z )are non-homogeneous polynomials of the third degree such thata 2,3=−(ν′)4(ν′′)2210(2+iν),(27)a 2,0=−iνν′′8−ν′u ′08u 0,b 2,0=iνν′′8−ν′v ′08v 0.Thus p 2(z )and q 2(z )are polynomials of the fourth degree with a single zero at z =0.Some of their coefficients arep 2,4=q 2,4=−(ν′)4(ν′′)24−(1+2iν)ν′′8u 0−ν(u ′0)24−(1−2iν)ν′′8v 0−ν(v ′0)22.Proof .The assertion holds true for j =0,1,2.Let it be correct for ∀j <j ′.Then a j ′(z )and b j ′(z )are defined as the sum of polynomials.The maximal de-grees of such polynomials are deg (p j ′−1f 0)′/f 0 =2j ′−1,deg (q j ′−1g 0)′/g 0 =72j′−1,anddeg 1z j′−1 α,β,γ=0α+β+γ=j′pαqβqγ =2j′−1. Thus deg a j′(z)=deg b j′(z)≤2j′−1,and deg p j′(z)=deg q j′(z)≤2j′.Multiplicity of the zero at z=0of a j′(z)and b j′(z)is no less than the min-imal multiplicity of the summed polynomials in(23),but the minor coefficients of the polynomials2∂z p j′−1and−(j−1)p j′−1/z,as well as of2∂z q j′−1and −(j−1)q j′−1/z may cancel each other.Let j′=2k be even.Thenm j′=min m j′−1;m j′−2+1;minα,β,γ=0,...,j′−1α+β+γ=j′mα+mβ+mγ =j′2 . Let j′=2k−1be odd.Then2m j′−1−(j′−1)=0,andm j′=min m j′−1+1;m j′−2+1;minα,β,γ=0,...,j′−1α+β+γ=j′mα+mβ+mγ =j′+12]p j,k z k,q j(z)=2jk=[j+12]z nn−[j+18k k!,g j(z)=v0∞n=[j+12]k=max{0;n−2j}q j,n−k(−i)k(ν′)2k2]k=max{0;n−2j}p j,n−ki k(ν′)2k2]k=max{0;n−2j}q j,n−k(−i)k(ν′)2kIn particular,the leading asymptotic term of these coefficients as n→∞and j fixed is given byu n,2n−j=u0p j,2j i n−2j(ν′)2(n−2j)n) ,v n,2n−j=v0q j,2j (−i)n−2j(ν′)2(n−2j)n) .(32)Thus we have reduced the problem of the evaluation of the asymptotics of the coefficients u n,2n−j v n,2n−j for large n to the computation of the leading coefficients of the polynomials p j(z),q j(z).In fact,using(24)or(26)and(23), it can be shown that the coefficients p j,2j,q j,2j satisfy the recurrence relationsp j,2j=−i (ν′)2ν′′2jj−1k,l,m=0k+l+m=jp k,2k p l,2l q m,2m++ν(ν′)2ν′′4j2j−1k,l,m=0k+l+m=jp k,2k(p l,2l−q l,2l)q m,2m,q j,2j=i (ν′)2ν′′2jj−1k,l,m=0k+l+m=jp k,2k q l,2l q m,2m−(33)−ν(ν′)2ν′′4j2j−1k,l,m=0k+l+m=jp k,2k(p l,2l−q l,2l)q m,2m.Similarly,the coefficients u n,0,v n,0for the non-logarithmic terms appears from(31)for j=2n,and are given simply byu n,0=u0p2n,n,v n,0=v0q2n,n.(34) Thus the problem of evaluation of the asymptotics of the coefficients u n,0,v n,0 for n large is equivalent to computation of the asymptotics of the minor coeffi-cients in the polynomials p j(z),q j(z).However,the last problem does not allow a straightforward solution because,according to(8),the sectional generating functions for the coefficients u n,0,v n,0are given byF(z,0)=∞n=0u n,0z n,G(z,0)=∞n=0v n,0z n,and solve the separated Nonlinear Schr¨o dinger equation−iFζ+izF z=νF+18zG′′+F G2.(35)93DiscussionOur consideration based on the use of generating functions of different types reveals the asymptotic behavior of the coefficients u n,2n−j,v n,2n−j as n→∞and jfixed for the long time asymptotic expansion(2)of the generic solution of the sNLS equation(1).The leading order dependence of these coefficients on n is described by the ratio a n2+d).The investigation of theRiemann-Hilbert problem for the sNLS equation yielding this estimate will be published elsewhere.Acknowledgments.We are grateful to the support of NSF Grant PHY-9988566.We also express our gratitude to P.Deift,A.Its and X.Zhou for discussions.A.K.was partially supported by the Russian Foundation for Basic Research under grant99-01-00687.He is also grateful to the staffof C.N.Yang Institute for Theoretical Physics of the State University of New York at Stony Brook for hospitality during his visit when this work was done. References[1]F.G¨o hmann,V.E.Korepin,Phys.Lett.A260(1999)516.[2]F.G¨o hmann,A.R.Its,V.E.Korepin,Phys.Lett.A249(1998)117.[3]F.G¨o hmann,A.G.Izergin,V.E.Korepin,A.G.Pronko,Int.J.Modern Phys.B12no.23(1998)2409.[4]V.E.Zakharov,S.V.Manakov,S.P.Novikov,L.P.Pitaevskiy,Soli-ton theory.Inverse scattering transform method,Moscow,Nauka,1980.[5]F.Calogero,A.Degasperis,Spectral transforms and solitons:toolsto solve and investigate nonlinear evolution equations,Amsterdam-New York-Oxford,1980.[6]M.J.Ablowitz,H.Segur,Solitons and the inverse scattering trans-form,SIAM,Philadelphia,1981.10[7]R.K.Dodd,J.C.Eilbeck,J.D.Gibbon,H.C.Morris,Solitons andnonlinear wave equations,Academic Press,London-Orlando-San Diego-New York-Toronto-Montreal-Sydney-Tokyo,1982.[8]L.D.Faddeev,L.A.Takhtajan,Hamiltonian Approach to the Soli-ton Theory,Nauka,Moscow,1986.[9]P.Deift,X.Zhou,Comm.Math.Phys.165(1995)175.[10]C.S.Gardner,J.M.Greene,M.D.Kruskal,R.M.Miura,Phys.Rev.Lett.19(1967)1095.[11]x,Comm.Pure Appl.Math.21(1968)467.[12]V.E.Zakharov,A.B.Shabat,Funkts.Analiz Prilozh.13(1979)13.[13]V.E.Zakharov,A.B.Shabat,JETP61(1971)118.[14]S.V.Manakov,JETP65(1973)505.[15]V.E.Zakharov,S.V.Manakov,JETP71(1973)203.[16]H.Segur,M.J.Ablowitz,J.Math.Phys.17(1976)710.[17]A.R.Its,A.G.Izergin,V.E.Korepin,G.G.Varzugin,Physica D54(1992)351.[18]H.Segur,J.Math.Phys.17(1976)714.[19]C.Kim,Z.-X.M.Shen,N.Motoyama,H.Eisaki,hida,T.To-hyama and S.Maekawa Phys Rev Lett.82(1999)802[20]A.R.Its,SR Izvestiya26(1986)497.11。
MULTI-FUNCTION TIMER WITH SHARED HARDWARE

专利名称:MULTI-FUNCTION TIMER WITH SHARED HARDWARE发明人:FISHER, Rollie, Morris,GUIDO, Samuel,James,GRAVENSTEIN, Martin, Gerard,VIGIL,Michael, Anthony申请号:EP01937812.4申请日:20010521公开号:EP1222513A1公开日:20020717专利内容由知识产权出版社提供摘要:A multi-function timer used to perform multiple input timing measurements and generate multiple timed output events on the I/O pins of the apparatus. The multi-function timer comprises a plurality of slots and a compute engine. Each of the slots represents one of a plurality of timing processes. The compute engine includes a micro-sequencer and a processor. The micro-sequencer identifies a current slot and associated plurality of instructions representing a process, and is configured to serially sequence through each of the slots. The processor performs the functions of the instructions associated with each current slot. Further, each slot is configured to perform any one of the following timing processes: pulse width modulation, high speed input, high speed output, or delta time input. The multi-function timer is advantageous in that it provides application design flexibility by eliminating the need for dedicated logic for input and output timing functions.申请人:Visteon Global Technologies, Inc.地址:Suite 728,Parklane Towers East,One Parklane Boulevard Dearborn,Michigan48126 US国籍:US代理机构:Solf, Alexander, Dr.更多信息请下载全文后查看。
微生物功能差异 统计学方法

微生物功能差异统计学方法Microbial Functional Differences and Statistical MethodsMicroorganisms play a crucial role in various ecosystems, including the human microbiome, soil, and marine environments. These microscopic organisms exhibitremarkable functional diversity, which contributes significantly to the overall functioning of these ecosystems. Understanding the differences in microbial functions and employing appropriate statistical methods to analyze them is essential for advancing our knowledge inthis field.微生物功能差异和统计学方法微生物在各种生态系统中起着至关重要的作用,包括人体微生物组、土壤和海洋环境等。
这些微观生物表现出显著的功能多样性,对于整个生态系统的运行起到重要作用。
了解微生物功能之间的差异,并采用适当的统计学方法进行分析,对于推动该领域的知识进展非常重要。
To study the functional differences among microorganisms, researchers utilize various approaches such as metagenomics, transcriptomics, proteomics, and metabolomics. Metagenomics involves sequencing the DNA or RNA from samples containing mixed microbial communities to identify and characterize their genetic potential. Transcriptomics focuses onstudying gene expression patterns using techniques like RNA sequencing (RNA-seq). Proteomics examines the composition and abundance of proteins present in microbial cells. Metabolomics analyzes the small molecule metabolites produced by microorganisms.为了研究微生物之间的功能差异,研究人员采用了多种方法,如宏基因组学、转录组学、蛋白质组学和代谢组学。
互相关函数 英文

互相关函数英文英语翻译:Cross correlation function双语例句1.在分散解耦的系统框架上,提出了基于MIMO过程互相关函数的神经网络解耦器在线学习算法。
Online learning algorithm of Neural Network Decoupler, which based on MIMO cross-correlation function, is proposed on the frame of distributed decoupling system.2.该算法定义了一组MIMO过程的互相关函数作为神经网络解耦器的指标函数,采用混合遗传算法在线训练神经网络。
The algorithm made a set of cross-correlation function of the MIMO act as the target function of neural decoupler, and adopted mixing genetic algorithm to train neural decoupler online.3.No Sequences互相关函数值的分配Distribution of Crosscorrelation Function Values of No Sequences4.得到CUT输入和输出之间的互相关函数后,可以采用方差特征分析法或者距离分类算法来判断电路有无故障。
The fault can be diagnosed by Variance Analysis or Distance classification after getting the correlation functions between the input and output of CUT.5.基于互相关函数相角特征的RBF神经网络来波方位估计Direction of Arrival Estimation Approach Based on Phase Angle Feature of Correlation Function Using RBF Neural Networks。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a r X i v :m a t h -p h /0701055v 1 22 J a n 2007The multi-time correlation functions,free white noise,and the generalized Poisson statistics in the low density limit A.N.Pechen Princeton University,Department of Chemistry,Frick Laboratory,Princeton,NJ 08544-1009E-mail:apechen@ Abstract.In the present paper the low density limit of the non-chronological multitime correlation functions of boson number type operators is investigated.We prove that the limiting truncated non-chronological correlation can be computed using only a sub-class of diagrams associated to non-crossing pair partitions and thus coincide with the non-truncated correlation functions of suitable free number operators.The independent in the limit subalgebras are found and the limiting statistics is investigated.In particular,it is found that the cumulants of certain elements coincide in the limit with the cumulants of the Poisson distribution.An explicit representation of the limiting correlation functions and thus of the limiting algebra is constructed in a special case through suitably defined quantum white noise operators.1.INTRODUCTIONThe reduced dynamics of a quantum open system interacting with a reservoir in certain physical regimes is approximated by Markovian master equations.These regimes include the weak system–reservoir interactions and dilute reservoirs and in the theoretical framework they are described by certain limits.For a weakly interacting system one considers the limit as the coupling constant goes to zero(Weak Coupling Limit,WCL) whereas for a dilute reservoir one considers the limit as the density of the reservoir goes to zero(Low Density Limit,LDL)and an appropriate time rescaling should be performed in order to get a non-trivial limit.The Markovian reduced dynamics in these limits is considered in the review papers by Spohn and Lebowitz1,2.The reduced dynamics in the LDL was considered in details later by D¨u mcke3using the method based on the quantum Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy.The total dynamics in these limits is governed by various quantum stochastic equations.There is a unique up to now approach,called the stochastic limit method, which allows an efficient derivation of the stochastic equations in the WCL.This approach is based on the quantum white noise technique and was developed by Accardi, Lu,and Volovich4.The convergence of the evolution operator of the total system in the LDL to a solution of a quantum stochastic equation was proved by Accardi and Lu5and by Rudnicki,Alicki,and Sadowski6.Recently the low density limit was investigated with the quantum white noise technique7,8.This technique,well developed for the WCL, was non-trivially modified to include the LDL and for this case was called the stochastic golden rule for the low density limit.This technique was applied to the derivation of the quantum stochastic equations in the LDL.An advantage of the obtained equations is that they,in contrast with the exact Schr¨o dinger equation,are explicitly solvable.At the same time they provide a good approximation of the exact dynamics.The approach of7,8uses the so called Fock-antiFock representation for the canonical commutation relations(CCR)algebra(this representation is unitary equivalent to the Gel’fand–Naimark–Segal representation).The difficulty with this approach is that the creation and annihilation operators in the Fock-antiFock Hilbert space do not describe creation and annihilation of physical particles and thus do not have direct physical meaning.To avoid this difficulty the investigation of the LDL directly in terms of the physicalfields was ing this approach the chronological correlation functions in the LDL were found and the corresponding stochastic equations derived.In the present paper we investigate the low density limit of the non-chronologically ordered correlation functions of boson number type operators.The investigation is related with ab initio derivations of quantum stochastic equations describing quantum dynamics of a test particle interacting with a dilute gas.Wefind the limiting truncated correlation functions of the number type operators and show that they can be computed by representing the number operators through creation and annihilation operators and then considering only a sub-class of diagrams associated to non-crossing pair partitions.This fact allows to represent the limiting truncated correlation functions as the non-truncated correlation functions of number operators of a free quantum white noise thus making a connection with the Voiculescu free probability theory.Wefind the limiting statistics and show that the cumulants of certain elements coincide in the limit with the cumulants of the Poisson distribution.The free probability theory was developed by Voiculescu around1985as a way to deal with von Neumann algebras of free groups.Then the theory was separated from this special context and began to develop as an independentfield.In particular, applications of the free independence theory to random matrices were found.The details of free probability theory and its applications to random matrices could be found,for example,in references10,11.Expectations of free random variables are characterized by diagrams associated to non-crossing pair partitions.The vanishing of crossing diagrams in the stochastic weak coupling limit for nonrelativistic QED and for the Anderson model was found in Refs4and12,respectively,thus making a connection between the WCL and free probability.The WCL is typically described by the quantum Boltzmann statistics4.In Ref13a generalized version of Boltzmann commutation relations,the so called entangled commutation relations,was found in the weak coupling limit for nonlinear interactions and possible applications to photon splitting cascades were discussed.The investigation of the multitime non-chronologically ordered correlation functions could have a connection with the behavior offluctuations in certain asymptotic regimes. The latter is described in the review paper by Andries,Benatti,De Cock and Fannes14. In that approach the limiting statistics is defined in terms of ground state distribution determined by non trivial pair partitions.The authors conjecture the appearance of exotic statistics in certain asymptotic regimes.The asymptoticfluctuations are the limiting correlation functions of appropriate centered elements and thus the results of the present paper could be applied to study thefluctuations in the low density limit.In Sec.II the truncated non-chronologically ordered correlation functions are defined and their low density limit is established(Theorem1).In Sec.III the irreducible diagrams(pair partitions)which contribute to the limiting correlation functions are found(Theorem2).In Sec.IV the limiting truncated correlation functions are represented as correlation functions of a suitable free white noise.In Sec.V we identify the independent in the limit subalgebras(Theorem4)and calculate the limiting cumulants which for some elements coincide with the cumulants of the Poisson distribution(Theorem5).In Sec.VI an explicit representation of the limiting correlation functions and thus of the limiting algebra is constructed for a special case by using suitable quantum white noise operators.2.THE CORRELATION FUNCTIONS IN THE LDLWe begin this section with construction of a general class of non-commutative probability spaces relevant for the investigation of the low density limit.The framework of a∗-probability space is used.A relation between the objects defined in this section and the model of a test particle interacting with a dilute gas is given in Appendix A.Definition1A∗-probability space is a pair(A,ω),where A is a unital∗-algebra over C andω:A→C is a state,i.e.,a linear normalized,ω(1A)=1,and strictly positive functional.Let H be a Hilbert space with inner product denoted by ·,· (called as one particle Hilbert space),{S t}t∈R a one parameter unitary group in H(a one particle free evolution),ˆn a bounded positive operator in H(density operator)such that∀t∈R, S−tˆn S t=ˆn,and B a countable set of real numbers.LetΓ(H)be the symmetric Fock space over H.For any trace class self-adjoint operator T acting in H we denote by N(T)≡dΓ(T)its second quantization operator inΓ(H)and extend this definition by complex linearity to the set of all trace class operators T(H).For any T∈T(H),ω∈B,and a positive numberε>0we define the following operator inΓ(H):e−i tω/εN T,ω,ε(t):=We will use for the correlation functions(2)and(3)also the shorter notations Wε(t1,...,t n)and Wε(ϕ1,...,ϕn).The reason for introducing the averaged operators N T,ω,ε(ϕ)and the averaged correlation functions(3)is that,as we will show below,the non-averaged operators N T,ω,ε(t)and the correlation functions(2)in the limit asε→0 become singular distributions.Clearly,one has the relationWε(ϕ1,...,ϕn)= d t1...d t n Wε(t1,...,t n)ϕ1(t1)...ϕn(t n)Definition2The truncated correlation functions W Tε(t1,...,t n)are defined for n=1 by W Tε(t1):=Wε(t1)and for n>1by induction through the relation:Wε(t1,...,t n)=W Tε(t1,...,t n)+nl=2′W Tε(t i1,...,t i k1)×W Tε(t i k1+1,...,t i k2)...W Tε(t i k l,...,t i n) where ′is the sum over i1<i2<...<i k1,i k1+1<...<i k2,...,i k l+1<...<i n.The truncated correlation functions are often used in quantumfield theory and in quantum kinetic theory15.They entirely determine the corresponding non-chronological correlation functions.Thus the investigation of the limit of the non-chronological correlation functions can be reduced to the investigation of the limit of the truncated correlation functions.We define the”projection”P E:=(2π)−1 d tS t e−i tE[it has the property P E P E′=δ(E−E′)P E]and for any k=1,2,...,n denote˜ωk=ωn+...+ωk.The following theorem states the low density limit of the truncated correlation functions.Theorem1One has the limit in the sense of distributions in variables t1,...,t n:lim ε→0W Tε,ˆn,T1,ω1,...,T n,ωn(t1,...,t n)=(2π)n−1δ(t2−t1)...δ(t n−t n−1)×δ˜ω1,0d E Tr ˆn P E+˜ω1T1P E+˜ω2T2...P E+˜ωn T n (4)where Tr denotes trace andδ˜ω1,0is the Kronecker delta symbol.The theorem is a corollary of Theorem2from Section3.3.THE NON-TRIVIAL DIAGRAMSIn the present section we investigate the low density limit of the non-chronologically ordered correlation functions for the particular case of operators of the form T l=|f l g l| andfind the diagrams which are non-trivial in the low density limit.In order to simplify the notations we will use the following energy representation for the creation and annihilation operators:A+ l :=e i t l E l/εεA+(P Elf l);A l:=1εA(S tl/εg l)(a slightly different version of the energy representation was introduced in7).One hasN Tl,ωl,ε(t l)=e−i t lωl/ε d E l A+l A l.Notice that the operator A+l is not the adjoint of A l.The symbols A l,A+lare used only to simplify the notations below.A multitime correlation function can be expressed using Gaussianity of the state ωˆn and the energy representation for the creation and annihilation operators asWε,ˆn,T1,ω1,...,T n,ωn(t1,...,t n)=exp −i n l=1ωl t l/ε ′ d E1...d E nωεˆn(A+i1A j1)...×ωεˆn(A+i k A j k)ωεˆn(A j k+1A+i k+1)...ωεˆn(A j n A+i n)(5) where ′is the sum over k=1,...,n,1=i1<i2<...<i k,j k+1<...<j n,i l≤j l for l=1,...,k and j l<i l for l=k+1,...,n.The sum contains terms of the formωεˆn(A+i1A j1)...ωεˆn(A+ikA jk)ωεˆn(A jk+1A+ik+1)...ωεˆn(A jnA+in)(6)To each such term we associate a diagram by pairing in the string A+1A1A+2A2...A+n A nthe operators A+il and A jlfor l=1,2,...n.Definition3We say that the expression(6)corresponds to a reducible diagram if there exists a nonempty subset I⊂{1,...,n}(strict inclusion)such that i l∈I⇔j l∈I. Otherwise we say that the expression(6)corresponds to an irreducible diagram.An important property of the truncated correlation functions(Def.2)is that they keep only all irreducible diagrams.The following are the examples of irreducible(first) and reducible(second)diagrams for n=2:A+1A1A+2A2A+1A1A+2A2(7) Given an reducible diagram,one can represent the set{1,...n}as a union of several disjoint subsets I1,...,I l such that the diagram contains only pairings between operators with indices from the same subsets.In this sense a general reducible diagram can be represented as a union of mutually disjoint irreducible diagrams.Examples of the truncated correlation functions,the corresponding irreducible diagrams,and their limits asε→0for n=1,2,3are given below.Example1n=1.The invariance of the state under the free evolution leads to the identity W Tε(t)≡Wε(t)≡Wε(0)= g1,ˆn f1 .Example2n=2.One hasW Tε(t1,t2)=Wε(t1,t2)−Wε(t1)Wε(t2)= d E1d E2ωεˆn(A+1A2)ωεˆn(A1A+2)= d E1d E2e i(t2−t1)(E2−E1)/εExample 3n =3.One hasW T ε(t 1,t 2,t 3)=d E 1d E 2d E 3 ωεˆn (A +1A 3)ωεˆn (A 1A +2)ωεˆn (A 2A +3)+ωεˆn (A +1A 2)ωεˆn (A 1A +3)ωεˆn (A +2A 3) This expression corresponds to the sum of the two irreducible diagrams:A +1A 1A +2A 2A +3A 3+A +1A 1A +2A 2A +3A 3In this case only the first diagram is non-zero in the limit and Lemma 1giveslimε→0W T ε(t 1,t 2,t 3)=(2π)2δ(t 3−t 2)δ(t 2−t 1) d E g 3,P E ˆn f 1 g 1,P E f 2 g 2,P E f 3 The case of arbitrary n is described by the following theorem.Theorem 2Let T l =|f l g l |,where f l ,g l ∈H for l =1,2,...,n .One has the limit in the sense of distributions in variables t 1,...,t n :lim ε→0W T ε,ˆn ,T 1,ω1,...,T n ,ωn (t 1,...,t n )=(2π)n −1δ(t 2−t 1)...δ(t n −t n −1)×δ˜ω1,0 d E g n ,P E ˆn f 1 g 1,P E +˜ω2f 2 ... g n −1,P E +˜ωn f n (9)For each n only the following irreducible diagram is non-zero as ε→0:εg j β,(1+εˆn )f i βone can write (6)as1εnexp i t n (E n −E αn )+...+t 1(E 1−E α1) ε εk F (E )+O (εk +1)and with the notations Ωl (E )=E n +...+E l −E αn −...−E αl for l =2,...,n as e i(t n −t n −1)Ωn (E )/εε εk −1F (E )+O (εk ) (12)If the expression(6)corresponds to an irreducible diagram then the functionsΩl(E) are linearly independent and,since they are linear in their arguments,the convolution δ(Ω2(E))...δ(Ωn(E))is well defined.In the case k>1,since for any l=2,...,n(see Lemma1):limε→0e i(t l−t l−1)Ωl(E)/εε...e i(t2−t1)Ω2(E)/εε...e i(t2−t1)(Ω2(E)−˜ω2)/εLet A be the algebra generated by the free white noise operators N T(t)and letφˆn be the state on A characterized byφˆn(N T(t))=Tr(ˆn T).Theorem3One has the equalitylim ε→0W Tε,ˆn,T1,0,...,T n,0(t1,...,t n)=φˆn(N T1(t1)...N Tn(t n))(16)Proof.By direct calculations using the Eq.(4)and the relation(15).The existence of the representation of the limiting truncated correlation functions by the free white noise number operators is related to the fact that only a sub-class of the non-crossing irreducible diagrams survives in the low density limit.We emphasize however,that the l.h.s.of Eq.(16)is the limit of a truncated correlation function whereas the r.h.s.contains the complete correlation function.5.INDEPENDENCE AND THE GENERALIZED POISSON STATISTICS IN THE LDLThe fact that the limiting truncated correlation functions are the distributions in variables t1,...,t n with support at t1=...=t n leads to the appearance of independent subalgebras in the low density limit.In the beginning of this section we remind the basic notions of independent subalgebras and of cumulants.Then wefind the asymptotically independent subalgebras of Aεand discuss the limiting statistics.We show that the cumulants and the moments of certain elements in the algebra Aεin the low density limit coincide with the cumulants and the moments of the Poisson distribution.Definition5Let(A,ω)be a∗-probability space.A family of unital∗-subalgebras {A i}i∈I,A i⊂A,is called independent ifω(a1...a n)=0whenever a l∈A i l,ω(a l)=0,and k=l implies i k=i l.Definition6Let(A,ω)be a∗-probability space.Cumulants of the space(A,ω)are the multilinear functionalsκn:A n→C,n≥1,uniquely determined byκ1(a):=ω(a),a∈A,and for n>1by induction through the relation:ω(a1...a n)=π,π=:{A1,...,A k}κ|Aj|((a1,...,a n)|A j)where the sum is over all partitionsπof the set{1,...,n}and”(a1,...,a n)|A”designates the set of a i with i∈A.Remark3The cumulantsκ(ε)n for a∗-probability space(Aε,ωεˆn)are directly related tothe truncated correlation ly,if a1=N T1,ω1,ε(ϕ1),...,a n=N Tn,ωn,ε(ϕn),thenκ(ε)n(a1,...,a n)=W Tε,ˆn,T1,ω1,...,T n,ωn(ϕ1,...,ϕn).For the analysis of independence in the low density limit we introduce the notion of asymptotically independent subalgebras for a∗-probability space(Aε,ωεˆn).Definition7Let(Aε,ωεˆn)be a∗-probability space for the LDL.We say that a family of subalgebras A1,ε,...,A l,εof Aεis asymptotically independent iflimε→0ωεˆn(a1,...,a n)=0whenever a l∈A i l,ε,ωεˆn(a l)=0,and k=l implies i k=i l.The next theorem identifies asymptotically independent subalgebras of Aε. Theorem4LetΛ1,...,Λl be a family of disjoint open subsets in R.Then the familyof subalgebras AΛ1,ε,...,AΛl,εis asymptotically independent.The proof follows from the fact that the truncated correlation functions become in the limit asε→0distributions in variables t1,...,t n with support at t1=t2=...=t n.Now let us analyze the statistics which appears in the low density limit.From Theorem1and the relation between the cumulants and the truncated correlation functions it follows that l-th cumulant for the element a=N T,ω,ε(ϕ)in the limit has the formκl(a,...,a)=limε→0W Tε,ˆn,T,ω,...,T,ω(ϕ,...,ϕ)=1|k||k′|)−1χ[0,√λ](|k′|),whereλis a positive number andχ[0,√λ].Letϕ0(t)=(2π)−1χ[0,2π](t).Theorem5Let aλ=N Tλ,ω,ε(ϕ0),where Tλandϕ0are defined as above.Then for anyl∈N one hasκl(aλ,...,aλ)=λδω,0or equivalently,the cumulants of the element aλwithω=0coincide in the low density limit with the cumulants of the Poisson distribution with expectation equal toλ. Proof.The proof of the theorem is based on the direct calculation of the cumulants using Eq.(17).One has1E,√λ](√Moments of the element aλwithω=0in the low density limit are equal to the sum over all partitions of the limiting cumulants and given by Touchard polynomials:lim ε→0ωεˆn(a nλ)=nk=1S(n,k)λkwhere S(n,k)is a Stirling number of the second kind,i.e.,the number of partitions of a set of size n into k disjoint non-empty subsets.The limiting moments coincide with the moments of the Poisson distribution with expectation equal toλ.For a1one has limε→0ωεˆn(a n1)=B nwhere B n is the n-th Bell number,i.e.,the number of partitions of a set of size n.The Bell numbers are the moments of the Poisson distribution with expectation equal to1.6.AN OPERATOR REPRESENTATION OF THE LIMITING CORRELATION FUNCTIONSIn the present section we explicitly realize the limiting correlation functions as correlation functions of certain operators acting in a suitable Hilbert space.Presence of delta functions in the limiting correlation functions suggests that they can be represented as correlation functions of certain white noise operators.Here such a representation is constructed in the special case using the results of7.Let g0,g1∈H satisfy the condition g0,S t g1 =0for any t∈R.Define for n,m=0,1the Hilbert space K nm:=L2(Spec H1,dµnm),where Spec H1⊂R is the spectrum of H1and dµnm:= g n,P E g n g m,P Eˆn g m d E.Let K:= n,m=0,1K nm and let H W N:=Γ(L2(R,K))be the symmetric Fock space over the Hilbert space of square integrable K-valued functions on R(abbreviation WN here stands for White Noise). Using the natural decomposition H W N= n,m=0,1Γ(L2(R,K nm))one can define the creation and annihilation operator valued distributions B±m,n(E,t)acting in H W N and satisfying the canonical commutation relations:[B−m,n(E,t),B+m′,n′(E′,t′)]=2πδ(t′−t)δ(E′−E) g m,P E g m′ g n′,P Eˆn g n (18) The operator valued distributions B±m,n(E,t)are called time-energy quantum white noise due to the presence ofδ(t′−t)δ(E−E′)in(18).Let define the number operators˜Nm,n(E,t):= n′=0,11Proof.r.h.s.of(19)has the formΩ,N g m1,g n1(t1)...N g m k,g n k(t k)Ω =d E1...d E k Ω,[˜N m1,n1(E1,t1)+B−n1,m1(E1,t1)+B+m1,n1(E1,t1)]...[˜N mk,n k(E k,t k)+B−nk,m k(E k,t k)+B+mk,n k(E k,t k)]ΩLet us denote˜N m,n(t):= d E˜N m,n(E,t).The truncated correlation function corresponds to the termd E d E′ Ω,B−n1,m1(E,t1)˜N m2,n2(t2)˜N m3,n3(t3)...˜N m k−1,n k−1(t k−1)B+m k,n k(E′,t k)Ω (20)Notice that˜N m,n(t)Ω=0.Therefore(20)equals tod E d E′ Ω,[...[[B−n1,m1(E,t1),˜N m2,n2(t2)],˜N m3,n3(t3)]...˜N m k−1,n k−1(t k−1)]B+m k,n k(E′,t k)ΩThe commutators can be calculated by induction using the canonical commutation relations(18).The result is(2π)k−2δ(t2−t1)...δ(t k−1−t k−2)d E d E′ g n1,P E g m2 ... g n k−2,P E g m k−1× Ω,B−n k−1,m1(E,t k−1)B+m k,n k(E′,t k)Ω (21) The last two-point correlation function can be calculated using the commutation relations(18).This gives for(21)the expression(2π)k−1δ(t2−t1)...δ(t k−t k−1)d E g n1,P E g m2 ... g n k−1,P E g m1 g n k,P Eˆn g m1which coincides with the r.h.s.of(9)in the caseω1=...=ωk=0. Remark4The limiting correlation functions could be represented as expectations of certain quantum white noise operators in the general case if one could construct a Hilbert space H W N,a vectorΩ∈H W N,and operator valued distributions B±f,g(E,t) and˜N f,g(E,t)in H W N with the property B−f,g(E,t)Ω=˜N f,g(E,t)Ω=0and satisfying the commutation relations[B−f,g(E,t),B+f′,g′(E′,t′)]=2πδ(t′−t)δ(E′−E) f,P E f′ g′,P Eˆn g (22)[B−f,g(E,t),˜N f′,g′(E′,t′)]=2πδ(t′−t)δ(E−E′) f,P E f′ B−g′,g(E,t)(23)[˜N f,g(E,t),˜N f′,g′(E′,t′)]=2πδ(t′−t)δ(E′−E)[ g,P E f′ N f,g′(E,t)− g′,P E f N f′,g(E,t)](24) Suppose there exist such operators.Define N f,g(t):= d E[˜N f,g(E,t)+B−g,f(E,t)+B+f,g(E,t)].Then one can prove exactly in the same way as in Theorem6thatlim ε→0Wε,ˆn,|f1 g1|,0,...,|f n g n|,0(t1,...,t n)= Ω,N f1,g1(t1)...N fn,g n(t n)ΩACKNOWLEDGEMENTSThe author is grateful to Luigi Accardi for useful discussions and for kind hospitality inthe Centro Vito Volterra of Rome University”Tor Vergata”where a significant part ofthis work was done.Special thanks to an anonymous referee for several suggestionsimproving the quality and content of the paper.The author acknowledges partialsupport from the grant RFFI-05-01-00884-a.APPENDIX AHere we make a connection between the objects defined in section II and the model ofa test particle interacting with a dilute Bose gas(see Ref.9for details).The one particle Hilbert space for this model has the form H≡L2(R3),where R3is the3-dimensional coordinate or momentum space.The one particle free evolutionis a unitary group S t≡e i tH1whose generator H1in the momentum representation is the multiplication operator by the functionω(k)=|k|2/2m,where m is the massof a gas particle.The test particle is characterized by its Hilbert space H S and itsfree Hamiltonian H S acting in H S which is assumed to have a discrete spectrum.Thediscrete set B is the set of all transition frequencies of the test particle,or equivalently,the spectrum of its free Liouvillean−i[H S,·].The dynamics of a test particle interacting with a gas is described by an evolutionoperator U(t)acting in H S⊗Γ(H)and satisfying in the interaction picture,after the time rescaling t→t/ε,the following Schr¨o dinger equationd U(t/ε)Lemma1One has the limit in S′(R)×S′(R)limε→0e i tx/εεf(x)φ(t)=limε→0 dτφ(ετ)d xe iτx f(x)=limε→0 dτφ(ετ)˜f(τ)Since˜f∈S(R),the functionφ(ετ)˜f(τ)satisfies the conditions of the Lebesgue lemma which allows to exchange the limit and integration in the last expression.Thus I=φ(0) dτ˜f(τ)=2πφ(0)f(0) 1H.Spohn and J.L.Lebowitz,Adv.Chem.Phys.38,109(1978).2H.Spohn,Rev.Mod.Phys.52,569(1980).3R.D¨u mcke,Comm.Math.Phys.97,331(1985).4L.Accardi,Y.G.Lu,and I.V.Volovich,Quantum Theory and Its Stochastic Limit (Springer,Berlin,2002).5L.Accardi and Y.G.Lu,Comm.Math.Phys.141,9(1991).6S.Rudnicki,R.Alicki,and S.Sadowski,J.Math.Phys.33,2607(1992).7L.Accardi,A.N.Pechen,and I.V.Volovich,J.Phys.A:Math.Gen.35,4889(2002). 8L.Accardi,A.N.Pechen,and I.V.Volovich,Infinite Dimen.Anal.,Quantum Probab.,Relat.Top.6,431(2003).9A.N.Pechen,J.Math.Phys.45,400(2004).10D.V.Voiculescu,K.J.Dykema,and A.Nica,Free Random Variables CRM monograph series1,American Mathematical Society,1992.11D.Voiculescu,Lectures on Free Probability Theory,Lecture Notes in Math.1738, 279–349(Springer,Berlin,2000).12L.Accardi,Y.G.Lu,and V.Mastropietro,Infinite Dimen.Anal.,Quantum Probab., Relat.Top.1,467(1998).13L.Accardi,I.Ya.Aref’eva,and I.V.Volovich,Proc.Steklov Inst.Math.228,106 (2000).14J.Andries,F.Benatti,M.De Cock,and M.Fannes,Rev.Math.Phys.12,921(2000). 15N.N.Bogoliubov,A.A.Logunov,A.I.Oksak,and I.T.Todorov,General Principles of Quantum Field Theory(Dordrecht,Boston,Kluwer Academic Publishers,1990).。
