《超级英雄》罗杰限时回归 金卡、红卡大放送
(自制)最最全面的WII游戏大全
0001 - Wario Ware Smooth Moves - 瓦里奥制造平滑移动0002 - Tony Hawks Downhill Jam - 托尼霍克滑板0003 - The Legend Of Zelda Twilight Princess - 塞尔达传说黎明公主0004 - Super Monkey Ball Banana Blitz - 超级猴子球香蕉闪电战0005 - Red Steel - 赤铁0006 - Rapala Tournament Fishing - 垂钓之旅0007 - Rayman Raving Rabbids/Rabbids Party - 雷曼疯狂兔子0008 - Marvel Ultimate Alliance - 漫画英雄联盟0009 - Kororinpa - 穿越迷地0010 - GT Pro Series - GT职业赛车0011 - Excite Truck - 疯狂卡车0012 - Elebits - 能源小精灵0013 - Cooking Mama - 烹饪老妈0014 - Call Of Duty 3 - 使命召唤30015 - Barnyard - 疯狂农庄0016 - Chicken Little Ace In Action - 四眼天鸡动作天王0017 - Ennichi no Tatsujin - 庙会达人0018 - Far Cry Vengeance - 孤岛惊魂复仇0019 - Ice Age 2 The Meltdown - 冰川时代2 消融0020 - Need For Speed Carbon - 极品飞车碳元素0021 - Sonic and The Secret Rings - 索尼克与神秘指环0022 - Super Swing Golf - 魔法高尔夫0023 - Madden NFL 07 - 美式橄榄球大联盟 070024 - Wii Sports - Wii运动0025 - Wii Play/Hajimete no Wii - 初次见面Wii0026 - Spongebob Squarepants Creature from Krusty Krab - 棉球方块历险记0027 - Rampage Total Destruction - 怪兽大破坏0028 - Monster 4x4 World Circuit - 怪物四驱世界巡回赛0029 - Splinter Cell Double Agent - 分裂细胞双重间谍0030 - Trauma Center Second Opinion - 超执刀再次执刀0031 - Super Fruit Fall - 超级水果瀑布0032 - Gottlieb Pinball Classics - 经典弹珠台0033 - Happy Feet - 快乐大脚0034 - Open Season - 狩猎季节0035 - Cars - 汽车总动员0036 - Avatar The Legend Of Aang - 降世神通最后的空气大师0037 - Metal Slug Anthology - 合金弹头精选集0038 - The Ant Bully - 别惹蚂蚁0039 - The Grim Adventures of Billy and Mandy - 企鹅也疯狂0040 - World Series of Poker Tournament of Champions 2007 Edition - 世界扑克冠军联赛20070041 - Dragon Ball Z Budokai Tenkaichi 2 - 龙珠Z 电光火石 20042 - SD Gundam Scad Hammers - SD高达革命0043 - Pokemon Battle Revolution - 口袋妖怪战斗革命0044 - Crayon Shinchan Saikyou Kazoku Kasukabe King Wii - 蜡笔小心最强家族春日部之王0045 - Necro Nesia/Escape From Bug Island - 巨虫魔岛0046 - Mahjong Taikai Wii - 麻将大赛Wii0047 - Bleach Wii Shiraha Kirameku Rinbukyoku - 死神 Wii白刃闪烁的轮舞曲0048 - Tamagotchi no Pikapika Daitoryo/Tamagotchi Party On Wii - 电子鸡宠物店0049 - Wing Island - 翼神之岛0050 - Fire Emblem - Akatsuki no Megami - 火炎纹章晓之女神0051 - Naruto Shippuuden Gekitou Ninja Taisen EX/Naruto Clash of Ninja Revolution - 火影忍者疾风传激斗忍者大战 EX0052 - SSX Blur - 极限滑雪0053 - Densha de GO Shinkansen EX Sanyou Shinkansen Hen - 电车Go!新干线EX 山阳新干线0054 - Eyeshield 21 Field no Saikyou Senshi Tachi - 光速蒙面侠21 赛场上的最强战士们0055 - Bomberman Land - 炸-弹人大陆0056 - Tiger Woods PGA Tour 07 - 泰格伍兹高尔夫巡回070057 - GI Jockey Wii - G1骑师Wii0058 - The Godfather Blackhand Edition - 教父黑手党0059 - Teenage Mutant Ninja Turtles - 忍者神龟旋风再起0060 - Puzzle Series Vol. 1 Sudoku - 解谜系列Vol.1 数独0061 - Sangokushi XI with Power Up Kit - 三国志11 威力加强版0062 - Blazing Angels Squadron Of WWII - 炽天使二战空骑兵0063 - Medal Of Honor Vanguard - 荣誉勋章先遣部队0064 - Disneys Meet the Robinsons - 迪斯尼拜访鲁滨逊一家0065 - Heatseeker - 热导追踪0066 - Prince Of Persia Rival Swords - 波斯王子宿敌之剑0067 - Mezase Tsuri Master - 目标!钓鱼王0068 - Super Paper Mario - 超级纸片马里奥0069 - Furu Furu Park - 摇摆回转公园0070 - Bust-A-Move BASH - 泡泡龙0071 - The Dog Island Hitotsu no Hana no Monogatari - 狗狗小岛花之物语0072 - One Piece Unlimited Adventure - 海贼王终极冒险0073 - Wii de Yawaraka Atama Juku/Big Brain Academy Wii Degree - 头脑柔软训练补习班0074 - Bionicle Heroes - 乐高生化战士0075 - Legend of the Dragon - 龙之传说0076 - Spider Man 3 - 蜘蛛侠30077 - Pirates of the Caribbean At World's End - 加勒比海盗世界的尽头0078 - Shrek the Third - 怪物史莱克30079 - Detective Conan Tsuioku no Gensou/Case Closed - One Truth Prevails The Mirapolis Investigation - 名侦探柯南追忆的幻想0080 - Mario Strikers Charged Football - 马里奥激情足球0081 - Sammys Collection Hokuto no Ken - 实战柏青哥·柏青嫂必胜法!Sammy合集北斗神拳Wii0082 - Mercury Meltdown Revolution/Tama Run - 水银溶化革命/水银溶化0083 - Mortal Kombat Armageddon - 真人快打0084 - Mario Party 8 - 马里奥聚会80085 - Biohazard 4 Wii Edition/Resident Evil 4 Wii Edition - 生化危机4 Wii版。
伯朗特操作说明书

超级英雄攻略技巧12.16

攻略(干货!重点!)新手嘛自然是玩新服比较好一点。
环境相对公平,起点一致,下面讲讲新服攻略。
不管是不是RMB玩家玩的顺一点少化点冤枉钱。
这游戏只要冲一次满天星就能玩会玩的还是去开启了同步的服务器比较好,钱比较值钱,各种英雄来的快。
充值技巧(不充可无视)不要一次冲完。
看你想充多少如果你充200,那请你第一天充一个98的第二天充一个68的第三天一个30的第四天一个月卡。
如果你是400档的就第一天换成198的,后面还是一样。
这个游戏每档充值都有首充。
而且每天充值30块都有豪华签到送免费的万能橙卡。
小R先买个月卡,然后礼包买奥创和斑一起升级。
斑练好了,练奥创-建议二转,换到六道之后可以把澳创换成六道,或者一起上。
然后攒钻满天星中R月卡,一个斑,然后每天6元豪华签到,换哈迪斯。
建议购买成长计划,一元=100钻。
然后攒钻满天星大R直接激活648.首冲双倍。
1.3W,然后购买成长计划128,月卡30月卡:120钻/天任务:200钻/天。
每天豪华签到,最低消费6元,激活充值有礼,还可以拿哈迪斯。
一天是66+168=234钻/天。
20天后满天星。
20*554+12960=2.4W钻总花费:806元满天星的档次28→280→880→2800→8800→18000→280001.8W无忧,然后2.4不够最后一次怎么办!?别忘了成长计划,还有升级,刷塔,竞技场,在线,关卡等各种奖励加上满天星转出来的。
2.8W 绝对够。
上了一次满天星,至少能有4W钻。
一次满天星,上一次活动(最好同步后,同步更值),一个月一次,3个月队伍就成形了。
转盘,海贼,招募,然后就是最强直接凑最终国家队,什么希腊,中国。
先练斑,6天后拿到哈迪斯。
随你喜欢练哪一个,记住一个个来。
土豪什么不说了,各种首冲翻倍,这卡那卡。
我们做个朋友吧!私信我啊,求带。
给一般玩家的建议:一、斑爷!对于我等广大平民必备神卡,获得方法:1.你去看看聊天里的广告,肯定有推广的,加群,按他的要求领到礼包。
Marvel与DC超级英雄商品详情说明书

Marvel: Captain Marvel Enamel Pin and Magnets9780762479993RP Minis$12.95 USD Marvel: Iron ManLight-Up Metal Helmet9780762475742RP Minis$14.95 USD Marvel: Light-Up Black Panther9780762478675RP Minis$13.95 USD Marvel: Thor Mjolnir9780762475711RP Minis$14.95 USDThe DC Book of Lists9780762472840Running Press Adult$24.00 USDWonder Woman:Chronicles of the Amazon Princess9780762468294Running Press Adult$20.00 USD Wonder Woman:Magnets, Pin, and Book Set9780762468324RP Minis$12.95 USDWonder Woman:You're Amazing!9780762467105RP Studio$12.00 USDWonder Woman Talking Figure and Illustrated Book9780762456949RP Minis$12.95 USDHarley Quinn Talking Figure and Illustrated Book9780762474684RP Minis$13.95 USD The Joker Talking Bust and Illustrated Book9780762494088RP Minis$12.95 USDWonder Woman Tiara Bracelet andIllustrated Book9780762458639RP Minis$9.95 USD Superman: Collectible Figurine and Pendant Kit9780762449088RP Minis$9.95 USD Justice League:Morphing Magnet Set9780762469840RP Minis$12.95 USD Marvel: The Amazing Spider-Man Light-Up Radioactive Spider9780762484355Running Press Adult $39.95 USDMarvel: Hulk Smash Button : With SmashingSound Effect 9780762484379RP Minis$13.95 USDMarvel: The Amazing Spider-Man Light-Up Spider-Signal9780762484362RP Minis$14.95 USDBatman: Chronicles of the Dark Knight9780762493210Running Press Adult $20.00 USD Batman: MetalDie-Cast Bat-Signal9780762462162Running Press Adult$42.95 USDCuphead BobblingFigurine9780762479313RP Minis$13.95 USD FORTNITE (Official):How to Draw 29780316704069L BYR$8.99 USDFORTNITE (Official)Loot Pack9780762468317RP Minis$9.95 USDFORTNITE (Official):The Chronicle9780316530279LBYR$12.99 USDThe Last Wish9780316333528Orbit$40.00 USDRuination9780316469050Orbit$28.00 USDFight, Magic, Items9780762479634Running Press Adult$17.99 USDMonster Kids9780762479504Running Press Adult$17.99 USDGamer Girls9780762474561Running Press Kids$17.99 USDA Kid's Guide toFandom9780762498758Running Press Kids$17.99 USDGeeky Baby's Guide toColors9780762470990Running Press Kids$8.99 USDStrange and Unsung All-Stars of the DCMultiverse: A Visual Encyclopedia9780762483440Running Press $27.00 USDPeacemaker Light-UpMetal Helmet9780762484645RP Minis$14.95 USDDungeons & Dragons:How to Be More D&D9780762478873Running Press Adult$18.00 USDDungeons & DragonsForgotten RealmsPoster Book9780762479016RP Studio$13.99 USDDungeons & Dragons:Mini Dice Dungeon9780762475919RP Minis$13.95 USDDungeons & Dragons:Beholder Figurine9780762478866RP Minis$13.95 USDDungeons & Dragons:Bag of Holding MagnetSet9780762475902RP Minis$9.95 USD。
魔法卡片数据20160808【含奖励】
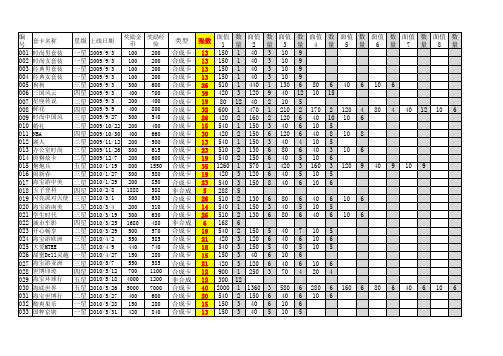
星级 三星 二星 一星 二星 三星 二星 二星 二星 二星 五星 二星 四星 四星 四星 二星 三星 四星 二星 四星 二星 二星 二星 四星 五星 四星 三星 四星 四星 四星 二星 三星 五星 五星 二星
上线日期 奖励金币奖励经验 类型 张数 面值1数量面值2数量面值3数量面值4数量面值5数量面值6 数量面值7数量面值8数量 2010/6/25 660 510 合成卡 20 420 2 120 6 40 6 10 6 2010/6/29 230 300 合成卡 16 540 1 150 3 40 6 10 6 2010/7/12 480 480 合成卡 15 150 3 40 6 10 6 2010/7/23 130 200 合成卡 14 250 2 70 6 20 6 2010/7/26 300 630 合成卡 26 510 2 130 6 80 6 40 6 10 6 2010/7/29 400 600 合成卡 20 540 2 150 6 40 6 10 6 2010/7/29 320 520 合成卡 15 540 2 150 4 40 4 10 5 2010/8/3 220 300 合成卡 15 540 1 150 3 40 5 10 6 2010/8/13 340 540 合成卡 18 540 2 150 4 40 6 10 6 2010/8/19 3950 5650 合成卡 38 1850 2 580 6 480 6 160 6 80 6 40 6 10 6 2010/8/20 330 520 合成卡 17 540 2 150 4 40 5 10 6 2010/9/1 650 1100 合成卡 29 780 1 320 2 210 5 120 10 40 4 10 7 2010/9/8 450 800 合成卡 34 580 2 260 3 120 9 80 4 40 10 10 6 2010/9/14 588 1288 非合成卡 5 198 5 2010/9/14 360 550 合成卡 18 540 2 150 5 40 6 10 5 2010/9/19 600 1100 合成卡 26 540 2 150 6 80 6 40 6 10 6 2010/9/25 588 1288 非合成卡 6 198 6 2010/9/26 300 500 合成卡 13 240 4 150 1 40 3 10 5 2010/10/22 1031 666 非合成卡 10 98 10 2010/11/2 450 250 合成卡 14 240 2 150 3 40 4 10 5 2010/11/8 500 300 合成卡 21 240 2 150 3 40 7 10 9 2010/11/15 550 350 合成卡 16 540 1 150 3 40 6 10 6 2010/11/18 1125 666 非合成卡 5 200 5 2010/11/23 2750 3500 合成卡 36 1180 2 480 5 340 5 160 5 80 6 40 6 10 7 2010/12/7 600 900 合成卡 29 1230 1 340 3 160 3 80 6 40 8 10 8 2010/12/9 1225 666 非合成卡 7 166 7 2010/12/22 800 1400 合成卡 30 540 3 410 3 240 3 150 7 40 7 10 7 2011/1/13 888 1666 合成卡 34 2011 1 588 3 280 4 150 4 40 11 10 11 2011/1/17 1888 688 非合成卡 7 288 7 2011/1/17 280 400 合成卡 18 540 2 150 4 40 6 10 6 2011/1/24 300 630 合成卡 26 510 2 130 6 80 6 40 6 10 6 2011/1/24 3900 5600 合成卡 37 1850 2 580 5 480 6 160 6 80 6 40 6 10 6 2011/2/23 3500 5000 合成卡 42 1850 2 580 3 480 5 160 8 80 8 40 8 10 8 2011/3/15 400 280 合成卡 19 540 1 150 5 40 5 10 8
《复仇者联盟》:英雄的集结,正义的胜利

《复仇者联盟》:英雄的集结,正义的胜利《复仇者联盟》是一部充满魅力的超级英雄电影系列。
影片中,一群天赋异禀、力量超凡的超级英雄集结在一起,为保卫地球而战。
他们携手合作,以拯救人类为己任,在正义与邪恶之间展开了一场激动人心的战斗。
在这个宇宙中,多样的超级英雄们各自拥有独特的能力和特殊的背景。
钢铁侠托尼·斯塔克机智聪明,凭借先进的科技武装自己,成为了一个活生生的铁人。
美国队长史蒂夫·罗杰斯是二战时期最优秀的士兵,通过接受超人药剂的改造成为美国队长,他坚定的意志力和无畏的英雄行动赢得了人们的尊敬。
雷神索尔则来自阿斯加德,他拥有强大的雷电之力,身披神铠,是一个灭顶之灾。
黑寡妇和鹰眼都是训练有素的间谍和顶尖战士,他们的敏锐和机智使他们成为不可或缺的团队成员。
而无法控制自己的浩克博士,以及机械天才小辣椒和维度能力超群的奇异博士,更是为这个超级英雄团队增添了更多的色彩。
这些英雄们因为各自的目标和信念而相聚在一起。
他们共同面对的威胁是毁灭人类的邪恶力量,无论是来自外星的入侵者、符石的威胁还是由超级反派导演的阴谋。
虽然每个英雄都有自己的个人问题和挑战,但他们懂得只有通过团队合作,才能最大化地发挥各自的力量与能力。
正是因为他们的团结一心,他们才能在危机关头,保护地球不受任何威胁。
《复仇者联盟》的魅力不仅在于其刺激的剧情和精彩的特效,更在于其揭示的一些人性的真相。
超级英雄们不仅是拥有超能力的角色,他们也是普通人,有着情感、矛盾和内心挣扎。
《复仇者联盟》中的英雄们有时候会犯错,会有争吵和分歧,但在面临共同的威胁时,他们能够团结一致,超越个人利益和矛盾,为了共同的目标而战斗。
这无疑给我们传达了一个重要的信息:只有在团结和合作的基础上,才能真正实现目标的突破,而不能仅仅依靠个人的力量。
除了对超级英雄们外,影片中也给我们展示了一些深度的主题。
例如,《复仇者联盟》关注的问题之一是权力的正确使用。
钢铁侠曾经因为个人的贪欲而落入了大反派洛基的陷阱,美国队长也曾怀疑政府对于超级英雄的掌控。
Super Star钢琴谱五线谱 完整版原版

>
35
!!
t
ttt
tt
ttttt
d tY
ttttt
d Yt
ttttt
d Yt
? !! Ðt t t t t t t t Ðt t t t t t t t Ðt t t t t t t t Ðt t t t t t t t
Page 3/Total 4
>
39
!!
tttt|
|Ç
tt tt Ett tt tt tt tt tt
t
t
t
t
t
t
Ð
>
19
!!
tt
tt tt tt
tt tt tt tt tt tt tt
tt tt tYt tt
tYt t t t t
? !!
|t t
t
t
| t
ttt
|ttt Ðt
|t t
t t
|t Ðt
t
t
| t
ttt
>
22
!!
|
tt tt 1. b
c tttt tttt tttttttttttt ¿
t bÇ
t t
t t
t t
d
t Yt
t t
t t
t t
t t
t t
t t
c tt t tt
ttt ttt
d
t Yt
ttt ttt
d
t Yt
>
28
!!
? !!
d Yt t t t t c
ttt d ttt
t Yt
ttt ttt ttt ttt
朗文supertots教材体系说明

视情幼儿英语SuperTots教材体系第一:教材内容总体教材分为三个级别,六册:1a, 1b,2a,2b, 3a,3b.●每个级别8个单元(配有8个自选手工活动)第一级围绕Beth认识小猫Sammy的故事展开。
第二级围绕孩子们出行游玩展开。
第三级围绕孩子们和祖母的探险故事展开。
●每个单元分为5个环节故事、对话、单词、TPR、语音(从1a第四单元开始)跨学科(从3a开始)●每个教学环节的特点Talk aboutit!(Storytime)1. 故事时间:看故事的标志2. 介绍主角,延续前一单元的故事3. 有语气的讲故事(图中发生的内容和人物的对话)4. 利用教辅材料(可爱的大图,吸引学生的注意力、引发学习动机,图中包含暗藏新学单词、相关肢体动作、发音单词,及学过单词的小图片)Sing it! / Chant it!ﻫ(Vocabulary & Dialog)1. 唱歌时间:歌唱的标志2. 单元故事继续发展3. 可爱大图提供歌曲、对话及单词的情境4. 利用歌曲重复演练对话或单词,KTV 版提供更自由的练习方式5. 书写形式的句子帮助教师及家长复习语言,也提倡幼儿早期的阅读(认字)技巧6. 适量单词:4Whatis it?(Vocabulary)1. 单词时间:问号标志2. 单元故事继续延续3. 贴纸提供个人化练习(Personalization)Doit! (Action)1. 运动时间:运动小猫标志2. 四个肢体反应运动3. 书写形式的句子帮助教师及家长复习语言,也提倡幼儿早期的阅读(认字)技巧4. 透过Do it! 吟唱帮助幼儿提升听力技巧,更增加学习乐趣Say it! (Sounds)1. 语音时间:大小写字母标志2. 利用学过单词,呈现主要发音,再透过歌曲加深对声音及单词的练习3. 更多同音单词以小图片呈现,训练幼儿的听力技巧4. 声音相对应的字母呈现在26个字母中Use it!(Dialog& Recycling)1. 对话时间:讲话小猫标志2. 复习及延伸学过的对话3. 透过歌曲或吟唱加强演练Ican do it!1. 贴纸奖赏时间:欢呼小猫标志2. 主题性的设计总结学习重点3. 5 张贴纸评价学习成果4. 增强学习的信心和成就感Discover it!(Content Connection - L3)☐跨学科时间:探险小猫标志☐单元故事的延续☐照片呈现对话、单词及活动的情境☐书写形式的句子帮助教师及家长复习语言,也提倡幼儿早期的阅读(认字)技巧第二:教学理念1. EarlyChildhoodEducation☐调动多重感官学习眼睛看、鼻子闻、耳朵听、嘴巴尝、手摸☐创设情景、提供机会,在“做”中学好奇心⇒尝试⇒模仿☐引入故事情节认同主角、情境、吸收讯息☐采用多变化的活动年龄适合、动静交替☐采取不同方式重复演练、鹦鹉学习☐了解幼儿世界利用幼儿喜欢且熟悉的事物☐培养交际能力礼仪、道德☐设计适合年龄的活动自我认同、手部肌力技巧、智能技巧、语言发展2.Crafts:手工教学1. 手工时间:剪刀小猫标志2. 四节额外的手工课,与节日或单元主题相结合3. 学生用书后面附的手工素材指引帮助教师及家长轻松带领4. 真实图片呈现过程和成品手工活动的好处☐幼儿喜爱做手工☐建立手部肌力的发展☐幼儿自由发挥,激发想像力与创造力☐“做”中学英语☐产生成就感、认同感☐促进多元智能发展Before making crafts做手工前☐桌下铺报纸或垃圾袋☐桌上铺数层垃圾袋☐请幼儿穿塑胶围裙、旧围裙或衣服☐确保每个幼儿有足够的空间☐确保每个幼儿有一套自己的基本工具☐要准备一些共用的学具☐教师提前准备材料和用具After making crafts做手工后☐展示成果Show me your (bear).What coloris it? It’s (brown).What’s your (bear’s) name?(Teddy).Doyoulike your (bear)? Do youlike (Jacky’s bear)?Goodbye bear.☐进行机会教育(关爱家人、学会合作、分享等)☐使用指令性语言与肢体动作--Clean up. Cleanup. (song)--Put our things away.--Pick up the books (crayons/paper).After makingcraftsﻫ做手工后☐使用成果回到对话中做角色扮演☐装饰学校、教室最好的宣传随时复习☐妥善保存校内校外3.TPR--成功的教学法之一☐幼儿好动,无法长时间坐著,TPR将幼儿的精力用来学英语☐幼儿以口语回应的能力非常有限,TPR成功的让幼儿以肢体做出回应☐TPR 提供大量的听力练习,幼儿接收(Receptive)语言的能力远超过产出(productive)的能力☐帮助幼儿拓展以肢体学习的方式☐最适合个性害羞的幼儿☐获得成就感TPR教学步骤☐说出指令并示范动作☐请幼儿一起做☐说出第三个指令并示范动作☐随意更换三个指令的顺序☐增加第四个指令,同上步骤☐随意指定幼儿做特定动作☐打开课本,请幼儿听,并指出图片☐将图卡随意贴在黑板上,请幼儿再听一次,并指出图片☐I am a teacher!Game!TPR延伸活动☐Fast commands☐Teacher says☐Do asI say,notas Ido.☐Teacher, wrong!4.歌曲管理教室☐用于游戏或活动的背景音乐☐用于手工时的背景音乐☐集合幼儿的背景音乐☐交给幼儿礼仪☐常规歌曲:Hello!SongClean upsongGoodbyesong第三:三个级别的内容联系SuperTots 教学内容的变化和联系⏹话题复现⏹故事教学⏹教学板块⏹教学目标⏹教学组织形式话题的复现⏹从学生感兴趣和熟悉的话题入手⏹话题的不断重复⏹话题的不断深入⏹知识的扩展故事教学⏹主人公有所变化⏹故事情节更加生动,吸引学生⏹故事的连续性更强⏹故事的内容更加广泛⏹故事教学的目标有所提高教学板块。
复仇者联盟里都有谁

复仇者联盟里都有谁复仇者联盟是一支由漫威漫画创办的超级英雄团队,该团队由多位强大的英雄组成,每个成员都有着独特的能力和背景故事。
在漫威的电影和漫画中,这个团队经历了许多惊心动魄的战斗和冒险。
现在让我们来看看究竟有哪些英雄加入了复仇者联盟。
第一位成员是钢铁侠,即托尼·斯塔克。
他是一个富有的工业家和天才发明家,他设计了一套高科技装甲,使他成为了钢铁侠。
他的装甲赋予了他超人的力量和无人机的战斗能力,使他能够在战斗中取得巨大的优势。
接下来是美国队长,即史蒂夫·罗杰斯。
他是二战时期的一名士兵,接受了一个实验性的药物注射,使他变成了一个超级士兵。
美国队长以他的勇气、力量和领导才能而闻名,他经常扮演复仇者联盟的领导角色。
绿巨人浩克也是复仇者联盟的一员。
布鲁斯·班纳是一个生物物理学家,在一次实验中不慎暴露于放射线下,从而变成了浩克。
浩克以他的巨大力量和无止境的怒火而闻名,成为了一个无敌的战士。
尽管他控制自己的怒火非常困难,但他的力量在战斗中是无与伦比的。
雷神索尔也是复仇者联盟的成员之一。
他是阿斯加德王国的王子,他拥有强大的雷霆之力。
索尔是一个战士和领导者,他的战锤和超能力使他成为了无与伦比的战士。
复仇者联盟还拥有一些非人类成员,如黑寡妇和鹰眼。
黑寡妇是一个出色的斗士和间谍,她拥有出色的格斗技巧和隐藏在她身体内的特殊项目。
鹰眼是一位精通弓箭技巧的神射手,他能够以惊人的准确性攻击敌人。
除了以上成员外,还有其他一些英雄也加入了复仇者联盟。
例如,奇异博士是一位拥有魔法能力的神秘医生,他可以操控时间和空间。
蚁人可以缩小并获得巨大的力量,他的战斗方式与其他成员完全不同。
猩红女巫拥有超能力,可以操纵现实并使用心灵控制。
还有许多其他的英雄,他们都为复仇者联盟做出了重要的贡献。
总而言之,复仇者联盟是一个由多位强大的超级英雄组成的团队,每个成员都有着独特的能力和背景故事。
他们共同战斗,保护地球免受各种邪恶势力的威胁。
switch乐高复联攻略

switch乐高复联攻略前言当我们首次通关故事模式的时候,我们所收集到的人物已经基本可以满足故事模式的黄砖挑战和红砖收集了。
每一关都有5个黄砖挑战,1个红砖收集。
黄砖挑战一般内容为:(1)完成挑战(过关):一周目通了,我们都有这个黄砖了。
(2)收集零件(金钱):金钱显示在你屏幕的左上方,随着关卡的推进,要求收集的金钱会越来越多。
(3)完成收集品:每一关都有3个收集品,其中2个角色收集和1个红砖收集。
(4)和(5)为个性任务,下面会逐一提到并告诉你怎样完成。
这时候我们点击屏幕左下方的小地图,然后点击地图右上方的谜之图标,进入回顾模式。
一、Prologue(序章)角色、红砖收集:HYDRA Sokovia Trooper第一个山坡上,干掉4个士兵之后,登上第一个山坡,小屋前使用黑寡妇操纵电脑打开房门,角色在屋内。
Baron Strucker在一条狭窄山路的右面,有一道大门紧闭的山洞。
使用特工考森Coulson(Shades)形态,使用大炮将铁门轰炸,角色在山洞内。
红砖在绿巨人出现后,屏幕的左下方出现一辆吉普车,使用猩红女巫Scarlet Witch的特殊技能(按O)将吉普车摧毁,收集到红砖。
黄砖挑战4:美国队长盾牌快速反弹第一个场景中,4个远程敌人。
黄砖挑战5:最终场景破坏战车无伤通关。
使用无敌红砖或者快速使用L键达成美国队长和雷神的特殊级,即可剧情杀。
二、HYDRA Fortress(九头蛇基地)角色、红砖收集:HYDRA Trooper在钢铁侠刚刚飞入九头蛇基地后院的时候,他出现在屏幕左下方。
Iron Legion九头蛇基地最后场景,使用飞行角色到达大海兽的左上方平台后,使用猩红女巫开门后得到。
红砖九头蛇基地最后场景中,中间的大海兽头的下方隐藏着一个充电机,使用雷神充能即可。
黄砖挑战4:开场摧毁九头蛇基地外围8个防御设施。
黄砖挑战5:在控制室中使用导弹消灭所有敌人。
三、Loki's Escape(洛基的逃跑)角色、红砖收集:SHIELD Scientist第一个驱车追逐场景,出现在屏幕中间的位置,撞碎柱子收集到。
线上商城微信小程序使用说明 一站式小程序通用版操作说明书

VX小程序操作指南目录一、概述 (20)一、官网小程序 (22)1. 选择行业 (22)2. 概览 (22)3. 店铺管理 (23)3.1. 模板市场 (23)3.2. 装修店铺 (23)3.3. 小程序跳转 (29)3.4. 微页面 (29)3.5. 图片库 (30)3.6. 个人中心 (31)3.7. 地址管理 (31)3.8. 支付方式........................................................................... 错误!未定义书签。
3.9. 连接WIFI ......................................................................... 错误!未定义书签。
3.10. 链接公众号图文 (32)3.11. 分享 (32)4. 客户管理 (33)4.1. 客户管理 (33)4.2. 用户表单 (33)4.3. 会员管理 (37)二、电商小程序 (38)1. 商品管理 (38)1.1. 商品管理 (38)1.2. 新建商品 (39)1.3. 商品分组 (41)1.4. 运费模板 (42)1.5. 打印小票 (48)2. 订单管理 (48)2.1. 所有订单 (48)2.2. 订单详情 (51)2.3. 订单设置 (52)2.5. 运单设置 (54)3. 商城店铺装修 (55)三、外卖零售小程序 (57)1. 外卖商品管理 (57)1.1. 外卖商品管理 (57)1.2. 新建外卖商品 (58)1.3. 商品分组 (59)1.4. 店铺配置 (60)1.5. 小票打印机 (63)1.6 桌号管理 (64)1.8 补充信息 (67)1.9 排队取号 (68)1. 外卖订单管理 (70)1.1. 所有外卖订单 (70)1.2. 订单详情 (71)2. 外卖店铺装修 (71)四、预约小程序 (71)1. 预约商品管理 (72)1.1. 预约商品管理 (72)1.2. 新建预约商品 (73)2. 预约订单管理 (77)2.1. 所有预约订单 (77)2.2. 订单详情 (78)3. 预约店铺装修 (78)五、营销插件 (79)1. 优惠券 (79)1.1. 优惠券管理 (79)1.2. 新建优惠券 (80)2. 全民拼团 (84)2.1. 全民拼团管理 (84)2.3. 全民拼团订单 (88)3. 疯狂砍价 (89)3.1. 疯狂砍价管理 (89)3.2. 新建疯狂砍价 (91)3.3. 疯狂砍价订单 (93)4. 秒杀活动 (93)4.1. 秒杀活动管理 (93)4.2. 新建秒杀活动 (95)4.3. 秒杀活动订单 (96)5. 新版拼团 (96)5.2. 新建活动 (98)5.3. 新版拼团订单 (101)6. 大转盘 (101)6.1. 大转盘活动管理 (101)6.2. 新建大转盘活动 (103)6.3. 大转盘中奖名单 (104)7. 摇钱树 (105)7.1. 摇钱树活动管理 (105)7.2. 新建摇钱树活动 (106)7.3. 摇钱树中奖名单 (107)8. 砸金蛋 (107)8.1. 砸金蛋活动管理 (107)8.2. 新建砸金蛋活动 (108)8.3. 砸金蛋中奖名单 (111)9. 心跳对对碰 (111)9.1. 心跳对对碰活动管理 (111)9.2. 新建心跳对对碰活动 (113)9.3. 心跳对对碰中奖名单 (115)10. 咻一咻 (116)10.1. 咻一咻活动管理 (116)10.2. 新建咻一咻活动 (117)11. 刮刮卡 (120)11.1. 刮刮卡活动管理 (120)11.2. 新建刮刮卡活动 (121)12. 当面付 (122)12.1. 当面付收款码管理 (123)12.2. 新建收款码 (124)12.3. 当面付订单 (125)13. 会员卡 (125)13.1. 会员卡管理 (125)13.2. 新建会员卡 (127)13.4. 等级会员卡 (129)14. 积分 (130)14.1. 积分规则 (130)14.2. 签到页面自定义 (132)14.3. 积分明细 (132)15. 积分商品 (132)15.1. 新增积分商品 (132)15.2. 积分商品管理 (134)16. 会员储值 (134)16.1. 会员储值 (134)16.3. 储值概况 (136)16.4. 收支记录 (136)17. 会员次卡 (137)17.1. 会员次卡 (137)17.2. 收入概况 (137)17.3. 次卡核销 (138)17.4. 核销方法 (138)18. 阶梯拼团 (138)18.1. 阶梯拼团活动管理 (139)18.2. 新建活动 (140)19. 预售 (143)19.1. 预售活动管理 (143)19.2. 新建预售活动 (145)19.3. 预售订单 (147)20. 首单立减 (147)20.1. 首单立减设置 (147)21. 社区管理 (148)21.1. 版块管理 (148)21.2. 新建版块 (150)21.3. 话题管理 (152)21.5. 话题详情 (153)21.6. 话题分类 (153)21.7. 用户管理 (154)22. 满包邮 (154)23. 满减 (154)24. 商品推广 (155)25. 支付推广 (155)26. 营销活动管理 (156)六、多门店管理 (156)1. 总店 (156)1.2. 新建子店 (158)1.3. 店铺分类 (159)1.4. 多门店组件 (159)1.5. 订单管理 (159)1.6. 收益管理 (161)1.7. 提现管理 (161)2. 子店 (162)3. 多门店规则 (162)七、分销管理 (163)1. 分销系统定义 (163)2.1. 分销开关 (165)2.2. 推广员准入条件 (165)2.3. 分销佣金 (165)2.4. 推广海报 (166)2.5. 佣金结算 (166)2.6. 支付佣金 (167)2.7. 分销页面设置 (167)3. 推广员管理 (168)4. 推广员分组 (170)5. 佣金管理 (171)八、其他 (171)1. 数据管理 (171)1.1. 概况趋势 (171)1.2. 地区分布 (171)1.3. 用户统计 (172)1.4. 数据助手 (172)2. 平台设置 (172)2.1. 模板消息 (172)2.2. 短信通知 (173)2.3. 修改密码 (174)2.4. 页面路径 (175)2.5. 权限账号 (175)2.6. 核销员管理 (176)2.7. 开放API ........................................................................... 错误!未定义书签。
A-GA~激动の惑星~流程图文攻略

A-GA~激動の惑星~流程图文攻略omega8315原创攻略——《A-GA~激動の惑星~》是ILLUSION提议的未来构想PC-THEATER-STATION的第一个步实现计划,是一部互动型动画电影,不是游戏!!!玩家的“互动”行为,就是操纵游戏角色完成电影片段之间的桥段连接。
由于不是游戏,因此不具有实际意义上的挑战性。
但是因为这毕竟是一个日文游戏,所以还是写了这篇攻略供遇到麻烦的玩友参考,至于达人们,博君一笑耳。
攻略集中于流程,剧情方面等3DHgame的汉化补丁出来再说。
在下为了下载游戏一夜不眠,为了写攻略又一宿没睡。
因此本攻略暂时只发3DH,未经许可,请勿转载。
电影操作:由鼠标和键盘操作游戏,也可以同时使用手柄。
1)选择模式:包括游戏主菜单的选择,游戏过程中的对话,道具与存档菜单的选择。
使用鼠标,按左键确认。
使用手柄,按方向键选择选项,按攻击键确认。
对话时,由上到下的选项依次是:对话:芙伊丽蒂娅其它:菜单下一步2)动画模式:播放动画时。
暂停:键盘“F3”跳过:单击鼠标左键。
(只有看过一遍的动画才可以跳过)3)行动模式:玩家操纵游戏角色行动。
使用键盘和鼠标:类似尾行转向:左右移动鼠标跑步:鼠标左键后退:鼠标右键攻击:键盘“Z”,或者鼠标左右键同时按下。
下蹲:键盘“X”,或者双击鼠标左键,再按一次就会站起来;蹲下后无法移动。
菜单:键盘“F1”观赏:键盘“F2”使用手柄的话,则可以自己设置以上键位。
建议使用鼠标与键盘搭配,便于操作。
4)水下模式:在水利活动时。
左右移动与浮沉:移动鼠标或手柄方向键在水下神殿,建议使用鼠标。
在铁丝网和水雷处,建议使用手柄。
5)观赏模式:按下键盘“F2”之后。
类似于尾行的观赏模式,用鼠标左右键配合移动,可以转换视角。
再次按下键盘“F2”后退出观赏模式。
6)枪击模式:进行BOSS战时。
开枪射击:鼠标左键或手柄攻击键改换目标:鼠标右键或手柄下蹲键左右移动:左右移动鼠标或手柄左右方向键建议使用手柄,易于操作。
EN 71-11-2005

© 2005 CEN
All rights of exploitation in any form and by any means reserved worldwide for CEN national Members.
Ref. No. prEN 71-11:2005: E
prEN 71-11:2005 (E)
Contents
Page Foreword..............................................................................................................................................................3 Introduction .........................................................................................................................................................4 1 2 3 4 5 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 Scope ......................................................................................................................................................5 Normative references ............................................................................................................................5 Terms and definitions ...........................................................................................................................5 Environmental, health and safety precautions...................................................................................6 Methods of analysis ..............................................................................................................................6 General....................................................................................................................................................6 Flame retardants ....................................................................................................................................6 Colourants ..............................................................................................................................................9 Primary aromatic amines ....................................................................................................................15 Monomers and solvents......................................................................................................................18 Wood preservatives.............................................................................................................................36 Preservatives........................................................................................................................................40 Plasticisers ...........................................................................................................................................43
big hero 6观后感

big hero 6观后感《大英雄天团》观后感《大英雄天团》(Big Hero 6)是由迪士尼影业和漫威动画工作室合作制作的一部3D动画电影。
该片于2014年在全球上映,取得了巨大的成功和口碑。
电影以精彩的故事情节、动人的情感和创新的动画技术成为了当年的一大亮点。
故事发生在一个虚构的未来城市“旧京山”中,这座城市集结了科技与创新的力量。
主人公是一个年轻的天才少年“小宏”,他是一名技术爱好者,擅长机器人技术。
小宏为了实现自己的梦想,加入了来自高尚大学的机器人博士“卡斯卡德”所带领的研究小组。
在这里,小宏结识了五位充满个性的天才科学家,“Baymax”是其中的一员,它是一个逗趣可爱的健康护理机器人。
然而,命运的捉弄让小宏面临了重大的挑战。
故事的起点发生在一个灾难的家庭场景中。
小宏的哥哥提尔是一个天才创造者,电子工艺和机器人技术方面具有非凡的天赋。
他开发了一种革命性的技术“微型液体连接器”,然而在一次综合实验中,提尔发生了意外并丧生。
小宏从失去亲人的痛苦中走出来后,他发现自己的提尔还留下了一件重要的遗物——一个失去记忆的机器人——Baymax。
Baymax是提尔为了保护人类而设计的护理机器人,具有巨大的可爱和幽默感。
在小宏的引导下,Baymax重新获得了记忆,并成为了他的搭档和朋友。
他们两个充满了活力和创造力,相互扶持去面对未来的挑战。
电影深入探讨了家庭与友情的重要性。
小宏与提尔是非常亲密的兄弟,提尔的离世对小宏是个巨大的打击。
这个悲伤的事件引发了小宏在成长过程中的内心成长和情感故事。
同时,小宏与Baymax之间的友情也让人感动。
他们相互关心、相互扶持,在遭遇困境和危险时,彼此始终不离不弃。
电影还通过温暖的情感和令人难以忘怀的角色塑造,探讨了科技与人性的关系。
Baymax作为一个机器人,被编码为保护和照顾人类。
然而,在与小宏的互动中,Baymax逐渐展现出情感和关怀。
他教会了小宏如何宽恕并释放内心的痛苦,以及如何用爱与关怀去对待他人。
迪士尼主题类体验乐园投融资模式与发展战略研究的启示——以漫威英雄体验乐园为例

迪士尼主题类体验乐园投融资模式与发展战略研究的启示——以漫威英雄体验乐园为例近50年来,主题乐园逐渐走入人们的视野,成为朋友聚会、家庭休闲娱乐的不错选择.其背后带来的反哺当地经济、就业的效应也是显著的,这使得主题乐园产业迅速崛起。
世界主题乐园权威研究机构美国主题娱乐协会(TEA)与美国ACOM集团联合发布的《2015年全球主题乐园调查报告》中显示,尽管15年经济持续低迷,但是排名前十的主题乐园共接待游客数量达4.2亿万人,同比增长7.2%,亚太地区的市场份额也在稳步上升,目前已经达到42%,成为主题乐园产业的重要目标市场。
主题乐园作为城市公共文化空间的重要组成部分,也是国家文化旅游事业发展的重要环节。
在主题乐园数量急剧增长的同时,也逐渐涌现了概念不清、盲目建设、模仿抄袭、低水平重复等问题。
在以“沉浸传播”、“体验经济”为标识的第三媒介时代,主题乐园应当围绕IP沉浸体验促进自身的可持续发展。
本文系统性介绍了香港、东京、上海迪士尼项目的驱动机制对其项目投融资模式差异,对漫威英雄体验乐园项目的发展战略提出建议。
一、主题类体验乐园主流投融资模式(一)东京迪士尼投资模式一特许经营模式东京迪士尼乐园是迪士尼集团第一个海外主题乐园,也是全世界最受欢迎的主题乐园之一。
东京迪士尼兴建之前,日本千叶县水质污染,难以继续维持渔业生产,政府设定进行填海造地,进行产业升级,此时引进了迪士尼乐园建设项目。
东京迪士尼乐园采取“许可经营模式”,由华特迪士尼公司将迪士尼的相关知识产权许可给OLC公司,乐园的日常经营由OLC公司负责。
在许可交易架构下,华特迪士尼公司不能直接参与到项目的运营管理,而是通过在日本设立Walt Disney Attractions Japanese(简称WDAJ)来实现迪士尼对其品牌的管理、协调和敦促OLC实施好迪士尼标准,确保项目在正确的轨道上推进。
“许可经营模式”中,华特迪士尼公司每年有一定比例的许可费收入,与项目营业总额挂钩,而与经营利润没有发生挂钩。
超级英雄传攻略

超级英雄传攻略1. 引言超级英雄是广受欢迎的文化现象,许多人都向往能够拥有超凡的能力并挑战邪恶势力。
然而,成为一名超级英雄并非易事。
在这份攻略中,我们将提供一些有关超级英雄的基本信息和建议,帮助你在追求正义的道路上取得成功。
2. 定义超级英雄超级英雄是指具备特殊能力或技能,致力于保护人类免受邪恶势力侵害的人物。
与普通人不同,超级英雄通常具备超人的力量、耐力和速度,或拥有特殊的能力,如超能力、变身能力等。
他们以自己独特的方式为社会服务,并努力维护正义和平等。
3. 选择超能力成为一名超级英雄的首要任务是选择合适的超能力。
超能力可以分为多个类别,如力量类、速度类、感知类、变身类等。
要根据自己的个性、优势和兴趣来选择合适的能力。
考虑自己的性格特点和目标,并找出适合的超能力来更好地发挥自己的潜力。
4. 训练和培养能力一旦选择了超能力,接下来就是不断训练和培养这些能力。
成为一名超级英雄需要付出大量的努力和时间来发展自己的技能和能力。
可以通过参加特训班、拜师学艺或进行自我训练来提升自己的实力。
同时,不应忽视身体和心理的锻炼,保持良好的体能和精神状态。
5. 制定行动计划超级英雄需要有一个明确的行动计划来应对各种威胁和危机。
制定行动计划可以帮助超级英雄更好地应对突发事件,并提高工作效率。
行动计划应包括收集情报、制定目标、选择适当的装备和工具等内容。
合理安排时间,确保在关键时刻能够及时行动。
6. 维护公众形象超级英雄在扮演自己的角色时,需要时刻维护自己的公众形象。
一个积极正面的形象可以赢得更多的支持和信任,帮助你更好地履行超级英雄的责任。
在公众面前保持自然、友好、专业的形象,避免过度暴力或挑战现行法律的行为。
7. 找到合适的伙伴在追求正义的道路上,一个人可能力量有限。
因此,与其他超级英雄或志同道合的人联手合作是明智的选择。
找到合适的伙伴可以相互补充优势、共同应对威胁,并分享经验和技巧。
建立强大的超级英雄团队,可以提高战斗效率并实现更大的目标。
A Practical Guide to Quantitative Finance Interview (Part)

Table of ContentsChapter 1 General Principles (1)1. Build a broad knowledge base (1)2. Practice your interview skills (1)3. Listen carefully (2)4. Speak your mind (2)5. Make reasonable assumptions (2)Chapter 2 Brain Teasers (3)2.1 Problem Simplification (3)Screwy pirates (3)Tiger and sheep (4)2.2 Logic Reasoning (5)River crossing (5)Birthday problem (5)Card game (6)Burning ropes (7)Defective ball (7)Trailing zeros (9)Horse race (9)Infinite sequence (10)2.3 Thinking Out of the Box (10)Box packing (10)Calendar cubes (11)Door to offer (12)Message delivery (13)Last ball (13)Light switches (14)Quant salary (15)2.4 Application of Symmetry (15)Coin piles (15)Mislabeled bags (16)Wise men (17)2.5 Series Summation (17)Clock pieces (18)Missing integers (18)Counterfeit coins I (19)2.6 The Pigeon Hole Principle (20)Matching socks (21)Handshakes (21)Have we met before? (21)Ants on a square (22)Counterfeit coins II (22)Contentsii 2.7 Modular Arithmetic (23)Prisoner problem (24)Division by 9 (25)Chameleon colors (26)2.8 Math Induction (27)Coin split problem (27)Chocolate bar problem (28)Race track (29)2.9 Proof by Contradiction (31)Irrational number (31)Rainbow hats (31)Chapter 3 Calculus and Linear Algebra (33)3.1 Limits and Derivatives (33)Basics of derivatives (33)Maximum and minimum (34)L’Hospital’s rule (35)3.2 Integration (36)Basics of integration (36)Applications of integration (38)Expected value using integration (40)3.3 Partial Derivatives and Multiple Integrals (40)3.4 Important Calculus Methods (41)Taylor’s series (41)Newton’s method (44)Lagrange multipliers (45)3.5 Ordinary Differential Equations (46)Separable differential equations (47)First-order linear differential equations (47)Homogeneous linear equations (48)Nonhomogeneous linear equations (49)3.6 Linear Algebra (50)Vectors (50)QR decomposition (52)Determinant, eigenvalue and eigenvector (53)Positive semidefinite/definite matrix (56)LU decomposition and Cholesky decomposition (57)Chapter 4 Probability Theory (59)4.1 Basic Probability Definitions and Set Operations (59)Coin toss game (61)Card game (61)Drunk passenger (62)A Practical Guide To Quantitative Finance InterviewsN points on a circle (63)4.2 Combinatorial Analysis (64)Poker hands (65)Hopping rabbit (66)Screwy pirates 2 (67)Chess tournament (68)Application letters (69)Birthday problem (71)100th digit (71)Cubic of integer (72)4.3 Conditional Probability and Bayes’ formula (72)Boys and girls (73)All-girl world? (74)Unfair coin (74)Fair probability from an unfair coin (75)Dart game (75)Birthday line (76)Dice order (78)Monty Hall problem (78)Amoeba population (79)Candies in a jar (79)Coin toss game (80)Russian roulette series (81)Aces (82)Gambler’s ruin problem (83)Basketball scores (84)Cars on road (85)4.4 Discrete and Continuous Distributions (86)Meeting probability (88)Probability of triangle (89)Property of Poisson process (90)Moments of normal distribution (91)4.5 Expected Value, Variance & Covariance (92)Connecting noodles (93)Optimal hedge ratio (94)Dice game (94)Card game (95)Sum of random variables (95)Coupon collection (97)Joint default probability (98)4.6 Order Statistics (99)Expected value of max and min (99)Correlation of max and min (100)Random ants (102)Chapter 5 Stochastic Process and Stochastic Calculus (105)iiiContentsiv 5.1 Markov Chain (105)Gambler’s ruin problem (107)Dice question (108)Coin triplets (109)Color balls (113)5.2 Martingale and Random walk (115)Drunk man (116)Dice game (117)Ticket line (117)Coin sequence (119)5.3 Dynamic Programming (121)Dynamic programming (DP) algorithm (122)Dice game (123)World series (123)Dynamic dice game (126)Dynamic card game (127)5.4 Brownian Motion and Stochastic Calculus (129)Brownian motion (129)Stopping time/ first passage time (131)Ito’s lemma (135)Chapter 6 Finance (137)6.1. Option Pricing (137)Price direction of options (137)Put-call parity (138)American v.s. European options (139)Black-Scholes-Merton differential equation (142)Black-Scholes formula (143)6.2. The Greeks (149)Delta (149)Gamma (152)Theta (154)Vega (156)6.3. Option Portfolios and Exotic Options (158)Bull spread (159)Straddle (159)Binary options (160)Exchange options (161)6.4. Other Finance Questions (163)Portfolio optimization (163)Value at risk (164)Duration and convexity (165)Forward and futures (167)Interest rate models (168)A Practical Guide To Quantitative Finance Interviews Chapter 7 Algorithms and Numerical Methods (171)7.1. Algorithms (171)Number swap (172)Unique elements (173)Horner's algorithm (174)Moving average (174)Sorting algorithm (174)Random permutation (176)Search algorithm (177)Fibonacci numbers (179)Maximum contiguous subarray (180)7.2. The Power of Two (182)Power of 2? (182)Multiplication by 7 (182)Probability simulation (182)Poisonous wine (183)7.3 Numerical Methods (184)Monte Carlo simulation (184)Finite difference method (189)vChapter 2 Brain TeasersIn this chapter, we cover problems that only require common sense, logic, reasoning, and basic—no more than high school level—math knowledge to solve. In a sense, they are real brain teasers as opposed to mathematical problems in disguise. Although these brain teasers do not require specific math knowledge, they are no less difficult than other quantitative interview problems. Some of these problems test your analytical and general problem-solving skills; some require you to think out of the box; while others ask you to solve the problems using fundamental math techniques in a creative way. In this chapter, we review some interview problems to explain the general themes of brain teasers that you are likely to encounter in quantitative interviews.2.1 Problem SimplificationIf the original problem is so complex that you cannot come up with an immediate solution, try to identify a simplified version of the problem and start with it. Usually you can start with the simplest sub-problem and gradually increase the complexity. You do not need to have a defined plan at the beginning. Just try to solve the simplest cases and analyze your reasoning. More often than not, you will find a pattern that will guide you through the whole problem.Screwy piratesFive pirates looted a chest full of 100 gold coins. Being a bunch of democratic pirates, they agree on the following method to divide the loot:The most senior pirate will propose a distribution of the coins. All pirates, including the most senior pirate, will then vote. If at least 50% of the pirates (3 pirates in this case) accept the proposal, the gold is divided as proposed. If not, the most senior pirate will be fed to shark and the process starts over with the next most senior pirate… The process is repeated until a plan is approved. You can assume that all pirates are perfectly rational: they want to stay alive first and to get as much gold as possible second. Finally, being blood-thirsty pirates, they want to have fewer pirates on the boat if given a choice between otherwise equal outcomes.How will the gold coins be divided in the end?Solution: If you have not studied game theory or dynamic programming, this strategy problem may appear to be daunting. If the problem with 5 pirates seems complex, we can always start with a simplified version of the problem by reducing the number of pirates. Since the solution to 1-pirate case is trivial, let’s start with 2 pirates. The seniorBrain Teasers4pirate (labeled as 2) can claim all the gold since he will always get 50% of the votes from himself and pirate 1 is left with nothing.Let’s add a more senior pirate, 3. He knows that if his plan is voted down, pirate 1 will get nothing. But if he offers private 1 nothing, pirate 1 will be happy to kill him. So pirate 3 will offer private 1 one coin and keep the remaining 99 coins, in which strategy the plan will have 2 votes from pirate 1 and 3.If pirate 4 is added, he knows that if his plan is voted down, pirate 2 will get nothing. So pirate 2 will settle for one coin if pirate 4 offers one. So pirate 4 should offer pirate 2 one coin and keep the remaining 99 coins and his plan will be approved with 50% of the votes from pirate 2 and 4.Now we finally come to the 5-pirate case. He knows that if his plan is voted down, both pirate 3 and pirate 1 will get nothing. So he only needs to offer pirate 1 and pirate 3 one coin each to get their votes and keep the remaining 98 coins. If he divides the coins this way, he will have three out of the five votes: from pirates 1 and 3 as well as himself.Once we start with a simplified version and add complexity to it, the answer becomes obvious. Actually after the case 5,n a clear pattern has emerged and we do not need to stop at 5 pirates. For any 21n pirate case (n should be less than 99 though), the most senior pirate will offer pirates 1,3,, and 21n each one coin and keep the rest for himself.Tiger and sheepOne hundred tigers and one sheep are put on a magic island that only has grass. Tigers can eat grass, but they would rather eat sheep. Assume: A . Each time only one tiger can eat one sheep, and that tiger itself will become a sheep after it eats the sheep. B . All tigers are smart and perfectly rational and they want to survive. So will the sheep be eaten?Solution: 100 is a large number, so again let’s start with a simplified version of the problem . If there is only 1 tiger (1n ), surely it will eat the sheep since it does not need to worry about being eaten. How about 2 tigers? Since both tigers are perfectly rational, either tiger probably would do some thinking as to what will happen if it eats the sheep. Either tiger is probably thinking: if I eat the sheep, I will become a sheep; and then I will be eaten by the other tiger. So to guarantee the highest likelihood of survival, neither tiger will eat the sheep.If there are 3 tigers, the sheep will be eaten since each tiger will realize that once it changes to a sheep, there will be 2 tigers left and it will not be eaten. So the first tiger that thinks this through will eat the sheep. If there are 4 tigers, each tiger will understandA Practical Guide To Quantitative Finance Interviews5that if it eats the sheep, it will turn to a sheep. Since there are 3 other tigers, it will be eaten. So to guarantee the highest likelihood of survival, no tiger will eat the sheep.Following the same logic, we can naturally show that if the number of tigers is even, the sheep will not be eaten. If the number is odd, the sheep will be eaten. For the case 100,n the sheep will not be eaten.2.2 Logic ReasoningRiver crossingFour people, A ,B ,C and D need to get across a river. The only way to cross the river is by an old bridge, which holds at most 2 people at a time. Being dark, they can't cross the bridge without a torch, of which they only have one. So each pair can only walk at the speed of the slower person. They need to get all of them across to the other side as quickly as possible. A is the slowest and takes 10 minutes to cross; B takes 5 minutes; C takes 2 minutes; and D takes 1 minute.What is the minimum time to get all of them across to the other side?1Solution: The key point is to realize that the 10-minute person should go with the 5-minute person and this should not happen in the first crossing, otherwise one of them have to go back. So C and D should go across first (2 min); then send D back (1min); A and B go across (10 min); send C back (2min); C and D go across again (2 min). It takes 17 minutes in total. Alternatively, we can send C back first and then D back in the second round, which takes 17 minutes as well.Birthday problemYou and your colleagues know that your boss A ’s birthday is one of the following 10 dates:Mar 4, Mar 5, Mar 8Jun 4, Jun 7Sep 1, Sep 5Dec 1, Dec 2, Dec 8A told you only the month of his birthday, and told your colleague C only the day. After that, you first said: “I don’t know A ’s birthday; C doesn’t know it either.” After hearing 1 Hint: The key is to realize that A andB should get across the bridge together.Brain Teasers6what you said, C replied: “I didn’t know A ’s birthday, but now I know it.” You smiled and said: “Now I know it, too.” After looking at the 10 dates and hearing your comments, your administrative assistant wrote down A ’s birthday without asking any questions. So what did the assistant write?Solution: Don’t let the “he said, she said” part confuses you. Just interpret the logic behind each individual’s comments and try your best to derive useful information from these comments.Let D be the day of the month of A ’s birthday, we have {1,2,4,5,7,8}.D If the birthday is on a unique day, C will know the A ’s birthday immediately. Among possible D s, 2 and 7 are unique days. Considering that you are sure that C does not know A ’s birthday, you must infer that the day the C was told of is not 2 or 7. C onclusion: the month is not June or December. (If the month had been June, the day C was told of may have been 2; if the month had been December, the day C was told of may have been 7.) Now C knows that the month must be either March or September. He immediately figures out A ’s birthday, which means the day must be unique in the March and September list. It means A ’s birthday cannot be Mar 5, or Sep 5. C onclusion: the birthday must be Mar 4, Mar 8 or Sep 1.Among these three possibilities left, Mar 4 and Mar 8 have the same month. So if the month you have is March, you still cannot figure out A ’s birthday. Since you can figure out A ’s birthday, A ’s birthday must be Sep 1. Hence, the assistant must have written Sep 1.Card gameA casino offers a card game using a normal deck of 52 cards. The rule is that you turn over two cards each time. For each pair, if both are black, they go to the dealer’s pile; if both are red, they go to your pile; if one black and one red, they are discarded. The process is repeated until you two go through all 52 cards. If you have more cards in your pile, you win $100; otherwise (including ties) you get nothing. The casino allows you to negotiate the price you want to pay for the game. How much would you be willing to pay to play this game?2Solution: This surely is an insidious casino. No matter how the cards are arranged, you and the dealer will always have the same number of cards in your piles. Why? Because each pair of discarded cards have one black card and one red card, so equal number of2Hint: Try to approach the problem using symmetry. Each discarded pair has one black and one red card. What does that tell you as to the number of black and red cards in the rest two piles?A Practical Guide To Quantitative Finance Interviews7red and black cards are discarded. As a result, the number of red cards left for you and the number of black cards left for the dealer are always the same. The dealer always wins! So we should not pay anything to play the game.Burning ropesYou have two ropes, each of which takes 1 hour to burn. But either rope has different densities at different points, so there's no guarantee of consistency in the time it takes different sections within the rope to burn. How do you use these two ropes to measure 45 minutes?Solution: This is a classic brain teaser question. For a rope that takes x minutes to burn, if you light both ends of the rope simultaneously, it takes /2x minutes to burn. So we should light both ends of the first rope and light one end of the second rope. 30 minutes later, the first rope will get completely burned, while that second rope now becomes a 30-min rope. At that moment, we can light the second rope at the other end (with the first end still burning), and when it is burned out, the total time is exactly 45 minutes. Defective ballYou have 12 identical balls. One of the balls is heavier OR lighter than the rest (you don't know which). Using just a balance that can only show you which side of the tray is heavier, how can you determine which ball is the defective one with 3 measurements?3Solution: This weighing problem is another classic brain teaser and is still being asked by many interviewers. The total number of balls often ranges from 8 to more than 100.Here we use 12nto show the fundamental approach. The key is to separate the original group (as well as any intermediate subgroups) into three sets instead of two. The reason is that the comparison of the first two groups always gives information about the third group.Considering that the solution is wordy to explain, I draw a tree diagram in Figure 2.1 to show the approach in detail. Label the balls 1 through 12 and separate them to three groups with 4 balls each. Weigh balls 1, 2, 3, 4 against balls 5, 6, 7, 8. Then we go on to explore two possible scenarios: two groups balance, as expressed using an “=” sign, or 1, 3Hint: First do it for 9 identical balls and use only 2 measurements, knowing that one is heavier than the rest.Brain Teasers82, 3, 4 are lighter than 5, 6, 7, 8, as expressed using an “<” sign. There is no need to explain the scenario that 1, 2, 3, 4 are heavier than 5, 6, 7, 8. (Why?4)If the two groups balance, this immediately tells us that the defective ball is in 9, 10, 11 and 12, and it is either lighter (L ) or heavier (H ) than other balls. Then we take 9, 10 and 11 from group 3 and compare balls 9, 10 with 8, 11. Here we have already figured out that 8 is a normal ball. If 9, 10 are lighter, it must mean either 9 or 10 is L or 11 is H . In which case, we just compare 9 with 10. If 9 is lighter, 9 is the defective one and it is L ; if 9 and 10 balance, then 11 must be defective and H ; If 9 is heavier, 10 is the defective one and it is L . If 9, 10 and 8, 11 balance, 12 is the defective one. If 9, 10 is heavier, than either 9 or 10 is H, or 11 is L.You can easily follow the tree in Figure 2.1 for further analysis and it is clear from the tree that all possible scenarios can be resolved in 3 measurements. In general if you have the information as to whether the defective ball is heavier or 4 Here is where the symmetry idea comes in. Nothing makes the 1, 2, 3, 4 or 5, 6, 7, 8 labels special. If 1, 2, 3, 4 are heavier than 5, 6, 7, 8, let’s just exchange the labels of these two groups. Again we have the case of 1, 2, 3, 4 being lighter than 5, 6, 7, 8.1/2L or 6H5H or 3L4L or 7/8H 12L or 12H 9/10H or 11L 9/10L or 11H 5,6,7,8+?1,2,53,6,9_1/2/3/4 L or 5/6/7/8 H1L 6H 2L 8H 4L 7H 3L 5H 2_18_79_39,108,11_9/10/11/12 L or H 9L 11H 10L 12H 11L 12L 10H 9H_912_8_9Figure 2.1 Tree diagram to identify the defective ball in 12 ballsA Practical Guide To Quantitative Finance Interviews9lighter, you can identify the defective ball among up to 3n balls using no more than n measurements since each weighing reduces the problem size by 2/3. If you have no information as to whether the defective ball is heavier or lighter, you can identify the defective ball among up to (33)/2n balls using no more than n measurements. Trailing zerosHow many trailing zeros are there in 100! (factorial of 100)?Solution: This is an easy problem. We know that each pair of 2 and 5 will give a trailing zero. If we perform prime number decomposition on all the numbers in 100!, it is obvious that the frequency of 2 will far outnumber of the frequency of 5. So the frequency of 5 determines the number of trailing zeros. Among numbers 1,2,,99, and 100, 20 numbers are divisible by 5 (5,10,,100 ). Among these 20 numbers, 4 are divisible by 52 (25,50,75,100). So the total frequency of 5 is 24 and there are 24 trailing zeros.Horse raceThere are 25 horses, each of which runs at a constant speed that is different from the other horses’. Since the track only has 5 lanes, each race can have at most 5 horses. If you need to find the 3 fastest horses, what is the minimum number of races needed to identify them?Solution: This problem tests your basic analytical skills. To find the 3 fastest horses, surely all horses need to be tested. So a natural first step is to divide the horses to 5 groups (with horses 1-5, 6-10, 11-15, 16-20, 21-25 in each group). After 5 races, we will have the order within each group, let’s assume the order follows the order of numbers (e.g., 6 is the fastest and 10 is the slowest in the 6-10 group)5. That means 1, 6, 11, 16 and 21 are the fastest within each group.Surely the last two horses within each group are eliminated. What else can we infer? We know that within each group, if the fastest horse ranks 5th or 4th among 25 horses, then all horses in that group cannot be in top 3; if it ranks the 3rd, no other horse in that group can be in the top 3; if it ranks the 2nd, then one other horse in that group may be in top 3; if it ranks the first, then two other horses in that group may be in top 3. 5 Such an assumption does not affect the generality of the solution. If the order is not as described, just change the labels of the horses.Chapter 4 Probability TheoryC hances are that you will face at least a couple of probability problems in most quantitative interviews. Probability theory is the foundation of every aspect of quantitative finance. As a result, it has become a popular topic in quantitative interviews. Although good intuition and logic can help you solve many of the probability problems, having a thorough understanding of basic probability theory will provide you with clear and concise solutions to most of the problems you are likely to encounter. Furthermore, probability theory is extremely valuable in explaining some of the seemingly-counterintuitive results. Armed with a little knowledge, you will find that many of the interview problems are no more than disguised textbook problems.So we dedicate this chapter to reviewing basic probability theory that is not only broadly tested in interviews but also likely to be helpful for your future career. 1 The knowledge is applied to real interview problems to demonstrate the power of probability theory. Nevertheless, the necessity of knowledge in no way downplays the role of intuition and logic. Quite the contrary, common sense and sound judgment are always crucial for analyzing and solving either interview or real-life problems. As you will see in the following sections, all the techniques we discussed in Chapter 2 still play a vital role in solving many of the probability problems.Let’s have some fun playing the odds.4.1 Basic Probability Definitions and Set OperationsFirst let’s begin with some basic definitions and notations used in probability. These definitions and notations may seem dry without examples—which we will present momentarily—yet they are crucial to our understanding of probability theory. In addition, it will lay a solid ground for us to systematically approach probability problems.Outcome (Ȧ):the outcome of an experiment or trial.Sample space/Probability space ( ):the set of all possible outcomes of an experiment.1 As I have emphasized in Chapter 3, this book does not teach probability or any other math topics due to the space limit—it is not my goal to do so, either. The book gives a summary of the frequently-tested knowledge and shows how it can be applied to a wide range of real interview problems. The knowledge used in this chapter is covered by most introductory probability books. It is always helpful to pick up one or two classic probability books in case you want to refresh your memory on some of the topics. My personal favorites are First Course in Probability by Sheldon Ross and Introduction to Probability by Dimitri P. Bertsekas and John N. Tsitsiklis.Probability Theory60()P Z : Probability of an outcome (()0,,()1P P Z Z Z Z :t : ¦).Event:A set of outcomes and a subset of the sample space.()P A : Probability of an event A , ()()AP A P Z Z ¦.A B : Union A B is the set of outcomes in event A or in event B (or both).A B or AB : Intersection A B (or AB ) is the set of outcomes in both A and B .c A : The complement of A , which is the event “not A ”.Mutually Exclusive :A B ) where ) is an empty set.For any mutually exclusive events 12,,N E E E ,11().N N i i i i P E P E §· ¨¸©¹¦ Random variable: A function that maps each outcome (Ȧ) in the sample space ( ) into the set of real numbers.Let’s use the rolling of a six-sided dice to explain these definitions and notations. A roll of a dice has 6 possible outcomes (mapped to a random variable): 1, 2, 3, 4, 5, or 6. Sothe sample space :is {1,2,3,4,5,6} and the probability of each outcome is 1/6 (assuming a fair dice). We can define an event A representing the event that the outcomeis an odd number {1,3,5},Athen the complement of A is {2,4,6}.c A Clearly ()P A (1)(3)(5)1/2.P P P Let B be the event that the outcome is larger than 3: {4,5,6}.B Then the union is {1,3,4,5,6}A B and the intersection is {5}.A B One popular random variable called indicator variable (a binary dummy variable) for event A is defined as the following:1,{1,3,5}.0,{1,3,5}A if x I if x ® ¯ Basically 1A I when A occurs and 0A I if c A occurs. The expected value of A I is []()A E I P A .Now, time for some examples.A Practical Guide To Quantitative Finance Interviews61Coin toss gameTwo gamblers are playing a coin toss game. Gambler A has (1)n fair coins; B has n fair coins. What is the probability that A will have more heads than B if both flip all their coins?2Solution: We have yet to cover all the powerful tools probability theory offers. What do we have now? Outcomes, events, event probabilities, and surely our reasoning capabilities! The one extra coin makes A different from B . If we remove a coin from A ,A and B will become symmetric. Not surprisingly, the symmetry will give us a lot of nice properties. So let’s remove the last coin of A and compare the number of heads in A ’s first n coins with B ’s n coins. There are three possible outcomes:1E :A ’s n coins have more heads than B ’s n coins;2E :A ’s n coins have equal number of heads as B ’s n coins;3E :A ’s n coins have fewer heads than B ’s n coins.By symmetry, the probability that A has more heads is equal to the probability that B has more heads. So we have 13()().P E P E Let’s denote 13()()P E P E x and 2().P E y Since ()1,P Z Z :¦ we have 2 1.x y For event 1,E A will always have more headsthan B no matter what A ’s (1)n th coin’s side is; for event 3E ,A will have no moreheads than B no matter what A ’s (1)n th coin’s side is. For event 2E ,A ’s (1)n thcoin does make a difference. If it’s a head, which happens with probability 0.5, it will make A have more heads than B . So the (1)n th coin increases the probability that A has more heads than B by 0.5y and the total probability that A has more heads is 0.50.5(12)0.5x y x x when A has (1)n coins.Card gameA casino offers a simple card game. There are 52 cards in a deck with 4 cards for each value jack queen king ace 2,3,4,5,6,7,8,9,10,,,,J Q K A . Each time the cards are thoroughly shuffled (so each card has equal probability of being selected). You pick up a card from the deck and the dealer picks another one without replacement. If you have a larger number, you win; if the numbers are equal or yours is smaller, the house wins—as in all other casinos, the house always has better odds of winning. What is your probability of winning? 2 Hint: What are the possible results (events) if we compare the number of heads in A ’s first n coins withB ’s n coins? By making the number of coins equal, we can take advantage of symmetry. For each event, what will happen if A ’s last coin is a head? Or a tail?。
凤凰佳影1.0操作手册

3.1.2 模糊查询.........................................................................................................20
3.1.3 开始下载.........................................................................................................21
2.4
座位图图示说明.....................................................................................................17
3 编排放映计划.........................................................................................................................18
广东粤科软件工程有限公司 Guangdong YueKe Software Engineering Co., Ltd
目录
1 系统结构图...............................................................................................................................4
4.2
卡后台.....................................................................................................................47
tp-link TL-R4238 TL-R4239 TL-R4299G 说明书

目
录
物 品 清 单 ......................................................................................1 第一章 用户手册简介 ....................................................................2 1.1 用途 ................................................................................................... 2 1.2 约定 ................................................................................................... 2 1.3 用户手册概述 ..................................................................................... 3 第二章 产品概述 ...........................................................................4 2.1 产品简介 ............................................................................................ 4 2.2 特性和规格说明 ................................................................................. 5 2.2.1 主要特性 ......................................................................................... 5 2.2.2 规格 ................................................................................................ 6 第三章 硬件安装 ..........................................................................9 3.1 面板布置 ............................................................................................ 9 3.1.1 前面板............................................................................................. 9 3.1.2 后面板........................................................................................... 10 3.2 系统需求 .......................................................................................... 11 3.3 安装环境 .......................................................................................... 11 3.4 硬件安装步骤 ................................................................................... 12 第四章 快速安装指南 ..................................................................14 4.1 建立正确的网络设置 ........................................................................ 14 4.2 快速安装指南 ................................................................................... 16 第五章 配置指南 .........................................................................19 5.1 启动和登录....................................................................................... 19 5.2 运行状态 .......................................................................................... 20 5.3 设置向导 .......................................................................................... 21 5.4 网络参数 ......................................................................................... 21
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《超级英雄》罗杰限时回归金卡、红卡大放送活动内容:
罗杰秘宝已被发现,海贼王罗杰为保护秘宝,强势降临乱世,罗杰能否在这乱世开启新海贼时代,我们拭目以待!
罗杰兑换活动即将开启,请各路英雄时刻关注最新公告!
【海贼之王罗杰】
大航海时代的开创者,海贼之王罗杰即将登陆超级英雄,作为最神秘与强大的海上霸主,罗杰拥有着辉煌而传奇的人生。
在《超级英雄》强大穿梭机的帮助下,神秘的海贼之王荣耀降临于动荡而危机四伏的英雄之地,罗杰能否拯救末世于倾覆,让我们拭目以待!
【海贼之王——技能篇】
武装色将武装色霸气附于武器之上,对敌人造成一定量的物理伤害,若敌人不属于理性宇宙则伤害提升100%。
心网战前技:通过运用见闻色的霸气预判对手的攻击,提升一定量的闪避,持续2回合。
霸王色运用王者才具备的霸王色霸气,对敌方全体造成一定量的物理伤害,并有一定概率使目标眩晕,持续1回合。
注:“一定量”受玩家技能等级影响
【海贼之王——命运篇】
神·傲世与六道和贝吉特同时出场时物攻、魔攻、防御、生命和速度+10%
英灵与斑爷和凤凰同时出场时物攻、生命和速度+15%
父与子与火拳同时出场时魔攻、生命和速度+15%
了解了这么多海贼之王的传奇与强大,你是否跃跃欲试了呢,快拿起你的手机吧,在超级
英雄,携手海贼之王——罗杰,开启属于你的伟大的航路吧!
温馨提示:此介绍如与游戏内公告冲突,以游戏内公告为准。
