专题11(3节)课堂精练
三年级上册课堂精练答案

三年级上册课堂精练答案自己的花是让别人看的1.划去括号中不恰当的读音或字。
耐人找寻(xún xué×)味莞(guǎn× wǎn)尔一笑姹(chà cà×)紫嫣红应接不(瑕× 暇)花团(锦绵×)簇脊(梁粱×)2.给加点字选择正确的意思,将序号写在括号里。
(1)③披针形;当作。
(2)①靠近;对着。
(3)②很,相当地。
3.先把下面的词语补充完整,再写三个描写花的成语。
花团(锦)簇 (姹)紫嫣(白)百花争艳百花齐放花枝招展光彩夺目竞相开放争奇斗艳万紫千红春暖花开鸟语花香花红柳绿锦上添花火树银花春花秋月过时黄花繁花似锦例如烟似霞4.品读课文片段,完成练习。
走到任何一条街,走跌向上看,家家户户的窗子前都就是花团锦簇、姹(chà)紫嫣(yān)白。
许多窗子相连接在一起,汇聚了一个(花掉的海洋),使我们看看的人西横堤(山阴道上),(应接不暇)。
每一家都就是这样,在屋子里的时候,自己的花是(使别人看看的);跑在街上的时候,自己又看看(别人的花)。
人人为我,我为人人。
我真的这一种境界就是颇(耐人寻味)的。
(1)按课文内容填空。
【答案见短文中划红线的句子。
】(2)念至文中划出横线的句子,你仿佛看见了怎样的景色?把自己的想象写下下来。
答:读到文中划横线的句子,我仿佛看到了家家户户窗前繁花似锦,一派春光。
(3)文中哪句话具体表现了“人人为我,我为人人”这种境界?用“ ”画出。
5.小练笔。
文中说“人人为我,我为人人”就是一种耐人寻味的境界,在生活中存有很多这样的事例,恳请你打听一打听,和同学交流交流,并刊登一下自己的见解。
①比如说扫地呀,当你扫地时,你扫得很干净,别人就会很舒心,当别人扫地的时候扫得很干净,你也会感到很舒心,这就是人人为我,我为人人的事例,其实,这是我们每个值日学生的职责,也是必须要这么做的。
②考试时,钢笔忽然没人管了,同桌还给了我一支他平时自己都不忍心用的钢笔,这就是“人人为我”;做作业时,同桌存有道题不能,我给他传授这道题,这就是“我为人人”。
《课课精练》语文九年级上册答案

《课课精练》语文九年级上册参考答案第一单元1沁园春雪一、预习与自学(一)D.(A. “惟.”读“wãi”;“折.”读“zhã”; B.“略.”读“lǜe”;C. “滔.”读“tāo”)(二)1.(1)莽莽 (2)分(3)俱(4)娇(5)竞(6)风2.(1)远眺长城内外,只剩下白茫茫的一片。
(2)奔腾的黄河顿时失去了滚滚滔滔的雄壮气势。
(3)可惜的是,秦皇汉武帝不擅“文治”,在思想文化上建树不多。
3.D(三)1.北国雪景,祖国山河壮丽;英雄人物,诗人的伟大抱负。
2.欲与天公试比高。
3.江山如此多娇,引无数英雄竞折腰。
4.在新时代,一定能涌现出更多的英雄人物,创造伟大的业绩,这也是作者自指,表现出作为革命家的伟大抱负。
5.一个风筝在半空中滑翔,终于,它可以在蓝天下自由地飞翔了,那是付出了小男孩的汗水、眼泪才得到的。
二、精读与赏析1.长城、黄河、山脉、高原等北国风貌的意象,营造出雄伟壮观、气势磅礴的意境。
2.示例(1):用“舞”字形容雪披群山的峰峦叠嶂,用“驰”字形容高原的奔腾耸动,以动写静,极为传神。
示例 (2):“看红妆素裹,分外妖娆”,用拟人的修辞,想像红日与白雪交相辉映的艳丽景象,表达出对壮丽山河的赞美之情。
3.惟余莽莽,漫天皆白。
4.相同点:都描写了雪景,都有雄壮、豪放的风格;不同点:《沁园春》描写雪景,借景抒怀;《减字木兰花》则是写景叙事,描写行军的一个场面。
三、拓展与迁移1.上阕:通过对湘江秋景的描写,暗示当时蓬勃发展的革命形势,提出了“谁主沉浮”的问题。
下阕:通过对往昔斗争生活的回忆,回答了“谁主沉浮”的问题。
号召人们发扬勇敢无畏的精神,为了民族的解放,担当起“主”中国革命“沉浮”的历史责任。
2.看山江天水3.“恰同学少年,风华正茂;书生意气,挥斥方遒。
指点江山,激扬文字,粪土当年万户侯。
”2雨说一、预习与自学(一)圃.pǔ锢.gù嚷.rǎng缕.lǚ蓑suō膏.gāo 跃.yuâ耸.sǒng 襁.褓qi ǎng(二)1.C (A. “暗”为“喑”; B.“倧”为“踪”; D.“悉”为“息”)2.我的爱心像丝缕那样把天地织在一起可别打开油伞将我抗拒我是四月的客人带来春的洗礼为什么不跟着我走,踩着我脚步的拍子?3.C(A项缺主语,“在……中”或“使”删去一个即可;B项不合逻辑,把“认真克服”与“随时发现……的缺点”调换位置;D项主语和谓语搭配不当,“笑脸”可以浮现,“教诲”不可以浮现,可改为“老师那和蔼可亲的笑脸总是浮现在我眼前,谆谆教诲总是回响在我耳畔”。
小学课堂精练讲解教案模板

课时:1课时年级:小学XX年级学科:XX学科教学目标:1. 让学生掌握XX学科的基础知识和技能。
2. 培养学生的思维能力和创新意识。
3. 提高学生的课堂参与度和学习兴趣。
教学重难点:1. 教学重点:XX学科的核心知识点。
2. 教学难点:XX学科中的难点问题。
教学过程:一、导入1. 引导学生回顾上一节课所学内容,为新知识的学习做好铺垫。
2. 通过提问、游戏等方式,激发学生的学习兴趣。
二、新课讲解1. 针对教学重点,进行详细讲解,结合实例,让学生理解并掌握。
2. 针对教学难点,采用多种教学方法,如分组讨论、小组合作等,引导学生共同解决。
三、课堂练习1. 设计针对性的练习题,让学生在课堂上进行练习,巩固所学知识。
2. 鼓励学生积极参与,对学生的答案进行及时点评和指导。
四、课堂小结1. 对本节课所学内容进行总结,帮助学生梳理知识体系。
2. 引导学生提出疑问,为下一节课的学习做好准备。
五、作业布置1. 布置适量的课后作业,巩固所学知识。
2. 作业内容应具有针对性,难度适中。
教学手段:1. 利用多媒体课件,丰富教学内容,提高教学效果。
2. 采用实物、图片、动画等多种教学手段,激发学生的学习兴趣。
教学评价:1. 通过课堂练习和课后作业,了解学生对本节课知识的掌握程度。
2. 关注学生在课堂上的表现,评价学生的参与度和学习兴趣。
教学反思:1. 教师应不断反思自己的教学方法和手段,提高教学质量。
2. 关注学生的学习需求,调整教学策略,使教学更加有效。
以下为教案模板的具体内容:一、导入1. 回顾上一节课内容,引导学生思考。
2. 提问:“同学们,上节课我们学习了什么?今天我们将学习什么新知识?”二、新课讲解1. 讲解XX学科的核心知识点,结合实例进行说明。
2. 针对教学难点,引导学生分组讨论,共同解决问题。
三、课堂练习1. 布置练习题,让学生在课堂上进行练习。
2. 鼓励学生积极参与,对学生的答案进行点评和指导。
四、课堂小结1. 总结本节课所学内容,帮助学生梳理知识体系。
专题11 二次函数-九年级数学专题讲座之剖析经典总结规律(解析版)

※知识精要1.形如2y ax bx c =++ (其中0, ,,a a b c ≠为常数 )的函数叫做二次函数。
2. 二次函数的性质:①抛物线的顶点坐标24,24b ac b a a ⎛⎫--⎪ ⎪⎝⎭,对称轴2b x a =- 。
②当时,抛物线向上开口;在对称轴左侧y 随x 的增大而减小,在对称轴右侧y 随x 的增大而增大,当2bx a=-时,y 有最小值,最小值是244ac b y a -= 。
当时,抛物线向下开口;在对称轴左侧y 随x 的增大而增大,在对称轴右侧y 随x 的增大而减小,当2bx a=-时,y 有最大值,最大值是244ac b y a -= 。
③a 越大抛物线的开口越小,a 越小抛物线的开口越大。
3.二次函数图象与系数的关系:对于二次函数,二次项系数a 决定抛物线的开口方向和大小:当时,抛物线向上开口;当时,抛物线向下开口;一次项系数b 和二次项系数a 共同决定对称轴的位置:当a 与b 同号时即,对称轴在y 轴左;当a 与b 异号时即,对称轴在y 轴右;常数项c 决定抛物线与y 轴交点位置:抛物线与y 轴交于;※要点突破1. 一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x 轴有两个交点时,可选择设其解析式为交点式来求解.2.二次函数综合运用.解题关键点:画出图形,数形结合分析问题,把问题转化为相应函数问题解决.※典例精讲例.已知二次函数y = 2x 2 -4x -6.(1)用配方法将y= 2x2 -4x-6化成y=a (x-h) 2 +k的形式;并写出对称轴和顶点坐标。
(2)在平面直角坐标系中,画出这个二次函数的图象;(3)当x取何值时,y随x的增大而减少?(4)当x取何值是,,y<0,(5)当时,求y的取值范围;(6)求函数图像与两坐标轴交点所围成的三角形的面积.【答案】(1)x=1,(1,-8);(2)图略;(3)x<1; (4)x=1或-3,x<-1或x>3,-1<x<3;(5);(6)12(2)如图所示:※课堂精练一、单选题1.抛物线的顶点坐标()A.(-3,4) B.(-3,-4)C.(3,-4) D.(3,4)【答案】D【解析】因为是抛物线的顶点式,根据顶点式的坐标特点,顶点坐标为(-3,4),2.为了得到函数的图象,可以将函数的图象A.先关于x轴对称,再向右平移1个单位,最后向上平移4个单位B.先关于x轴对称,再向右平移1个单位,最后向下平移4个单位C.先关于y轴对称,再向右平移1个单位,最后向上平移4个单位D.先关于y轴对称,再向右平移1个单位,最后向下平移4个单位【答案】A3.如图(1)是一个横断面为抛物线形状的拱桥.当水面在时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是()A.B.C.D.【答案】A【解析】由图中可以看出,所求抛物线的顶点在原点,对称轴为y轴,可设此函数解析式为:y=ax2,利用待定系数法求解.解:设此函数解析式为:y=ax2(a≠0),那么(2,-2)应在此函数解析式上.则-2=4a即得a=-,那么y=-x2.4.已知二次函数的部分图象如图所示,若连接该函数与坐标轴的交点所得到的三角形面积为20,则该函数的最大值为A.B.C.5 D.【答案】D5.在平面直角坐标系xOy中,二次函数的图象如图所示,下列说法正确的是A.,B.,C.,D.,【答案】A6.抛物线上部分点的横坐标x,纵坐标y的对应值如下表:小聪观察上表,得出下面结论:抛物线与x轴的一个交点为;函数的最大值为6;抛物线的对称轴是;在对称轴左侧,y随x增大而增大其中正确有A.B.C.D.【答案】D【解析】根据表中数据和抛物线的对称形,可得到抛物线的开口向下,当时,,即抛物线与x轴的交点为和;因此可得抛物线的对称轴是直线,再根据抛物线的性质即可进行判断.解:根据图表,当,,根据抛物线的对称形,当时,,即抛物线与x轴的交点为和;抛物线的对称轴是直线,根据表中数据得到抛物线的开口向下,当时,函数有最大值,而不是,或1对应的函数值6,并且在直线的左侧,y随x增大而增大,所以正确,错,故选D.【点睛】本题考查了抛物线的性质:抛物线是轴对称图形,它与x轴的两个交点是对称点,对称轴与抛物线的交点为抛物线的顶点;时,函数有最大值,在对称轴左侧,y随x增大而增大.7.抛物线的部分图象如图所示,与x轴的一个交点坐标为,抛物线的对称轴是下列结论中:;;方程有两个不相等的实数根;抛物线与x轴的另一个交点坐标为;若点在该抛物线上,则.其中正确的有A.5个B.4个C.3个D.2个【答案】B方程有两个不相等的实数根,故正确;抛物线与x轴的一个交点坐标为,抛物线的对称轴是,抛物线与x轴的另一个交点坐标为,故正确;抛物线的对称轴是,有最大值是,点在该抛物线上,,故正确,本题正确的结论有:,4个,故选B.【点睛】本题考查了二次函数图象与系数的关系:对于二次函数,二次项系数a 决定抛物线的开口方向和大小:当时,抛物线向上开口;当时,抛物线向下开口;一次项系数b 和二次项系数a共同决定对称轴的位置:当a与b同号时即,对称轴在y轴左;当a与b异号时即,对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于;也考查了抛物线与x轴的交点以及二次函数的性质.8.(题文)如图,已知二次函数的图象如图所示,有下列5个结论;;;;的实数其中正确结论的有A.B.C.D.【答案】B,故不正确;当时,,,故正确;由对称知,当时,函数值大于0,即,故正确;,,,,,故不正确;当时,y的值最大此时,,而当时,,所以,故,即,故正确,故正确,故选B.9.已知二次函数为常数,当自变量x的值满足时,与其对应的函数值y的最小值为5,则m的值为A.1或B.或5 C.1或D.1或3【答案】C10.如图,函数和(是常数,且)在同一平面直角坐标系的图象可能是()A.B.C.D.【答案】B11.已知函数y1=x2与函数y2=x+3的图象如图所示,若y1<y2,则自变量x的取值范围是()A.-<x<2 B.x>2或x<-C.-2<x<D.x<-2或x>【答案】C12.如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为()A.4 B.﹣4 C.﹣6 D.6【答案】C【解析】根据图象的旋转变化规律以及二次函数的平移规律得出平移后解析式,进而求出m的值,由2017÷5=403…2,可知点P(2018,m)在此“波浪线”上C404段上,求出C404的解析式,然后把P(2018,m)代入即可.解:当y=0时,﹣x(x﹣5)=0,解得x1=0,x2=5,则A1(5,0),∴OA1=5,∵将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…;如此进行下去,得到一“波浪线”,∴A1A2=A2A3=…=OA1=5,∴抛物线C404的解析式为y=(x﹣5×403)(x﹣5×404),即y=(x﹣2015)(x﹣2020),当x=2018时,y=(2018﹣2015)(2018﹣2020)=﹣6,即m=﹣6.故选:C.13.把二次函数y=x2﹣4x+3化成y=a(x﹣h)2+k的形式是_____.【答案】y=(x﹣2)2﹣114.若抛物线的顶点在第一象限,则m的取值范围为【答案】【解析】抛物线,顶点坐标为,顶点在第一象限,且,的取值范围为,故答案为:.15.若,,为二次函数的图象上的三点,则,,的大小关系是______.【答案】【解析】,,,,.故答案为:.16.已知抛物线与关于原点对称,我们称与互为“和谐抛物线”请写出抛物线的“和谐抛物线”______.【答案】【解析】抛物线的“和谐抛物线”是,化简,得,故答案为:.17.将抛物线向上平移一个单位,向右平移两个单位,直线恰好经过平移后的抛物线的顶点,则b的值是______.【答案】18.二次函数y=x2-2x-3,当m-2≤x≤m时函数有最大值5,则m的值可能为___________【答案】0或4【解析】根据二次函数的图像和解析式,判断出函数的最值的自变量x的值,然后根据m的范围求出m的值即可.解:令y=5,可得x2-2x-3=5,解得x=-2或x=4所以m-2=-2,m=4即m=0或4.故答案为:0或4.19.某数学课本上,用“描点法”画二次函数y=ax2+bx+c(a≠0)的图象时,列了如下表格:根据表格中的信息回答问题:当x=3时,y=____.【答案】-420.定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是___.【答案】【解析】在同一坐标系xOy中,画出函数二次函数y=-x2+1与正比例函数y=-x的图象,如图所示,设它们交于点A、B,令-x2+1=-x,即x2-x-1=0,解得:x=或,∴A(,),B(,),观察图象可知:当x≤时,min{-x2+1,-x}=-x2+1,函数值随x的增大而增大,其最大值为,当<x≤时,min{-x2+1,-x}=-x,函数值随x的增大而减小,没有最大值;当x>时,min{-x2+1,-x}=-x2+1,函数值随x的增大而减小,最大值为综上所示,min{-x2+1,-x}的最大值是,故答案为:21.已知二次函数的对称轴为x=2,且在x轴上截得的线段长为6,与y轴的交点为(0,﹣2),求此二次函数的解析式.【答案】y=x2﹣x﹣2.22.已知二次函数(为常数).(1)求证:不论为何值,该函数的图像与轴总有公共点;(2)当取什么值时,该函数的图像与轴的交点在轴的上方?【答案】(1)证明见解析;(2)时,该函数的图像与轴的交点在轴的上方.【解析】(1)首先求出与x轴交点的横坐标,,即可得出答案;(2)求出二次函数与y轴的交点纵坐标.根据交点纵坐标大于0即可求出.解:(1)证明:当时,.解得,.当,即时,方程有两个相等的实数根;当,即时,方程有两个不相等的实数根.所以,不论为何值,该函数的图像与轴总有公共点.(2)解:当时,,即该函数的图像与轴交点的纵坐标是.当,即时,该函数的图像与轴的交点在轴的上方.23.某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:(1)求y与x之间的函数关系式,并写出自变量x的取值范围;(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?(3)该经销商想要每天获得168元的销售利润,销售价应定为多少?【答案】(1)y与x之间的函数关系式y=-2x+60(10≤x≤18);(2)当销售价为18元时,每天的销售利润最大,最大利润是192元;(3)该经销商想要每天获得168元的销售利润,销售价应定为16元.(2)W=(x-10)(-2x+60)=-2x2+80x-600,对称轴x=20,在对称轴的左侧y随着x的增大而增大,∵10≤x≤18,∴当x=18时,W最大,最大为192.即当销售价为18元时,每天的销售利润最大,最大利润是192元(3)由168=-2x2+80x-600,解得x1=16,x2=24(不合题意,舍去)答:该经销商想要每天获得168元的销售利润,销售价应定为16元.24.如图,抛物线y=ax2+x+c(a≠0)与x轴交于点A,B两点,其中A(-1,0),与y轴交于点C(0,2).(1)求抛物线的表达式及点B坐标;(2)点E是线段BC上的任意一点(点E与B、C不重合),过点E作平行于y轴的直线交抛物线于点F,交x轴于点G.①设点E的横坐标为m,用含有m的代数式表示线段EF的长;②线段EF长的最大值是.【答案】(1)y=-x2+x+2,B(4,0);(2)①-m2+2m;②2当y=0时,x1=-1,x2=4,故B(4,0)(2)①设直线BC的函数表达式为y=kx+b,将B(4,0)、C(0,2)代入得:y=-x+2,EF=FG-GE=-m2+m+2-(-m+2)=-m2+2m② 226.如图,已知抛物线过点,,,顶点为D.求抛物线的解析式;设点,当的值最小时,求m的值;若P是抛物线上位于直线AC上方的一个动点,求的面积的最大值.【答案】(1);(2);(3).解得抛物线的解析式为配方,得,顶点D的坐标为作B点关于直线的对称点,如图1,则,由得,可求出直线的函数关系式为,当在直线上时,的值最小,则.,当时,的面积的最大值是;27.如图,在平面直角坐标系中,抛物线y =ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.点P、Q分别是AB、BC上的动点,当点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动.设P、Q同时运动的时间为t秒(0<t<2).(1)求抛物线的表达式;(2)设△PBQ的面积为S ,当t为何值时,△PBQ的面积最大,最大面积是多少?(3)当t为何值时,△PBQ是等腰三角形?【答案】(1)y=38x2−34x−3;(2)当t=1时,S△PBQ最大=910.;(3)当t的值是32秒或3023秒或4829秒时,△CPQ为等腰三角形.∴PB=6−3t.由题意得,点C的坐标为(0,−3).在Rt△BOC中,BC5=. 如图1,过点Q作QH⊥AB于点H.∴QH∥CO,∴△BHQ∽△BOC∴HQ BQOC BC=,即35HQ t=∴HQ=3 5 t.∴S△PBQ=12PB⋅HQ=12(6−3t)⋅35t=−910t2+95t=−910(t−1)2+910.∴当t=1时,S△PBQ最大=910. ()答:运动1秒使△PBQ的面积最大,最大面积是9 10;。
课时精练3

课时精练3只有中国特色社会主义才能发展中国一、选择题1.[2024·辽宁葫芦岛模拟]中国共产党第十二届中央委员会第三次全体会议,于1984年10月20日在北京召开。
全会一致通过了《中共中央关于经济体制改革的决定》,这次会议()①标志中国改革的重点从农村转向城市②加快推动以城市为重点的整个经济体制改革的步伐③就建立社会主义市场经济体制进行了全面部署④提出走自己的路,建设有中国特色的社会主义A.①②B.①③C.②④D.③④2.在我国改革开放40多年波澜壮阔的发展历程中,有许多标志性的事件。
下列选项对应正确的是()3.[2024·九省联考甘肃卷]2023年9月13日,国家主席习近平同来华进行国事访问的委内瑞拉总统会谈时,介绍了中国改革开放的有关情况,指出改革开放是中国大踏步赶上时代的重要法宝,是决定当代中国命运的关键一招,中国珍惜这一过程中取得的宝贵经验,将继续把改革开放推向前进。
下列说法正确的是()①改革开放完成了中华民族有史以来最为广泛而深刻的社会变革②改革开放奠定了中国特色社会主义的根本政治前提和制度基础③改革开放伟大觉醒孕育了中国共产党从理论到实践的伟大创造④改革开放实现了我国从封闭半封闭到全方位开放的历史性转变A.①②B.①③C.②④D.③④4.[2024·北京朝阳期末]2022年10月16日,中国共产党第二十次全国代表大会在北京隆重召开。
党的二十大报告提出的“三个务必”()①体现了我们党一以贯之加强法治建设、弘扬光荣传统的鲜明立场②与党的七届二中全会提出的“两个务必”既一脉相承又与时俱进③就是要激励全党永远与人民群众同呼吸、共命运,提高党的战斗力④意在告诫全党增强忧患意识,以确保做好防范化解重大风险的物质准备A.①②B.①④C.②③D.③④5.1978年,我国的经济总量仅占全球的1.8%;2023年,我国经济总量占全球经济比重超过18.5%。
1978年,贫穷是大多数中国人共同面对的难题。
七年级下册政治课堂精练人教版电子版

七年级下册政治课堂精练人教版电子版1、坚持和发展中国特色社会主义,要一以贯之体现在()[单选题] *A.发挥国家宏观调控配置资源的决定作用B.要毫不动摇地支持非公经济发展成为主导C.我正确处理好效率与公平的关系,维护稳定D.要坚持和发展我国现阶段的基本经济制度(正确答案)2、发展中国特色社会主义文化的指导思想是()[单选题] *A.促进传统文化和社会主义现代化文化的转化B.有效维护中国特色传统农耕文化的稳定性C.坚定坚持马克思主义的指导地位毫不动摇(正确答案)D.为中华民族伟大复兴提供社会主义道路自信3、第四课2单选题中国梦的本质是(? ) [单选题] *A.国家统一、维护主权、打击犯罪B.民族振兴、社会稳定、经济富足C.国家富强、社会安定、公民幸福D.国家富强、民主振兴、人民幸福(正确答案)4、实践的主体是()[单选题] *A.绝对精神B.具有思维能力、从事社会实践和认识活动的人(正确答案)C.人D.人的意识5、与理性认识相比较,感性认识有两个特点,一个是直接性,另一个是()[单选题] *A.生动性和具体性(正确答案)B.能动性和创造性C.客观性和普遍性D.抽象性和间接性6、改革开放以来,党的全部理论和实践的主题是()[单选题] *A.中国特色社会主义(正确答案)B.社会主义核心价值观C.不忘初心,牢记使命D.基本建成现代化强国7、96. 我国的民主党派是在我国社会主义建设时期建立起来的,它们为新中国的建立作出了积极贡献。
* [判断题] *对(正确答案)错8、2 单项选择题改革开放以来,中国取得一切成绩和进步的根本原因是(? ?)[单选题] *A.确立了中国特色社会主义道路、理论体系、制度和文化(正确答案)B.个体私营经济的发展,实现中华民族伟大复兴C.成功实行了“一国两制”的方针政策和科学构想D.确定了我国基层群众自治制度,促进公民政治参与9、十一届三中全会是新中国成立以来党的历史上最具有深远意义的伟大转折,这次全会作出实行改革开放的新决策,开始了中国从“以阶级斗争为纲”到(? ?)建设为中心,从僵化半僵化到全面改革,从封闭半封闭到对外开放的历史性转变。
3-第11讲-课堂练习(教师版)

(3)第十一讲课堂练习姓名_______1、54-54÷3+3×17=。
答案:87。
解析:原式=54-18+51=87。
2、有两辆车都从北京出发到某地,货车每小时行60千米,20小时可到达。
客车每小时行50千米,如果客车想与货车同时到达某地,它要比货车提前开出______小时。
答案:4。
解析:北京到某地的距离为60×20=1200(千米),客车到达某地需要的时间为1200÷50=24(小时),24-20=4(小时),所以客车要比货车提前开出4小时。
3、甲、乙两人同时匀速打字,4 分钟共打了320 个字,已知甲每分钟比乙多打28个字,甲每分钟打_______个字。
答案:54。
解析:本题关键在于找“暗和”,4 分钟共打了320 个字,那每分钟就应该是320÷4=80(个)字。
和:80;差:28;甲每分钟打字:(80+28)÷2=54(个)。
4、一辆汽车和一辆卡车分别从相距1000千米的甲、乙两地同时出发,相向而行,汽车每小时行60千米,卡车每小时行40千米,8小时后两车相距______千米。
答案:200。
解析:8 小时后两车相距 1000-(60+40)×8=200(千米)。
5、爸爸比儿子大30岁,妈妈比儿子大28岁。
当爸爸与妈妈的年龄和是100岁时,爸爸是______岁。
答案:51。
解析:爸爸与妈妈的年龄差为30-28=2(岁),当爸爸与妈妈的年龄和为100岁时,爸爸(100+2)÷2=51(岁)。
6、8个连续的奇数依序排列,最小的三个数的总和为45,最大的三个数的总和是_______。
答案:75。
解析:因为最小的三个数的总和为45,故第二小的数为45÷3=15,即8个连续奇数依序为13,15,17,19,21,23,25,27。
因此所求最大的三个数之和为23+25+27=75。
7、一个大正方形内有两个面积分别为 25 平方厘米及 4 平方厘米的小正方形,两个小正方形互不重叠,如下图,则阴影部分的周长为________厘米。
(新课标)高考物理一轮复习 高效课堂精讲精练11
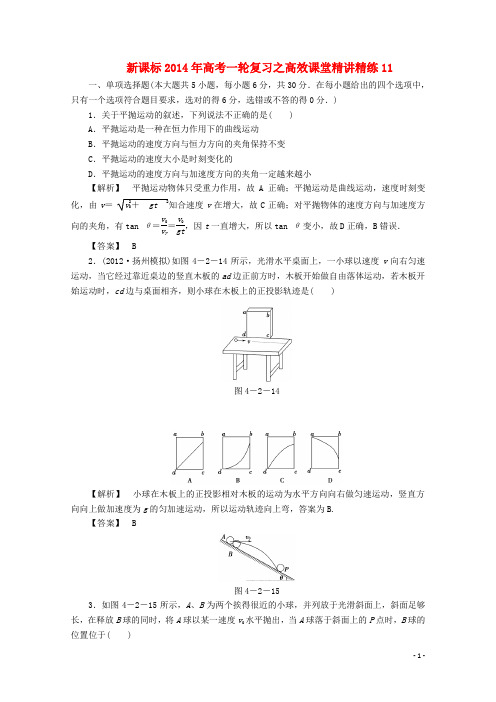
新课标2014年高考一轮复习之高效课堂精讲精练11一、单项选择题(本大题共5小题,每小题6分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求,选对的得6分,选错或不答的得0分.)1.关于平抛运动的叙述,下列说法不正确的是( ) A .平抛运动是一种在恒力作用下的曲线运动 B .平抛运动的速度方向与恒力方向的夹角保持不变 C .平抛运动的速度大小是时刻变化的D .平抛运动的速度方向与加速度方向的夹角一定越来越小【解析】 平抛运动物体只受重力作用,故A 正确;平抛运动是曲线运动,速度时刻变化,由v = v 20+gt2知合速度v 在增大,故C 正确;对平抛物体的速度方向与加速度方向的夹角,有tan θ=v 0v y =v 0gt,因t 一直增大,所以tan θ变小,故D 正确,B 错误.【答案】 B2.(2012·扬州模拟)如图4-2-14所示,光滑水平桌面上,一小球以速度v 向右匀速运动,当它经过靠近桌边的竖直木板的ad 边正前方时,木板开始做自由落体运动,若木板开始运动时,cd 边与桌面相齐,则小球在木板上的正投影轨迹是( )图4-2-14【解析】 小球在木板上的正投影相对木板的运动为水平方向向右做匀速运动,竖直方向向上做加速度为g 的匀加速运动,所以运动轨迹向上弯,答案为B.【答案】 B图4-2-153.如图4-2-15所示,A 、B 为两个挨得很近的小球,并列放于光滑斜面上,斜面足够长,在释放B 球的同时,将A 球以某一速度v 0水平抛出,当A 球落于斜面上的P 点时,B 球的位置位于( )A .P 点以下B .P 点以上C .P 点D .由于v 0未知,故无法确定【解析】 在竖直方向上A 球自由下落,加速度为g ,B 球在竖直方向加速度为g sin 2θ,故A 球先达P 点.【答案】 B4.(2012·海口模拟)如图4-2-16所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角φ满足( )图4-2-16A .tan φ=sin θB .tan φ=cos θC .tan φ=tan θD .tan φ=2tan θ【解析】 竖直速度与水平速度之比为:tan φ=gtv 0,竖直位移与水平位移之比为:tanθ=gt 22v 0t,故tan φ=2tan θ,D 正确.【答案】 D图4-2-175.(2012·佛山模拟)如图4-2-17所示,若质点以初速v 0正对倾角为θ=37°的斜面水平抛出,要求质点到达斜面时位移最小,则质点的飞行时间为( )A.3v 04g B.3v 08g C.8v 03gD.4v 03g【解析】 若使质点到达斜面时位移最小,则质点的位移应垂直斜面,如图所示: 有x =v 0t y =12gt 2且tan θ=x y =v 0t 12gt2=2v 0gt所以t =2v 0g tan θ=2v 0g tan 37°=8v 03g,选项C 正确.【答案】 C二、双项选择题(本大题共5小题,每小题8分,共40分.全部选对的得8分,只选1个且正确的得4分,有选错或不答的得0分.)6.(2011·福州模拟)如图4-2-18所示,三个小球从同一高度处的O 点分别以水平初速度v 1、v 2、v 3抛出,落在水平面上的位置分别是A 、B 、C ,O ′是O 在水平面上的射影点,且O ′A ∶O ′B ∶O ′C =1∶3∶5.若不计空气阻力,则下列说法正确的是( )图4-2-18A .v 1∶v 2∶v 3=1∶3∶5B .三个小球下落的时间相同C .三个小球落地的速度相同D .三个小球落地的动能相同【解析】 由于三个小球从同一高度处抛出,所以做平抛运动的时间相同,B 正确,由x =v 0t 可知选项A 正确;由于初速度不相同,但三种情况重力做功相同,由动能定理可得落地的动能不相同,速度也不相同,故选项C 、D 错误.【答案】 AB图4-2-197.(2012·珠海模拟)平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v -t 图线,如图4-2-19所示.若平抛运动的时间大于2t 1,下列说法中正确的是( )A .图线b 表示竖直分运动的v -t 图线B .t 1时刻的速度方向与初速度方向夹角为30°C .t 1时间内的位移方向与初速度方向夹角的正切值为12D .2t 1时间内的位移方向与初速度方向夹角为60°【解析】 图线b 表示匀加速直线运动,图线a 表示匀速直线运动,故A 项正确.当v x=v y 时,tan θ=v y v x =1,θ=45°,故B 项错.由tan θ=2tan φ,tan φ=12,C 项正确.时间2t 1时v y ′=2v x ,tan θ1=v y ′v x=2.由tan θ1=2tan φ1,tan φ1=1,φ1=45°,故D 项错.【答案】 AC图4-2-208.(2012·无锡模拟)甲、乙、丙三个小球分别位于如图4-2-20所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,水平面上的P 点在丙的正下方.在同一时刻甲、乙、丙开始运动,甲以水平速度v 0做平抛运动,乙以水平速度v 0沿水平面向右做匀速直线运动,丙做自由落体运动.则( )A .若甲、乙、丙三球同时相遇,则一定发生在P 点B .若甲、丙二球在空中相遇,此时乙球一定在P 点C .若只有甲、乙二球在水平面上相遇,此时丙球还未着地D .无论初速度v 0大小如何,甲、乙、丙三球一定会同时在P 点相遇【解析】 若要在P 处相遇,对甲:竖直方向h 甲=12gt 2,水平方向x 甲=v 0t .对乙:x乙=v 0t .对丙:h 丙=12gt 2.故甲与乙在水平方向运动相同,一定会相遇,相遇点一定在水平地面上某点.甲与丙在竖直方向的位置一定在同一高度,因此甲与丙相遇时一定在乙的正上方,即乙一定运动到P 处.若甲与丙在P 处相遇,则乙一定在P 处,即三者在P 处相遇,故A 、B 对;若甲与乙在水平面上相遇,则甲在竖直方向上的高度一定等于丙在竖直方向上的高度,即丙一定刚好落地,C 、D 错.【答案】 AB图4-2-219.(2012·深圳模拟)a 、b 两质点从同一点O 分别以相同的水平速度v 0沿x 轴正方向抛出,a 在竖直平面内运动,落地点为p 1,b 沿光滑斜面运动,落地点为p 2,p 1和p 2在同一水平面上,如图4-2-21所示,不计空气阻力,则下列说法中正确的是( )A .a 、b 的运动时间相同B .a 、b 沿x 轴方向的位移不同C .a 、b 落地时的速度大小相同D .a 、b 落地时的速度相同 【解析】质点a 在竖直平面内做平抛运动,质点b 在斜面上运动时,只受沿斜面方向垂直于斜面底边的重力的分力mg sin θ的作用,如图所示,质点b 做类平抛运动.分析如下:对a ,运动时间t a = 2h /g ;对b ,h sin θ=12g sin θt 2b ,所以运动时间t b =2h /g sin 2 θ≠t a ,则A 项错误;对a ,沿x 轴方向位移x a =v 0t a ,对b ,沿x 轴方向位移x b =v 0t b ≠x a ,则B 项正确;由动能定理知:mgh =12mv 2t -12mv 20,所以v t 的大小相等,则C 项正确;a 、b 落地时速度的方向不同,不能说速度相同,则D 项错误.【答案】 BC图4-2-2210.如图4-2-22所示,坐标方格每格边长为10 cm ,一物体做平抛运动时分别经过O 、a 、b 三点,重力加速度g 取10 m/s 2,则下列结论正确的是( )A .O 点就是抛出点B. a 点v a 与水平方向成45°角 C .速度变化量Δv aO =Δv ba D .小球抛出速度v =1 m/s【解析】 由于O 、a 、b 三点水平方向距离相等,说明t Oa =t ab ,若O 点为抛出点,则在竖直方向连续相等时间内通过的位移之比应为1∶3,而从题图看,竖直方向相等时间内位移之比为1∶2,所以O 点不是抛出点,故A 项错.因O 到a 的位移方向与水平方向成45°,所以物体经过a 点时速度方向与水平方向夹角肯定大于45°,故B 项错.平抛运动是匀变速曲线运动,加速度恒定,所以相等时间内速度变化量相等,Δv aO =Δv ba ,故C 项对.根据竖直方向匀变速直线运动公式a =Δx /t 2,a =g =10 m/s 2,得t = Δxg=0.1 s =t Oa =t ab ,水平方向匀速运动速度v x =x /t =1 m/s ,故D 项对.【答案】 CD三、非选择题(本题共2小题,共30分.要有必要的文字说明和解题步骤,有数值计算的要注明单位.)11.(14分)利用图4-2-23(a)实验可粗略测量人吹气产生的压强.两端开口的细玻璃管水平放置,管内塞有潮湿小棉球,实验者从玻璃管的一端A 吹气,棉球从另一端B 飞出,测得玻璃管内部截面积S ,距地面高度h ,棉球质量m ,开始时的静止位置与管口B 的距离x ,落地点C 与管口B 的水平距离l .然后多次改变x ,测出对应的l ,画出l 2-x 关系图线,如图4-2-23(b)所示,并由此得出相应的斜率k .图4-2-23(1)若不计棉球在空中运动时的空气阻力,根据以上测得的物理量可得,棉球从B 端飞出的速度v 0=________.(2)假设实验者吹气能保持玻璃管内气体压强始终为恒定值,不计棉球与管壁的摩擦,重力加速度g ,大气压强p 0均为已知,利用图(b)中倾斜直线的斜率k 可得,管内气体压强p =________.(3)考虑到实验时棉球与管壁间有摩擦,则(2)中得到的p 与实际压强相比________(填“偏大”或“偏小”).【解析】 (1)l =v 0t ,h =12gt 2,得v 0=lg 2h. (2)(p -p 0)Sx =12mv 20,故l 2=4p -p 0Sh mg x =kx ,因而有:p =p 0+kmg4Sh. (3)因没有考虑摩擦阻力的作用,求出的压强偏小了. 【答案】 (1)lg 2h (2)mgk4Sh+p 0 (3)偏小图4-2-2412.(16分)(2012·中山模拟)如图4-2-24所示,在竖直线OM 上某点P 平抛一个小球,仅在重力作用下小球运动轨迹恰在Q 点与ON 相切,已知OQ =L ,∠NOM =θ,求PO 的高度h .【解析】 如图所示,依题意小球从P 点做平抛运动,运动轨迹与OQ 相切.设小球初速度为v 0,末速度为v ,将末速度分解为水平速度v 0和竖直速度v y ,设运动时间为t .竖直方向做自由落体运动:v y =gt则tan θ=v 0v y =v 0gt水平方向匀速运动位移:x =v 0t 竖直方向自由落体运动位移:y =12gt 2由几何关系:tan θ=xy +h =v 0ty +h且h +y =L cos θ联立解得:h =0.5L cos θ. 【答案】 h =0.5L cos θ。
高中数学第1章三角函数112蝗制课后课时精练课件新人教A版必修4

休息时间到啦
同学们,下课休息十分钟。现在是休息时间,你们休息一 下眼睛,
看看远处,要保护好眼睛哦~站起来动一动,久坐对身体 不好哦~
2021/4/17
高中数学第1章三角函数112蝗制课后课时精练课件新人教 A版必修4
17
B 级:能力提升练 1.已知一扇形的中心角是 α,所在圆的半径是 R,若扇 形的周长是一定值 C(C>0),该扇形的最大面积为( )
10.扇形 AOB 的周长为 8 cm. (1)若这个扇形的面积为 3 cm2,求圆心角的大小; (2)求这个扇形的面积取得最大值时圆心角的大小和弦 长 AB.
解 (1)设扇形的圆心角为 θ,扇形所在圆的半径为 R.
2R+Rθ=8, 依题意有21θ·R2=3,
解得 θ=23或 6.
即圆心角的大小为23弧度或 6 弧度.
解析 ∵-9<-345<-8,∴-3π<-345<-3π+π2. ∴-345在第三象限,故 α 也在第三象限.
5.若一圆弧长等于其所在圆的内接正三角形的边长,
则其圆心角的弧度数的绝对值为( )
π
2π
A.3
B. 3
C. 3
D.2
解析 设所在圆的半径为 r,圆内接正三角形的边长为 2rsin60°= 3r,所以弧长 3r 的圆心角的弧度数为 r3r= 3.
三、解答题 9.用弧度制表示终边在图中阴影区域内角的集合(包括 边界),并判断 2019°是不是这个集合的元素.
解 ∵150°=56π, ∴终边在阴影区域内角的集合为 S=
{β56π+2kπ≤β≤32π+2kπ,k∈Z.
∵2019°=219°+5×360°=211890π+10π rad, 又 56π<211890π<32π,∴2019°∈S.
课堂精练七年级下册语文答案

课堂精练七年级下册语文答案1、54. 下列句子中加双引号成语使用恰当的一项是()[单选题] *A.在抗击疫情时期,众多“莘莘学子”通过空中课堂网络直播等方式在家学习。
B.中国戏曲“源远流长”,异彩纷呈,是中国传统文化的瑰宝。
(正确答案)C.夕阳西下,湖面光影交织,好一派“浮光掠影”的景象。
D.在演讲比赛中,钟明“夸夸其谈”,最终以优异表现获得一等奖。
2、25. 下列词语中加双引号字的字音、字形完全正确的一项是()[单选题] *A.“彷”徨páng“襁”褓qiáng接“踵”而至zhǒng“振”耳欲聋zhènB.推“搡”sang苍“劲”jìn 目“眩”神迷xuàn纷至“踏”来tàC.“抉”择jué“拾”级shè轻歌“曼”舞màn不修边“幅”fú(正确答案)D.“漩”涡xuàn“拙”劣zhuō“慢”不经心màn挑“拨”离间bō3、1“青出于蓝而胜于蓝”这句格言出自于荀子的《劝学》。
[判断题] *对(正确答案)错4、1《卖白菜》作者莫言,当代作家,原名管谟业,是第一个获得诺贝尔文学奖的中国籍作家,代表作有《红高粱》《蛙》《生死疲劳》等。
[判断题] *错(正确答案)5、下列词语中,加着重号字的注音正确的一项是()[单选题] *A、忖度(duó)濒临(pín)B、踽踽(jǔ)够呛(qiànɡ)(正确答案)C、沙砾(lì)娇嗔(zhēn)D、睿智(bì)醴酪(lǐ)6、10. 下面句子中的标点符号,运用正确的一项是()[单选题] *A.自然之美是一切艺术美的源头活水,正如古人所云“天地有大美而不言。
”B.《全景故宫》《全景兵马俑》等一批数字全景展厅项目,让观众宅在家中就能“漫游”文化遗产地。
(正确答案)C.网络让人类有限的大脑实现任意链接,但是谁也不知道网络搜索会不会让人变笨D.朗读不仅仅是一种学习方式;更是一种传递情感、传承精神的一种手段。
2021人教版物理八年级下册第11章功和机械能精讲精练(00001)

专题11.1 功课前预习1.在物理学中,把力和在力的方向上移动的____距离____的乘积叫做功。
2.做功的两个必要因素:一是有___力___作用在物体上,二是物体在力的方向上移动一段距离。
3.功计算公式:___W=Fs____.4.功单位是焦尔,用符号____ J____,1J=1N·m。
知识点解读与例题突破知识点1:力学中的功1.如果一个力作用在物体上,物体在力的方向上移动了一段距离,这个力的作用就显示出成效,力学里就说这个力做了功。
2.功的两个因素:一个是作用在物体上的力,另一个是在力的方向上移动的距离。
3.不做功的三种情况:①物体受到了力,但静止。
②物体由于惯性运动通过了距离,但不受力。
③物体受力的方向与运动的方向相互垂直,这个力也不做功。
【例题1】关于功的说法正确的是()A.小明用力推发生故障的汽车而未推动时,推力对汽车做了功B.吊车吊着重物沿水平匀速运动一段距离时,吊车的拉力对重物做了功C.足球在水平地面上滚动一段距离时,重力对足球做了功D.举重运动员从地面将杠铃举起的过程中,举重运动员对杠铃做了功【答案】D【解析】A.小明用力推发生故障的汽车而未推动时,推力对汽车做了功,错误,有力的作用,没有沿力的方向移动距离,没有做功;B.吊车吊着重物沿水平匀速运动一段距离时,吊车的拉力对重物做了功,错误,有力的作用,没有沿力的方向移动距离,没有做功;C.足球在水平地面上滚动一段距离时,重力对足球做了功,错误,错误,有力的作用,没有沿力的方向移动距离,没有做功;D.举重运动员从地面将杠铃举起的过程中,举重运动员对杠铃做了功,正确。
知识点2:功的计算(1)计算公式:物理学中,功等于力与力的方向上移动的距离的乘积。
即:W=Fs。
(2)符号的意义及单位:W表示功,单位是J,1J=1N·m;F表示力,单位是N;S表示距离,单位是m。
(3)计算时应注意的事项:①分清是哪个力对物体做功,即明确公式中的F。
课堂精练八下数学答案2021

课堂精练八下数学答案2021课堂精练八下数学答案20XX课堂精练八下数学答案数学(mathematics或maths),是研究数量结构变化空间以及信息等概念的一门学科,从某种角度看属于形式科学的一种。
下面是范文xxxx小编整理的课堂精练八下数学答案,供大家参考课堂精练八下数学答案一选择题(共15小题)1下列各式:,,,m,其中分式共有()A1个B2个C3个D4个答案:A解答:,,,m,其中分式共有:共有1个故选:A分析:直接利用分式的定义即可2下列各式中,是分式的是()ABCD答案:C解答:这个式子分母中含有字母,因此是分式其它式子分母中均不含有字母,是整式,而不是分式故选:C分析:根据分式的定义对上式逐个进行判断,得出正确答案3下列代数式中,是分式的是()ABCD答案:D解答:A分数,是单项式,故选项错误B分母是常数,是单项式,故选项错误C分母是常数,是单项式,故选项错误D正确故选D分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式4下列各代数式中是分式的是()A2xBCD答案:C解答:A2x,它是整式故本选项错误B的分母是常数2,所以它是整式故本选项错误C的分母是字母x,所以它是分式故本选项正确D是二次根式,故本选项错误故选C分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式5在下列式子,,,,,中,分式的个数是()A2个B4个C3个D5个答案:C解答:,,的分母中均不含有字母,因此它们是整式,而不是分式,,分母中含有字母,因此是分式故选:C分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式6在代数式,(xy),,,,中,分式有()A2个B3个C4个D5个答案:C解答:分母中含有字母的代数式有,,,,因为π是数字不是字母,故不是分式故分式有4个故选:C分析:分母中含有字母的代数式叫做分式,依据定义即可做出判断7下列各式:(1x)其中分式共有()A2个B3个C4个D5个答案:A解答:(1x),,的分母中均不含有字母,因此不是分式,是整式,分母中含有字母,因此是分式故选:A分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式8在中分式有()A1个B4个C3个D2个答案:D解答:分式有,共2个,故选D分析:找到分母含有字母的式子即可9在代数式6x2y中,分式有()A4个B3个C2个D1个答案:B解答:分式有,故选:B分析:根据分式的概念:一般地,如果A,B表示两个整式,并且B中含有字母,那么式子叫做分式可得答案10下列式子是分式的是()ABCD答案:B解答:,,的分母中均不含有字母,因此它们是整式,而不是分式分母中含有字母,因此是分式故选:B分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式11在中分式的个数有()A2个B3个C4个D5个答案:A解答:是分式,故选:A分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式12下列式子是分式的是()ABCD答案:B解答:A分母中不含有字母是整式,故A错误B分母中含有字母是分式,故B正确C分母中不含有字母是整式,故C错误D分母中不含有字母是整式,故D错误故选:B分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式13下列代数式中,属于分式的是()A5xBCD答案:C解答:根据分式的定义A是整式,答案错误B是整式,答案错误C是分式,答案正确D是根式,答案错误故答案选C分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式,从而得出答案14在中,分式的个数是()A2B3C4D5答案:B解答:在中,分式有,分式的个数是3个故选:B分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式15在式子中,分式的个数为()A2个B3个C4个D5个答案:B解答:,,这3个式子分母中含有字母,因此是分式其它式子分母中均不含有字母,是整式,而不是分式故选:B分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式二填空题(共5小题)16下列各式:,,x2y2,5,,中,分式是答案::,解答:,是分式,故答案为:,分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式17在,,,中,其中是分式答案:,解答:,的分母中均不含有字母,因此它们是整式,而不是分式,分母中含有字母,因此是分式分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式18在代数式,,,,,,,中,分式有答案:,,,解答:代数式,,,,,,中,分式有,,,故答案为:,,,分析:根据分式的定义得到在所给式子中分式有,,,19一般地,如果AB表示是,并且B中含有,叫做分式,其中A叫做分式的,B叫做分式的答案:两个整式字母分子分母解答:一般地,如果AB表示是两个整式,并且B中含有字母,叫做分式,其中A叫做分式的分子,B叫做分式的分母故答案是:两个整式,字母,分子,分母分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式20和统称有理式答案:分式整式解答:有理式,包括分式和整式故答案:分式,整式分析:分式和整式统称为有理式三解答题(共5小题)21已知两个式子,它们是否为分式,并给出理由答案:两个式子,它们是分式因为它们的分母中含有字母解答:两个式子,它们是分式,因为它们的分母中含有字母,因此是分式有字母则不是分式22下列各式中,那些是整式哪些不是整式两者有什么区别,2xy,,3a,5答案:整式:,2xy,,3a,5不是整式:,解答:整式:,2xy,,3a,5不是整式:,它们区别是分母中是否含有字母,若含有字母则不是整式,若不含有字母则是整式分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式23观察下面的一组分式:,,,,(1)求第10个分式是多少答案:解答:,,,,第10个分式是:(2)列出第n个分式答案:(1)n1解答:由(1)得到第n个分式为:(1)n1符号,奇数项为正数,偶数项为负数(2)根据(1)的推断过程得到通式24请从下列三个代数式a21,abb,a21,abb中任选两个构造一个分式,并化简该分式(1)构造的分式是:答案:解答:分式为(2)化简:答案:解答:化简得,25分式可以表示什么实际意义答案:解:用y表示某班要发新作业本的数目,x表示该班级原有人数,则分式可以表示新转来一名同学后,每人能发新作业本的数目。
八上数学课堂精练答案

八上数学课堂精练答案八上数学课堂精练答案八上数学课堂精练答案一.仔细选一选1.下列四个数中,结果为负数的是()A.﹣(﹣)B.|﹣|C.(﹣)2D.﹣|﹣|考点:正数和负数.分析:根据相反数,可判断A,根据负数的绝对值,可判断B,根据负数的偶次幂是正数,可判断C,根据绝对值的相反数,可判断D.解答:解:A、﹣(﹣)=>0,故A错误;B、|﹣|=>0,故B错误;C、(﹣)2=>0,故C错误;D、﹣|﹣|=﹣<0,故D正确;故选:D.点评:本题考查了正数和负数,小于零的数是负数,先化简再判断负数.2.下列计算正确的是()A.B.=﹣2C.D.(﹣2)3×(﹣3)2=72考点:实数的运算.分析:A、根据算术平方根的定义即可判定;B、根据立方根的定义即可判定;C、根据立方根的定义即可判定;D、根据乘方运算法则计算即可判定.解答:解:A、=3,故选项A错误;B、=﹣2,故选项B正确;C、=,故选项C错误;D、(﹣2)3×(﹣3)2=﹣8×9=﹣72,故选项D错误.故选B.点评:本题主要考查实数的运算能力,解决此类题目的关键是熟记二次根式、三次根式和立方、平方的运算法则.开平方和开立方分别和平方和立方互为逆运算.立方根的性质:任何数都有立方根,①正数的立方根是正数,②负数的立方根是负数,③0的立方根是0.3.用代数式表示:“a,b两数的平方和与a,b乘积的差”,正确的是()A.a2+b2﹣abB.(a+b)2﹣abC.a2b2﹣abD.(a2+b2)ab考点:列代数式.分析:先求得a,b两数的平方和为a2+b2,再减去a,b乘积列式得出答案即可.解答:解:“a,b两数的平方和与a,b乘积的差”,列示为a2+b2﹣ab.故选:A.点评:此题考查列代数式,找出题目蕴含的数量关系是解决问题的关键.4.据统计,2013年我国用义务教育经费支持了13940000名农民工随迁子女在城市里接受义务教育,这个数字用科学计数法可表示为()A.1.394×107B.13.94×107C.1.394×106D.13.94×105考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:解:13940000=1.394×107,故选:A.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5.若﹣2am﹣1b2与5abn可以合并成一项,则m+n的值是()A.1B.2C.3D.4考点:合并同类项.分析:根据可以合并,可得同类项,根据同类项是字母相同且相同字母的指数也相同,可得m、n的值,根据有理数的加法,可得答案.解答:解:由﹣2am﹣1b2与5abn可以合并成一项,得m﹣1=1,n=2.解得m=2,n=2.m+n=2+2=4,故选:D.点评:本题考查了合并同类项,利用了同类项得出m、n的值是解题关键.6.如图,A是直线l外一点,点B、C、E、D在直线l上,且AD⊥l,D为垂足,如果量得AC=8cm,AD=6cm,AE=7cm,AB=13cm,那么,点A到直线l的距离是()A.13cmB.8cmC.7cmD.6cm考点:点到直线的距离.分析:根据点到直线的距离是点与直线上垂足间线段的长,可得答案.解答:解:点A到直线l的距离是AD的长,故点A到直线l的距离是6cm,故选:D.点评:本题考查了点到直线的距离,点到直线的距离是点与直线上垂足间线段的长.7.下列式子变形正确的是()A.﹣(a﹣1)=﹣a﹣1B.3a﹣5a=﹣2aC.2(a+b)=2a+bD.|π﹣3|=3﹣π考点:合并同类项;绝对值;去括号与添括号.专题:常规题型.分析:根据去括号与添括号的法则以及合并同类项的定义对各选项依次进行判断即可解答.解答:解:A、﹣(a﹣1)=﹣a+1,故本选项错误;B、3a﹣5a=﹣2a,故本选项正确;C、2(a+b)=2a+2b,故本选项错误;D、|π﹣3|=π﹣3,故本选项错误.故选B.点评:本题考查去括号的方法:去括号时,运用乘法的分配律,先把括号前的数字与括号里各项相乘,再运用括号前是”+“,去括号后,括号里的各项都不改变符号;括号前是”﹣“,去括号后,括号里的各项都改变符号.运用这一法则去掉括号.同时要注意掌握合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变.8.若有理数m在数轴上对应的点为M,且满足m<1<﹣m,则下列数轴表示正确的是()A.B.C.D.考点:数轴;相反数;有理数大小比较.分析:根据m<1<﹣m,求出m的取值范围,进而确定M的位置即可.解答:解:∵m<1<﹣m,∴,解得:m<﹣1.故选:A.点评:此题主要考查了不等式组的解法以及利用数轴确定点的位置,根据已知得出m的取值范围是解题关键.9.下列说法:①两点确定一条直线;②射线AB和射线BA是同一条射线;③相等的角是对顶角;④三角形任意两边和大于第三边的理由是两点之间线段最短.正确的是()A.①③④B.①②④C.①④D.②③④考点:三角形三边关系;直线、射线、线段;直线的性质:两点确定一条直线;对顶角、邻补角.分析:利用确定直线的条件、射线的定义、对顶角的性质、三角形的三边关系分别判断后即可确定正确的选项.解答:解:①两点确定一条直线,正确;②射线AB和射线BA是同一条射线,错误;③相等的角是对顶角,错误;④三角形任意两边和大于第三边的理由是两点之间线段最短,正确,故选C.点评:本题考查了确定直线的条件、射线的定义、对顶角的性质、三角形的三边关系,属于基础知识,比较简单.10.已知线段AB=8cm,在直线AB上有一点C,且BC=4cm,点M是线段AC的中点,则线段AM的长为()A.2cmB.4cmC.2cm或6cmD.4cm或6cm考点:两点间的距离.分析:分类讨论:点C在线段AB上,点C在线段BC的延长线上,根据线段的和差,可得AC的长,根据线段中点的性质,可得AM 的长.解答:解:当点C在线段AB上时,由线段的和差,得AC=AB﹣BC=8﹣4=4(cm),由线段中点的性质,得AM=AC=×4=2(cm);点C在线段BC的延长线上,由线段的和差,得AC=AB+BC=8+4=12(cm),由线段中点的性质,得AM=AC=×12=6(cm);故选:C.点评:本题考查了两点间的距离,利用了线段的和差,线段中点的性质.二.认真填一填11.若∠1=40°50′,则∠1的余角为49°10′,∠1的补角为139°10′.考点:余角和补角;度分秒的换算.分析:根据余角的定义求出90°﹣∠1°,即可得出答案,根据补角的定义求出180°﹣∠1,即可得出答案.解答:解:∵∠1=40°50′,∴∠1的余角为90°﹣∠1=49°10′,∠1的补角为180°﹣∠1=139°10′,故答案为:49°10′,139°10′.点评:本题考查了余角和补角的应用,注意:∠1是的余角是90°﹣∠1,补角是180°﹣∠1.12.在实数,,0,,,﹣1.414,0.131131113…(两个“3”之间依次多一个“1”),﹣中,其中无理数是,,0.131131113…(两个“3”之间依次多一个“1”).考点:无理数.分析:无理数是指无限不循环小数,根据无理数的定义判断即可.解答:解:无理数有,,0.131131113…(两个“3”之间依次多一个“1”),故答案为:,,0.131131113…(两个“3”之间依次多一个“1”).点评:本题考查了对无理数的定义的应用,注意:无理数包括三方面的`数:①含π的,②开方开不尽的根式,③一些有规律的数.13.x的方程3x+2a=6的解是a﹣1,则a的值是.考点:一元一次方程的解.分析:把x=a﹣1代入方程计算即可求出a的值.解答:解:把x=a﹣1代入方程得:3a﹣3+2a=6,解得:a=,故答案为:.点评:此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.14.如果a﹣3b=6,那么代数式5﹣3a+9b的值是﹣13.考点:代数式求值.分析:将原式提取公因式,进而将已知代入求出即可.解答:解:∵a﹣3b=6,∴5﹣3a+9b=5﹣3(a﹣3b)=5﹣3×6=﹣13.故答案为:﹣13.点评:此题主要考查了代数式求值,正确应用已知得出是解题关键.15.若当x=3时,代数式(3x+4+m)与2﹣mx的值相等,则m=﹣.考点:解一元一次方程.专题:计算题.分析:把x=3代入两代数式,使其值相等求出m的值即可.解答:解:把x=3代入得:(13+m)=2﹣m,去分母得:4(13+m)=28﹣21m,去括号得:42+4m=28﹣21m,移项合并得:25m=﹣14,解得:m=﹣,故答案为:﹣点评:此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.16.下面每个正方形中的五个数之间都有相同的规律,根据这种规律,则第4个正方形中间数字m为29,第n个正方形的中间数字为8n﹣3.(用含n的代数式表示)考点:规律型:图形的变化类.分析:由前三个正方形可知:右上和右下两个数的和等于中间的数,根据这一规律即可求出m的值;首先求得第n个的最小数为1+4(n﹣1)=4n﹣3,其它三个分别为4n﹣2,4n﹣1,4n,由以上规律求得答案即可.解答:解:如图,因此第4个正方形中间数字m为14+15=29,第n个正方形的中间数字为4n﹣2+4n﹣1=8n﹣3.故答案为:29,8n﹣3.点评:此题考查图形的变化规律,通过观察,分析、归纳发现数字之间的运算规律,并应用发现的规律解决问题.三.全面答一答17.计算(1)(﹣2.25)﹣(+)+(﹣)﹣(﹣0.125)(2)﹣32+5×(﹣6)﹣(﹣4)2÷(﹣2)考点:有理数的混合运算.分析:(1)原式利用减法法则变形,计算即可得到结果;(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.解答:解:(1)原式=(﹣2.25﹣0.75)+(﹣0.625+0.125)=﹣3﹣0.5=﹣3.5;(2)原=﹣9﹣30+8=﹣31.点评:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.18.解方程(1)4x﹣2=3x﹣(2)=﹣2.考点:解一元一次方程.专题:计算题.分析:(1)方程移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.解答:解:(1)方程移项合并得:x=2﹣;(2)去分母得:4x+2=1﹣2x﹣12,移项合并得:6x=﹣13,解得:x=﹣.点评:此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把x系数化为1,求出解.19.如图,O在直线AC上,OD是∠AOB的平分线,OE在∠BOC内.(1)若OE是∠BOC的平分线,则有OD⊥OE,试说明理由;(2)若∠BOE=∠EOC,∠DOE=72°,求∠EOC的度数.考点:角平分线的定义.分析:(1)根据角平分线的定义可以求得∠DOE=∠AOC=90°;(2)设∠EOB=x度,∠EOC=2x度,把角用未知数表示出来,建立x的方程,用代数方法解几何问题是一种常用的方法.解答:解:(1)如图,∵OD是∠AOB的平分线,OE是∠BOC的平分线,∴∠BOD=∠AOB,∠BOE=∠BOC,∴∠DOE=(∠AOB+∠BOC)=∠AOC=90°,即OD⊥OE;(2)设∠EOB=x,则∠EOC=2x,则∠BOD=(180°﹣3x),则∠BOE+∠BOD=∠DOE,即x+(180°﹣3x)=72°,解得x=36°,故∠EOC=2x=72°.点评:本题考查了角平分线的定义.设未知数,把角用未知数表示出来,列方程组,求解.角平分线的运用,为解此题起了一个过渡的作用.20.在同一平面内有n条直线,当n=1时,如图①,一条直线将一个平面分成两个部分;当n=2时,如图②,两条直线将一个平面最多分成四个部分.(1)在作图区分别画出当n=3时,三条直线将一个平面分成最少部分和最多部分的情况;(2)当n=4时,请写出四条直线将一个平面分成最少部分的个数和最多部分的个数;(3)若n条直线将一个平面最多分成an个部分,(n+1)条直线将一个平面最多分成an+1个部分,请写出an,an+1,n之间的关系式.考点:规律型:图形的变化类.分析:(1)一条直线可以把平面分成两部分,两条直线最多可以把平面分成4部分,三条直线最少可以把平面分成4部分,最多可以把平面分成7部分,由此画出图形即可;(2)四条直线最少可以把平面分成5部分,最多可以把平面分成11部分;(3)可以发现,两条直线时多了2部分,三条直线比原来多了3部分,四条直线时比原来多了4部分,…,n条时比原来多了n部分..解答:解:(1)如图,(2)四条直线最少可以把平面分成5部分,最多可以把平面分成11部分;(3)当n=1时,分成2部分,当n=2时,分成4=2+2部分,当n=3时,分成7=4+3部分,当n=4时,分成11=7+4部分,…可以发现,有几条线段,则分成的部分比前一种情况多几部分,an、an+1、n之间的关系是:an+1=an+(n+1).点评:此题考查图形的变化规律,找出图形之间的联系,得出数字的运算规律,利用规律解决问题.21.在一条东西走向的马路旁,有青少年宫、学校、商场、医院四家公共场所.已知青少年宫在学校东500m处,商场在学校西300m处,医院在学校东600m处.若将马路近似地看作一条直线,以学校为原点,向东方向为正方向,用1个单位长度表示100m.(1)请画一条数轴并在数轴上表示出四家公共场所的位置;(2)列式计算青少年宫与商场之间的距离;(3)若小新家也位于这条马路旁,在青少年宫的西边,且到商场与青少年宫的距离之和等于到医院的距离,试求小新家与学校的距离.考点:数轴.分析:(1)规定向东为正,单位长度是以100米为1个单位,根据青少年宫、学校、商场、医院的位置画出数轴即可,(2)根据数轴上两点之间的距离是表示这两点的数的差的绝对值求值即可.(3)由题意可得小新家到医院的距离为800m,设小新家在数轴上为xm,列出方程求出x,即可确定小新家与学校的距离.解答:解:(1)如图,(2)青少年宫与商场之间的距离|500﹣(﹣300)|=800m,(3)①∵小新家在青少年宫的西边,且到商场与青少年宫的距离之和等于到医院的距离,∴小新家到医院的距离为800m,设小新家在数轴上为xm,则600﹣x=800,解得x=﹣200m,∴小新家与学校的距离为200m.②当小新家在商场的西边时,设小新家在数轴上为xm,则﹣300﹣x+500﹣x=600﹣x,解得x=﹣400m∴小新家与学校的距离为400m.点评:此题主要考查正负数在实际中的应用,所以学生在学这一部分时一定要联系实际,不能死学.22.图1为全体奇数排成的数表,用十字框任意框出5个数,记框内中间这个数为a(如图2).(1)请用含a的代数式表示框内的其余4个数;(2)框内的5个数之和能等于2015,2020吗?若不能,请说明理由;若能,请求出这5个数中最小的一个数,并写出最小的这个数在图1数表中的位置.(自上往下第几行,自左往右的第几个)考点:一元一次方程的应用.分析:(1)上下相邻的数相差18,左右相邻的数相差是2,所以可用a表示;(2)根据等量关系:框内的5个数之和能等于2015,2020,分别列方程分析求解.解答:解:(1)设中间的数是a,则a的上一个数为a﹣18,下一个数为a+18,前一个数为a﹣2,后一个数为a+2;(2)设中间的数是a,依题意有5a=2015,a=403,符合题意,这5个数中最小的一个数是a﹣18=403﹣18=385,2n﹣1=385,解得n=193,193÷9=21…4,最小的这个数在图1数表中的位置第22排第4列.5a=2020,a=404,404是偶数,不合题意舍去;即十字框中的五数之和不能等于2020,能等于2015.点评:本题考查一元一次方程的应用,关键是看到表格中中间位置的数和四周数的关系,最后可列出方程求解.23.某超市在“元旦”促销期间规定:超市内所有商品按标价的75%出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:消费金额a(元)的范围100≤a<400400≤a<600600≤a<800 获得奖券金额(元)40100130根据上述促销方法知道,顾客在超市内购物可以获得双重优惠,即顾客在超市内购物获得的优惠额=商品的折扣+相应的奖券金额,例如:购买标价为440元的商品,则消费金额为:440×75%=330元,获得的优惠额为:440×(l﹣75%)+40=150元.(1)购买一件标价为800元的商品,求获得的优惠额;(2)若购买一件商品的消费金额在450≤a<800之间,请用含a 的代数式表示优惠额;(3)对于标价在600元与900元之间(含600元和900元)的商品,顾客购买标价为多少元的商品时可以得到的优惠率?(设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价)考点:一元一次方程的应用.分析:(1)先求出标价为450元的商品按80%的价格出售,消费金额为360元,再根据消费金额360元在200≤x≤400之间,即可得出优惠额;(2)分两种情况:当400<a≤600时;当600≤a<800时;讨论可求该顾客获得的优惠额;(3)设购买标价为x元时,可以得到的优惠率,根据(2)的计算方法列出方程解答即可.解答:解:(1)优惠额为800×(l﹣75%)+130=330元;(2)消费金额在400<a≤600之间时,优惠额为(a÷70%)(1﹣75%)+100=a+100;消费金额在600≤a<800之间时,优惠额为(a÷70%)(1﹣75%)+130=a+130;(3)设购买标价为x元时,由题意得0.25x+130=x,或x+130=x,解得:x=832或x=(不合题意,舍去)答:购买标价为832元的商品时可以得到的优惠率.点评:此题考查一元一次方程的实际运用,列代数式,理解题意,找出运算的方法是解决问题的关键.下载全文。
【课堂精练八上数学答案】2021年课堂精练八年级数学下册北师大版山西专版

【课堂精练八上数学答案】2021年课堂精练八年级数学下册北师大版山西专版课堂精练八上数学答案20XX年课堂精练八年级数学下册北师大版山西专版数学(mathematics或maths),是研究数量结构变化空间以及信息等概念的一门学科,从某种角度看属于形式科学的一种。
下面是范文xxxx小编整理的20XX 年课堂精练八年级数学下册北师大版山西专版,供大家参考20XX年课堂精练八年级数学下册北师大版山西专版一选择题(共15小题)1如图,ABC是一个等腰直角三角形,DEFG是其内接正方形,H是正方形的对角线交点那么,由图中的线段所构成的三角形中相互全等的三角形的对数为() A12B13C26D30答案:C知识点:全等三角形的判定等腰直角三角形正方形的性质解析:解答:解:设AB3,图中所有三角形均为等腰直角三角形,其中,斜边长为1的有5个,它们组成10对全等三角形斜边长为的有6个,它们组成15对全等三角形斜边长为2的有2个,它们组成1对全等三角形共计26对故选C分析:根据全等三角形的判定可以确定全等三角形的对数,由于图中全等三角形的对数较多,可以根据斜边长的不同确定对数,可以做到不重不漏本题考查了全等三角形的判定,涉及到等腰直角三角形和正方形的性质,解题的关键是记熟全等三角形的判定方法并做到不重不漏2如图所示,EF分别是正方形ABCD的边CD,AD上的点,且CEDF,AE,BF 相交于点O,下列结论AEBFAEBFAOOESAOBS四边形DEOF中,错误的有()A1个B2个C3个D4个答案:A知识点:正方形的性质全等三角形的判定与性质解析:解答:解:四边形ABCD是正方形,CDADCEDFDEAFADEBAFAEBF,SADESBAF,DEAAFB,EADFBASAOBS四边形DEOFABFAFBDAEDEA90AFBEAF90AEBF一定成立错误的结论是:AOOE故选A分析:根据四边形ABCD是正方形及CEDF,可证出ADEBAF,则得到:AEBF,以及ADE和BAF的面积相等,得到SAOBS四边形DEOF可以证出ABOBAO90,则AEBF一定成立错误的结论是:AOOE本题考查了全等三角形的判定和正方形的判定和性质3如图,在正方形ABCD中,AB4,E为CD上一动点,AE交BD于F,过F作FHAE于H,过H作GHBD于G,下列有四个结论:AFFH,HAE45,BD2FG,CEH的周长为定值,其中正确的结论有()ABCD答案:D知识点:正方形的性质全等三角形的判定与性质解析:解答:解:(1)连接FC,延长HF交AD于点L,BD为正方形ABCD的对角线,ADBCDF45ADCD,DFDF,ADFCDFFCAF,ECFDAFALHLAF90,LHCDAF90ECFDAF,FHCFCH,FHFCFHAF(2)FHAE,FHAF,HAE45(3)连接AC交BD于点O,可知:BD2OA,AFOGFHGHFGFH,AFOGHFAFHF,AOFFGH90,AOFFGHOAGFBD2OA,BD2FG(4)延长AD至点M,使ADDM,过点C作CIHL,则:LIHC,根据MECMIC,可得:CEIM,同理,可得:ALHE,HEHCECALLIIMAM8CEM的周长为8,为定值故(1)(2)(3)(4)结论都正确故选D分析:(1)作辅助线,延长HF交AD于点L,连接CF,通过证明ADFCDF,可得:AFCF,故需证明FCFH,可证:AFFH(2)由FHAE,AFFH,可得:HAE45(3)作辅助线,连接AC交BD于点O,证BD2FG,只需证OAGF即可,根据AOFFGH,可证OAGF,故可证BD2FG(4)作辅助线,延长AD至点M,使ADDM,过点C作CIHL,则ILHC,可证ALHE,再根据MECMIC,可证:CIIM,故CEM的周长为边AM的长,为定值解答本题要充分利用正方形的特殊性质,在解题过程中要多次利用三角形全等4一个围棋盘由1818个边长为1的正方形小方格组成,一块边长为15的正方形卡片放在棋盘上,被这块卡片覆盖了一部分或全部的小方格共有n个,则n 的最大值是()A4B6C10D12答案:D知识点:正方形的性质解析:解答:解:卡片的边长为15,卡片的对角线长为23,且小方格的对角线长15故该卡片可以按照如图所示放置:图示为n取最大值的时候,n12故选D分析:要n取最大值,就让边长为15的正方形卡片边与小方格的边成一定角度本题考查的是已知正方形边长正方形对角线长的计算,旋转正方形卡片并且找到合适的位置使得n为最大值,是解题的关键5如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则AMD的度数是()A75B60C54D675答案:B知识点:正方形的性质线段垂直平分线的性质解析:解答:解:如图,连接BD,BCEBCDDCE9060150,BCEC,EBCBEC(180BCE)15BCMBCD45,BMC180(BCMEBC)120,AMB180BMC60AC是线段BD的垂直平分线,M在AC上,AMDAMB60故选B分析:连接BD,根据BD,AC为正方形的两条对角线可知AC为BD的垂直平分线,所以AMDAMB,要求AMD,求AMB即可本题考查的正方形的对角垂直平分的性质,根据垂直平分线的性质可以求得AMDAMB,确定AC和BD垂直平分是解题的关键6在平面直角坐标系中,称横纵坐标均为整数的点为整点,如下图所示的正方形内(包括边界)整点的个数是()A13B21C17D25答案:D知识点:正方形的性质坐标与图形性质解析:解答:解:正方形边上的整点为(0,3)(1,2)(2,1)(3,0)(4,5)(5,4)(6,3)(4,1)(5,2)(1,4)(2,5)(3,6)在其内的整点有(1,3)(2,2)(2,3)(2,4)(3,1)(3,2)(3,3)(3,4)(3,5)(4,2)(4,3)(4,4)(5,3)故选D分析:根据正方形边长的计算,计算出边长上的整点,并且根据边长的坐标找出在正方形范围内的整点本题考查的是正方形四条边上整点的计算,找到每条边上整点变化的规律是解本题的关键7在同一平面上,正方形ABCD的四个顶点到直线l的距离只取四个值,其中一个值是另一个值的3倍,这样的直线l可以有()A4条B8条C12条D16条答案:D知识点:正方形的性质点到直线的距离解析:解答:解:符合题目要求的一共16条直线,下图虚线所示直线均符合题目要求分析:根据正方形的性质,一个值为另一个值的3倍,所以本题需要分类讨论,该直线切割正方形,确定直线的位置该直线在正方形外,确定直线的位置本题考查了分类讨论计算点到直线的距离,找到直线的位置是解题的关键8如图,正方形ABCD的边长为1,E为AD中点,P为CE中点,F为BP中点,则F到BD的距离等于()ABCD答案:D知识点:正方形的性质三角形的面积解析:解答:解:连接DP,SBDPSBDCSDPCSBPC11,F为BP的中点,P到BD的距离为F到BD的距离的2倍SBDP2SBDF,SBDF,设F到BD的距离为h,根据三角形面积计算公式,SBDFBDh,计算得:h故选D分析:图中,F为BP的中点,所以SBDP2SBDF,所以要求F到BD的距离,求出P到BD的距离即可本题考查的是转化思想,先求三角形的面积,再根据三角形面积计算公式,计算三角形的高,即F到BD的距离9搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,xxxx将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点已知正方形ABCD的面积为576cm2,则被分隔开的CON的面积为()A96cm2B48cm2C24cm2D以上都不对答案:B知识点:正方形的性质三角形的面积相似三角形的判定与性质解析:解答:解:找到CD的中点E,找到AD的中点F,连接CF,AE,则CMEA,ANFC,BOMBKA,,同理可证:,故DKKOOB,BOC和BOA的面积和为正方形ABCD的面积,CNNBAMBM,OCN的面积为BOC和BOA的面积和,OCN的面积为48cm2,故选B分析:先证明BO为正方形ABCD的对角线BD的,再求证CNO,NBO,AMO,BMO的面积相等,即CON的面积为正方形面积的本题考查了正方形内中位线的应用,考查了正方形四边均相等的性质,解本题的关键是求证BOBD,OCN的面积为BOC和BOA的面积和10如图,正方形ABCD的对角线AC与BD相交于O点,在BD上截取BEBC,连接CE,点P是CE上任意一点,PMBD于M,PNBC于N,若正方形ABCD的边长为1,则PMPN()A1BCD1答案:C知识点:正方形的性质,三角形的面积解析:解答:解:连接BP,作EHBC,则PMPN分别为BPE和BCP的高,且底边长均为1,SBCE1SCDE,DEBDBE,CDE中CD边上的高为(1),SCDECD(1)SBCE1SCDE又SBCESBPESBPCBC(PMPN)PMPN故选C分析:连接BP,PMPN分别为BPE和BCP的高,且底边长均为1,因此根据面积计算方法可以求PMPN本题考查的用求三角形面积的方法求三角形的高的转化思想,考查正方形对角线互相垂直且对角线即角平分线的性质,面积转换思想是解决本题的关键11顶点为A(6,6),B(4,3),C(1,7),D(9,4)的正方形在第一象限的面积是()A25B36C49D30答案:B知识点:正方形的性质坐标与图形性质三角形的面积解析:解答:解:连接OA,过AD两点的直线方程是,即y16,解得它与x轴的交点E的横坐标是x78,同理求得过AB两点的直线方程是y42,解得它与y轴的交点E的纵坐标是y42,SAOE786234,SAFO426126,SAOESAFO23412636,即顶点为A(6,6),B(4,3),C(1,7),D(9,4)的正方形在第一象限的面积是36分析:根据正方形的顶点坐标,求出直线AD的方程,由方程式知AD与x轴的交点E的坐标,同理求得AB与y轴的交点F的坐标,连接OA,再去求两个三角形的面积,从而求得正方形在第一象限的面积解答本题要充分利用正方形的特殊性质注意在正方形中的特殊三角形的应用,利用直角三角形求面积,在本题中,借助直线方程求的点EF在坐标轴上的坐标,据此解得所求三角形的边长,代入面积公式求得结果12ABCD是边长为1的正方形,BPC是等边三角形,则BPD的面积为()ABCD答案:B知识点:正方形的性质三角形的面积等边三角形的性质解析:解答:解:BPD的面积等于BCP和CDP面积和减去BCD的面积因此本题求解BCPCDP面积和BCD的面积即可,SBCP,SCDP,SBCD11,SBPD故选B分析:根据三角形面积计算公式,找到BPD的面积等于BCP和CDP面积和减去BCD的面积的等量关系,并进行求解本题考查了三角形面积的计算,考查了正方形对角线平分正方形为2个全等的等腰直角三角形解决本题的关键是找到BPD 的面积等于BCP和CDP面积和减去BCD的面积的等量关系13如图,正方形ABCD的面积为16,ABE是等边三角形,点E在正方形ABCD 内,在对角线BD上有一点P,使PCPE的和最小,则这个最小值为()A4B2C2D2答案:A知识点:轴对称最短路线问题等边三角形的性质正方形的性质解析:解答:解:正方形ABCD,ACBD,OAOC,CA关于BD对称,即C关于BD的对称点是A,连接AE交BD于P,则此时EPCP的值最小,CA关于BD对称,CPAP,EPCPAE,等边三角形ABE,EPCPAEAB,正方形ABCD的面积为16,AB4,EPCP4,故选A分析:根据正方形的性质,推出CA关于BD对称,推出CPAP,推出EPCPAE,根据等边三角形性质推出AEABEPCP,根据正方形面积公式求出AB即可本题考查了正方形的性质,轴对称最短问题,等边三角形的性质等知识点的应用,解此题的关键是确定P的位置和求出EPCP的最小值是AE,题目比较典型,但有一定的难度,主要培养学生分析问题和解决问题的能力14如图是一张矩形纸片ABCD,AD10cm,若将纸片沿DE折叠,使DC落在DA 上,点C的对应点为点F,若BE6cm,则CD()A4cmB6cmC8cmD10cm答案:A知识点:正方形的性质翻折变换(折叠问题)解析:解答:解:四边形CEFD是正方形,ADBC10cm,BE6cm,CEEFCD1064(cm)分析:根据正方形的性质,即可轻松解答15如图,菱形ABCD中,B60,AB4,则以AC为边的正方形ACEF的周长为() A14B15C16D17答案:C知识点:正方形的性质菱形的性质解析:解答:解:四边形ABCD是菱形,ABBC,B60,ABC是等边三角形,ACAB4,正方形ACEF的周长是ACCEEFFA4416分析:根据正方形和菱形的性质,即可轻松解答二填空题(共5小题)1如图所示,将五个边长都为1cm的正方形按如图所示摆放,其中点ABCD分别是正方形对角线的交点如果有n个这样大小的正方形这样摆放,则阴影面积的总和是___cm2答案:知识点:正方形的性质探索图形规律解析:解答:解:点ABCD分别是正方形对角线的交点两个三角形之间的阴影面积为正方形总面积的,即11,当有三个三角形时,其面积为当有四个时,其面积为所以当n个三角形时,其面积为故答案为分析:求面积问题,因为点ABCD分别是正方形对角线的交点,所以两个三角形之间的阴影面积为正方形总面积的,由此便可求解熟练掌握正方形的性质,会运用正方形的性质进行一些简单的计算问题2如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系已知OA3,OC2,点E是AB的中点,在OA上取一点D,将BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FEFP,则P点坐标为答案:(0,4)或(0,0)知识点:正方形的性质坐标与图形性质全等三角形的判定与性质解析:解答:解:连接EF,OA3,OC2,AB2,点E是AB的中点,BE1,BFAB,CFBE1,FEFP,RtFCPRtFBE,PCBF2,P点坐标为(0,4)或(0,0),即图中的点P和点P故答案为:(0,4),(0,0)分析:连接EF,CFBE1,若EFFP,显然RtFCPRtFBE,由此确定CP的长本题考查了三角形翻折前后的不变量,利用三角形的全等解决问题3如图,边长为a的正方形ABCD和边长为b的正方形BEFG排放在一起,O1和O2分别是两个正方形的中心,则阴影部分的面积为,线段O1O2的长为答案:知识点:正方形的性质勾股定理相似三角形的判定与性质解析:解答:解:做O1HAE,使O2HO1H,交BG于P,K点,(1)BP,又O2HHO1,KPHO2,PKO1HO2O1,,KP,阴影部分的面积BK()(2)HO1,HO2,根据勾股定理O1O2故答案为:分析:阴影部分的面积可以看成两个三角形面积之和,所以求2个三角形面积即可线段O1O2的长根据勾股定理求解本题考查的相似三角形的证明即对应边比例相等的性质,三角形面积的计算,考查了根据勾股定理计算直角三角形斜边的应用,解决本题的关键是构建直角三角形HO1O24已知正方形ABCD在直角坐标系内,点A(0,1),点B(0,0),则点C,D坐标分别为和(只写一组)答案:(1,0)和(1,1)知识点:正方形的性质坐标与图形性质解析:解答:解:正方形ABCD的点A(0,1),点B(0,0),BDx轴,ACx轴,这样画出正方形,即可得出C与D的坐标,分别为:C(1,0),D(1,1)故答案为:(1,0),(1,1)分析:首先根据正方形ABCD的点A(0,1),点B(0,0),在坐标系内找出这两点,根据正方形各边相等,从而可以确定C,D的坐标本题主要考查了正方形的性质与坐标内图形的性质,确定已知点的坐标,从而根据正方形的性质,确定其它顶点的坐标是解决问题的关键5如图,在一个正方形被分成三十六个面积均为1的小正方形,点A与点B 在两个格点上在格点上存在点C,使ABC的面积为2,则这样的点C有个答案:5知识点:正方形的性质三角形的面积解析:解答:解:图中标出的5个点均为符合题意的点故答案为5分析:要使得ABC的面积为2,即Sah,则使得a2h2或者a4b1即可,在图示方格纸中找出C点即可本题考查了正方形各边长相等的性质,考查了三角形面积的计算公式,本题中正确地找全C点是解题的关键,考生容易漏掉一个或者几个答案三解答题(共5小题)1如图,在正方形ABCD中,对角线AC与BD相交于点O,AF平分BAC,交BD 于点F(1)求证:(2)点A1点C1分别同时从AC两点出发,以相同的速度运动相同的时间后同时停止,如图,A1F1平分BA1C1,交BD于点F1,过点F1作F1EA1C1,垂足为E,请猜想EF1,AB与三者之间的数量关系,并证明你的猜想(3)在(2)的条件下,当A1E16,C1E14时,则BD的长为答案:(1)见解析(2)ABEF1A1C1(3)知识点:正方形的性质全等三角形的判定与性质勾股定理解析:解答:解:(1)过F作FGAB于G,AF平分CAB,FOAC,FGAB,OFFG,AOFAGF90,AFAF,OFFG,AOFAGF,AOAG,直角三角形BGF中,DGA45,FGBGOF,ABAGBGAOOFACOF,ABOFAC(2)过F1作F1G1A1B,过F1作F1H1BC1,则四边形F1G1BH1是矩形同(1)可得EF1F1G,因此四边形F1G1BH1是正方形EF1G1F1F1H1,即:F1是三角形A1BC1的内心,EF1(A1BBC1A1C1)2A1BBC1ABA1ABCCC1,而CC1A1A,A1BBC12AB,因此式可写成:EF1(2ABA1C1)2,即ABEF1A1C1(3)由(2)得,F1是三角形A1BC1的内心,且E1G1H1都是切点A1E(A1C1A1BBC1)2,如果设CC1A1Ax,A1EA1C1(ABx)(ABx)2(102x)26,x1,在直角三角形A1BC1中,根据勾股定理有A1B2BC12AC12,即:(AB1)2(AB1)2100,解得AB7,BD7分析:(1)可通过构建全等三角形来求解,过F作FGAB于G,那么可通过角平分线上的点到角两边的距离相等得出OFFG,通过全等三角形AOF和AGF可得出AOAG,那么ABAOOF,而AC2OA,由此可得证(2)本题作辅助线的方法与(1)类似,过F1作F1G1AB,F1H1BC,那么可证得四边形F1G1BH1是正方形,EF1F1G1F1H1,那么可得出F1就是三角形A1BC1的内心,根据直角三角形的内心公式可得出EF1(A1BBC1A1C1)2,然后根据用AB分别表示出A1B,BC1,最后经过化简即可得出ABEF1A1C1(3)求BD的长,首先要求出AB的长,本题可借助(2)中,F1是三角形A1BC1的内心来解,那么我们不难看出E,G1,H1都应该是切点,根据切线长定理不难得出A1EA1G1A1C1A1BC1EBG1,由于C1EC1H1,BG1BH1,A1EA1G1因此式子可写成2A1EA1C1A1BBC1,而(A1BBC1)正好等于2A1A,由此可求出A1A的长,那么可根据勾股定理用AB表示出两条直角边,求出AB的长,然后即可得出BD的值本题主要考查了正方形的性质,三角形的内接圆与内心等知识点,要注意的是后两问中,结合圆的知识来解会使问题更简单2已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EAAF求证:DEBF答案:见解析知识点:全等三角形的判定与性质正方形的性质解析:解答:证明:FABBAE90,DAEBAE90,FABDAE,ABAD,ABFADE,AFBADE,DEBF分析:由同角的余角相等知,FABDAE,由正方形的性质知,ABAD,ABFADE90,则ASA证得AFBADEDEBF此题即考查了实数的运算又考查了正方形的性质学生对学过的知识要系统起来3如图,点EF分别在正方形ABCD的边DCBC上,AGEF,垂足为G,且AGAB,则EAF为多少度答案:45知识点:正方形的性质全等三角形的判定与性质解析:解答:解:在RtABF与RtAGF中,ABAG,AFAF,BG90,ABFAGF(HL),BAFGAF,同理易得:AGEADE,有GAEDAE即EAFEAGFAGDAGBAGDAB45,故EAF45分析:根据角平分线的判定,可得出ABFAGF,故有BAFGAF,再证明AGEADE,有GAEDAE所以可求EAF45主要考查了正方形的性质和全等三角形的判定4如图,正方形ABCD中,AB,点EF分别在BCCD上,且BAE30,DAF15度(1)求证:DFBEEF(2)求EFC的度数(3)求AEF的面积答案:(1)见解析(2)30(3)知识点:正方形的性质全等三角形的判定与性质解析:解答:解:(1)延长EB至G,使BGDF,连接AG,正方形ABCD,ABAD,ABGADFBAD90,ABGADF,AGAF,BAE30,DAF15,FAEGAE45,AEAE,FAEGAE,EFEGGBBEDFBE(2)AGEAFE,AFEAGE75,DFA90DAF75,EFC180DFAAFE180757530,EFC30(3)ABBC,BAE30,BE1,CE1,EFC30,CF3,SCEFCECF23,由(1)知,ABGADF,FAEGAE,SAEFS正方形ABCDSADFSAEBSCEFS正方形ABCDSAEFSCEF,SAEF(S正方形ABCDSAEFSCEF)3分析:(1)延长EB至G,使BGDF,连接AG利用正方形的性质,证明AGEAFE,FAEGAE,得出DFBEEF(2)根据AGEAFE及角之间的关系从而求得EFC的度数(3)SAEFS正方形ABCDSADFSAEBSCEFS正方形ABCDSAEFSCEF,关键求SCEF解答本题利用正方形的特殊性质,通过证明三角形全等,得出线段间的关系,同时考查了三角函数的运用,及组合图形的面积计算5已知正方形ABCD的边长为4cm,E,F分别为边DC,BC上的点,BF1cm,CE2cm,BE,DF相交于点G,求四边形CEGF的面积知识点:正方形的性质一次函数的性质两条直线相交或平行的问题解析:解答:解:以B点为坐标原点建立坐标系,如下图:由题意可得几个点的坐标A(0,4),B(0,0),C(4,0),D(4,4),E(4,2),F(1,0)设BE所在直线的解析式是ykx,因为BE所在直线经过E点,因此有4k2,k,因此BE所在直线的解析式是yx(1),同理可得出DF所在直线的解析式是y(x1)(2),联立(1)(2)可解得点G的坐标为(,)故可求四边形CEGF的面积SSBCESBFG421分析:本题的关键是求出G点的坐标,那么就要求出BE,DF所在直线的函数解析式,然后联立两个关系式求出交点坐标,再根据GECF的面积三角形BEC 的面积三角形BFG的面积,求出GECF的面积本题主要考查的是正方形的性质,一次函数等知识点的应用根据BE,DF所在直线求出交点的坐标是解题的关键。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.对下列句中加点的词的解释不.正确的一项是()A.既东封郑,又欲肆其西封.封:疆界B.群臣吏民,能面.刺寡人之过者面:当面C.上食埃土,下饮黄泉,用心一.也一:专一D.赵王之子孙侯者,其继.有在者乎继:继承解析:选D。
D项中的“继”属于动词用作名词,“继承人”的意思。
2.对下列句中加点的词的解释不.正确的一项是()A.于是相如前.进缶前:向前B.修守战之具,外连衡而斗.诸侯斗:使……斗C.邑人奇之,稍稍宾客..其父宾客:以……为宾客D.然皆祖.屈原之从容辞令祖:祖宗解析:选D。
D项中的“祖”属于名词用作动词,“效法、尊崇”的意思。
A项中的“前”属于名词用作状语;B项中的“斗”属于使动用法;C项中的“宾客”属于意动用法。
3.下列句中加点的词与“与苍梧太守吴巨有旧.,欲往投之”中的“旧”活用类型相同的一项是()A.殚其地之出.,竭其庐之入B.先破秦入咸阳者王.之C.小.学而大遗,吾未见其明也D.四更山吐月,残夜水明.楼解析:选C。
例句中的“旧”属于形容词用作名词,“交情”的意思。
C项中的“小”也属于形容词用作名词,“小的方面”的意思。
A项中的“出”属于动词用作名词,“出产的东西”的意思;B项中的“王”属于名词用作动词,“称王”的意思;D项中的“明”属于形容词用作动词,“照亮”的意思。
4.下列句中加点的词与“市中游侠儿得佳者笼.养之”中的“笼”活用方法不.同的一项是()A.天下云.集响应,赢粮而景从B.则尽其天年,人皆得以隶.使之C.五亩之宅,树之以桑,五十者可以衣.帛矣D.蒙故业,因遗策,南.取汉中,西举巴、蜀解析:选C。
例句中的“笼”本为名词,放在动词“养”的前面,又不作“养”的主语,属于名词用作状语,“用笼子”的意思。
C项中的“衣”放在名词“帛”的前面,名词用作动词,“穿”的意思。
A项中的“云”属于名词用作状语,“像云一样”的意思;B项中的“隶”属于名词用作状语,“像奴仆那样”的意思;D项中的“南”属于名词用作状语,“向南”的意思。
5.对下列加点的词的活用分类正确的一项是()①项伯乃夜.驰之沛公军②以事秦之心礼.天下之奇才③方其系燕父子以组,函.梁君臣之首④吾妻之美.我者,私我也⑤燕赵之收.藏.,韩魏之经营⑥亦以明.死生之大,匹夫之有重于社稷也⑦以先.国家之急而后私仇也⑧卒使上官大夫短.屈原于顷襄王⑨明.足以察秋毫之末,而不见舆薪⑩朱亥袖.四十斤铁椎椎杀晋鄙⑪故内.惑于郑袖,外欺于张仪⑫均之二策,宁许以负.秦曲A.①⑪/②③⑩/④/⑦/⑤/⑥⑧/⑨/⑫B.①⑪/②③⑩/④⑦⑫/⑤⑨/⑥⑧C.①⑪/②③/⑧④⑦/⑤⑥/⑨⑩/⑫D.①⑪②③/⑧④⑥/⑦⑤⑨/⑩/⑫解析:选A。
①⑪句是名词用作状语;②③⑩都是名词用作动词;④是形容词意动用法;⑦是名词的意动用法;⑤句是动词用作名词;⑥⑧句都是形容词用作动词;⑨句是形容词用作名词;⑫句是使动用法。
6.下列与“盖文王拘而演《周易》”句式不.同的一项是()A.荆州之民附操者,逼兵势耳B.六艺经传皆通习之,不拘于时,学于余C.生于忧患,死于安乐D.秦城恐不可得,徒见欺解析:选C。
例句的句式是被动句,“拘”字本身表被动,属意念上的被动句。
C项中尽管有“于”字,但“于”在这里是“在”的意思,属于介宾短语后置;A项中的“逼”字表被动;B项前一个“于”字表被动;D项中“见”字表被动。
7.括号中补出的被省略的成分,错误的一项是()A.夫战,勇气也。
一鼓作气,再(鼓)而衰,三(鼓)而竭B.吾妻之美我者,私我也;(吾)妾之美我者,畏我也C.臣与将军戮力而攻秦,将军战(之)河北,臣战(之)河南D.然力足以至焉(而未至),于人为可讥,而在己为有悔解析:选C。
C项省略的不是“之”而是介词“于”。
8.下列句中加点的“也”字的作用不.同于其他三项的一项是()A.廉颇者,赵之良将也.B.夫子欲之,吾二臣者皆不欲也.C.城北徐公,齐国之美丽者也.D.师者,所以传道受业解惑也.解析:选B。
B项中的“也”是语气助词,表陈述语气,不表判断。
A、C、D三项中的“也”都表示判断。
9.下列对宾语前置句式分类正确的一项是()①古之人不余欺也②吾孰与徐公美③保民而王,莫之能御也④沛公安在⑤是以后世无传焉,臣未之闻也⑥将子无怒,秋以为期⑦句读之不知,惑之不解⑧是以区区不能废远⑨惟兄嫂是依⑩子何恃而往A.①③⑦/②④⑥/⑤⑧/⑩⑨B.①③⑤/②④⑩/⑥⑧/⑦⑨C.①③⑦/④⑨/⑥⑤②/⑧⑩D.①③⑤/②④⑧/⑥⑩/⑦⑨解析:选B。
①③⑤句都属于否定句中代词作宾语,宾语前置;②④⑩句都属于疑问句中疑问代词作宾语,宾语前置;⑥⑧句都属于介词的宾语前置;⑦⑨句都属于特殊结构,用“之”、“是”将宾语提前,以加重语气。
10.下列句子中与“饰以篆文山龟鸟兽之形”句式相同的一项是()A.五亩之宅,树之以桑,五十者可以衣帛矣B.甚矣,汝之不惠C.一旦山陵崩,长安君何以自托于赵D.我持白璧一双,欲献项王,玉斗一双,欲与亚父解析:选A。
例句属于介宾短语后置句,A项也属于介宾短语后置句。
B项属于主谓倒装句;C项属于宾语前置句;D项属于定语后置句。
11.下列成语根据句式方面的特点分类,正确的一项是()①贻笑大方②一言九鼎③何去何从④持之以恒⑤饱以老拳⑥时不我待⑦名满天下⑧受制于人A.①⑧/②⑦/③⑥/④⑤B.①⑦/②⑧/③⑤/④⑥C.①⑤/②⑦/③⑥/④⑧D.①④②/⑤③⑧/⑥⑦解析:选A。
①⑧句都属于被动句;②⑦都属于省略句;③⑥句都属于宾语前置句;④⑤句都属于介宾短语后置句。
12.阅读下面的短文,完成文后问题。
吴王欲杀王子庆忌而莫之能杀,吴王患之。
要离曰:“臣能之。
”吴王曰:“汝恶能乎?吾尝以六马逐之江上矣,而不能及;射之矢,左右满把,而不能中。
今汝拔剑则不能举臂,上车则不能登轼,汝恶能?”要离曰:“士患不勇耳,奚患于不能,王诚能助,臣请必能。
”吴王曰:“诺。
”明旦加要离罪焉,挚执妻子,焚之而扬其灰。
要离走,往见王子庆忌于卫。
王子庆忌喜曰:“吴王之无道也,子之所见也,诸侯之所知也。
今子得免而去之,亦善矣。
”要离与王子庆忌居有间,谓王子庆忌曰:“吴之无道也愈甚,请与王子往夺之国。
”王子庆忌曰:“善。
”乃与要离俱涉于江。
中江,拔剑以刺王子庆忌。
王子庆忌捽之,投之于江,浮则又取而投之,如此者三。
其卒曰:“汝天下之国士也,幸汝以成而名。
”要离得不死,归于吴。
吴王大说,请与分国。
要离曰:“不可。
臣请必死!”吴王止之,要离曰:“夫杀妻子,焚之而扬其灰,以便事也,臣以为不仁。
夫为故主杀新主,臣以为不义。
夫捽而浮乎江,三入三出,特王子庆忌为之赐而不杀耳,臣已为辱矣。
夫不仁不义,又且已辱,不可以生。
”吴王不能止,果伏剑而死。
要离可谓不为赏动矣,故临大利而不易其义;可谓廉矣,廉,故不以贵富而忘其辱。
(选自《吕氏春秋》)(1)下列句中已补出被省略的成分,补出的内容错误的一项是()A.吾尝以六马逐之(于)江上矣B.中江,(要离)拔剑以刺王子庆忌C.吴王大说,请与(要离)分国D.夫(吴王)不仁不义,又且已辱,不可以生解析:选D。
D项在“不仁不义”前省略的是主语“吾”。
(2)对下列特殊句式的分析错误的一项是()A.吴王欲杀王子庆忌而莫之能杀宾语前置句B.吾尝以六马逐之江上矣,而不能及省略句C.臣已为辱矣被动句D.幸汝以成而名介宾短语后置句解析:选D。
D句不是介宾短语后置句,这里的“以”是用作连词的,而不是介词。
参考译文:吴王想要杀掉王子庆忌却总是杀不了,吴王很担忧。
要离说:“我能杀他。
”吴王说:“你怎么能?我曾经乘六匹马追他到江边,却没有追上;向他射箭,射空了身边的箭,也不能射中他。
现在你拔剑还不能举过肩,上车不能登上车上的横木,你怎么杀他?”要离说:“人就怕不勇敢,而不怕不能,如果您真的能帮助我,我一定能杀他。
”吴王说:“好。
”第二天吴王捏造要离的罪名,抓了他的妻子和儿子,并焚骨扬灰。
要离逃跑了,去见在卫国的王子庆忌。
王子庆忌高兴地说:“吴王无道,你看到了,诸侯也知道了。
如今你得以幸免而且离开了他,很好啊。
”要离和王子庆忌在一起不久,对王子庆忌说:“吴王更加昏庸了,请让我和您一起去夺取他的国家。
”王子庆忌说:“好。
”于是和要离一同渡江。
到了江中,要离拔出剑刺向王子庆忌。
王子庆忌揪住他,把他扔到江水里,他浮上来后王子庆忌又把他扔进水里,这样反复了多次。
最后王子庆忌说:“你是天下国士,我饶你不死来成就你的名声。
”要离得以不死,回到吴国。
吴王很高兴,愿意分给他一半国家。
要离说:“不行。
我一定要死!”吴王阻止他,要离说:“我杀了妻子儿女,并焚骨扬灰,是为了行刺而故意做的,我认为这样做不仁。
为了旧主人而杀新主人,我认为这样做不义。
被揪住扔进江里,三进三出,王子庆忌特意饶了我而不杀我,我觉得已经受到侮辱了。
不仁不义,又被侮辱,我不能再活了。
”吴王不能阻止他,他果然拔剑自刎而死。
要离可以说是没有为赏赐所打动,所以面临大的利益而不改变自己的心志;可以称得上廉洁,廉洁,就是不因为贵富而忘记了屈辱。
13.阅读下面文言文,完成文后问题。
孙沔征侬徭,请参军事,奏功得官,知巴州化城县。
巴俗尚鬼而废医,唯巫言是用,娶妇必责财,贫人女至老不得嫁。
可为约束,立制度,违者有罪,几变其习。
再调华原主簿。
富人有不占田籍而质人田券至万亩,岁责其租。
可晨驰至富家,发椟出券归其主。
郡吏赵至诚贪狡凶横,持守以下短长,前后莫能去。
可暴其罪,荷枷置狱,言于大府诛之,闻者快服。
下列各句中,与“唯巫言是用”句式相同的一项是()A.阙秦以利晋,唯君图之B.一日自远归,家以窭告C.言于大府诛之D.夫晋何厌之有解析:选D。
题干中“唯巫言是用”,“是”把宾语提前,构成宾语前置,正常语序为“用巫言”,译为“听巫师的话”。
选择项中只有D项为宾语前置,“何厌之有”是“之”作标志的宾语前置,正常语序为“夫晋有何厌”,译为“晋国,有什么满足的呢”。
参考译文:孙沔征讨侬徭(北宋时壮族首领),请侯可参与军事,建立功绩得到官,作巴州化城县知县。
巴地的风俗迷信鬼神而不信医道,只听信巫师的话,娶媳妇必要女人家的财物,穷人家的女孩子到老不能出嫁。
侯可制定规章,订立法度,违反的人有罪,差不多改变了当地的风气。
第二次调任华原主簿。
有个富人不占有田籍却抵押人家的田券达到一万亩,每年索取地租。
侯可一早骑马直奔富人家,打开木匣拿出田契归还给它的主人。
当地的衙役赵至诚贪婪狡诈凶蛮专横,掌握太守以下很多人的把柄,前前后后没有谁能除去他。
侯可揭露他的罪行,让他戴上重枷,投入大狱,报告给上一级官府杀了他,大快人心。
14.阅读下面的文言文,完成文后问题。
鹅笼夫人者,毗陵某氏女也。
幼时,父知女必贵,慎卜婿,得鹅笼文,即婿之。
母曰:“家云何?”曰:“吾恃其文为家也。
”家果贫,数年犹不能展一礼。
妹许某,家故豪,遽行聘。
