期末模拟卷01(B能力卷)-新教材高一数学尖子生培优卷(人教A版必修第二册)
人教A版高一数学必修第二册全册复习测试题卷含答案解析(60)

高一数学必修第二册全册复习测试题卷(共22题)一、选择题(共10题)1.设某项试验成功的概率是失败的概率的2倍,用随机变量X描述1次试验的成功次数,则P(X=0)等于( )A.0B.12C.13D.232.若∣a⃗∣=1,∣b⃗⃗∣=2,且(a⃗+b⃗⃗)⊥a⃗,则a⃗与b⃗⃗的夹角θ=( )A.π3B.−π3C.2π3D.2π3或−π33.已知i为虚数单位,若复数z满足z(1−i)=1+i,则z=( )A.i B.−12i C.1D.124.在复平面内,复数z1=3−i,z2=−1+2i对应的两点间的距离为( )A.2B.3C.4D.55.甲、乙两名同学在高考前的5次模拟考中的数学成绩如茎叶图所示,记甲、乙两人的平均成绩分别为x,y,下列说法正确的是( )A.x<y,且乙比甲的成绩稳定B.x>y,且乙比甲的成绩稳定C.x<y,且甲比乙的成绩稳定D.x>y,且甲比乙的成绩稳定6.复数z(1−i)=i(i为虚数单位),则z的共轭复数在复平面上对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限7.设a⃗=(32,sinα),b⃗⃗=(cosα,13),且a⃗∥b⃗⃗,则锐角α为( )A.45∘B.30∘C.75∘D.60∘8.已知实数a∈[−3,3],则复数z=a+i2−i在复平面内对应的点位于第二象限的概率为( )A.512B.12C.712D.349. 下列叙述中,错误的一项为 ( ) A .棱柱中两个互相平行的平面一定是棱柱的底面 B .棱柱的各个侧面都是平行四边形 C .棱柱的两底面是全等的多边形 D .棱柱的面中,至少有两个面相互平行10. 在 △ABC 中,a =5,b =3,则 sinA:sinB 的值是 ( ) A . 53B . 35C . 37D . 57二、填空题(共6题) 11. 思考辨析 判断正误两条直线无公共点,则这两条直线平行.( )12. 已知非零向量 a ⃗,b ⃗⃗ 满足 ∣a ⃗∣=∣∣a ⃗−b ⃗⃗∣∣,则 (a ⃗−12b ⃗⃗)⋅b ⃗⃗= .13. 设两个非零向量 a ⃗ 与 b ⃗⃗ 不共线.若 ka ⃗+b ⃗⃗ 与 a ⃗+kb ⃗⃗ 共线,则 k = .14. 已知 (a −i )2=2i ,其中 i 是虚数单位,那么实数 a = .15. 若复数 z 满足 2z +z =3−2i ,其中 i 为虚数单位,则 z = .16. 已知 O 为 △ABC 内一点,OA ⃗⃗⃗⃗⃗⃗+2OB ⃗⃗⃗⃗⃗⃗+3OC ⃗⃗⃗⃗⃗⃗=0⃗⃗,则 S△ABC S △AOC= .三、解答题(共6题)17. 一个盒子里装有完全相同的十个小球,分别标上 1,2,3,⋯,10 这 10 个数字,现随机地抽取两个小球,如果: (1)小球是不放回的; (2)小球是有放回的.分别求两个小球上的数字为相邻整数的概率.18. 正六边形 ABCDEF 中,O 是其中心,设 AB ⃗⃗⃗⃗⃗⃗=m ⃗⃗⃗,AF ⃗⃗⃗⃗⃗⃗=n ⃗⃗,用 m ⃗⃗⃗,n ⃗⃗ 表示 AD ⃗⃗⃗⃗⃗⃗,BD ⃗⃗⃗⃗⃗⃗⃗.19. 如图所示,某地出土的一种“钉”是由四条线段组成,其结构能使它任意抛至水平面后,总有一端所在的直线竖直向上,并记组成该“钉”的四条线段的公共点为 O ,钉尖为 A i (i =1,2,3,4).(1) 设OA1=a(a>0),当A1,A2,A3在同一水平面内时,求OA1与平面A1A2A3所成角的大小(结果用反三角函数值表示).(2) 若该“钉”的三个端尖所确定的三角形的面积为3√2cm2,要用某种线型材料复制100枚这种“钉”(损耗忽略不计),共需要该种材料多少米?⃗⃗⃗⃗⃗⃗对应的复数是1+2i,向量20.复平面内有A,B,C三点,点A对应的复数是2+i,向量BA⃗⃗⃗⃗⃗⃗对应的复数是3−i,求点C在复平面内的坐标.BC21.已知过球面上三点A,B,C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,求球面面积与球的体积.22.定义:对于两个非零向量p⃗和q⃗,如果存在不全为零的常数α,β,使αp⃗+βq⃗=0⃗⃗,那么称p⃗和q⃗是线性相关的,否则称p⃗和q⃗是线性无关的.已知a⃗=3i⃗−4j⃗,a⃗+b⃗⃗=4i⃗−3j⃗,试判断a⃗与b⃗⃗的线性关系(相关还是无关),并证明你的结论.答案一、选择题(共10题)1. 【答案】C【知识点】事件的关系与运算2. 【答案】C【解析】因为(a⃗+b⃗⃗)⊥a⃗,所以(a⃗+b⃗⃗)⋅a⃗=a⃗2+a⃗⋅b⃗⃗=1+2cosθ=0,解得cosθ=−12,又θ∈[0,π],所以θ=2π3.【知识点】平面向量的数量积与垂直3. 【答案】A【解析】由z(1−i)=1+i,得z=1+i1−i =(1+i)2(1−i)(1+i)=2i2=i.【知识点】复数的乘除运算4. 【答案】D【解析】在复平面内,复数z1=3−i,z2=−1+2i对应的两点的坐标分别为(3,−1),(−1,2),则两点间的距离为∣z2−z1∣=√(−1−3)2+[2−(−1)]2=5.【知识点】复数的加减运算、复数的几何意义5. 【答案】A【解析】由题,x=15×(101+102+105+114+138)=112,y=15×(108+118+117+124+123)=118,所以x<y,由茎叶图可知,乙的成绩更集中,故乙比甲的成绩稳定.【知识点】样本数据的数字特征6. 【答案】C【解析】因为z=i1−i =i(1+i)(1−i)(1+i)=−1+i2=−12+12i,所以z=−12−12i,对应点为(−12,−12),在第三象限.【知识点】复数的几何意义、复数的乘除运算7. 【答案】A【知识点】平面向量的数乘及其几何意义8. 【答案】A【解析】 z =a+i2−i =(a+i )(2+i )(2−i )(2+i )=2a+(a+2)i+i 24−i 2=2a−1+(a+2)i5,由于点位于第二象限, 所以 {2a −1<0,a +z >0,则 −2<a <12, P =∣∣12−(−2)∣∣∣3−(−3)∣=512.【知识点】复数的乘除运算、复数的几何意义9. 【答案】A【解析】在A 中,棱柱中两个互相平行的平面不一定是棱柱的底面, 例如正六棱柱的相对侧面互相平行,故A 错误;在B 中,由棱柱的定义知棱柱的各个侧面都是平行四边形,故B 正确; 在C 中,由棱柱的定义知棱柱的两底面是互相平行且全等的多边形,故C 正确; 在D 中,棱柱的定义是,有两个面互相平行,其余各面都是四边形, 相邻的公共边互相平行,有这些面围成的几何体是棱柱,由此得到D 正确. 【知识点】棱柱的结构特征10. 【答案】A【解析】根据正弦定理,得 sinAsinB =ab =53. 【知识点】正弦定理二、填空题(共6题) 11. 【答案】 ×【知识点】直线与直线的位置关系12. 【答案】 0【知识点】平面向量的数量积与垂直13. 【答案】 ±1【解析】因为 ka ⃗+b ⃗⃗ 与 a ⃗+kb⃗⃗ 共线,所以存在实数 λ,使 ka ⃗+b ⃗⃗=λ(a ⃗+kb ⃗⃗),即 (k −λ)a ⃗=(λk −1)b⃗⃗. 又 a ⃗,b ⃗⃗ 是两个不共线的非零向量,所以 k −λ=λk −1=0. 消去 λ,得 k 2−1=0,所以 k =±1. 【知识点】平面向量的数乘及其几何意义14. 【答案】 −1【解析】 a 2−2ai −1=a 2−1−2ai =2i ,a =−1. 【知识点】复数的乘除运算15. 【答案】 1−2i【解析】设 z =a +bi (a,b ∈R ), 则 z =a −bi , 因为 2z +z =3−2i ,所以 2a +2bi +a −bi =3−2i , 所以 3a =3,b =−2, 解得 a =1,b =−2, 所以 z =1−2i .【知识点】复数的加减运算16. 【答案】 3【解析】如图所示,取 BC 的中点 D ,AC 的中点 E ,连接 OD ,OE , 则OA ⃗⃗⃗⃗⃗⃗+2OB ⃗⃗⃗⃗⃗⃗+3OC ⃗⃗⃗⃗⃗⃗=(OA⃗⃗⃗⃗⃗⃗+OC ⃗⃗⃗⃗⃗⃗)+2(OB ⃗⃗⃗⃗⃗⃗+OC ⃗⃗⃗⃗⃗⃗)=2OE⃗⃗⃗⃗⃗⃗+4OD ⃗⃗⃗⃗⃗⃗⃗=0⃗⃗,所以 OE⃗⃗⃗⃗⃗⃗=−2OD ⃗⃗⃗⃗⃗⃗⃗, 所以 D ,O ,E 三点共线, 所以 DE ⃗⃗⃗⃗⃗⃗=32OE ⃗⃗⃗⃗⃗⃗, 又 DE 为 △ABC 的中位线,BA ⃗⃗⃗⃗⃗⃗=2DE ⃗⃗⃗⃗⃗⃗, 所以 BA⃗⃗⃗⃗⃗⃗=3OE ⃗⃗⃗⃗⃗⃗. 设在 △ABC 和 △AOC 中,AC 边上的高分别为 ℎ1,ℎ2,则 ℎ1=3ℎ2, 所以 S△ABC S △AOC=3.【知识点】平面向量的数乘及其几何意义三、解答题(共6题)17. 【答案】从十个小球中随机抽取两个小球,记事件 A 为“两个小球上的数字为相邻整数”,其所有可能的结果为 (1,2),(2,3),(3,4),(4,5),(5,6),(6,7),(7,8),(8,9),(9,10),(2,1),(3,2),(4,3),(5,4),(6,5),(7,6),(8,7),(9,8),(10,9),共 18 种.(1)如果小球是不放回的,按抽取顺序记录结果 (x,y ),则 x 有 10 种可能,y 有 9 种可能,共有 90 种可能的结果, 因此,事件 A 的概率是 1890=15.(2)如果小球是有放回的,按抽取顺序记录结果 (x,y ),则 x 有 10 种可能,y 有 10 种可能,共有 100 种可能的结果, 因此,事件 A 的概率是 18100=950. 【知识点】古典概型18. 【答案】 AD ⃗⃗⃗⃗⃗⃗=2AO ⃗⃗⃗⃗⃗⃗=2(m ⃗⃗⃗+n ⃗⃗),BD ⃗⃗⃗⃗⃗⃗⃗=BA ⃗⃗⃗⃗⃗⃗+AD ⃗⃗⃗⃗⃗⃗=m ⃗⃗⃗+2n ⃗⃗.【知识点】平面向量的数乘及其几何意义19. 【答案】(1) 根据题意,可知组成该种钉的四条线段长必相等,且两两所成的角相等,A 1,A 2,A 3,A 4 两两连接后得到的四面体 A 1A 2A 3A 4 为正四面体,延长 A 4O 交平面 A 1A 2A 3 于 B ,则 A 4B ⊥平面A 1A 2A 3,连接 A 1B ,则 A 1B 是 OA 1 在平面 A 1A 2A 3 上的射影, 所以 ∠OA 1B 即为 OA 1 与平面 A 1A 2A 3 所成角. 设 A 1A 4=l , 则 A 1B =√33l . 在 Rt △A 4A 1B 中,A 1A 42=A 1B 2+A 4B 2,即 l 2=(√33l)2+(a +√a 2−(√33l)2)2,所以 l =2√63a , 故 A 1B =√33×2√63a =2√23a ,cos∠OA 1B =A 1B OA 1=2√23(其中 0<∠OA 1B <π2),所以 ∠OA 1B =arccos2√23, 故 OA 1 与平面 A 1A 2A 3 所成角的大小为 arccos 2√23.(2) 12A 1A 22⋅√32=3√2,根据(1)可得 A 1A 2=2√63a ,所以 a =√2724cm ,1100⋅100⋅(4a )=4a =2√2164m . 答:复制 100 枚这种“钉”,共需材料 2√2164米.【知识点】棱锥的结构特征、线面角20. 【答案】因为 AC⃗⃗⃗⃗⃗⃗=BC ⃗⃗⃗⃗⃗⃗−BA ⃗⃗⃗⃗⃗⃗, 所以 AC⃗⃗⃗⃗⃗⃗ 对应的复数为 (3−i )−(1+2i )=2−3i , 设 C (x,y ),则 (x +yi )−(2+i )=2−3i ,所以 x +yi =(2+i )+(2−3i )=4−2i , 故 x =4,y =−2.所以点 C 在复平面内的坐标为 (4,−2). 【知识点】复数的加减运算、复数的几何意义21. 【答案】如图设球心为 O ,球的半径为 R ,作 OO 1⊥平面ABC 于点 O 1,则 OA =OB =OC =R ,且 O 1 是 △ABC 的外心,设 M 是 AB 的中点, 因为 AC =BC , 所以 O 1∈CM , 所以 O 1M ⊥AB , 设 O 1M =x ,则 O 1A =√22+x 2,O 1C =CM −O 1M =√62−22−x . 又 O 1A =O 1C ,所以 √22+x 2=√62−22−x ,解得 x =7√24. 所以 O 1A =O 1B =O 1C =9√24.在 Rt △OO 1A 中,O 1O =R 2,∠OO 1A =90∘,OA =R , 由勾股定理得 (R 2)2+(9√24)2=R 2,解得 R =3√62, 所以 S 球=4πR 2=54π,V 球=43πR 3=27√6π. 【知识点】球的表面积与体积22. 【答案】线性无关.对照定义,可求得 α=β=0.【知识点】平面向量的数乘及其几何意义。
人教A版高一数学必修第二册全册复习测试题卷含答案解析(56)

高一数学必修第二册全册复习测试题卷(共22题)一、选择题(共10题)1. 向量 a ⃗=(1,2),b ⃗⃗=(2,λ),且 a ⃗⊥b ⃗⃗,则实数 λ= ( ) A . 3 B . −3 C . 7 D . −12. 袋中共有完全相同的 4 只小球,编号为 1,2,3,4,现从中任取 2 只小球,则取出的 2 只球编号之和是偶数的概率为 ( ) A . 25B . 35C . 13D . 233. 下列命题正确的是 ( ) A .三点确定一个平面B .一条直线和一个点确定一个平面C .圆心和圆上两点可确定一个平面D .梯形可确定一个平面4. 复数 1+i 2= ( ) A . 0B . 2C . 2iD . 1−i5. 已知 ∣a ⃗∣=1,∣b ⃗⃗∣=2,a ⃗ 与 b ⃗⃗ 的夹角为 π3,则 a ⃗⋅b ⃗⃗ 等于 ( ) A . 1B . 2C . 3D . 46. 已知平面向量 a ⃗=(1,x ),b ⃗⃗=(y,1),若 a ⃗∥b ⃗⃗,则实数 x ,y 一定满足 ( ) A .xy −1=0B .xy +1=0C .x −y =0D .x +y =07. 在平行四边形 ABCD 中,A (1,2),B (3,5),AD ⃗⃗⃗⃗⃗⃗=(−1,2),则 AC ⃗⃗⃗⃗⃗⃗+BD ⃗⃗⃗⃗⃗⃗⃗= ( ) A . (−2,4)B . (4,6)C . (−6,−2)D . (−1,9)8. 若 AB ⃗⃗⃗⃗⃗⃗=(1,1),AD ⃗⃗⃗⃗⃗⃗=(0,1),BC ⃗⃗⃗⃗⃗⃗+CD ⃗⃗⃗⃗⃗⃗=(a,b ),则 a +b = ( ) A . −1B . 0C . 1D . 29. 已知直线 a 在平面 γ 外,则 ( ) A . a ∥γ B . a 与 γ 至少有一个公共点 C . a ∩γ=AD . a 与 γ 至多有一个公共点10. 下列四个长方体中,由图中的纸板折成的是 ( )A.B.C.D.二、填空题(共6题)11.思考辨析判断正误当向量的始点在坐标原点时,向量的坐标就是向量终点的坐标.( )12.复数加法与减法的运算法则设z1=a+bi,z2=c+di(a,b,c,d∈R)是任意两个复数,则(1)z1+z2=;(2)z1−z2=.13.利用“斜二测”法作多面体直观图时,需考虑个方向上的尺度.14.若向量a⃗与b⃗⃗的夹角为120∘,且∣a⃗∣=1,∣∣b⃗⃗∣∣=1,则∣∣a⃗−b⃗⃗∣∣=.15.当时,λa⃗=0⃗⃗.16.“直线a经过平面α外一点P”用集合符号表示为.三、解答题(共6题)=bsinA.17.△ABC的内角A,B,C的对边分别为a,b,c,已知asin A+C2(1) 求B;(2) 若△ABC为锐角三角形,且a=2,求△ABC面积的取值范围.18.画出如图水平放置的直角梯形的直观图.19.按图示的建系方法,画出水平放置的正五边形ABCDE的直观图.20. 根据图形用符号表示下列点、直线、平面之间的位置关系.(1) 点 P 与直线 AB ; (2) 点 C 与直线 AB ; (3) 点 M 与平面 AC ; (4) 点 A 1 与平面 AC ; (5) 直线 AB 与直线 BC ; (6) 直线 AB 与平面 AC ; (7) 平面 A 1B 与平面 AC .21. 有 4 条长为 2 的线段和 2 条长为 a 的线段,用这 6 条线段作为棱,构成一个三棱锥.问 a为何值时,可构成一个最大体积的三棱锥,最大值为多少?22. 类似于平面直角坐标系,我们可以定义平面斜坐标系:设数轴 x ,y 的交点为 O ,与 x ,y 轴正方向同向的单位向量分别是 i ⃗,j ⃗,且 i ⃗ 与 j ⃗ 的夹角为 θ,其中 θ∈(0,π2)∪(π2,π).由平面向量基本定理,对于平面内的向量 OP ⃗⃗⃗⃗⃗⃗,存在唯一有序实数对 (x,y ),使得 OP ⃗⃗⃗⃗⃗⃗=xi ⃗+yj ⃗,把 (x,y ) 叫做点 P 在斜坐标系 xOy 中的坐标,也叫做向量 OP⃗⃗⃗⃗⃗⃗ 在斜坐标系 xOy 中的坐标.在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如 θ=45∘ 时,方程x−24=y−1−5表示斜坐标系内一条过点 (2,1),且方向向量为(4,−5)的直线.),a⃗=(2,1),b⃗⃗=(m,6),且a⃗与b⃗⃗的夹角为锐角,求实数m的取值(1) 若θ=arccos(−13范围;(2) 若θ=60∘,已知点A(2,1)和直线l:3x−y+2=0.①求l一个法向量;②求点A到直线l的距离.答案一、选择题(共10题)1. 【答案】D【解析】由a⃗⊥b⃗⃗,所以有a⃗⋅b⃗⃗=1×2+2×λ=0⇒λ=−1.【知识点】平面向量数量积的坐标运算2. 【答案】C【解析】在编号为1,2,3,4的小球中任取2只小球,则有{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6种取法,则取出的2只球编号之和是偶数的有{1,3},{2,4},共2种取法,即取出的2只球编号之和是偶数的概率为26=13,故选:C.【知识点】古典概型3. 【答案】D【解析】由不共线的三点确定一个平面,故A错误;由一条直线和该直线外一点确定一个平面,故B错误;当圆心和圆上两点在圆的直径上,不能说明该三点确定一个平面,故C错误;由于梯形是有一组对边平行的四边形,可得梯形确定一个平面,故D正确.故选:D.【知识点】平面向量的概念与表示4. 【答案】A【解析】因为i2=−1,所以1+i2=0.故选:A.【知识点】复数的乘除运算5. 【答案】A【解析】a⃗⋅b⃗⃗=∣a⃗∣∣b⃗⃗∣cosπ3=1×2×cosπ3=1.【知识点】平面向量的数量积与垂直6. 【答案】A【解析】因为a⃗∥b⃗⃗,所以1×1−xy=0,即xy−1=0.【知识点】平面向量数乘的坐标运算7. 【答案】A【解析】在平行四边形ABCD中,因为 A (1,2),B (3,5),所以 AB⃗⃗⃗⃗⃗⃗=(2,3), 又 AD ⃗⃗⃗⃗⃗⃗=(−1,2), 所以 AC ⃗⃗⃗⃗⃗⃗=AB ⃗⃗⃗⃗⃗⃗+AD ⃗⃗⃗⃗⃗⃗=(1,5),BD ⃗⃗⃗⃗⃗⃗⃗=AD ⃗⃗⃗⃗⃗⃗−AB ⃗⃗⃗⃗⃗⃗=(−3,−1), 所以 AC ⃗⃗⃗⃗⃗⃗+BD ⃗⃗⃗⃗⃗⃗⃗=(−2,4), 故选A .【知识点】平面向量和与差的坐标运算8. 【答案】A【解析】 BC ⃗⃗⃗⃗⃗⃗+CD ⃗⃗⃗⃗⃗⃗=BD ⃗⃗⃗⃗⃗⃗⃗=AD ⃗⃗⃗⃗⃗⃗−AB⃗⃗⃗⃗⃗⃗=(0,1)−(1,1)=(−1,0), 故 a =−1,b =0, 所以 a +b =−1.【知识点】平面向量和与差的坐标运算9. 【答案】D【解析】直线在平面外,故直线与平面相交或直线与平面平行,直线 a 与平面 γ 平行时没有公共点,直线 a 与平面 γ 相交时有一个公共点,故选D . 【知识点】直线与平面的位置关系10. 【答案】A【解析】根据题图中纸板的形状及特殊面的阴影部分可以判断B ,C ,D 不正确,故选A . 【知识点】棱柱的结构特征二、填空题(共6题) 11. 【答案】 √【知识点】平面向量和与差的坐标运算12. 【答案】 (a +c)+(b +d)i ; (a −c)+(b −d)i【知识点】复数的加减运算13. 【答案】三【知识点】直观图14. 【答案】 √3【解析】因为向量 a ⃗ 与 b ⃗⃗ 的夹角为 120∘,∣a ⃗∣=1,∣∣b ⃗⃗∣∣=1,所以 a ⃗⋅b ⃗⃗=∣a ⃗∣∣∣b ⃗⃗∣∣cos120∘=−12,因此 ∣∣a ⃗−b ⃗⃗∣∣=√(a ⃗−b ⃗⃗)2=√∣a ⃗∣2+∣∣b ⃗⃗∣∣2−2a⃗⋅b ⃗⃗=√1+1+1=√3. 【知识点】平面向量的数量积与垂直15. 【答案】 λ=0 或 a ⃗=0⃗⃗【解析】若 λa ⃗=0⃗⃗,则 λ=0 或 a ⃗=0⃗⃗.【知识点】平面向量的数乘及其几何意义16. 【答案】 P ∈a ,P ∉α【知识点】平面的概念与基本性质三、解答题(共6题) 17. 【答案】(1) asinA+C 2=bsinA ,由正弦定理 sinAsinA+C 2=sinBsinA .因为 A ,B ,C 是 △ABC 的内角,sinA ≠0, 所以 sin A+C 2=sinB =sin (π−B )=sin (A +C ), 所以 sinA+C 2=2sinA+C 2cosA+C 2,因为 0<A +C <π, 所以 0<A+C 2<π2.所以 sinA+C 2≠0,cosA+C 2=12,A+C 2=π3,所以 A +C =2π3,B =π−(A +C )=π−2π3=π3(2) 由正弦定理得 asinA =bsinB =csinC =2sinA , 所以 c =2sinC sinA,由三角形内角和知 A +C =120∘, 所以 C =120∘−A , 所以 c =2sin (120∘−A )sinA=√3tanA+1,又 △ABC 为锐角三角形, 所以 120∘−A <90∘ 且 A <90∘, 即 30∘<A <90∘, 又 S △ABC =12acsinB =12ac ×√32=√32c =√32×(√3tanA +1),30∘<A <90∘,因为30∘<A<90∘,所以tanA>√33,得√3tanA <3,即1<√3tanA+1<4,所以S△ABC=√32×(√3tanA+1)∈(√32,2√3).【知识点】正弦定理18. 【答案】(1)在已知的直角梯形OBCD中,以OB所在直线为x轴,垂直于OB的腰OD所在直线为y轴建立平面直角坐标系.画出相应的xʹ轴和yʹ轴,使∠xʹOʹyʹ=45∘,如图①②所示.(2)在xʹ轴上截取OʹBʹ=OB,在yʹ轴上截取OʹDʹ=12OD,过点Dʹ作xʹ轴的平行线l,在l上沿xʹ轴正方向取点Cʹ,使得DʹCʹ=DC.连接BʹCʹ,如图②所示.(3)所得四边形OʹBʹCʹDʹ就是直角梯形OBCD的直观图,如图③所示.【知识点】直观图19. 【答案】画法:(1)在图①中作AG⊥x轴于G,作DH⊥x轴于H.(2)在图②中画相应的xʹ轴与yʹ轴,两轴相交于点Oʹ,使∠xʹOʹyʹ=45∘.(3)在图②中的xʹ轴上取OʹBʹ=OB,OʹGʹ=OG,OʹCʹ=OC,OʹHʹ=OH,yʹ轴上取OʹEʹ=1 2OE,分别过Gʹ和Hʹ作yʹ轴的平行线,并在相应的平行线上取GʹAʹ=12GA,HʹDʹ=12HD.(4)连接AʹBʹ,AʹEʹ,EʹDʹ,DʹCʹ,并擦去辅助线GʹAʹ,HʹDʹ,xʹ轴与yʹ轴,便得到水平放置的正五边形ABCDE的直观图五边形AʹBʹCʹDʹEʹ(如图③).【知识点】直观图20. 【答案】(1) 点P∈直线AB.(2) 点C∉直线AB.(3) 点M∈平面AC.(4) 点A1∉平面AC.(5) 直线AB∩直线BC=点B.(6) 直线AB⊂平面AC.(7) 平面A1B∩平面AC=直线AB.【知识点】点、线、面的位置关系、直线与平面的位置关系、平面与平面的位置关系、直线与直线的位置关系21. 【答案】构成三棱锥,这6条线段作为棱有两种摆放方式.(1)2条长为a的线段放在同一个三角形中.如图所示,不妨设底面 BCD 是一个边长为 2 的正三角形.欲使体积达到最大,必有 BA ⊥底面BCD ,且 BA =2,AC =AD =a =2√2, 此时 V =13×√34×22×2=23√3.(2)2 条长为 a 的线段不在同一个三角形中,此时长为 a 的两条线段必处在三棱锥的对棱,不妨设 AD =BC =a ,BD =CD =AB =AC =2. 取 BC 中点 E ,连接 AE ,DE (见下图).则 AE ⊥BC,DE ⊥BC ⇒BC ⊥平面AED ,V =13S △AED ⋅BC , 在 △AED 中,AE =DE =√4−a 24,AD =a ,S △AED =12a √4−a 24−a 24=12a √4−a 22,所以 V =16a 2√4−a 22=16√a 2a 2(16−2a 2)⋅14,由均值不等式 a 2a 2(16−2a 2)≤(163)3,等号当且仅当 a 2=163时成立,即 a =43√3, 所以此时 V max =16√(163)3⋅14=1627√3.【知识点】棱锥的表面积与体积22. 【答案】(1) 由已知 a ⃗=2i ⃗+j ⃗,b ⃗⃗=mi ⃗+6j ⃗,且 a ⃗⋅b ⃗⃗=2m +6+(12+m )(i ⃗⋅j ⃗)=53m +2>0,得 m >−65;若 a ⃗ 和 b ⃗⃗ 同向,则存在正数 t ,使得 t (2i ⃗+j ⃗)=mi ⃗+6j ⃗, 由 i ⃗ 和 j ⃗ 不平行得,{2t =m t =6 得 m =12.故所求为 m >−65,m ≠12.(2) ①方程可变形为x−01=y−23,方向向量为 d⃗=(1,3), 设法向量为 n ⃗⃗=(a,b ),由 n ⃗⃗⋅d ⃗=0 得 a +3b +12(3a +b )=52a +72b =0, 令 a =−7,b =−5,n ⃗⃗=(−7,5);②取直线 l 上一点 B (0,2),则 BA⃗⃗⃗⃗⃗⃗=(2,−1),所求为 ∣∣BA ⃗⃗⃗⃗⃗⃗⋅n ⃗⃗∣∣∣n⃗⃗∣=∣√(⃗+5j ⃗)2=7√3926.【知识点】直线的点法向式方程(沪教版)、平面向量数量积的坐标运算。
高一数学下学期(人教A版B卷)-(考试版)(范围:必修第二册第6、7、8章)

2022-2023学年高一下学期期中考前必刷卷数学(考试时间:120分钟试卷满分:150分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.测试范围:必修第二册第6、7、8章。
5.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,第1~8题只有一项符合题目要求,第9~12题有多项符合题目要求。
全部选对的得5分,选对但不全的得2分,有选错的得0分。
一、单选题1.在ABC 中,20,10,32a b B ===︒,则此三角形的解的情况是()A .有两解B .有一解C .有无数个解D .无解2.设a ,b是两个非零向量,下列四个条件中,使a a bb = 成立的充分条件是()A .a b =r r 且//a br r B .a b =-r r C .//a br r D .4a b= 3.已知正四面体S ABC -的外接球表面积为6π,则正四面体S ABC -的体积为()A B C .23D 4.一个正四棱锥的侧棱长为10,底面边长为台,正四棱台的侧棱长为5,则正四棱台的高为()A .5B .4C .3D .25.设1e ,2e是平面内不共线的两个向量,则以下各组向量中不能作为基底的是()A .122e e + 与212e e +u r u rB .2e 与12e e - C .122e e -与2142e e - D .12e e - 与12e e +6.如图四边形ABCD 为平行四边形,11,22AE AB DF FC == ,若AF AC DE λμ=+,则λμ-的值为A .12B .23C .13D .17.三棱锥-P ABC 的侧棱,,PA PB PC 上分别有E ,F ,G ,且111,,324PE PF PG PA PB PC ===,则三棱锥P EFG -的体积与三棱锥-P ABC 的体积之比是()A .124B .112C .16D .188.已知△ABC 的三边为3,4,5,其外心为O ,则OA AB OB BC OC CA ⋅+⋅+⋅的值为()A .-25B .52-C .0D .67二、多选题9.已知复数12z =,则下列结论正确的有()A .1z z ⋅=B .2z z=C .31z =-D .2020122z i=-+10.ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,则下列说法正确的是()A .若AB >,则sin cos A B>B .若30A = ,4b =,3a =,则ABC 有两解C .若ABC 为锐角三角形,则222a b c +>D .若60A = ,2a =,则ABC11.给出下列四个命题,其中正确的选项有()A .()()a b c a b c⋅⋅=⋅⋅r r r r r r B .若a c c b ⋅=⋅ ,则a b=C .若()()0AB AC AB AC +⋅-= ,则ABC 为等腰三角形D .非零向量a ,b 满足a b a b ==- ,则a 与a b +的夹角是30︒12.引入平面向量之间的一种新运算“⊗”如下:对任意的向量()11,m x y =u r,()22,n x y =r,规定1212m n x x y y ⊗=- ,则对于任意的向量a ,b ,c,下列说法正确的有()A .a b b a⊗=⊗ B .()()a b a b λλ⊗=⊗ C .()()a b c a b c⋅⊗=⊗⋅ D .||||||a b a b ⋅≥⊗ 二、填空题:本题共4小题,共20分。
人教版高一数学下学期必修第二册期末考试高分突破培优卷(含解析)

人教版高一数学下学期必修第二册期末考试高分突破培优卷(含解析)一、单项选择题:本题共8小题,每小题满分5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求,选对得5分,选错得0分.1.设a 、b 都是非零向量,下列四个条件中,使a b a b =成立的条件是()A .a b=-B .//a bC .2a b=D .//a b 且a b=2.一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,则原平面图形的面积为()A .82B .22C .43D .233.已知一组样本数据1x ,2x ,3x ,…,10x ,且222212310185x x x x ++++=,平均数4x =,则该组数据的方差2s =()A .1B .32C .2D .524.已知α、β是平面,m 、n 是直线,下列命题中不正确的是()A .若//m α,n αβ=,则//m nB .若//m n ,m α⊥,则n α⊥C .若m α⊥,m β⊥,则//αβD .若m α⊥,m β⊂,则αβ⊥5.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2a +b =2c cos B ,若CD 是角C 的平分线,AD =27,DB =7,求CD 的长.()A .3B .2C .22D .326.如图所示,在平面四边形ABCD 中,AD CD ⊥,6AD CD ==,AC BC ⊥,o 60B ∠=,现将ACD △沿AC 边折起,并连接BD ,当三棱锥D ABC -的体积最大时,其外接球的表面积为()A .4πB .8πC .12πD .16π7.已知O 为正三角形ABC 内一点,且满足()10OA OB OC λλ+++=,若OAB 的面积与OAC 的面积之比为3,则λ=()A .12B .14C .34D .328.已知长方体1111ABCD A B C D -的高12,26,AA AC ==11,AB x AD y ==,则当x y +最大时,二面角111A B D C --的余弦值为()A .155B .155-C .55D .55-二、多项选择题:本题共4小题,每小题满分5分,共20分.在每小题给出的四个选项中,有多项符合题目要求。
尖子班用必修1、2复习提优卷(100分)

尖子班用必修一二复习卷(100分)一、单选题(共10题;共40分)1.如图所示的两个光滑斜面,倾角分别为α,β 且α<β,顶端有一个定滑轮.两个质量分别为m1、m2的小物块用细线通过定滑轮连接起来,两物块静止且在同一个水平面上.某时刻把细线剪断,两物块均沿斜面向下滑动,最后下滑到地面上.关于两物块的运动情况,下列说法正确的是()A. 两物块沿斜面下滑到地面的时间相等B. 在下滑过程中,任一时刻两物块的速度大小相等C. 在下滑过程中,两物块的重力所做的功相等D. 在下滑到地面的瞬间两物块的重力的功率相等2.如图所示,用水平力F拉着三个物体A、B、C在光滑的水平面上一起运动.现在中间物体上另置一小物体,且拉力不变,那么中间物体两端绳的拉力大小T a和T b的变化情况是()A. T a增大,T b减小B. T a增大,T b增大C. T a减小,T b增大D. T a减小,T b 减小3.如图所示,重物A、B由刚性绳拴接,跨过定滑轮处于图中实际位置,此时绳恰好拉紧,重物静止在水平面上,用外力水平向左推A,当A的水平速度为v A时,如图中虚线所示,则此时B的速度为()A. v AB.C.D.4.2003年10月15日至16日,我国航天员杨利伟成功完成我国首次载人航天飞行。
其中有,神州五号载人飞船的竖直向上发射升空阶段和返回地球的向下减速阶段。
在这两个阶段中,航天员所经历的运动状态是()A. 超重、失重B. 超重、超重C. 失重、超重D. 失重、失重5.如图所示,质量m=2kg的小物体放在长直的水平地面上,用水平细线绕在半径R=0.5m的薄圆筒上.t=0时刻,圆筒由静止开始绕竖直的中心轴转动,其角速度随时间的变化规律如图乙所示,小物体和地面间的动摩擦因数μ=0.1,重力加速度g取10m/s2,则()A. 小物体的速度随时间的变化关系满足v=4tB. 细线的拉力大小为2NC. 细线拉力的瞬时功率满足P=4tD. 在0~4s内,细线拉力做的功为12J6.如图所示,光滑水平面上的两个小球A和B ,其质量分别为m A和m B,且m A<m B,B球固定一轻质弹簧,A、B球均处于静止状态.若A球以速度v撞击弹簧的左端(撞击后球A、球B均在同一直线上运动),则在撞击以后的过程中,下列说法中正确的是()A. 两球共速时,速度大小为B. 当两球速度相等时,弹簧恢复原长C. 当A球速度为零时,B球速度为VD. 当弹簧压缩量最大时,两球速度都为零7.物块A质量为m ,置于光滑水平地面上,其上表面固定一根轻弹簧,弹簧原长为,劲度系数为k ,如图所示.现将弹簧上端B缓慢的竖直向上提起一段距离L ,使物块A离开地面,若以地面为势能零点,则这时物块A具有的重力势能为()A. B. C.D.8.长度为L=0.50m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O 点为圆心,在竖直平面内做圆周运动,通过最高点时,小球的速率是v=2.0m/s,g取10m/s2,则细杆此时受到()A. 6.0 N拉力B. 6.0 N压力C. 24 N拉力D. 24 N压力9.质量为2kg的质点在xy平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是()A. 质点的初速度为3 m/sB. 质点所受的合外力为3 NC. 质点初速度的方向与合外力方向垂直D. 2 s末质点速度大小为6 m/s10.如图所示,质量分别为m1和m2的木块A 和B 之间用一轻质弹簧相连,然后将它们静置于一底端带有挡板的光滑斜面上,其中B 置于斜面底端的挡板上,设斜面的倾角为θ,弹簧的劲度系数为k.现用一平行于斜面的恒力F 拉木块A 沿斜面由静止开始向上运动,当木块B 恰好对挡板的压力为零时,木块 A 在斜面上运动的速度为v,则下列说法正确的是()A. 此时弹簧的弹力大小为m1gsinθB. 拉力F 在该过程中对木块A 所做的功为C. 弹簧在该过程中弹性势能增加了﹣mv2D. 木块A在该过程中重力势能增加了二、多选题(共5题;共20分)11.如图所示,A、B两物块静止叠放在水平地面上,A、B的质量分别为m A=3kg,m B=2kg,A、B之间的动摩擦因数为μ1=0.5,B与地面间的动摩擦因数为μ2=0.2.最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2.现对A施加一水平拉力F()A. 当F=12 N时,A,B都相对地面静止B. 当F>22.5 N时,A相对B滑动C. 当F=20 N时,A,B间的摩擦力为14ND. 无论F为何值,B的加速度不会超过5m/s212.如图所示,质量M=3kg的滑块套在水平固定着的轨道上并可在轨道上无摩擦滑动.质量m=2kg的小球(视为质点)通过长L=0.75m的轻杆与滑块上的光特轴O连接,开始时滑块静止、轻杆处于水平状态.现给小球一个v0=3m/s的竖直向下的初速度,取g=10m/s2则()A. 小球m从初始位置到第一次到达最低点的过程中,滑块M在水平轨道上向右移动了0.3 mB. 小球m从初始位置到第一次到达最低点的过程中,滑块对在水平轨道上向右移动了0.5 mC. 小球m相对于初始位置可以上升的最大高度为0.27 mD. 小球m从初始位置到第一次到达最大高度的过程中,滑块M在水平轨道上向右移动了0.54 m13.如图所示,在水平桌面上叠放着质量相等的A、B两块木板,在木板A上放着一个物块C,木板和物块均处于静止状态.已知物块C的质量为m,A、B、C之间以及B与地面之间的动摩擦因数均为μ.用水平恒力F向右拉动木板A使之做匀加速运动,物块C始终与木板A保持相对静止.设最大静摩擦力与滑动摩擦力大小相等,重力加速度为g.则以下判断正确的是()A. A 、C之间的摩擦力可能为零B. A 、B之间的摩擦力不为零,大小可能等于μmgC. A 、B之间的摩擦力大小一定小于FD. 木板B一定保持静止14.如图所示,在倾角为θ=30°的光滑斜面上有完全相同的质量为1kg的三个木块,A、B之间用轻弹簧相连,B、C之间用不可伸长的细绳相连,在手的恒定拉力F拉动下,达到稳定后,一起向上做匀加速运动,g大小取10m/s2,下列说法正确的是()A. 如果增大斜面的倾角,弹簧的弹力将增大B. 如果换成粗糙的斜面,弹簧的弹力和细绳的弹力将保持不变C. 如果一起运动加速度大小为5m/s2.在突然撤去拉力F瞬间BC之间的弹力大小为5ND. 如果一起运动加速度大小为5m/s2在突然撤去拉力F瞬间a A=5 m/s2,a B=a C=﹣10 m/s2(取沿斜面向上为正方向)15.一小船在静水中的速度为4m/s,要度过宽度为120m,水流速度为5m/s的河流,下列说法正确的是()A. 因为船速小于水速,所以船不能渡过此河B. 因为船速小于水速,所以船不能行使到正对岸C. 船渡河的最短时间为24sD. 船渡河的最小位移为150m三、实验探究题(共2题;每空两分,共16分)16.某探究学习小组的同学欲验证“动能定理”,他们在实验室组装了一套如图所示的装置,另外他们还找到了打点计时器所用的学生电源一台,导线、复写纸、纸带、小木块、细沙若干.当滑块连接上纸带,用细线通过滑轮挂上空的小沙桶时,释放小桶,滑块处于静止状态.1你是小组中的一位成员,要完成该项实验,则:①还需要补充的实验器材是________.2②某同学的实验步骤如下:用天平称量滑块的质量M.往沙桶中装入适量的细沙,让沙桶带动滑块加速运动,用打点计时器记录其运动情况,用天平称出此时沙和沙桶的总质量m.在打点计时器打出的纸带上取两点,测出这两点的间距L,算出这两点的速度v1与v2.他用沙和沙桶的总重力表示滑块受到的合外力,为了减小这种做法带来的实验误差,你认为在图示情况下还应该采取的一项操作是:________;应控制的实验条件是:________;③若挑选的一条点迹清晰的纸带如下,且已知滑块的质量为M,沙和沙桶的总质量为m,相邻两个点之间的时间间隔为T,从A点到B、C、D、E、F点的距离依次为S1、S2、S3、S4、S5(图中未标出S3、S4、S5),则由此可求得纸带上由B点到E点所对应的过程中,沙和沙桶的重力所做的功W=________;该滑块动能改变量的表达式为△E K=________.(结果用题中已知物理量的字母表示)17.A、B两物体在水平面上相向运动,其中物体A的质量为m A=4kg,两球发生相互作用前后的运动情况如图所示.则:(1)由图可知A、B两物体在________时刻发生碰撞,B物体的质量为m B________kg.(2)碰撞过程中,系统的机械能损失________J.四、计算题(共2题;共10分)18.如图所示,左侧的光滑斜面与右侧木板相连,把质量为m=l kg的滑块从斜面上高度h=0.1m处由静止释放,当右侧木板水平放置时,滑块在水平木板上滑行l=0.2m停止.欲使滑块从左侧斜面同一高度由静止下滑,并将右侧的木板向上转动一个锐角θ,形成斜面,使滑块在右侧木板上最远滑行0.l m,假设滑块由左侧斜面底端滑上右侧木板的瞬间速度大小不变.重力加速度g=10m/s2.求:θ的大小及滑块从冲上右侧木板到第一次返回最低点所用的时间.19.(2016•新课标Ⅲ)【物理-选修3-5】如图所示,水平地面上有两个静止的小物块a和b,其连线与墙垂直:a和b相距l;b与墙之间也相距l;a的质量为m,b的质量为m,两物块与地面间的动摩擦因数均相同,现使a以初速度向右滑动,此后a与b发生弹性碰撞,但b没有与墙发生碰撞,重力加速度大小为g,求物块与地面间的动摩擦力因数满足的条件。
人教A版高一数学必修第二册全册复习测试题卷含答案解析(54)
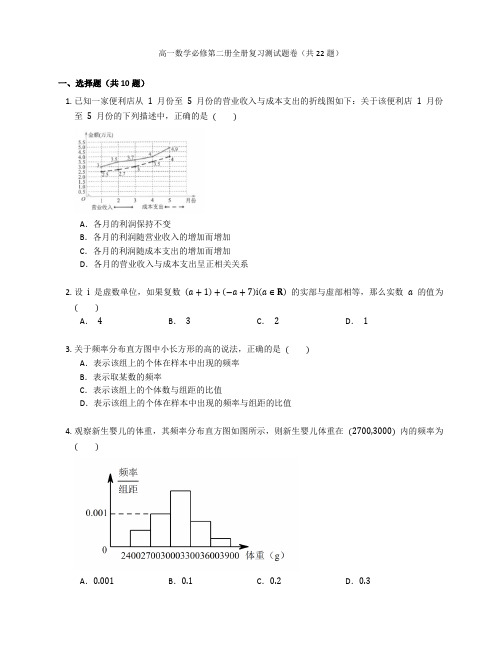
高一数学必修第二册全册复习测试题卷(共22题)一、选择题(共10题)1.已知一家便利店从1月份至5月份的营业收入与成本支出的折线图如下:关于该便利店1月份至5月份的下列描述中,正确的是( )A.各月的利润保持不变B.各月的利润随营业收入的增加而增加C.各月的利润随成本支出的增加而增加D.各月的营业收入与成本支出呈正相关关系2.设i是虚数单位,如果复数(a+1)+(−a+7)i(a∈R)的实部与虚部相等,那么实数a的值为( )A.4B.3C.2D.13.关于频率分布直方图中小长方形的高的说法,正确的是( )A.表示该组上的个体在样本中出现的频率B.表示取某数的频率C.表示该组上的个体数与组距的比值D.表示该组上的个体在样本中出现的频率与组距的比值4.观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿体重在(2700,3000)内的频率为( )A.0.001B.0.1C.0.2D.0.35. 如果一组数据“x 1,x 2,x 3,x 4,x 5”的平均数是 2,方差是 13,那么另一组数据“3x 1−2,3x 2−2,3x 3−2,3x 4−2,3x 5−2”的平均数和方差分别为 ( ) A . 2,13B . 2,1C . 4,23D . 4,36. 在 △ABC 中,∠BAC =π2,AB =AC =2,P 为 △ABC 所在平面上任意一点,则 PA⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ ) 的最小值为 ( ) A . 1B . −12C . −1D . −27. 已知互相垂直的平面 α,β 交于直线 l ,若直线 m ,n 满足 m ∥α,n ⊥β,则 ( ) A .m ∥lB .m ∥nC .n ⊥lD .m ⊥n8. 复数 i (2−i )= ( ) A . 1+2iB . 1−2iC . −1+2iD . −1−2i9. 若复数 z 满足 z (1+i )=2i ,其中 i 为虚数单位,则 z = ( ) A . 1−iB . 1+iC . −1+iD . −1−i10. 在 △ABC 中,B =30∘,AB =2√3,AC =2,则 △ABC 的面积是 ( )A . √3B . 2√3C . √3 或 2√3D . 2√3 或 4√3二、填空题(共6题) 11. 思考辨析,判断正误.在 △ABC 中,已知两边及夹角时,△ABC 不一定唯一.( )12. 根据党中央关于“精准脱贫”的要求,某市农业经济部门派甲、乙、丙 3 位专家对 A ,B 两个区进行调研,每个区至少派 1 位专家,则甲、乙两位专家均派遣至 A 区的概率为 .13. 已知向量 a =(2,1),b ⃗ =(−1,x ),若 (a +b ⃗ )∥(a −b ⃗ ),则实数 x 的值为 .14. 半径为 3 的球体表面积为 .15. 平面与平面垂直的性质定理:文字语言:两个平面垂直,如果一个平面内有一直线垂直于这两个平面的 ,那么这条直线与另一个平面 .符号语言:α⊥β,α∩β=l,,⇒a⊥β.图形语言:16.若复数z=2+i,其中i为虚数单位,则z在复平面内对应点的坐标为.1−2i三、解答题(共6题)17.已知圆柱的底面直径与高都等于球的直径.求证:(1) 球的表面积等于圆柱的侧面积;.(2) 球的表面积等于圆柱全面积的2318.在静水中划船的速度的大小是每分钟40m,水流速度的大小是每分钟20m,如果一小船从岸边某处出发,沿着垂直于水流的方向到达对岸,则小船的行进方向应指向哪里?19.在△ABC中,内角A,B,C所对的边分别为a,b,c,且满足b2+c2−a2=2bcsin(B+C).(1) 求角A的大小;,求△ABC的面积.(2) 若a=2,B=π320.应用面面平行判断定理应具备哪些条件?21.在北京市“危旧房改造”中,小强一家搬进了回龙观小区.这个小区冬季用家庭燃气炉取暖.为了估算冬季取暖第一个月使用天然气的开支情况,从11月15日起,小强连续八天每天晚上记录了天然气表显示的读数,如下表(注:天然气表上先后两次显示的读数之差就是这段时间内使用天然气的数量):日期15日16日17日18日19日20日21日22日小强的天然气表显示读数(单位:m3)220229241249259270279290妈妈11月15日买了一张面值600元的天然气使用卡,已知每立方米天然气1.70元,请你估算这张卡够小强家用一个月(按30天计算)吗?为什么?22.甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.(1) 结合平均数和方差分析谁更优秀;(2) 结合平均数和中位数分析谁的成绩好些;(3) 结合平均数和命中9环及以上的次数分析谁的成绩好些;(4) 从折线图上两人射击命中环数的走势分析谁更有潜力.答案一、选择题(共10题) 1. 【答案】D【知识点】频率分布直方图2. 【答案】B【解析】由题意得 a +1=−a +7,则 a =3.故选B . 【知识点】复数的乘除运算3. 【答案】D【解析】频率分布直方图中小长方形的高是 频率组距,面积表示频率.【知识点】频率分布直方图4. 【答案】D【知识点】频率分布直方图5. 【答案】D【知识点】样本数据的数字特征6. 【答案】C【解析】如图,以直线 AB ,AC 分别为 x ,y 轴建立平面直角坐标系, 则 A (0,0),B (2,0),C (0,2),设 P (x,y ),则 PA⃗⃗⃗⃗⃗ =(−x,−y ),PB ⃗⃗⃗⃗⃗ =(2−x,−y ),PC ⃗⃗⃗⃗⃗ =(−x,2−y ),PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ =(2−2x,2−2y ), 所以PA⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )=−x (2−2x )−y (2−2y )=2x 2−2x +2y 2−2y =2(x −12)2+2(y −12)2−1,当 x =12,y =12 时,PA ⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗ +PC⃗⃗⃗⃗⃗ ) 取得最小值,为 −1. 故选C .【知识点】平面向量数量积的坐标运算7. 【答案】C【解析】由题意知α∩β=l,所以l⊂β,因为n⊥β,所以n⊥l.【知识点】直线与直线的位置关系、点、线、面的位置关系8. 【答案】A【解析】i(2−i)=1+2i.【知识点】复数的乘除运算9. 【答案】B【解析】因为复数z满足z(1+i)=2i,所以z=2i1+i=1+i.【知识点】复数的乘除运算10. 【答案】C【解析】由AB=2√3,AC=2,B=30∘及正弦定理ACsinB =ABsinC得sinC=ABsinBAC=2√3×122=√32.由C为三角形的内角可知C=60∘或120∘.因此A=90∘或30∘.在△ABC中,由AB=2√3,AC=2,A=90∘或30∘,得面积S=12AC⋅AB⋅sinA=2√3或√3.【知识点】正弦定理二、填空题(共6题)11. 【答案】×【知识点】余弦定理12. 【答案】16【解析】该试验所有的样本点为(甲,乙丙),(乙,甲丙),(丙,甲乙),(甲乙,丙),(甲丙,乙),(乙丙,甲)(其中每个样本点表示的都是“派往A区调研的专家、派往B区调研的专家”),共6个,其中甲、乙两位专家均被派遣至 A 区的样本点有 1 个,因此,所求事件的概率为 16. 【知识点】古典概型13. 【答案】 −12【解析】因为 a =(2,1),b⃗ =(−1,x ), 所以 a +b ⃗ =(1,x +1),a −b ⃗ =(3,1−x ), 又 (a +b ⃗ )∥(a −b⃗ ), 所以 1−x −3(x +1)=0, 解得 x =−12.【知识点】平面向量数乘的坐标运算14. 【答案】 36π【知识点】球的表面积与体积15. 【答案】交线;垂直; a ⊂α ; a ⊥l【知识点】平面与平面垂直关系的性质16. 【答案】 (0,1)【知识点】复数的几何意义、复数的乘除运算三、解答题(共6题) 17. 【答案】(1) 略. (2) 略.【知识点】圆柱的表面积与体积、球的表面积与体积18. 【答案】如图所示,设向量 OA⃗⃗⃗⃗⃗ 的长度和方向表示水流速度的大小和方向,向量 OB ⃗⃗⃗⃗⃗ 的长度和方向表示船在静水中速度的大小和方向,以 OA⃗⃗⃗⃗⃗ ,OB ⃗⃗⃗⃗⃗ 为邻边作平行四边形 OACB ,连接 OC . 依题意得 OC ⃗⃗⃗⃗⃗ ⊥OA ⃗⃗⃗⃗⃗ ,∣∣BC ⃗⃗⃗⃗⃗ ∣∣=∣∣OA ⃗⃗⃗⃗⃗ ∣∣=20,∣∣OB ⃗⃗⃗⃗⃗ ∣∣=40,所以 ∠BOC =30∘.故船应向上游且与河岸夹角为 60∘ 的方向行进. 【知识点】平面向量的实际应用问题19. 【答案】(1) 因为 A +B +C =π, 所以 sin (B +C )=sinA , 所以 b 2+c 2−a 2=2bcsinA ,所以b 2+c 2−a 22bc=sinA ,由余弦定理得 cosA =sinA ,可得 tanA =1, 又因为 A ∈(0,π), 所以 A =π4.(2) 根据正弦定理得 b =a sinA ⋅sinB =√6,又 sinC =sin (A +B )=sin (π4+π3)=√6+√24, 所以S △ABC =12absinC =12⋅2⋅√6⋅√6+√24=3+√32.【知识点】余弦定理、正弦定理20. 【答案】①平面 α 内两条相交直线 a ,b ,即 a ⊂α,b ⊂α,a ∩b =P .②两条相交直线 a ,b 都与 β 平行,即 a ∥β,b ∥β. 【知识点】平面与平面平行关系的判定21. 【答案】 300×1.70<600,够用.【知识点】样本数据的数字特征22. 【答案】(1) 根据题意作出统计表:平均数方差中位数命中9环及以上次数甲7 1.271乙75.47.53因为平均数相同,且 s 甲2<s 乙2,所以甲的成绩比乙稳定,甲更优秀.(2) 因为平均数相同,甲的中位数 < 乙的中位数, 所以乙的成绩比甲好.(3) 因为平均数相同,且乙命中 9 环及以上的次数比甲多, 所以乙的成绩比甲好.(4) 因为甲的成绩在平均线附近波动,而乙的成绩整体处于上升趋势,从第 4 次开始射靶的环数没有比甲少的情况发生, 所以乙更有潜力.【知识点】样本数据的数字特征。
2022-2023学年高一下学期数学人教A版(2019)必修第二册期末模拟试题含答案

2022-2023学年高一第二学期期末模拟考试(新人教A 版)数学试题2023.61、满分为 150 分, 考试用时 120 分钟。
2.考试内容:必修第二册:第六章《平面向量及其应用 》,第七章《复数》,第八章《立体几何初步》,第九章《统计》,第十章《概率》 一、单项选择题(每小题5分,共40分)1、若(1)12(i z i +=−i 为虚数单位),则||(z =)A B C .52D 2、若夹角为3π的非零向量a,b 满足||1a = 且()a a b ⊥− ,则||(b = )A .1B C .2D .33、若m ,n 是两条不同的直线,α,β是两个不同的平面,则下列结论正确的是()A .若m α⊂,n β⊂,//αβ,则//m nB .若//m α,m β⊥,则αβ⊥C .若αβ⊥,m αβ= ,m n ⊥,则n β⊥D .若m n ⊥,m α⊥,m β⊥,则//n β4、掷一枚质地均匀的骰子,记事件A =“出现的点数不超过3”,事件B =“出现的点数是3或6”.则事件A 与B 的关系为( )A .事件A 与B 互斥 B .事件A 与B 对立 C .事件A 与B 独立D .事件A 包含于B5、如图所示,BC 是一条水平的靠山公路,测绘人员在山顶A 处测得B ,C 两点的俯角分别为30°,60°,若山顶到公路所在水平面的距离AD =,120BDC ∠=°,则BC =( )m .A 、B 、C 、D 、6、若向量(1,1)a − ,向量(4,3)b = ,则向量a在向量b 上的投影向量为()A .43(,)2525−B .43(,)2525−−C .11(,)22−D .43(,)55−−7、如图:已知正四面体ABCD 中E 在棱CD 上,2EC DE =,G 为ABC 的重心,则异面直线EG 与BD 所成角为( )A.30B.45°C.60°D.90°8、平面四边形PABC 中,2,2,3APC AB AC AC AB π∠⊥,则AP AB ⋅ 最小值()A.2−B.1− C.− D.二、多项选择题(每小题5分,共20分,有多项符合要求,全部选对得5分,部分选对得2分,有选错得0分)9、水稻是世界最重要的食作物之一,也是我国60%以上人口的主粮。
人教A版高一数学必修第二册全册复习测试题卷含答案解析(1)

高一数学必修第二册全册复习测试题卷11(共22题)一、选择题(共10题)1. △ABC 中,若 a =1,c =2,B =60∘,则 △ABC 的面积为 ( ) A . 12B . 1C .√32D . √32. 若书架中放有中文书 5 本,英文书 3 本,日文书 2 本,则抽出一本书为外文书的概率为 ( ) A . 15B . 310C . 25D . 123. 若 θ 为两个非零向量的夹角,则 θ 的取值范围为 ( ) A .(0,π) B .(0,π] C .[0,π) D .[0,π]4. 从一箱产品中随机地抽取一件,设事件 A = { 抽到一等品 },事件 B = { 抽到二等品 },事件 C = { 抽到三等品 } ,且已知 P (A )=0.65,P (B )=0.2,P (C )=0.1.则事件“抽到的是二等品或三等品”的概率为 ( ) A .0.7 B .0.65 C .0.35 D .0.35. 下列关于古典概型的说法中正确的是 ( ) ①试验中所有可能出现的样本点只有有限个; ②每个事件出现的可能性相等; ③每个样本点出现的可能性相等;④若样本点总数为 n ,随机事件 A 包含其中的 k 个样本点,则 P (A )=kn . A .②④ B .③④ C .①④ D .①③④6. 给定一组数据:102,100,103,104,101,这组数据的第 60 百分位数是 ( ) A . 102 B . 102.5 C . 103 D . 103.57. 为比较甲、乙两地某月 14 时的气温情况,随机选取该月中的 5 天,这 5 天中 14 时的气温数据(单位:∘C )如下:甲:2628293131乙:2829303132以下结论:①甲地该月 14 时的平均气温低于乙地该月 14 时的平均气温; ②甲地该月 14 时的平均气温高于乙地该月 14 时的平均气温;③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.其中根据数据能得到的统计结论的编号为( )A.①③B.①④C.②③D.②④8.下列说法正确的是( )A.任何事件的概率总是在(0,1)之间B.频率是客观存在的,与试验次数无关C.随着试验次数的增加,事件发生的频率一般会稳定于概率D.概率是随机的,在试验前不能确定9.用符号表示“点A在直线l上,l在平面α内”,正确的是( )A.A∈l,l∉αB.A⊂l,l⊄αC.A⊂l,l∈αD.A∈l,l⊂α10.半径为2的球的表面积为( )A.4πB.8πC.12πD.16π二、填空题(共6题)11.一家保险公司想了解汽车的挡风玻璃在一年时间里破碎的概率,公司收集了20000部汽车,时间从某年的5月1日到下一年的5月1日,共发现有600部汽车的挡风玻璃破碎,则一部汽车在一年时间里挡风玻璃破碎的概率约为.12.思考辨析 判断正误.( )做100次拋硬币的试验,结果51次出现正面朝上,因此,出现正面朝上的概率是5110013.若空间两个角的两条边分别平行,则这两个角的大小关系是.14.如图所示,在复平面内,网格中的每个小正方形的边长都为1,点A,B对应的复数分别是z1,=.z2,则z2z115.平均数:如果n个数x1,x2,⋯,x n,那么x=叫做这n个数的平均数.16.思考辨析判断正误为了更清楚地反映学生在这学期多次考试中数学成绩情况,可以选用折线统计图.( )三、解答题(共6题)17.如图所示,梯形ABCD中,AD∥BC,且AD<BC,当梯形ABCD绕AD所在直线旋转一周时,其他各边旋转围成了一个几何体,试描述该几何体的结构特征.18.小明是班里的优秀学生,他的历次数学成绩是96,98,95,93,45分,最近一次考试成绩只有45分的原因是他带病参加了考试.期末评价时,怎样给小明评价(90分及90分以上为优秀,75∼90分为良好)?19.类比绝对值∣x−x0∣的几何意义,∣z−z0∣(z,z0∈C)的几何意义是什么?20.如图,在三棱锥P−ABC中,平面PAC⊥平面ABC,∠ACB=90∘,PA=AC=2BC.(1) 若PA⊥PB,求证:平面PAB⊥平面PBC;(2) 若PA与平面ABC所成角的大小为60∘,求二面角C−PB−A的余弦值.21.应用面面平行判断定理应具备哪些条件?22.如图,在四棱锥P−ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,DC=6,AD=8,BC=10,PD=9,E为PA的中点.(1) 求证:DE∥平面BPC.(2) 在线段AB上是否存在一点F,满足CF⊥DB?若存在,试求出此时三棱锥B−PCF的体积;若不存在,请说明理由.答案一、选择题(共10题) 1. 【答案】C【解析】由题得 △ABC 的面积 S =12AB ⋅BC ⋅sin60∘=12×2×1×√32=√32. 【知识点】三角形的面积公式2. 【答案】D【解析】在 10 本书中,中文书 5 本,外文书为 3+2=5 本,由古典概型,在其中抽出一本书为外文书的概率为 510,即 12. 【知识点】古典概型3. 【答案】D【知识点】平面向量的数量积与垂直4. 【答案】D【解析】由题意知事件 A 、 B 、 C 互为互斥事件,记事件 D =“抽到的是二等品或三等品”,则 P (D )=P (B ∪C )=P (B )+P (C )=0.2+0.1=0.3. 【知识点】事件的关系与运算5. 【答案】D【解析】②中所说的事件不一定是样本点,所以②不正确;根据古典概型的特征及计算公式可知①③④正确. 【知识点】古典概型6. 【答案】D【解析】 5×0.6=3,第 60 百分位数是第三与第四个数的平均数, 即103+1042=103.5.【知识点】样本数据的数字特征7. 【答案】B【解析】因为 x 甲=26+28+29+31+315=29,x 乙=28+29+30+31+325=30,所以 x 甲<x 乙.又 s 甲2=9+1+0+4+45=185,s 乙2=4+1+0+1+45=2,所以 s 甲>s 乙,故由样本估计总体可知结论①④正确. 【知识点】样本数据的数字特征8. 【答案】C【解析】不可能事件的概率为 0,必然事件的概率为 1,故A 错误;频率是由试验的次数决定的,故B 错误;概率是频率的稳定值,故C 正确,D 错误. 【知识点】频率与概率9. 【答案】D【解析】点 A 在直线 l 上,表示为 A ∈l ,l 在平面 α 内,表示为 l ⊂α. 【知识点】平面的概念与基本性质10. 【答案】D【解析】因为球的半径为 r =2, 所以该球的表面积为 S =4πr 2=16π. 【知识点】球的表面积与体积二、填空题(共6题) 11. 【答案】 0.03【解析】 P =60020000=0.03.【知识点】频率与概率12. 【答案】 ×【知识点】频率与概率13. 【答案】相等或互补【知识点】直线与直线的位置关系14. 【答案】 −1−2i【解析】由题意,根据复数的表示可知z1=i,z2=2−i,所以z2z1=2−ii=(2−i)⋅(−i)i⋅(−i)=−1−2i.【知识点】复数的乘除运算、复数的几何意义15. 【答案】1n(x1+x2+⋯+x n)【知识点】样本数据的数字特征16. 【答案】√【知识点】频率分布直方图三、解答题(共6题)17. 【答案】如图所示,旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分构成的组合体.【知识点】组合体18. 【答案】小明5次考试成绩从小到大排列为45,93,95,96,98,中位数是95,应评定为“优秀”.【知识点】样本数据的数字特征19. 【答案】∣z−z0∣(z,z0∈C)的几何意义是复平面内点Z到点Z0的距离.【知识点】复数的加减运算20. 【答案】(1) 因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BC⊂平面ABC,BC⊥AC,所以BC⊥平面PAC,因为PA⊂平面PAC,所以PA⊥BC.又PA⊥PB,PB∩BC=B,所以PA⊥平面PBC,因为PA⊂平面PAB,所以平面PAB⊥平面PBC.(2) 如图,过P作PH⊥AC于点H,因为平面PAC⊥平面ABC,所以PH⊥平面ABC,所以∠PAH=60∘,不妨设PA=2,所以PH=√3,以 C 为原点,分别以 CA ,CB 所在直线为 x 轴,y 轴,以过 C 点且平行于 PH 的直线为 z 轴,建立如图所示的空间直角坐标系,则 C (0,0,0),A (2,0,0),B (0,1,0),P(1,0,√3),因此 AB⃗⃗⃗⃗⃗ =(−2,1,0),AP ⃗⃗⃗⃗⃗ =(−1,0,√3),CB ⃗⃗⃗⃗⃗ =(0,1,0),CP ⃗⃗⃗⃗⃗ =(1,0,√3). 设 n ⃗ =(x 1,y 1,z 1) 为平面 PAB 的一个法向量, 则 {n ⃗ ⋅AB⃗⃗⃗⃗⃗ =0,n ⃗ ⋅AP⃗⃗⃗⃗⃗ =0, 即 {−2x 1+y 1=0,−x 1+√3z 1=0,令 z 1=√3,可得 n ⃗ =(3,6,√3), 设 m ⃗⃗ =(x 2,y 2,z 2) 为平面 PBC 的一个法向量, 则 {m ⃗⃗ ⋅CB⃗⃗⃗⃗⃗ =0,m ⃗⃗ ⋅CP ⃗⃗⃗⃗⃗ =0, 即 {y 2=0,x 2+√3z 2=0,令 z 2=√3,可得 m ⃗⃗ =(−3,0,√3), 所以 cos⟨m ⃗⃗ ,n ⃗ ⟩=4√3×2√3=−14, 易知二面角 C −PB −A 为锐角, 所以二面角 C −PB −A 的余弦值为 14.【知识点】平面与平面垂直关系的判定、利用向量的坐标运算解决立体几何问题、二面角21. 【答案】①平面 α 内两条相交直线 a ,b ,即 a ⊂α,b ⊂α,a ∩b =P .②两条相交直线 a ,b 都与 β 平行,即 a ∥β,b ∥β. 【知识点】平面与平面平行关系的判定22. 【答案】(1) 取 PB 的中点 M ,连接 EM ,CM ,过点 C 作 CN ⊥AB ,垂足为 N ,如图所示. 因为 CN ⊥AB ,DA ⊥AB , 所以 CN ∥DA , 又 AB ∥CD ,所以四边形 CDAN 为矩形, 所以 CN =AD =8,DC =AN =6.在 Rt △BNC 中,BN =√BC 2−CN 2=√102−82=6, 所以 AB =12.因为 E ,M 分别为 PA ,PB 的中点, 所以 EM ∥AB 且 EM =6, 又 DC ∥AB ,且 CD =6, 所以 EM ∥CD 且 EM =CD , 则四边形 CDEM 为平行四边形, 所以 DE ∥CM .因为 CM ⊂平面BPC ,DE ⊄平面BPC ,所以 DE ∥平面BPC .(2) 存在.理由如下:由题意可得 DA ,DC ,DP 两两互相垂直,故以 D 为原点,DA ,DC ,DP所在直线分别为 x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系 Dxyz . 则 D (0,0,0),B (8,12,0),C (0,6,0),所以 DB⃗⃗⃗⃗⃗⃗ =(8,12,0). 假设 AB 上存在一点 F 使 CF ⊥BD ,设点 F 坐标为 (8,t,0)(0≤t ≤12), 则 CF⃗⃗⃗⃗⃗ =(8,t −6,0), 由 CF ⃗⃗⃗⃗⃗ ⋅DB ⃗⃗⃗⃗⃗⃗ =0,得 64+12(t −6)=12t −8=0, 所以 t =23,即 AF =23,故 BF =12−23=343.又 PD =9,所以 V 三棱锥B−PCF =V 三棱锥P−BCF =13×12×343×8×9=136.【知识点】直线与平面平行关系的判定、利用向量的坐标运算解决立体几何问题。
人教A版高一数学必修第二册全册复习测试题卷含答案解析(52)

高一数学必修第二册全册复习测试题卷(共22题)一、选择题(共10题)1. 在 △ABC 中,∠BAC =60∘,∠BAC 的平分线 AD 交 BC 边于点 D ,已知 AD =2√3,且λAB ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ −13AC ⃗⃗⃗⃗⃗ (λ∈R ),则 AB ⃗⃗⃗⃗⃗ 在 AD ⃗⃗⃗⃗⃗ 方向上的投影数量为 ( )A . 1B . 32C . 3D . 3√322. 在 △ABC 中,内角 A ,B ,C 的对边分别为 a ,b ,c .若 3bcosC =c (1−3cosB ),则 c:a = ( ) A . 1:3 B . 4:3 C . 3:1 D . 3:23. 已知 △ABC 中,内角 A ,B ,C 所对的边分别为 a ,b ,c 且 acosC +√32c =b ,若 a =1,√3c −2b =1,则角 B 为 A .π4B .π6C .π3D .π124. 已知向量 a =(2,x ),b ⃗ =(1,2),若 a ∥b ⃗ ,则实数 x 的值为 ( ) A .1B .2C .3D .45. 珠穆朗玛峰是印度洋板块和欧亚板块碰撞挤压形成的.这种挤压一直在进行,珠穆朗玛峰的高度也一直在变化.由于地势险峻,气候恶劣,通常采用人工攀登的方式为珠峰“量身高”.攀登者们肩负高精度测量仪器,采用了分段测量的方法,从山脚开始,直到到达山顶,再把所有的高度差累加,就会得到珠峰的高度.2020 年 5 月,中国珠峰高程测量登山队 8 名队员开始新一轮的珠峰测量工作.在测量过程中,已知竖立在 B 点处的测量觇标高 10 米,攀登者们在 A 处测得到觇标底点 B 和顶点 C 的仰角分别为 70∘,80∘,则 A ,B 的高度差约为 ( )A . 10 米B . 9.72 米C . 9.40 米D . 8.62 米6. 在 △ABC 中,A =120∘,AB =5,BC =7,则 sinB sinC= ( )A . 37B . 35C . 57D . 857. 若 O 为平行四边形 ABCD 的中心,AB ⃗⃗⃗⃗⃗ =2e 1⃗⃗⃗ ,BC ⃗⃗⃗⃗⃗ =3e 2⃗⃗⃗ ,则 32e 2⃗⃗⃗ −e 1⃗⃗⃗ 等于 ( )A . AO ⃗⃗⃗⃗⃗B . BO ⃗⃗⃗⃗⃗C . CO ⃗⃗⃗⃗⃗D . DO⃗⃗⃗⃗⃗⃗8. 在 △ABC 中,AB =2AC =6,BA⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ 2,点 P 是 △ABC 所在平面内的一点,则当 PA ⃗⃗⃗⃗⃗ 2+PB ⃗⃗⃗⃗⃗ 2+PC ⃗⃗⃗⃗⃗ 2 取得最小值时,AP ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ = ( ) A . 35B . −9C . 7D . −259. 在 △ABC 中,点 D 满足 BD ⃗⃗⃗⃗⃗⃗ =34BC ⃗⃗⃗⃗⃗ ,当点 E 在线段 AD 上移动时,若 AE ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ +μAC ⃗⃗⃗⃗⃗ (λ,μ∈R ),则 t =(λ−1)2+μ2 的最小值是 ( ) A .3√1010B .√824C . 910D .41810. 已知 a ,b ⃗ ,c 是三个不共线的向量,a 为给定向量,那么下列叙述中正确的是 ( )A .对任何非零实数 λ 及给定的向量 b ⃗ ,c ,均存在唯一的实数 μ,使得 a =λb ⃗ +μcB .对任何向量 b ⃗ 及给定的非零实数 λ,μ,均存在唯一的向量 c ,使得 a =λb ⃗ +μcC .若 ∣b ⃗ ∣=1,则对任何实数 λ,均存在单位向量 c 和实数 μ,使得 a =λb ⃗ +μcD .若 ∣b ⃗ ∣=1,则对任何实数 μ,均存在单位向量 c 和实数 λ,使得 a =λb ⃗ +μc二、填空题(共6题)11. 已知复数 a+i2−i 为纯虚数,那么实数 a = .12. 如图所示,三棱锥 P −ABC 外接球的半径为 1,且 PA 过球心,△PAB 围绕棱 PA 旋转 60∘后恰好与 △PAC 重合.若 PB =√3,则三棱锥 P −ABC 的体积为 .13. 思考辨析 判断正误频率分布直方图中所有小长方形面积之和为 1.14. 已知向量 a ,b ⃗ 满足 ∣a ∣=2,∣∣b ⃗ ∣∣=3,且已知向量 a,b ⃗ 的夹角为 60∘,(a −c )⋅(b ⃗ −c )=0,则 ∣c ∣ 的最小值是 .15. 已知向量 a =(1,2),b ⃗ =(2,−2),c =(1,λ).若 c ∥(2a +b ⃗ ),则 λ= .16. 在相距 2 km 的 A ,B 两点处测量目标点 C ,若 ∠CAB =75∘,∠CBA =60∘,则 A ,C 两点之间的距离为 .三、解答题(共6题)17. 如图,在五面体 ABCDEF 中,四边形 ABCD 是边长为 2 的正方形,EF ∥平面ABCD ,EF =1,FB =FC ,∠BFC =90∘,AE =√3,H 是 BC 的中点.(1) 求证:FH ∥平面BDE ; (2) 求证:AB ⊥平面BCF ; (3) 求五面体 ABCDEF 的体积.18. 对于任意实数 a ,b ,c ,d ,表达式 ad −bc 称为二阶行列式(determinant ),记作 ∣∣∣ab cd ∣∣∣. (1) 求下列行列式的值:① ∣∣∣1001∣∣∣; ② ∣∣∣1326∣∣∣; ③ ∣∣∣−2510−25∣∣∣;(2) 求证:向量 p =(a,b ) 与向量 q =(c,d ) 共线的充要条件是 ∣∣∣a b cd ∣∣∣=0.(3) 讨论关于 x ,y 的二元一次方程组 {a 1x +b 1y =c 1,a 2x +b 2y =c 2(a 1a 2b 1b 2≠0) 有唯一解的条件,并求出解.(结果用二阶行列式的记号表示)19. 有些同学说:实轴上的点表示实数,虚轴上的点表示虚数,这句话对吗?20. 在 △ABC 中,a ,b ,c 分别是内角 A ,B ,C 的对边,且 A =π6,a =2.(1) 若 B =π4,求 b 的值;(2) 若 △ABC 的面积为 √3,求 △ABC 的周长.21. 已知函数 f (x )=12sin2x −√3cos 2x .(1) 求函数 y =f (x ) 的最小正周期.(2) 在 △ABC 中,角 A ,B ,C 的对边分别为 a ,b ,c ,若锐角 A 满足 f (A )=1−√32,C =π6,c =2,求 △ABC 的面积.22. 在直角 △ABC 中,A =π2,D 为 AC 边上的一点,BD =√3.(1) 若 BC =3,∠BDC =2π3,求 △BDC 的面积.(2) 若 C =π3,求 △BCD 周长 l 的取值范围.答案一、选择题(共10题) 1. 【答案】D【解析】在 AC 上取点 E ,使 AE ⃗⃗⃗⃗⃗ =13AC ⃗⃗⃗⃗⃗ , 连接 DE ,过 D 作 DF ∥AC ,交 AB 于 F ,因为 λAB ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ −13AC ⃗⃗⃗⃗⃗ =ED ⃗⃗⃗⃗⃗ (λ∈R ),所以 ED ∥AB ,所以四边形 AFDE 为平行四边形, 又 AD 平分 ∠BAC , 所以四边形 AFDE 为菱形. 因为 AD =2√3,∠BAC =60∘, 所以 AE =2,则 AC =6. 设 FB =x , 因为 DF ∥AC , 所以 DFAC =FBAB , 即 26=x 2+x ,解得 x =1, 即 FB =1, 所以 AB =3.所以 AB ⃗⃗⃗⃗⃗ 在 AD ⃗⃗⃗⃗⃗ 方向上的投影数量为 ∣∣AB ⃗⃗⃗⃗⃗ ∣∣⋅cos30∘=3√32.【知识点】平面向量的数量积与垂直2. 【答案】C【解析】由 3bcosC =c (1−3cosB ) 及正弦定理可得 3sinBcosC =sinC (1−3cosB ),化简可得sinC=3sin(B+C).又A+B+C=π,所以sinC=3sinA,所以c:a=sinC:sinA=3:1.【知识点】正弦定理3. 【答案】B【解析】因为acosC+√32c=b,由正弦定理得sinAcosC+√32sinC=sinB=sin(B+C),整理得cosA=√32,所以A=π6,又因为a=1,√3c−2b=1,所以√3sinC−2sinB=sinA=12,即√3sin(5π6−B)−2sinB=12,整理得cos(B+π6)=12,所以B=π6.【知识点】正弦定理4. 【答案】D【解析】向量a=(2,x),b⃗=(1,2),a∥b⃗,可得x=4.【知识点】平面向量数乘的坐标运算5. 【答案】C【解析】根据题意画出如图的模型,则CB=10,∠OAB=70∘,∠OAC=80∘,所以∠CAB=10∘,∠ACB=10∘,所以AB=10,所以在Rt△AOB中,BO=10sin70∘≈9.4(米).【知识点】解三角形的实际应用问题6. 【答案】B【解析】由余弦定理得BC2=AB2+AC2−2⋅AB⋅AC⋅cosA,因此49=25+AC2+5AC,解得AC=3或AC=−8(舍去),因此由正弦定理得sinB sinC=AC AB=35.【知识点】正弦定理、余弦定理7. 【答案】B【解析】由 BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ =BD ⃗⃗⃗⃗⃗⃗ 得 3e 2⃗⃗⃗ −2e 1⃗⃗⃗ =BD ⃗⃗⃗⃗⃗⃗ ,即 2(32e 2⃗⃗⃗ −e 1⃗⃗⃗ )=BD ⃗⃗⃗⃗⃗⃗ =2BO ⃗⃗⃗⃗⃗ .【知识点】平面向量的数乘及其几何意义8. 【答案】B【知识点】平面向量的数量积与垂直9. 【答案】C【解析】如图,设存在实数 m 使得 AE⃗⃗⃗⃗⃗ =mAD ⃗⃗⃗⃗⃗ (0≤m ≤1), 因为AD ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BD⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +34BC ⃗⃗⃗⃗⃗ =AB⃗⃗⃗⃗⃗ +34(AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )=14AB ⃗⃗⃗⃗⃗ +34AC ⃗⃗⃗⃗⃗ , 所以 AE ⃗⃗⃗⃗⃗ =m (14AB ⃗⃗⃗⃗⃗ +34AC ⃗⃗⃗⃗⃗ )=m 4AB⃗⃗⃗⃗⃗ +3m 4AC ⃗⃗⃗⃗⃗ , 所以 {λ=m 4,μ=3m 4,所以t =(λ−1)2+μ2=(m4−1)2+(3m 4)2=58m 2−m2+1=58(m −25)2+910,当 m =25 时,t 取得最小值,为 910.【知识点】平面向量的分解10. 【答案】B【解析】对于A,由平面向量基本定理可得,有且仅有一对实数λ,μ,使得a=λb⃗+μc成立.故条件中的“对任何非零实数λ”说法不正确.故A错误.对于B,由平面向量基本定理可得结论正确,故B正确.对于C,当λ=0时,a=μc,与题设a,b⃗,c是三个不共线的向量矛盾.故C错误.对于D,当μ=0时,a=λb⃗,与题设a,b⃗,c是三个不共线的向量矛盾.故D错误.【知识点】平面向量的分解二、填空题(共6题)11. 【答案】12【知识点】复数的乘除运算12. 【答案】√38【解析】如图所示,由题意,PA过球心,故取PA中点为O,O即为球心.连接BO,CO,有△PAC由△PAB绕PA轴60∘后重合,故PC=PB,过B作BH⊥PA于H点,同理过C作CH⊥PA于H点,由于r=1,PB=PC=√3,过O点作OG⊥PB于G点,OP=OB=1,故有OG=√(PB2)2−OP2=12⇒∠BPH=π6,即有BH=PB⋅sinπ6=√32,又且∠BHC=60∘,BH=CH,故S△BHC=12×√32×34=3√316,则有V P−ABC=V P−BHC+V A−BHC=13S△BHC(PH+AH)=13×3√316×2=√38,故三棱锥P−ABC的体积为√38.【知识点】棱锥的表面积与体积13. 【答案】 √【知识点】频率分布直方图14. 【答案】√19−√72【解析】如图所示,设 OA ⃗⃗⃗⃗⃗ =a ,OB ⃗⃗⃗⃗⃗ =b ⃗ ,OC ⃗⃗⃗⃗⃗ =c ,由题,得 ∠AOB =π3,∣∣OA ⃗⃗⃗⃗⃗ ∣∣=2,∣∣OB ⃗⃗⃗⃗⃗ ∣∣=3,CA⃗⃗⃗⃗⃗ =a −c ,CB ⃗⃗⃗⃗⃗ =b ⃗ −c ,a ⋅b ⃗ =2×3×cos60∘=3, 又 (a −c )⋅(b ⃗ −c )=0,所以 CA⃗⃗⃗⃗⃗ ⊥CB ⃗⃗⃗⃗⃗ ,则点 C 在以 AB 为直径的圆上, 取 AB 的中点为 M ,则 OM ⃗⃗⃗⃗⃗⃗ =12(OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ ), 设以 AB 为直径的圆与线段 OM 的交点为 E ,则 ∣c ∣ 的最小值是 ∣∣OE ⃗⃗⃗⃗⃗ ∣∣, 因为∣∣OM ⃗⃗⃗⃗⃗⃗ ∣∣=√14(OA⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ )2=12√OA ⃗⃗⃗⃗⃗ 2+2OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ 2=12×√4+2×3+9=√192,又 AB =√OA 2+OB 2−2OA ⋅OB ⋅cos60∘=√4+9−2×2×3×12=√7, 所以 ∣c ∣ 的最小值是 ∣∣OE ⃗⃗⃗⃗⃗ ∣∣=OM −ME =OM −12AB =√19−√72.【知识点】平面向量的数量积与垂直、余弦定理15. 【答案】 12【解析】 2a +b⃗ =2(1,2)+(2,−2)=(4,2), 又因为 c ∥(2a +b ⃗ ), 所以 4×λ−2×1=0, 所以 λ=12.【知识点】平面向量数乘的坐标运算16. 【答案】√6km【知识点】正弦定理三、解答题(共6题)17. 【答案】(1) 连接AC,AC与BD相交于点O,则点O是AC的中点,连接OH,EO,因为H是BC的中点,AB=1.所以OH∥AB,OH=12因为EF∥平面ABCD,EF⊂平面ABFE,平面ABCD∩平面ABFE=AB,所以EF∥AB.因为EF=1,所以OH∥EF,OH=EF.所以四边形EOHF是平行四边形.所以EO∥FH,EO=FH.因为EO⊂平面BDE,FH⊄平面BDE,所以FH∥平面BDE.(2) 证法1:取AB的中点M,连接EM,则AM=MB=1,由(1)知,EF∥MB,且EF=MB,所以四边形EMBF是平行四边形.所以EM∥FB,EM=FB.在Rt△BFC中,FB2+FC2=BC2=4,又FB=FC,得FB=√2.所以EM=√2.在△AME中,AE=√3,AM=1,EM=√2,所以AM2+EM2=3=AE2.所以AM⊥EM.所以AM⊥FB,即AB⊥FB.因为四边形ABCD是正方形,所以AB⊥BC.因为FB∩BC=B,FB⊂平面BCF,BC⊂平面BCF,所以AB⊥平面BCF.证法2:在Rt△BFC中,H为BC的中点,BC=1.所以FH=12AC=√2,EO=FH=1,在△AEO中,AE=√3,AO=12所以AO2+EO2=AE2.所以AO⊥EO.因为 FH ∥EO , 所以 AO ⊥FH .因为 FH ⊥BC ,BC ⊂平面ABCD ,AO ⊂平面ABCD ,AO ∩BC =C , 所以 FH ⊥平面ABCD . 因为 AB ⊂平面ABCD , 所以 FH ⊥AB .因为四边形 ABCD 是正方形, 所以 AB ⊥BC .因为 BC ⊂平面BCF ,FH ⊂平面BCF ,BC ∩FH =H , 所以 AB ⊥平面BCF . (3) 连接 EC ,在 Rt △BFC 中,FH =12BC =1, 所以 EO =FH =1.由(2)知 AB ⊥平面BCF ,且 EF ∥AB , 所以 EF ⊥平面BCF .因为 FH ⊥平面ABCD ,EO ∥FH , 所以 EO ⊥平面ABCD .所以四棱锥 E −ABCD 的体积为 V 1=13⋅EO ⋅S 正方形ABCD =13×1×22=43.所以三棱锥 E −BCF 的体积为 V 2=13⋅EF ⋅S △BCF =13×1×12×(√2)2=13. 所以五面体 ABCDEF 的体积为 V =V 1+V 2=53.【知识点】棱锥的表面积与体积、直线与平面垂直关系的判定、直线与平面平行关系的判定18. 【答案】(1) ① ∣∣∣1001∣∣∣=1;② ∣∣∣1326∣∣∣=1×6−2×3=0;③ ∣∣∣−2510−25∣∣∣=(−2)×(−25)−5×10=0. (2) 若向量 p =(a,b ) 与向量 q =(c,d ) 共线,则 当 q ≠0⃗ 时,有 ad −bc =0,即 ∣∣∣a b c d ∣∣∣=0, 当 q =0⃗ 时,有 c =d =0,即 ∣∣∣a b c d ∣∣∣=ad −bc =0, 所以必要性得证. 反之,若 ∣∣∣a b cd ∣∣∣=0,即 ad −bc =0,当 c ,d 不全为 0 时,即 q ≠0⃗ 时, 不妨设 c ≠0,则 b =adc,所以 p =(a,ad c),因为 q =(c,d ),所以 p =ac q ,所以 p ∥q , 所以向量 p =(a,b ) 与向量 q =(c,d ) 共线,当 c =0 且 d =0 时,q =0⃗ , 所以向量 p =(a,b ) 与向量 q =0⃗ 共线, 充分性得证.综上,向量 p =(a,b ) 与向量 q =(c,d ) 共线的充要条件是 ∣∣∣ab c d ∣∣∣=0. (3) 用 b 2 和 b 1 分别乘上面两个方程的两端,然后两个方程相减,消去 y 得 (a 1b 2−a 2b 1)x =c 1b 2−c 2b 1, ⋯⋯① 同理,消去 x 得 (a 1b 2−a 2b 1)y =a 1c 2−a 2c 1, ⋯⋯② 所以,当 a 1b 2−a 2b 1≠0 时,即 ∣∣∣a 1b 1a 2b 2∣∣∣≠0 时, 由①②可得 x =c 1b 2−c 2b 1a 1b 2−a 2b 1=∣∣∣c 1b 1c 2b 2∣∣∣∣∣∣a 1b 1a 2b 2∣∣∣,y =a 1c 2−a 2c 1a1b 2−a 2b 1=∣∣∣a 1c 1a 2c 2∣∣∣∣∣∣a 1b 1a 2b 2∣∣∣, 所以,当 ∣∣∣a 1b 1a 2b 2∣∣∣≠0 时,方程组 {a 1x +b 1y =c 1,a 2x +b 2y =c 2 有唯一解且 x =∣∣∣c 1b 1c 2b 2∣∣∣∣∣∣a 1b 1a 2b 2∣∣∣,y =∣∣∣a 1c 1a 2c 2∣∣∣∣∣∣a 1b 1a 2b 2∣∣∣. 【知识点】平面向量数乘的坐标运算、二阶行列式19. 【答案】不正确.实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数,原点对应的有序实数对为 (0,0),它所确定的复数是 z =0+0i =0,表示的是实数.【知识点】复数的几何意义20. 【答案】(1) 2√2. (2) 4+2√3.【知识点】余弦定理、正弦定理21. 【答案】(1) f (x )=12sin2x −√32cos2x −√32=sin (2x −x3)−√32, T =π.(2) sin (2A −π3)=12,2A −π3=16π, A =π4,C =π6,B =712π, asinA =csinC , a =2√2,S =12acsinB =12×2√2×2×sin 712π=1+√3. 【知识点】Asin(ωx+ψ)形式函数的性质、正弦定理22. 【答案】(1) 由余弦定理得:BC 2=DB 2+DC 2−2DB ⋅DC ⋅cos2π3,即 DC 2+√3DC −6=0,解得 DC =√3,DC =−2√3(舍去).S △BDC =12BD ⋅DC ⋅sin∠BDC =12×√3×√3×sin 2π3=3√34.(2) 在 △BCD 中,C =π3,∠ABC =π6,BD =√3, 设 ∠DBC =α,所以BDsin π3=CD sinα=BC sin(2π3−α),故 CD =2sinα,BC =2sin (α+π3),所以 △BCD 的周长 l =BD +BC +CD =√3+2sinα+2sin (α+π3),即 l =√3+2√3sin (α+π6),因为 α∈(0,π6],所以 l ∈(2√3,3+√3].【知识点】余弦定理、Asin(ωx+ψ)形式函数的性质、正弦定理。
高中数学必修二 期末测试卷02-新教材-2021学年下学期期末考试全真模拟卷(人教A2019)

2020-2021学年高一数学下学期期末考试全真模拟卷(二)测试时间:120分钟 测试范围:人教A2019必修第一册+第二册满分:150分注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效. 3.考试结束后,将本试卷和答题卡一并交回.一、单项选择题(本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、若集合{}21A x x =-≤≤,{}2log 1B x x =≤,则A B =( )A .12x xB .{}01x x <≤C .{}22x x -≤≤D .{2x x <-或}2x >【答案】C 【详解】由{}2log 1B x x =≤,得{}02B x x =<≤. 又{}21A x x =-≤≤, 所以{}22AB x x =-≤≤.故选:C . 2、复数113i-的虚部是( )A .310-B .110-C .110D .310【答案】D 【详解】 因为1131313(13)(13)1010i z i i i i +===+--+, 所以复数113z i =-的虚部为310. 故选:D.3、某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是( ) A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半【答案】A 【详解】设新农村建设前的收入为M ,而新农村建设后的收入为2M ,则新农村建设前种植收入为0.6M ,而新农村建设后的种植收入为0.74M ,所以种植收入增加了,所以A 项不正确;新农村建设前其他收入我0.04M ,新农村建设后其他收入为0.1M ,故增加了一倍以上,所以B 项正确; 新农村建设前,养殖收入为0.3M ,新农村建设后为0.6M ,所以增加了一倍,所以C 项正确;新农村建设后,养殖收入与第三产业收入的综合占经济收入的30%28%58%50%+=>,所以超过了经济收入的一半,所以D 正确;4、已知向量a ,b 满足||5a =,||6b =,6a b ⋅=-,则cos ,=a a b +( )A .3135-B .1935-C .1735D .1935【答案】D 【详解】5a =,6b =,6a b ⋅=-,()225619a a b a a b ∴⋅+=+⋅=-=.()2222257a b a ba ab b +=+=+⋅+=-=,因此,()1919cos ,5735a a ba ab a a b⋅+<+>===⨯⋅+. 故选:D.5、埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A .514- B .512- C .514+ D .512+ 【答案】C 【详解】如图,设,CD a PE b ==,则22224a PO PE OEb =-=-,由题意212PO ab =,即22142a b ab -=,化简得24()210b b a a -⋅-=,解得154b a +=(负值舍去). 故选:C.6、已知π2tan tan()74θθ-+=,则tan θ=( )A .–2B .–1C .1D .2【答案】D 【详解】2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭,tan 12tan 71tan θθθ+∴-=-,令tan ,1t t θ=≠,则1271tt t+-=-,整理得2440t t -+=,解得2t =,即tan 2θ=. 故选:D.7、如图是我国古代著名的“赵爽弦图”的示意图,它由四个全等的直角三角形围成,其中3sin 5BAC ∠=,现将每个直角三角形的较长的直角边分别向外延长一倍,得到如图的数学风车,若在该数学风车内随机取一点,则该点恰好取自“赵爽弦图”外面(图中阴影部分)的概率为( )A .2543B .1843C .2549D .2449【答案】D 【详解】在Rt ABC ∆中,3sin 5BAC ∠=不妨设3BC =,则5AB =,4AC =则阴影部分的面积为1434242⨯⨯⨯=;数学风车的面积为224549+=∴所求概率2449P =本题正确选项:D 8、已知ABC ∆是面积为934的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则O 平面ABC 的距离为( )A .3B .32C .1D .32【答案】C 【详解】设球O 的半径为R ,则2416R ππ=,解得:2R =. 设ABC 外接圆半径为r ,边长为a ,ABC212a ∴=,解得:3a =,2233r ∴===,∴球心O 到平面ABC 的距离1d ==.故选:C.二、多项选择题(本题共4小题,每小题5分,共16分,在每小题给出的四个选项中,不止有一项是符合题目要求的)9、下列说法正确的是( ) A .随着试验次数的增加,频率一般会越来越接近概率B .连续10次掷一枚骰子,结果都是出现1点,可以认为这枚骰子质地不均匀C .某种福利彩票的中奖概率为11000,那么买1000张这种彩票一定能中奖D .某市气象台预报“明天本市降水概率为70%”,指的是:该市气象台专家中,有70%认为明天会降水,30%认为不降水 【答案】AB 【详解】对于A ,试验次数越多,频率就会稳定在概率的附近,故A 正确对于B ,如果骰子均匀,则各点数应该均匀出现,所以根据结果都是出现1点可以认定这枚骰子质地不均匀,故B 正确. 对于C ,中奖概率为11000是指买一次彩票,可能中奖的概率为11000,不是指1000张这种彩票一定能中奖,故C 错误.对于D ,“明天本市降水概率为70%”指下雨的可能性为0.7,故D 错. 故选:AB .10、有以下四种说法,其中正确的有( ) A .“2x >且3y >”是“5x y +>”的充要条件B .直线l ,m ,平面α,若m α⊂,则“l α⊥”是“l m ⊥”的充分不必要条件C .“3x =”是“2230x x --=”的必要不充分条件D .设,a b ∈R ,则“0a ≠”是“0ab =”的既不充分也不必要条件【答案】BD 【详解】对于A ,由“2x >且3y >”,根据不等式的性质可得5x y +>,充分性满足;反之,5x y +>推不出“2x >且3y >”,必要性不满足,故A 不正确; 对于B ,根据线面垂直的定义:“l α⊥”可推出“l m ⊥”,反之,由线面垂直的判定定理可知:仅“l m ⊥”,不一定得出“l α⊥”,故B 正确; 对于C ,“3x =”可得“2230x x --=”,充分性满足;反之,“2230x x --=”可得“3x =”或“1x =-”,必要性不满足, 所以“3x =”是“2230x x --=”的充分不必要条件,故C 不正确; 对于D ,若“0a ≠且0b =”可推出“0ab =”; 反之,若“0ab =”,可得“0a =”或“0b =”,所以“0a ≠”是“0ab =”的既不充分也不必要条件,故D 正确; 故选:BD11、已知函数()sin()f x x ωϕ=-(0,||2πωϕ><)的部分图象如图所示,则下列选项正确的是( )A .函数()f x 的最小正周期为3πB .5(,0)4π为函数()f x 的一个对称中心 C .1(0)2f =-D .函数()f x 向右平移2π个单位后所得函数为偶函数【答案】ACD 【分析】根据图象,先由144T ππ=-得,求ω,判断A 正确,再利用五点法定位确定ϕ得到解析式,结合利用正弦函数性质逐一判断BCD 的正误即可. 【详解】根据函数()sin(),0,||2f x x πωϕωϕ⎛⎫=-><⎪⎝⎭的部分图象,由144T ππ=-,所以3T π=,故A 正确; 由23ππω=,可得23ω=, 由点,04π⎛⎫⎪⎝⎭在函数图像上,可得2sin 034πϕ⎛⎫⨯-= ⎪⎝⎭,可得2,34k k πϕπ⨯-=∈Z ,解得,6k k πϕπ=-∈Z , 因为||2ϕπ<,可得6π=ϕ,可得2()sin 36f x x π⎛⎫=- ⎪⎝⎭,因为52523sin sin 0434632f ππππ⎛⎫⎛⎫=⨯-==≠⎪ ⎪⎝⎭⎝⎭,故B 错误; 由于1(0)sin 62f π⎛⎫=-=- ⎪⎝⎭,故C 正确; 将函数()f x 向右平移2π个单位后所得函数为2f x π⎛⎫- ⎪⎝⎭22sin cos 3263x x ππ⎡⎤⎛⎫=--=- ⎪⎢⎥⎝⎭⎣⎦为偶函数,故D正确. 故选:ACD.12、如图,棱长为1的正方体1111ABCD A B C D -中,点E 为11A B 的中点,则下列说法正确的是( )A .DE 与1CC 为异面直线B .DE 与平面11BCC B 所成角的正切值为24C .过,,D CE 三点的平面截正方体所得两部分的体积相等D .线段DE 在底面ABCD 的射影长为2【答案】ABC 【详解】由图可知:DE 与CC1为异面直线,∴A 正确;因为平面11//BCC B 平面11ADD A ,所以DE 与平面11BCC B 所成角即DE 与平面11ADD A 所成角,连接A1D ,显然,1A DE ∠是DE 与平面11ADD A 所成角.在直角三角形EA1D 中:111122tan 42A E A DE A D ∠===,∴B 正确;过D 、C 、E 三点的平面截正方体所得两部分的体积关系即为平面A1B1CD 截正方体所得两部分的体积关系,由正方体的对称性可知截得两部分几何体的体积相等,∴C 正确; 取AB 中点F ,连接EF 、DF ,∵EF //B1B 且B1B ⊥底面ABCD ,∴EF ⊥底面ABCD ,∴DF 的长为线段DE 在底面ABCD 的射影长,在直角三角形DFE 中:EF=1,DE=32,∴DF=2235122⎛⎫-= ⎪⎝⎭,∴D 错. 故选:ABC.三、填空题(本题共4小题,每小题5分,共20分)13、已知不等式220ax bx ++>的解集为{|12}x x -<<,则不等式220x bx a ++<的解集为__________________. 【答案】1{|1}?2x x -<< 【分析】 【详解】不等式220ax bx ++>的解集为{|12}x x -<<,220ax bx ∴++=的两根为1-,2,且0a <,即12b a-+=-,()212a -⨯=,解得1a =-,1b =,则不等式可化为2210x x +-<,解得112x -<<,则不等式220x bx a ++<的解集为1{|1}2x x -<<.14、在ABC ∆中,2cos ,4,33C AC BC ===,则tan B =____________.【答案】45【详解】设,,AB c BC a CA b ===22222cos 916234933c a b ab C c =+-=+-⨯⨯⨯=∴= 22221145cos sin 1()tan 452999a cb B B B ac +-==∴=-=∴=15、在四边形ABCD 中,AD BC ∥,23AB =,5AD =,30A ∠=︒,点E 在线段CB 的延长线上,且AE BE =,则BD AE ⋅=__________.【答案】1-. 【详解】建立如图所示的直角坐标系,则(23,0)B ,535(,)22D . 因为AD ∥BC ,30BAD ∠=︒,所以150CBA ∠=︒, 因为AE BE =,所以30BAE ABE ∠=∠=︒, 所以直线BE 的斜率为33,其方程为3(23)3y x =-,直线AE 的斜率为33-,其方程为33y x =-. 由3(23),333y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩得3x =,1y =-, 所以(3,1)E -.所以35(,)(3,1)122BD AE =-=-. 16、设函数()()21ln 11f x x x =+-+,则使()()21f x f x >-成立的x 的取值范围是____________. 【答案】1(,1)3【详解】试题分析:()()21ln 11f x x x =+-+,定义域为,∵,∴函数为偶函数,当时,函数单调递增,根据偶函数性质可知:得()()21f x f x >-成立,∴,∴,∴的范围为1,13⎛⎫⎪⎝⎭故答案为A.四、解答题(17题10分,其余每题12分,共70分,解答应写出文字说明、证明过程或演算步骤,考生根据要求作答)17、成年人收缩压的正常范围是(90,140)(单位:mmHg ),未在此范围的献血志愿者不适合献血,某血站对志愿者的收缩压进行统计,随机抽取男志愿者100名、女志愿者100名,根据统计数据分别得到如下直方图:(1)根据直方图计算这200名志愿者中不适合献血的总人数; (2)估计男志愿者收缩压的中位数;(3)估计女志愿者收缩压的平均值(同一组中的数据用该组区间的中点值为代表). 【答案】(1)20人;(2)115mmHg ;(3)125mmHg . 【详解】解:(1)由(0.0100.01520.0200.030)101m +++⨯+⨯=得0.005m =, 故这些男志愿者中有5人不适合献血;由(0.0050.01020.0200.035)101n ++++⨯=得0.015n =, 故这些女志愿者中有15人不适合献血. 综上所述,这些志愿者中共有20人不适合献血.(2)设男志愿者收缩压的中位数为(mmHg)x ,则110120x <<.由0.015100.02010(110)0.0300.5x ⨯+⨯+-⨯=得115x =, 因此,可以估计男志愿者收缩压的中位数为115(mmHg).(3)950.051050.101150.151250.351350.201450.15125⨯+⨯+⨯+⨯+⨯+⨯=, 因此,可以估计女志愿者收缩压的平均值为125(mmHg).18、在ABC ∆中,角,,A B C 所对的边分别为,,a b c.已知5,a b c === (Ⅰ)求角C 的大小; (Ⅰ)求sin A 的值; (Ⅰ)求πsin(2)4A +的值. 【答案】(Ⅰ)4C π;(Ⅰ)sin A =(Ⅰ)sin 2426A π⎛⎫+=⎪⎝⎭. 【详解】(Ⅰ)在ABC中,由5,a b c ===222cos 22a b c C ab +-===, 又因为(0,)C π∈,所以4Cπ;(Ⅰ)在ABC 中,由4Cπ,a c ==可得sin sin a CA c===13; (Ⅰ)由a c <知角A为锐角,由sin A =,可得cos A ==进而2125sin 22sin cos ,cos22cos 11313A A A A A ===-=,所以125sin(2)sin 2coscos2sin444132132A A A πππ+=+=⨯+⨯=26.19、如图,在长方体1111ABCD A B C D -中,点E ,F 分别在棱1DD ,1BB 上,且12DE ED =,12BF FB =.证明:(1)当AB BC =时,EF AC ⊥; (2)点1C 在平面AEF 内.【答案】(1)证明见解析;(2)证明见解析. 【详解】(1)因为长方体1111ABCD A B C D -,所以1BB ⊥平面ABCD ∴1AC BB ⊥,因为长方体1111,ABCD A B C D AB BC -=,所以四边形ABCD 为正方形AC BD ∴⊥ 因为11,BB BD B BB BD =⊂、平面11BB D D ,因此AC ⊥平面11BB D D ,因为EF ⊂平面11BB D D ,所以AC EF ⊥;(2)在1CC 上取点M 使得12CM MC =,连,DM MF ,因为111112,//,=D E ED DD CC DD CC =,所以11,//,ED MC ED MC = 所以四边形1DMC E 为平行四边形,1//DM EC ∴因为//,=,MF DA MF DA 所以M F A D 、、、四点共面,所以四边形MFAD 为平行四边形,1//,//DM AF EC AF ∴∴,所以1E C A F 、、、四点共面,因此1C 在平面AEF 内20、已知()22sin ,cos ,(3cos ,2),()a x x b x f x a b ===⋅. (1)求()f x 的最小正周期及单调递减区间; (2)求函数()f x 在区间π[0,]2上的最大值和最小值.【答案】(1)T π=,单调递减区间为2,,63k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z ;(2)见解析【详解】(1)2()23sin cos 2cos f x a b x x x =⋅=+2cos 212sin 216x x x π⎛⎫=++=++ ⎪⎝⎭,∴()f x 的最小正周期22T ππ==. 由3222,262k x k k Z πππππ+++∈,得2,63k x k k Z ππππ++∈, ∴()f x 的单调递减区间为2,,63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦.(2)∵0,2x π⎡⎤∈⎢⎥⎣⎦, ∴72,666x πππ⎡⎤+∈⎢⎥⎣⎦, 当7266x ππ+=,即2x π=时,函数()f x 取得最小值,为72sin106π+=; 当262x ππ+=,即6x π=时,函数()f x 取得最大值,为2sin 132π+=.故函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值为3,最小值为0.21、在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ,且2sin 0b A =. (I )求角B 的大小;(II )求cos cos cos A B C ++的取值范围. 【答案】(I )3B π=;(II)3]2【详解】(I)由2sin b A =结合正弦定理可得:2sin sin ,sin B A A B =∴= △ABC 为锐角三角形,故3B π=.(II )结合(1)的结论有:12cos cos cos cos cos 23A B C A A π⎛⎫++=++- ⎪⎝⎭11cos cos 22A A A =-+11cos 22A A =++1sin 62A π⎛⎫=++ ⎪⎝⎭.由203202A A πππ⎧<-<⎪⎪⎨⎪<<⎪⎩可得:62A ππ<<,2363A πππ<+<,则sin 32A π⎛⎤⎛⎫+∈ ⎥ ⎪ ⎝⎭⎝⎦,113sin ,2232A π⎛⎤⎛⎫++∈ ⎥ ⎪ ⎝⎭⎝⎦. 即cos cos cos A B C ++的取值范围是32⎤⎥⎝⎦.22、有一种鱼的身体吸收汞,当这种鱼身体中的汞含量超过其体重的1.00ppm (即百万分之一)时,人食用它,就会对人体产生危害.现从一批该鱼中随机选出30条鱼,检验鱼体中的汞含量与其体重的比值(单位:ppm ),数据统计如下:0.07 0.24 0.39 0.54 0.61 0.66 0.73 0.82 0.82 0.820.87 0.91 0.95 0.98 0.98 1.02 1.02 1.08 1.14 1.201.20 1.26 1.29 1.31 1.37 1.40 1.44 1.58 1.62 1.68(1)求上述数据的中位数、众数、极差,并估计这批鱼该项数据的80%分位数;(2)有A ,B 两个水池,两水池之间有10个完全相同的小孔联通,所有的小孔均在水下,且可以同时通过2条鱼.(Ⅰ)将其中汞的含量最低的2条鱼分别放入A 水池和B 水池中,若这2条鱼的游动相互独立,均有13的概率进入另一水池且不再游回,求这两条鱼最终在同一水池的概率;(Ⅰ)将其中汞的含量最低的2条鱼都先放入A 水池中,若这2条鱼均会独立地且等可能地从其中任意一个小孔由A 水池进入B 水池且不再游回A 水池,求这两条鱼由不同小孔进入B 水池的概率.【答案】(1)中位数为1;众数为0.82;极差为1.61;估计这批鱼该项数据的80百分位数约为1.34;(2)(Ⅰ)49;(Ⅰ)910. 【详解】解:(1)由题意知,数据的中位数为0.98 1.0212+=数据的众数为0.82数据的极差为1.680.07 1.61-=估计这批鱼该项数据的80百分位数约为1.31 1.371.342+= (2)(Ⅰ)记“两鱼最终均在A 水池”为事件A ,则212()339P A =⨯=记“两鱼最终均在B 水池”为事件B ,则212()339P B =⨯=∵事件A 与事件B 互斥,∴两条鱼最终在同一水池的概率为224()()()999P AB P A P B =+=+= (Ⅰ)记“两鱼同时从第一个小孔通过”为事件1C ,“两鱼同时从第二个小孔通过”为 事件2C ,依次类推;而两鱼的游动独立∴12111()()1010100P C P C ===⨯=记“两条鱼由不同小孔进入B 水池”为事件C ,则C 与1210...C C C 对立,又由事件1C ,事件2C ,10C 互斥∴121011()(...)1010010P C P C C C ==⨯=即12109()1(...)10P C P C C C =-=。
期末冲刺卷一 —2020-2021学年【新教材】人教A版(2019)高中数学必修第二册(含解析)

高高高高高高高高高高-高高高高高高高A高高2019高高高高高高高高高高高高高高高一、单选题1. 已知i 为虚数单位,纯虚数z 满足(z +a)i =1+i ,则实数a =( )A. −1B. 1C. 0D. 22. 如图,已知四边形ABCD 的直观图是一个边长为1的正方形,则原图形的周长为( )A. 2√2B. 6C. 8D. 4√2+23. 在△ABC 中,已知B =120°,AC =√19,AB =2,则BC =( )A. 1B. √2C. √5D. 34. 已知两个单位向量e 1⃗⃗⃗ ,e 2⃗⃗⃗ 的夹角为60°,向量m ⃗⃗⃗ =t e 1⃗⃗⃗ +2e 2⃗⃗⃗ (t <0),则( )A. |m ⃗⃗⃗ |t 的最大值为−√32 B. |m ⃗⃗⃗ |t 的最小值为−2 C. |m ⃗⃗⃗ |t 的最小值为−√32D. |m ⃗⃗⃗ |t的最大值为−2 5. 已知在正四棱柱ABCD −A 1B 1C 1D 1中,AA 1=√2AB ,M 是CC 1的中点,则( )A. 直线AM 与平面ABCD 所成角的正切值为√22B. 直线AM 与直线A 1B 1所成角的余弦值为√55C. AM ⊥A 1BD. 直线BM//平面AD 1C 16. 在△ABC 中,点D 在直线AC 上,且AD ⃗⃗⃗⃗⃗⃗ =23AC ⃗⃗⃗⃗⃗ ,点E 在直线BD 上,且BD ⃗⃗⃗⃗⃗⃗ =2DE ⃗⃗⃗⃗⃗⃗ ,若AE ⃗⃗⃗⃗⃗ =λ1AB ⃗⃗⃗⃗⃗ +λ2AC⃗⃗⃗⃗⃗ ,则λ1+λ2=( ) A. 0B. 12C. 79D. 897. 三棱锥P −ABC 中,PA ⊥平面ABC ,∠BAC =π2,AP =3,BC =6,则三棱锥外接球的表面积为( )A. 57πB. 63πC. 45πD. 84π8. 在某次高中学科竞赛中,4000名考生的参赛成绩统计如图所示,60分以下视为不及格,若同一组中数据用该组区间中点作代表,则下列说法中有误的是( )A. 成绩在[70,80)分的考生人数最多B. 不及格的考生人数为1000人C. 考生竞赛成绩的平均分约为70.5分D. 考生竞赛成绩的中位数为75分9. 如图,三棱柱ABC −A 1B 1C 1中,AB =4,AC =3,BC =5,AA 1=6,D 为CC 1中点,E 为BB 1上一点,BB 1⃗⃗⃗⃗⃗⃗⃗ =3BE ⃗⃗⃗⃗⃗ ,∠A 1AC =60°,M 为平面AA 1C 1C 上一点,且BM//平面ADE ,则点M 的轨迹的长度为( )A. 1B. √2C. √3D. 210. 已知函数f(x)={|log 2x|,0<x <2sin(π4x),2≤x ≤10,若存在实数x 1,x 2,x 3,x 4,满足x 1<x 2<x 3<x 4,且f(x 1)=f(x 2)=f(x 3)=f(x 4),则(x 3−2)(x 4−2)x 1x 2的取值范围是( )A. (0,12)B. (0,16)C. (9,21)D. (15,25)二、多选题11. 如图,棱长为1的正方体ABCD −A 1B 1C 1D 1中,M 为线段AB 1上的动点(含端点),则下列结论正确的是( )A. 平面BCM ⊥平面A 1AB 1B. 三棱锥B −MB 1C 体积最大值为16C. 当M 为AB 1中点时,直线B 1D 与直线CM 所成的角的余弦值为√23D. 直线CM 与A 1D 所成的角不可能是π412. 已知i 为虚数单位,以下四个说法中正确的是( )A. i +i 2+i 3+i 4=0B. 3+i >1+iC. 若z =(1+2i)2,则复平面内z −对应的点位于第四象限D. 已知复数z 满足|z −1|=|z +1|,则z 在复平面内对应的点的轨迹为直线13. 已知△ABC 三个内角A ,B ,C 的对应边分别为a ,b ,c ,且∠C =π3,c =2. ( )A. △ABC 面积的最大值为√3B. AC ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ 的最大值为2+4√33C. cosBcosA 的取值范围为(−2,+∞)D. bcosA +acosB =√214. 已知图1中的正三棱柱ABC −A 1B 1C 1的底面边长为2,体积为2√2,去掉其侧棱,再将上底面绕上下底面的中心所在直线逆时针旋转180°后,添上侧棱,得到图2所示的几何体,则下列说法正确的是( )A. A 2B 2//平面ABCB. AB 2=2√63C. 四边形ABA 2B 2为正方形D. 正三棱柱ABC −A 1B 1C 1与几何体ABCA 2B 2C 2的外接球的体积相等三、填空题15. 已知向量a ⃗ 、b ⃗ 为单位向量,a ⃗ ⋅b ⃗ =0,若c ⃗ =3a ⃗ +4b⃗ ,则c ⃗ 与b ⃗ 所成角的余弦值为______ . 16. 已知复数z 满足z =z+10i 3i,则z 的共轭复数z −的虚部______ .17. 《九章算术》把底面为直角三角形,且侧棱垂直于底面的三棱柱称为“堑堵”,把底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”.现有如图所示的“堑堵”ABC −A 1B 1C 1,其中AC ⊥BC ,AA 1=AC =1,当“阳马”四棱锥B −A 1ACC 1体积为13时,则“堑堵”即三棱柱ABC −A 1B 1C 1的外接球的体积为______ .18. 两个正实数a ,b 满足3a +b =1,则满足1a +3b ≥m 2−m 恒成立的m 取值范围为 .19. 某大学选拔新生补充进“篮球”,“电子竞技”,“国学”三个社团,据资料统计,新生通过考核选拔进入这三个社团成功与否相互独立,2020年某新生入学,假设他通过考核选拔进入该校的“篮球”,“电子竞技”,“国学”三个社团的概率依次为m ,13,n ,已知三个社团他都能进入的概率为124,至少进入一个社团的概率为34,且m >n.则m +n =____. 四、解答题20. (1)计算(1+i1−i )2021+(2−3i)(1+4i);(2)设复数z 1=2+ai ,z 2=b −4i.(其中a ,b ∈R),若z 1z 2是纯虚数,且z 1+z 2在复平面内对应的点在直线x +y −1=0上,求|z 1z 2|.21. 已知|a ⃗ |=5,|b ⃗ |=4, (1)若a ⃗ 与b ⃗ 的夹角为θ=120°.①求a ⃗ ·b ⃗ ; ②求a ⃗ 在b ⃗ 上的投影向量. (2)若a ⃗ // b ⃗ ,求a ⃗ ·b⃗ .22. 在复平面内,O 是原点,OA ⃗⃗⃗⃗⃗ ,OB⃗⃗⃗⃗⃗⃗ 对应的复数分别为2+icosx ,(2+√3sinx)+i(2+cosx),i 是虚数单位设函数f(x)=OA ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ . (1)求函数f(x)的解析式;(2)若函数y =f(x)−m 在区间[0,π2]上有2个零点,求实数m 的取值范围.23. 在①m ⃗⃗⃗ =(a +b,c −a),n⃗ =(a −b,c),且m ⃗⃗⃗ ⊥n ⃗ ,②2a −c =2bcosC ,,这三个条件中任选一个补充在下面的问题中,并给出解答. 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且______. (1)求角B ; (2)若b =4,求△ABC 周长的最大值.24. 已知四边形ABCD ,AB =AD =2,∠BAD =60°,∠BCD =30°.现将△ABD 沿BD边折起使得平面ABD ⊥平面BCD ,此时AD ⊥CD.点P 为线段AD 的中点. (1)求证:BP ⊥平面ACD ;(2)若M 为CD 的中点,求MP 与平面BPC 所成角的正弦值.25. 2020年初,世界各地相继爆发了“新冠肺炎”疫情,其最大特点是人传人,传播快,传播广,对人类生命形成巨大危害.而通过佩戴口罩可以防止外界的气体、飞沫进入口鼻呼吸道中,有效地降低病毒传染几率.若在某公共场合不戴口罩被感染的概率是12,戴口罩被感染的概率是110,现有在该公共场合活动的甲、乙、丙、丁、戊五人,每个人是否被感染相互独立. (1)若五人都不戴口罩,求其中恰有两人被感染的概率; (2)若五人中有3人戴口罩,求其中恰有两人被感染的概率;(3)分别计算戴口罩和不戴口罩五人全部感染“新冠肺炎”的概率,并得出你的结论.26. 如图,在多面体ABCDEF 中,平面ABCD ⊥平面CDEF ,四边形CDEF 是边长为2的正方形,四边形ABCD 是直角梯形,其中BC//AD ,BC ⊥CD ,且BC =CD =12AD .(1)证明:BE ⊥DF ;(2)求平面ABF 与平面CDEF 所成的锐二面角的余弦值.答案和解析一.单选题1.【答案】B【解析】解:设纯虚数z=bi,b∈R,则(z+a)i=1+i可化为bi2+ai=1+i,即(−b−1)+(a−1)i=0,所以a−1=0,解得a=1.故选:B.可设纯虚数z=bi,b∈R,代入方程利用复数相等求出a的值.本题考查了纯虚数的定义与复数相等的概念和应用问题,是基础题.2.【答案】C【解析】解:∵四边形ABCD的直观图是一个边长为1的正方形,∴原图形为平行四边形,一组对边长为1,另一组对边长为√(2√2)2+1=3,∴原图形的周长为2(1+3)=8.故选:C.根据四边形ABCD的直观图是一个边长为1的正方形,可得原图形为平行四边形,一组对边长为1,另一组对边长为√(2√2)2+1=3,即可求出原图形的周长.本题考查的知识点是平面图形的直观图,其中斜二测画法的规则,能够帮助我们快速的在直观图面积和原图面积之间进行转化.3.【答案】D【解析】解:设角A,B,C所对的边分别为a,b,c,结合余弦定理,可得19=a2+4−2×a×2×cos120°,即a2+2a−15=0,解得a=3(a=−5舍去),所以BC=3.故选:D.设角A,B,C所对的边分别为a,b,c,利用余弦定理得到关于a的方程,解方程即可求得a的值,从而得到BC的长度.本题考查了余弦定理,考查了方程思想,属基础题.4.【答案】A【解析】解:因为t <0,所以|m|t=√(te 1+2e 2)2t=√t2+4te 1⋅e 2+4t=√t 2+2t+4t=−√t 2+2t+4t 2=−√(2t +12)2+34,当2t =−12,即t =−4时,|m|t取得最大值,且最大值为−√32.故选:A . 利用|m|t=√(te 1+2e 2)2t=√t 2+4te 1⋅e 2+4t=√t 2+2t+4t=−√t 2+2t+4t 2=−√(2t +12)2+34,即可求解.本题考查了平面向量的模运算,考查了函数思想,属于中档题.5.【答案】C【解析】解:不妨设AB =2,对于A ,直线AM 与平面ABCD 所成角的正切值为MC AC=√22√2=12≠√22,所以A 错;对于B ,取A 1A 中点N ,连接NC 1、ND 1,因为A 1B 1//C 1D 1,AM//NC 1, 所以直线AM 与直线A 1B 1所成角的余弦值为cos∠NC 1D 1=C 1D 1NC 1=√10≠√55,所以B 错;对于C ,取C 1D 1中点P ,连接MP 、CD 1,PM//CD 1,CD 1//A 1B ,所以PM//A 1B , 连接AP 、AD 1,AD 1=√12,AP =√13,AM =√10,PM =√3, 所以AP 2=PM 2+AM 2,所以PM ⊥AM ,所以AM ⊥A 1B ,所以C 对; 对于D ,因为BM ∩平面AD 1C 1=B ,所以BM//平面AD 1C 1不成立,所以D 错. 故选:C .A 求直线AM 与平面ABCD 所成角的正切值判断;B 求AM 与直线A 1B 1所成角的余弦值判断;C 用勾股定理逆定理判断;D 直线BM 与平面AD 1C 1相交于B .本题以命题真假判断为载体,考查了异面直线成角问题,考查了直线与平面成角问题,属于中档题.6.【答案】B【解析】解:由三角形法则得:AE ⃗⃗⃗⃗⃗ =BE ⃗⃗⃗⃗⃗ −BA ⃗⃗⃗⃗⃗ =BE ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ ,∵BE ⃗⃗⃗⃗⃗ =BD ⃗⃗⃗⃗⃗⃗ +DE ⃗⃗⃗⃗⃗⃗ =BD ⃗⃗⃗⃗⃗⃗ +12BD ⃗⃗⃗⃗⃗⃗ =32BD ⃗⃗⃗⃗⃗⃗ =32(CD ⃗⃗⃗⃗⃗ −CB ⃗⃗⃗⃗⃗ )=32(CD ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )=32[−13AC ⃗⃗⃗⃗⃗ +(AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )]=AC ⃗⃗⃗⃗⃗ −32AB ⃗⃗⃗⃗⃗ , ∴AE⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −32AB ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −12AB ⃗⃗⃗⃗⃗ , ∴λ1+λ2=1−12=12, 故选:B .根据三角形法则表示出AE ⃗⃗⃗⃗⃗ 与BE ⃗⃗⃗⃗⃗ ,将BE ⃗⃗⃗⃗⃗ 代入表示出AE ⃗⃗⃗⃗⃗ ,确定出λ1与λ2的值,即可求出所求式子的值.此题考查了平面向量的基本定理及其意义,熟练掌握平面向量的数量积运算法则是解本题的关键.7.【答案】C【解析】解:如图,∵PA ⊥平面ABC ,∠BAC =π2,∴AB 、AC 、AP 两两互相垂直,把三棱锥P −ABC 变形为长方体,则长方体的外接球即三棱锥P −ABC 的外接球, 长方体的对角线长为√PA 2+AB 2+AC 2=√PA 2+BC 2=√9+36=√45, ∴三棱锥外接球的表面积为4π×(√452)2=45π.故选:C .由题意可知,AB 、AC 、AP 两两互相垂直,把三棱锥P −ABC 变形为长方体,则长方体的外接球即三棱锥P −ABC 的外接球,求出长方体的对角线长,可得外接球的半径,代入球的表面积公式得答案.本题考查多面体外接球表面积的求法,训练了分割补形法,是中档题.8.【答案】D【解析】 【分析】本题考查频率分布直方图和平均数、中位数、众数的计算,属基础题. 逐项进行分析判断即可得到答案. 【解答】解:通过频率分布直方图可看到成绩在70分∼80分的人的比重最大,所以人数也最多,所以A 正确;不及格的人数为4000×0.025×10=1000人,所以B 正确;根据公式算出平均分为0.01×10×45+0.015×10×55+0.02×10×65+0.03×10×75+0.015×10×85+0.01×10×95=70.5,故C 正确; ∵(0.01+0.015+0.02)×10=0.45<0.5,故中位数在70∼80之间,设为x ,则0.45+x ·0.03=0.5,解得x =53,故中位数是71.67,故D 错误; 故选D .9.【答案】C【解析】解:由题意得BE =2,CD =3,在CD 上取点M 1,使M 1D =2,M 1C =1,则M 1D//BE 且M 1D =BE ,所以四边形BEDM 1是平行四边形,所以BM 1//DE . 在AC 上取点M 2,使M 2A =2,M 2C =1,则CM 1M 1D=CM 2M2A=12,所以M 1M 2//AD . 又BM 1∩M 1M 2=M 1,DE ∩AD =D ,所以平面BM 1M 2//平面ADE ,所以点M 的轨迹就是线段M 1M 2, 在△CM 1M 2中,CM 1=CM 2=1,∠M 1CM 2=120°,由余弦定理得M 1M 2=√BM 12+BM 22−2BM 1⋅BM 2cos120°=√3.M 1M 2=√3, 故选:C .在CD 上取点M 1,使M 1D =2,M 1C =1,则证明BM 1//DE.在AC 上取点M 2,使M 2A =2,M 2C =1,证明面BM 1M 2//平面ADE ,推出点M 的轨迹就是线段M 1M 2,然后求解即可.本题考查空间中点、线、面的位置关系、直线与平面平行、平面与平面平行的判定定理、余弦定理,考查空间想象能力,考查直观想象、逻辑推理核心素养.10.【答案】A【解析】 【分析】作出函数f(x)的图象,由图象及对称性可得,x 1x 2=1,x 3+x 4=12,即为x 4=12−x 3,2<x 3<4,代入所求式子,运用二次函数的值域,结合单调性可得所求范围. 本题考查分段函数的运用:求取值范围,考查正弦函数的对称性和应用,以及二次函数的单调性的运用,考查运算能力,属于中档题. 【解答】解:作出函数f(x)={|log 2x|,0<x <2sin(π4x),2≤x ≤10的图象,存在实数x 1,x 2,x 3,x 4,满足x 1<x 2<x 3<x 4, 且f(x 1)=f(x 2)=f(x 3)=f(x 4), 可得−log 2x 1=log 2x 2,即有x 1x 2=1,且x 3+x 4=2×6=12,即为x 4=12−x 3,2<x 3<4, 则(x 3−2)(x 4−2)x 1x 2=(x 3−2)(x 4−2)=(x 3−2)(10−x 3)=−(x 3−6)2+16,可得在(2,4)递增, 即所求范围为(0,12). 故选A . 二.多选题11.【答案】ABC【解析】解:在正方体ABCD −A 1B 1C 1D 1中, BC ⊥面A 1AM ,BC ⊂面BCM , ∴面BCM ⊥面A 1AM , 故选项A 正确;设M 到面BB 1C 的距离为h ,V B−MB 1C =V M−B 1BC =13×12×1×1×ℎ=16ℎ,当M 点运动到线段AB 1的端点A 时,h 最大,且距离为1. ∴三棱锥B −MB 1C 的体积最大值为16, 故选项B 正确;如图,将A 1B 1延长至E ,使A 1B 1=B 1E ,连ME ,CE ,易得B 1D//CE ,∴直线CM 与直线CE 所成角即为直线B 1D 与直线CM 所成的角,即∠MCE , 易得|MC|=√62,|CE|=√3,|ME|=√102,∴cos∠MCE =|MC|2+|CE|2−|ME|22|MC|⋅|CE|=√23, 故选项C 正确;∵A 1D//B 1C ,∴直线CM 与直线B 1C 所成角就是∠MCB 1,当M 从点B 1沿着线段B 1A 向A 点运动时,∠MCB 1逐渐变大, ∴∠MCB 1max =∠ACB 1=π3>π4,故在点A 和点B 1之间,必定存在一点使得∠MCB 1=π4, 故选项D 错误. 故选:ABC .A 选项中,直接由正方体的性质证明即可;B 选项中将求体积的最大值转化为求M 到面BB 1C 的距离的最大值即可;C ,D 选项可利用平行四边形的方法,将异面直线夹角转化为求相交直线夹角即可; 本题考查了空间中面面垂直的判定,三棱锥的体积,以及异面直线所成的角,属于中档题.12.【答案】AD【解析】解:对于A ,i +i 2+i 3+i 4=i −1−i +1=0,故A 正确; 对于B ,两个虚数不能进行大小比较,故B 错误;对于C ,z =(1+2i)2=1+4i −4=−3+4i ,z −=−3−4i , 则复平面内z −对应的点的坐标为(−3,−4),位于第三象限,故C 错误;对于D ,已知复数z 满足|z −1|=|z +1|,则z 在复平面内对应的点的轨迹是以(1,0)和(−1,0)为端点的线段的垂直平分线,故D 正确. 故选:AD .利用虚数单位i 的运算性质判断A ;根据两个虚数不能进行大小比较判断B ;利用复数代数形式的乘除运算化简z 进一步求得z −的坐标判断C ;由复数模的几何意义判断D . 本题考查复数代数形式的乘除运算,考查复数的基本概念,考查复数的代数表示法及其几何意义,是基础题.13.【答案】AB【解析】解:对于A.因为∠C =π3,c =2,可得4=a 2+b 2−ab ≥2ab −ab =ab ,即ab 的最大值为4,可得△ABC 面积S =12absinC ≤12×4×√32=√3,即△ABC 面积的最大值为√3,当且仅当a =b =2时等号成立,可得A 正确; 对于B.设△ABC 的外接圆半径为R ,则2R =c sinC=4√33, 可得AC ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =bccosA =2bcosA =2×4√33sinBcosA =8√33sinBcosA ,因为B =2π3−A ,可得AC ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =8√33cosAsin(2π3−A)=8√33cosA(√32cosA +12sinA)=4cos 2A +4√33sinAcosA =2(1+cos2A)+2√33sin2A =2√33sin2A +2cos2A +2=4√33(12sin2A +√32cos2A)+2=4√33sin(2A +π3)+2.因为0<A <2π3,0<2A <4π3,所以π3<2A +π3<5π3,则当2A +π3=π2,即:A =π12时,AC ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ 取得最大值为4√33+2,可得B 正确; 对于C .cosBcosA=cos(2π3−A)cosA=cos2π3sinA+sin 2π3cosA cosA=−12tanA +√32,而tan A 的取值范围为(0,+∞)∪(−∞,−√3),所以cosBcosA 的取值范围为(√3,+∞)∪(−∞,√32),故C 错误;D .若bcosA +acosB =√2,则可得b ⋅b 2+c 2−a 22bc+a ⋅a 2+c 2−b 22ac=√2,可得2c 2=2√2c ,解得c =√2, 由于c =2,故D 错误. 故选:AB .对于A.由已知利用余弦定理,基本不等式可求ab 的最大值,进而根据三角形的面积公式即可求解;对于B.由题意根据正弦定理,平面向量数量积的运算,三角函数恒等变换的应用可求AC ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =4√33sin(2A +π3)+2,进而根据正弦函数的性质即可求解;对于C.利用三角函数恒等变换的应用可得cosBcosA=−12tanA +√32,根据正切函数的性质即可求解;对于D.由已知利用余弦定理即可求解.本题主要考查了余弦定理,基本不等式,三角形的面积公式,正弦定理,平面向量数量积的运算,三角函数恒等变换的应用,正弦函数的性质,正切函数的性质等知识的综合应用,考查了转化思想和函数思想,属于中档题.14.【答案】ACD【解析】解:对于A :因旋转前后,A 1,B 1,C 1,A 2,B 2,C 2,共面,由棱柱的性质得知:平面A 2B 2C 2//平面ABC , 从而A 2B 2//平面ABC ,故A 正确;对于B :因棱柱体积V =S △ABC ⋅AA 1=√34×22⋅AA 1=2√2,解得AA 1=2√63, 设H 为B 2在平面ABC 上的射影, 如图所示:则:点H 在BO 的延长线上,且OH =OB =2√33,又B 2H =OO 2=AA 1=2√63, 从而AH =AO =BO ,所以AB 2=√B 2H 2+AH 2=2,故B 错误;对于C :因为A 2B 2//A 1B 1//AB ,且A 1B 1=A 2B 2=AB , 故四边形ABB 2A 2为平行四边形,由对称性可知:AA 2=BB 2,又AB 2=AB =2, 所以四边形ABA 2B 2为正方形,故C 正确;对于D :因旋转前后正三棱柱ABC −A 1B 1C 1与几何体ABCA 2B 2C 2的外接球都是是以OO 2为直径的球G 上,故球的体积相等,故D 正确. 故选:ACD .直接利用柱体的旋转前后的面面和线线的位置关系,柱体的体积公式,几何体和球的位置关系的应用判断A 、B 、C 、D 的结论.本题考查的知识要点:柱体的旋转前后的面面和线线的位置关系,柱体的体积公式,几何体和球的位置关系,主要考查学生的运算能力和数学思维能力,属于中档题. 三.填空题15.【答案】45【解析】解:向量a ⃗ 、b ⃗ 为单位向量,a ⃗ ⋅b ⃗ =0,若c ⃗ =3a ⃗ +4b ⃗ , 设c ⃗ 与b ⃗ 所成角为θ, 则cosθ=c⃗ ⋅b ⃗ |c ⃗ ||b ⃗ |=b ⃗ ⋅(3a ⃗ +4b⃗ )|3a ⃗ +4b⃗ ||b ⃗ |=√9+16×1=45. 故答案为:45.利用向量的数量积,转化求解向量的夹角的余弦函数值即可. 本题考查向量的数量积的求法与应用,是中档题.16.【答案】1【解析】解:z =z+10i 3i,化为:z =−10i 1−3i =−10i(1+3i)(1−3i)(1+3i)=3−i ,则z 的共轭复数z −=3+i 的虚部为1. 故答案为:1.利用复数的运算法则、虚部的定义即可得出.本题考查了复数的运算法则、虚部的定义,考查了推理能力与计算能力,属于基础题.17.【答案】√32π【解析】解:由已知可得,BC ⊥平面A 1ACC 1, 则V B−AA 1C 1C =13×1×1×BC =13, 解得BC =1.此时“塹堵”即三棱柱ABC −A 1B 1C 1的外接球的直径A 1B =√12+12+12=√3, ∴三棱柱ABC −A 1B 1C 1的外接球的体积为V =43π×(√32)3=√32π.故答案为:√32π.首先利用锥体的体积公式求出BC 长度,进一步求出球的直径,再由球的体积公式得答案.本题考查锥体的体积公式的应用,多面体外接球体积的求法,考查空间想象能力和思维能力,考查运算求解能力,是中档题.18.【答案】[−3,4]【解析】 【分析】由基本不等式和“1”的代换,可得1a +3b 的最小值,再由不等式恒成立思想可得m 2−m 小于等于最小值,解不等式可得所求范围.本题考查基本不等式的运用,以及不等式恒成立问题解法,考查运算能力,属于中档题. 【解答】解:由3a +b =1,a >0,b >0, 可得1a+3b=(3a +b)(1a+3b)=6+ba+9a b ≥6+2√b a⋅9a b=12,当且仅当a =16,b =12上式取得等号, 由题意可得m 2−m ≤1a +3b 恒成立, 即有m 2−m ≤12,解得−3≤m ≤4. 故答案为[−3,4].19.【答案】34【解析】 【分析】本题考查相互独立事件同时发生的概率以及对立事件的应用,难度一般.根据相互独立事件的概率乘法公式得到m ×13×n =124⇒m ×n =18,再利用对立事件的概率简化得到(1−m )×23×(1−n )=14⇒1−m −n +m ×n =38,进而求解即可. 【解答】解:由题知三个社团都能进入的概率为124, 即m ×13×n =124⇒m ×n =18, 又因为至少进入一个社团的概率为34, 即一个社团都没能进入的概率为1−34=14,即(1−m )×23×(1−n )=14⇒1−m −n +m ×n =38, 整理得m +n =34. 故答案为34. 四.解答题20.【答案】解:(1)∵1+i1−i =(1+i)2(1−i)(1+i)=2i 2=i ,i 4=1,∴(1+i1−i )2021=i 2021=(i 4)505⋅i =i , ∴(1+i 1−i)2021+(2−3i)(1+4i)=i +(2−3i +8i −12i 2)=14+6i …(4分) (2)z 1z 2=2+ai b −4i =(2+ai)(b +4i)b 2+16=(2b −4a)+(8+ab)i b 2+16因为z 1z 2是纯虚数,所以{2b −4a =08+ab ≠0,即b =2a ,又因为z 1+z 2=(2+b)+(a −4)i =(2+2a)+(a −4)i , 所以z 1+z 2在复平面内对应的点为(2+2a,a −4), 所以2+2a +a −4−1=0得a =1,b =2…(8分) 因为z 1z 2=(2+i)(2−4i)=8−6i , 所以|z 1z 2|=√82+(−6)2=10…(10分)【解析】(1)计算1+i1−i =(1+i)2(1−i)(1+i)=i ,根据i 4=1,可得(1+i1−i )2021,利用复数的运算法则即可得出. (2)z 1z 2=2+ai b−4i =(2+ai)(b+4i)b 2+16=(2b−4a)+(8+ab)ib 2+16,利用z 1z 2是纯虚数,可得{2b −4a =08+ab ≠0,即b =2a.根据z 1+z 2在复平面内对应的点在直线x +y −1=0上,即可得出a ,b ,进而得出|z 1z 2|.本题考查了复数的运算法则、纯虚数的定义、几何意义、模的计算公式,考查了推理能力与计算能力,属于基础题.21.【答案】解:(1)①a ⃗ ·b ⃗ =|a ⃗ ||b ⃗ |cos θ=5×4×cos 120°=−10.②a ⃗ 在b ⃗ 上的投影向量为|a ⃗ |·cos θb⃗ |b ⃗ |=5×(−12)×b⃗ 4=−58b ⃗ . (2)∵a ⃗ // b ⃗ ,∴a ⃗ 与b ⃗ 的夹角为θ=0°或θ=180°. 当θ=0°时,a ⃗ ·b ⃗ =|a ⃗ ||b ⃗ |cos 0°=20. 当θ=180°时,a ⃗ ·b ⃗ =|a ⃗ ||b⃗ |cos180°=−20.【解析】本题考查向量的夹角 、向量的数量积 、投影向量以及平面向量共线的充要条件,属于中档题.(1)①利用数量积的定义即可求解; ②利用投影向量定义即可求解;(2)a ⃗ // b ⃗ ,分a ⃗ 与b⃗ 的夹角为θ=0°或180°两种情况即可求解;22.【答案】解:(1)由题意可得,OA ⃗⃗⃗⃗⃗ =(2,cosx),OB ⃗⃗⃗⃗⃗⃗ =(2+√3sinx,2+cosx), 则AB ⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ =(√3sinx,2),∴f(x)=OA ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =2√3sinx +2cosx =4sin(x +π6);(2)∵f(x)在[0,π3]上递增,在[π3,π2]上递减,且函数y =f(x)−m 在区间[0,π2]上有2个零点,∴max{f(0),f(π2)}≤m <f(π3)=4, ∵max{f(0),f(π2)}=max{2,2√3}=2√3, ∴2√3≤m <4.即实数m 的取值范围是[2√3,4).【解析】(1)由已知求得AB ⃗⃗⃗⃗⃗ 的坐标,再由数量积的坐标运算及两角和的正弦求函数f(x)的解析式;(2)由f(x)在区间[0,π2]上的单调性可得最值,结合函数y =f(x)−m 在区间[0,π2]上有2个零点,即可求得实数m 的取值范围.本题考查平面向量数量积的坐标运算,考查y =Asin(ωx +φ)型函数的图象与性质,考查函数零点的判定及应用,是中档题.23.【答案】解:(1)选①,∵m⃗⃗⃗ =(a +b,c −a),n ⃗ =(a −b,c),且, ∴(a +b)(a −b)+c(c −a)=0,化简得,a 2+c 2−b 2=ac , 由余弦定理得cosB =a 2+c 2−b 22ac =ac 2ac =12,又因为0<B <π,∴B =π3.选②,根据正弦定理,由2a −c =2bcosC 得2sinA −sinC =2sinBcosC , 又因为sin A =sin (B +C)=sin Bcos C +sin Ccos B ,所以2sinCcosB =sinC , 又因为sin C ≠0,所以cosB =12,又因为B ∈(0,π),所以B =π3. 选③,由sin (B +π6)=cos B +12,得√32sin B +12cos B =cos B +12,即√32sin B −12cos B =12,所以cos (B +π3)=−12, 又因为B ∈(0,π),所以B +π3=2π3,因此B =π3. (2)由余弦定理b 2=a 2+c 2−2accosB ,得16=(a +c)2−3ac . 又∵a+c 2⩾√ac ,∴ac ⩽(a+c)24,当且仅当a =c 时等号成立,∴3ac =(a +c)2−16⩽3(a+c)24,解得,a +c ≤8,当且仅当a =c =4时,等号成立.∴a +b +c ≤8+4=12. ∴△ABC 的周长的最大值为12.【解析】本题考查了正弦定理,余弦定理及向量的数量积运算,两角和的正余弦公式,以及基本不等式的应用,考查了推理能力与计算能力,属于中档题. (1)选①,利用向量的数量积及余弦定理,可推出cos B =12,由此可求出角B 的大小;选②根据正弦定理及两角和的正弦公式求解即可;选③,利用两角和的正余弦公式可推出cos (B +π3)=−12,进而可得B 的大小;(2)由题意,利用余弦定理及基本不等式进行求解即可.24.【答案】(1)证明:因为AB =AD ,∠BAD =60°,所以△ABD 为等边三角形,因为P 为AD 的中点,所以BP ⊥AD , 取BD 的中点E ,连结AE ,则AE ⊥BD ,因为平面ABD ⊥平面BCD ,平面ABD ∩平面BCD =BD ,所以AE ⊥平面BCD , 又CD ⊂平面BCD ,所以AE ⊥CD ,又因为CD ⊥AD ,AD ∩AE =A ,AE ,AD ⊂平面ABD ,所以CD ⊥平面ABD , 因为BP ⊂平面ABD ,所以CD ⊥BP , 又因为CD ∩AD =D ,CD ,AD ⊂平面ACD , 所以BP ⊥平面ACD ;(2)解:由(1)可知CD ⊥BD ,取BC 的中点F ,则EF ⊥DE ,即EA ,EF ,ED 两两垂直,以E 为坐标原点建立空间直角坐标系如图所示,则A(0,0,√3),B(0,−1,0),C(2√3,1,0),D(0,1,0),P(0,12,√32),M(√3,1,0),所以BP ⃗⃗⃗⃗⃗ =(0,32,√32),BC ⃗⃗⃗⃗⃗ =(2√3,2,0),设平面BPC 的法向量为n⃗ =(x,y,z), 则{n ⃗⋅BP ⃗⃗⃗⃗⃗ =0n ⃗ ⋅BC ⃗⃗⃗⃗⃗ =0,即{32y +√32z =02√3x +2y =0, 令x =1,则y =−√3,z =3,故n ⃗ =(1,−√3,3),又MP ⃗⃗⃗⃗⃗⃗ =(−√3,−12,√32),所以|cos <n ⃗ ,MP ⃗⃗⃗⃗⃗⃗ >|=|n ⃗⃗ ⋅MP⃗⃗⃗⃗⃗⃗⃗ ||n ⃗⃗ ||MP⃗⃗⃗⃗⃗⃗⃗ |=√32√13=√3926, 故MP 与平面BPC 所成角的正弦值为√3926.【解析】(1)利用面面垂直的性质定理,可得AE ⊥平面BCD ,再利用线面垂直的判定定理可证明CD ⊥平面ABD ,从而得到CD ⊥BP ,再利用等边三角形的性质得到BP ⊥AD ,即可证明BP ⊥平面ACD ;(2)建立空间直角坐标系,然后求出所需点的坐标,利用待定系数法求出平面BPC 的法向量,求出直线MP 的方向向量,再由向量的夹角公式求解即可.本题考查了线面垂直的判定定理的应用和线面角的求解,涉及了面面垂直的性质定理的应用,在求解空间角的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.25.【答案】解:(1)五人都不戴口罩,恰有两人被感染的概率是P =C 52×(12)2×(1−12)3=516;(2)当被感染的两人都没有戴口罩时,概率为P 1=(12)2×(1−110)3=7294000; 当被感染的两人中,一人戴口罩,一人没有戴口罩时,概率为P 2=C 31×110×(1−110)2×C 21×12×(1−12)=2432000; 当被感染的两人都有戴口罩时,概率为P 3=C 32×(110)2×(1−110)×(1−12)2=274000, 所以五人中有3人戴口罩,其中恰有两人感染的概率是: P =P 1+P 2+P 3=7294000+2432000+274000=6212000.(3)不戴口罩时,五人全部感染的概率为(12)5=132=3.125%, 戴口罩时,五人全部感染的概率为(110)5=0.001%,通过计算可知,戴口罩时被感染的概率远远低于不戴口罩时感染的概率, 因此建议在公共场合一定要佩戴口罩.【解析】本题主要考查相互独立事件的概率计算公式,概率的实际应用. (1)根据相互独立事件的概率计算即可. (2)分三种情况讨论计算,最后概率相加即可.(3)分别计算五个人戴口罩和不戴口罩感染的概率,比较大小即可.26.【答案】(1)证明:连结CE ,DF ,因为四边形CDEF 是正方形,所以DF ⊥CE.…………………………(1分) 因为BC ⊥CD ,平面ABCD ⊥平面CDEF ,所以BC ⊥平面CDEF ,从而DF ⊥BC.………………………(3分) 又BC ∩CE =C ,BC ,CE ⊂平面BCE ,所以DF ⊥平面BCE ,BE ⊂平面BCE ,所以BE ⊥DF.…………………(5分)(2)解:如图所示,以DA ,DC ,DE 分别为x ,y ,z 轴建立空间直角坐标系D −xyz , 依题意知A(4,0,0),B(2,2,0),F(0,2,2),D(0,0,0).……………………(7分) 设平面ABF 的法向量为m ⃗⃗⃗ =(x 1,y 1,z 1),AB ⃗⃗⃗⃗⃗ =(−2,2,0),AF⃗⃗⃗⃗⃗ =(−4,2,2),{−2x 1+2y 1=0−4x 1+2y 1+2z 1=0,令y 1=1,则{x 1=1y 1=1z 1=1,所以m ⃗⃗⃗ =(1,1,1)……………………(10分)取平面CDEF 的法向量为n⃗ =(1,0,0),………………(11分) 设该二面角的平面角为θ,所以cosθ=|m ⃗⃗⃗ ⋅n ⃗⃗ ||m ⃗⃗⃗ ||n ⃗⃗ |=√3×1=√33.………………(12分)【解析】(1)连结CE ,DF ,说明DF ⊥CE.结合BC ⊥CD ,平面ABCD ⊥平面CDEF ,推出DF ⊥BC ,证明DF ⊥平面BCE ,即可推出BE ⊥DF .(2)以DA ,DC ,DE 分别为x ,y ,z 轴建立空间直角坐标系D −xyz ,求出平面ABF 的法向量,平面CDEF 的法向量利用空间向量的数量积求解二面角的余弦函数值. 本题考查直线与平面垂直的判断定理的应用,二面角的平面积的求法,考查空间想象能力,转化思想以及计算能力,是中档题.。
期末模拟卷(A基础卷)(含答案)新教材高一数学尖子生培优AB卷(人教A版2019必修第二册)

期末模拟卷(A 基础卷)班级______ 姓名_______ 考号______一、单项选择题(本大题共8题,每小题5分,共计40分。
每小题列出的四个选项中只有一项是最符合题目要求的)1.复数2i z =-(i 为虚数单位)的虚部为( )A .1-B .1C .iD .i-【答案】A【详解】复数2i z =-的虚部是1-.故选:A2.已知向量()()1,2,1,0a b =-=r r ,那么向量3b a -r r 的坐标是( )A .()4,2-B .()4,2--C .()4,2D .()4,2-【答案】D【详解】解:因为()()1,2,1,0a b =-=r r ,所以()()()331,01,24,2b a -=--=-r r ;故选:D3.a ,b 是两个不同的平面,m ,n 是两条不同的直线,下列命题中正确的是( )A .如果m a Ì,n a Ë,m ,n 是异面直线,那么//n aB .若//m a ,//a b ,m b Ë,则//m bC .若//m a ,//m b ,则//a bD .如果//m a ,//n a ,m ,n 共面,那么//m n【答案】B【详解】对于A :如果m a Ì,n a Ë,m ,n 是异面直线,那么//n a 或n 与a 相交,A 不正确;对于B :若//m a ,则1l a $Ì,使得1//m l //a b ,则2l b $Ì,使得21//l l ∴2//m l ∵m b Ë,则//m bB 正确;对于C :若//m a ,//m b ,则a ,b 的位置关系为:平行或相交,C 不正确;对于D :如果//m a ,//n a ,m ,n 共面,则m ,n 的位置关系:相交或平行,D 不正确;故选:B .4.甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a ,再由乙猜甲刚才所想的数字,把乙猜的数字记为b ,其中{},1,2,3,4,5a b Î,则“a =b ”的概率为( )A .125B .225C .15D .25【答案】C【详解】解:甲乙猜数字时互不影响,故各有5种可能,故基本事件是5525´=种,则“a =b ”的基本事件有:()()()()()1,1,2,2,3,3,4,4,5,5,故5种,所以“a =b ”的概率为51255p ==,故选:C5.在ABC V BC =,且4A p=,则C =( )A .4pB .3pC .512p D .712p【答案】D【详解】解:在ABC V BC =a =,所以由正弦定理得:si n 1si n 2b AB a ==´=,因为b a <,所以B A <,所以6B p=,所以76412C p p pp =--=,故选:D6.已知2=r a ,向量a r 在向量b r a r 与b r 的夹角可以为()A .3pB .6pC .23pD .2p【答案】B【详解】解:记向量a r 与向量b r 的夹角为q ,[]0q p Î,,而2=r a ,a \r 在b r 上的投影为cos 2cos a q q =r ,a r Q 在b r 2cos q \=cos q \,[]0q p ÎQ ,,6pq \=.故选:B .7.某中学从甲、乙两个班中各选出7名学生参加2022年“希望杯”全国数学邀请赛,他们取得成绩的茎叶图如图,其中甲班学生成绩的中位数是84,乙班学生成绩的平均数是86,则xy 的值为( )A .36B .12C .10D .24【答案】D【详解】因为甲班学生成绩的中位数是84,所以根据茎叶图可得80x +为中位数,即8084x +=,解得4x =.又因为乙班学生成绩的平均数是86,即76818180919196867y +++++++=,解得6y =,故4624xy =´=.故选:D .8.中国古代数学名著《九章算术》的商功章记载了圆锥型几何体的体积公式,“水曰:下周自乘,以高乘之三十六而一”,其意思是:已知圆锥的底面周长C ,高h ,那么圆锥的体积公式是2112V C h p=,若一圆锥的轴截面是边长为 )A B .C D .【答案】C 【详解】因为圆锥的轴截面是边长为所以其底面直径,周长为,高h ==,故其体积为21812p p ´=.故选:C 二、多项选择题(本大题共4题,每小题5分,共计20分。
第七章 复数(B能力卷)(含答案)新教材高一数学尖子生培优AB卷(人教A版2019必修第二册)

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!第七章 复数(B 能力卷)班级______ 姓名_______ 考号______一、单项选择题(本大题共8题,每小题5分,共计40分。
每小题列出的四个选项中只有一项是最符合题目要求的)1.设复数z 满足()1i 1i z -=+,则z =( )A .1BC .2D .【答案】A 【详解】由已知可得()()()21i 1i 2i i 1i 1i 1i 2z ++====--+,因此,1z =.故选:A.2.已知复数53i1iz +=+,则下列说法正确的是( )A .z 的虚部为1-B .z 的共轭复数为4i-C .5z =D .z 在复平面内对应的点在第二象限【答案】A 【详解】由题意知,()()()()53i 1i 53i 82i4i 1i 1i 1i 2z +-+-====-+-+,对于A ,z 的虚部为1-,故A 正确;对于B ,z 的共轭复数为4i +,故B 错误;对于C =C 错误;对于D ,z 在复平面内对应的点在第四象限,故D 错误.故选:A3.已知()(),,2i i 3i a b a b Î++=-R (其中i 为虚数单位),则3a b -=( )A .4-B .2-C .2D .4【答案】D 【详解】()()2i i 2(2)ia b a b a b ++=-++由()()2i i 3i a b ++=-,可得2321a b a b -=ìí+=-î,解之得11a b =ìí=-î则()31314a b -=-´-=故选:D4.复数z 满足2220z z -+=,则||z =( )A .1BC .2D .1【答案】B 【详解】∵复数z 满足2220z z -+=,∴22i1i 2z ±==±,=故选:B.5.下面是关于复数22i 1i z =-(i 为虚数单位)的命题,其中真命题为( )A .2z =B .复数z 在复平面内对应点在直线y x =上C .z 的共轭复数为11i22-D .z 的虚部为1i2-【答案】B 【详解】∵22i 11i 1i 1i 2z ---===--,=A 错误;所以复数z 在复平面内对应点坐标为11(,)22--,在直线y x =上,B 正确;所以z 的共轭复数为11i 22-+,C 错误;所以z 的虚部为12-,D 错误.故选:B .6.设复数z 满足2i z z -=,2z =,复数z 所对应的点位于第一象限,则1=z( )A B C D 【答案】B设()i R,R z a b a b =+ÎÎ,则i z a b =-,由复数z 满足2i z z -=,2z =,复数z 所对应的点位于第一象限,则222240,0b a b a b =ìï+=íï>>î,解得1a b ==,∴1z ==故选:B.7.已知,a b 为实数,且2ii 1ib a +=++(i 为虚数单位),则i a b +=( )A .34i +B .12i +C .32i --D .32i+【答案】A 【详解】()()2i 1i 2i 22i i 22i 1i 2222b b b b b b +-+-+++-===++由题意知222=12b a b +ì=ïïí-ïïî,解得34a b =ìí=î,所以i 34ia b +=+故选:A8.已知复数()()4i z a a a =+-ÎR (i 为虚数单位),若z £a 的值为( )A .2-B .0C .1D .2【答案】D 【详解】由题意()()4i z a a a =+-ÎR,z ££()220a -£,所以20a -=,所以2a =,故选:D .二、多项选择题(本大题共4题,每小题5分,共计20分。
期末冲刺训练卷(含答案)高一下学期数学人教A版2019必修第二册

期末冲刺训练卷高一下学期数学人教A版2019必修第二册一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数,则的虚部为( )A.B.C.D.2.已知点A(0,1),B(3,2),向量=(﹣4,﹣3),则向量=( )A.(﹣7,﹣4)B.(7,4)C.(﹣1,4)D.(1,4)3.对于直线m,n和平面,,下列说法错误的是( )A.若,,m,n共面,则B.若,,m,n共面,则C.若,且,则D.若,且,则4.下列命题为真命题的有( )A.若随机变量的方差为,则B.已知经验回归方程,则与具有正线性相关关系C.对于随机事件与,若则事件与独立D.根据分类变量与的成对样本数据,计算得到,根据的独立性检验,有的把握认为与有关5.设的内角的边长分别是,且,则的值是( )A.2B.4C.6D.以上都不对6.一个内壁底面半径为2的圆柱体玻璃杯中盛有体积为V的水,若放入一个玻璃球(球的半径与圆柱体玻璃杯内壁的底面半径相同)后,水恰好淹没了玻璃球,则V=( )A.B.6πC.D.8π7.某高中共有学生2400人,其中高一、高二、高三的学生人数比为5∶4∶6,现用分层随机抽样的方法从该高中所有学生中抽取一个容量为120的样本,则应从高三年级抽取的人数为( )A.32B.40C.48D.568.如图,在各棱长均为1的的四面体中,E是PA的中点,Q为直线EB上的动点,则的最小值为( )A.B.C.D.2二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.小明在一次面试活动中,10位评委给他的打分分别为:70、85、86、88、90、90、92、94、95、100.则下列说法正确的有( )A.这10个分数的中位数为90B.这10个分数的第60百分位数为91C.这10个分数的平均数大于中位数D.去掉一个最低分和一个最高分后,平均分数会变大,而分数的方差会变小10.已知△ABC的内角A,B,C的对边分别是a,b,c,若,,,则C可能为( )A.B.C.D.11.如图,在直三棱妵中,D,G,E分别为所在棱的中点,,三棱柱挖去两个三棱锥,后所得的几何体记为,则( )A.有7个面B.有13条棱C.有7个顶点D.平面平面三、填空题:本题共3小题,每小题5分,共15分.12.设为虚数单位,复数为纯虚数,则实数为 .13.设,且,则 .14.如图,在扇形中,,点在扇形内部,,,则阴影部分的面积为 .四、解答题:本题共5小题,第15小题13分,第16、17小题15分,第18、19小题17分,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知是关于的方程的两个虚根,为虚数单位.(1)当时,求实数的值.(2)当,且,求实数的值.16.在中,内角A,B,C所对的边分别为a,b,c,已知.(1)求角A的大小;(2)若,求周长的取值范围.17.甲、乙两人参加猜成语活动,每轮活动由甲、乙各猜一个成语,已知甲每轮猜对的概率为,乙每轮猜对的概率为.在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响.(1)求经过两轮活动,两人共猜对2个成语的概率;(2)求经过两轮活动,两人猜对成语的个数不相同的概率.18.如图,某人位于临河的公路上,已知公路两个相邻路灯、之间的距离是,为了测量点与河对岸一点之间的距离,此人先后测得,.(1)求、两点之间的距离;(2)假设你只携带着量角器(可以测量以你为顶点的角的大小).请你设计一个通过测量角可以计算出河对岸两点、之间距离的方案,用字母表示所测量的角的大小,并用其表示出的长.19.如图,是半球的直径,为球心,依次是半圆上的两个三等分点,是半球面上一点,且,(1)证明:平面平面;(2)若点在底面圆内的射影恰在上,求二面角的余弦值.答案解析部分1.D2.A3.A4.C5.B6.C7.C8.B9.A,B,D10.A,C11.A,B,D12.213.014.15.(1)解:(2)解:16.(1)解:因为,所以,所以,又,所以;(2)解:由正弦定理可知:,则,所以,因为,所以,所以,所以,所以,所以周长的取值范围为.17.(1)解:设“甲第轮猜对”为事件,“乙第轮猜对”为事件,则,记“经过两轮活动,两人共猜对2个成语”为事件C,则事件有三种可能:甲全对、甲乙各对一个、乙全对,所以.(2)解:记“经过两轮活动,两人猜对成语的个数不相同”为事件D,则事件有三种可能:均全错、均错一个、均全对,所以,所以18.(1)解:在中,由正弦定理,有,即.答:、两点之间的距离为.(2)解:测得,,.在中,由正弦定理,有,即.在中,由余弦定理,有或. 19.(1)证明:连接OM,MN,如图,是半圆上的两个三等分点,则有,而,即有都为正三角形,因此,,四边形是菱形,,而,,平面,因此,平面,平面,所以平面平面.(2)解:由(1)知,平面平面,平面平面,则点在底面圆内的射影在上,因点在底面圆内的射影在上,因此,点在底面圆内的射影是与的交点,即平面,有,,,而,即有,取的中点,连,于是得,则有是二面角的平面角,在中,,所以,所以二面角的余弦值是.。
2020-2021学年高一数学尖子生同步培优题典2(人教A版)(解析版)

2020-2021 学年高一数学尖子生同步培优题典
D
、当
x
3
时,函数
f
(x)
2 sin(2 x
6
)
,
x
R
,
f
3
2
sin
2
3
6
2
所以 x 为 f (x) 图象的一条对称轴,正确. 3
2 sin(2 x
6
)
,
x
R
,
则 A 、 2 f (x) 2 正确,
B 、当 2x k ,k Z ,即 x k ,k Z ,f (x) 在区间 (0, ) 上只有 2 个零点,则 f (x)
6
2 12
在区间 (0, ) 上只有 1 个零点错误,
C 、 f (x) 的最小正周期为 ,正确
【解析】
cos(
2
)
cos[(
4
)
( 4
2
)]
cos(
4
)
cos
4
2
sin( 4
) sin( 4
2
)
,
而
(
,
3
)
,
(
,
)
,因此
sin(
)
2
2
,
sin(
)
6,
4
4 4 4 2 42
4
3
42 3
则 cos( ) 1 3 2 2 6 5 3 .故选:C 2 33 3 3 9
4 5
,
故
cos
3
2
2
cos
2
3
2
1
2
16 1 25
7 25
高一数学必修第二册综合测试(培优版)

必修第二册综合测试(培优版)时间:120分钟满分:150分命卷人:* 审核人:一、选择题(每小题5分,共60分)1. 如图所示的平面结构,绕中间轴旋转一周,形成的几何体形状为( )A. 一个球体B. 一个球体中间挖去一个圆锥C. 一个圆锥D. 一个球体中间挖去一个棱锥2. 已知点,则点到轴的距离为( )A. B.C. 5D.3. 如果两条直线与平行,那么等于( )A. 或B.C. D.4. 若直线始终平分圆的周长,则的最小值为( )A. B.C. D.5. 圆台轴截面的两条对角线互相垂直,且上、下底面半径比为,又其高为,则母线长为( )A. B.6. 如图所示,点在矩形所在平面外,,,面,,则与所成的角余弦值是( )A. B.C. D.7. 已知圆上到直线的距离等于的点恰有个,则实数的取值范围为( )A. B.C. D.8. 已知是直线,是平面,下列命题正确的是( )A. 若,则或B. 若,则C. 若,,,那么D.若,则9. 如图,网格纸上小正方形边长为,粗线画出的是某几何体的三视图,则该几何体中最长棱的长度为( )A. B.C. D.10. 已知点,点是圆上的动点,点是圆上的动点,则的最大值是( )A. B.C. D.11. 如图,正方体的棱长为,是棱的中点,是侧面内一点,若平面,则长度的范围为( )A. B.C. D.12. 如图,在等腰梯形中,,,为的中点.将与分别沿向上折起,使重合于点,则三棱锥的外接球的表面积为( )A. B. C. D.二、填空题(每小题5分,共20分)13. 已知直线与直线平行且与圆相切,则直线的方程是__________.14. 圆与圆:有__________条公切线.15. 在三棱锥中,为的重心,过点作三棱锥的一个截面,使截面平行于直线和,则截面的周长为__________.16. 在四棱锥中,底面为正方形,底面,且,为棱上的动点,若的最小值为,则__________.三、解答题(每小题10分,共60分)17. 已知的三个顶点. 求:(1)边上高所在的直线方程; (2)边中线所在的直线18. 在平面直角坐标系中,已知圆的方程为:,直线的方程为. (1)求证:直线恒过定点; (2)当直线被圆截得的弦长最短时,求直线的方程; (3)在(2)的前提下,若为直线上的动点,且圆上存在两个不同的点到点的距离为,求点的横坐标的取值范围.19. 如图,在四棱锥中,底面为平行四边形,点为中点,且.(1)证明:平面; (2)证明:平面平面.20. 已知直线,半径为的圆与相切,圆心在轴上且在直线的右下方. (1)求圆的方程; (2)过点的直线与圆交于两点(在轴上方),问在轴正半轴上是否存在定点,使得轴平分?若存在,请求出点的坐标;若不存在,请说明理由.,底面为直角梯形,,,平面底面,为的中点,是棱上的点,,.21. 如图,在四棱锥中(1)求证:平面平面; (2)若三棱锥的体积是四棱锥体积的,设,试确定的值.22. 如图,四棱锥中,底面为矩形,平面,,.(1)求异面直线与所成角的正切值; (2)求点到平面的距离.第1题:【答案】B【解析】圆绕中间轴旋转一周得到的几何体是球,三角形绕中间轴旋转一周得到的几何体是圆锥,则如图所示的平面结构,绕中间轴旋转一周,形成的几何体形状为一个球体中间挖去一个圆锥.第2题:【答案】C【解析】因为,所以点到轴的距离等于:.第3题:【答案】A【解析】当直线斜率不存在时,,此时直线斜率为,两条直线不平行, ∴直线斜率为,直线斜率为,两条直线平行, ∴,解方程得或, 经检验或时,与均不重合, ∴或.第4题:【答案】B【解析】把圆的方程化为标准方程得,∴圆心坐标为,半径. ∵直线始终平分圆的周长,∴直线过圆的圆心,把代入直线得即,点在直线上,是点到点的距离的平方,因为到直线的距离,所以的最小值为.第5题:【答案】D【解析】画出图象如下图所示,依题意,设上下底面半径分别为,由于截面等腰梯形两条对角线相互垂直,故,所以,同理,所以,在直角三角形中,即,解得,故母线长.第6题:【答案】D【解析】连接交于点,取中点,连接,所以, 因为面,,所以,, 因为在三角形中,是中点,所以,在直角三角形第7题:【答案】A【解析】由圆的方程,可得圆的圆心为原点,半径为, 若圆上恰有个点到直线的距离等于, 因为半径为,则圆心到直线的距离小于, ∴,解得.第8题:【答案】B【解析】若,则不一定在或内,即或不一定成立,故A不正确, 若,则.这是两个平面平行的性质定理,故B 正确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学单元测试AB 卷期末模拟卷01(B 能力卷)( 考试时间:120分钟 试卷满分:150分)姓名_____________ 班级_________ 考号_______________________ 注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.1.复数()()12z i i =+-,则z =( )A .3i +B .3i -C .4i +D .4i -【答案】B【详解】因为(1)(2)2213z i i i i i =+-=-++=+,所以3z i =-.故选:B.2.如图,已知3AB BP =,用OA ,OB 表示OP ,则OP 等于( )A .1433OA OB - B .1433OA OB + C .1433OA OB -+ D .1433OA OB -- 【答案】C【详解】解:3AB BP =, ()11413333OP OB BP OB AB OB OB OA OB OA ∴=+=+=+-=-, 故选:C. 3.有17名同学参加百米竞赛,预赛成绩各不相同,要取前8名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道17名同学成绩的( )A .平均数B .众数C .中位数D .方差【答案】C【详解】由题设,17名同学参加百米竞赛,要取前8名参加决赛,则成绩从高到低排列,确定17名同学成绩的中位数,即第9名的成绩便可判断自己是否能进入决赛. 故选:C. 4.已知水平放置的ABC 按斜二测画法,得到如图所示的直观图,其中2B O C O ''''==,3A O ''=,那么ABC 是一个( )A .直角三角形B .等边三角形C .钝角三角形D .三边互不相等的三角形【答案】B【详解】 A O ''在y '轴上,B C ''在x '轴,因此AO BC ⊥,在原图形中23,4AO BC ==,60ABC ACB ∠=∠=︒,三角形为等边三角形.故选:B .5.已知,a b 满足25,1045,a b a b a b +=⋅=+=+则a 与b 夹角的余弦值为( )A 25B 5C .12D 3【答案】A【详解】由题意,向量,a b 满足25,1045a b a b a b +=⋅=+=+, 可得22221045a b a b a b +=++⋅=+,所以2210a b +=,又由()222220a b a b a b +=++=,所以5a b =,设向量a 与b 夹角为θ,则25cos 5a b ba θ⋅==. 故选:A.6.如图,AB 为圆锥底面直径,点C 是底面圆O 上异于,A B 的动点,已知OA=3,圆锥侧面展开图是圆心角为3π的扇形,当PB 与BC 所成角为3π时,PB 与AC 所成角为( )A .3πB .6πC .4πD .56π 【答案】C【详解】设圆锥母线长为l ,则323l ππ=,解得2l =,PB PC =,PB ∴与BC 所成角3PBC π∠=,2BC ∴=, Rt ABC ∆∴中22AC =作BD AC 与圆O 交于点D ,连接AD ,四边形ABCD 为平行四边形,22BD AC ==,连接PD ,则PBD ∠为PB 与AC 所成角,PBD ∆中2PD PB ==,可得PD PB ⊥,4PBD π∴∠=,故选:C. 7.垃圾分类是对垃圾进行处置前的重要环节通过分类投放、分类收集,我们可以把有用物资从垃圾中分离出来重新回收、利用,变废为宝.某小区的分类垃圾箱如图所示,每组垃圾箱有四个垃圾投放桶,分别为有害垃圾、厨余垃圾、可回收垃圾、其他垃圾.该小区业主手提两袋垃圾,分别为有害垃圾和厨余垃圾,分别将其随机投入两个不同的垃圾投放桶,则恰有一袋投放正确的概率为( )A .19B .16C .13D .12【答案】C【详解】 记有害垃圾、厨余垃圾、可回收垃圾、其他垃圾四个垃圾投放桶分别为1,2,3,4,则两袋垃圾中恰有一袋投放正确的情况有(1,3),(1,4),(3,2),(4,2),共4种,而随机投放的情况有(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),共12种,所以所求概率41123P ==. 故选:C .8.在棱长为2的正方体1111ABCD A BC D -中,N 为BC 的中点.当点M 在平面11DCC D 内运动时,有//MN 平面1A BD ,则线段MN 的最小值为( )A .1B .62C .2D .3【答案】B【详解】取CD 中点P ,1DD 中点Q ,连接PQ 、PN 、QN ,如图所示:因为P 、N 分别为CD 、BC 中点,所以PN BD ∕∕,同理,P 、Q 分别为CD 、1DD 中点,所以11PQ DC A B ∕∕∕∕, 又PQ PN P ⋂=,,PQ PN ⊂平面PQN ,1A B BD B ⋂=,1,A B BD ⊂平面1A BD ,所以平面PQN ∕∕平面1A BD ,因为//MN 平面1A BD ,所以MN ⊂平面PQN ,又点M 在平面11DCC D 内运动,所以点M 在平面PQN 和平面11DCC D 的交线上,即M PQ ∈,在PQN 中,2PN =1122PQ CD ==22(2)26QN =+= 所以2221cos 22PN PQ QN NPQ PQ PN +-∠==-⨯, 所以120NPQ ∠=︒,所以N 点到PQ 的最小距离()6sin 180120d PN =⋅︒-︒=. 所以线段MN 的最小值为6. 二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符 合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.百年大计,教育为本.十四五发展纲要中,教育作为一个专章被提出.近日,救育部发布2020年全国教育事业统计主要结果.其中关于高中阶段教育(含普通高中、中等职业学校及其他适龄教育机构)近六年的在校规模与毛入学率情况图表及2020年高中阶段教育在校生结构饼图如下,根据图中信息,下列论断正确的有( )(名词解释:高中阶段毛入学率≡在校生规模÷适龄青少年总人数×100%)A .近六年,高中阶段在校生规模与毛入学率均持续增长B .近六年,高中阶段在校生规模的平均值超过4000万人C .2019年,未接受高中阶段教育的适龄青少年不足420万D .2020年,普通高中的在校生超过2470万人【答案】BD【详解】对A ,在前四年有下降的过程,故A 错误;对B ,六年的在校生总数为24037,平均值为4006以上,故B 正确;对C ,39950.1054680.895⨯≈,未接受高中阶段教育的适龄青少年有468万人以上,故C 错误; 对D ,41280.6012481⨯≈,故D 正确.故选:BD10.已知复数1z i =+,则下列结论正确的是( )A .z =B .复数z 的共轭复数为1z i =-C .20211122i i z =+ D .22z = 【答案】ABC【详解】对A ,z = A 正确;对B ,根据共轭复数的定义,1z i =-,B 正确;对C ,由41i =,所以2021(1)1111(1)(1)222⋅-+====+++-i i i i i i z i i i ,C 正确; 对D ,22(1)121=2=+=+-z i i i ,故D 错误.故选:ABC.11.已知,,a b c 是三个平面向量,则下列叙述错误的是( )A .若a b =,则a b =±B .若a b a c ⋅=⋅,且0a ≠,则b c =C .若//,//a b b c ,则//a cD .若a b ⊥,则a b a b +=- 【答案】ABC 【详解】A ,若a b =,可取()1,2a =,()2,1b =,则a b ≠±,故A 错误;B ,若a b a c ⋅=⋅,且0a ≠,当a b ⊥,a c ⊥ 时,则b 与c 不一定相等,故B 错误;C ,若//,//a b b c ,当0b =时,a 与c 不一定平行,故C 错误;D ,若a b ⊥,则0a b ⋅=,所以22222a b a b a b a b +=++⋅=+, 22222a b a b a b a b -=+-⋅=+,故a b a b +=-,故D 正确.故选:ABC12.已知正方体1111ABCD A BC D -中,以下结论正确的有( )A .点P 在直线BC 1上运动时,三棱锥A -D 1PC 的体积不变B .点P 在直线BC 1上运动时,直线AP 与平面AD 1C 所成角的大小不变C .点P 在直线BC 1上运动时,二面角P -AD 1-C 的大小不变D .M 是平面1111D C B A 上到点D 和C 1距离相等的点,则点M 的轨迹是过点D 1的直线【答案】ACD【详解】因为11A D PC P AD C V V --=,11//BC AD ,且1BC ⊄平面1AD C ,1AD ⊂平面1AD C ,所以1//BC 平面1AD C ,所以1BC 上的点到平面1AD C 的距离相等,所以三棱锥1A D PC -的体积不变,故A 正确;由图可知,当点P 在直线1BC 上运动时,直线AB 与平面1AD C 所成角和直线1AC 与平面1AD C 所成角不相等,故B 错误;因为AP ⊂平面11BC D A ,所以二面角1P AD C --的大小等于平面11BC D A 与平面1AD C 所成角的大小,所以二面角1P AD C --的大小不变,故C 正确;因为M 是平面1111D C B A 上到点D 和1C 距离相等的点,所以点M 的轨迹是平面1111D C B A 与线段1DC 的垂直平分线1DC 所在平面的交线,即点M 的轨迹是平面1111D C B A 与平面11A D C 的交线11A D ,所以点M 的轨迹是过点1D 的直线,故D 正确;三、填空题:本题共4小题,每小题5分,共20分13.某圆柱两个底面面积之和等于其侧面面积,则该圆柱底面半径与高的比值为________.【答案】1【详解】设圆柱底面半径为r ,高为h ,由题意222r rh ππ=,所以r h =,即1r h=.14.已知复数z 满足||||z i z i ++-=z 的最小值是_______.【答案】1【详解】由复数的几何意义,可得||||z i z i ++-=z 在椭圆2212y x +=上, 而z 表示椭圆上的点到椭圆对称中心()0,0的距离,当且仅当复数z 位于椭圆短轴端点(1,0)±时,z 取得最小值,z 的最小值为1. 故答案为:1.15.在ABC 中,2AB =,3AC =,且ABC 的面积为32,则BAC ∠=__________. 【答案】6π或56π 【详解】 ABC 中,2AB =,3AC =,且ABC 的面积为32, 所以13sin 22AB AC A ⋅⋅∠=,所以1323sin 22A ⨯⨯∠=,整理得:1sin 2A ∠=, 因为()0,A π∈,所以6BAC π∠=或56π, 故答案为:6π或56π 16.已知三棱柱111,ABC A BC -侧棱1AA ⊥底面,,ABC E F 分别是1,AB AA 的中点,且12,,4AC BC AC BC AA ==⊥=,过点E 作一个截面与平面1BFC 平行﹐则截面的周长为________________________.32225【详解】如图,取AF 中点G ,分别在1CC ,BC 上取点H ,M ,使1111,44HC CC BM BC ==, 连接,,,EG GH HM EM ,又,F G 分别是1,AA AF 中点,114FG AA ∴=, 又1111//,AA CC AA CC =,11//,FG HC FG HC ∴=,∴四边形1FGHC 为平行四边形, 1/GH FF ∴,1GH FC =,//GH ∴平面1BFC ,1111113,,//,444HC CC BM BC MH BC MH BC ==∴=,//MH ∴平面1BFC , 又MH GH H ⋂=,∴平面//EGHM 平面1BFC ,又1AA ⊥平面ABC ,2AC BC ==,,E F 分别是1,AB AA 的中点,1,4AC BC AA ⊥=, 122,2AB AF AF ∴===, 2211322EG BF AF AB ∴==+=22111122GH FC A F AC ==+= 2211113335442HM BC BB B C ==+= 在BEM △中,11,242BM BC BE ===45EBM ∠=, 22211252cos 452224224EM BM BE BM BE ∴=+-⋅=+-⨯=,5EM ∴= ∴所求截面的周长为353225322252EG GH HM EM +++==32225四、解答题:本小题共6小题,共70分。
