小学奥数16数阵图讲解学习
数阵图-奥数优秀课件

【经典例题】
例题1 把2~6这五个数分别填入下图的“○”中,使得横行三数之和与竖列三 数之和都等于13。
【经典例题】
例题1 把2~6这五个数分别填入下图的“○”中,使得横行三数之和与竖列三数之和都 等于13。
解析: 横行三数之和与竖列三数的和是 : 13×2=26 各个数的和是:
解析: 横行三数之和与竖列三数的和是 : 13×2=26 各个数的和是:
2+3+4+5+6=20 中间的数是 : 26-20=6 2+5=4+3=7
【经典例题】
例题1 把2~6这五个数分别填入下图的“○”中,使得横行三数之和与竖列三数之和都 等于13。
解析: 横行三数之和与竖列三数的和是 : 13×2=26 各个数的和是:
7个数字总和:(1+7)×7÷2=28
中间数字为:30-28=2
2÷2=1
边上的数字和:10-1=9,
2+7=4+5=3+6
(答案不唯一)
【课堂练习】
练习3: 把3~9这七个数字分别填入下图的各“○”中,使每条线上三个“○”内数的和等
于16.
【课堂练习】
练习3: 把3~9这七个数字分别填入下图的各“○”中,使每条线上三个“○”内数的和等
【思路导航】 设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3 +……+10+a+b=30×2,即55+a+b=60,a+b=5。在 1——10这十个数中1+4=5,2+3=5。 当a和b是1和4时,每个大圆上另外四个数分别是(2,6,8, 9)和(3,5,7,10);当a和b是2和3时,每个大圆上另 外四个数分别为(1,5,9,10)和(4,6,7,8)。
三年级奥数第16次课:数阵图(一)(学生版)

【我生命中最最最重要的朋友们,请你们认真听老师讲并且跟着老师的思维走。
学业的成功重在于考点的不断过滤,相信我赠予你们的是你们学业成功的过滤器。
谢谢使用!!!】数阵图(一)一、考点、热点回顾1、数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵。
2、观察下面两个图:左上图中有3个大圆,每个圆周上都有四个数字,有意思的是,每个圆周上的四个数字之和都等于13。
右上图就更有意思了,1~9九个数字被排成三行三列,每行的三个数字之和与每列的三个数字之和,以及每条对角线上的三个数字之和都等于15。
上面两个图就是数阵图。
二、典型例题例1、把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
例2 、把1~5这五个数填入下页左上图中的○里(已填入5),使两条直线上的三个数之和相等。
例3 、把1~5这五个数填入右图中的○里,使每条直线上的三个数之和相等。
例4 、将1~7这七个自然数填入左下图的七个○内,使得每条边上的三个数之和都等于10。
例5 、将 10~20填入左下图的○内,其中15已填好,使得每条边上的三个数字之和都相等。
辐射型辐射型数阵图只有一个重叠数,重叠次数是“直线条数”-1,即m-1。
对于辐射型数阵图,有:已知各数之和+重叠数×重叠次数=直线上各数之和×直线条数。
由此得到:(1)若已知每条直线上各数之和,则重叠数等于(直线上各数之和×直线条数-已知各数之和)÷重叠次数。
如例1、例4。
(2)若已知重叠数,则直线上各数之和等于(已知各数之和+重叠数×重叠次数)÷直线条数。
如例2、例5。
(3)若重叠数与每条直线上的各数之和都不知道,则要从重叠数的可能取值分析讨论,如例3。
三、习题练习1、将1~7这七个数分别填入左下图中的○里,使每条直线上的三个数之和都等于12。
如果每条直线上的三个数之和等于10,那么又该如何填?2、将1~9这九个数分别填入右上图中的○里(其中9已填好),使每条直线上的三个数之和都相等。
三年级上奥数第16讲 数阵图(一)
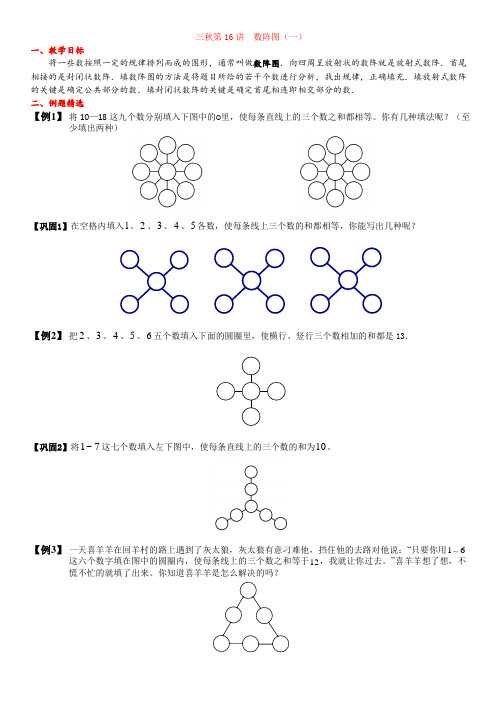
三秋第16讲 数阵图(一)一、教学目标将一些数按照一定的规律排列而成的图形,通常叫做数阵图.向四周呈放射状的数阵就是放射式数阵.首尾相接的是封闭状数阵.填数阵图的方法是将题目所给的若干个数进行分析,找出规律,正确填充.填放射式数阵的关键是确定公共部分的数.填封闭状数阵的关键是确定首尾相连即相交部分的数. 二、例题精选【例1】 将10—18这九个数分别填入下图中的○里,使每条直线上的三个数之和都相等。
你有几种填法呢?(至少填出两种)【巩固1】在空格内填入1、2、3、4、5各数,使每条线上三个数的和都相等,你能写出几种呢?【例2】 把2、3、4、5、6五个数填入下面的圆圈里,使横行、竖行三个数相加的和都是13.【巩固2】将7~1这七个数填入左下图中,使每条直线上的三个数的和为10。
【例3】 一天喜羊羊在回羊村的路上遇到了灰太狼,灰太狼有意刁难他,挡住他的去路对他说:“只要你用16这六个数字填在图中的圆圈内,使每条线上的三个数之和等于12,我就让你过去。
”喜羊羊想了想,不慌不忙的就填了出来。
你知道喜羊羊是怎么解决的吗?【巩固3】从1、2、3、4、5、6中选取适合的数填在圆圈里,使每个圆上四个数的和都等于15.【例4】将1~9这九个数分别填入下左图中,使每个三角形的顶点上的三个数的和相等。
【巩固4】将1,2,3,5,6,7这六个数填入下左表中,使每行中三个数的和相等,同时使每列两个数的和也相等。
【例5】在下左图中,三个圆圈两两相交成7块小区域,分别填上1~7这七个自然数,在一些小区域中已填好数字,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都是15。
375【例6】在下左列表格中填上0~8这9个数字,使得各行各列的和都恰好等于表格边上的数。
(每个数字只能用1次)21312121014。
人教版小学三年级数学第讲 数阵图(一)

第16讲数阵图(一)在神奇的数学王国中,有一类非常有趣的数学问题,它变化多端,引人入胜,奇妙无穷。
它就是数阵,一座真正的数字迷宫,它对喜欢探究数字规律的人有着极大的吸引力,以至有些人留连其中,用毕生的精力来研究它的变化,就连大数学家欧拉对它都有着浓厚的兴趣。
那么,到底什么是数阵呢?我们先观察下面两个图:左上图中有3个大圆,每个圆周上都有四个数字,有意思的是,每个圆周上的四个数字之和都等于13。
右上图就更有意思了,1~9九个数字被排成三行三列,每行的三个数字之和与每列的三个数字之和,以及每条对角线上的三个数字之和都等于15,不信你就算算。
上面两个图就是数阵图。
准确地说,数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵。
要排出这样巧妙的数阵图,可不是一件容易的事情。
我们还是先从几个简单的例子开始。
例1把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了,七拼八凑就写出了右上图的答案,可是却搞不清其中的道理。
下面我们就一起来分析其中的道理,只有弄懂其中的道理,才可能解出复杂巧妙的数阵问题。
分析与解:中间方格中的数很特殊,横行的三个数有它,竖列的三个数也有它,我们把它叫做“重叠数”。
也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次,即重叠了一次,其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9,所以(1+2+3+4+5)+重叠数=9+9,重叠数=(9+9)-(1+2+3+4+5)=3。
重叠数求出来了,其余各数就好填了(见右上图)。
例2把1~5这五个数填入下页左上图中的○里(已填入5),使两条直线上的三个数之和相等。
分析与解:与例1不同之处是已知“重叠数”为5,而不知道两条直线上的三个数之和都等于什么数。
所以,必须先求出这个“和”。
根据例1的分析知,两条直线上的三个数相加,只有重叠数被加了两遍,其余各数均被加了一遍,所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5]÷2=10。
小学奥数之数阵图解题方法(完整版)

小学奥数之数阵图解题方法1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.模块一、封闭型数阵图【例 1】 把1~8的数填到下图中,使每个四边形中顶点的数字和相等。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】学而思杯,3年级,第6题 【解析】5-1-3-1.数阵图教学目标知识点拨例题精讲【答案】【例 2】 将1~8这八个自然数分别填入下图中的八个○内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?【考点】封闭型数阵图 【难度】2星 【题型】填空 【解析】 为了叙述方便,先在各圆圈内填上字母,如下图(2).由条件得出以下四个算式:a+b+c=14(1) c+d+e=14 (2) e+f+g=14 (3)a+h+g=14 (4)由(1)+(3),得:a+b+c+e+f+g=28,(a+b+c+d+e+f+g+h )-(d+h )=28,d+h=(1+2+3+4+5+6+7+8)-28=8,由(2)+(4),同样可得b+f=8, 又1,2,3,4,5,6,7,8中有1+7=2+6=3+5=8.又1要出现在顶点上,d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性,不妨设b=2,f=6,d=3,h=5. a ,c ,e ,g 可取到1,4,7,8若a=1,则c=14-(1+2)=11,不在1,4,7,8中,不行.若c=1,则a=14-(1+2)=11,不行. 若e=1,则c=14-(1+3)=10,不行. 若g=1,则a=8,c=4,e=7. 说明:例题为封闭型数阵,由它的分析思考过程可以看出,确定各边顶点所应填的数为封闭型数8765432187654321()(2)h gf ed c ba阵的解题突破口.【答案】【例 3】 在如图6所示的○内填入不同的数,使得三条边上的三个数的和都是12,若A 、B 、C 的和为18,则三个顶点上的三个数的和是 。
奥数精编训练-数阵图(一)

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.模块一、封闭型数阵图【例 1】 把1~8的数填到下图中,使每个四边形中顶点的数字和相等。
例题精讲知识点拨教学目标5-1-3-1.数阵图【例 2】 将1~8这八个自然数分别填入下图中的八个○内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?(1)【例 3】 在如图6所示的○内填入不同的数,使得三条边上的三个数的和都是12,若A 、B 、C的和为18,则三个顶点上的三个数的和是 。
CBA【例 4】 将1至6这六个数字填入图中的六个圆圈中(每个数字只能使用一次),使每条边上的数字和相等.那么,每条边上的数字和是 .789fedcba 789【例 5】 将1到8这8个自然数分别填入如图数阵中的8个圆圈,使得数阵中各条直线上的三个数之和都相等,那么A 和B 两个圆圈中所填的数之差(大数减小数)是______.BA【例 6】如图所示,圆圈中分别填人0到9这10个数,且每个正方形顶点上的四个数之和都是18,则中间两个数A与B的和是________。
BA【例 7】把2~11这10个数填到右图的10个方格中,每格内填一个数,要求图中3个22的正方形中的4个数之和相等.那么,这个和数的最小值是多少?11109 8765432【例 8】下图中有五个正方形和12个圆圈,将1~12填入圆圈中,使得每个正方形四角上圆圈中的数字之和都相等.那么这个和是多少?861102912311457【例 9】如图,大、中、小三个正方形组成了8个三角形,现在把2、4、6、8四个数分别填在大正方形的四个顶点;再把2、4、6、8分别填在中正方形的四个顶点上;最后把2、4、6、8分别填在小正方形的四个顶点上.⑴能不能使8个三角形顶点上数字之和都相等?⑵能不能使8个三角形顶点上数字之和各不相同?如果能,请画图填上满足要求的数;如果不能,请说明理由.246824688642【例 10】 将1~16分别填入下图(1)中圆圈内,要求每个扇形上四个数之和及中间正方形的四个数之和都为34,图中已填好八个数,请将其余的数填完.【例 11】 一个3 3的方格表中,除中间一格无棋子外,其余梅格都有4枚一样的棋子,这样每边三个格子中都有12枚棋子,去掉4枚棋子,请你适当调整一下,使每边三格中任有12枚棋子,并且4个角上的棋子数仍然相等(画图表示)。
一起学奥数有趣的数阵图资料讲解

因为1-12是一个等差数列,确定1-4为四个顶角,且按逆时针方向排列后,可以把剩下 的分成5-8,9-12两组,分别填在直线上对应的位置。
最后一步的规律必须让学生领会。可以把和都为22的条件去掉做讲解
例4、把1~7这七个数分别填入下图中的各个圆圈内,使每条线段上三个 ○内的数的和相等。
7
2
1
4 5
上两题相比较,图形特征与数字特征存在雷同性,但每条线上 三个数字和受限制。因此需要确定公共圆圈的值。
五条线段上的数字和相加为: 22×5=110 11个圆圈内的数字和为: 11×12÷2=66 则公共圆圈的数字为: (110-66)÷(5-1)=11
剩余圆圈上的填法,与之前题目相同。对剩下的10个数首尾取 数即可。
而 A+B+C+D+E+F+G+H+I=45
F
C
对上面等式进行简化,则: (D+E+F)-(G+H+I)=18
对1~9这9个数进行分析,最大三个数的和为: 7+8+9=24;最小为: 1+2+3=6 两者差为18。所以D+E+F=18
试试枚举法解这个题目(对枚举法也可以做初步分析)
例:将1~10这十个数填入下图的圆圈内,使每个正方形的四个数字之 和都等于23,应怎样填?
接着从这八个数中找出4个和为34的数的组合,放在正方形中。(1、4、13、16)、 (2、4、12、16)
没有条件四个数之和为34,是否可以解答本题?
例:把数字1~9分别填入下图的9个圈内,要求三角形ABC和三角形 DEF的每条边上三个圈内数字之和都等于18.下图中D、E、F的三个圈 中所填数之和为什么?
小学数学-数阵图讲解学习
第一题图
第二题图
第三题图
例题3(书例2):
将1-9九个数字分别填在下图 圆圈内,使三角形 每条边上四个数的和是17.
1+2+3+……+9=45
每条边上的和是17,共有3条
17
17
边那么总和是17×3=51.
每个角上的数都被用了两次也 就是每个角上的数都加了一次。
17
51-45=6 6=1+2+3
17—1—2=14 14=5+9
3、(选做)把1--8这八个自然数分别填入图 中,使每个正方形四个角及每个对角线上四 个数的和均是18。(P17综3)
(书例4)把1--7七个数分别填入下图,使每条 线上三个数之和等于12
先看竖着的三条线,有一个公用数 12x3=36,1+2+3+4+5+6+7+8=28 36-28=8,公用数用了两次8÷2=4
三组数都用到了最中间的数,那么每组都减去 中间的那个数剩下的两个数的和相等
1 2 34567
7
1
4
23
6
5
1 1+7=2+6=3+5 2 2+7=3+6=4+5 3 1+6=2+5=3+4
7
2
1
43
5
6
1
6
7 45
3221来自54376
2 3
5 1 4 76
2
1 4
7
3
6
5
1. P16综1 2. P17能1 3. P16基1
不论是辐射型数阵阵、封闭型数还是复合型 数阵解题的要点都是先确定公共部分的数。
小学思维数学讲义:数阵图(一)-含答案解析

数阵图(一)1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.模块一、封闭型数阵图【例 1】 把1~8的数填到下图中,使每个四边形中顶点的数字和相等。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】学而思杯,3年级,第6题 【解析】87654321【答案】例题精讲知识点拨教学目标87654321【例 2】 将1~8这八个自然数分别填入下图中的八个○内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?(1)【考点】封闭型数阵图 【难度】2星 【题型】填空 【解析】 为了叙述方便,先在各圆圈内填上字母,如下图(2).由条件得出以下四个算式:(2)h gf ed c baa+b+c=14(1)c+d+e=14 (2) e+f+g=14 (3)a+h+g=14 (4)由(1)+(3),得:a+b+c+e+f+g=28,(a+b+c+d+e+f+g+h )-(d+h )=28,d+h=(1+2+3+4+5+6+7+8)-28=8,由(2)+(4),同样可得b+f=8, 又1,2,3,4,5,6,7,8中有1+7=2+6=3+5=8.又1要出现在顶点上,d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性,不妨设b=2,f=6,d=3,h=5. a ,c ,e ,g 可取到1,4,7,8若a=1,则c=14-(1+2)=11,不在1,4,7,8中,不行.若c=1,则a=14-(1+2)=11,不行. 若e=1,则c=14-(1+3)=10,不行. 若g=1,则a=8,c=4,e=7.说明:例题为封闭型数阵,由它的分析思考过程可以看出,确定各边顶点所应填的数为封闭型数阵的解题突破口.【答案】【例 3】 在如图6所示的○内填入不同的数,使得三条边上的三个数的和都是12,若A 、B 、C 的和为18,则三个顶点上的三个数的和是 。
数阵图(二)(含详细解析)

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.复合型数阵图【例 1】 由数字1、2、3组成的不同的两位数共有9个,老师将这9个数写在一个九宫格上,让同学选数,每个同学可以从中选5个数来求和.小刚选的5个数的和是120,小明选的5个数的和是111.如果两人选的数中只有一个是相同的,那么这个数是_____________.313233212223131211【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】迎春杯,中年级,决赛,3题【分析】 这9个数的和:111213212223313233++++++++10203031233198=++⨯+++⨯=()()例题精讲知识点拨教学目标5-1-3-2.数阵图由小刚和小明选的数中只有一个是相同的,可知他们正好把这9个数全部都取到了,且有一个数取了两遍.所以他们取的数的总和比这9个数的和多出来的部分就是所求的数.那么,这个数是12011119833+-=.【答案】33【例 2】 如图1,圆圈内分别填有1,2,……,7这7个数。
如果6个三角形的顶点处圆圈内的数字的和是64,那么,中间圆圈内填入的数是 。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】希望杯,五年级,复赛,第5题,5分【解析】 2 【答案】2【例 3】 如下图(1)所示,在每个小圆圈内填上一个数,使得每一条直线上的三个数的和都等于大圆圈上三个数的和.(1)17894【考点】复合型数阵图 【难度】3星 【题型】填空 【解析】 为叙述方便,先在每个圆圈内标上字母,如图(2),(2)a cb49817则有a+4+9=a+b+c (1)b+8+9=a+b+c (2)c+17+9=a+b+c (3)(1)+(2)+(3):(a+b+c )+56=3(a+b+c ),a+b+c=28,则 a=28-(4+9)=15,b=28-(8+9)=11,c=28-(17+9)=2解:见图.1789411215【答案】17 89411215【例 4】请你将数字1、2、3、4、5、6、7填在下面图(1)所示的圆圈内,使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填?【考点】复合型数阵图【难度】3星【题型】填空【解析】为了叙述方便,将各圆圈内先填上字母,如图(2)所示.设A+B+C=A+F+G=A+D+E=B+D+F=C+E+G=k (A+B+C)+(A+F+G)+(A+D+E)+(B+D+F)+(C+E+G)=5k,3A+2B+2C+2D+2E+2F+2G=5k,2(A+B+C+D+E+F+G)+A=5k,2(1+2+3+4+5+6+7)+A=5k,56+A=5k.,因为56+A为5的倍数,得A=4,进而推出k=12,因为在1、2、3、5、6、7中,1+5+6=7+3+2=12,不妨设B=1,F=5,D=6,则C=12-(4+1)=7,G=12-(4+5)=3,E=12-(4+6)=2.,解:得到一个基本解为:(见图)7654321【答案】7654321【例 5】在左下图的每个圆圈中填上一个数,各数互不相等,每个圆圈有3个相邻(即有线段相连的圆圈)的圆圈。
(完整版)小学三年级奥数--数阵图

数阵图(一)在神奇的数学王国中,有一类非常有趣的数学问题,它变化多端,引人入胜,奇妙无穷。
它就是数阵,一座真正的数字迷宫,它对喜欢探究数字规律的人有着极大的吸引力,以至有些人留连其中,用毕生的精力来研究它的变化,就连大数学家欧拉对它都有着浓厚的兴趣。
那么,到底什么是数阵呢?我们先观察下面两个图:左上图中有3个大圆,每个圆周上都有四个数字,有意思的是,每个圆周上的四个数字之和都等于13。
右上图就更有意思了,1~9 九个数字被排成三行三列,每行的三个数字之和与每列的三个数字之和,以及每条对角线上的三个数字之和都等于15,不信你就算算。
上面两个图就是数阵图。
准确地说,数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵。
要排出这样巧妙的数阵图,可不是一件容易的事情。
我们还是先从几个简单的例子开始。
例1 把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了,七拼八凑就写出了右上图的答案,可是却搞不清其中的道理。
下面我们就一起来分析其中的道理,只有弄懂其中的道理,才可能解出复杂巧妙的数阵问题。
分析与解:中间方格中的数很特殊,横行的三个数有它,竖列的三个数也有它,我们把它叫做“重叠数”。
也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次,即重叠了一次,其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9,所以(1+2+3+4+5)+重叠数=9+9,重叠数=(9+9)-(1+2+3+4+5)=3 。
重叠数求出来了,其余各数就好填了(见右上图)。
试一试:练习与思考第1 题。
例2 把1~5 这五个数填入下页左上图中的○里(已填入5),使两条直线上的三个数之和相等。
分析与解:与例1 不同之处是已知“重叠数”为5,而不知道两条直线上的三个数之和都等于什么数。
所以,必须先求出这个“和”。
根据例1 的分析知,两条直线上的三个数相加,只有重叠数被加了两遍,其余各数均被加了一遍,所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5] ÷2=10。
数阵图讲解
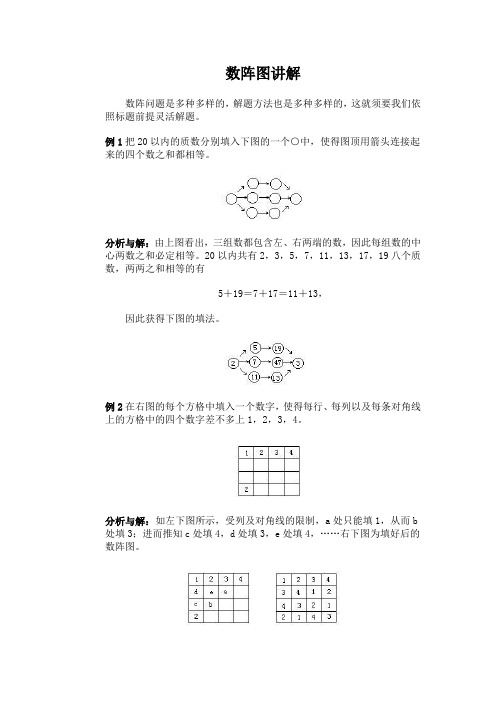
数阵图讲解数阵问题是多种多样的,解题方法也是多种多样的,这就须要我们依照标题前提灵活解题。
例1把20以内的质数分别填入下图的一个○中,使得图顶用箭头连接起来的四个数之和都相等。
分析与解:由上图看出,三组数都包含左、右两端的数,因此每组数的中心两数之和必定相等。
20以内共有2,3,5,7,11,13,17,19八个质数,两两之和相等的有5+19=7+17=11+13,因此获得下图的填法。
例2在右图的每个方格中填入一个数字,使得每行、每列以及每条对角线上的方格中的四个数字差不多上1,2,3,4。
分析与解:如左下图所示,受列及对角线的限制,a处只能填1,从而b 处填3;进而推知c处填4,d处填3,e处填4,……右下图为填好后的数阵图。
例3将1~8填入左下图的○内,要求按照天然数次序相邻的两个数不克不及填入有直线连接的相邻的两个○内。
分析与解:因为中心的两个○各自只与一个○不相邻,而2~7中的任何一个数都与两个数相邻,因此这两个○内只能填1和8。
2只能填在与1不相邻的○内,7只能填在与8不相邻的○内。
其余数的填法见右上图。
例4在右图的六个○内各填入一个质数(可取雷同的质数),使它们的和等于20,同时每个三角形(共5个)顶点上的数字之和都相等。
分析与解:因为大年夜三角形的三个顶点与中心倒三角形的三个顶点正好是图中的六个○,又因为每个三角形顶点上的数字之和相等,因此每个三角形顶点上的数字之和为20÷2=10。
10分为三个质数之和只能是2+3+5,由此获得右图的填法。
例5在右图所示立方体的八个顶点上标出1~9中的八个,使得每个面上四个顶点所标数字之和都等于k,同时k不克不及被未标出的数整除。
分析与解:设未被标出的数为a,则被标出的八个数之和为1+2+…+9-a =45-a。
因为每个顶点都属于三个面,因此六个面的所有顶点数字之和为6k=3×(45-a),2k=45-a。
2k是偶数,45-a也应是偶数,因此a必为奇数。
小学数学-数阵图讲解学习25页PPT

小学数学-数阵图讲解学习
51、山气日夕佳,飞鸟相与还。 52、木欣欣以向荣,泉涓涓而始流。
53、富贵非吾愿,帝乡不可期。 54、雄发指危冠,猛气冲长缨。 55、土地平旷,屋舍俨然,有良田美 池桑竹 之属, 阡陌交 通,鸡 犬相闻 。
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
小学奥数:数阵图(一).专项练习及答案解析

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格); 第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.模块一、封闭型数阵图【例 1】 把1~8的数填到下图中,使每个四边形中顶点的数字和相等。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】学而思杯,3年级,第6题 【解析】例题精讲知识点拨教学目标5-1-3-1.数阵图【答案】【例 2】 将1~8这八个自然数分别填入下图中的八个○内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?(1)【考点】封闭型数阵图 【难度】2星 【题型】填空 【解析】 为了叙述方便,先在各圆圈内填上字母,如下图(2).由条件得出以下四个算式:(2)h gf ed c baa+b+c=14(1) c+d+e=14 (2) e+f+g=14 (3)a+h+g=14 (4)由(1)+(3),得:a+b+c+e+f+g=28,(a+b+c+d+e+f+g+h )-(d+h )=28,d+h=(1+2+3+4+5+6+7+8)-28=8,由(2)+(4),同样可得b+f=8, 又1,2,3,4,5,6,7,8中有1+7=2+6=3+5=8.又1要出现在顶点上,d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性,不妨设b=2,f=6,d=3,h=5. a ,c ,e ,g 可取到1,4,7,8若a=1,则c=14-(1+2)=11,不在1,4,7,8中,不行.若c=1,则a=14-(1+2)=11,不行.若e=1,则c=14-(1+3)=10,不行.若g=1,则a=8,c=4,e=7.说明:例题为封闭型数阵,由它的分析思考过程可以看出,确定各边顶点所应填的数为封闭型数阵的解题突破口.【答案】【例 3】在如图6所示的○内填入不同的数,使得三条边上的三个数的和都是12,若A、B、C的和为18,则三个顶点上的三个数的和是。
小学奥数 数阵图

数阵图数阵图:就是将一些数按照一定要求排列而成的某种图形。
分为:封闭型、辐射型、复合型。
例如:特点:直线上的数字和相等。
名词:边和,重叠数(阵眼)(★★)将1~7这七个数字,分别填入图中各个○内,使每条线段上的三个○内数的和都等于14。
(★★★)把1~9这9个数分别填入下图的圆圈中,使得每条直线上的3个数的和都相等。
(★★★)将1~8这8个数分别填入下图中,使两个大圆上4个数的和都相等,那么这个和最大=______。
(★★★)请将1、2、4、6这四个数填入到下图中各空白区域内,使得每个圆圈里的四个数字和都等于15。
【铺垫】(★★)把1至8分别填入图的八个方格内,使得各列上两个数之和都相等,各行四个数之和也相等。
(★★★★★)请将数字1、2、3、4、5、6、7填在下图,使得每个圆圈上的三个数字之和与每条直线上的三个数之和相等。
【超常大挑战】(★★★★★)有一个长方形的城堡,四周有10个掩体。
守城的士兵有10件武器,各种武器的威力如下表。
为了使城堡四边上的武器威力总数都相同,并且尽量大,应如何在十个掩体中配备武器?【知识大总结】数阵图1.特点,新名词。
2.口诀1:数边和,看重叠,列等式,整除关系推一推等式:边和×次数=数字和+重叠数×(次数-1)本质:找边和与数字和、重叠数三者关系难点:重叠数有几个,各自用了多少次。
3.口诀2:掐头、去尾、取中间,首尾配对组相等。
适用:等差数列填入到放射型数阵图中。
4.复合型数阵图,先满足部分,保证不破坏已有边和前提下,微调,满足全部。
【今日讲题】例2,例3,例5【讲题心得】___________________________________________________________________________________________ ___________________________________________________________________________________________ __________________________________________________________________________________________。
四年级奥数之《数阵图》 教参+配套练习 覆盖面广,类型全面,针对性强,可直接下载

数阵图
数阵图,就是把一些数按照一定的规则,填在某一特定图形的规定位置上,这种图形,我们称它为数阵图。
数阵图的种类繁多、绚丽多彩,这里我们将主要介绍两种数阵图,即封闭型数阵图和开放型数阵图。
解答这类问题时,常用以下知识:
等差数列的求和公式:总和﹦(首项+末项)x项数÷2
计算中的奇偶问题:
奇数±奇数﹦偶数
偶数±偶数﹦偶数
奇数±偶数﹦奇数
10以内数字有如下关系:
(1)1+9=2+8=3+7=4+6
(2)1+8=2+7=3+6=4+5
(3)2+9=3+8=4+7=5+6
在解答这类问题时,要善于确定所求的和与关键数字间的关系式,用试验的方法,找到相等的和与关键数字;要会对基本解中的数进行适当调整,得到其他的解,从而培养自己的观察能力、思维的灵活性和严密性。
例1:
把1,2,3,4,5,6这六个数填在下图的6个○中,使每条边上的三个数之和都等于9。
例2:
把1—12这十二个数,分别填在下图中正方形四条边上的十二个○内,使每条边上四个○内数的和都等于22,试求出一个基本解。
随堂练习1
1、(1)将5—10这六个数字分别填入左下图中三角形三条边的六个○内,使每条边上三个○内数的和都是24。
二年级奥数.计算.数阵图

数阵图是小学奥数阶段一个很重要的专题。
在这节课中,我们的教学目标就是让学生初步认识数阵,并能通过一系列的练习,找到解数阵的一般方法。
今天我们重点研究的方法,就是通过找中心数来解题,会根据题目中给出的已知条件来求中心数。
在例题的设计中,我们也是层层深入,让学生能通过简单的例题来发现规律找到解题的方法,通过例题难度的加深来拓展应用。
希望这节课的学习能使学生的思维能力得到培养,能让学生对数阵产生兴趣,为今后的继续学习奠定基础。
在神奇的数学王国里,有一类非常有趣的数学问题,它变化多端,引人入胜, 奇妙无穷.它就是数阵图.到底什么是数阵图呢?我们先观察下面两个图:数阵图就是将一些数按照一定要求排列而成的某种图形.它一般分为辐射型(图1)和封闭型(2)两种.要把一些数字按一定的规则填入图形中,并不是一件容易的事,这需要我们多观察,找关系,仔细推理才能完成.下面我们就一起来找一找数阵图的秘密吧【例1】 把1,2,3,4,5这 5个数分别填入图中的圆圈内,(1)使得横行 3个数的和与竖列 3个数的和都等于10。
(2)使得横行3个数的和与竖列3个数的和都相等.一共有多少种不同的填法?知识框架数阵图例题精讲【例2】把4~8这五个数填入图中(已填入6),使两条直线上的三个数之和相等.【例3】把1,2,3,4,5,6,7 这7个数分别填入圆圈中,使得每条直线上的3个数的和等于12.【例4】把1~9这九个数字填入下列圆圈内,使每条线上的三个圆圈内的数之和都等于15。
【例5】1~7这七个数分别填入图中的各○内,使每条直线上三个○里数的和相等.一共有多少种方法?【例6】把1~9这9个数分别填入下图的圆圈中,使得每条直线上的3个数的和都等于15。
【例7】 将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.【例8】 把1,2,3,4,5,6这6个数分别填入右图的6个圆圈中,(1)使得三角形每条边上的3个数的和都等于10.(2)使得三角形每条边上的三个数之和都相等.还有几种不同的填法?【例9】 将1、2、3、4、5、6、7、8、9这9个数字分别填入图中的小圆圈里,使得每条边上4个数字的和是17.【例10】 把1~8这八个数分别填入图中的圆内,使每条线上的三个数相加的和等于12.【随练1】 将1、2、3、4、5、6六个数填在图中的空灯里,使每个大圆上的四盏灯里的数相加都等于14.课堂检测【随练2】把2、3、4、5、6、7、8、9、10填入方格里,使每一横行、每一竖行、每一斜行的3个数的和都是18.【作业1】在下面的○里填上适当的数,使每条线上的三个数之和都是16.【作业2】在空格内填入适当的数,使得每行、每列和两条对角线上的三个数的和都为18.【作业3】在空格内填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.【作业4】把数字1、2、3、4、5分别填入下图中的方格内,使横行3个数的和与竖列3个数的和都等于9.【作业5】把5,6,7,8,9这5个数填在下图的◇内,使横行、竖列3个数的和都相等.家庭作业【作业6】将1~9填入小方格里,使横行和竖列上五个数之和相等.【作业7】把10,20,30,40,50,60,70这7个数填在圆圈里,使每条直线上和每个圆周上的三个数的和都是120.【作业8】把3、5、7、9、11、13、15这7个数分别填入图中的圆圈内,使每条直线上的3个数都等于27.【作业9】把1~6填入○里,使每个圆圈上的四个数之和都相等16.【作业10】把4~9这6个数分别填入下图的6个圆圈中,使得三角形每条边上的3个数的和都等于21.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学奥数16数阵图1.10.5数阵图1.10.5.1基础知识数阵是由幻方演化出来的另一种数字图。
幻方一般均为正方形。
图中纵、横、对角线数字和相等。
数阵则不仅有正方形、长方形,还有三角形、圆、多边形、星形、花瓣形、十字形,甚至多种图形的组合。
变幻多姿,奇趣迷人。
一般按数字的组合形式,将其分为三类,即辐射型数阵、封闭型数阵、复合型数阵。
数阵的特点是:每一条直线段或由若干线段组成的封闭线上的数字和相等。
它的表达形式多为给出一定数量的数字,要求填入指定的图中,使其具备数阵的特点。
解数阵问题的一般思路是:1.求出条件中若干已知数字的和。
2.根据“和相等”,列出关系式,找出关键数——重复使用的数。
3.确定重复用数后,对照“和相等”的条件,用尝试的方法,求出其他各数。
有时,因数字存在不同的组合方法,答案往往不是唯一的。
1.10.5.2辐射型数阵例1 将1~5五个数字,分别填入下图的五个○中,使横、竖线上的三个数字和都是10。
解:已给出的五个数字和是:1+2+3+4+5=15题中要求横、竖每条线上数字和都是10,两条线合起来便是20了。
20-15=5,怎样才能增加5呢?因为中心的一个数是个重复使用数。
只有5连加两次才能使五个数字的和增加5,关键找到了,中心数必须填5。
确定中心数后,按余下的1、2、3、4,分别填在横、竖线的两端,使每条线上数的和是10便可。
例2将1~7七个数字,分别填入图中的各个○内,使每条线上的三个数和相等。
解:图中共有3条线,若每条线数字和相等,三条线的数字总和必为3的倍数。
设中心数为a,则a被重复使用了2次。
即,1+2+3+4+5+6+7+2a=28+2a,28+2a应能被3整除。
(28+2a)÷3=28÷3+2a÷3其中28÷3=9…余1,所以2a÷3应余2。
由此,便可推得a只能是1、4、7三数。
当a=1时,28+2a=30 30÷3=10,其他两数的和是10-1=9,只要把余下的2、3、4、5、6、7,按和为9分成三组填入两端即可。
同理可求得a=4、a=7两端应填入的数。
例3将从1开始的连续自然数填入各○中,使每条线上的数字和相等。
解:图中共有三条线,若每条线数字和相等,三条线的数字总和必为3的倍数。
设中心数为a,a被重复使用了两次,即:1+2+3+……+10+2a=55+2a,55+2a应能被3整除。
(55+2a)÷3=55÷3+2a÷3其中,55÷3=18余1,所以2a÷3应余2。
由此,可推知a只能在1、4、7中挑选。
在a=1时,55+2a=57,57÷3=19,即中心数若填1,各条线上的数字和应为19。
但是除掉中心数1,在其余九个数字中,只有两组可满足这一条件,即:9+7+2=18,8+6+4=18,7+5+3=15所以,a不能填1。
经试验,a=7时,余下的数组合为12(19-7=12),也不能满足条件。
因此,确定a只能填4。
例4将1~9九个数字,填入下图各○中,使纵、横两条线上的数字和相等。
解:1~9九个数字和是:1+2+3+……+9=5×9=45,把45平分成两份:45÷2=22余1。
这就是说,若使每行数字和为23,则需把1重复加一次,即中心数填1;若使数字和为24,中心数应填3……。
总之,因45÷2余数是1,只能使1、3、5、7、9各个奇数重复使用,才有可能使横、竖行的数字和相等。
因而,此题可有多种解法。
但中心数必须是9以内的奇数。
例5 将1~11十一个数字,填入下图各○中,使每条线段上的数字和相等。
解:图中共有五条线段,全部数字的总和必须是5的倍数,每条线上的数字和才能相等。
1~11十一个数字和为66,66÷5=13余1,必须再增加4,可使各线上数字和为14。
共五条线,中心数重复使用4次,填1恰符合条件。
此题的基本解法是:中心数重复使用次数与中心数的积,加上原余数1,所得的和必须是5的倍数。
据此,中心数填6、11均可得解。
1.10.5.3封闭型数阵例1把2、3、4、5、6、7六个数字,分别填入○中,使三角形各边上的数字和都是12。
解:要使三角形每边上的数字和都是12,则三条边的数字和便是12×3=36,而2+3+4+5+6+7=27,36与27相差9。
三个角顶的数字都重复使用两次,只有这三个数字的和是9,才能符合条件。
确定了角顶的数字,其他各数通过尝试便容易求得了!这题还可有许多解法,上图只是其中一种。
例2把1~9九个数字,分别填入下图○中,使每边上四个数的和都是21。
解:要使三角形每条边上的数字和是21,则三条边的数字和便是:21×3=63。
而1~9九个数字的和只有45。
45比63少18,只有使三角形三个顶角的数字和为18,重复使用两次,才能使总和增加18。
所以应确定顶点的三个数。
下面是填法中的一种。
确定了顶角的数后,其他各数便容易了。
例3下图是四个互相联系的三角形。
把1~9九个数字,填入○中,使每个三角形中数字的和都是15。
解:每个三角形数字和都是15,四个三角形的数字和便是:15×4=60,而1~9九个数字和只有45。
45比60少15。
怎样才能使它增加15呢?靠数字重复使用才能解决。
中间的一个三角形,每个顶角都联着其他三角形,每个数字都被重复使用两次。
因此,只要使中间的一个三角形数字和为15,便可以符合条件。
因此,它的三个顶角数字,可以分别为:1、9、5 2、8、5 2、7、6 4、6、5及2、9、4 3、8、4 3、7、5 8、6、1。
把中间的三角形各顶角数字先填出,其他各个三角形便容易解决了。
前页下图是其中的一种。
例4 把2~10九个数字,分别填入下图○中,使每条直线上的三个数和为15。
解:2~10九个数字的和为:2+3+4+……+10=6×9=54若排成每个三角形每边的数字和都是15,图中含有每边都三个数字的三角形有两个,共六条边,数字总和应是15×6=90。
54比90少36。
在外围的六个数都被重复使用了两次,它们又分属于两个三角形。
所以,每个三角形三个顶角的数和应为:36÷2=18。
这样,便可以先填外三角形三个顶角的数。
三个数和为18的有很多组,可以通过试验筛选出适宜的一组。
填好了外围三角形各个数后,里面的三角形,因为顶角的数已知,其他各数便容易填写了。
上面是填法中的一种。
例5 把1~10十个数字,分别填入下图○中,使每个三角形三个顶角的三个数字和相等。
解:图中有三个三角形,顶角数字互不联系,中心的一个数独立于各个三角形之外。
因此,要使各三角形顶角的数字和相等。
去掉中心数后,数字总和应是3的倍数,而且三角形顶角的数字三组中不能出现重复。
如:以10为中心数,可填为如上图样。
例6 将1~12分别填入下图○中,使图中每个三角形周边上的六个数的和都相等。
解:图中共有四个三角形,共有六个边。
1~12的数字和是78。
每条边上的数字和应为:78÷6=13。
这样,我们可以推想:因为内部的三条边都被重复计算两次,只要每个数增加1,十二个数的总和便增加6,它们同样可以填出来,因而,本题的解法是很多的。
7、把127125433212161413121、、、、、、、、九个数分别填入下图○中,使每条直线上的三个数的和都相等。
解:九个分数排成方阵,使纵、横、对角线的三个数和相等,这已经符合幻方的要求了,因此,可以按幻方的制作方法求解。
这十二个分数,按从小到大的顺序排列是:433212721125314161121、、、、、、、、 把它们按序排列为斜方形:将上、下两数,左、右两数对调,再把中间四数向外拉出,这样重新组成的数阵,便是求得的解了。
例8 将1~8八个数字,分别填入下图○中,使每个小三角形顶点上三数之和为12。
解:图中共有四个小三角形,每个三角形顶点数字的和若都是12,数字总和便是12×4=48,可是1~8八个数字总和只有36。
36比48少12。
只有靠共用顶角上数的重复使用,才能解决。
因此,必须把四个公用顶角的数字和填成12。
把1~8八个数四个一组,和为12的有:6+3+2+15+4+2+1上述两组中,经验证,只有6+3+2+1可以作公用顶点的数字。
例9 在下图五个○内,各填入一个自然数,使图中八个三角形中顶点的数字和各不相同。
求能满足这个条件的自然数中最小的五个数。
解:能满足使八个三角形顶点数字和各不相同的任意自然数有很多组,但自然数中能满足这个条件的最小自然数却只有一组。
最小的一组自然数中的五个数,若有两个相同的,其中三个数的和可以多到有7个不同值,因此,五个数互不相同。
如果这五个数是1,2,3,4,5,则其中三个数的和有如下组合方式:1+2+3=6 2+3+4=9 3+4+5=121+2+4=7 1+3+4=8 2+3+5=102+4+5=11这样,总共只有七种不同的和,而图中共八个三角形,可知1,2,3,4,5五个自然数不能满足条件。
例10 在下列图中三个正方形中,每个正方形的四个顶点上,只填入1,2,3,4四数,使图中八个三角形顶点数字和互不相同。
解:图中,顶角在大正方形边上的四个三角形,顶角都分别为两个三角形共用,只有正方形的四个角分别只属于一个三角形,所以,四个三角形顶点数字的和应等于:(1+2+3+4)×3=3030不是4的倍数,因而,外面的四个三角形顶点数字和不可能相等。
同理,里面的四个三角形顶点数字和也不可能相等。
题中要求,每个三角形顶点数字和不相同,1~4四个数之和最小值是1+1+2=4,最大值是4+4+3=11,这样共可组成八组数,将八组数分别填入各个三角形顶点,便可符合条件。
例11 将1~8八个数字,分别填入下图○中,使每个面的四个数和相等。
解:数字图是个正立方体,共有六个面。
每个面四个顶点上的数都是三个面重复使用的。
1~8八个数的数字总和是:1+2+3+……+8=36因为每个顶点的数都被重复使用三次,所以六个面的数字总和是:36×3=108每个面的数字和便是:108÷6=18这样,便可填为下图或其他形式。
