过程设备设计计算题
过程设备设计期末考卷及答案

过程设备设计期末考卷一、选择题(每题2分,共20分)1. 过程设备设计的主要目的是()。
A. 提高设备性能B. 降低生产成本C. 保证设备安全D. 满足生产工艺要求2. 下列哪种设备不属于过程设备?()A. 反应釜B. 蒸馏塔C. 风机D. 泵3. 过程设备设计的基本原则不包括()。
A. 安全性B. 可靠性C. 经济性D. 实用性A. 生产能力B. 操作压力C. 设备材质D. 设备形状5. 下列哪种设备适用于高温、高压工况?()A. 球罐B. 圆柱形储罐C. 立式储罐D. 卧式储罐6. 过程设备设计中,下列哪种应力属于一次应力?()A. 温差应力B. 外压应力C. 重力应力D. 装饰应力A. GB 150B. ASMEC. JB 4732D. API8. 在过程设备设计中,下列哪种因素对设备的疲劳寿命影响最大?()A. 材料性能B. 设备尺寸C. 工作温度D. 工作压力9. 下列哪种设备密封形式适用于有毒、易燃介质?()A. 填料密封B. 垫片密封C. 橡胶密封D. 齿轮密封10. 过程设备设计中,下列哪种结构不利于设备的散热?()A. 折流板B. 挡板C. 支承D. 拉杆二、填空题(每题2分,共20分)1. 过程设备设计的主要内容包括:____、____、____、____和____。
2. 压力容器的设计压力分为三个等级:____、____和____。
3. 设备的公称直径是指____的直径。
4. 过程设备设计中,常用的焊接方法有:____、____、____和____。
5. 在设备设计中,为了保证设备的强度和稳定性,通常需要对____、____、____和____等部位进行加强。
6. 设备的腐蚀裕量应根据____、____和____等因素确定。
7. 过程设备设计中,常用的法兰标准有:____、____和____。
8. 设备的绝热层分为____、____和____三个等级。
9. 设备的抗震设计应考虑____、____和____等因素。
过程设备设计第五到八章习题答案

第五章储运设备1 设计双鞍座卧式容器时,支座位置应按哪些原则确定?说明理由。
双鞍座卧式储罐的受力状态可简化为受均布载荷的外伸简支梁,由材料力学可知当外伸长度A=0.207时,跨度中央的弯矩与支座截面处弯矩绝对值相等,所以一般近似取A≤0.02L,其中L为两封头切线间的距离,A为鞍座中心线至封头切线间距离2)当鞍座邻近封头时,封头对支座处的筒体有局部加强作用,为充分利用加强效应,在满足A≤0.2L下应尽量满足A≤0.5R0 (R0为筒体外径)3卧式容器支座截面上部有时出现“扁塌”现象是什么原因?措施?原因:当支座截面处的圆筒不设加强圈,且A<0.5Ri时,由于支座处截面受剪力作用而产生周向弯矩,在周向弯矩作用下,导致支座处圆筒上半部发生变形,产生所“扁塌”现象。
措施:1)设置加强圈2)A<0.5Ri,使支座靠近封头布置,利用加强圈或封头的加强作用3)补设加强圈,且A<0.5Ri4 双鞍座卧式容器中应计算哪些应力?分析这些应力如何产生的?(1)圆筒上的轴向应力,由轴向弯矩引起2)支座截面处圆筒和封头上的切应力和封头的附加拉伸应力,由横向剪力引起3)支座截面处圆筒的周向弯曲应力,由截面上切应力引起4)支座截面处圆筒的周向压缩应力,通过鞍座作用于圆筒上的载荷所导致5 鞍座包角对卧式容器筒体应力和鞍座自身强度有何影响?鞍座包角θ时鞍式支座设计时需要的一个重要参数,其大小不仅影响鞍座处圆筒截面上的应力分布,而且也影响卧式储罐的稳定性及储罐支座系统的重心高低。
鞍座包角小,则鞍座重量轻,但是储罐一支座系统的重心较高,且鞍座处筒体上的应力较大。
常用包角有120,135,1506 在什么情况下应对双鞍座卧式容器进行加强圈加强?如卧式储罐支座因结构原因不能设置在靠近封头处,且圆筒不足以承受周向弯矩时,需设置加强圈以便与圆筒一起承载。
7 球形储罐特点?设计球罐时应考虑哪些载荷?各种储罐体形式的特点球形储罐应力分布均匀,承载能力大,设计时应考虑压力载荷,重量载荷,风载荷,雪载荷,地震载荷,和环境温度变化引起的载荷。
过程设备设计习题解答(Syni修改)

一氧化碳一、补充作业 1:划定下列容器类别序号设计压力 p() 介质容器(m 3) 设计温度(℃) 容器类别10.6 4 5020.5 氧气 10 50 31.6臭氧4050·压 力 容 器 分 类 方法:①先按照介质特性,选择相应的分类图,②再根据设计压力 p (单位)和容积 V (单位 m 3), 标出坐标点,③确定容器类别。
第一组 是易燃性质,容器类别是类;第二组 属于 类;第三组 高度毒性,属于 类。
二、补充作业 2:压力容器十大主要受压元件1.壳体;②封头(端盖);③膨胀节;④设备法兰;⑤球罐球壳板;⑥换热器的管板; ⑦换热管;⑧M36(含 36)以上的设备主螺柱;⑨公称直径大于或等于250 的接管;⑩公称 直径大于或等于 250 的管法兰三、问答题:国外产品图纸可否采用我国的材料及 150 标准制造压力容器?答: 不能,因为:1.安全系数 n 数值不一样,则应力许用值[σ ]t 不一样,计算壁厚不一 样;2.钢材几何尺寸偏差不一样,国外小一些,负偏差小;3.钢材化学成分和机械性能不 一样,国外严,国内松;4.制造、检验要求不一样,如,水压试验=1.5P[σ ]/[σ ]t ,而 我国水压试验=1.25P[σ ]/[σ ]t第二章一、一壳体成为回转薄壳轴对称的条件是什么?⑴满足薄壳条件: (t / R)≤0.1;⑵结构对称:结构的几何形状对称于回转轴;⑶载荷对 称:壳体任一横截面上的载荷对称于回转轴,但是沿轴线方向的载荷可以按照任意规律化。
⑷边界对称:支承壳体的边界对称于轴线。
⑸材质对称:壳体的材料性质对称于轴线。
二、试分析标准椭圆形封头采用长短轴之比 a / 2 的原因?原因是其应力的分布特点及加工工艺性: ⑴应力绝对值从小到大为:a /b <2 → a / 2 → a / b >2 ;⑵加工工艺性从易到难为:a /b >2 → a / 2 → a / b <2 ;可以看到,标准椭圆形封头的应力分布及加工工艺性比其它的非标准椭圆形封头综合性好。
过程设备设计课后习题答案

习题1. 一内压容器,设计(计算)压力为0.85MPa ,设计温度为50℃;圆筒内径D i =1200mm ,对接焊缝采用双面全熔透焊接接头,并进行局部无损检测;工作介质列毒性,非易燃,但对碳素钢、低合金钢有轻微腐蚀,腐蚀速率K ≤0.1mm/a ,设计寿命B=20年。
试在Q2305-A ·F 、Q235-A 、16MnR 三种材料中选用两种作为圆筒材料,并分别计算圆筒厚度。
解:p c =1.85MPa ,D i =1000mm ,φ=0.85,C 2=0.1×20=2mm ;钢板为4.5~16mm 时,Q235-A 的[σ]t =113 MPa ,查表4-2,C 1=0.8mm ;钢板为6~16mm 时,16MnR 的[σ]t = 170 MPa ,查表4-2,C 1=0.8mm 。
材料为Q235-A 时:[]mmC C ppD t1412.524mm 28.0724.99.724mm85.185.01132100085.12n 21n ==++=++≥=-⨯⨯⨯=-=δδδφσδ取材料为16MnR 时:[]mmC C ppD t109.243mm 28.0443.6mm443.685.185.01702100085.12n 21n ==++=++≥=-⨯⨯⨯=-=δδδφσδ取2. 一顶部装有安全阀的卧式圆筒形储存容器,两端采用标准椭圆形封头,没有保冷措施;内装混合液化石油气,经测试其在50℃时的最大饱和蒸气压小于1.62 MPa (即50℃时丙烷饱和蒸气压);圆筒内径D i =2600mm ,筒长L=8000mm ;材料为16MnR ,腐蚀裕量C 2=2mm ,焊接接头系数φ=1.0,装量系数为0.9。
试确定:○1各设计参数;○2该容器属第几类压力容器;○3圆筒和封头的厚度(不考虑支座的影响);○4水压试验时的压力,并进行应力校核。
解:○1p=p c =1.1×1.62=1.782MPa ,D i =2600mm ,C 2=2mm ,φ=1.0,钢板为6~16mm 时,16MnR 的[σ]t = 170 MPa ,σs =345 MPa ,查表4-2,C 1=0.8mm 。
过程设备设计过程设备设计试卷(练习题库)(2023版)

过程设备设计过程设备设计试卷(练习题库)1、所谓高温容器是指下列哪一种:()2、GB150适用下列哪种类型容器:()3、一个载荷稳定均匀的内压厚壁圆筒最好采用哪种设计准则:()4、有关《容规》适用的压力说法正确的是:()5、=0.2MPam3的低压容器应定为几类容器〃target—_b1ank〃>毒性为高度或极度危害介质PV>=0.2MPam3的低压容器应定为几类容器:()6、影响过程设备安全可靠性的因素主要有:材料的强度、韧性和与介质的相容性;设备的刚度、抗失稳能力和密封性7、毒性为中度危害的化学介质最高容许质量浓度为:()8、内压容器中,设计压力大小为50MPa的应划分为:()9、下列属于分离压力容器的是:()10、在厚壁圆筒中,如果由内压引起的应力与温差所引起的热应力同时存在,下列说法正确的是:()11、通过对最大挠度和最大应力的比较,下列关于周边固支和周边简支的圆平板说法正确的是:()12、下列有关受均布外压作用圆筒的失稳情况的叙述,错误的是:()13、下列不属于提高厚壁圆筒屈服承载能力的措施为:()14、下列有关不连续应力的叙述,错误的为:()15、下列关于局部载荷说法正确的是:()16、外压的短圆筒,失稳时,出现的波形个数为:()17、下列关于薄壳应力分析中应用的假设,错误的是:()18、关于薄圆平板的应力特点,下列表述错误的是:()19、在压力容器制造过程中应用最广的焊接方法是:()20、一般—容器的平盖制造用的钢材是:()21、在焊接中力学性能得到明显改善,是焊接接头中组织和性能最好的区域是:()22、下列不属于压力容器焊接结构的设计应遵循的原则的是:()23、下列焊接接头中可能出现的缺陷,最危险的是:()24、下列金属会产生低温变脆的是:()25、磁粉检测属于:O26、下列关于硫化学成分在钢材中的作用说法正确的是:()27、钢材的可焊性主要取决于它的化学成分,其中影响最大的是:()28、金属塑性变形可分为热变形和冷变形,其中分界线是:()29、下列关于氢腐蚀与氢脆的说法错误的是:()30、平垫密封属于:()31、同一承载能力下,仅受内压作用的圆筒按哪种计算方法计算的壁厚最薄: ()32、下列有关压力容器失效形式的叙述,正确的是:()33、下列有关压力容器失效判据与设计准则的叙述,错误的是:()34、在按弹性失效设计准则进行内压厚壁圆筒设计时,采用不同的强度理论会得到不同的结果,下列叙述错误的是:(35、下列有关圆筒设计的叙述,正确的是:()36、下列有关压力容器设计技术参数的叙述,正确的是:()37、下列有关焊接接头系数和材料设计系数的表述错误的是:()38、下列有关压力容器密封装置的叙述错误的是:()39、设计卧式储存罐双鞍座支承时,两支座的状态应采用:()40、低温球罐的支柱与球壳连接处最好采用:()41、卧式储罐发生扁塌现象的根本原因是:()42、随着石油业的发展,在大型球罐上最常采用的罐体组合方式是:()43、不属于管壳式换热器的是O44、常见的管壳式换热器和板式换热器属于以下哪种类型的换热器:()45、下面那种类型的换热器不是利用管程和壳程来进行传热的:()46、下列关于管式换热器的描述中,错误的是:O47、下列措施中,不能起到换热器的防振效果的有:()48、介质危害性有多种,其中影响压力容器分类的是:()49、下列属于第三类压力容器的是:()50、《容规》适用于具备下列哪些条件的压力容器:()51、过程设备在生产技术领域中应用十分广泛,是化工、炼油、轻工、交通、食品、制药、冶金、纺织、城建、海洋工52、下列关于压力容器的分类错误的是:()53、下列哪些是无力矩理论的应用条件:()54、《压力容器安全技术规程》适用于同时具备下类条件的压力容器:()55、下列对GB150,JB4732和JB/T4735三个标准的有关表述中,正确的有:O56、下列哪些是压力容器的安全附件:()57、按承载方式分类,压力容器可分为:()58、下列压力容器分类正确的是:()59、为降低局部应力,下列结构设计合理的是:()60、承受内压的薄椭球壳应力的大小与哪些因素有关:()61、下列哪些是较常用的实验应力分析方法:()62、深水容器由于长期工作于水底并承受较大的外压,常会出现以下几种失效方式:()63、不同结构组合壳的连接边缘处存在有边缘应力,边缘应力的特性有:O64、内压作用下,下列关于单层厚壁圆筒中应力分部规律的表述正确的有: ()65、下列有关热应力的说法正确的有:()66、下列关于形状缺陷对圆筒稳定性影响说法正确的是:()67、通过合理地设计结构,可以降低局部应力,例如以下措施正确的有:O68、下列关于厚壁圆筒应力分析正确的是:()69、下列选项中,那些属于高温下材料性能的劣化:()70、局部腐蚀有哪些形式:()71、属于应力腐蚀开裂的特征的有:()72、蠕变的结果是使压力容器材料产生如下哪些变化:()73、下列属于非破坏性检验的有:()74、焊接接头的组成一般有:()75、按化学成份分类,压力容器用钢可分为:()76、下列关于钢材化学成分的说法正确的是:()77、下列关于压力容器常用钢材形状说法正确的是:()78、压力容器的工作环境对材料性能的影响因素,主要有:()79、下列关于焊接应力和变形的说法正确的有:()80、为减少焊接应力和变形,可采取的措施有:()81、压力容器局部腐蚀的主要形式有:()82、下列说法中,正确的有:()83、压力容器失效的最终表现形式均为:()84、—密封的特点有O85、椭圆形封头是目前中、低压容器中应用较多的封头之一,下列关于椭圆形封头说法正确的有:()86、下列说法中选项正确的是:()87、压力容器接管补强结构通常采用局部补强结构,主要有:()88、关于压力容器应力中二次应力说法错误的是:()89、以下载荷属于交变载荷的有:()90、下列有关压力容器设计准则的叙述,正确的有:()91、为提高外压圆筒稳定性,需设置加强圈,下列有关加强圈的设计,正确的有:()92、压力容器封头较多,下列叙述正确的有:()93、下列属于提高—密封性能的措施有:()94、安全阀的优点包括:()95、在立式容器支座中,中小型直立容器常采用O高大的塔设备则广泛采用(),大型卧式储存采用()96、韧性断裂的原因包括:()97、按照换热设备热传递原理或传递方式进行分类可以分为以下几种主要形式:()98、下面属于管壳式换热器结构的有:()99、引起流体诱导振动的原因有:()100、传热强化的措施有:()101、下列关于管壳式换热器的描述中,错误的是:()102、压力容器主要是由筒体、封头、开孔与接管、支座以及安全附件组成。
过程设备设计课后习题答案

习题1. 一内压容器,设计(计算)压力为0.85MPa ,设计温度为50℃;圆筒内径D i =1200mm ,对接焊缝采用双面全熔透焊接接头,并进行局部无损检测;工作介质列毒性,非易燃,但对碳素钢、低合金钢有轻微腐蚀,腐蚀速率K ≤0.1mm/a ,设计寿命B=20年。
试在Q2305-A ·F 、Q235-A 、16MnR 三种材料中选用两种作为圆筒材料,并分别计算圆筒厚度。
解:p c =1.85MPa ,D i =1000mm ,φ=0.85,C 2=0.1×20=2mm ;钢板为4.5~16mm 时,Q235-A 的[σ]t =113 MPa ,查表4-2,C 1=0.8mm ;钢板为6~16mm 时,16MnR 的[σ]t = 170 MPa ,查表4-2,C 1=0.8mm 。
材料为Q235-A 时:[]mmC C ppD t1412.524mm 28.0724.99.724mm85.185.01132100085.12n 21n ==++=++≥=-⨯⨯⨯=-=δδδφσδ取材料为16MnR 时:[]mmC C ppD t109.243mm 28.0443.6mm443.685.185.01702100085.12n 21n ==++=++≥=-⨯⨯⨯=-=δδδφσδ取2. 一顶部装有安全阀的卧式圆筒形储存容器,两端采用标准椭圆形封头,没有保冷措施;内装混合液化石油气,经测试其在50℃时的最大饱和蒸气压小于1.62 MPa (即50℃时丙烷饱和蒸气压);圆筒内径D i =2600mm ,筒长L=8000mm ;材料为16MnR ,腐蚀裕量C 2=2mm ,焊接接头系数φ=1.0,装量系数为0.9。
试确定:○1各设计参数;○2该容器属第几类压力容器;○3圆筒和封头的厚度(不考虑支座的影响);○4水压试验时的压力,并进行应力校核。
解:○1p=p c =1.1×1.62=1.782MPa ,D i =2600mm ,C 2=2mm ,φ=1.0,钢板为6~16mm 时,16MnR 的[σ]t = 170 MPa ,σs =345 MPa ,查表4-2,C 1=0.8mm 。
过程设备设计第5章课后习题试题

第五章储存设备单选题5.1双鞍座设计卧式储存罐双鞍座支承时,两支座的状态应采用:()A.两个都固定B.两者均可移动C.一个固定,一个移动D.以上均可5.2柱式支座低温球罐的支柱与球壳连接处最好采用:()A.接连接结构形式B.加托板结构C.U型柱结构形式D.支柱翻边结构5.3扁塌现象卧式储罐发生扁塌现象的根本原因是:()A.支座处截面受剪力作用而产生周向弯矩B.圆筒上不设置加强圈C.支座的设置位置不适合D.设计压力过高5.4球罐随着石油业的发展,在大型球罐上最常采用的罐体组合方式是:()A.纯桔瓣罐体B.足球瓣式罐体C.混合式罐体D.两个半球组成的罐体单选题5.1 C 单选题5.2 C 单选题5.3 A 单选题5.4 C无5.1 储罐的形式主要有卧式,立式和球形储罐,储存介质的性质是选择储罐形式和储存系统的一个重要因素。
5.2 鞍座包角越小,鞍角重量越轻,且储罐——支座系统的中心降低。
5.3 工程上可以将双鞍座卧式储存罐简化为均布载荷的外伸简支梁。
5.4 球罐支座中裙式支座用得最为广泛。
5.5 柱式支座的主要缺点是球罐的重心高,稳定性差。
5.6 需要开检查孔时,由于特殊原因而不能开设时,应相应缩短检查周期,或者对全部纵向环向焊缝作100%无损检测。
5.7 球罐接管除工艺特殊要求外,应尽量集中在上下极板上。
5.8 在用水压测试容器壁厚时,校合压力一般取1.25P.5.9 按形状改变比能屈服失效判剧计算出的内壁初始屈服压力和实际测量值最为接近。
判断题5.1 T判断题5.2 F判断题5.3 T判断题5.4 F判断题5.5 T判断题5.6T判断题5.7 T判断题5.8 T判断题5.9 T思考题5.1 设计双鞍座卧式容器时,支座位置应该按照那些原则确定?试说明理由。
5.2 双鞍座卧式容器受力分析与外伸梁承受均布载荷有何相同何不同,试用剪力图和弯距图比较。
5.3 “扁塌”现象的原因是什么?如何防止这一现象出现?5.4 双鞍座卧式容器设计中应计算那些应力?如何产生的?5.5 鞍座包角对卧式容器筒体应力和鞍座自身强度有何影响?5.6 在什么情况下应对卧式容器进行加强圈加强?5.7 球形储罐有哪些特点?设计球罐时应考虑那些载荷?各种罐体型式有何特点?5.8 球形储灌采用赤道正切柱式支座时,应遵循那些准则?5.9 液化气体存储设备设计时如何考虑环境对它的影响?思考题5.1根据JB4731规定,取A小于等于0.2L,最大不得超过0.25L,否则容器外伸端将使支座界面的应力过大。
过程设备设计第4章习题

C.二次应力是指由相邻部件的约束或结构的自身约束所引起的正应力或切应力。 D.二次应力是局部结构不连续性和局部热应力的影响而叠加道一次应力之上的应力增量 4.8 交变载荷 以下载荷属于交变载荷的有: ( ) A.压力波动 B.开车停车 C.加热或冷却时温度变化引起的热应力变化 D.振动或容器接管引起的附加载荷 4.9 设计准则 下列有关压力容器设计准则的叙述,正确的有: ( ) A.弹性失效设计准则以容器整个危险面屈服作为实效状态。 B.弹塑性失效设计准则认为只要载荷变化范围达到安定载荷,容器就失效。 C.弹性失效设计准则较塑性失效设计准则更保守。 D.爆破失效设计准则认为压力达到全屈服压力时容器失效。 4.10 加强圈 为提高外压圆筒稳定性,需设置加强圈,下列有关加强圈的设计,正确的有: ( ) A.加强圈的最小间距应小于失稳临界长度。 B.在设计过程中,有可能通过增加加强圈的数量使圆筒厚度减薄。 C.加强圈与圆筒的连接可采用连续的或间断地焊接。 D.加强圈不可设置在筒体内部 4.11 封头 压力容器封头较多,下列叙述正确的有: ( ) A.凸形封头包括半球形封头、椭圆形封头、碟形封头、球冠形封头和锥壳。 B.由筒体与封头连接处的不连续效应产生的应力增强影响以应力增强系数的形式引入厚度 计算式。 C.半球形封头受力均匀,因其形状高度对称,整体冲压简单。 D.椭圆形封头主要用于中、低压容器。 4.12 高压密封 下列属于提高高压密封性能的措施有: ( ) A.改善密封接触表面 B.改进垫片结构 C.采用焊接密封元件 D.增加预紧螺栓数量 4.13 安全阀 安全阀的优点包括: () A.完全密封 B.多次使用 C.泄压反应快 D.只排出高于规定压力的部分压力 4.14 支座 在立式容器支座中,中小型直立容器常采用( )高大的塔设备则广泛采用( ) ,大型卧式 储存采用( ) A.耳式支座 B.裙式支座
过程设备设计习题..

目录第一章压力容器导言 (1)第二章压力容器应力分析 (5)第三章压力容器材料及环境和时间对其性能的影响 (13)第四章压力容器设计 (16)第五章储存设备 (23)第六章换热设备 (24)第七章塔设备 (26)第八章反应设备 (26)【概念题参考答案】 (27)第一章压力容器导言【教学基本内容和要求】1.了解压力容器基本组成和主要零部件;2.了解介质的毒性和易燃性,掌握压力容器几种不同分类方法;3.了解压力容器的质量保证体系的内容,了解常用压力容器标准和规范。
一.【思考题】1.介质的毒性程度和易燃特性对压力容器的设计、制造、使用和管理有何影响?2.压力容器主要由哪几部分组成?分别起什么作用?3.《容规》在确定压力容器类别时,为什么不仅要根据压力高低,还要视压力与容积的乘积pV大小进行分类?4.《容规》与GB150的适用范围是否相同?为什么?5.GB150、JB4732和JB/T4735三个标准有何不同?它们的适用范围是什么?6.过程设备的基本要求有哪些?要求的因素有哪些?7.在我们做压力容器爆破实验时发现,容器首先破坏的地方一般在离封头与筒体连接处一段距离的地方,而并非处于理论上应力集中的连接处的地方,请问原因何在?二.【判断题】1.压力容器主要是由筒体、封头、开孔与接管、支座以及安全附件组成。
()2.易燃介质是指与空气混合的爆炸下限小于10%或爆炸上限和下限之差小于等于20%的气体。
()3.高压容器(代号H)和超高压容器(代号U)是典型的第一类压力容器。
()4.压力容器中,封头与筒体之间一定要有密封装置。
()5.压力容器在设计时只要满足企业要求就行了,不需要满足GB150。
()6.盛装毒性程度为高度危害介质的容器制造时,容器上的A、B类焊接接头应进行100%射线或超声检测。
()7.压力容器分为三类:第一类压力容器,第二类压力容器,第三类压力容器,其中低压的具有极度毒性的压力容器属于第一类压力容器。
化工过程设备设计在线考试

中国石油大学(北京)远程教育学院期末考试《化工过程设备设计》学习中心:_ 姓名:_ __ 学号:__ ___关于课程考试违规作弊的说明1、提交文件中涉嫌抄袭内容(包括抄袭网上、书籍、报刊杂志及其他已有论文),带有明显外校标记,不符合学院要求或学生本人情况,或存在查明出处的内容或其他可疑字样者,判为抄袭,成绩为“0”。
2、两人或两人以上答题内容或用语有50%以上相同者判为雷同,成绩为“0”。
3、所提交试卷或材料没有对老师题目进行作答或提交内容与该课程要求完全不相干者,认定为“白卷”或“错卷”,成绩为“0”。
一、简答题(每题10分,共60分。
注:学号末尾数为奇数的考生请对1、3、5、7、9、11题进行作答,学号末尾数为偶数的考生请对2、4、6、8、10、12题进行作答)1.写出计算厚度与名义厚度的区别?答:GB150-98规定,计算厚度是指按各章公式计算得到的厚度:设计厚度是指计算厚度与腐蚀裕量之和名义厚度指设计厚度加上钢板厚度负偏差后向上圆整至钢材标准规格厚度,即标注在图样上的厚度:有效厚度指名义厚度减去腐蚀裕量和钢板厚度负偏差。
我们这里讨论的厚度是名义厚度从定义中可以看出,名义厚度不包括加工减薄量,元件的加工减薄量由制造单位根据各自的加工工艺和加工能力自行选取,只要保证产品的实际厚度不小于名义厚度减去钢材厚度负偏差就可以。
这样可以使制造单位根据自身条件调节加工减薄量,从而更能主动地保证产品强度所要求的厚度,更切合实际地符合制造要求。
名义厚度就是计算厚度加上腐蚀裕量加上材料负偏差再向上圆整至钢材标准规格厚度2.写出计算厚度与设计厚度的区别?3.什么是压力容器的公称直径?答:《压力容器公称直径(GB/T9019-2001)》是在已实施的GB/T9019-1988《压力容器公称直径》的基础上,总结了多年来压力容器在各行业的使用情况,本着满足需要的原则加以充实、完善而修订的。
本标准有下列变动:一标准适用范围包括常压容器。
过程装备试卷

一、填空题(25分)1、工业生产对过程装备的基本要求是(安全性)、(经济性)和(稳定性)等。
2、压差式流量计的核心部件是(节流装置),常见的节流装置有(孔板)、(喷嘴)和(文都利管)等。
3、液位是指(容器内液体介质液面的高低),常用的液位计有(浮力式)、(静压式)、(电容式)(光纤式)等。
4、在PID 调节器中,需要整定的参数为(比例度)、(积分时间)和(微分时间)。
5、调节阀的选型主要包括(阀的口径选择)、(型式选择)、(固有流量特性选择)和(材质选择)等内容。
6、计算机在过程控制中的应用类型一般可分为(直接数字控制系统)、(监督控制系统)、(分级控制系统)、(集散控制系统)等几种类型。
7、PLC 的程序表达方式常采用(梯形图)、(语句表)和(逻辑功能图)等方法。
梯形图程序、系统恢复数据、逻辑功能图程序二、判断改正题(10分)1、一单纯比例控制的液位对象,只要比例度选择的合适,系统就能跟踪并最终稳定到设定值。
(X) 单纯的比例控制不可能消除余差。
2、自动调节系统中,滞后的存在总不利于调节的。
(X )控制通道的滞后总是不利的,但干扰通道中的容量滞后可以缓和干扰的影响,对控制系统有利。
3、时间常数越大,表示对象受干扰作用后,到达新稳态值所需的时间越短。
(X )时间常数越大,表示对象受干扰作用后,到达新稳态值所需的时间越长。
4、控制系统中直接产生控制作用的是控制信号。
(X )控制系统中直接产生控制作用的是操纵变量。
5、串联管路中,随S 值下降,调节阀的等百分比流量特性畸变趋近于直线特性。
(正确)三、简答题(20分)1、何为调节器参数的工程整定法,并简述临界比例度法进行参数整定的过程。
所谓的工程整定法,就是避开被控对象的特性和数学描述,在被控对象运行时,直接在控制系统中,通过改变调节器参数,观察被控变量的过渡过程,来获取调节器参数的最佳数值。
临界比例度法整定参数的步骤是:首先将调节器的积分、微分作用全部去除,在纯比例作用调节比例度,直至得到等幅振荡的阶跃干扰过渡过程,此时的比例度和振荡周期称为临界比例度和临界周期,最后按照相应的经验公式计算出调节器各参数的整定数值。
过程设备设计答案(简答题和计算题)

1. 压力容器主要由哪几部分组成?分别起什么作用?答:压力容器由筒体、封头、密封装置、开孔接管、支座、安全附件六大部件组成。
筒体的作用:用以储存物料或完成化学反应所需要的主要压力空间.封头的作用:与筒体直接焊在一起,起到构成完整容器压力空间的作用.密封装置的作用:保证承压容器不泄漏.开孔接管的作用:满足工艺要求和检修需要。
支座的作用:支承并把压力容器固定在基础上.安全附件的作用:保证压力容器的使用安全和测量、控制工作介质的参数,保证压力容器的使用安全和工艺过程的正常进行。
2. 介质的毒性程度和易燃特性对压力容器的设计、制造、使用和管理有何影响?答:介质毒性程度越高,压力容器爆炸或泄漏所造成的危害愈严重,对材料选用、制造、检验和管理的要求愈高。
如Q235—A 或Q235-B 钢板不得用于制造毒性程度为极度或高度危害介质的压力容器;盛装毒性程度为极度或高度危害介质的容器制造时,碳素钢和低合金钢板应力逐张进行超声检测,整体必须进行焊后热处理,容器上的A 、B 类焊接接头还应进行100%射线或超声检测,且液压试验合格后还得进行气密性试验.而制造毒性程度为中度或轻度的容器,其要求要低得多。
毒性程度对法兰的选用影响也甚大,主要体现在法兰的公称压力等级上,如内部介质为中度毒性危害,选用的管法兰的公称压力应不小于1.0MPa ;内部介质为高度或极度毒性危害,选用的管法兰的公称压力应不小于1。
6MPa ,且还应尽量选用带颈对焊法兰等。
易燃介质对压力容器的选材、设计、制造和管理等提出了较高的要求。
如Q235—A ·F 不得用于易燃介质容器;Q235—A 不得用于制造液化石油气容器;易燃介质压力容器的所有焊缝(包括角焊缝)均应采用全焊透结构等.3. 《压力容器安全技术监察规程》在确定压力容器类别时,为什么不仅要根据压力高低,还要视压力与容积的乘积pV 大小进行分类?答:因为pV 乘积值越大,则容器破裂时爆炸能量愈大,危害性也愈大,对容器的设计、制造、检验、使用和管理的要求愈高.1. 一壳体成为回转薄壳轴对称问题的条件是什么?几何形状承受载荷边界支承材料性质均对旋转轴对称2. 推导无力矩理论的基本方程时,在微元截取时,能否采用两个相邻的垂直于轴线的横截面代替教材中与经线垂直、同壳体正交的圆锥面?为什么?答:不能.如果采用两个相邻的垂直于轴线的横截面代替教材中与经线垂直、同壳体正交的圆锥面,这两截面与壳体的两表面相交后得到的两壳体表面间的距离大于实际壳体厚度,不是实际壳体厚度。
第2章过程设备设计课后习题课

s max
pR4 64D
5 1
5 0.3 2.915 4.077 2.915 11.884mm 1 0.3
板的最大应力: max
33 pR2
8t 2
33 0.3 3 5002
8 382
3 0.3 389.543 1.65 389.543
2
642.746MPa
简支时的最大挠度是固支时的4.077倍;简支时的最大应力是固支时的1.65倍。
10
10
cos0 0.7
(2)支承以上部分,任一φ角处的应力: R1=R2=R,pz=-[p+ ρg R(cosφ0-cosφ)],r=Rsinφ,dr=Rcosφdφ
sin0
102 72 51
10
10
cos0 0.7
2R t sin2
2
r r0
p
cos0
cos
Rgrdr
2 p
12 1 2 12 1 0.32
p h g 0.815009.81 11772Pa 0.012MPa
周边简支圆平板中心挠度
ws max
pR4 64D
5 1
0.012 7504 64 7.50 107
5 0.3 1 0.3
3.22mm
挠度控制在1mm以下需要的塔板厚度:
塔板刚度需增加的倍数: 3.22 3.22 1
rd
w r
w r
物理方程
1 E
r
z
仅承受内压时的Lamè公式:
r
pi Ri2 R02 Ri2
1
R02 r2
K
pi 2
1
1
R02 r2
pi Ri2 R02 Ri2
2011春季模拟试卷—化工过程设备设计

《化工过程设备设计》模拟试题一一、名词解释1.外压容器2.边缘应力3.基本风压值4.计算厚度5.低压容器6.等面积补强法7.回转壳体8.公称压力9.计算压力10.20R11.设计压力12.强制式密封13.强度14.临界压力15.主应力二、判断是非题(正确的划√,错误划×)1.内压圆筒开椭圆孔时,其长轴应与轴线平行。
2.设计压力为4MPa的容器为高压容器。
3.容器的名义厚度与计算厚度的差值是壁厚附加量。
4.受内压作用的容器必须按强度计算进行壁厚设计。
5.一常压塔最大压应力应发生在安装检修时的设备迎风侧。
6.在补强圈上开有一个M10的小螺纹孔。
7.压力容器无论制造完毕后或检修完毕后,必须进行压力试验。
8.边缘应力具有自限性和局限性。
9.当焊缝系数一定时,探伤比例随焊缝系数的增加而减小。
10.容器的强度反映了外压容器抵抗失稳的能力。
11.压力容器的设计寿命是从腐蚀裕量中体现出来12.法兰密封中,法兰的刚度与强度具有同等重要的意义。
13.当材质与压力一定时,壁厚大的容器的应力总是比壁厚小的容器应力小14.塔的最大质量出现在其水压试验时15.塔的稳定性计算也可用计算法进行计算。
16.从管理角度出发,低压容器一定是一类容器。
17.内、外压容器的壁厚设计均是按强度设计方法进行设计。
18.以无缝钢管制成的压力容器其公称直径为钢管的内径。
19.按无力矩理论求得的应力为薄膜应力,薄膜应力是沿壁厚均匀分布的。
20.法兰联结结构中,垫片是一个不可缺少的元件之一。
三、简答题1.设置加强圈目的是什么?2.压力容器计算中壁厚名称有几种?3.为何要限定水压试验时的试验温度?4.为何在薄壁容器的壁厚设计公式中引入焊缝系数?5.设计某一钢制外压短圆筒时,发现20g钢板算得的临界压力比设计要求低10%,能否改用屈服限比20g高35%的16MnR钢板来满足设计要求?6.一管法兰为碳钢。
操作温度为300℃,操作压力为1.5MPa,试选择法兰型式及公称压力?7.一外压钢制圆筒,已知其临界压力为1.2MPa,试问当外压为0.6MPa,内压为0.1MPa时能否使用该圆筒?8.管法兰按联接方式分有哪些类型?9.指出球壳上任意一点的第一与第二曲率半径。
《过程装备设计》试卷

8.在螺栓法兰连接结构设计中,有垫片比压力 y 和垫片系数 m 两个参数,它们各 表示什么物理意义?
PDF 文件使用 "pdfFactory Pro" 试用版本第创5建页ÿ
类别
1 φ1500,设计压力为 2.0MPa 的管壳式余热锅炉 2 设计压力为 0.4MPa 的剧毒介质容器 P·V<0.1MPa·m3 3 设计压力 0.4MPa、设计温度 150℃的冷凝器(普通介质)
4 工作压力为 23.5MPa 的尿素合成塔
2. 绘图题。画出图 1 所示半圆形膨胀节上 A 点的第一曲率半径 R1 和第二曲率半径 R2。
三、计算题(每题 10 分,共 30 分) 1. 某化工厂设计一台卧式液氨储罐,其内直径 Di=1200mm,罐长 L=4000mm,工
作温度为-10℃-50℃,考虑饱和蒸汽压后取设计压力为 2.2MPa。试确定储罐各部 分的尺寸(考虑水压试验)。已知,材料选用 16MnR 钢板,要求采用双面 100% 无损探伤检查,取腐蚀裕量 C2=2mm,标准椭圆封头的直边长为 25mm。
是否完整正确,为什么?
PDF 文件使用 "pdfFactory Pro" 试用版本第创4建页
6. 图 2 中 A、B、C 点表示三个受外压的钢制 圆筒,材质为碳素钢,σs=216MPa,E=206GPa, 试回答: (1)A、B、C 三个圆筒各属于哪一类圆筒? 他们失稳时的波形数 n 等于(或大于)几? (2)当圆筒改为铝合金制造时(σs=108MPa, E=68.7GPa,),它的许用外压有何变化?变化 的幅度大约是多少?(用[p]铝/ [p]钢=?表示) 图2
过程设备设计期末考试题
p
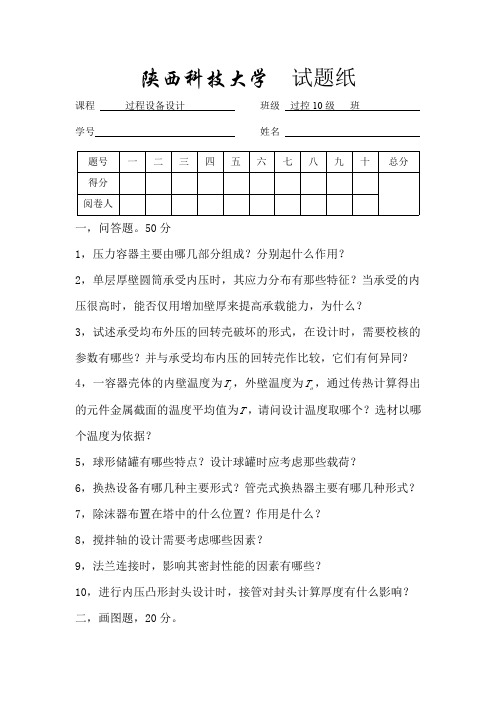
K +1 <= φ [σ ]t 2(k − 1)
由上式可得
δ=
pc Di 4[σ ]t φ − pc
10,简述爆破片的作用,并与安全阀相对比,简述其特点 答: 爆破片是一种断裂型安全泄放装置, 它个爆破片在标定爆破压力下即发生断裂来达到泄 压目的,泄压后爆破片不能继续有效使用,容器也就被迫停止运行。与安全阀相比,它有两 个特点:一是密闭性能好,能作到完全密封;二是破裂速度快,泄压反应迅速。 11,预应力法提高厚壁圆筒屈服承载能力的基本原理是什么? 答:通过压缩预应力,使内层材料受到压缩而外层材料受到拉伸。当厚壁圆筒承受工作压力 时, 筒壁内的应力分布由按拉美公式确定的弹性应力和残余应力叠加而成, 内壁处的总 应力有所下降,外壁处的总压力有所上升,均化沿筒壁厚度方向的应力分布,从而提高 圆筒的初始屈服压力。 12, 什么是不连续效应?并简述局部应力产生的原因。 不连续效应就是由于容器总体结构的不连续, 组合壳在连接处附近的局部区域出现衰减很快 的应力增大现象,称为不连续效应。产生原因:由几种简单的壳体组成的壳体,在两壳体的 连接处,若把两壳体作为自由体,即在内压作用下自由变形,在连接处的薄膜位移一般不相
π 2 D p 4 i
必与轴向内力 π Dδσ ϕ 相等。对于薄壳体,可近似认为内直径 Di 等与壳体的中面直径 D
π 2 D p = π Dδσ ϕ 4 i
由此得
σϕ =
pD 4δ pD t <= φ [σ ] 4δ
由强度理论知 用D=
σϕ =
K +1 K −1 Di , δ = Di 代入上式,经化简得 2 2
=
3 + µ µ = 0.3 ⎯⎯ ⎯→ 1.65 2
过程设备设计课后习题答案解析

习题1. 一内压容器,设计(计算)压力为0.85MPa ,设计温度为50℃;圆筒内径D i =1200mm ,对接焊缝采用双面全熔透焊接接头,并进行局部无损检测;工作介质列毒性,非易燃,但对碳素钢、低合金钢有轻微腐蚀,腐蚀速率K ≤0.1mm/a ,设计寿命B=20年。
试在Q2305-A ·F 、Q235-A 、16MnR 三种材料中选用两种作为圆筒材料,并分别计算圆筒厚度。
解:p c =1.85MPa ,D i =1000mm ,φ=0.85,C 2=0.1×20=2mm ;钢板为4.5~16mm 时,Q235-A 的[σ]t =113 MPa ,查表4-2,C 1=0.8mm ;钢板为6~16mm 时,16MnR 的[σ]t = 170 MPa ,查表4-2,C 1=0.8mm 。
材料为Q235-A 时:[]mmC C ppDt1412.524mm 28.0724.99.724mm85.185.01132100085.12n 21n ==++=++≥=-⨯⨯⨯=-=δδδφσδ取材料为16MnR 时:[]mmC C ppDt109.243mm 28.0443.6mm443.685.185.01702100085.12n 21n ==++=++≥=-⨯⨯⨯=-=δδδφσδ取2. 一顶部装有安全阀的卧式圆筒形储存容器,两端采用标准椭圆形封头,没有保冷措施;内装混合液化石油气,经测试其在50℃时的最大饱和蒸气压小于1.62 MPa (即50℃时丙烷饱和蒸气压);圆筒内径D i =2600mm ,筒长L=8000mm ;材料为16MnR ,腐蚀裕量C 2=2mm ,焊接接头系数φ=1.0,装量系数为0.9。
试确定:○1各设计参数;○2该容器属第几类压力容器;○3圆筒和封头的厚度(不考虑支座的影响);○4水压试验时的压力,并进行应力校核。
解:○1p=p c =1.1×1.62=1.782MPa ,D i =2600mm ,C 2=2mm ,φ=1.0,钢板为6~16mm 时,16MnR 的[σ]t = 170 MPa ,σs =345 MPa ,查表4-2,C 1=0.8mm 。
期末复习题答案——化工过程设备设计

《化工过程设备设计》期末复习题答案一、名词解释1.外压容器内外的压力差小于零的压力容器叫外压容器。
2.边缘应力由于容器的结构不连续等因素造成其变形不协调而产生的附加应力为边缘应力。
3.基本风压值以一般空旷平坦的地面、离地面10米高处,统计得到的30年一遇10分钟平均最大风速为标准计算而得的值叫基本风压值。
4.计算厚度由计算公式而得的壁厚叫计算壁厚。
5.低压容器对内压容器当其设计压力为 1.6MPa P 1MPa 0<≤.时为低压容器。
6.等面积补强法在有效的补强范围内,开孔接管处的有效补强金属面积应大于或等于开孔时减小的金属面积。
7.回转壳体一平面曲线绕同一平面的轴旋转一周形成的壳体为回转壳体。
8.公称压力将压力容器所受到的压力分成若干个等级,这个规定的标准等级就是公称压力。
9.计算压力在相应设计温度下,用以确定容器壁厚的压力为计算压力。
10.20R20表示含碳量为0.2%,R 表示容器用钢。
11.设计压力设定在容器顶部的最高压力,与相应的设计温度一起作为设计载荷,其值不低于工作压力。
12.强制式密封完全依靠螺栓力压紧垫片使之密封为强制式密封。
13.强度构件在外力作用下不至发生过大变形或断裂的能力。
14.临界压力导致外压圆筒失稳的外压为临界压力。
15.主应力在单元体的三对相互垂直的平面上只作用有正应力而无剪应力,这样的平面为主平面。
在主平面上作用的正应力为主应力。
16.内压容器内外压力差大于零的压力容器叫内压容器。
17.强度构件抵抗外力作用不致发生过大变形或断裂的能力。
18.无力矩理论因为容器的壁薄,所以可以不考虑弯矩的影响,近似的求得薄壳的应力,这种计算应力的理论为无力矩理论。
19.压力容器内部含有压力流体的容器为压力容器。
20.薄膜应力由无力矩理论求得的应力为薄膜应力。
二、判断是非题(正确的划√,错误划×)1.内压圆筒开椭圆孔时,其长轴应与轴线平行。
(×)2.设计压力为4MPa的容器为高压容器。
过程设备设计计算题

过程设备设计计算题(总22页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除计算题2.1无力矩方程 应力试用无力矩理论的基本方程,求解圆柱壳中的应力(壳体承受气体内压p ,壳体中面半径为R ,壳体厚度为t )。
若壳体材料由20R[σ(b)=400Mpa,σ(s)=245MPa]改为16MnR[σ(b)=510MPa,σ(s)=345MPa]时,圆柱壳中的应力如何变化为什么2.3 短圆筒 临界压力1、 三个几何尺寸相同的承受周向外压的短圆筒,其材料分别为(MPa y 220=σ,3.0,1025=⨯=μMPa E )、铝合金(3.0,107.0,1105=⨯==μσMPa E MPa y )和铜(31.0,101.1,1005=⨯==μσMPa E MPa y ),试问哪一个圆筒的临界压力最大,为什么?2.4临界压力 爆破压力有一圆筒,其内径为1000mm ,壁厚为10mm ,长度为20m ,材料为20?R(3.0,102,245,4005=⨯===μσσMPa E MPa MPa y b )。
①在承受周向外压时,求其临界压力cr p 。
②在承受内压力时,求其爆破压力b p ,并比较其结果。
2.5临界压力有一圆筒,其内径为1000mm ,壁厚为10mm ,长度为20m ,材料为20?R(3.0,102,245,4005=⨯===μσσMPa E MPa MPa y b )。
①在承受周向外压时,求其临界压力cr p 。
②在承受内压力时,求其爆破压力b p ,并比较其结果。
2.6无力矩理论 应力对一标准椭圆形封头(如图所示)进行应力测试。
该封头中面处的长轴D =1000mm,厚度t=10mm,测得E 点(x=0)处的周向应力为50MPa 。
此时,压力表A 指示数为1MPa ,压力表B 的指示数为2MPa ,试问哪一个压力表已失灵,为什么?2.7封头,厚度试推导薄壁半球形封头厚度计算公式2.8无力矩理论 应力有一锥形底的圆筒形密闭容器,如图2-54所示,试用无力矩理论求出锥形壳中的 最大薄膜应力θσ与ϕσ的值及相应位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算题2.1无力矩方程 应力试用无力矩理论的基本方程,求解圆柱壳中的应力(壳体承受气体内压p ,壳体中面半径为R ,壳体厚度为t )。
若壳体材料由20R[σ(b) =400Mpa,σ(s) =245MPa]改为16MnR[σ(b) =510MPa, σ(s) =345MPa]时,圆柱壳中的应力如何变化?为什么?2.3 短圆筒 临界压力1、 三个几何尺寸相同的承受周向外压的短圆筒,其材料分别为(MPa y 220=σ,3.0,1025=⨯=μMPa E )、铝合金(3.0,107.0,1105=⨯==μσMPa E MPa y )和铜(31.0,101.1,1005=⨯==μσMPa E MPa y ),试问哪一个圆筒的临界压力最大,为什么?2.4临界压力 爆破压力有一圆筒,其内径为1000mm ,壁厚为10mm ,长度为20m ,材料为20 R(3.0,102,245,4005=⨯===μσσMPa E MPa MPa y b )。
①在承受周向外压时,求其临界压力cr p 。
②在承受内压力时,求其爆破压力b p ,并比较其结果。
2.5临界压力有一圆筒,其内径为1000mm ,壁厚为10mm ,长度为20m ,材料为20 R(3.0,102,245,4005=⨯===μσσMPa E MPa MPa y b )。
①在承受周向外压时,求其临界压力cr p 。
②在承受内压力时,求其爆破压力b p ,并比较其结果。
2.6无力矩理论 应力对一标准椭圆形封头(如图所示)进行应力测试。
该封头中面处的长轴D =1000mm,厚度t=10mm,测得E 点(x=0)处的周向应力为50MPa 。
此时,压力表A 指示数为1MPa ,压力表B 的指示数为2MPa ,试问哪一个压力表已失灵,为什么?2.7 封头,厚度试推导薄壁半球形封头厚度计算公式2.8无力矩理论 应力有一锥形底的圆筒形密闭容器,如图2-54所示,试用无力矩理论求出锥形壳中的 最大薄膜应力θσ与ϕσ的值及相应位置。
已知圆筒形容器中面半径R ,厚度t ;锥形底的半锥角α,厚度t ,内装有密度为 ρ的液体,液面高度为H ,液面上承受气体压力C P2.9无力矩理论 应力一单层厚壁圆筒,承受内压力i p =36MPa 时,测得(用千分表)筒壁外表面的径向位移o w =0.365mm ,圆筒外直径o D =980mm ,E=5210⨯MPa ,μ=0.3。
试求圆筒内外壁面应力值。
2.10无力矩理论 应力有一容器端盖是由经线2/y x a =所形成的回转薄壳,如图所示,其中气体的压力为1Mpa ,筒体直径为1600mm ,盖及筒体的厚度为12mm ,试用无力矩理论计算A 、B 两点的压力。
(参考公式:曲线第一曲率半径()3/22'1''1y R y⎡⎤+⎢⎥⎣⎦=)2.11圆板有一周边固支的圆板,半径R=500mm ,板厚t=38mm ,板面上承受横向均布载荷 P=3MPa ,试求板的最大挠度和应力(取板材的E=2*e5MPa ,泊松比0.3 )。
上题中的圆平板周边改为简支,试计算其最大挠度和应力,并将计算结果与上题作一分析比较2.12 圆板 圆形塔板一穿流式泡沫塔其内径为mm 1500,塔板上最大液层为mm 800(液体重为34/105.1m N ⨯=γ),塔板厚度为mm 6,材料为低碳钢(MPa E 5102⨯=,3.0=μ)。
周边支承可视为简支,试求塔板中心处的挠度;若挠度必须控制在mm 3以下,试问塔板的厚度应增加多少?2.13环板如图中所示,外周边简支,已知b 所示内周边受均布力矩的环板与c 所示内周边受均布力环板的解,求a 所示内周边固支环板的解。
2.14 薄壳如图所示储满液体的锥壳,液体密度为 ,试写出应力表达式。
H αrxt R2.15 强度理论下图为一圆筒在内压作用时,压力与容积变化量的关系图。
看图回答下列问题并推导相关公式:(1) OA 段为直线,为什么?(2)A 、C 、D 点对应的压力分别称为什么?M M a.FFb.c.R RRR 1111附图(3)AC 段为弹塑性变形阶段,CD 段为爆破阶段,试分析曲线具有上图形状的原因。
(4)试推导出基于Tresca 屈服失效判据(又称为最大切应力屈服失效判据或第三强度理论)的i P 与C R 的关系(i P 为筒体所受内压,C R 为弹性区与塑性区分界面半径),假设材料为理想弹塑性材料,屈服点为s σ.并用所推导的公式写出S P (图中A 点压力)表达式。
2.16容器有一压力容器,一端为球形封头,另一端为椭圆形封头,如图所示。
已知圆筒的平均直径为2000 mm D =,封头和筒体壁厚均为20 mm ,最高工作压力 2 MPa p =,试确定:(1)筒身经向应力ϕσ和环向应力θσ;(2)球形封头的ϕσ和θσ(3)椭圆形封头/a b 值分别为2、2、3时,封头的最大应力所在位置。
试画出应力分布图。
参考公式:42221/2[(]2p a x a b t bϕσ--= 42221/244222[(][2]2()p a x a b a t b a x a b θσ--=---2.17无力矩理论 应力计算容器如图所示,圆筒中面半径为R ,壁厚为t ,圆锥与圆筒的壁厚相等,半锥顶角为α。
容器内承受气体压力p 的作用,且圆筒中液柱高为H1,圆锥液柱高为H2,液体密度为ρ,忽略壳体的自重。
(1)按无力矩理论推导A-A 、B-B 、C-C 、D-D 截面处的经向应力和周向应力的计算公式;(或推导壳体上各处的经向应力和周向应力的计算公式);(2)若H1 >H2,求出圆锥壳中最大应力作用点的位置及大小。
2.18薄膜应力半径为R ,厚度为t ,密度为ρ的球形盖,求因自身质量作用在容器中引起的薄膜应力。
2.19温差应力蒸汽管为Φ108×4mm 的无缝钢管,如果管道两端刚性固定,安装时温度t1=20℃,且无装配应力,工作时输送压力为0.1Mpa (绝)的蒸汽,求输送管外径不变、管壁厚度增大一倍时,求管壁温差应力及支座约束反力。
tqRrβ2.20应力 径向位移一仅受内压作用的单层厚壁圆筒,内压Pi =40MPa ,外径Do =1100mm ,内径Di=1000mm ,E=2*e5MPa ,μ=0.3 ,求圆筒外壁面的应力值和径向位移。
2.21薄膜应力*一离心机,用来沉降悬浮料液,物料密度31500/kg m ρ=。
转筒直径D=800mm ,壁厚t=8mm ,高H=700mm 。
材料为碳钢(密度37800/m kg m ρ=),弹性模量52.110E MPa =⨯,当以1500r/min 回转时,液体自由表面可近似与壁面平行。
回转半径r=300mm 。
(1)求环向薄壁应力θσ(2)求经向薄壁应力ϕσ.4.1内压容器 筒体厚度一内压容器,设计(计算)压力为0.85MPa ,设计温度为50℃;圆筒内径Di=1200mm ,对接焊缝采用双面全熔透焊接接头,并进行局部无损检测;工作介质无毒性,非易燃,但对碳素钢、低合金钢有轻微腐蚀,腐蚀速率K≤0.1mm/a ,设计寿命B=20年。
试在Q235-A•F 、Q235-A 、16MnR 三种材料中选用两种作为筒体材料,并分别计算筒体厚度。
4.2筒形储存一顶部装有安全阀的卧式圆筒形储存容器,两端采用标准椭圆形封头,没有保冷措施;内装混合液化石油气,经测试其在50℃时的最大饱和蒸气压小于1.62MPa (即50℃时丙烷的饱和蒸气压);筒体内径Di=2600mm ,筒长L=8000mm;材料为16MnR ,腐蚀裕量C2=2mm ,焊接接头系数φ=1.0,装量系数为0.9。
试确定(1)各设计参数;(2)该容器属第几类压力容器;(3)筒体和封头的厚度(不考虑支座的影响);(4)水压试验时的压力,并进行应力校核。
4.3封头形式今欲设计一台乙烯精榴塔。
已知该塔内径Di=600mm,厚度δn=7mm,材料选用16MnR,计算压力pc=2.2MPa,工作温度t=-20~-3℃。
试分别采用半球形、椭圆形、碟形和平盖作为封头计算其厚度,并将各种形式封头的计算结果进行分析比较,最后确定该塔的封头形式与尺寸。
4.4筒体的厚度一多层包扎式氨合成塔,内径D i=800mm,设计压力为31.4MPa,工作温度小于200℃,内筒材料为16MnR,层板材料为16MnRC,取C2=1.0mm,试确定筒体的厚度。
4.5容器下图所示为一立式夹套反应容器,两端均采用椭圆形封头。
反应器筒体内反应液的最高工作压力p w=3.0MPa,工作温度Tw=50℃,反应液密度ρ=1000kg/m3,顶部设有爆破片,筒体内径D i=1000mm,筒体长度L=4000mm,材料为16MnR,腐蚀裕量C2=2mm,对接焊缝采用双面全熔透焊接接头,且进行100%无损检测;夹套内为冷冻水,温度10℃,最高压力0.4MPa,夹套筒体内径D i=1100mm,腐蚀裕量C2=1mm,焊接接头系数φ=0.85。
试进行如下设计:(1)确定各设计参数;(2)计算并确定为保证足够的强度和稳定性,内筒和夹套的厚度;确定水压试验压力,并校核在水压试验时,各壳体的强度和稳定性是否满足要求。
有一受内压圆筒形容器,两端为椭圆形封头,内径D i=1000mm,设计(计算)压力为2.5MPa,设计温度300℃,材料为16MnR,厚度δn=14mm,腐蚀裕量C2=2mm,焊接接头系数φ=0.85;在筒体和封头上焊有三个接管(方位见题图),材料均为20号无缝钢管,接管a规格为φ89×6.0,接管b规格为φ219×8,接管c 规格为φ159×6,试问上述开孔结构是否需要补强?器设计规定”中推荐中径公式作为高压容器内壁相当应力的计算式,同时规定安全系数为1.6,试利用第四强度理论说明此种规定的合理性。
4.8塔,厚度一穿流式泡沫塔其内径为1500mm,塔板上最大液层为800mm(液体密度为1.5 kg/ ),塔板厚度为6mm,材料为低碳钢(E=2 MPa,u=0.3)。
周边支承可视为简支,试求塔板中心处的挠度;若挠度必须控制在3mm以下,试问塔板的厚度应增加多少?4.9 塔,焊接接头,腐蚀裕量今需要制造一台分馏塔,塔的内径D=2000mm,,塔身长(指圆桶长+两端椭圆形封头直边高度)L=6000mm,封头曲面深度h=500mm,塔在350摄氏度及真空条件下操作,腐蚀裕量为2mm,焊接接头系数为0.85。
现库存有8mm、6mm、4mm厚的Q235-A钢板,问能否用这三种钢板来制造这台设备。
4.10设计压力,腐蚀某圆柱形容器的设计压力为P=0.85MPa;设计温度为t=-50℃;内直径为1200mm;总高4000mm ;对接焊缝采用双面全熔透焊接接头,并进行局部无损检测,容器盛装液体介质,介质密度ρ=1500kg/m3,介质具有轻微的腐蚀性;腐蚀速率K≤0.1mm/年;设计寿命B=20年,试回答以下问题:1.该容器一般应选用什么材料?2.若在设计温度下材料的许用应力为[σ]t=170MPa ,求筒体的厚度?3.水压试验时的压力,并进行应力校核。
