最终版学习资料集合与函数概念单元测试.doc
高中数学必修一第一章《集合与函数概念》单元测试题(含答案)

⾼中数学必修⼀第⼀章《集合与函数概念》单元测试题(含答案)《集合与函数概念》单元测试题(第⼀章)(120分钟150分)⼀、选择题(本⼤题共12⼩题,每⼩题5分,共60分.在每⼩题给出的四个选项中,只有⼀项是符合题⽬要求的)1.集合A={0,1,2},B={x|-1A.{0}B.{1}C.{0,1}D.{0,1,2}2.设集合M={2,0,x},集合N={0,1},若N?M,则x的值为( )A.2B.0C.1D.不确定3.在下列由M到N的对应中构成映射的是( )4.已知函数f(x)=ax3+bx(a≠0),满⾜f(-3)=3,则f(3)= ( )A.2B.-2C.-3D.3【补偿训练】已知y=f(x)是偶函数,且f(4)=5,那么f(4)+f(-4)的值为( ) A.5 B.10C.8D.不确定5.已知⼀次函数y=kx+b为减函数,且kb<0,则在直⾓坐标系内它的⼤致图象是( )6.若f(x)=则f的值为( )A.-B.C.D.7.若f(g(x))=6x+3,且g(x)=2x+1,则f(x)= ( )A.3B.3xC.6x+3D.6x+18.下列四个图形中,不是以x为⾃变量的函数的图象是( )9.已知集合A={x|x2+x+1=0},若A∩R=?,则实数m的取值范围是( )A.m<4B.m>4C.0D.0≤m<410.函数f(x)=|x|和g(x)=x(2-x)的单调递增区间分别是( )A.(-∞,0]和(-∞,1]B.(-∞,0]和[1,+∞)C.[0,+∞)和(-∞,1]D.[0,+∞)和[1,+∞)11.对于任意两个正整数m,n,定义某种运算“※”如下:当m,n都为正偶数或正奇数时,m※n=m+n;当m,n中⼀个为正偶数,另⼀个为正奇数时,m※n=mn.则在此定义下,集合M={(a,b)|a※b=12,a∈N*,b∈N*}中的元素个数是( )A.10个B.15个C.16个D.18个12.设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则使<0的x的取值范围为( )A.(-1,0)∪(1,+∞)B.(-∞,-1)∪(0,1)C.(-∞,-1)∪(1,+∞)D.(-1,0)∪(0,1)⼆、填空题(本⼤题共4⼩题,每⼩题5分,共20分.请把正确答案填在题中横线上)13.已知集合A={x|1≤x<2},B={x|x14.已知a是实数,若集合{x|ax=1}是任何集合的⼦集,则a的值是.15.已知f(x)为偶函数,则f(x)=x1,1x0, ______,0x 1.+-≤≤≤≤16.定义在R上的奇函数f(x)为减函数,若a+b≤0,给出下列不等式:①f(a)f(b)≤0;②f(a)+f(b)≤f(-a)+f(-b);③f(b)f(-b)≤0;④f(a)+f(b)≥f(-a)+f(-b).其中正确的是.(把你认为正确的不等式的序号全写上).三、解答题(本⼤题共6⼩题,共70分.解答时应写出必要的⽂字说明、证明过程或演算步骤)17.(10分)设全集为R,集合A={x|3≤x<6},B={x|2(1)分别求A∩B,(eB)∪A.R(2)已知C={x|a18.(12分)已知函数f(x)=.(1)判断点(3,14)是否在f(x)的图象上.(2)当x=4时,求f(x)的值.(3)当f(x)=2时,求x的值.19.(12分)若函数f(x)=x2+4x+a的定义域和值域均为[-2,b](b>-2),求实数a,b的值.20.(12分)(2015·烟台⾼⼀检测)已知函数f(x)=ax+b,且f(1)=2,f(2)=-1.(1)求f(m+1)的值.(2)判断函数f(x)的单调性,并⽤定义证明..【拓展延伸】定义法证明函数单调性时常⽤变形技巧(1)因式分解:当原函数是多项式函数时,作差后的变形通常进⾏因式分解.(2)通分:当原函数是分式函数时,作差后往往进⾏通分,然后对分⼦进⾏因式分解.(3)配⽅:当原函数是⼆次函数时,作差后可考虑配⽅,便于判断符号.21.(12分)已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,⼜f(1)=-2.(1)判断f(x)的奇偶性.(2)求证:f(x)为R上的减函数.(3)求f(x)在区间[-3,3]上的值域.22.(12分)定义在(-1,1)上的函数f(x)满⾜:①对任意x,y∈(-1,1),都有f(x)+f(y)=f;②f(x)在(-1,1)上是单调递减函数,f=-1.(1)求f(0)的值.(2)求证:f(x)为奇函数.(3)解不等式f(2x-1)<1.《集合与函数概念》单元测试题参考答案(第⼀章)(120分钟150分)。
第一章__《集合与函数概念》单元测试题(含答案)

第⼀章__《集合与函数概念》单元测试题(含答案)《集合与函数概念》单元测试题⼀、选择题:1、在“①⾼⼀数学课本中的难题;②所有的正三⾓形;③⽅程220x +=的实数解”中,能够表⽰成集合的是( )(A )②(B )③(C )②③(D )①②③2、若{{}|0,|12A x x B x x =<<=≤<,则A B ?= ( )(A ){}|0x x ≤ (B ){}|2x x ≥(C ){0x ≤≤ (D ){}|02x x <<3、若{}{}0,1,2,3,|3,A B x x a a A ===∈,则A B ?= ( )(A ){}1,2 (B ){}0,1(C ){}0,3 (D ){}34、在映射中B A f →:,},|),{(R y x y x B A ∈==,且),(),(:y x y x y x f +-→,则与A 中的元素)2,1(-对应的B 中的元素为()(A ))1,3(- (B ))3,1( (C ))3,1(-- (D ))1,3(5、下列各组函数)()(x g x f 与的图象相同的是()(A )2)()(,)(x x g x x f == (B )22)1()(,)(+==x x g x x f(C )0)(,1)(x x g x f == (D )?-==x x x g x x f )(|,|)( )0()0(<≥x x 6、已知集合2{40}A x x =-=,集合{1}B x ax ==,若B A ?,则实数a 的值是()A .0B .12±C .0或12±D .0或127、已知集合{(,)2}A x y x y =+=,{(,)4}B x y x y =-=,则A B = ()A .{3,1}x y ==-B .(3,1)-C .{3,1}-D .{(3,1)}-8、设A 、B 为两个⾮空集合,定义{(,),}A B a b a A b B ⊕=∈∈,若{1,2,3}A =,{2,3,4}B =,则A B ⊕中的元素个数为()A .3B .7C .9D .129、已知集合2{1}A y y x ==+,集合2{26}B x y x ==-+,则A B = ()A .{(,)1,2}x y x y ==B .{13}x x ≤≤C .{13}x x -≤≤D .?10、如图所⽰,阴影部分的⾯积S 是h 的函数()H h ≤≤0。
高一数学必修1集合与函数概念单元测试题.doc

D. M= {x I x<-l, 或一 1<兀<(), 或 x>()=, N= {ylyHO}
6. 已知 A 、B 两地相距 150 千米,某人开汽车以 60 千米 / 小时的速度从 A 地到达 B 地, B 地停留 1 小时后再以 50 T 米/ 小时的速度返冋 A 地,把汽车离开 A 地的距离 x 表示 为时
C. { ax2+bx+c=O la, b, cGR} D. { ax2-^-bx+c=O I d, b, cWR,且 aHO}
2. 图中阴影部分所表示的集合是 (
)
A.BA [Cu(AUC)]
B.(AUB) U(BUC)
3. 设集合 P 二{ 立方后等于白身的数 }, 那么集合 P 的真子集个数是
16. (12 分) 集合 A={(x,y)*2 + inx — y + 2 = 0 } ,集合 B={(x,y) 卜一 y+ 1 = 0,且 05 兀 52}, 又 AC/H0, 求实数 m 的取值范围 .
17. (12 分) 已知砂
2 xe ( 一 8,1) 心 1,+8) '求两的值
18. (12 分) 如图,用长为 1 的铁丝弯成卜 - 部为矩形,上部为半圆形的框 架,
A. 3
B. 4
C. 7
4. 设 P 二{ 质数 } , Q= { 偶数 }, 贝 1JPPQ等于
A. C.(AUC ) n( CuB)
B. 2
C. {2}
D. [Cu(ACC)] UB
D. 8 D. N
1 f(x)= 』x_2 + J1 —兀启意义 ;
2 函数是其定义域到值域的映射; 3 函数 y=2x(xwN) 的图象是一直线 ;
集合与函数概念单元测试题

《集合与函数概念》单元测试题 (时间:100分钟,分数:100分)一、选择题:每小题4分,共40分1、在“①高一数学课本中的难题;②所有的正三角形; ③方程220x +=的实数解”中,能够表示成集合的是( ) A 、② B 、③ C 、②③ D 、①②③2、若{{}|0|12A x x x x =<<=≤<,则A B ⋃= ( )A 、{}|0x x ≤B 、{}|2x x ≥ C、{0x ≤≤D 、{}|02x x <<3、若{}{}0,1,2,3,|3,A B x x a a A ===∈,则A B ⋂= ( )A 、{}1,2B 、{}0,1C 、{}0,3D 、{}34、在映射中B A f →:,},|),{(R y x y x B A ∈==,且),(),(:y x y x y x f +-→,则与A 中的元素)2,1(-对应的B 中的元素为( )A 、)1,3(-B 、)3,1(C 、)3,1(--D 、)1,3( 5、下列各组函数)()(x g x f 与的图象相同的是( ) (A )2)()(,)(x x g x x f == (B )22)1()(,)(+==x x g x x f (C )0)(,1)(x x g x f ==(D )⎩⎨⎧-==x x x g x x f )(|,|)( )0()0(<≥x x 6、是定义在上的增函数,则不等式的解集是( )A 、(0 ,+∞)B 、(0 , 2)C 、 (2 ,+∞)D 、(2 ,716) 7、若奇函数()x f 在[]3,1上为增函数,且有最小值0,则它在[]1,3--上( ) A .是减函数,有最小值0 B .是增函数,有最小值0C .是减函数,有最大值0D .是增函数,有最大值08、若集合}1,1{-=A ,}1|{==mx x B , 且A B A =⋃,则m 的值为( ) A .1 B .1-C .1或1-D .1或1-或09、若{}21,,0,,b a aa b a ⎧⎫=+⎨⎬⎩⎭,则20052005a b+的值为( )A 、0B 、1C 、1-D 、1或1-10、奇函数f (x)在区间[-b, -a]上单调递减,且 f (x)>0,(0<a<b),那么| f (x)|在区间[a,b]上是( ) A 、单调递增B 、单调递减C 、不增也不减D 、无法判断二、填空题:每小题4分,共20分11、已知集合2{|4}M x x =<,2{|230}N x x x =--<,则集合M N = ;(用区间表示)12、已知)(x f y =为奇函数,当0≥x 时)1()(x x x f -=,则当0≤x 时,则=)(x f13、某班有学生55人,其中体育爱好者43人,音乐爱好者34人,还有4人既不爱好体育也不爱好音乐,则该班既爱好体育又爱好音乐的人数为 人。
集合与函数概念 单元测试题(附详解)
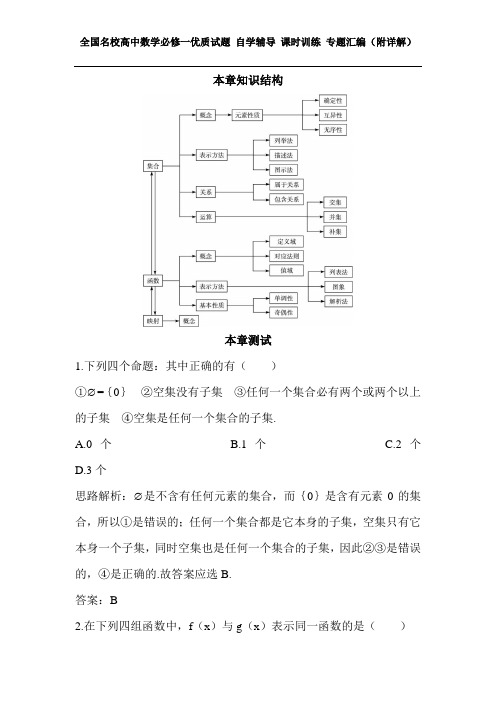
本章知识结构本章测试1.下列四个命题:其中正确的有()①∅={0}②空集没有子集③任何一个集合必有两个或两个以上的子集④空集是任何一个集合的子集.A.0个B.1个C.2个D.3个思路解析:∅是不含有任何元素的集合,而{0}是含有元素0的集合,所以①是错误的;任何一个集合都是它本身的子集,空集只有它本身一个子集,同时空集也是任何一个集合的子集,因此②③是错误的,④是正确的.故答案应选B.答案:B2.在下列四组函数中,f(x)与g(x)表示同一函数的是()A.f (x )=x-1,g (x )=112+-x x B.f (x )=|x+1|,g (x )=⎩⎨⎧-<---≥+.1,1,1,1x x x x C.f (x )=x+1,x ∈R ,g (x )=x+1,x ∈ZD.f (x )=x ,g (x )=(x )2思路解析:选项A 、C 、D 两个函数的定义域不同,所以不是同一个函数,应选B.答案:B3.已知M={x 2,2x-1,-x-1},N={x 2+1,-3,x+1},且M ∩N={0,-3},则x 的值为( )A.-1B.1C.-2D.2思路解析:∵M ∩N={0,-3},可知N 中有元素0,由于x 2+1≠0,故只能是x+1=0,解得x=-1,此时M={1,-3,0},N={2,-3,0},符合题意.应选A.答案:A4.y=f (x )(x ∈R )是奇函数,则它的图象必经过点( )A.(-a ,-f (-a ))B.(a ,-f (a ))C.(a ,f (1a ))D.(-a ,-f (a ))思路解析:由函数解析式的含义可知函数f (x )的图象经过点(a ,f(a )),又因为y=f (x )(x ∈R )是奇函数,所以有f (-a )=-f (a ),即函数图象经过点 (-a ,-f (a )),应选D.答案:D5.拟定从甲地到乙地通话m分钟的电话费由f(m)=1.06×(0.5·[m]+1)(元)决定,其中m>0,[m]是小于或等于m的最大整数,则从甲地到乙地通话时间为6.5分钟的电话费为()A.3.71元B.3.97元C.4.24元D.4.77元思路解析:根据题意知m=6.5,[m]=6,所以f(m)=1.06×(0.5·[m]+1)=1.06×4=4.24元,应选C.答案:C6.已知集合M、P、S,满足M∪P=M∪S,则()A.P=SB.M∩P=M∩SC.M∩(P∪S)=M∩(P∩S)D.(S∪M)∩P=(P∪M)∩S思路解析:特例法,举M={1,2},P={3},S={1,2,3},满足M∪P=M∪S,而P≠S,M∩P≠M∩S,M∩(P∪S)={1,2},M∩(P∩S)= ,所以A、B、C均是错误的,故正确答案应该为D.答案:D7.已知集合P={x∈N|1≤x≤10},集合Q={x∈R|x2+x-6≤0},则P∩Q等于( )A.{2}B.{1,2}C.{2,3}D.{1,2,3}思路解析:P={1,2,3,4,5,6,7,8,9,10},Q={-3,2},P∩Q={2}.答案:A8.函数y=ax 2+a 与y=xa(a ≠0)在同一坐标系中的图象可能是( )思路解析:从A 中的反比例图象可以看出a>0,此时y=ax 2+a 应是开口向上,且与x 轴没有交点的抛物线,故A 、B 、C 均是错误的;而对于D 可知a <0,y=ax 2+a 应是开口向下,且与x 轴没有交点的抛物线,所以D 是正确的.答案:D9.已知集合M={x |x ≥2或x ≤-1},N={x |x —a ≤0},若M ∩N ≠∅,则a 的取值范围是( )A.(-∞,2)B.(-1,+∞)C.(-∞,1) D(-∞,1]思路解析:由题意知M={x |-1<x <2=,N={x |x ≤-a},若M ∩N ≠∅,根据数轴,可得-a>-1即a <1,故选C.答案:C10.函数y=2)1(20++--x x x 的定义域为( )A.(-1, 2)B.(-1,1)∪(1,2)C.(-∞,1)∪(1,+∞)D.[-1,1]∪(1,2] 思路解析:要使函数有意义,则⎩⎨⎧>++-≠.02,12x x x 解得(-1,1)∪(1,2).答案:B11.函数f(x)=-x2+2(a-1)x+3在(-∞,4)上是增函数,则a的范围是()A.a≥5B.a≥3C.a≤3D.a ≤-5思路解析:本题作出函数f(x)=-x2+2(a-1)x+3的图象,可知此函数图象的对称轴是x=a-1,由图象可知,当a-1≥4,即当a≥5时,函数f(x)=-x2+2(a-1)x+2在(-∞,4)上是增函数.答案:A12.已知集合A={x|y=x2-2x-3,x∈R},B={y|y=x2-2x+2,x∈R},则A∩B=_________.思路解析:集合A={x|y=x2-2x-3,x∈R}表示函数y=x2?x-3的定义域,所以A=R;而B={y|y=x2-2x+2,x∈R}表示函数y=x2-2x+2的值域,应有B={y|y≥1},因此A∩B={y|y≥1}.答案:{y|y≥1}13.如右图,有一块边长为a的正方形铁皮,将其四个角各截去一个边长为x的小正方形,然后折成一个无盖的盒子,写出体积V以x 为自变量的函数式是_____________,这个函数的定义域为___________________.思路解析:围成的几何体是一个长方体,它的底面积为(a-2x)2,高为x ,所以体积V=x(a-2x)2,而x 满足a-2x >0且x >0,所以0<x <2a . 答案:V=x (a-2x )2 {x|0<x <2a }14.给定映射f :(x ,y )→(x ,x+y ),在映射f 下象(2,12)的原象是(a ,b ),则函数f (x )=ax 2+bx 的顶点坐标是____________________.思路解析:根据题意有a=2,a+b=12,解得a=4,b=8,所以函数f(x)=4x 2+8x=4(x+1)2-4,其顶点坐标为(-1,-4).答案:(-1,-4)15.函数f (x )=x 2-2|x |的单调减区间是____________________. 思路解析:因为f (-x )=x 2-2|x |=f (x ),所以f(x)是偶函数,我们可先考虑x >0的情况,当x >0时,f(x)=x 2-2x ,函数在(0,1)上为减函数,在[1,+∞)上为增函数;由于偶函数的图象关于y 轴对称,故函数在(-1,0)上为增函数,在(-∞,-1)上为减函数.答案:(0,1)和(-∞,-1]16.设A={x|x 2-x-12=0} ,B={x|x 2-2ax+b=0},若B ≠ ,且A ∪B=A,求a 、b 的值.思路解析:分别将每一个集合化简,再利用集合的运算进行求解. 解:∵A={x|x 2-x-12=0}={-3,4},若B ≠∅,且A ∪B=A ,则B ⊆A,当A=B 时,a=21,b=-12;当B={-3}时,a=-3,b=9;当B={4}时,a=4,b=16.因此,a=21,b=-12或A=-3,b=9或 a=4,b=16.17.设g(x)=⎩⎨⎧>≤,0,ln ,0,x x x e x 则g [g(21)]=__________________. 解:依题可知g(21)=ln 21=-ln2<0所以,g [g (21)]=g(-ln2)=21ln e =21. 18.已知函数f(x)=ax 2+2ax+4(0<a <3=,若x 1<x 2,x 1+x 2=1-a,则( )A.f(x 1)<f(x 2)B.f(x 1)=f(x 2)C.f(x 1)>f(x 2)D.f(x 1)与f(x 2)的大小不能确定思路解析:由f(x)=ax 2+2ax+4(0<a <3=,得f(x)为二次函数,且对称轴为x 0=-1,∵x 1+x 2=1-a,∴221x x +=21a -,即x 1,x 2中点横坐标为21a -,又∵0<a <3,∴21a ->-1.∵x 1<x 2, 如右图∴x1离对称轴的距离小于x2离对称轴的距离,∴f(x1)<f(x2).答案:A19.快艇和轮船分别从A地和C地同时开出,各沿箭头方向航行,如右图所示,快艇和轮船的速度分别是45千米/时和15千米/时,已知AC=150千米,经过多少时间后,快艇和轮船之间的距离最短?思路解析:解决有关函数的应用题,关键在于审清题意,正确列出函数模型.解:设经过x小时后快艇和轮船之间的距离最短,距离设为y,10),y=22)(xx+-(0<x≤4515150()3可求得当x=3时,y有最小值.答:经过3小时后,快艇和轮船之间的距离最短.20.设f(x)是定义在R上的增函数,f(xy)=f(x)+f(y),f(3)=1,求解不等式f(x)+f(x-2)>1.思路解析:对抽象不等式,常把常数看成某些变量的函数值,再利用函数的性质去“外层包装”,取出x,化成一元一次或二次不等式求解.解:由条件可得f(x)+f(x-2)=f[x(x-2)],1=f(3).所以f[x(x-2)]>f(3),又f(x)是定义在R上的增函数,所以有x (x-2)>3,可解得x >3或x <-1.答案:x >3或x <-121.已知函数f (x )=x+xm ,且f (1)=2. (1)求m ;(2)判断f (x )的奇偶性;(3)判断函数f (x )在[1,2]上的单调性,并求函数f (x )在[1,2]上的最值.思路解析:判断函数的奇偶性,首先观察函数的定义域是否关于原点对称,然后判断 f (-x )与f(x)的关系;而证明在某一区间上的单调性,常用定义进行证明,由于单调函数在闭区间内肯定有最值,可根据单调性求出最值.解:(1)f (1)=1+m=2,解得m=1.(2)f (x )=x+x 1,f (-x )=-x-x 1=-f (x ),∴f (x )是奇函数.(3)设x 1、x 2是[1,2]上的任意两个实数,且x 1<x 2,则 f (x 1)-f (x 2)=x 1+11x -(x 2+21x )=x 1-x 2+(11x -21x )=x 1-x 2-2121x x x x -=(x 1-x 2)21211x x x x -. 当1≤x 1<x 2≤2时,x 1x 2>1,x 1x 2-1>0,从而f (x 1)-f (x 2)<0, 即f (x 1)<f (x 2).∴函数f (x )=x1+x 在[1,2]上为增函数,其最小值为 f (1)=2,最大值为f (2)=25.。
(完整word版)集合与函数概念单元测试题

(完整word 版)集合与函数概念单元测试题第一章 《集合与函数概念》单元测试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟.第Ⅰ卷(选择题 共50分)一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列说法①高一数学课本中的难题能构成集合;②10以内的质数集合是{2,3,5,7}; ③方程x 2-4x +4=0的解集是{2,2};④0与{0}表示同一个集合;⑤由1,2,3组成的集合可表示为{1,2,3}或{3,2,1},其中正确的有 ( )A .①②B .②③C .②⑤D .①②③2.设集合A ={x |2x +1<3},B ={x |-3<x <2},则A ⋂B 等于 ( )A .{x |-3<x <1}B .{x |1<x <2}C .{x|x -3}D .{x|x 1} 3.拟定从甲地到乙地通话m 分钟的电话费由() 1.06(f m ==0.5[]1)m +(元)决定,其中0>m ,][m 是大于或等于m 的最小整数,(如[3]=3,[3.8]=4,[3.1]=4),则从甲地到乙地通话时间为5。
5分钟的电话费为 ( )A .3。
71元B .3。
97元C .4。
24元D .4。
77元4.已知函数32)1(+=+x x f 则)(x f 等于 ( ) A .32+x B .12+x C .22+x D .12-x5.下列四组中的),(),(x g x f 表示同一个函数的是 ( )A .0)(,1)(x x g x f == B .1)(,1)(2-=-=xx x g x x f C .42)()(,)(x x g x x f == D .393)(,)(x x g x x f ==6.已知函数f (n)= ⎩⎨⎧<+≥-)10)](5([)10(3n n f f n n ,其中n ∈N ,则f(8)等于 ( )A .2B .4C .6D .77.已知函数()533f x ax bx cx =-+-,()37f -=,则()3f 的值为 ( ) A .13 B .13- C .7 D .7-8.如图所示,阴影部分的面积S 是h 的函数()H h ≤≤0.则该函数的图象是 ( )ssHhS姓 名 班 级考 号 装订线内不要答卷A .B .C .D .9.设()11xf x x +=-,又记()()()()()11,,1,2,,k k f x f x f x f f x k +===则()2008f x =( )A .11x x +-B .11x x -+C .xD .1x -5.设偶函数()f x 在(0)+∞,上为增函数,且(1)0f =,则不等式()()0f x f x x+-<的解集为( )A .(10)(1)-+∞,,B .(1)(01)-∞-,,C .(1)(1)-∞-+∞,,D .(10)(01)-,,第II 卷(非选择题 共100分)二.填空题:本大题共5小题,每小题5分,共25分。
《集合与函数概念》单元测试题

第一章 《集合与函数概念》单元测试题一、选择题:每小题4分,共40分。
1、以下四个关系:φ}0{∈,∈0φ,{φ}}0{⊆,φ}0{,其中正确的个数是( ) A .1B .2 C .3D .42、若{}{}|02,|12A x x B x x =<<=≤<,则A B ⋃= ( ) A .{}|0x x ≤B .{}|2x x ≥C .{}02x ≤≤D .{}|02x x << 3、若{}21,,0,,b a a a b a ⎧⎫=+⎨⎬⎩⎭,则20092009b a +的值为( )A .0B .1C .1-D .1或1-4、在下列四组函数中,f (x )与g (x )表示同一函数的是( )A .x x y y ==,1B .1,112-=+⨯-=x y x x yC .55,x y x y ==D .2)(|,|x y x y ==5.已知集合M={R x x x y y ∈-+=,322},集合N={32≤-y y },则M =⋂N ( )。
(A ){4-≥y y } (B ){51≤≤-y y }(C ){14-≤≤-y y } (D )φ6、设集合{}06A x x =≤≤,{}02B y y =≤≤。
从A 到B 的对应法则f 不是映射的是() A .1:3f x y x −−→=B .1:2f x y x −−→= C .1:4f x y x −−→=D .1:6f x y x −−→= 7、若)1(-x f 的定义域为[1,2],则)2(+x f 的定义域为( )A .[0,1]B .[2,3]C .[-2,-1]D .无法确定8、是定义在上的增函数,则不等式的解集是( )A .(0 ,+∞)B .(0 , 2)C .(2 ,+∞)D .(2 ,716) 9、如果函数2()2(1)2f x x a x =+-+在区间(],4-∞上是减少的,那么实数a 的取值范围是( )A 、3a -≤B 、3a -≥C 、a ≤5D 、a ≥510、函数()f x 的定义域为),(b a ,且对其内任意实数12,x x 均有:1212()[()()]0x x f x f x --<,则()f x 在),(b a 上是A .增函数B .减函数C .奇函数D .偶函数二、填空题:每小题4分,共20分。
(完整word版)集合与函数概念单元测试题经典(含)

没有等出来的漂亮只有拼出来的绚烂第一章会合与函数观点测试题一:选择题1、以下会合中与会合{ x x2k1, k N } 不相等的是()A .{ x x2k3,k N}B.{ x x4k1, k N }C.{ x x2k1, k N}D.{ x x2k3, k3,k Z}2、图中暗影部分所表示的会合是()A.B ∩[ C U (A ∪C)]B.(A ∪ B)∪ (B∪ C)C.(A ∪ C)∩ (C U B)D. [ C U(A ∩C) ]∪ B3、已知会合A{ y y x21} ,会合 B{ x y22x6} ,则 A B()A .{( x, y) x 1, y 2}B.{ x 1 x 3}C.{ x 1 x 3}D.4、已知会合A{ x x240} ,会合 B{ x ax1} ,若 B A ,则实数a的值是()A .01C.0或11 B.2D.0或225、已知会合A{1,2,3, a},B2,则使得 (CU)B建立的 a 的值的个数为(){3, a }AA .2B.3C.4 D .56、设A、B为两个非空会合,定义A B{( a,b) a A,b B} ,若A}32,1{,B {2,3,4},则 A B 中的元素个数为()A .3B .7C.9D.127、已知 A 、B 两地相距 150千米,某人开汽车以60 千米 /小时的速度从 A 地抵达 B 地,在 B 地逗留 1小时后再以 50千米 /小时的速度返回 A 地,把汽车走开 A 地的距离 x 表示为时间 t(小时)的函数表达式是()A . x=60t B. x=60t+5060t ,(0t 2.5)60t,(0t 2.5)D .x= t 3.5)C. x=3.5)150 50t ,(t15050(t 3.5), (3.5 t 6.5)8、已知 g(x)=1-2x,f[g(x)]=1 x 20) ,则f(1()x 2(x)等于2A . 1B. 3C. 15 D . 309、函数 y=1x 29是()1x没有等出来的漂亮只有拼出来的绚烂A .奇函数B .偶函数C.既是奇函数又是偶函数 D .非奇非偶数10、设函数 f (x)是(-, + )上的减函数,又若 a R,则()A . f (a)>f (2a)B . f (a2)<f (a)C. f (a2+a)<f (a)D. f (a2+1)< f (a)二、填空题11、设会合 A={ x3x 2 },B={x2k1x k 2 1 },且A B,则实数 k 的取值范围是.12、已知 x[0,1], 则函数 y=x21x 的值域是.13、设函数y1的定义域为 ___________________; 值域为 _____________________________. 11x14 、设 f(x) 是定义在R上的偶函数,在区间(-∞, 0 )上单调递增,且满足 ,f ( a22a5) f (2 a2a1) 务实数a的取值范围_______________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
集合与函数概念单元测试
一、选择题
1.集合},{b a 的子集有 ( ) A .2个
B .3个
C .4个
D .5个
2、已知函数x
x f -=
21)(的定义域为M ,2)(+=x x g 的定义域为N ,则=⋂N M
A.{}
2-≥x x
B.{}2<x x
C.{}
22<<-x x
D. {}
22<≤-x x
3.下列各组函数中表示同一函数的是
(A )x x f =)(与2
)()(x x g = (B )||)(x x x f =与⎪⎩⎪⎨⎧-=22
)(x
x
x g )0()0(<>x x
(C )||)(x x f =与3
3)(x x g = (D )1
1)(2--=x x x f 与)1(1)(≠+=t t x g
4.
(A ) (B) (C ) (D)
5..已知()5412
-+=-x x x f ,则()x f 的表达式是( )
A .x x 62+
B .782++x x
C .322-+x x
D .1062
-+x x 6.已知函数y f x =+()1定义域是[]-23,,则y f x =-()21的定义域是( ) A []052
, B []-14, C []-55, D []-37,
7.函数是单调函数时,的取值范围 ( )
A .
B .
C .
D .
8.函数
在实数集上是增函数,则 ( )
A .
B .
C .
D .
9.已知在实数集上是减函数,若,则下列正确的是 ( )
A .
B .
C .
D .
x y 0 x y 0 x y 0 x
y 0
10.已知函数212x y x
⎧+=⎨-⎩ (0)
(0)x x ≤>,使函数值为5的x 的值是( )
A .-2
B .2或52-
C . 2或-2
D .2或-2或52
- 11.下列四个函数中,在(0,∞)上为增函数的是
(A )f (x )=3-x (B )f (x )=x 2
-3x (C )f (x )=-|x | (D )f (x )=-
2
3
+x 12、定义在R 上的偶函数在[0,7]上是增函数,在[7,+∞]上是减函数,又6)7(=f ,则)(x f A 、在[-7,0]上是增函数,且最大值是6 B 、在[-7,0]上是增函数,且最小值是6 C 、在[-7,0]上是减函数,且最小值是6 D 、在[-7,0]上是减函数,且最大值是6 二、填空题
13.已知集合M={(x ,y )|x +y =2},N={(x ,y )|x -y =4},那么集合M∩N= .
14.已知f (x )是偶函数,当x <0时,f (x )=x (2x -1),则当x >0时,f (x )=__
15. 设f(x)=2x+3,g(x+2)=f(x-1),则g(x)= .
16.定义域为2
[32,4]a a --上的函数f(x)是奇函数,则a= .
17.设32()3,()2f x x x g x x =-=-,则(())g f x = .
三.解答题
18..已知集合A={-1,a 2+1,a 2
-3},B={-4,a-1,a+1},且A∩B={-2},求a 的值.(13分)
19.已知集合A={}
71<≤x x ,B={x|2<x<10},C={x|x<a },全集为实数集R . (Ⅰ)求A ∪B ,(C R A)∩B ;
(Ⅱ)如果A ∩C ≠φ,求a 的取值范围.
20.集合A ={x |x 2-ax +a 2-19=0},B ={x |x 2
-5x +6=0}, C ={x |x 2+2x -8=0}. (Ⅰ)若A =B,求a 的值;
(Ⅱ)若∅A ∩B ,A ∩C =∅,求a 的值.
21.求下列函数的值域
(1)x x y -+=43 (2)3
425
2
+-=x x y (3)x x y --=21 (4)132222+-+-=x x x x y
22.已知函数2
()21f x x =-. (Ⅰ)用定义证明()f x 是偶函数;
(Ⅱ)用定义证明()f x 在(,0]-∞上是减函数;
(Ⅲ)作出函数()f x 的图像,并写出函数()f x 当[1,2]x ∈-时的最大值与最小值. y
o
x
23. 已知函数2
1
22()x x f x x
++
=,其中[1,)x ∈+∞,(1)试判断它的单调性;(2)试求它的最小
值.
24.已知函数()f x 的定义域是),0(+∞,且满足()()()f xy f x f y =+,1()12
f =, 如果对于0x y <<,都有()()f x f y >,(1)求(1)f ;(2)解不等式2)3()(-≥-+-x f x f 。
