NOIP2002普及组(复赛)

合集下载

noip普及组复赛模拟试题10答案

【试题描述】选拔考试即将开始，同学们陆续进入考场，哇，考场好大啊。

究竟star应该坐在哪张位置呢？考场门口贴了一张考场座位（m*n）明细表，其中考场里的有些位置是坏的不能坐，考号为1的同学的座位号是第一排第一列，即他的座位是1、1，2号同学的座位是1、2，以此类推，当然，如果某个座位是坏的，那么这个同学就往后延一个座位，后面的同学再依次排下去。

考场座位肯定够所有考生坐。

【输入描述】第1行：3个整数，m,n,k(m,n表示考场的座位是m行n列，k表示star的考号)m,n<=100;第2..m+1行：每行n个数代表考场明细0代表座位是好的，1代表座位是坏的）【输出描述】一行：两个整数代表star应该坐的位置【输入样例】4 4 50 0 0 00 0 1 00 0 0 10 0 0 0【输出样例】2 1【试题来源】常州长训班测试program ex1661;var k,i,j,s,m,n:integer;a:array[1..100,1..100] of 0..1;beginreadln(m,n,k);for i:=1 to m dofor j:=1 to n doread(a[i,j]);s:=0;for i:=1 to m dofor j:=1 to n dobeginif a[i,j]<>1 then inc(s);if s=k then begin writeln(i,' ',j); exit;end;end;end.输入 6 6 70 0 0 0 1 00 0 1 0 0 00 0 0 1 1 00 0 0 0 0 11 0 0 0 0 00 0 1 0 0 1 输出 2 2输入8 6 100 0 0 0 1 00 0 1 0 0 00 0 0 1 1 00 0 0 0 0 11 0 0 0 0 00 0 1 0 0 10 1 0 0 0 01 0 0 0 0 1输出 2 6【题目描述】一个农夫有n（n≤1000）头奶牛，可由于产奶太少，他决定把当天产奶最少的牛杀掉，但他有点舍不得，如果当天不只一头奶牛产奶，至少他便放过它们。

noip普及组复赛模拟试题12答案

【试题描述】读入二行整数，然后程序要完成如下的操作：第一步将2行数合并在一起，第二步将合并好的数由大到小排序，第三步重新排列，从第一个数起开始编号，然后将奇数号上的数（样例中的13，9，5）从前向后排，偶数号上的数（样例中的12，7，4）从后往前排。

第四步计算，将排好的数，第一个+第二个数的2倍+第三个数的3倍+…第五步：输出计算的结果。

【输入描述】第一行是一个整数 n(1≤n≤10)，第二行有n个整数，整数范围在1~100之间，数与数之间空格隔开。

第三行是一个整数 m(1≤m≤10)，第四行有m个整数，整数范围在1~100之间，数与数之间空格隔开。

【输出描述】一个整数（最后计算的结果）。

【输入样例】412 4 5 9213 7【输出样例】 169【解题提示】样例说明：第一步合并后为：12 4 5 9 13 7第二步上例中的数成为：13 12 9 7 5 4第三步得到：13 9 5 4 7 12第四步计算后为：13+2×9+3×5+4×4+5×7+6×12=169最后输出 169【试题来源】 2008年江苏省小学生信息学（计算机）奥赛program ex1731;var m,n,i,j,s,t,b1,b2:integer;a,b,c:array[1..20] of integer;sum:longint;beginreadln(n);for i:=1 to n do read(a[i]);readln(m);for i:=1 to m do read(a[i+n]);s:=m+n;for i:=1 to s-1 dofor j:=i+1 to s doif a[i]<a[j] then begint:=a[i];a[i]:=a[j];a[j]:=t;end;b1:=0;b2:=0;for i:=1 to s doif i mod 2=1 then begin inc(b1); b[b1]:=a[i];endelse begin inc(b2); c[b2]:=a[i];end;for i:=1 to b1 do a[i]:=b[i];for i:=1 to b2 do a[b1+i]:=c[b2-i+1];sum:=0;for i:=1 to s dosum:=sum+i*a[i];writeln(sum);end.输入 615 34 25 9 22 39423 17 46 57输出1496输入1015 34 25 9 22 39 47 12 33 99823 17 46 57 51 8 38 64输出5687SHLQSH数问题描述：我们把t1 , t2 (包括t1 , t2 (1<=t1<t2<=10000000))之间的所有数的约数个数和n称为t1 , t2的shlqsh数;问题是给出数据t1 , t2后,求t1 , t2的shlqsh数；输入输入文件shlqsh.in 仅包含一行，共有两个整数，表示t1 t2 (用空格分开)输出输出文件shlqsh.out 仅有一个整数，表示t1 , t2之间的shlqsh数。

2001-2002年普及复赛试题及分析

2001第七届全国青少年信息学（计算机）奥林匹克分区联赛复赛试题普及组题一数的计算(20分) 程序名:a01.pas/c/c++问题描述我们要求找出具有下列性质数的个数(包含输入的自然数n):先输入一个自然数n(n<=1000),然后对此自然数按照如下方法进行处理:1.不作任何处理;2.在它的左边加上一个自然数,但该自然数不能超过原数的一半;3.加上数后,继续按此规则进行处理,直到不能再加自然数为止.样例: 输入: 6 输入文件名:input1.txt满足条件的数为 6 (此部分不必输出) 输出文件名:output1.txt6162612636136问题描述输入二个正整数x0,y0(2<=x0<100000,2<=y0<=1000000),求出满足下列条件的P,Q的个数条件: 1.P,A是正整数2.要求P,Q以x0为最大公约数,以y0为最小公倍数.试求:满足条件的所有可能的两个正整数的个数.样例输入:x0=3 yo=60 输入文件名:input2.txt输出:4 输出文件名:output2.txt说明(不用输出)此时的P Q 分别为:3 6015 1212 1560 3所以:满足条件的所有可能的两个正整数的个数共4种.分析：1.数学方法枚举：根据数学性质枚举出所有可能，缺点存储量大,复杂度高p:=a*x0 ; q:=b*x0 （a,b互质）x0为其最大公约数p*q=a*x0*b*x0=y0*x0 y0为p,q最小公倍数则y0=a*b*x02.数学方法：p:=a*x0 ; q:=b*x0 （a,b互质）x0为其最大公约数p*q=a*x0*b*x0=y0*x0 y0为p,q最小公倍数则y0=a*b*x0题三求先序排列（30分）程序名:c03.pas/c/c++问题描述给出一棵二叉树的中序与后序排列。

求出它的先序排列。

（约定树结点用不同的大写字母表示，长度<=8）。

CSP-J（NOIP普及组）历年复赛真题考察内容（1998～2021）

CSP-J（NOIP普及组）历年复赛真题考察内容（1998～2021）1.CSP-J 2021思维、选择结构排序、归并排序⼤模拟双向链表、模拟2.CSP-J 2020位运算、进制转换桶排序栈、深搜动态规划(⾼级)3.CSP-J 2019字符串模拟、队列背包⼴搜、最短路4.NOIP2018 普及组字符串枚举、预处理动态规划(⾼级)⼆叉树5.NOIP2017 普及组顺序结构结构体排序深搜、剪枝⼆分、动态规划6.NOIP2016 普及组⼀重循环回⽂⼤模拟、队列枚举、前缀和7.NOIP2015 普及组⼀重循环⼆维数组组合数学贪⼼、优先队列8.NOIP2014 普及组模拟枚举、gcd模拟、找规律动态规划(⾼级)9.NOIP2013 普及组⼆重循环栈动态规划(⾼级)拓扑排序10.NOIP2012 普及组⼀重循环、质数模拟、取模背包、动态规划最短路11.NOIP2011 普及组进制转换字符串归并排序动态规划(⾼级)、栈12.NOIP2010 普及组⼆维数组模拟贪⼼贪⼼、博弈13.NOIP2009 普及组模拟结构体排序约数动态规划(⾼级)14.NOIP2008 普及组字符串贪⼼动态规划(⾼级)结构体排序贪⼼贪⼼⾼精度16.NOIP2006 普及组⼀维数组01背包模拟进制转换17.NOIP2005 普及组⼀维数组⼀维数组01背包⾼精度18.NOIP2004 普及组⼀重循环贪⼼递归、⼆叉树STL、深搜19.NOIP2003 普及组模拟动态规划(⾼级)组合数学、卡特兰数⾼精度20.NOIP2002 普及组⼀重循环深搜深搜递推、动态规划21.NOIP2001 普及组递推、递归枚举、gcd⼆叉树⼀元⼀次⽅程、模拟不等式、数论动态规划、⾼精度深搜23.NOIP1999 普及组找规律进制转换贪⼼24.NOIP1998 普及组简单数学、枚举、进制转换⾼精度深搜。

noip普及组复赛试题及答案

noip普及组复赛试题及答案一、选择题1. 在计算机科学中，以下哪个概念与数据结构最相关？A. 算法B. 操作系统C. 网络协议D. 编译原理答案：A2. 以下哪种排序算法的时间复杂度为O(n^2)？A. 快速排序B. 归并排序C. 堆排序D. 冒泡排序答案：D3. 在C++中，以下哪个关键字用于定义类？A. structB. unionC. enumD. typedef答案：A4. 以下哪个选项不是数据库管理系统（DBMS）的特性？A. 数据持久性B. 数据共享C. 数据加密D. 数据独立性答案：C5. 在计算机网络中，TCP和UDP协议分别属于哪一层？A. 传输层B. 应用层C. 网络层D. 物理层答案：A二、填空题1. 在计算机程序中，______ 用于定义数据的存储方式和组织形式。

答案：数据结构2. 一个算法的时间复杂度为O(1)，表示该算法的执行时间与输入数据的规模______。

答案：无关3. 在C++中，______ 是一种特殊的类，它提供了一种方式来定义数据类型。

答案：typedef4. 数据库管理系统（DBMS）通常包含数据定义语言（DDL）、数据操纵语言（DML）和______。

答案：数据控制语言（DCL）5. 在计算机网络中，______ 协议负责在网络层进行数据包的路由选择。

答案：IP三、简答题1. 请简述面向对象编程（OOP）的三个基本特征。

答案：封装、继承、多态2. 描述二分查找算法的基本步骤。

答案：二分查找算法的基本步骤包括：首先确定数组是有序的，然后取中间元素与目标值比较，如果中间元素等于目标值，则查找成功；如果目标值小于中间元素，则在左半部分继续查找；如果目标值大于中间元素，则在右半部分继续查找，直到找到目标值或查找范围为空。

四、编程题1. 编写一个函数，实现对整数数组的排序。

答案：以下是一个简单的冒泡排序算法实现：```cppvoid bubbleSort(int arr[], int n) {for (int i = 0; i < n-1; i++) {for (int j = 0; j < n-i-1; j++) {if (arr[j] > arr[j+1]) {swap(arr[j], arr[j+1]);}}}}```2. 编写一个函数，实现计算一个整数的阶乘。

NOIP2002普及组初赛试题及答案

第八届全国青少年信息学奥林匹克联赛(NOIP2002)试题(普及组PASCAL语言二小时完成)全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效一.选择一个正确答案代码(A/B/C/D,填入每题的括号内(每题1.5分,多选无分,共30分)1)微型计算机的问世是由于( ) 的出现。

A) 中小规模集成电路 B) 晶体管电路 C) (超)大规模集成电路 D) 电子管电路2)下列说法中正确的是( ) 。

A) 计算机体积越大,其功能就越强B) CPU的主频越高,其运行速度越快C) 两个显示器屏幕大小相同,则它们的分辨率必定相同D)点阵打印机的针数越多,则能打印的汉字字体越多3)Windows98中,通过查找命令查找文件时,若输入F*.? , 则下列文件( ) 可以被查到。

A) F.BAS B) FABC.BAS C) F.C D) EF.4)CPU处理数据的基本单位是字,一个字的字长( ) 。

A) 为8个二进制位 B) 为16个二进制位C) 为32个二进制位 D) 与芯片的型号有关5)资源管理器的目录前图标中增加"+"号,这个符号的意思是( ) 。

A) 该目录下的子目录已经展开 B) 该目录下还有子目录未展开C) 该目录下没有子目录 D) 该目录为空目录,6)下列哪一种程序设计语言是解释执行的( ) 。

A) Pascal B) GWBASIC C) C++ D) FORTRAN7)启动WORD的不正确方法是( ) 。

A) 单击Office工具栏上的Word图标B) 单击"开始"→"程序"→WordC) 单击"开始"→"运行",并输入Word按回车D) 双击桌面上的"Word快捷图标"8)多媒体计算机是指( ) 计算机。

A) 专供家庭使用的 B) 装有CDROM的C) 连接在网络上的高级 D) 具有处理文字、图形、声音、影像等信息的9)在树型目录结构中,不允许两个文件名相同主要是指( ) 。

noip 2002 普及组第四题

noip 2002 普及组第四题题目：有10个待排序的数，每个数都是非负整数，使用快速排序进行排序。

快速排序是一种常用的排序算法，其基本思想是选择一个基准元素，将数组分成两部分，一部分的元素都比基准元素小，另一部分的元素都比基准元素大，然后对这两部分分别进行快速排序。

快速排序的时间复杂度为O(nlogn)，其中n是待排序元素的个数。

以下是使用C++实现的快速排序算法的代码：c复制代码#include<iostream>#include<vector>using namespace std;void quicksort(vector<int>& nums, int left, int right) {if (left >= right) {return;}int pivot = nums[left];int i = left, j = right;while (i < j) {while (i < j && nums[j] >= pivot) {j--;}nums[i] = nums[j];while (i < j && nums[i] <= pivot) {i++;}nums[j] = nums[i];}nums[i] = pivot;quicksort(nums, left, i - 1);quicksort(nums, i + 1, right);}int main() {vector<int> nums = {5, 2, 9, 1, 5, 6, 8, 7, 4, 2}; quicksort(nums, 0, nums.size() - 1);for (int num : nums) {cout << num << " ";}cout << endl;return0;}在上述代码中，我们首先定义了一个快速排序函数quicksort，该函数接受一个待排序的vector<int> nums，以及左右边界left和right。

NOIP普及组复赛试题

P1909 买铅笔题目描述P教师需要去商店买n支铅笔作为小朋友们参加NOIP的礼物。

她发觉商店一共有3种包装的铅笔，不同包装内的铅笔数量有可能不同，价钱也有可能不同。

为了公平起见，P教师决定只买同一种包装的铅笔。

商店不许诺将铅笔的包装拆开，因此P教师可能需要购买超过n支铅笔才够给小朋友们发礼物。

此刻P教师想明白，在商店每种包装的数量都足够的情形下，要买够至少n支铅笔*最少*需要花费多少钱。

输入输出格式输入格式：输入的第一行包括一个正整数n，表示需要的铅笔数量。

接下来三行，每行用两个正整数描述一种包装的铅笔：其中第一个整数表示这种包装内铅笔的数量，第二个整数表示这种包装的价钱。

保证所有的7个数都是不超过10000的正整数。

输出格式：输出一行一个整数，表示P教师最少需要花费的钱。

输入输出样例输入样例#1：输出样例#1：输入样例#2：说明铅笔的三种包装别离是：•2支装，价钱为2;•50支装，价钱为30;•30支装，价钱为27。

P教师需要购买至少57支铅笔。

若是她选择购买第一种包装，那么她需要购买29份，共计2x29 = 58支，需要花费的钱为2x29 = 58。

事实上，P教师会选择购买第三种包装，如此需要买2份。

尽管最后买到的铅笔数量更多了，为30x2 = 60支，但花费却减少为27 x2 = 54，比第一种少。

关于第二种包装，尽管每支铅笔的价钱是最低的，但要够发必需买2份，实际的花费达到了30 x 2 = 60，因此P教师也可不能选择。

因此最后输出的答案是54。

【子任务】子任务会给出部份测试数据的特点。

若是你在解决题目中碰到了困难，能够尝试只解决一部份测试数据。

每一个测试点的数据规模及特点如下表：上表中“整倍数”的意义为：假设为“K”，表示对应数据所需要的铅笔数量n—定是每种包装铅笔数量的整倍数（这意味着必然能够不用多买铅笔)。

P2020 回文日期题目描述在日常生活中，通过年、月、日这三个要素能够表示出一个唯一确信的日期。

1995-2008 历届NOIP试题及详解

② 由编码求原数组：共 15 分（5%+5%+5%）
a 输入：N=5 B=（0，0，0，0，0）
输出： A=（4，3，2，1，0）
b 输入：N=10 B=（0，1，2，3，4，5，6，7，8，9）
输出： A=（0，1，2，3，4，5，6，7，8，9）
c 输入：N=7 B=（0，0，0，0，4，5，6）
R
Y Y
P2=B R N2R=2
Y
P3=Y R N3=R1
Y
Q
RR
Y
排列方案：排列总数： 105×2=210
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y
RRR
BB
Y BB
① 输10入5×2=210 3 4R 4 R4 4R 3 4 B B
1 2R 2 R2 2R 2 1 3B B
应打印出完整的图形R：（R12 分R）
BB
15 1R6 1R6 1R5 4 B B
Y Y Y Y Y
7 8 R 8R 8 R 7 7
BB
Y
3 4 R4 R4 R4 3 4 B B
Y
1 2 2R 2 R 2 R 2 1
19 18 17 16 15 14 13 12 11 10 <3> 本题 14 分

noip2002普及组第二题

noip2002普及组第二题【实用版】目录1.题目概述2.题目要求3.题目分析4.解题思路5.编程实现6.总结正文一、题目概述OIP2002 普及组第二题是一道涉及字符串操作的编程题。

题目要求我们编写一个程序，对给定的字符串进行操作，满足题目所给的条件。

二、题目要求题目要求我们编写一个程序，实现以下功能：1.读入一个仅包含大小写字母的字符串，长度不超过 1000 个字符；2.对字符串进行如下操作：a.将字符串中的所有字符转换为大写；b.删除字符串中的所有空格；c.计算字符串中每个字符出现的次数，并将结果按字典序排序；d.输出排序后的结果。

三、题目分析题目中涉及的操作都是字符串的基本操作，需要了解字符串的基本概念和操作方法。

对于每个操作，可以采用以下方法：1.转换为大写：可以使用 Python 的内置函数`ord()`和`chr()`以及字符串的遍历实现；2.删除空格：可以使用 Python 的字符串方法`replace()`实现；3.计算字符出现次数：可以使用 Python 的字典数据结构实现；4.按字典序排序：可以使用 Python 的内置函数`sorted()`实现。

四、解题思路根据题目要求和分析，可以设计以下解题思路：1.读入字符串，使用`ord()`和`chr()`以及字符串的遍历将字符串中的所有字符转换为大写；2.使用`replace()`方法删除字符串中的所有空格；3.遍历字符串，使用字典数据结构记录每个字符出现的次数；4.对字典进行排序，使用`sorted()`函数；5.输出排序后的结果。

五、编程实现以下是一个 Python 的示例代码：```pythons = input()s = s.upper()s = s.replace(" ", "")count = {}for c in s:if c in count:count[c] += 1else:count[c] = 1sorted_count = sorted(count.items())for c, v in sorted_count:print(c, v)```六、总结本题是一道涉及字符串操作的编程题，需要掌握字符串的基本概念和操作方法。

noip普及组复赛模拟试题15(附答案)

【基础】班委确定【试题描述】经过紧张而激烈的选拔考试，编程班终于浮出水面，一共有k位同学幸运的入选，这k位同学个个可都是精英，才华横溢，思维敏捷。

让谁做班长？让谁做学习委员？让谁做团委书记呢……？这可让班主任老师伤透了脑筋。

个个都优秀，个个都能干，实在是没有办法了。

抓阄吧！这个抓阄可不是普通的抓阄，老师让这k位同学围成一圈从一号位置开始顺时针报数报到m这个人就出圈（啊？猴子选大王啊！把我们当猴子啦？Of course not），出圈后就反向逆时针从下一个开始报数，报到n再出圈，然后再反向顺时针报到m出圈,反向逆时针报到n出圈……圈里的人越来越少，当还剩下5个人的时候那么这5个人就是编程班的班委。

Star很想当班委，为了能够当上班委，他想请你帮忙确定哪些位置是班委的位置。

【输入描述】一行：三个整数k,m和n【输出描述】一行：5个数，分别为5个班委位置的号码（号码从大到小排列）。

两个号码之间用一个空格隔开，最后一个号码没有空格【输入样例】 10 3 2【输出样例】 10 9 8 6 4【解题提示】样例说明：出圈顺序为：3 1 5 2 7 剩下4 6 8 9 10数据规模：10%的数据 k,n,m <= 1540%的数据 k,n,m <= 20060%的数据 k,n,m <= 50090%的数据 k,n,m <= 1000100%的数据 k<=1000 n,m <= 100000【试题来源】常州长训班测试var k,i,h,s,w:integer;t,z,m,n:int64;f:boolean; a:array[1..1000] of 0..1;b:array[1..5] of integer;begin readln(k,m,n); fillchar(a,sizeof(a),1);f:=true; s:=k; w:=0;while s>5 dobegint:=0;if f=true then begin h:=1;z:=m endelse begin h:=-1;z:=n end;while t<z dobeginw:=w+h; if w<=0 then w:=k+w;w:=w mod k;if w=0 then w:=k;t:=t+a[w];end;a[w]:=0;f:=not f;dec(s);end;t:=1;for i:=1 to k doif a[i]<>0 then begin b[t]:=i; inc(t);end;for i:=5 downto 2 do write(b[i],' ');write(b[1]);end.输入20 5 3 输出18 12 9 3 1输入40 9 5 输出31 25 16 2 1宝石手镯[Kolstad/Cox, 2006]贝茜在珠宝店闲逛时，买到了一个中意的手镯。

noip普及组复赛模拟试题16（附答案）

noip普及组复赛模拟试题16（附答案）【问题描述】任何一个整数N都能表示成另外两个整数a和b的平方差吗？如果能，那么这个数N就叫做Couple number。

你的工作就是判断一个数N是不是Couple number。

【输入文件】仅一行，两个长整型范围内的整数n1和n2，之间用1个空格隔开。

【输入文件】输出在n1到n2范围内有多少个Couple number。

注意：包括n1和n2两个数，且n1<="" <="10" n1="" p=""> 【输入样例】1 10【输出样例】7Couple numbera*a-b*b=n <=> (a+b)(a-b)=n如果n是奇数，则a，b一奇一偶，而n=1*n，所以，令a=(n+1)/2，b=(n-1)/2，即n一定是Couple number。

如果n是偶数，则a,b同奇同偶，此时如果n mod 4=2，则n一定是拆成一奇一偶的和，即x+y和x-y的值一定是一奇一偶，这种情况下x,y肯定无整数解，所以此时的n一定不是Couple number；如果n mod 4=0，则a=n/4+1，b=n/4-1，即n一定是Couple number。

参考程序：var x,y,i,ans:longint;begin assign(input,'couple.in'); reset(input);readln(x,y); close(input);ans:=0;for i:=x to y dobeginif odd(i) then inc(ans)else if i mod 4=0 then inc(ans);end;assign(output,'couple.out');rewrite(output);writeln(ans);close(output);end.10 90（60）5000 12000（5251）100000 200000（75001）对于某个数n,,我们这次的工作仅是求出小于n且和n互质的数的个数,,比如n=10时 1,3,7,9均与10互质//互质的定义是gcd(a,b)=1输入格式 InputFormat输入只有一行，一个数N（1<=N<=2,000,000,000）。

noip普及组复赛模拟试题6答案

计算机发明之前，数学家们需要手工进行数学计算。

遇到复杂计算往往要花去大量时间，而且正确率也不高。

现在可不一样了，有了计算机人们能快速而正确地求解数学问题。

小雪是个中学生，可已经能熟练的运用计算机编写程序了。

为了提高自己的计算机水平，小学经常将数学老师布置的题目用计算机加以求解。

有一次，数学老师提出这样一个问题：对于给定的一对自然数m 与n )(n m 在m 与n 之间（包含m 和n ）有多少素数呢？小雪很快得出了答案。

现在请你也编写程序实现。

（1不为素数）输入：文件的第一行为一个数k ，表示有k 对自然数。

以后k 行每行有两个自然数，第一个自然数为m ，第二个自然数为n 。

输出：依次输出每一对数之间的素数个数。

每个结果占一行。

例如：输入:21 510 20输出:34var n,i,s,x,y,j,t,h:longint;begin read(n);for i:=1 to n dobegin readln(x,y);h:=0;for t:=x to y dobegin s:=0;for j:=1 to t doif t mod j=0 then s:=s+1;if s=2 then h:=h+1;end;writeln(h);end;end.输入35 20输出6100 200 输出21500 1000 输出73当前有面值分别为a 分，b 分，c 分，d 分(a>b>c>d=1)的硬币，请给出找n 分钱的最佳方案（要求找出的硬币数目最少）输入:a,b,c,d,n输出:硬币各几个例:输入:25 10 5 1 36输出:25 10 5 11 1 0 1又例:输入:10 8 5 1 13输出: 10 8 5 10 1 1 0var a,b,c,d,min,s,n,t,a1,a2,a3,a4,b1,b2,b3,b4:integer;beginreadln(a,b,c,d,n);min:=9999;for a1:=0 to n div a dofor a2:=0 to n div b dofor a3:=0 to n div c dofor a4:=0 to n div d dobegint:=a1+a2+a3+a4;s:=a1*a+a2*b+a3*c+a4*d;if (s=n)and(t<min) then beginmin:=t;b1:=a1;b2:=a2;b3:=a3;b4:=a4;end;end;writeln(a:5,b:5,c:5,d:5);writeln(b1:5,b2:5,b3:5,b4:5)readln;end. 输入100 35 20 12 271输出100 35 20 122 1 0 3输入80 65 42 35 453 输出80 65 42 351 1 4 4在下面的算式中每个“#”都表示一个素数数字。

noip普及组复赛模拟试题11答案

机器人深海探测是一个极富挑战性的高技术科学研究项目。

小雪参加了这一项目的研究工作。

潜水机器人可以携带规定有限的能量。

在深海探测过程中，机器人需要消耗一定的能量，但可以在机器人之间通过接触传递能量。

用多个潜水机器人接力潜水可以极大地提高潜水机器人的潜水深度。

现给定2个潜水机器人。

第1个潜水机器人最多可以携带x1单位的能量，每下潜1米需要消耗能量y1单位。

第2个潜水机器人最多可以携带x2单位的能量，每下潜1米需要消耗能量y2单位。

开始时2个潜水机器人均处于同一海平面高度为0，并且每个机器人初始时都携带了规定最多的能量。

计算用这2个机器人进行不返回的接力深海探测可下潜的最大深度。

输入：每行一个整数，依次为x1,x2,y1,y2；输出: 这2个登山机器人可下潜的最大深度，精确到小数点后2位。

例如输入：50500.010.01输出:7500.00var x1,x2,y1,y2,x,y,s:real;beginreadln(x1); readln(x2); readln(y1); readln(y2);s:=0;if (x1/y1)>(x2/y2) thenbeginx:=x1;y:=y1;endelse beginx:=x2;y:=y2;end;repeatx1:=x1-y1;x2:=x2-y2;s:=s+1;until x1+x2<=x;s:=s+x/y;writeln(s:0:2);readln;end.输入：40 0.02↙50 0.01↙输出:6334.00输入25350.150.25输出254.671233211.55.1输出131.002035年，智能机器人在各行各业中的应用已经十分普遍了，毕竟它做事时的精度与力量比一个普通人是强多了。

王涛的运输队里就有一个，是用来装卸货物的。

这天，他们的任务是要把N（2 <= N <= 50 ）根废旧的条形钢材运送到钢铁厂重新冶炼。

这些钢材长短不同（有些还特别的长），为了便于运输，只好把它们切割成小段。

noip2002普及组第二题

noip2002普及组第二题摘要：一、引言1.介绍职业写手的身份和任务2.阐述本文的目的和结构二、文本分析1.简要分析文本内容2.突出文本中的关键信息三、编写文档1.根据文本内容，编写比赛规则文档2.强调文档的可读性和实用性四、总结与展望1.总结文档编写过程中的经验教训2.对未来职业写手工作的展望正文：作为一名职业写手，我的任务是根据所提供的文本完成一系列写作任务。

在此过程中，我需要充分挖掘文本中的关键信息，并以通俗易懂、富有逻辑的方式呈现出来。

本文将围绕noip2002普及组第二题的文本，进行分析和文档编写，以满足比赛规则文档的需求。

一、引言作为一名职业写手，我在处理文本时，不仅要确保内容的准确性，还要注重文档的可读性和实用性。

本文将以noip2002普及组第二题为例，详细介绍比赛规则，以便参赛者能够更好地了解比赛要求，提高参赛体验。

二、文本分析oip2002普及组第二题的文本主要介绍了比赛的基本信息、参赛资格、比赛形式、评分标准和奖品设置等内容。

在分析文本时，我们需要关注以下几点：1.文本的主题：了解比赛的背景和目的，为文档编写提供方向。

2.文本的结构：分析文本中的逻辑关系，确保文档的条理清晰。

3.关键信息：提炼文本中的重要信息，如参赛资格、比赛时间等。

三、编写文档在编写比赛规则文档时，我们需要遵循以下原则：1.语言简练：使用通俗易懂的语言，避免过多专业术语，使文档更具可读性。

2.逻辑清晰：根据文本分析，搭建文档结构，确保内容连贯、易懂。

3.重点突出：在文档中强调关键信息，便于读者快速掌握核心内容。

4.实用性：考虑读者需求，提供具体操作指南，使文档具有实际价值。

四、总结与展望在本次文档编写过程中，我们充分分析了文本内容，注重可读性和实用性，为广大参赛者提供了一份详尽的比赛规则指南。

展望未来，职业写手们将继续提升自身能力，为广大读者提供更多优质、实用的文档。

历年NOIP(普及组)难度分析

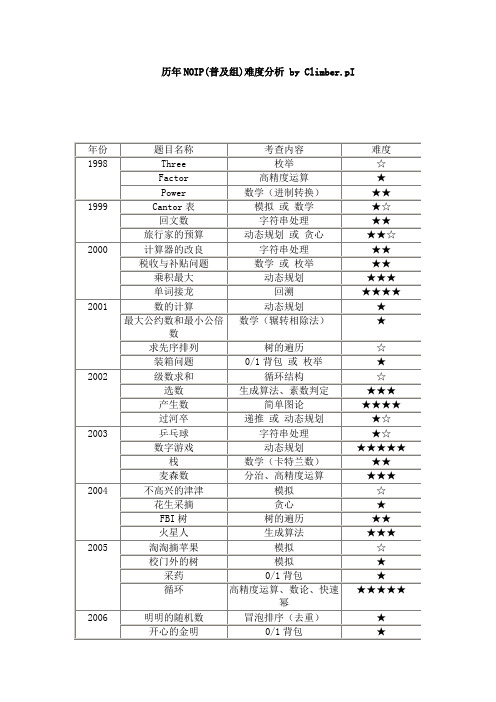
历年NOIP(普及组)难度分析 by Climber.pINOIP提高组复赛考察点详细分析12 模拟：10数学：5 图论：4搜索：4 构造：3贪心：2【动态规划】平均难度系数：0.55此项为历届NOIP考察次数最多的知识点。

主要有 1.区间模型 2.子序列模型 3.资源分配模型以及一些简单的多维状态设计技巧。

动态规划可以与图,树,高精度等知识点配合出题。

【模拟】平均难度系数：0.76平均每届NOIP都会出现1个模拟题。

这种题一般算法很简单，需要选手细心理解题目意思，注意细节。

考察选手的代码实现能力。

【数学】平均难度系数：0.46需要掌握质数及其性质，基础的实属操作，加法原理和乘法原理。

此类题需要选手对数学规律的灵感。

【图论】平均难度系数：0.50历届考察点基本上都是1.最短路问题和 2.特殊图的性质。

特殊图包括树，拓扑图，二分图等。

历届NOIP在图论上的考察并不是很多。

【搜索】平均难度系数：0.38历届搜索题一般都比较难，搜索算法本身简单，于是题目会提高选手对其他方面的要求。

主要有搜索优化和模拟。

写搜索题时应该以尽量多得分为目标。

【构造】平均难度系数：0.27构造类题目一般没有明确的算法，需要选手仔细分析题目的实质，并得出解法。

这个解法通常不是唯一的。

有时一个好的贪心可以得相当多的分。

有时搜索剪枝可以很大的提高效率。

同样以多得分为目标。

【【贪心】平均难度系数：0.75此类题需要选手对算法的直觉，贪心正确性一旦被证明，通常题目就简单了。

第八届全国青少年信息学奥林匹克联赛(NOIP2002)试题

第1页第八届全国青少年信息学奥林匹克联赛(NOIP2002)试题(普及组PASCAL 语言二小时完成)全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效一.选择一个正确答案代码(A/B/C/D,填入每题的括号内(每题1.5分,多选无分,共30分) 1)微型计算机的问世是由于( ) 的出现。

A) 中小规模集成电路 B) 晶体管电路 C) (超)大规模集成电路 D) 电子管电路 2)下列说法中正确的是( ) 。

A) 计算机体积越大,其功能就越强 B) CPU 的主频越高,其运行速度越快C) 两个显示器屏幕大小相同,则它们的分辨率必定相同D)点阵打印机的针数越多,则能打印的汉字字体越多3)Windows98中,通过查找命令查找文件时,若输入F*.? , 则下列文件( ) 可以被查到。

A) F.BAS B) FABC.BAS C) F.C D) EF. 4)CPU 处理数据的基本单位是字,一个字的字长( ) 。

A) 为8个二进制位 B) 为16个二进制位 C) 为32个二进制位 D) 与芯片的型号有关5)资源管理器的目录前图标中增加"+"号,这个符号的意思是( ) 。

A) 该目录下的子目录已经展开 B) 该目录下还有子目录未展开 C) 该目录下没有子目录 D) 该目录为空目录, 6)下列哪一种程序设计语言是解释执行的( ) 。

A) Pascal B) GWBASIC C) C++ D) FORTRAN 7)启动WORD 的不正确方法是( ) 。

A) 单击Office 工具栏上的Word 图标 B) 单击"开始"→"程序"→WordC) 单击"开始"→"运行",并输入Word 按回车 D) 双击桌面上的"Word 快捷图标" 8)多媒体计算机是指( ) 计算机。

A) 专供家庭使用的 B) 装有CDROM 的C) 连接在网络上的高级 D) 具有处理文字、图形、声音、影像等信息的 9)在树型目录结构中,不允许两个文件名相同主要是指( ) 。

NOIP2002普及组复赛试题

2002年全国青少年信息学（计算机）奥林匹克分区联赛复赛试题
（普及组竞赛用时：3 小时）
题一级数求和
（存盘名：NOIPC1）
[问题描述]:
已知：Sn= 1＋1／2＋1／3＋…＋1／n。

显然对于任意一个整数K，当n足够大的时候，Sn 大于K。

现给出一个整数K（1<=k<=15），要求计算出一个最小的n；使得Sn＞K。

[输入]
输入 k
[输出]
输出 n
[输入输出样例]
输人：1
输出：2
题二选数
（存盘名：NOIPC2）
[问题描述]:
已知 n 个整数 x1,x2,…,xn，以及一个整数 k（k＜n）。

从 n 个整数中任选 k 个整数相加，可分别得到一系列的和。

例如当 n=4，k＝3，4 个整数分别为 3，7，12，19 时，可得全部的组合与它们的和为： 3＋7＋12=22 3＋7＋19＝29 7＋12＋19＝38 3＋12＋19＝34。

现在，要求你计算出和为素数共有多少种。

例如上例，只有一种的和为素数：3＋7＋19＝29）。

[输入]：
输入格式为：
n , k （1<=n<=20，k＜n）
x1,x2，…,xn （1<=xi<=5000000）
[输出]：
输出格式为：
一个整数（满足条件的种数）。

[输入输出样例]:
输入：
4 3
3 7 12 19
输出：
1。

NOIPCSP普及组历年复赛真题题单（1998～2020）

NOIPCSP普及组历年复赛真题题单（1998～2020）**转载⾃： **1.CSP-J 2020T1 优秀的拆分位运算、进制转换T2 直播获奖桶排序T3 表达式栈、深搜T4 ⽅格取数动态规划2.CSP-J 2019T1 数字游戏字符串T2 公交换乘模拟、队列T3 纪念品背包T4 加⼯零件⼴搜、最短路3.NOIP2018 普及组T1 标题统计字符串T2 龙虎⽃枚举、预处理T3 摆渡车动态规划T4 对称⼆叉树⼆叉树4.NOIP2017 普及组T1 成绩枚举模拟T2 图书管理员结构体排序T3 棋盘深搜、剪枝T4 跳房⼦⼆分、动态规划5.NOIP2016 普及组T1 买铅笔枚举模拟T2 回⽂⽇期回⽂T3 海港⼤模拟、队列T4 魔法阵枚举、前缀和6.NOIP2015 普及组T1 ⾦币枚举模拟T2 扫雷游戏枚举模拟T3 求和组合数学T4 推销员贪⼼、优先队列7.NOIP2014 普及组T1 珠⼼算测验模拟T2 ⽐例简化枚举、gcdT3 螺旋矩阵模拟、找规律T4 ⼦矩阵动态规划8.NOIP2013 普及组T1 计数问题枚举模拟T2 表达式求值栈T3 ⼩朋友的数字动态规划T4 车站分级拓扑排序9.NOIP2012 普及组T1 质因数分解枚举模拟、质数T2 寻宝模拟、取模T3 摆花背包、动态规划T4 ⽂化之旅最短路10.NOIP2011 普及组T1 数字反转进制转换T2 统计单词数字符串T3 瑞⼠轮归并排序T4 表达式的值动态规划、栈11.NOIP2010 普及组T1 数字统计模拟枚举T2 接⽔问题模拟T3 导弹拦截贪⼼T4 三国游戏贪⼼、博弈12.NOIP2009 普及组T1 多项式输出模拟T2 分数线划定结构体排序T3 细胞分裂约数T4 道路游戏动态规划13.NOIP2008 普及组T1 ISBN 号码字符串T2 排座椅贪⼼T3 传球游戏动态规划T4 ⽴体图⼤模拟14.NOIP2007 普及组T1 奖学⾦结构体排序T2 纪念品分组贪⼼T3 守望者的逃离贪⼼T4 Hanoi 双塔问题⾼精度15.NOIP2006 普及组T1 明明的随机数枚举模拟T2 开⼼的⾦明 01背包T3 Jam 的计数法模拟T4 数列进制转换16.NOIP2005 普及组T1 陶陶摘苹果枚举模拟T2 校门外的树枚举模拟T3 采药 01背包T4 循环⾼精度17.NOIP2004 普及组T1 不⾼兴的津津模拟T2 花⽣采摘贪⼼T3 FBI 树递归、⼆叉树T4 ⽕星⼈ STL、深搜18.NOIP2003 普及组T1 乒乓球模拟T2 数字游戏动态规划T3 栈组合数学、卡特兰数T4 麦森数⾼精度19.NOIP2002 普及组T1 级数求和枚举T2 选数深搜T3 产⽣数深搜T4 过河卒递推、动态规划20.NOIP2001 普及组T1 数的计算递推、递归T2 最⼤公约数和最⼩公倍数问题枚举、GCD T3 求先序排列⼆叉树T4 装箱问题 01背包21.NOIP2000 普及组T1 计算器的改良⼀元⼀次⽅程、模拟T2 税收与补贴问题不等式、数论T3 乘积最⼤动态规划、⾼精度T4 单词接龙深搜22.NOIP1999 普及组T1 Cantor表找规律T2 回⽂数进制转换T3 旅⾏家的预算贪⼼23.NOIP1998 普及组T1 三连击简单数学、枚举、进制转换T2 阶乘和⾼精度T3 2的幂次⽅表⽰深搜。