小升初数学阴影面积专题

合集下载

小升初数学几何求阴影部分面积题带解析

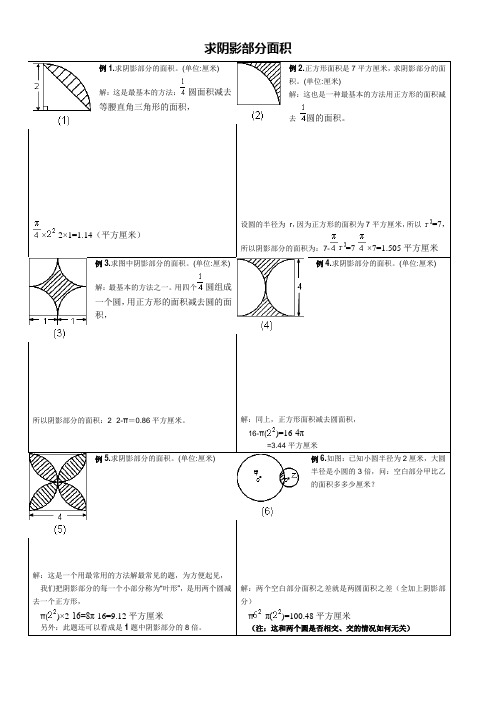
求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

(单位:厘米)解：把右面的正方形平移至左边的正方形部分，则阴影部分合成一个长方形，所以阴影部分面积为：2×3=6平方厘米例10.求阴影部分的面积。

小升初数学复习专题：求阴影部分面积(含答案解析)

小升初数学复习专题：求阴影部分面积（含答案解析）1、几何图形计算公式：1) 正方形：周长＝边长×4 C=4a面积=边长×边长S=a×a2) 正方体：表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3) 长方形：周长=(长+宽)×2 C=2(a+b)面积=长×宽S=ab4)长方体：表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)体积=长×宽×高V=abh5)三角形：面积=底×高÷2 s=ah÷26)平行四边形：面积=底×高s=ah7)梯形：面积=(上底+下底)×高÷2 s=(a+b)×h÷28)圆形：周长=直径×Π=2×Π×半径C=Πd=2Πr面积=半径×半径×Π9)圆柱体：侧面积=底面周长×高表面积=侧面积+底面积×2体积=底面积×高10)圆锥体：体积=底面积×高÷32、面积求解大致分为以下几类：Ø 从整体图形中减去局部；割补法：将不规则图形通过割补，转化成规则图形。

重难点：观察图形的特点，根据图形特点选择合适的方法求解图形的面积。

能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。

练习题例1.求阴影部分的面积。

(单位:厘米)例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)例3.求图中阴影部分的面积。

(单位:厘米)例4.求阴影部分的面积。

(单位:厘米)例5.求阴影部分的面积。

(单位:厘米)例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？例7.求阴影部分的面积。

不规则或组合平面图形阴影部分面积计算-2024年小升初数学复习热点题型专项训练(通用版)(含解析)

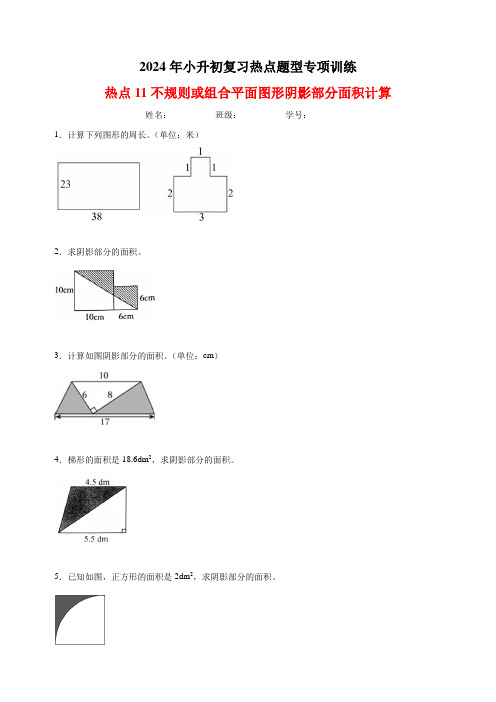
2024年小升初复习热点题型专项训练热点11不规则或组合平面图形阴影部分面积计算姓名：_________ 班级：_________ 学号：_________1．计算下列图形的周长。

（单位：米）2．求阴影部分的面积。

3．计算如图阴影部分的面积。

（单位：cm）4．梯形的面积是18.6dm2，求阴影部分的面积。

5．已知如图，正方形的面积是2dm2，求阴影部分的面积。

6．求阴影部分的周长。

7．求下列组合图形的面积。

（单位：cm）8．计算如图中阴影部分的面积。

9．计算下边阴影图形的周长。

10．求组合图形的面积。

（单位：米）11．求组合图形的面积。

（单位：cm）12．求图中阴影部分的面积（单位：厘米）13．如图中阴影部分的面积是多少？14．求如图阴影部分的周长和面积。

15．求阴影部分的面积（单位：厘米）。

16．求下面图形中阴影部分的面积。

17．求图中涂色部分的面积。

（单位：厘米）18．如图中，大圆的半径等于小圆的直径。

请计算阴影部分的周长。

19．计算如图阴影部分的面积。

20．求图形中阴影部分的面积。

（单位：分米）21．求下面图形阴影部分的周长和面积。

22．求下图中阴影部分的周长和面积。

23．求图中阴影部分的面积。

（单位：厘米）（取3.14）24．求阴影部分的面积。

（单位：厘米）25．求下面图中阴影部分的面积（单位：厘米）。

26．计算如图所示图形阴影部分的面积。

（单位：厘米；圆周率取3.14）27．求下面图形中阴影部分的周长和面积。

28．计算如图所示图形阴影部分的面积。

（单位：厘米；圆周率取3.14）29．求出下图中阴影部分的面积。

（单位：米）30．求出前两个图形的面积和第三个图形中涂色部分的面积。

参考答案1．122米；12米【分析】（1）长方形的周长＝（长＋宽）×2，代入数据即可解答；（2）把这个图形上方的小线段分别向上、向左及向右平移，则这个图形的周长就是边长为3米的正方形的周长，据此利用正方形的周长公式即可解答。

小升初面积计算真题专项

面积计算部分典型题总结1.填空（每小题2分，共4分）1.如右图，AB 平行于CD ，图中甲和图形乙的一组对边分别平行，它们的面积相比较，乙甲。

（填“＞”“=”或“＜”）2. 把长、宽分别为9厘米、6厘米的长方形划分为如图的4个三角形，其中的面积关系有4321s s s s +==，则3s = 平分厘米。

2.操作、应用（10分）1. 如图，等腰直角三角形的一腰的长是8厘米，以它的两腰为直径分别画了两个半圆，那么阴影部分的面积共有多少平方厘米？（π取3.14）3.求图形面积（6分）1. 如图，已知边长为8的正方形ABCD ，E 为AD 的中点，P 为CE 的中点，求△BDP 的面积。

4.求阴影部分的面积（共12分）（1）右图是由两个平行的四边形组成的，求阴影部分面积。

（6分）（2）求阴影部分的面积（6分）甲乙5.计算（共29分）1.右图中阴影部分占长方形的() ()。

（2分）2. 右图是圆柱沿一平面切掉一块后剩余部分，请计算它的体积。

（5分）6.我有办法（每小题4分，共8分）1.用四个一样的长方形拼成下图，一个长方形面积是864平方米，长比宽多12米，求长方形的长和宽。

2.求下面阴影部分的面积。

7.计算1.右图平行四边形的高是6厘米，它的面积是（）平方厘米（3分）A.35B.42C.30D.362.一个长5厘米，宽2.4厘米的长方形，沿对角线对折后，得到如右图所示的几何图形，阴影部分的周长是厘米（3分）3.在右图中，平行四边形的面积是20平方厘米，图中甲、乙、丙三个三角形的面积比是（3分）4.综合应用（每小题5分，共10分）（1）阅读理解：“数学小知识”“勾股定理”是指一个直角三角形中，两条直角边的平方和等于斜边的平方。

例如：两条直角边的长分别为3、4，则222543=+，即斜边的长为5。

已知图中两条直角边的长度，求图中以斜边为直角所作圆的面积。

（2）如右图，已知长方形ABCD 的面积是88平方厘米，E 和F 分别是长和宽的中点。

【精品】六年级下册数学试题——解决问题之阴影面积人教新课标(含答案)

小升初解决问题——阴影面积一、直接求法根据已知条件，从整体出发，直接求出阴影部分的面积。

例如：分析：从图形可知阴影部分是一个三角形，由于三角形的面积有特定的计算公式，因此，要计算三角形的面积只需知道三角形的底和高就可以了。

要注意的是先求出阴影三角形的“底”。

通过分析，阴影三角形的底为7厘米，高为14厘米解：阴影部分面积为：1/2x(15-8)x14=49(平方厘米)二、相减法这种方法就是阴影部分面积不能够直接算出来，但是总面积和空白部分的面积可以直接算出，因此可以用总面积减去空白部分面积，即得阴影之面积。

这是用得较多的一种方法，是求阴影面积的基础。

分析：由于阴影部分面积不能算出，但是总面积和空白部分面积是规则图形，可以根据计算公式计算出面积，然后用扇形面积减去三角形面积。

解：1/4x3.14x2x2-1/2x2x2=1.14(平方厘米)三、割补法这类题主要是阴影部分是一个不规则的图形。

但是通过割和补的方法，变成一个规则的图形，从而进行计算。

需要提醒的是，割补法重在割与补，割补后要有利于变整体为局部，化不规则为规则，化陌生为熟悉，化抽象为直观。

分析：通过看图发现连对角线后将"叶形"剪开移到右上面的空白部分，凑成正方形的一半。

解：8x8÷2=32(平方厘米)四、拼凑法这种方法就是把所有的阴影部分放到一块进行拼凑成一个图形，然后根据计算公式进行计算。

分析：通过看图阴影部分是三个扇形，但是扇形的圆心角不知道，好像无法计算。

但是，通过分析吧三个扇形通过拼可以一个半圆，这样问题也就迎刃而解。

解：1/2x3.14x3x3=14.13(平方厘米)五、等面积变换法它通过平面图形之间的等面积变换，化难为易，求出阴影部分的面积。

如下图(已知CD为6厘米)分析：图形中的阴影部分是不规则图形，面积较难计算，注意到点C、D为半圆的三等分点。

通过分析发现把P点移动到O点三角形CDP和三角形CDO同底等高，所以三角形CDP和三角形CDO的面积相等。

六年级下册数学试题——解决问题之阴影面积人教新课标(2014秋)(含答案)

小升初解决问题——阴影面积一、直接求法根据已知条件，从整体出发，直接求出阴影部分的面积。

要注意的是先求出阴影三角形的“底”。

这是用得较多的一种方法，是求阴影面积的基础。

分析：由于阴影部分面积不能算出，但是总面积和空白部分面积是规则图形，可以根据计算公式计算出面积，然后用扇形面积减去三角形面积。

解：1/4x3.14x2x2-1/2x2x2=1.14(平方厘米)三、割补法这类题主要是阴影部分是一个不规则的图形。

但是通过割和补的方法，变成一个规则的图形，从而进行计算。

需要提醒的是，割补法重在割与补，割补后要有利于变整体为局部，化不规则为规则，化陌生为熟悉，化抽象为直观。

分析：通过看图发现连对角线后将"叶形"剪开移到右上面的空白部分，凑成正方形的一半。

解：8x8÷2=32(平方厘米)四、拼凑法这种方法就是把所有的阴影部分放到一块进行拼凑成一个图形，然后根据计算公式进行计算。

分析：通过看图阴影部分是三个扇形，但是扇形的圆心角不知道，好像无法计算。

但是，通过分析吧三个扇形通过拼可以一个半圆，这样问题也就迎刃而解。

解：1/2x3.14x3x3=14.13(平方厘米)五、等面积变换法它通过平面图形之间的等面积变换，化难为易，求出阴影部分的面积。

如下图(已知CD为6厘米)分析：图形中的阴影部分是不规则图形，面积较难计算，注意到点C、D为半圆的三等分点。

通过分析发现把P点移动到O点三角形CDP和三角形CDO同底等高，所以三角形CDP和三角形CDO的面积相等。

数学六年级下人教新课标阴影部分面积专项练习(含答案)

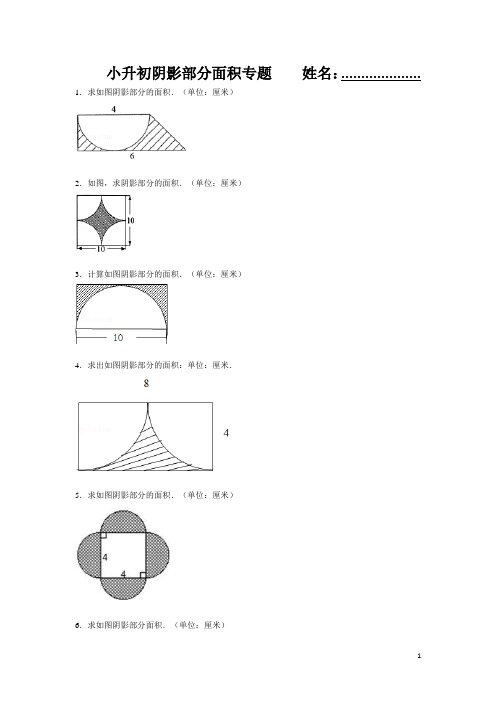
小升初阴影部分面积专题姓名：.................... 1．求如图阴影部分的面积．（单位：厘米）2．如图，求阴影部分的面积．（单位：厘米）3．计算如图阴影部分的面积．（单位：厘米）4．求出如图阴影部分的面积：单位：厘米．5．求如图阴影部分的面积．（单位：厘米）6．求如图阴影部分面积．（单位：厘米）7．计算如图中阴影部分的面积．单位：厘米．8．求阴影部分的面积．单位：厘米．9．如图是三个半圆，求阴影部分的周长和面积．（单位：厘米）10．求阴影部分的面积．（单位：厘米）11．求下图阴影部分的面积．（单位：厘米）12．求阴影部分图形的面积．（单位：厘米）13．计算阴影部分面积（单位：厘米）．14．求阴影部分的面积．（单位：厘米）15．求下图阴影部分的面积：（单位：厘米）16．求阴影部分面积（单位：厘米）．17．求阴影部分的面积．（单位：厘米）参考答案与试题解析1．求如图阴影部分的面积．（单位：厘米）考点：组合图形的面积；梯形的面积；圆、圆环的面积．分析：阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积，利用梯形和半圆的面积公式代入数据即可解答．解答：解：（4+6）×4÷2÷2﹣3.14×÷2，=10﹣3.14×4÷2，=10﹣6.28，=3.72（平方厘米）；答：阴影部分的面积是3.72平方厘米．点评：组合图形的面积一般都是转化到已知的规则图形中利用公式计算，这里考查了梯形和圆的面积公式的灵活应用．2．如图，求阴影部分的面积．（单位：厘米）考点：组合图形的面积．分析：根据图形可以看出：阴影部分的面积等于正方形的面积减去4个扇形的面积．正方形的面积等于（10×10）100平方厘米，4个扇形的面积等于半径为（10÷2）5厘米的圆的面积，即：3.14×5×5=78.5（平方厘米）．解答：解：扇形的半径是：10÷2，=5（厘米）；10×10﹣3.14×5×5，100﹣78.5，=21.5（平方厘米）；答：阴影部分的面积为21.5平方厘米．点评：解答此题的关键是求4个扇形的面积，即半径为5厘米的圆的面积．3．计算如图阴影部分的面积．（单位：厘米）考点：组合图形的面积．分析：分析图后可知，10厘米不仅是半圆的直径，还是长方形的长，根据半径等于直径的一半，可以算出半圆的半径，也是长方形的宽，最后算出长方形和半圆的面积，用长方形的面积减去半圆的面积也就是阴影部分的面积．解答：解：10÷2=5（厘米），长方形的面积=长×宽=10×5=50（平方厘米），半圆的面积=πr2÷2=3.14×52÷2=39.25（平方厘米），阴影部分的面积=长方形的面积﹣半圆的面积，=50﹣39.25，=10.75（平方厘米）；答：阴影部分的面积是10.75．点评：这道题重点考查学生求组合图形面积的能力，组合图形可以是两个图形拼凑在一起，也可以是从一个大图形中减去一个小图形得到；像这样的题首先要看属于哪一种类型的组合图形，再根据条件去进一步解答．4．求出如图阴影部分的面积：单位：厘米．考点：组合图形的面积．专题：平面图形的认识与计算．分析：由题意可知：阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积，代入数据即可求解．解答：解：8×4﹣3.14×42÷2，=32﹣25.12，=6.88（平方厘米）；答：阴影部分的面积是6.88平方厘米．点评：解答此题的关键是：弄清楚阴影部分的面积可以由哪些图形的面积和或差求出．5．求如图阴影部分的面积．（单位：厘米）考点：圆、圆环的面积．分析：由图可知，正方形的边长也就是半圆的直径，阴影部分由4个直径为4厘米的半圆组成，也就是两个圆的面积，因此要求阴影部分的面积，首先要算1个圆的面积，然后根据“阴影部分的面积=2×圆的面积”算出答案．解答：解：S=πr2=3.14×（4÷2）2=12.56（平方厘米）；阴影部分的面积=2个圆的面积，=2×12.56，=25.12（平方厘米）；答：阴影部分的面积是25.12平方厘米．点评：解答这道题的关键是重点分析阴影部分是由什么图形组成的，再根据已知条件去计算．6．求如图阴影部分面积．（单位：厘米）考点：长方形、正方形的面积；平行四边形的面积；三角形的周长和面积．分析：图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积；图二中阴影部分的面积=梯形的面积﹣平四边形的面积，再将题目中的数据代入相应的公式进行计算．解答：解：图一中阴影部分的面积=6×6÷2﹣4×6÷2=6（平方厘米）；图二中阴影部分的面积=（8+15）×（48÷8）÷2﹣48=21（平方厘米）；答：图一中阴影部分的面积是6平方厘米，图二中阴影部分的面积是21平方厘米．点评：此题目是组合图形，需要把握好正方形、三角形、梯形及平行四边形的面积公式，再将题目中的数据代入相应的公式进行计算．7．计算如图中阴影部分的面积．单位：厘米．考点：组合图形的面积．分析：由图意可知：阴影部分的面积=圆的面积，又因圆的半径为斜边上的高，利用同一个三角形的面积相等即可求出斜边上的高，也就等于知道了圆的半径，利用圆的面积公式即可求解．解答：解：圆的半径：15×20÷2×2÷25，=300÷25，=12（厘米）；阴影部分的面积：×3.14×122，=×3.14×144，=0.785×144，=113.04（平方厘米）；答：阴影部分的面积是113.04平方厘米．点评：此题考查了圆的面积公式及其应用，同时考查了学生观察图形的能力．8．求阴影部分的面积．单位：厘米．考点：组合图形的面积；三角形的周长和面积；圆、圆环的面积．分析：（1）圆环的面积等于大圆的面积减小圆的面积，大圆与小圆的直径已知，代入圆的面积公式，从而可以求出阴影部分的面积；（2）阴影部分的面积=圆的面积﹣三角形的面积，由图可知，此三角形是等腰直角三角形，则斜边上的高就等于圆的半径，依据圆的面积及三角形的面积公式即可求得三角形和圆的面积，从而求得阴影部分的面积．解答：解：（1）阴影部分面积：3.14×﹣3.14×，=28.26﹣3.14，=25.12（平方厘米）；（2）阴影部分的面积：3.14×32﹣×（3+3）×3，=28.26﹣9，=19.26（平方厘米）；答：圆环的面积是25.12平方厘米，阴影部分面积是19.26平方厘米．点评：此题主要考查圆和三角形的面积公式，解答此题的关键是找准圆的半径．9．如图是三个半圆，求阴影部分的周长和面积．（单位：厘米）考点：组合图形的面积；圆、圆环的面积．专题：平面图形的认识与计算．分析：观察图形可知：图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等，所以图中阴影部分的周长，就是直径为10+3=13厘米的圆的周长，由此利用圆的周长公式即可进行计算；阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积，利用半圆的面积公式即可求解．解答：解：周长：3.14×（10+3），=3.14×13，=40.82（厘米）；面积：×3.14×[（10+3）÷2]2﹣×3.14×（10÷2）2﹣×3.14×（3÷2）2，=×3.14×（42.25﹣25﹣2.25），=×3.14×15，=23.55（平方厘米）；答：阴影部分的周长是40.82厘米，面积是23.55平方厘米．点评：此题主要考查半圆的周长及面积的计算方法，根据半圆的弧长=πr，得出图中两个小半圆的弧长之和等于大半圆的弧长，是解决本题的关键．10．求阴影部分的面积．（单位：厘米）考点：圆、圆环的面积．分析：先用“3+3=6”求出大扇形的半径，然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积，进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可．解答：解：r=3，R=3+3=6，n=120，，=，=37.68﹣9.42，=28.26（平方厘米）；答：阴影部分的面积是28.26平方厘米．点评：此题主要考查的是扇形面积计算公式的掌握情况，应主要灵活运用．11．求下图阴影部分的面积．（单位：厘米）考点：组合图形的面积．分析：先求出半圆的面积3.14×（10÷2）2÷2=39.25平方厘米，再求出空白三角形的面积10×（10÷2）÷2=25平方厘米，相减即可求解．解答：解：3.14×（10÷2）2÷2﹣10×（10÷2）÷2=39.25﹣25=14.25（平方厘米）．答：阴影部分的面积为14.25平方厘米．点评：考查了组合图形的面积，本题阴影部分的面积=半圆的面积﹣空白三角形的面积．12．求阴影部分图形的面积．（单位：厘米）考点：组合图形的面积．分析：求阴影部分的面积可用梯形面积减去圆面积的，列式计算即可．解答：解：（4+10）×4÷2﹣3.14×42÷4，=28﹣12.56，=15.44（平方厘米）；答：阴影部分的面积是15.44平方厘米．点评：解答此题的方法是用阴影部分所在的图形（梯形）面积减去空白图形（扇形）的面积，即可列式解答．13．计算阴影部分面积（单位：厘米）．考点：组合图形的面积．专题：平面图形的认识与计算．分析：如图所示，阴影部分的面积=平行四边形的面积﹣三角形①的面积，平行四边形的底和高分别为10厘米和15厘米，三角形①的底和高分别为10厘米和（15﹣7）厘米，利用平行四边形和三角形的面积公式即可求解．解答：解：10×15﹣10×（15﹣7）÷2，=150﹣40，=110（平方厘米）；答：阴影部分的面积是110平方厘米．点评：解答此题的关键是明白：阴影部分的面积不能直接求出，可以用平行四边形和三角形的面积差求出．14．求阴影部分的面积．（单位：厘米）考点：梯形的面积．分析：如图所示，将扇形①平移到扇形②的位置，求阴影部分的面积就变成了求梯形的面积，梯形的上底和下底已知，高就等于梯形的上底，代入梯形的面积公式即可求解．解答：解：（6+10）×6÷2，=16×6÷2，=96÷2，=48（平方厘米）；答：阴影部分的面积是48平方厘米．点评：此题主要考查梯形的面积的计算方法，关键是利用平移的办法变成求梯形的面积．15．求下图阴影部分的面积：（单位：厘米）考点：组合图形的面积．分析：根据三角形的面积公式：S=ah，找到图中阴影部分的底和高，代入计算即可求解．解答：解：2×3÷2=6÷2=3（平方厘米）．答：阴影部分的面积是3平方厘米．点评：考查了组合图形的面积，本题组合图形是一个三角形，关键是得到三角形的底和高．16．求阴影部分面积（单位：厘米）．考点：组合图形的面积．分析：由图意可知：阴影部分的面积=梯形的面积﹣圆的面积，梯形的上底和高都等于圆的半径，上底和下底已知，从而可以求出阴影部分的面积．解答：解：（4+9）×4÷2﹣3.14×42×，=13×4÷2﹣3.14×4，=26﹣12.56，=13.44（平方厘米）；答：阴影部分的面积是13.44平方厘米．点评：解答此题的关键是明白：梯形的下底和高都等于圆的半径，且阴影部分的面积=梯形的面积﹣圆的面积．17．求阴影部分的面积．（单位：厘米）考点：组合图形的面积．分析：由图可知，阴影部分的面积=梯形的面积﹣半圆的面积．梯形的面积=（a+b）h，半圆的面积=πr2，将数值代入从而求得阴影部分的面积．解答：解：×（6+8）×（6÷2）﹣×3.14×（6÷2）2=×14×3﹣×3.14×9，=21﹣14.13，=6.87（平方厘米）；答：阴影部分的面积为6.87平方厘米．点评：考查了组合图形的面积，解题关键是看懂图示，把图示分解成梯形，半圆和阴影部分，再分别求出梯形和半圆的面积．。

【2020】小升初数学几何图形阴影部分面积题型大全(详细答案解析)

六年级阴影部分的面积1.求阴影部分的面积。

(单位:厘米)解：割补后如右图，易知，阴影部分面积为一个梯形。

梯形上底DE=7-4=3厘米，1S =S =DE AB)AD 2⨯+⨯阴梯形（=137)42⨯+⨯（=20(平方厘米)2、求阴影部分的面积。

<解：S =S 阴梯形，梯形的上底是圆的直径，下底、高是圆的半径，S =S 阴梯形=124)22⨯+⨯（=6(2cm )3、如图，平行四边形的高是6厘米，面积是54平方厘米，求阴影三角形的面积。

【解：S =AD AO ⨯ABCD =54平方厘米，且AO=6厘米，所以AD=9厘米。

由图形可知AED ∆是等腰直角三角形，所以AE=AD ，OE=OF=AE-AO=9-6=3cm ，BO=BC-OC=9-3=6cm 。

1S =BO OF 2⨯⨯阴=1S =632⨯⨯阴=92cm 。

4、如图是一个平行四边形，面积是50平方厘米，求阴影积分的面积。

解：方法一：过C 点作CF AD ⊥交AD 于点F ，可知AECF 是长方形，面积=5×6=302cm ，ABE CFD S =S ∆∆=(50-30)÷2=102cm 。

方法二：BC=S ABCD ÷AE=50÷5=10cm ，BE=BC-EC=10-6=4cm ，ABE S ∆=BE ×AE ÷2 =4×5÷2=102cm,5、下图是一个半圆形，已知ＡＢ＝10厘米，阴影部分的面积为平方厘米，求图形中三角形的高。

解：S =S -S ∆阴半圆=21AB 22π⎛⎫⨯⨯ ⎪⎝⎭=21103.1422⎛⎫⨯⨯ ⎪⎝⎭=152cm ，三角形的高=2S ∆÷AB=2×15÷10=3cm 。

@6、如图，一个长方形长是10cm ，宽是4cm ，以A 点和C 点为圆心各画一个扇形，求画中阴影部分的面积是多少平方厘米解：BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44⎛⎫- ⎪⎝⎭大圆小圆=ABCD 11S +S -S 44大圆小圆=()2213.1410-4-1044⨯⨯⨯ =2cm 。

小升初求圆的阴影面积的35种题型

小升初时，数学考试中常会涉及到求圆的阴影面积的题型。

这类题目被认为是数学中的难点之一，其解题方法和思路多种多样。

在此，将介绍35种不同类型的小升初求圆的阴影面积的题型，希望对广大学生能够有所帮助。

一、直接给出半径求圆的面积在这种类型的题目中，题目会明确给出圆的半径，要求求解圆的面积。

解题方法：根据圆的面积公式，直接将所给半径代入公式中进行计算即可。

二、直接给出直径求圆的面积在这种类型的题目中，题目会明确给出圆的直径，要求求解圆的面积。

解题方法：根据圆的面积公式和直径与半径之间的关系，将所给直径代入公式中进行计算即可。

三、给出半径求阴影面积在这种类型的题目中，题目会给出一个内接圆的半径，要求求解阴影的面积。

解题方法：利用内接圆的半径和外接正方形的边长之间的关系，结合圆和正方形的面积公式进行计算。

四、给出直径求阴影面积在这种类型的题目中，题目会给出一个内接圆的直径，要求求解阴影的面积。

解题方法：同样可以利用内接圆的直径和外接正方形的边长之间的关系，结合圆和正方形的面积公式进行计算。

五、给出正方形边长求阴影面积在这种类型的题目中，题目会给出一个正方形的边长，要求求解阴影的面积。

解题方法：结合正方形和圆的面积公式，可以直接计算出阴影的面积。

六、给出正方形的对角线长求阴影面积在这种类型的题目中，题目会给出一个正方形的对角线长度，要求求解阴影的面积。

解题方法：结合正方形和圆的性质，可以通过一些三角形的知识来求解阴影的面积。

七、给出阴影面积求半径在这种类型的题目中，题目会给出阴影的面积，要求求解内接圆的半径。

解题方法：利用阴影面积和内接圆的半径和正方形的边长之间的关系，可以逆向计算出圆的半径。

八、给出阴影面积求直径在这种类型的题目中，题目会给出阴影的面积，要求求解内接圆的直径。

解题方法：同样可以利用阴影面积和内接圆的直径和正方形的边长之间的关系，可以逆向计算出圆的直径。

九、给出阴影面积和正方形的两个边长求圆的半径在这种类型的题目中，题目会给出阴影的面积和正方形的两个边长，要求求解内接圆的半径。

2021年六年级数学小升初“圆”阴影部分面积习题及答案

2021年六年级数学小升初“圆”阴影部分面积习题及答案----16edfaf5-6ea2-11ec-b936-7cb59b590d7d
小升初“圆”阴影部分面积习题
1.找出图中阴影部分的面积（单位：厘米）
2．如图，求阴影部分的面积．（单位：厘米）
3.计算图中阴影部分的面积（单位：厘米）
4．求出如图阴影部分的面积：单位：厘米．
5.找出图中阴影部分的面积（单位：厘米）
6．求如图阴影部分面积．（单位：厘米）
7.计算阴影部分的面积，如图所示。

单位：厘米
8．求阴影部分的面积．单位：厘米．
9.如图所示，有三个半圆。

找出阴影部分的周长和面积。

（单位：厘米）
10．求阴影部分的面积．（单位：厘米）
11.在下图中找到阴影部分的面积。

（单位：厘米）
12．求阴影部分图形的面积．（单位：厘米）
13.计算阴影部分的面积（单位：厘米）
14．求阴影部分的面积．（单位：厘米）
15.在下图中找到阴影部分的面积：（单位：厘米）。

小升初数学求阴影部分图形面积新题型（含解答）

求阴影部分‎图形面积新‎题型近年来的中‎考数学试卷‎中，围绕图形面‎积的知识，出现了一批‎考查应用与‎创新能力的‎新题型，归纳起来主‎要有：一、规律探究型‎例1宏远广告公‎司要为某企‎业的一种产‎品设计商标‎图案，给出了如下‎几种初步方‎案，供继续设计‎选用（设图中圆的‎半径均为r‎）．（1）如图1，分别以线段‎O1O2的‎两个端点为‎圆心，以这条线段‎的长为半径‎作出两个互‎相交错的圆‎的图案，试求两圆相‎交部分的面‎积．（2）如图2，分别以等边‎△O1O2O‎3的三个顶‎点为圆心，以其边长为‎半径，作出三个两‎两相交的相‎同的圆，这时，这三个圆相‎交部分的面‎积又是多少‎呢？（3）如图3，分别以正方‎形O1O2‎O3O4的‎四个顶点为‎圆心，以其边长为‎半径作四个‎相同的圆，则这四个圆‎的相交部分‎的面积又是‎多少呢？（2005年‎黄冈市中考‎题）分析（1）利用“S阴=S菱形AO‎1B O2=4S弓形”即可；（2）利用“S阴=S△O1O2O‎3+3S弓”即可；（3）•直接求解比‎较困难，可利用求补‎法，即“S阴=S正方形O‎1O2O3‎O4-S空白”，考虑到四个‎圆半径相同‎，若延长O2‎O1交⊙O1•于A，则S空白=4SO1A‎B，由（1）根据对称性‎可求SO1‎B O4，再由“SO1AB‎=S扇形AO‎1O4-SO1BO‎4”，这样S空白‎可求．解答（1）设两圆交于‎A、B两点，连结O1A‎，O2A，O 1B，O2B．则S阴=S菱形AO‎1B O2+4S弓．∵S菱形=2S△AO1O2‎，△O1O2A‎为正△，其边长为r‎．∴S△AO1O2‎=r2，S弓=260360rπ2=26rπ2．∴S阴=22+4（6πr22）=23πr22．（2）图2阴影部‎分的面积为‎S阴=S△O1O2O‎3+3S弓．∵△O1O2O‎3为正△，边长为r．∴S△O1O2O‎32，S弓=260360rπ2．∴S阴r2+3（26rπ2）=2πr2r2．（3）延长O2O‎1与⊙O1交于点‎A，设⊙O1与⊙O4交于点‎B，由（1）知，SO1BO‎4=12（23πr2r2）．∵SO1AB‎=S扇形AO‎1O4-SO1BO‎4=290360rπ-12（23πr2r2）=24rπ-13πr2+4r2．则S阴=S正方形O‎1O2O3‎O4-4SO1A‎B=r2-4（24rπ-13πr2r2）=r 2+13πr 2-2=（13π+1-r 2．二、方案设计型‎例2 在一块长1‎6m ，宽12m 的‎矩形荒地上‎，要建造一个‎花园，要求花园所‎占面积为荒‎地面积的一‎半．下面分别是‎小明和小颖‎的设计方案‎．小明的设计‎方案：如图1，其中花园四‎周小路的宽‎度相等，经过解方程‎，•我得到路的‎宽为2m 或‎12m ．小颖的设计‎方案：如图2，其中花园中‎每个角上的‎扇形都相同‎．（1）你认为小明‎的结果对吗‎？请说明理由‎．（2）请你帮助小‎颖求出图中‎的x （精确到0．1m ）（3）你还有其它‎的设计方案‎吗？请在右边的‎矩形中画出‎你的设计草‎图，•并加以说明‎．（2004年‎新疆建设兵‎团中考题）分析（1）由小明的设‎计知，小路的宽应‎小于矩形荒‎地宽的一半‎，由此判断即‎可；（2）可由“花园面积为‎矩形面积一‎半”列方程求x ‎；（3）可由图形对‎称性来设计‎．解（1）小明的结果‎不对．设小路宽x ‎m ，则得方程（16-2x ）（12-2x ）=12×16×12解得：x 1=2，x 2=12．而荒地的宽‎为12m ，若小路宽为‎12m ，不符合实际‎情况，故x 2=12m 不合‎题意．（2）由题意，4×24x π=12×16×12x 2=96π，x ≈5.5m ．（3）方案有多种‎，下面提供5‎种供参考：三、网格求值型‎例3 图中的虚线‎网格我们称‎之为正三角‎形网格，它的每个小‎三角形都是‎边长为1个‎单位长度的‎正三角形，这样的三角‎形称为单位‎正三角形．（1）直接写出单‎位正三角形‎的高与面积‎；（2）图1中的A ‎BCD 含有‎多少个单位‎正三角形？ABCD 的‎面积是多少‎？（3）求出图1中‎线段AC 的‎长（可作辅助线‎）；（4）求出图2中‎四边形EF ‎G H 的面积‎．（2005年‎吉林省中考‎题）分析（1）由正三角形‎边角关系来‎求；（2）仔细观察图‎1便可找到‎答案；（3）考虑到图1‎中AB=3，BC=4，∠B=60°，可作△ABC 的高‎A K ，构造直角三‎角形，•再利用解直‎角三角形知‎识即可求得‎；（4）可利用网格‎构造特殊格‎点图形，再由求补法‎计算四边形‎E FGH•面积．解：（1）单位正三角‎形，（2）ABCD 含‎有24个单‎位正三角形‎，故其面积为‎24（3）如图1，过A 作AK ‎⊥BC 于K ，在Rt △ACK 中，AK=32KC=52．∴AC=（4）如图3，构造EQS ‎ R ，过F 作FT‎⊥QG 于T ，则S △FQG=12FT ·QG=12×2× 同理可求S △GSH S△EHR=6SEQSR ‎∴S 四边形E ‎F G H = SEQSR ‎ -S △FQG -S △GSH -S △EHR四、图形对称型‎例4 如图，半圆A 和半‎圆B 均与y ‎轴相切于点‎O ，其直径CD ‎、EF 均和x ‎轴垂直，以O 为顶点‎的两条抛物‎线分别经过‎C 、E 和D•、•F ，•则图中阴影‎部分的面积‎是____‎_____‎．•（2005年‎河南省中考‎题）分析由题意知，图中两半圆‎和两抛物线‎组成的图形‎关于y 轴对‎称，故y 轴左侧‎阴影部分面‎积等于半圆‎B 中的空白‎面积，所以所求阴‎影部分面积‎为半圆B 的‎面积，即S 阴=12π·12=12π．解答：2π．五、图形变换型‎例5 如图，矩形ABC ‎D 的长与宽‎分别是2c ‎m 和1cm ‎，AB 在直线‎L 上，依次为B 、C ′、•D ″，依次为B 、C ′、D ″为中心将矩‎形ABCD ‎按顺时针方‎向旋转90‎°．这样点A•走过的曲线‎依次为'AA 、 '''A A 、 '''''A A ，其中交CD ‎ 'AA于点P ．（1）求矩形A ′BC ′D ′的对角线A ‎′C ′的长；（2）求'AA 的长；（3）求图中部分的面积‎S ；（4）求图中部分的面积‎T ．（2005年‎吉林省中考‎题）分析（1）要求A ′C ′，因长宽分别‎为2和1，利用勾股定‎理即可；（2）要求'AA ，因所对圆心‎'AA 角为∠ABA ′=90°，半径AB=2，利用弧长公‎式即可；（3）因△A ′C ′D•′≌△A ″C ′D ″，故S=S 扇形A`C``A``；（4）连PB ，则PB=AB=2，又BC=1，故∠PBC=60°，∠ABP=30°，•欲求T ，由“T=S 扇形AB ‎P +S △BCP ”即可．解答（1）A ′C ′cm ）．（2） 'AA =90180π×2=π（cm ）．（3）S=S 扇形A`CA``54π（cm ）（4）连结BP ，在Rt △BCP 中，BC=1，BP=2， ∴∠BPC=30°，ABP=30°，∴T=S 扇形AB ‎P +S △PBC =30360π×22=（3π）cm 2．六、实际应用型‎例6 在栽植农作‎物时，一个很重要‎的问题是“合理密植”．如图是栽植‎一种蔬菜时‎的两种方法‎，A 、B 、C 、D 四珠顺次‎连结成为一‎个菱形，且AB=BD ；A ′、B ′、•C ′、D ′四株连结成‎一个正方形‎，这两种图形‎的面积为四‎株作物所占‎的面积，•两行作物间‎的距离为行‎距；一行中相邻‎两株作物的‎距离为株距‎；设这两种蔬‎菜充分生长‎后，每株在地面‎上的影子近‎似成一个圆‎面（相邻两圆如‎图相切），其中阴影部‎分的面积表‎示生长后空‎隙地面积．在株距都为‎a ，其他客观因‎素也相同的‎条件下，•请从栽植的‎行距，蔬菜所占的‎面积，充分生长后‎空隙地面积‎三个方面比‎较两种栽植‎方法．哪种方法能‎更充分地利‎用土地．分析：本题立意很‎新，要合理密植‎，充分利用土‎地，只需分别计‎算并比较两‎种方案的行‎距、阴影面积以‎及S 和S ．对应值小的‎即为合理密‎植．解连结AC 交‎B D 于点O ‎．在菱形AB ‎C D 中，有AB=AD ，AC ⊥BD ，BO=12BD ．∵AB=BD=a ，∴BO=OD=12a ．在Rt △AOD 中，AO=． ∴S 菱形AB ‎C D =2×12BD ·AO=22， S 正方形A ‎`B `C`D`=a 2．设方法（1）中空隙地面‎积为S 1，方法（2）中空隙地面‎积为S 2．则S 1=S 菱形AB ‎C D -S ☉A2-4πa 2，S 2=S 正方形A ‎`B `C`D`-S ☉A`=a 2-4πa 2．， ∴AO<A ′B ′，S 菱形AB ‎C D <S 正方形A ‎`B `C`D`，S 1<S 2．∴栽植方法（1）比栽植方法‎（2）能更充分地‎利用土地．。

小升初数学阴影部分算面积

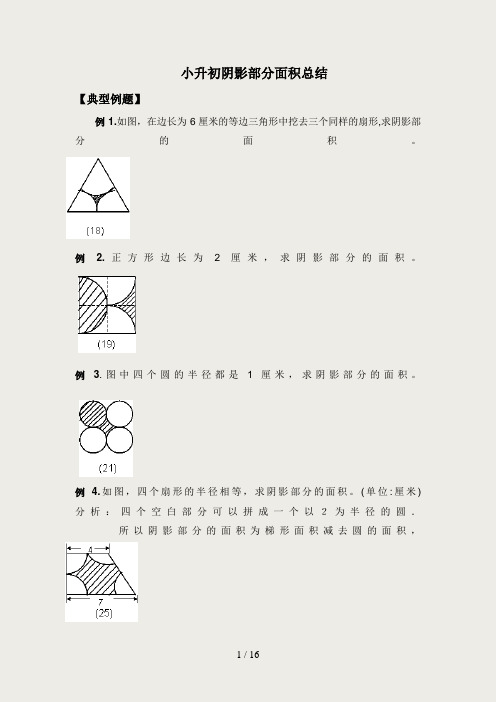
小升初阴影部分面积总结【典型例题】例1.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的面积。

例 2.正方形边长为2厘米，求阴影部分的面积。

例3.图中四个圆的半径都是1厘米，求阴影部分的面积。

例 4.如图，四个扇形的半径相等，求阴影部分的面积。

(单位:厘米) 分析：四个空白部分可以拼成一个以２为半径的圆．所以阴影部分的面积为梯形面积减去圆的面积，例22.如图，正方形ABCD的对角线AC=2厘米，扇形ACB是以AC为直径的半圆，扇形DAC是以D为圆心，AD为半径的圆的一部分，求阴影部分的面积。

例23.求阴影部分的面积。

(单位:厘米)例24.如图，三角形ABC是直角三角形，阴影部分甲比阴影部分乙面积大28平方厘米，AB=40厘米。

求BC的长度。

例 2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)【练习】1、求阴影部分的面积。

(单位:厘米)〖综合练习〗一、填空题。

1. 从直线外一点到这条直线可以画无数条线段，其中最短的是和这条直线（）的线段。

2. 下图中，∠1=（）度，∠2=（）度。

13023. 一个三角形中，最小的角是46°，按角分类，这个三角形是（）三角形。

4. 下图是三个半径相等的圆组成的图形，它有（）条对称轴。

5. 用百分数表示以下阴影部分是整个图形面积的百分之几。

6. 把一个底面直径2分米的圆柱体截去一个高1分米的圆柱体，原来的圆柱体表面积减少（）平方分米。

7. “”和“”的周长之比是（），面积之比是（）。

8.下图是由棱长1厘米的小正方体木块搭成的，这个几何体的表面积是（）平方厘米。

至少还需要（）块这样的小正方体才能搭成一个大正方体。

9. 画一个周长25.12厘米的圆，圆规两脚间的距离是（）厘米，画成的圆的面积是（）。

10. 下面的小方格边长为1厘米，估一估图①中“福娃”的面积，算一算图②中阴影部分的面积。

11. 一个梯形，上底长a厘米，下底长b厘米，高h厘米。

小升初数学求阴影部分图形面积新题型(含解答)

求阴影部分图形面积新题型近年来的中考数学试卷中，围绕图形面积的知识，出现了一批考查应用与创新能力的新题型，归纳起来主要有：一、规律探究型例1宏远广告公司要为某企业的一种产品设计商标图案，给出了如下几种初步方案，供继续设计选用（设图中圆的半径均为r）．（1）如图1，分别以线段O1O2的两个端点为圆心，以这条线段的长为半径作出两个互相交错的圆的图案，试求两圆相交部分的面积．（2）如图2，分别以等边△O1O2O3的三个顶点为圆心，以其边长为半径，作出三个两两相交的相同的圆，这时，这三个圆相交部分的面积又是多少呢？（3）如图3，分别以正方形O1O2O3O4的四个顶点为圆心，以其边长为半径作四个相同的圆，则这四个圆的相交部分的面积又是多少呢？（2005年黄冈市中考题）分析（1）利用“S阴=S菱形AO1BO2=4S弓形”即可；（2）利用“S阴=S△O1O2O3+3S弓”即可；（3）•直接求解比较困难，可利用求补法，即“S阴=S正方形O1O2O3O4-S空白”，考虑到四个圆半径相同，若延长O2O1交⊙O1•于A，则S空白=4S O1AB，由（1）根据对称性可求S O1BO4，再由“S O1AB=S扇形AO1O4-S O1BO4”，这样S空白可求．解答（1）设两圆交于A、B两点，连结O1A，O2A，O1B，O2B．则S阴=S菱形AO1BO2+4S弓．∵S菱形=2S△AO1O2，△O1O2A为正△，其边长为r．∴S△AO1O2=34r2，S弓=260360rπ3r2=26rπ32．∴S阴=232+4（6πr232）=23πr232．（2）图2阴影部分的面积为S阴=S△O1O2O3+3S弓．∵△O1O2O3为正△，边长为r．∴S△O1O2O332，S弓=260360rπ32．∴S阴32+3（26rπ32）=2πr23r2．（3）延长O2O1与⊙O1交于点A，设⊙O1与⊙O4交于点B，由（1）知，S O1BO4=12（23πr2-32r2）．∵S O1AB=S扇形AO1O4-S O1BO4=290360rπ-12（23πr232）=24rπ-13πr2+34r2．则S阴=S正方形O1O2O3O4-4S O1AB=r2-4（24rπ-13πr23r2）=r2+13πr2-3r2=（13π+1-3）r2．二、方案设计型例2 在一块长16m，宽12m的矩形荒地上，要建造一个花园，要求花园所占面积为荒地面积的一半．下面分别是小明和小颖的设计方案．小明的设计方案：如图1，其中花园四周小路的宽度相等，经过解方程，•我得到路的宽为2m或12m．小颖的设计方案：如图2，其中花园中每个角上的扇形都相同．（1）你认为小明的结果对吗？请说明理由．（2）请你帮助小颖求出图中的x（精确到0．1m）（3）你还有其它的设计方案吗？请在右边的矩形中画出你的设计草图，•并加以说明．（2004年新疆建设兵团中考题）分析（1）由小明的设计知，小路的宽应小于矩形荒地宽的一半，由此判断即可；（2）可由“花园面积为矩形面积一半”列方程求x；（3）可由图形对称性来设计．解（1）小明的结果不对．设小路宽xm，则得方程（16-2x）（12-2x）=12×16×12解得：x1=2，x2=12．而荒地的宽为12m，若小路宽为12m，不符合实际情况，故x2=12m不合题意．（2）由题意，4×24xπ=12×16×12x2=96π，x≈5.5m．（3）方案有多种，下面提供5种供参考：三、网格求值型例3 图中的虚线网格我们称之为正三角形网格，它的每个小三角形都是边长为1个单位长度的正三角形，这样的三角形称为单位正三角形．（1）直接写出单位正三角形的高与面积；（2）图1中的ABCD含有多少个单位正三角形？ABCD的面积是多少？（3）求出图1中线段AC 的长（可作辅助线）；（4）求出图2中四边形EFGH 的面积．（2005年吉林省中考题）分析（1）由正三角形边角关系来求；（2）仔细观察图1便可找到答案；（3）考虑到图1中AB=3，BC=4，∠B=60°，可作△ABC 的高AK ，构造直角三角形，•再利用解直角三角形知识即可求得；（4）可利用网格构造特殊格点图形，再由求补法计算四边形EFGH•面积．解：（133，（2）ABCD 含有24个单位正三角形，故其面积为2433（3）如图1，过A 作AK ⊥BC 于K ，在Rt △ACK 中，AK=323KC=52． ∴22AK KC +2235(3)()22+13（4）如图3，构造EQSR ，过F 作FT ⊥QG 于T ，则S △FQG =12FT ·QG=12×332×3．同理可求 S△GSH 3S△EHR3SEQSR3．∴S 四边形EFGH = SEQSR-S △FQG -S △GSH -S △EHR 33333．四、图形对称型例4 如图，半圆A 和半圆B 均与y 轴相切于点O ，其直径CD 、EF 均和x 轴垂直，以O 为顶点的两条抛物线分别经过C 、E 和D•、•F ，•则图中阴影部分的面积是_________．•（2005年河南省中考题）分析由题意知，图中两半圆和两抛物线组成的图形关于y 轴对称，故y 轴左侧阴影部分面积等于半圆B 中的空白面积，所以所求阴影部分面积为半圆B 的面积，即S 阴=12π·12=12π．解答：2π．五、图形变换型例5 如图，矩形ABCD 的长与宽分别是2cm 和1cm ，AB 在直线L 上，依次为B 、C ′、•D ″，依次为B 、C ′、D ″为中心将矩形ABCD 按顺时针方向旋转90°．这样点A•走过的曲线依次为'AA 、'''A A 、'''''A A ，其中'AA 交CD 于点P ．（1）求矩形A ′BC ′D ′的对角线A ′C ′的长；（2）求'AA 的长；（3）求图中部分的面积S ；（4）求图中部分的面积T ．（2005年吉林省中考题）分析（1）要求A ′C ′，因长宽分别为2和1，利用勾股定理即可；（2）要求'AA ，因'AA 所对圆心角为∠ABA ′=90°，半径AB=2，利用弧长公式即可；（3）因△A ′C ′D•′≌△A ″C ′D ″，故S=S 扇形A`C``A``；（4）连PB ，则PB=AB=2，又BC=1，故∠PBC=60°，∠ABP=30°，•欲求T ，由“T=S 扇形ABP +S △BCP ”即可．解答（1）A ′C ′2221+5cm ）．（2）'AA =90180π×2=π（cm ）．（3）S=S 扇形A`CA``290(5)π54π（cm ）（4）连结BP ，在Rt △BCP 中，BC=1，BP=2， ∴∠BPC=30°，3ABP=30°，∴T=S 扇形ABP +S △PBC =30360π×22+32=（3π+32）cm 2．六、实际应用型例6 在栽植农作物时，一个很重要的问题是“合理密植”．如图是栽植一种蔬菜时的两种方法，A 、B 、C 、D 四珠顺次连结成为一个菱形，且AB=BD ；A ′、B ′、•C ′、D ′四株连结成一个正方形，这两种图形的面积为四株作物所占的面积，•两行作物间的距离为行距；一行中相邻两株作物的距离为株距；设这两种蔬菜充分生长后，每株在地面上的影子近似成一个圆面（相邻两圆如图相切），其中阴影部分的面积表示生长后空隙地面积．在株距都为a ，其他客观因素也相同的条件下，•请从栽植的行距，蔬菜所占的面积，充分生长后空隙地面积三个方面比较两种栽植方法．哪种方法能更充分地利用土地．分析：本题立意很新，要合理密植，充分利用土地，只需分别计算并比较两种方案的行距、阴影面积以及S 和S ．对应值小的即为合理密植．解连结AC 交BD 于点O ．在菱形ABCD 中，有AB=AD ，AC ⊥BD ，BO=12BD ． ∵AB=BD=a ，∴BO=OD=12a ．在Rt △AOD 中，22AD OD -32a ．∴S 菱形ABCD =2×12BD ·3a 2，S 正方形A`B`C`D`=a 2．设方法（1）中空隙地面积为S 1，方法（2）中空隙地面积为S 2．则S 1=S 菱形ABCD -S ☉A 32-4πa 2， S 2=S 正方形A`B`C`D`-S ☉A`=a 2-4πa 2． 3<1，∴AO<A ′B ′，S 菱形ABCD <S 正方形A`B`C`D`，S 1<S 2．∴栽植方法（1）比栽植方法（2）能更充分地利用土地．。