2013年吉林省中考数学真题及答案解析

合集下载

2013年吉林省中考数学试卷-答案

在 Rt△AFB 中，ABF 90 ，AFB 43 ， tan AFB AB ， FB AB AB ，在 Rt△ABE 中，
FB
tan 43 0.93
ABE 90 ， AEB 32 ， tan AEB AB ， EB AB AB ， EF EB FB 且 EF 10 ，
EB
tan 32 0.62
AB AB 10 ，解得 AB 18.6 19 （米），所以教学楼的高度约 19 米． 0.62 0.93
【提示】若选择方法一，在 Rt△BGC 中，根据 CG BG 即可得出 CG 的长，同理，在 Rt△ACG 中， tan BCG
根据 tan ACG AG 可得出 AG 的长，根据 AB AG BG 即可得出结论． CG
8cm 即可，如 6cm，故答案为 6．【提示】根据勾股定理求出 AC，根据垂径定理求出 AB，即可得出 AP 的范围是大于等于 5cm 且小于等于 8cm，举出即可．【考点】垂径定理，勾股定理 14.【答案】 3a 2b 【解析】由轴对称可以得出 AB AB a ， BC b ， AC b a ．由轴对称可以得出 AC b a ， CD a 2(b a) ， CD 3a 2b ，故答案为 3a 2b ．
【提示】由轴对称可以得出 AB AB a ，就有 AC b a ，从而就有 AC b a ，就可以得出 CD a 2(b a) ，化简就可以得出结论．
【考点】翻折变换（折叠问题）
三、解答题 15.【答案】 1
2
【解析】原式
2b
ab
(a b)(a b) (a b)(a b)
ABB 1 (180 BAB) 1 (180 40) 70 ， ACB C 90 ， BC AB ，

吉林省中考数学真题试题1

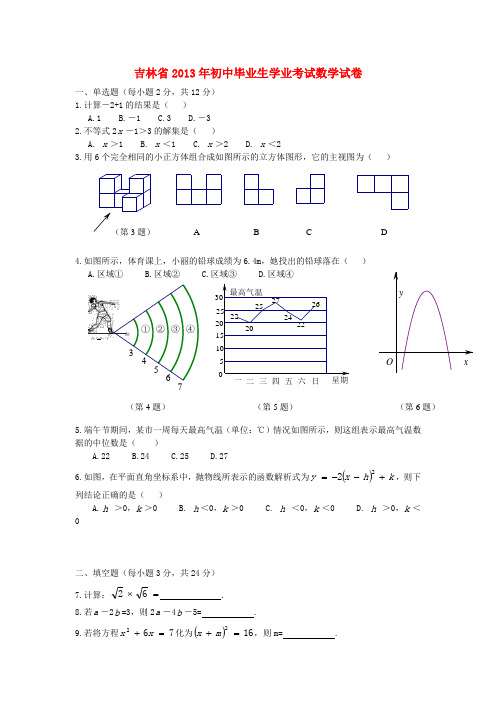
吉林省2013年初中毕业生学业考试数学试卷一、单选题（每小题2分，共12分） 1.计算－2+1的结果是（）A.1B.－1C.3D.－3 2.不等式2x －1＞3的解集是（）A. x ＞1B. x ＜1C. x ＞2D. x ＜23.用6个完全相同的小正方体组合成如图所示的立方体图形，它的主视图为（）4.如图所示，体育课上，小丽的铅球成绩为6.4m ，她投出的铅球落在（） A.区域① B.区域② C.区域③ D.区域④5.端午节期间，某市一周每天最高气温（单位：℃）情况如图所示，则这组表示最高气温数据的中位数是（）A.22B.24C.25D.27 6.如图，在平面直角坐标系中，抛物线所表示的函数解析式为()k h x y +--=22，则下列结论正确的是（）A.h ＞0，k ＞0B. h ＜0，k ＞0C. h ＜0，k ＜0D. h ＞0，k ＜0二、填空题（每小题3分，共24分） 7.计算：=⨯62 .8.若a －2b =3，则2a －4b －5= . 9.若将方程762=+x x 化为()162=+mx ，则m= .7日A B C D （第4题）（第5题）（第6题）10.分式方程132+=x x的解为x = . 11.如图，把Rt ⊿ABC 绕点A 逆时针旋转40°，得到Rt ⊿AB ′C ′，点C ′恰好落在边AB 上，连接BB ′，则∠BB ′C ′= 度.12.如图，在平面直角坐标系中，点A ，B 的坐标分别为（－6，0）、（0，8）.以点A 为圆心，以AB 长为半径画弧，交x 正半轴于点C ，则点C 的坐标为 . 13.如图，AB 是⊙O 的弦，OC ⊥AB 于点C ，连接OA 、OB.点P 是半径OB 上任意一点，连接AP.若OA=5cm ，OC=3cm ，则AP 的长度可能是 cm （写出一个符合条件的数值即可）14.如图，在矩形ABCD 中，AB 的长度为，BC 的长度为，其中b 32＜a ＜b .将此矩形纸片按下列顺序折叠，则C ′D ′的长度为（用含a 、b 的代数式表示）.三、解答题（每小题5分，共20分） 15.先化简，再求值：b a ba b ++-1222其中a =3，b =116.在一个不透明的箱子中装有3个小球，分别标有A ，B ，C.这3个小球除所标字母外，其它都相同.从箱子中随机地摸出一个小球，然后放回；再随机地摸出一个小球.请你用画树形图（或列表）的方法，求两次摸出的小球所标字不同的概率C/B /CB AA /B A /B A /DC B B（第11题）（第13题）（第14题）17.吉林人参是保健佳品.某特产商店销售甲、乙两种保健人参.甲种人参每棵100元，乙种人参每棵70元王叔叔用1200元在此特产商店购买这两种人参共15棵.求王叔叔购买每种人参的棵数.18.图①、图②都是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1.在每个网格中标注了5个格点.按下列要求画图：（1）在图①中以格点为顶点画一个等腰三角形，使其内部已标注的格点只有3个；（2）在图②中，以格点为顶点，画一个正方形，使其内部已标注的格点只有3个，且边长为无理数.四、解答题（每小题7分，共28分）19.“今天你光盘了吗？”这是国家倡导“厉行节约，反对浪费”以来的时尚流行语.某校团委随机抽取了部分学生，对他们进行了关于“光盘行动”所持态度的调查，并根据调查根据上述信息，解答下列问题：（1）抽取的学生人数为；（2）将两幅统计图补充完整；态度反对无所谓赞成赞成 %反对10%无所谓30%（第18题）图① 图② （第19题）（3）请你估计该校1200名学生中对“光盘行动”持赞成态度的人数.20.如图，在⊿ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为直角边作等腰三角形CDE，其中∠DCE=90°，连接BE.（1）求证：⊿ACD≌⊿BCE；（20若AC=3cm，则BE= cm.请你选择其中的一种．．方法，求教学楼的高度（结果保留整数）.22.在平面直角坐标系中，点A （－3，4）关于y 轴的对称点为点B ，连接AB ，反比例函数xky（x ＞0）的图象经过点B ，过点B 作BC ⊥x 轴于点C ，点P 是该反比例函数图象上任意一点，过点P 作PD ⊥x 轴于点D ，点Q 是线段AB 上任意一点，连接OQ 、CQ. （1）求k 的值；（2）判断⊿QOC 与⊿POD 的面积是否相等，并说明理由.五、解答题（每小题8分，共16分）23.如图，在⊿ABC 中，AB=BC 。

吉林2013年中考数学试题（word版）

吉林2013年中考数学试题（word版）
中考网为您提供中考试题及答案：《2014年中考真题》《2014年中考试题答案》
2013年中考数学考试已经圆满结束，2014年中考即将来临,()小编已为大家整理出吉林2013年中考数学试题（word版），帮助各位同学们对自己的数学成绩进行预估，敬请各位考生关注()中考频道其他科目的试题及答案的公布。

点击下载：吉林2013年中考数学试题（word版）.doc
点击下载：吉林2013年中考数学试题（word版）.doc
以上是()小编已为大家整理出的吉林2013年中考数学试题（word 版），更多内容请查看精品2013年中考试卷及答案专题。

吉林长春2013年中考数学试题（word版）

吉林长春2013年中考数学试题（word版）
中考网为您提供中考试题及答案：《2014年中考真题》《2014年中考试题答案》
2013年中考考试已经圆满结束，2014年中考即将来临,()小编已为大家整理出吉林长春2013年中考数学试题（word版），帮助各位同学们对自己的数学成绩进行预估，敬请各位考生关注()中考频道其他科目的试题及答案的公布。

点击下载：吉林长春2013年中考数学试题（word版）.doc
点击下载：吉林长春2013年中考数学试题（word版）.doc
以上是()小编已为大家整理出的吉林长春2013年中考数学试题（word版），更多内容请查看精品2013年中考试卷及答案专题。

2013长春中考数学试题(解析版)

吉林省长春市2013年中考数学试卷一、选择题（每小题3分，共24分）1．（3分）（2013•长春）的绝对值等于（）B的绝对值等于|=2．（3分）（2013•长春）如图是由四个相同的小长方体组成的立体图形，这个立体图形的正视图是（）B3．（3分）（2013•长春）我国第一艘航空母舰辽宁航空舰的电力系统可提供14 000 000瓦的B5．（3分）（2013•长春）如图，含30°角的直角三角尺DEF放置在△ABC上，30°角的顶点D在边AB上，DE⊥AB．若∠B为锐角，BC∥DF，则∠B的大小为（）6．（3分）（2013•长春）如图，△ABC内接于⊙O，∠ABC=71°，∠CAB=53°，点D在AC 弧上，则∠ADB的大小为（）7．（3分）（2013•长春）如图，∠ABD=∠BDC=90°，∠A=∠CBD，AB=3，BD=2，则CD 的长为（）B=，即=CD=8．（3分）（2013•长春）如图，在平面直角坐标系中，点A的坐标为（0，3），△OAB沿x 轴向右平移后得到△O′A′B′，点A的对应点在直线y=x上一点，则点B与其对应点B′间的距离为（）Bxx二、填空题（每小题3分，共18分）9．（3分）（2013•长春）计算：a2•5a=5a3．10．（3分）（2013•长春）吉林广播电视塔“五一”假期第一天接待游客m人，第二天接待游客n人，则这2天平均每天接待游客人（用含m、n的代数式表示）．天平均每天接待游客故答案为：．11．（3分）（2013•长春）如图，MN是⊙O的弦，正方形OABC的顶点B、C在MN上，且点B是CM的中点．若正方形OABC的边长为7，则MN的长为28．12．（3分）（2013•长春）如图，以△ABC的顶点A为圆心，以BC长为半径作弧；再以顶点C为圆心，以AB长为半径作弧，两弧交于点D；连结AD、CD．若∠B=65°，则∠ADC 的大小为65度．中，13．（3分）（2013•长春）如图，在平面直角坐标系中，边长为6的正六边形ABCDEF的对称中心与原点O重合，点A在x轴上，点B在反比例函数位于第一象限的图象上，则k的值为．AOB==60=3）在反比例函数3，．14．（3分）（2013•长春）如图，在平面直角坐标系中，抛物线y=ax2+3与y轴交于点A，过点A与x轴平行的直线交抛物线y=于点B、C，则BC的长值为6．y=时，三、解答题（本大题共10小题，共78分）15．（6分）（2013•长春）先化简，再求值：，其中x=．时，原式16．（6分）（2013•长春）甲、乙两人各有一个不透明的口袋，甲的口袋中装有1个白球和2个红球，乙的口袋中装有2个白球和1个红球，这些球除颜色外其他都相同．甲、乙两人分别从各自口袋中随机摸出1个球，用画树状图（或列表）的方法，求两人摸出的球颜色相同的概率．．17．（6分）（2013•长春）某班在“世界读书日”开展了图书交换活动，第一组同学共带图书24本，第二组同学共带图书27本．已知第一组同学比第二组同学平均每人多带1本图书，第二组人数是第一组人数的1.5倍．求第一组的人数．=，18．（7分）（2013•长春）在△ABC中，AB=AC，点D、E、F分别是AC、BC、BA延长线上的点，四边形ADEF为平行四边形．求证：AD=BF．19．（7分）（2013•长春）如图，岸边的点A处距水面的高度AB为2.17米，桥墩顶部点C 距水面的高度CD为23.17米．从点A处测得桥墩顶部点C的仰角为26°，求岸边的点A与桥墩顶部点C之间的距离．（结果精确到0.1米）（参考数据：sin26°=0.44，cos26°=0.90，tan26°=0.49）CAE=，==20．（7分）（2013•长春）某校学生会为了解学生在学校食堂就餐剩饭情况，随机对上周在食堂就餐的n名学生进行了调查，先调查是否剩饭的情况，然后再对其中剩饭的每名学生的剩饭次数进行调查．根据调查结果绘制成如下统计图．（1）求这n名学生中剩饭学生的人数及n的值．（2）求这n名学生中剩饭2次以上的学生占这n名学生人数的百分比．（3）按上述统计结果，估计上周在学校食堂就餐的1 200名学生中剩饭2次以上的人数．21．（8分）（2013•长春）甲、乙两工程队维修同一段路面，甲队先清理路面，乙队在甲队清理后铺设路面．乙队在中途停工了一段时间，然后按停工前的工作效率继续工作．在整个工作过程中，甲队清理完的路面长y（米）与时间x（时）的函数图象为线段OA，乙队铺设完的路面长y（米）与时间x（时）的函数图象为折线BC﹣CD﹣DE，如图所示，从甲队开始工作时计时．（1）分别求线段BC、DE所在直线对应的函数关系式．（2）当甲队清理完路面时，求乙队铺设完的路面长．25=（22．（9分）（2013•长春）探究：如图①，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD，AE⊥CD于点E．若AE=10，求四边形ABCD的面积．应用：如图②，在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，AE⊥BC于点E．若AE=19，BC=10，CD=6，则四边形ABCD的面积为152．BC××23．（10分）（2013•长春）如图，在平面直角坐标系中，抛物线y=ax2+bx﹣2 与x轴交于点A（﹣1，0）、B（4，0）．点M、N在x轴上，点N在点M右侧，MN=2．以MN为直角边向上作等腰直角三角形CMN，∠CMN=90°．设点M的横坐标为m．（1）求这条抛物线所对应的函数关系式．（2）求点C在这条抛物线上时m的值．（3）将线段CN绕点N逆时针旋转90°后，得到对应线段DN．①当点D在这条抛物线的对称轴上时，求点D的坐标．②以DN为直角边作等腰直角三角形DNE，当点E在这条抛物线的对称轴上时，直接写出所有符合条件的m值．（参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标为（，））x xy=﹣x=，x=x=x﹣m﹣．的值为DN=CN=CM=CN=2CM=2MNx x x=，﹣x x x=，解得m=x x x=，解得﹣x x x=x x x=，解得﹣﹣．24．（12分）（2013•长春）如图①，在▱ABCD中，AB=13，BC=50，BC边上的高为12．点P从点B出发，沿B﹣A﹣D﹣A运动，沿B﹣A运动时的速度为每秒13个单位长度，沿A ﹣D﹣A运动时的速度为每秒8个单位长度．点Q从点B出发沿BC方向运动，速度为每秒5个单位长度．P、Q两点同时出发，当点Q到达点C时，P、Q两点同时停止运动．设点P的运动时间为t（秒）．连结PQ．（1）当点P沿A﹣D﹣A运动时，求AP的长（用含t的代数式表示）．（2）连结AQ，在点P沿B﹣A﹣D运动过程中，当点P与点B、点A不重合时，记△APQ 的面积为S．求S与t之间的函数关系式．（3）过点Q作QR∥AB，交AD于点R，连结BR，如图②．在点P沿B﹣A﹣D运动过程中，当线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分时t的值．（4）设点C、D关于直线PQ的对称点分别为C′、D′，直接写出C′D′∥BC时t的值．时，根据三角形的面积公式分别求出＜时，当＜＜t=，==时，如图②．=t=．时，如图④．t=＜≤时，线段．t=．t=，t=。

2013吉林省中考数学试题及答案

A．
B．
C．
D．
考点：简单组合体的三视图．分析：找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．解答：解：从正面看易得第一层有 2 个正方形，第二层有 3 个正方形．
故选 A．点评：本题考查了三视图的知识，主视图是从物体的正面看得到的视图．
4．（2 分）（2013•吉林）如图所示，体育课上，小丽的铅球成绩为 6.4m，她投出的铅球落在（）
A．区域①
B．区②
C．区域③
D．区域④
考点：近似数和有效数字．分析：根据小丽的铅球成绩为 6.4m，得出其所在的范围，即可得出答案．解答：解：∵6＜6.4＜7，
∴她投出的铅球落在区域④；故选 D．点评：此题考查了近似数，关键是根据 6.4 求出其所在的范围，用到的知识点是近似数．
PDF pdfFactory Pro
解答：解：原式=
+
=
=，
当 a=3，b=1 时，原式= = ．
点评：本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
16．（5 分）（2013•吉林）在一个不透明的箱子中装有 3 个小球，分别标有 A，B，C．这 3 个小球除所标字母外，其它都相同．从箱子中随机地摸出一个小球，然后放回；再随机地摸出一个小球．请你用画树形图（或列表）的方法，求两次摸出的小球所标字不同的概率．考点：列表法与树状图法分析：依据题意画树状图法分析所有可能的出现结果即可解答．解答：解：如图所示：
PDF pdfFactory Pro

故原分式方程的解为：x=2．故答案为：2．点评：此题主要考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解；解分式方程一定注意要验根．

长春市2013年中考数学试卷(附答案)

长春市2013年中考数学试卷（附答案）（A）（B）（C）（D）5．如图，含30°角的直角三角尺DEF放置在△ABC上，30°角的顶点D 在边AB上，DE⊥AB．若为锐角，BC∥DF，则的大小为（A）30°.（B）45°.（C）60°.（D）75°.（第5题）（第6题）6．如图，△ABC内接于⊙O，∠ABC=71º，∠CAB=53°点D在AC弧上，则∠ADB的大小为（A）46°.（B）53°.（C）56°.（D）71°.7．如图，°,，AB=3，BD=2，则CD的长为（A）.（B）.（C）2.（D）3.（第7题）（第8题）8．如图，在平面直角坐标系中，点A的坐标为（0,3），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点在直线上一点，则点B与其对应点B′间的距离为（A）.（B）3.（C）4.（D）5.二、填空题（每小题3分，共18分）9．计算：＝.10．吉林广播电视塔“五一”假期第一天接待游客m人，第二天接待游客n人，则这2天平均每天接待游客人（用含m、n的代数式表示）. 11．如图，MN是⊙O的弦，正方形OABC的顶点B、C在MN上，且点B是CM的中点.若正方形OABC的边长为7，则MN的长为.（第11题）（第12题）12．如图，以△ABC的顶点A为圆心，以BC长为半径作弧；再以顶点C为圆心，以AB长为半径作弧，两弧交于点D；连结AD、CD．若∠B=65°，则∠ADC的大小为度.13．如图，在平面直角坐标系中，边长为6的正六边形ABCDEF的对称中心与原点O重合，点A在轴上，点B在反比例函数位于第一象限的图象上，则的值为.（第13题）（第14题）14．如图，在平面直角坐标系中，抛物线＝与y轴交于点A，过点A 与x轴平行的直线交抛物线＝于点B、C，则BC的长值为.三、解答题（本大题共10小题，共78分）15．（6分）先化简，再求值：，其中＝.16．（6分）甲、乙两人各有一个不透明的口袋，甲的口袋中装有1个白球和2个红球，乙的口袋中装有2个白球和1个红球，这些球除颜色外其他都相同．甲、乙两人分别从各自口袋中随机摸出1个球，用画树状图（或列表）的方法，求两人摸出的球颜色相同的概率. 17．（6分）某班在“世界读书日”开展了图书交换活动，第一组同学共带图书24本，第二组同学共带图书27本.已知第一组同学比第二组同学平均每人多带1本图书，第二组人数是第一组人数的1.5倍．求第一组的人数．18．（6分）在△ABC中，AB＝AC，点D、E、F分别是AC、BC、BA延长线上的点，四边形ADEF为平行四边形．求证：AD＝BF．19．（7分）如图，岸边的点A处距水面的高度AB为2.17米，桥墩顶部点C距水面的高度CD为23.17米．从点A处测得桥墩顶部点C的仰角为26°，求岸边的点A与桥墩顶部点C之间的距离．（结果精确到0.1米）【参考数据：sin26°=0.44，cos26°=0.90，tan26°=0.49】20．（7分）某校学生会为了解学生在学校食堂就餐剩饭情况，随机对上周在食堂就餐的n名学生进行了调查，先调查是否剩饭的情况，然后再对其中剩饭的每名学生的剩饭次数进行调查．根据调查结果绘制成如下统计图．（第20题）（1）求这n名学生中剩饭学生的人数及n的值．（2）求这n名学生中剩饭2次以上的学生占这n名学生人数的百分比．（3）按上述统计结果，估计上周在学校食堂就餐的1200名学生中剩饭2次以上的人数．21．（8分）甲、乙两工程队维修同一段路面，甲队先清理路面，乙队在甲队清理后铺设路面．乙队在中途停工了一段时间，然后按停工前的工作效率继续工作．在整个工作过程中，甲队清理完的路面长y（米）与时间x（时）的函数图象为线段OA，乙队铺设完的路面长y（米）与时间x（时）的函数图象为折线BC-CD-DE，如图所示，从甲队开始工作时计时．（1）分别求线段BC、DE所在直线对应的函数关系式．（2）当甲队清理完路面时，求乙队铺设完的路面长22．（9分）探究：如图①，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD,AE⊥CD于点E．若AE=10,求四边形ABCD的面积.应用：如图②，在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD,AE⊥BC 于点E.若AE=19，BC=10,CD=6,则四边形ABCD的面积为.23．（10分）如图，在平面直角坐标系中，抛物线y=ax2+bx-2与x轴交于点A（-1，0）、B（4，0）．点M、N在x轴上，点N在点M右侧，MN=2．以MN为直角边向上作等腰直角三角形CMN，∠CMN=90°．设点M的横坐标为m．（1）求这条抛物线所对应的函数关系式.（2）求点C在这条抛物线上时m的值.（3）将线段CN绕点N逆时针旋转90°后，得到对应线段DN.①当点D在这条抛物线的对称轴上时，求点D的坐标.②以DN为直角边作等腰直角三角形DNE,当点E在这条抛物线的对称轴上时，直接写出所有符合条件的m值.【参考公式：抛物线（a≠0）的顶点坐标为】24．（12分）如图①，在□ABCD中，AB＝13，BC＝50，BC边上的高为12．点P从点B出发，沿B-A-D-A运动，沿B-A运动时的速度为每秒13个单位长度，沿A-D-A运动时的速度为每秒8个单位长度．点Q从点B出发沿BC方向运动，速度为每秒5个单位长度.P、Q两点同时出发，当点Q到达点C时，P、Q两点同时停止运动．设点P的运动时间为t（秒）．连结PQ．（1）当点P沿A-D-A运动时，求AP的长（用含t的代数式表示）．（2）连结AQ，在点P沿B-A-D运动过程中，当点P与点B、点A不重合时，记△APQ的面积为S．求S与t之间的函数关系式.（3）过点Q作QR//AB，交AD于点R，连结BR，如图②．在点P沿B-A-D运动过程中，当线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分时t的值.（4）设点C、D关于直线PQ的对称点分别为、，直接写出//BC时t的值.（第24题）2013年长春市初中毕业生学业考试数学参考答案及评分标准一、选择题（本大题共8小题，每小题3分，共24分）1．A2．D3．B4．D5．C6．C7．B8．C二、填空题（本大题共6小题，每小题3分，共18分）9．10．11．2812．6513．14．6三、解答题（本大题共10小题，共78分）15．原式＝＝＝．（4分）当＝时，原式＝＝11．（6分）白红红白（白，白）（红，白）（红，白）白（白，白）（红，白）（红，白）红（白，红）（红，红）（红，红）16．（4分）∴P（两人摸出的球颜色相同）＝．（6分）17．设第一组有人．根据题意，得＝．（3分）解得＝.经检验，＝是原方程的解，且符合题意．答：第一组有6人．（6分）18.∵四边形ADEF为平行四边形，∴AD＝EF,AD∥EF.∴∠ACB＝∠FEB.（3分）∵AB＝AC,∴∠ACB＝∠B.∴∠FEB＝∠B.（5分）∴EF＝BF.∴AD＝BF.（7分）19．由题意知,DE＝AB＝2.17,∴＝＝＝10.在Rt△CAE中,∠CAE＝,＝,（3分）∴＝＝＝(米).答:岸边的点A与桥墩顶部点C之间的距离约为米.（7分）20．（1）58+41+6＝105（人），105÷70%＝150,所以这n名学生中剩饭的学生有105人，n的值为150.（3分）（2）＝4%,所以剩饭2次以上的学生占这n名学生人数的4%.（5分）（3）＝48（人）.所以估计上周在学校食堂就餐的1200名学生中剩饭2次以上的约有48人.（7分）21.（1）设线段BC所在直线对应的函数关系式为＝.∵图象经过（3，0）、（5，50）,∴∴线段BC所在直线对应的函数关系式为＝.（2分）设线段DE所在直线对应的函数关系式为＝.∵乙队按停工前的工作效率继续工作，∴＝25.∵图象经过（6.5，50）,∴＝50，解得＝.∴线段DE所在直线对应的函数关系式为＝.（5分）（2）甲队每小时清理路面的长为＝20，甲队清理完路面时,＝＝8.把＝8代入＝，得＝＝87.5.答：当甲队清理完路面时,乙队铺设完的路面长为87.5米.（8分）22．探究：过点A作AF⊥CB,交CB的延长线于点F.∵AE⊥CD，∠BCD＝，∴四边形AFCE为矩形.（2分）∴∠FAE＝.∴∠FAB＋∠BAE＝.∵∠EAD＋∠BAE＝，∴∠FAB＝∠EAD.∵AB＝AD，∠F＝∠AED＝，∴△AFB≌△AED.∴AF＝AE.∴四边形AFCE为正方形.∴＝＝＝＝100.（6分）拓展：.（9分）23．（1）∵抛物线经过点A(,0)、B(4,0)，∴解得∴抛物线所对应的函数关系式为＝.（2分）（2）由题意知，点C的坐标为(m,)，（3分）∵点C(m,2)在抛物线上，∴＝2，解得＝，＝.∴点C在这条抛物线上时，的值为或.（5分）（3）①由旋转得，点D的坐标为(m，-2).抛物线＝的对称轴为直线＝.∵点D在这条抛物线的对称轴上，∴点D的坐标为.（7分）②＝或＝或＝或＝.（10分）24.（1）当点P沿AD运动时，AP＝＝.当点P沿DA运动时，AP＝50×28＝108.（2分）（2）当点P与点A重合时，BP＝AB，t＝1.当点P与点D重合时，AP＝AD，＝50，t＝.当0＜t＜1时，如图①.作过点Q作QE⊥AB于点E.S△ABQ＝＝，∴QE＝＝＝.∴S＝.当1＜t≤时，如图②.S＝＝，∴S＝.（6分）（3）当点P与点R重合时，AP＝BQ，＝，t＝.当0＜t≤1时，如图③.∵＝，∴PM＝QM.∵AB∥QR，∴△BPM≌△RQM.∴BP＝AB，∴＝13，解得t＝1当1＜t≤时，如图④.∵BR平分阴影部分面积，∴P与点R重合.∴t＝.当＜t≤时，如图⑤.∵＝，∴＜.∴BR不能把四边形ABQP分成面积相等的两部分.综上，当t＝1或时，线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分.（9分）（4）t＝，t＝，＝.（12分）提示：当C′D′在BC上方且C′D′∥BC时，如图⑥. QC＝OC，∴＝，或＝，解得t＝7或t＝.当C′D′在BC下方且C′D′∥BC时，如图⑦.OD＝PD，∴＝，解得t＝.。

2013年吉林省中考数学试卷及答案(Word解析版)

吉林省2013年中考数学试卷一、单选题（每小题2分，共12分） 1．（2分）（2013•吉林）计算：﹣2+1的结果是（） A ． 1 B ． ﹣1 C ． 3 D ． ﹣3 2．（2分）（2013•吉林）不等式2x ﹣1＞3的解集（）A ． x ＞1B ． x ＞﹣2C ． x ＞2D ． x ＜ 2 3．（2分）（2013•吉林）用6个完全相同的小正方体组合成如图所示的立方体图形，它的主视图为（）A ．B ．C ．D ．4．（2分）（2013•吉林）如图所示，体育课上，小丽的铅球成绩为6.4m ，她投出的铅球落在（）A．区域① B ．区域② C ．区域③ D ．区域④ 5．（2分）（2013•吉林）端午节期间，某市一周每天最高气温（单位：℃）情况如图所示，则这组表示最高气温数据的中位数是（）A ．22 B ．24 C ．25 D ．276．（2分）（2013•吉林）如图，在平面直角坐标系中，抛物线所表示的函数解析式为y=﹣2（x﹣h）2+k，则下列结论正确的是（）A．h＞0，k＞0 B．h＜0，k＞0 C．h＜0，k＜0 D．h＞0，k＜0二、填空题（每小题3分，共24分）7．（3分）（2013•吉林）计算：=．8．（3分）（2013•吉林）若a﹣2b=3，则2a﹣4b﹣5=．9．（3分）（2013•吉林）若将方程x2+6x=7化为（x+m）2=16，则m=．10．（3分）（2013•吉林）分式方程的解为x=．11．（3分）（2013•吉林）如图，把Rt△ABC绕点A逆时针旋转40°，得到Rt△AB′C′，点C′恰好落在边AB上，连接BB′，则∠BB′C′=度．12．（3分）（2013•吉林）如图，在平面直角坐标系中，点A，B的坐标分别为（﹣6，0）、（0，8）．以点A为圆心，以AB长为半径画弧，交x正半轴于点C，则点C的坐标为．13．（3分）（2013•吉林）如图，AB是⊙O的弦，OC⊥AB于点C，连接OA、OB．点P是半径OB上任意一点，连接AP．若OA=5cm，OC=3cm，则AP的长度可能是cm（写出一个符合条件的数值即可）14．（3分）（2013•吉林）如图，在矩形ABCD中，AB的长度为a，BC的长度为b，其中b＜a＜b．将此矩形纸片按下列顺序折叠，则C′D′的长度为（用含a、b的代数式表示）．三、解答题（每小题5分，共20分）15．（5分）（2013•吉林）先化简，再求值：+，其中a=3，b=1．16．（5分）（2013•吉林）在一个不透明的箱子中装有3个小球，分别标有A，B，C．这3个小球除所标字母外，其它都相同．从箱子中随机地摸出一个小球，然后放回；再随机地摸出一个小球．请你用画树形图（或列表）的方法，求两次摸出的小球所标字不同的概率．17．（5分）（2013•吉林）吉林人参是保健佳品．某特产商店销售甲、乙两种保健人参．甲种人参每棵100元，乙种人参每棵70元王叔叔用1200元在此特产商店购买这两种人参共15棵．求王叔叔购买每种人参的棵数．18．（5分）（2013•吉林）图①、图②都是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．在每个网格中标注了5个格点．按下列要求画图：（1）在图①中以格点为顶点画一个等腰三角形，使其内部已标注的格点只有3个；（2）在图②中，以格点为顶点，画一个正方形，使其内部已标注的格点只有3个，且边长为无理数．四、解答题（每小题7分，共28分）19．（7分）（2013•吉林）“今天你光盘了吗？”这是国家倡导“厉行节约，反对浪费”以来的时尚流行语．某校团委随机抽取了部分学生，对他们进行了关于“光盘行动”所持态度的调查，并根据调查收集的数据绘制了如下两幅不完整的统计图：根据上述信息，解答下列问题：（1）抽取的学生人数为；（2）将两幅统计图补充完整；（3）请你估计该校1200名学生中对“光盘行动”持赞成态度的人数．20．（7分）（2013•吉林）如图，在△ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为直角边作等腰三角形CDE，其中∠DCE=90°，连接BE．（1）求证：△ACD≌△BCE；（2）若AC=3cm，则BE=6cm．21．（7分）（2013•吉林）某校数学课题学习小组在“测量教学楼高度”的活动中，设计了以下两种方案：课题测量教学楼高度方案一二图示测得数据CD=6.9m ，∠ACG=22°，∠BCG=13°， EF=10m ，∠AEB=32°，∠AFB=43° 参考数据 sin22°≈0.37，cos22°≈0.93， tan22°≈0.40sin13°≈0.22，cos13°≈0.97 tan13°≈0.23sin32°≈0.53，cos32°≈0.85，tan32°≈0.62 sin43°≈0.68，cos43°≈0.73，tan43°≈0.93 请你选择其中的一种方法，求教学楼的高度（结果保留整数）22．（7分）（2013•吉林）在平面直角坐标系中，点A（﹣3，4）关于y轴的对称点为点B，连接AB，反比例函数y=（x＞0）的图象经过点B，过点B作BC⊥x轴于点C，点P是该反比例函数图象上任意一点，过点P作PD⊥x轴于点D，点Q是线段AB上任意一点，连接OQ、CQ．（1）求k的值；（2）判断△QOC与△POD的面积是否相等，并说明理由．五、解答题（每小题8分，共16分）23．（8分）（2013•吉林）如图，在△ABC中，AB=BC．以AB为直径作圆⊙O交AC于点D，点E为⊙O上一点，连接ED并延长与BC的延长线交于点F．连接AE、BE，∠BAE=60°，∠F=15°，解答下列问题．（1）求证：直线FB是⊙O的切线；（2）若BE=cm，则AC=2cm．24．（8分）（2013•吉林）甲、乙两名大学生去距学校36千米的某乡镇进行社会调查．他们从学校出发，骑电动车行驶20分钟时发现忘带相机，甲下车前往，乙骑电动车按原路返回．乙取相机后（在学校取相机所用时间忽略不计），骑电动车追甲．在距乡镇13.5千米处追上甲后同车前往乡镇．乙电动车的速度始终不变．设甲方与学校相距y甲（千米），乙与学校相离y乙（千米），甲离开学校的时间为t（分钟）．y甲、y乙与x之间的函数图象如图所示，结合图象解答下列问题：（1）电动车的速度为0.9千米/分钟；（2）甲步行所用的时间为45分；（3）求乙返回到学校时，甲与学校相距多远？六、解答题（每小题10分，共20分）25．（10分）（2013•吉林）如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点D、E、F分别是边AB、BC、AC的中点，连接DE、DF，动点P，Q分别从点A、B同时出发，运动速度均为1cm/s，点P沿A F D的方向运动到点D停止；点Q沿BC的方向运动，当点P停止运动时，点Q也停止运动．在运动过程中，过点Q作BC的垂线交AB于点M，以点P，M，Q为顶点作平行四边形PMQN．设平行四边形边形PMQN与矩形FDEC 重叠部分的面积为y（cm2）（这里规定线段是面积为0有几何图形），点P运动的时间为x （s）（1）当点P运动到点F时，CQ=5cm；（2）在点P从点F运动到点D的过程中，某一时刻，点P落在MQ上，求此时BQ的长度；（3）当点P在线段FD上运动时，求y与x之间的函数关系式．26．（10分）（2013•吉林）如图①，在平面直角坐标系中，点P（0，m2）（m＞0）在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C1：y=x2于点A、B，交抛物线C2：y=x2于点C、D．原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD．【猜想与证明】填表：m 1 2 3由上表猜想：对任意m（m＞0）均有=．请证明你的猜想．【探究与应用】（1）利用上面的结论，可得△AOB与△CQD面积比为；（2）当△AOB和△CQD中有一个是等腰直角三角形时，求△CQD与△AOB面积之差；【联想与拓展】如图②过点A作y轴的平行线交抛物线C2于点E，过点D作y轴的平行线交抛物线C1于点F．在y轴上任取一点M，连接MA、ME、MD和MF，则△MAE与△MDF面积的比值为．吉林省2013年中考数学试卷一、单选题（每小题2分，共12分） 1．（2分）（2013•吉林）计算：﹣2+1的结果是（）A ． 1B ． ﹣1C ． 3D ． ﹣ 3考点：有理数的加法．分析：符号不相同的异号加减，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值，所以﹣2+1=﹣1．解答：解：﹣2+1=﹣1．故选B ．点评：此题主要考查了有理数的加法法则：符号不相同的异号加减，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值．2．（2分）（2013•吉林）不等式2x ﹣1＞3的解集（）A ． x ＞1B ． x ＞﹣2C ． x ＞2D ． x ＜2考点：解一元一次不等式；不等式的性质专题：计算题．分析：移项合并同类项得到2x ＞4，不等式的两边同除以2即可求出答案．解答：解：2x ﹣1＞3，移项得：2x ＞3+1，合并同类项得：2x ＞4，∴不等式的解集是x ＞2．故选C ．点评：本题主要考查对不等式的性质，解一元一次不等式等知识点的理解和掌握，能熟练地根据不等式的性质解不等式是解此题的关键．3．（2分）（2013•吉林）用6个完全相同的小正方体组合成如图所示的立方体图形，它的主视图为（）A ．B ．C ．D ．考点：简单组合体的三视图．分析：找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．解答：解：从正面看易得第一层有2个正方形，第二层有3个正方形．故选A ．点评：本题考查了三视图的知识，主视图是从物体的正面看得到的视图．4．（2分）（2013•吉林）如图所示，体育课上，小丽的铅球成绩为6.4m，她投出的铅球落在（）A．区域①B．区域②C．区域③D．区域④考点：近似数和有效数字．分析：根据小丽的铅球成绩为6.4m，得出其所在的范围，即可得出答案．解答：解：∵6＜6.4＜7，∴她投出的铅球落在区域④；故选D．点评：此题考查了近似数，关键是根据6.4求出其所在的范围，用到的知识点是近似数．5．（2分）（2013•吉林）端午节期间，某市一周每天最高气温（单位：℃）情况如图所示，则这组表示最高气温数据的中位数是（）A．22 B．24 C．25 D．27考点：中位数；折线统计图．分析：根据中位数的定义把这组数据从小到大排列，找出最中间的数即可．解答：解：把这组数据从小到大排列为：20，22，22，24，25，26，27，最中间的数是24，则中位数是24；故选B．点评：此题考查了中位数，掌握中位数的定义是本题的关键，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数）．6．（2分）（2013•吉林）如图，在平面直角坐标系中，抛物线所表示的函数解析式为y=﹣2（x﹣h）2+k，则下列结论正确的是（）A．h＞0，k＞0 B．h＜0，k＞0 C．h＜0，k＜0 D．h＞0，k＜0考点：二次函数图象与系数的关系专题：探究型．分析：根据抛物线所的顶点坐标在x轴的上方即可得出结论．解答：解：∵抛物线y=﹣2（x﹣h）2+k的顶点坐标为（h，k），由图可知，抛物线的顶点坐标在第一象限，∴h＞0，k＞0．故选A．点评：本题考查的是二次函数的图象与系数的关系，熟知二次函数的顶点式是解答此题的关键．二、填空题（每小题3分，共24分）7．（3分）（2013•吉林）计算：=2．考点：二次根式的乘除法分析：首先二次根式的乘法法则进行解答，然后化简．解答：解：原式=．故答案为2．点评：本题主要考查二次根式的乘法运算，关键在于正确的运用运算法则，最后要把结果化为最简根式．8．（3分）（2013•吉林）若a﹣2b=3，则2a﹣4b﹣5=1．考点：代数式求值．分析：把所求代数式转化为含有（a﹣2b）形式的代数式，然后将a﹣2b=3整体代入并求值即可．解答：解：2a﹣4b﹣5=2（a﹣2b）﹣5=2×3﹣5=1．故答案是：1．点评：本题考查了代数式求值．代数式中的字母表示的数没有明确告知，而是隐含在题设中，首先应从题设中获取代数式（a﹣2b）的值，然后利用“整体代入法”求代数式的值．9．（3分）（2013•吉林）若将方程x2+6x=7化为（x+m）2=16，则m=3．考点：解一元二次方程-配方法．分析：此题实际上是利用配方法解方程．配方法的一般步骤：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上一次项系数一半的平方．解答：解：在方程x2+6x=7的两边同时加上一次项系数的一半的平方，得x2+6x+32=7+32，配方，得（x+3）2=16．所以，m=3．故填：3．点评：本题考查了解一元二次方程﹣﹣配方法．用配方法解一元二次方程的步骤：（1）形如x2+px+q=0型：第一步移项，把常数项移到右边；第二步配方，左右两边加上一次项系数一半的平方；第三步左边写成完全平方式；第四步，直接开方即可．（2）形如ax2+bx+c=0型，方程两边同时除以二次项系数，即化成x2+px+q=0，然后配方．10．（3分）（2013•吉林）分式方程的解为x=2．考点：解分式方程．分析：观察可得最简公分母是x（x+1），方程两边乘最简公分母，可以把分式方程转化为整式方程求解．解答：解：去分母得：2（x+1）=3x，去括号得：2x+2=3x，移项得：2x﹣3x=﹣2，合并同类项得：﹣x=﹣2，把x的系数化为1得：x=2，检验：把x=2代入最简公分母x（x+1）=6≠0，故原分式方程的解为：x=2．故答案为：2．点评：此题主要考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解；解分式方程一定注意要验根．11．（3分）（2013•吉林）如图，把Rt△ABC绕点A逆时针旋转40°，得到Rt△AB′C′，点C′恰好落在边AB上，连接BB′，则∠BB′C′=20度．考点：旋转的性质．分析：根据旋转的性质可得AB=AB′，∠BAB′=40°，然后根据等腰三角形两底角相等求出∠ABB′，再利用直角三角形两锐角互余列式计算即可得解．解答：解：∵Rt△ABC绕点A逆时针旋转40°得到Rt△AB′C′，∴AB=AB′，∠BAB′=40°，在△ABB′中，∠ABB′=（180°﹣∠BAB′）=（180°﹣40°）=70°，∵∠AC′B′=∠C=90°，∴B′C′⊥AB，∴∠BB′C′=90°﹣∠ABB′=90°﹣70°=20°．故答案为：20．点评：本题考查了旋转的性质，等腰三角形的性质，直角三角形的两锐角互余，比较简单，熟记旋转变换只改变图形的位置不改变图形的形状与大小得到等腰三角形是解题的关键．12．（3分）（2013•吉林）如图，在平面直角坐标系中，点A，B的坐标分别为（﹣6，0）、（0，8）．以点A为圆心，以AB长为半径画弧，交x正半轴于点C，则点C的坐标为（4，0）．考点：勾股定理；坐标与图形性质分析：首先利用勾股定理求出AB的长，进而得到AC的长，因为OC=AC﹣AO，所以OC 求出，继而求出点C的坐标．解答：解：∵点A，B的坐标分别为（﹣6，0）、（0，8），∴AO=6，BO=8，∴AB==10，∵以点A为圆心，以AB长为半径画弧，∴AB=AC=10，∴OC=AC﹣AO=4，∵交x正半轴于点C，∴点C的坐标为（4，0），故答案为：（4，0）．点评：本题考查了勾股定理的运用、圆的半径处处相等的性质以及坐标与图形性质，解题的关键是利用勾股定理求出AB的长．13．（3分）（2013•吉林）如图，AB是⊙O的弦，OC⊥AB于点C，连接OA、OB．点P是半径OB上任意一点，连接AP．若OA=5cm，OC=3cm，则AP的长度可能是6cm（写出一个符合条件的数值即可）考点：垂径定理；勾股定理．专题：开放型．分析：根据勾股定理求出AC，根据垂径定理求出AB，即可得出AP的范围是大于等于5cm 且小于等于8cm，举出即可．解答：解：∵OC⊥AB，∴∠ACO=90°，∵OA=5cm，OC=3cm，∴由勾股定理得：AC==4cm，∴由垂径定理得：AB=2AC=8cm，只要举出的数大于等于5且小于等于8cm即可，如6cm，故答案为：6．点评：本题考查了勾股定理和垂径定理的应用，关键是求出AP的范围．14．（3分）（2013•吉林）如图，在矩形ABCD中，AB的长度为a，BC的长度为b，其中b＜a＜b．将此矩形纸片按下列顺序折叠，则C′D′的长度为3a﹣2b（用含a、b的代数式表示）．考点：翻折变换（折叠问题）分析：由轴对称可以得出A′B=AB=a，就有A′C=b﹣a，从而就有A′C′=b﹣a，就可以得出C′D′=a﹣2（b﹣a），化简就可以得出结论．解答：解：由轴对称可以得出A′B=AB=a，∵BC=b，∴A′C=b﹣a．由轴对称可以得出A′C′=b﹣a，∴C′D′=a﹣2（b﹣a），∴C′D′=3a﹣2b．故答案为：3a﹣2b．点评：本题考查了轴对称的运用，代数式的运用，折叠问题在实际问题中的运用，解答本题时利用折叠问题抓住在折叠变化中不变的线段是解答本题的关键．三、解答题（每小题5分，共20分）15．（5分）（2013•吉林）先化简，再求值：+，其中a=3，b=1．考点：分式的化简求值分析：先根据分式混合运算的法则把原式进行化简，再把a=3，b=1代入原式进行计算即可．解答：解：原式=+==，当a=3，b=1时，原式==．点评：本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．16．（5分）（2013•吉林）在一个不透明的箱子中装有3个小球，分别标有A，B，C．这3个小球除所标字母外，其它都相同．从箱子中随机地摸出一个小球，然后放回；再随机地摸出一个小球．请你用画树形图（或列表）的方法，求两次摸出的小球所标字不同的概率．考点：列表法与树状图法分析：依据题意画树状图法分析所有可能的出现结果即可解答．解答：解：如图所示：P（两次摸出的小球所标字母不同）==．点评：此题主要考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；用到的知识点为：概率=所求情况数与总情况数之比．17．（5分）（2013•吉林）吉林人参是保健佳品．某特产商店销售甲、乙两种保健人参．甲种人参每棵100元，乙种人参每棵70元王叔叔用1200元在此特产商店购买这两种人参共15棵．求王叔叔购买每种人参的棵数．考点：二元一次方程组的应用分析：设王叔叔购买了甲种人参x棵，购买了乙种人参y棵，根据条件可以建立方程x+y=15和100x+70y=1200，由这两个方程构成方程组求出其解即可．解答：解：设王叔叔购买了甲种人参x棵，购买了乙种人参y棵，由题意，得，解得：．答：王叔叔购买了甲种人参5棵，购买了乙种人参10棵．点评：本题考查了列二元一次方程组解实际问题的运用，二元一次方程组的解法的运用，解答时找到反应整个题意的两个等量关系建立方程是关键．18．（5分）（2013•吉林）图①、图②都是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．在每个网格中标注了5个格点．按下列要求画图：（1）在图①中以格点为顶点画一个等腰三角形，使其内部已标注的格点只有3个；（2）在图②中，以格点为顶点，画一个正方形，使其内部已标注的格点只有3个，且边长为无理数．考点：作图—应用与设计作图；等腰三角形的性质；勾股定理；正方形的性质分析：根据要求画图即可．（1）至少要有两条边相等；（2）四条边相等，四个角都是直角即可．解答：解：（1）部分画法如图所示：（2）部分画法如图所示：点评：本题考查的是应用与设计作图，熟知等腰三角形与正方形的性质是解答此题的关键．四、解答题（每小题7分，共28分）19．（7分）（2013•吉林）“今天你光盘了吗？”这是国家倡导“厉行节约，反对浪费”以来的时尚流行语．某校团委随机抽取了部分学生，对他们进行了关于“光盘行动”所持态度的调查，并根据调查收集的数据绘制了如下两幅不完整的统计图：根据上述信息，解答下列问题：（1）抽取的学生人数为200；（2）将两幅统计图补充完整；（3）请你估计该校1200名学生中对“光盘行动”持赞成态度的人数．考点：条形统计图；用样本估计总体；扇形统计图分析：（1）根据扇形统计图所给的数据，求出赞成的所占的百分比，再根据赞成的人数，即可求出总人数；（2）根据总人数和所占的百分比，即可补全统计图；（3）用赞成所占的百分比乘以总人数，即可得出该校1200名学生中对“光盘行动”持赞成态度的人数．解答：解：（1）赞成的所占的百分比是1﹣30%﹣10%=60%，抽取的学生人数为：120÷60%=200（人）；故答案为：200．（2）根据题意得：无所谓的人数是：200×30%=60（人），反对的人数是：200×10%=20（人），补图如下：（3）根据题意得：1200×60%=720（人），答：该校1200名学生中对“光盘行动”持赞成态度的人数有720人．点评：此题考查了条形统计图和扇形统计图，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．20．（7分）（2013•吉林）如图，在△ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为直角边作等腰三角形CDE，其中∠DCE=90°，连接BE．（1）求证：△ACD≌△BCE；（2）若AC=3cm，则BE=6cm．考点：全等三角形的判定与性质；等腰直角三角形分析：（1）求出∠ACD=∠BCE，根据SAS推出两三角形全等即可；（2）根据全等得出AD=BE，根据勾股定理求出AB，即可求出AD，代入求出即可．解答：（1）证明：∵△CDE是等腰直角三角形，∠DCE=90°，∴CD=CE，∵∠ACB=90°，∴∠ACB=∠DCE，∴∠ACB+∠BCD=∠DCE+∠BCD，∴∠ACD=∠BCE，在△ACD和△BCE中，∴△ACD≌△BCE；（2）解：∵AC=BC=3，∠ACB=90°，由勾股定理得：AB=3，又∵DB=AB，∴AD=2AB=6，∵△ACD≌△BCE；∴BE=AD=6，故答案为：6．点评：本题考查了等腰直角三角形性质，勾股定理，全等三角形的性质和判定的应用，主要考查学生运用定理进行推理的能力．21．（7分）（2013•吉林）某校数学课题学习小组在“测量教学楼高度”的活动中，设计了以下两种方案：课题测量教学楼高度方案一二图示测得数据CD=6.9m，∠ACG=22°，∠BCG=13°，EF=10m，∠AEB=32°，∠AFB=43°参考数据sin22°≈0.37，cos22°≈0.93，tan22°≈0.40sin13°≈0.22，cos13°≈0.97tan13°≈0.23sin32°≈0.53，cos32°≈0.85，tan32°≈0.62sin43°≈0.68，cos43°≈0.73，tan43°≈0.93请你选择其中的一种方法，求教学楼的高度（结果保留整数）考点：解直角三角形的应用分析：若选择方法一，在Rt△BGC中，根据CG=即可得出CG的长，同理，在Rt△ACG中，根据tan∠ACG=可得出AG的长，根据AB=AG+BG即可得出结论．若选择方法二，在Rt△AFB中由tan∠AFB=可得出FB的长，同理，在Rt△ABE 中，由tan∠AEB=可求出EB的长，由EF=EB﹣FB且EF=10，可知﹣=10，故可得出AB的长．解答：解：若选择方法一，解法如下：在Rt△BGC中，∠BGC=90°，∠BCG=13°，BG=CD=6.9，∵CG=≈=30，在Rt△ACG中，∠AGC=90°，∠ACG=22°，∵tan∠ACG=，∴AG=30×tan22°≈30×0.40=12，∴AB=AG+BG=12+6.9≈19（米）．答：教学楼的高度约19米．若选择方法二，解法如下：在Rt△AFB中，∠ABF=90°，∠AFB=43°，∵tan∠AFB=，∴FB=≈，在Rt△ABE中，∠ABE=90°，∠AEB=32°，∵tan∠AEB=，∴EB=≈，∵EF=EB﹣FB且EF=10，∴﹣=10，解得AB=18.6≈19（米）．答：教学楼的高度约19米．点评：本题考查的是解直角三角形的应用，熟知锐角三角函数的定义是解答此题的关键．22．（7分）（2013•吉林）在平面直角坐标系中，点A（﹣3，4）关于y轴的对称点为点B，连接AB，反比例函数y=（x＞0）的图象经过点B，过点B作BC⊥x轴于点C，点P是该反比例函数图象上任意一点，过点P作PD⊥x轴于点D，点Q是线段AB上任意一点，连接OQ、CQ．（1）求k的值；（2）判断△QOC与△POD的面积是否相等，并说明理由．考点：反比例函数综合题分析：（1）根据点B与点A关于y轴对称，求出B点坐标，再代入反比例函数解析式解可求出k的值；（2）设点P的坐标为（m，n），点P在反比例函数y=（x＞0）的图象上，求出S△POD，根据AB∥x轴，OC=3，BC=4，点Q在线段AB上，求出S△QOC即可．解答：解：（1）∵点B与点A关于y轴对称，A（﹣3，4），∴点B的坐标为（3，4），∵反比例函数y=（x＞0）的图象经过点B．∴=4，解得k=12．（2）相等．理由如下：设点P的坐标为（m，n），其中m＞0，n＞0，∵点P在反比例函数y=（x＞0）的图象上，∴n=，即mn=12．∴S△POD=OD•PD=mn=×12=6，∵A（﹣3，4），B（3，4），∴AB∥x轴，OC=3，BC=4，∵点Q在线段AB上，∴S△QOC=OC•BC=×3×4=6．∴S△QOC=S△POD．点评：本题考查了反比例函数综合题，涉及反比例函数k的几何意义，反比例函数图象上点的坐标特征等，综合性较强．五、解答题（每小题8分，共16分）23．（8分）（2013•吉林）如图，在△ABC中，AB=BC．以AB为直径作圆⊙O交AC于点D，点E为⊙O上一点，连接ED并延长与BC的延长线交于点F．连接AE、BE，∠BAE=60°，∠F=15°，解答下列问题．（1）求证：直线FB是⊙O的切线；（2）若BE=cm，则AC=2cm．考点：切线的判定分析：（1）欲证明直线FB是⊙O的切线，只需证明AB⊥FB；（2）通过解直角△AEB求得AB的长度；然后在等腰直角△ABC中，根据勾股定理来求斜边AC的长度即可．解答：（1）证明：∵AB是⊙O的直径，∴∠AEB=90°．∵∠BAE=60°，∴∠ABE=30°，∴∠ADE=∠ABE=30°，∴∠FDC=∠ADE=30°．∵∠F=15°，∴∠ACB=∠F+∠FDC=45°．又∵在△ABC中，AB=BC，∴∠ACB=∠CAB=45°，∴∠ABC=90°，即AB⊥FB．又∵AB是直径，∴直线FB是⊙O的切线；（2）解：∵在直角△AEB中，BE=cm，∠BAE=60°，∴AB===2（cm）．∴在△ABC中，∠ABC=90°，AB=BC，AB=2cm，则AC=AB=2cm．故答案是：2．点评：本题考查了切线的判定、解直角三角形．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．24．（8分）（2013•吉林）甲、乙两名大学生去距学校36千米的某乡镇进行社会调查．他们从学校出发，骑电动车行驶20分钟时发现忘带相机，甲下车前往，乙骑电动车按原路返回．乙取相机后（在学校取相机所用时间忽略不计），骑电动车追甲．在距乡镇13.5千米处追上甲后同车前往乡镇．乙电动车的速度始终不变．设甲方与学校相距y甲（千米），乙与学校相离y乙（千米），甲离开学校的时间为t（分钟）．y甲、y乙与x之间的函数图象如图所示，结合图象解答下列问题：（1）电动车的速度为0.9千米/分钟；（2）甲步行所用的时间为45分；（3）求乙返回到学校时，甲与学校相距多远？考点：一次函数的应用分析：（1）根据图象由速度=路程÷时间久可以求出结论；（2）先求出乙追上甲所用的时间，再加上乙返回学校所用的时间就是乙步行所用的时间．（3）先根据第二问的结论求出甲步行的速度，就可以求出乙回到学校时，甲与学校的距离．解答：解：（1）由图象，得18÷20=0.9故答案为：0.9；（2）乙从学校追上甲所用的时间为：（36﹣13.5）÷0.9=25分钟，∴甲步行所用的时间为：20+25=45分钟．故答案为：45；（3）由题意，得甲步行的速度为：（36﹣13.5﹣18）÷45=0.1．乙返回到学校时，甲与学校的距离为：18+0.1×20=20．答：乙返回到学校时，甲与学校相距20km．点评：本题考查了速度=路程÷时间的运用，追击问题的运用，解答本题时认真分析函数图象反应的数量关系是关键．六、解答题（每小题10分，共20分）25．（10分）（2013•吉林）如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点D、E、F分别是边AB、BC、AC的中点，连接DE、DF，动点P，Q分别从点A、B同时出发，运动速度均为1cm/s，点P沿A F D的方向运动到点D停止；点Q沿BC的方向运动，当点P停止运动时，点Q也停止运动．在运动过程中，过点Q作BC的垂线交AB于点M，以点P，M，Q为顶点作平行四边形PMQN．设平行四边形边形PMQN与矩形FDEC 重叠部分的面积为y（cm2）（这里规定线段是面积为0有几何图形），点P运动的时间为x （s）（1）当点P运动到点F时，CQ=5cm；（2）在点P从点F运动到点D的过程中，某一时刻，点P落在MQ上，求此时BQ的长度；（3）当点P在线段FD上运动时，求y与x之间的函数关系式．考点：相似形综合题分析：（1）当点P运动到点F时，求出AF=FC=3cm，BQ=AF=3cm，即可求出答案；（2）根据在点P从点F运动到点D的过程中，点P落在MQ上得出方程t+t﹣3=8，求出即可；（3）求出DE=AC=3，DF=BC=4，证△MBQ∽△ABC，求出MQ=x，分为三种情况：①当3≤x＜4时，重叠部分图形为平行四边形，根据y=PN•PD代入求出即可；②当4≤x＜时，重叠部分为矩形，根据图形得出y=3[（8﹣X）﹣（X﹣3））]；③当≤x≤7时，重叠部分图形为矩形，根据图形得出y=3[（x﹣3）﹣（8﹣x）]，求出即可．解答：解：（1）当点P运动到点F时，∵F为AC的中点，AC=6cm，∴AF=FC=3cm，∵P和Q的运动速度都是1cm/s，∴BQ=AF=3cm，∴CQ=8cm﹣3cm=5cm，故答案为：5．（2）设在点P从点F运动到点D的过程中，点P落在MQ上，如图1，则t+t﹣3=8，t=，BQ的长度为×1=（cm）；（3）∵D、E、F分别是AB、BC、AC的中点，∴DE=AC=×6=3，DF=BC=×8=4，∵MQ⊥BC，∴∠BQM=∠C=90°，∵∠QBM=∠CBA，∴△MBQ∽△ABC，∴=，∴=，MQ=x，分为三种情况：①当3≤x＜4时，重叠部分图形为平行四边形，如图2，。

吉林省长春市中考数学真题试题

2013年长春市初中毕业生学业考试数学本试卷包括三道大题，共24小题.共6页．全卷满分120分．考试时间为120分钟．考试结束后，将本试卷和答题卡一并交回．注意事项：1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内．2．答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试题卷上答题无效．一、选择题（每小题3分，共24分）1．14-的绝对值等于（A ）14. （B ）4. （C ）14-. （D ）4-.2．右图是由四个相同的小长方体组成的立体图形，这个立体图形的正视图是（A ）（B ）（C ）（D ） 3．我国第一艘航空母舰辽宁航空舰的电力系统可提供14 000 000瓦的电力．14 000 000这个数用科学记数法表示为（A ）61410⨯. （B）71.410⨯. （C ）81.410⨯. （D ）80.1410⨯. 4．不等式24x <-的解集在数轴上表示为（A ）（B ）（C ）（D ） 5．如图，含30°角的直角三角尺DEF 放置在△ABC 上，30°角的顶点D 在边AB 上，DE ⊥AB ．若B ∠为锐角，BC ∥DF ，则B ∠的大小为（A ）30°. （B ）45°. （C ）60°. （D ）75°.（第5题）（第6题）6．如图，△ABC 内接于⊙O ，∠ABC=71º，∠CAB=53 °点D 在AC 弧上，则∠ADB 的大小为（A ）46°. （B ）53°. （C ）56°. （D ）71°.7．如图，90ABD BDC ∠=∠=°,A CBD ∠=∠，AB=3，BD=2，则CD 的长为（第2题）（A ）34. （B ）43. （C ）2. （D ）3.（第7题）（第8题） 8．如图，在平面直角坐标系中，点A 的坐标为（0,3），△OAB 沿x 轴向右平移后得到△O ′A ′B ′，点A 的对应点在直线34y x=上一点，则点B 与其对应点B ′间的距离为（A ）94. （B ）3. （C ）4. （D ）5 .二、填空题（每小题3分，共18分）9．计算：25a a ⋅＝ .10．吉林广播电视塔“五一”假期第一天接待游客m 人，第二天接待游客n 人，则这2天平均每天接待游客人（用含m 、n 的代数式表示）.11．如图，MN 是⊙O 的弦，正方形OABC 的顶点B 、C 在MN 上，且点B 是CM 的中点.若正方形OABC 的边长为7，则MN 的长为 .（第11题）（第12题）12．如图，以△ABC 的顶点A 为圆心，以BC 长为半径作弧；再以顶点C 为圆心，以AB 长为半径作弧，两弧交于点D ；连结AD 、CD ．若∠B=65°，则∠ADC 的大小为度.13．如图，在平面直角坐标系中，边长为6的正六边形ABCDEF 的对称中心与原点O 重合，点A 在x 轴上，点B 在反比例函数ky x =位于第一象限的图象上，则k 的值为 .（第13题）（第14题）14．如图，在平面直角坐标系中，抛物线y ＝23ax +与y 轴交于点A ，过点A 与x 轴平行的直线交抛物线y＝213x于点B、C，则BC的长值为 .三、解答题（本大题共10小题，共78分）15．（6分）先化简，再求值：224()(2)1x xxx-+--，其中x＝7.16．（6分）甲、乙两人各有一个不透明的口袋，甲的口袋中装有1个白球和2个红球，乙的口袋中装有2个白球和1个红球，这些球除颜色外其他都相同．甲、乙两人分别从各自口袋中随机摸出1个球，用画树状图（或列表）的方法，求两人摸出的球颜色相同的概率.17．（6分）某班在“世界读书日”开展了图书交换活动，第一组同学共带图书24本，第二组同学共带图书27本.已知第一组同学比第二组同学平均每人多带1本图书，第二组人数是第一组人数的1.5倍．求第一组的人数．18．（6分）在△ABC中，AB＝AC，点D、E、F分别是AC、BC、BA延长线上的点，四边形ADEF 为平行四边形．求证：AD＝BF．（第18题）19．（7分）如图，岸边的点A处距水面的高度AB为2.17米，桥墩顶部点C距水面的高度CD为23.17米．从点A处测得桥墩顶部点C的仰角为26°，求岸边的点A与桥墩顶部点C 之间的距离．（结果精确到0.1米）【参考数据：sin26°=0.44，cos26°=0.90，tan26°=0.49】（第19题）20．（7分）某校学生会为了解学生在学校食堂就餐剩饭情况，随机对上周在食堂就餐的n 名学生进行了调查，先调查是否剩饭的情况，然后再对其中剩饭的每名学生的剩饭次数进行调查．根据调查结果绘制成如下统计图．（第20题）（1）求这n名学生中剩饭学生的人数及n的值．（2）求这n名学生中剩饭2次以上的学生占这n名学生人数的百分比．（3）按上述统计结果，估计上周在学校食堂就餐的1 200名学生中剩饭2次以上的人数．21．（8分）甲、乙两工程队维修同一段路面，甲队先清理路面，乙队在甲队清理后铺设路面．乙队在中途停工了一段时间，然后按停工前的工作效率继续工作．在整个工作过程中，甲队清理完的路面长y（米）与时间x（时）的函数图象为线段OA，乙队铺设完的路面长y （米）与时间x（时）的函数图象为折线BC-CD-DE，如图所示，从甲队开始工作时计时．（1）分别求线段BC、DE所在直线对应的函数关系式．（2）当甲队清理完路面时，求乙队铺设完的路面长．（第21题）22．（9分）探究：如图①，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD,AE⊥CD于点E．若AE=10,求四边形ABCD的面积.应用：如图②，在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD,AE⊥BC于点E.若AE=19，BC=10,CD=6,则四边形ABCD的面积为 .（第22题）23．（10分）如图，在平面直角坐标系中，抛物线y=ax2+bx-2 与x轴交于点A（-1，0）、B （4，0）．点M、N在x轴上，点N在点M右侧，MN=2．以MN为直角边向上作等腰直角三角形CMN，∠CMN=90°．设点M的横坐标为m．（1）求这条抛物线所对应的函数关系式.（2）求点C在这条抛物线上时m的值.（3）将线段CN绕点N逆时针旋转90°后，得到对应线段DN.①当点D在这条抛物线的对称轴上时，求点D的坐标.②以DN为直角边作等腰直角三角形DNE, 当点E在这条抛物线的对称轴上时，直接写出所有符合条件的m值.【参考公式：抛物线2y ax bx c=++（a≠0）的顶点坐标为24()24,b ac ba a--】（第23题）24．（12分）如图①，在□ABCD中，AB＝13，BC＝50，BC边上的高为12．点P从点B出发，沿B-A-D-A运动，沿B-A运动时的速度为每秒13个单位长度，沿A-D-A运动时的速度为每秒8个单位长度．点Q从点 B出发沿BC方向运动，速度为每秒5个单位长度. P、Q两点同时出发，当点Q到达点C时，P、Q两点同时停止运动．设点P的运动时间为t（秒）．连结PQ．（1）当点P沿A-D-A运动时，求AP的长（用含t的代数式表示）．（2）连结AQ，在点P沿B-A-D运动过程中，当点P与点B、点A不重合时，记△APQ的面积为S．求S与t之间的函数关系式.（3）过点Q作QR//AB，交AD于点R，连结BR，如图②．在点P沿B-A-D运动过程中，当线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分时t的值.C D//BC时t的值. （4）设点C、D关于直线PQ的对称点分别为'C、'D，直接写出''（第24题）2013年长春市初中毕业生学业考试数学参考答案及评分标准一、选择题（本大题共8小题，每小题3分，共24分） 1．A 2．D 3．B 4．D 5．C 6．C 7．B 8．C 二、填空题（本大题共6小题，每小题3分，共18分）9．35a 10．2m n+ 11．28 12．65 13．93 14．6三、解答题（本大题共10小题，共78分）15．原式＝24(1)441x x x x x -+-+-＝2444x x x +-+＝24x +．（4分）当x ＝7时，原式＝2(7)4+＝11．（6分） 16．（4分）∴P （两人摸出的球颜色相同）＝49．（6分）17．设第一组有x 人．根据题意，得24x ＝2711.5x +．（3分）解得x ＝6.经检验，x ＝6是原方程的解，且符合题意．答：第一组有6人．（6分）18. ∵四边形ADEF 为平行四边形， ∴AD ＝EF ,AD ∥EF.∴∠ACB ＝∠FEB. （3分）白红红白（白，白）（红，白）（红，白）白（白，白）（红，白）（红，白）红（白，红）（红，红）（红，红）或甲乙结果∵AB ＝AC, ∴∠ACB ＝∠B.∴∠FEB ＝∠B. （5分） ∴EF ＝BF.∴AD ＝BF. （7分） 19．由题意知,DE ＝AB ＝2.17, ∴CE ＝CD DE -＝12.17 2.17-＝10. 在Rt △CAE 中,∠CAE ＝26︒,sin CAE ∠＝CEAC , （3分） ∴AC ＝sin CE CAE ∠＝10sin 26︒＝100.4422.7≈(米) .答: 岸边的点A 与桥墩顶部点C 之间的距离约为22.7米. （7分）20．（1）58+41+6＝105（人），105÷70%＝150,所以这n 名学生中剩饭的学生有105人，n 的值为150. （3分）（2）6150100%÷⨯＝4%,所以剩饭2次以上的学生占这n 名学生人数的4%. （5分）（3）12004%⨯＝48（人）. 所以估计上周在学校食堂就餐的1 200名学生中剩饭2次以上的约有48人.（7分） 21.（1）设线段BC 所在直线对应的函数关系式为y ＝11k x b +. ∵图象经过（3，0）、（5，50）,∴11111130,25,550.75.k b k k b b +==⎧⎧⎨⎨+==-⎩⎩解得∴线段BC 所在直线对应的函数关系式为y ＝2575x -. （2分）设线段DE 所在直线对应的函数关系式为y ＝22k x b +. ∵乙队按停工前的工作效率继续工作， ∴2k ＝25. ∵图象经过（6.5，50）,∴26.525b ⨯+＝50，解得2b ＝112.5-.∴线段DE 所在直线对应的函数关系式为y ＝25112.5x -. （5分）（2）甲队每小时清理路面的长为 1005÷＝20，甲队清理完路面时,x ＝16020÷＝8.把x ＝8代入y ＝25112.5x -，得y ＝258112.5⨯-＝87.5.答：当甲队清理完路面时,乙队铺设完的路面长为87.5米. （8分） 22．探究：过点A 作AF ⊥CB,交CB 的延长线于点F. ∵AE ⊥CD ，∠BCD ＝90︒，∴四边形AFCE 为矩形. （2分） ∴∠FAE ＝90︒. ∴∠FAB ＋∠BAE ＝90︒. ∵∠EAD ＋∠BAE ＝90︒， ∴∠FAB ＝∠EAD.∵AB ＝AD ，∠F ＝∠AED ＝90︒， ∴△AFB ≌△AED. ∴AF ＝AE.∴四边形AFCE 为正方形. ∴ABCDS 四边形＝AFCES 正方形＝2AE ＝210＝100. （6分）拓展：152. （9分） 23．（1）∵抛物线经过点A(1-,0)、B(4,0)，∴20,16420.a b a b --=⎧⎨+-=⎩解得1,23.2a b ⎧=⎪⎪⎨⎪=-⎪⎩ ∴抛物线所对应的函数关系式为y ＝213222x x --. （2分）（2）由题意知，点C 的坐标为(m,2)，（3分）∵点C(m,2)在抛物线上，∴213222m m --＝2，解得1m 3412+，2m 3412-.∴点 C 在这条抛物线上时，m 3412+3412-（5分）（3）①由旋转得，点D 的坐标为(m ，-2).抛物线y ＝213222x x --的对称轴为直线x ＝32.∵点D 在这条抛物线的对称轴上，∴点D 的坐标为3(,2)2-. （7分）②m ＝52-或m ＝12-或m ＝32或m ＝72. （10分） 24. （1）当点P 沿A -D 运动时，AP ＝8(1)t -＝88t -.当点P 沿D -A 运动时，AP ＝50×2-8(1)t -＝108-8t . （2分）（2）当点P 与点A 重合时，BP ＝AB ，t ＝1.当点P 与点D 重合时，AP ＝AD ，88t -＝50，t ＝294.当0＜t ＜1时，如图①.作过点Q 作QE ⊥AB 于点E.S △ABQ ＝12AB QE ⋅＝1122BQ ⨯，∴QE ＝12BQ AB ＝12513t ⨯＝6013t.∴S ＝23030t t -+.当1＜t ≤294时，如图②.S ＝1122AP ⨯＝1(88)122t ⨯-⨯，∴S ＝4848t -. （6分）（3）当点P 与点R 重合时，AP ＝BQ ，88t -＝5t ，t ＝83. 当0＜t ≤1时，如图③.∵BPM S ∆＝BQM S ∆，∴PM ＝QM.∵AB ∥QR ，∴△BPM ≌△RQM.∴BP ＝AB ，∴13t ＝13，解得t ＝1 当1＜t ≤83时，如图④.∵BR 平分阴影部分面积，∴P 与点R 重合.∴t ＝83.当83＜t ≤294时，如图⑤.∵ABR S ∆＝QBR S ∆， ∴ABR S ∆＜BQPRS 四边形. ∴BR 不能把四边形ABQP 分成面积相等的两部分.综上，当t ＝1或83时，线段PQ 扫过的图形（阴影部分）被线段BR 分成面积相等的两部分. （9分）（4）t ＝7，t ＝9513，＝12113. （12分）提示：当C ′D ′在BC 上方且C ′D ′∥BC 时，如图⑥.QC ＝OC ，∴505t -＝58813t -+，或505t -＝85813t -+，解得t ＝7或t ＝9513.当C ′D ′在BC 下方且C ′D ′∥BC 时，如图⑦.OD ＝PD ，∴50513t -+＝858t -，解得t ＝12113.。

2013年吉林省长春市中考数学试卷

2013年吉林省长春市中考数学试卷一、选择题（每小题3分，共24分） 1.（ 3分）-的绝对值等于（）A . —B . 42. （3分）如图是由四个相同的小长方体组成的立体图形，这个立体图形的正视3. （3分）我国第一艘航空母舰辽宁航空舰的电力系统可提供 14 000 000瓦的电力.14 000 000这个数用科学记数法表示为（）A . 14X 105 6B . 1.4X 107C. 1.4X 108D . 0.14X 1084. （3分）不等式2x v- 4的解集在数轴上表示为（）A . 1 ■…B.-2 0 2厂-2 0 2 r11 ■•一C. -2 0 2 D .-2 0 25 （3分）如图，含30°角的直角三角尺DEF 放置在△ ABC 上, 30°角的顶点D 在C.-D .— 4BC// DF ,则/ B 的大小为（C. 60 D . 75 若/B 为锐角, B .45°则/ ADB的大小为（）A. 46°B. 53°C. 56°D. 71°7. （3 分）如图，/ ABD=Z BDC=90, / A=Z CBD AB=3, BD=2,贝U CD 的长为A. -B. -C. 2D. 38. （3分）如图，在平面直角坐标系中，点A的坐标为（0, 3）, △ OAB沿x轴向右平移后得到厶O' A',B点A的对应点在直线y^x上一点，则点B与其对应点B'间的距离为（）A. 一B. 3C. 4D. 5二、填空题（每小题3分，共18分）9. （3分）计算：a2?5a ______10. （3分）吉林广播电视塔五一”假期第一天接待游客m人，第二天接待游客n人，则这2天平均每天接待游客 ______ 人（用含m、n的代数式表示）. 11. （3分）如图，MN是。

O的弦，正方形OABC的顶点B、C在MN上，且点B是CM的中点.若正方形OABC的边长为7,则MN的长为___________ .以厶ABC的顶点A为圆心，以BC长为半径作弧；再以顶点C为圆心，以AB长为半径作弧，两弧交于点D;连结AD CD.若/ B=65,则/ ADC的大小为______ 度.13. （3分）如图，在平面直角坐标系中，边长为6的正六边形ABCDEF勺对称中14. （3分）如图，在平面直角坐标系中，抛物线y=aX2+3与y轴交于点A，过点心与原点0重合，点A在x轴上，点B在反比例函数-位于第一象限的图A与x轴平行的直线交抛物线y=- 于点B、C,则BC的长为10小题，共78分）15. （6分）先化简，再求值: 其中x=16. （6分）甲、乙两人各有一个不透明的口袋，甲的口袋中装有1个白球和2个红球，乙的口袋中装有2个白球和1个红球，这些球除颜色外其他都相同.甲、乙两人分别从各自口袋中随机摸出1个球，用画树状图（或列表）的方法，求两人摸出的球颜色相同的概率.17. （6分）某班在世界读书日”开展了图书交换活动，第一组同学共带图书24 本，第二组同学共带图书27本•已知第一组同学比第二组同学平均每人多带1本图书，第二组人数是第一组人数的1.5倍•求第一组的人数.18. （7分）在厶ABC中，AB=AC，点D、E F分别是AC BC BA延长线上的点，四边形ADEF为平行四边形.求证：AD=BF.19. （7分）如图，岸边的点A处距水面的高度AB为2.17米，桥墩顶部点C距水面的高度CD为12.17米.从点A处测得桥墩顶部点C的仰角为26°求岸边的点A 与桥墩顶部点C之间的距离.（结果精确到0.1米）（参考数据：sin26=0.44, cos26=0.90, tan26 =0.49）20. （7分）某校学生会为了解学生在学校食堂就餐剩饭情况，随机对上周在食堂就餐的n名学生进行了调查，先调查是否剩饭的情况，然后再对其中剩饭的每名学生的剩饭次数进行调查.根据调查结果绘制成如下统计图.（1）求这n名学生中剩饭学生的人数及n的值.（2）求这n名学生中剩饭2次以上的学生占这n名学生人数的百分比.（3）按上述统计结果，估计上周在学校食堂就餐的 1 200名学生中剩饭2次以上的人数.21. （8分）甲、乙两工程队维修同一段路面，甲队先清理路面，乙队在甲队清理后铺设路面•乙队在中途停工了一段时间，然后按停工前的工作效率继续工作•在整个工作过程中，甲队清理完的路面长 y （米）与时间x （时）的函数图象为线段0A ,乙队铺设完的路面长 y （米）与时间x （时）的函数图象为折线BC- CD- DE,如图所示，从甲队开始工作时计时.（1）分别求线段BC 、DE 所在直线对应的函数关系式.22. （9分）探究：如图①，在四边形 ABCD 中，/ BAD=Z BCD=90，AB=AD, AE 丄CD 于点E.若AE=1Q 求四边形ABCD 的面积.应用：如图②，在四边形 ABCD 中, / ABC+/ADC=180, AB=AD,AE 丄BC 于点E.若片名学①上周在般堂就軽制烘和不剩愎的人数扇彤统讣图脱名学生中上周测饭的学生劉饭次数的人散箓形统汁閨23. （10分）如图，在平面直角坐标系中，抛物线y=ax2+bx- 2与x轴交于点A（-1，0）、B（4，0）.点M、N在x轴上，点N在点M右侧，MN=2.以MN为直角边向上作等腰直角三角形CMN，Z CMN=90 .设点M的横坐标为m.（1）求这条抛物线所对应的函数关系式.（2）求点C在这条抛物线上时m的值.（3）将线段CN绕点N逆时针旋转90°后，得到对应线段DN.①当点D在这条抛物线的对称轴上时，求点D的坐标.②以DN为直角边作等腰直角三角形DNE当点E在这条抛物线的对称轴上时，直接写出所有符合条件的m值.（参考公式：抛物线y=a«+bx+c （a^ 0）的顶点坐标为（一， ------------ ））24. （12分）如图①，在？ABCD中，AB=13, BC=5Q BC边上的高为12.点P从点B出发，沿B-A- D- A运动，沿B-A运动时的速度为每秒13个单位长度，沿A-D-A 运动时的速度为每秒8个单位长度.点Q从点B出发沿BC 方向运动，速度为每秒5个单位长度.P、Q两点同时出发，当点Q到达点C 时，P、Q两点同时停止运动.设点P的运动时间为t （秒）.连结PQ.（1）当点P沿A-D-A运动时，求AP的长（用含t的代数式表示）.（2）连结AQ，在点P沿B- A-D运动过程中，当点P与点B、点A不重合时，记厶APQ的面积为S.求S与t之间的函数关系式.（3）过点Q作QR// AB，交AD于点R,连结BR,如图②.在点P沿B- A-D -A运动过程中，当线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分时t的值.（4）设点C D关于直线PQ的对称点分别为C'、D',直接写出C / BC时t的值.2013年吉林省长春市中考数学试卷参考答案与试题解析一、选择题（每小题3分，共24分）1.（3分）-的绝对值等于（）A. —B. 4【解答】解：--的绝对值等于-,故选：A.2. （3分）如图是由四个相同的小长方体组成的立体图形，这个立体图形的正视【解答】解：从正面看易得第一层有2个长方形.故选：D.3. （3分）我国第一艘航空母舰辽宁航空舰的电力系统可提供14 000 000瓦的电力.14 000 000这个数用科学记数法表示为（A. 14X 106B. 1.4X 107【解答】解：14 000 000=1.4X 107.)C. 1.4X108D. 0.14X 108故选：B.4. （3分）不等式2x v- 4的解集在数轴上表示为（)C.-D.—4【解答】解：解不等式得：X V- 2.故选：D .5. （3分）如图，含30°角的直角三角尺DEF 放置在△ ABC 上，30°角的顶点D 在 •••/ ADE=90,vZ FDE=30,•••/ ADF=90 - 30°60°,v BC// DF ,•••Z B=Z ADF=60,故选：C.6. （3 分）如图，△ ABC 内接于O O ,Z ABC=71,Z CAB=53，点 D 在AC 弧上, 则Z ADB 的大小为（）A . 46°B . 53° C. 56° D . 71【解答】解：vZ ABC=71,Z CAB=53,• Z ACB=180-Z ABC-Z BAC=56,v 弧AB 对的圆周角是Z ADB 和Z ACB• Z ADB=Z ACB=56,故选：C. 丄 1 * a--2 0 2 c.BC// DF ,则/ B 的大小为（ C. 60 D . 75若/B 为锐角,B . 45°【解答】解：：DE±AB ,7. （3 分）如图，/ ABD=Z BDC=90, / A=Z CBD AB=3, BD=2,贝U CD 的长为A. -B. -C. 2D. 3【解答】解：I/ ABD=Z BDC=90,Z A=Z CBD, AB=3, BD=2,•••△BDC,—=—，即 _=——,解得CD-.故选：B.8. （3分）如图，在平面直角坐标系中，点A的坐标为（0, 3）, △ OAB沿x轴向右平移后得到厶O' A', B点A的对应点在直线y^x上一点,则点B与其对应点B'间的距离为（）A. -B. 3C. 4D. 5【解答】解：如图，连接AA'、BB.•••点A的坐标为（0, 3）, △ OAB沿x轴向右平移后得到△ O A',B' •••点A的纵坐标是3.又•点A的对应点在直线yhx上一点, • 3hx,解得x=4.•••点A'的坐标是（4, 3）,••• AA =4•••根据平移的性质知BB =AA =4故选：C.卜4*1* *A S沪O0*二、填空题（每小题3分，共18分）9. （3分）计算：a2?5a= 5a3.【解答】解：原式=5a3.故答案为：5a3.10. （3分）吉林广播电视塔五一”假期第一天接待游客m人，第二天接待游客n人，则这2天平均每天接待游客------- 人（用含m、n的代数式表示）【解答】解：2天平均每天接待游客故答案为:11. （3分）如图，MN是。

吉林省长春市2013年中考数学试卷

吉林省长春市2013年中考数学试卷一、选择题（每小题3分，共24分）1．（3分）（2013•长春）的绝对值等于（） A ． B ． 4 C ． D ． ﹣4考点：绝对值．分析：根据负数的绝对值等于它的相反数解答．解答：解：﹣的绝对值等于，即|﹣|=．故选A ．点评：本题考查了绝对值，一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．2．（3分）（2013•长春）如图是由四个相同的小长方体组成的立体图形，这个立体图形的正视图是（）A ．B ．C ．D ．考点：简单组合体的三视图．分析：找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．解答：解：从正面看易得第一层有1个长方形，位于左边，第二层有2个长方形．故选D ．点评：本题考查了三视图的知识，主视图是从物体的正面看得到的视图．3．（3分）（2013•长春）我国第一艘航空母舰辽宁航空舰的电力系统可提供14 000 000瓦的电力．14 000 000这个数用科学记数法表示为（）A ． 14×106B ． 1.4×107C ． 1.4×108D ． 0.14×108考点：科学记数法—表示较大的数分析：科学记数法的表示形式为a ×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值是易错点，由于14 000 000有8位，所以可以确定n=8﹣1=7．解答：解：14 000 000=1.4×107．故选B ．点评：此题考查科学记数法表示较大的数的方法，准确确定a与n值是关键．4．（3分）（2013•长春）不等式2x＜﹣4的解集在数轴上表示为（）A．B．C．D．考点：在数轴上表示不等式的解集；解一元一次不等式分析：首先解不等式求得不等式的解集，根据数轴上点的表示法即可判断．解答：解：解不等式得：x＜﹣2．故选D．点评：把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．5．（3分）（2013•长春）如图，含30°角的直角三角尺DEF放置在△ABC上，30°角的顶点D 在边AB上，DE⊥AB．若∠B为锐角，BC∥DF，则∠B的大小为（）A．30°B．45°C．60°D．75°考点：平行线的性质；直角三角形的性质．分析：首先根据垂直定义可得∠ADE=90°，再根据∠FDE=30°，可得∠ADF=60°，然后根据两直线平行同位角相等可得∠B的大小．解答：解：∵DE⊥AB，∴∠ADE=90°，∵∠FDE=30°，∴∠ADF=90°﹣30°=60°，∵BC∥DF，∴∠B=∠ADF=60°，故选：C．点评：此题主要考查了平行线的性质，关键是掌握两直线平行同位角相等．6．（3分）（2013•长春）如图，△ABC内接于⊙O，∠ABC=71°，∠CAB=53°，点D在AC弧上，则∠ADB的大小为（）A．46°B．53°C．56°D．71°考点：圆周角定理．分析：根据三角形内角和定理求出∠ACB，根据圆周角定理得出∠C，求出即可．解答：解：∵∠ABC=71°，∠CAB=53°，∴∠ACB=180°﹣∠ABC﹣∠BAC=56°，∵弧AB对的圆周角是∠ADB和∠ACB，∴∠ADB=∠ACB=56°，故选C．点评：本题考查了圆周角定理和三角形内角和定理的应用，关键是求出∠ACB的度数和得出∠ACB=∠ADB．7．（3分）（2013•长春）如图，∠ABD=∠BDC=90°，∠A=∠CBD，AB=3，BD=2，则CD的长为（）A．B．C．2D．3考点：相似三角形的判定与性质．专题：探究型．分析：先根据题意判断出△ABD∽△BDC，再根据相似三角形的对应边成比例即可得出CD的长．解答：解：∵∠ABD=∠BDC=90°，∠A=∠CBD，AB=3，BD=2，∴△ABD∽△BDC，∴=，即=，解得CD=．故选B．点评：本题考查的是相似三角形的判定与性质，熟知相似三角形的对应边成比例是解答此题的关键．8．（3分）（2013•长春）如图，在平面直角坐标系中，点A的坐标为（0，3），△OAB沿x 轴向右平移后得到△O′A′B′，点A的对应点在直线y=x上一点，则点B与其对应点B′间的距离为（）A．B．3C．4D．5考点：一次函数图象上点的坐标特征；坐标与图形变化-平移分析：根据平移的性质知BB′=AA′．由一次函数图象上点的坐标特征可以求得点A′的坐标，所以根据两点间的距离公式可以求得线段AA′的长度，即BB′的长度．解答：解：如图，连接AA′、BB′．∵点A的坐标为（0，3），△OAB沿x轴向右平移后得到△O′A′B′，∴点A′的纵坐标是3．又∵点A的对应点在直线y=x上一点，∴3=x，解得x=4．∴点A′的坐标是（4，3），∴AA′=4．∴根据平移的性质知BB′=AA′=4．故选C．点评：本题考查了一次函数图象上点的坐标特征、坐标与图形变化﹣﹣平移．根据平移的性质得到BB′=AA′是解题的关键．二、填空题（每小题3分，共18分）9．（3分）（2013•长春）计算：a2•5a=5a3．考点：单项式乘单项式专题：计算题．分析：利用单项式乘单项式法则计算即可得到结果．解答：解：原式=5a3．故答案为：5a3．点评：此题考查了单项式乘单项式，熟练掌握运算法则是解本题的关键．10．（3分）（2013•长春）吉林广播电视塔“五一”假期第一天接待游客m人，第二天接待游客n人，则这2天平均每天接待游客人（用含m、n的代数式表示）．考点：列代数式分析：用两天接待的游客总人数除以天数，即可得解．解答：解：2天平均每天接待游客．故答案为：．点评：本题考查了列代数式，比较简单，熟练掌握平均数的求法是解题的关键．11．（3分）（2013•长春）如图，MN是⊙O的弦，正方形OABC的顶点B、C在MN上，且点B是CM的中点．若正方形OABC的边长为7，则MN的长为28．考点：垂径定理；正方形的性质．分析：根据正方形性质得出BC=7，∠OCB=90°，根据垂径定理得出CM=2BC，推出MN=4BC，代入求出即可．解答：解：∵四边形OABC是正方形，∴BC=7，∠OCB=90°，∴OC⊥MN，∴由垂径定理得：MN=2CM，∵点B是CM的中点，∴CM=2BC，∴MN=4BC=4×7=28，故答案为：28．点评：本题考查了垂径定理和正方形性质的应用，关键是推出MN=4BC．12．（3分）（2013•长春）如图，以△ABC的顶点A为圆心，以BC长为半径作弧；再以顶点C为圆心，以AB长为半径作弧，两弧交于点D；连结AD、CD．若∠B=65°，则∠ADC的大小为65度．考点：全等三角形的判定与性质．分析：根据作法可得AB=CD，BC=AD，然后利用“边边边”证明△ABC和△CDA全等，再根据全等三角形对应角相等解答．解答：解：∵以点A为圆心，以BC长为半径作弧；以顶点C为圆心，以AB长为半径作弧，两弧交于点D，∴AB=CD，BC=AD，在△ABC和△CDA中，，∴△ABC≌△CDA，∴∠ADC=∠B=65°．故答案为：65．点评：本题考查了全等三角形的判定与性质，根据作法得到全等三角形相等的边是解题的关键．13．（3分）（2013•长春）如图，在平面直角坐标系中，边长为6的正六边形ABCDEF的对称中心与原点O重合，点A在x轴上，点B在反比例函数位于第一象限的图象上，则k的值为．考点：正多边形和圆；反比例函数图象上点的坐标特征．分析：连接OB，过B作BM⊥OA于M，得出等边三角形AOB，求出OB，根据锐角三角函数求出BM和OM，即可得出B的坐标，代入即可求出答案．解答：解：连接OB，过B作BM⊥OA于M，∵六边形ABCDEF是正六边形，∴∠AOB==60°，∵OA=OB，∴△AOB是等边三角形，∴OA=OB=AB=6，∴BM=OB•sin∠BOA=6×sin60°=3，OM=OB•COS60°=3，即B的坐标是（3，3），∵B在反比例函数位于第一象限的图象上，∴k=3×3=9，故答案为：9．点评：本题考查了正多边形性质，锐角三角函数，反比例函数的性质，等边三角形的性质和判定的应用，关键是求出B的坐标．14．（3分）（2013•长春）如图，在平面直角坐标系中，抛物线y=ax2+3与y轴交于点A，过点A与x轴平行的直线交抛物线y=于点B、C，则BC的长值为6．考点：二次函数图象上点的坐标特征．分析：先由y轴上点的横坐标为0求出A点坐标为（0，3），再将y=3代入y=，求出x 的值，得出B、C两点的坐标，进而求出BC的长度．解答：解：∵抛物线y=ax2+3与y轴交于点A，∴A点坐标为（0，3）．当y=3时，=3，解得x=±3，∴B点坐标为（﹣3，3），C点坐标为（3，3），∴BC=3﹣（﹣3）=6．故答案为6．点评：本题考查了二次函数图象上点的坐标特征，两函数交点坐标的求法，平行于x轴上的两点之间的距离，比较简单．三、解答题（本大题共10小题，共78分）15．（6分）（2013•长春）先化简，再求值：，其中x=．考点：分式的化简求值专题：计算题．分析：将的分子因式分解，然后约分；再将（x﹣2）2展开，合并同类项后再代入求值即可．解答：解：原式==4x+x2﹣4x+4=x2+4．当x=时，原式==11．点评：本题考查了分式的化简求值，熟悉因式分解及约分、通分是解题的关键．16．（6分）（2013•长春）甲、乙两人各有一个不透明的口袋，甲的口袋中装有1个白球和2个红球，乙的口袋中装有2个白球和1个红球，这些球除颜色外其他都相同．甲、乙两人分别从各自口袋中随机摸出1个球，用画树状图（或列表）的方法，求两人摸出的球颜色相同的概率．考点：列表法与树状图法专题：计算题．分析：列表得出所有等可能的情况数，找出两人摸出的求颜色相同的情况数，即可求出所求的概率．解答：解：列表如下：甲乙结果白红红白（白，白）（红，白）（红，白）白（白，白）（红，白）（红，白）红（白，红）（红，红）（红，红）所有等可能的情况有9种，其中颜色相同的情况有4种，则P（两人摸出的球颜色相同）=．点评：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．17．（6分）（2013•长春）某班在“世界读书日”开展了图书交换活动，第一组同学共带图书24本，第二组同学共带图书27本．已知第一组同学比第二组同学平均每人多带1本图书，第二组人数是第一组人数的1.5倍．求第一组的人数．考点：分式方程的应用．分析：首先设第一组有x人，则第二组人数是1.5x人，根据题意可得等量关系：第一组同学共带图书24本÷第一组的人数﹣第二组同学共带图书27本÷第二组的人数=1，根据等量关系列出方即可．解答：解：设第一组有x人．根据题意，得=，解得x=6．经检验，x=6是原方程的解，且符合题意．答：第一组有6人．点评：此题主要考查了分式方程的应用，关键是正确理解题意，找出题目中的等量关系，列出方程，不要忘记检验．18．（7分）（2013•长春）在△ABC中，AB=AC，点D、E、F分别是AC、BC、BA延长线上的点，四边形ADEF为平行四边形．求证：AD=BF．考点：平行四边形的性质专题：证明题．分析：根据平行四边形的对边平行且相等可得AD=EF，AD∥EF，再根据两直线平行，同位角相等可得∠ACB=∠FEB，根据等边对等角求出∠ACB=∠B，从而得到∠FEB=∠B，然后根据等角对等边证明即可．解答：证明：∵四边形ADEF为平行四边形，∴AD=EF，AD∥EF，∴∠ACB=∠FEB，∵AB=AC，∴∠ACB=∠B，∴∠FEB=∠B，∴EF=BF，∴AD=BF．点评：本题考查了平行四边形对边平行且相等的性质，平行线的性质，等角对等边的性质，熟练掌握各性质是解题的关键．19．（7分）（2013•长春）如图，岸边的点A处距水面的高度AB为2.17米，桥墩顶部点C 距水面的高度CD为23.17米．从点A处测得桥墩顶部点C的仰角为26°，求岸边的点A与桥墩顶部点C之间的距离．（结果精确到0.1米）（参考数据：sin26°=0.44，cos26°=0.90，tan26°=0.49）考点：解直角三角形的应用-仰角俯角问题分析：在Rt△CAE中，利用CD、DE的长和已知的角的度数，利用正弦函数可求得AC的长．解答：解：由题意知，DE=AB=2.17，∴CE=CD﹣DE=12.17﹣2.17=10．在Rt△CAE中，∠CAE=26°，sin∠CAE=，∴AC===≈22.7（米）．答：岸边的点A与桥墩顶部点C之间的距离约为22.7米．点评：本题考查俯角、仰角的定义，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．20．（7分）（2013•长春）某校学生会为了解学生在学校食堂就餐剩饭情况，随机对上周在食堂就餐的n名学生进行了调查，先调查是否剩饭的情况，然后再对其中剩饭的每名学生的剩饭次数进行调查．根据调查结果绘制成如下统计图．（1）求这n名学生中剩饭学生的人数及n的值．（2）求这n名学生中剩饭2次以上的学生占这n名学生人数的百分比．（3）按上述统计结果，估计上周在学校食堂就餐的1 200名学生中剩饭2次以上的人数．考点：条形统计图；用样本估计总体；扇形统计图专题：计算题．分析：（1）由条形统计图中的数据相加即可求出n名学生中剩饭的学生人数，除以剩饭学生所占的百分比即可求出学生的总数，即为n的值；（2）根据条形统计图得到剩饭2次以上的人数，除以n的值，即可求出结果；（3）根据（2）中求出的百分比，乘以1200即可得到结果．解答：解：（1）根据题意得：这n名学生中剩饭学生的人数为58+41+6=105（人），n的值为105÷70%=150，则这n名学生中剩饭的学生有105人，n的值为150；（2）根据题意得：6÷150×100%=4%，则剩饭2次以上的学生占这n名学生人数的4%；（3）根据题意得：1200×4%=48（人）．则估计上周在学校食堂就餐的1200名学生中剩饭2次以上的约有48人．点评：此题考查了条形统计图，扇形统计图，以及用样本估计总体，弄清题意是解本题的关键．21．（8分）（2013•长春）甲、乙两工程队维修同一段路面，甲队先清理路面，乙队在甲队清理后铺设路面．乙队在中途停工了一段时间，然后按停工前的工作效率继续工作．在整个工作过程中，甲队清理完的路面长y（米）与时间x（时）的函数图象为线段OA，乙队铺设完的路面长y（米）与时间x（时）的函数图象为折线BC﹣CD﹣DE，如图所示，从甲队开始工作时计时．（1）分别求线段BC、DE所在直线对应的函数关系式．（2）当甲队清理完路面时，求乙队铺设完的路面长．考点：一次函数的应用分析：（1）先求出乙队铺设路面的工作效率，计算出乙队完成需要的时间求出E的坐标，再由待定系数法就可以求出结论．（2）由（1）的结论求出甲队完成的时间，把时间代入乙的解析式就可以求出结论．解答：（1）设线段BC所在直线对应的函数关系式为y=k1x+b1．∵图象经过（3，0）、（5，50），∴∴线段BC所在直线对应的函数关系式为y=25x﹣75．设线段DE所在直线对应的函数关系式为y=k2x+b2．∵乙队按停工前的工作效率为：50÷（5﹣3）=25，∴乙队剩下的需要的时间为：（160﹣50）÷25=，∴E（，160），∴，解得：∴线段DE所在直线对应的函数关系式为y=25x﹣112.5．（2）由题意，得甲队每小时清理路面的长为100÷5=20，甲队清理完路面的时间，x=160÷20=8．把x=8代入y=25x﹣112.5，得y=25×8﹣112.5=87.5．答：当甲队清理完路面时，乙队铺设完的路面长为87.5米．点评：本题考查了待定系数法求一次函数的解析式的运用，工作总量=工作效率×工作时间的运用，解答时求出函数的解析式是关键．22．（9分）（2013•长春）探究：如图①，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD，AE⊥CD于点E．若AE=10，求四边形ABCD的面积．应用：如图②，在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，AE⊥BC于点E．若AE=19，BC=10，CD=6，则四边形ABCD的面积为152．考点：全等三角形的判定与性质；正方形的判定与性质．分析：探究：过点A作AF⊥CB，交CB的延长线于点F，先判定四边形AFCE为矩形，根据矩形的四个角都是直角可得∠FAE=90°，然后利用同角的余角相等求出∠FAB=∠EAD，再利用“角角边”证明△AFB和△AED全等，根据全等三角形对应边相等可得AE=AF，从而得到四边形AFCE是正方形，然后根据正方形的面积公式列计算即可得解；应用：过点A作AF⊥CD交CD的延长线于F，连接AC，根据同角的补角相等可得∠ABC=∠ADF，然后利用“角角边”证明△ABE和△ADF全等，根据全等三角形对应边相等可得AF=AE，再根据S四边形ABCD=S△ABC+S△ACD列式计算即可得解．解答：探究：如图①，过点A作AF⊥CB，交CB的延长线于点F，∵AE⊥CD，∠BCD=90°，∴四边形AFCE为矩形，∴∠FAE=90°，∴∠FAB+∠BAE=90°，∵∠EAD+∠BAE=90°，∴∠FAB=∠EAD，∵在△AFB和△AED中，，∴△AFB≌△AED（AAS），∴AF=AE，∴四边形AFCE为正方形，∴S四边形ABCD=S正方形AFCE=AE2=102=100；应用：如图，过点A作AF⊥CD交CD的延长线于F，连接AC，则∠ADF+∠ADC=180°，∵∠ABC+∠ADC=180°，∴∠ABC=∠ADF，∵在△ABE和△ADF中，，∴△ABE≌△ADF（AAS），∴AF=AE=19，∴S四边形ABCD=S△ABC+S△ACD=BC•AE+CD•AF=×10×19+×6×19=95+57=152．故答案为：152．点评：本题考查了全等三角形的判定与性质，正方形的判定与性质，（1）作辅助线构造出全等三角形是解题的关键；（2）作辅助线构造出全等三角形并把四边形分成两个三角形是解题的关键．23．（10分）（2013•长春）如图，在平面直角坐标系中，抛物线y=ax2+bx﹣2 与x轴交于点A（﹣1，0）、B（4，0）．点M、N在x轴上，点N在点M右侧，MN=2．以MN为直角边向上作等腰直角三角形CMN，∠CMN=90°．设点M的横坐标为m．（1）求这条抛物线所对应的函数关系式．（2）求点C在这条抛物线上时m的值．（3）将线段CN绕点N逆时针旋转90°后，得到对应线段DN．①当点D在这条抛物线的对称轴上时，求点D的坐标．②以DN为直角边作等腰直角三角形DNE，当点E在这条抛物线的对称轴上时，直接写出所有符合条件的m值．（参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标为（，））考点：二次函数综合题分析：（1）将A（﹣1，0）、B（4，0）两点的坐标代入y=ax2+bx﹣2，运用待定系数法即可求出抛物线的解析式；（2）先根据等腰直角三角形的性质求出点C的坐标为（m，2），再将C的坐标代入y=x2﹣x﹣2，即可求出m的值；（3）①先由旋转的性质得出点D的坐标为（m，﹣2），再根据二次函数的性质求出抛物线y=x2﹣x﹣2的对称轴为直线x=，然后根据点D在直线x=上，即可求出点D的坐标；②以DN为直角边作等腰直角三角形DNE时，分别以D、N为直角顶点，在DN的两侧分别作出等腰直角三角形DNE，E点的位置分四种情况讨论．针对每一种情况，都可以先根据等腰直角三角形的性质求出点E的坐标，然后根据点E在直线x=上，列出关于m的方程，解方程即可求出m的值．解答：解：（1）∵抛物线经过点A（﹣1，0）、B（4，0），∴解得∴抛物线所对应的函数关系式为y=x2﹣x﹣2；（2）∵△CMN是等腰直角三角形CMN，∠CMN=90°，∴CM=MN=2，∴点C的坐标为（m，2），∵点C（m，2）在抛物线上，∴m2﹣m﹣2=2，解得m1=，m2=．∴点C在这条抛物线上时，m的值为或；（3）①∵将线段CN绕点N逆时针旋转90°后，得到对应线段DN，∴∠CND=90°，DN=CN=CM=MN，∴CD=CN=2CM=2MN，∴DM=CM=MN，∠DMN=90°，∴点D的坐标为（m，﹣2）．又∵抛物线y=x2﹣x﹣2的对称轴为直线x=，点D在这条抛物线的对称轴上，∴点D的坐标为（，﹣2）；②如图，以DN为直角边作等腰直角三角形DNE，E点的位置有四种情况：如果E点在E1的位置时，∵点D的坐标为（m，﹣2），MN=ME1=2，点N的坐标为（m+2，0），∴点E1的（m﹣2，0），∵点E1在抛物线y=x2﹣x﹣2的对称轴x=上，∴m﹣2=，解得m=；如果E点在E2的位置时，∵点D的坐标为（m，﹣2），点N的坐标为（m+2，0），∴点E2的（m+2，﹣4），∵点E2在抛物线y=x2﹣x﹣2的对称轴x=上，∴m+2=，解得m=﹣；如果E点在E3的位置时，∵点D的坐标为（m，﹣2），∴点E3的（m，2），∵点E3在抛物线y=x2﹣x﹣2的对称轴x=上，∴m=；如果E点在E4的位置时，∵点D的坐标为（m，﹣2），点N的坐标为（m+2，0），∴点E4的（m+4，﹣2），∵点E4在抛物线y=x2﹣x﹣2的对称轴x=上，∴m+4=，解得m=﹣；综上可知，当点E在这条抛物线的对称轴上时，所有符合条件的m的值为m=﹣或m=﹣或m=或m=．点评：本题是二次函数的综合题型，其中涉及到运用待定系数法求抛物线的解析式，二次函数的性质，等腰直角三角形的性质，旋转的性质等知识，综合性较强，难度适中．其中（3）②要注意分析题意分情况讨论E点可能的位置，这是解题的关键．24．（12分）（2013•长春）如图①，在▱ABCD中，AB=13，BC=50，BC边上的高为12．点P从点B出发，沿B﹣A﹣D﹣A运动，沿B﹣A运动时的速度为每秒13个单位长度，沿A ﹣D﹣A运动时的速度为每秒8个单位长度．点Q从点B出发沿BC方向运动，速度为每秒5个单位长度．P、Q两点同时出发，当点Q到达点C时，P、Q两点同时停止运动．设点P的运动时间为t（秒）．连结PQ．（1）当点P沿A﹣D﹣A运动时，求AP的长（用含t的代数式表示）．（2）连结AQ，在点P沿B﹣A﹣D运动过程中，当点P与点B、点A不重合时，记△APQ 的面积为S．求S与t之间的函数关系式．（3）过点Q作QR∥AB，交AD于点R，连结BR，如图②．在点P沿B﹣A﹣D运动过程中，当线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分时t的值．（4）设点C、D关于直线PQ的对称点分别为C′、D′，直接写出C′D′∥BC时t的值．考点：四边形综合题．分析：（1）分情况讨论，当点P沿A﹣D运动时，当点P沿D﹣A运动时分别可以表示出AP的值；（2）分类讨论，当0＜t＜1时，当1＜t＜时，根据三角形的面积公式分别求出S 与t的函数关系式；（3）分情况讨论，当0＜t＜1时，当1＜t＜时，当＜t＜时，利用三角形的面积相等建立方程求出其解即可；（4）分情况讨论当P在A﹣D之间或D﹣A之间时，如图⑥，根据轴对称的性质可以知道四边形QCOC′为菱形，根据其性质建立方程求出其解，当P在D﹣A之间如图⑦，根据菱形的性质建立方程求出其解即可．解答：解：（1）当点P沿A﹣D运动时，AP=8（t﹣1）=8t﹣8．当点P沿D﹣A运动时，AP=50×2﹣8（t﹣1）=108﹣8t．（2分）（2）当点P与点A重合时，BP=AB，t=1．当点P与点D重合时，AP=AD，8t﹣8=50，t=．当0＜t＜1时，如图①．作过点Q作QE⊥AB于点E．S△ABQ==，∴QE===．∴S=﹣30t2+30t．当1＜t≤时，如图②．S==，∴S=48t﹣48；（3）当点P与点R重合时，AP=BQ，8t﹣8=5t，t=．当0＜t≤1时，如图③．∵S△BPM=S△BQM，∴PM=QM．∵AB∥QR，∴∠PBM=∠QRM，∠BPM=∠MQR，在△BPM和△RQM中，∴△BPM≌△RQM．∴BP=RQ，∵RQ=AB，∴BP=AB∴13t=13，解得：t=1当1＜t≤时，如图④．∵BR平分阴影部分面积，∴P与点R重合．∴t=．当＜t≤时，如图⑤．∵S△ABR=S△QBR，∴S△ABR＜S四边形BQPR．∴BR不能把四边形ABQP分成面积相等的两部分．综上所述，当t=1或时，线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分．（4）如图⑥，当P在A﹣D之间或D﹣A之间时，C′D′在BC上方且C′D′∥BC时，∴∠C′OQ=∠OQC．∵△C′OQ≌△COQ，∴∠C′OQ=∠COQ，∴∠CQO=∠COQ，∴QC=OC，∴50﹣5t=50﹣8（t﹣1）+13，或50﹣5t=8（t﹣1）﹣50+13，解得：t=7或t=．当P在A﹣D之间或D﹣A之间，C′D′在BC下方且C′D′∥BC时，如图⑦．同理由菱形的性质可以得出：OD=PD，∴50﹣5t+13=8（t﹣1）﹣50，解得：t=．∴当t=7，t=，t=时，点C、D关于直线PQ的对称点分别为C′、D′，且C′D′∥BC．点评：本题考查了平行四边形的性质的运用，菱形的性质的运用，全等三角形的判定及性质的运用，分类讨论的数学思想的运用，轴对称的性质的运用，三角形的面积公式的运用，解答时灵活运用动点问题的解答方法确定分界点是解答本题的关键和难点．。

2013学年吉林省中考数学年试题

效 8
C. 4( 5 1) , 3
8 B. 4 5 ,
3
D.8,8
数学试卷第 1 页（共 4 页）
5.函数 f (x) 1 2x 1 的定义域为 x3
A. (3,0]
B. (3,1]
C. (, 3) (3,0]
D. (, 3) (3,1]
6.执行两次右图所示的程序框图,若第一次输入的 a 的值为
大值为
9
A.0
B.
C.2
8
()
9 D.
4
第Ⅱ卷(共 90 分)
二、填空题：本大题共 4 小题,每小题 4 分,共 16 分.
13.过点 (3,1) 作圆 (x 2)2 ( y 2)2 4 的弦,其中最短弦的长为
.
2x 3y 6≤0，
14.在平面直角坐标系 xOy 中, M 为不等式组 x y 2≥0，所表示的区域上一动点,
4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤.
参考公式：如果事件 A , B 互斥,那么 P(A B) P(A) P(B) .
第Ⅰ卷(共 60 分)
答一、选择题：本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
（Ⅰ）求数列{an} 的通项公式；
（Ⅱ）若数列{bn} 满足
b1 a1

b2 a2

bn an
1
1 2n
, n N* ,求{bn} 的前 n 项和Tn ；
21.（本小题满分 12 分）已知函数 f (x) ax2 bx ln x (a,b R) .
（Ⅰ）设 a≥0 ,求 f (x) 的单调区间；（Ⅱ）设 a＞0 ,且对于任意 x＞0 , f (x)≥f (1) .试比较 ln a 与 2b 的大小.