题型6
数轴动点问题6题型

数轴动点问题6题型
数轴动点问题是数学中常见的一类问题,涉及到数轴上点的移动和位置变化。
一般来说,数轴动点问题可以分为以下六种题型:
1. 绝对值不等式问题,这类问题涉及到数轴上的点在满足绝对值不等式时的位置。
例如,求解 |x 3| < 5 这样的不等式,需要在数轴上确定满足条件的 x 的取值范围。
2. 区间划分问题,这类问题要求根据给定条件在数轴上划分区间,例如求解不等式 2x 1 > 5 时,需要确定 x 的取值范围,从而将数轴划分成若干个区间。
3. 方程与不等式问题,涉及到方程和不等式的问题,例如求解x^2 4x + 3 > 0 这样的不等式时,需要确定 x 的取值范围,也就是数轴上点的位置。
4. 线段长度问题,这类问题需要根据数轴上点的位置来求解线段的长度,例如求解两点之间的距离。
5. 几何位置问题,涉及到几何位置关系的问题,例如求解点到
直线的距离等。
6. 运动问题,这类问题涉及到数轴上点的运动,例如求解两点之间的相对位置关系、速度等。
在解决数轴动点问题时,通常需要画出数轴图示,明确标出各个点的位置,然后根据题目要求进行分析和计算。
希望以上内容能够帮助你更好地理解数轴动点问题的不同题型。
函数性质的八大题型综合应用(解析版)-高中数学

函数性质的八大题型综合应用题型梳理【题型1函数的单调性的综合应用】【题型2函数的最值问题】【题型3函数的奇偶性的综合应用】【题型4函数的对称性的应用】【题型5对称性与周期性的综合应用】【题型6类周期函数】【题型7抽象函数的性质】【题型8函数性质的综合应用】命题规律从近几年的高考情况来看,本节是高考的一个热点内容,函数的单调性、奇偶性、对称性与周期性是高考的必考内容,重点关注单调性、奇偶性结合在一起,与函数图象、函数零点和不等式相结合进行考查,解题时要充分运用转化思想和数形结合思想,灵活求解.对于选择题和填空题部分,重点考查基本初等函数的单调性、奇偶性,主要考察方向是:判断函数单调性及求最值、解不等式、求参数范围等,难度较小;对于解答题部分,一般与导数相结合,考查难度较大.知识梳理【知识点1函数的单调性与最值的求解方法】1.求函数的单调区间求函数的单调区间,应先求定义域,在定义域内求单调区间.2.函数单调性的判断(1)函数单调性的判断方法:①定义法;②图象法;③利用已知函数的单调性;④导数法.(2)函数y=f(g(x))的单调性应根据外层函数y=f(t)和内层函数t=g(x)的单调性判断,遵循“同增异减”的原则.(3)函数单调性的几条常用结论:①若f(x)是增函数,则-f(x)为减函数;若f(x)是减函数,则-f(x)为增函数;②若f(x)和g(x)均为增(或减)函数,则在f(x)和g(x)的公共定义域上f(x)+g(x)为增(或减)函数;③若f(x)>0且f(x)为增函数,则函数f(x)为增函数,1f(x)为减函数;④若f(x)>0且f(x)为减函数,则函数f(x)为减函数,1f(x)为增函数.3.求函数最值的三种基本方法:(1)单调性法:先确定函数的单调性,再由单调性求最值.(2)图象法:先作出函数的图象,再观察其最高点、最低点,求出最值.(3)基本不等式法:先对解析式变形,使之具备“一正二定三相等”的条件后用基本不等式求出最值.4.复杂函数求最值:对于较复杂函数,可运用导数,求出在给定区间上的极值,最后结合端点值,求出最值.【知识点2函数的奇偶性及其应用】1.函数奇偶性的判断判断函数的奇偶性,其中包括两个必备条件:(1)定义域关于原点对称,这是函数具有奇偶性的必要不充分条件,所以首先考虑定义域;(2)判断f(x)与f(-x)是否具有等量关系,在判断奇偶性的运算中,可以转化为判断奇偶性的等价等量关系式(f(x)+f(-x)=0(奇函数)或f(x)-f(-x)=0(偶函数))是否成立.(3)运算函数的奇偶性规律:运算函数是指两个(或多个)函数式通过加、减、乘、除四则运算所得的函数,如f(x)+g(x),f(x)-g(x),f(x)×g(x),f(x)÷g(x).对于运算函数有如下结论:奇±奇=奇;偶±偶=偶;奇±偶=非奇非偶;奇×(÷)奇=偶;奇×(÷)偶=奇;偶×(÷)偶=偶.(4)复合函数y=f[g(x)]的奇偶性原则:内偶则偶,两奇为奇.(5)常见奇偶性函数模型奇函数:①函数f(x)=ma x+1a x-1(x≠0)或函数f(x)=m a x-1a x+1.②函数f(x)=±(a x-a-x).③函数f(x)=log a x+mx-m=log a1+2mx-m或函数f(x)=log a x-mx+m=log a1-2mx+m④函数f(x)=log a(x2+1+x)或函数f(x)=log a(x2+1-x).2.函数奇偶性的应用(1)利用函数的奇偶性可求函数值或求参数的取值,求解的关键在于借助奇偶性转化为求已知区间上的函数或得到参数的恒等式,利用方程思想求参数的值.(2)画函数图象:利用函数的奇偶性可画出函数在其对称区间上的图象,结合几何直观求解相关问题.【知识点3函数的周期性与对称性常用结论】1.函数的周期性常用结论(a是不为0的常数)(1)若f(x+a)=f(x),则T=a;(2)若f(x+a)=f(x-a),则T=2a;(3)若f(x+a)=-f(x),则T=2a;(4)若f(x+a)=f(1x),则T=2a;(5)若f(x+a)=f(1x),则T=2a;(6)若f(x+a)=f(x+b),则T=|a-b|(a≠b);2.对称性的三个常用结论(1)若函数f(x)满足f(a+x)=f(b-x),则y=f(x)的图象关于直线x=a+b2对称.(2)若函数f(x)满足f(a+x)=-f(b-x),则y=f(x)的图象关于点a+b2,0对称.(3)若函数f(x)满足f(a+x)+f(b-x)=c,则y=f(x)的图象关于点a+b2,c 2对称.3.函数的的对称性与周期性的关系(1)若函数y=f(x)有两条对称轴x=a,x=b(a<b),则函数f(x)是周期函数,且T=2(b-a);(2)若函数y=f(x)的图象有两个对称中心(a,c),(b,c)(a<b),则函数y=f(x)是周期函数,且T=2(b-a);(3)若函数y=f(x)有一条对称轴x=a和一个对称中心(b,0)(a<b),则函数y=f(x)是周期函数,且T=4(b-a).举一反三【题型1函数的单调性的综合应用】1(2023·广东深圳·统考模拟预测)已知函数f x 的定义域为R,若对∀x∈R都有f3+x= f1-x,且f x 在2,+∞上单调递减,则f1 ,f2 与f4 的大小关系是()A.f4 <f1 <f2B.f2 <f1 <f4C.f1 <f2 <f4D.f4 <f2 <f1【解题思路】由f3+x=f1-x,得到f1 =f3 ,利用单调性即可判断大小关系,即可求解.【解答过程】因为对∀x∈R都有f3+x=f1-x,所以f1 =f3-2=f[1-(-2)]=f3 又因为f x 在2,+∞上单调递减,且2<3<4,所以f4 <f3 <f2 ,即f4 <f1 <f2 .故选:A.【变式训练】1(2023·山西朔州·怀仁市第一中学校校考二模)定义在R上的函数f(x)满足f2-x=f x ,且当x ≥1时,f (x )单调递增,则不等式f 2-x ≥f (x +1)的解集为()A.12,+∞ B.0,12C.-∞,-12D.-∞,12【解题思路】根据函数的对称性和单调性即可.【解答过程】由f 2-x =f (x ),得f (x )的对称轴方程为x =1,故2-x -1 ≥x +1 -1 ,即(1-x )2≥x 2,解得x ≤12.故选:D .2(2023上·江西鹰潭·高三校考阶段练习)已知函数f x =-x 2+2ax +4,x ≤1,1x,x >1是-12,+∞ 上的减函数,则a 的取值范围是()A.-1,-12B.-∞,-1C.-1,-12D.-∞,-1【解题思路】首先分析知,x >1,函数单调递减,则x ≤1也应为减函数,同时注意分界点处的纵坐标大小关系即可列出不等式组,解出即可.【解答过程】显然当x >1时,f x =1x为单调减函数,f x <f 1 =1当x ≤1时,f x =-x 2+2ax +4,则对称轴为x =-2a2×-1=a ,f 1 =2a +3若f x 是-12,+∞上减函数,则a ≤-122a +3≥1解得a ∈-1,-12 ,故选:A .3(2023·四川绵阳·统考三模)设函数f x 为x -1与x 2-2ax +a +3中较大的数,若存在x 使得f x ≤0成立,则实数a 的取值范围为()A.-43,-1 ∪1,4 B.-∞,-43∪4,+∞ C.-∞,1-132∪1+132,4D.-1,1【解题思路】根据绝对值函数的图像和二次函数讨论对称轴判定函数的图像即可求解.【解答过程】因为f x =max x -1,x 2-2ax +a +3 ,所以f x 代表x -1与x 2-2ax +a +3两个函数中的较大者,不妨假设g (x )=|x |-1,h (x )=x 2-2ax +a +3g (x )的函数图像如下图所示:h(x)=x2-2ax+a+3是二次函数,开口向上,对称轴为直线x=a,①当a<-1时,h(x)=x2-2ax+a+3在-1,1上是增函数,需要h(-1)=(-1)2-2a(-1)+a+3=3a+4≤0即a≤-4 3,则存在x使得f x ≤0成立,故a≤-4 3;②当-1≤a≤1时,h(x)=x2-2ax+a+3在-1,1上是先减后增函数,需要h(x)min=h(a)=a2-2a⋅a+a+3=-a2+a+3≤0,即a2-a-3≥0,解得a≥1+132或a≤1-132,又1+132>1,1-132<-1故-1≤a≤1时无解;③当a>1时,h(x)=x2-2ax+a+3在-1,1上是减函数,需要h(1)=12-2a+a+3=-a+4≤0即a≥4,则存在x使得f x ≤0成立,故a≥4.综上所述,a的取值范围为-∞,-4 3∪4,+∞.故选:B.【题型2函数的最值问题】1(2023·江西九江·校考模拟预测)若0<x<6,则6x-x2有()A.最小值3B.最大值3C.最小值9D.最大值9【解题思路】根据二次函数的性质进行求解即可.【解答过程】令y =6x -x 2=-(x -3)2+9,对称轴为x =3,开口向下,因为0<x <6,所以当x =3时,6x -x 2有最大值9,没有最小值,故选:D .【变式训练】1(2023·全国·校联考三模)已知函数f x =bx -b +3 x 3在-1,1 上的最小值为-3,则实数b的取值范围是()A.-∞,-4B.9,+∞C.-4,9D.-92,9【解题思路】由已知可得当-1≤x <1时,可得bx 1+x ≥-3x 2+x +1 恒成立,通过分离变量,结合函数性质可求b 的取值范围【解答过程】因为f 1 =-3,函数f x =bx -b +3 x 3在-1,1 上的最小值为-3,所以对∀x ∈-1,1 ,f x ≥-3恒成立,所以bx -b +3 x 3≥-3恒成立,即bx 1-x 2 ≥-31-x 3 恒成立,当x =1时,b ∈R ,当-1≤x <1时,可得bx 1+x ≥-3x 2+x +1 恒成立.当x =0或x =-1时,不等式显然成立;当0<x <1时,b ≥-3x 2+x +1 x 1+x =-31+1x 2+x,因为x 2+x ∈0,2 ,所以1x 2+x ∈12,+∞ ,1+1x 2+x ∈32,+∞ ,-31+1x 2+x∈-∞,-92 ,所以b ≥-92;当-1<x <0时,b ≤-31+1x 2+x,因为x 2+x ∈-14,0 ,所以1x 2+x ∈-∞,-4 ,1+1x 2+x ∈-∞,-3 ,-31+1x 2+x∈9,+∞ ,所以b ≤9.综上可得,实数b 的取值范围是-92,9.故选:D .2(2023上·广东广州·高一校考阶段练习)定义一种运算min a ,b =a ,a ≤bb ,a >b,设f x =min 4+2x -x 2,x -t (t 为常数,且x ∈[-3,3],则使函数f x 的最大值为4的t 的值可以是()A.-2或4B.6C.4或6D.-4【解题思路】根据定义,先计算y=4+2x-x2在x∈-3,3上的最大值,然后利用条件函数f(x)最大值为4,确定t的取值即可.【解答过程】y=4+2x-x2=-x-12+5在x∈-3,3上的最大值为5,所以由4+2x-x2=4,解得x=2或x=0,所以x∈0,2时,y=4+2x-x2>4,所以要使函数f(x)最大值为4,则根据定义可知,当t≤1时,即x=2时,2-t=4,此时解得t=-2,符合题意;当t>1时,即x=0时,0-t=4,此时解得t=4,符合题意;故t=-2或4.故选:A.3(2023·广东惠州·统考一模)若函数f x 的定义域为D,如果对D中的任意一个x,都有f x > 0,-x∈D,且f-xf x =1,则称函数f x 为“类奇函数”.若某函数g x 是“类奇函数”,则下列命题中,错误的是()A.若0在g x 定义域中,则g0 =1B.若g x max=g4 =4,则g x min=g-4=1 4C.若g x 在0,+∞上单调递增,则g x 在-∞,0上单调递减D.若g x 定义域为R,且函数h x 也是定义域为R的“类奇函数”,则函数G x =g x h x 也是“类奇函数”【解题思路】对A,根据“类奇函数”的定义,代入x=0求解即可;对B,根据题意可得g-x=1g x,再结合函数的单调性判断即可;对C,根据g-x=1g x,结合正负分数的单调性判断即可;对D,根据“类奇函数”的定义,推导G x G-x=1判断即可.【解答过程】对于A,由函数g x 是“类奇函数”,所以g x g-x=1,且g x >0,所以当x=0时,g0 g-0=1,即g0 =1,故A正确;对于B,由g x g-x=1,即g-x=1g x,g-x随g x 的增大而减小,若g(x)max=g4 =4,则g(x)min=g-4=14成立,故B正确;对于C,由g x 在0,+∞上单调递增,所以g-x=1g x,在x∈0,+∞上单调递减,设t=-x∈-∞,0 ,∴g t 在t ∈-∞,0 上单调递增,即g x 在x ∈-∞,0 上单调递增,故C 错误;对于D ,由g x g -x =1,h x h -x =1,所以G x G -x =g x g -x h x h -x =1,所以函数G x =g x h x 也是“类奇函数”,所以D 正确;故选:C .【题型3 函数的奇偶性的综合应用】1(2023·广东·东莞市校联考一模)已知函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=ax +1,若f (-2)=5,则不等式f (x )>12的解集为()A.-∞,-12 ∪0,16B.-12,0 ∪0,16C.-∞,-12 ∪16,+∞ D.-12,0 ∪16,+∞ 【解题思路】根据条件可求得x >0时f (x )的解析式,根据函数为奇函数继而可求得当x <0时f (x )的解析式,分情况解出不等式即可.【解答过程】因为函数f (x )是定义在R 上的奇函数,所以f (-2)=-f (2)=5,则f (2)=-5,则2a +1=-5,所以a =-3,则当x >0时,f (x )=-3x +1,当x <0时,-x >0,则f (x )=-f (-x )=-[-3×(-x )+1]=-3x -1,则当x >0时,不等式f (x )>12为-3x +1>12,解得0<x <16,当x <0时,不等式f (x )>12为-3x -1>12,解得x <-12,故不等式的解集为-∞,-12 ∪0,16,故选:A .【变式训练】1(2023·全国·模拟预测)已知函数f (x ),g (x )的定义域均为R ,f (3x +1)为奇函数,g (x +2)为偶函数,f (x +1)+g (1-x )=2,f (0)=-12,则102k =1 g (k )=()A.-51B.52C.4152D.4092【解题思路】由题意,根据函数奇偶性可得f (x )的图象关于点(1,0)中心对称、g (x )的图象关于点(1,2)中心对称,进而可知g (x )是以4为周期的周期函数.求出g (1),g (2),g (3),g (4),结合周期即可求解.【解答过程】因为f (3x +1)为奇函数,所以f (x +1)为奇函数,所以f (x +1)=-f (-x +1),f (x )的图象关于点(1,0)中心对称,f (1)=0.因为g (x +2)为偶函数,所以g (x +2)=g (-x +2),g (x )的图象关于直线x =2对称.由f (x +1)+g (1-x )=2,得f (-x +1)+g (1+x )=2,则-f (x +1)+g (1+x )=2,所以g (x +1)+g (1-x )=4,g (x )+g (2-x )=4,所以g (x )的图象关于点(1,2)中心对称.因为g (x )的图象关于x =2轴对称,所以g (x )+g (2+x )=4,g (x +2)+g (x +4)=4,所以g (x +4)=g (x ),即g (x )是以4为周期的周期函数.因为f (1)=0,f (0)=-12,所以g (1)=2,g (2)=52,g (3)=g (1)=2,g (4)=g (0)=4-g (2)=32,所以102k =1g (k )=25×2+52+2+32 +2+52=4092.故选:D .2(2023·安徽亳州·蒙城第一中学校联考模拟预测)已知函数f x 是定义在R 上的偶函数,函数g x 是定义在R 上的奇函数,且f x ,g x 在0,+∞ 上单调递减,则()A.f f 2 >f f 3B.f g 2 <f g 3C.g g 2 >g g 3D.g f 2 <g f 3【解题思路】利用函数的单调性以及函数的奇偶性,判断各选项的正负即可.【解答过程】因为f x ,g x 在0,+∞ 上单调递减,f x 是偶函数,g x 是奇函数,所以g x 在R 上单调递减,f x 在-∞,0 上单调递增,对于A ,f 2 >f 3 ,但无法判断f 2 ,f 3 的正负,故A 不正确;对于B ,g 2 >g 3 ,但无法判断g 2 ,g 3 的正负,故B 不正确;对于C ,g 2 >g 3 ,g x 在R 上单调递减,所以g g 2 <g g 3 ,故C 不正确;对于D ,f 2 >f 3 ,g x 在R 上单调递减,g f 2 <g f 3 ,故D 正确.故选:D .3(2023·江西吉安·江西省遂川中学校考一模)若定义在R 上的函数f (x )满足:对任意x 1,x 2∈R有f (x 1+x 2)=f (x 1)+f (x 2)-2016,且x >0时,f (x )>2016,记f (x )在[-2017,2017]上的最大值和最小值为M ,N ,则M +N 的值为()A.2016B.2017C.4032D.4034【解题思路】先计算得到f (0)=2016,再构造函数g (x )=f (x )-2016,判断g (x )的奇偶性得出结论.【解答过程】解:令x 1=x 2=0得f (0)=2f (0)-2016,∴f (0)=2016,令x 1=-x 2得f (0)=f (-x 2)+f (x 2)-2016=2016,∴f (-x 2)+f (x 2)=4032,令g(x)=f(x)-2016,则g max(x)=M-2016,g min(x)=N-2016,∵g(-x)+g(x)=f(-x)+f(x)-4032=0,∴g(x)是奇函数,∴g max(x)+g min(x)=0,即M-2016+N-2016=0,∴M+N=4032.故选:C.【题型4函数的对称性的应用】1(2023·江西赣州·统考二模)已知函数f(x)的图像既关于点(-1,1)对称,又关于直线y=x对称,且当x∈[-1,0]时,f(x)=x2,则f174=()A.-194B.-92C.-72D.-174【解题思路】用Γ表示函数y=f x 的图像,设x0,y0∈Γ,根据中心对称性与轴对称性,得到4+y0,-4+x0∈Γ,令4+y0=174,求出y0,即可求出x0,即可得解.【解答过程】用Γ表示函数y=f x 的图像,对任意的x0∈-1,0,令y0=x20,则x0,y0∈Γ,且y0∈0,1,又函数f(x)的图像既关于点(-1,1)对称,且关于直线y=x对称,所以y0,x0∈Γ,则-2-y0,2-x0∈Γ,则2-x0,-y0-2∈Γ,则-4+x0,4+y0∈Γ,则4+y0,-4+x0∈Γ,令4+y0=174,即y0=14,此时x0=-12或x0=12(舍去),此时-4+x0=-4+-1 2=-92,即174,-92∈Γ,因此f174 =-92.故选:B.【变式训练】1(2023·四川绵阳·绵阳中学校考一模)若函数y=f x 满足f a+x+f(a-x)=2b,则说y=f x 的图象关于点a,b对称,则函数f(x)=xx+1+x+1x+2+x+2x+3+...+x+2021x+2022+x+2022x+2023的对称中心是()A.(-1011,2022)B.1011,2022C.(-1012,2023)D.1012,2023【解题思路】求出定义域,由定义域的对称中心,猜想a=-1012,计算出f(-1012+x)+f(-1012-x) =4046,从而求出对称中心.【解答过程】函数定义域为{x|x≠-1,x≠-2...,...x≠-2022,x≠-2023},定义域的对称中心为(-1012,0),所以可猜a=-1012,则f(-1012+x)=-1012+x-1011+x+-1011+x-1010+x+-1010+x-1009+x+...+1009+xx+1010+1010+x1011+x,f(-1012-x)=-1012-x-1011-x +-1011-x-1010-x+-1010-x-1009-x+...+1009-x1010-x+1010-x1011-x=1012+x 1011+x +1011+x1010+x+1010+x1009+x+...+1009-x1010-x+1010-x1011-x,故f(-1012+x)+f(-1012-x)=1010+x1011+x +1012+x 1011+x+1009+xx+1010+1011+x 1010+x⋯+-1012+x-1011+x +1010-x 1011-x=2×2023=4046所以y=f x 的对称中心为(-1012,2023),故选:C.2(2023·四川南充·四川省南充高级中学校考三模)函数f x 和g x 的定义域均为R,且y=f3+3x为偶函数,y=g x+3+2为奇函数,对∀x∈R,均有f x +g x =x2+1,则f7 g7 = ()A.615B.616C.1176D.2058【解题思路】由题意可以推出f x =f6-x,g x =-4-g6-x,再结合f x +g x =x2+1可得函数方程组,解出函数方程组后再代入求值即可.【解答过程】由函数f3+3x为偶函数,则f3+3x=f3-3x,即函数f x 关于直线x=3对称,故f x =f6-x;由函数g x+3+2为奇函数,则g x+3+2=-g-x+3-2,整理可得g x+3+g-x+3=-4,即函数g x 关于3,-2对称,故g x =-4-g6-x;由f x +g x =x2+1,可得f6-x+g6-x=(6-x)2+1,所以f x -4-g x =(6-x)2+1,故f x +g x =x2+1f x -4-g x =(6-x)2+1 ,解得f x =x2-6x+21,g x =6x-20,所以f7 =72-6×7+21=28,g7 =6×7-20=22,所以f7 g7 =28×22=616.故选:B.3(2023·甘肃张掖·高台县校考模拟预测)已知函数f(x)的定义域为R,f x-1的图象关于点(1,0)对称,f3 =0,且对任意的x1,x2∈-∞,0,x1≠x2,满足f x2-f x1x2-x1<0,则不等式x-1f x+1≥0的解集为()A.-∞,1∪2,+∞B.-4,-1∪0,1C.-4,-1∪1,2D.-4,-1∪2,+∞【解题思路】首先根据f(x-1)的图象关于点(1,0)对称,得出(x)是定义在R上的奇函数,由对任意的x1,x2∈(-∞,0),x1≠x2,满足f(x2)-f(x1)x2-x1<0,得出f(x)在(-∞,0)上单调递减,然后根据奇函数的对称性和单调性的性质,求解即可.【解答过程】∵f(x-1)的图象关于点(1,0)对称,∴f(x)的图象关于点(0,0)对称,∴f(x)是定义在R 上的奇函数,∵对任意的x1,x2∈(-∞,0),x1≠x2,满足f(x2)-f(x1)x2-x1<0,∴f(x)在(-∞,0)上单调递减,所以f(x)在(0,+∞)上也单调递减,又f3 =0所以f-3=0,且f0 =0,所以当x∈-∞,-3∪0,3时,f x >0;当x∈-3,0∪3,+∞时,f x <0,所以由x-1f x+1≥0可得x-1<0,-3≤x+1≤0或x-1>0,0≤x+1≤3或x-1=0,解得-4≤x≤-1或1≤x≤2,即不等式x-1f x+1≥0的解集为-4,-1∪1,2.故选:C.【题型5对称性与周期性的综合应用】1(2023·四川宜宾·统考一模)已知函数f x ,g x 的定义域为R,g x 的图像关于x=1对称,且g2x+2为奇函数,g1 =1,f x =g3-x+1,则下列说法正确的个数为()①g(-3)=g(5);②g(2024)=0;③f(2)+f(4)=-4;④2024n=1f(n)=2024.A.1B.2C.3D.4【解题思路】根据奇函数定义得到g-2x+2=-g2x+2,进而得到g x 的对称中心为,再根据对称轴求出周期,通过赋值得到答案.【解答过程】因为g2x+2为奇函数,所以g-2x+2=-g2x+2,则g-x+2=-g x+2,所以g x 对称中心为2,0,又因为g x 的图像关于x=1对称,则g-x+2=g x ,所以-g x+2=g x ,则g x+4=-g x+2=g x ,所以g x 的周期T=4,①g-3=g-3+8=g5 ,所以①正确;②因为g1 =1,g-x+2=g x ,g x 对称中心为2,0,所以g0 =g2 =0,所以g(2024)=g0 =0,所以②正确;③因为f x =g3-x+1,所以f2 =g1 +1=2,因为-g x+2=g x ,所以g-1=-g1 ,则f4 =g-1+1=-g1 +1=0,所以f(2)+f(4)=2,所以③错误;④因为f x =g 3-x +1且g x 周期T =4,所以f x +4 =g 3-x -4 +1=g 3-x +1=f x ,则f x 的周期为T =4,因为f 1 =g 2 +1=1,f 2 =2,f 3 =g 0 +1=1,f 4 =0,所以f 1 +f 2 +f 3 +f 4 =4,所以2024n =1 f (n )=506f 1 +f 2 +f 3 +f 4 =4 =506×4=2024,所以④正确.故选:C .【变式训练】1(2023·北京大兴·校考三模)已知函数f x 对任意x ∈R 都有f x +2 =-f x ,且f -x =-f x ,当x ∈-1,1 时,f x =x 3.则下列结论正确的是()A.函数y =f x 的图象关于点k ,0 k ∈Z 对称B.函数y =f x 的图象关于直线x =2k k ∈Z 对称C.当x ∈2,3 时,f x =x -2 3D.函数y =f x 的最小正周期为2【解题思路】根据f x +2 =-f x 得到f x +2 =f x -2 ,所以f x 的周期为4,根据f -x =-f x 得到f x 关于x =-1对称,画出f x 的图象,从而数形结合得到AB 错误;再根据f x =-f x -2 求出x ∈2,3 时函数解析式;D 选项,根据y =f x 的最小正周期,得到y =f x 的最小正周期.【解答过程】因为f x +2 =-f x ,所以f x =-f x -2 ,故f x +2 =f x -2 ,所以f x 的周期为4,又f -x =-f x ,所以f -x =f x -2 ,故f x 关于x =-1对称,又x ∈-1,1 时,f x =x 3,故画出f x 的图象如下:A 选项,函数y =f x 的图象关于点1,0 不中心对称,故A 错误;B 选项,函数y =f x 的图象不关于直线x =2对称,B 错误;C 选项,当x ∈2,3 时,x -2∈0,1 ,则f x =-f x -2 =-x -2 3,C 错误;D 选项,由图象可知y =f x 的最小正周期为4,又f x +2 =-f x =f x ,故y =f x 的最小正周期为2,D 正确.故选:D .2(2023·四川绵阳·绵阳校考模拟预测)已知函数f x 的定义域为R ,f 1 =0,且f 0 ≠0,∀x ,y∈R 都有f x +y +f x -y =2f x f y ,则下列说法正确的命题是()①f 0 =1;②∀x ∈R ,f -x +f x =0;③f x 关于点1,0 对称;④2023i =1 f (i )=-1A.①②B.②③C.①②④D.①③④【解题思路】利用特殊值法,结合函数的奇偶性、对称性和周期性进行求解即可.【解答过程】对于①,由于∀x ,y ∈R 都有f x +y +f x -y =2f x f y ,所以令x =y =0,则f 0 +f 0 =2f 0 f 0 ,即f 0 =f 20 ,因为f 0 ≠0,所以f 0 =1,所以①正确,对于②,令x =0,则f y +f -y =2f 0 f y =2f y ,所以f y =f -y ,即f x =f -x ,所以∀x ∈R ,f -x -f x =0,所以②错误,对于③,令x =1,则f 1+y +f 1-y =2f 1 f y =0,所以f 1+y =-f 1-y ,即f 1+x =-f 1-x ,所以f x 关于点1,0 对称,所以③正确,对于④,因为f 1+x =-f 1-x ,所以f 2+x =-f -x ,因为f x =f -x ,所以f 2+x =-f x ,所以f 4+x =-f 2+x ,所以f 4+x =f x ,所以f x 的周期为4,在f x +y +f x -y =2f x f y 中,令x =y =1,则f 2 +f 0 =2f 1 f 1 =0,因为f 0 =1,所以f (2)=-1,f (3)=f (-1)=f (1)=0,f (4)=f (0)=1,所以f (1)+f (2)+f (3)+f (4)=0+(-1)+0+1=0,所以2023i =1 f (i )=505×f (1)+f (2)+f (3)+f (4) +f (1)+f (2)+f (3)=-1,所以④正确,故选:D .3(2023·安徽合肥·合肥一中校考模拟预测)已知函数f x 与g (x )的定义域均为R ,f (x +1)为偶函数,且f (3-x )+g (x )=1,f (x )-g (1-x )=1,则下面判断错误的是()A.f x 的图象关于点(2,1)中心对称B.f x 与g x 均为周期为4的周期函数C.2022i =1f (i )=2022D.2023i =0g (i )=0【解题思路】由f (x +1)为偶函数可得函数关于直线x =1轴对称,结合f (3-x )+g (x )=1和f (x )-g (1-x )=1可得f x 的周期为4,继而得到g x 的周期也为4,接着利用对称和周期算出对应的值即可判断选项【解答过程】因为f x +1 为偶函数,所以f x +1 =f -x +1 ①,所以f x 的图象关于直线x =1轴对称,因为f x -g 1-x =1等价于f 1-x -g x =1②,又f 3-x +g x =1③,②+③得f 1-x +f 3-x =2④,即f 1+x +f 3+x =2,即f 2+x =2-f x ,所以f 4+x =2-f 2+x =f x ,故f x 的周期为4,又g x =1-f 3-x ,所以g x 的周期也为4,故选项B 正确,①代入④得f 1+x +f 3-x =2,故f x 的图象关于点2,1 中心对称,且f 2 =1,故选项A 正确,由f 2+x =2-f x ,f 2 =1可得f 0 =1,f 4 =1,且f 1 +f 3 =2,故f 1 +f 2 +f 3 +f 4 =4,故2022i =1 f (i )=505×4+f (1)+f (2)=2021+f (1),因为f 1 与f 3 值不确定,故选项C 错误,因为f 3-x +g x =1,所以g 1 =0,g 3 =0,g 0 =1-f 3 ,g 2 =1-f 1 ,所以g 0 +g 2 =2-f 1 +f 3 =0,故g 0 +g 1 +g 2 +g 3 =0,故2023i =0 g (i )=506×0=0,所以选项D 正确,故选:C .【题型6 类周期函数】1(2023·安徽合肥·合肥一六八中学校考模拟预测)定义在R 上的函数f x 满足f x +1 =12f x ,且当x ∈0,1 时,f x =1-2x -1 .当x ∈m ,+∞ 时,f x ≤332,则m 的最小值为()A.278B.298C.134D.154【解题思路】根据已知计算出f x =12n 1-2x -2n +1 ≤12n ,画出图象,计算f x =332,解得x =298,从而求出m 的最小值.【解答过程】由题意得,当x ∈1,2 时,故f x =12f x -1 =121-2x -3 ,当x ∈2,3 时,故f x =12f x -1 =141-2x -5 ⋯,可得在区间n ,n +1 n ∈Z 上,f x =12n 1-2x -2n +1 ≤12n ,所以当n ≥4时,f x ≤332,作函数y =f x 的图象,如图所示,当x ∈72,4 时,由f x =181-2x -7 =332,2x -7 =14,x =298,则m ≥298,所以m 的最小值为298故选:B .【变式训练】1(2023上·湖南长沙·高三校考阶段练习)定义域为R 的函数f x 满足f x +2 =2f x -1,当x∈0,2 时,f x =x 2-x ,x ∈0,1 1x,x ∈1,2.若x ∈0,4 时,t 2-7t 2≤f x ≤3-t 恒成立,则实数t 的取值范围是()A.1,2B.1,52C.12,2D.2,52【解题思路】由f (x +2)=2f (x )-1,求出x ∈(2,3),以及x ∈[3,4]的函数的解析式,分别求出(0,4]内的四段的最小值和最大值,注意运用二次函数的最值和函数的单调性,再由t 2-7t2≤f x ≤3-t 恒成立即为t 2-7t2≤f x min ,f x max ≤3-t ,解不等式即可得到所求范围【解答过程】当x ∈(2,3),则x -2∈(0,1),则f (x )=2f (x -2)-1=2(x -2)2-2(x -2)-1,即为f (x )=2x 2-10x +11,当x ∈[3,4],则x -2∈[1,2],则f (x )=2f (x -2)-1=2x -2-1.当x ∈(0,1)时,当x =12时,f (x )取得最小值,且为-14;当x ∈[1,2]时,当x =2时,f (x )取得最小值,且为12;当x ∈(2,3)时,当x =52时,f (x )取得最小值,且为-32;当x ∈[3,4]时,当x =4时,f (x )取得最小值,且为0.综上可得,f (x )在(0,4]的最小值为-32.若x ∈(0,4]时, t 2-7t2≤f x min 恒成立,则有t 2-7t 2≤-32.解得12≤t ≤3.当x ∈(0,2)时,f (x )的最大值为1,当x ∈(2,3)时,f (x )∈-32,-1 ,当x ∈[3,4]时,f (x )∈[0,1],即有在(0,4]上f (x )的最大值为1.由f x max ≤3-t ,即为1≤3-t ,解得t ≤2,综上,即有实数t 的取值范围是12,2.故选:C .2(2022·四川内江·校联考二模)定义域为R 的函数f (x )满足f (x +2)=3f (x ),当x ∈[0,2]时,f (x )=x 2-2x ,若x ∈[-4,-2]时,f (x )≥1183t-t 恒成立,则实数t 的取值范围是()A.-∞,-1 ∪0,3B.-∞,-3 ∪0,3C.-1,0 ∪3,+∞D.-3,0 ∪3,+∞【解题思路】根据题意首先得得到函数的具体表达式,由x ∈[-4,-2],所以x +4∈[0,2],所以f (x +4)=x 2+6x +8,再由f (x +4)=3f (x +2)=9f (x )可得出f (x )的表达式,在根据函数思维求出f (x )最小值解不等式即可.【解答过程】因为x ∈[-4,-2],所以x +4∈[0,2],因为x ∈[0,2]时,f x =x 2-2x ,所以f x +4 =(x +4)2-2(x +4)=x 2+6x +8,因为函数f x 满足f x +2 =3f x ,所以f x +4 =3f x +2 =9f x ,所以f x =19f x +4 =19x 2+6x +8 ,x ∈[-4,-2],又因为x ∈[-4,-2],f x ≥1183t-t 恒成立,故1183t -t ≤f x min =-19,解不等式可得t ≥3或-1≤t <0.故选C .3(2023上·浙江台州·高一校联考期中)设函数f x 的定义域为R ,满足f x =2f x -2 ,且当x∈0,2 时,f x =x 2-x .若对任意x ∈-∞,m ,都有f x ≤3,则m 的取值范围是()A.-∞,52B.-∞,72C.-∞,92D.-∞,112【解题思路】根据给定条件分段求解析式及对应函数值集合,再利用数形结合即得.【解答过程】因为函数f x 的定义域为R ,满足f x =2f x -2 ,且当x ∈0,2 时,f x =x 2-x =-x -1 2+1∈0,1 ,当x ∈(2,4],时,x -2∈(0,2],则f (x )=2f (x -2)=2x -2 2-x -2 =-2x -3 2+2∈0,2 ,当x ∈(4,6],时,x -4∈(0,2],则f (x )=4f (x -2)=4x -2-2 4-x -2 =-4x -5 2+4∈0.4 ,当x ∈(-2,0],时,x +2∈(0,2],则f (x )=12f (x +2)=12(x +2)-x =-12x +1 2+12∈0,12,作出函数f x 的大致图象,对任意x ∈-∞,m ,都有f x ≤3,设m 的最大值为t ,则f t =3,所以-4t -5 2+4=3,解得t =92或t =112,结合图象知m 的最大值为92,即m 的取值范围是-∞,92.故选:C .【题型7 抽象函数的性质】1(2023·新疆乌鲁木齐·统考二模)已知f x ,g x 都是定义在R 上的函数,对任意x ,y 满足f x -y=f x g y -g x f y ,且f -2 =f 1 ≠0,则下列说法正确的是()A.f 0 =1B.函数g 2x +1 的图象关于点1,0 对称C.g 1 +g -1 =0D.若f 1 =1,则2023n =1 f n =1【解题思路】利用赋值法结合题目给定的条件可判断AC ,取f x =sin2π3x ,g x =cos 2π3x 可判断B ,对于D ,通过观察选项可以推断f x 很可能是周期函数,结合f x g y ,g x f y 的特殊性及一些已经证明的结论,想到令y =-1和y =1时可构建出两个式子,两式相加即可得出f x +1 +f x -1 =-f x ,进一步得出f x 是周期函数,从而可求2023n =1 f n 的值.【解答过程】解:对于A ,令x =y =0,代入已知等式得f 0 =f 0 g 0 -g 0 f 0 =0,得f 0 =0,故A 错误;对于B ,取f x =sin 2π3x ,g x =cos 2π3x ,满足f x -y =f x g y -g x f y 及f -2 =f 1 ≠0,因为g 3 =cos2π=1≠0,所以g x 的图象不关于点3,0 对称,所以函数g 2x +1 的图象不关于点1,0 对称,故B 错误;对于C ,令y =0,x =1,代入已知等式得f 1 =f 1 g 0 -g 1 f 0 ,可得f 1 1-g 0 =-g 1 f 0 =0,结合f 1 ≠0得1-g 0 =0,g 0 =1,再令x =0,代入已知等式得f -y =f 0 g y -g 0 f y ,将f 0 =0,g 0 =1代入上式,得f -y =-f y ,所以函数f x 为奇函数.令x =1,y =-1,代入已知等式,得f 2 =f 1 g -1 -g 1 f -1 ,因为f -1 =-f 1 ,所以f 2 =f 1 g -1 +g 1 ,又因为f 2 =-f -2 =-f 1 ,所以-f 1 =f 1 g -1 +g 1 ,因为f 1 ≠0,所以g 1 +g -1 =-1,故C 错误;对于D ,分别令y =-1和y =1,代入已知等式,得以下两个等式:f x +1 =f x g -1 -g x f -1 ,f x -1 =f x g 1 -g x f 1 ,两式相加易得f x +1 +f x -1 =-f x ,所以有f x +2 +f x =-f x +1 ,即:f x =-f x +1 -f x +2 ,有:-f x +f x =f x +1 +f x -1 -f x +1 -f x +2 =0,即:f x -1 =f x +2 ,所以f x 为周期函数,且周期为3,因为f 1 =1,所以f -2 =1,所以f 2 =-f -2 =-1,f 3 =f 0 =0,所以f 1 +f 2 +f 3 =0,所以2023n =1 f n =1=f 1 +f 2 +f 3 +⋯+f 2023 =f 2023 =f 1 =1,故D 正确.故选:D .【变式训练】1(2023·福建宁德·福鼎市校考模拟预测)已知函数f x 及其导函数f x 的定义域均为R ,对任意的x ,y ∈R ,恒有f x +y +f x -y =2f x f y ,则下列说法正确的个数是()①f 0 =0;②fx 必为奇函数;③f x +f 0 ≥0;④若f (1)=12,则2023n =1f (n )=12.A.1B.2C.3D.4【解题思路】利用赋值法可判断①;利用赋值法结合函数奇偶性定义判断②;赋值,令y =x ,得出f 2x+f0 ≥0,变量代换可判断③;利用赋值法求出f(n)部分函数值,推出其值具有周期性,由此可计算2023n=1f(n),判断④,即可得答案.【解答过程】令x=y=0,则由f x+y+f x-y=2f x f y 可得2f0 =2f20 ,故f(0)=0或f0 =1,故①错误;当f(0)=0时,令y=0,则f(x)+f(x)=2f(x)f(0)=0,则f(x)=0,故f (x)=0,函数f (x)既是奇函数又是偶函数;当f(0)=1时,令x=0,则f(y)+f(-y)=2f(0)f(y),所以f-y=f y ,则-f (-y)=f (y),即f (-y)=-f (y),则f (x)为奇函数,综合以上可知f (x)必为奇函数,②正确;令y=x,则f2x+f0 =2f2x ,故f2x+f0 ≥0.由于x∈R,令t=2x,t∈R,即f t +f0 ≥0,即有f x +f0 ≥0,故③正确;对于D,若f1 =12,令x=1,y=0,则f1 +f1 =2f1 f0 ,则f(0)=1,令x=y=1,则f2 +f0 =2f21 ,即f2 +1=12,∴f2 =-12,令x=2,y=1,则f3 +f1 =2f2 f1 ,即f3 +12=-12,∴f(3)=-1,令x=3,y=1,则f4 +f2 =2f3 f1 ,即f4 -12=-1,∴f(4)=-12,令x=4,y=1,则f5 +f3 =2f4 f1 ,即f5 -1=-12,∴f(5)=12,令x=5,y=1,则f6 +f4 =2f5 f1 ,即f6 -12=12,∴f(6)=1,令x=6,y=1,则f7 +f5 =2f6 f1 ,即f7 +12=1,∴f(7)=12,令x=7,y=1,则f8 +f6 =2f7 f1 ,即f8 +1=12,∴f(8)=-12,⋯⋯,由此可得f(n),n∈N*的值有周期性,且6个为一周期,且f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=0,故2023n=1f n =337×[f(1)+f(2)+f(3)+f(4)+f(5)+f(6)]+f(1)=12,故④正确,即正确的是②③④,故选:C.2(2023·河南·校联考模拟预测)已知函数f x 对任意实数x,y恒有f(x-y)+f(x+y)=f(2x)成立,且当x<0时,f(x)>0.(1)求f(0)的值;(2)判断f x 的单调性,并证明;(3)解关于x的不等式:f x2-(a+2)x+f(a+y)+f(a-y)>0.【解题思路】(1)根据题意,令x=0,y=0,即可求得f(0)=0;(2)令x=0,得到f(-y)=-f(y),所以f x 为奇函数,在结合题意和函数单调性的定义和判定方法,即可求解;(3)化简不等式为f x2-(a+2)x>f(-2a),结合函数f x 的单调性,把不等式转化为x2-(a+2)x <-2a,结合一元二次不等式的解法,即可求解.【解答过程】(1)解:因为函数f(x)对任意实数x,y恒有f(x-y)+f(x+y)=f(2x)成立,令x=0,y=0,则f(0)+f(0)=f(0),所以f(0)=0.(2)解:函数f x 为R上的减函数.证明:令x=0,则f(-y)+f(y)=f(0)=0,所以f(-y)=-f(y),故f x 为奇函数.任取x1,x2∈R,且x1<x2,则x1-x2<0,因为当x<0时,f(x)>0,所以f x1-x2>0,所以f x1-f x2=f x1+f-x2=fx1-x22+x1+x22+f x1-x22-x1+x22=f x1-x2>0,即f x1>f x2,所以f x 是R上的减函数.(3)解:根据题意,可得f x2-(a+2)x>-[f(a+y)+f(a-y)]=-f(2a)=f(-2a),由(2)知f x 在R上单调递减,所以x2-(a+2)x<-2a,即x2-(a+2)x+2a<0,可得(x-2)(x-a)<0,当a>2时,原不等式的解集为(2,a);当a=2时,原不等式的解集为∅;当a<2时,原不等式的解集为(a,2).3(2023上·广东东莞·高一校联考期中)已知函数f x 对任意实数x,y恒有f x+y=f x +f y ,当x>0时,f x <0,且f1 =-2.(1)判断f x 的奇偶性;(2)判断函数单调性,求f x 在区间-3,3上的最大值;(3)若f x <m2-2am+2对所有的x∈-1,1,a∈-1,1恒成立,求实数m的取值范围.【解题思路】(1)令x=y=0,求得f0 =0,再令y=-x,从而得f-x=-f x ,从而证明求解. (2)设x1,x2∈R且x1<x2,结合条件用单调性的定义证明函数f x 的单调性,然后利用单调性求解区间-3,3上的最大值.(3)根据函数f x <m2-2am+2对所有的x∈-1,1,a∈-1,1恒成立,说明f x 的最大值2小于右边,因此先将右边看作a的函数,解不等式组,即可得出m的取值范围.【解答过程】(1)f x 为奇函数,证明如下:令x=y=0,则f0+0=2f0 ,所以f0 =0,令y=-x,则f x-x=f x +f-x=f0 =0,所以:f-x=-f x 对任意x∈R恒成立,所以函数f x 为奇函数.(2)f x 在R上是减函数,证明如下:任取x1,x2∈R且x1<x2,则x2-x1>0f x2-f x1=f x2+f-x1=f x2-x1<0,所以f x2<f x1,所以f x 在R上为减函数.当x∈-3,3时,f x 单调递减,所以当x=-3时,f x 有最大值为f-3,因为f3 =f2 +f1 =3f1 =-2×3=-6,所以f-3=-f3 =6,故f x 在区间-3,3上的最大值为6.(3)由(2)知f x 在区间-1,1上单调递减,所以f x ≤f-1=-f1 =2,因为f x <m2-2am+2对所有的x∈-1,1,a∈-1,1恒成立,即m2-2am>0对任意a∈-1,1恒成立,令g a =-2am+m2,则g-1>0g1 >0,即2m+m2>0-2m+m2>0,解得:m>2或m<-2.故m的取值范围为-∞,-2∪2,+∞.【题型8函数性质的综合应用】1(2023上·河北石家庄·高一校考阶段练习)已知函数f(x)=a x,g(x)=b⋅a-x+x,a>0且a≠1,若f(1)+g(1)=52,f(1)-g(1)=32,设h(x)=f(x)+g(x),x∈[-4,4].(1)求函数h(x)的解析式并判断其奇偶性;(2)判断函数h(x)的单调性(不需证明),并求不等式h(2x+1)+h(2x-1)≥0的解集.【解题思路】(1)由f(1)+g(1)=52、f(1)-g(1)=32代入可解出a、b,得到h(x),再计算h(x)与h(-x)的关系即可得到奇偶性;(2)分别判断h(x)中每一部分的单调性可得h(x)的单调性,结合函数的单调性与奇偶性解决该不等式即可得.【解答过程】(1)由f(1)+g(1)=52,f(1)-g(1)=32,即有a+ba+1=52a-ba-1=32,解得a=2b=-1,即f(x)=2x,g(x)=-2-x+x,则h(x)=2x-2-x+x,其定义域为R,h (-x )=2-x -2x -x =-2x -2-x +x =-h (x ),故h (x )为奇函数.(2)h (x )=2x -2-x +x ,由2x 在R 上单调递增,-2-x 在R 上单调递增,x 在R 上单调递增,故h (x )在R 上单调递增,由h (2x +1)+h (2x -1)≥0,且h (x )为奇函数,即有h (2x +1)≥-h (2x -1)=h 1-2x ,即有2x +1≥1-2x ,解得x ≥0,故该不等式的解集为x x ≥0 .【变式训练】1(2023上·上海·高一校考期中)已知定义在全体实数上的函数f x 满足:①f x 是偶函数;②f x 不是常值函数;③对于任何实数x 、y ,都有f x +y =f x f y -f 1-x f 1-y .(1)求f 1 和f 0 的值;(2)证明:对于任何实数x ,都有f x +4 =f x ;(3)若f x 还满足对0<x <1有f x >0,求f 13+f 23 +⋯+f 20263 的值.【解题思路】(1)取x =1,y =0代入计算得到f 1 =0,取y =0得到f x =f x f 0 ,得到答案.(2)取y =1,结合函数为偶函数得到f x +2 =-f x ,变换得到f x +4 =f x ,得到证明.(3)根据函数的周期性和奇偶性计算f 13 +f 23 +⋯+f 123 =0,取x =y =13和取x =13,y =-13得到f 13 =32,根据周期性得到f 13 +f 23 +⋯+f 20263=-f 13 -1,计算得到答案.【解答过程】(1)f x +y =f x f y -f 1-x f 1-y取x =1,y =0得到f 1 =f 1 f 0 -f 0 f 1 =0,即f 1 =0;取y =0得到f x =f x f 0 -f 1-x f 1 =f x f 0 ,f x 不是常值函数,故f 0 =1;(2)f x +y =f x f y -f 1-x f 1-y ,取y =1得到f x +1 =f x f 1 -f 1-x f 0 =-f 1-x ,f x 是偶函数,故f x +1 =-f x -1 ,即f x +2 =-f x ,f x +4 =-f x +2 =f x .(3)f x +2 +f x =0,f x 为偶函数,取x =-13,则f 53 +f -13 =0,即f 53 +f 13 =0;取x =-23,则f 43 +f -23 =0,即f 43 +f 23=0;故f 73+f 83 +f 103 +f 113 =-f 13 -f 23 -f 43 -f 53 =0,f 2 =-f 0 =-1,f 3 =f -1 =f 1 =0,f 4 =f 0 =1,故f 13+f 23 +⋯+f 123 =0,取x =y =13得到f 23 =f 213 -f 223,取x =13,y =-13得到f 0 =f 213 -f 23 f 43 =f 213 +f 223=1,f 13 >0,f 23 >0,解得f 13 =32,f 13+f 23 +⋯+f 20263 =-f 113 -f 123 =-f 13 -1=-32-1.2(2023下·山西运城·高二统考期末)已知f x =e x -1+e 1-x +x 2-2x +a ,(1)证明:f x 关于x =1对称;(2)若f x 的最小值为3(i )求a ;(ii )不等式f m e x +e -x +1 >f e x -e -x 恒成立,求m 的取值范围【解题思路】(1)代入验证f (x )=f (2-x )即可求解,(2)利用单调性的定义证明函数的单调性,即可结合对称性求解a =2,分离参数,将恒成立问题转化为m >e x -e -x -1e x +e -xmax ,构造函数F (x )=e x -e -x -1e x +e-x ,结合不等式的性质即可求解最值.【解答过程】(1)证明:因为f x =e x -1+e 1-x +x 2-2x +a ,所以f (2-x )=e 2-x -1+e1-(2-x )+(2-x )2-2(2-x )+a =e 1-x +e x -1+x 2-2x +a ,所以f (x )=f (2-x ),所以f (x )关于x =1对称.(2)(ⅰ)任取x 1,x 2∈(1,+∞),且x 1<x 2f x 1 -f x 2 =e x 1-1+e1-x 1+x 21-2x 1-ex 2-1+e1-x 2+x 22-2x 2=e x 1-1-ex 2-1+e1-x 1-e1-x 2+x 21-x 22 -2x 1-x 2=(ex 1-1-ex 2-1)(e x 1-1e x 2-1-1)ex 1-1ex 2-1+(x 1-x 2)(x 1+x 2-2)∵1<x 1<x 2,∴0<x 1-1<x 2-1,∴e x 1-1>1,ex 2-1>1,ex 1-1-ex 2-1<0,ex 1-1e x 2-1-1>0,x 1-x 2<0,x 1+x 2-2>0,∴f (x 1)<f (x 2),所以f (x )在1,+∞ 上单调递增,又f (x )关于x =1对称,则在-∞,1 上单调递减.所以f (x )min =f (1)=1+a =3,所以a =2.(单调性也可以用单调性的性质、复合函数的单调性判断、导数证明)(ⅱ)不等式f (m (e x +e -x )+1)>f (e x -e -x )恒成立等价于(m (e x +e -x )+1)-1 >e x -e -x -1 恒成立, 即m >ex-e -x -1 e x +e -x =e x -e -x -1e x +e -x恒成立,即m >e x -e -x -1e x +e -xmax令F (x )=e x -e -x -1e x +e -x ,则F (x )=e 2x -e x -1e 2x +1=1-e x +2e 2x +1,令e x +2=n ,n ∈2,+∞ ,则e x =n -2则g n =1-n n 2-4n +5=1-1n -4+5n,因为n ∈2,+∞ ,n -4+5n ≥25-4,n =5取等号,则g n ∈-52,1,所以g n ∈0,52,所以m >52,即m ∈-∞,-52 ∪52,+∞ .3(2023下·广东·高一统考期末)已知函数y =φx 的图象关于点P a ,b 成中心对称图形的充要条件是φa +x +φa -x =2b .给定函数f x =x -6x +1及其图象的对称中心为-1,c .(1)求c 的值;(2)判断f x 在区间0,+∞ 上的单调性并用定义法证明;(3)已知函数g x 的图象关于点1,1 对称,且当x ∈0,1 时,g x =x 2-mx +m .若对任意x 1∈0,2 ,总存在x 2∈1,5 ,使得g x 1 =f x 2 ,求实数m 的取值范围.【解题思路】(1)根据函数的对称性得到关于c 的方程,解出即可求出函数的对称中心;(2)利用函数单调性的定义即可判断函数f (x )单增,(3)问题转化为g (x )在[0,2]上的值域A ⊆[-2,4],通过讨论m 的范围,得到关于m 的不等式组,解出即可.【解答过程】(1)由于f (x )的图象的对称中心为-1,c ,则f (-1+x )+f (-1-x )=2c ,即(x -1)-6x -1+1+(-x -1)-6-x -1+1=2c ,整理得-2=2c ,解得:c =-1,故f (x )的对称中心为(-1,-1);(2)函数f (x )在(0,+∞)递增;设0<x 1<x 2,则f x 1 -f x 2 =x 1-6x 1+1-x 2+6x 2+1=x 1-x 2 +6x 1-x 2 x 2+1 x 1+1=x 1-x 2 1+6x 2+1 x 1+1,由于0<x 1<x 2,所以x 1-x 2<0, 6x 2+1 x 1+1>0,所以f x 1 -f x 2 <0⇒f x 1 <f x 2 ,故函数f (x )在(0,+∞)递增;。
6.题型六 函数的实际应用

题型六函数的实际应用1. 某超市以10元/个购进一批新型儿童玩具,当以17元/个出售时,每天可以售出50个.元旦期间,在确保不亏本的前提下超市采取降价促销的方式招揽顾客,经调查发现,当售价每降低0.5元时,每天可多卖出5个玩具,设售价降低了x元,每天可获利润为w元.(1)求w与x之间的函数关系式;(2)每件玩具的售价定为多少元时,商店每天获得的利润最大,最大利润是多少?此时每天的销售量是多少个?2. 游泳作为一项健康的有氧运动,越来越受到人们的欢迎.某游泳馆的普通卡售价30元/张,寒假为了促销,新推出两种优惠卡:①金卡售价900元/张,每次凭卡不再收费.②银卡售价300元/张,每次凭卡另收10元.普通卡正常出售,两种优惠卡仅限寒假使用,不限次数.设游泳x次时,所需总费用为y元.(1)分别写出选择银卡、普通卡消费时,y与x之间的函数关系式;(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点B、C、D的坐标;(3)根据三种方案,请你写出经济实惠的选择方案.第2题图3. (2019温州)某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.(1)求该旅行团中成人与少年分别是多少人?(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩,景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.①若由成人8人和少年5人带队,则所需门票的总费用是多少元?②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.4. 某地甲、乙两家超市出售同样的保温壶和水杯,保温壶和水杯在两家超市的售价一样.已知购买1个保温壶和2个水杯要花费70元,购买2个保温壶和3个水杯要花费130元.(1)求一个保温壶与一个水杯售价各是多少元?(2)为了迎接“五一劳动节”,两家超市都在搞促销活动,甲超市规定:两种商品都打九折;乙超市规定:买一个保温壶赠送一个水杯.若某单位想要购买保温壶和水杯共120个,且购买保温壶不超过50个,如果只能在一家超市购买,请问选择哪家超市购买更实惠?请说明理由.5. 为了美化环境,建设宜居城市,某市准备在一个广场上种植甲、乙两种花卉.经市场调查,乙种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,甲种花卉的种植费用为每平方米100元.(1)直接写出当0≤x≤300和x>300时,y与x的函数关系式;(2)花卉种植面积为200 m2时,计算种植甲、乙两种花卉的费用;(3)广场上甲、乙两种花卉的种植面积共1200 m2,若乙种花卉的种植面积不少于200 m2,且不超过甲种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?第5题图6. 已知A、B两地相距2.4 km,甲骑车匀速从A地前往B地,如图表示甲骑车过程中离A地的路程y(km)与行驶所用的时间x(min)之间的关系.根据图象解答下列问题:(1)甲骑车的速度是________ km/min;(2)若在甲出发时,乙在甲前方0.6 km处,两人均沿同一路线同时出发匀速前往B地,在第3分钟甲追上了乙,两人到达B地后停止.①请在下面同一平面直角坐标系中画出乙离A地的距离y乙(km)与所用时间x(min)的关系的大致图象;②乙在第几分钟到达B地?③两人在整个行驶过程中,何时相距0.2 km?第6题图7. (2019武汉)某商店销售一种商品,经市场调查发现,该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价,周销售量,周销售利润w(元)的三组对应值如下表:注:周销售利润=周销售量×(售价-进价)(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);②该商品进价是________元/件;当售价是____元/件时,周销售利润最大,最大利润是________元;(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值.8. 某宾馆共有80间客房,现规定每间房的价格不低于60元且不超过180元,对于顾客所入住的房间,宾馆每天需支出20元的其他费用,每天顾客入住房间数y(间)与房间单价x(元)之间满足的函数关系如图所示.(1)求y与x之间的函数关系式;(2)若宾馆某天客房的营业额为4250元,则这天每间客房的价格是多少元?(3)房价定为多少元时,宾馆每天获利最大?最大利润是多少?第8题图9. 某经销商去批发市场买某种水果,已知这种水果的批发量在20千克~50千克之间(含20千克和50千克)时,每千克的批发价是5元;若超过50千克时,批发的这种水果全部打八折.(1)求当所付的金额为320元时,批发量是多少千克;(2)此种水果的日销售量y(千克)受零售价x(元/千克)的影响较大,为此该经销商试销一周获得如下数据:根据以上数据求y与x之间的函数关系式;(3)如果每天批发的水果能够全部销售完,且当日零售价不变,那么零售价定为多少时,该经销商销售这种水果的当日利润最大?最大日利润为多少元?此时进货量是多少?参考答案题型六函数的实际应用1. 解:(1)由题意得,w=(50+10x).(17-10-x)=-10x2+20x+350,∴w=-10x2+20x+350;(2)由(1)知w =-10x 2+20x +350=-10(x -1)2+360, 由于进价是10元/个,因此价格不能低于10元,故0<x <7, ∵-10<0,∴当x =1时,w 最大,最大值为360.∴此时售价为17-1=16(元/个),每天的销售量为50+10×1=60(个).答:每件玩具的售价定为16元时,商店每天获得的利润最大,最大利润是360元,此时每天的销售量是60个.2. 解:(1)银卡:y =300+10x , 普通卡:y =30x ; (2)金卡:y =900,由题意得:当300+10x =900时, 解得x =60,则y =900, 当300+10x =30x 时, 解得x =15,则y =450, 当30x =900时, 解得x =30,则y =900,∴点B ,C ,D 的坐标为(15,450),(60,900),(30,900); (3)如题图所示:由点B ,D ,C 的坐标可知:当0<x <15时,普通卡消费更划算;当x =15时,银卡、普通卡费用相同,均比金卡划算;当15<x <60时,银卡消费更划算;当x =60时,金卡、银卡费用相同,均比普通卡划算;当x >60时,金卡消费更划算.3. 解:(1)设该旅行团中成人x 人,少年y 人,根据题意,得⎩⎪⎨⎪⎧x +y +10=32x =y +12,解得⎩⎪⎨⎪⎧x =17y =5.答:该旅行团中成人17人,少年5人. (2)①∵成人8人可免费带8名儿童,∴所需门票的总费用为:100×8+100×0.8×5+100×0.6×(10-8)=1320(元); ②设可以安排成人a 人、少年b 人带队,则1≤a ≤17,1≤b ≤5. 当10≤a ≤17时,(ⅰ)当a =10时,100×10+100×0.8≤1200,∴b ≤52,∴b 最大值=2,此时a +b =12,费用为1160元; (ⅱ)当a =11时,100×11+100×0.8≤1200,∴b ≤54,∴b 最大值=1,此时a +b =12,费用为1180元;(ⅲ)当a ≥12时,100a ≥1200,即成人门票至少需要1200元,不合题意,舍去. 当1≤a <10时,(ⅰ)当a =9时,100×9+100×0.8+60≤1200,∴b ≤3, ∴b 最大值=3,此时a +b =12,费用为1200元;(ⅱ)当a =8时,100×8+100×0.8+2×60≤1200,∴b ≤72,∴b 最大值=3,此时a +b =11<12.不合题意,舍去; (ⅲ)同理,当a <8时,a +b <12,不合题意,舍去.综上所述,最多可以安排成人和少年共12人带队,有三个方案:成人10人,少年2人;成人11人,少年1人;成人9人,少年3人;其中当成人10人,少年2人时购票费用最少.4. 解:(1)设一个保温壶售价是a 元,一个水杯售价是b 元,根据题意得⎩⎪⎨⎪⎧a +2b =702a +3b =130,解得⎩⎪⎨⎪⎧a =50b =10,答:一个保温壶售价是50元,一个水杯售价是10元; (2)设购买x 个保温壶(0<x ≤50),付款金额为W 元, 甲超市:W 甲=0.9[50x +10(120-x )]=36x +1080, 乙超市:W 乙=50x +10(120-2x )=30x +1200, 当36x +1080=30x +1200时,解得x =20,∴当x <20时,W 甲<W 乙,当20<x ≤50 时,W 甲>W 乙, ∴当购买保温壶少于20个时,选择甲超市更实惠; 当购买保温壶等于20个时,两个超市优惠活动效果相同; 当购买保温壶多于20个而不超过50个时,选择乙超市更实惠.5. 解:(1)y =⎩⎪⎨⎪⎧130x (0≤x ≤300)80x +15000(x >300);(2)种植甲种花卉的费用为:200×100=20000元;种植乙种花卉的费用为200×130=26000元; 答:种植甲种花卉的费用为20000元,种植乙种花卉的费用为26000元;(3)设总费用为W 元,乙种花卉种植面积为a m 2,则甲种花卉种植面积为(1200-a ) m 2;依题意得:200≤a ≤2(1200-a ),即200≤a ≤800,当200≤a ≤300时,W =130a +100(1200-a )=30a +120000; 故当a =200时,W min =126000, 当300<a ≤800时,W =80a +15000+100(1200-a )=-20a +135000; 故当a =800时,W min =119000. ∵119000<126000, ∴当a =800时总费用最少.答:当甲种花卉种植面积为400 m 2,乙种花卉种植面积为800 m 2时,种植总费用最少,最少总费用为119000元.6. 解:(1)0.4;【解法提示】根据图象可知,甲骑行2.4 km 用了6 min ,∴速度是2.4÷6=0.4 km /min .(2)画出图象如解图;第6题解图(3)设甲的函数的表达式为y 甲=kx (k ≠0),把x =6,y =2.4代入求得k =0.4,故函数表达式为y 甲=0.4x ,把x =3代入y =0.4x ,得y =1.2,设乙的函数表达式为y 乙=k ′x +b (k ′≠0),把x =0,y =0.6;x =3,y =1.2.代入得⎩⎪⎨⎪⎧b =0.6,3k ′+b =1.2,解得⎩⎪⎨⎪⎧k ′=0.2,b =0.6. 故函数表达式为y 乙=0.2x +0.6,把y =2.4代入y 乙=0.2x +0.6得x =9,∴乙在第9分钟到达B 地;(4)分为以下三种情况:①相遇前是y 乙-y 甲=0.2,即0.2x +0.6-0.4x =0.2,解得x =2,∴在第2分钟两人相距0.2 km ;②相遇后是y 甲-y 乙=0.2,即0.4x -(0.2x +0.6)=0.2,解得x =4,∴在第4分钟两人相距0.2 km ;③∵乙在甲前方0.6 km 处出发,且甲先到,故在y =2.2 km 处时,甲乙相距0.2 km ,把y =2.2代入y 乙=0.2x +0.6得x =8,∴第8分钟时两人相距0.2 km .综上所述,当两人在整个行驶过程中相距0.2 km 时,时间为2分钟或4分钟或8分钟.7. 解:(1)①设y =kx +b ,将x =50,y =100;x =60,y =80代入上式解得k =-2,b =200,故y =-2x +200;②40,70,1800;【解法提示】进价=50-1000÷100=40,利润w =(-2x +200)×(x -40)=-2x 2+280x -8000=-2(x -70)2+1800,∴当售价为70元/件时,最大利润w max =1800 元.(2)由题意可知w =(-2x +200)×(x -40-m )=-2x 2+(280+2m )x -8000-200m ,对称轴为x =140+m 2, ∵m >0,∴140+m 2>70>65, ∴当x =65时,w 取最大值1400,即(-2×65+200)×(65-40-m )=1400,解得m =5.8. 解:(1)设y 与x 之间的函数关系式为y =kx +b (k ≠0),将(70,75)、(80,70)代入得⎩⎪⎨⎪⎧70k +b =75,80k +b =70,解得⎩⎪⎨⎪⎧k =-0.5,b =110. 即y 与x 之间的函数关系式是y =-0.5x +110;(2)设宾馆每天客房的营业额为z ,则z =x (-0.5x +110)=-0.5x 2+110x ,将z =4250代入,得4250=-0.5x 2+110x ,解得x 1=170,x 2=50(舍),答:这天每间客房的价格是170元;(3)设宾馆每天获得的利润为w 元,w =(x -20)(-0.5x +110)=-0.5x 2+120x -2200=-0.5(x -120)2+5000,∵-0.5<0,60≤x ≤180,∴当x =120时,w 取得最大值,此时w =5000.答:房价定为120元时,宾馆每天获利最大,最大利润是5000元.9. 解:(1)∵50×5=250<320,∴当所付的金额为320元时,批发量超过50千克.设此时的批发量为z 千克,根据题意可得5×0.8z =320,解得z =80.∴当所付的金额为320元时,批发量是80千克;(2)由表格数据可知,y 与x 之间满足一次函数关系,设y =kx +b ,将点(5,90)、(6,60)代入,得⎩⎪⎨⎪⎧5k +b =90,6k +b =60,解得⎩⎪⎨⎪⎧k =-30,b =240, ∴y =-30x +240.∴y 与x 之间的函数关系式为y =-30x +240;(3)①当日销售量y 满足20≤y ≤50时,设日利润为W 1,则W 1=(x -5)·y =(x -5)(-30x +240)=-30x 2+390x -1200=-30(x -6.5)2+67.5(193≤x ≤223). ∴当x =6.5时,W 1最大,最大值为67.5,此时y =45;②当日销售量y 满足y >50时,设日利润为W 2,则W 2=(x -5×0.8)·y =(x -4)(-30x +240)=-30x 2+360x -960=-30(x -6)2+120(4<x <193). ∴当x =6时,W 2最大,最大值为120,此时y =60.∵67.5<120,∴当零售价定为6元/千克时,该经销商销售这种水果的当日利润最大,最大日利润为120元,此时进货量为60千克.。
数轴动点问题6题型

数轴动点问题6题型数轴动点问题是高中数学中常见的一类问题,主要涉及到点在数轴上运动的情况。
在解决这类问题时,可以利用数轴上的点的坐标与距离的关系,来求解点的位置、速度等信息。
本文将介绍数轴动点问题的6个典型题型,并通过解题步骤和例题来帮助读者更好地理解和掌握这类问题的解题方法。
题型一:根据速度求坐标如果一个点在数轴上以一定的速度运动,我们可以通过根据速度求坐标的方法来求解点的位置。
这个问题通常会给出点的初始位置和速度,要求我们求解点在某个给定的时间后的位置。
解决这类问题时,我们可以使用速度乘以时间的公式,即坐标 = 初始位置 + 速度 * 时间。
举例来说,假设一个点在数轴上初始位置为3,速度为2,我们需要求解它在10秒后的位置。
根据公式,我们可以得到坐标 = 3 + 2 * 10 = 23。
因此,在经过10秒后,点的位置为23。
题型二:根据坐标求速度与题型一相反,如果我们已知一个点在数轴上的初始位置和结束位置,并且需要求解点的速度,我们可以使用根据坐标求速度的方法。
解决这类问题时,我们可以使用坐标之差除以时间的公式,即速度 = (结束位置 - 初始位置) / 时间。
举例来说,假设一个点在数轴上初始位置为5,结束位置为25,并且经过10秒后到达结束位置。
我们可以使用公式速度 = (25 - 5) / 10 = 2来求解点的速度。
因此,这个点的速度为2。
题型三:两点相遇问题在数轴上,如果有两个点A和B,它们同时从不同的位置出发,以不同的速度运动,我们常常会遇到两点相遇的问题。
解决这类问题时,我们可以使用等速度的思想,通过设置一个相对速度来求解两点相遇的时间和位置。
举例来说,假设点A从位置1出发,速度为3,点B从位置9出发,速度为1,我们需要知道它们第一次相遇的时间和位置。
我们可以设置点A和点B的相对速度为3 - 1 = 2,根据题目描述,相对速度不变。
因此,这个问题可以转化为一个点以相对速度2运动的问题,我们可以使用速度乘以时间的公式,即坐标 = 初始位置 + 速度 * 时间,来求解它们的相遇时间和位置。
数轴动点问题6题型

数轴动点问题6题型数轴动点问题是数学中常见的问题之一,通过给定的条件,我们需要确定数轴上的某个点在未来的某个时刻的位置。
数轴动点问题可以分为六个不同的题型,包括直线匀速运动、自由落体运动、匀加速直线运动、正弦运动、周期性运动和复合运动。
一、直线匀速运动直线匀速运动是最简单的一个题型,其特点是物体在数轴上做匀速运动,即运动速度保持恒定。
在这种情况下,我们可以通过已知物体的初始位置和速度,以及经过的时间来确定物体在某个时刻的位置。
例如,已知小明从A点出发,以每小时30公里的速度向B点行进,经过2小时后,我们需要确定小明在这个时刻的位置。
解题思路如下:设小明从A点出发,以每小时30公里的速度向B点行进,经过2小时后小明行驶的距离为x公里。
根据速度的定义,速度等于位移与时间的比值,即速度=位移/时间。
因为小明的速度是恒定的,所以我们可以得到以下等式:30km/h = x km/2 h将等式化简,得到:x = 60 km因此,在经过2小时后,小明的位置在B点的60公里处。
二、自由落体运动自由落体运动是物体在重力作用下做垂直向下的运动。
在这种情况下,物体的初速度通常为0,所以我们只需考虑物体下落的距离和经过的时间。
例如,已知一个物体从高处下落,2秒后触地,我们需要确定物体下落的高度。
解题思路如下:设物体下落的高度为h米。
根据自由落体运动的公式:h = (1/2) * g * t^2其中,g为重力加速度,取9.8米/秒^2,t为时间,取2秒。
将这些数值代入公式中,我们可以计算出物体下落的高度:h = (1/2) * 9.8 * 2^2 = 19.6米因此,物体下落的高度为19.6米。
三、匀加速直线运动匀加速直线运动是物体在数轴上做匀加速运动,即运动的加速度保持恒定。
在这种情况下,我们需要根据已知的初始速度、加速度和时间来确定物体在某个时刻的位置。
例如,已知小车以每小时20公里的速度匀速行驶,并在10秒内加速到每小时60公里的速度,我们需要确定小车在这个时刻的位置。
高校行政结构化面试6大题型万能套话

高校行政结构化面试6大题型万能套话- 序:介绍主题,概述高校行政结构化面试的重要性和挑战性。
1. 题型1:自我介绍- 详细介绍高校行政结构化面试中常见的自我介绍题型,如何准备自我介绍,以及应该包括哪些内容。
- 重点强调自我介绍时要突出与高校行政工作相关的经验和技能。
2. 题型2:问答环节- 分析高校行政结构化面试中常见的问答环节,提及如何回答常见问题以展现自己的能力。
- 强调要注意语言表达和自信心,同时要展现对高校行政工作的热情和了解。
3. 题型3:案例分析- 探讨高校行政结构化面试中的案例分析题型,如何应对需要分析解决问题的情景。
- 强调要有逻辑性和条理性,同时结合个人经验和专业知识给出解决方案。
4. 题型4:领导力挑战- 分析高校行政结构化面试中可能出现的领导力挑战题型,如何展现自己的领导能力和应对挑战的能力。
- 强调要展现自己的决策能力、团队合作能力和解决问题的能力。
5. 题型5:未来规划- 探讨高校行政结构化面试中关于未来规划的题型,如何表达自己的发展规划和对高校行政工作的期待。
- 强调要展现自己的目标和抱负,同时与高校行政工作的发展紧密结合。
6. 题型6:个人素质评价- 分析高校行政结构化面试中的个人素质评价题型,如何展示自己的个人素质和特点。
- 强调要真实展现自己的优点和特长,同时要展现自己的成长态度和学习能力。
- 总结回顾:总结高校行政结构化面试的重要性,回顾每个题型的重点和应对方法,强调全面准备的重要性。
个人观点和理解:在我看来,高校行政结构化面试不仅是对个人能力的考察,更是对应聘者综合素质和适应性的考量。
在准备面试时,要做到充分了解高校行政工作的特点和要求,同时做到真实展现自己的能力和潜力。
只有全面准备,才能在面试中展现出自信、自信和能力,从而赢得面试官的青睐。
希望每一位应聘者都能在高校行政结构化面试中取得理想的成绩!(文章内容综述,深入浅出的解释了高校行政结构化面试的主要题型和准备方法,内容充实、丰富,思路清晰,言之有物。
题型六-新定义阅读理解题

题型六新定义阅读理解题1. (2016重庆B卷)我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=pq.例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所以3×4是12的最佳分解,所以F(12)=3 4.(1)如果一个正整数a是另外—个正整数b的平方,我们称正整数a是完全平方数.求证:对任意一个完全平方数m,总有F(m)=1;(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y是自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18.那么我们称这个数t为“吉祥数”.求所有“吉祥数”中F(t)的最大值.2. (2017重庆A卷)对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123.对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213 +321+132 =666,666÷111=6,所以,F(123) =6.(1)计算:F(243),F(617);(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=F(s)F(t).当F(s)+F(t)=18时,求k的最大值.3. (2015重庆A卷)如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数称为“和谐数”.例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,因此12321是一个“和谐数”.再如22,545,3883 ,345543,…,都是“和谐数”.(1)请你直接写出3个四位“和谐数”;请你猜想任意一个四位“和谐数”能否被11整除?并说明理由;(2)已知一个能被11整除的三位“和谐数”,设其个位上的数字为x(1≤x≤4,x 为自然数),十位上的数字为y,求y与x的函数关系式.4. (2017张家界)阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部.它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2-i)+(5+3i)=(2+5)+(-1+3)i=7+2i;(1+i)×(2-i)=1×2-i+2×i-i2=2+(-1+2)i+1=3+i;根据以上信息,完成下列问题:(1)填空:i3=________,i4=________;(2)计算:(1+i)×(3-4i);(3)计算:i+i2+i3+ (i2017)5. (2018原创)若整数m是8的倍数,那么称整数m为“发达数”.例如,因为16是8的倍数,所以16是“发达数”.(1)已知整数m等于某个奇数的平方减1,求证:m是“发达数”.(2)已知两位正整数t=10x+y(1≤x≤y≤9,其中x,y为自然数),交换其个位上的数字和十位上的数字得到新数s,如果s加上t的和是“发达数”,求所有符合条件的两位正整数t.6. (2017重庆南开模拟)若将自然数中能被3整除的数,在数轴上的对应点称为“3倍点”,取任意的一个“3倍点”P,到点P距离为1的点所对应的数分别记为a,b.定义:若数K=a2+b2-ab,则称数K为“尼尔数”.例如:若P所表示的数为3,则a=2,b=4,那么K=22+42-2×4=12;若P所表示的数为12,则a =11,b=13,那么K=132+112-13×11=147,所以12,147是“尼尔数”.(1)请直接判断6和39是不是“尼尔数”,并且证明所有“尼尔数”一定被9除余3;(2)已知两个“尼尔数”的差是189,求这两个“尼尔数”.7. (2017重庆一外一模)若一个三位数t=abc(其中a,b,c不全相等且都不为0),重新排列各数位上的数字必可得到一个最大数和一个最小数,此最大数和最小数的差叫作原数的差数,记为T(t).例如,357的差数T(357)=753-357=396. (1)已知一个三位数a1b(其中a>b>1)的差数T(a1b)=792,且各数位上的数字之和为一个完全平方数,求这个三位数.(2)若一个三位数ab2(其中a、b都不为0)能被4整除,将个位上的数字移到百位得到一个新数2ab被4除余1,再将新数的个位数字移到百位得到另一个新数b2a 被4除余2,则称原数为4的“闺蜜数”.例如:因为612=4×153,261=4×65+1,126=4×31+2,所以612是4的一个闺蜜数.求所有小于500的4的“闺蜜数”t,并求T(t)的最大值.8. (2017重庆八中一模)一个三位正整数M,其各位数字均不为零且互不相等,若将M的十位数字与百位数字交换位置,得到一个新的三位数,我们称这个三位数为M的“友谊数”,如:168的“友谊数”为“618”;若从M的百位数字、十位数字、个位数字中任选两个组成一个新的两位数,并将得到的所有两位数求和,我们称这个和为M的“团结数”,如:123的“团结数”为12+13+21+23+31+32=132.(1)求证:M与其“友谊数”的差能被15整除;(2)若一个三位正整数N,其百位数字为2,十位数字为a、个位数字为b,且各位数字互不相等(a≠0, b≠0).若N的“团结数”与N之差为24,求N的值.9. (2017重庆大渡口区模拟)我们知道:一个整数的个位数是偶数,则它一定能被2整除;一个整数的各位数字之和能被3整除,则它一定能被3整除.若一个整数既能被2整除又能被3整除,那么这个整数一定能被6整除.数字6象征顺利、吉祥,我们规定,能被6整除的四位正整数abcd(千位数字为a,百位数字为b,十位数字为c,个位数字为d)是“吉祥数”.请解答下面几个问题:(1)已知785x是“吉祥数”,则x=________.(2)若正整数abcd是“吉祥数”,试说明:d+4(a+b+c)能被2整除.(3)小明完成第(2)问后认为:四位正整数abcd是“吉祥数”,那么d+4(a+b+c)也能被6整除.你认为他说得对吗?请说明理由.10. —个正整数,由N个数字组成,若它的第一位数可以被1整除,它的前两位数可以被2整除,前三位数可以被3整除,…,一直到前N位数可以被N整除,则这样的数叫做“精巧数”.如:123的第—位“1”可以被1整除,前两位数“12”可以被2整除,“123”可以被3整除,则123是一个“精巧数”.(1)若四位数123k是一个“精巧数”,求k的值;(2)若一个三位“精巧数”2ab各位数字之和为—个完全平方数,请求出所有满足条件的三位“精巧数”.11. (2017重庆巴蜀模拟)阅读材料:欢喜数——若一个四位数的前2位数是后2位数的2倍,则称该数为“欢喜数”,如1005、2211等都是欢喜数;半和数——一个数,若各个数位上的数字之和等于十位上的数字的2倍,则称该数为“半和数”,如132等都是半和数;平方差数——一个三位数字,若十位上数字等于百位数字与个位数字的平方差,则称该数为“平方差数”.根据上面的材料,回答下列问题:(1)证明所有的三位“半和数”均能被11整除;(2)若一个四位正整数abbc是欢喜数,bmc既是半和数又是平方差数,求m的值.12. 一个三位自然数m,将它任意两个数位上的数字对调后得一个首位不为0的新三位自然数m′(m′可以与m相同),记m′=abc,在m′所有的可能情况中,当|a +2b-c|最小时,我们称此时的m′是m的“幸福美满数”,并规定K(m)=a2+2b2-c2.例如:318按上述方法可得新数有:381、813、138;因为|3+2×8-1|=18,|8+2×1-3|=7,|1+2×3-8|=1,1<7<18,所以138是318的“幸福美满数”,K(318)=12+2×32-82=-45.(1)若三位自然数t的百位上的数字与十位上的数字都为n(1≤n≤9,n为自然数),个位上的数字为0,求证:K(t)=0;(2)设三位自然数s=100+10x+y(1≤x≤9,1≤y≤9,x,y为自然数),且x<y.交换其个位与十位上的数字得到新数s′,若19s+8s′=3888,那么我们称s为“梦想成真数”,求所有“梦想成真数”中K(s)的最大值.13. (2018原创)如果一个自然数从高位到个位是由一个数字或几个数字重复出现组成,那么我们把这样的自然数叫循环数,被重复的一个或几个数字称为“循环节”,我们把“循环节”的数字个数叫做循环数的阶数,例如:252525,它由“25”依次重复出现组成,所以252525是循环数.它是2阶6位循环数;再如:11是1阶2位循环数,789789789是3阶9位循环数,345634563456是4阶12位循环数….(1)请你直接写出3个2阶6位循环数,猜想任意一个2阶6位循环数能否被7整除,并说明理由;(2)已知一个能被13整除的2阶4位循环数,设循环节为xy,(0<x<5),求y与x 之间的函数关系.14. (2018原创)若一个三位数,其个位数加上十位数等于百位数,可表示为t=100(x +y)+10y+x,则称实数t为“加成数”.将t的百位作为个位,个位作为十位,十位作为百位,组成一个新的三位数h,规定q=t-h,f(m)=q9.例如:321是一个“加成数”,将其百位作为个位,个位作为十位,十位作为百位,得到的数h=213,∴q=321-213=108,f(m)=1089=12.(1)当f(m)最小时,求此时对应的“加成数”t的值;(2)若f(m)是24的倍数,则称f(m)是“节气数”,猜想这样的“节气数”有多少个,并求出所有的“节气数”.15. (2017重庆渝中区校级二模)对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数abc(a≤c),在所有重新排列的三位数中,当|a+c-2b|最小时,称此时的abc为t的“最优组合”,并规定F(t)=|a-b|-|b -c|,例如:124重新排序后为:142、214,因为|1+4-4|=1,|1+2-8|=5,|2+4-2|=4,所以124为124的“最优组合”,此时F(124)=-1.(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能被1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值.16. (2018原创)如果两个实数a ,b ,使得a 2+b 与a +b 2都是有理数,我们则称(a ,b )是“完美数对”.如:(12)2+13=14+13=712,12+(13)2=12+19=1118,因为712,1118是有理数,所以(12,13)是“完美数对”;(2)2+1=3,2+12=1+2,因为1+2为无理数,所以(2,1)不是“完美数对”.(1)请判断(12+2,12-2)是否是“完美数对”,并说明理由;(2)若(a ,b )是“完美数对”,且a +b =2,证明:a ,b 都是有理数.17. 1742年6月7日,德国数学家哥德巴赫在写给著名数学家欧拉的一封信中,提出了两个大胆的猜想,其中的“任何不小于7的奇数,都可以表示为三个质数之和”称为“弱哥德巴赫猜想”,并已经得到了成功的证明.根据“弱哥德巴赫猜想”,任意一个不小于7的奇数m,都可以进行这样的拆分:m=a+b+c(a、b、c均为质数,且a≥b≥c),在m的所有这种拆分中,如果a、c两数之差a-c最小,我们就称a+b+c是m的最优拆分.并规定:P(m)=a-c.例如9可以分解成2+2+5,3+3+3,因为5-2>3-3,所以3+3+3是9的最优拆分,且P(9)=0.(1)由上述条件,可得:P(11)=________;若P(n)=1,则n=________;若P(n)=0,证明n必定能被3整除;(2)t是一个两位正整数,且t的十位数字、个位数字分别为x、y(1≤x≤y≤9,x、y为整数).若t的十位数字、个位数字和的8倍加上t所得的和为99,则我们称这个数t为“期盼数”,求所有“期盼数”中P(t)的最大值.18. 对于一个大于100的整数,若将它的后两位之前的数移到个位之后,重新得到一个新数,称之为原数的“兄弟数”. 比如:2017的兄弟数为1720, 168的兄弟数为681.根据以上阅读材料,回答下列问题.(1)求证:—个三位数与其兄弟数之差一定能被9整除;(2)已知一个六位数的兄弟数恰好是原六位数的4倍,求满足条件的原六位数.19. (2017重庆南开模拟)一个自然数m,若将其数字重新排列可得—个新的自然数n,如果m=3n,我们称m是一个“希望数”,例如:3105=3×1035,71253=3×23751,371250=3×123750.(1)请说明41不是希望数,并证明任意两位数都不可能是“希望数”;(2)一个四位“希望数”M记为abcd,已知abcd=3·cbad,且c=2,请求出这个四位“希望数”.20. (2017重庆西大附中月考)一个三位正整数N,各个数位上的数字互不相同且都不为0,若从它的百位、十位、个位上的数字任意选择两个数字组成两位数,所有这些两位数的和等于这个三位数本身,则称这样的三位数N为“公主数”.例如:132,选择百位数字1和十位效字3所组成的两位数为:13和31,选择百位数字1和个位数字2所组成的两位数为:12和21,选择十位数字3和个位数字2所组成的两位数为:32和23,因为13+31+12+21+32+23=132,所以132是“公主数”.—个三位正整数,若它的十位数字等于百位数字与个位数字的和,则称这样的三位数为“伯伯数”.(1)判断123是不是“公主数”?请说明理由.(2)证明:当一个“伯伯数”xyz是“公主数”时,则z=2x.(3)若一个“伯伯数”与132的和能被13整除,求满足条件的所有“伯伯数”.21. (2018原创)若实数a 可以表示成两个连续自然数的倒数差,即a =1n -1n +1,那么我们称a 为第n 个“1阶倒差数”,例如12=1-12,∴12是第1个“1阶倒差数”,16=12-13,∴16是第2个“1阶倒差数”.同理,若b =1n -1n +2,那么,我们称b 为第n 个“2阶倒差数”.(1)判断132是否为“1阶倒差数”;直接写出第5个“2阶倒差数”;(2)若c ,d 均是由两个连续奇数组成的“2阶倒差数”,且1d -1c =22,求c ,d 的值.22. (2017重庆八中二模)若在一个两位正整数N 的个位数字与十位数字之间添上数字2,组成一个新的三位数,我们称这个三位数为N 的“诚勤数”,如34的“诚勤数”为324;若将—个两位正整数M 加2后得到一个新数,我们称这个新数为M 的“立达数”,如34的“立达数”为36.(1)求证:对任意一个两位正整数A ,其“诚勤数”与”立达数”之差能被6整除;(2)若一个两位正整数B 的“立达数”的各位数字之和是B 的各位数字之和的一半,求B 的值.23. (2017重庆南岸区二模)若一个两位正整数m 的个位数为8,则称m 为“好数”.(1)求证:对任意“好数”m ,m 2-64一定为20的倍数;(2)若m=p2-q2,且p,q为正整数,则称数对(p,q)为“友好数对”.规定:H(m)=qp.例如68=182-162,称数对(18,16)为“友好数对”,则H(68)=1618=89.求小于50的“好数”中,所有“友好数对”的H(m)的最大值.24. (2018原创)定义,对于一个多位自然数a,若其从左向右各个数位上的数恰好是前一数位数字加1,我们称自然数a是“格调数”.例如,12,123,1234等都是“格调数”.根据数的特点,我们可以发现,最小的“格调数”是12,最大的“格调数”是123456789.而如果一个“格调数”有七位时,第一位上的数字最大只能是3,这样的“格调数”是3456789.(1)已知四位“格调数”m和n,若m-n=3333,求m的值;(2)规定:任意一个能被18整除的数,称为“发财数”.对于任意一个三位“格调数”t=100a+10(a+1)+(a+2),交换其个位和百位上的数字,得到新的三位数k,令q=k-t,猜想q是否为“发财数”,请说明理由.25. (2017重庆一中一模)人和人之间讲友情,有趣的是,数与数之间也有相类似的关系,若两个不同的自然数的所有真因数(即除了自身以外的正因数)之和相等,我们称这两个数为“亲和数”.例如:18的正因数有1、2、3、6、9、18,它的真因数之和为1+2+3+6+9=21;51的正因数有1、3、17、51,它的真因数之和为1+3+17=21,所以称18和51为“亲和数”.数还可以与动物形象地联系起来,我们称一个两头(首位与末位)都是1的数为“两头蛇数”.例如:121、1351等.(1)8的真因数之和为________;求证:一个四位的“两头蛇数”与它去掉两头后得到的两位数的3倍的差,能被7整除;(2)一个百位上的数为4的五位“两头蛇数”能被16的“亲和数”整除,若这个五位“两头蛇数”的千位上的数字小于十位上的数字,求满足条件的五位“两头蛇数”.26. (2018原创)依次排列的几个数,如:a,b,c,…,对任意相邻的两个数,都用右边的数减去左边的数,并将所得的差写在这两个数之间,从而产生一个新数串:a,b-a,b,c-b,c,…,我们称这样的一次操作为“差变增数列”.例如,对于依次排列的两个数,1,2,做一次“差变增数列”所得数串为1,1,2;再做一次“差变增数列”所得数串为1,0,1,1,2.(1)已知依次排列的3个数:2,8,7,做一次“差变增数列”,所得新数串所有数字的和是________;做m次“差变增数列”后,所得新数串所有数字的和为________(用含m的代数式表示);(2)若依次排列的3个数:x,8,y;其中,0≤x<y≤9,且x,y均为整数,做100次“差变增数列”后所得数串的所有数字和为216,求x和y的值.27. (2017重庆江北区一模)一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和平数”.例如:1423,x=1+4,y=2+3,因为x=y,所以1423是“和平数”.(1)直接写出:最小的“和平数”是________,最大的“和平数”是________;(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”;(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后的这两个“和平数”为一组“相关和平数”.例如:1423与4132为一组“相关和平数”.求证:任意的一组“相关和平数”之和是1111的倍数.28. (2017重庆南岸区一模)对任意一个正整数m,如果m=k(k+1),其中k是正整数,则称m为“矩数”,k为m的最佳拆分点.例如,56=7×(7+1),则56是一个“矩数”,7为56的最佳拆分点.(1)求证:若“矩数”m是3的倍数,则m一定是6的倍数;(2)把“矩数”p与“矩数”q的差记为D(p,q),其中p>q,D(p,q)>0.例如,20=4×5,6=2×3,则D(20,6)=20-6=14.若“矩数”P的最佳拆分点为t,“矩数”q的最佳拆分点为s,当D(p,q)=30时,求st的最大值.29. (2017重庆一外二模)若一个多位自然数t=abc…fg的各数位上的数字满足b-a=c-b=…=g-f=k(k≠0),则称该数为“k”类自然数,把自然数t各数位上的数字从左往右数,所有奇数位上的数字之和的平方减去所有偶数位上的数字之和的平方,记为F(t).例如:135是一个“2”类自然数.F(135)=(1+5)2-32=274321是一个“-1”类自然数.F(4321)=(4+2)2-(3+1)2=20(1)证明:任意一个三位“k”类自然数与它百位上的数字之和一定能被4整除;(2)如果—个四位自然数,交换其个位数字与千位数字得到的新数减去原数所得的差能够被18整除,则称这个数为“成年数”.若一个“k”类自然数t是“成年数”,求F(t)的最小值.30. 阅读下列材料解决问题:两个多位正整数,若它们各数位上的数字和相等,则称这两个多位数互为“调和数”.例如:37与82,它们各数位上的数字和分别为3+7,8+2,∵3+7=8+2=10,∴37与82互为“调和数”;又如:123与51,它们各数位上的数字和分别为1+2+3,5+1,∵1+2+3=5+1=6,∴123与51互为“调和数”.(1)若两个三位数a43、2bc(0≤b≤a≤9,0≤c≤9且a、b、c为整数)互为“调和数”,且这两个三位数之和是17的倍数,求这两个“调和数”;(2)若A、B是两个不相等的两位数,A=xy,B=mn,A、B互为“调和数”,且A 与B之和是B与A之差的3倍,求证:y=-x+9.答案1. (1)证明:∵m是一个完全平方数,∴m=p×q,当q=p时,p·q就是m的最佳分解,∴F(m)=pq=pp=1;(2)解:由题意得,(10y+x)-(10x+y)=18,得y=x+2,∴t=10x+y=10x+x+2=11x+2(1≤x≤7),则所有的吉祥数为:13,24,35,46,57,68,79共7个,∵13=1×13,24=1×24=2×12=3×8=4×6,35=1×35=5×7,46=1×46=2×23,57=1×57=3×19,68=1×68=2×34=4×17,79=1×79,则F(13)=113,F(24)=23,F(35)=57,F(46)=223,F(57)=319,F(68)=417,F(79)=179,∵57>23>417>319>223>113>179,∴“吉祥数”中F (t )的最大值为F (35)=57.2. 解:(1)F (243)=(423+342+234)÷111=9,F (617)=(167+716+671)÷111=14;(2)∵s ,t 都是相异数.∴F (s )=(302+10x +230+x +100x +23)÷111=x +5,F (t )=(510+y +100y +51+105+10y )÷111=y +6,∵F (s )+F (t )=18,∴x +5+y +6=x +y +11=18,∴x +y =7,∵1≤x ≤9,1≤y ≤9,且x ,y 都是正整数.∴⎩⎨⎧x =1y =6或⎩⎨⎧x =2y =5或⎩⎨⎧x =3y =4或⎩⎨⎧x =4y =3或⎩⎨⎧x =5y =2或⎩⎨⎧x =6y =1,∵s 是相异数,∴x ≠2,x ≠3,∵t 是相异数,∴y ≠1,y ≠5,∴满足条件的有⎩⎨⎧x =1y =6或⎩⎨⎧x =4y =3或⎩⎨⎧x =5y =2,∴⎩⎨⎧F (s )=6F (t )=12或⎩⎨⎧F (s )=9F (t )=9或⎩⎨⎧F (s )=10F (t )=8, ∴k =F (s )F (t )=612=12或k =F (s )F (t )=99=1或k =F (s )F (t )=108=54, ∵12<1<54,∴k 的最大值为54.3. 解:(1)1331,2442,1001;猜想:任意一个四位“和谐数”能被11整除.理由:设一个四位“和谐数”记为xyyx ,用十进制表示为: 1000x +100y +10y +x =1001x +110y =11(91x +10y ), ∵x 、y 是0~9之间的整数,∴11(91x +10y )能被11整除;∴任意一个四位“和谐数”能被11整除;(2)设这个三位的“和谐数”为xyx ,用十进制表示为: 100x +10y +x =101x +10y ,∵它是11的倍数,∴101x +10y 11为整数,∵101x +10y 11=99x +11y +2x -y 11=9x +y +2x -y 11,x ,y 是0~9之间的整数,∴2x -y 11是整数.又∵1≤x ≤4,0≤y ≤9,∴2≤2x ≤8,-9≤-y ≤0,∴-7≤2x -y ≤8,∵要使2x -y 11是整数,则2x -y 只能是0,∴2x -y =0,即y =2x ,∴y 与x 之间的函数关系式是y =2x (1≤x ≤4,x 为自然数).4. 解:(1)-i ;1;【解法提示】∵i 2=-1,∴i 3=i 2·i =-i ,i 4=i 2·i 2=(-1)×(-1)=1.(2)原式=3-4i +3i -4i 2=3-i +4=7-i ;(3)根据题意可得i =i ,i 2=-1,i 3=-i ,i 4=1,i 5=i ,i 6=-1,…,i 2016=1,i 2017=i ,∵i+i2+i3+i4=0,2016÷4=504,∴i+i2+i3+i4+…+i2017=i2017=i.5.解:(1)设这个奇数为2n+1,n为任意整数,由题意知m=(2n+1)2-1=4n2+4n+1-1=4n(n+1),4n(n+1)8=n(n+1)2,是整数,即4n(n+1)是8的倍数,∴m是“发达数”;(2)由题意知s=10y+x,∴s+t=10y+x+10x+y=11x+11y=11(x+y),又∵1≤x≤y≤9,∴2≤x+y≤18,要使11(x+y)是发达数,则x+y是发达数,∴x+y=8或x+y=16,当x+y=8时,x=1,y=7,t=17,x=2,y=6,t=26,x=3,y=5,t=35,x=4,y=4,t=44,当x+y=16时,x=7,y=9,t=79,x =8,y =8,t =88,故所有符合条件的两位正整数t 有17,26,35,44,79,88.6. 解:(1)6不是尼尔数,39是尼尔数.证明:设P 表示的数为3m ,则a =(3m -1),b =(3m +1),K =(3m -1)2+(3m +1)2-(3m -1)(3m +1)=9m 2+3,∵m 为整数,∴m 2为整数,∴9m 2+3被9除余3;(2)设这两个尼尔数分别是K 1,K 2,将P 1,P 2分别记为3m 1,3m 2.∴K 1-K 2=9m 12-9m 22=189,∴m 12-m 22=21,∵m 1,m 2都是整数,∴m 1+m 2=7,m 1-m 2=3,∴⎩⎨⎧m 1=5m 2=2, ∴⎩⎨⎧K 1=228K 2=39. 7. 解:(1)∵一个三位数a 1b (其中a >b >1)的差数T (a 1b )=792,∴a =9,∵三位数a1b(其中a>b>1)的各数位上的数字之和为一个完全平方数,∴1+a+b=n2,10<1+a+b≤19,∴n=4,∴b=16-9-1=6,∴这个三位数是916;(2)∵一个三位数ab2(其中a、b都不为0)能被4整除,∴b=1或3或5或7或9,∵将新数个位数字移到百位得到另一个新数b2a被4除余2并且a<5,∴a=2,∴所有小于500的4的“闺蜜数”t是212,232,252,272,292,T(t)的最大值是922-229=693.8. (1)证明:设M=xyz(x≠y≠z≠0),则M的友谊数是yxz,∴xyz-yxz=(100x+10y+z)-(100y+10x+z)=90x-90y=90(x-y)=15×6(x -y),∵6(x-y)是整数,∴xyz-yxz能被15整除.故M与其“友谊数”的差能被15整除;(2)解:由团结数定义可知,N 的团结数为:(20+a )+(20+b )+(10a +2)+(10a +b )+(10b +2)+(10b +a )=22a +22b +44,∵N 的团结数与N 之差为24,∴(22a +22b +44)-(200+10a +b )=24,即a =15-74b ,∵a 、b 为整数,1≤a ≤9,1≤b ≤9,a ≠b ,∴⎩⎨⎧a =8b =4或⎩⎨⎧a =1b =8, ∴N =284或218.9. 解:(1)4;(2)∵正整数abcd 能被6整除,∴d 能被2整除.设d =2k ( k 为自然数),则d +4(a +b +c )=2k +4(a +b +c )=2[k +2(a +b +c )].∴d +4(a +b +c )能被2整除;(3)小明的说法正确.理由如下:∵四位正整数abcd能被6整除,∴a+b+c+d能被3整除.设a+b+c+d=3m(m为自然数),则d+4(a+b+c)=(a+b+c+d)+3(a+b+c)=3m+3(a+b+c).∴d+4(a+b+c)既能被2整除,也能被3整除,∴也能被6整除.10.解:(1)根据精巧数的定义,得123k能被4整除,则1230+k能被4整除,∵1230+k=1228+(2+k),∴2+k能被4整除,又∵0≤k≤9,且k为整数,∴k=2或6;(2)∵2ab是“精巧数”,∴a为偶数,且2+a+b是3的倍数,∵a<10,b<10,∴2+a+b<22,∵2ab各位数字之和为一个完全平方数,∴2+a+b=32=9,∴当a=0时,b=7,当a=2时,b=5,当a=4时,b=3,当a=6时,b=1,∴所有满足条件的三位“精巧数”有:207,225,243,261.11. (1)证明:设三位数abc是一个半和数,则a+b+c=2b,∴a+c=b.∵这个三位数为100a+10b+c=100a+10(a+c)+c=110a+11c=11(10a+c),且10a+c为整数,∴这个三位数是11的倍数,能被11整除.(2)解:∵四位数abbc是欢喜数,∴10a+b=2(10b+c),∴10a-19b-2c=0①.∵bmc是半和数,∴b+c=m.∵bmc是平方差数,∴m=b2-c2=(b+c)(b-c),∴b -c =1,∴b =1+c ②,②代入①得a =21c +1910,∵a 是1~9的正整数,∴c =1,∴b =2,∴m =2+1=3.12. (1)证明:由题意得,t 按上述方法可得新数:n 0n ,nn 0,∵|n +2×0-n |=0,|n +2n -0|=3n ,0<3n ,∴n 0n 是t 的“幸福美满数”,K (t )=n 2+2×02-n 2=0;(2)解:s =100+10x +y ,s ′=100+10y +x ,19s +8s ′=3888,即19(100+10x +y )+8(100+10y +x )=3888.得到2x +y =12,∵x <y ,且均为自然数,∴⎩⎨⎧x =2y =8或⎩⎨⎧x =3y =6, ∴“梦想成真数”为128或136,通过计算,K (128)=-55,K (136)=-17或-25,又∵-55<-25<-17,∴K(s)的最大值为-17.13.解:(1)依照2阶6位循环数的定义,可任意写出3个2阶6位循环数:131313;272727;868686.任意一个2阶6位循环数能被7整除,理由如下:结合数字的特点可得知:2阶6位循环数为任意的一个两位数×10101得出的.∵10101÷7 =1443.∴任意一个2阶6位循环数能被7整除;(2)结合(1)的规律可知:2阶4位循环数为任意的一个两位数×101得出的.∵101为质数.∴xy为13的倍数,又∵0<x<5,∴y=3x.∵当x=4时,y=3×4=12,当x=5时,y=3×5=15均不符合题意.∴0<x<4,且x为整数,∴y与x之间的函数关系为y=3x(x=1,2,3).14.解:(1)根据题意知t=100(x+y)+10y+x,∴h=100y+10x+x+y,∴q=t-h=(100x+100y+10y+x)-(100y+10x+x+y)=90x+9y,∴f(m)=q9=90x+9y9=10x+y.∵0不能在百位,∴t的十位和百位均不可以为0,∴x的最小值为0,y的最小值为1,∴f(m)的最小值为1,此时“加成数”t为110;(2)∵f(m)是24的倍数,∴10x+y=24n(n=1,2,3,…),∵0≤x≤8,1≤y≤9,且1≤x+y≤9,∴当n=1时,10x+y=24,x=2,y=4,当n=3时,10x+y=72,x=7,y=2;综上,这样的“节气数”有2个,分别为24,72.15. (1)证明:∵三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,∴重新排序后,其中两个数位上数字的和是另一个数位上的数字的2倍,∴a+c-2b=0,∴F(t)=0;(2)解:∵m=200+10x+y是“善雅数”,∴x为偶数,且2+x+y是3的倍数,∵x<10,y<10,∴2+x+y<30,∵m的各位数字之和为一个完全平方数,∴2+x+y=32=9,∴当x=0时,y=7,当x=2时,y=5,当x=4时,y=3,当x=6时,y=1,∴所有符合条件的“善雅数”有:207,225,243,261,∴所有符合条件的“善雅数”中F(m)的最大值是|2-3|-|3-4|=0.16. (1)解:是.理由如下:∵(12+2)2+(12-2)=14+2+2+12-2=114,是有理数;(12+2)+(12-2)2=12+2+14-2+2=114,是有理数.∴(12+2,12-2)是“完美数对”;(2)证明:∵(a ,b )是“完美数对”,∴a 2+b 与a +b 2都是有理数,∴(a 2+b )-(a +b 2)=(a -b )(a +b -1)是有理数.设t =(a -b )(a +b -1)=(a -b )×(2-1)=a -b ,∴t =a -b 是有理数.解⎩⎨⎧a +b =2a -b =t ,得⎩⎪⎨⎪⎧a =1+t 2b =1-t 2, ∵t 是有理数,∴a ,b 都是有理数.17. 解:(1)2;8;证明:假设P (n )的质数为a ,b ,c ,由P (n )=0可知,a =b =c ,∴P (n )=a +a +a =3a ,∴3a÷3=a,为整数,∴若P(n)=0,n必定能被3整除;(2)(x+y)×8+10x+y=99,∴2x+y=11;∵1≤x≤y≤9,∴期盼数:35,27,19,35=11+11+13;27=7+7+13;19=7+7+5;P(35)=2,P(27)=6,P(19)=2,∴P(t)max=6.18. (1)证明:设原来的三位数为:100a+10b+c,其兄弟数为:100b+10c+a,则(100a+10b+c)-(100b+10c+a)=99a-90b-9c=9(11a-10b-c),∵(11a-10b-c)为整数,∴一个三位数与其兄弟数之差一定可以被9整除.(2)解:设这个六位数的前4位是M,后2位是N,则这个数可表示为:(100M+N),其兄弟数可表示为:(10000N+M),∴4×(100M+N)=10000N+M,∴化简得19M=476N,∴N一定是19的倍数,∵N是2位数,∴满足条件的N=19,38,57,76,95;又∵M是4位数,∴N=19,38都不满足条件,舍去;∴N=57,76,95,相应的:M=1428,1904,2380,∴满足条件的六位数有三个142857,190476,238095.19. (1)证明:∵3×14=42≠41,∴41不是希望数.假设存在两位数是希望数,记为ab,∴ab=3ba.∵3b为一位数,且b是3a的个位数,∴b=1,2,3.当b=1时,a=7,3×17=51≠71;当b=2时,a=4,3×24=72≠42;当b=3时,a=1,3×31=93≠13.综上可知:假设不成立,即任意两位数都不可能是“希望数”;(2)解:∵abcd=3·cbad,∴3d的个位是d,∴d=0或5.当d=0时,∵3a的个位是c,c=2,∴a=4,此时3c=6>4,不合适;当d=5时,∵3a的个位+1是c,c=2,∴a=7,又∵abcd=3·cbad,∴3b+2=10+b,解得:b=4.∴这个四位“希望数”为7425.20. (1)解:123的百位与十位数字组成的数为12,21,百位与个位数字组成的数为13,31, 十位与个位数字组成的数为23,32,则各数和为12+21+13+31+23+32=132≠123,显然不是公主数;(2)证明:∵xyz是一个公主数,∴(10x+y+10y+x)+(10x+z+10z+x)+(10y+z+10z+y) =100x+10y+z,∴78x=12y+21z①;∵xyz是一个伯伯数,∴y=x+z②,代入①得66x=33z,∴z=2x;(3)解:设这个伯伯数为xyz,则y=x+z,∴100x+10y+z=110x+11z.∵110x+11z+132=11(10x+z+12),∵能被13整除,∴10x+z+12是13的倍数.当10x+z+12=26时,x=1,z=4,y=5,这个数为154;当10x +z +12=39时,x =2,z =7,y =9,这个数为297;当10x +z +12=52时,x =4,z =0,y =4,这个数为440;当10x +z +12=65时,x =5,z =3,y =8,这个数为583;当10x +z +12=78时,x =6,z =6,y =12,不符合;当10x +z +12=91时,x =7,z =9,y =16,不符合.故满足条件的数有154,297,440,583.21. 解:(1)132不是“1阶倒差数”,235;【解法提示】∵32=1×32=2×16=4×8,不是两个连续自然数的积, ∴132不是“1阶倒差数”.第5个“2阶倒差数”为15-17=235.(2)设m 是由两个连续奇数2x -1,2x +1组成的“2阶倒差数”,则m =12x -1-12x +1=2x +1-(2x -1)(2x +1)(2x -1)=24x 2-1. ∵c ,d 是两个连续奇数组成的“2阶倒差数”,∴可设c =24y 2-1,d =24z 2-1,∵1d -1c =22,∴4z 2-12-4y 2-12=22,即z 2-y 2=11,∴(z +y )(z -y )=11>0,∴z >y .∵11=1×11,∴⎩⎨⎧z +y =11z -y =1,解得⎩⎨⎧y =5z =6, ∴c =24×52-1=299,d =24×62-1=2143. 22. (1)证明:设A =xy ,则其“诚勤数”为x 2y ,“立达数”为10x +y +2, ∴x 2y -(10x +y +2)=100x +20+y -10x -y -2=90x +18=6(15x +3), ∵15x +3为整数,∴6(15x +3)能被6整除,即对任意一个两位正整数A ,其“诚勤数”与“立达数”之差能被6整除;(2)解:设B =10a +b ,1≤a ≤9,0≤b ≤9(13加上2后各数字之和变小,说明个位发生了进位),B +2=10a +b +2,则B 的“立达数”为10(a +1)+(b +2-10),a +1+b +2-10=12(a +b ),整理得:a +b =14,∵1≤a ≤9,0≤b ≤9,∴⎩⎨⎧a =8(舍)b =6、⎩⎨⎧a =6b =8,⎩⎨⎧a =9(舍)b =5、⎩⎨⎧a =5b =9,经检验:86和95不符合题意舍去,∴所求两位数为68或59.23. (1)证明:设m =10t +8,1≤t ≤9,且t 为整数.∴m 2-64=(10t +8)2-64=100t 2+160t +64-64=20(5t 2+8t ).∵1≤t ≤9,t 为正整数,∴5t 2+8t 是正整数.∴m 2-64一定为20的倍数;(2)解:∵m =p 2-q 2,p ,q 为正整数,∴10t +8=(p +q )(p -q ),当t =1时,18=1×18=2×9=3×6,没有满足条件的p ,q .当t =2时,28=1×28=2×14=4×7.其中满足条件的p ,q 的数对有(8,6),即28=82-62,∴H (28)=68=34.当t =3时,38=1×38=2×19,没有满足条件的p ,q . 当t =4时,48=1×48=2×24=3×16=4×12=6×8.满足条件的p ,q 的数对为⎩⎨⎧p -q =2p +q =24或⎩⎨⎧p -q =4p +q =12或⎩⎨⎧p -q =6p +q =8,解得⎩⎨⎧p =13q =11或⎩⎨⎧p =8q =4或⎩⎨⎧p =7q =1. 即48=132-112=82-42=72-12.∴H (48)=1113或H (48)=48=12或H (48)=17.∵1113>34>12>17,∴H (m )的最大值为1113.24. 解:(1)∵m ,n 都是四位“格调数”,则设m =a (a +1)(a +2)(a +3),n =b (b +1)(b +2)(b +3), 即m =1000a +100(a +1)+10(a +2)+(a +3)=1111a +123, n =1000b +100(b +1)+10(b +2)+(b +3)=1111b +123, ∴m -n =1111a +123-(1111b +123)=1111(a -b )=3333, ∴a -b =3,即a =b +3.∵m是四位“格调数”,∴1≤a≤6,∴1≤b+3≤6,∴1≤b≤3,∴b为1,2或3,则a为4,5或6,∴m为4567,5678或6789;(2)q是“发财数”.∵t=100a+10(a+1)+(a+2)=111a+12,∴k=100(a+2)+10(a+1)+a=111a+210,∴q=k-t=(111a+210)-(111a+12)=210-12=198,∵198÷18=11,∴198是18的整倍数,即198是“发财数”,∴q是“发财数”.25. 解:(1)7;证明:设这个四位“两头蛇数”为1ab1,由题意得:1ab1-3ab=1001+100a+10b-30a-3b=1001+70a+7b=7(143+10a+b)∵a 、b 为整数,∴143+10a +b 为整数,∴一个四位的“两头蛇数”与它去掉两头后得到的两位数的三倍能被7整除;(2)∵16的真因数有:1,2,4,8.∴1+2+4+8=15,∵15=1+3+11,∴16的“亲和数”为33.设这个五位“两头蛇数”为1x 4y 1,由题意得:1x4y133为整数, ∴315+30x +10x +10y +633为整数, ∴10x +10y +6=66,∴x +y =6,∵0≤x ≤9,0≤y ≤9,且为整数,x <y∴⎩⎨⎧x =0y =6或⎩⎨⎧x =1y =5或⎩⎨⎧x =2y =4. ∴这个五位“两头蛇数”为10461或11451或12441.26.解:(1)22;17+5m.【解法提示】将3个数:2,8,7,做一次“差变增数列”,得到的数字为2,6,8,-1,7,所有数字的和为2+6+8+(-1)+7 =22;∵将数串a,b,c做一次“差变增数列”得到a,b-a,b,c-b,c,所有数字和的增加量M=(a+b-a+b+c-b+c)-(a+b+c)=c-a,∴将一个数串每做一次“差变增数列”,所有数字的和的增加量相同,均为原数最后一个数与第一个数的差∵数串2,8,7中,7-2=5.∴每做一次“差变增数列”,所有数字的和增加5,∴做m次“差变增数列”后,所得数字的和为2+8+7+5m,即17 +5m. (2)∵数串:x,8,y,∴做100次“差变增数列”,所得数字的和为x+8+y+100(y-x)=-99x+101y+8,根据题意得-99x+101y+8 =216,即y=208+99x101,∵y是整数,∴208+99x是101的正整数倍,当208+99x=101时,x无正整数解;。
中考英语题型组合选练(6)(阅读理解完形填空任务型阅读首字母)外研版

2019年中考英语选练(6)(阅读理解+完形填空+任务型阅读+首字母)(限时:20分钟)一、阅读理解。
A阅读下列短文,选出最佳选项。
Mark began to introduce the guest speaker to the listeners, but then stopped for a while. He had forgotten her name.Barbara hid her valuable things when she went on vacation. When she came back, she couldn’t remember where she’d put them.Perhaps you’ve had such experiences like these. Most people have. But most of them haven’t realized that they have a memory problem. Neither do they know a simple but important fact: Memory can be improved. If you’ll just accept that, the following will show you how.First, relax. If you are over worried about something, you’ll forget it. If you keep telling yourself that your memory is bad, your mind will come to believe it and you won’t remember things. When you forget something, don’t follow up with saying like “Oh, my god! I always forget things!” Such words will have a bad result on you and your memory.But relaxing isn’t enough. To improve your memory, you’ll need to take an active role. Like your body, your memory can be made strong through exercise. Look for opportunities to exercise your memory. For example, if you’re learning a language, try to actively remember a lot of new words.If you don’t take notice of things actively, you won’t remem ber them. So, youcan make pictures of what you see in your mind every day. For example, don’t just put your keys down! If you want to find them again, make a mind picture of the place where you’re putting them.1.The first two paragraphs just tell us .A.Barbara was a very rich person. B.examples of memory problemsC.Mark often forgot his friends’ names D.language problems of two persons 2.When you forget things, you _______.A.must be too careless B.shouldn’t take notice of t he result C.must accept the fact D.shouldn’t lose heart about your memory 3.The word “opportunities” in the fifth paragraph means “_______.”A.places B.doctors. C.chances D.positions 4.According to the passage, _____ can make your memory better.A.realizing your memory problems B.talking to your friendsC.doing sports every day D.making mind pictures of what you see 5.The purpose of the passage is to help you ______.A.to introduce the guest B.to improve your memoryC.to remember new words D.to forget unhappy things【参考答案】1—5、BDCDBB阅读下列短文,从每小题所给的A、B、C、D四个选项中选出最佳选项。
整式求值经典题型(9大类型)(原卷版)

专题2.2 整式求值经典题型(9大类型)【题型1 直接代入】【题型2 整体代入-配系数】【题型3整体代入-奇次项为相反数】【题型4 整体构造代入】【题型5不含无关】【题型6 化简求值】【题型7 绝对值化简求值】【题型8 非负性求值】【题型9 定义求值】【题型1 直接代入】【典例1】(2023•琼山区校级模拟)当x=﹣1时,代数式3x+1的值是()A.﹣4B.﹣2C.2D.4【变式1-1】(2023•秀英区模拟)当x=﹣2时,代数式3﹣2x的值是()A.﹣7B.7C.9D.﹣9【变式1-2】(2022秋•平泉市校级期末)当,计算代数式﹣x2﹣1=()A.0B.C.D.【变式1-3】(2021秋•济宁期末)当x=﹣1时,代数式2x2﹣5x的值为()A.5B.3C.﹣2D.7【题型2 整体代入-配系数】【典例2】(2023春•吴江区期中)当x2﹣3x=1时,代数式2x2﹣6x+3的值为()A.2B.3C.4D.5【变式2-1】(2022秋•平泉市期末)已知x﹣2y﹣4=﹣1,则代数式3+2x﹣4y 的值为()A.7B.6C.0D.9【变式2-2】(2023春•永安市期中)若x﹣3y=﹣5,则代数式5+2x﹣6y的值是()A.0B.﹣5C.﹣10D.﹣15(2023•香洲区一模)已知2a+3b=4,则整式﹣4a﹣6b+1的值是()【变式2-3】A.5B.3C.﹣7D.﹣10【题型3整体代入-奇次项为相反数】【典例3】(2023春•长治月考)当x=1时,代数式ax3﹣3bx+4的值是9,则当x=﹣1时,这个代数式的值是()A.9B.8C.﹣1D.﹣9(2020秋•越秀区校级期中)当x分别等于2或﹣2时,代数式ax4+bx2+1【变式3-1】的两个值()A.相等B.互为相反数C.互为倒数D.相差2【变式3-2】(2022秋•滦州市期末)当x=1时,多项式ax3+bx﹣2的值为2,则当x=﹣1时,该多项式的值是()A.﹣6B.﹣2C.0D.2【变式3-3】(2022秋•衡东县期末)当x=1时,代数式px3+qx+1的值为2022,则当x=﹣1时,px3+qx+4043的值为()A.2020B.﹣2020C.﹣2021D.2022【变式3-4】(2022秋•射洪市期末)已知:当x=3时,代数式ax2021+bx2019﹣1的值是8,则当x=﹣3时,这个代数式的值是()A.﹣10B.8C.9D.﹣8【题型4 整体构造代入】【典例4】(2023春•南宁期末)阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x =3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b),“整体思想”是中学教学课题中的一种重要的思想方法,它在方程、多项式的求值中应用极为广泛.(1)尝试应用:把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣5(a﹣b)2的结果是.(2)已知x﹣2y=1,求3x﹣6y﹣5的值.(3)拓展探索:已知a﹣2b=3,2b﹣c=﹣5,c﹣d=10,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.【变式4-1】(2022秋•翠屏区期末)若a+b=﹣5,b﹣c=﹣1,则c﹣a﹣2b的值为()A.6B.4C.﹣6D.﹣4【变式4-2】(2022秋•永年区期末)已知a+b=3,c﹣d=﹣2,则(b+c)﹣(d ﹣a)的值为()A.5B.﹣5C.1D.﹣1【变式4-3】(2022秋•沁县期末)我们知道:4x+2x﹣x=(4+2﹣1)x=5x,类似地,若我们把(a+b)看成一个整体,则有4(a+b)+2(a+b)﹣(a+b)=(4+2﹣1)(a+b)=5(a+b).这种解决问题的方法渗透了数学中的“整体思想”.“整体思想”是中学数学解题中的一种重要的思想方法,其应用极为广泛.请运用“整体思想”解答下面的问题:(1)把(a﹣b)看成一个整体,合并3(a﹣b)2﹣7(a﹣b)2+2(a﹣b)2;(2)已知:x2+2y=5,求代数式﹣3x2﹣6y+21的值;(3分)(3)已知a﹣2b=3,2b﹣c=﹣5,c﹣d=10,求(a﹣c)+(2b﹣d)﹣(2b ﹣c)的值.【题型5 不含无关】【典例5】(2022秋•青川县期末)已知多项式A=x2+xy+3y,B=x2﹣xy.(1)求2A﹣B;(2)x=﹣2,y=5时,求2A﹣B的值;(3)若2A﹣B的值与y的值无关,求x的值.【变式5-1】(2022秋•长沙期末)已知关于x,y的多项式mx2+2xy﹣x与3x2﹣2nxy+3y的差不含二次项,求n m的值()A.﹣1B.1C.3D.﹣3【变式5-2】(2023春•青阳县期末)如果多项式3x2﹣7x2+x+k2x2﹣5中不含x2项,则k的值为()A.2或﹣2B.﹣2C.0D.2【变式5-3】(2022秋•自贡期末)已知多项式A=x2+xy+3y,B=x2﹣xy.(1)求3A﹣2B的值;(2)若3A﹣2B的值与y的取值无关,求x的值.【变式5-4】(2022秋•栖霞市期末)已知A=2x2+3xy﹣2x,B=x2﹣xy+1,(1)求3A﹣6B;(2)若3A﹣6B的值与x的取值无关.求y的值.【题型6 化简求值】【典例6】(2022秋•华容区期末)先化简,再求值:,其中a=﹣3,b=﹣2.【变式6-1】(2022秋•澄海区期末)先化简,再求值:,其中,.【变式6-2】(2022秋•武陵区期末)先化简,再求值:5a2﹣[3a﹣(2a﹣3)+4a2],其中a=﹣2.【变式6-3】(2022秋•防城港期末)化简与求值:3(x﹣y)﹣(2x﹣y)+y,其中x=﹣2,y=1.【变式6-4】(2022秋•零陵区期末)先化简,再求值:(4x2y﹣2xy2+2)﹣3(x2y ﹣xy2+1),其中x=2,y=﹣1.【题型7 绝对值化简求值】【典例7】(2022秋•丰泽区校级期末)若用点A、B、C分别表示有理数a、b、c,如图:(1)判断下列各式的符号:a+b0;c﹣b0;c﹣a0(2)化简|a+b|﹣|c﹣b|﹣|c﹣a|【变式7-1】(2022秋•郫都区校级期末)有理数a、b、c在数轴上的位置如图:(1)判断正负,用“>”或“<”填空:b﹣c0,a+b0,c﹣a0.(2)化简:|b﹣c|+|a+b|﹣|c﹣a|.【变式7-2】(2021秋•农安县期末)有理数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简|c﹣a|+|c﹣b|+|a+b|.【变式7-3】(2022春•龙凤区期末)已知a、b、c三个数在数轴上对应点如图,其中O为原点,化简|b﹣a|﹣|2a﹣b|+|a﹣c|﹣|c|.【题型8 非负性求值】【典例8】(2023春•九龙坡区校级期末)先化简,再求值:4x2y﹣[(6x2y﹣3xy2)﹣2(3xy2﹣x2y)]﹣3x2y+1,其中x,y满足|x+2|+(y﹣1)2=0.【变式8-1】(2023春•九龙坡区校级期中)先化简,再求值:a3b﹣a2b3﹣(4ab ﹣6a2b3﹣1)+2(ab﹣a2b3),其中a,b满足|2a﹣1|+(b+4)2=0.【变式8-2】(2023春•通州区月考)已知(a﹣2)2+|b+3|=0,求代数式的值.【变式8-3】(2022秋•包河区期末)先化简,再求值:x2+(2xy﹣3y2)﹣2(x2+xy ﹣2y2),其中x、y满足|x+1|+(2y+4)2=0.【题型9定义求值】【典例9】(2022秋•晋州市期末)定义:若a+b+ab=10,则称a,b是“最佳拍档数”.例如:,因此3和是一组“最佳拍档数”.(1)8与是一组“最佳拍档数”;(2)有一个数与任何数都不能组成“最佳拍档数”,这个数是;(3)若m,n是一组“最佳拍档数”,请求出的值.【变式9-1】(2022秋•安乡县期末)定义如下:存在数a,b,使得等式+=成立,则称数a,b为一对“互助数”,记为(a,b).比如:(0,0)是一对“互助数”.(1)若(1,b)是一对“互助数”,则b的值为;(2)若(﹣2,x)是一对“互助数”,求代数式(﹣x2+3x﹣1)﹣(﹣x2+5x ﹣15)的值;(3)若(m,n)是一对“互助数”,满足等式m﹣n﹣(6m+2n﹣2)=0,求m和n的值.【变式9-2】(2022秋•昭阳区期中)定义新运算=ad﹣bc,例如=2×3﹣1×5=1.(1)化简;(2)当x=时,求的值.【变式9-3】(2022秋•东城区期末)给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“相伴有理数对”,记为(a,b).如:3﹣=3×+1,5﹣=5×+1,所以数对(3,),(5,)都是“相伴有理数对”.(1)数对(﹣2,),(﹣,﹣3)中,是“相伴有理数对”的是;(2)若(x+1,5)是“相伴有理数对”,则x的值是;(3)若(a,b)是“相伴有理数对”,求3ab﹣a+(a+b﹣5ab)+1的值.。
中考物理必考题型针对训练专题6 作图题
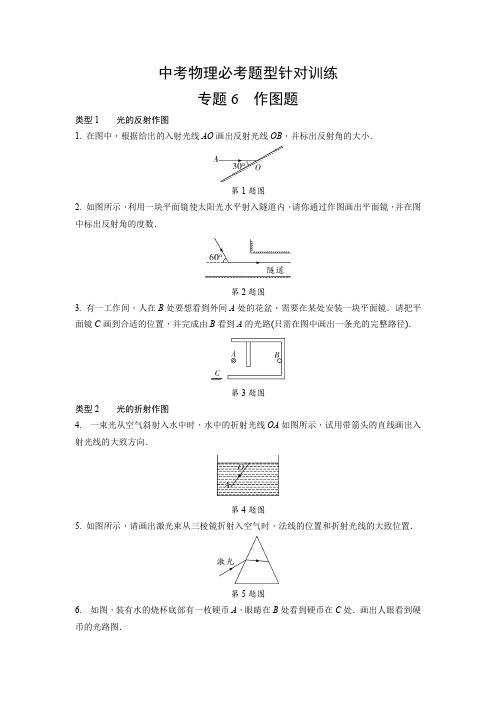
中考物理必考题型针对训练专题6作图题类型1光的反射作图1. 在图中,根据给出的入射光线AO画出反射光线OB,并标出反射角的大小.第1题图2. 如图所示,利用一块平面镜使太阳光水平射入隧道内,请你通过作图画出平面镜,并在图中标出反射角的度数.第2题图3. 有一工作间,人在B处要想看到外间A处的花盆,需要在某处安装一块平面镜.请把平面镜C画到合适的位置,并完成由B看到A的光路(只需在图中画出一条光的完整路径).第3题图类型2光的折射作图4. 一束光从空气斜射入水中时,水中的折射光线OA如图所示,试用带箭头的直线画出入射光线的大致方向.第4题图5. 如图所示,请画出激光束从三棱镜折射入空气时,法线的位置和折射光线的大致位置.第5题图6. 如图,装有水的烧杯底部有一枚硬币A,眼睛在B处看到硬币在C处.画出人眼看到硬币的光路图.第6题图类型3光的反射、折射综合作图7. 光从空气斜射向玻璃,发生反射和折射.请完成光路,并标出反射角的度数.第7题图8. 请画出:①折射光线的大致方向,标出折射角α;②经光滑墙壁反射后的反射光线.第8题图9. 如图所示为某同学利用标有角度的圆盘、激光器和半圆形玻璃砖“探究光的折射规律”的实验示意图,其中AO为激光器发出的从空气射向半圆形玻璃砖圆心的一束入射光线.请画出反射光线和玻璃砖中折射光线的大致方向.第9题图类型4平面镜成像特点作图Ⅰ. 像物互画10. 利用平面镜成像的特点在图中根据平面镜中的像A′B′画出物体AB.第10题图11. 如图所示,一束由A发出的光射到平面镜表面O点,画出物体AB在平面镜中的像,并画出入射光线AO的反射光线.第11题图Ⅰ.补画平面镜类12. 如图所示,A′B′是AB在平面镜中所成的像,请画出平面镜的位置(保留作图痕迹).第12题图Ⅰ .像点作图类13. 如图,请你画出烛焰上A点经平面镜MN所成的像A′(保留作图痕迹).第13题图14. 如图所示,S为发光点,请在图中画出发光点S在平面镜MN中所成像S′的位置,并画出由S点发出,经平面镜反射后通过P点的光线.第14题图15. 如图,在舞蹈室的墙面上装有一块平面镜,王老师用一激光笔从S点照向镜面,在地面上P点看到一光斑,请用平面镜成像特点完成光路图.第15题图类型5透镜作图)Ⅰ. 透镜的三条特殊光线作图16. 如图所示,探究凸透镜成像时,F是凸透镜的焦点,S是蜡烛火焰上的一点,试作出S 的像S′.第16题图17. 如图所示,一条入射光线过凹透镜光心,一条折射光线与主光轴平行.请将光路补画完整.第17题图Ⅰ.补画透镜18. 根据入射光线和折射光线,在图中虚线框内画出适当类型的透镜.第18题图19. 如图所示,请你根据近视眼的矫正方法,完成光路图.第19题图Ⅰ.透镜与平面镜结合作图20. 如图所示,平面镜垂直于凸透镜主光轴且在凸透镜左侧焦点上,请完成光路图.第20题图21. 如图所示,水平台上点光源S发出的一条光线经竖直放置的平面镜反射,再经凸透镜折射后,平行于凸透镜的主光轴射出.请在图中画出点光源S,并完成光路图.第21题图22. 如图所示,AB为遮光板,S′是点光源S在平面镜中所成的像,S发出的一条光线经平面镜反射后恰好经过凸透镜左侧焦点F.请画出:(1)光源S的位置;(2)光线EF的入射光线;(3)光线EF经凸透镜后的出射光线.第22题图23. 如图所示,水平放置的凹透镜,F是它的焦点,光线a经凹透镜折射后,再经平面镜反射,以图示的角度射到竖直放置的屏幕上.请在图中确定平面镜的位置,完成光路图并标出经平面镜反射时反射角的大小.第23题图Ⅰ.透镜与折射结合作图24. 如图所示,SA为水面上方的点光源S射向水面的一条光线,该光线射到水面的反射光线的方向刚好指向水面上方凹透镜右侧的焦点.请画出:(1)光线SA射入水中的折射光线;(2)经过凹透镜的折射光线.第24题图25. 如图所示,凸透镜的主光轴位于平静水面以下且与水面平行,F为其在水中的焦点.图中入射光线与主光轴平行,请画出经透镜后的折射光线及进入空气后的大致折射光线.第25题图类型6画指定力的示意图26. 如图所示,画出足球在空中飞行时所受重力的示意图.第26题图27. 如图所示,一个木块静止在水平桌面上.请画出木块所受支持力的示意图(重心已画出).第27题图28. 请在图中画出跳水运动员对跳板的压力.第28题图29. 将细线一端固定在烧杯底部,另一端固定在乒乓球上.烧杯加水后静置在斜面上,如图所示.不计乒乓球的重力,请以球心为作用点画出乒乓球受到的浮力和拉力的示意图.第29题图30. 如图所示,放在水平地面上的小车B与弹簧相连,弹簧处于伸长状态,物体A与小车B 均静止.请画出:①物体A的重力示意图(O为物体A的重心);②弹簧对小车B的弹力示意图.第30题图31. 在探究“推断物体不受力时的运动”实验中,小车从斜面顶端A自由滑下,在水平面上滑行经过B点,最终在C点静止.请以“O”为力的作用点,在图中作出小车经过B点时受到的摩擦力和重力示意图.第31题图类型7受力分析作图Ⅰ. 平衡状态32. 如图所示,物块置于长木板上表面,两者一起沿斜面匀速下滑,物块与木板始终保持相对静止.请在图中画出长木板对物块作用力的示意图(O点为力的作用点).第32题图33. 如图所示,太阳能汽车在水平公路上向右匀速行驶,请在图中画出汽车受力的示意图(力的作用点画在重心O点上).第33题图34. 如图所示,物体上系一细线,细线右端固定,物体静止在水中时细线恰好水平,请作出物体受力的示意图.第34题图35. 如图所示,用弹簧测力计悬挂着物体静止在水中,请画出此时物体所受力的示意图.第35题图Ⅰ.非平衡状态36. 如图所示是运动员百米赛跑时的情景,请画出他的右脚对地面作用力的示意图.(O点是力的作用点)第36题图37. 如图所示,木块沿光滑固定斜面下滑,请画出木块的受力示意图.第37题图38. 某同学用细线把他自己吹胀的气球悬挂在天花板下,当有水平向右的风吹来时的情景如图所示,请在图中画出气球所受力的示意图.第38题图类型8杠杆作图Ⅰ. 简单力臂作图39. 如图所示,硬棒OB能绕支点O转动,A处用绳子拉住固定在墙壁上.请画出拉力F 的力臂(用l表示).第39题图40. 如图所示,质量分布均匀的圆柱形细木棒一端放在地面上,另一端与支点O连接,请在图中画出木棒所受重力的示意图、重力的力臂.第40题图41. 如图是一个杠杆式简易起吊机,它上面装了一个定滑轮可以改变拉绳的方向,杠杆OBA 可绕O点转动.请在图上画出杠杆OBA的动力臂l和物体M所受重力的示意图.第41题图Ⅰ .画最小力、力臂42. 如图,请画出F A的力臂l,并在B端画出使杠杆平衡的最小力F B.第42题图43. 如图所示,甲图是正在使用的核桃夹,上、下两部分都是杠杆,乙图是上半部分杠杆的示意图.请在A点画出最小动力F1的示意图,在B点画出阻力F2的示意图及其力臂l2.第43题图44. 如图所示,在撬棒AD上作出撬起“石块1”的最小力F及对应的力臂l.第44题图类型9滑轮组绕线作图45. 如图所示,用滑轮组提升物体,已知滑轮质量均为2 kg,物体重100 N,绳子能承受的最大拉力为50 N.请画出绳子的正确绕法,并在绳的末端标出力的方向.(不考虑绳重及摩擦)第45题图类型10实物图与电路图互画46. 请根据图甲中电路图,用笔画线代替导线将实物图乙连接完整,使滑动变阻器的滑片P 向右移动时,接入电路的电阻变大.甲乙第46题图47. 根据下面的实物图画出与之对应的电路图.第47题图类型11按要求连接电路图(含纠错))48. 如图所示是“伏安法”测量小灯泡电功率的实物电路,用笔画线代替导线完成电路连接.第48题图49. 请在图中用笔画线代替导线连接电路.要求:两灯并联,开关S同时控制两盏灯泡.第49题图50. 某实验小组利用如图所示电路探究“导体中电流和电压的关系”,提供的实验器材有:电源(6 V)、电流表、电压表、定值电阻(10 Ω)、滑动变阻器(40 Ω0.5 A)、开关和导线若干.请用笔画线代替导线,将图中实物电路连接完整.第50题图51. 某同学利用如图所示的电路测量小灯泡的电功率.实验中电源电压保持不变,小灯泡的额定电压是2.5 V.该同学错接了一根导线,请你在这根导线上打“”,并补画出正确的那根导线.类型12电路设计作图52. 某额定电压为220 V的电动扶梯(已接地),只需在白天且有人时开启,利用红外线开关S1(有人时闭合、无人时断开)及可见光开关S2(白天闭合、夜间断开)即可实现自动控制.请在图中按要求正确完成电路连接.第52题图53. 常州汪芷瑶同学的专利《双手驾驶提醒装置》.可在汽车驾驶员双手脱离方向盘时发出警报.方向盘包裹气囊并通过导气管连接压力开关S1,压力开关S2置于坐垫内.压力开关受到压力时闭合,不受压力时断开.驾驶员坐在座椅上,当手握方向盘正常驾驶时灯亮、电铃不响,当双手脱离方向盘时,灯亮、电铃响.请以笔画线完成电路连接.第53题图类型13家庭电路作图54. 将灯泡与开关连接到图中的家庭电路中.第54题图55. 为判断如图所示的家庭电路中白炽灯L1是否短路,将火线上的熔丝断开,用另一只完好的白炽灯L2作为“校验灯”接入电路,然后闭合总开关,再闭合开关S,即可根据L2的亮暗做出判断.请在图中补画一根导线,将L2正确接入电路.第55题图类型14简单磁现象作图)56. 地球周围存在着磁场,如图所示,图中实线部分为地磁场的磁感线分布情况,请在图中用箭头标出地磁场的磁感线方向.第56题图57. 请在图中标出蹄形磁体的N、S极和磁感线的方向.第57题图类型15通电螺线管作图58. 如图所示,根据图中电流方向,标出磁感线方向、小磁针的N极.第58题图59. 如图所示,请按小磁针的指向,标出螺线管中的电流方向,并在括号中标明螺线管右端的极性.第59题图60. 通电螺线管的N、S极以及外部的一条磁感线如图.在图中标出磁感线的方向,并在括号中标出电源的正、负极.第60题图61. 小迪设计了如图所示的漂浮式指南针,铜片是“盐水电池”正极,锌片是负极.请标出:线圈中电流方向、磁感线方向,并在括号内标出通电螺线管左端的极性(用“N”或“S”表示).第61题图62. 通电螺线管外部的磁场与条形磁铁的磁场相似.螺线管通电后小磁针静止时的分布如图所示,请在图中标注螺线管电流方向、通电螺线管的N极和至少画出一条通电螺线管外的磁感线.第62题图63. 如图所示,闭合开关后,套在通电螺线管上的磁环会向右运动,已知磁环的左侧为N 极.请在图中标出:第63题图(1)通电螺线管左端的磁极(用“N”或“S”表示).(2)磁感线的方向.(3)电源右端的极性(用“+”或“-”表示).类型16电磁综合作图64. 如图,用笔画线代替导线将图中实物连接起来.要求:闭合开关后,使电磁铁的右端为N极,并且当滑动变阻器的滑片P向右移动时,电磁铁的磁性增强.第64题图65. 如图,是一种温度自动报警器原理示意图,当环境温度低于设定的警戒温度时,灯亮,电铃不响.当环境温度达到警戒温度值时,灯不亮电铃响,发出报警信号.①请在图中的虚线框内填入相应的电路元件符号并补全电路;②标出通电螺线管的N极(电铃符号).第65题图中考物理必考题型针对训练专题6作图题类型1光的反射作图1. 如答图所示第1题答图2. 如答图所示第2题答图3. 如答图所示第3题答图类型2光的折射作图4. 如答图所示第4题答图5. 如答图所示第5题答图6. 如答图所示第6题答图类型3光的反射、折射综合作图7. 如答图所示第7题答图8. 如答图所示第8题答图9. 如答图所示第9题答图类型4平面镜成像特点作图10. 如答图所示第10题答图11. 如答图所示第11题答图12. 如答图所示第12题答图13. 如答图所示第13题答图14. 如答图所示第14题答图15. 如答图所示第15题答图类型5透镜作图16. 如答图所示第16题答图17. 如答图所示第17题答图18. 如答图所示第18题答图19.如答图所示第19题答图20. 如答图所示第20题答图21. 如答图所示或第21题答图【解析】由于通过右侧焦点的光线经凸透镜折射后,折射光线与主光轴平行,据此可作出凸透镜的入射光线,反向延长该光线交平面镜于O,则该光线为经平面镜反射后的反射光线;再根据反射角等于入射角,作出入射光线,和水平台的交点即为光源S的位置.或延长凸透镜的入射光线与水平台面的延长线交于点S′,做S′关于平面镜的对称点即为光源S的位置,再连接S与O点,即为平面镜的入射光线.具体如答图所示.22. 如答图所示第22题答图23. 如答图所示第23题答图24. 如答图所示第24题答图25. 如答图所示第25题答图类型6画指定力的示意图26. 如答图所示第26题答图27. 如答图所示第27题答图28. 如答图所示第28题答图29. 如答图所示第29题答图30. 如答图所示第30题答图31. 如答图所示第31题答图类型7受力分析作图32. 如答图所示第32题答图33. 如答图所示第33题答图34. 如答图所示第34题答图35. 如答图所示第35题答图36. 如答图所示第36题答图37. 如答图所示第37题答图38. 如答图所示第38题答图类型8杠杆作图39. 如答图所示第39题答图40. 如答图所示第40题答图41. 如答图所示第41题答图42. 如答图所示第42题答图43. 如答图所示第43题答图44. 如答图所示第44题答图类型9滑轮组绕线作图45. 如答图所示第45题答图类型10实物图与电路图互画46. 如答图所示第46题答图47. 如答图所示第47题答图类型11按要求连接电路图(含纠错)48. 如答图所示第48题答图49. 如答图所示第49题答图50. 如答图所示第50题答图51. 如答图所示第51题答图类型12电路设计作图52. 如答图所示第52题答图53. 如答图所示第53题答图类型13家庭电路作图54. 如答图所示第54题答图55. 如答图所示第55题答图类型14简单磁现象作图56. 如答图所示第56题答图57. 如答图所示第57题答图类型15通电螺线管作图58. 如答图所示第58题答图59. 如答图所示第59题答图60. 如答图所示第60题答图61. 如答图所示第61题答图62. 如答图所示第62题答图63. 如答图所示第63题答图类型16电磁综合作图64. 如答图所示第64题答图65. 如答图所示第65题答图。
相似三角形的判定与性质(六大类型)(题型专练)(原卷版)

专题02 相似三角形的判定与性质(六大类型)【题型1 相似三角形的概念】【题型2 三边对应成比例,两三角形相似】【题型3两边对应成比例且夹角相等,两三角形相似】【题型4 两角对应相等,两三角形相似】【题型5 相似三角形的性质】【题型6相似三角形的性质与判定综合应用】【题型1 相似三角形的概念】1.(2023春•阳信县月考)下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与△ABC相似的是()A.B.C.D.2.(2022秋•道外区期末)下列三角形一定相似的是()A.两个等腰三角形B.两个等边三角形C.两个直角三角形D.有一角为70°的两个等腰三角形3.(2022秋•武城县期末)下列两个图形:①两个等腰三角形;②两个直角三角形;③两个正方形;④两个矩形;⑤两个菱形;⑥两个正五边形.其中一定相似的有()A.2组B.3组C.4组D.5组4.(2022秋•承德县期末)如图所示,网格中相似的两个三角形是()A.①与②B.①与③C.③与④D.②与③5.(2022秋•襄都区校级期末)下列判断中,不正确的有()A.三边对应成比例的两个三角形相似B.两边对应成比例,且有一个角相等的两个三角形相似C.斜边与一条直角边对应成比例的两个直角三角形相似D.有一个角是100°的两个等腰三角形相似【题型2 三边对应成比例,两三角形相似】6.(2022秋•常州期末)如图,△ABC∽△DEF,则DF的长是()A.B.C.2D.3 7.(2023•陇南模拟)两个相似三角形的相似比是4:9,则其面积之比是()A.2:3B.4:9C.9:4D.16:81 8.(2023•沙坪坝区校级模拟)如图,△ABO∽△CDO,若BO=6,DO=3,AB=4,则CD的长是()A.1B.2C.3D.49.(2022秋•鼓楼区期末)已知△ABC∽△DEF,若△ABC的三边分别长为6,8,10,△DEF的面积为96,则△DEF的周长为.10.(2023•惠城区校级一模)若△ABC∽△DEF,△ABC的面积为81cm2,△DEF的面积为36cm2,且AB=12cm,则DE=cm.11.(2022秋•于洪区期末)两个相似三角形的周长比是3:4,其中较小三角形的面积为18cm2,则较大三角形的面积为cm2.12.(2022秋•鸡西期末)如果两个相似三角形的周长比为1:6,那么这两个三角形的面积比为.13.(2023•长宁区一模)如果两个相似三角形的面积比是1:9,那么它们的周长比是.14.(2022秋•内乡县期末)如图,已知△ABC∽△ADE,AD=6,BD=3,DE =4,则BC=.15.(2022秋•零陵区期末)若△ABC∽△A′B′C′,且,△ABC 的面积为12cm2,则△A′B′C′的面积为cm2.【题型3两边对应成比例且夹角相等,两三角形相似】16.(2022秋•仓山区校级月考)如图,D、E分别是△ABC的边AB、AC上的点,AB=8,BD=5,AC=6,CE=2,求证:△ADE∽△ACB.17.(2021秋•武陵区期末)如图,已知∠BAE=∠CAD,AB=18,AC=48,AE=15,AD=40.求证:△ABC∽△AED.18.(2022秋•丰泽区校级期中)如图,E是△ABC的边BC上的点,已知∠BAE =∠CAD,,AB=18,AE=15.求证:△ABC∽△AED.19.(2022春•丰城市校级期末)如图,已知∠B=∠E=90°,AB=6,BF=3,CF=5,DE=15,DF=25.求证:△ABC∽△DEF.【题型4 两角对应相等,两三角形相似】20.(2022秋•蚌山区月考)已知:如图D、E分别是△ABC的边AB、AC上的点,∠A=40°,∠C=80°,∠AED=60°,求证:△ADE∽△ACB.21.(2022秋•龙胜县期中)如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高.求证:△ABC∽△CBD.22.(2022•江夏区模拟)如图,在△ABC和△DEC中,∠A=∠D,∠BCE=∠ACD.求证:△ABC∽△DEC.23.(2021秋•晋江市校级期末)如图,在△ABC中,点D在BC边上,点E在AC边上,且AD=AB,∠DEC=∠B.求证:△AED∽△ADC.24.(2022•南昌模拟)如图,在△ABC中,∠A=36°,AB=AC,BD是∠ABC 的平分线.求证:△ABC∽△BDC.【题型5 相似三角形的性质】25.(2020秋•思南县校级月考)判断图中的两个三角形是否相似,并说明理由.26.(大观区校级期中)如图,在边长为1的小正方形组成的网格中,△ABC 和△DEF的顶点都在格点上,请判断△ABC和△DEF是否相似,并说明理由.【题型6相似三角形的性质与判定综合应用】27.(2022秋•历城区校级月考)如图,AB∥CD,AC与BD交于点E,且AB=4,AE=2,AC=8.(1)求CD的长;(2)求证:△ABE∽△ACB.28.(2023•殷都区一模)如图,O是直线MN上一点,∠AOB=90°,过点A 作AC⊥MN于点C,过点B作BD⊥MN于点D.(1)求证:△AOC∽△OBD;(2)若OA=5,OC=OD=3,求BD的长.29.(2023•西湖区校级二模)如图,在菱形ABCD中,点M为对角线BD上一点,连接AM并延长交BC于点E,连接CM.(1)求证:CM=AM.(2)若∠ABC=60°,∠EMC=30°,求的值.30.(2023•港南区四模)如图,在△ABC中,D在AC上,DE∥BC,DF∥AB.(1)求证:△DFC∽△AED;(2)若CD=AC,求的值.31.(2023春•鼓楼区校级期末)如图,点C是△ABD边AD上一点,且满足∠CBD=∠A.(1)证明:△BCD∽△ABD;(2)若BC:AB=3:5,AC=16,求BD的长.32.(2022秋•顺平县期末)矩形ABCD中,E为DC上的一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.(1)求证:△ABF∽△FCE;(2)若AB=4,AD=8,求CE的长.33.(2022秋•南京期末)如图,在矩形ABCD中,点E,F分别在边BC,CD 上,AE,BF交于点G.(1)若=,求证AE⊥BF;(2)若E,F分别是BC,CD的中点,则的值为.34.(2023•桐乡市校级开学)如图,已知△ABC和△AED,边AB,DE交于点F,AD平分∠BAC,AF平分∠EAD,.(1)求证:△AED∽△ABC;(2)若BD=3,BF=2,求AB的长.35.(2022秋•海陵区校级期末)如图,矩形DEFG的四个顶点分别在等腰三角形ABC的边上.已知△ABC的AB=AC=10,BC=16,记矩形DEFG的面积为S,线段BE为x.(1)求S关于x的函数表达式;(2)当S=24时,求x的值.36.(2022秋•平城区校级期末)如图,已知在△ABC中,边BC=6,高AD=3,正方形EFGH的顶点F,G在边BC上,顶点E,H分别在边AB和AC上,求这个正方形的边长.。
数轴动点问题6题型

数轴动点问题6题型数轴动点问题是指在数轴上有一系列的点,然后通过一系列的规则或运算,使得这些点按一定的顺序进行移动。
在这些题型中,我们需要掌握一些基本的数学知识,如坐标表示、数轴上的运算等。
下面,我将为大家介绍六个不同类型的数轴动点问题。
一、给定一个数轴上的点A,求它关于原点的对称点B的坐标。
解法:对于给定的点A,我们可以通过计算其与原点的距离来求得它的对称点B。
对称点B的坐标可以表示为-x,其中x是点A的坐标。
例如,给定点A(3),那么对称点B的坐标为-3。
二、给定一个数轴上的点A,求它关于点B的对称点C的坐标。
解法:对于给定的点A,我们可以通过计算它与点B的距离,再将这个距离取负数,从而求得它的对称点C的坐标。
例如,给定点A(2)和点B(4),那么点C的坐标可以表示为2 * (4 - 2) = -2。
三、给定一个数轴上的点A和点B,求它们的中点C的坐标。
解法:对于给定的两个点A和B,我们可以通过它们的坐标求得它们的中点C的坐标。
中点C的坐标可以表示为(x1 + x2) / 2,其中x1和x2分别是点A和点B的坐标。
例如,给定点A(3)和点B(7),那么中点C的坐标可以表示为(3 +7) / 2 = 5。
四、给定一个数轴上的点A和点B,求它们之间的距离。
解法:对于给定的两个点A和B,我们可以通过它们的坐标求得它们之间的距离。
距离可以用绝对值来表示,在数轴上两个点的距离为|x1 - x2|,其中x1和x2分别是点A和点B的坐标。
例如,给定点A(3)和点B(7),那么它们之间的距离为|3 - 7| = 4。
五、给定一个数轴上的点A和一个正整数n,求点A向右移动n个单位后的坐标。
解法:对于给定的点A和一个正整数n,要求点A向右移动n个单位后的坐标,只需要将点A的坐标增加n。
例如,给定点A(5)和n=3,那么点A向右移动3个单位后的坐标为5 + 3 = 8。
六、给定一个数轴上的点A和一个正整数n,求点A向左移动n个单位后的坐标。
巧用运算规律简化有理数计算的六种方法(含答案)

巧用运算规律简化有理数计算的六种方法【题型1 归类法】【例1】阅读下面的解题过程并解决问题计算:53.27﹣(﹣18)+(﹣21)+46.73﹣(+15)+21解:原式=53.27+18﹣21+46.73﹣15+21(第一步)=(53.27+46.73)+(21﹣21)+(18﹣15)(第二步)=100+0+3(第三步)=103(1)计算过程中,第一步把原式化成的形式,体现了数学中的思想,为了计算简便,第二步应用了.(2)根据以上的解题技巧进行计算下列式子:−2123+314−(−23)−(+14).【分析】(1)根据有理数的加减混合运算步骤及运算定律可得答案;(2)仿照题意简便方法计算即可.【解答】解:(1)计算过程中,第一步把原式化成省略加号和括号的形式,体现了数学中的转化思想,为了计算简便,第二步应用了加法的交换律和结合律.故答案为:省略加号和括号,转化,加法的交换律和结合律;(2)−2123+314−(−23)−(+14) =﹣2123+314+23−14=(﹣2123+23)+(+314−14) =﹣21+3 =﹣18.【变式1-1】计算:(−23)+(516)+(−416)−913. 【分析】可利用结合律进行运算,最后得出结果.【解答】解:原式=(−23−913)+(516−416)=﹣10+1=﹣9 【变式1-2】计算:123+212−334+13−4.25.【分析】先算同分母分数,再相加即可求解; 【解答】解:123+212−334+13−4.25=(123+13)+212+(﹣334−4.25) =2+212−8=﹣312;【变式1-3】计算:3712+(﹣114)+(﹣3712)+114+(﹣418).【分析】先算同分母分数,再相加即可求解. 【解答】解:3712+(﹣114)+(﹣3712)+114+(﹣418)=(3712−3712)+(﹣114+114)+(﹣418)=0+0+(﹣418) =﹣418.【题型2 凑整法】将相加可得整数的数凑整,将相加得零的数(如互为相反数)相消. 【例2】计算:(﹣347)+12.5+(﹣1637)﹣(﹣2.5)【分析】运用加法的交换律和结合律计算可得. 【解答】解:原式=(﹣347−1637)+(12.5+2.5)=﹣20+15 =﹣5.【变式2-1】计算下列各题:(1)20.36+(﹣1.4)+(﹣13.36)+1.4; (2)(+325)+(﹣278)﹣(﹣535)+(−18).【分析】根据加法的运算律计算即可.【解答】解:(1)原式=(20.36﹣13.36)+(1.4﹣1.4)=7+0=7; (2)原式=(325+535)−(278+18)=9﹣3=6. 【变式2-2】计算:(1)(﹣0.1)﹣(﹣4.6)﹣(+8.9)+(+5.4) (2)(﹣1.75)﹣(﹣234)+(﹣345)﹣(﹣145)【分析】(1)根据有理数的加减运算法则计算即可; (2)根据有理数的加减运算法则计算即可. 【解答】解:(1)原式=﹣(0.1+8.9)+(4.6+5.4) =﹣9+10 =1;(2)原式=(﹣1.75+234)+(﹣345)+145=+(234−1.75)−(345−145) =1﹣2 =﹣1.【变式2-3】计算下列各题:(1)(0.5)+(+92)+(−192)+9.5; (2)(−12)+(−25)+(+32)+(185)+(+395);(3)﹣1.5+1.4﹣(﹣3.6)﹣4.3+(﹣5.2);(4)(﹣3.5)+(−43)+(−34)+(+72)+0.75+(−73).【分析】(1)应用加法交换律和结合律将两个小数和两个分数分别结合在一起计算; (2)先运用减法法则,再将分母相同的结合起来进行计算; (3)将正负数分别结合计算;(4)小数化分数,分母相同的结合计算. 【解答】解:(1)原式=(0.5+9.5)+(92−192)=10﹣5=5;(2)原式=−12−25+32+185+395=(32−12)+(185+395−25)=1+11=12;(3)原式=﹣1.5+1.4+3.6﹣4.3﹣5.2=(1.4+3.6)+(﹣1.5﹣4.3﹣5.2)=5﹣11=﹣6; (4)原式=−72−43−34+72+34−73=(72−72)+(34−34)+(−43−73)=−113. 【题型3 逆向法】【例3】计算:−52×(−115)+133×(−115)+56×2.2. 【分析】先变形,然后根据乘法分配律可以解答本题. 【解答】解:−52×(−115)+133×(−115)+56×2.2 =52×115−133×115+56×115 =(52−133+56)×115=(156−266+56)×115 =(﹣1)×115=−115.【变式3-1】计算:235×127+2.6÷711−135×67.【分析】先将题目式子中的带分数化为假分数,小数化为假分式,然后根据乘法分配律即可解答本题. 【解答】解:235×127+2.6÷711−135×67=135×97+135×117−135×67 =135×(97+117−67) =135×147 =265.【变式3-2】计算:−13×23−0.34×27+13×(−13)−57×0.34【分析】分别提取公因数﹣13和﹣0.34,即可简化计算,再合并即可; 【解答】解:−13×23−0.34×27+13×(−13)−57×0.34 =﹣13×(23+13)﹣0.34×(27+57)=﹣13﹣0.34 =﹣13.34【变式3-3】计算:0.7×149+234×(−15)+0.7×59+14×(−15); 【分析】根据乘法分配律可以解答本题;【解答】解:0.7×149+234×(−15)+0.7×59+14×(−15) =0.7×(149+59)+(234+14)×(﹣15)=0.7×2+3×(﹣15) =1.4+(﹣45) =﹣43.6; 【题型4 拆项法】【例4】阅读下面的计算过程,体会“拆项法” 计算:﹣556+(−923)+1734+(−312).解:原式=[(−5)+(−9)+17+(−3)]+[(−56)+(−23)+34+(−12)]=0+(−114)=(−114) 启发应用用上面的方法完成下列计算:(−3310)+(−112)+235−(212) 【分析】将原式利用“拆项法”得出原式=(﹣3﹣1+2﹣2)+(−310−12+35−12),再根据有理数的加减运算法则计算可得.【解答】解:原式=(﹣3﹣1+2﹣2)+(−310−12+35−12) =﹣4+(−710) =﹣4710.【变式4-1】阅读下列解题方法,然后根据方法计算.﹣516−(﹣923)=[(﹣5)﹣(﹣9)]+[(−16)﹣(−23)]=4+12=412.计算:(﹣201956)+(﹣201823)+4037+112【分析】利用加法的结合律,将整数、分数分别结合在一起先相加,运算简便. 【解答】解:(﹣201956)+(﹣201823)+4037+112=[(﹣2019)+(﹣2018)]+[(−56)+(−23)]+4037+112=﹣4037+(−32)+4037+32 =0【变式4-2】计算:﹣991517×34.【分析】根据乘法分配律简便计算. 【解答】解:﹣991517×34=(﹣100+217)×34 =﹣100×34+217×34 =﹣3400+4 =﹣3396.【变式4-3】计算:399498399×(−6) 【分析】根据乘法分配律简便计算. 【解答】解:399498399×(−6)=(400+33133)×(﹣6)=400×(﹣6)+33133×(﹣6)=﹣2400﹣165133=﹣240165133.【题型5 组合法】【例5】计算:1﹣3+5﹣7+9﹣11+…+97﹣99【分析】把原式写成(1﹣3)+(5﹣7)+(9﹣11)+…+(97﹣99),一个有25个﹣2,据此计算即可.【解答】解:原式=(1﹣3)+(5﹣7)+(9﹣11)+…+(97﹣99)=(﹣2)×25=﹣50.【变式5-1】计算:1﹣2+3﹣4+…+97﹣98+99.【分析】原式结合后,相加即可得到结果.【解答】解:原式=1+(﹣2+3)+(﹣4+5)+…+(﹣98+99)=1+1+…+1=50.【变式5-2】计算:1﹣2﹣3+4+5﹣6﹣7+8+…+2013﹣2014﹣2015+2016.【分析】原式四项四项结合,计算即可得到结果.【解答】解:1﹣2﹣3+4+5﹣6﹣7+8+…+2013﹣2014﹣2015+2016=(1﹣2﹣3+4)+(5﹣6﹣7+8)+…+(2009﹣2010﹣2011+2012)+(2013﹣2014﹣2015+2016)=0.【变式5-3】计算:1+2﹣3﹣4+5+6﹣7﹣8+9+10﹣11﹣12+…+2005+2006﹣2007﹣2008.【分析】将4个数字作为一组,分组计算即可.【解答】解:1+2﹣3﹣4+5+6﹣7﹣8+9+10﹣11﹣12+…+2005+2006﹣2007﹣2008=(1+2﹣3﹣4)+(5+6﹣7﹣8)+(9+10﹣11﹣12)+…+(2005+2006﹣2007﹣2008)=﹣4+(﹣4)+…+(﹣4)=﹣4×502=﹣2008.【题型6 裂项相消法】算变得简洁.【例6】阅读材料,回答下列问题. 通过计算容易发现: ①12−13=12×13;②14−15=14×15;③16−17=16×17(1)观察上面的三个算式,请写出一个像上面这样的算式: 17−18=17×18;(2)通过观察,计算11×2+12×3+13×4+14×5+15×6+16×7的值. (3)探究上述的运算规律,试计算11×3+13×5+15×7+17×9+19×11+⋯+197×99的值.【分析】(1)观察①②③三个算式,可知分母中两个乘数的差为1,分子的差也为1,直接写出一个类似的算式即可;(2)根据上述规律得原式=1−12+12−13+13−14+14−15+15−16+16−17,计算即可得出答案; (3)所给算式分母中两个乘数的差为2,但分子的差为1,故前面乘以12,则可以用裂项法进行计算.【解答】解:(1)17−18=17×18;故答案为:17−18=17×18;(2)11×2+12×3+13×4+14×5+15×6+16×7=1−12+12−13+13−14+14−15+15−16+16−17 =1−17=67; (3)11×3+13×5+15×7+17×9+19×11+⋯+197×99的值.=12(1−13+13−15+15−17+17−19+19−111+⋯+197−199) =12(1−199) =12×9899 =4999. 【变式6-1】12+13=2+32×3=56;13+14=3+43×4=712;14+15=4+54×5=920(1)请在理解上面计算方法的基础上,把下面两个数表示成两个分数的和的形式(分别写出表示的过程和结果)1342= = ,1772= = .(2)利用以上所得的规律进行计算:32−56+712−920+1130−1342+1556−1772【分析】(1)直接利用已知运算规律进而计算得出答案; (2)直接利用已知运算规律将原式变形进而计算得出答案. 【解答】解:(1)1342=16+17=6+76×7;1772=18+19=8+98×9;故答案为:16+17,6+76×7;18+19,8+98×9;(2)32−56+712−920+1130−1342+1556−1772=1+12−(12+13)+(13+14)﹣(14+15)+(15+16)﹣(16+17)+(17+18)﹣(18+19)=1−19 =89.【变式6-2】类比推理是一种重要的推理方法,根据两种事物在某些特征上相似,得出它们在其他特征上也可能相似的结论.在异分母的分数的加减法中,往往先化作同分母,然后分子相加减,例如:12−13=32×3−23×2=3−26=16,我们将上述计算过程倒过来,得到16=12×3=12−13,这一恒等变形过程在数学中叫做裂项.类似地,对于12×4可以用裂项的方法变形为:12×4=12×(12−14).类比上述方法,解决以下问题. (1)猜想并写出:1n(n+1)= .(2)探究并计算下列各式: ①11×2+12×3+13×4+⋅⋅⋅+149×50;②1−2×4+1−4×6+1−6×8+⋅⋅⋅+1−2018×2020.【分析】(1)根据题意和题目中的例子,可以解答本题;(2)①根据题目中的例子和式子的特点,可以求得所求式子的值; ②根据题目中的例子和式子的特点,可以求得所求式子的值. 【解答】解:(1)1n(n+1)=1n−1n+1,故答案为:1n −1n+1;(2)①11×2+12×3+13×4+⋅⋅⋅+149×50=1−12+12−13+13−14+⋯+149−150 =1−150=4950; ②1−2×4+1−4×6+1−6×8+⋅⋅⋅+1−2018×2020=−12×(12−14+14−16+16−18+⋯+12018−12020)=−12×(12−12020)=−12×10092020 =−10094040. 【变式6-3】阅读理解题 第1个等式:12=2−12×1=1−12; 第2个等式:16=3−23×2=12−13;第3个等式:112=4−34×3=13−14;……观察以上等式,请解答下列问题:(1)按以上规律列出第5个等式: ; (2)计算:11×5+15×9+19×13+⋯⋯+12017×2021.【分析】(1)仿照已知等式得到第5个等式即可; (2)原式利用得出的规律变形,计算即可求出值. 【解答】解:(1)第5个等式:130=6−56×5=15−16;(2)11×5+15×9+19×13+⋯⋯+12017×2021=14×(1−15+15−19+19−113+⋯⋯+12017−1 2021)=14×(1−12021)=14×20202021=5052021.故答案为:130=6−56×5=15−16.11。
2022年河南中考英语总复习题型组合练6(阅读理解+任务性阅读+完形填空+补全对话)

一、阅读理解[2020天津]Summer Fun at Happy Kids' Learning CentreAre you looking for something that can add colour to your summer holiday? If yes, here are the summer courses that you cannot miss!Children Can CookThe course is to improve children's knowledge in the kitchen.They will learn basic cooking skills, kitchen safety, and how to buy proper ingredients and follow steps in recipes. Children can sit comfortably and eat what they have cooked at the end of each lesson.Little WritersThe course is divided into two parts.In the first part, children are introduced to famous stories and their writers.In the second part, they are taught to write their own stories.Children also get the chance to write other text types, such as poems and plays.Acting for FunThis is a course that lets children enjoy the fun of acting.Through acting and speaking in front of people, children will be more confident.Parents are welcome to watch the performance given by the children at the end of the course.Watercolour PaintingThis course teaches children the basic skills of paintingpeople and animals.We encourage children to watch,imagine andcreate their own works.根据材料内容选择最佳答案。
三角函数专题三角函数中ω的取值范围问题(6大题型)(原卷版)

三角函数专题:三角函数中ω的取值范围问题一、求ω取值范围的常用解题思路 1、依托于三角函数的周期性因为f(x)=Asin(ωx +φ)的最小正周期是T =2π|ω|,所以ω=2πT,也就是说只要确定了周期T ,就可以确定ω的取值. 2、利用三角函数的对称性(1)三角函数两条相邻对称轴或两个相邻对称中心之间的“水平间隔”为T2,相邻的对称轴和对称中心之间的“水平间隔”为T4,也就是说,我们可以根据三角函数的对称性来研究其周期性,进而可以研究ω的取值。
(2)三角函数的对称轴比经过图象的最高点或最低点,函数的对称中心就是其图象与x 轴的交点(零点),也就是说我们可以利用函数的最值、零点之间的“差距”来确定其周期,进而可以确定ω的取值.3、结合三角函数的单调性函数f (x )=Asin(ωx +φ)的每一“完整”单调区间的长度(即两相邻对称轴的间距)恰好等于T 2,据此可用来求ω的值或范围。
反之,从函数变换的角度来看ω的大小变化决定了函数图象的横向伸缩,要使函数f (x )=Asin(ωx +φ)在指定区间上具有单调性,我们忘完可以通过调整周期长度来实现,犹如通过弹簧的伸缩来抬举三角函数在区间上的单调性和最值等。
二、已知函数y =Asin(ωx +φ)在给定区间上的单调性,求ω的取值范围已知函数y =Asin(ωx +φ)(A >0,ω>0),在[x 1,x 2]上单调递增(或递减),求ω的取值范围 第一步:根据题意可知区间[x 1,x 2]的长度不大于该函数最小正周期的一半,即x 2−x 1≤12T =πω,求得0<ω≤πx2−x 1.第二步:以单调递增为例,利用[ωx 1+φ,ωx 2+φ]⊆[−π2+2kπ,π2+2kπ],解得ω的范围; 第三步:结合第一步求出的ω的范围对k 进行赋值,从而求出ω(不含参数)的取值范围. 三、结合图象平移求ω的取值范围 1、平移后与原图象重合思路1:平移长度即为原函数周期的整倍数;思路2:平移前的函数()f x =平移后的函数()g x .2、平移后与新图象重合:平移后的函数()f x =新的函数()g x .3、平移后的函数与原图象关于y 轴对称:平移后的函数为偶函数;4、平移后的函数与原函数关于x 轴对称:平移前的函数()f x =平移后的函数()g x ;5、平移后过定点:将定点坐标代入平移后的函数中。
2021年广东省深圳市中考拉分题型专项训练6--书面表达

拉分题型专项训练6——书面表达(一)假定你是李华。
你的英国笔友Tom需要完成一个关于“中国龙文化”的课前小演讲,他来信向你咨询,请你用英语给他回信。
要点:1. 龙的象征意义:幸运,权力等;2. 相关节庆活动:赛龙舟等;3. 相关成语或习语。
参考词汇:the descendants of the dragon 龙的传人要求:1. 80词以上,短文的开头已给出,不计入总词数;2. 条理清楚,意思连贯,语句通顺,标点正确;3. 文中不得使用真实的校名与姓名。
Dear Tom,Thanks for your interesting question about the role of dragons in Chinese culture.I did a little research and here are some facts that may be helpful.Yours,Lihua 范文:Dear Tom,Thanks for your interesting question about the role of dragons in Chinese culture.I did a little research and here are some facts that may be helpful.Historically, legend says that Chinese are descendants of dragons, which symbolize good luck and highest power. As a result, only the emperor could wear garments featuring dragon designs in ancient China. Ordinary people shared the dragons’ blessings through celebrations, such as the Duanwu Festival’s dragon boat races and dragon dances performed during Chinese New Year.Dragons have also entered our daily vocabulary. “I wish you the spirit and vigor of a dragon” is one common idiom used to convey wishes for good health. I hope this information is useful for your presentation. If you have further questions, feel free to ask.Yours,Lihua目前,许多中学生利用周末和节假日上课外补习班,对此人们有不同的看法。
专题06 一元一次方程(归纳与讲解)(解析版)

专题06 一元一次方程【专题目录】技巧1:巧用一元一次方程求字母系数的值技巧2:特殊一元一次方程的解法技巧【题型】一、一元一次方程概念【题型】二、一元一次方程的解法【题型】三、一元一次方程应用之配套问题和工程问题【题型】四、一元一次方程应用之销售盈亏问题【题型】五、一元一次方程应用之比赛积分问题【考纲要求】1、了解等式、方程、一元一次方程的概念,掌握等式的基本性质.2、掌握一元一次方程的标准形式,熟练掌握一元一次方程的解法.3、会列方程(组)解决实际问题.【考点总结】一、一元一次方程【注意】一元一次方程的特征1.只含有一个未知数x2.未知数x的次数都是13.等式两边都是整式,分母中不含未知数。
2.解一元一次方程的一般步骤:(1)去分母;(2)去括号; (3)移项; (4)合并同类项; (5)未知数的系数化为1. 【技巧归纳】技巧1:巧用一元一次方程求字母系数的值【类型】一、利用一元一次方程的定义求字母系数的值1.已知方程(m -2)x |m|-1+16=0是关于x 的一元一次方程,求m 的值及方程的解. 2.已知方程(3a +2b)x 2+ax +b =0是关于x 的一元一次方程,求方程的解.3.已知(m 2-1)x 2-(m +1)x +8=0是关于x 的一元一次方程,求式子199(m +x)(x -2m)+9m +17的值.【类型】一、利用方程的解求字母系数的值 题型1:利用方程的解的定义求字母系数的值4.关于x 的方程a(x -a)+b(x +b)=0有无穷多个解,则( )A .a +b =0B .a -b =0C .ab =0D .ab =05.关于x 的方程(2a +b)x -1=0无解,则ab 是( )A .正数B .非正数C .负数D .非负数6.已知关于x 的方程9x -3=kx +14有整数解,那么满足条件的整数k =__________. 7.已知x =12是方程6(2x +m)=3m +2的解,求关于y 的方程my +2=m(1-2y)的解.8.当m 取什么整数时,关于x 的方程12mx -53=12⎝⎛⎭⎫x -43的解是正整数? 题型2:利用两个方程同解或解具有已知倍数关系确定字母系数的值9.如果方程x -43-8=-x +22的解与关于x 的方程2ax -(3a +5)=5x +12a +20的解相同,确定字母a 的值.题型3:利用方程的错解确定字母系数的值10.小马虎解方程2x -13=x +a2-1,去分母时,方程右边的-1忘记乘6,其他步骤都正确,这时方程的解为x =2,试求a 的值,并正确解方程. 参考答案1.解:由题意,得⎩⎪⎨⎪⎧|m|-1=1,m -2≠0,所以m =-2.将m =-2代入原方程,得-4x +16=0,解得x =4.2.解:由题意,得⎩⎪⎨⎪⎧3a +2b =0,a≠0,所以3a =-2b ,即a =-23b.当3a +2b =0时,原方程可化为ax +b =0,则x =-ba .将a =-23b 代入方程的解中,得x =-b a =32.3.解:由题意,得⎩⎪⎨⎪⎧m 2-1=0,m +1≠0,所以m =1.当m =1时,原方程可化为-2x +8=0,解得x =4.当m =1,x =4时,199(m +x)(x -2m)+9m +17=199×5×2+9×1+17=2 016. 4.A 5.B 6.8,-8,10或267.解:将x =12代入方程6(2x +m)=3m +2,得6⎝⎛⎭⎫2×12+m =3m +2,解得m =-43. 将m =-43代入方程my +2=m(1-2y),得-43y +2=-43(1-2y),解得y =56.点拨:已知一元一次方程的解,确定关于某一个未知数的方程中另外一个字母的值,只需把未知数的值(方程的解)代入原方程,即可得出含另一个字母的方程,通过求解确定另一个字母的值,从而进行关于其他字母的计算.8.解:原方程可化为12mx -53=12x -23,所以12(m -1)x =1,所以(m -1)x =2.因为x 必须为正整数且m 为整数,故m -1=1或2.当m -1=1,即m =2时,x =2; 当m -1=2,即m =3时,x =1.所以当m =2或3时,方程的解为正整数. 9.解:x -43-8=-x +22,去分母,得2(x -4)-48=-3(x +2).去括号、移项、合并同类项,得5x =50.系数化为1,得x =10.把x =10代入方程2ax -(3a +5)=5x +12a +20, 得2a×10-(3a +5)=5×10+12a +20, 去括号、移项,得20a -3a -12a =5+50+20. 合并同类项,得5a =75,系数化为1,得a =15. 10.解:由题意得4x -2=3x +3a -1,移项、合并同类项,得x =3a +1. 因为x =2,所以2=3a +1,则a =13.当a =13时,原方程为2x -13=x +132-1,解得x =-3.技巧2:特殊一元一次方程的解法技巧【类型】一、分子、分母含小数的一元一次方程 题型1:巧化分母为11.解方程:4x -1.60.5-3x -5.40.2=1.8-x0.1.2.解方程:2x +10.25-x -20.5=-10.题型2:巧化同分母3.解方程:x 0.6-0.16-0.5x0.06=1.题型3:巧约分去分母4.解方程:4-6x 0.01-6.5=0.02-2x0.02-7.5.【类型】二、分子、分母为整数的一元一次方程 题型1:巧用拆分法5.解方程:x -12-2x -36=6-x3.6.解方程:x 2+x 6+x 12+x20=1.题型2:巧用对消法7.解方程:x 3+x -25=337-6-3x15.题型3:巧通分8.解方程:x +37-x +25=x +16-x +44.【类型】三、含括号的一元一次方程 题型1:利用倒数关系去括号9.解方程:32⎣⎡⎦⎤23⎝⎛⎭⎫x 4-1-2-x =2. 题型2:整体合并去括号10.解方程:x -13⎣⎡⎦⎤x -13(x -9)=19(x -9). 题型3:整体合并去分母11.解方程:13(x -5)=3-23(x -5).题型4:不去括号反而添括号12.解方程:12⎣⎡⎦⎤x -12(x -1)=23(x -1). 题型5:由外向内去括号13.解方程:13⎣⎡⎦⎤14⎝⎛⎭⎫13x -1-6+2=0. 题型6:由内向外去括号14.解方程:2⎣⎡⎦⎤43x -⎝⎛⎭⎫23x -12=34x. 参考答案1.解:去分母,得2(4x -1.6)-5(3x -5.4)=10(1.8-x).去括号、移项、合并同类项,得3x =-5.8. 系数化为1,得x =-2915.点拨:本题将各分数分母化为整数1,从而巧妙地去掉了分母,给解题带来了方便 . 2.解:去分母、去括号,得8x +4-2x +4=-10.移项、合并同类项,得6x =-18. 系数化为1,得x =-3.点拨:由0.25×4=1,0.5×2=1,可巧妙地将分母化为整数1. 3.解:化为同分母,得0.1x 0.06-0.16-0.5x 0.06=0.060.06.去分母,得0.1x -0.16+0.5x =0.06. 解得x =1130.4.解:原方程可化为4-6x 0.01+1=0.01-x0.01.去分母,得4-6x +0.01=0.01-x. 解得x =45.点拨:本题将第二个分数通过约分处理后,使两个分数的分母相同,便于去分母.5.解:拆项,得x 2-12-x 3+12=2-x3.移项、合并同类项,得x2=2.系数化为1,得x =4.点拨:方程通过拆项处理后,便于合并同类项,使复杂方程简单化. 6.解:拆项,得⎝⎛⎭⎫x -x 2+⎝⎛⎭⎫x 2-x 3+⎝⎛⎭⎫x 3-x 4+⎝⎛⎭⎫x 4-x5=1. 整理得x -x 5=1.解得x =54.点拨:因为x 2=x -x 2,x 6=x 2-x 3,x 12=x 3-x 4,x 20=x 4-x5,所以把方程的左边每一项拆项分解后再合并就很简便 .7.解:原方程可化为x 3+x -25=247+x -25,即x 3=247.所以x =727. 点拨:此题不要急于去分母,通过观察发现-6-3x 15=x -25,两边消去这一项可避免去分母运算.8.解:方程两边分别通分后相加,得5(x +3)-7(x +2)35=2(x +1)-3(x +4)12.化简,得-2x +135=-x -1012.解得x =-36211.点拨:本题若直接去分母,则两边应同乘各分母的最小公倍数420,运算量大容易出错,但是把方程左右两边分别通分后再去分母,会给解方程带来方便. 9.解:去括号,得x4-1-3-x =2.移项、合并同类项,得-34x =6.系数化为1,得x =-8.点拨:观察方程特点,由于32与23互为倒数,因此让32乘以括号内的每一项,则可先去中括号,同时又去小括号,非常简便.10.解:原方程可化为x -13x +19(x -9)-19(x -9)=0.合并同类项,得23x =0.系数化为1,得x =0.11.解:移项,得13(x -5)+23(x -5)=3.合并同类项,得x -5=3.解得x =8.点拨:本题将x -5看成一个整体,通过移项、合并同类项进行解答,这样避免了去分母,给解题带来简便.12.解:原方程可化为12[(x -1)+1-12(x -1)]=23(x -1).去中括号,得12(x -1)+12-14(x -1)=23(x -1).移项、合并同类项,得-512(x -1)=-12.解得x =115.13.解:去中括号,得112⎝⎛⎭⎫13x -1-2+2=0.[来源:学科网] 去小括号,得136x -112=0.移项,得136x =112.系数化为1,得x =3.14.解:去小括号,得2[43x -23x +12]=34x.去中括号,得43x +1=34x.移项,合并同类项,得712x =-1.系数化为1,得x =-127.【题型讲解】【题型】一、一元一次方程概念例1、关于x 的一元一次方程224a x m -+=的解为1x =,则a m +的值为( ) A .9 B .8C .5D .4【详解】解:因为关于x 的一元一次方程2x a -2+m=4的解为x=1, 可得:a -2=1,2+m=4, 解得:a=3,m=2, 所以a+m=3+2=5, 故选:C .【题型】二、一元一次方程的解法例2、解一元一次方程11(1)123x x +=-时,去分母正确的是( )A .3(1)12x x +=-B .2(1)13x x +=-C .2(1)63x x +=-D .3(1)62x x +=-【答案】D【分析】根据等式的基本性质将方程两边都乘以6可得答案. 【详解】解:方程两边都乘以6,得:3(x +1)=6﹣2x ,故选:D . 例3、解方程:221123x x x ---=-【答案】27x =【分析】去分母、去括号、移项、合并同类项、系数化为1,依此即可求解. 【详解】解:221123x x x ---=-()()6326221x x x --=--636642x x x -+=-+ 634662x x x -+=-+ 72x =27x =【题型】三、一元一次方程应用之配套问题和工程问题例4、某车间有22名工人,每人每天可生产1200个螺钉或2000个螺母,1个螺钉需配2个螺母,为使生产的螺钉和螺母刚好配套,若设x 名工人生产螺钉,依题意列方程为( ) A .1200x =2000(22﹣x ) B .1200x =2×2000(22﹣x ) C .1200(22﹣x )=2000x D .2×1200x =2000(22﹣x )【答案】D【分析】首先根据题目中已经设出每天安排x 个工人生产螺钉,则(22-x )个工人生产螺母,由1个螺钉需要配2个螺母①可知螺母的个数是螺钉个数的2倍①从而得出等量关系,就可以列出方程. 【详解】解:设每天安排x 个工人生产螺钉,则(22-x )个工人生产螺母,利用一个螺钉配两个螺母.由题意得:2×1200x=2000①22-x ),即2×1200x=2000①22-x①①故选D① 【题型】四、一元一次方程应用之销售盈亏问题例5、随着传统节日“端午节”临近,某超市决定开展“欢度端午,回馈顾客”的活动,将进价为120元一盒的某品牌粽子按标价的8折出售,仍可获利20%,则该超市该品牌粽子的标价为__元.( )A .180B .170C .160D .150【答案】A【分析】设该超市该品牌粽子的标价为x 元,则售价为80%x 元,根据等量关系:利润=售价﹣进价列出方程,解出即可.【详解】解:设该超市该品牌粽子的标价为x 元,则售价为80%x 元, 由题意得:80%x ﹣120=20%×120, 解得:x =180.即该超市该品牌粽子的标价为180元. 故选:A .【题型】五、一元一次方程应用之比赛积分问题例6、一张试卷有25道选择题,做对一题得4分,做错一题得-1分,某同学做完了25道题,共得70分,那么他做对的题数是( ) A .17道 B .18道C .19道D .20道【答案】C【分析】设作对了x 道,则错了(25-x )道,根据题意列出方程进行求解. 【详解】设作对了x 道,则错了(25-x )道,依题意得4x -(25-x)=70,解得x=19 故选C.一元一次方程(达标训练)一、单选题1.(2020·浙江·模拟预测)下列各式:①253-+=;①235=3x x x -+;①211x +=;①21=x;①23x +;①4x =.其中是一元一次方程的有( ) A .1个 B .2个C .3个D .4个【答案】B【分析】根据一元一次方程的定义逐个判断即可 【详解】解:①不含未知数,故错 ①未知数的最高次数为2,故错①含一个未知数,次数为1,是等式且两边均为整式,故对 ①左边不是整式,故错 ①不是等式,故错①含一个未知数,次数为1,是等式且两边均为整式,故对故选:B【点睛】本题考查了一元一次方程的定义,熟练掌握并理解一元一次方程的定义是解本题的关键2.(2022·浙江温州·三模)解方程2233522x x x x x --+=--,以下去分母正确的是( )A .22335x x x ---=B .22335x x x --+=C .()223352x x x x ---=-D .()223352x x x x --+=-【答案】D【分析】利用等式的性质在分式方程两边分别乘()2x - 即可.【详解】A ,()223352,x x x x +--=-故此选项不符合题意. B ,()223352,x x x x +--=-故此选项不符合题意. C ,()223352,x x x x +--=-故此选项不符合题意. D ,()223352,x x x x +--=-故此选项符合题意.故选:D .【点睛】本题主要考查了解分式方程去分母,根据等式的性质在分式方程两边分别乘以分母的最简公分母,熟练掌握等式的性质是解此题的关键.3.(2022·重庆沙坪坝·一模)若关于x 的方程25x a +=的解是2x =,则a 的值为( ) A .9- B .9 C .1- D .1【答案】D【分析】把2x =代入方程计算即可求出a 的值. 【详解】解:把2x =代入方程得:45a +=, 解得1a =. 故选:D .【点睛】本题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值. 4.(2022·河北石家庄·二模)1x =是下列哪个方程的解( ) A .65x =- B .2233+=+x xC .21133x x x x -=-- D .2x x =【答案】D【分析】把x =1代入各选项进行验算即可得解. 【详解】解:A 、5−1=4≠6,故本选项错误; B 、2124⨯+=,3136⨯+=,4≠6,故本选项错误; C 、当x =1时,x -1=0即分式的分母为0,故本选项错误;D 、211=,故本选项正确. 故选:D .【点睛】本题考查了方程的解的概念,使方程的左右两边相等的未知数的值是方程的解. 5.(2022·广东·佛山市南海外国语学校三模)我国古代的《洛书》中记载了最早的三阶幻方—九宫图.在如图所示的幻方中,每一横行、每一竖列以及两条对角线上的数字之和都相等,则m 的值是( )A .5B .3C .1-D .2-【答案】A【分析】根据幻方中,每一横行、每一竖列以及两条对角线上的数字之和都相等列出方程,即可求解. 【详解】解:设幻方正中间的数字为a , 依题意得:124a m a ++=++, 解得:5m =. 故选A .【点睛】此题考查了一元一次方程的应用,正确理解题意是解题的关键.二、填空题6.(2022·四川达州·二模)方程2x -3=5的解为________. 【答案】x =4【分析】根据解一元一次方程的解法求解即可得. 【详解】解:2x -3=5, 移项得2x =8, 系数化为1得:x =4, 故答案为:x =4.【点睛】题目主要考查解一元一次方程,熟练掌握方法是解题关键.7.(2022·四川广元·二模)已知:A ,B 在数轴上对应的数分别用a ,b 表示,且2(4)|12|0a b ++-=.若点C 点在数轴上且满足3AC BC =,则C 点对应的数为________. 【答案】8或20##20或8【分析】先根据非负数的性质求出a ,b 的值,分C 点在线段AB 上和线段AB 的延长线上两种情况讨论,即可求解.【详解】解:①2(4)|12|0a b ++-= ①a +4=0,b −12=0 解得:a =−4,b =12①A 表示的数是−4,B 表示的数是12 设数轴上点C 表示的数为c ①AC =3BC ①|c +4|=3|c −12| 当点C 在线段AB 上时 则c +4=3(12−c ) 解得:c =8当点C 在AB 的延长线上时 则c +4=3(c −12) 解得:c =20综上可知:C 对应的数为8或20.【点睛】本题考查了非负数的性质,方程的解法,数轴两点之间的距离,运用分类讨论思想方程思想和数形结合思想是解本题的关键.三、解答题8.(2022·四川广元·一模)解方程:2(1)13x x x --=-. 【答案】12x =-【分析】先去括号,再移项,合并同类项,最后把未知数的系数化“1”,从而可得答案. 【详解】解:去括号,得2213x x x -+=-. 移项及合并同类项,得21x =-. 系数化为1,得12x =-.【点睛】本题考查的是一元一次方程的解法,掌握“解一元一次方程的步骤”是解本题的关键. 9.(2022·湖南·长沙市长郡双语实验中学二模)“小口罩,大温暖”,为有效防控疫情,缓解基层防疫物资短缺问题,2020年2月10日,福山区首批4万只口罩免费派发.烟台市政府紧急调拨的这批民用口罩包括A ,B 两种不同款型,其中A 型口罩单价100元,B 型口罩单价80元.(1)先进行试点发放,某社区环卫工人共收到A ,B 两种款型的口罩100盒,总价值共计9200元,求免费发放给该社区环卫工人的A 型口罩和B 型口罩各多少盒?(2)我区某街道办事处决定将此项公益活动在其整个街道社区全面铺开,按照试点发放中A,B两种款型的数量比共发放2000盒.若该社区人口平均每500人发放A型口罩m盒,B型口罩(328m-)盒.求该街道社区人口总数.【答案】(1)免费发放给该社区环卫工人的A型口罩60盒,B型口罩40盒(2)该街道社区人口总数为50000人【分析】(1)设免费发放给该社区环卫工人的A型口罩x盒,B型口罩y盒,根据题意,列出方程,即可求解;(2)根据题意可得3286040m m-=,从而得到m=12,即可求解.(1)解:设免费发放给该社区环卫工人的A型口罩x盒,B型口罩y盒,依题意得:100100809200x yx y+=⎧⎨+=⎩,解得:6040xy=⎧⎨=⎩.答:免费发放给该社区环卫工人的A型口罩60盒,B型口罩40盒.(2)解:依题意得:328 6040m m-=,解得:m=12,①m+3m−28=20.①该街道社区人口总数=200020×500=50000(人).答:该街道社区人口总数为50000人.【点睛】本题主要考查了一元一次方程的应用,二元一次方程组的应用,明确题意,准确得到等量关系是解题的关键.一元一次方程(提升测评)一、单选题1.(2022·湖北十堰·一模)《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数,羊价各是多少?如果我们设合伙人数为x ,则可列方程( ) A .54573x x +=+ B .54573x x -=-C .45357x x +=+D .45357x x-=+【答案】A【分析】根据每人出5钱,还差45钱;若每人出7钱,还差3钱,可以列出相应的一元一次方程,本题得以解决.【详解】解:设合伙人数为x ,则可列方程为 54573x x +=+;故选:A【点睛】本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程. 2.(2022·浙江温州·二模)若代数式()()2132x x +++的值为8,则代数式()()2231x x -+-的值为( ) A .0 B .11 C .7- D .15-【答案】C【分析】由()()2132x x +++的值为8,求得x =0,再将x =0代入计算可得. 【详解】解:①()()2132x x +++的值为8, ①2x +2+3x +6=8, ①x =0,当x =0时,()()2231x x -+-=2×(-2)+3×(-1)=-7. 故选:C .【点睛】本题考查了解一元一次方程,代数式的求值,掌握解一元一次方程的解法是解题的关键. 3.(2022·河北·石家庄市第四十一中学模拟预测)已知m n =,下列等式不成立的是( ) A .2m n m += B .0-=m n C .22m x n x -=- D .235m n n -=【答案】D【分析】根据等式的性质和合并同类项即可判断. 【详解】由m n =,得2m n m m m +=+=,故A 成立; 0m n m m -=-=,故B 成立;根据等式的性质,等式两边同加或减一个等式,左右两边仍相等,22m x n x -=-,故C 成立;2323m n n n n -=-=-,故D 不成立;故选D .【点睛】本题考查了等式的性质和合并同类项,熟记运算法则是解题的关键.4.(2022·河北保定·一模)已知分式:341()()32a a a a -+---■的某一项被污染,但化简的结果等于2a +,被污染的项应为( ) A .0 B .1 C .23a a -- D .32a a -- 【答案】B【分析】设被污染的部分为p ,然后根据等式的性质解关于p 的方程,求出p 的表达式即可. 【详解】解:设被污染的部分为p , 则341()()232a a p a a a -+-=+--, ①241()232a p a a a --=+--, ①()()()132222a p a a a a --=+⨯--+, ①3122a p a a -=+--, ①22a p a -=-, ①1p =. 故选:B .【点睛】本题主要考查了分式的混合运算和利用等式的性质解一元一次方程,解题的关键是根据等式的性质解方程和掌握分式混合运算顺序和运算法则. 5.(2022·重庆·三模)下列四种说法中正确的有( ) ①关于x 、y 的方程24107x y +=存在整数解.①若两个不等实数a 、b 满足()()244222a b a b +=+,则a 、b 互为相反数.①若2()4()()0a c a b b c ---=-,则2b a c =+. ①若222x yz y xz z xy ---==,则x y z ==. A .①① B .①① C .①①① D .①①①【答案】B【分析】将24x y +提公因式2得2(2)x y +,由x 、y 为整数,则2(3)x y +为偶数,因为107为奇数,即原等式不成立,即可判断①;将442222()()a b a b +=+,整理得222()0a b -=,即得出22a b =,由于实数a 、b 不相等,即得出a 、b 互为相反数,故可判断①;2()4()()0a c a b b c ---=-整理得2(2)0a c b +-=,即得20a c b +-=,即2a c b +=,故可判断①;由222x yz y xz z xy ---==,得出2222x xz y yz y xy z xz ⎧+=+⎨+=+⎩,即可变形为222211()()2211()()22x z y z y x z x ⎧+=+⎪⎪⎨⎪+=+⎪⎩,可以得出x y z ==或0x y z ++=,故可判断①. 【详解】解:①262(3)x y x y +=+, ①如果x 、y 为整数,那么2(3)x y +为偶数, ①107为奇数,①24107x y +=不存在整数解,故①错误; 442222()()a b a b +=+444422222a b a b a b +++=442220a b a b +-=222()0a b -=①22a b =,①实数a 、b 不相等,①a 、b 互为相反数,故①正确; 2()4()()0a c a b b c ---=-222244440a ac c ab ac b bc -+-++-=()()22440a c b a c b +-++=2(2)0a c b +-=①20a c b +-=,即2a c b +=,故①正确; ①222x yz y xz z xy ---==①2222x xz y yzy xy z xz ⎧+=+⎨+=+⎩, ①2222222211441144x xz z y yz z y xy x z xz x ⎧++=++⎪⎪⎨⎪++=++⎪⎩,即222211()()2211()()22x z y z y x z x ⎧+=+⎪⎪⎨⎪+=+⎪⎩,①11()2211()22x z y z y x z x ⎧+=±+⎪⎪⎨⎪+=±+⎪⎩,①x y z ==或0x y z ++=,故①不一定正确. 综上可知正确的有①①.故选B.【点睛】本题考查因式分解,整式的混合运算.熟练掌握完全平方公式是解题关键.二、填空题6.(2022·山东临沂·一模)如图,用一块长7.5cm、宽3cm的长方形纸板,和一块长6cm、宽1.5cm 的长方形纸板,与一块小正方形纸板以及另两块长方形纸板,恰好拼成一个大正方形,则小正方形的边长是______cm,拼成的大正方形的面积是______cm2.【答案】 4.581【分析】设小正方形的边长为x cm,然后表示出大正方形的边长,利用正方形的面积相等列出方程求得小正方形的边长,然后求得大正方形的边长即可求得面积.【详解】解:设小正方形的边长为x cm,则大正方形的边长为(6+7.5-x)cm或(x+3+1.5)cm,根据题意得:6+7.5-x=x+3+1.5,解得:x=4.5,则大正方形的边长为6+7.5-x=6+7.5-4.5=9(cm),大正方形的面积为92=81(cm2),故答案为:4.5;81.【点睛】此题主要考查了一元一次方程的应用,关键是正确理解题意,设出小正方形的边长并表示出大正方形的边长.7.(2022·上海静安·1=的解是________.【答案】x=1【分析】首先方程两边同时平方,把无理方程化为有理方程,再解方程即可求得【详解】解:方程两边同时平方,得3x-2=1,解得x=1,经检验,x=1是原方程的解,所以,原方程的解为x=1.故答案为:x=1.【点睛】本题考查了无理方程的解法,熟练掌握和运用无理方程的解法是解决本题的关键,注意要检验.三、解答题8.(2022·河北·育华中学三模)如图,数轴上a 、b 、c 三个数所对应的点分别为A 、B 、C ,已知b是最小的正整数,且a 、c 满足2(6)20c a -++=.(1)①直接写出数a 、c 的值 , ; ①求代数式222a c ac +-的值;(2)若将数轴折叠,使得点A 与点C 重合,求与点B 重合的点表示的数; (3)请在数轴上确定一点D ,使得AD =2BD ,则D 表示的数是 . 【答案】(1)①-2,6;①64 (2)3 (3)4或0【分析】(1)①根据平方和绝对值的非负性即可求出a 和c ,①把a 和c 的值代入222a c ac +-求值即可;(2)根据题意,求出b 的值,然后求出线段AC 的中点,即可求出结论;(3)设点D 表示的数为x ,然后根据点D 的位置分类讨论,分别根据2AD BD =列出方程即可分别求出结论. (1) 解:①①()2620c a -++=, ①20a +=,60c -=, 解得2a =-,6c =. 故答案为:-2,6.①把2a =-,6c =代入222a c ac +-,2224362464a c ac +-=++=;(2)解:①b 是最小的正整数,①1b =,①线段AC 的中点为()2622-+÷=,设与点B 重合的点表示的数为n ,则(1+n )÷2=2, 解得:n =3.①与点B 重合的点表示的数是3. 故答案为:3. (3)解:因为a =-2,b =1,c =6,设点D 表示的数为x ,若2AD BD =,分三种情况讨论: ①若点D 在点A 的左侧,则x <-2且()221x x --=-, 解得4x =(不符合题意,舍去);①若点D 在点A 、B 之间,则-2<x <1且()()221x x --=-, 解得0x =;①若点D 在点B 右侧,则x >1且x -(-2)=2(x -1), 解得:x =4.综上所述,点D 表示的数是0或4. 故答案为:0或4.【点睛】此题考查了非负性的应用、数轴上两点之间的距离、中点公式和一元一次方程的应用,解题的关键是掌握平方、绝对值的非负性、数轴上两点之间的距离公式、中点公式和等量关系.。
2022届新高考二轮复习新题型专项练习6——读后续写(人与动物)

2022届新高考二轮复习新题型专项练习6——读后续写(人与动物)1. 阅读下面材料,根据其内容和所给段落开头语续写两段,使之构成一篇完整的短文。
I took a job as a receptionist for a veterinarian(兽医) almost five decades ago. As an enthusiastic animal lover, I accepted the position on condition that I wouldn't have to assist with any wounded animals. I couldn't bear to see any creature in pain. At the end of my first week, we were closing the office for the day when a young man ran up to us holding a severely injured Doberman puppy in his arms and begging us to save his life. The four-month-old pup had been hit by a car.The doctor and I ran back into the operating room. The only place the skin was still attached to this poor little animal's body was around one shoulder. The vet worked tirelessly for what seemed like hours, stitching(缝合) him back together again. That was the easy part. The puppy had broken multiple bones, including his spine (脊柱). Even if he survived the next few days, we were quite sure he would never walk again.That day forever changed my life. The veterinarian guided me, and I became his assistant in all things. One of my first jobs was to give that Doberman puppy daily physical care. I remembered moving his tiny legs to try to keep his muscles from withering (萎缩). Weeks went by until one day, I felt this little fighter push back ever so slightly. And he continued to push back till he could finally use his legs. He recovered.A year later, I walked into the clinic's waiting room and saw a huge Doberman who had been standing quietly with his owner on the opposite side of the room. I called the name of the next client.注意:续写词数应为150左右。
三角函数的图象与性质6大题型

三角函数的图象与性质6大题型三角函数的图象与性质是高考的热点,函数sin()y A x ωϕ=+的图象变换以及三角函数的周期性、对称性、单调性之间逻辑关系则是重心。
随着新高考改革的推进,更加注重对以周期性为核心的三大性质之间的逻辑关系的考查,要求考生能用几何直观和代数运算来研究三角函数。
高考中的相关试题多以选择题、填空题的形式考查,难度中等或偏下。
一、三角函数性质问题相关方法1、周期的计算公式:函数)0()cos(),sin(>+=+=ωϕωϕωx A y x A y 的周期为ωπ2=T ,函数)0()tan(>+=ωϕωx A y 的周期为ωπ=T 求解.2、奇偶性的判断方法:三角函数中奇函数一般可化为x A y ωsin =或x A y ωtan =的形式,而偶函数一般可化为b x A y +=ωcos 的形式.3、解决对称性问题的关键:熟练掌握三角函数的对称轴、对称中心.方法:整体处理法、代入验证法对于函数)0()cos(),sin(>+=+=ωϕωϕωx A y x A y ,其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此在判断直线0x x =或点)0,(0x 是否是函数的对称轴或对称中心时,可通过检验)(0x f 的值进行判断.4、确定函数)0,0()sin(>>+=ωϕωA x A y 单调区间的方法采用“换元”法整体代换,将‘ϕω+x ’看作一个整体,可令“ϕω+=x z ”,即通过求z A y sin =的单调区间而求出函数的单调区间.若0<ω,则可利用诱导公式先将x 的系数转变为正数,再求单调区间.二、三角函数图形变换问题解决三角函数图像变换问题的两种方法分别为先平移后伸缩和先伸缩后平移.破解此类题的关键如下:1、定函数:一定要看准是将哪个函数的图像变换得到另一个函数的图像.2、变同名:函数的名称要一样.3、选方法:即选择变换方法.要注意:对于函数)0(sin >=ωωx y 的图像,向左平移ϕ个单位长度得到的是函数)(sin ϕω+=x y 的图象,而不是函数)sin(ϕω+=x y 的图像.【题型1【例1】(2023·湖南湘潭·统考二模)函数2cos2()sin xf x x+=的部分图象大致为()A .B .C .D .【变式1-1】(2023秋·云南·高三云南师大附中校考阶段练习)函数()21sin 2f x x x x =-的图象大致为()A .B .C .D .【变式1-2】(2022秋·河南·高三校联考阶段练习)函数()cos e =xf x 的部分图象大致为()A .B .C .D .【变式1-3】(2022秋·云南·高三校联考阶段练习)函数()cos ln xf x x xππ+=⋅-在(),ππ-上的图象大致为()A .B .C .D .【变式1-4】(2022秋·四川遂宁·高三遂宁中学校考阶段练习)函数()(tan sin 2)22x x y x x -=--的部分图象大致为()A .B .C .D .【题型2根据图象求三角函数解析式】【例2】(2023秋·湖南怀化·高三统考期末)已知函数()2cos()(0)f x x ωϕω=+>的部分图象如图所示,则()0f =()A .1B .1-CD .【变式2-1】(2022秋·贵州铜仁·高三校考阶段练习)已知A ,B ,C ,D ,E 是函数sin()y x ωϕ=+0,02πωϕ⎛⎫><< ⎪⎝⎭一个周期内的图像上的五个点,如图,A ,06π⎛⎫- ⎪⎝⎭,B 为y 轴上的点,C 为图像上的最低点,E 为该函数图像的一个对称中心,B 与D 关于点E 对称,CD 在x 轴上的投影为12π,则ωφ,的值为()A .2ω=,3πϕ=B .2ω=,6πϕ=C .12ω=,3πϕ=D .12ω=,6πϕ=【变式2-2】(2023秋·山西太原·高三山西大附中校考阶段练习)函数()sin()(0,0)f x x ωϕωϕπ=+><<的部分图象如图,BC x ∥轴,当π0,4x ⎡⎤∈⎢⎥⎣⎦时,若不等式()sin 2f x m x ≥-恒成立,则m 的取值范围是()A.⎛-∞ ⎝⎦B .1,2⎛⎤-∞ ⎥⎝⎦C .(-∞D .(],1-∞【变式2-3】(2023秋·北京朝阳·高三统考期末)已知函数π()sin()0,||2ωϕωϕ⎛⎫=+>< ⎪⎝⎭f x x ,若()()1g x f x ⋅=,且函数()g x 的部分图象如图所示,则ϕ等于()A .π3-B .π6-C .π6D .π3【变式2-4】(2023·全国·模拟预测)(多选)已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,若将()f x 的图象向右平移()0m m >个单位长度后得到函数()()sin 2g x A x ωϕ=-的图象,则m 的值可以是()A .π4B .π3C .4π3D .9π4【题型3三角函数图象变换问题】【例3】(2023秋·江西赣州·高三统考期末)函数()()sin f x x ωϕ=+(其中0ω>,π2ϕ<)的图象如图所示,为了得到cos y x ω=的图象,只需把()y f x =的图象上所有点()A .向左平移π6个单位长度B .向右平移π12个单位长度C .向左平移π12个单位长度D .向右平移π6个单位长度【变式3-1】(2022·四川·高三统考对口高考)为了得到函数sin 24y x π⎛⎫=+ ⎪⎝⎭的图象,只需把函数sin 24y x π⎛⎫=- ⎪⎝⎭的图象上所有的点()A .向左平移4π个单位B .向右平移4π个单位C .向左平移2π个单位D .向右平移2π个单位【变式3-2】(2022·陕西汉中·统考一模)为得到函数cos 23y x π⎛⎫=+ ⎪⎝⎭的图象,只需将sin2y x =的图象()A .向左平移512π个单位长度B .向右平移512π个单位长度C .向左平移23π个单位长度D .向右平移23π个单位长度【变式3-3】(2023秋·江苏南通·高三统考期末)已知函数π()3sin (0)6f x x ωω⎛⎫-> ⎪⎝⎭的图象向左平移()0ϕϕ>个单位长度后与其导函数()y f x '=的图象重合,则()f ϕ的值为()A .0B .32C .62D .32【变式3-4】(2022·全国·模拟预测)已知函数()3sin cos f x x x =-的图象向左平移ϕ(0ϕ>)个单位长度后得到()f x 的导函数()f x '的图象,则()f ϕ=()A .3-B .3C .1D .1-【变式3-5】(2023·河南信阳·河南省信阳市第二高级中学校联考一模)将函数()sin 2c 2πos π63f x x x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭图象上的所有点的横坐标缩短为原来的12(纵坐标不变),然后再将其图象向左平移()0θθ>单位得到图象()g x ,若函数()g x 图象关于y 轴对称,则θ的最小值为()A .π3B .π6C .π12D .π24【题型4三角函数的四种性质】【例4】(2023秋·河南南阳·高三统考期末)已知函数()()()sin cos f x x x ϕϕ=+++是偶函数,则3sin 2cos 2sin 3cos ϕϕϕϕ-=+______.【变式4-1】(2023秋·河北邢台·高三邢台市第二中学校考期末)函数9cos 24y x π⎛⎫=- ⎪⎝⎭的单调递减区间为______.【变式4-2】(2022秋·辽宁沈阳·高三沈阳市第一二〇中学校考期中)已知函数()tan tan f x x x =+,则下列结论中正确的是()A .()f x 的最小正周期为π2B .点π,02⎛⎫- ⎪⎝⎭是()f x 图象的一个对称中心C .()f x 的值域为[)0,∞+D .不等式()2f x >的解集为()ππ2,2πZ 42k k k π⎛⎫++∈ ⎪⎝⎭【变式4-3】(2023·四川内江·统考一模)已知函数()()1sin cos sin (0)2f x x x x ωωωω=-+>,若函数()f x 在π,π2⎛⎫⎪⎝⎭上单调递减,则ω不能取()A .23B .13C .58D .14【变式4-4】(2023秋·江苏南通·高三统考期末)(多选)设函数()()sin f x x ωϕ=+,x ∈R ,其中0ω>,3πϕ<.若1409f π⎛⎫-= ⎪⎝⎭,419f π⎛⎫=⎪⎝⎭,且()f x 的最小正周期大于52π,则()A .14ω=B .6πϕ=C .()f x 在()2,3ππ上单调递增D .()f x 在()0,3π上存在唯一的极值点【变式4-5】(2023·安徽淮南·统考一模)(多选)已知函数()()πsin ,12,2f x x ωϕωϕ⎛⎫=+<<< ⎪⎝⎭图像过点10,2⎛⎫- ⎪⎝⎭,且存在12,x x ,当122πx x -=时,()()120f x f x ==,则()A .()f x 的周期为4π3B .()f x 图像的一条对称轴方程为5π9x =-C .()f x 在区间4π10π,99⎡⎤⎢⎣⎦上单调递减D .()f x 在区间()0,5π上有且仅有4个极大值点【变式4-6】(2023秋·湖北·高三统考期末)(多选)已知函数()2sin sin 2f x x x =,则下列说法正确的是()A .π是()f x 的一个周期B .()f x 的图象关于点π,02⎛⎫⎪⎝⎭中心对称C .()f x 在区间[]0,2π上的零点个数为4D .()f x 的最大值为8【变式4-7】(2023春·浙江·高三校联考开学考试)(多选)已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭,则()A .()0f =B .()f x 的最小正周期为π2C .()f x 在π0,6⎛⎫⎪⎝⎭上单调递减D .()f x 在π,06⎛⎫- ⎪⎝⎭上单调递增【题型5三角函数的最值问题】【例5】(2022秋·北京·高三北京市八一中学校考阶段练习)定义运算,,,.a a b a b b a b ≤⎧=⎨>⎩※例如,121=※,则函数()sin cos f x x x =※的值域为()A .1,2⎡⎤-⎢⎥⎣⎦B .22⎡⎤⎢⎥⎣⎦C .2,12⎡⎤⎢⎥⎣⎦D .22⎡-⎢⎣⎦【变式5-1】(2023秋·湖南株洲·已知定义域为R 的函数(),()f x g x 满足()()πf x f x +=-,且()()cos π,g x x f x =++()()sin πf x x g x =-+,则当π0,4x ⎡⎤∈⎢⎥⎣⎦时,函数()()y f x g x =的最小值为()A .0B .2CD .38【变式5-2】(2022秋·安徽·高三石室中学校联考阶段练习)如图是函数()cos()(0)f x x ωϕω=+>的部分图象,则()f x 在,9045⎡⎤-⎢⎥⎣⎦π22π上的值域为()A .[]1,1-B .1322⎡⎢⎣⎦C .11,2⎡⎤-⎢⎥⎣⎦D .32⎡-⎢⎣⎦【变式5-3】(2023·河北衡水·河北衡水中学校考模拟预测)函数()25cos 4sin 53cos f x x x x -+的最大值为().A .22B .23C .5D .3【变式5-4】(2023秋·北京丰台·高三统考期末)已知函数π()sin (0)6f x x ωω⎛⎫=+>⎪⎝⎭,若ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,且()f x 在区间ππ,62⎛⎫⎪⎝⎭上有最小值无最大值,则ω=___________.【变式5-4】(2020秋·吉林白城·高三校考阶段练习)已知向量1(cos ,)2a x = ,(3,cos 2),Rb x x x =∈,设函数()f x a b =⋅ .(1)求()f x 的最小正周期;(2)求()f x 在π[0,]2上的最大值和最小值.【题型6三角函数的零点问题】【例6】(2022·四川宜宾·统考模拟预测)若函数()π2sin 213f x x ⎛⎫=+- ⎪⎝⎭,则()f x 在区间[]0,2π上零点的个数是_______.【变式6-1】(2023·全国·高三对口高考)已知0ω>,函数()πsin 16f x x ω⎛⎫=+- ⎪⎝⎭在区间[]0,π上有且仅有两个零点,则ω的取值范围是________.【变式6-2】(2022秋·河南濮阳·高三统考阶段练习)已知函数5π()cos (0)6f x x ωω⎛⎫=-> ⎪⎝⎭在π0,4⎛⎫⎪⎝⎭上有且仅有1个零点,则实数ω的取值范围为______.【变式6-3】(2023秋·福建宁德·高三校考阶段练习)若函数()1cos42f x x x m =-+-在π04⎡⎤⎢⎥⎣⎦,上存在两个零点,则实数m 的取值范围为()A .3522⎛⎤ ⎥⎝⎦,B .3522⎡⎫⎪⎢⎣⎭,C.1522⎛⎤+ ⎥⎝⎦,D.1522⎡⎫+⎪⎢⎪⎣⎭,【变式6-4】(2023秋·山西·高三校联考阶段练习)已知函数()()221sin 2π,,3213,,x a x a f x x a x a x a ⎧⎡⎤⎛⎫-+<⎪ ⎪⎢⎥=⎝⎭⎨⎣⎦⎪-+++≥⎩.若()f x 在()0,∞+上恰好有5个零点,则a 的取值范围是()A .411,36⎡⎫⎪⎢⎣⎭B .411717,,3636⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦C .1167,3⎡⎫⎪⎢⎣⎭D .43117,,3263⎛⎤⎛⎤⋃ ⎝⎦⎝⎦【变式6-5】(2022秋·广西桂林·高三校考阶段练习)已知定义在R 上的函数()y f x =是偶函数,当0x ≥时,()2sin ,01213,122x x x f x x π⎧≤≤⎪⎪=⎨⎛⎫⎪+> ⎪⎪⎝⎭⎩,若关于x 的方程()()()20,R f x af x b a b ++=∈⎡⎤⎣⎦,有且仅有6个不同实数根,则实数a 的取值范围是()A .34,2⎛⎫-- ⎪⎝⎭B .74,2⎛⎫-- ⎪⎝⎭C .7734,222⎛⎫⎛⎫--⋃-- ⎪⎝⎭⎝⎭D .324,1,27⎛⎫⎛⎫--⋃-- ⎪ ⎪⎝⎭⎝⎭【变式6-6】(2023秋·山东烟台·高三统考期末)已知定义在R 上的函数()f x 满足:2f x π⎛⎫- ⎪⎝⎭为偶函数,且()()8sin ,021,02x x f x f x x ππ⎧--≤≤⎪⎪=⎨⎪->⎪⎩;函数()lg 2g x x π=+,则当[]4,3x ππ∈-时,函数()()y f x g x =-的所有零点之和为()A .7π-B .6π-C .72π-D .3π-(建议用时:60分钟)1.(2022秋·河北唐山·高三开滦第二中学校考阶段练习)将函数()π3cos (0)6f x x ωω⎛⎫=+> ⎪⎝⎭的图象向右平移π6ω个单位长度,得到函数()g x 的图象,若函数()y g x =在π3π,24⎡⎤⎢⎥⎣⎦上单调递增,则ω的最大值为()A .2B .83C .103D .42.(2022秋·广西钦州·高三校考阶段练习)已知函数()()sin f x x ϕ=-且2cos πcos 3ϕϕ⎛⎫-= ⎪⎝⎭,则函数()f x 的图象的一条对称轴是()A .5π6x =B .7π12x =C .π3x =D .π6x =3.(2023·四川绵阳·统考模拟预测)函数()πcos()0,||2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图像如图所示,且()302f =.则下列选项正确的是()A .π3ϕ=-B .π122f ⎛⎫=-⎪⎝⎭C .()f x 在区间2π,π3⎡⎤⎢⎥⎣⎦上为减函数D .()102f f ⎛⎫> ⎪⎝⎭4.(2023·全国·高三专题练习)已知函数π()2sin (0)6f x x ωω⎛⎫=-> ⎪⎝⎭在[]0,π上单调递增,且2π()3f x f ⎛⎫≥-⎪⎝⎭恒成立,则ω的值为()A .2B .32C .1D .125.(2022·四川成都·成都市第二十中学校校考一模)已知函数()πsin 23f x x ⎛⎫=- ⎪⎝⎭,则下列结论不正确的是()A .π为函数()f x 的一个周期B .2π,03⎛⎫⎪⎝⎭是函数()f x 图象的一个对称中心C .函数()f x 在区间[],a a -上单调递增,则实数a 的最大值为5π12D .将函数()f x 的图象向右平移π12个单位长度后,得到一个偶函数的图象6.(2022·河北衡水·衡水市第二中学校考一模)已知()()()π2tan 0,,02f x x f ωϕωϕ⎛⎫=+><= ⎪⎝,周期π3ππ,,446T ⎛⎫⎛⎫∈ ⎪ ⎪⎝⎭⎝⎭是()f x 的对称中心,则π3f ⎛⎫⎪⎝⎭的值为()A .BC D .3-7.(2023秋·山东东营·高三东营市第一中学校考期末)(多选)关于函数2()cos 4cos 1f x x x =++,下列说法正确的是()A .函数()f x 在π3π,42⎡⎤⎢⎥⎣⎦上的最大值为6B .函数()f x 在π3π,42⎡⎤⎢⎥⎣⎦上的最小值为-2C .函数()f x 在π,02⎛⎫- ⎪⎝⎭上单调递增D .函数()f x 在π0,2⎛⎫⎪⎝⎭上单调递减8.(2022秋·河北唐山·高三开滦第二中学校考阶段练习)(多选)设()sin 22cos f x x x =+,x ∈R ,则().A .()f x 在区间[]0,2π上有2个零点B .()f x 的单调递增区间为π7ππ,π26k k ⎛⎫++⎪⎝⎭,k ∈Z C .()f x 的图象关于直线ππ3x k =+对称D .()f x 的值域为0,2⎡⎢⎣⎦9.(2023·湖南长沙·统考一模)已知函数()()()2sin 0f x x ωϕω=+>,若函数()f x 的图象关于点π,06⎛⎫⎪⎝⎭中心对称,且关于直线π3x =轴对称,则ω的最小值为______.10.(2022秋·四川遂宁·高三校考阶段练习)已知函数()()7ππsin 12f x x x ⎛⎫=---+ ⎪⎝⎭则函数()f x 的对称中心_________11.(2021·上海浦东新·华师大二附中校考模拟预测)已知函数23()sin sin cos (,,0)2f x a x x x a b a b a =-+<,(1)若当π0,2x ⎡⎤∈⎢⎥⎣⎦时,函数()f x 的值域为[]5,1-,求实数,a b 的值;(2)在(1)条件下,求函数()f x 图像的对称中心和单调区间.12.(2023秋·江苏扬州·高三校联考期末)已知函数()()(0,0f x x ωϕωϕ=+><<sin π的最小正周期为π,且直线π2x =-是其图像的一条对称轴.(1)求函数()f x 的解析式;(2)将函数()y f x =的图像向右平移π4个单位,再将所得的图像上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图像对应的函数记作()y g x =,已知常数R λ∈,*n ∈N ,且函数()()212sin F x x g x λ=-+在()0,πn 内恰有2021个零点,求常数λ与n 的值.参考答案【题型1三角函数的图象辨析】【例1】(2023·湖南湘潭·统考二模)函数2cos2()sin xf x x+=的部分图象大致为()A .B .C .D .【答案】A【解析】()f x 的定义域为{}π,Z x x k k ≠∈,关于原点对称,因为2cos(2)2cos2()()sin()sin x xf x f x x x+-+-==---,所以()f x 为奇函数,故排除C,D ,又π102f ⎛⎫=> ⎪⎝⎭,所以排除B,故选:A【变式1-1】(2023秋·云南·高三云南师大附中校考阶段练习)函数()21sin 2f x x x x =-的图象大致为()A .B .C .D .【答案】A【解析】()f x 的定义域为R ,2211()()()sin()sin ()22f x x x x x x x f x -=----=-=,所以()f x 为偶函数,图象关于y 轴对称,排除C ,D 选项;()21ππ02f =>,排除B 选项.所以A 选项正确.故选:A【变式1-2】(2022秋·河南·高三校联考阶段练习)函数()cos e =xf x 的部分图象大致为()A .B .C .D .【答案】C【解析】由题意得函数定义域为R ,且()()()cos cos ee --===x xf x f x ,∴()f x 为偶函数,故排除选项B ,∵()()cos e2πe xf x f k =≤=,Z k ∈,()0e f =为最大值,∴排除选项D ,∵()()()cos 2πcos 2πee x xf x f x ++===,∴()f x 是2π为周期的周期函数,∴排除选项A.故选:C【变式1-3】(2022秋·云南·高三校联考阶段练习)函数()cos ln xf x x xππ+=⋅-在(),ππ-上的图象大致为()A .B .C .D .【答案】B【解析】因为()()cos lnxf x x f x xππ--=⋅=-+,所以f (x )是奇函数,排除A ,D ,当0,2x π⎛⎫∈ ⎪⎝⎭时,cos 0x >,ln0xxπ+>π-,所以()0f x >,排除C ,故选:B .【变式1-4】(2022秋·四川遂宁·高三遂宁中学校考阶段练习)函数()(tan sin 2)22x x y x x -=--的部分图象大致为()A .B .C .D .【答案】A【解析】由题得函数的定义域为π{|π,}2x x k k Z ≠+∈,定义域关于原点对称.设()()(tan sin 2)22x xf x x x -=--,所以()()(tan sin 2)22x x f x x x --=-+-()(tan sin 2)22()x xx x f x -=--=,所以函数()f x 是偶函数,其图象关于y 轴对称,排除选项D.又(π)=0f ,所以排除选项B.当π2x →时,tan ,sin 20,x x →+∞→()220x x-->,所以此时()0f x >.故选:A【题型2根据图象求三角函数解析式】【例2】(2023秋·湖南怀化·高三统考期末)已知函数()2cos()(0)f x x ωϕω=+>的部分图象如图所示,则()0f =()A .1B .1-CD .【答案】C【解析】观察函数图象得,函数()f x 的周期413()3123T πππ=-=,则22Tπω==,而13212f π⎛⎫= ⎪⎝⎭,即13cos 16πϕ⎛⎫+= ⎪⎝⎭,则有132,Z 6k k πϕπ+=∈,因此132Z 6k k πϕπ=-∈,即有13()2cos(22)2cos(2)66f x x k x πππ=+-=-,所以()02cos()6f π=-故选:C【变式2-1】(2022秋·贵州铜仁高三校考阶段练习)已知A ,B ,C ,D ,E 是函数sin()y x ωϕ=+0,02πωϕ⎛⎫><< ⎪⎝⎭一个周期内的图像上的五个点,如图,A ,06π⎛⎫- ⎪⎝⎭,B 为y 轴上的点,C 为图像上的最低点,E 为该函数图像的一个对称中心,B 与D 关于点E 对称,CD在x 轴上的投影为12π,则ωφ,的值为()A .2ω=,3πϕ=B .2ω=,6πϕ=C .12ω=,3πϕ=D .12ω=,6πϕ=【答案】A【解析】因B 与D 关于点E 对称,CD 在x 轴上的投影为12π,则B 与图像最高点(最靠近B 点)连线所对应向量在x 轴上的投影为12π,又A ,06π⎛⎫- ⎪⎝⎭,则A 与图像最高点(最靠近B 点)连线对应向量在x 轴上的投影为πππ6124+=,故函数最小正周期为24πππ=4ω⨯=,又0ω>,则2ω=.又因函数图像过点,06π⎛⎫- ⎪⎝⎭,则2ππ,Z 3φk k -+=∈,得2ππ,Z 3φk k =+∈,又02πϕ<<,则0k =,得π3ϕ=.综上,有2ω=,π3ϕ=.故选:A【变式2-2】(2023秋·山西太原·高三山西大附中校考阶段练习)函数()sin()(0,0)f x x ωϕωϕπ=+><<的部分图象如图,BC x ∥轴,当π0,4x ⎡⎤∈⎢⎥⎣⎦时,若不等式()sin 2f x m x ≥-恒成立,则的取值范围是()A .⎛-∞ ⎝⎦B .1,2⎛⎤-∞ ⎥⎝⎦C .(-∞D .(],1-∞【答案】A【解析】因为//BC x 轴,所以()f x 图象的一条对称轴方程为1π2π7π()22312x =+=,所以7πππ41234T =-=,则πT =,所以2π2T ω==,又π2π2π3k ϕ⨯+=+,Z k ∈,且0πϕ<<,所以π3ϕ=,故π()sin(23f x x =+,因为当π[0,]4x ∈时,不等式()sin 2f x m x ≥-恒成立,所以π3π()sin 2sin(2)sin 2sin 2cos 2sin(2)3226m f x x x x x x x ≤+=++=++,令()π26g x x ⎛⎫=+ ⎪⎝⎭,因为π0,4x ⎡⎤∈⎢⎥⎣⎦,则ππ2π2,663x ⎡⎤+∈⎢⎥⎣⎦,所以π1sin 2,162x ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦所以π())6g x x +的最小值为2,所以2m ≤,即m ⎛∈-∞ ⎝⎦.故选:A .【变式2-3】(2023秋·北京朝阳·高三统考期末)已知函数π()sin()0,||2ωϕωϕ⎛⎫=+>< ⎪⎝⎭f x x ,若()()1g x f x ⋅=,且函数()g x 的部分图象如图所示,则ϕ等于()A .π3-B .π6-C .π6D .π3【答案】B【解析】由图可知,函数()g x 过点π,13⎛⎫⎪⎝⎭和点5π,16⎛⎫- ⎪⎝⎭,即π135π16g g⎧⎛⎫= ⎪⎪⎪⎝⎭⎨⎛⎫⎪=- ⎪⎪⎝⎭⎩,又因为()()1g x f x ⋅=,所以π135π16f f ⎧⎛⎫= ⎪⎪⎪⎝⎭⎨⎛⎫⎪=- ⎪⎪⎝⎭⎩,结合正弦型函数的性质可知,5ππ263T =-,解得πT =,所以2ππω=,解得2ω=±,因为0ω>,所以2ω=所以()sin(2)f x x ϕ=+,所以πsin(2)13ϕ⨯+=,即2ππ2π32k ϕ+=+,Z k ∈解得π2π6k ϕ=-+,Zk ∈因为π||2ϕ<,所以π6ϕ=-,故选:B.【变式2-4】(2023·全国·模拟预测)(多选)已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,若将()f x 的图象向右平移()0m m >个单位长度后得到函数()()sin 2g x A x ωϕ=-的图象,则m 的值可以是()A .π4B .π3C .4π3D .9π4【答案】AD【解析】由图象可知:2A =,最小正周期5ππ4π126T ⎛⎫=⨯-=⎪⎝⎭,2π2T ω∴==,ππ2sin 263f ϕ⎛⎫⎛⎫∴=+= ⎪ ⎪⎝⎭⎝⎭,()ππ2π32k k ϕ∴+=+∈Z ,解得:()π2π6k k ϕ=+∈Z ,又π2ϕ<,π6ϕ∴=,()π2sin 26f x x ⎛⎫∴=+ ⎪⎝⎭,()π2sin 23g x x ⎛⎫=- ⎪⎝⎭,()()π2sin 226f x m x m g x ⎛⎫-=-+= ⎪⎝⎭ ,()ππ22π63m k k ∴-+=-+∈Z ,解得:()ππ4m k k =-∈Z ,当0k =时,π4m =;当2k =-时,9π4m =.故选:AD.【题型3三角函数图象变换问题】【例3】(2023秋·江西赣州·高三统考期末)函数()()sin f x x ωϕ=+(其中0ω>,π2ϕ<)的图象如图所示,为了得到cos y x ω=的图象,只需把()y f x =的图象上所有点()A .向左平移π6个单位长度B .向右平移π12个单位长度C .向左平移π12个单位长度D .向右平移π6个单位长度【答案】C【解析】由图象可知,712344Tπππ-==,所以T π=,又因为2T πω=,所以2ω=,所以()()sin 2f x x ϕ=+,又因为771,sin 211212f ππϕ⎛⎫⎛⎫=-∴⨯+=-⎪ ⎪⎝⎭⎝⎭,又||2ϕπ<,所以,3πϕ=所以()sin 2cos 2cos 2cos 2332612f x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=+=+-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭又因为()cos 2g x x =,所以只需把()y f x =的图象上所有点向左平移π12个单位长度可得()cos 2g x x=的图象.故选:C.【变式3-1】(2022·四川·高三统考对口高考)为了得到函数sin 24y x π⎛⎫=+ ⎪⎝⎭的图象,只需把函数sin 24y x π⎛⎫=- ⎪⎝⎭的图象上所有的点()A .向左平移4π个单位B .向右平移4π个单位C .向左平移2π个单位D .向右平移2π个单位【答案】A【解析】依题意,sin(2)sin(2)sin[2()]42444y x x x πππππ=+=+-=+-,所以把函数sin 24y x π⎛⎫=- ⎪⎝⎭图象上所有的点向左平移4π个单位可以得到函数sin 24y x π⎛⎫=+ ⎪⎝⎭的图象,A 正确.故选:A 【变式3-2】(2022·陕西汉中·统考一模)为得到函数cos 23y x π⎛⎫=+ ⎪⎝⎭的图象,只需将sin2y x =的图象()A .向左平移512π个单位长度B .向右平移512π个单位长度C .向左平移23π个单位长度D .向右平移23π个单位长度【答案】A【解析】555cos 2cos 2sin 2sin 2362612y x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+=+-=+=+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦故可由sin2y x =的图象向左平移512π个单位长度得到.故选:A.【变式3-3】(2023秋·江苏南通·高三统考期末)已知函数π()sin (0)6f x x ωω⎛⎫-> ⎪⎝⎭的图象向左平移()0ϕϕ>个单位长度后与其导函数()y f x '=的图象重合,则()f ϕ的值为()A .0B .2C .2D .32【答案】D【解析】因为π()sin (0)6f x x ωω⎛⎫-> ⎪⎝⎭,所以()ππcos sin (0)63f x x x ωωω⎛⎫⎛⎫=-=+> ⎪ ⎪⎝⎭⎝⎭',而函数()f x 的图象向左平移()0ϕϕ>个单位长度后得到()()ππsin (0)66f x x x ϕωϕωωϕω⎡⎤⎛⎫++-+-> ⎪⎢⎥⎣⎦⎝⎭,由题意得()()f x f x ϕ+=',所以ππ2π,Z 63k k ωϕ=⎨-=+∈⎪⎩,解得1π2π,Z 2k k ωϕ=⎧⎪⎨=+∈⎪⎩且0ϕ>,所以πππ3()2π2632f k ϕ⎛⎫=+-= ⎪⎝⎭,故选:D 【变式3-4】(2022·全国·模拟预测)已知函数()3sin cos f x x x =-的图象向左平移ϕ(0ϕ>)个单位长度后得到()f x 的导函数()f x '的图象,则()f ϕ=()A .3-B .3C .1D .1-【答案】B【解析】因为()3sin cos f x x x =-,所以()3cos sin f x x x =+',而()()()3sin cos 3sin cos 3cos sin cos cos sin sin f x x x x x x x ϕϕϕϕϕϕϕ+=+-+=+-+()()3cos sin sin 3sin cos cos x x ϕϕϕϕ=++-⋅,由题意得()()f x f x ϕ+=',所以3cos sin 13sin cos 3ϕϕϕϕ+=⎧⎨-=⎩,解得sin 1cos 0ϕϕ=⎧⎨=⎩,所以()3sin cos 3f ϕϕ=-=,故选:B.另解:因为()3sin cos f x x x =-,所以()3cos sin f x x x =+',由题意知()()f x f x ϕ+='对一切实数x 恒成立,所以令0x =,得()()03cos 0sin 03f f ϕ'==+=,故选:B.【变式3-5】(2023·河南信阳·河南省信阳市第二高级中学校联考一模)将函数()sin 2c 2πos π63f x x x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭图象上的所有点的横坐标缩短为原来的12(纵坐标不变),然后再将其图象向左平移()0θθ>单位得到图象()g x ,若函数()g x 图象关于y 轴对称,则θ的最小值为()A .π3B .π6C .π12D .π24【答案】C 【解析】()πsin 2cos 2sin 2co i ππs 22s n26366πππ62f x x x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++-=+++-=+ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,由()π2sin 26f x x ⎛⎫=+ ⎪⎝⎭,横坐标缩短为原来的12(纵坐标不变)得到π2sin 46⎛⎫=+ ⎪⎝⎭y x ,将其图象向左平移()0θθ>单位得到图象()46π2sin 4g x x θ⎛⎫=++ ⎪⎝⎭,而()g x 图象关于y 轴对称,∴4π,Z 6π2πk k θ+=+∈,∵0θ>,∴当0k =时,θ取最小值π12.故选:C.【题型4三角函数的四种性质】【例4】(2023秋·河南南阳·高三统考期末)已知函数()()()sin cos f x x x ϕϕ=+++是偶函数,则3sin 2cos 2sin 3cos ϕϕϕϕ-=+______.【答案】15【解析】由题知数()()()sin cos f x x x ϕ=+++是R 上偶函数,所以()()ππ22f f =-,即()()()()ππππsin cos sin cos 2222ϕϕϕϕ+++=-++-+,即cos sin cos sin ϕϕϕϕ-=-+,即cos sin ϕϕ=,tan 1ϕ=,所以3sin 23sin 2cos 321cos 2sin 2sin 3cos 2353cos ϕϕϕϕϕϕϕϕ---===+++.故答案为:15【变式4-1】(2023秋·河北邢台·高三邢台市第二中学校考期末)函数9cos 24y x π⎛⎫=- ⎪⎝⎭的单调递减区间为______.【答案】()π5ππ,πZ 88k k k ⎡⎤++∈⎢⎥⎣⎦【解析】由9πcos 24y x ⎛⎫=-⎪⎝⎭=cos π24x ⎛⎫- ⎪⎝⎭=cos π24x ⎛⎫- ⎪⎝⎭,得2kπ≤2x -4π≤2k π+π(k ∈Z ),解得kπ+π8≤x ≤kπ+58π(k ∈Z ),所以函数的单调递减区间为π5ππ,π88k k ⎡⎤++⎢⎥⎣⎦(k ∈Z ).故答案为:()π5ππ,πZ 88k k k ⎡⎤++∈⎢⎥⎣⎦.【变式4-2】(2022秋·辽宁沈阳·高三沈阳市第一二〇中学校考期中)已知函数()tan tan f x x x =+,则下列结论中正确的是()A .()f x 的最小正周期为π2B .点π,02⎛⎫- ⎪⎝⎭是()f x 图象的一个对称中心C .()f x 的值域为[)0,∞+D .不等式()2f x >的解集为()ππ2,2πZ 42k k k π⎛⎫++∈ ⎪⎝⎭【答案】C【解析】()π2tan ,[π,π),Z 2tan tan π0,(π,π),Z 2x x k k k f x x x x k k k ⎧∈+∈⎪⎪=+=⎨⎪∈-+∈⎪⎩,作出()f x的图象,如图,观察图象,()f x 的最小正周期为π,A 错误;()f x 的图象没有对称中心,B 错误;()f x 的值域为[)0,∞+,C 正确;不等式()2f x >,即π[π,π)(Z)2x k k k ∈+∈时,2tan 2x >,得tan 1x >,解得ππππ,Z 42k x k k +<<+∈,所以()2f x >的解集为ππ(π,π)()42Z k k k +∈+,故D 错误.故选:C【变式4-3】(2023·四川内江·统考一模)已知函数()()1sin cos sin (0)2f x x x x ωωωω=-+>,若函数()f x 在π,π2⎛⎫⎪⎝⎭上单调递减,则ω不能取()A .23B .13C .58D .14【答案】A【解析】因为()()1sin cos sin 2f x x x x ωωω=-+21sin cos sin 2x x x ωωω=⋅-+11cos 21sin 2222x x ωω-=-+1(sin 2cos 2)2x x ωω=+(sin 2cos 2)222x x ωω=⋅⋅π)4x ω=+由ππ3π2π22π242k x k ω+≤+≤+,Z k ∈,得ππ5ππ88k k x ωωωω+≤≤+,Z k ∈,所以函数()f x 的单调递减区间为ππ5ππ,88k k ωωωω⎡⎤++⎢⎥⎣⎦()k ∈Z .又函数()f x 在π,π2⎛⎫ ⎪⎝⎭上单调递减,所以π,π2⎛⎫ ⎪⎝⎭⊆ππ5ππ,88k k ωωωω⎡⎤++⎢⎥⎣⎦()k ∈Z ,所以πππ825πππ8k k ωωωω⎧+≤⎪⎪⎨⎪+≥⎪⎩,Z k ∈,因为0ω>,所以15248k k ω+≤≤+,Z k ∈,当23ω=时,得1252438k k +≤≤+,得152424k ≤≤,不成立;所以23ω=不可取;当13ω=时,得1152438k k +≤≤+,得712412k -≤≤,因为Z k ∈,所以0k =时,13ω=可取到;当58ω=时,得1552488k k +≤≤+,得3016k ≤≤,因为Z k ∈,所以0k =时,58ω=可取到;当14ω=时,得1152448k k +≤≤+,得308k -≤≤,因为Z k ∈,所以0k =时,14ω=可取到.综上所述:ω不能取23.故选:A【变式4-4】(2023秋·江苏南通·高三统考期末)(多选)设函数()()sin f x x ωϕ=+,x ∈R ,其中0ω>,3πϕ<.若1409f π⎛⎫-= ⎪⎝⎭,419f π⎛⎫= ⎪⎝⎭,且()f x 的最小正周期大于52π,则()A .14ω=B .6πϕ=C .()f x 在()2,3ππ上单调递增D .()f x 在()0,3π上存在唯一的极值点【答案】BC【解析】函数()()sin f x x ωϕ=+的最小正周期为T ,由1409f π⎛⎫-= ⎪⎝⎭及419f π⎛⎫= ⎪⎝⎭得:414(21)()2,N 499T k k πππ*⋅-=--=∈,则8,N 21T k k π*=∈-,而52T π>,即有5822,N 1k k ππ*>∈-,解得21,N 10k k *<∈,即1k =或2k =,当1k =时,18,4T πω==,由419f π⎛⎫= ⎪⎝⎭得1114,Z 492k k ππϕπ⨯+=+∈,有117,Z 18k k πϕπ=+∈,而3πϕ<,显然不存在整数1k ,使得3πϕ<,当2k =时,83,34T πω==,由419f π⎛⎫= ⎪⎝⎭得2234,Z 492k k ππϕπ⨯+=+∈,有22,Z 6k k πϕπ=+∈,而3πϕ<,于是得20,6k πϕ==,符合题意,所以83,,346T ππωϕ===,A 不正确,B 正确;3()sin()46f x x π=+,当23x ππ<<时,532934612x πππ<+<,而函数sin y x =在529(,)312ππ上单调递增,所以函数()f x 在()2,3ππ上单调递增,C 正确;当03x π<<时,32964612x πππ<+<,而函数sin y x =在29(,)612ππ上两个极值点,一个极大值点,一个极小值点,所以函数()f x 在()0,3π上有两个极值点,一个极大值点,一个极小值点,D 不正确.故选:BC【变式4-5】(2023·安徽淮南·统考一模)(多选)已知函数()()πsin ,12,2f x x ωϕωϕ⎛⎫=+<<< ⎪⎝⎭图像过点10,2⎛⎫- ⎪⎝⎭,且存在12,x x ,当122πx x -=时,()()120f x f x ==,则()A .()f x 的周期为4π3B .()f x 图像的一条对称轴方程为5π9x =-C .()f x 在区间4π10π,99⎡⎤⎢⎣⎦上单调递减D .()f x 在区间()0,5π上有且仅有4个极大值点【答案】ACD【解析】因为()f x 图像过点10,2⎛⎫- ⎪⎝⎭且π2ϕ<,所以1sin 2ϕ=-,解得π6ϕ=-,因为存在12,x x ,当122πx x -=时,()()120f x f x ==,所以π2π2T k k ω⋅==,即2k ω=,*N k ∈,又因为12ω<<,所以32ω=,所以()3πsin 26f x x ⎛⎫=-⎪⎝⎭,选项A :()f x 的周期2π4π332T ==,正确;选项B :()f x 图像的对称轴为3πππ262x k -=+,解得4π2π93kx =+,Z k ∈,令5π4π2π993k-=+,k 无整数解,B 错误;选项C :当4π10π,99x ⎡⎤∈⎢⎥⎣⎦时,3ππ3π,2622x ⎡⎤-∈⎢⎣⎦,所以由正弦函数的图像和性质可得()f x 在区间4π10π,99⎡⎤⎢⎥⎣⎦上单调递减,C正确;选项D :当()0,5πx ∈时,3ππ22π,2663x ⎛⎫-∈- ⎪⎝⎭,所以由正弦函数的图像和性质可得()f x 在区间()0,5π有4个极大值点,3个极小值点,D 正确;故选:ACD【变式4-6】(2023秋·湖北·高三统考期末)(多选)已知函数()2sin sin 2f x x x =,则下列说法正确的是()A .π是()f x 的一个周期B .()f x 的图象关于点π,02⎛⎫ ⎪⎝⎭中心对称C .()f x 在区间[]0,2π上的零点个数为4D .()f x 的最大值为8【答案】ABD 【解析】对于A ,因为()2(π)sin (π)sin 2(π)f x x x +=++()22sin sin 2sin sin 2()x x x x f x =-==,所以π是()f x 的一个周期,故A 正确;对于B ,()2π(2)(π)sin (π)sin 2(π)2f x f x x x ⨯-=-=--22sin sin(2)sin sin 2()x x x x f x =-=-=-,所以()f x 的图象关于点π,02⎛⎫⎪⎝⎭中心对称,故B 正确;对于C ,由()2sinsin 2f x x x =0=,得πx k =或2πx k =,Z k ∈,得πx k =或π2k x =,Z k ∈,由0π2πk ≤≤及Z k ∈得0k =或1k =或2k =,所以0x =或2πx =或πx =,由π02π2k ≤≤及Z k ∈得0k =或1k =或2k =或3k =或4k =,所以0x =或π2x =或πx =或3π2x =或2πx =,所以()f x 在区间[]0,2π的零点为0x =,π2x =,πx =,3π2x =,2πx =,共5个,故C 错误;对于D ,()2sinsin 2f x x x =2sin 2sin cos x x x =⋅32sin cos x x =,所以()262()4sin cos f x x x =624sin (1sin )x x =-,设2sin [0,1]t x =∈,34(1)y t t =-3444(01)t t t =-≤≤,则23212164(34)y t t t t '=-=-,令0'>y ,得304t <<,令0'<y ,得314t <≤,所以3444(01)y t t t =-≤≤在3[0,)4上为增函数,在3(,1]4上为减函数,所以当3t 4=时,y 取得最大值为333274(1)4464⎛⎫⨯-= ⎪⎝⎭,0=t 或1t =时,y 取得最小值为0,所以()2()f x y =27[0,64∈,所以()[f x ∈,所以()f x D 正确;故选:ABD 【变式4-7】(2023春·浙江·高三校联考开学考试)(多选)已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭,则()A .()0f =B .()f x 的最小正周期为π2C .()f x 在π0,6⎛⎫ ⎪⎝⎭上单调递减D .()f x 在π,06⎛⎫- ⎪⎝⎭上单调递增【答案】BD【解析】()ππ0tan tan 66f ⎛⎫=-=-= ⎪⎝⎭A 错误;函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭的最小正周期为π2T =,故B 正确;π0,6x ⎛⎫∈ ⎪⎝⎭时,2,πππ666x ⎛⎫-∈- ⎪⎝⎭,故()f x 在π0,6⎛⎫⎪⎝⎭上单调递增,故C 错误;π,06x ⎛⎫∈- ⎪⎝⎭时,2,π626ππx ⎛⎫-∈-- ⎪⎝⎭,故()f x 在π,06⎛⎫- ⎪⎝⎭上单调递增,故D 正确.故选:BD .【题型5三角函数的最值问题】【例5】(2022秋·北京·高三北京市八一中学校考阶段练习)定义运算,,,.a a b a b b a b ≤⎧=⎨>⎩※例如,121=※,则函数()sin cos f x x x =※的值域为()A.1,2⎡⎤-⎢⎥⎣⎦B.22⎡⎤⎢⎥⎣⎦C.,12⎡⎤⎢⎥⎣⎦D.2⎡-⎢⎣⎦【答案】D【解析】根据题设中的新定义,得()sin ,sin cos cos ,sin cos x x x f x x x x≤⎧=⎨>⎩,由sin cos x x ≤可得sin cos 0x x -≤π04x ⎛⎫-≤ ⎪⎝⎭,所以π2ππ2π4k x k -≤-≤,Z k ∈,即3ππ2π2π+44k x k -≤≤,Z k ∈,由sin cos x x >可得sin cos 0x x ->π04x ⎛⎫-> ⎪⎝⎭,所以π2π2π+π4k x k <-<,Z k ∈,即π5π2π+2π+44k x k <<,Z k ∈,所以()3ππsin ,2π2π,Z 44π5πcos ,2π2π,Z44x k x k k f x x k x k k ⎧-≤≤+∈⎪⎪=⎨⎪+<<+∈⎪⎩,当3ππ2π2π+44x k x k ∈-≤≤,Z k ∈,()()()2πsin 2πsin f x x x f x +=+==,当π5π2π+2π+44x k x k ∈<<,Z k ∈时,()()()2πcos 2πcos f x x x f x +=+==,所以函数()f x 为周期函数,周期为2π,作出函数()f x 在一个周期内的图象(实线部分),观察图象,可知函数()f x 的值域为22⎡-⎢⎣⎦,故选:D.【变式5-1】(2023秋·湖南株洲·高三校联考期末)已知定义域为R 的函数(),()f xg x满足()()πf x f x +=-,且()()cos π,g x x f x =++()()sin πf x x g x =-+,则当π0,4x ⎡⎤∈⎢⎥⎣⎦时,函数()()y f x g x =的最小值为()A .0B .2CD 【答案】A【解析】()cos ()=-g x x f x ,()()()()πcos ππcos +=+-+=-+g x x f x x f x ,所以()sin cos ()f x x x f x =+-,得sin cos ()2x x f x +=,cos sin ()2x xg x -=,所以22cos sin 1()()cos 244x x y f x g x x -===,π0,4x ⎡⎤∈⎢⎥⎣⎦,所以0cos 21x ≤≤,10()()4≤≤f x g x ,得()()y f x g x =的最小值为0.故选:A.【变式5-2】(2022秋·安徽·高三石室中学校联考阶段练习)如图是函数()cos()(0)f x x ωϕω=+>的部分图象,则()f x 在,9045⎡⎤-⎢⎥⎣⎦π22π上的值域为()A .[]1,1-B .122⎡⎢⎣⎦C .11,2⎡⎤-⎢⎥⎣⎦D .⎡-⎢⎣⎦【答案】D【解析】由图象知函数的周期13ππ2π230103T ⎛⎫=⨯-=⎪⎝⎭,即2π2π=3ω,即3ω=,由五点对应法得ππ32π+()102k k ϕ⨯+=∈Z ,得π2π+5k ϕ=,则π()cos 35f x x ⎛⎫=+ ⎪⎝⎭,因为π22π,9045x ⎡⎤∈-⎢⎥⎣⎦,所以ππ5π3,563x ⎡⎤+∈⎢⎣⎦,所以πcos 31,52x ⎡⎛⎫+∈-⎢ ⎪⎝⎭⎣⎦.故选:D【变式5-3】(2023·河北衡水·河北衡水中学校考模拟预测)函数()3cos f x x 的最大值为().A .B .C .D .3【答案】D 【解析】2225cos 4sin 59cos 4cos 4sin 5x x x x x -+=--+()()22229cos 4sin 4sin 13cos 2sin 1x x x x x =+-+=+-,所以()3cos f x x ==故()f x 的最大值转化为点()3cos ,2sin P x x 到()0,1A 与()0,2sin B x 的距离之差的最大值,因为1sin 1x -≤≤,22sin 2x -≤-≤,112sin 3x -≤-≤,所以12sin 3PA PB AB x -≤=-≤,当且仅当sin 1x =-时,等号成立,则3PA PB -≤,经检验,此时cos 0x =,()303f x =⨯=,所以()3f x ≤,即()f x 的最大值为3.故选:D.【变式5-4】(2023秋·北京丰台·高三统考期末)已知函数π()sin (0)6f x x ωω⎛⎫=+>⎪⎝⎭,若ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,且()f x 在区间ππ,62⎛⎫ ⎪⎝⎭上有最小值无最大值,则ω=___________.【答案】4【解析】由于若ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,且()f x 在区间ππ,62⎛⎫ ⎪⎝⎭上有最小值无最大值,πππ6223+=,则πππsin 1336f ω⎛⎫⎛⎫=+=- ⎪ ⎪⎝⎭⎝⎭,所以πππ2π,62,Z 362k k k ωω+=-=-∈,又ππππ,62366T ωω=≥-=≤,由于0ω>,所以ω的值为4.故答案为:4。
数轴动点问题6题型

数轴动点问题6题型数轴动点问题是数学中的一种常见题型,通过将问题抽象成数轴上的点动态移动的方式来帮助学生理解和解决问题。
以下将介绍六种常见的数轴动点问题,并给出解题思路和方法。
题型一:从一个点出发,每次只能向左或向右移动固定的距离,求到达目标点的最短步数。
这种问题可以使用贪心算法来解决。
首先计算目标点和起始点之间的距离,然后判断目标点在起始点的左边还是右边。
每次移动,选择距离目标点最近的方向,继续移动直到到达目标点。
题型二:从一个点出发,每次可以向左或向右移动任意距离,求到达目标点的最短步数。
这类问题可以使用动态规划来解决。
首先计算目标点和起始点之间的距离,然后创建一个数组,数组的索引表示距离起始点的位置,数组的值表示到达该位置的最短步数。
通过迭代计算数组中的值,最终得到到达目标点的最短步数。
题型三:从一个点出发,每次可以向左或向右移动任意距离,每次移动的步数还会随着移动的次数改变,求到达目标点的最短步数。
对于这类问题,一种解决方法是使用二分查找。
首先确定移动次数的上界和下界,然后不断二分查找直到找到最短步数。
题型四:数轴上有若干个起点和终点,需要将它们连成线段,使得线段的总长度最短。
可以使用贪心算法解决这类问题。
首先将所有的起点和终点按照位置排序,然后依次连接相邻的起点和终点,计算连接线段的长度并累加。
最终得到线段的总长度。
题型五:数轴上有若干个起点和终点,需要将它们连成线段,使得线段的总长度最大。
对于这类问题,可以使用动态规划。
首先将所有的起点和终点按照位置排序,然后创建一个数组,数组的索引表示终点的位置,数组的值表示以该终点为结尾的最长线段的长度。
通过迭代计算数组中的值,最终得到线段的总长度。
题型六:数轴上有若干个点,需要找出一个点,使得该点到其他点的距离之和最小。
一种解决方法是通过数学推导得出结论:该点的位置应该在所有点的中位数处。
统计所有点的位置,然后找到它们的中位数,即为所求的点。
数轴动点问题是数学中的一类经典问题,解决这类问题需要熟练掌握贪心算法、动态规划和二分查找等知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题型6 功能关系的理解和应用1.(2014·重庆·2)某车以相同的功率在两种不同的水平路面上行驶,受到的阻力分别为车重的k 1和k 2倍,最大速率分别为v 1和v 2,则( )A .v 2=k 1v 1B .v 2=k 1k 2v 1 C .v 2=k 2k 1v 1D .v 2=k 2v 1 答案 B解析 车达到最大速度时,牵引力的大小等于阻力的大小,此时车的功率等于克服阻力做功的功率.故P =k 1mg v 1=k 2mg v 2,解得v 2=k 1k 2v 1,选项B 正确. 2.洒水车沿平直粗糙路面匀速行驶,设车所受阻力与车重成正比,洒水车行驶到某一路段时开始洒水,且牵引力保持恒定,则开始洒水后的一段时间内( )A .车仍保持原有速度做匀速直线运动B .车开始做匀加速直线运动C .车的发动机的输出功率不断增大D .车的发动机的输出功率保持不变答案 C解析 设洒水车的牵引力为F ,洒水车的质量为m ,阻力为kmg ,由牛顿第二定律有F -kmg=ma 得,a =F m-kg ,开始时F =kmg ,a =0,随着m 减小,a 逐渐增大,故洒水车做加速度逐渐增大的加速运动,故A 、B 错误.由于速度逐渐增加,而牵引力不变,由P =F v 可得输出功率变大,故C 正确,D 错误.3.(2014·新课标Ⅱ·16)一物体静止在粗糙水平地面上.现用一大小为F 1的水平拉力拉动物体,经过一段时间后其速度变为v .若将水平拉力的大小改为F 2,物体从静止开始经过同样的时间后速度变为2v .对于上述两个过程,用W F 1、W F 2分别表示拉力F 1、F 2所做的功,W f1、W f2分别表示前后两次克服摩擦力所做的功,则( )A .W F 2>4W F 1,W f2>2W f1B .W F 2>4W F 1,W f2=2W f1C .W F 2<4W F 1,W f2=2W f1D .W F 2<4W F 1,W f2<2W f1答案 C解析 根据x =v +v 02t 得,两过程的位移关系x 1=12x 2,根据加速度的定义a =v -v 0t,得两过程的加速度关系为a 1=a 22.由于在相同的粗糙水平地面上运动,故两过程的摩擦力大小相等,即F f1=F f2=f ,根据牛顿第二定律得,F 1-F f1=ma 1,F 2-F f2=ma 2,所以F 1=12F 2+12F f ,即F 1>F 22.根据功的计算公式W =Fl ,可知W f1=12W f2,W F 1>14W F 2,故选项C 正确,选项A 、B 、D 错误.图14.如图1所示,小球从A 点以初速度v 0沿粗糙斜面向上运动,到达最高点B 后返回A ,C 为AB 的中点.下列说法中正确的是( )A .小球从A 出发到返回A 的过程中,位移为零,外力做功为零B .小球从A 到C 过程与从C 到B 过程,减少的动能相等C .小球从A 到C 过程与从C 到B 过程,损失的机械能相等D .小球从A 到C 过程与从C 到B 过程,速度的变化量相等答案 BC解析 小球从A 出发到返回A 的过程中,重力做功为零,摩擦力一直做负功,所以外力做功不为零,故A 错误;小球从A 到C 与从C 到B ,重力与摩擦力做功之和相等,减少的动能相等,所以B 正确;小球从A 到C 与从C 到B ,克服摩擦力做功相等,故损失的机械能相等,所以C 正确;小球从A 到C 过程与从C 到B 过程,加速度相同,但运动的时间不同,故速度的变化量不相等,所以D 错误.5.如图2所示,传送带足够长,与水平面间的夹角α=37°,并以v =10m /s 的速度逆时针匀速转动着,在传送带的A 端轻轻地放一个质量为m =1 kg 的小物体,若已知物体与传送带之间的动摩擦因数μ=0.5,(g =10 m/s 2,sin37°=0.6,cos37°=0.8)则下列有关说法正确的是( )图2A .小物体运动1s 后,受到的摩擦力大小不适用公式f =μNB .小物体运动1s 后加速度大小为2m/s 2C .在放上小物体的第1s 内,系统产生50J 的热量D .在放上小物体的第1s 内,至少给系统提供能量70J 才能维持传送带匀速转动 答案 B解析 释放后A 由mg sin θ+μmg cos θ=ma 1,得a 1=10m /s 2,再根据v =a 1t =10 m/s ,可得:t =1s ,即1s 后物体与传送带速度相等,又因为mg sin θ>μmg cos θ,所以1s 后物体继续做加速运动,mg sin θ-μmg cos θ=ma 2,解得:a 2=2m/s 2,摩擦力为滑动摩擦力,故适用公式f =μN ,所以A 错误,B 正确;在第1s 内物体的位移x 1=12v t =5m ,传送带的位移x 2=v t =10m ,故相对位移Δx =x 2-x 1=5m ,所以系统产生的热量Q =μmg cos θΔx =20J ,故C 错误;物体增加的动能E k =12m v 2=50J ,系统提供能量E =E k +Q -mg sin θ·x 1,小于70J ,故D 错误. 6.(2014·福建·18)如图3所示,两根相同的轻质弹簧,沿足够长的光滑斜面放置,下端固定在斜面底部挡板上,斜面固定不动.质量不同、形状相同的两物块分别置于两弹簧上端.现用外力作用在物块上,使两弹簧具有相同的压缩量,若撤去外力后,两物块由静止沿斜面向上弹出并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块( )图3A .最大速度相同B .最大加速度相同C .上升的最大高度不同D .重力势能的变化量不同答案 C解析 当弹簧的弹力和滑块重力沿斜面向下的分力大小相等时,滑块的速度最大,由于两滑块的质量不同,故两滑块速度分别达到最大时,与质量大的滑块接触的弹簧的形变量较小,根据能量守恒定律可知,质量大的滑块的最大速度较小,选项A 错误.刚撤去外力时,根据牛顿第二定律得kx -mg sin θ=ma (θ为斜面倾角),a =kx m-g sin θ,若a >g sin θ,则此时两滑块的加速度最大,由于两滑块的质量不同,故两滑块的最大加速度不同,选项B 错误.整个过程中,弹簧的弹性势能全部转化为滑块的重力势能,由于两滑块质量不同,故上升的最大高度不同,选项C 正确.两滑块重力势能的变化量等于弹簧弹性势能的减少量,故重力势能的变化量相同,选项D 错误.7.两木块A 、B 用一轻弹簧连接,静置于水平地面上,如图4(a)所示.现用一竖直向上的力F 拉动木块A ,使木块A 向上做匀加速直线运动,如图(b)所示.从木块A 开始运动到木块B 将要离开地面的过程中,下述判断正确的是(设弹簧始终在弹性限度内)( )图4A .弹簧的弹性势能一直减小B .力F 一直增大C .木块A 的动能和重力势能之和一直增大D .两木块A 、B 和轻弹簧组成的系统的机械能先增大后减小答案 BC解析 在木块A 上升过程中,弹簧从压缩到伸长,所以弹簧的弹性势能先减小后增大,故A 错误;由牛顿第二定律即可解出此过程所需的拉力F 的大小,得出拉力一直增大,故B 正确;由于木块A 做匀加速运动,所以木块A 的速度增大,高度升高,则木块A 的动能和重力势能之和增大,故C 正确;在上升过程中,除重力与弹力做功外,还有拉力做正功,所以两木块A 、B 和轻弹簧组成的系统的机械能一直增大,故D 错误.8.将一物体以一定的初速度从某一高度处竖直上抛,一段时间后物体回到原出发点,已知空气阻力与其速度成正比,则下面说法正确的是( )A .上升过程所用时间与下降过程所用时间相等B .上升过程所用时间小于下降过程所用时间C .上升和下降过程,小球的机械能都减少,且上升过程机械能的减少量大于下降过程D .在出发点,上升时重力的瞬时功率小于下降时的瞬时功率答案 BC解析 空气阻力的大小F 阻=k v ,上升过程中由牛顿第二定律得加速度大小为a 1=g +k v m,下降过程中加速度为a 2=g -k v m,所以a 1>a 2,物体减速上升过程可看作初速度为零的加速下降过程,由x =12at 2可知上升过程的时间小于下降过程的时间,故选项A 错误,B 正确;由于需要克服阻力做功,所以在同一位置的速度上升时大于下降时的速度,即上升时的阻力大于下降时的阻力,所以上升过程中的阻力大于下降过程中阻力,即上升过程中克服阻力做的功大于下降过程中克服阻力做的功,故选项C 正确;因为上升和下降过程中克服阻力做功,物体回到出发点时的速度小于出发时的速度,所以在出发点,上升时重力的瞬时功率大于下降时重力的瞬时功率,故选项D 错误.9.如图5所示,斜面体固定在水平地面上,虚线以上部分斜面光滑,虚线以下部分斜面粗糙.质量分别为m 1、m 2(m 2>m 1)的两物体之间用细线连接,开始时m 1处在斜面顶端并被束缚住.当由静止释放m 1后,两物体开始沿斜面下滑,则下列说法正确的是( )图5A .m 2到达斜面底端前两物体一定不能相遇B .m 2到达斜面底端前两物体有可能相遇C .在虚线上方运动时细线对两物体均不做功D .在虚线上方运动时细线对m 1做正功,对m 2做负功答案 BC解析 虚线以上部分斜面光滑,物体受到重力和支持力作用,把两个物体看成整体,根据牛顿第二定律得:a =(m 1+m 2)g sin θm 1+m 2=g sin θ,两物体加速度相等,绳子拉直,但没有力的作用,此过程,细线对两物体均不做功,m 2先到达虚线下方,此时m 2受到重力、支持力、滑动摩擦力作用,若滑动摩擦力大于重力沿斜面的分量,则m 2做匀减速运动,此时m 1仍做匀加速运动,所以绳子处于松弛状态,m 1运动到虚线位置时的速度比m 2运动到虚线位置时的速度大,m 1进入虚线下方做匀减速运动,相同时间内m 1运动的位移比m 2运动的位移大,所以m 2到达斜面底端前两物体有可能相遇,故A 、D 错误,B 、C 正确.10.如图6所示,轻弹簧上端通过一轻绳固定,下端拴一小球,小球与光滑的三角形斜面接触,弹簧处于竖直状态.现用力F 竖直向上推斜面,使斜面缓慢向上运动直至弹簧与斜面平行,则在此过程中,以下说法正确的是( )图6A .小球对斜面的压力一直增大B .弹簧对小球不做功C .斜面对小球做正功D .推力F 做的功等于斜面与小球机械能的增加答案 AC解析 斜面在上升过程中,小球受斜面的支持力、重力和弹簧的拉力,由平衡条件知,N 和弹簧弹力F 弹的合力大小等于mg ,由三角形定则可知,N 一直增大,故A 正确;小球在弹力方向发生了位移,故弹力做功,故B 错误;斜面对小球的作用力与小球的位移成锐角,故斜面对小球做正功,故C 正确;推力做的功等于斜面与小球机械能增加量和弹簧弹性势能的变化量之和,故D 错误.11.如图7所示,倾角为θ的光滑斜面足够长,一质量为m 小物体,在沿斜面向上的恒力F 作用下,由静止从斜面底端沿斜面向上做匀加速直线运动,经过时间t ,力F 做功为60J ,此后撤去力F ,物体又经过相同的时间t 回到斜面底端,若以地面为零势能参考面,则下列说法正确的是( )图7A .物体回到斜面底端的动能为60JB .恒力F =2mg sin θC .撤去力F 时,物体的重力势能是45JD .动能与势能相等的时刻一定出现在撤去力F 之后答案 ACD解析 设撤去F 前、后的加速度为a 1、a 2,由运动学规律,有x =12a 1t 2和-x =a 1t 2-12a 2t 2,联立解得a 1a 2=13,由牛顿第二定律,有F -mg sin θ=ma 1和mg sin θ=ma 2,则F =43mg sin θ,选项B 错误;又W =Fx =43mgx sin θ=60J ,可得mgx sin θ=45J ,选项C 正确;物体从出发到回到斜面底端,由动能定理Fx =E k =60J ,选项A 正确;F 作用时,动能从0增加到15J ,重力势能从0增加到45J ,不可能出现动能与势能相等的位置,撤去力F 后,物体上滑时,动能减少,势能增大,不可能出现动能与势能相等的位置,物体下滑时,动能从0增加到60J ,重力势能从60J 减小到0,将能出现动能与势能相等的位置,选项D 正确.12.一质量为2kg 的物体,在水平恒定拉力的作用下以一定的初速度在粗糙的水平面上做匀速运动,当运动一段时间后,拉力逐渐减小,且当拉力减小到零时,物体刚好停止运动,图8中给出了拉力随位移变化的关系图像.已知重力加速度g =10m/s 2,由此可知( )图8A .物体与水平面间的动摩擦因数约为0.35B .减速过程中拉力对物体所做的功约为8JC .匀速运动时的速度约为6m/sD .减速运动的时间等于73s 答案 AC解析 物体与水平面间的动摩擦因数为μ=f N =F mg=0.35,A 正确;减速过程中拉力对物体所做的功可以用这段图线与横轴围成的面积来表达,可以粗略得到功应为12J ,B 错误.对减速过程应用动能定理得W F -μmgx =0-12m v 2,代入数据得v ≈6m /s ,C 正确;减速过程物体的加速度逐渐增大,平均速度小于3 m/s ,运动时间大于73s ,D 错误. 13.如图9所示,固定的光滑倾斜杆上套有一个质量为m 的圆环,圆环与竖直放置的轻质弹簧上端相连,弹簧的下端固定在水平地面上的A 点,开始弹簧竖直并且长度恰好为原长h .现让圆环由静止沿杆滑下,滑到杆的底端(未触及地面)时速度恰好为零,已知当地的重力加速度大小为g .则在圆环下滑的整个过程中( )图9A .圆环、弹簧和地球组成的系统机械能不守恒B .弹簧的弹性势能先增大后减小C .弹簧的弹性势能增大了mghD.弹簧的最大压缩量小于其最大伸长量答案CD解析圆环沿杆滑下,滑到杆的底端的过程中有两个力对圆环做功,即环的重力和弹簧的弹力;所以圆环的机械能不守恒,如果把圆环和弹簧组成的系统作为研究对象,则系统的机械能守恒,故A选项错误;弹簧的弹性势能随弹簧的形变量的变化而变化,由图知弹簧先缩短后伸长,故弹簧的弹性势能先增大再减小,最后再增大,故B选项错误;根据系统的机械能守恒,圆环的机械能减少了mgh,那么弹簧的机械能即弹性势能增大mgh,故C选项正确;由图可知,弹簧的最大压缩量在弹簧与杆垂直的时刻,此时的系统具有的能量为圆环的动能、重力势能和弹簧的弹性势能,当圆环速度减为零时,到达最底端,此时圆环的动能和势能都为零(以地面为零参考平面),系统所有的机械能全部转化成了弹簧的弹性势能,此时的弹簧处于最大伸长状态,所以弹簧的最大伸长量要大于最大压缩量,故D正确.。
