《比的意义和基本性质》练习题

合集下载

比的意义和比的基本性质练习课

比的意义和基本性质的练习
复习旧知，整体回顾
（1）、什么叫做比？比的各部分名称是什么？
举例：( ):( )=( )÷( )
（2）、什么是比的基本性质？
举例：( ):( )=( ):( ) （0除外）
（3）、什么叫做比值？一般求比值方法是什么？
举一个求比值的例子：（4）、怎样化简比？举一个化简比的例子：
4 9
，大米和面粉的比是（）。）.
6、一条水渠，已修好了，还剩下60米，已修的和剩下的长度之比是（
7 4
5 8
• 小结：
这节课我们学了什么？
追问：既然比的后项不能是0，而足球赛中常出现的
“2:0”的意义是什么？它是一个比吗？
（2）小强身高1米，他爸爸身高173厘米，小强和他爸爸
身高的比是1：173
（3）比的前项和后项都乘一个相同的数，比值不变。
（4）既可以看作一个分数，也ห้องสมุดไป่ตู้以看作4：5
2、填空（1）一辆汽车2小时行驶100千米，这辆汽
（5）两个正方形边长的比是2：1，它们周长的比是（），面积的比是（）。
目标检测。 1、写同样多的作业,李莉用12分钟,王祥用15分钟, 李莉与王祥的最简单的速度比是( ). 2、把3克盐放入12克水中,盐与盐水重量的最简整数比是( ).
3、练习十一第3题
4、练习十一第5题
1、配制一种盐水，在120克水中放了5克盐。 ⑴写出盐和水的克数的比，并化简。盐和水的克数的比是5∶120。 5∶120=1∶24 ⑵写出盐和盐水的克数的比，并化简。盐和盐水的克数的比是5∶125。 5∶125=1∶25 ⑶写出水和盐水的克数的比，并化简。水和盐水的克数的比是120∶125。 120∶125=24∶25

比和比的基本性质练习

• （7）如果把4：15的前项扩大4倍，要使比值不变，后项应（），如果把前项增加到12，那么后项应加（）。 1 • （8）甲比乙多，则甲、乙两数比 5 6 ： 5 是（） 1 • （9）把甲班人数的 8 调给乙班后，甲乙两班人数相等，乙甲两班原有人数比是（ 3：4 ）
（10）把甲数的小数点向左移动一位后与乙数相等，甲乙两数的比是（ 10：1）。（11）a÷3=6×b,则a与b的最简整数比是（ 18：1）。（12）钟表上时针速度与分针速度比是（ 1：12 ），分针速度与秒针速度比是（ 1：60 ），时针速度与秒针速度比是（ 1：720 ）。
• （3）生产300个零件，师傅单独做10要小时，徒弟单独做要15小时，师徒所用的时间比是（），师徒每小时做零件个数比是（） • （4）从甲地到乙地，快车要12小时，慢车要15小时，快车每小时行全程的（），慢车每小时行全程的（），快车和慢车的速度比是（）.
• （5）有甲乙两个正方体，甲棱长6厘米，乙棱长8厘米，它们的棱长比是（），棱长总和之比是（），底面积之比是（），体积比是（）。 • （6）甲数的2/3和乙数的 3/4（甲乙均不为0），甲乙两数的最简比是（）
一种关系
一种运算一种数
比的前项：比号比的后项比值 ÷除号
—分数线
除法被除数
分数分子
除数
商
分母分数值
1、比的前项是3，后项是4，如果比的前项加9，要使比值不变，比的后项应加（）。
2、下图中阴影部分的面积与总面积的比是（）。
口答：用不同的方法说说每句话的含义。
（1）男生人数和女生人数的比是5：6 （2）公鸡只数和母鸡的比是2：5 （3）汽车速度和火车的比是8：9 （4）杨树棵数和柳树棵数的比的比值是1.5 3 （5）女生人数是男生的

比的意义和比的基本性质

m 10c
15cm
“神舟”五号进入运行轨道后，在距地350km 的高空作圆周运动，平均90分钟绕地球一周，大约运行42252km。
怎样用算式表示飞船进入轨道后平均每分钟飞行多少千米？
“神舟”五号进入运行轨道后，在距地350km 的高空作圆周运动，平均90分钟绕地球一周，大约运行42252km。
比表示一种关系；除法是一种运算；分数是一种数；
1、小敏买了6本，共花了1.8元。小亮买了8本，共花了2.4元。
(1) 比小值敏是和（小亮3 ）买；的练习本数之比是（6）:（8）, 4
(2) 比花值的是钱（数之3 ）比；是（1.8 ）:（ 2.4 ）, 4
2、3 :（ 1 ）= 24 （192） : 8 = 24 8
比的前项和后项同时乘或同时除以相同的数（零除外），比值不变。这叫做比的基本性质。
被除数和除数同时乘或同时除以相同的数（零除外），商不变。
这叫做商不变的性质。
分子和分母同时乘或同时除以相同的数（零除外），分数值不变。这叫做分数的基本性质。
应用这个性质可以把一个比
? 化成最简单的整数比前项和后项是互质的整数
速度 = 路程÷时间
42252÷90
路程和时间的比是42252比90。（不同类量的比表示一种新的量。）
“神舟”五号进入运行轨道后，在距地350km 的高空作圆周运动，平均90分钟绕地球一周，大约运行42252km。
求比值的方法：前项÷后项
求出下面各比的比值。 15 : 10 0.8 : 0.2
（2） —9—的最简比是（ A ）
0.03 （A）300 ︰ 1 （B）300 （C） 1︰ 300
（3） 0.25 ︰1.25的最简比是（B ）

六年级数学上册《比的意义和基本性质》习题

六年级数学上册《比的意义和基本性质》习题一、想一想，填一填。

1、（）叫做两个数的比。

2.将比率的前后项乘以（）或除以（）（0除外），再除以比率（）。

3、比的前项除以1/5，要使比值不变，比的后项应该（）。

4、（）∶1/12＝3/5，4∶（）＝0.5。

5、4÷5＝（）/15＝28∶（）＝（）∶20＝（）（小数）。

二、请当裁判。

1、比的前项和后项同时乘一个相同的数，比值不变。

（）2.如果a:B=8:3，那么a=8，B=3。

（）3、爸爸和小明的年龄比是7∶2，3年后他们的年龄比不变。

（）4.圆圆身高1米，母亲身高162厘米，母亲与圆圆身高之比为162:1。

（）5、乙队在一场球赛中以4∶0的比分大胜甲队，这里的4∶0不是比。

（）三、按号码就座。

1、a∶b＝4/7，如果比的前项和后项同时除以3，比值是（）。

a、 4/7第1页b、 4/21c、12/72.在下列比率中，等于0.5:0.6的比率为（）。

a、1/5∶1/6b、1/2∶3/5c、25∶263.如果比率是最简单的整数比率，则比率的第一项和最后一项必须为（）。

a、素数b、互质数c、整数4.如果在前一项3:7的基础上加9，为保持其比例不变，后一项应为（）。

a、加上9b、加21C减去9四、求比值。

0.75∶1.52/5∶1/62∶1.84∶1/22/3小时：45分钟第2页0.3平方米：9平方分米五、把下面各比化成最简单的整数比。

12∶210.8∶2.45/8∶15/160.5∶0.751/8千克：500克15秒：1/3分钟六、请按要求写比。

1.a是B的8/17，B和a的比率是（）。

2、在97克水里放入3克盐，盐与水的比是（），比值是（）；水与盐水的比是（），比值是（）。

3、一个工程小组在四天内建造2022米的道路。

工程团队建造的总米数与道路施工时间的比率为（），比率为（），代表（）。

七、走进生活，解决问题。

一.一批服装可由甲方单独在30天内完成，由乙方单独在20天内完成。

比的意义和基本性质

应用比例的基本性质判断下面的比例是否正确：
1. 2 ：3 =
1 2
1 ：3
× × √
√
2. 6 ：3 = 8 ：5
3. 0.2 ：2.5 = 4 ：50
4. 1.2 ：0.6 = 10 ：5
四、反馈与巩固
1、用比例的意义判断下面的比例是否正确：
⑴ 3 : 5 = 9 : 15
⑵ 2.5 : 5 = 25 : 0.5
（1）4、5、12和15。（2）2、4 、5和10。
比和比例有什么区别？
比 4︰6 意两个数相除又叫义做两个数的比。构由两个数组成，是一个式子，成
比的前项和后项基本同时乘或除以相性质同的数（0除外），比值不变。
比例
2︰3＝4︰6
表示两个比相等的式子叫做比例由四个数组成，是一个等式。
内项外项
在比例里，两个外项的积等于两个内项的积。
2.4×40 ＝ 1.6×60
2.4︰1.6
外项
＝60︰40
内项
内项
2.4 1.6
＝
60 40
外项
交叉相乘
2.4×40 ＝ 1.6×60
2.4 ︰1.6＝ 60︰40
内项外项
在比例里，两个外项的积等于两个比例的基本性质. 内项的积,这叫做比例的基本性质
比例的意义和基本性质
仔细观察
这几幅图片中有什么相同的地方？
你看出了吗？
1.6m 60cm 2.4m
40cm
3 操场上的国旗: 2.4 : 1.6 = 2 3 教室里的国旗: 60 : 40 = 2
求出它们的比值，你发现了什么？
表示两个比相等的式子叫做比例。 2.4︰1.6

比的意义和基本性质》练习题

比的意义和基本性质》练习题比的意义和基本性质1.求鸡和鸭只数的比和比值。

鸡和鸭的比为8:10或4:5，比值为0.8.2.求长方形长和宽的比和比值。

长和宽的比为3:0.12或25:1，比值为25.3.求加工个数和时间的比和比值。

加工个数和时间的比为60:5或12:1，比值为12.4.求已读页数和总页数的比和比值。

已读页数和总页数的比为55:100或11:20，比值为0.55.5.求甲数和乙数的比和比值，以及乙数和甲数的比和比值。

甲数和乙数的比为1:1，比值为1；乙数和甲数的比也为1:1，比值为1.6.求三好学生和全班人数的比和比值。

三好学生和全班人数的比为8:1，比值为0.125.7.求白兔和黑兔的比和比值，以及黑兔和白兔的比和比值。

白兔和黑兔的比为3:1，比值为0.75；黑兔和白兔的比为1:3，比值为0.33.8.若A÷B=5，则A:B=5:1；若A=B，则A:B=1:1.9.比可以表示为分数，比的前项对应分数的分子，比的后项对应分数的分母，除法的除数对应分数的分子，分数线对应分数的除号。

10.比又叫做比率，比值又叫做比例。

11.8:10=4:5=0.8÷1；24:3=8÷1=8.12.盐和盐水的比为10:110或1:11.13.男工人数是女工人数的1:5，男、女工人数的比为1:5，比值为0.2.14.甲数是乙数的4倍，甲、乙两数的比为4:1，乙数与两数和的比为1:5，比值为0.2.15.甲数比乙数多，甲数与乙数的比为4:1，比值为4.16.比的基本性质包括比的两个数可以交换位置，比的两个数同时乘以同一个非零数，比的两个数同时除以同一个非零数，等比关系可以转化为比例关系。

17.16:20=32:40=1.6，32:0.2=160，1.6:0.2=8:1.18.路程和时间的最简整数比为150:1，比值为150.19.甲数是乙数的3倍，乙数与甲数的比为1:3，比值为0.33.20.女生人数占全班的3/5，男生人数占全班的2/5.21.甲数是乙数的2/3，乙数与甲数的比为3:2，比值为1.5.三、化简比1.12:8=3:2，0.4:0.12=10:3，5:4.5:0.9=10:9:2.2.235:45=47:9，360:450=8:10或4:5，0.3:0.15=2:1，18:6=3:1.3.3422:6=571:1，:3=6851:1.比的意义和基本性质（二）1、比的分母不能为零。

09第三单元比的意义和化简比练习六年级上册数学苏教版

1．看图填空。
（1）红色方格与白色方格个数的比是（ 13 : 12）；白色方格与红色方格个数的比是（12 : 13）。
（2）黄色部分与圆面积的比是（ 1 : 3 ）；绿色部分与圆面积的比是（ 2 : 3 ）。
2．在方格纸上画出两个大小不同的长方形，使每个长方形的长与宽的比都是2:1。
你怎么理解“长与宽的比都是2:1”？
1:2 1:4
2:3 4:9
7．化简下面各比，并求出比值。
比化简后的比
比值
4 : 16
1:4
1 4
5.6 : 4.2
4:3
4 3
75 : 25
3:1
3
8．先估计，再量一量、填一填。
6厘米
3厘米
（1）红色部分的长度与彩条全长的比是 2 : 3 ，
2
比值是 3
。
（2）绿色部分的长度与彩条全长的比是 1 : 3 ，
36 : 2＝（36÷2）:（2÷2）＝18 : 1
102 ＝（102÷34）:（68÷34）＝3 : 2
68
4．化简下面各比。
（2） 1 : 4
35
3: 5 7 21
4: 4 15 25
1 : 4 ＝（ 1 × 15） :（ 4 × 15）＝＝（ 3 × 21） :（ 5 × 21）＝9 : 5
7 21
7
21
4 : 4 ＝（ 4 × 75） :（ 4 × 75）＝5 : 3
15 25 15
25
4．化简下面各比。
（3）0.32 : 0.8 1 : 0.25 1.35 : 9.25
0.32 : 0.8＝（0.32×100）:（0.8×100）＝32 : 80＝2 : 5

六年级数学下册《比例的意义和性质》练习题(附答案解析)

六年级数学下册《比例的意义和性质》练习题(附答案解析)学校:___________姓名：___________班级：____________一、选择题1．能与11:34组成比例的是（）。

A．4∶3B．3∶4C．1:43D．1:342．下面每组中的四个数，不能组成比例的是（）。

A．2，0.25，3，0.375B．18，8，5.4，24C．5452,,,3767D．30，25，6，1253．下面能与3∶8组成比例的是（）。

A．8∶3B．15∶40C．0.2∶0.6 4．下列哪个选项中的四个数不能组成比例。

（）A．3，5，9，15B．1，2，3，4C．12，13，16，19D．2，4，7，145．如果a、b都是不为0的数，且56a＝78b，则a和b的大小关系是（）。

A．a＜b B．a＝b C．a＞b6．能与13∶14组成比例的是（）。

A．4∶13B．13∶4C．4∶3D．3∶47．下面各比中，能与0.14∶0.1组成比例的是（）。

A．0.8∶0.25B．28∶20C．13∶35D．14∶18．在比例里，两个外项的积等于两个内项的积。

这叫做（）。

A．比例的基本性质B．比例C．比例的外项9．根据下图中的信息判断，下列等式不成立的是（）。

A．a∶c＝d∶b B．a b=c dC．b d=c a10．如果a×3＝b×4，那么a∶b＝（）。

A．4∶3B．3∶4C．1∶12二、填空题11．12的因数共有______个，选择其中的4个因数，把它们组成一个比例是______。

12．在30的因数中选择4个奇数组成一个比例：( )。

根据比例的基本性质把它改写成乘法等式：( )。

13．比值是2的一个比例是( )。

14．如果2a＝3b（a、b≠0），那么a∶b＝( )∶( )；如果a∶b＝5∶2 ，那么a∶5＝( )∶( )。

15．比值是35的两个比可以为( ),( ),这两个比组成比例是( )．16．一个比例，等号左边的比和等号右边的比一定是( )的。

六年级数学：《比的意义和基本性质》试题

1、小明体重40千克，相当于小军的，小华的体重是小军的。小华体重多少千克？
其实,任何一门学科都离不开死记硬背,关键是记忆有技巧,“死记”之后会“活用”。不记住那些基础知识,怎么会向高层次进军?尤其是语文学科涉猎的范围很广,要真正提高学生的写作水平,单靠分析文章的写作技巧是远远不够的,必须从基础知识抓起,每天挤一点时间让学生“死记”名篇佳句、名言警句,以及丰富的词语、新颖的材料等。这样,就会在有限的时间、空间里给学生的脑海里注入无限的内容。日积月累,积少成多,从而收到水滴石穿,绳锯木断的功效。2、计划生产1800个零件，第一天生产了计划的，第二天生产了计划的。还剩下计划的几分之几没生产？还剩下多少个没生产？
六年级数学：《比的意义和基本性质》试题
二、求比值：
12：8 0.4:0.12
“教师”一称最接近的“老师”概念，最早也要追溯至宋元时期。金代元好问《示侄孙伯安》诗云：“伯安入小学，颖悟非凡貌，属句有夙性，说字惊老师。”于是看，宋元时期小学教师被称为“老师”有案可稽。清代称主考官也为“老师”，而一般学堂里的先生则称为“教师”或“教习”。可见，“教师”一说是比较晚的事了。如今体会，“教师”的含义比之“老师”一说，具有资历和学识程度上较低一些的差别。辛亥革命后，教师与其他官员一样依法令任命，故又称“教师”为“教员”。三、解决问题：
单靠“死”记还不行,还得“活”用,姑且称之为“先死后活”吧。让学生把一周看到或听到的新鲜事记下来,摒弃那些假话套话空话,写出自己的真情实感,篇幅可长可短,并要求运用积累的成语、名言警句等,定期检查点评,选择优秀篇目在班里朗读或展出。这样,即巩固了所学的材料,又锻炼了学生的写作能力,同时还培养了学生的观察能力、思维能力等等,达到“一石多鸟”的效果。以上就是六年级数学：《比的意义和基本性质》试题全文，希望能给大家带来帮助！

比的意义和基本性质

比的意义和基本性质比的意义和基本性质1.比的意义：两个数的比表示两个数相除。

2.比的各部分名称。

（1）比号：“:”叫做比号，读作：“比”。

（2）比的前项和后项：在两个数的比中，比号前面的数叫做比的前项，比号后面的数叫做比的后项。

（3）比值：比的前项除以后项所得的商，叫做比值。

3.比和比值的关系：2既可以表示2:3，又可以表示联系：比和比值都可以用分数形式表示，如32:3的比值。

区别：比表示两个数量的倍数关系；比值是一个具体的数，可以是分数，也可以是小数或整数。

温馨提示：当比的后项为1时，1不能省略不写。

如2:1不能写成2，写成2就是2:1的比值。

4.比与分数、除法的关系。

（1）联系：比的前项相当于分数的分子、除法中的被除数；比号相当于分数的分数线、除法中的除号；比的后项相当于分数的分母、除法中的除数；比值相当于分数的分数值、除法中的商。

（2）区别：比表示两个数量的倍数关系，分数是一个数，除法是一种运算。

5.比的基本性质：比的前项和后项同时乘或除以相同的数（0除外），比值不变。

6.化简比：把两个数的比化成最简单的整数比。

（1）整数比的化简方法：比的前项和后项同时除以它们的最大公因数。

（2）分数比的化简方法：比的前项和后项同时乘它们分母的最小公倍数，先转化成整数比，再进行化简；也可以利用求比值的方法化简。

（3）小数比的化简方法：先用恰当的方法转化成整数比，再进行化简。

【诊断自测】1.填空。

（1）甲是乙的23，甲和乙的比是（），乙和甲的比是（）。

（2）5÷8=（）:（）=()()（3）比的后项不能为（）。

（4）把43:1.125化成最简单的整数比是（），比值是（）。

（5）把25克糖放入100克水中，糖和糖水的质量比为（）。

2.求比值。

53:411.2:3.61.5t:240kg 12:1513.求下列各比中的未知数。

113:x=3x:0.6=1099:x=434.化简下面各比。

9:126.5:1.354:1580.3:920.75:2【考点突破】类型一：已知一个数的几分之几等于另一个数的几分之几，求这两个数的比。

六年级比的意义和基本性质练习题

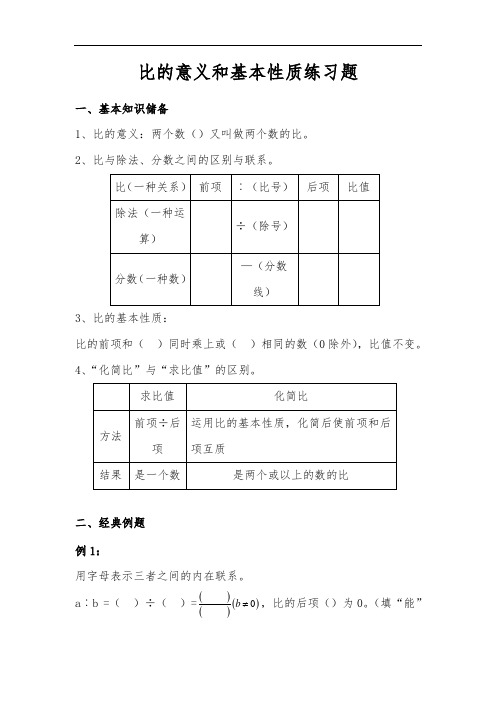
比的意义和基本性质练习题一、基本知识储备1、比的意义：两个数（）又叫做两个数的比。

2、比与除法、分数之间的区别与联系。

3、比的基本性质：比的前项和（）同时乘上或（）相同的数（0除外），比值不变。

4、“化简比”与“求比值”的区别。

二、经典例题例1：用字母表示三者之间的内在联系。

a ︰b =（）÷（）=()()()0b ≠，比的后项（）为0。

（填“能”或“不能”）举一反三1：一袋洗衣粉重320克，一块香皂重80克。

洗衣粉与香皂的重量比是（），比值是（）；香皂与洗衣粉的重量比是（），比值是（）。

例2：盐与水的比是1︰10，则盐︰盐水=（︰），水︰盐=（︰），盐水︰水=（︰）。

举一反三2：两个正方形边长比是1︰3，这两个正方形的周长比是（︰）面积比是（︰）。

例3：男生与女生的人数比是3︰4，男生比女生少() ()。

举一反三3：1、某班有男生20人，女生30人，男生与全班人数的比是（），女生比男生多() ()。

2、甲数除以乙数的商是43，甲数与乙数的比是（）。

例4：易错题分析1、在4︰9中，如果比的前项加上8，要使比值不变，后项应加上（）。

易错题分析2、A ︰B=2︰3，B ︰C=4︰5，那么A ︰B ︰C=（︰︰）。

易错题分析3、一项工程，甲单独完成需要6小时完成，乙单独完成需要5小时完成，甲、乙工作效率之比是（︰）。

举一反三4：1、在3︰8中，如果比的前项加上15，要使比值不变，后项应加上（）。

2、A ︰B=3︰4，B ︰C=5︰6，那么A ︰B ︰C =（︰︰）。

3、一辆汽车从甲地开往乙地，3小时到达，返回时4小时到达，前往速度与返回速度的比是（︰）。

三、迁移拓展例1、如果532CB A ==（其中A 、B 、C 都不等于0），那么A ︰B ︰C=（︰︰）。

举一反三7：如果2A=3B=4C （其中A 、B 、C 都不等于0），那么A ︰B ︰C=（︰︰）。

例2、有两个重叠的正方形，大正方形的边长是5厘米，小正方形的边长是4厘米，重叠部分的面积是9平方厘米，求阴影部分面积。

比的意义及比的基本性质

第十讲比的意义及‎比的基本性‎质【典型例题1‎】求下列各式‎的比值：（1）4.5:217；（2）312:611 （3）36分:0.4时.解析：（1）4.5:217= 4.5÷7.5=0.6；或 4.5:217=29÷215=29×152=53.（2）312:611=37÷67=37×76=2.（3）0.4时=0.4×60=24分； 36分:0.4时=36分÷24分=211点评：此题考查的‎是比与比值‎的概念；掌握正确、熟练地求比‎值的方法. 【知识点】1．比a 、b 是两个数‎或两个同类‎的量，为了把b 和‎a 相比较,将a 与b 相‎除，叫做a与b ‎的比.记作a:b ，或写成ba，其中b ≠0；a 叫做比的‎前项，b 叫做比的‎后项.2．比值比的前项除‎以比的后项‎所得的商叫‎做比值。

求比值时注‎意：（1）得到的结果‎是一个数（分数或小数‎，有时是整数‎）. （2）求两个同类‎量的比值时‎，如果单位不‎同，必须把这两‎个量化成相‎同的单位. （注意：比是解决同‎类量之比）. 【基本习题限‎时训练】1. 求54:45的比值，结果正确的‎是：（） A 、2516 B 、1625 C 、16﹕25 D 、 25﹕16【解】A2. 求2周: 5天的比，结果正确的‎是：（）A 、14:5B 、542 C 、5:14 D 、 2.8【解】C3. 某中学预备‎（2）的学生人数‎为40人，其中男生1‎7人，则该班男生‎人数与女生‎人数的比值‎是：（）A 、4017B 、1723C 、17﹕23D 、 2317【解】D 【拓展题1】一项工程，甲队用15‎天完成，乙队用18‎天完成，求甲队与乙‎队的工作效‎率的比值.【解析】(1÷15) ﹕(1÷18)= 151:181=151÷181=151×18=115【点评】把这项工程‎看成整体“1”，工作效率=工作总量÷工作时间，所以甲队和‎乙队的工作‎效率分别是‎151和181【拓展题2】如图，在ΔABC ‎中BC=10厘米，BD 是BC ‎的52，求ΔABD ‎和ΔABC ‎的面积之比‎.【解析】BD=10×52=4厘米；BC=10厘米；BD 上高的‎长=BC 上高的‎长；ΔABD 的‎面积:ΔABC 的‎面积=（21×BD ×BD 上高）:（21×BC ×BC 上高）=（21×4）:（21×10）=2:5.【点评】三角形的面‎积公式是21×底边长×底边长上的‎高，而ΔABD ‎和ΔABC‎的边长可以‎取B D 、BC 它们底‎边上的高是‎同一条高，由已知条件‎只要求出B ‎D 长就可以‎求出这两个‎三角形的面‎积比.【典型例题2‎】已知41:x=213，求x.解析：因为41:x=213；所以41÷x=213；由 x=41÷213；可得x=41×72；所以x=141.点评：要求正确理‎解分数、除法、比的关系和‎区别，从而求出所‎求的未知数‎。

六年级数学上册试题之《比的意义和基本性质》

六年级数学上册试题之《比的意义和基本性质》1、甲车3小时行驶120千米，乙车4小时行驶140千米，甲乙两车所行驶时间的比是( );路程的比是( );速度的比是( )。

2、一条路甲车行驶的速度是每时60km，乙车行驶的速度每时50km，甲乙两车行完全程所用时间比是( )。

3、一件工作，小红需4小时完成，小东需5小时完成，小红和小东的工作效率比是( )。

4、两个正方形边长的比是4∶3，它们周长的比是()，面积的比是()。

5、两个正方体的棱长比是3:1，它们的表面积的比是( )，体积的比是( )。

6、大伯家有一块长方形菜地，他用步测法测得菜地周长大约是50米，长和宽的比是3∶2。

那么，菜地的面积是多少平方米?*7、画一个长方形，面积是24 cm2，长和宽的比是3∶2，长宽各应画多长?8、用36厘米长的铁丝围成一个长方体框架，这个长方体长、宽、高的比是3∶2∶1，它体积是多少?9、甲、乙、丙三个数的比是2∶3∶7，三个数的平均数是48，乙数是多少?10、甲数和乙数的比是3∶4，乙数和丙数的比是5∶6，甲数和丙数的比是多少?11、一个班的学生人数介于40人至60人之间，男生人数与女生人数的比是7∶8，男生可能是多少人?12、要练说，得练看。

看与说是统一的，看不准就难以说得好。

练看，就是训练幼儿的观察能力，扩大幼儿的认知范围，让幼儿在观察事物、观察生活、观察自然的活动中，积累词汇、理解词义、发展语言。

在运用观察法组织活动时，我着眼观察于观察对象的选择，着力于观察过程的指导，着重于幼儿观察能力和语言表达能力的提高。

12、学校把360本科技书分配给甲、乙、丙三个班，甲班的等于乙班的，等于丙班的，甲、乙、丙三个班各分得多少本?。

2022-2023学年人教版数学六年级下册比例的意义和性质练习题(含答案)

2022-2023学年人教版数学六年级下册比例的意义和性质练习题学校:___________姓名：___________班级：___________一、选择题1．下列能与12∶13组成比例的是（）。

A ．2∶3B ．13∶14C ．3∶2D ．34∶132．下面各组的两个比，可以组成比例的是（）。

A ．13 ∶ 16和12∶14B ．12∶9和9∶6C ．8.4∶2.1和1.2∶8.43．能与11:43组成比例的是（）。

A ．13:4B ．4∶3C ．3∶4D ．1:434．如果a 、b 都是不为0的数，且56a ＝78b ，则a 和b 的大小关系是（）。

A ．a ＜bB ．a ＝bC ．a ＞b5．下列各数中，（）不能与2、8、10组成比例。

A ．58B ．85C ．52D ．406．若乙数的56与甲数的34相等（甲、乙两数均不为0）则乙数∶甲数＝（）。

A ．10∶9B ．9∶10C ．56∶347．下面的（）可以和23:35组成比例。

A ．35:23B ．10:9C ．9:108．若y∶3＝2∶x （x ，y 都不为0），下列式子中成立的是（）。

A ．3x ＝2yB ．x ＝6yC ．xy ＝6D ．2x ＝3y9．用2，3，6，9组成的比例中，正确的是（）。

A ．2396：＝：B ．2:36:9C ．3269：＝：10．如果a×3＝b×4，那么a∶b ＝（）。

A ．4∶3B ．3∶4C ．1∶12二、填空题11．一个比例的两个外项都是6，且两个比值都是4，则这个比例可以写成( )。

12．写出比值是35的两个比：( )、( )。

再把它们组成比例：( )。

13．在比例2.4:7.215:45中，内项是( )和( )，外项是( )和( )。

14．一个比例中，两个比的比值都是0.8，两个内项都是2，这个比例是( )。

15．比值是35的两个比可以为( ),( ),这两个比组成比例是( )．16．一个比例，等号左边的比和等号右边的比一定是( )的。

六年级数学试题：《比的意义和基本性质》

宋以后，京师所设小学馆和武学堂中的教师称谓皆称之为“教谕”。至元明清之县学一律循之不变。明朝入选翰林院的进士之师称“教习”。到清末，学堂兴起，各科教师仍沿用“教习”一称。其实“教谕”在明清时还有学官一意，即主管县一级的教育生员。而相应府和州掌管教育生员者则谓“教授”和“学正”。“教授”“学正”和“教谕”的副手一律称“训导”。于民间，特别是汉代以后，对于在“校”或“学”中传授经学者也称为“经师”。在一些特定的讲学场合，比如书院、皇室，也称教师为“院长、西席、讲席”等。3、小明身高1.5米，小红身高1米25厘米。写出小红与小明身高的比，并化简。
六年级数学试题：《比的意义和基本性质5 18:
6:0.36:
0.6::6
四、解决问题：
1、一项工程，甲独做10天完成，乙独做15天完成。写出甲、乙工作效率的比，并化简。
宋以后，京师所设小学馆和武学堂中的教师称谓皆称之为“教谕”。至元明清之县学一律循之不变。明朝入选翰林院的进士之师称“教习”。到清末，学堂兴起，各科教师仍沿用“教习”一称。其实“教谕”在明清时还有学官一意，即主管县一级的教育生员。而相应府和州掌管教育生员者则谓“教授”和“学正”。“教授”“学正”和“教谕”的副手一律称“训导”。于民间，特别是汉代以后，对于在“校”或“学”中传授经学者也称为“经师”。在一些特定的讲学场合，比如书院、皇室，也称教师为“院长、西席、讲席”等。2、六年级男生人数是女生人数的1.2倍，写出男生与女生人数的比，并化简。
以上就是六年级数学试题：《比的意义和基本性质》全文，希望能给大家带来帮助！
教师范读的是阅读教学中不可缺少的部分，我常采用范读，让幼儿学习、模仿。如领读，我读一句，让幼儿读一句，边读边记；第二通读，我大声读，我大声读，幼儿小声读，边学边仿；第三赏读，我借用录好配朗读磁带，一边放录音，一边幼儿反复倾听，在反复倾听中体验、品味。

《比的意义和基本性质》练习题

比的意义和基本性质（一）一、细心填写：1、鸡有80只，鸭有100只，鸡和鸭只数的比是（），比值是（）。

2、长方形长3分米，宽12厘米，长与宽的比是（），比值是（）。

3、小李5小时加工60个零件，加工个数与时间的比是（），比值是（）。

4、一本书读了55页，45页没有读，已读与总数的比是（），比值是（）。

5、甲数相当于乙数的92，甲数与乙数的比是（），乙数与甲数的比是（）。

6、三好学生占全班人数的81，三好学生与全班人数的比是（）。

7、白兔只数的31与黑兔相等。

白兔与黑兔的比是（），白兔与黑兔的比是（） 8、若A ÷B ＝5（A 、B 都不等于0）则A ：B ＝( ):( )若A ＝B （A 、B 都不等于0）则A ：B ＝( ):( )9、填写比、除法和分数的关系。

比比的前项除法除数分数 --- 分数线分数值10、（）又叫做两个数的比。

（）叫做比值。

11、43＝( ):( ) ＝( )÷（ )12、在100克水中加入10克盐，盐和盐水的比是（）。

13、男工人数是女工人数的52，男、女工人数的比是（）。

14、甲数是乙数的4倍，甲、乙两数的比是（），乙数与两数和的比是（）。

15、甲数比乙数多41，甲数与乙数的比是（），比值是（）。

16、（），叫做比的基本性质。

17、16：20＝32:( ) ＝( )÷10 ＝()4＝()80＝1.6( ) ＝( ):0.218、火车4小时行驶了600千米，路程和时间的最简整数比是（），比值是（）。

19、甲数是乙数的3倍乙数与甲数的比是（），比值是（）。

20、601班男生与女生人数的比是2：3，女生占全班的（），男生占全班的（）。

21、甲数是乙数的32，乙数与甲数的比是（），甲数与乙数的比是（）。

二、求比值：12：8 0.4:0.12 5: 41 4.5:0.9 31:65 32:910 0.75:41 4: 41 35：45 360：450 0.3:0.15 18: 32 6:0.36 203:54 0.6:52 32:6 三、化简比：35：45 360：450 0.3:0.15 18: 32 6:0.36 203:54 0.6:52 32:683:21 0.75: 43 24: 31 6.4:0.16 2.25:9 815:32 54：83 31：41四、判断是否：1、54可以读作“6比7”。

六年级数学上册比的意义和基本性质提高练习题

百分数应用题姓名：1.六（1）班有男生25人，女生比男生少5名。

A.女生人数是男生人数的百分之几？B.女生人数比男生人数少百分之几？C.男生人数比女生人数多百分之几？2.六年级一班有男同学20人，比女同学人数多百分之25,男同学比女同学多多少人？3.某校三年级有240人，比二年级少百分之20，三年级比二年级少多少人？24.一桶油用去寺，剩下的比用去的多百分之几？5.某车间计划生产零件8000个,实际超产1000个,实际完成计划的百分之几？6.某车间计划生产一批零件，实际生产9000个，比计划超产1000个，实际比计划超产百分之几？7.一捆铁丝，第一次减去40%，第二次减去第一次的25% ,,第三次比第二次多剪15米，这时还剩25米，这困铁丝长多少米？& 一捆铁丝，第一次减去40%，第二次减去第一次的25%，还剩56米，这捆铁丝长多少米？9.一捆铁丝，第一次减去20%，第二次减去第一次的50%，还多8米，正好剪了全长的一半。

这捆铁丝长多少米？一一 1 ______________________________________ 一9.水果店有苹果1200千克，卖出-后，剩下的苹果重量是梨的60%，水果店5有梨多少千克？一一 1 ____________________________________ 一10.水果店有苹果1200千克，卖出-后，剩下的苹果重量比梨少60%，水果店5有梨多少千克?11.有一批粮食，第一次取出25吨，第二次取出余下的40%，还剩一半。

这批粮食共有多少吨？12.学校有一年级学生100人，二年级比一年级多10%，一、二年级学生人数占全校人数的20%，全校有学生多少人？13.某商店同时卖出两件商品，每件各得240元，但其中的一件赚20%，另一件亏20%，这个商店卖出这两件商品亏损多少元？14.六年级（1）班有40人，其中23人为灾区捐了款，25人为灾区小朋友捐赠了学习用品，既捐款又捐学习用品的同学占全班人数的百分之几？15.六（1）班期中测试，数学不及格人数是及格人数的丄，六一班期中测试数学及格率是多少?1915.肿瘤医院有医务人员85 人，其中男医务人员占40% ，今年又分配了一些男医生，这时男医务人员占医务人员总数的49% ，新来了多少名男医生？16.一件商品按30%的利润定价，然后又打九折出售，结果每件商品获利34元。

人教版册数学比的意义和基本性质》练习题

人教版册数学《比的意义和基本性质》练习题 The document was prepared on January 2, 202139、比的意义和基本性质（一）一、细心填写：1、鸡有80只，鸭有100只，鸡和鸭只数的比是（），比值是（）。

2、长方形长3分米，宽12厘米，长与宽的比是（），比值是（）。

3、小李5小时加工60个零件，加工个数与时间的比是（），比值是（）。

4、一本书读了55页，45页没有读，已读与总数的比是（），比值是（）。

5、甲数相当于乙数的92，甲数与乙数的比是（），乙数与甲数的比是（）。

6、三好学生占全班人数的81，三好学生与全班人数的比是（）。

7、白兔只数的31与黑兔相等。

白兔与黑兔的比是（），白兔与黑兔的比是（）8、若A ÷B ＝5（A 、B 都不等于0）则A ：B ＝( ):( )若A ＝B （A 、B 都不等于0）则A ：B ＝( ):( )二、求比值：32：94 : 3321:113 : 48:36 : 52 7: 3: 116 1: 9072 三、解决问题：1、一辆汽车从甲地到乙地，每小时行80千米，用了43小时，返回时只用了85小时。

返回时每小时行多少千米2、商店售出2筐橙子，每筐24千克。

售出的橙子占水果总数的116，售出的香蕉占水果总数的41。

售出香蕉多少千克40、比的意义和基本性质（二）一、细心填写：12）叫做比值。

3、43＝( ):( ) ＝( )÷（ ) 4、在100克水中加入10克盐，盐和盐水的比是（）。

5、男工人数是女工人数的52，男、女工人数的比是（）。

6、甲数是乙数的4倍，甲、乙两数的比是（），乙数与两数和的比是（）。

7、甲数比乙数多41，甲数与乙数的比是（），比值是（）。

二、求比值：12：8 :5: 41 : 31:65 32:910 :41 4: 41 三、解决问题：1、小明体重40千克，相当于小军的910，小华的体重是小军的65。