2017_2018学年八年级数学上册第十四章整式的乘法与因式分解14.2.2完全平方公式同步精练新版
八年级数学人教版上册第14章整式的乘除与因式分解14.2.2完全平方公式(第1课时图文详解)

八年级上册第14章整式的乘除与因式分解
一位老人非常喜欢孩子.每当有孩子到他家做客时, 老人都要拿出糖果招待他们.来一个孩子,老人就给这个 孩子一块糖,来两个孩子,老人就给每个孩子两块塘,… (1)第一天有a个男孩去了老人家,老人一共给了这些孩
子多少块糖? a2
(2)第二天有b个女孩去了老人家,老人一共给了这些孩
八年级上册第14章整式的乘除与因式分解
(2)(-a2+b3)2 【解析】原式= (b3-a2)2
=b6-2 a2 b3+a4 ∵(a-b)2 =(b-a)2 ∴(-a2 +b3)2 = (a2 -b3)2
八年级上册第14章整式的乘除与因式分解
【例2】运用完全平方公式计算:
(1) 1022;
(2) 992.
(2) (4x-3y)2 =16x2-24xy+9y2
(4)(-2m-1)2 =4m2+4m+1
八年级上册第14章整式的乘除与因式分解
1.(日照·中考)由m(a+b+c)=ma+mb+mc,可得a+b)(a2- ab+b2)=a3-a2b+ab2+a2b-ab2+b3=a3+b3,即(a+b)(a2-ab+b2) =a3+b3 ①.我们把等式①叫做多项式乘法的立方公式. 下列应用这个立方公式进行的变形不正确的是( ) (A)(x+4y)(x2-4xy+16y2)=x3+64y3 (B)(2x+y)(4x2-2xy+y2)=8x3+y3 (C)(a+1)(a2+a+1)=a3+1 (D) x3+27=(x+3)(x2-3x+9) 【解析选】C.根据乘法的立方公式(a+b)(a2-ab+b2)
14.2.2 第2课时 乘法公式的综合运用

14.2.2 第2课时 乘法公式的综合运用
学习指 知 南识 管 归 理类 探 当 究堂 测 分 评层 作
业
教学目标 1.掌握添括号法则;
学习指 南
Байду номын сангаас
2.综合运用乘法公式进行计算.
情景问题引入
图书阅览室里有 a 人正在看书, b 人看完后出去了,又有 c 人回教室上课
了,此时阅览室中还有多少人?小刚得出的答案是 a-(b+c),小芳得出的答案是
里;
(2)把后三项括到带有“-”号的括号里;
(3)把四次项括到带有“+”号的括号里,把二次项括到带有“-”号的括号
里.
解:(1)5a3b-2ab+3ab3-2b2=(5a3b-2ab)-(-3ab3+2b2). (2)5a3b-2ab+3ab3-2b2=5a3b-(2ab-3ab3+2b2). (3)5a3b-2ab+3ab3-2b2=(5a3b+3ab3)-(2ab+2b2).
6.[2018·邵阳]先化简,再求值:(a-2b)(a+2b)-(a-2b)2+8b2,其中 a=-2, b=12.
解:原式=a2-4b2-(a2-4ab+4b2)+8b2 =a2-4b2-a2+4ab-4b2+8b2 =4ab. 当 a=-2,b=12时, 原式=4×(-2)×12=-4.
7.[2018 春·延庆区期末]先化简,再求值:(x-1)2-(x+2)(x-2)+(x-4)(x+ 5),其中 x2-x-5=0.
(2)(x-3y-1)(x+3y-1) =[(x-1)-3y][(x-1)+3y] =(x-1)2-(3y)2 =x2-2x+1-9y2.
(3)3x-2y+142 =3x-2y+142 =(3x-2y)2+2×(3x-2y)×14+142 =(3x)2-2×3x×2y+(2y)2+12(3x-2y)+116 =9x2-12xy+4y2+32x-y+116.
人教版数学八年级上册14.2.2完全平方公-添括号法则教案

(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与完全平方公式相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。通过实际计算几个完全平方公式的例子,让学生直观感受公式的作用。
突破方法:引导学生观察表达式中的常数项,是否为某数的平方,然后尝试将中间项分解为两倍的乘积。
(3)难点:在解决实际问题如(2x-3)(2x+3)=4x²-9时,学生可能难以将右侧转换为完全平方形式;
突破方法:通过示例展示如何将4x²-9视为(2x)²-3²,进而应用平方差公式(a²-b²)=(a+b)(a-b),引导学生理解。
此外,课堂总结环节,学生们对于完全平方公式的掌握程度有了明显的提升,但仍有个别学生在应用时出现错误。针对这一问题,我计划在下一节课中,通过更多的实际例题和练习,帮助他们巩固知识,提高解题能力。
总体来说,今天的课堂氛围较好,学生们对完全平方公式的学习兴趣浓厚。但我也意识到,在今后的教学中,需要更加关注学生的个体差异,采取有针对性的教学方法,帮助他们突破难点,提高学习效果。同时,要加强课堂互动,鼓励学生提问和表达自己的观点,使他们在课堂中真正成为主体,从而提高数学素养和解决问题的能力。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“完全平方公式在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
人教版八年级数学上册第十四章 14.2.2完全平方公式

两个数的和(或差)的平方,等于它们的平 方和,加上(或减去)它们的积的2倍.
你能将上面发现的规律推导出来吗?
(a+b)2 =a2+ab+ab+b2 =a2+b2+2ab
(a-b)2 =a2-ab-ab+b2 =a2+b2-2ab
其中解x:=1原,式y==2(.2x2-x2+y2)(x2-y2+2y2) =(x2+y2)2 =x4+2x2y2+y4
当x=1,y=2时,原式=1+8+16=25.
课堂小结
S1
S2
S3
S4
S= (a+b)2 =S1+S2+S3+S4a=2+b2+2ab .
课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题。
(2)若4x2+mx+9是完全平方式,则 ±12
m=解析:(. 1)∵(x-5)2=x2-10x+25=x2+kx+25, ∴k=-10. (2)∵4x2+mx+9是完全平方式, ∴4x2+mx+9=(2x±3)2,∴m=±12.
2.化简求值:[2x2-(x+y)(x-y)][(-x-y)(yx)+2y2],
(a+b)2=a2+b2+2ab (a-b)2=a2+b2-2ab
即两个数的和(或差)的平方,等于它们的平 方和,加上(或减去)它们的积的2倍.这个公 式叫完全平方公式.
思考 你能根据下图中图形的面积说明完全平方公式吗?
人教版八年级数学上册14.2.2完全平方公式

D 3.下列计算正确的是( A.(x+y)2=x2+y2 )
B.(x-y)2=x2-2xy-y2
C.(x+2y)(x-2y)=x2-2y2 D.(-x+y)2=x2-2xy+y2
16m2-8mn+n2 ; 4.计算:(4m-n)2=________________ 1 2 4x2+2x+1 (2x+ ) =____________________ ; 4 2
2 2 a + b 19.已知 a(a-1)+(b-a2)=7,求 -ab 的值. 2
(a-b)2 49 解:由已知得 b-a=7,∴原式= = 2 2
20.(1)化简:(a-b)2+(b-c)2+(c-a)2; (2)利用上题结论,已知a-b=10,b-c=5,求a2+b2+c2-ab-bc -ac的值.
解:(1)原式=2a2+2b2+2c2-2ab-2bc-2ac (2)∵a-b=10,b- 1 2 1 2 2 c=5, ∴a-c=15, ∴原式= (2a +2b +2c -2ab-2bc-2ac)= [(a 2 2 -b)2+(b-c)2+(c-a)2]=175
解:9960.04
1 解:420 4
8.用简便方法计算:
10002-2000×1001+10012.
解:1
知识点3:添括号法则 9.下列添括号正确的是( A.a-b+c=a-(b+c) B.a-b+c=a-(-b-c) C.a-b+c=a-(b-c) D.a-b+c=a+(b-c)
C
)
10.对于下列计算(a-b+c)(a+b-c)的变形过程中,正确的 A 是( ) A.[a-(b-c)][a+(b-c)] B.[(a-c)+b][(a-c)-b] C.[(a-b)+c][(a-b)-c] D.[a-(b+c)][a+(b-c)]
14.2.2完全平方公式(第一课时)

3.选择题 (1)如果x2+mx+4是一个完全平方公式,那么 m的值是( c ) A .4 B.-4 C.±4 D.±8 (2)将正方形的边长由acm增加6cm,则正方形 的面积增加了( c ) A.36cm2 B.12acm2 C.(36+12a)cm2 D.以上都不对
(a+b)2=(a+b) (a+b) = a2+ab+ab+b2 =a2+2ab+b2.
(a -b )2 = ( a - b ) (a - b ) = a2-ab-ab+b2
=a2-2ab+b2
完全平方公式的数学表达式:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2 完全平方公式的文字叙述: 两数和(或差)的平方,等于它们的平方和, 加上(或减去)它们的积的2倍.
(3)已知 a+b=4,ab=-12,则a2+b2= 40
(4)已知 m+n=3,mn=5, 求:(m+3)(n+3)的值. (5)已知x+y=4,xy=-13, 求: x2-3xy+y2的值. (6)已知:(a+b)2=4, (a-b)2=36 求a2-ab+b2的值. ab=-8 28
.
23 81
第十四章 整式的乘法与因式分解
14.2.2完全平方公式 (第一课时)
复习与回顾 1.多项式的乘法法则是什么? 用一个多项式的每一项乘以另一个多项式的每一 项,再把所得的积相加.
(a+b) (m+n) = am+an + bm+bn
第14章“整式的乘法与因式分解”简介
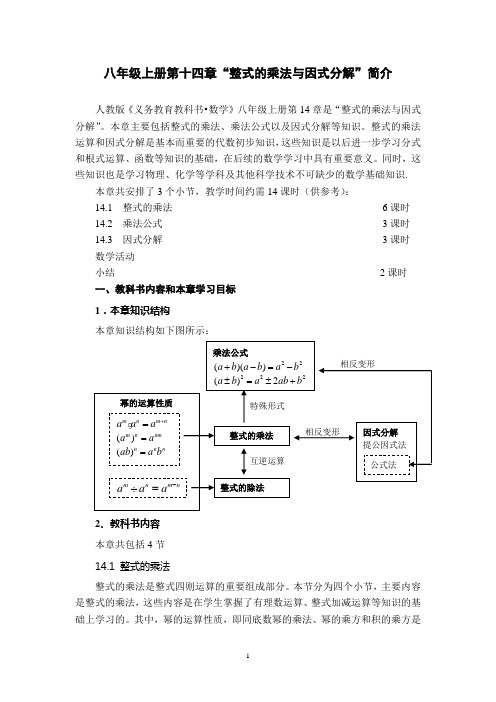
八年级上册第十四章“整式的乘法与因式分解”简介人教版《义务教育教科书•数学》八年级上册第14章是“整式的乘法与因式分解”。
本章主要包括整式的乘法、乘法公式以及因式分解等知识。
整式的乘法运算和因式分解是基本而重要的代数初步知识,这些知识是以后进一步学习分式和根式运算、函数等知识的基础,在后续的数学学习中具有重要意义。
同时,这些知识也是学习物理、化学等学科及其他科学技术不可缺少的数学基础知识.本章共安排了3个小节,教学时间约需14课时(供参考):14.1 整式的乘法6课时14.2 乘法公式3课时14.3 因式分解3课时数学活动小结2课时一、教科书内容和本章学习目标1.本章知识结构本章知识结构如下图所示:2.教科书内容本章共包括4节14.1 整式的乘法整式的乘法是整式四则运算的重要组成部分。
本节分为四个小节,主要内容是整式的乘法,这些内容是在学生掌握了有理数运算、整式加减运算等知识的基础上学习的。
其中,幂的运算性质,即同底数幂的乘法、幂的乘方和积的乘方是整式乘法的基础,教科书把它们依次安排在前三个小节中,教学中应适当复习幂、指数、底数等概念,特别要弄清正整数指数幂的意义。
在学生掌握了幂的运算性质后,作为它们的一个直接应用,教科书在第四小节安排一般整式乘法的教学内容。
首先是单项式与单项式相乘,由于进行单项式与多项式、多项式与多项式相乘的前提是熟练地进行单项式与单项式相乘,因此,对于单项式与单项式相乘的教学应该予以充分重视。
在学生掌握了单项式与单项式相乘的基础上,教科书利用分配律等进一步引入单项式与多项式相乘、多项式与多项式相乘,这样使整式乘法运算的教学从简到繁,由易到难,层层递进。
整式的除法也是整式四则运算的重要组成部分,是今后学习(因式分解、整数指数幂、分式运算)必须的内容。
考虑到课标没有单列条目,因此不单独成节。
在讲完整式乘法后,从逆运算角度介绍同底数幂的除法、单项式除以单项式,多项式除以单项式等必须内容。
人教版八年级数学上册课时练 第十四章 整式的乘法与因式分解 14.2.2 完全平方公式

人教版八年级数学上册课时练 第十四章 整式的乘法与因式分解 14.2.2 完全平方公式一、选择题1.已知(x -2015)2+(x -2017)2=34,则(x -2016)2的值是( ) A .4B .8C .12D .162.已知a 2﹣2a﹣1﹣0,则a 4﹣2a 3﹣2a+1等于﹣ ﹣ A .0B .1C .2D .33.已知2210x x +-=,则4252x x x -+的值为( ) A .0B .1-C .2D .14.三种不同类型的长方形地砖长宽如图所示,现有A 类1块,B 类4块,C 类5块.小明在用这些地砖拼成一个正方形时,多出其中1块地砖,那么小明拼成正方形的边长是( )A .m+nB .2m+2nC .2m+nD .m+2n5.已知18221n ++是一个有理数的平方,则n 不能为( ) A .20-B .10C .34D .366.设2017a x =-,2019b x =-,2018c x =-.若2234a b +=,则2c 的值是( ) A .16B .12C .8D .47.用如图所示的正方形和长方形卡片若干张,拼成一个边长为2+a b 的正方形,需要B 类卡片的张数为( )A .6B .2C .3D .48.下列运算中,结果正确的是( ) A .235a b ab += B .()2a a b a b -+=-C .()222a b a b +=+ D .236a a a ⋅=9.设2020x y z ++=,且201920202021x y z ==,则3333x y z xyz ++-=( ) A .673 B .20203 C .20213D .67410.若229x kxy y -+是一个完全平方式,则常数k 的值为( ) A .6 B .6- C .6±D .无法确定二、填空题11.已知关于x 的代数式()2x -1x 9a ++是完全平方式,则a =____________12.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了n(a b)(n +为非负整数)展开式的项数及各项系数的有关规律.例如:0(a b)1+=,它只有一项,系数为1;系数和为1﹣1(a b)a b +=+,它有两项,系数分别为1﹣1,系数和为2﹣222(a b)a 2ab b +=++,它有三项,系数分别为1﹣2﹣1,系数和为4﹣33223(a b)a 3a b 3ab b +=+++,它有四项,系数分别为1﹣3﹣3﹣1,系数和为8﹣⋯﹣则n(a b)+的展开式共有______项,系数和为______﹣13.用4张长为a 、宽为b ()a b >的长方形纸片,按如图的方式拼成一个边长为()a b +的正方形,图中空白部分的面积为1S ,阴影部分的面积为2S .若122S S =,则a b 、之间存在的数量关系是__________.14.若241x mx +-是完全平方式,则m 的值是________________.15.如图,//PQ MN ,A 、B 分别为直线MN 、PQ 上两点,且45BAN ∠=︒,若射线AM 绕点顺时针旋转至AN 后立即回转,射线BQ 绕点B 逆时针旋转至BP 后立即回转,两射线分别绕点A 、点B 不停地旋转,若射线AM 转动的速度是a ︒/秒,射线BQ 转动的速度是b ︒/秒,且a 、b 满足()2510a b -+-=.若射线AM 绕点A 顺时针先转动18秒,射线BQ 才开始绕点B 逆时针旋转,在射线BQ 到达BA 之前,问射线AM 再转动_______秒时,射线AM 与射线BQ 互相平行.三、解答题16.若x 满足(7﹣x )(x ﹣4)=2,求(x ﹣7)2+(4﹣x )2的值:解:设7﹣x =a ,x ﹣4=b ,则(7﹣x )(x ﹣4)=ab =2,a +b =(7﹣x )+(x ﹣4)=3 所以(x ﹣7)2+(4﹣x )2=(7﹣x )2+(x ﹣4)2=a 2+b 2=(a +b )2﹣2ab =32﹣2×2=5 请仿照上面的方法求解下面的问题(1)若x 满足(8﹣x )(x ﹣3)=3,求(8﹣x )2+(x ﹣3)2的值;(2)已知正方形ABCD 的边长为x ,E ,F 分别是AD ,DC 上的点,且AE =2,CF =5,长方形EMFD 的面积是28,分别以MF 、DF 为边作正方形,求阴影部分的面积.17.认真阅读以下材料,然后解答问题.我们学习了多项式的运算法则,类似地,我们可以计算出多项式的展开式.如:1222323223(),()2,()()()33,a b a b a b a ab b a b a b a b a a b ab b +=++=+++=++=+++.我们依次对()n a b +展开式的各项系数进一步研究发现,当n 取正整数时可以单独列成以下形式:1()a b + 1 1 2()a b + 1 2 13()a b + 1 3 3 14()a b + 1 4 6 4 15()a b + 1 5 10 10 5 1 6()a b + 1 6 15 20 15 6 1……上面的多项式展开系数表称为“杨辉三角”,仔细观察“杨辉三角”,用你发现的规律回答下列问题: (1)多项式()n a b +(n 取正整数)的展开式是一个几次几项式?并预测第三项的系数.(2)结合上述材料,推断出多项式()n a b +(n 取正整数)的展开式的各项系数之和.(结果用含字母n 的代数式表示) 18.把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.例如,由图1,可得等式:(a+2b )(a+b )=a 2+3ab+2b 2(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c 的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c =11,ab+bc+ac =38,求a 2+b 2+c 2的值.(3)如图3,将两个边长分别为a 和b 的正方形拼在一起,B ,C ,G 三点在同一直线上,连接BD 和BF .若这两个正方形的边长满足a+b =10,ab =20,请求出阴影部分的面积.19.先化简,再求值:已知代数式2(3)(24)ax x x b -+--化简后,不含有x 2项和常数项. (1)求a﹣b 的值;(2)求2()()()(2)b a a b a b a a b ---+---+的值. 20.先阅读材料,再解答问题:例:已知x =123456789×123456786,y =123456788×123456787,试比较x 、y 的大小. 解:设123456788=a ,则x =(a +1)(a -2)=22a a --,y =a(a -1)=2-a a ,∵x -y =()()222a a a a ----=-2, ∴x <y .问题:已知x =20182018×20182022-20182019×20182021,y =20182019×20182023-20182020×20182022,试比较x 、y 的大小.21.在求234561222222++++++的值时,小明发现:从第二个加数起每一个加数都是前一个数的2倍,于是他设:234561222222S =++++++①,然后在①式的两边都乘以2,得:23456722222222S =++++++②;②-①得7221S S -=-(1)求234561333333++++++的值; (2)求12310012222----+++++的值;(3)求232019a a a a -----(0a ≠且1a ≠)的值.22.先化简,再求值:3(2x ﹣y )2+(2x +y )(2x ﹣y )+(﹣3x )(4x ﹣3y ),其中x =﹣1,y =1. 23.探究阅读材料:“若x 满足()()806030x x --=,求()()228060x x -+-的值”解:设()80x a -=,()60x b -=,则()()806030x x ab --==,()()806020a b x x +=-+-=, 所以()()22228060x x a b -+-=+()22220230340a b ab =+-=-⨯=. 解决问题:(1)若x 满足()()451520x x --=-,求()()224515x x -+-的值.(2)若x 满足()()22202020184040x x -+-=,求()()20202018x x --的值.(3)如图,正方形ABCD 的边长为x ,20AE =,30CG =,长方形EFGD 的面积是700,四边形NGDH 和MEDQ 都是正方形,PQDH 是长方形,求图中阴影部分的面积(结果必须是一个具体的数值). 【参考答案】1.D 2.C 3.A 4.D 5.D 6.A 7.D 8.B 9.B 10.C 11.5或-712.n 1+ n 2 13.a =2b 14.4± 15.15或22.5 16.(1)19;(2)33. 17.(1)n 次1n +项式,(1)2n n -;(2)2n . 18.(1)(a+b+c )2=a 2+b 2+c 2+2ab+2bc+2ac ;(2)45;(3)20. 19.(1)1;122a b ==-;(2)-620.x y =21.(1)()71312-;(2)10022--;(3)20201a a a --22.9.23.(1)940;(2)2018;(3)2900。
2017-2018学年八年级数学上册(人教版)教案第十四章整式的乘法与因式分解

4.数学运算:提高学生准确熟练地进行整式的乘法与因式分解运算的能力,培养严谨的计算习惯。
5.数据分析:通过对整式的乘法与因式分解的练习,使学生能够分析数据,发现规律,为解决更复杂问题奠定基础。
6.空间想象:在学习过程中,培养学生对整式结构的空间想象能力,为高中阶段数学学习打下基础。
2017-2018学年八年级数学上册(人教版)教案第十四章整式的乘法与因式分解
一、教学内容
《2017-2018学年八年级数学上册(人教版)》第十四章整式的乘法与因式分解,主要包括以下内容:
1.单项式乘单项式:掌握同类项与合并同类项的方法,运用法则进行计算。
2.单项式乘多项式:学会将单项式分别与多项式的每一项相乘,再将所得积相加。
五、教学反思
在今天的教学过程中,我发现学生们对整式的乘法与因式分解这一章节表现出很大的兴趣。在导入新课的时候,通过联系日常生活中的例子,成功引起了学生们的注意力。他们积极参与讨论,提出了许多有关整式乘法的问题,这是一个很好的开始。
在新课讲授环节,我注意到学生们在理解整式乘法的基本概念上并没有太大困难。但在进行案例分析时,有些学生在运用乘法法则进行计算时出现了错误。针对这个问题,我及时进行了纠正和指导,强调需要注意的细节,例如同类项的合并和多项式乘多项式的运算顺序。
举例:平方差公式a^2 - b^2 = (a + b)(a - b),完全平方公式(a + b)^2 = a^2 + 2ab + b^2。
(3)因式分解方法:掌握提公因式法、应用公式法、十字相乘法等方法,并能解决实际问题。
举例:如多项式4x^2 + 4x,可以提取公因式4x,得到4x(x + 1)。
人教版八年级数学上册第十四章 14.2.2完全平方公式3

知识要点
知识点一:去括号、添括号的法则 (1)去括号法则 括号前面是“+”号,去掉“+”号和括号,括号里的各项
不改变符号 ; 括号前面是“-”号,去掉“-”号和括号,括号里的各项都
改变符号 .
(2)添括号法则 所添括号前面是“+”号,括到括号里的各项都 不改变符号 ; 所添括号前面是“-”号,括到括号里的各项都 改变符号 . (3)添括号与去括号是互逆的,可以相互进行检验添括号或去 括号的正确性.
14.1.1 同底数幂的乘法
14.2.2 完全平方公式
知识点1 完全平方公式的几何意义
知识点2 完全平方公式的运用
知识点3 添括号法则及其运用
1.下列计算正确的是( C )
A.(x+y)2=x2+y2
B.(x-y)2=x2-2xy-y2
C.(x+1)(x-1)=x2-1
D.(x-1)2=x2-1
解:原式=[a+(b-2)][a-(b-2)] =a2-b2+4b-4. 小结:能把-b+2 改写成-(b-2)是关键.
10.运用乘法公式计算:(2x+y+z)(2x-y-z). 解:原式=[2x+(y+z)][2x-(y+z)] =(2x)2-(y+z)2 =4x2-(y2+2yz+z2) =4x2-y2-2yz-z2.
小结:用去括号法则可以检验添括号后是否正确.
变式练习
9.在括号里填上适当的项: (1)a+2b-c=a+( 2b-c ); (2)a-b-c+d=a-( b+c-d ); (3)(a+b-c)(a-b+c)=[a+( b-c
)][a-(
b-c )].
6.【例 2】运用乘法公式计算:(a+b-2)(a-b+2).
2.计算(-a-b)2的结果是( C )
八年级数学上册第十四章《整式的乘法与因式分解》14.2乘法公式14.2.2完全平方公式14.2.2

2018年秋八年级数学上册第十四章《整式的乘法与因式分解》14.2 乘法公式14.2.2 完全平方公式14.2.2.2 添括号法则课时作业(新版)新人教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018年秋八年级数学上册第十四章《整式的乘法与因式分解》14.2 乘法公式14.2.2 完全平方公式14.2.2.2 添括号法则课时作业(新版)新人教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018年秋八年级数学上册第十四章《整式的乘法与因式分解》14.2 乘法公式14.2.2 完全平方公式14.2.2.2 添括号法则课时作业(新版)新人教版的全部内容。
第2课时添括号法则知识要点基础练知识点1添括号法则1.不改变代数式a2-(2a+b+c)的值,把它括号前面的符号变为相反的符号,应为(B)A.a2+(-2a+b+c)B.a2+(—2a—b-c)C。
a2+(-2a)+b+cD。
a2—(—2a-b-c)2.将多项式3x3-2x2+4x—5添括号后正确的是(B)A。
3x3-(2x2+4x-5)B.(3x3+4x)-(2x2+5)C。
(3x3-5)+(-2x2-4x)D。
2x2+(3x3+4x-5)3.在下列各式的括号内填上适当的项.(1)x3-3x2y+3xy2—y3=x3+(—3x2y+3xy2—y3);(2)2—x2+2xy-y2=2-(x2—2xy+y2)。
知识点2添括号法则在乘法公式中的应用4.为了应用平方差公式计算(m-n+1)(m-n—1),下列变形正确的是(A)A.[(m—n)+1][(m-n)-1]B。
[m—(n-1)][m-(n+1)]C。
八年级数学上册第十四章整式的乘法与因式分解14.2乘法公式教学

2021/12/13
第十五页,共二十四页。
此处可先让学生独立思考,然后自主发言,口述 解题思路,可先不给出题目中“运用完全平方公式 计算”的要求,允许他们(tā men)算法的多样化,但要 求明白每种算法的局限和优越性.
2021/12/13
第十六页,共二十四页。
四、再探新知
1.现有下图所示三种规格的卡片各若干(ruògān)张,请你根据 二次三项式a2+2ab+b2,选取相应种类和数量的卡片,尝
2021/12/13
第十九页,共二十四页。
反过来,就得到添括号法则:
a+b+c=a+(b+c);
a-b-c=a-(b+c). 也就是说,添括号时,如果括号前面是正号,括到括 号里的各项都不改变(gǎibiàn)符号;如果括号前面是负号,括
到括号里的各项都改变(gǎibiàn)符号.
2021/12/13
2ab+b2.
2021/12/13
第十八页,共二十四页。
3.添括号法则 运用(yùnyòng)乘法公式计算,有时要在式子中添括号.
我们学过去括号法则,即 a+(b+c)=a+b+c; a-(b+c)=a-b-c.
教师带领学生回顾去括号法则:括号前的符号是“+”时,去 括号后,括号内各项的符号不变;括号前的符号是“-”时,去 括号后,括号内各项的符号改变.
2021/12/13
第十一页,共二十四页。
通过几个这样的运算例子,让学生观察(guānchá)算式与结果间的结 构特征.
归纳:公式
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2 语言叙述:两个数的和(或差)的平方,等于它们的平方和, 加上(或减去)它们积的2倍.这两个公式叫做(乘法的)完全平 方公式.
完全平方公式

(a -b) 2 = a2-2ab +b2.
即两数和(或差)的平方,等于它们的平方和,加(或 减)它们的积的2倍. 这两个公式叫做(乘法的)完全平方公式.
知识回顾
学习新知
当堂训练
小结归纳
布置作业
环节4
讨论
你能根据教材中图1和图2中的面积说明完全平 方公式吗?
b a a b a 图1 b 图2 a b
教材分析
目标分析
教法学法分析
教学过程分析
教学评价分析
3.情感与态度目标: 了解数学的历史,激发学习数学的兴趣.鼓励学生自 己探索算法的多样化,有意识地培养学生的创新能力.
教材分析
目标分析
教法学法分析
教学过程分析
教学评价分析
教学重点:
1.完全平方公式的推导过程、结构特点、几何解释; 2.完全平方公式的应用.
布置作业
环节2 计算(a+b)2, (a-b)2
(a+b)2=(a+b) (a+b) = a2+ab+ab+b2
=a2+2ab+b2.
(a-b)2 = (a-b) (a-b) = a2-ab-ab+b2 =a2-2ab+b2 .
知识回顾
学习新知
当堂训练
小结归纳
布置作业
环节3
一般地,我们有
(a+b)2=a2+2ab+b2,
知识回顾
探求新知
当堂训练
小结归纳
布置作业
(四)小结:完全平方公式
(a+b)2=a2+2ab+b2, (a -b) 2 = a2-2ab +b2.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14.2.2 完全平方公式
1.两项和(或差)的平方,等于它们的__平方和__加上(或减去)它们乘积的2倍,公式a±b2=__a2+b2±2ab___.
为()
2.计算:(1)(x+2y)2=__x2+4xy+4y2__;
(2)(x-2y)2=__x2-4xy+4y2__.
■易错点睛■
计算:(1)(-a+b)2;
(2)(-a-b)2.
【解】(1)a2-2ab+b2;
(2)a2+2ab+b2.
【点睛】(-a+b)2=(b-a)2,
(-a-b)2=[-(a+b)]2=(a+b)2.
知识点完全平方公式
1.计算(a-1)2的结果是( B )
A.a2-1 B.a2-2a+1
C.a2-2a-1 D.a2+1
2.计算(2x+y)2的结果是( B )
A.4x2-4xy+y2B.4x2+4xy+y2
C.-4x2+4xy-y2D.4x2-4xy-y2
3.(-a+b)2等于( B )
A.a2+b2B.a2-2ab+b2
C.a2-b2D.a2+2ab+b2
4.下列各式中计算正确的是( D )
A.(a-b)2=a2-b2B.(a+2b)2=a2+2ab+4b2
C.(a2+1)2=a4+2a+1 D.(m+n)2=m2+2mn+n2
5.填空:x2+10x+25 =(x+ 5 )2.
6.计算:
(1)992;
【解题过程】
解:9801;
【解题过程】 解:10404; (3)(3+5p )2
; 【解题过程】 解:9+30p +25p 2
; (4)(7x -2)2
; 【解题过程】 解:49x 2
-28x +4; (5)(-2x +3y )2
; 【解题过程】 解:4x 2
-12xy +9y 2
; (6)(ab +2)2
; 【解题过程】 解:a 2b 2
+4ab +4; (7)(-x -y )2
; 【解题过程】 解:x 2
+2xy +y 2; (8)(x +y )2
+(x -y )2
; 【解题过程】 解:2x 2
+2y 2; (9)(a +3)2
-(a -3)2
. 【解题过程】 解:12a .
7.若x 2
+a x +9=(x +3)2
,则a 的值为( C ) A .3 B .±3 C .6
D .±6
8.(2017·杭州)若a +b =3,a -b =7,则ab =( A ) A .-10 B .-40 C .10
D .40
9.若a +1a =4,则a 2
+1a
2=__14__.
10.(2016·陕西)已知(a +b )2=25,(a -b )2=9,求ab 与a 2+b 2
的值. 【解题过程】
解:ab=4,a2+b2=17.
11.已知a+b=6,ab=9.
(1)求a2+b2的值;
【解题过程】
解:18
(2)求(a-b)2的值;
【解题过程】
解:0
(3)求a2-ab+b2的值;
【解题过程】
解:9
(4)求a2+b2+3ab的值.
【解题过程】
解:45
12.解方程与不等式:
(1)(3y-1)2+(2y-1)2=13(y+1)(y-1);
【解题过程】
解:y=1.5.
(2)(2x-3)2+(3x+1)2>13(x2-2).
【解题过程】
解:x<6.
13. 先化简,再求值:(2x-1)2+(x+2)(x-2)-4x(x-1),其中x=2.
【解题过程】
解:原式=x2-3=1.
14.如图,长方形ABCD的周长是20cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为68cm2,求长方形ABCD的面积.(导学号:58024264)
【解题过程】
解:设AB=x,AD=y,根据题意得x2+y2=68①,2(x+y)=20②,由①得(x+y)2-2xy
=68,∴2xy=100-68=32,
∴xy=16,长方形ABCD的面积为16cm2.。
