1.4.3. 特殊平行四边形(复习3)(jlsh2015)

合集下载

鲁教版特殊的平行四边形复习课33页PPT

鲁教版特殊的平行四边形复习课
31、别人笑我太疯癫，我笑他人看不穿。(名言网) 32、我不想听失意者的哭泣，抱怨者的牢骚，这是羊群中的瘟疫，我不能被它传染。我要尽量避免绝望，辛勤耕耘，忍受苦楚。我一试再试，争取每天的成功，避免以失败收常在别人停滞不前时，我继续拼搏。
33、如果惧怕前面跌宕的山岩，生命就永远只能是死水一潭。别眨眼!你会看到世界由清晰变模糊的全过程，心会在你泪水落下的那一刻变得清澈明晰。盐。注定要融化的，也许是用眼泪的方式。
35、不要以为自己成功一次就可以了，也不要以为过去的光荣可以被永远肯定。
31、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。——洛克

特殊的平行四边形复习讲义(完整资料).doc

【最新整理，下载后即可编辑】沃根金榜一对一学科教师辅导讲义学生姓名：年级：老师：上课日期：上课时间：上课次数：______年级第______单元课题______ ——————————————————————————————————[ 课前准备]课前检查：作业完成情况：优（）良（）中（）差（）复习预习情况：优（）良（）中（）差（）——————————————————————————————————[ 学习内容]特殊的平行四边形讲义考试考点综述：特殊平行四边形即矩形、菱形、正方形，它们是初二的必考内容之一，主要出现的题型多样，注重考查学生的基础证明和计算能力，以及灵活运用数学思想方法解决问题的能力。

内容主要包括：矩形、菱形、正方形的性质与判定，以及相关计算，了解平行四边形与矩形、菱形、正方形之间的联系，掌握平行四边形是矩形、菱形、正方形的条件。

知识目标掌握矩形、菱形、正方形等概念，掌握矩形、菱形、正方形的性质和判定，通过定理的证明和应用的教学，使学生逐步学会分别从题设和结论出发，寻找论证思路分析法和综合法。

重难点：1.矩形、菱形性质及判定的应用2. 相关知识的综合应用教学过程知识点归纳一．矩形有一角是直角的平行四边形叫做矩形．【强调】矩形（1）是平行四边形；（2）一一个角是直角．矩形的性质性质1矩形的四个角都是直角；性质2 矩形的对角线相等，具有平行四边形的所以性质。

矩形的判定矩形判定方法1:对角线相等的平行四边形是矩形．注意此方法包括两个条件：（1）是一个平行四边形；（2）对角线相等矩形判定方法2:四个角都是直角的四边形是矩形．矩形判断方法3：有一个角是直角的平行四边形是矩形。

例1：若矩形的对角线长为8cm，两条对角线的一个交角为600，则该矩形的面积为例2：菱形具有而矩形不具有的性质是（）A．对角线互相平分； B.四条边都相等； C.对角相等； D.邻角互补例3：已知：如图，□ABCD各角的平分线分别相交于点E，F，G，•H，求证：•四边形EFGH是矩形．二．菱形有一组邻边相等的平行四边形叫做菱形．【强调】菱形（1）是平行四边形；（2）一组邻边相等．菱形的性质性质1菱形的四条边都相等；性质2 菱形的对角线互相平分，并且每条对角线平分一组对角；菱形的判定菱形判定方法1:对角线互相垂直的平行四边形是菱形．注意此方法包括两个条件：（1）是一个平行四边形；（2）两条对角线互相垂直．菱形判定方法2:四边都相等的四边形是菱形．例1已知：如图，四边形ABCD是菱形，F是AB上一点，DF交AC于E．求证：∠AFD=∠CBE．例2已知：如图ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F．求证：四边形AFCE 是菱形．例3、如图，在中，O 是对角线AC 的中点，过点O 作AC 的垂线与边AD 、BC 分别交于E 、F ，求证：四边形AFCE 是菱形.例4、已知如图，菱形ABCD 中，E 是BC 上一点，AE 、BD 交于M ，若AB=AE,∠EAD=2∠BAE 。

北师大版九年级数学上册特殊平行四边形复习

D
(2)若按正
方形设计,
请画出你
设计的示
意图.
B
C
倍
速课
(3)你在(2)所设计的正方形鱼塘中,
时学
有无最大面积？为什么？
练
你知道吗？
C
DE
当直角三角
形的斜边一定 A
∟
B
时,两直角边
O
满足什么条件
倍速
时直角三角形
课时
的面积最大？
学
练
倍速课时学练
考考你
1、检查一个门框是矩形的方法是（ B）
A、测量两条对角线是否相等. B、测量有三个角是直角.
C、测量两条对角线是否互相平分.
D、测量两条对角线是否互相垂直.
倍
速课
2、顺次连接矩形各边中点所得的四边形是（ B
时学
A、矩形 B、菱形 C、梯形 D、正方形
练
3、菱形的周长等于高的8倍，则其最大内角
等于（ D）
60° B、90°
D
CA
1、定义：有一外角是直角的平行四边形是矩形. 2、三个角是直角的四边形是矩形. 3、对角线相等的平行四边形是矩形. 1、定义：一组邻边相等的平行四边形是菱形. 2、四条边都相等的四边形是菱形. 3、对角线互相垂直的平行四边形是菱形. 1、定义：一组邻边相等且有一个角是直角的平行四边形是正方形. 2、有一组邻边相等的矩形是正方形. 3、有一个角是直角的菱形是正方形.
解：
AE AB
6 9
2 ，AD 3 AC
4 6
2 3
AE AD AB AC
又 EAD BAC
B
E
6
A
9
7

特殊平行四边形知识点复习

矩形菱形正方形定义有一角是直角的平行四边形叫做矩形有一组邻边相等的平行四边形叫做菱形有一组邻边相等并且有一个角是直角的平行四边形叫做正方形性质边对边平行且相等对边平行，四边相等对边平行，四边相等角四个角都是直角对角相等，邻角互补四个角都是直角对角线互相平分且相等互相垂直平分，且每条对角线平分一组对角互相垂直平分且相等,每条对角线平分一组对角判定·有三个角是直角;·有一个角是直角的平行四边形;·两条对角线相等的平行四边形.·四边相等的四边形；·有一组邻边相等的平行四边形；·对角线互相垂直的平行四边形。

·有一组邻边相等的矩形；·对角线互相垂直的的矩形；·有一组邻边相等的矩形；·两条对角线相等的的菱形。

(矩形+菱形）对称性(条数）既是轴对称图形，又是中心对称图形2条对称轴2条对称轴4条对称轴面积长*宽对角线乘积的一半对角线乘积的一半特殊性具有平行四边形具有的一切性质具有菱形和矩形具有的一切性质特殊的平行四边形知识点归纳平行四边形的定义：1. 定义：两组对边分别平行的四边形是平行四边形．2. 平行四边形的性质（1）边：平行四边形的对边平行且相等．（2）角：平行四边形的对角相等，邻角互补．（3）对角线：平行四边形的对角线互相平分．（4）对称性：平行四边形是中心对称图形，对角线的交点为对称中心．3. 平行四边形的判定方法（1）定义识别：两组对边分别平行的四边形是平行四边形．（2）用平行四边形的判定定理识别：判定定理①：两组对边分别相等的四边形是平行四边形．判定定理②：对角线互相平分的四边形是平行四边形．判定定理③：一组对边平行且相等的四边形是平行四边形．4. 三角形中位线（1）定义：连接三角形两边中点的线段叫做三角形的中位线．每个三角形都有三条中位线．（2）三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．5. 直角三角形特殊性质（1）直角三角形斜边上的中线等于斜边的一半。

特殊的平行四边形复习课课件

02
对边相等
矩形的对边相等。
03
对角相等
矩形的对角相等。
04
邻边垂直
矩形的邻边互相垂直。
判定方法
01
02
03
有一个角是直角
根据矩形定义，有一个角是直角的平行四边形是矩形。
对角线相等
对角线相等的平行四边形是矩形。
邻边垂直
邻边互相垂直的平行四边形是矩形。
面积与周长计算
面积计算
矩形的面积 = 长 x 宽。
。
解答
01 02 03 04
判断题：×。改正：两组对边分别平行的四边形是平行四边形，两组对边分别相等的四边形也是平行四边形。
填空题：平行,相等,互相平分。
简答题：平行四边形对角线是连接平行四边形两对对角的线段，且对角线互相平分。
画图题：（略）
THANKS FOR WATCHING
感谢您的观看
分类与判定
矩形判定
对角线相等的平行四边形是矩形；有一个角是直角的平行四边形是矩形。
菱形判定
四边相等的平行四边形是菱形；对角线互相垂直的平行四边形是菱形。
面积与周长计算
矩形面积=长×宽；矩形周长=2(长+宽)。菱形面积=底×高；菱形周长=4×边长。
02
矩形
定义与性质
01
矩形定义
有一个角是直角的平行四边形是矩形。
判定方法
定义判定
四条边都相等的平行四边形是正方形。
角判定
四个角都是直角的平行四边形是正方形。
对角线判定
对角线相等且互相平分的平行四边形是正方形。
面积与周长计算
要点一
面积计算
正方形的面积 = 边长 × 边长。

特殊的平行四边形综合复习教学课件

特殊的平行四边形综合复习教学课件2023-10-27CATALOGUE 目录•复习导入•新课学习•课堂练习•小结与作业01复习导入定义、性质、判定矩形定义、性质、判定菱形定义、性质、判定正方形特殊平行四边形的定义和性质角是直角的平行四边形是矩形；矩形的对角线相等；矩形的四个角都是直角矩形菱形正方形四边相等的平行四边形是菱形；菱形的对角线互相垂直平分；菱形的对角线平分一组对角对角线相等的菱形是正方形；有一个角是直角的菱形是正方形；对角线互相垂直的矩形是正方形03特殊平行四边形的判定方法0201矩形面积 = 长 x 宽菱形面积 = (对角线乘积) / 2正方形面积 = 边长 x 边长特殊平行四边形的面积计算02新课学习矩形与菱形的判定方法及性质01矩形的判定方法02有一个角是直角的平行四边形是矩形03对角线相等的平行四边形是矩形04菱形的判定方法05一组邻边相等的平行四边形是菱形06对角线互相垂直的平行四边形是菱形正方形与长方形的性质与判定方法•正方形的性质•四边相等，四个角都是直角•对角线相等且互相垂直平分•正方形的判定方法•有一组邻边相等的矩形是正方形•有一个角是直角的菱形是正方形•长方形的性质•对边相等，四个角都是直角•对角线相等且互相平分•长方形的判定方法•有一个角是直角的平行四边形是长方形•对角线相等的平行四边形是长方形梯形的定义与性质梯形的定义：一组对边平行，另一组对边不平行的四边形叫做梯形梯形是平行四边形，所以具有平行四边形的所有性质梯形的性质梯形中有一组对边平行，另一组对边不平行，所以具有这个特性所带来的所有性质03课堂练习详细描述通过讲解矩形的对角线平分对角和邻边互相垂直的性质以及菱形的四边相等和对应边互相垂直的性质，使学生能够灵活运用这些性质进行证明和计算。

矩形与菱形的判定练习总结词熟练掌握矩形的判定方法和菱形的判定方法详细描述通过对比矩形和菱形的判定方法，使学生能够熟练掌握矩形的对角线相等且为直角的判定方法和菱形的四边相等的判定方法。

特殊平行四边形知识点归纳

特殊的平行四边形复习矩形菱形正方形定义有一角是直角的平行四边形叫做矩形有一组邻边相等的平行四边形叫做菱形有一组邻边相等．．．．．．并且有一个．．．角是直角．．．．的平行四边形．．．．．叫做正方形性质边对边平行且相等对边平行，四边相等对边平行，四边相等角四个角都是直角对角相等四个角都是直角对角线互相平分且相等互相垂直平分，且每条对角线平分一组对角互相垂直平分且相等,每条对角线平分一组对角判定·有三个角是直角;·是平行四边形且有一个角是直角;·是平行四边形且两条对角线相等.·对角线相等且互相平分的四边形是矩形·四边相等的四边形；·是平行四边形且有一组邻边相等；·是平行四边形且两条对角线互相垂直。

·对角线互相垂直平分的是四边形·是矩形，且有一组邻边相等；·是菱形，且有一个角是直角。

(矩形+菱形）对称性(条数）既是轴对称图形，又是中心对称图形2 2 4面积长*宽对角线乘积的一半/底乘高补充由矩形的性质，可以得到直角三角形的一个重要性质，直角三角形斜边上的中线等于斜边的一半．·菱形对角线的平方和等于边长平方的4倍·在有一个角是60°角的菱形中，较短的对角线等于边长，较长的对角线是较短的对角线的√3倍正方形具有平行四边形、菱形、矩形的一切性质与特性。

平行四边形及特殊平行四边形知识点(经典完整版)

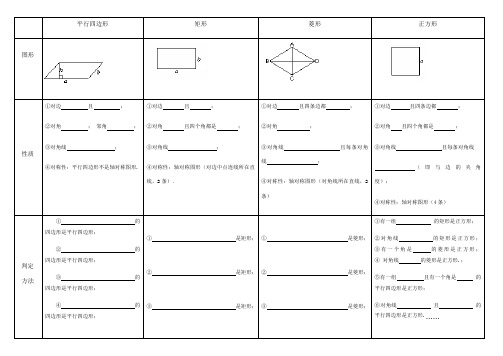
平行四边形矩形菱形正方形图形性质①对边且；②对角；邻角；③对角线；④对称性：平行四边形不是轴对称图形.①对边且；②对角且四个角都是；③对角线；④对称性：轴对称图形（对边中点连线所在直线，2条）．①对边且四条边都；②对角；③对角线且每条对角线；④对称性：轴对称图形（对角线所在直线，2条）①对边且四条边都；②对角且四个角都是；③对角线且每条对角线（即与边的夹角度）；④对称性：轴对称图形（4条）判定方法①的四边形是平行四边形；②的四边形是平行四边形；③的四边形是平行四边形；④的四边形是平行四边形；①是矩形；②是矩形；③是矩形；①是菱形；②是菱形；③是菱形；①有一组的矩形是正方形；②对角线的矩形是正方形；③有一个角是的菱形是正方形；④对角线的菱形是正方形.；⑤有一组且有一个角是的平行四边形是正方形；⑥对角线且的平行四边形是正方形.⋅⋅⋅⋅⋅⋅⑤的四边形是平行四边形；正方形的判定方法很多，所有以平行四边形，矩形，菱形三者的判定作为条件的四边形都是正方形.面积一、本章知识框架图正方形与平行四边形、矩形、菱形之间的关系有怎样的包含关系？请填入下图中.平行四边形二、几种特殊四边形的常用说理方法与解题思路分析（1）判定矩形的常用方法（3种）①先说明四边形ABCD为平行四边形，再说明平行四边形ABCD的有一个角为直角．②先说明四边形ABCD为平行四边形，再说明平行四边形ABCD的对角线相等．③说明四边形ABCD的三个角是直角．（2）判定菱形的常用方法（3种）①先说明四边形ABCD为平行四边形，再说明平行四边形ABCD的任一组邻边相等．②先说明四边形ABCD为平行四边形，再说明对角线互相垂直．③说明四边形ABCD的四条边相等．（3）判定正方形的常用方法①先说明四边形ABCD矩形，再说明对角线互相垂直．②先说明四边形ABCD为矩形，再说明一组邻边相等．③先说明四边形ABCD为菱形，再说明菱形ABCD的一个角为直角．④先说明四边形ABCD为菱形，再说明菱形ABCD对角线相等．⑤先说明四边形ABCD为平行四边形，再说明平行四边形ABCD的一个角为直角（或对角线相等）且有一组邻边相等（对角线互相垂直）．即一般思路为先说明是平行四边形，再说明是矩形（菱形），最后说明是菱形（矩形）.。