2006年陕西省中考数学试题及答案
2006年陕西初中毕业学业考试大纲卷

2006年陕西省初中毕业学业考试(大纲卷)第I 卷(选择题 共30分)A 卷一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的) 1.下列计算正确的是( ) A .321-+=B .|2|2-=-C .3(3)9⨯-=-D .0211-=2.如图,123,,∠∠∠的大小关系为( ) A .213>>∠∠∠ B .132>>∠∠∠ C .321>>∠∠∠D .123>>∠∠∠3.2005年11月1日零时,全国总人口为130628万人.60岁及以上的人口占总人口的11.03%,则全国60岁及以上的人口用科学记数法表示(保留三位有效数字)约为( ) A .81.4410⨯人B .81.4510⨯人C .714.410⨯人D .41.4410⨯人4.一件标价为600元的上衣,按8折(即按标价的80%)销售仍可获利20元.设这件上衣的成本价为x 元,根据题意,下面所列方程正确的是( ) A .6000.820x ⨯-= B .600820x ⨯-= C .6000.820x ⨯=-D .600820x ⨯=-5.如图,O 是ABC △的外接圆,AD 是O 的直径,连结CD ,若O 的半径322r AC ==,,则cos B 的值是( )A .32B.3C.2D .236.下列图形中,是中心对称图形的是( )7.若圆锥的侧面展开图是一个弧长为36π的扇形,则这个圆锥的底面半径是( )(第5题图)123(第2题图)A .B .C .D .A .36B .18C .9D .68.有一块多边形草坪,在市政建设设计图纸上的面积为2300cm ,其中一条边的长度为5cm .经测量,这条边的实际长度为15m ,则这块草坪的实际面积是( )A .2100mB .2270mC .22700mD .290000m9.如图,抛物线的函数表达式是( ) A .22y x x =-+B .22y x x =++C .22y x x =--+D .22y x x =-++10.如图,矩形()ABCG AB BC <与矩形CDEF 全等,点B C D ,,在同一条直线上,APE ∠的顶点P 在线段BD 上移动,使APE ∠为直角的点P 的个数是( )A .0B .1C .2D .3第II 卷(非选择题 共90分)二、填空题(共6小题,每小题3分,计18分) 11.分解因式:233a -= .12.选做题...(要求在(1)、(2)中任选一题作答) (1)用计算器估算:若2.6456 2.6459<<,则a 的整数值是 .(2(填“>”、“=”、“<”). 13.不等式组210x x >-⎧⎨-⎩≤的解集为 .14.如图,小河对岸有一座塔AB .分别在点DC ,处测得塔尖点A 处的仰角为128=∠,241=∠,且25CD =米.则塔的高度AB 约为 米(精确到0.1米).(第10题图)E(第9题图)(可用计算器求,也可用下列参考数据求:sin 280.4695sin 410.6561,≈≈ cos 280.8829cos 410.7547,≈≈ tan 280.5317tan 410.8693,≈≈)15.观察下列等式:22(12)4114+-⨯=+ 22(22)4224+-⨯=+ 22(32)4334+-⨯=+…则第n 个等式可以表示为 .16.将一个无盖正方体纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②).则所剪得的直角三角形较短的与较长的直角边的比是 .三、解答题(共9小题,计72分.解答应写出过程) 17.(本题满分5分)解分式方程:23222x x x -=+-. 18.(本题满分6分)如图,在直角坐标系中:(1)描出下列各点,并将这些点用线段依次..(24)(38)(84)(31)(24)----,,,,,,,,,;(2)作出(1)中的图形关于y 轴的对称图形.12ABCD(第14题图)(第16题图①)(第16题图②)x(第18题图)19.(本题满分7分)如图,O 为ABCD 的对角线AC 的中点,过点O 作一条直线分别与AB CD ,交于点M N ,,点E F ,在直线MN 上,且OE OF =.(1)图中共有几对全等三角形,请把它们都写出来; (2)求证:MAE NCF =∠∠.20.(本题满分8分)2003~2005年陕西省财政收入情况如图所示.根据图中的信息,解答下列问题: (1)陕西省这三年平均年财政收入为多少亿元?(2)陕西省2004~2005年财政收入的年增长率约为多少?(精确到1%)(3)如果陕西省2005~2006年财政收入的年增长率与(2)中求得的年增长率基本相同,请估计陕西省2006年财政收入约为多少亿元?(精确到1亿元)21.(本题满分8分)如图,在Rt ABC △中,90BAC =∠,E F ,分别是BC AC ,的中点,延长BA 到点D ,使12AD AB =.连结DE DF ,. (1)求证:AF 与DE 互相平分; (2)若4BC =,求DF 的长.22.(本题满分8分)ADFCEB(第21题图)2003 2004 2005 年份/年(第20题图)A E MD FCBO 1 2(第19题图) N甲、乙两车从A 地出发,沿同一条高速公路行驶至距A 地400千米的B 地.12l l ,分别表示甲、乙两车行驶路程y (千米)与时间x (时)之间的关系(如图所示).根据图象提供的信息,解答下列问题:(1)求2l 的函数表达式(不要求写出x 的取值范围);(2)甲、乙两车哪一辆先到达B 地?该车比另一辆车早多长时间到达B 地?23.(本题满分8分) 如图,O的直径430AB ABC BC ===,,∠D 是线段BC 的中点.(1)试判断点D 与O 的位置关系,并说明理由;(2)过点D 作DE AC ⊥,垂足为点E ,求证直线DE 是O 的切线.24.(本题满分10分)某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信.这五封信的重量分别是72g ,90g ,215g ,340g ,400g .根据这五所学校的地址及信件的重量范围,在邮局查得相关..邮费标准如下:B(第23题图)444(时)(第22题图)(1)重量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?(2)这五封信分别以怎样的方式寄出最合算?请说明理由.(3)通过解答上述问题,你有何启示?(请你用一、两句话说明)25.(本题满分12分)30cm,下底为120cm,高为60cm的直角梯形板子(如图①).王师傅想将这两块板子裁成两块全等的矩形板材.他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCFE围成的区域(如图②).由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点.(1)求FC的长;(2)利用图②求出矩形顶点B所对的顶点.....到BC边的距离x(cm)为多少时,矩形的面积y(2cm)最大?最大面积是多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长.AB CE DGF(第25题图②)(第25题图①)。
链接陕西省中考数学第24题

9 ,2 6),D′(6,
9 )2
亲!你做对吗
2 , 解之,得 a′=- 3
,
∴a≠a′
∴经过A′、E′、D′三点的抛物线不能由(1)中的抛物线平移得到。…(8分)
2007年陕西省中考24题(1)答案
24.解:(1)过点C作CE OD于点E,则四边形 OBCE 为矩形.
∴ CE OB 8
y
7 6 5 4 3 2 1
(2008年陕西省中考试题)
E A D x B C 1 2 3 4 5 6 7 (第24题图)
O
y
7 6 5 4 3 E 2 A D 1
B C O 1 2 3 4 5 6 7
(第24题图)
x
24.(本题满分10分) OB 2 OA OB OA 如图,在平面直角坐标系中, ,且 ,点A 的坐标是(-1,2) . (1)求点B的坐标; (2)求过点A、O、B的抛物线的表达式; (3)连接AB,在(2)中的抛物线上求出点P, 使得 S△ABP S△ABO . y
(2011年陕西省中考试题)
y A o
B x
2012年陕西省中考试题 2 24.(10分)如果一条抛物线y=ax +bx+c(a≠0)与x轴有两个交点,那么 以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线 的 “抛物线三角形”.
(1)“抛物线三角形”一定是_____________三角形; 求b的值.
(3)如图,△OAB是抛 2 物线y=-x +b’x(b’>o)的 “抛物线三角形”,是否 存在以原点为对称中心的 矩形ABCD?若存在,求 出过O、C、D三点的抛物 线的表达式,若不存在, 说明理由.
y A
数学f1初中数学2006年中考试题分类汇编-三角形 (2)

本文为自本人珍藏 版权所有 仅供参考 本文为自本人珍藏 版权所有 仅供参考2006年中考试题分类汇编—三角形1.(2006·陕西省)如图,在△ABC 中,D 、E 、F 分别是边AB 、BC 、AC 的中点,若△ABC 的周长为20cm ,则△DEF 的周长为( B )A .5cmB .10cmC .12cmD .15cm2.(2006·陕西省)如图,△ABC 是不等边三角形DE =BC ,以D 、E 为两个顶点作位置不同....的三角形,使所作三角形与△ABC 全等,这样的三角形可以画出 ( B )A .2个B .4个C .6个D .8个 3.(2006·湛江市)在下列长度的四根木棒中,能与3cm ,7cm 两根木棒围成一个三角形的是( )A A .7cm B .4cm C .3cm D .10cm4.(2006·广东省)如图,若△OAD≌△OBC,且∠0=65°,∠C=20°,则∠OAD= 95° .5.(2006·株洲市)如图,AE AD =,要使ABD ACE △≌△,请你增加一个..条件是 .(只需要填一个..你认为合适的条件)B C ∠=∠6.(2006·永州市)如右图,已知142ABE =∠,72C =∠,则A =∠ ,ABC =∠ .A ∠7.(2006·永州市)示,钉上两条斜拉的木条,8.(2006·永州市)如图所示,在等腰三角形第4题图ABCE14272D(第10题)12cm AB AC ==,30ABC =∠,那么底边上的高 AD = cm .69. (2006·江 西 省)在△ABC 中,∠A = 80°,∠B = 60°,则∠C = . 40°10. ( 2006·湖州市)已知Rt △ABC 中,∠C=90º。
中考数学试题陕西省2006年初中毕业学业考试数学试题(课改卷)

陕西省2006年初中毕业学业考试数学试题(课改卷)第Ⅰ卷(选择题 共30分)A卷一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的) 1.下列计算正确的是( ) A.321-+=B.22-=-C.()339⨯-=-D.0211-=2.如图,几何体的左.视图是( )3.一件标价为600元的上衣,按8折销售仍可获利20元.设这件上衣的成本价为x 元,根据题意,下面所列的方程正确的是( ) A.6000.820x ⨯-= B.600820x ⨯-= C.6000.820x ⨯=-D.600820x ⨯=-4.如图,O 是ABC △的外接圆,AD 是O 的直径,连接CD ,若O 的半径32r =,2AC =,则cos B 的值是( )A.32B.53C.52D.235.如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( ) A.5月1日 B.5月2日 C.5月3日 D.5月5日 6.若圆锥的侧面展开图是一个弧长为36π的扇形,则这个圆锥的底面半径是( ) A.36 B.18 C.9 D.6A. B. C. D. (第2题图)(第4题图)0 1 2 3 4 5 6 7 12 1314 15 16 1724 25 26 27 温度(℃)(第5题图)日最低气温日最高气温7.直线332y x=-+与x 轴,y轴所围成的三角形的面积为()A.3B.6C.34D.328.如图,抛物线的函数表达式是()A.22y x x=-+B.22y x x=--+C.22y x x=++D.22y x x=-++9.有一块多边形草坪,在市政建设设计图纸上的面积为2300cm,其中一条边的长度为5cm.经测量,这条边的实际长度为15m,则这块草坪的实际面积是()A.2100mB.2270mC.22700mD.290000m10.如图,矩形()ABCG AB BC<与矩形CDEF全等,点B C D,,在同一条直线上,APE∠的顶点P在线段BD上移动,使APE∠为直角的点P的个数是()A.0B.1C.2D.3第Ⅱ卷(非选择题共90分)二、填空题(共6小题,每小题3分,计18分)11.不等式()231x x-+≤的解集为.12.选做题...(要求在(1),(2)中任选一题作答).(1)2005年11月1日零时,全国总人口为130628万人.60岁及以上的人口占总人口的11.03%,则全国60岁及以上的人口用科学记数法表示约为万人(用计算器计算,保留3个有效数字).(2)用计算器比较大小:3176_____0-(填“>”、“=”、“<”).13.在同一时刻,小明测得一棵树的影长是身高为1.6米的小华影长的4.5倍,则这棵树的高度为米.14.观察下面图形,按规律在两个..箭头所指的“田”字格内分别画上适当图形.(第10题图)(第14题图)(第8题图)15.双曲线8y x=与直线2y x =的交点坐标为 . 16.将一个无盖正方体纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②).则所剪得的直角三角形较短的与较长的直角边的比是 .三、解答题(共9小题,计72分.解答应写出过程) 17.(本题满分5分)解分式方程:23222x x x -=+-. 18.(本题满分6分)观察下面网格中的图形,解答下列问题: (1)将网格中左图沿水平方向向右.........平移,使点A 移至点A '处,作出平移后的图形; (2)(1)中作出的图形与右边原有的图形,组成一个新的图形.这个新图形...是中心对称图形,还是轴对称图形?19.(本题满分7分)2003~2005年陕西省财政收入情况如图所示.根据图中的信息,解答下列问题: (1)陕西省这三年财政收入共为多少亿元?(2)陕西省2004~2005年财政收入的年增长率约为多少?(精确到1%)(第18题图)(第16题图①) (第16题图②)(3)如果陕西省2005~2006年财政收入的年增长率与(2)中求得的年增长率基本相同,请估计陕西省2006年财政收入约为多少亿元?(精确到1亿元)20.(本题满分8分)如图,O 为ABCD 的对角线AC 的中点,过点O 作一条直线分别与AB CD ,交于点M N ,,点E F ,在直线MN 上,且OE OF =.(1)图中共有几对全等三角形,请把它们都写出来; (2)求证:MAE NCF =∠∠.21.(本题满分8分)甲、乙两车从A 地出发,沿同一条高速公路行驶至距A 地400千米的B 地.12l l ,分别表示甲、乙两车行驶路程y (千米)与时间x (时)之间的关系(如图所示).根据图象提供的信息,解答下列问题:(1)求2l 的函数表达式(不要求写出x 的取值范围);(2)甲、乙两车哪一辆先到达B 地?该车比另一辆车早多长时间到达B 地?528 415 326 02003 2004 2005 年份/年 陕西省财政收入/亿元(第19题图)AE M DFCBO 1 2(第20题图)N400 300 y (千米) x (时) (第21题图)22.(本题满分8分)有两个可以自由转动的均匀转盘A B ,,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:①分别转动转盘A B ,;②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).(1)用列表法(或树状图)分别求出数字之积为3的倍数和数字之积为5的倍数的概率;(2)小亮和小芸想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小亮得2分;数字之积为5的倍数时,小芸得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.23.(本题满分8分) 如图,O 的直径43043AB ABC BC ===,,∠,D 是线段BC 的中点.(1)试判断点D 与O 的位置关系,并说明理由;(2)过点D 作DE AC ⊥,垂足为点E ,求证直线DE 是O 的切线.24.(本题满分10分)某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信.这五封信的重量分别是72g ,90g ,215g ,340g ,400g .根据这五所学校的地址及信件的重量范围,在邮局查得相关..邮费标准如下: 业务种类计费单位资费标准(元) 挂号费 (元/封)特制信封 (元/个)挂号信首重100g 内,每重20g0.8 30.5续重101~2 000g ,每重100g2.0012 3 A 4 6 5B (第22题图) AO B D C E(第23题图)特快专递 首重1 000g 内 5.00 3 1.0(1)重量为90g 的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?(2)这五封信分别以怎样的方式寄出最合算?请说明理由.(3)通过解答上述问题,你有何启示?(请你用一、两句话说明)25.(本题满分12分)王师傅有两块板材边角料,其中一块是边长为60cm 的正方形板子;另一块是上底为30cm ,下底为120cm ,高为60cm 的直角梯形板子(如图①).王师傅想将这两块板子裁成两块全等的矩形板材.他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCFE 围成的区域(如图②).由于受材料纹理的限制,要求裁出的矩形要以点B 为一个顶点. (1)求FC 的长;(2)利用图②求出矩形顶点B 所对的顶点.....到BC 边的距离x (cm )为多少时,矩形的面积y (2cm )最大?最大面积是多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长.信函资费常识.挂号信: 首重、续重计费方法: 如:信的重量为260g ,则其中100g为“首重”,每20g 按0.8元计费(不足20g 按20g 计费);其余160g 为“续重”,每100g 按2元计费.160g 超过100g ,但不足200g ,按200g 计费.邮寄费(每封)=首重资费+续重资费+挂号费+特制信封费.特快专递: 如:首重不超过1 000g ,则邮寄费(每封)=首重资费(5元)+挂号费(3元)+特制信封费(1元) A B C E D G F (第25题图②)(第25题图①)。
中考数学试题分析【精选】

3
2
3
⒍若圆锥的侧面展开图是一个弧长为36 的扇
形,则这个圆锥的底面半径是( )设新的情境来考查“双基”. 在变化的情境中运用“双基”解决问题. 学生必须以不变应万变,透过现象把握 本质,才能将问题转化为熟知的或运用 知识能处理的情形.
(例: 5, 8, 10, 14, 16)
角
数 的
三应几
角
用
何 问
容
换
形应
形题题
用
⒊试题特点
(1)试题求稳,注重考查课本中最核心、最
基本的内容,着眼于能力,立足于学生发展;
扎实的“三基”是提高数学素养,发展创新能力与实践能力的基础, 是学生发展的必要条件。试卷把考查学生的数学基础知识与基本能力放在 首位,不出人为编造的繁难偏旧的试题,充分体现数学学科的教育价值。 试卷中如选择题1~9, 填空题11~15,解答题第17、18、19、20共18个 题,占总题数的72%.这些题都植根于本届考生所学的教材,对一些重要的 数学概念、公式、定理、法则,数、式的基本运算和变形及几何图形的简 单属性等进行了考查.大多属简单题或中等难度的题,尽可能少失分是中 考成败的关键因素,这也是好多有经验的老师在后期复习中根据学生情况 所要侧重的,“题海战术”、“难题战术”是要坚决摒弃。
⒐有一块多边形草坪,在市政建设设计图 纸上的面积为300cm²,其中一条边的长度为5cm, 经测量,这条边的实际长度为15m,则这块草坪 的实际面积是( )
A.100m² B.270m² C.2700m² D.90000m²
(2)突出考查学生对数学思想方 法的理解与简单应用
数学思想方法是数学的灵魂,掌握了它, 就能驾驭知识,形成能力。本份试卷能注意 联系课改精神,培养学生的数感、符号感、 统计意识、合情推理等能力,可以说是千方 百计、挖苦心思地渗透数形结合、运动变化 以及函数、方程、归纳、分类等思想。
历年陕西中考数学试题及答案3(word版)
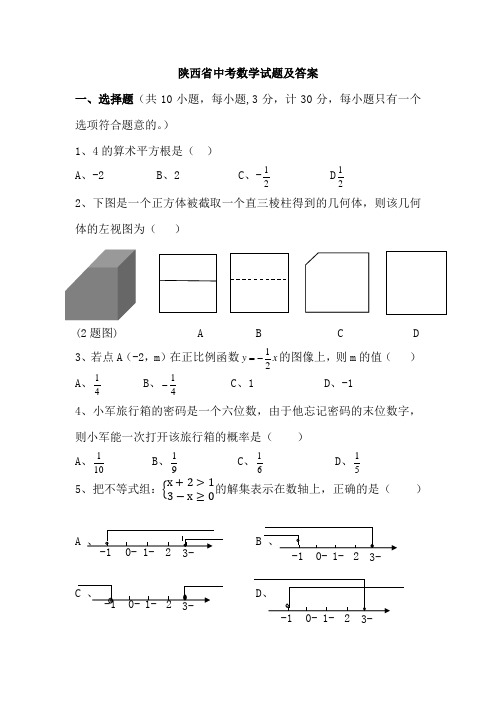
陕西省中考数学试题及答案一、选择题(共10小题,每小题,3分,计30分,每小题只有一个选项符合题意的。
) 1、4的算术平方根是( )A 、-2B 、2C 、-21 D 212、下图是一个正方体被截取一个直三棱柱得到的几何体,则该几何体的左视图为( )(2题图) A B C D 3、若点A (-2,m )在正比例函数x y 21-=的图像上,则m 的值( ) A 、41 B 、41- C 、1 D 、-14、小军旅行箱的密码是一个六位数,由于他忘记密码的末位数字,则小军能一次打开该旅行箱的概率是( ) A 、101 B 、91 C 、61 D 、515、把不等式组:{x +2>13−x ≥0的解集表示在数轴上,正确的是( )A 、B 、C 、D 、1- -10- 3- 2 1- -10- 3- 2 1- -10- 3-2 1- -10- 3-26、某区10名学生参加市级汉子听写大赛,他们得分情况如下表: 人数 3 4 2 1 分数80859095那么这10名学生所得分数的平均数和众数分别是多少?( ) A 、85和82.5 B 、 85.5和85 C 、85和85 D 、85.5和807、如图AB ‖CD,∠A=45°,∠C=28°,则∠AEC 的大小为( ) A 、17° B 、o 62 C 、o 63 D 、o 738、若2-=x 是关于x 的一元二次方程02522=+-a ax x 的一个根,则a 的值是( )A 、1或4B 、-1或-4C 、-1或4D 、1或-4 9、如图,在平行四边形ABCD 中,5=AB ,对角线6=AC ,若过点A 作BC AE ⊥,垂足为E,则AE 的长( ) A 、4 B 、512 C 、524D 、510、二次函数)0(2≠++=a c bx ax y 的图象如图所示,则下列结论正确的是( )A 、c ˃-1B 、b ˃0C 、02≠+b aD 、b c a 392〉+E YX-1 4 -ABEDC第8题图第10题图BCDA第7题图第II 卷(非选择题90分)二、填空题(共6小题,每小题3分,计18分) 11、计算=-2)31(____。
2006年陕西省中考数学试题及答案
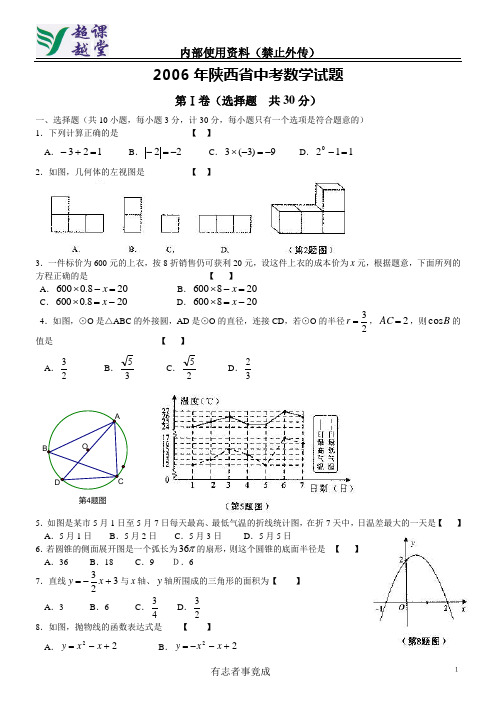
2006年陕西省中考数学试题第Ⅰ卷(选择题 共30分)一、选择题(共10小题,每小题3分,计30分,每小题只有一个选项是符合题意的) 1.下列计算正确的是 【 】A .123=+-B .22-=-C .9)3(3-=-⨯ D .1120=- 2.如图,几何体的左视图是 【 】3.一件标价为600元的上衣,按8折销售仍可获利20元,设这件上衣的成本价为x 元,根据题意,下面所列的方程正确的是 【 】A .208.0600=-⨯xB .208600=-⨯xC .208.0600-=⨯xD .208600-=⨯x4.如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,连接CD ,若⊙O 的半径23=r ,2=AC ,则B cos 的值是 【 】 A .23 B .35 C.25D .32 第4题图5.如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在折7天中,日温差最大的一天是【 】 A .5月1日 B .5月2日 C .5月3日 D .5月5日 6.若圆锥的侧面展开图是一个弧长为π36的扇形,则这个圆锥的底面半径是 【 】 A .36 B .18 C .9 D.67.直线323+-=x y 与x 轴、y 轴所围成的三角形的面积为【 】 A .3 B .6 C .43 D .238.如图,抛物线的函数表达式是【 】C .22++=x x yD .22++-=x x y9.有一块多边形草坪,在市政建设射击图纸上的面积为3002cm ,其中一条边的长度为5cm ,经测量,这条边的实际长度为15m ,则这块草坪的实际面积是 【 】 A .1002m B .2702m C .27002m D .900002m10.如图,矩形ABCG (BC AB )与矩形CDEF 全等,点B 、C 、D 在同一条直线上,APE ∠的顶点P 在线段BD 上移动,使APE ∠为直角的点P 的个数是【】A .0B .1C .2D .3第Ⅱ卷(非选择题 共90分)二、填空题(共6小题,每小题3分,共18分) 11.不等式)1(32+≤-x x 的解集为 12.选做题...(要求在(1)、(2)中任选一题作答)。
2006年陕西省初中毕业学业考试理化试卷及答案

陕西省2006年初中毕业学业考试理化试卷一、选择题(共14小题。
每小题2分。
计28分。
每小题只有一个选项是符合题意的)1.我省华县的“皮影戏”是一种具有悠久历史的民间艺术形式,在皮影戏演出时,人们从影幕上看到的“影像”形成的主要原因是A.光的直线传播B.光的反射D.光的折射D.平面镜成像2.跳水运动员自跳台上跳下,从接触水面到完全浸入水中的过程中,关于运动员受到水的压强和浮力的变化情况,下列说法正确的是A.压强减小,浮力减小B.压强减小,浮力增大C.压强增大,浮力减小D.压强增大,浮力增大3.下列关于声现象的说法正确的是A.铁路工人用铁锤敲打车轮,根据发声的响度判断车轮是否完好B.在城市道路两旁植树,可以减弱噪声C.敲鼓时用力大小不同,鼓声的音调不同D.演奏员拧紧或放松琴弦,可以改变乐器发声的音色4.老师上课时,用小磁块把图片固定在竖直悬挂的磁性黑板上,小磁块静止在黑板上不会滑落的原因是A.磁块受到的重力太小B.磁块受到黑板的吸引力大于重力C.磁块受到的重力和摩擦力是一对平衡力D.磁块受到的摩擦力大于重力5.关于厨房里的物理现象,下列说法不正确的是A.做饭时锅盖内表面会有许多小水珠,这是水蒸气液化形成的B.烧水时被水蒸气烫伤比沸水烫伤更严重,因为水蒸气液化吸热C.煤气燃烧时,化学能转化为内能D.炒菜时的香味会四处飘散,因为分子在不停地做无规则运动6.如图所示电路中,电源电压为3V且保持不变,R=10Ω,滑动变阻器的最大阻值R′=20Ω.当开关S闭合后,在将滑动变阻器的滑片由A端移动到B端的过程中,电流表示数的变化是由A.0.3 A~0.1 AB.0 A~0.1 AC.0.1 A~0.3 AD.0.3A~0 A7.小明在实验考核时连接了如图所示电路,闭合开关后他看到灯泡L1发光,L2不发光,电压表有示数.关于电路中L1、L2的连接方式和L2不发光的原因,以下判断正确的是A.L l与L2串联,L2被短路B.L1与L2串联,L2的实际功率比额定功率小得多C.L1与L2并联,L2与灯座接触不良D.L1与L2并联,L2的灯丝断了陕西省2006年初中毕业学业考试理化试卷第Ⅱ卷(非选择题共92分)五、填空题(共5小题。
2006年陕西省中考数学试题及答案

第Ⅰ卷(选择题共30分)A 卷一、选择题(共10小题,每小题3分,计30分,每小题只有一个选项是符合题意的) 1.下列计算正确的是【C 】A .123=+-B .22-=-C .9)3(3-=-⨯D .1120=- 2.如图,几何体的左视图是【B 】3.一件标价为600元的上衣,按8折销售仍可获利20元,设这件上衣的成本价为x 元,根据题意,下面所列的方程正确的是【A 】 A .208.0600=-⨯x B .208600=-⨯x C .208.0600-=⨯x D .208600-=⨯x4.如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,连接CD ,若⊙O 的半径23=r ,2=AC ,则B cos 的值是【B 】 A .23B .35C .25D .32 5.如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在折7天中,日温差最大的一天市A .5月1日B .5月2日C .5月3日D .5月5日6.若圆锥的侧面展开图市一个弧长为π36的扇形,则这个圆锥的底面半径是【B 】 A .36B .18C .9D.67.直线323+-=x y 与x 轴、y 轴所围成的三角形的面积为【A 】A .3B .6C .43D .238.如图,抛物线的函数表达式是【D 】 A .22+-=x x y B .22+--=x x y C .22++=x x y D .22++-=x x y9.有一块多边形草坪,在市政建设射击图纸上的面积为3002cm ,其中一条边的长度为5cm ,经测量,这条边的实际长度为15m ,则这块草坪的实际面积是【C 】A .1002m B .2702m C .27002m D .900002m10.如图,矩形ABCG (BC AB )与矩形CDEF全等,点B 、C 、D 在同一条直线上,APE ∠的顶点P 在线段BD 上移动,使APE ∠为直角的点P 的个数是【C 】 A .0B .1C .2D .3第Ⅱ卷(非选择题共90分)二、填空题(共6小题,每小题3分,共18分) 11.不等式)1(32+≤-x x 的解集为25-≥x 。
陕西省2006年初中毕业学业考试数学试题(大纲卷,含答案)1-

陕西省2006年初中毕业学业考试数 学 试 题(大纲)第I 卷(选择题 共30分)A 卷一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的) 1.下列计算正确的是( ) A .321-+= B .|2|2-=- C .3(3)9⨯-=-D .0211-=2.如图,123,,∠∠∠的大小关系为( )A .213>>∠∠∠B .132>>∠∠∠C .321>>∠∠∠D .123>>∠∠∠ 3.2005年11月1日零时,全国总人口为130628万人.60岁及以上的人口占总人口的11.03%,则全国60岁及以上的人口用科学记数法表示(保留三位有效数字)约为( ) A .81.4410⨯人B .81.4510⨯人C .714.410⨯人D .41.4410⨯人4.一件标价为600元的上衣,按8折(即按标价的80%)销售仍可获利20元.设这件上衣的成本价为x 元,根据题意,下面所列方程正确的是( ) A .6000.820x ⨯-= B .600820x ⨯-=C .6000.820x ⨯=-D .600820x ⨯=- 5.如图,O 是ABC △的外接圆,AD 是O 的直径,连结CD , 若O 的半径322r AC ==,,则cos B 的值是( )A .32B .53C .52D .236.下列图形中,是中心对称图形的是( )7.若圆锥的侧面展开图是一个弧长为36π的扇形,则这个圆锥的底面半径是( ) A .36 B .18 C .9 D .6 8.有一块多边形草坪,在市政建设设计图纸上的面积为2300cm ,其中一条边的长度为5cm .经测量,这条边的实际长度为15m ,则这块草坪的实际面积是( )(第5题图)ABCDO123(第2题图) A . B . C . D .A .2100mB .2270mC .22700mD .290000m9.如图,抛物线的函数表达式是( ) A .22y x x =-+ B .22y x x =++ C .22y x x =--+ D .22y x x =-++10.如图,矩形()ABCG AB BC <与矩形CDEF 全等,点B C D ,,在同一条直线上,APE ∠的顶点P 在线段BD 上移动,使APE ∠为直角的点P 的个数是( )A .0B .1C .2D .3第II 卷(非选择题 共90分)二、填空题(共6小题,每小题3分,计18分) 11.分解因式:233a -= .12.选做题...(要求在(1)、(2)中任选一题作答) (1)用计算器估算:若2.6456 2.6459<<,则a 的整数值是 .(2(填“>”、“=”、“<”). 13.不等式组210x x >-⎧⎨-⎩≤的解集为 .14.如图,小河对岸有一座塔AB .分别在点D C ,处测得塔尖点A 处的仰角为128=∠,241=∠,且25CD =米.则塔的高度AB 约为 米(精确到0.1米). (可用计算器求,也可用下列参考数据求:sin 280.4695sin 410.6561,≈≈ cos 280.8829cos 410.7547,≈≈ tan 280.5317tan 410.8693,≈≈)(第10题图)E12ABCD(第9题图)15.观察下列等式:22(12)4114+-⨯=+ 22(22)4224+-⨯=+ 22(32)4334+-⨯=+…则第n 个等式可以表示为 . 16.将一个无盖正方体纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②).则所剪得的直角三角形较短的与较长的直角边的比是 .三、解答题(共9小题,计72分.解答应写出过程) 17.(本题满分5分)解分式方程:23222x x x -=+-. 18.(本题满分6分)如图,在直角坐标系中:(1)描出下列各点,并将这些点用线段依次..连结起来: (24)(38)(84)(31)(24)----,,,,,,,,,;(2)作出(1)中的图形关于y 轴的对称图形.(第16题图①) (第16题图②)x(第18题图)如图,O 为ABCD 的对角线AC 的中点,过点O 作一条直线分别与AB CD ,交于点M N ,,点E F ,在直线MN 上,且OE OF =.(1)图中共有几对全等三角形,请把它们都写出来; (2)求证:MAE NCF =∠∠.20.(本题满分8分)2003~2005年陕西省财政收入情况如图所示.根据图中的信息,解答下列问题: (1)陕西省这三年平均年财政收入为多少亿元?(2)陕西省2004~2005年财政收入的年增长率约为多少?(精确到1%) (3)如果陕西省2005~2006年财政收入的年增长率与(2)中求得的年增长率基本相同,请估计陕西省2006年财政收入约为多少亿元?(精确到1亿元)2003 2004 2005 年份/年(第20题图)AE M D FC B O12 (第19题图)N如图,在Rt ABC △中,90BAC =∠,E F ,分别是BC AC ,的中点,延长BA 到点D ,使12AD AB =.连结DE DF ,. (1)求证:AF 与DE 互相平分; (2)若4BC =,求DF 的长.22.(本题满分8分)甲、乙两车从A 地出发,沿同一条高速公路行驶至距A 地400千米的B 地.12l l ,分别表示甲、乙两车行驶路程y (千米)与时间x (时)之间的关系(如图所示).根据图象提供的信息,解答下列问题:(1)求2l 的函数表达式(不要求写出x 的取值范围);(2)甲、乙两车哪一辆先到达B 地?该车比另一辆车早多长时间到达B 地?ADFEB(第21题图)444 (时) (第22题图)如图,O 的直径430AB ABC BC ===,,∠D 是线段BC 的中点.(1)试判断点D 与O 的位置关系,并说明理由;(2)过点D 作DE AC ⊥,垂足为点E ,求证直线DE 是O 的切线.24.(本题满分10分)某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信.这五封信的重量分别是72g ,90g ,215g ,340g ,400g .根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下: (1)重量为90g 的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?(2)这五封信分别以怎样的方式寄出最合算?请说明理由.(3)通过解答上述问题,你有何启示?(请你用一、两句话说明)B (第23题图)25.(本题满分12分)王师傅有两块板材边角料,其中一块是边长为60cm的正方形板子;另一块是上底为30cm,下底为120cm,高为60cm的直角梯形板子(如图①).王师傅想将这两块板子裁成两块全等的矩形板材.他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCFE围成的区域(如图②).由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点.(1)求FC的长;(2)利用图②求出矩形顶点B所对的顶点.....到BC边的距离x(cm)为多少时,矩形的面积y(2cm)最大?最大面积是多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长.AB CE DGF(第25题图②)(第25题图①)陕西省2006年初中毕业学业考试参考答案数 学 试 题(大纲) 第I 卷(选择题 共30分)A 卷一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的) 1.C 2.D 3.A 4.A 5.B 6.D 7.B 8.C 9.D 10.C (B 卷)一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的) 1.D 2.B 3.D 4.D 5.C 6.A 7.C 8.B 9.A 10.B 二、填空题(共6小题,每小题3分,计18分)11.3(1)(1)a a +- 12.(1)7,(2)> 13.21x -<≤ 14.34.2 15.22(2)44n n n +-=+ 16.1:2三、解答题(共9小题,计72分.解答应写出过程) 17.(本题满分6分)解:22(2)3(2)2(4)x x x x --+=-. ··················································· (1分)22243628x x x x ---=-, 72x -=-, 27x =. ·························································· (4分) 经检验:27x =是原方程的解. ∴原方程的解为27x =. ······························································ (5分)18.(本题满分6分)······················· (每问3分,共6分)19.(本题满分7分) 解:(1)有4对全等三角形.分别为AMO CNOOCF OAE ,△≌△△≌△, AME CNF ABC CDA ,△≌△△≌△. ················································ (4分)(第18题图)(2)证明:12OA OC OE OF ===,,∠∠,OAE OCF ∴△≌△,EAO FCO ∴=∠∠. ·········································· (6分) 在ABCD 中,AB CD ∥, BAO DCO EAM NCF ∴=∴=.∠∠∠∠. ············································ (7分) 20.(本题满分8分)解:(1)1(326415528)4233x =++=(亿元), ∴陕西省这三年平均年财政收入为423亿元. ·········································· (2分)(2)528415100%27%415-⨯≈,∴陕西省2004~2005年财政收入的年增长率约为27%. ······························ (5分)(3)528(127%)670.56671+=≈(亿元), ∴2006年财政收入约为671亿元. ························································ (8分)21.(本题满分8分) 证明:(1)连结EF AE ,. ·································································· (1分) 点E F ,分别为BC AC ,的中点, 12EF AB EF AB ∴=,∥. 又12AD AB =, EF AD ∴=. 又EF AD ∥, ∴四边形AEFD 是平行四边形. ··························································· (3分) ∴AF 与DE 互相平分. ····································································· (4分) (2)在Rt ABC △中,E 为BC 的中点,4BC =,122AE BC ∴==.又四边形AEFD 是平行四边形,2DF AE ∴==. ············································································· (8分) 22.(本题满分8分)解:(1)设2l 的函数表达式是2y k x b =+,则22304194004k b k b ⎧=+⎪⎪⎨⎪=+⎪⎩,.··············································································· (2分) 解之,得210075k b ==-,.∴2l 的函数表达式为10075y x =-. ····················································· (4分)(2)乙车先到达B 地.······································································· (5分) ADF EB (第21题图)15300100754x x =-∴=,. ····························································· (6分) 设1l 的函数表达式是1y k x =, 图象过点153004⎛⎫⎪⎝⎭,, 180k ∴=,即80y x =.当400y =时,4008x =,5x ∴=.191544∴-=(小时). ∴乙车比甲车早14小时到达B 地. ························································ (8分)23.(本题满分8分)解:(1)点D 在O 上. ···································································· (1分)连结OD ,过点O 作OF BC ⊥于点F . ················································ (2分) 在Rt BOF △中,12302OB AB B ===,∠, 2cos303BF ∴==.12BD BC == DF ∴=在Rt ODF △中,312OD OB =+==,∴点D 在O 上. ············································································· (5分) (2)D 是BC 的中点,O 是AB 的中点, OD AC ∴∥. 又DE AC ⊥,90EDO ∴=∠.又OD 是O 的半径,DE ∴是O 的切线. ········································································· (8分) 24.(本题满分10分)解:(1)重量为90g 的信以“挂号信”方式寄出,则邮寄费为50.830.57.5⨯++=(元); 以“特快专递”方式寄出,邮寄费为 5319++=(元). ············································································ (2分) (2)这五封信的重量均小于1 000g ,∴若以“特快专递”方式寄出,邮寄费为5319++=(元).B(第23题图)..由(1)得知,重量为90g 的信以“挂号信”方式寄出,费用为7.5元小于9元; 72g<90g ,∴重量为72g 的信以“挂号信”方式寄出小于9元; ································· (4分) 若重量为215g 的信以“挂号信”方式寄出,则邮寄费为50.82230.511.5⨯+⨯++=(元)>9(元). ···························· (6分) 400g>340g>215g ,∴重量为400g ,340g 的信以“挂号信”方式寄出,费用均超过9元.因此,将这五封信的前两封以“挂号信”方式寄出,后三封以“特快专递”方式寄出最合算. ················································ (8分)(3)学生言之有理即可. ·································································· (10分)25.(本题满分12分)解:(1)由题意,得DEF CGF △∽△,603060DF DE FC FC CG FC -∴=∴=,, 40(cm)FC ∴=. ············································································· (3分)(2)如图,设矩形顶点B 所对顶点为P ,则①当顶点P 在AE 上时,60x =,y 的最大值为260301800(cm )⨯=.……………………………………(4分)②当顶点P 在EF 上时,过点P 分别作PN BG ⊥于点N ,PM AB ⊥于点M .根据题意,得GFC GPN △∽△. 3312022PN FC NG x BN x NG CG ∴=∴=∴=-,,. 233(120)(40)240022y x x x ∴=-=--+. ∴当40x =时,y 的最大值为22400(cm ). ··········································· (7分) ③当顶点P 在FC 上时,y 的最大值为260402400(cm )⨯=. ··················· (8分) 综合①②③,得40cm x =时,矩形的面积最大,最大面积为22400cm . ··············································· (9分)(3)根据题意,正方形的面积2(cm )y 与边长(cm)x 满足的函数表达式为: 231202y x x =-+. 当2y x =时,正方形的面积最大,2231202x x x ∴=-+. 解之,得10x =(舍),248(cm)x =.∴面积最大的正方形的边长为48cm . ··················································· (12分)B NC G (第25题图②)。
2006年陕西省中考数学试题

陕西省2006年中考数学试题及答案(课改实验区A 卷)第Ⅰ卷(选择题 共30分)A 卷一、选择题(共10小题,每小题3分,计30分,每小题只有一个选项是符合题意的) 1.下列计算正确的是 【 C 】A .123=+-B .22-=-C .9)3(3-=-⨯D .1120=- 2.如图,几何体的左视图是 【 B 】3.一件标价为600元的上衣,按8折销售仍可获利20元,设这件上衣的成本价为x 元,根据题意,下面所列的方程正确的是 【 A 】 A .208.0600=-⨯x B .208600=-⨯x C .208.0600-=⨯x D .208600-=⨯x4.如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,连接CD ,若⊙O 的半径23=r ,2=AC ,则B cos 的值是 【 B 】A .23 B .35 C .25 D .32 第4题图5.如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在折7天中,日温差最大的一天市A .5月1日B .5月2日C .5月3日D .5月5日6.若圆锥的侧面展开图市一个弧长为π36的扇形,则这个圆锥的底面半径是 【 B 】 A .36 B .18 C .9 D.6 7.直线323+-=x y 与x 轴、y 轴所围成的三角形的面积为【 A 】A .3B .6C .43 D .23 8.如图,抛物线的函数表达式是 【 D 】 A .22+-=x x y B .22+--=x x y C .22++=x x y D .22++-=x x y 9.有一块多边形草坪,在市政建设射击图纸上的面积为3002cm ,其中一条边的长度为5cm ,经测量,这条边的实际长度为15m ,则这块草坪的实际面积是 【 C 】A .1002m B .2702m C .27002m D .900002m 10.如图,矩形ABCG (BC AB )与矩形CDEF 全等,点B 、C 、D 在同一条直线上,APE ∠的顶点P 在线段BD 上移动,使APE ∠为直角的点P 的个数是 【 C 】 A .0 B .1 C .2 D .3第Ⅱ卷(非选择题 共90分)二、填空题(共6小题,每小题3分,共18分) 11.不等式)1(32+≤-x x 的解集为25-≥x 。
历年陕西中考数学试题及答案3(word版)
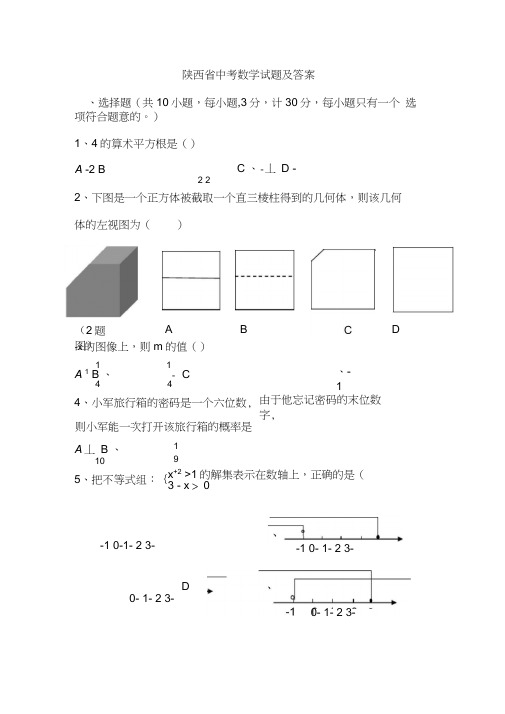
陕西省中考数学试题及答案、选择题(共10小题,每小题,3分,计30分,每小题只有一个选项符合题意的。
)1、4的算术平方根是()C 、-丄D -2 22、下图是一个正方体被截取一个直三棱柱得到的几何体,则该几何体的左视图为()-x的图像上,则m的值()(2题图)A B D1 1A1 B 、- C4 44、小军旅行箱的密码是一个六位数,、-1由于他忘记密码的末位数字,则小军能一次打开该旅行箱的概率是A丄B 、105、把不等式组:{19x+2 >1的解集表示在数轴上,正确的是(3 - x > 0-1 0-1- 2 3- -1 0- 1- 2 3-D0- 1- 2 3-0- 1- 2 3-A -2 B9、如图,在平行四边形 ABCD 中,AB 5,对角线AC 6,若过点A作AE BC ,垂足为E,则AE 的长( A 4B 12、5 C 24D、5510、二次函数y 是() A c ?-1 C 2a b 02ax bx c(aB b?0 、9a 2 0)的图象如图所示,则下列结论正确的c 3b6、某区10名学生参加市级汉子听写大赛,他们得分情况如下表: 人数 3 4 2 1 分数80859095那么这10名学生所得分数的平均数和众数分别是多少?()A 、85 和 82.5 C 、85 和 857、如图 AB|| CD,/ A=45°,Z C=28° ,则/AEC 的大小为(&若x 2是关于x 的一元二次方程x 2 -ax a 2 0的一个根,则a 的2值是()A 、1 或 4B 、-1 或-4C 、-1 或 4D 、1 或-4、85.5 和 85 、85.5 和 80A 、17B 、 620C 630D 、730X第10题图第II 卷(非选择题90分)二、填空题(共6小题,每小题3分,计18分) 11、 计算(I )2。
3--------12、 _________________________________________ 因式分解: m (x y ) n(x y ) ___________________________________________ 。
历年陕西省中考数学试卷及答案

最新中考模拟题 数学试卷第Ⅰ卷(选择题 共30分)一、选择题(共10小题,每小题3分,计30分)1.如果零上5 ℃记做+5 ℃,那么零下7 ℃可记作( ) A .-7 ℃ B .+7 ℃ C .+12 ℃ D .-12 ℃ 2.如图,是由三个相同的小正方体组成的几何体,该几何体的左视图是( )3.计算23)5(a -的结果是( )A .510a -B .610aC .525a -D .625a4.某中学举行歌咏比赛,以班为单位参赛,评委组的各位评委给九年级三班的演唱打分情况(满分100分)如下表,从中去掉一个最高分和一个最低分,则余下的分数的平均分是( )分数(分) 89 92 95 96 97 评委(位) 12211 A .92分B .93分C .94分D .95分5.如图,在BE AD ABC ,中,∆是两条中线,则=∆∆ABC EDC S S :( )A .1∶2B .2∶3C .1∶3D .1∶46.下列四组点中,可以在同一个正比例函数图象上的一组点是( ) A .(2.-3),(-4,6) B .(-2,3),(4,6) C .(-2,-3),(4,-6) D .(2,3),(-4,6) 7.如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,OE AB ⊥,垂足为E ,若=130ADC ∠︒,则AOE ∠的大小为( )A .75°B .65°C .55°D .50° 8.在同一平面直角坐标系中,若一次函数533-=+-=x y x y 与图象交于点M ,则点M 的坐标为( ) A .(-1,4) B .(-1,2) C .(2,-1) D .(2,1)9.如图,在半径为5的圆O 中,AB ,CD 是互相垂直的两条弦,垂足为P ,且AB =CD =8,则OP 的长为( )A .3B .4C .32D .2410.在平面直角坐标系中,将抛物线62--=x x y 向上(下)或向左(右)平移了m 个单位,使平移后的抛物线恰好经过原点,则m 的最小值为( )A .1B .2C .3D .6第Ⅱ卷(非选择题 共90分)二、填空题(共6小题,每小题3分,计18分)11.计算:()2cos 45-38+1-2=︒ .12.分解因式:3223-2+=x y x y xy .13.请从以下两个小题中任选一个....作答,若多选,则按所选的第一题计分. A .在平面内,将长度为4的线段AB 绕它的中点M ,按逆时针方向旋转30°,则线段AB 扫过的面积为 .B .用科学计算器计算:7sin 69︒≈ (精确到0.01).14.小宏准备用50元钱买甲、乙两种饮料共10瓶.已知甲饮料每瓶7元,乙饮料每瓶4元,则小宏最多能买 瓶甲饮料.15.在同一平面直角坐标系中,若一个反比例函数的图象与一次函数=-2+6y x 的图象无.公共点,则这个反比例函数的表达式是 (只写出符合条件的一个即可).16.如图,从点()02A ,发出的一束光,经x 轴反射,过点()43B ,,则这束光从点A 到点B 所经过路径的长为 .三、解答题(共9小题,计72分.解答应写过程) 17.(本题满分5分) 化简:22a bb a b a b a b a b--⎛⎫÷⎪+-+⎝⎭-. 18.(本题满分6分)如图,在ABCD 中,ABC ∠的平分线BF 分别与AC 、AD 交于点E 、F . (1)求证:AB AF =; (2)当35AB BC ==,时,求AEAC的值.19.(本题满分7分)某校为了满足学生借阅图书的需求,计划购买一批新书.为此,该校图书管理员对一周内本校学生从图书馆借出各类图书的数量进行了统计,结果如下图.请你根据统计图中的信息,解答下列问题:(1)补全条形统计图和扇形统计图;(2)该校学生最喜欢借阅哪类图书?(3)该校计划购买新书共600本,若按扇形统计图中的百分比来相应地确定漫画、科普、文学、其它这四类图书的购买量,求应购买这四类图书各多少本?20.(本题满分8分)如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A 处测得湖心岛上的迎宾槐C处位于北偏东65︒方向,然后,他从凉亭A处沿湖岸向正东方向走了100、、在同一水平面上).请你米到B处,测得湖心岛上的迎宾槐C处位于北偏东45︒方向(点A B C利用小明测得的相关数据,求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离(结果精确到1米).(参考数据:,,,,sin250.4226cos250.9063tan250.4663sin650.9063︒≈︒≈︒≈︒≈,)cos650.4226tan65 2.1445︒≈︒≈21.(本题满分8分)科学研究发现,空气含氧量y (克/立方米)与海拔高度x (米)之间近似地满足一次函数关系.经测量,在海拔高度为0米的地方,空气含氧量约为299克/立方米;在海拔高度为2000米的地方,空气含氧量约为235克/立方米. (1)求出y 与x 的函数表达式;(2)已知某山的海拔高度为1200米,请你求出该山山顶处的空气含氧量约为多少? 22.(本题满分8分)小峰和小轩用两枚质地均匀的骰子做游戏,规则如下:每人随机掷两枚骰子一次(若掷出的两枚骰子摞在一起,则重掷),点数和大的获胜;点数和相同为平局. 依据上述规则,解答下列问题:(1)随机掷两枚骰子一次,用列表法求点数和为2的概率;(2)小峰先随机掷两枚骰子一次,点数和是7,求小轩随机掷两枚骰子一次,胜小峰的概率. (骰子:六个面分别刻有1、2、3、4、5、6个小圆点的立方块.点数和:两枚骰子朝上的点数之和.) 23.(本题满分8分)如图,PA PB 、分别与O 相切于点A B 、,点M 在PB 上,且//OM AP ,MN AP ,垂足为N . (1)求证:=OM AN ;(2)若O 的半径=3R ,=9PA ,求OM 的长. 24.(本题满分10分)如果一条抛物线()2=++0y ax bx c a ≠与x 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. (1)“抛物线三角形”一定是 三角形;(2)若抛物线()2=-+>0y x bx b 的“抛物线三角形”是等腰直角三角形,求b 的值;(3)如图,△OAB 是抛物线()2=-+''>0y x bx b 的“抛物线三角形”,是否存在以原点O 为对称中心的矩形ABCD ?若存在,求出过O C D 、、三点的抛物线的表达式;若不存在,说明理由. 25.(本题满分12分) 如图,正三角形ABC 的边长为3+3.(1)如图①,正方形EFPN 的顶点E F 、在边AB 上,顶点N 在边AC 上.在正三角形ABC 及其内部,以A 为位似中心,作正方形EFPN 的位似正方形''''EFPN ,且使正方形''''EFPN 的面积最大(不要求写作法);(2)求(1)中作出的正方形''''EFPN 的边长; (3)如图②,在正三角形ABC 中放入正方形DEMN 和正方形EFPH ,使得DE EF 、在边AB 上,点P N 、分别在边CB CA 、上,求这两个正方形面积和的最大值及最小值,并说明理由.参考答案1、【答案】A【解析】通过题意我们可以联想到数轴,零摄氏度即原点,大于零摄氏度为正方向,数值为正数, 小于零摄氏度为负数.故选A . 2、【答案】C【解析】三视图主要考查学生们的空间想象能力,是近几年中考的必考点,从图中我们可以知道正 面为三个正方形,(下面两个,上面一个),左视图即从左边观看,上边有一个正方形,下 面两个正方体重叠,从而看到一个正方形,故选C . 3、【答案】D【解析】本题主要考查了数的乘方以及幂的乘方,从整体看,外边是个平方,那么这个数肯定是正 数,排除A ,C ,然后看到5的平方,是25,3a 的平方是6a ,积为625a ,选D . 4、【答案】C【解析】统计题目也是年年的必考题,注重学生们的实际应用能力,根据题目规则,去掉一个最高 分和一个最低分,也就是不算89分和97分,然后把其余数求平均数,得到94分.其实这 种计算有个小技巧,我们看到都是90多分,所以我们只需计算其个位数的平均数,然后再 加上90就可以快速算出结果.个位数平均数为45)62522(=÷+⨯+⨯,所以其余这些数 的平均数为94分.故选C . 5、【答案】D【解析】本题主要考查了三角形的中位线的性质,由题意可知,ED 为ABC ∆的中位线,则面积比 =∆∆ABC EDC S S :4:1)21()(22==AB ED ,故选D . 6、【答案】A【解析】本题考查了一次函数的图象性质以及应用,若干点在同一个正比例函数图像上,由kx y =, 可知,y 与x 的比值是相等的,代进去求解,可知,A 为正确解.选A . 7、【答案】B【解析】本题考查了菱形的性质,我们知道菱形的对角线互相平分且垂直,外加OE AB ⊥,即可得 出︒=︒⨯=∠⨯=∠=∠651302121ABC OBE AOE .选B . 8、【答案】D【解析】一次函数交点问题可以转化为二元一次方程组求解问题,解得x=2,y=1.选D . 9、【答案】C 【解析】本题考查圆的弦与半径之间的边角关系,连接OB ,OD ,过O 作OH AB ⊥,交AB 于点H . 在OBH Rt ∆中,由勾股定理可知,OH =3,同理可作AB OE ⊥,OE =3,且易证 OPH OPE ∆≅∆,所以OP =23,选C . 10、【答案】B【解析】本题考查了抛物线的平移以及其图像的性质,由)2)(3(62+-=--=x x x x y ,可知其与 x 轴有两个交点,分别为()()30-20,,,.画图,数形结合,我们得到将抛物线向右平移2个单位,恰好使得抛物线经过原点,且移动距离最小.选B . 11、【答案】【解析】原式=22⨯⨯12、【答案】()2-xy x y【解析】()()2322322-2-2-x y x y xy xy x xy y xy x y +=+=13、A 【答案】23π【解析】将长度为4的线段AB 绕它的中点M ,按逆时针方向旋转30°,则线段AB 扫过部分的形状为半径为2,圆心角度数为30°的两个扇形,所以其面积为230222=3603ππ⨯⨯. B 【答案】2.4714、【答案】3【解析】设小宏能买x 瓶甲饮料,则买乙饮料()10-x 瓶.根据题意,得 ()7+410-50x x ≤ 解得133x ≤ 所以小宏最多能买3瓶甲饮料.15、【答案】18=y x (只要=k y x 中的k 满足9>2k 即可) 【解析】设这个反比例函数的表达式是=ky x()0k ≠.由==-2+6ky xy x ⎧⎪⎨⎪⎩,,得22-6+=0x x k . 因为这个反比例函数与一次函数的图象没有交点,所以方程22-6+=0x x k 无解. 所以()2=-6-42=36-8<0k k ∆⨯,解得9>2k .16、【解析】方法一:设这一束光与x 轴交与点C ,过点C 作x 轴的垂线CD ,过点B 作BE x ⊥轴于点E .根据反射的性质,知ACO BCE ∠=∠.所以Rt ACORt BCE ∆∆.所以=AO BECO CE. 已知=2AO ,=3BE ,+=4OC CE ,则23=4-CE CE. 所以12=5CE ,8=5CO .由勾股定理,得AC =BC =+AB AC BC方法二:设设这一束光与x 轴交与点C ,作点B 关于x 轴的对称点'B ,过'B 作'B D y ⊥轴 于点D .由反射的性质,知'A C B ,,这三点在同一条直线上. 再由对称的性质,知'=BC BC . 则=+=''AB AC CB AC CB AB +=.由题意易知=5AD ,'=4BD ,由勾股定理,得AB =AB AB17、【答案】解:原式=(2)()()()()2a b a b b a b a ba b a b a b---++⋅+--=22222()(2)a ab ab b ab b a b a b --+----=224()(2)a aba b a b ---=2(2)()(2)a ab a b a b ---=2aa b-. 18、【答案】解:(1)如图,在ABCD 中,//AD BC , ∴23∠=∠.∵BF 是ABC ∠的平分线, ∴12∠=∠. ∴13∠=∠. ∴AB AF =.(2)23AEF CEB ∠=∠∠=∠,, ∴△AEF ∽△CEB , ∴35AE AF EC BC ==,∴38AE AC =. 19、【答案】解:(1)如图所示一周内该校学生从图书馆借出各类图书数量情况统计图(2)该学校学生最喜欢借阅漫画类图书.(3)漫画类:600×40%=240(本),科普类:600×35%=210(本), 文学类:600×10%=60(本),其它类:600×15%=90(本). 20、【答案】解:如图,作CD AB ⊥交AB 的延长线于点D ,则4565BCD ACD ∠=︒∠=︒,. 在Rt △ACD 和Rt △BCD 中, 设AC x =,则sin 65AD x =︒, cos65BD CD x ==︒.∴100cos65sin65x x +︒=︒.∴100207sin 65cos65x =≈︒-︒(米). ∴湖心岛上的迎宾槐C 处与凉亭A 处之间距离约为207米.21、【答案】解:(1)设+y kx b =,则有299,2000235.b k b =⎧⎨+=⎩解之,得4125299.k b ⎧=-⎪⎨⎪=⎩,∴4299125y x =-+. (2)当1200x =时,41200299260.6125y =-⨯+=(克/立方米).∴该山山顶处的空气含氧量约为260.6克/立方米. 22、【答案】解:(1)随机掷两枚骰子一次,所有可能出现的结果如右表:右表中共有36种等可能结果,其中点数和 为2的结果只有一种. ∴P (点数和为2)=136. (2)由右表可以看出,点数和大于7的结果 有15种.∴P (小轩胜小峰)= 1536=512.23、【答案】解:(1)证明:如图,连接OA ,则OA AP ⊥. ∵MN AP ⊥, ∴//MN OA . ∵//OM AP ,∴四边形ANMO 是矩形. ∴=OM AN .(2)连接OB ,则OB BP ⊥.∵=OA MN ,=OA OB ,//OM AP , ∴=OB MN ,=OMB NPM ∠∠. ∴Rt OBM Rt MNP ∆≅∆. ∴=OM MP .设=OM x ,则=9-NP x .在Rt MNP ∆中,有()222=3+9-x x .∴=5x .即=5OM . 24、【答案】解:(1)等腰(2)∵抛物线()2=-+>0y x bx b 的“抛物线三角形”是等腰直角三角形,∴该抛物线的顶点224b b ⎛⎫ ⎪⎝⎭,满足2=24b b ()>0b .∴=2b .(3)存在.如图,作△OCD 与△OAB 关于原点O 中心对称, 则四边形ABCD 为平行四边形.当=OA OB 时,平行四边形ABCD 为矩形. 又∵=AO AB ,∴△OAB 为等边三角形. 作AE OB ⊥,垂足为E . ∴=AE 3OE .∴()2''=3'>042b b b ⋅. 骰子2 骰子11 2 3 4 5 61 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5 6 7 8 91056 7 8 910 116 78910 11 12。
2006年陕西省初三上学期中考预测数学试卷(一

2006年陕西省初三上学期中考预测数学试卷(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
全卷120分,时间:120分钟。
第Ⅰ卷(选择题共30分)一、选择题 (共10小题,每小题3分,计30分,每小题只有一个选项是符合题意的) 1.小马虎在下面的计算中只做对了一道题,他做对的题目是( ) A .(a -b )2=a 2-b 2 B .(-2a 3)2=4a 6 C .a 3+a 2=2a 5D .-(a -1)=-a -12.如图1是小明用八块小正方体搭的积木,该几何体的俯视图是 ( )图13.一件衣服标价132元,若以9折降价出售,仍可获利10%,则这件衣服的进价是( ). A .106元 B .105元 C .118元 D .108元4.如图2,AB 是⊙O 的直径,点D 、E 是半圆的三等分点,AE 、BD 的延长线交于点C 。
若CE =2,则图中阴影部分的面积是( ) A .34π-3 B .32πC .32π-3 D .31π 图25.小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作圆锥形的生日礼帽。
如图3,圆锥帽底半径为9 cm ,母线长为36 cm ,请你帮助他们计算制作一个这样的生日礼帽需要纸板的面积为( ) A .648π cm 2B .432π cm 2图3C .324π cm 2D .216π cm 26.数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图(如图4),根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为( )图4A .8,8B .8,9C .9,9D .9,8 7.已知矩形的面积为10,则它的长y 与宽x 之间的关系用图象大致可表示为( )ABCD8.已知二次函数y =ax 2+bx +c 的图象如图5所示,则在“①a <0,②b >0,③c <0,④b 2-4ac >0”中正确的判断是( )A .①②③④B .④C .①②③D .①④9.将矩形ABCD 沿AE 折叠,得到如图6所示的图形,已知∠CED =60°,则∠AED 的大小是( ) A .60° B .50° C .75°D .55° 图610.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则!98!100的值为( ) 图5A .4950 B .99! C .9 900 D .2!第Ⅱ卷(非选择题共90分)二、填空题 (共6小题,每小题3分,计18分)11.某公司成立3年以来,积极向国家上缴利税,由第一年的200万元增长到800万元,则平均每年增长的百分数是 。
2006年陕西省中考数学试卷(课标卷)
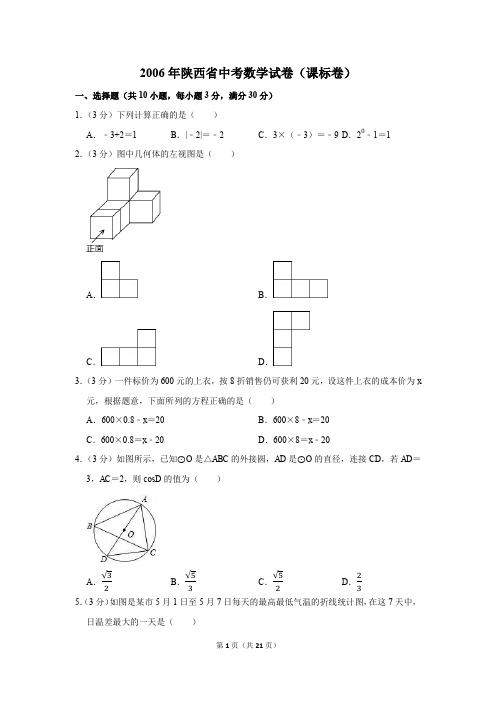
2006年陕西省中考数学试卷(课标卷)一、选择题(共10小题,每小题3分,满分30分)1.(3分)下列计算正确的是()A.﹣3+2=1B.|﹣2|=﹣2C.3×(﹣3)=﹣9D.20﹣1=1 2.(3分)图中几何体的左视图是()A.B.C.D.3.(3分)一件标价为600元的上衣,按8折销售仍可获利20元,设这件上衣的成本价为x 元,根据题意,下面所列的方程正确的是()A.600×0.8﹣x=20B.600×8﹣x=20C.600×0.8=x﹣20D.600×8=x﹣204.(3分)如图所示,已知⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若AD=3,AC=2,则cos D的值为()A.B.C.D.5.(3分)如图是某市5月1日至5月7日每天的最高最低气温的折线统计图,在这7天中,日温差最大的一天是()A.5月1日B.5月2日C.5月3日D.5月5日6.(3分)若圆锥的侧面展开图是一个弧长为36π的扇形,则这个圆锥的底面半径是()A.36B.18C.9D.67.(3分)直线y x+3与x轴、y轴所围成的三角形的面积为()A.3B.6C.D.8.(3分)如图,抛物线的函数表达式是()A.y=x2﹣x+2B.y=x2+x+2C.y=﹣x2﹣x+2D.y=﹣x2+x+2 9.(3分)有一多边形草坪,在市政建设设计图纸上的面积为300cm2,其中一条边的长度为5cm.经测量,这条边的实际长度为15m,则这块草坪的实际面积是()A.100m2B.270m2C.2700m2D.90000m2 10.(3分)如图,矩形ABCG(AB<BC)与矩形CDEF全等,点B,C,D在同一条直线上,∠APE的顶点P在线段BD上移动,使∠APE为直角的点P的个数是()A.0B.1C.2D.3二、填空题(共5小题,每小题3分,满分15分)11.(3分)不等式x﹣2≤3(x+1)的解集为.12.(3分)(1)2005年11月1日零时,全国总人口为130 628万人,60岁及以上的人口占总人口的11.03%,则全国60岁及以上的人口用科学记数法表示约为万人(用计算器计算,保留3位有效数字).(2)用计算器比较大小:0(填“>“、“=“、“<“).13.(3分)在同一时刻,小明测得1米的杆子影长为1.6米,一棵树的影长是4.5米,则这棵树的高度为米.15.(3分)双曲线与直线y=2x的交点坐标为.16.(3分)将一个无盖正方体纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②).则所剪得的直角三角形较短的与较长的直角边的比是.三、解答题(共10小题,满分75分)14.(3分)观察下面图形,按规律在两个箭头所指的“田”字格内分别画上适当图形(只对一个2分)17.(5分)解分式方程:.18.(6分)观察下面网格中的图形,解答下列问题:(1)将网格中左图沿水平方向向右平移,使点A移至点A′处,作出平移后的图形:(2)(1)中作出的图形与右边原有的图形,组成一个新的图形,这个新图形是中心对称图形,还是轴对称图形?19.(7分)2003~2005年陕西省财政收入情况如图所示.根据图中的信息,解答下列问题:(1)陕西省这三年平均年财政收入为多少亿元?(2)陕西省2004~2005年财政收入的年增长率约为多少?(精确到1%)(3)如果陕西省2005~2006年财政收入的年增长率与(2)中求得的年增长率基本相同,请估计陕西省2006年财政收入约为多少亿元?(精确到1亿元)20.(8分)如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.(1)图中共有几对全等三角形,请把它们都写出来;(2)求证:∠MAE=∠NCF.21.(8分)甲、乙两车从A地出发,沿同一条高速公路行驶至距A地400千米的B地.l1,l2分别表示甲、乙两车行驶路程y(千米)与时间x(时)之间的关系(如图所示).根据图象提供的信息,解答下列问题:(1)求l2的函数表达式(不要求写出x的取值范围);(2)甲、乙两车哪一辆先到达B地该车比另一辆车早多长时间到达B地?22.(8分)有两个可以自由转动的均匀转盘A、B,都被分成了3等份,并在每份内均标有数字,如图所示,规则如下:①分别转动转盘A、B.②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).(1)用列表法(或树状图)分别求出数字之积为3的倍数和为5的倍数的概率;(2)小亮和小芸想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小亮得2分;数字之积为5的倍数时,小芸得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏双方公平.23.(8分)如图,⊙O的直径AB=4,∠ABC=30°,BC,D是线段BC的中点.(1)试判断点D与⊙O的位置关系,并说明理由;(2)过点D作DE⊥AC,垂足为点E,求证:直线DE是⊙O的切线.24.(10分)某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信.这五封信的重量分别是72g,90g,215g,340g,400g.根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:(1)重量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?(2)这五封信分别以怎样的方式寄出最合算?请说明理由.(3)通过解答上述问题,你有何启示?(请你用一、两句话说明)25.(12分)王师傅有两块板材边角料,其中一块是边长为60cm的正方形板子;另一块是上底为30cm,下底为120cm,高为60cm的直角梯形板子(如图①).王师傅想将这两块板子裁成两块全等的矩形板材.他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCFE围成的区域(如图②).由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点.(1)求FC的长;(2)利用图②求出矩形顶点B所对的顶点到BC边的距离x(cm)为多少时,矩形的面积y(cm2)最大?最大面积是多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长.2006年陕西省中考数学试卷(课标卷)参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.(3分)下列计算正确的是()A.﹣3+2=1B.|﹣2|=﹣2C.3×(﹣3)=﹣9D.20﹣1=1【解答】解:A中:﹣3+2=﹣1.B中:|﹣2|=2.C中:3×(﹣3)=﹣9.D中:20﹣1=0.故选:C.2.(3分)图中几何体的左视图是()A.B.C.D.【解答】解:从物体左面看,第一层3个正方形,第二层左上角1个正方形.故选:B.3.(3分)一件标价为600元的上衣,按8折销售仍可获利20元,设这件上衣的成本价为x 元,根据题意,下面所列的方程正确的是()A.600×0.8﹣x=20B.600×8﹣x=20C.600×0.8=x﹣20D.600×8=x﹣20【解答】解:设上衣的成本价为x元,由已知得上衣的实际售价为600×0.8元,然后根据利润=售价﹣成本价,可列方程:600×0.8﹣x=20故选:A.4.(3分)如图所示,已知⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若AD=3,AC=2,则cos D的值为()A.B.C.D.【解答】解:∵AD是⊙O的直径,∴∠ACD=90°.∵AD=3,AC=2,∴CD.∴cos D.故选:B.5.(3分)如图是某市5月1日至5月7日每天的最高最低气温的折线统计图,在这7天中,日温差最大的一天是()A.5月1日B.5月2日C.5月3日D.5月5日【解答】解:在图中,从5月1日至5月7日找出实线与虚线差距最大的一天,为5月5日;故答案为D.6.(3分)若圆锥的侧面展开图是一个弧长为36π的扇形,则这个圆锥的底面半径是()A.36B.18C.9D.6【解答】解:设底面半径是r.∵弧长为圆锥的周长,∴36π=2πr,∴r=18,圆锥的底面半径是18.故选:B.7.(3分)直线y x+3与x轴、y轴所围成的三角形的面积为()A.3B.6C.D.【解答】解:当x=0时,y=3,即与y轴交点是(0,3),当y=0时,x=2,即与x轴的交点是(2,0),所以与x轴、y轴所围成的三角形的面积为2×3=3.故选:A.8.(3分)如图,抛物线的函数表达式是()A.y=x2﹣x+2B.y=x2+x+2C.y=﹣x2﹣x+2D.y=﹣x2+x+2【解答】解:根据题意,设二次函数的表达式为y=ax2+bx+c,抛物线过(﹣1,0),(0,2),(2,0),所以,解得a=﹣1,b=1,c=2,这个二次函数的表达式为y=﹣x2+x+2.故选:D.9.(3分)有一多边形草坪,在市政建设设计图纸上的面积为300cm2,其中一条边的长度为5cm.经测量,这条边的实际长度为15m,则这块草坪的实际面积是()A.100m2B.270m2C.2700m2D.90000m2【解答】解:设草坪的实际面积是x平方米,则有,解得x=2700m2.故选:C.10.(3分)如图,矩形ABCG(AB<BC)与矩形CDEF全等,点B,C,D在同一条直线上,∠APE的顶点P在线段BD上移动,使∠APE为直角的点P的个数是()A.0B.1C.2D.3【解答】解:设两个矩形的长是a,宽是b.连接AE,如图在△AEQ中,根据勾股定理可得:AE;过AE的中点M作MN⊥BD于点N.则MN是梯形ABDE的中位线,则MN(a+b);以AE为直径的圆,半径是,(a+b)a b,而只有a=b是等号才成立,因而(a+b)<,即圆与直线BD相交,则直角顶点P的位置有两个.故选:C.二、填空题(共5小题,每小题3分,满分15分)11.(3分)不等式x﹣2≤3(x+1)的解集为x.【解答】解:去括号得:x﹣2≤3x+3.移项及合并得:﹣2x≤5.∴x.12.(3分)(1)2005年11月1日零时,全国总人口为130 628万人,60岁及以上的人口占总人口的11.03%,则全国60岁及以上的人口用科学记数法表示约为 1.44×104万人(用计算器计算,保留3位有效数字).(2)用计算器比较大小:>0(填“>“、“=“、“<“).【解答】解:(1)130628×11.03%≈1.44×104;(2)∵ 2.571, 2.449,∴>0.故填空答案:(1)1.44×104;(2)>.13.(3分)在同一时刻,小明测得1米的杆子影长为1.6米,一棵树的影长是4.5米,则这棵树的高度为米.【解答】解:据相同时刻的物高与影长成比例,设这棵树的高度为xm,则解得x.∴这棵树的高度为米.15.(3分)双曲线与直线y=2x的交点坐标为(2,4)和(﹣2,﹣4).【解答】解:依题意有,解得与.即交点坐标为(2,4)和(﹣2,﹣4).故答案为:(2,4)和(﹣2,﹣4).16.(3分)将一个无盖正方体纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②).则所剪得的直角三角形较短的与较长的直角边的比是1:2.【解答】解:由图可得,所剪得的直角三角形较短的边是原正方体棱长的一半,而较长的直角边正好是原正方体的棱长,所以所剪得的直角三角形较短的与较长的直角边的比是1:2.三、解答题(共10小题,满分75分)14.(3分)观察下面图形,按规律在两个箭头所指的“田”字格内分别画上适当图形(只对一个2分)【解答】解:由图可看出每8个田字是一个循环.箭头所指的是第9个和第十个田字.那么根据第一个循环中,第一个田字和第二个田字的图形,便可画出所求的图形.17.(5分)解分式方程:.【解答】解:方程两边都乘(x+2)(x﹣2),得2x(x﹣2)﹣3(x+2)=2(x2﹣4),解得x.检验:当x时,(x+2)(x﹣2)≠0.∴x是原方程的解.18.(6分)观察下面网格中的图形,解答下列问题:(1)将网格中左图沿水平方向向右平移,使点A移至点A′处,作出平移后的图形:(2)(1)中作出的图形与右边原有的图形,组成一个新的图形,这个新图形是中心对称图形,还是轴对称图形?【解答】解:(1)如图所示.(作图正确3分)(2)新图形是轴对称图形.(6分)19.(7分)2003~2005年陕西省财政收入情况如图所示.根据图中的信息,解答下列问题:(1)陕西省这三年平均年财政收入为多少亿元?(2)陕西省2004~2005年财政收入的年增长率约为多少?(精确到1%)(3)如果陕西省2005~2006年财政收入的年增长率与(2)中求得的年增长率基本相同,请估计陕西省2006年财政收入约为多少亿元?(精确到1亿元)【解答】解:(1)∵(326+415+528)=423(亿元),∴陕西省这三年平均年财政收入为423亿元;(2)∵100%≈27%,∴陕西省2004~2005年财政收入的年增长率约为27%;(3)∵528(1+27%)=670.56≈671(亿元),∴2006年财政收入约为671亿元.20.(8分)如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.(1)图中共有几对全等三角形,请把它们都写出来;(2)求证:∠MAE=∠NCF.【解答】(1)解:有4对全等三角形.分别为△AMO≌△CNO,△OCF≌△OAE,△AME≌△CNF,△ABC≌△CDA;(2)证明:∵OA=OC,∠1=∠2,OE=OF,∴△OCF≌△OAE.∴∠EAO=∠FCO.在平行四边形ABCD中,AB∥CD,∴∠BAO=∠DCO.∴∠EAM=∠NCF.21.(8分)甲、乙两车从A地出发,沿同一条高速公路行驶至距A地400千米的B地.l1,l2分别表示甲、乙两车行驶路程y(千米)与时间x(时)之间的关系(如图所示).根据图象提供的信息,解答下列问题:(1)求l2的函数表达式(不要求写出x的取值范围);(2)甲、乙两车哪一辆先到达B地该车比另一辆车早多长时间到达B地?【解答】解:(1)设L2的函数表达式是y=k2x+b,则,解之得k2=100,b=﹣75,∴L2的函数表达式为y=100x﹣75.(2)由图可知,乙先到达B地.∵300=100x﹣75,∴x=3.75.设l1的函数表达式是y=k1x.∵该函数过点(3.75,300),∴k1=80,即y=80x.当y=400时,400=80x,∴x=5.∴5﹣4(小时)∴乙车比甲车早小时到达B地.22.(8分)有两个可以自由转动的均匀转盘A、B,都被分成了3等份,并在每份内均标有数字,如图所示,规则如下:①分别转动转盘A、B.②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).(1)用列表法(或树状图)分别求出数字之积为3的倍数和为5的倍数的概率;(2)小亮和小芸想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小亮得2分;数字之积为5的倍数时,小芸得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏双方公平.【解答】解:(1)每次游戏可能出现的所有结果列表如下:表格中共有9种等可能的结果,则数字之积为3的倍数的有五种,其概率为;数字之积为5的倍数的有三种,其概率为.(2)这个游戏对双方不公平.∵小亮平均每次得分为(分),小芸平均每次得分为(分),∵,∴游戏对双方不公平.修改得分规定为:若数字之积为3的倍数时,小亮得3分;若数字之积为5的倍数时,小芸得5分即可.23.(8分)如图,⊙O的直径AB=4,∠ABC=30°,BC,D是线段BC的中点.(1)试判断点D与⊙O的位置关系,并说明理由;(2)过点D作DE⊥AC,垂足为点E,求证:直线DE是⊙O的切线.【解答】(1)解:点D在⊙O上;理由如下:设⊙O与BC交于点M,连接AM,∵AB是直径,∴∠AMB=90°,在直角△ABM中,BM=AB•cos∠ABC=42,∵BC,∴M是BC的中点,则M与D重合.∴点D在⊙O上;(2)证明:连接OD,∵D是BC的中点,O是AB的中点,∴DO是△ABC的中位线,∴OD∥AC,则∠EDO=∠CED又∵DE⊥AC,∴∠CED=90°,∠EDO=∠CED=90°∴DE是⊙O的切线.24.(10分)某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信.这五封信的重量分别是72g,90g,215g,340g,400g.根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:(1)重量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?(2)这五封信分别以怎样的方式寄出最合算?请说明理由.(3)通过解答上述问题,你有何启示?(请你用一、两句话说明)【解答】解:(1)重量为90g的信以“挂号信”方式寄出,则邮寄费为5×0.8+3+0.5=7.5(元);以“特快专递”方式寄出,邮寄费为5+3+1=9(元).(2)信的质量只要超过100克,挂号信最低收取9.5元,比9元大,选择特快.故大于100的用特快,小于等于100的用挂号.(3)学生言之有理即可.如:在生活中遇到花钱的问题要多计算一下,选最优方案.25.(12分)王师傅有两块板材边角料,其中一块是边长为60cm的正方形板子;另一块是上底为30cm,下底为120cm,高为60cm的直角梯形板子(如图①).王师傅想将这两块板子裁成两块全等的矩形板材.他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCFE围成的区域(如图②).由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点.(1)求FC的长;(2)利用图②求出矩形顶点B所对的顶点到BC边的距离x(cm)为多少时,矩形的面积y(cm2)最大?最大面积是多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长.【解答】解:(1)由题意,得△DEF∽△CGF,∴,又∵DE=AD﹣AE=60﹣30=30,DF=DC﹣FC=60﹣FC,CG=120﹣60=60,∴,∴FC=40(cm);(3分)(2)如图,设矩形顶点B所对顶点为P,则①当顶点P在AE上时,x=60,y的最大值为60×30=1800(cm2).(4分)②当顶点P在EF上时,过点P分别作PN⊥BG于点N,PM⊥AB于点M.根据题意,得△GFC∽△GPN.∴,∴NG x,∴BN=120x.∴y=x(120x)(x﹣40)2+2400.∴当x=40时,y的最大值为2400(cm2).(7分)③当顶点P在FC上时,y的最大值为60×40=2400(cm2).(8分)综合①②③,得x=40cm时,矩形的面积最大,最大面积为2400cm2;(9分)(3)根据题意,正方形的面积y(cm2)与边长x(cm)满足的函数表达式为:y=x(120x)x2+120x.当y=x2时,正方形的面积最大,∴x2x2+120x.解之,得x1=0(舍),x2=48(cm).∴面积最大的正方形的边长为48cm.(12分)第21页(共21页)。
2006年陕西省中考数学试卷(大纲卷)

2006年陕西省中考数学试卷(大纲卷)一、选择题(共10小题,每小题3分,满分30分)1.(3分)下列计算正确的是()A.﹣3+2=1B.|﹣2|=﹣2C.3×(﹣3)=﹣9D.20﹣1=1 2.(3分)如图,∠1、∠2、∠3的大小关系为()A.∠2>∠1>∠3B.∠1>∠3>∠2C.∠3>∠2>∠1D.∠1>∠2>∠3 3.(3分)2005年11月1日零时,全国总人口为130 628万人.60岁及以上的人口占总人口的11.03%,则全国60岁及以上的人口用科学记数法表示(保留三位有效数字)约为()A.1.44×108人B.1.45×108人C.14.4×107人D.1.44×104人4.(3分)一件标价为600元的上衣,按8折销售仍可获利20元,设这件上衣的成本价为x 元,根据题意,下面所列的方程正确的是()A.600×0.8﹣x=20B.600×8﹣x=20C.600×0.8=x﹣20D.600×8=x﹣205.(3分)如图所示,已知⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若AD=3,AC=2,则cos D的值为()A.B.C.D.6.(3分)下列图形中,是中心对称图形的是()A.B.C.D.7.(3分)若圆锥的侧面展开图是一个弧长为36π的扇形,则这个圆锥的底面半径是()A.36B.18C.9D.68.(3分)有一多边形草坪,在市政建设设计图纸上的面积为300cm2,其中一条边的长度为5cm.经测量,这条边的实际长度为15m,则这块草坪的实际面积是()A.100m2B.270m2C.2700m2D.90000m29.(3分)如图,抛物线的函数表达式是()A.y=x2﹣x+2B.y=x2+x+2C.y=﹣x2﹣x+2D.y=﹣x2+x+2 10.(3分)如图,矩形ABCG(AB<BC)与矩形CDEF全等,点B,C,D在同一条直线上,∠APE的顶点P在线段BD上移动,使∠APE为直角的点P的个数是()A.0B.1C.2D.3二、填空题(共6小题,每小题3分,满分18分)11.(3分)分解因式:3x2﹣3=.12.(3分)(1)用计算器估算:若2.6456<<2.6459,则a的整数值是.(2)用计算器比较大小:0(填“>”、“=”、“<”).>的解集为.13.(3分)不等式组:14.(3分)如图,小河对岸有一座塔AB.分别在点D、C处测得塔尖点A处的仰角为∠1=28°、∠2=41°,且CD=25米.则塔的高度AB约为米(精确到0.1米).(可用计算器求,也可用下列参考数据求:sin28°≈0.4659,sin41°≈0.6561cos28°≈0.8829,cos41°≈0.7547tan28°≈0.5317,tan41°≈0.8693).15.(3分)观察下列等式:(1+2)2﹣4×1=12+4(2+2)2﹣4×2=22+4(3+2)2﹣4×3=32+4…则第n个等式可以表示为.16.(3分)将一个无盖正方体纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②).则所剪得的直角三角形较短的与较长的直角边的比是.三、解答题(共9小题,满分72分)17.(5分)解分式方程:.18.(6分)如图,在直角坐标系中:(1)描出下列各点,并将这些点用线段依次连接起来:(﹣2,4),(﹣3,8),(﹣8,4),(﹣3,1),(2,4);(2)作出(1)中的图形关于y轴的对称图形.19.(7分)如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.(1)图中共有几对全等三角形,请把它们都写出来;(2)求证:∠MAE=∠NCF.20.(8分)2003~2005年陕西省财政收入情况如图所示.根据图中的信息,解答下列问题:(1)陕西省这三年平均年财政收入为多少亿元?(2)陕西省2004~2005年财政收入的年增长率约为多少?(精确到1%)(3)如果陕西省2005~2006年财政收入的年增长率与(2)中求得的年增长率基本相同,请估计陕西省2006年财政收入约为多少亿元?(精确到1亿元)21.(8分)如图,在Rt△ABC中,∠BAC=90°,E,F分别是BC,AC的中点,延长BA 到点D,使AD AB.连接DE,DF.(1)求证:AF与DE互相平分;(2)若BC=4,求DF的长.22.(8分)甲、乙两车从A地出发,沿同一条高速公路行驶至距A地400千米的B地.l1,l2分别表示甲、乙两车行驶路程y(千米)与时间x(时)之间的关系(如图所示).根据图象提供的信息,解答下列问题:(1)求l2的函数表达式(不要求写出x的取值范围);(2)甲、乙两车哪一辆先到达B地该车比另一辆车早多长时间到达B地?23.(8分)如图,⊙O的直径AB=4,∠ABC=30°,BC,D是线段BC的中点.(1)试判断点D与⊙O的位置关系,并说明理由;(2)过点D作DE⊥AC,垂足为点E,求证:直线DE是⊙O的切线.24.(10分)某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信.这五封信的重量分别是72g,90g,215g,340g,400g.根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:(1)重量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?(2)这五封信分别以怎样的方式寄出最合算?请说明理由.(3)通过解答上述问题,你有何启示?(请你用一、两句话说明)25.(12分)王师傅有两块板材边角料,其中一块是边长为60cm的正方形板子;另一块是上底为30cm,下底为120cm,高为60cm的直角梯形板子(如图①).王师傅想将这两块板子裁成两块全等的矩形板材.他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCFE围成的区域(如图②).由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点.(1)求FC的长;(2)利用图②求出矩形顶点B所对的顶点到BC边的距离x(cm)为多少时,矩形的面积y(cm2)最大?最大面积是多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长.2006年陕西省中考数学试卷(大纲卷)参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.(3分)下列计算正确的是()A.﹣3+2=1B.|﹣2|=﹣2C.3×(﹣3)=﹣9D.20﹣1=1【解答】解:A中:﹣3+2=﹣1.B中:|﹣2|=2.C中:3×(﹣3)=﹣9.D中:20﹣1=0.故选:C.2.(3分)如图,∠1、∠2、∠3的大小关系为()A.∠2>∠1>∠3B.∠1>∠3>∠2C.∠3>∠2>∠1D.∠1>∠2>∠3【解答】解:∵∠2是△ABF的外角,∴∠2>∠3;∵∠1是△AEF的外角,∴∠1>∠4;又∵∠4=∠2∴∠1>∠2.∠1、∠2、∠3的大小关系为:∠1>∠2>∠3.故选:D.3.(3分)2005年11月1日零时,全国总人口为130 628万人.60岁及以上的人口占总人口的11.03%,则全国60岁及以上的人口用科学记数法表示(保留三位有效数字)约为()A.1.44×108人B.1.45×108人C.14.4×107人D.1.44×104人【解答】解:130 628万×11.03%=144 082 684≈144 000 000=1.44×108人.故选A.4.(3分)一件标价为600元的上衣,按8折销售仍可获利20元,设这件上衣的成本价为x 元,根据题意,下面所列的方程正确的是()A.600×0.8﹣x=20B.600×8﹣x=20C.600×0.8=x﹣20D.600×8=x﹣20【解答】解:设上衣的成本价为x元,由已知得上衣的实际售价为600×0.8元,然后根据利润=售价﹣成本价,可列方程:600×0.8﹣x=20故选:A.5.(3分)如图所示,已知⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若AD=3,AC=2,则cos D的值为()A.B.C.D.【解答】解:∵AD是⊙O的直径,∴∠ACD=90°.∵AD=3,AC=2,∴CD.∴cos D.故选:B.6.(3分)下列图形中,是中心对称图形的是()A.B.C.D.【解答】解:A、不是中心对称图形,故本选项不符合题意;B、不是中心对称图形,故本选项不符合题意;C、是中心对称图形,故本选项符合题意;D、不是中心对称图形,故本选项不符合题意;故选:C.7.(3分)若圆锥的侧面展开图是一个弧长为36π的扇形,则这个圆锥的底面半径是()A.36B.18C.9D.6【解答】解:设底面半径是r.∵弧长为圆锥的周长,∴36π=2πr,∴r=18,圆锥的底面半径是18.故选:B.8.(3分)有一多边形草坪,在市政建设设计图纸上的面积为300cm2,其中一条边的长度为5cm.经测量,这条边的实际长度为15m,则这块草坪的实际面积是()A.100m2B.270m2C.2700m2D.90000m2【解答】解:设草坪的实际面积是x平方米,则有,解得x=2700m2.故选:C.9.(3分)如图,抛物线的函数表达式是()A.y=x2﹣x+2B.y=x2+x+2C.y=﹣x2﹣x+2D.y=﹣x2+x+2【解答】解:根据题意,设二次函数的表达式为y=ax2+bx+c,抛物线过(﹣1,0),(0,2),(2,0),所以,解得a=﹣1,b=1,c=2,这个二次函数的表达式为y=﹣x2+x+2.故选:D.10.(3分)如图,矩形ABCG(AB<BC)与矩形CDEF全等,点B,C,D在同一条直线上,∠APE的顶点P在线段BD上移动,使∠APE为直角的点P的个数是()A.0B.1C.2D.3【解答】解:设两个矩形的长是a,宽是b.连接AE,如图在△AEQ中,根据勾股定理可得:AE;过AE的中点M作MN⊥BD于点N.则MN是梯形ABDE的中位线,则MN(a+b);以AE为直径的圆,半径是,(a+b)a b,而只有a=b是等号才成立,因而(a+b)<,即圆与直线BD相交,则直角顶点P的位置有两个.故选:C.二、填空题(共6小题,每小题3分,满分18分)11.(3分)分解因式:3x2﹣3=3(x+1)(x﹣1).【解答】解:3x2﹣3,=3(x2﹣1),=3(x+1)(x﹣1).12.(3分)(1)用计算器估算:若2.6456<<2.6459,则a的整数值是7.(2)用计算器比较大小:>0(填“>”、“=”、“<”).【解答】解:(1)∵2.6456,2.6459.所以a的整数值是7.(2) 2.571﹣2.449≈0.12>0.故填空答案:(1)7;(2)>.>的解集为﹣2<x≤1.13.(3分)不等式组:【解答】解:由(2)x≤1,又x>﹣2,所以解集为:﹣2<x≤1.14.(3分)如图,小河对岸有一座塔AB.分别在点D、C处测得塔尖点A处的仰角为∠1=28°、∠2=41°,且CD=25米.则塔的高度AB约为34.2米(精确到0.1米).(可用计算器求,也可用下列参考数据求:sin28°≈0.4659,sin41°≈0.6561cos28°≈0.8829,cos41°≈0.7547tan28°≈0.5317,tan41°≈0.8693).【解答】解:在△ABC中,有BC=AB÷tan∠2.在ABD中,有BD=AB÷tan∠1.∵CD=BD﹣BC=25.∴AB≈34.2米.15.(3分)观察下列等式:(1+2)2﹣4×1=12+4(2+2)2﹣4×2=22+4(3+2)2﹣4×3=32+4…则第n个等式可以表示为(n+2)2﹣4n=n2+4.【解答】解:(n+2)2﹣4n=n2+4.16.(3分)将一个无盖正方体纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②).则所剪得的直角三角形较短的与较长的直角边的比是1:2.【解答】解:由图可得,所剪得的直角三角形较短的边是原正方体棱长的一半,而较长的直角边正好是原正方体的棱长,所以所剪得的直角三角形较短的与较长的直角边的比是1:2.三、解答题(共9小题,满分72分)17.(5分)解分式方程:.【解答】解:方程两边都乘(x+2)(x﹣2),得2x(x﹣2)﹣3(x+2)=2(x2﹣4),解得x.检验:当x时,(x+2)(x﹣2)≠0.∴x是原方程的解.18.(6分)如图,在直角坐标系中:(1)描出下列各点,并将这些点用线段依次连接起来:(﹣2,4),(﹣3,8),(﹣8,4),(﹣3,1),(2,4);(2)作出(1)中的图形关于y轴的对称图形.【解答】解:19.(7分)如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.(1)图中共有几对全等三角形,请把它们都写出来;(2)求证:∠MAE=∠NCF.【解答】(1)解:有4对全等三角形.分别为△AMO≌△CNO,△OCF≌△OAE,△AME≌△CNF,△ABC≌△CDA;(2)证明:∵OA=OC,∠1=∠2,OE=OF,∴△OCF≌△OAE.∴∠EAO=∠FCO.在平行四边形ABCD中,AB∥CD,∴∠BAO=∠DCO.∴∠EAM=∠NCF.20.(8分)2003~2005年陕西省财政收入情况如图所示.根据图中的信息,解答下列问题:(1)陕西省这三年平均年财政收入为多少亿元?(2)陕西省2004~2005年财政收入的年增长率约为多少?(精确到1%)(3)如果陕西省2005~2006年财政收入的年增长率与(2)中求得的年增长率基本相同,请估计陕西省2006年财政收入约为多少亿元?(精确到1亿元)【解答】解:(1)∵(326+415+528)=423(亿元),∴陕西省这三年平均年财政收入为423亿元;(2)∵100%≈27%,∴陕西省2004~2005年财政收入的年增长率约为27%;(3)∵528(1+27%)=670.56≈671(亿元),∴2006年财政收入约为671亿元.21.(8分)如图,在Rt△ABC中,∠BAC=90°,E,F分别是BC,AC的中点,延长BA 到点D,使AD AB.连接DE,DF.(1)求证:AF与DE互相平分;(2)若BC=4,求DF的长.【解答】(1)证明:连接EF,AE.∵点E,F分别为BC,AC的中点,∴EF∥AB,EF AB.又∵AD AB,∴EF=AD.又∵EF∥AD,∴四边形AEFD是平行四边形.∴AF与DE互相平分.(2)解:在Rt△ABC中,∵E为BC的中点,BC=4,∴AE BC=2.又∵四边形AEFD是平行四边形,∴DF=AE=2.22.(8分)甲、乙两车从A地出发,沿同一条高速公路行驶至距A地400千米的B地.l1,l2分别表示甲、乙两车行驶路程y(千米)与时间x(时)之间的关系(如图所示).根据图象提供的信息,解答下列问题:(1)求l2的函数表达式(不要求写出x的取值范围);(2)甲、乙两车哪一辆先到达B地该车比另一辆车早多长时间到达B地?【解答】解:(1)设L2的函数表达式是y=k2x+b,则,解之得k2=100,b=﹣75,∴L2的函数表达式为y=100x﹣75.(2)由图可知,乙先到达B地.∵300=100x﹣75,∴x=3.75.设l1的函数表达式是y=k1x.∵该函数过点(3.75,300),∴k1=80,即y=80x.当y=400时,400=80x,∴x=5.∴5﹣4(小时)∴乙车比甲车早小时到达B地.23.(8分)如图,⊙O的直径AB=4,∠ABC=30°,BC,D是线段BC的中点.(1)试判断点D与⊙O的位置关系,并说明理由;(2)过点D作DE⊥AC,垂足为点E,求证:直线DE是⊙O的切线.【解答】(1)解:点D在⊙O上;理由如下:设⊙O与BC交于点M,连接AM,∵AB是直径,∴∠AMB=90°,在直角△ABM中,BM=AB•cos∠ABC=42,∵BC,∴M是BC的中点,则M与D重合.∴点D在⊙O上;(2)证明:连接OD,∵D是BC的中点,O是AB的中点,∴DO是△ABC的中位线,∴OD∥AC,则∠EDO=∠CED又∵DE⊥AC,∴∠CED=90°,∠EDO=∠CED=90°∴DE是⊙O的切线.24.(10分)某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信.这五封信的重量分别是72g,90g,215g,340g,400g.根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:(1)重量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?(2)这五封信分别以怎样的方式寄出最合算?请说明理由.(3)通过解答上述问题,你有何启示?(请你用一、两句话说明)【解答】解:(1)重量为90g的信以“挂号信”方式寄出,则邮寄费为5×0.8+3+0.5=7.5(元);以“特快专递”方式寄出,邮寄费为5+3+1=9(元).(2)信的质量只要超过100克,挂号信最低收取9.5元,比9元大,选择特快.故大于100的用特快,小于等于100的用挂号.(3)学生言之有理即可.如:在生活中遇到花钱的问题要多计算一下,选最优方案.25.(12分)王师傅有两块板材边角料,其中一块是边长为60cm的正方形板子;另一块是上底为30cm,下底为120cm,高为60cm的直角梯形板子(如图①).王师傅想将这两块板子裁成两块全等的矩形板材.他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCFE围成的区域(如图②).由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点.(1)求FC的长;(2)利用图②求出矩形顶点B所对的顶点到BC边的距离x(cm)为多少时,矩形的面积y(cm2)最大?最大面积是多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长.【解答】解:(1)由题意,得△DEF∽△CGF,∴,又∵DE=AD﹣AE=60﹣30=30,DF=DC﹣FC=60﹣FC,CG=120﹣60=60,∴,∴FC=40(cm);(3分)(2)如图,设矩形顶点B所对顶点为P,则①当顶点P在AE上时,x=60,y的最大值为60×30=1800(cm2).(4分)②当顶点P在EF上时,过点P分别作PN⊥BG于点N,PM⊥AB于点M.根据题意,得△GFC∽△GPN.∴,∴NG x,∴BN=120x.∴y=x(120x)(x﹣40)2+2400.∴当x=40时,y的最大值为2400(cm2).(7分)③当顶点P在FC上时,y的最大值为60×40=2400(cm2).(8分)综合①②③,得x=40cm时,矩形的面积最大,最大面积为2400cm2;(9分)(3)根据题意,正方形的面积y(cm2)与边长x(cm)满足的函数表达式为:y=x(120x)x2+120x.当y=x2时,正方形的面积最大,∴x2x2+120x.解之,得x1=0(舍),x2=48(cm).∴面积最大的正方形的边长为48cm.(12分)第21页(共21页)。
2006-2015陕西中考数学真题分类整理

1、 主考初一引入的负数知识,同时里边又用倒数、相反数、绝对值、零次方、相反数的意义去考察。
(必考题)(06)1.下列计算正确的是 ( )A .123=+-B .22-=-C .9)3(3-=-⨯D .1120=- (07)1.2-的相反数为 ( ) A .2B .2-C .12D .12-(08)1、零上13℃记作+13℃,零下2℃可记作 ( ) A .2 B .-2 C . 2℃ D .-2℃ (09)1.12-的倒数是( ) A.2 B .2- C .12 D .12-(10) 1. 13-= ( ) A. 3 B-3 C 13 D-13(11)1、的倒数为( )A 、B 、C 、D 、(12)1.如果零上5 ℃记做+5 ℃,那么零下7 ℃可记作( )A .-7 ℃B .+7 ℃C .+12 ℃D .-12 ℃(13)1.下列四个数中最小的数是( )A .-2 B.0 C.31-(14)11.计算(- 13)-2 = .(15)1.计算(- 23)0=( )A . 1 B . - 23 C . 0 D . 232、考察组合体的三视图,或展开图中的邻居和对门的试题(必考题) (06)2.如图,几何体的左视图是 【 】(07)2.下面四个图形中,经过折叠能围成如图只有三个面上印有图案的正方体纸盒的是( )A .B .D .(第2题图)120° (第7题图) (08)2、如图,这个几何体的主视图是 ( )(09) 7.若用半径为9,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是( ).A .1.5 B .2 C .3 D .6(10) 4. 如图是由正方体和圆锥组成的几何体,他的俯视图是 ( )A .B .C .D .(11)2、下面四个几何体中,同一个几何体的主视图和俯视图相同的共有( )A 、1个B 、2个C 、3个D 、4个(12)2.如图,是由三个相同的小正方体组成的几何体,该几何体的左视图是( )(13)2.如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是( )(14)2.下图是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是( )(15)2.如图是一个螺母的示意图,它的俯视图是( )A .B .C .D .3、不等式、不等式组和不等式组解集的表示(2011版的数学课程标准下,不在考察不等式组的应用) (06) 11.不等式)1(32+≤-x x 的解集为25-≥x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第Ⅰ卷(选择题 共30分)A 卷一、选择题(共10小题,每小题3分,计30分,每小题只有一个选项是符合题意的) 1.下列计算正确的是 【 C 】A .123=+-B .22-=-C .9)3(3-=-⨯D .1120=- 2.如图,几何体的左视图是 【 B 】3.一件标价为600元的上衣,按8折销售仍可获利20元,设这件上衣的成本价为x 元,根据题意,下面所列的方程正确的是 【 A 】 A .208.0600=-⨯x B .208600=-⨯x C .208.0600-=⨯x D .208600-=⨯x4.如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,连接CD ,若⊙O 的半径23=r ,2=AC ,则B cos 的值是 【 B 】A .23 B .35 C .25 D .32 第4题图5.如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在折7天中,日温差最大的一天市A .5月1日B .5月2日C .5月3日D .5月5日6.若圆锥的侧面展开图市一个弧长为π36的扇形,则这个圆锥的底面半径是 【 B 】 A .36 B .18 C .9 D.6 7.直线323+-=x y 与x 轴、y 轴所围成的三角形的面积为【 A 】A .3B .6C .43 D .23 8.如图,抛物线的函数表达式是 【 D 】 A .22+-=x x y B .22+--=x x y C .22++=x x y D .22++-=x x y 9.有一块多边形草坪,在市政建设射击图纸上的面积为3002cm ,其中一条边的长度为5cm ,经测量,这条边的实际长度为15m ,则这块草坪的实际面积是 【 C 】A .1002m B .2702m C .27002m D .900002m 10.如图,矩形ABCG (BC AB )与矩形CDEF 全等,点B 、C 、D 在同一条直线上,APE ∠的顶点P 在线段BD 上移动,使APE ∠为直角的点P 的个数是 【 C 】 A .0 B .1 C .2 D .3第Ⅱ卷(非选择题 共90分)二、填空题(共6小题,每小题3分,共18分) 11.不等式)1(32+≤-x x 的解集为25-≥x 。
12.选做题...(要求在(1)、(2)中任选一题作答)。
(1)2005年11月1日零时,全国总人口为130628万人,60岁及以上的人口占总人口的11.03%,则全国60岁及以上的人口用科学记数法表示约为 41044.1⨯ 万人(用计算器计算,保留3个有效数字)。
(2)用计算器比较大小:173-(填””、“”、““ =)13.在同一时刻,小明测得一棵树的影长为1.6米的小华影长的4.5倍,则这棵树的高度 为 7.2米。
14.观察下面图形,按规律在两个..箭头所指的“田”字格内分别画上适当图形(只对一个2分)第10题图P15.双曲线xy 8=与直线x y 2=的交点坐标为(2,4),(2-,4- ) 。
16.将一个无盖正方形纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②),则所剪得得直角三角形较短得与较长得直角边的比是 1∶2 。
三、解答题(共9小题,计72分。
解答应写出过程) 17.(本题满分5分) 解分式方程:22322=--+x x x 解:)4(2)2(3)2(22-=+--x x x x ……………………………………………(1分) 82634222-=---x x x x 27-=-x 72=x ………………………………………………………………(4分) 经检验:72=x 是原方程的解 ∴原方程的解为72=x …………………………………………………………(5分)18.(本题满分6分)观察下面网格中的图形,解答下列问题: (1)将网格中左图沿水平方向向右.........平移,使点A 移至点A '处,作出平移后的图形: (2)(1)中作出的图形与右边原有的图形,组成一个新的图形,这个新图形...是中心对称图形,还是轴对称图形?解:(1)如图所示。
(作图正确3分)(2)新图形是轴对称图形。
…………………………………………(6分) 19.(本题满分7分)2003~2005年陕西省财政收入情况如图所示,根据图中的信息,解答下列问题: (1)陕西省这三年财政收入共为多少亿元?(2)陕西省2004~2005年财政收入的年增长率约为多少?(精确到1%)(3)如果陕西省2005~2006年财政收入的年增长率与(2)中求得的年增长率基本相同。
请估计陕西省2006年财政收入约为多少亿元?(精确到1亿元) 解:(1)∵1269528415326=++(亿元)∴陕西省这三年的财政收入共为 1269亿元(2分) (2)∵%27%100415415528≈⨯-∴陕西省2004~2005年财政收入的 年增长率为27%(4分)(3)∵67156.670%)271(528≈=+(亿 元)∴2006年财政收入约为671亿元(7 分)20.(本题满分8分) 如图。
O 为的对角线AC 的中点,过点O 左一条直线分别与AB 、CD 交于点M 、N ,E 、F 在直线MN 上,且OF OE =解:(1)有四对全等三角形……………………(1分) 分别为△AMO ≌△CNO ,△OCF ≌△OAE△AME ≌△CNF ,△ABC ≌△CDA …………(5分) (2)证明:∵OF OE OC AO =∠=∠=,21,, ∴△AME ≌△CNF ,∴FCO EAO ∠=∠。
…………(7分) 在中,AB ∥CD ∴DCO BAO ∠=∠,∴NCF EAM ∠=∠………………(8分)21.(本题满分8分)甲、乙两车从A 地出发,沿同一条高速公路行驶至距A 地400千米的B 地,21l l 、分别表示甲、乙两车行驶路程y (千米)与时间x (时)之间的关系(如图所示)。
根据图像提供的信息,解答下列问题:(1)求2l 的函数表达式(不要求写出x 的取值范围)(2)甲、乙两车哪一辆先到达B 地?该车比另一辆车早多长时间到达B 地?解:(1)设2l 的函数表达式是b x k y +=2,则⎪⎪⎩⎪⎪⎨⎧+=+=bk b k 22419400430………………(2分)解之,得75,1002-=b k ………(4分) (2)乙车先到达B 地……………(5分) ∵75100300-=x ,∴415=x ……………………(6分) 设1l 的函数表达式是x k y 1=, ∵图像过点(415,300), ∴801=k ,即x y 80=。
当400=y 时,x 80400=,∴5=x∴414195=-(小时)∴乙车比甲车早41小时到达B 地………………(8分)22.(本题满分8分)有两个可以自由转动的均匀转盘A 、B ,都被分成了3等份,并在每份内均标有数字,如图所示,规则如下:①分别转动转盘A 、B ②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停在等分线上,那么重转一次,直到指针指向某一份为止)。
(1)用列表法(或树状图)分别求出数字之积为3的倍数和为5的倍数的概率;(2)小亮和小芸想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小亮得2分;数字之积为5的倍数时,小芸得3分。
这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏双方公平。
表格中共有9种等可能的结果,则数字之积为3的倍数的有五种,其概率为95;…………………………(2分) 数字之积为5的倍数的有三种,其概率为93。
…………………………(4分)(2)这个游戏对双方不公平.…………………………………………………(5分)∵小亮平均每次得分为910952=⨯(分), 小芸平均每次得分为99933=⨯(分) ∵1910≠,∴游戏对双方不公平。
……………………………………(6分) 修改得分规定为:若数字之积为3的倍数时,小亮得3分;若数字之积为5的倍数时,小芸得5分即可………………………………………………………………(8分) 23.(本题满分8分) 如图,⊙O 的直径34,30,4=︒=∠=BC ABC AB ,D 时线段BC 的中点,(1)试判断点D 与⊙O 的位置关系,并说明理由;(2)过点D 作AC DE ⊥,垂足为点E ,求证直线DE 是⊙O 的切线。
解:(1)点D 在⊙O 上,………………………………(1分) 连接OD ,过点O 作BC OF ⊥于点F 。
……(2分) 在Rt △BOF 中,︒=∠==30,221B AB OB , ∴330cos 2=︒∙=BF 。
∵3221==BC BD ,∴3=DF 。
在Rt △ODF 中,∵OB OD ==+=213,∴点D 在⊙O 上……………………………………(5分) (2)∵D 是BC 的中点,O 是AB 的中点,∴OD ∥AC又∵AC DE ⊥,∴︒=∠90EDO ,又∵OD 是⊙O 的半径, ∴DE 是⊙O 的切线。
………………(8分)24.(本题满分10分)某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信。
这五封信的重量分别是72g 、90g 、215g 、340g 、400g 。
根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:第23题图(寄出呢?(2)这五封信分别以怎样得方式寄出最合算?请说明理由。
(3)通过解答上述问题,你有何启示?(请你用一、两句话说明) 解:(1)重量为90g 的信以“挂号信”方式寄出,则邮寄费为5.75.038.05=++⨯(元);以“特快专递”方式寄出,邮寄费为 9135=++(元)…………(2分) (2)∵这五封信的重量均小于1000g ,∴若以“特快专递”方式寄出,邮寄费为 9135=++(元) 由(1)得知,重量为90g 的信以“挂号信”方式寄出,费用为7.5元小于9元; ∵g g 9072 ,∴重量为72g 的信以“挂号信”方式寄出 小于9元;………………(4分)若重量为215g 的信以“挂号信”方式寄出,则邮寄费为9(5.115.03228.05 元)=++⨯+⨯(元)………………………………………………………………(6分)g g g 215340400 ,∴重量为400g ,340g 的信以“挂号信”方式寄出,费用均超过9元。
因此,将这五封信的前两封以“挂号信”方式寄出,后三封以“特快专递”方式寄出最合算。
…………………………………………………………(8分) (3)学生言之有理即可……………………………………………(10分) 25.(本题满分12分)王师傅有两块板材边角料,其中一块是边长为60cm 的正方形板子;另一块是上底为30cm ,下底为120cm ,高为60cm 的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材。
