七年级数学上册整式计算题专项练习(含答案)
七年级数学上册整式计算题专项练习(有答案)

整式的乘除计算训练(1)1. )2()(b a b a -++-2. (x+2)(y+3)-(x+1)(y-2)3. 22)2)(2(y y x y x ++-4.x(x -2)-(x+5)(x -5)5. ⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛--y x y x224 6.)94)(32)(23(22x y x y y x +---7. ()()3`122122++-+a a 8.()()()2112+--+x x x9. (x -3y)(x+3y)-(x -3y)2 10. 23(1)(1)(21)x x x +---11. 22)23()23(y x y x --+ 12.22)()(y x y x -+13. 0.125100×810014. 3022)2(21)x (4554---÷⎪⎭⎫⎝⎛--π-+⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛15. (1211200622332141)()()()-⨯+----16—19题用乘法公式计算16.999×1001 17.1992-18.298 19.2010200820092⨯-20.化简求值:)4)(12()12(2+-+-a a a ,其中2-=a 。
21. 化简求值2(2)2()()2(3)x y x y x y y x y +--++-,其中12,2x y =-=。
22. 5(x-1)(x+3)-2(x-5)(x-2) 23. (a-b)(a2+ab+b2)24. (3y+2)(y-4)-3(y-2)(y-3) 25. a(b-c)+b(c-a)+c(a-b)1y2)2 26. (-2mn2)2-4mn3(mn+1) 27. 3xy(-2x)3·(-428. (-x-2)(x+2) 29. 5×108·(3×102) 30. (x-3y)(x+3y)-(x-3y)231. (a+b-c)(a-b-c)答案1. 2. 3. 4.5. 6. 7. 8.9. 10. 11. 12.13. 14. 15.16. 原式=(1000-1)(1000+1) 17. 原式=(99+1)(99-1)=1000000-1 =10098=999999 =980018. 原式=(900-2)2 19. 原式=20092-(2009+1)(2009-1)=10000-400+4 =20092-20092+1=9604 =120.原式=,当时,原式=21.原式=,当,时,原式=22. 23. 24. 25. 0 26. 27. 28. 29.30. 31.北师大七年级数学上册《整式及其加减》计算题专项练习一一.解答题(共12小题)1.计算题①12﹣(﹣8)+(﹣7)﹣15;②﹣12+2×(﹣5)﹣(﹣3)3÷;③(2x﹣3y)+(5x+4y);④(5a2+2a﹣1)﹣4(3﹣8a+2a2).2.(1)计算:4+(﹣2)2×2﹣(﹣36)÷4;(2)化简:3(3a﹣2b)﹣2(a﹣3b).3.计算:(1)7x+4(x2﹣2)﹣2(2x2﹣x+3);(2)4ab﹣3b2﹣[(a2+b2)﹣(a2﹣b2)];(3)(3mn﹣5m2)﹣(3m2﹣5mn);(4)2a+2(a+1)﹣3(a﹣1).4.化简(1)2(2a2+9b)+3(﹣5a2﹣4b)(2)3(x3+2x2﹣1)﹣(3x3+4x2﹣2)5.(2009•柳州)先化简,再求值:3(x﹣1)﹣(x﹣5),其中x=2.6.已知x=5,y=3,求代数式3(x+y)+4(x+y)﹣6(x+y)的值.7.已知A=x2﹣3y2,B=x2﹣y2,求解2A﹣B.8.若已知M=x2+3x﹣5,N=3x2+5,并且6M=2N﹣4,求x.9.已知A=5a2﹣2ab,B=﹣4a2+4ab,求:(1)A+B;(2)2A﹣B;(3)先化简,再求值:3(A+B)﹣2(2A﹣B),其中A=﹣2,B=1.10.设a=14x﹣6,b=﹣7x+3,c=21x﹣1.(1)求a﹣(b﹣c)的值;(2)当x=时,求a﹣(b﹣c)的值.11.化简求值:已知a、b满足:|a﹣2|+(b+1)2=0,求代数式2(2a﹣3b)﹣(a﹣4b)+2(﹣3a+2b)的值.12.已知(x+1)2+|y﹣1|=0,求2(xy﹣5xy2)﹣(3xy2﹣xy)的值.北师大七年级数学上册《整式及其加减》计算题专项练习一参考答案与试题解析一.解答题(共12小题)1.计算题①12﹣(﹣8)+(﹣7)﹣15;②﹣12+2×(﹣5)﹣(﹣3)3÷;③(2x﹣3y)+(5x+4y);④(5a2+2a﹣1)﹣4(3﹣8a+2a2).考点:整式的加减;有理数的混合运算.专题:计算题.分析:(1)直接进行有理数的加减即可得出答案.(2)先进行幂的运算,然后根据先乘除后加减的法则进行计算.(3)先去括号,然后合并同类项即可得出结果.(4)先去括号,然后合并同类项即可得出结果.解答:解:①原式=12+8﹣7﹣15=﹣2;②原式=﹣1﹣10+27÷=﹣11+81=70;③原式=2x﹣3y+5x+4y=7x+y;④原式=5a2+2a﹣1﹣12+32a﹣8a2=﹣3a2+34a﹣13.点评:本题考查了整式的加减及有理数的混合运算,属于基础题,解答本题的关键熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.2.(1)计算:4+(﹣2)2×2﹣(﹣36)÷4;(2)化简:3(3a﹣2b)﹣2(a﹣3b).考点:整式的加减;有理数的混合运算.分析:(1)按照有理数混合运算的顺序,先乘方后乘除最后算加减;(2)运用整式的加减运算顺序计算:先去括号,再合并同类项.解答:解:(1)原式=4+4×2﹣(﹣9)=4+8+9=17;(2)原式=9a﹣6b﹣2a+6b=(9﹣2)a+(﹣6+6)b=7a.点评:在混合运算中要特别注意运算顺序:先三级,后二级,再一级;熟记去括号法则:﹣﹣得+,﹣+得﹣,++得+,+﹣得﹣;及熟练运用合并同类项的法则:字母和字母的指数不变,只把系数相加减.3.计算:(1)7x+4(x2﹣2)﹣2(2x2﹣x+3);(2)4ab﹣3b2﹣[(a2+b2)﹣(a2﹣b2)];(3)(3mn﹣5m2)﹣(3m2﹣5mn);(4)2a+2(a+1)﹣3(a﹣1).考点:整式的加减.分析:(1)先去括号,再合并同类项即可;(2)先去括号,再合并同类项即可;(3)先去括号,再合并同类项即可;(4)先去括号,再合并同类项即可.解答:解:(1)7x+4(x2﹣2)﹣2(2x2﹣x+3)=7x+4x2﹣8﹣4x2+2x﹣6=9x﹣14;(2)4ab﹣3b2﹣[(a2+b2)﹣(a2﹣b2)]=4ab﹣3b2﹣[a2+b2﹣a2+b2]=4ab﹣3b2﹣2b2=4ab﹣5b2;(3)(3mn﹣5m2)﹣(3m2﹣5mn)=3mn﹣5m2﹣3m2+5mn=8mn﹣8m2;(4)2a+2(a+1)﹣3(a﹣1)=2a+2a+2﹣3a+3=a+5.点评:本题考查了整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.4.化简(1)2(2a2+9b)+3(﹣5a2﹣4b)(2)3(x3+2x2﹣1)﹣(3x3+4x2﹣2)考点:整式的加减.专题:计算题.分析:(1)原式利用去括号法则去括号后,合并同类项即可得到结果;(2)原式利用去括号法则去括号后,合并同类项即可得到结果.解答:解:(1)原式=4a2+18b﹣15a2﹣12b=﹣11a2+6b;(2)原式=3x3+6x2﹣3﹣3x3﹣4x2+2=2x2﹣1.点评:此题考查了整式的加减,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握法则是解本题的关键.5.(2009•柳州)先化简,再求值:3(x﹣1)﹣(x﹣5),其中x=2.考点:整式的加减—化简求值.分析:本题应对方程去括号,合并同类项,将整式化为最简式,然后把x的值代入即可.解答:解:原式=3x﹣3﹣x+5=2x+2,当x=2时,原式=2×2+2=6.点评:本题考查了整式的化简.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.6.已知x=5,y=3,求代数式3(x+y)+4(x+y)﹣6(x+y)的值.考点:整式的加减—化简求值.分析:先把x+y当作一个整体来合并同类项,再代入求出即可.解答:解:∵x=5,y=3,∴3(x+y)+4(x+y)﹣6(x+y)=x+y=5+3=8.点评:本题考查了整式的加减的应用,主要考查学生的计算能力,用了整体思想.7.已知A=x2﹣3y2,B=x2﹣y2,求解2A﹣B.考点:整式的加减.分析:直接把A、B代入式子,进一步去括号,合并得出答案即可.解答:解:2A﹣B=2(x2﹣3y2)﹣(x2﹣y2)=2x2﹣6y2﹣x2+y2=x2﹣5y2.点评:此题考查整式的加减混合运算,掌握去括号法则和运算的方法是解决问题的关键.8.若已知M=x2+3x﹣5,N=3x2+5,并且6M=2N﹣4,求x.考点:整式的加减;解一元一次方程.专题:计算题.分析:把M与N代入计算即可求出x的值.解答:解:∵M=x2+3x﹣5,N=3x2+5,∴代入得:6x2+18x﹣30=6x2+10﹣4,解得:x=2.点评:此题考查了整式的加减,熟练掌握运算法则是解本题的关键.9.已知A=5a2﹣2ab,B=﹣4a2+4ab,求:(1)A+B;(2)2A﹣B;(3)先化简,再求值:3(A+B)﹣2(2A﹣B),其中A=﹣2,B=1.考点:整式的加减;整式的加减—化简求值.专题:计算题.分析:(1)把A与B代入A+B中计算即可得到结果;(2)把A与B代入2A﹣B中计算即可得到结果;(3)原式去括号合并得到最简结果,把A与B的值代入计算即可求出值.解答:解:(1)∵A=5a2﹣2ab,B=﹣4a2+4ab,∴A+B=5a2﹣2ab﹣4a2+4ab=a2+2ab;(2)∵A=5a2﹣2ab,B=﹣4a2+4ab,∴2A﹣B=10a2﹣4ab+4a2﹣4ab=14a2﹣8ab;(3)原式=3A+3B﹣4A+2B=﹣A+5B,把A=﹣2,B=1代入得:原式=2+5=7.点评:此题考查了整式的加减,熟练掌握运算法则是解本题的关键.10.设a=14x﹣6,b=﹣7x+3,c=21x﹣1.(1)求a﹣(b﹣c)的值;(2)当x=时,求a﹣(b﹣c)的值.考点:整式的加减;代数式求值.专题:计算题.分析:(1)把a,b,c代入a﹣(b﹣c)中计算即可得到结果;(2)把x的值代入(1)的结果计算即可得到结果.解答:解:(1)把a=14x﹣6,b=﹣7x+3,c=21x﹣1代入得:a﹣(b﹣c)=a﹣b+c=14x﹣6+7x﹣3+21x﹣1=42x ﹣10;(2)把x=代入得:原式=42×﹣10=10.5﹣10=0.5.点评:此题考查了整式的加减,以及代数式求值,熟练掌握运算法则是解本题的关键.11.化简求值:已知a、b满足:|a﹣2|+(b+1)2=0,求代数式2(2a﹣3b)﹣(a﹣4b)+2(﹣3a+2b)的值.考点:整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.专题:计算题.分析:原式去括号合并得到最简结果,利用非负数的性质求出a与b的值,代入计算即可求出值.解答:解:原式=4a﹣6b﹣a+4b﹣6a+4b=﹣3a+2b,∵|a﹣2|+(b+1)2=0,∴a=2,b=﹣1,则原式=﹣6﹣2=﹣8.点评:此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.12.已知(x+1)2+|y﹣1|=0,求2(xy﹣5xy2)﹣(3xy2﹣xy)的值.考点:整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.分析:因为平方与绝对值都是非负数,且(x+1)2+|y﹣1|=0,所以x+1=0,y﹣1=0,解得x,y的值.再运用整式的加减运算,去括号、合并同类项,然后代入求值即可.解答:解:2(xy﹣5xy2)﹣(3xy2﹣xy)=(2xy﹣10xy2)﹣(3xy2﹣xy)=2xy﹣10xy2﹣3xy2+xy=(2xy+xy)+(﹣3xy2﹣10xy2)=3xy﹣13xy2,∵(x+1)2+|y﹣1|=0∴(x+1)=0,y﹣1=0∴x=﹣1,y=1.∴当x=﹣1,y=1时,3xy﹣13xy2=3×(﹣1)×1﹣13×(﹣1)×12=﹣3+13=10.答:2(xy﹣5xy2)﹣(3xy2﹣xy)的值为10.点评:整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.代入求值时要化简.。
人教版七年级上册数学《整式》练习题(含答案)

2.1整 式一.判断题 (1)31+x 是关于x 的一次两项式. ( ) (2)-3不是单项式.( )(3)单项式xy 的系数是0.( )(4)x 3+y 3是6次多项式.( )(5)多项式是整式.( )二、选择题1.在下列代数式:21ab ,2b a +,ab 2+b+1,x 3+y2,x 3+ x 2-3中,多项式有( ) A .2个 B .3个 C .4个 D5个2.多项式-23m 2-n 2是( )A .二次二项式B .三次二项式C .四次二项式D 五次二项式3.下列说法正确的是( )A .3 x 2―2x+5的项是3x 2,2x ,5B .3x -3y 与2 x 2―2xy -5都是多项式 C .多项式-2x 2+4xy 的次数是3D .一个多项式的次数是6,则这个多项式中只有一项的次数是64.下列说法正确的是( )A .整式abc 没有系数B .2x +3y +4z 不是整式 C .-2不是整式 D .整式2x+1是一次二项式5.下列多项式中,是二次多项式的是( )A 、132+xB 、23xC 、3xy -1D 、253-x6.下列单项式次数为3的是( )×3×4 417.下列代数式中整式有( )x 1, 2x +y , 31a 2b , πy x -, xy 45, , a 个 个 个 个8.下列整式中,单项式是( )+1 -y D.21+x 9.下列各项式中,次数不是3的是( )A .xyz +1B .x 2+y +1C .x 2y -xy 2D .x 3-x 2+x -110.下列说法正确的是( )A .x(x +a)是单项式B .π12+x 不是整式C .0是单项式D .单项式-31x 2y 的系数是31 11.在多项式x 3-xy 2+25中,最高次项是( )A .x 3B .x 3,xy 2C .x 3,-xy 2D .2512.单项式-232xy 的系数与次数分别是( ) A .-3,3 B .-21,3 C .-23,2 D .-23,313.下列说法正确的是( )A .x 的指数是0B .x 的系数是0C .-10是一次单项式D .-10是单项式14.已知:32y x m -与n xy 5是同类项,则代数式n m 2-的值是( )A 、6-B 、5-C 、2-D 、5 15.系数为-21且只含有x 、y 的二次单项式,可以写出( ) A .1个B .2个C .3个D .4个 三.填空题1填一填 整式-ab πr 2 232ab - -a+b 2453-+y x A 3b 2-2a 2b 2+b 3-7ab+5 系数次数项2.单项式: 3234y x -的系数是 ,次数是 ; 3.220053xy 是 次单项式;4.y x 342-的一次项系数是 ,常数项是 ;5.单项式21xy 2z 是_____次单项式. 6.多项式a 2-21ab 2-b 2有_____项,其中-21ab 2的次数是 . 7.整式①21,②3x -y 2,③23x 2y ,④a ,⑤πx +21y ,⑥522a π,⑦x +1中 单项式有 ,多项式有8.x+2xy +y 是 次多项式.9.b 的311倍的相反数是 ; 10.设某数为x ,10减去某数的2倍的差是 ;11.42234263y y x y x x --+-的次数是 ;12.当x =2,y =-1时,代数式||||x xy -的值是 ;13.当y = 时,代数式3y -2与43+y 的值相等; 14.-23ab 的系数是 ,次数是 次.15.多项式x 3y 2-2xy 2-43xy -9是___次___项式,其中最高次项的系数是 ,二次项是 ,常数项是 .16.若2313m x y z -与2343x y z 是同类项,则m = . 17.在x 2, 21 (x +y),π1,-3中,单项式是 ,多项式是 ,整式是 .18.单项式7532c ab 的系数是____________,次数是____________.19.多项式x2y+xy-xy2-53中的三次项是____________.20.当a=____________时,整式x2+a-1是单项式.21.多项式xy-1是____________次____________项式.22.当x=-3时,多项式-x3+x2-1的值等于____________.23.一个n次多项式,它的任何一项的次数都____________.24.如果3x k y与-x2y是同类项,那么k=____ ____.四、合并下列多项式中的同类项(1)3x2+4x-2x2-x+x2-3x-1;(2)-a2b+2a2b(3)a3-a2b+ab2+a2b-2ab2+b3;(4)2a2b+3a2b-12a2b(5)(2x+3y)+(5x-4y);(6)(8a-7b)-(4a-5b)(7)(8x-3y)-(4x+3y-z)+2z;(8)(2x-3y)-3(4x-2y)(9)3a2+a2-2(2a2-2a)+(3a-a2)(10)3b-2c-[-4a+(c+3b)]+c五.先去括号,再合并同类项:(1)(2x+3y )+(5x -4y ); (2)(8a -7b )-(4a -5b )(3)(8x -3y )-(4x+3y -z )+2z (4)(2x -3y )-3(4x -2y )(5)3a 2+a 2-2(2a 2-2a )+(3a -a 2) (6)3b -2c -[-4a+(c+3b )]+c六、求代数式的值1.当x =-2时,求代数式132--x x 的值。
人教版数学七年级上册整式计算专项练习200题及答案详解

1当2已知,当3当4当5当当6若代数式7已知当8当9 C. D.如图所示的运算程序中,若开始输入的10B.C. D.按如图所示的程序计算:若开始输入的11 B.C.D.已知,则代数式的值是().12 B.C.D.已知,则式子的值为().13不能确定已知代数式的值是,则代数式的值是().14当时,代数式值为,那么当时,代数式的值是 ().1516化简17当18已知19已知代数式20化简21若22已知23如果24已知代数式25若代数式26整式化简求值:先化简,再求值:27已知整式化简求值:先化简,再求值:28已知三个有理数29已知30先化简,再求值31已知代数式32按照如图的运算顺序,输入33如图是一个数值转换机.若输入的34当35若36已知37已知多项式时,多项式的值是38已知.3940设41用整体思想解题:为了简化问题,我们往往把一个式子看成一个数42已知当43已知当44已知45先化简再求值:46设若代数式47若48已知49先化简再求值50若51已知52先化简,再求值:53先化简,在求值:5456当57化简求值:58化简:59请回答下列各题:60已知62已知63先化简,再求值:64先化简,再求值:65先化简,再求值:66回答下面问题;67先化简,再求值:68先化简,再求值:69化简再求值:70阅读框图并回答下列问题:.71先化简,再求值:72先化简,再求值.求73对于74先化简,再求值:75若76已知77已知78已知79奕铭在化简多项式80先化简,再求值81先化简,再求值:82先化简,再求值:83若84已知:85先化简再求值:86先化简,再求值:87已知88已知89已知90先化简,再求值:91已知92先化简,再求值:93若单项式94求多项式95设96已知97已知98求99若100若代数式1 23 4 5 67 8 9 10 11 1213 14 15 16 17 18 1920 21 22 23 24 25 26 2728 29 30 31 32 33 34 3536 37 38 39 40 41 4243 44 45 46 47 48 4950 51 52 53 54 55 5657 58 59 60 61 62 63 6465 66 67 68 69 70 7173 74 75 76 77 78 7981 82 83 84 85 8687 88 89 90 91 9293 94 9596 9798 99 100。
七年级上册 数学 第二章 整式的加减-专项练习100题含答案

整式的加减专项练习1、3(a+5b)-2(b-a)2、3a-(2b-a)+b3、2(2a2+9b)+3(-5a2-4b)4、(x3-2y3-3x2y)-(3x3-3y3-7x2y)5、3x2-[7x-(4x-3)-2x2]6、(2xy-y)-(-y+yx)7、5(a2b-3ab2)-2(a2b-7ab)8、(-2ab+3a)-2(2a-b)+2ab 9、(7m2n-5mn)-(4m2n-5mn)10、(5a2+2a-1)-4(3-8a+2a2).11、-3x2y+3xy2+2x2y-2xy2;12、2(a-1)-(2a-3)+3.13、-2(ab-3a2)-[2b2-(5ab+a2)+2ab]14、(x2-xy+y)-3(x2+xy-2y)15、3x2-[7x-(4x-3)-2x2]16、a2b-[2(a2b-2a2c)-(2bc+a2c)];17、-2y3+(3xy2-x2y)-2(xy2-y3).18、2(2x-3y)-(3x+2y+1)19、-(3a2-4ab)+[a2-2(2a+2ab)].20、5m-7n-8p+5n-9m-p ;21、(5x 2y-7xy 2)-(xy 2-3x 2y ); 22、3(-3a 2-2a )-[a 2-2(5a-4a 2+1)-3a].23、3a 2-9a+5-(-7a 2+10a-5); 24、-3a 2b-(2ab 2-a 2b )-(2a 2b+4ab 2).25、(5a-3a 2+1)-(4a 3-3a 2); 26、-2(ab-3a 2)-[2b 2-(5ab+a 2)+2ab]27、(8xy -x 2+y 2)+(-y 2+x 2-8xy ); 28、(2x 2-21+3x )-4(x -x 2+21);29、3x 2-[7x -(4x -3)-2x 2]. 30、5a+(4b-3a )-(-3a+b );31、(3a 2-3ab+2b 2)+(a 2+2ab-2b 2); 32、2a 2b+2ab 2-[2(a 2b-1)+2ab 2+2].33、(2a 2-1+2a )-3(a-1+a 2); 34、2(x 2-xy )-3(2x 2-3xy )-2[x 2-(2x 2-xy+y 2)].35、 -32ab +43a 2b +ab +(-43a 2b )-1 36、(8xy -x 2+y 2)+(-y 2+x 2-8xy );37、2x -(3x -2y +3)-(5y -2); 38、-(3a +2b )+(4a -3b +1)-(2a -b -3)39、4x 3-(-6x 3)+(-9x 3) 40、3-2xy +2yx 2+6xy -4x 2y41、 1-3(2ab +a )十[1-2(2a -3ab )].42、 3x -[5x +(3x -2)];43、(3a 2b -ab 2)-(ab 2+3a 2b ) 44、()[]{}y x x y x --+--3233245、(-x 2+5+4x 3)+(-x 3+5x -4) 46、(5a 2-2a+3)-(1-2a+a 2)+3(-1+3a-a 2).47、5(3a 2b-ab 2)-4(-ab 2+3a 2b ). 48、4a 2+2(3ab-2a 2)-(7ab-1).49、 21xy+(-41xy )-2xy 2-(-3y 2x ) 50、5a 2-[a 2-(5a 2-2a )-2(a 2-3a )]51、5m-7n-8p+5n-9m+8p 52、(5x 2y-7xy 2)-(xy 2-3x 2y )53、 3x2y-[2x2y-3(2xy-x2y)-xy] 54、5556、(a2+4ab-4b2)-3(a2+b2)-7(b2-ab).57、a2+2a3+(-2a3)+(-3a3)+3a2;58、5ab+(-4a2b2)+8ab2-(-3ab)+(-a2b)+4a2b2; 59、(7y-3z)-(8y-5z);60、-3(2x2-xy)+4(x2+xy-6).61、(x3+3x2y-5xy2+9y3)+(-2y3+2xy2+x2y-2x3)-(4x2y-x3-3xy2+7y3)62、-3x2y+2x2y+3xy2-2xy2; 63、3(a2-2ab)-2(-3ab+b2);64、5abc-{2a2b-[3abc-(4a2b-ab2]}.65、5m2-[m2+(5m2-2m)-2(m2-3m)].66、-[2m-3(m-n+1)-2]-1.67、31a-( 21a-4b-6c)+3(-2c+2b) 68、 -5a n -a n -(-7a n )+(-3a n ) 69、x 2y-3xy 2+2yx 2-y 2x70、 41a 2b-0.4ab 2- 21a 2b+ 52ab 2;71、3a-{2c-[6a-(c-b )+c+(a+8b-6)]}72、-3(xy-2x 2)-[y 2-(5xy-4x 2)+2xy];73、化简、求值21x 2-2212- (x + y )2⎡⎤⎢⎥⎣⎦-23(-32x 2+31y 2),其中x =-2, y =-3474、化简、求值21x -2(x -31y 2)+(-23x +31y 2),其中x =-2,y =-32.75、x x x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛---其中x =-121;76、 化简,求值(4m+n )-[1-(m-4n )],m=52 n=-13177、化简、求值2(a2b+2b3-ab3)+3a3-(2ba2-3ab2+3a3)-4b3,其中a=-3,b=278、化简,求值:(2x3-xyz)-2(x3-y3+xyz)+(xyz-2y3),其中x=1,y=2,z=-3.79、化简,求值:5x2-[3x-2(2x-3)+7x2],其中x=-2.80、若两个多项式的和是2x2+xy+3y2,一个加式是x2-xy,求另一个加式.81、若2a2-4ab+b2与一个多项式的差是-3a2+2ab-5b2,试求这个多项式.82、求5x2y-2x2y与-2xy2+4x2y的和.83、求3x2+x-5与4-x+7x2的差.84、计算 5y+3x+5z2与12y+7x-3z2的和85、计算8xy2+3x2y-2与-2x2y+5xy2-3的差86、 多项式-x 2+3xy-21y 与多项式M 的差是-21x 2-xy+y ,求多项式M87、当3(x 2-2xy )-[3x 2-2y+2(xy+y )]的值.88、化简再求值5abc-{2a 2b-[3abc-(4ab 2-a 2b )]-2ab 2},其中a=-2,b=3,c=-4189、已知A=a 2-2ab+b 2,B=a 2+2ab+b 2(1)求A+B ; (2)求41(B-A);90、小明同学做一道题,已知两个多项式A ,B ,计算A+B ,他误将A+B 看作A-B ,求得9x 2-2x+7,若B=x 2+3x-2,你能否帮助小明同学求得正确答案?91、已知:M=3x 2+2x-1,N=-x 2-2+3x ,求M-2N .92、已知222244,5A x xy y B x xy y =-+=+-,求3A -B93、已知A =x 2+xy +y 2,B =-3xy -x 2,求2A -3B .94、已知2 a +(b +1)2=0,求5ab 2-[2a 2b -(4ab 2-2a 2b )]的值.95、化简求值:5abc-2a 2b+[3abc-2(4ab 2-a 2b )],其中a 、b 、c 满足|a-1|+|b-2|+c 2=0.96、已知a ,b ,z 满足:(1)已知|x-2|+(y+3)2=0,(2)z 是最大的负整数,化简求值:2(x 2y+xyz )-3(x 2y-xyz )-4x 2y .97、已知a+b=7,ab=10,求代数式(5ab+4a+7b )+(6a-3ab )-(4ab-3b )的值.98、已知m 2+3mn=5,求5m 2-[+5m 2-(2m 2-mn )-7mn-5]的值99、设A=2x 2-3xy+y 2+2x+2y ,B=4x 2-6xy+2y 2-3x-y ,若|x-2a|+(y-3)2=0,且B-2A=a ,求a 的值.100、有两个多项式:A =2a 2-4a +1,B =2(a 2-2a )+3,当a 取任意有理数时,请比较A 与B 的大小.整式的加减专项练习答案:1、3(a+5b )-2(b-a )=5a+13b2、3a-(2b-a )+b=4a-b .3、2(2a 2+9b )+3(-5a 2-4b )=—11a 2+6b 2 4、(x 3-2y 3-3x 2y )-(3x 3-3y 3-7x 2y )= -2x 3+y 3+4x 2y5、3x 2-[7x-(4x-3)-2x 2] = 5x 2 -3x-36、(2xy-y )-(-y+yx )= xy7、5(a 22b-3ab 2)-2(a 2b-7ab ) = -a 2b+11ab 8、(-2ab+3a )-2(2a-b )+2ab= -2a+b9、(7m 2n-5mn )-(4m 2n-5mn )= 3m 2n10、(5a 2+2a-1)-4(3-8a+2a 2)= -3a 2+34a-1311、-3x 2y+3xy 2+2x 2y-2xy 2= -x 2y+xy 212、2(a-1)-(2a-3)+3.=413、-2(ab-3a 2)-[2b 2-(5ab+a 2)+2ab]= 7a 2+ab-2b 214、(x 2-xy+y )-3(x 2+xy-2y )= -2x 2-4xy+7y15、3x 2-[7x-(4x-3)-2x 2]=5x 2-3x-3 16、a 2b-[2(a 2b-2a 2c )-(2bc+a 2c )]= -a 2b+2bc+6a 2c17、-2y 3+(3xy 2-x 2y )-2(xy 2-y 3)= xy 2-x 2y18、2(2x-3y )-(3x+2y+1)=2x-8y-1 19、-(3a 2-4ab )+[a 2-2(2a+2ab )]=-2a 2-4a20、5m-7n-8p+5n-9m-p = -4m-2n-9p21、(5x 2y-7xy 2)-(xy 2-3x 2y )=4xy 2-4x 2y22、3(-3a 2-2a )-[a 2-2(5a-4a 2+1)-3a]=-18a 2 +7a+223、3a 2-9a+5-(-7a 2+10a-5)=10a 2-19a+1024、-3a 2b-(2ab 2-a 2b )-(2a 2b+4ab 2)= -4a 2b-64ab 225、(5a-3a 2+1)-(4a 3-3a 2)=5a-4a 2+126、-2(ab-3a 2)-[2b 2-(5ab+a 2)+2ab]=7a 2+ab-2b 2 27、(8xy -x 2+y 2)+(-y 2+x 2-8xy )=028、(2x 2-21+3x )-4(x -x 2+21) = 6x 2-x-25 29、3x 2-[7x -(4x -3)-2x 2]= 5x 2-3x -330、5a+(4b-3a )-(-3a+b )= 5a+3b31、(3a 2-3ab+2b 2)+(a 2+2ab-2b 2)= 4a 2-ab32、2a 2b+2ab 2-[2(a 2b-1)+2ab 2+2].= -133、(2a 2-1+2a )-3(a-1+a 2)= -a 2-a+234、2(x 2-xy )-3(2x 2-3xy )-2[x 2-(2x 2-xy+y 2)]=-2x 2+5xy-2y 235、-32ab +43a 2b +ab +(-43a 2b )-1 = 31ab-1 36、(8xy -x 2+y 2)+(-y 2+x 2-8xy )=037、2x -(3x -2y +3)-(5y -2)=-x-3y-138、-(3a +2b )+(4a -3b +1)-(2a -b -3)= -a-4b+439、4x 3-(-6x 3)+(-9x 3)= x 340、3-2xy +2yx 2+6xy -4x 2y = -2 x 2y+441、 1-3(2ab +a )十[1-2(2a -3ab )]=2-7a42、 3x -[5x +(3x -2)]=-5x+243、(3a 2b -ab 2)-(ab 2+3a 2b )= -2ab 244、()[]{}y x x y x --+--32332 = 5x+y45、(-x 2+5+4x 3)+(-x 3+5x -4)= 3x 3-x 2+5x+146、(5a 2-2a+3)-(1-2a+a 2)+3(-1+3a-a 2)=a 2+9a-147、5(3a 2b-ab 2)-4(-ab 2+3a 2b ).=3a 2b-ab 248、4a 2+2(3ab-2a 2)-(7ab-1)=1-ab49、 21xy+(-41xy )-2xy 2-(-3y 2x )=41xy+xy 2 50、5a 2-[a 2-(5a 2-2a )-2(a 2-3a )]=11a 2-8a51、5m-7n-8p+5n-9m+8p=-4m-2n59、(7y-3z )-(8y-5z )=-y+2z60、-3(2x 2-xy )+4(x 2+xy-6)=-2x 2+7xy-24 61、(x 3+3x 2y-5xy 2+9y 3)+(-2y 3+2xy 2+x 2y-2x 3)-(4x 2y-x 3-3xy 2+7y 3)=0 62、-3x 2y+2x 2y+3xy 2-2xy 2 = -x 2y+xy 263、3(a 2-2ab )-2(-3ab+b 2)=3a 2-2b 264、5abc-{2a 2b-[3abc-(4a 2b-ab 2]}=8abc-6a 2b+ab 265、5m 2-[m 2+(5m 2-2m )-2(m 2-3m )]=m 2-4m66、-[2m-3(m-n+1)-2]-1=m-3n+467、31a-( 21a-4b-6c)+3(-2c+2b)= -61a+10b 68、 -5a n -a n -(-7a n )+(-3a n )= -2a n69、x 2y-3xy 2+2yx 2-y 2x=3x 2y-4xy 271、 41a 2b-0.4ab 2- 21a 2b+ 52ab 2 = -41a 2b 71、3a-{2c-[6a-(c-b )+c+(a+8b-6)]}= 10a+9b-2c-672、-3(xy-2x 2)-[y 2-(5xy-4x 2)+2xy]= 2x 2-y 2 73、化简、求值21x 2-2212- (x + y )2⎡⎤⎢⎥⎣⎦-23(-32x 2+31y 2),其中x =-2, y =-34 原式=2x 2+21y 2-2 =698 74、化简、求值21x -2(x -31y 2)+(-23x +31y 2),其中x =-2,y =-32. 原式=-3x+y 2=694 75、x x x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛---其中x =-121; 原式=x 3+x 2-x+6=683 76、 化简,求值(4m+n )-[1-(m-4n )],m=52 n=-131 原式=5m-3n-1=577、化简、求值2(a 2b +2b 3-ab 3)+3a 3-(2ba 2-3ab 2+3a 3)-4b 3,其中a =-3,b =2原式=-2ab 3+3ab 2=1278、化简,求值:(2x 3-xyz )-2(x 3-y 3+xyz )+(xyz-2y 3),其中x=1,y=2,z=-3.原式=-2xyz=679、化简,求值:5x 2-[3x-2(2x-3)+7x 2],其中x=-2.原式=-2x 2+x-6=-1680、若两个多项式的和是2x 2+xy+3y 2,一个加式是x 2-xy ,求另一个加式.(2x 2+xy+3y 2 ) ——( x 2-xy )= x 2+2xy+3y 281、若2a 2-4ab+b 2与一个多项式的差是-3a 2+2ab-5b 2,试求这个多项式.( 2a 2-4ab+b 2 )—(-3a 2+2ab-5b 2)=5a 2 -6ab+6b 282、求5x 2y -2x 2y 与-2xy 2+4x 2y 的和.(5x 2y -2x 2y )+(-2xy 2+4x 2y )=3xy 2+2x 2y83、 求3x 2+x -5与4-x +7x 2的差.(3x 2+x -5)—(4-x +7x 2)=—4x 2+2x -984、计算 5y+3x+5z 2与12y+7x-3z 2的和(5y+3x+5z 2)+(12y+7x-3z 2)=17y+10x+2z 285、计算8xy 2+3x 2y-2与-2x 2y+5xy 2-3的差(8xy 2+3x 2y-2)—(-2x 2y+5xy 2-3)=5x 2y+3xy 2+186、 多项式-x 2+3xy-21y 与多项式M 的差是-21x 2-xy+y ,求多项式M23y 87、当3(x 2-2xy )-[3x 2-2y+2(xy+y )]的值. 原式=-8xy+y= —1588、化简再求值5abc-{2a 2b-[3abc-(4ab 2-a 2b )]-2ab 2},其中a=-2,b=3,c=-41 原式=83abc-a 2b-2ab 2=3689、已知A=a 2-2ab+b 2,B=a 2+2ab+b 2 (1)求A+B ;(2)求41(B-A); A+B=2a 2+2b 2 41(B-A)=ab 90、小明同学做一道题,已知两个多项式A ,B ,计算A+B ,他误将A+B 看作A-B ,求得 9x 2-2x+7,若B=x 2+3x-2,你能否帮助小明同学求得正确答案?A=10x 2+x+5 A+B=11x 2+4x+391、已知:M=3x 2+2x-1,N=-x 2-2+3x ,求M-2N .M-2N=5x 2-4x+392、已知222244,5A x xy y B x xy y =-+=+-,求3A -B3A -B=11x 2-13xy+8y 293、已知A =x 2+xy +y 2,B =-3xy -x 2,求2A -3B .2A -3B= 5x 2+11xy +2y 294、已知2-a +(b +1)2=0,求5ab 2-[2a 2b -(4ab 2-2a 2b )]的值. 原式=9ab 2-4a 2b=3495、化简求值:5abc-2a 2b+[3abc-2(4ab 2-a 2b )],其中a 、b 、c 满足|a-1|+|b-2|+c 2=0. 原式=8abc-8a 2b=-3296、已知a ,b ,z 满足:(1)已知|x-2|+(y+3)2=0,(2)z 是最大的负整数,化简求值: 2(x 2y+xyz )-3(x 2y-xyz )-4x 2y .原式=-5x 2y+5xyz=9097、已知a+b=7,ab=10,求代数式(5ab+4a+7b )+(6a-3ab )-(4ab-3b )的值. 原式=10a+10b-2ab=5098、已知m 2+3mn=5,求5m 2-[+5m 2-(2m 2-mn )-7mn-5]的值原式=2m 2+6mn+5=1599、设A=2x 2-3xy+y 2+2x+2y ,B=4x 2-6xy+2y 2-3x-y ,若|x-2a|+(y-3)2=0,且B-2A=a ,求a 的值. B-2A=-7x-5y=-14a-15=a a=-1100、有两个多项式:A =2a 2-4a +1,B =2(a 2-2a )+3,当a 取任意有理数时,请比较A与B 的大小. A=2a 2-4a +1 B =2a 2-4a +3 所以A<B。
七年级上册数学整式加减计算题

七年级上册数学整式加减计算题一、整式加减基础运算题(1 - 10)1. 计算:(3a + 2b)-(a - b)- 解析:- 去括号法则:括号前是正号,把括号和它前面的正号去掉后,原括号里各项的符号都不改变;括号前是负号,把括号和它前面的负号去掉后,原括号里各项的符号都要改变。
- 所以(3a + 2b)-(a - b)=3a + 2b - a + b。
- 然后合并同类项,3a - a+2b + b = 2a+3b。
2. 计算:2(x^2-3x + 1)-3(2x^2+x - 4)- 解析:- 先使用乘法分配律去括号,2(x^2-3x + 1)=2x^2-6x + 2,3(2x^2+x -4)=6x^2+3x - 12。
- 然后进行整式的减法:(2x^2-6x + 2)-(6x^2+3x - 12)=2x^2-6x + 2 - 6x^2-3x + 12。
- 合并同类项得(2x^2-6x^2)+(-6x - 3x)+(2 + 12)= - 4x^2-9x + 14。
3. 计算:(5a^2-3b^2)+(a^2+b^2)-(5a^2+3b^2)- 解析:- 先去括号,(5a^2-3b^2)+(a^2+b^2)-(5a^2+3b^2) = 5a^2-3b^2+a^2+b^2-5a^2-3b^2。
- 再合并同类项,(5a^2+a^2-5a^2)+(-3b^2+b^2-3b^2)=a^2-5b^2。
4. 计算:3x^2y-(2xy - 2(xy-(3)/(2)x^2y)+xy)- 解析:- 先去小括号,3x^2y-(2xy - 2(xy-(3)/(2)x^2y)+xy)=3x^2y-(2xy-2xy +3x^2y+xy)。
- 再去中括号,3x^2y - 2xy + 2xy - 3x^2y - xy=-xy。
5. 计算:(4m^3-2m^2+m - 1)-(2m^3+3m^2-m + 2)- 解析:- 去括号得4m^3-2m^2+m - 1 - 2m^3-3m^2+m - 2。
北师大版七年级数学上册整式计算题专项练习(附答案)
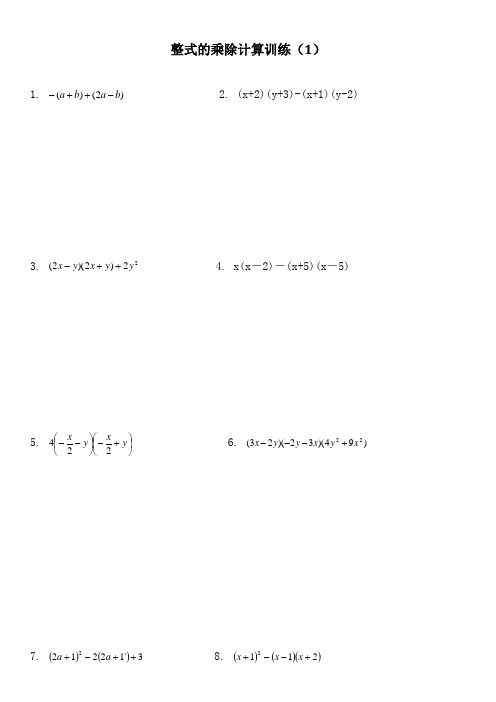
整式的乘除计算训练(1)1. )2()(b a b a -++-2. (x+2)(y+3)-(x+1)(y-2)3. 22)2)(2(y y x y x ++-4. x(x -2)-(x+5)(x -5)5. ⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--y x y x224 6. )94)(32)(23(22x y x y y x +---7. ()()3`122122++-+a a 8. ()()()2112+--+x x x9. (x -3y)(x+3y)-(x -3y)2 10. 23(1)(1)(21)x x x +---11. 22)23()23(y x y x --+ 12. 22)()(y x y x -+13. ×810014. 3022)2(21)x (4554---÷⎪⎭⎫⎝⎛--π-+⎪⎭⎫⎝⎛-÷⎪⎭⎫ ⎝⎛15. (1211200622332141)()()()-⨯+----16—19题用乘法公式计算×1001 17.1992-18.298 19.2010200820092⨯-20.化简求值:)4)(12()12(2+-+-a a a ,其中2-=a 。
21. 化简求值2(2)2()()2(3)x y x y x y y x y +--++-,其中12,2x y =-=。
22. 5(x -1)(x +3)-2(x -5)(x -2) 23. (a -b )(a 2+ab +b 2)24. (3y+2)(y-4)-3(y-2)(y-3) 25. a(b-c)+b(c-a)+c(a-b)1y2)226. (-2mn2)2-4mn3(mn+1) 27. 3xy(-2x)3·(-428. (-x-2)(x+2) 29. 5×108·(3×102) 30. (x-3y)(x+3y)-(x-3y)2 31. (a+b-c)(a-b-c)答案1. a-2b2. 5x+y+83. 4x2+y24. -2x+255. x2-4y26. 16y4-81x47. 4a2+28. x+39. 6xy-18y2 10. -x2+4x-4 11. 24xy 12. x4-2x2y2+y413. 1 14. 10 15. 161216. 原式=(1000-1)×(1000+1) 17. 原式=(99+1)×(99-1)=1000000-1 =100×98=999999 =980018. 原式=(900-2)2 19. 原式=20092-(2009+1)(2009-1)=10000-400+4 =20092-20092+1=9604 =120.原式=6a2+3a-3,当a=2时,原式=6×(-2)2+3×(-2)-3=1521.原式=-x2+6xy,当x=2,y=12时,原式=-(-2)2+6×(-2)×12=-1022. -3x2+24x-35 23. a3-b3 24. 5y-26 25. 026. -4mn3 27. -3x4y5 28. -x2-4x-4 29. 1.5×1011230. 6xy-18y2 31. a2-2ac+c2-b22014年北师大七年级数学上册《整式及其加减》计算题专项练习一一.解答题(共12小题)1.计算题①12﹣(﹣8)+(﹣7)﹣15;②﹣12+2×(﹣5)﹣(﹣3)3÷;③(2x﹣3y)+(5x+4y);④(5a2+2a﹣1)﹣4(3﹣8a+2a2).2.(1)计算:4+(﹣2)2×2﹣(﹣36)÷4;(2)化简:3(3a﹣2b)﹣2(a﹣3b).3.计算:(1)7x+4(x2﹣2)﹣2(2x2﹣x+3);(2)4ab﹣3b2﹣[(a2+b2)﹣(a2﹣b2)];(3)(3mn﹣5m2)﹣(3m2﹣5mn);(4)2a+2(a+1)﹣3(a﹣1).4.化简(1)2(2a2+9b)+3(﹣5a2﹣4b)(2)3(x3+2x2﹣1)﹣(3x3+4x2﹣2)5.(2009?柳州)先化简,再求值:3(x﹣1)﹣(x﹣5),其中x=2.6.已知x=5,y=3,求代数式3(x+y)+4(x+y)﹣6(x+y)的值.7.已知A=x2﹣3y2,B=x2﹣y2,求解2A﹣B.8.若已知M=x2+3x﹣5,N=3x2+5,并且6M=2N﹣4,求x.9.已知A=5a2﹣2ab,B=﹣4a2+4ab,求:(1)A+B;(2)2A﹣B;(3)先化简,再求值:3(A+B)﹣2(2A﹣B),其中A=﹣2,B=1.10.设a=14x﹣6,b=﹣7x+3,c=21x﹣1.(1)求a﹣(b﹣c)的值;(2)当x=时,求a﹣(b﹣c)的值.11.化简求值:已知a、b满足:|a﹣2|+(b+1)2=0,求代数式2(2a﹣3b)﹣(a﹣4b)+2(﹣3a+2b)的值.12.已知(x+1)2+|y﹣1|=0,求2(xy﹣5xy2)﹣(3xy2﹣xy)的值.2014年北师大七年级数学上册《整式及其加减》计算题专项练习一参考答案与试题解析一.解答题(共12小题)1.计算题①12﹣(﹣8)+(﹣7)﹣15;②﹣12+2×(﹣5)﹣(﹣3)3÷;③(2x﹣3y)+(5x+4y);④(5a2+2a﹣1)﹣4(3﹣8a+2a2).考点:整式的加减;有理数的混合运算.专题:计算题.分析:(1)直接进行有理数的加减即可得出答案.(2)先进行幂的运算,然后根据先乘除后加减的法则进行计算.(3)先去括号,然后合并同类项即可得出结果.(4)先去括号,然后合并同类项即可得出结果.解答:解:①原式=12+8﹣7﹣15=﹣2;②原式=﹣1﹣10+27÷=﹣11+81=70;③原式=2x﹣3y+5x+4y=7x+y;④原式=5a2+2a﹣1﹣12+32a﹣8a2=﹣3a2+34a﹣13.点评:本题考查了整式的加减及有理数的混合运算,属于基础题,解答本题的关键熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.2.(1)计算:4+(﹣2)2×2﹣(﹣36)÷4;(2)化简:3(3a﹣2b)﹣2(a﹣3b).考点:整式的加减;有理数的混合运算.分析:(1)按照有理数混合运算的顺序,先乘方后乘除最后算加减;(2)运用整式的加减运算顺序计算:先去括号,再合并同类项.解答:解:(1)原式=4+4×2﹣(﹣9)=4+8+9=17;(2)原式=9a﹣6b﹣2a+6b=(9﹣2)a+(﹣6+6)b=7a.点评:在混合运算中要特别注意运算顺序:先三级,后二级,再一级;熟记去括号法则:﹣﹣得+,﹣+得﹣,++得+,+﹣得﹣;及熟练运用合并同类项的法则:字母和字母的指数不变,只把系数相加减.3.计算:(1)7x+4(x2﹣2)﹣2(2x2﹣x+3);(2)4ab﹣3b2﹣[(a2+b2)﹣(a2﹣b2)];(3)(3mn﹣5m2)﹣(3m2﹣5mn);(4)2a+2(a+1)﹣3(a﹣1).考点:整式的加减.分析:(1)先去括号,再合并同类项即可;(2)先去括号,再合并同类项即可;(3)先去括号,再合并同类项即可;(4)先去括号,再合并同类项即可.解答:解:(1)7x+4(x2﹣2)﹣2(2x2﹣x+3)=7x+4x2﹣8﹣4x2+2x﹣6=9x﹣14;(2)4ab﹣3b2﹣[(a2+b2)﹣(a2﹣b2)]=4ab﹣3b2﹣[a2+b2﹣a2+b2]=4ab﹣3b2﹣2b2=4ab﹣5b2;(3)(3mn﹣5m2)﹣(3m2﹣5mn)=3mn﹣5m2﹣3m2+5mn=8mn﹣8m2;(4)2a+2(a+1)﹣3(a﹣1)=2a+2a+2﹣3a+3=a+5.点评:本题考查了整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.4.化简(1)2(2a2+9b)+3(﹣5a2﹣4b)(2)3(x3+2x2﹣1)﹣(3x3+4x2﹣2)考点:整式的加减.专题:计算题.分析:(1)原式利用去括号法则去括号后,合并同类项即可得到结果;(2)原式利用去括号法则去括号后,合并同类项即可得到结果.解答:解:(1)原式=4a2+18b﹣15a2﹣12b=﹣11a2+6b;(2)原式=3x3+6x2﹣3﹣3x3﹣4x2+2=2x2﹣1.点评:此题考查了整式的加减,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握法则是解本题的关键.5.(2009?柳州)先化简,再求值:3(x﹣1)﹣(x﹣5),其中x=2.考点:整式的加减—化简求值.分析:本题应对方程去括号,合并同类项,将整式化为最简式,然后把x的值代入即可.解答:解:原式=3x﹣3﹣x+5=2x+2,当x=2时,原式=2×2+2=6.点评:本题考查了整式的化简.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.6.已知x=5,y=3,求代数式3(x+y)+4(x+y)﹣6(x+y)的值.考点:整式的加减—化简求值.分析:先把x+y当作一个整体来合并同类项,再代入求出即可.解答:解:∵x=5,y=3,∴3(x+y)+4(x+y)﹣6(x+y)=x+y=5+3=8.点评:本题考查了整式的加减的应用,主要考查学生的计算能力,用了整体思想.7.已知A=x2﹣3y2,B=x2﹣y2,求解2A﹣B.考点:整式的加减.分析:直接把A、B代入式子,进一步去括号,合并得出答案即可.解答:解:2A﹣B=2(x2﹣3y2)﹣(x2﹣y2)=2x2﹣6y2﹣x2+y2=x2﹣5y2.点评:此题考查整式的加减混合运算,掌握去括号法则和运算的方法是解决问题的关键.8.若已知M=x2+3x﹣5,N=3x2+5,并且6M=2N﹣4,求x.考点:整式的加减;解一元一次方程.专题:计算题.分析:把M与N代入计算即可求出x的值.解答:解:∵M=x2+3x﹣5,N=3x2+5,∴代入得:6x2+18x﹣30=6x2+10﹣4,解得:x=2.点评:此题考查了整式的加减,熟练掌握运算法则是解本题的关键.9.已知A=5a2﹣2ab,B=﹣4a2+4ab,求:(1)A+B;(2)2A﹣B;(3)先化简,再求值:3(A+B)﹣2(2A﹣B),其中A=﹣2,B=1.考点:整式的加减;整式的加减—化简求值.专题:计算题.分析:(1)把A与B代入A+B中计算即可得到结果;(2)把A与B代入2A﹣B中计算即可得到结果;(3)原式去括号合并得到最简结果,把A与B的值代入计算即可求出值.解答:解:(1)∵A=5a2﹣2ab,B=﹣4a2+4ab,∴A+B=5a2﹣2ab﹣4a2+4ab=a2+2ab;(2)∵A=5a2﹣2ab,B=﹣4a2+4ab,∴2A﹣B=10a2﹣4ab+4a2﹣4ab=14a2﹣8ab;(3)原式=3A+3B﹣4A+2B=﹣A+5B,把A=﹣2,B=1代入得:原式=2+5=7.点评:此题考查了整式的加减,熟练掌握运算法则是解本题的关键.10.设a=14x﹣6,b=﹣7x+3,c=21x﹣1.(1)求a﹣(b﹣c)的值;(2)当x=时,求a﹣(b﹣c)的值.考点:整式的加减;代数式求值.专题:计算题.分析:(1)把a,b,c代入a﹣(b﹣c)中计算即可得到结果;(2)把x的值代入(1)的结果计算即可得到结果.解答:解:(1)把a=14x﹣6,b=﹣7x+3,c=21x﹣1代入得:a﹣(b﹣c)=a﹣b+c=14x﹣6+7x﹣3+21x﹣1=42x﹣10;(2)把x=代入得:原式=42×﹣10=﹣10=.点评:此题考查了整式的加减,以及代数式求值,熟练掌握运算法则是解本题的关键.11.化简求值:已知a、b满足:|a﹣2|+(b+1)2=0,求代数式2(2a﹣3b)﹣(a﹣4b)+2(﹣3a+2b)的值.考点:整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.专题:计算题.分析:原式去括号合并得到最简结果,利用非负数的性质求出a与b的值,代入计算即可求出值.解答:解:原式=4a﹣6b﹣a+4b﹣6a+4b=﹣3a+2b,∵|a﹣2|+(b+1)2=0,∴a=2,b=﹣1,则原式=﹣6﹣2=﹣8.点评:此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.12.已知(x+1)2+|y﹣1|=0,求2(xy﹣5xy2)﹣(3xy2﹣xy)的值.考点:整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.分析:因为平方与绝对值都是非负数,且(x+1)2+|y﹣1|=0,所以x+1=0,y﹣1=0,解得x,y的值.再运用整式的加减运算,去括号、合并同类项,然后代入求值即可.解答:解:2(xy﹣5xy2)﹣(3xy2﹣xy)=(2xy﹣10xy2)﹣(3xy2﹣xy)=2xy﹣10xy2﹣3xy2+xy=(2xy+xy)+(﹣3xy2﹣10xy2)=3xy﹣13xy2,∵(x+1)2+|y﹣1|=0∴(x+1)=0,y﹣1=0∴x=﹣1,y=1.∴当x=﹣1,y=1时,3xy﹣13xy2=3×(﹣1)×1﹣13×(﹣1)×12=﹣3+13=10.答:2(xy﹣5xy2)﹣(3xy2﹣xy)的值为10.点评:整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.代入求值时要化简.。
(必考题)七年级数学上册第二单元《整式加减》-解答题专项经典题(含答案解析)

一、解答题1.如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化,(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)(2)求出当a=20,b=12时的绿化面积.解析:(1)(5a2+3ab)平方米;(2)2720平方米【分析】(1)根据割补法,用含有a,b的式子表示出整个长方形的面积,然后用含有a,b的式子表示出中间空白处正方形的面积,然后两者相减,即可求出绿化部分的面积.(2)将a=20,b=12分别代入(1)问中求出的关系式即可解决.【详解】解:(1)(3a+b)(2a+b)﹣(a+b)2=6a2+3ab+2ab+b2﹣(a2+2ab+b2)=6a2+3ab+2ab+b2﹣a2﹣2ab﹣b2=5a2+3ab,答:绿化的面积是(5a2+3ab)平方米;(2)当a=20,b=12时5a2+3ab=5×202+3×20×12=2000+720=2720,答:当a=20,b=12时的绿化面积是2720平方米.【点睛】(1)本题考查了割补法,多项式乘多项式和完全平方式的运算法则,解决本题的关键是正确理解题意,能够熟练掌握多项式乘多项式的运算法则.(2)本题考查了整式的化简求值,解决本题的关键是熟练掌握整式的运算法则和步骤.2.生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条x,分别回答下列的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为cm问题:(1)为了保证能折成图④的形状(即纸条两端均超出点P ),试求P 的取值范围. (2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M 与点P 的距离(用P 表示) 解析:(1) x <5.2(2) 13-1.5x【详解】分析:(1)按图中方式折叠后可得到除去两端,纸条使用的长度为5x ,那么纸条使用的长度应大于0,小于纸条总长度.(2)是轴对称图形,那么AM=AP+x .解答:解:(1)由折纸过程可知0<5x <26,∴0<x <5.2.(2)∵图④为轴对称图形,∴AM=2652x -+x=13-1.5x , 即点M 与点A 的距离是(13-1.5x )cm . 点评:本题考查学生的动手操作能力,难点是得到纸条除去两端使用的纸条的长度. 3.如图,将面积为2a 的小正方形和面积为2b 的大正方形放在同一水平面上(0b a >>)(1)用a 、b 表示阴影部分的面积;(2)计算当3a =,5b =时,阴影部分的面积.解析:(1)22111222a ab b ++;(2)492【分析】(1)阴影部分为两个直角三角形,根据面积公式即可计算得到答案;(2)将3a =,5b =代入求值即可.【详解】(1)()21122a ab b ⨯++, 22111222a ab b =++; (2)当3a =,5b =时, 原式221113355222=⨯+⨯⨯+⨯492=. 【点睛】 此题考察列式计算,根据图形边长正确列式表示图形的面积即可.4.某商店出售一种商品,其原价为m 元,现有如下两种调价方案:一种是先提价10%,在此基础上又降价10%;另一种是先降价10%,在此基础上又提价10%.(1)用这两种方案调价的结果是否一样?调价后的结果是不是都恢复了原价?(2)两种调价方案改为:一种是先提价20%,在此基础上又降价20%;另一种是先降价20%,在此基础上又提价20%,这时结果怎样?(3)你能总结出什么规律吗?解析:(1)这两种方案调价的结果一样,都没有恢复原价;(2)这两种方案调价的结果一样,都没有恢复原价;(3)在原价基础上,先提价百分之多少,在此基础上再降价同样的百分数,与先降价百分之多少,再提价同样的百分数,最后结果一样,但都没有恢复原价..【分析】(1)先提价10%为110m%,再降价10%后价钱为99m%;先降价10%为90m%,再提价10%后价钱为99m%,据此可得答案;(2)先提价20%为120%m ,再降价20%后价钱为96%m ;先降价20%为80%m ,再提价20%后价钱为96%m ,据此可得答案;(3)根据(1)(2)的结果得出规律即可.【详解】解:(1)方案一:先提价10%价钱为()110%110%m m +=,再降价10%后价钱为()110%110%99%m m ⨯-=;方案二:先降价10%价钱为()110%90%m m -=,再提价10%后价钱为()90%110%99%m m ⨯+=,故这两种方案调价的结果一样,都没有恢复原价;(2)方案一:先提价20%价钱为()120%120%m m +=,再降价20%后价钱为()120%120%96%m m ⨯-=;方案二:先降价20%价钱为()120%80%m m -=,再提价20%后价钱为()80%120%96%m m ⨯+=,故这两种方案调价的结果一样,都没有恢复原价;(3)在原价基础上,先提价百分之多少,在此基础上再降价同样的百分数,与先降价百分之多少,再提价同样的百分数,最后结果一样,但都没有恢复原价.【点睛】本题考查了列代数式的知识,解题的关键是能够表示出降价或涨价后的量,难度不大. 5.当0.2x =-时,求代数式22235735x x x x -+-+-的值。
七年级上册数学第二章整式的加减-专项练习100题含答案

整式的加减专项练习1、3(a+5b)-2 (b-a ) 2 、 3a- (2b-a ) +b3、2(2a2+9b)+3( -5a 2-4b )4、( x3-2y 3-3x 2y)- (3x3 -3y 3-7x 2y) 5 、 3x2-[7x- ( 4x-3 ) -2x 2] 6、( 2xy-y )- (-y+yx ) 7、 5( a2b-3ab 2) -2 (a2b-7ab )8、( -2ab+3a) -2 (2a-b )+2ab2 29 、(7mn-5mn)- (4mn-5mn)10 、(5a2+2a-1)-4 ( 3-8a+2a2).11、-3x 2y+3xy2 +2x2y-2xy 2;12、2(a-1 )- (2a-3 )+3. 13、-2 (ab-3a 2)-[2b 2 - ( 5ab+a2) +2ab]14、( x2-xy+y )-3 ( x2 +xy-2y )15、 3x2-[7x- (4x-3 ) -2x 2]16、a2b-[2 (a2 b-2a 2c) - ( 2bc+a2c)] ;17、-2y 3+(3xy2-x 2y)-2 ( xy2-y 3).18、2(2x-3y ) - (3x+2y+1)19、- (3a2-4ab )+[a 2 -2 (2a+2ab) ] .120、5m-7n-8p+5n-9m-p;21、( 5x2y-7xy 2)- ( xy2-3x 2y);22 、3( -3a 2-2a )-[a 2 -2 (5a-4a 2 +1)-3a] .23、3a2-9a+5- ( -7a 2+10a-5);24 、-3a 2b- ( 2ab2-a 2b) - ( 2a2b+4ab2).25、( 5a-3a 2+1)- (4a3-3a 2);26 、 -2 (ab-3a 2)-[2b 2- (5ab+a2)+2ab]27、(8xy-x2+ y2)+- y2+x2-xy;、x2- 1 +x-4(x- x2+1);( 8 ) 28(2 3 )22x2-[x-(4x-3)- x2].30、()(-3a+b);29、37 2 5a+ 4b-3a -2 2 2 2 2 2 2 2.31、(3a -3ab+2b)+( a +2ab-2b);32、2a b+2ab -[2(a b-1 )+2ab +2]33 (、2a2 -1+2a)-3( a-1+a2); 34 、(2x2-xy )-3(2x2-3xy )-2[x 2(-2x2-xy+y 2)] .35、-2 ab+3 a2b+ ab+( -3 a2 b) -1 36 、(8 xy- x2+y2) +( -y2+x2-8xy) ;3 4 4237、2x-(3 x- 2y+3) -(5 y-2) ; 38 、-(3 a+2b) + (4 a-3b+ 1) -(2 a-b-3) 39、4x3-( -6x3 ) +( -9x3) 40 、 3- 2xy+ 2yx 2+6xy- 4x2y41、 1 - 3(2 ab+a) 十 [1 -2(2 a-3ab)] .42、 3 x-[5 x+(3 x-2)] ;43、(3 a2b-ab2)-ab2+a2b44、 2x3 y 3x 2 3x y( 3 )45 、( -x2+5+4x3 ) + ( - x3+5x- 4) 46 、( 5a2-2a+3 )-(1-2a+a2)+3(-1+3a-a 2).47 、 5( 3a2b-ab 2)-4 (-ab 2+3a2 b).48 、 4a2+2( 3ab-2a 2)- (7ab-1 ).49、1 xy+( -1 xy)-2xy 2- (-3y 2x)50 、5a2-[a 2- (5a2-2a )-2 ( a2-3a )]2 451 、 5m-7n-8p+5n-9m+8p 52 、( 5x2y-7xy 2)- (xy2-3x 2y)353、 3x 2y-[2x 2 y-3 ( 2xy-x 2y)-xy] 54 、 3x2-[5x-4( 1 x2-1)]+5x 2255、2a3b- 1 a3 b-a 2b+ 1 a2b-ab 2;2 256、( a2+4ab-4b2)-3 (a2+b2)-7 ( b2-ab ). 57、a2+2a3+(-2a 3)+(-3a 3) +3a2;58 、5ab+(-4a 2 b2)+8ab2- ( -3ab ) +( -a 2b)+4a2b2; 59 、( 7y-3z )- (8y-5z );60、 -3 (2x2-xy )+4( x2 +xy-6 ).61、(x3+3x2 y-5xy 2+9y3) +( -2y 3+2xy2+x2y-2x 3)- (4x2y-x 3 -3xy 2+7y3)62、-3x 2y+2x2y+3xy2-2xy 2;63 、3(a2-2ab ) -2 (-3ab+b2);2 2 2 2 2 2 264、5abc-{2a b-[3abc- (4a b-ab ]} .65、5m-[m +( 5m-2m) -2 (m-3m) ] .66、-[2m-3 (m-n+1) -2]-1 .467、1 a-(1 a-4b-6c)+3(-2c+2b)3 268、 -5a n-a n- (-7a n) +( -3a n)69 、x2y-3xy 2 +2yx2-y 2x70、1 a2b-0.4ab 2- 1 a2b+ 2 ab2;71、 3a-{2c-[6a-(c-b )+c+( a+8b-6)]}4 2 572、-3 ( xy-2x 2)-[y 2 - ( 5xy-4x 2)+2xy] ;73、化简、求值1 x2-2-(1 22 -3(-2 x2+1 y2),其中 x=-, y=-4 22 x +y ) 2 33 2 374、化简、求值1 x- 2( x-1 y2) +( -3 x+1 y2 ) ,其中 x=- 2, y=-22 3 2 3 375、1 x 3 3x2 2 x 3 1 x 2 (4x 6) 5x其中 x=- 1 1;3 2 3 2 276、化简,求值( 4m+n)-[1- (m-4n)] ,m=2 n=-1 15 3577、化简、求值 2( a2b+2b3-ab3 ) + 3a3- (2 ba2-3ab2+3a3) -4b3,其中 a=- 3,b=278、化简,求值:(2x3-xyz )-2 (x3-y 3 +xyz)+(xyz-2y 3),其中 x=1,y=2,z=-3 .79、化简,求值: 5x2-[3x-2 ( 2x-3 ) +7x2] ,其中 x=-2 .80、若两个多项式的和是2x2 +xy+3y2,一个加式是 x2-xy ,求另一个加式.81、若 2a2-4ab+b2与一个多项式的差是 -3a 2 +2ab-5b2,试求这个多项式.82、求 5x2y-2x2y 与- 2xy2+4x2 y 的和.83、求 3x2+x-5 与 4- x+ 7x2的差.84、计算 5y+3x+5z 2与 12y+7x-3z 2的和85、计算 8xy 2 +3x 2 y-2 与-2x 2 y+5xy 2 -3 的差686、多项式 -x 2 +3xy- 1 y 与多项式 M的差是 - 1 x2-xy+y ,求多项式 M2 212287、当 x=- , y=-3 时,求代数式 3(x -2xy )-[3x -2y+2 (xy+y)] 的值.88、化简再求值 5abc-{2a 2 b-[3abc- (4ab 2 -a 2 b)]-2ab 2 } ,其中 a=-2 ,b=3,1c=-489、已知 A=a2 -2ab+b 2,B=a2 +2ab+b2(1)求 A+B;(2)求1 (B-A) ;490、小明同学做一道题,已知两个多项式 A,B,计算 A+B,他误将 A+B看作 A-B,求得 9x2 -2x+7 ,若 B=x2+3x-2 ,你能否帮助小明同学求得正确答案?2 291、已知: M=3x+2x-1 ,N=-x -2+3x ,求 M-2N.92、已知 A 4x24xy y2 , B x2xy 5 y2,求 3A-B93、已知 A=x2+xy+ y2,B=- 3xy- x2,求 2A-3B.794、已知 a 2 +( b+ 1) 2= 0,求 5ab2-[2 a2b-(4 ab2-2a2b)] 的值.22295、化简求值: 5abc-2a b+[3abc-2 ( 4ab -a b)] ,其中 a、b、c 满足2|a-1|+|b-2|+c =0.96、已知 a,b, z 满足:(1)已知 |x-2|+ (y+3)2=0,(2)z 是最大的负整数,化简求值:2 ( x2 y+xyz)-3 ( x2y-xyz )-4x 2 y.97、已知 a+b=7,ab=10,求代数式( 5ab+4a+7b)+(6a-3ab )- (4ab-3b )的值.2 2 2 298、已知 m+3mn=5,求 5m-[+5m- (2m-mn)-7mn-5]的值99、设 A=2x2 -3xy+y 2+2x+2y,B=4x2-6xy+2y 2-3x-y ,若 |x-2a|+ ( y-3 )2 =0,且B-2A=a,求 a 的值.100、有两个多项式: A= 2a2- 4a+1,B=2( a2-2a) +3,当 a 取任意有理数时,请比较A 与 B 的大小.8整式的加减专项练习答案:1、 3( a+5b) -2 ( b-a ) =5a+13b2、 3a- ( 2b-a ) +b=4a-b .3、 2( 2a2+9b) +3( -5a 2-4b ) =—11a 2 +6b 23323323+3+424、( x -2y -3x y) - ( 3x -3y -7x y) = -2x y x y 6、( 2xy-y ) - ( -y+yx ) = xy7、 5( a 22b-3ab2 ) -2( a2b-7ab ) = -a2b+11ab8、( -2ab+3a ) -2 ( 2a-b ) +2ab= -2a+b9、( 7m2 n-5mn) - ( 4m2 n-5mn) = 3m 2 n10 、( 5a2+2a-1 ) -4 ( 3-8a+2a 2)= -3a 2+34a-1311 、 -3x 2 y+3xy 2 +2x 2 y-2xy 2 = -x 2 y+xy 212 、 2( a-1 ) - ( 2a-3 ) +3.=413、 -2 ( ab-3a 2) -[2b 2 - ( 5ab+a 2) +2ab]= 7a 2 +ab-2b 214、( x 2-xy+y ) -3 ( x 2 +xy-2y )= -2x 2 -4xy+7y15、 3x 2-[7x- ( 4x-3 ) -2x 2 ]=5x 2 -3x-316、 a2b-[2 (a2b-2a 2c) - ( 2bc+a2c)]= -a2b+2bc+6a2c 17、 -2y 3+( 3xy 2-x 2y) -2 ( xy 2-y 3) = xy 2-x 2y18、 2(2x-3y ) - ( 3x+2y+1)=2x-8y-119、-(3a2-4ab )+[a2-2 ( 2a+2ab) ]=-2a2 -4a20、 5m-7n-8p+5n-9m-p = -4m-2n-9p21、( 5x 2y-7xy 2) - ( xy 2-3x 2y) =4xy 2-4x 2y22、 3( -3a 2-2a )-[a 2-2 ( 5a-4a 2+1) -3a]=-18a 2 +7a+223、 3a2-9a+5- ( -7a 2+10a-5 ) =10a2-19a+1024、 -3a 2b- (2ab2-a 2b) - ( 2a2b+4ab2) = -4a 2b-64ab 225、( 5a-3a 2+1) - ( 4a3-3a 2) =5a-4a 2+126、 -2 ( ab-3a 2)-[2b 2 - ( 5ab+a2)+2ab]=7a 2 +ab-2b227、 (8 xy-x2+ y2) + ( -y2+ x2-8xy)=028、 (2 x2-1+3x) - 4( x- x2+1 )= 6x 2 -x- 52 2 229、 3x2-[ 7x- (4 x-3) - 2x2] = 5 x2- 3x- 330、 5a+( 4b-3a ) - ( -3a+b ) = 5a+3b31、( 3a 2 -3ab+2b 2) +( a 2 +2ab-2b 2) = 4a 2 -ab32、 2a 2 b+2ab 2 -[2 ( a 2 b-1 ) +2ab 2 +2] . = -1933 、( 2a 2-1+2a ) -3 ( a-1+a 2) = -a 2-a+234、 2( x 2-xy ) -3 ( 2x 2-3xy ) -2[x 2- ( 2x 2-xy+y 2) ]=-2x 2+5xy-2y 235、- 2+ 3 2 ++(-3 2 )-1 = 1ab-1 3 ab a b ab a b 3 4 436、 (8 xy -x 2+ y 2) + ( - y 2+ x 2- 8xy)=0 37、 2x - (3 x - 2y +3) - (5 y -2)=-x-3y-138、- (3 a + 2b) + (4 a - 3b +1) - (2 a -b - 3)= -a-4b+439、 3 3 3 x 3 4x - ( -6x ) + ( -9x ) =40、 3- 2xy + 2yx 2+ 6xy - 4x 2y = -2 x 2y+441、 1 - 3(2 ab + a) 十 [1 - 2(2 a -3ab)]=2-7a42、 3 - [5 x + (3 - 2)]=-5x+2x x43、 (3 a 2b - ab 2) - ( ab 2+ 3a 2b)= -2 ab 244、 2x3y 3x2 3x y= 5x+y45、(- x 2+5+4 x 3)+(- x 3+ 5 x -4)= 3x 3 - x 2+ 5 x+146、( 5a 2-2a+3 ) - ( 1-2a+a 2) +3( -1+3a-a 2) =a 2+9a-12 2 2 2 2 247、 5( 3a b-ab ) -4 ( -ab +3a b ). =3a b-ab48 、 4a 2+2( 3ab-2a 2) - ( 7ab-1 )=1-ab49、1xy+( - 1xy ) -2xy 2 -( -3y2x ) = 1xy+xy22 4 450 、 5a 2-[a 2- (5a 2-2a ) -2 ( a 2-3a ) ]=11a 2-8a 51 、 5m-7n-8p+5n-9m+8p=-4m-2n52、( 5x 2y-7xy 2) - ( xy 2-3x 2y ) =8x 2y-6xy 253 、 3x 2y-[2x 2y-3( 2xy-x 2y ) -xy]=-2x 2y+7xy54、 3x 2-[5x-4( 1 x 2-1)]+5x2 = 10x 2 -5x-4 255、 2a 3b- 1a 3b-a 2b+ 1a 2b-ab 2= 3a 3b- 1a 2b-ab 222 2 22 2 2 2 2 2 256、( a +4ab-4b ) -3 ( a +b ) -7 ( b -ab ) =-2a +11ab-14b58、 5ab+(-4a 2b 2) +8ab 2- ( -3ab ) +( -a 2b ) +4a 2b 2=8ab+8ab 2-a 2b 59 、( 7y-3z ) - ( 8y-5z ) =-y+2z60 、 -3 ( 2x 2-xy ) +4(x 2+xy-6 ) =-2x 2+7xy-24322 332 232 3 2 361、( x +3x y-5xy +9y ) +(-2y +2xy +x y-2x ) -(4x y-x -3xy +7y )=062、 -3x 2y+2x2y+3xy 2-2xy 2= -x 2y+xy263、 3( a2-2ab ) -2 ( -3ab+b 2) =3a 2 -2b 264、 5abc-{2a 2 2 2 2 2b-[3abc- ( 4a b-ab ]}=8abc-6a b+ab2 2 2 2 265、 5m-[m +(5m-2m) -2 ( m-3m)]=m -4m66、 -[2m-3( m-n+1) -2]-1=m-3n+467、1 a-( 1 a-4b-6c)+3(-2c+2b)=- 1 a+10b3 2 6n n n n n68、 -5a -a - ( -7a ) +( -3a ) = -2a1071、1 a 2b-0.4ab 2- 1 a 2b+2 ab 2=- 1 a 2b 4 2 5 4 71、 3a-{2c-[6a- ( c-b ) +c+( a+8b-6 ) ]}=10a+9b-2c-672、 -3 ( xy-2x 2) -[y2- (5xy-4x 2)+2xy]= 2x 2 -y 273、化简、求值 1 2 - 2- ( 1 2 2 )- 3 2 2 1 2 ) ,其中 x =- 2, y =- 42 x 2 x + y( - 3 x + 3 y 32 原式 =2x 2+ 1y 2- 2 =6 82 974、化简、求值 1x - 2( x - 1y 2) + ( - 3x + 1y 2) ,其中 x =- 2, y =-223 2 33原式 =-3x+y 2=6 4975、 1 x 33 x 2 2 x 3 1 x 2( 4x 6) 5x 其中 x =- 1 1; 32 32233276、 化简,求值( 4m+n ) -[1- ( m-4n ) ] , m=2n=-1 15 3原式 =5m-3n-1=577、化简、求值 2( a 2b +2b 3- ab 3) +3a 3- (2 ba 2- 3ab 2+ 3a 3) -4b 3,其中 a =- 3, b =2原式 =-2 ab 3+3ab 2= 1278、化简,求值: ( 2x 3-xyz ) -2 ( x 3-y 3+xyz ) +( xyz-2y 3),其中 x=1, y=2, z=-3 . 原式 =-2xyz=679、化简,求值: 5x 2-[3x-2 ( 2x-3 ) +7x 2] ,其中 x=-2 .原式 =-2x 2+x-6=-1680、若两个多项式的和是 2x 2+xy+3y 2,一个加式是 x 2-xy ,求另一个加式.( 2x 2+xy+3y 2)——( x 2-xy ) = x 2+2xy+3y 281、若 2a 2-4ab+b 2与一个多项式的差是-3a 2+2ab-5b 2,试求这个多项式.( 2a 2-4ab+b 2)—( -3a 2+2ab-5b 2) =5a 2-6ab+6b 282、求 5x 2y -2x 2y 与- 2xy 2+ 4x 2y 的和.( 5x 2y - 2x 2y )+(- 2xy 2+ 4x 2y )=3xy 2+ 2x 2y 83、 求 3x 2+x - 5 与 4- x + 7x 2的差.( 3x 2+ x - 5)—( 4- x + 7x 2) =— 4x 2+2x - 9 84 、计算 5y+3x+5z 2与 12y+7x-3z 2的和( 5y+3x+5z 2) +( 12y+7x-3z 2) =17y+10x+2z 285、计算 8xy 2 +3x 2 y-2 与 -2x 2 y+5xy 2 -3 的差(8xy 2 +3x 2 y-2 )—( -2x 2 y+5xy 2 -3 ) =5x 2 y+3xy 2 +11186、 多项式 -x 2+3xy- 1 y 与多项式 M 的差是- 1 x 2-xy+y ,求多项式 M2 2M=- 1x 2+4xy — 3y2 287、当 x=- 1, y=-3 时,求代数式 3( x 2-2xy ) -[3x 2-2y+2 ( xy+y ) ] 的值.2原式 =-8xy+y= — 1588、化简再求值 5abc-{2a2 b-[3abc- (4ab 2-a 2b )]-2ab 2} ,其中 a=-2 ,b=3,c=- 1 原4式=83abc-a 2b-2ab 2=3689、已知 A=a 2-2ab+b 2, B=a 2+2ab+b 2(1)求 A+B ;( 2)求 1(B-A) ;4 A+B=2a 2 +2b 21 (B-A)=ab4290、小明同学做一道题, 已知两个多项式 ,A ,B ,计算 A+B ,他误将 A+B 看作 A-B ,求得 9x -2x+7若 B=x 2+3x-2 ,你能否帮助小明同学求得正确答案?A=10x 2+x+5 A+B=11x 2+4x+3 91、已知: M=3x 2+2x-1 , N=-x 2-2+3x ,求 M-2N .M-2N=5x 2- 4x+392、已知 A 4x 24xy y 2 , B x 2xy 5 y 2,求 3A - B 3A- B=11x 2-13xy+8y293、已知 A = x 2+ xy + y 2,B =- 3xy - x 2,求 2A - 3B .2A -2 2 3B= 5 x +11 xy + 2y 94、已知 a 2 +( b +1) 2= 0,求 5ab 2-[2 a 2b - (4 ab 2- 2a 2b)] 的值.原式 =9 2-4 2ab a b=3495、化简求值: 5abc-2a 2b+[3abc-2 ( 4ab 2-a 2b )] ,其中 a 、b 、c 满足 |a-1|+|b-2|+c2=0.原式=8abc-8a 2b=-3296、已知 a , b , z 满足:( 1)已知 |x-2|+( y+3) 2=0,(2) z 是最大的负整数,化简求值: 2( x 2y+xyz ) -3 (x 2y-xyz ) -4x 2y .原式 =-5x 2y+5xyz=9097、已知 a+b=7, ab=10,求代数式( 5ab+4a+7b ) +( 6a-3ab ) - ( 4ab-3b )的值.原式 =10a+10b-2ab=502 2 -[+5m 22298、已知 m+3mn=5,求 5m - ( 2m-mn) -7mn-5] 的值原式=2m+6mn+5=1599、设 A=2x2-3xy+y 2+2x+2y , B=4x2 -6xy+2y 2-3x-y ,若 |x-2a|+( y-3 )2 =0,且 B-2A=a,求a 的值.B-2A=-7x-5y=-14a-15=a a=-1100、有两个多项式: A=22-4+ 1, B=2(a2-2a)+3,当a取任意有理数时,请比较Aa a与 B 的大小.A=2 a2-4a+ 1 B = 2a2- 4a+3所以 A<B12。
人教版数学七年级上册整式计算专项练习200题及答案解析

1写出下列单项式的系数和次数:2找出下列各代数式中的单项式(画3把多项式4计算:5化简:6解答下列问题:7解答下列各题:8请回答下列问题:9先化简,再求值:10先化简后求值:已知11已知12化简:13化简:14已知15合并同类项.16“1718先化简,再求值:19已知当20已知21先化简再求值.22化简:23已知24课堂上李老师给出了一道整式求值的题目,李老师把要求的整式25若关于26先化简,再求值:27已知28有这样一道题29有这样一道题:30先化简,再求值31已知32小明做一道题33已知多项式34先化简,再求值:35已知老师在黑板上书写了一个正确的演算过程随后用手掌捂住了如图所示的一个二次三项式,形式如36化简:37计算:38计算:39计算:40计算:41化简下列各式4243先化简,再求值:44若多项式45已知46已知47小红做一道数学题48先化简,再求值:49先化简,再求值:50已知:51先化简,后求值:已知52若53先化简再求值:54先化简,再求值:55解答下列各题:56完成下列小题.57化简求值,先化简代数式:58先化简,再求值:59先化简,再求值:60小明同学做数学题:已知两个多项式61回答问题.62先化简,再求值:63先化简,再求值:64先化简,再求值:65先化简,再求值:66化简:67先化简,再求值:68先化简,再求值:先化简,再求值:69化简:70已知:多项式71先化简,再求值:72先化简,再求值:73化简求值:74先化简,再求值:7576化简:77计算:78先化简,再求值:79化简:80已知81化简:82先化简,再求值:83阅读下面的解题过程并回答问题.84计算:8586解答下列问题.先化简,再求值:87先化简,再求值:88下列去括号正确的是(89下列去括号或添括号:90当9192如果单项式93单项式9495关于多项式9697先化简,再求值:98若代数式99若100观察下列运算并填空.1 23 4 5 67 8 9 10 11 1213 14 15 16 17 18 1920 21 22 23 24 25 26 2728 29 30 31 32 33 34 3536 37 38 39 40 41 4243 44 45 46 47 48 4950 51 52 53 54 55 5657 58 59 60 61 62 63 6465 66 67 68 69 70 7173 74 75 76 77 78 7981 82 83 84 85 8687 88 89 90 91 9293 94 9596 9798 99 100。
七年级数学上册第二单元《整式加减》-解答题专项测试题

一、解答题1.让我们规定一种运算a b ad cb c d=-, 如232534245=⨯-⨯=-. 再如14224x x =-. 按照这种运算规定,请解答下列问题,(1)计算60.5142= ;-3-245= ;2-335x x=- (2)当x=-1时,求223212232x x x x -++-+---的值(要求写出计算过程).解析:(1)1;-7;-x ;(2)-7 【分析】(1)根据新运算的定义式,代入数据求出结果即可;(2)根据新运算的定义式将原式化简为-x-8,代入x=-1即可得出结论. 【详解】解:(1)60.5160.543211242=⨯-⨯=-=; -3-23524158745=-⨯--⨯=---=-()(); 2-3253310935xx x x x x x=⨯---⨯=---=--()()().故答案为:1;-7;-x .(2)原式=(-3x 2+2x+1)×(-2)-(-2x 2+x-2)×(-3), =(6x 2-4x-2)-(6x 2-3x+6), =-x-8,当x=-1时,原式=-x-8=-(-1)-8=-7.∴当x=-1时,223212232x x x x -++-+---的值为-7.【点睛】本题考查了整式的化简求值以及有理数的混合运算,读懂题意掌握新运算并能用其将整式进行化简是解题的关键. 2.若单项式21425m n x y +--与413n mx y +是同类项,求这两个单项式的积 解析:10453x y -【分析】根据题意,可得到关于m ,n 的二元一次方程组,求出m ,n 的值,即可求得答案. 【详解】∵单项式21425m n x y +--与413n mx y +是同类项, ∴21442m n n m +=+⎧⎨-=⎩,解得21m n =⎧⎨=⎩,∴21425252441011355533n m m n x y xy x y x y x y ++--⋅-⋅=-=【点睛】本题主要考查同类项的定义和单项式乘单项式的法则,根据同类项的定义,列出关于m ,n 的二元一次方程组,是解题的关键.3.已知22332A x y xy =+-,2222B xy y x =--. (1)求23A B -.(2)若|23|1x -=,29y =,且||x y y x -=-,求23A B -的值.解析:(1)2212127x y xy +-;(2)114或99.【分析】(1)把22332A x y xy =+-,2222B xy y x =--代入23A B -计算即可;(2)根据|23|1x -=,29y =,且||x y y x -=-求出x 和y 的值,然后代入(1)中化简的结果计算即可. 【详解】 解:(1)()()2222232332322A B x y xy xy y x-=+----2222664366x y xy xy y x =+--++ 2212127x y xy =+-;(2)由题意可知:231x -=±,3=±y , ∴2x =或1,3=±y ,由于||x y y x -=-, ∴2x =,3y =或1x =,3y =. 当2x =,3y =时,23114A B -=. 当1x =,3y =时,2399A B -=. 所以,23A B -的值为114或99. 【点睛】本题考查了整式的加减运算,绝对值的意义,以及分类讨论的数学思想,熟练掌握整式的加减运算法则是解(1)的关键,分类讨论是解(2)的关键.4.为鼓励居民节约用电,某市采用价格调控手段达到省电目的,该市电费收费标准如下表(按月结算):(2)设某月的用电量为x 度(0300x <≤),试写出不同电量区间应缴交的电费.解析:(1)该居民12月份应缴电费94.5元;(2)0.5,01500.6522.5,1502500.860,250300x x x x x x <≤⎧⎪-<≤⎨⎪-<≤⎩【分析】(1)根据用电量类型分别进行计算即可;(2)分三种情况进行讨论,当x 不超过150度时,x 超过150度,但不超过时250度时和x 超过250度时,再分别代入计算即可. 【详解】解:(1)由题意,得150×0.50+(180-150)×0.65=94.5(元) 答:该居民12月应缴交电费94.5元;(2)若某户的用电量为x 度,则当x≤150时,应付电费:0.50x 元; 当150<x≤250时,应付电费:0.65(x -150)+75=0.65x 22.5-(元); 当250<x <300,应付电费:0.80(x -250)+140=0.8x 60-(元).∴不同电量区间应缴交的电费为:0.5,01500.6522.5,1502500.860,250300x x x x x x <≤⎧⎪-<≤⎨⎪-<≤⎩.【点睛】本题考查了列代数式,读懂题目信息,理解阶梯电价的收费方法和电费的计算方法是解题的关键.5.已知一个多项式加上223x y xy -得222x y xy -,求这个多项式. 佳佳的解题过程如下:解:222223x y xy x y xy ---①224x y xy =-②请问佳佳的解题过程是从哪一步开始出错的?并写出正确的解题过程. 解析:是从第①步开始出错的,见解析 【分析】根据多项式的加减运算法则进行运算即可求解. 【详解】解:佳佳是从第①步开始出错的,正确的解题过程如下: 根据题意,得:()()222223x y xyxy xy ---222223x y xy x y xy =--+222x y xy =+,∴这个多项式为222x y xy +. 故答案为222x y xy +. 【点睛】本题考查了多项式的加减混合运算,注意:只有同类项才能进行加减运算. 6.已知222242,325A ab b a B b a ab =--=-+,当11.5,2a b ==-时,求34B A -的值.解析:12【分析】根据题意,先根据整式的混合运算法则化简34B A -,再将a ,b 的值代入即可. 【详解】()()2222222234332544296151684B A b a ab ab b a b a ab ab b a -=-+---=-+-++=22172b a ab --,当11.5,2a b ==-时,原式22111931172 1.5 1.517224242⎛⎫⎛⎫=⨯--⨯-⨯-=⨯-+= ⎪ ⎪⎝⎭⎝⎭. 【点睛】本题主要考查了整式的化简求值,熟练掌握整式的混合运算法则以及有理数的运算是解决本题的关键.7.有这样一道题“求多项式3323323763363101a a b a b a a b a b a -+++--+的值,其中99.01,123.89a b ==-”,有一位同学把99.01a =抄成99.01,123.89a b =-=-抄成123.89b =,结果也正确,为什么?解析:见解析 【分析】原式合并同类项得到最简结果为常数1,这个多项式的值与a 、b 的值无关,故a ,b 的值抄错后,答案仍然是1 【详解】解:∵3323323763363101a a b a b a a b a b a -+++--+()()()33333227310663311a a a a b a b a b a b =+-+-++-+=;∴这个多项式的值与,a b 的值无关,故,a b的值抄错后结果也正确.【点睛】此题考查了整式的加减——化简求值,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握运算法则是解本题的关键.8.(规律探究题)用计算器计算下列各式,将结果填写在横线上.99999×11=__________;99999×12=__________;99999×13=__________;99999×14=__________.(1)你发现了什么?(2)不用计算器,你能直接写出99999×19的结果吗?解析:1099989;1199988;1299987;1399986;(1)如果n是11,12,13,…,20中的任何一个数,则:99999×n=(n-1)9998(20-n),其中(n-1)9998(20-n)是1个7位数,前2位是n-1,个位是20-n,中间4个数字总是9998;(2)99999×19=1899981【分析】用计算器分别进行计算,再根据结果找出规律,最后根据规律即可直接写出99999×19的结果.【详解】解:99999×11=1099989;99999×12=1199988;99999×13=1299987;99999×14=1399986.故答案为:1099989;1199988;1299987;1399986.(1)通过计算观察可发现以下规律:如果n是11,12,13,…,20中的任何一个数,则:99999×n=(n-1)9998(20-n),其中(n-1)9998(20-n)是1个7位数,前2位是n-1,个位是20-n,中间4个数字总是9998.(2)根据以上规律可直接写出:99999×19=1899981.【点睛】此题考查了计算器−有理数,解题的关键是通过用计算器计算,找出规律,通过规律进行解答.9.上海与南京间的公路长为364km,一辆汽车以xkm/h的速度开往南京,请用代数式表示:(1)汽车从上海到南京需多少小时?(2)如果汽车的速度增加2km/h,从上海到南京需多少小时?(3)如果汽车的速度增加2km/h,可比原来早到几小时?解析:(1)364xh;(2)3642x+h;(3)3643642x x⎛⎫-⎪+⎝⎭h【分析】(1)根据题意,可以用代数式表示出汽车从上海到南京需要的时间;(2)根据题意,可以用代数式表示出汽车的速度增加2千米/时,从上海到南京需要的时间;(3)根据题意,可以用代数式表示出如果汽车的速度增加2千米/时,可比原来早到几小时. 【详解】解:(1)汽车从上海到南京需364xh ; (2)如果汽车的速度增加2km/h ,从上海到南京需3642x +h ; (3)如果汽车的速度增加2km/h ,可比原来早到3643642xx ⎛⎫- ⎪+⎝⎭h . 【点睛】本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式. 10.先化简,再求值:-2x 2-2[3y 2-2(x 2-y 2)+6],其中x =-1,y =-2. 解析:2221012x y --,-50. 【分析】根据整式的加减及合并同类项先对原式进行化简,得到2221012x y --,再将1,2x y =-=-代入即可求解,需要注意本题中两次遇到去括号,注意符号的改变.【详解】原式=2222223226x y x y ⎡⎤---++⎣⎦ =2222264412x y x y --+-- =2222246412x x y y -+--- =2221012x y --,当1,2x y =-=-时,原式=222(1)10(2)1250⨯--⨯--=-.【点睛】本题主要考查了去括号,整式的加减,合并同类项,乘法的分配律等相关内容,熟练掌握各项计算法则是解决本题的关键,注意去括号中符号的改变原则. 11.数学课上,老师出示了这样一道题目:“当1,22a b ==-时,求多项式3233233733631061a a b a a b a b a a b +++----的值”.解完这道题后,张恒同学指出:“1,22a b ==-是多余的条件”师生讨论后,一致认为这种说法是正确的,老师及时给予表扬,同学们对张恒同学敢于提出自己的见解投去了赞赏的目光. (1)请你说明正确的理由;(2)受此启发,老师又出示了一道题目,“无论x 取任何值,多项式2233x mx nx x -++-+的值都不变,求系数m 、n 的值”.请你解决这个问题.解析:(1)见解析;(2)3n =,1m =.【分析】(1)将原式进行合并同类项,然后进一步证明即可;(2)将原式进行合并同类项,根据“无论x 取任何值,多项式值不变”进一步求解即可. 【详解】(1)3233233733631061a a b a a b a b a a b +++---- =3332233731033661a a a a b a b a b a b +-+-+-- =1-,∴该多项式的值与a 、b 的取值无关, ∴1,22a b ==-是多余的条件. (2)2233x mx nx x -++-+ =2233x nx mx x -++-+ =2(3n)(1)3x m x -++-+ ∵无论x 取任何值,多项式值不变, ∴30n -+=,10m -=, ∴3n =,1m =. 【点睛】本题主要考查了多项式运算中的无关类问题,熟练掌握相关方法是解题关键.12.已知多项式234212553x x x x ++-- (1)把这个多项式按x 的降冥重新排列;(2)请指出该多项式的次数,并写出它的二次项和常规项.解析:(1)432215253x x x x -+++-;(2)该多项式的次数为4,二次项是22x ,常数项是13-. 【分析】(1)按照x 的指数从大到小的顺序把各项重新排列即可;(2)根据多项式的次数的定义找出次数最高的项即是该多项式的次数,再找出次数是2的项和不含字母的项即可得二次项和常数项. 【详解】(1)按的降幂排列为原式432215253x x x x -+++-. (2)∵234212553x x x x ++--中次数最高的项是-5x 4, ∴该多项式的次数为4,它的二次项是22x ,常数项是13-.【点睛】本题考查多项式的定义,正确掌握多项式次数及各项的判定方法及多项式升幂、降幂排列方法是解题关键.13.国庆期间,广场上设置了一个庆祝国庆70周年的造型(如图所示).造型平面呈轴对称,其正中间为一个半径为b 的半圆,摆放花草,其余部分为展板.求: (1)展板的面积是 .(用含a ,b 的代数式表示) (2)若a =0.5米,b =2米,求展板的面积.(3)在(2)的条件下,已知摆放花草部分造价为450元/平方米,展板部分造价为80元/平方米,求制作整个造型的造价(π取3).解析:(1)12ab 平方米;(2)12 (平方米);(3)3660元. 【分析】(1)利用分割法求解即可.(2)把a ,b 的值代入(1)中代数式求值即可.(3)分别求出摆放花草部分造价,展板部分造价即可解决问题. 【详解】(1)由题意:展板的面积=12a •b (平方米). 故答案为:12ab (平方米).(2)当a =0.5米,b =2米时,展板的面积=12×0.5×2=12(平方米). (3)制作整个造型的造价=12×8012+π×4×450=3660(元). 【点睛】本题考查轴对称图形,矩形的性质,圆的面积等知识,解题的关键是熟练掌握基本知识. 14.化简与求值:(1)若1a =-,则式子21a -的值为______; (2)若1a b +=,则式子12a b++的值为______; (3)若534a b +=-,请你仿照以上求式子值的方法求出()()2422a b a b +++-的值. 解析:(1)0;(2)32;(3)-10. 【分析】(1)把a 的值代入计算即可; (2)把a+b 的值代入计算即可;(3)原式去括号转化为含有(5a+3b)的式子,然后代入5a+3b 的值计算即可. 【详解】解:(1)()221110a -=--=;(2)1311222a b ++=+=; (3)()()()()24221062253224210a b a b a b a b +++-=+-=+-=⨯--=-. 【点睛】本题考查的是整式的化简求值和整体代换的思想.只要原式化简出含有已知的式子,再代入求值即可.15.如图,某市有一块长为(3a+b )米,宽为(2a+b )米的长方形地块,中间是边长为(a+b )米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化,(1)绿化的面积是多少平方米?(用含字母a 、b 的式子表示) (2)求出当a =20,b =12时的绿化面积.解析:(1)(5a 2+3ab )平方米;(2)2720平方米 【分析】(1)根据割补法,用含有a,b 的式子表示出整个长方形的面积,然后用含有a,b 的式子表示出中间空白处正方形的面积,然后两者相减,即可求出绿化部分的面积. (2)将a =20,b =12分别代入(1)问中求出的关系式即可解决. 【详解】解:(1)(3a+b )(2a+b )﹣(a+b )2=6a 2+3ab+2ab+b 2﹣(a 2+2ab+b 2)=6a 2+3ab+2ab+b 2﹣a 2﹣2ab ﹣b 2=5a 2+3ab , 答:绿化的面积是(5a 2+3ab )平方米; (2)当a =20,b =12时 5a 2+3ab =5×202+3×20×12=2000+720=2720, 答:当a =20,b =12时的绿化面积是2720平方米. 【点睛】(1)本题考查了割补法,多项式乘多项式和完全平方式的运算法则,解决本题的关键是正确理解题意,能够熟练掌握多项式乘多项式的运算法则.(2)本题考查了整式的化简求值,解决本题的关键是熟练掌握整式的运算法则和步骤. 16.在数学活动课上,李老师设计了一个游戏活动,四名同学分别代表一种运算,四名同学可以任意排列,每次排列代表一种运算顺序,剩余同学中,一名学生负责说一个数,其他同学负责运算,运算结果既对又快者获胜,可以得到一个奖品. 下面我们用四个卡片代表四名同学(如下):(1)列式,并计算:①3-经过A ,B ,C ,D 的顺序运算后,结果是多少? ②5经过B ,C ,A ,D 的顺序运算后,结果是多少?(2)探究:数a 经过D ,C ,A ,B 的顺序运算后,结果是45,a 是多少? 解析:(1)①7;②206;(2)256a =或256a =- 【分析】(1)把-3和5经过A ,B ,C ,D 的运算顺序计算即可; (2)根据已知条件列列出关于a 的方程计算即可; 【详解】(1)①2[(3)2(5)]67-⨯--+=;②2[5(5)]26206--⨯+=;(2)()()226545a +--=,()2620a +=, 解得256a =或256a =-. 【点睛】本题主要考查了规律型数字变化类,一元二次方程的求解,准确计算是解题的关键. 17.观察下列单项式:﹣x ,2x 2,﹣3x 3,…,﹣9x 9,10x 10,…从中我们可以发现: (1)系数的规律有两条: 系数的符号规律是 系数的绝对值规律是 (2)次数的规律是(3)根据上面的归纳,可以猜想出第n 个单项式是 .解析:(1)奇数项为负,偶数项为正;与自然数序号相同;(2)与自然数序号相同;(3)(1)n nnx -【分析】通过观察题意可得:奇数项的系数为负,偶数项的系数为正,且系数的绝对值与自然数序号相同,次数也与与自然数序号相同.由此可解出本题. 【详解】(1)奇数项为负,偶数项为正, 与自然数序号相同; (2)与自然数序号相同;(3)(1)n nnx -.【点睛】本题考查了单项式的有关概念.确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.分别找出单项式的系数和次数的规律也是解决此类问题的关键.18.若关于x ,y 的多项式my 3+3nx 2y +2y 3-x 2y +y 不含三次项,求2m +3n 的值. 解析:-3.【分析】先合并同类项,根据已知得出m+2=0,3n-1=0,求出m 、n 的值后代入进行计算即可.【详解】my 3+3nx 2y +2y 3-x 2y +y =(m +2)y 3+(3n -1)x 2y +y ,∵此多项式不含三次项,∴m +2=0,3n -1=0,∴m =-2,n =13, ∴2m +3n =2×(-2)+3×13=-4+1=-3. 【点睛】本题考查了合并同类项和解一元一次方程的应用,关键是求出m 、n 的值.19.数a 、b 、c 在数轴上对应的位置如图所示,化简a c c b a b +-++-.解析:0;【分析】由数轴可得a >0>b >c ,并从数轴上可得出a ,b ,c 绝对值的大小,从而可以得出各项式子的正负,去绝对值可得出答案.【详解】解:由数轴得,c b 0a <<<,且c a b >>,a c cb a b +-++-a c cb a b =--+++-0=.【点睛】本题考查了数轴上数的大小,去绝对值,熟悉掌握定义是解决本题的关键.20.父母带着孩子(一家三口)去旅游,甲旅行社报价大人为a 元,小孩为a 2元;乙旅行社报价大人、小孩均为a 元,但三人都按报价的90%收费,则乙旅行社收费比甲旅行社贵多少元?(结果用含a 的代数式表示)解析:乙旅行社收费比甲旅行社贵0.2a 元.【分析】根据题意分别表示出甲乙两旅行社的费用,相减即可得到结果.【详解】根据题意得:(a+a+a )×90%-(a+a+12a ) =2.7a-2.5a=0.2a (元), 则乙旅行社收费比甲旅行社贵0.2a 元.【点睛】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.21.已知多项式﹣3x 2+mx+nx 2﹣x+3的值与x 无关,求(2m ﹣n )2017的值.解析:-1【分析】先把多项式进行合并同类项得(n-3)x 2+(m-1)x+3,由于关于字母x 的二次多项式-3x 2+mx+nx 2-x+3的值与x 无关,即不含x 的项,所以n-3=0,m-1=0,然后解出m 、n ,代入计算(2m-n )2017的值即可.【详解】合并同类项得(n ﹣3)x 2+(m ﹣1)x+3,根据题意得n ﹣3=0,m ﹣1=0,解得m=1,n=3,所以(2m ﹣n )2017=(﹣1)2017=﹣1.【点睛】考查了多项式及相关概念:几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数. 22.国庆期间,王老师计划组织朋友去晋西北游览两日.经了解,现有甲、乙两家旅行社针对组团两日游的游客报价均为每人500元,且提供的服务完全相同.甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按八折收费.假设组团参加甲、乙两家旅行社两日游的人数均为x 人. (1)请列式表示甲、乙两家旅行社收取组团两日游的总费用;(2)若王老师组团参加两日游的人数共有30人,请你通过计算,在甲、乙两家旅行社中,帮助王老师选择收取总费用较少的一家.解析:(1)甲旅行社收取组团两日游的总费用为425x 元;若人数不超过20人时,乙旅行社收取组团两日游的总费用为450x 元;若人数超过20人时,乙旅行社收取组团两日游的总费用为(4001000x +)元;(2)王老师应选择甲旅行社.【分析】(1)根据总费用等于人数乘以打折后的单价,易得甲旅行社的费用=500 x×0.85,对于乙家旅行社的总费用,应分类讨论:当0≤x≤20时,乙旅行社的费用=500 x×0.9;当x >20时,乙旅行社的费用=500×20×0.9+500(x-20)×0.8;(2)把x=30分别代入(1)中对应关系计算甲旅行社的费用和乙旅行社的费用的值,然后比较大小即可.【详解】(1)甲旅行社收取组团两日游的总费用为:5000.85425x x ⨯=元若人数不超过20人时,乙旅行社收取组团两日游的总费用为:5000.9450x x ⨯=元 若人数超过20人时,乙旅行社收取组团两日游的总费用为:()500(20)0.8500200.94001000-⨯+⨯⨯=+x x 元(2)因为王老师组团参加两日游的人数共有30人,所以甲旅行社收取组团两日游的总费用为:4253012750⨯=元乙旅行社收取组团两日游的总费用为40030100013000⨯+=元1275013000<,王老师应选择甲旅行社.【点睛】本题考查了代数式,能根据具体情境列代数式并求代数式的值是关键.23.将正整数1,2,3,4,5,……排列成如图所示的数阵:(1)十字框中五个数的和与框正中心的数11有什么关系?(2)若将十字框上下、左右平移,可框住另外五个数,这五个数的和与框正中心的数还有这种规律吗?请说明理由;(3)十字框中五个数的和能等于180吗?若能,请写出这五个数;若不能,请说明理由; (4)十字框中五个数的和能等于2020吗?若能,请写出这五个数;若不能,请说明理由.解析:(1)十字框中五个数的和是正中心数的5倍;(2)十字框中五个数的和是正中心数的5倍,理由见解析;(3)不能,理由见解析;(4)这五个数是404,403,405,397,411.【分析】(1)把框住的数相加即可求解;(2)设中心的数为a ,则其余4个数分别为1a -,1a +,7a -,7a +,相加即可得到规律;(3)由(2)得五个数的和为5a ,令5a=180,根据解得情况即可求解;(4)由(2)得五个数的和为5a ,令5a=2020,根据解得情况即可求解;【详解】解:(1)十字框中五个数的和是正中心数的5倍.∵十字框中五个数的和41011121855511=++++==⨯,∴十字框中五个数的和是正中心数的5倍.(2)五个数的和与框正中心的数还有这种规律.设中心的数为a ,则其余4个数分别为1a -,1a +,7a -,7a +.11775a a a a a a +-+++-++=,∴十字框中五个数的和是正中心数的5倍.(3)十字框中五个数的和不能等于180.∵当5180a =时,解得36a =,36751÷=,36在数阵中位于第6排的第1个数,其前面无数字,∴十字框中五个数的和不能等于180.(4)十字框中五个数的和能等于2020.∵当52020a =时,解得404a =,4047575÷=,404在数阵中位于第58排的第5个数,∴十字框中五个数的和能等于2020,这五个数是404,403,405,397,411.【点睛】此题主要考查一元一次方程的应用,解题的关键是设中心的数为a ,求出十字框中五个数的和为5a.24.已知A =2a 2+3ab ﹣2a ﹣1,B =﹣a 2+1223ab + (1)当a =﹣1,b =﹣2时,求4A ﹣(3A ﹣2B )的值;(2)若(1)中式子的值与a 的取值无关,求b 的值.解析:(1)4ab ﹣2a+13;(2)b=12 【分析】(1)将a=﹣1,b=﹣2代入A=2a 2+3ab ﹣2a ﹣1,B=﹣a 2+12ab+23,求出A 、B 的值,再计算4A ﹣(3A ﹣2B )的值即可;(2)把(1)结果变形,根据结果与a 的值无关求出b 的值即可.【详解】(1)4A ﹣(3A ﹣2B )=4A ﹣3A+2B=A+2B ,∵A=2a 2+3ab ﹣2a ﹣1,B=﹣a 2+12ab+23, ∴A+2B=2a 2+3ab ﹣2a ﹣1+2(﹣a 2+12ab+23) =2a 2+3ab ﹣2a ﹣1﹣2a 2+ab+43 =4ab ﹣2a+13; (2)因为4ab ﹣2a+13 =(4b ﹣2)a+13, 又因为4ab ﹣2a+13的值与a 的取值无关, 所以4b ﹣2=0,所以b=12. 【点睛】本题考查了整式的加减、化简求值,熟练掌握运算法则是解答本题的关键.25.学习了整式的加减运算后,张老师给同学们布置了一道课堂练习题“当2a =-,2018b =,求222221(324)2(23)2()12a b ab a a b a ab a b -+--++-的值”.小明做完后对同桌说:“老师给的条件2018b =是多余的,这道题不给b 的值,照样可以求出结果来”.同桌不相信他的话.亲爱的同学们,你相信小明的说法吗?解析:-21【分析】首先化简代数式,通过去括号、合并同类项,得出结论即含有b 的代数式相加为0,即可说明.【详解】解()()222221324223212a b ab a a b a ab a b ⎛⎫-+--++- ⎪⎝⎭=222223244621a b ab a a b a ab a b -+-+++-=101a -当2a =-时原式=()1021⨯--=-21.【点睛】考查整式的化简求值,熟练掌握去括号法则以及合并同类项法则是解题的关键. 26.已知230x y ++-=,求152423x y xy --+的值. 解析:-24.【分析】首先根据绝对值的非负性求出x ,y ,然后代入代数式求值.【详解】解:∵230x y ++-=,∴x+2=0,y-3=0,∴x=-2,y=3, ∴152423x y xy --+ ()()552342323=-⨯--⨯+⨯-⨯ ()5524=-+-24=-.【点睛】本题考查了代数式求值,利用非负数的和为零得出x 、y 的值是解题关键.27.已知:A=2x 2+ax ﹣5y+b ,B=bx 2﹣32x ﹣52y ﹣3. (1)求3A ﹣(4A ﹣2B )的值;(2)当x 取任意数值,A ﹣2B 的值是一个定值时,求(a+314A )﹣(2b+37B )的值. 解析:(1)(2b ﹣2)x 2﹣(a+3)x ﹣(b+6);(2)﹣312. 【分析】(1)先化简原式,再分别代入A 和B 的表达式,去括号并合并类项即可;(2)先代入A 和B 的表达式并去括号并合并类项,由题意可令x 和x 2项的系数为零,求解出a 和b 的数值,再化简原式后代入相关数值即可求解.【详解】解:(1)∵A=2x 2+ax ﹣5y+b ,B=bx 2﹣32x ﹣52y ﹣3, ∴原式=3A ﹣4A+2B=﹣A+2B=﹣2x 2﹣ax+5y ﹣b+2bx 2﹣3x ﹣5y ﹣6=(2b ﹣2)x 2﹣(a+3)x ﹣(b+6);(2)∵A=2x 2+ax ﹣5y+b ,B=bx 2﹣32x ﹣52y ﹣3, ∴A ﹣2B=2x 2+ax ﹣5y+b ﹣2bx 2+3x+5y+6=(2﹣2b )x 2+(a+3)x+(b+6),由x 取任意数值时,A ﹣2B 的值是一个定值,得到2﹣2b=0,a+3=0,解得:a=﹣3,b=1,则原式=a ﹣2b+314(A ﹣2B )=﹣3﹣2+32=﹣312. 【点睛】理解本题中x 取任意数值时A ﹣2B 的值均是一个定值的意思是整式化简后的x 和x 2项的系数均为零是解题关键.28.有一长方体形状的物体,它的长,宽,高分别为a ,b ,c(a>b>c),有三种不同的捆扎方式(如图所示的虚线).哪种方式用绳最少?哪种方式用绳最多?说明理由.解析:方式甲用绳最少,方式丙用绳最多.【解析】试题分析:根据长方形的对称性分别得到三种方式所需要的绳子的长度,然后将这三个代数式进行作差比较大小.试题方式甲所用绳长为4a +4b +8c ,方式乙所用绳长为4a +6b +6c ,方式丙所用绳长为6a +6b +4c ,因为a>b>c ,所以方式乙比方式甲多用绳(4a +6b +6c)-(4a +4b +8c)=2b -2c ,方式丙比方式乙多用绳(6a +6b +4c)-(4a +6b +6c)=2a -2c.因此,方式甲用绳最少,方式丙用绳最多.29.先化简,再求值(1)()223421332a a a a -+-+-,其中23a =- (2)()()22352542m mn mn m -+--+,其中22m mn -=解析:(1)原式=23362a a --+;256;(2)原式()2111m mn =-+;23. 【分析】(1)根据整式的运算法则,先将整式进行化简,再将字母的值代入计算求值即可.(2)根据整式的运算法则,去括号合并同类项,将整式化成最简,然后将字母的值代入计算即可.【详解】解(1)原式=22333-4233222a a a a ⨯-⨯++-=22363332a a a a --++-=23362a a --+ 将23a =-代入得:222336332⎛⎫⎛⎫-⨯--⨯-+ ⎪ ⎪⎝⎭⎝⎭=256; (2)原式=()()2222352542351084m mn mn m m mn mn m -+--+=+-+-- ()2111m mn =-+将22m mn -=代入得:11×2+1=23【点睛】本题考查了整式的化简求值,解决本题的挂件是正确理解题意,熟练掌握整式的运算法则,将整式正确进行化简.30.先化简,再求值:()()22222322a b ab a b ab a b -+---,其中1a =,2b =-. 解析:2ab -,4-.【分析】先去括号,再合并同类项,再将1a =,2b =-代入原式求值即可.【详解】原式22222423a b ab a b ab a b +=-+-- 22(112)(34)a b ab =--++-2ab =-,当1a =,2b =-时,原式21(2)4=-⨯-=-【点睛】本题考查了整式的化简求值问题,掌握整式化简的方法、合并同类项的方法是解题的关键.。
七年级上册数学整式的加减计算题50道(含答案)

七年级数学整式的加减计算题50道1.化简求值:−12a−2(a−12b2)−(32a−13b2),其中a=−2,b=32.2.已知a、b互为相反数,x、y互为倒数,m的绝对值是2,求:13(a+b)2−6xy+m3的值。
3.已知代数式A=x2+xy−2y,B=2x2−2xy+x−1(1)求2A−B;(2)若2A−B的值与x的取值无关,求y的值.4.计算:(1)12+(−34)+(−23)(2)(3x2−xy−2y2)−2(x2+xy−2y2)5.先化简,再求值:(3a2−ab+7)−(−4a2+2ab+7),其中a=−1,b=26.化简:(1)−3m+3n−5m−7n(2)5a2−[3a−2(a−3)+4a2]7.若−2a m b与a2b n是同类项,求2mn2−[2m2n−3(m2n−2mn2)]的值.8.化简下列各式(1)3ab−a2−2ab−3a2(2)−2(x2−3xy)+6(x2−12 xy)9.计算与化简:(1)30−48×(16+34−112)(2)−14−2×(−3)2÷(−16)(3)5(x+y)−4(3x−2y)+3(2x−y)(4)6ab2−[a2b+2(a2b−3ab2)]10.化简11.先化简,再求值:5x2−[2xy−3(13xy+2)+4x2]。
其中x=−2,y=12。
12.化简(1)4x2y−8xy2−9−4x2y+12xy2+5;(2)−(2a2b−5ab)+2(−ab+a2b−1).13.计算:(1)(3a−2)−3(a−5)(2)(4a2b−5ab2)−(3a2b−4ab2)14. 合并下列多项式中的同类项:(1)3a 2+4b 2+ab −3a 2−4b 2;.15. 已知A =3ax 3−bx ,B =−ax 3−2bx +8.(1)求A +B ;(2)当x =−1时,A +B =10,求代数式3b −2a 的值.16. 计算:(1)16÷(−12)×(−38)−(+4)(2)−12020÷(−5)2×(−53)−|0.8−1| (3)2a +(3a 1)(a 5)(4)3x 2y 4xy 23+5x 2y +2xy 2+5.17.化简.(1)(8a−7b)−(−4a+5b)(2)a+(2a+b)−2(a−2b)18.化简:(l)m−2n+3(m+n);(2)5(a2b−ab)−2(−a2b+3ab)。
部编数学七年级上册专题06整式的化简与求值专项训练40题(解析版)含答案

专题06 整式的化简与求值 专项训练40题1.(2022·山东青岛·七年级阶段练习)先化简,再求值:()3222231322362b a a ab a b æö---+-ç÷èø,其中2a =,1b =-.2.(2022·内蒙古赤峰·七年级期末)先化简,再求值:()()22222322x y xy x y x xy y +----,其中x ,y 的值满足()2220x y ++-=3.(2022·山东威海·期末)计算:(1)()()222433224ab b ab b +--+-; (2)()2323132424424433xy x xy x æö-+---+ç÷èø.(3)先化简,再求值:13(2)3(2)2a ab a b --+-+,其中4a =-,12b =.4.(2022·湖南常德·七年级期中)先化简,再求值:221123(4)22ab ab a b a ---êúêú,其中122a b =-=,5.(2021·黑龙江哈尔滨·七年级期末)先化简,再求值:()224222éù---+ëûx y xy xy x y xy ,其中x 与y 互为倒数.【答案】4xy -;4-【分析】根据x 与y 互为倒数,可得1xy =,原式去括号合并同类项后得到最简结果,再把1xy =代入计算即可求出值.【详解】解:原式()224222=--++x y xy xy x y xy 2244242=-+--x y xy xy x y xy 4xy=-∵x 与y 互为倒数,∴1xy =,∴原式4414=-=-´=-xy .【点睛】本题考查整式的加减—化简求值,熟练掌握去括号法则与合并同类项法则是解题的关键.6.(2021·湖北咸宁·七年级期中)先化简后求值:2223322()2x y xy yx x y éù---êú,其中15,5x y ==-.7.(2022·贵州铜仁·七年级期末)先化简,再求值:()222242x xy y x xy y -+--+,其中11,2x y =-=-.8.(2022·山东烟台·期末)先化简,再求值:()()22333244b a ab b a ab éùéù----+-ëûëû,其中a =-4,14b =.9.(2022·黑龙江大庆·期中)先化简再求值:22113122223a a b a b æöæö-----ç÷ç÷,其中2a =-,32b =.10.(2022·内蒙古鄂尔多斯·七年级期末)先化简,再求值:(1)3(2a 2b ﹣ab 2)﹣(5a 2b ﹣4ab 2),其中a =2,b =1;(2)若a 2+2b 2=5,求多项式(3a 2﹣2ab +b 2)﹣(a 2﹣2ab ﹣3b 2)的值.【答案】(1)a 2b +ab 2,-2 (2)10【分析】(1)先合并同类项,再代入计算即可;(2)原式去括号合并整理后,把已知等式代入计算即可求出值.(1)解:3(2a 2b ﹣ab 2)﹣(5a 2b ﹣4ab 2)=6a 2b ﹣3ab 2﹣5a 2b +4ab 2=a 2b +ab 2,当a =2,b =﹣1时,原式=22×(﹣1)+2×(﹣1)2=﹣2;(2)解:当a 2+2b 2=5时,原式=3a 2﹣2ab +b 2﹣a 2+2ab +3b 2=2a 2+4b 2=2(a 2+2b 2),=2×5=10.【点睛】本题考查了整式加减的化简求值,正确的化简代数式是解题的关键.11.(2022·河南安阳·七年级期末)先化简,再求值:3(a ﹣ab )12-(6a ﹣b )12-b ,其中a =1,b =﹣2.12.(2022·黑龙江·哈尔滨市第十七中学校七年级阶段练习)先化简,再求值:()()2254452x x x x -++---,其中2x =-.【答案】291,13x x ++-【分析】原式先去括号,再合并得到最简结果,最后把2x =-代入求值即可.【详解】解:()()2254452x x x x-++---=2254452x x x x -++-++291x x =++当2x =-时,原式=2(2)9(2)1-+´-+13=-【点睛】本题考查整式的运算,解题的关键是熟练运用整式的运算法则.13.(2022·江苏南京·七年级期中)已知2(1)|2|0x y +++=,求代数式322332311543222xy x y xy y x xy x y --+--的值.14.(2022·陕西咸阳·七年级开学考试)化简:()()22222332133a b ab a b ab --+-+,若12b =-,请给a 取一个非零有理数代入化简后的式子中求值.15.(2022·浙江绍兴·七年级期中)先化简,再求值:2(2)()a a b a b -++,其中3a =-,5b =【答案】222a b +,43【分析】由单项式乘以多项式法则,结合完全平方公式进行化简,再代入数值计算即可.【详解】解:原式=22222a ab a ab b -+++= 222a b +当3a =-,5b =时,原式=()2223543´-+=.【点睛】本题考查整式加减的化简求值,涉及完全平方公式,掌握相关知识是解题关键.16.(2021·河南洛阳·七年级期中)化简求值:22225[(52)2(3)]a a a a a a -+---,其中12a =.17.(2021·四川广元·七年级期末)先化简,再求值:已知|a +1|+(b ﹣2)2=0,求代数式3a 2b ﹣[2ab 2﹣2(a 2b +3ab 2)]﹣4ab 2的值.【答案】25a b ;10【分析】根据整式的加减化简代数式,然后根据非负数的性质求得,a b 的值,代入化简后的代数式进行计算即可求解.【详解】解:原式()2222232264a b ab a b ab ab=----=2222232264a b ab a b ab ab -+-+25a b =;∵|a +1|+(b ﹣2)2=0,∴1,2a b =-=,∴原式=()251210´-´=.【点睛】本题考查了整式加减化简求值,非负数的性质,正确的去括号是解题的关键.18.(2021·河南周口·七年级期中)先化简,再求值:﹣xy +3x 2﹣(2xy ﹣x 2)﹣3(x 2﹣xy +y 2),其中x ,y 满足(x +1)2+|y ﹣2|=0.【答案】x 2﹣3y 2,-11【分析】先根据整式的加减混合运算法则化简原式,再根据平方式和绝对值的非负性求出x 、y ,代入化简式子中求解即可.【详解】解:﹣xy +3x 2﹣(2xy ﹣x 2)﹣3(x 2﹣xy +y 2)=﹣xy +3x 2﹣2xy +x 2﹣3x 2+3xy -3y 2=x 2﹣3y 2,∵x ,y 满足(x +1)2+|y ﹣2|=0,且(x +1)2≥0,|y ﹣2|≥0,∴x +1=0,y -2=0,解得:x =-1,y =2,∴原式=(-1)2-3×22=1-12=-11.【点睛】本题考查整式加减中的化简求值、平方式和绝对值的非负性,熟记整式加减混合运算法则是解答的关键.19.(2022·黑龙江·哈尔滨市虹桥初级中学校七年级期中)先化简,求值2222223723323535x x xy y x xy y æöæö-+-+++ç÷ç÷,其中12x =-,2y =-.【点睛】本题主要考查了整式的化简求值,掌握整式加减运算法则是解题的关键.20.(2022·黑龙江·哈尔滨市第十七中学校期中)先化简再求值:()()3322x xyz x xyz xyz --++,其中1x =,2y =,3z =-.【答案】2xyz -,12【分析】先去括号,再合并同类项,然后把x 、y 的值代入计算即可.【详解】(2x ³-xyz )-2(x ³+xyz )+xyz =2x ³-xyz -2x ³-2xyz +xyz =-2xyz当x =1,y =2,z =-3时,原式=-2×1×2×(-3)=12.【点睛】本题主要考查了整式的化简求值,熟练掌握去括号法则是解题的关键.21.(2022·陕西·紫阳县师训教研中心七年级期末)先化简,再求值:()()2222x xy y x xy --+-+,其中3,2x y ==-.【答案】22x y -,5【分析】先去括号,然后再进行整式的加减运算,最后代值求解即可.【详解】解:原式=2222x xy y x xy ---+=22x y -;把3,2x y ==-代入得:原式=945-=.【点睛】本题主要考查整式的化简求值,熟练掌握整式的运算是解题的关键.22.(2022·黑龙江·哈尔滨工业大学附属中学校期中)先化简,再求值:22137(43)2x x x x éù----êú,其中1x =-.23.(2022·陕西·紫阳县师训教研中心七年级期末)先化简,再求值:()()222222122+----a b ab a b ab ab ,其中2a =-,12b =.24.(2022·河北承德·七年级期末)(1)计算:()()322231--´-+;2111941836æöæö-+¸-ç÷ç÷èøèø.(2)先化简,再求值:()221532x xy x xy æö+--ç÷èø,其中x 、y 的取值如图所示.25.(2022·河北承德·七年级期末)(1)计算:()()322231--´-+;2111941836æöæö-+¸-ç÷ç÷èøèø.(2)先化简,再求值:()221532x xy x xy æö+--ç÷èø,其中x 、y 的取值如图所示.整式的加减运算.26.(2022·江苏南京·七年级期末)先化简,再求值:5(3a 2b -ab 2)+4(ab 2-3a 2b ),其中a =-2,b =3.【答案】223a b ab -,54【分析】原式去括号合并同类项得到最简结果,再把a 与b 的值代入计算即可求出值.【详解】解:原式=2222155412a b ab ab a b -+-=223a b ab -当a =-2,b =3时,原式=()()2232323´-´--´=34329´´+´=54【点睛】此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.27.(2022·全国·七年级课时练习)(1)先化简,再求值:()()2222523625x y xy y x -++-,其中13x =,12y =-;(2)设2345A a ab =++,22B a ab =-.当a ,b 互为倒数时,求3A B -的值.28.(2022·新疆昌吉·七年级期末)先化简下式,再求值:222345256x x x x x +----+,其中2x =-.【答案】1x -,-3【分析】先合并同类项化简,再把2x =-代入,即可求解.【详解】解∶ 222345256x x x x x+----+()()()222325645x x x x x --+-++-=1x =-当2x =-时,原式213=--=-【点睛】本题主要考查了整式加减中的化简求值,熟练掌握整式加减混合运算法则是解题的关键.29.(2022·湖南岳阳·七年级期末)先化简,再求值.()()22224235x xy y x xy y -+--+,其中1x =-,12y =-.30.(2022·湖南湘西·七年级期末)先化简,再求值:()()2222221x x x x +----,其中12x =-.【点睛】此题考查了整式的加减-化简求值,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握运算法则是解本题的关键.31.(2022·山东滨州·七年级期末)(1)计算:23100422(1)593æö-¸´-+-´ç÷èø;(2)先化简再求值:22113122323a a b a b æöæö--+-+ç÷ç÷,其中22,3a b =-=.32.(2022·安徽滁州·七年级期末)已知4x =-,2y =,求代数式()()2222332x y xy x y xy ---的值.【答案】25xy ;-80【分析】先化简整式,再代入求值即可.【详解】原式2222336x y xy x y xy =--+25xy =,当4x =-,2y =时,原式()254280=´-´=-.【点睛】本题考查整式化简求值,熟练掌握整加减运算法则是解题的关键.33.(2022·河南南阳·七年级期末)先化简,再求值:()22463421x y xy xy x y éù----+ëû.其中,2x =-,12y =.【答案】2565+-x y xy ,-1【分析】原式去括号合并得到最简结果,把x 与y 的值代入计算即可求值。
北师大版七年级数学上册整式计算题专项练习(附答案)

北师大版七年级数学上册整式计算题专项练习(附答案)1.将表达式化简:$-a-b+2a-b=-b+a$2.将表达式化简:$(x+2)(y+3)-(x+1)(y-2)=xy+3x+2y+6-xy+x-2y+2=x+3x+2+6+x-2y+2=4x-2y+10$3.将表达式化简:$(2x-y)(2x+y)+2y2=4x2-y2+2y2=4x2$4.将表达式化简:$\frac{x(x-y)}{x-2}+\frac{2y}{x-2}=\frac{x(x-y)+2y}{x-2}=\frac{x^{2}-xy+2y}{x-2}$6.将表达式化简:$(2a+1)^{2}-2(2a+1)+3=4a^{2}+8a+4-4a-2+3=4a^{2}+4a+5$8.将表达式化简:$-(x-5)(x+5)-\frac{(3x-2y)(-2y-3x)}{x+1}=\frac{-(x^{2}-25)(x+1)+(9x^{2}-12xy+4y^{2})}{x+1}=\frac{-x^{3}-10x^{2}-21x+4y^{2}}{x+1}$10.将表达式化简:$3(x+1)(x-1)-(2x-1)(x+y)2(x-y)2=3(x^{2}-1)-2x^{3}+x^{2}y+xy^{2}-2xy^{2}+2y^{3}=3x^{2}-3-2x^{3}+x^{2}y-y^{2}$15.将表达式化简:$-\frac{1}{2}-(-1)^{2006}+\frac{2^{11}\times(-3)^{432}}{2}= -\frac{1}{2}-1+2^{10}\times3^{432}=2^{10}\times3^{432}-\frac{3}{2}$20.将表达式化简:$(2a-1)^{2}+(2a-1)(a+4)=4a^{2}-4a+1+2a^{2}+7a-4=6a^{2}+3a-3$21.将表达式化简:$(x+2y)^{2}-2(x-y)(x+y)+2y(x-3y)=x^{2}+4xy+4y^{2}-2(x^{2}-y^{2})+2xy-6y^{2}=x^{2}+6xy-8y^{2}$22.将表达式化简:$5(x-1)(x+3)-2(x-5)(x-2)=5(x^{2}+2x-3)-2(x^{2}-3x+10)=3x^{2}+16x-40$23.将表达式化简:$(a-b)(a^{2}+ab+b^{2})=a^{3}-b^{3}$24.将表达式化简:$(3y+2)(y-4)-3(y-2)(y-3)=3y^{2}-5y-18$25.将表达式化简:$a(b-c)+b(c-a)+c(a-b)=ab-ac+bc-bc+ac-ab=0$26.将表达式化简:$(-2mn^{2})^{2}-4mn^{3}(mn+1)=4m^{2}n^{4}-4m^{2}n^{4}-4mn^{3}= -4mn^{3}$28.将表达式化简:$-(x+2)(x-2)=-(x^{2}-4)=-x^{2}+4$30.将表达式化简:$(x-3y)(x+3y)-(x-3y)=x^{2}-9y^{2}-x+3y$1.原式=2.原式=-400+4=9604;原式=-+1=13.原式=900×219;原式=-(2009+1)(2009-1)=2xxxxxxxxxxxx=-xxxxxxx4.原式=6a^2+3a-3,当a=2时,原式=6×(-2)^2+3×(-2)-3=24-6-3=155.原式=-x^2+6xy,当x=2,y=2时,原式=-(-2)^2+6×(-2)×2=-4-24=-286.原式=-3x^2+24x-357.原式=a^3-b3=(a-b)(a^2+ab+b^2)8.原式=5y-269.原式=6xy-18y210.原式=(a-c+b)^2-b^2=a^2-2ac+2bc+c^2-b^211.原式=15×10^912.原式=2a+2解答题:1.①原式=12-(-8)+(-7)-15=38②原式=-1+2×(-5)-(-3)÷(-1)=-1+(-10)-3=-14③原式=2x-3y+5x+4y=7x+y④原式=5a+2a^-1-4(3-8a+2a)=5a+2a^-1-12+32a-8a=34a+2a^-1-122.1) 原式=4-2×2-(-36)÷4=4-4+9=92) 原式=9a-6b-2a+6b=7a3.①原式=7x+4(x-2)-2(2x-x+3)=7x+4x-8-2x+2=9x-6②原式=4ab-3b-[(a+b)-(a-b)]=4ab-3b-a-b+a+b=4ab-3b-a③原式=3mn-5m-3m+5mn=8mn-8m④原式=2a+2(a+1)-3(a-1)=2a+2a+2-3a+3=4a+54.①原式=4a+18b-15a-12b=4a-15a+18b-12b=-11a+6b②原式=3x+6x^-1-3x-4x^-1=2x+2x^-15.原式=3(x-1)-(x-5)=3x-3-x+5=2x+26.原式=3(x+y)+4(x+y)-6(x+y)=7(x+y)=7(5+3)=567.原式=2(x-3y)-(x-y)=2x-6y-x+y=x-5y8.由6M=2N-4得M=N/3-2/3,代入M=x+3x-5和N=3x+5中得到:x+3x-5=N/3-2/3+3x-5解得x=7/69.原式=A+B=5a-2ab-4a+4ab=a先化简,再求值:3(A+B)﹣2(2A﹣B),其中A=﹣2,B=1.分析:先代入数值,再按照整式的加减运算顺序进行计算.解答:代入A=﹣2,B=1得:3(A+B)﹣2(2A﹣B)=3(﹣2+1)﹣2(2(﹣2)﹣1)=3﹣4﹣(﹣5)=9.点评:本题考查了整式的加减及代数式的化简,解答本题的关键在于熟练掌握整式的加减运算顺序及代入数值的方法.10.设a=14x﹣6,b=﹣7x+3,c=21x﹣1.1)求a﹣(b﹣c)的值;2)当x=时,求a﹣(b﹣c)的值.分析:先代入数值,再按照整式的加减运算顺序进行计算.解答:代入a=14x﹣6,b=﹣7x+3,c=21x﹣1得:1)a﹣(b﹣c)=14x﹣6﹣(﹣7x+3﹣21x+1)=14x﹣6﹣﹣7x+3﹣21x﹣1=6x﹣4;2)当x=时,a﹣(b﹣c)=6×﹣4﹣4=﹣28.点评:本题考查了整式的加减及代数式的化简,解答本题的关键在于熟练掌握整式的加减运算顺序及代入数值的方法.11.化简求值:已知a、b满足:|a﹣2|+(b+1)=0,求代数式2(2a﹣3b)﹣(a﹣4b)+2(﹣3a+2b)的值.分析:先化简|a﹣2|+(b+1)=0得a=2,b=﹣1,再代入求值.解答:代入a=2,b=﹣1得:2(2a﹣3b)﹣(a﹣4b)+2(﹣3a+2b)=2(2×2﹣3(﹣1))﹣(2﹣4(﹣1))+2(﹣3×2+2(﹣1))=4+9+6=19.点评:本题考查了整式的加减及代数式的化简,解答本题的关键在于熟练掌握绝对值的性质及代入求值的方法.12.已知(x+1)+|y﹣1|=0,求2(xy﹣5xy)﹣(3xy﹣xy)的值.分析:先解方程|x﹣1|+(y+1)=0,得x=﹣1,y=﹣2,再代入求值.解答:解方程得x=﹣1,y=﹣2,代入得:2(xy﹣5xy)﹣(3xy﹣xy)=2(﹣1×﹣2﹣5﹣1×﹣2)﹣(3﹣1×﹣2)=4﹣(3+2)=﹣1.点评:本题考查了整式的加减及代数式的化简,解答本题的关键在于熟练掌握绝对值的性质及代入求值的方法.解答:将3(x+y)+4(x+y)﹣6(x+y)化简得:(3+4-6)(x+y)=x+y=-2代入x=5,y=3,得到3(5+3)+4(5+3)﹣6(5+3)=24 所以,代数式3(x+y)+4(x+y)﹣6(x+y)的值为24.点评:本题考查了整式的加减、化简和求值,需要熟练掌握去括号、合并同类项和代入数值的方法。
人教版数学七年级上册第二章《整式的加减》计算题专项训练

人教版七年级数学上册《整式的加减》计算题训练附答案解析第二章整式的加减第一节整式的加减法(高效训练1--20)1、计算下列各式2、化简:1、计算下列各式2、化简:3、先化简再求值:其中,4、先化简,再求值.,其中与互为相反数1、合并同类项2、化简:先化简,后求值:,其中.3、有这样一道题:计算的值,其中。
某同学把抄成了,但计算结果也是正确的,试说明理由,并求出这个结1、计算下列各式2、计算下列各式3、已知a是绝对值等于4的负数,b是最小的正整数,c的倒数的相反数是,求a,b,c的值;求:、1、计算下列各式计算:计算:化简:化简并求值:;其中,;2、计算下列各式3、先化简,再求值.已知,求的值.1、计算下列各式2、计算下列各式3、已知:,求的值;若的值与x无关,求y的值.1、计算下列各式若,,求:当时,的值.已知,,求代数式的值.2、在关于x,y的多项式中,无论x,y取任何数,多项式的值都不变,求a,b的值.3、已知,求的值1、计算下列各式(2)2、合并下列多项式中的同类项.3、先化简,再求值:,其中,1、计算下列各式2、化简:3、化简求值:已知,求代数式的值1、计算下列各式2、已知代数式,马小虎同学在做整式加减运算时,误将“”看成“”了,计算的结果是.请你帮马小虎同学求出正确的结果;是最大的负整数,将x代入问的结果求值3、已知,,且,求C1、计算下列各式2、计算下列各式化简:先化简,再求值:,其中,3、已知:已知,.求B;当时,求的1、计算下列各式2、化简下列各式:.3、老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图:求所捂的二次三项式;若,求所捂二次三项式的值1、计算下列各式2、化简下列各式先化简,再求值.,其中,.已知,,求代数式的值3、已知,.求;若,求的值;试将用A与B的式子表示出来.1、计算下列各式2、求值:,其中,3、先化简,再求值:,其中.,其中,.1、计算下列各式2、已知,,按要求完成下列各小题.若的结果中不存在含x的一次项,求a的值;当时,求的结果.3、已知,求的值.1、先化简,再求值:,其中.,其中,2、先化简,再求值:,其中,.有一道题是一个多项式减去“”,小强误当成了加法计算,得到的结果是“”,请求出正确的计算结果.3、已知,.若化简是常数的结果中没有常数项,求m的值;当时,求的值.1、计算下列各式,其中.,其中,.2、若代数式中不含xy项,求:的值.3、已知多项式与多项式A的和为,且式子的计算结果中不含关于x的一次项,求多项式A.求m的值1、计算下列各式2、已知,.求;若,求的值.3、化简或求值化简:;化简求值:,其中,.1、计算下列各式2、已知,求的值3、如果代数式的值与字母x取值无关,试求代数式的值.4、若,求的值高效训练20 第周星期1、计算下列各式先化简,再求值:,其中,.已知整式,整式M与整式N之差是,求出整式N.2、有这样一道题:计算的值,其中,甲同学把“”错抄成了“”但他计算的结果也是正确的,请你通过计算说明原因.3、已知:,求的值;当x的取任意数值,的值是一个定值时,求的值4、如果关于x的多项式的值与x的取值无关,且该多项式的次数是三次.求m,n的值.参考答案与解析高效训练11.原式原式原式原式原式原式2.解:原式;原式.高效训练21.原式;原式.2.原式原式3.解:4.解:原式,,,原式高效训练31.原式.原式原式原式2.原式;原式;原式,原式.3..当时,原式.因为化简的结果中不含x,所以原式的值与x值无关.高效训练41.(1).(2).(3).2.(1);(2).3.由题意可知:,,当,,时,原式高效训练51.原式;原式;原式;原式.原式.2.原式原式.3.=10高效训练61.解:原式;原式;原式原式2.原式;原式3.原式;原式要使原式的值与x无关,则,解得:.高效训练71.原式;原式;,,,当时,原式;,,原式.2.解:,无论x,y取任何数,多项式的值都不变,,,解得:,3.解:,,原式高效训练81.(1);(2);;(4).2.原式;原式;原式;原式.3.原式原式高效训练91.原式;原式;原式;原式;原式;原式.2.原式;原式;原式;原式.3.原式原式高效训练101.原式;原式;原式;原式;原式;原式.2.根据题意知,则;是最大的负整数,,则原式.3.,,,高效训练111.原式;原式;原式;原式.2.原式;原式,原式.3.(1)B;(2),原式.高效训练121.原式原式原式.2.(1)原式(2)原式(3)原式.3.根据题意得:;当时,原式.高效训练131.原式;原式;原式;原式2.原式,当,时,原式;原式,当,时,原式.3.(1)(2)原式;.高效训练141.(1).(2)(3).(4).2.原式,当,时,原式3.(1),当时,原式.(2),当,时,原式.高效训练151.原式;原式;原式;原式.2.,,,由结果中不含x的一次项,得到,解得:;,,,3.原式,当,时,原式.高效训练161.原式,原式;原式,当,时,原式.2.原式,当,时,原式;原式则正确的计算结果.3.(1),由结果不含常数项,得到,解得:;(2)原式,当时,原式.高效训练171.原式当时,原式.原式当,时,原式.2.原式,由结果不含xy项,得到,解得:,则原式.3.根据题意得:;,结果不含关于x的一次项,,即高效训练181.原式;原式;原式;原式.2.(2)解得,,.3.(1);(2);(3).高效训练191.原式;原式2.原式当时,原式3.,根据题意知且,解得:、,4.,,,,当,时,原式.高效训练201.(1),当,时,原式;整式.2.原式,此题的结果与x的取值无关.3...当x的取任意数值,的值是一个定值,即的值是一个定值,.4.由题意得,,,解得,,.。
2022-2023学年七年级上数学:整式(附答案解析)

2022-2023学年七年级上数学:整式一.选择题(共5小题)1.如图,正方形ABCD与正方形AEFG的边长分别为x,y.若xy=10,BE=,则图中阴影部分的面积为()A.5B.C.D.2.S市今年第二季度的工业总产值为8000亿元,比第一季度增长了2.5%,那么第一季度工业总产值是多少亿元?下列列式正确的是()A.8000×(1﹣2.5%)B.8000÷(1﹣2.5%)C.8000×(1+2.5%)D.8000÷(1+2.5%)3.已知并排放置的正方形ABCD和正方形BEFG如图,其中点E在直线AB上,那么△DEG 的面积S1和正方形BEFG的面积S2大小关系是()A.S1=S2B.S1=S2C.S2=2S2D.S1=S2 4.甲、乙、丙三家商店对一种定价相同的文具开展促销活动.甲商店一次性降价30%;乙商店连续两次降价15%;丙商店先降价20%后又降价10%.若小雪准备在促销活动中,购买此种文具,则下列说法中,正确的是()A.小雪到甲商店购买这种文具更合算B.小雪到乙商店购买这种文具更合算C.小雪到丙商店购买这种文具更合算D.在促销活动中,三家商店的这种文具售价相同,小雪可任选一家购买5.如图,从A地到B地,小明沿直径AB上方的半圆走到B地,小丽先沿直径AC下方半圆走到AB上的C地,再沿直径CB下方半圆走到B地,他们走过的路程相比较()A.小明的路程长B.小丽的路程长C.两人路程一样D.无法确定二.填空题(共5小题)6.多项式a2b+2ab+b+1的次数是.7.若当x=2时,ax3+bx+3的值是﹣2,则当x=﹣2时,ax3+bx+3的值是.8.对单项式“7x”可以解释为:长方形的长为x,宽为7,则此长方形的面积为7x.请你对“7x”再赋予一个含义:.9.小淇同学在元旦晚会上表演了一个节目:他准备了♥(红桃)和♠(黑桃)的扑克牌各10张,洗匀后将这些牌的牌面朝下,排成两列:一列m(m>10)张,一列(20﹣m)张,他立刻报出长的一列中的♠(黑桃)比短的一列中的♥(红桃)多了张.(结果用含有m的代数式表示)10.如下表是某面包店的价目表.小明原本拿了4个面包去结账,结账时收银员告诉小明,店内有优惠活动,优惠方式为每买5个面包,其中1个价格最低的面包就免费.因此,小明又去拿了一个,他挑选了香蒜面包.如果小明原本的结账金额为a元,则小明后来的结账金额为元.(用含a的式子表示)面包品种甜甜圈芒果面包香蒜面包切片面包奶香片奶油面包单价5元6元7.5元11元12元12元三.解答题(共5小题)11.北宋科学家沈括在《梦溪笔谈》中曾记载了宋代行军时的后勤供应情况:人负米六斗,卒自携一斗,人食日二升.其大意为,在行军过程中,民夫可以背负六斗(60升)米,士兵可以自己背一斗(10升)米,民夫(士兵)每人一天行军会消耗2升米.(1)若每个士兵雇佣4个民夫随其一同行军,则在没有其他粮食补充的情况下,背负的米支持行军的天数为天;(2)若每个士兵雇佣n个民夫随其一同行军,则在没有其他粮食补充的情况下,背负的米支持行军的天数为(用含有n的代数式表示);如果每个士兵雇佣的民夫数量没有上限,在没有其他粮食补充的情况下,背负的米支持的行军天数有没有上限?(回答“有”或者“没有”)请你说明理由.12.对于数轴上的A,B,C三点,给出如下定义:若其中一个点到另外两个点的距离恰好满足n(n是大于1的整数)倍的数量关系,则称该点是另外两个点的“n倍和谐点”.例如:数轴上点A,B,C所表示的数分别为1,2,4,此时点B是点A,C的“2倍和谐点”;(1)若点A表示数是﹣1,点C表示的数是5,点B1,B2,B3,依次表示﹣4,,7各数,其中是点A,C的“3倍和谐点”的是;(2)点A表示的数是﹣20,点C表示的数是40,点Q是数轴上一个动点.①若点Q是点A,C的“4倍和谐点”,求此时点Q表示的数;②若点Q在点A的右侧,且点Q是点A,C的“n倍和谐点”,用含有n的式子直接写出此时点Q所表示的数.13.某单位购买了30台A、B、C三种型号的空调,根据下表提供的信息,解答以下问题:空调类型A B C购买的台数(台)129每台空调的销售价(元)18003000(1)该单位购买的A型号的空调占购买全部空调的百分之几?(2)如果每台A型号空调的销售价比每台C型号空调的售价便宜10%,那么每台C型号空调的销售价是多少元?(3)在第(2)题的条件下,为了促销,现商家搞优惠活动:若购买B类空调的台数超过10台,超过部分,可以享受9折优惠.那么本次购买空调该单位一共需要支付多少元钱?14.点O为数轴的原点,点A、B在数轴上的位置如图所示,点A表示的数为5,线段AB 的长为线段OA长的1.2倍.点C在数轴上,M为线段OC的中点.(1)点B表示的数为;(2)若线段BM=5,则线段OM的长为;(3)若线段AC=a(0<a<5),求线段BM的长(用含a的式子表示).15.如图,某校的“图书码”共有7位数字,它是由6位数字代码和校验码构成,其结构分别代表“种类代码、出版社代码、书序代码和校验码”.其中校验码是用来校验图书码中前6位数字代码的正确性,它的编制是按照特定的算法得来的.以上图为例,其算法为:步骤1:计算前6位数字中偶数位数字的和a,即a=9+1+3=13;步骤2:计算前6位数字中奇数位数字的和b,即b=6+0+2=8;步骤3:计算3a与b的和c,即c=3×13+8=47;步骤4:取大于或等于c且为10的整数倍的最小数d,即d=50;步骤5:计算d与c的差就是校验码X,即X=50﹣47=3.请解答下列问题:(1)《数学故事》的图书码为978753Y,则“步骤3”中的c的值为,校验码Y 的值为.(2)如图①,某图书码中的一位数字被墨水污染了,设这位数字为m,你能用只含有m 的代数式表示上述步骤中的d吗?从而求出m的值吗?写出你的思考过程.(3)如图②,某图书码中被墨水污染的两个数字的差是4,这两个数字从左到右分别是多少?请直接写出结果.2022-2023学年七年级上数学:整式参考答案与试题解析一.选择题(共5小题)1.如图,正方形ABCD与正方形AEFG的边长分别为x,y.若xy=10,BE=,则图中阴影部分的面积为()A.5B.C.D.【分析】根据题图可判断S阴影=S△CDF+S△BEF,而后列代数式计算即可.【解答】解:根据题意得:S阴影=S△CDF+S△BEF=x(x﹣y)+y(x﹣y)=(x+y)(x﹣y),∵BE=,∴x﹣y=,∵(x+y)2﹣4xy=(x﹣y)2,xy=10,∴(x+y)2=(x﹣y)2+4xy=()2+40==()2,∴x+y=,∴S阴影=(x﹣y)(x+y)=××=.故选:B.【点评】本题考查了根据题图来求阴影面积,将阴影面积转化并灵活运用已知条件是解题的关键.2.S市今年第二季度的工业总产值为8000亿元,比第一季度增长了2.5%,那么第一季度工业总产值是多少亿元?下列列式正确的是()A.8000×(1﹣2.5%)B.8000÷(1﹣2.5%)C.8000×(1+2.5%)D.8000÷(1+2.5%)【分析】根据第二季度的工业总产值=第一季度的工业总产值×(1+2.5%),可得到答案.【解答】解:∵第二季度的工业总产值为8000亿元,比第一季度增长了2.5%,∴第一季度工业总产值是8000÷(1+2.5%).故选:D.【点评】本题考查了列代数式,解答本题的关键是明确题意,写出相应的代数式.3.已知并排放置的正方形ABCD和正方形BEFG如图,其中点E在直线AB上,那么△DEG 的面积S1和正方形BEFG的面积S2大小关系是()A.S1=S2B.S1=S2C.S2=2S2D.S1=S2【分析】连接BD,可得BD∥EG,则有S△DEG=S△BEG=S正方形BEFG.从而得出答案.【解答】解:连接BD,∵四边形ABCD、BEFG是正方形,∴∠ABD=∠BEG=45°,∴BD∥EG,∴S△DEG=S△BEG=S正方形BEFG,∴S1=S2,故选:A.【点评】本题主要考查了正方形的性质,平行线的判定与性质等知识,证明BD∥EG是解题的关键.4.甲、乙、丙三家商店对一种定价相同的文具开展促销活动.甲商店一次性降价30%;乙商店连续两次降价15%;丙商店先降价20%后又降价10%.若小雪准备在促销活动中,购买此种文具,则下列说法中,正确的是()A.小雪到甲商店购买这种文具更合算B.小雪到乙商店购买这种文具更合算C.小雪到丙商店购买这种文具更合算D.在促销活动中,三家商店的这种文具售价相同,小雪可任选一家购买【分析】首先把这种文具原来的价格看作单位“1”,根据百分数乘法的运算方法,分别求出在甲、乙、丙三家商店买这种文具各需要多少钱;然后比较大小,判断出小雪购买这种文具应该去的商店是哪个即可.【解答】解:在甲商店买这种文具需要:1×(1﹣30%)=1×70%=0.7,在乙商店买这种文具需要:1×(1﹣15%)×(1﹣15%)=1×85%×85%=0.7225,在丙商店买这种文具需要:1×(1﹣20%)×(1﹣10%)=1×80%×90%=0.72,因为0.7<0.72<0.7225,所以小雪购买这种文具应该去的商店是甲.故选:A.【点评】此题主要考查了列代数式问题,要熟练掌握,解答此题的关键是分别求出在甲、乙、丙三家商店买这种文具各需要多少钱.5.如图,从A地到B地,小明沿直径AB上方的半圆走到B地,小丽先沿直径AC下方半圆走到AB上的C地,再沿直径CB下方半圆走到B地,他们走过的路程相比较()A.小明的路程长B.小丽的路程长C.两人路程一样D.无法确定【分析】小明所走的路程长为以AB为直径的半圆弧长,小丽所走的路程长为以AC和BC为直径的两个半圆弧长的和,然后根据圆的周长公式进行计算,再比较大小即可.【解答】解:小明所走的路程长:π×AB,小丽所走的路程长:π×AC+π×BC=π×(AC+BC)=π×AB,故他们走过的路程相比较两人路程一样.故选:C.【点评】本题考查了列代数式,圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).记住圆的周长公式.二.填空题(共5小题)6.多项式a2b+2ab+b+1的次数是3.【分析】根据多项式的次数的定义(多项式中次数最高项的次数是多项式的次数)解决此题.【解答】解:a2b+2ab+b+1含四项,分别是a2b、2ab、b、1,次数分别是3、2、1、0,则这个多项式的次数是3.故答案为:3.【点评】本题主要考查多项式,熟练掌握多项式的次数的定义是解决本题的关键.7.若当x=2时,ax3+bx+3的值是﹣2,则当x=﹣2时,ax3+bx+3的值是8.【分析】将x=2代入可求得﹣8a﹣2b=5,当x=﹣2时,可得到ax3+bx+3=﹣8a﹣2b+3,从而可求得问题的答案.【解答】解:将x=2代入得:8a+2b+3=﹣2,∴8a+2b=﹣5,∴﹣8a﹣2b=5,当x=﹣2时,ax3+bx+3=﹣8a﹣2b+3=5+3=8.故答案为:8.【点评】本题主要考查的是求代数式的值,得到当x=2时,8a+2b=﹣5是解题的关键.8.对单项式“7x”可以解释为:长方形的长为x,宽为7,则此长方形的面积为7x.请你对“7x”再赋予一个含义:笔记本的单价为每本7元,买x个笔记本的总钱数(答案不唯一).【分析】根据代数式的意义即可解答.【解答】解:同一个式子可以表示不同的含义,例如对单项式“7x”可以解释为:长方形的长为x,宽为7,则此长方形的面积为7x,也可以表示更多的含义,请你给7x再赋予一个含义:笔记本的单价为每本7元,买x个笔记本的总钱数,故答案为:笔记本的单价为每本7元,买x个笔记本的总钱数(答案不唯一).【点评】本题考查了列代数式,熟练掌握代数式的意义是解题的关键.9.小淇同学在元旦晚会上表演了一个节目:他准备了♥(红桃)和♠(黑桃)的扑克牌各10张,洗匀后将这些牌的牌面朝下,排成两列:一列m(m>10)张,一列(20﹣m)张,他立刻报出长的一列中的♠(黑桃)比短的一列中的♥(红桃)多了(m﹣10)张.(结果用含有m的代数式表示)【分析】设一列m(m>10)张的黑桃有n张,则红桃有(m﹣n)张,再求出短的一列中红桃有10﹣(m﹣n)=(10﹣m+n)张,两种牌数作差即可﹒【解答】解:设一列m(m>10)张的黑桃有n张,则红桃有(m﹣n)张,短的一列中红桃有10﹣(m﹣n)=(10﹣m+n)张,:.长的一列中的(黑桃)比短的一列中的(红桃)多:n﹣(10﹣m+n)=(m﹣10)张.故答案为:(m﹣10).【点评】本题考查用代数式表示数,整式的加减法运算,掌握用代数式表示数的方法,整式的加减法运算去括号合并同类项是解题关键﹒10.如下表是某面包店的价目表.小明原本拿了4个面包去结账,结账时收银员告诉小明,店内有优惠活动,优惠方式为每买5个面包,其中1个价格最低的面包就免费.因此,小明又去拿了一个,他挑选了香蒜面包.如果小明原本的结账金额为a元,则小明后来的结账金额为a或(a+1.5)或(a+2.5)元.(用含a的式子表示)面包品种甜甜圈芒果面包香蒜面包切片面包奶香片奶油面包单价5元6元7.5元11元12元12元【分析】分小明原本拿了4个面包最低价钱是5元或6元或大于等于7.5元进行讨论即可求解.【解答】解:小明原本拿了4个面包最低价钱是5元,小明后来的结账金额为a+7.5﹣5=(a+2.5)元;或小明原本拿了4个面包最低价钱是6元,小明后来的结账金额为a+7.5﹣6=(a+1.5)元;或小明原本拿了4个面包最低价钱是大于等于7.5元,小明后来的结账金额为a元.故小明后来的结账金额为a或(a+1.5)或(a+2.5)元.故答案为:a或(a+1.5)或(a+2.5).【点评】本题考查了列代数式,关键是理解店内优惠活动,注意分类思想的应用.三.解答题(共5小题)11.北宋科学家沈括在《梦溪笔谈》中曾记载了宋代行军时的后勤供应情况:人负米六斗,卒自携一斗,人食日二升.其大意为,在行军过程中,民夫可以背负六斗(60升)米,士兵可以自己背一斗(10升)米,民夫(士兵)每人一天行军会消耗2升米.(1)若每个士兵雇佣4个民夫随其一同行军,则在没有其他粮食补充的情况下,背负的米支持行军的天数为25天;(2)若每个士兵雇佣n个民夫随其一同行军,则在没有其他粮食补充的情况下,背负的米支持行军的天数为(用含有n的代数式表示);如果每个士兵雇佣的民夫数量没有上限,在没有其他粮食补充的情况下,背负的米支持的行军天数有没有上限?有(回答“有”或者“没有”)请你说明理由.【分析】(1)用所带的粮食除以每天消耗的粮食,即得支持行军的天数;(2)每个士兵雇佣n个民夫随其一同行军,根据题意列代数式即可得答案.【解答】解:(1)每个士兵雇佣4个民夫随其行军,则士兵和民夫共携带了60×4+10=250升粮食,而250÷(2×4+2)=250÷10=25,∴最多可以支持25天的行军;故答案为:25;(2)每个士兵雇佣n个民夫随其一同行军,则在没有其他粮食补充的情况下,背负的米支持行军的天数为,有;原式不可能超过30,随着n的增加,的值越来越贴近30,因此最多可以支持29天(或者30天).故答案为:;有.【点评】本题考查列代数式.解答此题关键是读懂题意,根据题目中的数量关系列代数式.12.对于数轴上的A,B,C三点,给出如下定义:若其中一个点到另外两个点的距离恰好满足n(n是大于1的整数)倍的数量关系,则称该点是另外两个点的“n倍和谐点”.例如:数轴上点A,B,C所表示的数分别为1,2,4,此时点B是点A,C的“2倍和谐点”;(1)若点A表示数是﹣1,点C表示的数是5,点B1,B2,B3,依次表示﹣4,,7各数,其中是点A,C的“3倍和谐点”的是B1,B2;(2)点A表示的数是﹣20,点C表示的数是40,点Q是数轴上一个动点.①若点Q是点A,C的“4倍和谐点”,求此时点Q表示的数;②若点Q在点A的右侧,且点Q是点A,C的“n倍和谐点”,用含有n的式子直接写出此时点Q所表示的数.【分析】(1)根据“3倍和谐点”的定义即可求解;(2)①分三种情况:Ⅰ.如图,当点Q1在点A,C之间,且靠近点A时,4AQ1=Q1C.Ⅱ.如图,当点Q2在点A,C之间,且靠近点C时,4Q2C=AQ2.Ⅲ.如图,当点Q3在点A 左侧时,4Q3A=CQ3.Ⅳ.如图,当点Q3在点C右侧时,4CQ4=AQ4.进行讨论即可求解;②点Q在点A的右侧,有三种情况,根据“n倍和谐点”的定义即可求解.【解答】解:(1)∵[5﹣(﹣4)]÷[﹣1﹣(﹣4)]=3,∴B1是点A,C的“3倍和谐点”,∵(5﹣)÷[﹣(﹣1)]=×=3,∴B2是点A,C的“3倍和谐点”,∵[7﹣(﹣1)]÷(7﹣5)]=8÷2=4,∴B3不是点A,C的“3倍和谐点”.故答案为:B1,B2;(2)①设点Q表示的数为x,Ⅰ.如图,当点Q1在点A,C之间,且靠近点A时,4AQ1=Q1C.则4[x﹣(﹣20)]=40﹣x,解得x=﹣8.所以点Q1表示的数为﹣8.Ⅱ.如图,当点Q2在点A,C之间,且靠近点C时,4Q2C=AQ2.则4(40﹣x)=x﹣(﹣20),解得x=28.所以点Q2表示的数为28.Ⅲ.如图,当点Q3在点A左侧时,4Q3A=CQ3.则4(﹣20﹣x)=40﹣x,解得x=﹣40.所以点Q3表示的数为﹣40.Ⅳ.如图,当点Q3在点C右侧时,4CQ4=AQ4.则4(x﹣40)=x﹣(﹣20),解得x=60.所以点Q4表示的数为60.综上所述,若点Q是点A,C的“4倍和谐点”,此时点Q表示的数﹣40,﹣8,28,60.②﹣20+(或),40﹣(或),40+(或).【点评】本题考查了一元一次方程的应用,数轴及列代数式,认真理解新定义:若其中一个点到另外两个点的距离恰好满足n(n是大于1的整数)倍的数量关系,则称该点是另外两个点的“n倍和谐点”.13.某单位购买了30台A、B、C三种型号的空调,根据下表提供的信息,解答以下问题:空调类型A B C购买的台数(台)129每台空调的销售价(元)18003000(1)该单位购买的A型号的空调占购买全部空调的百分之几?(2)如果每台A型号空调的销售价比每台C型号空调的售价便宜10%,那么每台C型号空调的销售价是多少元?(3)在第(2)题的条件下,为了促销,现商家搞优惠活动:若购买B类空调的台数超过10台,超过部分,可以享受9折优惠.那么本次购买空调该单位一共需要支付多少元钱?【分析】(1)由购买了30台A、B、C三种型号的空调可求出购买A型号的空调的数量,再除以30即可;(2)根据“每台A型号空调的销售价比每台C型号空调的售价便宜10%”,可直接列式计算.(3)分别求出三种型号空调的总销售价再相加即可.【解答】解:(1)(30﹣12﹣9)÷30=30%.答:该单位购买的A型号的空调占购买全部空调的30%.(2)1800÷(1﹣10%)=2000(元).答:每台C型号空调的销售价是2000元.(3)10×3000+2×3000×90%+9×1800+9×2000=30000+5400+16200+18000=69600(元).答:本次购买空调该单位一共需要支付69600元.【点评】本题属于商品销售类应用题,第(2)问也可以利用一元一次方程去解决问题,解题的关键是正确找出题中的数量关系,属于基础题型.14.点O为数轴的原点,点A、B在数轴上的位置如图所示,点A表示的数为5,线段AB 的长为线段OA长的1.2倍.点C在数轴上,M为线段OC的中点.(1)点B表示的数为﹣1;(2)若线段BM=5,则线段OM的长为4或6;(3)若线段AC=a(0<a<5),求线段BM的长(用含a的式子表示).【分析】(1)由题意可求得AB=6,则可求得OB=1,根据题意可得结果;(2)分点M位于点B左侧和右侧两种情况可求得结果;(3)分点C位于点A左侧和右侧两种情况,表示出OM的长,再求出BM的长即可.【解答】解:(1)由题意得AB=1.2OA=1.2×5=6,∴OB=6﹣5=1,∴点B表示的数为﹣1,故答案为:﹣1;(2)当点M位于点B左侧时,点M表示的数为﹣1﹣5=﹣6,当点M位于点B右侧时,点M表示的数为﹣1+5=4,∴OM=|﹣6|=6,或OM=|4|=4,故答案为:4或6.(3)∵AC=a且0<a<5,∴点C始终在原点右侧,当点C位于点A左侧时,OC=5﹣a,∴OM=,则BM=+1=,当点C位于点A右侧时,OC=5+a,∴OM=,则BM=+1=.【点评】此题考查了数形结合与分类讨论解决问题的能力,关键是能确定数轴上的点表示的数与对满足条件的点的不同情况的全面考虑.15.如图,某校的“图书码”共有7位数字,它是由6位数字代码和校验码构成,其结构分别代表“种类代码、出版社代码、书序代码和校验码”.其中校验码是用来校验图书码中前6位数字代码的正确性,它的编制是按照特定的算法得来的.以上图为例,其算法为:步骤1:计算前6位数字中偶数位数字的和a,即a=9+1+3=13;步骤2:计算前6位数字中奇数位数字的和b,即b=6+0+2=8;步骤3:计算3a与b的和c,即c=3×13+8=47;步骤4:取大于或等于c且为10的整数倍的最小数d,即d=50;步骤5:计算d与c的差就是校验码X,即X=50﹣47=3.请解答下列问题:(1)《数学故事》的图书码为978753Y,则“步骤3”中的c的值为73,校验码Y 的值为7.(2)如图①,某图书码中的一位数字被墨水污染了,设这位数字为m,你能用只含有m 的代数式表示上述步骤中的d吗?从而求出m的值吗?写出你的思考过程.(3)如图②,某图书码中被墨水污染的两个数字的差是4,这两个数字从左到右分别是多少?请直接写出结果.【分析】(1)根据特定的算法代入计算即可求解;(2)根据特定的算法依次求出a,b,c,d,再根据d为10的整数倍即可求解;(3)根据校验码为8结合两个数字的差是4即可求解.【解答】解:(1)∵《数学故事》的图书码为978753Y,∴a=7+7+3=17,b=9+8+5=22,则“步骤3”中的c的值为3×17+22=73,校验码Y的值为80﹣73=7.故答案为:73,7;(2)依题意有a=m+1+2=m+3,b=6+0+0=6,c=3a+b=3(m+3)+6=3m+15,d=c+X=3m+15+6=3m+21,∵d为10的整数倍,∴3m的个位数字只能是9,∴m的值为3;(3)可设这两个数字从左到右分别是p,q,依题意有a=p+9+2=p+11,b=6+1+q=q+7,c=3(p+11)+(q+7)=3p+q+40,∵校验码为8,∴3p+q的个位是2,∵|p﹣q|=4,∴p=4,q=0或p=9,q=5或p=2,q=6.故这两个数字从左到右分别是4,0或9,5或2,6.【点评】本题考查了列代数式、正确理解题意,学会探究规律、利用规律是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
整式的乘除计算训练(1)1. )2()(b a b a -++-2. (x+2)(y+3)-(x+1)(y-2)3. 22)2)(2(y y x y x ++-4. x(x -2)-(x+5)(x -5)5. ⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--y x y x 224 6. )94)(32)(23(22x y x y y x +--- 7. ()()3`122122++-+a a 8. ()()()2112+--+x x x9. (x -3y)(x+3y)-(x -3y)2 10. 23(1)(1)(21)x x x +--- 11. 22)23()23(y x y x --+ 12. 22)()(y x y x -+13. 0.125100×8100 14. 30022)2(21)x (4554---÷⎪⎭⎫ ⎝⎛--π-+⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛ 15. (1211200622332141)()()()-⨯+---- 16—19题用乘法公式计算16.999×1001 17.1992-18.298 19.2010200820092⨯-20.化简求值:)4)(12()12(2+-+-a a a ,其中2-=a 。
21. 化简求值2(2)2()()2(3)x y x y x y y x y +--++-,其中12,2x y =-=。
22. 5(x -1)(x +3)-2(x -5)(x -2) 23. (a -b )(a 2+ab +b 2)24. (3y +2)(y -4)-3(y -2)(y -3) 25. a (b -c )+b (c -a )+c (a -b )26. (-2mn 2)2-4mn 3(mn +1) 27. 3xy (-2x )3·(-41y 2)228. (-x -2)(x +2) 29. 5×108·(3×102)30. (x -3y )(x +3y )-(x -3y )2 31. (a +b -c )(a -b -c )答案1. 2. 3. 4.5. 6. 7. 8.9. 10. 11. 12.13. 14. 15.16. 原式=(1000-1)(1000+1) 17. 原式=(99+1)(99-1)=1000000-1 =10098=999999 =980018. 原式=(900-2)2 19. 原式=20092-(2009+1)(2009-1)=10000-400+4 =20092-20092+1=9604 =120.原式=,当时,原式=21.原式=,当,时,原式=22. 23. 24. 25. 026. 27. 28. 29.30. 31.2014年北师大七年级数学上册《整式及其加减》计算题专项练习一一.解答题(共12小题)1.计算题①12﹣(﹣8)+(﹣7)﹣15;②﹣12+2×(﹣5)﹣(﹣3)3÷;③(2x﹣3y)+(5x+4y);④(5a2+2a﹣1)﹣4(3﹣8a+2a2).2.(1)计算:4+(﹣2)2×2﹣(﹣36)÷4;(2)化简:3(3a﹣2b)﹣2(a﹣3b).3.计算:(1)7x+4(x2﹣2)﹣2(2x2﹣x+3);(2)4ab﹣3b2﹣[(a2+b2)﹣(a2﹣b2)];(3)(3mn﹣5m2)﹣(3m2﹣5mn);(4)2a+2(a+1)﹣3(a﹣1).4.化简(1)2(2a2+9b)+3(﹣5a2﹣4b)(2)3(x3+2x2﹣1)﹣(3x3+4x2﹣2)5.(2009•柳州)先化简,再求值:3(x﹣1)﹣(x﹣5),其中x=2.6.已知x=5,y=3,求代数式3(x+y)+4(x+y)﹣6(x+y)的值.7.已知A=x2﹣3y2,B=x2﹣y2,求解2A﹣B.8.若已知M=x2+3x﹣5,N=3x2+5,并且6M=2N﹣4,求x.9.已知A=5a2﹣2ab,B=﹣4a2+4ab,求:(1)A+B;(2)2A﹣B;(3)先化简,再求值:3(A+B)﹣2(2A﹣B),其中A=﹣2,B=1.10.设a=14x﹣6,b=﹣7x+3,c=21x﹣1.(1)求a﹣(b﹣c)的值;(2)当x=时,求a﹣(b﹣c)的值.11.化简求值:已知a、b满足:|a﹣2|+(b+1)2=0,求代数式2(2a﹣3b)﹣(a﹣4b)+2(﹣3a+2b)的值.12.已知(x+1)2+|y﹣1|=0,求2(xy﹣5xy2)﹣(3xy2﹣xy)的值.2014年北师大七年级数学上册《整式及其加减》计算题专项练习一参考答案与试题解析一.解答题(共12小题)1.计算题①12﹣(﹣8)+(﹣7)﹣15;②﹣12+2×(﹣5)﹣(﹣3)3÷;③(2x﹣3y)+(5x+4y);④(5a2+2a﹣1)﹣4(3﹣8a+2a2).考点:整式的加减;有理数的混合运算.专题:计算题.分析:(1)直接进行有理数的加减即可得出答案.(2)先进行幂的运算,然后根据先乘除后加减的法则进行计算.(3)先去括号,然后合并同类项即可得出结果.(4)先去括号,然后合并同类项即可得出结果.解答:解:①原式=12+8﹣7﹣15=﹣2;②原式=﹣1﹣10+27÷=﹣11+81=70;③原式=2x﹣3y+5x+4y=7x+y;④原式=5a2+2a﹣1﹣12+32a﹣8a2=﹣3a2+34a﹣13.点评:本题考查了整式的加减及有理数的混合运算,属于基础题,解答本题的关键熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.2.(1)计算:4+(﹣2)2×2﹣(﹣36)÷4;(2)化简:3(3a﹣2b)﹣2(a﹣3b).考点:整式的加减;有理数的混合运算.分析:(1)按照有理数混合运算的顺序,先乘方后乘除最后算加减;(2)运用整式的加减运算顺序计算:先去括号,再合并同类项.解答:解:(1)原式=4+4×2﹣(﹣9)=4+8+9=17;(2)原式=9a﹣6b﹣2a+6b=(9﹣2)a+(﹣6+6)b=7a.点评:在混合运算中要特别注意运算顺序:先三级,后二级,再一级;熟记去括号法则:﹣﹣得+,﹣+得﹣,++得+,+﹣得﹣;及熟练运用合并同类项的法则:字母和字母的指数不变,只把系数相加减.3.计算:(1)7x+4(x2﹣2)﹣2(2x2﹣x+3);(2)4ab﹣3b2﹣[(a2+b2)﹣(a2﹣b2)];(3)(3mn﹣5m2)﹣(3m2﹣5mn);(4)2a+2(a+1)﹣3(a﹣1).考点:整式的加减.分析:(1)先去括号,再合并同类项即可;(2)先去括号,再合并同类项即可;(3)先去括号,再合并同类项即可;(4)先去括号,再合并同类项即可.解答:解:(1)7x+4(x2﹣2)﹣2(2x2﹣x+3)=7x+4x2﹣8﹣4x2+2x﹣6=9x﹣14;(2)4ab﹣3b2﹣[(a2+b2)﹣(a2﹣b2)]=4ab﹣3b2﹣[a2+b2﹣a2+b2]=4ab﹣3b2﹣2b2=4ab﹣5b2;(3)(3mn﹣5m2)﹣(3m2﹣5mn)=3mn﹣5m2﹣3m2+5mn=8mn﹣8m2;(4)2a+2(a+1)﹣3(a﹣1)=2a+2a+2﹣3a+3=a+5.点评:本题考查了整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.4.化简(1)2(2a2+9b)+3(﹣5a2﹣4b)(2)3(x3+2x2﹣1)﹣(3x3+4x2﹣2)考点:整式的加减.专题:计算题.分析:(1)原式利用去括号法则去括号后,合并同类项即可得到结果;(2)原式利用去括号法则去括号后,合并同类项即可得到结果.解答:解:(1)原式=4a2+18b﹣15a2﹣12b=﹣11a2+6b;(2)原式=3x3+6x2﹣3﹣3x3﹣4x2+2=2x2﹣1.点评:此题考查了整式的加减,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握法则是解本题的关键.5.(2009•柳州)先化简,再求值:3(x﹣1)﹣(x﹣5),其中x=2.考点:整式的加减—化简求值.分析:本题应对方程去括号,合并同类项,将整式化为最简式,然后把x的值代入即可.解答:解:原式=3x﹣3﹣x+5=2x+2,当x=2时,原式=2×2+2=6.点评:本题考查了整式的化简.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.6.已知x=5,y=3,求代数式3(x+y)+4(x+y)﹣6(x+y)的值.考点:整式的加减—化简求值.分析:先把x+y当作一个整体来合并同类项,再代入求出即可.解答:解:∵x=5,y=3,∴3(x+y)+4(x+y)﹣6(x+y)=x+y=5+3=8.点评:本题考查了整式的加减的应用,主要考查学生的计算能力,用了整体思想.7.已知A=x2﹣3y2,B=x2﹣y2,求解2A﹣B.考点:整式的加减.分析:直接把A、B代入式子,进一步去括号,合并得出答案即可.解答:解:2A﹣B=2(x2﹣3y2)﹣(x2﹣y2)=2x2﹣6y2﹣x2+y2=x2﹣5y2.点评:此题考查整式的加减混合运算,掌握去括号法则和运算的方法是解决问题的关键.8.若已知M=x2+3x﹣5,N=3x2+5,并且6M=2N﹣4,求x.考点:整式的加减;解一元一次方程.专题:计算题.分析:把M与N代入计算即可求出x的值.解答:解:∵M=x2+3x﹣5,N=3x2+5,∴代入得:6x2+18x﹣30=6x2+10﹣4,解得:x=2.点评:此题考查了整式的加减,熟练掌握运算法则是解本题的关键.9.已知A=5a2﹣2ab,B=﹣4a2+4ab,求:(1)A+B;(2)2A﹣B;(3)先化简,再求值:3(A+B)﹣2(2A﹣B),其中A=﹣2,B=1.考点:整式的加减;整式的加减—化简求值.专题:计算题.分析:(1)把A与B代入A+B中计算即可得到结果;(2)把A与B代入2A﹣B中计算即可得到结果;(3)原式去括号合并得到最简结果,把A与B的值代入计算即可求出值.解答:解:(1)∵A=5a2﹣2ab,B=﹣4a2+4ab,∴A+B=5a2﹣2ab﹣4a2+4ab=a2+2ab;(2)∵A=5a2﹣2ab,B=﹣4a2+4ab,∴2A﹣B=10a2﹣4ab+4a2﹣4ab=14a2﹣8ab;(3)原式=3A+3B﹣4A+2B=﹣A+5B,把A=﹣2,B=1代入得:原式=2+5=7.点评:此题考查了整式的加减,熟练掌握运算法则是解本题的关键.10.设a=14x﹣6,b=﹣7x+3,c=21x﹣1.(1)求a﹣(b﹣c)的值;(2)当x=时,求a﹣(b﹣c)的值.考点:整式的加减;代数式求值.专题:计算题.分析:(1)把a,b,c代入a﹣(b﹣c)中计算即可得到结果;(2)把x的值代入(1)的结果计算即可得到结果.解答:解:(1)把a=14x﹣6,b=﹣7x+3,c=21x﹣1代入得:a﹣(b﹣c)=a﹣b+c=14x﹣6+7x﹣3+21x﹣1=42x﹣10;(2)把x=代入得:原式=42×﹣10=10.5﹣10=0.5.点评:此题考查了整式的加减,以及代数式求值,熟练掌握运算法则是解本题的关键.11.化简求值:已知a、b满足:|a﹣2|+(b+1)2=0,求代数式2(2a﹣3b)﹣(a﹣4b)+2(﹣3a+2b)的值.考点:整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.专题:计算题.分析:原式去括号合并得到最简结果,利用非负数的性质求出a与b的值,代入计算即可求出值.解答:解:原式=4a﹣6b﹣a+4b﹣6a+4b=﹣3a+2b,∵|a﹣2|+(b+1)2=0,∴a=2,b=﹣1,则原式=﹣6﹣2=﹣8.点评:此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.12.已知(x+1)2+|y﹣1|=0,求2(xy﹣5xy2)﹣(3xy2﹣xy)的值.考点:整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.分析:因为平方与绝对值都是非负数,且(x+1)2+|y﹣1|=0,所以x+1=0,y﹣1=0,解得x,y的值.再运用整式的加减运算,去括号、合并同类项,然后代入求值即可.解答:解:2(xy﹣5xy2)﹣(3xy2﹣xy)=(2xy﹣10xy2)﹣(3xy2﹣xy)=2xy﹣10xy2﹣3xy2+xy=(2xy+xy)+(﹣3xy2﹣10xy2)=3xy﹣13xy2,∵(x+1)2+|y﹣1|=0∴(x+1)=0,y﹣1=0∴x=﹣1,y=1.∴当x=﹣1,y=1时,3xy﹣13xy2=3×(﹣1)×1﹣13×(﹣1)×12=﹣3+13=10.答:2(xy﹣5xy2)﹣(3xy2﹣xy)的值为10.点评:整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.代入求值时要化简.。
