11年海淀初三上期末
北京市各区县2011-2012学年度初三期末试题及答案汇总

北京市各区县2011-2012学年度初三期末试题及答案汇总内容预览:东城区2011-2012学年第一学期期末统一检测初三语文试卷2102.1学校班级姓名考号考生须知1.本试卷共8页,共六道大题,26道小题。
满分120分。
考试时间150分钟。
2.在试卷和答题卡上准确填写学校名称、班级、姓名和考号。
3.所有试题均在答题卡上作答,在试卷上作答无效。
4.在答题卡上,第一大题用2B铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,请将答题卡和试卷一并交回。
一、选择。
下列各题均有四个选项,其中只有一个符合题意,选出答案后在答题卡上用2B铅笔把对应题目的选项字母涂黑涂满。
(共14分。
每小题2分)1.下列词语中加点字读音完全正确的一项是A.襁褓(qiánɡ) 阴晦(huì) 妖娆(ráo) 陟罚臧否(fǒu)B.拮据(jū) 睿智(ruì) 商酌(zhuó) 为民请命(wèi)C.诓骗(kuānɡ) 逞辩(chénɡ) 狡黠(xié) 强聒不舍(ɡuō)D.汲取(xī) 抽噎(yē) 陨落(yùn) 夙夜忧叹(sù)2.下列句子中没有错别字的一项是A.苍黄的天底下,远近横着几个箫索的荒村,没有一些活气。
B.将全副精力集中到一件事上头,一点不旁务,便是敬。
C.“正确答案只有一个”这种思维模式,在我们头脑中已不知不觉地根深蒂固。
我在东京太师府里做奶公时,门下军官见了无千无万,都向着我喏喏连声。
D.慢慢的你能够从客观的立场分析前因后果,做将来的借鉴,以免重蹈覆辄。
3.下面语段中依次填入关联词语最恰当的一项是“黄叶”与“红叶”,是两种很相似的东西,在我们的观感上,各有不同的情调。
如果容我做点譬喻,,黄叶就像清高的隐士,红叶是艳妆的美人了。
北京海淀区北京市十一学校2022-2023学年九年级上学期期末数学试题及解析

北京海淀区北京市十一学校2022-2023学年九年级上学期期末数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.若)(250y x xy =≠,则下列比例式正确的是( ) A .52x y=B .25x y= C .25x y = D .25y x = 2.在Rt ABC △中,90C ∠=︒,4AB =,3BC =,则sin A 的值是( )A B .34C .35D .453.在平面直角坐标系xOy 中,抛物线2y x =向上平移2个单位长度得到的抛物线为( ) A .)(22y x =+B .)(22y x =-C .22y x =-D .22y x =+4.在平面直角坐标系xOy 中,抛物线)(20y ax bx c a =++≠的示意图如图所示,下列说法中正确的是( )A .a<0B .0b <C .0c >D .0∆>5.在平面直角坐标系xOy 中,若函数)(0ky x x=<的函数值y 随着自变量x 的增大而增大,则函数)(0ky x x=<的图象所在的象限为( ) A .第一象限B .第二象限C .第三象限D .第四象限6.如图,四边形ABCD 内接于O ,若四边形ABCO 是菱形,则D ∠的度数为( )A .45°B .60°C .90°D .120°7.正方形的面积y 与它的周长x 满足的函数关系是( ) A .正比例函数B .一次函数C .二次函数D .反比例函数8.在平面直角坐标系xOy 中,点123(1)(2)(4)y y y -,,,,,在抛物线22y ax ax c =-+上,当0a >时,下列说法一定正确的是( ) A .若120y y <,则30y > B .若230y y >,则10y < C .若130y y <,则20y >D .若1230y y y =,则20y =二、填空题 9.如图,ABCD ,AD ,BC 交于点O ,12AO OD =.若3BO =,则OC 的长为______.10.在半径为3的圆中,60°的圆心角所对的劣弧长等于_____. 11.如图,在平面直角坐标系xOy 中,P 为函数)(0my x x=>图象上一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为M ,N .若矩形PMON 的面积为3,则m 的值为______.12.如图,ABC 的高AD ,BE 相交于点O ,写出一个与AOE △相似的三角形,这个三角形可以是______.13.如图,PA ,PB 是O 的切线,切点分别为A ,B .若30OBA ∠=︒,3PA =,则AB 的长为________.14.有一块三角形的草坪,其中一边的长为10m .在这块草坪的图纸上,这条边的长为5cm .已知图纸上的三角形的周长为15cm ,则这块草坪的周长为______m . 15.北京冬奥会雪上项目竞赛场地“首钢滑雪大跳台”巧妙地融入了敦煌壁画“飞天”元素.如图,赛道剖面图的一部分可抽象为线段AB .已知坡AB 的长为30m ,坡角ABH∠约为37°,则坡AB 的铅直高度AH 约为______m .(参考数据:sin370.60︒≈,cos370.80︒≈,tan370.75︒≈.)16.如图,在平面直角坐标系xOy 中,P 为x 轴正半轴上一点.已知点)(0,2A ,)(0,8B ,M 为ABP 的外接圆.(1)点M 的纵坐标为______;(2)当APB ∠最大时,点P 的坐标为______.三、解答题17)(0604cos 451π︒-︒--18.如图,AE 平分BAC ∠,D 为AE 上一点,B C ∠=∠.(1)求证:ABEACD ;(2)若D 为AE 中点,4BE =,求CD 的长.19.在平面直角坐标系xOy 中,已知抛物线243y x x =-+. (1)求它的顶点坐标; (2)求它与x 轴的交点坐标.20.下面是小石设计的“过三角形一个顶点作其对边的平行线”的尺规作图过程. 已知:如图,ABC .求作:直线BD ,使得BD AC ∥. 作法:如图,①分别作线段AC ,BC 的垂直平分线1l ,2l ,两直线交于点O ; ①以点O 为圆心,OA 长为半径作圆;①以点A 为圆心,BC 长为半径作弧,交AB 于点D ; ①作直线BD .所以直线BD 就是所求作的直线. 根据小石设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹) (2)完成下面的证明. 证明:连接AD ,①点A ,B ,C ,D 在O 上,AD BC =, ①AD =______.①DBA CAB ∠=∠(______)(填推理的依据). ①BD AC ∥.21.如图,在ABC 中,45B ∠=︒,2tan 3C =,AC =BC 的长.22.在平面直角坐标系xOy 中,二次函数图象上部分点的横坐标x ,纵坐标y 的对应值如下表:(1)求这个二次函数的表达式; (2)画出这个二次函数的图象;(3)若3y <-,结合函数图象,直接写出x 的取值范围.23.如图,AB 为O 的直径,点C 在O 上,连接AC ,BC ,过点O 作OD BC ⊥于点D ,过点C 作O 的切线交OD 的延长线于点E .(1)求证:E B ∠=∠;(2)连接AD .若CE =8BC =,求AD 的长.24.如图,排球运动场的场地长18m ,球网高度2.24m ,球网在场地中央,距离球场左、右边界均为9m .一名球员在场地左侧边界练习发球,排球的飞行路线可以看作是对称轴垂直于水平面的抛物线的一部分.某次发球,排球从左边界的正上方发出,击球点的高度为2m ,当排球飞行到距离球网3m 时达到最大高度2.5m .小石建立了平面直角坐标系xOy (1个单位长度表示1m ),求得该抛物线的表达式为215722y x =-+.根据以上信息,回答下列问题:(1)画出小石建立的平面直角坐标系; (2)判断排球能否过球网,并说明理由.25.在平面直角坐标系xOy 中,反比例函数)(0ky k x=≠的图象过点)(2,3A . (1)求k 的值;(2)过点)()(,00P m m ≠作x 轴的垂线,分别交反比例函数)(0ky k x =≠,4y x=-的图象于点M ,N .①当2m =-时,求MN 的长;①若5MN ≥,直接写出m 的取值范围.26.在平面直角坐标系xOy 中,()11,A m y -,()23,B y 是抛物线2224y x mx m =-+-上两点.(1)将2224y x mx m =-+-写成()2y a x h k =-+的形式; (2)若1m =,比较1y ,2y 的大小,并说明理由; (3)若12y y <,直接写出m 的取值范围.27.如图,AD 是ABC 的高,点B 关于直线AC 的对称点为E ,连接CE ,F 为线段CE 上—点(不与点E 重合),AF AB =.(1)比较AFE ∠与ABC ∠的大小;(2)用等式表示线段BD ,EF 的数量关系,并证明.(3)连接BF ,取BF 的中点M ,连接DM .判断DM 与AC 的位置关系,并证明.28.在平面直角坐标系xOy 中,O 的半径为2.点P ,Q 为O 外两点,给出如下定义:若O 上存在点M ,N ,使得P ,Q ,M ,N 为顶点的四边形为矩形,则称点P ,Q 是O 的“成对关联点”.(1)如图,点A ,B ,C ,D 横、纵坐标都是整数.在点B ,C ,D 中,与点A 组成O 的“成对关联点”的点是______;(2)点)(,E t t 在第一象限,点F 与点E 关于x 轴对称.若点E ,F 是O 的“成对关联点”,直接写出t 的取值范围;(3)点G 在y 轴上.若直线4y =上存在点H ,使得点G ,H 是O 的“成对关联点”,直接写出点G 的纵坐标G y 的取值范围.参考答案:1.C【分析】根据“内项之积等于外项之积”对四个选项进行计算,然后与条件进行对比即可判断. 【详解】解:A 、52xy =,得25x y =,故选项A 不符合题意; B 、 25x y=,得10xy =,故选项B 不符合题意; C 、25x y =,得52x y =,故选项C 符合题意; D 、25y x =,得52y x =,故选项D 不符合题意; 故选:C .【点睛】此题主要考查了比例的性质,正确将已知变形是解题关键. 2.B【分析】根据锐角的正弦为对边比斜边求出sin A 的值即可. 【详解】解:在Rt ABC △中,90C ∠=︒,4AB =,3BC =, ①3sin 4BC A AB ==. 故选:B .【点睛】本题考查锐角三角函数的定义及运用,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边. 3.D【分析】抛物线的平移规律:左加右减,上加下减,利用平移规律直接可得答案. 【详解】解:抛物线2y x =向上平移2个单位长度得到的抛物线为22,y x故选D【点睛】本题考查的是抛物线的平移,掌握“抛物线的上下平移规律”是解本题的关键. 4.A【分析】根据抛物线开口方向可得a<0,可对A 进行判断;根据对称轴位置可得b >0,可对B 进行判断;根据抛物线与y 轴交点位置可得c <0,可对C 进行判断;根据抛物线与x 轴无交点可得①<0,可对D 进行判断;综上即可得答案. 【详解】①抛物线开口向下, ①a<0,故A 选项正确, ①对称轴在y 轴右侧,①2ba->0, ①b >0,故B 选项错误, ①抛物线与y 轴交于y 轴负半轴, ①c <0,故C 选项错误, ①抛物线与x 轴无交点, ①①<0,故D 选项错误, 故选:A .【点睛】本题考查二次函数图象与系数的关系,当a =0时,抛物线开口向上,当a <0时,开口向下;当对称轴在y 轴左侧时,a 、b 同号,当对称轴在y 轴右侧时,a 、b 异号;c 的符号由图象与y 轴的交点位置决定;当①>0时,图象与x 轴有2个交点,当①=0时,图象与x 轴有1个交点;①<0时,图象与x 轴没有交点;熟练掌握相关知识是解题关键. 5.B【分析】根据反比例函数的性质求解. 【详解】解:反比例函数)(0ky x x=<的函数值y 随着自变量x 的增大而增大, 所以双曲线的两支分别位于第二、第四象限,而x <0,则分支在第二象限. 故选:B .【点睛】本题考查了反比例函数的性质:反比例函数ky x=(k ≠0)的图象是双曲线;当k >0,双曲线的两支分别位于第一、第三象限,在每一象限内y 随x 的增大而减小;当k <0,双曲线的两支分别位于第二、第四象限,在每一象限内y 随x 的增大而增大. 6.B【分析】设①ADC =α,①ABC =β,由菱形的性质与圆周角定理可得18012,求出β即可解决问题.【详解】解:设①ADC =α,①ABC =β; ①四边形ABCO 是菱形, ①①ABC =①AOC β=; ∴ ①ADC =12β;四边形ABCD 为圆的内接四边形,∴α+β=180°,①18012,解得:β=120°,α=60°,则①ADC =60°, 故选:B .【点睛】该题主要考查了圆周角定理及其应用,圆的内接四边形的性质,菱形的性质;掌握“同圆或等圆中,一条弧所对的圆周角是它所对的圆心角的一半”是解本题的关键. 7.C【分析】由周长,先求出正方形的边长,然后结合面积公式,即可得到答案. 【详解】解:①正方形的周长为x ,①正方形的边长为4x,①正方形的面积221()416x y x ==; 故选:C .【点睛】本题考查了函数表达式,解题的关键是掌握正方形的面积和周长公式. 8.A【分析】根据二次函数解析式可得抛物线对称轴及开口方向,根据各点横坐标可判断312y y y >>,进而求解.【详解】解:①22y ax ax c =-+中0a >, ①抛物线开口向上,对称轴为直线212ax a-=-=, ①411(1)21->-->-, ①312y y y >>,当120y y <时,12y y ,异号, ①1200y y ><,,①310y y >>,选项A 正确. 当3120y y y >>>时,230y y >, ①选项B 错误,当130y y <时,3100y y ><,, ①210y y <<,选项C 错误.当1230y y y =时,123y y y ,,中有1个值为0即可, ①选项D 错误. 故选:A .【点睛】本题考查二次函数图象上点的坐标特征,解题关键是掌握二次函数的性质,掌握二次函数图象与系数的关系. 9.6【分析】根据ABCD 可以证明ODC OAB △∽△,进而得出比例式,再根据12AO OD =和3BO =即可求出OC 的长度. 【详解】解:①ABCD ,AD ,BC 交于点O ,①D A ∠=∠,C B ∠=∠. ①ODC OAB △∽△. ①OD OCOA OB=. ①12AO OD =, ①2ODOA=. ①2OCOB=. ①3BO =, ①6OC =. 故答案为:6.【点睛】本题考查相似三角形的判定定理和性质,综合应用这些知识点是解题关键. 10.π【分析】弧长公式为l =n 180rπ,把半径和圆心角代入公式计算就可以求出弧长. 【详解】解:半径为3的圆中,60°的圆心角所对的劣弧长=603180π⨯=π, 故答案为:π.【点睛】本题主要考查了弧长计算,关键是掌握弧长计算公式.11.3【分析】根据反比例函数的解析式是m y x=,设点(,)P a b ,根据已知得出3ab =,即3xy =,求出即可.【详解】解:设反比例函数的解析式是my x=, 设点(,)P a b 是反比例函数图象上一点, 矩形PMON 的面积为3,3ab ∴=,即3m xy ==, 故答案为:3.【点睛】本题考查了矩形的面积和反比例函数的有关内容的应用,解题的关键是主要考查学生的理解能力和运用知识点解题的能力. 12.ACD ∆(答案不唯一)【分析】根据已知条件得到90AEO BDO ∠=∠=︒,AOE BOD ∠=∠,推出AOE BOD ∆∆∽;同理AOE ACD ∆∆∽,根据相似三角形的性质得到AFE C ∠=∠,又90AEO BEC ∠=∠=︒,于是得到AOE BCE ∆∆∽.【详解】解:本题答案不唯一;与AOE ∆相似的三角形有:BOD ∆,ACD ∆,BCE ∆, 选择求证:ACD AOE ∆∆∽.证明:ABC ∆的高AD ,BE 交于点O ,90ADC AEO ∴∠=∠=︒. CAD OAE ∠=∠, ACD AOE ∴∆∆∽,故答案是:ACD ∆.【点睛】本题考查了相似三角形的判定,三角形的高的定义,解题的关键是掌握有两角对应的两个三角形相似. 13.3【分析】根据切线长定理和切线的性质,得出PA PB =,90PBO ∠=︒,再根据等腰三角形的判定定理,得出PAB 为等腰三角形,再根据角之间的数量关系,得出60PBA ∠=︒,再根据等边三角形的判定定理,得出PAB 为等边三角形,再根据等边三角形的性质,得出AB PA =,进而即可得出答案.【详解】解:①PA ,PB 分别为O 的切线, ①PA PB =,90PBO ∠=︒, ①PAB 为等腰三角形, ①30OBA ∠=︒,①60PBA PBO OBA ∠=∠-∠=︒, ①PAB 为等边三角形, ①AB PA =, ①3PA =, ①3AB =. 故答案为:3【点睛】本题考查了切线长定理、切线的性质、等腰三角形的判定定理、等边三角形的判定与性质,解本题的关键在熟练掌握相关的性质定理. 14.30【分析】设这块草坪的周长为x m ,由实际的三角形草坪与图纸上的三角形草坪是相似三角形,再利用相似三角形的性质列方程即可. 【详解】解:设这块草坪的周长为x m ,由题意可得:实际的三角形草坪与图纸上的三角形草坪是相似三角形,10,155x解得:30x =,所以这块草坪的周长为30m. 故答案为:30【点睛】本题考查的是相似三角形的性质,掌握“相似三角形的周长之比等于相似比”是解本题的关键. 15.18【分析】由30,37,90,AB ABHAHB 结合sin 37,AHAB再解方程即可. 【详解】解:由题意得:30,37,90,AB ABH AHBsin 37,AHAB300.6018AHm ,故答案为:18【点睛】本题考查的是解直角三角形的实际应用,掌握“由锐角的正弦求解直角三角形的边长”是解本题的关键. 16. 5 (4,0)【分析】(1)根据点M 在线段AB 的垂直平分线上求解即可;(2)点P 在①M 切点处时,APB ∠最大,而四边形OPMD 是矩形,由勾股定理求解即可. 【详解】解:(1)①①M 为△ABP 的外接圆, ①点M 在线段AB 的垂直平分线上, ①A (0,2),B (0,8), ①点M 的纵坐标为:8252+=, 故答案为:5;(2)过点)(0,2A ,)(0,8B ,作①M 与x 轴相切,则点M 在切点处时,APB ∠最大, 理由:若点P '是x 轴正半轴上异于切点P 的任意一点, 设AP '交①M 于点E ,连接AE ,则①AEB =①APB , ①①AEB 是ΔA P 'E 的外角, ①①AEB>①A P 'B ,①①APB >①A P 'B ,即点P 在切点处时,①APB 最大, ①①M 经过点A (0,2)、B (0,8),①点M 在线段AB 的垂直平分线上,即点M 在直线y =5上,①①M 与x 轴相切于点P ,MP ①x 轴,从而MP =5,即①M 的半径为5,设AB 的中点为D ,连接MD 、AM ,如上图,则MD ①AB ,AD =BD =12AB =3,BM =MP =5,而①POD =90°,①四边形OPMD 是矩形,从而OP =MD , 由勾股定理,得MD 4=, ①OP =MD =4,①点P 的坐标为(4,0),故答案为:(4,0).【点睛】本题考查了切线的性质,线段垂直平分线的性质,矩形的判定及勾股定理,正确作出图形是解题的关键. 17.2【分析】将特殊角的三角函数值代入,然后利用二次根式的运算法则计算即可得.()0604cos 451π︒-︒--41-+31=-+2=.【点睛】题目主要考查特殊角的三角函数值的计算,二次根式的混合运算,0次幂的运算,熟记特殊角的三角函数值是解题关键. 18.(1)证明见详解;(2)CD 的长为2.【分析】(1)由角平分线的定义可得BAE EAC ∠=∠,根据相似三角形的判定定理即可证明; (2)由中点的定义可得12AD AE =,再由(1)中结论相似三角形的性质即可得. 【详解】解:(1)证明∵AE 平分BAC ∠, ∴BAE EAC ∠=∠, 在ABE ∆与ACD ∆中, ∵BAE EAC ∠=∠,B C ∠=∠,∴~ABE ACD ∆∆;(2)∵D 为AE 中点, ∴12AD AE =, ∵~ABE ACD ∆∆, ∴12AD CD AE BE ==, ∴122CD BE ==, ∴CD 的长为2.【点睛】题目主要考查相似三角形的判定和性质,角平分线和线段中点的性质,熟练掌握相似三角形的判定和性质是解题关键. 19.(1)()2,1-;(2)1,0,3,0. 【分析】(1)把抛物线化为顶点式即可;(2)令0,y = 则2430,x x -+=再利用因式分解法解一元二次方程即可. 【详解】解:(1)224321,yx x x所以抛物线的顶点坐标为:2,1. (2)令0,y = 则2430,x x -+=()()130,x x ∴--=10x ∴-=或30,x -=解得:121,3,x x ==所以抛物线与x 轴的交点坐标为:1,0,3,0.【点睛】本题考查的是求解抛物线的顶点坐标,抛物线与x 轴的交点坐标,掌握“把抛物线化为顶点式以及把0y =代入抛物线求解与x 轴的交点坐标”是解本题的关键. 20.(1)作图见解析;(2),BC 在同圆中,等弧所对的圆周角相等 【分析】(1)根据题干的作图步骤依次作图即可;(2)由作图可得AD BC =,证明AD BC =,利用圆周角定理可得DBA CAB ∠=∠,从而可得答案.【详解】解:(1)如图,直线BD 就是所求作的直线(2)证明:连接AD ,①点A ,B ,C ,D 在O 上,AD BC =, ①AD BC =.①DBA CAB ∠=∠(在同圆中,等弧所对的圆周角相等). ①BD AC ∥.故答案为:,BC 在同圆中,等弧所对的圆周角相等【点睛】本题考查的是作线段的垂直平分线,三角形的外接圆,平行线的作图,圆周角定理的应用,掌握“圆周角定理”是理解作图的关键. 21.10【分析】过点A 作AD ①BC ,结合三角函数值,分别求出BD 、CD 的长度,即可得到答案. 【详解】解:根据题意,过点A 作AD ①BC ,如图:①①ABD ,①ACD 都是直角三角形, ①2tan 3AD C CD ==, 设2AD x =,3CD x =,①AC == 解得:2x =(负值已舍去), ①4=AD ,6CD =, ①45B ∠=︒, ①4BD AD ==, ①4610BC =+=;【点睛】本题考查了三角函数,勾股定理,等腰直角三角形的性质,解题的关键是正确的求出BD 、CD 的长度.22.(1)22y x x =-+;(2)图象见解析;(3)1x <-或x >3【分析】(1)设二次函数的表达式为2y ax bx c =++,根据三组横坐标x 和纵坐标y 的值列出方程组求出a ,b ,c 的值即可得到二次函数的表达式;(2)计算并补充出一些横坐标x 和纵坐标y 的对应值,然后在平面直角坐标系中描点,并用平滑曲线连接即可;(3)根据二次函数的图象应用数形结合思想即可得到x 的取值范围. 【详解】解:(1)设二次函数的表达式为2y ax bx c =++. 将三组横坐标x ,纵坐标y 的值代入可得222000,111,022a b c a b c a b c ⎧=⨯++⎪=⨯++⎨⎪=⨯++⎩.解得1,2,0a b c =-⎧⎪=⎨⎪=⎩.所以二次函数的表达式为22y x x =-+. (2)横坐标x 与纵坐标y 的对应值如下表:建立平面直角坐标系,描点并用平滑曲线连接即可得到该二次函数的图象.(3)3y <-,即223x x -+<-.根据(2)中二次函数图象可以看出当1x <-或x >3时,3y <-. 所以x 的取值范围是1x <-或x >3.【点睛】本题考查二次函数的解析式,二次函数的图象和性质,熟练掌握这些知识点是解题关键.23.(1)证明见解析;(2)AD 【分析】(1)连接OC 通过垂径定理和等腰三角形性质证明①E =①B(2)连接AD 通过计算发现BC =EC ,再通过证明①CED ①①ABC 得到AC =DC =4. 【详解】(1)证明:连接OC 如图:OD ①CB①OB =OC ,①B =OCD又CE 为圆O 的切线①OC ①CE①①ECD +①DCO =①ECD +①E =90°①①E =①DCO =①B①①E =①B(2)连接AD 如图①①EDC 为R t①①DE由(1)得①E =①B又AB 为直径①①BCA =90°在①CED 和①ABC 中 ①B E EDC BCA ED BC ∠=∠⎧⎪∠=∠⎨⎪=⎩①①CED ①①ABC (AAS )①AC =DC =12BC =4①AD ==【点睛】本题考查垂径定理和全等三角形的判定与性质,掌握这些是本题解题关键.24.(1)见解析;(2)排球能过球网,理由见解析【分析】(1)根据该抛物线的表达式为215722y x =-+,可得抛物线的顶点坐标为50,2⎛⎫⎪⎝⎭,从而得到小石建立的平面直角坐标系是以O 为坐标原点,OB 所在的直线为x 轴,OA 所在的直线为y 轴,即可求解;(2)根据题意得:当3x = 时,2153 2.375 2.24722y =-⨯+=> ,即可求解. 【详解】解:(1)如图,①该抛物线的表达式为215722y x =-+, ①抛物线的顶点坐标为50,2⎛⎫ ⎪⎝⎭ ,①当排球飞行到距离球网3m 时达到最大高度2.5m .根据题意得:点A 的坐标为50,2⎛⎫ ⎪⎝⎭,①小石建立的平面直角坐标系是以O 为坐标原点,OB 所在的直线为x 轴,OA 所在的直线为y 轴,如下图:(2)排球能过球网,理由如下:根据题意得:点B 的横坐标为3,①当3x = 时,2153 2.375 2.24722y =-⨯+=> , ①排球能过球网.【点睛】本题主要考查了建立二次函数的图象和性质,建立适当的平面直角坐标系,熟练掌握二次函数的图象和性质是解题的关键.25.(1)6;(2)①5;①20m -<<或02m <<【分析】(1)把(2,3)A 代入k y x =中即可得出k 的值; (2)①令2x =-代入6y x =和4y x =-中,求出点M 、N 的坐标,即可得出MN 的长; ①令x m =代入6y x =和4y x=-中,求出点M 、N 的坐标,即可得出MN 含m 的表达式,由5MN >即可求出m 的取值范围.【详解】(1))把(2,3)A 代入k y x=中得:32k =, ①6k =;(2)①令2x =-代入6y x =中得:632y ,①(2,3)M --, 令2x =-代入4y x =-中得:422y =-=-, ①(2,2)N -,①235MN =+=;①令x m =代入6y x =中得:6y m =, ①6(2,)M m-, 令x m =代入4y x=-中得:4y m =-, ①4(2,)N m --,①6410+MN m m m==, 当0m >时,105MN m=>, 解得:2m <,①02m <<, 当0m <时,105MN m=->, 解得:2m >-,①20m -<<, 综上述所,m 的取值范围为20m -<<或02m <<.【点睛】本题考查反比例函数的综合应用,掌握待定系数法求解析式以及两点长度的表示是解题的关键.26.(1)()24y x m =-- (2)12y y <(3)2m <或4m >【分析】(1)利用完全平方公式即可求解;(2)当1m =时,确定函数解析式,根据点A ,点B 到对称轴的距离即可判断1y ,2y 的大小; (3)先求出抛物线的对称轴,根据12y y <可知点A 到对称轴的距离小于点B 到对称轴的距离,解不等式即可.【详解】(1)解:2224y x mx m =-+-()24x m =--;(2)解:12y y <,理由如下:若1m =,则抛物线的解析式为()214y x =--,()10,A y ,()23,B y , ∴对称轴为1x =,0131-<-,∴点()23,B y 到对称轴的距离大于点()10,A y 到对称轴的距离,0a >,∴12y y <;(3)解:()24y x m =--的图象开口向上,对称轴为x m =, ∴点()11,A m y -到对称轴的距离为11m m --=,点()23,B y 到对称轴的距离为3m -,12y y <, ∴31m ->,∴31m ->或31m -<-,∴2m <或4m >.【点睛】本题考查二次函数的顶点式,利用函数图象判断函数值的大小,解一元一次不等式等,熟练掌握二次函数的图象和性质是解题的关键.27.(1)AFE ABC ∠=∠,理由见详解;(2)2EF BD =,理由见详解;(3)DH①AC .【分析】(1)过点A 作AG ①CE ,然后利用HL 证明Rt ①ABD ①Rt ①AFG ,即可得到结论成立; (2)连接AE ,则AE =AF ,则AG 垂直平分EF ,则BD FG EG ==,即可得到答案;(3)连接BF ,取BF 的中点M ,连接AM ,DM 并延长交AC 于H ,由等腰三角形的性质知①BAM+①ABM=90°,再利用四边形内角和定理说明①ACB+①BAM=90°,则①ACD=①ABM ,由①AMB=①ADB=90°,由四点A 、B 、D 、M 共圆解决问题.【详解】解:(1)AFE ABC ∠=∠;理由如下:过点A 作AG ①CE ,如图:根据题意,点B 关于直线AC 的对称点为E ,①AC 平分①BCE ,①AD ①BC ,AG ①CE ,①AD =AG ,①AF =AB ,①Rt①ABD①Rt①AFG(HL),∠=∠;①AFE ABC(2)2=;EF BD理由如下:连接AE,如图:①Rt①ABD①Rt①AFG,=,①BD FG①点B关于直线AC的对称点为E,①AB=AE,①AE=AF,①AG垂直平分EF,=,①FG EG==,①BD FG EG①2=;EF BD(3)DM①AC,理由如下:连接BF,取BF的中点M,连接AM,DM并延长交AC于H,①AB=AF,点M为BF的中点,①AM①BF,①①BAM+①ABM=90°,①点B 关于直线AC 的对称点为E ,①①ACB=①ACF ,①①ABC=①AFE ,①①ABC+①AFC=180°,①①BAF+①BCF=180°,①①ACB+①BAM=90°,①①ACD=①ABM ,①①AMB=①ADB=90°,①四点A 、B 、D 、M 共圆,①①ABM=①ADM ,①①ADM+①HDC=90°,①①ACD+①HDC=90°,①DH①AC .【点睛】本题考查了轴对称的性质,全等三角形的判定和性质,垂直平分线的性质,角平分线的性质定理,解题的关键是熟练掌握所学的知识,正确的作出辅助线,从而进行解题.28.(1)B 和C ;(22t ≤;(3)42G y <≤+【分析】(1)根据图形可确定与点A 组成O 的“成对关联点”的点;(2)如图,点E 在直线y x =上,点F 在直线y x =-上,当点E 在线段01E E 上,点F 在线段01F F 上时,有O 的“成对关联点”,求出即可得出t 的取值范围;(3)分类讨论:点G 在4y =上,点G 在4y =的下方和点G 在4y =的上方,构造O 的“成对关联点”,即可求出G y 的取值范围.【详解】(1)如图所示:在点B ,C ,D 中,与点A 组成O 的“成对关联点”的点是B 和C ,故答案为:B 和C ;(2)①(,)E t t①(,)E t t 在直线y x =上,①点F 与点E 关于x 轴对称,①(,)F t t -在直线y x =-,如下图所示:直线y x =和y x =-与O 分别交于点0E ,0F ,与直线2x =分别交于1E ,1F ,由题可得:0E ,当点E 在线段01E E 上时,有O 的“成对关联点”2t ≤;(3)如图,当点G 在4y =上时,GH x ∥轴,在O 上不存在这样的矩形;如图,当点G 在4y =下方时,也不存在这样的矩形;如图,当点G 在4y =上方时,存在这样的矩形GMNH ,当恰好只能构成一个矩形时,设(0,)G m ,直线4y =与y 轴相交于点K ,则GHK OGM ∠=∠,2OM =,OG m =,4GH MN ==,4GK m =-,①sin sin GHK OGM ∠=∠,即GK OM GH OG =, ①424m m-=,解得:2m =+2m =-,综上:当42G y <≤+G ,H 是O 的“成对关联点”.【点睛】本题考查几何图形综合问题,属于中考压轴题,掌握“成对关联点”的定义是解题的关键.。
北京市海淀区九年级(上)期末英语试卷(含答案)

九年级(上)期末英语试卷题号I II III IV总分得分一、单项选择题(本大题共11 小题,共5.5 分)1.-Do you know ______ ?-Last year.()A.when will Professor Lee visit ChinaB.when Professor Lee will visit ChinaC.when did Professor Lee visit ChinaD.when Professor Lee visited China2. Many people like to see golden leaves ______ autumn .()A. inB. onC. atD. to3.Today is Mark's birthday ,and he ______ a big party with his family in the garden now .()A. hadB. is havingC. has hadD. was having4. Colin's home is far from school and he ______ to school by bus every day .()A. goesB. has goneC. was goingD. will go5. Taron ______ a cold yesterday , so he had to go to see a doctor.()A. has caughtB. is catchingC. catchesD. caught6.-______ is your favorite writer ?-Charles Dickens . He wrote A Christmas Carol in 1843 .()A. WhatB. WhoC. WhyD. Whose7. Emma ______ a car when her phone rang.()A. drivesB. will driveC. was drivingD. is driving8.Jessica really enjoys travelling ,and she ______ many foreign countries since 2010 .()A. visitsB. has visitedC. will visitD. was visiting9. My uncle likes books , ______ he doesn't have much time to read.()A. forB. orC. butD. so10. -Do you know Paul is ______ boy in Class 5 ?-Yes. He is very good at playing basketball .()A. tallB. tallerC. tallestD. the tallest11. Miss Brown knows a lot about biology .We all like to ask ______ about it .()A. sheB. heC. herD. him二、阅读理解(本大题共13 小题,共 26.0 分)AMindfulness MattersmeditationIn recent years, some schools have begun to introduce meditation , or mindfulness training ,into their classrooms . During mindfulness training , students may be asked to sit quietly and observe their own thoughts and feelings to avoid being controlled by them . Mindfulness training can help students overcome anxiety (忧虑), control their behavior , and improve their ability to pay attention in class . Students are expected to learn how to meditate in order to reduce stress and do better in their schoolwork .Among schools that already teach meditation , the results have been positive . In onestudy , teachers reported that after five weeks of mindfulness practice , their students were more focused.They also participated more fully in class .A middle school in San Francisco reported that a student meditation program led to higher attendance rates and bettergrades . Another study suggested that meditation helped students perform better on tests by improving their working memory and reducing their anxiety .Many supporters believe that meditation training programs can also help students overcome stress.For example,Headstand is a mindfulness education program designed to help students overcome anxiety . A study concluded that ninety-eight percent of participating students felt less stressed after they completed the Headstand program.In another study,researchers in New Haven ,Connecticut ,followed students who participated in meditation and yoga classes three times a week.They found that after each class,participants had lower levels ofcortisol ,a stress hormone (激素), in their bodies .Despite the positive results seen so far, critics also point out that much of the current research is not rigorous (谨慎的) enough.Associate Professor Tamar Mendelson agrees that research on meditation in children is still in its early stages .However ,even she insists that she has seen the positive impact of meditation on children . Others express worries that meditation is not a valuable use of class time . But many disagree . Denise Pope, a professor from the Stanford University ,says,"This is something teachers can do immediately . You get a lot of bang for your buck and anyone who is against it isn't thinking clearly . "Indeed , additional studies will surely strengthen our understanding of the benefits of mindfulness .Although still in its early stages , research shows that meditation can help students learn todeal with anxiety and stress.As an added bonus,students of mindfulness training also report better concentration and gains in their academic performances.Therefore ,meditation should be a part of every student's school day . Participating in"stillness"can be just as productive as other school-related activities .12.Why do some schools introduce mindfulness training into classes ? ______A.To control students'working memory .B.To reduce students'stress and anxiety.C.To increase students'attendance rates.D.To research students'thoughts and feelings.13.What can we learn from the passage? ______A.Mindfulness training is not a valuable use of class time at school .B. Mindfulness training is more productive than other school activities.C. Students felt more stressful after joining yoga classes three times a week.D. Students paid closer attention in class after weeks of mindfulness practice.14. The words"a lot of bang for your buck"in Paragraph 4probably mean" ______ ".A. challengesB. complaintsC. advantagesD. influences15.The writer probably agrees that ______ .A.further studies will prove the benefits of mindfulness trainingB.students will become more talented with mindfulness trainingC.doctors will do researches on the spread of mindfulness trainingD.mindfulness training decides students'mental and physical health .BNowadays ,many teens are badly addicted to using phones.It probably won't surprise youthat teens are texting more than ever before.Instead of sleeping,Kenny Alarcon ,16,often texts with his friends through the night .FrancesGarcia,a high school senior,sends and receives about 1000texts each day.Both Frances and Kenny wake up several times during the night to text . Kenny even sleeps with his phone beneath his pillow .Dr . Elizabeth Dowdell , a professor at Villanova University in Pennsylvania,says that it's common for teens to be interrupted by texts while sleeping . "If they often lose sleep ,"Dr .Dowdell says ,"teens may become angry,or depressed.A lack of sleep can lead to weight gain and even obesity because many people turn to junk food for quick energy whenthey are tired . "Some experts are worried about how texting is affecting teenagers'lives .One concern is that students might not learn correct grammar and spelling if most of the writing they do is made up of text messages. Some people also worry that teens don't spend enough time talking with others face-to-face , which could be hurting their relationships with friends andfamily .Moreover ,all that texting takes away hours that could be spent studying,exercising, taking up a hobby ,or just relaxing .According to Dr . Dowdell , teens need to learn that they can and should turn off their phones sometimes. She had Kenny and Frances do an experiment. These were the rules:No phone for 48hours . No computer or Internet either , unless it was for schoolwork .After 48phone-free hours ,Kenny and Frances were interviewed . "Wow , it was pure torture (摧残),"Kenny joked .Kenny missed his friends,and he was sad at times.But he also felt relief from the constant texting .He spent time reading books and talking with his family ,which he really enjoyed . Frances had an even happier result. "I loved it!"she said , "I was going to the gym and hanging out with friends and playing basketball.I had a wonderful experience."Frances decided to continue the experiment for a while . "I think I'll be so much smarter and healthier, "she explained , "everybody in the world should try it."16. If teens keep waking up to text while sleeping , they may ______ .A. get overweightB. become happierC. disturb their parentsD. feel more relaxed17.What is Paragraph 4mainly about ? ______A.Mistakes in teens'text writing .B.Time wasted on meaningless texting .C.Worries about how texting affects teens .D.Encouragement to teens'talking face-to-face .18. The writer mentions the experiment on Frances and Kenny to ______.A.advise people what to do without phonesB.show teens can live well without phonesC.explain phones are important in teens'livesD.introduce how they make good use of phones .CFinally HomeLast year, my parents moved to this town . I had to go to a new school and found no one to be friends with because I wasn't interested in the topics most of my classmates liked ."Maybe I'll never have real friends , "I thought .I closed my eyes and imagined playing my drums . Suddenly , I heard the sound of aguitar . I followed the sound and found out that was a band . I recognized the guitar player at my first sight and so did he ."Hey , you're Cassie from my class!"his voice surprised me ."I'm sorry ,"I said ."I just haven't heard any live music in this town before!You sound great-didyou guys write that song ? ""Yeah-well , we're still working on it.I'm Matt."He stood up and held out his hand."Mind if I listen in?"I asked in a low voice."Not at all , "Matt said , smiling . "Maybe you can give us some suggestions!"The song was pretty good and I could really improve it with my drum skills . Behind my drumset was the one place I felt completely like myself .But I wasn't sure if I wanted to open thatdoor to the world ."Hey , do you play drums ? "Matt asked suddenly .His question surprised me . How did he know ?And then I followed his eyes to my hands ,which had been beating a rhythm (节奏) on the floor .I tried to say no,but my heartstopped me from refusing ."Sure , I've been playing for a few years , "I said finally ."Oh , wow!You've got to join us!"Matt said."I have some drums over here."I looked at their shiny faces . "Absolutely . I would love to play!"I replied."One , two , three, four!"Matt counted and began singing , and I knew I was finally home.19. When the writer first went to a new school , she ______ .A. joined a music clubB. had no close friendsC. could play the guitarD. developed a new hobby20. How did the writer feel when Matt asked if she played drums ? ______A. Surprised.B. Scared.C. Worried.D. Excited.21. The writer said she was finally home because ______ .A.she learned to play the drumsB.she decided to leave the townC.she loved her home very muchD.she made some friends finally .DNew Year's ResolutionPosted by Lauren Conrad December 28 , 2017You guys , I can not believe it's about to be 2018!If you haven't thought of your2018New Year's resolution yet , start by choosing one word from the list below .Love Peace KindnessJoy Patience Self-controlKathieDecember29, 2017The word that I choose from the list is joy. Whether that meansjogging with my classmates in the morning, walking my dog in the neighborhood,or enjoying dinner with my parents,I am going to make sure I take the time to have fun!SofiaDecember 30, 2017Self-control would be my word for the coming year.This year I amgoing to be a morning person!I'll wake up early and start my day at 5 am instead of 6 am. Imagine what I could do with 5 more hours every week!TaylorDecember31, 2017My word isn't on your list . But this year I'd like"SLOW"to guide me , which means many things to me . I will try to avoid too muchhomework in order to think deeply , slowly read a book instead of quickly looking through social media ,and go to bed earlier in order to have slower mornings .22. When did Kathie make her resolution ? ______A. On December 28 .B. On December 29 .C. On December 30 .D. On December 31 .23. What is Sofia's word for the coming year ? ______A..B.Kindness .PeaceC. Patience .D. Self-control .24. What is Taylor probably going to do in 2018 ? ______A. To jog in the morning .B. To look through social media quickly .C. To read a book slowly .D. To walk his dog in the neighborhood .三、任务型阅读(本大题共1 小题,共 10.0 分)25. Can you imagine a world without a writing system for your language ? It may be hard topicture it now ,but a man named Sequoyah lived in such a world .Sequoyah was a memberof a native American tribe , the Cherokee .Cherokee people speak their own language , but for hundreds of years they did not have a system of writing .Without a writingsystem , the Cherokee had no newspapers or books before 1809.Sequoyah was probably born around the year 1770and lived with his mother in a small village in the mountains of Tennessee .When he grew up ,he became ablacksmith .When he was doing business with those"English-speaking people" ,he noticed that they used paper with marks to record their thoughts and ideas .Sequoyah called these pieces of paper with marks"talking leaves" .He began to wonder why people who spoke Cherokee did not have a way to write down their words .In 1809, Sequoyah decided to give the Cherokee their own"talking leaves" . At first he tried to make a different symbol for every word in the Cherokee language .But in that case , there would be so many symbols and too hard for people to remember ,so he decided to make a picture for each syllable (音节). After much hard work , Sequoyah invented 85symbols . In order to see whether it would work ,he helped his six-year-old daughter Ayoka learn each symbol and found she could learn to read and write very quickly . Sequoyah's invention was a success!Before long ,Sequoyah's writing system had spread far and wide .Cherokee people living in all different parts of the country learned to read and write .In 1825 ,Sequoyah's system was made the official written language for Cherokee people . To this day , Cherokee speakers still use Sequoyah's writing system .In some parts of the United States ,you can see street signs and billboards written in both English and Cherokee . Sequoyah will always be remembered for his important contribution to Cherokee people .Did the Cherokee have newspapers before 1809?______What did Sequoyah call the pieces of paper with marks ?______How many symbols did Sequoyah invent in the Cherokee language ?______When was Sequoyah's system made the official written language ?______Why will Sequoyah always be remembered ?______ .四、书面表达(本大题共 2 小题,共30.0 分)26.和睦是一种美德.和睦社会由一个个和睦的家庭组成.建立和睦家庭是我们每一个人的责任.和睦的家庭赐予我们精神支持,并使我们倍感幸福.若是你是李华,你家被社区评为 "和睦家庭 ".请你用英语写一篇短文,给某英文网站投稿,说说你的家庭是什么样子,为使家庭和睦你常常做些什么,以及你的感觉.提示词语: harmony (和睦), get on well with , support, happy提示问题:●What'syour harmonious family like ?●Whatdo you usually do ?●Howdo you feel ?Everyone wants to live in a harmonious family . ______.27. 从下边两个题目中任选一题,依据中文和英文提示,达成一篇许多于50 词的文段....写作.文中已给出内容不计入总词数.所给提示词语仅供采用.请不要写出你的校名和姓名.若是你是李华,寒假马上到来,为了方便外籍教师和留学生在假期使用图书室,请你写一则英文通知,告诉他们图书室假期开放时间,每次可借阅图书的数目和借阅限期,以及需要注意的事项.提示词语: return, renew (续借), ID card提示问题:●When will the school library be open during the winter vacation ?●How many books can be borrowed and how long can they be kept ?●Whatrules should be followed ?NoticeDear foreign teachers and students,Winter vacation is coming . ______.答案和分析1.【答案】D【分析】答案:D依据第一句问句可知是宾语从句,宾语从句要用陈说语序.依据这一规则,可清除 AC,由于 AC 是疑问语序.再依据答语 last year,可知是一般过去时.故可清除 B.应选 D.-你知道李教授什么时间接见中国的? - 昨年.做单项选择填空的技巧是:清除比较法.即利用上下文的时间状语,推测出适合的时态,清除错误的答案,而后再比较剩下的选择项,进而做出正确的答案.2.【答案】A【分析】答案:A在季节前面应当用介词 in,联合句意:很多人喜爱在秋季看金黄的树叶,应选A.很多人喜爱在秋季看金黄的树叶.此题考察介词的辨析,介词的用法一般都是固定的.熟记介词的用法及联合语境是解答本题的重点.3.【答案】B【分析】答案:B.此刻进行时表示此时此刻正在进行的动作,其组成是:am/is/are+此刻分词.依据时间状语 now,此刻,所以可知这个句子要用此刻进行时来填空,因此可知这句话的意思是 " 今日是马克的诞辰,他此刻正在花园里和朊友举行一个浩大的聚会. "应选 B.今日是马克的诞辰,他此刻正在花园里和朊友举行一个浩大的聚会.第一要掌握这个句子的意思,而后联合详细的题目,就能够确立正确答案.4.【答案】A【分析】答案:A .考察动词第三人称单数.A 第三人称单数.B 此刻达成时态.C 过去进行时态.D 一般未来时态.由every day每日,可知,一般此刻时态,主语 he 他,第三人称单数.谓语动词用第三人称单数 goes去.答案是 A .柯林的家离学校很远,他每日乘公共汽车上学.实义动词的第三人称单数.往常用于一般此刻时态,要联合主语的单复数变化,选择适合的实义动词形式,注意实义动词第三人称单数变化规则.5.【答案】D【分析】答案:D.一般过去时表示在过去的某个时间发生的动作或存在的状态.基本构造:主语 +谓语(动词过去式)+句子其余成分;主语 +was/were+形容词/名词/介词短语 +过去时过去时间;依据时间状语 yesterday,这是一个表过去的时间状语,所以要用一般过去时来填空,所以可知这句话的意思是 "塔伦昨天感冒了,所以他不得不去看医生. " 应选 D.塔伦昨天感冒了,所以他不得不去看医生.第一要掌握这个句子的意思,而后联合详细的题目,就能够确立正确答案.6.【答案】B【分析】答案:B.what 意思是 "什么 "who 意思是 "谁"why 意思是 "为何 "whose 意思是 "谁的 "根据答语 Charles Dickens查理?狄更斯,所以可知上一句问的是谁,所以可知这句话的意思是 "-- 谁是你最喜欢的作家? --查理?狄更斯.他在 1843 年写了《圣诞颂歌》"应选 B.--谁是你最喜欢的作家?--查理?狄更斯.他在 1843 年写了《圣诞颂歌》第一要掌握这个句子的意思,而后联合详细的题目,就能够确立正确答案.7.【答案】C【分析】答案:C.when 指引的时间状语从句,表示一个动作进行时,另一个动作正在由rang 过去式.可知,应当用过去进行时态.构造是 was/were+动词的此刻分词.主语 Emma ,用was.应选 C.艾玛正在开车,这时她的电话响了.第一要掌握这个句子的意思,而后联合详细的题目,就能够确立正确答案.8.【答案】B【分析】答案:B.visit" 观光,接见 ",是动词原形,visits 是第三人称的单数形式,用于一般此刻时;has visited 已经接见,用于此刻达成时;will visit 将观光,用于一般未来时;was visiting 正在接见,用于过去未来时.由since 2010,"自从 2010 年 ",表示一段时间,用此刻达成时,故用has visited.由题干"杰西卡确实喜欢旅行,自从 2010 年她已接见很多外国国家." 可知,故答案选择 B.杰西卡确实喜欢旅行,自从 2010 年她已接见很多外国国家.此题考察时态,做这种题要注意时间状语,依据句意,进而选出正确答案.9.【答案】C【分析】答案:C依据题意:我叔叔喜爱书,可是他没有太多的时间去阅读.可知前后是住在你和应选,联合选项,A.为了 B.或许 C.可是 D.所以,应选 C.我叔叔喜欢书,可是他没有太多的时间去阅读.熟习并列连词的基本用法,联合题意,给出答案.10.【答案】D【分析】答案:D.依据 Do you know Paul is ______ boy in Class 5,可知这里 in Class 5一般用于最高等之中,而最高等前面一般加冠词 the.应选 D.--你知道保罗是 5 班里最高的男孩吗?--是的,他很善于打篮球.解答这种试题时 ,务必充足理解上下文的 语境和前后文的 逻辑关系,找到解题的依照,同时正确划分 选项的细微差异,正确作答.11.【答案】 C【分析】答案:C .she"她 "是主格,he "他 "是主格,her"她 "是宾格,him" 他 "是宾格,ask"问,咨询 "是动词,后跟宾格,依据 Miss Brown" 布朗小姐 "可知,是女性,故用her .由题干"布朗小姐对于生物学知道好多.对于生物学的知 识我们都喜爱问她."可知,故答案选择 C .布朗小姐对于生物学知道好多.对于生物学的知 识我们都喜爱问她.此题考察人称代词的分析,在熟知所供 词含义的基础上,依据句意,判断出正确答案.12.【答案】【小题 1 】 B【小题 2 D【小题 3 】 C【小题 4 】 A】【分析】54.B ,细节理解题,research shows that meditation can help students learn to deal with anxiety and stress 经过冥想,能够提升学生的注意力, 缓解忧虑,还可以提升他 们的抗压能力,选择 B .55.D ,细节理解题,As an added bonus ,students of mindfulness training also report better concentration and gains in theiracademic performances 经过冥想,学生们的注意力获得了提升, 选择 D . 56.C ,句意猜想题,anyone who is against it isn't thinking clearly 任何不认可这一点的人都是不理智的,前文提到的一个人在 说冥想的缺点,由此可知是那个人不承 认冥想的好 处及长处,由此确立选择 C .57.A ,细节理解题,Indeed ,additional studies will surely strengthen our understanding of the benefits of mindfulness 深入的研究有益于人们更好理解冥想的好处,选择 A .文章粗心文章主要叙述的是一种提升学生综合素质的方法,那就是冥想.经过冥想,学生们的注意力会获得明显的提升,同时还会提升他们的抗压能力,缓解焦虑,让他们在学习和考试中表现的更为优秀.对于阅读表达题,必定要记得第一通读全文,认识文章粗心,而后再依据文章重点词,重点句,掌握细节问题,并进行推理判断,再去回答详细的问题.16.【答案】【小题 1】 A【小题2】C【小题3】B【分析】答案:51.A 细节理解题.依据第三段最后一句"A lack of sleep can lead to weight gain and even obesity because many people tu rn to junk food for quick energy when they are tired"可知,睡眠不足会致使体重增添甚至肥胖,由于好多人累的时候都会用垃圾食品来获得迅速的能量.故答案为 A.52.C 段落粗心题.依据第四段第一句"Some experts are worried about how texting is affecting teenagers'lives""一些专家担忧发短信会影响青少年的生活" 和整段的内容可知,本段主要叙述担忧短信对青少年的影响,故答案为 C.53.B 细节理解题.依据最后一段两个做实验的孩子说的话可知,没有手机孩子们会更聪慧、更健康;所以说作者提到了弗朗西丝和肯尼的实验,表示青少年没有手机生活得很好.故答案为 B.文章粗心:此刻好多青少年都对使用电话上瘾了.青少年发短信比过去任何时候都多.一些专家担忧短信会对青少年的生活造成怎样的影响.专家对两个孩子 Kenny 和 Frances的实验表示,不用手机和网络,孩子会更聪慧、更健康.阅读理解的做题技巧:先阅读所给的问题以及选择项,而后带着问题在通读原文的基础上迅速地找到答案,而后再回过头来检查一遍,保证万无一失.还有,最好把答案所在的句子划出来,以便回来检查时更为的省时省力.19.【答案】【小题 1】 B【小题2】A【小题3】D【分析】48.B,细节理解题,I had to go to a new school and found no one to be friends with去了新学校,没有人能够做朊友,选择 B.49.A,细节理解题,His question surprised me当对方问到自己能否打鼓的时候,他很吃惊,选择 A .50.D,细节理解题,I looked at their shiny faces."Absolutely .I would love to play!"I replied .他最终给出的答案是很想加入,由此可知会有好多朊友,选择D.文章粗心本文主要叙述的是一个新迁居少年找寻到朊友的过程.他新搬了家,没有朊友.有一天听见一个乐队在演奏,就上前往听,最后乐队的人发现他会打鼓,就邀请他加入,以后他就赞同加入,和他们做了朊友.对于阅读表达题,必定要记得第一通读全文,认识文章粗心,而后再依据文章重点词,重点句,掌握细节问题,并进行推理判断,再去回答详细的问题.22.【答案】【小题 1】 B【小题2】D【小题3】C【分析】45.B,细节理解题,December 29,2017文中提到 Kathie 是在 2017年 12 月29 日决定的,选择 B.46.D,细节理解题,Self-control would be my word for the coming year 文中提到 Sofia 选择的但此时自我控制,选择 D.47.C,细节理解题,slowly read a book instead of quickly looking through social media 念书的时候会放慢速度,选择 C.文章粗心文章主要提到的是有对于2018 年计划的事情.文中提到了几个不一样的单词,代表着不一样的含义,这几个单词分别是爱,和平,平和,乐趣,忍受和自我控制.对于阅读表达题,必定要记得第一通读全文,认识文章粗心,而后再依据文章重点词,重点句,掌握细节问题,并进行推理判断,再去回答详细的问题.25.【答案】【小题1】No.【小题 2】Talking leaves .【小题 3】85.【小题 4】In 1825 .【小题 5】Because of/For his important contribution to Cherokee people ./Because he created the writing system for Cherokee language . /Because he made the official written language for Cherokee people【分析】1.No.细节理解题,依据 Without a writing system,the Cherokee had no newspapers or books before 1809.可知在 1809 以前没有报纸,故答案为 No.2.Talking leaves.细节理解题,依据Sequoyah called these pieces of paper with marks"talking leaves".可知Sequoyah把这些纸条叫做 "讲话树叶 ",故答案为 Talking leaves.3. 85.细节理解题,依据 Sequoyah invented 85symbols,可知是 85 种符号,故答案为 85.4.In 1825.细节理解题,依据 In 1825,Sequoyah's system was made the official written language for Cherokee people.可知在 1825年,成为切罗基人官方的书面语言,故答案为 In 1825.5.Because of/For his important contribution to Cherokee people./Because he created the writing system for Cherokee language./Because he made the officialwritten language for Cherokee people.细节理解题,依据Sequoyah will always be remembered for his important contribution to Cherokeepeople.可知是由于他对切罗基人的重要贡献,故答案为 Because of/For hisimportant contribution to Cherokee people./Because he created the writing system for Cherokee language./Because he made the official written language for Cherokee people.文章主要介绍了 Sequoyah在语言上对切罗基人的重要贡献.主若是依据前提问题来做出相应的要求内的答案,题型比较灵巧可是考查了学生多方面的知识和技术,要做好这种题,就要注意平常知识的累积,包含单词、词组、句型等.26.【答案】I live in a harmonious family full of laughter.Each of the family members gets on well with each other .We often sit together to share our problems and happiness and everyone feels relaxed at home .As for me ,I respect and love my parents.When I'm at school ,I always study hard and try not to make my parents worried about my schoolwork . When I'm at home, I often help them with some housework,so they can have more time to do what they love to do.When my sister is in trouble , I usually try my best to help her .I love my harmonious family and feel comfortable at home .I think everyone should take responsibility to create a harmonious family .【分析】I live in a harmonious family full of laughter .【高分句型一】Each of the family members gets on well with each other.We often sit together to share our problemsand happiness and everyone feels relaxed at home.【介绍自己家庭是什么样子的】As for me,I respect and love my parents.When I'm at school,I always study hard and try not to make my parents worried about my schoolwork.When I'm at home, I often help them with some housework,so they can have more time to do what they love to do.When my sister is in trouble,I usually try my best to help her.【我在家庭中都做什么】I love my harmonious family and feel comfortable at home.I think everyoneshould take responsibility to create a harmonious family.【高分句型二】总【结并提出自己的看法】【高分句型一】I live in a harmonious family full of laughter .我居住在一个充满欢笑的家庭.full of laughter 做 family 的定语,修饰 family .【高分句型二】I think everyone should take responsibility to create a harmonious family.我以为每一个人都应当肩负起创建和睦家庭的责任.take responsibility to 肩负起的责任,固定搭配.纲要作文写作时注意知识点要全面,而且语法知识的运用要正确.27.【答案】Here are the things you need to know in order to use the library well during the vacation .First , the library will be open only from 9 a . m. to 4 p. m. from Monday toFriday . And it will be closed for 7 days during the Spring Festival .Second,only 3 books can be borrowed each time and kept for 20 days,but you can renew them if you haven't finished reading them on time .Magazines and newspapers can not be borrowed, and you can only read them in the library .Be sure to have your ID card with you if you want to borrow books or read in thelibrary . Besides, no food or drinks are allowed in the library.Ask the library staff for further information if you still have questions.Wish you a great winter vacation and happy Spring Festival!The School Library【分析】NoticeJanuary 18,2018Dear foreign teachers and students,Winter vacation is coming.Here are the things you need to know in order to use thelibrary well during the vacation .【高分句型一】总【述】First,the library will be open only from 9 a.m.to 4 p.m.from Monday to Friday.And it will be closed for 7 days during the Spring Festival.Second,only 3 books can be borrowed each time and kept for 20 days,but you can renew them if you haven't finished reading them on time.Magazines and newspapers can not be borrowed,and you can only read them in the library.Be sure to have your ID card with you if you want to borrow books or read in the library .【高分句型二】Besides,no food or drinks are allowed in the library.Ask the library staff for further information if you still have questions .【分述图书使用的注意事项】Wish you a great winter vacation and happy Spring Festival!【总结,提出梦想】The School Library【高分句型一】Here are the things you need to know in order to use the library well during the vacation.为了在假期更好地使用图书室,有些事情是你需要知道的.in order to 固定搭配,译为为了【高分句型二】Be sure to have your ID card with you if you want to borrow books or read in thelibrary .假如你想在图书室借书或念书的话,保证带着你的身份证.Be sure to do保证做某事,want to do 想要做某事,注意固定搭配写作时应注意联合给出知识点并综合运用有关语法知识进行连结.。
北京海淀区20112012学年九年级数学上册期末模拟试题及答案
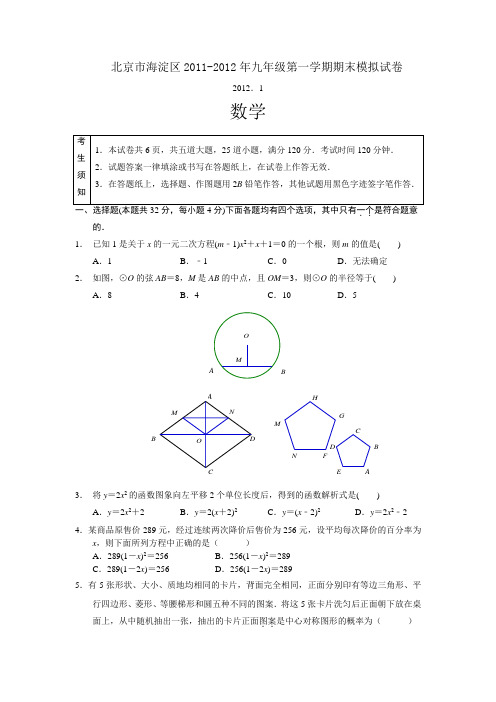
北京市海淀区2011-2012年九年级第一学期期末模拟试卷2012.1数学考生须知1.本试卷共6页,共五道大题,25道小题,满分120分.考试时间120分钟. 2.试题答案一律填涂或书写在答题纸上,在试卷上作答无效.3.在答题纸上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答.一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的.1. 已知1是关于x 的一元二次方程(m ﹣1)x 2+x +1=0的一个根,则m 的值是( )A .1B .﹣1C .0D .无法确定2. 如图,⊙O 的弦AB =8,M 是AB 的中点,且OM =3,则⊙O 的半径等于( )A .8B .4C .10D .5MBAONOM BCDADEA BCFGHMN3. 将y =2x 2的函数图象向左平移2个单位长度后,得到的函数解析式是( )A .y =2x 2+2B .y =2(x +2)2C .y =(x ﹣2)2D .y =2x 2﹣24.某商品原售价289元,经过连续两次降价后售价为256元,设平均每次降价的百分率为x ,则下面所列方程中正确的是( ) A .289(1-x )2=256 B .256(1-x )2=289 C .289(1-2x )=256 D .256(1-2x )=289 5.有5张形状、大小、质地均相同的卡片,背面完全相同,正面分别印有等边三角形、平行四边形、菱形、等腰梯形和圆五种不同的图案.将这5张卡片洗匀后正面朝下放在桌面上,从中随机抽出一张,抽出的卡片正面图案..是中心对称图形的概率为( )A .51 B .52 C .53 D .54 6. 如图,正五边形FGHMN 是由正五边形ABCDE 经过位似变换得到的,若AB ︰FG =2︰3,则下列结论正确的是( )A .2DE =3MNB .3DE =2MNC .3∠A =2∠FD .2∠A =3∠F7. 定义[,,a b c ]为函数2y ax bx c =++的特征数,下面给出特征数为[2m ,1–m ,–1–m ]的函数的一些结论:①当m =-3时,函数图象的顶点坐标是(31,38); ②当m >0时,函数图象截x 轴所得的线段长度大于23; ③当m <0时,函数在x >41时,y 随x 的增大而减小; ④当m ≠0时,函数图象经过同一个点. 其中正确的结论有 A .①②③④B .①②④C .①③④D .②④8.如图所示,P 是菱形ABCD 的对角线AC 上一动点,过P 垂直于AC 的直线交菱形ABCD的边于M 、N 两点,设AC =2,BD =1,AP =x ,△AMN 的面积为y ,则y 关于x 的函数图象的大致形状是( )OPBCMNDA21O xyyxO 1221O xyyxO 12A .B .C .D .二、填空题(本题共16分,每小题4分)9. 如图,已知AB 为⊙O 的直径,∠CAB =30°,则∠D =________.ODB CAPO DABCM B CDEN A10.如图,在等腰Rt △ABC 中,∠A =90°,AC =9,点O 在AC 上,且AO =2,点P 是AB上一动点,连接OP 将线段OP 绕O 逆时针旋转90°得到线段OD ,要使点D 恰好落在BC 上,则AP 的长度等于________.11.如图,直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =4,BC =6,将腰CD 以D 为中心顺时针旋转90°至ED ,过点D 作DM ⊥BC 于M ,过点E 作EN ⊥AD 延长线于N ,连接AE 、CE ,则△AED 的面积为________.12.如图,在ABC △中,1086AB AC BC ===,,,经过点C 且与边AB 相切的动圆与CB CA ,分别相交于点E F ,,则线段EF 长度的最小值是________.三、解答题(本题共30分,每小题5分) 13.解方程:2410x x --=14.如图,等腰直角三角形ABC 的直角边AB 的长为6cm ,将△ABC 绕点A 逆时针旋转15°后得到△AB ′C ′,画出图形,计算图中阴影部分面积等于_________cm 2.BC EF ACB A※15.已知关于x 的方程x 2﹣2x ﹣2n =0有两个不相等的实数根. (1)求n 的取值范围;(2)若n <5,且方程的两个实数根都是整数,求n 的值.16.如图,二次函数y =﹣x 2+bx +c 的图象经过坐标原点,与x 轴交于点A (﹣2,0). (1)求此二次函数的解析式及点B 的坐标;(2)在抛物线上有一点P ,满足S △AOP =3,请直接写出点P 的坐标.17.在下列8×8的方格纸中每个小格都是边长为1的正方形,A 1,A 2两点在小方格的顶点上,⊙A 1的半径为1,⊙A 2的半径为2,且⊙A 1与⊙A 2外切于P (如图).请你在小方格的顶点上确定五个点A 3,A 4,A 5,A 6,A 7,使以这些点为圆心,半径为3的圆同时与⊙A 1,⊙A 2相切(只标出圆心,不必画出圆);A 2A 118.如图,在Rt △ABC 中,∠C =90°,O 、D 分别为AB 、BC 上的点.经过A 、D 两点的⊙O分别交AB 、AC 于点E 、F ,且D 为EF 的中点. (1)求证:BC 与⊙O 相切;(2)当AD =23,∠CAD =30°时.求AD 的长.EDBF OCA四、解答题(本题共20分,其中第19题4分,第20题6分,第21、22题各5分)19.如图,△ABC ,是一张锐角三角形的硬纸片,AD 是边BC 上的高,BC =40cm ,AD =30cm ,从这张硬纸片上剪下一个长HG 是宽HE 的2倍的矩形EFGH ,使它的一边EF 在BC 上,顶点G 、H 分别在AC ,AB 上,AD 与HG 的交点为M . (1)求证:;AM HGAD BC(2)求这个矩形EFGH 的周长.20.利民商店经销甲、乙两种商品.现有如下信息:请根据以上信息,解答下列问题: (1)甲、乙两种商品的进货单价各多少元?(2)该商店平均每天卖出甲商品500件和乙商品300件.经调查发现,甲、乙两种商品零售单价分别每降0.1元,这两种商品每天可各多销售100件.为了使每天获取更大的利润,商店决定把甲、乙两种商品的零售单价都下降m 元.在不考虑其他因素的条件下,当m 定为多少时,才能使商店每天销售甲、乙两种商品获取的利润最大?每天的最大利润是多少?信息1:甲、乙两种商品的进货单价之和是5元; 信息2:甲商品零售单价比进货单价多1元,乙商品零售单价比进货单价的2倍少 1元.信息3:按零售单价购买 甲商品3件和乙商品2件, 共付了19元.BE DF HMGCA21.如图,AB 是⊙O 的直径,AC 是弦,CD 是⊙O 的切线,C 为切点,AD ⊥CD 于点D .求证:(1)∠AOC =2∠ACD ;(2)AC 2=AB ·AD .22.阅读下面的情境对话,然后解答问题 老师:“我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.” 小华:“等边三角形一定是奇异三角形!” 小明:“那直角三角形中是否存在奇异三角形呢?”(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是否正确?________(填“正确”或“不正确”)(2)在Rt ∆ABC 中, ∠ACB =90°,AB =c ,AC =b ,BC =a ,且b >a ,若Rt ∆ABC 是奇异三角形,那么a ︰b ︰c =_______________.(3)如图,AB 是⊙O 的直径,C 是上一点(不与点A 、B 重合),D 是半圆 ⌒ABD 的中点,CD 在直径AB 的两侧,若在⊙O 内存在点E 使得AE =AD ,CB =CE .○1求证:∆ACE 是奇异三角形; ○2当∆ACE 是直角三角形时,∠AOC 的度数为________°. EDOBCA五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.已知一元二次方程x 2﹣4x +k =0有两个不相等的实数根 (1)求k 的取值范围;(2)如果k 是符合条件的最大整数,且一元二次方程x 2﹣4x +k =0与x 2+mx ﹣1=0有一个相同的根,求此时m 的值.24.已知菱形ABCD 的边长为1,∠ADC =60º,等边△AEF 两边分别交DC 、CB 于点E 、F .(1)特殊发现:如图1,若点E 、F 分别是DC 、CB 的中点,求证菱形ABCD 对角母AC 、BD 的交点O 即为等边△AEF 的外心;(2)若点E 、F 始终分别在边DC 、CB 上移动,记等边△AEF 的外心为点P .①猜想验证:如图2,猜想△AEF 的外心P 落在哪一直线上,并加以证明;②拓展运用:如图3,猜想△AEF 面积最小时,过点P 任作一直线分别交边DA 于点M ,交边DC 的延长线于点N ,试判断11DM DN是否为定值,若是,请求出该定值;若不是,请说明理由.图1OEFDCBA图2PABCDEF图3N M P ABCDEF25.如图,在平面直角坐标系xOy 中,一抛物线的顶点坐标是(0,1),且过点(-2,2),平行四边形OABC 的顶点A 、B 在此抛物线上,AB 与y 轴相交于点M .已知点C 的坐标是(-4,0),点Q (x ,y )是抛物线上任意一点. (1)求此抛物线的解析式及点M 的坐标;(2)在x 轴上有一点P (t ,0),若PQ ∥CM ,试用x 的代数式表示t ;(3)在抛物线上是否存在点Q ,使得ΔBAQ 的面积是ΔBMC 的面积的2倍?若存在,求此时点Q 的坐标.参考答案:一、选择题1.B .2.D .3.B .4.A .5.C .6.B .7.B . 8.当0<x <1时,因为△AMN ∽△ABD ,所以=AO AP BD MN ,即=1x 1MN,所以MN =x ,所以y =21x 2;当1<x <2时,因为△CMN ∽△CBD ,所以=CO CP BD MN ,即=-12x 1MN,所以MN =2-x ,所以y =21x (2-x ).选C . 二、填空题 9.60°.10.解:过点D 作DE ⊥AC 于E ,则△DEO ≌△OAP ,∴DE =OA =CE =2,∴AP =OE=9﹣4=5.11.解:∵将腰CD 以D 为中心顺时针旋转90°至ED ,∴CD =ED ,∠CDE =90°;∵DM ⊥BC ,AD ∥BC ;∴∠DMC =∠ADM =90°;∴∠NDE =∠MDC ;∵EN ⊥AD ;∴∠ENA =90°;∴∠ENA =∠DMC ;∴△END ≌△DMC ;∴EN =MC =BC ﹣BM =BC ﹣AD =2;∴△AED 的面积=0.5×4×2=4.故填4. 12.4.8.13.因为a =1,b =-4,c =-1,所以425252x ±==±,即125x =+,225x =- 14.如图,面积为63.15.解:(1)∵于x 的方程x 2﹣2x ﹣2n =0的二次项系数a =1、一次项系数b =﹣2、常数项c =﹣2n ,∴△=b 2﹣4ac =4+8n >0,解得,n >﹣12; (2)由原方程,得(x ﹣1)2=2n +1,∴x =1±21n +; ∵方程的两个实数根都是整数,且n <5, ∴0<2n +1<11,且2n +1是完全平方形式,∴2n +1=1,2n +1=4或2n +1=9,解得,n =0,n =1.5或n =4.CB′C′BAA 7A 6A 5A 4A 3A 2A 116.解:将A 、O 两点坐标代入解析式y =﹣x 2+bx +c ,解得b =-2,c =0.∴此二次函数的解析式为:y =﹣x 2﹣2x ,变化形式得:y =﹣(x +1)2+1, 顶点坐标B (﹣1,1).(2)P 1(﹣3,﹣3),P 2(1,﹣3). 17.解:(1)如图,A 3,A 4,A 5,A 6,A 7;18.解:(1)证明:连接OD ,则OD =OA .∴∠OAD =∠ODA (等边对等角);∵DE DF =,∴∠OAD =∠CAD ,∴∠ODA =∠CAD ,∴OD ∥AC ; 又∵∠C =90°,∴∠ODC =90°,即BC ⊥OD ,∴BC 与⊙O 相切; (2)连接DE ,则∠ADE =90°.∵∠OAD =∠ODA =∠CAD =30°,∴∠AOD =120°; 在Rt △ADE 中,易求AE =23cos 32AD EAD =∠=4,∴⊙O 的半径r =2, ∴AD 的长=120241803ππ⨯=.19.(1)方法一:证明:∵四边形EFGH 为矩形,∴EF ∥GH ,∴△AHG ∽△ABC , 又∵AD ⊥BC ,∴AM ⊥HG ,∴;AM HGAD BC= 方法二:证明:∵四边形EFGH 为矩形,∴EF ∥GH ,∴△AHG ∽△ABC ;△AHM ∽△ABD ∴HG AH BC AB =;AM AH AD AB =,∴;AM HGAD BC= (2)由(1)得;AM HGAD BC=设HE =x ,则HG =2x , ∵AD ⊥BC ,∴DM =HE∴AM =AD -DM =AD -HE =30-x 可得3023040x x-=,解得,x =12,2x =24 所以矩形EFGH 的周长为2×(12+24)=72cm .20.(1)设甲商品的进货单价是x 元,乙商品的进货单价是y 元.根据题意,得53(1)2(21)19x y x y +=⎧⎨++-=⎩解得23x y =⎧⎨=⎩答:甲商品的进货单价是2元,乙商品的进货单价是3元. (2)设商店每天销售甲、乙两种商品获取的利润为s 元,则s =(1-m )(500+100×0.1m )+(5-3-m )(300+100×0.1m ) 即s =-2000m 2+2200m +1100=-2000(m -0.55)2+1705. ∴当m =0.55时,s 有最大值,最大值为1705.答:当m 定为0.55时,才能使商店每天销售甲、乙两种商品获取的利润最大,每天的最大利润是1705元.21.证明:(1)∵CD 是⊙O 的切线,∴∠OCD =90°,即∠ACD +∠ACO =90°.…① ∵OC =OA ,∴∠ACO =∠CAO ,∴∠AOC =180°-2∠ACO ,即21∠AOC +∠ACO =90°. ②. 由①,②,得:∠ACD -21∠AOC =0,即∠AOC =2∠ACD ;(2)如图,连接BC .∵AB 是直径,∴∠ACB =90°. 在Rt △ACD 与△Rt ACD 中,∵∠AOC =2∠B ,∴∠B =∠ACD , ∴△ACD ∽△ABC ,∴ACADAB AC =,即AC 2=AB ·AD . 22.解:(1)正确.(2)在Rt ∆ABC 中a 2+b 2= c 2, ∵c >b >a >0∴2c 2>a 2+b 2,2a 2<c 2+b 2∴若Rt ∆ABC 是奇异三角形,一定有2b 2=c 2+ a 2∴2b 2=a 2+(a 2+b 2) ∴b 2=2a 2得:b =2a∵c 2=b 2+ a 2=3a 2∴c =3a∴a :b :c =1:2: 3(3)①∵AB 是⊙O 的直径ACBADB =90° 在Rt ∆ABC 中,AC 2+BC 2=AB 2 在Rt ∆ADB 中,AD 2+BD 2=AB 2 ∵点D 是半圆 ⌒ABD 的中点 ∴ ⌒AD = ⌒BD ∴AD =BD∴AB2=AD2+BD2=2AD2∴AC2+CB2=2AD2又∵CB=CE,AE=AD∴AC2=CE2=2AE2∴∆ACE是奇异三角形②由①可得∆ACE是奇异三角形∴AC2=CE2=2AE2当∆ACE是直角三角形时由(2)可得AC:AE:CE=1:2:3或AC:AE:CE=3:2:1(Ⅰ)当AC:AE:CE=1:2:3时AC:CE=1:3即AC:CB=1: 3∵∠ACB=90°∴∠ABC=30°∴∠AOC=2∠ABC=60°(Ⅱ)当AC:AE:CE=3:2:1时AC:CE=3:1即AC:CB=3:1∵∠ACB=90°∴∠ABC=60°∴∠AOC=2∠ABC=120°∴∠AOC=2∠ABC=120°∴∠AOC的度数为60°或120°23.解:(1)因为一元二次方程x2﹣4x+k=0有两个不相等的实数根,所以△=b2﹣4ac>0,即(﹣4)2﹣4×1×k>0,解得k<4.(2)当k取最大整数时,即k=3,x1=1,x2=3.当相同根为x=1时,有1+m﹣1=0,m=0;当相同根为x=3时,有m=﹣83.∴m的值是0或﹣83.24.(1)证明:如图1,分别连接OE、OF ∵四边形ABCD是菱形∴AC⊥BD,BD平分∠ADC,AD=DC=BC ∴∠COD=∠COB=∠AOD=90º,∠ADO=116030 22ADC∠=⨯︒=︒又∵E、F分别为DC、CB中点∴OE=12CD,OF=12BC,AO=12AD∴OE=OF=OA, ∴点O即为△AEF的外心A BC D FEO图1JIFEDC BAP图2FEDC BAPMN图3FEDC BAPMN图4(2)①猜想:外心P一定落在直线DB上证明:如图2,分别连接PE、P A,过点P分别作PI⊥CD于I,PJ⊥AD于J ∴∠PIE=∠PJD=90º∵ADG=60º∴∠IPJ=360º-∠PIE-∠PJD-∠JDI=360º-90º-90º-60º=120º∵点P是等边△AEF的外心∴∠EP A=120º,PE=P A∴∠IPJ=∠EP A∴∠IPE=∠JP A∴△PIE≌△PJA,∴PI=PJ∴点P在∠ADC的平分线上,即点P落在直线DB上②11DM DN+为定值2当AE⊥DC时,△AEF面积最小此时点E、F分别为DC、CB中点连接BD、AC交于点P,由(1)可得点P即为△AEF的外心解法一:如图3,设MN交BC于点G设DM=x,DN=y(x≠0,y≠0),则CN=y-1∵BC//DA∴△GBP≌△MDP, ∴BG=DM=x ∴CG=1-x, ∵BC//DA , ∴△NCG∽△NDM∴CN CGDN DM=,∴11y xy x--=,∴xy-x=y-xy∴x+y=2xy, ∴112x y+=,即11DM DN+=2.解法二:如图4,连接PE∵P、E分别为AC、DC的中点∴PE=1122DA=,PE//DA∴△NEP∽△NDM,∴NE EP DN DM=,设DM=x,DN=y,则NE=12 y-∴1122yy x-=,∴1122xy x y-=∴112x y+=,即11DM DN +=2.25.(1)因为抛物线的顶点坐标是(0,1),且过点(-2,2),故设其解析式为12+=ax y则有,1)2(22+-=a ,得41=a 所以此抛物线的解析式为:1412+=x y 因为四边形OABC 是平形四边形 所以AB =OC =4,AB ∥OC 又因为y 轴是抛物线的对称轴所以点A 与B 是抛物线上关于y 轴的对称点 则MA =MB =2,即点A 的横坐标是2 则其纵坐标12412+⨯=y =2,即点A (2,2),故点M (0,2) (2)作QH ⊥x 轴,交x 轴于点H则90QHP MOC ∠=∠=,因为PQ ∥CM ,所以QPH MCO ∠=∠ 所以ΔPQH ∽ΔCMO 所以MO QHCO PH =,即24y t x =-而1412+=x y ,所以)141(2142+=-x t x所以2212-+-=x x t(3)设ΔABQ 的边AB 上的高为h ,因为221=⋅=OM BM S BCM Δ 24212==⋅==h h AB S S BCM ABQ ,所以所以ΔΔ 所以点Q 的纵坐标为4,代入1412+=x y ,得32±=x 因此,存在符合条件的点Q ,其坐标为),)或(,(432-432.。
2011年海淀区初三数学二模试题及答案(word_版)

D FC北京市海淀区2010--2011学年第二学期初三综合练习(二)数 学 试 卷学校 姓名 考号2011.6 一、选择题(本题共32分,每小题4分) 1. 6-的绝对值是( )A. 6B. 6-C.16D. 16-2. 下列运算正确的是( )A. 22a a a += B. 236a a a ⋅= C. 33a a ÷= D. 33()a a -=- 3. 如图,R tA B C 中,90AC B ∠=︒,过点C 的直线DF 与B A C ∠的平分线AE 平行,若50B ∠=︒,则B C F ∠=( ) A. 100︒ B. 80︒C. 70︒D. 50︒4. 已知关于x 的一元二次方程21104x x m -+-=有实数根,则m 的取值范围是( )A. 2m ≥B. 5m ≤C. 2m >D. 5m <5. 在6张完全相同的卡片上分别画有线段、等边三角形、直角梯形、正方形、正五边形和圆各一个图形。
从这6张卡片随机地抽取一张卡片,则这张卡片上的图形是中心对称图形的概率是( ) A.16B.13C.12D.236. 两个半径不等的圆相切,圆心距为6cm ,且大圆半径是小圆半径的2倍,则小圆的半径为( )A. 3B. 4C. 2或4D. 2或67. 农科所连续四年在两块环境相同的实验田里种植甲、乙两种不同品种的小麦。
亩产量(单位:公斤)统计如下表。
设甲、乙品种四年亩产量的平均数依次为x 甲,x 乙,四年亩产量的方差依次为2S 甲,2S 乙,则下列关系中完全正确的是( )A. x 甲<x 乙,2S 甲>2S 乙B. x 甲>x 乙,2S 甲<2S 乙C. x 甲>x 乙,2S甲>2S乙D. x 甲<x 乙,2S 甲<2S 乙8. 一个不透明的小方体的的6个面上分别写有数学1,2,3,4,5,6,任意两对面上所写的两个数字之和为7。
海淀区2010-2011学年度第一学期初三期末数学答案.doc

海淀区九年级第一学期期末练习数 学参考答案及评分标准 2011.1说明: 合理答案均可酌情给分,但不得超过原题分数 一、选择题(本题共32分,每小题4分)二、填空题(本题共16分,每小题4分)注:第12题答对一个给2分,答对两个给4分 三、解答题(本题共30分,每小题5分)13.解:原式=…………………………….…………………………….2分=…………………………….…………………………….4分 =6 …………………………….…………………………….5分 14.(1)解: 48,…………………………….…………………………….1分 0.81…………………………….…………………………….2分 (2)解:()90.8P =射中环以上…………………………….…………………………….4分从频率的波动情况可以发现频率稳定在0.8附近,所以这名运动员射击一次时“射中9环以上”的概率是0.8. …………………………….…………………………….5分 注:简述的理由合理均可给分 15.解法一:因式分解,得()()620x x +-= …………………………….…………………………….2分于是得 60x +=或20x -=126,2x x =-= …………………………….…………………………….5分解法二:1,4,12a b c ===-2464b ac ∆=-= …………………………….…………………………….2分482x -±==…………………………….…………………………….4分126,2x x =-= …………………………….…………………………….5分16.解:在ABC △中,60,75B C ∠=︒∠=︒Q ,45A ∴∠=︒. …………………………….…………………………….2分AB Q 是⊙O 的直径,⊙O 与AC 交于点D, ∴290DOB A ∠=∠=︒. …………………………….…………………………….5分17.解:(1)D ;90︒. …………………………….…………………………….2分 (2)DCF DEA Q △旋转后恰好与△重合, DCF DAE ∴∆∆≌.3,2AE CF BF ∴===又. 5BC BF CF ∴=+=. AED BFDE ABFD S S S ∆∴=+四边形四边形DCF ABFD S S ∆=+四边形 ABCD S =正方形2BC =25=…………………………….…………………………….5分 18.解:设该地区2009年到2011年高效节能灯年销售量的平均增长率为x . ……………….1分依据题意,列出方程 ()210114.4x += ……………………….…………………………….2分 化简整理,得: ()21 1.44x +=,解这个方程,得 1 1.2x +=±, ∴ 120.2, 2.2x x ==-.∵ 该地区2009年到2011年高效节能灯年销售量的平均增长率不能为负数.∴ 2.2x =-舍去.∴ 0.2x =. …………………….…………………………….4分 答:该地区2009年到2011年高效节能灯年销售量的平均增长率为20%. …………….5分 四、解答题(本题共20分,每小题5分) 19.(1)解:连结OD ,OE ,OC ,∵半圆与AC ,BC 分别相切于点D ,E . ∴OD AC ⊥,且DCO ECO ∠=∠. ∵AC BC =,∴CO AB ⊥且O 是AB 的中点. ∴122AO AB ==. ∵120C ∠=︒,∴60DCO ∠=︒. ∴30A ∠=︒.∴在R t AOD △中,112OD AO ==. 即半圆的半径为1.…………………………….…………………………….3分(2)设CO =x ,则在R t AOC △中,因为30A ∠=︒,所以AC =2x ,由勾股定理得: 222AC OC AO -= 即 222(2)2x x -= 解得x =x =舍去)∴11422ABC S AB OC =⋅=⨯=△. ……….…………………………….4分∵ 半圆的半径为1, ∴ 半圆的面积为2π,∴2S π=-阴影 …………………………….…………………………….5分20.(1)解:过O 作ON CD ⊥于N ,连结OM ,则OM BC ⊥.∵ AC 是正方形ABCD 的对角线,∴ AC 是BCD ∠的平分线. ∴ OM =ON.即圆心O 到CD 的距离等于⊙O 半径,∴ CD 与⊙O 相切. …………………………….…………………………….3分 (2)由(1)易知MOC △为等腰直角三角形,OM 为半径, ∴ OM =MC =1.∴ 222112OC OM MC =+=+=, ∴OC∴1AC AO OC =+=+ 在R t ABC △中,AB =BC ,有 222AC AB BC =+ ∴ 222AB AC =∴AB =…………………………….…………………………….5分故正方形ABCD的边长为22. 21.(1)解:依题意画出树状图(或列表)如下或123123312m n…………………………….…………………………….2分(2)解:当240m n ->时,关于x 的方程20x mx n ++=有两个不相等实数根,而使得240m n ->的m ,有2组,即(3,1)和(3,2). ………….…………………………….4分则关于x 的方程20x mx n ++=有两个不相等实数根的概率是13.∴P (有两个不等实根)=13…………………….5分22.(1)证明:如图一,连结OC ,则OC EF ⊥,且OC=OA , 易得OCA OAC ∠=∠.∵ AD EF ⊥,∴OC//AD.∴OCA ∠=CAD ∠,∴CAD ∠=OAC ∠. 即 CAD BAC ∠=∠.…………………………….…………………………….2分 (2)解:与CAD ∠相等的角是BAG ∠.…………………………….…………………………….3分证明如下: 如图二,连结BG .∵ 四边形ACGB 是O e 的内接四边形, ∴ 180ABG ACG ∠+∠=︒. ∵ D ,C ,G 共线, ∴ 180ACD ACG ∠+∠=︒. ∴ ACD ABG ∠=∠. ∵ AB 是O e 的直径, ∴90BAG ABG ∠+∠=︒ ∵ AD EF ⊥∴90CAD ACD ∠+∠=︒ ∴ CAD BAG ∠=∠.…………………………….…………………………….5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8图一图一23.(1)解:如图一,连结AQ .由题意可知:OQ =OA =1. ∵OP =2,∴A 为OP 的中点.∵PQ 与O e 相切于点Q ,∴OQP △为直角三角形. …………1分∴112AQ OP OQ OA ==== . …………2分即ΔOAQ 为等边三角形. ∴∠QOP =60°. …………3分(2)解:由(1)可知点Q 运动1秒时经过的弧长所对的圆心角为30°,若Q 按照(1)中的方向和速度继续运动,那么再过5秒,则Q 点落在O e 与y 轴负半轴的交点的位置(如图二).设直线PQ 与O e 的交点为D ,过O 作OC ⊥QD 于点C ,则C 为QD 的中点. …………4分 ∵∠QOP =90°,OQ =1,OP =2, ∴QP=. (5)∵1122OQ OP QP OC ⋅=⋅, ∴OC . …………6分∵OC ⊥QD ,OQ =1,OC ,∴QC ∴QD …………7分 24.(1)解:∵关于x 的方程为221(1)04x a -++=为一元二次方程,且有实根.故满足:220,1(4(1)0.4a a ≥⎧⎪⎨∆=--⨯⨯+≥⎪⎩ ……….…………………………….2分(注:每个条件1分) 整理得 20,(1)0.a a ≥⎧⎨-≤⎩∴1a =……….…………………………….4分(2)由(1)可知1a =,故(2)中的方程2(1)0mx m x a +--=可化为2(1)10mx m x +--=.①当m =0时,原方程为10x -=,根为1x =,符合题意.………………………….5分图二②当m ≠0时,2(1)10mx m x +--=为关于x 的一元二次方程,Δ=2222(1)4(1)12421(1)0m m m m m m m m --⨯⨯-=-++=++=+≥.此时,方程的两根为 1211,x x m==-. ∵两根均为整数, ∴m =1±.………………………….7分综上所述,m 的值为1-,0 或1.25.(1)证明:如图一,∵1O ,2O ,F 分别是AB ,AC ,BC 边的中点,∴1O F ∥AC 且1O F =A 2O ,2O F ∥AB 且2O F =A 1O , ∴∠B 1O F=∠BAC ,∠C 2O F=∠BAC , ∴∠B 1O F=∠C 2O F∵点D 和点E 分别为两个半圆圆弧的中点, ∴1O F =A 2O =2O E ,2O F =A 1O =1O D , ………………………….2分∠B 1O D =90°,∠C 2O E =90°, ∴∠B 1O D=∠C 2O E . ∴∠D 1O F=∠F 2O E .∴12DO F FO E △≌△. ………………………….3分(2)解:如图二,延长CA 至G ,使AG =AQ ,连接BG 、AE .∵点E 是半圆2O 圆弧的中点, ∴AE=CE=3∵AC 为直径 ∴∠AEC =90°,∴∠ACE =∠EAC =45°,AC∵AQ 是半圆2O 的切线,∴CA ⊥AQ ,∴∠CAQ =90°, ∴∠ACE =∠AQE =45°,∠GAQ =90° ∴AQ =AC =AG=图一图二同理:∠BAP =90°,AB =AP=∴CG=∠GAB =∠QAP ∴AQP AGB △≌△.……………………..5分∴PQ =BG ∵∠ACB =90°,∴BC∴BG∴PQ=……………………..6分(3) 证法一:如图三,设直线F A 与PQ 的垂足为M ,过C 作CS ⊥MF 于S ,过B 作BR ⊥MF 于R ,连接DR 、AD 、DM.∵F 是BC 边的中点,∴ABF ACF S S =△△. ∴BR=CS ,由(2)已证∠CAQ =90°, AC =AQ, ∴∠2+∠3=90°∵FM ⊥PQ , ∴∠2+∠1=90°, ∴∠1=∠3, 同理:∠2=∠4,∴AMQ CSA △≌△,∴AM=CS , ∴AM=BR ,同(2)可证AD=BD ,∠ADB =∠ADP =90°,∴∠ADB =∠ARB =90°, ∠ADP =∠AMP =90°∴A 、D 、B 、R 四点在以AB 为直径的圆上,A 、D 、P 、M 四点在以AP 为直径的圆上, 且∠DBR+∠DAR =180°,∴∠5=∠8, ∠6=∠7, ∵∠DAM +∠DAR =180°, ∴∠DBR =∠DAM ∴DBR DAM △≌△, ∴∠5=∠9, ∴∠RDM =90°, ∴∠5+∠7=90°, ∴∠6+∠8=90°, ∴∠P AB =90°,∴P A ⊥AB ,又AB 是半圆1O 直径, ∴P A 是半圆1O 的切线.……………………..8分证法二:假设P A 不是是半圆1O 的切线,如图四,过点A 作半圆1O 的切线交BD 的延长线于点P ',图三则点P '异于点P ,连结P Q ',设直线F A 与PQ 的 垂足为M ,直线F A 与P Q '的交点为M '.延长AF 至N ,使得AF =FN ,连结BN ,CN ,由于点F 是 BC 中点,所以四边形ABNC 是平行四边形. 易知,180BAC ACN ∠+∠=︒, ∵AQ 是半圆2O 的切线,∴∠QAC =90°,同理90P AB '∠=︒. ∴180P AQ BAC '∠+∠=︒. ∴P AQ ACN '∠=∠.由(2)可知,,AQ AC AB AP '==,∴P AQ NCA '△≌△. ∴NAC P QA '∠=∠. ∵90QAC ∠=︒,∴90NAC M AQ '∠+∠=︒. 即 90AQM M AQ ''∠+∠=︒.∴90AM Q '∠=︒. 即 P Q AF '⊥.∵ PQ AF ⊥,∴ 过点Q 有两条不同的直线P Q '和PQ 同时与AF 垂直.这与在平面内过一点有且仅有一条直线与已知直线垂直相矛盾,因此假设错误.所以P A 是是半圆1O 的切线.Q图四。
2011年北京市海淀区初三一模试题和答案

海淀区九年级第二学期期中练习数 学 2011.5一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.-2的相反数是 A .12-B .12C. -2D. 22.据报道,北京市今年开工及建设启动的8条轨道交通线路,总投资约82 000 000 000元.将82 000 000 000 用科学计数法表示为A .110.8210⨯B .108.210⨯C .98.210⨯D .98210⨯ 3.在下列几何体中,主视图、左视图和俯视图形状都相同的可能是4. 一个布袋中有1个红球,3个黄球,4个蓝球,它们除颜色外完全相同. 从袋中随机取出一个球,取到黄球的概率是 A.18B.38C.13D.125. 用配方法把代数式245x x -+变形,所得结果是A .2(2)1x -+B .2(2)9x --C .2(2)1x +-D .2(2)5x +-6. 如图,A B C D 中,AB =10,BC =6,E 、F 分别是AD 、DC 的中点,若EF =7,则四边形EACF 的周长是A .20B .22C .29D .317.有20名同学参加“英语拼词”比赛,他们的成绩各不相同,按成绩取前10名参加复赛. 若小新知道了自己的成绩,则由其他19名同学的成绩得到的下列统计量中,可判断小新能否进入复赛的是 A .平均数 B .极差 C .中位数 D .方差ABD CEF BCDA8.如图,在R t ABC △中,∠C =90°,AB =5cm ,BC =3cm ,动点P 从点A 出发,以每秒1cm 的速度,沿A →B →C 的方向运动,到达点C 时停止.设2y PC =, 运动时间为t 秒,则能反映y 与t 之间函数关系的大致图象是二、填空题(本题共16分,每小题4分) 9.若分式14x -有意义,则x 的取值范围是 .10. 分解因式: 269mx mx m -+= .11. 如图,CD 是⊙O 的直径,弦AB ⊥CD 于点H ,若∠D =30°,CH =1cm ,则AB = cm .12.如图,矩形纸片ABC D中,AB BC ==第一次将纸片折叠,使点B 与点D 重合,折痕与BD交于点1O ;设1O D 的中点为1D ,第二次将纸片折叠使点B 与点1D 重合,折痕与BD 交于点2O ;设21O D 的中点 为2D ,第三次将纸片折叠使点B 与点2D 重合,折痕与BD 交于点3O ,… .按上述方法折叠,第n 次折叠后的折痕与BD交于点n O ,则1BO = ,n BO = .…第一次折叠 第二次折叠 第三次折叠 …CDC A B DBADCBA CBAD CBA DC三、解答题(本题共30分,每小题5分) 13.计算:0211)()4sin 452-+-︒.14.解不等式组:48011.32x x x -<⎧⎪+⎨-<⎪⎩,15.如图,点C 、D 在线段AB 上,E 、F 在AB 同侧,DE 与CF 相交于点O ,且AC =BD , CO =DO ,A B ∠=∠. 求证:AE =BF .16.已知m 是方程220x x --=的一个实数根,求代数式22()(1)m m m m--+的值.17.如图,一次函数y kx b =+与反比例函数m y x=的图象交于A (2,1),B (-1,n )两点.(1)求k 和b 的值;(2)结合图象直接写出不等式0m kx b x+->的解集.18.列方程或方程组解应用题:“五一”节日期间,某超市进行积分兑换活动,具体兑 换方法见右表. 爸爸拿出自己的积分卡,对小华说:“这里 积有8200 分,你去给咱家兑换礼品吧”.小华兑换了两种礼品,共10件,还剩下了200分,请问她兑换了哪两种 礼品,各多少件?AC D BE FO四、解答题(本题共20分,每小题5分)19.如图,在梯形ABCD 中,AD ∥BC ,∠B=60°,∠ADC=105°,AD =6,且AC ⊥AB ,求AB 的长.20. 如图,AB 为⊙O 的直径,AB =4,点C 在⊙O 上, CF ⊥OC ,且CF =BF . (1)证明BF 是⊙O 的切线;(2)设AC 与BF 的延长线交于点M ,若MC =6,求∠MCF 的大小.21.为了解学生的课余生活情况,某中学在全校范围内随机抽取部分学生进行问卷调查. 问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图和条形统计图(如图所示).(1)请根据所给的扇形图和条形图,填写出扇形图中缺失的数据,并把条形图补充完整;(2)在问卷调查中,小丁和小李分别选择了音乐类和美术类,校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动,用列表或画树状图的方法求小丁和小李恰好都被选中的概率; (3)如果该学校有500名学生,请你估计该学校中最喜欢体育运动的学生约有多少名?A DCB A FCOBM32%其他16%音乐12%美术%体育音乐美术体育其他2468类别扇形统计图条形统计图合),记△DEF 的周长为p .(1)若D 、E 、F 分别是AB 、BC 、AC 边上的中点,则p =_______;(2)若D 、E 、F 分别是AB 、BC 、AC 边上任意点,则p 的取值范围是 .小亮和小明对第(2)问中的最小值进行了讨论,小亮先提出了自己的想法:将ABC △以AC 边为轴翻折一次得1AB C △,再将1AB C △以1B C 为轴翻折一次得11A B C △,如图2所示. 则由轴对称的性质可知,112DF FE E D p ++=,根据两点之间线段最短,可得2p DD ≥. 老师听了后说:“你的想法很好,但2DD 的长度会因点D 的位置变化而变化,所以还得不出我们想要的结果.”小明接过老师的话说:“那我们继续再翻折3次就可以了”.请参考他们的想法,写出你的答案.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的方程2(3)40x m x m --+-=.(1)求证:方程总有两个实数根;(2)若方程有一个根大于4且小于8,求m 的取值范围;(3)设抛物线2(3)4y x m x m =--+-与y 轴交于点M ,若抛物线与x 轴的一个交点关于直线y x =-的对称点恰好是点M ,求m 的值.24.已知平面直角坐标系xOy 中, 抛物线2与直线的一个公共点为.ABDFC E 1图AB DFCE 1F 1A 1B 2D 1D 1E 2图(备图)(1)求此抛物线和直线的解析式;(2)若点P 在线段OA 上,过点P 作y 轴的平行线交(1)中抛物线于点Q ,求线段PQ 长度的最大值; (3)记(1)中抛物线的顶点为M ,点N 在此抛物线上,若四边形AOMN 恰好是梯形,求点N 的坐标及梯形AOMN 的面积.25.在Rt △ABC 中,∠ACB =90°,tan ∠BAC =12. 点D 在边AC 上(不与A ,C 重合),连结BD ,F 为BD中点.(1)若过点D 作DE ⊥AB 于E ,连结CF 、EF 、CE ,如图1. 设C F kEF ,则k = ;(2)若将图1中的△ADE 绕点A 旋转,使得D 、E 、B 三点共线,点F 仍为BD 中点,如图2所示. 求证:BE -DE =2CF ;(3)若BC =6,点D 在边AC 的三等分点处,将线段AD 绕点A 旋转,点F 始终为BD 中点,求线段CF长度的最大值.(备图1)(备图2)BCA DEFB DEA FCBAC1图2图备图海淀区九年级第二学期期中练习数 学参考答案及评分标准 2011.5说明: 合理答案均可酌情给分,但不得超过原题分数 一、选择题(本题共32分,每小题4分)二、填空题(本题共16分,每小题4分)注:第12题答对一个给2分,答对两个给4分 三、解答题(本题共30分,每小题5分) 13.解:原式=14+-…………………………….……………………………4分 = 3.…………………………….……………………………5分 14.解:解不等式480x -<,得 2x <,…………………………….……………………………2分解不等式1132x x +-<,得 2263x x +-<,即 4x >-, …………………………….……………………………4分 所以,这个不等式组的解集是42x -<<. …………………………….……………………………5分15.证明:在△COD 中,∵ CO =DO ,∴ ∠ODC =∠OCD .…………………………….……………………………1分 ∵ AC =BD ,∴ AD =BC .…………………………….……………………………2分在△ADE 和△BCF 中,∵,,,A B AD BC ED A FC B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ △ADE ≌△BCF . …………………………….……………………………4分 ∴ AE =BF .…………………………….……………………………5分16.解:∵ m 是方程220x x --=的一个根,∴ 220m m --=.∴ 22m m -=,22m m -=.…………………………….……………………………2分∴ 原式=222()(1)m m m m--+ …………………………….……………………………3分 =2(1)m m⨯+ …………………………….……………………………4分 =22⨯=4.…………………………….……………………………5分17.解:(1)∵ 反比例函数m y x=的图象过点A (2,1), ∴ m =2.…………………………….……………………………1分 ∵ 点B (-1,n )在反比例函数2y x=的图象上,∴ n = -2 .∴ 点B 的坐标为(-1,-2).…………………………….……………………………2分∵ 直线y kx b =+过点A (2,1),B (-1,-2),∴ 21,2.k b k b +=⎧⎨-+=-⎩解得1,1.k b =⎧⎨=-⎩ …………………………….……………………………3分(2)10x -<<或2x >. (写对1个给1分) …………….……………………………5分18.解:因为积分卡中只有8200分,要兑换10件礼品,所以不能选择兑换电茶壶.设小华兑换了x 个保温杯和y 支牙膏, …………….……………………………1分 依题意,得10,20005008200200.x y x y +=⎧⎨+=-⎩…………….……………………………3分解得2,8.x y =⎧⎨=⎩ …………….……………………………4分答:小华兑换了2个保温杯和8支牙膏. …………….……………………………5分四、解答题(本题共20分,每小题5分)19.解:过点D 作DE ⊥AC 于点E ,则∠AED =∠DEC =90°.………….……………………1分∵ AC ⊥AB ,∴ ∠BAC =90°. ∵ ∠B =60°, ∴ ∠ACB =30°.∵ AD ∥BC ,ADCBE∴ 在Rt △ADE 中,DE =12AD =3,AE=,∠ADE =60°. ….………3分∵ ∠ADC=105°,∴ ∠EDC =45°.∴ 在Rt △CDE 中, CE =DE =3.…………….……………………………4分∴ AC =AE +CE=3.∴ 在Rt △ABC 中,AB =AC ⋅tan ∠ACB=3)33⨯=+. …….……………………5分20.证明:连接OF . (1) ∵ CF ⊥OC,∴ ∠FCO =90°. ∵ OC =OB , ∴ ∠BCO =∠CBO . ∵ FC =FB , ∴ ∠FCB =∠FBC .…………………………..1分∴ ∠BCO +∠FCB =∠CBO +∠FBC . 即 ∠FBO =∠FCO =90°. ∴ OB ⊥BF .∵ OB 是⊙O 的半径, ∴ BF 是⊙O 的切线.…………………………..2分(2) ∵ ∠FBO =∠FCO =90°,∴ ∠MCF +∠ACO =90°,∠M +∠A =90°. ∵ OA =OC , ∴ ∠ACO =∠A. ∴ ∠FCM =∠M. ……………………………………3分易证△ACB ∽△ABM, ∴AC AB ABAM=.∵ AB =4,MC =6, ∴ AC =2.………………………………………………..4分∴ AM =8,BM =∴cos ∠MC F = cos M =BM AM=2. ∴ ∠MCF =30°.………………………………………………..5分AFCOBM21.(1)…………………………….……………………………2分(2)易知选择音乐类的有4人,选择美术类的有3人.记选择音乐类的4人分别是12,,,A A A 小丁;选择美术类的3人分别是12,,B B 小李.可画出树状图如下:由树状图可知共有12中选取方法,小丁和小李都被选中的情况仅有1种,所以小丁和小李恰好都被选中的概率是112. .…………………………….……………………………4分由表可知共有12中选取方法,小丁和小李都被选中的情况仅有1种,所以小丁和小李恰好都被选中的概率是112..…………………………….……………………………4分(3)由(1)可知问卷中最喜欢体育运动的的学生占40%,得50040%20⨯= 所以该年级中最喜欢体育运动的学生约有200名.…………….……………………………5分22. 解:(1)32p =; .…………………………….……………………………2分 (2)332p <≤..…………………………….……………………………5分音乐美术体育其他类别扇形统计图条形统计图32%其他16%音乐12%美术40%体育1A 1B 2B 小李2A 1B 2B 小李3A 1B 2B 小李1B 2B 小李小丁五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.证明:(1)22224(3)4(4)1025(5)b ac m m m m m ∆=-=---=-+=-≥0,所以方程总有两个实数根..…………………………….……………………………2分解:(2)由(1)2(5)m ∆=-,根据求根公式可知,方程的两根为:2x =即:11x =,24x m =-,由题意,有448m <-<,即812m <<.……………………….……………………………5分(3)易知,抛物线2(3)4y x m x m =--+-与y 轴交点为M (0,4m -),由(2)可知抛物线与x 轴的交点为(1,0)和(4m -,0),它们关于直线y x =-的对称点分别为(0,1-)和(0, 4m -), 由题意,可得:14m -=-或44m m -=-,即3m =或4m =. ……….……………………………7分24.解:(1)由题意,可得8164(1)a a =-+及84k =,解得1,2a k ==,所以,抛物线的解析式为22y x x =-,直线的解析式为2y x =.…………………………2分(2)设点P 的坐标为4(,2)(0)t t t ≤≤,可得点Q 的坐标为2(,2)t t t -,则 2222(2)4(2)4P Q t t t t t t =--=-=--+ 所以,当2t =时,PQ 的长度取得最大值为4.………………………………4分(3)易知点M 的坐标为(1,-1).过点M 作直线OA 的平行线交抛物线于点N ,如图所示,四边形AOMN为梯形.直线MN 可看成是由直线OA 向下平移b 个单位得到,所以直线MN 的方程为2y x b =-.因为点M 在直线2y x b =-上,解得b =3,即直线MN 的方程为23y x =-,将其代入22y x x =-,可得2232x x x -=-即 2430x x -+= 解得 11x =,23x = 易得 11y =-,23y =所以,直线MN 与抛物线的交点N 的坐标为(3,3).…………5分如图,分别过点M 、N 作y 轴的平行线交直线OA 于点显然四边形MNHG 是平行四边形.可得点G (1,2),H 113(10)[2(1)]222OM G S M G =⨯-⨯=⨯--=△113(43)(63)222ANH S NH =⨯-⨯=⨯-=△(31)236MNHG S NH =-⨯=⨯=△所以,梯形AOMN 的面积9OMG MNHG ANH AOMN S S S S =++=△△△梯形. ……………………7分25. 解:(1)k =1;……………………….……………………………2分(2)如图2,过点C 作CE 的垂线交BD 于点G ,设BD 与AC 的交点为Q .由题意,tan ∠BAC =12,∴12BC D E ACAE==.∵ D 、E 、B 三点共线, ∴ AE ⊥DB .∵ ∠BQC =∠AQD ,∠ACB =90°,∴ ∠QBC =∠EAQ.∵ ∠ECA+∠ACG =90°,∠BCG+∠ACG =90°, ∴ ∠ECA =∠BCG . ∴ BC G AC E △∽△. ∴12BC GB ACAE==.∴ GB =DE. ∵ F 是BD 中点, ∴ F 是EG 中点. 在R t EC G △中,12C F EG=,∴ 2BE D E EG C F -==..…………………………….……………………………5分(3)情况1:如图,当AD =13A C 时,取AB 的中点M ,连结MF 和CM ,∵∠ACB =90°, tan ∠BAC =12,且BC = 6,∴AC =12,AB=∵M 为AB 中点,∴CM=∵AD =13A C,∴AD =4.∵M 为AB 中点,F 为BD 中点, ∴FM =12AD = 2.∴当且仅当M 、F 、C 三点共线且M 在线段CF 上时CF 最大,此时CF =CM +FM=2+..…………………………….……………………………6分CB2图BDEAFC GQ情况2:如图,当AD=23AC时,取AB的中点M,连结MF和CM,类似于情况1,可知CF的最大值为4+.………….……………………………7分综合情况1与情况2,可知当点D在靠近点C的三等分点时,线段CF的长度取得最大值为4+..…………………………….……………………………8分C。
2022-2023学年北京市海淀区九年级(上)期末数学试卷+答案解析(附后)

2022-2023学年北京市海淀区九年级(上)期末数学试卷1. 刺绣是中国民间传统手工艺之一.下列刺绣图案中,是中心对称图形的为( )A. B.C. D.2. 点关于原点对称的点的坐标为( )A. B. C. D.3. 二次函数的图象向左平移1个单位长度,得到的二次函数解析式为( )A. B.C. D.4. 如图,已知正方形ABCD,以点A为圆心,AB长为半径作,点C与的位置关系为( )A. 点C在外B. 点C在内C. 点C在上D. 无法确定5. 若点,在抛物线上,则m的值为( )A. 2B. 1C. 0D.6. 勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形.如图,该勒洛三角形绕其中心O旋转一定角度a后能与自身重合,则该角度a可以为( )A. B.C. D.7. 如图,过点A作的切线AB,AC,切点分别是B,C,连接过上一点D作的切线,交AB,AC于点E,若,的周长为4,则BC的长为( )A. 2B.C. 4D.8. 遥控电动跑车竞速是青少年喜欢的活动.如图是某赛道的部分通行路线示意图,某赛车从入口A驶入,行至每个岔路口选择前方两条线路的可能性相同,则该赛车从F口驶出的概率是( )A. B. C. D.9. 二次函数的图象与y轴的交点坐标为_____________.10. 半径为3,圆心角120度的扇形面积为__________.11. 如表记录了一名球员在罚球线上投篮的结果.投篮次数n50100150200300400500投中次数m284978102153208255投中频率根据以上数据,估计这名球员在罚球线上投篮一次,投中的概率为__________.12. 关于x的一元二次方程有两个不相等的实数根,则m的取值范围为__________.13. 二次函数的图象如图所示,则ab__________填“>”“<”或“=”14. 如图,是的内接三角形,于点E,若的半径为,,则__________.15. 对于二次函数,y与x的部分对应值如表所示.x在某一范围内,y 随x的增大而减小,写出一个符合条件的x的取值范围__________.X…0123…y…1331…16. 如图,AB,AC,AD分别是某圆内接正六边形、正方形、等边三角形的一边.若,下面四个结论中,①该圆的半径为2;②的长为;③AC 平分;④连接BC,CD,则与的面积比为1:,所有正确结论的序号是__________.17. 解方程:18. 已知抛物线过点和,求该抛物线的解析式.19. 已知a为方程的一个根,求代数式的值.20. 如图,四边形ABCD内接于,AB为直径,若,求的度数.21. 为了发展学生的兴趣爱好,学校利用课后服务时间开展了丰富的社团活动.小明和小天参加的篮球社共有甲、乙、丙三个训练场.活动时,每个学生用抽签的方式从三个训练场中随机抽取一个场地进行训练.小明抽到甲训练场的概率为____;用列表或画树状图的方法,求小明和小天在某次活动中抽到同一场地训练的概率.22. 已知:如图,AP是的切线,A为切点.求作:的另一条切线PB,B为切点.作法:以P为圆心,PA长为半径画弧,交于点B;作直线直线PB即为所求.根据上面的作法,补全图形保留作图痕迹;完成下面证明过程.证明:连接OA,OB,是的切线,A为切点,在与中,( )≌于点是的半径,是的切线____填推理的依据23. 紫砂壶是我国特有的手工制造陶土工艺品,其制作过程需要几十种不同的工具,其中有一种工具名为“带刻度嘴巴架”,其形状及,使用方法如图当制壶艺人把“带刻度嘴巴架”上圆弧部分恰好贴在壶口边界时,就可以保证需要粘贴的壶嘴、壶把、壶口中心在一条直线上.图2是正确使用该工具时的示意图.如图3,为某紫砂壶的壶口,已知A,B 两点在上,直线l过点O,且于点D,交于点若,,求这个紫砂壶的壶口半径r的长.24. 如图,AB是的直径,点C在上.过点C作的切线l,过点B作于点求证:BC 平分;连接OD,若,,求OD的长.25. 学校举办“科技之星”颁奖典礼,颁奖现场入口为一个拱门.小明要在拱门上顺次粘贴“科”“技”“之”“星”四个大字如图,其中,“科”与“星”距地面的高度相同,“技”与“之”距地面的高度相同,他发现拱门可以看作是抛物线的一部分,四个字和五角星可以看作抛物线上的点.通过测量得到拱门的最大跨度是10米,最高点的五角星距地面米.请在图2中建立平面直角坐标系xOy,并求出该抛物线的解析式;“技”与“之”的水平距离为2a米.小明想同时达到如下两个设计效果:①“科”与“星”的水平距离是“技”与“之”的水平距离的2倍;②“技”与“科”距地面的高度差为米.小明的设计能否实现?若能实现,直接写出a的值;若不能实现,请说明理由.26. 在平面直角坐标系xOy中,抛物线过点求用含a的式子表示;抛物线过点,,,①判断:____填“>”“<”或“=”;②若M,N,P恰有两个点在x轴上方,求a的取值范围.27. 如图,在中,,是AB边上一点,交CA的延长线于点用等式表示AD与AE的数量关系,并证明;连接BE,延长BE至F,使连接DC,CF,①依题意补全图形;②判断的形状,并证明.28. 在平面直角坐标系xOy中,对于点P和线段AB,若线段PA或PB的垂直平分线与线段AB有公共点,则称点P为线段AB的融合点.已知,,①在点,,中,线段AB的融合点是____;②若直线上存在线段AB的融合点,求t的取值范围;对称线段为若对于实数a,存在直线l,使得上有的融合点,直接写出a的取值范围.答案和解析1.【答案】B【解析】【分析】根据中心对称图形的概念判断.把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.【解答】解:选项A、C、D中的图形都不能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形.选项B中的图形能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形.故选:2.【答案】A【解析】【分析】根据关于原点对称的两个点的坐标特征判断即可.【解答】解:点关于原点对称的点的坐标是故选:3.【答案】D【解析】【分析】根据“上加下减、左加右减”的原则进行解答即可.【解答】解:,将二次函数的图象在平面直角坐标系中向左平移1个单位长度所得函数解析式为:,故选:4.【答案】A【解析】【分析】根据正方形的性质得到,于是得到结论.【解答】解:正方形ABCD的对角线,点C在外,故选:5.【答案】B【解析】【分析】根据抛物线的对称性即可求解.【解答】解:因为点,的纵坐标相同,都是5,所以对称轴为直线,故m的值为故选:6.【答案】C【解析】【分析】由于是等边三角形,那么,所以要使等边三角形旋转后与自身重合,那么它们就是旋转角,而它们的和为,由此即可求出绕中心旋转的角度.【解答】解:如图,连接OA、OB、是等边三角形,,它们都是旋转角,而它们的和为,将该勒洛三角形绕其中心O旋转后能与自身重合.故选:7.【答案】B【解析】【分析】根据切线长定理得到,再根据切线长定理、三角形的周长公式计算,得到答案.【解答】解:、AC为的切线,,、FC为的切线,,同理,,的周长,,故选:8.【答案】B【解析】【分析】画树状图,共有4种等可能的结果,其中该赛车从F口驶出的结果有1种,再由概率公式求解即可.【解答】解:画树状图如下:共有4种等可能的结果,其中该赛车从F口驶出的结果有1种,该赛车从F口驶出的概率为,故选:9.【答案】【解析】【分析】将代入解析式求解.【解答】解:将代入得,抛物线与y轴交点坐标为,故答案为:10.【答案】【解析】【分析】根据扇形的面积公式计算即可.【解答】解:,故答案为:11.【答案】【解析】【分析】根据频率估计概率的方法结合表格数据可得答案.【解答】解:由频率分布表可知,随着投篮次数越来越大时,频率逐渐稳定到常数附近,这名球员在罚球线上投篮一次,投中的概率为,故答案为:12.【答案】【解析】【分析】若一元二次方程有两个不相等的实数根,则根的判别式,建立关于m 的不等式,求出m的取值范围.【解答】解:方程有两个不相等的实数根,,,,解得,故答案为:13.【答案】<【解析】【分析】根据二次函数的图象与性质即可求出答案.【解答】解:由图象可知:,,,故答案为:14.【答案】1【解析】【分析】连接AO,BO,根据圆周角定理得到,根据等腰直角三角形的性质即可得到结论.【解答】解:连接AO,BO,,,,,,,,故答案为:15.【答案】【解析】【分析】根据表格确定二次函数的对称轴,然后结合x、y的值确定答案即可.【解答】解:观察表格知:二次函数的图象经过点和,对称轴为,当时,y随x的增大而减小,故答案为:16.【答案】①③④【解析】【分析】设圆的圆心是O,半径是r,连接OA,OB,OC,OD,作交AB延长线于M,于N,应用圆内接正多边形的性质,圆周角定理,弧长计算公式,三角形面积的计算公式,可以解决问题.【解答】解:设圆的圆心是O,半径是r,连接OA,OB,OC,OD,作交AB延长线于M,于N,是圆内接正六边形的一边,的度数,是等边三角形,,该圆的半径为是圆内接正方形的一边,的度数,的度数,是圆内接正三边形的一边,的度数,的度数,,,平分的长,,,中,,,平分,,,,::正确的有①③④.故答案为:①③④.17.【答案】解:,,即,,,【解析】利用配方法求解即可.18.【答案】解:抛物线过点和,,解得,所以,该二次函数的解析式为【解析】将,代入求得b,c的值,得到此函数的解析式.19.【答案】解:原式为方程的一个根,,原式【解析】直接利用平方差公式以及单项式乘多项式计算,进而合并同类项,把已知数据整体代入得出答案.20.【答案】解:如图,连接,,,为直径,,【解析】【分析】连接AC,根据圆周角定理得到,再利用AB为直径得到,然后利用直角三角形两锐角互余计算的度数.21.【答案】解:画树状图如下:共有9种等可能的结果,其中小明和小天在某次活动中抽到同一场地训练的结果有3种,小明和小天在某次活动中抽到同一场地训练的概率为【解析】【分析】直接由概率公式求解即可;画树状图,共有9种等可能的结果,其中小明和小天在某次活动中抽到同一场地训练的结果有3种,再由概率公式求解即可.22.【答案】解:如图,PB为所作;;经过半径的外端且与半径垂直的直线是圆的切线【解析】【分析】根据几何语言画出对应的几何图形即可;先根据切线的性质得再证明≌得到,然后根据切线的判定定理得到PB是的切线.23.【答案】解:连接OB,若,在中,,,,,解得答:这个紫砂壶的壶口半径r的长为【解析】【分析】连接OB,根据垂径定理求出BD,在中,根据勾股定理即可求出24.【答案】证明:连接,是的切线,OC是的半径,,,,,平分解:连接OD,过点O作于点G,得矩形OCDG,在中,,设,,则,,在中,根据勾股定理得:【解析】【分析】连接OC,由题意可证,进而证明BC平分;连接OD,过点O作于点G,得矩形OCDG,可得,由勾股定理求出OB的长,再由勾股定理可得出答案.25.【答案】解:以过拱顶为原点,以过拱顶平行于地面的直线为x轴建立如图所示坐标系.设抛物线解析式为,抛物线过点,,解得,抛物线解析式为能实现,由知抛物线解析式为,设“之”的坐标为,则“星”的坐标为,,,,解得,,,能实现,【解析】【分析】建立如图所示坐标系,由待定系数法求函数解析式即可;根据题意求出“之”和“星”的坐标,然后求出a 的值即可.26.【答案】解:将代入抛物线表达式得:,解得:由得,抛物线的表达式为:,则抛物线的对称轴为直线,将点M 、N 、P 的坐标代入抛物线表达式得:,,,①,故答案为:②当时,由点M、N、P的坐标知,点N的函数值最小,则点M、P在x轴上方,即且,解得:当时,同理可得:点N、P在x轴上方,即且,解得:;综上所述,a的取值范围的为:或【解析】【分析】将代入抛物线表达式得:,即可求解;①,即可求解;②当时,由点M、N、P的坐标知,点N的函数值最小,则点M、P在x轴上方,进而求解;当时,同理可解.27.【答案】解:结论:理由:,,,,,①图形如图所示:②结论:是等边三角形.证明:延长BA至点H使,连接CH,FH,如图.,,是等边三角形.,,,,,,,≌,是等边三角形.【解析】【分析】结论:利用直角三角形30度角的性质证明即可;①根据要求作出图形即可;②结论:是等边三角形.延长BA至点H使,连接CH,FH,.证明≌,推出,,可得结论.28.【答案】解:①,②线段AB的融合点在以A、B为圆心,AB为半径的圆及内部,,,,当与圆相切时,或,当时,直线上存在线段AB 的融合点.由可知,的融合点在以、为圆心,为圆心的圆及内部,,,上有的融合点,圆O 与圆、有交点,圆O 与圆、圆的公共区域为以O 为圆心2为半径,以O 为圆心6为半径的圆环及内部区域,当时,a 的最大值为,最小值为,;当时,a 的最大值为,最小值为,综上所述:a 的取值范围为或【解析】【分析】①,,的线段垂直平分线与x 轴的交点为,是线段AB的融合点.,,设直线的垂直平分线与x轴的交点为,,解得,直线的垂直平分线与x轴的交点为,不是线段AB的融合点.,,设直线的垂直平分线与x轴的交点为,,解得,直线的垂直平分线与x轴的交点为,是线段AB的融合点.故答案为:,②线段AB的融合点在以A、B为圆心,AB为半径的圆及内部,当与圆有交点时,直线上存在线段AB的融合点;由可知,的融合点在以、为圆心,为圆心的圆及内部,圆O与圆、圆的公共区域为以O为圆心2为半径,以O为圆心6为半径的圆环及内部区域满足题意,当时,a的最大值为,最小值为,当时,a的最大值为,最小值为,由此可求a的取值范围为或。
北京海淀区2011-2012学年度初三数学上册期

海淀区九年级第一学期期末练习数学试卷答案及评分说明: 与参考答案不同, 但解答正确相应给分.一、选择题(本题共32分,每小题4分)1. B2.D3.A4.B5. B6. C7.D8. C二、填空题(本题共16分,每小题4分)9. x =0或x =4 10. 15 11. 1 12. π(2分); 32π12n + (2分)三、解答题(本题共29分,第13题~第15题各5分,第16题4分,第17题、第18题各5分)13.解法一: a=1, b=-8, c=1, …………………………1分 24600b ac ∆=-=>. …………………………2分860b x -±∆±==. …………………………3分∴ 154,15421-=+=x x . …………………………5分解法二:281x x -=-.2816116x x -+=-+. …………………………1分 2(4)15x -=. …………………………2分 415x -=±. …………………………3分 ∴154,15421-=+=x x . …………………………5分14.证明: 在△AED和△ACB中,∵∠A=∠A, ∠AED =∠C, ……………………………2分∴△AED∽△ACB. ……………………………3分∴.ABADACAE=……………………………4分∴.64 5= AE∴.310=AE……………………………5分15.(1)①(-2 ,0), (1, 0);②8; ③增大(每空1分) ……………………………3分(2)依题意设抛物线解析式为y=a (x+2) (x-1).由点(0, -4)在函数图象上,得-4=a(0+2) (0-1). ……………………………………4分解得a =2.∴y=2 (x+2) (x-1). …………………………………………………5分即所求抛物线解析式为y=2x2+2x-4.16.(1)正确画图(1分)标出字母(1分)……………………………………2分(2)正确画图(1分),结论(1分)………………………………………………4分17.解:由题意得{220,[2(2)]4(2)(1)0.kk k k-≠∆=---+≥…………………1分由①得2k≠. ………………………………………………………2分由②得2k≤. ………………………………………………………4分∴2k<.∵k为正整数,∴1k=. ……………………………………………………5分18.解法一:由题意画树形图如下:…………………3分从树形图看出,所有可能出现的结果共有9个,这些结果出现的可能性相等,标号之和等于4的结果共有3种. ………………………………………………………4分所以P(标号之和等于4)=3193=. ………………………………………………………5分解法二:①②第二次摸球第一次摸球312321233211……………………………………3分由上表得出,所有可能出现的结果共有9个,这些结果出现的可能性相等,标号之和等于4的结果共有3种. ………………………………………………………4分所以P(标号之和等于4)=3193=. ………………………………………………………5分 四、解答题(本题共21分, 第19题、第20题各5分, 第21题6分,第22题5分)19.(1)(20)(280)(20)y w x x x =-=-+- ……………………………………2分 221201600x x =-+-.(2)22(30)200y x =--+. ∵2040x ≤≤, a =-2<0,∴当30x =时,200y =最大值. ……………………………………4分 答:当销售单价定为每双30元时,每天的利润最大,最大利润为200元. ………5分20.(1)∵二次函数y 的图象与x 轴交于点 (x1, 0)和(x2, 0), ∴ 令0y =,即 .………………………………………………1分∵m>0,0.解得 1x =或x = …………………………………………………………2分∵ x1 <x2,103<<-m ,∴21x =. ……………………………………………………………3分(2)由(1)1x =3x -.由1x =是方程的根,∴………5分 21.解:(1)证明:∵CE AB ⊥, ∴ 90CEB ∠=.∵ CD 平分ECB ∠, BC=BD,∴ 12∠=∠, 2D ∠=∠.∴ 1D ∠=∠. …………………………1分 ∴ CE ∥BD . ∴ 90DBA CEB ∠=∠=.∵ AB 是⊙O 的直径,∴ BD 是⊙O 的切线. ………………………………………………………2分 (2)连接AC ,∵ AB 是⊙O 直径, ∴ 90ACB ∠=. ∵CE AB ⊥,可得 2CE AE EB =⋅.∴ .162==AE CE EB ………………………………………………………3分在Rt △CEB 中,∠CEB=90︒, 由勾股定理得20.BC == ……………4分∴ 20BD BC ==.∵ 1D ∠=∠, ∠EFC =∠BFD,∴ △EFC ∽△BFD. ………………………………………………………5分∴BF EFBD EC =. ∴ 101620BF BF -=. ∴ BF=10. ………………………………………………………………………6分 22.(1)画图: 图略(1分); 填空: a (1分) …………………………………2分 (2)a 85(1分), a n n 1212++ (2分) ……………………………………………5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.(1)∵A(a, -3)在4a y x +=的图象上,∴43a a +=-. 解得1a =-. ……………………………………1分∴反比例函数的解析式为3y x =. ……………………………………2分(2)过A 作AC ⊥y 轴于C. ∵ A(-1, -3),∴ AC=1,OC=3. ∵ ∠ABO=135︒,∴ ∠ABC=45︒. 可得 BC=AC=1. ∴ OB=2.∴ B (0, -2). …………………3分由抛物线2y ax bx c =++与y 轴交于B ,得c= -2.∵ a= -1,∴22y x bx =-+-. ∵ 抛物线过A(-1,-3), ∴ 123b ---=-. ∴ b=0.∴ 二次函数的解析式为22y x =--. ……………………………………4分 (3)将22y x =--的图象沿x 轴翻折,得到二次函数解析式为22y x =+. ……………5分 设将22y x =+的图象向右平移后的二次函数解析式为2()2y x m =-+ (m>0). ∵ 点P (x0, 6)在函数3y x =上,∴036.x =∴012x =.∴2()2y x m =-+的图象过点1(,6)2P .∴62)21(2=+-m .可得1253,22m m ==-(不合题意,舍去). ∴ 平移后的二次函数解析式为25()22y x =-+. …………………………6分∵ a=1>0,∴ 当2521≤≤x 时,62≤≤y ; 当325≤<x 时,492≤<y . ∴ 当132x ≤≤时,26y ≤≤. ……………………………………7分∴ 平移后的二次函数y 的取值范围为 26y ≤≤.24. (1)CD=AF+BE. …………………1分 (2)解:(1)中的结论仍然成立.证明:延长EA 到G ,使得AG=BE ,连结DG . ∵ 四边形ABCD 是平行四边形, ∴ AB=CD, AB ∥CD ,AD=BC. ∵ AE ⊥BC 于点E,∴ ∠AEB=∠AEC=90︒.∴∠AEB=∠DAG=90︒. ∴ ∠DAG=90︒. ∵ AE=AD,∴ △ABE ≌△DAG . …………………………………………………………………3分 ∴∠1=∠2, DG=AB. ∴∠GFD=90︒-∠3. ∵ DF 平分∠ADC, ∴∠3=∠4.∴∠GDF=∠2+∠3=∠1+∠4=180︒-∠FAD-∠3=90︒-∠3.∴∠GDF=∠GFD. ………………………………………………………………4分 ∴ DG=GF.∴ CD=GF=AF+AG= AF + BE.即 CD = AF +BE. ………………………………………………………………5分(3)a CD AF BE b =+或bCD aAF bBE =+或b b CD AF BEa a =+. …………………7分 25. 解:(1)∵ 抛物线过原点和A(0-), ∴ 抛物线对称轴为3-=x . ∴B(3).设抛物线的解析式为23y a x =+(.∵ 抛物线经过(0, 0),∴ 0=3a+3. ∴ a=-1. ∴3)3(2++-=x y ……………………………………………1分=.322x x -- 4321GDAFC E B∵ C 为AB 的中点,A(0-)、B(3), 可得C(32) . 可得直线OC 的解析式为xy 33-=. ……………………………………………2分(2)连结OB. 依题意点E 为抛物线x x y 322--=与直线xy 33-=的交点(点E 与点O 不重合).由2,y x y x ⎧=⎪⎨⎪=--⎩,解得5,3x y ⎧=⎪⎪⎨⎪=⎪⎩ 或0,0.x y =⎧⎨=⎩(不合题意,舍).∴ E(53) …………………………3分 过E 作EF ⊥y 轴于F, 可得OF=53, ∵ OE=DE ,EF ⊥y 轴, ∴ OF=DF.∴ DO=2OF=103.∴ D(0, 10)3.∴(3)E 点的坐标为(32)或(12-). 说明:此问少一种结果扣1分.。
2010-2011学年海淀区九年级上数学期末统一试卷及答案

海淀区九年级数学第一学期期末练习 2011.1一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.2(-=( )A .3B .3-C .3±D .92.已知两圆的半径分别为2和3,圆心距为5,则这两圆的位置关系是 ) A .外离B .外切C .相交D .内切3.将一枚硬币抛掷两次,则这枚硬币两次正面都向上的概率为( )A .12B .13C .14D .164.如图,⊙O 是△ABC 的外接圆,已知∠ABO =30º,则∠ACB 的大小为( )A .60ºB .30ºC .45ºD .50º5.下列一元二次方程中没有..实数根的是( ) A .2240x x +-= B .2440x x -+= C .2250x x --=D .2340x x ++=6.如图,有一枚圆形硬币,如果要在这枚硬币的周围摆放几枚与它完全相同的硬币,使得周围的硬币都和这枚硬币相外切,且相邻的硬币相外切,则这枚硬币周围最多可摆放( )A .4枚硬币B .5枚硬币C .6枚硬币D .8枚硬币7.圆锥的母线长是3,底面半径是1,则这个圆锥侧面展开图圆心角的度数为( )A .90°B .120°C .150°D .180°8.如图,E ,B ,A ,F 四点共线,点D 是正三角形ABC 的边AC 的中点,点P 是直线AB 上异于A ,B 的一个动点,且满足30CPD ∠=︒,则( )A .点P 一定在射线BE 上B .点P 一定在线段AB 上C .点P 可以在射线AF 上 ,也可以在线段AB 上D .点P 可以在射线BE 上 ,也可以在线段 二、填空题(本题共16分,每小题4分)9.已知P 是⊙O 外一点,P A 切⊙O 于A ,PB 切⊙O 于B .若P A =6,则PB = . 10x 的取值范围是 .11.如图,圆形转盘中,A ,B ,C 三个扇形区域的圆心角分别为150°,120°和90°. 转动圆盘后,指针停止在任何位置的可能性都相同(若指针停在分界线上,则重新转动圆盘),则转动圆盘一次,指针停C12.(1) 如图一,等边三角形MNP 的边长为1,线段AB 的长为4,点M 与A 重合,点N 在线段AB 上. △MNP 沿线段AB 按A B →的方向滚动, 直至△MNP 中有一个点与点B 重合为止,则点P 经过 的路程为 ;(2)如图二,正方形MNPQ 的边长为1,正方形ABCD 的边长为2,点M 与点A 重合,点N 在线段AB 上, 点P 在正方形内部,正方形MNPQ 沿正方形ABCD 的边按A B C D A →→→→→ 的方向滚动,始终保持M ,N ,P ,Q 四点在正方形内部或边界上,直至正方形MNPQ 回到初始位置为 止,则点P 经过的最短路程为 .(注:以△MNP 为例,△MNP 沿线段AB 按A B →的方向滚动指的是先以顶点N 为中心顺时针旋转, 当顶点P 落在线段AB 上时, 再以顶点P 为中心顺时针旋转,如此继续. 多边形沿直线滚动与此类 似.)三、解答题(本题共30分,每小题5分) 13.计算:.14(1)根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);(2)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),并简述理由.15.解方程:24120x x +-=. ()A N P图二图一图三(A Q16.如图,在ABC △中,AB 是⊙O 的直径,⊙O 与AC 交于点D,60,75AB B C =∠=︒∠=︒,求B O D ∠的度数;17.如图,正方形ABCD 中,点F 在边BC 上,E 在边BA 的延长线上. (1)若DCF △按顺时针方向旋转后恰好与DAE △重合.则旋转中心是点 ;最少旋转了 度;(2)在(1)的条件下,若3,2AE BF ==,求四边形BFDE 的面积.18.列方程解应用题:随着人们节能意识的增强,节能产品的销售量逐年增加.某地区高效节能灯的年销售量2009年为10万只,预计2011年将达到14.4万只.求该地区2009年到2011年高效节能灯年销售量的平均增长率.四、解答题(本题共20分,每小题5分)19.如图,在△ABC 中,120,C ∠=︒,4AC BC AB ==,半圆的圆心O 在AB 上,且与AC ,BC 分别相切于点D ,E . (1)求半圆O 的半径;(2)求图中阴影部分的面积. ADCBODCFBEA20.如图,O 为正方形ABCD 对角线AC 上一点,以O 为圆心,OA 长为半径的⊙O 与BC 相切于点M . (1)求证:CD 与⊙O 相切;(2)若⊙O 的半径为1,求正方形ABCD 的边长.21.一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m ,再从剩下的两张中任取一张,将其编号记为n .(1)请用树状图或者列表法,表示事件发生的所有可能情况; (2)求关于x 的方程20x mx n ++=有两个不相等实数根的概率.22.如图一,AB 是O 的直径,AC 是弦,直线EF 和O 相切与点C ,AD EF ⊥,垂足为D . (1)求证CAD BAC ∠=∠;(2)如图二,若把直线EF 向上移动,使得EF 与O 相交于G ,C 两点(点C 在点G 的右侧),连结AC ,AG ,若题中其他条件不变,这时图中是否存在与CAD ∠相等的角?若存在,找出一个这样 的角,并证明;若不存在,说明理由.图一图二五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.以坐标原点为圆心,1为半径的圆分别交x ,y 轴的正半轴于点A ,B .(1)如图一,动点P 从点A 处出发,沿x 轴向右匀速运动,与此同时,动点Q 从点B 处出发,沿圆周按顺时针方向匀速运动.若点Q 的运动速度比点P 的运动速度慢,经过1秒后点P 运动到点(2,0),此时PQ 恰好是O 的切线,连接OQ . 求QOP ∠的大小;(2)若点Q 按照(1)中的方向和速度继续运动,点P 停留在点(2,0)处不动,求点Q 再经过5秒后直线PQ 被O 截得的弦长.24.已知关于x的方程221(1)04x a -++=有实根.(1)求a 的值;(2)若关于x 的方程2(1)0mx m x a +--=的所有根均为整数,求整数m 的值.图一图二(备用图)25.如图一,在△ABC 中,分别以AB ,AC 为直径在△ABC 外作半圆1O 和半圆2O ,其中1O 和2O 分别为两个半圆的圆心. F 是边BC 的中点,点D 和点E 分别为两个半圆圆弧的中点. (1)连结1122,,,,,O F O D DF O F O E EF ,证明:12DO F FO E △≌△;(2)如图二,过点A 分别作半圆1O 和半圆2O 的切线,交BD 的延长线和CE 的延长线于点P 和点Q ,连结PQ ,若∠ACB=90°,DB=5,CE=3,求线段PQ 的长;(3)如图三,过点A 作半圆2O 的切线,交CE 的延长线于点Q ,过点Q 作直线F A 的垂线,交BD 的延长线于点P ,连结P A . 证明:P A 是半圆1O 的切线. 图一图二Q图三海淀区九年级数学第一学期期末练习参考答案及评分标准 2011.1说明: 合理答案均可酌情给分,但不得超过原题分数三、解答题(本题共30分,每小题5分)13.解:原式=…………………………….…………………………….2分= …………………………….…………………………….4分 =6 …………………………….…………………………….5分 14.(1)解: 48,…………………………….…………………………….1分 0.81…………………………….…………………………….2分 (2)解:()90.8P =射中环以上…………………………….…………………………….4分从频率的波动情况可以发现频率稳定在0.8附近,所以这名运动员射击一次时“射中9环以上” 的概率是0.8. …………………………….…………………………….5分 注:简述的理由合理均可给分 15.解法一:因式分解,得()()620x x +-= …………………………….…………………………….2分 于是得 60x +=或20x -= 126,2x x =-= ………………………….5分 解法二:1,4,12a b c ===-2464b ac ∆=-=…………………………….…………………………….2分482x -±== …………………………….…………………………….4分126,2x x =-= …………………………….…………………………….5分16.解:在ABC △中,60,75B C ∠=︒∠=︒ ,45A ∴∠=︒. …………………………….…………………………….2分AB 是⊙O 的直径,⊙O 与AC 交于点D, ∴290DOB A ∠=∠=︒. …………………………….…………………………….5分17.解:(1)D ;90︒. …………………………….…………………………….2分 (2)DCF DEA △旋转后恰好与△重合, DCF DAE ∴△≌△.3,2AE CF BF ∴===又. 5BC BF CF ∴=+=.AED BFDE ABFD S S S ∴=+△四边形四边形DCF ABFD S S ∆=+四边形ABCD S =正方形2BC =25= 5分18.解:设该地区2009年到2011年高效节能灯年销售量的平均增长率为x .……………….1分依据题意,列出方程 ()210114.4x += ……………………….…………………………….2分 化简整理,得: ()21 1.44x +=, 解这个方程,得 11.2x +=±, ∴ 120.2, 2.2x x ==-. ∵ 该地区2009年到2011年高效节能灯年销售量的平均增长率不能为负数. ∴ 2.2x =-舍去. ∴ 0.2x =. …………………….…………………………….4分四、解答题(本题共20分,每小题5分) 19.(1)解:连结OD ,OC ,∵半圆与AC ,BC 分别相切于点D ,E . ∴DCO ECO ∠=∠,且OD AC ⊥. ∵AC BC =,∴CO AB ⊥且O 是AB 的中点.∴122AO AB ==. ∵120C ∠=︒,∴60DCO ∠=︒. ∴30A ∠=︒.∴在R t AOD △中,112OD AO ==.即半圆的半径为1. …………………………….…………………………….3分(2)设CO =x ,则在R t AOC △中,因为30A ∠=︒,所以AC =2x ,由勾股定理得: 222AC OC AO -= 即 222(2)2x x -= 解得x =(x =舍去)∴11422ABC S AB OC =⋅=⨯=△……….…………………………….4分∵ 半圆的半径为1,∴ 半圆的面积为2π,∴2S π=-=阴影…………………………….…………………………….5分20.(1)解:过O 作ON CD ⊥于N ,连结OM ,则OM BC ⊥. ∵ AC 是正方形ABCD 的对角线, ∴ AC 是BCD ∠的平分线. ∴ OM =ON.即圆心O 到CD 的距离等于⊙O 半径, ∴ CD 与⊙O 相切.…………………………….…………………………….3分(2)由(1)易知MOC △为等腰直角三角形,OM 为半径, ∴ OM =MC =1.∴ 222112OC OM MC =+=+=, ∴OC =.∴1AC AO OC =+= 在R t ABC △中,AB =BC ,有 222A C A BB C=+ ∴ 222AB AC = ∴AB =…………………………….…………………………….5分故正方形ABCDN21.(1)解:依题意画出树状图(或列表)如下或…………………………….…………………………….2分注:画出一种情况就可给2分(2)解:当240m n ->时,关于x 的方程20x mx n ++=有两个不相等实数根,而使得240m n ->的m ,n 有2组,即(3,1)和(3,2). ………….…………………………….4分则关于x 的方程20x mx n ++=有两个不相等实数根的概率是13.∴P (有两个不等实根)=13. …………………….5分22.(1)证明:如图一,连结OC ,则OC EF ⊥,且OC=OA ,易得OCA OAC ∠=∠.∵ AD EF ⊥,∴OC//AD.∴OCA ∠=CAD ∠,∴CAD ∠=OAC ∠. 即 C A D B A C ∠=∠.…………………………….…………………………….2分 (2)解:与CAD ∠相等的角是BAG ∠.…………………………….…………………………….3分证明如下: 如图二,连结BG .∵ 四边形ACGB 是O 的内接四边形, ∴ 180ABG ACG ∠+∠=︒. ∵ D ,C ,G 共线,∴ 180ACD ACG ∠+∠=︒. ∴ ACD ABG ∠=∠.∵ AB 是O 的直径, ∴ 90BAG ABG ∠+∠=︒ ∵ AD EF ⊥ ∴ 90CAD ACD ∠+∠=︒ ∴ CAD BAG ∠=∠. …………………………….…………………………….5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.(1)解:如图一,连结AQ .由题意可知:OQ =OA =1. ∵OP =2, ∴A 为OP 的中点. ∵PQ 与O 相切于点Q ,∴OQP △为直角三角形. …………1分∴112AQ OP OQ OA ==== . …………2分即ΔOAQ 为等边三角形.123123312m n 图一图二(2)解:由(1)可知点Q 运动1秒时经过的弧长所对的圆心角为30°,若Q 按照(1)中的方向和速度继续运动,那么再过5秒,则Q 点落在O 与y 轴负半轴的交点处(如图二).设直线PQ 与O 的另外一个交点为D ,过O 作OC ⊥QD 于点C ,则C 为QD 的中点. …………4分 ∵∠QOP =90°,OQ =1,OP =2,∴QP…………5分 ∵1122OQ OP QP OC ⋅=⋅, ∴OC. …………6分∵OC ⊥QD ,OQ =1,OC∴QC∴QD. …………7分24.(1)解:∵关于x的方程为221(1)04x a -++=为一元二次方程,且有实根.故满足:220,1(4(1)0.4a a ≥⎧⎪⎨∆=--⨯⨯+≥⎪⎩ ……….…………………………….2分(注:每个条件1分) 整理得 20,(1)0.a a ≥⎧⎨-≤⎩ ∴1a =……….…………………………….4分(2)由(1)可知1a =,故方程2(1)0mx m x a +--=可化为2(1)10mx m x +--=.①当m =0时,原方程为10x -=,根为1x =,符合题意. ………………………….5分②当m ≠0时,2(1)10mx m x +--=为关于x 的一元二次方程,2222(1)4(1)12421(1)0m m m m m m m m ∆=--⨯⨯-=-++=++=+≥.此时,方程的两根为 1211,x x m==-. ∵两根均为整数, ∴m =1±.………………………….7分综上所述,m 的值为1-,0 或1.图二1125.(1)证明:如图一,∵1O ,2O ,F 分别是AB ,AC ,BC 边的中点,∴1O F ∥AC 且1O F =A 2O ,2O F ∥AB 且2O F =A 1O , ∴∠B 1O F=∠BAC ,∠C 2O F=∠BAC , ∴∠B 1O F=∠C 2O F∵点D 和点E 分别为两个半圆圆弧的中点, ∴1O F =A 2O =2O E ,2O F =A 1O =1O D ,分 ∠B 1O D =90°,∠C 2O E =90°, ∴∠B 1O D=∠C 2O E . ∴∠D 1O F=∠F2O E .∴12DO F FO E △≌△.………………………….3分(2)解:如图二,延长CA 至G ,使AG =AQ ,连接BG 、AE .∵点E 是半圆2O 圆弧的中点, ∴AE=CE=3 ∵AC 为直径 ∴∠AEC =90°,∴∠ACE =∠EAC =45°,AC = ∵AQ 是半圆2O 的切线, ∴CA ⊥AQ ,∴∠CAQ =90°,∴∠ACE =∠AQE =45°,∠GAQ =90° ∴AQ =AC =AG =同理:∠BAP =90°,AB =AP = ∴CG =∠GAB =∠QAP ∴AQP AGB △≌△. ……………………..5分∴PQ =BG ∵∠ACB =90°,∴BC ∴BG ∴PQ=……………………..6分(3) 证法一:如图三,设直线F A 与PQ 的垂足为M ,过C 作CS ⊥MF 于S ,过B 作BR ⊥MF 于R ,连接DR 、AD 、DM.∵F 是BC 边的中点,∴ABF ACF S S =△△. ∴BR=CS ,由(2)已证∠CAQ =90°, AC =AQ,∴∠2+∠3=90° ∵FM ⊥PQ , ∴∠2+∠1=90°, ∴∠1=∠3, 同理:∠2=∠4,∴AMQ CSA △≌△, ∴AM=CS , ∴AM=BR ,图一图二图三12同(2)可证AD=BD ,∠ADB =∠ADP =90°,∴∠ADB =∠ARB =90°, ∠ADP =∠AMP =90° ∴A 、D 、B 、R 四点在以AB 为直径的圆上,A 、D 、P 、M 四点在以AP 为直径的圆上, 且∠DBR+∠DAR =180°, ∴∠5=∠8, ∠6=∠7, ∵∠DAM +∠DAR =180°, ∴∠DBR =∠DAM ∴DBR DAM △≌△, ∴∠5=∠9, ∴∠RDM =90°,∴∠5+∠7=90°, ∴∠6+∠8=90°, ∴∠P AB =90°,∴P A ⊥AB ,又AB 是半圆1O 直径, ∴P A 是半圆1O 的切线.……………………..8分证法二:假设P A 不是是半圆1O 的切线,如图四,过点A 作半圆1O 的切线交BD 的延长线于点P ', 则点P '异于点P ,连结P Q ',设直线F A 与PQ 的 垂足为M ,直线F A 与P Q '的交点为M '.延长AF 至N ,使得AF =FN ,连结BN ,CN ,由于点F 是 BC 中点,所以四边形ABNC 是平行四边形. 易知,180BAC ACN ∠+∠=︒, ∵AQ 是半圆2O 的切线,∴∠QAC =90°,同理90P AB '∠=︒. ∴180P AQ BAC '∠+∠=︒. ∴P AQ ACN '∠=∠.由(2)可知,,AQ AC AB AP '==,∴P AQ NCA '△≌△. ∴NAC P QA '∠=∠. ∵90QAC ∠=︒,∴90NAC M AQ '∠+∠=︒.即 90AQM M AQ ''∠+∠=︒.∴90AM Q '∠=︒. 即 P Q A F '⊥.∵ PQ AF ⊥,∴ 过点Q 有两条不同的直线P Q '和PQ 同时与AF 垂直.这与在平面内过一点有且仅有一条直线与已知直线垂直相矛盾,因此假设错误.所以P A 是是半圆1O 的切线.Q图四。
2011-2012学年北京市海淀区九年级(上)期末数学试卷

2011-2012 学年北京市海淀区九年级(上)期末数学试卷一、选择题(本题共32 分,每小题4 分)下面各题均有四个选项,其中只有一个是符合题意的.1.(4分)下列说法正确的是()A.掷两枚硬币,一枚正面朝上,一枚反面超上是不可能事件B.随意地翻到一本书的某页,这页的页码为奇数是随机事件C.经过某市一装有交通信号灯的路口,遇到红灯是必然事件D.某一抽奖活动中奖的概率为买100 张奖券一定会中奖2.(4 分)下列图形,既是轴对称图形,又是中心对称图形的是()A. B.C. D.3.(4 分)将抛物线y=x2 平移得到抛物线y=x2+3,则下列平移过程正确的是()A.向上平移3 个单位B.向下平移3 个单位C.向左平移3 个单位D.向右平移3 个单位4.(4分)下列一元二次方程有两个相等实数根的是()A.x2﹣x+1=0 B.2x2﹣3x﹣1=0 C.x2﹣6x+9=0 D.x2﹣4x+2=0 5.(4分)已知圆锥的底面半径为2cm,母线长为5cm,则圆锥的侧面积是()A.20cm2 B.20πcm2 C.10πcm2 D.5πcm26.(4 分)如图,为了测量某棵树的高度,小明用长为2m 的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m,与树相距15m,则树的高度是()A.7m B.6m C.5m D.4m7.(4 分)已知二次函数y=ax2+bx+c 的图象如图所示,则下列结论正确的是()A.a>0 B.c<0 C.b2﹣4ac<0 D.a+b+c>0 8.(4分)已知O 为圆锥顶点,OA、OB 为圆锥的母线,C 为OB 中点,一只小蚂蚁从点C 开始沿圆锥侧面爬行到点A,另一只小蚂蚁也从C 点出发,绕着圆锥侧面爬行到点B,它们所爬行的最短路线的痕迹如右图所示.若沿OA 剪开,则得到的圆锥侧面展开图为()A. B.C. D.二、填空题(本题共16 分,每小题4 分)9.(4 分)方程x2﹣4x=0 的解为.10.(4 分)如图,△ABD 与△AEC 都是等边三角形,若∠ADC=15°,则∠ABE=.11.(4 分)若(x,y,z 均不为0),则的值为.12.(4 分)用两个全等的含30°角的直角三角形制作如图1 所示的两种卡片,两种卡片中扇形的半径均为1,且扇形所在圆的圆心分别为长直角边的中点和30°角的顶点,按先A 后B 的顺序交替摆放A、B 两种卡片得到图2 所示的图案.若摆放这个图案共用两种卡片8 张,则这个图案中阴影部分的面积之和为;若摆放这个图案共用两种卡片(2n+1)张(n 为正整数),则这个图案中阴影部分的面积之和为.(结果保留π )三、解答题(本题共29 分,第13 题~第15 题各5 分,第16 题4 分,第17 题、第18 题各5 分)13.(5 分)解方程:x2﹣4x﹣1=0.14.(5 分)如图,在△ABC 中,D、E 分别是AC、AB 边上的点,∠AED=∠C,AB=6,AD=4,AC=5,求AE 的长.15.(5 分)抛物线y=ax2+bx+c 上部分点的横坐标x,纵坐标y 的对应值如下表:x…﹣2 ﹣1 0 1 2 …y…0 ﹣4 ﹣4 0 8 …(1)根据上表填空:①抛物线与x 轴的交点坐标是和;②抛物线经过点(﹣3,);③在对称轴右侧,y 随x 增大而;(2)试确定抛物线y=ax2+bx+c 的解析式.16.(4 分)如图,在正方形网格中,△ABC 的顶点和O 点都在格点上.(1)在图1 中画出与△ABC 关于点O 对称的△A′B′C′;(2)在图2 中以点O 为位似中心,将△ABC 放大为原来的2 倍(只需画出一种即可).17.(5 分)已知关于x 的方程(k﹣2)x2+2(k﹣2)x+k+1=0 有两个实数根,求正整数k 的值.18.(5 分)在一个口袋中有3 个完全相同的小球,把它们分别标号为1,2,3,随机地摸出一个小球记下标号后放回,再随机地摸出一个小球记下标号,求两次摸出小球的标号之和等于4 的概率.四、解答题(本题共21 分,第19 题、第20 题各5 分,第21 题6 分,第22 题5 分)19.(5 分)某商店销售一种进价为20 元/双的手套,经调查发现,该种手套每天的销售量w(双)与销售单价x(元)满足w=﹣2x+80(20≤x≤40),设销售这种手套每天的利润为y(元).(1)求y 与x 之间的函数关系式;(2)当销售单价定为多少元时,每天的利润最大?最大利润是多少?20.(5 分)已知二次函数y=x2+(3﹣)x﹣3(m>0)的图象与x 轴交于点(x1,0)和(x2,0),且x1<x2.(1)求x2 的值;2 2(2)求代数式mx1 + x1 +(3﹣)x1+ x1+9 的值.21.(6 分)如图,AB 是⊙O 的直径,点C 在⊙O 上,CE⊥AB 于E,CD 平分∠ECB,交过点B 的射线于D,交AB 于F,且BC=BD.(1)求证:BD 是⊙O 的切线;(2)若AE=9,CE=12,求BF 的长.22.(5 分)已知△ABC 的面积为a,O、D 分别是边AC、BC 的中点.(1)画图:在图中将点D 绕点O 旋转180°得到点E,连接AE、CE.填空:四边形ADCE 的面积为;(2)在(1)的条件下,若F1 是AB 的中点,F2 是AF1 的中点,F3 是AF2 的中点,…,F n 是AF n﹣1 的中点(n 为大于1 的整数),则△F2CE 的面积为;△F n CE 的面积为.五、解答题(本题共22 分,第23 题7 分,第24 题7 分,第25 题8 分)23.(7 分)已知二次函数y=ax2+bx+c 的图象与反比例函数的图象交于A(a,﹣3),与y 轴交于点B.(1)试确定反比例函数的解析式;(2)若∠ABO=135°,试确定二次函数的解析式;(3)在(2)的条件下,将二次函数y=ax2+bx+c 的图象先沿x 轴翻折,再向右平移到与反比例函数的图象交于点P(x0,6).当x0≤x≤3 时,求平移后的二次函数y 的取值范围.24.(7 分)已知在□ABCD 中,AE⊥BC 于E,DF 平分∠ADC 交线段AE 于F.(1)如图1,若AE=AD,∠ADC=60°,请直接写出线段CD 与AF+BE 之间所满足等量关系;(2)如图2,若AE=AD,你在(1)中得到的结论是否仍然成立,若成立,对你的结论加以证明,若不成立,请说明理由;(3)如图3,若AE:AD=a:b,试探究线段CD、AF、BE 之间所满足的等量关系,请直接写出你的结论.25.(8 分)如图,已知抛物线经过坐标原点O 及A(,0),其顶点为B(m,3),C 是AB 中点,点E 是直线OC 上的一个动点(点E 与点O 不重合),点D 在y 轴上,且EO=ED.(1)求此抛物线及直线OC 的解析式;(2)当点E 运动到抛物线上时,求BD 的长;(3)连接AD,当点E 运动到何处时,△AED 的面积为?请直接写出此时E 点的坐标.2011-2012 学年北京市海淀区九年级(上)期末数学试卷参考答案与试题解析一、选择题(本题共32 分,每小题4 分)下面各题均有四个选项,其中只有一个是符合题意的.1.(4分)下列说法正确的是()A.掷两枚硬币,一枚正面朝上,一枚反面超上是不可能事件B.随意地翻到一本书的某页,这页的页码为奇数是随机事件C.经过某市一装有交通信号灯的路口,遇到红灯是必然事件D.某一抽奖活动中奖的概率为买100 张奖券一定会中奖【分析】根据已知及一定会发生的事件为必然事件.可能发生也可能不发生,是随机事件作出判断.【解答】解:A、掷两枚硬币,一枚正面朝上,一枚反面超上可能发生也可能不发生,是随机事件,故本选项错误;B、随意地翻到一本书的某页,这页的页码为奇数是随机事件正确,故本选项正确;C、经过某市一装有交通信号灯的路口,遇到红灯也可能遇到绿灯,所以是随机事件,故本选项错误;D、某一抽奖活动中奖的概率为买100 张奖券一定会中奖,只是说获奖的概率是,但买100 张不一定有奖,故本选项错误.故选:B.【点评】此题考查的知识点是随机事件,解决本题要正确理解必然事件、不可能事件、随机事件的概念,理解概念是解决基础题的主要方法.用到的知识点为:必然事件指在一定条件下一定发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.2.(4 分)下列图形,既是轴对称图形,又是中心对称图形的是()A.B.C. D.【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.【解答】解:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,也不是轴对称图形,故此选项错误;B、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;C、此图形旋转180°后能与原图形重合,此图形是中心对称图形,不是轴对称图形,故此选项错误;D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.故选:D.【点评】此题主要考查了中心对称图形与轴对称的定义,根据定义得出图形形状是解决问题的关键.3.(4 分)将抛物线y=x2 平移得到抛物线y=x2+3,则下列平移过程正确的是()A.向上平移3 个单位B.向下平移3 个单位C.向左平移3 个单位D.向右平移3 个单位【分析】根据“上加下减”的原则直接进行解答即可.【解答】解:由“上加下减”的原则可知,将抛物线y=x2 向上平移得到抛物线y=x2+3.故选:A.【点评】本题考查的是二次函数的图象与几何变换,熟知“上加下减”的原则是解答此题的关键.4.(4 分)下列一元二次方程有两个相等实数根的是()A.x2﹣x+1=0 B.2x2﹣3x﹣1=0 C.x2﹣6x+9=0 D.x2﹣4x+2=0 【分析】判断上述方程的根的情况,只要看根的判别式△=b2﹣4ac 的值的符号就可以了.有两个相等实数根的一元二次方程就是判别式的值是0 的一元二次方程.【解答】解:A、△=12﹣4×1×1<0,无实数根;B、△=(﹣3)2﹣4×2×(﹣1)>0,有两个不相等实数根;C、△=62﹣4×9=0,有两个相等实数根;D、△=42﹣4×1×2>0,有两个相等实数根.故选:C.【点评】本题考查了根的判别式,总结:一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.5.(4 分)已知圆锥的底面半径为2cm,母线长为5cm,则圆锥的侧面积是()A.20cm2 B.20πcm2 C.10πcm2 D.5πcm2【分析】圆锥的侧面积=π×底面半径×母线长,把相应数值代入即可求解.【解答】解:圆锥的侧面积=π×2×5=10πcm2,故选:C.【点评】本题考查圆锥侧面积的求法.6.(4分)如图,为了测量某棵树的高度,小明用长为2m 的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m,与树相距15m,则树的高度是()A.7m B.6m C.5m D.4m【分析】此题中,竹竿、树以及经过竹竿顶端和树顶端的太阳光构成了一组相似三角形,利用相似三角形的对应边成比例即可求得树的高度.【解答】解:如图;AD=6m,AB=21m,DE=2m;由于DE∥BC,所以△ADE∽△ABC,得:,即,解得:BC=7m,故树的高度为7m.故选:A.【点评】此题考查了相似三角形在测量高度时的应用;解题的关键是找出题中的相似三角形,并建立适当的数学模型来解决问题.7.(4 分)已知二次函数y=ax2+bx+c 的图象如图所示,则下列结论正确的是()A.a>0 B.c<0 C.b2﹣4ac<0 D.a+b+c>0【分析】由抛物线的开口方向判断a 与0 的关系,由抛物线与y 轴的交点得出c 的值,然后根据抛物线与x 轴交点的个数及x=1 时二次函数的值的情况进行推理,进而对所得结论进行判断.【解答】解:A、由二次函数的图象开口向下可得a<0,故选项错误;B、由抛物线与y 轴交于x 轴上方可得c>0,故选项错误;C、由抛物线与x 轴有两个交点可以看出方程ax2+bx+c=0 的根的判别式b2﹣4ac>0,故选项错误;D、把x=1 代入y=ax2+bx+c得:y=a+b+c,由函数图象可以看出x=1 时二次函数的值为正,正确.故选:D.【点评】主要考查图象与二次函数系数之间的关系,二次函数与方程之间的转换,根的判别式的熟练运用.会利用特殊值代入法求得特殊的式子,如:y=a+b+c,y=a﹣b+c,然后根据图象判断其值.8.(4分)已知O 为圆锥顶点,OA、OB 为圆锥的母线,C 为OB 中点,一只小蚂蚁从点C 开始沿圆锥侧面爬行到点A,另一只小蚂蚁也从C 点出发,绕着圆锥侧面爬行到点B,它们所爬行的最短路线的痕迹如右图所示.若沿OA 剪开,则得到的圆锥侧面展开图为()A. B.C. D.【分析】要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果,再利用做对称点作出另一只小蚂蚁绕着圆锥侧面爬行到点B,它们所爬行的最短路线.【解答】解:∵C 为OB 中点,一只小蚂蚁从点C 开始沿圆锥侧面爬行到点A,∴侧面展开图BO 为扇形对称轴,连接AC 即可是最短路线,∵另一只小蚂蚁绕着圆锥侧面爬行到点B,作出C 关于OA 的对称点,再利用扇形对称性得出关于BO 的另一对称点,连接即可;故选:C.【点评】此题主要考查了圆锥侧面展开图以及做对称点得出最短路径,根据做对称点得出最短路径问题是中考中考查重点也是难点,同学们应重点掌握.二、填空题(本题共16 分,每小题4 分)9.(4 分)方程x2﹣4x=0 的解为 x1=0,x2=4 .【分析】x2﹣4x 提取公因式x,再根据“两式的乘积为0,则至少有一个式子的值为0”求解.【解答】解:x2﹣4x=0x(x﹣4)=0 x=0 或x﹣4=0x1=0,x2=4故答案是:x1=0,x2=4.【点评】本题考查简单的一元二次方程的解法,在解一元二次方程时应当注意要根据实际情况选择最合适快捷的解法.该题运用了因式分解法.10.(4 分)如图,△ABD 与△AEC 都是等边三角形,若∠ADC=15°,则∠ABE= 15 ° .【分析】因为△ABD 和△ACE 都是等边三角形,所以有AD=AB,AC=AE,又因为∠DAB+∠BAC=∠EAC+∠BAC,所以∠DAC=∠BAE,故可根据SAS 判定△ADC≌△ABE,根据全等三角形的性质即可得出∠ABE 的度数.【解答】解:∵△ABD 和△ACE 都是等边三角形,∴AD=AB,AC=AE,又∵∠DAB+∠BAC=∠EAC+∠BAC,∴∠DAC=∠BAE,∴△ADC≌△ABE(SAS).又∵∠ADC=15°,∴∠ABE=∠ADC=15°.故答案为:15°.【点评】本题考查等边三角形的性质及三角形全等的判定方法,解答本题的关键是根据题意判断出△ADC≌△ABE,难度一般.11.(4 分)若(x,y,z 均不为0),则的值为 1 .【分析】首先根据比例的等比性质与已知得出,,然后将化为:+2•﹣,再代入求值.【解答】解:已知(x,y,z 均不为0),由比例的性质得:==,=,则=+2•﹣=+﹣1=1,故答案为:1.【点评】此题考查的知识点是比例的性质,关键是准确掌握其性质进行运算.12.(4 分)用两个全等的含30°角的直角三角形制作如图1 所示的两种卡片,两种卡片中扇形的半径均为1,且扇形所在圆的圆心分别为长直角边的中点和30°角的顶点,按先A 后B 的顺序交替摆放A、B 两种卡片得到图2 所示的图案.若摆放这个图案共用两种卡片8 张,则这个图案中阴影部分的面积之和为π;若摆放这个图案共用两种卡片(2n+1)张(n 为正整数),则这个图案中阴影部分的面积之和为π.(结果保留π)【分析】分别求出A、B 两种扇形的面积,再求图形中A、B 两种扇形的个数,求阴影部分的面积,注意按先A 后B 的顺序交替摆放A、B 两种卡片.【解答】解:依题意,A 种图中扇形圆心角为60°,半径为1,面积为=,B 种图中扇形圆心角为30°,半径为1,面积为=,故图2 中阴影部分面积和为4×(+)=π,摆放这个图案共用两种卡片(2n+1)张,需要A 种图(n+1)张,需要B 种图n 张,则这个图案中阴影部分的面积和为(n+1)×+n×=π.故答案为:π,π.【点评】本题考查了图形的变化规律型的计算.关键是先计算每一个基本图形的面积,再确定组合中含基本图形的个数.三、解答题(本题共29 分,第13 题~第15 题各5 分,第16 题4 分,第17 题、第18 题各5 分)13.(5 分)解方程:x2﹣4x﹣1=0.【分析】配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.【解答】解:∵x2﹣4x﹣1=0,∴x2﹣4x=1,∴x2﹣4x+4=1+4,∴(x﹣2)2=5,∴x=2±,∴x1=2+,x2=2﹣.【点评】此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确应用.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2 的倍数.14.(5 分)如图,在△ABC 中,D、E 分别是AC、AB 边上的点,∠AED=∠C,AB=6,AD=4,AC=5,求AE 的长.【分析】利用有两角相等的三角形相似先判定△AED∽△ACB,再利用相似三角形的性质:对应边的比值相等即可求出AE 的长.【解答】证明:在△AED 和△ACB 中,∵∠A=∠A,∠AED=∠C,∴△AED∽△ACB,∴ ,∵AB=6,AD=4,AC=5,∴∴AE=.【点评】此题考查了相似三角形的判定和相似三角形的性质:对应边的比相等的性质,做题时注意:边之间的对应.15.(5 分)抛物线y=ax2+bx+c 上部分点的横坐标x,纵坐标y 的对应值如下表:x…﹣2 ﹣1 0 1 2 …y…0 ﹣4 ﹣4 0 8 …①抛物线与x 轴的交点坐标是(﹣2,0)和(1,0);②抛物线经过点(﹣3, 8 );③在对称轴右侧,y 随x 增大而增大;(2)试确定抛物线y=ax2+bx+c 的解析式.【分析】(1)①由表格可知:x=﹣2 及1 时,y 的值为0,从而确定出抛物线与x 轴的交点坐标;②由x=﹣1 及x=0 时的函数值y 相等,x=﹣2 及1 时的函数值也相等,可得抛物线的对称轴为x=﹣0.5,由函数的对称性可得x=2 及x=﹣3 时的函数值相等,故由x=2 对应的函数值可得出x=﹣3 所对应的函数值,从而得出正确答案;③由表格中y 值的变化规律及找出的对称轴,得到抛物线的开口向上,在对称轴右侧为增函数,故在对称轴右侧,y 随x 的增大而增大;(2)由第一问得出抛物线与x 轴的两交点坐标(﹣2,0),(1,0),可设出抛物线的两根式方程为y=a(x+2)(x﹣1),除去与x 轴的交点,在表格中再找出一个点坐标,代入所设的解析式即可求出a 的值,进而确定出函数解析式.【解答】解:(1)①(﹣2,0),(1,0);②8;③增大(每空1 分)…(3 分)(2)依题意设抛物线解析式为y=a(x+2)(x﹣1),由点(0,﹣4)在函数图象上,代入得﹣4=a(0+2)(0﹣1),…(4 分)解得:a=2.∴y=2(x+2)(x﹣1),即所求抛物线解析式为y=2x2+2x﹣4.…(5 分)故答案为:(﹣2,0),(1,0);8;增大.【点评】此题考查了利用待定系数法求二次函数的解析式,二次函数最值的求法,以及二次函数与不等式的关系,利用了转化及数形结合的数学思想,其中待定系数法确定函数解析式一般步骤为:设出函数解析式,把图象上点的坐标代入所设的解析式,得到方程组,求出方程组的解可得出系数的值,从而确定出函数解析式.16.(4 分)如图,在正方形网格中,△ABC 的顶点和O 点都在格点上.(1)在图1 中画出与△ABC 关于点O 对称的△A′B′C′;(2)在图2 中以点O 为位似中心,将△ABC 放大为原来的2 倍(只需画出一种即可).【分析】(1)找到A、B、C 关于点O 的对称点A′,B′,C′,连接A′,B′,C′即可;(2)分别作出三角形的对应点,扩大对应边2 倍即可得出答案.【解答】解(1)如图1 所示:(2)如图2 所示:【点评】此题考查了作图﹣﹣旋转变换和位似图形的画法,找到各点关于点O 的对称点并连接各点是解题的关键.17.(5 分)已知关于x 的方程(k﹣2)x2+2(k﹣2)x+k+1=0 有两个实数根,求正整数k 的值.【分析】根据一元二次方程有两个实数根,则根的判别式△=b2﹣4ac≥0,建立关于k 的不等式,求出k 的取值范围即可,在解题时要注意二次项系数不能为0 即k≠2;【解答】解:由题意得:k﹣2≠0①,△=[2(k﹣2)]2﹣4(k﹣2)(k+1)≥0②.由①得k≠2.由②得k≤2.∴k<2.∵k 为正整数,∴k=1.【点评】此题主要考查了根的判别式以及一元一次不等式的整数解,一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数.18.(5 分)在一个口袋中有3 个完全相同的小球,把它们分别标号为1,2,3,随机地摸出一个小球记下标号后放回,再随机地摸出一个小球记下标号,求两次摸出小球的标号之和等于4 的概率.【分析】用树状图列举出所有情况,看两次摸出小球的标号之和等于4 的情况数占总情况数的多少即可.【解答】解:由题意画树形图如下:从树形图看出,所有可能出现的结果共有9 个,这些结果出现的可能性相等,标号之和等于4 的结果共有3 种.所以P(标号之和等于4)==.【点评】考查概率的求法;用到的知识点为:概率=所求情况数与总情况数之比.得到所求的情况数是解决本题的关键.四、解答题(本题共21 分,第19 题、第20 题各5 分,第21 题6 分,第22 题5 分)19.(5 分)某商店销售一种进价为20 元/双的手套,经调查发现,该种手套每天的销售量w(双)与销售单价x(元)满足w=﹣2x+80(20≤x≤40),设销售这种手套每天的利润为y(元).(1)求y 与x 之间的函数关系式;(2)当销售单价定为多少元时,每天的利润最大?最大利润是多少?【分析】(1)用每双手套的利润乘以销售量得到每天的利润;(2)由(1)得到的是一个二次函数,利用二次函数的性质,可以求出最大利润以及销售单价.【解答】解:(1)y=w(x﹣20)=(﹣2x+80)(x﹣20)=﹣2x2+120x﹣1600;(2)y=﹣2(x﹣30)2+200.∵20≤x≤40,a=﹣2<0,∴当x=30 时,y 最大值=200.答:当销售单价定为每双30 元时,每天的利润最大,最大利润为200 元.【点评】本题考查的是二次函数的应用,(1)根据题意得到二次函数.(2)利用二次函数的性质求出最大值.(3)由二次函数的值求出x 的值.20.(5 分)已知二次函数y=x2+(3﹣)x﹣3(m>0)的图象与x 轴交于点(x1,0)和(x2,0),且x1<x2.1 1 1 1 1(1)求 x 2 的值;22(2)求代数式 mx 1 +x 1 +(3﹣ )x 1+x 1+9 的值.【分析】(1)令 y =0,得到关于 x 的一元二次方程x 2+(3﹣)x ﹣3=0,再利用因式分解法解二元一次方程即可求出两交点的坐标,然后根据 x 1<x 2 即可得解;(2)根据(1)的结论,先整理得到 x 2+(3﹣)x =3,再把 x 的值代入进行计算即可得解.【解答】解:(1)∵二次函数 y =x 2+(3﹣ )x ﹣3 (m >0)的图象与 x 轴交于点 (x 1,0)和(x 2,0), ∴令 y =0,即x 2+(3﹣)x ﹣3=0,(x +3)(x ﹣1)=0,∵m >0, ∴>0,解得 x =1 或 x =﹣,∵x 1<x 2,﹣<0<1,∴x 2=1;(2)由(1)x 1=﹣,得 x 1=﹣3,∵x 1=﹣是方程 x 2+(3﹣ )x ﹣3=0 的根,∴x 2+(3﹣)x =3,222∴mx 1 + x 1 +(3﹣ )x 1+6 x 1+9=mx 1 +3+6 x 1+9, =m •(﹣)2+3+6 ×(﹣)+9,=9+3﹣18+9, =21﹣18, =3.【点评】本题考查了抛物线与 x 轴的交点问题,通常令 y =0,求关于 x 的二元一次方程 得到交点,(2)题先利用方程的概念把代数式化简然后再代入 x 1 的值进行计算更加简 便.21.(6 分)如图,AB 是⊙O 的直径,点 C 在⊙O 上,CE ⊥AB 于 E ,CD 平分∠ECB ,交过点B 的射线于D,交AB 于F,且BC=BD.(1)求证:BD 是⊙O 的切线;(2)若AE=9,CE=12,求BF 的长.【分析】(1)要证明BD 是⊙O 的切线,由已知条件转化为证明∠DBA=90°即可;(2)连接AC,利用三角形相似求出BE 的值,由勾股定理求出BC 的值,由已知条件再证明△EFC∽△BFD,相似三角形的性质利用:对应边的比值相等即可求出BF 的长.【解答】(1)证明:∵CE⊥AB,∴∠CEB=90°.∵CD 平分∠ECB,BC=BD,∴∠1=∠2,∠2=∠D.∴∠1=∠D,∴CE∥BD,∴∠DBA=∠CEB=90°,∵AB 是⊙O 的直径,∴BD 是⊙O 的切线;(2)解:连接AC,∵AB 是⊙O 直径,∴∠ACB=90°.∵CE⊥AB,∴∠AEC=∠BEC=90°,∵∠A+∠ABC=90°,∠A+∠ACE=90°,∴∠ACE=∠ABC,∴△ACE∽△CBE,∴=,即CE2=AE•EB,∵AE=9,CE=12,∴EB=16,在Rt△CEB 中,∠CEB=90,由勾股定理得BC=20,∴BD=BC=20,∵∠1=∠D,∠EFC=∠BFD,∴△EFC∽△BFD,∴=,即∴BF=10.【点评】本题考查了切线的判定定理、圆周角定理、相似三角形判定和相似三角形的性质以及勾股定理的运用,题目综合性很强,难度不大.22.(5 分)已知△ABC 的面积为a,O、D 分别是边AC、BC 的中点.(1)画图:在图中将点D 绕点O 旋转180°得到点E,连接AE、CE.填空:四边形ADCE 的面积为 a ;(2)在(1)的条件下,若F1 是AB 的中点,F2 是AF1 的中点,F3 是AF2 的中点,…,F n 是AF n﹣1 的中点(n 为大于1 的整数),则△F2CE 的面积为 a ;△F n CE 的面积为 a .【分析】(1)根据平行四边形的判定的平行四边形ADCE,推出AE=CD,AD=CE,根据SSS 证△ADC 和△CEA 全等,即可求出答案;(2)设△ABC 边AB 上的高是h,则AB×h=a,求出DE∥AB,推出△EAF2 的边AF2 上的高和△BCF2 上的边BF2 上的高相等,都是h,根据△F2CE 的面积为:S△ABD+S 四边形ADCE﹣﹣,代入求出即可;求出BF1=AB,AF1=AB,BF2=AB,AF2=AB,BF3=AB,AF3=AB,根据线段的结果推出BF n=AB,AF n=AB,根据△F n CE 的面积为S△ABD+S 四边形ADCE﹣﹣,代入求出即可.【解答】(1)解:如图:∵AO=OC,DO=OE,∴四边形ADCE 是平行四边形,∴AE=DC,CE=AD,在△ADC 和△CEA 中,∴△ADC≌△CEA,∴S△ADC=S△CEA=a,∴四边形ADCE 的面积是a+a=a,故答案为:a.(2)解:过C 作CM⊥AB 于M,设△ABC 边AB 上的高是CM=h,则AB×h=a,∵BD=DC,AO=CO,∴DE∥AB,∴△EAF2 的边AF2 上的高和△BAD 上的边BF2 上的高相等,都是h,∴△F2CE 的面积为:S△ABD+S 四边形ADCE﹣﹣,=a+a﹣×AB×h﹣×AB×h═a,∵BF1=AB,AF1=AB,BF2=AB,AF2=AB,BF3=AB,AF3=AB,…∴BF n=AB,AF n=AB,∴;△F n CE 的面积为S△ABD+S 四边形ADCE﹣﹣,=a+a﹣×AB×h﹣×AB×h,=a+a﹣a﹣a,=a.故答案为:a,a.【点评】本题考查了三角形的面积,平行四边形的性质和判定,全等三角形的性质和判定,三角形的中位线定理,旋转的性质等知识点的应用,关键是根据线段的结果得出BF n,AF n 的长,本题有一定的难度,对学生提出了较高的要求,主要培养学生的观察能力和总结规律的能力.五、解答题(本题共22 分,第23 题7 分,第24 题7 分,第25 题8 分)23.(7 分)已知二次函数y=ax2+bx+c 的图象与反比例函数的图象交于A(a,﹣3),与y 轴交于点B.(1)试确定反比例函数的解析式;(2)若∠ABO=135°,试确定二次函数的解析式;(3)在(2)的条件下,将二次函数y=ax2+bx+c 的图象先沿x 轴翻折,再向右平移到与反比例函数的图象交于点P(x0,6).当x0≤x≤3 时,求平移后的二次函数y 的取值范围.【分析】(1)把点A 的坐标代入反比例函数解析式,然后解方程求出a 的值,代入反比例函数解析式整理即可;(2)过点A 作AC⊥y 轴于C,根据∠ABO=135°求出∠ABC=45°,再根据等角对等边的性质得到BC=AC=1,然后求出OB 的长度,从而可得点B 的坐标,再把点A 的坐标代入二次函数解析式求出b 的值,从而得到二次函数的解析式;(3)先求出翻折平移后的二次函数解析式,再把点P 的坐标代入反比例函数解析式求出点P 的坐标,然后把点P 的坐标代入并求出二次函数解析式,然后根据二次函数图象的增减性分段求出y 的取值范围,从而得解.【解答】解:(1)∵A(a,﹣3)在y=的图象上,∴=﹣3,解得a=﹣1,∴y==,∴反比例函数的解析式为y=;(2)过A 作AC⊥y 轴于C.∵A(﹣1,﹣3),∴AC=1,OC=3,∵∠ABO=135°∴∠ABC=45°,可得BC=AC=1,∴OB=2,∴B(0,﹣2),由抛物线y=ax2+bx+c 与y 轴交于B,得c=﹣2.∵a=﹣1,∴y=﹣x2+bx﹣2,∵抛物线过A(﹣1,﹣3),∴﹣1﹣b﹣2=﹣3,∴b=0,∴二次函数的解析式为y=﹣x2﹣2;(3)将y=﹣x2﹣2 的图象沿x 轴翻折,得到二次函数解析式为y=x2+2,设将y=x2+2 的图象向右平移后的二次函数解析式为y=(x﹣m)2+2(m>0),∵点P(x0,6)在函数y=上,∴6=,解得x0=,∴y=(x﹣m)2+2 的图象过点P(,6),∴(﹣m)2+2=6,解得m1=,m2=﹣,(不合题意,舍去),∴平移后的二次函数解析式为y=(x﹣)2+2,∵a=1>0,∴①当≤x≤时,2≤y≤6,②当<x≤3 时,2<y≤,∴当≤x≤3 时,2≤y≤6,∴平移后的二次函数y 的取值范围为2≤y≤6.【点评】本题是对反比例函数的综合考查,主要有待定系数法求函数解析式,等腰直角三角形的性质,函数图象的平移,以及二次函数图象的增减性,综合性较强,难度较大,特别是第(3)小题,求出点P 的坐标是解题的关键.24.(7 分)已知在□ABCD 中,AE⊥BC 于E,DF 平分∠ADC 交线段AE 于F.(1)如图1,若AE=AD,∠ADC=60°,请直接写出线段CD 与AF+BE 之间所满足等量关系;。
初三物理海淀试题及答案

初三物理海淀试题及答案一、选择题(每题2分,共20分)1. 光在真空中的传播速度是:A. 3×10^8 m/sB. 3×10^7 m/sC. 3×10^6 m/sD. 3×10^5 m/s2. 一个物体的体积是5×10^-3 m^3,密度为2.5×10^3 kg/m^3,它的质量是:A. 12.5 kgB. 1.25 kgC. 2.5 kgD. 0.125 kg3. 以下哪个选项是正确的温度单位?A. 摄氏度B. 华氏度C. 开尔文D. 所有选项都是4. 根据欧姆定律,电阻R、电流I和电压U之间的关系是:A. R = I/UB. R = U/IC. I = R/UD. U = I/R5. 一个物体从静止开始做匀加速直线运动,经过时间t,位移为s,那么它的加速度a是:A. a = s/tB. a = s/t^2C. a = 2s/t^2D. a = s^2/t^2二、填空题(每题2分,共20分)6. 声音在空气中的传播速度大约是______ m/s。
7. 一个物体的动能与其质量成正比,与速度的平方成正比,其公式为______。
8. 根据牛顿第三定律,作用力与反作用力______、方向______、作用在______物体上。
9. 电流的单位是______,电压的单位是______。
10. 一个物体在水平面上做匀速直线运动,摩擦力等于______。
三、简答题(每题10分,共30分)11. 请简述牛顿第一定律的内容。
12. 什么是电磁感应现象?请给出一个实际应用的例子。
13. 请解释什么是热机效率,并给出一个提高热机效率的方法。
四、计算题(每题15分,共30分)14. 一个质量为2 kg的物体从静止开始自由下落,忽略空气阻力,请计算物体下落5秒后的速度和位移。
15. 一个电阻为10Ω的电路中,通过它的电流为0.5A,求该电路的电压。
答案:一、选择题1. A2. A3. D4. B5. C二、填空题6. 3407. E_k = 1/2 mv^28. 相等、相反、不同9. 安培、伏特10. 牵引力三、简答题11. 牛顿第一定律,也称为惯性定律,指出一切物体在没有受到外力作用时,总保持静止状态或匀速直线运动状态。
北京市海淀区十一学校2024-2025学年九年级上学期开学测试数学试题

北京市海淀区十一学校2024-2025学年九年级上学期开学测试数学试题一、单选题1.在《2023北京市数字经济标杆企业评价报告》中,昌平区共有7家重点企业成功获评北京市数字经济标杆企业. 以下是四家标杆企业的商标,其中商标图形是中心对称图形的是( )A .B .C .D .2.在ABC V 中,A B C ∠∠∠,, 的对边分别为a ,b ,c ,下列条件中可以判断90A ∠=︒的是( )A .345a b c ===,,B .654a b c ===,,C .2a b c ==,D .12,,==a b c 3.如图,在平行四边形ABCD 中,6AD =,E 为AD 上一动点,M ,N 分别为BE ,CE 的中点,则MN 的长为( )A .3B .4C .5D .不确定4.某商店销售5种领口大小分别为38,39,40,41,42(单位:cm )的衬衫,一个月内的销量如下表:你认为商店最感兴趣的是这组数据的( ) A .平均数B .中位数C .众数D .方差5.函数y ax a =-与(0)ay a x=≠在同一平面直角坐标系中的图象可能是( )A .B .C .D .6.如图,AB 是O e 的弦,CD 是O e 的直径,CD AB ⊥于点E .在下列结论中,不一定成立的是( )A .AE BE =B .90CBD ∠=︒C .2COBD ∠=∠ D .COB C ∠=∠7.如图,以40m/s 的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h (单位:m )与飞行时间t (单位:s )之间具有函数关系h =20t ﹣5t 2.下列叙述正确的是( )A .小球的飞行高度不能达到15mB .小球的飞行高度可以达到25mC .小球从飞出到落地要用时4sD .小球飞出1s 时的飞行高度为10m8.如图,四边形ABCD 是正方形, 点E F ,分别在AB BC ,的延长线上, 且BE CF =,设AD a AE b AF c ===,,. 给出下面三个结论:①a b c +>;②22ab c <;2a .上述结论中,所有正确结论的序号是( )A .①②B .②③C .①③D .①②③二、填空题9.函数y =x 的取值范围是. 10.若关于x 的一元二次方程28160kx x -+=有实数根,则k 的取值范围是. 11.如图,在正方形ABCD 中.点E ,F ,G 分别在边CD ,AD ,BC 上,FD CG <.若F G A E =,1a ∠=,则2∠的度数为(用含a 的式子表示).12.在平面直角坐标系xOy 中,将直线1:2l y x m =-+向左平移3个单位长度,得到直线2:21l y x =-+,则m =.13.如图,将△ABC 纸片绕点C 顺时针旋转40°得到A B C '''V ,连接AA ',若AC ⊥A B '',则AA B ''∠的度数为 ,14.在平面直角坐标系xOy 中,已知点()12,n y -,()21,n y -,()31,n y +在抛物线()2220y ax ax a =--<上,若01n <<,则1y ,2y ,3y 的大小关系为(用“<”表示)15.如图,AB 为O e 的直径,PB ,PC 分别与⊙O 相切于点B ,C ,过点C 作AB 的垂线,垂足为E ,交O e 于点D.若60,BPC CD ∠=︒=PB 的长为.16.已知反比例函数6y x=-.则:(1)当26x ≤≤时,y 的取值范围为; (2)当3x ≤-时,y 的取值范围为;(3)当26x -≤≤且0x ≠时,y 的取值范围为.三、解答题17.(1)计算:()21202352⎛⎫-++- ⎪⎝⎭. (2)解不等式组:()2531432x x x x ⎧-≤-⎪⎨--<⎪⎩18.已知40a b -=,求分式22223a ab b a b -++的值.19.已知y 是z 的反比例函数,z 是x 的正比例函数.(1)当23z =-时,6y =.当6x =时,4z =.求y 与x 之间的函数关系式;(2)证明:y 是x 的反比例函数.20.如图,在四边形ABCD 中,AB DC AB AD =∥,,对角线AC BD ,交于点,O AC 平分角BAD ∠,过点C 作CE AB ⊥交AB 的延长线于点E ,连接OE .(1)求证:四边形ABCD 是菱形;(2)若4AB BD ==,求OE 的长.21.小明的爸爸买了甲、乙两种不同的一年期理财产品共20万元.甲种理财产品的预期年利率为8%,乙种理财产品的预期年利率为6%.按预期,小明的爸爸一年共可获得收益14400元.小明的爸爸购买甲、两种不同的理财产品各多少万元?22.在平面直角坐标系xOy 中,一次函数()0y kx b k =+≠的图象与函数2y x =的图象平行,且过点()1,3A .(1)求这个一次函数的表达式;(2)当2x >时,对于x 的每一个值,函数()0y mx m =≠的值都大于函数()0y kx b k =+≠的值,直接写出m 的取值范围.23.糖类是一类有机化合物,有研究表明,不同种类的糖熔化过程中的温度变化不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海淀区九年级数学第一学期期末练习 2011.1一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的.1.2(-=( )A .3B .3-C .3±D .92.已知两圆的半径分别为2和3,圆心距为5,则这两圆的位置关系是 ) A .外离B .外切C .相交D .内切3.将一枚硬币抛掷两次,则这枚硬币两次正面都向上的概率为( )A .12B .13C .14D .164.如图,⊙O 是△ABC 的外接圆,已知∠ABO =30º,则∠ACB 的大小为( )A .60ºB .30ºC .45ºD .50º5.下列一元二次方程中没有..实数根的是( ) A .2240x x +-= B .2440x x -+= C .2250x x --=D .2340x x ++=6.如图,有一枚圆形硬币,如果要在这枚硬币的周围摆放几枚与它完全相同的硬币,使得周围的硬币都和这枚硬币相外切,且相邻的硬币相外切,则这枚硬币周围最多可摆放( )A .4枚硬币B .5枚硬币C .6枚硬币D .8枚硬币7.圆锥的母线长是3,底面半径是1,则这个圆锥侧面展开图圆心角的度数为( )A .90°B .120°C .150°D .180°8.如图,E ,B ,A ,F 四点共线,点D 是正三角形ABC 的边AC 的中点,点P 是直线AB 上异于A ,B 的一个动点,且满足30CPD ∠=︒,则( )A .点P 一定在射线BE 上B .点P 一定在线段AB 上C .点P 可以在射线AF 上 ,也可以在线段AB 上D .点P 可以在射线BE 上 ,也可以在线段 二、填空题(本题共16分,每小题4分)9..已知...P .是.⊙.O .外一点,....PA ..切.⊙.O .于.A .,.PB ..切.⊙.O .于.B ...若.PA ..=.6.,则..PB ..=. ..C10x 的取值范围是 . 11.如图,圆形转盘中,A ,B ,C 三个扇形区域的圆心角分别为150°,120°和90°. 转动圆盘后,指针停止在任何位置的可能性都相同(若指针停在分界线上,则重新转动圆盘),则转动圆盘一次,指针停在B 区域的概率是 .12.(1) 如图一,等边三角形MNP 的边长为1,线段AB 的长为4,点M 与A 重合,点N 在线段AB 上.△MNP 沿线段AB 按A B →的方向滚动, 直至△MNP 中有一个点与点B 重合为止,则点P 经过的路程为 ;(2)如图二,正方形MNPQ 的边长为1,正方形ABCD 的边长为2,点M 与点A 重合,点N 在线段AB 上, 点P 在正方形内部,正方形MNPQ 沿正方形ABCD 的边按A B C D A →→→→→的方向滚动,始终保持M ,N ,P ,Q 四点在正方形内部或边界上,直至正方形MNPQ 回到初始位置为止,则点P 经过的最短路程为 .(注:以△MNP 为例,△MNP 沿线段AB 按A B →的方向滚动指的是先以顶点N 为中心顺时针旋转,当顶点P 落在线段AB 上时, 再以顶点P 为中心顺时针旋转,如此继续. 多边形沿直线滚动与此类似.)三、解答题(本题共30分,每小题5分) 13.计算:(1)根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精(A N P图二图一图三(A Q确到0.01);(2)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),并简述理由.15.解方程:24120x x +-=.16.如图,在ABC △中,AB 是⊙O 的直径,⊙O 与AC 交于点D,60,75AB B C =∠=︒∠=︒,求BOD ∠的度数;17.如图,正方形ABCD 中,点F 在边BC 上,E 在边BA 的延长线上. (1)若DCF △按顺时针方向旋转后恰好与DAE △重合.则旋转中心是点 ;最少旋转了 度;(2)在(1)的条件下,若3,2AE BF ==,求四边形BFDE 的面积.18.列方程解应用题:随着人们节能意识的增强,节能产品的销售量逐年增加.某地区高效节能灯的年销售量2009年为10万只,预计2011年将达到14.4万只.求该地区2009年到2011年高效节能ADCBODCFBEA灯年销售量的平均增长率.四、解答题(本题共20分,每小题5分)19.如图,在△ABC 中,120,C ∠=︒,4AC BC AB ==,半圆的圆心O 在AB 上,且与AC ,BC 分别相切于点D ,E . (1)求半圆O 的半径;(2)求图中阴影部分的面积.20.如图,O 为正方形ABCD 对角线AC 上一点,以O 为圆心,OA 长为半径的⊙O 与BC 相切于点M .(1)求证:CD 与⊙O 相切;(2)若⊙O 的半径为1,求正方形ABCD 的边长.21.一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m ,再从剩下的两张中任取一张,将其编号记为n .(1)请用树状图或者列表法,表示事件发生的所有可能情况; (2)求关于x 的方程20x mx n ++=有两个不相等实数根的概率.22.如图一,AB 是O 的直径,AC 是弦,直线EF 和O 相切与点C ,AD EF ⊥,垂足为D .(1)求证CAD BAC ∠=∠;(2)如图二,若把直线EF 向上移动,使得EF 与O 相交于G ,C 两点(点C 在点G 的右侧),连结AC ,AG ,若题中其他条件不变,这时图中是否存在与CAD ∠相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.以坐标原点为圆心,1为半径的圆分别交x ,y 轴的正半轴于点A ,B .(1)如图一,动点P 从点A 处出发,沿x 轴向右匀速运动,与此同时,动点Q 从点B 处出发,沿圆周按顺时针方向匀速运动.若点Q 的运动速度比点P 的运动速度慢,经过1秒后点P 运动到点(2,0),此时PQ 恰好是O 的切线,连接OQ . 求QOP ∠的大小;图一图一图二(2)若点Q 按照(1)中的方向和速度继续运动,点P 停留在点(2,0)处不动,求点Q 再经过5秒后直线PQ 被O 截得的弦长.24.已知关于x的方程221(1)04x a -++=有实根.(1)求a 的值;(2)若关于x 的方程2(1)0mx m x a +--=的所有根均为整数,求整数m 的值.25.如图一,在△ABC 中,分别以AB ,AC 为直径在△ABC 外作半圆1O 和半圆2O ,其中1O 和2O 分别为两个半圆的圆心. F 是边BC 的中点,点D 和点E 分别为两个半圆圆弧的中点.(1)连结1122,,,,,O F O D DF O F O E EF ,证明:12DO F FO E △≌△;图二(备用图)图一(2)如图二,过点A 分别作半圆1O 和半圆2O 的切线,交BD 的延长线和CE 的延长线于点P 和点Q ,连结PQ ,若∠ACB=90°,DB=5,CE=3,求线段PQ 的长;(3)如图三,过点A 作半圆2O 的切线,交CE 的延长线于点Q ,过点Q 作直线F A 的垂线,交BD 的延长线于点P ,连结P A . 证明:P A 是半圆1O 的切线.海淀区九年级数学第一学期期末练习参考答案及评分标准2011.1说明: 合理答案均可酌情给分,但不得超过原题分数图二Q图三三、解答题(本题共30分,每小题5分)13.解:原式=…………………………….…………………………….2分= …………………………….…………………………….4分 =6 …………………………….…………………………….5分 14.(1)解: 48, …………………………….…………………………….1分0.81…………………………….…………………………….2分 (2)解:()90P =射中环以上 …………………………….…………………………….4分从频率的波动情况可以发现频率稳定在0.8附近,所以这名运动员射击一次时“射中9环以上”的概率是0.8. …………………………….…………………………….5分 注:简述的理由合理均可给分 15.解法一:因式分解,得()()620x x +-= …………………………….…………………………….2分于是得60x +=或20x -=126,2x x =-= ………………………….5分 解法二:1,4,12a b c ===- 2464b ac ∆=-=…………………………….…………………………….2分482x -±==…………………………….…………………………….4分126,2x x =-=…………………………….…………………………….5分 16.解:在ABC △中,60,75B C ∠=︒∠=︒ , 45A ∴∠=︒.…………………………….…………………………….2分AB 是⊙O 的直径,⊙O 与AC 交于点D, ∴290DOB A ∠=∠=︒.…………………………….…………………………….5分 17.解:(1)D ;90︒.…………………………….…………………………….2分 (2)DCF DEA △旋转后恰好与△重合, DCF DAE ∴△≌△.3,2AE CF BF ∴===又.5BC BF CF ∴=+=.AED BFDE ABFD S S S ∴=+△四边形四边形DCF ABFD S S ∆=+四边形ABCD S =正方形2BC =25= 5分18.解:设该地区2009年到2011年高效节能灯年销售量的平均增长率为x . ……………….1分依据题意,列出方程()210114.4x += ……………………….…………………………….2分 化简整理,得: ()21 1.44x +=, 解这个方程,得 11.2x +=±, ∴ 120.2, 2.2x x ==-. ∵ 该地区2009年到2011年高效节能灯年销售量的平均增长率不能为负数. ∴ 2.2x =-舍去. ∴ 0.2x =.…………………….…………………………….4分答:该地区2009年到2011年高效节能灯年销售量的平均增长率为20%. …………….5分四、解答题(本题共20分,每小题5分) 19.(1)解:连结OD ,OC ,∵半圆与AC ,BC 分别相切于点D ,E . ∴DCO ECO ∠=∠,且OD AC ⊥. ∵AC BC =,∴CO AB ⊥且O 是AB 的中点.∴122AO AB ==. ∵120C ∠=︒,∴60DCO ∠=︒. ∴30A ∠=︒.∴在R t AOD △中,112OD AO ==.即半圆的半径为1.…………………………….…………………………….3分(2)设CO =x ,则在R t AOC △中,因为30A ∠=︒,所以AC =2x ,由勾股定理得: 222AC OC AO -= 即 222(2)2x x -=解得x =x =舍去)∴11422ABC S AB OC =⋅=⨯=△……….…………………………….4分 ∵ 半圆的半径为1,∴ 半圆的面积为2π,∴2S π==阴影 …………………………….…………………………….5分20.(1)解:过O 作ON CD ⊥于N ,连结OM ,则OM BC ⊥.∵ AC 是正方形ABCD 的对角线, ∴ AC 是BCD ∠的平分线.∴ OM =ON.即圆心O 到CD 的距离等于⊙O 半径, ∴ CD 与⊙O 相切.…………………………….…………………………….3分(2)由(1)易知MOC △为等腰直角三角形,OM 为半径, ∴ OM =MC =1.∴ 222112OC OM MC =+=+=, ∴OC = ∴1AC AO OC =+= 在R t ABC △中,AB =BC ,有 222A C A BB C=+ ∴ 222AB AC = ∴AB =.…………………………….…………………………….5分 故正方形ABCD. 21.(1)解:依题意画出树状图(或列表)如下或…………………………….…………………………….2分注:画出一种情况就可给2分(2)解:当240m n ->时,关于x 的方程20x mx n ++=有两个不相等实数根,而使得240m n ->的m ,n 有2组,即(3,1)和(3,2). ………….…………………………….4分则关于x 的方程20x mx n ++=有两个不相等实数根的概率是13.∴P (有两个不等实根)=13.…………………….5分 22.(1)证明:如图一,连结OC ,则OC EF ⊥,且OC=OA ,123123312m n易得OCA OAC∠=∠.∵AD EF⊥,∴OC//AD.∴OCA∠=CAD∠,∴CAD∠=OAC∠.即C A D B A C∠=∠.…………………………….…………………………….2分(2)解:与CAD∠相等的角是BAG∠.…………………………….…………………………….3分证明如下:如图二,连结BG.∵四边形ACGB是O的内接四边形,∴180ABG ACG∠+∠=︒.∵D,C,G共线,∴180ACD ACG∠+∠=︒.∴ACD ABG∠=∠.∵AB是O的直径,∴90BAG ABG∠+∠=︒∵AD EF⊥∴90CAD ACD∠+∠=︒∴CAD BAG∠=∠.…………………………….…………………………….5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.(1)解:如图一,连结AQ.由题意可知:OQ=OA=1.∵OP=2,∴A为OP的中点.∵PQ与O相切于点Q,∴OQP△为直角三角形. …………1分∴112AQ OP OQ OA====. …………2分即ΔOAQ为等边三角形.∴∠QOP=60°.…………3分(2)解:由(1)可知点Q运动1秒时经过的弧长所对的圆心角为30°,若Q按照(1)中的方向和速度继续运动,那么再过5秒,则Q点落在O与y轴负半轴的交点处(如图二).设直线PQ与O的另外一个交点为D,过O作OC⊥QD于点C,则C为QD的中点.…………4分∵∠QOP=90°,OQ=1,OP=2,∴QP=…………5分∵1122OQ OP QP OC⋅=⋅,∴OC. …………6分∵OC⊥QD,OQ=1,OC,图一图二图二∴QC. ∴QD. …………7分24.(1)解:∵关于x的方程为221(1)04x a -++=为一元二次方程,且有实根.故满足:220,1(4(1)0.4a a ≥⎧⎪⎨∆=--⨯⨯+≥⎪⎩……….…………………………….2分(注:每个条件1分) 整理得 20,(1)0.a a ≥⎧⎨-≤⎩ ∴1a =……….…………………………….4分(2)由(1)可知1a =,故方程2(1)0mx m x a +--=可化为2(1)10mx m x +--=.①当m =0时,原方程为10x -=,根为1x =,符合题意.………………………….5分②当m ≠0时,2(1)10mx m x +--=为关于x 的一元二次方程,2222(1)4(1)12421(1)0m m m m m m m m ∆=--⨯⨯-=-++=++=+≥.此时,方程的两根为 1211,x x m==-. ∵两根均为整数, ∴m =1±.………………………….7分 综上所述,m 的值为1-,0 或1.25.(1)证明:如图一,∵1O ,2O ,F 分别是AB ,AC ,BC 边的中点,∴1O F ∥AC 且1O F =A 2O ,2O F ∥AB 且2O F =A 1O , ∴∠B 1O F=∠BAC ,∠C 2O F=∠BAC ,∴∠B 1O F=∠C 2O F∵点D 和点E 分别为两个半圆圆弧的中点, ∴1O F =A 2O =2O E ,2O F =A 1O =1O D ,………………………….2分∠B 1O D =90°,∠C 2O E =90°, ∴∠B 1O D=∠C 2O E . ∴∠D 1O F=∠F 2O E .∴12DO F FO E △≌△.………………………….3分(2)解:如图二,延长CA 至G ,使AG =AQ ,连接BG 、AE .∵点E 是半圆2O 圆弧的中点, ∴AE=CE=3 ∵AC 为直径 ∴∠AEC =90°,∴∠ACE =∠EAC =45°,AC, ∵AQ 是半圆2O 的切线, ∴CA ⊥AQ ,∴∠CAQ =90°,∴∠ACE =∠AQE =45°,∠GAQ =90° ∴AQ =AC =AG=同理:∠BAP =90°,AB =AP=∴CG=,∠GAB =∠QAP ∴AQP AGB △≌△.……………………..5分 ∴PQ =BG ∵∠ACB =90°, ∴BC=∴BG∴PQ=……………………..6分(3) 证法一:如图三,设直线F A 与PQ 的垂足为M ,过C 作CS ⊥MF 于S ,过B 作BR ⊥MF 于R ,连接DR 、AD 、DM.∵F 是BC 边的中点,∴ABF ACF S S =△△. ∴BR=CS ,由(2)已证∠CAQ =90°, AC =AQ,∴∠2+∠3=90° ∵FM ⊥PQ , ∴∠2+∠1=90°, ∴∠1=∠3, 同理:∠2=∠4,图二∴AMQ CSA △≌△, ∴AM=CS , ∴AM=BR ,同(2)可证AD=BD ,∠ADB =∠ADP =90°, ∴∠ADB =∠ARB =90°, ∠ADP =∠AMP =90° ∴A 、D 、B 、R 四点在以AB 为直径的圆上,A 、D 、P 、M 四点在以AP 为直径的圆上, 且∠DBR+∠DAR =180°, ∴∠5=∠8, ∠6=∠7, ∵∠DAM +∠DAR =180°, ∴∠DBR =∠DAM ∴DBR DAM △≌△, ∴∠5=∠9, ∴∠RDM =90°,∴∠5+∠7=90°, ∴∠6+∠8=90°, ∴∠P AB =90°,∴P A ⊥AB ,又AB 是半圆1O 直径, ∴P A 是半圆1O 的切线.……………………..8分证法二:假设P A 不是是半圆1O 的切线,如图四,过点A 作半圆1O 的切线交BD 的延长线于点P ', 则点P '异于点P ,连结P Q ',设直线F A 与PQ 的 垂足为M ,直线F A 与P Q '的交点为M '.延长AF 至N ,使得AF =FN ,连结BN ,CN ,由于点F 是 BC 中点,所以四边形ABNC 是平行四边形. 易知,180BAC ACN ∠+∠=︒, ∵AQ 是半圆2O 的切线,∴∠QAC =90°,同理90P AB '∠=︒. ∴180P AQ BAC '∠+∠=︒. ∴P AQ ACN '∠=∠.由(2)可知,,AQ AC AB AP '==,∴P AQ NCA '△≌△. ∴NAC P QA '∠=∠. ∵90QAC ∠=︒,∴90NAC M AQ '∠+∠=︒.即 90AQM M AQ ''∠+∠=︒.∴90AM Q '∠=︒.Q图四'⊥.即P Q A F∵PQ AF⊥,∴过点Q有两条不同的直线P Q'和PQ同时与AF垂直.这与在平面内过一点有且仅有一条直线与已知直线垂直相矛盾,因此假设错误.所以P A是是半圆O的切线.1。
