福建省泉州市2018届九年级5月质量检测数学试题(含答案)

合集下载

2018年福建省泉州市中考数学试卷含答案

福建省泉州市2018年中考数学试卷一、选择题<每小题3分，共21分）：每小题有四个答案，其中有且只有一个答案是正确的，请在答题卡上相应题目的答题区域内作答，答对的得3分，答错或不答一律得0分．D．的形状是体的正视图是< ）C ．D ．4．<3分）<2018•泉州）把不等式组的解集在数轴上表示出来，正确的是B ．D ．解：，，7，则圆积V<m3）一定的污水处理池，池的底面积S<m2）与其深度h<m）满足关系式：C ．D ．<h要掌握它的性质才能灵活解题．反比例函数y=8．<4分）<2018•泉州）的立方根是．考点：立方根分析：根据立方根的定义即可得出答案．解答：解：的立方根是；故答案为：．点评：此题考查了立方根，求一个数的立方根，应先找出所要求的这个数是哪一个数的立方，由开立方和立方是互逆运算，用立方的方法求这个数的立方根．注意一个数的立方根与原数的性质符号相同．考点：因式分解-运用公式法专题：因式分解．分析：分解因式1﹣x2中，可知是2项式，没有公因式，用平方差公式分解即可．解答：解：1﹣x2=<1+x）<1﹣x）．故答案为：<1+x）<1﹣x）．点评：本题考查了因式分解﹣运用公式法，熟练掌握平方差公式的结构特点是解题的关键．千M，考点：科学记数法—表示较大的数分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n 为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：解：110000=1.1×105，故答案为：1.1×105．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．OA D，若QC=QD，则∠AOQ= 35 °．5PCzVD7HxAAOQ=A0B=×70°=35°．13．<4分）<2018•泉州）计算：+= 1 ．解：原式=14．<4分）<2018•泉州）方程组的解是．故原方程组的解为．F、G、H，则四边形EFGH的形状一定是平行四边形．jLBHrnAILgAC AC和BD相交于点O，AC：BD=1：2，则AO：BO= 1：2 ，菱形ABCD的面积S=16 ．xHAQX74J0XAO8AB=2S==16直平分，菱形的四条边相等和菱形的面积为两对角线乘积的一x的值是7，可发现第1次输出的结果是12，第2次输出的结果是6，第3次输出的结果是 3 ，依次继续下去…，第2018次输出的结果是 3 ．LDAYtRyKfEx代入x第6次输出的结果为×4=2；．÷x=．x=、C作BE⊥AD于点E，CF⊥AD交AD的延长线于点F，求证：BE=CF．Zzz6ZB2Ltk外没有任何区别，现将它们放在盒子里搅匀．dvzfvkwMI1<1）随机地从盒子里抽取一张，求抽到数字3的概率；<2）随机地从盒子里抽取一张，将数字记为x，不放回再抽取第二张，将数字记为y，请你用画树状图或列表的方法表示所有等可能的结果，并求出点<x，y）在函数y=图象上的概率．rqyn14ZNXI比例图象上的情况数，即可求出所求的概率．的概率为；P==<1）求a的值；<2）若点A<m，y1）、B<n，y2）<m＜n＜3）都在该抛物线上，试比较y1与y2的动，设有征文、独唱、绘画、手抄报四个工程，该校共有800人次参加活动．下面是该校根据参加人次绘制的两幅不完整的统计图，请根据图中提供的信息，解答下面的问题．EmxvxOtOco<1）此次有200 名同学参加绘画活动，扇形统计图中“独唱”部分的圆心角是36 度．请你把条形统计图补充完整．SixE2yXPq5<2）经研究，决定拨给各工程活动经费，标准是：征文、独唱、绘画、手抄报每人次分别为10元、12元、15元、12元，请你帮学校计算开展本次活动共需多少扇形统计图中“独唱”部分的圆心角是296×10+80×12+200×15+224×12=9608动，小明设计了点做圆周运动的一个雏形，如图所示，甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动，甲运动的路程l<cm）与时间t<s）满足关系：l=t2+t<t≥0），乙以4cm/s的速度匀速运动，半圆的长度为21cm．kavU42VRUs<1）甲运动4s后的路程是多少？<2）甲、乙从开始运动到第一次相遇时，它们运动了多少时间？<3）甲、乙从开始运动到第二次相遇时，它们运动了多少时间？l=t2+t=8+6=14<cm甲走过的路程为t2+t则t2+t+4t=21则t2+t+4t=63B、C，点A<﹣2，0），P是直线BC上的动点．y6v3ALoS89<1）求∠ABC的大小；<2）求点P的坐标，使∠APO=30°；<3）在坐标平面内，平移直线BC，试探索：当BC在不同位置时，使∠APO=30°的点P的个数是否保持不变？若不变，指出点P的个数有几个？若改变，指出点P的个数情况，并简要说明理由．M2ub6vSTnP。

(完整)2018年泉州市初三质检数学试题及答案,推荐文档

2018年泉州市初三质检数学试题一、选择题(本题共10小题，每小题4分，共40分) (1)化简|-3|的结果是（）． (A)3 (B)-3 (C)±3 (D)31(2)如图是由八个相同小正方体组合而成的几何体，则其主视图是（）．(3)从泉州市电子商务中心获悉，近年来电子商务产业蓬勃发展截止到2018年3月，我市电商从业人员已达873 000人，数字873 000可用科学记数法表示为（）． (A)8.73×103 (B)87.3×104 (C)8.73×105 (D)0.873×106 (4)下列各式的计算结果为a 5的是（） (A)a 7-a 2 (B)a 10÷a 2 (C)(a 2)3 (D)( -a )2·a 3 (5)不等式组⎩⎨⎧≥+->-06301x x 的解集在数轴上表示为（）．(6)下列图形中，是中心对称图形，但不是轴对称图形的是（）．(7)去年某市7月1日到7日的每一天最高气温变化如折线图所示，则关于这组数据的描述正确的是（）． (A)最低温度是32℃ (B)众数是35℃ (C)中位数是34℃ (D)平均数是33℃(8)在《九章算术》中有“盈不足术”的问题，原文如下：今有共买物，人出八，盈三；人出七，不足四．问人数几何?大意为：现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元．问人数是多少?若设人数为x ，则下列关于x 的方程符合题意的是（）． (A)8x -3=7x +4 (B)8(x -3)=7(x +4) (C)8x +4=7x -3 (D)81371=-x x +4 (9)如图，在3×3的网格中，A ，B 均为格点，以点A 为圆心，以AB 的长为半径作弧，图中的点C 是该弧与格线的交点，则sin ∠BAC 的值是（）．(A)21 (B) 32(C) 35 (D) 552(10)如图，反比例函数y=xk的图象经过正方形ABCD 的顶点A 和中心E ，若点D 的坐标为(-1，0)，则k 的值为（）． (A)2 (B) 2- (C)1 (D) 1- A B C D(A) (B) (C) (D) A BC D EO xy(A) (B) (C) (D)二、填空题(本题共6小题，每小题4分，共24分) (11)已知a =(21)°，b=2-1，则a _______b (填“>”，“<”或“=”) ． (12)正八边形的每一个内角的度数为________．(13)一个暗箱中放有除颜色外其他完全相同的m 个红球，6个黄球，3个白球现将球搅匀后，任意摸出1个球记下颜色，再放回暗箱，通过大量重复试验后发现，摸到黄球的频率稳定在30%附近，由此可以估算m 的值是________．(14)如图，将△ABC 绕点A 顺时针旋转120°，得到 △ADE ．这时点D 、E 、B 恰好在同一直线上，则 ∠ABC 的度数为________．(15)已知关于x 的一元二次方程(m -1)x 2- (2m -2)x -1=0 有两个相等实数根，则m 的值为________．(16)在平行四边形ABCD 中，AB=2，AD=3，点E 为BC 中点，连结AE ，将△ABE 沿AE 折叠到△AB'E 的位置，若∠BAE=45°，则点B'到直线BC 的距离为________．三、解答题：(本题共9小题，共86分) (17)( 8分)解方程：23-x 312+-x =1．(18) (8分)先化简，再求值：3223393a aa a a a +÷⎪⎪⎭⎫ ⎝⎛---，其中a =22．(19)(8分)如图，在锐角△ABC 中，AB=2cm ，AC=3cm ． (1)尺规作图：作BC 边的垂直平分线分别交AC ，BC 于点D 、E(保留作图痕迹，不要求写作法)； (2)在(1)的条件下，连结BD ，求△ABD 的周长．(20)(8分)为进一步弘扬中华优秀传统文化，某校决定开展以下四项活动：A 经典古诗文朗诵；B 书画作品鉴赏；C 民族乐器表演；D 围棋赛。

福建省泉州市2018-2019年最新最全5月初中毕业班质量检测数学试题(含答案解析)

2019届福建省泉州市初中学业质量检查数学试题(试卷满分：150分；考试时间：120分钟)友情提示：所有答案必须填写在答题卡相应的位置上．一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上相应题目的答题区域内作答．1. 下列各式正确的是( )A. －(－2018)＝2018B. |－2018|＝±2018C. 20180＝0D. 2018－1＝－20182. 计算(－2a2)3的结果是( )A. －6a2B. －8a5C. 8a5D. －8a63. 某几何体如下左图所示，该几何体的右视图是( )第3题图4. 一个正多边形的边长为2，每个外角都为60°，则这个多边形的周长是( )A. 8B. 12C. 16D. 185. 不等式组⎩⎪⎨⎪⎧x －1≤0－x ＜2，的整数解的个数为( ) A. 0个 B. 2个 C. 3个 D. 无数个6. 如图，▱ABCD 的对角线AC 与BD 相交于点O ，要使它成为矩形，需再添加的条件是( )A. OA ＝OCB. AC ＝BDC. AC ⊥BDD. BD 平分∠ABC第6题图7. 在学校演讲比赛中，10名选手的成绩折线统计图如图所示，则下列说法正确的是( )A. 最高分90B. 众数是5C. 中位数是90D. 平均分为87.5第7题图8. 如图，在△ABC 中，点D 、E 分别是边AB 、AC 上的点，且DE ∥BC ，若AD DB ＝12，DE ＝3，则BC 的长度是( ) A. 6 B. 8 C. 9 D. 10第8题图 9. 实数a 、b 、c 、d 在数轴上的对应点从左到右依次是A 、B 、C 、D ，若b ＋d ＝0，则a ＋c 的值( )A. 小于0B. 等于0C. 大于0D. 与a 、b 、c 、d 的取值有关10. 已知双曲线y ＝k x经过点(m ，n)，(n ＋1，m －1)，(m2－1，n2－1)，则k 的值为( )A. 0或3B. 0或－3C. －3D. 3二、填空题：本大题共6小题，每小题4分，共24分．把答案填在答题卡的相应位置．11. 已知x ＝0是方程x2－5x ＋2m －1＝0的解，则m 的值是________．12. 分解因式：x3－4x ＝________．13. 某口袋中装有2个红球和若干个黄球，每个球除颜色外其它都相同，搅匀后从中摸出一个球恰为红球的概率是15，则袋中黄球的个数为________．14. 抛物线y ＝x2－6x ＋7的顶点坐标是________．15. 在直角坐标系中，点M(3，1)绕着原点O 顺时针旋转60°后的对应点的坐标是________．16. 如图，在面积为16的四边形ABCD 中，∠ADC ＝∠ABC ＝90°，AD ＝CD ，DP ⊥AB 于点P ，则DP 的长是________．第16题图三、解答题：本大题共9小题，共86分．解答应写出文字说明，证明过程或演算步骤．在答题卡的相应位置内作答．17. (8分)先化简，再求值：x(x ＋2)＋(x －1)(x ＋1)－2x ，其中x ＝2.18. (8分)解方程组：⎩⎪⎨⎪⎧x －y ＝13x ＋y ＝7.19. (8分)如图，在四边形ABCD 中，AB ＝AD ＝3，DC ＝4，∠A ＝60°，∠D ＝150°，试求BC 的长度．第19题图20. (8分)如图，E、F是▱ABCD的对角线AC上的两点，AE＝CF，求证：DF＝BE.第20题图21. (8分)某中学采用随机的方式对学生掌握安全知识的情况进行测评，并按成绩高低分成优、良、中、差四个等级进行统计，绘制了下面两幅尚不完整的统计图．请根据有关信息解答：第21题图(1)接受测评的学生共有________人，扇形统计图中“优”部分对应扇形的圆心角为________°，并补全条形统计图；(2)若该校共有学生1200人，请估计该校对安全知识达到“良”程度的人数；(3)测评成绩前五名的学生恰好是3个女生和2个男生，现从中随机抽取2人参加市安全知识竞赛，请用树状图或列表法求出抽到1个男生和1个女生的概率．22. (10分)某学校在“校园读书节”活动中，购买甲、乙两种图书共100本作为奖品，已知乙种图书的单价比甲种图书的单价高出50%.同样用360元购买乙种图书比购买甲图书少4本．(1)求甲、乙两种图书的单价各是多少元；(2)如果购买图书的总费用不超过3500元，那么乙种图书最多能买多少本？23. (10分)如图，在矩形ABCD 中，对角线AC ，BD 相交于点O ，E 是边AD 的中点，且AC ＝5，DC ＝1.(1)求证：AB ＝DE ；(2)求tan ∠EBD 的值．第23题图24. (13分)如图，AB 为⊙O 的直径，F 为弦AC 的中点，连接OF 并延长交AC ︵于点D ，过点D 作DE ∥AC ，交BA 的延长线于点E ，连接AD 、CD.(1)求证：DE 是⊙O 的切线；(2)若OA ＝AE ＝2时，①求图中阴影部分的面积；②以O 为原点，AB 所在的直线为x 轴，直径AB 的垂直平分线为y 轴，建立如图所示的平面直角坐标系，试在线段AC 上求一点P ，使得直线DP 把阴影部分的面积分成1∶2的两部分．第24题图25. (13分)如图，在直角坐标系中，抛物线y＝－x2＋bx＋2与x轴交于A、B两点，与直线y＝2x交于点M(1，m)．(1)求m，b的值；(2)已知点N，点M关于原点O对称，现将线段MN沿y轴向上平移s(s ＞0)个单位长度．若线段MN与抛物线有两个不同的公共点，试求s的取值范围；(3)利用尺规作图，在该抛物线上作出点G，使得∠AGO＝∠BGO，并简要说明理由．(保留作图痕迹)第25题图2019届福建省泉州市初中学业质量检查1. A 【解析】2. D 【解析】(－2a2)3＝(－2)3(a2)3＝－8a6，故选D.3. D 【解析】本题考查几何体的右视图，从右往左看，可看到两个矩形，一上一下叠放在一起，且所有棱都能看到，故轮廓线均为实线，符合条件的只有D.4. B 【解析】正多边形的每个外角都为60°，360°÷60°＝6，所以这个多边形为正六边形，正六边形的周长为6×2＝12.5. C 【解析】不等式组的解为－2<x ≤1，其中的整数解有－1，0，1，共3个．6. B 【解析】对角线相等的平行四边形是矩形，故选B.7. C 【解析】由折线统计图可知，十名选手的最高分为95分，A 错误；众数为90，B 错误；把成绩从低到高排，中间两数都为90，所以中位数为90，C 正确；x －＝1080×2＋85＋90×5＋95×2＝88.5(分)，故D 错误．8. C 【解析】∵DE ∥BC ，∴AB AD ＝BC DE，∵DB AD ＝21，∴BC DE ＝31，∵DE ＝3，∴BC ＝9.9. A 【解析】根据数轴上右边的数总比左边的大，得a<b<c<d ，∵b＋d＝0，∴b＋c<0，∵b>a，∴a＋c<0.10. D 【解析】把点(m，n)，(n＋1，m－1)，(m2－1，n2－1)代入双曲线y＝x k得，k＝mn①，k＝(n＋1)(m－1)②，k＝(m2－1)(n2－1)③，①代入②得m－n＝1；②代入③中得，1＝(m＋1)(n－1)，1＝mn＋n－m－1，mn＝2＋(m－n)＝3，所以k＝3.11. 21【解析】把x＝0代入方程得2m－1＝0，∴m＝21.12. x(x＋2)(x－2) 【解析】x3－4x＝x(x2－4)＝x(x＋2)(x－2)13. 8 【解析】口袋中球的个数为2÷51＝10个，袋中黄球的个数为10－2＝8个．14. (3，－2) 【解析】y＝x2－6x＋7＝(x2－6x＋9)－9＋7＝(x－3)2－2，所以抛物线的顶点坐标为(3，－2)．15. (，－1) 【解析】如解图，由旋转的性质可知∠MOB＝60°，OM ＝OB，又∵M(，1)，可得∠MOC＝30°，∴∠COB＝30°，过点B作BC⊥OC 于点C，结合OB＝OM可知，点B与点M关于x轴对称，∴B(，－1)．第15题解图16. 4 【解析】如解图所示，过D点作DE⊥BC交BC的延长线于点E.∵∠ADC＝∠ABC＝90°，∴四边形DPBE是矩形．∴∠PDE＝90°，∴∠ADP ＝∠CDE.∵AD＝DC，∴Rt△APD≌Rt△CED，∴DP＝DE，∴四边形PDEB是正方形，又∵四边形ABCD的面积为16，∴正方形DPBE的面积也为16，∴DP＝DE＝4.第16题解图17. 解：原式＝x2＋2x ＋x2－1－2x ＝2x2－1当x ＝时，原式＝2×()2－1＝4－1＝3. 18. 解：3x ＋y ＝7 ②x －y ＝1 ①， ①＋②得4x ＝8，∴x ＝2，将x ＝2代入①得y ＝1. 所以该方程组的解为y ＝1x ＝2. 19. 解：如解图，连接DB ，第19题解图∵AB ＝AD ，∠A ＝60°， ∴△ABD 是等边三角形， ∴BD ＝AD ＝3，∠ADB ＝60°，又∵∠ADC ＝150°，∴∠CDB ＝∠ADC －∠ADB ＝150°－60°＝90°， ∵DC ＝4， ∴BC ＝＝＝5.20. 证明：在▱ABCD 中，CD ∥AB ，DC ＝AB ， ∴∠DCA ＝∠BAC ，在△DCF 和△BAE 中，CF ＝AE ∠DCA＝∠BAC，∴△DCF ≌△BAE(SAS)， ∴DF ＝BE.21. (1)80，135，补全条形统计图如解图①所示；第21题解图①【解法提示】接受测评的学生共有20÷25%＝80(人)，安全知识达到“良”的人数为80－30－20－5＝25(人)，扇形统计图中“优”部分对应扇形的圆心角为8030×360°＝135°.(2)该校对安全知识达到“良”程度的人数为： 1200×8030＋25＝825(人)； (3)列表如下：所有等可能的结果为20种，其中抽到一男一女的为12种，所以P(抽到1男1女)＝2012＝53. 或画树状图如解图②：第21题解图②所有等可能的结果为20种，其中抽到一男一女的为12种，所以P(抽到1男1女)＝2012＝53.22. 解：(1)设甲种图书的单价是x 元，则乙种图书的单价是1.5x 元，依题意得：x 360－1.5x 360＝4. 解得：x ＝30，经检验x ＝30是原方程的解，且x ＝30，1.5x ＝45符合题意．答：甲种图书的单价是30元，乙种图书的单价是45元. (2)设乙种图书能买m 本，依题意得：45m ＋30(100－m)≤3500，解得：m ≤3100＝3331，因为m 是正整数，所以m 最大值为33，答：乙种图书最多能买33本.23. (1)证明：在矩形ABCD中，∠ADC＝90°，AB＝DC＝1，∵AC＝，DC＝1，∴在Rt△ADC中，AD＝＝＝2，∵E是边AD的中点，∴AE＝DE＝1，又∵AB＝1，∴AB＝DE；(2)解：如解图，过点E作EM⊥BD于点M，第23题解图∵BD＝AC＝，在Rt△DEM和Rt△DBA中，sin∠ADB＝ED EM＝BD BA，即1EM＝51，解得：EM＝55，又∵在Rt△ABE中，BE＝＝＝，∴在Rt△BEM中，BM＝＝）25＝55，∴在Rt△BEM中，tan∠EBD＝BM EM＝55＝31.第24题解图24. (1)证明：如解图，连接OC ， ∵OA ＝OC ，F 为AC 的中点， ∴OD ⊥AC ，又∵DE ∥AC ， ∴OD ⊥DE ， ∵OD 为⊙O 的半径， ∴DE 是⊙O 的切线； (2)解：①由(1)得OD ⊥DE ， ∴∠EDO ＝90°， ∵OA ＝AE ＝2， ∴OA ＝OD ＝AD ＝2， ∴△AOD 是等边三角形， ∴∠AOD ＝∠DAO ＝60°， ∴∠ACD ＝21∠AOD ＝30°，又∵AC ⊥OD ，∴∠CAO ＝∠CAD ＝30°， ∴∠ACD ＝∠CAO ， ∴CD ∥AB ， ∴S △ACD ＝S △OCD ， ∴S 阴＝S 扇形OCD ，∵∠CAD ＝∠OAD －∠OAC ＝60°－30°＝30°， ∴∠COD ＝2∠CAD ＝60°， ∴S 阴＝36060π×22＝32π；②由已知得：A(－2，0)，C(1，)， ∴直线AC 的表达式为y ＝33x ＋33，如解图，过点P1分别作P1M ⊥x 轴，P1N ⊥AD ，垂足分别M ，N ，由①得AC 平分∠OAD ， ∴P1M ＝P1N ，设P1(x ，33x ＋33)(－2≤x ≤1)， P1M ＝P1N ＝33x ＋33，∵直线DP1把阴影部分面积分成1∶2的两部分，若S △AP1D ＝31S 阴，即21×2·(33x ＋33)＝31×32π，解得：x ＝93π－18，此时P1(93π－18，92π)，若S △AP2D ＝32S 阴，同理可求得P2(93π－18，94π)，综上所述：满足条件的点P 的坐标为P1(93π－18，92π)和P2(93π－18，94π).25. 解：(1)把M(1，m)代入y ＝2x 得m ＝2×1＝2，把M(1，2)代入y ＝－x2＋bx ＋2得2＝－12＋b ＋2，即b ＝1； (2)由(1)得y ＝－x2＋x ＋2，M(1，2)，因为点N ，点M 关于原点O 对称，所以N(－1，－2)，如解图①，过点N 作CN ⊥x 轴，交抛物线于C ，则C 的横坐标为－1，所以C 的纵坐标为－(－1)2＋(－1)＋2＝0，第25题解图①所以C(－1，0)与A 重合，则CN ＝AN ＝2，即当s ＝2时线段MN 与抛物线有两个公共点，设平移后的直线表达式为y ＝2x ＋s ，由y ＝－x2＋x ＋2y ＝2x ＋s得x2＋x ＋s －2＝0，由Δ＝12－4(s －2)＝0，得s ＝49，即当s ＝49时，线段MN 与抛物线只有一个公共点，所以，当线段MN 与抛物线有两个公共点时，s 的取值范围为2≤s ＜49； (3)如解图②，在x 轴上取一点P(－2，0)，以P 为圆心，OP 为半径作圆，⊙P 与抛物线的交点，即是所求作的点G(解图②中的G 与G ′)，理由：第25题解图②当点G 在x 轴上方时，由作图可知，PG ＝2，PA ＝1，PB ＝4，则PG PA＝PB PG＝21， ∵∠GPA ＝∠BPG ， ∴△GPA ∽△BPG ， ∴∠PBG ＝∠PGA ， ∵GP ＝PO ， ∴∠POG ＝∠PGO ，又∵∠POG ＝∠PBG ＋∠OGB ， ∠PGO ＝∠PGA ＋∠AGO ，∴∠AGO＝∠BGO，同理可证：当点G′在x轴的下方时，结论也成立.。

2018年泉州市初中学业质量检查数学参考答案及评分标准

…………………………………4 分
证明： ∵四边形 ABCD 是矩形， ∴ AB CD, ABC DCB 90 ．…………………………………………………………6 分
在 ABC 与 DCB 中，
AB DC ABC DCB BC CB
……………………………………………………………………………7 分
三、解答题（共 86 分）（17）（本小题 8 分）
（15） 0
（16） 2 2 . 3
解：去分母，得 3(x 3) 2(2x 1) 6, ……………………………………………………3 分
3 x 9 4 x 2 6, ………………………………………………………5 分
3 x 4 x 6 9 2, ………………………………………………………6 分
由 A 3,0， C1,2 可求得直线 AC 的解析式为 y x 1 ．
由题意设点 F m, 1 m2 m 3 (其中 m 1)，则点 Em, m 1，
2
2
∴ EF 1 m2 m 3 m 1 1 m2 1 4 ，………………………………………7 分
∴ AEB ≌ AFD ．…………………………4 分
∴ AF AE , ∴ CD 是⊙A 的切线．…………………………5 分
（Ⅱ）解：在菱形 ABCD 中， AB BC 6, AB CD ， ∴ B C 180 ． ∵ C 135， ∴ B180135=45．……………………6 分
解法二：画树状图如下：
由树状图可知，共有 16 种等可能的结果，其中他们参加的项目相同的有 4 种，
所以 P （项目相同）= 4 1 ．………………………………………………………………8 分 16 4

2018年5月份泉州市质检数学试卷答案

3)

a3
aa
3
a2 ．………………………………………………………………………………6 分
当 a 2 时， 2
原式
2 2

2
……………………………………………………………………………7 分
= 1 ．……………………………………………………………………………………8 分 2
…………………………………4 分
证明： ∵四边形 ABCD 是矩形， ∴ AB CD, ABC DCB 90 ．…………ABC 与 DCB 中，
AB DC ABC DCB BC CB
……………………………………………………………………………7 分
2018 年泉州市初中学业质量检查
数学参考答案及评分标准
说明：
（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分．（二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原
则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分．
（19）（本小题 8 分）
解：（Ⅰ）如图所示，直线 DE 为所求作的；………………3 分（Ⅱ）∵ DE 垂直平分 BC ，
∴ BD CD ．………………………………………5 分 ABD 的周长= AB AD BD
AB AD CD AB AC
2018 年泉州市初中学业质量检查数学参考答案
∴ AEB ≌ AFD ．…………………………4 分
∴ AF AE , ∴ CD 是⊙A 的切线．…………………………5 分
（Ⅱ）解：在菱形 ABCD 中， AB BC 6, AB CD ， ∴ B C 180 ． ∵ C 135， ∴ B180135=45．……………………6 分

2018年福建省泉州市中考数学试卷(含答案)

2018年福建省泉州市初中毕业、升学考试数学试题（满分150分，考试时间120分钟）友情提示：所有答案都必须填涂在答题卡的相应的位置上，答在本试卷一律无效.毕业学校_________________姓名___________考生号_________一、选择题(共7小题，每题3分，满分21分；每小题只有一个正确的选项，请在答题卡的相应位置填涂) 1. 7-的相反数是（）.A. 7-B. 7C.71- D. 71解：应选B 。

⒉42)(a 等于（）.A.42a B.24a C.8a D. 6a 解：应选C 。

⒊把不等式01≥+x 在数轴上表示出来，则正确的是（）.解：应选B 。

⒋下面左图是两个长方体堆积的物体，则这一物体的正视图是（）.解：应选A 。

⒌若4-=kx y 的函数值y 随着x 的增大而增大，则k 的值可能是下列的（）.A .4- B.21- C.0 D.3 解：应选D 。

⒍下列图形中，有且只有两条对称轴的中心对称图形是（）. A .正三角形 B.正方形 C.圆 D.菱形解：应选D 。

⒎如图，点O 是△ABC 的内心，过点O 作EF ∥AB ，与AC 、BC 分别交于点E 、F ，则（）A .EF>AE+BF B. EF<AE+BFC.EF=AE+BFD.EF ≤AE+BF C 解：应选C 。

B （第七题图）二、填空题(每题4分，共40分；请将正确答案填在答题卡相应位置) ⒏比较大小：5-__________0.（用“＞”或“＜”号填空〕解：＜。

⒐因式分解：x x 52-=__________. 解：)5(-x x 。

⒑光的速度大约是300 000 000米/秒，将300 000 000用科学计数法法表示为__________. 解：8103⨯。

⒒某校初一年段举行科技创新比赛活动，各个班级选送的学生数分别为3、2、2、6、6、5，则这组数据的平均数是__________. 解：4.⒓n 边形的内角和为900°，则n =__________.解：7. ⒔计算：=---111m m m __________. 解：1. D⒕如图，在△ABC 中，AB=AC ，BC=6，AD ⊥BC 于点D ，则BD 的长是__________. 解：3.C D （第十四题图） ⒖如图，在△ABC 中,∠A=60°，∠B=40°，点D 、E 分别在BC 、AC 的延长线上，则∠1=_ °. 解：80°。

2018年福建省泉州质检数学试题及答案

2018年5月福建9地市初三数学5月质检分类汇编(圆)含答案

2018年九地市质检圆的汇编（2018年福州质检)如图，AD 是半圆O 的直径，AD ＝12，B ，C 是半圆O 上两点．若AB BC CD ==，则图中阴影部分的面积是（Ａ）（A ）6π （B ）12π （C ）18π（D ）24π（2018年福州质检）如图，AB 是⊙O 的直径，点C 在⊙O 上，过点C 的直线与AB 延长线相交于点P ．若∠COB=2∠PCB ，求证：PC 是⊙O 的切线．证法一：连接A C ．............................1分∵CB =CB ，∴∠COB =2∠CA B ． ···················· 2分 ∵∠COB =2∠PCB ， ∴∠CAB =∠PC B ． ····················· 3分 ∵OA =OC ，∴∠OAC =∠OCA ， ∴∠OCA =∠PC B ． ·········· 4分 ∵AB 是⊙O 的直径， ∴∠ACB =90°， ············ 5分 ∴∠OCA +∠OCB =90°， ∴∠PCB +∠OCB =90°，即∠OCP =90°， ····················· 6分 ∴OC ⊥CP ． ························ 7分 ∵OC 是⊙O 的半径，∴PC 是⊙O 的切线． ···················· 8分证法二：过点O 作OD ⊥BC 于D ，则∠ODC =90°， ·········· 1分∴∠OCD +∠COD =90°． ················· 2分 ∵OB =OC ，∴OD 平分∠COB ，∴∠COB =2∠CO D ． ·········· 3分 ∵∠COB =2∠PCB ，∴∠COD =∠PCB ， ·········· 4分 ∴∠PCB +∠OCD =90°，即∠OCP =90°， ····················· 6分 ∴OC ⊥CP ． ························ 7分 ∵OC 是⊙O 的半径，∴PC 是⊙O 的切线． ···················· 8分证法三：设∠PCB =x °， ······················ 1分则∠COB =2x °． ····················· 2分 ∵OB =OC ，∴∠OCB =18022x ︒-︒=90°-x °， ···· 4分∴∠OCP =∠OCB +∠PCB=90°-x °+x °=90°， ···· 6分DA B C O A BPC O A B P CD O A B P C O A B PC O∴OC ⊥P C ． ·············· 7分 ∵OC 是⊙O 的半径，∴PC 是⊙O 的切线． ···················· 8分（2018年厦门质检）如图4，已知AB 是⊙O 的直径，C ，D 是圆上两点，∠CDB ＝45°，AC ＝1，则AB 的长为____2____．（2018年厦门质检）已知AB ＝8，直线l 与AB 平行，且距离为4．P 是l 上的动点，过点P 作PC ⊥AB 交线段AB 于点C ，点C 不与A 、B 重合．过A 、C 、P 三点的圆与直线PB 交于点D ． (1)如图9，当D 为PB 的中点时，求AP 的长；(2)如图10，圆的一条直径垂直AB 于点E ，且与AD 交于点M ．当ME 的长度最大时，判断直线PB 是否与该圆相切?并说明理由．解法一：如图6，∵ PC ⊥AB ， ∴ ∠ACP ＝90°．∴ AP 是直径．…………………2分∴ ∠ADP ＝90°． …………………3分即AD ⊥P B ．又∵ D 为PB 的中点，∴ AP ＝AB ＝8．…………………5分解法二：如图7，设圆心为O ，PC 与AD 交于点N ，连接OC ，O D ．∵ ︵CD ＝︵CD ，∴ ∠CAD ＝12∠COD ，∠CPD ＝12∠CO D ．∴ ∠CAD ＝∠CP D ．…………………1分∵ ∠ANC ＝∠PND ，又∵ 在△ANC 和△PND 中，∠NCA ＝180°－∠CAN －∠ANC ， ∠NDP ＝180°－∠CPN －∠PND ，∴ ∠NCA ＝∠NDP ． …………………2分 ∵ PC ⊥AB ，O · 图7N∴ ∠NCA ＝90°．∴ ∠NDP ＝90°． …………………3分即AD ⊥P B ．又∵ D 为PB 的中点，∴ AP ＝AB ＝8．…………………5分（2）（本小题满分6分）解法一：当ME 的长度最大时，直线PB 与该圆相切．理由如下：如图8，设圆心为O ，连接OC ，O D ． ∵ ︵CD ＝︵CD ，∴ ∠CAD ＝12∠COD ，∠CPD ＝12∠CO D ．∴ ∠CAD ＝∠CP D ．又∵ PC ⊥AB ，OE ⊥AB ， ∴ ∠PCB ＝∠MEA ＝90°．∴ △MEA ∽△BCP ． …………………7分 ∴ ME BC ＝AE PC．∵ OE ⊥AB ，又∵ OA ＝OC ， ∴ AE ＝E C ．设AE ＝x ，则BC ＝8－2x ．由ME BC ＝AE PC ，可得ME ＝－12（x －2）2＋2．…………………8分 ∵ x ＞0，8－2x ＞0， ∴ 0＜x ＜4．又∵ －12＜0，∴ 当x ＝2时，ME 的长度最大为2．…………………9分连接AP ，∵ ∠PCA ＝90°， ∴ AP 为直径．∵ AO ＝OP ，AE ＝EC ， ∴ OE 为△ACP 的中位线． ∴ OE ＝12P C ．∵ l ∥AB ，PC ⊥AB ， ∴ PC ＝4． ∴ OE ＝2．∴ 当ME ＝2时，点M 与圆心O 重合．…………………10分即AD 为直径．图8O ·也即点D 与点P 重合．也即此时圆与直线PB 有唯一交点．所以此时直线PB 与该圆相切．…………………11分解法二：当ME 的长度最大时，直线PB 与该圆相切．理由如下：如图8，设圆心为O ，连接OC ，O D ． ∵ OE ⊥AB ，又∵ OA ＝OC ， ∴ AE ＝E C ．设AE ＝x ，则CB ＝8－2x ． ∵ ︵CD ＝︵CD ，∴ ∠CAD ＝12∠COD ，∠CPD ＝12∠CO D ．∴ ∠CAD ＝∠CP D ．又∵ PC ⊥AB ，OE ⊥AB ， ∴ ∠PCB ＝∠MEA ＝90°．∴ △MEA ∽△BCP ． …………………7分 ∴ ME BC ＝AE PC．可得ME ＝－12（x －2）2＋2．…………………8分∵ x ＞0，8－2x ＞0， ∴ 0＜x ＜4．又∵ －12＜0，∴ 当x ＝2时，ME 的长度最大为2．…………………9分连接AP ，∵ AE ＝x ＝2，∴ AC ＝BC ＝PC ＝4． ∵ PC ⊥AB ， ∴ ∠PCA ＝90°，∴ 在Rt △ACP 中，∠P AC ＝∠APC ＝45°．同理可得∠CPB ＝45°． ∴ ∠APB ＝90°．即AP ⊥P B ． …………………10分又∵ ∠PCA ＝90°， ∴ AP 为直径．∴ 直线PB 与该圆相切．…………………11分图8O ·（2018年泉州质检）如图，菱形ABCD 中，BC ＝6，∠C ＝135°，以点A 为圆心的⊙A 与BC 相切于点E ． (1)求证：CD 是⊙A 的切线； (2)求图中阴影部分的面积．（2018年宁德质检）如图，在△ABC 中，∠ACB ＝90°，O 是AB 上一点，以OA为半径的⊙O 与BC 相切于点D ，与AB 交于点E ，连接ED 并延长交AC 的延长线于点F . （1）求证：AE ＝AF ；（2）若DE ＝3，sin ∠BDE ＝13，求AC 的长．解：（1）证明：连接O D .∵ OD ＝OE ，∴∠ODE ＝∠OE D ． ········· 1分∵直线BC 为⊙O 的切线， ∴OD ⊥B C ．∴∠ODB ＝90°． ·········· 2分 ∵∠ACB ＝90°，F A E C D BO∴OD ∥AC ． ············ 3分∴∠ODE ＝∠F ．∴∠OED ＝∠F ． ················ 4分 ∴AE ＝AF ． ·················· 5分（2）连接A D ．∵AE 是⊙O 的直径∴∠ADE ＝90°． ··············· 6分 ∵AE ＝AF ， ∴DF ＝DE ＝3. ∵∠ACB ＝90°．∴∠DAF ＋∠F ＝90°，∠CDF ＋∠F ＝90°， ∴∠DAF ＝∠CDF ＝∠BDE ． ····· 7分在Rt △ADF 中，1sin sin 3∠DF DAF BDE AF ==∠=， ∴39AF DF ==． ·········· 8分在Rt △CDF 中，1sin sin 3∠CF CDF BDE DF ==∠=， ∴113CF DF ==． ·········· 9分∴AC ＝AF －CF ＝8. ········ 10分（2018年漳州质检）如图，AB 是⊙O 的直径，AC 是弦，D 是BC 的中点，过点D 作EF 垂直于直线AC ，垂足为F ,交AB 的延长线于点E .（1）求证：EF 是⊙O 的切线；（2）若tan A ＝43,AF ＝6,求⊙O 的半径. 解：（1）方法一：如图1，连接O D . ∵EF ⊥AF ,∴∠F ＝90°.∵D 是BC 的中点,∴BD DC =.∴∠1＝∠2＝12∠BO C . ………………………………………………1分 ∵∠A ＝12∠BOC , ∴∠A ＝∠1 . ………………………………………2分 ∴OD ∥AF .∴∠EDO ＝∠F ＝90°.∴OD ⊥EF . ……………………………………………………………3分F A E C D B O图2∴EF 是⊙O 的切线. ……………………………………………………4分方法二：如图2，连接OD ，BC .∵D 是BC 的中点,∴BD DC =.∴∠1＝∠2. …………………………………………………………1分∵OB ＝OC ，∴OD ⊥B C . ……………………………2分∵AB 是⊙O 的直径，∴∠ACB ＝90°. ∵AF ⊥EF ，∴∠F ＝∠ACB ＝90°.∴BC ∥EF .∴OD ⊥EF . ……………………………………………………………3分∴EF 是⊙O 的切线. …………………………………………………4分（2）设⊙O 半径为r ,则OA ＝OD ＝OB ＝r .方法一：在Rt △AFE 中，tan A ＝43，AF ＝6, ∴EF ＝AF ·tan A ＝8.∴10AE ==. ………………5分∴OE ＝10－r .∵cos A ＝ 35AF AE=, ………………………………………………………6分∴cos ∠1＝ cos A ＝3105OD r OE r ==-. ……………………………………7分 ∴r ＝154，即⊙O 的半径为154. ……………………………………8分方法二：在Rt △AFE 中，tan A ＝43，AF ＝6, ∴EF ＝AF ·tan A ＝8.∴10AE ==. ………………5分∴EO ＝10－r .∵∠A ＝∠1，∠E ＝∠E ,∴△EOD ∽△EAF . ……………………………………………………6分 ∴OD EO AFEA= . …………………………………………………………7分∴10610r r -=.∴r ＝154，即⊙O 的半径为154. ……………………………………8分DC（2018年龙岩质检）如图，在ABC ∆中，90,BAC ∠=︒AB AC ==AD BC ⊥，垂足为D ，过,A D 的O 分别与,AB AC 交于点,E F ，连接,,EF DE DF ．（Ⅰ）求证：ADE ∆≌CDF ∆；（Ⅱ）当BC 与O 相切时，求O 的面积解：（Ⅰ）证明：∵,90AB AC BAC =∠=︒∴45C ∠=︒ …………1分又∵,AD BC AB AC ⊥=∴1145,,902BAC BD CD ADC ∠=∠=︒=∠=︒…………2分又∵90,BAC BD CD ∠=︒=∴AD CD =…………3分又∵90EAF ∠=︒ ∴,E F 是O 直径∴90EDF ∠=︒…………4分 ∴2490∠+∠=︒又∵3490∠+∠=︒ ∴23∠=∠ 又∵1C ∠=∠…………5分∴ADE ∆≌()CDF ASA ∆. …………6分（Ⅱ）当BC 与O 相切时，AD 是直径 (7)分在Rt ADC ∆中，45,C AC ∠=︒=8分∴sin ADC AC∠=∴1AD =…………9分∴O 的半径为12∴O 的面积为4π…………10分（2018年莆田质检）如图，AB 是⊙O 的切线，A 为切点，连接OB 交⊙O 于点C .若OA ＝3,tan ∠AOB ＝34，则BC 的长为（）(A ) 2 (B ) 3 (C ) 4 (D ) 5（2018年莆田质检）如图，⊙O 的直径CD ，AB 是⊙O 的弦，AB ⊥CD ，垂足为N .连（第23题图）O F E D C B A接A C .(I ) 若ON ＝1，BN ＝3.求长度； (II ) 若点E 在AB 上，且AB AE AC ⋅=2.求证：∠CEB ＝2∠CA B . (I )解：∵AB ⊥CD ，垂足为N ∴∠BNO ＝90°在Rt △ABC 中，∵ON ＝1，BN ＝3∴222=+=ON BN BO ，3tan ==∠ONBNBON ┄┄┄┄┄┄┄┄┄┄┄┄3分 ∴∠BON ＝60° ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分∴. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄5分(II )证明：如图，连接BC∵CD 是⊙O 的直径，AB ⊥CD ， ∴. ┄┄┄┄┄┄┄┄┄┄┄┄6分∴∠1＝∠CAB∵AB AE AC ⋅=2，且∠A ＝∠A∴△ACE ∽△ABC ┄┄┄┄┄┄┄┄┄┄┄┄┄8分 ∴∠1＝∠2 ∴∠CAB ＝∠2∴∠CEB ＝∠CAB ＋∠2＝2∠CA B . ┄┄┄┄┄┄┄┄┄┄┄┄┄10分BCBDC(2018三明质检)如图，在△ABC 中，∠A ＝45°，以AB 为直径的⊙O 经过AC 的中点D ，E 为⊙O 上的一点，连接DE ，BE ，DE 与AB 交于点F . （Ⅰ）求证：BC 为⊙O 的切线；（Ⅱ）若F 为OA 的中点,⊙O 的半径为2，求BE 的长. 解法一：连接OD ，∵OA ＝OD , ∠A ＝45°，∴∠ADO ＝∠A ＝45°,∴∠AOD ＝90°. …………………1分 ∵D 是AC 的中点，∴AD ＝C D .∴OD ∥B C . ……………………2分∴∠ABC ＝∠AOD ＝90°. ……………………3分∴BC 是⊙O 的切线. ……………………4分解法二：连接BD ，∵AB 为⊙O 的直径，∴BD ⊥A C . …………………1分∵D 是AC 的中点，∴BC ＝A B . …………………2分 ∴∠C ＝∠A ＝45°.∴∠ABC ＝90°. ……………………3分 ∴BC 是⊙O 的切线. ……………………4分（Ⅱ）连接OD ，由（Ⅰ）可得∠AOD ＝90°.∵⊙O 的半径为2, F 为OA 的中点，∴OF ＝1,BF ＝3，AD (5)分∴DF =……………6分∵BD BD =, ∴∠E ＝∠A . ……………7分 ∵∠AFD ＝∠EFB ,∴△AFD ∽△EF B . ……………8分 ∴DF BF AD BE =,3BE =. ……………………9分∴BE ……………………10分（2018南平质检）如图，AB 为半圆O 的直径，弦CD 与AB 的延长线相交于点E ．（Ⅰ）求证: ∠COE ＝2∠BDE ；（Ⅱ）当OB ＝BE ＝2，且∠BDE ＝60°时，求tan E ．（Ⅰ）证明：连接AC ，∵∠A ＋∠CDB ＝180， ………1分 ∠BDE ＋∠CDB ＝180°，………2分 ∴∠A ＝∠BDE ， ……………3分EA OBCD （第23题图）∵∠COE ＝2∠A ， ……………4分∴∠COE ＝2∠BDE ；…………5分（Ⅱ）解：过C 点作CF ⊥AE 于F 点，∵∠BDE ＝60°，∴∠A ＝60°， …………………………………………………………6分又∵OA ＝OC ，∴△AOC 是等边三角形，∵OB ＝2，∴OA ＝AC ＝2， ∴121===AO FO AF ， …………………………………………7分在Rt △AFC 中，∴，…………………………8分在Rt △CEF 中，EF ＝FO ＋OB ＋BE ＝5，∴53tan ==EF CF E ． ………………………………………………10分（2018石狮质检）如图，AB 是⊙O 的直径，点C 是⊙O 上一点，点D 是OB 的中点，过点D 作AB 的垂线交AC 的延长线于点F ，过点C 作⊙O 的切线交FD 于点E ．（1）求证：CE ＝EF ；（2）如果sin F ＝53，EF ＝5，求AB 的长．（1）证明：连结OC ．∵CE 切⊙O 于点E ， ∴OC ⊥CE . ……………………………… 2分∴︒=∠+∠9021°.∵FD AB ⊥， ∴︒=∠+∠90F A ．又∵OC ＝OA ， ∴1∠=∠A . ………………………………….3分∴F ∠=∠2.∴CE EF =. …………………………………………………………….4分（2）∵FD AB ⊥，3sin 5F =， ∴设3AD k =，5AF k =，可得4FD k =． …………… 5分∵D 为OB 的中点， ∴DB k =，k AB 4=．………… 6分连结CB 交FD 于点G ．∵AB 为⊙O 直径， ∴90ACB FCB ∠=∠=°．∴F B ∠=∠．∵︒=∠=∠90GDB FDA ，∴△FAD ∽△BDG ，……………………………………… 7分 ∴DB FD DG AD =，即k k DG k 43=，解得k DG 43=，可得134FG k =． ……………………………………………… 8分 ∵90FCB ∠=°， ∴324∠+∠=∠+∠F ．∵2∠=∠F ， ∴43∠=∠．312222=-=-=AF AC CF A B F O D EC G∴CE EF EG ==． ………………………………………… 9分∵5EF =， ∴10FG =． ∴13104k =，4013k =． ∴131604==k AB ． ………… 10分（2018晋江质检）如图，在平面直角坐标系中，直线l ：y ＝kx ＋1(k ＞0)与x 轴、y 轴分别相交于点A 、B ，tan ∠ABO ＝3．（1）求k 的值；（2）若直线l ：y ＝kx ＋1与双曲线y ＝xm (0≠m ) 的一个交点Q 在一象限内，以BQ 为直径的⊙I 与x 轴相明于点T ，求m 的值．解：(I )在()10y kx k =+>中，令0=x ，则1=y ，∴1=OB …………………………………………………1分在AOB Rt ∆中，31tan ===∠AO BO AO ABO ， ∴3=AO ，()0,3-A .………………………………2分把点()0,3-A 代入1+=kx y 中得：130+-=k ，解得：33=k .…………………………………3分 (II )∵3tan =∠ABO ，∴︒=∠60ABO ，︒=∠30BAO .………………………………………………4分连接IT ，∵⊙I 与x 轴相切于点T ，∴AT IT ⊥，︒=∠90ITA ，在AOB Rt ∆中，︒=∠30BAO ，1=OB ，∴2=AB ，……………………………………………………………………………………………………5分在ATI Rt ∆中，︒=∠30IAT ，设r IT =，则2+=r AI ，TI AI 2=，∴r r 22=+，解得：2=r ，6=AQ ，……………………………………………………7分作x QC ⊥轴于点C ,在ACQ ∆中，︒=∠30QAC ，362121=⨯==AQ QC ,…………………………………………………8分 3330cos =︒⋅=AQ AC ， ∴32333=-=-=AO AC OC ，……………………………………………………………………9分∴()3Q ，把点()3Q 代入xm y =得：36=m .………………………………………………………………10分。

泉州市2018-2019学年度上学期初中教学质量监测初三数学参考答案及评分标准(定稿阅卷)

3 1 = . ……………………………………………………………………7 分 6 2 1 ∴游戏者获胜的概率为 .…………………………………………………………………………8 分 2
∴ P (“配橙色”)=
2018 年秋季九年级期末跟踪质量检测数学试题参考答案
第 1 页共 6 页
（19）（本小题 8 分）解：（Ⅰ） A' B' C ' 为所求画的三角形；…………………5 分（Ⅱ） A' (0, 4 ) ， B' (− 2, 0) ， C ' (4, − 2) . ………………………………………………………………8 分 B’ B
100(1 + x )(1 + 2 x ) = 132 ，………………………………………………………………4 分
整理得： x + 1.5 x − 0.16 = 0 ，
2
解得： x1 = 0.1 ， x2 = −1.6 （不合题意，舍去）………………………………………………7 分 ∴只取 x = 0.1 = 10% 答：第二个月的增长率为 10% ．…………………………………………………………………8 分（22）（本小题 10 分）画图正确………………………………………1 分已知：如图， ABC ∽ A' B ' C ' ， ABC 和 A
泉州市 2018-2019 学年度上学期初三教学质量检测初三数学参考答案及评分标准
一、选择题（每小题 4 分，共 40 分）（1）D （2）A （3）B （4）B （5）D （6）D （7）D 二、填空题（每小题 4 分，共 24 分）（11）18 （12） x1 = 0 ， x2 = 3 （13）（8）B （9） C （10）A （15）

泉州市2018—2019学年度上学期初三教学质量检测数学试卷

2018年福建泉州中考数学试卷及答案解析版

2018 年福建省泉州市初中毕业、升学考试( 满分： 150 分；考试时间： 120 分钟 )友谊提示：全部答案一定填写到答题卡相应的地点上.毕业学校姓名考生号一、选择题 ( 每题 3 分，共 21 分 ) ：每题有四个答案，此中有且只有一个答案是正确的. 请答题卡上相应题目的答题地区内作答. 答对的得 3 分，答错或不答一律得0 分.1. （ 2018 福建泉州， 1， 3 分） 4 的相反数是（)A. 4B. -4C. 1 1D.4 4【答案】 B2. （ 2018 福建泉州， 2， 3 分）在△ ABC 中，∠ A = 20°，∠ B = 60°，则△ ABC 的形状是 ( )A. 等边三角形B.锐角三角形C. 直角三角形D. 钝角三角形【答案】 D3.（ 2018 福建泉州， 3，3 分）以下左图是由六个完整同样的正方体堆成的物体，则这一物体的正视图是( )【答案】 Ax2,4. （ 2018 福建泉州， 4， 3 分）把不等式组的解集在数轴上表示出来，正确的选项是( )2x 6【答案】 A5. （ 2018 福建泉州，9.3 环，方差以下表：5， 3 分）甲、乙、丙、丁四位选手各射击10 次，每人的均匀成绩都是则这四人中成绩发挥最稳固的是( )A. 甲B. 乙C. 丙D. 丁【答案】 B6. （ 2018 福建泉州， 6，3 分）已知⊙ O1 与⊙ O 订交，它们的半径分别是4、 7，则圆心距 O O22 1可能是 ( )A.2B.3C. 6D. 12【答案】 C7. （ 2018 福建泉州， 7，3 分）为了更好保护水资源，造福人类. 某工厂计划建一个容积V(m3) 一．定的污水办理池，池的底面积S(m2) 与其深度 h(m) 知足关系式： V = Sh( V≠0) ，则 S 对于 h 的函．。

2018年5月福建省泉州市初中毕业班质量检测数学试题含精品解析

(25)(13 分)已知：二次函数 y=ax2+bx+c(a≠0)的图象与 x 轴交于点 A、B(-3，0)，顶点为 C(-1，-2) (1)求该二次函数的解析式； (2)如图，过 A、C 两点作直线，并将线段 AC 沿该直线向上平移，记点 A、C 分别平移到点 D、E 处．若点 F 在这个二次函数的图象上，且△DEF 是以 EF 为斜边的等腰直角三角形，求
(C)8x+4=7x-3
(D)
1 1 x 3 x+4 7 8
(9)如图，在 3×3 的网格中，A，B 均为格点，以点 A 为圆心，以 AB 的长为半径作弧，图中的点 C 是该弧与格线的交点，则 sin∠BAC 的值是（）． (A)
1 2
(B)
2 3(C)5 3(D)2 5 5
(10)如图，反比例函数 y=
B
C
(20)(8 分)为进一步弘扬中华优秀传统文化，某校决定开展以下四项活动：A 经典古诗文朗诵；B 书画作品鉴赏；C 民族乐器表演；D 围棋赛。学校要求学生全员参与，且每人限报一项．九年级 (1)班班长根据本班报名结果，绘制出了如下两个尚不完整的统计图，请结合图中信息解答下列问题： (1)直接填空：九年级(1)班的学生人某校九年级(1)班参加项目情况某校九年级(1)班参加项目情况数是_______，在扇形统计图中，条形统计图扇形统计图 B 项目所对应的扇形的圆心角度 B 数是_______； A (2)将条形统计图补充完整； 30% (3)用列表或画树状图的方法，求该 C D 班学生小聪和小明参加相同项目活动的概率．
x 3 2x 1 =1． 2 3
(18) (8 分)先化简，再求值：
a2 2 9 a 2 3a ，其中 a= ． 3 2 a a 3 a 3

泉州市2018—2019学年度上学期初三教学质量检测数学试卷((含答案)

泉州市2018—2019学年度上学期初三教学质量检测数学试题（满分：150分考试时间：120分钟）一、选择题：本题共10小题，每小题4分，共40分． 1．下列各数中，能使5-x 有意义的是（）．A ．0B ．2C ．4D ．6 2．下列二次根式中与2是同类二次根式的是（）．A ．8B ．2.0C ．12D ．323．若35=b a ，则aba -的值为（）． A ．32 B ．52 C ．53 D ．32- 4．用配方法解方程0162=+-x x ，下列配方正确的是（）．A ．8)3(2=+xB ．8)3(2=-xC ．9)3(2=+xD ．9)3(2=-x 5．下列事件为不可能事件的是（）．A ．掷一枚质地均匀的正方体骰子，掷得的点数不是奇数就是偶数B ．从一副扑克牌中任意抽出一张，花色是黑桃C ．抛一枚普通的硬币，正面朝上D ．从装满红球的袋子中摸出一个白球6．若三角形的各边长分别是8cm 、10cm 和16cm ，则以各边中点为顶点的三角形的周长为（）． A ．34cm B ．30cm C ．29cm D ．17cm7．从一个由4个男生、3个女生组成的学习小组中，随机选出1人担任小组长，则选出“男生”为小组长的概率是（）．A ．41B ．21C ．73D ．748．某斜坡的坡度=i 1︰33，则该斜坡的直角为（）． A ．75° B ．60° C ．45° D ．30°9．如图，在△ABC 中，点G 为△ABC 的重心，过点G 作DE ∥BC ，分别交AB 、AC 于点D 、E ，则△ADE 与四边形DBCE 的面积比为（）．第9题图A ．32 B ．43 C ．54 D ．94 10．若关于x 的一元二次方程02=++c bx ax （0≠ac ）有一根为2019=x ，则关于y 的一元二次方程02=++a by cy （0≠ac ）必有一根为（）．A ．20191B ．20191-C ．2019D ．2019-二、填空题：本题共6小题，每小题4分，共24分． 11．计算：=2)23( ．12．方程032=-x x 的解是．13．在Rt △ABC 中，∠C = 90°，BC = 3，AC = 4，则sin A = ．14．如图，直线1l ∥2l ∥3l ，直线AC 分别交1l 、2l 、3l 于点A 、B 、C ，直线DF 交于1l 、2l 、3l 点D 、E 、F ，AB = 3，BC = 5，DE = 2，则EF = ．15．我国古代数学著作《九章算术》中有题如下：“今有勾五步，股十二步，问勾中容方几何”其大意译为：如图，在Rt △ABC 中，∠ACB = 90°，BC = 5，AC = 12，四边形CDEF 是Rt △ABC 的内接正方形，点D 、E 、F 分别在边BC 、AB 、AC 上，则正方形CDEF 边长为． 16．若在△ABC 内有一点D ，使得∠ADB =∠ADC ，AD = a ，CD = b ，则当BD = 时，△ABD 与△ACD 相似．三、解答题：本题共9小题，共86分． 17．（8分）计算：︒+-⨯30cos 282426．18．（8分）小玲为毕业联欢会设计了一个“配橙色”的游戏，使用的是如图所示两个可以自由转动的转盘，每个转盘被分成面积相等的若干个扇形，不同扇形分别填涂颜色，分界线可忽略，游戏者同时转动两个转盘，两个转盘停止转动时，若有一个转盘的指针指向红色，另一个转盘的指针指向黄色，则“配橙色”游戏成功，游戏者获胜．求游戏者获胜的概率．AB CF DEl 1 l 2 l3第14题图第15题图ACD E F 转盘1转盘2ABC 19．（8分）如图，在8 × 8的网格图中，△ABC 三个顶点坐标分别为A （0，2）、B （1-，0）、C （2，1-）．（1）以O 为位似中心，将△ABC 放大为△A′B ′C ′，使得△A′B ′C ′与△ABC 的位似比为2︰1，请在网格图中画出△A′B ′C ′；（2）直接写出（1）中点A′、B ′、C ′的坐标．20．（8分）如图，一架遥控无人机在点A 处测得某高楼顶点B 的仰角为60°，同时测得其底部点C 的俯角为30°，点A 与点B 的距离为60米，求这栋楼高BC 的长．21．（8分）某钢铁厂第一个月生产钢铁100万吨，从第二个月起改进技术增大产量，第三个月生产钢铁132万吨，若钢铁产量第三个月增长率是第二个月增长率的2倍，求第二个月钢铁产量的增长率．22．（10分）求证：相似三角形对应高的比等于相似比．（请根据题意补全图形，写出已知、求证并证明）23．（10分）已知1x 、2x 是关于x 的一元二次方程0332=-++k x x 的两个实数根．A B COxy1 1-1-1 ABC A BCPAB DQA （1）求k 的取值范围；（2）若322121=+++k x x x ，试求k 的值．24．（13分）如图，已知直线b x y +=43与x 轴、y 轴分别交于点B 、A ，点P 是y 轴上一动点，PQ ⊥AB 于点Q ，点A 的坐标为（0，3）．（1）求直线AB 的解析式；（2）若54=AB AQ ，求点P 的坐标；（3）当P 在y 轴负半轴时，连接BP 、OQ ，分别取BP 、OQ 的中点E 、F ，连接EF 交PQ 于点G ，当OQ ∥BP 时，求证：PQ PG PB ⋅=22．25．（13分）如图，在正方形ABCD 中，AB = 4，点P 、Q 分别是AD 、AC 边上的动点．（1）填空：AC = ；（2）若AP = 3PD ，且点A 关于PQ 的对称点A′落在CD 边上，求tan ∠A′QC 的值；（3）设AP = a ，直线PQ 交直线BC 于点T ，求△APQ 与△CTQ 面积之和S 的最小值．（用含a 的代数式表示）泉州市2018-2019学年度上学期初三教学质量检测初三数学参考答案及评分标准一、选择题（每小题4分，共40分）（1）D （2）A （3）B （4）B （5）D （6）D （7）D （8）B （9） C （10）A 二、填空题（每小题4分，共24分）（11）18 （12）01=x ，32=x （13）53 （14（15（16）b 或b a 2.三、解答题（共86分）（17）（本小题8分）解：原式=3332+-……………………………………………………………………………6分32=…………………………………………………………………………………………8分（18）（本小题8分）解：方法一：画树状图如下：………………………………………………………………………………………………………4分由树状图可知，共有6种等可能结果，其中“配橙色”即“一红一黄”的有3种结果.∴P (“配橙色”)=2163=. ……………………………………………………………………7分 ∴游戏者获胜的概率为21.…………………………………………………………………………8分方法二：列表如下：ABD备用图红1 红黄红2红黄黄红黄………………………………………………………………………………………………………4分由树状图可知，共有6种等可能结果，其中“配橙色”即“一红一黄”的有3种结果.∴P (“配橙色”)=2163=. ……………………………………………………………………7分 ∴游戏者获胜的概率为21.…………………………………………………………………………8分（19）（本小题8分）解：（Ⅰ）'''C B A ∆为所求画的三角形；…………………5分（Ⅱ）()4,0'A ，()0,2'-B ，()2,4'-C .………………………………………………………………8分（20）（本小题8分）解：由已知条件得：︒=∠30ABC ，︒=︒+︒=∠903060BAC ……………………………2分在ABC Rt ∆中，………………………………………3分 ∴BCABABC =∠cos ， ∴ABCABBC ∠=cos︒=30cos AB……………………………………………………………6分2360=340=（米） …………………………………………………………………………7分C(第20题图)(第19题图)答：这栋高楼的高BC 为340米 ……………………………………………8分（21）（本小题8分）解：设第二个月钢铁产量的增长率为x ，则第三个月的增长率为x 2，依题意得： ……………1分()()132********=++x x ，………………………………………………………………4分整理得：016.05.12=-+x x ，解得：1.01=x ，6.12-=x （不合题意，舍去）………………………………………………7分 ∴只取%101.0==x答：第二个月的增长率为%10．…………………………………………………………………8分（22）（本小题10分）画图正确………………………………………1分已知：如图，ABC ∆∽'''C B A ∆，ABC ∆和'''C B A ∆的相似比为k ，AD 、''D A 分别是ABC ∆和'''C B A ∆的高．……………………………………3分求证：k D A AD=''………………………………4分证明：∵ABC ∆∽'''C B A ∆，∴'B B ∠=∠，…………………………………………………………………………6分 ∵AD 、''D A 分别是ABC ∆和'''C B A ∆的高， ∴︒=∠=∠90'''A D B BDA ，∴ABD ∆∽'''D B A ∆，…………………………………………………………………………9分 ∴k B A ABD A AD ==''''，…………………………………………………………………………10分（23）（本小题10分）解：（I ）∵一元二次方程0332=-++k x x 有两个实数根（II ）∵1x 是关于x 的一元二次方程0332=-++k x x 的根，∴033121=-++k x x ，即33121+--=k x x ………………………………………………5分(第22题图)'DB∵322121=+++k x x x ，∴3233211=++++--k x x k x ……………………………………………………………7分 ∴12x x =…………………………………………………………………………………………8分 ∴()031432=-⨯⨯-=∆k …………………………………………………………………9分解得： 421=k .…………………………………………………………………………………10分 (24)（本小题13分）解：(Ⅰ) ∵直线b x y +=43经过点A ()30，， ∴3=b .∴直线AB 的解析式为343+=x y .…………………3分 (Ⅱ) 在343+=x y 中，令0=y ，则4-=x ，()04，-B ，由(Ⅰ)得：A ()30，，3=OA ，在OAB Rt ∆中，由勾股定理得：5=AB .①当点Q 在y 轴的左侧时，如图1， ∵AB PQ ⊥，OA OB ⊥， ∴︒=∠=∠90AOB PQA ，又PAG BAO ∠=∠， ∴PAQ ∆∽BAO ∆，∴AB APOA AQ =， ∵54=AB AQ ，∴455454=⨯==AB AQ . ∴534AP =，解得：320=AP ，∴3113320=-=OP ，∴点P 的坐标为⎪⎭⎫⎝⎛-3110，.……………………………………………………………………6分 ②当点Q 在y 轴的右侧时，同①可得：320=AP ， ∴3293320=+=OP ，（第24题图1）∴点P 的坐标为⎪⎭⎫ ⎝⎛3290，.综上，点P 的坐标为⎪⎭⎫ ⎝⎛-3110，或⎪⎭⎫⎝⎛3290，.……………………………………………………8分 (Ⅲ)解法一：如图2，连接QE 、QO .在BPQ Rt ∆中，EQ 是BPQ Rt ∆斜边BP 边上的中线，∴BP EQ 21=，同理，BP EO 21= ∴EO EQ =，即EQO ∆是等腰三角形.又EF 是EQO ∆的中线，∴OQ EF ⊥.…………………………………………………9分 ∴︒=∠90QFE ， ∵OQ ∥BP ，∴︒=∠=∠90QFE GEP ，又GPE BPQ ∠=∠，∴BPQ ∆∽GPE ∆，…………………………………………………………………………11分 ∴PQPEPB PG =， ∴PQ PG PB PE ⋅=⋅， ∵PB PE 21=， ∴PQ PG PB PB ⋅=⋅21∴PQ PG PB ⋅=22.…………………………………………………………………………13分解法二：如图3，连接QE 、QO .在BPQ Rt ∆中，EQ 是BPQ Rt ∆斜边BP 边上的中线，∴BP EQ 21=，同理，BP EO 21= ∴EO EQ =，即EQO ∆是等腰三角形.又EF 是EQO ∆的中线，∴OQ EF ⊥. …………………………………………………………………………………9分 ∴︒=∠90QFE ， ∵OQ ∥BP ，∴︒=∠=∠90QFE GEP ， ∴BP EF ⊥.延长PQ 至点'P ，使得：PQ Q P ='，连接B P '、BG ， ∵BQ 为'PP 的垂直平分线， ∴BP BP ='， ∴P BP BPP ''∠=∠①（第24题图2）（第24题图3）∵GE 为BP 的垂直平分线， ∴PG BG =， ∴PBG BPG ∠=∠②由①②可得：PBG P BP BPP ∠=∠=∠''，∴'BPP ∆∽GPB ∆，…………………………………………………………………………11分 ∴PBPP PG PB '=即'2PP PG PB ⋅=，又PQ PP 2'=，∴PQ PG PB ⋅=22. …………………………………………………………………………13分(25)（本小题13分）解：（I ）24；…………………………………………………………………………………………2分（II ）∵点A 关于PQ 的对称点'A ，即APQ ∆与PQ A '∆关于PQ 对称， ∴︒=∠=∠=∠45'QCD P QA DAC ，'PA AP =， ∵D PA P QA D QA '''∠+∠=∠， QC A QCD D QA ''∠+∠=∠，∴QC A D PA ''∠=∠.…………………………………………………………………………………4分 ∵4=AB ，PD AP 3=，∴1=PD ，3'==PA AP ，在'PDA Rt ∆中，由勾股定理得：22'=D A ，42221'tan ==∠QC A .……………………………………………………………………………7分（III ）过点Q 作直线AD MN ⊥于点M ，交BC 于点N ，则BC MN ⊥. ∵AP ∥CT , ∴APQ ∆∽CTQ ∆，∴QNQMCT AP =，设h QM =，则h QN -=4，∴hh CT a -=4，∴()h h a CT -=4，(第25题图2)B(第25题图1)A∴()h h a ah S 24212-+=，………………………………………………………………………………9分整理得：()0842=++-a h S a ah （*）， ∵关于h 的一元二次方程（*）有实根，∴∆≥0， ………………………………………………10分 ∴()a a a S 1624822⋅⨯-+=∆≥0， ()282a S +≥2128a ，又082>+a S ，∴a S 82+≥a 28，S ≥()a 424-，当()a S 424-=时，由方程（*）可得22=h 满足题意，……………………………………12分故当22=h 时，APQ ∆与CTQ ∆面积之和S 的最小值为()a 424-.…………………………13分。

福建省泉州市洛江区2018年中考质量检查数学试题及答案

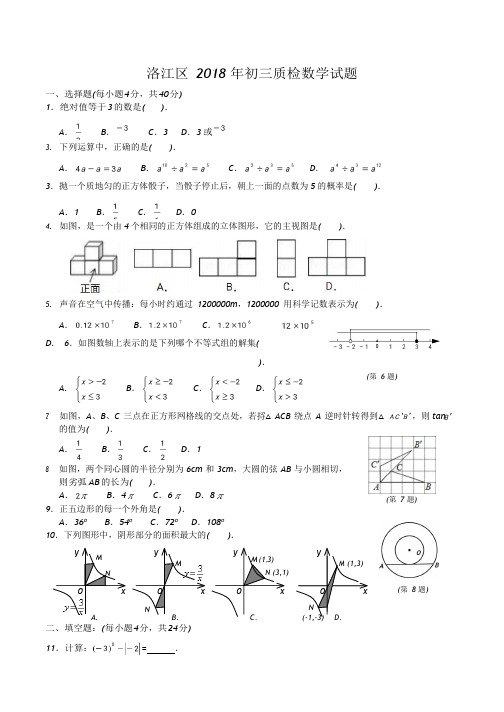
yMx NyM Nx洛江区 2018 年初三质检数学试题一、选择题(每小题 4 分，共 40 分) 1．绝对值等于 3 的数是( )．A ．B ．C ．3D ．3 或3. 下列运算中，正确的是( )．A ．B ．C ．D ．3．抛一个质地匀的正方体骰子，当骰子停止后，朝上一面的点数为 5 的概率是()．A ．1B ．C ．D ．04. 如图，是一个由 4 个相同的正方体组成的立体图形，它的主视图是()．5. 声音在空气中传播：每小时约通过 1200000m ，1200000 用科学记数表示为( )．A ．B ．C ．D ． 6．如图数轴上表示的是下列哪个不等式组的解集()．A.B ．C ．D ．(第 6 题)7.如图，A 、B 、C 三点在正方形网格线的交点处，若捋△ACB 绕点 A 逆时针转得到△，则 tan的值为( )． A ． B ． C ． D ．18.如图，两个同心圆的半径分别为 6cm 和 3cm ，大圆的弦 AB 与小圆相切，则劣弧 AB 的长为( )．A ．B ．4C ．6D ．89．正五边形的每一个外角是( )．A ．36oB ．54oC ．72oD ．108o 10．下列图形中，阴形部分的面积最大的( )． yM (1,3)N (3,1)x (第 7 题)(第 8 题)A.B ．C ．二、填空题：(每小题 4 分，共 24 分) 11．计算：=．yM (1,3)xN(-1,-3)D ．12. 因式分解：= ．13. 如图，路灯距离地面 8 米：身高 1.6 米的小明在距离灯的底部（点 O ）20 米的 A 处，则小明的影子AM 长为．14. 已知某校学生“科技创社团”成员的年龄与人数情况如右表所示，那么“科技创斯社团”成员年龄的中位数是岁．15．已知 A (-2,y 1)，B (-1,y 2)，C (4,y 3)都在反比例函数的图象上，则 y 1、y 2、y 3 的大小关系(从大到小)为．16．在每个小正方形的边长为 1 的网格中，点 A 、B 、C 均在格点上，在 △ABC 的内部有一点 P ，满足 S △PAB ：S △PBC ：S △PCA = 1：2：3，请在如图所示的网格中，用无刻度直尺画出点 P （保留画图痕迹）三、解答题：(本大颗共 9 小西，共 86 分) 17．（8 分）化简：．（按要求填空）(第 16 题)18．（8 分）如图，点 E 、F 在 B C 上，B E =C F ，A B =D C ，∠ B=∠ C ，求证：∠ A=∠ DAD19．（8 分）如图，已知锐角△A B C （1）过点 A 作 BC 边的垂线 MN ，交 BC 于 D（尺规作图，保留痕迹，不要求写作法）（2）在(1)条件下，若 BC=5，AD=4，tan ∠ BAD=，求 DC 的长．BEF CAB C(第 13 题)20．（8 分）阅读下列材料，回答问题：解方程，这是一个一元四次方程，根据该方程的特点，它的解法通常是：设，那么，于是原方程可变为①，解得 y 1=1，y 2=4．当 y 1=1 时，，∴ ；当 y 2=4 时，，∴；∴ 原方程有四个解： x 1=1，x 2=，x 3=2，x 4=,（1）在解原方程得到方程①的过程中，利用法达到降次目的，体现了数学的转化思想；（2）解方程：21．（8 分）为了发展旅游，建设美丽洛江，某中学九年级一班同学积积极参加了植树活动，今年四月份该班同学植树情况部分如图所示，且植树 2 株的人数占 32%．(1) 求该班的总人数、植树株数的众数，并把条形统计图补充完整；(2) 若将该班同学的植树人数所占比例绘制成扇形统计图时，求“植树 3 株”对应扇形的圆心角的度数； (3) 从该班参加植树的学生中任意抽取一名，其植树株数超过该班植树株数的平均数的概率．22．（10 分）某经销商销售一种产品，这种产品的成本价为 10元/千克，市场调查发现，该产品每天的销售 y （千克）与销售价 x （元/千克，且 1018）之间的函数关系如图所示：（1）求 y （千克）与销售价 x 之间的函数关系；（2）该经销商想要获得 150 元的销售利润，销售价应定为多少？y(千克)4024O1018 x(元/千克)23．(10 分)如图，已知：△ABC 中，AB=AC ，以 AB 为直径的⊙ O 交 BC 于点 D ，过 DDE ⊥ AC 于 E ．（1）求证：直线 DE 是⊙ O 的切线；（2）若 CD=，∠ ACB=300，分别求 AB 、OE 的大小．9724．(12 分)已知抛物线y= 经过点A(2，0) ．(1)求抛物线的解析式和顶点坐标；(2)若点B(m，n)是抛物线上的一动点，点B 关于原点的对称点为C．①若B、C 都在抛物线上，求m 的值；②若点C 在第四象限，当AC2的值最小时，求m 的值．25．(14 分)如图，在Rt△ABC 中，∠ A=900，AB=12，AC=16，点 D 为边BC 的中点，DE⊥BC 交边AC 于点E，点P 为射线AB 上的一动点，点Q 为直线AC 上的一动点，且∠ PDQ=900．(1)求ED、EC 的长；(2)若BP=2，求CQ 的长；(3)若线段PQ 与线段DE 交点为F，当△PDF 为等腰三角形时，求BP 的长洛江区2018 年初三质检数学参考答案。

福建省泉州市2018届九年级5月质量检测数学试题(含答案)

2018年福建省泉州市中考数学试卷含答案

(完整)2018年泉州市初三质检数学试题及答案,推荐文档

福建省泉州市2018-2019年最新最全5月初中毕业班质量检测数学试题(含答案解析)

2018年泉州市初中学业质量检查数学参考答案及评分标准

2018年5月份泉州市质检数学试卷答案

2018年福建省泉州市中考数学试卷(含答案)

2018年福建省泉州质检数学试题及答案

最新-2018年泉州市初中学业质量检查数学试题精品

2018年5月福建9地市初三数学5月质检分类汇编(圆)含答案

泉州市2018-2019学年度上学期初中教学质量监测初三数学参考答案及评分标准(定稿阅卷)

泉州市2018—2019学年度上学期初三教学质量检测数学试卷

2018年福建泉州中考数学试卷及答案解析版

最新福建省泉州市2018-2019年最新5月初中毕业班质量检测数学试题(含答案解析)

2018年5月福建省泉州市初中毕业班质量检测数学试题含精品解析

泉州市2018—2019学年度上学期初三教学质量检测数学试卷((含答案)

福建省泉州市洛江区2018年中考质量检查数学试题及答案

福建省泉州市2018届九年级5月质量检测数学试题(含答案)

2018年福建省泉州市中考数学试卷含答案

(完整)2018年泉州市初三质检数学试题及答案,推荐文档

福建省泉州市2018-2019年最新最全5月初中毕业班质量检测数学试题(含答案解析)

2018年泉州市初中学业质量检查数学参考答案及评分标准

2018年5月份泉州市质检数学试卷答案

2018年福建省泉州市中考数学试卷(含答案)

2018年福建省泉州质检数学试题及答案

最新-2018年泉州市初中学业质量检查数学试题 精品

2018年5月福建9地市初三数学5月质检分类汇编(圆)含答案

泉州市2018-2019学年度上学期初中教学质量监测初三数学参考答案及评分标准(定稿阅卷)

泉州市2018—2019学年度上学期初三教学质量检测数学试卷

2018年福建泉州中考数学试卷及答案解析版

最新福建省泉州市2018-2019年最新5月初中毕业班质量检测数学试题(含答案解析)

2018年5月福建省泉州市初中毕业班质量检测数学试题含精品解析

泉州市2018—2019学年度上学期初三教学质量检测数学试卷((含答案)

福建省泉州市洛江区2018年中考质量检查数学试题及答案

最新-2018年泉州市初中学业质量检查数学试题精品