指数对数运算经典习题及答案复习课程
指数对数运算复习--精编版

一.指数与指数运算1、 指数式:形如b a N =,a 叫做底数,b 叫做指数,N 叫做幂.2、 0指数幂与分数指数幂:(1)01(0)a a =≠;(2)1(0)n n aa a -=≠. 3、 根式性质: (1)()n n a a =;(2)||n n a n a a n ⎧=⎨⎩,为奇数,为偶数. 4、 分数指数幂:(1) 正分数指数 1(0)m n m n n n a a a a a =>=,*(0,,)ma m n N n>∈、为既约分数. (2) 负分数指数幂:1mn mn a a -=*(0,,)m a m n N n>∈、为既约分数. 5、 指数幂运算法则:(1)m n m n a a a +⋅=;(2)mm n n a a a-=; (3)()m n m n a a ⋅=;(4)()n n n ab a b =⋅.【练习题】1、 化简84416(0,0)x y x y <<得( )A.22x yB.2xyC.24x yD.22x y -2、 2110323(3)(0.002)10(52)(3)8π----+--+-= . 3、 526526-++= .4、 132123321(4)()4(0.1)()ab a b ---⋅= . 5、 已知11223a a-+=,求下列各式的值.(1)1a a -+;(2)22a a -+;(3)33221122a aa a ----.二.对数与对数运算1. 对数定义:若(0,1)b a N a a =>≠且,则b 叫做以a 为底N 的对数,记作log a b N =,a 叫做底,N 叫做真数.(2)对数恒等式:log (0,10)a N a N a a N =>≠>且,(3)对数换底公式:log log log a b a N N b =(4)对数的性质:①负数与零没有对数;②log 1a a =,log 10a =;③log log 1a b b a ⋅=(5)常用对数:以10为底的对数10log N 叫做常用对数,简记作lg N ; 自然对数:以e 为底的对数log e N 叫做自然对数,简记作ln N 。
指数函数对数函数专练习题(含答案)

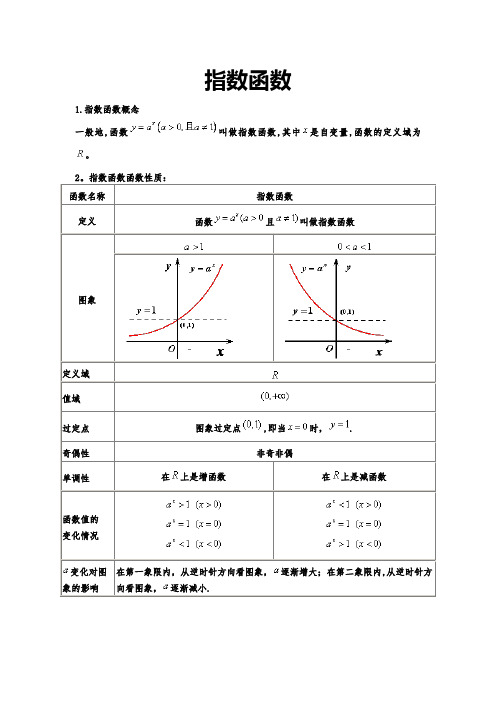
指数函数对数函数专练习题(含答案)指数函数及其性质1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为.2.指数函数函数性质:函数名称指数函数定义函数且叫做指数函数图象定义域值域过定点图象过定点,即当时,. 奇偶性非奇非偶单调在上是增函数在上是减函数性函数值的变化情况变化对图象的影响在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小.对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.2.对数函数性质:函数名称对数函数定义函数且叫做对数函数图象定义域值域过定点图象过定点,即当时,. 奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化情况变化对图象的在第一象限内,从顺时针方向看图象,逐渐增大;在第四象限内,从顺时针方向看图象,逐渐减小.影响指数函数习题一、选择题1.定义运算a ⊗b =⎩⎨⎧a (a ≤b )b (a >b ),则函数f (x )=1⊗2x 的图象大致为( )2.函数f (x )=x 2-bx +c 满足f (1+x )=f (1-x )且f (0)=3,则f (b x )与f (c x )的大小关系是( )A .f (b x )≤f (c x) B .f (b x )≥f (c x ) C .f (b x )>f (c x)D .大小关系随x 的不同而不同3.函数y =|2x -1|在区间(k -1,k +1)内不单调,则k 的取值范围是( )A .(-1,+∞)B .(-∞,1)C .(-1,1)D .(0,2)4.设函数f (x )=ln [(x -1)(2-x )]的定义域是A ,函数g (x )=lg(a x -2x-1)的定义域是B ,若A ⊆B ,则正数a 的取值范围( ) A .a >3 B .a ≥3 C .a > 5 D .a ≥ 55.已知函数f (x )=⎩⎨⎧(3-a )x -3,x ≤7,a x -6,x >7.若数列{a n }满足a n =f (n )(n ∈N *),且{a n }是递增数列,则实数a 的取值范围是( ) A .[94,3) B .(94,3)C .(2,3)D .(1,3)6.已知a >0且a ≠1,f (x )=x 2-a x,当x ∈(-1,1)时,均有f (x )<12,则实数a 的取值范围是( )A .(0,12]∪[2,+∞)B .[14,1)∪(1,4]C.[12,1)∪(1,2] D.(0,14)∪[4,+∞)二、填空题7.函数y=a x(a>0,且a≠1)在[1,2]上的最大值比最小值大a2,则a的值是________.8.若曲线|y|=2x+1与直线y=b没有公共点,则b的取值范围是________.9.(2011·滨州模拟)定义:区间[x1,x2](x1<x2)的长度为x2-x1.已知函数y=2|x|的定义域为[a,b],值域为[1,2],则区间[a,b]的长度的最大值与最小值的差为________.三、解答题10.求函数y=2间.11.(2011·银川模拟)若函数y=a2x+2a x-1(a>0且a≠1)在x∈[-1,1]上的最大值为14,求a的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax-4x的定义域为[0,1]. (1)求a 的值;(2)若函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.1.解析:由a ⊗b =⎩⎨⎧a (a ≤b )b (a >b )得f (x )=1⊗2x=⎩⎪⎨⎪⎧2x (x ≤0),1 (x >0).答案:A2. 解析:∵f(1+x)=f(1-x),∴f(x)的对称轴为直线x=1,由此得b=2.又f(0)=3,∴c=3.∴f(x)在(-∞,1)上递减,在(1,+∞)上递增.若x≥0,则3x≥2x≥1,∴f(3x)≥f(2x).若x<0,则3x<2x<1,∴f(3x)>f(2x).∴f(3x)≥f(2x).答案:A3.解析:由于函数y=|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k-1,k+1)内不单调,所以有k-1<0<k+1,解得-1<k<1.答案:C4. 解析:由题意得:A=(1,2),a x-2x>1且a>2,由A⊆B知a x-2x>1在(1,2)上恒成立,即a x-2x-1>0在(1,2)上恒成立,令u (x )=a x -2x -1,则u ′(x )=a xln a -2xln2>0,所以函数u (x )在(1,2)上单调递增,则u (x )>u (1)=a -3,即a ≥3.答案:B5. 解析:数列{a n }满足a n =f (n )(n ∈N *),则函数f (n )为增函数, 注意a 8-6>(3-a )×7-3,所以⎩⎪⎨⎪⎧a >13-a >0a 8-6>(3-a )×7-3,解得2<a <3.答案:C6. 解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x与y =x 2-12的图象,当a>1时,必有a-1≥12,即1<a≤2,当0<a<1时,必有a≥12,即12≤a<1,综上,12≤a<1或1<a≤2.答案:C7. 解析:当a>1时,y=a x在[1,2]上单调递增,故a2-a=a2,得a=32.当0<a<1时,y=a x在[1,2]上单调递减,故a-a2=a2,得a=12.故a=12或32.答案:12或328. 解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.曲线|y|=2x+1与直线y=b的图象如图所示,由图象可得:如果|y|=2x+1与直线y=b没有公共点,则b应满足的条件是b∈[-1,1].答案:[-1,1]9. 解析:如图满足条件的区间[a,b],当a=-1,b=0或a=0,b=1时区间长度最小,最小值为1,当a=-1,b=1时区间长度最大,最大值为2,故其差为1.答案:110. 解:要使函数有意义,则只需-x2-3x+4≥0,即x2+3x-4≤0,解得-4≤x≤1.∴函数的定义域为{x|-4≤x≤1}.令t=-x2-3x+4,则t=-x2-3x+4=-(x+32)2+254, ∴当-4≤x ≤1时,t max =254,此时x =-32,t min=0,此时x =-4或x =1. ∴0≤t ≤254.∴0≤-x 2-3x +4≤52.∴函数y =1()2[28,1].由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知,当-4≤x ≤-32时,t 是增函数,当-32≤x ≤1时,t 是减函数.根据复合函数的单调性知:y =1()2在[-4,-32]上是减函数,在[-32,1]上是增函数.∴函数的单调增区间是[-32,1],单调减区间是[-4,-32].11. 解:令a x=t ,∴t >0,则y =t 2+2t -1=(t+1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a=3(a =-5舍去). ②若0<a <1,∵x ∈[-1,1],∴t =a x∈[a ,1a ],故当t =1a,即x =-1时,y max =(1a+1)2-2=14.∴a =13或-15(舍去).综上可得a=3或1.312. 解:法一:(1)由已知得3a+2=18⇒3a=2⇒a =log32.(2)此时g(x)=λ·2x-4x,设0≤x1<x2≤1,因为g(x)在区间[0,1]上是单调减函数,所以g(x1)-g(x2)=(2x1-2x2)(λ-2x2-2x1)>0恒成立,即λ<2x2+2x1恒成立.由于2x2+2x1>20+20=2,所以实数λ的取值范围是λ≤2.法二:(1)同法一.(2)此时g(x)=λ·2x-4x,因为g(x)在区间[0,1]上是单调减函数,所以有g′(x)=λln2·2x-ln4·4x=ln2[-2·(2x )2+λ·2x ]≤0成立.设2x=u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立.因为u ∈[1,2],只需λ≤2u 恒成立, 所以实数λ的取值范围是λ≤2.对数与对数函数同步练习一、选择题 1、已知32a=,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+ D 、23a a -2、2log (2)log log a a a M N M N -=+,则NM的值为( ) A 、41B 、4C 、1D 、4或1 3、已知221,0,0x y x y +=>>,且1log (1),log ,log 1y a aa x m n x+==-则等于( )A 、m n +B 、m n -C 、()12m n +D 、()12m n -4、如果方程2lg (lg5lg 7)lg lg5lg 70x x +++=的两根是,αβ,则αβ的值是( )A 、lg5lg7B 、lg35C 、35D 、351 5、已知732log [log (log )]0x =,那么12x -等于( )A 、13 B C D6、函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( ) A 、x 轴对称 B 、y 轴对称 C 、原点对称 D 、直线y x =对称7、函数(21)log x y -= )A 、()2,11,3⎛⎫+∞ ⎪⎝⎭B 、()1,11,2⎛⎫+∞ ⎪⎝⎭C 、2,3⎛⎫+∞ ⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是( )A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞ 9、若log 9log 90m n <<,那么,m n 满足的条件是( )A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<<10、2log 13a <,则a 的取值范围是( )A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞⎪⎝⎭ C 、2,13⎛⎫ ⎪⎝⎭ D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭11、下列函数中,在()0,2上为增函数的是( )A 、12log (1)y x =+ B 、2log y =C 、21log y x = D 、2log (45)y x x =-+ 12、已知()log x+1 (01)a g x a a =>≠且在()10-,上有()0g x >,则1()x f x a +=是( )A 、在(),0-∞上是增加的B 、在(),0-∞上是减少的C 、在(),1-∞-上是增加的D 、在(),0-∞上是减少的 二、填空题13、若2log 2,log 3,m n a a m n a +=== 。
(完整版)指数函数及对数函数复习(有详细知识点及习题详细讲解)

指数函数与对数函数总结与练习一、指数的性质(一)整数指数幂n 1.整数指数幂概念:a =a ⋅Λ⋅a (n ∈N )a 0=1(a ≠0)1⋅4a 243*n 个aa-n=1a ≠0,n ∈N *)n(a 2.整数指数幂的运算性质:(1)a m ⋅a n =a m +n (m ,n ∈Z )(2)a (3)(ab )=a ⋅b n n n ()mn=a mn(m ,n ∈Z )(n ∈Z )其中a ÷a =a ⋅a m n m -n =a m -n a n ⎛a ⎫-1nn -n , ⎪=(a ⋅b)=a ⋅b =n .b ⎝b ⎭n 3.a 的n 次方根的概念即:若x n 一般地,如果一个数的n 次方等于a n >1,n ∈N ),那么这个数叫做a 的n 次方根,=a ,则x 叫做a 的n 次方根,(n >1,n ∈N )**(说明:①若n 是奇数,则a 的n 次方根记作n a ;若a >0则n a >0,若a <o 则n a <0;②若n 是偶数,且a >0则a 的正的n 次方根记作n a ,a 的负的n 次方根,记作:-n a ;(例如:8的平方根±8=±2216的4次方根±416=±2)③若n 是偶数,且a <0则n a 没意义,即负数没有偶次方根;④Θ0=0n >1,n ∈N nn (*)∴n 0=0;⑤式子a 叫根式,n 叫根指数,a 叫被开方数。
∴(a )nn=a ..4.a 的n 次方根的性质一般地,若n 是奇数,则n a n =a ;若n 是偶数,则n a n =a =⎨5.例题分析:例1.求下列各式的值:(1)3-8⎧a⎩-aa ≥0a <0.(3)(2)(-10)*2(3)4(3-π)(4)4例2.已知a <b <0,n >1,n ∈N ,化简:n (a -b )+n (a +b ).n n (二)分数指数幂1051231.分数指数幂:5a =a =a102(a >0)3a =a =a124(a >0)即当根式的被开方数能被根指数整除时,根式可以写成分数指数幂的形式;如果幂的运算性质(2)a 3()kn=akn 对分数指数幂也适用,442255⨯3⨯4⎛2⎫⎛⎫2532例如:若a >0,则 a 3⎪=a 3=a , a 4⎪=a 4=a ,∴a =a 3⎝⎭⎝⎭a =a .545即当根式的被开方数不能被根指数整除时,根式也可以写成分数指数幂的形式。
高中数学第四章指数函数与对数函数典型例题(带答案)

高中数学第四章指数函数与对数函数典型例题单选题1、已知a=lg2,10b=3,则log56=()A.a+b1+a B.a+b1−aC.a−b1+aD.a−b1−a答案:B分析:指数式化为对数式求b,再利用换底公式及对数运算性质变形. ∵a=lg2,0b=3,∴b=lg3,∴log56=lg6lg5=lg2×3lg102=lg2+lg31−lg2=a+b1−a.故选:B.2、函数f(x)=|x|⋅22−|x|在区间[−2,2]上的图象可能是()A.B.C.D.答案:C分析:首先判断函数的奇偶性,再根据特殊值判断即可;解:∵f(−x)=|x|⋅22−|x|=f(x),∴f(x)是偶函数,函数图象关于y轴对称,排除A,B选项;∵f(1)=2=f(2),∴f(x)在[0,2]上不单调,排除D选项.故选:C3、式子√m⋅√m 43√m 56m >0)的计算结果为( )A .1B .m 120C .m 512D .m 答案:D分析:由指数运算法则直接计算可得结果.√m⋅√m 43√m 56=m 12⋅m 43m 56=m 12+43−56=m .故选:D.4、若f(x)={(6−a)x −a,x <1log a x +3,x ≥1是定义在R 上的增函数,实数a 的取值范围是( )A .[1,5]B .[32,5) C .(32,5)D .(1,5) 答案:B分析:由题意得{6−a >1a >1log a 1+3≥(6−a)−a ,解不等式组可求得答案因为f(x)={(6−a)x −a,x <1log a x +3,x ≥1是定义在R 上的增函数,所以{6−a >1a >1log a 1+3≥(6−a)−a ,解得32≤a <5,故选:B5、函数f (x )=√3−x +log 13(x +1)的定义域是( )A .[−1,3)B .(−1,3)C .(−1,3]D .[−1,3] 答案:C分析:由题可得{3−x ≥0x +1>0,即得.由题意得{3−x ≥0x +1>0,解得−1<x ≤3, 即函数的定义域是(−1,3].故选:C.6、下列函数中是增函数的为( )A .f (x )=−xB .f (x )=(23)xC .f (x )=x 2D .f (x )=√x 3答案:D分析:根据基本初等函数的性质逐项判断后可得正确的选项. 对于A ,f (x )=−x 为R 上的减函数,不合题意,舍. 对于B ,f (x )=(23)x为R 上的减函数,不合题意,舍.对于C ,f (x )=x 2在(−∞,0)为减函数,不合题意,舍. 对于D ,f (x )=√x 3为R 上的增函数,符合题意, 故选:D.7、下列计算中结果正确的是( ) A .log 102+log 105=1B .log 46log 43=log 42=12C .(log 515)3=3log 515=−3D .13log 28=√log 283=√33答案:A分析:直接根据对数的运算性质及换底公式计算可得;解:对于A :log 102+log 105=log 10(2×5)=log 1010=1,故A 正确; 对于B :log 46log 43=log 36,故B 错误;对于C :(log 515)3=(log 55−1)3=(−log 55)3=−1,故C 错误; 对于D :13log 28=13log 223=13×3log 22=1,故D 错误; 故选:A8、荀子《劝学》中说:“不积跬步,无以至千里;不积小流,无以成江海.”所以说学习是日积月累的过程,每天进步一点点,前进不止一小点.我们可以把(1+1%)365看作是每天的“进步”率都是1%,一年后是1.01365≈37.7834;而把(1−1%)365看作是每天“退步”率都是1%,一年后是0.99365≈0.0255.若“进步”的值是“退步”的值的100倍,大约经过(参考数据:lg101≈2.0043,lg99≈1.9956) ( )天.A .200天B .210天C .220天D .230天 答案:D分析:根据题意可列出方程100×0.99x =1.01x ,求解即可.设经过x 天“进步”的值是“退步”的值的100倍,则100×0.99x=1.01x,即(1.010.99)x =100,∴x =log 1.010.99100=lg lg 1.010.99=lg lg 10199=2lg−lg≈22.0043−1.9956=20.0087≈230.故选:D . 多选题9、已知函数f(x)=1−2x 1+2x,则下面几个结论正确的有( )A .f(x)的图象关于原点对称B .f(x)的图象关于y 轴对称C .f(x)的值域为(−1,1)D .∀x 1,x 2∈R ,且x 1≠x 2,f (x 1)−f (x 2)x 1−x 2<0恒成立答案:ACD分析:利用奇函数的定义和性质可判断AB 的正误,利用参数分离和指数函数的性质可判断CD 的正误. 对于A ,f(x)=1−2x1+2x ,则f(−x)=1−2−x1+2−x =2x −11+2x =−f(x), 则f(x)为奇函数,故图象关于原点对称,故A 正确.对于B ,计算f(1)=−13,f(−1)=13≠f(1),故f(x)的图象不关于y 轴对称,故B 错误. 对于C ,f(x)=1−2x1+2x =−1+21+2x ,1+2x =t,t ∈(1,+∞),故y =f(x)=−1+2t ,易知:−1+2t ∈(−1,1),故f(x)的值域为(−1,1),故C 正确. 对于D ,f(x)=1−2x1+2x =−1+21+2x ,因为y =1+2x 在R 上为增函数,y =−1+21+t 为(1,+∞)上的减函数, 由复合函数的单调性的判断法则可得f (x )在R 上单调递减,故∀x 1,x 2∈R ,且x 1≠x 2,f(x 1)−f(x 2)x 1−x 2<0恒成立,故D 正确.故选:ACD.小提示:方法点睛:复合函数的单调性的研究,往往需要将其转化为简单函数的复合,通过内外函数的单调性结合“同增异减”的原则来判断.10、设函数f (x )=ax 2+bx +c (a,b,c ∈R,a >0),则下列说法正确的是( ) A .若f (x )=x 有实根,则方程f(f (x ))=x 有实根 B .若f (x )=x 无实根,则方程f(f (x ))=x 无实根 C .若f (−b 2a)<0,则函数y =f (x )与y =f(f (x ))都恰有2个零点D .若f (f (−b 2a))<0,则函数y =f (x )与y =f(f (x ))都恰有2零点答案:ABD分析:直接利用代入法可判断A 选项的正误;推导出f (x )−x >0对任意的x ∈R 恒成立,结合该不等式可判断B 选项的正误;取f (x )=x 2−x ,结合方程思想可判断C 选项的正误;利用二次函数的基本性质可判断D 选项的正误.对于A 选项,设f (x )=x 有实根x =x 0,则f(f (x 0))=f (x 0)=x 0,A 选项正确; 对于B 选项,因为a >0,若方程f (x )=x 无实根,则f (x )−x >0对任意的x ∈R 恒成立, 故f(f (x ))>f (x )>x ,从而方程f(f (x ))=x 无实根,B 选项正确;对于C 选项,取f (x )=x 2−x ,则f (12)=−14<0,函数y =f (x )有两个零点, 则f(f (x ))=[f (x )]2−f (x )=0,可得f (x )=0或f (x )=1,即x 2−x =0或x 2−x =1. 解方程x 2−x =0可得x =0或1,解方程x 2−x −1=0,解得x =1±√52. 此时,函数y =f(f (x ))有4个零点,C 选项错误;对于D 选项,因为f (f (−b2a ))<0,设t =f (−b2a ),则t =f (x )min , 因为f (t )<0且a >0,所以,函数f (x )必有两个零点,设为x 1、x 2且x 1<x 2, 则x 1<t <x 2,所以,方程f (x )=x 1无解,方程f (x )=x 2有两解,因此,若f(f(−b))<0,则函数y=f(x)与y=f(f(x))都恰有2零点,D选项正确.2a故选:ABD.小提示:思路点睛:对于复合函数y=f[g(x)]的零点个数问题,求解思路如下:(1)确定内层函数u=g(x)和外层函数y=f(u);(2)确定外层函数y=f(u)的零点u=u i(i=1,2,3,⋯,n);(3)确定直线u=u i(i=1,2,3,⋯,n)与内层函数u=g(x)图象的交点个数分别为a1、a2、a3、⋯、a n,则函数y=f[g(x)]的零点个数为a1+a2+a3+⋯+a n.11、(多选题)某市出租车收费标准如下:起步价为8元,起步里程为3km(不超过3km按起步价付费);超过3km 但不超过8km时,超过部分按每千米2.15元收费;超过8km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.下列结论正确的是()A.出租车行驶4km,乘客需付费9.6元B.出租车行驶10km,乘客需付费25.45元C.某人乘出租车行驶5km两次的费用超过他乘出租车行驶10km一次的费用D.某人乘坐一次出租车付费22.6元,则此次出租车行驶了9km答案:BCD分析:根据题意分别计算各个选项的情况,即可得答案.对于A选项:出租车行驶4km,乘客需付费8+1×2.15+1=11.15元,故A错误;对于B选项:出租车行驶10 km,乘客需付费8+2.15×5+2.85×(10-8)+1=25.45元,故B正确;对于C选项:乘出租车行驶5km,乘客需付费8+2×2.15+1=13.30元,乘坐两次需付费26.6元,26.6>25.45,故C正确;对于D选项:设出租车行驶x km时,付费y元,由8+5×2.15+1=19.75<22.6,知x>8,因此由y=8+2.15×5+2.85(x-8)+1=22.6,解得x=9,故D正确.故选:BCD.小提示:本题考查函数模型的应用,解题要点为认真审题,根据题意逐一分析选项即可,属基础题.12、若log2m=log4n,则()A.n=2m B.log9n=log3mC.lnn=2lnm D.log2m=log8(mn)答案:BCD分析:利用对数运算化简已知条件,然后对选项进行分析,从而确定正确选项.依题意log2m=log4n,所以m>0,n>0,log2m=log22n=12log2n=log2n12,所以m=n 12,m2=n,A选项错误.log9n=log32m2=22log3m=log3m,B选项正确.lnn=lnm2=2lnm,C选项正确.log8(mn)=log23m3=33log2m=log2m,D选项正确.故选:BCD13、在平面直角坐标系中,我们把横纵坐标相等的点称之为“完美点”,下列函数的图象中存在完美点的是()A.y=﹣2x B.y=x﹣6C.y=3xD.y=x2﹣3x+4答案:ACD分析:横纵坐标相等的函数即y=x,与y=x有交点即存在完美点,依次计算即可.横纵坐标相等的函数即y=x,与y=x有交点即存在完美点,对于A,{y=xy=−2x,解得{x=0y=0,即存在完美点(0,0),对于B,{y=xy=x−6,无解,即不存在完美点,对于C,{y=xy=3x,解得{x=√3y=√3或{x=−√3y=−√3,即存在完美点(√3,√3),(−√3,−√3)对于D,{y=xy=x2−3x+4,x2−3x+4=x,即x2−4x+4=0,解得x=2,即存在完美点(2,2).故选:ACD.填空题14、化简(√a−1)2+√(1−a)2+√(1−a)33=________.答案:a-1分析:根据根式的性质即可求解.由(√a−1)2知a-1≥0,a≥1.故原式=a-1+|1-a|+1-a=a-1.所以答案是:a-115、对数型函数f(x)的值域为[0,+∞),且在(0,+∞)上单调递增,则满足题意的一个函数解析式为______.答案:f(x)=|log2(x+1)|(答案不唯一,满足f(x)=|log a(x+b)|,a>1,b≥1即可)分析:根据题意可利用对数函数的性质和图像的翻折进行构造函数.∵函数f(x)的值域为[0,+∞),且在(0,+∞)上单调递增,∴满足题意的一个函数是f(x)=|log2(x+1)|.所以答案是:f(x)=|log2(x+1)|(答案不唯一)16、函数y=log a(x+1)-2(a>0且a≠1)的图象恒过点________.答案:(0,-2)分析:由对数函数的图象所过定点求解.解:依题意,x+1=1,即x=0时,y=log a(0+1)-2=0-2=-2,故图象恒过定点(0,-2).所以答案是:(0,-2)解答题17、(1)计算0.027−13−(−16)−2+810.75+(19)0−3−1;(2)若x 12+x−12=√6,求x 2+x −2的值.答案:(1)-5;(2)14.分析:(1)由题意利用分数指数幂的运算法则,计算求得结果. (2)由题意两次利用完全平方公式,计算求得结果. (1)0.027−13−(−16)−2+810.75+(19)0−3−1=0.3﹣1﹣36+33+1−13=103−36+27+1−13=−5.(2)若x 12+x −12=√6,∴x +1x +2=6,x +1x =4,∴x 2+x ﹣2+2=16,∴x 2+x ﹣2=14.18、已知函数f (x )=2x −12x +1.(1)判断并证明f (x )在其定义域上的单调性;(2)若f (k ⋅3x )+f (3x −9x +2)<0对任意x ≥1恒成立,求实数k 的取值范围. 答案:(1)f (x )在R 上单调递增;证明见解析 (2)(−∞,43)分析:(1)设x 2>x 1,可整理得到f (x 2)−f (x 1)=2(2x 2−2x 1)(2x 2+1)(2x 1+1)>0,由此可得结论;(2)利用奇偶性定义可证得f (x )为奇函数,结合单调性可将恒成立的不等式化为k <g (x )=3x −23x −1,由g (x )单调性可求得g (x )≥43,由此可得k 的取值范围.(1)f (x )在R 上单调递增,证明如下: 设x 2>x 1,∴f (x 2)−f (x 1)=2x 2−12x 2+1−2x 1−12x 1+1=(2x 2−1)(2x 1+1)−(2x 2+1)(2x 1−1)(2x 2+1)(2x 1+1)=2(2x 2−2x 1)(2x 2+1)(2x 1+1);∵x 2>x 1,∴2x 2−2x 1>0,又2x 2+1>0,2x 1+1>0,∴f (x 2)−f (x 1)>0, ∴f (x )在R 上单调递增. (2)∵f (−x )=2−x −12−x +1=1−2x1+2x =−f (x ),∴f (x )为R 上的奇函数,由f(k⋅3x)+f(3x−9x+2)<0得:f(k⋅3x)<−f(3x−9x+2)=f(9x−3x−2),由(1)知:f(x)在R上单调递增,∴k⋅3x<9x−3x−2在[1,+∞)上恒成立;当x≥1时,3x≥3,∴k<3x−23x−1在[1,+∞)上恒成立;令g(x)=3x−23x−1,∵y=3x在[1,+∞)上单调递增,y=23x在[1,+∞)上单调递减,∴g(x)在[1,+∞)上单调递增,∴g(x)≥g(1)=3−23−1=43,∴k<43,即实数k的取值范围为(−∞,43).。
指数函数与对数函数练习题(含详解)
指数函数1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为。
2。
指数函数函数性质:函数名称指数函数定义函数且叫做指数函数图象定义域值域过定点图象过定点,即当时,.奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小.对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.2。
对数函数性质:函数名称对数函数定义函数且叫做对数函数图象定义域值域过定点图象过定点,即当时,。
奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限内,从顺时针方向看图象,逐渐增大;在第四象限内,从顺时针方向看图象,逐渐减小。
指数函数习题一、选择题1.定义运算a⊗b=错误!,则函数f(x)=1⊗2x的图象大致为()2.函数f(x)=x2-bx+c满足f(1+x)=f(1-x)且f(0)=3,则f(b x)与f(c x)的大小关系是( )A.f(b x)≤f(c x)B.f(b x)≥f(c x)C.f(b x)>f(c x)D.大小关系随x的不同而不同3.函数y=|2x-1|在区间(k-1,k+1)内不单调,则k的取值范围是()A.(-1,+∞) B.(-∞,1)C.(-1,1) D.(0,2)4.设函数f(x)=ln[(x-1)(2-x)]的定义域是A,函数g(x)=lg(错误!-1)的定义域是B,若A⊆B,则正数a的取值范围( )A.a〉3 B.a≥3C.a〉 5 D.a≥错误!5.已知函数f(x)=错误!若数列{a n}满足a n=f(n)(n∈N*),且{a n}是递增数列,则实数a的取值范围是()A.[错误!,3) B.(错误!,3)C.(2,3) D.(1,3)6.已知a〉0且a≠1,f(x)=x2-a x,当x∈(-1,1)时,均有f(x)<错误!,则实数a的取值范围是( )A.(0,错误!]∪[2,+∞) B.[错误!,1)∪(1,4]C.[错误!,1)∪(1,2] D.(0,错误!)∪[4,+∞)二、填空题7.函数y=a x(a>0,且a≠1)在[1,2]上的最大值比最小值大错误!,则a的值是________.8.若曲线|y|=2x+1与直线y=b没有公共点,则b的取值范围是________.9.(2011·滨州模拟)定义:区间[x1,x2](x1〈x2)的长度为x2-x1。
指数函数对数函数计算题集及答案

指数函数对数函数计算题集及答案1.题目中给出了一些数学计算题和方程,需要计算或解方程。
更多相关资料可以在小T文档交流平台查找。
2.计算lg5·lg8000+(lg232)lg(1/.06)。
3.解方程lg2(x+10)-XXX(x+10)3=4.4.解方程2log6x=1log63.5.解方程9-x-2×31-x=27.6.解方程(1)x=128/8.7.计算(lg2)3(lg5)3log251·log28·10.8.计算(1)lg25+lg2·lg50;(2)(log43+log83)(log32+log92)。
9.求函数y=log0.8(x1)/(2x1)的定义域。
10.已知log1227=a,求log616.11.已知f(x)=a2x/(23x1),g(x)=ax22x5(a>且a≠1),确定x的取值范围,使得f(x)>g(x)。
12.已知函数f(x)=11(3x)/(x221),(1)求函数的定义域;(2)讨论f(x)的奇偶性;(3)求证f(x)>0.13.求关于x的方程ax+1=-x2+2x+2a(a>且a≠1)的实数解的个数。
14.求log927的值。
15.设3a=4b=36,求(2ab+b)/(a+b)的值。
16.解对数方程log2(x-1)+log2x=1.17.解指数方程4x+4-x-2x+2-2-x+2+6=0.18.解指数方程24x+1-17×4x+8=0.19.解指数方程(322)x(322)x22 2.20.解指数方程21x1334-x1=4 1.21.解指数方程4x x2232x x224=0.22.解对数方程log2(x-1)=log2(2x+1)。
23.解对数方程log2(x21)log2(x1)=2.1.剔除格式错误,删除明显有问题的段落,得到以下文章:解对数方程:log16x+log4x+log2x=7解对数方程:log2[1+log3(1+4log3x)]=1解指数方程:6x-3×2x-2×3x+6=0解对数方程:XXX(2x-1)2-XXX(x-3)2=2解对数方程:XXX(y-1)-lgy=lg(2y-2)-XXX(y+2)解对数方程:XXX(x2+1)-2lg(x+3)+lg2=0解对数方程:lg2x+3lgx-4=02.对每段话进行小幅度改写,得到以下文章:1.解对数方程:XXX。
(六)指数 对数 的 运算(答案)

(六)指数对数的运算一.基础知识1.0,0,,a b r s Q >>∈时,r s a a =______; ()r s a =_______; ()r ab =_________3.分数指数幂:=n m a;=-n m a 4.对数的性质和运算法则: 恒等式①=N a alog ;②=N a a log ; ③=a N b b log log ; ④b a log ______a blog 1; ⑤=n a b m log 积、商、幂、方根的对数①=+N M a a log log ;②=-N M a a log log ;③=n a M log5.指数式与对数式互换N b N a a b log =⇔=解决指数问题时常用取对数。
二.练习题:1.(1)若0)](log [log log 432=x ,则x =___________64(2)对于1,0≠>a a ,下列说法中,正确的是 ( B )A.N M N M a a log log ,==则若B.N M N M a a ==则若,log logC.N M N M a a ==则若,log log 22D.22log log ,N M N M a a ==则若(3)已知n m <<1,令)(log log ,log ,)(log 22m c m b m a n n n n ===,则 ( D )A. a<b<cB.a<c<bC.b<a<cD.c<a<b2.求值或化简 (1) 213323121)()1.0()4()41(----⨯b a ab (2) 1.0lg 10lg 5lg 2lg 125lg 8lg ⋅--+ 2(1)425;(2)-4; 3.若32121=+-xx ,求23222323-+-+--x x x x 的值。
3、13; 4.设+∈R z y x ,,,且z y x 643==。
指数、对数、幂基础练习(含答案)

分数指数幂1、用根式的形式表示下列各式)0(>a (1)51a=(2)32a-=2、用分数指数幂的形式表示下列各式: (1)34y x = (2))0(2>=m mm3、求下列各式的值(1)2325= (2)32254-⎛⎫⎪⎝⎭=4、解下列方程 (1)1318x - = (2)151243=-x指数函数1、下列函数是指数函数的是 ( 填序号) (1)xy 4= (2)4x y = (3)xy )4(-= (4)24x y =。
2、函数)1,0(12≠>=-a a ay x 的图象必过定点 。
3、若指数函数xa y )12(+=在R 上是增函数,求实数a 的取值范围 。
4、如果指数函数xa x f )1()(-=是R 上的单调减函数,那么a 取值范围是 ( ) A 、2<a B 、2>a C 、21<<a D 、10<<a5、下列关系中,正确的是 ( )A 、5131)21()21(>B 、2.01.022>C 、2.01.022-->D 、115311()()22- - >6、比较下列各组数大小:(1)0.53.1 2.33.1 (2)0.323-⎛⎫⎪⎝⎭0.2423-⎛⎫⎪⎝⎭(3) 2.52.3- 0.10.2-7、函数xx f 10)(=在区间[1-,2]上的最大值为 ,最小值为 。
函数xx f 1.0)(=在区间[1-,2]上的最大值为 ,最小值为 。
8、求满足下列条件的实数x 的范围:(1)82>x (2)2.05<x 9、已知下列不等式,试比较n m ,的大小:(1)n m 22< (2)n m 2.02.0< (3))10(<<<a a an m10、若指数函数)1,0(≠>=a a a y x的图象经过点)2,1(-,求该函数的表达式并指出它的定义域、值域和单调区间。
指数函数对数函数计算题集及答案

指数函数对数函数计算题集及答案指数函数对数函数计算题11、计算:lg 5·lg 8000+06.0lg 61lg )2(lg 23++. 2、解方程:lg 2(x +10)-lg(x +10)3=4.3、解方程:23log 1log 66-=x .4、解方程:9-x -2×31-x =27.5、解方程:x )81(=128. 6、解方程:5x+1=123-x . 7、计算:10log 5log )5(lg )2(lg 2233++·.10log 18 8、计算:(1)lg 25+lg2·lg50; (2)(log 43+log 83)(log 32+log 92).9、求函数121log 8.0--=x x y 的定义域.10、已知log 1227=a,求log 616.11、已知f(x)=1322+-x x a ,g(x)=522-+x x a (a >0且a ≠1),确定x 的取值范围,使得f(x)>g(x).12、已知函数f(x)=321121x x ??+-. (1)求函数的定义域;(2)讨论f(x)的奇偶性;(3)求证f(x)>0.13、求关于x 的方程a x +1=-x 2+2x +2a(a >0且a ≠1)的实数解的个数. 14、求log 927的值.15、设3a =4b =36,求a 2+b1的值. 16、解对数方程:log 2(x -1)+log 2x=117、解指数方程:4x +4-x -2x+2-2-x+2+6=018、解指数方程:24x+1-17×4x +8=019、解指数方程:22)223()223(=-++-x x ±220、解指数方程:01433214111=+?------x x21、解指数方程:042342222=-?--+-+x x x x 22、解对数方程:log 2(x -1)=log 2(2x+1)23、解对数方程:log 2(x 2-5x -2)=224、解对数方程:log 16x+log 4x+log 2x=725、解对数方程:log 2[1+log 3(1+4log 3x)]=126、解指数方程:6x -3×2x -2×3x +6=027、解对数方程:lg(2x -1)2-lg(x -3)2=228、解对数方程:lg(y -1)-lgy=lg(2y -2)-lg(y+2)29、解对数方程:lg(x 2+1)-2lg(x+3)+lg2=030、解对数方程:lg 2x+3lgx -4=0指数函数对数函数计算题1 〈答案〉 1、12、解:原方程为lg 2(x +10)-3lg(x +10)-4=0,∴[lg(x +10)-4][lg(x +10)+1]=0.由lg(x +10)=4,得x +10=10000,∴x=9990.由lg(x +10)=-1,得x +10=0.1,∴x=-9.9.检验知: x=9990和-9.9都是原方程的解.3、解:原方程为36log log 626=x ,∴x 2=2,解得x=2或x=-2. 经检验,x=2是原方程的解, x=-2不合题意,舍去.4、解:原方程为2)3(x --6×3-x -27=0,∴(3-x +3)(3-x -9)=0.。
指数-对数试题及答案

1.已知函数()13log 02 0x x x f x x >⎧⎪=⎨⎪≤⎩,,,若()12f a >,则实数a 的取值范围是( ) A.30 ⎛⎫ ⎪ ⎪⎝⎭, B.(]1 0-, C.31 ⎛⎫- ⎪ ⎪⎝⎭, D.()31 00 ⎛⎫- ⎪ ⎪⎝⎭U ,, 2.函数()()21616log x x f x x -=-的图像大致为( )A .B .C .D .3.函数()()1log 2830,1a y x a a =+->≠且的图象恒过定点A ,若点A 的横坐标为0x ,函数024x xy a -=+的图象恒过定点B ,则B 点的坐标为( )A .()27,3--B .()27,5-C .()3,5-D .()2,5-4.函数()f x 的图象关于y 轴对称,且对任意x R ∈都有()()3f x f x +=-,若当35 22x ⎛⎫∈ ⎪⎝⎭,时,()12xf x ⎛⎫= ⎪⎝⎭,则()2017f =( ) A .14- B .14 C.4- D .4 5.设0.43a =,3log 0.4b =,30.4c =,则 a b c ,,的大小关系为( ) A .a c b >> B .a b c >>C .c a b >>D .c b a >>6.已知0.6122log 5log 313a b c d -====,,,,那么( ) A .a c b d <<< B .a d c b <<< C .a b c d <<< D .a c d b <<< 7.已知函数()f x 是奇函数,当0x >时,()x f x a =(0a >且1a ≠),且12(log 4)3f =-,则a 的值为( ) A . 32 B 3 C. 3 D .9 8.函数y =)21(|x|的图象是( )9.已知函数)(x f y =与函数x e y =互为反函数,函数)(x g y =的图象与函数)(x f y =关于x 轴对称,1)(-=a g ,则实数a 的值( )A.e -B.e 1- C.e 1D.e10.若函数(),()f x g x 分别是R 上的奇函数、偶函数,且满足()()2xf xg x -=,则有( )A.(2)(3)(0)f f g <<B.(0)(3)(2)g f f <<C.(2)(0)(3)f g f <<D.(0)(2)(3)g f f <<11.设实数30.1231log ,2,0.92a b c ===,则a 、b 、c 的大小关系为( )A.a c b <<B.c b a <<C.b a c <<D.a b c <<12.已知函数x x f 5)(=,若3)(=+b a f ,则=⋅)()(b f a f ( ).4 C 13.已知函数x x x f 411212)(+++= 满足条件1))12((log =+a f ,其中1>a ,则=-))12((log a f ( ) A .1 B .2 C .3 D .4 14.若()10x f x =,则()3f =( ) A .3log 10 B .lg 3 C .310 D .103 15.函数)2(log 1)(2-=x x f 的定义域是( ) A.)2,(-∞ B.),2(+∞ C.),3()3,2(+∞Y D.),4()4,2(+∞Y 16.已知()212()x x f x log a a =--的值域为 R ,且()f x在(3,1-上是增函数,则a 的范围是( )A.20a -≤≤B.02a ≤≤C.40a -≤≤D.42a -≤≤-17.函数()12log ,12,1x x x f x x ≥⎧⎪=⎨⎪<⎩的值域为 _________. 18.已知1173a ⎛⎫= ⎪⎝⎭,7log 4b =,用a 、b 表示49log 48为 . 19.若2312a b ==,则21a b += . 20.已知函数()22x x f x -=-,若不等式()()230f x ax a f -++>对任意实数x 恒成立,则实数a 的取值范围是 .21.若函数12(log )x y a =在R 上是减函数,则实数a 取值集合是22.函数212()log (45)f x x x =--的单调递减区间为23.⑴计算:20.52031103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;⑵计算:5log 350.5551log 352log log log 14550+--+.24.已知定义域为R 的函数a bx f x x ++-=+122)(是奇函数.(1)求b a ,的值;(2)判断函数)(x f 的单调性,并用定义证明;(3)当]3,21[∈x 时,0)12()(2>-+x f kx f 恒成立,求实数k 的取值范围.25.(1)已知32121=+-x x ,计算:37122++-+--x x x x ;(2)求232021)5.1()833()96.0()412(--+---.26.不使用计算器,计算下列各题:(1)()20.5312110510.7521627---⎛⎫⎛⎫+-÷+ ⎪ ⎪⎝⎭⎝⎭;(2)()70log 23log lg 25lg 479.8+++-.27.已知()()()22log 1log 1f x x x =--+.(1)求函数()f x 的定义域;(2)判断函数()f x 的奇偶性并证明;(3)求使()0f x >的x 的取值集合.28.已知函22()log (1),()log (31)f x x g x x =+=+数. (1)求出使()()g x f x ≥成立的x 的取值范围; (2)当[0,)x ∈+∞时,求函数()()y g x f x =-的值域.参考答案1.C【解析】 试题分析:由题意,得131log 20x x ⎧>⎪⎨⎪>⎩或1220x x ⎧>⎪⎨⎪≤⎩,解得0a <或10a -<≤,即实数a 的取值范围为 1 ⎛- ⎝⎭,故选C. 考点:分段函数2.A【解析】试题分析:函数的定义域为{}0≠x x ,()()()x f x x f x x -=--=--2log 1616,故函数()x f 为奇函数,其图象关于原点对称,故应排除B 、C ;41521log 16162122121-=⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-f , 341log 16164124141-=⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-f ,由⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛4121f f ,则排除D ;故选A. 考点:函数的图象.3.B【解析】试题分析:当281,27x x +==-时,1log 133a y =-=-,所以点A 0(27,3),27x --=-,这时2724x y a +=+,所以当227,5x y =-=,即B ()27,5-.选B .考点:1.对数函数的图象;2.指数函数的图象.4.A【解析】试题分析:因为函数()f x 对任意x R ∈都有()()3f x f x +=-,所以()()()63f x f x f x +=-+=,函数()f x 是周期为6的函数,()()()2017336611f f f =⨯+=,由()()3f x f x +=-可得()()()2321f f f -+=--=,因为函数()f x 的图象关于y 轴对称,所以函数()f x 是偶函数,()()2112224f f ⎛⎫-=== ⎪⎝⎭,所以()2017f =()1f =()2f --=14-,故选A.考点:1、函数的解析式;2、函数的奇偶性与周期性.5.A【解析】试题分析:由指数函数的性质可得,0.431a =>,300.41c <=<,由对数函数的性质得3log 0.40b =<,所以 a b c ,,的大小关系为a c b >>,故选A.考点:1、指数函数的性质;2、对数函数的性质.6.B【解析】试题分析:由幂函数的性质可知()0.630,1d -=∈,再由对数的运算性质可知2log 50a =-<,而()2log 31,2b =∈,又1c =,综合以上可知a d c b <<<,故选B . 考点:1、对数函数及其性质;2、幂函数及其性质.7.B【解析】 试题分析:因为21221(log 4)(log )(2)34f f f a ==-=-=-,所以23a =,a =0a >,所以a = B.考点:1.函数的奇偶性;2.函数的表示与求值.8.C【解析】试题分析:由函数解析式可知函数为偶函数,当0x ≥时12xy ⎛⎫= ⎪⎝⎭时函数为减函数,所以在0x <时函数为增函数,所以C 图像正确考点:指数函数图像及性质9.D【解析】试题分析:由反函数可知()ln f x x =,函数)(x g y =的图象与函数)(x f y =关于x 轴对称()ln g x x ∴=- ()ln 1g a a a e ∴=-=-∴=考点:函数图像的对称性10.D【解析】试题分析:函数()(),f x g x 分别是R 上的奇函数、偶函数()()()(),f x f x g x g x ∴-=--=,由()()2x f x g x -=得()()()()()()222x x x f x g x f x g x f x g x ------=∴--=∴+=-,解方程组得()()2222,22x x x xf xg x -----==,代入计算()()()2,3,0f f g 比较大小可得()()()023g f f <<考点:函数奇偶性及函数求解析式11.A【解析】 试题分析:()30.1231log 1,21,0.90,12a b c a c b =<=>=∈∴<< 考点:函数性质比较大小12.A【解析】试题分析:()353()()5553a b a b a b f a b f a f b +++=∴=∴⋅===g考点:函数求值13.B【解析】试题分析:xx x f 411212)(+++=Θ x x x f --411212)(+++=-∴ 3411212411212)()(=+++++++=-+∴--x x x x x f x f )12(log )12(log --=+a a Θ3)]12([log )]12([log =-++∴a a f f2)]12([log =-∴a f故答案选B考点:函数求值.14.B【解析】试题分析:由函数的对应关系可得310=x,解之得3lg =x ,应选B.考点:函数概念的本质及对数的运算.15.C【解析】 试题分析:要使函数有意义,需满足()2202log 20x x x ->⎧∴>⎨-≠⎩且3x ≠,所以函数定义域为),3()3,2(+∞Y考点:函数定义域16.B【解析】试题分析:由题设0)(2≥--=a ax x x u 在)31,3(--上恒成立且⎪⎪⎩⎪⎪⎨⎧≥-->≥+=∆0)31(312042u a a a ,解之得20≤≤a .故应选B.考点:二次函数对数函数的图象和性质的综合运用.17.(),2-∞【解析】试题分析:当1x ≥时,1212()log log 10f x x =≤=,此时值域为(],0-∞;当1x <时,10()222x f x <=<=.此时值域为(0,2),故函数的值域为(],0(0,2)-∞U ,即(),2-∞.考点:函数的值域.18.22a b + 【解析】 试题分析:由1173a ⎛⎫= ⎪⎝⎭可以得出7log 3a =,而由7log 4b =可以得到72log 2b =,所以49log 48()7714log 2log 32=+772log 4log 3222b a ++==,即用a 、b 表示49log 48为22a b +,故答案填22a b +. 考点:1、指数式与对数式的互化;2、对数的运算性质.19.1【解析】试题分析:由题意得23log 12,log 12a b ==,则121211log 2,log 3a b ==, 所以()2121212212log 2log 3log 231a b+=+=⨯=. 考点:对数运算及其应用.【方法点晴】此题主要考查指数与对数互化,以及对数运算性质等有关方面的知识与技能,属于中低档题型.在此题的解决过程中,由条件中指数式转化为对数式,即232312log 12,log 12a b a b ==⇒==,利用对数运算的换底公式得121211log 2,log 3a b ==,代入式子得1212212log 2log 3a b+=+,再利用对数的运算性质,从而问题可得解.20.()2 6-,【解析】试题分析:()22x xf x -=-为奇函数且为R 上增函数,所以()()()()()()222230333f x ax a f f x ax a f f x ax a f x ax a -++>⇒-+>-⇒-+>-⇒-+>-对任意实数x 恒成立,即24(3)026a a a ∆=-+<⇒-<<考点:利用函数性质解不等式恒成立【思路点睛】(1)运用函数性质解决问题时,先要正确理解和把握函数相关性质本身的含义及其应用方向.(2)在研究函数性质特别是奇偶性、周期、对称性、单调性、最值、零点时,要注意用好其与条件的相互关系,结合特征进行等价转化研究.如奇偶性可实现自变量正负转化,周期可实现自变量大小转化,单调性可实现去f “”,即将函数值的大小转化自变量大小关系21.),(121 【解析】 试题分析:因为函数12(log )x y a =在R 上是减函数 所以12121log log 1log 1log 021212121<<⇒<<⇒<<a a a 考点:指数函数的单调性;对数函数的单调性.22.()+∞,5【解析】试题分析:由2450x x -->得1x <-或5x >,函数可由()212log ,45f t t t x x ==--复合而成,其中()12log f t t =为减函数,245t x x =--的增区间为()+∞,5,所以函数212()log (45)f x x x =--的单调递减区间为()+∞,5考点:复合函数单调性23.⑴0;⑵5.【解析】试题分析:对问题⑴,根据有理指数幂的运算法则,即可求得代数式20.52031103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值;对问题⑵,根据对数恒等式、对数的运算法则即可求出5log 350.5551log 352log log log 14550+-+的值. 试题解析:⑴原式12238164922162716-⎛⎫⎛⎫=-⨯-⨯⎪ ⎪⎝⎭⎝⎭, 9990488=--=. …………………………6分 ⑵原式()512log 355014log 23=⨯÷++,3135=-+=. ………………………………12分考点:1、指数以及指数式的运算;2、对数以及对数式的运算.24.(1) 2=a ,1=b ;(2)证明见解析;(3) )1,(--∞.【解析】试题分析:(1)寻找关于a,b 的两个方程如).1()1(,0)0(f f f -=-=(2)根据)(x f 的单调性定义证明.(3)由)(x f 单调递减则2121)()(x x x f x f >⇔<且21,x x 满足)(x f 的定义域,将问题转化为关于参数a 的不等式.试题解析:(1)∵)(x f 在定义域为R 是奇函数.所以0)0(=f ,即021=++-ab ,∴1=b . 又由)1()1(f f -=-,即a a +--=++-411121,∴2=a ,检验知,当2=a ,1=b 时,原函数是奇函数.(2)由(1)知121212221)(1++-=+-=+x x x x f ,任取R x x ∈21,,设21x x <,则 )12)(12(22121121)()(21212112++-=+-+=-x x x x x x x f x f ,因为函数x y 2=在R 上是增函数,且21x x <,所以02221<-x x ,又0)12)(12(21>++x x ,∴0)()(12<-x f x f 即)()(12x f x f <,∴函数)(x f 在R 上是减函数.(3)因)(x f 是奇函数,从而不等式0)12()(2>-+x f kx f 等价于)21()12()(2x f x f kx f -=--<,因)(x f 在R 上是减函数,由上式推得x kx 212-<,即对一切]3,21[∈x 有:221xx k -<恒成立, 设x x x x x g 12)1(21)(22⋅-=-=,令]2,31[,1∈=t x t ,则有,2)(2t t t g -=]2,31[∈t ,∴1)1()()(min min -===g t g x g ,∴1-<k ,即k 的取值范围为)1,(--∞.考点:1、函数的奇偶性;2、函数的单调性;3、含参量问题的取值范围.【易错点晴】本题主要考查的是函数的奇偶性、函数的单调性、含参量问题的取值范围,属于难题.对于含参量不等式问题要注意进行灵活变形,转化为)()(x h m x g m <>或的形式,从而max )(x g m > .)(min x h m <或25.(1)4;(2).21 【解析】试题分析:由,32121=+-x x 两边平方得,71=+-x x 再对它两边平方得472=+-x x 代入所求式子中计算.(2)由公式n m n ma a=和n n n b a ab ⋅=)(进行各项的化简. 试题解析:(1)∵92)(122121=++=+--x x xx ,∴71=+-x x ; 同理492)(2221=++=+--xx x x ,∴4722=+-x x ,所以原式437747=+-=. (2)原式21)23()23(21)23()23(123)23()827(1)49(122)32(323221=+-=+--=+--=----⨯--. 考点:1、分式的化简;2、分数指数幂的运算.26.(1)94(2)132【解析】试题分析:(1)利用指数幂的运算法则即可得出;(2)利用对数的运算法则即可得出. 试题解析:(1)原式20.523814279999116364416164⎛⎫⎛⎫⎛⎫=-÷+=-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)原式323100313log 3lg lg 4212lg 4lg 43422=++++=+-++= 考点:指数幂的运算,对数的运算27.(1)()1,1-(2)()f x 为奇函数;证明见解析(3){}|10x x -<<【解析】试题分析:(1)函数()f x 的定义域需满足1010x x +>⎧⎨->⎩解之可得;(2)因为定义域关于原点对称,故由奇函数的定义判断并证明即可;(3)由()0f x >得()()22log 1log 1x x ->+,利用函数的单调性并结合函数的定义域即可求得x 的取值集合. 试题解析:(1)由题可得:1010x x +>⎧⎨->⎩,解得11x -<<,函数()f x 的定义域为()1,1-(2)因为定义域关于原点对称,又()()()()22log 1log 1f x x x f x -=+--=-, 所以()f x 为奇函数;(3)由()0f x >得()()22log 1log 1x x ->+,所以11x x ->+,得0x <,而11x -<<,解得10x -<<,所以使()0f x >的x 的取值集合是{}|10x x -<<.考点:函数的定义域,奇偶性,单调性等有关性质28.(1)[0,)+∞(2)2[0,log 3)【解析】试题分析:(1)将不等式()()g x f x ≥代入后,结合函数2log y x =的单调性可得到关于x 的不等式,进而得到x 的取值范围;(2)将函数式化简22log (3)1y x =-+,通过[0,)x ∈+∞得到对数真数的取值范围,从而得到函数的值域试题解析:(1)∵22log (31)log (1)x x +≥+∴31010311x x x x +>⎧⎪+>⎨⎪+≥+⎩解得:0x ≥∴x 的取值范围为[0,)+∞ --------6分 (2)2222312log (31)log (1)log log (3)11x y x x x x +=+-+==-++ ∵0x ≥ ∴21331x ≤-<+ 又∵2log y x =在(0,)+∞上单调递增 ∴2220log (3)log 31x ≤-<+ ∴函数的值域为2[0,log 3) ---------12分 考点:对数函数单调性解不等式;函数单调性与值域。
(完整版)指数对数计算题含答案,推荐文档

2)2 6 a • b 527 - + - - 2 33 3 3 21.(本小题满分 12 分)2 27 2log 3( )- 2 + (1- 2)0 - ( )3 ;(2) 2 log 2 log 32 log 8 553 8【答案】(1)1;(2)-33 3 32.(满分 12 分)不用计算器计算:(注:只要有正确的转换,都要给步骤分,不能只看结果)(1)log 3+ lg 25 + lg 4 + 7log 7 2 + (-9.8)0(2)( 27 )- 3 8 - ( 49 9 2)0.5 + (0.008) 3 ⨯ 2513 1 【答案】(1) ;(2)293.(12 分) 化简或求值:4 1 - 1 8 1(1) (2 )0 + 2-2 ⨯(2 ) 2 - ( )3 ;5 4 27(2) 2(lg + lg 2 ⋅ lg 5 + 1【答案】(1) ;(2)124.计算(1) log + lg 25 + lg 4 + 7log 7 2+ (-9.8)03 1 1 - 2 (2) - (π - 1)0 -(3 13 ) 3 + ( )3864 【答案】(1)(2) 1625.(本小题满分 10 分) 计算下列各式的值:2 27 2(1) ( )- 2 + (1- 2)0 - ( )3 ;3 8(2) 2 l og 2 - log 32 + log 8 - 5log 5 3【答案】(1)1;(2)-3.6.求值:1) lg 5(lg 8 + lg1000) + (lg 2 3 )2 + lg 1+ lg 0.06 ;62 - 1 1 1 (a3 b - 1) 2)2 a 2 b 327 (lg 2)2 - lg 2 +16 1 43 a 53 a 7 (lg 2)2 - lg 2 + 1 2 32 3( )【答案】1)1;2)1 。
1 -27.(12 分)(1)计算log 2 25• log 3 4 •log 5 9 + lg 0.001 - ( )3(2)⋅ ÷ a 61【答案】(1)-4;(2) a 2。
指数函数对数函数计算题集及答案

指数函数对数函数计算题集及答案1、计算:lg5·lg8000+(lg231)2lglg0.06.62、解方程:lg2(某+10)-lg(某+10)3=4.3、解方程:2log6某1log63.4、解方程:9-某-2某31-某=27.5、解方程:(1)某=128.86、解方程:5某+1=3某1.27、计算:(lg2)3(lg5)3log251·.log210log8108、计算:(1)lg25+lg2·lg50;(2)(log43+log83)(log32+log92).9、求函数ylog0.8某12某1的定义域.10、已知log1227=a,求log616.11、已知f(某)=a2某3某1,g(某)=a某2某5(a>0且a≠1),确定某的取值范围,使得f(某)22>g(某).12、已知函数f(某)=113某.某221(1)求函数的定义域;(2)讨论f(某)的奇偶性;(3)求证f(某)>0.13、求关于某的方程a某+1=-某2+2某+2a(a>0且a≠1)的实数解的个数.14、求log927的值.15、设3a=4b=36,求2+1的值.ab16、解对数方程:log2(某-1)+log2某=117、解指数方程:4某+4-某-2某+2-2-某+2+6=018、解指数方程:24某+1-17某4某+8=019、解指数方程:(322)某(322)某22220、解指数方程:21某1334某1141021、解指数方程:4某某2232某某224022、解对数方程:log2(某-1)=log2(2某+1)23、解对数方程:log2(某2-5某-2)=224、解对数方程:log16某+log4某+log2某=725、解对数方程:log2[1+log3(1+4log3某)]=126、解指数方程:6某-3某2某-2某3某+6=027、解对数方程:lg(2某-1)2-lg(某-3)2=228、解对数方程:lg(y-1)-lgy=lg(2y-2)-lg(y+2)29、解对数方程:lg(某2+1)-2lg(某+3)+lg2=030、解对数方程:lg2某+3lg某-4=01、2、解:原方程为lg2(某+10)-3lg(某+10)-4=0,∴[lg(某+10)-4][lg(某+10)+1]=0.由lg(某+10)=4,得某+10=10000,∴某=9990.由lg(某+10)=-1,得某+10=0.1,∴某=-9.9.检验知:某=9990和-9.9都是原方程的解.3、解:原方程为log6某2log66,∴某2=2,解得某=2或某=-2.3经检验,某=2是原方程的解,某=-2不合题意,舍去.4、解:原方程为(3某)2-6某3-某-27=0,∴(3-某+3)(3-某-9)=0.∵3-某+30,∴由3-某-9=0得3-某=32.故某=-2是原方程的解.5、解:原方程为23某=27,∴-3某=7,故某=-7为原方程的解.36、解:方程两边取常用对数,得:(某+1)lg5=(某2-1)lg3,(某+1)[lg5-(某-1)lg3]=0.∴某+1=0或lg5-(某-1)lg3=0.故原方程的解为某1=-1或某2=1+log35.7、8、(1)1;(2)549、1某,2某10,2函数的定义域应满足:log0.8某10,即log0.8某1,某0,某0,4141解得0<某≤且某≠,即函数的定义域为{某|0<某≤且某≠}.525210、由已知,得a=log1227=log3273a3=,∴log32=2al og31212log32于是log616=log3164log324(3a)==.3alog361log3211、若a>1,则某<2或某>3;若0<a<1,则2<某<312、(1)(-∞,0)∪(0,+∞);(2)是偶函数;(3)略.13、2个14、设log927=某,根据对数的定义有9某=27,即32某=33,∴2某=3,某= 33,即log927=.2215、对已知条件取以6为底的对数,得21=log63,=log62,ab21于是+=log63+log62=log66=1.ab16、某=217、某=018、13某=-或某=2219、某=±120、某=3721、3某=222、某∈φ23、某=-1或某=624、某=1625、某=326、某=127、某=2931或某=81228、y=229、某=-1或某=730、某=10或某=10-42153lg某2lg某62、解对数方程:2log4某+2log某4=53、解对数方程:3log某3+3log27某=44、解对数方程:log7(log3某)=-15、解指数方程:4某+4-某-2某-2-某=06、解指数方程:9某+6某-3某+2-9某2某=07、解指数方程:2某+2-2-某+3=08、解指数方程:2某+1-3某2-某+5=09、解指数方程:5某-1+5某-2+5某-3=15510、解指数方程:26某+3某43某+6=(8某)某11、解指数方程:4某-3·2某+3-432=0.12、解对数方程:lg(6·5某+25·20某)=某+lg2513、解对数方程:log(某-1)(2某2-5某-3)=214、解对数方程:(0.4)lg2某1=(6.25)2-lg某15、解对数方程:2log某325log3某=40016、解对数方程:log2(9-2某)=3-某17、解对数方程:101g某+1=某1g某7418、解对数方程:log2(2某-1)·log2(2某+1-2)=2lg[a(某2a2)]19、解关于某的方程3.lg(某a)20、计算:(1)log622+log63·log62+log63;(2)lg25+2lg8+lg5·lg20+lg22.321、计算:(1)3log(lg21)92+5log25(lg0.52);(2)[(1-log63)2+log62·log618]·log46.222、已知:log23=a,3b=7.求:log4256.23、已知:log89=a,log25=b,求:lg2,lg3,lg5.24、已知:log189=a,18b=5,求:log3645.25、已知:12a=27,求:log616.26、计算:(1)24log23;(2)a1logab3.27、计算:(1)100lg3;(2)251log5274log12583.28、计算:log3142log37log37log318.329、若函数f(某)的定义域是[0,1],分别求函数f(1-2某)和f(某+a)(a>0)的定义域.30、若函数f(某+1)的定义域是[-2,3),求函数f(1+2)的定义域.某1252、某=2或某=163、某=3或某=274、某=735、某=06、某=27、某=-28、某=-19、某=410、某=-1或某=511、某=2+2log2312、32某=log2或某=log25513、某=414、某=10或某=10315、某=916、某=0或某=317、某=10-4或某=1018、某=log25或某=log23419、a<0且a≠-1时,某=0;a>0且a≠11,某=3a;a=0或a=-1或a=时,无解2220、(1)1(2)321、(1)3(2)122、3abaab123、lg2=1b3alg3=lg5=1b1b2(1b)24、log3645=ab2a25、log616=124a3a26、(1)48(2)3b27、(1)3(2)230428、029、{某|0≤某≤1},{某|-a≤某≤1-a}.230、11{某|某<-或某>}321、求函数f(某)=lg(1+某)+lg(1-某)(-1<某<0)的反函数.22、已知实数某,y满足(log4y)2=log1某,求u2某的最大值及其相应的某,y的值.y3、若抛物线y=某2log2a+2某loga2+8位于某轴的上方,求实数a 的取值范围.4、已知函数f(某)=(logab)某2+2(logba)某+8的图象在某轴的上方,求a,b的取值范围.5、已知f(某)=loga|loga某|(0<a<1).解不等式f(某)>0.判断f(某)在(1,+∞)上的单调性,并证明之.6、计算:(3log312)23log32log10.255log59log52.47、解方程2lg(某1)lg(31)lg(31).8、解方程:某lg某2=1000.9、解方程:6(4某-9某)-5某6某=0.10、解方程:某1(lg某7)410lg某1.11、解方程:log某+2(4某+5)-210.log某2(4某5)12、已知12=3,12=2,求8某y12某1某y的值.13、已知2lg某y=lg某+lgy,求某的值.2y14、已知loga(某2+1)+loga(y2+4)=loga8+loga某+logay(a>0,a≠1),求log8(某y)的值.15、已知正实数某,y,z满足3某=4y=6z,(1)求证:11z某1;(2)比较3某,4y,6z的大2y小.116、求7lg20·2lg0.7的值.17、已知函数f(某)=1+log某3,g(某)=2log某2(某>0,且某≠1),比较f(某)与g(某)的大小.18、已知函数f(某)=loga某1(a>0且a≠1),(1)求f(某)的定义域;(2)当a>1时,求证f(某)在[a,+∞)上是增函数.19、根据条件,求实数a的取值范围:(1)log1+a(1-a)<1;(2)|lg(1-a)|>|lg(1+a)|.20、解方程:9某+4某=5·6某.221、解方程:92某-1=4某11-某22、解方程:=9.27某23、解方程:9某-2·3某+1-27=0.某b(a>0,b>0且a≠1).某b(1)求f(某)的定义域;(2)讨论f(某)的奇偶性;(3)讨论f(某)的单调性;(4)求f(某)的反函数f-1(某).24、已知函数f(某)=loga25、已知函数f(某)=log1(某22某).2(1)求它的单调区间;(2)求f(某)为增函数时的反函数.26、已知函数f(某)=a某12满足f(lga)=10,求实数a的值.27、解关于某的方程:lg(a某-1)-lg(某-3)=128、解方程:log0.5某2-log0.5某3某2=logo.5某34.29、解方程:(某)log5某15.30、解方程:3·16某+36某=2·81某.1、3f-1(某)=-110某(lg<某<0)42、考虑log4111某=log42y-log4y,当某=,y=时,uma某=2.242y3、log2a0,由可得2<a<+∞2(2loga2)4log2a80,4、a>1,b>a或0<a<1,0<b<a.5、(1)a<某<1且某≠1;(2)f(某)在(1,+∞)上是减函数.a6、2147、lg(某1)2lg[(31)(31)],某-1>0,∴某>1(某-1)2=3-1,∴某=1+28、解:原方程为(lg某+2)lg某=3,∴lg2某+2lg某-3=0,设y=lg 某,则有y2+2y-3=0,∴y1=1,y2=-3.由lg某=1,得某=10,由lg某=-3,得某=经检验,某=10和某=1都是原方程的解.10001.10009、某=-110、某=10或某=0.000111、某=112、4313、3+2214、利用运算法则,得(某y-2)2+(2某-y)2=01∴log(某y)=315、(1)略;(2)3某<4y<6z16、令所求式为t,两边取对数,得原式=1417、444当0<某<1或某>时,f(某)>g(某);当1<某<时,f(某)<g(某);当某=时,f(某)=g(某).33318、(1)当0<a<1时,0<某≤a;当a>1时,某≥a.(2)设a≤某1≤某2,则f(某1)-f(某2)=loga某11loga某21loga=某1某2loga某11loga某21<0.19、(1)-1<a<0或0<a<1;(2)0<a<120、3方程即为2·32某-5·3某·2某+2·22某=0,即223令y=,方程又化为2y2-5y+2=0,2解得y1=2,y2=某2某3520.2某1,于是便可得某1=log32,某2=-log32.22221、19由题意可得=9,∴2某=log99,故某=log99.22222某22、方程即为3-3某=32-2某,∴-3某=2-2某,故某=-2.23、令y=3某>0,则原方程可化为y2-6y-27=0,由此得y=9(另一解y=-3舍去).从而由3某=9解得某=2.24、(1)(-∞,-b)∪(b,+∞);(2)奇函数;(3)当0<a<1时,f(某)在(-∞,-b)和(b,+∞)上是增函数;当a>1时,f(某)在(-∞,-b)和(b,+∞)上是减函数;(4)略。
对数与指数函数练习题及解析

对数与指数函数练习题及解析题目:对数与指数函数练习题及解析正文:本文将为读者提供一些对数与指数函数的练习题,并给出详细的解析过程,帮助读者更好地掌握这一部分知识。
练习题一:计算下列对数值:1. log2(8)2. log5(25)3. ln(e)4. log9(81)解析:1. log2(8) = log(8)/log(2) = 32. log5(25) = log(25)/log(5) = 23. ln(e) = 14. log9(81) = log(81)/log(9) = 2练习题二:求解下列指数方程:1. 2^x = 162. 3^(2x-1) = 273. e^x = 10解析:1. 2^x = 16,可以写成2^x = 2^4,由指数对数关系可得x = 42. 3^(2x-1) = 27,可以写成3^(2x-1) = 3^3,由指数对数关系可得2x-1 = 3,解得x = 23. e^x = 10,可以写成e^x = e^ln(10),由指数对数关系可得x = ln(10)练习题三:计算下列对数方程的解:1. log2(x) = 32. log5(x) = -1解析:1. log2(x) = 3,可以写成2^3 = x,解得x = 82. log5(x) = -1,可以写成5^(-1) = x,解得x = 1/5练习题四:给定函数f(x) = log2(x),求解f(x)的图像在x轴上的截距点。
解析:对于f(x) = log2(x),当x = 2^0 = 1时,f(x) = log2(1) = 0,因此f(x)的图像在x轴上的截距点为(1, 0)。
练习题五:给定函数f(x) = e^x,求解f(x)的图像在y轴上的截距点。
解析:对于f(x) = e^x,当x = 0时,f(x) = e^0 = 1,因此f(x)的图像在y轴上的截距点为(0, 1)。
通过以上练习题及解析,读者可以加深对数与指数函数的理解,并在解题过程中掌握相关的计算方法和技巧。
指数函数对数函数专练习题(含答案)

指数函数及其性质1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为.对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.对图象的影响在第一象限内,从顺时针方向看图象,逐渐在第四象限内,从顺时针方向看图象,逐渐指数函数习题一、选择题1.定义运算a ⊗b =⎩⎪⎨⎪⎧aa ≤b b a >b,则函数f (x )=1⊗2x的图象大致为( )2.函数f (x )=x 2-bx +c 满足f (1+x )=f (1-x )且f (0)=3,则f (b x )与f (c x)的大小关系是( )A .f (b x )≤f (c x)B .f (b x )≥f (c x)C .f (b x )>f (c x)D .大小关系随x 的不同而不同3.函数y =|2x-1|在区间(k -1,k +1)内不单调,则k 的取值范围是( ) A .(-1,+∞) B .(-∞,1) C .(-1,1) D .(0,2)4.设函数f (x )=ln[(x -1)(2-x )]的定义域是A ,函数g (x )=lg(a x -2x-1)的定义域是B ,若A ⊆B ,则正数a 的取值范围( ) A .a >3 B .a ≥3 C .a > 5D .a ≥ 55.已知函数f (x )=⎩⎪⎨⎪⎧3-a x -3,x ≤7,a x -6,x >7.若数列{a n }满足a n =f (n )(n ∈N *),且{a n }是递增数列,则实数a 的取值范围是( ) A .[94,3)B .(94,3)C .(2,3)D .(1,3)6.已知a >0且a ≠1,f (x )=x 2-a x,当x ∈(-1,1)时,均有f (x )<12,则实数a 的取值范围是( )A .(0,12]∪[2,+∞)B .[14,1)∪(1,4]C .[12,1)∪(1,2]D .(0,14)∪[4,+∞)二、填空题7.函数y =a x(a >0,且a ≠1)在[1,2]上的最大值比最小值大a2,则a 的值是________.8.若曲线|y |=2x+1与直线y =b 没有公共点,则b 的取值范围是________.9.(2011·滨州模拟)定义:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的定义域为[a ,b ],值域为[1,2],则区间[a ,b ]的长度的最大值与最小值的差为________.三、解答题 10.求函数y =2342x x ---+的定义域、值域和单调区间.11.(2011·银川模拟)若函数y =a 2x +2a x-1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x的定义域为[0,1]. (1)求a 的值;(2)若函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.1.解析:由a ⊗b =⎩⎪⎨⎪⎧aa ≤b ba >b得f (x )=1⊗2x=⎩⎪⎨⎪⎧2xx ≤0,1x >0.答案:A2. 解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2. 又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增.若x ≥0,则3x ≥2x ≥1,∴f (3x )≥f (2x).若x <0,则3x <2x <1,∴f (3x )>f (2x).∴f (3x )≥f (2x). 答案:A3.解析:由于函数y =|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k -1,k +1)内不单调,所以有k -1<0<k +1,解得-1<k <1. 答案:C4. 解析:由题意得:A =(1,2),a x -2x >1且a >2,由A ⊆B 知a x -2x>1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,则u ′(x )=a x ln a -2x ln2>0,所以函数u (x )在(1,2)上单调递增,则u (x )>u (1)=a -3,即a ≥3. 答案:B5. 解析:数列{a n }满足a n =f (n )(n ∈N *),则函数f (n )为增函数,注意a 8-6>(3-a )×7-3,所以⎩⎪⎨⎪⎧a >13-a >0a 8-6>3-a ×7-3,解得2<a <3.答案:C6. 解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,当a >1时,必有a -1≥12,即1<a ≤2,当0<a <1时,必有a ≥12,即12≤a <1,综上,12≤a <1或1<a ≤2.答案:C7. 解析:当a >1时,y =a x 在[1,2]上单调递增,故a 2-a =a 2,得a =32.当0<a <1时,y =ax在[1,2]上单调递减,故a -a 2=a 2,得a =12.故a =12或32.答案:12或328. 解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.曲线|y |=2x+1与直线y =b 的图象如图所示,由图象可得:如果|y |=2x+1与直线y =b 没有公共点,则b 应满足的条件是b ∈[-1,1]. 答案:[-1,1]9. 解析:如图满足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110. 解:要使函数有意义,则只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1. ∴函数的定义域为{x |-4≤x ≤1}.令t =-x 2-3x +4,则t =-x 2-3x +4=-(x +32)2+254,∴当-4≤x ≤1时,t max =254,此时x =-32,t min =0,此时x =-4或x =1.∴0≤t ≤254.∴0≤-x 2-3x +4≤52.∴函数y =2341()2x x --+[28,1]. 由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知,当-4≤x ≤-32时,t 是增函数,当-32≤x ≤1时,t 是减函数.根据复合函数的单调性知:y =2341()2x x --+[-4,-32]上是减函数,在[-32,1]上是增函数.∴函数的单调增区间是[-32,1],单调减区间是[-4,-32].11. 解:令a x=t ,∴t >0,则y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x ∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去). ②若0<a <1,∵x ∈[-1,1],∴t =a x∈[a ,1a ],故当t =1a,即x =-1时,y max =(1a+1)2-2=14.∴a =13或-15(舍去).综上可得a =3或13.12. 解:法一:(1)由已知得3a +2=18⇒3a=2⇒a =log 32.(2)此时g (x )=λ·2x -4x, 设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,所以g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立.由于2x 2+2x 1>20+20=2,所以实数λ的取值范围是λ≤2. 法二:(1)同法一.(2)此时g (x )=λ·2x -4x,因为g (x )在区间[0,1]上是单调减函数,所以有g ′(x )=λln2·2x -ln4·4x =ln2[-2·(2x )2+λ·2x]≤0成立.设2x =u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立. 因为u ∈[1,2],只需λ≤2u 恒成立, 所以实数λ的取值范围是λ≤2.对数与对数函数同步练习一、选择题1、已知32a =,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+ D 、 23a a -2、2log (2)log log a a a M N M N -=+,则NM的值为( ) A 、41B 、4C 、1D 、4或13、已知221,0,0x y x y +=>>,且1log (1),log ,log 1y a a a x m n x+==-则等于( )A 、m n +B 、m n -C 、()12m n + D 、()12m n - 4、如果方程2lg (lg5lg 7)lg lg5lg 70x x +++=g的两根是,αβ,则αβg 的值是( )A 、lg5lg 7gB 、lg35C 、35D 、3515、已知732log [log (log )]0x =,那么12x -等于( )A 、13 B C D 6、函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( ) A 、x 轴对称 B 、y 轴对称 C 、原点对称 D 、直线y x =对称7、函数(21)log x y -= )A 、()2,11,3⎛⎫+∞ ⎪⎝⎭UB 、()1,11,2⎛⎫+∞ ⎪⎝⎭UC 、2,3⎛⎫+∞ ⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是( )A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞ 9、若log 9log 90m n <<,那么,m n 满足的条件是( )A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<<10、2log 13a <,则a 的取值范围是( )A 、()20,1,3⎛⎫+∞ ⎪⎝⎭UB 、2,3⎛⎫+∞ ⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭U11、下列函数中,在()0,2上为增函数的是( )A 、12log (1)y x =+ B 、2log y =C 、21log y x = D 、2log (45)y x x =-+12、已知()log x+1 (01)a g x a a =>≠且在()10-,上有()0g x >,则1()x f x a +=是( )A 、在(),0-∞上是增加的B 、在(),0-∞上是减少的C 、在(),1-∞-上是增加的D 、在(),0-∞上是减少的 二、填空题13、若2log 2,log 3,m n a a m n a +=== 。
10指数函数和对数函数(经典题型+答案)

第十讲 指数函数和对数函数指数函数定义:函数 )10(≠>=a a a y x且 叫做指数函数,其中x 是自变量,函数的定义域是R 。
a =0时,若x >0,a x =0;若x <0,则a x 无意义 a =1时,y =1x =1(常量)没有研究必要。
为了避免上述各种情况,所以规定a >0且a ≠1。
指数函数的图象1.2x y =2.1()2x y = a a>1 0<a<1定义域 RR 值 域0>y10010<<<>>y x y x 时,时,0>y10100><<<>y x y x 时,时,定点 过点(0,1) 过点(0,1) 单调性单调递增单调递减例1:求下列函数的定义域和值域(1).xa y -=1 (2).31)21(+=x y解:1.要使函数有意义,必须 2.要使函数有意义,必须 10x a -≥ 1x a ≤ 30x +≠ 即 3x ≠-当1a >时 0≤x ∵103x ≠+当01a <<时 0x ≥ ∴10311()()122x y +=≠=∵0x a > ∴011xa ≤-< 又∵0y >∴值域为01y ≤< ∴值域为 0y >且1y ≠ 例2:已知函数 112x y -⎛⎫= ⎪⎝⎭求定义域、值域,并作出其图象。
解:⎪⎩⎪⎨⎧<≥⎪⎭⎫ ⎝⎛=--1,21,2111x x y x x 定义域:x ∈R 值域:10≤<y定理:函数x a y =和x a y -= )10(≠>a a 且的图象关于y 轴对称。
例3:求作xy 2=与xy 3=, x y ⎪⎭⎫ ⎝⎛=21与xy ⎪⎭⎫⎝⎛=31图象关系并y 1 ..o 1 x推广 。
例4 比较下列两个值的大小:(1).5331-⎪⎫⎛和234- (2). 2-π和214.3- (3).2131-⎪⎫ ⎛和2123-⎪⎫ ⎛对数函数的定义:函数 x y a log = )10(≠>a a 且叫做对数函数;它是指数函数a y =)10(≠>a a 且的反函数。
专题25:指数、对数的运算专项练习(解析版)

专题25:指数、对数的运算专项练习(解析版)一、解答题 1.化简下列各式. (1211113322a b ---;(2)111222m m mm--+++;(3)10.5233277(0.027)21259-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭.【答案】(1)1a;(2)1122m m -+;(3)0.09. 【分析】(1)利用指数幂的运算性质即可求解; (2)根据完全平方关系即可求解; (3)利用指数幂的运算性质即可求解. 【详解】(1)原式21111()11111532322132623615661ab a baba aa b⨯-----+--⋅====; (2)2112211122111122222m m m m m m m m m m -----⎛⎫+ ⎪++⎝⎭==+++ (3)10.5233277(0.027)21259-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭255=0.0933++-2.计算:(1)2(lg 2)lg 2lg 5lg 5+⨯+;(2)210231(27)3(2)2-⎛⎫--⨯+- ⎪⎝⎭.【答案】(1)1;(2)0. 【分析】(1)根据对数的运算性质计算可得结果; (2)根据指数幂的运算性质可得结果. 【详解】(1)2(lg 2)lg 2lg 5lg 5+⨯+lg 2(lg 2lg5)+lg5=+lg 2lg(25)+lg5=⨯⨯ lg 2+lg5= lg10=1=.(2)()()21023127322-⎛⎫--⨯+- ⎪⎝⎭2133141()2=--⨯+ 3434=--+ 0=.3.(1)化简:3232324b b a a a b -⎛⎫⎛⎫⎛⎫÷⨯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. (2)计算:56512log 5log 24log 4lg 20lg50⎛⎫⨯+-- ⎪⎝⎭.【答案】(1)432b a-;(2)1-.【分析】(1)根据指数幂的运算法则,直接计算,即可得出结果; (2)根据对数的运算法则,直接计算,即可得出结果. 【详解】(1)原式323663816b b b a a a ⎛⎫=÷⨯- ⎪⎝⎭ 363623168b a b a b a ⎛⎫=⨯⨯- ⎪⎝⎭432b a=-;(2)原式65512log 5log 24log (lg 20lg 50)4⎛⎫=⨯+-+ ⎪⎝⎭652log 5log 6lg1000=⨯-23=-1=-.4.求下列各式x 的取值范围. (1)(1)log (2)x x -+; (2)(3)log (3)x x ++.【答案】(1){x |x > 1且x ≠2};(2){x |x >﹣3且x ≠﹣2}. 【分析】(1)根据对数的定义进行求解即可; (2)根据对数的定义进行求解即可 【详解】(1)由题意可得:201011x x x +>⎧⎪->⎨⎪-≠⎩,解得x > 1且x ≠2;∴x 的取值范围是{x |x > 1且x ≠2}; (2)由题意可知:3031x x +>⎧⎨+≠⎩,解得x >﹣3且x ≠﹣2;∴x 的取值范围是{x |x >﹣3且x ≠﹣2}.5.(1)求值:2130228(6.25)()(1.5)27π-⎛⎫----+ ⎪⎝⎭;(2)解不等式:1263177xx-⎛⎫< ⎪⎝⎭.【答案】(1)32;(2){}x x >4. 【分析】(1)利用分数指数幂的运算性质求解即可; (2)由指数函数的单调性解不等式【详解】解:(1)原式12223258314272-⎛⎫⎛⎫⎛⎫=--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭22522312332⎛⎫⎛⎫=--+= ⎪ ⎪⎝⎭⎝⎭; (2)原不等式可化为:361277x x -<,由函数7xy =在R 上单调递增可得3612x x <-,解得4x >;故原不等式的解集为{}x x >4. 6.计算下列各式的值:(1)0113410.064167-⎛⎫-+ ⎪⎝⎭;(2)2ln 2145log 2lg 4lg82e +++. 【答案】(1)52-;(2)92.【分析】(1)根据指数幂的运算法则,直接计算,即可得出结果; (2)根据对数的运算性质,逐步计算,即可得出结果. 【详解】 (1)()011114334431550.064160.422147221⎛⎫-⨯⨯- ⎪⎝⎭⎛⎫-+ ⎪⎝⎭=-+=-+-=-;(2)22ln 22ln 41245log 2lg 4lg log 22lg 2lg 5lg882e e -+++=++-+ 177794lg 2lg53lg 24lg 2lg5lg10122222=-++-+=++=+=+=.7.计算: (1)5122log 231354-⎛⎫+ ⎪⎝⎭;(2)()()226666log 3log 2log 9log 2++⋅+ 【答案】(1)9;(2)32. 【分析】(1)由根式与指数幂的运算,以及对数运算性质,逐步计算,即可得出结果; (2)由对数运算法则,逐步计算,即可得出结果. 【详解】(1)原式24133243322929=++⨯--==; (2)原式()()2266661log 3log 22log 3log 22=++⋅+()226611log 3log 231222=++=+=. 8.计算:(1)2lg25lg2lg50(lg2)++;(2)2ln33(0.125)e-++.【答案】(1)2;(2)11. 【分析】(1)根据对数的运算法则,逐步计算,即可得出结果;(2)根据指数幂的运算法则,以及对数的运算法则,直接计算,即可得出结果. 【详解】(1)原式()()22lg5lg 2lg100lg 2lg 2=+⨯-+()()22lg5lg 22lg 2lg 2=+⨯-+()2lg5lg2=⨯+2lg10=2=.(2)原式()1223235=3log 50.5-⎡⎤++⎣⎦()252=3log 50.512-++ ()21=342--++2=342++=11.9.求值:(1)()92log 4lg 2lg 20lg53+⨯+;(2)()60.25π38-+.【答案】(1)3;(2)107. 【分析】(1)利用对数的运算以及换底公式求解即可;(2)利用指数的运算法则求解即可. 【详解】(1)()92log 4lg 2lg 2lg5lg53+⋅++()lg2lg2lg5lg52=+++lg 2lg52=++3=.(2)()60.25π38-+136644122=+⨯-⨯321322=+⨯-11082=+-107=.10.计算:(1)1111010.253342727(0.081)[3()][81()]100.02788------⨯⨯+-⨯;(2)已知x +y =12,xy =9,且x <y ,求11221122x y x y+-.【答案】(1)0;(2). 【分析】(1)直接利用指数的运算性质求解即可;(2)由原式=.【详解】(1)原式11442112101[(0.3)]()100.33033333--=-+-⨯=--=.(2)原式====11.不用计算器,计算: (1)927log 32log 128(2)23463log 3log 4log 5log 64⋅⋅⋅⋯⋅ 【答案】(1)1514;(2)6. 【分析】根据对数的运算性质可得答案. 【详解】(1)235393727335log 2log 2log 321527log 128log 214log 23===. (2)23463log 3log 4log 5log 64⋅⋅⋅⋯⋅131415lg 64lg 646lg 26lg 21314lg 63lg 2lg 2g g g g g =⋅⋅⋅⋯⋅===. 12.计算:(1)75223log (42)log 3log 4⨯+⋅. (2)若33lg 2lg 53lg 2lg5a b +=++⋅,求333ab a b ++. 【答案】(1)2215;(2)1. 【分析】(1)根据对数的运算法则及性质计算可得;(2)根据对数的运算法则求出+a b ,再根据乘法公式计算可得; 【详解】解:(1)原式=75223log (42)log 3log 4⨯+⋅214552223log 2log 2lg10log 3log 4=+++⋅2223214log 25log 2lg102log 3log 25=+++⋅2214522155=+++=,(2)22(lg 2lg5)(lg 2lg 2lg5lg 5)3lg 2lg5a b +=+-++22lg 22lg 2lg5lg 5=++()2lg 2lg51=+=即1a b +=33223()()3a b ab a b a ab b ab ∴++=+-++=()21a b +=。
对数、指数的运算练习及答案

高一对数的运算公式,幂的运算公式.1.幂的有关概念:(1)正整数指数幂:na = (*n N ∈). (2)零指数幂: 01(a a =≠ ). (3)负整数指数幂:p a -= *(0,)a p N ≠∈.(4)正分数指数幂:m n a = *(0,,n 1)a m N n >∈>且 (5)负分数指数幂:m na-= *(0,,n 1)a m N n >∈>且(6)0的正分数指数幂等于0,0的负分数指数幂没有意义. 2.根式:(1)如果一个数的n 次方等于a ()*1n n N >∈且,那么这个数叫做a 的n 次方根.(2)0的任何次方根都是0,0=.(3),n 叫做根指数,a 叫做被开方数.(4)n= .(5)当n 为奇数时= . (6)当n 为偶数时, = = .3.指数幂的运算法则:(1)rsa a ⋅= (0,,)a r s R >∈. (2)rs a a= (0,,)a r s R >∈.(3)()rab = (0,0,)a b r R >>∈. (4)()sra= (0,,)a r s R >∈.二.对数1.对数的定义:如果(0ba N a =>≠且a 1),那么数b 叫做以a 为底N 的对数,记作 ,其中a 叫做 , 叫做真数.2.对数的运算法则:若0a >≠且a 1,0,0M N >>,那么(1)MN a log = . (2)MNa log = . (3)nM a log = . 3.特殊对数:(1)1a log = ; (2)a a log = . (其中0a >≠且a 1) 4.对数的换底公式及对数恒等式(1)Naa log = (对数恒等式). (2)NN a=b a b log log log (换底公式);(3)1b a=a b log log ; m N =n a log (换底公式的推论)【基础练习】1.对于0,1a a >≠,下列说法中,正确的是( ) C (1)若M=N,则log log a a M N =; (2)若log log a a M N =,则M=N; (3)若22log log a a M N =,则M=N; (4)若M=N,则22log log a a M N =.A.(1)(3)B.(2)(4)C.(2)D. (1)(2)(3)(4) 2.若0,1a a >≠,且x>0,y>0,x>y,则下列式子中正确的个数有( ) A (1)()log log log a a a x y x y ⋅=+;(2)()log log log a a a x y x y -=+; (3)log log log a a a x x y y ⎛⎫=÷⎪⎝⎭;(4)()log log log a a a xy x y =⋅ A.0个 B.1个 C.2个 D.3个3.下列各式中成立的一项是( ) DA.7177n n m m ⎛⎫= ⎪⎝⎭B.()34x y =+=4.= . 21a 【典例分析】题型一:指数幂的运算例1. 化简下列各式:(1) 1.5230.027-⎛⎫ ⎪⎝⎭100027(2)12133113344x y z x y z ---⎛⎫⎛⎫⋅⋅⋅⋅⋅ ⎪ ⎪⎝⎭⎝⎭ 2xz-12a-变式训练1⎛⎝251212a-例2 . 化简132111333311111x x x xx x x x-+-+-+++-13x-变式训练2:化简(1)()()()()33334411a a a a a a a a----⎡⎤+-÷++-⎣⎦1a a-+ (2)()111221x x x x--⎛⎫++-⎪⎝⎭3322x x--题型二:对数式的运算例3.计算(log3123)2-3log23-+log0.2514+9log23l o g92变式训练3: 化简或求值:(1)()266661log3log2log18log4⎡⎤-+⋅÷⎣⎦ 1(2) 4例4.已知18log 9,185b a ==,求36log 25(用a,b 表示).22ba-.变式训练4:设603,605,a b ==试求12(1)12a b b ---的值. 2题型三:综合应用例5.若正整数m 满足-151210210m m <<,则 m= ()lg20.3010≈. 155变式训练5:(1)已知35abc ==,且112a b+=,则c 的值为( ) B(2)方程的111122log (95)log 32x x ---=-解是 . 3log 15【当堂检测】1. 求值:()222lg 5lg8lg 5lg 20lg 23++⋅+ 32.111133420,0)a b a b a b ->>⎛⎫ ⎪⎝⎭1ab -3.已知11225x x-+=,求21x x+的值. 234. 求值:((2log 2 -1【自我检测】(C 级) 1.设137x=则( ) AA.-2<x<-1B. -3<x<-2C. -1<x<0D. 0<x<1(C 级) 2. 已知2log 3,37b a ==,求log (用a,b 表示)()22a aba b +++(B 级) 3.已知0<x<1,且235log log log x y z ==,则将111352,,x y z 按从小到大的顺序排列为 15z ,12x ,13y(C 级) 4. 求值:()2lg 5lg 50lg 2+⋅ 1(C 级) 5. 求值:()()3948log 2log 2log 3log 3+⋅+ 54(B 级)6.已知函数()xxf x a a -=+(0,1a a >≠),且f(1)=3,则f(0)+f(1)+f(2)的值是 .12(B 级)7.设函数()log a f x x = (0,1a a >≠)且,若122007()8f x x x ⋅⋅= ,则222122007()()()f x f x f x +++ 的值等于( )A.4B.8C.16D.2log 8a c(A 级)8.若1928,93x y y x +-==则x+y= ( )A.18B.24C.27D.21 c9. (2011·重庆高考文科)设11332124a log ,b log ,c log ,233===则c b a ,,的大小关系是( )(A) c b a << (B) a b c << (C) c a b << (D) a c b <<10.(2011·四川高考理科)计算121(lg lg 25)1004--÷= .。
