自贡市富顺县2017-2018年八年级下六校联考第一次段考试卷含答案
四川省自贡市富顺县下学期八年级(新.)

2017-2018学年度下学期富顺县直属中学六校联考第一次段考八 年 级 数 学 科 试 卷说明:试卷来源于富顺县六所直属中学联考一 重新制版:郑宗平一.选择题(本大题共8个小题,每小题3分,共30分) 1.A. a =-24a b =2.在△ABC 90,周长为长分别是 A. 5,4,13,12,5 C.10,8,6 D. 26,24,10 3.化简)x0的结果是( )A.y 2x -y C. 2x y - D. y -4.( )2=B. 2=x 1=-=5. 已知直角三角形中30°角所对的直角边长是cm ,则另一条直角边的长是 ( )m C.,90AC =8.如图,分别以直角⊿ABC 的三边AB,BC,CA 为直径向外作半 圆.设直线AB 左边的阴影部分的面积为1S ,右边的阴影部分的面 积和为2S 则 ( )A.=12S SB.12S S ≥ C 12S S ≤ D.12S S >9. )A. 4±11.12.三) 90,CD ⊥23.小明将一副三角板按如图所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长;若已知CD 2=,求AC 的长?90 ,AC24.在一次“探究性学习”课中,老师设计了如下数表:C2017 – 2018下学期富顺县六校联考一八年级数学 参考答案一.选择题(本大题共10个小题,每小题3分,共30分)10题辅助线示意图:二三.解答题(本题有5个小题,17 – 20题每题5分,21题6.)17. 7- ;18. -; 19. 0 ;; 21.化简结果:2a 6a +;计算结果:3。
四.解答题(本题有4个小题,22、 23题每题6分,24、25题每题7分,共26分.) 22.(1).90,AC (2).∴=CD 12 .23.∴632=x∴24.略解:连接BD (见图)∵CD CP ⊥,CD PC 2== ∴⊿PCD 为等腰直角三角形. ∴∠=CPD 45 .∵∠+∠=∠+∠=ACP BCP BCP BCD 90 ∴∠=∠ACP BCD ∵=CA CB∴⊿CAP ≌⊿CBD (SAS ) ∴==DB PA 3在Rt ⊿CPD 中,82222222=+=+=CD CP DP .又∵,==2PB 1DP 8∴918222=+=+=PB DP DB .∴∠=DPB 90∴∠=∠+∠=+=CPB CPD DPB 4390551 .25.略解:⑴.a = 2n 1-, b = 2n , c = 2n 1+ ; ⑵.答:以,,a b c 为边的三角形是直角三角形.证明:∵a = 2n 1-, b = 2n , c = 2n 1+∴()()()+=-+=-++=+=22222242222a b n 12n n 2n 14n n 1c ,∴ 以,,a b c 为边的三角形是直角三角形.说明:以上答案仅供参考!2018.4.7A。
四川省自贡市2017-2018学年八年级下学期半期考试语文试题

八年级下册半期语文试题一、(20分)1.用行楷书写下面的句子。
(2分)关河梦断何处?尘暗旧貂裘。
2.选出加点字的注音和词语解释有误的一项是()(2分)A 忸怩..不安(niŭ ní):形容不好意思或不大方的样子。
B 喋喋..不休(dié):形容说话没完没了。
C 情郁.于中(yŭ):感情忧郁在心中。
D觥.筹交错(gōng):形容宴饮尽欢的样子。
3.填入下面横线上的句子,排列恰当的一项是(2分)从大门通向公园深处,尽植芙蓉。
___饱赏着多姿多彩的芙蓉花,我不禁联想到:芙蓉花傲霜而开,体现的正是她敢于抗争的勇气;而不吝美艳,彰显的则是她无私奉献的精神。
①远远望去,似绿云接天,如彩练当空。
②置身花丛,但见“大红芙蓉”花大质丽,灼灼照人,时而薄雾笼罩,若隐若现,犹如戴上面纱的少女,别有一番情致。
③只见坡上坡下,花连花,树挨树,层层叠叠,红绿交替,使人仿佛身临千年前那遍植芙蓉、高下相照的古“锦城”。
④当秋阳普照,寒霜下的“醉芙蓉”闪闪烁烁,似朗星点点,色泽由白色渐渐变成粉成,进而转为大红,奇趣无穷。
A.③①④② B.④③①② C.②④①③ D.①③②④4.下列搭配正确的是(2分)A.《大堰河——我的保姆》——长篇叙事诗——艾青B.《细柳营》——《史记》——东汉——司马光C.《桃花源记》——《陶渊明集》——东晋——陶渊明D.《长相思》——《纳兰词》——元——纳兰性德5.概括下面语段内容。
(不超过18个字)(2分)4月18日至19日,自贡大安区教育局和区公安分局联合举办首次学校保安集中业务培训,全区各学校幼儿园分管安全的领导和保安人员120余人参加培训。
本次培训是加强全区学校幼儿园安全工作的一个组成部分,培训采取理论与实践相结合的方式进行,安排了校园治安保卫工作尝试、危机处置应对程序和安保器械设备设施实践操作等内容,使培训活动针对性和实效性强。
参加本次培训的都是经过各学校推荐、筛选上来的校园分管干部和得力保安人员。
【全国市级联考】四川省自贡市2017-2018学年下学期八年级期末统一考试数学试题(解析版)

自贡市2017-2018学年下学期八年级期末统考数学试题一、选择题(本题有8个小题,每小题3分,满分24分,每小题只有一个选项符合题意)1. 与可以合并的二次根式是()A. B. C. D.【答案】C【解析】分析:将各选项中的二次根式化简,被开方数是5的根式即为正确答案.详解:A.与不是同类二次根式,不可以合并,故本选项错误;B.与不是同类二次根式,不可以合并,故本选项错误;C.=2,故与是同类二次根式,故本选项正确;D.=5,故与不是同类二次根式,故本选项错误.故选:C.点睛:本题考查了同类二次根式的定义,同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式.2. 直线不经过()A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】B【解析】试题分析:一次函数的性质:当时,图象经过第一、二、三象限;当时,图象经过第一、三、四象限;当时,图象经过第一、二、四象限;当时,图象经过第二、三、四象限.∵∴直线经过第一、三、四象限,不经过第二象限故选B.考点:一次函数的性质点评:本题属于基础应用题,只需学生熟练掌握一次函数的性质,即可完成.3. 若代数式在实数范围内有意义,则的取值范围是()A. B. C. D. 且【答案】D【解析】分析:根据被开方数大于等于0,分母不等于0列式计算即可得解.详解:由题意得,x+1≥0且x≠0,解得x≥-1且x≠0.故选:D.4. 下列曲线中不能表示是的函数的是()A. (A)B. (B)C. (C)D. (D)【答案】B【解析】分析:函数的定义:设在一个变化过程中有两个变量x与y,对于x的每一个确定的值,y都有唯一的值与其对应,那么就说y是x的函数,x是自变量.由此即可判断.详解:当给x一个值时,y有唯一的值与其对应,就说y是x的函数,x是自变量.选项B中的曲线,不满足对于自变量的每一个确定的值,函数值有且只有一个值与之对应,即单对应.故B 中曲线不能表示y是x的函数.故选:B.点睛:考查了函数的概念,理解函数的定义,是解决本题的关键.5. 已知直角三角形的两直角边分别是12和5,则斜边的中线长是()A. 34B. 26C. 8.5D. 6.5【答案】D【解析】由勾股定理得,斜边==13,所以,斜边上的中线长=×13=6.5.故选:D.6. 为了解某班学生双休日户外活动情况,对部分学生参加户外活动的时间进行抽样调查,结果如下表:则关于“户外活动时间”这组数据的众数、中位数、平均数分别是()A. B.C. D.【答案】A【解析】分析:根据中位数、平均数和众数的概念求解即可.详解:∵共10人,∴中位数为第5和第6人的平均数,∴中位数=(3+3)÷3=5;平均数=(1×2+2×2+3×4+6×2)÷10=3;众数是一组数据中出现次数最多的数据,所以众数为3.故选:A.点睛:本题考查平均数、中位数和众数的概念.一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数;在一组数据中出现次数最多的数叫做这组数据的众数;将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.7. 实数在数轴上对应点如图所示,则化简的结果是()A. B. C. D.【答案】B【解析】分析:先根据数轴确定a,b的范围,再根据二次根式的性质进行化简,即可解答.详解:由数轴可得:a<0<b,a- b<0,∴=|b|+| a-b|-| a|,=b-(a-b)+a,=b-a+b+a,=2b.故选:B.点睛:本题考查了实数与数轴,解决本题的关键是根据数轴确定a,b的范围.8. 如图,长方形的高为,底面长为,宽为,蚂蚁沿长方体表面,从点到(点见图中黑圆点)的最短距离是()A. B. C. D.【答案】D【解析】分析:要求蚂蚁爬行的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.详解:根据题意可能的...最短路线有6条,重复的不算,可以通过三条来计算比较.(见图示)根据他们相应的展开图分别计算比较:图①:;图②:;图③:.∵.故应选D.点睛:考查了轴对称-最短路线问题,本题是一道趣味题,将长方体展开,根据两点之间线段最短,运用勾股定理解答即可.二、填空题(本题有6个小题,每小题3分,共计18分)9. 一组数据,则这组数据的方差是__________ .【答案】2【解析】分析:先求出这5个数的平均数,然后利用方差公式求解即可.详解:平均数为=(1+2+3+4+5)÷5=3,S2=[(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2]=2.故答案为:2.点睛:本题考查了方差的知识,牢记方差的计算公式是解答本题的关键,难度不大.10. 命题“直角三角形斜边上的中线等于斜边的一半”的逆命题是___________________ .它是________命题(填“真”或“假”).【答案】(1). 如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形(2). 真【解析】分析:把一个命题的条件和结论互换就得到它的逆命题.命题“直角三角形斜边上的中线等于斜边的一半”的条件是直角三角形,结论是斜边上的中线等于斜边的一半,故其逆命题:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.详解:定理“直角三角形斜边上的中线等于斜边的一半”的逆命题:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.它是真命题.故答案为:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形;真.点睛:本题考查了互逆命题的知识及命题的真假判断,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.11. 已知函数,当= _______时,直线过原点;为_______数时,函数随的增大而增大 .【答案】(1). (2). m>0【解析】分析:(1)根据正比例函数的性质可得出m的值;(2)根据一次函数的性质列出关于m的不等式,求出m的取值范围即可.详解:直线过原点,则;即,解得:;函数随的增大而增大,说明,即,解得:;故分别应填:;m>0 .点睛:本题考查的是一次函数的图象与系数的关系,熟知一次函数的定义及增减性是解答此题的关键.12. 观察分析下列数据:,则第17个数据是_______ .【答案】【解析】分析:将原数变形为:1×,2×,3×,4×…,根据规律可以得到答案.详解:将原数变形为:1×,2×,3×,4×…,所以第17个数据是:17×=51.故答案为:51.点睛:本题考查了算术平方根,解题的关键是将所得二次根式变形,找到规律解答.13. 如图,四边形是矩形,是延长线上的一点,是上一点,;若,则= ________ .【答案】【解析】分析:由矩形的性质得出∠BCD=90°,AB∥CD,AD∥BC,证出∠FEA=∠ECD,∠DAC=∠ACB=21°,由三角形的外角性质得出∠ACF=2∠FEA,设∠ECD=x,则∠ACF=2x,∠ACD=3x,由互余两角关系得出方程,解方程即可.详解:∵四边形ABCD是矩形,∴∠BCD=90°,AB∥CD,AD∥BC,∴∠FEA=∠ECD,∠DAC=∠ACB=21°,∵∠ACF=∠AFC,∠FAE=∠FEA,∴∠ACF=2∠FEA,设∠ECD=x,则∠ACF=2x,∴∠ACD=3x,∴3x+21°=90°,解得:x=23°.故答案为:23°.点睛:本题考查了矩形的性质、平行线的性质、直角三角形的性质、三角形的外角性质;熟练掌握矩形的性质和平行线的性质是解决问题的关键.14. 如图,正方形中,,点在边上,且;将沿对折至,延长交边于点,连结,下列结论:①.;②.;③. .其中,正确的结论有__________________.(填上你认为正确的序号)【答案】①②③【解析】分析:根据折叠的相知和正方形的性质可以证明⊿≌⊿;根据勾股定理可以证得;先证得,由平行线的判定可证得;由于⊿和⊿等高的 .故由⊿:⊿求得面积比较即解得.详解:∵,,∴⊿≌⊿(),∴,故①正确的.∵,∴,,设,则,,在⊿中,根据勾股定理有:,即,解得即,则,∴,∴,∵且满足,∴,∴故②正确的.∵,且⊿和⊿等高的 .∴⊿:⊿=,∵⊿= ,∴⊿=⊿= ,故③正确的.故答案为:①②③ .点睛:本题是一道综合性较强的几何题,其中勾股定理与方程思想的结合起来为破解②③提供了有力的支撑,技巧性比较强,也是本题的难点所在,对于大多数同学来说具有一定的挑战性.三、解答题(本题有5个小题,每小题5分,共计25分)15. 计算:.【答案】19【解析】分析:先化简括号里面的,再合并,最后计算相乘,即可得到结果.详解:原式= = =.点睛:本题主要考查二次根式的化简,二次根式的乘法法则,合并同类二次根式,关键在于熟练运用相关的运算法则,正确认真的进行计算.16. 在甲地到乙地有一块山地正在开发,现有一处需要爆破,已知点与公路上的停靠站的距离为300米,与公路上另一停靠站的距离为400米,且 .如图,为了安全起见,爆破点周围半径250米范围内不得进入,问在进行爆破时,公路段是否有危险,是否需要暂时封锁?请通过计算进行说明.【答案】公路段有一定的危险,需要暂时封锁,证明见解析.【解析】分析:如图,本题需要判断点C到AB的距离是否小于250米,如果小于则有危险,大于则没有危险.因此过C作CD⊥AB于D,然后根据勾股定理在直角三角形ABC中即可求出AB的长度,然后利用三角形的公式即可求出CD,然后和250米比较大小即可判断需要暂时封锁.详解:如图,过C作CD⊥AB于D,∵BC=400米,AC=300米,∠ACB=90°,∴根据勾股定理得AB=500米,∵AB•CD=BC•AC,∴CD=240米.∵240米<250米,故有危险,因此AB段公路需要暂时封锁.点睛:本题考查正确运用勾股定理,善于观察题目的信息是解题以及学好数学的关键.17. 如图,将四边形的四边中点依次连接起来,得四边形到是平行四边形吗?请说明理由.【答案】四边形到是平行四边形.理由见解析.【解析】分析:连接一条对角线把转化成三角形的中位线来进行推理说明.详解:四边形到是平行四边形.理由如下:连接.∵点是四边形的四边中点∴∥,∥∴∴四边形到是平行四边形点睛:本题考查了平行四边形的判断及三角形的中位线定理的应用,三角形的中位线平行于第三边,并且等于第三边的一半.18. 在同一坐标系中,画出函数与的图像,观察图像写出当时,的取值范围.【答案】画图见解析,当时,的取值范围为 .【解析】分析:(1)利用两点法作出一次函数的图象,根据图象直接确定自变量的取值范围即可.详解:建立平面直角坐标系过画该直线(如图)过画该直线.(如图)∵解得∴两直线的交点为(如图)根据图象当时,的取值范围为.点睛:本题考查了一次函数的图象,作一次函数的图象时,可以利用两点法作图.19. 在四个互不相等的正整数中,最大的数是8,中位数是4,求这四个数(按从小到大的顺序排列)【答案】这四个数为或或.【解析】分析:根据中位数的定义得出第二个数和第三个数的和是8,再根据这四个数是不相等的正整数,得出这两个数是3、5或2、6,再根据这些数都是正整数得出第一个数是2或1,再把这四个数相加即可得出答案.详解:∵中位数是4,最大的数是8,∴第二个数和第三个数的和是8,∵这四个数是不相等的正整数,∴这两个数是3、5或2、6,∴这四个数是1,3,5,8或2,3,5,8或1,2,6,8,故答案为:1, 2, 6, 8或1, 3, 5, 8 或2, 3, 5, 8.点睛:此题考查了中位数,掌握中位数的概念是本题的关键;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.20. 国家规定:“中小学每天在校体育锻炼时间应不小于1小时”.某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.根据以上信息,回答下列问题:(1)A组的人数是,并补全条形统计图;(2)本次调查的中位数落在组;(3)根据统计图估计该地区2.5万名中学生中,达到国家规定的每天在校体育锻炼时间的约有多少人?【答案】(1)250,50;补全条形图见解析;(2)时间的平均数落在组;(3)2.5万名学生中“体育锻炼时间应不小于1小时” 人数为14000人......................试题解析:()由统计图可得,组人数为:,因此,本题正确答案是:,补全的条形统计图如图所示.()由补全的条形统计图可得,中位数落在组,因此,本题正确答案是:.()根据题意可得,该地区名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有:(人),因此,本题正确答案是:.21. 如图,⊿是直角三角形,且,四边形是平行四边形,为的中点,平分,点在上,且.求证:【答案】证明见解析.【解析】分析:延长DE交AB于点G,连接AD.构建全等三角形△AED≌△DFB(SAS),则由该全等三角形的对应边相等证得结论.详解:证明:延长DE交AB于点G,连接AD.∵四边形BCDE是平行四边形,∴ED∥BC,ED=BC.∵点E是AC的中点,∠ABC=90°,∴AG=BG,DG⊥AB.∴AD=BD,∴∠BAD=∠ABD.∵BD平分∠ABC,∴∠ABD=∠BAD=45°,即∠BDE=∠ADE=45°.又BF=BC,∴BF=DE.∴在△AED与△DFB中,,∴△AED≌△DFB(SAS),∴AE=DF,即DF=AE.点睛:本题考查了平行四边形的性质,全等三角形的判定与性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.22. 已知一次函数与正比例函数都经过点,的图像与轴交于点,且.(1)求与的解析式;(2)求⊿的面积.【答案】(1)或;⊿的面积为15个平方单位.【解析】分析:本题的⑴求正比例函数解析式可通过来解决.而要求的解析式则还需要一个点的坐标,这个通过来解决;⑵问通过结合⑴问的坐标来确定⊿解底边长和高长,利用三角形的面积公式求解.详解:⑴.∵正比例函数过点;∴解得:∴根据勾股定理可求设点的坐标为.又∵,则解得或∴点的坐标为或又∵一次函数同时也过点∴或;分别解得或∴或⑵.根据⑴的解答画出示意图,过作轴∵,的坐标为或∴∴⊿=⊿=∴综上所解,⊿的面积为15个平方单位.点睛:本题要注意两点:其一.所需线段的长度可以由坐标直接求出,也可能借助于勾股定理计算;其二.要注意根据绝对值的意义进行分类讨论,也就是可能有多解.23. 如图,直线与轴、轴分别交于,点的坐标为,是直线在第一象限内的一个动点(1)求⊿的面积与的函数解析式,并写出自变量的取值范围?(2)过点作轴于点, 作轴于点,连接,是否存在一点使得的长最小,若存在,求出的最小值;若不存在,请说明理由?【答案】(1),;(2)的最小值为【解析】分析:本题的⑴问直接根据坐标来表示⊿的底边和底边上的高,利用三角形的面积公式得出函数解析式;本题的⑵抓住四边形是矩形,矩形的对角线相等即,从而把转化到上来解决,当的端点运动到时最短,以此为切入点,问题可获得解决.详解:⑴.∵的坐标为,是直线在第一象限的一个动点,且轴.∴,∴整理得:自变量的取值范围是:⑵. 存在一点使得的长最小.求出直线与轴交点的坐标为, 与轴交点的坐标为∴∴根据勾股定理计算: .∵轴, 轴,轴轴∴∴四边形是矩形∴当的端点运动到(实际上点恰好是的中点)时的最短(垂线段最短)(见示意图)又∵∴点为线段中点(三线合一)∴(注:也可以用面积方法求解)∴即的最小值为点睛:本题的⑴问直接利用三角形的面积公式并结合点的坐标可以求解析式;本题的⑵问要打破平时求最小值的思路,把问题进行转化,通过求的最小值来得到的最小值,构思巧妙!24. 如图,在正方形内任取一点,连接,在⊿外分别以为边作正方形和.⑴.按题意,在图中补全符合条件的图形;⑵.连接,求证:⊿≌⊿;⑶.在补全的图形中,求证:∥.【答案】(1)补全图形见解析;(2)证明见解析;(3)证明见解析.【解析】分析:⑴问要注意“在⊿外”作正方形;本题的⑵问根据正方形的性质得出的结论为三角形全等提供条件,比较简单;本题额⑶问可以连接正方形的对角线后,然后利用“内错角相等,两直线平行.”来证明.详解:⑴.如图1,在⊿外.分别以为边作正方形和.(要注意是在“⊿外.”作正方形,见图1)⑵.在图1的基础上连接.∵四边形、和都是正方形∴∴∴∴⊿≌⊿()⑶. 继续在图1的基础上连接.(见图2)∵四边形是正方形,且已证∴∴∵⊿≌⊿∴∴∴即∴∥.点睛:本题的⑴问要注意的是在“在⊿外”作正方形,所以不要作在三角形内部;本题的⑵问主要是利用正方形提供的条件来证明两个三角形全等,比较简单,常规证法;本题的⑶问巧妙利用与正方形的对角线构成的内错角来提供平行的条件,需正方形和全等三角形来综合提供.。
四川省自贡市2017-2018学年度八年级(下)期末试题及答案
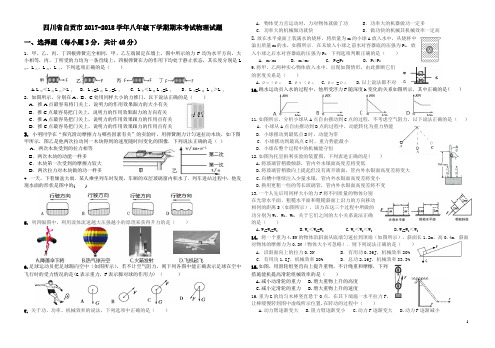
四川省自贡市2017-2018学年八年级下学期期末考试物理试题一、选择题(每小题3分,共计48分)1. 甲、乙、丙、丁四根弹簧完全相同,甲、乙左端固定在墙上,图中所示的力F均为水平方向,大小相等,丙、丁所受的力均为一条直线上,四根弹簧在力的作用下均处于静止状态,其长度分别是L 甲、L乙、L丙、L丁,下列选项正确的是()A.L甲<L丙L 乙>L丁 B.L甲=L丙 L乙=L丁 C.L甲<L丙L乙=L丁 D.L甲=L丙 L乙>L丁2.如图所示,分别在A、B、C处用同样大小的力推门,以下说法正确的是()A.推A点最容易将门关上,说明力的作用效果跟力的大小有关B.推C点最容易把门关上,说明力的作用效果跟力的方向有关C.推A点最容易把门关上,说明力的作用效果跟力的作用点有关D.推C点最容易把门关上,说明力的作用效果跟力的作用点有关3.小明同学在“探究滑动摩擦力与哪些因素有关”的实验时,用弹簧测力计匀速拉动木块,如下图甲所示,图乙是他两次拉动同一木块得到的速度随时间变化的图像.下列说法正确的是()A.两次木块受到的拉力相等B.两次木块的动能一样多C.木块第一次受到的摩擦力较大D.两次拉力对木块做的功一样多4. 一天,下着倾盆大雨.某人乘坐列车时发现,车厢的双层玻璃窗内积水了.列车进站过程中,他发现水面的形状是图中的()5.列四幅图中,利用流体流速越大压强越小的原理来获得升力的是()6.足球运动员把足球踢向空中(如图所示),若不计空气阻力,则下列各图中能正确表示足球在空中飞行时的受力情况的是(G表示重力,F表示脚对球的作用力) ()7.关于功、功率、机械效率的说法,下列选项中正确的是()A.物体受力且运动时,力对物体就做了功 B.功率大的机器做功一定多C.功率大的机械做功就快 D.做功快的机械其机械效率一定高8.放在水平桌面上装满水的烧杯,将质量为m1的小球A放入水中,从烧杯中溢出质量m2的水,如图所示.在未放入小球之前水对容器底的压强为P1,放入小球之后水对容器底的压强为P2.下列选项判断正确的是()A. m1<m2B. m1>m2C. P1=P2D. P1>P29.将甲、乙两种实心物体放入水中,出现如图情形,由此推断它们的密度关系是()A.ρ甲>ρ乙B.ρ甲<ρ乙C.ρ甲=ρ乙D.以上说法都不对10.跳水运动员入水的过程中,他所受浮力F随深度h变化的关系如图所示,其中正确的是( )11.如图所示,分析小球从A点自由摆动到C点的过程,不考虑空气阻力,以下说法正确的是()A.小球从A点自由摆动到B点的过程中,动能转化为重力势能B.小球摆动到最低点B时,动能为零C.小球摆动到最高点C时,重力势能最小D.小球在整个过程中的机械能守恒12.如图为托里拆利实验的装置图,下列表述正确的是( )A.将玻璃管稍微倾斜,管内外水银面高度差将变低B.将玻璃管稍微向上提起但没有离开液面,管内外水银面高度差将变大C.向槽中继续注入少量水银,管内外水银面高度差将变小D.换用更粗一些的等长玻璃管,管内外水银面高度差将不变13.一个人先后用同样大小的力F将不同质量的物体分别在光滑水平面、粗糙水平面和粗糙斜面上沿力的方向移动相同的距离S(如图所示),该力在这三个过程中所做的功分别为W1、W2、W3,关于它们之间的大小关系说法正确的是()A.W1=W2=W3B.W1<W2=W3C.W1<W2<W3D.W1=W2<W314.将一个重为4.5N的物体沿斜面从底端匀速拉到顶端(如图所示),斜面长1.2m,高0.4m,斜面对物体的摩擦力为0.3N(物体大小可忽略).则下列说法正确的是()A.沿斜面向上的拉力0.3N B.有用功0.36J,机械效率20%C.有用功1.8J,机械效率20% D.总功2.16J,机械效率83.3%15.如图,用滑轮组竖直向上提升重物,不计绳重和摩檫,下列措施能机提高滑轮组械效率的是()A.减小动滑轮的重力B.增大重物上升的高度C.减小定滑轮的重力D.增大重物上升的速度16.重为G的均匀木棒竖直悬于O点,在其下端施一水平拉力F,让棒缓慢转到图中虚线所示位置.在转动的过程中()A.动力臂逐渐变大B.阻力臂逐渐变小C.动力F逐渐变大D.动力F逐渐减小二、填空题(每空1分,共计12分)17.如图所示的物理教材中的插图,坐在船中的人用力向前推动另一艘船时,发现自己坐的船向后退,说明力可以改变物体的,还可说明物体间.18.如图所示,用20N的压力F将重5N的物体压在墙上时,物体恰好竖直向下匀速运动,此时该物体受到墙壁给它的摩擦力大小为_________N,若把压力F减小,该物体与墙壁之间的摩擦力将__________(选填“变大”、“变小”或“不变”)。
2017-2018学年四川省自贡市初中八年级下学期期末统一考试数学试题word版含答案
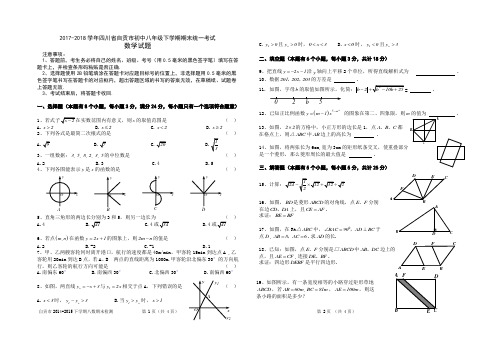
自贡市2014-2015下学期八数期末检测 第 1页(共 4页)第 2页 (共 4页)2017-2018学年四川省自贡市初中八年级下学期期末统一考试数学试题注意事项:1、答题前,考生务必将自己的姓名、班级、考号(用0.5毫米的黑色签字笔)填写在答题卡上,并检查条形码粘贴是否正确.2、选择题使用2B 铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米的黑色签字笔书写在答题卡的对应框内,超出答题区域的书写的答案无效,在草稿纸、试题卷上答题无效.3、考试结束后,将答题卡收回.一、选择题(本题有8个小题,每小题3分,满分24分,每小题只有一个选项符合题意)1x 的取值范围是 ( )A.x 2>B.x 2≤C.x 2<D.x 2≥2、下列各式是最简二次根式的是 ( )3、一组数据:,,,,,358235的中位数是 ( )A.2B.3C.4D.54、下列各图能表示y 是x 的函数的是 ( )5、直角三角形的两边长分别为3和5,则另一边长为 ( ) C.46、若点(),m n 在函数y 2x 1=+的图象上,则2m n -的值是 ( )A.2B.-2C.-1D.17、甲、乙两艘客轮同时离开港口,航行的速度都是40m/min ,甲客轮15min 到达点A ,乙客轮用20min 到达B 点,若A 、B 两点的直线距离为1000m.甲客轮沿北偏东30°的方向航行,则乙客轮的航行方向可能是 ( ) A.南偏东60° B.南偏西30° C.北偏西30° D.南偏西60°8、如图,两直线2y x 3=-+与1y 2x =相交于点A ,下列错误的是 )A.x 3<时,12y y 3->B.当12y y >时,x 1>C.1y 0>且2y 0>时,0x 3<<D.x 0<时,1y 0<且2y 3>二、填空题(本题有6个小题,每小题3分,共计18分)9、把直线y 2x 1=--沿y 轴向上平移2个单位,所得直线解析式为 .10、数据201202203,,的方差是 . 11. 如图,字母b 的取值如图所示,化简:b 2-= .12、已知正比例函数()25m y m 1x -=- 的图象在第二、四象限,则m 的值为 .13、如图,22⨯的方格中,小正方形的边长是1,点A B C 、、都 在格点上,则△ABC 中AB 边上的高长为 .14、如图,将两张长为6cm,宽为3cm 的矩形纸条交叉,使重叠部分 是一个菱形,那么菱形周长的最大值是 . 三、解答题(本题有5个小题,每小题5分,共计25分) 15 16、如图,BD 是菱形ABCD 的对角线,点E F 、分别 在边CD DA 、上,且CE AF =. 求证:BE BF = 17、如图,在Rt △ABC 中,BAC 90AD BC ∠=⊥,于 点D ,AB 8AC 6==,.求AD 的长. 18、已知:如图,点E F 、分别是□ABCD 中AB DC 、边上的点,且AE CF =,连接DE BF 、.求证:四边形DEBF 是平行四边形.19、如图所示,有一条宽度相等的小路穿过矩形草地 ABCD ,若,AB 60m =BC 81m =,AE 100m =,则这条小路的面积是多少?A D 0b 5自贡市2014-2015下学期八数期末检测 第 3页(共 4页) 第 4页 (共 4页)四、解答题(本题有3道小题,每小题6分,共计18分)20、正方形ABCD 中,点M 是边DC 上的任意一点,BE AM ⊥ 于点E ,DF AM ⊥于点F ,若,BE 7DF 4==,求EF 的长.21、某公司为了了解员工每人所创年利润情况,公司从各部抽取部分员工对每年所创年利润情况进行统计,并绘制如图1,图2统计图.⑴.将图形补充完整;⑵.每人所创年利润的平均数是 . ⑶.若每人创造利润10万元及以上为优秀员工,在公司1200名员工中估计有多少可以评为优秀员工?22、点(),P x y 在直线x y 8+=上,且,x 0y 0>>,点A 的坐标为(),A 60 , 设△OPA 的面积为S .⑴.求S 与x 的函数关系式,并直接写出x 的取值范围; ⑵.当S 9=时,求点P 的坐标.五、解答下列各题(第23题7分,第24题8分,共计1523、阅读下列材料,然后回答问题:一样的式子,其实我们还可以将其进一步化简:==;(Ⅰ)==;(Ⅱ) )22212111⨯⨯===- . (Ⅲ) 以上这种化简的步骤叫分母有理化.还可以用以下方法化简:221111-====.(Ⅳ)⑴.请用不同方法化简①.参照(Ⅲ)式得= ;②.参照(Ⅳ)式得= .⑵.化简:2n ++++24、如图1,在平面直角坐标系xoy 中,等腰直角△AOB 的斜边OB 在x 轴上,顶点A 的坐标为(),22⑴.求直线OA 的解析式;⑵.如图2,如果点P 是x 轴正半轴上的一动点,过点P 作PC ∥y 轴,叫直线OA 于点C ,设点P 的坐标为(),m 0,以A C P B 、、、为顶点的四边形面积为S ,求S 与m 之间的函数关系式; ⑶.如图3,如果(),D 1a 在直线AB 上.过点O D 、作直线OD ,交直线PC 于点E ,在CE 的右侧作矩形CGFE ,其中3CG 2=,请你直接写出矩形CGFE 与△AOB 重叠部分为轴对称图形时m 的取值范围.图 1图 2图 3图 102468101214163581015每年所创利润/万元图 2自贡市14-15下期八数期末考试 答题卡 第1页 共6页 第 2页 共6页 第3页 共6页2017~2018学年八年级下学期期末考试数 学 答 题 卡 请在各题目的答题区域内作答,超出答题区域的答案无效准考证号姓 名 设计:郑宗平14-15下期八数期末考试 答题卡 第4页 共6页 第 5页 共6页 第6页 共6页请在各题目的答题区域内作答,超出答题区域的答案无效请在各题目的答题区域内作答,超出答题区域的答案无效 ..。
最新-自贡市富顺县直属中学六校联考2018届中考数学一模试卷含答案解析 精品

2018年四川省自贡市富顺县直属中学六校联考中考数学一模试卷一、选择题(共10个小题,每小题4分,共40分)1.若函数为反比例函数,则m的值为()A.±1 B.1 C.D.﹣12.在Rt△ABC中,∠C=90°,BC=5,CA=12,则cosB=()A.B.C.D.3.在△ABC中,,则△ABC为()A.直角三角形B.等边三角形C.含60°的任意三角形D.是顶角为钝角的等腰三角形4.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是()A.B.C.D.5.若点(﹣5,y1),(﹣3,y2),(3,y3)都在反比例函数图象上,则()A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y1>y3>y26.将一副三角板按如图叠放,△ABC是等腰直角三角形,△BCD是有一个角为30°的直角三角形,则△AOB与△DCO的面积之比等于()A.B.C.D.7.已知函数图象如图,以下结论,其中正确有()个:①m<0;②在每个分支上y随x的增大而增大;③若A(﹣1,a),点B(2,b)在图象上,则a<b④若P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.A.4个B.3个C.2个D.1个8.从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是()A.(6+6)米 B.(6+3)米 C.(6+2)米 D.12米9.如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为()时,△ABE与以D、M、N为顶点的三角形相似.A.B. C.或D.或10.如图,已知矩形OABC面积为,它的对角线OB与双曲线相交于D且OB:OD=5:3,则k=()A.6 B.12 C.24 D.36二、填空题11.若tan(x+10°)=1,则锐角x的度数为.12.如图,在△ABC中,∠A=30°,∠B=45°,AC=,则AB的长为.13.如图,在▱ABCD中,E为CD上一点,DE:CE=2:3,连接AE、BE、BD,且AE、BD交于点F,则S△DEF:S△EBF:S△ABF=.14.如图:M为反比例函数图象上一点,MA⊥y轴于A,S△MAO=2时,k=.15.如图,第一角限内的点A在反比例函数的图象上,第四象限内的点B 在反比例函数图象上,且OA⊥OB,∠OAB=60度,则k值为.三、解答题16.计算:(﹣1)2018﹣(π﹣3)0+tan45°﹣sin60°cos30°+.17.已知:如图,是由一个等边△ABE和一个矩形BCDE拼成的一个图形,其中B,C,D点的坐标分别为(1,2),(1,1),(3,1).(1)求E点和A点的坐标;(2)试以点P(0,2)为位似中心,作出相似比为3的位似图形A1B1C1D1E1,并写出各对应点的坐标.四.解答题18.如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数的图象在第一象限内的交点为M,若△OBM的面积为2.(1)求一次函数和反比例函数的表达式;(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.19.如图,在△ABC中,AD是BC边上的高,tanC=,AC=3,AB=4,求△ABC的周长.五.解答题20.如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.(1)求证:△ABF∽△DFE;(2)若sin∠DFE=,求tan∠EBC的值.21.如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟,据了解,该材料在加热过程中温度y与时间x成一次函数关系,已知该材料在加热前的温度为15℃,加热5分钟使材料温度达到60℃时停止加热.停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系.(1)分别求出该材料加热过程中和停止加热后y与x之间的函数表达式,并写出x的取值范围;(2)根据工艺要求,在材料温度不低于30℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理所用的时间是多少?六.解答题(本小题12分)22.如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.(1)求该轮船航行的速度;(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据:,)七.解答题(本小题12分)23.已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D,OC交AB于E.(1)求∠D的度数;(2)求证:AC2=AD•CE;(3)求的值.八.解答题(本小题14分)24.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A 出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t的值.2018年四川省自贡市富顺县直属中学六校联考中考数学一模试卷参考答案与试题解析一、选择题(共10个小题,每小题4分,共40分)1.若函数为反比例函数,则m的值为()A.±1 B.1 C.D.﹣1【考点】反比例函数的定义.【分析】根据反比例函数的定义即可求出m的值.【解答】解:根据题意得:m2﹣2=﹣1,且m﹣1≠0解得:m=﹣1.故选D.【点评】本题考查了反比例函数的定义,重点是将一般式y=(k≠0)转化为y=kx﹣1(k≠0)的形式.2.在Rt△ABC中,∠C=90°,BC=5,CA=12,则cosB=()A.B.C.D.【考点】锐角三角函数的定义.【分析】先根据勾股定理求出AB=13,再根据三角函数的定义即可求得cosB的值.【解答】解:∵Rt△ABC中,∠C=90°,BC=5,CA=12,∴根据勾股定理AB==13,∴cosB==,故选C.【点评】本题主要考查了勾股定理以及余弦函数的定义:直角三角形中邻边与斜边的比叫做余弦,难度适中.3.在△ABC中,,则△ABC为()A.直角三角形B.等边三角形C.含60°的任意三角形D.是顶角为钝角的等腰三角形【考点】特殊角的三角函数值;非负数的性质:绝对值;非负数的性质:偶次方.【分析】首先结合绝对值以及偶次方的性质得出tanA﹣3=0,2cosB﹣=0,进而利用特殊角的三角函数值得出答案.【解答】解:∵(tanA﹣3)2+|2cosB﹣|=0,∴tanA﹣3=0,2cosB﹣=0,∴tanA=,cosB=,∠A=60°,∠B=60°,∴△ABC为等边三角形.故选:B.【点评】此题主要考查了绝对值以及偶次方的性质和特殊角的三角函数值等知识,熟练记忆特殊角的三角函数值是解题关键.4.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是()A.B.C.D.【考点】相似三角形的判定与性质.【分析】易证△DEF∽△DAB,△BEF∽△BCD,根据相似三角形的性质可得=,=,从而可得+=+=1.然后把AB=1,CD=3代入即可求出EF的值.【解答】解:∵AB、CD、EF都与BD垂直,∴AB∥CD∥EF,∴△DEF∽△DAB,△BEF∽△BCD,∴=,=,∴+=+==1.∵AB=1,CD=3,∴+=1,∴EF=.故选C.【点评】本题主要考查的是相似三角形的判定与性质,发现+=1是解决本题的关键.5.若点(﹣5,y1),(﹣3,y2),(3,y3)都在反比例函数图象上,则()A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y1>y3>y2【考点】反比例函数图象上点的坐标特征.【专题】计算题.【分析】根据反比例函数图象上点的坐标特征,分别计算出y2、y1、y3的值,然后比较大小即可.【解答】解:当x=﹣5时,y1=﹣;当x=﹣3时,y2=﹣;当x=3时,y3=,所以y2<y1<y3.故选C.【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.6.将一副三角板按如图叠放,△ABC是等腰直角三角形,△BCD是有一个角为30°的直角三角形,则△AOB与△DCO的面积之比等于()A.B.C.D.【考点】相似三角形的判定与性质.【专题】压轴题.【分析】根据已知可得到△AOB∽△DCO,从而得到相似比,根据面积比是相似比的平方即可得到其面积比.【解答】解:设BC=a,则AB=BC=a,CD= a∴AB:CD=1:∵AB∥CD∴△AOB∽△COD∴AB:CD=1:∴△AOB与△DCO的面积之比为1:3故选C.【点评】通过两个直角三角形的公共边找到两个三角形之间的联系是解决本题的关键.7.已知函数图象如图,以下结论,其中正确有()个:①m<0;②在每个分支上y随x的增大而增大;③若A(﹣1,a),点B(2,b)在图象上,则a<b④若P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.A.4个B.3个C.2个D.1个【考点】反比例函数的性质;反比例函数图象上点的坐标特征.【分析】利用反比例函数的性质及反比例函数的图象上的点的坐标特征对每个小题逐一判断后即可确定正确的选项.【解答】解:①根据反比例函数的图象的两个分支分别位于二、四象限,可得m<0,故正确;②在每个分支上y随x的增大而增大,正确;③若点A(﹣1,a)、点B(2,b)在图象上,则a<b,错误;④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上,正确,故选:B.【点评】本题考查了反比例函数的性质及反比例函数的图象上的点的坐标特征,解题的关键是熟练掌握其性质,难度不大.8.从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是()A.(6+6)米 B.(6+3)米 C.(6+2)米 D.12米【考点】解直角三角形的应用-仰角俯角问题.【专题】几何图形问题.【分析】在Rt△ABC求出CB,在Rt△ABD中求出BD,继而可求出CD.【解答】解:在Rt△ACB中,∠CAB=45°,AB⊥DC,AB=6米,∴BC=6米,在Rt△ABD中,∵tan∠BAD=,∴BD=AB•tan∠BAD=6米,∴DC=CB+BD=6+6(米).故选:A.【点评】本题考查仰角俯角的定义,要求学生能借助仰角俯角构造直角三角形并解直角三角形,难度一般.9.如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为()时,△ABE与以D、M、N为顶点的三角形相似.A.B. C.或D.或【考点】相似三角形的判定;正方形的性质.【分析】根据AE=EB,△ABE中,AB=2BE,所以在△MNC中,分CM与AB和BE是对应边两种情况利用相似三角形对应边成比例求出CM与CN的关系,然后利用勾股定理列式计算即可.【解答】解:∵四边形ABCD是正方形,∴AB=BC,∵BE=CE,∴AB=2BE,又∵△ABE与以D、M、N为顶点的三角形相似,∴①DM与AB是对应边时,DM=2DN∴DM2+DN2=MN2=1∴DM2+DM2=1,解得DM=;②DM与BE是对应边时,DM=DN,∴DM2+DN2=MN2=1,即DM2+4DM2=1,解得DM=.∴DM为或时,△ABE与以D、M、N为顶点的三角形相似.故选C.【点评】本题考查相似三角形的判定与性质、正方形的性质.解决本题特别要考虑到①DM与AB 是对应边时,②当DM与BE是对应边时这两种情况.10.如图,已知矩形OABC面积为,它的对角线OB与双曲线相交于D且OB:OD=5:3,则k=()A.6 B.12 C.24 D.36【考点】反比例函数系数k的几何意义.【分析】先找到点的坐标,然后再利用矩形面积公式计算,确定k的值.【解答】解:由题意,设点D的坐标为(x D,y D),则点B的坐标为(x D,y D),矩形OABC的面积=|x D×y D|=,∵图象在第一象限,∴k=x D•y D=12.故选B.【点评】本题考查了反比例函数与几何图形的结合,综合性较强,同学们应重点掌握.二、填空题11.若tan(x+10°)=1,则锐角x的度数为20°.【考点】特殊角的三角函数值.【分析】利用特殊角的三角函数值得出x+10°的值进而求出即可.【解答】解:∵tan(x+10°)=1,∴tan(x+10°)==,∴x+10°=30°,∴x=20°.故答案为:20°.【点评】此题主要考查了特殊角的三角函数值,正确记忆相关角对应的函数值是解题关键.12.如图,在△ABC中,∠A=30°,∠B=45°,AC=,则AB的长为3+.【考点】解直角三角形.【专题】几何图形问题.【分析】过C作CD⊥AB于D,求出∠BCD=∠B,推出BD=CD,根据含30度角的直角三角形求出CD,根据勾股定理求出AD,相加即可求出答案.【解答】解:过C作CD⊥AB于D,∴∠ADC=∠BDC=90°,∵∠B=45°,∴∠BCD=∠B=45°,∴CD=BD,∵∠A=30°,AC=2,∴CD=,∴BD=CD=,由勾股定理得:AD==3,∴AB=AD+BD=3+.故答案为:3+.【点评】本题考查了勾股定理,等腰三角形的性质和判定,含30度角的直角三角形性质等知识点的应用,关键是构造直角三角形,题目具有一定的代表性,是一道比较好的题目.13.如图,在▱ABCD中,E为CD上一点,DE:CE=2:3,连接AE、BE、BD,且AE、BD交于点F,则S△DEF:S△EBF:S△ABF=4:10:25.【考点】平行四边形的性质.【分析】由平行四边形的性质得AB=CD=DE+CE,则DE:AB=2:5,由CD∥AB得△DEF∽△ABF,根据面积比等于相似比的平方求S△DEF:S△ABF,△DEF与△BEF等高,其面积比为DF:FB,由此可求三个三角形的面积比.【解答】解:∵在▱ABCD中,AB=CD=DE+CE,DE:CE=2:3,∴DE:AB=2:5,又∵CD∥AB,∴△DEF∽△ABF,∴S△DEF:S△ABF=DE2:AB2=4:25,∵△EBF与△ABF等高,∴S△EBF:S△ABF=EF:AF=2:5=10:25,∴S△DEF:S△EBF:S△ABF=4:10:25.故答案为:4:10:25.【点评】本题考查了平行四边形的性质.关键是利用平行四边形的对边相等,得到相应线段的比,利用平行四边形的对边平行,得到相似三角形.14.如图:M为反比例函数图象上一点,MA⊥y轴于A,S△MAO=2时,k=﹣4.【考点】反比例函数系数k的几何意义.【分析】根据反比例函数y=(k≠0)系数k的几何意义得到S△AOM=|k|=2,然后根据k<0去绝对值得到k的值.【解答】解:∵AB⊥x轴,∴S△AOM=|k|=2,∵k<0,∴k=﹣4.故答案为﹣4.【点评】本题考查了反比例函数y=(k≠0)系数k的几何意义:从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.15.如图,第一角限内的点A在反比例函数的图象上,第四象限内的点B 在反比例函数图象上,且OA⊥OB,∠OAB=60度,则k值为﹣6.【考点】反比例函数图象上点的坐标特征;相似三角形的判定与性质.【专题】计算题.【分析】作AC⊥y轴于C,BD⊥y轴于D,如图,根据反比例函数图象上点的坐标特征,设A(a,),B(b,),再证明Rt△OAC∽Rt△BOD,根据相似的性质得==,而在Rt△AOB中,根据正切的定义得到tan∠OAB==,即==,然后利用比例性质先求出ab的值再计算k的值.【解答】解:作AC⊥y轴于C,BD⊥y轴于D,如图,设A(a,),B(b,),∵∠AOB=90°,∴∠AOC+∠DOB=90°,而∠AOC+∠OAC=90°,∴∠OAC=∠DOB,∴Rt△OAC∽Rt△BOD,∴==,∵在Rt△AOB中,tan∠OAB=tan60°==,∴==,即==,∴ab=2,∴k=﹣ab=﹣×2=﹣6.故答案为﹣6.【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了相似三角形的判定与性质.三、解答题16.计算:(﹣1)2018﹣(π﹣3)0+tan45°﹣sin60°cos30°+.【考点】实数的运算;零指数幂;特殊角的三角函数值.【专题】计算题.【分析】原式第一项利用乘方的意义计算,第二项利用零指数幂法则计算,第三、四项利用特殊角的三角函数值计算,最后一项利用算术平方根的定义计算即可得到结果.【解答】解:原式=﹣1﹣1+1﹣×+2=.【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.17.已知:如图,是由一个等边△ABE和一个矩形BCDE拼成的一个图形,其中B,C,D点的坐标分别为(1,2),(1,1),(3,1).(1)求E点和A点的坐标;(2)试以点P(0,2)为位似中心,作出相似比为3的位似图形A1B1C1D1E1,并写出各对应点的坐标.【考点】作图-位似变换.【分析】(1)首先过点A作AF⊥BE,由△ABE是等边三角形,可求得AF的长,继而可求得E 点和A点的坐标;(2)首先根据题意画出图形,由位似图形的性质即可求得各对应点的坐标.【解答】解:(1)过点A作AF⊥BE,∵△ABE是等边三角形,∴AB=BE=2,∠ABE=60°,∴AF=AB•sin60°=2×=,∴点A的坐标为:(2,2+),点E的坐标为:(3,2);(2)如图:A1(6,2+3),B1(3,2),C1(3,﹣1),D1(9,﹣1),E1(9,2).【点评】此题考查了位似图形的性质与矩形、等边三角形的性质.注意作位似图形时找准位似中心与位似比.四.解答题18.如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数的图象在第一象限内的交点为M,若△OBM的面积为2.(1)求一次函数和反比例函数的表达式;(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.【考点】反比例函数与一次函数的交点问题.【专题】探究型.【分析】(1)根据一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)可得到关于b、k1的方程组,进而可得到一次函数的解析式,设M(m,n)作MD⊥x轴于点D,由△OBM的面积为2可求出n的值,将M(m,4)代入y=2x﹣2求出m的值,由M(3,4)在双曲线上即可求出k2的值,进而求出其反比例函数的解析式;(2)过点M(3,4)作MP⊥AM交x轴于点P,由MD⊥BP可求出∠PMD=∠MBD=∠ABO,再由锐角三角函数的定义可得出OP的值,进而可得出结论.【解答】解:(1)∵直线y=k1x+b过A(0,﹣2),B(1,0)两点∴,∴∴一次函数的表达式为y=2x﹣2.∴设M(m,n),作MD⊥x轴于点D∵S△OBM=2,∴,∴∴n=4∴将M(m,4)代入y=2x﹣2得4=2m﹣2,∴m=3∵M(3,4)在双曲线上,∴,∴k2=12∴反比例函数的表达式为(2)过点M(3,4)作MP⊥AM交x轴于点P,∵MD⊥BP,∴∠PMD=∠MBD=∠ABO∴tan∠PMD=tan∠MBD=tan∠ABO==2∴在Rt△PDM中,,∴PD=2MD=8,∴OP=OD+PD=11∴在x轴上存在点P,使PM⊥AM,此时点P的坐标为(11,0)【点评】本题考查的是反比例函数与一次函数的交点问题,涉及到的知识点为用待定系数法求一次函数与反比例函数的解析式、锐角三角函数的定义,熟知以上知识是解答此题的关键.19.如图,在△ABC中,AD是BC边上的高,tanC=,AC=3,AB=4,求△ABC的周长.【考点】解直角三角形;勾股定理.【专题】计算题.【分析】在Rt△ADC中,根据正切的定义得到tanC==,则可设AD=k,CD=2k,接着利用勾股定理得到AC=k,则k=3,解得k=3,所以AD=3,CD=6,然后在Rt△ABD中,利用勾股定理计算出BD=,再根据三角形的周长的定义求解.【解答】解:在Rt△ADC中,tanC==,设AD=k,CD=2k,AC==k,∵AC=3,∴k=3,解得k=3,∴AD=3,CD=6,在Rt△ABD中,BD===,∴△ABC的周长=AB+AC+BD+CD=4+3++6=10+3+.【点评】本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了勾股定理.五.解答题20.如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.(1)求证:△ABF∽△DFE;(2)若sin∠DFE=,求tan∠EBC的值.【考点】相似三角形的判定与性质;矩形的性质;翻折变换(折叠问题);解直角三角形.【专题】几何综合题;压轴题.【分析】(1)根据矩形的性质可知∠A=∠D=∠C=90°,△BCE沿BE折叠为△BFE,得出∠BFE=∠C=90°,再根据三角形的内角和为180°,可知∠AFB+∠ABF=90°,得出∠ABF=∠DFE,即可证明△ABF∽△DFE,(2)已知sin∠DFE=,设DE=a,EF=3a,DF==2a,可得出CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,由(1)中△ABF∽△DFE,可得tan∠EBC=tan∠EBF= =.【解答】(1)证明:∵四边形ABCD是矩形∴∠A=∠D=∠C=90°,∵△BCE沿BE折叠为△BFE,∴∠BFE=∠C=90°,∴∠AFB+∠DFE=180°﹣∠BFE=90°,又∵∠AFB+∠ABF=90°,∴∠ABF=∠DFE,∴△ABF∽△DFE,(2)解:在Rt△DEF中,sin∠DFE==,∴设DE=a,EF=3a,DF==2a,∵△BCE沿BE折叠为△BFE,∴CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,又由(1)△ABF∽△DFE,∴===,∴tan∠EBF==,tan∠EBC=tan∠EBF=.【点评】本题考查了矩形的性质以及相似三角形的证明方法,以及直角三角形中角的函数值,难度适中.21.如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟,据了解,该材料在加热过程中温度y与时间x成一次函数关系,已知该材料在加热前的温度为15℃,加热5分钟使材料温度达到60℃时停止加热.停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系.(1)分别求出该材料加热过程中和停止加热后y与x之间的函数表达式,并写出x的取值范围;(2)根据工艺要求,在材料温度不低于30℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理所用的时间是多少?【考点】反比例函数的应用.【分析】(1)确定两个函数后,找到函数图象经过的点的坐标,用待定系数法求得函数的解析式即可;(2)分别令两个函数的函数值为30,解得两个x的值相减即可得到答案.【解答】解:(1)设加热过程中一次函数表达式为y=kx+b(k≠0),∵该函数图象经过点(0,15),(5,60),∴,解得,∴一次函数的表达式为y=9x+15(0≤x≤5),设加热停止后反比例函数表达式为y=(a≠0),∵该函数图象经过点(5,60),∴=60,解得:a=300,∴反比例函数表达式为y=(x≥5);(2)∵y=9x+15,∴当y=30时,9x+15=30,解得x=,∵y=,∴当y=30时,=30,解得x=10,10﹣=,所以对该材料进行特殊处理所用的时间为分钟.【点评】本题考查了反比例函数的应用,解题的关键是从实际问题中整理出函数模型,利用函数的知识解决实际问题.六.解答题(本小题12分)22.如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.(1)求该轮船航行的速度;(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据:,)【考点】解直角三角形的应用-方向角问题.【专题】压轴题.【分析】(1))过点A作AC⊥OB于点C.可知△ABC为直角三角形.根据勾股定理解答.(2)延长AB交l于D,比较OD与AM、AN的大小即可得出结论.【解答】解(1)过点A作AC⊥OB于点C.由题意,得OA=千米,OB=20千米,∠AOC=30°.∴(千米).∵在Rt△AOC中,OC=OA•cos∠AOC==30(千米).∴BC=OC﹣OB=30﹣20=10(千米).∴在Rt△ABC中,==20(千米).∴轮船航行的速度为:(千米/时).(2)如果该轮船不改变航向继续航行,不能行至码头MN靠岸.理由:延长AB交l于点D.∵AB=OB=20(千米),∠AOC=30°.∴∠OAB=∠AOC=30°,∴∠OBD=∠OAB+∠AOC=60°.∴在Rt△BOD中,OD=OB•tan∠OBD=20×tan60°=(千米).∵>30+1,∴该轮船不改变航向继续航行,不能行至码头MN靠岸.【点评】本题考查了解直角三角形的应用,此题结合方向角,考查了阅读理解能力、解直角三角形的能力.计算出相关特殊角和作出辅助线构造相似三角形是解题的关键.七.解答题(本小题12分)23.已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D,OC交AB于E.(1)求∠D的度数;(2)求证:AC2=AD•CE;(3)求的值.【考点】平行线的判定;圆周角定理;相似三角形的判定与性质.【专题】代数几何综合题.【分析】(1)根据圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.等边对等角及平行线的性质可求∠D的度数;(2)乘积的形式通常可以转化为比例的形式,通过证明三角形相似得出.(3)延长BO交DA的延长线于F,连接OA.通过证明△BOC∽△BFD得出的值.【解答】(1)解:如图,连接OB∵⊙O的内接△ABC中,∠BAC=45°,∴∠BOC=2∠BAC=90°∵OB=OC,∴∠OBC=∠OCB=45°∵AD∥OC,∴∠D=∠OCB=45°(2)证明:∵∠BAC=45°,∠D=45°,∴∠BAC=∠D∵AD∥OC,∴∠ACE=∠DAC∴△ACE∽△DAC∴∴AC2=AD•CE(3)解:方法一:如图,延长BO交DA的延长线于F,连接OA∵AD∥OC,∴∠F=∠BOC=90°∵∠ABC=15°,∴∠OBA=∠OBC﹣∠ABC=30°∵OA=OB,∴∠FOA=∠OBA+∠OAB=60°,∠OAF=30°、∴OF=OA∵AD∥OC,∴△BOC∽△BFD∴∴=2,即的值为2方法二:作OM⊥BA于M,设⊙O的半径为r,可得BM=,OM=,∠MOE=30°,ME=OM•tan30°=,BE=,AE=,所以=2【点评】本题主要考查了相似三角形的判定和性质,同时考查了圆周角定理和平行线的性质,综合性较强,难度较大.八.解答题(本小题14分)24.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A 出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t的值.【考点】相似三角形的判定;全等三角形的判定与性质;勾股定理.【专题】压轴题.【分析】(1)在Rt△ABC中,利用勾股定理可求得AB的长,即可得到AD、t的值,从而确定AE 的长,由DE=AE﹣AD即可得解.(2)若△DEG与△ACB相似,要分两种情况:①AG:DE=DH:GE,②AH:EG=DH:DE,根据这些比例线段即可求得t的值.(需注意的是在求DE的表达式时,要分AD>AE和AD<AE两种情况)【解答】解:(1)∵∠ACB=90°,AC=3,BC=4,∴AB==5.∵AD=5t,CE=3t,∴当AD=AB时,5t=5,即t=1;∴AE=AC+CE=3+3t=6,DE=6﹣5=1.(2)∵EF=BC=4,G是EF的中点,∴GE=2.当AD<AE(即t<)时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,若△DEG与△ACB相似,则或,∴或,∴t=或t=;当AD>AE(即t>)时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,若△DEG与△ACB相似,则或,∴或,解得t=或t=;综上所述,当t=或或或时,△DEG与△ACB相似.【点评】此题考查了勾股定理、轴对称的性质、平行四边形及梯形的判定和性质、解直角三角形、相似三角形等相关知识,综合性强,是一道难度较大的压轴题.。
自贡市富顺县2017-2018年八年级下六校联考第一次段考试卷含答案

2017-2018学年度下学期富顺县直属中学六校联考第一次段考八 年 级 数 学 科 试 卷说明:试卷来源于富顺县六所直属中学联考一 重新制版:郑宗平一.选择题(本大题共8个小题,每小题3分,共30分) 1.A. a =-24a b =2.在△ABC 90,周长为长分别是 A. 5,4,13,12,5 C.10,8,6 D. 26,24,10 3.化简)x 0的结果是( )A.y 2x -y C. 2x y - D. y -4.( )2=B. 2=x 1=-=5. 已知直角三角形中30°角所对的直角边长是cm ,则另一条直角边的长是 ( ),90AC =8.如图,分别以直角⊿ABC 的三边AB,BC,CA 为直径向外作半 圆.设直线AB 左边的阴影部分的面积为1S ,右边的阴影部分的面 积和为2S 则 ( )A.=12S SB.12S S ≥ C 12S S ≤ D.12S S >9. )A. 4±11.12.三) 90,CD ⊥23.小明将一副三角板按如图所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长;若已知CD 2=,求AC 的长?90 ,AC ;求BPC ∠24.在一次“探究性学习”课中,老师设计了如下数表:C2017 – 2018下学期富顺县六校联考一八年级数学 参考答案一.选择题(本大题共10个小题,每小题3分,共30分)10题辅助线示意图:二三.解答题(本题有5个小题,17 –20题每题5分,21题6.)17. 7- ;18. -; 19. 0 ;; 21.化简结果:2a 6a +;计算结果:3-。
四.解答题(本题有4个小题,22、 23题每题6分,24、25题每题7分,共26分.) 22.(1).90,AC +=215(2).∴=CD 12 .23.∴632=x∴24.略解:连接BD (见图)∵CD CP ⊥,CD PC 2== ∴⊿PCD 为等腰直角三角形. ∴∠=CPD 45 .∵∠+∠=∠+∠=ACP BCP BCP BCD 90 ∴∠=∠ACP BCD ∵=CA CB∴⊿CAP ≌⊿CBD (SAS ) ∴==DB PA 3在Rt ⊿CPD 中,82222222=+=+=CD CP DP .又∵,==2PB 1DP 8∴918222=+=+=PB DP DB .∴∠=DPB 90∴∠=∠+∠=+=CPB CPD DPB 4390551 .25.略解:⑴.a = 2n 1-, b = 2n , c = 2n 1+ ; ⑵.答:以,,a b c 为边的三角形是直角三角形.证明:∵a = 2n 1-, b = 2n , c = 2n 1+∴()()()+=-+=-++=+=22222242222a b n 12n n 2n 14n n 1c ,∴ 以,,a b c 为边的三角形是直角三角形.说明:以上答案仅供参考!2018.4.7A。
2017-2018学年第二学期期末调研考试八年级数学试题及答案(含评分标准与解析)
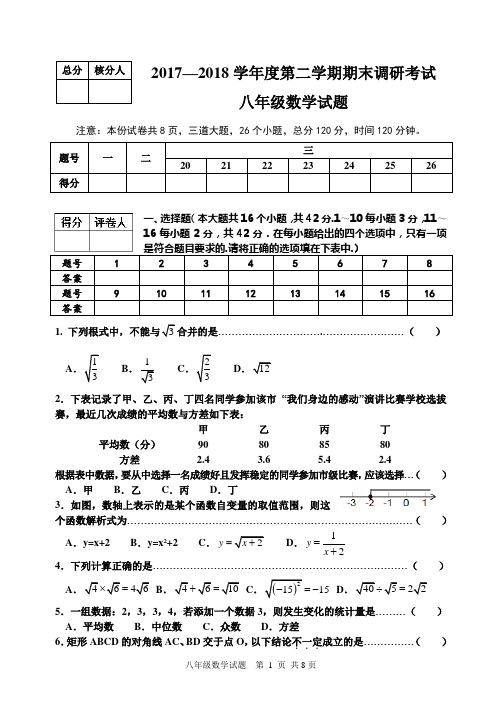
2017—2018学年度第二学期期末调研考试八年级数学试题注意:本份试卷共8页,三道大题,26个小题,总分120分,时间120分钟。
题号 一 二 三20 21 22 23 24 25 26 得分一、选择题(本大题共16个小题,共42分.1~10每小题3分,11~16每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确的选项填在下表中.) 题号1 2 3 4 5 6 7 8 答案 题号 9 10 11 12 13 14 15 16 答案1. 下列根式中,不能与3合并的是………………………….……………………( )A .13 B .13C .23D .12 2.下表记录了甲、乙、丙、丁四名同学参加该市 “我们身边的感动”演讲比赛学校选拔赛,最近几次成绩的平均数与方差如下表:甲 乙 丙 丁 平均数(分) 90 80 85 80方差 2.4 3.6 5.4 2.4根据表中数据,要从中选择一名成绩好且发挥稳定的同学参加市级比赛,应该选择…( ) A .甲 B .乙 C .丙 D .丁3.如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式为…………………………………………………………………………( ) A .y=x+2 B .y=x 2+2 C .2y x =+ D .12y x =+ 4.下列计算正确的是…………………………………………………………………( ) A .4646⨯= B .4610+= C .()21515-=- D .40522÷=5.一组数据:2,3,3,4,若添加一个数据3,则发生变化的统计量是………( ) A .平均数 B .中位数 C .众数 D .方差 6.矩形ABCD 的对角线AC 、BD 交于点O ,以下结论不一定...成立的是……………( ) 总分 核分人A .∠BCD=90°B .AC ⊥BD C .AC=BD D .OA=OB7.一组数据:3,2,5,3,7,5,x ,它们的众数为5,则这组数据的中位数是…( ) A .2 B .3 C .5 D .7 8.已知:2xy =,521x y -=-,则(x+1)(y ﹣1)的值为……………………( ) A .42- B .622- C .62 D .无法确定9.在四边形ABCD 中AC 、BD 相交于点O ,下列说法错误..的是……………………( ) A .AB ∥CD ,AD=BC ,则四边形ABCD 是平行四边形B .AO=CO ,BO=DO 且AC ⊥BD ,则四边形ABCD 是菱形 C .AO=OB=OC=OD ,则四边形ABCD 是矩形D .∠A=∠B=∠C=∠D 且AB=BC ,则则四边形ABCD 是正方形10.如图,在四个均由十六个小正方形组成的正方形网格中,各有一个三角形ABC ,那么这四个三角形中,不是..直角三角形的是……………………………………………( ) A . B . C . D .11.关于函数y=﹣x ﹣2的图象,有如下说法:①图象过(0,﹣2)点;②图象与x 轴交点是(﹣2,0);③从图象知y 随x 增大而增大;④图象不过第一象限;⑤图象是与y=﹣x 平行的直线.其中正确说法有………( ) A .2个 B .3个 C .4个 D .5个 12.如图,在△ABC 中,∠ACB=90°,D 在BC 上,E 是AB 的中点,AD 、CE 相交于F ,且AD=DB .若∠B=20°,则∠DFE 等于……( ) A .30° B .40° C .50° D .60° 13.若式子()011k k -+-有意义,则一次函数y=(1﹣k )x+k ﹣1的图象可能是…( )A .B .C .D .14.平面直角坐标系中,O 是坐标原点,点A 的坐标是(4,0),点P 在直线y=﹣x+m 上,且AP=OP=4.则m 的值为……………………………………………………( ) A .223+或223- B .4或﹣4 C .23或23- D .423+或423-15.如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,动点P从B点出发,沿B→C→A运动.如图(1)所示,设S△DPB=y,点P运动的路程为x,若y与x之间的函数图象如图(2)所示,则图(2)中Q点的坐标是……………………………()A.(4,4)B.(4,3)C.(4,6)D.(4,12)16.如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E、F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=25.以上结论中,你认为正确的是………………………………………………………()A.①②③B.①③④C.①②④D.②③④二、填空题(本大题共3小题,共10分.17~18小题各3分;19小题有2个空,每空2分.把答案写在题中横线上)17.如图,函数y=ax+m和y=bx的图象相交于点A,则不等式bx≥ax+m的解集为.18.如图,平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,∠ABC=75°,∠DBC=30°,BC=2,则BD的长度为.19.如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第3个等腰直角三角形A3B2B3顶点B3的横坐标为,第2018个等腰直角三角形A2018B2017B2018顶点B2018的横坐标为.三、解答题(本大题共7小题,共68分.解答应写出文字说明、证明过程或演算步骤)20.计算(本题共2小题,每小题4分,满分8分)(1)11484320.583⎛⎫⎛⎫---⎪ ⎪⎪ ⎪⎝⎭⎝⎭;(2)()()()215225382-+--+⨯.21.(本题满分9分)有一块边长为40米的正方形绿地ABCD,如图所示,在绿地旁边E处有健身器材,BE=9米.由于居住在A 处的居民去健身践踏了绿地(图中AE),小明想在A处树立一个标牌“少走米,踏之何忍”.请你计算后帮小明在标牌的处填上适当的数.22.(本题满分9分)某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.回答下列问题:(1)写出条形图中存在的错误,并说明理由;(2)这20名学生每人植树量的众数是,中位数是;(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的:①小宇的分析是从哪一步开始出现错误的?②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.23.(本题满分9分)如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为点E.连接DE,则线段DE与线段AC有怎样的数量关系?请证明你的结论.24.(本题满分10分)如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.(1)求直线AB的解析式.(2)求△OAC的面积.(3)当△OMC的面积是△OAC的面积的14时,求出这时点M的坐标.25.(本题满分11分)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)。
精品解析:【市级联考】四川省自贡市2017-2018学年八年级下学期期末考试物理试题(解析版)

四川省自贡市2017-2018学年下学期期末考试八年级物理试题一、选择题1.【2016·威海卷】图中甲、乙、丙、丁四根弹簧完全相同,甲、乙左端固定在墙上,图中所示的力F 均为水平方向,大小相等,丙、丁所受的力均在一条直线上,四根弹簧在力的作用下均处于静止状态,其长度分别是L甲、L乙、L丙、L丁。
下列选项正确的是()A. L甲<L丙L乙>L丁B. L甲= L丙L乙= L丁C. L甲<L丙L乙= L丁D. L甲= L丙L乙>L丁【答案】B【解析】由图可知,图甲和丙的力都会使弹簧伸长,图乙和图丁的力都会使弹簧压缩;在图甲中,力F通过弹簧传递给墙,力的作用是相互的,墙对弹簧施加的力等于F,方向水平向左,所以图甲和图丙的作用力情况相同,效果相同,故它们伸长的长度相同,所以L甲=L丙;在图乙中,力F通过弹簧传递给墙,力的作用是相互的,墙对弹簧施加的力等于F,方向水平向右,所以图乙和图丁的作用力情况相同,效果相同,故它们缩短的长度相同.所以L乙=L丁.故选D.2.如图所示,分别在A、B、C处用同样大小的力推门,以下说法正确的是A. 推A点最容易将门关上,说明力的作用效果跟力的大小有关B. 推C点最容易把门关上,说明力的作用效果跟力的方向有关C. 推A点最容易把门关上,说明力的作用效果跟力的作用点有关D. 推C点最容易把门关上,说明力的作用效果跟力的作用点有关【答案】C【解析】【详解】力的大小、方向、作用点叫做力的三要素,力的三要素影响力的作用效果。
分别在A、B、C处用同样大小的力推门,可以感受到在A点用力容易把门推开,这是因为力的作用点不同,说明力的作用效果跟力的作用点有关,故C正确,故选C。
3.小明同学在“探究滑动摩擦力与哪些因素有关”的实验时,用弹簧测力计匀速拉动木块,如下图甲所示,图乙是他两次拉动同一木块得到的速度随时间变化的图像.下列说法正确的是A. 两次木块受到的拉力相等B. 两次木块的动能一样多C. 木块第一次受到的摩擦力较大D. 两次拉力对木块做的功一样多【答案】A【解析】试题分析:由于两次都是匀速运动,所以在水平方向上受力是平衡的,在水平方向上只受拉力和摩擦力,由于两次拉的时候压力与接触面都相同,所以摩擦力是相等的,因此可知两次的拉力相等,A正确;因为两次的速度不相等所以动能就不一样多,B错;两次的摩擦力相等,所以C错;由于拉木块的时间不确定,所以无法判断出做功的多少,D错;应选A。
自贡市富顺县2017-2018年八年级下六校联考第一次段考试卷含答案

2017-2018学年度下学期富顺县直属中学六校联考第一次段考八 年 级 数 学 科 试 卷说明:试卷来源于富顺县六所直属中学联考一 重新制版:郑宗平一.选择题(本大题共8个小题,每小题3分,共30分) 1.A. a =-24a b =2.在△ABC 90,周长为长分别是 A. 5,4,13,12,5 C.10,8,6 D. 26,24,10 3.化简)x0的结果是( )A. y2x -y C. 2x y - D. y -4.( )2=B. 2=x 1=-=5. 已知直角三角形中30°角所对的直角边长是cm ,则另一条直角边的长是 ( )m C.,90AC =8.如图,分别以直角⊿ABC 的三边AB,BC,CA 为直径向外作半 圆.设直线AB 左边的阴影部分的面积为1S ,右边的阴影部分的面 积和为2S 则 ( )A.=12S SB.12S S ≥ C 12S S ≤ D.12S S >9. )A. 4±11.12.三21.先化简,再求值:()()()2a 3a 3a a 66+---+ ,其中a 21=- .) 22.如图,在Rt ⊿ABC 中,ACB 90∠=,CD AB ⊥于D ,,AC 20BC 15== .⑴.求AB 的长; ⑵.求CD 的长.23.小明将一副三角板按如图所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长;若已知CD 2=,求AC 的长?23.如图,在⊿ABC 中,ACB 90∠= ,AC BC =,P 是⊿ABC 内的一点,且PA 3=,PB 1=,CD PC 2==, CD CP ⊥;求BPC ∠的度数.24.在一次“探究性学习”课中,老师设计了如下数表:⑴.请你分别观察,,a b c 与n 之间的关系,用含自然数()n n 0> 的代数式表示,,a b c ,则a = ,b = ,c = ;⑵.猜想:以,,a b c 为三边的三角形是否为直角三角形?证明你的结论.n 23 4 5 a 221- 231- 241- 251-b 4 6 8 10c 221+ 231+ 241+ 251+D CA D C AB P2017 – 2018下学期富顺县六校联考一八年级数学 参考答案一.选择题(本大题共10个小题,每小题3分,共30分)10题辅助线示意图:二三.解答题(本题有5个小题,17 –20题每题5分,21题6.)17. 7- ;18. -; 19. 0 ;; 21.化简结果:2a 6a +;计算结果:3。
富顺县2017-2018年初二第二次月考英语试题及答案含听力

童寺片区八年级英语第二次段考测试Class: ______ Name: ______ Full marks: 100 Your marks: ______第Ⅰ卷(选择题,共65分)第一部分:听力(共两节,满分20分)第一节:(共5小题;每小题1分,满分5分)听下面5段小对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
每段对话读一遍。
( )1. What does Lisa need?( )2. What are the boy and the girl talking about?( )3. What does Andy like playing?( )4. What is Jake’s favorite Chinese food?( )5. What will the classmates do for LinHong?第二节:(共15小题;每小题1分,满分15分)听下面几段材料,每段材料后有一个或几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
每段材料读两遍。
( )6. What does Brian think of action movies?A. Meaningless.B. Boring.C. Exciting.( )7. Which cinema does Tony like best?A. Rose Cinema.B. Town Cinema.C. Park Cinema.( )8. When does the bus to Guangzhou leave?A. At 3:15 p.m.B. At 3:45 p.m.C. At 4:15 p.m.( )9. What did Alice watch last night?A. A talk show.B. A game show.C. A talent show.( )10. Who will watch a cartoon this afternoon?A. Sara.B. Jenny.C. Betty.听下面一段材料,回答11-12题( )11. When does Linda’s birthday party start?A. At 7:50 p.m.B. At 8:10 p.m.C. At 8:50 p.m. ( )12. What might Mike do this evening?A. Go to Linda’s party.B. Go to the concert.C. Look after his grandmother.听下面一段材料,回答13-15题( )13. How often does Robert play basketball?A. Once a week.B. Twice a week.C. Three times a week. ( )14. When does Robert play soccer?A. On Tuesdays.B. On Thursdays.C. On Saturdays.( )15. What sport does Robert play on Sundays?A. Baseball.B. V olleyball.C. Basketball.听下面一段材料,回答16-20题( )16. When did “Walking Street” open?A. Two days ago.B. Two months ago.C. Two years ago.( )17. What’s on “Walking Street”?A. There are lots of interesting markets.B. There are lots of new markets.C. There are lots of big markets.( )18. What can you find at “Friendship” market?A. All kinds of fruits.B. All kinds of bags.C. All kinds of clothes. ( )19. Where can you buy flowers?A. At “Sweet” market.B. At “One Plus One” market.C. At “Happiness” market.( )20. Where is “One Plus One” market?A. Across from the station.B. Across from the post office.C. Across from the hospital.第二部分:基础知识运用(共两节,满分20分)第一节:单项填空(共10小题;每小题1分,满分10分)从A、B、C三个选项中选出最佳选项。
2017-2018年上学期八年级数学六校联考第一次段考(新人教版.含答题卡.含答案)

2017-2018上学期八数六校联考一 第 1页(共 4页) 第 2页 (共 4页)2017-2018学年度上学期富顺县直属中学六校联考第一次段考八 年 级 数 学 科 试 卷命题人:学校 赵化中学 教师 郑宗平注意事项:1.答题前,考生务必将自己的姓名、考号(用0.5毫米的黑色签字笔)填写在答题卡上,并检查条形码粘贴是否正确.2.选择题使用2B 铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米的黑色签字笔书写在答题卡的对应框内,超出答题区域的书写的答案无效,在草稿、试卷上答题无效.3.考试结束后,将答题卡收回.一.选择题(本大题共8个小题,每小题3分,共24分) 1.下列哪组数据能组成三角形 ( ) A. 4cm,4cm,9cm B.1cm,2cm,4cm C.1cm,2cm,3cm D.2cm,3cm,4cm 2.下列四个图形中,线段BE 是△ABC 的高的是 ( )3.已知在 △ABC 中有A B C ∠=∠+∠,那么△ABC 是 ( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上三种情况都有可能4.下列说法不正确的是 ( )A.三角形的重心是指三角形三条中线的交点B.邻边相等的长方形一定是正多边形C.三角形和四边形都具有稳定性D.从n 边形一个顶点出发可引()n 3-条对角线 5. 如图,A B C D E F G ∠+∠+∠+∠+∠+∠+∠ = ( ) A.180° B.360° C.540° D.720°6.如图,用尺规作图的办法作'''A B C ABC ∠=∠(见作图痕迹),其作图的理论依据是首先运用了三角形判定方法中的)A.SSSB.SASC.ASAD.HL7.下列条件中,能利用“SAS ”判定△ABC ≌△'''A B C 的是 ( )A.'','','AB A B AC A C C C ==∠=∠ B.'',',''AB A B A A BC B C =∠=∠= C.'',','',AC A C C CBC B C =∠=∠= D.'',',''AC A C A A BC B C =∠=∠= 8.如图,点B C E 、、三点在同一直线上,且,,AB AD AC AE==若12394∠+∠+∠= ,则3∠的度数为 ( A.49° B.47° C.45° D.43°二.选择题(本大题共6个小题,每小题3分,共18分)9.一个三角形的三个内角中最多有 个钝角(或直角) 10.根据右图中标出的已知条件可求出α∠的度数为 .11. 如图,已知在△ABC 中,BC 5cm =;将△ABC 沿边BC 的直线平移至△DEF (见图);若EC 2cm =,则CF = cm12.如图,某同学不小心把一块三角形玻璃打碎成了三块(见右面的示意图)是带 去(填序号),依据的是 .(填写简写或简记形式) 13.如图,在Rt △ABC 中C 90∠= ,点D 为边CB 上的一点,连结AD ;若,AC 12AD 13==,△DCA 的周长为30;要使AD 恰好是 △ABC 的角平分线,那么点D 到边AB 的距离应为 .14.如图.在梯形ABCD 中,AD ∥BC ,若E 为AB 的中点;若梯形ABCD 的面积为34个平方单位,则△ECD (阴影部分)的 面积为 个平方单位.三.解答题(本题有5个小题,每小题5分,共25分.)15.若一个等腰三角形有两边长分别为5和9,求这个等腰三角形的周长.16.一个多边形的内角和比它的外角的和大1080°,这个多边形的边数是多少?;C A C 'B C B B B A ED AB2017-2018上学期八数六校联考一 第 3页(共 4页) 第 4页 (共 4页) 17.如图,B 在A 处的南偏西50°方向,C 在A 处的南偏东20°方向,C 在B 处的北偏东75°方向.⑴.求ABC ∠的度数;(2分) ⑵.求ACB ∠的度数.(3分)18.推理填空(按步给分)如图,,E F 12∠=∠∠=∠;求证:△ABE ≌△ABF . 证明:∵,1ABF 1802ABE 180∠+∠=∠+∠= 12∠=∠ ∴∠=∠(等角的补角相等) 在△ABE ≌△ABF 中⎧⎪⎪⎨⎪⎪⎩∴△ABE ≌△ABF ().19.作图解答:如图,已知AOB ∠.⑴.作出AOB ∠的角平分线OC ;(本问用尺规作图,不写作法但要保留作图痕迹) (3分) ⑵.在AOB ∠的角平分线OC 取一点P (端点除外),过P 分别作线段,PD OA PE OB ⊥⊥,垂足分别为D E 、,并直接写出PD 与PE 的数量关系.(本问可不用尺规作图)(2分)四.解答题(本题有3个小题,共18分) 20.已知,在△ABC ,三个内角的度数满足::::ABC C A 567∠∠∠=,BD 是△ABC 的角平分线,DE 是△DBC 的高,D 是垂足点.⑴.求△ABC 各内角的度数;(3分)⑵.求图中1∠的度数. (3分)21.作图解答:已知n 边形(图中虚线表示点4A 到n A 没画出来的其它部分的边).从一个点出发分别依次连接n 边形的顶点将n 边形分成三角形. ⑴.在下面分别画出不同情况下连接的线条意图;(注意三角形之间无交叉重叠情况)(3分) ⑵.用含n 的代数式表示出分成的三角形个数,并直接写在该个示意图的下面括号里.(3分)22. 如图,已知点A B C D 、、、在同一直线上,且A D ∠=∠,AB CD = ⑴.清添加一个条件能使△ACE ≌△DBF .(2分)⑵.在⑴问的基础上证明△ACE ≌△DBF .(4分)五.解答题(本题有2个小题,第23题7分,第24题8分,共15分)23.如图,已知AOB COD 90∠=∠= ,,AB CD OA OC ==求证:⑴.△AOB ≌△COD (3分) ⑵.DE BF =(4分)24.如图,AD 为△ABC 边BC 上的高,点E 是AD 上的一点,若,DA DB =DC DE =;清探究BE 与AC 之间的关系,并对你探究的结论加以证明.BO A分成( )三角形A 3A 4分成( )三角形A 3A 4分成( )三角形A 3A 4请在各题目的答题区域内作答,超出答题区域的答案无效2017~2018学年上学期八年级六校联考一数学答题卡设计:郑宗平准考证号姓 名请在各题目的答题区域内作答,超出答题区域的答案无效2017-2018上六联考一 八数 参考答案 第 1页(共 4页) 第 2页 (共 4页)2017 - 2018上富顺县六校联考一八年级数学 参考答案一.选择题(本大题共8个小题,每小题3分,共24分)二.选择题(本大题共6个小题,每小题3分,共18分)9. 1 ; 10. 109° ;11. 3 cm ; 12. ③ , ASA ; 13. 5 ; 14. 17 .三.解答题(本题有5个小题,每小题5分,共25分.)15.若一个等腰三角形有两边长分别为5和9,求这个等腰三角形的周长. 解(略);等腰三角形的周长分别为19和23.(注:两种情况若没有讨论两腰之和是否大于底边,则分别扣1分)16.一个多边形的内角和比它的外角的和大1080°,这个多边形的边数是多少?;解(略):设这个多边形的边数为n 条,则:()n 21801080360-⋅=+ ;解得:n 10=.17.如图,B 在A 处的南偏西50°方向,C 在A 处的南偏东20°方向,C 在B 处的北偏东75°方向.⑴.求ABC ∠的度数;(2分) ⑵.求ACB ∠的度数.(3分)解(略):本题方法多种.⑴.2ABC 5∠= ;⑵.8ACB 5∠= .18.填空(按步给分)如图,,E F 12∠=∠∠=∠;求证:△ABE ≌△ABF . 证明:∵,1ABF 1802ABE 180∠+∠=∠+∠= 12∠=∠∴ABF ABE ∠=∠(等角的补角相等)在△ABE ≌△ABF 中E FABF ABE AB AB⎧∠=⎪⎪⎨∠∠=∠=⎪⎪⎩ ∴△ABE ≌△ABF ()AAS .19.作图解答:如图,已知AOB ∠.⑴.作出AOB ∠的角平分线OC ;(本问用尺规作图,不写作法但要保留作图痕迹) (3分) ⑵.在AOB ∠的角平分线OC 取一点P (端点除外),过P 分别作线段,PD OA PE OB ⊥⊥,垂足分别为D E 、,并直接写出PD 与PE 的数量关系.(本问可不用尺规作图)(2分)解(略):⑴.见图;(注:按痕迹各给1分)⑵.见图.PD PE =.(注:垂线段和数量关系各给1四.解答题(本题有3个小题,共18分) 20.已知,在△ABC ,三个内角的度数满足::::ABC C A 567∠∠∠=,BD 是△ABC 的角平分线,DE 是△DBC 的高,D 是垂足点. ⑴.求△ABC各内角的度数;(3分)⑵.求图中1∠的度数. (3分)解(略):⑴.,,ABC C A 506070∠=∠=∠= ⑵.615∠= .21.作图解答:已知n 边形(图中虚线表示点4A 到n A 没画出来的其它部分的边),从一个点出发分别依次连接n 边形的顶点将n 边形分成三角形. ⑴.在下面分别画出不同情况下连接的线条意图;(注意三角形之间无交叉重叠情况)(3分) ⑵.用含n 的代数式表示出分成的三角形个数,并直接写在该个示意图的下面括号里.(3分)A分成( )三角形A 3A 4n 2-分成( )三角形A 13A 4n 1-分成( )三角形A 13A 4n2017-2018上六联考一 八数 参考答案 第 3页(共 4页) 第 4页 (共 4页)22. 如图,已知点A B C D 、、、在同一直线上,且A D ∠=∠,AB⑴.清添加一个条件能使△ACE ≌△DBF .(2分) ⑵.在⑴问的基础上证明△ACE ≌△DBF .(4分)解(略):⑴.添加条件不唯一. ⑵.由于添加的添加不唯一.根据⑴问添加的条件可利用SAS 或ASA 或AAS 等来判定△ACE ≌△DBF .五.解答题(本题有2个小题,第23题7分,第24题8分,共15分) 23.如图,已知AOB COD 90∠=∠= ,,AB CD OA OC ==. 求证:⑴.△AOB ≌△COD (3分)⑵.DE BF =(4分) 证明(略):⑴.利用HL 来证明△AOB ≌△COD ; ⑵.∵△AOB ≌△COD∴OD OB = A C ∠=∠∵AOB COD 90∠=∠=∴AOB EOF COD EOF ∠-∠=∠-∠ 即AOE COF ∠=∠ 在△AOE ≌△COF 中AOE COF OA OC A C⎧∠=⎪⎪⎨∠=∠=∠⎪⎪⎩∴△AOE ≌△COF ()ASA ∴OE OF = ∵OD OB =∴OD OE OB OF -=- 即DE BF =24.如图,AD 为△ABC 边BC 上的高,点E 是AD 上的一点,若,DA DB =DC DE =;清探究BE 与AC 之间的关系,并对你探究的结论加以证明.解(略):BE 与AC 之间的⑴.数量关系:BE AC =;⑵.位置关系:BE AC ⊥. (2分) 理由如下(6分):延长BE 交AC 于F⑴. ∵AD 为△ABC 边BC 上的高. ∴AD BC ⊥∴BDE ADC 90∠=∠= 在△BDE ≌△ADC 中DA DB BDE ADC DC DE⎧⎪⎪⎨=∠=∠=⎪⎪⎩∴△BDE ≌△ADC ()SAS ∴BE AC =⑵. ∵ △BDE ≌△ADC ∴2C ∠=∠∵ BDE 90∠= ∴1290∠+∠= ∴1C 90∠+∠=∴390∠=∴BF AC ⊥ 即BE AC ⊥说明:以上答案仅供参考!2017.10.9O。
自贡市2017--2018学年人教版八年级下学期期末考试数学试题0912

A
E
B
形,四边形 ABCD 还应满足的一个条件使
.
13. 已知直线 y ax a 2 ( a 为常数)不经过第四象限,则 a
A
的取值范围是
.
E
D
14.7 张如图 1 的长为 a ,宽为 b a b 的小长方形纸片,按如 b
F
图 2 的方式不重叠地放在矩形 ABCD 内,未被覆盖的部分(两a
Q H
G
个矩形)用阴影表示 . 设左上角与右下角的阴影部分的面积差为 B S ,当 BC 的长度变化时,按照同样的放置方式, S 始终保持不图 1
y1 ( )
5. 如图,直线 y1
3
x 与直线 2
y2
1 x 2 交于点 A ,若
2
2
A
1
y1 y2 ,则
x ( ) – 1 O 1 2 3 4 5 y 2
A. x 1 B. x 1 C. x 3 D. x 3
–1
2
2
6. 在直线 L 上依次放着三个正方形,已知斜放的正方形的面积为 2,正
放的两个正方形的面积分别为 S1, S2 ,则 S1 S2 的值为
则关于 x 的一次函数 y min x, 2x 1 可以表示为
()
x,
x1
A. y x B. y 2x 1 C. y
D.
2x 1, x 1
x,
x1
y
2x 1, x 1
二、填空题(本题有 6 个小题,每小题 3 分,共计 18 分)
2
9. 计算
3=
.
10. 甲、乙两人进行射击测试, 每 10 次射击成绩的平均数都是 8.5 环,方差分别是:
A. 2
最新四川省自贡市-2018学年八年级下学期期末考试数学试题

自贡市2017-2018学年八年级下学期期末考试数学试卷 重新制版:河口镇学校 李祖林一、选择题(本题有8个小题,每小题3分,满分24分,每小题只有一个选项符合题意) 1.)A.2.直线y =x -1不经过( )A.第一象限 B .第二象限 C.第三象限 D .第四象限 3在实数范围内有意义,则x 的取值范围是( ) A .x >一1 B .≥-1 C .x≠0 D.x≥-1且x≠0 4.下列曲线中不能表示y 是x 的函数的是( )5.已知直角三角形的两直角边分别是12和5,则斜边上的中线长是( ) A.34 B.26 C.8.5 D.6.56,为了解某班学生双休户外活动情况,对部分学生参加户外活动的时间进行抽样调查,结果如下表:则关于“户外活动时间”这组数的众数、中位数、平均数分别是( ) A.3,3,3 B.6,2,3 C.3,3,2 D.3,2,37.实数a ,ba 的结果是( )A.2aB.2bC.-2bD.-2a8.如图,长方体的高为2cm ,底面长为3cm ,宽为1cm ,蚂蚁沿长方体表面爬行,从点1A 到点2C 的最短距离是( )A BC .D .二、填空题(本题有6个小题,每小题3分,共计18分) 9.一组数1、2、3、4、5,则这组数据的方差是_________.10.命题“直角三角形斜边上的中线等于斜边的一半”的逆命题是____________________ _______________.它是________命题,(填“真”或“假)11.己知函数253y mx m =--,当m =_______时,直线过原点;m 为______数时,函数 y 随x 的增大而减小12按上述规律,第17个数据是__________.13.如图,四边形ABCD 是矩形,E 是BA 延长线上一点,F 是CE 上一点, ,.ACF AFC FAE FEA ∠=∠∠=∠若∠ACB =21︒,则∠ECD=_________ 14.如图,正方形ABCD 中,AB =3,点E 在边CD 上,且CE =2ED .将△A DE 沿AE 对折至△A FE ,延长EF 交边BC 于点G ,连结AG 、CF. 下列结论:①BG=GC ;②AG∥CF;③910FGC S ∆=。
2017-2018学年四川省自贡市八年级(下)期末数学试卷(解析版)
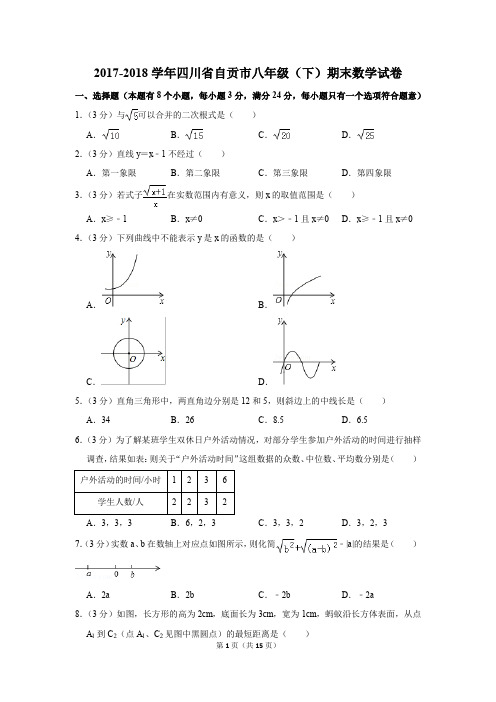
3.(3 分)若式子
在实数范围内有意义,则 x 的取值范围是( )
A.x≥﹣1
B.x≠0
C.x>﹣1 且 x≠0 D.x≥﹣1 且 x≠0
4.(3 分)下列曲线中不能表示 y 是 x 的函数的是( )
A.
B.
C.
D.
5.(3 分)直角三角形中,两直角边分别是 12 和 5,则斜边上的中线长是( )
A.34
时,直线过原点;m 为
数时,
函数 y 随 x 的增大而增大.
12.(3 分)观察分析下列数据: ,2 ,6,4 ,……,则第 17 个数据是
.
13.(3 分)如图,四边形 ABCD 是矩形,E 是 BA 延长线上的一点,F 是 CE 上一点,∠ACF
=∠AFC,∠FAE=∠FEA;若∠ACB=21°,则∠ECD=
四、解答题(本题有 3 个小题,每小题 6 分,共计 18 分) 20.(6 分)国家规定,“中小学生每天在校体育锻炼时间不小于 1 小时”,某地区就“每天
在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不 完整).其中分组情况:A 组:时间小于 0.5 小时;B 组:时间大于等于 0.5 小时且小于 1 小时;C 组:时间大于等于 1 小时且小于 1.5 小时;D 组:时间大于等于 1.5 小时.
2017-2018 学年四川省自贡市八年级(下)期末数学试卷
2017-2018 学年四川省自贡市八年级(下)期末数学试卷
一、选择题(本题有 8 个小题,每小题 3 分,满分 24 分,每小题只有一个选项符合题意)
1.(3 分)与 可以合并的二次根式是(
A.
B.
2.(3 分)直线 y=x﹣1 不经过( )
四川省自贡市八年级下学期物理第一阶段考试试卷

四川省自贡市八年级下学期物理第一阶段考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)以下估测比较接近实际的是()A . 一枚鸡蛋的重力大约是1 NB . 一瓶矿泉水的重力大约是50 NC . 小李同学受到的重力大约是550 ND . 一只鸡受到的重力大约是4 N2. (2分) (2015八下·龙湖期中) 如图是足球运动员踢足球时的情景,下列说法正确的是()A . 球被脚踢出去,说明只有球才受到力的作用B . 脚踢球使球飞出去,说明力是物体运动的原因C . 足球在空中飞行过程中,运动状态一定发生改变D . 空中飞行的足球,若它所受的力全部消失,它一定沿水平方向做匀速直线运动3. (2分) (2017八下·荔湾期末) 用力拉弹簧,弹簧就伸长;用力压弹簧,弹簧就缩短,这个现象说明力产生效果()A . 跟力的作用点有关B . 跟力的大小有关C . 跟力的方向有关D . 跟力的大小、方向和作用点有关4. (2分)(2017·高安模拟) 如图是太阳能汽车在平直公路上匀速行驶的情形,若不计空气对汽车的影响,则下列说法正确的是()A . 汽车受到两对平衡力的作用B . 汽车的重力和地面对汽车的支持力是相互作用力C . 汽车急刹车时不能立即停止,是由于速度大惯性大D . 汽车对地面的压力和地面对汽车的支持力是平衡力5. (2分)随着生活质量的提高,轿车进入了越来越多的城市家庭,我们的生活也与轿车产生了越来越紧密的关系.下面是关于轿车的一些说法,其中正确的是()A . 轿车行驶时,只要不鸣喇叭,就不会产生噪声B . 轿车静止时没有惯性,所以靠近静止着的轿车是安全的C . 轿车上凸下平近似流线型的设计,使它行驶时,底部比顶部受到的气流的压强小D . 汽车轮胎上的花纹是为了增大与地面间的摩擦6. (2分)(2020·朝阳模拟) 关于惯性,下列说法正确的是()A . 铅球被推出离开手后,仍然向前运动,是因为铅球受到惯性的作用B . 汽车关闭发动机后仍能继续前进,是因为汽车的惯性大于它所受到的阻力C . 网球被竖直向上抛出后,由于它具有惯性而继续向上运动D . 重返大气层的神舟飞船,运动得越来越快,是由于飞船具有惯性7. (2分)跳伞运动员在空中张开降落伞后,跳伞运动员匀速下降,这是因为跳伞运动员()A . 没有受到力的作用B . 受到的重力小于阻力C . 受到的重力等于阻力D . 受到的重力大于阻力8. (2分)妈妈做饭时,小军在旁边仔细观察。
2018-2019学年度上学期四川省自贡市富顺县直属中学六校联考第一次段考八 年 级 数 学 科 试 卷

2018-2019学年度上学期直属中学六校联考第一次段考一.选择题1.下列所给的各组线段,能组成三角形的是 ( ) A.,,.15cm 15cm 35cm B.,,.20cm 30cm 40cmC.,,.17cm 27cm 47cmD.,,.10cm 40cm 50cm 2.下列四个图形中,线段B E 是△ABC 的高的是 ( )3.已知在 △ABC 中有A B C∠=∠+∠,那么△ABC 是 ( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上三种情况都有可能 4.下列说法不正确的是 ( )A.三角形的重心是指三角形三条中线的交点B.邻边相等的长方形一定是正多边形C.三角形和四边形都具有稳定性D.从n 边形一个顶点出发可引()n 3-条对角线5.下列说法正确的是 ( )A . 全等三角形是指形状相同大小相等的三角形B . 全等三角形是指面积相等的三角形C . 周长相等的三角形是全等三角形D . 所有的等边三角形都是全等三角形6.如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成2011个三角形,那么这个多边形是 ( )A . 2012边形B . 2013边形C . 2014边形D . 2015边形7. 如图,A B C D E F G ∠+∠+∠+∠+∠+∠+∠ = ( ) A.180° B.540° C.360° D.720° 8.如图,点B C E 、、三点在同一直线上,且,,A B A D A C A E B C D E ===; 若12394∠+∠+∠=o,则3∠的度数为 ( ) A.49° B.47° C.45° D.43° 二.选择题(本大题共6个小题,每小题3分,共18分)11. 如图,已知在△ABC 中,B C 5c m=;将△ABC 沿边B C 所在 的直线平移至△DEF (见图);若E C 2c m =,则CF =cm . 12.已知等腰三角形的一边长等于3,一边长等于7,则它的周长为 .13.已知a b c 、、为三角形的三边,化简a b c b a c +----的结果是 . 14.如图,,DE BC BE EC ⊥=,且,AB 5AC 8==,则△ABD 的周长为 .一、选择题(共10小题,每小题3分,共30分) 1.以下列各组长度的线段为边,能构成三角形的是( )A .7 cm ,5 cm ,12 cmB .6 cm ,8 cm ,15 cmC .4 cm ,6 cm ,5 cmD .8 cm ,4 cm ,3 cm 2.在△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,则此三角形是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .等腰三角形 3.如图,△ABC ≌△DEF ,则∠E 的度数为( )A .80°B .40°C .62°D .38°4.某同学把一块三角形的玻璃打碎成3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )A .带①去B .带②去C .带③去D .带①②③去5.如果等腰三角形两边长是6 cm 和3 cm ,那么它的周长是( )A .9 cmB .12 cmC .12 cm 或15 cmD .15 cm6.一个多边形的每个内角为144°,则这个多边形是( )边形A .8B .9C .10D .127.如图,△ABC 中,D 、E 分别为BC 、AD 的中点,S △ABC =1,则阴影部分的面积是( )A .81B .61C .41D .218.下列说法正确的是( )A .四边形具有稳定性B .各边都相等的多边形是正多边形C .面积相等的两个三角形全等D .半径相等的两个圆是全等形 9.如图,在方格纸中,以AB 为一边作△ABP ,使之与△ABC 全等,从P 1、P 2、P 3、P 4四个点中找出符合条件的点P ,则点P 有( )A .1个B .2个C .3个D .4个EFDB AC 123DE B AC A B E DC GF A C B E B E A C B A E A C B C E BCA D EB CD A第4题A B C E D 第10题 10.如图,△ABC 中,AC=BC ,∠ACB=90°,AE 平分∠BAC 交BC 于E ,BD ⊥AE于D ,DM ⊥AC 于M ,连CD ,下列结论:①AC+CE=AB ;②BD=12AE ;③∠CDB=120°;④AC AB AM+为定值,其中正确的有( )个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018下学期八数六校联考一 第 1页(共 4页) 第 2页 (共 4页) 2017-2018学年度下学期富顺县直属中学六校联考第一次段考
八 年 级 数 学 科 试 卷
说明:试卷来源于富顺县六所直属中学联考一 重新制版:郑宗平
一.选择题(本大题共8个小题,每小题3分,共30分) 1.
A. a =-24a b =2.在△ABC 90,周长为长分别是 A. 5,4,13,12,5 C.
10,8,6 D. 26,
24,10 3.化简)
x
0的结果是
( )
A. y
2x -y C. 2x y - D. y -
4.
( )
2
=
B. 2
=
x 1=-=
5. 已知直角三角形中30°角所对的直角边长是cm ,则另一条直角边的长是 ( )
,90AC =8.如图,分别以直角⊿ABC 的三边AB,BC,CA 为直径向外作半 圆.设直线AB 左边的阴影部分的面积为1S ,右边的阴影部分的面 积和为2S 则 ( )
A.=12S S
B.12S S ≥ C 12S S ≤ D.12S S >
9. )
A. 4±
11.12.三
2017-2018下学期八数六校联考一 第 3页(共 4页) 第 4页 (共 4页)
) 90
,CD ⊥
23.小明将一副三角板按如图所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长;若已知CD 2=,求AC 的长?
90 ,AC ;求BPC ∠
24.在一次“探究性学习”课中,老师设计了如下数表:
C
2017-2018下学期六联考一 八数 参考答案 第 1页(共 4页) 第 2页 (共 4页) 2017 – 2018下学期富顺县六校联考一八年级数学 参考答案
一.选择题(本大题共10个小题,每小题3分,共30分)
10题辅助线示意图:
二
三.
解答题(本题有5个小题,17 – 20
题每题5分,21题6
.)
17. 7- ;
18. -; 19. 0 ;;
21.化简结果:2
a 6a +;计算结果:3。
四.解答题(本题有4个小题,22、 23题每题6分,24、25题每题7分,共26分.) 22.(1).90,AC +=215(2).∴=CD 12 .
23.
∴632=x
∴
24.略解:
连接BD (见图)
∵CD CP ⊥,CD PC 2== ∴⊿PCD 为等腰直角三角形. ∴∠=CPD
45 .
∵∠+∠=∠+∠=ACP BCP BCP BCD 90 ∴∠=∠ACP BCD ∵=CA CB
∴⊿CAP ≌⊿CBD (SAS ) ∴==DB PA 3
在Rt ⊿CPD 中,8222
2
2
2
2
=+=+=CD CP DP .
又∵,==2
PB 1DP 8
∴918222=+=+=PB DP DB . ∴∠=DPB 90
∴∠=∠+∠=+=CPB CPD DPB 4390551 .
25.略解:
⑴.a = 2
n 1-, b = 2n , c = 2
n 1+ ; ⑵.答:以,,a b c 为边的三角形是直角三角形.
证明:∵a = 2n 1-, b = 2n , c = 2
n 1+
∴(
)
()()
+=-+=-++=+=2
2
2
22
2
4
2
2
2
2a b n 12n n 2n 14n n 1
c ,
∴ 以,,a b c 为边的三角形是直角三角形.
说明:以上答案仅供参考!
2018.4.7
A。
