2015高一三角函数测试卷2(详细答案)

合集下载

2015高一三角函数2015全国高考数学题选tttt

2015年高考数学试题分类汇编(三角函数)1.（15年新课标1理科）sin20°cos10°-con160°sin10°=（A）（B（C ）12- （D ）122.(15年新课标1理科) 函数f(x)=的部分图像如图所示，则f （x ）的单调递减区间为 (A)（）,k(b)（）,k(C)（）,k (D)（）,k3.（15年陕西文科）如图，某港口一天6时到18时的谁深变化曲线近似满足函数y ＝3sin (6πx ＋Φ)＋k ，据此函数可知，这段时间水深(单位：m )的最大值为____________.4.（15年天津文科）已知函数()()sin cos 0,,f x x x x ωωω=+>∈R 若函数()f x 在区间(),ωω-内单调递增,且函数()f x 的图像关于直线x ω=对称,则ω的值为．5. A.512πB.3π C.4π D.6π 6.（15年福建文科）若5sin 13α=-，且α为第四象限角，则tan α的值等于（）A ．125B ．125-C ．512D ．512-7（15年江苏）已知tan 2α=-，()1tan 7αβ+=，则tan β的值为_______.1.（15北京理科）已知函数2()cos 222x x xf x ．(Ⅰ) 求()f x 的最小正周期；(Ⅱ) 求()f x 在区间[π0]-，上的最小值．8.（15北京文科）已知函数()2sin 2x f x x =-．（Ⅰ）求()f x 的最小正周期；（Ⅱ）求()f x 在区间20,3π⎡⎤⎢⎥⎣⎦上的最小值．9.（15年广东文科）已知tan 2α=．()1求tan 4πα⎛⎫+ ⎪⎝⎭的值；()2求2sin 2sin sin cos cos 21ααααα+--的值．10.（15年安徽文科）已知函数2()(sin cos )cos2f x x x x =++ （1）求()f x 最小正周期；（2）求()f x 在区间[0,]2π上的最大值和最小值.11.（15年福建理科）已知函数f()x 的图像是由函数()cos g x x =的图像经如下变换得到：先将()g x 图像上所有点的纵坐标伸长到原来的2倍（横坐标不变），再将所得到的图像向右平移2p个单位长度. (Ⅰ)求函数f()x 的解析式，并求其图像的对称轴方程；(Ⅱ)已知关于x 的方程f()g()x x m +=在[0,2)p 内有两个不同的解,a b ．（1)求实数m 的取值范围；（2)证明：22cos ) 1.5m a b -=-(12.（15年福建文科）已知函数()2cos 10cos 222x x xf x =+．（Ⅰ）求函数()f x 的最小正周期；（Ⅱ）将函数()f x 的图象向右平移6π个单位长度，再向下平移a （0a >）个单位长度后得到函数()g x 的图象，且函数()g x 的最大值为2．（ⅰ）求函数()g x 的解析式；（ⅱ）证明：存在无穷多个互不相同的正整数0x ，使得()00g x >．。

三角函数与解三角形测试卷(二)

三角函数与解三角形测试卷（二）一、单选题1．在△ABC 中，60A ∠=︒，6a =，4b =，则满足条件的△ABC （） A ．无解B ．有一解C ．有两解D ．不能确定2．下列四个函数中，以π为最小正周期，且在区间π,π2⎛⎫⎪⎝⎭上单调递减的是（）A ．cos y x =B ．sin y x =C ．cos 2xy =D ．tan y x =3．函数2sin ()||2xf x x =+的部分图象大致为（） A ． B ．C ．D ．4．圣·索菲亚教堂是哈尔滨的标志性建筑，其中央主体建筑集球、圆柱、棱柱于一体，极具对称之美．为了估算圣·索菲亚教堂的高度，某人在教堂的正东方向找到一座建筑物AB ，高约为36m ，在它们之间的地面上的点M （B ，M ，D 三点共线）处测得建筑物顶A 、教堂顶C 的仰角分别是45和60，在建筑物顶A 处测得教堂顶C 的仰角为15，则可估算圣·索菲亚教堂的高度CD 约为（）A ．54mB ．47mC ．50mD ．44m5．已知函数()13π2sin (0,)6f x x m x ⎡⎤=-∈⎢⎥⎣⎦有三个不同的零点123,,x x x ，且123x x x <<，则1232x x x ++=（） A ．4πB ．2πC ．4π3D ．7π36．已知sin sin 13πθθ⎛⎫++= ⎪⎝⎭，则tan 6πθ⎛⎫+= ⎪⎝⎭（）A ．63B ．33C ．±2D ．±227．tan10tan 503tan10tan 50++的值为（） A ．33B ．3C ．1D ．3-8．已知()1sin 5αβ+=，()3sin 5αβ-=，则tan tan αβ的值为（）A ．2B ．2-C ．12D ．12-9．已知函数()()sin 20,02f x x πωϕωϕ⎛⎫=+><< ⎪⎝⎭的部分图象如图所示，则下列结论正确的是（）A ．()f x 的图象关于点,03π⎛⎫- ⎪⎝⎭对称B ．()f x 的图象向右平移6π个单位后得到sin 2y x =的图象 C ．()f x 在区间0,2π⎡⎤⎢⎥⎣⎦的最小值为3D ．6f x π⎛⎫+ ⎪⎝⎭为偶函数10．在ABC 中，A ，B ，C 分别为ABC 三边a ，b ，c 所对的角，若cos 32B B =，且cos cos 2sin sin 3sin B C A Bb c C+=，则a c +的最大值是（） A ．1 B 3C ．2 D ．2311．在ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，若2222022a b c +=，则()2tan tan tan tan tan A BC A B +的值为（）A ．0B ．1C ．2021D ．202212．已知M 是ABC 内的一点，且2AB AC ⋅=，4BAC π∠=，12MBC ABC S S =△△，则11MABMACS S +△△的最小值是（）A ．8B ．4C ．2D ．1二、填空题13．已知cos(75°＋α)＝13，求cos(105°－α)＋sin(15°－α)＝________.14．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，满足22230b c ac --=，sin()2sin A B A +=，则cos C ___________．15．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知()sin sin sin a A b B c b C =++，若角A 的内角平分线AD 的长为2，则△ABC 面积的最小值为______．16．已知函数()2sin f x x ω=（0>ω）在区间3,43ππ⎡⎤-⎢⎥⎣⎦上单调递增，且函数()2sin 2g x x ω=+在[]2,0π-上有且仅有一个零点，则实数ω的取值范围是_______. 三、解答题17．设ABC 的内角A 、B 、C 所对的边分别为a 、b 、c ，已知3c =，且()cos 2A B C ++=.(1)求角C 的大小；(2)若向量()sin ,1m A =-与()2,sin n B =互相垂直，求a 、b 的值.18．从①)sin sin sin c C a A b B -=-；② sin 22A A =补充到下面横线处，并解答：在ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，AB =(1)求角A ；(2)若ABC 外接圆的圆心为O ，11cos 14AOB ∠=，求BC 的长. 注：如果选择多个条件分别解答；按第一个解答计分.19．在ABC 中．3sin cos 64A A π⎛⎫-= ⎪⎝⎭．(1)求角A ；(2)若8AC =，点D 是线段BC 的中点，DE AC ⊥于点E ，且DE =CE 的长．20．在ABC 中，内角,,A B C 的对边分别为,,a b c ，tan tan b A b B += (1)求角B ；(2)D 是AC 边上的点，若1CD =，3AD BD ==，求sin A 的值． 21．如图，在平面四边形ABCD 中，3,2,4B BC ABC π∠==的面积 2.ABCS =(1)求AC 的长；(2)从条件①､条件②､条件③这三个条件中任选两个作为已知，判断DCA BCA ∠=∠是否可能成立，并说明理由. 条件①：4D π∠=；条件②：4=AD ；条件③：6CD =.22．在ABC 中，内角,,A B C 的对边分别为,,a b c ，且()()sin sin 2sin sin sin a A c C B b C B =-++．(1)求角A ；(2)若ABC )32b c a-的取值范围．参考答案：1．A 【解析】【分析】根据正弦定理进行判断即可. 【详解】由正弦定理可知：4sin 1sin sin sin a bB A B B==⇒=，显然不存在这样的角B ，故选：A 2．B 【解析】【分析】利用最小正周期为π排除选项AC ；利用在区间π,π2⎛⎫⎪⎝⎭上单调递减排除选项D ；选项B 以π为最小正周期，且在区间π,π2⎛⎫⎪⎝⎭上单调递减，判断正确.【详解】选项A ：cos y x =最小正周期为2π.判断错误；选项B ：sin y x =最小正周期为π，且在区间π,π2⎛⎫⎪⎝⎭上单调递减.判断正确；选项C ：cos 2xy =最小正周期为4π.判断错误；选项D ：tan y x =在区间π,π2⎛⎫⎪⎝⎭上单调递增. 判断错误.故选：B 3．B 【解析】【分析】根据奇偶性及函数值的正负判断即可. 【详解】因为2sin ()2x f x x =+，定义域为R所以2sin()2sin ()()22x xf x f x x x --==-=--++所以()f x 为奇函数，且(0)0f =，排除CD 当()0,x π∈时，sin 0x >，即()0f x >，排除A 故选：B. 4．A 【解析】【分析】根据题意求得AM =AMC 中由正弦定理求出CM ，即可在直角CDM 中求出CD .【详解】由题可得在直角ABM 中，45AMB ∠=︒，36AB =，所以AM = 在AMC 中，180604575AMC ∠=︒-︒-︒=︒，154560MAC ∠=︒+︒=︒，所以180756045ACM ∠=︒-︒-︒=︒，所以由正弦定理可得sin 45sin 60AM CM=︒︒，所以CM ==则在直角CDM 中，sin6054CD CM =⋅︒=，即圣·索菲亚教堂的高度约为54m. 故选：A. 5．A 【解析】【分析】根据正弦函数的对称性，结合函数零点的定义进行求解即可. 【详解】令()2sin 02sin f x x m m x =-=⇒=，当13π0,6x ⎡⎤∈⎢⎥⎣⎦时，函数有三个零点，因此函数,2sin y m y x ==的图象有三个不同的交点，因为13ππ12sin2sin 21662==⨯=，所以[0,1]m ∈，显然有123π13π0π<2π26x x x ≤<<≤≤≤，而12,x x 关于直线π2x =对称，23,x x 关于直线3π2x =对称，所以21231232π3π224π22x x x x x x x ++=+++=⨯+⨯=，故选：A 6．D 【解析】【分析】根据两角和的正弦公式展开，之后再用辅助角公式可得sin 6πθ⎛⎫+= ⎪⎝⎭函数的关系求解即可. 【详解】sin sin()13πθθ++=，则1sin sin 12θθθ+=，即3sin 12θθ+=，1cos 2θθ+=sin 6πθ⎛⎫+= ⎪⎝⎭cos 6πθ⎛⎫+== ⎪⎝⎭，所以tan 6πθ⎛⎫+== ⎪⎝⎭故选：D 7．B 【解析】【分析】由()tan 60tan 10503=+=，利用两角和差正切公式可整理得到结果. 【详解】()tan10tan 50tan 60tan 105031tan10tan 50+=+==-，tan10tan 5033tan10tan 50∴+=-，tan10tan 503tan10tan 503∴++=. 故选：B. 8．B 【解析】【分析】首先根据正弦两角和差公式得到2sin cos 51cos sin 5αβαβ⎧=⎪⎪⎨⎪=-⎪⎩，再利用同角三角函数的商数关系求解即可. 【详解】由题知：()()1sin sin cos cos sin 53sin sin cos cos sin 5αβαβαβαβαβαβ⎧+=+=⎪⎪⎨⎪-=-=⎪⎩，解得2sin cos 51cos sin 5αβαβ⎧=⎪⎪⎨⎪=-⎪⎩，所以tan sin cos 2tan cos sin ααββαβ==-. 故选：B 9．D 【解析】【分析】先由函数图象求出函数解析式，然后再逐个分析判断【详解】因为()f x 的图象过点10,2⎛⎫⎪⎝⎭，所以1sin 2ϕ=，因为02πϕ<<，所以6π=ϕ，因为()f x 的图象过点2,13π⎛⎫- ⎪⎝⎭，所以由五点作图法可知43362πππω⋅+=，得1ω=，所以()sin 26f x x π⎛⎫+ ⎝=⎪⎭，对于A ，因为2sin sin 13362f ππππ⎛⎫⎛⎫⎛⎫-=-+=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以3x π=-为()f x 的图象的一条对称轴，所以A 错误，对于B ，()f x 的图象向右平移6π个单位后，得sin 2sin 2666y x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，所以B错误，对于C ，当0,2x π⎡⎤∈⎢⎥⎣⎦时，52,666x πππ⎡⎤-∈-⎢⎥⎣⎦，所以1sin 2126x π⎛⎫-≤-≤ ⎪⎝⎭，所以()f x 在区间0,2π⎡⎤⎢⎥⎣⎦的最小值为12-，所以C 错误，对于D ，sin 2sin 2cos 26662f x x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫+=++=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，令()cos 26g x f x x π⎛⎫=+= ⎪⎝⎭，因为()cos(2)cos 2()g x x x g x -=-==，所以()cos 26g x f x x π⎛⎫=+= ⎪⎝⎭为偶函数，所以D 正确，故选：D 10．D 【解析】【分析】根据已知条件求得,B b ，再利用正弦定理将角化边，将问题转化为求6A π⎛⎫+ ⎪⎝⎭的最大值问题求解即可. 【详解】cos 2B B =得sin 16B π⎛⎫+= ⎪⎝⎭，又7666B πππ<+<，所以3B π=. 在ABC 中，由正弦定理得：cos cos cos cos sin cos sin cos sin 2sin sin sin sin 3sin B C c B b C C B B C A A Bb c bc b C b C C+++====所以32sin b B=()2sin sin 2sin 2sin sin 36b a c A C A A A B ππ⎛⎫⎛⎫+=+=+-=+ ⎪ ⎪⎝⎭⎝⎭.故当62A ππ+=，即3A π=时，a c +取得最大值故选：D 11．C 【解析】【分析】将给定三角式切化弦，再利用正弦定理角化边，借助余弦定理及已知计算作答. 【详解】在ABC 中，由余弦定理得：22222cos 2021ab C a b c c =-=+，所以sin sin 22tan tan 2sin sin cos cos cos sin sin sin tan (tan tan )sin (sin cos cos sin )()cos cos cos A BA B A B C A B C A B C A B C A B A B C A B⋅⋅==+++ 222sin sin cos 2sin sin cos 2cos 2021sin sin()sin A B C A B C ab CC A B C c ====+.故选：C 12．A 【解析】【分析】利用向量数量积公式及三角形面积公式可得ABC 的面积，结合已知可得12MAB MACS S+=，再根据基本不等式即可求解. 【详解】∵2AB AC ⋅=，4BAC π∠=，∴cos 222AB AC AB AC BAC AB AC ⋅=⋅∠=⇒⋅= ∴1sin 4512ABCSAB AC =⋅︒=，因为ABCMBCMABMACS SSS=++，12MBC ABC S S =△△，所以1122MAB MACABCSSS +==，所以()22221122442MAC MAC MAB MABMABMACMABMAC MAB MAC MAB MACS S S S S SS S S S S S ⎛⎫++=++≥+⋅ ⎪⎝⎭， 448=+=，当且仅当22MAC MABMAB MACS S S S =，即14MACMABS S==时取等. 故选：A. 13．0 【解析】【分析】利用诱导公式化简每一个式子，再把已知代入即得解. 【详解】因为(105°－α)＋(75°＋α)＝180°，(15°－α)＋(α＋75°)＝90°，所以cos(105°－α)＝cos[180°－(75°＋α)]＝－cos(75°＋α)＝－13，sin(15°－α)＝sin[90°－(α＋75°)]＝cos(75°＋α)＝13.所以cos(105°－α)＋sin(15°－α)＝－13＋13＝0.故答案为：0 14【解析】【分析】利用正弦定理角化边及其余弦定理即可求解. 【详解】∵sin()2sin A B A +=，∴sin 2sin C A =, 由正弦定理得2c a =，∵ 22230b c ac --=，∴22222b c c ac -=+，由余弦定理得：2222cos b c a ac B -=-，∴2224cos a ac B c ac -=+， ∴ 222228cos 42a a B a a -=+， ∴228cos 4a B a -=，解得1cos 2B =-，又∵0πB <<，∴2π3B =, 将2c a =代入22230b c ac --=得b =, 由正弦定理可得sin sin b c B C =，即22πsin sin 3c C =，解得sin 7C =，又∵π02C <<，∴cos C ===. 15．【解析】【分析】利用正弦定理进行边角互化，再利用余弦定理即可求出角A ，由三角形面积相等，结合基本不等式求面积的最小值. 【详解】本题考查解三角形的应用，考查逻辑推理的核心素养．因为()sin sin sin a A b B c b C =++，所以222a b c bc =++．由余弦定理易得1cos 2A =-，又0A π<<所以23A π=．因为AD 平分角A ，所以∠BAD ＝∠CAD ＝60°．由ABCABDACDSSS=+，得111sin120sin 60sin 60222bc c AD b AD ︒=⋅︒+⋅︒，即()2bc b c =+≥16bc ≥，当且仅当b ＝c 时，等号成立，所以△ABC 面积的最小值为故答案为： 16．12,43⎡⎤⎢⎥⎣⎦【解析】【分析】第一步，函数()2sin f x x ω=（0>ω）在区间3ππ,43⎡⎤-⎢⎥⎣⎦上单调递增结合()2sin f x xω=（0>ω）在ππ22ωω⎡⎤-⎢⎥⎣⎦，单调递增得到3ππππ,4322ωω⎡⎤⎡⎤-⊆-⎢⎥⎢⎥⎣⎦⎣⎦，，得出203ω<≤ . 第二步，()2sin 2g x x ω=+在[]2,0π-上有且仅有一个零点，可得12π2π452π2π4ωω⎧⨯≤⎪⎪⎨⎪⨯>⎪⎩，解出实数ω的取值范围.第三步，求出交集即可. 【详解】由题及ππ22x ω-≤≤得()2sin f x x ω=（0>ω）在ππ,22ωω⎡⎤-⎢⎥⎣⎦单调递增，又函数()2sin f x x ω=（0>ω）在区间3ππ,43⎡⎤-⎢⎥⎣⎦上单调递增，所以，3ππππ,4322ωω⎡⎤⎡⎤-⊆-⎢⎥⎢⎥⎣⎦⎣⎦，，得203ω<≤ . ()2sin 2g x x ω=+在[]2,0π-上有且仅有一个零点，可得12π2π452π2π4ωω⎧⨯≤⎪⎪⎨⎪⨯>⎪⎩，所以，1544ω≤<，所以，1243ω≤≤. 故答案为：1243⎡⎤⎢⎥⎣⎦，.17．(1)3C π=(2)a =b = 【解析】【分析】（1）利用三角恒等变换化简得出sin 61C π⎛⎫+= ⎪⎝⎭，结合角C 的取值范围可求得角C 的值；（2）由平面向量垂直的坐标表示以及正弦定理可得出2b a =，再利用余弦定理可求得a 、b 的值. (1)()cos cos 2sin 26A B C C C C π⎛⎫++=+=+= ⎪⎝⎭，所以，sin 61C π⎛⎫+= ⎪⎝⎭，0C π<<，则7666C πππ<+<，62C ππ∴+=，解得3C π=. (2)解：由已知2sin sin 0m n A B ⋅=-=，则2b a =，由余弦定理可得22222292cos 3c a b ab C a b ab a ==+-=+-=，因此，a =b =18．(1)π6A =(2)BC =【解析】【分析】（1）选择条件①可以用正弦定理进行角化边即可求解，选择条件②利用辅助角公式进行三角恒等变换即可.（2）利用圆的角度关系和正弦定理即可求解. (1)解：选择条件①：因为)sin sin sin c C a A b B -=-，由正弦定理，可得)22c a bb -=-，即222b c a +-=，所以222cos 2b c A bc a +===-. 因为()0,πA ∈，所以π6A =.选择条件②：因为sin 22A A =所以π2sin 23A ⎛⎫+= ⎪⎝⎭πsin 23A ⎛⎫+=⎪⎝⎭因为()0,πA ∈所以ππ7π2,333A ⎛⎫+∈ ⎪⎝⎭所以π2π233A +=，π6A =.(2)由题意，O 是ABC 外接圆的圆心，所以2AOB C ∠=，所以211cos cos 212sin 14AOB C C ∠==-=故此sin C =. 在ABC 中，由正弦定理，sin sin AB BC C A=12BC=，解得BC =19．(1)3A π=(2)134【解析】【分析】（1）利用两角和差余弦公式、二倍角和辅助角公式化简可得sin 216A π⎛⎫-= ⎪⎝⎭，由此可求得A ；（2）利用面积桥可求得AB ，利用余弦定理求得BC 后可得CD ，由勾股定理可得结果.(1)21sin cos sin cos cos sin sin cos sin 6662A A A A A A A Aπππ⎛⎫⎛⎫-=+=+ ⎪ ⎪⎝⎭⎝⎭311113sin 2cos 2sin 24442644A x A π⎛⎫=-+=-+= ⎪⎝⎭，sin 216A π⎛⎫∴-= ⎪⎝⎭；()0,A π∈，112,666A πππ⎛⎫∴-∈- ⎪⎝⎭，262A ππ∴-=，解得：3A π=.(2)D 是BC 中点，1228632ABCADCSSAC DE DE ∴==⨯⋅==又1sin 23632ABCSAB AC A AB =⋅==3AB =；在ABC 中，由余弦定理得：2222cos 9642449BC AB AC AB AC A =+-⋅=+-=， 7BC ∴=，则72CD =，224927134164CE CD DE ∴=-=-. 20．(1)3B π=(2)21sin A = 【解析】【分析】（1）利用正弦定理边化角、切化弦，结合三角恒等变换公式可化简已知等式求得cos B ，由此可得B ；（2）设ABD BAD θ∠=∠=；在ABC 和BDC 分别利用正弦定理和余弦定理可构造关于sin θ的方程，解方程可求得结果.(1)由3tan tan c b A b B +=sin sin 3cos cos A B c A B +=由正弦定理得：()sin sin sin sin cos cos sin 3sin cos cos cos cos cos cos A B A B A B A B CA B A B A B +++===()()sin sin sin A B C C π+=-=，又()0,C π∈，sin 0C ∴≠，sin cos 3cos cos B A A B ∴=；tan A 有意义，cos 0A ∴≠，sin 3cos B B ∴=，即tan 3B =，又()0,B π∈，3B π∴=.(2)AD BD =，ABD BAD ∴∠=∠，设ABD BAD θ∠=∠=，则2BDC θ∠=，在ABC 中，由正弦定理得：sin sin BC AC ABCθ=∠，即4sin 83sin 3BC θθπ==；在BDC 中，由余弦定理得：2222cos 2106cos 2BC BD CD BD CD θθ=+-⋅=-；()2264sin 106cos 210612sin 3θθθ∴=-=--，解得：23sin 7θ=，即23sin 7A =，又()0,A π∈，21sin A ∴=21．(1)25(2)答案见解析【解析】【分析】（1）由面积公式先求出AB 的长，进而根据余弦定理求出AC 的长.（2）由题设，可以随意选择两个条件，去判断DCA ∠与BCA ∠是否可能相等.但是优先选择哪两个条件思维逻辑最清晰､解题过程最简洁是同学们应该思考的.由第一问可知，ABC 是唯一确定的三角形，sin ,cos BCA BCA ∠∠都是可求的，而要判断DCA ∠与BCA ∠是否可能相等，可转化为判断它们的某一个三角函数值是否相等，因此首选条件②和条件③，此时ADC 中的三条边长都知道，容易计算余弦值.如果看到条件①4D π∠=，正好满足D B π∠+∠=，能够想到四点共圆，那么圆周角相等则对应的弦长相等，因此选条件①和条件②也非常简单.最麻烦的是选择条件①和条件③，因为此时ADC 中知道的条件是边边角，ADC 不一定唯一确定，需要讨论. (1) 因为3,2,24ABCB BC S π∠===，所以在ABC 中，由1sin 2ABCSAB BC B =⋅⋅，得2sin ABC S AB BC B ===⋅由余弦定理2222cos AC ABBC AB BC B =-+⋅，得2842220AC ⎛=+-⋅⋅= ⎝⎭，所以AC =(2)选择条件②：4=AD 和条件③：6CD =，在ADC 中由余弦定理可得222cos 2CD CA AD DCA CD CA ∠+-==⋅，在ABC 中由余弦定理可得222cos 2CB CA AB BCA CB CA ∠+-=⋅，因为cos cos DCA BCA ∠∠≠，所以DCA BCA ∠∠≠；选择条件①：4D π∠=和条件②：4=AD ，在ADC 中，由正弦定理可得sin sin AC ADD DCA∠=，在ABC 中，由正弦定理可得sin sin AC ABB BCA=∠，所以，若DCABCA ∠=∠，则AD AB =，与4,AD AB == 所以DCA BCA ∠∠≠；选择条件①：4D π∠=和条件③：6CD =，在ABC 中由余弦定理可得222cos 2CB CA AB BCA CB CA ∠+-=⋅. 在ADC 中，由余弦定理2222cos AC ADDC AD DC D =+-⋅，可得2160AD -+=，所以AD =AD =当AD=ADC中，由余弦定理可得222cos2CD CA ADDCACD CA∠+-==⋅因为cos cosDCA BCA∠∠=，且(),0,DCA BCA∠∠π∈，所以DCA BCA∠=∠.当AD=ADC中，由余弦定理可得222cos2CD CA ADDCACD CA∠+-=⋅，因为cos cosDCA BCA∠∠≠，所以DCA BCA∠∠≠.所以选择条件①和条件③时，当AD=DCA BCA∠=∠成立；当AD= DCA BCA∠∠≠.22．(1)3Aπ=；(2)11,22⎛⎫-⎪⎝⎭.【解析】【分析】（1）角换边，在利用余弦定理求解；（2）边换角，将待求表达式表示成关于B的三角函数，利用锐角三角形条件求出B的范围，最后再求表达式的范围即可.(1)因为()()sin sin2sin sin sina A c C Bb C B=-++，所以由正弦定理得()()22a c cb bc b=-++，整理得222b c a bc+-=，由余弦定理得2221cos22b c aAbc+-==．因为0Aπ<<，所以3Aπ=．(2)由正弦定理得)sin sin2sin sin sin sin sin2sin33b c B CB C B B Ba Aππ--⎛⎫⎛⎫==-=--=-⎪ ⎪⎝⎭⎝⎭．因为ABC为锐角三角形，所以0,220,32BBπππ⎧<<⎪⎪⎨⎪<-<⎪⎩解得62B ππ<<，所以636B πππ-<-<，所以11sin 232B π⎛⎫-<-< ⎪⎝⎭，故)2b c a-的取值范围为11,22⎛⎫- ⎪⎝⎭．。

高一年级数学三角函数单元测试题二

三角函数单元测试题二一、选择题：本大题共12小题：每小题5分：共60分在每小题给出的四个选项中：只有一项是符合题目要求的．（1）的值为（）．A． B． C． D．（2）函数的定义域是（）．（A）（B）（C）取（D）（3）已知：是第二象限角：且：则等于（）．A． B．C．－7 D．7（4）函数的最小正周期是（）．A． B． C． D．（5）（文）当时：函数的最大值为（）．（A）0 （B）5 （C）（D）3（理）函数的值域为（）．A． B．C． D．（6）若：则的值为（）．A． B． C． D．（7）设：则、、的大小是（）．A． B． C． D．（（8）．函数的单调递增区间是（）．（A）（B）（C）（D）（9）函数的图象可由函数的图象向右平移（）个单位而得到．（A）（B）（C）（D）（10）设：那么是函数为奇函数的（）．A．充分非必要条件B．必要非充分条件C．充分必要条件D．既非充分也非必要条件（11）如果：那么的值为（）．A． B．－ C． D．－（12）函数的图象与函数的图象在闭区间上（）．A．可能没有公共点 B．只有一个公共点C．一定有两个公共点 D．至少有一个公点二、填空题：本大题共4小题：每小题4分：共16分把答案填在题中横线上（13）中：：那么这个三角形的最大角的度数为．（14）已知,那么的值等于．（15）函数的图象的两条相邻的对称轴之间的距离为：则．（16）是定义在R上的奇函数：且对任意成立：则的值= ．三、解答题：本大题共6小题：共74分解答应写出文字说明：证明过程和演算步骤（17）（本小题满分12分）．已知：求的值．（18）（本小题满分12分）设函数满足（Ⅰ）求、的值：（Ⅱ）求使成立的的取值集合．（19）（本小题满分12分）求函数的最大值和最小值．（20）（本小题满分12分）在：角A、B、C的对边分别为、、：若：且：求的值．（21）（本小题满分12分）在中：于D：作：交AC于F：BC于E．求当x 取什么值时：的面积最大：并求这面积的最大值．（22）（本小题满分14分）已知：求的最大值．单元测试题答案一、选择题（1）B （2）C （3）D （4）C （5）(文)B、（理）A （6）A （7）A （8）A （9）B （10）C （11）D （12）D提示：（3）由得：又（4）经变形：得（5）（理）由：根据反余弦函数的图象：可得函数的值域为．（6）由已知可得且（7）（10）必要性显然：若：即：则∴是奇函数．（11）令：则（12）取特例作研究：设：则结合图象作分析时：注意两函数相邻两个公共点间距离为：区间的长度也为．二、填空题：（13）（14）（15）3 （16）0提示：（13）本题即：求角C：可用余弦定理．（15）本题即的最小正周期之半为（16）易有：又：故三、解答题（17）∵：故∴：∴∴（18）（Ⅰ）由：即：故又：即：故（Ⅱ）∴：即∴∴∴所求的取值集合为（１９）设：则由可得到．又．故：可得时：的最大值为：时：的最小值为.（20）由,得：∴：∴又：依正弦定理有∴：即由此可得（２１）如图：设：（均定值）：则在：中：分别可得：于是因此当即时：的最大面积为.。

三角函数测试题及答案

三角函数测试题及答案一、选择题1. 已知角A的正弦值为\( \sin A = \frac{1}{2} \)，则角A的余弦值\( \cos A \)是：A. \( \frac{1}{2} \)B. \( \frac{\sqrt{3}}{2} \)C. \( -\frac{1}{2} \)D. \( -\frac{\sqrt{3}}{2} \)2. 函数\( y = \sin x + \cos x \)的周期是：A. \( \pi \)B. \( 2\pi \)C. \( \pi/2 \)D. \( 4\pi \)3. 已知\( \cos x = \frac{1}{3} \)，且\( x \)在第一象限，求\( \sin x \)的值：A. \( \frac{2\sqrt{2}}{3} \)B. \( \frac{2\sqrt{5}}{3} \)C. \( \frac{4\sqrt{2}}{9} \)D. \( \frac{4\sqrt{5}}{9} \)二、填空题4. 根据正弦定理，如果三角形ABC的边a和角A相对，且\( a = 5 \)，\( \sin A = \frac{3}{5} \)，则边b的长度为______（假设\( \sin B = \frac{4}{5} \)）。

5. 已知\( \tan x = -1 \)，求\( \sin 2x \)的值。

三、解答题6. 求以下列三角方程的解：\( \sin^2 x + \cos^2 x = 1 \)7. 证明：\( \sin(2\theta) = 2\sin(\theta)\cos(\theta) \)。

四、应用题8. 在直角三角形ABC中，角C为直角，已知AB = 10，AC = 6，求BC 的长度。

答案：一、选择题1. C2. B3. B二、填空题4. 45. 1 或 -1三、解答题6. 该方程对所有\( x \)都成立，因为它是三角恒等式。

2015年高中数学三角函数组卷解析

2015年高中数学三角函数组卷一．解答题（共28小题）1．（2015•北京）已知函数f（x）=sinx﹣2sin2（1）求f（x）的最小正周期；（2）求f（x）在区间[0，]上的最小值．2．（2015•山东）设f（x）=sinxcosx﹣cos2（x+）．（Ⅰ）求f（x）的单调区间；（Ⅱ）在锐角△ABC中，角A，B，C的对边分别为a，b，c，若f（）=0，a=1，求△ABC 面积的最大值．3．（2015•湖北）某同学将“五点法”画函数f（x）=Asin（wx+φ）（w＞0，|φ|＜）在某一π（2）将y=f（x）图象上所有点向左平移个单位长度，得到y=g（x）图象，求y=g（x）的图象离原点O最近的对称中心．4．（2012•陕西）函数（A＞0，ω＞0）的最大值为3，其图象相邻两条对称轴之间的距离为，（1）求函数f（x）的解析式；（2）设，则，求α的值．5．（2015•天津）已知函数f（x）=sin2x﹣sin2（x﹣），x∈R．（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）在区间[﹣，]内的最大值和最小值．6．（2015•北京）已知函数f（x）=sin cos﹣sin．（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）在区间[﹣π，0]上的最小值．7．（2015•广东）已知tanα=2．（1）求tan（α+）的值；（2）求的值．8．（2015•重庆）已知函数f（x）=sin（﹣x）sinx﹣x（Ⅰ）求f（x）的最小正周期和最大值；（Ⅱ）讨论f（x）在上的单调性．9．（2015•浙江）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知tan（+A）=2．（Ⅰ）求的值；（Ⅱ）若B=，a=3，求△ABC的面积．10．（2014•红塔区校级模拟）△ABC中，D为边BC上的一点，BD=33，sinB=，cos∠ADC=，求AD．11．（2014•广东）已知函数f（x）=Asin（x+），x∈R，且f（）=．（1）求A的值；（2）若f（θ）﹣f（﹣θ）=，θ∈（0，），求f（﹣θ）．12．（2013•四川）在△ABC中，角A，B，C的对边分别为a，b，c，且2cos2cosB﹣sin（A﹣B）sinB+cos（A+C）=﹣．（Ⅰ）求cosA的值；（Ⅱ）若a=4，b=5，求向量在方向上的投影．13．（2013•湖南）已知函数f（x）=sin（x ﹣）+cos（x ﹣），g（x）=2sin 2．（Ⅰ）若α是第一象限角，且f（α）=，求g（α）的值；（Ⅱ）求使f（x）≥g（x）成立的x的取值集合．14．（2013•北京）已知函数f（x）=．（Ⅰ）求f（x）的最小正周期及最大值；（Ⅱ）若α∈（，π），且f（α）=，求α的值．15．（2012•广东）已知函数，x∈R ，且（1）求A的值；（2）设，，，求cos（α+β）的值．16．（2009•惠州模拟）在△ABC 中，，．（Ⅰ）求sinC的值；（Ⅱ）设BC=5，求△ABC的面积．17．（2009•浙江）在△ABC中，角A、B、C所对应的边分别为a、b、c，且满足=，•=3．（Ⅰ）求△ABC的面积；（Ⅱ）若c=1，求a的值．18．（2008•江西）已知，，α，β∈（0，π）（1）求tan（α+β）的值；（2）求函数的最大值．19．（2007•安徽）已知0＜α＜，β为f（x）=cos（2x+）的最小正周期，=（tan（a+），﹣1），=（cosα，2），且=m ，求．20．（2007•福建）在△ABC中，tanA=，tanB=．第3页（共27页）（Ⅰ）求角C的大小；（Ⅱ）若AB边的长为，求BC边的长．21．（2005•浙江）已知函数f（x）=2sinxcosx+cos2x（Ⅰ）求的值；（Ⅱ）设α∈（0，π），，求sinα的值、22．（2005•福建）已知﹣＜x＜0，sinx+cosx=．（1）求sinx﹣cosx的值；（2）求的值．23．（2005•福建）已知﹣＜x＜0，则sinx+cosx=．（I）求sinx﹣cosx的值；（Ⅱ）求的值．24．（2006•湖南）如图，D是直角△ABC斜边BC上一点，AB=AD，记∠CAD=a，∠ABC=β．（1）证明sina+cos2β=0；（2）若AC=DC，求β的值．25．（2012•重庆）设f（x）=4cos（ωx﹣）sinωx﹣cos（2ωx+π），其中ω＞0．（Ⅰ）求函数y=f（x）的值域（Ⅱ）若f（x）在区间上为增函数，求ω的最大值．26．（2014•四川）已知函数f（x）=sin（3x+）．（1）求f（x）的单调递增区间；（2）若α是第二象限角，f（）=cos（α+）cos2α，求cosα﹣sinα的值．27．（2014•江苏）已知α∈（，π），sinα=．（1）求sin （+α）的值；（2）求cos （﹣2α）的值．28．（2013•山东）设函数f（x）=﹣sin2ωx﹣sinωxcosωx（ω＞0），且y=f（x）的图象的一个对称中心到最近的对称轴的距离为，（Ⅰ）求ω的值（Ⅱ）求f（x）在区间[]上的最大值和最小值．第5页（共27页）2015年高中数学三角函数组卷一．解答题（共28小题）1．（2015•北京）已知函数f（x）=sinx﹣2sin2（1）求f（x）的最小正周期；（2）求f（x）在区间[0，]上的最小值．x+）﹣]x+∈[22×=sinx+﹣）﹣=2]∈[，）x+）﹣，﹣]上的最小值为：﹣．2．（2015•山东）设f（x）=sinxcosx﹣cos2（x+）．（Ⅰ）求f（x）的单调区间；（Ⅱ）在锐角△ABC中，角A，B，C的对边分别为a，b，c，若f（）=0，a=1，求△ABC 面积的最大值．，由，，（=0时等号成立，从而可求bcsinA﹣sin2x﹣≤2k ≤，≤2k≤，[k，[k（=0，cosA=1+bcbcsinA面积的最大值为3．（2015•湖北）某同学将“五点法”画函数f（x）=Asin（wx+φ）（w＞0，|φ|＜）在某π第7页（共27页）（2）将y=f（x）图象上所有点向左平移个单位长度，得到y=g（x）图象，求y=g（x）的图象离原点O最近的对称中心．2））图象上所有点向左平移（）﹣]2x+）=k﹣，．（﹣4．（2012•陕西）函数（A＞0，ω＞0）的最大值为3，其图象相邻两条对称轴之间的距离为，（1）求函数f（x）的解析式；（2）设，则，求α的值．）通过，求出，=））∵，所以5．（2015•天津）已知函数f（x）=sin2x﹣sin2（x﹣），x∈R．（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）在区间[﹣，]内的最大值和最小值．sin），]﹣（）﹣[1）（1+cos2x+（﹣cos2x+sin=，]∈﹣，第9页（共27页）），sin），]，]内的最大值和最小值分别为，﹣6．（2015•北京）已知函数f（x）=sin cos﹣sin．（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）在区间[﹣π，0]上的最小值．sin cos﹣sin（=sinxcos+cosxsin﹣）﹣，≤≤1﹣）取得最小值﹣﹣（1）求tan（α+）的值；（2）求的值．+===18．（2015•重庆）已知函数f（x）=sin（﹣x）sinx﹣x（Ⅰ）求f（x）的最小正周期和最大值；（Ⅱ）讨论f（x）在上的单调性．∈在﹣﹣﹣（﹣﹣）﹣=．∈∈≤时，[，]≤≤π[，]第11页（共27页）9．（2015•浙江）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知tan（+A）=2．（Ⅰ）求的值；（Ⅱ）若B=，a=3，求△ABC的面积．tanA=，A+）+A，=．，，cosA=及正弦定理b=3）absinC=910．（2014•红塔区校级模拟）△ABC中，D为边BC上的一点，BD=33，sinB=，cos∠ADC=，求AD．确定角ADC=＜＜，可得，，可得ADC=ADCsinB=．AD=．11．（2014•广东）已知函数f（x）=Asin（x+），x∈R，且f（）=．（1）求A的值；（2）若f（θ）﹣f（﹣θ）=，θ∈（0，），求f（﹣θ）．x+）=，）﹣x+））（）=Asin））﹣））﹣（cos=3sin，第13页（共27页）﹣）．12．（2013•四川）在△ABC中，角A，B，C的对边分别为a，b，c，且2cos2cosB ﹣sin（A﹣B）sinB+cos（A+C）=﹣．（Ⅰ）求cosA的值；（Ⅱ）若a=4，b=5，求向量在方向上的投影．，，（Ⅱ）由正弦定理，，所以，B=在方向上的投影：．13．（2013•湖南）已知函数f（x）=sin（x﹣）+cos（x﹣），g（x）=2sin2．（Ⅰ）若α是第一象限角，且f（α）=，求g（α）的值；（Ⅱ）求使f（x）≥g（x）成立的x的取值集合．，结合，利用同角三角函数的基本关系算出；sinx x+=sinxcos cosxsin=sinx﹣）=cosxcos+sinxsin cosx+sinx（cosx（cosx+，∴=，sinx移项，得x+），可得≤+2k≤+2k14．（2013•北京）已知函数f（x）=．（Ⅰ）求f（x）的最小正周期及最大值；第15页（共27页）（Ⅱ）若α∈（，π），且f（α）=，求α的值．（Ⅱ）通过，且T=，函数的最大值为：，，，又∵15．（2012•广东）已知函数，x∈R，且（1）求A的值；（2）设，，，求cos（α+β））将）先将，）），．16．（2009•惠州模拟）在△ABC中，，．（Ⅰ）求sinC的值；，得，，得．（Ⅱ）由正弦定理得的面积=17．（2009•浙江）在△ABC中，角A、B、C所对应的边分别为a、b、c，且满足=，•=3．第17页（共27页）（Ⅰ）求△ABC的面积；（Ⅱ）若c=1，求a的值．，利用•=3=2﹣，=，•bcsinA=2==218．（2008•江西）已知，，α，β∈（0，π）（1）求tan（α+β）的值；解之；，=．19．（2007•安徽）已知0＜α＜，β为f（x）=cos（2x+）的最小正周期，=（tan（a+），﹣1），=（cosα，2），且=m，求．的值，进而根据β+2x+）的最小正周期，故=m，又=cosββ，所以）第19页（共27页）20．（2007•福建）在△ABC中，tanA=，tanB=．（Ⅰ）求角C的大小；﹣C=（Ⅱ）由，．21．（2005•浙江）已知函数f（x）=2sinxcosx+cos2x （Ⅰ）求的值；（Ⅱ）设α∈（0，π），，求sinα的值、）后，将得用和角公式化成（Ⅱ）．．，故22．（2005•福建）已知﹣＜x＜0，sinx+cosx=．（1）求sinx﹣cosx的值；（2）求的值．）欲求）把两边平方得，有，）由，得，与解得有第21页（共27页）23．（2005•福建）已知﹣＜x＜0，则sinx+cosx=．（I）求sinx﹣cosx的值；（Ⅱ）求的值．，进而根据﹣，平方得，．．＜﹣==sinxcosx ））（1）证明sina+cos2β=0；（2）若AC=DC，求β的值．）利用诱导公式可求得）根据正弦定理可求得代入）∵中由正弦定理）得或25．（2012•重庆）设f（x）=4cos（ωx﹣）sinωx﹣cos（2ωx+π），其中ω＞0．（Ⅰ）求函数y=f（x）的值域（Ⅱ）若f（x）在区间上为增函数，求ω的最大值．第23页（共27页））在区间﹣cos sin[][所以，解不等式得=[）在区间上为增函数⊆[．解得，故的最大值是26．（2014•四川）已知函数f（x）=sin（3x+）．（1）求f（x）的单调递增区间；（2）若α是第二象限角，f（）=cos（α+）cos2α，求cosα﹣sinα的值．﹣3x+，（+）=））=+．再由）﹣3x+，﹣≤+，故函数的增区间为[﹣，]（+）=））=））coscos sin=（sin）=﹣﹣或﹣．27．（2014•江苏）已知α∈（，π），sinα=．（1）求sin（+α）的值；（2）求cos（﹣2α）的值．（（（．∴﹣=+=sin cos﹣+．，=，第25页（共27页）﹣=cos sin2﹣）的值为：﹣28．（2013•山东）设函数f（x）=﹣sin2ωx﹣sinωxcosωx（ω＞0），且y=f（x）的图象的一个对称中心到最近的对称轴的距离为，（Ⅰ）求ω的值（Ⅱ）求f（x）在区间[]上的最大值和最小值．[]﹣，故周期为，所以）时，，，[]上的最大值和最小值分别为：第27页（共27页）。

2015课标卷(Ⅱ)三角函数

2015年新课标卷Ⅱ《三角函数》1．（2015年新课标卷Ⅱ文科）ABC ∆中，D 是BC 上的点，AD 平分BAC ∠，2BD DC =.（I ）求sin sin BC ∠∠ ；（II ）若60BAC ∠= ,求B ∠.【解析】（I ）由正弦定理得,,sin sin sin sin ADBDADDCB BADC CAD ==∠∠∠∠因为AD 平分∠BAC ,BD =2DC ,所以sin 1.sin 2BDCC BD ∠==∠ （角平分线定理：ABBDAC CD =能不能用？）（II ）因为()180,60,C BAC B BAC ∠=-∠+∠∠=所以()1sin sin sin .2C BAC B B B ∠=∠+∠=∠+∠ 由（I ）知2sin sin B C ∠=∠,所以tan ,30.3B B ∠=∠=2.（2015年新课标卷Ⅱ理科）ABC ∆中，D 是BC 上的点，AD 平分BAC ∠，ABD ∆的面积是ADC ∆面积的2倍.（I ）求sin sin B C∠∠ ； (Ⅱ) 若AD =1，DC =22，求BD 和AC 的长. 【解析】（I ）2,2ABD ADC S S BD DC ∆∆=∴= ，由角平分线定理得12AC CD AB DB == 正弦定理sin 1sin 2B AC C AB ∠==∠ （角平分线定理：AB BD AC CD=能不能用？似乎此题就是在推证角平分线定理）(Ⅱ)由（I ）知2BD DC =ABD ∆和ADC ∆中，由余弦定理得 2222cos AB AD BD AD BD ADB=+-⋅∠，2222cos AC AD DC AD DC ADC =+-⋅∠． 222222326AB AC AD BD DC +=++=．由(Ⅰ)知2AB AC =，所以1AC =．【点评】此题第二问也是2014年文科题的延续。

近几年的三角形考查偏向于应用意识，在众多的边角问题上组建等量关系式，加强了思维含量的考查，这也是高考以能力立意的一个好的素材。

高一2015级数学三角函数单元测试卷

高2015级三角函数单元测试卷一、选择题：（50分）1、角α在第二象限，且cos cos ,222ααα=-则在（） A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限2、角0600的终边上有一点4),a -（，则a 的值为（）A、± B、、-3、若sin cos αα+=，则α在（） A 、第一象限 B 、第一、二象限 C 、第二象限 D 、第二、四象限 4、若α是第三象限角，且445sin cos ,sin cos 9αααα+==则（） A、3 B、3- C 、13 D 、13- 5、函数2sin()2x y φφ=+=是偶函数，则（） A 、π- B 、2π C 、4π- D 、8π- 6、若4sin()5x π+=，且x 在第四象限，则cos(2)x π-= （） A 、35- B 、35 C 、35± D 、457、若00cos110,tan(80)k =-=则（）A、k - B、k C、k± D 、都不对 8、函数sin sin y x x =-的值域是（）A 、[-1，0]B 、[0，1]C 、[-1，1]D 、[-2，0]9、方程2sin x x =的解的个数为（）A 、一个B 、两个C 、三个D 、无数个10、1sin ()lg cos x f x x+=是（） A 、奇函数 B 、偶函数 C 非奇函数非偶函数 D 、奇且偶函数二、填空题（30分） 11、若11tan 21sin 1sin x x x=+=+-，则，。

12、若θ为锐角，则2sin 1(1)tan log θθ+= 。

13、函数cos(2)4y x π=-的单调增区间。

14、若()sin ,6n f n n N π+=∈，则(1)(2)(2008)f f f +++= 。

15、函数2sin(2)6y x π=+，,123x ππ⎡⎤∈⎢⎥⎣⎦的值域。

人教版高中数学必修第一册第五单元《三角函数》测试题(有答案解析)(2)

一、选择题1．已知5π2sin 63α⎛⎫+= ⎪⎝⎭，则πcos 23α⎛⎫-= ⎪⎝⎭（）A ．B ．19-C ．3D ．192．已知α为第二象限角，且π3cos 25α⎛⎫-= ⎪⎝⎭，则tan α=（）． A ．34-B ．43-C ．53-D ．45-3．已知函数()sin()(0)f x x ωω=>在区间,123ππ⎛⎤- ⎥⎝⎦上单调递增，在区间5,312ππ⎡⎫⎪⎢⎣⎭上单调递减，则ω=（）A ．362k -，k ∈N B ．362k +，k ∈N C ．32D ．34．计算cos 20cos80sin160cos10+=（）．A ．12B C ．12-D ． 5．已知3sin 7a π=，4cos 7b π=，3tan()7c π=-，则a ，b ，c 的大小关系为（） A ．a b c <<B ．b c a <<C ．c b a <<D ．c a b <<6．把函数sin y x =的图象上所有的点向左平行移动6π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数解析式是（） A ．sin 23y x π⎛⎫=- ⎪⎝⎭B ．sin 26x y π⎛⎫=+⎪⎝⎭ C ．sin 26y x π⎛⎫=-⎪⎝⎭D ．sin 26y x π⎛⎫=+⎪⎝⎭7．sin 20cos10cos160sin10-=（）A ．B ．12C ．12-D ．28．若1sin 63πα⎛⎫-= ⎪⎝⎭，则2cos 23πα⎛⎫+ ⎪⎝⎭等于（）.A ．79-B ．13-C ．13D ．799．若将函数3sin(2)3y x π=+的图象向左平移6π个单位长度，则平移后图象的一个对称中心是（） A ．,06π⎛⎫ ⎪⎝⎭B ．,06π⎛⎫-⎪⎝⎭C ．,012π⎛⎫⎪⎝⎭D ．,03π⎛⎫⎪⎝⎭10．刘徽是中国魏晋时期杰出的数学家，他提出“割圆求周”方法:当n 很大时，用圆内接正n 边形的周长近似等于圆周长，并计算出精确度很高的圆周率 3.1416π≈.在《九章算术注》中总结出“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”的极限思想，可以说他是中国古代极限思想的杰出代表．运用此思想，当π取3.1416时可得cos89︒的近似值为（） A ．0.00873B ．0.01745C ．0.02618D ．0.0349111．已知tan 2α=，则sin sin 44ππαα⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭（） A ．310-B ．310 C ．35D ．3512．已知2cos 432θπ⎛⎫= ⎪⎝⎭-，则sin θ=（） A ．79 B ．19C ．－19D ．－79二、填空题13．已知()sin()cos()1f x a x b x παπβ=++-+，其中α，β，a ，b 均为非零实数，若()20202f =，则()2021f =________.14．已知函数sin cos y x x =-，其图象的对称轴中距离y 轴最近的一条对称轴方程为x =________.15．已知锐角α满足1cos()35πα+=，则sin α=______． 16．若()()2sin 03f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为4π，则()()tan 06g x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为______．17．已知1tan()3πα+=-，则sin 2cos 5cos sin αααα+=-______． 18．已知tan 2α=，则cos2=α__． 19．已知tan 2α=，则cos 22πα⎛⎫-= ⎪⎝⎭___________.20．若2sin 63πα⎛⎫+= ⎪⎝⎭，则sin 26πα⎛⎫-= ⎪⎝⎭________．三、解答题21．已知函数2()2sin 23sin cos 1f x x x x =++．求：（1）()f x 的最小正周期；（2）()f x 在0,2π⎡⎤⎢⎥⎣⎦上的最值． 22．已知函数()cos f x x =.（1）已知α，β为锐角，()5f αβ+=-，4tan 3α=，求cos2α及()tan βα-的值；（2）函数()()321g x f x =+，若关于x 的不等式()()()2133g x a g x a ≥+++有解，求实数a 的最大值.23．如图为一个观览车示意图，该观览车圆半径为4.8m ，圆上最低点与地面距离为0.8m ，60秒转动一圈.图中OA 与地面垂直，以OA 为始边，逆时针转动θ到OB .设B 点与地面的距离为h .（1）求h 与θ的函数关系式；（2）设从OA 开始转动，经过10秒到达OB ，求h . 24．已知函数25()23cos()2cos (0)32f x wx wx wx w π=+-+>的图像上相邻的两个最低点的距离为π. （1）求w 的值；（2）求函数()f x 的单调递增区间. 25．已知函数2()sin(2)2cos 1(0)6f x x x πωωω=-+->的最小正周期为π，（1）求ω的值（2）求()f x 在区间70,12π⎡⎤⎢⎥⎣⎦上的最大值和最小值.26．已知α∈(0,)2π，tan α＝12，求tan 2α和sin ()4πα-的值．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】先用诱导公式化为5cos 2cos 233ππαα⎛⎫⎛⎫-=+⎪ ⎪⎝⎭⎝⎭，再用二倍角公式计算．【详解】225521cos 2cos 212sin 1233639a a πππα⎛⎫⎛⎫⎛⎫⎛⎫-=+=-+--⨯= ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选：D 2．A解析：A 【分析】由已知求出3sin 5α=，即可得cos α，进而求出所求. 【详解】 ∵π3cos 25α⎛⎫-=⎪⎝⎭，∴3sin 5α=，∵α为第二象限角，∴4cos 5α==-， ∴sin 3tan cos 4ααα==-．故选：A ．3．C解析：C 【分析】由题意知，当3x π=时，函数()f x 取得最大值，可求得362k ω=+，k ∈N .再由函数的单调区间得出不等式组，解之可得选项. 【详解】由题意知，当3x π=时，函数()f x 取得最大值，所以232k ππωπ⋅=+，k Z ∈.得362k ω=+，k ∈N .因为()f x 在区间,123ππ⎛⎤-⎥⎝⎦上递增，在5,312ππ⎡⎫⎪⎢⎣⎭上递减，所以312πππω≥+且5123πππω≥-，解得1205ω<≤.因此32ω=.故选：C.4．A解析：A 【分析】将160化为20,10化为80后，利用两角差的余弦公式可求得结果. 【详解】cos 20cos80sin160cos10+cos 20cos80sin 20sin80=+()cos 8020=-cos60=12=．故选：A ．5．C解析：C 【分析】3sin07a π=>,4cos 07b π=<，a b >且均属于()1,1-，而1c <-，大小关系即可确定. 【详解】解：3sin7a π=>；427πππ<<， 4cos coscos 72πππ∴<<，即10b -<<. 又正切函数在(0,)2π上单调递增，347ππ<； 3tantan 174ππ∴>=；33tan()tan 177c ππ∴=-=-<-， 01a b c ∴>>>->，故选：C. 6．D解析：D 【分析】根据三角函数的图象变换规律可得解析式．【详解】函数sin y x =的图象上所有的点向左平行移动6π个单位长度，得sin 6y x π⎛⎫=+ ⎪⎝⎭，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），可得sin 26y x π⎛⎫=+ ⎪⎝⎭. 故选：D ．7．B解析：B 【分析】利用诱导公式cos160cos 20=-，再利用两角和的正弦公式即可求解. 【详解】sin 20cos10cos160sin10-()sin 20cos10cos 18020sin10=-- sin 20cos10cos 20sin10=+()sin 2010=+sin30=12=故选：B8．A解析：A 【分析】根据1sin 63πα⎛⎫-=⎪⎝⎭，利用诱导公式得到cos 3πα⎛⎫+ ⎪⎝⎭，再由2cos 2cos 233ππαα⎛⎫⎛⎫⎛⎫+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，利用二倍角公式求解. 【详解】因为1sin sin 6233πππαα⎛⎫⎛⎫⎛⎫-=-+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以1cos 33πα⎛⎫+=⎪⎝⎭，所以227cos 2cos 22cos 13339πππααα⎛⎫⎛⎫⎛⎫⎛⎫+=+=+-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，故选：A9．A解析：A 【分析】先求出平移后的解析式为23sin 23y x π⎛⎫=+ ⎪⎝⎭，令()223x k k Z ππ+=∈解方程即可求解. 【详解】将函数3sin(2)3y x π=+的图象向左平移6π个单位长度得：23sin 23sin 2633y x x πππ⎡⎤⎛⎫⎛⎫=++=+⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，令()223x k k Z ππ+=∈，解得：()32kx k Z ππ=-+∈，当1k =时，326x πππ=-+=，所以平移后图象的一个对称中心为,06π⎛⎫⎪⎝⎭，故选：A10．B解析：B 【分析】根据cos89sin1︒=，将一个单位圆分成360个扇形，由这360个扇形的面积之和近似为单位圆的面积求解. 【详解】因为()cos89cos 901sin1︒=-=，所以将一个单位圆分成360个扇形，则每一个扇形的圆心角为1︒，所以这360个扇形的面积之和近似为单位圆的面积，即2136011sin112π⨯⨯⨯⨯≈，所以 3.1416sin10.01745180180π≈≈≈，故选：B11．B解析：B【分析】利用两角和与差的正弦公式、同角三角函数的基本关系式化简所求表达式，由此求得所求表达式的值. 【详解】sin sin sin cos cos sin sin cos cos sin 444444ππππππαααααα⎛⎫⎛⎫⎛⎫⎛⎫-+=-⋅+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭()22222211sin cos sin cos 22sin cos αααααα-=-=⨯+ 221tan 114132tan 124110αα--=⨯=⨯=++. 故选：B12．C解析：C 【分析】根据题中条件，由诱导公式，以及二倍角公式，即可求出结果. 【详解】因为2cos 432θπ⎛⎫=⎪⎝⎭-，所以241sin cos 2cos 12124299ππθθθ⎛⎫⎛⎫=-=--=⨯-=- ⎪ ⎪⎝⎭⎝⎭.故选：C二、填空题13．0【分析】由题设条件结合周期性及诱导公式运算即可得解【详解】由题意所以所以故答案为：0解析：0 【分析】由题设条件结合周期性及诱导公式运算即可得解. 【详解】由题意，()sin(2020)cos(2020)1sin cos()12020a b a b f παπβαβ++-++-=+=sin cos 12a b αβ=++=，所以sin cos 1αβ+=a b ，所以()sin(2021)cos(202)201211f a b παπβ++-+=sin()cos()1sin cos 1110a b a b παπβαβ==++-+-+=-+=-.故答案为：0.14．【分析】函数令求解【详解】已知函数令解得所以其图象的对称轴中距离轴最近的一条对称轴方程为故答案为：解析：4π-【分析】函数4y x π⎛⎫=- ⎪⎝⎭，令42x k πππ-=+求解.【详解】已知函数sin cos 4y x x x π⎛⎫=-=- ⎪⎝⎭，令,42x k k Z πππ-=+∈，解得 3,4x k k Z ππ=+∈，所以其图象的对称轴中距离y 轴最近的一条对称轴方程为x =4π-. 故答案为：4π-15．【分析】利用余弦的两角和公式展开结合代入计算即可【详解】解得根据代入计算解得故答案为：【分析】利用余弦的两角和公式展开，结合22sin cos 1αα+=，代入计算即可．【详解】1cos cos 2513πααα⎛⎫+=⋅= ⎪⎝⎭，解得2cos 5αα=+，根据22sin cos 1αα+=，代入计算，解得sin α=. 16．【分析】先由的最小正周期求出的值再由的最小正周期公式求的最小正周期【详解】的最小正周期为即则所以的最小正周期为故答案为：解析：8π 【分析】先由()f x 的最小正周期，求出ω的值，再由()tan y x ωϕ=+的最小正周期公式求()g x的最小正周期. 【详解】()()2sin 03f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为4π，即24ππω=，则8ω=所以()tan 86g x x π⎛⎫=+ ⎪⎝⎭的最小正周期为8T π=故答案为：8π 17．【分析】由已知条件求出再根据同角公式弦化切可解得结果【详解】故答案为：【点睛】关键点点睛：弦化切求解是解题关键解析：516【分析】由已知条件求出1tan 3α=-，再根据同角公式弦化切可解得结果. 【详解】1tan()3πα+=-，1tan 3α∴=-，sin 2cos tan 25cos sin 5tan αααααα++∴=--123153-+=⎛⎫-- ⎪⎝⎭516=．故答案为：516【点睛】关键点点睛：弦化切求解是解题关键.18．【分析】利用余弦的倍角公式和三角函数的基本关系式即可求解【详解】由又由故答案为：解析：35【分析】利用余弦的倍角公式和三角函数的基本关系式，即可求解. 【详解】由tan 2α=，又由22222222cos sin cos 2cos sin cos sin 1tan 1431tan 145ααααααααα--===-++-=-==+. 故答案为：35． 19．【分析】本题首先可通过三角恒等变换将转化为然后代入即可得出结果【详解】因为所以故答案为：【点睛】关键点点睛：本题考查给值求值问题能否合理利用同角三角函数关系诱导公式二倍角公式是解决本题的关键考查计算解析：45【分析】本题首先可通过三角恒等变换将cos 22πα⎛⎫- ⎪⎝⎭转化为22tan tan 1αα+，然后代入tan 2α=即可得出结果. 【详解】因为tan 2α=，所以2222sin cos 2tan 4cos 2sin 22sin cos tan 15παααααααα⎛⎫-==== ⎪++⎝⎭，故答案为：45. 【点睛】关键点点睛：本题考查给值求值问题，能否合理利用同角三角函数关系、诱导公式、二倍角公式是解决本题的关键，考查计算能力，是中档题.20．【分析】由结合诱导公式和二倍角公式得出答案【详解】故答案为：解析：19-【分析】由sin 2sin 2632πππαα⎡⎤⎛⎫⎛⎫-=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，结合诱导公式和二倍角公式得出答案．【详解】2sin 63πα⎛⎫+= ⎪⎝⎭，21cos 212sin 369ππαα⎛⎫⎛⎫∴+=-+= ⎪ ⎪⎝⎭⎝⎭．22326πππαα⎛⎫+=+- ⎪⎝⎭， 1sin 2sin 2cos 263239ππππααα⎡⎤⎛⎫⎛⎫⎛⎫∴-=+-=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦．故答案为：19-三、解答题21．（1）π；（2）最小值为1，最大值为4．【分析】（1）由二倍角降幂，由两角差的正弦公式化函数为一个角的一个三角函数形式，然后结合正弦函数性质可求得最小正周期；（2）求出26x π-的范围，然后由正弦函数性质得最值．【详解】（1）因为2()2sin cos 1f x x x x =++1cos2cos 1x x x =-++2cos 22x x =-+2sin 226x π⎛⎫=-+ ⎪⎝⎭，所以()f x 的最小正周期22T ππ==．（2）因为02x π≤≤，所以52666x πππ-≤-≤．所以1sin 2126x π⎛⎫-≤-≤ ⎪⎝⎭．所以()2sin 22[1,4]6f x x π⎛⎫=-+∈ ⎪⎝⎭．即()f x 的最小值为1，最大值为4．【点睛】方法点睛：本题考查两角差的正弦公式，二倍角公式，考查正弦函数的性质．此类问题的解题方法是：利用二倍角公式降幂，利用诱导公式、两角和与差的正弦（余弦）公式展开与合并，最终把函数化为()sin()f x A x m ωϕ=++形式，然后结合正弦函数性质求解． 22．（1）7cos 225α=-，()2tan 11βα-=；（2）a 的最大值为3. 【分析】（1）利用二倍角公式，求出cos2α，然后分别求出()cos αβ+，sin()αβ+，进而求出()tan αβ+，最后，利用()()tan tan 2βααβα-=+-求解即可（2）由()()[]3213cos212,4g x f x x =+=+∈-，得关于x 的不等式()()()2133g x a g x a ≥+++有解，化简得，即()()()213g x a g x ≥++⎡⎤⎣⎦有解，令()3t g x =+，然后，利用对勾函数的性质求解即可【详解】解：（1）∵4tan 3α=，∴222222cos sin cos 2cos sin cos sin ααααααα-=-=+2222411tan 73251tan 413αα⎛⎫- ⎪-⎝⎭===-+⎛⎫+ ⎪⎝⎭，∵α，β为锐角，即α，0,2πβ⎛⎫∈ ⎪⎝⎭， ∴()20,απ∈，()0,αβπ+∈.22422tan 243tan 21tan 7413ααα⨯===--⎛⎫- ⎪⎝⎭， ∵()cos f x x =，∴()()cos 5f αβαβ+=+=-， ∴()sin αβ+==，∴()()()sin tan 2cos αβαβαβ++==-+， ∴()()()()242tan tan 227tan tan 2241tan tan 211127αβαβααβααβα-++--=+-===+++⨯. 综上，7cos 225α=-，()2tan 11βα-=. （2）()()[]3213cos212,4g x f x x =+=+∈-，关于x 的不等式()()()2133g x a g x a ≥+++有解，即()()()213gx a g x ≥++⎡⎤⎣⎦有解，令()3t g x =+，则[]1,7t ∈，()()231t a t -≥+有解，即916a t t+≤+-有解， max97a t t ⎛⎫+≤+ ⎪⎝⎭，设()9h t t t =+，则()h x 在[)1,3上单调递减，在(]3,7上单调递增，则()(){}max9max 1,710t h h t ⎛⎫+== ⎪⎝⎭， ∴3a ≤，故实数a 的最大值为3. 【点睛】关键点睛：（1）利用二倍角公式，以及正切函数的两角和差公式求解；（2）通过化简，把问题转化为()()()213gx a g x ≥++⎡⎤⎣⎦有解，令()3t g x =+，然后，利用对勾函数的性质求解；主要考查学生的转化化归思想以及运算能力，属于中档题 23．（1） 5.6 4.8cos h θ=-；（2）3.2m. 【分析】（1）建立平面直角坐标系，结合条件求出点B 的坐标后可得h 与θ间的函数关系式；（2）由60秒转动一圈，易得点A 在圆上转动的角速度是/30rad s π，再计算出经过10秒后转过的弧度数为3π，然后代入（1）中所求函数解析式计算即可得到答案. 【详解】（1）以圆心O 原点，建立如图所示的坐标系，如下图所示，则以Ox 为始边，OB 为终边的角为2πθ-，故点B 坐标为 4.8cos ,4.8sin 22ππθθ⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ∴ 5.6 4.8sin 5.6 4.8cos 2h πθθ⎛⎫=+-=- ⎪⎝⎭；（2）点A 在圆O 上逆时针运动的角速度是/30rad s π，∴经过t 秒后转过的角度30t πθ=，则经过10秒后转过的角度为3πθ=，∴ 5.6 4.8cos 5.6 2.4 3.23h π=-=-=（m ）.【点睛】关键点点睛：本题考查的知识点是在实际问题中建立三角函数模型，在建立函数模型的过程中，以圆心O 为原点，以水平方向为x 轴方向，以竖直方向为y 轴方向建立平面直角坐标系，是解决本题的关键． 24．（1）1；（2）()36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦，.【分析】本题考查三角函数的图像和性质、三角恒等变换，根据三角恒等变换公式()f x 化简函数解析式，根据图像和性质求单调递增区间. 【详解】（1）5()23(cos cossin sin )(1cos 2)332f x wx wx wx wx ππ=--++23sin 23sin cos 222wx wx wx =--+1cos 2323cos 222wx wx wx -=-⨯-+12cos 22wx wx =+ sin(2)6wx π=+又因为()f x 图象上相邻的两个最低点间的距离为π，0w >，所以22w，解得1w =.（2）据（1）求解知，()sin(2)6f x x π=+令222()262k x k k Z πππππ-+≤+≤+∈，所以()36k x k k Z ππππ-+≤≤+∈，所以所求的单调递增区间是()36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦，.【点睛】思路点睛：三角恒等变换综合应用的解题思路：（1）利用降幂、升幂公式将()f x 化为sin cos a x b x 的形式；（2）构造())f x x x +；（3）和差公式逆用，得())f x x ϕ=+ (其中ϕ为辅助角，tan b aϕ=)；（4）利用())f x x ϕ=+研究三角函数的性质；（5）反思回顾，查看关键点、易错点和答题规范．25．（1）1ω=；（2）最大值为1；最小值为. 【分析】（1）根据三角函数的倍角公式以及辅助角公式将函数进行化简即可．（2）求出角的取值范围，结合三角函数的最值性质进行判断求解即可．【详解】解：（1）因为2π()sin(2)(2cos 1)6f x x x ωω=-+-ππ(sin 2cos cos 2sin )cos 266x x x ωωω=-+12cos22x x ωω=+ πsin(2)6x ω=+，所以()f x 的最小正周期2ππ2T ω==，0>ω，解得1ω=.（2）由（1）得π()sin(2)6f x x =+. 因为7π12x ≤≤0，所以ππ4π2663x +≤≤. 所以，当ππ262x +=，即π6x =时，()f x 取得最大值为1；当π4π263x +=，即7π12x =时，()f x取得最小值为. 26．an 2α＝43，sin ()4πα-＝. 【分析】先由tan α＝12可得tan 2α＝43，再由sin cos αα＝12，结合角的范围可得sin α和cos α的值，再由in ()4πα-的展开求解即可.【详解】∵tan α＝12，∴tan 2α＝22tan 1tan a a -＝122114⨯-＝43. 且sin cos αα＝12，即cos α＝2sin α. 又sin 2α＋cos 2α＝1，∴5sin 2α＝1.而α∈(0,)2π，∴sin α，cos α. ∴sin ()4πα-＝sin αcos4π－cos αsin 4π。

2015年高考数学—三角函数(解答+答案)

2015年高考数学—三角函数（解答+答案）1.(2015新课标Ⅰ文数（17）（本小题满分12分）)已知a ，b ，c 分别为△ABC 内角A ，B ，C 的对边，sin 2B=2sinAsinC （Ⅰ）若a=b ，求cosB ；（Ⅱ）设B=90°，且a=2，求△ABC 的面积2.（2015新课标II 文数17．（本小题满分12分））ΔABC 中，D 是BC 上的点，AD 平分∠BAC ，BD=2DC 。

（1）求sin sin BC∠∠；（2）若60BAC ∠=o，求B ∠。

3.（2015安徽文数16.（本小题满分12分））已知函数2()(sin cos )cos 2f x x x x =++（Ⅰ）求()f x 的最小正周期；（Ⅱ）求()f x 在区间[0,]2π上的最大值和最小值.4.（2015北京文数（15）（本小题13分））已知函数2()sin 2f x x π=-（Ⅰ）求()f x 的最小正周期；（Ⅱ）求()f x 在区间20,3π⎡⎤⎢⎥⎣⎦上的最小值。

5.（2015重庆文数18）已知函数21()sin 22f x x x =. （Ⅰ）求()f x 的最小周期和最小值；（Ⅱ）将函数()f x 的图像上每一点的横坐标伸长到原来的两倍，纵坐标不变，得到函数()g x 的图像.当,2x ππ⎡⎤∈⎢⎥⎣⎦时，求()g x 的值域.6.(2015福建文数21.（本小题满分12分）)已知函数()2cos 10cos 222x x x f x =+．（Ⅰ）求函数()f x 的最小正周期；（Ⅱ）将函数()f x 的图象向右平移6π个单位长度，再向下平移a （0a >）个单位长度后得到函数()g x 的图象，且函数()g x 的最大值为2．（ⅰ）求函数()g x 的解析式；（ⅱ）证明：存在无穷多个互不相同的正整数0x ，使得()00g x >．7.（2015广东文数16、（本小题满分12分））已知tan 2α=．()1求tan 4πα⎛⎫+ ⎪⎝⎭的值；()2求2sin 2sin sin cos cos 21ααααα+--的值．8.（2015湖北文数18.（本小题满分12分））某同学用“五点法”画函数π()sin()(0,||)2f x A x ωϕωϕ=+><在某一个周期内的图象时，列表并填入了部分数据，如下表：（Ⅰ）请将上表数据补充完整，填写在答题卡上相应位置．．．．．．．．．．．，并直接写出函数()f x 的解析式；（Ⅱ）将()y f x =图象上所有点向左平行移动π6个单位长度，得到()y g x =图象，求()y g x =的图象离原点O 最近的对称中心.9.（2015湖南文数17. （本小题满分12分））设△ABC 的内角,,A B C 的对边分别为,,,tan a b c a b A =. （Ⅰ）证明：sin cos B A =；（Ⅱ）若3sin sin cos 4C A B -=，且B 为钝角，求,,A B C .10.（2015山东文数17．（本小题满分12分））AB C ∆中，角C B,A,所对的边分别为c b a ,,，已知33cos =B ，sin()A B +=ac =，求A sin 和c 的值.11.（2015陕西文数17．）ABC ∆的内角,,A B C 所对的边分别为,,a b c ，向量(,3)m a b =u r 与(cos ,sin )n A B =r平行.（Ⅰ）求A ；（Ⅱ）若7,2a b ==求ABC ∆的面积.12.（2015上海文数21. （本题满分14分））如图，,,O P Q 三地有直道相通，3OP =千米，4PQ =千米，5OQ =千米，现甲、乙两警员同时从O 地出发匀速前往Q 地，经过t 小时，他们之间的距离为()f t （单位：千米）.甲的路线是OQ ，速度为5千米/小时，乙的路线是OPQ ，速度为8千米/小时，乙到达Q 地后在原地等待.设1t t =时，乙到达P 地，2t t =时，乙到达Q 地.（1）求1t 与1()f t 的值；（2）已知警员的对讲机的有效通话距离是3千米，当12t t t ≤≤时，求()f t 的表达式，并判断()f t 在12[,]t t 上的最大值是否超过3？说明理由.13.（2015四川文数19、(本小题满分12分)）已知A 、B 、C 为ABC ∆的内角，tan ,tan A B 是关于方程2310()x px p p R +-+=∈的两个实根.（Ⅰ）求C 的大小；（Ⅱ）若3,6AB AC ==，求p 的值14.（2015天津文数16.（13分））△ABC 中，内角A,B,C 所对的边分别为a ，b ，c ，已知△ABC 的面积为315，12,cos ,4b c A -==-（Ⅰ）求a 和sin C 的值；（Ⅱ）求cos 26A π⎛⎫+ ⎪⎝⎭的值。

2015-三角函数高考真题教师版

2015-2017三角函数高考真题1、（2015全国1卷2题）o o o o sin 20cos10cos160sin10- =（）（A）（B（C ）12- （D ）12【答案】D【解析】原式=o o o o sin 20cos10cos 20sin10+ =o sin30=12，故选D. 2、（2015全国1卷8题）函数()f x =cos()x ωϕ+的部分图像如图所示，则()f x 的单调递减区间为（）（A ）13(,),44k k k Z ππ-+∈ （B ）13(2,2),44k k k Z ππ-+∈ （C ）13(,),44k k k Z -+∈ （D ）13(2,2),44k k k Z -+∈【答案】D【解析】由五点作图知，1+4253+42πωϕπωϕ⎧=⎪⎪⎨⎪=⎪⎩，解得=ωπ，=4πϕ，所以()cos()4f x x ππ=+，令22,4k x k k Z πππππ<+<+∈，解得124k -＜x ＜324k +，k Z ∈，故单调减区间为（124k -，324k +），k Z ∈，故选D. 考点：三角函数图像与性质3、（2015全国1卷12题）在平面四边形ABCD 中，∠A=∠B=∠C=75°，BC=2，则AB 的取值范围是 .【答案】【解析】如图所示，延长BA ，CD 交于E ，平移AD ，当A 与D 重合与E 点时，AB 最长，在△BCE 中，∠B=∠C=75°，∠E=30°，BC=2，由正弦定理可得sin sin BC BEE C=∠∠，即o o2sin 30sin 75BE=，解得BE，平移AD ，当D 与C 重合时，AB 最短，此时与AB 交于F ，在△BCF 中，∠B=∠BFC =75°，∠FCB=30°，由正弦定理知，sin sin BF BCFCB BFC=∠∠，即o o2sin 30sin 75BF =，解得-AB 的取值范围为）.考点：正余弦定理；数形结合思想4、（2015全国2卷10题）如图，长方形ABCD 的边2AB =，1BC =，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，记BOP x ∠=．将动P 到A 、B 两点距离之和表示为x 的函数()f x ，则()y f x =的图像大致为（）【解析】由已知得，当点P 在BC 边上运动时，即04x π≤≤时，tan PA PB x +=；当点P 在CD 边上运动时，即3,442x x πππ≤≤≠时，PA PB +=，当2x π=时，PA PB +=当点P 在AD 边上运动时，即34x ππ≤≤时，tan PA PB x +=，从点P 的运动过程可以看出，轨迹关于直线2x π=对称，且()()42f f ππ>，且轨迹非线型，故选B ．考点：函数的图象和性质．5、（2015全国2卷17题）ABC ∆中，D 是BC 上的点，AD 平分BAC ∠，ABD ∆面积是ADC ∆面积的2倍．（Ⅰ）求sin sin BC∠∠；（Ⅱ）若1AD =，2DC =，求BD 和AC 的长．【解析】（Ⅰ）1sin 2ABD S AB AD BAD ∆=⋅∠，1sin 2ADC S AC AD CAD ∆=⋅∠，因为2ABDADC S S ∆∆=，BAD CAD ∠=∠，所以2AB AC =．由正弦定理可得sin 1sin 2B AC C AB ∠==∠．（Ⅱ）因为::ABD ADC S S BD DC ∆∆=，所以BD =ABD ∆和ADC ∆中，由余弦定理得DPCB OAx2222cos AB AD BD AD BD ADB =+-⋅∠，2222cos AC AD DC AD DC ADC =+-⋅∠．222222326AB AC AD BD DC +=++=．由（Ⅰ）知2AB AC =，所以1AC =．考点：1、三角形面积公式；2、正弦定理和余弦定理．6、（2016全国1卷12题）已知函数()sin()(0),24f x x+x ππωϕωϕ=>≤=-，为()f x 的零点,4x π=为()y f x =图像的对称轴,且()f x 在51836ππ⎛⎫⎪⎝⎭，单调,则ω的最大值为（A ）11 （B ）9 （C ）7 （D ）5 【答案】B考点：三角函数的性质【名师点睛】本题将三角函数单调性与对称性结合在一起进行考查,叙述方式新颖,是一道考查能力的好题.注意本题解法中用到的两个结论:①()()()sin 0,0f x A x A ωϕω=+≠≠的单调区间长度是半个周期;②若()()()sin 0,0f x A x A ωϕω=+≠≠的图像关于直线0x x = 对称,则()0f x A = 或()0f x A =-.7、（2016全国1卷17题）ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知2cos (cos cos ).C a B+b A c =（I ）求C ；（II ）若c ABC =∆求ABC V 的周长．试题分析：（I ）先利用正弦定理进行边角代换化简得得1cos C 2=,故C 3π=；（II ）根据1sin C 2ab =．及C 3π=得6ab =．再利用余弦定理得 ()225a b +=．再根据c =可得C ∆AB 的周长为5+．考点：正弦定理、余弦定理及三角形面积公式【名师点睛】三角形中的三角变换常用到诱导公式,()()sin sin ,cos cos ,A B C A B C +=+=-()tan tan A B C+=-,就是常用的结论,另外利用正弦定理或余弦定理处理条件中含有边或角的等式,常考虑对其实施“边化角”或“角化边.”8、（2016全国2卷7题）若将函数y =2sin 2x 的图像向左平移π12个单位长度，则平移后图象的对称轴为（A ）()ππ26k x k =-∈Z （B ）()ππ26k x k =+∈Z （C ）()ππ212Z k x k =-∈ （D ）()ππ212Z k x k =+∈ 解析：平移后图像表达式为，令，得对称轴方程：，故选B ．9、（2016全国2卷9题）若π3cos 45α⎛⎫-= ⎪⎝⎭，则sin2α=（A ）725 （B ）15（C ）15- （D ）725-【解析】D ∵，，10、（2016全国2卷13题）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，若4cos 5A =，5cos 13C =，1a =，则b = ．【解析】 ∵，，，，，由正弦定理得：解得．11、（2016全国3卷5题）若3tan 4α= ，则2cos 2sin 2αα+=（） (A)6425 (B) 4825 (C) 1 (D)1625【答案】A【解析】试题分析：由3tan 4α=，得34sin ,cos 55αα==或34sin ,cos 55αα=-=-，所以2161264cos 2sin 24252525αα+=+⨯=，故选A ．考点：1、同角三角函数间的基本关系；2、倍角公式．【方法点拨】三角函数求值：①“给角求值”将非特殊角向特殊角转化，通过相消或相约消去非特殊角，进而求出三角函数值；②“给值求值”关键是目标明确，建立已知和所求之间的联系．12、（2016全国3卷8题）在ABC △中，π4B =，BC 边上的高等于13BC ,则cos A =（）（A （B （C ）- （D ）- 【答案】C 【解析】试题分析：设BC 边上的高线为AD ，则3BC AD =，所以AC ==，AB =．由余弦定理，知222222cos2AB AC BC A AB AC +-===⋅，故选C ．考点：余弦定理．13、（2016全国3卷14题）函数sin y x x =的图像可由函数sin y x x =的图像至少向右平移_____________个单位长度得到．【答案】32π 考点：1、三角函数图象的平移变换；2、两角和与差的正弦函数．【误区警示】在进行三角函数图象变换时，提倡“先平移，后伸缩”，但“先伸缩，后平移”也经常出现在题目中，所以也必须熟练掌握，无论是哪种变形，切记每一个变换总是对字母x 而言，即图象变换要看“变量”起多大变化，而不是“角”变化多少．14、（2017年全国1卷9题）9、已知曲线1:cos C y x =，22π:sin 23C y x ⎛⎫=+ ⎪⎝⎭，则下面结论正确的是（）A ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CB ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2CC ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CD ．把1C 上各点的横坐标缩短到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2C 【答案】D【解析】1:cos C y x =，22π:sin 23⎛⎫=+ ⎪⎝⎭C y x首先曲线1C 、2C 统一为一三角函数名，可将1:cos C y x =用诱导公式处理．πππcos cos sin 222⎛⎫⎛⎫==+-=+ ⎪ ⎪⎝⎭⎝⎭y x x x ．横坐标变换需将1=ω变成2=ω，即112πππsin sin 2sin 2224⎛⎫⎛⎫⎛⎫=+−−−−−−−−−→=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C 上各坐短它原y x y x x 点横标缩来 2ππsin 2sin 233⎛⎫⎛⎫−−→=+=+ ⎪ ⎪⎝⎭⎝⎭y x x ．注意ω的系数，在右平移需将2=ω提到括号外面，这时π4+x 平移至π3+x ，根据“左加右减”原则，“π4+x ”到“π3+x ”需加上π12，即再向左平移π12． 15、（2017年全国1卷17题）17、ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知ABC △的面积为23sin a A．（1）求sin sin B C ；（2）若6cos cos 1B C =，3a =，求ABC △的周长．【解析】本题主要考查三角函数及其变换，正弦定理，余弦定理等基础知识的综合应用.（1）∵ABC △面积23sin a S A=.且1sin 2S bc A =∴21sin 3sin 2a bc A A = ∴223sin 2a bc A =∵由正弦定理得223sin sin sin sin 2A B C A =，由sin 0A ≠得2sin sin 3B C =. （2）由（1）得2sin sin 3B C =，1cos cos 6B C = ∵πA B C ++=∴()()1cos cos πcos sin sinC cos cos 2A B C B C B B C =--=-+=-=又∵()0πA ∈，∴60A =︒，sin A =1cos 2A =由余弦定理得2229a b c bc =+-= ① 由正弦定理得sin sin a b B A =⋅，sin sin ac C A=⋅ ∴22sin sin 8sin a bc B C A=⋅= ②由①②得b c +=∴3a b c ++=+ABC △周长为316、（2017年全国2卷14题）函数()23sin 4f x x x =-（0,2x π⎡⎤∈⎢⎥⎣⎦）的最大值是．【命题意图】本题考查三角函数同角基本关系及函数性质—最值，意在考查考生转化与化归思想和运算求解能力【解析】∵ ()23sin 0,42f x x x x π⎛⎫⎡⎤=-∈ ⎪⎢⎥⎣⎦⎝⎭，22sin cos 1x x +=∴ ()21cos 4f x x x =-+设cos t x =，[]0,1t ∈，∴ ()214f x t =-+函数对称轴为[]0,1t =，∴ ()max 1f x = 17、（2017年全国2卷17题）ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知2sin()8sin 2BA C +=． (1)求cos B(2)若6a c += , ABC ∆面积为2,求.b 【命题意图】本题考查三角恒等变形，解三角形．【试题分析】在第（Ⅰ）中，利用三角形内角和定理可知A C B π+=-，将2sin 8)sin(2B C A =+转化为角B 的方程，思维方向有两个：①利用降幂公式化简2sin 2B ，结合22sin cos 1B B +=求出cos B ；②利用二倍角公式，化简2sin 8sin 2BB =，两边约去2sin B ，求得2tan B，进而求得B cos .在第（Ⅱ）中，利用（Ⅰ）中结论，利用勾股定理和面积公式求出a c ac +、，从而求出b ．（Ⅰ）【基本解法1】由题设及2sin 8sin ,2BB C B A ==++π，故 sin 4-cosB B =（1）上式两边平方，整理得 217cos B-32cosB+15=0 解得 15cosB=cosB 171（舍去），= 【基本解法2】由题设及2sin 8sin ,2B BC B A ==++π，所以2sin 82cos 2sin 22B B B =，又02sin ≠B，所以412tan =B ，17152tan 12tan 1cos 22=+-=B BB（Ⅱ）由158cosB sin B 1717==得，故14a sin 217ABC S c B ac ∆== 又17=22ABC S ac ∆=，则由余弦定理及a 6c +=得2222b 2cos a 2(1cosB)1715362(1)2174a c ac Bac =+-=-+=-⨯⨯+=（+c ）所以b=2【知识拓展】解三角形问题是高考高频考点，命题大多放在解答题的第一题，主要利用三角形的内角和定理，正、余弦定理、三角形面积公式等知识解题，解题时要灵活利用三角形的边角关系进行“边转角”“角转边”，另外要注意22,,a c ac a c ++三者的关系，这样的题目小而活，备受老师和学生的欢迎．18、（2017全国3卷6题）设函数π()cos()3f x x =+，则下列结论错误的是（）A ．()f x 的一个周期为2π-B ．()y f x =的图像关于直线8π3x =对称 C ．()f x π+的一个零点为π6x =D ．()f x 在π(,π)2单调递减【答案】D【解析】函数()πcos 3f x x ⎛⎫=+ ⎪⎝⎭的图象可由cos y x =向左平移π3个单位得到，如图可知，()f x 在π,π2⎛⎫⎪⎝⎭上先递减后递增，D 选项错误，故选D.19、（2017全国3卷17题）ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，已知sin 0A A =，a =，2b =．（1）求c ；（2）设D 为BC 边上一点，且AD AC ⊥，求ABD △的面积．【解析】（1）由sin 0A A =得π2sin 03A ⎛⎫+= ⎪⎝⎭，即()ππ3A k k +=∈Z ，又()0,πA ∈， ∴ππ3A +=，得2π3A =.由余弦定理2222cos a b c bc A =+-⋅.又∵12,cos 2a b A ===-代入并整理得()2125c +=，故4c =.（2）∵2,4AC BC AB ===，由余弦定理222cos 2a b c C ab +-==. ∵AC AD ⊥，即ACD △为直角三角形，则cos AC CD C =⋅，得CD =由勾股定理AD =又2π3A =，则2πππ326DAB ∠=-=， 1πsin 26ABD S AD AB =⋅⋅=△。

必修2三角函数检测题高一下学期数学测试卷(二)

高一下学期数学测试卷（二）只有一个正确，请将答案代号填在答卷相应的题号下的空格中。

）1、)600cos(︒-的值是（）（A ）21 （B ） 23 （C ）21- （D ）23-2、角α的终边经过点)0(),3,4(<-a a a P ,则αsin = ( ) (A)53 (B) 54 (C) 54± (D) 53± 3、已知0tan ,0sin ><θθ，则θ2sin 1-化简的结果为 ( ) (A) θcos (B) θcos - (C) θcos ± (D) 以上都不对4、已知53sin -=α,且α是第四象限角,则αtan 的值为 ( ) (A) 53- (B) 43- (C) 43 (D) 345、已知5cos 5sin 3cos 2sin -=+-αααα，则=αtan ( )(A) －2 (B) 2 (C) 2316(D) －23166、若扇形的圆心角为3π，半径为2，则扇形的面积为（） (A)31 (B)32 (C) 3π (D) 32π7、下列函数是奇函数的是 ( )(A)R x x x y ∈+=,cos 2(B)x y sin 2=,R x ∈(C) 2,tan 2ππ+≠=k x x y (D)R x x x y ∈=,sin 28、函数)62sin(3π+=x y 的图像的一条对称轴方程是 ( )(A) 0=x (B) 12π-=x (C) 6π=x (D) 3π=x9、已知1sin cos ,0,cos sin 84πααααα=<<-且则的值为 ( ) (A)23 (B) 43 (C) 23- (D) 43- 10、函数1cos 2+=x y 的定义域是（）（A ）)(322,322z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ （B ）)(62,62z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ （C ）)(322,32z k k k ∈⎥⎦⎤⎢⎣⎡++ππππ （D ）)(32,32z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ 11、若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ，两点，则MN 的最大值为（）（A ）1（B（C（D ）212、函数x x x x f cos sin 3sin )(2+=在区间⎥⎦⎤⎢⎣⎡2,4ππ上的最大值是 ( ) (A) 1 (B)231+ (C) 23(D) 31+ 二、填空题（每小题5分，共20分，请将答案填在答卷相应的题号下的空格中。

2015-2019年三角函数高考真题.docx

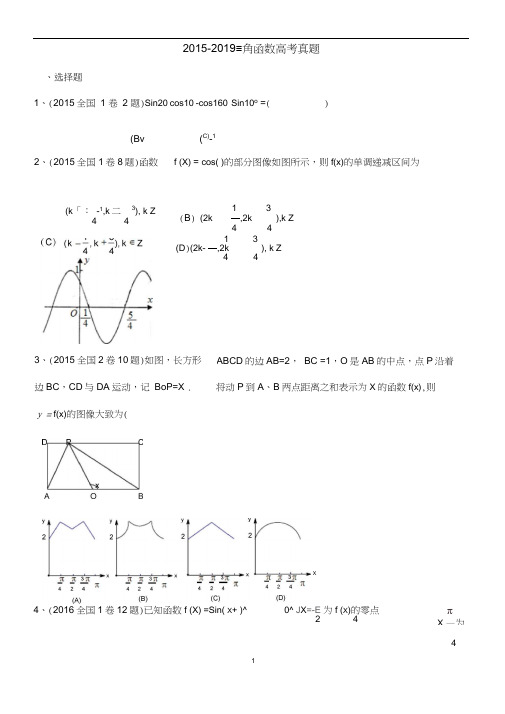
2015-2019≡角函数高考真题、选择题1、(2015全国1 卷2 题)Sin20°cos10°-cos160°Sin10o =( )(Bv (C)-14、(2016全国1卷12题)已知函数f (X) =Sin( X+ )^ 0^ J X=-E 为f (X)的零点2 42、(2015全国1卷8题)函数 f (X) = cos( )的部分图像如图所示，则f(x)的单调递减区间为(k「：-1,k二3), k Z4 41 3(B) (2k —,2k ),k Z4 41 3(D)(2k- —,2k ), k Z4 43、(2015全国2卷10题)如图，长方形ABCD的边AB=2，BC =1，O是AB的中点，点P沿着边BC，CD与DA运动，记BoP=X .将动P到A、B两点距离之和表示为X的函数f(x),则y = f(x)的图像大致为(Xπ,X —为4y=f(x)图像的对称轴且f(x)在任,竺单调,则技的最大值为(18 36 J(A) 11 (B) 9 (C) 7 (D) 55、(2016全国2卷7题)若将函数y=2sin 2x的图像向左平移1∏个单位长度，则平移后图象的对称轴为( )(A) X 斗-∏ k∙ Z (B) x=k∏ 上2 6 2& (2016全国2卷9题)若cos -(A) 25 1(B) 1 (C)5 -k Z(C)J5，15 (D)7、(2016全国3卷5题) ,则X忙訂Z (D) X=Z」k Z2 127252cos ‘：亠2sin2：=64(A)—25 (B)48258、(2016全国3卷8题) 在厶ABC中,(A)迈(B)卫10 109、(2017年全国1卷9题)16(D)—25B= - , BC边上的高等于-BC ,则cosA=( 4 3(D)-辽10(C) 1(C)-卫10、『2 JV已知曲线C i : y =CoSX , O ：y =sin 2χ■2-,则下面结论正确的是()A .把G上各点的横坐标伸长到原来的 2 倍, 纵坐标不变，再把得到的曲线向右平移才个单位长度，得到曲线C2B.把G上各点的横坐标伸长到原来的 2 倍, 纵坐标不变，再把得到的曲线向左平移度，得到曲线C2C.把C l上各点的横坐标缩短到原来的纵坐标不变，再把得到的曲线向右平移三个单位长6度，得到曲线C2D .把G上各点的横坐标缩短到原来的 2倍,纵坐标不变，再把得到的曲线向左平移度，得到曲线C2 .10、( 2017全国3卷6题)设函数f(x^cos(x π),则下列结论错误的是()3B. y =f (X)的图像关于直线A. f (x)的一个周期为-2πX哼对称—C. f(χ V)的一个零点为X=- D . f (x)在(∏, ∏单调递减611、(2018年全国1 ∙8)已知函数f X =2cos2χ-sin2x • 2 ,贝U ( )A. f X的最小正周期为π,最大值为3B. f X的最小正周期为π,最大值为4C. f (X )的最小正周期为2π,最大值为3 D . f (X )的最小正周期为2 π,最大值为412. (2018年全国1 • 11)已知角〉的顶点为坐标原点，始边与X轴的非负半轴重合，终边上有两点2A(1, a ), B (2 , b ),且cos2α =—,则a —b =( )3A. -B. -5C. 2-5 D . 15 5 513. (2018 年全国2 • 7).在厶ABC 中，CoSC=逅,BC =1 , AC =5 ,则AB=(2 5A . 4.2 B. .. 30 C. 29 D . 2 514. (2018年全国2 • 10)若f(x) =COSX-sinx在［0, a］是减函数，贝U a的最大值是(A. πB. πC.3πD.π42415. (2018年全国3 • 4) 若Sin「^—,则cos2 ：■=()3A 8r 778 A.-B.C. D.999916. (2018年全国3 • 6) 函数f (X)=tan X的最小正周期为 ( )1 tan2XMπ… πA.-B.-C. πD. 24217、(2018年全国3∙ 11) △ ABC的内角A , B , C的对边分别为a , b , C .若△ ABC的面积为2-CJl λJl fAA. -B. -C. —D.-2 3 4 6Sin X + X18、(2019年全国1 • 5)函数f(x)= ------------- 2在［—π,π］的图像大致为cos X 十X19、 (2019年全国1 ∙11)关于函数f(x) =sin∣x∣ |sin x|有下述四个结论：①f(x)是偶函数②f(x)在区间(-√:)单调递增2③f(x)在［-二，二］有4个零点④f(x)的最大值为2其中所有正确结论的编号是A.①②④B.②④C.①④D.①③20、 (2019年全国2 • 9)下列函数中，以二为周期且在区间(二,)单调递增的是2 4 2A. f (X)=∣COS 2x IB. f (X)=∣Sin 2x ∣C. f (X)= COS | X | D . f (X) = Sin | X |___ -JT21、(2019年全国2 • 10)已知α∈0,—」，2sin 2 α= coS∣2 贝α Sin α=()2A. 1B. §C.仝 D .空5 5 3 5二、填空题1、(2015全国1卷12题)在平面四边形ABCD中，∠ A= ∠ B= ∠ C=75 ° , BC=2 ,贝U AB的取值范围是_________ .4 5 2、(2016全国2卷13题)A ABC的内角A, B, C的对边分别为a, b, c,若cosA=-, cosC -,5 13a =1 ,贝Ub =_____ .3、(2016全国3卷14题)函数y =sinx---3cosx的图像可由函数y=sinχ∙ ■■一3cosx的图像至少向右平移______________ 单位长度得到.函数2厂 3 （- 7r ］）的最大值是 ____________________.f （x ）=sin x +J 3cosx -一 X E ：0 二4f 2」5. （2018年全国 1 ∙16） △ ABC 的内角 A , B , C 的对边分别为 a , b , C ,已知 bsinC +csin B =4asin BsinC ,b 2c 2 -a 2 -8 ,则△ ABC 的面积为 _______________ 。

高一三角函数月考卷(附解析)

绝密★启用前2015-2016学年度2015级4班12月三角函数测试卷注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题（5*12）1．已知),0(πα∈，且1sin cos 2αα+=，则α2cos 的值为（） A ．47± B ．47 C ．47- D ．43-2．已知函数()sin 3f x x x π=+-, 则12340292015201520152015f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的值为（） A ．4029 B ．4029- C ．8058 D ．8058- 3．若sin()cos()=3sin()cos()α-π+π-απ+α-π+α，则tan （π+α）=（）（A ）21（B ）2 （C ）1 （D ）-2 4．o o o osin 20cos10cos160sin10- =（）（A ）（B （C ）12- （D ）125．已知点(tan ,cos )P αα在第三象限，则角α的终边在（）（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限6．tan 2θ=，则22sin sin cos 2cos θθθθ+-=（）（A ）43-（B ）54 （C ）34- （D ）457．设角θ的终边经过点(3,4)P -，那么sin 2cos θθ+=（） A ．15B ．15-C ．25- D ．258．sin(690)-︒的值为（）A．12- C ．12D．9．若35)2cos(=-απ且)0,2(πα-∈，则=-)sin(απA ．35-B ．32-C ．31-D ．32± 10．已知31)22015sin(=+απ，则)2cos(a -π的值为（） A ．31 B ．31- C ．97 D ．97-11．已知函数()sin(2)()2f x x x R π=-∈下列结论错误的是（）A ．函数()f x 的最小正周期为πB ．函数()f x 是偶函数C ．函数()f x 的图象关于直线4x π=对称D ．函数()f x 在区间[0,]2π上是增函数12．若函数()2sin()3f x x πω=+，且()2,()0f f αβ=-=，αβ-的最小值是2π，则()f x 的单调递增区间是（） A ．5[,]()1212k k k Z ππππ-+∈ B ．[,]()36k k k Z ππππ-+∈ C ．2[2,2]()33k k k Z ππππ-+∈ D ．5[2,2]()66k k k Z ππππ-+∈第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题（4*5）13．若θsin +1cos 5θ=，θ∈（0，π），则tan θ=． 14．已知函数3sin )(-+=x x x f π, 则)20154029()20152()20151(f f f +++ 的值为． 15．给出如下五个结论： ①存在)2,0(πα∈使31cos sin =+a a ②存在区间（,a b ）使x y cos =为减函数而x sin ＜0 ③x y tan =在其定义域内为增函数 ④)2sin(2cos x x y -+=π既有最大、最小值，又是偶函数⑤) ⎝⎛+=62sin πx y 最小正周期为π其中正确结论的序号是 16．关于函数)62sin(2)(π+=x x f 下列结论:①()f x 的最小正周期是π； ②()f x 在区间[,]66ππ-上单调递增； ③函数()f x 的图象关于点(,0)12π成中心对称图形； ④将函数()f x 的图象向左平移512π个单位后与2sin 2y x =-的图象重合；其中成立的结论序号为．三、解答题（题型注释）17．（本题满分10分）已知α为第三象限角，()3s i n ()c o s ()t a n ()22tan()sin()f ππααπαααπαπ-+-=----，（1）化简()fα；（2）若31cos()25πα-=，求()f α的值． π部分图象如图所示．（1）试确定函数()f x 的解析式；（2）若1()23f απ=，求2cos()3πα-的值． 19．（本题满分12分）（1）已知角α的顶点在原点，始边与x 轴的非负半轴重合，终边经过点)4,3(-P ，求)2cos()cos(απαπ++-的值。

2015高一三角函数测试卷2(详细答案)总结

三角函数阶段测试(2)一．选择题：1．如果1弧度的圆心角所对的弦长为2，那么这个圆心角所对的弧长为（）A ．B．sin0.5C．2sin0.5D．tan0.52．已知α为第三象限角，则所在的象限是（）A ．第一或第二象限B．第二或第三象限C．第一或第三象限D．第二或第四象限3．已知sinα＞sinβ，那么下列命题成立的是（）A．若α、β是第一象限角，则cosα＞cosβB．若α、β是第二象限角，则tanα＞tanβC．若α、β是第三象限角，则cosα＞cosβD．若α、β是第四象限角，则tanα＞tanβ4．若，则sinαcosα=（）A ．B．C．D．5．在△ABC中，已知cos=，则cos=（）A．﹣B．C．D．﹣6．三角形ABC中角C为钝角，则有（）A．sinA＞cosBB．sinA＜cosBC．sinA=cosBD．sinA与cosB大小不确定7．已知=（）A ．B．C．D．8．设函数f（x）=3sin（ωx+φ）（ω＞0，﹣＜φ＜）的图象关于直线x=对称，它的周期是π，则（）A．f（x ）的图象过点（0，），B．f（x）的一个对称中心是（，0）C．f（x）在[，]上是减函数D．将f（x）的图象向右平移|φ|个单位得到函数y=3sin ωx的图象9．在函数①y=cos丨2x丨，②y=丨cosx丨，③y=cos（2x+）④y=tan（2x﹣）中，最小正周期为π的所有函数为（）A ．①②③B．①③④C．②④D．①③10．设，则不等式xf（x）＜0在上的解集是（）A ．B．C．D．二．填空题：11．已知f（x）=atanx﹣bcosx+4（其中以a、b为常数且ab≠0），如果f（3）=5，则f（2013π﹣3）的值为．12．已知角α的顶点在原点，始边与x轴正半轴重合，点P（﹣4m，3m）（m＜0）是角α终边上一点，则2sinα+cosα= ．13．给出下列六种图象变换方法：（1）图象上所有点的纵坐标不变，横坐标缩短到原来的；（2）图象上所有点的纵坐标不变，横坐标伸长到原来的2倍；（3）图象向右平移个单位；（4）图象向左平移个单位；（5）图象向右平移个单位；（6）图象向左平移个单位．请用上述变换中的两种变换，将函数y=sinx的图象变换到函数y=sin（+）的图象，那么这两种变换正确的标号是（要求按变换先后顺序填上一种你认为正确的标号即可）．14．设函数f（x）=sin（2x+），现有下列结论：（1）f（x）的图象关于直线x=对称；（2）f（x）的图象关于点（，0）对称（3）把f（x）的图象向左平移个单位，得到一个偶函数的图象；（4）f（x）的最小正周期为π，且在[0，]上为增函数．其中正确的结论有（把你认为正确的序号都填上）三．解答题：15．已知2sinθ﹣cosθ=1，求的值．16．已知﹣＜x＜0，sinx+cosx=．（1）求sin2x﹣cos2x的值；（2）求的值．17．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的一段图象如下所示．（1）求f（x）的解析式；（2）求f（x）的单调减区间，并指出f（x）的最大值及取到最大值时x的集合．18．函数的图象上一个最高点的坐标为，与之相邻的一个最低点的坐标为．（1）求f（x）的表达式；（2）当，求函数f（x）的单调递增区间和零点．参考答案一．选择题：1．如果1弧度的圆心角所对的弦长为2，那么这个圆心角所对的弧长为（）A ．B ．sin0.5C ．2sin0.5D ．tan0.5考点：弧长公式．专题：计算题．分析：连接圆心与弦的中点，则得到一个弦一半所对的角是1弧度的角，由于此半弦是1，故可解得半径为，弧长公式求弧长即可．解答：解：连接圆心与弦的中点，则由弦心距，弦长的一半，半径构成一个直角三角形，半弦长为1，其所对的圆心角也为1故半径为这个圆心角所对的弧长为1×=故选A ．点评：本题考查弧长公式，求解本题的关键是利用弦心距，弦长的一半，半径构成一个直角三角形求半径，熟练记忆弧长公式也是正确解题的关键．2．已知α为第三象限角，则所在的象限是（）A ．第一或第二象限B ．第二或第三象限 C ．第一或第三象限 D ．第二或第四象限考点：象限角、轴线角；角的变换、收缩变换．分析： α为第三象限角，即k ∈Z ，表示出，然后再判断即可．解答：解：因为α为第三象限角，即k ∈Z ，所以，k ∈Z 当k 为奇数时它是第四象限，当k 为偶数时它是第二象限的角．故选D ．点评：本题考查象限角，角的变换，是基础题．可以推广到其它象限．3．已知sinα＞sinβ，那么下列命题成立的是（）A．若α、β是第一象限角，则cosα＞cosβB．若α、β是第二象限角，则tanα＞tanβC．若α、β是第三象限角，则cosα＞cosβD．若α、β是第四象限角，则tanα＞tanβ考点：象限角、轴线角．专题：计算题．分析：由于题中条件没有给出角度的范围，不妨均假定0≤α，β≤2π，结合三角函数的单调性加以解决．解答：解：若α、β同属于第一象限，则，cosα＜cosβ；故A错．第二象限，则，tanα＜tanβ；故B错．第三象限，则，cosα＜cosβ；故C错．第四象限，则，tanα＞tanβ．（均假定0≤α，β≤2π．）故D正确．答选为D．点评：本题考查三角函数的性质，三角函数的性质是三角部分的核心，主要指：函数的定义域、值域，函数的单调性、对称性、奇偶性和周期性．4．若，则sinαcosα=（）A ．B．C．D．考点：同角三角函数间的基本关系；二倍角的正弦．专题：计算题．分析：由已知中，由于分子是二次三角表达式，故可以利用弦化切思想，将式子转化成一个只含α正切的式子，代入即可得到答案．解答：解：∵，∴sinαcosα===故选D点评：本题考查的知识点是同角三角函数间的基本关系，其中利用弦化切思想，找到已知式与求知式之间的关系是解答本题的关键．5．在△ABC中，已知cos =，则cos=（）A ．﹣B．C．D．﹣考点：运用诱导公式化简求值．专题：三角函数的求值．分析：已知等式左边中的角度变形后，利用诱导公式化简求出sin的值，再利用同角三角函数间的基本关系即可求出cos的值．解答：解：∵cos=cos（﹣）=sin=，且为锐角，∴cos==．故选：C．点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．6．三角形ABC中角C为钝角，则有（）A ．sinA＞cosB B．sinA＜cosBC ．sinA=cosB D．sinA与cosB大小不确定考点：诱导公式的作用．专题：计算题．分析：由C＞90°，A+B+C=180°，知A+B＜90°，90°﹣B＞A，所以sin（90°﹣B）=cosB＞sinA．解答：解：△ABC中，∠C为钝角，cosB=sin（90°﹣B），∵∠C＞90°，A+B+C=180°，∴A+B＜90°，90°﹣B＞A∴sin（90°﹣B）＞sinA，∴cosB＞sinA．故选B．点评：本题考查诱导公式的应用，解题时要认真审题，仔细解答，注意三角函数的恒等变换．7．已知=（）A ．B．C．D．考点：诱导公式的作用；同角三角函数间的基本关系．专题：三角函数的求值．分析：利用诱导公式即可得出．解答：解：===，故选C．点评：熟练掌握诱导公式是解题的关键．8．设函数f（x）=3sin（ωx+φ）（ω＞0，﹣＜φ＜）的图象关于直线x=对称，它的周期是π，则（）A．f（x）的图象过点（0，），B．f（x）的一个对称中心是（，0）C．f（x）在[，]上是减函数D．将f（x）的图象向右平移|φ|个单位得到函数y=3sinωx的图象考点：正弦函数的图象．专题：三角函数的图像与性质．分析：先根据已知，求出周期，ω，φ的值，从而可得函数解析式，再根据三角函数的单调性、周期性、对称性即可判断．解答：解：因为函数的周期为π，所以ω=2，又函数图象关于直线x=π对称，所以由f（x）=3sin（2x+φ）（ω＞0，﹣＜φ＜），可知2×π+φ=kπ+，φ=kπ﹣，﹣＜φ＜，所以k=1时φ=．∴函数的解析式为：f（x）=3sin（2x+）．当x=0时f（0）=，所以A不正确．当x=时f（x）=0．函数的一个对称中心是（，0）B正确；当＜x＜，2x+∈[，]，函数不是单调减函数，C不正确；f（x）的图象向右平移|φ|个单位得到函数y=3sin（ωx+φ﹣ωφ）的图象，不是函数y=3sinωx的图象，D不正确；故选：B．点评：本题主要考查了正弦函数的单调性、周期性、对称性，三角函数解析式的求法，属于基础题．9．在函数①y=cos丨2x丨，②y=丨cosx丨，③y=cos（2x+）④y=tan（2x﹣）中，最小正周期为π的所有函数为（）A ．①②③B．①③④C．②④D．①③考点：三角函数的周期性及其求法．专题：三角函数的图像与性质．分析：根据三角函数的周期性，求出各个函数的最小正周期，从而得出结论．解答：解：∵函数①y=cos丨2x丨=cos2x，它的最小正周期为=π，②y=丨cosx丨的最小正周期为=π，③y=cos（2x+）的最小正周期为=π，④y=tan（2x﹣）的最小正周期为，故选：A．点评：本题主要考查三角函数的周期性及求法，属于基础题．10．设，则不等式xf（x）＜0在上的解集是（）A ．B．C．D．考点：正弦函数的单调性；其他不等式的解法；余弦函数的单调性．专题：计算题．分析：根据正弦（余弦）函数的性质对解析式进行化简，由解析式、定义域和正弦（余弦）值的符号求出不等式的解集．解答：解：由正弦（余弦）函数的性质得，，当时，f（x）=cosx＞0，有xf（x）＜0；当时，cosx＞0且sinx＞0，xf（x）＞0，则所求的解集为．故选D．点评：本题考查了正弦（余弦）函数的性质的应用，即根据正弦（余弦）函数的性质化简解析式，并且根据正弦（余弦）值的符号，求不等式的解集，考查了分析和解决问题的能力．二．填空题：11．已知f（x）=atanx﹣bcosx+4（其中以a、b为常数且ab≠0），如果f（3）=5，则f（2013π﹣3）的值为3．考点：运用诱导公式化简求值；函数奇偶性的性质；函数的值．专题：三角函数的求值．分析：直接利用已知条件化简结果，化简所求表达式，代入所求表达式求解即可．解答：解：f（3）=5，atan3﹣bcos3+4=5，∴atan3﹣bcos3=1f（2013π﹣3）=atan（2013π﹣3）﹣bcos（2013π﹣3）+4=﹣atan3+bcos3+4=﹣1+4=3．故答案为：3．点评：本题主要考察诱导公式的应用，奇函数的性质，属于中档题．12．已知角α的顶点在原点，始边与x轴正半轴重合，点P（﹣4m，3m）（m＜0）是角α终边上一点，则2sinα+cosα=．考任意角的三角函数的定义．点：专题：计算题．分析：可先求r==﹣5m（m＜0），由三角函数的定义可得，sin，可分别可求sinα，cosα，进而可求2sinα+cosα解答：解：由题意可得点P到原点的距离r==﹣5m（m＜0）由三角函数的定义可得，sin=﹣，=2sinα+cosα=，故答案为：点评：本题主要考查的三角函数的定义：若角α的终边上有一点P（x，y），OP=r则sin的应用，属于基础试题13．给出下列六种图象变换方法：（1）图象上所有点的纵坐标不变，横坐标缩短到原来的；（2）图象上所有点的纵坐标不变，横坐标伸长到原来的2倍；（3）图象向右平移个单位；（4）图象向左平移个单位；（5）图象向右平移个单位；（6）图象向左平移个单位．请用上述变换中的两种变换，将函数y=sinx的图象变换到函数y=sin（+）的图象，那么这两种变换正确的标号是（4）（2）或（2）（6）（要求按变换先后顺序填上一种你认为正确的标号即可）．考点：函数y=Asin（ωx+φ）的图象变换．专题：综合题．分析：（法一）y=sinx（法二）y=sinx．解答：解：（法一）y=sinx→y=（法二）：故答案为：（4）（2）或（2）（6）点评：本题考查了三角函数的平行移与周期变换的综合运用：熟悉y=sinx→y=sin （ωx+φ）的变换的途径有两个①y=sinx→y=sin （x+φ）→y=sin （ωx+φ）②y=sinx→y=sinωx→y=sin（ωx+φ），要注意两种变换中的平移量的不同．14．设函数f （x ）=sin （2x+），现有下列结论：（1）f （x ）的图象关于直线x=对称；（2）f （x ）的图象关于点（，0）对称（3）把f （x ）的图象向左平移个单位，得到一个偶函数的图象；（4）f （x ）的最小正周期为π，且在[0，]上为增函数．其中正确的结论有（3）（把你认为正确的序号都填上）考点：正弦函数的对称性；三角函数的周期性及其求法；正弦函数的单调性；函数y=Asin （ωx+φ）的图象变换．分析：利用正弦函数的单调性，对称性和三角函数图象的平移法则，对四个结论逐一验证，答案可得．解答：解：根据正弦函数的性质可知f （x ）=sin （2x+）的对称轴为2x+=kπ+（k ∈Z ），即x=+（k ∈Z ）∴直线x=不是函数f （x ）的对称轴，结论（1）错误根据正弦函数的性质可知f （x ）=sin （2x+）的对称中心横坐标为2x+=kπ，即x=，∴点（，0）不是函数的对称中心．结论（2）错误．f （x ）的图象向左平移个单位，得f （x ）=sin （2x+）=cos2x ，为偶函数，∴结论（3）正确． f （x ）的最小正周期为π，且2kπ﹣≤2x+≤2kπ+时，即kπ﹣π≤x≤kπ+函数单调增，∴结论（4）不正确．故答案为（3）点评：本题主要考查了正弦函数的基本性质．属基础题．三．解答题：15．已知2sinθ﹣cosθ=1，求的值．考同角三角函数基本关系的运用．点：三角函数的求值．专题：分已知等式利用二倍角的正弦、余弦函数公式化简得到2sin=cos或cos=0，原式利用同角三角析：函数间基本关系，完全平方公式，以及平方差公式变形，约分后代入计算即可求出值．解解：已知等式变形得：2sinθ=1+cosθ，即4sin cos=2cos2，答：即2sin=cos或cos=0，当2sin=cos时，原式=====2；当cos=0时，原式=0．点此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．评：16．已知﹣＜x＜0，sinx+cosx=．（1）求sin2x﹣cos2x的值；（2）求的值．考同角三角函数基本关系的运用．点：三角函数的求值．专题：由题意可得sinx和cosx的值，代入要求的式子化简即可．分析：解解：（1）∵﹣＜x＜0，∴sinx＜0且cosx＞0答：又sinx+cosx=，sin2x+cos2x=1∴sinx=，cosx=，∴sin2x﹣cos2x=；（2）由（1）知tanx==，∴==点评：本题考查同角三角函数的基本关系，属基础题．17．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的一段图象如下所示．（1）求f（x）的解析式；（2）求f（x）的单调减区间，并指出f（x）的最大值及取到最大值时x的集合．考点：由y=Asin（ωx+φ）的部分图象确定其解析式；正弦函数的单调性；三角函数的最值．专题：三角函数的图像与性质．分析：（1）由图象直接得到振幅A，和四分之三周期，所以周期可求，则ω可求，然后根据五点作图的第一点求得Φ，则函数解析式可求；（2）直接由三角函数符号后面的相位在正弦函数的减区间内求得函数的减区间，由终边在y轴正半轴上的角的正弦值最大求出使函数取得最大值时的角x的集合．解答：解：（1）由图象可以得到函数f（x）的振幅A=3，设函数周期为T，则，所以T=5π，则ω=，由ωx0+Φ=0，得Φ=0，所以Φ=﹣，所以f（x）=3sin．（2）由，得，所以函数的减区间为（+5kπ，4π+5kπ）k∈Z．函数f（x）的最大值为3，当且仅当，即时函数取得最大值．所以函数的最大值为3，取得最大值时的x的集合为{x|x=}．点评：本题考查了根据函数的部分图象求函数解析式问题，考查了复合函数的增减性，解答此题的关键是求初相，运用的是五点作图的第一点，具体办法是看图象在y轴右侧与x轴的第一个交点是上升趋势还是下降趋势，若是上升趋势有ωx0+Φ=0，若是下降趋势则有ωx0+Φ=π．18．函数的图象上一个最高点的坐标为，与之相邻的一个最低点的坐标为．（1）求f（x）的表达式；（2）当，求函数f（x）的单调递增区间和零点．考点：由y=Asin（ωx+φ）的部分图象确定其解析式；正弦函数的图象．专题：综合题．分析：（1）由已知中函数的图象上一个最高点的坐标为，与之相邻的一个最低点的坐标为．我们可根据两个最值点的纵坐标求出A，B的值，根据横坐标求出周期T，进而得到ω及φ的值，从而求出求f（x）的表达式；（2）根据由（1）的结论，及正弦型函数单调区间的求法，及零点的定义，我们易得到结论．解答：解：（1）依题意的，所以T=π，于是（2分）由解得（4分）把代入f（x）=2sin（2x+φ）+1，可得，所以，所以，因为，所以综上所述，（7分）（2）令f（x）=0，得，又∵∴∴故函数f（x）的零点是（10分）∵∴由得∴函数f（x）的单调递增区间是（13分）点评：本题考查的知识点是由y=Asin（ωx+φ）的部分图象确定其解析式，正弦型函数的性质及函数的零点，其中根据已知中的条件求出函数的解析式，是解答本题的关键．。

完整word版,高中三角函数测试题及答案(K12教育文档)

完整word版,高中三角函数测试题及答案(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（完整word版,高中三角函数测试题及答案(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为完整word版,高中三角函数测试题及答案(word版可编辑修改)的全部内容。

三角函数测试1、已知A=｛第一象限角｝,B={锐角},C=｛小于90°的角},那么A 、B 、C 关系是（） A ．B=A ∩CB ．B ∪C=C C ．A CD ．A=B=C2、将分针拨慢5分钟，则分钟转过的弧度数是 ( ）A ．3π B ．－3πC ．6πD ．－6π3、已知sin 2cos 5,tan 3sin 5cos ααααα-=-+那么的值为（ )A ．－2B ．2C ．2316D ．－23164、已知角α的余弦线是单位长度的有向线段;那么角α的终边( ）A ．在x 轴上B ．在直线y x =上C ．在y 轴上D ．在直线y x =或y x =-上 5、若(cos )cos2f x x =,则(sin15)f ︒等于 ( ) A ．32-B ．32C ．12D ． 12-6、要得到)42sin(3π+=x y 的图象只需将y=3sin2x 的图象（ )A ．向左平移4π个单位B ．向右平移4π个单位C ．向左平移8π个单位D ．向右平移8π个单位7、如图，曲线对应的函数是（）A ．y=|sin x ｜B ．y=sin|x ｜C ．y=－sin|x ｜D ．y=－|sin x ｜8、化简1160-︒2sin 的结果是（）A ．cos160︒B ．cos160-︒C ．cos160±︒D ．cos160±︒ 9、A 为三角形ABC 的一个内角,若12sin cos 25A A +=，则这个三角形的形状为（） A. 锐角三角形 B 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。