已知两点大地坐标求第三点大地坐标
大地坐标与直角空间坐标转换计算公式

⼤地坐标与直⾓空间坐标转换计算公式⼤地坐标与直⾓空间坐标转换计算公式⼀、参⼼⼤地坐标与参⼼空间直⾓坐标转换1名词解释:A :参⼼空间直⾓坐标系:a) 以参⼼0为坐标原点;b) Z轴与参考椭球的短轴(旋转轴)相重合;c) X轴与起始⼦午⾯和⾚道的交线重合;d) Y轴在⾚道⾯上与 X轴垂直,构成右⼿直⾓坐标系O-XYZ ;e) 地⾯点P的点位⽤(X,Y,Z)表⽰;B :参⼼⼤地坐标系:a) 以参考椭球的中⼼为坐标原点,椭球的短轴与参考椭球旋转轴重合;b) ⼤地纬度B :以过地⾯点的椭球法线与椭球⾚道⾯的夹⾓为⼤地纬度 B ;c) ⼤地经度L:以过地⾯点的椭球⼦午⾯与起始⼦午⾯之间的夹⾓为⼤地经度L;d) ⼤地⾼H:地⾯点沿椭球法线⾄椭球⾯的距离为⼤地⾼H ;e) 地⾯点的点位⽤(B,L,H)表⽰。
2参⼼⼤地坐标转换为参⼼空间直⾓坐标:X =(N +H )* cosB* cosLY =(N +H )* cosB* sin L ?Z =[N * (I _e2) +H]* sin B”公式中,N为椭球⾯卯⾣圈的曲率半径,e为椭球的第⼀偏⼼率,a、b椭球的长短半径,f椭球扁率,W为第⼀辅助系数a2 -b22* f -1e 或e =a fW = . (1 -g*sin2BN aW西安80椭球参数:长半轴 a=6378140⼟ 5( m)短半轴 b=6356755.2882m扁率a =1/298.2573参⼼空间直⾓坐标转换参⼼⼤地坐标Z* (N + H) (X2 Y2)* N* (1 -e2) HX2 Y2cosB⼆⾼斯投影及⾼斯直⾓坐标系1、⾼斯投影概述⾼斯-克吕格投影的条件:1.是正形投影;2.中央⼦午线不变形⾼斯投影的性质: 1.投影后⾓度不变; 2.长度⽐与点位有关,与⽅向⽆关;3.离中央⼦午线越远变形越⼤为控制投影后的长度变形,采⽤分带投影的⽅法。
常⽤3度带或6度带分带,城市或⼯程控制⽹坐标可采⽤不按 3度带中央⼦午线的任意带。
大地坐标与平面坐标之间的区别与转换

南方CASS和南方平差易可以计算,正反算,坐标换带下面收集的文章总结,相互转换需根据文章计算方法:1.大地坐标系:WGS84(世界坐标系)坐标以经纬度显示,GPS测得2.平面直角坐标系:高斯投影平面直角坐标系:北京54全国80,平面坐标以数字显示,由WGS84坐标系根据椭球参数转换而得。
北京54和全国80坐标系之间可以相互转换3.全站仪放样测得坐标属于平面直角坐标;GPS测得坐标属于大地坐标,高程是海拔高程。
4.同一个坐标系之间的转换高斯投影坐标系中坐标换带的计算见以下文章,比如80坐标系的6度带坐标,要换带计算为80坐标系的3度带,需要平面坐标先转换为大地坐标后根据经纬度调整再转换为另一度带坐标5.全站仪采用极坐标放样原理:把坐标输入全站仪,全站仪自动转换成方位角和距离,根据后视基准边的夹角和距离来放样。
具体参考WORD直角坐标与极坐标的区别和转换例题:高斯坐标和北京54,西安80坐标有什么区别,举例说一下,行吗?举个例子,野外采集GPS数据,数据是用大地坐标表示的,也就是用经纬度和高程表示。
而采集的数据要在地图上显示出来,就需要将经纬度转化为平面坐标,也就是通常说的x,y 坐标。
因为我国地形图一般采用高斯投影,所以通常转化成高斯平面坐标显示到地图上。
而在经纬度向平面坐标转化的过程中,需要用到椭球参数,因此要考虑所选的坐标系,我国常用的坐标系有北京54,西安80,WGS-84坐标系,不同的坐标系对应的椭球体是不一样的,这里你可能会不明白根椭球体有啥关系,是这样的,我们所说的地理数据都是为了描述大地水准面上的某一个点,而大地水准面是不规则的,我们用一个规定的椭球面去拟合这个水准面,用椭球面上的点来近似表示地球上的点。
每个国家地理情况不同,采用的椭球体也不尽相同。
北京54坐标系采用的是克拉索夫斯基(Krassovsky)椭球体,而西安80采用的是IAG 75地球椭球体WGS84坐标与北京54坐标转换(转)2007-09-20 12:03转自GIS中的坐标系定义与转换戴勤奋1. 椭球体、基准面及地图投影GIS中的坐标系定义是GIS系统的基础,正确定义GIS系统的坐标系非常重要。
大地、地心空间直角和球面三种坐标的转换

第一章大地坐标第一节大地坐标系统科技名词定义中文名称:大地坐标系英文名称:geodetic coordinate system定义:以参考椭球中心为原点、起始子午面和赤道面为基准面的地球坐标系。
应用学科:测绘学(一级学科);大地测量学(二级学科)大地坐标系(geodetic coordinate system)是大地测量中以参考椭球面为基准面建立起来的坐标系。
地面点的位置用大地经度、大地纬度和大地高度表示。
大地坐标系的确立包括选择一个椭球、对椭球进行定位和确定大地起算数据。
一个形状、大小和定位、定向都已确定的地球椭球叫参考椭球。
参考椭球一旦确定,则标志着大地坐标系已经建立。
大地坐标系亦称为地理坐标系。
大地坐标系是用来表述地球上点的位置的一种地区坐标系统。
它采用一个十分近似于地球自然形状的参考椭球作为描述和推算地面点位置和相互关系的基准面。
一个大地坐标系统必须明确定义其三个坐标轴的方向和其中心的位置。
通常人们用旋转椭球的短轴与某一规定的起始子午面分别平行干地球某时刻的平均自转轴和相应的真起始子午面来确定坐标轴的方向。
若使参考椭球中心与地球平均质心重合,则定义和建立了地心大地坐标系。
它是航天与远程武器和空间科学中各种定位测控测轨的依据。
若椭球表面与一个或几个国家的局部大地水准面吻合最好,则建立了一个国家或区域的局部大地坐标系。
大地坐标系中点的位置是以其大地坐标表示的,大地坐标均以椭球面的法线来定义。
其中,过某点的椭球面法线与椭球赤道面的交角为大地纬度;包含该法线和大地子午面与起始大地子午面的二面角为该点的大地经度;沿法线至椭球面的距离为该点的大地高。
大地纬度、大地经度和大地高分别用大写英文字母B、L、H表示。
大地坐标系是以地球椭球赤道面和大地起始子午面为起算面并依地球椭球面为参考面而建立的地球椭球面坐标系。
它是大地测量的基本坐标系,其大地经度L、大地纬度B和大地高H为此坐标系的3个坐标分量。
它包括地心大地坐标系和参心大地坐标系。
【测量学】导线测量常用计算公式

一、方位角的计算公式二、平曲线转角点偏角计算公式三、平曲线直缓、缓直点的坐标计算公式四、平曲线上任意点的坐标计算公式五、竖曲线上点的高程计算公式六、超高计算公式七、地基承载力计算公式八、标准差计算公式九、坐标中线测量与计算十、全站仪的使用方法和坐标测量步骤一、 方位角的计算公式1. 字母所代表的意义:x 1:QD 的X 坐标 y 1:QD 的Y 坐标 x 2:ZD 的X 坐标 y 2:ZD 的Y 坐标 S :QD ~ZD 的距离 α:QD ~ZD 的方位角2. 计算公式:()()212212y y x x S -+-=1)当y 2- y 1>0,x 2- x 1>0时:1212x x y y arctg--=α 2)当y 2- y 1<0,x 2- x 1>0时:1212360x x y y arctg --+︒=α 3)当x 2- x 1<0时:1212180x x y y arctg--+︒=α 二、 平曲线转角点偏角计算公式1. 字母所代表的意义:α1:QD ~JD 的方位角 α2:JD ~ZD 的方位角β:JD 处的偏角2. 计算公式:β=α2-α1(负值为左偏、正值为右偏)三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义:U :JD 的X 坐标 V :JD 的Y 坐标 A :方位角(ZH ~JD )T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=D :JD 偏角,左偏为-、右偏为+2. 计算公式:直缓(直圆)点的国家坐标:X ′=U+T cos(A+180°)Y ′=V+Tsin(A+180°)缓直(圆直)点的国家坐标:X ″=U+T cos(A+D)Y ″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义:P :所求点的桩号B :所求边桩~中桩距离,左-、右+ M :左偏-1,右偏+1C :JD 桩号 D :JD 偏角 L s :缓和曲线长 A :方位角(ZH ~JD ) U :JD 的X 坐标 V :JD 的Y 坐标T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=I=C-T :直缓桩号 J=I+L :缓圆桩号s L DRJ H -+=180π:圆缓桩号K=H+L :缓直桩号2. 计算公式: 1)当P<I 时中桩坐标:X m =U+(C-P)cos(A+180°) Y m =V+(C-P)sin(A+180°)边桩坐标:X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°)2)当I<P<J 时()s230RL I P MA O π-︒+= ()()2390R I P I P G ---=中桩坐标:X m =U+Tcos(A+180°)+GcosO Y m =V+Tsin(A+180°)+GsinO()s290RL I P W π-︒=边桩坐标:X b =X m +Bcos(A+MW+90°) Y b =Y m +Bsin(A+MW+90°)3)当J<P<H 时()()R J P L M A R J P R L M A O s s πππ-+︒+=⎪⎭⎫⎝⎛-︒+︒+=909090 ()RJ P R G π-︒=90sin2中桩坐标:()O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()RJ P W π-︒=90边桩坐标:X b =X m +Bcos(O+MW+90°)Y b =Y m +Bsin(O+MW+90°)4)当H<P<K 时()sRL K P MMD A O π230180-︒-︒++= ()2390R P K P K G ---=中桩坐标:X m =U+Tcos(A+MD)+GcosO Y m =V+Tsin(A+MD)+GsinO()s290RL K P W π-︒=边桩坐标:X b =X m +Bcos(A+MD-MW+90°) Y b =Y m +Bsin(A+MD-MW+90°)5)当P>K 时中桩坐标:X m =U+(T+P-K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标:X b =X m +Bcos(A+MD+90°) Y b =Y m +Bsin(A+MD+90°)注:计算公式中距离、长度、桩号单位:“米”;角度测量单位:“度”;若要以“弧度”为角度测量单位,请将公式中带°的数字换算为弧度。
大地测量学知识点

第一章大地测量学定义广义:大地测量学是在一定的时间-空间参考系统中,测量和描绘地球及其他行星体的一门学科。
狭义:大地测量学是测量和描绘地球表面的科学。
包含测定地球形状与大小,测定地面点几何位置,确定地球重力场,以及在地球上进行必须顾及地球曲率的那些测量工作。
大地测量学最基本的任务是测量和描绘地球并监测其变化,为人类活动提供关于地球等行星体的空间信息。
P1 P4 P6(了解几个阶段、了解展望)大地测量学的地位和作用:1、大地测量学在国民经济各项建设和社会发展中发挥着基础先行性的重要保证作用2、大地测量学在防灾、减灾、救灾及环境监测、评价与保护中发挥着独具风貌的特殊作用3、大地测量是发展空间技术和国防建设的重要保障4、大地测量在当代地球科学研究中的地位显得越来越重要5、大地测量学是测绘学科的各分支学科(其中包括大地测量、工程测量、海洋测量、矿山测量、航空摄影测量与遥感、地图学与地理信息系统等)的基础科学现代大地测量学三个基本分支:几何大地测量学、物理大地测量学、空间大地测量学第二章开普勒三大行星运动定律:1、行星轨道是一个椭圆,太阳位于椭圆的一个焦点上2、行星运动中,与太阳连线哎单位时间内扫过的面积相等3、行星绕轨道运动周期的平方与轨道长半轴的立方之比为常数地轴方向相对于空间的变化(岁差和章动)(可出简答题)地轴相对于地球本体内部结构的相对位置变化(极移)历元:对于卫星系统或天文学,某一事件相应的时刻。
对于时间的描述,可采用一维的时间坐标轴,有时间原点、度量单位(尺度)两大要素,原点可根据需要进行指定,度量单位采用时刻和时间间隔两种形式。
任何一个周期运动,如果满足如下三项要求,就可以作为计量时间的方法:1、运动是连续的2、运动的周期具有足够的稳定性3、运动是可观测的多种时间系统以地球自转运动为基础:恒星时和世界时以地球公转运动为基础:历书时→太阳系质心力学时、地球质心力学时以物质内部原子运动特征为基础:原子时协调世界时(P23)大地基准:建立大地基准就是求定旋转椭球的参数及其定向(椭球旋转轴平行于地球的旋转轴,椭球的起始子午面平行于地球的起始子午面)和定位(旋转椭球中心与地球中心的相对关系)。
大地测量学知识点

第一章大地测量学定义广义:大地测量学是在一定的时间-空间参考系统中,测量和描绘地球及其他行星体的一门学科。
狭义:大地测量学是测量和描绘地球表面的科学。
包含测定地球形状与大小,测定地面点几何位置,确定地球重力场,以及在地球上进行必须顾及地球曲率的那些测量工作。
大地测量学最基本的任务是测量和描绘地球并监测其变化,为人类活动提供关于地球等行星体的空间信息。
P1 P4 P6(了解几个阶段、了解展望)大地测量学的地位和作用:1、大地测量学在国民经济各项建设和社会发展中发挥着基础先行性的重要保证作用2、大地测量学在防灾、减灾、救灾及环境监测、评价与保护中发挥着独具风貌的特殊作用3、大地测量是发展空间技术和国防建设的重要保障4、大地测量在当代地球科学研究中的地位显得越来越重要5、大地测量学是测绘学科的各分支学科(其中包括大地测量、工程测量、海洋测量、矿山测量、航空摄影测量与遥感、地图学与地理信息系统等)的基础科学现代大地测量学三个基本分支:几何大地测量学、物理大地测量学、空间大地测量学第二章开普勒三大行星运动定律:1、行星轨道是一个椭圆,太阳位于椭圆的一个焦点上2、行星运动中,与太阳连线哎单位时间内扫过的面积相等3、行星绕轨道运动周期的平方与轨道长半轴的立方之比为常数地轴方向相对于空间的变化(岁差和章动)(可出简答题)地轴相对于地球本体内部结构的相对位置变化(极移)历元:对于卫星系统或天文学,某一事件相应的时刻。
对于时间的描述,可采用一维的时间坐标轴,有时间原点、度量单位(尺度)两大要素,原点可根据需要进行指定,度量单位采用时刻和时间间隔两种形式。
任何一个周期运动,如果满足如下三项要求,就可以作为计量时间的方法:1、运动是连续的2、运动的周期具有足够的稳定性3、运动是可观测的多种时间系统以地球自转运动为基础:恒星时和世界时以地球公转运动为基础:历书时→太阳系质心力学时、地球质心力学时以物质内部原子运动特征为基础:原子时协调世界时(P23)大地基准:建立大地基准就是求定旋转椭球的参数及其定向(椭球旋转轴平行于地球的旋转轴,椭球的起始子午面平行于地球的起始子午面)和定位(旋转椭球中心与地球中心的相对关系)。
大地测量学复习资料#(精选.)

1.垂线偏差:地面一点上的重力向量g和相应椭球面上的法线向量n之间的夹角定义为该点的垂线偏差。
2.参考椭球:具有确定参数(长半径a和扁率α),经过局部定位和定向,同某一地区大地水准面最佳拟合的地球椭球,叫参考椭球。
3.大地线:椭球面上两点间的最短程曲线叫做大地线。
4.力高:水准面在纬度45度处的正常高。
5.大地主题解算:已知某些大地元素推求另一些大地元素的计算工作叫大地主题解算。
6.大地主题正算:已知P1点的大地坐标(L1,B1),P1至P2的大地线长S及其大地方位角,计算P2点的大地坐标(L2,B2)和大地线S在P2点的反方位角A21,这类问题叫做大地主题正算。
7.大地基准:是指能够最佳拟合地球形状的地球椭球的参数及椭球定位和定向8.高斯投影:横轴椭圆柱等角投影(假象有一个椭圆柱横套在地球椭球体外,并与某一条子午线相切,椭球柱的中心轴通过椭球体中心,然后用一定投影方法,将中央子午线两侧各一定范围内的地区投影到椭圆柱上,再将此柱面展开成投影面)。
9.大地测量学:是指在一定的时间与空间参考系中,测量和描绘地球形状及其重力场并监测其变化,为人类活动提供关于地球的空间信息的一门科学。
10.理论闭合差:由水准面不平行而引起的水准环线闭合差,称为理论闭合差。
11.地心坐标系:地心坐标系是在大地体内建立的O-XYZ坐标系。
原点O设在大地体的质量中心,用相互垂直的X,Y,Z三个轴来表示,X轴与首子午面与赤道面的交线重合,向东为正。
Z轴与地球旋转轴重合,向北为正。
Y 轴与XOZ平面垂直构成右手系。
12.高斯投影正、反算公式进行换带计算的步骤。
这种方法的实质是把椭球面上的大地坐标作为过度坐标。
首先把某投影带内有关点的平面坐标(x,y)1利用高斯投影反算公式换算成椭球面上的大地坐标(B,l),进而得到L=L0+l,然后再由大地坐标(B,l),利用投影正算公式换算成相邻带的平面坐标(x,y)2在计算时,要根据第2带的中央子午线来计算经差l,亦即此时l=L-L0。
高斯投影及换带计算

02
1.投影与变形
6.1 地图投影概述
投影面上的边长与原面上的相应长度之比,称为长度比。 长度比:
2、地图投影的分类
1)按变形性质分类 (1)等角投影 又称为正形投影。投影面上某点的任意两方向线夹角与椭球面上相应两线段夹角相等,即角度变形为零。等角投影在一点上任意方向的长度比都相等,但在不同地点长度比是不同的。 (2)等积投影 在投影平面上任意一块面积与椭球面上相应的面积相等,即面积变形等于零。 (3)等距投影 定义为沿某一特定方向的距离,投影前后保持不变,即沿着该特定方向长度比为1。在这种投影图上并不是不存在长度变形,它只是在特定方向上没有长度变形。
若已知某点的经度为L,则该点的6º带的带号N由下式计算:
1
若已知某点的经度为L,则该点所在3º带的带号按下式计算:
2
(四舍五入)
3
高斯平面直角坐标系的建立:
x轴 — 中央子午线的投影 y轴 — 赤道的投影 原点O — 两轴的交点
O
x
y
P
(X,Y)
高斯自然坐标
注:X轴向北为正, y轴向东为正。
4、常用的几种地图投影
从世界范围看,各国大中比例尺地形图所使用的投影很不统一,据不完全统计有十几种之多,最常用的有横轴等角椭圆柱投影等。中华人民共和国成立后,我国大中比例尺地形图一律规定采用以克拉索夫斯基椭球体元素计算的高斯-克吕格投影。我国新编1:100万地形图,采用的则是边纬与中纬变形绝对值相等的正轴等角圆锥投影。
赤道
中央子午线
平行圈
子午线
O
x
y
(4) 除赤道外的其余纬线,投影后为凸向赤道的曲线,并以赤道为对称轴。 (5)经线与纬线投影后仍然保持正交。 (6) 所有长度变形的线段,其长度变形比均大于l。 (7)离中央子午线愈远,长度变形愈大。
现代普通测量学(第2版)课后习题参考答案

《现代普通测量学》习题参考答案第1章 绪 论略第2章 测量学的基础知识一、学习目的与要求1.掌握测量学的基础知识,清楚参照系的选择和地面点定位的概念。
2.了解水准面与水平面的关系。
3.明确测量工作的大体概念。
4.深刻理解测量工作的大体原则。
5.充分熟悉普通测量学的主要内容。
二、课程内容与知识点1.地球特征,大地水准面的形成,地球椭球选择与定位。
地球形状和大小。
水准面的特性。
参考椭球面。
2.肯定点位的概念。
点的平面位置和高程位置。
3.测量中常常利用的坐标系统,坐标系间的坐标转换。
天文坐标(λ,φ),大地坐标(L ,B ),空间直角坐标(X ,Y ,Z ),高斯平面直角坐标(x ,y ),独立平面直角坐标(x ,y )。
高斯投影中计算带号的公式:()()取整数部分取整数部分=+︒-==+=13/'30116/P P n N λλ计算中央子午线的公式:n N 33636=︒-︒=︒︒λλ 4.地面点的高程。
1985年国家黄海高程基准。
高程与高差的关系:''A B A B AB H H H H h -=-=。
5.用水平面代替水准面的限度。
对距离的影响:223RD D D ≈∆ 对水平角的影响:"6.0≤ε 对高差的影响:R D h 2/2=∆ 6.测量工作的大体概念。
测量工作的原则:从整体到局部、先控制后碎部;步步检核。
测量工作的内容:地形图测绘,施工测量。
三、习题与思考题1.何谓大地水准面?它在测量工作中起何作用?答:静止平衡状态下的平均海水面, 向大陆岛屿延伸而形成的闭合水准面。
特性: 唯一性、等位面、 不规则曲面; 作用:测量野外工作的基准面。
2. 测量中常常利用的坐标系有几种?各有何特点?不同坐标系间如何转换坐标? 答:测量中常常利用的坐标系统有:天文坐标系、大地坐标系、高斯平面直角坐标系、独立平面直角坐标系。
3. 北京某点的大地经度为116º20′,试计算它所在的六度带和三度带带号,相应六度带和三度带的中央子午线的经度是多少?答:()().391]3/'301[;201191]6[=+︒-==+=+=P P n N λλ L 0=6 ºN -3 º=117 º ;L ’0 =3ºn=117 º。
已知两个点的大地坐标求第三个点的大地坐标.1

5、n2=a2+b2(a为A点到D点的垂直距离,b为D点到A点的垂直距离) 6、h2=c2+d2(c为B点到D点的垂直距离,d为D点到B点的垂直距离)
7、A点到B点的坐标方位角:α=arctan【(Yb- Ya)/( Xb- Xa)】 8、A点到D点的坐标方位角:Ф=α+β 9、Xd=Xa+ncosФ 10、Yd=Ya+nsinФ 11、再校核用B、D两点的坐标计算出来的距离是否与图纸上的距离 相等,若相等则计算正确。
1、 Xa 2、 Ya 3、 Xb
4、 Yb
5、 Xa-Xb 6、 Ya-Yb 7、 (Xa-Xb)2 8、 (Ya-Yb)2
9、 m2 10、 m
3456789.345 4567834.123 3456989.345
编制计算程序
4567534.123 -200 300 40000 90000
130000 360.5551275
已知两个点的大地坐标求第三个点的大地坐标
已知条件:A(Xa,Ya),B(Xb,Yb),m为A、B两点之间的距离, n为A、D两点之间的距离,h为B、D两点之间的距离。 (n、h的长度可以在图纸上计算出来。) 求:D点的大地坐标(Xd,Yd)。如图所示。
1、m2=(Xa-Xb)ቤተ መጻሕፍቲ ባይዱ+(Ya-Yb)2
2、β= arccos【(m2+n2-h2)/2mn】(β=∠BAD) 3、θ= arccos【(m2+ h2- n2)/2mh】(θ=∠ABD)
坐标
距离,
。) 离
施工坐标(A,B)与大地测量坐标(X,Y)之间的几种换算方法

施工坐标(A,B)与大地测量坐标(X,Y)之间的几种换算方法施工坐标(,B)与大地测量坐标(,y)之间的几种换算方法杨成贵(四川石油蔷面葡察设计研究院).『]3'摘要总图设计施工图阶段,常常引入施工坐标系,施工坐标值与大地测量坐标值之间就存在一个换算问题本文针对建北与磁北不一致时(即施工坐标系与大地测量坐标系之问有一旋转角),结合工程实践,归纳总结出五种简便易行的坐标换算方法.主翘词大地测量施工坐标值计算方法AB坐标系(即施工坐标系).然后在AB坐标问题的提出系下以设定的基准点为参照,推算确定各个工程设计中,为方便设计和施工放线,常建构筑物的AB坐标,来达到给建构筑物定常在XY坐标系(即测量坐标系)基础上引入位的目的.图l某油库征地边界线示意图(xY坐标AB坐标)建北成都某油库(圉1).由测量成果表可得征地界址点的XY坐标.为方便施工定位,我*扬成贵,助理工程师,1971年生;1994年毕业于武汉测绘科技大学城镇建设学院城市规划专业,获工学学士.现主要从事总图设计工作.地址:(6iO0l7)四川省成都市小关庙后街28号.电话:(028)6917700389.十天然气与石油们以点为基准点,MP为纵轴设置AB坐标系,且建北与磁北夹角为北偏东37.45(由和P两点得出),继而在AB坐标系下确定出各构筑的AB坐标,但是图面上界址点和库内建构筑分属两套坐标系统(XY坐标系和AB坐标系),界址点就难以用现有坐标值有效直观地控制库内建构筑的定位.速就要求我们统一坐标系,即要求我们将各界址点的XY坐标换算成AB坐标靖边至西安输气管道工程某基地平面布置图中(图2).引入了AB坐标,以站3(.一55912.63,y0—627599.45)相当于A0—500.00,B.一500.00为基准,建北与磁北夹角为北偏东l7..然后在AB坐标系下较简便地给基地内各建构筑物定了位,而某些特殊要求的建构筑物(如该基地综合楼上通讯塔,即图2中点D(A一464.00,B=354.10),仅知道AB坐标是不够的,应通讯专业要求,还要给出其相应的XY坐标.如何将AB坐标换算成相应的XY坐标就又摆在了设计人面前.下面就以图2中通讯塔坐标换算为例,详细讲述五种坐标换算方法.数学公式法图2某工矿基地平面布置示意图(AB坐标xY坐标)首先得强调的是:工程中AB坐标系(或XY坐标系)与数学笛卡尔直角坐标系(或计算机图形处理器)的纵横轴是不匹配的(图3).工程图纸上的点(,B)(或(,))对应于数学笛卡尔坐标系(或计算机图形)中的点(,)或(,).坐标值进出计算机和套用数学公式时应注意.方法一:坐标轴平移和旋转公式法新坐标系Y,}.系的原点不在,y系的原点,却在X,系中有坐标=Xo和y=ro;并有OX轴与OX轴之间有旋转角0(弧度,逆时针方向为正)则有数学公式:』一'一...+'r—in(1)lY一(一.)sin~(—D)c0f—o+Xcc~+YsinO{—+置sjn+c0s(2)在工程上,以(o,)为基准点M(山,)设置AB坐标系,且建北与磁北有夹角(逆时针(即北偏西)为正).则有公式(参见图4):rA.+'.c~o(Y (3)lB一0+(X一0)sinO+(Y一】0)cosO=X0+(AAncos+(BBnsing{—.一(一.)s.n+(—.)c.s第l6卷第l期扬成贵:施工坐标(^,口)与大地测量坐标(,y)之间的几种换算方法}^J一0'X=100P(1O.O,蚰工程图中:纵轴为轴()轴数学坐标系及计算机图形器中l轴为()轴^(盛北)/.一Xain口L-/,^\//o\ArI\△h口图4具体到图2中通讯塔坐标转换,有:^=464,00,A0=500.00,Xo=55912,63B=354.10,BD=500.O0,Yo=627599.45日一一17.(建北为北偏东故取负值)将上述值代入公式(4)中,则可得D点相应的XY坐标:X一55912,63+(464—5O0)coS(一17)+(354,10--500)sin(一17)一55912.63(一36)×cos(一17)+(一145.9)×sin(一17)=55912,63—34.427+42.657=55920.86r=627599.45一(464—500)sin(一17)354.1—500)cos(一17)一627599.45一l0.525到∞\l刺乙,O图5XY坐标系下P(r,d)AB坐标系下P(r,)其中——点P的向径ia,——点P在极坐标系的角弧度有(0≤d,fl<~360.)#~a--O天然气与石油极轴分别为OY,OB算成直角坐标值本方法就是借助极坐标来实现转换,再将转换后的极坐标折算成直角坐标.具体步骤:(1)数据预处理,求出AA,AB.AA=A--n==464--500一——36△=B—B0=354.1—500=一145.9(2)在AB坐标系,求出D点相对于M点的极坐标(r,),(注意是以MB方向为极轴.)r=&B2==丽_1一150.275=a…g(面A,4)ecg(二)一(180+13.86)=193.86(O≤fl~360.,注意象限)图(3)参照图5画出AB坐标系及XY坐标系之间的旋转关系及D点位置(如图6),以极坐标方法实现D点的坐标转换,即在XY 坐标系下点D的极坐极为:D(r,)其中一+口(口在建北为北偏西时为正)具体到通讯塔,有=150.276,d一193.86+(一l7),即:D(150.276,176.86)(4)在XY坐标系下,将极坐标O(r,a)换AX=rsina=rsin(+)=150.276sin(176.86)=8.23AY=rcosa=rcos(+)一l50.276c∞(176.86)一一l50.05(5)在J】lf点XY坐标值基础上,纵横轴值分别加上AX,△y即为D点的XY坐标. X—X0+AX一559l2.63+8.23=55920.86Y=Yo+AY一527599.45一l5O.05=627449.40方法二较之方法一,公式分解后较简单易记.但步骤较多并面临一个确定象限角的问题,还涉及反三角函数等.计算机图形处理法从前面两种方法中,我们不难看出:数学公式法计算麻烦,需要不断进行逐点校对.因此,我们都希望用直观的换等方法来代替传统的,抽象的数学公式法.计算机图形编辑器及相关工程软件的出现,给我们带来了极大的便利.方法三:GPCAD软件法GPCAD是杭州飞时达电脑技术公司开发的规划总圈设计软件包.利用该软件包中"设置坐标系"这一功能菜单,按照具体设计要求在XY坐标系下设置好AB坐标系.用IDD命令点取图中任意位置,程序自动计算出该点的AB坐标,并将该点的XY坐标一并读出.具体步骤:(1)进入GPCAD工作环境;(2)点取功能菜单{系统H设置坐标,图层…—设置坐标系(3)选择"建立"选项,程序提示:选择参考点<O,O>:[选定当前坐标系建,二北磁第l6卷第l期杨成贵:施工坐标,B)与大地测量坐标(x,y)之间的几种换算方法47中的某一点<可用捕捉>]627599.25.559l2.63取该点的坐标值d0,O>;[给定参考点在新坐标系中的坐标]500.00,500.00输入+B轴旋转角度(定义+轴角度):一17.[给定新建坐标系(AB坐标系)与原坐标系(XY坐标系)水平轴之间的旋转角<逆时针为正>];(4)在新建坐标系下,画线MD,以确定待求点D的位置:Command:Linefrompoint:500,500topoint:354.10,464.00(5)用IDD命令点取D点(端点捕捉),从计算机上读出D点:B施工坐标(354.10,464.10)对应x—r测量坐标(627449.40,55920.86)调换一下计算机提供的纵横轴值,即可得点D的XY坐标(55920.86,627449.40).该方法对各数据不进行任何的预处理,直接机械地将相关数据输入计算中,完全由计算机软件来完成换算.若本身是用GPCAD软件设计出图,已设置好新坐标系,直接用步骤(5)就可得出换算结果,很是方便简单.但其局限性也是显而易见的——要购有GP-CAD软件包,而GPCAD本身远不及Auto_ CAD软件普及;下面就介绍两种基于AuCAD软件功能来实现坐标换算的方法.方法四:AutoCAD软件UCS法AutoCAD有UCS命令设置用户坐标系,用该命令来建立AB坐标系,也可实现坐标转换.具体步骤:(1)数据预处理,求出待求点D相对于基准点Ⅳ的,A(同方法二).(2)进入AutoCAD图形编辑器,在当前(XY)坐标系下找到点M(627599.45, 55912.63).并画出方向角为0的直线(建北为北偏西时,0取正).(3)运行UCS命令,用三点法设置用户坐标系(以埘为原点,MN为水平轴).(4)在新建坐标系下,画线MD(0,0)(A,△).'5)再运行UCS命令,空回车.恢复到原始坐标系.(6)运行ID命令,端点捕捉方法读出D点坐标为(627449.40,55920.86).与方法三同理,调换计算机屏幕上的纵横轴值,即得D点XY坐标(55920.86,627449.40).方法五:AutoCAD软件ROTATE法利用AutoCAD软件ROTATE旋转功能,亦可实现坐标旋转转换.具体步骤:(I)数据预处理,求出AA,△(同方法二)(2)进入Aq~oCAD图形编辑器,视当前坐标系为AB坐标系,基准点为坐标原点(0,0).画线MD(O,0)一(△占,△)以确定D点相对于点的位置.(3)运行ROTATE命令,以点为基点旋转一(建北为北偏西时,0取正).(4)运行ID命令,用端捕捉方式得出D点旋转后的坐标值D(△y,△x)为(一l5O.05,8.23).再调换纵横轴值与点的XY坐标值相加,即得点D的XY坐标:x一o+AX=55912.63+8.23—55920.86Y—d-△y627599.45—15O.05=627449.40结束语I.五种换算方法的比较(表I),设计人员可据自身习惯以及手上现有软件和工具,选择相应的坐标换算法.有条件的,笔者建议天然气与石油1998芷用计算机图形处理法,特别对于需要对多个具体工程中,可用一种方法来换算计算,点进行坐标换算时(如图1),更显其优越性.表1五种方法综台比较表数学公式法方法一,坐标轴平移和旋转公式法方法二,投坐标公式法计算器计算器公式只一十,一次性出结果但:公式长,运算易错公式有五十,公式易记但:要分五步才得出结果,井涉及象限角,运算易错方法三,GPCAD软件法方法四,AutoCAD软件UCS法处理法方法五,Aut0cAD软件ROTATE法计算机(带GPCAD软件包)计算机(带AutoCAD软件)计算机(带AutoCAD软件)最简单,直观,明了但:局限性大(要购有GPCAD为前提)简单,直观,明了通用性强(AutoCAD很普及),但:有少量的数据预处理直观根普及)注:AB坐标xY坐标,建北为北偏西时,取正值.用另一种方法来校对,验算,达到自检的目的.2.本文是以由AB坐标换算成相应的XY坐标为例论述的.若是XY坐标换算成AB坐标(如图1).则:方法一,用公式3;方法三,同理;方法二,四,五,用x,y(或AX,)换A,B(找AA,△B)来上机操作或代八公式亦可实现转换,值则在建北为北偏东时取正值3.本文重点论述的是建北与磁北之间有一夹角0.当建北与磁北一致时,换算较简单:参照基准点倒有:AA=AX,AB=AY,在倒点相应的坐标轴上简单的增减AX,AY(或AA,△日).即可实现转换.当然,上述五种转换法对建北,磁北一致时仍适用,只是夹角一O了.参考文献l[美]A?科恩M?科恩.国民强等译.数学手册.工人出版杜,1987,122陈高波等.GPCAD操作手册.杭州飞时达电脑技术公司,t995,123邱玉春.AutoCAD操作手册.电子工业出敝社,1989,54王莉等.计算机图形学殛其在工程中的应用.交通出版社,1992,3f审稿人高级工程师杨秀田lI收稿日期1997--10--14)』计算机图形D理处预糍濑通但。
《大地测量学基础》复习题及参考答案

《大地测量基础》复习题及参考答案一、名词解释:1、子午圈:过椭球面上一点的子午面同椭球面相截形成的闭合圈。
2、卯酉圈:过椭球面上一点的一个与该点子午面相垂直的法截面同椭球面相截形成的闭合的圈。
3、椭园偏心率:第一偏心率 a b a e 22-=第二偏心率bb a e 22-=' 4、大地坐标系:以大地经度、大地纬度和大地高来表示点的位置的坐标系。
5、空间坐标系:以椭球体中心为原点,起始子午面与赤道面交线为X 轴,在赤道面上与X 轴正交的方向为Y 轴,椭球体的旋转轴为Z 轴,构成右手坐标系O-XYZ 。
6、法截线:过椭球面上一点的法线所作的法截面与椭球面相截形成圈。
7、相对法截线 :设在椭球面上任意取两点A 和B ,过A 点的法线所作通过B 点的法截线和过B 点的法线所作通过A 点的法截线,称为AB 两点的相对法截线。
8、大地线:椭球面上两点之间的最短线。
9、垂线偏差改正:将以垂线为依据的地面观测的水平方向观测值归算到以法线为依据的方向值应加的改正。
10、标高差改正:由于照准点高度而引起的方向偏差改正。
11、截面差改正:将法截弧方向化为大地线方向所加的改正。
12、起始方位角的归算:将天文方位角以测站垂线为依据归算到椭球面以法线为依据的大地方位角。
13、大地元素:椭球面上点的大地经度、大地纬度,两点之间的大地线长度及其正、反大地方位角。
14、大地主题解算:如果知道某些大地元素推求另外一些大地元素,这样的计算称为大地主题解算。
15、大地主题正算:已知P 1点的大地坐标,P 1至P 2的大地线长及其大地方位角,计算P 2点的大地坐标和大地线在 P 2点的反方位角。
16、大地主题反算:如果已知两点的大地坐标,计算期间的大地线长度及其正反方位角。
17、地图投影: 将椭球面上各个元素(包括坐标、方向和长度)按一定的数学法则投影到平面上。
18、高斯投影:横轴椭圆柱等角投影(假象有一个椭圆柱横套在地球椭球体外,并与某一条子午线相切,椭球柱的中心轴通过椭球体中心,然后用一定投影方法,将中央子午线两侧各一定范围内的地区投影到椭圆柱上,再将此柱面展开成投影面)。
控制测量学试题六及参考答案

控制测量学试题六及参考答案一、名词解释:1、子午圈2、卯酉圈3、椭圆偏心率4、大地坐标系5、空间坐标系6、法截线7、相对法截线8、大地线9、垂线偏差改正10、标高差改正11、截面差改正12、起始方位角的归算13、勒让德尔定理14、大地元素15、地图投影16、高斯投影17、平面子午线收敛角18、方向改化19、长度比20、参心坐标系21、地心坐标系二、填空题:1、旋转椭球的形状和大小是由子午椭圆的个基本几何参数来决定的,它们分别是。
2、决定旋转椭球的形状和大小,只需知道个参数中的个参数就够了,但其中至少有一个。
3、传统大地测量利用天文大地测量和重力测量资料推算地球椭球的几何参数,我国1954年北京坐标系应用是椭球,1980年国家大地坐标系应用的是椭球,而全球定位系统(GPS)应用的是椭球。
4、两个互相垂直的法截弧的曲率半径,在微分几何中统称为主曲率半径,它们是指和。
5、椭球面上任意一点的平均曲率半径R等于该点和的几何平均值。
6、克莱洛定理(克莱洛方程)表达式为。
7、拉普拉斯方程的表达式为。
8、若球面三角形的各角减去,即可得到一个对应边相等的平面三角形。
9、投影变形一般分为、和变形。
10、地图投影中有、和投影等。
11、高斯投影是投影,保证了投影的的不变性,图形的性,以及在某点各方向上的的同一性。
12、采用分带投影,既限制了,又保证了在不同投影带中采用相同的简便公式进行由于引起的各项改正数的计算。
13、长度比只与点的有关,而与点的无关。
14、高斯—克吕格投影类中,当m0=1时,称为,当m0=0.9996时,称为。
15、写出工程测量中几种可能采用的直角坐标系名称(写出其中三种):、、。
16、所谓建立大地坐标系,就是指确定椭球的,以及。
17、参考椭球的定位和定向,就是依据一定的条件,将具有确定参数的椭球与确定下来。
18、参考椭球的定位和定向,应选择六个独立参数,即表示参考椭球定位的三个参数和表示参考椭球定向的三个参数。
大地坐标和经纬度之间的换算
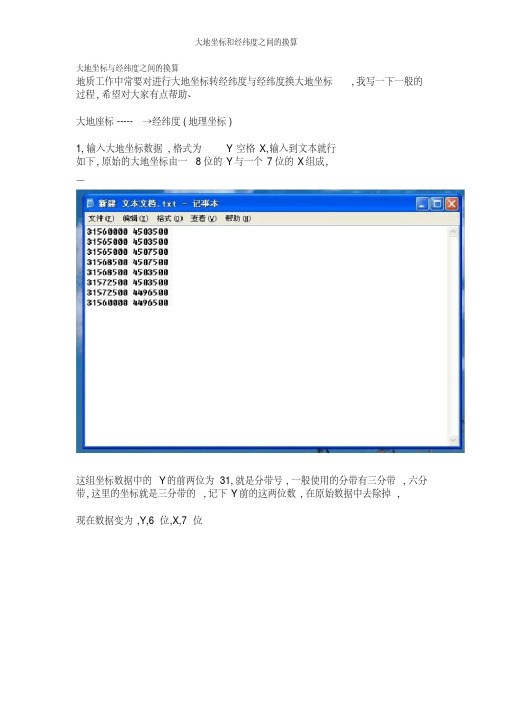
大地坐标与经纬度之间的换算地质工作中常要对进行大地坐标转经纬度与经纬度换大地坐标,我写一下一般的过程,希望对大家有点帮助、大地座标-----→经纬度(地理坐标)1,输入大地坐标数据,格式为 Y空格X,输入到文本就行如下,原始的大地坐标由一8位的Y与一个7位的X组成,这组坐标数据中的Y的前两位为31,就是分带号,一般使用的分带有三分带,六分带,这里的坐标就是三分带的,记下Y前的这两位数,在原始数据中去除掉,现在数据变为,Y,6位,X,7位保存这个TXT的文本文件。
2,打开MAPGIS,启动坐标投影变形程序接下来选择投影转换>>>>用户文件投影转换点打开文件,打开刚才的大地坐标的文本文件,设置输入数据的格式,点击用户投影参数,并完成设置。
这里我们的大地座标为3度带的第31带,注意填好,坐标单位为米好了以为设置输出的格式,我们要求输出的就是经纬度,点结果转换参数,完成以下设置我们输出的经纬度的单位应该就是DDDMMMSS。
SS注意点写到文件,保存就大功告成了,注意保存的文件要写上、TXT的后缀下面就是计算出的结果文件XP为经度,1234234。
357就就是123度42分34。
357秒,YP为纬度,403950。
225就就是40度39分50。
255秒(纬度没有最多90,所以没有三位数)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 经纬度——→大地座标输入文件格式如下,这里面的数据前面的为经度,格式为DDDMMSS,后面的为纬度,格式为DDMMSS接下来的转换过程与大地坐标转换一样,只要将刚才的用户转换参数与结果转换参数交换即可,要注意分带号的确定,如果您不知道分带号,就应该先计算分带号,算法就是经度/3得到的整数为三度带的分带号经度/6得到的整数为六度带的分带号其中的XP为地图上的Y坐标,记得在前面加上带号,其中的YP为地图上的X坐标。
大地坐标系与站心地平直角坐标系的坐标转换

大地坐标系与站心地平直角坐标系的坐标转换
凌震莹 (第七一五研究所,杭州,310012)
摘要 介绍了大地坐标系和站心地平直角坐标系之间的转换算法,并结合实例数据对算法运算精度和速 度进行了仿真分析和评价,可解决声呐浮标搜潜系统中实时将测量所得的目标位置信息从大地坐标系转换到
作战区域所在的站心地平直角坐标系中问题,供定位和跟踪之用。
心直角坐标值(X、Y、Z)。
3.2 球心直角坐标转换为大地坐标
该步骤是从球心直角坐标(X、Y、Z)转换到 大地坐标(L、B、H),如图 1 如示,经度 L 可以 直接计算:
L = arctan Y X
(11)
纬度 B 计算比较复杂,有直接法和迭代法等多 种算法[3],本系统选择精度较高的迭代法,算法流 程如图 3 所示。
即:
(9)
⎡ ⎢ ⎢ ⎢⎣
x⎤ y⎥⎥ x⎥⎦
=
⎡⎢1 ⎢0 ⎢ ⎢⎣0
0
cos(90 − B) −sin(90 − B)
0
⎤ ⎥
sin(90 − B)⎥i
⎥
cos(90 − B)⎥⎦
⎡ X ⎤ ⎡− sin L
⎢ ⎢
Y
⎥ ⎥
=
⎢ ⎢
cos
L
⎢⎣ Z ⎥⎦ ⎢⎣ 0
− sin B cos L −sin B sin L
⎢ ⎢
Y
⎥ ⎥
=
⎢ ⎢
x
sin
L
⎥ ⎥
⎢⎣ Z ⎥⎦ ⎢⎣ y ⎥⎦
(1)
1 坐标系定义
文中用到了三个坐标系:大地坐标系、站心地 平直角坐标系和球心直角坐标系[1]。大地坐标系是 基于椭球体的曲线曲面坐标系,该坐标系中的任一 点用 L(经度)、B(纬度)和 H(高度)表示;站 心地平直角坐标系是三维坐标系(右手系),Y 轴指 向北,X 轴指向东,O 点法线为 Z 轴(指向天顶为 正);球心直角坐标系以椭球中心为原点,起始子 午面与赤道的交线为 X 轴,椭球的短轴为 Z 轴(向 北为正),在赤道面上与 X 轴正交的方向为 Y 轴, 构成右手直角坐标系。
【干货】2000国家大地坐标系转换指南

【干货】2000国家大地坐标系转换指南一、2000国家大地坐标系的定义国家大地坐标系的定义包括坐标系的原点、三个坐标轴的指向、尺度以及地球椭球的4个基本参数的定义.2000国家大地坐标系的原点为包括海洋和大气的整个地球的质量中心;2000国家大地坐标系的Z轴由原点指向历元2000.0的地球参考极的方向,该历元的指向由国际时间局给定的历元为1984.0的初始指向推算,定向的时间演化保证相对于地壳不产生残余的全球旋转,X轴由原点指向格林尼治参考子午线与地球赤道面(历元2000.0)的交点,Y轴与Z轴、X轴构成右手正交坐标系.采用广义相对论意义下的尺度.2000国家大地坐标系采用的地球椭球参数的数值为:长半轴a=6378137m扁率f=1/298.25722210114m3s-2地心引力常数GM=3.986004418×10-5rads-1自转角速度ω=7.292l15×10其它参数见下表:采用2000国家大地坐标系后仍采用无潮汐系统.二、点位坐标转换方法(一)模型选择全国及省级范围的坐标转换选择二维七参数转换模型;省级以下的坐标转换可选择三维四参数模型或平面四参数模型.对于相对独立的平面坐标系统与2000国家大地坐标系的联系可采用平面四参数模型或多项式回归模型.坐标转换模型详见本指南第六部分.(二)重合点选取坐标重合点可采用在两个坐标系下均有坐标成果的点.但最终重合点还需根据所确定的转换参数,计算重合点坐标残差,根据其残差值的大小来确定,若残差大于3倍中误差则剔除,重新计算坐标转换参数,直到满足精度要求为止;用于计算转换参数的重合点数量与转换区域的大小有关,但不得少于5个.(三)模型参数计算用所确定的重合点坐标,根据坐标转换模型利用最小二乘法计算模型参数.(四)精度评估与检核用上述模型进行坐标转换时必须满足相应的精度指标,具体精度评估指标及评估方法见附件中相关内容.选择部分重合点作为外部检核点,不参与转换参数计算,用转换参数计算这些点的转换坐标与已知坐标进行比较进行外部检核.应选定至少6个均匀分布的重合点对坐标转换精度进行检核.(五)数据库中点位坐标转换模型参数计算的区域选取对于1980西安坐标系下的数据库,采用全国数据计算的一套模型参数可满足1:5万及1:25万比例尺数据库转换的精度要求;采用全国数据计算的六个分区的模型参数可满足1:1万比例尺数据库转换的精度要求.对于1954年北京坐标系下的数据库的转换,采用全国数据计算的六个分区的模型参数可满足1:5万及1:25万比例尺数据库转换的精度要求;按(2°×3°)进行分区计算模型参数可满足1:1万比例尺数据库转换的精度要求.三、1:2.5-1:25万数据库的转换(一)按国家基本比例尺地形图分幅组织的数据库按国家基本比例尺地形图分幅组织的图形数据(DLG、DEM、DRG),依据以下方案进行转换.1、1:2.5-1:10万DLG数据库转换(1)1954年北京坐标系下1:2.5-1:10万DLG数据库转换a、依据相应比例尺分幅进行区域划分,分两步完成坐标转换.首先进行椭球体变换,再利用对应的比例尺图幅区域的X、Y坐标平移量进行坐标平移;b、依据2000国家大地坐标系下对应的比例尺标准分幅图廓进行数据裁切,区域边缘图幅中的数据空白区利用相邻图幅数据进行补充;c、添加2000国家大地坐标系下的方里格网层,删除原方里格网数据层;d、完成图廓更改、数据编辑、数据接边、拓扑重建、数据入库等数据后处理及建库工作;e、图幅换带接边:采用右图(1954年北京坐标系)接左图(2000国家大地坐标系)时,先进行右图的椭球体与换带转换,在左带中利用左图的平移量进行右图的坐标平移,完成接边后保存在左带中的右图(备份)成果.返回右图取消先前换带接边加入的平移量,并进行投影变换,最后利用右带自身的平移量完成平移后,方可与其相邻的右图接边;f、对基础地理信息数据库元数据相关条目进行更改.(2)1980西安坐标系下1:2.5-1:10万DLG数据库转换依据相应比例尺分幅进行区域划分,不考虑椭球体变换,直接利用对应的比例尺图幅区域的X、Y坐标平移量进行坐标平移;然后按照1954年北京坐标系下DLG 数据库转换的b~f对应步骤进行.2、1:2.5-1:10万DRG数据库转换原数据为300~500dpi的原版印刷地图经扫描纠正生成的RGB栅格数据,无图幅间要素的接边处理.(1)1954年北京坐标系下1:2.5-1:10万DRG数据库转换a、考虑椭球变换及对应图廓角点的X、Y坐标平移量,计算1954年北京坐标系分幅图廓角点在2000国家大地坐标系下的坐标,并修改数据头文件中相应的定位坐标;b、在DRG数据上叠加2000国家大地坐标系下新的大地控制基础层(图廓及方里格网等),新图廓中数据空白或数据出图区域不做图纹补充和裁减;c、在图例中添加2000国家大地坐标系下新的控制基准说明条款;d、完成数据合层,并保持DRG数据的原有分辨率;e、更改元数据中相关内容,增加1954年北京坐标系标准分幅的图廓四角点在2000国家大地坐标系下坐标,计算2000国家大地坐标系标准分幅的图廓四角点的坐标.转换后数据为2000国家大地坐标系坐标、1954年北京坐标系分幅.(2)1980西安坐标系下1:2.5-1:10万DRG数据库转换获取图幅对应比例尺图幅图廓角点的X、Y坐标平移量,根据平移量计算图幅定位坐标,修改数据头文件;然后按照1954年北京坐标系到2000国家大地坐标系的1:2.5-1:10万DRG数据库转换的b~e步骤进行.转换后数据为2000国家大地坐标系坐标、1980年西安坐标系分幅.3、1:2.5-1:10万DEM数据库转换原数据为25米分辨率的灰阶(256个)栅格数据,建库数据图幅间接边处理完好.此数据转换可有两种方式:一种是依据2000国家大地坐标系下DLG相关图层数据(等高线、高程点)重新生成DEM(见DEM数据生产规范),一种是进行DEM数据的转换.以下给出DEM数据转换方法.(1)1954年北京坐标系下1:2.5-1:10万DEM数据库转换a、按照比例尺对应图幅分块,在需补充内容的邻接边各增加一个相应比例尺图幅;b、考虑椭球变换及相应的比例尺图幅的X、Y坐标平移量,求得X、Y坐标改正值;c、根据坐标改正值进行图幅坐标平移,同时,参考像素分辨率确定起算坐标进行数据重采样;d、按2000国家大地坐标系新的图廓及重叠像素进行图幅裁切,更改数据头文件中定位坐标;e、修改元数据相关条目.(2)1980西安坐标系下1:2.5-1:10万DEM数据库转换a、按照相应比例尺对应图幅分块,在需补充内容的邻接边各增加一个相应比例尺图幅;b、依据相应的比例尺图幅的X、Y坐标平移量,进行图幅坐标平移,并参考像素分辨率确定起算坐标完成数据重采样;c、d按1954年北京坐标系1:2.5-1:10万DEM数据库转换的d、e步骤进行.4、1:25万DLG数据库转换(1)将1:25万分幅的平面坐标平移量转换为对应的经、纬度平移量或直接获取对应图幅的经、纬度平移量;(2)根据1:25万分幅的经、纬度平移量,完成1:25万经纬度数据到2000国家大地坐标系经纬度数据的转换(1954年北京坐标系需同时考虑椭球体变化和平移量);(3)依据2000国家大地坐标系下对应的1:25万标准分幅图廓进行数据裁切,区域边缘图幅中的数据空白区利用相邻图幅数据进行补充;(4)数据后处理,包括:图廓更改、新格网层添加、数据编辑、数据接边、拓扑重建、数据入库等;(5)更改元数据文件.5、1:25万DEM数据库转换(1)利用2000国家大地坐标系对应的DLG数据层,重新内插生成DEM;(2)依据新的DEM更改元数据文件.(二)按其它方式建立的数据库1、按区域建立的图形数据库按区域(省、地区、流域等)建立的图形数据库(DLG、DEM、DRG),可先分带分块分层完成转换,参照以上相应比例尺基础地理信息数据库的转换方案转换后拼接合成.1:10万-1:25万数据库,依1:25万数据库转换方案逐块进行转换,再整体拼接合成;按非高斯投影方式组织的,将原数据经纬网30′×30′或15′×15′交点作为坐标转换参考点,计算这些参考点在2000国家大地坐标系下的坐标,利用地理信息软件进行图形纠正,完成数据转换.2、按线性条带建立的图形数据库按线性条带(境界、河流、交通线、管道线等)建立的图形数据库,可依据条带的方向、长短等分段进行,再拼接合成;也可通过条带中一定密度地物点的两套坐标,通过软件逐点进行纠正.具体方法:分块纠正:对于1:1万分块,按1:1万数据转换方案逐块纠正后接边合成;对于1:5万分块,按1:2.5-1:10万数据转换方案逐块纠正后接边合成;逐点纠正:依据数据精度,建立一定密度(1:1万100米格网点、1:5万2000米格网点)的坐标转换参考点,计算这些参考点在新坐标系下的坐标,利用地理信息软件完成数据转换.3、按无固定分幅分区建立的图形数据库按无固定分幅分区建立的图形数据,根据坐标系、比例尺及数据主体所在的图幅、数据的组织方式、产品类型(DLG、DEM、DRG)等,参照相应比例尺的转换方案,实施数据转换.4、DOM数据库转换原数据为航空或航天遥感获取的黑白或彩色影像数据,是连续的灰度(全色)或RGB(彩色)栅格数据,分辨率有多种方式(主要包括用于1:5地形图测绘的各种分辨率航空影像,以及用于专题调查的10米、15米、30米等卫星影像).影像数据转换可参照下列方式进行.对于已按数据库组织方式加工与处理的DOM数据,可采用1:2.5-1:10万DEM的数据转换方法,也可采用计算各景影像有效图边的4点在2000国家大地坐标系下的坐标来重新定位的方式.对于尚未按数据库组织方式加工与处理的DOM数据,可采用1:2.5-1:10万DRG的数据转换方法,不再添加新的控制基础信息.分辨率5米-30米的数据,需依据其数据主体所在的1:25万图幅区域来选用1:25万对应图幅的综合坐标改正值;对于分辨率在2米到5米间的数据,需依据其数据主体所在的1:5万图幅区域来选用1:5万对应图幅的综合坐标改正值;由此确定各自的X、Y方向平移像素数对应的坐标值(直接取1:25万或1:5万综合坐标改正值,或由像素数×像素分辨率求得).按高斯投影、分像对(分景)组织的高分辨率影像数据,参照1:1万DOM转换技术方案进行转换.四、1:1万及1:5千基础地理信息数据库的转换(一)1:1万及1:5千格网点坐标转换改正量计算1、1980西安坐标系坐标转换改正量计算1:1万以上大比例尺一般按(2°×3°)进行分区,并对每个分区向外扩充约20′,分别解算出各分区的转换参数后,利用确定的转换方法与转换模型分别计算全国1:1万及1:5千格网点的2000国家大地坐标系坐标B2000,L2000,进而求出各点的1980西安坐标系与2000国家大地坐标系的差值DB802000,DL802000(B2000-B80,L2000-L80),形成全国1:1万及1:5千格网点的1980西安坐标系与2000国家大地坐标系的转换改正量DB802000,DL802000.2、1954年北京坐标系坐标转换改正量计算全国1954年北京坐标系向2000国家大地坐标系转换改正量计算采用两步法:首先计算1954年北京坐标系转换向1980西安坐标系转换改正量,其次计算1980西安坐标系向2000国家大地坐标系转换改正量,最后将两改正量叠加形成1954年北京坐标系向2000国家大地坐标系转换坐标转换改正量.①1954年北京坐标系向1980西安坐标系转换坐标改正量计算新旧坐标系统(1954年北京坐标系与1980年西安坐标系)的转换大地坐标改正量计算公式:式中:△a,△e2分别为IAG-75椭球与克拉索夫斯基椭球长半径,第一偏心率平方之差.即.则各个点在1980西安坐标系中的大地坐标为:●根据转换的B80,L80,采用高斯投影正算公式计算相应的高斯平面坐标X80,Y80.●求取全国1:1万以大比例尺格网点的转换改正量●平差改正量的计算1954年北京坐标系所提供的大地点成果没有经过整体平差,1980西安坐标系提供的大地点成果是经过整体平差的数据,所以新旧系统转换还要考虑平差改正量的问题.计算平差改正量比较麻烦,没有一定的数学模式,不同地区,平差改正量差别很大,在我国中部某些地区,平差改正量在1米以下,而在东北地区的某些图幅则在10米以上.在实际计算中,在全国均匀地选择一定数量的一、二等大地点,利用它们新(1980西安坐标系)旧(1954年北京坐标系)坐标系的坐标进行多种分析试算并剔除粗差点,然后分别计算它们的坐标差值,根据这些差值和它们的大地坐标分别绘制两张平差改正量分布图(即dX,dY分布图),这样在分布图上可以直接内插出全国1:1万以大比例尺格网点的平差改正量DX2,DY2.●根据全国1:1万以大比例尺格网点的转换改正量DX1,DY1和平差改正量DX2,DY2按下列公式计算1954年北京坐标系向1980西安坐标系转换坐标转换改正量DX,DY.●将DX,DY换算成1:1万以大比例尺格网点大地坐标转换改正量DB5480,DL5480.②1954年北京坐标系向2000国家大地坐标系转换坐标转换改正量计算将全国1:1万以大比例尺格网点的1954年北京坐标系向1980西安坐标系的转换改正量DB5480与1980西安坐标系向2000国家大地坐标系的转换改正量DB802000叠加,得到全国1:1万以大比例尺格网点1954年北京坐标系向2000国家大地坐标系转换的坐标转换改正量DB542000.即:DB542000=DB5480+DB802000DL542000=DL5480+DL802000(二)1:1万及1:5千DLG数据库转换转换流程如图1所示:1、1954年北京坐标系下1:1万、1:5千DLG数据库转换(1)每个图幅的四个图廓点坐标改正量选用1954年北京坐标系向2000国家大地坐标系转换方法计算;(2)图幅内各要素点的坐标改正量根据选用的本图幅的四个图廓点坐标改正量,按双线性内插等方法计算;(3)根据图幅四个图廓点坐标改正量和图幅内各要素点的坐标改正量,计算2000国家大地坐标系下的图幅四个图廓点坐标和图幅内各要素点的坐标;(4)与周边图幅拼接;(5)按照2000国家大地坐标系下对应1:1万、1:5千标准分幅计算新的公里格网数据,即添加2000国家大地坐标系下新的公里格网层;(6)完成图廓更改、数据编辑、换带接边、拓扑重建;(7)对空间数据库元数据相关条目进行更改;(8)数据入库等数据后处理工作.2、1980西安坐标系下1:1万、1:5千DLG数据库转换(1)每个图幅的四个图廓点坐标改正量选用1980西安坐标系向2000国家大地坐标系转换方法计算;(2)~(8)参照1954年北京坐标系到2000国家大地坐标系1:1万、1:5千DLG数据库转换的对应步骤进行.(三)1:1万及1:5千DRG数据库转换在保持原分辨率不变的情况下,利用逐格网纠正的方法进行数据转换.1、1954年北京坐标系下1:1万、1:5千DRG数据库转换(1)在2000国家大地坐标系下生成图廓坐标及公里格网,逐公里格网点纠正1:1万、1:5千DRG数据;(2)修改元数据相关条目;(3)修改相关的图外整饰.2、1980西安坐标系下1:1万、1:5千DRG数据库转换参照1954年北京坐标系到2000国家大地坐标系1:1万、1:5千DRG数据库转换的对应步骤进行.(四)1:1万及1:5千DEM数据库转换利用DEM生产过程中形成的矢量数据与DEM离散点数据完成数据转换.1、1954年北京坐标系下1:1万、1:5千DEM数据库转换(1)矢量数据与DEM离散点数据转换方法;a、每个图幅的四个图廓点坐标改正量选用1954年北京坐标系向2000国家大地坐标系转换方法计算;b、图幅内各要素点的坐标改正量根据选用的本图幅的四个图廓点坐标改正量,按双线性内插等方法计算;c、根据图幅四个图廓点坐标改正量和图幅内各要素点的坐标改正量,计算2000国家大地坐标系下的图幅四个图廓点坐标和图幅内各要素点的坐标;d、与周边图幅拼接.(2)构造TIN;(3)按相关规范或规定内插DEM;(4)对检查点坐标文件进行点对点坐标转换;(5)修改元数据条目.2、1980西安坐标系下1:1万、1:5千DEM数据库转换(1)每个图幅的四个图廓点坐标改正量选用1980西安坐标系向2000国家大地坐标系转换方法计算;(2)~(5)参照1954年北京坐标系1:1万、1:5千DEM数据库转换的对应步骤进行.(五)1:1万及1:5千DOM数据库转换原数据为航空或航天遥感获取的黑白或彩色影像数据,是连续的灰度或RGB 栅格数据,在转换中应保持原影像分辨率.1、在原DOM上叠加相应坐标系统的内图廓及公里格网,在2000国家大地坐标系下生成图廓坐标及公里格网,逐公里格网点纠正1:1万、1:5千DOM数据;2、转换后,删除内图廓及公里格网;3、修改元数据相关条目.五、相对独立的平面坐标系统与2000国家大地坐标系建立联系的方法(一)相对独立的平面坐标系统控制点建立联系的方法可通过现行国家大地坐标系的平面坐标过渡,利用坐标转换方法将相对独立的平面坐标系统下控制点成果转换到2000国家大地坐标系下.选取相对独立的平面坐标系统与2000国家大地坐标系的重合点的原则如下:择优选取地方控制网的起算点及高精度控制点、周围国家高精度的控制点,大中城市至少选取5个重合点(城外4个,市内中心1个);小城市在城市外围至少选取4个重合点,重合点要分布均匀,包围城市区域,并在城市内部选定至少6个均匀分布的重合点对坐标转换精度进行检核.建立相对独立的平面坐标系统与2000国家大地坐标系联系时,坐标转换模型要同时适用于地方控制点转换和城市数字地图的转换.一般采用平面四参数转换模型,重合点较多时可采用多元逐步回归模型.当相对独立的平面坐标系统控制点和数字地图均为三维地心坐标时,采用Bursa七参数转换模型.坐标转换中误差应小于0.05米.(二)相对独立的平面坐标系统下数字地形图转换采用点对点转换法完成相对独立的平面坐标系统下数字地形图到2000国家大地坐标系的转换,转换后相邻图幅不存在接边问题.具体步骤如下:利用控制点的转换模型和参数,对相对独立的平面坐标系统下数字地形图进行转换,形成2000国家大地坐标系地形图.根据转换后的图幅四个图廓点在2000国家大地坐标系下的坐标,重新划分公里格网线,原公里格网线删除.根据2000国家大地坐标系下的图廓坐标,对每幅图进行裁剪和补充.六、坐标转换方法(一)坐标转换模型1、二维七参数转换模型其中:△B,△L---同一点位在两个坐标系下的纬度差、经度差,单位为弧度,△a,△f---椭球长半轴差(单位米)、扁率差(无量纲),△X,△Y,△Z---平移参数,单位为米,εx,εy,εz---旋转参数,单位为弧度,m---尺度参数(无量纲).2、平面四参数转换模型属于两维坐标转换,对于三维坐标,需将坐标通过高斯投影变换得到平面坐标再计算转换参数.平面直角坐标转换模型:其中,x0,y0为平移参数,α为旋转参数,m为尺度参数.x2,y2为2000国家大地坐标系下的平面直角坐标,x1,y1为原坐标系下平面直角坐标.坐标单位为米.3、综合法坐标转换所谓综合法即就是在相似变换(Bursa七参数转换)的基础上,再对空间直角坐标残差进行多项式拟合,系统误差通过多项式系数得到消弱,使统一后的坐标系框架点坐标具有较好的一致性,从而提高坐标转换精度.综合法转换模型及转换方法:●利用重合点先用相似变换转换Bursa七参数坐标转换模型式中,3个平移参数[△X△Y△Z]T,3个旋转参数[εxεyεz]T和1个尺度参数m.●对相似变换后的重合点残差Vx,Vy,Vz采用多项式拟合式中:B,L单位:弧度;K为拟合阶数;aij为系数,通过最小二乘求解.4、三维七参数坐标转换模型(二)高斯正反算公式1、高斯投影正算公式子午线弧长X计算见附录.2、高斯投影反算公式(三)坐标转换精度评定和评估方法对于1954年北京坐标系、1980西安坐标系与2000国家大地坐标系转换分区转换及数据库转换点位的平均精度应小于图上的0.1mm.具体:对于1:5千坐标转换,1980西安坐标系与2000国家大地坐标系转换分区转换平均精度≤0.5m;1954年北京坐标系与2000国家大地坐标系转换分区转换平均精度≤1.0m;1:5万基础地理信息数据库坐标转换精度≤5.0m;1:1万基础地理信息数据库坐标转换精度≤1.0m;1:5千基础地理信息数据库坐标转换精度≤0.5m.依据计算坐标转换模型参数的重合点的残差中误差评估坐标转换精度.对于n 个点,坐标转换精度估计公式如下:①V(残差)=重合点转换坐标-重合点已知坐标②空间直角坐标X残差中误差③空间直角坐标Y残差中误差④空间直角坐标Z残差中误差点位中误差⑤平面坐标x残差中误差⑥平面坐标y残差中误差⑦大地高H残差中误差平面点位中误差为2000国家大地坐标系转换常见问题分析摘要:在现有成果向2000国家大地坐标系转换工作中,各省市都做了很多理论研究和实际转换工作.本文阐述了现有成果向2000国家大地坐标系转换的方法,对不同数据、不同方法转换过程中常见的问题进行汇总、整理,并分析问题产生的原因及对成果的影响,为今后现有成果向2000国家大地坐标系转换工作提供参考和建议,以确保成果转换的质量.关键词:CGCS2000;坐标转换;大地控制点;基础地理信息数据;GNSS基准站;三角点;4D产品自2008年7月1日起,我国启用2000国家大地坐标系(CGCS2000),各地有关部门开展了现有各类测绘信息成果到CGCS2000的转换工作,积极推进CGCS2000的推广使用.为做好启用CGCS2000的实施工作,国家测绘地理信息局于2008年7月组织编制了《启用2000国家大地坐标系实施方案》和《现有测绘成果转换到2000国家大地坐标系技术指南》.为加快CGCS2000推广使用工作,进一步指导各部门、各单位顺利完成原有坐标系成果向CGCS2000转换,确保转换技术方法正确,国家测绘地理信息局于2013年6月组织编制了《2000国家大地坐标系推广使用技术指南》和《大地测量控制点坐标转换技术规程》.CGCS2000转换涉及的测绘地理信息成果主要包括大地控制点类成果(GNSS基准站、GNSS控制点、三角点)和基础地理信息数据成果(DLG、DOM、DEM、DRG).文献[1—2]从总体上介绍了CGCS2000的构建、精化、维持和更新,以及可用于转换工作的国家级成果.文献[3—11]研究了GNSS基准站、大地控制点、4D产品的转换方法.文献[12]探讨了转换的检查方法.本文对省级坐标转换中存在的常见问题进行梳理和分析.一坐标转换方法1.大地控制点类成果(1)坐标归算本方法适用于非CGCS2000的省级GNSS基准站和卫星大地控制点坐标向CGCS2000的坐标转换.即对拟转换点采用与周边稳定的IGS 站及国家级的GNSS连续运行基准站进行联测的方法,获得各站点在现ITRF框架、观测历元下的位置,经过历元归算、板块运动改正、框架转换。
地理坐标与大地坐标的转换

地理坐标与大地坐标的转换把文件输出为DXF格式(DXFOUT)在正式版CAD中打开生成的DXF文件,打印时不会提示版本问题。
打印时无教育版打印戳记哈哈,问题解决了!关键词:地图投影,坐标系,TIC点,标准分幅。
前言:MAPGIS是国家科技部和建设部推广的国产GIS软件,是国内优秀GIS平台之一,目前在城市勘测单位使用越来越广泛,很多单位用它来做矢量化、数据编辑、入库的平台。
但由于大部分城市勘测单位都是做1:500到1:2000的大比例尺地形图,对投影变换用的比较少,偶尔要用到地方坐标系和国家坐标系的转换,以及换带计算等就觉得非常困难,笔者经过大量的生产实践发现:巧用MAPGIS 的投影变换不仅可以轻松解决各种坐标系之间的转换问题,还可以进行坐标展点及高斯坐标的正反算等,下面就对这些问题的参数设置、操作过程进行详细的说明。
在具体说明之前,先对几个关键词的含义进行说明。
地图投影即按某种数学规则将椭球球面上一点与地图平面上的一点相对应。
地图投影的参数有椭球的长半径,短半径,扁率,第一偏心率,第二偏心率。
数学规则有等角映射、等面积映射等。
我国地图制图普遍采用的是高斯-克吕格(GAUSS-KRUGER)投影,它是一种等角横切椭圆柱投影,该投影以中央经线和赤道投影后为坐标轴,为控制长度变形,一般采取分带投影。
我国1:2.5-1:50万的地形图均采用6度分带,1:1万及更大比例尺地形图采用3度分带。
MAPGIS的坐标系为数学坐标系,与投影平面直角坐标系中的X、Y坐标相反,即横坐标为X,纵坐标为Y,未经投影变化之前均为毫米表示。
MAPGIS的用户坐标系是指由用户指定的相对二维坐标系,一般与实际地物定位无关;地理坐标系是以经纬度表示的,经度的起点在格林威治,向东为正,纬度自赤道起,向北为正,常用来坐标定位;投影平面直角坐标系是将地球球面投影到平面后所设定的坐标系。
我们常说的1954年北京坐标系,1980年西安坐标系均为高斯投影的投影平面直角坐标系,只不过它们采用了不同的椭球参数;北京坐标系使用克拉索夫斯基椭球,西安坐标系采用IAG1975年推荐椭球。
大地坐标转换
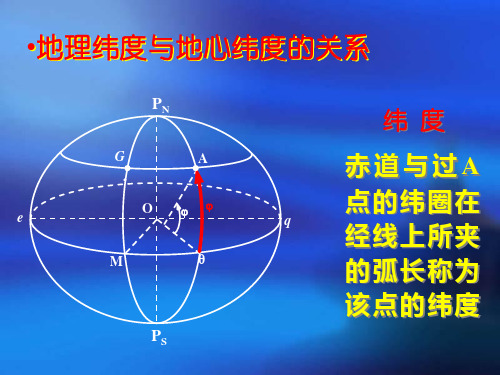
参考椭球体
q′
O
大地球体
q
2、绝对定位
⑴ 椭球体中心与地球质心重合 ⑵ 椭球体基准大地子午面与基
准天文子午面重合 ⑶ 椭球体短轴与地轴重合 ⑷ 椭球体面与整个大地水准面
充分接近
地心坐标系
总椭球体
大地水准面等高线图 (美国NWL-8D)
二、大地坐标转换
N N
为大地坐标改正值
大地坐标改正值
一、纬圈半径
PN
r G
O
e
x
M
PS
子午圈方程:
x2 y2
A
a2 b2 1
y
90+
q
A点切线的斜率:
dy tg 90 ctg
dx
x2 y2 a2 b2 1
求导
dy dx
b2 a2
x y
dy tg 90 ctg
dx
b2 x
y a2 ctg
x2 a2
y2 b2
1
r x acos 1 e2sin 2
⑵ =90时,M最大:M
a 1-e2
3
1 e2 2
a2 b
a
结论:M随纬度的升高而增大
三、东西圈曲率半径
东西圈(卯酉圈)
PN
r
A
包含地球椭球体面
上某点的法线与该
E
点子午圈垂直的平
N
e
O
q 面,与地球椭球体
表面的交线。
nW
N r
PS
cos
分析:
a
N
1
1 e2sin 2 2
⑴ = 0 时,N=a,这时N>M
1918年东京系
-140
地理坐标系转换公式

青岛海洋地质研究所 戴勤奋 译 (Email: qddqinfen@) 本 文 译 自 国 际 石 油 技 术 软 件 开 放 公 司 ( ) 文 献 “ Coordinate Conversions and Transformations including Formulas ” part 2 – – “ Formulas for Coordinate Operations other than Map Projections ” 。原文献由 EPSG(欧洲石油勘探组织)编写,初稿时 间 1995,最新更新时间 2004 年 1 月。世界各国参考椭球体参数及基准面转换参数,可参考 (/military/library/policy/army/fm/6-2/appe2.htm#tabe_22) 。
式中:Xt = 新坐标系的坐标值, Xs = 原坐标系的坐标值, A 为新坐标系的原点在原坐标系中的坐标值, m 为单位方向因子 (如果两坐标系轴向一致 m=1; 如果两坐标系轴向不一致 m = -1) , Us 、Ut 和 UA 分别为原坐标、新坐标和偏移参数的坐标单位与米的比值。
3.2 三参数转换( EPSG 坐标运算方法 9603)
基(Molodenski)提出了相应三参数的直接转换方法。方法假定原坐标系与新坐标系的坐标 轴相互平行,正如前面已提到的,该假设不一定成立,由此得到的转换结果只能达到中等精 度,对范围大的区域尤其如此。 赫尔默特(Helmert)7 参数转换法提高了转换精度。由于三个旋转参数有两种相反的符 号协定,EPSG(欧洲石油勘探组织)将其分为两种不同的转换方法,其一称位置矢量法, 另一称坐标框架法,其中位置矢量法也称布尔莎-沃尔夫(Bursa-Wolf)转换法。赫尔默特方 法的关键在于转换参数的符号要与遵循的约定一致。 鉴于赫尔默特方法的平移和旋转参数之 间具有很强的相关性,有碍于实际应用,莫洛金斯基-巴德克斯(Molodenski-Badekas )提出 了改进的赫尔默特 7 参数转换法,避免了上述相关性问题。 根据研究区内一系列已知点的大地坐标或网格坐标改正量进行插值, 也是一种坐标系转 换方法。北美 1927 基准面(基于 Clarke 1966 椭球体)与北美 1983 基准面(基于 GRS 1980 椭球体)之间的坐标系转换就是其中一例。北美测量控制网是用传统大地测量方法建立的, 由于早期的仪器精度不足、网平差不完善等因素,基于 Clarke 1966 椭球体、并且只有一个 基准点(位于堪萨斯州 Meades Ranch)的老坐标网精度低、且误差分布不均匀;新坐标网 采用了卫星技术、 现代先进的测量仪器和电子计算机技术, 其精确度与可靠性完全能得到保 障。由此造成北美大陆网内,不同地区、甚至不同位置点的转换参数都有可能不一致,所以 如仅采用莫洛金斯基( Molodenski)和赫尔默特( Helmert)方法对付上述新、旧坐标系的 转换显然不合适,为此需要用到 EPSG(欧洲石油勘探组织)所谓的“双线性插值”转换技 术。到北美 NAD83 的坐标转换就是通过格网双线性插值实现的,其中采用了美国海岸带与 大地测绘局(US Coast & Geodetic Survey)的 NADCON 控制点网。注:美国以西经为正, 而 EPSG 文献中 NAD27 与 NAD83 坐标系的设定均以东经为正;加拿大的网格文件格式也 被澳大利亚与新西兰采用;英国采用北向与东向的双线性网格插值。 此外,经纬度多项式也可以用于坐标系转换,挪威在海岸带调查中,就采用这种方法进 行新(ED87— 欧洲 1987 基准面) 、旧(ED50— 欧洲 1950 基准面)坐标系之间的转换。挪 威地调局 Statens Kartwerk 发表的文献中列出了包含 15 个系数的经纬度 4 次多项式展开公 式。 上述格网插值及多项式拟合方法更适合于早期基准面与新建基准面之间的坐标值转换。 坐标系转换时,选择正确的转换参数符号非常重要,转换前应该明确转换的“从 (From) ”……“到(To) ” ……,避免符号混淆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4、γ=arccos(n2+h2-m2)/2hn(γ=∠ACB)
(此时应检验β+θ+γ是否等于180度,若等于180度则计算正确。)
5、h2=a2+b2(a为A点到C点的垂直距离,b为C点到A点的垂直距离)
6、n2=c2+d2(c为B点到C点的垂直距离,d为C点到B点的垂直距离)
已知两点大地坐标求第三点大地坐标
已知条件:大地坐标A(Xa,Ya)、B(Xb,Yb),m为A、B两点之间的距离,n为A、C两点之间的距离,h为B、C两点之间的距离。求:C点的大地坐标(Xc,Yc)。如图所示。
1、m2=(Xa-Xb)2+(Ya-Yb)2
2、θ=arccos(m2+n2-h2)/2mn(θ=∠ABC)
7、A点到B点的坐标方)
8、A点到C点的坐标方位角:Ф=α+β
9、Xc=Xa+hcosФ
10、Yc=Ya+hsinФ
11、再校核用B、C两点的坐标计算出来的距离是否与图纸上的距离相等,若相等则计算正确。
