余干县二元一次方程及方程组试卷
二元一次方程练习题及答案

二元一次方程练习题及答案一、二元一次方程的概念和解法二元一次方程是代数学中的基础内容,它由两个未知数和一个或多个含有这两个未知数的一次方程组成。
在解二元一次方程时,我们需要找到一个满足方程的有序数对,使得方程两边的值相等。
二、二元一次方程练习题1. 问题:解下列方程组:(1) 2x + y = 5x - y = 1(2) 3x - y = 72x + y = 12. 问题:求下列方程的解:(1) 3x + 2y = 102x - y = 4(2) 5x - 3y = 74x + 6y = 163. 问题:解方程组:(1) 2x + 3y = 13x - 2y = -5(2) 4x - 5y = 63x + 2y = 144. 问题:求下列方程的解:(1) 3x + 4y = 9x - 2y = -2(2) 2x - 5y = 1x + y = 3三、二元一次方程的解答1. 解答:(1) 解:将第二个方程中的x表示为y的函数:x = y + 1代入第一个方程中得:2(y+1) + y = 5,化简得:3y + 2 = 5解得:y = 1将y = 1代入x = y + 1得:x = 2所以方程组的解为:x = 2, y = 1(2) 解:将两个方程相加得:5x = 8,解得:x = 8/5将x代入第一个方程得:y = 3 - 2x = 3 - 2(8/5) = 3 - 16/5 = -1/5所以方程组的解为:x = 8/5, y = -1/52. 解答:(1) 解:将第二个方程中的x表示为y的函数:x = (4 + y)/2代入第一个方程中得:3((4 + y)/2) + 2y = 10,化简得:3y + 8 = 10解得:y = 2将y = 2代入x = (4 + y)/2得:x = (4 + 2)/2 = 3所以方程组的解为:x = 3, y = 2(2) 解:将第一个方程乘以2,得到2(5x - 3y) = 2(7),化简得:10x - 6y = 14将第二个方程乘以3,得到3(4x + 6y) = 3(16),化简得:12x + 18y = 48将两个方程相加得:22x = 62,解得:x = 62/22 = 31/11将x代入第一个方程得:5(31/11) - 3y = 7,化简得:155/11 - 3y = 7解得:y = (155 - 77)/33 = 78/33 = 26/11所以方程组的解为:x = 31/11, y = 26/11(1) 解:将第二个方程中的x表示为y的函数:x = (6 + 5y)/4代入第一个方程中得:2((6 + 5y)/4) + 3y = 13,化简得:3y + 3 = 13解得:y = 10/3将y = 10/3代入x = (6 + 5y)/4得:x = (6 + 5(10/3))/4 = (6 +50/3)/4 = 56/12 = 14/3所以方程组的解为:x = 14/3, y = 10/3(2) 解:将第一个方程乘以2,得到2(4x - 5y) = 2(6),化简得:8x - 10y = 12将第二个方程乘以5,得到5(3x + 2y) = 5(14),化简得:15x + 10y = 70将两个方程相加得:23x = 82,解得:x = 82/23将x代入第一个方程得:4(82/23) - 5y = 6,化简得:328/23 - 5y = 6解得:y = (328 - 138)/115 = 190/115 = 38/23所以方程组的解为:x = 82/23, y = 38/23(1) 解:将第二个方程中的x表示为y的函数:x = 5 - 2y代入第一个方程中得:3(5 - 2y) + 4y = 9,化简得:15 - 6y + 4y = 9解得:y = 6将y = 6代入x = 5 - 2y得:x = 5 - 2(6) = -7所以方程组的解为:x = -7, y = 6(2) 解:将第二个方程中的x表示为y的函数:x = 1 - y代入第一个方程中得:2(1 - y) - 5y = 1,化简得:2 - 2y - 5y = 1解得:y = -2将y = -2代入x = 1 - y得:x = 1 - (-2) = 3所以方程组的解为:x = 3, y = -2四、总结通过以上的习题练习,我们学习了解二元一次方程的方法。
初中数学二元一次方程组经典练习题(含答案)

初中数学二元一次方程组经典练习题(含答案)解下列二元一次方程组:1. {x +y = 2 3x +7y =10;2.{x +3y = 810x −y =18;3.{3x +2y =1364x −3y =1;4.{ x+52+y−43=2x+20.3−y+70.4= −10 ;5.{ 4x −3y =−1 x 5=y 7 ;6. {3(x +2)=2(y +3)4(x −2)=3(y −3);7.{ x 5+y 7=10 x 3−y 4=3;8.{x 2+y 3=42x +7y =50 ;9.{12(x +3)+13(y −4)=52(x −3)+5(y +4)=70 ;10.{0.2x +0.5y =9x+22+y+105=15 ;11.{4(x −1) +3(y +1) =320%(x +1)+80%(y −1)=−3;12.{x+2y 2 +x−2y 3 = 113(x +2y )−4(x −2y )=30 ;参考答案1. {x +y = 23x +7y =10 ;解: {x +y = 2−−−−−−①3x +7y =10−−−−②①×3,得3x+3y=6-------③②-③,得4y=4,即y=1将y=1代入①,解得x=1故原方程组的解是: {x =1y =12.{x +3y = 810x −y =18; 解:{x +3y = 8−−−−−−−①10x −y =18−−−−−−②②×3,得 30x-3y=54----③①+③,得31x=62,即x=2将x=2代入①,得2+3y=8,y=2故原方程组的解是: {x =2y =23.{3x +2y =1364x −3y =1; 解:{3x +2y =136−−−−−−①4x −3y =1−−−−−−② ①×3,得9x+6y= 132------③ ②×2,得8x-6y=2-----④③+④,得17x= 172 ,x= 12 将x= 12代入②,2-3y=1,y= 13 故原方程组的解是: {x = 12y = 134.{ x+52+y−43=2 x+20.3−y+70.4= −10; 解:{ x+52+y−43=2 −−−−−−−① x+20.3−y+70.4= −10−−−−−−②①等号两边同时乘以6,得3(x+5)+2(y-4)=123x+15+2y-8=12整理,得3x+2y=5----------③②等号两边同时乘以0.3×0.4,得0.4(x+2)-0.3(y+7)=-1.2两边同时乘以10,得4(x+2)-3(y+7)=-124x+8-3y-21=-12整理,得4x-3y=1--------④③×3,得9x+6y=15------⑤④×2,得8x-6y=2-------⑥⑤+⑥,得17x=17,即x=1将x=1代入③,得3+2y=5,y=1故原方程组的解是: {x =1y =15.{ 4x −3y =−1 x 5=y 7 ; 解:{ 4x −3y =−1 −−−−−−−−−−−① x 5=y 7−−−−−−−−−−−−−−−② ②变化为x= 57 y--------------③ 将③代入①,得4×57y -3y=-1 20−217 y =-1,整理得y=7将y=7代入③,得x= 57 ×7,x=5 故原方程组的解是: {x =5y =76. {3(x +2)=2(y +3)4(x −2)=3(y −3); 解:{3(x +2)=2(y +3)4(x −2)=3(y −3)方程组去括号,得{3x +6=2y +64x −8=3y −9整理得{3x −2y =0−−−−①4x −3y +1=0−−②①×3,得9x-6y=0--------③②×2, 得8x-6y+2=0------④③-④,得x-2=0,即x=2将x=2代入①,得6-2y=0,y=3故原方程组的解是: {x =2y =37.{ x 5+y 7=10 x 3−y 4=3; 解:{ x 5+y 7=10 x 3−y 4=3 方程组去分母,得{ 7x +5y =350−−−−−−①4x −3y =36−−−−−−−②①×3,得21x+15y=1050---③②×5,得20x-15y=180----④③+④,得41x=1230,即x=30将x=30代入①,得210+5y=350,y=28故原方程组的解是: {x =30y =288.{x 2+y 3=4 2x +7y =50; 解:{x 2+y 3=4 2x +7y =50方程组去分母,得{3x +2y =24−−−−−−−① 2x +7y =50−−−−−−−②①×2,得6x+4y=48-----③②×3,得6x+21y=150---④④-③,得17y=102,即y=6将y=6代入① ,得3x+12=24,x=4故原方程组的解是: {x =4y =69.{12(x +3)+13(y −4)=52(x −3)+5(y +4)=70 ; 解:{12(x +3)+13(y −4)=5−−−−① 2(x −3)+5(y +4)=70−−−②①去分母,得3(x+3)+2(y-4)=30去括号,得3x+9+2y-8=30整理,得3x+2y-29=0-----------③②去括号,得2x-6+5y+20=70整理,得2x+5y-56=0-----------④③×2,得6x+4y-58=0------------⑤④×3,得6x+15y-168=0----------⑥⑥-⑤,得11y-110=0,即y=10将y=10代入③,得3x+20-29=0,x=3故原方程组的解是:{x=3 y=1010.{0.2x+0.5y=9x+2 2+y+105=15 ;解:{0.2x+0.5y=9−−−−−①x+22+y+105=15−−−−−−②①等号两边同时乘以10,得2x+5y=90------------------③②去分母,得5(x+2)+2(y+10)=150去括号,整理得5x+2y=120---④③×5,得10x+25y=450------⑤④×2,得10x+4y=240-------⑥⑤-⑥,得21y=210,即y=10将y=10代入③,得2x+50=90,x=20故原方程组的解是:{x=20 y=1011.{4(x −1) +3(y +1) =320%(x +1)+80%(y −1)=−3; 解:{4(x −1) +3(y +1) =3−−−−−−−−−①20%(x +1)+80%(y −1)=−3−−−−−−② ①去括号,得4x-4+3y+3=3,整理得4x+3y=4-----③ ②去百分号,得0.2(x+1)+0.8(y-1)=-3等号两边同时乘以10,得2(x+1)+8(y-1)=-30 去括号,得2x+2+8y-8=-30,整理得x+4y=-12----④ ④×4,得4x+16y=-48------------------------⑤ ⑤-③,得13y=-52,即y=-4将y=-4代入④,得x-16=-12,x=4故原方程组的解是: {x =4y =−412.{x+2y 2 +x−2y 3 = 11 3(x +2y )−4(x −2y )=30; 解:{x+2y 2 +x−2y 3 = 11 −−−−−−−−−−−−−−① 3(x +2y )−4(x −2y )=30−−−−−−② ①×6,得3(x+2y )+2(x-2y )=66----------------③③-②,得6(x-2y )=36,即x-2y= 6 -------④①×12,得6(x+2y )+4(x-2y )=132---------------⑤⑤+②,得9(x+2y)=162,即x+2y=18---⑥④+⑥,得2x=24,即x=12④-⑥,得-4y=-12,即y=3故原方程组的解是:{x=12 y=3。
(完整版)二元一次方程组练习题含答案

二元一次方程组专题训练1.⎩⎨⎧=-=+33651643y x y x 2. ⎩⎨⎧=+=-6251023x y x y ⎩⎨⎧=-=+19542023b a b a 1、 2、 3、 ⎩⎨⎧=-=+1572532y x y x4、⎩⎨⎧=+-=18435276t s t s 5、 ⎩⎨⎧=-=+574973p q q p 6、⎩⎨⎧=-=+42634y x y x7、⎩⎨⎧-=-=+22223n m n m 8、⎩⎨⎧=--=-495336y x y x 9、10、⎩⎨⎧=-=-yx y x 23532 11、⎩⎨⎧=-=+124532n m n m12、⎩⎨⎧=+=+10232556y x y x13、⎩⎨⎧=+=+2.54.22.35.12y x y x 14、⎪⎩⎪⎨⎧=-+-=+6)(3)1(26132y x x y x15、⎪⎩⎪⎨⎧=+--=-+-04235130423512y x y x 16、⎪⎩⎪⎨⎧=--=+-4323122y x y x yx17、⎪⎩⎪⎨⎧-=-++=-+52251230223x y x y x二元一次方程组练习题一、选择题:1.下列方程中,是二元一次方程的是( ) A .3x -2y=4z B .6xy+9=0 C .1x+4y=6 D .4x=2.下列方程组中,是二元一次方程组的是( )A .228423119...23754624x y x y a b xBCD x y b c y x x y +=+=-=⎧⎧=⎧⎧⎨⎨⎨⎨+=-==-=⎩⎩⎩⎩3.二元一次方程5a -11b=21 ( )A .有且只有一解B .有无数解C .无解D .有且只有两解4.方程y=1-x 与3x+2y=5的公共解是( )A .3333...2422x x x x B C D y y y y ==-==-⎧⎧⎧⎧⎨⎨⎨⎨===-=-⎩⎩⎩⎩5.若│x -2│+(3y+2)2=0,则的值是( )A .-1B .-2C .-3D .326.方程组43235x y kx y -=⎧⎨+=⎩的解与x 与y 的值相等,则k 等于( )7.下列各式,属于二元一次方程的个数有( )①xy+2x -y=7; ②4x+1=x -y ; ③1x+y=5; ④x=y ; ⑤x 2-y 2=2⑥6x -2y ⑦x+y+z=1 ⑧y (y -1)=2y 2-y 2+x A .1 B .2 C .3 D .48.某年级学生共有246人,其中男生人数y 比女生人数x 的2倍少2人,•则下面所列的方程组中符合题意的有( ) A .246246216246 (22222222)x y x y x y x y B C D y x x y y x y x +=+=+=+=⎧⎧⎧⎧⎨⎨⎨⎨=-=+=+=+⎩⎩⎩⎩ 二、填空题9.已知方程2x+3y -4=0,用含x 的代数式表示y 为:y=_______;用含y 的代数式表示x 为:x=________. 10.在二元一次方程-12x+3y=2中,当x=4时,y=_______;当y=-1时,x=______.11.若x 3m -3-2y n -1=5是二元一次方程,则m=_____,n=______.12.已知2,3x y =-⎧⎨=⎩是方程x -ky=1的解,那么k=_______.13.已知│x -1│+(2y+1)2=0,且2x -ky=4,则k=_____.14.二元一次方程x+y=5的正整数解有______________. 15.以57x y =⎧⎨=⎩为解的一个二元一次方程是_________. 16.已知2316x mx y y x ny =-=⎧⎧⎨⎨=--=⎩⎩是方程组的解,则m=_______,n=______.三、解答题17.当y=-3时,二元一次方程3x+5y=-3和3y -2ax=a+2(关于x ,y 的方程)•有相同的解,求a 的值.18.如果(a -2)x+(b+1)y=13是关于x ,y 的二元一次方程,则a ,b 满足什么条件?19.二元一次方程组437(1)3x y kx k y +=⎧⎨+-=⎩的解x ,y 的值相等,求k .20.已知x,y是有理数,且(│x│-1)2+(2y+1)2=0,则x-y的值是多少?21.已知方程12x+3y=5,请你写出一个二元一次方程,使它与已知方程所组成的方程组的解为41xy=⎧⎨=⎩.22.根据题意列出方程组:(1)明明到邮局买0.8元与2元的邮票共13枚,共花去20元钱,•问明明两种邮票各买了多少枚?(2)将若干只鸡放入若干笼中,若每个笼中放4只,则有一鸡无笼可放;•若每个笼里放5只,则有一笼无鸡可放,问有多少只鸡,多少个笼?23.方程组2528x yx y+=⎧⎨-=⎩的解是否满足2x-y=8?满足2x-y=8的一对x,y的值是否是方程组2528x yx y+=⎧⎨-=⎩的解?24.(开放题)是否存在整数m ,使关于x 的方程2x+9=2-(m -2)x 在整数范围内有解,你能找到几个m 的值?你能求出相应的x 的解吗?《二元一次方程组》单元测试题一、选择题(每题3分,共30分) 1.下列方程组中,是二元一次方程组的是( ). (A ) 2311089x y x y ⎧+=⎨-=-⎩ (B )426xy x y =⎧⎨+=⎩ (C )21734x y y x-=⎧⎪⎨-=-⎪⎩(D )24795x y x y +=⎧⎨-=⎩ 2.二元一次方程组⎩⎨⎧==+xy y x 2,102的解是( ) (A )⎩⎨⎧==;3,4y x (B )⎩⎨⎧==;6,3y x (C )⎩⎨⎧==;4,2y x (D )⎩⎨⎧==.2,4y x 3.根据图1所示的计算程序计算y 的值,若输入2=x , 则输出的y 值是( )(A )0 (B )2- (C )2 (D )44.如果2315a b 与114x x y a b ++-是同类项,则x ,y 的值是( )(A )⎩⎨⎧==31y x (B )⎩⎨⎧==22y x (C )⎩⎨⎧==21y x (D )⎩⎨⎧==32y x 5.已知12x y =⎧⎨=⎩ 是方程组错误!未找到引用源。
(完整版)二元一次方程组测试题及答案

二元一次方程组(时间:45分钟 满分:100分) 姓名一、选择题(每小题5分,共20分)1. 下列不是二元一次方程组的是( )A .141y x x y ⎧+=⎪⎨⎪-=⎩ B .43624x y x y +=⎧⎨+=⎩C .44x y x y +=⎧⎨-=⎩ D .35251025x y x y +=⎧⎨+=⎩2.由132x y-=,可以得到用x 表示y 的式子是( )A .223x y -=B .2133x y =-C .223x y =-D .223xy =-3.方程组327413x y x y +=⎧⎨-=⎩的解是( )A .13x y =-⎧⎨=⎩ B .31x y =⎧⎨=-⎩C .31x y =-⎧⎨=-⎩ D .13x y =-⎧⎨=-⎩4.方程组125x y x y -=⎧⎨+=⎩的解是( )A .12x y =-⎧⎨=⎩ B .21x y =⎧⎨=-⎩C .12x y =⎧⎨=⎩D .21x y =⎧⎨=⎩二、填空题(每小题6分,共24分)5.在349x y +=中,如果2y = 6,那么x = 。
6.已知18x y =⎧⎨=-⎩是方程31mx y -=-的解,则m = 。
7.若方程m x + n y = 6的两个解是11x y =⎧⎨=⎩,21x y =⎧⎨=-⎩,则m = ,n = 。
8.如果2150x y x y -+=+-=,那么x = ,y = 。
三、解下列方程组(每小题8分,共16分)9.1323334m nm n ⎧+=⎪⎪⎨⎪-=⎪⎩10.()()344126x y x y x y x y⎧+--=⎪⎨+-+=⎪⎩四、综合运用(每小题10分,共40分)11.用16元买了60分、80分两种邮票共22枚。
60分与80分的邮票各买了多少枚?12.已知梯形的面积是42cm2,高是6cm,它的下底比上底的2倍少1cm,求梯形的上下底。
13.〈〈一千零一夜〉〉中有这样一段文字:有一群鸽子,其中一部分在树上欢歌,另一部分在地上觅食,树上的一只鸽子对地上觅食的鸽子说:“若从你们中飞上来一只,则树下的鸽子就是整个鸽群的13,若从树上飞下去一只,则树上、树下的鸽子就一样多了。
二元一次方程组习题及答案

初一数学下第8章《二元一次方程组》试题及答案§8.1二元一次方程组一、填空题1、二元一次方程4x-3y=12,当x=0,1,2,3时,y=____2、在x+3y=3中,若用x 表示y ,则y= ,用y 表示x ,则x=3、已知方程(k 2-1)x 2+(k+1)x+(k-7)y=k+2,当k=______时,方程为一元一次方程;当k=______时,方程为二元一次方程。
4、对二元一次方程2(5-x)-3(y-2)=10,当x=0时,则y=____;当y=0时,则x=____。
5、方程2x+y=5的正整数解是______。
6、若(4x-3)2+|2y+1|=0,则x+2= 。
7、方程组⎩⎨⎧==+b xy a y x 的一个解为⎩⎨⎧==32y x ,那么这个方程组的另一个解是 。
8、若21=x 时,关于y x 、的二元一次方程组⎩⎨⎧=-=-212by x y ax 的解互为倒数,则=-b a 2 。
二、选择题1、方程2x-3y=5,xy=3,33=+yx ,3x-y+2z=0,62=+y x 中是二元一次方程的有( )个。
A、1 B、2 C、3 D、4 2、方程2x+y=9在正整数范围内的解有( )A 、1个B 、2个C 、3个D 、4个3、与已知二元一次方程5x-y=2组成的方程组有无数多个解的方程是( )A 、10x+2y=4B 、4x-y=7C 、20x-4y=3D 、15x-3y=6 4、若是m y x 25与2214-++n m n y x 同类项,则n m -2的值为 ( )A 、1B 、-1C 、-3D 、以上答案都不对 5、在方程(k 2-4)x 2+(2-3k)x+(k+1)y+3k=0中,若此方程为二元一次方程,则k 值为( ) A 、2 B 、-2 C 、2或-2 D 、以上答案都不对.6、若⎩⎨⎧-==12y x 是二元一次方程组的解,则这个方程组是( )A 、⎩⎨⎧=+=-5253y x y x B 、⎩⎨⎧=--=523x y x y C 、⎩⎨⎧=+=-152y x y x D 、⎩⎨⎧+==132y x yx7、在方程3)(3)(2=--+x y y x 中,用含x 的代数式表示y ,则 ( )A 、35-=x yB 、3--=x yC 、35+=x yD 、35--=x y 8、已知x=3-k,y=k+2,则y与x的关系是( )A、x+y=5 B、x+y=1 C、x-y=1 D、y=x-1 9、下列说法正确的是( )A、二元一次方程只有一个解 B、二元一次方程组有无数个解C、二元一次方程组的解必是它所含的二元一次方程的解 D、三元一次方程组一定由三个三元一次方程组成10、若方程组⎩⎨⎧=+=+16156653y x y x 的解也是方程3x+ky=10的解,则k的值是( =)A、k=6 B、k=10 C、k=9 D、k=101三、解答题1、解关于x 的方程)1(2)4)(1(+-=--x a x a a2、已知方程组⎩⎨⎧=+=+c y ax y x 27,试确定c a 、的值,使方程组:(1)有一个解;(2)有无数解;(3)没有解3、关于y x 、的方程3623-=+k y kx ,对于任何k 的值都有相同的解,试求它的解。
二元一次方程组单元测试题及答案(2套)

二元一次方程组解法练习题一.解答题(共16小题) 1.解下列方程组 (1)(2)(3))(6441125为已知数a a y x ay x ⎩⎨⎧=-=+(4)(5)(6).(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x(9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2.求适合的x,y的值.3.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?1.解下列方程组(1)(2);(3);(4)(5).(6)(7)(8)(9)(10);2.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.二元一次方程组解法练习题精选参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:解二元一次方程组.考点:计算题.专题:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.分析:解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点;二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.评:4.解方程组:考点:解二元一次方程组.专题:计算题.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.分析:(1)将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k、b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.点评:解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.二元一次方程组单元测试题及答案(一)一、选择题(每题3分,共24分)1、表示二元一次方程组的是( )A 、⎩⎨⎧=+=+;5,3x z y xB 、⎩⎨⎧==+;4,52y y xC 、⎩⎨⎧==+;2,3xy y xD 、⎩⎨⎧+=-+=222,11xy x x y x 2、方程组⎩⎨⎧=-=+.134,723y x y x 的解是( ) A 、⎩⎨⎧=-=;3,1y x B 、⎩⎨⎧-==;1,3y x C 、⎩⎨⎧-=-=;1,3y x D 、⎩⎨⎧-=-=.3,1y x 3、设⎩⎨⎧=+=.04,3z y y x ()0≠y 则=z x ( ) A 、12 B 、121-C 、12-D 、.121 4、设方程组()⎩⎨⎧=--=-.433,1by x a by ax 的解是⎩⎨⎧-==.1,1y x 那么b a ,的值分别为( )A 、;3,2-B 、;2,3-C 、;3,2-D 、.2,3-5、方程82=+y x 的正整数解的个数是( )A 、4B 、3C 、2D 、16、在等式n mx x y ++=2中,当3.5,3;5,2=-=-===x y x y x 则时时时,=y ( )。
二元一次方程组(例题、解方程组、练习及答案)
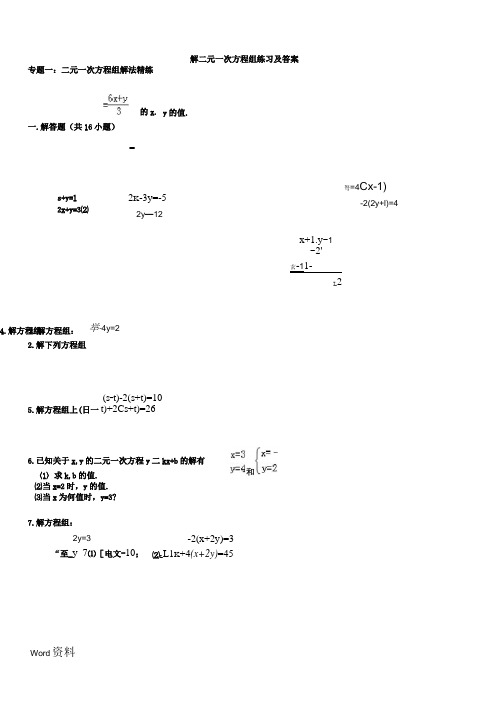
的x. y 的值.s+y=l 2x+y=3⑵2K -3y=-52y —12弩=4Cx-1)-2(2y+l)=43.解方程组:举-4y=24.解方程组: x+1.y~1 ~2'玄-11-L 2-2(x+2y)=3⑵L L1K +4(x+2y)=45解二元一次方程组练习及答案专题一:二元一次方程组解法精练一.解答题(共16小题)2.解下列方程组(s _t)-2(s+t)=10 5.解方程组上(日一t)+2Cs+t)=266.已知关于x,y 的二元一次方程y 二kx+b 的解有 (1)求k,b 的值. ⑵当x=2时,y 的值. ⑶当x 为何值时,y=3?7.解方程组:2y=3“至_y_7⑴[电文-10;=13_X "12,乙看错了方程组中的b.蓋二- £时,由于粗心,甲看错了方程组中的a,而得解为 (沪5而得解为尸°.(1)甲把a 看成了什么,乙把b 看成了什么? (2)求出原方程组的正确解.亠一空二5 14.I X0.315.解下列方程组:8.解方程组:卩(旳)(K -3y)=159.解方程组:10.解下列方程组: fs-y=4 ⑴4贵 11.解方程组: "T⑵[4(葢十7)-5(K-y)=212.解二元一次方程组: f 9s+2y=20(1).办十4尸10;乜(K -1)-4(y-4)=0⑵占〔厂"二3匕+5)鮎曲+5尸1013.在解方程组(1) 匹站3y=15 “x+1_y+4 ⑵f2x+y=4 16.解下列方程组:(1)时戈产5 p+y=l(2)■20^1+30^25^X2专题二:方程组解法强化训练 ■>二1+尸j3^-2/=6 2(右十为*175x+y+z=145 15 3.x+y —2z-5 仝%+4®二1124.5. 17 r0.25x+3ty+3)=156.匚(工十1)—1.5(^十刀二35 r 3(x-y 十E 二0'mJ4耳+2了+£=3i4 l 税25t+5v+z=6O 盲8.9.—2 4 J2 3 XH -/=60 J y +z =40 x+i=50 10. H 十JJ-H-Z=11<3A +J 二25z=4^11.L》+z -了工二号 5-3^+4-7y=1121」心+5我彳z +z-3j=5 13.乐十》)-4&p )二4土+二=118.21. fi-2j=7y x+1—二36y-1=3fx+|)16.y—1x二y-I2_y+2.2x=+13T" 33(x-0=4(卩一4)17.+500,[60%^+80%-7=500x72%.19.宝”一1)=3(兀+5)20.卜223A-3J-9=^±13r2(z+^+3(x-y)=1322.j-2z+3y=1123.尸(*)亠4决2刃=8724. 25. 弘+»=198jc-3y=6727. =-1=4IZ尹-1=128.30. SI兰工_气2十3-5巧P=〔23-_答案专题一1.x=6"X=1 「K=3、「K=3「⑵•卄8•解万程组:9•解方程组:1歼-1(y=0\y=0工二3114V——3⑷•y=-3•解方程组fl4•解方程组:鳥I尸4,尸亍6••(1)求k,b的值.k二言,b二号•7⑵当x=2时,y的值•把x=2代入,得y=p•(3)当x为何值时,y=3?把y=3代入,得x=1 7•解方程组:10•解下列方程组:17 \=60:'尸-2411•解方程组:⑴12⑵¥二广1712•解二元一次方程组:13.(1)甲把a看成了什么,乙把b看成了什么?fa=-2 [b=6(2)求出原方程组的正确解.P=152•解下列方程组专题二:=50rz=4rz=5K=5[75rz=-70rA=61.2.3.4.5.6.g1715•解下列方程组:⑴16•解下列方程组:⑴rx=-2cm =49.严=35L=2510.厂=30 12.J=_10 严=-17/4K=_19/413r=_5厂=17/15 厂1=714."11⑴15.J=-316.=1厂=20017.J=300 18. J -A =-1/4丫尹=3/819.29/6 -7/422. 23.CI ;rz =2324.f A =-11/2 25.f A =826.5=-127.rz=428.J -A =4.5 29.rz=6.530.。
七年级初一下学期数学 二元一次方程组考试卷及答案

七年级初一下学期数学 二元一次方程组考试卷及答案一、选择题1.已知1,2x y =⎧⎨=⎩是二元一次方程24x ay +=的一组解,则a 的值为( )A .2B .2-C .1D .1-2.若关于x y ,的二元一次方程组232320x y kx y k +=⎧⎨-=⎩的解也是二元一次方程236x y +=的解,则k 的值为( ) A .34-B .34C .43D .43-3.我市某九年一贯制学校共有学生3000人,计划一年后初中在校生增加8%,小学在校生增加11%,这样全校在校生将增加10%,设这所学校现初中在校生x 人,小学在校生y 人,由题意可列方程组( ) A .30008%11%300010%x y x y +=⎧⎨+=⨯⎩B .30008%11%3000(110%)x y x y +=⎧⎨+=+⎩C .()()300018%111%300010%x y x y +=⎧⎨+++=⨯⎩D .30008%11%10%x y x y +=⎧⎨+=⎩4.已知方程组43235x y kx y -=⎧⎨+=⎩的解满足x y =,则k 的值为( )A .1B .2C .3D .45.若二元一次方程组,3x y a x y a-=⎧⎨+=⎩的解是二元一次方程3570x y --=的一个解,则a 为( ) A .3 B .5 C .7 D .96.甲是乙现在的年龄时,乙10岁,乙是甲现在的年龄时,甲25岁,那么( ) A .甲比乙大5岁 B .甲比乙大10岁 C .乙比甲大10岁 D .乙比甲大5岁7.如图,将正方形ABCD 的一角折叠,折痕为AE ,点B 落在点B ′处,B AD ∠'比BAE ∠大48︒.设BAE ∠和B AD ∠'的度数分别为x ︒和y ︒,那么x 和y 满足的方程组是( )A .4890y x y x -=⎧⎨+=⎩B .482y x y x -=⎧⎨=⎩C .48290x y y x -=⎧⎨+=⎩D .48290y x y x -=⎧⎨+=⎩8.三元一次方程组236216x y z x y z ==⎧⎨++=⎩①②的解是( )A .135x y z =⎧⎪=⎨⎪=⎩B .556x y z =⎧⎪=⎨⎪=⎩C .632x y z =⎧⎪=⎨⎪=⎩D .642x y z =⎧⎪=⎨⎪=⎩9.关于x ,y 的方程组2318517ax y x by +=⎧⎨-+=⎩(其中a ,b 是常数)的解为34x y =⎧⎨=⎩,则方程组2()3()18()5()17a x y x y x yb x y ++-=⎧⎨+--=-⎩的解为( ) A .34x y =⎧⎨=⎩B .71x y =⎧⎨=-⎩C . 3.50.5x y =⎧⎨=-⎩D . 3.50.5x y =⎧⎨=⎩10.如图,在数轴上标出若干个点,每相邻的两个点之间的距离都是1个单位,点A 、B 、C 、D 表示的数分别是整数a 、b 、c 、d ,且满足2319ad,则b c +的值为( )A .3-B .2-C .1-D .011.以方程组21x y y x +=⎧⎨=-⎩的解为坐标的点(x ,y )在平面直角坐标系中的位置是( )A .第一象限B .第二象限C .第三象限D .第四象限12.已知方程组222x y kx y +=⎧⎨+=⎩的解满足x+y=2,则k 的算术平方根为( )A .4B .﹣2C .﹣4D .2 二、填空题13.某水稻种植中心培育了甲、乙、丙三种水稻,将这三种水稻分别种植于三块大小各不相同的试验田里.去年,三种水稻的平均亩产量分别为300kg ,500kg ,400kg ,总平均亩产量为450kg ,且丙种水稻的的总产量是甲种水稻总产量的4倍,今年初,研究人员改良了水稻种子,仍按去年的方式种植,三种水稻的平均亩产量都增加了.总平均亩产量增长了20%,甲、丙两种水稻的总产量增长了30%,则乙种水稻平均亩产量的增长率为_____. 14.已知方程组1122a x y c a x y c +=⎧⎨+=⎩解为510x y =⎧⎨=⎩,则关于x ,y 的方程组1112223232a x y a c a x y a c +=+⎧⎨+=+⎩的解是_______.15.若关于x ,y 的方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解为32x y =⎧⎨=⎩,则方程组11122252605260a x b y c a x b y c +-=⎧⎨+-=⎩的解为__________. 16.若m 满足关系式35223x y m xy m +--++-199199x y x y =--⋅-+,则m =________.17.2019年秋,重庆二外初2021级将开启“大阅读”活动,为了充实书吧藏书,学生会号召全年级学生捐书,得到各班的大力支持.同时,年级部分备课组的老师也购买藏书充实到年级书吧,其中数学组购买了甲、乙两种自然科学书籍若干本,用去699元;语文组购买了A 、B 两种文学书籍若干本,用去6138元,已知A 、B 的数量分别与甲、乙的数量相等,且甲种书与B 种书的单价相同,乙种书与A 种书的单价相同.若甲种书的单价比乙种书的单价多7元,则乙种书籍比甲种书籍多买了__________本.18.在某一个学校的运动俱乐部里面有三大筐数量相同的球,甲每次从第一个大筐中取出9个球;乙每次从第二个大筐中取出7个球;丙则是每次从第三个大筐中取出5个球.到后来甲、乙、丙三人都记不清各自取过多少次球了,于是管理人员查看发现第一个大筐中还剩下7个球,第二个大筐还剩下4个球,第三个大筐还剩下2个球,那么根据上述情况可以推知甲至少取了______次.19.方程组1111121132x y x z y z ⎧+=⎪⎪⎪+=⎨⎪⎪+=⎪⎩的解为______.20.历代数学家称《九章算术》为“算经之首”.书中有这样一道题的记载,译文为:今有5只雀、6只燕,分别聚集在一起称重,称得雀重,燕轻.若将一只雀、一只燕交换位置,则重量相等;将5只雀、6只燕放在一起称量,则总重量为1斤.问雀、燕每1只各重多少斤?若设雀每只重x 斤,燕每只重y 斤,则可列方程组为________________ 21.如图,长方形ABCD 被分成若干个正方形,已知32cm AB =,则长方形的另一边AD =_________cm .22.在平面直角坐标系中,当点M (x,y )不在坐标轴上时,定义点M 的影子点为M /(,)y x x y -.已知点P 的坐标为(a,b ),且a 、b 满足方程组3401416a c b c ⎧++-=⎪-=-(c 为常数).若点P 的影子点是点P /,则点P /的坐标为___.23.我校第二课堂开展后受到了学生的追捧,学期结束后对部分学生做了一次“我最喜爱的第二课堂”问卷调查(每名学生都填了调査表,且只选了一个项目),统计后趣味数学、演讲与口才、信息技术、手工制作榜上有名.其中选信息技术的人数比选手工制作的少8人;选趣味数学的人数不仅比选手工制作的人多,且为整数倍;选趣味数学与选手工制作的人数之和是选演讲与口才与选信息技术的人数之和的5倍;选趣味数学与选演讲与口才的人数之和比选信息技术与选手工制作的人数之和多24人.则参加调查问卷的学生有________人.24.一个二元一次方程和一个二元二次方程组成的二元二次方程组的解是24x y =⎧⎨=⎩和24x y =-⎧⎨=-⎩,试写出符合要求的方程组________(只要填写一个即可). 三、解答题25.某生态柑橘园现有柑橘21吨,计划租用A ,B 两种型号的货车将柑橘运往外地销售.已知满载时,用2辆A 型车和3辆B 型车一次可运柑橘12吨;用3辆A 型车和4辆B 型车一次可运柑橘17吨.(1)1辆A 型车和1辆B 型车满载时一次分别运柑橘多少吨?(2)若计划租用A 型货车m 辆,B 型货车n 辆,一次运完全部柑橘,且每辆车均为满载.①请帮柑橘园设计租车方案;②若A 型车每辆需租金120元/次,B 型车每辆需租金100元/次.请选出最省钱的租车方案,并求出最少租车费.26.为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A 型节能灯和5只B 型节能灯共需50元,2只A 型节能灯和3只B 型节能灯共需31元. (1)求1只A 型节能灯和1只B 型节能灯的售价各是多少元?(2)学校准备购买这两种型号的节能灯共200只,要求A 型节能灯的数量不超过B 型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由. 27.在平面直角坐标系中,点A 、B 在坐标轴上,其中()0,A a 、(),0Bb 满足|21|280a b a b --++-=.(1)求A 、B 两点的坐标;(2)将线段AB 平移到CD ,点A 的对应点为()2,C t -,如图1所示,若三角形ABC 的面积为9,求点D 的坐标;(3)平移线段AB 到CD ,若点C 、D 也在坐标轴上,如图2所示.P 为线段AB 上的一动点(不与A 、B 重合),连接OP 、PE 平分OPB ∠,2BCE ECD ∠=∠.求证:3()BCD CEP OPE ∠=∠-∠.28.阅读下列材料,然后解答后面的问题.已知方程组372041027x y z x y z ++=⎧⎨++=⎩,求x+y+z 的值.解:将原方程组整理得2(3)()203(3)()27x y x y z x y x y z ++++=⎧⎨++++=⎩①②,②–①,得x+3y=7③, 把③代入①得,x+y+z=6.仿照上述解法,已知方程组6422641x y x y z +=⎧⎨--+=-⎩,试求x+2y –z 的值.29.为鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市居民“一户一表”生活用水阶梯式计费价格表的部分信息,请解答:(1)小王家今年3月份用水20吨,要交水费___________元;(用a ,b 的代数式表示) (2)小王家今年4月份用水21吨,交水费48元;邻居小李家4月份用水27吨,交水费70元,求a ,b 的值.(3)在第(2)题的条件下,若交水费76.5元,求本月用水量.(4)在第(2)题的条件下,小王家5月份用水量与4月份用水量相同,却发现要比4月份多交9.6元钱水费,小李告诉小王说:“水价调整了,表中表示单位的a ,b 的值分别上调了整数角钱(没超过1元),其他都没变.”到底上调了多少角钱呢?请你帮小王求出符合条件的所有可能情况.30.甲从A 地出发步行到B 地,乙同时从B 地步行出发至A 地,2小时后在中途相遇,相遇后,甲、乙步行速度都提高了1千米/小时.若设甲刚出发时的速度为a 千米/小时,乙刚出发的速度为b 千米/小时.(1)A 、B 两地的距离可以表示为 千米(用含a ,b 的代数式表示); (2)甲从A 到B 所用的时间是: 小时(用含a ,b 的代数式表示); 乙从B 到A 所用的时间是: 小时(用含a ,b 的代数式表示).(3)若当甲到达B 地后立刻按原路向A 返行,当乙到达A 地后也立刻按原路向B 地返行.甲乙二人在第一次相遇后3小时36分钟又再次相遇,请问AB 两地的距离为多少?31.如图,已知∠a 和β∠的度数满足方程组223080αββα︒︒⎧∠+∠=⎨∠-∠=⎩,且CD //EF,AC AE ⊥.(1)分别求∠a 和β∠的度数;(2)请判断AB 与CD 的位置关系,并说明理由; (3)求C ∠的度数。
二元一次方程20道题

二元一次方程20道题一、基础型题目(1 - 10题)1. 已知方程2x + 3y=12,当x = 3时,求y的值。
- 解析:将x = 3代入方程2x+3y = 12中,得到2×3+3y=12,即6 + 3y=12。
方程两边同时减去6,得到3y=12 - 6=6,解得y = 2。
2. 解方程组x + y=5 x - y = 1- 解析:将两个方程相加,(x + y)+(x - y)=5 + 1,即2x=6,解得x = 3。
把x = 3代入x + y=5中,得到3+y = 5,解得y=2。
3. 若3x - 2y=11,且y = 2x - 4,求x和y的值。
- 解析:把y = 2x-4代入3x - 2y=11中,得到3x-2(2x - 4)=11,展开括号得3x-4x + 8 = 11,移项得3x-4x=11 - 8,即-x = 3,解得x=-3。
把x = - 3代入y = 2x-4,得y=2×(-3)-4=-6 - 4=-10。
4. 解方程组2x+3y = 8 3x - 2y=-1- 解析:给第一个方程2x + 3y=8两边同时乘以2,得到4x + 6y = 16;给第二个方程3x-2y=-1两边同时乘以3,得到9x-6y=-3。
将这两个新方程相加,(4x +6y)+(9x-6y)=16+(-3),即13x = 13,解得x = 1。
把x = 1代入2x + 3y=8中,2×1+3y = 8,3y=8 - 2 = 6,解得y = 2。
5. 已知x、y满足方程4x - 3y=1,且x = 2y - 2,求x和y的值。
- 解析:将x = 2y-2代入4x-3y = 1中,得到4(2y-2)-3y = 1,展开括号得8y-8 - 3y=1,移项得8y-3y=1 + 8,5y=9,解得y=(9)/(5)。
把y=(9)/(5)代入x = 2y-2,得x=2×(9)/(5)-2=(18)/(5)-(10)/(5)=(8)/(5)。
二元一次方程组练习题(含答案)

二元一次方程组练习题(含答案)1.解下列方程组:1) 5x + 2y = 11a,-4y = 6a;2) 4x + 3y - 1 = 0,2x + y - 2 = 0;3) x + 2y/3 - 1/3 = 2,x/3 + 1 - y/2 = 1/2;4) x - y/2 = 1,x + y/2 = 3.2.求解以下方程组:1) 2x + 3y = 7,x - y = 1;2) x + 2y = 5,2x + y = 7;3) 3x + 2y = 8,4x - 3y = -11.3.已知二元一次方程y = kx + b的解有(2,5)和(-1,0)。
1) 求k,b的值;2) 当x = 2时,y的值;3) 当y = 3/5时,x的值。
4.在解方程组2x + y = 5,x - y = 1时,甲看错了方程组中的a,而得到解x = 2,y = 1.乙看错了方程组中的b,而得到解x = 3,y = -1.1) 甲把a看成了什么,乙把b看成了什么?2) 求出原方程组的正确解。
参考答案与解析:1.解下列方程组:1) 5x + 2y = 11a,-4y = 6a。
将第二个方程式化简为y = -3/2a,代入第一个方程式中得到5x + 2(-3/2a) = 11a,化简得到x = (23/10)a,y = (-9/5)a。
2) 4x + 3y - 1 = 0,2x + y - 2 = 0.将第二个方程式中的y用第一个方程式中的x表示,得到y = 2 - 2x,代入第一个方程式中得到4x + 3(2 - 2x) - 1 = 0,化简得到x = 1/2,y = 1.3) x + 2y/3 - 1/3 = 2,x/3 + 1 - y/2 = 1/2.将第二个方程式中的x用第一个方程式中的y表示,得到x = 6 - 2y,代入第一个方程式中得到6 - 4y/3 = 2,化简得到y = 3/2,x = 0.4) x - y/2 = 1,x + y/2 = 3.将两个方程式相加得到2x = 4,化简得到x = 2,代入第一个方程式中得到y = 2.2.求解以下方程组:1) 2x + 3y = 7,x - y = 1.将第二个方程式中的x用第一个方程式中的y表示,得到x = y + 1,代入第一个方程式中得到2(y + 1) + 3y = 7,化简得到y = 1,x = 2.2) x + 2y = 5,2x + y = 7.将第一个方程式中的x用第二个方程式中的y表示,得到x = (7 - y)/2,代入第一个方程式中得到(7 - y)/2 + 2y = 5,化简得到y = 1,x = 2.3) 3x + 2y = 8,4x - 3y = -11.将第一个方程式中的x用第二个方程式中的y表示,得到x = (3y - 11)/4,代入第一个方程式中得到3(3y - 11)/4 + 2y = 8,化简得到y = 1,x = 1.3.已知二元一次方程y = kx + b的解有(2,5)和(-1,0)。
(完整版)二元一次方程计算题含答案(最新整理)

∴原方程组可化为
,
解得 ,
∴
∴原方程组的解为 .
点评:此题考查了学生的计算能力,解题时要细心. 12.解二元一次方程组:
(1)
;
(2)
.
考点:解二元一次方程组. 809625
专题:计算题. 分析:(1)运用加减消元的方法,可求出 x、y 的值;
(2)先将方程组化简,然后运用加减消元的方法可求出 x、y 的值. 解答:
11.解方程组:
(1)
(2)
考点:解二元一次方程组. 809625
专题:计算题;换元法. 分析:方程组(1)需要先化简,再根据方程组的特点选择解法;
方程组(2)采用换元法较简单,设 x+y=a,x﹣y=b,然后解新方程组即可求解.
解答:
解:(1)原方程组可化简为
,
解得
.
(2)设 x+y=a,x﹣y=b,
(2)
考点:解二元一次方程组. 809625
分析:观察方程组中各方程的特点,用相应的方法求解. 解答:
解:(1)①×2﹣②得:x=1,
将 x=1 代入①得: 2+y=4, y=2.
∴原方程组的解为 ;
(2)原方程组可化为
,
①×2﹣②得:
﹣y=﹣3, y=3. 将 y=3 代入①得: x=﹣2.
∴原方程组的解为
解答:
解:原方程组可化为
,
①×4﹣②×3,得
7x=42, 解得 x=6. 把 x=6 代入①,得 y=4. 所以方程组的解为 .
点评:注意:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的 方法有代入法和加减法.
4.解方程组:
考点:解二元一次方程组. 809625
二元一次方程及方程组解法测试题

二元一次方程及方程组测试题一、选择题(每题3分,共18分)1.下列方程是一元一次方程的是---------------------------------------------------------------------------------------( )A .3x -2y =4zB .6xy =1C .641=+y xD .424-=y x 2.下列方程组中是二元一次方程组的是------------------------------------------------------------------------------( )A .⎩⎨⎧=+=+7324y x y xB .⎩⎨⎧=+=-733432c b b aC .⎩⎨⎧==y x x 342D .⎩⎨⎧=+=+842y x y x 3.二元一次方程5x -11y =21---------------------------------------------------------------------------------------------( )A .有且只有一个解B .有无数解C .无解D .有且只有两个解4.方程5231=+-=y x x y 与的公共解是--------------------------------------------------------------------------() A .⎩⎨⎧==23y x B .⎩⎨⎧=-=23y x C .⎩⎨⎧-==23y x D .⎩⎨⎧-=-=23y x 5.若()022=++-x y x ,则的值是y x ------------------------------------------------------------------------() A .-1 B .2- C .4 D .236.关于x ,y 的方程组⎩⎨⎧=+=-532y 34y x kx 的解x 与y 的值相等,则k 的值为--------------------------------------() A .4 B .3 C .2 D .1二、填空题(每题3分,共18分)7.已知方程x -y =4,用含x 的代数式表示y 为:y = .8.在二元一次方程===+-y x y x 时,中,当42321.9.若5232=---m n m y x 是二元一次方程,则m = ;n = .10.已知⎩⎨⎧=-=32y x ,是方程x -☆y =1的解,那么☆= .11.二元一次方程x +y =3的正整数解....有 .12.以⎩⎨⎧==75y x 为解的一个二元一次方程是 .三、解答题 13.用代入消元法.....解方程组(每题6分,共24分)⎩⎨⎧=+-=82332.1y x x y ⎩⎨⎧-=++=1562.2y x x y ⎩⎨⎧=+=-332274.3y x y x ⎩⎨⎧=+=-1541153.4y x y x14.用加减消元法.....解方程组(每题6分,共24分) ⎩⎨⎧=-=+35.1y x y x ⎩⎨⎧=-=+7332.2y x y x ⎩⎨⎧=+=+53723.3y x y x ⎩⎨⎧-=-=+2321635.4y x y x15.已知的值?,是同类项,求和y x b a b a y x x y 4223542-+-(本题6分)16.关于x ,y 的二元一次方程组⎩⎨⎧=-+=+3)1(7y 34y k kx x 的解x ,y 的值相等,求k .(本题6分)17.是否存在整数m ,使关于x 的方程x m x )2(292--=+在整数范围内有解,你能找到几个m 的值?你能求出相应的x 的解吗?(本题4分)。
二元一次方程组测试卷

二元一次方程组测试卷一、选择题(每题3分,共30分)1. 下列方程中,是二元一次方程的是()A. x + (1)/(y)=2B. xy = 9C. 3x - 2y = 4D. x^2+y = 62. 方程2x + y = 9在正整数范围内的解有()A. 1组。
B. 2组。
C. 3组。
D. 4组。
3. 若x = 2 y = 1是关于x、y的二元一次方程ax - 3y = 1的解,则a的值为()A. 2.B. -2.C. 5.D. -5.4. 二元一次方程组x + y = 5 x - y = 3的解是()A. x = 4 y = 1B. x = 1 y = 4C. x = 2 y = 3D. x = 3 y = 25. 用代入法解方程组y = 1 - x x - 2y = 4时,代入正确的是()A. x - 2 - x = 4B. x - 2 - 2x = 4C. x - 2 + 2x = 4D. x - 2 + x = 46. 已知x = m y = n和x = n y = m是方程2x - 3y = 1的解,则m - n的值为()A. 1.B. -1.C. 0.D. 2.7. 若方程组ax + by = 2 ax - by = 2与2x + 3y = 4 4x - 5y = -6的解相同,则a,b的值为()A. a = (23)/(11) b = (4)/(11)B. a = (23)/(11) b = -(4)/(11)C. a = -(23)/(11) b = (4)/(11)D. a = -(23)/(11) b = -(4)/(11)8. 某班有x名学生,其中女生人数占45%,则男生人数为()A. 0.45xB. 0.55xC. (x)/(0.45)D. (x)/(0.55)9. 甲、乙两人练习跑步,如果乙先跑10米,则甲跑5秒就可追上乙;如果乙先跑2秒,则甲跑4秒就可追上乙,设甲的速度为x米/秒,乙的速度为y米/秒,下列方程组正确的是()A. 5x = 5y + 10 4x = 4y + 2yB. 5x - 5y = 10 4x - 2x = 4yC. 5x + 10 = 5y 4x - 4y = 2D. 5x - 5y = 10 4x - 4y = 2y10. 关于x,y的方程组3x - y = m x + my = n的解是x = 1 y = 1,则| m - n|的值是()A. 5.B. 3.C. 2.D. 1.二、填空题(每题3分,共15分)1. 若x^2m - 1+5y^3n - 2m=7是二元一次方程,则m=_ ,n=_ 。
初中数学七年级下册-二元一次方程及方程组测试题

(七年级数学)第八章二元一次及方程方程组测验卷第 周 星期 班别: 姓名: 学号:Ⅰ卷一、选择题(每题3分,共30分)1、下列各式中,是二元一次方程的是( )A 、3+xB 、02=+x xC 、y x 2=D 、0=++z y x2、下列各式中是二元一次方程组的是( )。
A 、⎩⎨⎧=+=+;5,3x z y xB 、⎩⎨⎧==+;4,52y y xC 、⎪⎩⎪⎨⎧=+=+9114y x y x D 、⎩⎨⎧=+=y x y x 2,11 3、如果34172=--y x k 是二元一次方程,那么k 的值是( )。
A 、0 B 、1 C 、2 D 、34、若⎩⎨⎧-==12y x 是二元一次方程组的解,则这个方程组可能是( )。
A 、⎩⎨⎧=+=-5253y x y x B 、⎩⎨⎧=--=523x y x y C 、⎩⎨⎧=+=-152y x y x D 、⎩⎨⎧+==132y x y x 5、方程组⎩⎨⎧=--=82352y x x y ,消去y 后得到的方程是( )。
A 、01043=--x x B 、8543=+-x xC 、8)25(23=--x xD 、81043=+-x x6、方程组⎩⎨⎧=-=+.134,723y x y x 的解是( )。
A 、⎩⎨⎧=-=;3,1y x B 、⎩⎨⎧-==;1,3y x C 、⎩⎨⎧-=-=;1,3y x D 、⎩⎨⎧-=-=.3,1y x7、在方程10)3(2=-+x y 中,用含x 的代数式表示y ,则 ( )。
A 、x y 218-=B 、x y 212-=C 、x y 212+= D 、x y +=8 8、若532=-y x ,则=+-y x 646( )A 、1B 、-4C 、-1D 、49、某校七年级学生参加植树活动,甲、乙两个组共植树50棵,乙组植树的棵树是甲组的41。
问每组各植树多少棵?设甲组植树x 棵,乙组植树y 棵,则列方程组是( )。
二元一次方程试题

二元一次方程试题1. 求解下列方程组:2x + 3y = 74x - 5y = 11解:首先我们可以尝试使用消元法解决这个方程组。
将第一个方程乘以5,第二个方程乘以3,得到:10x + 15y = 3512x - 15y = 33接下来我们将两个方程相加,得到:22x = 68将上式解得 x = 3。
将 x 的值代入第一个方程,得到:2(3) + 3y = 76 + 3y = 73y = 1y = 1/3最终的解为 x = 3,y = 1/3。
2. 求解下列方程组:3x - 2y = 8解:这个方程组可以使用消元法解决。
将第一个方程乘以4,第二个方程乘以2,得到:12x - 8y = 3210x + 8y = 2接下来我们将两个方程相加,得到:22x = 34将上式解得 x = 17/11。
将 x 的值代入第一个方程,得到:3(17/11) - 2y = 851/11 - 2y = 8-2y = 8 - 51/11-2y = 29/11y = -29/22最终的解为 x = 17/11,y = -29/22。
3. 求解下列方程组:2x + 5y = 13x - 4y = 5解:同样使用消元法,将第一个方程乘以4,第二个方程乘以5,得到:15x - 20y = 25接下来我们将两个方程相加,得到:23x = 29将上式解得 x = 29/23。
将 x 的值代入第一个方程,得到: 2(29/23) + 5y = 158/23 + 5y = 15y = 1 - 58/235y = -35/23y = -7/23最终的解为 x = 29/23,y = -7/23。
4. 求解下列方程组:7x - 3y = 25x + 2y = 3解:将第一个方程乘以2,第二个方程乘以3,得到:14x - 6y = 415x + 6y = 9接下来我们将两个方程相加,得到:29x = 13将上式解得 x = 13/29。
将 x 的值代入第一个方程,得到:7(13/29) - 3y = 291/29 - 3y = 2-3y = 2 - 91/29-3y = 47/29y = -47/87最终的解为 x = 13/29,y = -47/87。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、若(a 2-1)x 2+(a -1)x +(2a -3)y =0是二元一次方程,则a 的值为 。
2、方程组⎩⎨⎧=+-=+81043y x x m my mx 有唯一的解,那么m 的值为 。
3、x +y =5且x ,y 的绝对值都小于5的整数解共有 组4、在方程4x -3y =7里,如果用x 的代数式表示y ,则 。
5、任何一个二元一次方程都有( )(A )一个解; (B )两个解;(C )三个解; (D )无数多个解;6、一个两位数,它的个位数字与十位数字之和为6,那么符合条件的两位数的个数有( )(A )5个 (B )6个 (C )7个 (D )8个7、、如果⎩⎨⎧=+=-423y x a y x 的解都是正数,那么a 的取值范围是( )(A )a <2; (B )34->a ; (C )342<<-a ; (D )34-<a ; 8、关于x 、y 的方程组⎩⎨⎧=-=+m y x m y x 932的解是方程3x +2y =34的一组解,那么m 的值是( )(A )2; (B )-1; (C )1; (D )-2;9、与已知二元一次方程5x -y =2组成的方程组有无数多个解的方程是( )(A )15x -3y =6 (B )4x -y =7 (C )10x +2y =4 (D )20x -4y =310、下列方程组中,是二元一次方程组的是( )(A )⎪⎩⎪⎨⎧=+=+9114y x y x (B )⎩⎨⎧=+=+75z y y x(C )⎩⎨⎧=-=6231y x x (D )⎩⎨⎧=-=-1y x xy y x11、若|3x +y +5|+|2x -2y -2|=0,则2x 2-3xy 的值是( )(A )14 (B )-4 (C )-12 (D )121.已知⎩⎨⎧=+=+25ay bx by ax 的解是⎩⎨⎧==34y x ,则a 、b 的值是( ) A ⎩⎨⎧==12b a B ⎩⎨⎧-==12b a C ⎩⎨⎧=-=12b a D ⎩⎨⎧-=-=12b a 4.出境旅游者问某童,有几个兄弟、几个姐妹,答:“有几个兄弟就有几个姐妹。
”再问他的妹妹有几个兄弟、几个姐妹。
她答:“我的兄弟是姐妹的2倍。
”试问:他们兄弟姐妹的人数各是( )A 兄弟4人,姐妹3人B 兄弟3人,姐妹4人C 兄弟2人,姐妹5人D 兄弟5人,姐妹2人4、关于x 、y 的方程组51x ay y x +=⎧⎨-=⎩有正整数解,则正整数a 为( )A . 1、2B .2、5C .1、5D .1、2、525、在方程3x +4y =16中,当x =3时,y =________,当y =-2时,x =_______若x 、y 都是正整数,那么这个方程的解为___________;26、方程2x +3y =10中,当3x -6=0时,y =_________;27、如果0.4x -0.5y =1.2,那么用含有y 的代数式表示的代数式是_____________;28、若⎩⎨⎧-==11y x 是方程组⎩⎨⎧-=-=+1242a y x b y ax 的解,则⎩⎨⎧==______________b a ;29、方程|a |+|b |=2的自然数解是_____________;30、如果x =1,y =2满足方程141=+y ax ,那么a =____________;31、已知方程组⎩⎨⎧-=+=+m y x ay x 26432有无数多解,则a =______,m =______;32、若方程x -2y +3z =0,且当x =1时,y =2,则z =______;33、若4x +3y +5=0,则3(8y -x )-5(x +6y -2)的值等于_________;34、若x +y =a ,x -y =1同时成立,且x 、y 都是正整数,则a 的值为________;35、从方程组)0(030334≠⎩⎨⎧=+-=--xyz z y x z y x 中可以知道,x :z =_______;y :z =________;36、已知a -3b =2a +b -15=1,则代数式a 2-4ab +b 2+3的值为__________37、2.若x 3a-2b-2 – 2y a+b =5是二元一次方程,则a= , b= 。
5.方程组⎩⎨⎧=+=+7322y x ay x 的解是二元一次方程x-y=1的一个解,则a= 。
7.若x ,y 的值既满足x-3y=5,又满足2x+y=3,则x+3y= 。
5.已知方程组⎩⎨⎧=-=+31y x y x 与方程组⎩⎨⎧=-=+21by ax by ax 的解相同,则a= b= 。
6.已知y=kx+b ,当x=1,-2时,y=3,-6;当x= -1时,y= 。
三.解答下列各题:一.用代入法解下列方程组:1.⎩⎨⎧=++=8323y x y x 2.⎩⎨⎧-==-x y y x 5717343.⎩⎨⎧=+-=-10235y x y x 4.⎩⎨⎧-=-=-2.32872x y y x 三.用代入法解二元一次方程组: 1.⎩⎨⎧=+=+1894842y x y x 2.⎩⎨⎧+=++=-3)2(22)2(3x y y x 1.已知:⎩⎨⎧=-=21y x 是关于x 、y 的方程组⎩⎨⎧=-=+4213by x y ax 的解,求a+b 的值。
2.已知关于x 、y 的方程组⎩⎨⎧=-=-m y x y x 3523的解中x= -1,求y 的值及m 的值。
方程组23352x y k x y k +=⎧⎨+=+⎩中, x 与y 的和12,求k 的值.3.若方程x-3y+2k-2=0的一个解是方程组⎩⎨⎧+=-=212k y k x 的解,则k 的值为多少? 2.如图所示,将正方形ABCD 的一角折叠,折痕为AE ,∠BAD 比∠BAE 大48°。
设∠BAE 和∠BAD 的度数分别为x ,y ,那麽x ,y 所适合的方程组是( ) BC DA EA ⎩⎨⎧︒=+︒=-9048x y x yB ⎩⎨⎧=︒=-x y x y 248C ⎩⎨⎧︒=+︒=-90248x y x yD ⎩⎨⎧︒=+︒=-90248x y y x 四.解答题:已知方程组⎩⎨⎧=+=+4535y ax y x 与⎩⎨⎧=+=-1552by x y x 有相同的解,求a 、b 的值。
1.解关于x 、y 的方程组⎩⎨⎧=-=+872y cx by ax ,甲正确地解出⎩⎨⎧-==23y x ,乙因把c 抄错了,解得⎩⎨⎧=-=22y x ,求a,b,c 。
列方程组解应用题:1.某中学初二学生去烈士陵园扫墓,若每辆汽车坐35个学生,则有16个学生没有座位;若每辆汽车坐52个学生,则空出一辆汽车,问共有几辆汽车和多少学生?2.运往某地两批货物,第一批360t,用6节火车皮再加上15辆汽车正好装完;第二批440t,用8节火车皮加上10辆汽车正好装完,求每节火车皮和每辆汽车平均各装多少吨?2.李明家和陈刚家都从甲乙两供水点购买同样的一种桶装矿泉水,李明家第一季度从甲乙两供水点分别购买了10桶和6桶,共需花51元;陈刚家第一季度从甲乙两供水点分别购买了8桶和12桶,且在乙供水点比在甲供水点多花18元。
若只考虑价格因素,通过计算说明到哪家供水点购买这种桶装矿泉水更便宜一些?3.为了保护环境,某校环保小组成员收集废电池,第一天收集1号电池4节,5号电池5节,总重量为460克,第二天收集1号电池2节,5号电池3节,总重量为240克,试问1号电池和5号电池每节分别重多少克?29、为了提倡节约用水,自来水公司规定了如下收费标准:若每户每月用水不超过53m,则每立方米收费1.8元;若每户每月用水超过53m,则超过的部分每立方米收费2元,已知小雪家每月水费都不少于15元,则小雪家每月用水量至少是多少?30、今年春天以来,由于积雪融化,伊犁哈萨克自治州某镇遭受严重水涝灾害,群众失去家园。
民政局为解决灾民群众困难,紧急组织了一批救灾帐篷和食品准备送到灾区.已知这批物资中,帐篷和食品共680件,且帐篷比食品多200件.(1)帐篷和食品各有多少件?(2)现计划租用A、B两种货车共16辆,一次性将这批物资送到群众手中,已知A 种货车可装帐蓬40件和食品10件,B种货车可装帐篷20件和食品20件,试通过计算帮助民政局设计几种运输方案?(3)在(2)条件下,A种货车每辆需付运费800元,B种货车每辆需付运费720元,民政局应选择哪种方案,才能使运输费用最少?最少费用是多少?4.某商场对顾客购物实行优惠,规定:(1)一次性购物不超过100元不优惠;(2)一次性购物超过100元但不超过300元,按标价的9折优惠;(3)一次性购物超过300元的,300元内的部分按规定(2)优惠,超过300元的部分按8折优惠。
老王第一次去购物享受了9折优惠,第二次去购物享受了8折优惠。
商场告诉他:如果他一次性购买同样多的商品还可少花19元,如果商品不打折,他将比现在多花67元钱。
问老王第一次、第二次购物实际各支付了多少钱?3.甲乙二人都以不变的速度在环形路上跑步,如果同时同地出发,相向而行,每隔2分钟相遇一次;如果同向而行,每隔6分钟相遇一次。
已知甲比乙跑得快,甲、乙每分钟各跑多少圈?4.某铁路桥长1000米,一列火车从桥上通过,从上桥到离开桥共用1分钟,整列火车全在桥上的时间为40 秒钟,求火车的长度和速度。
5.某地生产一种绿色蔬菜,在市场上直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元。
当地一家农工商公司收购这种蔬菜140吨,该公司加工能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但这两种加工方式不能同时进行。
因受季节等条件限制,公司必须用15天的时间将这批蔬菜全部销售或加工完毕,为此,公司研究出了三种可行方案:方案一:将蔬菜全部进行粗加工。
方案二:尽可能多地对蔬菜进行精加工,没来得及加工的到市场直接销售。
方案三:将一部分粗加工,其余部分进行精加工,并恰好用15天完成。
你认为选择哪种方案获利最多?为什麽?17、某城市规定:出租车起步价允许行驶的最远路程为3千米,超过3千米的部分按每千米另收费.甲说:“我乘这种出租车走了11千米,付了17元”;乙说:“我乘这种出租车走了23千米,付了35元”.请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?。
