平面向量中的三角形四心问题

合集下载

平面向量与三角形四心

一、四心的概念介绍（1）重心——中线的交点：重心将中线长度分成2：1；（2）垂心——高线的交点：高线与对应边垂直；（3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等；（4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。

二、四心与向量的结合（1）OA OB OC0++=⇔O 是∆ABC 的重心.证法1：设O x y A x y B x y C x y 112233(,),(,),(,),(,)OA OB OC 0++=⇔x x x x x x y y y y y y 123123()()()0()()()0-+-+-=-+-+-=⎧⎨⎩x x x x y y y y 12312333⇔=++=++⎧⎨⎪⎪⎩⎪⎪⇔O 是∆ABC的重心. 证法2：如图++OA OB OCOA OD =+=20∴=2AO OD∴、、A O D 三点共线，且O 分AD为2：1∴O 是∆ABC 的重心（2）OA OB OB OCOC OA ⋅=⋅=⋅⇔O 为∆ABC 的垂心.证明：如图所示O 是三角形ABC 的垂心，BE 垂直AC ，AD 垂直BC ， D 、E 是垂足.OA OB OB OCOB OA OC OB CA ⋅=⋅⇔-=⋅=()0⇔⊥OB AC同理⊥OA BC ，⊥OC AB⇔O 为∆ABC 的垂心（3）设a ,b ,c 是三角形的三条边长，O 是∆ABC 的内心0++=⇔aOA bOB cOC O 为∆ABC 的内心.证明：、AB c AC b分别为、AB AC 方向上的单位向量，∴+AB c AC b平分∠BAC,D CB 平面向量与三角形四心(λ=∴AO bACc AB +)，令cb a bc++=λ∴cb a bcAO ++=（b AC c AB +) 化简得0)(=++++AC c AB b OA c b a∴0=++OC c OB b OA a（4==⇔O 为的外心。

平面向量与三角形“四心”

解题技巧与方法JIETI JIQIAO YU FANGFA 121平面向量与三角形“四心”◎胡建勋刘健( 永吉实验高中132200)平面向量是高中数学的重要工具之一，它不仅可以把几何问题转化为代数问题求解，也可以把代数问题转化为几何问题求解．它与高中数学的许多模块( 三角函数，平面解析几何，立体几何，数列，不等式等) 都有紧密联系．借助平面向量研究三角形“四心”问题更会起到意想不到的效果．本文仅从几个方面加以说明，以餐读者．一、“三角形四心”的向量表示1．三角形重心的向量表示→ → →G 是△ABC 重心 GA + GB + GC = 0 若 D ，E ，F 分别为→ → → → → →AB ，BC ，CA 中点则CG = 2 GD ( 或AG = 2 GE ，BG = 2GF ) 2．三角形外心的向量表示 →→ →O 是 △ABC 外心，==OB OC ( → →→ → →→ → →→OA + OB )·AB = ( OB + OC )·BC = ( OA + OC ) ·AC = 0．3．三角形内心的向量表示 (→ → )→ →I 是 △ABC 内心IA ·= IB ·( → → ( →→= IC·= 0．4．三角形垂心的向量表示H 是 △ABC→→ → → → →垂心 HA ·BC = HB ·AC = HC ·AB→ → → → → →HA·HB = HB·HC = HC·HA ．二、“三角形四心”相关问题 1．“三角形四心”的判定解题策略利用向量运算化简题干中的向量等式，再据“三角形四心”的向量表示判定．例，(→→)1 点 O 为 △ABC 所在平面内一点OA + OB ·→ ( → →) → ( → →) →AB = OB + OC ·BC = OA + OC ·OB = 0，则 O 是△ABC() ．A ．重心B ．外心C ．内心D ．垂心→解析设 D 为 AB→ →边中点，( OA + OB ) = 2 OD ，由→ →→ → →( OA + OB )·AB = 0，∴ OD·AB = 0，O 在 AB 垂直平分线上，同理 O 应在 BC ，AC 垂直平分线上．∴ O 是△ABC 外心．应选 B ．例 2 点 O 为△ABC 所在平面内一点，且满足→2 +OA BC → 2 = OB → 2 + AC → 2 = OC → 2 +AB →2 ，则 O 是 △ABC的( ) ． A ．重心 B ．外心 C ．内心 D ．垂心解析由→2 +→2 = → 2 +→ 2得，OABC OB AC → → → →→ → →→→ ( AC － BC ) ( AC + BC ) + ( OB － OA ) ( OB + OA ) =0， AB( → →) →( → →)AC + BC + AB OB + OA = 0．→ →2 AB·OC = 0，则 O 是△ABC 中 AB 边的高上，同理 O 应在△ABC 中 AC ，BC 边的高上， ∴O 是△ABC 垂心．应选 D ．2．“三角形四心”与动点轨迹解题策略: 探究动点经过特殊点问题，首先据题干给出的向量等式，利用向量运算化简后，结合向量运算的几何意义，判定动点轨迹特征．例 3 点 O 是△ABC 所在平面内一定点，P 是△ABC 所→ →( → → )，则 P 点轨在平面内一动点，若OP = OA + λ 迹一定通过△ABC 的() ．A ．重心B ．外心C ．内心D ．垂心( → → )解析由若+ →OP = OA + λ→→AP =→→→→分别为→，→同向的单位向λ量，AP 与∠A 平分线所在直线共线， ∴ P 过△ABC 内心，应选 C ．例 4 点 O 是△ABC 所在平面内一定点，P 是△ABC 所( → →) ( → →)在平面内一动点，若 OP － OA · AB － AC = 0，则 P 点轨迹一定通过△ABC 的A ．重心B ．外心C ．内心D ．垂心解析→ → → → → →→ →AB － AC = CB ，OP － OA = AP ，又∵ ( OP － OA )·( → →)AB － AC= 0，→ →→ →∴ AP·CB = 0，AP ⊥BC ． ∴ P 在过 A 点且垂直于 BC 的垂线上，点 P 轨迹过 △ABC 的垂心应选 D ．例 5 点 O 是△ABC 所在平面内一定点，P 是△ABC 所→ →→→，则 P 点轨迹一定通过△ABC 的() ． A ．重心 B ．外心C ．内心 D．垂心→ → →→得:解析由OA = OP + λ+→→，→ →= λ= 0．→ →∴ PA ⊥BC ．∴ P 在过 A 点且垂直于 BC 的直线上，( 转下页)数学学习与研究 2016. 9解题技巧与方法122 JIETI JIQIAO YU FANGFA数列{ n2 }和 S n 的新求法◎郑晶晶 ( 永嘉县东瓯街道办事处消防办，浙江温州 325100) 【摘要】介绍数列{ n2}和 S n的新求法．【关键词】数列; 初等数学= 4 + 4 + 4 + 4笔者在文中介绍了数列{ n2}和 S n的新求法．其很好的= 3 + 3 + 3 = 2 + 2展现了数学之美且易懂．= 1．即: T n + S n =［1 + 2 + 3 + 4 + … + ( n － 1) + n］一式: n2 = 1 + 3 + 5 + 7 + … + ( 2n － 3) + ( 2n － 1) +［1 + 2 + 3 + 4 + … + ( n － 1) + n］= 2 + 4 + 6 + 8 + … + ( 2n － 2) + 2n － n=［1 + 2 + 3 + 4 + … + ( n － 1) + n］·2 － n．+［1 + 2 + 3 + 4 + … + ( n － 1) + n］得到三式:( n2 + n) /2 = 1 + 2 + 3 + 4 + … + ( n － 1) + n +［1 + 2 + 3 + 4 + … + ( n － 1) + n］(在这里我们把等号的右边部分看作数列{ n( n + 1) /2}其+［1 + 2 + 3 + 4 + … + ( n － 1) + n］．和 T n．(上共有( n + 1)个［1 + 2 + 3 + 4 + … + ( n － 1) + n］相T n =［1 + 2 + 3 + 4 + … + ( n － 1) + n］+ 加)［1 + 2 + 3 + … + ( n － 1)］所以容易得出T n + S n =［1 + 2 + 3 + 4 + … + ( n － 1) + n］·( n + 1) + ( 1 + 2 + 3 + 4) = n·( n + 1) /2·( n + 1)+ ( 1 + 2 + 3) =［n·( n + 1)2］/2．+ ( 1 + 2) 又因为 T n为数列{ n( n + 1) /2}和，+ 1．因为 n( n + 1) /2 = ( n2 + n) /2，二式: n2 = n + n + n + … + n + n．(此处共有 n 个 n 相所以 Tn=［n( n + 1) /2 + S ］/2．加) 所以 T n + S n =［n( n + 1) /2 + S n］/2 + S n．所以所以［n( n + 1) /2 + S n］/2 + S n =［n·( n + 1)2］/2．S n = n + n + n + … + n + n．(此处共有 n 个 n 相加) 最后得出 S n = n( n + 1) ( 2n + 1) /6．= n + n + n + … + n(此处共有 n － 1 个 n － 1 相加)( 接上页)∴ P 在 BC 边高上，应过△ABC 的垂心，应选 D．→例 6 在△ABC 中，动点 M →2 －→2 →满足AC AB = 2 AM·BC，则点 M 一定通过△ABC 的( ) ．A．重心B．外心C．内心→2－→2D．垂心→ →→→解析由 AC AB = 2 AM · BC 得: ( AC － AB )→ →→→( AC + AB) = 2 AM·BC→→→→→→设 D 为 BC 中点，AC + AB = 2 AD，2 BC·AD = 2 AM·→ → →BC，BC·MD = 0．M 点应在 BC 的垂直平分线上．应选B．3．“三角形四心”的应用解题策略: 利用向量法解决有关“三角形四心”相关问题，首先确定一组基底，再根据“三角形四心”的向量表示，用向量线性运算，模的运算，向量数量积运算等简化( 经常利用正弦定理和余弦定理) 题干条件．例 7 G 是△ABC 的重心，AB，AC 的边长为 2 和 1，→→) ．∠BAC = 60°，则AG·BG等于(A．8 B．－1099C．5 －槡3 D．－5 + 槡39 9→ 1 → →解析AG = ( AB + AC)，3→ 1 →→ 1 →→BG = ( BC + BA) = ( AC － 2 AB)．3 3→ → 1 →→ 1 →→AG·BG = ( AB + AC) ×( AC － 2 AB)3 31 →2 →→→2)8= ( AC － AB·AC － 2 AB = －．9 9→例 8 O 是外接圆半径为 1 的△ABC 外心，且满足了 3 →→→→OA + 4 OB + 5 OC = 0，则OA·BC =→→→→→→解法 1 →→→OA·BC = OA ( OC － OB) = ，OA ·OC － OA ·→= →= →，OB又∵OA OB OC→→→3 OA +4 OB +5 OC = 0，∴ 9 → 2 →→→= 25 → 2OA + 12 OA·OB + 16 OB OC→→→→→→ 2 →→OA·OB = 0，3 OA + 5 OC = － 4 OB，9 OA + 30 OA·→ 2 = 16 → 2OC + 25 OC OB→ → 3 → → 3∴ OA·OC = －，∴ OA·BC = －．5 5→→解法 2 →→→→由 3 OA + 4 OB + 5 OC = 0，则以 3 OA，4 OB，5 →→OC为边可构成一个边长为3，4，5 的三角形，OA ·BC =→·→cos ∠AOC －→·→cos ∠AOB = cos OA OC OA OB∠AOC － cos∠AOB．∵ cos∠AOB = ，cos∠AOC = －3 →→ 3，∴ OA·BC = －．5 5数学学习与研究2016. 9。

平面向量中的四心问题总结

平面向量中的四心问题总结平面向量中的四心问题是数学中的一个经典问题，涉及到平面向量的几何性质和运算规律。

在平面向量中，有四个重要的“心”，重心、垂心、外心和内心。

这四个心点在平面向量的运算和几何关系中起着重要的作用，对于理解平面向量的性质和应用具有重要意义。

首先，重心是指由若干个向量确定的几何图形的中心点。

在平面向量中，如果有n个向量A1，A2，...，An，那么它们的重心G可以表示为G=(A1+A2+...+An)/n。

重心在平面向量的平移和旋转中具有重要的作用，可以帮助我们理解向量的平均位置和集中趋势。

其次，垂心是指在三角形中，从顶点到对边的垂线的交点。

在平面向量中，如果有三个向量A、B、C分别代表三角形的三个顶点，那么垂心H可以表示为H=(A+B+C)。

垂心在平面向量中可以帮助我们理解三角形的垂线性质和垂心定理，对于解决相关的几何问题具有重要的作用。

第三，外心是指在三角形中，三条中垂线的交点。

在平面向量中，如果有三个向量A、B、C分别代表三角形的三个顶点，那么外心O可以表示为O=(A+B+C)/2。

外心在平面向量中可以帮助我们理解三角形的外接圆性质和外心定理，对于解决相关的几何问题具有重要的作用。

最后，内心是指在三角形中，三条角平分线的交点。

在平面向量中，如果有三个向量A、B、C分别代表三角形的三个顶点，那么内心I可以表示为I=(aA+bB+cC)/(a+b+c)，其中a、b、c分别代表三角形的三个内角的平分线。

内心在平面向量中可以帮助我们理解三角形的内切圆性质和内心定理，对于解决相关的几何问题具有重要的作用。

总的来说，平面向量中的四心问题涉及到重心、垂心、外心和内心这四个重要的几何点，在理论研究和实际应用中都具有重要的地位。

通过对这些问题的研究和理解，可以更深入地理解平面向量的性质和应用，为解决相关的数学和几何问题提供重要的理论基础。

专题：平面向量与三角形四心问题

专题:平面向量与三角形四心问题三角形四心指的是三角形的垂心、重心、内心和外心，在高考中常常结合平面向量的知识进行考察，是高中数学的一个难点.很多学生对三角形四心总是产生混淆，面对与四心有关的问题也常常束手无策，为了解决广大学子的困扰，本文以四心的常见结论出发，借助几道经典的例题，对三角形四心问题进行系统梳理，希望能够为读者提供帮助.如果读者是在校高中生，则标注了星号的内容可作为拓展知识. 一、三角形的内心（1）定义：三角形内切圆的圆心，即三角形三条角平分线的交点（如图1）. （2）向量表示：若O 为△ABC 的内心→→→→=⋅+⋅+⋅⇔0OC c OB b OA a . （注：本文中的边a ，b ，c 分别表示BC ，AC ，AB .角A ，B ，C 分别表示BAC ∠，ABC ∠，ACB ∠.）证明：→→→→→→→→→→=+⋅++⋅+⋅⇔=⋅+⋅+⋅0)()(0AC OA c AB OA b OA a OC c OB b OA a→→→→=⋅+⋅+⋅++⇔0)(AC c AB b OA c b a →→→⋅+⋅=⋅++⇔AC c AB b AO c b a )(||||||||)(→→→→→→→⋅⋅+⋅⋅=⋅++⇔AC AC AC c AB AB AB b AO c b a)||||()(→→→→→+⋅=⋅++⇔AC ACAB ABbc AO c b a)||||(→→→→→+⋅++=⇔AC ACAB AB c b a bc AO （图1）⇔点O 在角A 的角平分线上，同理点O 也在角B 、C 的角平分线上. ⇔O 为△ABC 的内心.（3）常用性质性质1：))(||||(R AC ACAB AB∈+⋅→→→→λλ所在的直线与A ∠的角平分线重合（经过内心）.证明：如图所示，||→→AB AB 表示→AB 上的单位向量，不妨记作→AD ，||→→AC AC 表示→AC 上的单位向量，不妨记作→AE .设→→→+=AE AD AP ，由平行四边形法则知，四边形ADPE 为菱形，故直线AP 为A ∠的角平分线.))(||||(RAC ACAB AB∈+⋅∴→→→→λλ所在的直线与A ∠的角平分线重合（经过内心）.性质2：r c b a S ABC ⋅++=∆)(21（r △ABC 内切圆的半径）. 证明：由等面积法易证.性质3：O 为△ABC 的内心c b a S S S OAB OAC OBC ::::=⇔∆∆∆. 证明：由面积公式易证. （4）典例剖析例1-1：在△ABC 中，O 为平面内一个定点，动点P 满足)||||(→→→→→→++=AC ACAB ABOA OP λ,),0(+∞∈λ.则动点P 的轨迹经过△ABC 的（）A .内心B .外心C .垂心D .重心解析：由性质1知，答案为A .例1-2：已知O 是△ABC 所在平面上的一点，若cb a PCc PB b PA a PO ++++=→→→→（其中P 是△ABC 所在平面内任意一点），则O 是△ABC 的（）A .内心B .外心C .垂心D .重心解析：由题意知→→→→→→++=++PC c PB b PA a PO c PO b aPO ，即+-→→)(PO PA a→→→→→=-+-0)()(PO PC c PO PB b ，化简得→→→→=⋅+⋅+⋅0OC c OB b OA a .根据内心的向量表示知，O 是△ABC 的内心，答案为A .例1-3：已知O 是△ABC 内的一点，且满足0)||||(=-⋅→→→→→AC ACAB ABOA ，则OA 所在的直线一定经过三角形的（）A .内心B .外心C .垂心D .重心解析：||→→AB AB 表示→AB 上的单位向量，不妨记作→1e ，||→→AC AC 表示→AC 上的单位向量，不妨记作→2e .故0)(21=-⋅→→→e e OA ，即→→→→⋅=⋅21e OA e OA ,即>>=<<→→→→21,,e OA e OA .∴直线OA 与A ∠的角平分线重合，故OA 所在的直线一定经过三角形的内心，答案A .二、三角形的外心（1）定义：三角形外接圆的圆心，即三角形三边中垂线的交点（如图2）. （2）向量表示：若O 为△ABC 的外心||||||→→→==⇔OC OB OA . （3）常用性质：奔驰定理*：已知O 为△ABC 内的一点（不一定为外心），则→→∆→∆→∆=⋅+⋅+⋅0OC S OB S OA S OAB OAC OBC .（该定理反之也成立）证明：不妨延长AO 到D （如下图），则（图2）=++===∆∆∆∆∆∆∆∆ACD ABD OAC OAB ACD OAC ABD OAB S S S S S S S S AD AO ABC OACOAB S S S ∆∆∆+，即→∆∆∆→+=AD S S S AO ABCOAC OAB .且根据B ，D ,C 三点共线知，→∆∆∆→∆∆∆→+++=AB S S S AC S S S AD OAC OAB OACOAC OAB OAB ，故→∆∆→∆∆→+=AB S S AC S S AO ABC OAC ABC OAB ，即)()(→→∆∆→→∆∆→-+-=-OA OB S S OA OC S S OA ABCOAC ABC OAB . →→∆→∆→∆=⋅+⋅+⋅∴0OC S OB S OA S OAB OAC OBC （反之易证）性质1*：O 为△ABC 的外心C B A S S S OAB OAC OBC 2sin :2sin :2sin ::=⇔∆.证明：如图2所示，O 为△ABC 的外心A R BOC R S OBC 2sin 212sin 2122=∠=⇔∆，B R AOC R S OAC 2sin 212sin 2122=∠=∆，C R AOB R S OAB 2sin 212sin 2122=∠=∆ C B A S S S OAB OAC OBC 2sin :2sin :2sin ::=⇔∆（R 为△ABC 外接圆半径）.性质2*：O 为△ABC 的外心→→→→=⋅+⋅+⋅⇔0)2(sin )2(sin )2(sin OC C OB B OA A . 证明：结合性质1与奔驰定理易证.（4）典例剖析例2-1：在△ABC 中，O 为平面内一个定点，动点P 满足++=→→→2OCOB OP )cos ||cos ||(CAC AC BAB AB →→→→+λ，),0(+∞∈λ.则动点P 的轨迹一定经过△ABC 的（）A .内心B .外心C .垂心D .重心解析：设线段BC 的中点为D ，故)cos ||cos ||(C AC AC BAB AB OD OP →→→→→→++=λ，即)cos ||cos ||(CAC AC BAB AB DP →→→→→+=λ,而)cos ||cos ||(CAC BC AC BAB BC AB BC DP →→→→→→→→⋅+⋅=⋅λ，即)cos ||cos ||||cos ||)cos(||||(CAC CBC AC B AB B BC AB BC DP →→→→→→→→⋅+-⋅=⋅πλ0|)|||(=+-=→→BC BC λ 即→→⊥BC DP ，故点P 在线段BC 的垂直平分线上. ∴动点P 的轨迹一定经过△ABC 的外心，答案B .例2-2：在△ABC 中，动点O 满足→→→→⋅=-BC AO AB AC 222，则点O 一定经过△ABC 的（）A .内心B .外心C .垂心D .重心解析：由题知→→→→→→⋅=+-BC AO AB AC AB AC 2))((，设D 为BC 的中点，则=⋅→→AD BC 2→→⋅BC AO 2,故0=⋅→→OD BC ,即→→⊥OD BC ，O ∴在BC 的垂直平分线上，故点O 一定经过△ABC 的外心，答案B .例2-3：已知O 为△ABC 所在平面内的一点，满足→→→→⋅=⋅BA OB AB OA ，=⋅→→BC OB→→⋅CB OC ，则O 为△ABC 的（）A .内心B .外心C .垂心D .重心解析：由→→→→⋅=⋅BA OB AB OA 知0)(=+⋅→→→OA OB AB ,即0)()(=+⋅-→→→→OA OB OA OB ，即||||→→=OA OB ,同理可得：||||→→=OC OB ，O ∴为△ABC 的外心，答案B .三、三角形的垂心（1）定义：三角形三条高的交点（如图3）.（2）向量表示：若O 为△ABC 的垂心→→→→→→⋅=⋅=⋅⇔OC OB OC OA OB OA . 证明：→→→→→→→→→→→⊥⇔=⋅=-⋅⇔⋅=⋅BC OA BC OA OB OC OA OC OA OB OA 0)(.同理→→⊥AC OB ,O AB OC ⇔⊥→→为△ABC 的垂心.（3）常用性质性质1*：O 为锐角△ABC 的垂心⇔=∆∆∆OAB OAC OBC S S S ::C B A tan :tan :tan . （图3）证明：ACDOC b BCDOC a OF b OE a S S OAC OBC ∠⋅⋅∠⋅⋅=⋅⋅=∆∆sin sin ,且在直角△BCD 和直角△ACD 中有 B BCD cos sin =∠，A ACD cos sin =∠.故BAA B B A A b B a S S OAC OBC tan tan cos sin cos sin cos cos =⋅⋅=⋅⋅=∆∆. 同理，CBS S OAB OAC tan tan =∆∆. C B A S S S OAB OAC OBC tan :tan :tan ::=∴∆∆∆，反之易证.性质2*：当O 为锐角△ABC 的垂心→→→→=⋅+⋅+⋅⇔0tan tan tan C OC B OB A OA .证明：利用性质1和“奔驰定理”易证. （4）典例剖析例3-1：在△ABC 中，O 为平面内一个定点，动点P 满足)cos ||cos ||(CAC AC BAB AB OA OP →→→→→→++=λ，),0(+∞∈λ，则动点P 的轨迹一定经过△ABC 的（）A .内心B .外心C .垂心D .重心解析：由题知)cos ||cos ||(CAC AC BAB AB AP →→→→→+=λ,得=⋅+-⋅=⋅+⋅=⋅→→→→→→→→→→→→→→)cos ||cos ||||cos ||)cos(||||()cos ||cos ||(CAC CBC AC B AB B BC AB CAC BC AC BAB BC AB BC AP πλλ0|)|||(=+-→→BC BC λ，即→→⊥BC AP .P ∴在BC 边上的高上，过垂心，答案C .例3-2：已知O 为△ABC 所在平面内的一点，且满足=+=+→→→→2222||||||||AC OB BC OA22||||→→+AB OC ,则O 是△ABC 的（）A .内心B .外心C .垂心D .重心解析：由题知2222||||||||→→→→-=-BC AC OB OA ，即=+⋅-→→→→)()(OB OA OB OA)()(→→→→+⋅-BC AC BC AC ，即0)()(=+⋅++⋅→→→→→→OB OA AB BC AC AB ,即02=⋅→→OC AB ，故→→⊥OC AB ，同理→→⊥OB AC ，→→⊥OA BC∴O 是△ABC 的垂心，答案C .例3-3：设O 是△ABC 的外心，点P 满足→→→→=++OP OC OB OA ,则P 是△ABC 的（）A .内心B .任意一点C .垂心D .重心解析：由题知→→→→→=-=+CP OC OP OB OA ，由于O 是△ABC 的外心，故→→→=+OD OB OA 2（D 为线段AB 的中点）且→→⊥AB OD ，即→→=OD CP 2，→→⊥∴AB CP ，同理→→⊥AC BP ，→→⊥BC AP ，故P 是△ABC 的垂心，答案C .四、三角形的重心（1）定义：三角形三条中线的交点（如图4）.（2）向量表示：若O 为△ABC 的重心→→→→=++⇔0OC OB OA . （3）常用性质（图4 ）性质1：若O 为△ABC 的重心ABC OBC OAC OAB S S S S ∆∆∆∆===⇔31性质2：若O 为△ABC 的重心→→=⇔AF AO 32，→→=BD BO 32，→→=CF CO 32性质3：已知),(11y x A ，),(22y x B ,),(33y x C .若O 为△ABC 的重心)3,3(321321y y y x x x O ++++⇔.（4）典例剖析例4-1：在△ABC 中，O 为平面内一个定点，动点P 满足)sin ||sin ||(CAC AC BAB AB OA OP →→→→→→++=λ，),0(+∞∈λ，则动点P 的轨迹一定经过△ABC的（）A .内心B .外心C .垂心D .重心解析：由题知)sin ||sin ||(CAC AC BAB AB AP →→→→→+=λ，其中hC AC B AB ==→→sin ||sin ||（h 表示BC 边上的高），故)(hACh AB AP →→→+=λ→=AF h λ2（F 为线段BC 的中点）. P ∴在BC 边上的中线上，故动点P 的轨迹一定经过△ABC 的重心，答案D .例4-2：在△ABC 中，O 为平面内一个定点，动点P 满足])21()1()1[(31→→→→++-+-=OC OB OA OP λλλ，R ∈λ，则动点P 的轨迹一定经过△ABC 的（）A .内心B .外心C .垂心D .重心解析：设AB 的中点为D ，故])21()1(2[31→→→++-=OC OD OP λλ，由于+-3)1(2λ1321=+λ，即点P ，C ，D 三点共线. P ∴在AB 边上的中线上，故动点P 的轨迹一定经过△ABC 的重心，答案D .例4-3：已知O 在△ABC 内，且满足→→→→=++0432OC OB OA ，现在到△ABC 内随机取一点，次点取自△OAB ，△OAC ，△OBC 的概率分别记为1P 、2P 、3P ,则（）A .321P P P ==B .123P P P >>C .321P P P >>D .312P P P >> 解析：法一：如图，延长OA ，OB ，OC 使得OA OD 2=,OB OE 3=，OC OF 4=, 故→→→→=++0OF OE OD ，即O 是△DEF 的重心，即△OED 、△ODF 、 △OEF 的面积相等，不妨令它们的面积都为1. 61=∴∆OAB S ，81=∆OAC S ，121=∆OBC S ,故321P P P >>，答案C . 法二：由“奔驰定理”知，k S OBC 2=∆，k S OAC 3=∆，kS OAB 4=∆（k 为比例系数），故321P P P >>，答案C .法三：根据三角形内心的向量表示，不妨设O 是以2k ，3k ，4k （k 为比例系数）为边长的三角形的内心，所以OBC OAC OAB S S S ∆∆∆>>,即321P P P >>，答案C .五、等腰（边）三角形的四心（1）等腰三角形等腰三角形只有顶角的角平分线与中线、高三线重合，其余的线不重合.另外，等腰三角形的四心不重合. （2）等边三角形性质1：若△ABC 为等边三角形⇔△ABC 四心合一. 性质2：若△ABC 为等边三角形⇔△ABC 三线合一. 六、欧拉线*瑞士数学家欧拉（1707~1783）于1765年在他的著作《三角形的几何学》中首次提出：（如图5）任意△ABC （非等边三角形）的垂心D 、重心E 、外心F 三点共线，即欧拉线. （图5）特别地，（如图6）当△ABC 为直角三角形时（A 为直角），垂心D 与A 重合，外心F 在BC 的中点上，欧拉线为直角△ABC 的外接圆半径（或BC 边上的中线）.（图6）性质1：在任意三角形中，垂心与重心的距离是重心与外心距离的2倍，即EF DE 2=.。

微专题平面向量痛点问题之三角形“四心”问题(解析版)

微专题平面向量痛点问题之三角形“四心”问题【题型归纳目录】题型一：重心定理题型二：内心定理题型三：外心定理题型四：垂心定理【知识点梳理】一、四心的概念介绍：(1)重心：中线的交点，重心将中线长度分成2：1．(2)内心：角平分线的交点(内切圆的圆心)，角平分线上的任意点到角两边的距离相等．(3)外心：中垂线的交点(外接圆的圆心)，外心到三角形各顶点的距离相等．(4)垂心：高线的交点，高线与对应边垂直．二、三角形四心与推论：(1)O 是△ABC 的重心：S △BOC :S △COA :S △A 0B =1:1:1⇔OA +OB +OC =0 ．(2)O 是△ABC 的内心：S △B 0C :S △COA :S △AOB =a :b :c ⇔aOA +bOB +cOC =0 ．(3)O 是△ABC 的外心：S △B 0C :S △COA :S △AOB =sin2A :sin2B :sin2C ⇔sin2AOA +sin2BOB +sin2COC =0 ．(4)O 是△ABC 的垂心：S △B 0C :S △COA :S △AOB =tan A :tan B :tan C ⇔tan AOA +tan BOB +tan COC =0 ．【方法技巧与总结】(1)内心：三角形的内心在向量AB AB +AC AC 所在的直线上. AB ⋅PC +BC ⋅PC +CA ⋅PB =0 ⇔P 为△ABC 的内心.(2)外心：PA =PB =PC ⇔P 为△ABC 的外心.(3)垂心：PA ⋅PB =PB ⋅PC =PC ⋅PA ⇔P 为△ABC 的垂心.(4)重心：PA +PB +PC =0 ⇔P 为△ABC 的重心.【典型例题】题型一：重心定理例1.(2023春·山东聊城·高一山东聊城一中校考阶段练习)已知点G 是三角形ABC 所在平面内一点，满足GA +GB +GC =0 ，则G 点是三角形ABC 的( )A.垂心B.内心C.外心D.重心【答案】D【解析】因为GA +GB +GC =0 ，所以GA +GB =-GC =CG .以GA 、GB 为邻边作平行四边形GADB ，连接GD 交AB 于点O .如图所示:则CG =GD ，所以GO =13CO ，CO 是AB 边上的中线，所以G 点是△ABC 的重心.故选：D例2.(2023春·山东·高一阶段练习)已知G 是△ABC 的重心，点D 满足BD =DC ，若GD =xAB +yAC ，则x +y 为( )A.13B.12C.23D.1【答案】A【解析】因为BD =DC ，所以D 为BC 中点，又因为G 是△ABC 的重心，所以GD =13AD ，又因为D 为BC 中点，所以AD =12AB +12AC ，所以GD =1312AB +12AC =16AB +16AC ，所以x =y =16，所以x +y =13.故选：A例3.(2023春·上海金山·高一上海市金山中学校考期末)记△ABC 内角A ,B ,C 的对边分别为a ,b ,c ，点G 是△ABC 的重心，若BG ⊥CG ,5b =6c 则cos A 的取值是( )A.5975B.5775C.1115D.6175【答案】D【解析】依题意，作出图形，因为点G 是△ABC 的重心，所以M 是BC 的中点，故AM =12AB +AC ，由已知得BC =a ,AC =b ,AB =c ，因为BG ⊥CG ，所以GM =12BC =12a ，又因为点G 是△ABC 的重心，所以GM =12GA ，则AM =12a +a =32a ，又因为AM 2=14AB +AC 2，所以94a 2=14c 2+b 2+2bc cos A ，则9a 2=c 2+b 2+2bc cos A ，又由余弦定理得a 2=c 2+b 2-2bc cos A ，所以9c 2+b 2-2bc cos A =c 2+b 2+2bc cos A ，整理得2c 2+2b 2-5bc cos A =0，因为5b =6c ，令b =6k k >0 ，则c =5k ，所以2×5k 2+2×6k 2-5×6k ×5k cos A =0，则cos A =122150=6175.故选：D .题型二：内心定理例4.(2023春·江苏宿迁·高一沭阳县修远中学校考期末)已知点P 为△ABC 的内心，∠BAC =23π,AB =1,AC =2，若AP =λAB +μAC ，则λ+μ=______．【答案】9-372【解析】在△ABC ，由余弦定理得BC =AC 2+AB 2-2AC ⋅AB cos ∠BAC =7,设O ,Q ,N 分别是边AB ,BC ,AC 上的切点，设AN =AO =x ，则NC =QC =2-x ,BO =BQ =1-x ，所以BC =BQ +QC =1-x +2-x =7⇒x =3-72，由AP =λAB +μAC 得，AP ⋅AB =λAB +μAC ⋅AB ，即AO ⋅AB =λAB 2+μAC ⋅AB ⇒AO =λ-μ，①同理由AP ⋅AC =λAB +μAC ⋅AC ⇒2AN =-λ+4μ,②联立①②以及AN =AO =x 即可解得：λ+μ=3x =3×3-72=9-372，故答案为：9-372例5.(2023春·陕西西安·高一陕西师大附中校考期中)已知O 是平面上的一个定点，A ､B ､C 是平面上不共线的三点，动点P 满足OP =OA +λAB AB +AC ACλ∈R ，则点P 的轨迹一定经过△ABC 的( )A.重心B.外心C.内心D.垂心【答案】C 【解析】因为AB AB 为AB 方向上的单位向量，AC AC 为AC 方向上的单位向量，则AB |AB |+AC |AC |的方向与∠BAC 的角平分线一致，由OP =OA +λAB AB +AC AC ，可得OP -OA =λAB AB +AC AC，即AP =λAB AB +AC AC，所以点P 的轨迹为∠BAC 的角平分线所在直线，故点P 的轨迹一定经过△ABC 的内心.故选：C .例6.(2023·全国·高一假期作业)已知I 为△ABC 所在平面上的一点，且AB =c ,AC =b ,BC =a .若aIA+bIB +cIC =0 ，则I 是△ABC 的( )A.重心B.内心C.外心D.垂心【答案】B 【解析】因为IB =IA +AB ,IC =IA +AC ，所以aIA +bIB +cIC =aIA +b IA +AB +c IA +AC =a +b +c IA +bAB +cAC =0 ，所以(a +b +c )IA =-(b ⋅AB +c ⋅AC )，所以IA =-(b ⋅AB +c ⋅AC )a +b +c =-b a +b +c ⋅AB +c a +b +c AC =-1a +b +c b ⋅AB +c ⋅AC=-bc a +b +c AB c +AC b=-bc a +b +c AB AB +AC AC ，所以IA 在角A 的平分线上，故点I 在∠BAC 的平分线上，同理可得，点I 在∠BCA 的平分线上，故点I 在△ABC 的内心，故选：B .例7.(2023春·四川成都·高一树德中学校考竞赛)在△ABC 中，cos A =34，O 为△ABC 的内心，若AO =xAB +yAC x ,y ∈R ，则x +y 的最大值为( )A.23B.6-65C.7-76D.8-227【答案】D【解析】如图：圆O 在边AB ,BC 上的切点分别为E ,F ，连接OE ,OF ，延长AO 交BC 于点D设∠OAB =θ，则cos A =cos2θ=1-2sin 2θ=34，则sin θ=24设AD =λAO =λxAB +λyAC∵B ,D ,C 三点共线，则λx +λy =1，即x +y =1λ1λ=AO AD =AO AO +OD ≤AO AO +OF =11+OF AO =11+OE AO=11+sin θ=11+24=8-227即x +y ≤8-227故选：D ．题型三：外心定理例8.(2023春·湖北武汉·高一校联考期末)在△ABC 中，AB =2,AC =3,N 是边BC 上的点，且BN =NC ,O 为△ABC 的外心，则AN ⋅AO =( )A.3B.134C.92D.94【答案】B【解析】因为BN =NC ，则N 是BC 的中点，所以AN =12AB +12AC ，设外接圆的半径为r ，所以AO ⋅AN =AO ⋅12AC +12AB =12AO ⋅AC +12AO ⋅AB =12r ×3×cos ∠OAC +12r ×2×cos ∠OAB =12×3×32+12×2×1=134．故选：B ．例9.(2023春·河南许昌·高一统考期末)已知P 在△ABC 所在平面内，满足PA =PB =PC ，则P 是△ABC 的( )A.外心B.内心C.垂心D.重心【答案】A 【解析】PA =PB =PC 表示P 到A ,B ,C 三点距离相等，P 为外心．故选：A ．例10.(2023春·四川自贡·高一统考期末)直角△ABC 中，∠C =90∘,AB =4,O 为△ABC 的外心，OA ⋅OB +OB ⋅OC +OC ⋅OA =( )A.4B.-4C.2D.-2【答案】B 【解析】∵直角△ABC 中，∠C =90°，AB =4，O 为△ABC 的外心，∴O 为AB 的中点，即OA =OB =2，∴OA +OB =0 且OA ⋅OB =|OA |⋅|OB |⋅cos180°=-4，∴OA ⋅OB +OB ⋅OC +OC ⋅OA =-4+OC ⋅(OA +OB )=-4+0=-4，故选：B ．例11.(2023春·辽宁丹东·高一凤城市第一中学校考阶段练习)已知O 为△ABC 的外心，若AB =1，则AB ⋅AO =( )A.-12B.12C.-1D.23【答案】B【解析】因为点O 为△ABC 的外心，设AB 的中点为D ，连接OD ，则OD ⊥AB ，如图所以AB ⋅AO =AB ⋅(AD +DO )=AB ⋅AD +AB ⋅DO =12AB 2+0=12×12=12.故选：B .题型四：垂心定理例12.(2023春·河南南阳·高一统考期中)若H 为△ABC 所在平面内一点，且HA 2+BC 2=HB 2+CA 2=HC 2+AB 2则点H 是△ABC 的( )A.重心B.外心C.内心D.垂心【答案】D 【解析】HA 2+BC 2=HB 2+CA 2⇒HA 2+BH +HC 2=HB 2+CH +HA 2，得BH ⋅HC =CH ⋅HA ⇒HC ⋅BA =0，即HC ⊥BA ；HA 2+BC 2=HC 2+AB 2⇒HA 2+BH +HC 2=HC 2+AH +HB 2，得BH ⋅HC =AH ⋅HB ⇒BH ⋅AC =0，即BH ⊥AC ；HB 2+CA 2=HC 2+AB 2⇒HB 2+CH +HA 2=HC 2+AH +HB 2，CH ⋅HA =AH ⋅HB ⇒HA ⋅CB =0，即HA ⊥CB ，所以H 为△ABC 的垂心.故选：D .例13.(多选题)(2023春·湖南长沙·高一长沙市明德中学校考期中)已知O ，N ，P ，I 在△ABC 所在的平面内，则下列说法正确的是( )A.若OA =OB =OC ，则O 是△ABC 的外心B.若PA ⋅PB =PB ⋅PC =PC ⋅PA ，则P 是△ABC 的垂心C.若NA +NB +NC =0，则N 是△ABC 的重心D.若CB ⋅IA =AC ⋅IB =BA ⋅IC =0，则I 是△ABC 的垂心【答案】ABCD【解析】对A ，根据外心的定义，易知A 正确；对B ，PB ⋅PA -PC =PB ⋅CA =0⇒PB ⊥CA ，同理可得：PA ⊥CB ,PC ⊥AB ，所以P 是垂心，故B 正确；对C ，记AB 、BC 、CA 的中点为D 、E 、F ，由题意NA +NB =2ND =-NC ，则|NC |=2|ND |，同理可得：|NA |=2|NE |,|NB |=2|NF |，则N 是重心，故C 正确；对D ，由题意，CB ⊥IA ,AC ⊥IB ,BA ⊥IC ，则I 是垂心，故D 正确故选：ABCD .例14.(2023春·河南商丘·高一商丘市第一高级中学校考阶段练习)设H 是△ABC 的垂心，且4HA +5HB +6HC =0 ，则cos ∠AHB =_____．【答案】-2211【解析】∵H 是△ABC 的垂心，∴HA ⊥BC ，HA ⋅BC =HA ⋅HC -HB =0，∴HA ⋅HB =HC ⋅HA ，同理可得，HB ⋅HC =HC ⋅HA ，故HA ⋅HB =HB ⋅HC =HC ⋅HA ，∵4HA +5HB +6HC =0 ，∴4HA 2+5HA ⋅HB +6HA ⋅HC =0，∴HA ⋅HB =-411HA 2，同理可求得HA ⋅HB =-12HB 2，∴cos ∠AHB =HB ⋅HA HB HA =-411HA 2HB HA ，cos ∠AHB =HB ⋅HA HB HA =-12HB 2HB HA，∴cos 2∠AHB =211，即cos ∠AHB =-2211.故答案为：-2211．【同步练习】一、单选题1.(2023·四川泸州·泸县五中校考二模)已知△ABC 的重心为O ，则向量BO =( )A.23AB +13ACB.13AB +23ACC.-23AB +13ACD.-13AB +23AC 【答案】C【解析】设E ,F ,D 分别是AC ,AB ,BC 的中点，由于O 是三角形ABC 的重心，所以BO =23BE =23×AE -AB =23×12AC -AB =-23AB +13AC .故选：C .2.(2023·全国·高三专题练习)对于给定的△ABC ，其外心为O ，重心为G ，垂心为H ，则下列结论不正确的是( )A.AO ⋅AB =12AB 2B.OA ⋅OB =OA ⋅OC =OB ⋅OCC.过点G 的直线l 交AB 、AC 于E 、F ，若AE =λAB ，AF =μAC ，则1λ+1μ=3D.AH 与ABAB cos B +AC ACcos C 共线【答案】B【解析】如图，设AB 中点为M ，则OM ⊥AB ，∴AO cos ∠OAM =AM ，∴AO ·AB =AO AB cos ∠OAB =AB AO cos ∠OAB =AB ⋅AB 2=12AB2，故A 正确；OA ·OB =OA ·OC 等价于OA ·OB -OC =0等价于OA ·CB =0，即OA ⊥BC ，对于一般三角形而言，O 是外心，OA 不一定与BC 垂直，比如直角三角形ABC 中，若B 为直角顶点，则O 为斜边AC 的中点，OA 与BC 不垂直，故B 错误；设BC 的中点为D ，则AG =23AD =13AB +AC =131λAE +1μAF =13λAE +13μAF ，∵E ，F ，G 三点共线，∴13λ+13μ=1，即1λ+1μ=3，故C 正确；AB AB cos B +AC AC cos C ⋅BC =AB ⋅BC AB cos B +AC ⋅BC AC cos C=AB BC cos π-B AB cos B +AC BC cos C AC cos C =-BC +BC =0，∴AB AB cos B +AC AC cos C与BC 垂直，又∵AH ⊥BC ，∴AB AB cos B +AC AC cos C与AH 共线，故D 正确.故选：B .3.(2023·四川·校联考模拟预测)在平行四边形ABCD 中，G 为△BCD 的重心，AG =xAB +yAD ，则3x +y =( )A.73B.2C.83D.3【答案】C【解析】如图，设AC 与BD 相交于点O ，由G 为△BCD 的重心，可得O 为BD 的中点，CG =2GO ，则AG =AO +OG =AO +13OC =43AO =43×12AB +AD =23AB +23AD ，可得x =y =23，故3x +y =83.故选：C .4.(2023秋·河南信阳·高三校考阶段练习)过△ABC 的重心任作一直线分别交AB 、AC 于点D 、E ，若AD =xAB ，AE =yAC ，且xy ≠0，则1x +1y=( )A.4B.3C.2D.1【答案】B【解析】设△ABC 的重心为点G ，延长AG 交BC 于点M ，则M 为线段BC 的中点，因为D 、G 、E 三点共线，设DG =λDE ，即AG -AD =λAE -AD ，所以，AG =1-λ AD +λAE =1-λ xAB +λyAC ，因为M 为BC 的中点，则AM =AB +BM =AB +12BC =AB +12AC -AB =12AB +12AC ，因为G 为△ABC 的重心，则AG =23AM =13AB +13AC ，所以，1-λ x =λy =13，所以，1x +1y=31-λ +3λ=3.故选：B .5.(2023秋·上海·高二专题练习)O 是平面上一定点，A 、B 、C 是该平面上不共线的3个点，一动点P 满足：OP =OA +λ(AB +AC ),λ>0，则直线AP 一定通过△ABC 的( )A.外心B.内心C.重心D.垂心【答案】C【解析】取线段BC 的中点E ，则AB +AC =2AE ．动点P 满足：OP =OA +λ(AB +AC )，λ>0，则OP -OA =2λAE 则AP =2λAE .则直线AP 一定通过△ABC 的重心．故选：C ．6.(2023秋·湖北·高二校联考期中)O 是△ABC 的外心，AB =6,AC =10，AO =xAB +yAC ,2x +10y=5，则cos ∠BAC =( )A.12B.13C.35D.13或35【答案】D【解析】当O 在AC 上，则O 为AC 的中点，x =0,y =12满足2x +10y =5，符合题意，∴AB ⊥BC ，则cos ∠BAC =AB AC =35；当O 不在AC 上，取AB ,AC 的中点D ,E ，连接OD ,OE ，则OD ⊥AB ,OE ⊥AC ，则AB ⋅AO =AB AO cos ∠OAD =AB ×AO ×AD AO =12AB 2=18，同理可得：AC ⋅AO =12AC 2=50∵AB ⋅AO =AB ⋅xAB +yAC =xAB 2+yAB ⋅AC =36x +60y cos ∠BAC =18，AC ⋅AO =AC ⋅xAB +yAC =xAC ⋅AB +yAC 2=60x cos ∠BAC +100y =50，联立可得36x +60y cos ∠BAC =1860x cos ∠BAC +100y =502x +10y =5，解得x =14y =920cos ∠BAC =13 ，故选：D .7.(2023·湖南·高考真题)P 是△ABC 所在平面上一点，若PA ⋅PB =PB ⋅PC =PC ⋅PA ，则P 是△ABC 的( )A.外心B.内心C.重心D.垂心【答案】D 【解析】因为PA ⋅PB=PB ⋅PC ，则PB ⋅PC -PA =PB ⋅AC =0，所以，PB ⊥AC ，同理可得PA ⊥BC ，PC ⊥AB ，故P 是△ABC 的垂心.故选：D .8.(2023·全国·高一专题练习)已知点O ,P 在△ABC 所在平面内，满OA +OB +OC =0 ，PA =PB=PC ，则点O ,P 依次是△ABC 的( )A.重心，外心B.内心，外心C.重心，内心D.垂心，外心【答案】A【解析】设AB 中点为D ，因为OA +OB +OC =0 ，所以OA +OB +OC =2OD +OC =0 ，即-2OD =OC ，因为OD ,OC有公共点O ，所以，O ,D ,C 三点共线，即O 在△ABC 的中线CD ，同理可得O 在△ABC 的三条中线上，即为△ABC 的重心；因为PA =PB=PC ，所以，点P 为△ABC 的外接圆圆心，即为△ABC 的外心综上，点O ,P 依次是△ABC 的重心，外心.故选：A9.(2023·全国·高一专题练习)已知O ,A ,B ,C 是平面上的4个定点，A ,B ,C 不共线，若点P 满足OP =OA +λAB +AC ，其中λ∈R ，则点P 的轨迹一定经过△ABC 的( )A.重心B.外心C.内心D.垂心【答案】A【解析】根据题意，设BC 边的中点为D ，则AB +AC =2AD ，因为点P 满足OP =OA+λAB +AC ，其中λ∈R所以，OP -OA=AP =λAB +AC =2λAD ，即AP =2λAD ，所以，点P 的轨迹为△ABC 的中线AD ，所以，点P 的轨迹一定经过△ABC 的重心.故选：A10.(2023春·安徽安庆·高一安庆一中校考阶段练习)在△ABC 中，设O 是△ABC 的外心，且AO =13AB +13AC，则∠BAC 等于( )A.30°B.45°C.60°D.90°【答案】C【解析】依题意，因为AO =13AB +13AC ，所以O 也是△ABC 的重心，又因为O 是△ABC 的外心，所以△ABC 是等边三角形，所以∠BAC =60°.11.(2023·全国·高三专题练习)在△ABC 中,AB =2,∠ACB =45°,O 是△ABC 的外心,则AC ⋅BC +OC ⋅AB的最大值为( )A.1B.32C.3D.72【答案】C【解析】解:由题知,记△ABC 的三边为a ,b ,c ,因为O 是△ABC 的外心,记AB 中点为D ,则有OD ⊥AB ,所以OD ⋅AB =0且CD =12CA +CB ,所以AC ⋅BC +OC ⋅AB =CA ⋅CB +OD +DC ⋅AB =CA ⋅CB +OD ⋅AB +DC ⋅AB =CA ⋅CB -12CA +CB ⋅AB=CA ⋅CB -12CA +CB ⋅CB -CA=CA ⋅CB +12CA 2-CB 2=b ⋅a ⋅cos ∠ACB +12b 2-a 2=122ab +b 2-a 2 ①,在△ABC 中,由余弦定理得:cos ∠ACB =a 2+b 2-c 22ab =22,即a 2+b 2-c 2=2ab ,即a 2+b 2-2=2ab ,代入①中可得:AC ⋅BC +OC ⋅AB=b 2-1,在△ABC 中,由正弦定理得:a sin A=b sin B =csin C =222=2,所以b =2sin B ≤2,所以AC ⋅BC +OC ⋅AB=b 2-1≤3,当b =2,a =c =2,A =C =45∘,B =90∘时取等,故AC ⋅BC +OC ⋅AB的最大值为3.12.(2023·全国·高三专题练习)在△ABC 中，AB =3，AC =4，BC =5，O 为△ABC 的内心，若AO=λAB +μBC ，则λ+μ=( )A.23B.34C.56D.35【答案】C【解析】由AO =λAB +μBC 得AO =λOB -OA +μOC -OB ，则1-λ OA +λ-μ OB +μOC =0，因为O 为△ABC 的内心，所以BC OA +AC OB +AB OC =0，从而1-λ :λ-μ :μ=5:4:3，解得λ=712，μ=14，所以λ+μ=56.故选：C .13.(2023秋·四川绵阳·高二四川省绵阳南山中学校考开学考试)若O ，M ，N 在△ABC 所在平面内，满足|OA |=|OB |=|OC |,MA ⋅MB =MB ⋅MC=MC ⋅MA ，且NA +NB +NC =0 ，则点O ，M ，N 依次为△ABC 的( )A.重心，外心，垂心B.重心，外心，内心C.外心，重心，垂心D.外心，垂心，重心【答案】D【解析】因为|OA |=|OB |=|OC |，所以OA =OB =OC ，所以O 为△ABC 的外心；因为MA ⋅MB =MB ⋅MC=MC ⋅MA ，所以MB ⋅(MA-MC )=0，即MB ⋅CA=0，所以MB ⊥AC ，同理可得：MA ⊥BC ，MC ⊥AB ，所以M 为△ABC 的垂心；因为NA +NB +NC =0 ，所以NA +NB =-NC ，设AB 的中点D ，则NA +NB =2ND，所以-NC =2ND，所以C ，N ，D 三点共线，即N 为△ABC 的中线CD 上的点，且NC =2ND ，所以N 为△ABC 的重心．故选：D ．14.(2023春·浙江绍兴·高二校考学业考试)已知点O ，P 在△ABC 所在平面内，且OA =OB=OC ，PA ⋅PB =PB ⋅PC =PC ⋅PA ，则点O ，P 依次是△ABC 的( )A.重心，垂心B.重心，内心C.外心，垂心D.外心，内心【答案】C【解析】由于OA =OB =OC ，所以O 是三角形ABC 的外心.由于PA ⋅PB =PB ⋅PC ，所以PA -PC ⋅PB =0,CA ⋅PB=0⇒CA ⊥PB ，同理可证得AB ⊥PC ,BC ⊥PA ，所以P 是三角形ABC 的垂心.故选：C二、多选题15.(2023春·河南·高一校联考期中)已知△ABC 的重心为O ，边AB ,BC ,CA 的中点分别为D ,E ,F ，则下列说法不正确的是( )A.OA +OB =2ODB.若△ABC 为正三角形，则OA ⋅OB +OB ⋅OC +OC ⋅OA=0C.若AO ⋅AB -AC=0，则OA ⊥BCD.OD +OE +OF =0【答案】BD【解析】对于A ，在△OAB 中，因为D 为AB 的中点，所以OD =12(OA +OB )，所以OA +OB =2OD ，所以A 正确，对于B ，因为△ABC 为正三角形，O 为△ABC 的重心，所以OA =OB =OC ，∠AOB =∠BOC =∠AOC =120°，设OA =OB =OC =a ，则OA ⋅OB +OB ⋅OC +OC ⋅OA =OA ⋅OB cos ∠AOB +OB ⋅OC cos ∠BOC +OC ⋅OAcos ∠AOC=a 2cos120°+a 2cos120°+a 2cos120°=-32a 2≠0，所以B 错误，对于C ，因为AO ⋅AB -AC =0，所以AO ⋅CB =0，所以AO ⊥CB，所以OA ⊥BC ，所以C 正确，对于D ，因为边AB ,BC ,CA 的中点分别为D ,E ,F ，所以OD =12(OA +OB )，OE =12(OB +OC )，OF =12(OA +OC)，因为O 为△ABC 的重心，所以CO =2OD ，所以2OD =-OC，所以OD +OE +OF =12(OA +OB )+12(OC +OB )+12(OA+OC )=OA +OB +OC=2OD +OC=-OC +OC =0 ，所以D 错误，故选：BD16.(2023·全国·高三专题练习)如图，M 是△ABC 所在平面内任意一点，O 是△ABC 的重心，则( )A.AD +BE =CFB.MA +MB +MC=3MOC.MA +MB +MC =MD +ME +MFD.BC ⋅AD+CA ⋅BE +AB ⋅CF =0【答案】BCD【解析】对于A 选项，由题意可知，D 、E 、F 分别为BC 、AC 、AB 的中点，所以，AD =AB +12BC =AB +12AC -AB =12AB +AC ，同理可得BE =12BA +BC ，CF =12CA +CB，所以，AD +BE =12AB +AC +12BA +BC =12AC +BC =-CF ，A 错；对于B 选项，由重心的性质可知AD =32AO ，BE =32BO ，CF =32CO，由A 选项可知，AD +BE +CF =32AO +BO +CO =0，所以，MA +MB +MC =MO +OA +MO +OB +MO +OC =3MO -AO +BO +CO =3MO ，B 对；对于C 选项，由重心的性质可知OD =12AO ，OE =12BO ，OF =12CO ，所以，MD +ME +MF=MO +OD +MO +OE +MO +OF =3MO +12AO +BO +CO=3MO ，C 对；对于D 选项，BC ⋅AD =12AC -AB ⋅AC +AB =12AC 2-AB 2，同理可得CA ⋅BE =12BA 2-BC 2 ，AB ⋅CF =12CB 2-CA 2，因此，BC ⋅AD+CA ⋅BE +AB ⋅CF =0，D 对.故选：BCD .17.(2023秋·重庆渝北·高二重庆市两江育才中学校校考阶段练习)设O 为△ABC 的外心，且满足2OA+3OB +4OC =0 ，OA=1，则下列结论中正确的是( )A.OB ⋅OC =-78B.AB =62C.∠A =2∠CD.sin ∠A =14【答案】ABC【解析】有题意可知：OA =OB =OC =1．对于A ：2OA +3OB +4OC =0 ⇒2OA =-3OB -4OC．两边同时平方得到：4OA 2=9OB 2+16OC 2+24OB ⋅OC．解得OB ⋅OC =-78，故A 正确．对于B ：2OA +3OB +4OC =0 ⇒2OA -2OB =-5OB -4OC ⇒2AB =5OB +4OC．两边再平方得到：4AB 2=25OB 2+16OC 2+40OB ⋅OC．结合A 可得：AB =62．所以B 正确．对于C ：2OA +3OB +4OC =0 ⇒3BO =2OA +4OC．两边平方得到：9BO 2=4OA 2+16OC 2+16OA OCcos ∠AOC ．解得cos ∠AOC =-1116．同理可得cos ∠AOB =14，cos ∠BOC =-78．∵∠AOB =2∠C ，∠COB =2∠A ．∴cos2∠C =14<12，所以π3<2∠C <π2，则2π3<4∠C <π，cos2∠A =-78<-22，所以3π4<2∠A <π，∵cos4∠C =2cos 22∠C -1=2×142-1=-78=cos2∠A ，2∠A =4∠C ．∴∠A =2∠C ．故C 正确；由cos2∠A =2cos 2∠A -1=-78，所以cos 2∠A =116，所以sin 2∠A =1516，所以sin ∠A =±154，显然sin ∠A =154，故D 错误．故选：ABC ．18.(2023春·安徽淮北·高一淮北师范大学附属实验中学校考阶段练习)生于瑞士的数学巨星欧拉在1765年发表的《三角形的几何学》一书中有这样一个定理：“三角形的外心、垂心和重心都在同一直线上．”这就是著名的欧拉线定理．在△ABC 中，O ，H ，G 分别是外心、垂心和重心，D 为BC 边的中点，下列四个选项中正确的是( )A.GH =2OGB.GA +GB +GC =0C.AH =2ODD.S △ABG =S △BCG =S △ACG【答案】ABCD【解析】在△ABC 中，O ，H ，G 分别是外心、垂心和重心，画出图形，如图所示．对于B 选项，根据三角形的重心性质由重心的性质可得G 为AD 的三等分点，且GA =-2GD ，又D 为BC 的中点，所以GB +GC =2GD ，所以GA +GB +GC =-2GD+GD =0 ，故选项B 正确；对于A 与C 选项，因为O 为△ABC 的外心，D 为BC 的中点，所以OD ⊥BC ，所以AH ∥OD ，∴△AHG ∽△DOG ，∴GH OG =AH OD =AGDG=2，∴GH =2OG ，AH =2OD ，故选项A ，C 正确；对于D ，过点G 作GE ⊥BC ，垂足为E ，∴△DEG ∽△DNA ，则GE AN =DG DA=13，∴△BGC 的面积为S △BGC =12×BC ×GE =12×BC ×13×AN =13S △ABC ；同理，S △AGC =S △AGB =13S △ABC ，选项D 正确.故选：ABCD19.(2023·全国·模拟预测)在△ABC 中，点D ，E 分别是BC ，AC 的中点，点O 为△ABC 内的一点，则下列结论正确的是( )A.若AO =OD ，则AO =12OB +OCB.若AO =2OD ，则OB =2EOC.若AO =3OD ，则OB =58AB +38ACD.若点O 为△ABC 的外心，BC =4，则OB ⋅BC=-4【答案】AB【解析】选项A ：因为AO =OD ，所以O 为AD 中点，由题易知AO =OD =12OB +OC ，故A 正确．选项B ：若AO =2OD ，则点O 为△ABC 的重心，(三角形重心的性质)则OB =2EO，故B 正确．选项C ：若AO =3OD ，则OB =OD +DB =14AD +12CB =14×12AB +AC +12AB -AC=58AB -38AC，故C 错误．选项D ：若点O 为△ABC 的外心，BC =4，则OD ⊥BC ，(三角形外心的性质)故OB ⋅BC =OD +DB ⋅BC =-12BC 2=-8，故D 错误．故选：AB20.(2023春·河北石家庄·高一统考期末)著名数学家欧拉提出了如下定理：三角形的外心、重心、垂心依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半，此直线被称为三角形的欧拉线，该定理被称为欧拉线定理．已知△ABC 的外心为O ，垂心为H ，重心为G ，且AB =3，AC =4，下列说法正确的是( )A.AH ⋅BC =0B.AG ⋅BC =-73 C.AO ⋅BC =72D.OH =OA +OB +OC【答案】ACD【解析】对于A 选项，由垂心的性质可知AH ⊥BC ，则AH ⋅BC=0，A 对；对于B 选项，设D 为BC 的中点，则AG =23AD，AD =AB +BD =AB +12BC =AB +12AC -AB =12AB +AC ，所以，AG =23AD =13AB +AC ，所以，AG ⋅BC =13AC +AB ⋅AC -AB =13AC 2-AB 2 =73，B错；对于C 选项，由外心的性质可知OB =OC ，则OD ⊥BC ，∴AO ⋅BC =AD +DO ⋅BC =AD ⋅BC =12AB +AC ⋅AC -AB =12AC 2-AB 2 =72，C 对；对于D 选项，由AH ⎳OD 得AH OD =AGGD=2，所以AH =2OD ，因为OD =OB +BD =OB +12BC =OB +12OC -OB =12OB +OC，所以OH -OA =AH =2OD =OB +OC ，即OH =OA +OB +OC，D 对.故选：ACD .三、填空题21.(2023秋·上海长宁·高二上海市延安中学校考期中)已知△ABC 的顶点坐标A -6,2 、B 6,4 ，设G 2,0 是△ABC 的重心，则顶点C 的坐标为_________.【答案】6,-6 【解析】设点C a ,b ，∵G (2,0)是△ABC 的重心，所以，-6+6+a 3=22+4+b 3=0，解得a =6b =-6 ，故点C 的坐标为6,-6 .故答案为：6,-6 .22.(2023秋·山西吕梁·高三统考阶段练习)设O 为△ABC 的外心，且满足2OA +3OB +4OC =0，OA=1，下列结论中正确的序号为______．①OB ⋅OC =-78；②AB =2；③∠A =2∠C ．【答案】①③【解析】由题意可知：OA =OB =OC =1．①2OA +3OB +4OC =0 ，则2OA =-3OB -4OC ，两边同时平方得到：4=9+24OB ⋅OC +16，解得：OB ⋅OC =-78，故①正确．②2OA +3OB +4OC =0 ，则2OA -2OB =-5OB -4OC ，2BA =-5OB -4OC ，两边再平方得到：4AB 2=25+16+40OB ⋅OC=6．所以|AB =62，所以②不正确．③2OA +3OB +4OC =0 ，4OC =-3OB -2OA ，两边平方得到：16=9+4+12OA ⋅OB =13+12OA OB cos ∠AOB ，cos ∠AOB =14，∠AOB ∈0,π2，同理可得：cos ∠BOC =-78，∠BOC ∈π2,π ，∠AOB =2∠C ，∠COB =2∠A ．故cos2C =14，cos2A =-78，且∠C ∈0,π4 ，∠A ∈π4,π2，cos4C =2cos 22C -1=2×14 2-1=-78=cos2A ，即∠A =2∠C ．故③正确．故答案为：①③23.(2023·河北·模拟预测)已知O 为△ABC 的外心，AC =3，BC =4，则OC ⋅AB=___________．【答案】-72【解析】如图：E ,F 分别为CB ,CA 的中点，则OE ⊥BC ,OF ⊥AC∴OC ⋅AB =OC ⋅CB -CA =OC ⋅CB -OC ⋅CA=OE +EC ⋅CB -OF +FC ⋅CA=OE ⋅CB +EC ⋅CB -OF ⋅CA -FC ⋅CA=-12|CB |2--12|CA |2 =12CA |2- CB |2 =12×9-16 =-72.故答案为：-72.24.(2023秋·上海嘉定·高二上海市嘉定区第一中学校考期中)已知A ､B ､C 为△ABC 的三个内角，有如下命题：①若△ABC 是钝角三角形，则tan A +tan B +tan C <0；②若△ABC 是锐角三角形，则cos A +cos B <sin A +sin B ；③若G ､H 分别为△ABC 的外心和垂心，且AB =1,AC =3，则HG ⋅BC =4；④在△ABC 中，若sin B =25,tan C =34，则A >C >B ，其中正确命题的序号是___________.【答案】①②③④【解析】对于①，若△ABC 是钝角三角形，由tan C =-tan (A +B )=-tan A +tan B1-tan A tan B得tan A +tan B +tan C =tan A tan B tan C <0，故①正确，对于②，若△ABC 是锐角三角形，则A +B >π2，有0<π2-B <A <π2且0<π2-A <B <π2，则cos B =sin π2-B<sin A ，同理得cos A <sin B ，故cos A +cos B <sin A +sin B ，故②正确，对于③，由HG ⋅BC =(AG -AH )⋅BC =AG ⋅(AC -AB )=12(AC 2-AB 2)=4，故③正确，对于④，若sin B =25,tan C =34，则sin C =35，sin B <sin C <22，则B <C <π4，故A >π2>C >B ，故④正确，故答案为：①②③④25.(2023秋·天津南开·高三南开大学附属中学校考开学考试)在△ABC 中，AB =3，AC =5，点N 满足BN =2NC ，点O 为△ABC 的外心，则AN ⋅AO 的值为__________.【答案】596【解析】分别取AB ,AC 的中点E ,F ，连接OE ,OF ，因为O 为△ABC 的外心，∴OE ⊥AB ,OF ⊥AC ，∴AB ⋅OE =0,AC ⋅OF =0，∵BN =2NC ，∴BN =23BC ，∴AN =AB +BN =AB +23BC =AB +23(AC -AB )=13AB +23AC ，∴AO ⋅AB =12AB +EO ⋅AB =12AB 2=92，AO ⋅AC =12AC +FO ⋅AC =12AC 2=252，∴AN ⋅AO =13AB +23AC ⋅AO =13AB ⋅AO +23AC ⋅AO =13×92+23×252=596故答案为：59626.(2023·全国·高三专题练习)已知G 为△ABC 的内心，且cos A ⋅GA +cos B ⋅GB +cos C ⋅GC =0 ，则∠A =___________．【答案】π3【解析】首先我们证明一个结论：已知O 是△ABC 所在平面上的一点，a ,b ,c 为△ABC 的三边长，若a ⋅OA +b ⋅OB +c ⋅OC =0 ,则O 是△ABC 的内心.证明:OB =OA +AB ,OC =OA +AC ,则a ⋅OA +b ⋅OB +c ⋅OC =0 ⇔(a +b +c )⋅OA +b ⋅AB +c ⋅AC =0 ,等式两边同时除以a +b +c 得，AO =bc a +b +c AB |AB |+AC |AC | ，AB |AB |表示AB 方向上的单位向量，同理AC |AC |表示AC 方向上的单位向量，则由平行四边形定则可知bc a +b +c AB |AB |+AC |AC |表示∠BAC 的角平分线方向上的向量，则AO 为∠BAC 的角平分线，同理BO 、CO 分别为∠ABC ,∠ACB 的角平分线，所以O 是△ABC 的内心.于是我们得到本题的一个结论aGA +bGB +cGC =0 ．又∵cos A ⋅GA +cos B ⋅GB +cos C ⋅GC =0 ，∴由正弦定理与题目条件可知sin A :sin B :sin C =a :b :c =cos A :cos B :cos C ．由sin A :sin B =cos A :cos B 可得sin A cos B -cos A sin B =sin (A -B )=0，可得A =B ，同理可得B =C ,C =A ，即A =B =C =π3．故答案为：π3.27.(2023·全国·高三专题练习)在△ABC 中，cos ∠BAC =13，若O 为内心，且满足AO =xAB +yAC ，则x +y 的最大值为______．【答案】3-32【解析】延长AO 交BC 于D ，设BC 与圆O 相切于点E ，AC 与圆O 相切于点F ，则OE =OF ，则OE ≤OD ，设AD =λAO =λxAB +λyAC ，因为B 、C 、D 三点共线，所以λx +λy =1，即x +y =1λ=AO AD =AO AO +OD ≤AO AO +OE =11+OE OA =11+OF OA=11+sin A 2，因为cos A =1-2sin 2A 2=13，0<A <π,0<A 2<π2，所以sin A 2=33，所以x +y ≤11+33=3-32．故答案是：3-3228.(2023·全国·高三专题练习)设I 为△ABC 的内心，若AB =2，BC =23，AC =4，则AI ⋅BC =___________【答案】6-23【解析】解法1：不难发现，△ABC 是以B 为直角顶点的直角三角形，如图，设圆I 与AB ､AC ､BC 分别相切于点D ､E ､F ，设圆I 的半径为r ，则ID =IE =IF =r ，显然四边形BDIF 是正方形，所以BD =BF =r ，从而AD =2-r ，CF =23-r ，易证AE =AD ，CE =CF ，所以AE =2-r ，CE =23-r ，故AE +CE =2+23-2r =AC =4，从而r =3-1，AD =2-r =3-3，AI ⋅BC =AI ⋅AC -AB =AI ⋅AC -AI ⋅AB =AI ⋅AC ⋅cos ∠IAC -AI ⋅AB ⋅cos ∠IAB=AE ⋅AC -AD ⋅AB =AD AC -AB =2AD =6-23.故答案为:6-23.解法2：按解法1求得△ABC 的内切圆半径r =3-1，由图可知AI在BC 上的投影即为3-1，所以AI ⋅BC =3-1 ×23=6-23.故答案为:6-23.。

平面向量与三角形的“四心”问题

平面向量与三角形的“四心”综合问题【例题精讲】例题1 已知O ，N ，P 在△ABC 所在平面内，且|OA ―→|＝|OB ―→|＝|OC ―→|，NA ―→＋NB ―→＋NC ―→＝0，且P A ―→·PB ―→＝PB ―→·PC ―→＝PC ―→·P A ―→，则点O ，N ，P 依次是△ABC 的( )A ．重心外心垂心B ．重心外心内心C ．外心重心垂心D ．外心重心内心【解析】由|OA ―→|＝|OB ―→|＝|OC ―→|知，O 为△ABC 的外心；由NA ―→＋NB ―→＋NC ―→＝0知，N 为△ABC 的重心；因为P A ―→·PB ―→＝PB ―→·PC ―→，所以(P A ―→－PC ―→)·PB ―→＝0，所以CA ―→·PB ―→＝0，所以CA ―→△PB ―→，即CA △PB ，同理AP △BC ，CP △AB ，所以P 为△ABC 的垂心，故选C.例题2 在△ABC 中，AB ＝5，AC ＝6，cos A ＝15，O 是△ABC 的内心，若OP ―→＝x OB ―→＋y OC ―→，其中x ，y △[0,1]，则动点P 的轨迹所覆盖图形的面积为( ) A.1063B ．1463C ．4 3D ．62【解析】根据向量加法的平行四边形法则可知，动点P 的轨迹是以OB ，OC 为邻边的平行四边形及其内部，其面积为△BOC 的面积的2倍．在△ABC 中，设内角A ，B ，C 所对的边分别为a ，b ，c ，由余弦定理a 2＝b 2＋c 2－2bc cos A ，得a ＝7.设△ABC 的内切圆的半径为r ，则12bc sin A ＝12(a ＋b ＋c )r ，解得r ＝263，所以S △BOC ＝12×a ×r ＝12×7×263＝763.故动点P 的轨迹所覆盖图形的面积为2S △BOC ＝1463，故选B.【知识小结】三角形“四心”的向量表示(1)在△ABC 中，若|OA ―→|＝|OB ―→|＝|OC ―→|或OA ―→2＝OB ―→2＝OC ―→2，则点O 是△ABC 的外心．(2)在△ABC 中，若GA ―→＋GB ―→＋GC ―→＝0，则点G 是△ABC 的重心．(3)对于△ABC ，O ，P 为平面内的任意两点，若OP ―→－OA ―→＝λ⎝ ⎛⎭⎪⎫AB ―→＋12BC ―→，λ△(0，＋∞)，则直线AP 过△ABC 的重心． (4)OA ―→·OB ―→＝OB ―→·OC ―→＝OC ―→·OA ―→或者|OA ―→|2＋|OB ―→|2＝|OB ―→|2＋|OC ―→|2＝|OC ―→|2＋|OA ―→|2，则点O 为三角形的垂心．(5)|BC ―→|·OA ―→＋|AC ―→|·OB ―→＋|AB ―→|·OC ―→＝0，则点O 为三角形的内心．(6)对于△ABC ，O ，P 为平面内的任意两点，若OP ―→＝OA ―→＋λ⎝ ⎛⎭⎪⎪⎫AB ―→|AB ―→|＋AC ―→|AC ―→|(λ>0)，则直线AP 过△ABC 的内心．【变式练习】1．已知O 是平面上的一定点，A ，B ，C 是平面上不共线的三个动点，若动点P 满足OP ―→＝OA ―→＋λ(AB ―→＋AC ―→)，λ△(0，＋∞)，则点P 的轨迹一定通过△ABC 的( )A ．内心B ．外心C ．重心D ．垂心【解析】选C 由原等式，得OP ―→－OA ―→＝λ(AB ―→＋AC ―→)，即AP ―→＝λ(AB ―→＋AC ―→)，根据平行四边形法则，知AB ―→＋AC ―→＝2AD ―→(D 为BC 的中点)，所以点P 的轨迹必过△ABC 的重心．故选C.2．在△ABC 中，|AB ―→|＝3，|AC ―→|＝2，AD ―→＝12AB ―→＋34AC ―→，则直线AD 通过△ABC 的( )A ．重心B ．外心C ．垂心D ．内心解析：选D △|AB ―→|＝3，|AC ―→|＝2，△12|AB ―→|＝34|AC ―→|＝32.设AE ―→＝12AB ―→，AF ―→＝34AC ―→，则|AE ―→|＝|AF ―→|.△AD ―→＝12AB ―→＋34AC ―→＝AE ―→＋AF ―→，△AD 平分△EAF ，△AD 平分△BAC ，△直线AD 通过△ABC 的内心。

平面向量中三角形四心问题

平面向量中的三角形四心问题向量是高中数学中引入的重要概念，是解决几何问题的重要工具。

本文就平面向量与三角形四心的联系做一个归纳总结。

在给出结论及证明结论的过程中，可以体现数学的对称性与推论的相互关系。

一、重心(baryce nter)三角形重心是三角形三边中线的交点。

重心到顶点的距离与重心到对边中点的距离之比为2：1。

在重心确定上，有著名的帕普斯定理。

结论1 :若G为/ ABC所在平面内一点，贝U GA • GB • GC = 6 二G是三角形的重心证明：设BC中点为D，则2GD二GB • GCGA GB GC = 6二-GA = GB GC-GA = 2GD,B 这表明，G在中线AD上同理可得G在中线BE,CF上故G为厶ABC 的重心1 一——若P为ABC所在平面内一点，贝U PG (PA，PB PC)3=G是厶ABC的重心—i - 一—(PG - PA) (PG - PB) (PG - PC) = 0证明：PG (PA PB PC)u =GA GBGC = 0二G是厶ABC的重心二、垂心(orthocenter)三角形的三条高线的交点叫做三角形的垂心。

结论3:若H为厶ABC所在平面内一点，则HA HB二HB HC二HC HA=H是厶ABC的垂心证明：HAHB 二HB HC= HB (HA-HC) = 0 二HB AC = 0= HB — AC 同理，有HA —CB,HC 一AB故H为三角形垂心2 ------ 2 ------ 2 ------ 2 -------- 2 ------ 2若H为丄ABC所在平面内一点，贝U HA BC = HB AC = HC AB =H 是ABC的垂心-- '2 ------ 2 ------ 2 2 2 ■ * ------------------------------------ 2 * 证明：由HA BC 二HB CA 得,HA (HB - HC)2二HB (HC - HA)2 =HB HC 二HC HA同理可证得，HA HB = HB HC = HC HA由结论3可知命题成立三、外心(circumcenter)三角形三条边的垂直平分线(中垂线)的相交点。

重难点专题02+平面向量痛点问题之三角形“四心”问题(四大题型)(课件)

＝2，∠BAC为钝角，M是边BC的中点，则 ⋅ =
【答案】5
【解析】如图所示，
取AB的中点E，连接OE，
因为为△ABC的外心，则 ⊥ ，
所以 ⋅ = cos < , >
= | | × 2 | | =
1
1
2
同理： ⋅ =
1
（2）是△ 的内心：△0 : △ : △ = : : ⇔ + + = 0．
（3）是△ 的外心：
△0 : △ : △ = sin2: sin2: sin2 ⇔ sin2 + sin2 + sin2 = 0．
A．1
B．
1+ 2
2
1
的最小值为（
2 −1
D．1 + 2 2
C．2
【答案】A
【解析】若是的中点，连接，
2
点G是△ 的重心，则必过，且 = 3 ，
2
1
1
由题设 = 3 = 3 + = 3 ( + )，又, , 共线，
所以 + = 3，即2 − 1 + 2 − 1 = 4，注意, ∈ (1, +∞)，
，

+ ��
sin

= || ( + ) = 2|| ，
所以点在三角形的中线上，则动点P的轨迹一定经过△ 的重心．故选：D．
典型例题
题型二：内心定理
【典例2-1】（2024·高一课时练习）已知点O是边长为 6的等边△ABC的内心，
则 + ⋅ + ＝
所以 + − 3 = 0 ，必要性成立，故选： C．

平面向量与三角形的四心

平面向量与三角形的四心一、三角形的心（在△ABC 中，内角A 、B 、C 所对的边分别为a 、b 、c ）1.三角形的外心（Circumcenter ）：三角形三条边的垂直平分线相交于一点，它是这个三角形外接圆的圆心，即外心.①外心到三顶点的距离相等，即|OA →|＝|OB →|＝|OB →|； ②外接圆半径R ＝a 2sin A ＝b 2sin B ＝c 2sin C ＝abc4S △ABC，直角三角形的外接圆半径R ＝c2（c 为斜边长）；③AO →·BC →＝12(b 2－c 2).2.三角形的内心（Incenter ）：三角形三条内角平分线交于一点，这一点到这个三角形的三边的距离相等，是这个三角形的内切圆的圆心，即内心.①内切圆半径r ＝2S △ABC a ＋b ＋c＝S △ABCp ＝(p －a )(p －b )(p －c )p ，Rr ＝abc2(a ＋b ＋c )，（其中R 为△ABC 外接圆半径，p ＝a ＋b ＋c2），直角三角形的内切圆半径r ＝a ＋b －c 2＝aba ＋b ＋c（其中c 为斜边长，a 、b 为直角边长）；② a IA →＋b IB →＋c IC →＝0→； ③ID IA ＝a b ＋c ，IE IB ＝b c ＋a ，IF IC ＝c a ＋b. 3.三角形的重心：三角形三条中线相交于一点，它是这个三角形的重心．①GD GA ＝GE GB ＝GF GC ＝12，AD ＝122b 2＋2c 2－a 2，BE ＝122c 2＋2a 2－b 2，CF ＝122a 2＋2b 2－c 2； ② S △GBC ＝S △GCA ＝S △GAB ，重心G 到三条边的距离与三条边的长成反比；③重心G 的坐标为(x 1＋x 2＋x 33，y 1＋y 2＋y 33)；④GA →+GB →+GC →＝0→； ⑤AG →·BC →＝13(b 2－c 2).4.三角形的垂心（Orthocenter ）：三角形三条高或其所在的直线的交点叫做这个三角形的垂心，锐角三角形的垂心在三角形内，直角三角形的垂心在直角顶点，钝角三角形的垂心在三角形外．BDBC二、三角形的心与向量的关系 1、三角形四心与各个顶点的关系⑴|OA →|＝|OB →|＝|OB →|； ⑵a IA →＋b IB →＋c IC →＝0→⑶GA →+GB →+GC →＝0→； ⑷HA →·HB →＝HB →·HC →＝HC →·HA → 2、轨迹经过三角形的外心、内心、重心、垂心若O 是平面ABC 内的一定点，那么⑴若OP →＝OA →＋λ (AB →+AC →) (λ∈R )，则点P 的轨迹经过△ABC 的重心； ⑵若OP →＝OA →＋λ (AB →—|AB →|＋AC →—|AC →|) (λ∈R )，则点P 的轨迹经过△ABC 的内心；⑶若OP →＝OA →＋λ (AB →—|AB →|cos B ＋AC →—|AC →|cos C ) (λ∈R )，则点P 的轨迹经过△ABC 的垂心； ⑷若OP →＝OB →＋OC →2＋λ (AB →—|AB →|cos B ＋AC →—|AC →|cos C ) (λ∈R )，则点P 的轨迹经过△ABC 的外心；⑸若AP →·AB →—|AB →|＝AP →·AC →—|AC →|，则点P 的轨迹经过△ABC 的内心. 4、当O 是△ABC 的各心时有下列结论：⑴若O 是重心，则OA →＋OB →＋OC →＝0→，反之亦然； ⑵若O 是内心，则a OA →＋b OB →＋c OC →＝0→，反之亦然；⑶若O 是外心，则sin2A OA →＋sin2B OB →＋sin2C OC →＝0→，反之亦然； ⑷若O 是垂心，则tan A OA →＋tan B OB →＋tan C OC →＝0→，反之亦然；三、三角形的重要线段及面积 1、若AD 是△ABC 的中线，则⑴AD →＝12(AB →＋AC →)；拓展，若点D 在BC 边上，BD ：DC ＝m ；n ，则AD →＝n m ＋n AB →＋m m ＋n AC →⑵AB 2＋AC 2＝2(BD 2＋AD 2)，或AD ＝122b 2＋2c 2－a 2；2、若AD 为∠A 的平分线，则⑴BD DC ＝AB AC ；⑵AD →＝ (→AB —|AB →|＋→AC—|AC →|). 3、若AD 是BC 边上的高，则AD →·BC →＝04、三角形面积S △＝12ab sin C ＝p (p －a )(p －b )(p －c )＝2R 2sin A sin B sin C ＝abc4R【练习题】1.（09海南宁夏）已知O ，N ，P 在△ABC 所在平面内，且|OA →|＝|OB →|＝|OC →|，NA →＋NB →＋NC →＝0→，且P A →·PB →＝PB →·PC →＝PC →·P A →，则点O ，N ，P 依次是△ABC 的（ C ） A. 重心、外心、垂心 B. 重心、外心、内心C. 外心、重心、垂心D. 外心、重心、内心（注：三角形的三条高线交于一点，此点为三角型的垂心）2.（2010湖北）已知△ABC 和点M 满足MA →＋MB →＋MC →＝0→．若存在实数m 使得AB →＋AC →＝m AM →成立，则m ＝ ······························································································· （ B ）A ．2B ．3C ．4D ．53.（2010全国Ⅱ）△ABC 中，点D 在AB 上，CD 平分∠ACB ．若CB →＝a →，CA →＝b →，|a →|＝1，|b →|＝2，则CD →＝ ···························································································· （ A ）A. 13a →＋23b → B. 23a →＋13b → C. 35a →＋45b → D. 45a →＋35b → 4.（2005年全国I 文科）点O 是△ABC 所在平面内的一点，满足OA →·OB →＝OB →·OC →＝OC →·OA →，则点O 是△ABC 的 ············································································· （ D ） A. 三个内角的角平分线的交点 B. 三条边的垂直平分线的交点C. 三条中线的交点D. 三条高的交点5.（2012年大纲）△ABC 中，AB 边上的高为CD ，若CB →＝a →，CA →＝b →，a →·b →＝0，|a→|＝1，|b →|＝2，则AD →＝ ··························································································· （ D ）A ．13a →－13b →B ． 23a →－23b →C ．35a →－35b →D ．45a →－45b →6.（2005年全国I 理科）△ABC 的外接圆的圆心为O ，两条边上的高的交点为H ， OH →＝m (OA →＋OB →＋OC →)，则实数m = ；【1】7. （2014全国1高考理15）已知A ，B ，C 为圆O 上的三点，若AO →＝12(AB →＋AC →)，则AB→与AC →的夹角为．【90 】8.给定直线l ：y ＝2x －16，抛物线C ：y 2＝ax （a ＞0）. ⑴当抛物线C 的焦点在直线l 上时，求抛物线的方程；⑵若△ABC 的三个顶点在⑴确定的抛物线上，且点A 的纵坐标y A ＝8，△ABC 的重心恰好时抛物线的焦点，求直线BC 的方程.【简答】⑴y 2＝32x ；⑵4x ＋y －40＝09.（北京2002年理科数学第21题）已知O (0，0)，B (1，0)，C (b ，c )是△OBC 的三个顶点.⑴写出△OBC 的重心G ，外心F ，垂心H 的坐标，并证明G 、F 、H 三点共线； ⑵当直线FH 与OB 平行时，求顶点C 的轨迹.。

高中数学平面向量与三角形的“四心”

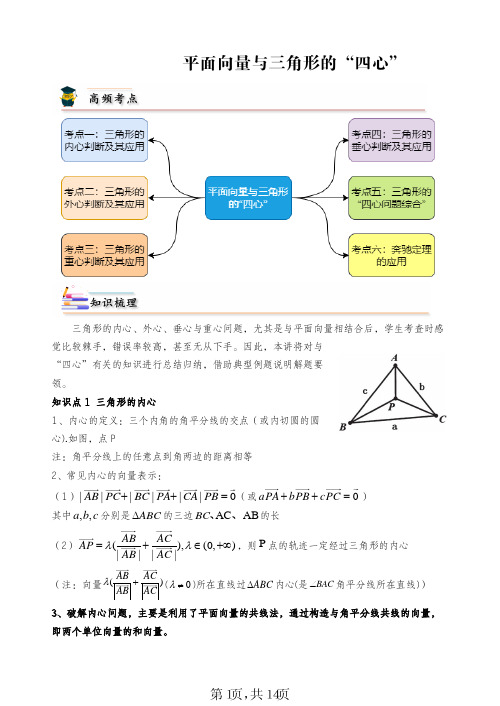
培优专题1 平面向量与三角形的“四心”三角形的内心、外心、垂心与重心问题，尤其是与平面向量相结合后，学生考查时感觉比较棘手，错误率较高，甚至无从下手。

因此，本讲将对与“四心”有关的知识进行总结归纳，借助典型例题说明解题要领。

知识点1 三角形的内心1、内心的定义：三个内角的角平分线的交点（或内切圆的圆心).如图，点P注：角平分线上的任意点到角两边的距离相等 2、常见内心的向量表示：（1）||||||0AB PC BC PA CA PB ++=（或0aPA bPB cPC ++=）其中,,a b c 分别是ABC ∆的三边AC AB BC 、、的长（2）(),(0,)||||AB ACAP AB AC λλ=+∈+∞，则P 点的轨迹一定经过三角形的内心（注：向量()AB AC ABACλ+(0λ≠)所在直线过ABC ∆内心(是BAC ∠角平分线所在直线)）3、破解内心问题，主要是利用了平面向量的共线法，通过构造与角平分线共线的向量，即两个单位向量的和向量。

拓展：是平面上一定点，，，是平面上不共线的三个点，动点满足，证明的轨迹一定通过的内心．【解析】证明：、分别表示与、方向相同的单位向量，的方向与的角平分线方向一致；又，；的方向与的角平分线方向一致，点的轨迹一定通过的内心．知识点2 三角形的外心1、外心的定义：三角形三边的垂直平分线的交点（或外接圆的圆心）注：外心到三角形各顶点的距离相等. 2、常用外心的向量表示：（1）222||||||OA OB OC OA OB OC ==⇔==（2）()()()0OA OB AB OB OC BC OA OC AC +⋅=+⋅=+⋅= 变形：P 为平面ABC 内一动点，若()()()()()()0OA OB PB PA OB OC PC PB OA OC PC PA +⋅−=+⋅−=+⋅−=，则O 为三角形的外心3、破解外心问题，关键是运用平面向量的加减法和数量积的运算，结合数量积的运算律从而得到三角形的外心。

5.4平面向量与三角形的“四心”问题

平面向量与三角形的“四心”问题
三角形“四心”的向量特征：
（1）垂心：三角形三边上的高交于一点H，这一点叫三角形的垂心。 A
HA BC=HB AC=HC AB=0 HA HB=HA HC=HB HC
uuu r uuu r uu u r uu u r AB AC 变形：（1） OP OA ( uuu uuu ), (0, ) r r AB sin B AC sin C
Ｃ
uuu r uuu r uu u r uu u r AB AC （2） OP OA ( uuu r sin C uuu r sin B), (0, ) AB AC uuu r uuu r uu u r uu u r AB AC (3)OP OA ( uuu uuu ), (0, ) r r AB cos B AC cos C uuu r uuu r uu u r uuu r AB AC （4） PB PC ( uuu uuu ), (0, ) r r AB cos B AC cos C

AI bc a b c | AB | | AC |
AB AC ) (A，B，C所对的边分别是a,b.c) (
aIA bIB cIC 0
F c

I
Da
E
b
SIBC IA SIAC IB SIAB IC 0

B
C
例1. O是平面上一定点，A、B、C是平面上不共线的三个点，
AB AC 动点P满足 OP = OA +λ ( + ), λ ∈[0,+∞). |AB| |AC|

平面向量在三角形四心中的应用

平面向量在三角形四心中的应用平面向量在三角形四心中的应用，乍一听，好像有点高深莫测，但其实它不难理解。

你要是能把三角形的四个“心”理解透了，平面向量就像一把钥匙，帮你打开这些奥秘的大门。

别看这些名字听起来很复杂，什么重心、外心、内心、垂心，一听就让人头大，其实呢，每个“心”都有它自己独特的作用。

就像你自己也是三角形的一部分一样，每个点都有自己的使命，发挥着不容忽视的作用。

咱们从最常见的“重心”说起。

重心，简单来说，就是三角形的“平衡点”。

你想象一下，拿一块三角形的纸板，想让它平稳地悬挂在一根细线上，放哪里最稳？答案就是它的重心。

这个点，其实就是通过三角形三个顶点的连线中线交汇的地方。

其实也没啥复杂的，只是每个小小的向量，通过加法的方式，帮助我们找到了这个点。

换句话说，重心就是三个顶点之间的“心机”。

如果你用向量表示每个顶点的坐标，然后通过加法“调和”，就能计算出这个“重心”的位置。

接着是“外心”。

说起外心，你可能会问：那它又是个啥？简单来说，外心就是三角形外接圆的圆心。

记住了，是外接圆！这个外接圆，就是能完美地包住三角形的那个圆。

外心的位置，基本上是通过三角形三个边的垂直平分线交点来确定的。

你试想，三个边的垂直平分线把三角形围住，那个交点就是外心。

它的位置就是用向量计算出来的，基本就是通过从每个顶点向垂直平分线投射向量，然后找交点的方式来求解。

是不是有点像数学里的“反向操作”？说实话，搞定了这个，你就等于掌握了三角形的“外面世界”。

再说说“内心”。

内心的位置，顾名思义，它就是三角形内角平分线的交点。

它就是三角形“心”的存在。

每条内角平分线把三角形的一个角分成两部分，它们交汇的地方，就是内心。

内心的位置不仅仅是由几何关系确定，还可以用向量表示。

通过向量的比值关系，我们可以计算出这个点的准确位置。

你要是能通过向量公式算出它的坐标，就能说你已掌握了三角形的“内心”奥秘！它不仅是几何的“心脏”，也是在三角形中最神秘、最让人着迷的点之一。

(完整版)平面向量与三角形四心问题

平面向量基本定理与三角形四心已知0是 ABC 内的一点，BOC, AOC, AOB 的面积分别为 S A , S B , S C ,求证:S A ?0A S B ?0B S C ?0C 00D罟0B 誥0C0DS B0D S C0D S B0D S C0D S A0AS B0AE OAS B0AS C0AS BS C0D S BS CS A ?0A S B ?0B S C ?0C 0推论o 是ABC 内的一点，且x ?0A y ?0B z ?0c 0，则S B0C : S C0A : S A0B X ： y ： z如图2延长0A 与BC 边相交于点D 则BD DCS A BD S B0D S ABD S B0DS ACD S C0DSACDS C0DS CS鱼 0B 生 0C S B S C SBS C0AoAS BS BS CS B S C0B二0C有此定理可得三角形四心向量式O是ABC的重心S BOC : S COA : S AOB 1：1：1 O A OB O C 0是SABC的内心BOC :S COA :S AOB■a:b:c a ?OA b?oB c?oC 00是ABC的外心S BOC : S COA :S AOB sin 2A:sin 2B :sin 2C sin 2A?OA sin2B ?O B sin2C ?OC 0O是ABC的垂心S BOC : S COA : S AOB tan A: tan B: tanCtan A?OA tan B?OB tan C ?OC 0tanA 竺,tanBAD CDDBtan A: tanB DB: ADS BOC : S COA DB: ADS BOC : S COA tan A:tan B同理得S COA : S AOB tan B :tanC, S BOC：S AOB tan A:tanC S BOC : S COA : S AOB tan A: tan B : tanC奔驰定理是三角形四心向量式的完美统证明：如图0为三角形的垂心,X一•知识梳理:四心的概念介绍：UUUT UUU UUU UL11T OP OA (AB AC),A .重点B .外心 C.内心 D .垂心 €( 0, +x )),则动点P 的轨迹一定通过厶ABC 的()A .内心B .重心 C.外心D .垂心4.2三角形“四心”的相关向量问题(1)重心：中线的交点，重心将中线长度分成⑵ 垂心：高线的交点，高线与对应边垂直； ⑶ 内心：角平分线的交点(内切圆的圆心)(4)外心：中垂线的交点(外接圆的圆心)与"重心”有关的向量问题1已知G 是△ ABC 所在平面上的一点，A. 重点 B .外心 C.内心2 : 1；，角平分线上的任意点到角两边的距离相，外心到三角形各顶点的距离相等。

(完整版)平面向量四心问题(最全)

近年来，对于三角形的“四心”问题的考察时有发生，尤其是和平面向量相结合来考察很普遍，难度上偏向中等，只要对于这方面的知识准备充分，就能应付自如.下面就平面向量和三角形的“四心”问题的类型题做一阐述：一、重心问题三角形“重心”是三角形三条中线的交点，所以“重心”就在中线上.例1 已知O是平面上一定点，A，B，C是平面上不共线的三个点，动点P 满足：，则P的轨迹一定通过△ABC的（）Ａ外心Ｂ内心 C 重心 D 垂心解析：如图1，以AB，AC为邻边构造平行四边形ABCD，E为对角线的交点，根据向量平行四边形法则，因为，所以，上式可化为，E在直线AP上，因为AE为的中线，所以选 C.点评：本题在解题的过程中将平面向量的有关运算与平行四边形的对角线互相平分及三角形重心性质等相关知识巧妙结合.二、垂心问题三角形“垂心”是三角形三条高的交点，所以“垂心”就在高线上.例2 P是△ABC所在平面上一点，若，则P是△ABC的（）.A．外心 B．内心 C．重心 D．垂心解析:由.即.则，所以P为的垂心. 故选D.点评：本题考查平面向量有关运算，及“数量积为零，则两向量所在直线垂直”、三角形垂心定义等相关知识.将三角形垂心的定义与平面向量有关运算及“数量积为零，则两向量所在直线垂直” 等相关知识巧妙结合.三、内心问题三角形“内心”是三角形三条内角平分线的交点，所以“内心”就在内角平分线线上.例3 已知P是△ABC所在平面内的一动点，且点P满足，则动点P一定过△ABC的〔〕.A、重心B、垂心C、外心 D、内心解析：如图2所示，因为是向量的单位向量设与方向上的单位向量分别为，又，则原式可化为，由菱形的基本性质知AP平分，那么在中，AP平分，则知选B.点评：这道题给人的印象当然是“新颖、陌生”，首先是什么？想想一个非零向量除以它的模不就是单位向量？此题所用的都必须是简单的基本知识，如向量的加减法、向量的基本定理、菱形的基本性质、角平分线的性质等，若十分熟悉，又能迅速地将它们迁移到一起，这道题就迎刃而解了.四、外心问题三角形“外心”是三角形三条边的垂直平分线的交点，所以“外心”就在垂直平分线线上.例4 已知O 是△ABC 内的一点，若，则O 是△ABC 的〔〕.A ．重心 B.垂心 C.外心 D.内心解析：，由向量模的定义知到的三顶点距离相等.故是的外心，选C.点评：本题将平面向量模的定义与三角形外心的定义及性质等相关知识巧妙结合三角形的“四心”与平面向量向量本身是一个几何概念，具有代数形式和几何形式两种表示方法，易于数形结合，而且向量问题在进行数形结合时具有新形式、新特点，因此可称为高中数学的一个交汇点。

妙用三角形“四心”的性质解答向量问题

四、妙用三角形垂心的性质
三角形的垂心是三角形三条边上的高的交点.其
性质有：（1）若 O、H 分别为 △ABC 的外心和垂心，则
O∠AB∙AOOB==∠OHB∙AOCC，=∠OACB∙OHA=.∠在O解BC答，向∠量BC问O题= ∠时H，C可A ；以（根2）
据三角形垂心的定义推断出垂心的位置，也可以通过关系式 OA∙OB = OB∙OC = OC∙OA 来判定三角形的垂
意确定三角形的外心，然后根据题意明确外心与三角
形三个顶点、三个角之间的关系，灵活运用三角形外
心的性质来解题.
共
例 2. 线的
已知 O 是平三点. 若动
面内一点点P满
，A,B,C 是平足 OP = OB
面内不
+ 2
O C
+
| | | | æ
λçç è
ABAcBos B +
ACAcCos
C
ö ÷ ÷ ø
三角形边的AB距C离的相外等心，，则都等aO于A 内+ b切OB圆 +的cO半C径= 0；（；（3）4）若∠OBO为C三=
90°+
∠
A 2
，∠BOA
=90°+
∠
C 2
，∠AOC
=90°+
∠
B 2
.在解
答向量问题时，需根据三角形内心的定义确定内心的
位置及其与三条角平分线之间的关系，便可根据三角
形内心的性质来解题.
，λμ A=P45=.m
AD
，
∴
AD
=
λ m
AB
+
μ m
AC
，
∵

平面向量与三角形四心关系

平面向量与三角形四心在向量问题中经常出现形如0=++→→→OC r OB n OA m 的式子（其实它是OP m OA n OB →→→=+的一个升级版），对此类式子的几何意义做如下解释：若O 为ABC ∆内一点，则m n r S S S OC r OB n OA m OBC OAC OAB ::::0=⇔=++∆∆∆→→→证明如下(几何法更易理解)：第一步：作出：OE m OA →→=,OF n OB→→=三角形面积1sin 2OEF S OE OF AOB ∆=⋅⋅∠1sin 2OAB mOA nOB AOB mnS ∆=⋅⋅∠= 又12OEF OEGFOGF S S S ∆∆==第二步同理对OB,OC 同样操作得OFh OBC S npS ∆∆= 又因为OG=OH 所以OFh OGF S S ∆∆=即OAB OBC mnS npS ∆∆=所以OAB OBC S pS m∆∆= 所以原题得证，同理可推出必要性由此性质从面积比例出发推出四心与向量的关系列表如下 1:若O 为ABC ∆的重心，则ABC OBCOAC OAB S S S S ∆∆∆∆===31，OA OB OC →→→→++=证明：如图ABC ∆，O 为重心，故OC OD 31=。

分别过C O ,作AB 的垂线，21,h h ，则3121==OC OD h h ，所以ABC OAB S S 31=。

同理可证ABC OAC S S 31=，ABCOBC S S 31= 2:若O 为ABC ∆的垂心，则A B C S S S O BC O AC O AB tan :tan :tan ::=∆∆∆，故0tan tan tan=⋅+⋅+⋅→→→OA A OB B OC C证明：如图ABC ∆，O 为垂心，则 BE OA S OAB ⋅=21，CE OA S OAC ⋅=21因此BC CE AE AE BE CE BE S S OACOAB tan tan =⋅== 同理可证ABS S OBC OAC tan tan =。

平面向量四心问题

三角形“四心”向量形式的充要条件及其应用1.三角形的“四心”定理的平面几何证明①三角形三边的中垂线交于一点，这一点为三角形外接圆的圆心，称外心。

证明: 设AB 、BC 的中垂线交于点O ，则有OA=OB=OC ，故O 也在AC 的中垂线上，因为O 到三顶点的距离相等，故点O 是ΔABC 外接圆的圆心．因而称为外心．②三角形三边上的高交于一点，这一点叫三角形的垂心。

证明: AD 、BE 、CF 为ΔABC 三条高，过点A 、B 、C 分别作对边的平行线，相交成ΔA ′B ′C ′，AD 为B ′C ′的中垂线；同理BE 、CF 也分别为 A ′C ′、A ′B ′的中垂线，由外心定理，它们交于一点，命题得证．③三角形三边中线交于一点，这一点叫三角形的重心。

设中线BE,CF 交于点(G 证明,连同一法):结EF, 则EF//BC,且EF:BC=FG:GC=EG:GB=1:2.' 同理中线AD,BE 交于G ,连结DE,则:'''''DE//AB,且EG :G B=DG :G A=DE:AB=1:2,故G,G 重合.④三角形三内角平分线交于一点，这一点为三角形内切圆的圆心，称内心。

证明 : 设∠A 、∠C 的平分线相交于I,过I 作ID ⊥BC ，IE ⊥AC ， IF ⊥AB ，则有IE=IF=ID ．因此I 也在∠C 的平分线上，即三角形三内角平分线交于一点．2.三角形的“四心” 定理的平面向量表达式及其证明①O 是123PP P ∆的重心⇔1230OP OP OP ++=(其中,,a b c 是123PP P ∆三边) 证明：充分性1230OP OP OP ++=⇒O 是123PP P ∆的重心若1230OP OP OP ++=，则123OP OP OP +=-，以1OP ，2OP为邻边作P 12PP 3OP平行四边形132'O P P P ，设/3OP 与12P P 交于点P ，则P 为12P P 的中点，有'123OP OP OP +=，得'33OP OP =-，即'33,,,O PP P 四点共线，故3P P 为123PP P ∆的中线，同理，12,PO P O 亦为123PP P ∆的中线，所以，O 为的重心。