升力螺旋桨在桨盘上的诱导速度分布

螺旋桨基础理论分解

2-9
作用在桨叶上的力及力矩
三、螺旋桨的作用力由上面的分析可知，在给定螺旋桨的进速VA和转速n时．如能求得诱导速度ua及ut，则可根据机翼理论求出任意半径处叶元体上的作用力，进而求出整个螺旋桨的作用力。取半径r处dr 段的叶元体进行讨论，其速度多角形如图3 一10 所示。当水流以合速度VR、攻角α K流向此叶元体时，便产生了升力dL和阻力dD。将升力dL分解为沿螺旋桨轴向的分力dLa和旋转方向的分力dLt，阻力dD 相应地分解为dDa和dDt 。因此该叶元体所产生的推力dT及遭受的旋转阻力dF是：
对于有限翼展机翼，由于机翼上下表面的压差作用，下表面高压区的流体会绕过翼梢流向上表面的低压区．翼梢的横向绕流与来流的共同作用，使机翼后缘形成旋涡层。这些旋涡称为自由涡。它们在后方不远处卷成两股大旋涡而随流速V 延伸至无限远处，如图3 一8 所示。
2-7
作用在桨叶上的力及力矩
由于自由涡的存在，在空间产生一个诱导速度场。在机翼后缘处，诱导速度垂直于运动方向，故也称下洗速度。由于产生下洗速度，使机翼周围的流动图形有所改变，相当于无限远处来流速度V 发生偏转，真正的攻角发生变化，如图3 一9 所示。由于机翼处下洗速度un／2 ，使得原来流速V 改变为VR，真正的攻角由α ’k改变为α k, α ’k为三元的名义弦线攻角，α k 称为有效几何攻角。 △α =α ’k-α k称为下洗角，一般约为2º ～3º，因此可近似地2认- 8为
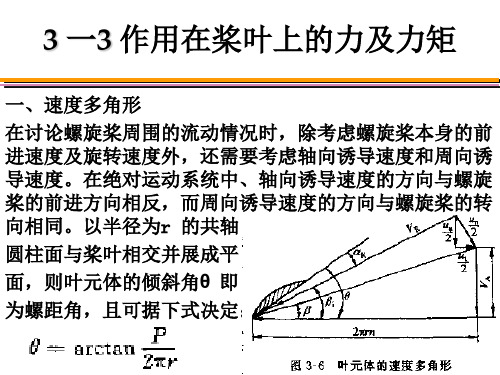
3 一3 作用在桨叶上的力及力矩
一、速度多角形在讨论螺旋桨周围的流动情况时，除考虑螺旋桨本身的前进速度及旋转速度外，还需要考虑轴向诱导速度和周向诱导速度。在绝对运动系统中、轴向诱导速度的方向与螺旋桨的前进方向相反，而周向诱导速度的方向与螺旋桨的转向相同。以半径为r 的共轴圆柱面与桨叶相交并展成平面，则叶元体的倾斜角θ 即为螺距角，且可据下式决定：

诱导速度

0 引言直升机是一种重于空气的飞行器，它依靠发动机驱动旋翼转动产生拉力而飞行。

飞行员操纵直升机改变飞行状态就是靠改变旋翼拉力的大小和方向来完成的。

从本质上讲，旋翼是一个能量转换部件，它把发动机通过旋翼轴传来的旋转动能转换成旋翼拉力。

旋翼产生拉力的同时，空气因受旋翼作用而加速向下流动，随之产生了诱导速度。

诱导速度与旋翼拉力、需用功率和飞行状态有着密切联系，因此，研究直升机的飞行问题，就应该掌握旋翼诱导速度的相关知识，结合理论与实践，解决飞行中所出现的问题，提高飞行技能和学习质量，保证任务的顺利完成。

文章将对旋翼诱导速度的产生、分布规律、直升机在轴流和斜流两种不同飞行状态下诱导速度的特点以及诱导速度在特殊状态对直升机的影响进行分析和说明。

1 诱导速度的产生、特点及分布规律1.1 诱导速度的产生、特点根据旋翼产生拉力的原理可以知道，旋翼依靠发动机带动旋转，旋翼旋转时，在桨盘上下一定范围内，空气受到旋翼作用，桨盘上面的空气压力小，下面的空气压力大，这样，处于旋翼桨盘上方的空气将从上面被吸入桨盘旋转平面，空气通过桨盘受到桨叶作用后，会一边旋转一边向下加速流动。

空气受到旋翼作用产生的向下加速流动并略带扭转的气流称为滑流。

如果不考虑滑流扭转，通常把空气受到旋翼作用向下加速流动所增加的速度叫诱导速度。

在旋翼影响范围之内的空气，被旋翼吸入之后向下流动，产生诱导速度，离旋翼越近，空气受到旋翼的吸力越大，产生的流速越大。

空气在旋翼作用下从初速度υ0= 0 开始，在桨盘平面上，诱导速度增至υ1。

通过桨盘后，空气受旋翼桨叶的排压作用，诱导速度继续增大。

这里可以假设空气是没有粘性的不可压缩的理想气体，根据不可压的一维定常流动方程：VA = C （米3/秒）其中：V ——截面处的流速（米/秒）A ——截面面积（米2）可以得知，在不可压缩的一维定常流动中，同一流管各截面上的流速与截面面积成反比，即：流速小的地方滑流截面积大，流速大的地方滑流截面积小。

船舶推进概念

1-1 推进器：在船上需设有把能源（发动机）发出的功率转换为推船前进的功率的专门的装置或机构。

1-2 快速性：指船舶在给定主机功率情况下，在一定装载下（以一定的航速航行的能力）于水中航行的快慢问题。

1-3 对快速性的要求四方面：①船舶于航行时所遭受的阻力要小，即所谓的优良线型的选择问题②选择推力足够，且效率高的推进器③选取合适的主机④推进器与船体和主机之间协调一致。

1-4 推进器类型及特点：①螺旋桨：构造简单、价格低廉、使用方便、效率较高②风帆：可利用无代价的风力，但推力依赖于风向和风力，故船的速度和操纵性能都受到限制③明轮：机构笨重，在波涛中操纵性差且易损坏④直叶推进器：操纵性能好，效率较高，汹涌海面下，工作情况也较好，但机构复杂，造价昂贵，叶片易损坏⑤喷水推进器：具有良好的保护性，操纵性能好，但减少了船的有效载重，且推进效率低⑥水力锥形推进器：构造简单，设备轻便，常用于航行在浅水及阻塞航道中的船。

1-5 有效功率（推进器所产生的实际有效功率）：船以速度 v 航行时所遭受的阻力为R，则阻力 R 在单位时间内所消耗的功为Rv，而有效推力 T e在单位时间内所作的功为T e v，两者数值相等，故 T e v（或 Rv ）为有效功率 P E。

1-6 推进系数 PC ：有效功率与主机功率之比，为多种效率相乘之综合名称，通常可以表示用某种机器及推进器以推进船舶之全面性能，推进系数越高，船舶的推进性能越好。

1-7 本课程主要研究：推进器在水中运动时产生推力的基本原理以及它的性能好坏（效率高低）等问题，然后解决如何根据实际的要求设计出一个性能优良的推进器问题。

①推进器（效率、空泡、强度、振动）②船 -桨 -机配合问题③螺旋桨设计。

2-1 螺旋桨各部分名称（通常由桨叶和桨毂构成）：①桨毂：螺旋桨与尾轴连接部分②毂帽：为减小水阻力，在桨毂后端加的整流罩，与桨毂形成一光顺流线型体③叶面及叶背：由船尾后面向前看时所见到的螺旋桨桨叶的一面为叶面，另一面为叶背④叶根：桨叶与毂连接处⑤叶梢：桨叶的外端⑥导边及随边：螺旋桨正车旋转时桨叶边缘在前面者为导边，另一边为随边⑦梢圆：螺旋桨旋转时（设无前后运动）叶梢的圆形轨迹⑧螺旋桨直径 D：梢圆的直径⑨螺旋桨的盘面积 A o：梢圆的面积⑩右（左）旋桨：当螺旋桨正车旋转时，由船后向前看去所见到的旋转方向为顺时针者为右旋桨，反之为左旋桨。

倾转旋翼飞行器飞行力学建模及验证分析

倾转旋翼飞行器飞行力学建模及验证分析鲁可;刘春生;汪正中;陈仁良【摘要】In order to improve the modeling precision of the tilt-rotor aircraft, the rotor aerodynamic force calculation model is established by using a finite-state wake model and considering the rotor flapping motion.Considered the effect of the rotor wake on the wing, a wing aerodynamic model is established.For the problem of control redundancy, a mathematical control strategy model is established for the whole flight modes.Finally, the model is verified by the generic tilt-rotor aircraft simulation (GTRS) model and flight test data.The simulation results show that the flight dynamics model has good precision and is suitable for analysis of other problems of flight dynamics.%为了进一步提高倾转旋翼飞行器的建模精度,考虑旋翼挥舞运动、采用有限状态尾迹模型描述旋翼诱导速度,进而建立旋翼气动力数学模型;考虑旋翼/机翼/干扰,建立相应气动力数学模型;针对倾转旋翼飞行器操纵冗余问题,建立了适用于全模态的操纵策略数学模型.最后以通用倾转旋翼飞行器数学模型和飞行试验数据,对建立的数学模型进行验证.仿真结果表明建立的飞行动力学模型具有良好的精度,适用于飞行动力学其他问题的分析研究.【期刊名称】《系统工程与电子技术》【年(卷),期】2017(039)004【总页数】7页(P910-916)【关键词】倾转旋翼飞行器;飞行动力学;有限状态尾迹模型;气动干扰;配平;动态响应【作者】鲁可;刘春生;汪正中;陈仁良【作者单位】南京航空航天大学自动化学院, 江苏南京 210016;中国直升机设计研究所直升机旋翼动力学重点实验室, 江西景德镇 333001;南京航空航天大学自动化学院, 江苏南京 210016;中国直升机设计研究所直升机旋翼动力学重点实验室, 江西景德镇 333001;南京航空航天大学直升机旋翼动力学国家级重点实验室, 江苏南京 210016【正文语种】中文【中图分类】V211倾转旋翼飞行器兼顾直升机和固定翼飞行器共同的优点,同时具备悬停和垂直起降性能和高速前飞的能力,在军民两用都有广阔的应用前景。

一种求解船用螺旋桨最佳径向环量分布的方法

讨论。计算结果表明，该最佳环量分布的求解方法是可行、有效和正确的。关键词：船用螺旋桨；最佳径向环量分布；升力线模型；粒子群算法
中图分类号：Ｕ６６１．３１３
文献标识码：Ａ
ｄｏｉ：１０．３９６９／ｊ．ｉｓｓｎ．１ＯＯ７ — ７２９４．２０１３．１１．００４
ＣＡＩＨａｏ－ｐｅｎｇ，ＭＡＣｈｅｎｇ，ＱＩＡＮＺｈｅｎｇ－ｆａｎｇ１，２ＣＨＥＮＫｅ，ＺＨＡＮＧＨｅ
（１ＩｎｓｔｉｔｕｔｅｏｆＮａｖａｌＡｃａｄｅｍｙｏｆＡｒｍａｍｅｎｔ，Ｂｅｉｊｉｎｇ１００１６１，Ｃｈｉｎａ；２ＮａｖａｌＵｎｉｖＷｕｈａｎ４３００３３，Ｃｈｉｎａ；
第１７卷第１ｌ期
２０１３年１１月
文章编号：１００７ — ７２９４（２０１３）１１－１２４４ — ０９
船舶力学
ＪｏｕｒｎａｌｏｆＳｈｉｐＭｅｃｈａｎｉｃｓ
Ｖ０１．１７Ｎｏ．１ｌ
Ａｍｅｔｈｏｄｔｏｄｅｔｅｒｍｉｎｅｔｈｅｏｐｔｉｍｕｍｒａｄｉａｌｃｉｒｃｕｌａｔｉｏｎ
ｄｉｓｔｒｉｂｕｔｉｏｎｏｆｔｈｅｍａｒｉｎｅｐｒｏｐｅｌｌｅｒ

船舶螺旋桨理论(第四章)

如要计算在叶面区内控制点 P(x,r,) 处的诱导速度，以uf 2、uf 3 和 u A2 A3分别表示由A2区、A3区和（A2＋A3）区的自由涡系在P点产生的诱导速度，则有
uf2uA2A3uf3
如果P点的位置处于上图的情况，全部涡系在P点的诱导速度为
w 0 u ( u b u f1 u f3 ) ( w 0 u l)
卞保琦方法中采用附着涡分布函数的定义与前面所讲的
略有不同，这里用来表示。它与前面讲的之间的关系
为：
b(r0,0)bc(r0o,sP 0()rr0 0)RP
故：
Γ(r0)ltb (r0,0)d0
b
的物理意义是把附着涡在单位圆周角内的涡强度作
为密度。
为了便于解析表达及数值计算，陈美生的计算方法把
从（4-127）式不难理解有
u f3 n (r,) R 1 Pr 1 H d Γ d ( r 0 r 0 )d r 0 t(r 0 )K f( n r,;r 0 ,0 )d0
求得 f 及α后，按式（4-188）有
s
fc(r,s) sb(2r)fscd s(sb(2r))
螺距角按（4-189）式有
计算中需要知道附着涡的弦向分布。分布的形式可由设计者选定，但须满足以下两个条件：
（1）满足附着涡的总环量的条件，即 RPltb(cr0o , 0 sP)(rr00d)0Γ(r0)
（2）随边须满足库塔条件。由薄翼理论知道，这个条件意味着随边处等于零。即
b(r0,t)0
为了进行计算，把 b(r0,0) 用解析的形式来表达。
下面介绍克尔文的方法，该方法仍采用升力线理论计算所得的
w0n )
1 WT
(ubn
uf 1n

对转螺旋桨升力面设计方法

η２— ——后桨敞水效率；
ＫＴ１＝
Ｔ１
２４
!ｎＤ１
ＫＴ２＝
Ｔ２
２４
!ｎＤ１
ＫＱ１＝
Ｑ１
２５
!ｎＤ１
ＫＴ２
ＫＱ＝ＫＱ１＋ＫＱ２
"１＝
Ｊ２#
·ＫＴ１ＫＱ１
%＝Ｊ ·ＫＴ２$ ＫＱ
３．２设计过程
"２＝
Ｊ２$
·ＫＴ２ＫＱ２
Ｊ＝ＶｎＤ１
采用上述对转桨设计程序进行设计，首先输入前后桨的主参数，先进行前桨的设计，此时后桨在
前桨桨盘面处的诱导速度ｕ２１（ｒ）设为零，前桨的进流条件即为前桨的伴流分数ｗ１（ｒ），通过对前桨的设计计算可求出前桨在后桨桨盘
面处的诱导速度ｕ１２（ｒ），将其作为前桨对后桨的干扰；然后进行后桨的设计，此时后桨的
ｒ／Ｒ０．２３５０．３
０．４
Ｃ／Ｄ０．１１８００．１４１２０．１７８４
Ｔ／Ｃ０．３０８７０．２３０１０．１４８４
Ｔ／Ｄ０．０３６４０．０３２５０．０２６５
Ｆ（ｒ）－０．２３９４－０．４６８０－０．６９２０
ｗｘ（ｒ）０．４６０２０．３９８６０．３１３７
０．５０．１７７６０．０９０２０．０２２８０．８７２９０．３６３５０．６０．１９８８０．０６２６０．０１８０１．０００００．２７２１０．７０．２１４４０．０４２９０．０１３４１．０２９４０．１９２７０．８０．２２３００．０３０８０．００９６０．９５２４０．１２７３
在设计计算中，前桨和后桨均定义为右旋桨，这里建立了两个坐标系：一个是柱坐标系（ｘ，ｒ， !），与螺旋桨固定在一起，以桨叶参考线与桨轴交点为坐标原点，ｘ仍以向下游为正，以１号叶片的桨叶参考线定义 !＝０， ! 方向按右手定则定义正方向，ｒ向外为正；另一个是直角坐标系（ｘ，ｙ，ｚ），ｘ方向与柱坐标系相同，ｙ方向是竖直向上为正，ｚ方向是与ｘ，ｙ方向满足右手定则。

直升机空气动力学-涡流理论

小结：轴向
园筒涡系在桨盘处的诱导速度
ì vy = 0 当 r> r ï ï ï í kG W ï vy = 当 r< r ï 4p V1 ï ï î
径向
kG r W 2 1 r 2 + r 2 (r + r )2 vr＝( （ ) ） [ KE] 4p V1 p r + r 2rr 2rr
ì vy = 0 (r > r ) ï ï ï 式中 r 计算此处的诱速 í k G ï vy = (r < r ) ï ρ涡柱半径 ï 4p r î
第二步，沿方位角θ积分，并注意到：
ì 1 2 p [r - r cos(y - q )]d q 1 ï ï = (当 r > r ) 或 0 （当r < r ) 2 ò ï 0 l0 r ï ï 2p í 2 2 2 2 p cos( y - q )d q ï 1 2 1 r + r (r + r ) ï ＝（） [ KE] ï ò ï 0 l0 p r + r 2rr 2rr ï î 2p
不受力条件，让涡线随气流自由延伸。
流速分布与涡线形状同
步迭代计算，逐步近似直至收敛。计入了涡系形状的畸变。讨论：三类涡系的优缺点和适用性
第三节旋翼圆筒涡系
3-1 基本假定
除假定空气是无粘性、不可压缩的气体外，还假定：
气流是定常的（相当于无限多片桨叶）；桨叶环量沿半径不变（只在桨尖有尾涡逸出）；
4-1 轴向（y 向）诱导速度
4-1-1 圆筒涡面的轴向诱导速度 r 筒面上任一点 A 处的涡元 ds ，在桨盘平面上M0 (r , ) 点的轴向诱导速度为：
dq dv y = [(- l0 cos f )(- ds0 cos q ) 3 4p l - ( l0 sin f )(- ds0 sin q )