武汉理工大学专业基础实践Matlab运算与受控源电阻电路分析
MATLAB在电路分析中的应用

《MATLAB语言》课程论文MATLAB在电路分析中的应用姓名:李娜学号:专业:2010级通信工程班级:(1)班指导老师:汤全武学院:物理电气信息学院完成日期:MATLAB在电路分析中的应用(李娜 2010级通信1班)■[摘要]本文将Mat lab软件的模拟功能用于电路分析研究,以基本电路理论中典型的直流电阻电路和含有复数运算的正弦稳态电路的计算为例,详述了如何分别运用MATLAB语言编程的方法来对电路进行仿真分析和计算。
结论表明,应用这两种方法可以是复杂电路的分析和计算变得非常快捷•方便,从而为电路分析提供了一个有效的辅助工具。
[关键词]MATLAB;电路分析:模拟:正弦稳态:向量图一、问题的提出MATLAB语言结构紧凑.语句精炼,指令表达式和数字表达式非常接近,仅需儿条简单的语句,就可以完成一大审其他高级语言才能完成的任务,可大大节省编程时间,提高计算效率。
基本电路是电类专业非常重要的专业基本课,不仅为后继课程提供了深厚的理论基础,也为电路的分析计算提供了各种方法。
其中,在电路分析理论中一般将关于时间的微分方程转化为复数方程求解,在一些电路比较复杂的.方程数量多的情况下,都可以运用MATLAB程序来解决。
运用该程序不仅可以节约时间,还可以非常方便的调试电路参数,直观的观察电路中的电流.电压和功率波形。
二、应用1典型直流电阻电路的分析计算图1所示为典型的直流电阻电路,含有电压控制的受控电流源VCCS,其中,R1 二 1 Q, R2=2 Q, R3二3 Q, Us=10v, Is=15A, VCCS二,现需分析计算电流i x和电压u2U1图1 典型直流电阻电路基本电路分析的基本方法实现建立数学模型,一般是电路方程组。
然后通过求解方程组,得到各支路电压和电流。
对图1应用回路电流法,可列出如下方程组:fRllIal^R12lni2*Ri3l D3=U2US R21 Ial+R:;I XI2+R:3 ID3—U:22 [R31I D1^R32I XI2+R33I D3=U S33Rss二R2+R3, R沪也=一&, R13二R31 二-R:,R23二弘二一%Us/Us,UE, U533=-U3而11二1山一12,If二I尸15, I D3=, (Inl"Io3)整理以上方程,并写岀形如AX二BU的矩阵方程形式,可得R H Rl30 X*、厂1-Ri?Ra R33-1 0 J 二0 -RmRsi R320 1 U:0 -Rs:0 0 u30 oj JMATLA语言编程法应用MATLAB语言编程如下: CLEAR;US=1O;IS=15;R1=1;R2=2;R3=3; % 为给定元件赋值R11=R1+R2;R12=-R1;R21=-R1;R13=-R2;R31=-R2; % 为系数矩阵各元素赋值R22=R1+R3;R23二-R3;R32二-R3;R33二R2+R3;A=[RU R13 0 0;R21 R23 -1 0;R31 R33 0 1;*R2 *R2 0 0]; % 列出系数矩阵 A B二[1 -R12;0 -R22;0 -R23;0 0] ;USS二[US; IS]; % 列出系数矩阵 BX二A\B*USS; % 解岀 XU二X⑴-IS %显示要求的分量II和U2U2=2*(X(1)-X(2))程序运行结果11= , U2=202典型的正弦稳态电路的分析与计算图2所示为典型的正弦稳态电路,其中|J S =10Z-45°,VCCS = O.5|J 1, Rl = IQ, R2 = 20丄1 = 0.4///H. Cl = 1000//F, o = 1000 幺,现需分析该含源一端口在b-o端口间戴维南等效电路其中,Rn二Ri+R:,R::二R1+R3,图2 典型的正弦稳态电路图3 在b-。
武汉理工大学电路MATLAB仿真基础强化训练报告
训练目的:1.掌握Matlab基本语法结构及调试方法;2.熟悉Matlab函数调用,熟练其用于电工电子的一些计算;3.学会用Matlab/Simulink进行简单电路的仿真。
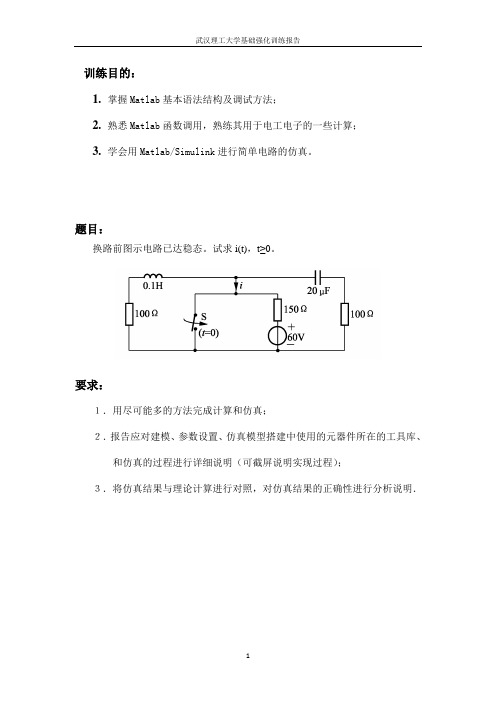
题目:换路前图示电路已达稳态。
试求i(t),t≥0。
要求:1.用尽可能多的方法完成计算和仿真;2.报告应对建模、参数设置、仿真模型搭建中使用的元器件所在的工具库、和仿真的过程进行详细说明(可截屏说明实现过程);3.将仿真结果与理论计算进行对照,对仿真结果的正确性进行分析说明.目录摘要 2 1.电路模型求解 3 1.1 初始值的求解 3 1.2 利用微分方程求解 31.3 利用拉普拉斯求解 42. 利用MATLAB计算和仿真 5 2.1 用微分方程设计程序 5 2.2 用微分方程建立仿真模型 62.3 用拉普拉斯变换设计程序 93.仿真结果与理论值的比较 104.总结与体会 115.参考文献 11摘要本次基础强化训练的问题是求一电路的零输入响应,并且通过matlab的编程计算或matlab的simulink工具箱进行仿真.我先通过基础电路当中所学的电路知识,通过两种方法进行求解:一种方法是通过微分方程求解,另一种方法是通过拉普拉斯变换及其逆变换,得到相应的零输入响应.求解电路完之后,我再利用matlab编程和matlab中的simulink工具箱进行仿真,仿真中也采用三种方法进行仿真:一种是利用微分方程设计程序计算,一种是利用微分方程进行simulink 仿真,另一种是利用拉普拉斯变换设计程序计算,得到仿真图形,与实际理论值进行比较。
关键字:simulink工具箱;微分方程;拉普拉斯变换基础强化训练论文1.电路模型求解:试求下图电路的零输入响应i(t),t≥0。
1.1初始值的求解图 1-1由图1-1,用KVL 定律,易求得 (0)(0)24c c u u V+-== 11(0)(0)0.24i i A+-==-1.2利用微分方程求解图1-2 KVL 电压与电流定律图形由KVL 电压定律,得到如下表达式:1110di L R di dt += .....................( 1 )20c c du R C u dt += ...................... ( 2 )又由于22c u R i = 代入2式得2220di R Ci dt += ...................... ( 3 )初始值:1(0)0.24i A+=- ...................... ( 4 )22(0)24(0)0.24100c u i A R ++=== .................... ( 5 )代入数值到1式和3式得到:111000di i dt =- ...................... ( 6 )22500di i dt =- ..................... ( 7 )分析电路易知:12i i i =+ .................... ( 8 )做到这一步之后,我已经基本解决了该问题,剩下的是通过高等数学的微分方程知识来求解该微分方程:从而解得微分方程得到:5001000()0.240.24t ti t e e --=- (t≥0)1.2 利用拉普拉斯变换来求解该模型:在电路中我们学习过利用拉普拉斯来求解电路响应,首先要将电路转化为拉普拉斯变换的形式,再通过相应的电路定律来求解电路.我通过电路转化,得到如下的拉普拉斯电路形式:图1-3 拉普拉斯变换电路图形同理,我利用KVL 电压定律有得到下面的拉普拉斯方程:111()(0)()0s L I s L i R Is --+= ..........................( 9 )222(0)1()()0u I s R I s sC s -++= ...........................( 10 )12()()()I s I s I s =- .........................( 11 )解得 ,66()25250002512500I s s s -=+++ ...........................( 12 )得到所需求响应的拉普拉斯形式之后,再利用拉普拉斯逆变换来求得响应的时间域响应形式,得到下面的表达式:5001000()0.240.24t ti t e e --=- (t≥0)2.电路仿真:2.1利用微分方程设计程序搭建微分方程: 111000di i dt =-22500dii dt =-12i i i =+M 程序为: i1=dsolve('Di1=-1000*i1','i1(0)=-0.24');i2=dsolve('Di2=-500*i2','i2(0)=0.24'); i0=char(i1+i2);ezplot(i0,[0,0.01])得到仿真图像为:图2-12.2利用微分方程搭建电路仿真模型有:搭建微分方程:111000 dii dt=-22500diidt=-12i i i=+图2-2 微分方程模型图Gain的参数设置为:图2-3Gain1的参数设置为:图2-4 Gain1参数设置图Step1和Step2的参数设置均为:图2-5 step参数设置图通过上面的参数设置之后,我得到了关于时间t与i(t)的图像,下面就是仿真图像:图2-6 i(t)仿真图形2.3利用拉普拉斯变换设计程序:拉普拉斯变换得到的最后结果为:2120()1500500000I s s s =++M 程序为: syms s; b=[120];a=[1,1500,500000];is=poly2sym(b,s)/poly2sym(a,s); it=ilaplace(is); ezplot(it,[0,0.01])得到图像为:图2-73.仿真结果与理论值的比较:通过1中的理论计算和2中的仿真运用,我们可以看到仿真结果与理论计算比较吻合,能够很好的反应出理论值,因此我可以认为仿真结果是正确的.不过,仿真的缺点是不能到达时间为无穷远处,只能仿真出在有限时间内的图形.同时为了能够更好的得到仿真结果与理论值的比较,我根据所求得的理论表达式得到理论图形如图2-1和图2-7。
matlab课程设计
课程设计任务书学生姓名:张华专业班级:通信1201班指导教师:刘新华工作单位:信息工程学院题目:MATLAB课程设计之利用MATLAB仿真软件系统进行图像的数据分析要求完成的主要任务:1. 利用MATLAB仿真软件系统进行图像的数据分析要求:读取图像并求出图像的最大值、最小值、均值、中值、和、标准差、两图像的协方差、相关系数等课程设计的目的:课程设计的主要目的是为了巩固课堂理论学习,并能用所学理论知识正确分析图像的数据。
时间安排:序阶段内容所需时间号1 方案设计1天2 软件设计2天3 系统调试3天4 答辩1天合计7天指导教师签名:年月日系主任(或责任教师)签字:年月日目录摘要 (III)Abstract (IV)1.Matlab简介及其在图像处理与分析的应用 (V)2.数据采集 (VI)2.1 MA TLAB的读取方法 (VI)3图像数据统计处理 (9)3.1 图像数据处理原理 (9)3.2各像素点中最大值的获取 (10)3.3各像素点中最小值 (11)3.4各像素点值的均值 (12)3.5各像素点值的中值 (13)3.6各像素点值的和 (14)3.7各像素点值的标准差 (15)3.8各像素点值的方差 (16)3.9两图中各像素点值的协方差 (17)3.10两图的相对系数 (17)心得体会 (18)参考文献 (19)附件 (20)本科生课程设计成绩评定表 (21)摘要MATLAB软件是矩阵实验室的简称,是美国MathWorks公司出品的商业数学软件,可用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,广泛用于数字信号分析,系统识别,时序分析与建模,神经网络、动态仿真等方面有着广泛的应用。
而且随着信息时代和数字世界的到来,数字信号处理也已成为当今一门极其重要的学科和技术领域。
目前数字信号处理在通信、语音、图像、自动控制、雷达、军事、航空航天、医疗和家用电器等众多领域得到了广泛的应用。
MATLAB课程设计1武汉理工

课程设计任务书学生姓名:吴桥专业班级:电信1001班指导教师:李庆工作单位:武汉理工大学题目:MATLAB应用课程设计-利用MATLAB实现多项式拟合初始条件:1.Matlab6.5以上版本软件;2.先修课程:高等数学;要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、已知数据点来自函数2()), -1x1=+f x1/(125x≤≤,根据生成的数据点进行多项式曲线拟合,绘出拟合曲线,观察拟合效果;2、画出程序设计框图,编写程序代码,上机运行调试程序,记录实验结果(含计算结果和图表等),并对实验结果进行分析和总结;3、课程设计说明书按学校统一规范来撰写,具体包括:⑴目录;⑵理论分析;⑶程序设计;⑷程序运行结果及图表分析和总结;⑸课程设计的心得体会(至少800字,必须手写。
);⑹参考文献(不少于5篇)。
时间安排:周一、周二查阅资料,了解设计内容;周三、周四程序设计,上机调试程序;周五、整理实验结果,撰写课程设计说明书。
指导教师签名:年月日系主任(或责任教师)签名:年月日摘要 (I)Abstract (II)1概述 (1)2理论分析 (3)3根据函数生成数据点 (4)3.1简介 (4)3.2 根据函数生成数据点 (4)4图形界面曲线拟合 (5)5拟合残差图形绘制 (10)5.1拟合残差图形 (10)5.2拟合结果保存 (11)6心得体会 (13)7参考文献 (15)MATLAB是一种高性能的工程计算语言。
它集计算,可视化,可编程于一体,并在一个易于使用的环境下用熟悉的数学符号解决问题。
典型用途包括数学计算,算法,开发,日期,采集,建模,仿真,可视化,科学和工程图形,包括图形界面的应用开发。
MATLAB有可以用于曲线拟合的内建函数。
MathWorks公式也提供了很多工具箱可以用于曲线拟合。
这些方法可以用来做线性或者非线性曲线拟合。
MATLAB也有一个开放的工具箱――曲线拟合工具箱(Curve Fitting Toolbox),它可以用于参数拟合,也可以用于非参数拟合。
武汉理工大学matlab课设

课程设计任务书学生姓名:专业班级:电子科学与技术1103班指导教师:娄平工作单位:信息工程学院题目: 终端开路TEM传输线中的驻波一、设计目的《MATLAB应用实践》课程是电子科学与技术专业学科实践性课程,要了解MATLAB软件的基本知识,基本的程序设计,软件在高等数学和工程数学中的应用,学会使用软件进行数值计算和控制工程中的应用。
二、设计内容和要求1、分析无损传输线中,终端开路时的电流,电压,输入阻抗。
画出电流,电压,输入阻抗的波形。
2、并将画出的图形与《电磁场与电磁波理论基础》教材上的图形进行比较。
三、时间安排1、2014年01月06日,课程设计任务布置、选题、查阅资料。
2、2014年01月07日,学习MATLAB语言的概况。
3、2014年01月08日到2014年01月09日,学习MATLAB语言的基本知识。
4、2014年01月10日到2014年01月11日,学习MATLAB语言的应用环境、调试命令,绘图功能函数和几个主要工具箱。
5、2014年01月11日到2014年01月16日,课程设计。
6、2014年01月17日,提交设计说明及答辩。
指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要 (I)1 绪论 (1)2 设计内容及要求 (2)2.1设计的目的及主要任务 (2)2.1.1设计的目的 (2)2.1.2 设计任务及主要技术指标 (2)2.2设计思路 (2)3 MATLAB软件功能简介 (3)3.1图形用户界面 (4)3.2二维函数图形绘制基本指令 (5)3.2.1 plot函数介绍 (5)3.2.2 图形修饰函数 (5)3.2.3绘制图形的形式 (6)3.2.4 axis函数介绍 (6)3.2.5 legend函数介绍 (7)3.2.6其他函数介绍 (7)4 电磁场理论知识 (8)4.1分布参数电路 (8)4.2传输线终端开路工作状态 (8)5 MATLAB程序设计 (11)6 仿真与调试 (12)7 心得体会 (14)8 参考文献 (15)附录源程序 (16)摘要随着科学技术的飞速发展,微波技术被广泛应用于工业,农业,生物医学,军事,气象探测,遥感探测,交通管理以及各种通信业务中,学科之间的相互渗透不断加剧,在其他学科中应用微波理论和技术进一步深入研究的范例不断增多,传输线作为传输电磁波的导波系统,对电磁波的传输特性能直接关系到电磁波信息能量的传送,越来越收到人们的重视,成为了很有意义的研究对象。
武大电气matlab电路仿真实验报告

实验一:直流电路1.电阻电路的计算程序:1电阻电路的计算第1题%本题选用回路法,列出的方程为Z*I=U的形式,求出回路电流,然后进一步求解Z=[ 20 -12 0; %阻抗矩阵-12 32 -12;0 -12 18];U=[10 0 0]'; %电压向量I=inv(Z)*U; %回路电路向量i3=I(1)-I(2); %求i3u4=I(2)*8; %求u4u7=I(3)*2; %求u7fprintf('(1) i3= %8.4fA\n u4= %8.4fV\n U7= %8.4fV\n',i3,u4,u7)us=10/u4*4; %根据电路线性性质,由上题的u4变化的倍数求出usUb=[us 0 0]'; %变化后的电压向量Ib=inv(Z)*Ub; %变化后的回路电流向量ib3=Ib(1)-Ib(2); %变化后的i3ub7=Ib(3)*2; %变化后的u7fprintf('(2) us= %8.4fV\n i3= %8.4fA \n U7= %8.4fV\n',us,ib3,ub7)输出结果:(1) i3= 0.3571Au4= 2.8571VU7= 0.4762V(2) us= 14.0000Vi3= 0.5000AU7= 0.6667V2、求解电路里的电压程序:%导纳矩阵AA=[ 0.6 0.125 -0.125 -0.1 0 -5 01 -1 0 0 0 0 -100 -0.125 0.325 -0.2 0 0 00 0 1 -1 0 0 5-0.1 0 -0.2 0.55 -0.25 0 00 0 0 0 1 0 01 0 0 -1 0 -1 0];%电流矩阵BB=[0 0 5 0 0 24 0]';V=inv(A)*B;fprintf('V(1)=%f V\nV(2)=%f V\nV(3)=%f V\nV(4)=%f V\nV(5)=%f V\n',V(1),V(2),V(3),V(4),V(5));输出结果:V(1)=117.479167V(2)=299.770833V(3)=193.937500V(4)=102.791667V(5)=24.0000001.求解含有受控源的电路里的电流程序:%A为阻抗方程A=[ 0 0 1 0 0 04 0 -4 12 -4 -4-4 0 0 -4 8 00 0.5 0 0 0 10 -1 0 0 1 0-1 0 0 1 0 -1];B=[2 0 0 0 0 0]';%B为电压方程I=inv(A)*B;fprintf('i1= %.0f A\ni2= %.0f A\n',I(1),I(2));输出结果:i1= 1 Ai2= 1 A实验二:直流电路(2)1.求最大功率损耗程序:A=[ 1 0-1/10000 1/10000];is=0;B=[10 is]'x 104-3V=A\B; Uoc=V(2); is=1;B=[0 is]'; V=A\B;Req=[V(2)-V(1)]/is; Pmax=Uoc.^2/(4.*Req)fprintf('The maximum power occurs at %f ¦¸\n',Req) fprintf('The maximum powerdissipation is %f W',Pmax) RL=0:50000;VL=10.*RL./(10000+RL); PL=VL.^2./RL;figure(1),plot(RL,PL),grid输出结果:The maximum power occurs at 10000.000000 ΩThe maximum powerdissipation is 0.002500 W输出图形如下则从图上可验证当RL 为10K Ω时,最大功率约为2.5×W2. 求消耗的功率程序: A=[1 0 0 0-1/5 1/5+1/2+1/20 -1/2 0 0 -1/2 1/2+1/24+1/1.2 -1/1.2 0 0 -1/1.2 1/1.2]; V1=inv(A)*[75 0 0 0]'; Uoc=V1(4); is=1;V2=inv(A)*[0 0 0 is]'; Req=V2(4)/is;RL=[0 2 4 6 10 18 24 42 90 186];REQ=[Req Req Req Req Req Req Req Req Req Req];B=REQ+RL;for i=1:1:10;UL=Uoc.*RL(i)/B(i);IL=Uoc./B(i);PL=UL.*IL;fprintf('(%2d)',i);fprintf(' RL= %6.0f ¦¸',RL(i));fprintf(' IL= %6.3f A',IL);fprintf(' UL= %6.3f V',UL);fprintf(' PL= %6.3f W\n',PL);end输出结果:( 1) RL= 0 Ω IL= 8.000 A UL= 0.000 V PL= 0.000 W ( 2) RL= 2 Ω IL= 6.000 A UL= 12.000 V PL= 72.000 W( 3) RL= 4 Ω IL= 4.800 A UL= 19.200 V PL= 92.160 W( 4) RL= 6 Ω IL= 4.000 A UL= 24.000 V PL= 96.000 W( 5) RL= 10 Ω IL= 3.000 A UL= 30.000 V PL= 90.000 W( 6) RL= 18 Ω IL= 2.000 A UL= 36.000 V PL= 72.000 W( 7) RL= 24 Ω IL= 1.600 A UL= 38.400 V PL= 61.440 W( 8) RL= 42 Ω IL= 1.000 A UL= 42.000 V PL= 42.000 W( 9) RL= 90 Ω IL= 0.500 A UL= 45.000 V PL= 22.500 W(10) RL= 186 Ω IL= 0.250 A UL= 46.500 V PL= 11.625 W 实验三:正弦稳态1.求各支路的电流相量和电压相量程序:%设置变量R1=2;R2=3;R3=4;XL=2;XC1=3;XC2=5;Us1=8;Us2=6;Us3=8;Us4=15;%求阻抗Z1=(j*XL*R1)/(j*XL+R1);Z2=R2*(-j*XC1)/[(R2-j*XC1)];Z3=R3*(-j*XC2)/(R3-j*XC2);Y1=1/Z1;Y2=1/Z2;Y3=1/Z3;%导纳矩阵YY=[Y1+Y2 -Y2-Y2 Y2+Y3];%电流矩阵II=[Us1/(j*XL)+Us2/R2902701800 Us3/R3-Us4/(j*XC2)-Us2/R2]; U=inv(Y)*I;ua=U(1),ub=U(2),I1=ua*Y1,I2=(ub-ua)*Y2,I3=-ub*Y3, I1R=ua/R1,I1L=(ua)/(j*XL), I2R=-(ua-ub)/R2,I2C=-(ua-ub)/(-j*XC1), I3R=(ub)/R3, I3C=ub/(-j*XC2),compass([ua,ub,I1,I2,I3,I1R,I1L,I2R,I2C,I3R,I3C]); 输出结果:ua = 3.7232 - 1.2732i ub = 4.8135 + 2.1420iI1 = 1.2250 - 2.4982iI2 = -0.7750 + 1.5018i I3 = -0.7750 - 1.4982i I1R = 1.8616 - 0.6366i I1L = -0.6366 - 1.8616iI2R = 0.3634 + 1.1384i I2C = -1.1384 + 0.3634i I3R = 1.2034 + 0.5355i I3C = -0.4284 + 0.9627i输出图形为:2. 含互感的电路:复功率程序: %设置变量R1=4;R2=2;R3=2;XL1=10;XL2=8;XM=4;XC=8;US=10;IS=10;Z1=R1*(-j*XC)/(R1-j*XC);Z2=j*(XL1-XM);Z3=j*XM;Z4=j*(XL2-XM)+R2;Z5=R3;Y1=1/Z1;Y2=1/Z2;Y3=1/Z3;Y4=1/Z4;Y5=1/Z5;%导纳矩阵YY=[Y1+Y2 -Y2 0-Y2 Y2+Y3+Y4 -Y40 -Y4 Y4+Y5];I=[US/R1 0 IS]';U=inv(Y)*I;ua=U(1);ub=U(2);uc=U(3);i1=(US-ua)/R1;Pus=US*conj(i1),Pis=uc*conj(IS)输出结果:Pus = -4.0488 - 9.3830iPis = 1.7506e+02 + 3.2391e+01i3.正弦稳态电路:求未知参数程序:US=100;I1=0.1;P=6;XL1=1250;XC=750;P=6;Z1=j*XL1;Z2=-j*XC;cos_a=P/(US*I1);a=acos(cos_a);I1=0.1*exp(-a*1i);UL1=I1*Z1;UC2=US-UL1;IC2=UC2/Z2;IL3=I1-IC2;ZL=UC2/IL3;IC2=UC2/Z2;IZ3=I1-IC2;Z3=UC2/IZ3R3=real(Z3)XL3=imag(Z3)输出结果:Z3 = 7.5000e+02 + 3.7500e+02iR3 = 750.0000XL3 = 375.00004.正弦稳态电路,利用模值求解程序:%变量初始化syms XL;U2=200;IR=10;XC=10;R=U2/IR;%解方程的语句f=R*XL-sqrt((XC*XL)^2+[R*(XL-XC)]^2);XL=solve(f,XL);XL1=XL(1)XL2=XL(2)输出结果:XL1 = 20*3^(1/2) + 40XL2 = 40 - 20*3^(1/2)实验四:交流分析和网络函数1.求解电流和电压程序:%本程序计算回路电流I1,I2%Z是阻抗矩阵,U是电压向量,I是电流矩阵Z=[10-7.5i -6+5i-6+5i 16+3i];Zc=-10i;U1=5;U2=-2*exp(75i*pi/180);U=[U1 U2]';I=Z\U;I1_abs=abs(I(1));I1_ang=angle(I(1))*180/pi;Ic=I(1)-I(2);Uc=Ic*Zc;Uc_abs=abs(Uc);Uc_ang=angle(Uc)*180/pi;fprintf('current I1,magnitude: %f \n current I1,angle in degree:%f\n',I1_abs,I1_ang);fprintf('voltage Uc,magnitude: %f \n voltage Uc,angle in degree:%f\n',Uc_abs,Uc_ang);运行结果:current i1,magnitude: 0.387710current i1, angle in degree: 15.019255voltage vc,magnitude: 4.218263voltage vc,angle in degree:-40.8616912.求解三相不平衡相电压程序:%U为电压矩阵,I为电流矩阵,Z为总阻抗矩阵,ZL为负载阻抗矩阵U1=110;U2=110*exp(-120i*pi/180);U3=110*exp(120i*pi/180);U=[U1 U2 U3]';Z1=[6+13i 4+2i 6-12.5i]';ZL=[5+12i 3+4i 5-12i]';I=U./Z1;Vn=I.*ZL;Vna_abs=abs(Vn(1));Vna_ang=angle(Vn(1))*180/pi;Vnb_abs=abs(Vn(2));Vnb_ang=angle(Vn(2))*180/pi;Vnc_abs=abs(Vn(3));Vnc_ang=angle(Vn(3))*180/pi;fprintf('phasor vlotage Vna,magnitude:%f \n phasor voltage Vna,angle in dgree: %f \n',Vna_abs,Vna_ang);fprintf('phasor vlotage Vnb,magnitude:%f \n phasor voltage Vnb,angle in dgree: %f \n',Vnb_abs,Vnb_ang);fprintf('phasor vlotage Vnc,magnitude:%f \n phasor voltage Vnc,angle in dgree: %f \n',Vnc_abs,Vnc_ang);运行结果:phasor vlotage Vna,magnitude:99.875532phasor voltage Vna,angle in dgree: -2.155276phasor vlotage Vnb,magnitude:122.983739phasor voltage Vnb,angle in dgree: 93.434949phasor vlotage Vnc,magnitude:103.134238phasor voltage Vnc,angle in dgree: -116.978859实验五:动态电路1.正弦激励的一阶电路程序:%变量初始化R=2;C=0.5;Uc0=4;Um=10;Ulong=Um;%作图t=0:0.01:20;time=R*C;Uct=Ulong+(Uc0-Ulong)*exp(-t/time); figure(1),plot(t,Uct),grid运行结果:2.二阶欠阻尼电路的零输入响应程序:L=0.5;R=1;C=0.02;%输入元件参数 Uc0=1;IL0=0;alpha=R/2/L;wn=sqrt(1/(L*C));%输入给定参数 p1=-alpha+sqrt(alpha^-wn^2);%方程的两个根 p2=-alpha-sqrt(alpha^2-wn^2) dt=0.01;t=0:dt:1; %设定时间组 %用公式Uc1=(p2*Uc0-IL0/C)/(p2-p1)*exp(p1*t);%Uc 的第一个分量 Uc2=-(p1*Uc0-IL0/C)/(p2-p1)*exp(p2*t);%Uc 的第二个分量 IL1=p1*C*(p2*Uc0-IL0/C)/(p2-p1)*exp(p1*t); IL2=-p2*C*(p1*Uc0-IL0/C)/(p2-p1)*exp(p2*t); Uc=Uc1+Uc2; IL=IL1+IL2;%分别画出两种数据曲线subplot(2,1,1),plot(t,Uc),grid subplot(2,1,2),plot(t,IL),grid运行结果:0246810121416182045678910R=1R=200.10.20.30.40.50.60.70.80.91-1-0.500.5100.10.20.30.40.50.60.70.80.910.511.52R=300.10.20.30.40.50.60.70.80.91-0.06-0.04-0.0200.0200.10.20.30.40.50.60.70.80.9100.20.40.60.81R=400.10.20.30.40.50.60.70.80.91-0.06-0.04-0.0200.0200.10.20.30.40.50.60.70.80.9100.20.40.60.8100.10.20.30.40.50.60.70.80.91-0.08-0.06-0.04-0.0200.0200.10.20.30.40.50.60.70.80.9100.20.40.60.81R=60.10.20.30.40.50.60.70.80.91-0.08-0.06-0.04-0.0200.0200.10.20.30.40.50.60.70.80.9100.20.40.60.8100.10.20.30.40.50.60.70.80.91-0.08-0.06-0.04-0.0200.0200.10.20.30.40.50.60.70.80.9100.20.40.60.81R=80.10.20.30.40.50.60.70.80.91-0.08-0.06-0.04-0.0200.0200.10.20.30.40.50.60.70.80.9100.20.40.60.8100.10.20.30.40.50.60.70.80.91-0.08-0.06-0.04-0.0200.0200.10.20.30.40.50.60.70.80.91-0.50.51R=100.10.20.30.40.50.60.70.80.91-0.08-0.06-0.04-0.0200.0200.10.20.30.40.50.60.70.80.91-0.50.5100.10.20.30.40.50.60.70.80.91-0.08-0.06-0.04-0.02000.10.20.30.40.50.60.70.80.9100.20.40.60.81实验六:频率响应1.一阶低通电路的频率响应程序:ww=0:0.2:4;%设定频率数组 ww=w/wcH=1./(i+j*ww);%求复频率响应figure(1)subplot(2,1,1),plot(ww,abs(H)),%绘制幅频特性grid,xlabel('ww'),ylabel('angle(H)')subplot(2,1,2),plot(ww,angle(H)),%绘制相频特性grid,xlabel('ww'),ylabel('angle(H)')figure(2) %绘制对数频率特性subplot(2,1,1),semilogx(ww,20*log10(abs(H)))%纵坐标为分贝grid,xlabel('ww'),ylabel('分贝')subplot(2,1,2),semilogx(ww,angle(H))%绘制相频特性grid,xlabel('ww'),ylabel('angle(H)')运行结果:00.51 1.52 2.53 3.540.20.40.60.81wwa n g l e (H )0.511.52 2.533.54-3-2.5-2-1.5-1-0.5wwa n g l e (H )100ww分贝10wwa n g l e (H )2.频率响应:二阶低通电路程序:for Q=[1/3,1/2,1/sqrt(2),1,2,5]ww=logspace(-1,1,50);%设无量纲频率数组ww=w/w0H=1./(1+j*ww/Q+(j*ww).^2);%求复频率响应figure(1)subplot(2,1,1),plot(ww,abs(H)),hold onsubplot(2,1,2),plot(ww,angle(H)),hold onfigure(2)subplot(2,1,1),semilogx(ww,20*log10(abs(H))),hold on%纵坐标为分贝subplot(2,1,2),semilogx(ww,angle(H)),hold on%绘制相频特性endfigure(1),subplot(2,1,1),grid,xlabel('w'),ylabel('abs(H)')subplot(2,1,2),grid,xlabel('w'),ylabel('angle(H)')figure(2),subplot(2,1,1),grid,xlabel('w'),ylabel('abs(H)')subplot(2,1,2),grid,xlabel('w'),ylabel('abs(H)')运行结果:012345678910246wa b s (H )012345678910-4-3-2-10wa n g l e (H )3. 频率响应:二阶带通电路程序:clear,format compact H0=1;wn=1;for Q=[5,10,20,50,100]w=logspace(-1,1,50);%设频率数组w H=H0./(1+j*Q*(w./wn-wn./w)); figure(1)%横坐标为线性坐标subplot(2,1,1),plot(w,abs(H)),grid,hold on %绘制幅频特性 subplot(2,1,2),plot(w,angle(H)),grid,hold on %绘制相频特性 figure(2)subplot(2,1,1),semilogx(w,20*log10(abs(H))),grid,hold on %纵坐标为分贝subplot(2,1,2),semilogx(w,angle(H)),grid,hold on %绘制相频特性 end运行结果:10-1100101-60-40-20020wa b s (H )10-1100101-4-3-2-10wa b s (H )01234567891000.20.40.60.81012345678910-2-112复杂谐振电路的计算程序:clear,format compactR1=2;R2=3;L1=0.75e-3;L2=0.25e-3;C=1000e-12;Rs=28200;L=L1+L2;R=R1+R2;Rse=Rs*(L/L1)^2%折算内阻f0=1/(2*pi*sqrt(C*L))Q0=sqrt(L/C)/R,R0=L/C/R;%空载Q0值Re=R0*Rse/(R0+Rse)%折算内阻与回路电阻的并联Q=Q0*Re/R0,B=f0/Q,%实际Q 值和带通s=log10(f0);f=logspace(s-.1,s+.1,501);w=2*pi*f;%设定计算的频率及范围及数组 z1e=R1+j*w*L;z2e=R2+1./(j*w*C);%等效单回路中量纲电抗支路的阻抗 ze=1./(1./z1e+1./z2e+1./Rse);%等效回路中三个支路的并联阻抗subplot(2,1,1),loglog(w,abs(ze)),grid%画对数幅频特性axis([min(w),max(w),0.9*min(abs(ze)),1.1*max(abs(ze))]) 10-1100101-60-40-202010-1100101-2-112subplot(2,1,2),semilogx(w,angle(ze)*180/pi)axis([min(w),max(w),-100,100]),gridfh=w(find(abs(1./(1./z1e+1./z2e))>50000))/2/pi;%求回路阻抗大于50千欧的频带fhmin=min(fh),fhmax=max(fh)运行结果:10610106。
武汉理工大学MATLAB课设报告

课程设计任务书学生姓名:专业班级:指导教师:江雪梅工作单位:信息工程学院题目: MATLAB的基本运算与绘图初始条件:1. Matlab实验软件2. 实验程序要求完成的主要任务:1. 采用MATLAB选用适当的函数或矩阵进行如下计算(1)极限的计算、微分的计算、积分的计算、级数的计算、求解代数方程、求解常微分方程;(2)矩阵的最大值、最小值、均值、方差、转置、逆、行列式、特征值的计算、矩阵的相乘、右除、左除、幂运算;(3)多项式加减乘除运算、多项式求导、求根和求值运算、多项式的部分分式展开、多项式的拟合、插值运算。
2. MATLAB的绘图(1)绘制四个不同的一维函数y=f(x)。
把四个函数用不同曲线、不同标识符显示在同一幅图中;用同一种曲线、同一种标识符把四个函数显示在同一界面的不同窗口;要求显示网格、有图形标题、有坐标轴标志、有图形标注函数。
(2)选择合适的二维函数z= f(x,y)分别绘制其空间曲线图、三维网线图和三维曲面图(3)选择一幅图像,画出图像的频谱图。
(4)对图像加入噪声,再画出图像的频谱图。
时间安排:1.第15周排任务,分组2.16—17周设计仿真,撰写报告3.第18周完成设计,提交报告,答辩指导教师签名:年月日系主任(或责任教师)签名:年月日学号:课程设计题目 MATLAB原理与应用课程设计学院信息工程学院专业通信工程班级姓名指导教师江雪梅2016 年 1 月9 日摘要Matlab是一个高级的矩阵/阵列语言,它包含控制语句、函数、数据结构、输入和输出和面向对象编程特点。
用户可以在命令窗口中将输入语句与执行命令同步,也可以先编写好一个较大的复杂的应用程序(M文件)后再一起运行。
新版本的MATLAB语言是基于最为流行的C++语言基础上的,因此语法特征与C++语言极为相似,而且更加简单,更加符合科技人员对数学表达式的书写格式。
使之更利于非计算机专业的科技人员使用。
而且这种语言可移植性好、可拓展性极强,这也是MATLAB能够深入到科学研究及工程计算各个领域的重要原因。
LC并联谐振MATLAB仿真 武汉理工大学 基础强化训练
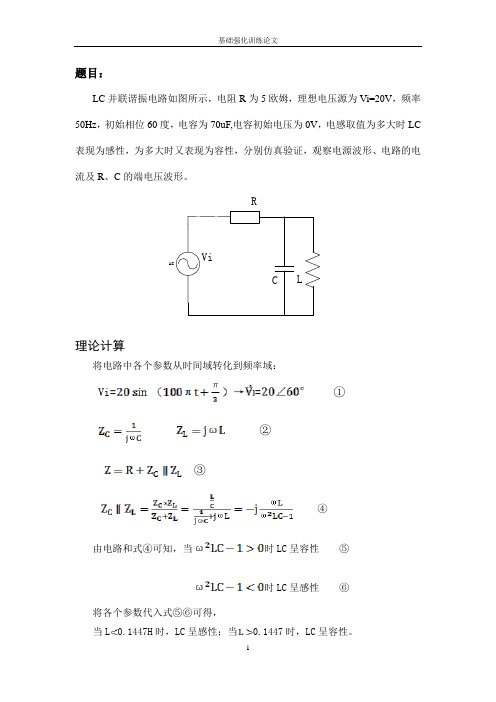
题目:LC并联谐振电路如图所示,电阻R为5欧姆,理想电压源为Vi=20V,频率50Hz,初始相位60度,电容为70uF,电容初始电压为0V,电感取值为多大时LC 表现为感性,为多大时又表现为容性,分别仿真验证,观察电源波形、电路的电流及R、C的端电压波形。
RAC理论计算将电路中各个参数从时间域转化到频率域:Vi=→=①②③④由电路和式④可知,当时LC呈容性⑤时LC呈感性⑥将各个参数代入式⑤⑥可得,当L0.1447H时,LC呈感性;当0.1447时,LC呈容性。
MATLAB电路仿真要想得到什么时候LC呈感性什么时候呈容性,必须借助电路中得示波器,或者MATLAB中得一些重要功能来观察电路中电源电压的相位和干路电流的相位的关系,如果电压超前于电流,则LC呈感性,如果电流超前于电压则LC呈容性。
仿真过程1.打开MATLAB软件2.在软件打开后的界面上点击工具栏的simulink键,弹出一个窗口如下图所示3.点击菜单栏中得File菜单新建一个模型4.在libraries中找到SinmpowerSystem,它的子菜单中可以找到电路所需的各种元件,包括正弦电压源,串联RLC电路,并联RLC电路,电压表,电流表。
示波器在Simulink的子菜单sink里面。
如图所示5.每找到一个元件将其拖到新建的模型中6. 所有的元件的参数都应该按照题目所有的条件来设定,由于电感是待求量,但又必须设定出一个确定的值才能观察电路的波形以及相位关系,所以这里我们取一系列的电感值,在理论值得附近取值稍微密一点。
6.1电源参数6.2 电阻参数6.3电容参数6.4设定初值6.5 示波器的设定由于要同时观察电源电压以及干路电流的波形,则设置双踪同时观察7. 电路参数全部设置完成后电路连接好如下图8.对电感设置不同的参数,观察波形及相位关系。
① L=0.12H时,电压超前于电流,呈感性②L=0.13H时,电压超前于电流,呈感性③L=0.14H时,电压超前于电流,呈感性④L=0.145H时,电压超前于电流,呈感性,电流波形失真⑤L=0.15H时,电压滞后于电流,呈容性⑥L=0.16H时,电压滞后于电流,呈容性为了验证公式中L趋近于0时电路呈纯阻性这一特点,另外添加两组数据如下⑦L=0.01H时,电压电流的相位比较接近,但依然是电压超前于电流,呈感性⑧ L=0.0001H时,电压电流的相位非常接近,几乎同相位,电路接近纯阻性。
武汉理工大学Matlab课设报告-PSK和DPSK信号的仿真分析

课程设计任务书学生姓名:张亚男专业班级:通信1104班指导教师:张小梅工作单位:信息工程学院题目: PSK和DPSK信号的仿真分析初始条件:在MATLAB仿真软件系统中设计并实现PSK和DPSK信号系统的仿真,并进行调试和仿真波形分析。
要求完成的主要任务: (包括课程设计工作量及技术要求,以及说明书撰写等具体要求)1、课程设计工作量:5天。
2、技术要求:调制信号:300Hz正弦信号,经过μ律PCM编码;载波频率:100kHz;要求:画出调制信号、已调信号、解调信号的波形、频谱以及误码率与输入信噪比的关系曲线3、查阅至少5篇参考文献。
按《武汉理工大学课程设计工作规范》要求撰写设计报告书。
全文用A4纸打印,图纸应符合绘图规范。
时间安排:1、2013年5 月16 日,布置课设具体实施计划与课程设计报告格式的要求说明。
2、2013年6 月27 日至2013年6 月29 日,方案选择和电路设计。
3、2013年6 月30 日至2013年7 月3 日,电路调试和设计说明书撰写。
4、2013年7 月5 日,上交课程设计成果及报告,同时进行答辩。
指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要....................................................... 错误!未定义书签。
Abstract.................................................... 错误!未定义书签。
1 方案设计................................................. 错误!未定义书签。
1.1 调制部分方案选择..................................... 错误!未定义书签。
1.2 解调部分方案选择..................................... 错误!未定义书签。
武汉理工Matlab实验报告程序

1、利用zeros 和ones 函数来产生单位阶跃序列。
函数格式: zeros(1,n) ones(1,n) n 为序列长度。
程序如下: n1=-2;n2=8;k=0; n=n1:n2; nt=length(n); nk=abs(k -n1)+1;x=[zeros(1,nk -1),ones(1,nt -nk+1)]; stem(n,x)2、已知信号x1(n)=3e −0.25n (4<n<10)x2(n)=u(n+1) (-2<n<6) 求x(n)=x1(n)*x2(n),并画出对应波形。
程序如下:function[x,n]=stepseq(n1,n2,n0) n=[n1:n2]; x=[(n -n0)>=0];function [y,ny]=conv_m(x,nx,h,nh,p) nyb=nx(1)+nh(1);nyc=nx(length(x))+nh(length(h)); ny=[nyb:p:nyc]; y=conv(x,h); p=1;n1=[-4:p:10];f1=3*exp(-0.25*n1); n2=[-2:p:6];[f2,n2]=stepseq(-2,6,-1);[y,ny]=conv_m(f1,n1,f2,n2,p); subplot(3,1,1);stem(n1,f1) subplot(3,1,2);stem(n2,f2) subplot(3,1,3);stem(ny,y)图1 单位阶跃序列图2 对应波形验证线性性质:如果有两个有限长序列分别为x1(n)和x2(n),长度分别为N1和N2,且y(n)=ax1(n)+bx2(n),(a ,b 均为常数),则该y(n)的N 点DFT 为 Y(k)=DFT[y(n)]=aX1(k)+bX2(k) (0<=k<=N -1) 其中:N=max(N1,N2),X1(k)和X2(k)分别为x1(n)和x2(n)的N 点DFT 。
matlab基础强化训练—含受控源的电阻直流电路

课程设计题目含受控源的电阻直流电路学院自动化学院专业Xxxxxxxx班级Xxxxxxxx姓名Xxxxxxxx指导教师Xxxxxxxx2011 年7 月12 日课程设计任务书学生姓名:Xxxxxxxx专业班级:Xxxxxxxx指导教师:Xxxxxxxx 工作单位:Xxxxxxxx题目: MATLAB/SIMULINK在阻抗匹配网络中的分析与应用初始条件:(2)Matlab6.5以上版本软件;(2)课程设计辅导资料:“Matlab语言基础及使用入门”、“Matlab教程”、“Matlab 宝典”、“Matlab及在电子信息课程中的应用”、MATLAB及其在理工课程中的应用指南等;先修课程:电路基础、模拟电路、数字电路、Matlab应用实践及信号处理类课程等。
要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)(1)熟悉Matlab的相关界面以及操作,掌握MATLAB的数值计算、符号运算、基本绘图等功能,使用文本编辑器编辑m文件,并且运行,熟悉Simulink仿真环境;(2)对阻抗匹配网络进行原理分析、经过必要的推导建立数学模型,并求解得出正确的计算结果;(3)编写程序代码(含注释);(4)上机调试运行程序,给出程序运行结果和图表、以及实验结果分析和总结;(5)采用WORD撰写课程设计说明书,说明书中涉及的表格、电路图、图形等采用Word、Visol、Autocad、Matlab、Simulink等软件绘制。
说明书不少于8页(A4),课程设计的心得体会(至少500字)。
时间安排:指导教师签名:年月日系主任(或责任教师)签名:年月日目录MATLAB简介 (1)1. 含受控源的电阻直流电路 (2)1.1 对含受控源的电阻直流电路原理的分析 (2)1.2 建模 (3)1.3应用MATLAB对上面的题目编程 (4)1.4绘图 (5)1.5MATLAB中函数功能介绍 (7)2.对结果的对比与分析 (8)3.心得与体会 (9)参考文献 (10)MATLAB简介MATLAB是由美国MathWorks公司推出的用于数值计算和图形处理计算系统环境,除了具备卓越的数值计算能力外,它还提供了专业水平的符号计算,文字处理,可视化建模仿真和实时控制等功能.MATLAB的基本数据单位是矩阵,它的指令表达式与数学,工程中常用的形式十分相似,故用MATLAB来解算问题要比用C、FORTRAN等语言简捷得多.MATLAB是国际公认的优秀数学应用软件之一。
武汉理工大学基于MATLAB的二进制移相键控(2PSK)调制与解调

课程设计任务书学生姓名:专业班级:指导教师:工作单位:题目:信号分析处理课程设计-基于MATLAB的二进制移相键控(2PSK)调制与解调分析初始条件:1.Matlab6.5以上版本软件;2.先修课程:通信原理等;要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、利用MATLAB中的simulink工具箱中的模块进行二进制移相键控(2PSK)调制与解调,观察波形变化;2、画出程序设计框图,编写程序代码,上机运行调试程序,记录实验结果(含计算结果和图表等),并对实验结果进行分析和总结;3、课程设计说明书按学校统一规范来撰写,具体包括:⑴目录;⑵理论分析;⑶程序设计;⑷程序运行结果及图表分析和总结;⑸课程设计的心得体会(至少800字,必须手写。
);⑹参考文献(不少于5篇)。
时间安排:周一、周二查阅资料,了解设计内容;周三、周四程序设计,上机调试程序;周五、整理实验结果,撰写课程设计说明书。
指导教师签名:年月日系主任(或责任教师)签名:年月日目录1 理论分析 (1)1.1基础知识 (1)1.2二进制相移键控基本原理 (1)1.3二进制相移键控调制 (2)1.4二进制相移键控解调 (4)2 程序设计与仿真模型建立 (6)2.1设计与仿真基础 (6)2.2程序设计实现 (7)2.3 Simulink仿真模型建立 (12)3 程序运行结果与仿真结果 (20)3.1程序运行结果与分析 (20)3.2 Simulink仿真结果与分析 (21)4 心得体会 (23)参考文献 (25)1 理论分析1.1基础知识数字信号的传输方式分为基带传输和带通传输。
然而,实际中的大多数信道(如无线信道)因具有带通特性而不能直接传送基带信号,这是因为数字基带信号往往具有丰富的低频分量。
为了使数字信号在带通信道中传输,必须用数字基带信号对载波进行调制,以使信号与信道的特性相匹配。
这种用数字基带信号控制载波,把数字基带信号变换为数字带通信号(已调信号)的过程称为数字调制。
基础强化训练之MATLAB 在交流稳态电路中的分析应用

武汉理工大学《基础技能强化训练》课程设计说明书1 训练目的就自动化专业的需要,在平时的学习中我们会经常针对各种电路进行分析,在这个过程会遇到各种各样的问题。
但是随着电路规模的加大,微积分方程阶数以及联立方程的个数的增多,解题运算会变得越来困难。
而此次基础强化训练的主要内容是通过实践学习并掌握MATLAB语言工具,结合《线性代数》、《电路原理》等课程,强化、巩固专业理论基础,掌握MATLAB语言的编程技巧,为后续专业课程的仿真学习打下良好的基础,以解决更加复杂的电路问题等等。
据了解,MATLAB语言的两个最显著特点,即其强大的矩阵运算能力和完美的图形可视化功能,使它成为控制界应用最广的科学计算工具。
此外,它还具有用于各种不同领域解决实际问题的计算工具箱。
通过分析研究发现,用MATLAB语言进行电工、电子电路的分析、设计与仿真,简单、高效,可以避免复杂的数学计算编程(比如矩阵的计算),并且借助其绘图函数可方便实现计算结果的可视化,若采用MATALAB进行电路的调试、仿真、验证,不仅省时、省力,而且还可以节约大量的成本。
MATALB语言不但可作为从事电工、电子专业的技术人员提供强大的设计和论证方面的保障,也可以作为学习、了解掌握电工、电子知识的一种更方便、更可靠的开发工具,还可以作为大中专学校实践教学手段的一种扩充和补充,将其引入电工电子电路的教学和科研中,显得十分必要。
这次基础强化训练的目的,就是让我们了解和熟悉MATLAB,利用MATLAB去掌握相关的理论知识及实际处理方法,熟练使用MATLAB语言编写所需应用程序,上机调试,输出实验结果,并对实验结果进行分析。
解决一些简单的电路分析,为今后学习和工作中遇到的大规模电路分析做准备。
2 训练要求2.1题目:图2-1所示示正弦交流电路中,已知()︒10sinUs t V,R=10Ω,100+=15 L=0. 1H,C=100μF。
求电压is。
图2-1 基本电路图2.2要求:1)用尽可能多的方法(计算/仿真)以求出题目的未知量;2)报告应对建模、参数设置、仿真模型搭建中使用的元器件所在的工具库、和仿真的过程进行详细说明(可截屏说明实现过程);3)将仿真结果与理论计算进行对照,对仿真结果的正确性进行分析说明3 理论计算()()) 1.30)A(-0t 0 0.901sin(1 A4.74100sin 901.0A 4.74901.04.890982.11/15104.890982.11 11.0976i + 0.1220)2/11/1/(1/110L 2XL 00110C 1/1C .100,1.0,10,15100sin 10su弧度制所在支路中串联支路中、欧姆定律,得:、通过=︒-=︒-∠=︒∠︒∠=∴⨯=Ω︒∠=Ω=⇒+=Ω==Ω-=+===Ω=︒+=t is I XI U X X X X X j j j j R X R KCL KVL F C H L R t ωωμ4 设计分析4.1整体分析图2-1为一交流电压源经电容、电感、电阻串并联组成的简单一阶响应电路,题目要求求us 输出的干路电流is 。
利用MATLAB分析电阻电路

利用MATLAB分析电阻电路学院:物理电气信息学院专业:通信工程姓名:顾川学号:12010245242指导老师:汤全武利用MATLAB 分析电阻电路[摘要] 在电路分析中,随着电路复杂程度的增加,联立方程的数量会越来越多,即使是相对简单的电阻电路,当电路复杂到一定程度时,无论网孔分析还是节点分析,都会引入大量方程(组),手工求解异常繁杂且容易出错。
MATLAB 具有强大的数学方程求解能力,尤其是对由网孔分析和节点分析列出的线性方程组,利用MATLAB 求解有着得天独厚的优势。
[关键词]电阻电路;MATLAB一. 电阻电路分析电阻电路:由电阻、受控源和独立源组成的电路称为电阻电路。
利用MATLAB ,可以手工建立电路方程,表示为Ax=B (A 是系数矩阵,取决于电路元件的值;x 是由电路中一些电压和电流构成的列向量;B 是右端列向量,与电压源电压和电流源电流有关)再用MATLAB 求解线性代数方程,指令为x=A\B 。
分析电路的基本依据是KVL 和KCL ,列方程的基本原则是利用节点(包括广义节点)和回路(包括假设回路)的互相约束关系,建立含未知数最少、求解最容易的方程组。
例1:如图:A I s 3= ,Ω=211R ,Ω=312R ,V U s 5=。
求?=s U解:设三个回路电流分别为1m I 、2m I 、3m I 则:31=m I)(10102113m m m I I I I -==053)3121(2321=++++-m m m I I I 图1 图233032=++U I I m m 由此可以解出A I m 31=、A 4.52=m I 、A 24-3=m I 、V U 2.60=(当然如果把并联的受控电流源等效后回简单些)。
一般的回路方程,左边是回路电路与无源元件表示,右边用电源表示,在此处经过分析,真正的未知数其实是回路2的回路电流和所要求的电压,于是原方程组整理后写成矩阵形式再利用MATLAB 把矩阵写成Ax=B ,];[02U I x m =指令和结果如下:a=[5/6-10/3 0;1/3-10/3 1];b=[3/2-5-30/3;-30/3];x=a\a %求解方程组运行结果是:x =5.40006.2000例2:如图,已知Ω=1R ,V U s 14=,求支路电流i 和支路电压U解:设三个回路电流分别为1m I 、2m I 、3m I ,则:03114)11(U I I m m -=-+032)11(U I I m m =-+u I m 5.03-=图3 图4补充方程为:i I I m m =-31i I I m m 5.012=-u I I m m =-32由此可以解出A I m 11=、A I m 32=、A I m 33-=、A i 4=、A u 6=。
matlab在直流电路中电阻电路的应用

初始条件:试用叠加原理计算图中所示电路中的电流I和电压U ab。
b设计任务:1.根据已知分析电路(包括电路变换及简化);2.完成在MATLAB中的参数设定及模型建立;3.完成仿真输出波形显示,并分析结果。
4.整理设计过程,总结心得,完成报告。
摘要《电路原理》是电类专业必修的一门重要的技术基础课,它具有基础科学和技术科学的二重性,不仅是电类学生学习后续课程的基础,也直接为解决电工电子工程中的一些实际问题服务。
大一下学期开始,通过对本课程的学习,我初步掌握了近代电路理论的一些基本知识和概念,能分析计算一些常见的,比较简单的基本电路,初步具有了解决实际问题的能力,并为后续课程的学习准备了必要的电路理论知识。
其分析电路的常见方法有:节点电压法,网孔电流法,叠加原理分析法,戴维宁定理和诺顿定理等等。
本文主要讨论用叠加原理分析法来分析直流电路中关于电阻电路的计算方法。
在这个分析解决问题的过程中需要运用到MATLAB软件。
MATLAB是矩阵实验室(Matrix Laboratory)的简称,是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink 两大部分。
本文就是通过对MATLAB编程计算出的结果和Simulink仿真出的结果两大部分。
本文就是通过对MATLAB编程计算出的结果和直流电路中电阻电路的计算1题目分析1.1设计题目试用叠加原理计算图1中所示电路中的电流I和电压U ab。
b图1 电路图1.2理论分析题图1中有一个电压源和一个电流源,根据叠加原理可以将电路图进行分解成图2和图3叠加。
aI2Ωb图2 分解图一20ΩI 10图3 分解图二列方程得I 1+I 2=3 10 I 1-20 I 2=0 (10+20)I 3=-12对上面三个方程,可将其写成如下所示的矩阵形式:=求解线性方程组得I 1 =2A I 2=1A I 3=-0.4A由叠加原理得I= I 1+I 3=1.6A由电路性质得U ab =10I=16V上面的过程,为理论上的解题方法。
基于MATLAB的电路分析

基于MATLAB的电路分析MATLAB是一种用于科学计算和工程应用的高级计算机语言和环境。
它提供了许多功能强大的工具,可以用于电路分析和模拟。
使用MATLAB进行电路分析可以帮助工程师和研究人员快速而准确地分析和设计电路。
在MATLAB中,电路分析可以通过多种方法和工具来完成。
以下是一些基于MATLAB的电路分析的方法和工具:1.电路建模和仿真:在MATLAB中,可以使用Simulink工具箱来建立电路的数学模型,并进行仿真。
Simulink提供了丰富的电路元件库,可以轻松地建立复杂的电路模型。
通过在模型中添加适当的输入信号和参数,可以模拟电路的响应,并分析电路的性能。
2.网络方程求解:利用MATLAB的符号计算工具箱,可以求解复杂电路中的网络方程。
符号计算工具箱可以自动化地进行符号计算,可以求解电路中的方程组,得到电路的节点电压和支路电流。
3.频率响应分析:通过使用MATLAB的信号处理工具箱,可以对电路进行频率响应分析。
可以使用傅立叶分析和滤波器设计工具来分析电路在不同频率下的响应,例如幅频响应曲线、相频响应曲线和频率特性等。
4.参数优化和参数估计:在电路设计和分析过程中,通常需要优化电路参数以满足特定的性能要求。
MATLAB提供了优化工具箱,可以使用不同的优化算法来自动寻找最佳参数组合。
另外,也可以使用统计和机器学习工具箱来进行参数估计和预测。
5.可视化和数据分析:MATLAB具有强大的可视化功能,可以帮助用户更好地理解电路的性能和行为。
可以使用MATLAB的绘图工具来绘制电路的电压、电流和功率等变量随时间的变化图表。
通过对数据进行分析和处理,可以获得更多有关电路性能的信息。
总结而言,MATLAB是一个强大的工具,可以帮助工程师和研究人员进行电路分析和设计。
它提供了多种方法和工具,可以用于电路建模、仿真、方程求解、频率响应分析、参数优化和可视化等方面。
MATLAB的灵活性和易用性使其成为电路分析的首选工具之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专业基础实践任务书学生姓名: 专业班级:电信1406班指导教师:阙大顺工作单位:信息工程学院题目:Matlab运算与受控源电阻电路分析初始条件:1.Matlab7.1以上版本软件;2.专业基础实践辅导资料:“Matlab语言基础及使用入门”、“Matlab及在电子信息课程中的应用”、“线性代数”及“信号处理类”相关书籍等;3.先修课程:高等数学、线性代数、电路、Matlab应用实践及信号处理类基础课程等。
要求完成的主要任务:1.实践内容:根据指导老师给定的7套题目,按规定选择其中1套独立完成;2.本专业基础实践统一技术要求:研读辅导资料对应章节,对选定的设计题目进行理论分析,完成针对具体设计部分的原理分析、建模、必要的推导和可行性分析,画出程序设计框图,编写程序代码(含注释),上机调试运行程序,记录实验结果(含计算结果和图表等),并对实验结果进行分析和总结。
具体设计要求包括:①初步了解Matlab、熟悉Matlab界面、进行简单操作等;②Matlab的数值计算:创建矩阵、矩阵运算、多项式运算、线性方程组、数值统计等;③基本绘图函数:了解plot, plot3, mesh, surf等,要求掌握以上绘图函数的用法、简单图形标注、简单颜色设定等;④使用文本编辑器编辑m文件,会函数调用等;⑤能完成简单电路的Matlab编程分析;⑥按要求参加专业基础实践的实验演示和答辩等。
3.课程设计说明书按学校“课程设计工作规范”中的“统一书写格式”撰写,具体包括:①目录;②与设计题目相关的理论分析、归纳和总结;③与设计内容相关的原理分析、建模、推导、可行性分析;④程序设计框图、程序代码(含注释)、程序运行结果和图表、实验结果分析和总结;⑤课程设计的心得体会(至少500字);⑥参考文献(近5年的、不少于5篇);⑦其它必要内容等。
时间安排:12.22-12.28一周指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要.................................................................... І1. 方案选择与论证..................................... 错误!未定义书签。
1.1方案框图 (1)1.1.1RC网络................................... 错误!未定义书签。
1.1.2放大器................................... 错误!未定义书签。
1.1.3反馈网络................................. 错误!未定义书签。
1.2方案设计与论证 (1)1.2.1方案设计................................. 错误!未定义书签。
1.2.2方案选择 (5)1.2.3元器件选择 (6)2. 单元电路设计与元件参数计算 (7)2.1传递函数 (7)2.2低通滤波器[1] (8)2.3高通滤波器[2] (9)2.4带通滤波器[2]................................... 错误!未定义书签。
3. 电路仿真分析 (10)3.1低通滤波器 (10)3.2高通滤波器 (11)3.3带通滤波器 (12)4.直流稳压电源设计与实物焊接 (13)5.总结 (15)6.附录一参考文献 (15)Matlab运算与受控源电阻电路分析摘要MATLAB是美国MathWorks公司出品用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境的商业数学软件,本次专业基础实践,用MATLAB软件完成了对受控源电阻电路的分析。
关键词:MATLAB 受控源分析1.MATLAB概述1.1简介MATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
MATLAB是matrix&laboratory两个词的组合,意为矩阵工厂(矩阵实验室)。
是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。
它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,代表了当今国际科学计算软件的先进水平。
MATLAB和Mathematica、Maple并称为三大数学软件。
它在数学类科技应用软件中在数值计算方面首屈一指。
MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
MATLAB的基本数据单位是矩阵,它的指令表达式与数学、工程中常用的形式十分相似,故用MATLAB来解算问题要比用C,FORTRAN等语言完成相同的事情简捷得多,并且MATLAB也吸收了像Maple等软件的优点,使MATLAB成为一个强大的数学软件。
在新的版本中也加入了对C,FORTRAN,C++,JAVA的支持。
1.2主要功能数值分析数值和符号计算工程与科学绘图控制系统的设计与仿真数字图像处理数字信号处理通讯系统设计与仿真财务与金融工程1.3优势特点1) 高效的数值计算及符号计算功能,能使用户从繁杂的数学运算分析中解脱出来;2) 具有完备的图形处理功能,实现计算结果和编程的可视化;3) 友好的用户界面及接近数学表达式的自然化语言,使学者易于学习和掌握;4) 功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) ,为用户提供了大量方便实用的处理工具。
1.4MATLAB基本命令1.4.1运算符+:加,-:减,*:乘,/:除,\:左除^:幂,‘:复数的共轭转置,():制定运算顺序。
1.4.2常用函数表sin( ) 正弦(变量为弧度)Cot( ) 余切(变量为弧度)sind( ) 正弦(变量为度数)Cotd( ) 余切(变量为度数)asin( ) 反正弦(返回弧度)acot( ) 反余切(返回弧度)Asind( ) 反正弦(返回度数)acotd( ) 反余切(返回度数)cos( ) 余弦(变量为弧度)exp( ) 指数cosd( ) 余弦(变量为度数)log( ) 对数acos( ) 余正弦(返回弧度)log10( ) 以10为底对数acosd( ) 余正弦(返回度数)sqrt( ) 开方tan( ) 正切(变量为弧度)realsqrt( ) 返回非负根tand( ) 正切(变量为度数)abs( ) 取绝对值atan( ) 反正切(返回弧度)angle( ) 返回复数的相位角atand( ) 反正切(返回度数)mod(x,y) 返回x/y的余数sum( ) 向量元素求和1.4.3常用常数的值:pi 3.1415926…….realmin 最小浮点数,2^-1022i 虚数单位realmax 最大浮点数,(2-eps)2^1022 j 虚数单位Inf 无限值eps 浮点相对经度=2^-52NaN 空值1.5MATLAB基本操作1.5.1矩阵的创建>> x = [1 2 3] % 一维 1x3 阵列>> x = [1 2 3; 4 5 6]%二维 2x3 矩阵,以;区隔各列的元素>> x = [1 2 3 %二维 2x3 矩阵,各列的元素分二行键入4 5 6] %矩阵的尺寸不必预先定义假设要计算 y = sin (x), 0=<x<=π而x = 0, 0.2π, 0.4π,...,π,即可用数组方式运算,例如>> x = [0 0.2*pi 0.4*pi 0.6*pi 0.8*pi pi] %注意数组内也可作运算x =0 0.6283 1.2566 1.8850 2.5133 3.1416>> y=sin(x)y =0 0.5878 0.9511 0.9511 0.5878 0.00001.5.2在命令窗口输入矢量并绘图y=[0 0.6 2.3 5 8.3 11.7 15 17.7 19.4 20];plot(y)在命令窗口输入两个矢量并绘图:x=0:0.05:4*pi; %生成0至4π,间隔为0.05的自变量y=sin(x);plot(x,y)注意,绘制双矢量曲线图时,矢量x与y必须具有同样的长度。
1.5.3绘制线性坐标图和3种对数坐标图y=[0 0.6 2.3 5 8.3 11.7 15 17.7 19.4 20];subplot(2,2,1) %创建第一个子图plot(y)title('plot(y)')subplot(2,2,2) %创建第二个子图semilogx(y)title('semilogx(y)')subplot(2,2,3) %创建第三个子图semilogy(y)title('semilogy(y)')subplot(2,2,4) %创建第四个子图loglog(y)title('loglog(y)')1.5.4绘制函数y=sin2tcos2t 的极坐标图形 在命令窗口创建角度矢量t ,以函数y=sin2tcos2t 为半径绘图: t=0:.01:2*pi;polar(t,sin(2*t).*cos(2*t))2.设计题目1.计算y1=51)3.0sin(2+π和y2=51)3.0cos(2+π;2.画出衰减震荡曲线t e y t 3sin )3/(-=及其他的包络线)3/(0t e y -=,t 的取值范围是[0,4π].3.画出2222sin y x y x z ++=所表示的三维曲面。
x,y 的取值范围是[-8,8]。
4.分析下面每条指令的功能并运行,观察执行结果。
(1) X=0:0.1:1;Y=X.*exp(-X);plot(X,Y),xlabel(‘x ’), ylabel(‘y ’),title(‘y=x*exp(-x)’);(2) A=zeros(2,5)A(:)=-4:5L=abs(A)>3islogical(L)X=A(L)(3) A=[1:4;5:8]pow2(A)(4) A=zeros(2,3)A(:)=1:6A=A*(1+i)A1=A.’;B1=A ’;(5) A=ones(1,2)B=ones(2)C=eye(3)D=diag(C)E=repmat(C,1,3)5.计算1001.045-+=x x y 在x=0.1与10处的值。
