辽宁省沈阳市2014年中考数学试卷
2014年辽宁省沈阳市中考数学试卷-答案

辽宁省沈阳市2014年中等学校招生统一考试数学答案解析第Ⅰ卷(选择题)一、选择题1.【答案】C【解析】0既不是正数也不是负数,而是正负数的分界线;0是整数,不是无理数,故选C.【考点】数的分类.2.【答案】B【解析】科学记数法是将一个数写成10n a ⨯的形式,其中110a ≤<,n 为整数.其中a 是只有一位整数的数;当原数的绝对值10≥时,n 为正整数,n 等于原数的整数位数减1;当原数的绝对值1<时,n 为负整数,n的绝对值等于原数中左起第一个非零数字前零的个数(含整数位上的零).4850008.510=⨯,故选B.【考点】科学记数法.3.【答案】C【解析】三视图都为矩形的只有长方体,故选C.【考点】由三视图判断几何体形状.4.【答案】A【解析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不只一个;平均数为所有数据的和除以数据的个数;方差为每一数据与平均数的差的平方和除以数据个数.将数据从小到大排列为1,2,3,3,6,共5个数,最中间的数为3,故中位数为3;3出现的次数最多,故众数为3;平均数为(12336)53++++÷=,所以平均数为3;方差2222221114[(31)(32)(33)(33)(36)](41009)555s =⨯-+-+-+-+-=⨯++++=,所以正确的是A ,故选A.【考点】数据的特征.5.【答案】A【解析】解不等式1x ≥,将不等式的解集表示在数轴上时,应注意“方向”与“点型”,大于向右,小于向左;含有等号时用实心圆圈,故选A.【考点】不等式解集在数轴上的表示.【提示】忽略空心圆圈与实心点的区别而致错.6.【答案】B【解析】沿某直线折叠,直线两旁部分能够重合的图形为轴对称图形,正方形通过折叠可以找到对角线所在直线及各边垂直平分线所在的直线共4条对称轴,故选B.【考点】轴对称图形对称轴的确定.7.【答案】D【解析】326()x x -=,故A 错误;4442x x x +=,故B 错误;235x x x =,故C 错误;43()xy xy y ÷-=-,故选D.【考点】整式的相关计算.8.【答案】C【解析】因为D E B C ∥,所以::AD AB DE BC =,因为2B D A D =,所以:1:3A D A B =,所以:5:1:3D E B C B C ==,所以15BC =,故选C. 【考点】相似三角形的性质与判定.第Ⅱ卷(选择题)二、填空题9.【答案】33,故填3.【考点】平方根的运算.10.【答案】2(5)m n +【解析】分解因式的题目首先提公因式,然后再运用公式来分解因式,如果提公因式后是两项看能否用平方差公式分解因式,如果是三项看能否运用完全平方公式分解因式.此题22102(5)m m m m +=+, 【考点】因式分解.11.【答案】40【解析】如图,因为a b ∥,所以13∠=∠,因为PM l ⊥,所以2390∠+∠=︒,因为150∠=︒,所以350∠=︒,2903905040∠=︒-∠=︒-︒=︒.【考点】平行线的性质,垂线的性质.12.【答案】11x - 【解析】原式1111x x x x =⨯=--. 【考点】考查分式的化简.13.【答案】6【解析】由交点的横坐标为2得213y =+=,所以交点的纵坐标为3,所以由反比例函数的解析式得6k xy ==.【考点】反比例函数与一次函数的应用.【提示】不能由交点坐标将两个函数解析式联系起来二致错.14.【答案】516【解析】由三角形中位线定理得:1:2DE AB =,所以14DC EDEF A B C S S S ==△△△.同理11416FMP DEF ABC S S S ==△△△.所以516DCE FMP ABC S S S +=△△△,所以这个点取在阴影部分的概率为516. 【考点】三角形中位线的性质,概率的计算. 【提示】不能表示出阴影部分与整个三角形面积之比而出错.15.【答案】25【解析】利润22(30)(20)50600(25)25y x x x x x =--=-+-=--+,所以若使利润最大,每件的售价应为25元.【考点】二次函数最值的求解.【提示】由于不能根据题意列出二次函数解析式而致错或由于不能正确配方而致错.16.【答案】5;13【解析】因为四边形EFMH 为平行四边形ABCD 四个内角平分线围成的四边形,所以此四边形为矩形.因为3FM =,4EF =,由勾股定理得5EM =.由题意知BHC BEA MFE △△△,设3BH x =,则4CH x =,5BC x =,33BE x =+,44AE x =+,215AB x =-,所以222(33)(44)(215)x x x +++=-.解得85x =,所以58BC x ==,21813AB =-=.【考点】平行四边形的性质,角平分线的性质,矩形的判定和性质,勾股定理.三、解答题17.【答案】20【解析】解:22[()()]a b a b a +--2222(22)a ab b a ab b a =++-+-4ab a =24a b =,当1a =-,5b =时,原式24(1)520=⨯-⨯=.【考点】整式的化简求值.18.【答案】见解析 【解析】证明:四边形ABCD 为矩形,90ADC BCD ∴∠=∠=︒,AC BD =,12OD BD =,12OC AC =.OD OC ∴=.ODC OCD ∴∠=∠.ADC ODC BCD OCD ∴∠-∠=∠-∠,即EDO FCO ∠=∠.又DE DF =,ODE OCF ∴≅△△,OE OF ∴=.【考点】矩形的性质,三角形全等的判定方法.19.【答案】23【解析】解:列表得或画树状(形)图得由表格(或树状图/树形图)可知,共有9种可能出现的结果,每种结果出现的可能性相同,其中小明两次摸出的球颜色不同的有6中:(红球,白球),(红球,黑球),(白球,红球),(白球,黑球),(黑球,红球),(黑球,白球),所以6293P =(小明两次摸出的球颜色不同)=. 【考点】列表法或树状图法求概率.20.【答案】(1)30%a =,5%b =.(2)见解析.(3)1 440【解析】(1)30%a =,5%b =.(2)预测最有可能获得世界杯冠军球队的条形统计图(3)480030%1440⨯=(人).答:大约有1 440人预测德国队最有可能获得冠军.【考点】统计表与条形图综合应用.21.【答案】20%.【解析】解:设这个增长率为x ,依题意得220(1)20(1) 4.8x x +-+=,解得10.2x =,2 1.2x =-(不合题意,舍去),0.220%=.答:这个增长率为20%.【考点】用一元二次方程解决平均增长率问题.22.【答案】(1)见解析.(2)12. 【解析】(1)证明:AB 为O 的直径,90ACB ∴∠=︒.又OD BC ∥,90AEO ACB ∴∠=∠=︒.OC AC ∴⊥,AD CD ∴=,AD CD ∴=.(2)10AB =,152OA OD AB ∴===. OD BC ∥,AOE ABC ∴∠=∠.在Rt AEO △中,3cos cos 535OE OA AOE OA ABC =∠=∠=⨯=. 532DE OD OE ∴=-=-=.由勾股定理得4AE ==.在Rt AED △中,21tan 42DE DAE AE ∠===. 又DBC DAE ∠=∠,1tan 2DBC ∴∠=. 【考点】圆周角定理,垂径定理,勾股定理,三角函数.23.【答案】(1)见解析.(2).(3)①122m t =+②(2,0),32(,0)3 【解析】解:(1)证明:过点A 作AM x ⊥轴于点M ,点A 的坐标为,2OM ∴=,AM =∴在Rt AOM △中,tan AM AOM OM ∠=== 60AOM ∴∠=︒.由勾股定理得4OA ,4OD =,OA OD ∴=.AOD ∴△是等边三角形.(2)过点A 作AN BC ⊥于点N ,BC OC ⊥,AM x ⊥轴,90BCM CMA ANC ∴∠=∠=∠=︒.∴四边形ANCM 为矩形.AN MC ∴=,AM NC =.60B ∠=︒,AB =∴在Rt ABN △中,sin 6AN AB B ===, 1cos 2BN AB B ===6AN MC ∴==,CN AM ==268OC OM MC ∴=+=+=.BC BN CN =+=+=.(3)①122m t =+.②(2,0),32(,0)3. 【考点】平面直角坐标系,勾股定理,等边三角形的判定,矩形的判定及性质,用函数解析式表示图形的运动变化.24.【答案】(1)5.(2)见解析.(3)【解析】解:(1)四边形ABCD 为菱形,AC BD ∴⊥,12OB OD BD ==. 24BD =,12OB ∴=,在Rt OAB △中,13AB =,5OA ∴.(2)证明:四边形ABCD 为菱形,BD ∴垂直平分AC ,FA FC ∴=.FAC FCA ∴∠=∠.由已知AF AM =,60MAF ∠=︒.AMF ∴△为等边三角形,60M AFM ∴∠=∠=︒.点M ,F ,C 三点在同一直线上,60FAC FCA AFM ∴∠+∠=∠=︒.30FAC FCA ∴∠=∠=︒.603090MAC MAF FAC ∴∠=∠+∠=︒+︒=︒.在Rt ACM △中,tan AC M AM =,tan 60AC AM ∴︒=,AC ∴=.(3)AFM △的周长为【考点】菱形的性质,勾股定理,等边三角形的判定与性质,三角函数的应用.25.【答案】(1)(9,0)-,(9,0).(2)①见解析.②152n -或215n -. ③24164279y x x =-++或243212279y x x =-+-. 【解析】解:(1)(9,0)-,(9,0).(2)①证明:AB CD ∥,MN BC ∥,∴四边形BMNC 为平行四边形.BM CN ∴=.BM AP =,AP CN ∴=.9OC OB ==,又AO BC ⊥, AB AC ∴=,AB BM AC AP ∴-=-.AM PC ∴=.AB CD ∥,MAP PCN ∴∠=∠.PAM NCP ∴≅△△.②152n -或215n -. ③24164279y x x =-++或243212279y x x =-+-. 【考点】二次函数的相关性质,平行四边形的判定与性质,三角形全等的证明,待定系数法求二次函数的解析式.。
2014年沈阳市中考数学试题及答案

却M年咖魏学词题★试题满分150分考试时间12盼钟X公氏:抛轲孙dzc的耐是卜务特对称轴足宜如吗.—■建择■(下列各■的■速答赛中,只有一个答SftiFa 的.每小題3分.共24分)1-03人数足8.如图,?FAABC中.点D在边ABk , BD=2AD. DE〃BC交AC于点E,若线段DE=5・则线段BC的怅为A. 7.5B. 10C. 15D. 20D.xy4 * (・xy) =-y3C.整数D.无理数2.201£年端午15小长假期间.沈阳杲景区按待游客约为85000人.将数据85000用科学记数法表示为A.85X103B.8.5x 10'C.0.85x 10°D£.5x 10*3荒几何体的三视ffijnffl所示.这个几何体足主視图口左视图B. 三棱柱C. 长方体D. 圆俳4 •已知一组数据1下列说法正确的足2, 6・ 3. 3,俯视图A. 众数足3B. 中懺数足6C. 平均数足4D. 方差足55•—元一次不需式X"的解集在数粒上農示正•的是A B C D6.正方形足轴对称图形.A.2条Cg7 .下列运算正确的是A.(-x3r«-x c 它的对称轴有B.4条D.8条B U=: J二.填空题侮小题4分.共32分)10 •分鋼因式2m\l0m = _H.如图,克线a/7b.直线I 与Mg交于点P.与直馥b相交于点Q. PM11于点P.若乙1=50°• fU2= °・12.化简(U—_)•丄x-1 x13•已知一次国数存“1的图欽与反比例函数存上的图鮫相x交.其中令一个交点的零來标足2.14•如图.AABC三边的中点D t E. F组戍△ DEF, ADEF三边的中点M. N. P组成△MNP。
将Z^FPM与AECD涂成阴影隈设可以馳意右厶ABC中1R点.那么这个点取存阴彩部分的概率为8中考版20□■刊則k的值为________毎件进价为20元.调冷裘明亦果段时问内若以每件x元(2gxw30・且x为整数!出隹.可卖出(30-x)件.若使利卿18大.毎件的隹价应为________________ 元.16•如图,OABCD中.AB>AD. AE・BE. CM. DM分别为厶DAB・厶ABC,乙BCD. ZCDA的平分线.AE与DM相交于卢、F. BE 与CM相文于点H. iittEM,若OABCD的周长为42cm. FM=3cm, EF=4cm, g|EMs 1 cm» AB= 2 cm.三、解答题〔第17、18小题各8分,第19小毬10分,共26别17. 先化简.再承值1»$七・$卜"其中b=5.18. 如图.存矩形ABCD中.对角线AC. BD相交于点0・点E, F号别右边AD, BC上.且DE=CF,连接OE. OF.求证I OE-OF.第18题图19. 在一个不透明的塞子里有红球.白球、黑球各一个.它们除了倾色外其余都相PT小胡从盒子甲陆机授出一球.记录下倾色后放回盒子甲.充牙摇匀后.再馳机技出一球.并记录下颇色请用列表法或画树状图(树形图)法求小明两次授出的球颜色不同的礙邈.: 21.M公司今年情售一种产品.1月份获得利濟20万元.由于:产品輔舖.利润逐月绘加.3月份的利润比2月份的利洵绘加4.8:万元,假设该产品利涓每月的塔长率相同.求这个増长率.:五.(本题10力)22. 如图.00足4ABC的外接圆,AB为鱼逻.OD〃BC交O0于点D.文AC于点E, S«AD. BD. CD.(1)求证AD=CD.六、(本越12分)23. 如图,存平面垃角给标系中.四边影OABC的顶点0为半标原点,点C在x轴的正半50 上.且BC丄0C于点C.点A的坐标为(2.2\7T , AB=4\/T・四、每小题10分.共20分:20.2014年世界杯足球赛于北京时间6月13B2讨冇巴西开足球样目从參加世界杯球队中选出五支传统强队意大利队、徳国队、西班牙队、巴西队、阿根廷队.对哪支球队最有可能获得冠军进行了问卷调杏•为了使调今结果有效.每付菠调Q者只能頃写一份6卷.存冋卷中必须选鏗这五支球队中的一队作为调吝结果.这样的问卷才能成为有效何柱.从收集到的4800份耳效问牲中随机给取辭分何卷进行了线计.绘制了统计图表的一曲分如下根据统计便表捉供的信息.解答下列问苏(1)a»« b. :(2)根据以上信息.诸皐券存答题卡中补全条形统计图:(3)恨据抽样洞白结g「请你估计在提供有效问卷的这4800人中韦多少人戎测现国队E4可能获得J0军.ZB=6O°•点D足线«0C上一点.且0D=4・连按AD.(1)求证AAODj®畀边三角形.(2)求点B的坐标(3)平行于AD的直线I从原点0出发,沿x轴正方向平務.设直线I破四边形0ABCii得的线饺长为m.直线I与*仙交点做横生标为t.1当直线I与x轴的交点亦线段CD上(交点不与点G D亜合)时.请更孚写出m与t的函数关系式(不必写出自变金t的取值范用)2^m=2t请直樓写出此时直线I与x轴的交点半标.• •七.(木题12分)24. 如图1・在憂影ABCD中,对角线AC与BD相交于点6 AB=13,BD=24.农茎形ABCD的外邮以AB为边作*边三E形ABE.点F足对対线BD上一动点(点F不与点B匝合).将线段AF绕点A順时针方向检铸60=得到线段AM.连按FM.(1>求A0的长;(2)如图2.当点F在线段B0上.旦点M, F, C三点存同一条直线上时.求证AC= \/TAM⑶S«EM.若AAEM的血枳为40,请孚学三;出ZLAFM 的周长.温■提示:彦生可以根据鬆意.存备用图中补充图形.以便作答.(2)若AB = 10, cosz.ABC= • ^tanzDBC 的值.球队名称百分比意大利17%鶴国 a西班牙10%巴再38%mas b曲拥・4可11就傅g參加撕血◎叫匙坎狗色畀补“牛译臥硏补於攻计is二.填空题(包小越4分,共32分)9.3 10.2m(m+5:11.40 12.——x-1片13.6 14.—15.25 16 1 5; 21316三、解答题(第17、18小趁各8分,第19小題10分•共26分)17JI Ja4b)7-(a-bJ2l*®s(a\2ab*b-a\2ab-b-)-ae4ab*a=4『b八.(本题14分)25.AnSl.存平面直角半标系中•二次函fty=-Ax\l2的27图獄与y辘交于卢A.与x轴交于B・C两点(点8存点C的方侧)■连IIAB. AC.⑴点B的坐标为 _______ •点C的坐标为 _______ ;(2皿点C作射线CD AB.成M足线I殳AB上的动点.点P足线RAC 1的动点■冃始経満足BM=AP(点M不与点A.点B审合).过点"作MN/ BC分别交AC干点Q,交射线CD于点N (点Q不与点P 車合).连接PM. PN.设线段AP的长为n.1 JnE2,当n<—AC时.求证:APAM^ANCP;22直«!用含门的代数式表示线段PQ的长;• •3若PM的长为X/ST.当二次®fty=-Ax\l2的图象线过^aa-1.b=5 时•原式»4x(-1)18•证明・・•四边形ABCD为矩形..•.ZADC=ZBCD=9O°,AC=BD,OD=丄BD・2OC=J-AC ・.-.OD=OC.2/. r ODC=厶OCD.x5 = 20.・・・ Z.ADC- zODCs /.BCD- ZOCD,即ZL EDO» Z FCO. 又vDE.CF,/.AODEffiAOCF.A OE=OF19.解列表得-、第二次红球白球红球(红球,红球)(红球•白球)(红球球)白球(白璋■红球)(白球,白球)(白球.累球)(wv.tr 球)(尿球•白球)(用諫•禺球)或画树狀(形)图得平穆同时过点P和点N时.出此时的二次函欽农达式.示I老冷可以根・亦各用图中补充阴形.W 便作答. (trM・ttMt)(“M・Art)(灯球.Xi*)(口廉・tfflt)(r<«. nM)(白球.JE 球)(JE 球.tltf)(広球.白球)(盛球.泉球)—■选择题(毎小題3分,共24分)1.C2.B3.C4.A5.A6.B7.D8.C由表格(或拇状图/树形图)可知•共有9种可能出现的结果•每种结果出现的可能性相同•其中小明两次換出的球嫌色不同的结果有6种(红球■白球)(红球,黑球)(白球•红球)(白球•黑球)(黑球•红球X黑白球)■所以只小鋼两次授出的球顾色不同9 3中考S2O14 jffl四、每小题10分.共20分)20. ( 1 )a=30% b=5% (2)预测用有可能获得tit 界杯冠军球队的条形疣计图人敷200 ................. «血・・.固边矽ANCM 为知形./.ANxMC.AMsNC.・.・ rB=60° ・AB=4 \ T …・.ff RtAABN 中•AN =AB.s.n B =4VTx<L =6, BN=AB*cosB=4 v**T x *=2\ TT(314800 x30%«1440(人)答大约有1440人预测徳国队E 有可能跃得冠军. 21. 惬设这个塔长率为X.依题意得 20( 1 +x 匚20( 1 +x >=4.8解得心・62上汙-1.2(不合題童“広),0.2 = 20% 答这个増长率为20%. 五、(本題10分)22. ( 1 )uF 明 vABDOOS??•/. ZACB=9O° 又・・・0D 力BC-••厶AEO 二乙ACB=90°・・・・ OD 丄 AC./. ZkD=Cb..\ AD=CD.(21 解:・. AB= 10, /.OA = OD=—AB = 5.2・・・OD 〃BC.・・・乙AOE=ZABC. SRtAAE O 中. AAN=MC==:AM=2v r T.AOC=OM4MC=2*6=8.BC=BN>CN=2\ T ♦ 2 V"T « 4 \/T.・••点B 的第标为(8.4W⑶ 1 m= -L U 2. 212.0).(21.0).23七.(直题12分)24」1 )解・・•四边形ABCD 为菱形.・・・AC 丄BD,OB=OD=—BD.2•/BD.24. /.0B=12.?FRtA0AB4>t vAB»13, ...OA=VAB J -OB 2X V132-12J =5(2)证明厂••四边形ABCD 为菱妙 FA=FC..\ Z. FAC= Z FCA. 由已5tf)AF=AM.zMAF=6O° ・ •■•△AMF 为祥边三角形. AZMcZ AFM=60° ・・.•点M.F.C 三应在同一条直线上•・.厶 FAC+ 厶 FCA=ZAFM=6O J3OE=0Acos Z AOE=OAcos z_ ABC = 5x — = 3.5 /.DE=OD-OE=5-3=2.田勾股定 ,At= V^AO^Ot 2 = V57-32 =4. ??RtAAED^ JanzDAE = —= £ = ±.AE 42Xvz.DBC=厶 DAEtan L DBC=丄.2 六、(本超12分)23. ( 1 )]证明过克A 作AM 丄xSfi 于方M・・•点 A 的坐标为(2,2 V3") 1 /. OM=2, AM=2 \T. /.iTRtAAOM 中仙乙A0M=竺1二 2、丁 八OM 2 ・・・乙AOM=60° •由勾股定理得• OV 0M\AM ? = V2%(2VT f =4 ・・• OD=4. A r MAC= L MAF f ZL FAC=6(r +30。
辽宁省沈阳市2014年中考数学试题及答案【word解析版】

XX省XX市20XX中考数学试卷一、选择题〔每小题3分,共24分〕1.〔3分〕〔2014•XX〕0这个数是〔〕A.正数B.负数C.整数D.无理数考点:有理数.分析:根据0的意义,可得答案.解答:解:A、B、0不是正数也不是负数,故A、B错误;C、是整数,故C正确;D、0是有理数,故D错误;故选:C.点评:本题考查了有理数,注意0不是正数也不是负数,0是有理数.2.〔3分〕〔2014•XX〕20XX端午节小长假期间,XX某景区接待游客约为85000人,将数据85000用科学记数法表示为〔〕A.85×103B.8.5×104C.0.85×105D.8.5×105考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:解:将85000用科学记数法表示为:8.5×104.故选:B.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以与n的值.3.〔3分〕〔2014•XX〕某几何体的三视图如图所示,这个几何体是〔〕A.圆柱B.三棱柱C.长方体D.圆锥考点:由三视图判断几何体.分主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.析:解答:解:由于主视图和左视图为长方形可得此几何体为柱体,由俯视图为长方形可得为长方体.故选C.点评:本题考查了由三视图来判断几何体,还考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间的想象能力.4.〔3分〕〔2014•XX〕已知一组数据:1,2,6,3,3,下列说法正确的是〔〕A.众数是3 B.中位数是6 C.平均数是4 D.方差是5考点:众数;算术平均数;中位数;方差.分析:利用众数、算术平均数、中位数与方差的定义分别求解后即可确定正确的选项.解答:解:A、数据3出现2次,最多,故众数为3正确;B、排序后位于中间位置的数为3,故中位数为3,故选项错误;C、平均数为3,故选项错误;D、方差为2.4,故选项错误.故选A.点评:本题考查了众数、算术平均数、中位数与方差的定义,属于基础题,比较简单.5.〔3分〕〔2014•XX〕一元一次不等式x﹣1≥0的解集在数轴上表示正确的是〔〕A.B.C.D.考点:在数轴上表示不等式的解集;解一元一次不等式.分析:先求出不等式的解集,再在数轴上表示出来即可.解答:解:移项得,x≥1,故此不等式组的解集为:x≥1.在数轴上表示为:.故选A.点评:本题考查的是在数轴上表示不等式的解集,熟知“小于向左,大于向右〞是解答此题的关键.6.〔3分〕〔2014•XX〕正方形是轴对称图形,它的对称轴有〔〕A.2条B.4条C.6条D.8条考点:轴对称图形.分析:正方形既是矩形,又是菱形,具有矩形和菱形的轴对称性,由此可知其对称轴.解答:解:正方形的对称轴是两对角线所在的直线,两对边中点所在的直线,对称轴共4条.故选:B.点评:本题考查了正方形的轴对称性.关键是明确正方形既具有矩形的轴对称性,又具有菱形的轴对称性.7.〔3分〕〔2014•XX〕下列运算正确的是〔〕A.〔﹣x3〕2=﹣x6B.x4+x4=x8C.x2•x3=x6D.x y4÷〔﹣xy〕=﹣y3考点:整式的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.专题:计算题.分析:A、原式利用幂的乘方与积的乘方运算法则计算得到结果,即可作出判断;B、原式合并得到结果即可找出判断;C、原式利用同底数幂的乘法法则计算得到结果,即可找出判断;D、原式利用单项式除以单项式法则计算即可得到结果.解答:解:A、原式=x6,故选项错误;B、原式=2x4,故选项错误;C、原式=x5,故选项错误;D、原式=﹣y3,故选项正确.故选:D.点评:此题考查了整式的除法,合并同类项,同底数幂的乘法,以与幂的乘方与积的乘方,熟练掌握运算法则是解本题的关键.8.〔3分〕〔2014•XX〕如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC 于点E,若线段DE=5,则线段BC的长为〔〕A.7.5 B.10 C.15 D.20考点:相似三角形的判定与性质.分析:由DE∥BC,可证得△ADE∽△ABC,然后由相似三角形的对应边成比例求得答案.解答:解:∵DE∥BC,∴△ADE∽△ABC,∴=,∵BD=2AD,∴=,∵DE=5,∴=,∴DE=15.故选C.点评:此题考查了相似三角形的判定与性质.此题比较简单,注意掌握数形结合思想的应用.二、填空题〔每小题4分,共32分〕9.〔4分〕〔2014•XX〕计算:=3.考点:算术平方根.分析:根据算术平方根的定义计算即可.解答:解:∵32=9,∴=3.点评:本题较简单,主要考查了学生开平方的运算能力.10.〔4分〕〔2014•XX〕分解因式:2m2+10m=2m〔m+5〕.考点:因式分解-提公因式法.分析:直接提取公因式2m,进而得出答案.解答:解:2m2+10m=2m〔m+5〕.故答案为:2m〔m+5〕.点评:此题主要考查了提取公因式法分解因式,正确提取公因式是解题关键.11.〔4分〕〔2014•XX〕如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2=40°.考点:平行线的性质;垂线.分析:根据两直线平行,内错角相等,即可求得∠3=∠1,根据PM⊥l于点P,则∠MPQ=90°,即可求解.解答:解:∵直线a∥b,∴∠3=∠1=50°,又∵PM⊥l于点P,∴∠MPQ=90°,∴∠2=90°﹣∠3=90°﹣50°=40°.故答案是:40.点评:本题重点考查了平行线的性质与垂直的定义,是一道较为简单的题目.12.〔4分〕〔2014•XX〕化简:〔1+〕=.考点:分式的混合运算.专题:计算题.分析:原式括号中两项通分并利用同分母分式的加法法则计算,约分即可得到结果.解答:解:原式=•=•=.故答案为:.点评:此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.13.〔4分〕〔2014•XX〕已知一次函数y=x+1的图象与反比例函数y=的图象相交,其中有一个交点的横坐标是2,则k的值为6.考点:反比例函数与一次函数的交点问题.分析:把x=2代入一次函数的解析式,即可求得交点坐标,然后利用待定系数法即可求得k 的值.解答:解:在y=x+1中,令x=2,解得y=3,则交点坐标是:〔2,3〕,代入y=得:k=6.故答案是:6.点评:本题考查了用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.14.〔4分〕〔2014•XX〕如图,△ABC三边的中点D,E,F组成△DEF,△DEF三边的中点M,N,P组成△MNP,将△FPM与△ECD涂成阴影.假设可以随意在△ABC中取点,那么这个点取在阴影部分的概率为.考点:三角形中位线定理;几何概率.分析:先设阴影部分的面积是x,得出整个图形的面积是,再根据几何概率的求法即可得出答案.解答:解:∵D、E分别是BC、AC的中点,∴DE是△ABC的中位线,∴ED∥AB,且DE=AB,∴△CDE∽△CBA,∴==,∴S△CDE=S△CBA.同理,S△FPM=S△FDE=S△CBA.∴S△FPM=+S△CDE=S△CBA.则=.故答案是:.点评:本题考查了三角形中位线定理和几何概率.几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件〔A〕;然后计算阴影区域的面积在总面积中占的比例,这个比例即事件〔A〕发生的概率.15.〔4分〕〔2014•XX〕某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元〔20≤x≤30,且x为整数〕出售,可卖出〔30﹣x〕件.若使利润最大,每件的售价应为25元.考点:二次函数的应用.分析:本题是营销问题,基本等量关系:利润=每件利润×销售量,每件利润=每件售价﹣每件进价.再根据所列二次函数求最大值.解答:解:设最大利润为w元,则w=〔x﹣20〕〔30﹣x〕=﹣〔x﹣25〕2+25,∵20≤x≤30,∴当x=25时,二次函数有最大值25,故答案是:25.点评:本题考查了把实际问题转化为二次函数,再利用二次函数的性质进行实际应用.此题为数学建模题,借助二次函数解决实际问题.16.〔4分〕〔2014•XX〕如图,▱ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点H,连接EM.若▱ABCD的周长为42cm,FM=3cm,EF=4cm,则EM=5cm,AB=13cm.考点:矩形的判定与性质;勾股定理的应用;平行四边形的性质;相似三角形的应用.专题:综合题.分析:由条件易证∠AEB=∠AFD=∠DMC=90°.进而可证到四边形EFMN是矩形与∠EFM=90°,由FM=3cm,EF=4cm可求出EM.易证△ADF≌△CBN,从而得到DF=BN;易证△AFD∽△AEB,从而得到4DF=3AF.设DF=3k,则AF=4k.AE=4〔k+1〕,BE=3〔k+1〕,从而有AD=5k,AB=5〔k+1〕.由▱ABCD的周长为42cm 可求出k,从而求出AB长.解解:∵AE为∠DAB的平分线,答:∴∠DAE=∠EAB=∠DAB,同理:∠ABE=∠CBE=∠ABC,∠BCM=∠DCM=∠BCD,∠CDM=∠ADM=∠ADC.∵四边形ABCD是平行四边形,∴∠DAB=∠BCD,∠ABC=∠ADC,AD=BC.∴∠DAF=∠BCN,∠ADF=∠CBN.在△ADF和△CBN中,.∴△ADF≌△CBN〔ASA〕.∴DF=BN.∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAB+∠ABC=180°.∴∠EAB+∠EBA=90°.∴∠AEB=90°.同理可得:∠AFD=∠DMC=90°.∴∠EFM=90°.∵FM=3,EF=4,∴ME==5〔cm〕.∵∠EFM=∠FMN=∠FEN=90°.∴四边形EFMN是矩形.∴EN=FM=3.∵∠DAF=∠EAB,∠AFD=∠AEB,∴△AFD∽△AEB.∴=.∴=.∴4DF=3AF.设DF=3k,则AF=4k.∵∠AFD=90°,∴AD=5k.∵∠AEB=90°,AE=4〔k+1〕,BE=3〔k+1〕,∴AB=5〔k+1〕.∵2〔AB+AD〕=42,∴AB+AD=21.∴5〔k+1〕+5k=21.∴k=1.6.∴AB=13〔cm〕.故答案为:5、13.点评:本题考查了平行四边形的性质、平行线的性质、矩形的判定与性质、相似三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识,综合性较强.三、解答题〔17、18各8分,19题10分,共26分〕17.〔8分〕〔2014•XX〕先化简,再求值:{〔a+b〕2﹣〔a﹣b〕2}•a,其中a=﹣1,b=5.考点:整式的混合运算—化简求值.分析:先利用完全平方公式和整式的乘法计算化简,再进一步代入求得数值即可.解答:解:[〔a+b〕2﹣〔a﹣b〕2]•a =〔a2+2ab+b2﹣a2+2ab﹣b2〕•a =4ab•a=4a2b;当a=﹣1,b=5时,原式=4×〔﹣1〕2×5=20.点评:此题考查整式的混合运算与化简求值,注意先利用公式计算化简,再进一步代入求得数值即可.18.〔8分〕〔2014•XX〕如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.考点:全等三角形的判定与性质;矩形的性质.专题:证明题.分析:欲证明OE=OF,只需证得△ODE≌△OCF即可.解答:证明:如图,∵四边形ABCD是矩形,∴∠ADC=∠BCD=90°,AC=BD,OD=BD,OC=AC,∴OD=OC,∴∠ODC=∠OCD,∴∠ADC﹣∠ODC=∠BCD﹣∠OCD,即∠EDO=∠FCO,∴在△ODE与△OCF中,,∴△ODE≌△OCF〔SAS〕,∴OE=OF.点评:本题考查了全等三角形的判定与性质,矩形的性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.19.〔10分〕〔2014•XX〕在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图〔树形图〕法求小明两次摸出的球颜色不同的概率.考点:列表法与树状图法.分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小明两次摸出的球颜色不同的情况,再利用概率公式即可求得答案.解答:解:画树状图得:∵共有9种等可能的结果,小明两次摸出的球颜色不同的有6种情况,∴小明两次摸出的球颜色不同的概率为:=.点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.四、每小题10分,共20分20.〔10分〕〔2014•XX〕20XX世界杯足球赛于时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:球队名称百分比意大利17%德国 a西班牙10%巴西38%阿根廷0根据统计图表提供的信息,解答下列问题:〔1〕a=30%,b=5%;〔2〕根据以上信息,请直接在答题卡中补全条形统计图;〔3〕根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.考点:条形统计图;用样本估计总体.分析:〔1〕首先根据意大利有85人,占17%,据此即可求得总人数,则根据百分比的定义求得b的值,然后利用1减去其它各组的百分比即可求得a的值;〔2〕根据百分比的定义求得德国、西班牙的人数,即可解答;〔3〕利用总人数4800,乘以对应的百分比即可求解.解答:解:〔1〕总人数是:85÷17%=500〔人〕,则b==5%,a=1﹣17%﹣10%﹣38%﹣5%=30%;〔2〕〔3〕4800×30%=1440〔人〕.点评:本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.21.〔10分〕〔2014•XX〕某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.考点:一元二次方程的应用.专题:增长率问题.分析:设每月获得的利润的增长率是x,然后用x分别表示出2月份和3月份,根据“3月份的利润比2月份的利润增加4.8万元〞列方程求解.解答:解:设这个增长率为x.依题意得:200〔1+x〕2﹣20〔1+x〕=4.8,解得x1=0.2,x2=﹣1.2〔不合题意,舍去〕.0.2=20%.答:这个增长率是20%.点评:本题考查了一元二次方程的应用.此题中要求学生能够根据利润率分别用x表示出每一年的利润.能够熟练运用因式分解法解方程.五、本题10分22.〔10分〕〔2014•XX〕如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD.〔1〕求证:AD=CD;〔2〕若AB=10,cos∠ABC=,求tan∠DBC的值.考点:圆周角定理;勾股定理;圆心角、弧、弦的关系;解直角三角形.分析:〔1〕由AB为直径,OD∥BC,易得OD⊥AC,然后由垂径定理证得,=,继而证得结论;〔2〕由AB=10,cos∠ABC=,可求得OE的长,继而求得DE,AE的长,则可求得tan∠DAE,然后由圆周角定理,证得∠DBC=∠DAE,则可求得答案.解答:〔1〕证明:∵AB为⊙O的直径,∴∠ACB=90°,∵OD∥BC,∴∠AEO=∠ACB=90°,∴OD⊥AC,∴=,∴AD=CD;〔2〕解:∵AB=10,∴OA=OD=AB=5,∵OD∥BC,∴∠AOE=∠ABC,在Rt△AEO中,OE=OA•cos∠AOE=OA•cos∠ABC=5×=3,∴DE=OD=OE=5﹣3=2,∴AE===4,在Rt△AED中,tan∠DAE===,∵∠DBC=∠DAE,∴tan∠DBC=.点评:此题考查了圆周角定理、垂径定理以与勾股定理.此题难度适中,注意掌握数形结合思想的应用.六、本题12分23.〔12分〕〔2014•XX〕如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,点A的坐标为〔2,2〕,AB=4,∠B=60°,点D是线段OC上一点,且OD=4,连接AD.〔1〕求证:△AOD是等边三角形;〔2〕求点B的坐标;〔3〕平行于AD的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形OABC截得的线段长为m,直线l与x轴交点的横坐标为t.①当直线l与x轴的交点在线段CD上〔交点不与点C,D重合〕时,请直接写出m与t 的函数关系式〔不必写出自变量t的取值X围〕②若m=2,请直接写出此时直线l与x轴的交点坐标.考点:一次函数综合题.分析:〔1〕过点A作AM⊥x轴于点M,根据已知条件,依据三角函数求得∠AOM=60°,根据勾股定理求得OA=4,即可求得.〔2〕过点A作AN⊥BC于点N,则四边形AMCN是矩形,在Rt△ABN中,根据三角函数求得AN、BN的值,从而求得OC、BC的长,得出点B的坐标.〔3〕①如图3,因为∠B=60°,BC=4,所以PC=12,EM=m,因为OC=8,所以PO=4,OF=t,DF=t﹣m,所以PD=4+〔t﹣m〕,根据△PDE∽△PCB即可求得m=t+2;②如图4,△OEF是等边三角形所以OF=EF=m=2,在Rt△PCF'中∠CF'P=60°,∠BPE'=∠CPF'=30°,所以BP=PE'÷sin∠B=,PC=4﹣=,根据勾股定理求得CF'=,所以OF'=8+=.解答:解:〔1〕如图2,证明:过点A作AM⊥x轴于点M,∵点A的坐标为〔2,2〕,∴OM=2,AM=2∴在Rt△AOM中,tan∠AOM===∴∠AOM=60°由勾股定理得,OA===4∵OD=4,∴OA=OD,∴△AOD是等边三角形.〔2〕如图2,解:过点A作AN⊥BC于点N,∵BC⊥OC,AM⊥x轴,∴∠BCM=∠CMA=∠ANC=90°∴四边形ANCM为矩形,∴AN=MC,AM=NC,∵∠B=60°,AB=4,∴在Rt△ABN中,AN=AB•SinB=4×=6,BN=AB•CosB=4×=2∴AN=MC=6,CN=AM=2,∴OC=OM+MC=2+6=8,BC=BN+CN=2+2=4,∴点B的坐标为〔8,4〕.〔3〕①如图3,m=t+2;②如图4,〔2,0〕,〔,0〕.点评:本题考查了等边三角形的性质,矩形的性质,直角三角函数的应用以与勾股定理的应用.七、本题12分24.〔12分〕〔2014•XX〕如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点〔点F不与点B重合〕,将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.〔1〕求AO的长;〔2〕如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=AM;〔3〕连接EM,若△AEM的面积为40,请直接写出△AFM的周长.考点:四边形综合题.分析:〔1〕在RT△OAB中,利用勾股定理OA=求解,〔2〕由四边形ABCD是菱形,求出△AFM为等边三角形,∠M=∠AFM=60°,再求出∠MAC=90°,在RT△ACM中tan∠M=,求出AC.〔3〕求出△AEM≌△ABF,利用△AEM的面积为40求出BF,在利用勾股定理AF===,得出△AFM的周长为3.解答:解:〔1〕∵四边形ABCD是菱形,∴AC⊥BD,OB=OD=BD,∵BD=24,∴OB=12,在RT△OAB中,∵AB=13,∴OA===5,〔2〕如图2,∵四边形ABCD是菱形,∴BD垂直平分AC,∴FA=FC,∠FAC=∠FCA,由已知AF=AM,∠MAF=60°,∴△AFM为等边三角形,∴∠M=∠AFM=60°,∵点M,F,C三点在同一条直线上,∴∠FAC+∠FCA=∠AFM=60°,∴∠FAC=∠FCA=30°,∴∠MAC=∠MAF+∠FAC=60°+30°=90°,在RT△ACM中∵tan∠M=,∴tan60°=,∴AC=AM.〔3〕如图,连接EM,∵△ABE是等边三角形,∴AE=AB,∠EAB=60°,由〔1〕知△AFM为等边三角形,∴AM=AF,∠MAF=60°,∴∠EAM=∠BAF,在△AEM和△ABF中,,∴△AEM≌△ABF〔SAS〕,∵△AEM的面积为40,△ABF的高为AO ∴BF•AO=40,BF=16,∴FO=BF﹣BO=16﹣12=4AF===,∴△AFM的周长为3.点评:本题主要考查四边形的综合题,解题的关键是灵活运用等过三角形的性质与菱形的性质.八、本题14分25.〔14分〕〔2014•XX〕如图1,在平面直角坐标系中,二次函数y=﹣x2+12的图象与y 轴交于点A,与x轴交于B,C两点〔点B在点C的左侧〕,连接AB,AC.〔1〕点B的坐标为〔﹣9,0〕,点C的坐标为〔9,0〕;〔2〕过点C作射线CD∥AB,点M是线段AB上的动点,点P是线段AC上的动点,且始终满足BM=AP〔点M不与点A,点B重合〕,过点M作MN∥BC分别交AC于点Q,交射线CD于点N 〔点Q不与点P重合〕,连接PM,PN,设线段AP的长为n.①如图2,当n<AC时,求证:△PAM≌△NCP;②直接用含n的代数式表示线段PQ的长;③若PM的长为,当二次函数y=﹣x2+12的图象经过平移同时过点P和点N时,请直接写出此时的二次函数表达式.考点:二次函数综合题.分析:〔1〕由二次函数y=﹣x2+12的图象与y轴交于点A,与x轴交于B,C两点,代入y=0,即可解出B,C坐标.〔2〕①求证三角形全等.易发现由平行可得对应角相等,由平行四边形对边相等与已知BM=AP,可得对应角的两个邻边对应相等,则利用SAS得证.②上问中以提示n<AC,则我们可以分n<AC,n=AC,n>AC三种情形讨论.又已得△PAM≌△NCP,顺推易得PQ与n的关系.③上问中已得当n<AC时,PQ=15﹣2n;当n>AC时,PQ=2n﹣15,则也要分两种情形讨论,易得两种情形的P,N.由图象为二次函数y=﹣x2+12平移后的图形,所以可设解析式为y=﹣〔x+k〕2+12+h,代入即得.解答:〔1〕答:〔﹣9,0〕,〔9,0〕.解:B、C为抛物线与x轴的交点,故代入y=0,得y=﹣x2+12=0,解得x=﹣9或x=9,即B〔﹣9,0〕,C〔9,0〕.〔2〕①证明:∵AB∥CN,∴∠MAP=∠PCN,∵MN∥BC,∴四边形MBCN为平行四边形,∴BM=CN,∵AP=BM,∴AP=CN,∵BO=OC,OA⊥BC,∴OA垂直平分BC,∴AB=AC,∴AM=AB﹣BM=AC﹣AP=CP.在△MAP和△PCN中,,∴△MAP≌△PCN〔AAS〕.②解:1.当n<AC时,如图1,,∵四边形MBCN为平行四边形,∴∠MBC=∠QNC,∵AB=AC,MN∥BC,∴∠MBC=∠QCB=∠NQC,∴∠NQC=∠QNC,∴CN=CQ,∵△MAP≌△PCN,∴AP=CN=CQ,∵AP=n,AC===15,∴PQ=AC﹣AP﹣QC=15﹣2n.2.当n=AC时,显然P、Q重合,PQ=0.3.当n>AC时,如图2,∵四边形MBCN为平行四边形,∴∠MBC=∠QNC,BM=CN∵AB=AC,MN∥BC,∴∠MBC=∠QCB=∠NQC,∴∠NQC=∠QNC,∴BM=CN=CQ,∵AP=BM,∴AP=CQ,∵AP=n,AC=15,∴PQ=AP+QC﹣AC=2n﹣15.综上所述,当n≤AC时,PQ=15﹣2n;当n>AC时,PQ=2n﹣15.③或.分析如下:1.当n≤AC时,如图3,过点P作x轴的垂线,交MN于E,交BC于F.此时△PEQ∽△PFC∽△AOC,PQ=15﹣2n.∵PM=PN,∴ME=EN=MN=BC=9,∴PE===4,∵OC:OA:AC=3:4:5,△PEQ∽△PFC∽△AOC,∴PQ=5,∴15﹣2n=5,∴AP=n=5,∴PC=10,∴FC=6,PF=8,∵OF=OC﹣FC=9﹣6=3,EN=9,EF=PF﹣PE=8﹣4=4,∴P〔3,8〕,N〔12,4〕.设二次函数y=﹣x2+12平移后的解析式为y=﹣〔x+k〕2+12+h,∴,解得,∴y=﹣〔x+6〕2+12+8=﹣x2+x+4.2.当n>AC时,如图4,过点P作x轴的垂线,交MN于E,交BC于F.此时△PEQ∽△PFC∽△AOC,PQ=2n﹣15...∵PM=PN ,∴ME=EN=MN=BC=9,∴PE===4,∵OC :OA :AC=3:4:5,△PEQ ∽△PFC ∽△AOC ,∴PQ=5,∴2n ﹣15=5,∴AP=n=10,∴PC=5,∴FC=3,PF=4,∵OF=OC ﹣FC=9﹣3=6,EN=9,EF=PF+PE=4+4=8,∴P 〔6,4〕,N 〔15,8〕.设二次函数y=﹣x 2+12平移后的解析式为y=﹣〔x+k 〕2+12+h , ∴,解得, ∴y=﹣〔x ﹣12〕2+12﹣=﹣x 2+x ﹣12.点评: 本题考查了二次函数的图象与性质,三角形全等、相似的证明与性质,函数平移与待定系数法求过定点函数解析式等知识.回答题目是一定注意多问综合题目问题之间的相关性,顺着题目思路递推易得思路.本题计算量稍大,难度适中,适合学生训练.。
沈阳市中考数学试卷及答案解析
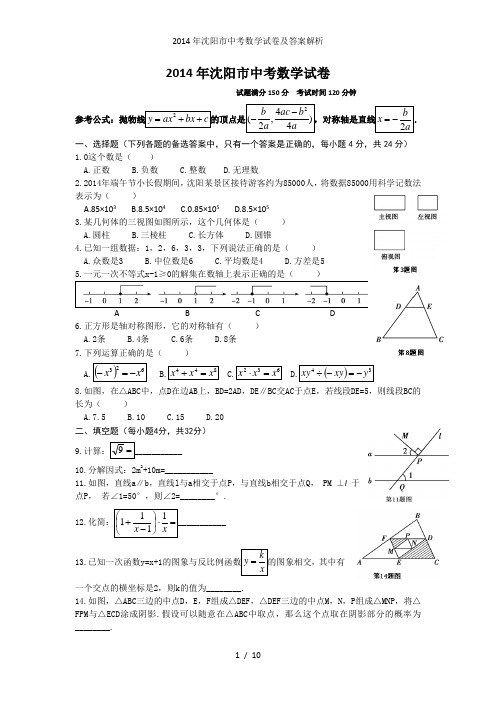
2014年沈阳市中考数学试卷试题满分150分 考试时间120分钟 参考公式:抛物线2y ax bx c =++的顶点是24(,)24b ac b a a --,对称轴是直线2b x a =-. 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题4分,共24分) 1.0这个数是( )A.正数B.负数C.整数D.无理数2.2014年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为( )A.85×103B.8.5×104C.0.85×105D.8.5×1053.某几何体的三视图如图所示,这个几何体是( )A.圆柱B.三棱柱C.长方体D.圆锥4.已知一组数据:1,2,6,3,3,下列说法正确的是( )A.众数是3B.中位数是6C.平均数是4D.方差是55.一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A B C D6.正方形是轴对称图形,它的对称轴有( )A.2条B.4条C.6条D.8条7.下列运算正确的是( )A.()623x x -=-B.844x x x =+C.632x x x =⋅D.()34y xy xy -=-÷8.如图,在△ABC 中,点D 在边AB 上,BD=2AD ,DE ∥BC 交AC 于点E ,若线段DE=5,则线段BC 的长为( )A.7.5B.10C.15D.20二、填空题(每小题4分,共32分)9.计算:=9___________10.分解因式:2m 2+10m=___________11.如图,直线a ∥b ,直线l 与a 相交于点P ,与直线b 相交于点Q , PM ⊥l 于点P , 若∠1=50°,则∠2=________°.12.化简:=⋅⎪⎭⎫ ⎝⎛-+xx 1111___________ 13.已知一次函数y=x+1的图象与反比例函数xk y =的图象相交,其中有一个交点的横坐标是2,则k 的值为________.14.如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M ,N ,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在△ABC 中取点,那么这个点取在阴影部分的概率为________.15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数) 出售,可卖出(30-x)件.若使利润最大,每件的售价应为________元16.如图,□ABCD 中,AB >AD ,AE ,BE ,CM ,DM 分别为∠DAB ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM= ① cm ,AB= ② cm.三、解答题(第17、18小题各8分,第19小题10分,共26分)17.先化简,再求值:()()a b a b a ⋅--+22,其中a=-1,b=5.18.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE=CF ,连接OE ,OF.求证:OE=OF.19.在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.四、(每小题10分,共20分)20.2014年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a=________,b=________;(2)根据以上信息,请直接..在答题卡中补全条形统计图; (3) 根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.21.某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.五、(本题10分)22.如图,⊙O 是△ABC 的外接圆,AB 为直径,OD ∥BC 交⊙O 于点D ,交AC 于点E ,连接AD ,BD ,CD(1)求证:AD=CD ;(2)若AB=10,cos ∠ABC=53,求tan ∠DBC 的值.六、(本题12分)23.如图,在平面直角坐标系中,四边形OABC 的顶点O 为坐标原点,点C 在x 轴的正半轴上,且BC ⊥OC 于点C ,点A 的坐标为 (2,32),AB=34,∠B=60°,点D 是线段OC 上一点,且OD=4,连接AD.(1)求证:△AOD 是等边三角形;(2)求点B 的坐标;(3)平行于AD 的直线l 从原点O 出发,沿x 轴正方向平移.设直线l 被四边形OABC 截得的线段长为m ,直线l 与x 轴交点的横坐标为t.①当直线l 与x 轴的交点在线段CD 上(交点不与点C ,D 重合)时,请直接..写出m 与t 的函数关系式(不必写出自变量t 的取值范围)②若m=2,请直接..写出此时直线l 与x 轴的交点坐标.七、(本题12分)24.如图1,在菱形ABCD 中,对角线AC 与BD 相交于点O ,AB=13,BD=24,在菱形ABCD 的外部以AB 为边作等边三角形ABE.点F 是对角线BD 上一动点(点F 不与点B 重合),将线段AF 绕点A 顺时针方向旋转60°得到线段AM ,连接FM.(1)求AO 的长;(2)如图2,当点F 在线段BO 上,且点M ,F ,C 三点在同一条直线上时,求证:AC=3AM ;(3) 连接EM ,若△AEM 的面积为40,请直接..写出△AFM 的周长. 温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.八、(本题14分)25.如图1,在平面直角坐标系中,二次函数122742+-=x y 的图象与y 轴交于点A ,与x 轴交于B ,C 两点(点B 在点C 的左侧),连接AB ,AC.(1)点B 的坐标为________,点C 的坐标为________;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP(点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n.①如图2,当AC n 21<时,求证:△PAM ≌△NCP ; ②直接..用含n 的代数式表示线段PQ 的长; ③若PM 的长为97,当二次函数122742+-=x y 的图象经过平移同时过点P 和点N 时,请直.接.写出此时二次函数表达式 温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.。
2014年沈阳市中考数学试卷

2014年沈阳市中考数学试卷试题满分150分 考试时间120分钟参考公式:抛物线2y ax bx c =++的顶点是24(,)24b ac b a a --,对称轴是直线2b x a =-. 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题4分,共24分)1.0这个数是( )A.正数B.负数C.整数D.无理数2.2014年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为( )A.85×103B.8.5×104C.0.85×105D.8.5×1053.某几何体的三视图如图所示,这个几何体是( )A.圆柱B.三棱柱C.长方体D.圆锥4.已知一组数据:1,2,6,3,3,下列说法正确的是( )A.众数是3B.中位数是6C.平均数是4D.方差是55.一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A B C D6.正方形是轴对称图形,它的对称轴有( )A.2条B.4条C.6条D.8条7.下列运算正确的是( )A.()623x x -=-B.844x x x =+C.632x x x =⋅D.()34y xy xy -=-÷8.如图,在△ABC 中,点D 在边AB 上,BD=2AD ,DE ∥BC 交AC 于点E ,若线段DE=5,则线段BC 的长为( ) A.7.5 B.10 C.15 D.20填空题(每小题4分,共32分)9.计算:=9___________10.分解因式:2m 2+10m=___________11.如图,直线a ∥b ,直线l 与a 相交于点P ,与直线b 相交于点Q , PM ⊥l 于点P , 若∠1=50°,则∠2=________12.化简:=⋅⎪⎭⎫ ⎝⎛-+xx 1111___________ 13.已知一次函数y=x+1的图象与反比例函数x k y =的图象相交,其中有一个交点的横坐标是2,则k 的值为________.14.如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M ,N ,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在△ABC 中取点,那么这个点取在阴影部分的概率为________.15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数) 出售,可卖出(30-x)件.若使利润最大,每件的售价应为________元16.如图,□ABCD 中,AB >AD ,AE ,BE ,CM ,DM 分别为∠DAB ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM= ① cm ,AB= ② cm.三、解答题(第17、18小题各8分,第19小题10分,共26分)17.先化简,再求值:()()a b a b a ⋅--+22,其中a=-1,b=5.18.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE=CF ,连接OE ,OF.求证:OE=O F.19、在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.(每小题10分,共20分)20.2014年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a=________,b=________;(2)根据以上信息,请直接..在答题卡中补全条形统计图; (3) 根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.21、某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.22、如图,⊙O 是△ABC 的外接圆,AB 为直径,OD ∥BC 交⊙O 于点D ,交AC 于点E ,连接AD ,BD ,CD(1)求证:AD=CD ;(2)若AB=10,cos ∠ABC=53,求tan ∠DBC 的值.23、如图,在平面直角坐标系中,四边形OABC 的顶点O 为坐标原点,点C 在x 轴的正半轴上,且BC ⊥OC 于点C ,点A 的坐标为 (2,32),AB=34,∠B=60°,点D 是线段OC 上一点,且OD=4,连接AD.(1)求证:△AOD 是等边三角形;(2)求点B 的坐标;(3)平行于AD 的直线l 从原点O 出发,沿x 轴正方向平移.设直线l 被四边形OABC 截得的线段长为m ,直线l 与x 轴交点的横坐标为t.①当直线l 与x 轴的交点在线段CD 上(交点不与点C ,D 重合)时,请直接..写出m 与t 的函数关系式(不必写出自变量t 的取值范围) ②若m=2,请直接..写出此时直线l 与x 轴的交点坐标.24.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;(3)连接EM,若△AEM的面积为40,请直.接.写出△AFM的周长.25、如图1,在平面直角坐标系中,二次函数122742+-=x y 的图象与y 轴交于点A ,与x 轴交于B ,C 两点(点B 在点C 的左侧),连接AB ,AC.(1)点B 的坐标为________,点C 的坐标为________;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP(点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n.①如图2,当AC n 21<时,求证:△PAM ≌△NCP ; ②直接..用含n 的代数式表示线段PQ 的长; ③若PM 的长为97,当二次函数122742+-=x y 的图象经过平移同时过点P 和点N 时,请直接..写出此时二次函数表达式温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.。
辽宁省沈阳市2014年中考数学真题试题(含扫描答案)

辽宁省沈阳市2014年中考数学真题试题试题满分150分 考试时间120分钟参考公式:抛物线2y ax bx c =++的顶点是24(,)24b ac b a a --,对称轴是直线2b x a =-. 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题4分,共24分)1.0这个数是( )A.正数B.负数C.整数D.无理数2.2014年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为( )A.85×103B.8.5×104C.0.85×105D.8.5×105 3.某几何体的三视图如图所示,这个几何体是( )A.圆柱B.三棱柱C.长方体D.圆锥4.已知一组数据:1,2,6,3,3,下列说法正确的是( )A.众数是3B.中位数是6C.平均数是4D.方差是55.一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A B C D6.正方形是轴对称图形,它的对称轴有( )A.2条B.4条C.6条D.8条7.下列运算正确的是( )A.()623x x -=-B.844x x x =+C.632x x x =⋅D.()34y xy xy -=-÷8.如图,在△ABC 中,点D 在边AB 上,BD=2AD ,DE ∥BC 交AC 于点E ,若线段DE=5,则线段BC 的长为( ) A.7.5 B.10 C.15 D.20二、填空题(每小题4分,共32分)9.计算:=9___________10.分解因式:2m 2+10m=___________11.如图,直线a ∥b ,直线l 与a 相交于点P ,与直线b 相交于点Q , PM ⊥l 于点P , 若∠1=50°,则∠2=________°.12.化简:=⋅⎪⎭⎫ ⎝⎛-+xx 1111___________ 13.已知一次函数y=x+1的图象与反比例函数x k y =的图象相交,其中有一个交点的横坐标是2,则k 的值为________.14.如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M ,N ,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在△ABC 中取点,那么这个点取在阴影部分的概率为________.15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数) 出售,可卖出(30-x)件.若使利润最大,每件的售价应为________元16.如图,□ABCD 中,AB>AD ,AE ,BE ,CM ,DM 分别为∠DAB ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM= ① cm ,AB= ② cm.三、解答题(第17、18小题各8分,第19小题10分,共26分)17.先化简,再求值:()()a b a b a ⋅--+22,其中a=-1,b=5.18.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE=CF ,连接OE ,OF.求证:OE=O F.19.在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.四、(每小题10分,共20分)20.2014年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a=________,b=________;(2)根据以上信息,请直接..在答题卡中补全条形统计图; (3) 根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.21.某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.五、(本题10分)22.如图,⊙O 是△ABC 的外接圆,AB 为直径,OD ∥BC 交⊙O 于点D ,交AC 于点E ,连接AD ,BD ,CD(1)求证:AD=CD ;(2)若AB=10,cos ∠ABC=53,求tan ∠DBC 的值.六、(本题12分)23.如图,在平面直角坐标系中,四边形OABC 的顶点O 为坐标原点,点C 在x 轴的正半轴上,且BC ⊥OC 于点C ,点A 的坐标为 (2,32),AB=34,∠B=60°,点D 是线段OC 上一点,且OD=4,连接AD.(1)求证:△AOD 是等边三角形;(2)求点B 的坐标;(3)平行于AD 的直线l 从原点O 出发,沿x 轴正方向平移.设直线l 被四边形OABC 截得的线段长为m ,直线l 与x 轴交点的横坐标为t.①当直线l 与x 轴的交点在线段CD 上(交点不与点C ,D 重合)时,请直接..写出m 与t 的函数关系式(不必写出自变量t 的取值范围)②若m=2,请直接..写出此时直线l与x轴的交点坐标.七、(本题12分)24.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;(3)连接EM,若△AEM的面积为40,请直.接.写出△AFM的周长.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.八、(本题14分)25.如图1,在平面直角坐标系中,二次函数122742+-=x y 的图象与y 轴交于点A ,与x 轴交于B ,C 两点(点B 在点C 的左侧),连接AB ,AC.(1)点B 的坐标为________,点C 的坐标为________;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP(点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n.①如图2,当AC n 21<时,求证:△PAM ≌△NCP ; ②直接..用含n 的代数式表示线段PQ 的长;③若PM 的长为97,当二次函数122742+-=x y 的图象经过平移同时过点P 和点N 时,请直接..写出此时二次函数表达式温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.。
2014年沈阳市数学中考题详解

2014年辽宁省沈阳市中考试题数学(满分150分,考试时间120分钟)参考公式:抛物线y=ax2+bx+c的顶点坐标是(-b2a,4ac-b24a).对称轴是直线x=-b2a.一、选择题(下面各题的备选答案中,只有一个答案是正确的,每小题3分,共24分)1.(2014年辽宁省沈阳市,1,3分) 0这个数是()A.正数 B.负数 C.整数 D.无理数【答案】C2.(2014年辽宁省沈阳市,2,3分)2014年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为()A.85×103 B.8.5×104 C.0.85×105 D.8.5×105【答案】B3.(2014年辽宁省沈阳市,3,3分)某几何体的三视图如图所示,这个几何体是()A.圆柱 B.三棱柱C.长方体 D.圆锥【答案】C4.(2014年辽宁省沈阳市,4,3分)已知一组数据:1,2,6,3,3,下列说法正确的是()A.众数是3 B.中位数是6 C.平均数是4 D.方差是5【答案】A5.(2014年辽宁省沈阳市,5,3分)一元一次不等式x-1≥0的解集在数轴上表示正确的是( )【答案】A6.(2014年辽宁省沈阳市,6,3分)正方形是轴对称图形,它的对称轴有()A.2条 B.4条 C.6条 D.8条【答案】B7.(2014年辽宁省沈阳市,7,3分) 下列运算正确的是()A.(-x3)2=-x6 B.x4+x4=x8C.x2•x3=x6 D.xy4÷(-xy)=-y3【答案】D8.(2014年辽宁省沈阳市,8,3分)如图,在△ABC中,点D在边AB上,BD=2AD,DE//BC交AC于点E,若线段DE=5,则线段BC的长为()A. 7.5B. 10C.15D.20【答案】C二、填空题(每小题4分,共32分)9.(2014年辽宁省沈阳市,9,4分) 计算:9=__________.【答案】310. (2014年辽宁省沈阳市,10,4分) 分解因式:2m2+10m=__________. 【答案】2m(m+5)11. (2014年辽宁省沈阳市,11,4分) 如图,直线a//b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50 °,则∠2= °.【答案】4012. (2014年辽宁省沈阳市,12,4分)化简:(1+1x -1)·1x=___________. 【答案】1x -113. (2014年辽宁省沈阳市,13,4分)已知一次函数y =x +1的图象与反比例函数y =k x的图象相交,其中一个交点的横坐标是2,则k 的值为_________. 【答案】614. (2014年辽宁省沈阳市,14,4分) 如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M,N,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在ABC △中取点,那么这个点取在阴影部分的概率为__________.【答案】51615.(2014年辽宁省沈阳市,15,4分)某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数)出售,可卖出(30-x )件.若使利润最大,每件的售价应为__________元.【答案】16.(2014年辽宁省沈阳市,16,4分)(每题7分,共14分)如图,□ABCD 中,AB>AD ,AE,BE,CM,DM 分别为∠DBA ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM= cm ,AB= cm.【答案】5;13三、解答题(第17、18小题各8分,第19小题10分,共26分)17. (2014年辽宁省沈阳市,17,8分)先化简,再求值:(a +b )2-(a -b )2éëùû·a ,其中a =-1,b =5.【答案】解: (a +b )2-(a -b )2éëùû·a=a 2+2ab +b 2-a 2+2ab -b 2éëùû·a=4ab ·a=4a 2b当a =-1,b=5时,原式=4×(-1)2×5=20.18.(2014年辽宁省沈阳市,18,8分)如图,在矩形ABCD 中,对角线AC,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE=CF ,连接OE ,OF. 求证:OE=OF.【答案】证明:∵四边形ABCD为矩形,∴∠ADC=∠BCD=90°,AC=BD,OD=12BD,OC=12AC.OD=OC.∴∠ODC=∠OCD.∴∠ADC-∠ODC =∠BCD-∠OCD,即∠EDO=∠FCO.又∵DE=CF,∴△ODE≌△OCF. ∴OE=OF.19.(2014年辽宁省沈阳市,19,10分) 在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率. 【答案】解:或画树状(形)图得:由表格(或树状图/树形图)可知,共有9种可能出现的结果,每种结果出现的可能性相同,其中小明两次摸出的球颜色不同的结果有6种:(红球,白球)(红球,黑球)(白球,红球)(白球,黑球)(黑球,红球)(黑球,白球),所以P (小明两次摸出的球的颜色不同)=69=23.四、(每小题10分,共20分)20. (2014年辽宁省沈阳市,20,10分)2014年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查都只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a= ,b= ;(2)根据以上信息,请直接..在答题卡中补全条形统计图; (3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.【答案】解:(1) a=30%,b=5% (2)(3)4800×30%=1440(人)答:大约有1440人预测德国队最有可能获得冠军.21.(2014年辽宁省沈阳市,21,10分)某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.【答案】解:设这个增长率为x.依题意得:20(1+x )2-20(1+x )=4.8解得:x 1=0.2,x 2=-1.2(不合题意,舍去),0.2=20%答:这个增长率为20%.五、(本题10分)22.(2014年辽宁省沈阳市,22,10分)如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD.(1)求证:AD=CD;(2)若AB=10,cos∠ABC=35,求tan∠DBC的值.【答案】解:(1)证明:∵AB为⊙O直径,∴∠ACB=90°. 又∵OD∥BC, ∴∠AEO=∠ACB=90°.∴OD⊥AC. ∴AD=CD.∴AD=CD.(2)解:∵AB=10,∴OA=OD=12AB=5.∵OD∥BC,∴∠AOE=∠ABC.在Rt△AEO中,OE=OAcos∠AOE= OAcos∠ABC=5×35=3.∴DE=OD-OE=5-3=2.由勾股定理得,AE=AO2-OE2=52-32=4.在Rt△AED中,tan∠DAE=DEAE=24=12.又∵∠DBC=∠DAE, ∴tan∠DBC=12.六、(本题12分)23.(2014年辽宁省沈阳市,23,12分)如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,点(),AB=43,∠B=60°,点D是线段OC上一点,且OD=4,A的坐标为2,23连接AD.(1)求证:△AOD是等边三角形;(2)求点B的坐标;(3)平行于AD的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形OABC截得的线段长为m,直线l与x轴交点的横坐标为t.①当直线l与x轴的交点在线段CD上(交点不与点以,D重合)时,请直接写出m与t的函数关系式(不必写出自变量t的取值范围);②若m=2,请直接..写出此时直线l与x轴的交点坐标.【答案】解: (1)证明:过点作AM⊥x轴于点M,∵点A的坐标为2,23(),∴OM=2,AM=23.∴在Rt△AOM中,tan∠AOM=AMOM=232=3,∴∠AOM=60°.由勾股定理得,OA=OM2+AM2=22+23()2=4∵OD=4,∴OA=OD.∴△AOD是等边三角形.(2)解:过点A作AN⊥BC于点N,∵BC⊥OC,AM⊥x轴,∴∠BCM=∠CMA=∠ANC =90°.∴四边形ANCM为矩形,∴AN=MC,AM=NC.∵∠B=60°,AB=43,∴在Rt△ABN中,AN=AB·sinB=43´32=6,∴BN=AB·cosB= 43´12=23.∴AN=MC=6,CN=AM=23.∴OC=OM+MC=2+6=8, BC=BN+CN=23+23=43.∴点B的坐标为(8,43).(3)①m=12t+2. ②(2,0),(323,0)七、(本题12分)24.(2014年辽宁省沈阳市,24,12分)如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A 在顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;(3)连接EM,若△AEM的面积为40,请直接..写出△AFM的周长.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.【答案】解:(1)解:∵四边形ABCD为菱形,∴AC⊥BD,OB=OD=12 BD.∵BD=24,∴OB=12. ∴在Rt△OAB中,∵AB=13,∴OA=AB2-OB2=132-122=5.(2)证明:∵四边形ABCD为菱形,∴BD垂直平分AC.∴FA=FC. ∠FAC=∠FCA.由已知AF=AM.∴∠MAF=60°.∴△AMF为等边三角形.∴∠M=∠AFM=60°.∵点M,F,C三点在同一条直线上∴∠FAC+∠FCA=∠AFM=60°. ∴∠FAC=∠FCA=30°.∴∠MAC=∠MAF+∠FAC=60°+30°=90°.在Rt △ACM 中,tanM=AC AM ,∴tan60°=AC AM. ∴AC=3AM.(3) △AFM 的周长为341.八、(本题14分)25.(2014年辽宁省沈阳市,25,14分) 如图1,在平面直角坐标系中,二次函数y =-427x 2+12的图象与y 轴交于点A ,与x 轴交于点B ,C 两点(点B 在点C 的左侧),连接AB ,AC.(1)点B 的坐标为 ,点C 的坐标为 ;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP (点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n.①如图2,当n <12AC 时,求证:△PAM ≌△NCP ; ②直接..用含n 的代数式表示线段PQ 的长;③若PM的长为97,当二次函数y=-427x2+12的图象经过平移同时过点P和点N时,请直接..写出此时的二次函数的表达式.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答【答案】解:(1)(-9,0),(9,0).(2)①证明:∵AB∥CD,MN∥BC,∴四边形BMNC为平行四边形.∴BM=CN.∵BM=AP,∴AP=CN.∵OC=OB=9,又∵AO⊥BC,∴AB=AC,∴AB-BM=AC-AP.∴AM=PC.∵AB∥CD,∴∠MAP=∠PCN.∴△PAM≌△NCP.②15-2n或2n-15.③y=-427x2+169x+4或y=-427x2+329x-12.。
中考数学试卷2014年沈阳卷(有答案)

2014年沈阳市中等学校招生统一考试数学试题(含答案全解全析)参考公式:抛物线y=ax2+bx+c的顶点是--,对称轴是直线x=-.第Ⅰ卷(选择题,共24分)一、选择题(下列各题的备选答案中,只有一个答案是正确的.每小题3分,共24分)1.0这个数是( )A.正数B.负数C.整数D.无理数2.2014年端午节小长假期间,沈阳某景区接待游客约为85 000人,将数据85 000用科学记数法表示为( )A.85×103B.8.5×104C.0.85×105D.8.5×1053.某几何体的三视图如图所示,这个几何体是( )A.圆柱B.三棱柱C.长方体D.圆锥4.已知一组数据:1,2,6,3,3,下列说法正确的是( )A.众数是3B.中位数是6C.平均数是4D.方差是55.一元一次不等式x-1≥0的解集在数轴上表示正确的是( )6.正方形是轴对称图形,它的对称轴有( )A.2条B.4条C.6条D.8条7.下列运算正确的是( )A.(-x3)2=-x6B.x4+x4=x8C.x2·x3=x6D.xy4÷(-xy)=-y38.如图,在△ABC中,点D在边AB上 BD= AD DE∥BC交AC于点E,若线段DE=5,则线段BC 的长为( )A.7.5B.10C.15D.20第Ⅱ卷(非选择题,共126分)二、填空题(每小题4分,共32分)9.计算:= .10.分解因式:2m2+10m= .11.如图,直线a∥b 直线l与a相交于点P,与直线b相交于点Q PM⊥l于点P,若∠1=50° 则∠ =°.·1= .12.化简:11-113.已知一次函数y=x+1的图象与反比例函数y=的图象相交,其中有一个交点的横坐标是2,则k的值为.14.如图 △ABC三边的中点D,E,F组成△DEF △DEF三边的中点M,N,P组成△MNP 将△FPM 与△ECD涂成阴影.假设可以随意在△ABC中取点,那么这个点取在阴影部分的概率为.15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元( 0≤x≤30 且x为整数)出售,可卖出(30-x)件.若使利润最大,每件的售价应为元.16.如图,▱ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB ∠ABC ∠BCD ∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点H,连结EM,若▱ABCD的周长为42 cm,FM=3 cm,EF=4 cm,则EM= cm,AB= cm.三、解答题(第17、18小题各8分,第19小题10分,共26分)17.先化简,再求值:[(a+b)2-(a-b)2]·a 其中a=-1,b=5.18.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连结OE,OF.求证:OE=OF.19.在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.四、(每小题10分,共20分)20.2014年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4 800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:预测最有可能获得世界杯冠军球队的条形统计图根据统计图表提供的信息,解答下列问题:(1)a= ,b= ;(2)根据以上信息,请补全条形统计图;(3)根据抽样调查结果,请你估计在提供有效问卷的这4 800人中有多少人预测德国队最有可能获得冠军.21.某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.五、(本题10分)22.如图 ☉O是△ABC的外接圆,AB为直径 OD∥BC交☉O于点D,交AC于点E,连结AD,BD,CD.(1)求证:AD=CD;(2)若AB=10 cos∠ABC=3,求tan∠DBC的值.5六、(本题12分)23.如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,点A的坐标为(2,23),AB=43 ∠B=60° 点D是线段OC上一点,且OD=4,连结AD.(1)求证:△AOD是等边三角形;(2)求点B的坐标;(3)平行于AD的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形OABC截得的线段长为m,直线l与x轴交点的横坐标为t.写出m与t的函数①当直线l与x轴的交点在线段CD上(交点不与点C,D重合)时,请直接··关系式(不必写出自变量t的取值范围);写出此时直线l与x轴的交点坐标.②若m=2,请直接··七、(本题12分)24.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF 绕点A顺时针方向旋转60°得到线段AM,连结FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;写出△AFM的周长.(3)连结EM,若△AEM的面积为40,请直接··温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.图1 图2 备用图八、(本题14分)25.如图1,在平面直角坐标系中,二次函数y=-x2+12的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连结AB,AC.(1)点B的坐标为,点C的坐标为;(2)过点C作射线CD∥AB 点M是线段AB上的动点,点P是线段AC上的动点,且始终满足BM=AP(点M不与点A,点B重合),过点M作MN∥BC分别交AC于点Q,交射线CD于点N(点Q 不与点P重合),连结PM,PN,设线段AP的长为n.①如图2,当n<1AC时,求证:△PAM≌△NCP;②直接..用含n的代数式表示线段PQ的长;③若PM的长为,当二次函数y=-x2+12的图象经过平移同时过点P和点N时,请直接写··出此时的二次函数表达式.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.图1 图2 备用图答案全解全析:一、选择题1.C 0不是正数,也不是负数,是有理数,是整数,故选C.2.B 85 000=8.5×104,故选B.3.C 由于三视图都为长方形,所以此几何体为长方体,故选C.评析 本题考查由三视图来判断几何体形状、学生的空间想象能力,属容易题.4.A 1、2、3、3、6这一组数据的众数是3,中位数是3,平均数=1 3 3 65=3,方差=15[(1-3)2+(2-3)2+(3-3)2+(3-3)2+(6-3)2]=1 5,只有A 是正确的,故选A.5.A 解不等式x-1≥0得x≥1 故选A.6.B 如图所示,正方形有4条对称轴,故选B.7.D (-x 3)2=x 6,x 4+x 4=2x 4,x 2·x 3=x 2+3=x 5,故A 、B 、C 选项都是错误的,故选D.8.C 由题意可得△ADE∽△ABC 相似比为13,所以BC=3DE=15,故选C. 评析 本题考查相似三角形的判定与性质,属容易题. 二、填空题 9.答案 3解析 = 3=3.10.答案 2m(m+5)解析 2m 2+10m=2m(m+5). 11.答案 40解析 如图,因为a∥b 所以∠1=∠3=50° 又PM⊥l 所以∠ = 0° 所以∠ =180°- 0°-∠3= 0°.12.答案1-1解析 1 1-1 ·1 =-1 1-1·1 =1-1.13.答案 6解析 由题意可得该交点为(2,3),将(2,3)代入y=,得k=6. 14.答案516解析 题图中的三角形都是相似三角形,S △EDC =1 S △ABC ,S △FMP =1 S △FED =116S △ABC ,所以S 阴影=516S △ABC ,点取在阴影部分的概率为P= 阴影 △=516.评析 本题综合考查了相似三角形的性质、随机事件的概率计算,属中等难度题. 15.答案 25解析 设利润为y 元,则y=(x-20)(30-x)=-x 2+50x-600=-(x-25)2+25,所以当每件的售价为25元时,利润最大. 16.答案 5;13解析 由题意可得四边形EFMH 是矩形,所以EM= F =5 cm.如图,延长CM 交AB 于点I,延长AE 交CD 于点J,连结FH,易证△BHI≌△BHC 所以BC=BI,CH=HI,则H 为IC 的中点.同理,AD=DJ,F 为AJ 的中点.所以AI=FH=EM=5 cm.因为▱ABCD 的周长为42 cm,所以AB+BC=21 cm,所以2BC+AI=21 cm,所以BC=8 cm,AB=13 cm.评析 本题考查平行四边形的性质,直角三角形的性质,属较难题. 三、解答题17.解析 [(a+b)2-(a-b)2]·a =(a 2+2ab+b 2-a 2+2ab-b 2)·a = ab·a =4a 2b.当a=-1,b=5时,原式= ×(-1)2×5= 0. 18.证明 ∵四边形ABCD 为矩形, ∴∠ADC=∠BCD= 0°AC=BD,OD=1BD,OC=1AC.∴OD=OC.∴∠ODC=∠OCD.∴∠ADC -∠ODC=∠BCD -∠OCD 即∠EDO=∠FCO.又∵DE=CF ∴△ODE≌△OCF ∴OE=OF. 19.解析或画树状(形)图:由表格(或树状图/树形图)可知,共有9种可能出现的结果,每种结果出现的可能性相同,其中小明两次摸出的球颜色不同的结果有6种:(红球,白球),(红球,黑球),(白球,红. 球),(白球,黑球),(黑球,红球),(黑球,白球),所以P(小明两次摸出的球颜色不同)=6=3四、20.解析(1)30%;5%.(2)补全的条形统计图如图所示.预测最有可能获得世界杯冠军球队的条形统计图(3) 800×30%=1 0(人).答:大约有1 440人预测德国队最有可能获得冠军.评析本题考查分析数据,用样本估计总体,属容易题.21.解析设这个增长率为x.依题意得20(1+x)2-20(1+x)=4.8,解得x1=0.2,x2=-1.2(不合题意,舍去).0.2=20%.答:这个增长率为20%.五、22.解析(1)证明:∵AB为☉O直径 ∴∠ACB= 0°.又∵OD∥BC ∴∠AEO=∠ACB= 0°.∴OD⊥AC.∴=.∴AD=CD.( )∵AB=10∴OA=OD=1AB=5.∵OD∥BC∴∠AOE=∠ABC.在Rt△AEO中,OE=OAcos∠AOE=OAcos∠ABC=5×3=3.5∴DE=OD-OE=5-3=2.由勾股定理得,AE=-O=5-3=4.在Rt△AED中 tan∠DAE===1.又∵∠DBC=∠DAE ∴tan∠DBC=1.评析本题综合考查了圆的知识,解直角三角形,属中等难度题.六、23.解析(1)证明:过点A作AM⊥x轴于点M,∵点A的坐标为(2,23) ∴OM= AM= 3.∴在Rt△AOM中 tan∠AOM==3=,∴∠AOM=60°.由勾股定理得,OA=A=( 3)=4.∵OD= ∴OA=OD.∴△AOD是等边三角形.(2)过点A作AN⊥BC于点N,∵BC⊥OC AM⊥x轴,∴∠BCM=∠CMA=∠ANC= 0°.∴四边形ANCM为矩形.∴AN=MC AM=NC.∵∠B=60° AB= 3 ∴在Rt△ABN中,AN=AB·sin B= 3×3=6,BN=AB·cos B= 3×1=23.∴AN=MC=6 CN=AM= .∴OC=OM+MC= +6=8BC=BN+CN=23+23=43.∴点B的坐标为(8,4).(3)①m=1t+2.②( 0) 30.3评析本题考查在直角坐标系中探究图形的形状,根据图形的性质求某个点的坐标,综合性较强,属中等难度题.七、24.解析(1)∵四边形ABCD为菱形,∴AC⊥BD OB=OD=1BD.∵BD= ∴OB=1 .在Rt△OAB中 ∵AB=13∴OA=-O=13-1 =5.(2)证明:∵四边形ABCD为菱形 ∴BD垂直平分AC.∴FA=FC.∴∠FAC=∠FCA.∵AF=AM ∠MAF=60°∴△AMF为等边三角形.∴∠M=∠AFM=60°.∵点M,F,C三点在同一条直线上,∴∠FAC+∠FCA=∠AFM=60°.∴∠FAC=∠FCA=30°.∴∠MAC=∠MAF+∠FAC=60°+30°= 0°.在Rt△ACM中,tan M=,即tan 60°=,∴AC=3AM.(3)△AFM的周长为3 1.评析本题考查了菱形、等边三角形的性质,通过旋转图形,考查学生的发散思维能力,属难题.八、25.解析(1)(-9,0);(9,0).( )①证明:∵AB∥CD MN∥BC∴四边形BMNC为平行四边形.∴BM=CN.∵BM=AP ∴AP=CN.∵OC=OB= AO⊥BC∴AB=AC ∴AB-BM=AC-AP.∴AM=PC.∵AB∥CD ∴∠MAP=∠PCN.∴△PAM≌△NCP.②15-2n或2n-15.③y=-x2+16x+4或y=-x2+3 x-12.评析本题综合考查了平行四边形、二次函数的性质,综合性较强,属难题.。
沈阳市中考数学试卷及答案解析

2014年沈阳市中考数学试卷试题满分150分 考试时间120分钟参考公式:抛物线2y ax bx c =++的顶点是24(,)24b ac b a a --,对称轴是直线2b x a=-. 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题4分,共24分)这个数是( )A.正数B.负数C.整数D.无理数年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为( )×103 104 C 某几何体的三视图如图所示,这个几何体是( )A.圆柱B.三棱柱C.长方体D.圆锥4.已知一组数据:1,2,6,3,3,下列说法正确的是( )A.众数是3B.中位数是6C.平均数是4D.方差是55.一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A B C D6.正方形是轴对称图形,它的对称轴有( )条 条 条 条7.下列运算正确的是( )A.()623x x -=- B.844x x x =+ C.632x x x =⋅ D.()34y xy xy -=-÷ 8.如图,在△ABC 中,点D 在边AB 上,BD=2AD ,DE ∥BC 交AC 于点E ,若线段DE=5,则线段BC 的长为( )A.7.5 .10 C二、填空题(每小题4分,共32分)9.计算:=9___________ 10.分解因式:2m 2+10m=___________11.如图,直线a ∥b ,直线l 与a 相交于点P ,与直线b 相交于点Q , PM ⊥l 于点P , 若∠1=50°,则∠2=________°.12.化简:=⋅⎪⎭⎫ ⎝⎛-+x x 1111___________13.已知一次函数y=x+1的图象与反比例函数x k y =的图象相交,其中有一个交点的横坐标是2,则k 的值为________.14.如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M ,N ,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在△ABC 中取点,那么这个点取在阴影部分的概率为________.15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数) 出售,可卖出(30-x)件.若使利润最大,每件的售价应为________元16.如图,□ABCD 中,AB>AD ,AE ,BE ,CM ,DM 分别为∠DAB ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM= ①cm ,AB= ② cm.三、解答题(第17、18小题各8分,第19小题10分,共26分)17.先化简,再求值:()()a b a b a ⋅--+22,其中a=-1,b=5.18.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE=CF ,连接OE ,OF.求证:OE=OF.19.在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.四、(每小题10分,共20分)年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a=________,b=________;(2)根据以上信息,请直接..在答题卡中补全条形统计图;(3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.21.某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加万元,假设该产品利润每月的增长率相同,求这个增长率.五、(本题10分)22.如图,⊙O 是△ABC 的外接圆,AB 为直径,OD ∥BC 交⊙O 于点D ,交AC 于点E ,连接AD ,BD ,CD(1)求证:AD=CD ;(2)若AB=10,cos ∠ABC=53,求tan ∠DBC 的值.六、(本题12分)23.如图,在平面直角坐标系中,四边形OABC 的顶点O 为坐标原点,点C 在x轴的正半轴上,且BC ⊥OC 于点C ,点A 的坐标为 (2,32),AB=34,∠B=60°,点D 是线段OC 上一点,且OD=4,连接AD.(1)求证:△AOD 是等边三角形;(2)求点B 的坐标;(3)平行于AD 的直线l 从原点O 出发,沿x 轴正方向平移.设直线l 被四边形OABC 截得的线段长为m ,直线l 与x 轴交点的横坐标为t.①当直线l 与x 轴的交点在线段CD 上(交点不与点C ,D 重合)时,请直接..写出m 与t 的函数关系式(不必写出自变量t 的取值范围)②若m=2,请直接..写出此时直线l 与x 轴的交点坐标.七、(本题12分)24.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;(3)连接EM,若△AEM的面积为40,请直接..写出△AFM的周长.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.八、(本题14分)25.如图1,在平面直角坐标系中,二次函数122742+-=x y 的图象与y 轴交于点A ,与x 轴交于B ,C 两点(点B 在点C 的左侧),连接AB ,AC.(1)点B 的坐标为________,点C 的坐标为________;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP(点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n. ①如图2,当AC n 21<时,求证:△PAM ≌△NCP ; ②直接..用含n 的代数式表示线段PQ 的长; ③若PM 的长为97,当二次函数122742+-=x y 的图象经过平移同时过点P 和点N 时,请直接..写出此时二次函数表达式 温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.。
2014年沈阳市中考数学试卷

2014年沈阳市中考数学试卷试题满分150分 考试时间120分钟参考公式:抛物线2y ax bx c =++的顶点是24(,)24b ac b a a --,对称轴是直线2b x a =-. 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题4分,共24分)1.0这个数是( )A.正数B.负数C.整数D.无理数2.2014年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为( )A.85×103B.8.5×104C.0.85×105D.8.5×1053.某几何体的三视图如图所示,这个几何体是( )A.圆柱B.三棱柱C.长方体D.圆锥4.已知一组数据:1,2,6,3,3,下列说法正确的是( )A.众数是3B.中位数是6C.平均数是4D.方差是55.一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A B C D6.正方形是轴对称图形,它的对称轴有( )A.2条B.4条C.6条D.8条7.下列运算正确的是( )A.()623x x -=-B.844x x x =+C.632x x x =⋅D.()34y xy xy -=-÷8.如图,在△ABC 中,点D 在边AB 上,BD=2AD ,DE ∥BC 交AC 于点E ,若线段DE=5,则线段BC 的长为( ) A.7.5 B.10 C.15 D.20二、填空题(每小题4分,共32分)9.计算:=9___________10.分解因式:2m 2+10m=___________11.如图,直线a ∥b ,直线l 与a 相交于点P ,与直线b 相交于点Q , PM ⊥l 于点P , 若∠1=50°,则∠2=________°.12.化简:=⋅⎪⎭⎫ ⎝⎛-+xx 1111___________ 13.已知一次函数y=x+1的图象与反比例函数x k y =的图象相交,其中有一个交点的横坐标是2,则k 的值为________.14.如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M ,N ,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在△ABC 中取点,那么这个点取在阴影部分的概率为________.15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数) 出售,可卖出(30-x)件.若使利润最大,每件的售价应为________元16.如图,□ABCD 中,AB >AD ,AE ,BE ,CM ,DM 分别为∠DAB ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM= ① cm ,AB= ② cm.三、解答题(第17、18小题各8分,第19小题10分,共26分)17.先化简,再求值:()()a b a b a ⋅--+22,其中a=-1,b=5.18.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE=CF ,连接OE ,OF.求证:OE=O F.19.在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.四、(每小题10分,共20分)20.2014年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a=________,b=________;(2)根据以上信息,请直接..在答题卡中补全条形统计图; (3) 根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.21.某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.五、(本题10分)22.如图,⊙O 是△ABC 的外接圆,AB 为直径,OD ∥BC 交⊙O 于点D ,交AC 于点E ,连接AD ,BD ,CD(1)求证:AD=CD ;(2)若AB=10,cos ∠ABC=53,求tan ∠DBC 的值.六、(本题12分)23.如图,在平面直角坐标系中,四边形OABC 的顶点O 为坐标原点,点C 在x 轴的正半轴上,且BC ⊥OC 于点C ,点A 的坐标为 (2,32),AB=34,∠B=60°,点D 是线段OC 上一点,且OD=4,连接AD.(1)求证:△AOD 是等边三角形;(2)求点B 的坐标;(3)平行于AD 的直线l 从原点O 出发,沿x 轴正方向平移.设直线l 被四边形OABC 截得的线段长为m ,直线l 与x 轴交点的横坐标为t.①当直线l 与x 轴的交点在线段CD 上(交点不与点C ,D 重合)时,请直接..写出m 与t 的函数关系式(不必写出自变量t 的取值范围)②若m=2,请直接..写出此时直线l与x轴的交点坐标.七、(本题12分)24.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;(3)连接EM,若△AEM的面积为40,请直接..写出△AFM的周长.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.八、(本题14分)25.如图1,在平面直角坐标系中,二次函数122742+-=x y 的图象与y 轴交于点A ,与x 轴交于B ,C 两点(点B 在点C 的左侧),连接AB ,AC.(1)点B 的坐标为________,点C 的坐标为________;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP(点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n.①如图2,当AC n 21<时,求证:△PAM ≌△NCP ; ②直接..用含n 的代数式表示线段PQ 的长;③若PM 的长为97,当二次函数122742+-=x y 的图象经过平移同时过点P 和点N 时,请直接..写出此时二次函数表达式温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.。
沈阳市中考数学试卷及答案解析

2014年沈阳市中考数学试卷试题满分150分 考试时间120分钟参考公式:抛物线2y ax bx c =++的顶点是24(,)24b ac b a a --,对称轴是直线2b x a=-. 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题4分,共24分)这个数是( )A.正数B.负数C.整数D.无理数年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为( )×103 104 C 某几何体的三视图如图所示,这个几何体是( )A.圆柱B.三棱柱C.长方体D.圆锥4.已知一组数据:1,2,6,3,3,下列说法正确的是( )A.众数是3B.中位数是6C.平均数是4D.方差是55.一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A B C D6.正方形是轴对称图形,它的对称轴有( )条 条 条 条7.下列运算正确的是( )A.()623x x -=- B.844x x x =+ C.632x x x =⋅ D.()34y xy xy -=-÷ 8.如图,在△ABC 中,点D 在边AB 上,BD=2AD ,DE ∥BC 交AC 于点E ,若线段DE=5,则线段BC 的长为( )A.7.5 .10 C二、填空题(每小题4分,共32分)9.计算:=9___________ 10.分解因式:2m 2+10m=___________11.如图,直线a ∥b ,直线l 与a 相交于点P ,与直线b 相交于点Q , PM ⊥l 于点P , 若∠1=50°,则∠2=________°.12.化简:=⋅⎪⎭⎫ ⎝⎛-+x x 1111___________13.已知一次函数y=x+1的图象与反比例函数x k y =的图象相交,其中有一个交点的横坐标是2,则k 的值为________.14.如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M ,N ,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在△ABC 中取点,那么这个点取在阴影部分的概率为________.15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数) 出售,可卖出(30-x)件.若使利润最大,每件的售价应为________元16.如图,□ABCD 中,AB>AD ,AE ,BE ,CM ,DM 分别为∠DAB ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM= ①cm ,AB= ② cm.三、解答题(第17、18小题各8分,第19小题10分,共26分)17.先化简,再求值:()()a b a b a ⋅--+22,其中a=-1,b=5.18.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE=CF ,连接OE ,OF.求证:OE=OF.19.在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.四、(每小题10分,共20分)年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a=________,b=________;(2)根据以上信息,请直接..在答题卡中补全条形统计图;(3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.21.某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加万元,假设该产品利润每月的增长率相同,求这个增长率.五、(本题10分)22.如图,⊙O 是△ABC 的外接圆,AB 为直径,OD ∥BC 交⊙O 于点D ,交AC 于点E ,连接AD ,BD ,CD(1)求证:AD=CD ;(2)若AB=10,cos ∠ABC=53,求tan ∠DBC 的值.六、(本题12分)23.如图,在平面直角坐标系中,四边形OABC 的顶点O 为坐标原点,点C 在x轴的正半轴上,且BC ⊥OC 于点C ,点A 的坐标为 (2,32),AB=34,∠B=60°,点D 是线段OC 上一点,且OD=4,连接AD.(1)求证:△AOD 是等边三角形;(2)求点B 的坐标;(3)平行于AD 的直线l 从原点O 出发,沿x 轴正方向平移.设直线l 被四边形OABC 截得的线段长为m ,直线l 与x 轴交点的横坐标为t.①当直线l 与x 轴的交点在线段CD 上(交点不与点C ,D 重合)时,请直接..写出m 与t 的函数关系式(不必写出自变量t 的取值范围)②若m=2,请直接..写出此时直线l 与x 轴的交点坐标.七、(本题12分)24.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;(3)连接EM,若△AEM的面积为40,请直接..写出△AFM的周长.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.八、(本题14分)25.如图1,在平面直角坐标系中,二次函数122742+-=x y 的图象与y 轴交于点A ,与x 轴交于B ,C 两点(点B 在点C 的左侧),连接AB ,AC.(1)点B 的坐标为________,点C 的坐标为________;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP(点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n. ①如图2,当AC n 21<时,求证:△PAM ≌△NCP ; ②直接..用含n 的代数式表示线段PQ 的长; ③若PM 的长为97,当二次函数122742+-=x y 的图象经过平移同时过点P 和点N 时,请直接..写出此时二次函数表达式 温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.。
沈阳市中考数学试卷及答案解析(优选.)甄选.

沈阳市中考数学试卷及答案解析(优选.)2014年沈阳市中考数学试卷试题满分150分 考试时间120分钟参考公式:抛物线2y ax bx c =++的顶点是24(,)24b ac b a a --,对称轴是直线2b x a =-. 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题4分,共24分)1.0这个数是( )A.正数B.负数C.整数D.无理数2.2014年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为( )A.85×103B.8.5×104C.0.85×105D.8.5×1053.某几何体的三视图如图所示,这个几何体是( )A.圆柱B.三棱柱C.长方体D.圆锥4.已知一组数据:1,2,6,3,3,下列说法正确的是( )A.众数是3B.中位数是6C.平均数是4D.方差是55.一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A B CD6.正方形是轴对称图形,它的对称轴有( )A.2条B.4条C.6条D.8条7.下列运算正确的是( ) A.()623x x -=- B.844x x x =+ C.632x x x =⋅ D.()34y xy xy -=-÷ 8.如图,在△ABC 中,点D 在边AB 上,BD=2AD ,DE ∥BC 交AC 于点E ,若线段DE=5,则线段BC 的长为( )A.7.5B.10C.15D.20二、填空题(每小题4分,共32分)9.计算:=9___________10.分解因式:2m 2+10m=___________ 11.如图,直线a ∥b ,直线l 与a 相交于点P ,与直线b 相交于点Q , PM ⊥l 于点P , 若∠1=50°,则∠2=________°.12.化简:=⋅⎪⎭⎫ ⎝⎛-+xx 1111___________ 图象相交,其中有一个交点的横坐标13.已知一次函数y=x+1的图象与反比例函数x ky =的是2,则k 的值为________.14.如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M ,N ,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在△ABC 中取点,那么这个点取在阴影部分的概率为________.15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数) 出售,可卖出(30-x)件.若使利润最大,每件的售价应为________元16.如图,□ABCD 中,AB>AD ,AE ,BE ,CM ,DM 分别为∠DAB ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM= ① cm ,AB= ② cm.三、解答题(第17、18小题各8分,第19小题10分,共26分) 17.先化简,再求值:()()a b a b a ⋅--+22,其中a=-1,b=5.18.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE=CF ,连接OE ,OF.求证:OE=OF.19.在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.四、(每小题10分,共20分)20.2014年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a=________,b=________;(2)根据以上信息,请直接..在答题卡中补全条形统计图;(3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.21.某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.五、(本题10分)22.如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD3,求tan∠DBC的值.(1)求证:AD=CD;(2)若AB=10,cos∠ABC=5六、(本题12分)23.如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC 于点C,点A的坐标为(2,34,∠B=60°,点D是线段OC上一点,且OD=4,连接AD.2),AB=3(1)求证:△AOD是等边三角形;(2)求点B的坐标;(3)平行于AD的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形OABC截得的线段长为m,直线l与x 轴交点的横坐标为t.①当直线l与x轴的交点在线段CD上(交点不与点C,D重合)时,请直接..写出m与t的函数关系式(不必写出自变量t的取值范围)②若m=2,请直接..写出此时直线l与x轴的交点坐标.七、(本题12分)24.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;(3)连接EM,若△AEM的面积为40,请直接..写出△AFM的周长.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.八、(本题14分)25.如图1,在平面直角坐标系中,二次函数122742+-=x y 的图象与y 轴交于点A ,与x 轴交于B ,C 两点(点B 在点C 的左侧),连接AB ,AC.(1)点B 的坐标为________,点C 的坐标为________;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP(点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n.①如图2,当AC n 21<时,求证:△PAM ≌△NCP ; ②直接..用含n 的代数式表示线段PQ 的长; ③若PM 的长为97,当二次函数122742+-=x y 的图象经过平移同时过点P 和点N 时,请直接..写出此时二次函数表达式温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.感谢您使用本店文档您的满意是我们永恒的追求!(本句可删)------------------------------------------------------------------------------------------------------------。
【初中数学】辽宁省沈阳市2014年中考数学试卷 人教版

沈阳市2014年中考数学试卷试题满分150分 考试时间120分钟参考公式:抛物线2y ax bx c =++的顶点是24(,)24b ac b a a--,对称轴是直线2b x a =-.一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题4分,共24分)1.0这个数是( )A.正数B.负数C.整数D.无理数2.2014年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为( ) A.85×103 B.8.5×104 C.0.85×105 D.8.5×1053.某几何体的三视图如图所示,这个几何体是( ) A.圆柱 B.三棱柱 C.长方体 D.圆锥4.已知一组数据:1,2,6,3,3,下列说法正确的是( ) A.众数是3 B.中位数是6 C.平均数是4 D.方差是55.一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A B C D 6.正方形是轴对称图形,它的对称轴有( ) A.2条 B.4条 C.6条 D.8条 7.下列运算正确的是( ) A.()623x x -=- B.844x x x =+ C.632x x x =⋅ D.()34y xy xy -=-÷8.如图,在△ABC 中,点D 在边AB 上,BD=2AD ,DE ∥BC 交AC 于点E ,若线段DE=5,则线段BC 的长为( )A.7.5B.10C.15D.20二、填空题(每小题4分,共32分) 9.计算:=9___________10.分解因式:2m 2+10m=___________11.如图,直线a ∥b ,直线l 与a 相交于点P ,与直线b 相交于点Q , PM ⊥l 于点P , 若∠1=50°,则∠2=________°.12.化简:=⋅⎪⎭⎫ ⎝⎛-+xx 1111___________ 13.已知一次函数y=x+1的图象与反比例函数xky =的图象相交,其中有一个交点的横坐标是2,则k 的值为________.14.如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M ,N ,P 组成△MNP ,将△FPM与△ECD 涂成阴影.假设可以随意在△ABC 中取点,那么这个点取在阴影部分的概率为________.15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数)出售,可卖出(30-x)件.若使利润最大,每件的售价应为________元16.如图,□ABCD 中,AB >AD ,AE ,BE ,CM ,DM 分别为∠DAB ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM= ① cm ,AB= ② cm.三、解答题(第17、18小题各8分,第19小题10分,共26分)17.先化简,再求值:()()a b a b a ⋅--+22,其中a=-1,b=5.18.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE=CF ,连接OE ,OF.求证:OE=OF.19.在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.四、(每小题10分,共20分)20.2014年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a=________,b=________; (2)根据以上信息,请直接..在答题卡中补全条形统计图; (3) 根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.21.某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.五、(本题10分)22.如图,⊙O 是△ABC 的外接圆,AB 为直径,OD ∥BC 交⊙O 于点D ,交AC 于点E ,连接AD ,BD ,CD(1)求证:AD=CD ;(2)若AB=10,cos ∠ABC=53,求tan ∠DBC 的值.六、(本题12分)23.如图,在平面直角坐标系中,四边形OABC 的顶点O 为坐标原点,点C 在x 轴的正半轴上,且BC ⊥OC 于点C ,点A 的坐标为 (2,32),AB=34,∠B=60°,点D 是线段OC 上一点,且OD=4,连接AD.(1)求证:△AOD 是等边三角形;(2)求点B的坐标;(3)平行于AD的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形OABC截得的线段长为m,直线l与x轴交点的横坐标为t.①当直线l与x轴的交点在线段CD上(交点不与点C,D重合)时,请直接..写出m与t的函数关系式(不必写出自变量t的取值范围)②若m=2,请直接..写出此时直线l与x轴的交点坐标.七、(本题12分)24.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB 为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;(3)连接EM,若△AEM的面积为40,请直接..写出△AFM的周长.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.八、(本题14分)25.如图1,在平面直角坐标系中,二次函数122742+-=x y 的图象与y 轴交于点A ,与x 轴交于B ,C 两点(点B 在点C 的左侧),连接AB ,AC.(1)点B 的坐标为________,点C 的坐标为________;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP(点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n. ①如图2,当AC n 21<时,求证:△PAM ≌△NCP ; ②直接..用含n 的代数式表示线段PQ 的长;③若PM 的长为97,当二次函数122742+-=x y 的图象经过平移同时过点P 和点N 时,请直接..写出此时二次函数表达式温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.。
(完整版)沈阳市中考数学试题含答案Word版,推荐文档

②若 m=2,请直接写出此时直线l与x轴的交点坐标.
7、(本题12分) 24.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边 三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段 AM,连接FM. (1)求AO的长;
①如图2,当 n 1 AC 时,求证:△PAM≌△NCP; 2
②直接用含n的代数式表示线段PQ的长;
③若PM的长为 97 ,当二次函数 y 4 x2 12 的图象经过平移同时过点P和点N时,请直接写出此时二 27
次函数表达式 温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
那么这
个点取在阴影部分的概率为________.
15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数) 出售,可
卖出(30-x)件.若使利润最大,每件的售价应为________元
16.如图,□ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分 线,AE与DM相交
5、(本题10分) 22.如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD
3
(1)求证:AD=CD;(2)若AB=10,cos∠ABC= ,求 tan∠DBC的值.
5
6、(本题12分) 23.如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC
2014年辽宁省沈阳市中考试题(word版含答案)

2014年辽宁省沈阳市中考试题数学(满分150分,考试时间120分钟)参考公式:抛物线y=ax2+bx+c的顶点坐标是(-b2a,4ac-b24a).对称轴是直线x=-b2a.一、选择题(下面各题的备选答案中,只有一个答案是正确的,每小题3分,共24分)1.(2014年辽宁省沈阳市,1,3分) 0这个数是()A.正数B.负数C.整数D.无理数2.(2014年辽宁省沈阳市,2,3分)2014年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为()A.85×103B.8.5×104C.0.85×105 D.8.5×1053.(2014年辽宁省沈阳市,3,3分)某几何体的三视图如图所示,这个几何体是()A.圆柱B.三棱柱C.长方体D.圆锥4.(2014年辽宁省沈阳市,4,3分)已知一组数据:1,2,6,3,3,下列说法正确的是()A.众数是3 B.中位数是6 C.平均数是4 D.方差是55.(2014年辽宁省沈阳市,5,3分)一元一次不等式x-1≥0的解集在数轴上表示正确的是( )6.(2014年辽宁省沈阳市,6,3分)正方形是轴对称图形,它的对称轴有()A.2条B.4条C.6条D.8条7.(2014年辽宁省沈阳市,7,3分) 下列运算正确的是()A.(-x3)2=-x6B.x4+x4=x8C.x2•x3=x6D.xy4÷(-xy)=-y38.(2014年辽宁省沈阳市,8,3分)如图,在△ABC中,点D在边AB上,BD=2AD,DE//BC 交AC于点E,若线段DE=5,则线段BC的长为()A. 7.5B. 10C.15D.20二、填空题(每小题4分,共32分)9.(2014年辽宁省沈阳市,9,4分) 计算:9=__________.10. (2014年辽宁省沈阳市,10,4分) 分解因式:2m2+10m=__________.11. (2014年辽宁省沈阳市,11,4分) 如图,直线a//b,n直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50 °,则∠2= °.12. (2014年辽宁省沈阳市,12,4分)化简:(1+1x-1)·1x=___________.13. (2014年辽宁省沈阳市,13,4分)已知一次函数y=x+1的图象与反比例函数y=kx的图象相交,其中一个交点的横坐标是2,则k的值为_________.14. (2014年辽宁省沈阳市,14,4分) 如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M,N,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在ABC △中取点,那么这个点取在阴影部分的概率为__________.15.(2014年辽宁省沈阳市,15,4分)某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数)出售,可卖出(30-x )件.若使利润最大,每件的售价应为__________元.16.(2014年辽宁省沈阳市,16,4分)(每题7分,共14分)如图,□ABCD 中,AB>AD ,AE,BE,CM,DM 分别为∠DBA ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM= cm ,AB= cm.三、解答题(第17、18小题各8分,第19小题10分,共26分)17. (2014年辽宁省沈阳市,17,8分)先化简,再求值:(a +b )2-(a -b )2éëùû·a ,其中a =-1,b =5.18.(2014年辽宁省沈阳市,18,8分)如图,在矩形ABCD 中,对角线AC,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE=CF ,连接OE ,OF.求证:OE=OF.19.(2014年辽宁省沈阳市,19,10分) 在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.四、(每小题10分,共20分)20. (2014年辽宁省沈阳市,20,10分)2014年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查都只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a= ,b= ;(2)根据以上信息,请直接..在答题卡中补全条形统计图;(3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.21.(2014年辽宁省沈阳市,21,10分)某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.五、(本题10分)22.(2014年辽宁省沈阳市,22,10分)如图,⊙O是△ABC的外接圆,AB为直径,OD ∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD.(1)求证:AD=CD;(2)若AB=10,cos∠ABC=35,求tan∠DBC的值.23.(2014年辽宁省沈阳市,23,12分)如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,点A的坐标为(),AB=43,∠B=60°,点D是线段OC上一点,且OD=4,连接AD.2,23(1)求证:△AOD是等边三角形;(2)求点B的坐标;(3)平行于AD的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形OABC截得的线段长为m,直线l与x轴交点的横坐标为t.①当直线l与x轴的交点在线段CD上(交点不与点以,D重合)时,请直接写出m与t的函数关系式(不必写出自变量t的取值范围);②若m=2,请直接..写出此时直线l与x轴的交点坐标.24.(2014年辽宁省沈阳市,24,12分)如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A在顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;(3)连接EM,若△AEM的面积为40,请直接..写出△AFM的周长.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.八、(本题14分)25.(2014年辽宁省沈阳市,25,14分)如图1,在平面直角坐标系中,二次函数y=-427x2+12的图象与y轴交于点A,与x轴交于点B,C两点(点B在点C的左侧),连接AB,AC.(1)点B的坐标为,点C的坐标为;(2)过点C作射线CD∥AB,点M是线段AB上的动点,点P是线段AC上的动点,且始终满足BM=AP(点M不与点A,点B重合),过点M作MN∥BC分别交AC于点Q,交射线CD于点N(点Q不与点P重合),连接PM,PN,设线段AP的长为n.①如图2,当n<12AC时,求证:△PAM≌△NCP;②直接..用含n的代数式表示线段PQ的长;③若PM的长为97,当二次函数y=-427x2+12的图象经过平移同时过点P和点N时,请直接..写出此时的二次函数的表达式.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答2014年辽宁省沈阳市中考试题数学参考答案一、选择题(下面各题的备选答案中,只有一个答案是正确的,每小题3分,共24分)1.【答案】C2.【答案】B3.【答案】C4.【答案】A5【答案】A6.【答案】B7.【答案】D8.【答案】C二、填空题(每小题4分,共32分)9.【答案】310.【答案】2m(m+5)11.【答案】4012.【答案】1x -113.【答案】614.【答案】51615.【答案】16.【答案】5;13三、解答题(第17、18小题各8分,第19小题10分,共26分) 17.【答案】解: (a +b )2-(a -b )2éëùû·a=a 2+2ab +b 2-a 2+2ab -b 2éëùû·a=4ab ·a=4a 2b当a =-1,b=5时,原式=4×(-1)2×5=20.18.【答案】证明:∵四边形ABCD 为矩形,∴∠ADC=∠BCD=90°,AC=BD,OD=12BD,OC=12AC. OD=OC.∴∠ODC=∠OCD.∴∠ADC-∠ODC =∠BCD-∠OCD,即∠EDO=∠FCO.又∵DE=CF,∴△ODE≌△OCF.∴OE=OF.19.【答案】解:或画树状(形)图得:由表格(或树状图/树形图)可知,共有9种可能出现的结果,每种结果出现的可能性相同,其中小明两次摸出的球颜色不同的结果有6种:(红球,白球)(红球,黑球)(白球,红球)(白球,黑球)(黑球,红球)(黑球,白球),所以P(小明两次摸出的球的颜色不同)=69=23.四、(每小题10分,共20分)20.【答案】解:(1) a=30%,b=5% (2)(3)4800×30%=1440(人)答:大约有1440人预测德国队最有可能获得冠军.21.【答案】解:设这个增长率为x.依题意得:20(1+x)2-20(1+x)=4.8解得:x1=0.2,x2=-1.2(不合题意,舍去),0.2=20%答:这个增长率为20%.五、(本题10分)22.【答案】解:(1)证明:∵AB为⊙O直径,∴∠ACB=90°. 又∵OD∥BC, ∴∠AEO=∠ACB=90°.∴OD⊥AC. ∴AD=CD.∴AD=CD.(2)解:∵AB=10,∴OA=OD=12AB=5.∵OD∥BC,∴∠AOE=∠ABC.在Rt△AEO中,OE=OAcos∠AOE= OAcos∠ABC=5×35=3.∴DE=OD-OE=5-3=2.由勾股定理得,AE=AO2-OE2=52-32=4.在Rt△AED中,tan∠DAE=DEAE=24=12.又∵∠DBC=∠DAE,∴tan∠DBC=1 2 .六、(本题12分)23.【答案】解:(1)证明:过点作AM⊥x轴于点M,∵点A的坐标为2,23(),∴OM=2,AM=23.∴在Rt△AOM中,tan∠AOM=AMOM=232=3,∴∠AOM=60°.由勾股定理得,OA=OM2+AM2=22+23()2=4∵OD=4,∴OA=OD.∴△AOD是等边三角形.(2)解:过点A作AN⊥BC于点N,∵BC⊥OC,AM⊥x轴,∴∠BCM=∠CMA=∠ANC =90°.∴四边形ANCM为矩形,∴AN=MC,AM=NC.∵∠B=60°,AB=43,∴在Rt△ABN中,AN=AB·sinB=43´32=6,∴BN=AB·cos B= 43´12=23.∴AN=MC=6,CN=AM=23.∴OC=OM+MC=2+6=8, BC=BN+CN=23+23=43.∴点B的坐标为(8,43).(3)①m=12t+2.②(2,0),(323,0)七、(本题12分)24.【答案】解:(1)解:∵四边形ABCD为菱形,∴AC⊥BD,OB=OD=12 BD.∵BD=24,∴OB=12. ∴在Rt△OAB中,∵AB=13,∴OA=AB2-OB2=132-122=5.(2)证明:∵四边形ABCD为菱形,∴BD垂直平分AC.∴FA=FC. ∠FAC=∠FCA.由已知AF=AM.∴∠MAF=60°.∴△AMF为等边三角形.∴∠M=∠AFM=60°.∵点M,F,C三点在同一条直线上∴∠FAC+∠FCA=∠AFM=60°. ∴∠FAC=∠FCA=30°.∴∠MAC=∠MAF+∠FAC=60°+30°=90°.在Rt△ACM中,tanM=ACAM,∴tan60°=ACAM.∴AC=3AM.(3)△AFM的周长为341.八、(本题14分)25.【答案】解:(1)(-9,0),(9,0).(2)①证明:∵AB∥CD,MN∥BC,∴四边形BMNC为平行四边形.∴BM=CN.∵BM=AP,∴AP=CN.∵OC=OB=9,又∵AO⊥BC,∴AB=AC,∴AB-BM=AC-AP.∴AM=PC.∵AB∥CD,∴∠MAP=∠PCN.∴△PAM≌△NCP.②15-2n或2n-15.③y=-427x2+169x+4或y=-427x2+329x-12.。
沈阳市中考数学试题含答案Word版

2014年沈阳市中考数学试卷试题满分150分 考试时间120分钟参考公式:抛物线2y ax bx c =++的顶点是24(,)24b ac b a a --,对称轴是直线2b x a=-. 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题4分,共24分)1.0这个数是( )A.正数B.负数C.整数D.无理数 2.2014年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为( )A.85×103B.8.5×104C.0.85×105D.8.5×1053.某几何体的三视图如图所示,这个几何体是( ) A.圆柱 B.三棱柱 C.长方体 D.圆锥4.已知一组数据:1,2,6,3,3,下列说法正确的是( ) A.众数是3 B.中位数是6 C.平均数是4 D.方差是55.一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A B C D 6.正方形是轴对称图形,它的对称轴有( ) A.2条 B.4条 C.6条 D.8条 7.下列运算正确的是( ) A.()623x x -=- B.844x x x =+ C.632x x x =⋅ D.()34y xy xy -=-÷8.如图,在△ABC 中,点D 在边AB 上,BD=2AD ,DE ∥BC 交AC 于点E ,若线段DE=5,则线段BC 的长为( ) A.7.5 B.10 C.15 D.20二、填空题(每小题4分,共32分) 9.计算:=9___________10.分解因式:2m 2+10m=___________11.如图,直线a ∥b ,直线l 与a 相交于点P ,与直线b 相交于点Q , PM ⊥l 于点P ,若∠1=50°,则∠2=________°.12.化简:=⋅⎪⎭⎫ ⎝⎛-+xx 1111___________ 13.已知一次函数y=x+1的图象与反比例函数xky =的图象相交,其中有一个交点的横坐标是2,则k 的值为________.14.如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M ,N ,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在△ABC 中取点,那么这个点取在阴影部分的概率为________.15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数) 出售,可卖出(30-x)件.若使利润最大,每件的售价应为________元16.如图,□ABCD 中,AB >AD ,AE ,BE ,CM ,DM 分别为∠DAB ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM= ① cm ,AB= ② cm.三、解答题(第17、18小题各8分,第19小题10分,共26分) 17.先化简,再求值:()()a b a b a ⋅--+22,其中a=-1,b=5.18.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE=CF ,连接OE ,OF.求证:OE=O F.19.在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.四、(每小题10分,共20分)20.2014年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a=________,b=________; (2)根据以上信息,请直接..在答题卡中补全条形统计图; (3) 根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.21.某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.五、(本题10分)22.如图,⊙O 是△ABC 的外接圆,AB 为直径,OD ∥BC 交⊙O 于点D ,交AC 于点E ,连接AD ,BD ,CD(1)求证:AD=CD ;(2)若AB=10,cos ∠ABC=53,求tan ∠DBC 的值.六、(本题12分)23.如图,在平面直角坐标系中,四边形OABC 的顶点O 为坐标原点,点C 在x 轴的正半轴上,且BC ⊥OC 于点C ,点A 的坐标为 (2,32),AB=34,∠B=60°,点D 是线段OC 上一点,且OD=4,连接AD. (1)求证:△AOD 是等边三角形; (2)求点B 的坐标;(3)平行于AD 的直线l 从原点O 出发,沿x 轴正方向平移.设直线l 被四边形OABC 截得的线段长为m ,直线l 与x 轴交点的横坐标为t.①当直线l 与x 轴的交点在线段CD 上(交点不与点C ,D 重合)时,请直接..写出m 与t 的函数关系式(不必写出自变量t 的取值范围)②若m=2,请直接..写出此时直线l与x轴的交点坐标.七、(本题12分)24.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;(3)连接EM,若△AEM的面积为40,请直接..写出△AFM的周长.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.八、(本题14分)25.如图1,在平面直角坐标系中,二次函数122742+-=x y 的图象与y 轴交于点A ,与x 轴交于B ,C 两点(点B 在点C 的左侧),连接AB ,AC.(1)点B 的坐标为________,点C 的坐标为________;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP(点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n. ①如图2,当AC n 21<时,求证:△PAM ≌△NCP ; ②直接..用含n 的代数式表示线段PQ 的长;③若PM 的长为97,当二次函数122742+-=x y 的图象经过平移同时过点P 和点N 时,请直接..写出此时二次函数表达式温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辽宁省沈阳市2014年中考数学试卷
一、选择题(每小题3分,共24分)
1.(3分)(2014•沈阳)0这个数是()
2.(3分)(2014•沈阳)2014年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为()
3.(3分)(2014•沈阳)某几何体的三视图如图所示,这个几何体是()
4.(3分)(2014•沈阳)已知一组数据:1,2,6,3,3,下列说法正确的是()
5.(3分)(2014•沈阳)一元一次不等式x﹣1≥0的解集在数轴上表示正确的是()..D
6.(3分)(2014•沈阳)正方形是轴对称图形,它的对称轴有()
7.(3分)(2014•沈阳)下列运算正确的是()
8.(3分)(2014•沈阳)如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC 于点E,若线段DE=5,则线段BC的长为()
=,
=,
=,
二、填空题(每小题4分,共32分)
9.(4分)(2014•沈阳)计算:=3.
∴
10.(4分)(2014•沈阳)分解因式:2m2+10m=2m(m+5).
11.(4分)(2014•沈阳)如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2=40°.
12.(4分)(2014•沈阳)化简:(1+)=.
=•
=•
=
故答案为:
13.(4分)(2014•沈阳)已知一次函数y=x+1的图象与反比例函数y=的图象相交,其中有一个交点的横坐标是2,则k的值为6.
得:
14.(4分)(2014•沈阳)如图,△ABC三边的中点D,E,F组成△DEF,△DEF三边的中点M,N,P组成△MNP,将△FPM与△ECD涂成阴影.假设可以随意在△ABC中取点,
那么这个点取在阴影部分的概率为.
=
∴=
S
则.
故答案是:
15.(4分)(2014•沈阳)某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x≤30,且x为整数)出售,可卖出(30﹣x)件.若使利润最大,每件的售价应为25元.
16.(4分)(2014•沈阳)如图,▱ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点H,连接EM.若▱ABCD的周长为42cm,FM=3cm,EF=4cm,则EM=5cm,AB=13cm.
∠
∠∠
∠
=5
∴=
∴=
三、解答题(17、18各8分,19题10分,共26分)
17.(8分)(2014•沈阳)先化简,再求值:{(a+b)2﹣(a﹣b)2}•a,其中a=﹣1,b=5.
18.(8分)(2014•沈阳)如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F 分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.
BD AC
中,
19.(10分)(2014•沈阳)在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.
∴小明两次摸出的球颜色不同的概率为:=
四、每小题10分,共20分
20.(10分)(2014•沈阳)2014年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:
根据统计图表提供的信息,解答下列问题:
(1)a=30%,b=5%;
(2)根据以上信息,请直接在答题卡中补全条形统计图;
(3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.
=5%
21.(10分)(2014•沈阳)某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.
五、本题10分
22.(10分)(2014•沈阳)如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,C D.
(1)求证:AD=CD;
(2)若AB=10,cos∠ABC=,求tan∠DBC的值.
,然后由垂径定理证得,=
,可求得
∴=
AB
=5×
==4
==,
=
六、本题12分
23.(12分)(2014•沈阳)如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,点A的坐标为(2,2),AB=4,∠B=60°,点D是线段OC上一点,且OD=4,连接A D.
(1)求证:△AOD是等边三角形;
(2)求点B的坐标;
(3)平行于AD的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形OABC截得的线段长为m,直线l与x轴交点的横坐标为t.
①当直线l与x轴的交点在线段CD上(交点不与点C,D重合)时,请直接写出m与t的函数关系式(不必写出自变量t的取值范围)
②若m=2,请直接写出此时直线l与x轴的交点坐标.
=4
m﹣
t
=4﹣= '='=8+=
)
=
=
=4
=4×=6=4×=2
,
=2+2,
)
t
(
七、本题12分
24.(12分)(2014•沈阳)如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.
(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=AM;(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
,求出
==.
=
=
=
∴
==
八、本题14分
25.(14分)(2014•沈阳)如图1,在平面直角坐标系中,二次函数y=﹣x2+12的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,A C.
(1)点B的坐标为(﹣9,0),点C的坐标为(9,0);
(2)过点C作射线CD∥AB,点M是线段AB上的动点,点P是线段AC上的动点,且始终满足BM=AP(点M不与点A,点B重合),过点M作MN∥BC分别交AC于点Q,交射线CD于点N(点Q不与点P重合),连接PM,PN,设线段AP的长为n.
①如图2,当n<AC时,求证:△P AM≌△NCP;
②直接用含n的代数式表示线段PQ的长;
③若PM的长为,当二次函数y=﹣x2+12的图象经过平移同时过点P和点N时,请直接写出此时的二次函数表达式.
x
<AC AC AC
<>
x
﹣
﹣
AC
=
AC
>
AC AC ③.
≤
MN BC
==4
x﹣∴
,
(x
>
MN BC
==4
x﹣∴
,
(=x+。
