山东省平邑县蒙阳新星学校八年级数学下册第18章平行四边形自测题1(新版)新人教版【含解析】

合集下载

人教版八年级下数学《第18章平行四边形》单元测试(含答案)

人教版八年级下数学《第18章平行四边形》单元测试（含答案）第18章平行四边形一、选择题1.下面几组条件中，能判断一个四边形是平行四边形的是（）A. 一组对边相等B. 两条对角线互相平分C. 一组对边平行D. 两条对角线互相垂直2.如图，在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片，则图中空白部分的面积为（）A. ﹣12+8B. 16﹣8C. 8﹣4D. 4﹣23.如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个钝角为100°的菱形，剪口与折痕所成的角的度数应为（）A. 25°或50°B. 20°或50°C. 40°或50°D. 40°或80°4.如图，过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH，那么图中的过平行四边形AEMG的面积S1与▱HCFM的面积S2的大小关系是（）A. S1＞S2B. S1=S2C. S1＜S2D. 不能确定5.如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=﹣的图象上，若点A的坐标为（﹣2，﹣2），则k的值为（）A. 4B. ﹣4C. 8D. ﹣86.下列对正方形的描述错误的是（）A. 正方形的四个角都是直角B. 正方形的对角线互相垂直C. 邻边相等的矩形是正方形D. 对角线相等的平行四边形是正方形7.如图，在平行四边形ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，则AB的长为（）A. 4B. 3C.D. 28.矩形各个内角的平分线围成一个四边形，则这个四边形一定是（）A. 正方形B. 菱形C. 矩形D. 平行四边形9.如图，等腰梯形ABCD中，AD∥BC，AE∥DC，∠AEB =60°，AB =AD= 2cm，则梯形ABCD的周长为( )A. 6cmB. 8cmC. 10cmD. 12cm10.已知AC为矩形ABCD的对角线，则图中∠1与∠2一定不相等的是（）A. B. C. D.11.如图，在四边形ABCD中，E、F分别是AB、AD的中点，若EF=4，BC=10，CD=6，则tanC等于（）A. B. C. D.12.如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则EF的长为（）A. 1B.C.D.二、填空题13.如图，△ABC,△ACE,△ECD都是等边三角形，则图中的平行四边形有哪些________．14.已知菱形的两条对角线长为8和6，那么这个菱形面积是________，菱形的高________．15.如图，A、B是直线m上两个定点，C是直线n上一个动点，且m∥n．以下说法：①△ABC的周长不变；②△ABC的面积不变；③△ABC中，AB边上的中线长不变．④∠C的度数不变；⑤点C到直线m的距离不变．其中正确的有________ （填序号）．16.如图，在矩形ABCD中，AB=8，BC=10，E是AB上一点，将矩形ABCD沿CE折叠后，点B落在AD边的点F 上，则AF的长为________．17.在▱ABCD中，AB=15，AD=9，AB和CD之间的距离为6，则AD和BC之间的距离为________18.如图，已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm，AE⊥BC于点E，则AE的长是________．19.如图，如果要使ABCD成为一个菱形，需要添加一个条件，那么你添加的条件是________。

人教版初二数学8年级下册第18章(平行四边形)单元测试题(含答案)

人教版八年级数学下册第十八章平行四边形单元测试题一、选择题（30分）1．甲、乙、丙、丁四位同学到木工厂参观时，一木工师傅要他们拿尺子帮助检测一个窗框是否是矩形，他们各自做了如下检测，你认为最有说服力的是（）A ．甲量得窗框的一组邻边相等B ．乙量得窗框两组对边分别相等C ．丙量得窗框的对角线长相等D ．丁量得窗框的两组对边分别相等且两条对角线也相等2．菱形ABCD 的边长为5，一条对角线长为6，则菱形面积为（）A ．20B ．24C ．30D ．483．平行四边形ABCD 中，若∠A ＝2∠B ，则∠C 的度数为（）A ．120°B ．60°C ．30°D ．15°4．如图，正方形ABCD 中，对角线AC ，BD 相交于点O ，H 为CD 边中点，正方形ABCD 的周长为8，则OH 的长为（）A ．4B ．3C ．2D ．15．如图，菱形ABCD 的面积为24cm 2，对角线BD 长6cm ，点O 为BD 的中点，过点A 作AE ⊥BC 交CB 的延长线于点E ，连接OE ，则线段OE 的长度是（）A ．3cmB ．4cmC ．4.8cmD ．5cm 6．如图，矩形中，，如果将该矩形沿对角线折叠，那么图中阴影部分的面积是22.5，则（）ABCD 6AB =BD BED BC =A．8B．10C．12D．147．将图1所示的长方形纸片对折后得到图2，图2再对折后得到图3，沿图3中的虚线剪下并展开，所得的四边形是（）A．矩形B．菱形C．正方形D．梯形8．如图，为了测量池塘边A、B两地之间的距离，在线段AB的一侧取一点C，连接CA并延长至点D，连接CB并延长至点E，使A、B分别是CD、CE的中点，若DE＝16m，则线段AB的长度是（）A．12m B．10m C．9m D．8m9．如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（）A．OA＝OC，OB＝OD B．AB＝CD，AO＝COC．AB＝CD，AD＝BC D．∠BAD＝∠BCD，AB∥CD10．如图，在平行四边形ABCD 中，，，以点C 为圆心，适当长为半径画弧，交BC 于点P ，交CD 于点Q ，再分别以点P ，Q 为圆心，大于的长为半径画弧，两弧相交于点N，射线CN 交BA 的延长线于点E ，则AE 的长是（）A ．1B ．2C ．3D ．4二、填空题（15分）11．已知矩形一条对角线长8cm ，两条对角线的一个交角是60°，则矩形较短的边长为 _____cm ．12．已知一直角三角形的两直角边长分别为6和8，则斜边上中线的长度是_____．13．如图，菱形ABCD 的周长为40，面积为80，P 是对角线BC 上一点，分别作P 点到直线AB ．AD 的垂线段PE ．PF ，则等于______．14．如图，矩形ABCD 的两条对角线AC ，BD 交于点O ，∠AOB ＝60°，AB ＝3，则矩形的周长为 _____．15．如图，四边形ABDE 和四边形ACFG 都是正方形，CE 与BG 交于点M ，点M 在△ABC 的外部．①；②；③．上述结论正确的是__________．4AB =5BC =12PQ PE PF +BG CE =CE BG ⊥120AME ∠=︒三、解答题（75分）16．如图，点O 是△ABC 外一点，连接OB 、OC ，线段AB 、OB 、OC 、AC 的中点分别为D 、E 、F 、G ，连接DE 、EF 、FG 、GD ．（1）判断四边形DEFG 的形状，并说明理由；（2）若M 为EF 的中点，OM =2，∠OBC 和∠OCB 互余，求线段DG 的长．17．如图，已知菱形ABCD 的对角线相交于点O ，延长AB 至点E ，使BE =AB ，连结CE ．(1)求证：BD =EC ．(2)当∠DAB =60°时，四边形BECD 为菱形吗?请说明理由．18．如图，四边形是平行四边形．求：（1）和的度数；（2）和的长度．19．如图，在矩形ABCD 中，已知AB ＝4，∠DBC ＝30°，求AC的长．ABCD ADC ∠BCD ∠AB BC20．如图，在中，点E ，H ，F ，G 分别在边上，，，与相交于点O ，图中共有多少个平行四边形？21．如图，A ，B 两地被池塘隔开，在没有任何测量工具的情况下，小明通过下面的方法估测出了A ，B 间的距离：先在外选一点C ，然后步测出的中点M ，N ，并测出的长，如果M ，N 两点之间还有阻隔，你有什么解决办法？说明你的理由．22．如图，在平行四边形中，过点作于点，点在边上，且，连接、．（1）求证：四边形是矩形；（2）若平分，，，求的长．23．如图，在四边形ABCD 中，，，对角线AC 、BD 交于点O ，AC 平分∠BAD ，过点C 作交AB 的延长线于点E．ABCD ,,,AB BC CD DA //AD EF //CD GH EFGH AB ,AC BCMN ABCD D DE AB ⊥E F CD FC A E =AFBF DEBF AF DAB ∠6FC =10DF =BF AB DC ∥AB AD =CE AB⊥(1)求证：四边形ABCD 是菱形；(2)若，，求CE 的长．【参考答案】1．D 2．B 3．A 4．D 5．B 6．C 7．B 8．D 9．B 10．A11．412．513．814．15．①②16．解：（1）四边形DEFG 是平行四边形，理由是：∵线段AB 、OB 、OC 、AC 的中点分别为D 、E 、F 、G ，∴EF ∥BC ，EF=BC ，DG ∥BC ，DG =BC ，∴EF ∥DG ，EF =DG ，∴四边形DEFG 是平行四边形；（2）∵∠OBC 和∠OCB 互余，∴∠OBC +∠OCB =90°，∴∠BOC =180°﹣90°=90°，∴∠EOF =90°，△EOF 为直角三角形，∵M 为EF 的中点，OM =2，∴EF =2OM =4，∵EF =DG ，∴DG =4．17．（1）证明：四边形ABCD 是菱形，∴AB =CD ，AB ∥CD ，又∵BE =AB ，∴BE =CD ，BE ∥CD ，∴四边形BECD 是平行四边形，∴BD =EC ；（2）解：结论：四边形BECD 是菱形．理由：∵四边形ABCD 是菱形，8AC =6BD =6+1212∴AD =AB ，∵∠DAB =60°，∴△ADB ，△DCB 都是等边三角形，∴DC =DB ，∵四边形BECD 是平行四边形，∴四边形BECD 是菱形．18．解：（1）∵四边形ABCD 是平行四边形∴ ,∵∴（2）∵四边形ABCD 是平行四边形∴∵∴19．解：∵四边形ABCD 是矩形，∴CD ＝AB ＝4，AC ＝BD ，∠BCD ＝90°，又∵∠DBC ＝30°，∴BD ＝2CD ＝2×4＝8，∴AC ＝8．20．四边形是平行四边形，，，，平行四边形有：ABCD ，ABHG ，CDGH ，BCFE ，ADFE ，AGOE ，BEOH ，OFCH ，OGDF 共9个，共有9个平行四边形．21．解：用步测出CM ，CN 中点D 、E ，只要测量出DE 长便可求出AB ，∵点D 、E 分别为CM ，CN 的中点，∴DE =（三角形的中位线平行于第三边，并且等于第三边的一半），又∵点M ，N 分别为的中点，∴MN =（三角形的中位线平行于第三边，并且等于第三边的一半），∴AB =2MN =4DE ．∴只要测量出DE 长便可求AB ．=ADC B ∠∠180B BCD ∠+∠=56B =∠5618056124ADC BCD ∠=∠=-=，=,AB DC BC AD=25,30DC AD ==25,30AB BC == ABCD ∴//,//AB CD AD BC //AD EF //CD GH //,//AB GH BC EF∴∴ ∴12MN ,AC BC 12AB22．解：（1）证明：∵四边形是平行四边形，∴，，∵，∴，即，∴四边形是平行四边形，又∵，∴，∴平行四边形是矩形；（2）∵平分，∴，∵，∴，∴，∴，在中，，由勾股定理得：，由（1）得四边形是矩形，∴．23．(1)证明：∵，∴，∵AC 平分∠BAD ，∴，∴，∴，∵AB=AD ，∴，∵，ABCD //CD AB CD AB =FC A E =CD FC AB AE -=-DF BE =DEBF DE AB ⊥90DEB ∠=︒DEBF AF DAB ∠DAF BAF ∠=∠//CD AB DFA BAF ∠=∠DFA DAF ∠=∠10AD DF ==Rt AED △6AE FC ==8DE ===DEBF 8BF DE ==//AB DC OAB DCA ∠=∠OAB DAC ∠=∠DAC DCA ∠=∠CD AD =AB CD =//AB DC∴四边形ABCD 是平行四边形，又∵，∴四边形ABCD 是菱形；(2)∵四边形ABCD 是菱形，BD ＝6，AC =8，∴，，，∴，在中，根据勾股定理可知，，∴菱形的面积，∵，∴菱形面积，∴AB AD =118422OA OC AC ===⨯=BD AC ⊥116322OB OD BD ===⨯=90AOB ∠=︒Rt AOB△5AB ===11862422S AC BD ==⨯⨯= CE AB ⊥524S AB CE CE === 245CE =。

人教版数学八年级下《第18章平行四边形》单元检测题(含答案)

人教版数学八年级下《第18章平行四边形》单元检测题（含答案）《平行四边形》单元检测题一、选择题（每小题只有一个正确答案）1．在下列条件中，不能判定四边形为平行四边形的是（）A. 对角线互相平分B. 一组对边平行且相等C. 两组对边分别平行D. 一组对边平行，另一组对边相等2．已知O为平行四边形ABCD对角线的交点，△AOB的面积为1，则平行四边形的面积为（）A. 1B. 2C. 3D. 43．如图，在▱ABCD中，对角线AC的垂直平分线分别交AD、BC于点E、F，连接CE，若▱ABCD的周长为20，则△CED 的周长为（）A. 5B. 10C. 15D. 204．在□ABCD中，∠B＝100°，则∠A，∠D的度数分别是（）A. ∠A＝80°，∠D＝80°B. ∠A＝80°，∠D＝100°C. ∠A＝100°，∠D＝80°D. ∠A＝100°，∠D＝100°5．如图，E是平行四边形内任一点，若S□ABCD=8，则图中阴影部分的面积是（）A. 3B. 4C. 5D. 66．已知菱形的一条对角线与边长相等,则菱形的邻角度数分别为（）A. 45°, 135°B. 60°, 120°C. 90°, 90°D. 30°, 150°7．如图，已知在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，若∠DAE∶∠BAE＝3∶1，则∠EAC 的度数是( )A. 18°B. 36°C. 45°D. 72°8．如图放置的两个正方形，大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），M在BC边上，且BM=b，连接AM，MF，MF交CG于点P，将△ABM绕点A旋转至△ADN，将△MEF绕点F旋转至△NGF，给出以下五个结论：①∠MAD=∠AND；②CP=；③△ABM≌△NGF；④；⑤A，M，P，D四点共圆，其中正确的个数是（）A. 2B. 3C. 4D. 59．如图，在△ABC中，∠BAC＝45°，AB＝AC＝8，P为AB边上一动点，以PA，PC为边作□PAQC，则对角线PQ 长度的最小值为（）A. 6B. 810．在面积为12的平行四边形ABCD中，过点A作直线BC的垂线交直线BC于点E，过点A作直线CD的垂线交直线CD于点F，若AB=4，BC=6，则CE+CF的值为( )A. 10+B. 10-C. 10+或2D. 10+或10-二、填空题11．如图，在□ABCD 中，点P是对角线BD上的一个动点(点P与点B、点D不重合)，过点P作EF∥BC，GH∥AB，则图中面积始终相等的平行四边形有_________ 对．12．如图，在▱ABCD中，∠C＝40°，过点D作CB的垂线，交AB于点E，交CB的延长线于点F，则∠BEF的度数为____．13．如图，△ABC中，D是边AB上一点，O是边AC的中点，连接DO并延长到点E，使OE=DO，连接DC，CE，EA，则四边形ADCE的形状是_______________.14．如图，把一张矩形纸片ABCD按如图方式折叠，使顶点B和点D重合，折痕为EF，若AB=3cm，BC=4cm．则线段EF=_____cm．15．如图，在边长为4的正方形ABCD中，P是BC边上一动点（不含B、C两点），将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE 交CD于点N，连接MA，NA．则以下结论中正确的有__________（写出所有正确结论的序号）①△CMP∽△BP A；②四边形AMCB的面积最大值为10；③当P为BC中点时，AE为线段NP的中垂线；④线段AM的最小值为；⑤当△ABP≌△ADN时，BP=．三、解答题16．如图所示，在平行四边形ABCD中，O是对角线AC、BD的交点，BE⊥AC，DF⊥AC，垂足分别为E、F.那么OE与OF是否相等？为什么？17．如图，已知□ABCD中，E为AD的中点，CE的延长线交BA的延长线于点E.（1）试说明线段CD与FA相等的理由；（2）若使∠F＝∠BCF，□ABCD的边长之间还需再添加一个什么条件？请你补上这个条件，并说明你的理由(不要再增添辅助线).18．如图，四边形ABCD中，AB∥DC，∠B＝90°，F为DC上一点，且FC＝AB，E为AD上一点，EC交AF于点G.(1)求证：四边形ABCF是矩形；(2)若ED＝EC，求证：EA＝EG.19．如图，在等腰三角形ABC中，AB=AC，AH⊥BC，点E是AH上一点，延长AH至点F，使FH=EH.(1)求证：四边形EBFC是菱形；(2)如果∠BAC=∠ECF，求证：AC⊥CF.20．四边形ABCD是边长为4的正方形，点E在边AD所在直线上，连接CE，以CE为边，作正方形CEFG（点D，点F在直线CE的同侧），连接BF．（1）如图1，当点E与点A重合时，请直接写出BF的长；（2）如图2，当点E在线段AD上时，AE=1；①求点F到AD的距离；②求BF的长；（3）若BF=，请直接写出此时AE的长．参考答案1．D2．D3．B4．B5．B6．B7．C8．D9．D10．C11．312．50°13．平行四边形14．15 415．①②⑤．16．相等．解析：在平行四边形ABCD中，OB＝OD，∵BE⊥AC，DF⊥AC∴∠BEO＝∠DFO，又∵∠BOE＝∠DOF∴△BOE≌△DOF∴OE＝ OF.17．解析：（1）证明：∵四边形ABCD是平行四边形，∴CD∥AB．又∵CE的延长线交BA的延长线于点F，∴∠CDA=∠DAF．∵E是AD中点，∴DE=AE．∵∠CED=∠AEF，∴△CDE≌△AEF．∴CD=AF．（2）要使∠F=∠BCF，需平行四边形ABCD的边长之间是2倍的关系，即BC=2AB，证明：∵由（1）知，△CED≌△FEA，∴CD=AF．又∵四边形ABCD是平行四边形，∴CD=AB．∴AB=AF，即BF=2AB．∵BC=2AB．∴BF=BC，∴∠F=∠BCF．18．解析：（1）证明：∵AB∥DC，FC=AB，∴四边形ABCF是平行四边形．∵∠B=90°，∴四边形ABCF是矩形．（2）证明：由（1）可得，∠AFC=90°，∴∠DAF=90°-∠D，∠CGF=90°-∠ECD．∵ED=EC，∴∠D=∠ECD．∴∠DAF=∠CGF．∵∠EGA=∠CGF，∴∠EAG=∠EGA．∴EA=EG．19．解析：证明：（1）∵AB=AC，AH⊥CB，∴BH=HC．∵FH=EH，∴四边形EBFC是平行四边形．又∵AH⊥CB，∴四边形EBFC是菱形．（2）证明：如图，∵四边形EBFC是菱形．∴∠2＝∠3＝12∠ECF．∵AB=AC，AH⊥CB，∴∠4＝12∠BAC．∵∠BAC=∠ECF∴∠4=∠3．∵AH⊥CB∴∠4+∠1+∠2=90°．∴∠3+∠1+∠2=90°．即：AC⊥CF．20．解析：（1）作FH⊥AB于H，如图1所示：则∠FHE=90°，∵四边形ABCD和四边形CEFG是正方形，∴AD=CD=4，EF=CE，∠ADC=∠DAH=∠BAD=∠CEF=90°，∴∠FEH=∠CED，在△EFH和△CED中，∵∠FHE=∠EDC=90°，∠FEH=∠CED，EF=CE，∴△EFH≌△CED（AAS），∴FH=CD=4，AH=AD=4，∴BH=AB+AH=8，∴BF===；（2）过F作FH⊥AD交AD的延长线于点H，作FM⊥AB于M，如图2所示：则FM=AH，AM=FH，①∵AD=4，AE=1，∴DE=3，同（1）得：△EFH≌△CED（AAS），∴FH=DE=3，EH=CD=4，即点F到AD的距离为3；②∴BM=AB+AM=4+3=7，FM=AE+EH=5，∴BF=；（3）分两种情况：①当点E在边AD的左侧时，过F作FH⊥AD交AD的延长线于点H，交BC延长线于K，如图3所示：同（1）得：△EFH≌△CED，∴FH=DE=4+AE，EH=CD=4，∴FK=8+AE，在Rt△BFK中，BK=AH=EH﹣AE=4﹣AE，由勾股定理得：（4﹣AE）2+（8+AE）2=（）2，解得：AE=1或AE=﹣5（舍去），∴AE=1；②当点E在边AD的右侧时，过F作FH⊥AD交AD的延长线于点H，交BC延长线于K，如图4所示：同理得：AE=；综上所述：AE的长为1或．。

八年级数学(下)第十八章《平行四边形》测试卷含答案

八年级数学（下）第十八章《平行四边形》测试卷（测试时间：90分钟满分：120分）一.选择题（共10小题，每题3分，共30分）1．已知四边形ABCD是平行四边形，则下列各图中∠1与∠2一定不相等的是（）2．下列命题中正确的是（）A.有一组邻边相等的四边形是菱形B.有一个角是直角的平行四边形是矩形C.对角线垂直的平行四边形是正方形D.一组对边平行的四边形是平行四边形3．如图，在平行四边形ABCD中，∠B＝80°，AE平分∠BAD交BC于点E，CF∥AE交AE于点F，则∠1＝（）A．40° B．50° C．60° D．80°4．如图，在中，AD=8，点E，F分别是BD，CD的中点，则EF等于（）A．2 B．3 C．4 D．55．已知一矩形的两边长分别为7cm和12 cm，其中一个内角的平分线分长边为两部分，这两部分的长分别为（）.A．6cm和6cm B．7cm和5cm C．4cm和8cm D．3cm和9cm6．在菱形ABCD中，AB=5，对角线AC=6，若过点A作AE⊥BC于E，则AE=（）A、4B、5C、4.8D、2.47．如图，在平行四边形ABCD中，AB=3cm，BC=5cm，对角线AC，BD相交于点O，则OA的取值范围是（）A．2cm＜OA＜5cmB．2cm＜OA＜8cmC．1cm＜OA＜4cmD．3cm＜OA＜8cm8．如图，菱形ABCD中，∠B=60°，AB=4，则以AC为边长的正方形ACEF的周长为（）A．14 B．15 C．16 D．179．如图所示，将一张边长为8的正方形纸片ABCD折叠，使点D落在BC的中点E处，点A落在点F处，折痕为MN，则线段MN的长为（）2A．10 B．45 C．89 D．2110．已知在四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC ②AD=BC ③OA=OC ④OB=OD.从中任选两个条件，能使四边形ABCD为平行四边形的选法有（）A．2种 B.3种 C.4种 D.5种二、填空题（共10小题，每题3分，共30分）11．如图，在四边形ABCD中，对角线AC、BD交于点O，AD∥BC，请添加一个条件：，使四边形ABCD 为平行四边形（不添加任何辅助线）．12．平行四边形的两条对角线长分别为8和10,则其中每一边长x的取值范围是。

新人教版八年级数学(下)第十八章-平行四边形测试题

八年级数学第十八章平行四边形测试题一、选择题（每小题3分，共36分）1.①两组对边分别平行②两组对边分别相等③有一组对边平行且相等④对角线相等。

以上四个条件中可以判定四边形是平行四边形的有（）（A ） 1个（B ） 2个（C ） 3个（D ） 4个 2.菱形具有而矩形不具有的性质是（）（A ）对角线互相平分（B ）四条边都相等（C ）对角相等（D ）邻角互补 3．矩形、菱形、正方形都具有的性质是（）A 、对角线相等B 、对角线互相平分C 、对角线互相垂直D 、对角线平分对角 4.如图，将一个边长分别为4、8的长方形纸片ABCD 折叠，使C 点与A 点重合，则折痕EF 的长是( )AB．CD．5.顺次连结对角线相等．．．．．的四边形各边中点所得的四边形必定是（）（A ）菱形（B ）矩形（C ）正方形（D ）平行四边形 6.如图，AD ∥BC ，若△ABC 面积是15，则△DBC 的面积是（） A 、12 B 、13 C 、14 D 、15 7.能够判定一个四边形是矩形的条件是（） A 、对角线互相平分且相等 B 、对角线互相垂直平分 C 、对角线相等且互相垂直 D 、对角线互相垂直8在四边形ABCD 中，O 是对角线的交点，能判定这个四边形是正方形的条件是( ) A ．AC ＝BD ，AB ＝CD ，AB ∥CD B ．AD //BC ，∠A ＝∠CC ．AO ＝BO ＝CO ＝DO ，AC ⊥BD D ．AO ＝CO ，BO ＝DO ，AB ＝BC9. 如图4，菱形花坛 ABCD 的边长为6m ，∠B ＝60°，其中由两个正六边形组成的图形部分种花，则种花部分的图形的周长（粗线部分）为（）B.20mC.22mD.24m10.如图，菱形ABCD 中对角线相交于点O ，且OE ⊥AB ，若AC=8，BD=6，则OE 的长是（）（A ）2.5 （B ）5 （C ） 2.4 （D ）不清楚11．下列说法正确的是（）A ．对角线互相平分且相等的四边形是菱形B ．对角线相等且互相垂直的四边形是菱形C ．对角线互相平分且垂直的四边形是正方形D ．对角线互相垂直平分且相等的四边形是正方形12在四边形ABCD 中，若有下列四个条件：①AB//CD ；②AD=BC ；③∠A=∠C ；④AB=CD ，现以其中的两个条件为一组，能判定四边形ABCD 是平行四边形的条件有（） A ．3组 B ．4组 C ．5组 D ．6组二、填空题（每空3分，共24分）13.平行四边形ABCD 中，∠A=50°，AB=30cm ，则∠B=__ __，DC=__ __.14在□ABCD 中，若添加一个条件________，则四边形ABCD 是矩形；若添加一个条件_______，则四边形ABCD 是菱形．15.菱形的两条对角线分别长10cm ，24cm ，则菱形的边长为____cm ，面积为____cm 2． 16.在Rt △ABC 中，∠ACB=90°，若CA=8，BC=6，点D 、E 分别是AC 、AB 的中点，则DE= ， CE= ..17在平面直角坐标系中，四边形AOBC 是菱形。

人教版八年级下册《第18章平行四边形》单元测试试卷及答案(共五套)

人教版八年级下册《第18章平行四边形》单元测试试卷（一）一、选择题(每题4分,共40分)1．不能判定四边形ABCD为平行四边形的题设是（）（A）AB平行且等于CD。

（B）∠A=∠C，∠B=∠D。

（C）AB=AD，BC=CD。

（D）AB=CD，AD=BC。

2．正方形具有而菱形不一定具有的性质是（）（A）四条边相等（B）对角线互相垂直平分（C）对角线平分一组对角（D）对角线相等3、顺次连结任意四边形四边中点所得的四边形一定是（）A、平行四边形B、矩形C、菱形D、正方形4.正多边形的一个内角是120°,则这个正多边形的边数为( )A.4B.8C.6D.125.如图,□ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )A.18°B.36°C.72°D.108°6．下列命题中，真命题是（）A、有两边相等的平行四边形是菱形B、对角线垂直的四边形是菱形C、四个角相等的菱形是正方形D、两条对角线相等的四边形是矩形7.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )A.6B.7C.8D.98.菱形的周长是它的高的4倍,则菱形中较大的一个角是( )A.100°B.120°C.135°D.150°9.如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是( )A.20B.15C.10D.510.如图,梯形ABCD中,AB∥CD,点E,F,G分别是BD,AC,DC的中点.已知两底之差是6,两腰之和是12,则△EFG的周长是( )A.8B.9C.10D.12二、填空题(每题4分,共24分)11、菱形ABCD的周长为36，其相邻两内角的度数比为1:5，则此菱形的面积为_________。

12、对角线长为2的正方形的周长为___________，面积为__________。

八年级数学下册人教版第十八章平行四边形测试卷(含答案)

第十八章平行四边形测试题一、选择题（每小题3分，共24分）1.下列命题中正确的是（） A.平行四边形的对角线相等 B.矩形的对角线互相垂直 C.菱形的对角线互相垂直且平分 D.四边形的对角线相等2.在平行四边形ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC 等于（）A．1.5cm B．2cm C．2.5cm D．3cm3.如图1，在菱形ABCD中，对角线AC，BD交于点O，∠BAD=120°，AC=4，则该菱形的面积是（）A．163B．16C．83D．84．要测量一个门框是否是矩形，下列方法中正确的是（）A．测量对角线是否平分C．测量一组对角是直角B．测量上下边是否相等D．测量三个角是直角5．如图2，将正方形纸片ABCD折叠，使边AB，CB均落在对角线BD上，得折痕BE，BF，则∠EBF的大小为（）A．15°B．30°C．45°D．60°6．已知下列四个命题：①对角线互相垂直平分的四边形是正方形；②对角线互相垂直且相等的四边形是菱形；③对角线互相平分且相等的四边形是矩形；④对角线互相平分、相等且垂直的四边形是正方形．其中真命题的个数是（）A．1B．2C．3D．47．如图3，把一个长方形纸片对折两次，然后剪下一个角，为了得到一个内角为120°的菱形，剪口与第二次折痕所成角的度数应为（）A．15°或30°C．45°或60°B．30°或45°D．30°或60°8.如图4，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE，则∠DEC的大小为（）A．78°B．75°C．60°D．45°二、填空题（每小题4分，共32分）9.在矩形ABCD中，对角线AC，BD相交于点O，若∠AOB=60°，AC=10，则AB=________.10．点A，B，C是同一平面内不在同一条直线上的三点，点D是平面内任意一点.若A，B，C，D四点恰能构成一个平行四边形，则在这个平面内符合这样条件的点D有________个.11.已知正方形ABCD，以CD为边作等边三角形CDE，则∠AED的度数是________.12.如图5，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值是________.13.如图6□，在ABCD中，AE⊥BC于点E，AF⊥CD于点F.若AE＝4，为AF＝6□，ABCD的周长为40，则□S ABCD________.14.如图7，在矩形ABCD中，O是两对角线的交点，AE⊥BD，垂足为E．若OD＝2OE，AE＝3，则DE的长为________.15.如图8，四边形ABCD是对角线互相垂直的四边形，且OB=OD，请你添加一个适当的条件：________，使ABCD为菱形（只需添加一个即可）.16.如图9，O为四边形ABCD的对角线AC，BD的交点，EF过点O且与边AD，BC分别交于点E，F.若BF＝DE，AD∥BC，则图中的平行四边形分别是________．三、解答题（共64分）17．（12分）在□ABCD中，∠A比∠B小30°，求这个平行四边形各个内角的度数.18．（12分）如图10，四边形ABCD是矩形，E是AB上一点，且DE＝AB，过C作CF⊥DE，垂足为F．猜想AD与CF的大小关系，并说明理由．19.（12分）如图11，在菱形ABCD中，F是BC上任意一点，连接AF交对角线BD于点E，连接EC.（1）求证：AE=EC；（2）当∠ABC=60°，∠CEF=60°时，点F在线段BC上的什么位置？说明理由.20．（14分）如图12，点O是菱形ABCD对角线的交点，DE∥AC，CE∥BD，DE与CE交于点E，连接OE．求证：OE=BC．21．（14分）如图13-①，在正方形ABCD中，E，F分别是边AD，DC上的点，且AF⊥BE．（1）求证：AF=BE；（2）如图13-②，在正方形ABCD中，M，N，P，Q分别是边AB，BC，CD，DA上的点，且MP⊥NQ，那么MP与NQ是否相等？并说明理由．第十八章平行四边形测试题一、1.C 2.B 3.C 4.D 5.C 6.B7.D8.B二、9.510.311.15°或75°12.1013.4814.315.OC=OA（答案不唯一）16.□BFDE□，AECF□，ABCD三、17.□ABCD的四个内角的度数分别是75°，105°，75°，105°.18．解：AD＝CF．理由：因为四边形ABCD是矩形，所以AB∥DC，AB＝CD.所以∠AED＝∠FDC．又DE＝AB，所以DE＝CD．因为CF⊥DE，所以∠CFD＝∠A＝90°．所以ADE≌△FCD．所以AD＝CF．△19.（1）证明：连接AC.因为BD，AC是菱形ABCD的对角线，所以BD垂直平分AC.所以AE=EC.（2）解：点F是线段BC的中点.理由：在菱形ABCD中，AB=BC，又∠ABC=60°，所以△ABC是等边三角形，即∠BAC=60°.因为AE=EC，∠CEF=60°，所以∠EAC=30°.所以AF是∠BAC的平分线.所以AF是BC边上的中线，即点F是线段BC的中点.20.证明：因为DE∥AC，CE∥BD，所以四边形OCED是平行四边形.因为四边形ABCD是菱形，所以∠COD=90°，所以四边形OCED是矩形，所以OE=CD.因为四边形ABCD是菱形，所以BC=CD.所以OE=BC．21.（1）证明：在正方形ABCD中，AB=AD，∠BAE=∠D=90°，所以∠DAF+∠BAF=90°.因为AF⊥BE，所以∠ABE+∠BAF=90°，所以∠ABE=∠DAF.所以△ABE≌△DAF.所以AF=BE.（2）解：MP与NQ相等．理由：过点A作AF∥MP交CD于点F，过点B作BE∥NQ交AD于点E，则与（1）的情况完全相同，可得AF=BE，从而MP=NQ.。

人教版八年级下册数学第十八章平行四边形考试试题及答案

人教版八年级下册数学第十八章平行四边形一、选择题（每小题3分，共30分）1．菱形和矩形一定都具有的性质是()A．对角线相等B．对角线互相垂直C．对角线互相平分且相等D．对角线互相平分2．能够判定一个四边形是矩形的条件是()A．对角线互相平分且相等B．对角线互相垂直平分C．对角线相等且互相垂直D．对角线互相垂直3．已知正方形的边长为4cm，则其对角线长是()A．8cm B．16cm C．32cm D．4cm4．在矩形ABCD中，AB=3，BC=4，则点A到对角线BD的距离为()A．B．2C．D．5．如图，▱ABCD中，CE⊥AB，垂足为E，如果∠A=115°，则∠BCE等于()A．65°B．25°C．30°D．15°6．如图，在正方形ABCD中∠DAE=25°，AE交对角线BD于E点，那么∠BEC等于()A．45°B．60°C．70°D．75°7．四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是()A．AB∥DC，AD∥BC B．AB=DC，AD=BC C．AO=CO，BO=DO D．AB∥DC，AD=BC8．如图，菱形ABCD中对角线相交于点O，且OE⊥AB，若AC=8，BD=6，则OE的长是()A．2.5B．5C．2.4D．不确定9．如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD=8，则HE等于()A．20B．16C．12D．810．如图，△ABC中，AB=AC，点D、E分别是边AB、AC的中点，点G、F在BC边上，四边形DEFG是正方形．若DE=2cm，则AC的长为()A．cm B．4cm C．cm D．cm二、填空题（每小题3分，共18分）11．菱形的两条对角线分别长10cm，24cm，则菱形的边长为cm，2．面积为cm12．如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD2．的面积为cm13．如图，▱ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点．若AC+BD=24厘米，△OAB的周长是18厘米，则EF=厘米．14．如图，在平面直角坐标系中，四边形AOBC是菱形．若点A的坐标是（3，4），则菱形的周长为，点B的坐标是．15．如图，四边形ABCD是正方形，P在CD上，△ADP旋转后能够与△ABP′重合，若AB=3，DP=1，则PP′=．16．如图，在正方形ABCD的外侧，作等边△ADE，则∠AEB=．三、解答题（共52分）17．如图，点D、E、F分别是△ABC各边中点．求证：四边形ADEF是平行四边形．18．如图，BD是菱形ABCD的对角线，点E、F分别在边CD、DA上，且CE=AF．求证：BE=BF．19．如图，正方形ABCD的对角线AC、BD相交于点O，∠OCF=∠OBE．求证：OE=OF．20．已知：如图，在Rt△ABC中，∠ACB=90°，CD平分∠ACB，DE⊥BC，DF⊥AC，垂足分别为E、F，求证：四边形CFDE是正方形．21．已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，（1）求证：四边形ADCE为矩形；（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．参考答案一、选择题（每小题3分，共30分）1．菱形和矩形一定都具有的性质是()A．对角线相等B．对角线互相垂直C．对角线互相平分且相等D．对角线互相平分考点：菱形的性质；矩形的性质．分析：根据矩形的对角线的性质（对角线互相平分且相等），菱形的对角线性质（对角线互相垂直平分）可解．解答：解：菱形的对角线互相垂直且平分，矩形的对角线相等且平分．菱形和矩形一定都具有的性质是对角线互相平分．故选：D．点评：此题主要考查矩形、菱形的对角线的性质．熟悉菱形和矩形的对角线的性质是解决本题的关键．2．能够判定一个四边形是矩形的条件是()A．对角线互相平分且相等B．对角线互相垂直平分C．对角线相等且互相垂直D．对角线互相垂直考点：矩形的判定．分析：根据矩形的判定定理逐一进行判定即可．解答：解：A、对角线互相平分且相等的四边形是矩形，故正确；B、对角线互相垂直平分的是菱形，故错误；C、对角线相等且互相垂直的四边形不一定是矩形，故错误；D、对角线互相垂直的四边形不一定是矩形，故错误，故选A．点评：本题主要考查了对矩形定义和判定的理解．矩形的判定定理有：（1）有一个角是直角的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．（3）对角线互相平分且相等的四边形是矩形．3．已知正方形的边长为4cm，则其对角线长是()A．8cm B．16cm C．32cm D．4cm考点：勾股定理．分析：作一个边长为4cm的正方形，连接对角线，构成一个直角三角形如下图所示：由勾2=AB2+BC2，求出AC的值即可．股定理得AC解答：解：如图所示：四边形ABCD是边长为4cm的正方形，在Rt△ABC中，由勾股定理得：AC==4cm．所以对角线的长：AC=4cm．故选：D．点评：本题主要考查勾股定理的应用，应先构造一个直角三角形，在直角三角形中斜边的平方等于两直角边的平方和，作图可以使整个题变得简洁明了4．在矩形ABCD中，AB=3，BC=4，则点A到对角线BD的距离为()A．B．2C．D．考点：矩形的性质．分析：本题只要根据矩形的性质，利用面积法来求解．×3×4=6，解答：解：因为BC=4，故AD=4，AB=3，则S△DBC=×5AE，故×5AE=6，AE=．又因为BD==5，S△ABD=故选A．点评：本题考查矩形的性质，矩形具有平行四边形的性质，又具有自己的特性，要注意运用矩形具备而一般平行四边形不具备的性质．5．如图，▱ABCD中，CE⊥AB，垂足为E，如果∠A=115°，则∠BCE等于()A．65°B．25°C．30°D．15°考点：平行四边形的性质．分析：由平行四边形的性质得出邻角互补，求出∠B，再由角的互余关系求出∠BCE即可．解答：解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠A+∠B=180°，∴∠B=180°﹣115°=65°，∵CE⊥AB，∴∠BEC=90°，∴∠BCE=90°﹣∠B=90°﹣65°=25°；故选：B．点评：本题考查了平行四边形的性质、角的互余关系；熟练掌握平行四边形的性质，并能进行推理计算是解决问题的关键．6．如图，在正方形ABCD中∠DAE=25°，AE交对角线BD于E点，那么∠BEC等于()A．45°B．60°C．70°D．75°考点：正方形的性质．分析：首先证明△AED≌△CED，即可证明∠ECD=∠DAE=25°，从而求得∠BEC，再根据三角形内角和定理即可求解．解答：解：在△AED和△CED中，，∴△AED≌△CED，∴∠ECD=∠DAE=25°，又∵在△DEC中，∠CDE=45°，∴∠CED=180°﹣25°﹣45°=110°，∴∠BEC=180°﹣110°=70°．故选：C．点评：此题主要考查了正方形的性质，正确理解，证明△AED≌△CED是解题的关键．7．四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是()A．AB∥DC，AD∥BC B．AB=DC，AD=BCC．AO=CO，BO=DO D．AB∥DC，AD=BC考点：平行四边形的判定．分析：根据平行四边形判定定理进行判断．解答：解：A、由“AB∥DC，AD∥BC”可知，四边形ABCD的两组对边互相平行，则该四边形是平行四边形．故本选项不符合题意；B、由“AB=DC，AD=BC”可知，四边形ABCD的两组对边相等，则该四边形是平行四边形．故本选项不符合题意；C、由“AO=CO，BO=DO”可知，四边形ABCD的两条对角线互相平分，则该四边形是平行四边形．故本选项不符合题意；D、由“AB∥DC，AD=BC”可知，四边形ABCD的一组对边平行，另一组对边相等，据此不能判定该四边形是平行四边形．故本选项符合题意；故选D．点评：本题考查了平行四边形的判定．（1）两组对边分别平行的四边形是平行四边形．（2）两组对边分别相等的四边形是平行四边形．（3）一组对边平行且相等的四边形是平行四边形．（4）两组对角分别相等的四边形是平行四边形．（5）对角线互相平分的四边形是平行四边形．8．如图，菱形ABCD中对角线相交于点O，且OE⊥AB，若AC=8，BD=6，则OE的长是()A．2.5B．5C．2.4D．不确定考点：菱形的性质；勾股定理．分析：根据菱形的性质可得AC⊥DB，AO=AC，BO=BD，然后利用勾股定理计算出AB长，再根据菱形的面积公式得到S菱形ABCD=×8×6=24，进而得到△AOB的长，然后根据直角三角形的面积计算出EO长即可．解答：解：∵四边形ABCD是菱形，∴AC⊥DB，AO=AC，BO=BD，∵AC=8，BD=6，×8×6=24，∴AO=4，BO=3，S菱形ABCD=，∴AB==5，S△AOB=6∵•AB•EO=×AO×BO，∴5EO=4×3，EO=，故选：C．点评：此题主要考查了菱形的性质、面积，以及勾股定理，关键是掌握菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．9．如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD=8，则HE等于()A．20B．16C．12D．8考点：三角形中位线定理；直角三角形斜边上的中线．分析：利用三角形中位线定理知DF=AC；然后在直角三角形AHC中根据“直角三角形斜边上的中线等于斜边的一半”即可将所求线段EH与已知线段DF联系起来了．解答：解：∵D、F分别是AB、BC的中点，∴DF是△ABC的中位线，∴DF=AC（三角形中位线定理）；又∵E是线段AC的中点，AH⊥BC，∴EH=AC，∴EH=DF=8．故选D．点评：本题综合考查了三角形中位线定理、直角三角形斜边上的中线．三角形的中位线平行于第三边且等于第三边的一半．10．如图，△ABC中，AB=AC，点D、E分别是边AB、AC的中点，点G、F在BC边上，四边形DEFG是正方形．若DE=2cm，则AC的长为()A．cm B．4cm C．cm D．cm考点：三角形中位线定理；等腰三角形的性质；勾股定理；正方形的性质．专题：计算题．分析：根据三角形的中位线定理可得出BC=4，由AB=AC，可证明BG=CF=1，由勾股定理求出CE，即可得出AC的长．解答：解：∵点D、E分别是边AB、AC的中点，∴DE=BC，∵DE=2cm，∴BC=4cm，∵AB=AC，四边形DEFG是正方形．∴△BDG≌△CEF，∴BG=CF=1，∴EC=，∴AC=2cm．故选D．点评：本题考查了相似三角形的判定、勾股定理、等腰三角形的性质以及正方形的性质，是基础题，比较简单．二、填空题（每小题3分，共18分）11．菱形的两条对角线分别长10cm，24cm，则菱形的边长为13cm，面积为120cm2．考点：菱形的性质．分析：根据菱形的对角线性质，得出两条对角线的一半为5与12．然后可用勾股定理求出其边长．利用菱形的面积公式：对角线之积的一半进行计算．解答：解：根据题意可得AC=10cm，BD=24cm，∵四边形ABCD是菱形，∴AO=AC，BO=BD，AC⊥BD，∵AC=10cm，BD=24cm，∴AO=5cm，BO=12cm，∴AB==13cm，2）．面积：AC•BD=×10×24=120（cm故答案为：13；120．点评：此题主要考查了菱形的性质，以及勾股定理的应用，关键是掌握菱形四边相等，对角线互相垂直平分．12．如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD2．的面积为2cm考点：菱形的性质；勾股定理．分析：因为DE丄AB，E是AB的中点，所以AE=1cm，根据勾股定理可求出DE的长，菱形的面积=底边×高，从而可求出解．解答：解：∵E是AB的中点，∴AE=1cm，∵DE丄AB，∴DE==cm．2．∴菱形的面积为：2×=2cm故答案为：2．点评：本题考查菱形的性质，四边都相等，菱形面积的计算公式以及勾股定理的运用等．13．如图，▱ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点．若AC+BD=24厘米，△OAB的周长是18厘米，则EF=3厘米．考点：三角形中位线定理；平行四边形的性质．分析：根据平行四边形的性质可知OA=AC，OB=BD，结合AC+BD=24厘米，△OAB 的周长是18厘米，求出AB的长，利用三角形中位线定理求出EF的长．解答：解：∵▱ABCD的对角线AC，BD相交于点O，∴点O是AC、BD的中点，∵AC+BD=24厘米，∴OB+0A=12厘米，∵△OAB的周长是18厘米，∴AB=18﹣12=6厘米，∵▱ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点，∴AB=2EF，∴EF=6÷2=3厘米，故答案为：3．点评：本题主要考查了三角形中位线定理以及平行四边形的性质的知识，解答本题的关键是求出AB的长，此题难度不大．14．如图，在平面直角坐标系中，四边形AOBC是菱形．若点A的坐标是（3，4），则菱形的周长为20，点B的坐标是（5，0）．考点：菱形的性质；坐标与图形性质．分析：过A作AE⊥x轴于点E，根据勾股定理可求出OA的长，进而可求出菱形的周长，再由菱形的性质可得AO=AC=BO=BC=5，即可求出点B的坐标．解答：解：过A作AE⊥x轴于点E，∵点A的坐标是（3，4），∴OE=3，AE=4．∴AO==5，∵四边形AOBC是菱形，∴AO=AC=BO=BC=5，∴菱形的周长=4AB=20，点B的坐标是（5，0），故答案为：20，（5，0）．点评：此题主要考查了菱形的性质，解题的关键是利用勾股定理求出OA的长，是2015届中考常见题型，比较简单．15．如图，四边形ABCD是正方形，P在CD上，△ADP旋转后能够与△ABP′重合，若AB=3，DP=1，则PP′=2．考点：旋转的性质．分析：由正方形的性质得出AB=AD=3，∠ABC=∠D=∠BAD=90°，由勾股定理求出AP，再由旋转的性质得出△ADP≌△ABP′，得出AP′=AP=，∠BAP′=∠DAP，证出△PAP′是等腰直角三角形，得出PP′=AP，即可得出结果．解答：解：∵四边形ABCD是正方形，∴AB=AD=3，∠ABC=∠D=∠BAD=90°，∴AP==，∵△ADP旋转后能够与△ABP′重合，∴△ADP≌△ABP′，∴AP′=AP=，∠BAP′=∠DAP，∴∠PAP′=∠BAD=90°，∴△PAP′是等腰直角三角形，∴PP′=AP=2；故答案为：2．点评：本题考查了旋转的性质、勾股定理、全等三角形的性质、等腰直角三角形的性质；熟练掌握正方形和旋转的性质是解决问题的关键．16．如图，在正方形ABCD的外侧，作等边△ADE，则∠AEB=15°．考点：正方形的性质；等边三角形的性质．专题：计算题分析：由四边形ABCD为正方形，三角形ADE为等比三角形，可得出正方形的四条边相等，三角形的三边相等，进而得到AB=AE，且得到∠BAD为直角，∠DAE为60°，由∠BAD+∠DAE求出∠BAE的度数，进而利用等腰三角形的性质及三角形的内角和定理即可求出∠AEB的度数．解答：解：∵四边形ABCD为正方形，△ADE为等边三角形，∴AB=BC=CD=AD=AE=DE，∠BAD=90°，∠DAE=60°，∴∠BAE=∠BAD+∠DAE=150°，又∵AB=AE，∴∠AEB==15°．故答案为：15°．点评：此题考查了正方形的性质，以及等边三角形的性质，利用了等量代换的思想，熟练掌握性质是解本题的关键．三、解答题（共52分）17．如图，点D、E、F分别是△ABC各边中点．求证：四边形ADEF是平行四边形．考点：三角形中位线定理；平行四边形的判定．专题：证明题．分析：根据三角形的中位线定理可得DE∥AC，EF∥AB，再根据两组对边分别平行的四边形是平行四边形证明即可．解答：证明：∵D、E分别为AB、BC的中点，∴DE∥AC，∵E、F分别为BC、AC中点，∴EF∥AB，∴四边形ADEF是平行四边形．点评：此题主要考查了三角形的中位线定理，勾股定理以及平行四边形的判定定理，关键是掌握三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．18．如图，BD是菱形ABCD的对角线，点E、F分别在边CD、DA上，且CE=AF．求证：BE=BF．考点：菱形的性质；全等三角形的判定与性质．专题：证明题．分析：根据菱形的性质可得AB=BC，∠A=∠C，再证明△ABF≌△CBE，根据全等三角形的性质可得BF=BE．解答：证明：∵四边形ABCD是菱形，∴AB=BC，∠A=∠C，∵在△ABF和△CBE中，，∴△ABF≌△CBE（SAS），∴BF=BE．点评：此题主要考查了菱形的性质，以及全等三角形的判定与性质，关键是掌握菱形的四条边都相等．19．如图，正方形ABCD的对角线AC、BD相交于点O，∠OCF=∠OBE．求证：OE=OF．考点：正方形的性质；全等三角形的判定与性质．专题：证明题．分析：根据正方形的性质及全等三角形的判定得到△OCF≌△OBE，从而可得到结论．解答：证明：∵四边形ABCD是正方形，∴AC⊥BD，即∠AOB=∠BOC=90°，∴BO=OC，∵∠OCF=∠OBE，∴△OCF≌△OBE，∴OE=OF．点评：本题利用了正方形的性质（正方形的四个角都是直角，对角线互相垂直平分且相等），还利用了全等三角形的判定．20．已知：如图，在Rt△ABC中，∠ACB=90°，CD平分∠ACB，DE⊥BC，DF⊥AC，垂足分别为E、F，求证：四边形CFDE是正方形．考点：正方形的判定；角平分线的性质；矩形的判定与性质．专题：证明题．分析：由题意可得，四边形CFDE是矩形，根据角平分线的性质得到DE=DF，根据有一组邻边相等的矩形是正方形，四边形CFDE是正方形．解答：证明：∵∠ACB=90°，DE⊥BC，DF⊥AC，∴四边形CFDE是矩形．又∵CD平分∠ACB，DE⊥BC，DF⊥AC，∴DE=DF．∴四边形CFDE是正方形（有一组邻边相等的矩形是正方形）．点评：本题是考查正方形的判别方法，判别一个四边形为正方形主要根据正方形的概念，途经有两种：①先说明它是矩形，再说明有一组邻边相等；②先说明它是菱形，再说明它有一个角为直角．21．已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，（1）求证：四边形ADCE为矩形；（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．考点：矩形的判定；角平分线的性质；等腰三角形的性质；正方形的判定．专题：证明题；开放型．分析：（1）根据矩形的有三个角是直角的四边形是矩形，已知CE⊥AN，AD⊥BC，所以求证∠DAE=90°，可以证明四边形ADCE为矩形．（2）根据正方形的判定，我们可以假设当AD=BC，由已知可得，DC=BC，由（1）的结论可知四边形ADCE为矩形，所以证得，四边形ADCE为正方形．解答：（1）证明：在△ABC中，AB=AC，AD⊥BC，∴∠BAD=∠DAC，∵AN是△ABC外角∠CAM的平分线，∴∠MAE=∠CAE，∴∠DAE=∠DAC+∠CAE=180°=90°，又∵AD⊥BC，CE⊥AN，∴∠ADC=∠CEA=90°，∴四边形ADCE为矩形．（2）当△ABC满足∠BAC=90°时，四边形ADCE是一个正方形．理由：∵AB=AC，∴∠ACB=∠B=45°，∵AD⊥BC，∴∠CAD=∠ACD=45°，∴DC=AD，∵四边形ADCE为矩形，∴矩形ADCE是正方形．∴当∠BAC=90°时，四边形ADCE是一个正方形．点评：本题是以开放型试题，主要考查了对矩形的判定，正方形的判定，等腰三角形的性质，及角平分线的性质等知识点的综合运用．。

八年级数学(下)第十八章《平行四边形》测试题含答案

八年级数学（下）第十八章《平行四边形》测试题（测试时间：90分钟满分：120分）一、选择题（共10小题，每题3分，共30分）1．下列说法错误的是（）A. 对角线互相平分的四边形是平行四边形B. 两组对边分别相等的四边形是平行四边形C. 一组对边平行且相等的四边形是平行四边形D. 一组对边相等，另一组对边平行的四边形是平行四边形2．如图，在平行四边形中，，，的平分线交于点，则的长为（）．A. B. C. D.3．已知四边形ABCD是平行四边形，对角线AC、BD交于点O，E是BC的中点，以下说法错误的是（）A. OE＝DCB. OA=OCC. ∠BOE＝∠OBAD. ∠OBE＝∠OCE4．如图，过平行四边形对角线交点的直线交于，交于，若，，，那么四边形周长是（）．A. B. C. D.5．如图，在四边形中，是边的中点，连结并延长，交的延长线于点，．添加一个条件，使四边形是平行四边形，你认为下面四个条件中可选择的是（）．A. B. C. D.6．如图，四边形ABCD，AEFG均为正方形，点E在BC上，且B,E两点不重合，连接BG.根据图中标示的角判断，下列关系正确的是（）A. ∠1＜∠2B. ∠1＞∠2C. ∠3＜∠4D. ∠3＞∠47．如图，在长方形ABCD中，AB=3，BC=4，若沿折痕EF折叠，使点C与点A重合，则折痕EF的长为（）A. B. C. D. 158．如图，在ABC中，5AC=，点D，E，F分别是ABC三边中点，则DEFBC=，7AB=，6的周长为（）．A. 9B. 10C. 11D. 129．如图，在平行四边形ABCD中，过对角线BD上一点P作EF∥AB，GH∥AD，与各边交点分别为点E，F，G，H，则图中面积相等的平行四边形的对数为( )A. 3对B. 4对C. 5对D. 6对10．如图，正方形ABCD的对角线AC与BD相交于O点，在BD上截取BE＝BC，连接CE，点P是CE上任意一点，PM⊥BD于M，PN⊥BC于N，若正方形ABCD的边长为1，则PM＋PN＝（）A. 1B.C.D. 1＋二、填空题（共10小题，每题3分，共30分）11．如图，▱ABCD中，∠DCE=70°，则∠A=__．12．在平行四边形中，若再增加一个条件__________，使平行四边形能成为矩形（填写一个你认为正确的即可）．13．若直角三角形斜边上的高和中线分别是和，则斜边长为__________，面积为__________．14．如图，在四边形中，，若加上，则四边形为平行四边形，现在请你添加一个适当的条件：__________，使得四边形为平行四边形．（图中不再添加点和线）15．如图，等边三角形在正方形内，连接，则__________．16．已知：在平行四边形中，，，的平分线交于点，交的延长线于点，则__________．17．如图，矩形ABCD的对角线AC，BD相交于点O，分别过点C，D作BD，AC的平行线，相交于点E．若AD=6，则点E到AB的距离是________．18．如图所示，将两张等宽的长方形纸条交叉叠放，重叠部分是一个四边形ABCD，若AD=4cm，∠ABC=30°，则长方形纸条的宽度是__cm．19．如图，在矩形ABCD中，E是AB边上的中点，将△BCE沿CE翻折得到△FCE，连接AF．若∠EAF=75°，那么∠BCF的度数为_____．20．如图，在矩形ABCD中，AB=5，B C=7，点E为BC上一动点，把△ABE沿AE折叠，当点B的对应点B′落在∠ADC的角平分线上时，则点B′到BC的距离为_______．三、解答题（共60分）21.（6分）如图，在平行四边形ABCD中，E、F是对角线AC上的两点，且AE=CF.（1）写出图中所有的全等三角形；（2）求证：BE=DF.22．（6分）已知：如图，E，F是四边形ABCD的对角线AC上的两点，AF=CE，连接DE，DF，BE，BF，四边形DEBF为平行四边形.求证：四边形ABCD是平行四边形.23．（8分）如图，已知点E、F在四边形ABCD的对角线延长线上，AE=CF，DE∥BF，∠1=∠2．（1）求证：△AE D≌△CFB；（2）若AD⊥CD，四边形ABCD是什么特殊四边形？请说明理由．24．（6分）如图，矩形ABCD中，点E在CD边的延长线上，且∠EAD=∠CAD．求证：AE=BD．25.（9分）已知：如图，在△ABC中，90⊥，CE∥AD．如果AC=2，CE=4．ACB∠=︒，D是BC的中点，DE BC（1）求证：四边形ACED是平行四边形；（2）求四边形ACEB的周长；（3）直接写出CE和AD之间的距离．26．（8分）如图，在正方形ABCD中，点E、F在对角线BD上，且BF＝DE．⑴求证：四边形AECF是菱形．⑵若AB＝2，BF＝1，求四边形AECF的面积．27．(8分 )如图，平行四边形ABCD的边CD的垂直平分线与边DA，BC的延长线分别交于点E，F，与边CD 交于点O，连结CE，DF．（1）求证：DE=CF；（2）请判断四边形ECFD的形状，并证明你的结论．28．（9分）如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F，另一边交CB的延长线于点G.（1）求证：EF＝EG；（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变．（1）中的结论是否仍然成立？若成立，情给予证明；若不成立，请说明理由；答案（测试时间：90分钟满分：120分）一、选择题（共10小题，每题3分，共30分）1．下列说法错误的是（）A. 对角线互相平分的四边形是平行四边形B. 两组对边分别相等的四边形是平行四边形C. 一组对边平行且相等的四边形是平行四边形D. 一组对边相等，另一组对边平行的四边形是平行四边形【答案】D【解析】一组对边相等，另一组对边平行不能判定四边形为平行四边形，故D选项错误.故选D.2．如图，在平行四边形中，，，的平分线交于点，则的长为（）．A. B. C. D.【答案】D3．已知四边形ABCD是平行四边形，对角线AC、BD交于点O，E是BC的中点，以下说法错误的是（）A. OE＝DC B. OA=OC C. ∠BOE＝∠OBA D. ∠OBE＝∠OCE【答案】D【解析】4．如图，过平行四边形对角线交点的直线交于，交于，若，，，那么四边形周长是（）．A. B. C. D.【答案】C【解析】在平行四边形中，，，，∴，∵，∴≌，∴，，∵，，∴，，∵，∴，∴四边形的周长是：，故选．5．如图，在四边形中，是边的中点，连结并延长，交的延长线于点，．添加一个条件，使四边形是平行四边形，你认为下面四个条件中可选择的是（）．A. B. C. D.【答案】D6．如图，四边形ABCD，AEFG均为正方形，点E在BC上，且B,E两点不重合，连接BG.根据图中标示的角判断，下列关系正确的是（）A. ∠1＜∠2B. ∠1＞∠2C. ∠3＜∠4D. ∠3＞∠4【答案】D7．如图，在长方形ABCD中，AB=3，BC=4，若沿折痕EF折叠，使点C与点A重合，则折痕EF的长为（）A. B. C. D. 15【答案】B【解析】连接AF．根据折叠的性质，得EF垂直平分AC，则设则在中，根据勾股定理，得解得在中，根据勾股定理，得AC=5，则AO=2.5．在中，根据勾股定理，得根据全等三角形的性质，可以证明则故选B．8．如图，在ABC中，5AC=，点D，E，F分别是ABC三边中点，则DEF AB=，6BC=，7的周长为（）．A. 9B. 10C. 11D. 12【答案】A9．如图，在平行四边形ABCD中，过对角线BD上一点P作EF∥AB，GH∥AD，与各边交点分别为点E，F，G，H，则图中面积相等的平行四边形的对数为( )A. 3对B. 4对C. 5对D. 6对【答案】A【解析】∵ABCD为平行四边形，∴AB∥CD，AD∥BC．∵EF∥AB，GH∥AD，∴EF∥AB∥CD，GH∥AD∥BC，∴AGPE，ABFE，AGHD，PFCH，BCHG，FCDE是平行四边形．∵ABCD为平行四边形，BD为对角线，∴S△ABD=S△BCD．同理S△BFP=S△BGP，S△PED=S△HPD．∵S△BCD－S△BFP－S△PHD=S PFCH，S△ABD－S△GBD－S△EPD=S AGPE，∴S PFCH=S AGPE，∴S AGHD=S EFCD，S ABFE=S BCHG，∴有3对面积相等的平行四边形．故选A．10．如图，正方形ABCD的对角线AC与BD相交于O点，在BD上截取BE＝BC，连接CE，点P是CE上任意一点，PM⊥BD于M，PN⊥BC于N，若正方形ABCD的边长为1，则PM＋PN＝（）A. 1B.C.D. 1＋【答案】C二、填空题（共10小题，每题3分，共30分）11．如图，▱ABCD中，∠DCE=70°，则∠A=__．【答案】110°12．在平行四边形中，若再增加一个条件__________，使平行四边形能成为矩形（填写一个你认为正确的即可）．【答案】或【解析】∵有一个角为的平行四边形为矩形；对角线相等的平行四边形为矩形∴可增加一个条件是：或.13．若直角三角形斜边上的高和中线分别是和，则斜边长为__________，面积为__________．【答案】【解析】∵直角三角形斜边中线是，高是，∴斜边是，面积是：．14．如图，在四边形中，，若加上，则四边形为平行四边形，现在请你添加一个适当的条件：__________，使得四边形为平行四边形．（图中不再添加点和线）【答案】【解析】连结，交于点，∵，，∴四边形是平行四边形，∴，，∵，∴，∴四边形为平行四边形．15．如图，等边三角形在正方形内，连接，则__________．【答案】15°16．已知：在平行四边形中，，，的平分线交于点，交的延长线于点，则__________．【答案】317．如图，矩形ABCD的对角线AC，BD相交于点O，分别过点C，D作BD，AC的平行线，相交于点E．若AD=6，则点E到AB的距离是________．【答案】918．如图所示，将两张等宽的长方形纸条交叉叠放，重叠部分是一个四边形ABCD，若AD=4cm，∠ABC=30°，则长方形纸条的宽度是__cm．【答案】2【解析】过点A作BC的垂线可得直角三角形,在30度角的直角三角形中,30度角所对直角边等于斜边的一半,可得长方形纸条的宽度是2,故答案为:2.学科.网19．如图，在矩形ABCD中，E是AB边上的中点，将△BCE沿CE翻折得到△FCE，连接AF．若∠EAF=75°，那么∠BCF的度数为_____．【答案】30°【解析】∵四边形ABCD是矩形，∴∠B=90°，20．如图，在矩形ABCD中，AB=5，B C=7，点E为BC上一动点，把△ABE沿AE折叠，当点B的对应点B′落在∠ADC的角平分线上时，则点B′到BC的距离为_______．【答案】2或1【解析】连接B′D,过点B′作B′M⊥AD于M.∵点B的对应点B′落在∠ADC的角平分线上，∴设DM=B′M=x，则AM=7−x，又由折叠的性质知AB=AB′=5，∴在直角△AMB′中,由勾股定理得到：，即(7−x)2=25−x2，解得x=3或x=4，则点B′到BC的距离为2或1.故答案为：2或1.三、解答题（共60分）21.（6分）如图，在平行四边形ABCD中，E、F是对角线AC上的两点，且AE=CF.（1）写出图中所有的全等三角形；（2）求证：BE=DF.【答案】（1）图中全等的图形有：△ADF≌△CBE，△ABE≌△CDF，△ABC≌△DCA；（2）证明见解析．学科.网【解析】22．（6分）已知：如图，E，F是四边形ABCD的对角线AC上的两点，AF=CE，连接DE，DF，BE，BF，四边形DEBF为平行四边形.求证：四边形ABCD是平行四边形.【答案】证明见解析.【解析】考点：平行四边形的判定和性质.23．（8分）如图，已知点E、F在四边形ABCD的对角线延长线上，AE=CF，DE∥BF，∠1=∠2．（1）求证：△AED≌△CFB；（2）若AD⊥CD，四边形ABCD是什么特殊四边形？请说明理由．【答案】（1）证明见解析（2）四边形ABCD是矩形；理由见解析【解析】试题分析：（1）根据DE∥BF可得∠E=∠F，再由“角角边”证明△AED和△CF B全等即可；（2）由（1）可得AD=BC，∠DAE=∠BCF，再求出∠DAC=∠BCA，然后可得AD∥BC，再根据一组对边平行且相等的四边形是平行四边形证明四边形ABCD是平行四边形，再根据有一个角是直角的平行四边形是矩形即可得．试题解析：（1）∵DE∥BF，∴∠E=∠F，又∵AE=CF，∠1=∠2，∴△AED≌△CFB（AAS）；（2）四边形ABCD是矩形．理由如下：∵△AED≌△CFB，∴AD=BC，∠DAE=∠BCF，∴∠DAC=∠BCA，∴AD∥BC，∴四边形ABCD是平行四边形，又∵AD⊥CD，∴四边形ABCD是矩形．考点：1、全等三角形的判定与性质；2、矩形的判定24．（6分）如图，矩形ABCD中，点E在CD边的延长线上，且∠EAD=∠CAD．求证：AE=BD．【答案】证明见解析.【解析】考点：1.矩形的性质；2.全等三角形的判定与性质．25.（9分）已知：如图，在△ABC中，90∠=︒，D是BC的中点，DE BC⊥，CE∥AD．如果AC=2，CE=4．ACB（1）求证：四边形ACED是平行四边形；（2）求四边形ACEB的周长；（3）直接写出CE和AD之间的距离．【答案】（1）证明见解析；（2）四边形ACEB的周长是 10+132；（3）CE和AD之间的距离是3；学*科网【解析】试题分析：（1）首先证明AC∥DE，再加上CE∥AD可根据两组对边平行的四边形是平行四边形可证明四边形考点：1、平行四边形的判定与性质；2、勾股定理26．（8分）如图，在正方形ABCD中，点E、F在对角线BD上，且BF＝DE．⑴求证：四边形AECF是菱形．⑵若AB＝2，BF＝1，求四边形AECF的面积．【答案】（1）证明见解析；（2）四边形AECF的面积为4﹣22．【解析】试题分析：（1）根据正方形的性质，可得正方形的四条边相等，对角线平分对角，根据 SAS，可得△ABF 与△CBF与△CDE与△ADE的关系，根据三角形全等，可得对应边相等，再根据四条边相等的四边形，可得证明结果；（2）根据正方形的边长、对角线，可得直角三角形，根据勾股定理，可得AC、EF的长，根据菱形的面积公式，可得答案．试题解析：（1）正方形ABCD中，对角线BD，∴AB=BC=CD=DA，∠ABF=∠CBF=∠CDE=∠A DE=45°．∵BF=DE，∴△ABF≌△CBF≌△DCE≌△DAE（SAS）．∴AF=CF=CE=AE，∴四边形AECF是菱形；（2）在Rt△ABD中，由勾股定理，得AD=2222+=+=，BC=AD=22，AB BD2222EF=BC﹣BF﹣DE=22﹣1﹣1，四边形AECF的面积=AD•EF÷2=22×（22﹣2）÷2=4﹣22．考点：1.正方形的性质2.菱形的判定与性质．27．(8分 )如图，平行四边形ABCD的边CD的垂直平分线与边DA，BC的延长线分别交于点E，F，与边CD 交于点O，连结CE，DF．（1）求证：DE=CF；（2）请判断四边形ECFD的形状，并证明你的结论．【答案】（1）证明见解析；（2）四边形ECFD是菱形，证明见解析【解析】考点：1.菱形的判定；2.全等三角形的判定与性质；3.平行四边形的性质28．（9分）如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F，另一边交CB的延长线于点G.（1）求证：EF＝EG；（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变．（1）中的结论是否仍然成立？若成立，情给予证明；若不成立，请说明理由；【答案】（1）证明见解析；（2）是，证明见解析.【解析】考点：1.正方形的性质；2.全等三角形的判定与性质．学科￥网。

(完整版)人教版八年级数学下册第十八章平行四边形单元测试题(含答案).docx

人教版八年级数学下册第十八章平行四边形单元测试题一、选择题1. 如图，在平行四边形ABCD中，CE⊥ CD，C为垂足，如果∠ A=1250，则∠ BCE的度数为（ B）A．550B．350C．250D．300第 6 题图2. 如图，矩形 ABCD对角线相交于点O，∠ AOB=60°，AB=4，则矩形的对角线AC为（B）A.4B. 8C. 4 √3D. 103．在□ABCD中，对角线 AC、BD交于点 O，下列式子中一定成立的是（B）A． AC⊥ BD B ． OA=OC C ． AC=BD D ． AO=OD4.如图，在菱形 ABCD中， AB=13，对角线 BD=24，若过点 C 作 CE⊥ AB，垂足为 E，则 CE的长为（ A ）120B. 10C. 12240A. D.1313AB， BC， CD， DA的长度之比，其中能满足四边形ABCD是平5. 下面给出的是四边形ABCD中行四边形的是(C)A． 1∶ 2∶ 3∶ 4B． 2∶ 2∶ 3∶ 3C． 2∶ 3∶ 2∶ 3D． 2∶ 3∶ 3∶ 26.顺次连接：①矩形；②菱形；③对角线相等的四边形；④对角线垂直的四边形，各边中点所构成的四边形中，为菱形的有（C）A．①B．①②C．①③D．①③④7. 四边形中，有两条边相等，另两条边也相等，则这个四边形（C）A．一定是平行四边形B．一定不是平行四边形C．可以是平行四边形，也可以不是平行四边形D．上述答案都不对8.已知四边形 ABCD中，∠ A=∠ B=∠ C=900，如果添加一个条件，可推出四边形是正方形，那么这个条件可以是（D）A．∠ D=900B． AB=CD C．AD=BC D．BC=CD9．如图，在四边形 ABCD中，对角线 AC，BD相交于点 E，∠ CBD＝ 90°， BC＝ 4，BE＝ ED＝ 3，AC＝ 10，则四边形 ABCD的面积为 (D)A． 6 B ． 12C． 20D． 2410.如图，在正方形 ABCD中， E 为 AB 上一点，且 AE=1，DE=2，那么正方形的面积为（ C ）A．3B．5C．3D．23二、填空题2 BC ，则AD= 9，CD= 6．11. □ABCD的周长是30cm，AB312.如图，在△ ABC中， AD⊥ BC，垂足为 D，E、 F 分别是 AB、AC的中点，连接 DE、DF，当△ABC满足条件AB=AC 或∠ B=∠C 等时，四边形AEDF是菱形（填写一个即可）．13. 如图，在四边形ABCD中， AB＝ CD， BC＝ AD.若∠ A＝ 110°，则∠ C＝ 110__°．14.如图，将正方形纸片按如图折叠， AM为折痕，点 B 落在对角线 AC上的点 E 处，则∠ CME=___45° ___ ．15.如图，四边形 ABCD是矩形，点 E 在线段 CB的延长线上，连接 DE交 AB于点 F，∠ AED=2∠CED，点 G是 DF 的中点，若BE=2， DF=8，则 AB的长为 ___2√3___ ．16．在 ?ABCD中， AE⊥ BC于点 E，若 AB＝ 10 cm， BC＝ 15 cm， BE＝6 cm，则 ?ABCD的面积为120__cm2．三、解答题17.如图，矩形 ABCD中， AB=4，点 E， F 分别在 AD，BC边上，且 EF⊥ BC，若矩形 ABFE∽矩形 DEFC，且相似比为 1： 2，求 AD的长．解：∵矩形ABFE∽矩形 DEFC，且相似比为1： 2，∴AB =AE =1，DE DC 2∵四边形ABCD为矩形，∴C D=AB=4∴4 =AE =1，DE 42∴D E=8， AE=2，∴A D=AE+DE=2+8=10．18.如图，在 ?ABCD中， E， F 是对角线 AC上的两点，且 AE＝ CF，求证：∠ AED＝∠ CFB.证明：∵四边形ABCD是平行四边形，∴AD＝BC， AD∥BC.∴∠ DAE＝∠ BCF.在△ ADE和△ CBF中，AD＝ CB，∠DAE＝∠ BCF，AE＝ CF，∴△ ADE≌△ CBF(SAS)．∴∠ AED＝∠ CFB.19.如图，点 E、 F 在正方形 ABCD的边 BC、 CD上， BE=CF．（1） AE与 BF 相等吗？为什么？（2） AE与 BF 是否垂直？说明你的理由．（ 1）相等；证明：∵四边形ABCD是正方形，∴∠ABC=∠ C， AB=BC，又∵ BE=CF，∴△ ABE≌△ BCF，∴ AE=CF．（2）垂直，证明：∵△ ABE≌△ BCF，∴∠ AEB=∠ BFC．∵∠ FBC+∠ BFC=900，∴∠ FBC+∠ AEB=900．∴∠ BGE=900，故 AE⊥ BF．20. 如图，□ ABCD与□ABEF中， BC=BE，∠ ABC=∠ ABE，求证：四边形EFDC是矩形。

山东省平邑县蒙阳新星学校八年级数学下册第18章《平行四边形》自测题(4)

初中数学试卷灿若寒星整理制作第18 章自测题（四）一、选择题：1. 能够判定一个四边形是矩形的条件是（）.A．对角线互相平分且相等 B.对角线互相垂直平分C.对角线相等且互相垂直D.对角线互相垂直2．如图所示，在平行四边形ABCD中，∠B=110°，延长AD至F，延长CD至E，连接EF，则∠E+∠F 等于（）A．110°B．30°C．50°D．70°3．如图所示，在菱形ABCD中，对角线AC与BD相交于点O，OE∥DC交BC于点E，AD=6cm，则OE 的长为（）A．6cm B．4cm C．3cm D．2cm4．若四边形的两条对角线相等，则顺次连结该四边形各边中点所得的四边形是（）A．梯形B．矩形C．菱形D．正方形5.四边形ABCD的对角线互相平分，要使它变为矩形，需要添加的条件是（）A．AB=CD B．AD=BCC．AB=BC D．AC=BD6．如图，矩形ABCD中，点E在边AB上，将矩形ABCD沿直线DE折叠，点A恰好落在边BC的点F 处．若AE=5，BF=3，则CD的长是（）A． 7 B．8 C．9 D．107．如图，等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD，则下列结论：①AD=BC；②BD、AC互相平分；③四边形ACED是菱形．其中正确的个数是（）A . 0 B． 1 C．2 D．38.如图，矩形ABCD中，E为CD的中点，连接AE并延长交BC的延长线于点F，连接BD．DF，则图中全等的直角三角形共有（）A．3对B．4对C．5对D．6对9.如图在矩形ABCD中，若AC=2AB，则∠AOB的大小是（）A. 30°B. 45°C. 60°D.90°10.如图，在四边形ABCD中，E是BC边的中点，连结DE并延长，交AB的延长线于F点，AB=BF．添加一个条件，使四边形ABCD是平行四边形．你认为下面四个条件中可选择的是（）A．AD=BC B．CD=BFC．∠A=∠C D．∠F=∠CDE二、填空题11．ABCD中两邻角∠A：∠B=1：2，则∠C=_______度．12.如图，在ABCD中，AD=8，点E、F分别是BD、CD的中点，则EF= .13．如图所示，正方形ABCD的周长为16cm，顺次连结正方形ABCD各边的中点，得到四边形EFGH，则四边形EFGH的周长等于______cm，四边形EFGH的面积等于______cm2．14．如图所示，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD=120°，AB=2．5，则AC的长为______．三、解答下列各题15．如图，已知D是△ABC的边AB上一点，CE∥AB，DE交AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明．16.已知：如图，在正方形ABCD中，AC，BD交于点O，延长CB到点E，使BE=BC，连结DE交AB于点F，求证：OF=12 BE．17.如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点N，连接BM，DN．（1）求证：四边形BMDN是菱形；（2）若AB=4，AD=8，求MD的长．18.如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．（1）求证：四边形AEBD是矩形；（2）当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．第18 章自测题（四）一、选择题：题号 1 2 3 4 5 6 7 8 9 10 答案 A D C C D C D B C D 二、填空题11．60 12. 4 13．82；8cm214．5三、解答下列各题15．证明：∵CE∥AB，∴∠DAO=∠ECO，∵OA=OC，∴△ADO≌△ECO，∴AD=CE，∴四边形ADCE是平行四边形，∴CD∥AE，CD =AE．16.证明：∵四边形ABCD是正方形，∴BC=AD．又∵BE=BC，∴BE=AD．∵AD∥BE，∴∠E=∠ADF，∠AFD=∠EFB．∴△ADF≌△BEF．∴DF=FE．又∵DO=OB．∴OF为△BDE的中位线．∴OF=12 BE．17.（1）证明：∵四边形ABCD是矩形，∴AD∥BC，∠A=90°，∵MN是BD的中垂线，∴OB=OD，BD⊥MN，=，∴BM=DM，∵OB=OD，∴四边形BMDN是平行四边形，∵MN⊥BD，∴平行四边形BMDN是菱形．（2）解：∵四边形BMDN是菱形，∴MB=MD，设MD长为x，则MB=DM=x，在Rt△AMB中，BM2=AM2+AB2即x2=（8﹣x）2+42，解得：x=5，答：MD长为5．18.（1）证明：∵点O为AB的中点，连接DO并延长到点E，使OE=OD，∴四边形AEBD是平行四边形，∵AB=AC，AD是△ABC的角平分线，∴AD⊥BC，∴∠ADB=90°，∴平行四边形AEBD是矩形；（2）当∠BAC=90°时，理由：∵∠BAC=90°，AB=AC，AD是△ABC的角平分线，∴AD=BD=CD，∵由（1）得四边形AEBD是矩形，∴矩形AEBD是正方形．。

山东省平邑县蒙阳新星学校八年级数学下册第18章《平行四边形》自测题(1).docx

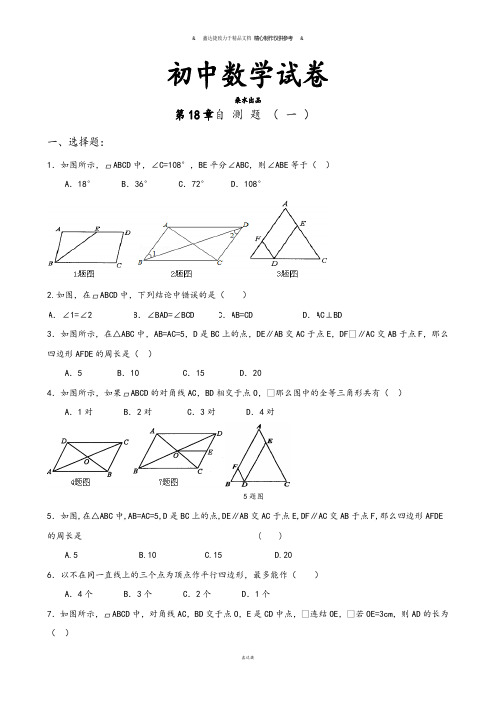
初中数学试卷桑水出品第18章自测题（一）一、选择题：1．如图所示，ABCD中，∠C=108°，BE平分∠ABC，则∠ABE等于（） A．18° B．36° C．72° D．108°2.如图，在ABCD中，下列结论中错误的是（）A．∠1=∠2 B．∠BAD=∠BCD C．A B=CD D．A C⊥BD3．如图所示，在△ABC中，AB=AC=5，D是BC上的点，DE∥AB交AC于点E，DF•∥AC交AB于点F，那么四边形AFDE的周长是（）A．5 B．10 C．15 D．204．如图所示，如果ABCD的对角线AC，BD相交于点O，•那么图中的全等三角形共有（）A．1对 B．2对 C．3对 D．4对5题图5．如图,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE 的周长是 ( )A.5B.10C.15D.206．以不在同一直线上的三个点为顶点作平行四边形，最多能作（）A．4个 B．3个 C．2个 D．1个7．如图所示，ABCD中，对角线AC，BD交于点O，E是CD中点，•连结OE，•若OE=3cm，则AD的长为（）A ．3cmB ．6cmC ．9cmD ．12cm8．在△ABC 中，D ，E ，F 分别是AB ，BC ，AC 的中点，若△ABC 的周长为20cm ，则△DEF•的周长为（）A ．5cmB ．10cmC ．12cmD ．15cm二．填空题：9.平行四边形的周长为24cm,相邻两边长的比为3:1,则其较短的边长为 cm.10．如图所示，ABCD 的对角线AC 和BD 交于点O ，若AC=6，BD=10，AB=•4，•则△AOB 的周长等于______．11．如图中，已知AD ∥BC ，要使四边形ABCD 为平行四边形，需要添加的条件是______．（只要填一个你认为正确的条件即可）12．如图所示，E ，F 是ABCD 对角线BD 上的两点，•请你添加一个适当的条件：_______，使四边形AECF 是平行四边形．13．如图所示，EF 过ABCD 的对角线的交点O 交AD 于E ，交BC 于F ，若AB=4，•BC=5，OE=1.5，则四边形EFCD 的周长为______．14．如图所示，EF 是△ABC 的中位线，BD 平分∠ABC 交EF 于D ，若DE=2，•则EB=_______．15.如图， ABCD 中，E 是BA 延长线上一点，AB ＝AE ，连结CE 交AD 于点F ，若CF 平分∠BCD ，AB ＝3，则BC 的长为．16.如图，D ，E ，F 分别为△ABC 三边的中点，△ABC 的周长是18cm ，则△DEF 的周长是__________．三、解答题17.如图，四边形ABCD 中，AD ∥BC,AE ⊥AD 交BD 于点E ，CF ⊥BC 交BD 于点F ，且AE=CF.求证：四边形ABCD 是平行四边形．18．如图，在ABCD 中，AE ⊥BC 于E ，在AD 边上取一点G ，使GD=AB ，过点G 作GF ⊥CD 于点F ，求证：AE=GF ．19．如图，ABCD 的对角线相交于点O ，EF 过点O 分别与AD ，BC 相┌┙EF C A交于点E，F．（1）求证：△AOE≌△COF；（2）若AB=4，BC=7，OE=3，试求四边形EFCD的周长．20．如图，ABCD中，点E是AD的中点，BE的延长线与CD的延长线交于点F．（1）求证：△ABE≌△DFE；（2）试连结BD，AF，判断四边形ABDF的形状，并证明你的结论．第18章自测题（一）一、选择题：二．填空题：9．6cm 10．12． 11．AB ∥CD 或AD=BC(答案不唯一)12．BE=DF （答案不唯一）． 13．12． 14．2. 15．6．16．9cm 三、解答题17.证明：∵AE ⊥AD ，CF ⊥BC ，∴∠EAD=∠FCB=90°，∵AD ∥BC ，∴∠ADE=∠CBF ，在Rt △AED 和Rt △CFB 中， ∵90ADE CBFEAD FCB AE CF∠=∠⎧⎪∠=∠=⎨⎪=⎩∴Rt △AED ≌Rt △CFB （AAS ），∴AD=BC ，∵AD ∥BC ，∴四边形ABCD 是平行四边形．18．证明：在 ABCD 中，∠B=∠D ，GD=AB ，AE ⊥BC ，GF ⊥CD ，∴△ABE ≌△GDF ．∴AE=GF ．19．（1）证明：∵AD ∥BC ，∴∠EAO=∠FCO ．又∵∠AOE=∠COF ，OA=OC ，在△AOE 和△COF 中，EAO FCOOA OC AOE COF∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AOE ≌△COF ．（2）∵△AOE ≌△COF∴AE=FC ，OF=OE又∵在ABCD 中，BC=AD CD=AB∴FC+DE=AE+ED=AD=BC=7∴S 四边形EFCD=EF+FC+CD+ED=6+7+4=1720．（1）证明：∵四边形ABCD 是平行四边形，∴AB∥CF．∴∠1=∠2，∠3=∠4∵E是AD的中点，∴AE=DE．∴△ABE≌△DFE．（2）解：四边形ABDF是平行四边形．∵△ABE≌△DFE，∴AB=DF又∵AB∥DF∴四边形ABDF是平行四边形．。

人教版数学八年级下册第十八章《平行四边形》测试题(含答案)

第十八章《平行四边形》测试题一、单选题（每小题只有一个正确答案）1．在下列给出的条件中，能判定四边形ABCD 为平行四边形的是（）A ．AB ＝BC ，CD ＝DAB ．AB //CD ，AD ＝BC C ．AB //CD ，∠A ＝∠C D ．∠A ＝∠B ，∠C ＝∠D2．在平行四边形ABCD 中，∠A ∶∠B ∶∠C ∶∠D 的值可以是( )A ．4∶3∶3∶4B ．7∶5∶5∶7C ．4∶3∶2∶1D ．7∶5∶7∶53．如图，▱ABCD 的周长为36，对角线AC 、BD 相交于点O ，点E 是CD 的中点，BD=12，则△DOE 的周长为（）A ．15B ．18C ．21D ．244．如图所示，在四边形ABCD 中，AD//BC ，要使四边形ABCD 成为平行四边形还需要条件（）A ．AB DC = B ．D B ∠=∠ C ．AB AD = D ．12∠=∠5．如图，在ABC ∆中，,D E 分别是,AB BC 的中点，点F 在DE 延长线上，添加一个条件使四边形ADFC 为平行四边形，则这个条件是（）A ．B F ∠=∠ B ．B BCF ∠=∠C ．AC CF =D ．AD CF =6．如下图，在t R ABC ∆中，90BAC ∠=．，D E 、分别是AB BC 、的中点，F 在CA 延长线上, ∠FDA=∠B，AC=6，AB=8，则四边形AEDF 的周长为（）A ．14B ．15C ．16D ．187．正方形有而矩形不一定有的性质是（）A ．四个角都是直角B ．对角线相等C ．对角线互相平分D ．对角线互相垂直8．如图，在矩形ABCD 中，对角线AC ，BD 交于点O ，已知∠AOD=120°，AC=16，则图中长度为8的线段有（）A ．2条B ．4条C ．5条D ．6条9．如图，菱形ABCD 的对角线AC BD ，相交于点O ，DH AB ⊥于点H ，连接OH ，若AH DH =，则DHO ∠的度数是( )A ．25°B ．22.5°C ．30°D ．15°10．如图，四边形ABCD 是菱形，8AC =，6DB =，DH AB ⊥于点H ．则DH =（）A ．6B ．245C ．485D ．511．如图，在周长为12的菱形ABCD 中，AE =1，AF =2，若P 为对角线BD 上一动点，则EP +FP 的最小值为（）A．1 B．2 C．3 D．412．如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（）A．（2，10）B．（﹣2，0）C．（2，10）或（﹣2，0）D．（10，2）或（﹣2，0）二、填空题13．如图，四边形ABCD的对角线相交于点O，AO=CO，请添加一个条件_________（只添一个即可），使四边形ABCD是平行四边形．于O，14．如图，平行四边形ABCD的周长为20cm，AC与BD交于点O，EO BDEO交AD于点E，则ABE△的周长为__________cm．15．如图，在平行四边形ABCD中，AE⊥BC于E，AC＝AD，∠CAE＝56°，则∠D＝_____．16．如图，剪两张对边平行的纸条，随意交叉叠放在一起，重合部分构成了一个四边形ABCD ，当线段AD ＝5时，线段BC 的长为_____．17．如图，在正方形ABCD 中，点E 在对角线AC 上，EF ⊥AB 于点F ，EG ⊥BC 于点G ，连接DE ，若AB ＝10，AE ＝，则ED 的长度为__．三、解答题18．如图，平行四边形ABCD ，E 、F 两点在对角线BD 上，且BE=DF ，连接AE ，EC ，CF ，FA ．求证：四边形AECF 是平行四边形．19．过正方形ABCD 的顶点D 作DE ∥AC ，交BC 的延长线于点E ．（1）判断四边形ACED 的形状，并说明理由；（2）若CE =4，求AC 的长．20．如图，△ABC 中，AB=AC ，AD 是△ABC 的角平分线，点O 为AB 的中点，连接DO 并延长到点E ，使OE=OD ，连接AE ，BE ，（1）求证：四边形AEBD是矩形；（2）当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．21．如图，在▱ABCD中，点O是对角线AC、BD的交点，点E是边CD的中点，点F在BC的延长线上，且CF＝12BC，求证：四边形OCFE是平行四边形．22．如图，在□ABCD中，点E、F分别在边CB、AD的延长线上，且BE＝DF，EF分别与AB、CD交于点G、H，求证：AG＝CH.23．如图，已知点E、F分别在▱ABCD的边AB、CD上，且AE=CF．求证：DE=BF．24．如图，矩形ABCD的对角线AC、BD交于点O，且DE∥AC，CE∥BD．(1)求证：四边形OCED是菱形；(2)若∠BAC=30°，AC=4，求菱形OCED的面积．参考答案1．C 2．D 3．A 4．B 5．B 6．C 7．D 8．D 9．B 10．B 11．C 12．C 13．BO=DO． 14．10 15．73° 16．5 1718．解：连接AC交BD于点O，∵四边形ABCD为平行四边形，∴OA=OC，OB=OD．∵BE=DF，∴OE=OF．∴四边形AECF为平行四边形．19．解：（1）四边形ACED是平行四边形，理由是：在正方形ABCD中，AD//BC，即AD//CE．又∵DE//AC，∴四边形ACED是平行四边形．（2）∵四边形ACED是平行四边形，∴AD=CE=4．在正方形ABCD中，∠ABC=90°，AB=BC=AD=4．在Rt△ABC中，AC=20．解：（1）证明：∵点O为AB的中点，连接DO并延长到点E，使OE=OD，∴四边形AEBD是平行四边形．∵AB=AC，AD是△ABC的角平分线，∴AD⊥BC．∴∠ADB=90°．∴平行四边形AEBD是矩形．（2）当∠BAC=90°时，矩形AEBD是正方形．理由如下：∵∠BAC=90°，AB=AC，AD是△ABC的角平分线，∴AD=BD=CD．∵由（1）得四边形AEBD是矩形，∴矩形AEBD是正方形．21．解：∵四边形ABCD是平行四边形，∴点O是BD的中点．又∵点E 是边CD 的中点，∴OE 是△BCD 的中位线，∴OE∥BC，且OE=12BC ．又∵CF=12BC ，∴OE=CF．又∵点F 在BC 的延长线上，∴OE∥CF，∴四边形OCFE 是平行四边形．22．解：∵在四边形ABCD 是平行四边形，∴AD ∥BC ，AD=BC ，∠A=∠C ，∴∠E=∠F ，又∵BE ＝DF ，∴AD+DF=CB+BE ，即AF=CE ，在△CEH 和△AFG 中，E F EC FA C A ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△CEH ≌△AFG ，∴CH=AG.23．证明：∵四边形ABCD 是平行四边形，∴AB=CD，AB∥CD．∵AE=CF．∴BE=FD，BE∥FD，∴四边形EBFD 是平行四边形，∴DE=BF．24．解：()1证明：CE //OD Q ，DE //OC ，∴四边形OCED 是平行四边形，Q 矩形ABCD ，AC BD ∴=，1OC AC 2=，1OD BD 2=， OC OD ∴=，∴四边形OCED 是菱形；()2在矩形ABCD 中，ABC 90o ∠=，BAC 30∠=o ，AC 4=，BC 2∴=，AB DC ∴== 连接OE ，交CD 于点F ，Q 四边形OCED 为菱形， F ∴为CD 中点， O Q 为BD 中点， 1OF BC 12∴==， OE 2OF 2∴==，OCED 11S OE CD 222∴=⨯⨯=⨯⨯=菱形。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平行四边形
一、选择题：
1．如图所示，ABCD中，∠C=108°，BE平分∠ABC，则∠ABE等于（）
A．18°B．36°C．72°D．108°
AC交AB于点F，那么四边形AFDE的周长是（）
A．5 B．10 C．15 D．20
4．如图所示，如果ABCD的对角线AC，BD相交于点O，•那么图中的全等三角形共有（）A．1对B．2对C．3对D．4对
5题图
5．如图,在△ABC中,AB=AC=5,D是BC上的点,D E∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
A.5
B.10
C.15
D.20
6．以不在同一直线上的三个点为顶点作平行四边形，最多能作（）
A．4个B．3个C．2个D．1个
7．如图所示，ABCD中，对角线AC，BD交于点O，E是CD中点，•连结OE，•若OE=3cm，则AD 的长为（）
A．3cm B．6cm C．9cm D．12cm
8．在△ABC中，D，E，F分别是AB，BC，AC的中点，若△ABC的周长为20cm，则△DEF•的周长为（）
A．5cm B．10cm C．12cm D．15cm
二．填空题：
9.平行四边形的周长为24cm,相邻两边长的比为3:1,则其较短的边长为cm.
10．如图所示，ABCD的对角线AC和BD交于点O，若AC=6，BD=10，AB=•4，•则△AOB的周长等于______．
11．如图中，已知AD ∥BC ，要使四边形ABCD 为平行四边形，需要添加的条件是______．（只要填一个你认为正确的条件即可）
12．如图所示，E ，F 是ABCD 对角线BD 上的两点，•请你添加一个适当的条件：_______，使四边形AECF 是平行四边形．
13．如图所示，EF 过ABCD 的对角线的交点O 交AD 于E ，交BC 于F ，若AB=4，•BC=5，OE=1.5，则四边形EFCD 的周长为______．
14．如图所示，EF 是△ABC 的中位线，BD 平分∠ABC 交EF 于D ，若DE=2，•则EB=_______．
15.如图， ABCD 中，E 是BA 延长线上一点，AB ＝AE ，连结CE 交AD 于点F ，若CF 平分∠BCD ，AB ＝3，则BC 的长为．
16.如图，D ，E ，F 分别为△ABC 三边的中点，△ABC 的周长是18cm ，则△DEF 的周长是__________．
三、解答题 17.如图，四边形ABCD 中，AD ∥BC,AE ⊥AD 交BD 于点E ，CF ⊥BC 交BD 于点F ，且AE=CF.求证：四边形ABCD 是平行四边形．
18．如图，在ABCD 中，AE ⊥BC 于E ，在AD 边上取一点G ，使GD=AB ，过点G 作GF ⊥CD 于点F ，求证：AE=GF ．
19．如图，AB CD 的对角线相交于点O ，EF 过点O 分别与AD ，BC 相交于点E ，F ．
（1）求证：△AOE ≌△COF ；
（2）若AB=4，BC=7，OE=3，试求四边形EFCD 的周长．
20．如图，ABCD中，点E是AD的中点，BE的延长线与CD的延长线交于点F．（1）求证：△ABE≌△DFE；
（2）试连结BD，AF，判断四边形ABDF的形状，并证明你的结论．
第18章自测题（一）
二．填空题：
9．6cm 10．12． 11．AB ∥CD 或AD=BC(答案不唯一)
12．BE=DF （答案不唯一）．
13．12． 14．2. 15．6． 16．9cm
三、解答题
17.证明：∵AE ⊥AD ，CF ⊥BC ，
∴∠EAD=∠
FCB=90°，
∵AD ∥BC ，
∴∠ADE=∠CBF ，
在Rt △AED 和Rt △CFB 中，
∵90ADE CBF
EAD FCB AE CF
∠=∠⎧⎪∠=∠=⎨⎪=⎩ ∴Rt △AED ≌Rt △CFB （AAS ），
∴AD=BC ，
∵AD ∥BC ，
∴四边形ABCD 是平行四边形．
18．证明：在 ABCD 中，∠B=∠D ，GD=AB ，AE ⊥BC ，GF ⊥CD ， ∴△ABE ≌△GDF ．
∴AE=GF ．
19．（1）证明：∵AD ∥BC ，
∴∠EAO=∠FCO ．
又∵∠AOE=∠COF ，OA=OC ，
在△AOE 和△COF 中，
EAO FCO
OA OC AOE COF
∠=∠⎧⎪=⎨
⎪∠=∠⎩，
∴△AOE ≌△COF ．
（2）∵△AOE ≌△COF
∴AE=FC ，OF=OE
又∵在ABCD 中，BC=A D CD=AB
∴FC +DE=AE+ED=AD=BC=7
∴S 四边形EFCD=EF+FC+CD+ED
=6+7+4
=17
20．（1）证明：∵四边形ABCD 是平行四边形，
∴AB ∥CF ．
∴∠1=∠2，∠3=∠4
∵E 是AD 的中点，
∴AE=DE ．
∴△ABE ≌△DFE ．
（2）解：四边形ABDF是平行四边形．∵△ABE≌△DFE，
∴AB=DF
又∵AB∥DF
∴四边形ABDF是平行四边形．。