金陵中学2005—2006学年第一学期高一数学月考试卷

高一2005——2006年度第一次月考试题

高一2005～2006年度第二学期月考试题一．选择题：（每小题4分，共40分）1. 已知集合A={第一象限的角}；B={锐角}；C={小于90 的角}则下列四个命题①A=B=C ； ②B A ⊂ ③B C A =⊂ ④ A C ⊂ ⑤ B C A = ；中正确的命题个数是（） A ．0 B. 1 C. 2 D. 以上答案均错误2.一中心角为3π,半径为R 的扇形面积之比为 ( ) A ．231R π B. 261R π C. 2121R π D. R π313. 已知函数()2cos xx f = ,则下列等式成立的是( )A ．()()x f x f =-π2 B. ()()x f x f =+π2 C.()()x f x f -=- D. ()()x f x f =- 4. 已知0cos sin <αα则α在 ( )A ．第三象限或第四象限B ．第二象限或第四象限C ．第二象限或第三象限D ．第一象限或第二象限 5.函数x x y 2cos 2sin 2=是A ．周期为2π的奇函数 B.周期为2π的偶函数 C.周期为4π的奇函数 D. 周期为4π的偶函数6.=-2sin 1 ( )A ．1sin 2 B.1cos 2 C. ()1cos 1sin -± D. 1cos 1sin -7.80cos 60cos 40cos 20cos 的值等于 ( )A ．41 B. 81 C. 161 D. 321 8. 已知⎪⎭⎫⎝⎛∈2,4ππα则αsin ， α，αtan 的大小顺序是 ( ) A ．αsin <α<αtan B. αtan <αsin < αC.αsin <α < αtanD. αsin <α<αtan 9. 在△ABC 中,已知tanA,tanB 是方程0132=--x x 的两个实数根,则 tanC 等于( )A ．21 B. 21- C. -2 D. 以上都不对 10. 已知31tan =α，则ααα2cos cos sin 21+的值是（）A ． 310 B. 38- C.310- D. 38二.填空题 (每小题4分,共16分 )11.=+-15tan 115tan 1______________ 12. 已知角β终边过点( -3 , 4 )求_______2cos _______,sin ==ββ13. _______22sin 23sin 22cos 23cos =-________75tan 75tan 12=-14.若 ()()()x x x f sin 1log sin 1log 2121++-=则________4=⎪⎭⎫⎝⎛πf≠ ≠ ≠高一2005～2006年度第二学期第一次月考数学试卷一．选择题：（每小题4分，共40分）二.填空题 (每小题4分,共16分 )11．_________ 12. ________ _________13. _________ __________ 14. ________________ 三.解答题(５分×２＋６分＋６分＋６分＋８分＋８分＝44分) 15. 化简: ① ()()()()()πααπαπαπαπ----+-sin 3sin cos cos 2sin ② ()10tan 3140cos +16. 已知：71cos =α ,()1411cos -=+βα且⎪⎭⎫ ⎝⎛∈2,0,πβα,求βcos 的值．17. 若A+B=4π,求：()()B A tan 1tan 1++的值.18. 证明：()αββαβαβα222tan tan 1cos sin )sin(sin 2-=-+19. 有一块半径为R 的半圆形材料,问怎样裁能获得一面积最大的矩形,最大面积是多少?20. 求函数x x x x y 22cos 3cos sin 2sin ++=（R x ∈）的单调增区间，周期及最大值。

金陵中学高一分班测试模拟试卷(数学)

金陵中学高一分班测试模拟试卷（数学）一、选择题（共10小题，每小题3分，满分30分）1．已知，ab＞0，化简二次根式a的正确结果是（）A．B． C．﹣D．﹣2．观察下列算式：21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256…，用你发现的规律得出22015的末位数字是（）A．3 B．4 C．6 D．83．把方程=化成整式方程，得（）A．x2+3y2+6x﹣9=0 B．x2+3y2﹣6x﹣9=0C．x2+y2﹣2x﹣3=0 D．x2+y2+2x﹣3=04．若不等式组的解集为空集，则a的取值范围是（）A．a＞3 B．a≥3 C．a＜3 D．a≤35．股票每天的涨跌幅均不超过10%，即当涨了原价的10%后，便不能再涨，叫做涨停；当跌了原价的10%后，便不能再跌，叫做跌停．已知一支股票某天涨停，之后两天时间又跌回原价，若这两天此股票股价的平均下跌的百分率为x，则x满足的方程是（）A．1﹣2x=B．（1﹣x）2=C．1﹣2x=D．（1﹣x）2=6．若实数a≠b，且a，b满足a2﹣8a+5=0，b2﹣8b+5=0，则代数式的值为（）A．﹣20 B．2 C．2或﹣20 D．2或207．如图，AB是⊙O的弦，C是AB的三等分点，连接OC并延长交⊙O于点D．若OC=3，CD=2，则圆心O到弦AB的距离是（）A．6B．9﹣C．D．25﹣38．如图，在平面直角坐标系中，直线y=﹣3x+3与x轴、y轴分别交于A、B两点，以AB为边在第一象限作正方形ABCD，点D在双曲线（k≠0）上．将正方形沿x轴负方向平移a个单位长度后，点C恰好落在该双曲线上，则a的值是（）A．1 B．2 C．3 D．49．如图，分别过点P i（i，0）（i=1、2、…、n）作x轴的垂线，交的图象于点A i，交直线于点B i．则的值为（）A． B．2 C．D．10．如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2），且与x轴交点的横坐标分别为x1、x2，其中﹣2＜x1＜﹣1，0＜x2＜1，下列结论：①4a﹣2b+c＜0；②2a﹣b＜0；③a＜﹣1；④b2+8a＞4ac．其中正确的有（）A．1个 B．2个 C．3个 D．4个二、填空题（共5小题，每小题4分，满分20分）11．某小区20户家庭的日用电量（单位：千瓦时）统计如下：这20户家庭日用电量的众数、中位数分别是．12．已知实数a、b、c满足a+b=ab=c，有下列结论：①若c≠0，则+=1；②若a=3，则b+c=9；③若a=b=c，则abc=0；④若a、b、c中只有两个数相等，则a+b+c=8．其中正确的是（把所有正确结论的序号都选上）．13．如图，在⊙O的内接五边形ABCDE中，∠CAD=40°，则∠B+∠E=°．14．如图，在平面直角坐标系中，四边形OABC是边长为4的正方形，M（4，m）、N（n，4）分别是AB、BC上的两个动点，且ON⊥MN，当OM最小时，m+n=．15．若关于x的方程（x﹣2）（x2﹣4x+m）=0有三个根，且这三个根恰好可以作为一个三角形的三条边的长，则m的取值范围是．三、解答题（共5小题，满分50分）16．解方程：x2﹣2|x﹣1|﹣2=0．17．已知在Rt△ABC中，∠C=90°，AD是∠BAC的角平分线，以AB上一点O为圆心，AD为弦作⊙O．（1）在图中作出⊙O；（不写作法，保留作图痕迹）（2）求证：BC为⊙O的切线；（3）若AC=3，tanB=，求⊙O的半径．18．如图1，某超市从底楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN 上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，求二楼的层高BC（精确到0.1米）．（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）19．设p，q都是实数，且p＜q．我们规定：满足不等式p≤x≤q的实数x的所有取值的全体叫做闭区间，表示为[p，q]．对于一个函数，如果它的自变量x与函数值y满足：当p≤x≤q时，有p≤y≤q，我们就称此函数是闭区间[p，q]上的“闭函数”．（1）反比例函数y=是闭区间[1，2016]上的“闭函数”吗？请判断并说明理由；（2）若一次函数y=kx+b（k≠0）是闭区间[m，n]上的“闭函数”，求此一次函数的解析式．20．已知二次函数f（x）=ax2+bx+c，其中a＞0．（1）若方程f（x）+2x=0有两个实根x1=1，x2=3，且方程f（x）+6a=0有两个相等的根，f（x）解析式；（2）若f（x）得图象与x轴交于A（﹣3，0），B（m，0）两点，且当﹣1≤x≤0时，f（x）≤0恒成立，求实数m的取值范围．注：f（x）是一个函数的记号，相当于函数y．金陵中学高一分班测试模拟试卷（数学）参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．已知，ab＞0，化简二次根式a的正确结果是（）A．B．C．﹣D．﹣【考点】二次根式的性质与化简．【分析】直接利用二次根式的性质进而化简得出答案．【解答】解：∵ab＞0，∴a=a×=﹣．故选：D．2．观察下列算式：21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256…，用你发现的规律得出22015的末位数字是（）A．3B．4C．6D．8【考点】尾数特征．【分析】因为21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，观察发现：2n的个位数字是2，4，8，6四个一循环，所以根据2015÷4=503…3，得出22015的个位数字与23的个位数字相同，是8．【解答】解：∵21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，…．2015÷4=503…3，∴22015的末位数字和23的末位数字相同，是8．故选：D．3．把方程=化成整式方程，得（）A．x2+3y2+6x﹣9=0B．x2+3y2﹣6x﹣9=0C．x2+y2﹣2x﹣3=0D．x2+y2+2x﹣3=0【考点】无理方程．【分析】先将方程两边都平方即可去掉根号，再根据去分母化为整式方程，最后整理整式方程即可得．【解答】解：方程两边平方，得：，∴4（x2+y2）=（x+3）2+y2，去括号，得：4x2+4y2=x2+6x+9+y2，移项、合并，得：3x2+3y2﹣6x﹣9=0，两边都除以3，得：x2+y2﹣2x﹣3=0，故选：C．4．若不等式组的解集为空集，则a的取值范围是（）A．a＞3B．a≥3C．a＜3D．a≤3【考点】解一元一次不等式组．【分析】根据不等式组的解集为空集时的条件列出不等式，即可求出a的取值范围．【解答】解：，由①得：x＜3，∵不等式组的解集为空集，∴a的取值范围是：a≥3；故选B．5．股票每天的涨跌幅均不超过10%，即当涨了原价的10%后，便不能再涨，叫做涨停；当跌了原价的10%后，便不能再跌，叫做跌停．已知一支股票某天涨停，之后两天时间又跌回原价，若这两天此股票股价的平均下跌的百分率为x，则x满足的方程是（）A．1﹣2x=B．（1﹣x）2=C．1﹣2x=D．（1﹣x）2=【考点】由实际问题抽象出一元二次方程．【分析】设这两天此股票股价的平均下跌的百分率为x，根据“涨停后的价格为（1+10%），两天时间又跌回原价”，即可列出关于x的一元二次方程，整理后即可得出结论．【解答】解：设这两天此股票股价的平均下跌的百分率为x，涨停后的价格为（1+10%），根据题意得：（1+10%）×（1﹣x）2=1，整理得：（1﹣x）2=．故选B．6．若实数a≠b，且a，b满足a2﹣8a+5=0，b2﹣8b+5=0，则代数式的值为（）A．﹣20B．2C．2或﹣20D．2或20【考点】根与系数的关系；分式的化简求值．【分析】由于实数a≠b，且a，b满足a2﹣8a+5=0，b2﹣8b+5=0，则a，b可看着方程x2﹣8x+5=0的两根，根据根与系数的关系得a+b=8，ab=5，然后把通分后变形得到，再利用整体代入的方法计算．【解答】解：∵a，b满足a2﹣8a+5=0，b2﹣8b+5=0，∴a，b可看着方程x2﹣8x+5=0的两根，∴a+b=8，ab=5，====﹣20．故选A．7．如图，AB是⊙O的弦，C是AB的三等分点，连接OC并延长交⊙O于点D．若OC=3，CD=2，则圆心O到弦AB的距离是（）A．6B．9﹣C．D．25﹣3【考点】垂径定理；勾股定理．【分析】过圆心O作弦的垂线，垂足为G，得到Rt△OBG和Rt△OCG，在这两个三角形中用勾股定理计算可以求出OG的值，也就是圆心到弦的距离．【解答】解：如图：过O作OG⊥AB于G，根据垂径定理有：AG=BG，设AC=2a，则CB=4a，CG=a，GB=3a，在Rt△OCG中，OC2=OG2+CG2=OG2+a2①在Rt△OBG中，OB2=OG2+GB2=OG2+9a2②又OC=3，OB=5，代入①②中，解方程得：a2=2，OG2=7．所以圆心到弦的距离是．故选C．8．如图，在平面直角坐标系中，直线y=﹣3x+3与x轴、y轴分别交于A、B两点，以AB为边在第一象限作正方形ABCD，点D在双曲线（k≠0）上．将正方形沿x轴负方向平移a个单位长度后，点C恰好落在该双曲线上，则a的值是（）A．1B．2C．3D．4【考点】反比例函数综合题．【分析】作CE⊥y轴于点E，交双曲线于点G．作DF⊥x轴于点F，易证△OAB≌△FDA≌△BEC，求得A、B的坐标，根据全等三角形的性质可以求得C、D的坐标，从而利用待定系数法求得反比例函数的解析式，进而求得G的坐标，则a的值即可求解．【解答】解：作CE⊥y轴于点E，交双曲线于点G．作DF⊥x轴于点F．在y=﹣3x+3中，令x=0，解得：y=3，即B的坐标是（0，3）．令y=0，解得：x=1，即A的坐标是（1，0）．则OB=3，OA=1．∵∠BAD=90°，∴∠BAO+∠DAF=90°，又∵直角△ABO中，∠BAO+∠OBA=90°，∴∠DAF=∠OBA，∵在△OAB和△FDA中，，∴△OAB≌△FDA（AAS），同理，△OAB≌△FDA≌△BEC，∴AF=OB=EC=3，DF=OA=BE=1，故D的坐标是（4，1），C的坐标是（3，4）．代入y=得：k=4，则函数的解析式是：y=．∴OE=4，则C的纵坐标是4，把y=4代入y=得：x=1．即G的坐标是（1，4），∴CG=2．故选：B．9．如图，分别过点P i（i，0）（i=1、2、…、n）作x轴的垂线，交的图象于点A i，交直线于点B i．则的值为（）A．B．2C．D．【考点】二次函数综合题．【分析】根据A i的纵坐标与B i纵坐标的绝对值之和为A i B i的长，分别表示出所求式子的各项，拆项后抵消即可得到结果．【解答】解：根据题意得：A i B i=x2﹣（﹣x）=x（x+1），∴==2（﹣），∴++…+=2（1﹣+﹣+…+﹣）=．故选A10．如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2），且与x轴交点的横坐标分别为x1、x2，其中﹣2＜x1＜﹣1，0＜x2＜1，下列结论：①4a﹣2b+c＜0；②2a﹣b＜0；③a＜﹣1；④b2+8a＞4ac．其中正确的有（）A．1个B．2个C．3个D．4个【考点】二次函数图象与系数的关系．【分析】首先根据抛物线的开口方向得到a＜0，抛物线交y轴于正半轴，则c＞0，而抛物线与x轴的交点中，﹣2＜x1＜﹣1，0＜x2＜1，说明抛物线的对称轴在﹣1～0之间，即x=﹣＞﹣1，根据这些条件以及函数图象上一些特殊点的坐标来进行判断．【解答】解：由图知：抛物线的开口向下，则a＜0；抛物线的对称轴x=﹣＞﹣1，且c＞0．①由图可得：当x=﹣2时，y＜0，即4a﹣2b+c＜0，故①正确；②已知x=﹣＞﹣1，且a＜0，所以2a﹣b＜0，故②正确；③已知抛物线经过（﹣1，2），即a﹣b+c=2（1），由图知：当x=1时，y＜0，即a+b+c ＜0（2），由①知：4a﹣2b+c＜0（3）；联立（1）（2），得：a+c＜1；联立（1）（3）得：2a﹣c＜﹣4；故3a＜﹣3，即a＜﹣1；所以③正确；④由于抛物线的对称轴大于﹣1，所以抛物线的顶点纵坐标应该大于2，即：＞2，由于a＜0，所以4ac﹣b2＜8a，即b2+8a＞4ac，故④正确；因此正确的结论是①②③④．故选D．二、填空题（共5小题，每小题4分，满分20分）11．某小区20户家庭的日用电量（单位：千瓦时）统计如下：4567810日用电量（单位：千瓦时）户数136541这20户家庭日用电量的众数、中位数分别是6，6.5．【考点】众数；中位数．【分析】根据众数和中位数的定义求解即可，众数是一组数据中出现次数最多的数；中位数是将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．【解答】解：这20户家庭日用电量的众数是6，中位数是（6+7）÷2=6.5，故答案为：6，6.5．12．已知实数a、b、c满足a+b=ab=c，有下列结论：①若c≠0，则+=1；②若a=3，则b+c=9；③若a=b=c，则abc=0；④若a、b、c中只有两个数相等，则a+b+c=8．其中正确的是①③④（把所有正确结论的序号都选上）．【考点】分式的混合运算；解一元一次方程．【分析】按照字母满足的条件，逐一分析计算得出答案，进一步比较得出结论即可．【解答】解：①∵a+b=ab≠0，∴+=1，此选项正确；②∵a=3，则3+b=3b，b=，c=，∴b+c=+=6，此选项错误；③∵a=b=c，则2a=a2=a，∴a=0，abc=0，此选项正确；④∵a、b、c中只有两个数相等，不妨a=b，则2a=a2，a=0，或a=2，a=0不合题意，a=2，则b=2，c=4，∴a+b+c=8．当a=c时，则b=0，不符合题意，b=c时，a=0，也不符合题意；故只能是a=b=2，c=4；此选项正确其中正确的是①③④．故答案为：①③④．13．如图，在⊙O的内接五边形ABCDE中，∠CAD=40°，则∠B+∠E=220°．【考点】圆周角定理．【分析】连接CE，根据圆内接四边形对角互补可得∠B+∠AEC=180°，再根据同弧所对的圆周角相等可得∠CED=∠CAD，然后求解即可．【解答】解：如图，连接CE，∵五边形ABCDE是圆内接五边形，∴四边形ABCE是圆内接四边形，∴∠B+∠AEC=180°，∵∠CED=∠CAD=40°，∴∠B+∠E=180°+40°=220°．故答案为：220．14．如图，在平面直角坐标系中，四边形OABC是边长为4的正方形，M（4，m）、N（n，4）分别是AB、BC上的两个动点，且ON⊥MN，当OM最小时，m+n= 5．【考点】正方形的性质；坐标与图形性质；全等三角形的判定与性质；勾股定理．【分析】证明△OCN∽△NBM，列比例式得：m==（n﹣2）2+3，即当n=2时，m有最小值为3，在Rt△OAM中，因为OA是定值，AM的大小决定OM 的大小，由m的最小值计算OM的最小值．【解答】解：由题意得：OA=4，AM=m，OC=4，CN=n，BN=4﹣n，BM=4﹣m，∵四边形OABC是矩形，∴∠OCB=∠ABC=90°，∴∠CNO+∠CON=90°，∵ON⊥MN，∴∠ONM=90°，∴∠CNO+∠MNB=90°，∴∠CON=∠MNB，∴△OCN∽△NBM，∴，∴=，m==（n﹣2）2+3，即当n=2时，m有最小值为3，在Rt△OAM中，OA是定值，AM的大小决定OM的大小，当AM为最小时，OM为最小，∴当AM=m=3时，OM最小，此时m+n=3+2=5，故答案为：5．15．若关于x的方程（x﹣2）（x2﹣4x+m）=0有三个根，且这三个根恰好可以作为一个三角形的三条边的长，则m的取值范围是3＜m≤4．【考点】根与系数的关系；三角形三边关系．【分析】根据原方程可知x﹣2=0，和x2﹣4x+m=0，因为关于x的方程（x﹣2）（x2﹣4x+m）=0有三个根，所以x2﹣4x+m=0的根的判别式△＞0，然后再由三角形的三边关系来确定m的取值范围．【解答】解：∵关于x的方程（x﹣2）（x2﹣4x+m）=0有三个根，∴①x﹣2=0，解得x1=2；②x2﹣4x+m=0，∴△=16﹣4m≥0，即m≤4，∴x2=2+，x 3=2﹣，又∵这三个根恰好可以作为一个三角形的三条边的长，且最长边为x2，∴x1+x3＞x2；解得3＜m≤4，∴m的取值范围是3＜m≤4．故答案为：3＜m≤4．三、解答题（共5小题，满分50分）16．解方程：x2﹣2|x﹣1|﹣2=0．【考点】解一元二次方程﹣因式分解法；解一元二次方程﹣配方法．【分析】当x≥1时，方程为x2﹣2x=0，因式分解法求解得出x的值；当x＜1时，方程为x2+2x﹣4=0，公式法求解可得x的值．【解答】解：当x≥1时，方程为x2﹣2x=0，即x（x﹣2）=0，解得x=0（舍）或x=2；当x＜1时，方程为x2+2x﹣4=0，解得：x==﹣1±，即x=﹣1﹣，综上x=2或x=﹣1﹣．17．已知在Rt△ABC中，∠C=90°，AD是∠BAC的角平分线，以AB上一点O为圆心，AD为弦作⊙O．（1）在图中作出⊙O；（不写作法，保留作图痕迹）（2）求证：BC为⊙O的切线；（3）若AC=3，tanB=，求⊙O的半径．【考点】切线的判定；作图—复杂作图．【分析】（1）作图思路：可做AD的垂直平分线，这条垂直平分线与AB的交点就是所求圆的圆心，这个圆心和A点或D点的距离就是圆的半径．（2）要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．本题中可先连接OD再证明OD⊥BC即可．（3）在Rt△ABC中，由“tanB=，AC=3”求得BC=4，AB=5；然后在Rt△ODB中，利用∠B的正切值求得=；设一份为x，则OD=OA=3x，则BD=4x，OB=5x．列出关于x的方程，解方程即可．【解答】解：（1）如图；（2）连接OD；∵AD平分∠BAC，∴∠BAD=∠DAC；又∵OD=OA，∴∠ODA=∠OAD，∴∠ODA=∠DAC，∴OD∥AC，∴∠ODC=∠C=90°，∴BC为⊙O的切线．（3）在Rt△ABC中，∠C=90°，tanB=，AC=3，∴BC=4，AB=5，在Rt△ODB中，tanB==，设OD=OA=3x，则BD=4x，OB=5x，∴AB=8x，∴8x=5，解得x=，∴半径OA=．18．如图1，某超市从底楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN 上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，求二楼的层高BC（精确到0.1米）．（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）【考点】解直角三角形的应用﹣仰角俯角问题；解直角三角形的应用﹣坡度坡角问题．【分析】延长CB交PQ于点D，根据坡度的定义即可求得BD的长，然后在直角△CDA中利用三角函数即可求得CD的长，则BC即可得到．【解答】解：延长CB交PQ于点D．∵MN∥PQ，BC⊥MN，∴BC⊥PQ．∵自动扶梯AB的坡度为1：2.4，∴．设BD=5k米，AD=12k米，则AB=13k米．∵AB=13米，∴k=1，∴BD=5米，AD=12米．在Rt△CDA中，∠CDA=90゜，∠CAD=42°，∴CD=AD•tan∠CAD≈12×0.90≈10.8米，∴BC≈5.8米．答：二楼的层高BC约为5.8米．19．设p，q都是实数，且p＜q．我们规定：满足不等式p≤x≤q的实数x的所有取值的全体叫做闭区间，表示为[p，q]．对于一个函数，如果它的自变量x与函数值y满足：当p≤x≤q时，有p≤y≤q，我们就称此函数是闭区间[p，q]上的“闭函数”．（1）反比例函数y=是闭区间[1，2016]上的“闭函数”吗？请判断并说明理由；（2）若一次函数y=kx+b（k≠0）是闭区间[m，n]上的“闭函数”，求此一次函数的解析式．【考点】反比例函数的性质；一次函数的性质．【分析】（1）根据反比例函数y=的单调区间进行判断；（2）根据新定义运算法则列出关于系数k、b的方程组或，通过解该方程组即可求得系数k、b的值．【解答】解：（1）是；由函数的图象可知，当1≤x≤2014时，函数值y随着自变量x的增大而减少，而当x=1时，y=2014；x=2014时，y=1，故也有1≤y≤2014，所以，函数是闭区间[1，2014]上的“闭函数”．（2）因为一次函数y=kx+b（k≠0）是闭区间[m，n]上的“闭函数”，所以根据一次函数的图象与性质，必有：①当k＞0时，，解之得k=1，b=0．∴一次函数的解析式为y=x．②当k＜0时，，解之得k=﹣1，b=m+n．∴一次函数的解析式为y=﹣x+m+n．故一次函数的解析式为y=x或y=﹣x+m+n．20．已知二次函数f（x）=ax2+bx+c，其中a＞0．（1）若方程f（x）+2x=0有两个实根x1=1，x2=3，且方程f（x）+6a=0有两个相等的根，f（x）解析式；（2）若f（x）得图象与x轴交于A（﹣3，0），B（m，0）两点，且当﹣1≤x≤0时，f（x）≤0恒成立，求实数m的取值范围．注：f（x）是一个函数的记号，相当于函数y．【考点】抛物线与x轴的交点；一元二次方程的解．【分析】（1）由题意可知：把x1=1和x2=3代入ax2+bx+c+2x=0，再利用方程f（x）+6a=0的△=0，求出a、b、c的值即可，注意a＞0的条件；（2）由题意可知：对称轴为x=，根据对称轴的位置分三种情况进行讨论．【解答】解：（1）由题意可知：f（x）+2x=0，即：ax2+bx+c+2x=0，∴把x1=1和x2=3代入ax2+bx+c+2x=0，可得：a+b+c+2=0，9a+3b+c+6=0，解得：a=c，b=﹣2﹣c，∵f（x）+6a=0有两个相等的根，∴ax2+bx+c+6a=0有两个相等的根，∴△=b2﹣4a（c+6a）=0，∴（﹣2﹣c）2﹣4×c（c+2c）=0，∴解得：c=﹣或c=3，∵a＞0，∴c＞0，∴c＞0，∴c=3，∴a=1，b=﹣6，∴f（x）=x2﹣6x+3，（2）由题意可知：对称轴为x=，由根与系数的关系可知：﹣3m=，﹣3+m=﹣∴c=﹣3ma，b=（3﹣m）a，∵a＞0，∴抛物线开口向上，当≤﹣1时，即m≤1，f（x）在﹣1＜x＜0上，y随x的增大而减小，∴﹣1≤x≤0时，f（x）≤0恒成立，只需要f（0）≤0即可，∴c≤0即可，∴﹣3ma≤0，∴m≥0，∴0≤m≤1，当﹣1＜＜0时，即：1＜m＜3，f（x）在﹣1＜x＜上，y随x的增大而减小，在＜x＜0上，y随x的增大而增大，∴﹣1≤x≤0时，f（x）≤0恒成立，∴即f（﹣1）≤0且f（0）≤0，∴a﹣b+c≤0，且c≤0，∴a﹣（3﹣m）a﹣3ma≤0，且﹣3ma≤0，解得：m≥﹣1且m≥0，∴1＜m＜3，当≥0时，即m≥3，f（x）在﹣1＜x＜0上，y随x的增大而减小，∴﹣1≤x≤0时，f（x）≤0恒成立，只需f（﹣1）≤0即可，∴a﹣b+c≤0，∴a﹣（3﹣m）a﹣3ma≤0，解得：m≥﹣1，∴m≥3，综上所述，m≥0时，当﹣1≤x≤0时，f（x）≤0恒成立．。

金陵中学下册高一数学期中试卷-精校

金陵中学2005－2006学年度第二学期高一数学期中试卷一、选择题（每小题3分，共36分）1．若x 是第四象限的角，且cos x ＝45，则tan x 的值是( )． (A)35 (B)－35(C) －43 (D)－342．函数y ＝2sin(x ＋π4)的图象的一个对称中心的坐标是( )． (A)（π4，2） (B)（3π4，0） (C)（ 5π4，－2） (D) （π4，0） 3．已知sin α2＝13，α∈(0，π)，则sin α的值为( )． (A)229 (B)－ 229 (C) 429 (D) － 4294．已知向量a ＝（2，1），b ＝（1，m )．若a ∥b ，则实数m 的值是( )．(A)12 (B)－2 (C)2 (D)－125．设０＜α＜π2＜β＜π，且sin α＝35，cos β＝－1213，则cos(α－β)的值是( )． (A)1665 (B) 3365 (C)－ 1665 (D)－ 33656．已知A （1，－1），B （3，1），C （－2，4），则与→AC －→BC 方向相同的单位向量的坐标是( )．(A)（1，1） (B)（－1，－1） (C)（－22 ，－22 ） (D)（22 ，22） 7．在△ABC 中，若(1＋tan A )(1＋tan B )＝2，则A ＋B 等于( )．(A)π4 (B) 3π4 (C) 5π4 (D) 7π48．在边长为1的正△ABC 中，记→AB ＝c ，→BC ＝a ，→AC ＝b ，则a ·b ＋c ·b ＋c ·a 的值等于( )．(A)32 (B)－32 (C)12 (D)－129．将函数y ＝f (x )的图象沿x 轴向左平移π6个单位后，再将图象上每一个点的横坐标变为原来的2倍（纵坐标不变），得到函数y ＝cos x 的图象，则函数f (x )的解析式是( )．(A)f (x )＝cos(2x ＋π6) (B)f (x )＝cos(2x －π6) (C)f (x )＝cos(2x ＋π3) (D)f (x )＝cos(2x －π3) 10．若cos(π4－x )＝－35，x ∈(3π4，π)，则1－tan x 1＋tan x的值是( )． (A)34 (B)－34 (C) 43 (D) －4311．若点O 是△ABC 所在平面内的一点，且→OA ·→OB ＝→OC ·→OB ＝→OC ·→OA ，则点O 是△ABC的( )．(A)三个内角角平分线的交点 (B)三条边垂直平分线的交点(C)三条中线的交点 (D)三条高的交点12．设f (x )是定义在区间(－∞，＋∞)上的奇函数，在区间(0，＋∞)内单调递增，且f (12)＝0．若△ABC 的内角A 满足f (cos A )＜0，则角A 的取值范围是( )．(A)(π3，π) (B)(π3，π2) (C)(π3，π2)∪(2π3，π) (D)(0，π3)∪(2π3，π) 二、填空题（每小题4分，共16分）13．计算：2tan15°1－tan 215°＝． 14．若向量a ＝(cos x ，sin x )，b ＝(12，－32)，则| a －b |的最大值是． 15．函数y ＝cos(12x －π4)的最小正周期是． 16．给出如下四个命题：①若a ，b 为两个不共线向量，且| a |＝| b |，则( a －b )⊥( a ＋b )；②在四边形ABCD 中，必有→AB ＋→BC ＋→CD ＋→AD ＝0；③若x a ＝x b ，x ∈R ，则a ＝b ；④若a ，b 为两个不共线向量，且x a ＋y b ＝0，则x ＝y ＝0．其中真命题的序号是．三、解答题（本大题共48分）17．(1)已知sin(π＋α)＝513，求cos(3π2－α)的值； (2)已知sin α＝23，cos(α＋β)＝－35，且α∈(π2，π)，β∈(π2，π)，求sin β的值． 18．设e 1，e 2是两个不共线的向量，设→AB ＝2e 1＋k e 2，→CB ＝e 1＋3e 2，→CD ＝2e 1－e 2，且A ，B ，D 三点共线．(1)求实数k 的值；(2)若|e 1|＝|e 2|＝1，e 1与e 2的夹角为60°，求|→AB |．19．如图，是一个物体作简谐运动的装置，点O 为简谐运动的平衡位置，取向右的方向为物体位移的正方向．已知振幅为4cm ，周期为3s ，且物体向右第一次运动到点O 时开始计时．(1)求物体对于平衡位置的位移y (cm)和时间t (s)之间的函数关系；(2)求该物体在t ＝10s 时的位置．20．已知A (sin x ，cos x )，B (sin x ，sin x )，C (－1，0)．(1)若x ＝π6，求→OC 与→OA 的夹角； (2)设函数f (x )＝m →OA ·→OB ，其中m ∈R ．①若m ＝1，求f (x )的单调增区间；②当x ∈［－π4，π4］时，f (x )的最大值是12，求m 的值． O C D21．在△ABC 中， a ，b ，c 分别是角A ，B ，C 的对边，且a ＋c ＝10，C ＝2A ，cos A ＝34． (1)求a c的值；(2)求sin B 和b 的值．金陵中学05－06学年度第二学期高一数学期中考试答题纸一、选择题（答案填涂在答题卡上）二、填空题13．．14．．15．．16．．三、解答题17．(1)(2)18．19．20．21．。

(数学)2016年金陵中学第一次数学月考试卷

8. 【答案】 −3 ．
9. 【答案】 [−1 , + ∞) ．
10. 【答案】 x2 − 2x + 1 ．
11. 【答案】 [10 , +∞) ．
12. 【答案】 −13 ．
【解析】 g= ( x) f ( x) + 2 为奇函数 ⇒ g (−1) =−g (1) =−11 ⇒ f (−1) =−13 ． 13. 【答案】 (−2, 2) ．
x
16. 已知集合=A {x | x2 − 3x +=2 0} ．
⑴若集合=B {x | mx= +1 0} 满足 B ⊆ A ，求实数 m 的值；
⑵若集合=C {x | x2 − 2x +=m 0} 满足 C A = A ，试确定实数 m 的范围．
17.
若函数
f
(x)
=
ax x2
+b +1
是R
上的奇函数，且
两式相减得： 1 − 1 = b − a ⇒ ab = 1，显然不可能，综上：不可能． ab
金陵中学高一年级阶段调研测试卷
数学
一、填空题（本大题共 14 小题，每小题 4 分，共 56 分，请将答案填在答卷纸上）
1. 已知集合 P= {x |1 < x < 6} ，集合 Q= {x | x − 3 > 0} ，则 P Q =
．
2. 已知全集U = {1,2,3,4} ，集合 A = {1,3} ， B = {1,3,4} ，则 A (U B)
1 2
=
2 ⇒ a = 1； 5
⑵
f
(x)
=
x x2 +1
，任取
x1
<

南京市金陵中学高一数学12月月考试卷 (1)

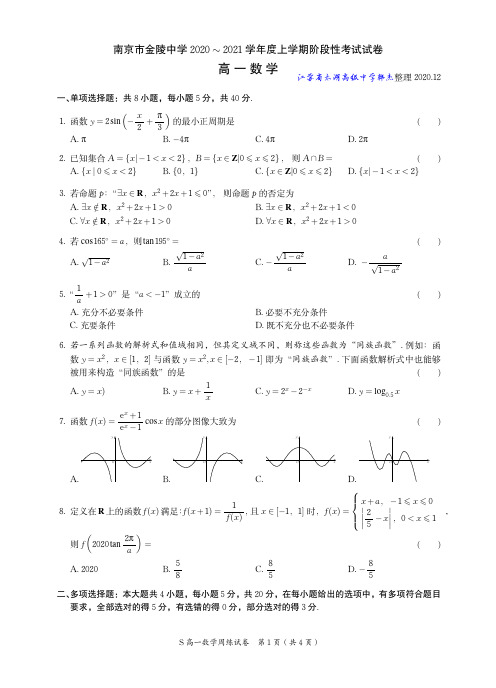
19.（12 分）已知函数 y = f(x) 定义域为 D，对于定义域 D 上的任意不等实数 x1，x2，试比较下列
函数中的 f(x1) + f(x2) 与f x1 + x2 的大小关系.
被用来构造“同族函数”的是
()
A. y = x)
B. y = x + 1 x
C. y = 2x − 2−x
D. y = log0.5 x
7.
函数 f(x) =
ex + 1 ex − 1
cos x 的部分图像大致为
y
y
y
()
y
O
x
O
x
O
x
O
x
A.
B.
C.
D.
8.
定义在 R 上的函数 f(x) 满足：f(x + 1) =
实数 a 的取位范围.Robin 老师告诉该同学“函数:g(x) = ex − x − 1 的单调区间是 [0， + ∞) 和
(−∞，0], 且函数 h(x) = x − 3 ln x 在 (1， + ∞) 有零点”. 根据 Robin 老师的提示，可求得问题中
实数 a 的取值范围是
.
四、解答题：共 6 小题，共 70 分，解答应写出文字说明、证明过程或演算步骤.
A. 充分不必要条件 C. 充要条件
B. 必要不充分条件 D. 既不充分也不必要条件
()
6. 若一系列函数的解析式和值域相同，但其定义域不同，则称这些函数为“同族函数”. 例如：函
数 y = x2，x ∈ [1，2] 与函数 y = x2, x ∈ [−2， − 1] 即为“同族函数”. 下面函数解析式中也能够

【精】金陵中学下册高一数学期中试卷

金陵中学2005－2006学年度第二学期高一数学期中试卷一、选择题（每小题3分，共36分）1．若x 是第四象限的角，且cos x ＝45，则tan x 的值是( )． (A)35 (B)－35(C) －43 (D)－342．函数y ＝2sin(x ＋π4)的图象的一个对称中心的坐标是( )． (A)（π4，2） (B)（3π4，0） (C)（ 5π4，－2） (D) （π4，0） 3．已知sin α2＝13，α∈(0，π)，则sin α的值为( )． (A)229 (B)－ 229 (C) 429 (D) － 4294．已知向量a ＝（2，1），b ＝（1，m )．若a ∥b ，则实数m 的值是( )．(A)12 (B)－2 (C)2 (D)－125．设０＜α＜π2＜β＜π，且sin α＝35，cos β＝－1213，则cos(α－β)的值是( )． (A)1665 (B) 3365 (C)－ 1665 (D)－ 33656．已知A （1，－1），B （3，1），C （－2，4），则与→AC －→BC 方向相同的单位向量的坐标是( )．(A)（1，1） (B)（－1，－1） (C)（－22 ，－22 ） (D)（22 ，22） 7．在△ABC 中，若(1＋tan A )(1＋tan B )＝2，则A ＋B 等于( )．(A)π4 (B) 3π4 (C) 5π4 (D) 7π48．在边长为1的正△ABC 中，记→AB ＝c ，→BC ＝a ，→AC ＝b ，则a ·b ＋c ·b ＋c ·a 的值等于( )．(A)32 (B)－32 (C)12 (D)－129．将函数y ＝f (x )的图象沿x 轴向左平移π6个单位后，再将图象上每一个点的横坐标变为原来的2倍（纵坐标不变），得到函数y ＝cos x 的图象，则函数f (x )的解析式是( )．(A)f (x )＝cos(2x ＋π6) (B)f (x )＝cos(2x －π6) (C)f (x )＝cos(2x ＋π3) (D)f (x )＝cos(2x －π3) 10．若cos(π4－x )＝－35，x ∈(3π4，π)，则1－tan x 1＋tan x的值是( )． (A)34 (B)－34 (C) 43 (D) －4311．若点O 是△ABC 所在平面内的一点，且→OA ·→OB ＝→OC ·→OB ＝→OC ·→OA ，则点O 是△ABC的( )．(A)三个内角角平分线的交点 (B)三条边垂直平分线的交点(C)三条中线的交点 (D)三条高的交点12．设f (x )是定义在区间(－∞，＋∞)上的奇函数，在区间(0，＋∞)内单调递增，且f (12)＝0．若△ABC 的内角A 满足f (cos A )＜0，则角A 的取值范围是( )．(A)(π3，π) (B)(π3，π2) (C)(π3，π2)∪(2π3，π) (D)(0，π3)∪(2π3，π) 二、填空题（每小题4分，共16分）13．计算：2tan15°1－tan 215°＝． 14．若向量a ＝(cos x ，sin x )，b ＝(12，－32)，则| a －b |的最大值是． 15．函数y ＝cos(12x －π4)的最小正周期是． 16．给出如下四个命题：①若a ，b 为两个不共线向量，且| a |＝| b |，则( a －b )⊥( a ＋b )；②在四边形ABCD 中，必有→AB ＋→BC ＋→CD ＋→AD ＝0；③若x a ＝x b ，x ∈R ，则a ＝b ；④若a ，b 为两个不共线向量，且x a ＋y b ＝0，则x ＝y ＝0．其中真命题的序号是．三、解答题（本大题共48分）17．(1)已知sin(π＋α)＝513，求cos(3π2－α)的值； (2)已知sin α＝23，cos(α＋β)＝－35，且α∈(π2，π)，β∈(π2，π)，求sin β的值． 18．设e 1，e 2是两个不共线的向量，设→AB ＝2e 1＋k e 2，→CB ＝e 1＋3e 2，→CD ＝2e 1－e 2，且A ，B ，D 三点共线．(1)求实数k 的值；(2)若|e 1|＝|e 2|＝1，e 1与e 2的夹角为60°，求|→AB |．19．如图，是一个物体作简谐运动的装置，点O 为简谐运动的平衡位置，取向右的方向为物体位移的正方向．已知振幅为4cm ，周期为3s ，且物体向右第一次运动到点O 时开始计时．(1)求物体对于平衡位置的位移y (cm)和时间t (s)之间的函数关系；(2)求该物体在t ＝10s 时的位置．20．已知A (sin x ，cos x )，B (sin x ，sin x )，C (－1，0)．(1)若x ＝π6，求→OC 与→OA 的夹角； (2)设函数f (x )＝m →OA ·→OB ，其中m ∈R ．①若m ＝1，求f (x )的单调增区间；②当x ∈［－π4，π4］时，f (x )的最大值是12，求m 的值． O C D21．在△ABC 中， a ，b ，c 分别是角A ，B ，C 的对边，且a ＋c ＝10，C ＝2A ，cos A ＝34． (1)求a c的值；(2)求sin B 和b 的值．金陵中学05－06学年度第二学期高一数学期中考试答题纸一、选择题（答案填涂在答题卡上）二、填空题13．．14．．15．．16．．三、解答题17．(1)(2)18．19．20．21．。

江苏省南京市金陵中学2006届高三数学综合练习一

南京市金陵中学2006届高三数学综合练习一(按2006年江苏省考试说明出题,选择10道,填空6道,解答5道)本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．满分150分，考试时间120钟．第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.命题“若a 、b 都是奇数，则a +b 是偶数”的否命题是（） A ．若a +b 不是偶数，则a 、b 都不是奇数 B ．若a +b 是偶数，则a 、b 都是奇数 C ．若a +b 不是偶数，则a 、b 不都是奇数 D ．若a 、b 不都是奇数，则a +b 不是偶数 2．已知向量a =(x 1,y 1)，b =(x 2,y 2)，则下列为a 与b 共线的充要条件是 ( ) A ．存在一个实数λ，使得a =λbB ．1122x y x y =C ．x 1x 2-y 1y 2=0D ．x 1y 2-x 2y 1=03.曲线 2cos 2sin x y θθ=⎧⎨=⎩ （θ为参数，—π≤θ≤—3π）的长度为（）A.34π B.32π C.35π D.3π4、若2()f x x ax b =++,且1(1)2,2(1)4f f ≤-≤≤≤,则点(a ,b )在a O b 平面上的区域是一个（）A. 三角形B.矩形C. 菱形D. 直角梯形5、函数3221x e y -⋅=π的部分图象大致是（）（A ）（B ）（C ）（D ）6、已知ω>0，若函数()2cos2sin4xxx f ωω∙=在⎥⎦⎤⎢⎣⎡-3,4ππ上单调递增，则ω的取值范围是 ( )A.]32,0(B.]23,0( C.]2,0( D.),2[+∞图7－ 57．如图，在正三角形ABC 中，D 、E 、F 分别为各边的中点，G 、H 、I 分别为DE 、FC 、EF 的中点，将△ABC 沿DE 、EF 、DF 折成三棱锥以后，BG 与IH 所成的角的弧度数为（）A ．6πB ．3π C ．32arccos D ．33arccos8．若0,0a b >>且a b ≠,在a ,b 之间插入n 个正数12,,,n x x x ,使之成为等比数列()*2,n n N ≥∈,记M =,2a bN +=,则M 与N 的大小关系是 ( ) A.M>N B.M=N C.M<N D.不能确定9. 一种专门占据内存的计算机病毒开始时占据内存2KB ，工作时3分钟自身复制一次，（即复制后所占内存是原来的2倍），那么，开机后（）分钟，该病毒占据64MB （1210MB KB =). A. 45B. 48C. 51D. 4210.若直线 )0,(022>=+-b a by ax 过圆014222=+-++y x y x 的圆心,则ab 的最大值是 ( ) A.41 B. 21C. 1D. 2 第Ⅱ卷（非选择题，共90分）二、填空题：本大题4个小题，每小题4分，共16分．11．若32(1)1nnx x ax bx +=+++++，且a :b =3:1,那么(1)nx -的展开式中系数最大的项是 . 12．若函数1()()x f x ax R -=∈的反函数()1f x -的图像经过点（4，2），则()12f -的值为 .13．甲、乙两名射击运动员参加某大型运动会的预选赛，他们分别射击了5次，成绩如下表(单位：环)：人入选，则入选的应是． 15．给出下列四个命题：图7－7① 已知函数()f x =()()43f f >；② 函数223sin sin y x x=+的最小值是 ③ 函数()()log 20,1x a y a a a =+>≠在R 上是增函数；④ 函数2sin 26y x π⎛⎫=-⎪⎝⎭的图象的一个对称点是,012π⎛⎫⎪⎝⎭；其中正确命题的序号是（把你认为正确的都写上）.16. 在数列{}n a 中，如果存在非零常数T ，使得n T n a a +=对于任意的非零自然数n 均成立，那么就称数列{}n a 为周期数列，其中T 叫做数列{}n a 的周期。

金陵中学~学年度高一年级第一学期阶段考试.doc

金陵中学2006~2007第一学期高一年级阶段考试化学2006.10命题：高一备课组审核：江敏相对原子质量：H－1 C－12 N－14 O－16 Na－23 S－32 Cl－35.5 K－39 Ca－40 本试卷分第I卷（选择题）和第II卷（非选择题）两部分。

第I卷（选择题）部分请在答题卡上填涂，第II卷（非选择题）部分请在答卷纸上作答。

本卷满分100分，考试用时100分钟。

第Ⅰ卷（选择题共40分）一．选择题（本题包括8小题，每小题2分，共16分。

每小题只有一个．．．．选项符合题意）1．以下是一些常用的危险品标志，装运乙醇的包装箱应贴的图标是A B C D2．已知溴在有机溶剂中的溶解度比在水中的大很多，可用作萃取溴水中的溴是①四氯化碳②直馏汽油③酒精④白葡萄酒A.①和④B.①和②C.①和③D.①②③④3．观察右图，量筒中液体的体积读数是A. 0.5mlB. 2.4mlC. 1.6mlD. 1.7ml4．下列实验操作中: ①过滤②蒸发③溶解④取液体试剂⑤取固体试剂，一定要用到玻璃棒的是A. ①②③B.④⑤C. ①④D. ①③⑤5．下列实验仪器中，不能直接用于混合物的分离或提纯的是A．分液漏斗B.普通漏斗C.蒸馏烧瓶D.量筒6．向装有碘水的试管中加四氯化碳振荡，静置后，你观察到的现象是A．下层几乎无色，上层紫红色B. 上层几乎无色，下层紫红色C. 下层橙色，上层几乎无色D. 不分层，紫红色7．实验室进行NaCl溶液蒸发时，一般有以下操作过程：①放置酒精灯；②固定铁圈位置；③放置蒸发皿；④加热搅拌；⑤停止加热，余热蒸干。

其正确的操作顺序为A．②③④⑤①B．①②③④⑤C．②③①④⑤D．②①③④⑤8．O2、SO2、SO3三者的质量比为2 : 4 : 5时，它们的物质的量之比为A．2 : 4 : 5 B．1 : 2 : 3 C．1 : 1 : 1 D．2 : 2 : 3二．选择题(本题包括8小题。

每小题3分，共24分。

2005-2006学年度第一学期高一数学期考试卷(1)

2005-2006学年度第一学期高一数学期考试卷2006.1.12测试时间：100分钟，满分：150分一、选择题（10×5=50分）1.方程的解集是()255log (21)log (2)x x +=-(A) {3} (B) {-1} (C) {-1,3} (D) {1,3} 2.下列说法中正确的是( )(A)三点确定一个平面. (B)两条直线确定一个平面. (C)三条直线两两相交,则这三条直线共面.(D)空间四点中如果有三点共线,则这四点共面.3.给出下列命题:（1）同垂直于一直线的两直线平行.（2）同平行于一平面的两直线平行. （3）同平行于一直线的两直线平行.（4）平面内不相交的两直线平行. 其中正确的命题个数是( )(A) 1 (B)2 (C)3 (D) 44设集合，则下列关系式中正确的是（） 2{10}M x x =>A ． B ． C ． D ． 3M ⊆{3}M ⊆3R C M ∈3M ∈5.以点A （－5，4）为圆心且与x 轴相切的圆的标准方程是（） A ．(x+5)2+(y －4)2=25;B ．(x+5)2+(y －4)2=16;C ．(x －5)2+(y ＋4)2=16;D ．(x －5)2+(y ＋)2=25;6.偶函数f(x)的定义域[-5，5]，其在[0，5]的图象如下所示,则>0的解集为( ) ()f x (A) {x|2<x<4}(B) {x|<4}2x ≤(D){x|2<x<4或7.函数）()f x （A ）是奇函数但不是偶函数（B ）是偶函数但不是奇函数（C ）既是奇函数又是偶函数（D ）既不是奇函数又不是偶函数 8.两条异面直线在同一平面的正投影不可能是（）（A ）两条平行直线 (B)两条相交直线（C ）一个点和一条直线（D ）两个点9.设是正方体的一条对角线，则这个正方体中面对角线与异面的有1BD 1111ABCD A B C D -1BD （）（A ）0条（B ）4条（C ）6条（D ）12条10．已知三角形ABC 的顶点A （2，2，0），B （0，2，0），C(0，1，4)，则三角形ABC 是（） A ．直角三角形； B ．锐角三角形； C ．钝角三角形； D ．等腰三角形；二、填空(4×5=20分) 11.已知=,则=____________()f x {200x x x x ≥< ((2))f f -12.用”<”从小到大排列、、、______________________ 32log 10.5-32-30.5log 13.一球的表面积与它的体积的数量相等,则球的半径为______3_____________14. 下列函数：y=； y = x 2; y= |x| －1; ○1x lg ○2;2xy =○3○4其中有2个零点的函数的序号是。

2005-2006年第二学期扬州中学高三第一次月考数学试卷

2005-2006年第二学期扬州中学高三第一次月考数学试卷2006．2本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分。

第Ⅰ卷 (选择题共60分)一、选择题：（本大题共计12小题，每小题5分，共60 分）1.设()2x x f =，集合A ＝{x|f(x)＝x,x ∈R}，B ＝{x|f[f(x)]＝x,x ∈R},则A 与B 的关系是（）A ．A ∩B ＝A B ．A ∩B ＝φC ．A ∪B ＝RD ．A ∪B ＝{－1，0，1}2．抛物线214y x =的焦点坐标是（）A 、1(0,)16B 、1(,0)16 C 、(1,0) D 、(0,1)3．已知等差数列{}n a 的前n 项和为n S ，若5418a a =-，则8S 等于（）A 、144B 、72C 、54D 、364．4男5女排成一排，4男顺序一定，5女顺序也一定的排法种数为（）A. 15120B. 126C. 3024D. 以上答案都不对5．若R ∈k ，则“3>k ”是“方程13322=+--k y k x 表示双曲线”的 ( ) （A ）充分不必要条件. （B ）必要不充分条件.（C ）充要条件. （D ）既不充分也不必要条件. 6．若b a c b a >∈,R 、、，则下列不等式成立的是 ( ) （A ）ba11<. （B ）22b a >. （C ）1122+>+c bc a . （D ）||||c b c a >. 7．若向量a =(－2,1),b =(3,－x)，且a 与b的夹角为钝角，则x 的取值范围为（）A.｛x|x>－6｝B.｛x|x<－6｝C.｛x|x ≥－6｝D.｛x|x>－6且x ≠32｝8．设直线0543=-+y x 的倾斜角为θ ，则该直线关于直线a x =（R a ∈）对称的直线的倾斜角为（） A.θπ-2 B. 2πθ- C. θπ-2 D.θπ-9．过点（1，2）总可以作两条直线与圆x 2+y 2+kx+2y+k 2-15=0相切，则实数k 的取值范围（）（A ）k>2 （B ）-3<k<2 （C ）k<-3或k>2 （D ）都不对10．如图所示，在正方体ABCD －A 1B 1C 1D 1的侧面AB 1内有一动点P 到直线A 1B 1的距离是点P 到直线BC 的距离的2倍，则动点P 的轨迹为（） A. 圆弧B. 椭圆的一部分C. 双曲线的一部分D. 抛物线的一部分11．在△ABC 中，有下列命题：①A>B 的充要条件为sinA>sinB ； ②A<B 的充要条件为cosA>cosB ；③若A,B 为锐角，则sinA+sinB>cosA+cosB ； ④tan 2A B +tan 2C为常数其中正确的命题的个数为（） A. 1个 B. 2个 C. 3个 D. 4个 12．如图，正方形ABCD 的顶点(0,)2A，(2B ，顶点CD 、位于第一象限，直线:(0)l x t t =≤将正方形ABCD()f t ，则函数()S f t =的图象大致是A 、3-B 、2-C 、1-D 、第二卷（非选择题共90分）二. 填空题：（本大题共6小题，每小题4分，共24分，请把答案直接填在题中横线上） 13．把函数y=2x 2-4x+5的图象按向量a 平移,得到y=2x 2的图象,且a ⊥b,c=(1,-1),b •c=4,则b= 。

【精选】金陵中学下册高一数学期中试卷

金陵中学2005－2006学年度第二学期高一数学期中试卷一、选择题（每小题3分，共36分）1．若x 是第四象限的角，且cos x ＝45，则tan x 的值是( )． (A)35 (B)－35(C) －43 (D)－342．函数y ＝2sin(x ＋π4)的图象的一个对称中心的坐标是( )． (A)（π4，2） (B)（3π4，0） (C)（ 5π4，－2） (D) （π4，0） 3．已知sin α2＝13，α∈(0，π)，则sin α的值为( )． (A)229 (B)－ 229 (C) 429 (D) － 4294．已知向量a ＝（2，1），b ＝（1，m )．若a ∥b ，则实数m 的值是( )．(A)12 (B)－2 (C)2 (D)－125．设０＜α＜π2＜β＜π，且sin α＝35，cos β＝－1213，则cos(α－β)的值是( )． (A)1665 (B) 3365 (C)－ 1665 (D)－ 33656．已知A （1，－1），B （3，1），C （－2，4），则与→AC －→BC 方向相同的单位向量的坐标是( )．(A)（1，1） (B)（－1，－1） (C)（－22 ，－22 ） (D)（22 ，22） 7．在△ABC 中，若(1＋tan A )(1＋tan B )＝2，则A ＋B 等于( )．(A)π4 (B) 3π4 (C) 5π4 (D) 7π48．在边长为1的正△ABC 中，记→AB ＝c ，→BC ＝a ，→AC ＝b ，则a ·b ＋c ·b ＋c ·a 的值等于( )．(A)32 (B)－32 (C)12 (D)－129．将函数y ＝f (x )的图象沿x 轴向左平移π6个单位后，再将图象上每一个点的横坐标变为原来的2倍（纵坐标不变），得到函数y ＝cos x 的图象，则函数f (x )的解析式是( )．(A)f (x )＝cos(2x ＋π6) (B)f (x )＝cos(2x －π6) (C)f (x )＝cos(2x ＋π3) (D)f (x )＝cos(2x －π3) 10．若cos(π4－x )＝－35，x ∈(3π4，π)，则1－tan x 1＋tan x的值是( )． (A)34 (B)－34 (C) 43 (D) －4311．若点O 是△ABC 所在平面内的一点，且→OA ·→OB ＝→OC ·→OB ＝→OC ·→OA ，则点O 是△ABC的( )．(A)三个内角角平分线的交点 (B)三条边垂直平分线的交点(C)三条中线的交点 (D)三条高的交点12．设f (x )是定义在区间(－∞，＋∞)上的奇函数，在区间(0，＋∞)内单调递增，且f (12)＝0．若△ABC 的内角A 满足f (cos A )＜0，则角A 的取值范围是( )．(A)(π3，π) (B)(π3，π2) (C)(π3，π2)∪(2π3，π) (D)(0，π3)∪(2π3，π) 二、填空题（每小题4分，共16分）13．计算：2tan15°1－tan 215°＝． 14．若向量a ＝(cos x ，sin x )，b ＝(12，－32)，则| a －b |的最大值是． 15．函数y ＝cos(12x －π4)的最小正周期是． 16．给出如下四个命题：①若a ，b 为两个不共线向量，且| a |＝| b |，则( a －b )⊥( a ＋b )；②在四边形ABCD 中，必有→AB ＋→BC ＋→CD ＋→AD ＝0；③若x a ＝x b ，x ∈R ，则a ＝b ；④若a ，b 为两个不共线向量，且x a ＋y b ＝0，则x ＝y ＝0．其中真命题的序号是．三、解答题（本大题共48分）17．(1)已知sin(π＋α)＝513，求cos(3π2－α)的值； (2)已知sin α＝23，cos(α＋β)＝－35，且α∈(π2，π)，β∈(π2，π)，求sin β的值． 18．设e 1，e 2是两个不共线的向量，设→AB ＝2e 1＋k e 2，→CB ＝e 1＋3e 2，→CD ＝2e 1－e 2，且A ，B ，D 三点共线．(1)求实数k 的值；(2)若|e 1|＝|e 2|＝1，e 1与e 2的夹角为60°，求|→AB |．19．如图，是一个物体作简谐运动的装置，点O 为简谐运动的平衡位置，取向右的方向为物体位移的正方向．已知振幅为4cm ，周期为3s ，且物体向右第一次运动到点O 时开始计时．(1)求物体对于平衡位置的位移y (cm)和时间t (s)之间的函数关系；(2)求该物体在t ＝10s 时的位置．20．已知A (sin x ，cos x )，B (sin x ，sin x )，C (－1，0)．(1)若x ＝π6，求→OC 与→OA 的夹角； (2)设函数f (x )＝m →OA ·→OB ，其中m ∈R ．①若m ＝1，求f (x )的单调增区间；②当x ∈［－π4，π4］时，f (x )的最大值是12，求m 的值． O C D21．在△ABC 中， a ，b ，c 分别是角A ，B ，C 的对边，且a ＋c ＝10，C ＝2A ，cos A ＝34． (1)求a c的值；(2)求sin B 和b 的值．金陵中学05－06学年度第二学期高一数学期中考试答题纸一、选择题（答案填涂在答题卡上）二、填空题13．．14．．15．．16．．三、解答题17．(1)(2)18．19．20．21．。

金陵中学下册高一数学期中试卷-精编

金陵中学2005－2006学年度第二学期高一数学期中试卷一、选择题（每小题3分，共36分）1．若x 是第四象限的角，且cos x ＝45，则tan x 的值是( )． (A)35 (B)－35(C) －43 (D)－342．函数y ＝2sin(x ＋π4)的图象的一个对称中心的坐标是( )． (A)（π4，2） (B)（3π4，0） (C)（ 5π4，－2） (D) （π4，0） 3．已知sin α2＝13，α∈(0，π)，则sin α的值为( )． (A)229 (B)－ 229 (C) 429 (D) － 4294．已知向量a ＝（2，1），b ＝（1，m )．若a ∥b ，则实数m 的值是( )．(A)12 (B)－2 (C)2 (D)－125．设０＜α＜π2＜β＜π，且sin α＝35，cos β＝－1213，则cos(α－β)的值是( )． (A)1665 (B) 3365 (C)－ 1665 (D)－ 33656．已知A （1，－1），B （3，1），C （－2，4），则与→AC －→BC 方向相同的单位向量的坐标是( )．(A)（1，1） (B)（－1，－1） (C)（－22 ，－22 ） (D)（22 ，22） 7．在△ABC 中，若(1＋tan A )(1＋tan B )＝2，则A ＋B 等于( )．(A)π4 (B) 3π4 (C) 5π4 (D) 7π48．在边长为1的正△ABC 中，记→AB ＝c ，→BC ＝a ，→AC ＝b ，则a ·b ＋c ·b ＋c ·a 的值等于( )．(A)32 (B)－32 (C)12 (D)－129．将函数y ＝f (x )的图象沿x 轴向左平移π6个单位后，再将图象上每一个点的横坐标变为原来的2倍（纵坐标不变），得到函数y ＝cos x 的图象，则函数f (x )的解析式是( )．(A)f (x )＝cos(2x ＋π6) (B)f (x )＝cos(2x －π6) (C)f (x )＝cos(2x ＋π3) (D)f (x )＝cos(2x －π3) 10．若cos(π4－x )＝－35，x ∈(3π4，π)，则1－tan x 1＋tan x的值是( )． (A)34 (B)－34 (C) 43 (D) －4311．若点O 是△ABC 所在平面内的一点，且→OA ·→OB ＝→OC ·→OB ＝→OC ·→OA ，则点O 是△ABC的( )．(A)三个内角角平分线的交点 (B)三条边垂直平分线的交点(C)三条中线的交点 (D)三条高的交点12．设f (x )是定义在区间(－∞，＋∞)上的奇函数，在区间(0，＋∞)内单调递增，且f (12)＝0．若△ABC 的内角A 满足f (cos A )＜0，则角A 的取值范围是( )．(A)(π3，π) (B)(π3，π2) (C)(π3，π2)∪(2π3，π) (D)(0，π3)∪(2π3，π) 二、填空题（每小题4分，共16分）13．计算：2tan15°1－tan 215°＝． 14．若向量a ＝(cos x ，sin x )，b ＝(12，－32)，则| a －b |的最大值是． 15．函数y ＝cos(12x －π4)的最小正周期是． 16．给出如下四个命题：①若a ，b 为两个不共线向量，且| a |＝| b |，则( a －b )⊥( a ＋b )；②在四边形ABCD 中，必有→AB ＋→BC ＋→CD ＋→AD ＝0；③若x a ＝x b ，x ∈R ，则a ＝b ；④若a ，b 为两个不共线向量，且x a ＋y b ＝0，则x ＝y ＝0．其中真命题的序号是．三、解答题（本大题共48分）17．(1)已知sin(π＋α)＝513，求cos(3π2－α)的值； (2)已知sin α＝23，cos(α＋β)＝－35，且α∈(π2，π)，β∈(π2，π)，求sin β的值． 18．设e 1，e 2是两个不共线的向量，设→AB ＝2e 1＋k e 2，→CB ＝e 1＋3e 2，→CD ＝2e 1－e 2，且A ，B ，D 三点共线．(1)求实数k 的值；(2)若|e 1|＝|e 2|＝1，e 1与e 2的夹角为60°，求|→AB |．19．如图，是一个物体作简谐运动的装置，点O 为简谐运动的平衡位置，取向右的方向为物体位移的正方向．已知振幅为4cm ，周期为3s ，且物体向右第一次运动到点O 时开始计时．(1)求物体对于平衡位置的位移y (cm)和时间t (s)之间的函数关系；(2)求该物体在t ＝10s 时的位置．20．已知A (sin x ，cos x )，B (sin x ，sin x )，C (－1，0)．(1)若x ＝π6，求→OC 与→OA 的夹角； O C D(2)设函数f (x )＝m →OA ·→OB ，其中m ∈R ．①若m ＝1，求f (x )的单调增区间；②当x ∈［－π4，π4］时，f (x )的最大值是12，求m 的值． 21．在△ABC 中， a ，b ，c 分别是角A ，B ，C 的对边，且a ＋c ＝10，C ＝2A ，cos A ＝34． (1)求a c的值；(2)求sin B 和b 的值．金陵中学05－06学年度第二学期高一数学期中考试答题纸一、选择题（答案填涂在答题卡上）二、填空题13．．14．．15．．16．．三、解答题17．(1)(2)18．19．20．21．。

单元测验-金陵中学

南京市金陵中学2005/2006第一学期高一年级化学月考第一章从实验学化学单元测验高一（）班姓名: 学号: .可能用到的相对原子质量：H-1 C-12 N-14 O-16 S-32 Na-23 Mg-24 Cu-64 Ba-137 Cl-35.5第I 卷（选择题）一、选择题（本题包括8小题。

每小题只有一个选项符合题意。

）1．下列实验基本操作（或实验注意事项）中，主要是出于实验安全考虑的是（）A ．实验剩余的药品不能放回原试剂瓶B ．可燃性气体的验纯C ．气体实验装置在实验前进行气密性检查D ．滴管不能交叉使用2．在盛放浓硫酸的试剂瓶的标签上应印有下列警示标记中的（）3．除去下列物质中的杂质所选用的试剂（括号内）正确的是（）A. 碳酸钠溶液中的碳酸氢钠（盐酸）B. 二氧化碳中的水蒸气（浓硫酸）C. 氢氧化钠溶液中的碳酸钠（氯化钙）D. 二氧化碳中的一氧化碳（氧气） 4．30mL 1mol/L NaCl 溶液和40mL 0.5mol/L CaCl 2溶液混合后（忽略混合时体积变化），混合液中Cl －浓度为：（）A ．0.5mol/LB ．0.6mol/LC ．1.00mol/LD ．2mol/L 5．与标准状况下Ｖ L CO 2所含氧原子数目相同的水的质量是（） A ．4.2244Vg B ．4.22Vg C ．4.2236Vg D ．4.2218Vg 6．用N A 表示阿伏加德罗常数的值，下列说法中不正确．．．的是（） A ．磷酸的摩尔质量（以g/mol 为单位）与N A 个磷酸分子的质量（以g 为单位）在数值上相等B ．N A 个氮分子和N A 个氢分子的质量比等于14∶1C ．1 molCH 3+ (碳正离子)中含有电子数为10 N AD ．32 g 氧气所含的原子数目为2N A7．已知KNO 3、K 2SO 4、K 3PO 4在溶液中完全解离，物质的量浓度相同的KNO 3、K 2SO 4、K 3PO 4 3种溶液中，若要使K ＋的物质的量相等，则这3种溶液的体积比为 ( ) A ．3∶2∶1 B ．6∶3∶2 C ．2∶3∶6 D ．1∶2∶38．有三种盐的混合溶液，其中含有Na ＋、Mg 2＋、SO -24和Cl －，其物质的量分别为Na ＋0.2 mol 、Mg 2＋0.25 mol 、Cl －0.4 mol ，则SO -24的物质的量为（） A ．0.15 mol B ．0.2 mol C ．0.25 molD ．0.05 mol二、选择题(本题包括10小题。

高一数学期中试卷金陵中学

金陵中学2005—2006学年高一数学第一学期期中试卷命题：吴祥华审核：张松年 05．11．2一、选择题1．幂函数n x y =的图象（）．A ．一定经过点（0，0）B ．一定经过点1(-，)1-C ．一定经过点1(-，)1D ．一定经过点1(，)12．若全集1{=U ，2，3，}4，集合1{=A ，}2，则满足U B A = 的集合B 有（）． A ．1个 B ．2个 C ．3个 D ．4个 3．当x ≥3-时，化简-+2)3(x 33)3(-x 得（）． A ．6 B ．x 2C ．6或x 2-D ．x 2-或6或x 2 4．设10<<a ，则函数()5log +=x y a 的图象不经过（）．A ．第一象限B ．第二象限C ．第三象限D ．第四象限 5．若函数x m y )1(-=是R 上的减函数，则实数m 的取值范围是（）． A ．1(，)∞+ B ．0(，)1 C ．-∞(，)1 D ．1(-，)16．已知函数)(x f y =的图象如右图所示，则函数|)(|x f y =的图象为（）．7．下列关于函数x y 2log =的结论中，正确的是（）．A ．是函数2x y =的反函数B ．图象过点1(，)0C ．图象与直线x y -=无交点D ．定义域为0[，)∞+8．23.0，3.0log 2与3.02的大小关系是（）．A ．3.0log 23.023.02<<B ．3.02223.0log 3.0<<C ．23.023.023.0log <<D ．3.02223.03.0log <<9．若函数)(x f 的定义域是1[-，]1，则函数)1(+x f 的定义域是（）．A ．1[-，]1B ．0[，]2C ．2[-，]0D ．0[，)2 10．若函数c bx x x f ++=2)(满足)3()1(f f =-，则（）． A ．)1()1(->>f c f B ．)1()1(-<<f c fC ．)1()1(f f c >->D ．)1()1(f f c <-<11．已知函数32)(2+-=x x x f 在闭区间0[，]m 上的值域是2[，]3，则实数m 的取值范围是（）． A ．1[，)∞+ B ．[0，2]ABCC ．-∞(，]2-D ．1[，]212．已知指数函数x a y =在[0，]1上的最大值与最小值的和为3，则实数a 的值为（）． A ．41 B ．21C ．2D ．4 二、填空题13．已知集合}02|{2=--=x x x P ，集合x x T <-=1|{≤}2，则集合=T P ． 14．若)(x f 是R 上的奇函数，当0>x 时，)1()(+=x x x f ，则当0<x 时，)(x f = ． 15．若函数)26(log 22+-=x mx y 的定义域为R ，则实数m 的取值范围是．16．已知)(x f 与)(x g 是定义在R 上的非奇非偶函数，且)()(x g x f ⋅是定义在R 上的偶函数，试写出满足条件的一组函数：=)(x f ，=)(x g ．（只要写出满足条件的一组即可）三、解答题17．对于集合A ，B ，我们把集合{(a ，b )|A a ∈，B b ∈}记作B A ⨯．例如：=A {1，2}，=B {3，4}，则有=⨯B A {(1，3)，(1，4)，(2，3)，(2，4)}， =⨯A B {(3，1)，(3，2)，(4，1)，(4，2)}， =⨯A A {(1，1)，(1，2)，(2，1)，(2，2)}， =⨯B B {(3，3)，(3，4)，(4，3)，(4，4)}，据此，试解答下列问题：（1）已知=C {m }，=D {1，2，3}，求D C ⨯；（2）已知=⨯B A {(1，2)，(2，2)}，求集合A ，B ；（3）若A 中有3个元素，B 中有4个元素，试确定B A ⨯有几个元素．18．完成下列填空，并按要求画出函数的简图，不写画法，请保留画图过程中的痕迹，痕迹用虚线表示，最后成图部分用实线表示．（1）函数|32|2--=x x y 的零点是，利用函数322--=x x y 的图象，在直角坐标系（1）中画出函数|32|2--=x x y 的图象．（2）函数12||+=x y 的定义域是，值域是，是函数（填“奇”、“偶”或“非奇非偶”）．利用x y 2=的图象，通过适当的变换，在直角坐标系（2）中画出函数12||+=x y 的图象．)2(19．计算：（1）已知0>a 且32=xa ，求xx xx a a a a --++33的值；（2）求1.0lg 10lg 5lg 2lg 125lg 8lg ⋅--+的值．20．已知函数1212log )(21+-=x x x f （-∞∈(x ，21()21 -，)∞+）．（1）判断函数)(x f 的奇偶性，并说明理由；（2）指出函数)(x f 在区间21(，)∞+上的单调性，并加以证明．21．某旅游点有50辆自行车供游客租赁使用，管理这些自行车的费用是每日115元．根据经验，若每辆自行车的日租金不超过6元，则自行车可以全部租出；若超过6元，则每提高1元，租不出去的自行车就增加3辆．规定：每辆自行车的日租金不超过20元，每辆自行车的日租金x 元只取整数，并要求出租所有自行车一日的总收入必须超过一日的管理费用，用y 表示出租所有自行车的日净收入（即一日中出租所有自行车的总收入减去管理费后的所得）．（1）求函数)(x f y =的解析式及定义域；（2）试问日净收入最多时每辆自行车的日租金应定为多少元？日净收入最多为多少元？高一数学期中试卷答题纸一．选择题（涂在答题卡上）二．填空题13．=T P ．14．当0<x 时，=)(x f ． 15．． 16．=)(x f ，=)(x g ．三．解答题 17．18．（1）函数|32|2--=x x y 的零点是，利用函数322--=x x y 的图象，在直角坐标系（1）中画出函数|32|2--=x x y 的图象．（2）函数12||+=x y 的定义域是，值域是，是函数（填“奇”、“偶”或“非奇非偶”）．利用x y 2=的图象，通过适当的变换，在直角坐标系（2）中画出函数12||+=x y 的图象． 19．（1）（2） 20．)2(21．附加题22．设)(x f 是定义在1[-，]1上的奇函数，且对任意的1[,-∈b a ，]1，当0≠+b a 时，都有ba b f a f ++)()(＞0．（1）若a ＞b ，试比较)(a f 与)(b f 的大小；（2）解不等式)21(-x f ＜)41(-x f ；（3）如果)()(c x f x g -=和)()(2c x f x h -=这两个函数的定义域的交集是空集，求c 的取值范围．金陵中学2005—2006学年高一数学第一学期期中试卷命题：吴祥华审核：张松年 05．11．2一、选择题1．幂函数n x y =的图象（）．DA ．一定经过点（0，0）B ．一定经过点)1,1(--C ．一定经过点1(-，)1D ．一定经过点1(，)12．若全集1{=U ，2，3，}4，集合1{=A ，}2，则满足U B A = 的集合B 有（）． A ．1个 B ．2个 C ．3个 D ．4个选D ．}4,3{，}4,3,1{，}4,3,2{，}4,3,2,1{． 3．当x ≥3-时，化简-+2)3(x 33)3(-x 得（）． A A ．6 B ．x 2C ．6或x 2-D ．x 2-或6或x 2 4．设10<<a ，则函数()5log +=x y a 的图象不经过（）． AA ．第一象限B ．第二象限C ．第三象限D ．第四象限 5．若函数x m y )1(-=在R 上是减函数，则m 的取值范围是（）． BA ．1(，)∞+ C ．-∞(，)1 6．已知函数)(x f y =的图象为（）． B7．下列关于函数x y 2log =的结论中正确的是（）． BA ．是函数2x y =的反函数B ．图象恒过定点1(，)0C ．图象与直线x y -=无交点D ．定义域为0[，)∞+ 8．23.0，3.0log 2与3.02的大小关系是（）． DA ．3.0log 23.023.02<<0B ．3.02223.0log 3.0<<C ．23.023.023.0log <<D ．3.02223.03.0log <<9．若函数)(x f 的定义域是1[-，]1，则函数)1(+x f 的定义域是（）． C A ．1[-，]1 B ．0[，]2 C ．2[-，]0 D ．0[，)2 10．若二次函数c bx x x f ++=2)(，且)3()1(f f =-，则（）． A ．)1()1(->>f c f B ．)1()1(-<<f c fC ．)1()1(f f c >->D ．)1()1(f f c <-< 解选B ．∵)3()1(f f =-，∴函数c bx x x f ++=2)(的对称轴是直线1=x ，画出)(x f 的草图（如图），又∵c f =)0(，)(x f 在1[-，]1上递减，故)1()1(-<<f c f ，∴选B ．11．已知函数32)(2+-=x x x f 在闭区间0[，]m 上的值域是2[，]3则m 的取值范围是（）．DA ．1[，)∞+B ．[0，2]C ．-∞(，]2-D ．1[，]212．已知指数函数x a y =在[0，]1上的最大值与最小值的和为3，则a 的值为（）．C A ．41 B ．21C ．2D ．4 二、填空题13．已知集合}02|{2=--=x x x P ，集合x x T <-=1|{≤}2，则集合=T P ． }2{．14．若)(x f 是R 上的奇函数，当0>x 时，)1()(+=x x x f ，则当0<x 时，)(x f = ． )1()(x x x f -= 15．若函数)26(log 22+-=x mx y 的定义域为R ，则m 的取值范围是． (∈m ),29+∞． 16．已知)(x f 与)(x g 是定义在R 上的非奇非偶函数，且)()(x g x f ⋅是定义在R 上的偶函数，写出满足条件的一组函数：=)(x f ，=)(x g ． 1)(+=x x f ，1)(-=x x g （答案不惟一）三、解答题17．对于集合A ，B ，我们把集合{(a ，b )|A a ∈，B b ∈}记作B A ⨯．例如：=A {1，2}，=B {3，4}，则有B=⨯B A {(1，3)，(1，4)，(2，3)，(2，4)}， =⨯A B {(3，1)，(3，2)，(4，1)，(4，2)}， =⨯A A {(1，1)，(1，2)，(2，1)，(2，2)}， =⨯B B {(3，3)，(3，4)，(4，3)，(4，4)}，据此，试解答下列问题：（1）已知=C {m }，=D {1，2，3}，求D C ⨯；（2）已知=⨯B A {(1，2)，(2，2)}，求集合A ，B ；（3）若A 中有3个元素，B 中有4个元素，试确定B A ⨯有几个元素．解：（1）由题知=⨯D C {(m ，1)，(m ，2)，(m ，3)}．（2）因为=⨯B A {(1，2)，(2，2)}，所以A 中有元素1，2，B 中含有元素2，即=A {1，2}，=B {2}．（3）B A ⨯中含有12个元素．18．完成下列填空，并按要求画出函数的简图，不写画法，请保留画图过程中的痕迹，痕迹用虚线表示，最后成图部分用实线表示．（1）函数|32|2--=x x y 的零点是，利用函数322--=x x y 的图象，在直角坐标系（1）中画出函数|32|2--=x x y 的图象．（2）函数12||+=x y 的定义域是，值域是，是函数（填“奇”、“偶”或“非奇非偶”）．利用x y 2=的图象，通过适当的变换，在直角坐标系（2）中画出函数12||+=x y 的图象．19．计算：（1）已知0>a ，32=xa ，求xx xx a a a a --++33的值；（2）求1.0lg 10lg 5lg 2lg 125lg 8lg ⋅--+的值．解：（1）原式x x x x x x a a a a a a ---++-+=)1)((22112-+=xa a 371313=-+=．（2）原式10lg )1(10lg 215lg 2lg 5lg 2lg 33-⨯--+=21)5lg 2(lg 2-+=10lg 4-=4-=． 20．已知函数1212log )(21+-=x x x f （-∞∈(x ，21()21 -，)∞+）．（1）判断函数)(x f 的奇偶性，并说明理由；（2）指出函数)(x f 在区间21(，)∞+上的单调性，并加以证明．解（1）因为1212log )(21+---=-x x x f 1212log 21-+=x x 1211212log -⎪⎭⎫⎝⎛+-=x x )(x f -=，所以函数)(x f 是奇函数．（3）设1212)(+-=x x x g 1221+-=x ．设21x x m <<-，则)()(21x g x g -)12)(12(42112++-⋅-=x x x x ，因为0<m ，2121x x <<，所以012>-x x ，0121>+x ，0122>+x ，所以0)12)(12(42112<++-⋅-x x x x ，即)()(21x g x g <，因为x y 21log =是减函数，所以)(log )(log 221121x g x g >，即)()(21x f x f >，所以)(x f 在21(，)∞+上是减函数．21．某旅游点有50辆自行车供游客租赁使用，管理这些自行车的费用是每日115元．根据经验，若每辆自行车的日租金不超过6元，则自行车可以全部租出；若超过6元，则每提高1元，租不出去的自行车就增加3辆．规定：每辆自行车的日租金不超过20元，每辆自行车的日租金x 元只取整数，并要求出租所有自行车一日的总收入必须超过一日的管理费用，用y 表示出租所有自行车的日净收入（即一日中出租所有自行车的总收入减去管理费后的所得）．（1）求函数)(x f y =的解析式及定义域；（2）试问日净收入最多时每辆自行车的日租金应定为多少元？日净收入最多为多少元？解：（1）当x ≤6时，11550-=x y ，令011550>-x ，解得3.2>x ．∵∈x N ，∴x ≥3，∴3≤x ≤6，且∈x N ．当x <6≤20时，115)]6(350[---=x x y 1156832-+-=x x ．综上可知⎩⎨⎧∈≤<-+-∈≤≤-=).,206(,115683),,63(,115502N N x x x x x x x y （2）当3≤x ≤6，且∈x N 时，∵11550-=x y 是增函数，∴当6=x 时，185max =y 元．当x <6≤20，∈x N 时，1156832-+-=x x y 3811)334(32+--=x ， ∴当11=时，270max =y 元．综上所述，当每辆自行车日租金定在11元时才能使日净收入最多，为270元．附加题22．设)(x f 是定义在1[-，]1上的奇函数，且对任意的1[,-∈b a ，]1，当0≠+b a 时，都有ba b f a f ++)()(＞0．（1）若a ＞b ，试比较)(a f 与)(b f 的大小；（2）解不等式)21(-x f ＜)41(-x f ；（3）如果)()(c x f x g -=和)()(2c x f x h -=这两个函数的定义域的交集是空集，求c 的取值范围．解：设1-≤1x ＜2x ≤1，由奇函数的定义和题设条件，得)()()()()()()()(1212121212x x x x x f x f x f x f x f x f --+-+=-+=-＞0，∴)(x f 在]1,1[-上是增函数．∵∈b a ,]1,1[-，a ＞b ，∴)(a f ＞)(b f ．（2）∵)(x f 是]1,1[-上的增函数，∴不等式)21(-x f ＜)41(-x f 等价于⎪⎪⎪⎩⎪⎪⎪⎨⎧-<-≤-≤-≤-≤-,4121,1411,1211x x x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧≤--<--≤-⇔,141,4121,211x x x x ∴原不等式的解集是}4521|{≤≤-x x ．（3）设函数)(),(x h x g 的定义域分别是P 和Q ，则1|{-=x P ≤c x -≤}11|-=c x ≤x ≤}1+c ，1|{-=x Q ≤2c x -≤}11|{2-=c x ≤x ≤}12+c ．于是=Q P φ的充要条件是1+c ＜12-c 或12+c ＜1-c ．解得c 的取值范围是-∞(，2()1 -，)+∞．。

金陵中学2005~2006年度高一年级第一学期第二次阶段性考试

金陵中学2005~2006年度高一年级第一学期第二次阶段性考试化学试题可能用到的相对原子质量：H-1C-12N-14O-16Na-23Mg-24S-32Cl-35.5K-39Ca-40Mn-55Cu-64Ba-137第I卷（选择题）一、选择题（本题包括8小题，每小题只有一个选项符合题意）1．随着人们生活节奏的加快，方便的小包装食品已被广泛接受。

为了延长食品的保质期，防止食品受潮及富脂食品氧化变质，在包装袋中应放入的化学物质是A．无水硫酸铜、蔗糖B．硅胶、硫酸亚铁C．食盐、硫酸亚铁D．生石灰、食盐2．人体血红蛋白中含有Fe2+离子，如果误食亚硝酸盐，会使人中毒，因为亚硝酸盐会使Fe2+离子转变成Fe3+离子，生成高铁血红蛋白而丧失与O2结合的能力。

服用维生素C可缓解亚硝酸盐的中毒，这说明维生素C具有A．酸性B．碱性C．氧化性D．还原性3．下列有关物质用途的叙述中不正确的是A．氧化亚铜均匀分布在玻璃中形成红色玻璃B．氢氧化铝可作色素的吸附剂C．小苏打用于治疗胃溃疡病人的胃酸过多D．明矾可用作净水剂4．纯碱和小苏打是厨房中两种常见的用品，它们都是白色固体。

下列区分这两种物质的方法正确的是A．分别用炒锅加热两种样品，全部分解挥发，没有残留物的是小苏打B．用洁净铁丝蘸取两种样品在煤气火焰上灼烧，使火焰颜色发生明显现象的是小苏打C．在两只玻璃杯中分别加入少量的两种样品，再加入等量食醋，产生气泡快的是小苏打D．先将两样品配成溶液，分别加入石灰水，无白色沉淀生成的是小苏打5．为提纯下列物质（括号内物质为杂质），所选用的试剂和分离方法正确的是6．等质量的钠进行下列实验，其中生成氢气最多的是A．将钠投入到足量水中B．将钠用铝箔包好并刺一些小孔，再放人足量的水中C．将钠放入足量稀硫酸中D．将钠放入足量稀盐酸中7．已知浓H2SO4和Fe3+都可以将Cu氧化（Fe3+与Cu的反应为：2Fe3++Cu=2Fe2++Cu2+），浓H2SO4还可以将Br-氧化成Br2，Fe与Br2反应生成FeBr3，则有关物质氧化性强弱的顺序为A．H2SO4(浓)>Cu2+>Fe3+>Br2B．H2SO4(浓)>Br2>Fe3+>Cu2+C．Br2>H2SO4(浓)>Cu2+>Fe3+D．Cu2+>Fe3+>Br2>H2SO4(浓)8．在氯化铁、氯化铜和盐酸的混合溶液中加入铁粉，待反应结束所剩余的固体滤出后能被磁铁吸引，则反应后溶液中存在的较多的阳离子是A．Cu2+B．Fe3+C．Fe2+D．H+二、选择题（本题包括12小题，每小题有1~2个选项符合题意）9．下列各组离子能大量共存，当溶液中c(H+)=0.1mol/L时，有气体产生；而当溶液中c(OH-)=0.1mol/L时，又能生成沉淀。

金陵中学2004-2005年度第一学期高一期中试题

金陵中学2004-2005年度第一学期高一期中试题可能用到的相对原子质量：H-1 He-4 C-12 N-14 O-16 F-19 Na-23 Mg-24 Al-27 Si-28 P-31 S-32 Cl-35.5 K-39 Ca-40 Fe-56 Cu-64 Zn-65一．选择题：（本题包括12小题，每小题有一个选项符合题意，每小题3分，共36 分） 1．下列物质属于非电解质的是（）A ．醋酸B ．硫酸钡Ｃ．石墨 D ．二氧化碳 2．下列反应中，需加入氧化剂才能发生的是（）A ．Na→NaOHB ．Na 2CO 3→NaHCO 3C ．Na 2O 2→NaOHD ．Na 2O→NaOH 3．若向某一电解质溶液中逐渐滴入另一溶液时，用电解质溶液导电性装置实验，得到溶液导电性与所滴加的溶液体积的关系如下图所示。

则符合图像的是下列中的（） A ．醋酸中逐滴加入氨水 B ．硫酸中逐滴加入氢氧化钠溶液 C ．盐酸中逐滴加入氢氧化钡溶液 D ．硫酸铜中逐滴加入氢氧化钡溶液4．下列离子方程式中正确的是（） A ．Fe 2O 3与稀硫酸反应 O 2－+2H +H 2OB ．Ca(HCO 3)2和Ca(OH)2溶液反应 Ca 2+ + HCO 3－+OH －CaCO 3↓+H 2O C ．碳酸钙和稀盐酸反应 CO 32－+ 2H + H 2O + CO 2↑D ．Ba(OH)2和稀硫酸反应 Ba 2+ + H + + OH －+ SO 42－BaSO 4↓+ H 2O5．下列反应中盐酸作还原剂的是（）A ．CuO +2HCl =CuCl 2 +H 2OB ．Fe(OH)3+3HCl =FeCl 3 +3H 2OC ． Zn+2HCl=ZnCl 2 +H 2 ↑D ．2KMnO 4 + 16HCl =2KCl+2MnCl 2 +5 Cl 2↑+ 8H 2O 6．在一试管中加入水和苯（密度：0.88 g/cm 3）各5 mL 。