【学练优】2016春九年级数学下册 1.6 利用三角函数测高课件 (新版)北师大版
合集下载
北师大版数学九年级下册1.6利用三角函数测高课件

你能测量出
楼顶的旗杆
的高度吗?
教学过程
新
知
新
授
议一议
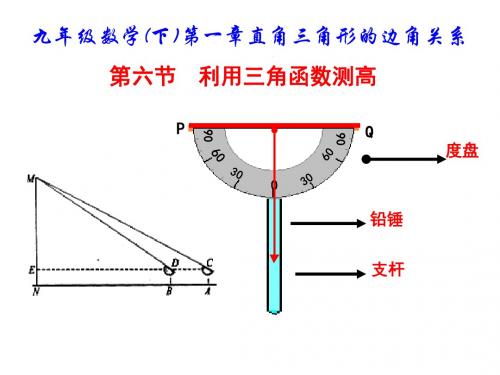
利用三角函数可以测量物体的高度,我们需要
用到一种仪器——侧倾器,侧倾器的构造如下
图:
刻度盘
铅垂线
枝干
教学过程
新
知
新
授
做一做
活动一、用侧倾器测倾斜角
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅垂
线和度盘的0°刻度线重合,这时度盘的顶线PQ在
水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此
时铅垂线所指的度数
教学过程
新
知
新
授
做一做
M
根据测量数据,你能求出目标
M的仰角或俯角吗?说说你的
理由.
Q
O
N
P
B
A
教学过程
新
知
新
授
做一做
活动二、测量底部可以到达的物体的高度
测量工具:测倾器(或经纬仪、测角仪
等)、皮尺等
测量步骤:1.在测点A处安置测倾器,
素的过程,叫做解直角三角形.
2.解直角三角形时至少要知道几个元素?
直角三角形中,除了直角外的5个元素中只要知
道其中两个元素(其中至少要有一边),就可以
求出其余的三个元素.
教学过程
新
课
引
入
议一议
我们学过了用全等三角形、类似三角形测量物
体高度的方法,我们学了三角函数后,可不可
以利用三角函数测量物体的高度呢?
α.
2.在测点A与物体之间的B处安置测倾器(A、B与
N在一条直线上,且A,B之间的距离可以直接测
楼顶的旗杆
的高度吗?
教学过程
新
知
新
授
议一议
利用三角函数可以测量物体的高度,我们需要
用到一种仪器——侧倾器,侧倾器的构造如下
图:
刻度盘
铅垂线
枝干
教学过程
新
知
新
授
做一做
活动一、用侧倾器测倾斜角
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅垂
线和度盘的0°刻度线重合,这时度盘的顶线PQ在
水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此
时铅垂线所指的度数
教学过程
新
知
新
授
做一做
M
根据测量数据,你能求出目标
M的仰角或俯角吗?说说你的
理由.
Q
O
N
P
B
A
教学过程
新
知
新
授
做一做
活动二、测量底部可以到达的物体的高度
测量工具:测倾器(或经纬仪、测角仪
等)、皮尺等
测量步骤:1.在测点A处安置测倾器,
素的过程,叫做解直角三角形.
2.解直角三角形时至少要知道几个元素?
直角三角形中,除了直角外的5个元素中只要知
道其中两个元素(其中至少要有一边),就可以
求出其余的三个元素.
教学过程
新
课
引
入
议一议
我们学过了用全等三角形、类似三角形测量物
体高度的方法,我们学了三角函数后,可不可
以利用三角函数测量物体的高度呢?
α.
2.在测点A与物体之间的B处安置测倾器(A、B与
N在一条直线上,且A,B之间的距离可以直接测
北师大版九年级数学下册1.6利用三角函数测高讲义1(共18张PPT)

M
讲授正课
(3)到目前为止,你有那些测量物体高度的方法?
解书习本题P1:.23 如图,作EM垂直CD于M点,根据题意,可知
解: 在Rt△AEG中,EG=AG/tan30°=1.
E=301°7B.,=45°1,.460mm,∠DEM=30°,BC=EM=30 m,
解:如图,作EM垂直CD于M点,根据题意,可知
?
D
A
C
随堂练习
2. 一测量船在海平面A点测得岸上山顶C的仰角 为30°,该船向前行驶100米后到达点B,测得岸上 山顶C的仰角为60°求山的高CD。
C
?
60°
D
B
30°
100
A
小结与拓展
如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得 主楼顶部的仰角是30°,而当时侧倾器离地面1. (2)误差的解决办法---用平均值 一测量船在海平面A点测得岸上山顶C的仰角为30°,该船向前行驶100米后到达点B,测得岸上山顶C的仰角为60°求山的高CD。 解: 在Rt△AEG中,EG=AG/tan30°=1. (3)到目前为止,你有那些测量物体高度的方法?
章直角三角形的边角关系
1.6利用三角函数 测高
情景导入
➢ 活动课题:利用直角三角形的边角关系测量物体的高度. ➢ 活动方式:分组活动,全班交流研讨. ➢ 活动工具:测倾器(或经纬仪,测角仪),皮尺等.
讲授正课
➢ 活动一: 测量倾斜角.
测量倾斜角可以用测倾 器.简单的侧倾器由度盘、 铅锤和支杆组成
3、量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据 测量数据,可求出物体MN的高度.
讲授正课
(3)到目前为止,你有那些测量物体高度的方法?
解书习本题P1:.23 如图,作EM垂直CD于M点,根据题意,可知
解: 在Rt△AEG中,EG=AG/tan30°=1.
E=301°7B.,=45°1,.460mm,∠DEM=30°,BC=EM=30 m,
解:如图,作EM垂直CD于M点,根据题意,可知
?
D
A
C
随堂练习
2. 一测量船在海平面A点测得岸上山顶C的仰角 为30°,该船向前行驶100米后到达点B,测得岸上 山顶C的仰角为60°求山的高CD。
C
?
60°
D
B
30°
100
A
小结与拓展
如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得 主楼顶部的仰角是30°,而当时侧倾器离地面1. (2)误差的解决办法---用平均值 一测量船在海平面A点测得岸上山顶C的仰角为30°,该船向前行驶100米后到达点B,测得岸上山顶C的仰角为60°求山的高CD。 解: 在Rt△AEG中,EG=AG/tan30°=1. (3)到目前为止,你有那些测量物体高度的方法?
章直角三角形的边角关系
1.6利用三角函数 测高
情景导入
➢ 活动课题:利用直角三角形的边角关系测量物体的高度. ➢ 活动方式:分组活动,全班交流研讨. ➢ 活动工具:测倾器(或经纬仪,测角仪),皮尺等.
讲授正课
➢ 活动一: 测量倾斜角.
测量倾斜角可以用测倾 器.简单的侧倾器由度盘、 铅锤和支杆组成
3、量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据 测量数据,可求出物体MN的高度.
1.6北师大版九年级数学下册课件第一章第六节利用三角函数测高
练习
复习题9
求图中避雷针的长度(结果精确到0.01m). 解:如图,根据题意,可知 AB=20m,∠CAB=50°,∠DAB=56° 在Rt△DBA中, ∠DBA=90°. DB=AB· tan56°≈20×1.4826=29.652(m) 在Rt△CBA中, ∠CBA=90°. CB=AB· tan50°≈ 20×1.1918 =23.836(m) 所以避雷针的长度 DC=DB-CB=29.652-23.836≈5.82(m).
1.(2014•浙江宁波)如图,从 A 地到 B 地的公路需经过 C 地, 图中 AC=10 千米,∠CAB=25° ,∠CBA=37° ,因城市规划的需 要,将在 A、B 两地之间修建一条笔直的公路. (1)求改直的公路 AB 的长; (sin25° ≈0.42,cos25° ≈0.91,sin37° ≈0.60,tan37° ≈0.75) 解: (1)作 CH⊥AB 于 H. 在 Rt△ACH 中,CH=AC•sin∠CAB =AC•sin25°≈10× 0.42=4.2 千米, AH=AC•cos∠CAB=AC•cos25° ≈10× 0.91=9.1 千米, CH 在 Rt△BCH 中,BH= H tan∠CBA 4.2 4.2 = ≈ =5.6 千米, 0.75 tan37° 中考链接 ∴AB=AH+BH=9.1+5.6=14.7 千米. 故改直的公路 AB 的长 14.7 千米;
2、转动度盘,使度盘的直径对准目标M,记下此时铅垂线 所指的读数。 M P
30°
Q
活动二:测量底部可以到达的物体的高度. 所谓“底部可以到达”, 就是在地面上可以无障碍 地直接测得测点与被测物 体底部之间的距离. 如图,要测量物体MN的高 度,可以按下列步骤进行: 1.在测点A处安置测倾器,测得M的仰角∠MCE=α. 2.量出测点A到物体底部N的水平距离AN=l. 3.量出测倾器的高度AC=a(即顶线PQ水平位置时它与 地面的距离).
九年级数学北师大版初三下册--第一单元1.6《利用三角函数测高》课件

44° 35’ 45° 25’
G B
CD的长
60.11m 59.89m
(1)到目前为止,你有哪些测量物体高度的方法? (2)如果一个物体的高度已知或容易测量,那么 如何测量某测点到该物体的水平距离?
讨 与同伴交流一下,谈谈你的想法? 论 :
1.如图1-16,在高20米的建筑物CD的顶部C测得塔顶A的仰角
=L·tanα
α
C
L
aA
MN=ME+EN=ME+AC=L·tanα+ a
课题 测量学校旗杆MN的高度(底部可以到达)
测
M
量
MN=Ltanα+ a
示 意 图
E N
α
L
C aA
测量项目
第一次
第二次
平均值
测
得
倾斜角α α=30°15′
α=19°49 ′
α=30°2 ′
数 据
测倾器高a a =1.23m
a =1.21 m a =1.22m
活动1:测量倾斜角
水平线
根据刚才测 量数据,你能求 出目标M的仰角 或俯角吗?说说 你的理由.
同角的余角 相等
活动1:测量倾斜角
水平线
1
2
4
3
活动2:测量底部可以到达的物体的高度.
所谓“底部可以到达”,就是在地面上可以无障碍地直接
测得测点与被测物体底部之间的距离. 如图,要测量物体MN的高度,需测量哪些数据?
为60°,测得塔底B的俯角为30°,则塔高AB =
米;
2.如图1-17,小明想测量电线杆AB的高度,发现电线杆的影
子恰好落在地面BC和斜坡的坡面CD上,测得BC = 10米,CD =
北师大版九年级数学下册《利用三角函数测高》PPT课件

(2)DE=AC=610(米), 在Rt△BDE中,tan∠BDE=
故BE=DE tan39°. 因为 CD=AE,所以 CD=AB-DE·tan39°=610-610×tan39°≈116(米)
4. 小明家所在居民楼的对面有一座大厦 AB,AB=80
米.为测量居民楼与这座大厦之间的距离,小明从自
∠α
第一次 30°16'
第二次 29°44'
平均值
30°
G B
∠β 45° 5' 44°25’'
45°
CD 的长 60.11 m 59.89 m
60 m
解:由表格中数据,得α = 30° ,β = 45°,
tan AG , tan AG ,
EG
FG
EG AG AG 3AG,
tan tan 30
E
或 BN 的长度.
A
B
N
问题 2:测量东方明珠的高度的步骤是怎么样的M 呢?
ME ME b, MN ME a
tan tan
CαD β
E
AB
N
1. 在测点 A 处安置测倾器,测得此时 M 的仰角∠MCE=α;
2. 在测点 A 与物体之间的 B 处安置测倾器,测得此时
M 的仰角 ∠MDE = β;
D′
C′
B′
x
50
25 3 43.3(mD)
tan 60 tan 30
C
B
x 43.3 1.5 45(m)
3.目前世界上最高的电视塔是广州新电视塔.如图所示,
新电视塔高 AB 为 610 米,远处有一栋大楼,某人在楼 底 C 处测得塔顶 B 的仰角为 45°,在楼顶 D 处测得塔 顶 B 的仰角为 39°.(tan39° ≈ 0.81) (1)求大楼与电视塔之间的距离 AC; (2)求大楼的高度 CD(精确到 1 米) 解:(1)由题意,AC=AB=610(米);
故BE=DE tan39°. 因为 CD=AE,所以 CD=AB-DE·tan39°=610-610×tan39°≈116(米)
4. 小明家所在居民楼的对面有一座大厦 AB,AB=80
米.为测量居民楼与这座大厦之间的距离,小明从自
∠α
第一次 30°16'
第二次 29°44'
平均值
30°
G B
∠β 45° 5' 44°25’'
45°
CD 的长 60.11 m 59.89 m
60 m
解:由表格中数据,得α = 30° ,β = 45°,
tan AG , tan AG ,
EG
FG
EG AG AG 3AG,
tan tan 30
E
或 BN 的长度.
A
B
N
问题 2:测量东方明珠的高度的步骤是怎么样的M 呢?
ME ME b, MN ME a
tan tan
CαD β
E
AB
N
1. 在测点 A 处安置测倾器,测得此时 M 的仰角∠MCE=α;
2. 在测点 A 与物体之间的 B 处安置测倾器,测得此时
M 的仰角 ∠MDE = β;
D′
C′
B′
x
50
25 3 43.3(mD)
tan 60 tan 30
C
B
x 43.3 1.5 45(m)
3.目前世界上最高的电视塔是广州新电视塔.如图所示,
新电视塔高 AB 为 610 米,远处有一栋大楼,某人在楼 底 C 处测得塔顶 B 的仰角为 45°,在楼顶 D 处测得塔 顶 B 的仰角为 39°.(tan39° ≈ 0.81) (1)求大楼与电视塔之间的距离 AC; (2)求大楼的高度 CD(精确到 1 米) 解:(1)由题意,AC=AB=610(米);
北师大版九年级数学下册《利用三角函数测高》直角三角形的边角关系PPT精品课件

CM=BE=1.4m
在Rt△DEM中,
DM=EMtan30°≈30×0.577 =17.32(m),
CD=DM+CM=17.32+1.4≈18.72(m).
∴学校主楼的高度约为18.72m.
A
E
B
30°
M
C
总结:与仰角(或俯角)有关的计算问题的解决方法:
首先弄清哪个角是仰角(或俯角),再选择或构造恰当的
AB=b.
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
β
α
b
a
议一议
(1)到目前为止,你有哪些测量物体高度的方法?
一、测量底部可以到达的物体的高度,如图
M
E
N
C
A
二、测量底部不可以直接到达的物体的高度,如图
M
E
N
D
C
B
ቤተ መጻሕፍቲ ባይዱ
A
(2)如果一个物体的高度已知或容易测量,那么如何
测量某测点到该物体的水平距离?
相信大家就能轻松解决上面的问题了.
问题1:如何测量长度? 测量长度可以用皮尺或卷尺,
问题2:如何测量倾斜角?
90
测量倾斜角可以用测倾器,
----简单的侧倾器由度盘、铅锤和支杆组成.
P
Q
度盘
0
铅锤
支杆
M
活动一:测量倾斜角
⬥使用测倾器测量倾斜角的
步骤如下:
1.把支杆竖直插入地面,使支
杆的中心线、铅锤线和度盘
留整数).
(参考数据:tan28°≈0.53, cos28°≈0.88,sin28°≈0.47,
≈1.41)
【详解】解:延长BE交CD于点G,交CF于点H,
最新北师大版九年级数学下1.6利用三角函数测高ppt公开课优质课件

第一章 直角三角形的边角关系
1.6 利用三角函数测高
导入新课 讲授新课 当堂练习 课堂小结
学习目标
1.能够设计活动方案、自制测倾器和运用测倾器进行实地
测量以及撰写活动报告的过程;
2.能够对所得的数据进行整理、分析和矫正;(重点) 3.能够综合运用直角三角形边角关系的知识解决实际问题. (难点)
导入新课
器测得塔顶的仰角∠BAC为25°(在视线与水平线所成
的角中,视线在水平线上方的叫作仰角,在水平线下 方的叫作俯角),仪器距地面高为1.7m. 求上海东方明珠塔的高BD.(结果精确到1m.)
解:如图,在Rt△ABC中,∠BAC =25°,AC =1000m,
BC BC 因此 tan 25 AC 1000
观察与思考
某探险者某天到达如图
所示的点A 处时,他准备估
算出离他的目的地——海拔 为3 500 m的山峰顶点B处的 水平距离.他能想出一个可行 的办法吗?
B
.
A .
通过这节课的学习,相
信你也行.
Байду номын сангаас
讲授新课
一 测量倾斜角
问题1:如何测量倾斜角? 测量倾斜角可以用测倾器, ----简单的侧倾器由度盘、铅锤和支杆组成 P Q 度盘 90 90 0
首页
解:如图,作EM垂直CD于M点, 根据题意,可知 EB=1.4m∠DEM=30°,BC=EM= M
30 m, CM=BE=1.4m 在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m),
CD=DM+CM=17.32+1.4=18.72(m).
三 测量底部不可以到达的物体的高度
从而 BC=1000×tan25°≈466.3(m) 因此,上海东方明珠塔的高度
1.6 利用三角函数测高
导入新课 讲授新课 当堂练习 课堂小结
学习目标
1.能够设计活动方案、自制测倾器和运用测倾器进行实地
测量以及撰写活动报告的过程;
2.能够对所得的数据进行整理、分析和矫正;(重点) 3.能够综合运用直角三角形边角关系的知识解决实际问题. (难点)
导入新课
器测得塔顶的仰角∠BAC为25°(在视线与水平线所成
的角中,视线在水平线上方的叫作仰角,在水平线下 方的叫作俯角),仪器距地面高为1.7m. 求上海东方明珠塔的高BD.(结果精确到1m.)
解:如图,在Rt△ABC中,∠BAC =25°,AC =1000m,
BC BC 因此 tan 25 AC 1000
观察与思考
某探险者某天到达如图
所示的点A 处时,他准备估
算出离他的目的地——海拔 为3 500 m的山峰顶点B处的 水平距离.他能想出一个可行 的办法吗?
B
.
A .
通过这节课的学习,相
信你也行.
Байду номын сангаас
讲授新课
一 测量倾斜角
问题1:如何测量倾斜角? 测量倾斜角可以用测倾器, ----简单的侧倾器由度盘、铅锤和支杆组成 P Q 度盘 90 90 0
首页
解:如图,作EM垂直CD于M点, 根据题意,可知 EB=1.4m∠DEM=30°,BC=EM= M
30 m, CM=BE=1.4m 在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m),
CD=DM+CM=17.32+1.4=18.72(m).
三 测量底部不可以到达的物体的高度
从而 BC=1000×tan25°≈466.3(m) 因此,上海东方明珠塔的高度
