苏教版高中数学选修2-2《1.1.2 瞬时变化率——导数(2)》教案
高中数学第一章导数及其应用1.1.2瞬时变化率--导数学案苏教版选修2

1.1.2 瞬时变化率——导数导数定义求函数的导函数.1.瞬时速度(1)在物理学中,运动物体的位移与所用时间的比称为__________.(2)一般地,如果当Δt __________0时,运动物体位移s (t )的平均变化率s (t 0+Δt )-s (t 0)Δt无限趋近于一个______,那么这个______称为物体在t =t 0时的__________,也就是位移对于时间的____________.预习交流1做一做:如果质点A 按规律s =3t 2运动,则在t =3 s 时的瞬时速度为__________. 2.瞬时加速度一般地,如果当Δt __________时,运动物体速度v (t )的平均变化率v (t 0+Δt )-v (t 0)Δt无限趋近于一个_______,那么这个________称为物体在t =t 0时的_________,也就是速度对于时间的____________.3.导数(1)设函数y =f (x )在区间(a ,b )上有定义,x 0∈(a ,b ),若Δx 无限趋近于0时,比值Δy Δx =f (x 0+Δx )-f (x 0)Δx无限趋近于一个______A ,则称f (x )在x =x 0处______,并称该______A 为函数f (x )在x =x 0处的______,记为______.(2)导数f ′(x 0)的几何意义就是曲线y =f (x )在点P (x 0,f (x 0))处切线的________. (3)若f (x )对于区间(a ,b )内任一点都可导,则f (x )在各点的导数也随着自变量x 的变化而变化,因而也是自变量x 的函数,该函数称为f (x )的________,记作________.预习交流2做一做:设函数f (x )可导,则当Δx →0时,f (1+Δx )-f (1)3Δx等于__________.预习交流3做一做:函数y =x +1x在x =1处的导数是__________.预习交流4利用导数求曲线切线方程的步骤有哪些?预习导引1.(1)平均速度 (2)无限趋近于 常数 常数 瞬时速度 瞬时变化率预习交流1:提示:s (3+Δt )=3(3+Δt )2=3[9+6Δt +(Δt )2]=27+18Δt +3(Δt )2.s (3)=3×32=27.Δs =s (3+Δt )-s (3)=18Δt +3(Δt )2, ∴Δs Δt =18+3Δt ,当Δt →0时,ΔsΔt→18. 2.无限趋近于0 常数 常数 瞬时加速度 瞬时变化率3.(1)常数 可导 常数 导数 f ′(x 0) (2)斜率 (3)导函数 f ′(x )预习交流2:提示:f (1+Δx )-f (1)3Δx =13·f (1+Δx )-f (1)Δx,当Δx →0时,f (1+Δx )-f (1)Δx =f ′(1),∴原式=13f ′(1).预习交流3:提示:∵函数y =f (x )=x +1x,∴Δy =f (1+Δx )-f (1)=1+Δx +11+Δx -1-1=(Δx )21+Δx.∴Δy Δx =Δx 1+Δx ,当Δx →0时,Δy Δx →0,即y =x +1x在x =1处的导数为0. 预习交流4:提示:利用导数的几何意义求曲线的切线方程的步骤: (1)求出函数y =f (x )在点x 0处的导数f ′(x 0);(2)根据直线的点斜式方程,得切线方程为y -y 0=f ′(x 0)(x -x 0); (3)将所得切线方程化为一般式.一、求瞬时速度一辆汽车按规律s =at 2+1做直线运动,当汽车在t =2 s 时的瞬时速度为12 m/s ,求a .思路分析:先根据瞬时速度的求法得到汽车在t =2 s 时的瞬时速度的表达式,再代入求出a 的值.1.一个物体的运动方程为s =1-t +t 2.其中s 的单位是m ,t 的单位是s ,那么物体在3 s 末的瞬时速度是__________.2.子弹在枪筒中运动可以看作是匀变速运动,如果它的加速度是a =5×105 m/s 2,子弹从枪口射出时所用的时间为t 0=1.6×10-3s .求子弹射出枪口时的瞬时速度.根据条件求瞬时速度的步骤:(1)探究非匀速直线运动的规律s =s (t );(2)由时间改变量Δt 确定路程改变量Δs =s (t 0+Δt )-s (t 0);(3)求平均速度v =ΔsΔt;(4)运用逼近思想求瞬时速度,当Δt →0时,ΔsΔt→v (常数).二、利用导数的定义求函数的导数已知f (x )=x 2-3.(1)求f (x )在x =2处的导数; (2)求f (x )在x =a 处的导数.思路分析:根据导数的定义进行求解.深刻理解概念是正确解题的关键.1.若函数f (x )=ax -2在x =3处的导数等于4,则a =__________.2.(1)求函数f (x )=1x +1在x =1处的导数;(2)求函数f (x )=2x 的导数.结合函数,先求出Δy =f (x 0+Δx )-f (x 0),再求ΔyΔx=f (x 0+Δx )-f (x 0)Δx ,当Δx →0时,求ΔyΔx 的值,即f ′(x 0).三、导数的几何意义已知y =2x 3上一点A (1,2),求点A 处的切线斜率.思路分析:为求得过点(1,2)的切线斜率,可以从经过点(1,2)的任意一条直线(割线)入手.1.抛物线y =14x 2在点Q (2,1)处的切线方程为__________.2.已知曲线y =3x 2-x ,求曲线上一点A (1,2)处的切线的斜率及切线方程.1.导数的几何意义是指:曲线y =f (x )在(x 0,y 0)点处的切线的斜率就是函数y =f (x )在x =x 0处的导数,而切线的斜率就是切线倾斜角的正切值.2.运用导数的几何意义解决曲线的切线问题时,一定要注意所给的点是否是在曲线上,若点在曲线上,则该点的导数值就是该点处的曲线的切线的斜率;若点不在曲线上,则该点的导数值不是切线的斜率.3.若所给的点不在曲线上,应另设切点,然后利用导数的几何意义建立关于所设切点横坐标的关系式进行求解.1.若一物体的运动方程为s =2-12t 2,则该物体在t =6时的瞬时速度为__________.2.已知曲线y =12x 2-2上一点P ⎝⎛⎭⎪⎫1,-32,则过点P 的切线的倾斜角为__________. 3.函数f (x )=1-3x 在x =2处的导数为__________.4.一质点按规律s =2t 3运动,则t =2时的瞬时速度为__________.5.如图,函数y =f (x )的图象在点P 处的切线是l ,则f (2)+f ′(2)=__________.答案:活动与探究1:解:∵s =at 2+1,∴s (2+Δt )=a (2+Δt )2+1=4a +4a ·Δt +a ·(Δt )2+1.于是Δs =s (2+Δt )-s (2)=4a +4a ·Δt +a ·(Δt )2+1-(4a +1)=4a ·Δt +a ·(Δt )2,∴Δs Δt =4a ·Δt +a ·(Δt )2Δt=4a +a ·Δt . 当Δt →0时,ΔsΔt→4a ,依题意有4a =12,∴a =3. 迁移与应用:1.5 m/s 解析:s (3+Δt )=1-(3+Δt )+(3+Δt )2=(Δt )2+5Δt +7,所以s (3+Δt )-s (3)=(Δt )2+5Δt , 故s (3+Δt )-s (3)Δt=Δt +5,于是物体在3 s 末的瞬时速度,即Δt →0时,ΔsΔt→5(m/s).2.解:运动方程为s =12at 2.∵Δs =12a (t 0+Δt )2-12at 20=at 0·Δt +12a ·(Δt )2,∴Δs Δt =at 0+12a ·Δt ,∴Δt →0时,ΔsΔt→at 0. 由题意知a =5×105(m/s 2),t 0=1.6×10-3(s),故at 0=8×102=800(m/s).即子弹射出枪口时的瞬时速度为800 m/s.活动与探究2:解:(1)因为Δy Δx =f (2+Δx )-f (2)Δx=(2+Δx )2-3-(22-3)Δx=4+Δx ,当Δx 无限趋近于0时,4+Δx 无限趋近于4, 所以f (x )在x =2处的导数等于4.(2)因为Δy Δx =f (a +Δx )-f (a )Δx=(a +Δx )2-3-(a 2-3)Δx=2a +Δx ,当Δx 无限趋近于0时,2a +Δx 无限趋近于2a , 所以f (x )在x =a 处的导数等于2a .迁移与应用:1.4 解析:由题意知f ′(3)=4,而f ′(3)=Δy Δx =a (3+Δx )-2-(3a -2)Δx=a ,当Δx →0时,ΔyΔx→a ,故a =4.2.解:(1)(导数定义法)∵Δy =f (1+Δx )-f (1)=12+Δx -12=-Δx 2(2+Δx ),∴ΔyΔx=-12(2+Δx ),从而Δx →0时,2+Δx →2,∴f (x )在x =1处的导数等于-14.(导函数的函数值法)∵Δy =1x +Δx +1-1x +1=-Δx (x +Δx +1)(x +1),∴ΔyΔx=-1(x +Δx +1)(x +1),从而Δx →0时,Δy Δx →-1(x +1)2,于是f ′(1)=-1(1+1)2=-14.(2)∵Δy =f (x +Δx )-f (x )=2x +Δx -2x ,∴Δy Δx =2x +Δx -2x Δx =(2x +Δx -2x )(x +Δx +x )Δx (x +Δx +x )=2x +Δx +x,从而Δx →0时,Δy Δx →1x.活动与探究3:解:设A (1,2),B (1+Δx,2(1+Δx )3),则割线AB 的斜率为k AB =2(1+Δx )3-2Δx =6+6Δx +2(Δx )2,当Δx 无限趋近于0时,k AB 无限趋近于常数6,从而曲线y =2x 3在点A (1,2)处的切线斜率为6.迁移与应用:1.x -y -1=0 解析:∵y =14x 2,Δy =14(2+Δx )2-14×22=Δx +14(Δx )2,Δy Δx=1+14Δx , ∴当Δx →0时,Δy Δx →1,即f ′(2)=1,由导数的几何意义得抛物线y =14x 2在点Q (2,1)处的切线的斜率为1.∴切线方程为y -1=x -2,即x -y -1=0.2.解:因为Δy Δx =3(1+Δx )2-(1+Δx )-(3×12-1)Δx=5+3Δx ,当Δx 无限趋近于0时,5+3Δx 无限趋近于5,所以曲线y =3x 2-x 在点A (1,2)处的切线斜率是5.切线方程为y -2=5(x -1),即5x -y -3=0. 当堂检测1.-6 解析:Δs Δt =s (6+Δt )-s (6)Δt =2-12(6+Δt )2-(-16)Δt =-12Δt -6,∴当Δt →0时,ΔsΔt→-6.2.45° 解析:∵Δy Δx =12(1+Δx )2-2-12×1+2Δx =Δx +12(Δx )2Δx =1+12Δx ,当Δx无限趋近于0时,1+12Δx 无限趋近于1,∴曲线y =12x 2-2在点P ⎝⎛⎭⎪⎫1,-32处的切线斜率为1,∴倾斜角为45°.3.-3 解析:Δy =f (2+Δx )-f (2)=-3Δx ,Δy Δx =-3,则Δx 趋于0时,ΔyΔx=-3.∴f (x )在x =2处的导数为-3.4.24 解析:Δs =s (2+Δt )-s (2)=2(2+Δt )3-2×23=2×[8+6(Δt )2+12Δt +(Δt )3]-16=24Δt +12(Δt )2+2(Δt )3, ∴Δs Δt =24+12Δt +2(Δt )2,则当Δt →0时,Δs Δt →24. 5.98解析:由题图可知,直线l 的方程为9x +8y -36=0. 当x =2时,y =94,即f (2)=94.又切线斜率为-98,即f ′(2)=-98,∴f (2)+f ′(2)=98.欢迎您的下载,资料仅供参考!。
(教师用书)高中数学 1.1.2 瞬时变化率 导数同步备课课件 苏教版选修2-2

1.曲线上一点处的切线 设 Q 为曲线 C 上不同于 P 的一点,这时,直线 PQ 称
割线 ,随着点 Q 沿曲线 C 向点 P 运动,割线 PQ 为曲线的______ 逼近 曲线 C.当点 Q__________ 无限逼近 点 P 时, 在点 P 附近越来越______
逼近 曲线的直线 l,这条 直线 PQ 最终就成为在点 P 处最______
常数 ,则称 f(x)在 x=x0 处______ 可导 ,并 限趋近于一个_____A 常数 为函数 f(x)在 x=x0 处的______ 导数 ,记作 f′(x0). 称该_____A
2.导数的几何意义 导数 f′(x0)的几何意义就是曲线 y=f(x)在点 P(x0,f(x0))
斜率 处 的 切 线 的 _______ , 切 线
●教学建议 新课标对“导数及其应用”内容的处理有较大的变化, 它不介绍极限的形式化定义及相关知识,而是按照“平均变 化率——曲线在某一点处的切线——瞬时速度(加速度)—— 瞬时变化率 ——导数的概念”这样的顺序来安排,用“逼 近”的方法来定义导数,这种概念建立的方式直观、形象、 生动,又易于理解,突出导数概念的形成过程. 因此,在教学中采用教师启发诱导与学生动手操作、自 主探究、合作交流相结合的教学方式,引导学生动手操作、 观察、分析、类比、抽象、概括,并借助 excel 及几何画板 演示,调动学生参与课堂教学的主动性和积极性.
y-f(x0)=f′(x0)(x-x0) ___________________________ .
PT
的 方 程 是
求瞬时速度、瞬时加速度
已知质点 M 的运动速度与运动时间的关系为 v= 3t2+2(速度单位:cm/s,时间单位:s), Δv (1)当 t=2,Δ t=0.01 时,求 ; Δt (2)求质点 M 在 t=2 时的瞬时加速度. 【思路探究】
苏教版高二数学选修2-2 1.1.2瞬时变化率——导数 学案

1.1.2 瞬时变化率——导数学习目标 1.理解切线的含义.2.理解瞬时速度与瞬时加速度.3.掌握瞬时变化率——导数的概念,会根据定义求一些简单函数在某点处的导数.知识点一 曲线上某一点处的切线如图,P n 的坐标为(x n ,f (x n ))(n =1,2,3,4,…),点P 的坐标为(x 0,y 0).思考1 当点P n →点P 时,试想割线PP n 如何变化?答案 当点P n 趋近于点P 时,割线PP n 趋近于确定的位置,即曲线上点P 处的切线位置. 思考2 割线PP n 的斜率是什么?它与切线PT 的斜率有何关系. 答案 割线PP n 的斜率k n =f (x n )-f (x 0)x n -x 0;当P n 无限趋近于P 时,k n 无限趋近于点P 处切线的斜率k .梳理 (1)设Q 为曲线C 上的不同于P 的一点,这时,直线PQ 称为曲线的割线.随着点Q 沿曲线C 向点P 运动,割线PQ 在点P 附近越来越逼近曲线C .当点Q 无限逼近点P 时,直线PQ 最终就成为在点P 处最逼近曲线的直线l ,这条直线l 称为曲线在点P 处的切线. (2)若P (x ,f (x )),过点P 的一条割线交曲线C 于另一点Q (x +Δx ,f (x +Δx )),则割线PQ 的斜率为k PQ =f (x +Δx )-f (x )Δx ,当Δx →0时,f (x +Δx )-f (x )Δx 无限趋近于点P (x ,f (x ))处的切线的斜率.知识点二 瞬时速度与瞬时加速度——瞬时变化率 1.平均速度在物理学中,运动物体的位移与所用时间的比称为平均速度. 2.瞬时速度一般地,如果当Δt 无限趋近于0时,运动物体位移S (t )的平均变化率S (t 0+Δt )-S (t 0)Δt无限趋近于一个常数,那么这个常数称为物体在t =t 0时的瞬时速度,也就是位移对于时间的瞬时变化率. 3.瞬时加速度一般地,如果当Δt 无限趋近于0时,运动物体速度v (t )的平均变化率v (t 0+Δt )-v (t 0)Δt 无限趋近于一个常数,那么这个常数称为物体在t =t 0时的瞬时加速度,也就是速度对于时间的瞬时变化率. 知识点三 导数 1.导数设函数y =f (x )在区间(a ,b )上有定义,x 0∈(a ,b ),若Δx 无限趋近于0时,比值Δy Δx=f (x 0+Δx )-f (x 0)Δx 无限趋近于一个常数A ,则称f (x )在x =x 0处可导,并称该常数A 为函数f (x )在x =x 0处的导数,记作f ′(x 0). 2.导数的几何意义导数f ′(x 0)的几何意义就是曲线y =f (x )在点P (x 0,f (x 0))处的切线的斜率. 3.导函数(1)若f (x )对于区间(a ,b )内任一点都可导,则f (x )在各点的导数也随着自变量x 的变化而变化,因而也是自变量x 的函数,该函数称为f (x )的导函数,记作f ′(x ).在不引起混淆时,导函数f ′(x )也简称为f (x )的导数.(2)f (x )在x =x 0处的导数f ′(x 0)就是导函数f ′(x )在x =x 0处的函数值.类型一 求曲线上某一点处的切线例1 已知曲线y =x +1x 上的一点A (2,52),用切线斜率定义求:(1)点A 处的切线的斜率; (2)点A 处的切线方程. 解 (1)∵Δy =f (2+Δx )-f (2)=2+Δx +12+Δx -(2+12)=-Δx 2(2+Δx )+Δx ,∴Δy Δx =-Δx 2Δx (2+Δx )+ΔxΔx =-12(2+Δx )+1. 当Δx 无限趋近于零时,Δy Δx 无限趋近于34,即点A 处的切线的斜率是34.(2)切线方程为y -52=34(x -2),即3x -4y +4=0.反思与感悟 根据曲线上一点处的切线的定义,要求曲线过某点的切线方程,只需求出切线的斜率,即在该点处,Δx 无限趋近于0时,ΔyΔx无限趋近的常数.跟踪训练1 (1)已知曲线y =2x 2+4x 在点P 处的切线的斜率为16,则点P 坐标为________. 答案 (3,30)解析 设点P 坐标为(x 0,y 0), 则f (x 0+Δx )-f (x 0)(x 0+Δx )-x 0=2(Δx )2+4x 0Δx +4Δx Δx=4x 0+4+2Δx .当Δx 无限趋近于0时,4x 0+4+2Δx 无限趋近于4x 0+4, 因此4x 0+4=16,即x 0=3, 所以y 0=2×32+4×3=18+12=30. 即点P 坐标为(3,30).(2)已知曲线y =3x 2-x ,求曲线上一点A (1,2)处的切线的斜率及切线方程. 解 设A (1,2),B (1+Δx,3(1+Δx )2-(1+Δx )), 则k AB =3(1+Δx )2-(1+Δx )-(3×12-1)Δx =5+3Δx ,当Δx 无限趋近于0时,5+3Δx 无限趋近于5, 所以曲线y =3x 2-x 在点A (1,2)处的切线斜率是5. 切线方程为y -2=5(x -1),即5x -y -3=0. 类型二 求瞬时速度例2 某物体的运动路程s (单位:m)与时间t (单位:s)的关系可用函数s (t )=t 2+t +1表示,求物体在t =1 s 时的瞬时速度.解 在1到1+Δt 的时间内,物体的平均速度v =Δs Δt =s (1+Δt )-s (1)Δt=(1+Δt )2+(1+Δt )+1-(12+1+1)Δt=3+Δt ,∴当Δt 无限趋近于0时,v 无限趋近于3, ∴物体在t =1处的瞬时变化率为3. 即物体在t =1 s 时的瞬时速度为3 m/s. 引申探究1.若本例中的条件不变,试求物体的初速度.解 求物体的初速度,即求物体在t =0时的瞬时速度. ∵Δs Δt =s (0+Δt )-s (0)Δt=(0+Δt )2+(0+Δt )+1-1Δt=1+Δt ,∴当Δt →0时,1+Δt →1,∴物体在t =0时的瞬时变化率为1, 即物体的初速度为1 m/s.2.若本例中的条件不变,试问物体在哪一时刻的瞬时速度为9 m/s. 解 设物体在t 0时刻的速度为9 m/s. 又Δs Δt =s (t 0+Δt )-s (t 0)Δt=(2t 0+1)+Δt .∴当Δt →0时,ΔsΔt →2t 0+1.则2t 0+1=9,∴t 0=4.则物体在4 s 时的瞬时速度为9 m/s.反思与感悟 (1)求瞬时速度的题目的常见错误是不能将物体的瞬时速度转化为函数的瞬时变化率.(2)求运动物体瞬时速度的三个步骤①求时间改变量Δt 和位移改变量Δs =s (t 0+Δt )-s (t 0). ②求平均速度v =Δs Δt. ③求瞬时速度,当Δt 无限趋近于0时,ΔsΔt无限趋近于的常数v 即为瞬时速度.跟踪训练2 一质点M 按运动方程s (t )=at 2+1做直线运动(位移单位:m ,时间单位:s),若质点M 在t =2 s 时的瞬时速度为8 m/s ,求常数a 的值.解 质点M 在t =2 s 时的瞬时速度即为函数在t =2 s 处的瞬时变化率. ∵质点M 在t =2 s 附近的平均变化率为 Δs Δt =s (2+Δt )-s (2)Δt =a (2+Δt )2-4a Δt =4a +a Δt , ∴当Δt →0时,ΔsΔt →4a =8,即a =2.类型三 求函数在某点处的导数 例3 已知f (x )=x 2-3. (1)求f (x )在x =2处的导数;(2)求f (x )在x =a 处的导数. 解 (1)因为Δy Δx =f (2+Δx )-f (2)Δx=(2+Δx )2-3-(22-3)Δx=4+Δx ,当Δx 无限趋近于0时,4+Δx 无限趋近于4, 所以f (x )在x =2处的导数等于4. (2)因为Δy Δx =f (a +Δx )-f (a )Δx=(a +Δx )2-3-(a 2-3)Δx=2a +Δx ,当Δx 无限趋近于0时,2a +Δx 无限趋近于2a , 所以f (x )在x =a 处的导数等于2a .反思与感悟 求一个函数y =f (x )在x =x 0处的导数的步骤 (1)求函数值的改变量Δy =f (x 0+Δx )-f (x 0). (2)求平均变化率Δy Δx =f (x 0+Δx )-f (x 0)Δx .(3)令Δx 无限趋近于0,求得导数.跟踪训练3 (1)设f (x )=ax +4,若f ′(1)=2,则a =________. 答案 2解析 ∵f (1+Δx )-f (1)Δx =a (1+Δx )+4-a -4Δx =a ,∴f ′(1)=a ,即a =2.(2)将原油精炼为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热,如果第x h ,原油的温度(单位:℃)为f (x )=x 2-7x +15(0≤x ≤8).求函数y =f (x )在x =6处的导数f ′(6),并解释它的实际意义.解 当x 从6变到6+Δx 时,函数值从f (6)变到f (6+Δx ),函数值y 关于x 的平均变化率为 f (6+Δx )-f (6)Δx=(6+Δx )2-7(6+Δx )+15-(62-7×6+15)Δx=5Δx +(Δx )2Δx=5+Δx .当Δx →0时,平均变化率趋近于5,所以f ′(6)=5,导数f ′(6)=5表示当x =6时原油温度的瞬时变化率即原油温度的瞬时变化速度.也就是说,如果保持6 h 时温度的变化速度,每经过1 h 时间,原油温度将升高5 ℃.1.一个做直线运动的物体,其位移S 与时间t 的关系是S =3t -t 2,则此物体在t =2时的瞬时速度为________. 答案 -1解析 由于ΔS =3(2+Δt )-(2+Δt )2-(3×2-22) =3Δt -4Δt -(Δt )2=-Δt -(Δt )2, 所以ΔS Δt =-Δt -(Δt )2Δt=-1-Δt .当Δt 无限趋近于0时,ΔSΔt 无限趋近于常数-1.故物体在t =2时的瞬时速度为-1.2.已知曲线y =f (x )=2x 2上一点A (2,8),则点A 处的切线斜率为________. 答案 8解析 因为Δy Δx =f (2+Δx )-f (2)Δx=2(2+Δx )2-8Δx=8+2Δx ,当Δx →0时,8+2Δx 趋近于8.即k =8. 3.函数y =x +1x 在x =1处的导数是________.答案 0解析 ∵函数y =f (x )=x +1x ,∴Δy =f (1+Δx )-f (1)=1+Δx +11+Δx -1-1=(Δx )21+Δx ,∴Δy Δx =Δx 1+Δx ,当Δx →0时,Δy Δx→0, 即y =x +1x在x =1处的导数为0.4.设函数f (x )在点x 0附近有定义,且有f (x 0+Δx )-f (x 0)=a Δx +b (Δx )2(a ,b 为常数),则f ′(x 0)的值为________. 答案 a解析 由导数定义,得f (x 0+Δx )-f (x 0)Δx=a Δx +b (Δx )2Δx=a +b Δx ,故当Δx →0时,其值趋近于a ,故f ′(x 0)=a .5.如果一个物体的运动方程S (t )=⎩⎪⎨⎪⎧t 2+2,0≤t <3,29+3(t -3)2,t ≥3,试求该物体在t =1和t =4时的瞬时速度. 解 当t =1时,S (t )=t 2+2,则ΔS Δt =S (1+Δt )-S (1)Δt =(1+Δt )2+2-3Δt =2+Δt , 当Δt 无限趋近于0时,2+Δt 无限趋近于2, 所以v (1)=2; ∵t =4∈[3,+∞),∴S (t )=29+3(t -3)2=3t 2-18t +56,∴ΔS Δt =3(4+Δt )2-18(4+Δt )+56-3×42+18×4-56Δt =3(Δt )2+6Δt Δt=3Δt +6,∴当Δt 无限趋近于0时,3Δt +6→6,即ΔSΔt →6,所以v (4)=6.1.平均变化率和瞬时变化率的关系平均变化率Δy Δx =f (x 0+Δx )-f (x 0)Δx ,当Δx 无限趋近于0时,它所趋近于的一个常数就是函数在x =x 0处的瞬时变化率.即有:Δx 无限趋近于0是指自变量间隔Δx 越来越小,能达到任意小的间隔,但始终不能为0.即对于瞬时变化率,我们通过减小自变量的改变量以致无限趋近于零的方式,实现用割线斜率“逼近”切线斜率,用平均速度“逼近”瞬时速度.一般地,可以用平均变化率“逼近”瞬时变化率.2.求切线的斜率、瞬时速度和瞬时加速度的解题步骤(1)计算Δy .(2)求Δy Δx .(3)当Δx →0时,ΔyΔx 无限趋近于哪个常数.课时作业一、填空题1.函数f (x )=x 2在x =3处的导数等于________. 答案 6解析 Δy Δx =(3+Δx )2-32Δx =6+Δx ,当Δx →0时,得f ′(3)=6.2.若曲线y =x 2+ax +b 在点(0,b )处的切线方程是x -y +1=0,则a =________,b =________. 答案 1 1解析 Δy Δx =(0+Δx )2+a (0+Δx )+b -b Δx =a +Δx ,当Δx →0时,Δy Δx→a .∵切线x -y +1=0的斜率为1, ∴a =1.∵点(0,b )在直线x -y +1=0上,∴b =1.3.已知曲线y =12x 2-2上一点P ⎝⎛⎭⎫1,-32,则过点P 的切线的倾斜角为________. 答案 45°解析 ∵y =12x 2-2,∴Δy Δx =12(x +Δx )2-2-⎝⎛⎭⎫12x 2-2Δx =12(Δx )2+x ·Δx Δx=x +12Δx .故当Δx →0时,其值无限趋近于x ,∴y ′|x =1=1.∴点P ⎝⎛⎭⎫1,-32处切线的斜率为1,则切线的倾斜角为45°. 4.设曲线y =ax 2在点(1,a )处的切线与直线2x -y -6=0平行,则a =________. 答案 1解析 Δy Δx =a (1+Δx )2-aΔx =2a +a Δx ,当Δx →0时,ΔyΔx →2a ,∴可令2a =2,∴a =1.5.已知曲线y =13x 3上一点P (2,83),则该曲线在点P 处切线的斜率为________.答案4解析 由y =13x 3,得Δy Δx =13(x +Δx )3-13x 3Δx=13[3x 2+3x ·Δx +(Δx )2], 当Δx →0时,其值无限趋近于x 2. 故y ′=x 2,y ′|x =2=22=4,结合导数的几何意义知,曲线在点P 处切线的斜率为4. 6.在曲线y =x 2上切线倾斜角为π4的点的坐标为________.答案 (12,14)解析 ∵Δy Δx =(x +Δx )2-x 2Δx =2x +Δx ,当Δx →0时,其值趋近于2x . ∴令2x =tan π4=1,得x =12,∴y =⎝⎛⎭⎫122=14,所求点的坐标为⎝⎛⎭⎫12,14. 7.已知曲线y =f (x )=2x 2+4x 在点P 处的切线斜率为16,则点P 坐标为________. 答案 (3,30)解析 设点P (x 0,2x 20+4x 0), 则Δy Δx =f (x 0+Δx )-f (x 0)Δx=2(Δx )2+4x 0·Δx +4Δx Δx=2Δx +4x 0+4,当Δx →0时,其值无限趋近于4+4x 0. 令4x 0+4=16,得x 0=3,∴P (3,30).8.如图,函数y =f (x )的图象在点P 处的切线方程是y =-x +8,则f (5)+f ′(5)=________.答案 2解析 ∵点P 在切线上,∴f (5)=-5+8=3,f ′(5)=k =-1, ∴f (5)+f ′(5)=3-1=2.9.已知函数f (x )的图象在点M (1,f (1))处的切线方程是y =12x +2,则f (1)+f ′(1)=________.答案 3解析 由在点M 处的切线方程是y =12x +2,得f (1)=12×1+2=52,f ′(1)=12.∴f (1)+f ′(1)=52+12=3.10.若抛物线y =x 2-x +c 上一点P 的横坐标是-2,抛物线过点P 的切线恰好过坐标原点,则c 的值为________. 答案 4解析 设在点P 处切线的斜率为k ,∵Δy Δx =(-2+Δx )2-(-2+Δx )+c -(6+c )Δx =-5+Δx , ∴当Δx →0时,ΔyΔx →-5,∴k =-5,∴切线方程为y =-5x .∴点P 的纵坐标为y =-5×(-2)=10, 将P (-2,10)代入y =x 2-x +c ,得c =4. 二、解答题11.已知质点运动方程是s (t )=12gt 2+2t -1(g 是重力加速度,常量),求质点在t =4 s 时的瞬时速度(其中s 的单位是m ,t 的单位是s). 解Δs Δt =s (4+Δt )-s (4)Δt=[12g (4+Δt )2+2(4+Δt )-1]-(12g ·42+2×4-1)Δt=12g (Δt )2+4g ·Δt +2Δt Δt=12g Δt +4g +2. ∵当Δt →0时,ΔsΔt→4g +2,∴S ′(4)=4g +2,即v (4)=4g +2,∴质点在t =4 s 时的瞬时速度为(4g +2) m/s.12.求曲线y =f (x )=x 3-x +3在点(1,3)处的切线方程.解 因为点(1,3)在曲线上,且f (x )在x =1处可导,Δy Δx =(1+Δx )3-(1+Δx )+3-(1-1+3)Δx=(Δx )3+3(Δx )2+2Δx Δx=(Δx )2+3Δx +2,当Δx →0时,(Δx )2+3Δx +2→2,故f ′(1)=2.故所求切线方程为y -3=2(x -1),即2x -y +1=0.13.已知直线l 1为曲线y =x 2+x -2在点(1,0)处的切线,l 2为该曲线的另一条切线,且l 1⊥l 2.(1)求直线l 2的方程;(2)求直线l 1,l 2与x 轴所围成的三角形的面积.解 (1)Δy Δx =(1+Δx )2+(1+Δx )-2-(12+1-2)Δx=Δx +3,当Δx →0时,Δy Δx→3, ∴直线l 1的斜率k 1=3,∴直线l 1的方程为y =3(x -1),即y =3x -3.设直线l 2过曲线y =x 2+x -2上的点P (x 0,x 20+x 0-2),则直线l 2的方程为y -(x 20+x 0-2)=(2x 0+1)(x -x 0).∵l 1⊥l 2,∴3(2x 0+1)=-1,解得x 0=-23. ∴直线l 2的方程为y =-13x -229. (2)解方程组⎩⎪⎨⎪⎧ y =3x -3,y =-13x -229,得⎩⎨⎧ x =16,y =-52.又∵直线l 1,l 2与x 轴的交点坐标分别为(1,0),(-223,0), ∴所求三角形的面积为S =12×|-52|×(1+223)=12512.三、探究与拓展14.设P 为曲线C :y =x 2+2x +3上的点,且曲线C 在点P 处的切线倾斜角的范围为⎣⎡⎦⎤0,π4,则点P 横坐标的取值范围为________.答案 ⎣⎡⎦⎤-1,-12 解析 ∵Δy Δx =(x +Δx )2+2(x +Δx )+3-(x 2+2x +3)Δx=(2x +2)·Δx +(Δx )2Δx=Δx +2x +2. 故当Δx →0时,其值无限趋近于2x +2.∴可设点P 横坐标为x 0,则曲线C 在点P 处的切线斜率为2x 0+2.由已知,得0≤2x 0+2≤1,∴-1≤x 0≤-12,∴点P 横坐标的取值范围为⎣⎡⎦⎤-1,-12. 15.已知抛物线y =2x 2+1分别满足下列条件,求出切点的坐标.(1)切线的倾斜角为45°;(2)切线平行于直线4x -y -2=0.解 设切点坐标为(x 0,y 0),则Δy =2(x 0+Δx )2+1-2x 20-1=4x 0·Δx +2(Δx )2,∴Δy Δx=4x 0+2Δx , 当Δx →0时,Δy Δx→4x 0,即f ′(x 0)=4x 0. (1)∵抛物线的切线的倾斜角为45°,∴斜率为tan 45°=1,即f ′(x 0)=4x 0=1,解得x 0=14, ∴切点坐标为(14,98). (2)∵抛物线的切线平行于直线4x -y -2=0,∴k =4,即f ′(x 0)=4x 0=4,解得x 0=1,∴切点坐标为(1,3).。
《1.1.2 瞬时变化率——导数》教学案
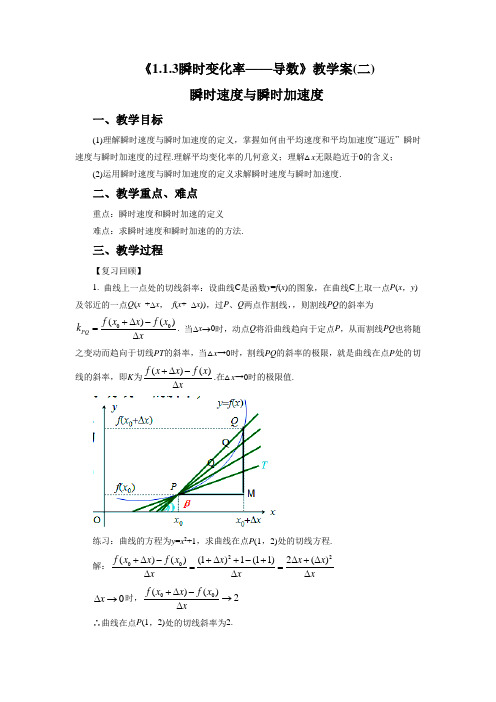
《1.1.3瞬时变化率——导数》教学案(二)瞬时速度与瞬时加速度一、教学目标(1)理解瞬时速度与瞬时加速度的定义,掌握如何由平均速度和平均加速度“逼近” 瞬时速度与瞬时加速度的过程.理解平均变化率的几何意义;理解△x 无限趋近于0的含义;(2)运用瞬时速度与瞬时加速度的定义求解瞬时速度与瞬时加速度.二、教学重点、难点重点:瞬时速度和瞬时加速的定义 难点:求瞬时速度和瞬时加速的的方法.三、教学过程【复习回顾】1. 曲线上一点处的切线斜率:设曲线C 是函数y =f (x )的图象,在曲线C 上取一点P (x ,y )及邻近的一点Q (x +∆x , f (x + ∆x )),过P 、Q 两点作割线,,则割线PQ 的斜率为00()()PQ f x x f x k x+∆-=∆. 当∆x →0时,动点Q 将沿曲线趋向于定点P ,从而割线PQ 也将随之变动而趋向于切线PT 的斜率,当△x →0时,割线PQ 的斜率的极限,就是曲线在点P 处的切线的斜率,即K 为()()f x x f x x+∆-∆.在△x →0时的极限值.练习:曲线的方程为y =x 2+1,求曲线在点P (1,2)处的切线方程.解:2200()()(1)1(11)2()f x x f x x x x x x x+∆-+∆+-+∆+∆==∆∆∆ 0x ∆→时,00()()2f x x f x x+∆-→∆∴曲线在点P (1,2)处的切线斜率为2.因此,点p (1,2)切线的方程为y -2=2(x -1),即 y =2x.【问题情境1】平均速度:物体的运动位移与所用时间的比称为平均速度.平均速度反映物体在某一段时间段内运动的快慢程度.那么如何刻画物体在某一时刻运动的快慢程度?【问题情境2】跳水运动员从10m 高跳台腾空到入水的过程中,不同时刻的速度是不同的.假设t 秒后运动员相对于水面的高度为()24.9 6.510H t t t =-++,那么我们就会计算任意一段的平均速度v ,通过平均速度v 来描述其运动状态,但用平均速度不一定能反映运动员在某一时刻的瞬时速度,那么如何求运动员的瞬时速度呢?问题:2秒时的瞬时速度是多少?我们现在会算任意一段的平均速度,先来观察一下2秒附近的情况.关于这些数据,下面的判断对吗?2.当t ∆趋近于0时,即无论t 从小于2的一边,还是t 从大于2的一边趋近于2时,平均速度都趋近于一个确定的值-13.1s m /.3. 靠近-13.1且比-13.1大的任何一个数都可以是某一段[]2,2t ∆+上的平均速度; 4. 靠近-13.1且比-13.1小的任何一个数都可以是某一段[]t ∆+2,2上的平均速度; 5.-13.1表示在2秒附近,运动员的速度大约是-13.1s m /.分析:2=t 秒时有一个确定的速度,2秒附近的任何一段上的平均速度都不等于瞬时速度,所以比-13.1大的数作为2秒的瞬时速度不合理,比-13.1小的数作为2秒的瞬时速度也不合理,因此,运动员在2秒时的瞬时速度是-13.1s m /.【构建数学】 瞬时速度和瞬时加速度(1)平均速度: 物理学中,运动物体的位移与所用时间的比称为平均速度. (2) 位移的平均变化率:tt s t t s ∆-∆+)()(00(3)瞬时速度:当t ∆无限趋近于0时,tt s t t s ∆-∆+)()(00无限趋近于一个常数,这个常数称为0t t =时的瞬时速度.“逼近”思想和以直代曲思想;如何得到求瞬时速度的步骤?a 、先求时间改变量t ∆和位置改变量)()(00t s t t s s -∆+=∆b 、再求平均速度t s v ∆∆=c 、后求瞬时速度:当t ∆无限趋近于0,ts ∆∆无限趋近于常数v 为瞬时速度.(4)速度的平均变化率:tt v t t v ∆-∆+)()(00(5)瞬时加速度:当t ∆无限趋近于0 时,tt v t t v ∆-∆+)()(00无限趋近于一个常数,这个常数称为0t t =时的瞬时加速度注:瞬时加速度是速度对于时间的瞬时变化率,感受速度的平均变化率与加速度的关系,以及加速度与瞬时加速度的“逼近”关系.三、例题分析例题1 物体做自由落体运动,运动方程为212S gt =,其中位移单位是m ,时间单位是s ,210/g m s =.求例2 设一辆轿车在公路上做加速直线运动,假设()t s 时的速度为2()3v t t =+,求0()t t s =时轿车的加速度.分析:(1)先求轿车在[]00,t t t t ∈+∆时,轿车的平均加速度.(2)当0t ∆→时,平均加速度a 逼近一个常数,这个常数就是2t s =时运动员的瞬时速度.由例1和例2我们能发现一个问题:位移在时间上的改变量就是速度,而速度在时间上的改变量就是加速度.例3 将原油精炼为汽油、柴油、塑胶等各种不同产品,需对原油进行冷却和加热.如果在第x h 时原油的温度)(C为157)(2+-=x x x f )80(≤≤x .计算第2 h 和第6 h 时,原油的瞬时变化率,并说明意义.四、课堂练习1.质点沿x 轴运动,设距离为()x m ,时间为()t s 时,2105x t =+,则当00t t t t ≤≤+∆时,质点的平均速度为 ;当0t t =时,质点的瞬时速度为 ;当00t t t t ≤≤+∆时,质点的平均加速度为 ;当0t t =时,质点的瞬时加速度为 .2.一质点的运动方程为210s t =+(位移单位:m ,时间单位:s ),试求该质点在3t s =的瞬时速度.3.自由落体运动的位移()s m 与时间()t s 的关系为212s gt =(g为常数). (1)求0()t t s =时的瞬时速度; (2)分别求1,2,3t s =时的瞬时速度.五、课堂小结本节课主要学习了物体运动的瞬时速度与瞬时加速度的定义,掌握如何由平均速度和平均加速度“逼近” 瞬时速度与瞬时加速度的过程.运用瞬时速度与瞬时加速度的定义求解瞬时速度与瞬时加速度.充分理解由平均速度的“逼近”转化成瞬时速度与瞬时加速度的过程,培养学生解决实际问题的能力,学会用运动学的观点理解和解决实际问题.充分感受到学习数学的乐趣,体会到数学的研究方法和内在美.六、课后作业位是1gt 例1:物体作自由落体运动,运动方程为:其中位移单m,时间单位是s,g=10m/s 2.求:(1) 物体在时间区间[2,2.1]上的平均速度;(2) 物体在时间区间[2,2.01]上的平均速度;(3) 物体在t =2(s)时的瞬时速度.22s =1.已知物体做自由落体运动的方程为21(),2s s t gt ==若t 无限趋近于0时, (1)(1)s t s t+∆-∆无限趋近于9.8/m s ,那么正确的说法是( )A .9.8/m s 是在0~1s 这一段时间内的速度B .9.8/m s 是在1~(1+t )s 这段时间内的速度C .9.8/m s 是物体在1t s =这一时刻的速度D .9.8/m s 是物体从1s 到(1+t ∆)s 这段时间内的平均速度.2.如果质点M 按规律23S t =+运动,则在一小段时间[2,2.1]中相应的平均速度等于( )A .4B .4.1C .0.41D .33.如果某物体的运动方程是22(1)s t =-,则在 1.2t =秒时的瞬时速度是( ) A .4 B .4- C .4.8 D .0.84.设一物体在t 秒内所经过的路程为s 米,并且32423s t t t =+-,则物体在运动开始的速度为( )A .3/m sB .-3/m sC .0/m sD .2/m s5.任一做直线运动的物体,其位移s 与时间t 的关系是23t t s -=,则物体的初速度是( )A.0B.3C.-2D.t 23-6.枪弹在枪筒中可以看成是匀加速运动,如果它的加速度是525.010/m s ⨯.枪弹从枪筒弹出的时间为31.610s -⨯,求枪弹弹出枪口时的瞬时速度.(位移公式是212s at =,其中a 是加速度,t 是时间)7.设一物体在t 秒内所经过的路程为s 米,并且3242-+=t t s ,试求物体分别在运动开始及第5秒末的速度.8、一块岩石在月球表面上以24m s的速度垂直上抛,()t s 时达到的高度为2240.8h t t =-(单位:m ).(1)求岩石在()t s 时的速度、加速度; (2)多少时间后岩石达到最高点.9.一作直线运动的物体其位移s 与时间t 的关系是23s t t =-. (1)求此物体的初速度;(2)求此物体在t =2秒时的瞬时速度; (3)求t =0到t =2时的平均速度.。
2018版高中数学苏教版选修2-2学案:1.1.2瞬时变化率——导数(二)

1.1.2 瞬时变化率一一导数(二)【学习目标】1•理解导数的概念2会求曲线过某点的的切线方程.3•能利用导数的几何意义解决一些实际问题.问题导学新知探究点点落实知识点导函数思考1 已知f(x) = X2,求f'⑴与f'(X).思考2 试说明思考1中的f' (1)与f' (x)的区别与联系.从求函数f(x)在X= X0处导数的过程可以看到,当X= X0时,f' (X o)是一个确定的数.这样,当X变化时,f' (x)便是X的一个函数,它们称它为f(x)的导函数(简称导数).y= f(x)的导函数有时也记作y'.题型探究車点理点仆击坯类型一导函数例1求函数f(x) = x2+ 1的导函数.厨进行变形是解答本题的反思与感悟充分把握导函数的定义,恰当地运用分子有理化对关键.跟踪训练1已知f(x)= X —1若f' (x0) = 5,试求x0的值.x ' 4类型二求曲线过某点的切线方程例2试求过点P(3,5)且与曲线y= x2相切的直线方程.反思与感悟求曲线y= f(x)过点P的切线方程的步骤:⑴设切点为坐标为M(x o, y o);(2) 利用M(x o, y o)求曲线在M处切线的斜率f' (x o); (3)由斜率公式,求出ki MP;(4)利用f'(X。
) =k MP,从而求得点M的坐标及k MP; (5)根据直线的点斜式方程写出所求切线的方程.跟踪训练2求过点P( —1,0)并与抛物线y= x2+ x+ 1相切的直线方程.类型三导数几何意义的应用例3 (1)已知函数f(x)在区间[0,3]上的图象如图所示,记k1 =f' (1), k2= f' (2), k3= f(2)—f(1),则k1, k2, k3之间的大小关系为 _________ .(请用“ >”连接)⑵设点P是曲线y= x3—』3x+彳上的任意一点,P点处的切线倾斜角为a贝V a的取值范围3登录91淘燥I网■:www.31 }.听名师桁讲谍程——异徵的几何意义反思与感悟导数几何意义的综合应用问题的解题关键还是对函数进行求导,利用题目所提供的诸如直线的位置关系、斜率最值范围等关系求解相关问题,此处常与函数、方程、不等式等知识相结合.b ]上的图象可能是 ________1⑵曲线y =-和y = X 1 2在它们交点处的两条切线与X达标检测(-------- ■■规律与方法■■ ---------- 11. f ' (x o )与f ' (x)的区别与联系:f ' (x o )是函数y = f(x)在x = x o 处的导数,是一个具体的函 数值.f ' (x)是函数y = f(x)的导函数,它随x 的变化而变化.求f '(X 0)可用定义求,也可以先求 f ' (x),再求 f ' (x o ).2•利用导数求过曲线外一点的切线方程的步骤:⑴设切点坐标为(xo, f(x 。
苏教版数学高二-苏教版数学选修2-2 第1课时 瞬时变化率 导数

1.1.2 瞬时变化率——导数第1课时课时目标 1.知道导数的几何意义.2.用导数的定义求曲线的切线方程.1.导数的几何意义:函数y =f (x )在点x 0处的导数f ′(x 0)的几何意义是:__________________________.2.利用导数的几何意义求曲线的切线方程的步骤:(1)求出函数y =f(x)在点x 0处的导数f ′(x 0);(2)根据直线的点斜式方程,得切线方程为________________.一、填空题1.曲线y =1x在点P(1,1)处的切线方程是________. 2.已知曲线y =2x 3上一点A(1,2),则A 处的切线斜率为________.3.曲线y =4x -x 3在点(-1,-3)处的切线方程是____________.4.若曲线y =x 2的一条切线l 与直线x +4y -8=0垂直,则l 的方程为______________.5.曲线y =2x -x 3在点(1,1)处的切线方程为______.6.设函数y =f(x)在点x 0处可导,且f ′(x 0)>0,则曲线y =f(x)在点(x 0,f(x 0))处切线的倾斜角的范围是________.7.曲线f(x)=x 3+x -2在点P 处的切线平行于直线y =4x -1,则P 点的坐标为______________.8.已知直线x -y -1=0与曲线y =ax 2相切,则a =________.二、解答题9.已知曲线y =4x在点P(1,4)处的切线与直线l 平行且距离为17,求直线l 的方程.10.求过点(2,0)且与曲线y =1x相切的直线方程.能力提升11.已知曲线y =2x 2上的点(1,2),求过该点且与过该点的切线垂直的直线方程.12.设函数f(x)=x3+ax2-9x-1 (a<0).若曲线y=f(x)的斜率最小的切线与直线12x+y=6平行,求a的值.1.利用导数可以解决一些与切线方程或切线斜率有关的问题.2.利用导数求曲线的切线方程,要注意已知点是否在曲线上.如果已知点在曲线上,则切线方程为y-f(x0)=f′(x0) (x-x0);若已知点不在切线上,则设出切点(x0,f(x0)),表示出切线方程,然后求出切点.答案知识梳理1.曲线y=f(x)上过点x0的切线的斜率2.(2)y-y0=f′(x0)·(x-x0)作业设计1.x+y-2=0解析ΔyΔx=11+Δx-1Δx=-Δx1+ΔxΔx=-11+Δx,当Δx无限趋近于0时,ΔyΔx无限趋近于-1,∴k=-1,∴切线方程为y-1=-(x-1),即x+y-2=0.2.6解析∵y=2x3,∴ΔyΔx=2(x+Δx)3-2x3Δx=2(Δx )3+6x (Δx )2+6x 2(Δx )Δx=2(Δx )2+6x (Δx )+6x 2.∴当Δx 无限趋近于0时,Δy Δx无限趋近于6x 2, ∴点A (1,2)处切线的斜率为6.3.x -y -2=0解析 Δy Δx =4(x +Δx )-(x +Δx )3-4x +x 3Δx=4-(Δx )2-3x 2-3x (Δx ),当Δx 无限趋近于0时,Δy Δx无限趋近于4-3x 2, ∴f ′(-1)=1.所以在点(-1,-3)处的切线的斜率为k =1,所以切线方程是y =x -2.4.4x -y -6=0解析 与直线x +4y -8=0垂直的直线l 为4x -y +m =0,即y =x 2在某一点的导数为4,而y ′=2x ,所以y =x 2在(2,2)处导数为4,此点的切线方程为4x -y -6=0.5.x +y -2=0解析 Δy Δx=2-(Δx )2-3x 2-3x (Δx ), 当Δx 无限趋近于0时,Δy Δx无限趋近于2-3x 2, ∴y ′=2-3x 2,∴k =2-3=-1.∴切线方程为y -1=-(x -1),即x +y -2=0.6.⎝⎛⎭⎫0,π2 解析 k =f ′(x 0)>0,∴tan θ>0,∴θ∈⎝⎛⎭⎫0,π2. 7.(1,0)或(-1,-4)解析 设P (x 0,y 0),由f (x )=x 3+x -2,Δy Δx=(Δx )2+3x 2+3x (Δx )+1, 当Δx 无限趋近于0时,Δy Δx无限趋近于3x 2+1. ∴f ′(x )=3x 2+1,令f ′(x 0)=4,即3x 20+1=4,得x 0=1或x 0=-1,∴P (1,0)或P (-1,-4).8.14解析 Δy Δx =a (x +Δx )2-ax 2Δx=2ax +a (Δx ), 当Δx 无限趋近于0时,2ax +a (Δx )无限趋近于2ax ,∴f ′(x )=2ax . 设切点为(x 0,y 0),则f ′(x 0)=2ax 0,2ax 0=1,且y 0=x 0-1=ax 20,解得x 0=2,a =14.9.解 Δy Δx =f (x +Δx )-f (x )Δx=4x +Δx -4x Δx =-4Δx x (Δx )(x +Δx )=-4x (x +Δx ), 当Δx 无限趋近于0时,-4x (x +Δx )无限趋近于-4x 2,即f ′(x )=-4x 2.k =f ′(1)=-4,切线方程是y -4=-4(x -1), 即为4x +y -8=0,设l :4x +y +c =0,则17=|c +8|42+12,∴|c +8|=17,∴c =9,或c =-25,∴直线l 的方程为4x +y +9=0或4x +y -25=0.10.解 (2,0)不在曲线y =1x 上,令切点为(x 0,y 0),则有y 0=1x 0.① 又Δy Δx =1x +Δx -1x Δx =-1x (x +Δx ),当Δx 无限趋近于0时,-1x (x +Δx )无限趋近于-1x 2.∴k =f ′(x 0)=-1x 20.∴切线方程为y =-1x 20(x -2).而y 0x 0-2=-1x 20.② 由①②可得x 0=1,故切线方程为x +y -2=0.11.解 ΔyΔx =2(1+Δx )2-2Δx =4Δx +2(Δx )2Δx =4+2Δx ,当Δx 无限趋近于0时,ΔyΔx 无限趋近于4,∴f ′(1)=4.∴所求直线的斜率为k =-14.∴y -2=-14(x -1),即x +4y -9=0.12.解 ∵Δy =f (x 0+Δx )-f (x 0)=(x 0+Δx )3+a (x 0+Δx )2-9(x 0+Δx )-1-(x 30+ax 20-9x 0-1)=(3x 20+2ax 0-9)Δx +(3x 0+a )(Δx )2+(Δx )3,∴Δy Δx=3x 20+2ax 0-9+(3x 0+a )Δx +(Δx )2. 当Δx 无限趋近于零时,Δy Δx无限趋近于3x 20+2ax 0-9. 即f ′(x 0)=3x 20+2ax 0-9.∴f ′(x 0)=3⎝⎛⎭⎫x 0+a 32-9-a 23. 当x 0=-a 3时,f ′(x 0)取最小值-9-a 23. ∵斜率最小的切线与12x +y =6平行, ∴该切线斜率为-12.∴-9-a 23=-12.解得a =±3. 又a <0,∴a =-3.。
2019-2020学年苏教版选修2-2 瞬时变化率——导数 教案

2019-2020学年苏教版选修2-2 瞬时变化率——导数教案教学重点:理解并掌握曲线在一点处的切线的斜率的定义以及切线方程的求法.教学难点:用“无限逼近”、“局部以直代曲”的思想理解某一点处切线的斜率.教学过程:一、问题情境1.问题情境.如何精确地刻画曲线上某一点处的变化趋势呢?如果将点P附近的曲线放大,那么就会发现,曲线在点P附近看上去有点像是直线.如果将点P附近的曲线再放大,那么就会发现,曲线在点P附近看上去几乎成了直线.事实上,如果继续放大,那么曲线在点P附近将逼近一条确定的直线l,该直线l是经过点P的所有直线中最逼近曲线的一条直线.因此,在点P附近我们可以用这条直线l来代替曲线,也就是说,点P附近,曲线可以看出直线(即在很小的范围内以直代曲).2.探究活动.如图所示,直线l 1,l 2为经过曲线上一点P 的两条直线,(1) 试判断哪一条直线在点P 附近更加逼近曲线;(2) 在点P 附近能作出一条比l 1,l 2更加逼近曲线的直线l 3吗?(3) 在点P 附近能作出一条比l 1,l 2,l 3更加逼近曲线的直线吗?二、建构数学切线定义: 如图,设Q 为曲线C 上不同于P 的一点,直线PQ 称为曲线的割线. 随着点Q 沿曲线C 向点P 运动,割线PQ 在点P 附近逼近曲线C ,当点Q 无限逼近点P 时,直线PQ 最终就成为经过点P 处最逼近曲线的直线l ,这条直线l 也称为曲线在点P 处的切线.这种方法叫割线逼近切线.思考:如上图,P 为已知曲线C 上的一点,如何求出点P 处的切线方程?三、数学运用例1 试求2()f x x =在点(2,4)处的切线斜率.解法一 分析:设P (2,4),Q (x Q ,f (x Q )),则割线PQ 的斜率为:2()44222Q Q PQ Q Q Q f x x k x x x --===+--当Q 沿曲线逼近点P 时,割线PQ 逼近点P 处的切线,从而割线斜率逼近切线斜率;当Q 点横坐标无限趋近于P 点横坐标时,即x Q 无限趋近于2时,k PQ 无限趋近于常数4.从而曲线f (x )=x 2在点(2,4)处的切线斜率为4.解法二 设P (2,4),Q (x Q ,x Q 2),则割线PQ 的斜率为:22(2)444∆∆∆∆∆∆PQ x k x x x x x+-=+==+ 当∆x 无限趋近于0时,k PQ 无限趋近于常数4,从而曲线f (x )=x 2,在点(2,4)处的切线斜率为4.练习 试求2()1f x x =+在x =1处的切线斜率.解:设P (1,2),Q (1+Δx ,(1+Δx )2+1),则割线PQ 的斜率为:22[(1)1]222∆∆∆∆∆∆PQ x k xx x xx++-=+==+ 当∆x 无限趋近于0时,k PQ 无限趋近于常数2,从而曲线f (x )=x 2+1在x =1处的切线斜率为2.小结 求曲线()y f x =上一点处的切线斜率的一般步骤:(1)找到定点P 的坐标,设出动点Q 的坐标;(2)求出割线PQ 的斜率;(3)当∞→∆x 时,割线逼近切线,那么割线斜率逼近切线斜率.思考 如上图,P 为已知曲线C 上的一点,如何求出点P 处的切线方程? 解 设0000(())(())∆∆P x f x Q x x f x x ,,+,+000000()()()()()∆∆∆∆PQ f x x f x f x x f x k x x x x+-+-∴==+- 所以,当x ∆无限趋近于0时,00()()∆∆f x x f x x--无限趋近于点00(())P x f x ,处的切线的斜率.变式训练 1.已知2()f x x =,求曲线()y f x =在1x =-处的切线斜率和切线方程;2.已知1()f x x -=,求曲线()y f x =在1x =-处的切线斜率和切线方程;3.已知()f x ,求曲线()y f x =在12x =处的切线斜率和切线方程. 课堂练习已知()f x 求曲线()y f x =在12x =处的切线斜率和切线方程. 四、回顾小结1.曲线上一点P 处的切线是过点P 的所有直线中最接近P 点附近曲线的直线,则P 点处的变化趋势可以由该点处的切线反映(局部以直代曲).2.根据定义,利用割线逼近切线的方法, 可以求出曲线在一点处的切线斜率和方程.五、课外作业。
苏教版高中数学选修2-2《瞬时变化率—导数:曲线上一点处的切线》教学教案

1.1.2《瞬时变化率-导数》教案(一)曲线上一点处的切线一、教学目标1.理解并掌握曲线在某一点处的切线的概念;2.掌握用割线逼近切线的方法;3.会求曲线在一点处的切线的斜率与切线方程.二、教学重点、难点重点:理解曲线在一点处的切线和切线的斜率的定义,掌握曲线在一点处切线斜率的求法难点:理解曲线在一点处的切线的定义,特别是对“无限逼近”、“局部以直代曲”的理解三、教学过程【问题情景】导数是解决函数的最大值、最小值问题的有力工具.导数的知识形成一门学科,就是我们通常所说的微积分.微积分除了解决最大值、最小值问题,还能解决一些复杂曲线的切线问题.导数的思想最初是法国数学家费马(Fermat)为解决极大、极小问题而引入的.但导数作为微分学中最主要概念,却是英国科学家牛顿(Newton)和德国数学家莱布尼兹(Leibniz)分别在研究力学与几何学过程中建立的.微积分能成为独立的科学并给整个自然科学带来革命性的影响,主要是靠了牛顿和莱布尼兹的工作.但遗憾的是他们之间发生了优先权问题的争执.其实,他们差不多是在相同的时间相互独立地发明了微积分.方法类似但在用语、符号、算式和量的产生方式稍有差异.牛顿在1687年以前没有公开发表,莱布尼兹在1684年和1686年分别发表了微分学和积分学. 所以,就发明时间而言,牛顿最于莱布尼兹,就发表时间而言,莱布尼兹则早于牛顿.关于谁是微积分的第一发明人,引起了争论.而我们现在所用的符号大多数都是莱布尼兹发明的.而英国认为牛顿为第一发明人,拒绝使用莱布尼兹发明的符号,因此,使自己远离了分析【学生活动,建构数学】(一)点P 附近的曲线1.平均变化率:函数()f x 在区间[]12x x ,上的平均变化率为 . 即曲线上两点的连线(割线)的斜率。
显然平均变化率近似地刻画了曲线在某个区间上的变化趋势。
2.如何精确地刻画曲线上某一点处的变化趋势呢?(点P 附近的曲线的研究)(从直线上某点的变化趋势的研究谈起,结合“天圆地方”的故事带来“宏观上曲,微观上直”,“曲绝对,直相对”的初步感受,后提出“放大图形”的朴素方法.)C1C2(1)观察“点P 附近的曲线”,随着图形放大,你看到了怎样的现象?曲线有点像直线(2)这种现象下,这么一条特殊位置的曲线从其趋势看几乎成了直线 这种思维方式就叫做“逼近思想”。
高中数学瞬时变化率—导数苏教版选修2-2 教案

瞬时变化率—导数教学目的:知识与技能:掌握用极限给瞬时速度下的精确的定义.过程与方法:会运用瞬时速度的定义,求物体在某一时刻的瞬时速度. 情感、态度与价值观:理解足够小、足够短的含义教学重点:知道了物体的运动规律,用极限来定义物体的瞬时速度,学会求物体的瞬时速度. 教学难点:理解物体的瞬时速度的意义教具准备:与教材内容相关的资料。
教学设想:提供一个舞台, 让学生展示自己的才华,这将极大地调动学生的积极性,增强学生的荣誉感,培养学生独立分析问题和解决问题的能力,体现了“自主探究”,同时,也锻炼了学生敢想、敢说、敢做的能力。
教学过程:学生探究过程: 我们物理中学习直线运动的速度时,已经学习了物体的瞬时速度的有关知识,现在我们从数学的角度重新来认识一下瞬时速度一、复习引入: 1.曲线的切线如图,设曲线c 是函数()y f x =的图象,点00(,)P x y 是曲线 c 上一点作割线PQ 当点Q 沿着曲线c无限地趋近于点P ,割线PQ 无限地趋近于某一极限位置PT 我们就把极限位置上的直线PT ,叫做曲线c在点P 处的切线y=f(x)β∆x∆yQ MPxOy2.确定曲线c 在点00(,)P x y 处的切线斜率的方法:因为曲线c 是给定的,根据解析几何中直线的点斜是方程的知识,只要求出切线的斜率就够了设割线PQ 的倾斜角为β,切线PT 的倾斜角为α,既然割线PQ 的极限位置上的直线PT 是切线,所以割线PQ 斜率的极限就是切线PQ 的斜率tan α,即tan α=0lim→∆x =∆∆x y0lim→∆x 0x∆ 二、讲解新课:1.瞬时速度定义:运动物体经过某一时刻(某一位置)的速度,叫做瞬时速度.2. 确定物体在某一点A 处的瞬时速度的方法:要确定物体在某一点A 处的瞬时速度,从A 点起取一小段位移AA 1,求出物体在这段位移上的平均速度,这个平均速度可以近似地表示物体经过A 点的瞬时速度.当位移足够小时,物体在这段时间内运动可认为是匀速的,所得的平均速度就等于物体经过A 点的瞬时速度了.我们现在已经了解了一些关于瞬时速度的知识,现在已经知道物体做直线运动时,它的运动规律用函数表示为s =s (t ),也叫做物体的运动方程或位移公式,现在有两个时刻t 0,t 0+Δt ,现在问从t 0到t 0+Δt 这段时间内,物体的位移、平均速度各是:位移为Δs =s (t 0+Δt )-s (t 0)(Δt 称时间增量) 平均速度tt s t t s t s v ∆-∆+=∆∆=)()(00 根据对瞬时速度的直观描述,当位移足够小,现在位移由时间t 来表示,也就是说时间足够短时,平均速度就等于瞬时速度.现在是从t 0到t 0+Δt ,这段时间是Δt . 时间Δt 足够短,就是Δt 无限趋近于0. 当Δt →0时,平均速度就越接近于瞬时速度,用极限表示瞬时速度瞬时速度tt s t t s v v t t ∆-∆+==→∆→∆)()(limlim 0000所以当Δt →0时,平均速度的极限就是瞬时速度三、讲解范例:例1物体自由落体的运动方程s =s (t )=21gt 2,其中位移单位m ,时间单位s ,g =9.8 m/s 2. 求t =3这一时段的速度.解:取一小段时间[3,3+Δt ],位置改变量Δs =21g (3+Δt )2-21g ·32=2g(6+Δt )Δt ,平均速度21=∆∆=t s v g (6+Δt )瞬时速度m/s 4.293)(21lim lim 00==∆+==→∆→∆g t t g v v t t由匀变速直线运动的速度公式得v =v 0+at =gt =g ·3=3g =29.4 m/s例2已知质点M 按规律s =2t 2+3做直线运动(位移单位:cm ,时间单位:s),(1)当t =2,Δt =0.01时,求ts ∆∆. (2)当t =2,Δt =0.001时,求ts∆∆.(3)求质点M 在t =2时的瞬时速度.分析:Δs 即位移的改变量,Δt 即时间的改变量,t s ∆∆即平均速度,当Δt 越小,求出的ts ∆∆越接近某时刻的速度.解:∵tt t t t t s t t s t s ∆+-+∆+=∆-∆+=∆∆)32(3)(2)()(22=4t +2Δt ∴(1)当t =2,Δt =0.01时,ts∆∆=4×2+2×0.01=8.02 cm/s (2)当t =2,Δt =0.001时,ts∆∆=4×2+2×0.001=8.002 cm/s (3)v =00lim lim→∆→∆=∆∆t t t s(4t +2Δt )=4t =4×2=8 cm/s四、巩固练习:1.一直线运动的物体,从时间t 到t t +∆时,物体的位移为s ∆,那么0lim t s t∆→∆∆为( )A.从时间t 到t t +∆时,物体的平均速度; B.在t 时刻时该物体的瞬时速度; C.当时间为t ∆时物体的速度; D.从时间t 到t t +∆2.一球沿一斜面自由滚下,其运动方程是s =s (t )=t 2(位移单位:m ,时间单位:s),求小球在t =5解:瞬时速度v =2200(5)(5)(5)5lim lim t t s t s t t t∆→∆→+∆-+∆-=∆∆lim t ∆→=(10+Δt )=10 m/s.∴瞬时速度v =2t =2×5=10 m/s.3.质点M 按规律s =2t 2+3做直线运动(位移单位:cm ,时间单位:s),求质点M 在t =2时的瞬时速度.解:瞬时速度v =tt t s t s t t ∆+⋅-+∆+=∆-∆+→∆→∆)322(3)2(2lim)2()2(lim 2200 =0lim →∆t (8+2Δt )=8 cm/s.点评:求瞬时速度,也就转化为求极限,瞬时速度我们是通过在一段时间内的平均速度的极限来定义的,只要知道了物体的运动方程,代入公式就可以求出瞬时速度了.运用数学工具来解决物理方面的问题,是不是方便多了.所以数学是用来解决其他一些学科,比如物理、化学等方面问题的一种工具,我们这一节课学的内容以及上一节课学的是我们学习导数的一些实际背景五、教学反思 :这节课主要学习了物体运动的瞬时速度的概念,它是用平均速度的极限来定义的,主要记住公式瞬时速度v =tt ∆→∆lim。
瞬时变化率——导数知识 学案 2017-2018学年高中数学 苏教版 选修2-2

1.1.1 平均变化率1.1.2 瞬时变化率——导数知识梳理1.函数f(x)在区间[x 1,x 2]上的平均变化率为___________.2.设物体运动的路程与时间的关系是s=f(t),当Δt 趋近于0时,函数f(t)在t 0+Δt 之间的平均变化率tt f t t f ∆-∆+)()(00趋近于常数.我们把这个常数称为t 0时刻的____________. 3.函数y=f(x)在x 0处的导数f′(x 0)的几何意义,就是曲线y=f(x)在(x 0,f(x 0))处切线的斜率,即k=f′(x 0)=_____________.知识导学要学好本节内容,最重要的是理解平均变化率和瞬时变化率的概念.本节的重点是导数的定义及其几何意义,难点是利用割线逼近的方法求曲线在某点处的导数,及两种变化率之间的关系.疑难突破1.正确理解平均变化率和瞬时变化率的关系.剖析:平均变化率和瞬时变化率都是反映事物变化程度的量,平均变化率表示的是曲线在某区间上的变化趋势;瞬时变化率表示的是曲线上某一点处的变化趋势.2.怎样理解导数的定义及几何意义?剖析:导数是函数在某一点处的瞬时变化率,导数的几何意义就是曲线y=f(x)在点P(x 0,f(x 0))处的切线的斜率.导数的概念就是变量变化速度在数学上的一种抽象,深刻理解导数的定义是本节的关键.典题精讲【例1】 已知f(x)=x 2,求曲线y=f(x)在x=3处的切线斜率.思路分析:为求得过点(3,9)处的切线斜率,我们从经过点(3,9)的任意一条直线(割线)入手.解:设P(3,9),Q(3+Δx,(3+Δx)2),则割线PQ 的斜率为k PQ =x x ∆-∆+9)3(2=6+Δx. 当Δx 无限趋近于0时,k PQ 无限趋近于常数6,从而曲线y=f(x)在点P(3,9)处的切线斜率为6.绿色通道:利用割线逼近切线的方法,求曲线在某一点处的切线斜率的方法是一种比较直观的解题方法.变式训练:已知f(x)=2x 2,求曲线y=f(x)在x=1处的切线斜率.思路分析:为求得过点(1,2)处的切线斜率,我们从经过点(1,2)的任意一条直线(割线)入手.解:设P(1,2),Q(1+Δx,2(1+Δx)2),则割线PQ 的斜率为k PQ =xx ∆-∆+2)1(22=4+2Δx. 当Δx 无限趋近于0时,k PQ 无限趋近于常数4,从而曲线y=f(x)在点P(1,2)处的切线斜率为4.【例2】 已知f(x)=x 2+3.(1)求f(x)在x=1处的导数;(2)求f(x)在x=a 处的导数.思路分析:函数在某一点处的导数实际上就是相应函数图象在该点切线的斜率,深刻理解概念是正确解题的关键.解:(1)因为xx x f x f x y ∆+-+∆+=∆-∆+=∆∆)31(3)1()1()1(22=2+Δx , 当Δx 无限趋近于0时,2+Δx 无限趋近于2,所以f(x)在x=1处的导数等于2.(2)因为xa x a x a f x a f x y ∆+-+∆+=∆-∆+=∆∆)3(3)()()(22=2a+Δx , 且当Δx 无限趋近于0时,2a+Δx 无限趋近于2a,所以f(x)在x=a 处的导数等于2a. 绿色通道:本题主要考查对导数概念的理解程度,及应用定义解题的熟炼程度.变式训练:已知f(x)=3x+5,求当x=2时的导数.思路分析:函数在某一点处的导数的几何意义就是函数图象在该点切线的斜率.解:因为3)523(5)2(3)2()2(=∆+⨯-+∆+=∆-∆+=∆∆xx x f x f x y . 所以f(x)在x=2时的导数为3.【例3】 已知曲线y=3x 2-x,求曲线上一点A(1,2)处的切线的斜率及切线方程.思路分析:求曲线上某点的切线斜率就是求函数在那一点的导数值.解:因为x xx x x y ∆+=∆-⨯-∆+-∆+=∆∆35)113()1()1(322, 当Δx 趋近于0时,5+3Δx 就趋近于5,所以曲线y=3x 2-x 在点A(1,2)处的切线斜率是5. 切线方程为y-2=5(x-1),即5x-y-3=0.绿色通道:根据导数的定义将切线的斜率求出,再根据点斜式方程求出切线方程,这是用导数求某点处切线的一般方法.变式训练:已知曲线y=331x 上一点P(2,38),求点P 的切线斜率及点P 处的切线方程. 思路分析:先求出某点处的切线斜率,即求该函数在某点处的导数,然后利用导数定义求解.解:因为xx x y ∆⨯-∆+=∆∆33231)2(31 xx x x x x x x ∆∆+∆+∆=∆∆+∆⨯+∆⨯=323223124])()(2323[31=4+2Δx+231x ∆, 当Δx 趋近于0时,4+2Δx+2 31x ∆就趋近于4, 所以曲线y=331x 上点P(2,38)处的切线斜率为4,切线方程为)2(438-=-x y ,即03164=--y x 问题探究问题:某钢管厂生产钢管的利润函数为P(n)=-n 3+600n 2+67 500n-1 200 000,其中n 为工厂每月生产该钢管的根数,利润P(n)的单位是元.(1)求边际利润函数P′(n)=0时n 的值;(2)解释(1)中n 的实际意义.导思:这是一道有关边际函数的实际应用题,由于利润函数已给出,只需先求边际利润函数P′(n),再根据P′(n)=0解出n 的值即可.探究:(1)因为nn n n n n n n y ∆-∆++∆++∆+-=∆∆1200000)(67500)(600)(23 =(-3n 2+1 200n+67 500)+Δn.当Δn 无限趋近于0时,-3n 2+1 200n+67 500+Δn 无限趋近于-3n 2+1 200n+67 500.∴P′(n)=-3n 2+1 200n+67 500.由P′(n)=0,即-3n 2+1 200n+67 500=0.解得n=450或n=-50(舍).即当边际利润函数P′(n)=0时,n 的值为450.(2)P′(n)=0时,n 的值为450表示的实际意义是当工厂生产450根钢管时,利润增加量为零.。
高中数学 瞬时变化率 导数导学案 苏教版选修22

瞬时变化率—导数 NO.2【教学目标】(1)理解并掌握曲线在某一点处的切线的概念(2)会运用瞬时速度的定义求物体在某一时刻的瞬时速度和瞬时加速度(3)理解导数概念 实际背景,培养学生解决实际问题的能力,进一步掌握在一点处 的导数的定义及其几何意义,培养学生转化问题的能力及数形结合思想【重点难点】导数概念的理解,以及运用导数解决问题的能力。
一、复习引入1、什么叫做平均变化率;2、曲线上两点的连线(割线)的斜率与函数f(x)在区间[x A ,x B ]上的平均变化率3、如何精确地刻画曲线上某一点处的变化趋势呢?二、新课讲解设曲线C 上一点P(x ,f(x)),过点P 的一条割线交曲线C 于另一点Q (x x +∆,()f x x +∆)则割线PQ 的斜率为()()()()()PQ f x x f x f x x f x k x x x x +∆-+∆-==+∆-∆ 1、曲线上一点处的切线斜率当点Q 沿曲线C 向点P 运动,并无限靠近点P 时,割线PQ 逼近点P 的切线l,从而割线的斜率逼近切线l 的斜率,即当△x 无限趋近于0时,()()f x x f x x+∆-∆无限趋近点P(x ,f(x))处的切线的斜率。
()()f x x f x k x+∆-=∆,当△x 无限趋近于0时,k 值即为(x ,f(x))处切线的斜率。
2.瞬时速度与瞬时加速度(1)平均速度: 物理学中,运动物体的位移与所用时间的比称为平均速度(2)位移的平均变化率:tt s t t s ∆-∆+)()(00 (3)瞬时速度:当t ∆无限趋近于0 时,运动物体的位移S( t)的平均变化率tt s t t s ∆-∆+)()(00无限趋近于一个常数,这个常数称为物体在t=t 0时的瞬时速度,也就是位移对时间的瞬时变化率求瞬时速度的步骤:1.先求时间改变量t ∆和位置改变量)()(00t s t t s s -∆+=∆2.再求平均速度ts v ∆∆= 3.后求瞬时速度:当t ∆无限趋近于0,t s ∆∆无限趋近于常数v 为瞬时速度 (4)速度的平均变化率:tt v t t v ∆-∆+)()(00 (5)瞬时加速度:当t ∆无限趋近于0 时,t t v t t v ∆-∆+)()(00无限趋近于一个常数,这个常数称为t=t 0时的瞬时加速度注:瞬时加速度是速度对于时间的瞬时变化率3.导数:函数在某点的瞬时变化率)0()()(00→∆→∆-∆+=∆∆x A xx f x x f x y 记作)(0x f ' 三、数学应用例1、已知f(x)=x 2,求曲线在x=2处的切线的斜率。
苏教版高中数学选修(2-2)-1.1《瞬时变化率—导数:瞬时速度与瞬时加速度》导学案

1.1.2《瞬时变化率——导数》导学案(二)瞬时速度与瞬时加速度一、学习目标1.理解瞬时速度与瞬时加速度的定义,掌握如何由平均速度和平均加速度“逼近” 瞬时速度与瞬时加速度的过程.理解平均变化率的几何意义;理解△x无限趋近于0的含义;2.运用瞬时速度与瞬时加速度的定义求解瞬时速度与瞬时加速度.二、学习重点、难点重点:瞬时速度和瞬时加速的定义难点:求瞬时速度和瞬时加速的的方法.三、学习过程【复习回顾】1. 曲线上一点处的切线斜率:设曲线C是函数y=f(x)的图象,在曲线C上取一点P(x,y)及邻近的一点Q(x +∆x, f(x+ ∆x)),过P、Q两点作割线,,则割线PQ的斜率k=. 当∆x→0时,动点Q将沿曲线趋向为PQ于定点P,从而割线PQ也将随之变动而趋向于切线PT的斜率,当△x→0时,割线PQ的斜率的极限,就是曲线在点P处的切线的斜率,即K为.在△x→0时的极限值.练习:曲线的方程为y=x2+1,求曲线在点P(1,2)处的切线方程.【问题情境1】平均速度:物体的运动位移与所用时间的比称为平均速度.平均速度反映物体在某一段时间段内运动的快慢程度.那么如何刻画物体在某一时刻运动的快慢程度?【问题情境2】跳水运动员从10m 高跳台腾空到入水的过程中,不同时刻的速度是不同的.假设t 秒后运动员相对于水面的高度为()24.9 6.510H t t t =-++,那么我们就会计算任意一段的平均速度v ,通过平均速度v 来描述其运动状态,但用平均速度不一定能反映运动员在某一时刻的瞬时速度,那么如何求运动员的瞬时速度呢? 问题:2秒时的瞬时速度是多少?我们现在会算任意一段的平均速度,先来观察一下2秒附近的情况.问题:1.你能描述一下你算得的这些数据的变化规律吗?关于这些数据,下面的判断对吗?2.当t ∆趋近于0时,即无论t 从小于2的一边,还是t 从大于2的一边趋近于2时,平均速度都趋近于一个确定的值-13.1s m /.3.靠近-13.1且比-13.1大的任何一个数都可以是某一段[]2,2t ∆+上的平均速度;4.靠近-13.1且比-13.1小的任何一个数都可以是某一段[]t ∆+2,2上的平均速度;。
1.1.2 瞬时变化率——导数 学案(苏教版高中数学选修2-2)

1.1.2 瞬时变化率——导数学案(苏教版高中数学选修2-2)112瞬时变化率瞬时变化率导数导数学习目标1.了解切线的含义.2.理解瞬时速度与瞬时加速度.3.掌握瞬时变化率导数的概念,会根据定义求一些简单函数在某点处的导数知识点一曲线上某一点处的切线如图,Pn的坐标为xn,fxnn1,2,3,4,,点P的坐标为x0,y0思考1当点Pn点P时,试想割线PPn如何变化答案当点Pn趋近于点P时,割线PPn趋近于确定的位置,即曲线上点P处的切线位置思考2割线PPn的斜率是什么它与切线PT的斜率有何关系答案割线PPn的斜率knfxnfx0xnx0;当Pn无限趋近于P时,kn无限趋近于点P处切线的斜率k.梳理1设Q为曲线C上的不同于P的一点,这时,直线PQ称为曲线的割线随着点Q沿曲线C向点P运动,割线PQ在点P 附近越来越逼近曲线C.当点Q无限逼近点P时,直线PQ最终就成为在点P处最逼近曲线的直线l,这条直线l称为曲线在点P处的切线2若Px,fx,过点P的一条割线交曲线C于另一点Qxx,fxx,则割线PQ的斜率为kPQfxxfxx,当x0时,fxxfxx无限趋近于点Px,fx处的切线的斜率知识点二瞬时速度与瞬时加速度瞬时变化率1平均速度在物理学中,运动物体的位移与所用时间的比称为平均速度2瞬时速度一般地,如果当t无限趋近于0时,运动物体位移St的平均变化率St0tSt0t无限趋近于一个常数,那么这个常数称为物体在tt0时的瞬时速度,也就是位移对于时间的瞬时变化率3瞬时加速度一般地,如果当t无限趋近于0时,运动物体速度vt的平均变化率vt0tvt0t无限趋近于一个常数,那么这个常数称为物体在tt0时的瞬时加速度,也就是速度对于时间的瞬时变化率知识点三导数1导数设函数yfx在区间a,b上有定义,x0a,b,若x 无限趋近于0时,比值yxfx0xfx0x无限趋近于一个常数A,则称fx在xx0处可导,并称该常数A为函数fx在xx0处的导数,记作fx02导数的几何意义导数fx0的几何意义就是曲线yfx在点Px0,fx0处的切线的斜率3导函数1若fx对于区间a,b内任一点都可导,则fx在各点的导数也随着自变量x的变化而变化,因而也是自变量x的函数,该函数称为fx的导函数,记作fx在不引起混淆时,导函数fx也简称为fx的导数2fx在xx0处的导数fx0就是导函数fx在xx0处的函数值1曲线上给定一点P,过点P 可以作该曲线的无数条割线2有的曲线过它上面的某一点可作两条切线3函数fx在区间a,b内可导就是fx对于任意x0a,b都有fx0存在4fx0表示函数fx在xx0处的导数,是对一个点x0而言的,它是一个确定的值类型一求曲线上某一点处的切线例1已知曲线yfxx1x上的一点A2,52,用切线斜率定义求1点A处的切线的斜率;2点A处的切线方程解1yf2xf22x12x212x22xx,yxx2x2xxx122x1.当x无限趋近于零时,yx无限趋近于34,即点A处的切线的斜率是34.2切线方程为y5234x2,即3x4y40.反思与感悟根据曲线上一点处的切线的定义,要求曲线在某点处的切线方程,只需求出切线的斜率,即在该点处,x无限趋近于0时,yx无限趋近的常数跟踪训练11已知曲线yfx2x24x在点P处的切线的斜率为16,则点P坐标为________答案3,30解析设点P坐标为x0,y0,则fx0xfx0x0xx02x24x0x4xx4x042x.当x 无限趋近于0时,4x042x无限趋近于4x04,因此4x0416,即x03,所以y023*******30.即点P坐标为3,302已知曲线y3x2x,求曲线上一点A1,2处的切线的斜率及切线方程解设A1,2,B1x,31x21x,则kAB31x21x3121x53x,当x无限趋近于0时,53x无限趋近于5,所以曲线y3x2x在点A1,2处的切线斜率是5.切线方程为y25x1,即5xy30.类型二求瞬时速度例2某物体的运动路程s单位m与时间t单位s 的关系可用函数stt2t1表示,求物体在t1s时的瞬时速度解在1到1t的时间内,物体的平均速度vsts1ts1t1t21t11211t3t,当t 无限趋近于0时,v无限趋近于3,物体在t1处的瞬时变化率为3.即物体在t1s时的瞬时速度为3m/s.引申探究1若本例中的条件不变,试求物体的初速度解求物体的初速度,即求物体在t0时的瞬时速度sts0ts0t0t20t11t1t,当t0时,1t1,物体在t0时的瞬时变化率为1,即物体的初速度为1m/s.2若本例中的条件不变,试问物体在哪一时刻的瞬时速度为9m/s.解设物体在t0时刻的速度为9m/s.又stst0tst0t2t01t.当t0时,st2t01.则2t019,t04.则物体在4s时的瞬时速度为9m/s.反思与感悟1求瞬时速度的题目的常见错误是不能将物体的瞬时速度转化为函数的瞬时变化率2求运动物体瞬时速度的三个步骤求时间改变量t和位移改变量sst0tst0求平均速度vst.求瞬时速度,当t无限趋近于0时,st无限趋近于的常数v即为瞬时速度跟踪训练2有一做直线运动的物体,其速度v单位m/s与时间t单位s 的关系是v3tt2,求此物体在t2s时的瞬时加速度解因为v2tv232t2t232223t4tt2tt2,所以v2tv2t1t,所以当t趋于0时,1t无限趋近于1.所以该物体在t2s时的瞬时加速度为1m/s2.类型三求函数在某点处的导数例3已知fxx23.1求fx在x2处的导数;2求fx在xa处的导数解1因为yxf2xf2x2x23223x4x,当x无限趋近于0时,4x无限趋近于4,所以fx在x2处的导数等于4.2因为yxfaxfaxax23a23x2ax,当x无限趋近于0时,2ax 无限趋近于2a,所以fx在xa处的导数等于2a.反思与感悟求一个函数yfx在xx0处的导数的步骤1求函数值的改变量yfx0xfx02求平均变化率yxfx0xfx0x.3令x无限趋近于0,求得导数跟踪训练31设fxax4,若f12,则a________.答案2解析f1xf1xa1x4a4xa,f1a,即a2.2将原油精炼为汽油.柴油.塑胶等各种不同产品,需要对原油进行冷却和加热,如果第xh原油的温度单位为fxx27x150x8求函数yfx在x6处的导数f6,并解释它的实际意义解当x从6变到6x时,函数值从f6变到f6x,函数值y关于x的平均变化率为f6xf6x6x276x15627615x5xx2x5x.当x0时,5x趋近于5,所以f65,导数f65表示当x6时原油温度大约以5/h的速度上升1设函数fx可导,则当x0时,f13xf13x趋近于________答案f1解析当x0时,f13xf13xf12若函数fx在点A1,2处的导数是1,那么过点A的切线方程是________________答案xy30解析kf11,切线方程是y2x1,即xy30.3已知函数yfx在点2,1处的切线与直线3xy20平行,则f2________.答案3解析因为直线3xy20的斜率为3,所以由导数的几何意义可知f23.4已知曲线yfx2x2上一点A2,8,则点A处的切线斜率为________答案8解析因为yxf2xf2x22x28x82x,当x0时,82x趋近于8.即k8.5函数yfxx1x在x1处的导数是________答案0解析函数yfxx1x,yf1xf11x11x11x21x,yxx1x,当x0时,yx0,即yfxx1x 在x1处的导数为0.1平均变化率和瞬时变化率的关系平均变化率yxfx0xfx0x,当x无限趋近于0时,它所趋近于的一个常数就是函数在xx0处的瞬时变化率即有x无限趋近于0是指自变量间隔x 越来越小,能达到任意小的间隔,但始终不能为0.即对于瞬时变化率,我们通过减小自变量的改变量以致无限趋近于零的方式,实现用割线斜率“逼近”切线斜率,用平均速度“逼近”瞬时速度一般地,可以用平均变化率“逼近”瞬时变化率2求切线的斜率.瞬时速度和瞬时加速度的解题步骤1计算y.2求yx.3当x0时,yx无限趋近于一个常数4常数即为所求值.。
数学:1.1.2《瞬时变化率-导数》教案(苏教版选修2-2)

1。
1。
2瞬时变化率-导数(三)导数的概念一、教学目标1.理解导数的概念,知道瞬时变化率就是导数,体会导数的思想及其内涵.2. 会求函数在某点的导数。
二、例题讲解例 1(1)以初速度为)0(00>v v做竖直上抛运动的物体,t 秒时的高度为2021)(gt t v t s -=,求物体在时刻0t 处的瞬时速度。
(2)求122+=xy 在0x 到x x ∆+0之间的平均变化率. (3)设2)(x x f =+1,求)('x f,)1('-f ,)2('f例2、函数)(x f 满足2)1('=f ,则当x 无限趋近于0时,(1)=-+x f x f 2)1()1( (2)=-+xf x f )1()21( 变式:设f (x)在x=x 0处可导,(3)x x f x xf ∆-∆+)()4(00无限趋近于1,则)(0x f '=___________ (4)xx f x x f ∆-∆-)()4(00无限趋近于1,则)(0x f '=________________ (5)当△x 无限趋近于0,xx x f x xf ∆∆--∆+)2()2(00所对应的常数与)(0x f '的关系. 例3.(1)求函数y =3x 2在x =1处的导数.(2)求函数f (x )=x x +-2在1x =-附近的平均变化率,并求出在该点处的导数.例4:已知函数x x f =)(,求)(x f 在2=x 处的切线.例 5.某工厂每日产品的总成本C 是日产量x 的函数,即2571000)(x x x C ++=,试求:(1)当日产量为100时的平均成本;(2)当日产量由100增加到125时,增加部分的平均成本;(3)当日产量为100时的边际成本.三、课堂练习1.函数xx y 1+=, 在1=x 处的导数是 2.将半径为R 的球加热,若球的半径增加R ∆,则球的表面积增加S ∆等于( )AR R ∆π8 B ()248R R R ∆+∆ππ C ()244R R R ∆+∆ππ D ()24R ∆π 3. 在曲线12+=xy 的图象上取一点(1,2)及附近一点()y x ∆+∆+2,1,则x y ∆∆为( ) A 21+∆+∆x x B 21-∆-∆x x C 2+∆x D xx ∆-∆+12 四、课后作业1.函数)(x f y =在0x x =处的导数)(0/x f 的几何意义是( ) A 在点0x x =处的函数值 B 在点))(,(00x f x 处的切线与x 轴所夹锐角的正切值C 曲线)(x f y =在点))(,(00x f x 处的切线的斜率D 点))(,(00x f x 与点(0,0)连线的斜率2.已知曲线3x y =上过点(2,8)的切线方程为01612=--ax x ,则实数a 的值为( )3.设4)(+=ax x f ,若2)1('=f ,则a 的值( )4.任一做直线运动的物体,其位移s 与时间t 的关系是23t t s -=,则物体的初速度是( )5、求下列函数在相应位置的导数(1)1)(2+=xx f ,2=x (2)12)(-=x x f ,2=x (3)3)(=x f ,2=x6.已知曲线331x y =上的一点)38,2(P ,求(1)点P 处切线的斜率;(2)点P 处的切线方程.变式:已知曲线331x y =,求与直线084=++y x 垂直,并与该曲线相切的直线方程。
高中数学教案选修22《1.1.2瞬时变化率——导数》

Word 文档仅限参照教课目的:1.理解并掌握刹时速度的定义;2.会运用刹时速度的定义求物体在某一时辰的刹时速度和刹时加快度;3.理解刹时速度的实质背景,培育学生解决实质问题的能力.教课要点:会运用刹时速度的定义求物体在某一时辰的刹时速度和刹时加快度.教课难点:理解刹时速度和刹时加快度的定义.教课过程:一、问题情境1.问题情境.均匀速度:物体的运动位移与所用时间的比称为均匀速度.问题一均匀速度反应物体在某一段时间段内运动的快慢程度.那么怎样刻画物体在某一时辰运动的快慢程度?问题二跳水运动员从10m 高跳台凌空到入水的过程中, 不一样时辰的速度是不一样的.假定 t 秒后运动员相关于水面的高度为h( t) =- 4. 9t2+ 6. 5t+10, 试确立t=2s 时运动员的速度 .2.研究活动:( 1) 计算运动员在2s 到 2. 1s( t∈) 内的均匀速度.( 2) 计算运动员在2s 到( 2+ ?t)s( t∈) 内的均匀速度.( 3) 怎样计算运动员在更短时间内的均匀速度.研究结论:Word 文档仅限参照时间区间?t 均匀速度0.1-13.590. 01- 13. 1490. 001- 13. 10490. 0001- 13. 100490. 00001- 13. 100049 0. 000001- 13. 1000049当 ?t 0 时, v -13.1,该常数可作为运动员在 2s 时的刹时速度.即 t = 2s 时, 高度关于时间的刹时变化率.二、建构数学1.均匀速度.设物体作直线运动所经过的行程为=, 以 t 0 为开端时辰 , 物体在 t 时间内s f (t )的均匀速度为 v = s =f (t+t)-f (t0 ).ttv 可作为物体在 t 0 时辰的速度的近似值 , t 越小 , 近似的程度就越好.因此当t 0 时, v 极限就是物体在 t 0 时辰的刹时速度.三、数学运用例 1 物体作自由落体运动 ,运动方程为= 12 ,此中位移单位是m, 时Sgt2间单位是 s, =2,求:g 10 m/ s( 1) 物体在时间区间 s 上的均匀速度;Word 文档仅限参照( 2) 物体在时间区间上的均匀速度;( 3) 物体在 t =2s 时的刹时速度.剖析s = s(t 0+ t)- s(t 0 )=2g t + 1g ( t )2__2s = s(t 0+ t)- s(t 0 ) =2g + 1v = g ( t )__t t 2解 = s= 1v + t )t2 gg (2__( 1)将 ?t =0. 1 代入上式 , 得: v ==.__( 2)将 ?t =0.0 1 代入上式 , 得: v ==.__( 3)当 t 0,2+ t2,进而均匀速度 v 的极限为:__s= 2g =20m/ s.v = lim v = limt 0t 0t例 2设一辆轿车在公路上作直线运动 ,假定 t (s) 时的速度为2= +v(t ) t 3 ,求当 t = t 0 (s) 时轿车的刹时加快度 a .解+-a = v =f (tt ) f (t 0 )= 2t 0+ xtt∴当 ?t 无穷趋于 0 时, a 无穷趋于 2t 0 ,即 a = 2t 0 . 练习课本 P12— 1, 2.四、回首小结问题 1本节课你学到了什么?① 理解刹时速度和刹时加快度的定义;② 实质应用问题中刹时速度和刹时加快度的求解;问题 2解决刹时速度和刹时加快度问题需要注意什么?注意当 t 0 时, 刹时速度和刹时加快度的极限值.问题 3本节课表现了哪些数学思想方法?② 极限的思想方法.③ 特别到一般、从详细到抽象的推理方法.五、课外作业。
1.1.2瞬时变化率导数(苏教版选修2-2)

知新益能
•1.割线逼近切线的方法 •设Q为曲线C上不同于P的一点,这时直线PQ称为曲线的_____.随着点Q沿曲线C向P点运动,
割线PQ在点P附近越来越逼近曲线C.当点Q无限逼近点P时,直线PQ最终成为经过点P处最逼近
曲线的直线l,这条直线l称为曲线在点P处的_____.
割线
切线
•2.用割线逼近切线的方法计算曲线上某点处切线的斜率 •设曲线C上一点P(x,f(x)),过点P的一条割线交曲线C于另一点Q(x+Δx,f(x+Δx)),则割线PQ 的斜率为 •kPQ=______________=_______________. •当点Q沿曲线C向点P运动,并无限靠近点P时,割线PQ逼近过点P的切线l,从而割线的斜率逼 近过
st0+Δt-st0 无限趋近于一个常数,那么这个常数 Δt 瞬时速度 . 称为物体在 t=t0 时的_________ (2) 一般地,我们计算运动物体速度的平均变化率 vt0+Δt-vt0 ,如果当 Δt 无限趋近于 0 时, Δt vt0+Δt-vt0 无限趋近于一个常数,那么这个常数 Δt 瞬时加速度 . 称为物体在 t=t0 时的___________
导数的几何意义的应用 函数 f(x) 在 x = x0 处的导数 f′(x0) 的几何意义是曲线 y
=f(x)在 x=x0处切线的斜率,故该曲线在 x= x0处的
切线方程y-f(x0)=f′(x0)(x-x0).
例3
1 (本题满分 14 分)已知曲线 y=x+x上一点
5 A(2, ),用斜率定义求: 2 (1)点 A 处的切线的斜率; (2)点 A 处的切线方程.
•2.求曲线的切线时需要注意:(1)在求曲线的切线方程时,要注意区分所求切线是曲线上某点处 的切线(只有当此点在曲线上时,此点处的切线的斜率才是f′(x0)),还是过某点的切线;(2)求过 某一点的切线方程时也是通过切点坐标来求.
高中数学学案选修2-2《2.1.2瞬时变化率》

第二章变化率与导数
第2课时
课题名称
时间
第周星期
课型
新授课
主备课人
陈锋
目标
1.理解并掌握曲线在某一点处的切线的概念;
2.会运用瞬时速度的定义求物体在某一时刻的瞬时速度.
重点
求切线及瞬时速度
二次备课
难点
求切线及瞬时速度
自
主
学
习
提出问题:(阅读课本回答)
1.平均变化率:
2.平均速度:
例2一作直线运动的物体其位移s与时间t的关系是 .
(1)求此物体的初速度;
(2)求此物体在t=2秒时的瞬时速度;Байду номын сангаас
(3)求t=0到t=2时的平均速度.
达
标
训
练
1.课本30页练习1
2.如果质点M按规律 运动,则在一小段时间中相应的平均速度等于()
A.4 B. C. D.3
3.如果某物体的运动方程是 ,则在 秒时的瞬时速度是()
3.曲线上两点的连线(割线)的斜率与函数f(x)在区间上的平均变化率
有何关系?
问题生成记录:
精
讲
互
动
1.瞬时速度:
如何理解瞬时速度?它与平均速度有何关系?
2.求瞬时速度的步骤:
1)先求时间改变量 和位置改变量
2)再求平均速度
3)后求瞬时速度:当 无限趋近于0, 无限趋近于常数v为瞬时速度
例1自由落体运动的位移s (m)与时间t(s)的关系为s= ,求t=3s时的瞬时速度
A.4 B. C. D.
4.设一物体在t秒内所经过的路程为s米,并且 ,则物体在运动开始的速度为()
A.3 B.-3 C.0 D.2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学目标:
1.理解并掌握瞬时速度的定义;
2.会运用瞬时速度的定义求物体在某一时刻的瞬时速度和瞬时加速度;
3.理解瞬时速度的实际背景,培养学生解决实际问题的能力.
教学重点:
会运用瞬时速度的定义求物体在某一时刻的瞬时速度和瞬时加速度.
教学难点:
理解瞬时速度和瞬时加速度的定义.
教学过程:
一、问题情境
1.问题情境.
平均速度:物体的运动位移与所用时间的比称为平均速度.
问题一平均速度反映物体在某一段时间段内运动的快慢程度.那么如何刻画物体在某一时刻运动的快慢程度?
问题二跳水运动员从10m高跳台腾空到入水的过程中,不同时刻的速度是不同的.假设t 秒后运动员相对于水面的高度为h(t)=-4.9t2+6.5t+10,试确定t=2s时运动员的速度.
2.探究活动:
(1)计算运动员在2s到2.1s(t∈)内的平均速度.
(2)计算运动员在2s到(2+∆t)s(t∈)内的平均速度.
(3)如何计算运动员在更短时间内的平均速度.
探究结论:
当∆t →0时,v →-13.1,
该常数可作为运动员在2s 时的瞬时速度. 即t =2s 时,高度对于时间的瞬时变化率. 二、建构数学 1.平均速度.
设物体作直线运动所经过的路程为()s f t =,以0t 为起始时刻,物体在∆t 时间内的平均速度为00()()
∆∆∆∆f t t f t s v t t
+-=
=. v 可作为物体在0t 时刻的速度的近似值,∆t 越小,近似的程度就越好.所以当
∆t →0时,v 极限就是物体在0t 时刻的瞬时速度.
三、数学运用
例1 物体作自由落体运动,运动方程为21
2
S gt =,其中位移单位是m ,时
间单位是s ,210m/s g =,求:
(1) 物体在时间区间 s 上的平均速度;
(2) 物体在时间区间上的平均速度; (3) 物体在t =2s 时的瞬时速度.
分析 2001
()()2()2
s s t t s t g t g t =+-=+∆∆∆∆
__
00()()12()2s t t s t s v g g t t t +-===+∆∆∆∆∆
解 __
1
2()2
s v g g t t ==+∆∆∆
(1)将∆t =0.1代入上式,得:__
v =2.05g =20.5m/s . (2)将∆t =0.01代入上式,得:__
v =2.005g =20.05m/s . (3)当∆t →0,2+∆t →2,从而平均速度__
v 的极限为:
__
0lim lim
2g 20m/s.→→t t s
v v t
====∆∆∆∆ 例2 设一辆轿车在公路上作直线运动,假设)(s t 时的速度为2()3v t t =+, 求当0(s)t t =时轿车的瞬时加速度a .
解 v
a t =
∆∆00()()∆∆f t t f t t
+-=02∆t x =+ ∴当∆t 无限趋于0时,a 无限趋于02t ,即a =02t . 练习
课本P12—1,2. 四、回顾小结
问题1 本节课你学到了什么? ① 理解瞬时速度和瞬时加速度的定义;
② 实际应用问题中瞬时速度和瞬时加速度的求解; 问题2 解决瞬时速度和瞬时加速度问题需要注意什么? 注意当∆t →0时,瞬时速度和瞬时加速度的极限值. 问题3 本节课体现了哪些数学思想方法? ② 极限的思想方法.
③ 特殊到一般、从具体到抽象的推理方法. 五、课外作业。
