19页小升初“圆”阴影部分面积例题及答案
小学六年级圆-阴影部分面积(含答案)

求阴影部分面积例 2. 正方形面积是 7 平方厘米,求阴影部分的面积。
设圆的半径为 r ,因为正方形的面积为 7平方厘米,所以=7,=平方厘米解:这是一个用最常用的方法解 最常见的题,为方便起见,我们把阴影部分的每一个小 部分称为 “叶形 ”,是用两个圆减π -π( )=平方厘米所以阴影部分的面积为:7- ×7=平方厘例 3.求图中阴影部分的面积。
(单位:厘米 )例 4.求阴影部分的面积。
(单位 :圆组成一个圆, 去圆的面积, 所以阴影部分的面积:解:最基本的方法之一。
用四个 面积,厘米)解:同上,正方形面积减去圆 =平方厘米。
16-π()=16-4π例 5.求阴影部分的面积。
(单位 : 厘米 )例 6. 如图:已知小圆半径为 2 厘米,大圆半径是小圆的 3 倍,问:空白部分甲比乙的面积多多少厘米?去一个正方形,例 1.求阴影部分的面积。
(单位 : 厘米 )(单位 :厘米)解:这也是一种最基本的方法用正方形的面积减去 圆的面积。
解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)另外:此题还可以看成是 1 题中阴影部分的 8 关) 倍。
厘米(注 :以上几个题都可以直接用图形的差来求,无需割、补、增、减变形 )例 9.求阴影部分的面积。
(单位 : 厘米 ) 例 10.求阴影部分的面积。
(单位 : 厘米 )2× 1=2平方厘米(注: 8、9、10 三题是简单割、补或平移 )×21-6=8π-16=平方厘米注:这和两个圆是否相交、交的情况如何无例 7.求阴影部分的面积。
(单位 : 厘米 ) 长 ÷2,求 ) 正方形面积为: 解:正方形面积可用 所以阴影面积为:π ÷=平方解:右面正方形上部阴 影部分的面积,等于左面正方形下部空白部分面积,割补以后为 圆,例 8.求阴影部分的面积。
(单位:厘米 ) 解:把右面的正方形平移至左 边的正方形部分,则阴影部分 合成一个长方形, 解:同上,平移左右两部分至中间部分,则合成一 个长方形,所以阴影部分面积为所以阴影部分面积为: 2×3=6平方厘米例 11.求阴影部分的面积。
圆_阴影部分面积(含答案)

求阴影部分面积解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还能够看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
圆_阴影部分面积(含答案)

例12.求阴影部分的面积。(单 位:厘米) 解:这种图形称为环形,可以 用两个同心圆的面积差或差的 解:三个部分拼成一个半圆面 积.
一部分来求。 (π -π )× = ×3.14=3.66平方厘米 例13.求阴影部分的面积。(单 位:厘米)
π( )÷2=14.13平方厘米
例14.求阴影部分的面积。(单 位:厘米)
解:这是最基本的方法: 圆面积减去等腰直角三角形的 面积, × -2×1=1.14(平方厘米)
解:这也是一种最基本的方法 用正方形的面积减去 圆的面积。 设圆的半径为 r,因为正 方形的面积为7平方厘米,所 以 =7, 所以阴影部分的面积为: 7=7×7=1.505平方厘米
例3.求图中阴影部分的面积。 (单位:厘米)
解:两个空白部分面积之差就 是两圆面积之差(全加上阴影 部分) π -π( )=100.48平方厘米 (注:这和两个圆是否相 交、交的情况如何无关)
例7.求阴影部分的面积。(单 位:厘米) 解:正方形面积可用(对角线长 ×对角线长÷2,求)
例8.求阴影部分的面积。(单位: 厘米) 解:右面正方形上部阴影部分 的面积,等于左面正方形下部 空白部分面积,割补以后为
例25.如图,四个扇形的半径相 例26.如图,等腰直角三角形 等,求阴影部分的面积。(单 ABC和四分之一圆DEB, 位:厘米) AB=5厘米,BE=2厘米,求图 中阴影部分的面积。
分析:四个空白部分可以拼成 一个以2为半径的圆. 所以阴影部分的面积为 梯形面积减去圆的面积, 4×(4+7)÷2-π
例30.如图,三角形ABC是直角 三角形,阴影部分甲比阴影部 分乙面积大28平方厘米, AB=40厘米。求BC的长度。 解:两部分同补上空白部分后 为直角三角形ABC,一个为半 圆,设BC长为X,则 40X÷2-π ÷2=28 所以40X-400π=56 X=32.8厘米
19页小升初圆阴影部分面积例题及答案

小升初“圆”阴影部分面积例题及答案1求如图阴影部分的面积.(单位:厘米)2.如图,求阴影部分的面积. (单位:厘米)3.计算如图阴影部分的面积. (单位:厘米)4.求出如图阴影部分的面积: 单位:厘米.S5.求如图阴影部分的面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米. 8求阴影部分的面积.单位:厘米.6.求如图阴影部分面积.(单位:厘米)9. 如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10. 求阴影部分的面积.(单位:厘米)11. 求下图阴影部分的面积.(单位:厘米)13. 计算阴影部分面积(单位:厘米).12.求阴影部分图形的面积. (单位:厘米)14. 求阴影部分的面积.(单位:厘米)15. 求下图阴影部分的面积:(单位:厘米)3 216. 求阴影部分面积(单位:厘米).17. (2012?长泰县)求阴影部分的面积.(单位:厘米)参考答案与试题解析1求如图阴影部分的面积.(单位:厘米)考 组合图形的面积;梯形的面积;圆、圆环的面积. 1526356占:八、、•分 阴影部分的面积等于梯形的面积减去直径为 4厘米的半圆的面积,析:梯形和半圆的面积公式代入数据即可解答.. 2解 解:(4+6) >4吃吃-3.14X 寺 吃,答: =10 - 3.14X4吃,=10 - 6.28,=3.72 (平方厘米);答:阴影部分的面积是 3.72平方厘米.点 组合图形的面积一般都是转化到已知的规则图形中利用公式计算,评:考查了梯形和圆的面积公式的灵活应用.2. 如图,求阴影部分的面积.(单位:厘米)考 组合图形的面积.1526356利用 这里点:八、、•分根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面析:积.正方形的面积等于(10X10)100平方厘米,4个扇形的面积等于半径为(10吃)5厘米的圆的面积,即: 3.14X5X5=78.5 (平方厘米).解解:扇形的半径是:答:10吃,=5 (厘米);10X0—3.14X5X5,100 - 78.5,=21.5 (平方厘米);答:阴影部分的面积为21.5平方厘米.点解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.评:3. 计算如图阴影部分的面积.(单位:厘米)考组合图形的面积.1526356占:八、、•分分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径析:等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解解:10吃=5 (厘米),答:长方形的面积=长>宽=10 >5=50 (平方厘米),半圆的面积=n2吃=3.14 >52吃=39.25 (平方厘米),阴影部分的面积=长方形的面积-半圆的面积,=50 - 39.25,=10.75 (平方厘米);答:阴影部分的面积是10.75 .点这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形评:拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4. 求出如图阴影部分的面积:单位:厘米.考组合图形的面积.1526356占:八、、•专平面图形的认识与计算.题:分由题意可知:阴影部分的面积=长方形的面积-以4厘米为半径的半圆的析:面积,代入数据即可求解.解解:8 >4 - 3.14 >42吃,答:=32 - 25.12,=6.88 (平方厘米);答:阴影部分的面积是6.88平方厘米.点解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差评:求出.5. 求如图阴影部分的面积.(单位:厘米)考圆、圆环的面积.1526356占:八、、•分由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4析:厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据阴影部分的面积=2>圆的面积”算出答案.解解:S=n2答:=3.14 >(4 吃)2=12.56 (平方厘米);阴影部分的面积=2个圆的面积,=2 X12.56,=25.12 (平方厘米);答:阴影部分的面积是25.12平方厘米.点解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已评:知条件去计算.6.求如图阴影部分面积.(单位:厘米)考长方形、正方形的面积;平行四边形的面积;三角形的周长和面点:积.1526356分图一中阴影部分的面积=大正方形面积的一半-与阴影部分相邻的小三析:角形的面积;图二中阴影部分的面积=梯形的面积-平四边形的面积,再将题目中的数据代入相应的公式进行计算.解解:图一中阴影部分的面积=6>6吃-4>6吃=6 (平方厘米);答:图二中阴影部分的面积=(8+15)X(48七)乜-48=21 (平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的评:面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考组合图形的面积.1526356占:八、、•分由图意可知:阴影部分的面积 =二圆的面积,又因圆的半径为斜边上的高,析:利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解解:圆的半径:15 >20吃>2吃5,答:=300 吃5,=12 (厘米);阴影部分的面积:4>3.14X122,4弓>3.14X144,=0.785 X44,=113.04 (平方厘米);答:阴影部分的面积是113.04平方厘米.点此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.评:&求阴影部分的面积.单位:厘米.考组合图形的面积;三角形的周长和面积;圆、圆环的面积. 1526356占:八、、•分(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,析:代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积二圆的面积-三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解解:(1 )阴影部分面积:2 2答: 3.14弋)-3.14"》,=28.26 - 3.14,=25.12 (平方厘米);(2)阴影部分的面积:3.14X32 --X (3+3) X3,=28.26 - 9,=19.26 (平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米. 点此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径. 评:9. 如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考组合图形的面积;圆、圆环的面积. 1526356占:八、、•专平面图形的认识与计算.题:分观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧析:长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积二大半圆的面积-以10乜=5厘米为半径的半圆的面积-以3吃=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解解:周长:3.14X (10+3),答:=3.14 X13,=40.82 (厘米);面积:丄>3.14>[ (10+3)吃]2—丄>3.14X( 10^2) 2—丄X3.14X ( 3 吃)2,遥X3.14X (42.25 - 25 - 2.25),=* >3.14X5,=23.55 (平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=n,得出评:图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10. 求阴影部分的面积.(单位:厘米)考圆、圆环的面积.1526356占:八、、•分先用3+3=6 ”求出大扇形的半径,然后根据析:出大扇形的面积和小扇形的面积,进而根据面积=阴影部分的面积”解答即可.扇形的面积「j ”分别计算360大扇形的面积-小扇形的解解:r=3, R=3+3=6 , n=120,答:=—「1-」,=37.68 - 9.42,=28.26 (平方厘米);答:阴影部分的面积是28.26平方厘米.点此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.评:11. 求下图阴影部分的面积.(单位:厘米)考组合图形的面积.1526356占:八、、•分先求出半圆的面积3.14 X(10吃)2-2=39.25平方厘米,再求出空白三角形析:的面积10 X(10吃)-42=25平方厘米,相减即可求解.解解:3.14X (10 吃)2-2- 10X(10 吃)吃答:=39.25 - 25=14.25 (平方厘米).答:阴影部分的面积为14.25平方厘米.点考查了组合图形的面积,本题阴影部分的面积=半圆的面积-空白三角形评:的面积.12. 求阴影部分图形的面积.(单位:厘米)考组合图形的面积.1526356点:八、、•分 求阴影部分的面积可用梯形面积减去圆面积的 析:解 解:(4+10) >4吃-3.14>42泊, 答:=28 - 12.56,= 15.44 (平方厘米);答:阴影部分的面积是 15.44平方厘米. 点 解答此题的方法是用阴影部分所在的图形 (梯形)面积减去空白图形(扇评:形)的面积,即可列式解答.13. 计算阴影部分面积(单位:厘米).10考 组合图形的面积.1526356 占: 八、、•专 平面图形的认识与计算. 题:分 如图所示,阴影部分的面积 =平行四边形的面积-三角形 ①的面积,平析:行四边形的底和高分别为 10厘米和15厘米,三角形 ①的底和高分别 为10厘米和(15 - 7)厘米,利用平行四边形和三角形的面积公式即可 求解.令列式计算即可.解解:10X15- 10X( 15- 7)吃,答:=150 - 40,=110 (平方厘米);答:阴影部分的面积是110平方厘米.点解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四评:边形和三角形的面积差求出.14. 求阴影部分的面积.(单位:厘米)考梯形的面积.1526356占:八、、•分如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成析:了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解解:(6+10)>6 吃,答:=16 >6 吃,=96 吃,=48 (平方厘米);答:阴影部分的面积是48平方厘米.点此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯评:形的面积.15. 求下图阴影部分的面积:(单位:厘米)考组合图形的面积.1526356占:八、、•分根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即析:可求解.解解:2 >3吃答:=6吃=3 (平方厘米).答:阴影部分的面积是3平方厘米.点考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形评:的底和高.16. 求阴影部分面积(单位:厘米).考组合图形的面积.1526356占:八、、•分由图意可知:阴影部分的面积=梯形的面积-二圆的面积,梯形的上底和析:高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解解:(4+9)>4吃-3.14X42%,答:=13 >4 吃—3.14X4,=26 - 12.56,=13.44 (平方厘米);答:阴影部分的面积是13.44平方厘米.点解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分评:的面积=梯形的面积-扌圆的面积.17. (2012?长泰县)求阴影部分的面积.(单位:厘米)考组合图形的面积.1526356点:八、、•分由图可知,阴影部分的面积二梯形的面积-半圆的面积.梯形的面积七析:(a+b)h,半圆的面积 =n2,将数值代入从而求得阴影部分的面积.解解:2>(6+8) X(6吃)-丄314X(6吃)2乙£答: =g X4>3-g>3.14>9,=21 - 14.13,=6.87(平方厘米);答:阴影部分的面积为6.87 平方厘米.点考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半评:圆和阴影部分,再分别求出梯形和半圆的面积.。
小升初“圆”阴影部分面积例题及答案
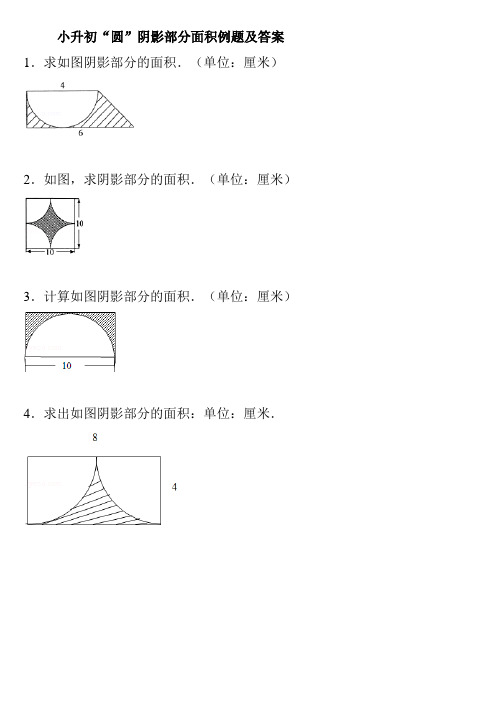
小升初“圆”阴影部分面积例题及答案1.求如图阴影部分的面积.(单位:厘米)2.如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.(2012•长泰县)求阴影部分的面积.(单位:厘米)参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点:组合图形的面积;梯形的面积;圆、圆环的面积.分析: 阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答: 解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评: 组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点:组合图形的面积.分析: 根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米). 解答: 解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评:解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点:组合图形的面积.分析:分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答: 解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr 2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评:这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点:组合图形的面积.专题:平面图形的认识与计算.分析: 由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答: 解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评: 解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点:圆、圆环的面积.分析:由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案. 解答: 解:S=πr 2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评: 解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点: 长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析: 图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答: 解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评: 此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点:组合图形的面积.分析: 由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答: 解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122, =×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评:此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点:组合图形的面积;三角形的周长和面积;圆、圆环的面积. 分析: (1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积. 解答: 解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米. 点评:此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点:组合图形的面积;圆、圆环的面积.专题:平面图形的认识与计算.分析: 观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答: 解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2, =×3.14×(42.25﹣25﹣2.25), =×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评: 此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr ,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点:圆、圆环的面积.分析: 先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答:解:r=3,R=3+3=6,n=120,, =,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评:此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点:组合图形的面积.分析: 先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答: 解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评: 考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点:组合图形的面积.分析: 求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答: 解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评: 解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点:组合图形的面积.专题:平面图形的认识与计算.分析: 如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答: 解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评: 解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点:梯形的面积.分析:如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答: 解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评: 此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点:组合图形的面积.分析: 根据三角形的面积公式:S=ah ,找到图中阴影部分的底和高,代入计算即可求解.解答: 解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评: 考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点:组合图形的面积.分析: 由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答: 解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评:解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点:组合图形的面积.分析:由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b )h ,半圆的面积=πr 2,将数值代入从而求得阴影部分的面积. 解答: 解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2 =×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评: 考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
圆阴影部分面积含答案

求阴影部分面积例1.求阴影部分的面积..单位:厘米解:这是最基本的方法:圆面积减去等腰直角三角形的面积;×-2×1=1.14平方厘米例2.正方形面积是7平方厘米;求阴影部分的面积..单位:厘米解:这也是一种最基本的方法用正方形的面积减去圆的面积..设圆的半径为r;因为正方形的面积为7平方厘米;所以=7;所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积..单位:厘米解:最基本的方法之一..用四个圆组成一个圆;用正方形的面积减去圆的面积;所以阴影部分的面积:2×2-π=0.86平方厘米.. 例4.求阴影部分的面积..单位:厘米解:同上;正方形面积减去圆面积;16-π=16-4π=3.44平方厘米例5.求阴影部分的面积..单位:厘米解:这是一个用最常用的方法解最常见的题;为方便起见;我们把阴影部分的每一个小部分称为“叶形”;是用两个圆减去一个正方形;π×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍.. 例6.如图:已知小圆半径为2厘米;大圆半径是小圆的3倍;问:空白部分甲比乙的面积多多少厘米解:两个空白部分面积之差就是两圆面积之差全加上阴影部分π-π=100.48平方厘米注:这和两个圆是否相交、交的情况如何无关例7.求阴影部分的面积..单位:厘米解:正方形面积可用对角线长×对角线长÷2;求正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米注:以上几个题都可以直接用图形的差来求;无需割、补、增、减变形例8.求阴影部分的面积..单位:厘米解:右面正方形上部阴影部分的面积;等于左面正方形下部空白部分面积;割补以后为圆;所以阴影部分面积为:π=3.14平方厘米例9.求阴影部分的面积..单位:厘米解:把右面的正方形平移至左边的正方形部分;则阴影部分合成一个长方形;所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积..单位:厘米解:同上;平移左右两部分至中间部分;则合成一个长方形;所以阴影部分面积为2×1=2平方厘米注: 8、9、10三题是简单割、补或平移例11.求阴影部分的面积..单位:厘米解:这种图形称为环形;可以用两个同心圆的面积差或差的一部分来求..π-π×=×3.14=3.66平方厘米例12.求阴影部分的面积..单位:厘米解:三个部分拼成一个半圆面积.π÷2=14.13平方厘米例13.求阴影部分的面积..单位:厘米解: 连对角线后将"叶形"剪开移到右上面的空白部分;凑成正方形的一半.所以阴影部分面积为:8×8÷2=32平方厘米例14.求阴影部分的面积..单位:厘米解:梯形面积减去圆面积;4+10×4-π=28-4π=15.44平方厘米 .例15.已知直角三角形面积是12平方厘米;求阴影部分的面积..分析: 此题比上面的题有一定难度;这是"叶形"的一个半.解: 设三角形的直角边长为r;则=12;=6圆面积为:π÷2=3π..圆内三角形的面积为12÷2=6;阴影部分面积为:3π-6×=5.13平方厘米例16.求阴影部分的面积..单位:厘米解:π+π-π=π116-36=40π=125.6平方厘米例17.图中圆的半径为5厘米;求阴影部分的面积..单例18.如图;在边长为6厘米的等边三角形中挖去三位:厘米解:上面的阴影部分以AB为轴翻转后;整个阴影部分成为梯形减去直角三角形;或两个小直角三角形AED、BCD面积和..所以阴影部分面积为:5×5÷2+5×10÷2=37.5平方厘米个同样的扇形;求阴影部分的周长..解:阴影部分的周长为三个扇形弧;拼在一起为一个半圆弧;所以圆弧周长为:2×3.14×3÷2=9.42厘米例19.正方形边长为2厘米;求阴影部分的面积..解:右半部分上面部分逆时针;下面部分顺时针旋转到左半部分;组成一个矩形..所以面积为:1×2=2平方厘米例20.如图;正方形ABCD的面积是36平方厘米;求阴影部分的面积..解:设小圆半径为r;4=36;r=3;大圆半径为R;=2=18;将阴影部分通过转动移在一起构成半个圆环;所以面积为:π-÷2=4.5π=14.13平方厘米例21.图中四个圆的半径都是1厘米;求阴影部分的面积..解:把中间部分分成四等分;分别放在上面圆的四个角上;补成一个正方形;边长为2厘米;所以面积为:2×2=4平方厘米例22.如图;正方形边长为8厘米;求阴影部分的面积..解法一: 将左边上面一块移至右边上面;补上空白;则左边为一三角形;右边一个半圆.阴影部分为一个三角形和一个半圆面积之和. π÷2+4×4=8π+16=41.12平方厘米解法二: 补上两个空白为一个完整的圆.所以阴影部分面积为一个圆减去一个叶形;叶形面积为:π÷2-4×4=8π-16所以阴影部分的面积为:π-8π+16=41.12平方厘米例23.图中的4个圆的圆心是正方形的4个顶点;;它们的公共点是该正方形的中心;如果每个圆的半径都是1厘米;那么阴影部分的面积是多少例24.如图;有8个半径为1厘米的小圆;用他们的圆周的一部分连成一个花瓣图形;图中的黑点是这些圆的圆心..如果圆周π率取3.1416;那么花瓣图形的的解:面积为4个圆减去8个叶形;叶形面积为:π-1×1=π-1 所以阴影部分的面积为:4π-8π-1=8平方厘米面积是多少平方厘米分析:连接角上四个小圆的圆心构成一个正方形;各个小圆被切去个圆;这四个部分正好合成3个整圆;而正方形中的空白部分合成两个小圆.解:阴影部分为大正方形面积与一个小圆面积之和.为:4×4+π=19.1416平方厘米例25.如图;四个扇形的半径相等;求阴影部分的面积..单位:厘米分析:四个空白部分可以拼成一个以2为半径的圆.所以阴影部分的面积为梯形面积减去圆的面积;4×4+7÷2-π=22-4π=9.44平方厘米例26.如图;等腰直角三角形ABC和四分之一圆DEB;AB=5厘米;BE=2厘米;求图中阴影部分的面积..解: 将三角形CEB以B为圆心;逆时针转动90度;到三角形ABD位置;阴影部分成为三角形ACB 面积减去个小圆面积;为: 5×5÷2-π÷4=12.25-3.14=9.36平方厘米例27.如图;正方形ABCD的对角线AC=2厘米;扇形ACB是以AC为直径的半圆;扇形DAC是以D为圆心;AD为半径的圆的一部分;求阴影部分的面积..解: 因为2==4;所以=2以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积;π-2×2÷4+π÷4-2=π-1+π-1=π-2=1.14平方厘米例28.求阴影部分的面积..单位:厘米解法一:设AC中点为B;阴影面积为三角形ABD面积加弓形BD的面积;三角形ABD的面积为:5×5÷2=12.5弓形面积为:π÷2-5×5÷2=7.125所以阴影面积为:12.5+7.125=19.625平方厘米解法二:右上面空白部分为小正方形面积减去小圆面积;其值为:5×5-π=25-π阴影面积为三角形ADC减去空白部分面积;为:10×5÷2-25-π=π=19.625平方厘米例29.图中直角三角形ABC的直角三角形的直角边AB=4厘米;BC=6厘米;扇形BCD所在圆是以B为圆心;半径为BC的圆;∠CBD=;问:阴影部分甲比乙面积小多少解: 甲、乙两个部分同补上空白部分的三角形后合成一个扇形BCD;一个成为三角形ABC;此两部分差即为:π×-×4×6=5π-12=3.7平方厘米例30.如图;三角形ABC是直角三角形;阴影部分甲比阴影部分乙面积大28平方厘米;AB=40厘米..求BC 的长度..解:两部分同补上空白部分后为直角三角形ABC;一个为半圆;设BC长为X;则40X÷2-π÷2=28所以40X-400π=56 则X=32.8厘米例31.如图是一个正方形和半圆所组成的图形;其中P为半圆周的中点;Q为正方形一边上的中点;求阴影部分的面积..解:连PD、PC转换为两个三角形和两个弓形;两三角形面积为:△APD面积+△QPC面积=5×10+5×5=37.5两弓形PC、PD 面积为:π-5×5所以阴影部分的面积为:37.5+π-25=51.75平方厘米例32.如图;大正方形的边长为6厘米;小正方形的边长为4厘米..求阴影部分的面积..解:三角形DCE的面积为:×4×10=20平方厘米梯形ABCD的面积为:4+6×4=20平方厘米从而知道它们面积相等;则三角形ADF面积等于三角形EBF面积;阴影部分可补成圆ABE的面积;其面积为:π÷4=9π=28.26平方厘米例33.求阴影部分的面积..单位:厘米解:用大圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积;为例34.求阴影部分的面积..单位:厘米解:两个弓形面积为:π-3×4÷2=π-6 阴影部分为两个半圆面积减去两个弓形面积;结果为π+π-6=×13π-6=4.205平方厘米π+π-π-6=π4+-+6=6平方厘米例35.如图;三角形OAB是等腰三角形;OBC是扇形;OB=5厘米;求阴影部分的面积..解:将两个同样的图形拼在一起成为圆减等腰直角三角形π÷4-×5×5÷2=π-÷2=3.5625平方厘米。
圆-阴影部分面积(含标准答案)

求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
圆_阴影部分面积(含答案)

+π )-6 = ×13π-6 =4.205平方厘米 )+6=6平方厘米
例35.如图,三角形OAB是等 腰三角形,OBC是扇形, OB=5厘米,求阴影部分的面
积。
解:将两个同样的图形拼在一 起成为 圆减等腰直角三角形 [π ÷4-
×5×5]÷2 =(
π)÷2=3.5625平方厘米
例33.求阴影部分的面积。(单 位:厘米)
例34.求阴影部分的面积。(单 位:厘米) 解:两个弓形面积为:π -3×4÷2= π-6 阴影部分为两个半圆面积 减去两个弓形面积,结果为 π +π -( π-6)=π(4+
解:用 大圆的面积减去长方形面积再 加上一个以2为半径的 圆ABE面积,为 (π
× - ×4×6=5π-12=3.7平方厘米 例31.如图是一个正方形和半圆 所组成的图形,其中P为半圆 周的中点,Q为正方形一边上 的中点,求阴影部分的面积。 例32.如图,大正方形的边长为 6厘米,小正方形的边长为4厘 米。求阴影部分的面积。 解:三角形DCE的面积为: ×4×10=20平方厘米 梯形ABCD的面积为: 解:连PD、PC转换为两个三 角形和两个弓形, 两三角形面积为:△APD 面积+△QPC面积= (5×10+5×5)=37.5 两弓形PC、PD面积为: π -5×5 所以阴影部分的面积为: 37.5+ π-25=51.75平方厘米 (4+6)×4=20平方厘米 从而知道 它们面积相等,则三角形ADF面 积等于三角形EBF面积,阴影 部分可补成 圆ABE的面积,其面积为: π ÷4=9π=28.26平方厘米
例25.如图,四个扇形的半径相 例26.如图,等腰直角三角形 等,求阴影部分的面积。(单 ABC和四分之一圆DEB, 位:厘米) AB=5厘米,BE=2厘米,求图 中阴影部分的面积。
圆_阴影部分面积(含答案)

求阴影部分面积之袁州冬雪创作例1.求阴影部分的面积.(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积.(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积.设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积.(单位:厘米) 解:最基本的方法之一.用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米. 例4.求阴影部分的面积.(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积.(单位:厘米)解:这是一个用最常常使用的方法解最罕见的题,为方便起见,我们把阴影部分的每个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米别的:此题还可以当作是1题中阴影部分的8倍. 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空缺部分甲比乙的面积多多少厘米?解:两个空缺部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积.(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接例8.求阴影部分的面积.(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空缺部分面积,割补以后为圆,所以阴影部分用图形的差来求,无需割、补、增、减变形)面积为:π(例9.求阴影部分的面积.(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积.(单位:厘米)解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11.求阴影部分的面积.(单位:厘米)解:这种图形称为环形,可以用两个同心圆的面积差或差的一部分来求.(π-π)×=×3.14=3.66平方厘米例12.求阴影部分的面积.(单位:厘米)解:三个部分拼成一个半圆面积.π()÷2=14.13平方厘米例13.求阴影部分的面积.(单位:厘米)解: 连对角线后将"叶形"剪开移到右上面的空缺部分,凑成正方形的一半.所以阴影部分面积为:8×8÷2=32平方厘米例14.求阴影部分的面积.(单位:厘米)解:梯形面积减去圆面积,(4+10)×4-π=28-4π=15.44平方厘米.例15.已知直角三角形面积是12平方厘米,求阴影部分的面积.分析: 此题比上面的题有一定难度,这是"叶形"的一个半.解: 设三角形的直角边长为r ,则=12,=6 例16.求阴影部分的面积.(单位:厘米)解:[π+π-π]=π(116-36)=40π=125.6平方厘米圆面积为:π÷2=3π.圆内三角形的面积为12÷2=6,阴影部分面积为:(3π-6)×=5.13平方厘米例17.图中圆的半径为5厘米,求阴影部分的面积.(单位:厘米)解:上面的阴影部分以AB为轴翻转后,整个阴影部分成为梯形减去直角三角形,或两个小直角三角形AED、BCD面积和.所以阴影部分面积为:5×5÷2+5×10÷2=37.5平方厘米例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长.解:阴影部分的周长为三个扇形弧,拼在一起为一个半圆弧,所以圆弧周长为:2×3.14×3÷2=9.42厘米例19.正方形边长为2厘米,求阴影部分的面积.解:右半部分上脸部分逆时针,下脸部分顺时针旋转到左半部分,组成一个矩形.所以面积为:1×2=2平方厘米例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积.解:设小圆半径为r,4=36, r=3,大圆半径为R ,=2=18,将阴影部分通过转动移在一起构成半个圆环,所以面积为:π(-)÷2=4.5π=14.13平方厘米例21.图中四个圆的半径都是1厘米,求阴影部分的面积.解:把中间部分分成四等分,分别放在上面圆的四个角上,补成一个正方形,边长为2厘米,所以面积为:2×2=4平方厘米例22. 如图,正方形边长为8厘米,求阴影部分的面积.解法一: 将左边上面一块移至右边上面,补上空缺,则左边为一三角形,右边一个半圆.阴影部分为一个三角形和一个半圆面积之和.π()÷2+4×4=8π+16=41.12平方厘米解法二: 补上两个空缺为一个完整的圆.所以阴影部分面积为一个圆减去一个叶形,叶形面积为:π()÷2-4×4=8π-16所以阴影部分的面积为:π()-8π+16=41.12平方厘米例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那末阴影部分的面积是多少?解:面积为4个圆减去8个叶形,叶形面积为:π-1×1=π-1所以阴影部分的面积为:4π-8(π-1)=8平方厘米例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心.如果圆周π率取3.1416,那末花瓣图形的的面积是多少平方厘米?分析:毗连角上四个小圆的圆心构成一个正方形,各个小圆被切去个圆,这四个部分正好合成3个整圆,而正方形中的空缺部分合成两个小圆.解:阴影部分为大正方形面积与一个小圆面积之和.为:4×4+π=19.1416平方厘米例25.如图,四个扇形的半径相等,求阴影部分的面积.(单位:厘米)分析:四个空缺部分可以拼成一个以2为半径的圆.所以阴影部分的面积为梯形面积减去圆的面积,4×(4+7)÷2-π=22-4π=9.44平方厘米例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中阴影部分的面积.解: 将三角形CEB以B为圆心,逆时针转动90度,到三角形ABD位置,阴影部分成为三角形ACB 面积减去个小圆面积,为: 5×5÷2-π÷4=12.25-3.14=9.36平方厘米例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积.解: 因为2==4,所以=2以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+[π÷4-2]=π-1+(π-1)=π-2=1.14平方厘米例28.求阴影部分的面积.(单位:厘米)解法一:设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积,三角形ABD的面积为:5×5÷2=12.5弓形面积为:[π÷2-5×5]÷2=7.125所以阴影面积为:12.5+7.125=19.625平方厘米解法二:右上面空缺部分为小正方形面积减去小圆面积,其值为:5×5-π=25-π阴影面积为三角形ADC减去空缺部分面积,为:10×5÷2-(25-π)=π=19.625平方厘米例29.图中直角三角形ABC的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD 所在圆是以B为圆心,半径为BC的圆,∠CBD=,问:阴影部分甲比乙面积小多少?解: 甲、乙两个部分同补上空缺部分的三角形后合成一个扇形BCD,一个成为三角形ABC,此两部分差即为:π×-×4×6=5π-12=3.7平方厘米例30.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米.求BC的长度.解:两部分同补上空缺部分后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π÷2=28所以40X-400π=56 则X=32.8厘米例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积. 例32.如图,大正方形的边长为6厘米,小正方形的边长为4厘米.求阴影部分的面积.解:连PD、PC转换为两个三角形和两个弓形,两三角形面积为:△APD面积+△QPC面积=(5×10+5×5)=37.5 两弓形PC、PD 面积为:π-5×5所以阴影部分的面积为:37.5+π-25=51.75平方厘米解:三角形DCE的面积为:×4×10=20平方厘米梯形ABCD的面积为:(4+6)×4=20平方厘米从而知道它们面积相等,则三角形ADF 面积等于三角形EBF 面积,阴影部分可补成圆ABE的面积,其面积为:π÷4=9π=28.26平方厘米例33.求阴影部分的面积.(单位:厘米)解:用大圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积,为(π+π)-6=×13π-6=4.205平方厘米例34.求阴影部分的面积.(单位:厘米)解:两个弓形面积为:π-3×4÷2=π-6阴影部分为两个半圆面积减去两个弓形面积,成果为π+π-(π-6)=π(4+-)+6=6平方厘米例35.如图,三角形OAB是等腰三角形,OBC 是扇形,OB=5厘米,求阴影部分的面积.解:将两个同样的图形拼在一起成为圆减等腰直角三角形[π÷4-×5×5]÷2 =(π-。
【小升初数学训练】 求圆的阴影面积专项

求圆的阴影面积专项1.求下图阴影部分的面积.(单位:厘米)解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.2.求阴影部分图形的面积.(单位:厘米)解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56=15.44(平方厘米)答:阴影部分的面积是15.44平方厘米.3.求下图阴影部分的面积.(单位:厘米)解:3.14×(2÷2)2+2×(2÷2)÷2×2=3.14+2=5.14(平方厘米)答:阴影部分的面积是5.14平方厘米.求圆的阴影面积专项4.求图中阴影部分图形的面积.解:6÷2=3(厘米)6×3-3.14×32÷2=18-14.13=3.87(平方厘米)答:阴影部分的面积是3.87平方厘米.5.计算如图阴影部分的面积.解:10÷2=5(厘米)3.14×5×5÷2=78.5÷2=39.25(平方厘米)10×5=50(平方厘米)50-39.25=10.75(平方厘米)答:阴影部分的面积是10.75平方厘米.求圆的阴影面积专项6.求阴影部分的面积(单位:cm)阴影部分的面积=梯形的面积-半圆的面积解:(5+12)×4÷2-3.14×(4÷2)2÷2=17×4÷2-3.14×4÷2=34-6.28=27.72(平方厘米)答:阴影部分的面积是27.72平方厘米.7.求阴影部分的面积(单位:cm)根据环形面积公式:环形面积=大圆的面积-小圆的面积,解:3.14×52-3.14×32=3.14×(25-9)=3.14×16=50.24(平方厘米).。
圆阴影部分面积(含答案)

求阴影部分面积求阴影部分面积例1.求阴影部分的面积。
(单位:厘米) 解:解:这是最基本的方法:这是最基本的方法: 圆面积减去等腰直角三角形的面积,×-2×-2×1=1.141=1.14(平方厘米)米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米) 解:这也是一种最基本的方法用正方形的面积减去形的面积减去 圆的面积。
圆的面积。
设圆的半径为设圆的半径为 r ,因为正方形的面积为7平方厘米,所以平方厘米,所以 =7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米平方厘米例3.求图中阴影部分的面积。
(单位:厘米) 解:最基本的方法之一。
用四个 圆组成一个圆,用正方形的面积减去圆的面积,去圆的面积,所以阴影部分的面积:2×2×2-2-2-ππ=0.86平方厘米。
平方厘米。
例4.求阴影部分的面积。
(单位:厘米) 解:同上,正方形面积减去圆面积,面积, 16-16-π(π()=16-)=16-4π4π=3.44平方厘米平方厘米例5.求阴影部分的面积。
(单位:厘米) 解:这是一个用最常用的方法解最常见的题,为方便起见,最常见的题,为方便起见, 我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,去一个正方形,π()×)×2-2-2-16=8π16=8π16=8π-16=9.12-16=9.12平方厘米方厘米另外:此题还可以看成是1题中阴影部分的8倍。
倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)部分)π-π()=100.48平方厘米厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求) 正方形面积为:5×5×5÷5÷5÷2=12.5 2=12.5 所以阴影面积为:π÷4-12.5=7.125平方厘米平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
圆_阴影部分面积(含答案)

供阳影部分里积之阳早格格创做例1.供阳影部分的里积.(单位:厘米)解:那是最基原的要领:圆里积减去等腰曲角三角形的里积,×-2×1=1.14(仄圆厘米)例2.正圆形里积是7仄圆厘米,供阳影部分的里积.(单位:厘米)解:那也是一种最基原的要领用正圆形的里积减去圆的里积.设圆的半径为r,果为正圆形的里积为7仄圆厘米,所以=7,所以阳影部分的里积为:7-=7-×7=1.505仄圆厘米例3.供图中阳影部分的里积.(单位:厘米) 解:最基原的要领之一.用四个圆组成一个圆,用正圆形的里积减去圆的里积,所以阳影部分的里积:2×2-π=0.86仄圆厘米. 例4.供阳影部分的里积.(单位:厘米)解:共上,正圆形里积减去圆里积,16-π()=16-4π=3.44仄圆厘米例5.供阳影部分的里积.(单位:厘米)解:那是一个用最时常使用的要领解最罕睹的题,为便当起睹,咱们把阳影部分的每一个小部分称为“叶形”,是用二个圆减去一个正圆形,π()×2-16=8π-16=9.12仄圆厘米其余:此题还不妨瞅成是1题中阳影部分的8倍. 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空黑部分甲比乙的里积多几厘米?解:二个空黑部分里积之好便是二圆里积之好(齐加上阳影部分)π-π()=100.48仄圆厘米(注:那战二个圆是可相接、接的情况怎么样无闭)例7.供阳影部分的里积.(单位:厘米) 解:正圆形里积可用(对于角线少×对于角线少÷2,供)正圆形里积为:5×5÷2=12.5所以阳影里积为:π÷4-12.5=7.125仄圆厘米(注:以上几个题皆不妨间接例8.供阳影部分的里积.(单位:厘米)解:左里正圆形上部阳影部分的里积,等于左里正圆形下部空黑部分里积,割补以去为圆,所以阳影部分用图形的好去供,无需割、补、删、减变形)里积为:π(例9.供阳影部分的里积.(单位:厘米)解:把左里的正圆形仄移至左边的正圆形部分,则阳影部分合成一个少圆形,所以阳影部分里积为:2×3=6仄圆厘米例10.供阳影部分的里积.(单位:厘米)解:共上,仄移安排二部分至中间部分,则合成一个少圆形,所以阳影部分里积为2×1=2仄圆厘米(注: 8、9、10三题是简朴割、补或者仄移)例11.供阳影部分的里积.(单位:厘米)解:那种图形称为环形,不妨用二个共心圆的里积好或者好的一部分去供.(π-π)×=×3.14=3.66仄圆厘米例12.供阳影部分的里积.(单位:厘米)解:三个部分拼成一个半圆里积.π()÷2=14.13仄圆厘米例13.供阳影部分的里积.(单位:厘米)解: 连对于角线后将"叶形"剪启移到左上头的空黑部分,凑成正圆形的一半.所以阳影部分里积为:8×8÷2=32仄圆厘米例14.供阳影部分的里积.(单位:厘米)解:梯形里积减去圆里积,(4+10)×4-π=28-4π=15.44仄圆厘米.例15.已知曲角三角形里积是12仄圆厘米,供阳影部分的里积.分解: 此题比上头的题有一定易度,那是"叶形"的一个半.解: 设三角形的曲角边少为r ,则=12,=6 例16.供阳影部分的里积.(单位:厘米)解:[π+π-π]=π(116-36)=40π=125.6仄圆厘米圆里积为:π÷2=3π.圆内三角形的里积为12÷2=6,阳影部分里积为:(3π-6)×=5.13仄圆厘米例17.图中圆的半径为5厘米,供阳影部分的里积.(单位:厘米)解:上头的阳影部分以AB为轴翻转后,所有阳影部分成为梯形减去曲角三角形,或者二个小曲角三角形AED、BCD里积战.所以阳影部分里积为:5×5÷2+5×10÷2=37.5仄圆厘米例18.如图,正在边少为6厘米的等边三角形中掘去三个共样的扇形,供阳影部分的周少.解:阳影部分的周少为三个扇形弧,拼正在所有为一个半圆弧,所以圆弧周少为:2×3.14×3÷2=9.42厘米例19.正圆形边少为2厘米,供阳影部分的里积.解:左半部分上头部分顺时针,底下部分顺时针转化到左半部分,组成一个矩形.所以里积为:1×2=2仄圆厘米例20.如图,正圆形ABCD的里积是36仄圆厘米,供阳影部分的里积.解:设小圆半径为r,4=36, r=3,大圆半径为R ,=2=18,将阳影部分通过转化移正在所有形成半个圆环,所以里积为:π(-)÷2=4.5π=14.13仄圆厘米例21.图中四个圆的半径皆是1厘米,供阳影部分的里积.解:把中间部分分成四仄分,分别搁正在上头圆的四个角上,补成一个正圆形,边少为2厘米,所以里积为:2×2=4仄圆厘米例22. 如图,正圆形边少为8厘米,供阳影部分的里积.解法一: 将左边上头一齐移至左边上头,补上空黑,则左边为一三角形,左边一个半圆.阳影部分为一个三角形战一个半圆里积之战.π()÷2+4×4=8π+16=41.12仄圆厘米解法二: 补上二个空黑为一个完备的圆.所以阳影部分里积为一个圆减去一个叶形,叶形里积为:π()÷2-4×4=8π-16所以阳影部分的里积为:π()-8π+16=41.12仄圆厘米例23.图中的4个圆的圆心是正圆形的4个顶面,,它们的大众面是该正圆形的核心,如果每个圆的半径皆是1厘米,那么阳影部分的里积是几?解:里积为4个圆减去8个叶形,叶形里积为:π-1×1=π-1所以阳影部分的里积为:4π-8(π-1)=8仄圆厘米例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的乌面是那些圆的圆心.如果圆周π率与3.1416,那么花瓣图形的的里积是几仄圆厘米?分解:对接角上四个小圆的圆心形成一个正圆形,各个小圆被切去个圆,那四个部分正佳合成3个整圆,而正圆形中的空黑部分合成二个小圆.解:阳影部分为大正圆形里积与一个小圆里积之战.为:4×4+π=19.1416仄圆厘米例25.如图,四个扇形的半径相等,供阳影部分的里积.(单位:厘米)分解:四个空黑部分不妨拼成一个以2为半径的圆.所以阳影部分的里积为梯形里积减去圆的里积,4×(4+7)÷2-π=22-4π=9.44仄圆厘米例26.如图,等腰曲角三角形ABC战四分之一圆DEB,AB=5厘米,BE=2厘米,供图中阳影部分的里积.解: 将三角形CEB以B为圆心,顺时针转化90度,到三角形ABD位子,阳影部分成为三角形ACB 里积减去个小圆里积,为: 5×5÷2-π÷4=12.25-3.14=9.36仄圆厘米例27.如图,正圆形ABCD的对于角线AC=2厘米,扇形ACB是以AC为曲径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,供阳影部分的里积.解: 果为2==4,所以=2以AC为曲径的圆里积减去三角形ABC里积加上弓形AC里积,π-2×2÷4+[π÷4-2]=π-1+(π-1)=π-2=1.14仄圆厘米例28.供阳影部分的里积.(单位:厘米)解法一:设AC中面为B,阳影里积为三角形ABD里积加弓形BD的里积,三角形ABD的里积为:5×5÷2=12.5弓形里积为:[π÷2-5×5]÷2=7.125所以阳影里积为:12.5+7.125=19.625仄圆厘米解法二:左上头空黑部分为小正圆形里积减去小圆里积,其值为:5×5-π=25-π阳影里积为三角形ADC减去空黑部分里积,为:10×5÷2-(25-π)=π=19.625仄圆厘米例29.图中曲角三角形ABC的曲角三角形的曲角边AB=4厘米,BC=6厘米,扇形BCD 地圆圆是以B为圆心,半径为BC的圆,∠CBD=,问:阳影部分甲比乙里积小几?解: 甲、乙二个部分共补上空黑部分的三角形后合成一个扇形BCD,一个成为三角形ABC,此二部分好即为:π×-×4×6=5π-12=3.7仄圆厘米例30.如图,三角形ABC是曲角三角形,阳影部分甲比阳影部分乙里积大28仄圆厘米,AB=40厘米.供BC的少度.解:二部分共补上空黑部分后为曲角三角形ABC,一个为半圆,设BC少为X,则40X÷2-π÷2=28所以40X-400π=56 则X=32.8厘米例31.如图是一个正圆形战半圆所组成的图形,其中P为半圆周的中面,Q为正圆形一边上的中面,供阳影部分的里积.解:连PD、PC变换为二个三角形战二个弓形,二三角形里积为:△APD里积+△QPC里积=(5×10+5×5)=37.5二弓形PC、PD 里积为:π-5×5所以阳影部分的里积为:37.5+π-25=51.75仄圆厘米例32.如图,大正圆形的边少为6厘米,小正圆形的边少为4厘米.供阳影部分的里积.解:三角形DCE的里积为:×4×10=20仄圆厘米梯形ABCD的里积为:(4+6)×4=20仄圆厘米进而知讲它们里积相等,则三角形ADF 里积等于三角形EBF 里积,阳影部分可补成圆ABE的里积,其里积为:π÷4=9π=28.26仄圆厘米例33.供阳影部分的里积.(单位:厘米)解:用大圆的里积减去少圆形里积再加上一个以2为半径的圆ABE里积,为(π+π)-6=×13π-6=4.205仄圆厘米例34.供阳影部分的里积.(单位:厘米)解:二个弓形里积为:π-3×4÷2=π-6阳影部分为二个半圆里积减去二个弓形里积,截止为π+π-(π-6)=π(4+-)+6=6仄圆厘米例35.如图,三角形OAB是等腰三角形,OBC 是扇形,OB=5厘米,供阳影部分的里积.解:将二个共样的图形拼正在所有成为圆减等腰曲角三角形[π÷4-×5×5]÷2=(π-。
圆-阴影部分面积(含答案)
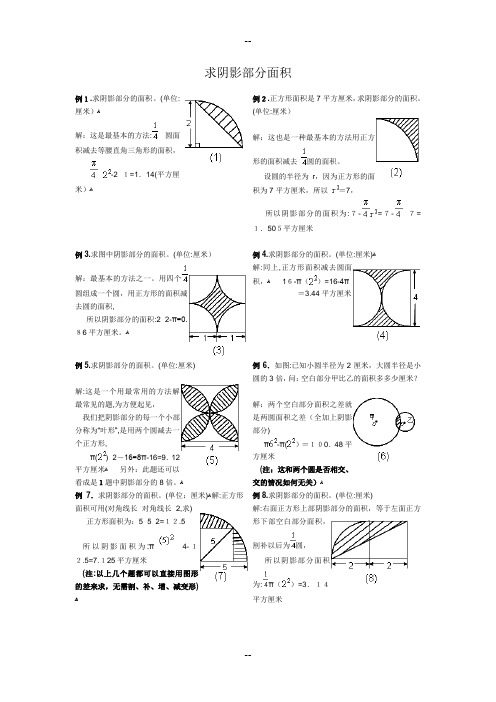
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)ﻫ解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)ﻫ例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
ﻫ例4.求阴影部分的面积。
(单位:厘米)ﻫ解:同上,正方形面积减去圆面积,ﻫ16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米ﻫ另外:此题还可以看成是1题中阴影部分的8倍。
ﻫ例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)ﻫ例7.求阴影部分的面积。
(单位:厘米)ﻫ解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)ﻫ例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
圆-阴影部分面积(含标准答案)

求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
圆阴影部分面积含标准答案(终审稿)

圆阴影部分面积含标准答案TPMK standardization office【 TPMK5AB- TPMK08- TPMK2C- TPMK18】求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为 r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米) 解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米) 解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求) 正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
圆阴影部分面积含标准答案

圆阴影部分面积含标准答案YUKI was compiled on the morning of December 16, 2020求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为 r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米) 解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米) 解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求) 正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小升初“圆”阴影部分面积例题及答案1.求如图阴影部分的面积.(单位:厘米)2.如图,求阴影部分的面积单位:厘米)3.计算如图阴影部分的面积单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.单位:厘米)6.求如图阴影部分面积.(单位:厘米)8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.(2012?长泰县)求阴影部分的面积.(单位:厘米)参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考组合图形的面积;梯形的面积;圆、圆环的面积.点:八、、•分阴影部分的面积等于梯形的面积减去直径为4 厘米的半圆的面积,利用析:梯形和半圆的面积公式代入数据即可解答.解解:(4+6)X 4-2-2-X + 2,答:=10-X 4-2,=(平方厘米);答:阴影部分的面积是平方厘米.点组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里评:考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考组合图形的面积.1526356点:八、、•分根据图形可以看出:阴影部分的面积等于正方形的面积减去4 个扇形的面析:积.正方形的面积等于(10X 10)100平方厘米,4个扇形的面积等于半径为(10-2)5厘米的圆的面积,即:x 5X 5=(平方厘米).解解:扇形的半径是:答:10-2,=5(厘米);10x 10-x 5x 5,100-,=(平方厘米);答:阴影部分的面积为平方厘米.点解答此题的关键是求4 个扇形的面积,即半径为5 厘米的圆的面积.评:3.计算如图阴影部分的面积.(单位:厘米)考组合图形的面积.1526356点:八、、•分分析图后可知,10 厘米不仅是半圆的直径,还是长方形的长,根据半径析:等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解解:10+ 2=5 (厘米),答:长方形的面积=长乂宽=10X 5=50 (平方厘米),半圆的面积=nr2+ 2=X52+ 2=(平方厘米),阴影部分的面积=长方形的面积-半圆的面积,=50 -,=(平方厘米);答:阴影部分的面积是.点这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形评:拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考组合图形的面积.1526356点:八、、• 专平面图形的认识与计算.题:分由题意可知:阴影部分的面积二长方形的面积-以4厘米为半径的半圆的析:面积,代入数据即可求解.解解:8X4-X4 2+ 2,答: =32-,=(平方厘米);答:阴影部分的面积是平方厘米.点解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差评:求出.5.求如图阴影部分的面积.(单位:厘米)考圆、圆环的面积.1526356点:八、、•分由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4 析:厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2X圆的面积”算出答案.解解:S=nr 2答: =X( 4-2)=(平方厘米);阴影部分的面积=2 个圆的面积,=2X,=(平方厘米);答:阴影部分的面积是平方厘米.点解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已评:知条件去计算.6.求如图阴影部分面积.(单位:厘米)考长方形、正方形的面积;平行四边形的面积;三角形的周长和面点:积.1526356分图一中阴影部分的面积二大正方形面积的一半-与阴影部分相邻的小三析:角形的面积;图二中阴影部分的面积=梯形的面积-平四边形的面积,再将题目中的数据代入相应的公式进行计算.解解:图一中阴影部分的面积=6X6+2-4X6+2=6 (平方厘米);答:图二中阴影部分的面积=(8+15)X(48+ 8)+ 2- 48=21 (平方厘米)答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是平方厘米.点此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的评:面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考组合图形的面积.1526356点:八、、•分由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,析:利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解解:圆的半径:15X 20-2X 2-25,答:=300- 25,=12(厘米);阴影部分的面积:xx 122,=xx 144,=x 144,=(平方厘米);答:阴影部分的面积是平方厘米.点此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.评:8.求阴影部分的面积.单位:厘米.考组合图形的面积;三角形的周长和面积;圆、圆环的面积.1526356点:八、、• 分 ( 1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,析:代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积二圆的面积-三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解解:( 1)阴影部分面积:答:x-x,一 ?=(平方厘米);( 2)阴影部分的面积:2x32-x( 3+3 )x 3,=- 9,=(平方厘米);答:圆环的面积是平方厘米,阴影部分面积是平方厘米.点此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.评:9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考组合图形的面积;圆、圆环的面积.1526356点:八、、•专平面图形的认识与计算.题:分观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧析:长相等,所以图中阴影部分的周长,就是直径为10+3=13 厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积-以10+ 2=5厘米为半径的半圆的面积-以3+2= 厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解解:周长:X( 10+3),答:=x 13,=(厘米);面积:xx [ ( 10+3)+2 ]2-xx( 10+ 2) 2-xx( 3+2) 2,= xx(- 25-),=xx 15,=(平方厘米);答:阴影部分的周长是厘米,面积是平方厘米.点此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=n r,得评:出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考圆、圆环的面积.1526356点:分先用“ 3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算析:出大扇形的面积和小扇形的面积, 进而根据“大扇形的面积-小扇形的面积=阴影部分的面积”解答即可.解解:r=3 ,R=3+3=6,n=120,答:一 ?一 ?=(平方厘米);答:阴影部分的面积是平方厘米.点此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.八、、11.求下图阴影部分的面积.(单位:厘米)考组合图形的面积.1526356点:八、、•分先求出半圆的面积X( 10+ 2) 2+ 2=平方厘米,再求出空白三角形的面积析:10X( 10+ 2)+ 2=25平方厘米,相减即可求解.解解:X( 10+ 2) 2+ 2- 10X( 10+ 2)+2答:=-25=(平方厘米).答:阴影部分的面积为平方厘米.点考查了组合图形的面积,本题阴影部分的面积=半圆的面积-空白三角形评:的面积.12.求阴影部分图形的面积.(单位:厘米)考组合图形的面积.1526356点:八、、•分求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.析:解解:(4+10)X 4-2-X4 2+ 4,答:=28-,=(平方厘米);答:阴影部分的面积是平方厘米.点解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形评:形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考组合图形的面积.1526356点:八、、•专平面图形的认识与计算.题:分如图所示,阴影部分的面积=平行四边形的面积-三角形①的面积,平析:行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15 - 7)厘米,利用平行四边形和三角形的面积公式即可求解.解解:10X 15- 10X(15 - 7)+ 2,答:=150- 40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四评:边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考梯形的面积.1526356点:八、、•分如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了析:求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解解:(6+10)X 6-2,答: =16X 6+2,=96+ 2,=48(平方厘米);答:阴影部分的面积是48 平方厘米.点此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯评:形的面积.15.求下图阴影部分的面积:(单位:厘米)考组合图形的面积.1526356点:八、、•分根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即析:可求解.解解:2X3+2答:=6+2=3(平方厘米).答:阴影部分的面积是3平方厘米.点考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形评:的底和高.16.求阴影部分面积(单位:厘米).考组合图形的面积.1526356点:八、、•分由图意可知:阴影部分的面积=梯形的面积-圆的面积,梯形的上底和高析:都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解解:(4+9)X 4-2-X4 2X,答: =13X4-2-X 4,=26-,=(平方厘米);答:阴影部分的面积是平方厘米.点解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分评:的面积=梯形的面积-圆的面积.17.(2012?长泰县)求阴影部分的面积.(单位:厘米)考组合图形的面积.1526356点:分由图可知,阴影部分的面积=梯形的面积-半圆的面积.梯形的面积析(a+b)h,半圆的面积=nr2,将数值代入从而求得阴影部分的面积.:解解:X( 6+8)X( 6-2)-xx( 6-2) 2答=x 14X3-xx 9,:=21-,=(平方厘米);答:阴影部分的面积为平方厘米.点考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半评:圆和阴影部分,再分别求出梯形和半圆的面积.。
