计算机理论导引实验报告3-图灵机(Turing)的模拟
理论计算机科学中的图灵机

理论计算机科学中的图灵机图灵机是理论计算机科学中的一个重要概念。
它被认为是能够计算任何可计算问题的最基本的计算机模型。
理解图灵机对于对计算机科学的学习和研究都至关重要。
一、图灵机的定义和原理图灵机是由英国数学家图灵提出的一种计算模型。
它包括一个有限控制器和一条无限长的纸带。
纸带被划分为一系列的单元格,每个单元格上可以写上一个字符。
控制器通过读取纸带上的字符和控制器内部的状态来进行计算。
它可以进行有限的计算,而且可以处理无限长的输入。
在图灵机模型中,所有的操作都是基于读取和写入单元格上的字符来进行。
图灵机具有非常简单的结构,但它却能够计算出任何可计算问题。
二、图灵机的应用图灵机能够计算出任何可计算问题,因此它在理论计算机科学中有着非常重要的应用。
它被用于证明计算机科学中的许多重要问题,例如停机问题和可计算性问题。
通过证明一个问题是不可计算的,我们可以得出它是无法用计算机解决的。
这对于计算机的设计和实现都有着重要的指导意义。
此外,图灵机还被广泛应用于计算机语言和自动机理论的研究中。
我们可以使用图灵机来描述计算机语言的语法和语义,并且使用它来定义自动机模型。
这在编程语言的编译、解释和分析中都有着广泛的应用。
三、图灵机的限制尽管图灵机是一种非常强大的计算模型,它仍然存在着一些限制。
其中最明显的一点是图灵机的速度。
尽管图灵机能够计算出任何可计算问题,但某些问题可能需要非常长的时间才能得到结果。
例如,计算出一个长文本的哈希值可能需要几分钟,而对于一个复合的问题,甚至需要几个世纪才能计算得出。
此外,图灵机还无法解决某些问题,例如非计算问题和不规则问题。
这些问题之所以无法用图灵机解决,是因为它们没有确定的方法来解决它们。
这些问题是无法用算法来解决的,并且需要人类直接进行解决。
四、结语图灵机是理论计算机科学中最重要的概念之一。
它被认为是能够计算出任何可计算问题的最基本计算机模型。
通过图灵机的研究,我们可以深入理解计算机科学的基本原理,理解计算机能力和限制。
图灵机模型

2.1.1 基本图灵机
(2)处理输入串0001的过程中经历的ID变换序 列如下:
q00001├M 0q0001├M 00q001 ├M 000q01├M 0001q1├M 0001Bq2 (3)处理输入串000101的过程中经历的ID变换 序列如下:
q0000101├M 0q000101├M 00q00101 ├M 000q0101├M 0001q101├M 00010q11
3
直观物理模型
4
2.1.1 基本图灵机
图灵机(Turing machine)/基本的图灵机 M=(Q, ∑, Γ, δ,q0 , B , F) ,
Q为状态的有穷集合,q∈Q,q为M的一个 状态;
q0∈Q,是M的开始状态,对于一个给定的输 入串,M从状态q0启动,读头正注视着输入带 最左端的符号;
B∈Γ,被称为空白符(blank symbol),含有 空白符的带方格被认为是空的;
∑Γ-{B}为输入字母表,a∈∑,a为M的一 个输入符号。除了空白符号B之外,只有∑中 的符号才能在M启动时出现在输入带上;
7
2.1.1 基本图灵机
δ:Q×ΓQ×Γ×{R, L},为M的移动函数 (transaction function)。
δ(q , X)=(p , Y, R)表示M在状态q读入符号X, 将状态改为p,并在这个X所在的带方格中印 刷符号Y,然后将读头向右移一格;
δ(q , X)=(p , Y , L)表示M在状态q读入符号X, 将状态改为p,并在这个X所在的带方格中印 刷符号Y,然后将读头向左移一格。
8
例子2-1说明
的符号串或者是M的输入带最左端到M的读头注视 的带方格中的符号组成的符号串 – M正注视着α2的最左符号。
图灵机计算机的理论模型

图灵机——计算机的理论模型
机器的程序是五元组{Si , X , Y , L(R或N) , Sj}形式的指 令集,定义了机器在一个特定状态下读入一个特定字符时所 采取的动作。 五个元素的含义如下:
①Si 表示机器当前的状态;
②X 表示机器从方格中读入的内容,也即当前内容; ③Y 表示机器用来代替X 写入方格中的内容; ④L、R、N 分别表示左移一格、右移一格和不移动; ⑤Sj 表示机器下一步的状态。
图灵机——计算机的理论模型
图灵机的计算开始于初始状态,设为S0,终止于停止(HALT)状态,设为SH。 例: 设计能够实现“a+1”运算的图灵机,计算完成后要求读写头回到原位。
图灵机进行“a+1”运算的控制规则表
输入
当前状态 (Si) S0 S1 S1 S1 S2 S2 S2 S3 S3 S3 S4 当前内容 (X ) b 0 1 b 0 1 b 0 1 b 任意 重写的新内容 (Y) b 1 0 b 1 0 1 0 1 b b
英国科学家阿兰.图灵 (1912-1954)
图灵证明,只有图灵机能解决的 计算问题,实际计算机才能解决。
“图灵奖”是美国计算机协会于1966年设立的。
什么是图灵机? 图灵机由一条无限长的纸带、读/写头及控制
器构成。
图灵机模型
控制器内包括控制规则表,它能够通过读/写头对纸带上 的符号进行读或写,读写头可以在纸带上左右移动。 纸带分成了一个个的小方格,每个方格中可以记录机器 字母表里的符号,如0或1等。
பைடு நூலகம்输出
读写头移动方向 (L,R或N) L R L R R L L R R N R 进入的新状态 (Sj) S1 S3 S2 SH S3 S2 S4 S3 S3 SH S3
turingmachine图灵机

图灵机的意义
图灵机模型理论是计算科学最核心的理论之一 图灵机模型为计算机设计指明了方向 图灵机模型是算法分析和程序语言设计的基础
理论
图灵机概述
所谓的图灵机就是指一个抽象的机器,它有 一条无限长的纸带,纸带分成了一个一个的 小方格,每个方格有不同的颜色。有一个机 器头在纸带上移来移去。机器头有一组内部 状态,还有一些固定的程序。在每个时刻, 机器头都要从当前纸带上读入一个方格信息, 然后结合自己的内部状态查找程序表,根据 程序输出信息到纸带方格上,并转换自己的 内部状态,然后进行移动。
读写头
状态控制器
图灵机的组成
一个确定型单带图灵机由以下四个部分组成 (见上页图): ·无限长的带子 TAPE,带子划成小格, 格子标记 … , -3,-2,-1,0,1,2, 3,… ·读写头HEAD ·控制规则表TABLE ·状态存储器
图灵机的组成-TAPE
纸带被划分为一个接一个的小格子,每个格 子上包含一个来自有限字母表的符号,字母 表中有一个特殊的符号 表示空白。纸带上 的格子从左到右依此被编号为 0, 1, 2, ... , 纸带的右端可以无限伸展。
图灵机的基本思想
用机器来模拟人们用纸笔进行数学运算的过 程,该过程可分为如下两个简单动作:
➢在纸上写上或擦除某个符号 ➢把注意力从纸的一个位置移动到另一个位置
而在每个阶段,人要决定下一步的动作,依 赖于:
➢此人当前所关注的纸上某个位置的符号 ➢此人当前思维的状态。
… -2 -1 0 1 2 3 …
图灵机计算思想
计算机系统应该有: 存储器(相当于存储带)
中央处理器(控制器及其状态)
为了能够将数据保存到存储器并将计算结 果从存储器送出来展示给用户,计算机系 统还应该有输入设备和输出设备如键盘、 鼠标、显示器和打印机等。
计算模型图灵机课件

图灵机为计算机安全领域提供了理论 基础,如分析病毒、黑客攻击等。
04
图灵机的启示
对人工智能的影响
1 2
奠定人工智能理论基础
图灵机作为计算模型,为人工智能领域提供了理 论基础,推动了人工智能的发展。
启发机器学习算法
图灵机的计算原理启发了众多机器学习算法,如 神经网络、深度学习等。
3
强化智能系统设计
特点
非确定型图灵机具有更高的计算能力,可以模拟更复杂的算法和问 题。
应用
非确定型图灵机在理论计算机科学中有着重要的地位,例如在自动 机理论和形式语言等领域中的应用。
概率图灵机
定义
概率图灵机是一种能够进行概率计算的图灵机模型,即机器在执行 操作时具有一定的概率分布。
特点
概率图灵机可以模拟随机过程和不确定性,适用于处理概率性和统 计性的问题。
05
图灵机的扩展
多带图灵机
定义
多带图灵机是指具有多个磁带,并且每个磁带都可以独立进行读 写操作的图灵机。
特点
多带图灵机可以同时处理多个任务,提高了计算效率和并行处理 能力。
应用
多带图灵机在计算机科学和人工智能领域中有着广泛的应用,例 如并行算法、分布式计算和云计算等。
非确定型图灵机
定义
非确定型图灵机是指具有不确定性的计算模型,即存在多个可能的 计算路径,但最终都能得到正确的结果。
计算模型图灵机课 件
contents
目录
• 图灵机简介 • 图灵机的工作原理 • 图灵机的应用 • 图灵机的启示 • 图灵机的扩展
01
图灵机简介
图灵机的发明者
01
图灵机的发明者是英国数学家阿 兰·图灵(Alan Turing),他在 1936年提出了图灵机的概念。
【计算理论】图灵机(图灵机示例)
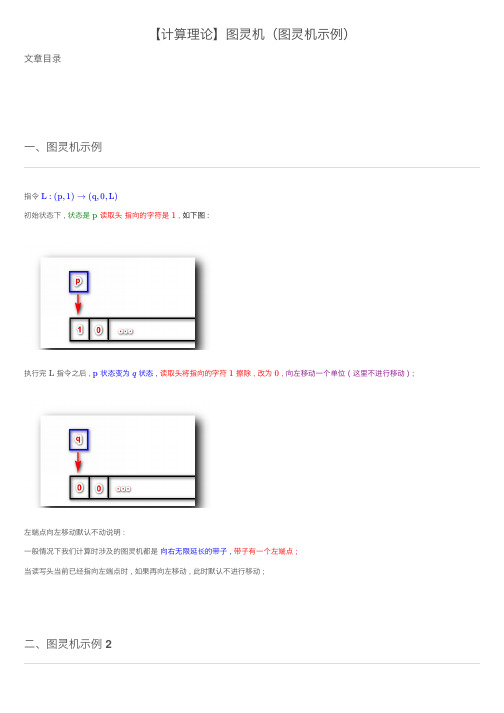
【计算理论】图灵机(图灵机⽰例)⽂章⽬录⼀、图灵机⽰例指令 初始状态下 , 状态是 读取头 指向的字符是 ,如下图 :执⾏完 指令之后 , 状态变为 状态 , 读取头将指向的字符 擦除 , 改为 ,向左移动⼀个单位 ( 这⾥不进⾏移动 ) ;左端点向左移动默认不动说明 :⼀般情况下我们计算时涉及的图灵机都是 向右⽆限延长的带⼦ , 带⼦有⼀个左端点 ;当读写头当前已经指向左端点时 , 如果再向左移动 , 此时默认不进⾏移动 ;⼆、图灵机⽰例 2L :(p,1)→(q,0,L)p 1L p q 10任务 : 设计⼀个图灵机 , 给定输⼊之后 , 图灵机会 在输⼊中寻找 字符 ;算法 :如果 找到了 字符 , 就会将该字符转变成 字符 , 然后将当前状态改为接受状态 , 然后停下来 ;如果带⼦上的字符都读取完毕后 , 没有找到 , 只找到了空⽩字符 , 将该空⽩字符改为 , 然后向左移动⼀格 , 然后停下来 ;( ⾃动机停下的前提是处于可接受状态 )根据上述算法 , 构造图灵机 ;图灵机设计 :① 状态集 , 其中 是开始状态 , 是接受状态 ;② 输⼊字符集 ;③ 带⼦字符集 , 其中 是空⽩字符 ;④ 指令 ⑤ 指令 ⑥ 指令 上述图灵机设计中 , 最关键的部分是三条指令 ;图灵机处于开始状态 , 读头指向 字符 , 左端的 是输⼊字符 , 查看图灵机是否接受 字符串 ;下⾯图灵机后续都是空⽩字符 ;根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;如下图 :110f 11Q ={q,f}q f Σ={0,1}Γ={0,1,B}B δ(q,0)=(q,0,R)δ(q,1)=(f,0,R)δ(q,B)=(q,1,L)q 00000B δ(q,0)=(q,0,R)q 0q,0,R q 0此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;如下图 :此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向左移动⼀个字符 ;如下图 :δ(q,0)=(q,0,R)q 0q,0,R q 0δ(q,B)=(q,1,L)q B q,1,L q 1此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;如下图 :此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;此时的状态 是接受状态 , ⾃动机停⽌运⾏ ;如下图 :δ(q,0)=(q,0,R)q 0q,0,R q 0δ(q,1)=(f,0,R)q 1f,0,R f 0f图灵机 与 ⾃动机 接受的条件是不同的 ;图灵机计算过程中 , ⼀旦到达接受状态 , ⽴刻停机 , 不再继续进⾏计算 ; 并且称该图灵机是可接受的 ;⾃动机即使到达接受状态 , 也要把⾃动机读取的字符读取完毕 , 才停⽌计算 ; 然后在查看最终的状态是否是接受状态 ;。
计算理论实验灵机模拟与可计算性验证

计算理论实验灵机模拟与可计算性验证计算理论是计算机科学的重要分支,研究了计算的本质和边界。
在计算理论中,实验灵机模拟以及可计算性验证是两个重要的概念。
本文将介绍实验灵机模拟和可计算性验证的概念、应用以及其在计算理论中的重要性。
一、实验灵机模拟实验灵机模拟是指使用计算机程序对图灵机的行为进行模拟和仿真。
图灵机是由阿兰·图灵提出的一种理论计算模型,可以模拟现代计算机的工作原理。
实验灵机模拟的目的是通过计算机程序模拟图灵机的运行过程,以便对计算理论进行实验和验证。
实验灵机模拟允许计算机科学家们在计算理论研究中进行大规模的实验。
它可以帮助我们更好地理解计算的本质,研究计算过程的性质和行为。
通过实验灵机模拟,我们可以验证算法的正确性、分析计算问题的可解性以及研究不同计算模型之间的联系和差异。
二、可计算性验证可计算性验证是指判断一个问题是否可由计算机算法进行有效求解的过程。
在计算理论中,可计算性验证的核心问题是确定一个问题是否可被计算机程序表示和求解。
可计算性验证是计算理论的核心问题之一,它研究了计算过程的边界和限制。
可计算性验证的内容包括可计算问题和不可计算问题的判定。
可计算问题是指可以通过计算机算法进行求解的问题,而不可计算问题是指不存在有效的计算机算法来求解的问题。
通过可计算性验证,我们可以确定某个问题是否存在解决方案,以及该问题是否可以用计算机算法进行有效求解。
三、实验灵机模拟与可计算性验证的重要性实验灵机模拟和可计算性验证是计算理论研究中的重要工具和方法。
它们不仅有助于我们理解计算的本质和边界,还可以帮助我们验证和验证计算理论中的各种概念和结论。
首先,实验灵机模拟允许我们在计算机上模拟和仿真复杂的计算过程。
通过实验灵机模拟,我们可以测试和验证算法的正确性、分析算法的性能和行为,从而改进和优化现有的算法。
其次,可计算性验证可以帮助我们确定一个问题是否可被计算机算法求解。
通过可计算性验证,我们可以确定哪些问题是可计算的,哪些问题是不可计算的,从而引导我们将精力集中在可计算问题的研究和解决上。
图灵机实验报告

图灵机实验报告图灵机实验报告引言:图灵机是由英国数学家艾伦·图灵在1936年提出的一种理论计算模型,它被认为是现代计算机的理论基础之一。
本实验旨在通过模拟图灵机的工作原理,探索计算机科学的基本概念和算法设计。
一、图灵机的基本原理图灵机由一个无限长的纸带和一个可移动的读写头组成。
纸带被划分为一系列格子,每个格子上可以写入一个字符。
读写头可以在纸带上左右移动,并根据当前所处格子上的字符执行相应的操作。
二、图灵机的操作图灵机的操作分为三种:读取、写入和移动。
读取操作是指读取当前格子上的字符,并根据字符执行相应的算法。
写入操作是指将指定的字符写入当前格子上。
移动操作是指将读写头在纸带上向左或向右移动一个格子。
三、图灵机的程序设计图灵机的程序设计是通过一系列规则来描述的。
每个规则包含三个部分:当前状态、当前字符和下一步操作。
通过这些规则,图灵机可以执行各种复杂的计算任务。
四、图灵机的应用图灵机的应用非常广泛,它可以用来解决各种计算问题。
例如,可以使用图灵机来模拟其他计算机的工作原理,设计和验证算法,甚至用来解决一些数学难题。
五、图灵机的局限性尽管图灵机是一种非常强大的计算模型,但它也有一些局限性。
首先,图灵机只能处理离散的输入和输出。
其次,图灵机的计算能力是有限的,它无法解决一些无法被计算的问题。
六、图灵机的发展与未来图灵机的概念为计算机科学的发展奠定了基础,它不仅帮助人们理解计算机的本质,还推动了算法设计和计算理论的发展。
未来,随着技术的不断进步,图灵机的应用将会更加广泛,同时也会面临更多的挑战和机遇。
结论:通过本次图灵机实验,我们深入了解了图灵机的基本原理、操作和程序设计。
图灵机作为计算机科学的基石,为我们理解和应用计算机提供了重要的思维工具。
通过不断探索和研究,我们相信图灵机的概念将会在未来的科学研究和技术创新中发挥更加重要的作用。
图灵机器的原理和应用

图灵机器的原理和应用图灵机器是一种理论上的计算模型。
它是由英国数学家阿兰·图灵在1936年提出的。
按照图灵的定义,一台图灵机器包括一个有限的控制器和一条无限长、多分支的纸带,纸带上有一个一个的符号,控制器扫描这些符号并执行一系列的指令,来完成特定的计算任务。
图灵机器的工作原理图灵机器是由控制器和纸带两部分组成。
其控制器包括有限状态自动机和一个读写头。
无论是读取纸带上的符号,还是执行某种指令,都是由其状态自动机所完成的。
假设图灵机器的某个输入具有以下形式:10111001那么图灵机器会首先扫描第一个符号,然后根据其预设的指令,在纸带上进行如下操作:在其状态自动机中找到对应程序,在磁带上将该符号改为下一个字符。
该过程会循环迭代直至结束。
图灵机器的应用目前,图灵机器的应用主要体现在两个方面:人工智能和密码破解。
下面逐一进行阐述。
1.人工智能传统的计算机模型和算法仅适用于指定的问题,而人工智能则可以通过机器学习和数据挖掘等一系列技术,完成许多人类所难以完成的任务。
图灵机器的概念提出之初即旨在真正实现人工智能。
到目前为止,图灵机器已经成为了开发出各种人工智能算法和技术的理论基础。
2.密码破解密码破解在各种计算机安全领域有着重要的应用。
用图灵机器进行密码破解的原理就是先设想一个加密算法,并用图灵机器来对其加密的结果进行破解。
在这种情况下,图灵机器可以解决计算难度较高的问题,如确定密码本身的长度、密码包含的字符数、密码中各类字符出现的频率等。
图灵机器是一种强大而灵活的计算模型,它在计算领域的应用有着广泛的前景,因为其理论完备性和普适性,所以可以应用于各种不同领域的计算。
在人工智能和计算机安全等众多领域,图灵机器作为重要的理论基础已经深入人心,并成为了不可或缺的计算模型和工具。
计算理论导引总结分章节版

定义概念题目:第三章:1. 图灵机:是一种精确的通用计算机模型,能模拟实际计算机的所有计算行为,它的核心是转移函数δ,它说明了机器如何从一个格局走到下一个格局。
对于图灵机,δ的形式如下:Q×Γ→Q×Γ{L,R},图灵机是一个7元组(Q,∑,Γ,δ,q 0,q accept,q reject).其中Q,∑,Γ都是有穷集合,并且1)Q是状态集;2)∑是输入字母表,不包括特殊空白符号凵,3)Γ是带字母表,其中凵∈Г,∑∈Г4)δ2. 格局:图灵机的计算过程中,当前状态,当前内容和读写头当前位置组合在一起。
例如:1011q701111:当前状态q7,当前读写头位置在第二个0上。
定义3.2 如果一个语言能被某一个图灵机识别,则称该语言是图灵可识别的(递归可枚举语言)定义3.2 如果一个语言能被某一个图灵机判定,则称该语言是图灵可判定的简称可判定的(递归语言)3.图灵机的变形:多带图灵机、非确定型图灵机、枚举器。
每个4.枚举器:他是图灵机的一种变形,是带有打印机的图灵机,图灵机把打印机当作输出设备,从而可以打印串,每当图灵机想在打印序列中增加一个串时,就把此串送到打印机。
一个语言是图灵可识别的,当且仅当有枚举器枚举它。
5.图灵机的术语:形式化描述,实现描述,高水平描述。
第四章:1.可判定的语言有:(A DFA、A NFA、A REX、E DFA、EQ DFA 是正则语言)、(A CFG、E CFG 是上下无关语言)❶每个上下文无关语言都是可判定的。
2.不可判定的语言有::EQ CFG、A TM 、停机问题、HALT TM 、E TM、REGULAR TM 、EQ TM 、 E LBA 、ALL CFG 、PCPA TM ={<M,ω>|M是TM,ω是串,M接受ω}是不可判定的。
证明:假设证A TM 是可判定的,下面将由之导出矛盾。
设H是A TM 的判定器。
令M是一个TM,ω是一个串。
图灵机的原理

图灵机的原理图灵机是英国数学家艾伦·图灵于1936年提出的一种抽象的数学模型,用来描述一种能够模拟任何计算机算法的理论计算机。
图灵机的原理是基于一种简单的计算模型,它包括一个无限长的纸带和一个能够读写纸带上符号的读写头,以及一系列状态和状态转移规则。
图灵机的设计思想和工作原理对于理解计算机科学的基本概念和原理具有重要的意义。
图灵机的核心是其状态转移规则,它描述了在给定状态下,图灵机应该如何根据当前读取的符号和内部状态来进行下一步的操作。
这种简单的状态转移规则使得图灵机能够模拟任何可以被算法描述的计算过程,从而成为了计算理论的基础模型之一。
图灵机的工作原理可以简单描述为,读写头在纸带上移动,读取当前符号并根据当前状态和读取的符号进行状态转移,然后根据状态转移规则进行下一步操作。
这个过程不断重复,直到图灵机进入停机状态或者无限循环。
图灵机的原理具有重要的理论意义,它证明了存在一种通用的计算模型,能够模拟任何可以被算法描述的计算过程。
这个理论结果被称为“图灵完备性”,它表明只要一种计算模型具有和图灵机相同的能力,就能够模拟任何计算过程。
这也是为什么图灵机被认为是计算机科学的基础理论之一。
除了理论意义,图灵机的原理还对计算机科学和人工智能领域有着重要的启发作用。
图灵机的设计思想和工作原理启发了人们对计算机和算法的理解,也为人工智能的发展提供了重要的理论基础。
图灵机的原理对于理解计算机科学的基本概念和原理具有重要的意义。
总的来说,图灵机的原理是计算机科学领域中非常重要的理论概念,它描述了一种能够模拟任何计算机算法的理论计算机模型。
图灵机的工作原理基于简单的状态转移规则,能够模拟任何可以被算法描述的计算过程,具有重要的理论意义和启发作用。
图灵机的原理对于理解计算机科学的基本概念和原理具有重要的意义,也为人工智能的发展提供了重要的理论基础。
计算理论导论(英文版)图灵机

Exa. : 判定A = { 0j | j=2n ,n
0}
Example 3.4 Describe a TM M that recognizes the language consisting of all strings of 0s whose length is a power of 2. It decides the language A = { 0j | j=2n ,n0}. Solution: To give the formal description of M= (Q,S,G,d,q0,qaccept,qreject) as follows. 1. Q = {q1,q2,q3,q4,q5, qaccept,qreject), 2. S ={0}, and 3. G = {0, x, _ } , 4. q1 start state Q 5. qaccept accept state Q 6. qreject reject state Q 7. To describe the transition function d with the following 21 state diagram. (fig. 3.4 p132)
6
Input Convention
7
Input Convention
8
Output Convention
9
Turing Machine
元组式定义 A Turing machine M is defined by a 7-tuple (Q,S,G,d,q0,qaccept,qreject), with 1. Q finite set of states 状态集合,相当于程序标号 2. S finite input alphabet (without “_”) 输入字母表 3. G finite tape alphabet with { _ } S G 带字母表 4. q0 start state Q 开始状态 5. qaccept accept state Q 接受状态 6. qreject reject state Q 拒绝状态 7. d the transition function 转移函数相当于移动+goto
计算机系统3-现代计算机基石图灵机理论

计算机系统3-现代计算机基⽯图灵机理论在理解CPU之前,我们有必要先了解⼀下现代计算机理论的基⽯——图灵机,这个抽象模型决定了现代计算机可以被实现。
这个模型的⼯作原理也投射到了CPU的⼯作实现上。
图灵机的知识可深可浅,换句话说,上⼿容易,但是意义深远。
下⾯是⼀个可以在线学习图灵机的⽹站:主要参考1. 《嵌⼊式C语⾔⾃我素养》2. 百度百科以及⼤佬博客3. b站视频4. 《数字逻辑》课程00 内容概括图灵机的概念产⽣于英国数学家艾伦·图灵在1936年在《伦敦数学协会会刊》上发表的那篇改变世界的论⽂——《论可计算数及其在判定问题中的应⽤》,论⽂本⾝很难很复杂,但对于计算机科学⽽⾔,可以简单概括为:“任何复杂的运算都可以分解为基本运算指令。
”⽽图灵机则是图灵机理论中提出的理想模型,可以⽤简若⼲指令的组合就实现任意复杂的计算。
01 基本构造图灵机的构造如下图所⽰:1. ⼀条⽆限长的纸带-Tape这是要处理的对象,被划分为⼀个个⼤⼩相等的⼩⽅格。
每个⼩⽅格都可以存放⼀个符号,可以存放数字、字母、空⽩等。
2. ⼀个读写头-Head可以在纸带上左右移动,它能读出当前所指的格⼦上的符号,并能改变当前格⼦上的符号。
3. ⼀套控制规则/状态转换规则-Table根据当前机器所处的状态以及当前读写头所指的格⼦上的符号来确定读写头下⼀步的动作,并改变状态寄存器的值,令机器进⼊⼀个新的状态。
4. ⼀个状态寄存器⽤来保存图灵机当前所处的状态。
图灵机的所有可能状态的数⽬是有限的,并且有⼀个特殊的状态,称为停机状态。
02 ⼯作原理与思想02-1 ⼯作原理这个东西是有数学推导的,我在此简化具体⼀下:想象⾃⼰是⼀只⼩猫,我们会有饿和饱的状态,⾯对不同的⾷物,我们吃或者不吃,最终是饱或者饿。
上图就是我们理想化的Table,即状态转换规则。
在这个例⼦中,猫就是⼀个读写头Head,可以存储⼀个状态我们假设猫会根据⾃⼰饿与不饿以及格⼦⾥是否是⾷物来决定“吃”或是“等待”。
Turing机器测试搭建以及AI异常生成算法探索

Turing机器测试搭建以及AI异常生成算法探索Turing机器测试是人工智能(AI)领域中重要且不可或缺的环节。
它的目的是验证AI的智能水平和能力,通过进行一系列测试来评估机器的表现。
在本文中,我们将讨论Turing机器测试的搭建过程,并探索AI异常生成算法的应用。
Turing机器测试的核心思想是通过对机器进行对话或其他形式的交互,以模拟人类对机器的评估。
这种测试方法是基于英国数学家艾伦·图灵于1950年提出的“图灵测试”。
图灵测试的目标是使机器的参与者(通常为人类评判者)无法区分出他们与机器进行的对话是否与与人对话。
首先,为了搭建Turing机器测试,我们需要一个可靠的测试平台。
这个平台应该能够模拟真实的对话环境,提供与机器进行交互的接口,以及记录和分析对话数据。
一种常用的测试平台是通过构建聊天机器人来进行测试。
聊天机器人可以通过自然语言处理技术来理解输入并生成回答。
为了提高机器的表现,我们可以使用机器学习和深度学习技术对机器进行训练,使其能够更好地理解和回复用户的问题。
在Turing机器测试中,还需要精心设计合适的测试用例和评判标准。
测试用例应该涵盖各种语义和语法的不同情况,以便全面评估机器的能力。
评判标准可以根据对话的流畅性、逻辑性和信息准确性等因素进行评估,以获得机器在不同方面的得分。
然而,Turing机器测试中最大的挑战之一是如何避免机器通过“猜测”或使用特定的技巧来回答问题。
为了解决这个问题,一种常见的方法是引入AI异常生成算法。
AI异常生成算法的目标是通过添加特定的扰动或噪音来改变输入,从而测试机器的鲁棒性和应对能力。
这些异常可能是语法错误、意义歧义或其他形式的干扰。
通过对机器在这些异常情况下的表现进行评估,我们可以更准确地判断机器的表现是否真正具有人类智能的水平。
在探索AI异常生成算法时,我们还需要注意算法的合理性和可解释性。
这意味着生成的异常应该是合理的,并且能够被解释为机器在特定情况下的处理方法。
人工智能_图灵及图灵测试

在定义智慧时,英国科学家图灵做出了贡献, 如果一台机器能够通过称之为图灵实验的实验, 那它就是智慧的
图灵实验的本质
就是让人在不看外型的情况 下不能区别是机器的行为还是人的行为时,这 个机器就是智慧的。
不要以为图灵只做出这一点贡献就会名垂表史,
如果你是学计算机的就会知道,对于计算机人 士而言,获得图灵奖就等于物理学家获得诺贝 尔奖一样,图灵在理论上奠定了计算机产生的 基础,没有他的杰出贡献世界上根本不可能有 这个东西,更不用说什么网络了。
• Computer needs to posses:Natural language processing, Knowledge representation, Automated reasoning, and Machine learning • Problem: 1) Turing test is not reproducible, constructive, and amenable to mathematic analysis. 2) What about physical interaction with interrogator and environment? • Total Turing Test: Requires physical interaction and needs perceptio(Turing)
英国数学家Turing(图灵)(1912-1954) 1936年提出了一种理想计算机的数 学模型(图灵机,论文“理想计算 机”)。 1950年提出了图灵试验,发表了 “计算机与智能”的论文(“计算机 能思维吗”),提出机器能够思维的 论述。 图灵奖。
如果希望做出一台能够思考的机器,那就必须知道 什么是思考,更进一步讲就是什么是智慧,它的表 现是什么? 你可以说科学家有智慧,可你决不会说一个路人什 么也不会,没有知识,你同样不敢说一个孩子没有 智慧,可对于机器你就不敢说它有智慧。 那么智慧是如何分辨的呢? 我们说的话,我们做的事情,我们的想法如同泉 水一样从大脑中流出,如此自然,可是机器不行 什么样的机器才是智慧的?汽车,火车,飞机, 收音机等,它们模仿我们身体器官的功能,但是 不能模仿人类大脑的功能。 到目前为止,我们仅仅知道大脑由数十亿个神经 细胞组成,模仿它是非常困难。
图灵机简介和原理分析

图灵机简介和原理分析摘要:1936年,阿兰·图灵提出了一种抽象的计算模型——图灵机 (Turing Machine)。
图灵机是指一个抽象的机器,可被视作任意解决有限数学逻辑过程的机器,它提供了一种简单有效的解决逻辑过程的方法,加快了后来诺依曼设计的计算机的出现。
本文将对图灵机的原理和历史等进行简介和分析。
关键字:图灵机,计算模型。
一.图灵机的历史发展图灵机被公认为现代计算机的原型,这台机器可以读入一系列的零和一,这些数字代表了解决某一问题所需要的步骤,按这个步骤走下去,就可以解决某一特定的问题。
这种观念在当时是具有革命性意义的,因为即使在50年代的时候,大部分的计算机还只能解决某一特定问题,不是通用的,而图灵机从理论上却是通用机。
1936年,图灵向伦敦权威的数学杂志投了一篇论文,题为"论数字计算在决断难题中的应用"。
在这篇开创性的论文中,图灵给"可计算性"下了一个严格的数学定义,并提出著名的图灵机"(Turing Machine)的设想。
"图灵机"不是一种具体的机器,而是一种思想模型,可制造一种十分简单但运算能力极强的计算装置,用来计算所有能想像得到的可计算函数。
"图灵机"与"冯•诺伊曼机"齐名,被永远载入计算机的发展史中。
1950年10月,图灵又发表了另一篇题为"机器能思考吗"的论文,成为划时代之作。
也正是这篇文章,为图灵赢得了"人工智能之父"的桂冠。
在图灵看来,这台机器只用保留一些最简单的指令,一个复杂的工作只用把它分解为这几个最简单的操作就可以实现了,在当时他能够具有这样的思想确实是很了不起的。
图灵机的产生一方面奠定了现代数字计算机的基础(要知道后来冯•诺依曼就是根据图灵的设想才设计出第一台计算机的)。
另一方面,根据图灵机这一基本简洁的概念,我们还可以看到可计算的极限是什么。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
int currentpos;//记录当前位置
int halt;//退出
int i;//临时辅助变量
int s;//临时存储状态
char tape[N];//纸带长度
char number[M];//存储x
char c1;//临时存储字符
char c2;//临时存储字符
}
for(i = S;i < S + M && number[i-S] != '\0';i++) //将数字写入纸带
tape[i] = number[i-S];
currentpos = S;//初始化
halt = 1;//此时state = 1
d = 'R';//初始为右移
cout<<endl<<"其五元组如下:"<<endl;
print();
}
}
void state6()//此时d = 'L';
{
while(state == 6)
{
c1 = c2 = tape[currentpos];//暂存
s = state;
if(tape[currentpos] == 'B')//返回状态1
{
state = 1;
currentpos++;
}
else//进入状态2
{
state = 2;
currentpos++;//进入2时d='R'
}
print();
}
}
void state2()//此时d = 'R'
{
while(state == 2)
{
c1 = c2= tape[currentpos];//暂存
s = state;
if(tape[currentpos] == 'B')//进入状态3
char d;//方向输出
void start()
{
for(i = 0;i < N - 1;i++)//初始化纸带
tape[i] = 'B';
tape[N-1] = '\0';
cout<<"使用图灵机计算f(x) = 2^x。其中x为二进制数字。"<<endl;
while(1)//判断二进制
{
state = 1;
for(i = 0;i < N;i++)
if(tape[i] != 'B' && tape[i] != '\0')
{
cout<<tape[i];
outfile<<tape[i];
}
cout<<")二进制"<<endl<<endl;
outfile<<")二进制"<<endl;
}
void main()
{
outfile<<"请输入二进制数字x = ";
outfile<<number<<endl;
outfile<<endl<<"其五元组如下:"<<endl;
}
void print()//输出函数
{
cout<<"<Q"<<s<<","<<c1<<","<<c2<<","<<d<<",Q"<<state<<">"<<endl;
{
state = 4;
c2 = tape[currentpos] = '0';
currentpos--;
d = 'L';//进入4时d='L';
}
else
currentpos++;
print();
}
}
void state4()//此时d='L';
{
while(state == 4)
{
c1 = c2 = tape[currentpos];//暂存
s = state;
if(tape[currentpos] == '0')
c2 = tape[currentpos] = '1';
else
if(tape[currentpos] == '1')//进入状态6
{
state = 6;
c2 = tape[currentpos] = '0';
}
currentpos--;//进入6时d='L';
state = 3;
currentpos++;//进入3时d='R';
print();
}
}
void state3()//此时d = 'R';
{
while(state == 3)
{
c1 = c2 = tape[currentpos];//暂存
s = state;
if(tape[currentpos] == '输入二进制数字x = ";
cin>>number;
for(i = 0;i < M && number[i]!= '\0';i++)
if(number[i] >'1' || number[i] < '0')
state = 0;
if(state)
break;
else
cout<<"无效数字。";
三、实验代码
/*****************************************************************
图灵机的模拟过程
计科二班20110801212张琦佳
*****************************************************************/
}
void homework()//写入文件
{
outfile<<"图灵机的实现过程"<<endl;
outfile<<" Turing.........."<<endl;
outfile<<"计科2班张琦佳"<<endl<<endl;
outfile<<"使用图灵机计算f(x) = 2^x。其中x为二进制数字。"<<endl;
start();
homework();
while(halt)
switch(state)
{
case 1 : state1();
case 2 : state2();
case 3 : state3();
case 4 : state4();
case 5 : state5();
case 6 : state6();
if(tape[currentpos] == '0')
currentpos++;
else
if(tape[currentpos] == 'B')//进入状态7
{
state = 7;
c2 = tape[currentpos] = '1';
currentpos--;
d = 'L';//进入7时d='L';
HUNANUNIVERSITY
计算理论导引
实验报告
题目:
图灵机(Turing)的模拟
学生姓名:
学生学号:
专业班级:
计算机科学与技术2班
上课老师:
实验日期:
2014-1-6
一、
1、掌握Turing机的概念。
2、掌握Turing机的运行过程,了解每一个格局的转化。
二、
对于任意给定的一台Turing机和任意给定的字符串w(w不含空格),编程模拟此Turing机的运行过程,要求输出从开始运行起的每一格局。
d = 'R';//进入1时d='R';
}
else
currentpos--;
print();
}
}
void state7()//此时d= 'L';
{
while(state == 7)
{
c1 = c2 = tape[currentpos];//暂存
s = state;
if(tape[currentpos] == '0')//清零
outfile<<"<Q"<<s<<","<<c1<<","<<c2<<","<<d<<",Q"<<state<<">"<<endl;
