【2015红桥二模】天津市红桥区2015届高三第二次模拟考试数学文科答案

合集下载

天津市红桥区高三二模数学(文)试卷.docx

2016年天津市红桥区高三二模数学（文）试卷一、单选题（共8小题）1．已知集合，则（）A．B．C．D．2．已知抛物线上一点的横坐标为3，且满足，则抛物线的方程为( )A．B．C．D．3．某程序框图如图所示，若输出的，则判断框内为（）A ．B．C．D．4．函数的零点所在的区间是（）A．B．C．D．5．“”是“”成立的（）A．既不充分也不必要条件B．充要条件C．必要而不充分条件D．充分而不必要条件6．函数，将函数的图象上向右平移个单位重复，得到函数的图象，则在区间上的最小值为( )A ．B．C．D．7．已知双曲线，以C的右焦点为圆心，以为半径的圆与C的一条渐近线交于A、B两点，若，则双曲线C的离心率为( ) A．B．C．D．8．已知函数是定义域为R的偶函数，且，若在上是减函数，记，则A ．B．C ．D．二、填空题（共7小题）9.已知是虚数单位，则10.若直线过点且与直线垂直，则直线的方程是11.设，则不等式的解集为12.如图，是一个几何体的三视图，其中正视图是等腰直角三角形，侧视图与俯视图均为边长为1的正方形，则该几何体外接球的表面积为13.如图，已知圆内接四边形，边延长线交延长线于点，连接，若，则14.矩形中，，点E在BC上，满足，点F在CD 上，若，则15.在钝角中，内角所对的边分别为，已知。

（1）求边和角的大小；（2）求的值。

三、解答题（共4小题）16.某工厂要安排生产Ⅰ，Ⅱ两种产品，这些产品要在四种不同的设备上加工，按工艺规定，在一天内，每件产品在各设备上需要加工的时间，及各设备限制最长使用时间如下表：设计划每天生产产品Ⅰ的数量为（件），产品Ⅱ的数量为（件），（Ⅰ）用，列出满足设备限制使用要求的数学关系式，并画出相应的平面区域；（Ⅱ）已知产品Ⅰ每件利润（万元）产品Ⅱ每件利润（万元），在满足设备限制使用要求的情况下，问该工厂在每天内产品Ⅰ，产品Ⅱ各生产多少会使利润最大，并求出最大利润.17.如图，在四棱锥中，底面是菱形，侧面是直角三角形，，点是PC的中点，且平面平面。

天津市红桥区2015-2016学年高二下学期期中数学试卷(文科) 含解析

2015-2016学年天津市红桥区高二（下）期中数学试卷（文科）一、选择题（每小题4分,共48分，每小题有且仅有一个正确答案)1．i是虚数单位,复数=(）A． +i B．﹣1+i C．1﹣i D．﹣+i2．复平面内表示复数i(1﹣2i)的点位于(）A．第一象限B．第二象限C．第三象限D．第四象限3．阅读如图所示的程序框图,若输入的a、b、c分别是1、2、7，则输出的a、b、c分别是(）A．7、2、1 B．1、2、7 C．2、1、7 D．7、1、24．执行如图所示的程序框图,则输出S的值为（）A．10 B．19 C．21 D．365．若函数f（x）=ax4+bx2+c满足f′（1）=2，则f′(﹣1)=（)A．﹣1 B．﹣2 C．2 D．06．下列函数求导运算正确的有（）①（3x）′=3x log3e；②（log2x）′=；③（e x）′=e x;④（)′=x；⑤（x•e x)=e x(1+x）A．1个 B．2个 C．3个 D．4个7．如图所示,4个散点图中，不适合用线性回归模型拟合其中两个变量的是（) A．B．C．D．8．设某大学的女生体重y（单位：kg)与身高x（单位：cm)具有线性相关关系，根据一组样本数据（x i，y i)（i=1，2，…,n)，用最小二乘法建立的回归方程为=0.85x ﹣85。

71，则下列结论中不正确的是(）A．y与x具有正的线性相关关系B．回归直线过样本点的中心(，）C．若该大学某女生身高增加1cm，则其体重约增加0.85kgD．若该大学某女生身高为170cm，则可断定其体重必为58.79kg9．在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（）A．若K2的观测值为k=6.635，我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病B．若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误C．从独立性检验可知有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他有99％的可能患有肺病D．以上三种说法都不正确10．如图是函数y=f（x）的导函数f′（x）的图象，则下面判断正确的是（）A．在区间（﹣2，1）上f（x）是增函数B．在（1,3）上f（x）是减函数C．当x=4时，f（x)取极大值D．在(4，5）上f（x）是增函数11．函数y=xlnx在区间（)A．（0,+∞）上单调递减 B．上单调递减C．上单调递减D．（0，+∞)上单调递增12．已知函数f(x）=ax3﹣3x2+1,若f(x）存在唯一的零点x0，且x0＞0，则实数a 的取值范围是（）A．（1，+∞）B．(2，+∞）C．（﹣∞，﹣1）D．（﹣∞，﹣2）二、填空题(每小题4分,共24分）13．复数的实部等于．14．如图所示的程序框图，输出的n的值是．15．已知某车间加工零件的个数x与所花费时间y(h）之间的线性回归方程为=0.01x+0。

天津市红桥区2015届高三第二次模拟考试文综试题带答案(扫描版)

1-11题，每题4分，共44分。

DCCDA DDBBB A12．（16分）（1）旅游、文化等（一点即可得2分）（2）传承民族文化和文明（2分）（3）丰富了人文旅游景点（提高了人文旅游资源的开发价值）；突出了人文旅游景观特色（增强了人文旅游景点的吸引力）；增加了游客（增加旅游业的收入）。

（6分）（4）（6分）13．（18分）（1）③（2分）（2）甲（2分）南北纬30°-40°的大陆西岸（2分）甲地气温年较差比乙地小（2分）甲地夏季降水量比乙地少（甲地降水季节变化比乙地大）（2分）（3）沟通大西洋东岸地区与太平洋西岸地区（亚欧大陆东西岸）之间的联系（2分）（4）①地理位置优越，交通便捷；②经济发达，商贸往来频繁；③历史悠久，旅游资源丰富；④人口众多，城市规模大。

（答出任三项即可得6分）14．（22分）（1）低山丘陵（2分）（2）在地转偏向力的作用下，海浪向北偏折，使北岸易于遭受侵蚀；夏秋季节，盛行东南风，北岸成为迎风岸，也易遭受海浪的冲刷。

（4分）（3）沿高速公路、铁路等交通线分布，沿城市分布。

（4分）（4）自西南向东北（2分）水量大，水位季节变化大，无结冰期，汛期长等。

（4分）（5）地处我国东部沿海；滨海平原面积较大；气候温暖湿润。

海岸线曲折，多港湾；大陆架宽阔，海洋资源(海洋生物资源、海底矿产资源、海洋旅游资源)丰富。

（三点即可得6分高三历史答案Ⅱ卷共3题，共56分。

12.（18分）（1）中国丝绸制作精良，质量上乘，中国丝绸深受古罗马人的喜爱追捧；运输的曲折艰难。

（3分）（2）状况：长期居于领先地位；近代以来虽有下降，但到1870年仍居世界第一位。

（2分）领先原因：中国古代农业、手工业发达，长期领先世界并远销海外；新航路的开辟和殖民扩张使世界市场出现并得到拓展。

（3分）下降原因：鸦片战争以后，西方列强的经济侵略，瓦解着中国的自然经济，客观促进商品经济的发展，手工业品和农产品在商品流通中的比重加大，国内外市场不断扩大，到1870年虽有下降仍居世界第一。

天津市红桥区高三二模数学(文)试题 Word版含答案

高三数学（文史类）第Ⅰ卷一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求的） 1、已知集合2{|1},{|0}A x x B x x x =<=-≤，则AB =A ．{|11}x x -≤≤B ．{|01}x x ≤≤C ．{|01}x x <≤D ．{|01}x x ≤<2、盒子装有形状、大小完全相同的5个球，其中红色球3个，黄色球2个，若从中随机取出2个球，则所有取出的2个球颜色不同的概率等于 A ．310 B ．25 C ．35 D ．123、根据如下图所示的框图，对大于2的正数N ，输出的数列的通项公式是A ．2n a n =B ．2(1)n a n =-C ．2n n a =D ．12n n a -=4、某几何体的三视图如上图所示，且该几何体的体积是3，则正视图中的x 的值 A ．2 B ．3 C ．32 D ．925、设:{|lg(1)},:{|21}xp x x y x q x x -∈=-∈<，则p 是q 的A ．充分且不必要条件B ．必要且不充分条件C ．充要条件D ．既不充分也不必要条件 6、在ABC ∆中，0120,2,3,,ABC BA BC D E ∠===是线段AC 的三等分点，则BD BE ⋅的值为 A ．659 B ．119 C ．419 D ．139-7、将函数()2sin(2)4f x x π=+的图象向右平移(0)ϕϕ>个单位，再讲图象上没一点的横坐标缩短到原来的12（纵坐标不变），所得图象关于直线4x π=对称，则ϕ的最小值为A ．18πB ．14πC ．38πD ．12π 8、已知函数()2log ,02sin(),2104x x f x x x π⎧<<⎪=⎨≤≤⎪⎩，若存在实数1234,,,x x x x 满足1234()()()()f x f x f x f x ===，且1234x x x x <<<，则3412(1)(1)x x x x --的取值范围是A ．(9,21)B ．(20,32)C ．(8,24)D ．(15,25)第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上.. 9、设i 为虚数单位，复数z 满足3(2)z i i -=，则复数z 的虚部为 10、()21ln 2f x x x =-+在1[,]e e上的最大值是 11、已知函数()12cos (0),()2,()0f x wx wx w f x f x +>=-=，且12x x -的最小值等于π，则w = 12、已知直线:l y =，点(,)P x y 是圆22(2)1x y -+=上的动点，则点P 到直线l 的距离的最小值为13、如图，12,F F 是双曲线22221(0,0)x y a b a b-=>>的左右焦点，过1F 的直线与双曲线的左右两支分别交于点,A B ，若2ABF ∆为等边三角形，则双曲线的离心率为 14、已知下列命题： ①函数()f x =有最小值2；②“2450x x --=”的一个必要不充分条件是“5x =”；③命题:,tan 1p x R x ∃∈=；命题2:,10q x R x x ∀∈-+>，则命题“()p q ∧⌝”是假命题； ④函数()3231f x x x =-+在点(2,(2))f 处的切线方程为3y =-.其中正确命题的序号是三、解答题：本大题共6小题，满分70分，解答应写出文字说明、证明过程或演算步骤 17、（本小题满分13分）在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且3,sin 2sin a b C A ===. （1）求c 的值；（2）求sin(2)4A π-的值.18、（本小题满分13分）某人准备投资1200万元办一所中学，为了考虑社会效益和经济效益，对该地区教育市场进行调查，得出一组数据，列表如下（以班级为单位）：市场调查表：根据物价部门的有关文件，初中是义务教育阶段，收费标准适当控制，预计除书本费、办公费外，初中每人每年可以取600元，高中每人每年可收取1500元，因生源和环境等条件限制，办学规模以20至30个班为宜（含20个与30个），教师实行聘任制，初、高中的教育周期均为三年，设初中编制为x 个班，高中编制为y 个班，请你合理安排招生计划，使年利润最大.17、（本小题满分13分）如图，在四棱锥P ABCD -中，底面ABCD 是边长为2的正方形，侧面PAD ⊥底面ABCD ，且,,2PA PD AD E F ==分别为,PC BD 的中点. （1）求证：平面//EF 平面PAD ；（2）求证：平面PAB ⊥平面PDC ；18、（本小题满分13分）已知数列{}n a 满足1221,3,32(,2)n n a a a a n N n ++===-∈≥.（1）证明：数列{}1n n a a +-是等比数列，并求出{}n a 的通项公式；（2）设数列{}n b 满足242log (1)n n b a =+，证明：对一切正整数n ，有2221211111112n b b b +++<--- .19、（本小题满分14分）已知椭圆2222:1(0)x y Ca b a b+=>>. （1）求椭圆C 的方程；（2）设与圆223:4O x y +=相切的直线l 交椭圆C 于,A B 两点，求OAB ∆面积的最大值，及取得最大值时直线l 的方程.20、（本小题满分14分已知函数()3212()32a f x x x x a R =-+-∈. （1）当3a =时，求函数()f x 的单调区间；（2）若对于任意[1,)x ∈+∞都有()2(1)f x a '<-成立，求实数a 的取值范围；（3）过过点1(0,)3-可作函数()y f x =图象的三条不同切线，求实数a 的取值范围.高三数学（文）（1705）一、选择题（每小题5分，共40分）二、填空题（每小题5分，共30分）9．52-10．21- 11．12121 13．7 14．③④ 三、解答题（本大题共6小题，共80分）（15）（本小题满分13分）（Ⅰ）根据正弦定理，， (2)因为，所以． (5)（Ⅱ）根据余弦定理，得， (8)于是，从而，， (11)． (13)（16）（本小题满分13分）设初中编制为个班，高中编制为个班，则依题意有 (4)又设年利润为万元，那么，即 (7)在直角坐标系中作出不等式组所表示的可行域，如图所示． (10)问题转化为在如图所示的阴影部分中，求直线在轴上的截距的最大值．显然图中的点是符合题意的最优解．解方程组得即． (11)所以．故学校规模以初中个班、高中个班年利润最大 (13)（17）（本小题满分13分）（Ⅰ）连接，为正方形，为中点，为中点．所以在中，，且，所以． (4)（Ⅱ）因为，为正方形，，所以． (6)所以， (7)又，所以是等腰直角三角形，且即 (9)，且所以又，所以． (13)（18）（本小题满分13分）（Ⅰ）因为，所以，因为，，所以， (3)所以数列是以为首项，为公比的等比数列，则所以 (7)（Ⅱ）nn 2)112(log 224=+-= (9)则 (13)（19）（本小题满分14分）（Ⅰ）由题意可得：2212133a bc a⎧+=⎪⎪⎨⎪=⎪⎩ ..........................2 22223,1,13x a b y ==∴+= (4)（Ⅱ）①当k不存在时，x y =∴=，1324OAB S ∆∴== (5)②当k 存在时，设直线为y kx m =+，()()1122,,,,A x y B x y222221,(13)63303x y k x km m y kx m ⎧+=⎪+++-=⎨⎪=+⎩....................8 212122263313,13km m x x x x k k --+==++ (9)2243(1)d r m k =⇒=+ (10)||AB ===2=≤ (12)当且仅当2219,k k =即k =时等号成立..........................13 11222OAB S AB r ∆∴=⨯≤⨯=∴OAB ∆面积的最大值为，此时直线方程1y x =±. (14)（20）（本小题满分14分）（Ⅰ）当时，，得． (1)因为232-+-=x x x f ）（’=)1(2---x x ）（，所以当时，，函数单调递增；当或时，，函数单调递减．所以函数的单调递增区间为，单调递减区间为．...........4 （Ⅱ）方法1：由x x a x x f 2231)(23-+-=，得．因为对于任意都有成立，即对于任意都有成立，即对于任意都有成立，令，要使对任意都有成立，必须满足或即或所以实数的取值范围为． (9)方法2：由x x a x x f 2231)(23-+-=，得，因为对于任意都有成立，所以问题转化为，对于任意都有．因为，其图象开口向下，对称轴为．①当时，即时，在上单调递减，所以，由，得，此时．②当时，即时，在上单调递增，在上单调递减，所以，由，得，此时．综上①②可得，实数的取值范围为． (9)（Ⅲ）设点是函数图象上的切点，则过点的切线的斜率为，所以过点的切线方程为．因为点在切线上，所以即．若过点可作函数图象的三条不同切线，则方程有三个不同的实数解．令，则函数与轴有三个不同的交点．令，解得或．因为，，所以必须，即．所以实数的取值范围为． (14)。

天津市红桥区高三数学第二次模拟考试试题文(含解析)

2013年天津市红桥区高考数学二模试卷（文科）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）（2013•红桥区二模）i是虚数单位，复数的共轭复数是（）=2．（5分）（2013•红桥区二模）“x＞l”是“x＞0”的（）因为“x解：∵“x可得“x“x∴“x＞1”是“x0.224．（5分）（2013•红桥区二模）把函数y=sin（x+）图象上所有点向右平移个单位，再将所得图象的横坐标变为原来的倍（纵坐标不变），所得图象的单调递增区间是（）+k+k，+k≤2x≤2k+）图象上所有点向右平移+倍（纵坐标不变）﹣﹣++k，5．（5分）（2013•红桥区二模）设变量x，y满足约束条件，则目标函数z=﹣2x+y6．（5分）（2013•红桥区二模）集合A={x||x﹣2|≤2}，B={y|y=﹣x2，﹣1≤x≤2}，则A∩B=7．（5分）（2013•红桥区二模）己知抛物线y2=4x的准线与双曲线=1两条渐近=4﹣x（﹣，﹣=4，x交于∴A（﹣（﹣，．8．（5分）（2013•红桥区二模）阅读如图所示的程序框图，运行相应的程序（其中“r=a MOD 4”表示“r等于a除以4的余数”），输出S值等于（）二、填空题：本大题共6个小题，每小题5分，共30分．9．（5分）（2013•红桥区二模）一学校从一个年级的两个班中抽出部分同学进行一项问卷调查，已知理科班有56名同学，文科班有42名同学，采用分层抽样的方法，抽出一个容量为28的样本．那么这个样本中的文科学生、理科学生的比是3：4 ．10．（5分）（2013•红桥区二模）若直线（m﹣l）x﹣y+2=0与直线3x+my+3=0垂直，则实数m的值等于．，11．（5分）（2013•红桥区二模）如图，边长为1的菱形OABC中，AC交OB于点D，∠AOC=60°，M，N分别为对角线AC，OB上的点，满足，则•= ．，AC⊥OB，再利|OB|==+=+﹣•=故答案为：12．（5分）（2013•红桥区二模）已知某几何体的三视图如图所示，则该几何体的体积为．V=（）•1•3=故答案为：13．（5分）（2013•红桥区二模）如图，C，B，D，E四点共圆，ED与CB的延长线交于点A．若AB=4，BC=2，AD=3，则DE= 5 ．14．（5分）（2013•红桥区二模）某人要在自家的院内建造一间背面靠墙的小房，地面面积为10m2，房屋正面造价每平米约为1000元，房屋两个侧面造价均为每平米约800元，屋顶总造价约为5000元，如果计划把小屋墙高建到2m，且不计房屋背面和地面的费用，则房屋主人至少要准备资金21000 元．+3200x+5000≥2=3200x三、解答题：本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．15．（13分）（2013•红桥区二模）如图，在四边形ABCD中，AC平分∠DAB，已知∠B=60°，AC=7．AD=6，面积（1）求sin∠DAC和cos∠DAB的值；（2）求边BC，AB的长度．由sin∠DAC=中，sin∠BAC=sin∠DAB=）∵=•AD•AC•sin∠DAC=×6×7×sin∠DAC，解得sin∠DAC==中，sin∠BAC=sin∠DAB=﹣14AB•16．（13分）（2013•红桥区二模）某学校高三（1）班学生举行新年联欢活动，准备了5张标有1，2，3，4，5的外表完全相同的卡片，规定通过游戏来决定抽奖机会，每个获得抽奖机会的同学，一次从中任意抽取2张卡片，两个卡片中的数字之和为5时获一等奖，两个卡片中的数字之和能被3整除时获二等奖，其余情况均没有奖．（1）共有几个一等奖？几个二等奖？（2）求从中任意抽取2张，获得一等奖的概率；（3）一名同学获得两次抽奖机会，求①获得一个一等奖和一个二等奖的概率：②两次中至少一次获奖的概率．P=①获得一个一等奖和一个二等奖的概率两次中至少一次获奖的概率为．（2013•红桥区二模）如图，四边形ABCD与BDEF均为菱形，已知∠DAB=∠DBF=60°，17．（13分）且FA=FC，AC=．（1）求证：AC⊥平面BDEF；（2）求直线CF与平面BDEF所成的角；（3）求异面直线AF与BD所成的角．AC=，BD=OF=BD=18．（13分）（2013•红桥区二模）已知等比数列{a n}的公比q≠1，a1=3，且3a2、2a3、a4成等差数列．（1）求数列{a n}的通项公式；（2）设b n=21og3a n，求证：数列{b n}成等差数列；（3）是否存在非零整数λ，使不等式…．对一切，n∈N*都成立？若存在，求出λ的值；若不存在，说明理由．，则不等式等价于（﹣．∵a；，∴，=．，即综上，，由19．（14分）（2013•红桥区二模）已知椭圆：=l（a＞b＞0）的一个顶点坐标为B（0，1），若该椭圆的离心率等于．（1）求椭圆的方程．（2）Q是椭圆上位于x轴下方的一点，F1F2分别是椭圆的左、右焦点，直线QF1的倾斜角为，求△QF1F2的面积；（3）以B为直角顶点作椭圆的内接等腰直角三角形ABC，判断这样的三角形存在吗？若存在，有几个？若不存在，请说明理由．，得x+1，因为离心率等于，，解得所以椭圆方程为：；（﹣，代入中，，，=x+1①，②，，得：，，，k=20．（14分）（2013•红桥区二模）已知函数f（x）=ax2﹣e x（a∈R），f′（x）是f（x）的导函数（e为自然对数的底数）．（1）当a=1时，求曲线y=f（x）在点（0，f（0））处的切线方程；（2）若f（x）有两个极值点x1，x2，求实数a的取值范围；（3）若当x≥0时，不等式f（x）≤﹣x﹣1恒成立，求实数a的最大值．即，此时a≤时的情况：．。

天津市五区县2015届高三数学二模考试试卷-文(含解析)

天津市五区县2015届高考数学二模试卷（文科）一、选择题（共8小题，每小题5分，满分40分）1．设集合M={x|（x+3）（x﹣2）＜0，x∈R}，N={0，1，2}，则M∩N=( )A．{0，1，2} B．{0，1} C．{x|0＜x＜2} D．{x|﹣3＜x＜2}2．设变量x，y满足约束条件，则目标函数z=x+3y的最小值为( )A．﹣3 B．0 C．3 D．123．已知φ∈R，则“φ=0”是“f（x）=sin（2x+φ）为奇函数”的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件4．阅读如图所示的框图，运行相应的程序，则输出S的值为( )A．30 B．45 C．63 D．845．若直线y=x+4与圆（x+a）2+（y﹣a）2=4a（0＜a≤4）相交于A，B两点，则弦AB长的最大值为( ) A．2B．4C．D．26．若直线2x+y﹣2=0过双曲线=1（a＞0，b＞0）的一个焦点，且与双曲线的一条渐近线垂直，则双曲线的方程为( )A．B．x2﹣C．D．7．已知函数f（x）=sin（ωx+）+sin（ωx﹣）（ω＞0，x∈R）的最小正周期为π，则( ) A．f（x）为偶函数B．f（x）在上单调递增C．x=为f（x）的图象的一条对称轴D．（，0）为f（x）的图象的一个对称中心8．定义在R上的函数y=f（x）的图象是连续不断的，且满足f（3﹣x）=f（x），当x≠时总有（x﹣）f′（x）＞0（f′（x）是f（x）的导函数），若x1＜x2，且x1+x2＞3，则( )A．f（x1）＞f（x2）B．f（x1）＜f（x2）C．f（x1）=f（x2）D．f（x2）与f（x2）的大小无法确定二、填空题（共6小题，每小题5分，满分30分）9．i是虚数单位，若（2+ai）（1﹣i）=4．则实数a=__________．10．某几何体的三视图如图所示，其中正视图和侧视图均为等腰直角三角形，俯视图是圆心角为直角的扇形，则该几何体的体积为__________．11．如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于点D，DE⊥AC，交AC的延长线于点E．若AE=8，AB=10，则CE的长为__________．12．若x＞0，y＞0，x+3y=1，则+的最小值为__________．13．已知函数f（x）=|x+a|﹣2x（a＜0），若f（x）≤0的解集M⊆{x|x≥2}，则实数a的取值范围是__________．14．如图，在△ABC中，点D是BC延长线上的点，=3，O在线段CD上且不与端点重合，若=x+（1﹣x），则x的取值范围是__________．三、解答题（共6小题，满分80分）15．某网站对中国好歌曲的参赛选手A、B、C三人进行网上投票，结果如下观众年龄支持A 支持B 支持C25岁以下（含25岁） 180 240 36025岁以上 120 120 180在所有参与该活动的人中，按照观众的年龄和所支持选手不同用分层抽样的方法抽取n人，其中有5人支持A（1）求n的值（2）记抽取n人中，且年龄在25岁以上，支持选手B的为B1（i=1，2…），支持选手C的为C1（i=1，2，…），从B1，C1中随机选择两人进行采访，求两人均支持选手C的概率．16．已知A，B，C为△ABC的三个内角，其所对的边分别为a，b，c，2cos2﹣cos（B+C）=0（1）求角A的值（2）若a=2，b+c=4，求△ABC的面积．17．如图，△ACB，△ADC都为等腰直角三角形，M为AB的中点，且平面ADC⊥平面ACB，AB=4，AC=2，AD=2（1）求证：BC⊥平面ACD（2）求直线MD与平面ADC所成的角．18．在等比数列{a n}中，a1=1，a3，a2+a4，a5成等差数列．（1）求数列{a n}的通项公式（2）若数列{b n}满足b1++…+（n∈N+），{b n}的前n项和为S n，求证S n≤n•a n（n∈N+）19．已知函数f（x）=ax2﹣（2a+1）x+2lnx（a∈R）（1）若曲线f（x）在x=1和x=3处的切线互相平行，求函数f（x）的单调区间（2）若函数f（x）既有极大值又有极小值，求a的取值范围．20．已知椭圆C经过点P（，），两焦点分别为F1（﹣，0），F2（，0）（1）求椭圆C的标准方程（2）已知点A（0，﹣1），直线l与椭圆C交于两点M，N，若△AMN是以A为直角顶点的等腰直角三角形，试求直线l方程．天津市五区县2015届高考数学二模试卷（文科）一、选择题（共8小题，每小题5分，满分40分）1．设集合M={x|（x+3）（x﹣2）＜0，x∈R}，N={0，1，2}，则M∩N=( )A．{0，1，2} B．{0，1} C．{x|0＜x＜2} D．{x|﹣3＜x＜2}考点：交集及其运算．专题：集合．分析：求出M中不等式的解集确定出M，找出M与N的交集即可．解答：解：由M中不等式解得：﹣3＜x＜2，即M=（﹣3，2），∵N={0，1，2}，∴M∩N={0，1}，故选：B．点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．设变量x，y满足约束条件，则目标函数z=x+3y的最小值为( ) A．﹣3 B．0 C．3 D．12考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对应的平面区域，利用目标函数的几何意义，求最小值．解答：解：作出不等式组对应的平面区域如图：（阴影部分）．由z=x+3y得y=﹣，平移直线y=﹣，由图象可知当直线y=﹣经过点A时，直线y=﹣的截距最小，此时z最小．由，解得，即A（﹣6，3），代入目标函数得z=﹣6+3×3=﹣6+9=3．即z=x+3y的最小值为3．故选：C．点评：本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．3．已知φ∈R，则“φ=0”是“f（x）=sin（2x+φ）为奇函数”的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件考点：充要条件．专题：简易逻辑．分析：由f（x）=sin（2x+φ）为奇函数，可得φ=kπ+π，k∈Z，即可判断出．解答：解：f（x）=sin（2x+φ）为奇函数，则φ=kπ+π，k∈Z，∴“φ=0”是“f（x）=sin（2x+φ）为奇函数”的充分不必要条件，故选：A．点评：本题考查了充要条件的判定方法、三角函数的奇偶性，考查了推理能力与计算能力，属于基础题．4．阅读如图所示的框图，运行相应的程序，则输出S的值为( )A．30 B．45 C．63 D．84考点：循环结构．专题：图表型；算法和程序框图．分析：模拟执行程序框图，依次写出每次循环得到的i，S的值，当i=6时满足条件i＞5，退出循环，输出S的值为63．解答：解：模拟执行程序框图，可得S=0，i=1S=3，不满足条件i＞5，i=2，S=9不满足条件i＞5，i=3，S=18不满足条件i＞5，i=4，S=30不满足条件i＞5，i=5，S=45不满足条件i＞5，i=6，S=63满足条件i＞5，退出循环，输出S的值为63．故选：C．点评：本题主要考查了循环结构的程序框图，正确依次写出每次循环得到的i，S的值是解题的关键，属于基本知识的考查．5．若直线y=x+4与圆（x+a）2+（y﹣a）2=4a（0＜a≤4）相交于A，B两点，则弦AB长的最大值为( ) A．2B．4C．D．2考点：直线与圆相交的性质．专题：计算题；直线与圆．分析：圆的圆心坐标为（﹣a，a），代入直线y=x+4，可得a=2，求出圆的半径，即可求出AB长的最大值．解答：解：圆的圆心坐标为（﹣a，a），代入直线y=x+4，可得a=2，所以圆的半径为2，所以弦AB长的最大值为4，故选：B．点评：本题考查直线与圆的相交的性质，考查学生的计算能力，比较基础．6．若直线2x+y﹣2=0过双曲线=1（a＞0，b＞0）的一个焦点，且与双曲线的一条渐近线垂直，则双曲线的方程为( )A．B．x2﹣C．D．考点：双曲线的简单性质；直线的一般式方程与直线的垂直关系．专题：综合题；圆锥曲线的定义、性质与方程．分析：令y=0可得双曲线=1（a＞0，b＞0）的一个焦点，利用直线2x+y﹣2=0与双曲线的一条渐近线垂直，可得=，即可求出a，b，从而可得双曲线的方程．解答：解：令y=0可得，x=，∵直线2x+y﹣2=0过双曲线=1（a＞0，b＞0）的一个焦点，∴c=，∵直线2x+y﹣2=0与双曲线的一条渐近线垂直，∴=，∴a=2，b=1，∴双曲线的方程为，故选：A．点评：本题考查双曲线的方程与性质，考查学生的计算能力，比较基础．7．已知函数f（x）=sin（ωx+）+sin（ωx﹣）（ω＞0，x∈R）的最小正周期为π，则( )A．f（x）为偶函数B．f（x）在上单调递增C．x=为f（x）的图象的一条对称轴D．（，0）为f（x）的图象的一个对称中心考点：两角和与差的正弦函数．专题：三角函数的图像与性质．分析：利用两角和差的正弦公式将函数f（x）进行化简，利用函数的周期求出ω即可得到结论．解答：解：f（x）=sin（ωx+）+sin（ωx﹣）=f（x）=sin（ωx+）+sin（ωx+﹣）=sin（ωx+）﹣cosωx+）=2sin（ωx+﹣）=2sinωx．∵f（x）的最小正周期为π，∴T=，解得ω=2，即f（x）=2sin2x．∵f（）=2sin（2×）=2sinπ=0，∴（，0）为f（x）的图象的一个对称中心．故选：D点评：本题主要考查三角函数的图象和性质，利用两角和差的正弦公式求出ω是解决本题的关键．8．定义在R上的函数y=f（x）的图象是连续不断的，且满足f（3﹣x）=f（x），当x≠时总有（x﹣）f′（x）＞0（f′（x）是f（x）的导函数），若x1＜x2，且x1+x2＞3，则( ) A．f（x1）＞f（x2）B．f（x1）＜f（x2）C．f（x1）=f（x2）D．f（x2）与f（x2）的大小无法确定考点：利用导数研究函数的单调性．专题：数形结合；导数的综合应用．分析：根据已知条件便可得到f（x）关于x=对称，在区间上单调递减，而在上单调递增，从而可以画出f（x）的大致图象，根据图象上的点关于对称轴的对称点的横坐标之和为3并结合图象即可判断出f（x1）和f（x2）的大小关系．解答：解：根据f（3﹣x）=f（x）知f（x）关于x=对称；当x时，总有；∴时f（x）单调递减，时f（x）单调递增；∴f（x）的大致形状如下图所示：x1+x2＞3，∴（1）若，作点（x1，f（x1））关于x=的对称点为（x3，f（x3）），则：x1+x3=3；∴x2＞x3；∴f（x2）＞f（x3）=f（x1）；即f（x2）＞f（x1）；（2）若，x1＜x2；∴f（x1）＜f（x2）；∴综上得f（x1）＜f（x2）．故选B．点评：考查由f（a﹣x）=f（x）能得到f（x）关于对称，函数导数符号和函数单调性的关系，以及数形结合解题的方法．二、填空题（共6小题，每小题5分，满分30分）9．i是虚数单位，若（2+ai）（1﹣i）=4．则实数a=2．考点：复数代数形式的混合运算．专题：数系的扩充和复数．分析：利用复数的运算法则、复数相等即可得出．解答：解：∵（2+ai）（1﹣i）=4，∴2+a+（a﹣2）i=4，∴2+a=4，a﹣2=0，解得a=2．故答案为：2．点评：本题考查了复数的运算法则、复数相等，属于基础题．10．某几何体的三视图如图所示，其中正视图和侧视图均为等腰直角三角形，俯视图是圆心角为直角的扇形，则该几何体的体积为．考点：由三视图求面积、体积．专题：计算题；空间位置关系与距离．分析：根据几何体的三视图，得出该几何体是圆锥的一部分，结合三视图中的数据，求出几何体的体积．解答：解：根据几何体的三视图，得；该几何体是圆锥的一部分，且底面是半径为2的圆面，高为2，∴该几何体的体积为：V几何体=×π•22×2=．故答案为：．点评：本题考查了利用几何体的三视图求体积的应用问题，解题的根据是由三视图得出几何体的结构特征，是基础题目．11．如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于点D，DE⊥AC，交AC的延长线于点E．若AE=8，AB=10，则CE的长为1．考点：与圆有关的比例线段．专题：直线与圆．分析：连接OD，BC，根据角平分线定义和等腰三角形性质推行∠CAD=∠ODA，推出OD∥AC，根据平行线性质和切线的判定推出即可；解答：解：连接OD，可得∠ODA=∠OAD=∠DAC∴OD∥A E．又AE⊥DE，∴DE⊥OD．而OD为半径，∴DE是⊙O的切线；连接BC，交OD于G，AB是圆的直径，所以AC⊥BC，所以四边形CEDG是矩形，∵OD∥AE，O是AB中点，∴G是BC中点，∴CG=DE=BC=3，∴BG=3，OG=4，∴DG=1，所以CE=1；故答案为：1．点评：本题考查了圆周角定理以及切线的判断、矩形的判断等知识点；比较综合，但难度不大．12．若x＞0，y＞0，x+3y=1，则+的最小值为4．考点：基本不等式．专题：不等式的解法及应用．分析：利用基本不等式，问题得以解决．解答：解：（方法一）∵x+3y=1，∴+==2+=4．当且仅当x=，y=等号成立．（方法二）+=（+）（x+3y）=2×=4．当且仅当x=，y=等号成立．故答案为：4．点评：本题主要考查基本不等式的应用，属于基础题．13．已知函数f（x）=|x+a|﹣2x（a＜0），若f（x）≤0的解集M⊆{x|x≥2}，则实数a的取值范围是（﹣∞，﹣6]．考点：绝对值不等式的解法；集合的包含关系判断及应用．专题：不等式的解法及应用．分析：分类讨论解绝对值不等式求的M，再根据M⊆{x|x≥2}，求得实数a的取值范围．解答：解：不等式f（x）≤0即|x+a|≤2x，等价于①或②，解①求得x≥﹣a，解②求得﹣≤x＜﹣a，故原不等式的解集M={x|x≥﹣ }．由于M⊆{x|x≥2}，则﹣≥2，解得a≤﹣6，故答案为：（﹣∞，﹣6]．点评：本题主要考查绝对值不等式的解法，体现了转化、分类讨论的数学思想，属于基础题．14．如图，在△ABC中，点D是BC延长线上的点，=3，O在线段CD上且不与端点重合，若=x+（1﹣x），则x的取值范围是（，0）．考点：平面向量的基本定理及其意义．专题：平面向量及应用．分析：结合图形，根据向量加法，，可以想着用来表示，根据已知条件知，其中0＜k＜1，从而便可得到，从而x=，从而根据k的范围即可求出x的范围．解答：解：；O在线段CD上且不与端点重合；∴存在k，0＜k＜1，使；又；∴；∴=；又；∴；∴；∴x的取值范围是．故答案为：（，0）．点评：考查向量加法、减法的几何意义，共线向量基本定理，向量数乘的运算．三、解答题（共6小题，满分80分）15．某网站对中国好歌曲的参赛选手A、B、C三人进行网上投票，结果如下观众年龄支持A 支持B 支持C25岁以下（含25岁） 180 240 36025岁以上 120 120 180在所有参与该活动的人中，按照观众的年龄和所支持选手不同用分层抽样的方法抽取n人，其中有5人支持A（1）求n的值（2）记抽取n人中，且年龄在25岁以上，支持选手B的为B1（i=1，2…），支持选手C的为C1（i=1，2，…），从B1，C1中随机选择两人进行采访，求两人均支持选手C的概率．考点：古典概型及其概率计算公式．专题：概率与统计．分析：（1）根据分层抽样时，各层的抽样比相等，结合已知构造关于n的方程，解方程可得n值．（2）计算出“支持选手B”和“支持选手C且年龄在25岁以上的人数，代入古典概率概率计算公式，可得答案解答：解：（1）∵利用层抽样的方法抽取n个人时，从“支持选手A”的人中抽取了5人，总人数为120+180+240+120+360+180=1200人∴=，解得n=20；（2）从“支持选手B”的人中，用分层抽样的方法抽取人数且龄在25岁以上有20××=2人，记为a，b，从“支持选手C”的人中，用分层抽样的方法抽取人数且龄在25岁以上有20××=3人，记为1，2，3，从则这5人中任意选取2人，共有10种不同情况，分别为：（1，2），（1，3），（1，a），（1，b），（2，3），（2，a），（2，b），（3，a），（3，b），（a，b），两人均支持选手C事件有：（1，2），（1，3），（2，3）共3种．故两人均支持选手C的概率P=．点评：本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键．16．已知A，B，C为△ABC的三个内角，其所对的边分别为a，b，c，2cos2﹣cos（B+C）=0（1）求角A的值（2）若a=2，b+c=4，求△ABC的面积．考点：余弦定理的应用．专题：计算题；解三角形．分析：（1）由三角函数恒等变换化简已知等式可得cosA=﹣，结合A的范围，即可求得A的值．（2）结合已知由余弦定理可可求得：12=16﹣bc，解得：bc=4，由三角形面积公式即可求解．解答：解：（1）∵2cos2﹣cos（B+C）=0⇒1+cosA+cosA=0⇒cosA=﹣，∵A，B，C为△ABC的三个内角，∴A=．（2）∵a=2，b+c=4，∴由余弦定理可知：a2=12=b2+c2﹣2bccosA=b2+c2+bc=（b+c）2﹣bc=16﹣bc，可解得：bc=4，∴S△ABC=bcsinA==．点评：本题主要考查了余弦定理，三角函数恒等变换，三角形面积公式的应用，综合性较强，属于基本知识的考查．17．如图，△ACB，△ADC都为等腰直角三角形，M为AB的中点，且平面ADC⊥平面ACB，AB=4，AC=2，AD=2（1）求证：BC⊥平面ACD（2）求直线MD与平面ADC所成的角．考点：直线与平面所成的角；直线与平面垂直的判定．专题：空间位置关系与距离；空间角；空间向量及应用．分析：（1）根据所给边的长度和△ACB，ADC都为等腰直角三角形即可知道∠ADC=90°，BC⊥AC，而根据平面ADC⊥平面ACB即可得到BC⊥平面ACD；（2）取AC中点E，连接ME，DE，便容易说明∠E DM是直线MD与平面ADC所成的角，由已知条件即知ME=DE=，从而得到∠EDM=45°．解答：解：（1）证明：根据已知条件便知∠ADC=90°，∠ACB=90°；∴BC⊥AC；∵平面ADC⊥平面ACB，平面ADC∩平面ACB=AC；∴BC⊥平面ACD；（2）如图，取AC中点E，连接ME，DE，∵M为AB中点，则：ME∥BC，ME=，DE=；由（1）BC⊥平面ACD；∴ME⊥平面ACD；∴∠MDE为直线MD和平面ADC所成角；∴在Rt△MDE中，直角边ME=DE；∴∠MDE=45°；即直线MD与平面ADC所成的角为45°．点评：考查直角三角形边的关系，面面垂直的性质定理，以及中位线的性质，线面角的概念及求法．18．在等比数列{a n}中，a1=1，a3，a2+a4，a5成等差数列．（1）求数列{a n}的通项公式（2）若数列{b n}满足b1++…+（n∈N+），{b n}的前n项和为S n，求证S n≤n•a n（n∈N+）考点：数列与不等式的综合．专题：等差数列与等比数列．分析：（1）通过将a2、a3、a4、a5用公比q表示及条件a3、a2+a4、a5成等差数列，可求出q=2，利用等比数列的通项公式计算即可；（2）当n=1时，b1=a1=1，显然有S1=1×a1；当n≥2时，利用=a n﹣a n﹣1可得b n=n•2n﹣2，求出S n、2S n，两者相减，利用错位相减法解得S n，计算即可．解答：（1）解：设数列{a n}的公比为q，∵a1=1，∴a2=q，a3=q2，a4=q3，a5=q4，又∵a3，a2+a4，a5成等差数列，∴2（a2+a4）=a3+a5，即2（q+q3）=q2+q4，解得q=2或0（舍），∴a n=2n﹣1；（2）证明：∵数列{b n}满足b1++…+=a n（n∈N+），∴当n=1时，b1=a1=1，此时S1=1×a1；当n≥2时，=a n﹣a n﹣1=2n﹣1﹣2n﹣2=2n﹣2，∴b n=n•2n﹣2，∴S n=1+2×20+3×21+4×22+…+（n﹣1）×2n﹣3+n×2n﹣2，∴2S n=2×20+2×21+3×22+4×23+…+（n﹣1）×2n﹣2+n×2n﹣1，两式相减，得﹣S n=1+21+22+23+…+2n﹣2﹣n×2n﹣1，∴S n=n×2n﹣1﹣1﹣（21+22+23+…+2n﹣2）=n×2n﹣1﹣1﹣=（n﹣1）×2n﹣1﹣1=n×2n﹣1﹣（1+2n﹣1）＜n×2n﹣1=n•a n，综上所述，S n≤n•a n（n∈N+）．点评：本题考查考查等差、等比数列的性质，考查分类讨论的思想，考查分析问题的能力与计算能力，利用错位相减法求S n是解决本题的关键，属于中档题．19．已知函数f（x）=ax2﹣（2a+1）x+2lnx（a∈R）（1）若曲线f（x）在x=1和x=3处的切线互相平行，求函数f（x）的单调区间（2）若函数f（x）既有极大值又有极小值，求a的取值范围．考点：利用导数研究函数的极值；利用导数研究曲线上某点切线方程．专题：计算题；导数的概念及应用；导数的综合应用．分析：先确定函数f（x）=ax2﹣（2a+1）x+2lnx的定义域，（1）求导f′（x）=ax﹣（2a+1）+，从而可得f′（1）=f′（3），从而求得a=；从而得到f′（x）=x﹣+=；从而确定函数的单调性；（2）化简f′（x）=ax﹣（2a+1）+==，从而可得，从而解得．解答：解：函数f（x）=ax2﹣（2a+1）x+2lnx的定义域为（0，+∞），（1）f′（x）=ax﹣（2a+1）+，∵曲线f（x）在x=1和x=3处的切线互相平行，∴f′（1）=f′（3），即a﹣（2a+1）+2=3a﹣（2a+1）+，解得，a=；故f′（x）=x﹣+=；故f（x）在（0，）上是增函数，在（，2）上是减函数，在（2，+∞）上是增函数．（2）∵f′（x）=ax﹣（2a+1）+==，∵函数f（x）既有极大值又有极小值，∴，故a的取值范围为（0，）∪（，+∞）．点评：本题考查了导数的综合应用及导数几何意义的应用，属于中档题．20．已知椭圆C经过点P（，），两焦点分别为F1（﹣，0），F2（，0）（1）求椭圆C的标准方程（2）已知点A（0，﹣1），直线l与椭圆C交于两点M，N，若△AMN是以A为直角顶点的等腰直角三角形，试求直线l方程．考点：直线与圆锥曲线的综合问题．专题：圆锥曲线的定义、性质与方程．分析：（1）通过焦点坐标可设椭圆C的标准方程且a2﹣b2=3，将点P（，）代入椭圆方程，计算即得结论；（2）通过△AMN是以A为直角顶点的等腰直角三角形可得直线l与x轴平行，利用k AM•k AN=﹣1计算即可．解答：解：（1）∵两焦点分别为F1（﹣，0），F2（，0），∴可设椭圆C的标准方程为：（a＞b＞0），a2﹣b2=3，①又∵椭圆C经过点P（，），∴，②联立①②，解得a2=4，b2=1，∴椭圆C的标准方程为：；（2）由（1）知，点A（0，﹣1）即为椭圆的下顶点，∵△AMN是以A为直角顶点的等腰直角三角形，∴直线l与x轴平行，设直线l方程为y=t（﹣1＜t＜1），则M（﹣2，t），N（2，t），∵k AM=﹣，k AN=，∴k AM•k AN=﹣•=﹣1，解得：t=或t=﹣1（舍），∴直线l方程为：y=．点评：本题考查椭圆的定义及标准方程，考查直线与椭圆的位置关系，注意解题方法的积累，属于中档题．。

天津市红桥区2015-2016学年高二下学期期末数学试卷(文科) 含解析

2015-2016学年天津市红桥区高二(下）期末数学试卷（文科）一、选择题：本大题共12小题，每小题2分，共24分，在每个小题给出的四个选项中,只有一个符合题目要求的.1．不等式的解集是（）A．（﹣∞，2）B．（2，+∞）C．（0，2) D．（﹣∞，0）∪（2,+∞）2．不等式＜0的解集为（）A．{x｜x＜﹣1或1＜x＜2｝B．｛x｜1＜x＜2} C．{x|﹣1＜x＜2且x≠1｝D．{x|x ＜2且x≠1｝3．不等式9x2+6x+1≤0的解集是（)A．｛x｜x≠﹣｝B．｛x|﹣≤x≤｝C．∅D．｛x｜x=﹣}4．不等式｜x+2|≤5的解集是（）A．｛x|x≤1或x≥2}B．｛x｜﹣7≤x≤3｝C．{x｜﹣3≤x≤7｝D．{x|﹣5≤x≤9} 5．下列不等式中，解集为实数集R的是（)A．x2+4x+4＞0 B．|x｜＞0 C．x2﹣x+1≥0 D．﹣1＜6．不等式ax＞b的解集不可能是（)A．B．R C．D．∅7．关于x的不等式组有解，则实数a的取值范围是(）A．[﹣3，1］B．（﹣3,1）C．［﹣1，3] D．（﹣1，3）8．关于x的不等式ax﹣b＞0的解集为(1，+∞）,则关于x的不等式＞0的解集为（）A．(﹣1，2）B．（1，2) C．(﹣∞，﹣1）∪（2,+∞）D．（﹣∞，﹣2）∪（1，+∞）9．已知如图，四边形ABCD为圆内接四边形,AB是直径，MN切⊙O于C点，∠BCM=38°,那么∠ABC的度数是（）A．38°B．52°C．68°D．42°10．如图所示，在⊙O中，弦AB与半径OC相交于点M，且OM=MC，AM=1.5,BM=4，则OC=（）A．2B．2C．2D．11．如图，AD,AE，BC分别与圆切D，E,F于点，延长AF与圆O交于另一点G,给出下列三个结论：①AD+AE=AB+BC+CA②△AFB～△ADG③AF•AG=AD•AE其中正确结论的序号是（)A．①②B．②③C．①③D．①②③12．已知a∈［﹣1,1]，不等式x2+（a﹣4）x+4﹣2a＞0恒成立，则x的取值范围为（）A．（﹣∞，2）∪（3，+∞) B．(﹣∞,1)∪（2，+∞) C．（﹣∞,1)∪（3，+∞）D．（1，3）二、填空题：本大题共8个小题，每小题4分.、共32分.13．不等式组的解集是．14．不等式＜0解集为．15．不等式|5x﹣4|＜6的解集为．16．在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，AB=2,DB=1，则DC=．17．如图所示,在平行四边形ABCD中，BC=24，E，F为BD的三等分点，则DN=．18．如图，在△ABC中，∠C=90°，∠A=60°，AB=20，过C作△ABC的外接圆的切线CD，BD⊥CD，BD与外接圆交于点E,则DE的长为．19．（几何证明选讲选做题)如图，圆O的半径为5cm,点P是弦AB的中点，OP=3cm，弦CD过点P，且=，则CD的长为cm．20．如图所示，AB是圆O的直径，直线MN切圆O于C，CD⊥AB，AM⊥MN，BN⊥MN，给出下列四个结论：①∠1=∠2=∠3；②AM•CN=CM•BN；③CM=CD=CN；④△ACM∽△ABC∽△CBN．则其中正确结论的序号是．三、解答题：本大题共4小题，共44分,解答应写出文字说明、证明过程或演算步骤。

【2015红桥二模】天津市红桥区2015届高三第二次模拟考试物理扫描版含答案

2015红桥二模物理高三物理答案Ⅰ卷共8题，每小题分，共48分。

一．B 2．A 3．D 4．A 5．D二．6．ABC 7．BD 8．BCR v l B F 22=Ⅱ卷共4题，共72分。

9．（18分）（一）（共6分）(1) BD （3分） (2) k42π （3分）（二）（共4分） (1)C （2分）（2） D （2分）（三）（共8分）（每空2分）（1）如右图所示；（2）4.5 1.0 （3）0.00四、计算题10．（16分）解：(1)设该星球表面的重力加速度为g 0,圆轨道的半径为r .当H =5 m 时,有: mg 0(H -2r )=12mv 02 mv 02r =mg 0 解得:r =25H =2 m. （6分） (2)当H 1=10 m 时,有: mg 0(H 1-2r )=12mv 2 mv 2r =mg 0+F 由F -H 图象可得:g 0=5 m/s 2 （6分）该星球的第一宇宙速度v =g 0R =5 km/s. （4分）11．（18分）解析：设带电粒子经电压为U 的电场加速后速度为v ，qU ＝12m v 2 ① （4分）带电粒子进入磁场后，洛伦兹力提供向心力，由牛顿第二定律：qB v ＝m v 2r ② 依题意可知：r ＝d ③联立①②③可解得：B ＝2qUm qd④ （6分）带电粒子在电场中偏转，做类平抛运动，设经时间t 从P 点到达C 点，由d ＝v t ⑤ d ＝12qE m t 2 ⑥联立①⑤⑥可解得：E ＝4U d。

（8分）12、(20分) 解：⑴由于线圈完全处于磁场中时不产生电热，所以线圈进入磁场过程中产生的电热Q 就是线圈从图中2位置到4位置产生的电热，而2、4位置动能相同，由能量守恒Q =mgd=0.50J （6分）⑵3位置时线圈速度一定最小，而3到4线圈是自由下落运动因此有v 02-v 2=2g (d-l )，得v =22m/s （6分）⑶2到3是减速过程，因此安培力减小，由F-mg =mah d l 1 2 3 4 v 0 v 0v知加速度减小，到3位置时加速度最小，a=4.1m/s2 （8分）。

2015红桥二模高清版含答案天津市红桥区2015届高三第二次模拟考试数学文扫描版含答案

高三数学（文）答案一、选择题：每小题5分，共40分．题号1 2 3 4 5 6 7 8 答案 C D A B D C B C二、填空题：每小题5分，共30分．题号 910 11 12 13 14 答案错误！未找到引用源。

错误！未找到引用源。

三、解答题：共6小题，共80分．（15）（本小题满分13分）甲、乙两位学生参加数学竞赛培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次．得到甲、乙两位学生成绩的茎叶图．（Ⅰ）现要从中选派一人参加数学竞赛，对预赛成绩的平均值和方差进行分析，你认为哪位学生的成绩更稳定?请说明理由；（Ⅱ）若将频率视为概率，求乙同学在一次数学竞赛中成绩高于84分的概率；（Ⅲ）在甲同学的8次预赛成绩中，从不小于80分的成绩中随机抽取2个成绩，列出所有结果，并求抽出的2个成绩均大于85分的概率．解：（Ⅰ）派甲参加比较合适，理由如下：85)35124889290480270(81=++++++++⨯+⨯+⨯=甲x ，错误！未找到引用源。

， …………………………… 3分222222)8585()8583()8580()8579()8578(81-+-+-+---=甲S ])8595()8592()8590(222-+-+-+=35.5，222222)8585()8583()8580()8580()8575[(81-+-+-+-+-=乙S ])8595()8592()8590(222-+-+-+=41， ……………………………… 6分22,乙甲乙甲S S x x <= ， ∴甲的成绩比较稳定． …………………………………………………………… 7分（Ⅱ）错误！未找到引用源。

． …………………………………………………………… 9分（Ⅲ）从不小于80分的成绩中随机抽取2个成绩，所有结果为错误！未找到引用源。

2015-2016学年天津市红桥区高二上学期期末文科数学试卷(带解析)

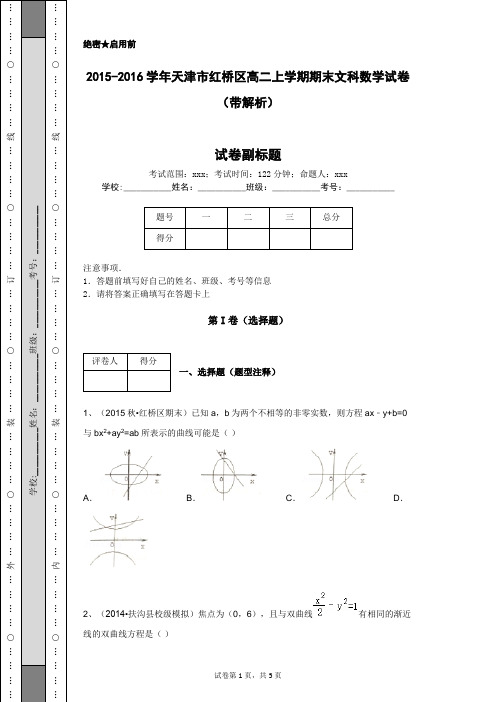
绝密★启用前2015-2016学年天津市红桥区高二上学期期末文科数学试卷（带解析）试卷副标题考试范围：xxx ；考试时间：122分钟；命题人：xxx学校:___________姓名：___________班级：___________考号：___________注意事项．1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题（题型注释）1、（2015秋•红桥区期末）已知a ，b 为两个不相等的非零实数，则方程ax ﹣y+b=0与bx 2+ay 2=ab 所表示的曲线可能是（）A ．B ．C ．D ．2、（2014•扶沟县校级模拟）焦点为（0，6），且与双曲线有相同的渐近线的双曲线方程是（）B．C．D．3、（2015秋•红桥区期末）已知双曲线方程为，过P（1，0）的直线L与双曲线只有一个公共点，则L的条数共有（）A．4条 B．3条 C．2条 D．1条4、（2015秋•红桥区期末）已知抛物线的顶点在原点，焦点在y轴上，其上的点P（m，﹣3）到焦点的距离为5，則抛物线方程为（）A．x2=8y B．x2=4y C．x2=﹣4y D．x2=﹣8y5、（2015秋•红桥区期末）抛物线y=2x2的焦点坐标是（）A．（0，） B．（，0） C．（1，0） D．（0，）6、（2003•天津）双曲线虚轴的一个端点为M，两个焦点为F1、F2，∠F1MF2=120°，则双曲线的离心率为（）A． B． C． D．7、（2015秋•红桥区期末）双曲线的焦距是（）A．4 B． C．8 D．与m有关8、（2015秋•红桥区期末）已知椭圆=1（a＞5）的两个焦点为F1、F2，且|F1F2|=8，弦AB过点F1，则△ABF2的周长为（）A．10 B．20 C． D．A． B． C． D．10、（2015秋•红桥区期末）过点P（﹣2，m）和Q（m，4）的直线斜率等于1，那么m的值等于（）A．1或3 B．4 C．1 D．1或4第II卷（非选择题）二、填空题（题型注释）11、（2015秋•红桥区期末）已知M为抛物线y2=4x上一动点，F为这条抛物线的焦点，有一个定点A（3，2），则|MA|+|MF|的最小值= ．12、（2015秋•红桥区期末）离心率e=，一个焦点是F（0，﹣3）的椭圆标准方程为．13、（2015秋•红桥区期末）圆（x﹣4）2+（y﹣1）2=5内一点P（3，0），则过P点的最短弦的弦长为．14、（2015秋•红桥区期末）已知圆的﹣条直径的两端点是（2，0），（2，﹣2）．则此圆方程是．15、（2015秋•红桥区期末）已知直线l过点A（﹣2，0）且与直线x+2y﹣l=0平行．则直线l的方程是．16、（2015秋•红桥区期末）在直角坐标系中，直线x+y﹣3=0的倾斜角是．三、解答题（题型注释）17、已知椭圆的离心率，过点A（0，﹣b）和B（a，0）的直线与原点的距离为．（1）求椭圆的方程；（2）已知定点E（﹣1，0），若直线y=kx+2（k≠0）与椭圆交于C、D两点，问：是否存在k的值，使以CD为直径的圆过E点？请说明理由．18、（2012•镜湖区校级模拟）已知双曲线与椭圆共焦点，它们的离心率之和为，求双曲线方程．19、（2015秋•红桥区期末）圆的方程为x2+y2﹣6x﹣8y=0，过坐标原点作长为8的弦，求弦所在的直线方程．20、（2015秋•红桥区期末）已知两条直线l1：x﹣ay=0（a≠0），l2：x+y﹣3=0．（1）若l1⊥l2，求a的值；（2）在（1）的条件下，如果直线l3经过l1与l2的交点，且经过点A（2，4），求直线l3的方程．参考答案1、C2、B3、B4、D5、A6、B7、C8、D9、A10、C11、412、13、2．14、（x﹣2）2+（y+1）2=115、x+2y+2=0．16、150°．17、（1）．（2）经验证k=使得①成立综上可知，存在k=使得以CD为直径的圆过点E．18、19、y=或x=0．20、（1）a=1；（2）5x﹣y﹣6=0【解析】1、试题分析：先把曲线方程整理成=1的形式，直线方程整理成y=ax+b，通过观察选项中的直线判断出a和b与0的关系，进而推断曲线方程形式推断其图象．解：把曲线方程整理成=1的形式，整理直线方程得y=ax+bA，C选项中，直线的斜率a＞0，截距b＜0，则曲线方程为双曲线，焦点在x轴，故C 正确，A错误．B项中直线斜率a＜0，则曲线一定不是椭圆，故B项错误．对于D选项观察直线图象可知a＞0，b＞0，则曲线的方程的图象一定是椭圆，故D不符合．故选：C．考点：曲线与方程．2、试题分析：设所求的双曲线方程是，由焦点（0，6）在y 轴上，知k＜0，故双曲线方程是，据c2=36 求出k值，即得所求的双曲线方程．解：由题意知，可设所求的双曲线方程是，∵焦点（0，6）在y 轴上，∴k ＜0，所求的双曲线方程是，由﹣k+（﹣2k）=c2=36，∴k=﹣12，故所求的双曲线方程是，故选B．考点：双曲线的简单性质．3、试题分析：由双曲线方程可知其渐近线为y=y=±2x，分别考虑所求直线的情况有①直线的斜率不存在②与渐近线平行由题意可得：双曲线x2﹣=1的渐近线方程为：y=±2x，点P（1，0）是双曲线的右顶点，故直线x="1" 与双曲线只有一个公共点；过点P （1，0）平行于渐近线y=±2x时，直线L与双曲线只有一个公共点，有2条所以，过P（1，0）的直线L与双曲线只有一个公共点，这样的直线共有3条故选B考点：直线与圆锥曲线的关系．4、试题分析：先假设抛物线的方程，利用抛物线上一点A（m，﹣3）到焦点F的距离为5，建立两个方程，即可求得正数m的值，及此抛物线的方程．解：依题意，设抛物线方程为为x2=﹣2py （p＞0）点P在抛物线上，到准线的距离为5，又点P到x轴的距离为3，所以准线到x轴的距离为2，∴=2，∴p=4，∴抛物线方程为x2=﹣8y．故选：D．考点：抛物线的简单性质．5、试题分析：先将方程化成标准形式，即x2=y，求出p=，即可得到焦点坐标．解：抛物线y=2x2的方程即x2=y，∴p=，故焦点坐标为（0，），故选：A．考点：抛物线的简单性质．6、试题分析：根据双曲线对称性可知∠OMF2=60°，在直角三角形MOF2中可得tan∠OMF2==，进而可得b和c的关系式，进而根据a=求得a和b的关系式．最后代入离心率公式即可求得答案．解：根据双曲线对称性可知∠OMF2=60°，∴tan∠OMF2===，即c=b，∴a==b，∴e==．故选B．考点：双曲线的简单性质．7、试题分析：由双曲线的方程可先根据公式c2=a2+b2求出c的值，进而可求焦距2c 解：由题意可得，c2=a2+b2=m2+12+4﹣m2=16∴c="4" 焦距2c=8故选C考点：双曲线的简单性质．8、试题分析：根据椭圆=1，得出b=5，再由|F1F2|=8，可得c=4，求得a=，运用定义整体求解△ABF2的周长为4a，即可求解．解：由|F1F2|=8，可得2c=8，即c=4，由椭圆的方程=1（a＞5）得：b=5，则a==，由椭圆的定义可得，△ABF2的周长为c=|AB|+|BF2|+|AF2|=|AF1|+|BF1|+|BF2|+|AF2|=（|AF1|+|AF2|）+（|BF1|+|BF2|）=4a=4．故选：D．考点：椭圆的简单性质．9、试题分析：由题意画出椭圆在平面坐标系中的图象，由图象可知三角形ABC为等比三角形，所以得到2b等于a并用b表示a，又根据椭圆的基本性质可知a2=b2+c2，把a等于2b代入即可用b表示出c，然后根据离心率e=，分别把a与c的式子代入，约分后即可得到值．解：由题意画出椭圆的图象，得到△ABC为等比三角形，则a=2b，则根据椭圆的性质得到：a2=b2+c2=4b2，解得c=b，所以e===．故选A．考点：椭圆的简单性质．10、试题分析：利用直线的斜率公式求解．解：∵过点P（﹣2，m）和Q（m，4）的直线斜率等于1，∴k==1，解得m=1．故选：C．考点：直线的斜率．11、试题分析：设点M在准线上的射影为D，则根据抛物线的定义可知|MF|=|MD|进而把问题转化为求|MA|+|MD|取得最小，进而可推断出当D，M，A三点共线时|MA|+|MD|最小，答案可得．解：设点M在准线上的射影为D，则根据抛物线的定义可知|MF|=|MD|，∴要求|MA|+|MF|取得最小值，即求|MA|+|MD|取得最小，当D，M，A三点共线时|MA|+|MD|最小，为3﹣（﹣1）=4．故答案为：4．考点：抛物线的简单性质．12、试题分析：先设出椭圆方程，根据条件列出关于a，b，c的方程，求出a，b，c即可得到结论．解：由题设椭圆的焦点在y轴上，设方程为：，由题得：解得所以椭圆标准方程为故答案为：．考点：椭圆的标准方程．13、试题分析：过点P的最短弦就是垂直于OP的弦，根据垂径定理和勾股定理可求得．解：由圆的标准方程：（x﹣4）2+（y﹣1）2=5，可得圆的圆心坐标为O（4，1），半径为，由于最短弦就是垂直于OP的弦，OP=所以过P点的最短弦的弦长为2=2．故答案为：2．考点：直线与圆相交的性质．14、试题分析：根据条件求出圆心和半径即可得到结论．解：∵圆的﹣条直径的两端点是（2，0），（2，﹣2）．∴圆心坐标为（，），即（2，﹣1），则半径r=1，则圆的方程为（x﹣2）2+（y+1）2=1，故答案为：（x﹣2）2+（y+1）2=1考点：圆的一般方程．15、试题分析：设与直线x+2y﹣l=0平行的直线方程为+2y+c=0，再把点A（﹣2，0）代入，求出c，从而得到结果．解：设与直线x+2y﹣l=0平行的直线方程为x+2y+c=0，把点A（﹣2，0）代入，得﹣2+0+c=0，解得c=2，∴过点A（﹣2，0）且与直线x+2y﹣l=0平行的直线方程为x+2y+2=0．故答案为：x+2y+2=0．考点：直线的一般式方程与直线的平行关系．16、试题分析：由已知方程得到直线的斜率，根据斜率对于得到倾斜角．解：由已知直线的方程得到直线的斜率为，设倾斜角为α，则tanα=，α∈[0，180°），所以α=150°；故答案为：150°．考点：直线的一般式方程；直线的倾斜角．17、试题分析：（1）直线AB方程为bx﹣ay﹣ab=0，依题意可得：，由此能求出椭圆的方程．（2）假设存在这样的值．，得（1+3k2）x2+12kx+9=0，再由根的判别式和根与系数的关系进行求解．解：（1）直线AB方程为bx﹣ay﹣ab=0，依题意可得：，解得：a2=3，b=1，∴椭圆的方程为．（2）假设存在这样的值．，得（1+3k2）x2+12kx+9=0，∴△=（12k）2﹣36（1+3k2）＞0…①，设C（x1，y1），D（x2，y2），则而y1•y2=（kx1+2）（kx2+2）=k2x1x2+2k（x1+x2）+4，要使以CD为直径的圆过点E（﹣1，0），当且仅当CE⊥DE时，则y1y2+（x1+1）（x2+1）=0，∴（k2+1）x1x2+（2k+1）（x1+x2）+5=0…③将②代入③整理得k=，经验证k=使得①成立综上可知，存在k=使得以CD为直径的圆过点E．考点：圆与圆锥曲线的综合；椭圆的标准方程．18、试题分析：先根据椭圆方程求得椭圆的焦点和离心率，进而根据题意求得双曲线的焦点和离心率，进而求得双曲线方程得长轴和短轴，则双曲线方程可得．解：依题意可知椭圆方程中a=5，b=3，∴c==4∴椭圆焦点为F（O，±4），离心率为e=所以双曲线的焦点为F（O，±4），离心率为2，从而双曲线中求得c=4，a=2，b=．所以所求双曲线方程为考点：双曲线的标准方程；椭圆的简单性质；双曲线的简单性质．19、试题分析：求出圆心，求出半径，设直线方程，注意斜率存在时设为k，用圆心到直线的距离公式，求出k的值可得直线方程．斜率不存在时直线为x=0，只需验证弦长是否是8即可，是则此直线也符合要求．解：x2+y2﹣6x﹣8y=0即（x﹣3）2+（y﹣4）2=25，斜率存在时设所求直线为y=kx．∵圆半径为5，圆心M（3，4）到该直线距离为3，∴，∴9k2﹣24k+16=9（k2+1），∴．∴所求直线为y=；当斜率不存在是直线为x=0，验证其弦长为8，所以x=0也是所求直线．故所求直线为：y=或x=0．考点：直线与圆的位置关系．20、试题分析：（1）利用直线垂直，得到系数的关系，求a；（2）利用（1）的结论，解方程组求出直线的交点，然后利用待定系数法求直线方程．解：（1）由l1⊥l2，∴A1B2﹣A2B1=0，…2'∴1﹣a=0即a=1（2）交点坐标为（1.5，1.5）设直线l3的方程为：y=kx+b由直线l3过点（2，4）和点（1.5，1.5），得直线l3的方程为5x﹣y﹣6=0考点：待定系数法求直线方程；直线的一般式方程与直线的垂直关系．。

天津市红桥区高三数学第二次模拟考试试题文(红桥二模)新人教A版

天津市红桥区2013届高三第二次模拟考试数学文试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

答卷前，考生务必将自己的姓名、准考号填写在答题卡上，并在规定位置粘贴考试用条形码。

答题时，务必将答案涂写在答题卡上，答在试卷上的无效。

考试结束后，将本试卷和答题卡一并交回。

参考公式：●如果事件A ，B 互斥，那么P （A U B ）=P （A ）+P （B ）． ●如果事件A ，B 相互独立，那么P （A·B）=P （A ）P （B ）． ●如果在1次试验中某事件A 发生的概率是p ，那么在n 次独立重复试验中这个事件恰好发生k 次的概率是P n （k ）=C kn p k（1－P ）n －k．●柱体体积公式：V=sh ，其中s 表示柱体底面积，h 表示柱体的高，●锥体体积公式：V=13sh ，其中s 表示锥体底面积,h 表示锥体的高． ●球体体积公式：V=343R π，其中R 表示球体的半径．第Ⅰ卷注意事项：1．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

2．本卷共8题，共40分。

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．i 是虚数单位，复数71ii+-的共轭复数是 A ． 4－3i B ．4+4iC ． 3+3iD ．3+4i2．“x>l”是“x 1x->0”的 A ．必要不充分条件 B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件 3．已知a=log 2 0.3，b=30.2，c=0.32，则 A ．a<c<b B ．a<b<c C ．c<b<aD ．c<a<b4．把函数y=sin （x+3π）图象上所有点向右平移3π个单位，再将所得图象的横坐标变为原的12倍（纵坐标不变），所得图象的单调递增区间是 A ．[（4k －1）π，（4k+l ）π]，k ∈Z B ．[,],1212k k k Z ππππ-++∈C ．[,],44k k k Z ππππ-++∈D ．7[,],1212k k k Z ππππ-+-+∈5．设变量x ，y 满足约束条件222200x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩，则目标函数z= －2x+y 的最大值是A ．23- B ．1 C ．2 D ．46．集合 A = {x| |x －2|≤ 2}, B = {y | y= －x 2,－1≤ x≤ 2} , 则 A I B =A ． {x|－4≤x≤4} B．{x|x≠0}C ． {0}D ．∅7．己知抛物线y 23x 的准线与双曲线2222x y a b-=1两条渐近线分别交于A ，B 两点，且|AB|=2，则双曲线的离心率e 为A ．2B ．43C 2D 238．阅读右图所示的程序框图，运行相应的程序（其中“r=a MOD 4”表示“r 等于a 除以4的余数”），输出S 值等于 A ．2508 B ．2509 C ．2510 D ．2511第Ⅱ卷注意事项：用黑色墨水的钢笔或签字笔将答案写在答题卡上．．．．．．．．．．二、填空题：本大题共6个小题，每小题5分，共30分． 9．一学校从一个年级的两个班中抽出部分同学进行一项问卷调查，已知理科班有56名同学，文科班有42名同学，采用分层抽样的方法，抽出一个容量为28的样本．那么这个样本中的文科学生、理科学生的比是． 10．若直线（m －l ）x －y+2 =0与直线3x+my+3=0垂直，则实数m 的值等于．11．如图，边长为1的菱形OABC 中，AC 交OB 于点D ，∠AOC =60o，M ，N 分别为对角线AC, OB上的点，满足11,33CM CD DN DB ==u u u u r u u u r u u u r u u u r，则OM u u u u r ·MN u u u u r= ．12．已知某几何体的三视图如图所示，则该几何体的体积为。

天津市南开区2015届高考第二次模拟考试数学文科试卷及答案

南开区2014～2015学年度第二学期高三年级总复习质量检测（二）数学试卷（文史类）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．共150分，考试时间120分钟．第Ⅰ卷1至2页，第Ⅱ卷3至9页．祝各位考生考试顺利！第 Ⅰ 卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂在答题卡上；2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．3．本卷共8小题，每小题5分，共40分．参考公式：·如果事件A ，B 互斥，那么 ·球的体积公式V 球=34πR 3， P (A ∪B )=P (A )+P (B )．其中R 表示球的半径．·棱柱的体积公式V 柱体=Sh ，其中S 表示棱柱的底面积，h 表示棱柱的高．一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．（1）设i 是虚数单位，则复数ii65-=（）．（A ）6–5i （B ）6+5i （C ）–6+5i （D ）–6–5i （2）已知命题p ：x 1，x 2∈R ，(f (x 2)–f (x 1))(x 2–x 1)≥0，则⌝p 是（）．（A ）x 1，x 2∈R ，(f (x 2)–f (x 1))(x 2–x 1)≤0 （B ）x 1，x 2∈R ，(f (x 2)–f (x 1))(x 2–x 1)≤0 （C ）x 1，x 2∈R ，(f (x 2)–f (x 1))(x 2–x 1)＜0 （D ）x 1，x 2∈R ，(f (x 2)–f (x 1))(x 2–x 1)＜0（3）某单位有840名职工，现采用系统抽样方法，抽取42人做问卷调查，将840人按1，2，…，840随机编号，则抽取的42人中，编号落入区间[481，720]的人数为（）．（A ）10 （B ）11 （C ）12（D ）13（4）下列函数是奇函数的是（）．（A ）f (x )=–|x | （B ）f (x )=lg (1+x )–lg (1–x ) （C ）f (x )=2x +2–x （D ）f (x )=x 3–1（5）如图所示的程序框图表示求算式“2×4×8×16×32×64”的值，则判断框内可以填入（）．（A ）k ＜132? （B ）k ＜70? （C ）k ＜64? （D ）k ＜63?（6）已知双曲线C ：22x a –22y b=1的焦距为10，点P (2，1)在C 的渐近线上，则C 的方程为（）．（A ）220x –25y =1 （B ）25x –220y =1（C ）280x –220y =1 （D ）220x –280y =1（7）已知函数f (x )=sin (ωx +4π)（x ∈R ，ω＞0）的最小正周期为π，将y=f (x )的图象向左平移|ϕ|个单位长度，所得图象关于y 轴对称，则ϕ的一个值是（）．（A ）2π（B ）83π（C ）4π （D ）8π（8）在△ABC 中，若|AB +AC |=|AB –AC |，AB=2，AC=1，E ，F 为BC 边的三等分点，则AE •AF =（）．（A ）98 （B ）910 （C ）925（D ）926南开区2014～2015学年度第二学期高三年级总复习质量检测（二）答题纸（文史类）题号二三总分(15)(16) (17) (18) (19) (20) 得分第 Ⅱ 卷注意事项：1．用黑色墨水的钢笔或签字笔答题； 2．本卷共12小题，共110分．得分评卷人二、填空题：本大题共6个小题，每小题5分，共30分．请将答案填在题中横线上。

《解析》天津市红桥区2015-2016学年高二下学期期末数学试卷(文科)Word版含解析

2015-2016学年天津市红桥区高二（下）期末数学试卷（文科）一、选择题：本大题共12小题，每小题2分，共24分，在每个小题给出的四个选项中，只有一个符合题目要求的.1．不等式的解集是（）A．（﹣∞，2）B．（2，+∞）C．（0，2）D．（﹣∞，0）∪（2，+∞）2．不等式＜0的解集为（）A．{x|x＜﹣1或1＜x＜2} B．{x|1＜x＜2}C．{x|﹣1＜x＜2且x≠1} D．{x|x＜2且x ≠1}3．不等式9x2+6x+1≤0的解集是（）A．{x|x≠﹣}B．{x|﹣≤x≤}C．∅D．{x|x=﹣}4．不等式|x+2|≤5的解集是（）A．{x|x≤1或x≥2}B．{x|﹣7≤x≤3}C．{x|﹣3≤x≤7}D．{x|﹣5≤x≤9} 5．下列不等式中，解集为实数集R的是（）A．x2+4x+4＞0 B．|x|＞0 C．x2﹣x+1≥0 D．﹣1＜6．不等式ax＞b的解集不可能是（）A．B．R C．D．∅7．关于x的不等式组有解，则实数a的取值范围是（）A．[﹣3，1] B．（﹣3，1）C．[﹣1，3] D．（﹣1，3）8．关于x的不等式ax﹣b＞0的解集为（1，+∞），则关于x的不等式＞0的解集为（）A．（﹣1，2）B．（1，2）C．（﹣∞，﹣1）∪（2，+∞）D．（﹣∞，﹣2）∪（1，+∞）9．已知如图，四边形ABCD为圆内接四边形，AB是直径，MN切⊙O于C点，∠BCM=38°，那么∠ABC的度数是（）A．38°B．52°C．68°D．42°10．如图所示，在⊙O中，弦AB与半径OC相交于点M，且OM=MC，AM=1.5，BM=4，则OC=（）A．2B．2C．2D．11．如图，AD，AE，BC分别与圆切D，E，F于点，延长AF与圆O交于另一点G，给出下列三个结论：①AD+AE=AB+BC+CA②△AFB～△ADG③AF•AG=AD•AE其中正确结论的序号是（）A．①②B．②③C．①③D．①②③12．已知a∈[﹣1，1]，不等式x2+（a﹣4）x+4﹣2a＞0恒成立，则x的取值范围为（）A．（﹣∞，2）∪（3，+∞）B．（﹣∞，1）∪（2，+∞）C．（﹣∞，1）∪（3，+∞）D．（1，3）二、填空题：本大题共8个小题，每小题4分.、共32分.13．不等式组的解集是．14．不等式＜0解集为．15．不等式|5x﹣4|＜6的解集为．16．在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，AB=2，DB=1，则DC=．17．如图所示，在平行四边形ABCD中，BC=24，E，F为BD的三等分点，则DN=．18．如图，在△ABC中，∠C=90°，∠A=60°，AB=20，过C作△ABC的外接圆的切线CD，BD⊥CD，BD与外接圆交于点E，则DE的长为．19．（几何证明选讲选做题）如图，圆O的半径为5cm，点P是弦AB的中点，OP=3cm，弦CD过点P，且=，则CD的长为cm．20．如图所示，AB是圆O的直径，直线MN切圆O于C，CD⊥AB，AM⊥MN，BN⊥MN，给出下列四个结论：①∠1=∠2=∠3；②AM•CN=CM•BN；③CM=CD=CN；④△ACM∽△ABC∽△CBN．则其中正确结论的序号是．三、解答题：本大题共4小题，共44分，解答应写出文字说明、证明过程或演算步骤. 21．解下列不等式．（1）6x2﹣x﹣1≥0；（2）﹣x2+2x﹣＞0；（3）≥3；（4）≥1．22．解关于x的不等式＜0 （a∈R）．23．记关于x的不等式的解集为P，不等式|x﹣1|≤1的解集为Q．（Ⅰ）若a=3，求P；（Ⅱ）若Q⊆P，求正数a的取值范围．24．设函数f（x）=2|x﹣1|+x﹣1，g（x）=16x2﹣8x+1．记f（x）≤1的解集为M，g（x）≤4的解集为N．（Ⅰ）求M；（Ⅱ）当x∈M∩N时，证明：x2f（x）+x[f（x）]2≤．2015-2016学年天津市红桥区高二（下）期末数学试卷（文科）参考答案与试题解析一、选择题：本大题共12小题，每小题2分，共24分，在每个小题给出的四个选项中，只有一个符合题目要求的.1．不等式的解集是（）A．（﹣∞，2）B．（2，+∞）C．（0，2）D．（﹣∞，0）∪（2，+∞）【考点】其他不等式的解法．【分析】移项通分化为分式不等式，解答即可．【解答】解：由得：，即x（2﹣x）＜0，所以x＜0或x＞2故选D．2．不等式＜0的解集为（）A．{x|x＜﹣1或1＜x＜2} B．{x|1＜x＜2}C．{x|﹣1＜x＜2且x≠1} D．{x|x＜2且x ≠1}【考点】其他不等式的解法．【分析】利用平方差公式化简不等式，等价转化后利用穿根法求出不等式的解集．【解答】解：由题意得，则，所以（x+1）（x﹣1）（x﹣2）＜0，如图所示：由图得，不等式的解集是{x|x＜﹣1或1＜x＜2}，故选：A．3．不等式9x2+6x+1≤0的解集是（）A．{x|x≠﹣}B．{x|﹣≤x≤}C．∅D．{x|x=﹣}【考点】一元二次不等式的解法．【分析】把不等式化为（3x+1）2≤0，即可求出它的解集．【解答】解：不等式9x2+6x+1≤0可化为（3x+1）2≤0，解得x=﹣；所以该不等式的解集是{x|x=﹣}．故选：D．4．不等式|x+2|≤5的解集是（）A．{x|x≤1或x≥2}B．{x|﹣7≤x≤3}C．{x|﹣3≤x≤7}D．{x|﹣5≤x≤9}【考点】绝对值不等式的解法．【分析】利用绝对值表达式的解法求解即可．【解答】解：不等式|x+2|≤5，等价于﹣5≤x+2≤5，可得：﹣7≤x≤3．不等式|x+2|≤5的解集是：{x|﹣7≤x≤3}．故选：B．5．下列不等式中，解集为实数集R的是（）A．x2+4x+4＞0 B．|x|＞0 C．x2﹣x+1≥0 D．﹣1＜【考点】一元二次不等式的解法．【分析】分别利用不等式的解法确定即可．【解答】解：对于A的解集是{x|x≠﹣2}，对于B的解集是{x|x≠0}，对于C：x2﹣x+1=+＞0，解集是R，对于D的解集是{x|x≠0}，故选：C．6．不等式ax＞b的解集不可能是（）A．B．R C．D．∅【考点】其他不等式的解法．【分析】分a等于0，小于0，大于0三种情况考虑，分别求出不等式的解集，即可做出判断．【解答】解：当a=0时，b＞0，不等式无解；b＜0，不等式解集为R；当a＞0时，解得：x＞，此时不等式的解集为（，+∞）；当a＜0时，解得：x＜，此时不等式的解集为（﹣∞，），则不等式的解集不可能为（﹣∞，﹣）．故选A7．关于x的不等式组有解，则实数a的取值范围是（）A．[﹣3，1] B．（﹣3，1）C．[﹣1，3] D．（﹣1，3）【考点】其他不等式的解法．【分析】根据题意和一元一次不等式的解法求出不等式组的解集，由非空集合的条件列出不等式，由一元二次不等式的解法求出实数a的取值范围．【解答】解：由题意得，，则，∵关于x的不等式组有解，∴不等式的解集是[1+a2，4+2a），且1+a2＜4+2a，则a2﹣2a﹣3＜0，解得﹣1＜a＜3，∴实数a的取值范围是（﹣1，3），故选D．8．关于x的不等式ax﹣b＞0的解集为（1，+∞），则关于x的不等式＞0的解集为（）A．（﹣1，2）B．（1，2）C．（﹣∞，﹣1）∪（2，+∞）D．（﹣∞，﹣2）∪（1，+∞）【考点】其他不等式的解法．【分析】根据关于x的不等式ax﹣b＞0的解集为（1，+∞），可得a=b，a＞0，进而不等式＞0可化为：，由此可求不等式的解集．【解答】解：∵关于x的不等式ax﹣b＞0的解集为（1，+∞），∴a＞0，a﹣b=0∴a=b，a＞0∴不等式＞0可化为：∴（x+1）（x﹣2）＞0∴x＜﹣1，或x＞2∴关于x的不等式＞0的解集为（﹣∞，﹣1）∪（2，+∞）故选C．9．已知如图，四边形ABCD为圆内接四边形，AB是直径，MN切⊙O于C点，∠BCM=38°，那么∠ABC的度数是（）A．38°B．52°C．68°D．42°【考点】弦切角．【分析】连结AC，由直径所对的圆周角为直角，结合三角形的内角和定理可得∠B+∠BAC=90°，根据弦切角定理可得∠BCM=∠BAC=38°，因此可以得到∠ABC=90°﹣∠BAC=52°．【解答】解：连结AC，可得∵直线MN切圆O于C，∴∠BCM=∠BAC=38°，∵AB是圆O的直径，∴∠BCA=90°，可得∠B+∠BAC=90°，由此可得∠B=90°﹣∠BAC=90°﹣38°=52°，即∠ABC=52°．故选：B10．如图所示，在⊙O中，弦AB与半径OC相交于点M，且OM=MC，AM=1.5，BM=4，则OC=（）A．2B．2C．2D．【考点】与圆有关的比例线段．【分析】过C、O作直径CD，用OC表示出DM、CM的长，然后运用相交弦定理，列方程求解．【解答】解：如图，延长CO，交⊙O于D，则CD为⊙O的直径；∵OM=MC，∴OC=2MC=2OM，DM=3OM=3MC；由相交弦定理得：DM•MC=AM•BM，即：3MC2=1.5×4，解得MC=；∴OC=2MC=2，故选：B．11．如图，AD，AE，BC分别与圆切D，E，F于点，延长AF与圆O交于另一点G，给出下列三个结论：①AD+AE=AB+BC+CA②△AFB～△ADG③AF•AG=AD•AE其中正确结论的序号是（）A．①②B．②③C．①③D．①②③【考点】弦切角；与圆有关的比例线段．【分析】由切线性质，能推导出AD+AE=AB+BC+CA；连接FD，若△AFB～△ADG，则有∠ABF=∠DGF，不成立；由切割定理可得AF•AG=AD2=AD•AE．【解答】解：在①中：由切线性质，得BD=BF，CF=CE，∴AD+AE=AB+BC+CA，故①正确；在②中：连接FD（如图），若△AFB～△ADG，则有∠ABF=∠DGF．通过图象结合圆的性质，得：∠ABF=∠BFD+∠BDF=2∠DGF，不成立，故②错误；在③中，由切线性质得AD=AE，∴由切割定理可得AF•AG=AD2=AD•AE，故③正确．故选：C．12．已知a∈[﹣1，1]，不等式x2+（a﹣4）x+4﹣2a＞0恒成立，则x的取值范围为（）A．（﹣∞，2）∪（3，+∞）B．（﹣∞，1）∪（2，+∞）C．（﹣∞，1）∪（3，+∞）D．（1，3）【考点】函数恒成立问题．【分析】把不等式看作是关于a的一元一次不等式，然后构造函数f（a）=（x﹣2）a+x2﹣4x+4，由不等式在[﹣1，1]上恒成立，得到，求解关于a的不等式组得x得取值范围．【解答】解：令f（a）=（x﹣2）a+x2﹣4x+4，则不等式x2+（a﹣4）x+4﹣2a＞0恒成立转化为f（a）＞0恒成立（a∈[﹣1，1]）．∴有，即，整理得：，解得：x＜1或x＞3．∴x的取值范围为（﹣∞，1）∪（3，+∞）．故选：C．二、填空题：本大题共8个小题，每小题4分.、共32分.13．不等式组的解集是（﹣1，5）．【考点】其他不等式的解法．【分析】根据题意和一元一次不等式的解法求出不等式组的解集．【解答】解：由题意得，，则，所以不等式的解集是（﹣1，5），故答案为：（﹣1，5）．14．不等式＜0解集为{x|﹣1＜x＜2} ．【考点】其他不等式的解法．【分析】由不等式不等式，可得（x﹣2）（x+1）＜0，由此解得它的解集．【解答】解：由不等式不等式，可得（x﹣2）（x+1）＜0，解得﹣1＜x＜2，故答案为{x|﹣1＜x＜2}．15．不等式|5x﹣4|＜6的解集为（﹣，2）．【考点】绝对值不等式的解法．【分析】根据绝对值非负的性质，将不等式两边平方得到关于x的一元二次不等式，化简得（5x+2）（5x﹣10）＜0，即可求出原不等式的解集．【解答】解：∵|5x﹣4|≥0∴不等式|5x﹣4|＜6的两边平方，可得（5x﹣4）2＜36化简得（5x+2）（5x﹣10）＜0，解之得﹣＜x＜2因此，原不等式的解集为（﹣，2）故答案为：（﹣，2）16．在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，AB=2，DB=1，则DC=3．【考点】三角形中的几何计算．【分析】由射影定理可得，AB2=BD•BC，数据代入可得结论．【解答】解：由射影定理可得，AB2=BD•BC，∵AB=2，DB=1，∴22=1×（1+DC），∴DC=3．故答案为：3．17．如图所示，在平行四边形ABCD中，BC=24，E，F为BD的三等分点，则DN=6．【考点】线段的定比分点．【分析】根据AD∥BC，得出=，=，从而求出AD与DN的关系，再由AD=BC求出DN的值．【解答】解：如图所示，平行四边形ABCD中，BC=24，E，F为BD的三等分点，所以DE=2BE，且BF=2DF；又AD∥BC，所以==，==2，可得BM=AD=2DN，所以DN=AD，又AD=BC，所以DN=BC=×24=6．故答案为：6．18．如图，在△ABC中，∠C=90°，∠A=60°，AB=20，过C作△ABC的外接圆的切线CD，BD⊥CD，BD与外接圆交于点E，则DE的长为5．【考点】与圆有关的比例线段．【分析】利用直角△ABC的边角关系即可得出BC，利用弦切角定理可得∠BCD=∠A=60°．利用直角△BCD的边角关系即可得出CD，BD．再利用切割线定理可得CD2=DE•DB，即可得出DE．【解答】解：在△ABC中，∠C=90°，∠A=60°，AB=20，∴BC=AB•sin60°=．∵CD是此圆的切线，∴∠BCD=∠A=60°．在Rt△BCD中，CD=BC•cos60°=，BD=BC•sin60°=15．由切割线定理可得CD2=DE•DB，∴，解得DE=5．故答案为5．19．（几何证明选讲选做题）如图，圆O的半径为5cm，点P是弦AB的中点，OP=3cm，弦CD过点P，且=，则CD的长为6cm．【考点】与圆有关的比例线段．【分析】连接OA，根据垂径定理可知OP⊥AB，AP=AB，在Rt△AOP中运用勾股定理即可求出AP的长，再利用相交弦定理，可得结论．【解答】解：连接OA，∵点P是弦AB的中点，∴OP⊥AB，AP=AB，∵OA=5cm，OP=3cm，∴在Rt△AOP中，AP=4∴AP×PB=CP×PD∵∴16=×∴CD=故答案为：20．如图所示，AB是圆O的直径，直线MN切圆O于C，CD⊥AB，AM⊥MN，BN⊥MN，给出下列四个结论：①∠1=∠2=∠3；②AM•CN=CM•BN；③CM=CD=CN；④△ACM∽△ABC∽△CBN．则其中正确结论的序号是①③④．【考点】命题的真假判断与应用；弦切角；与圆有关的比例线段．【分析】利用圆周角判断①的正误；相似三角形判断②的正误；三角形全等判断③的正误；三角形相似判断④的正误．即可得出结论．【解答】解：∵AB是圆O的直径，CD⊥AB，∴∠2=∠3，∵直线MN切圆O于C，∴∠1=∠2，∴∠1=∠2=∠3，①对；利用△AMN∽△CNB得=，∴AM•BN=CM•CN，②错．利用△AMN≌△ADC，可得CM=CD，△CDB≌△CNB，可得CD=CN，∴CM=CD=CD，③对；利用等角的余角相等得到△ACM∽△ABC∽△CBN，④对．故答案为：①③④．三、解答题：本大题共4小题，共44分，解答应写出文字说明、证明过程或演算步骤. 21．解下列不等式．（1）6x2﹣x﹣1≥0；（2）﹣x2+2x﹣＞0；（3）≥3；（4）≥1．【考点】其他不等式的解法；一元二次不等式的解法．【分析】（1）由一元二次方程的解法求出对应方程的根，由一元二次不等式的解法求出不等式的解集；（2）先化简不等式，由一元二次方程的解法求出对应方程的根，由一元二次不等式的解法求出不等式的解集；（3）先化简分式不等式，再等价转化为一元二次不等式组，由一元二次不等式的解法求出不等式的解集；（4）先化简分式不等式，再等价转化为对应不等式组，由穿根法求出高次不等式的解集．【解答】解：（1）由6x2﹣x﹣1=0得（3x+1）（2x﹣1）=0，解得x=或x=， (2)所以不等式6x 2﹣x ﹣1≥0 的解集为{x |x或x } (4)（2）由﹣x 2+2x ﹣＞0得3x 2﹣6x +2＜0，因为3＞0，且方程3x 2﹣6x +2=0的解是：x 1=，x 2=，所以原不等式的解集是{x |} (8)（3）由得，则，即，所以，解得，则不等式的解集是{x |} (12)（4）原不等式化为：，整理得0即，如图所以原不等式的解集为{x |x ≤1或2＜x ≤3或x ＞4} (16)22．解关于x 的不等式＜0 （a ∈R ）．【考点】其他不等式的解法．【分析】把不等式转化为同解不等式，对a 分类讨论解答即可．【解答】解：＜0⇔（x ﹣a ）（x ﹣a 2）＜0，①当a=0或a=1时，原不等式的解集为Φ；②当a ＜0或a ＞1时，a ＜a 2，此时a ＜x ＜a 2；③当0＜a ＜1时，a ＞a 2，此时a 2＜x ＜a ．综上，当a ＜0或a ＞1时，原不等式的解集为{x |a ＜x ＜a 2}；当0＜a ＜1时，原不等式的解集为{x |a 2＜x ＜a }；当a=0或a=1时，原不等式的解集为Φ．23．记关于x 的不等式的解集为P ，不等式|x ﹣1|≤1的解集为Q ．（Ⅰ）若a=3，求P ；（Ⅱ）若Q⊆P，求正数a的取值范围．【考点】集合的包含关系判断及应用；其他不等式的解法；绝对值不等式的解法．【分析】（I）分式不等式的解法，可转化为整式不等式（x﹣a）（x+1）＜0来解；对于（II）中条件Q⊆P，应结合数轴来解决．【解答】解：（I）由，得P={x|﹣1＜x＜3}．（II）Q={x||x﹣1|≤1}={x|0≤x≤2}．由a＞0，得P={x|﹣1＜x＜a}，又Q⊆P，结合图形所以a＞2，即a的取值范围是（2，+∞）．24．设函数f（x）=2|x﹣1|+x﹣1，g（x）=16x2﹣8x+1．记f（x）≤1的解集为M，g（x）≤4的解集为N．（Ⅰ）求M；（Ⅱ）当x∈M∩N时，证明：x2f（x）+x[f（x）]2≤．【考点】其他不等式的解法；交集及其运算．【分析】（Ⅰ）由所给的不等式可得①，或②，分别求得①、②的解集，再取并集，即得所求．（Ⅱ）由g（x）≤4，求得N，可得M∩N=[0，]．当x∈M∩N时，f（x）=1﹣x，不等式的左边化为﹣，显然它小于或等于，要证的不等式得证．【解答】解：（Ⅰ）由f（x）=2|x﹣1|+x﹣1≤1 可得①，或②．解①求得1≤x≤，解②求得0≤x＜1．综上，原不等式的解集为[0，]．（Ⅱ）证明：由g（x）=16x2﹣8x+1≤4，求得﹣≤x≤，∴N=[﹣，]，∴M∩N=[0，]．∵当x∈M∩N时，f（x）=1﹣x，∴x 2f （x ）+x [f （x ）]2=xf （x ）[x +f （x ）]=﹣≤，故要证的不等式成立．2016年8月17日。

【2015红桥二模全科答案】天津市红桥区2015届高三第二次模拟考试

【2015红桥二模全科答案】天津市红桥区2015届高三第二次模拟考试2015红桥二模高三语文答案 (1)2015红桥二模高三英语答案 (4)2015红桥二模高三数学（文）答案 (4)2015红桥二模高三数学（理）答案 (10)2015红桥二模高三政治答案 (17)2015红桥二模高三历史答案 (17)2015红桥二模高三地理答案 (19)2015红桥二模高三物理答案 (20)2015红桥二模高三化学答案 (21)2015红桥二模高三生物答案 (22)2015红桥二模高三语文答案一、1.B 2.C 3.D 4.A 5.D二、6. C（亲情背景下的社会互助和应急保障只能“小范围”“小社会”，笼统地表述为“促进社会救助，实现社会的应急保障”则会让人觉得不可思议。

）7. A（作者于文中所言“‘八婆’特征”是缘于私人场合之下且带有亲情色彩的“叽叽喳喳地说个不停”，与通常意义的“八婆”有着本质的区别，作者以此表明沟通交流的重要，并非认为“八婆”值得效仿。

）8. D（由原文可知，作者不赞同由政府承担全部的社会保障义务，但现代社会的普遍观点是“把社会保障的责任全部放在政府身上”，两者并不一致。

只不过“政府要承担全部社会保障责任”与“现代社会不主张政府的权力太大”两者又形成了矛盾。

）三、9.C 10.D 11.B 12.C四、13.（1）这之后纯粹、古朴、隐隐约约、旷远之声音才出现，然而从中能有所领悟、喜欢听的人，十个人中没有一两个。

【3分】（2）柯孝廉于是和韫修各自弹奏一曲，音律高低交错，不能分辨出是两个人弹的。

【2分】（3）然则，没有琴弦弹琴，已经足以改变人的性情，何况是像成连、伯牙那类妙手呢？【3分】14.（1）不能。

“似觉”含有不确定之意。

诗人多年来仕途奔波，宦海沉浮，似乎觉得谙练世情，但又感到政治风云变幻难测。

“似觉”一词准确地写出了诗人对前途把握不定的心理态度，能很好地呼应下句中的“空更”一词。

“犹觉”则没有这样的表达效果。

2014-2015学年天津市红桥区高二(上)期末数学试卷(文科)

2014-2015学年天津市红桥区高二（上）期末数学试卷（文科）学校:___________姓名：___________班级：___________考号：___________一、选择题(本大题共8小题，共32.0分)1.已知点P（3，m）在直线x+y-1=0上，则m的值为（）A.5B.2C.-2D.-6【答案】C【解析】解：∵点P（3，m）在直线x+y-1=0上，∴3+m-1=0，解得m=-2故选：C由题意可得3+m-1=0，解方程可得．本题考查直线的一般式方程，属基础题．2.已知直线y=（a-a2）x-2和y=（3a+1）x+1互相平行，则a的值等于（）A.2B.1C.0D.-1【答案】D【解析】解：∵直线y=（a-a2）x-2和y=（3a+1）x+1互相平行，∴a-a2=3a+1，即a2+2a+1=0，解得a=-1故选：D由平行关系可得a-a2=3a+1，解方程可得．本题考查直线的一般式方程和平行关系，属基础题．3.圆心在（2，-1），且过点（3，0）的圆的方程为（）A.（x+2）2+（y-1）2=2B.（x-2）2+（y+1）2=2C.（x+2）2+（y-1）2=D.（x-2）2+（y+1）2=【答案】B【解析】解：圆心在（2，-1），且过点（3，0）的圆的半径R=，则圆的标准方程为（x-2）2+（y+1）2=2，故选：A根据条件求出圆的半径即可．本题主要考查圆的标准方程的求解，根据圆的性质求出圆的半径是解决本题的关键．4.圆（x+1）2+（y+）2=1的切线方程中有一条是（）A.x=0B.x+y=0C.y=0D.x-y=0【答案】A【解析】解：圆心坐标为（-1，-），半径R=1，B．若x+y=0，则圆心到直线的距离d=≠1，不满足相切．C．若y=0，则圆心到直线的距离d=≠1，不满足相切．D．若x-y=0，则圆心到直线的距离d=≠1，不满足相切．故选：A根据直线和圆相切的条件判断即可．本题主要考查直线和圆相切的判断，根据圆心到直线的距离d=R是解决本题的关键．5.若抛物线x2=ay的焦点坐标为（0，2），则实数a的值为（）A.-8B.-4C.8D.4【答案】C【解析】解：∵抛物线x2=ay的焦点坐标为（0，2），可知抛物线开口向上，∴=2，解得a=8．故选：C．由抛物线x2=ay的焦点坐标为（0，2），可得=2，解出即可．本题考查了抛物线的标准方程及其性质，考查了计算能力，属于基础题．6.椭圆+y2=1的左、右焦点分别为F1、F2，过F1的直线l交椭圆于A、B两点，则△ABF2的周长为（）A.4B.8C.12D.16【答案】B【解析】解：椭圆+=1的a=4，由椭圆的定义可得，△AF2B的周长为c=|AB|+|AF2|+|BF2|=（|AF2|+|AF1|）+（|BF1|+|BF2|）=2a+2a=4a=8．故选B．求得椭圆的a=2，再由椭圆的定义可得△AF1B的周长为c=4a=8．本题考查椭圆的定义、方程和性质，主要考查椭圆的定义的运用，考查运算能力，属于基础题．7.若双曲线-y2=1（a＞0）的离心率为2，则该双曲线的渐近线方程为（）A.y=±xB.y=±3xC.y=±xD.y=±x【答案】D解：双曲线-y2=1（a＞0）的c=，则离心率e===2，解得，a=．则双曲线的渐近线方程为y=x，即为y=x．故选D．求出双曲线的c，由离心率公式，解方程求得a，再由双曲线的渐近线方程即可得到．本题考查双曲线的方程和性质，考查渐近线方程的求法和离心率公式的运用，考查运算能力，属于基础题．8.如图，过抛物线y2=2px（p＞0）焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为（）A.y2=3xB.y2=9xC.y2=xD.y2=x【答案】A【解析】解：设A（x1，y1），B（x2，y2），作AM、BN垂直准线于点M、N，则|BN|=|BF|，又|BC|=2|BF|，得|BC|=2|BN|，∴∠NCB=30°，有|AC|=2|AM|=6，设|BF|=x，则2x+x+3=6⇒x=1，而x1+=3，x2+=1，且x1x2=，∴（3-）（1-）=，解得p=．得y2=3x．故选A．根据过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B，作AM、BN垂直准线于点M、N，根据|BC|=2|BF|，且|AF|=3，和抛物线的定义，可得∠NCB=30°，设A（x1，y1），B（x2，y2），|BF|=x，而x1+=3，x2+=1，且x1x2=，即有（3-）（1-）=，可求得p的值，即求得抛物线的方程．此题是个中档题．考查抛物线的定义以及待定系数法求抛物线的标准方程．体现了数形结合的思想，特别是解析几何，一定注意对几何图形的研究，以便简化计算．二、填空题(本大题共5小题，共20.0分)9.双曲线2x2-y2=8的实轴长是______ ．4【解析】解：双曲线2x2-y2=8化为标准方程为∴a2=4∴a=2∴2a=4即双曲线2x2-y2=8的实轴长是4故答案为：4双曲线2x2-y2=8化为标准方程为，即可求得实轴长．本题重点考查双曲线的几何性质，解题的关键是将双曲线方程化为标准方程，属于基础题．10.准线方程x=-1的抛物线的标准方程为______ ．【答案】y2=4x【解析】解：∵抛物线的准线方程为x=-1，∴可设抛物线方程为y2=2px（p＞0），由准线方程x=-，得p=2．∴抛物线的标准方程为y2=4x．故答案为：y2=4x．直接由抛物线的准线方程设出抛物线方程，再由准线方程求得p，则抛物线标准方程可求．本题考查了抛物线的标准方程，考查了抛物线的简单几何性质，是基础题．11.已知直线l1：3x+4y-3=0，直线l2：3x+4y+2=0，则l1与l2之间的距离为______ ．【答案】1【解析】解：∵直线l1与l2是平行直线，∴l1与l2之间的距离d==1．故答案为：1．利用两条平行线之间的距离公式即可得出．本题考查了两条平行线之间的距离公式，属于基础题．12.已知圆C：（x-1）2+（y-2）2=5与y轴交于A、B两点，则△ABC的面积是______ ．【答案】2【解析】解：圆心C（1，2），当x=0时，（y-2）2=4，解得y=4或y=0，即A（0，4），B（0，0），则△ABC的面积为，故答案为：2根据条件求出A，B，C的坐标即可．本题主要考查三角形的面积的计算，根据圆的方程求出A，B，C的坐标是解决本题的关键．比较基础．13.分别过椭圆的左、右焦点F1、F2所作的两条互相垂直的直线l1、l2的交点在此椭圆的内部，则此椭圆的离心率的取值范围是______ ．【答案】，【解析】解：由题意可知椭圆内存在点P使得直线PF1与直线PF2垂直，可得|OP|=c＜b，所以c2＜b2=a2-c2，∴e∈，．故答案为：，．根据椭圆内存在点P使得直线PF1与直线PF2垂直，可得|OP|=c＜b，从而可求椭圆离心率e的取值范围；本题考查椭圆的几何性质，离心率的求法，考查计算能力．三、解答题(本大题共4小题，共48.0分)14.已知点A（2，-2），B（4，6）．（Ⅰ）求直线AB的方程；（Ⅱ）求过点C（-2，0）且与AB垂直的直线方程．【答案】解：（Ⅰ）由已知，直线AB的斜率，所以直线AB的方程为y+2=4（x-2），即4x-y-10=0．（Ⅱ）设所求直线l的斜率为k'，则k•k'=-1，解得．所以直线l的方程为，即x+4y+2=0．【解析】（I）利用斜率计算公式、点斜式即可得出；（II）利用相互垂直的直线斜率之间的关系、点斜式即可得出．本题考查了斜率计算公式、相互垂直的直线斜率之间的关系、点斜式，属于基础题．15.已知关于x，y的方程C：x2+y2-2x-4y+m=0，直线l：x+2y-4=0．（Ⅰ）当方程C表示圆时，求m的取值范围；（Ⅱ）若直线l被圆C截得的弦长为时，求m的值．【答案】解：（Ⅰ）方程C化为（x-1）2+（y-2）2=5-m，由5-m＞0，解得m＜5．（Ⅱ）圆心C的坐标为（1，2），点C到直线l的距离，所以，所以5-m=1，解得m=4．【解析】（Ⅰ）根据圆的一般方程满足的条件即可求m的取值范围；（Ⅱ）根据直线和圆相交的弦长公式进行求解即可．本题主要考查圆的方程的应用以及直线弦长公式的应用，比较基础．16.已知椭圆C的两焦点为F1（-，0），F2（，0），长轴长是短轴长的2倍．（Ⅰ）求椭圆C的方程；（Ⅱ）过点（1，0）的直线l与椭圆C交于M（x1，y1），N（x2，y2）两点，若x1x2+y1y2=0，求直线l的方程．【答案】解：（Ⅰ）由已知，，解得a2=4，b2=1，所以椭圆的方程为；（Ⅱ）设直线l的方程为y=k（x-1），由，，消去y，得（1+4k2）x2-8k2x+4k2-4=0，所以，．==0，所以k2-4=0，解得k=±2．所以直线l的方程为y=2x-2或y=-2x+2．【解析】（Ⅰ）由题意可得a=2b，a，b，c的关系，计算即可得到a，b，进而得到椭圆方程；（Ⅱ）设直线l的方程为y=k（x-1），代入椭圆方程，运用韦达定理，化简整理即可得本题考查椭圆的方程和性质，主要考查椭圆的方程和运用，联立直线方程，运用韦达定理，考查化简整理和运算求解能力，属于中档题．17.如图，已知直线l：y=kx-2与抛物线C：x2=-2py（p＞0）交于A，B两点，线段AB的中点坐标为（-2，-6）．（Ⅰ）求直线l和抛物线C的方程；（Ⅱ）求线段AB的长；（Ⅲ）抛物线上一动点P从A到B运动时，求△ABP面积最大值．【答案】解：（Ⅰ）由已知，点（-2，-6）在直线l上，所以-6=-2k-2，解得k=2，所以直线l的方程为y=2x-2．设A（x1，y1），B（x2，y2），由，，消去y，得x2+4px-4p=0，所以x1+x2=-4p，x1•x2=-4p．所以-4p=-4，解得p=1．所以抛物线的方程为x2=-2y．（Ⅱ）．（Ⅲ）当点P到直线AB的距离h最大时，△ABP的面积最大．设与AB平行的直线l'的方程为y=2x+m，由，，消去y，得x2+4x+2m=0，由△=0，解得m=2．所以l'的方程为y=2x+2．所以．所以△ABP面积的最大值为．【解析】（Ⅰ）代入点（-2，-6），求得k=2，联立直线方程和抛物线方程，运用韦达定理，由题意可得p=1，即可得到抛物线的方程；（Ⅱ）运用弦长公式：|AB|=•|x1-x2|，计算即可得到；（Ⅲ）当点P到直线AB的距离h最大时，△ABP的面积最大．设与AB平行的直线l'的方程为y=2x+m，联立抛物线方程，由判别式为0，可得m=2，由两平行直线的距离公式即可求得h的最大值，计算可得面积的最大值．本题考查抛物线的方程的性质，主要考查直线方程和抛物线方程联立，运用韦达定理和弦长公式，同时考查点到直线的距离公式的运用，属于中档题．。

2015年天津市红桥区中考数学二模试卷(解析版)

2015年天津市红桥区中考数学二模试卷一、选择题（本大题共12小题，每小题3分，共36分）每小题给出4个答案，其中只有一个是正确的1．（3分）计算（﹣3）﹣（﹣5）的结果等于（）A．8 B．﹣8 C．2 D．﹣22．（3分）计算6tan45°﹣2cos60°的结果是（）A．4 B．4 C．5 D．53．（3分）下列图形中，不是中心对称图形有（）A．B．C．D．4．（3分）如图，下面几何体的俯视图是（）A．B．C．D．5．（3分）我国的陆地面积约为9600000km2，用科学记数法表示应为（）A．0.96×107B．9.6×106C．96×105D．960×1046．（3分）正六边形的边心距与边长之比为（）A．：3 B．：2 C．1：2 D．：27．（3分）甲乙两组各10名学生，进行趣味数学抢答比赛，共10道题，两组答对题数的有关数据统计如下（）A．甲组比乙组的成绩稳定B．乙组比甲组的成绩稳定C．两个组的成绩一样稳定D．无法比较8．（3分）如图，AB是⊙O的直径，延长AB至点P，使PB等于半径OB，过点P作⊙O的切线，切点为C，则∠ABC的度数等于（）A．45°B．50°C．55°D．60°9．（3分）反比例函数y=（k≠0）的图象经过点（﹣1，﹣2），且自变量x＞1时，函数值y的取值范围是（）A．0＜y＜2 B．y＞2 C．y＜1 D．y＞110．（3分）某服装店原计划按每套200元的价格销售一批保暖内衣，但上市后销售不佳，为减少库存积压，两次连续降价打折处理，最后价格调整为每套128元．若两次降价折扣率相同，则每次降价率为（）A．8% B．18% C．20% D．25%11．（3分）如图，菱形ABCD中，点M，N在AC上，ME⊥AD，NF⊥AB．若NF=NM=2，ME=3，则AN=（）A．3 B．4 C．5 D．612．（3分）已知二次函数y=ax2+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根，有下列结论：①b2﹣4ac＞0；②abc＜0；③m＞2．其中，正确结论的个数是（）A．0 B．1 C．2 D．3二、填空题（本大题共6小题，每小题3分，共18分）13．（3分）计算﹣（x4）3的结果等于．14．（3分）抛物线y=x2﹣4x+3的顶点坐标是．15．（3分）若一次函数y=kx+1（k为常数，k≠0）的图象经过第一、二、三象限，则k的取值范围是．16．（3分）同时掷两个质地均匀的骰子，观察向上一面的点数，两个骰子点数之和是9的概率为．17．（3分）如图为正三角形ABC与正方形DEFG的重叠情形，其中D、E两点分别在AB、BC上，且BD=BE．若AC=18，GF=6，则F点到AC的距离为．18．（3分）某同学遇到这样一个问题：已知在△ABC中，AB，BC，AC三边的长分别为、、，求△ABC的面积．他是这样解决问题的：如图1，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处）．从而借助网格就能计算出△ABC的面积．他把这种解决问题的方法称为构图法．请回答：（1）图1中△ABC的面积为；（2）图2是一个6×6的正方形网格（每个小正方形的边长为1）．利用构图法在图2中画出三边长分别为、2、的格点△DEF；（3）如图3，已知△PQR，以PQ、PR为边向外作正方形PQAF、PRDE，连EF．若PQ=2，PR=，QR=．则六边形AQRDEF的面积为．三、解答题（本大题共7小题，共66分。