第十七届“华罗庚金杯”少年数学邀请赛网上初赛试卷(小学中低年级组)

合集下载

第十七届华罗庚金杯少年数学邀请赛_试题及答案_小学高年级组

第十五届华罗庚金杯少年数学邀请赛初赛试卷（小学组）一、选择题（每小题10分，满分60分。

以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内。

）1．如图所示，平行四边形内有两个大小一样的正六边形，那么阴影部分的面积占平行四边形面积的（）。

2．两条纸带，较长的一条为23cm，较短的一条为15 cm。

把两条纸带剪下同样长的一段后，剩下的两条纸带中，要求较长的纸带的长度不少于较短的纸带长度的两倍，那么剪下的长度至少是（）cm。

（A）6 （B）7 （C）8 （D）93．两个水池内有金鱼若干条，数目相同。

亮亮和红红进行捞鱼比赛，第一个水池内的金鱼被捞完时，亮亮和红红所捞到的金鱼数目比是3：4；捞完第二个水池内的金鱼时，亮亮比第一次多捞33条，与红红捞到的金鱼数目比是5：3。

那么每个水池内有金鱼（）条。

（A）112 （B）168 （C）224 （D）3364．从中去掉两个数，使得剩下的三个数之和与最接近，去掉的两个数是（）。

5．恰有20个因数的最小自然数是（）。

（A）120 （B）240 （C）360 （D）4326．如图的大正方形格板是由81个1平方厘米的小正方形铺成，B，C是两个格点。

若请你在其它的格点中标出一点A，使得△ABC的面积恰等于3平方厘米，则这样的A点共有（）个。

（A）6 （B）5 （C）8 （D）107．算式的值为，则m+n 的值是。

8．“低碳生活”从现在做起，从我做起。

据测算，1公顷落叶阔叶林每年可吸收二氧化碳14吨。

如果每台空调制冷温度在国家提倡的26℃基础上调到27℃，相应每年减排二氧化碳21千克。

某市仅此项减排就相当于25000公顷落叶阔叶林全年吸收的二气化碳；若每个家庭按3台空调计，该市家庭约有万户。

（保留整数）9．从0、1、2、3、4、5、6、7、8、9这十个数字中，选出九个数字，组成一个两位数、一个三位数和一个四位数，使这三个数的和等于2010，那么其中未被选中的数字是。

2017“华杯赛”初赛试卷小中组试卷

第二十二届华罗庚金杯少年数学邀请赛初赛试卷（小学中年级组）第二十二届华罗庚金杯少年数学邀请赛初赛试卷（小学中年级组）一、选择题1.两个小三角形不重叠放置可以拼成一个大三角形, 那么这个大三角形不可能由（）拼成.（A）两个锐角三角形（B）两个直角三角形（C）两个钝角三角形（D）一个锐角三角形和一个钝角三角形2.从1至10这10个整数中, 至少取（）个数, 才能保证其中有两个数的和等于10.（A）4 （B）5 （C）6 （D）73.小明行李箱锁的密码是由两个数字8与5构成的三位数. 某次旅行, 小明忘记了密码, 他最少要试（）次, 才能确保打开箱子.（A）9（B）8（C）7（D）64.猎豹跑一步长为2米, 狐狸跑一步长为1米. 猎豹跑2步的时间狐狸跑3步.猎豹距离狐狸30米, 则猎豹跑动（）米可追上狐狸.（A）90（B）105（C）120（D）1355.图1中的八边形是将大长方形纸片剪去一个小长方形得到.则至少需要知道（）条线段的长度, 才可以计算出这个八边形的周长.（A）4（B）3（C）5 （D）10图1第二十二届华罗庚金杯少年数学邀请赛初赛试卷（小学中年级组）6.一个数串219, 从第4个数字开始, 每个数字都是前面3个数字和的个位数.下面有4个四位数：1113, 2226, 2125, 2215, 其中共有（）个不出现在该数串中.（A）1（B）2（C）3（D）4二、填空题(每小题 10 分, 满分40分.)7.计算=----1643842571000.8.已知动车的时速是普快的两倍, 动车的时速提高%25即达到高铁的时速, 高铁与普快的平均时速比特快快15千米/小时, 动车与普快的平均时速比特快慢10千米/小时, 则高铁和普快列车的时速分别是千米/小时和千米/小时.9.《火星救援》中, 马克不幸没有跟上其他5名航天员飞回地球, 独自留在了火星, 马克必须想办法生存, 等待救援. 马克的居住舱内留有每名航天员5天的食品和50千克的非饮用水, 还有一个足够大的菜园, 马克计划用来种植土豆, 30天后每平方米可以收获5.2千克,但是需要灌溉4千克的水.马克每天需要吃875.1千克土豆, 才可以维持生存, 则食品和土豆可供马克最多可以支撑天.10.图2五角星中, 位于顶点处的“华”、“罗”、“庚”、“金”、“杯”5个汉字分别代表1至5的数字, 不同的汉字代表不同的数字.每条线段两端点上的数字和恰为5个连续自然数.如果“杯”代表数字“1”, 则“华”代表的数字是或.奥数要从小学抓起,培养孩子的数学思维能力。

第十七届华罗庚金杯少年数学邀请赛答案及解析过程(初一网络版)

word 专业资料-可复制编辑-欢迎下载第十七届华罗庚金杯少年数学邀请赛初赛试卷（初一网络版）一、选择题1. A 解析：根据题意可知，a 、b 异号，且a 为正，b 为负；2. C 解析：根据题意可知：B+D=9，A+C=13，根据竖式加法原理可知X=1，Y=3，则X+Y=43. D 解析：划过的面积为底边长为6，高为CD 的平行四边形的面积和ABC ∆的面积之和，在ADB ∆ 中，由勾股定理知：，3452222=-=-=AD AB BD 则CD=3+6=9，6646215496=⨯⨯+=+⨯=∆ABC S S 4. B 解析：第一个正方形为—，第二个正方形为X ，第三个正方形为+，第四个正方形为÷5. C 解析：32%2.6%5%8==+⨯+⨯乙甲乙甲乙甲，解得m m m m m m ，现在所求表达式为：%5.6%10032%561%83241%100%561%841=⨯+⨯⨯+⨯⨯=⨯+⨯⨯+⨯⨯乙乙乙乙乙甲乙甲m m m m m m m m 6. B 解析：设最小的一个数为a,则最大的那个数为a+n-1,根据连续n 个数的和的公式可知：20122)1=-++n n a a （，化简可知：2)1(2012--=n n a ，又503222012⨯⨯=,且a,n 均为正数，因此，（n-1）必须为偶数，故n 只能为奇数，且必须为2012的约数，所以n=503。

二、填空题7. 2010 解析：[][]=⨯⨯⨯=+⨯=+⨯⨯=2013-2013201220132010-201020122013-12012201220132010-2-201220122013-2012201220132010-20122-201222222323）（）（）（原式[]201020131-2012201320101-201222=⨯⨯⨯）（）（ 8. 0 解析：本题通过取特殊值法解题，发现当时，0====d c b a 等式成立，故0=+++d c b a9. 77 解析：取AG 中点I,因为，27)166(21)(21=+⋅⨯=+⋅=∆IC GH AB IC S ACG 解得1127=IC ,由IH BI GH AB GHI ABI =∆∆相似得与,解得：83=IH BI ,又113911276=-=-=IC BC BI ,所以1110438113938=⨯=⨯=BI IH ,7112711104=-=-=IE IH CH ,77)166(721)(21=+⨯⨯=+⨯⨯=HG CD CH S DHGC 10. 12，解析：令,32,6-=+=m a m b 则要使原式为整数，即要ab 为整数即可，又152=-a b ，两边同时处以1152+=b a 得：,为使取值如下：与只能为奇数，为整数，则m a a b 15 则。

第十七届华罗庚金杯少年数学邀请赛小学高年级网络版答案及解析过程

第1 页/共 1页第十七届华罗庚金杯少年数学邀请赛小学高年级网络版初赛试卷一、选择题1. B 解析：因为)(C A +的值超过10，则9=+D B ,所以13=+C A 即31==Y X ，,所以4=+Y X 2. D 解析：32%2.6%5%8==+⨯+⨯乙甲乙甲乙甲，解得m m m m m m ，现在所求表达式为：%5.6%10032%561%83241%100%561%841=⨯+⨯⨯+⨯⨯=⨯+⨯⨯+⨯⨯乙乙乙乙乙甲乙甲m m m m m m m m 3. C 解析：能把100整除又能被20整除的数为20和100，则这两个数只能为20和100，两数的乘积为2000，两数都扩大10倍，则最大公约数扩大10倍，最小公倍数扩大10倍，两数的乘积此时扩大100倍，故（1）、（3）和（4）对。

4. C 解析：满足条件的数队排列如下：41,39,52,44,45,55,47；41,44,52,45,47,55,39;44,45,52,47,39,55,41,第四个数最大值为47.5. A 解析：数阴影部分所占的格子数量，数后发现，完整格子数为12，占半格子数为13，则转化为整格子数为18.5，那么一个格子代表的面积为：25.1837=÷，整个区域的面积为：80240=⨯空白区域的面积为：433780=-6. A 解析：是9的倍数的前提条件为各位上的数字之和必须为9的倍数，则满足要求的数分别为9，二、填空题7． 1 解析：满足要求的数为11118． 305 解析：填入符号后应为3051717171717=÷-+⨯9． 66 解析：划过的面积为底边长为6，高为CD 的平行四边形的面积和ABC ∆的面积之和，在ADB ∆ 中，由勾股定理知：，3452222=-=-=AD AB BD 则CD=3+6=9，6646215496=⨯⨯+=+⨯=∆ABC S S 10． 2040 解析：设甲的速度为x,乙的速度为y,10分钟后甲乙离O 点距离相等，则有,136,10101360y x y x -==-即40分钟后甲乙在B 点相遇，则32,13604040=-=-y x y x 即；联立两式得：51,85==y x ，则20405140=⨯=OB。

第十七届“华罗庚金杯”少年数学邀请赛网上初赛试卷(小学高年级组)

2012年第十七届“华罗庚金杯”少年数学邀请赛网上初赛试卷（小学高年级组）一、选择题（共6小题，每小题3分，满分18分）1．（3分）在如图所示的两位数的加法运算式中，已知A+B+C+D＝22，则X+Y ＝（）A．2 B．4 C．7 D．132．（3分）已知甲瓶盐水浓度为8%，乙瓶盐水浓度为5%，混合后浓度为6.2%，那么四分之一的甲瓶盐水与六分之一的乙瓶盐水混合后的浓度为（）A．7.5% B．5.5% C．6% D．6.5%3．（3分）两个数的最大公约数是20，最小公倍数是100，下面说法正确的有（）个．（1）两个数的乘积是2000．（2）两个数都扩大10倍，最大公约数扩大100倍．（3）两个数都扩大10倍，最小公倍数扩大10倍．（4）两个数都扩大10倍，两个数乘积扩大100倍．A．1 B．2 C．3 D．44．（3分）将39、41、44、45、47、52、55这7个数重新排成一列，使得其中任意相邻的三个数的和都为3的倍数．在所有这样的排列中，第四个数的最大值是（）A．44 B．45 C．47 D．525．（3分）如图所示，在5×8的方格中，阴影部分的面积为37cm2．则非阴影部分的面积为（）cm2．A．43 B．74 C．80 D．1116．（3分）在由1、3、4、7、9组成的没有重复数字的数中，是9的倍数的有（）个．A．1 B．2 C．3 D．4二、填空题（共4小题，每小题3分，满分12分）7．（3分）满足下列两个条件的四位数共有个．（1）任意相邻两位数字之和均不大于2；（2）任意相邻三位数字之和均不小于3．8．（3分）在17□17□17□17□17的四个□中填入“+”、“﹣”、“×”、“÷”运算符号各一个．所成的算式的最大值是．9．（3分）图中，ABC是一个钝三角形．BC＝6厘米，AB＝5厘米，BC边的高AD等于4厘米，若此三角形以每秒3厘米的速度沿DA的方向向上移动．2秒后，此三角形扫过的面积是平方厘米．10．（3分）一条公路上有A、O、B三个地点，O在A与B之间，A与O相距1360米．甲、乙两人同时分别从A点和O点出发向B点进行．出发后第10分钟，甲、乙两人离O点的距离相等：第40分钟甲与乙两人在B点相遇．那么O与B两点的距离是米．2012年第十七届“华罗庚金杯”少年数学邀请赛网上初赛试卷（小学高年级组）参考答案与试题解析一、选择题（共6小题，每小题3分，满分18分）1．（3分）在如图所示的两位数的加法运算式中，已知A+B+C+D＝22，则X+Y ＝（）A．2 B．4 C．7 D．13【分析】根据和的个位数字是9可得：B+D＝9，则A+C＝22﹣9＝13，所以可得x＝1，y＝3，据此即可求出x+y的值．【解答】解：根据题干分析可得：B+D＝9，则A+C＝22﹣9＝13，所以可得x＝1，y＝3，则x+y＝1+3＝4．故选：B．2．（3分）已知甲瓶盐水浓度为8%，乙瓶盐水浓度为5%，混合后浓度为6.2%，那么四分之一的甲瓶盐水与六分之一的乙瓶盐水混合后的浓度为（）A．7.5% B．5.5% C．6% D．6.5%【分析】我们分别设甲瓶盐水质量为a，乙瓶盐水的质量是b．根据它们混合后浓度为6.2%为等量关系求出ab之间的数量关系，然后再进一步求出四分之一的甲瓶盐水与六分之一的乙瓶盐水混合后的浓度．【解答】解：设甲瓶盐水质量为a，乙瓶盐水的质量是b．（8%a+5%b）÷（a+b）＝6.2%，解得：a＝b；（a×8%+b×5%）÷（a+b），＝（a+b）÷（b+b），＝（b b）÷（b），＝b×，＝6.5%；故选：D．3．（3分）两个数的最大公约数是20，最小公倍数是100，下面说法正确的有（）个．（1）两个数的乘积是2000．（2）两个数都扩大10倍，最大公约数扩大100倍．（3）两个数都扩大10倍，最小公倍数扩大10倍．（4）两个数都扩大10倍，两个数乘积扩大100倍．A．1 B．2 C．3 D．4【分析】根据“两个数的最大公约数是20，最小公倍数是100”，可知这两个数分别是20和100，据此逐项进行分析判断得解．【解答】解：根据题意，可知这两个数分别是20和100；（1）20×100＝2000，所以两个数的乘积是2000，所以原说法正确的；（2）两个数都扩大10倍，最大公约数变为20×10＝200，是扩大了10倍，所以原说法错误；（3）两个数都扩大10倍，最小公倍数变为100×10＝1000，是扩大了10倍，所以原说法正确；（4）两个数都扩大10倍，变为200和1000，乘积变为200000，也即两个数乘积扩大100倍，所以原说法正确；正确的说法有3个．故选：C．4．（3分）将39、41、44、45、47、52、55这7个数重新排成一列，使得其中任意相邻的三个数的和都为3的倍数．在所有这样的排列中，第四个数的最大值是（）A．44 B．45 C．47 D．52【分析】将给出的每个数分别除以3，余数分别是：0、2、2、0、2、1、1；把余数排列，相邻三个数的和都为3，则重新排列为：2、1、0、2、1、0、2；因为第四个数是2，余数为2的最大的数是47．【解答】解：因为39÷3＝13，41÷3＝13…2，44÷3＝14…2，45÷3＝15，47÷3＝15…2，52÷3＝17…1，55÷3＝18…1，余数分别是：0、2、2、0、2、1、1；按相邻三个数的和都为3，把余数重新排列为：2、1、0、2、1、0、2；因为第四个数是2，余数为2的最大的数是47．故选：C．5．（3分）如图所示，在5×8的方格中，阴影部分的面积为37cm2．则非阴影部分的面积为（）cm2．A．43 B．74 C．80 D．111【分析】如图所示，在5×8的方格中，阴影部分占了18.5个格，非阴影就分占21.5格；阴影面积为37cm2，据此可求出每格的面积，进而求出则非阴影部分的面积．【解答】解：如图，阴影部分占了18.5个格，面积为37cm2，每格的面积是：37÷18.5＝2（cm2）；非阴影就分占21.5格，其面积是：21.5×2＝43（cm2）；答：则非阴影部分的面积为43cm2；故选：A．6．（3分）在由1、3、4、7、9组成的没有重复数字的数中，是9的倍数的有（）个．A．1 B．2 C．3 D．4【分析】一个数如果能被9整除那么这个数的各位数字和必须能被9整除，由此选择数字解答即可．【解答】解：如果能被9整除，那么这个数的各位数字和必须能被9整除，这样的组合可能是由一个数字9组成数是9，这样共有1种．故选：A．二、填空题（共4小题，每小题3分，满分12分）7．（3分）满足下列两个条件的四位数共有 1 个．（1）任意相邻两位数字之和均不大于2；（2）任意相邻三位数字之和均不小于3．【分析】由（1）可知，这个四位数每个数位上的数字只能是0，1，2，并且1与2，2与2不能相邻，再结合（2）可知，每个数位上的数字不能是0．综上可知每个数位上的数字只能是1，即这个四位数是1111．【解答】解：由分析可知，满足条件的四位数是1111，只有1个．故答案为：1．8．（3分）在17□17□17□17□17的四个□中填入“+”、“﹣”、“×”、“÷”运算符号各一个．所成的算式的最大值是305 ．【分析】题目要求只填运算符号，不加括号；那么运算顺序是先算乘除，再算加减，要使运算的结果最大只要减的数最小即可．【解答】解：因为减号只能用一次，减数不能为0，那么17÷17＝1做减数时，运算的结果最大：17×17+17﹣17÷17，＝289+17﹣1，＝305．故答案为：305．9．（3分）图中，ABC是一个钝三角形．BC＝6厘米，AB＝5厘米，BC边的高AD等于4厘米，若此三角形以每秒3厘米的速度沿DA的方向向上移动．2秒后，此三角形扫过的面积是66 平方厘米．【分析】平移时图形的每个点都在移动及整个图形沿同一方向移动同样的距离，将三角形以每秒3厘米的速度沿高的方向向上移动2秒，就是沿高的方向移动了3×2＝6cm，三角形扫过的面积应该是一个正方形的面积加上一个三角形的面积，再加上平行四边形ABFE的面积．【解答】解：扫过的面积应该是正方形BCDF的面积加上上面三角形的面积，再加上平行四边形ABFE的面积，因为AD＝4，AB＝5，且AB2﹣AD2＝BD2，即52﹣42＝32，所以DB＝3厘米，3×2＝6厘米，6×6+×6×4÷2+6×3，＝36+12+18，＝66（平方厘米）．答：此三角形扫过的面积是66平方厘米．故答案为：66．10．（3分）一条公路上有A、O、B三个地点，O在A与B之间，A与O相距1360米．甲、乙两人同时分别从A点和O点出发向B点进行．出发后第10分钟，甲、乙两人离O点的距离相等：第40分钟甲与乙两人在B点相遇．那么O与B两点的距离是2040 米．【分析】第40分钟甲与乙两人在B点相遇，即此时甲行了1360米，则甲的速度为每分钟1360÷40米，所以10分钟甲行了1360÷40×10＝340米，距0点1360﹣340＝1020米，又出发后第10分钟，甲、乙两人离O点的距离相等，则乙每分钟行1020÷10＝102米．由于第第40分钟甲与乙两人在B点相遇，此时乙行了2个0B，则O与B两点的距离是 102×40÷2米．【解答】解：（1360﹣1360÷40×10）÷10×40÷2＝（1360﹣340）÷10×40÷2，＝1020×40÷2，＝2040（米）．答：O与B两点的距离是 2040米．故答案为：2040．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2019/5/7 10:56:04；用户：小学奥数；邮箱：pfpxxx02@；学号：20913800。

第十七届华罗庚金杯少年数学邀请赛网上初赛试卷-中年级组.docx

第十七届华罗庚金杯少年数学邀请赛网上初赛试卷（小学中年级组）一、选择题（每小题10分，以下每题的四个选项中，仅有一个是正确的，请单击选择答案） 1•如图，适中上的表针从（1）转到（2）最少经过了（）A 、2小时30分B 、2小时45分C 、3小时30分D 、3小时45分【分析】：考点：钟表问题难度：★★ 解：表（1）显示的是12:45分，表（2）显示的是3： 30也可以表示为15:30分，两个表同表示为下午的时间就是最近的。

15:30-22:45=2:45分答案：[B]2.在2012年，1月1日是星期口，并且（）【分析】: 考点：周期问题难度：★★★ 解：1月有31天，所以前三天所表示的星期数会出现5次，其它的出现4次，而1月份前三天分别是星期日、一、二。

所以星期三只有4个。

这样1月最后一天就是星期二，而2 月第一天是星期三。

注意到2012年是闰年，2月份有29天。

所以，2月份的第一天表示的星期数回出现5次。

所以2月份有4个星期三，2月份有5个星期三。

答案：[D]3•有大小不同的4个数,从中任取3个数相加,所得到的和分别是180,197,208和222,那么，第二小的数所在的和一定不是（）A 、 180B 、 197C 、 208D 、 222【分析】：考点：推理难度：★★ 解：因为是三个数的和，所以可以看做是4个数的总和减去其中的一个。

那么和减去最小的数一定是最大的222。

减去第二小的一定是第二大的，即208答案：[C]4.四百米比赛进入冲刺阶段，甲在乙前面30米，丙在丁后面60米，乙在丙前而20米，这时，跑在最前面的两位同学相差（）米 A 、 10 B 、 20 C 、 50 D 、60A 、 1月份有5个星期三,B 、 1月份有5个星期三,C 、 1月份有4个星期三,D 、 1月份有4个星期三, 2月份只有4个星期三 2月份也有5个星期三 2月份也有4个星期三 2月份有5个星期三【分析】：考点：推理问题难度：★★解：先根据中乙芮的位置关系容易得到下图內刼乙30 S 10 T所以，前两名甲与丁的距离是10米。

第17届“华杯赛”网上决赛试题以及答案(小中组)

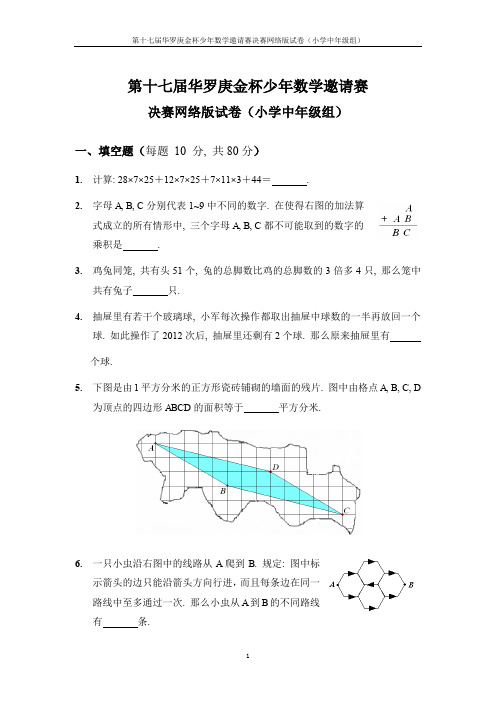
3. 鸡兔同笼, 共有头 51 个, 兔的总脚数比鸡的总脚数的 3 倍多 4 只, 那么笼中共有兔子只.
4. 抽屉里有若干个玻璃球, 小军每次操作都取出抽屉中球数的一半再放回一个球. 如此操作了 2012 次后, 抽屉里还剩有 2 个球. 那么原来抽屉里有个球. 5. 下图是由 1 平方分米的正方形瓷砖铺砌的墙面的残片. 图中由格点 A, B, C, D 为顶点的四边形 ABCD 的面积等于平方分米.
6. 一只小虫沿右图中的线路从 A 爬到 B. 规定: 图中标示箭头的边只能沿箭头方向行进，而且每条边在同一路线中至多通过一次. 那么小虫从 A 到 B 的不同路线有条.
1
第十七届华罗庚金杯少年数学邀请赛决赛网络版试卷（小学中年级组）
7. 有一些自然数，它们中的每一个与 7 相乘, 其积的末尾四位数都为 2012, 那么在这些自然数中, 最小的数是 .
8. 将棱长为 1 米的正方体木块分割成棱长为 1 厘米的小正方体积木, 设想孙悟空施展神力将所有的小积木一个接一个地叠放起来, 成为一根长方体 “神棒”, 直指蓝天. 已知珠穆朗玛峰的海拔高度为 8844 米, 则“神棒”的高度超过珠穆朗玛峰的海拔高度米.
二、回答下列各题（每题 10 分, 共 40 分, 写出答案即可）
第十七届华罗庚金杯少年数学邀请赛决赛网络版试卷（小学中年级组）
第十届华罗庚金杯少年数学邀请赛
决赛网络版试卷（小学中年级组）
一、填空题（每题 10 分, 共 80 分）
1. 计算: 28× 7× 25＋12× 7× 25＋7× 11× 3＋44＝ .
2. 字母 A, B, C 分别代表 1~9 中不同的数字. 在使得右图的加法算式成立的所有情形中, 三个字母 A, B, C 都不可能取到的数字的乘积是 .

第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷(小中组)

2012年第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷（小中组）一、填空题（每题10分，共80分）1．（10分）计算：28×7×25+12×7×25+7×11×3+44＝．2．（10分）字母 A，B，C 分别代表 1～9 中不同的数字．在使得如图的加法算式成立的所有情形中，三个字母 A，B，C 都不可能取到的数字的乘积是．3．（10分）鸡兔同笼，共有头51个，兔的总脚数比鸡的总脚数的3倍多4只，那么笼中共有兔子只．4．（10分）抽屉里有若干个玻璃球，小军每次操作都取出抽屉中球数的一半再放回一个球．如此操作了2012次后，抽屉里还剩有2个球．那么原来抽屉里有个球．5．（10分）如图是由1平方分米的正方形瓷砖铺砌的墙面的残片．问：图中由格点 A，B，C，D 为顶点的四边形ABCD的面积等于多少平方分米？6．（10分）一只小虫沿如图中的线路从A爬到B．规定：图中标示箭头的边只能沿箭头方向行进，而且每条边在同一路线中至多通过一次．问：小虫从A到B的不同路线有多少条？7．（10分）有一些自然数，它们中的每一个与7相乘，其积的末尾四位数都为2012，那么在这些自然数中，最小的数是．8．（10分）将棱长为1米的正方体木块分割成棱长为1厘米的小正方体积木，设想孙悟空施展神力将所有的小积木一个接一个地叠放起来，成为一根长方体“神棒”，直指蓝天．已知珠穆朗玛峰的海拔高度为8844米，则“神棒”的高度超过珠穆朗玛峰的海拔高度米．二、回答下列各题（每题10分，共40分，写出答案即可）9．（10分）已知被除数比除数大78，并且商是 6，余数是 3，求被除数与除数之积．10．（10分）今年甲、乙俩人年龄的和是70岁．若干年前，当甲的年龄只有乙现在这么大时，乙的年龄恰好是甲年龄的一半．问：甲今年多少岁？11．（10分）有三个连续偶数，它们的乘积是一个五位数，该五位数个位是0，万位是2，十位、百位和千位是三个不同的数字，那么这三个连续偶数的和是多少？12．（10分）在等式“爱国×创新×包容+厚德＝北京精神”中，每个汉字代表 0～9 的一个数字，爱、国、创、新、包、容、厚、德分别代表不同的数字．当四位数北京精神最大时，厚德为多少？2012年第十七届“华罗庚金杯”少年数学邀请赛网试决赛试卷（小中组）参考答案与试题解析一、填空题（每题10分，共80分）1．（10分）计算：28×7×25+12×7×25+7×11×3+44＝7275 ．【分析】根据乘法的结合律与分配律简算即可，注意计算中的11×25的乘法时根据“两边拉，中间加”巧算．【解答】解：28×7×25+12×7×25+7×11×3+44＝7×25×（28+12）+11×21+11×4＝7×（25×40）+11×（21+4）＝7×1000+11×25＝7000+275＝7275故答案为：7275．2．（10分）字母 A，B，C 分别代表 1～9 中不同的数字．在使得如图的加法算式成立的所有情形中，三个字母 A，B，C 都不可能取到的数字的乘积是8 ．【分析】首先分析出A是加上进位等于B，那么A比B小1，并且A与B 的和是有..进位的，枚举出所有情况排除即可．【解答】解：依题意可知：A加上进位等于B，那么这两个数字相差1，可以是A＝5，B＝6，C＝1．A＝6，B＝7，C＝3．A＝7，B＝8，C＝5．A＝8，B＝9，C＝7．那么A，B，C不可能取道的数字有2，4即2×4＝8故答案为：83．（10分）鸡兔同笼，共有头51个，兔的总脚数比鸡的总脚数的3倍多4只，那么笼中共有兔子31 只．【分析】根据题意可知如果少一只兔子，则兔的总脚数是鸡的总脚数的3倍，因一只兔脚的只数是一只鸡脚只数的4÷2＝2倍，所以当兔的只数是鸡的只数的3÷2＝1.5倍时兔的总脚数是鸡的总脚数的3倍，据此可只鸡的头数是（51﹣1）÷（1.5+1）＝20只，进而可求出兔子的只数．【解答】解：4÷2＝2（51﹣1）÷（3÷2+1）＝50÷2.5＝20（只）51﹣20＝31（只）答：笼子中共有兔子31只．故答案为：31．4．（10分）抽屉里有若干个玻璃球，小军每次操作都取出抽屉中球数的一半再放回一个球．如此操作了2012次后，抽屉里还剩有2个球．那么原来抽屉里有 2 个球．【分析】还原问题每次拿走一半再放回一个，倒推就是每次拿走一个再加一倍．2个拿走1个，剩下1个加一倍是2个．重复周期问题．【解答】解：还原问题的倒推图操作第一次：（2﹣1）×2＝2（个）操作第二次：（2﹣1）×2＝2（个）操作第三次：（2﹣1）×2＝2（个）每一次结果都是2个，属于周期问题．无论操作多少次结果都是2个．故答案为：25．（10分）如图是由1平方分米的正方形瓷砖铺砌的墙面的残片．问：图中由格点 A，B，C，D 为顶点的四边形ABCD的面积等于多少平方分米？【分析】这属于正方形格点问题，根据正方形格点毕克定理S＝N﹣1+L÷2可以直接求出面积，其中N表示内部的格点数，L表示边界上的格点数．【解答】解：内部的格点数是12，边界点的数是6，根据公式列出算式是12﹣1+6÷2＝14答：四边形ABCD的面积等于14平方分米．6．（10分）一只小虫沿如图中的线路从A爬到B．规定：图中标示箭头的边只能沿箭头方向行进，而且每条边在同一路线中至多通过一次．问：小虫从A到B的不同路线有多少条？【分析】小虫从A到B，第一个六边形的分叉口上下均有2条，B所在的六边形也上下有2条，于是有2×2+2×2＝8条，中间往回走的箭头有2条路线，一共有10条．【解答】解：小虫从A到B，第一个六边形的分叉口上下均有2条，B所在的六边形也上下有2条，于是有2×2+2×2＝8条，中间往回走的箭头有2条路线，一共有10条．答：小虫从A到B的不同路线有10条．7．（10分）有一些自然数，它们中的每一个与7相乘，其积的末尾四位数都为2012，那么在这些自然数中，最小的数是1716 ．【分析】首先分析本题可以反过来求解，想找到最小的乘数可以转换找到最小的乘积，2012不是7的倍数，那么需要在前面加上一位数字是最小的即可．【解答】解：首先发现2012不是7的倍数，那么要找到最小就需要看看在2012前加一个最小的数字组成7的倍数．在首位加上数字1，12012÷7＝1716．那么最小就是1716．故答案为：1716．8．（10分）将棱长为1米的正方体木块分割成棱长为1厘米的小正方体积木，设想孙悟空施展神力将所有的小积木一个接一个地叠放起来，成为一根长方体“神棒”，直指蓝天．已知珠穆朗玛峰的海拔高度为8844米，则“神棒”的高度超过珠穆朗玛峰的海拔高度1156 米．【分析】1米＝100厘米，则1立方米＝1000000立方厘米，即1 米的正方体木块分割成棱长为 1 厘米的小正方体积1000000个，即可求解．【解答】解：1立方米＝1000000立方厘米，即1米的正方体木块分割成棱长为1厘米的小正方体积1000000个；它们相互叠加组成“神棒”的高度＝1000000×0.01＝10000（米）；即比珠穆朗玛峰的海拔高度高10000﹣8848＝1156（米），故填1156．故答案为：1156．二、回答下列各题（每题10分，共40分，写出答案即可）9．（10分）已知被除数比除数大78，并且商是 6，余数是 3，求被除数与除数之积．【分析】被除数＝除数×商+余数，所以被除数是除数的6倍多3，78就是除数的5倍多3．【解答】解：除数＝（78﹣3）÷（6﹣1）＝25，被除数＝除数×商+余数＝6×25+3＝153，那么被除数与除数之积是153×25＝3825．故答案为：3825．10．（10分）今年甲、乙俩人年龄的和是70岁．若干年前，当甲的年龄只有乙现在这么大时，乙的年龄恰好是甲年龄的一半．问：甲今年多少岁？【分析】根据题意，可得：若干年前乙的年龄等于今年乙的年龄的一半，所以今年甲的年龄等于若干年前甲的年龄的1.5（1+0.5＝1.5）倍，所以今年甲的年龄等于今年乙的年龄的1.5倍，再根据今年甲、乙两人年龄的和是70岁．求出甲今年多少岁即可．【解答】解：因为当甲的年龄只有乙现在这么大时，乙的年龄恰好是甲年龄的一半，所以今年甲的年龄等于若干年前甲的年龄的：1+0.5＝1.5倍，所以今年甲的年龄等于今年乙的年龄的1.5倍，70÷（1+1.5）×1.5＝70÷2.5×1.5＝28×1.5＝42（岁）答：甲今年42岁．11．（10分）有三个连续偶数，它们的乘积是一个五位数，该五位数个位是0，万位是2，十位、百位和千位是三个不同的数字，那么这三个连续偶数的和是多少？【分析】26×26×26＝17576，31×31×31＝29791，所以三个连续偶数在24，26，28，30，32之间，考虑个位为0，应有因数2，5．【解答】解：26×26×26＝17576，31×31×31＝29791，所以三个连续偶数在24，26，28，30，32之间，考虑个位为0，应有因数2，5，26×28×30＝21840，符合要求．28×30×32＝26880，不合要求，30×32×34＝32640，不符合要求．所以这三个连续偶数的和为26+28+30＝84．故答案为：84．12．（10分）在等式“爱国×创新×包容+厚德＝北京精神”中，每个汉字代表 0～9 的一个数字，爱、国、创、新、包、容、厚、德分别代表不同的数字．当四位数北京精神最大时，厚德为多少？【分析】由题意，14×20×35+98＝9898，即可得出结论．【解答】解：由题意，14×20×35+98＝9898，∴当四位数北京精神最大时，厚德为98．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2019/5/7 10:49:20；用户：小学奥数；邮箱：pfpxxx02@；学号：20913800。

第十七届华罗庚金杯少年数学邀请赛网上初赛(小学高年级组)试题

（C）80
（D）111
第6题（选择题）：
（A）1
（B）2
（C）3
（D）4
第7题（填空题）：ຫໍສະໝຸດ 请输入答案：第8题（填空题）：
请输入答案：
第9题（填空题）：
请输入答案：
第10题（填空题）：
请输入答案：
重要提示:
答案交卷之前都可以修改，答题完毕必须点击交卷按钮。考生必须在规定的时间内完成考试。开考时间没到，选手无法进入考试程序；交卷时间一到，选手不可以再继续答题。答题完成之后必须点击交卷按钮提交答案。
第十七届华罗庚金杯少年数学邀请赛网上初赛
(
第1题（选择题）：
（A）2
（B）4
（C）7
（D）9
第2题（选择题）：
（A）7.5%
（B）5.5%
（C）6%
（D）6.5%
第3题（选择题）：
（A）1
（B）2
（C）3
（D）4
第4题（选择题）：
（A）44
（B）45
（C）47
（D）52
第5题（选择题）：
（A）43
（B）74

2012第十七届华杯赛决赛笔试(小学高年级组三份试卷ABC全部)试题及答案

三、解答下列各题（每小题 15 分，共 30 分，要求写出详细过程）
13. 请写出所有满足下面三个条件的正整数 a 和 b: 1) a ≤ b ; 2) a + b 是个三位数 , 且三个数字从小到大排列等差 ; 3) a × b 是一个五位数 , 且五个数字相同. 14. 记一百个自然数 x, x + 1, x + 2, , x + 99 的和为 a, 如果 a 的数字和等于 50, 则 x 最小为多少?
N 被 3 除的余数是多少？ 11. 王大妈拿了一袋硬币去银行兑换纸币 , 袋中有一分、二分、五分和一角四种硬币 , 二分硬币的枚数是一分的的枚数是五分的
3 3 , 五分硬币的枚数是二分的 , 一角硬币 5 5
3 少 7 枚. 王大妈兑换到的纸币恰好是大于 50 小于 100 的 5 整元数. 问这四种硬币各有多少枚?
4. 甲、乙两个粮库原来各存有整袋的粮食, 如果从甲粮库调 90 袋到乙粮库, 则乙粮库存粮的袋数是甲粮库的 2 倍．如果从乙粮库调若干袋到甲粮库 , 则甲粮库存粮的袋数是乙粮库的 6 倍．那么甲粮库原来最少存有袋的粮食 .
5. 现有 211 名同学和四种不同的巧克力, 每种巧克力的数量都超过 633 颗. 规定每名同学最多拿三颗巧克力 , 也可以不拿. 若按照所拿巧克力的种类和数量都是否相同分组 , 则人数最多的一组至少有名同学 .
边长都为
7. 一条路上有 A, O, B 三个地点, O 在 A 与 B 之间, A 与 O 相距 1620 米. 甲、乙两人同时分别从 A 和 O 点出发向 B 点行进. 出发后第 12 分钟, 甲、乙两人离 O 点的距离相等；第 36 分钟甲与乙两人在 B 点相遇 . 那么 O 与 B 两点的距离是 8. 从 1 到 1000 中最多可以选出和. 米.

第十七届华罗庚金杯少年数学邀请赛初赛试卷小学中年级组

第十七届华罗庚金杯少年数学邀请赛初赛试卷（小学中年级组笔试版）〔吋间:2012年3月17日10:00-11:00 〕一、选择题（每小题10分.以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内）1.在右面的加法算式中，每个汉字代表一个非零数字，不同的汉字代表不同的数字.当算式成立吋，贺＋新＋春＝（）.（A）24 〔B〕22 (C) 20 (D) 182.北京吋间16吋，小龙从镜子里看到挂在身后墙上的4个钟表(如下图)，其中最接近16吋的是〔〕.3.平面上有四个点，任意三个点都不在-条直线上.以这四个点为端点连接六条线段，在所组成的图形中，最少可以形成（）个三角形.(A）3 （B）4 (C) 6 (D) 84.在10口10口10口10口10的四个口中填入“＋”“－”“×”“÷”运算符号各一个，所成的算式的最大值是〔〕.（A）104 〔B〕109 (C) 114 (D) 1195.牧羊人用15段每段长2米的篱笆，一面靠墙围成一个正方形或长方形羊圈，则羊圈的最大面积是〔〕平方米.（A）100 〔B〕108 (C) 112 (D) 1226.小虎在19x19的围棋盘的格点上摆棋子，先摆成了一个长方形的实心点阵.然后再加上45枚棋子，就正好摆成-边不变的较大的长方形的实心点阵.那么小虎最多用了〔〕枚棋子.(A)285 〔B〕171 (C) 95 (D)57二、填空题(每小题10分，满分40分）7.三堆小球共有2012颗，如杲从每堆取走相同数目的小球贩笫二堆还剩下17颗小球，并且笫一堆剩下的小球数是笫三堆剩下的2倍，那么笫三堆原有______颗小球.8.右图的计数器三个档上各有10个算珠，将每档算珠分成上下两部分，技数位得到两个三位数，要求上面的三位数的数字不同，且是下面三位数的倍数，那么满足题意的上面的三位数是________.9.把一块长90厘米，宽42厘米的长方形纸板恰无剩余地剪成边长都是整数厘米、面积都相等的小正方形纸片，最少能剪出_____块，这种剪法剪成的所有正方形纸片的周长之和是_______厘米.10.体育馆正在进行乒乓球单打、双打比赛，双打比赛的运动员比单打的运动员多4名，比赛的乒乓球台共有13张，那么双打比赛的运动员有________名.第十七届全国华罗庚金杯少年数学邀请赛初赛试题（小学中年级组笔试版）答案―、选择题（每小题10分，满分60分）二、填空理（每小题10分，满分40分）。

2012第十七届华罗庚金杯少年数学邀请赛决赛网络版试题与详细解答(小学高年级组)

其中 ⎜
1 ⎞ 1 ⎞ ⎛1 1 1 ⎛1 1 1 + + + … + ⎟ 的整数部分小于 1，且 5 × ⎜ + + + … + ⎟ < 4 ， 20 ⎠ 20 ⎠ ⎝ 11 12 13 ⎝ 11 12 13
因此原式的整数部分为 46 6. 把 CE 和 DA 延长相交于点 H，则 AH=BC，
1 1 FC = BC = DH ， 3 6
⎛ 10 11 12 13 14 15 16 17 18 19 ⎞ 原式 = 5 × ⎜ + + + + + + + + + ⎟ ⎝ 11 12 13 14 15 16 17 18 19 20 ⎠ 1 1 1 ⎞ ⎛ = 5 × ⎜1 − + 1 − + … + 1 − ⎟ 12 20 ⎠ ⎝ 11 ⎡ 1 ⎞⎤ ⎛1 1 1 = 5 × ⎢10 − ⎜ + + + … + ⎟⎥ 20 ⎠⎦ ⎝ 11 12 13 ⎣ 1 ⎞ ⎛1 1 1 = 50 - 5 × ⎜ + + + … + ⎟ 20 ⎠ ⎝ 11 12 13
所以
S ∆GFC FG FC 1 = = = ， S ∆DGC DG DH 6
6 6 1 1 S ∆DFC = × × S ABCD = 120 7 7 3 2
S ∆DGC =
于是
S ADGE = S ABCD − S ∆BEC − S ∆DGC = 840 − 210 − 120 = 510
7. 三位数的回文数一共有 90 个，如下图
3. 设 B 龙头放水的效率为 x ，则 A 龙头的工作效率为剩下的工作总量为 1 -

2012年第十七届“华罗庚金杯”奥数初赛试卷（小学中低年级组）

2012年第十七届“华罗庚金杯”少年数学邀请赛网上初赛试卷（小学中低年级组）一、选择题（共6小题,每小题3分,满分18分）1．（3分）如图,时钟上的针从（1）转到（2）最少经过了（）A．2小时30分B．2小时45分C．3小时50分D．3小时45分2．（3分）在2012年,1月1日是星期日,并且（）A．1月份有5个星期三,2月份只有4个星期三B．1月份有5个星期三,2月份也有5个星期三C．1月份有4个星期三,2月份也有4个星期三D．1月份有4个星期三,2月份有5个星期三3．（3分）有大小不同的4个数,从中任取3个数相加,所得到的和分别是180、197、208和222．那么,第二小的数所在的和一定不是（）A．180B．197C．208D．2224．（3分）四百米比赛进入冲刺阶段,甲在乙前面30米,丙在丁后面60米,乙在丙前面20米．这时,跑在前面的两位同学相差（）米．A．10B．20C．50D．605．（3分）在如图所示的两位数的加法运算式中,已知A+B+C+D＝22,则X+Y＝（）A．2B．4C．7D．136．（3分）小明在正方形的边上标出若干个点,每条边上恰有3个,那么所标出的点最少有（）个．A．12B．10C．8D．6二、填空题（共4小题,每小题3分,满分12分）7．（3分）如图,用一条线段把一个周长是30cm的长方形分割成一个正方形和一个小的长方形．如果小长方形的周长是16cm,则原来长方形的面积是 cm2．8．（3分）将10、15、20、30、40和60填入图中的圆圈中,使A,B,C三个小三角形顶点上的3个数的积都相等．那么相等的积最大为．9．（3分）用3,5,6,18,23这五个数组成一个四则运算式,得到的结果是最小的非零自然数, ．（要求列出该算式）10．（3分）里山镇到省城的高速路全长189千米,途径县城．县城离里山镇54千米．早上8：30一辆客车从里山镇开往县城,9：15到达．停留15分钟后开往省城,午前11：00能够到达．另有一辆客车于当日早上9：00从省城径直开往里山镇．每小时行驶60千米．两车相遇时,省城开往里山镇的客车行驶了分钟．2012年第十七届“华罗庚金杯”少年数学邀请赛网上初赛试卷（小学中低年级组）参考答案与试题解析一、选择题（共6小题,每小题3分,满分18分）1．（3分）如图,时钟上的针从（1）转到（2）最少经过了（）A．2小时30分B．2小时45分C．3小时50分D．3小时45分【分析】先分别得到时钟上的表针的两个时刻,再用结束的时刻﹣开始的时刻即为中间的时间．【解答】解：表针（1）的时刻是0时45分,表针（2）的时刻是3时30分,最少经过的时间为：3时30分﹣0时45分＝2小时45分．答：时钟上的秒针从（1）转到（2）最少经过了2小时45分．故选：B．2．（3分）在2012年,1月1日是星期日,并且（）A．1月份有5个星期三,2月份只有4个星期三B．1月份有5个星期三,2月份也有5个星期三C．1月份有4个星期三,2月份也有4个星期三D．1月份有4个星期三,2月份有5个星期三【分析】先分别推算出2012年1月,2012年2月的天数,然后用经过的天数除以7,求出一共是几周,还余几天,然后根据余数判断．【解答】解：因为2012年1月有31天,2月有29天,31÷7＝4（星期）…3（天）,29÷7＝4（星期）…1（天）,所以1月份有4个星期三,2月份有5个星期三．故选：D．3．（3分）有大小不同的4个数,从中任取3个数相加,所得到的和分别是180、197、208和222．那么,第二小的数所在的和一定不是（）A．180B．197C．208D．222【分析】设这四个不同的数分别为a,b,c,d．由题意可知,（a+b+c）+（a+c+d）+（b+c+d）+（a+b+d）＝3（a+b+c+d）＝180+197+208+222＝807,则a+b+c+d＝269．由此能求出第二小的数不在的和是哪个．【解答】解：设这四个不同的数分别为a,b,c,d．则（a+b+c）+（a+c+d）+（b+c+d）+（a+b+d）＝3（a+b+c+d）,＝180+197+208+222,＝807;所以,a+b+c+d＝807÷3＝269．因此最小数应为：269﹣222＝47,第二小的数为：269﹣208＝61．即第二小的数所在的和一定不是208．故选：C．4．（3分）四百米比赛进入冲刺阶段,甲在乙前面30米,丙在丁后面60米,乙在丙前面20米．这时,跑在前面的两位同学相差（）米．A．10B．20C．50D．60【分析】根据题意画出线段图如下：跑在前面的两位同学是丁和甲,相差60﹣20﹣30＝10米．【解答】解：由分析得出：跑在前面的两位同学是丁和甲,相差60﹣20﹣30＝10（米）．答：跑在前面的两位同学相差10米;故选：A．5．（3分）在如图所示的两位数的加法运算式中,已知A+B+C+D＝22,则X+Y＝（）A．2B．4C．7D．13【分析】根据和的个位数字是9可得：B+D＝9,则A+C＝22﹣9＝13,所以可得x＝1,y＝3,据此即可求出x+y的值．【解答】解：根据题干分析可得：B+D＝9,则A+C＝22﹣9＝13,所以可得x＝1,y＝3,则x+y＝1+3＝4．故选：B．6．（3分）小明在正方形的边上标出若干个点,每条边上恰有3个,那么所标出的点最少有（）个．A．12B．10C．8D．6【分析】要使每条边上所标出的点最少,则正方形的四个顶点处都要标点,由此利用正方形的四周点数＝每边点数×4﹣4即可求出最少标出的点数．【解答】解：3×4﹣4,＝12﹣4,＝8（个）,答：标出的点最少有8个．故选：C．二、填空题（共4小题,每小题3分,满分12分）7．（3分）如图,用一条线段把一个周长是30cm的长方形分割成一个正方形和一个小的长方形．如果小长方形的周长是16cm,则原来长方形的面积是　56　cm2．【分析】由大长方形到小长方形周长减少了：30﹣16＝14（厘米）,相当于减少了两条正方形的边长,所以正方形的边长是：14÷2＝7（厘米）,也就是原来长方形的宽是7厘米;那么原来长方形的长为：16÷2﹣7+7＝8（厘米）,面积是：8×7＝56cm2．【解答】解：根据分析可得,30﹣16＝14（厘米）,正方形的边长：14÷2＝7（厘米）,原来长方形长：16÷2﹣7+7＝8（厘米）,面积：8×7＝56（平方厘米）;答：原来长方形的面积是56cm2．故答案为：56．8．（3分）将10、15、20、30、40和60填入图中的圆圈中,使A,B,C三个小三角形顶点上的3个数的积都相等．那么相等的积最大为　18000　．【分析】设A,B,C三个小三角形顶点上的3个数的积是S,那么中间3个数被计算了两次,设这三个数的积是d,则（10×15×20×30×40×60）×d＝S3,把每个因数分解质因数即29×56×33×d＝S3,由于29、56、33都是立方数,所以d也应是立方数,由于要使积d最大,必须有60这个因数,60＝22×3×5,要使d是立方数,还需要1个2、2个3、2个5,即2×32×52＝15×30,由此,可知d＝60×15×30,经过调整可得A,B,C三个小三角形顶点上的3个数的积是：60×20×15＝60×30×10＝15×30×40＝18000;据此解答．【解答】解：根据分析可得,设A,B,C三个小三角形顶点上的3个数的积是S,那么中间3个数被计算了两次,设这三个数的积是d,则（10×15×20×30×40×60）×d＝S3,29×56×33×d＝S3,由于29、56、33都是立方数,所以d也应是立方数,由于要使积d最大,必须有60这个因数,60＝22×3×5,要使d是立方数,还需要1个2、2个3、2个5,即2×32×52＝15×30,由此,可知d＝60×15×30,经过调整可得A,B,C三个小三角形顶点上的3个数的积是：60×20×15＝60×30×10＝15×30×40＝18000;．9．（3分）用3,5,6,18,23这五个数组成一个四则运算式,得到的结果是最小的非零自然数,　23﹣18+5﹣6﹣3或（23﹣3）÷5﹣18÷6　．（要求列出该算式）【分析】最小的非零自然数是1,看能否算出1,转化为跟算24类似的问题;化繁为简,先用最大的二个数相减：23﹣18＝5;进一步转化为3,5,6,5四个数要算出来是1即可．【解答】解：由分析可得：23﹣18+5﹣6﹣3＝1;或：（23﹣3）÷5﹣18÷6＝1．故答案为：23﹣18+5﹣6﹣3或（23﹣3）÷5﹣18÷6．10．（3分）里山镇到省城的高速路全长189千米,途径县城．县城离里山镇54千米．早上8：30一辆客车从里山镇开往县城,9：15到达．停留15分钟后开往省城,午前11：00能够到达．另有一辆客车于当日早上9：00从省城径直开往里山镇．每小时行驶60千米．两车相遇时,省城开往里山镇的客车行驶了　72　分钟．【分析】先求出从8：30到9：15,客车行驶的时间,依据速度＝路程÷时间,求出客车从里山镇到县城时的速度,再求出客车从县城出发时,以及到达省城时的时间,依据速度＝路程÷时间,求出此时客车的速度;客车9：15到达．停留15分钟后开往省城,相当于客车是从9：30分开车,根据路程＝速度×时间,求出另一辆客车30分钟行驶的路程,再求出两车共同行驶的路程,最后根据时间＝路程÷速度,求出两车的相遇时间,再加30分钟即可解答．【解答】解：9：15+15分钟＝9：30,11：00﹣9：30＝1.5小时,30分钟＝0.5小时,（189﹣54）÷1.5,＝135÷1.5,＝90（千米）,189﹣54﹣60×0.5,＝189﹣54﹣30,＝135﹣30,＝105（千米）,105÷（60+90）,＝105÷150,＝0.7（小时）＝42（分钟）,42+30＝72分钟,答：省城开往里山镇的客车行驶了72分钟,故应填：72．11。

第十七届“华罗庚金杯”少年数学邀请赛初赛试卷(小高组笔试)

2012年第十七届“华罗庚金杯”少年数学邀请赛初赛试卷（小高组笔试）一、选择题（每小题3分.以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内）1．（3分）计算：[（0.8）×24+6.6]﹣7.6＝（）A．30 B．40 C．50 D．602．（3分）以平面上4个点为端点连接线段，形成的图形中最多可以有〔〕个三角形．A．3 B．4 C．6 D．83．（3分）一个奇怪的动物庄园里住着猫和狗，狗比猫多180只．有20%的狗错认为自己是猫；有20%的猫错认为自己是狗．在所有的猫和狗中，有32%认为自己是猫，那么狗有（）只．A．240 B．248 C．420 D．8424．（3分）图中的方格纸中有五个编号为1，2，3，4，5的小正方形，将其中的两个涂上阴影，与图中阴影部分正好组成正方体的展开图，这两个正方形的编号可以是（）A．1，2 B．2，3 C．3，4 D．4，55．（3分）在图所示的算式中，每个字母代表一个非零数字，不同的字母代表不同的数字，则和的最小值是（）A．369 B．396 C．459 D．5496．（3分）如图由相同的正方形和相同的等腰直角三角形构成，则正方形的个数为（）A．83 B．79 C．72 D．65二、填空题（每小题3分，满分12分）7．（3分）如图的计数器三个档上各有10个算珠，将每档算珠分成上下两部分，得到两个三位数．要求上面部分是各位数字互不相同的三位数，且是下面三位数的倍数，则上面部分的三位数是．8．（3分）四支排球队进行单循环比赛，即每两队都要赛一场，且只赛一场．如果一场比赛的比分是3：0或3：1．则胜队得3分，负队得0分；如果比分是3：2，则胜队得2分，负队得1分．比赛的结果各队得分恰好是四个连续的自然数，则笫一名的得分是分．9．（3分）甲、乙两车分别从A、B两地同吋出发，且在A、B两地往返来回匀速行驶．若两车笫一次相遇后，甲车继续行驶4小吋到达B，而乙车只行驶了1小吋就到达A，则两车笫15次（在A，B两地相遇次数不计）相遇吋，它们行驶了小吋．10．（3分）正方形ABCD的面积为9平方厘米，正方形EFGH的面积为64平方厘米．如图所示，边BC落在EH上．已知三角形ACG的面积为6.75平方厘米，则三角形ABE的面积为平方厘米．2012年第十七届“华罗庚金杯”少年数学邀请赛初赛试卷（小高组笔试）参考答案与试题解析一、选择题（每小题3分.以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内）1．（3分）计算：[（0.8）×24+6.6]﹣7.6＝（）A．30 B．40 C．50 D．60【分析】先算小括号内的，再算中括号内的乘法，然后算中括号内的加法，最后算括号外的除法和减法．【解答】解：[（0.8）×24+6.6]﹣7.6＝[（0.8+0.2）×24+6.6]﹣7.6＝[1×24+6.6]﹣7.6＝30.6﹣7.6＝30.6×﹣7.6＝47.6﹣7.6＝40．故选：B．2．（3分）以平面上4个点为端点连接线段，形成的图形中最多可以有〔〕个三角形．A．3 B．4 C．6 D．8【分析】如下图：4个小的三角形，再就是由两个三角形组成的大三角形，有4个，所以一共有8个，据此解答．【解答】解：4+4＝8（个）故选：D．3．（3分）一个奇怪的动物庄园里住着猫和狗，狗比猫多180只．有20%的狗错认为自己是猫；有20%的猫错认为自己是狗．在所有的猫和狗中，有32%认为自己是猫，那么狗有（）只．A．240 B．248 C．420 D．842【分析】仔细分析题目，发现本题其实是一个简单的浓度问题：有20%的狗认为自己是猫，由“有20%的猫认为它们是狗”，那么有80%的猫认为自己是猫，而将猫和狗混合在一起，所有的猫和狗中，有32%的认为自己是猫．那么根据浓度问题，狗和猫的数量之比是：（80%﹣32%）：（32%﹣20%）＝4：1，而狗比猫多180只，所以狗的数量为：180÷（4﹣1）×4，解决问题．【解答】解：狗和猫的数量之比是：（1﹣20%﹣32%）：（32%﹣20%），＝48%：12%，＝4：1；狗的数目为：180÷（4﹣1）×4，＝180÷3×4，＝60×4，＝240（只）；答：狗的数目是240只．故选：A．4．（3分）图中的方格纸中有五个编号为1，2，3，4，5的小正方形，将其中的两个涂上阴影，与图中阴影部分正好组成正方体的展开图，这两个正方形的编号可以是（）A．1，2 B．2，3 C．3，4 D．4，5【分析】根据正方体展开图的11种特征，只有把4、5或3、5阴影，才能与已涂阴影的4个正方形组成正方体展开图的“1﹣3﹣2”结构．【解答】解：如图，故选：D．5．（3分）在图所示的算式中，每个字母代表一个非零数字，不同的字母代表不同的数字，则和的最小值是（）A．369 B．396 C．459 D．549【分析】根据题干，和的最高位最小是3，若H＝3，则A和D分别是1和2，则剩下的数字是4、5、6、7、8、9，个位与十位的数字怎么排，都会发生进位，则H不能是3，那么H只能最小是4，A和D还是1和2，则剩下的数字是3、5、6、7、8、9，明显可知相加时十位要向前一位进1，又因为每个数字表示的数字不同，所以经过计算实验可得：73+86＝59，即本题和最小是173+286＝459，据此即可选择．【解答】解：根据题干分析可得：答：和的最小值是459．故选：C．6．（3分）如图由相同的正方形和相同的等腰直角三角形构成，则正方形的个数为（）A．83 B．79 C．72 D．65【分析】因为所有的正方形都是斜着的，所以先数边长为1的正方形有2+4+6+8+8+6+4+2＝40；边长为2的正方形有1+3+5+7+5+3+1＝25个，边长为3的正方形有2+4+4＝2＝12个，边长为4的正方形有1+3+1＝5个，还有一个大正方形，据此解答．【解答】解：边长为1的正方形有2+4+6+8+8+6+4+2＝40；边长为2的正方形有1+3+5+7+5+3+1＝25个，边长为3的正方形有2+4+4+2＝12个，边长为4的正方形有1+3+1＝5个，还有一个大正方形；共有：40+25+12+5+1＝83个．故选：A．二、填空题（每小题3分，满分12分）7．（3分）如图的计数器三个档上各有10个算珠，将每档算珠分成上下两部分，得到两个三位数．要求上面部分是各位数字互不相同的三位数，且是下面三位数的倍数，则上面部分的三位数是925 ．【分析】因为上面三位数是下面三位数的倍数，假设下面三位数为abc，则上面三位数表示为k•abc．计数器三个档上各有10个算珠，所以上下两数之和为（k|1）abc＝|00×10|10×10|1×10＝1110，把1110分解质因数：1110＝2×3×5×37，因为上面的各位数字互不相同，所以下面的数可以是5×37﹣185，上面的数是185×（2×3﹣1）＝925．【解答】解：设下面三位数为abc，则上面三位数表示为k•abc．上下两数之和为（k|1）abc＝|00×10|10×10|1×10＝1110，1110＝2×3×5×37，因为上面的各位数字互不相同，所以下面的数可以是5×37﹣185，上面的数是185×（2×3﹣1）＝925．故答案为：925．8．（3分）四支排球队进行单循环比赛，即每两队都要赛一场，且只赛一场．如果一场比赛的比分是3：0或3：1．则胜队得3分，负队得0分；如果比分是3：2，则胜队得2分，负队得1分．比赛的结果各队得分恰好是四个连续的自然数，则笫一名的得分是 6 分．【分析】根据握手问题可知：四支队单循环赛，共有6场比赛，无论每场的结果如何，每场的得分之和是3分；那么总得分是：3×6＝18（分），把18分解成3个连线的自然数的和即可求解．【解答】解：一个赛：4×（4﹣1）÷2＝6（场）；总分：6×3＝18（分）3+4+5+6＝18，所以最高的6分．答：笫一名的得分是6分．故答案为：6．9．（3分）甲、乙两车分别从A、B两地同吋出发，且在A、B两地往返来回匀速行驶．若两车笫一次相遇后，甲车继续行驶4小吋到达B，而乙车只行驶了1小吋就到达A，则两车笫15次（在A，B两地相遇次数不计）相遇吋，它们行驶了86 小吋．【分析】设两车出发t小时相遇，甲的速度是v1，乙的速度是v2，由题意得：4v1＝tv2，（t+4）v1＝（t+1）v2，解得t＝2．所以跑完全程甲要6小时，乙要3小时，巧的是甲跑完一趟，乙就跑完整个来回，所以A、B两地相遇次数不计时，6小时就相遇一次，相向出发2小时候相遇，同向出发4小时相遇，第15趟是相向出发，6×14+2＝86（小时）．【解答】解：设两车出发t小时相遇，甲的速度为v1，乙的速度为v2，则：4v1＝tv2，（t+4）v1＝（t+1）v2，解得t＝2．所以跑完全程甲要6小时，乙要3小时，A、B两地相遇次数不计时，6小时就相遇一次，相向出发2小时候相遇，同向出发4小时相遇，第15趟是相向出发，则两车笫15次相遇吋，它们行驶了：6×（15﹣1）+2＝6×14+2＝84+2＝86（小时）答：两车笫15次相遇吋，它们行驶了86小吋．故答案为：86．10．（3分）正方形ABCD的面积为9平方厘米，正方形EFGH的面积为64平方厘米．如图所示，边BC落在EH上．已知三角形ACG的面积为6.75平方厘米，则三角形ABE的面积为 2.25 平方厘米．【分析】延长AB与FG交于M，如图所示，设正方形ABCD的面积求出边长a，EB＝b，CH＝c，用CH+BC表示出BH，即为MG，由三角形ABC的面积+直角梯形BCGM的面积﹣三角形AMG的面积＝三角形ACG的面积，分别利用梯形的面积公式，三角形的面积公式及已知三角形ACG的面积列出关系式，由正方形ABCD的面积为9，求出a2的值为9，整理后将a2的值代入，得到ab的值，即为三角形ABE的面积．【解答】解：延长AB与FG交于点M，如图所示：设正方形ABCD的边长为a厘米，EB＝b厘米，CH＝c厘米，则AB＝BC＝a厘米，BM＝EH＝EB+BC+CH＝（a+b+c）厘米，MG＝BH＝（a+c）厘米，因为S△ACG＝S△ABC+S梯形BCGM﹣S△AMG＝6.75，所以a2+（a+b+c）（2a+c）﹣（2a+b+c）（a+c）＝6.75，整理得：a2+ab＝6.75，又正方形ABCD的面积为9平方厘米，即a2＝9，所以S△ABE＝AB•EB＝ab＝6.75﹣×9＝6.75﹣4.5＝2.25（平方厘米）．答：三角形ABE的面积为 2.25平方厘米．故答案为：2.25．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2019/5/7 10:52:34；用户：小学奥数；邮箱：****************；学号：20913800。

第十七届华罗庚金杯少年数学邀请赛初赛试卷(初一组笔试版)

第十七届华罗庚金杯少年数学邀请赛初赛试卷（初一组笔试版）〔吋间:2012年3月17曰10:00-11:00 〕一、选择题（每小题10分.以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内）1.平面上四个点，任意三个点都不在一条直线上，在连接这四个点的六条线段所形成的图形中，最少可以形成〔〕个三角形.(A）3 （B）4 (C) 6 (D) 82.在右图所示的三位数加法算式中，每个字母代表非零数字，不同的字母代表不同的数字，则和“”的最小值是〔〕.（A）459 〔B〕457 （C）456 (D) 4533.内角都小于180度的七边形的内角至少有〔〕个钝角.(A）6 〔B〕5 (C) 4 （D）34.四支排球队进行单循环比赛，即每两队都要赛-场，且只赛一场.如果一场比赛的比分是3:0或3:1，则胜队得3分，负队得0分；如杲比分是3:2，则胜队得2分，负队得1分.如杲比赛后各队得分恰好是四个连续的自然数，那么笫一名的得分是〔〕分.(A）3 〔B〕4 (C) 5 (D) 65.如图所示，M为平行四边形ABCD中BC边上一点，BM：MC＝2：3.己知三角形CMN的面积为45 cm2.则平行四边形ABCD的面积为〔〕cm2.(A)30 (B)45(C)90(D)1006.如果正整数x与y使得的值为质数：那么x＋y共有〔〕种可能的值.(A) 1 (B) 2 （C）3 （D）4二、填空题〈每小题10分，满分40分）7.计算：1.2345 ×0.2345 ×2.469－123455－1.2345 X 0.23452＝________.8.己知关于x的一元一次方程7x＋（3＋x）＝k＋bx方程有非零解，且这个方程的解是方程7x+（3+x) = k－bx解的1/3,那么b的值为_______.9.己知甲、乙两车分别从A、B两地同吋出发，且在A，B地住返来回勻速行驶.若两车笫一次相遇后，甲车继续行驶4小吋到达B，而乙车只行驶了1小吋就到达A，则两车笫15次相遇（在A，B两地相遇次数不计）吋，它们行驶了______小吋.10.设a、b、c代表三个不同的非零数字，由它们组成一个最大的三位数和一个最小的三位数，记这两个三位数的差为m，且m的数字和恰好整除m，则所有不同的m的值之和为_______.(A）30 〔B〕45 (C)90 (D) 100第十七届全国华罗庚金杯少年数学邀请赛初赛试题（初一组笔试版）答案―、迭择题(每小题10分，满分60分）二、填空题〈每小题10分，满分40分）。

(完整版)年第17届“华罗庚金杯”少年数学邀请赛决赛试卷c(小学高年级组).doc解答_共8页

÷（）﹣的值为．3．（10分）设某圆锥的侧面积是10π，表面积是19π，则它的侧面展开图的圆心角是．4．（10分）设a△b和a▽b分别表示取a和b两个数的最小值和最大值，如，3△4=3，3▽4=4，那么对于不同的数x，5▽[4▽（x△4）]的取值共有个．5．（10分）某水池有A，B两个水龙头．如果A，B同时打开需要30分钟可将水池注满．现在A和B同时打开10分钟，6．（10分）如图是一个五棱柱的平面展开图．图中的正方形边长都为2．按图所示数据，这个五棱柱的体积等7．（10分）一条路上有A、O、B三个地点，O在A与B之间，A与O相距1620，米，甲、乙两人同时分别从A和O8．（10分）从1到1000中最多可以选出个数，使得这些数中任意两个数的差都不整除它们的和．二．解答下列各题（每题10分，要求写出简要过程）。

N=++…+，问12．（10分）小明拿着100元人民币去商店买文具，回来后数了数找回来的人民币有4张不同币值的纸币，4枚不同的硬币．纸币面值大于一元，硬币的面值小于1元．并且所有纸币的面值和以“元”为单位可以被3整除，所有硬币的面值13．（10分）能否用540个图所示的1×2的小长方形拼成一个6×180的大长方形，使得6×180的长方形的每一行、每一列都有奇数个星？请说明理由．14．（10分）已知100个互不相同的质数p1，p2，…，p100，记N=p12+p12+…+p1002，问：N被3除的余数是多少？15．（15分）王大妈拿了一袋硬币去银行兑换纸币，袋中有一分、二分、五分和一角四种硬币，二分的枚数是一分的，五分硬币的枚数是二分的，一角硬币的枚数是五分的少7枚．王大妈兑换到的纸币恰好是大于50小于100的整元数．问这四种硬币各有多少枚？16．（15分）右图四一个三角形网格，由16个小的等边三角形构成．网格中由3个相邻的小三角形构成的图形称为“3﹣梯形”．如果在每个小三角形内填上数字1﹣9中的一个，那么能否给出一种填法，使得任意两个“3﹣梯形”中的3个数之和均不相同？如果能，请举出一例；如果不能，请说明理由．三．解答下列各题（每小题15分，共60分，要求写出详细过程）17．（15分）图中，ABCD是平行四边形，E在AB边上，F在DC边上，G为AF与DE的交点，H为CE与BF的交点．已知，平行四边形ABCD的面积是1，=，三角形BHC的面积是，求三角形ADG的面积．18．（15分）记一千个自然数x、x+1、x+2、…，x+999的和的和为a，如果a的数字和等于50，则x最小为多少？19．（15分）请写出所有满足下面三个条件的正整数a和b；（1）a≤b；（2）a+b 是个三位数，且三个数字从小到大排列等差；（3）a×b 是一个五位数，且五个数字相同．20．（15分）记一百个自然数x，x+1，x+2，…，x+99的和为a，如果a的数字和等于50，则x最小为多少？．。

第十七届“华罗庚金杯”少年数学邀请赛网上初赛补考试卷(小学高年级组)

2012年第十七届“华罗庚金杯”少年数学邀请赛网上初赛补考试卷（小学高年级组）一、选择题（每小题3分．以下每题的四个选项，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内．）1．（3分）如果a÷0.3＝0.6，那么a＝（）A．2 B．1 C．0.2 D．0.182．（3分）a和b是非零自然数，如果＜，则（）A．是一个假分数B．是一个真分数C．是一个假分数3．（3分）用四个数码1，3，4和6所组成的没有重复数字的所有整数中，是6的倍数的有（）A．1 B．2 C．3 D．44．（3分）如图所示是一个5×7的网格，每个小方格的面积是1，内有1个灰色方格．水平线和竖直线的交点格点，适当选择4个格点，可以画出一个以这4个格点为顶点的不包含灰色方格、也和灰色方格不相交并且面积是15的长方形，共可以画出这样的长方形（）个．A．6 B．8 C．10 D．125．（3分）a＝，b＝，c＝，则有（）A．a＞b＞c B．a＞c＞b C．a＜b＜c D．a＜c＜b6．（3分）一副扑克牌有54张，将大小王视为0点，A视为1点，J视为11点，Q视为12点，K视为13点，任意抽出若干张牌，不计花色，如果要求每次抽出的牌中必定有2张牌的点数之和等于14，那么至少要取（）张牌．A．26 B．27 C．28 D．29三、标题7．（3分）植树节有一批树苗需要种植，甲单独种植所需时间比乙单独种植所需时间多，如果甲和乙一起种植，植完这批树苗，乙比甲多植36棵，那么这批树苗一共有棵．8．（3分）将一个个位不是零的整数的数码，重新从右至左排列后所得到的整数，称为这个原整数的反序数，例如325的反序数是523，1376的反序数是6731．有两个三位数，和是1372，他们的反序数的和最大是．9．（3分）图中，ABC是一个钝三角形．BC＝6厘米，AB＝5厘米，BC边的高AD等于4厘米，若此三角形以每秒3厘米的速度沿DA的方向向上移动．2秒后，此三角形扫过的面积是平方厘米．10．（3分）将自然数1，2，3，4，5，6，7，8，9，依次重复写下去组成一个2012位整数，这个整数被9除的余数是．2012年第十七届“华罗庚金杯”少年数学邀请赛网上初赛补考试卷（小学高年级组）参考答案与试题解析一、选择题（每小题3分．以下每题的四个选项，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内．）1．（3分）如果a÷0.3＝0.6，那么a＝（）A．2 B．1 C．0.2 D．0.18【分析】因为a÷0.3＝0.6，根据“被除数＝商×除数”，那么a＝0.3×0.6，计算出结果即可．【解答】解：0.3×0.6＝0.18；故选：D．2．（3分）a和b是非零自然数，如果＜，则（）A．是一个假分数B．是一个真分数C．是一个假分数【分析】a和b是非零自然数，如果＜，把不等式去分母后，可得ab+a ＜ab+b，不等式两边同时再减去ab，进而可确定a＜b，再根据a和b的大小关系解答即可．【解答】解：＜，ab+a＜ab+b，a＜b；所以是一个真分数；是一个假分数，排除A、B，因此选择C．故选：C．3．（3分）用四个数码1，3，4和6所组成的没有重复数字的所有整数中，是6的倍数的有（）A．1 B．2 C．3 D．4【分析】根据被2整除数的特征，可得个位数字为4或6；当个位数字为4时，根据被3整除数的特征，可得用其余三个数字所组成的没有重复数字的所有整数中，没有3的倍数；当个位数字为6时，根据被3整除数的特征，可得用其余三个数字所组成的没有重复数字的所有整数中，有3的倍数，分别是6或36．【解答】解：由分析可知，用四个数码1，3，4和6所组成的没有重复数字的所有整数中，是6的倍数的有36和6这两个数．故选：B．4．（3分）如图所示是一个5×7的网格，每个小方格的面积是1，内有1个灰色方格．水平线和竖直线的交点格点，适当选择4个格点，可以画出一个以这4个格点为顶点的不包含灰色方格、也和灰色方格不相交并且面积是15的长方形，共可以画出这样的长方形（）个．A．6 B．8 C．10 D．12【分析】如图1所示，数出如图的长5宽3的长方形的个数；如图2所示，数出如图的长5宽3的长方形的个数；再相加即可得到这样的长方形个数．【解答】解：如图1所示，如图符合题意的长5宽3的长方形的个数是2个；如图2所示，如图符合题意的长5宽3的长方形的个数是3×2＝6个；这样的长方形个数为2+6＝8（个）．答：这样的长方形有8个．故选：B．5．（3分）a＝，b＝，c＝，则有（）A．a＞b＞c B．a＞c＞b C．a＜b＜c D．a＜c＜b【分析】一个真分数，当分子与分母的差一定时，分母越大，这个分数也就越大．【解答】解：＜，＜，＜，所以：×＜×＜×，即＜＜，所以，a＜b＜c故选：C．6．（3分）一副扑克牌有54张，将大小王视为0点，A视为1点，J视为11点，Q视为12点，K视为13点，任意抽出若干张牌，不计花色，如果要求每次抽出的牌中必定有2张牌的点数之和等于14，那么至少要取（）张牌．A．26 B．27 C．28 D．29【分析】54张牌按照下面的分成四个部分：大王和小王、1﹣6、7、8﹣13，考虑最差情况：怎么取得最多的牌而没有任何两张牌之和等于14呢？在这四个部分里，当取到1﹣6区间的时候，就不能取8﹣13区间的牌，反之一样；而且7只能取一个，大小王必取．这样我们就可以这样取牌：大小王、1﹣6全取、1个7（或大小王、1个7、8﹣13全取）总共27张牌，再随便取一张牌就必定有2张牌的和等于14了．所以要满足题目至少要取27+1＝28张．【解答】解：根据题干分析可得，可以这样取牌：大小王、1﹣6全取、1个7（或大小王、1个7、8﹣13全取）总共27张牌，再随便取一张牌就必定有2张牌的和等于14了．所以要满足题目至少要取27+1＝28张．故选：C．三、标题7．（3分）植树节有一批树苗需要种植，甲单独种植所需时间比乙单独种植所需时间多，如果甲和乙一起种植，植完这批树苗，乙比甲多植36棵，那么这批树苗一共有252 棵．【分析】我们把乙用的时间看作1，甲的时间是1×（1+），求出它们的工作效率的差，用36除以就是乙载的棵数，进一步求出总共的棵数．【解答】解：乙的工作效率是：1÷1＝11÷[1×（1+）]，＝1÷，＝；36÷（1﹣）×（1），＝36×4×，＝252（棵）；答：这批树苗一共有252棵．故答案为：252．8．（3分）将一个个位不是零的整数的数码，重新从右至左排列后所得到的整数，称为这个原整数的反序数，例如325的反序数是523，1376的反序数是6731．有两个三位数，和是1372，他们的反序数的和最大是1372 ．【分析】设原来的两个三位可数分别是b 1c1，a2b2c2．根据题意知：100×（+a2）+10×（b 1+b2）+（c1+c2）＝1372（式1），其中、b1、c1、a 2、b2、c2均为一位数字，求100×（c1+c2）+10×（b1+b2）+（+a2）（式2）的最大值，先看c1+c2，由1372可知，c1+c2＝12或2，要使式2的值最大，则c 1+c2＝12，此时可知：1b1+b2＝6或者16，当b1+b2＝6，+a2＝13，此时式2＝1273，当b 1+b2＝16，+a2＝12，此时式2＝1372．据此解答．【解答】解：设原来的两个三位可数分别是b 1c1，a2b2c2．根据题意知：100×（+a2）+10×（b 1+b2）+（c1+c2）＝1372（式1），其中、b1、c1、a2、b2、c2均为一位数字，求100×（c 1+c2）+10×（b1+b2）+（+a2）（式2）的最大值，先看c1+c2，由1372可知，c1+c2＝12或2，要使式2的值最大，则c1+c2＝12，此时可知：1b 1+b2＝6或者16，当b1+b2＝6，+a2＝13，此时式2＝1273，当b 1+b2＝16，+a2＝12，此时式2＝1372．故答案为：1372．9．（3分）图中，ABC是一个钝三角形．BC＝6厘米，AB＝5厘米，BC边的高AD等于4厘米，若此三角形以每秒3厘米的速度沿DA的方向向上移动．2秒后，此三角形扫过的面积是66 平方厘米．【分析】平移时图形的每个点都在移动及整个图形沿同一方向移动同样的距离，将三角形以每秒3厘米的速度沿高的方向向上移动2秒，就是沿高的方向移动了3×2＝6cm，三角形扫过的面积应该是一个正方形的面积加上一个三角形的面积，再加上平行四边形ABFE的面积．【解答】解：扫过的面积应该是正方形BCDF的面积加上上面三角形的面积，再加上平行四边形ABFE的面积，因为AD＝4，AB＝5，且AB2﹣AD2＝BD2，即52﹣42＝32，所以DB＝3厘米，3×2＝6厘米，6×6+×6×4÷2+6×3，＝36+12+18，＝66（平方厘米）．答：此三角形扫过的面积是66平方厘米．故答案为：66．10．（3分）将自然数1，2，3，4，5，6，7，8，9，依次重复写下去组成一个2012位整数，这个整数被9除的余数是 6 ．【分析】如果一个数字能够被9整除，那么它的每个位数相加所得的数值一定也能被9整除，那么连续9个数的和一定能被9整除，求出2012除以9的余数是几，再根据余数推算．【解答】解：2012÷9＝223…5；所以余数是：（1+2+3+4+5）÷9，＝15÷9，＝1…6；故答案为：6．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2019/5/7 10:55:49；用户：小学奥数；邮箱：pfpxxx02@；学号：20913800。