第四届_华罗庚杯_少年数学邀请赛复赛部分试题以及答案讲解
历届“华杯赛”初赛决赛试题汇编【小中组(附答案)】

二、简答题(每小题 15 分, 共 60 分, 要求写出简要过程)
9. 用 4 个数码 4 和一些加、减、乘、除号和小括号, 写出值分别等于 2、3、4、 5、6 的五个算式. 10. 右图是 U, V, W, X 四辆不同类型的汽车每百千米的耗油 量. 如果每辆车都有 50 升油, 那么这四辆车最多可行驶 的路程总计是多少千米? 11. 某商店卖出一支钢笔的利润是 9 元, 一个小熊玩具的进 价为 2 元. 一次, 商家采取 “买 4 支钢笔赠送一个小熊玩具”的打包促销, 共 获利润 1922 元. 问这次促销最多卖出了多少支钢笔? 12. 编号从 1 到 10 的 10 个白球排成一行, 现按照如下方法涂红色: 1)涂 2 个球; 2)被涂色的 2 个球的编号之差大于 2. 那么不同的涂色方法有多少种?
四百米比赛进入冲刺阶段,甲在乙前面 30 米,丙在丁后面 60 米,乙在丙前面 20 米. 这时,跑在最前面的两位同学相差( (A)10 (B)20 )米. (D)60
(C)50
5.
在右图所示的两位数的加法算式中, 已知 A B C D 22 , ). (B)4 (C)7 (D)13
一、选择题 (每小题 10 分, 满分 60 分. 以下每题的四个选项中, 仅 有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号 内.)
2012年-2017年华罗庚金杯少年数学邀请赛初赛真题合集(小高组)附答案

目录第二十二届华罗庚金杯少年数学邀请赛 (1)第二十一届华罗庚金杯少年数学邀请赛 (3)第二十一届华罗庚金杯少年数学邀请赛 (5)第二十届华罗庚金杯少年数学邀请赛 (7)第二十届华罗庚金杯少年数学邀请赛 (9)第十九届华罗庚金杯少年数学邀请赛 (11)第十九届华罗庚金杯少年数学邀请赛 (13)第十八届华罗庚金杯少年数学邀请赛 (15)第十八届华罗庚金杯少年数学邀请赛 (17)第十七届华罗庚金杯少年数学邀请赛 (19)第十七届华罗庚金杯少年数学邀请赛 (21)第二十二届华罗庚金杯少年数学邀请赛答案 (23)第二十一届华罗庚金杯少年数学邀请赛答案 (24)第二十一届华罗庚金杯少年数学邀请赛答案 (25)第二十届华罗庚金杯少年数学邀请赛答案 (26)第二十届华罗庚金杯少年数学邀请赛答案 (27)第十九届华罗庚金杯少年数学邀请赛答案 (28)第十九届华罗庚金杯少年数学邀请赛答案 (29)第十八届华罗庚金杯少年数学邀请赛答案 (30)第十八届华罗庚金杯少年数学邀请赛答案 (31)第十八届华罗庚金杯少年数学邀请赛答案 (32)第十七届华罗庚金杯少年数学邀请赛答案 (33)第十七届华罗庚金杯少年数学邀请赛答案 (34)A B 第二十二届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组)(时间 2016 年 12 月 10 日 10:00-11:00)一、选择题.(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 两个有限小数的整数部分分别是 7 和 10,那么这两个有限小数的积的整数部分有( )种可能的取值.A .16B .17C .18D .192. 小明家距学校,乘地铁需要 30 分钟,乘公交车需要 50 分钟,某天小明因故先乘地铁,再换乘公交车,用了 40 分钟到达学校,其中换乘过程用了 6 分钟,那么这天小明乘坐公交车用了( )分钟. A .6 B .8 C .10 D .123. 将长方形 ABCD 对角线平均分成 12 段,连接成右图,长方形 ABCD 内部空白部分面积总和是 10 平方厘米,那么阴影部分面积总和是( )平方厘米.A .14B .16C .18D .204.请在图中的每个方框中填入适当的数字,使得乘法竖式成立.那么乘积是( ).A .2986B .2858C .2672D .27545. 在序列 20170……中,从第 5 个数字开始,每个数字都是前面 4 个数字和的个位数,这样的序列可以一直写下去.那么从第 5 个数字开始,该序列中一定不会出现的数组是( )A .8615B .2016C .4023D .20176. 从 0 至 9 选择四个不同的数字分别填入方框中的四个括号中,共有( )种填法使得方框中话是正确的.× 71 0 2罗华金杯ABG FHDEC二、填空题.(每小题 10 分,共 40 分)7. 若( 1 5 245 3— )× 9 2 5 7 ÷ 2 +2.25=4,那么A 的值是 .3 34 1A8. 右图中,“华罗庚金杯”五个汉字分别代表 1-5 这五个不同的数字,将各线段两端点的数字相加得到五个和,共有 种情况使得这五个和恰为五个连续自然数.9. 右图中,ABCD 是平行四边形,E 为 CD 的中点,AE 和 BD 的交点为 F ,AC 和 BE 的交点为 H ,AC 和BD 的交点为 G ,四边形 EHGF 的面积是 15 平方厘米,则 ABCD 的面积是平方厘米.10. 若 2017,1029 与 725 除以 d 的余数均为 r ,那么 d -r 的最大值是 .庚第二十一届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组A 卷) (时间:2015 年 12 月 12 日 10:00~11:00一、选择题.(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内) 1. 算式999 9 × 999 9 的结果中含有( )个数字 0.2016个92016个9A .2017B .2016C .2015D .20142. 已知 A ,B 两地相距 300 米.甲、乙两人同时分别从 A 、B 出发,相向而行,在距 A 地 140 米处相遇;如果乙每秒多行 1 米,则两人相遇处距 B 地 180 米.那么乙原来的速度是每秒( )米.A . 2 2B . 2 4C .3D . 3 15 5 53. 在一个七位整数中,任何三个连续排列的数字都构成一个能被 11 或 13 整除的三位数,则这个七位数最大是( )A .9981733B .9884737C .9978137D .98717734. 将 1,2,3,4,5,6,7,8 这 8 个数排成一行,使得 8 的两边各数之和相等,那么共有( )种不同的排法. A .1152B .864C .576D .2885. 在等腰梯形 ABCD 中,AB 平行于 CD ,AB =6,CD =14,∠AEC 是直角,CE =CB ,则 AE 2 等于( )A .84B .80C .75D .646. 从自然数 1,2,3,…,2015,2016 中,任意取 n 个不同的数,要求总能在这 n 个不同的数中找到 5个数,它们的数字和相等.那么 n 的最小值等于( ). A .109 B .110 C .111 D .112EABD C二、填空题.(每小题 10 分,共 40 分)AP M O7. 两个正方形的面积之差为 2016 平方厘米,如果这样的一对正方形的边长都是整数厘米,那么满足上述条件的所有正方形共有对.8. 如下图,O ,P ,M 是线段 AB 上的三个点,AO = 4 AB ,BP = 2AB ,M 是 AB 的中点,且 OM =2,那5 3么 PM 长为 .9. 设 q 是一个平方数.如果 q -2 和 q +2 都是质数,就称 q 为 p 型平方数.例如,9 就是一个 p 型平方数.那么小于 1000 的最大 p 型平方数是 .10. 有一个等腰梯形的纸片,上底长度为 2015,下底长度为 2016.用该纸片剪出一些等腰梯形,要求剪出的梯形的两底边分别在原来梯形的底边上,剪出的梯形的两个锐角等于原来梯形的锐角,则最多可以剪出 个同样的等腰梯形.第二十一届华罗庚金杯少年数学邀请赛初赛试卷 B (小学高年级组)(时间:2015 年 12 月 12 日 10:00~11:00)一、选择题.(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内) 1. “凑 24 点”游戏规则是:从一副扑克牌中抽去大小王剩下 52 张,(如果初练也可只用 1 至 10 这 40 张牌)任意抽取 4 张牌(称牌组),用加、减、乘、除(可加括号)把牌面上的数算成 24.每张牌必须用一次且只能用一次,并不能用几张牌组成一个多位数,如抽出的牌是 3,8,8,9,那么算式为(9- 8)×8×3 或(9-8÷8)×3 等.在下面 4 个选项中,唯一无法凑出 24 点的是( ). A .1,2,2,3 B .1,4,6,7 C .1,5,5,5 D .3,3,7,72. 有一种数,是以法国数学家梅森的名字命名的,它们就是形如 2n -1( n 为质数)的梅森数,当梅森数是质数时就叫梅森质数,是合数时就叫梅森合数.例如:22-1=3 就是一个梅森质数.第一个梅森合数是( ).A .4B .15C .127D .20473. 有一种饮料包装瓶的容积是 1.5 升.现瓶里装了一些饮料,正放时饮料高度为 20 厘米,倒放时空余部分的高度为 5 厘米,如下图.那么瓶内现有饮料( )升.A .1B .1.2C .1.25D .1.3754. 已知 a ,b 为自然数, 4 = 1 + 1,那么 a +b 的最小值是( ).15 a bA .16B .20C .30D .65. 如下图,平面上有 25 个点,每个点上都钉着钉子,形成 5×5 的正方形钉阵.现有足够多的橡皮筋,最多能套出( )种面积不同的正方形.A .4B .6C .8D .106. 在一个七位整数中,任何三个连续排列的数字都构成一个能被 11 或 13 整除的三位数,那么这个七位数最大是( ).A .9981733B .9884737C .9978137D .9871773二、填空题.(每小题 10 分,共 40 分)华 杯 赛 三 十 年× 杯 杯今 年 认 真 赛 好今 年 认 真 赛 好 三 十 年 华 杯 赛 好7. 计算:20152+20162-2014×2016-2015×2017= .8. 在下边的算式中,相同汉字代表相同数字,不同汉字代表不同数字.当杯代表 5 时,“华杯赛”所代表的三位数是 .9. 于 2015 年 10 月 29 日闭幕的党的十八届五中全会确定了允许普遍二孩的政策.笑笑的爸爸看到当天的新闻后跟笑笑说:我们家今年的年龄总和是你年龄的 7 倍,如果明年给妳添一个弟弟或妹妹,我们家 2020 年的年龄总和就是你那时年龄的 6 倍.那么笑笑今年 岁.10. 教育部于 2015 年 9 月 21 日公布了全国青少年校园足球特色学校名单,笑笑所在的学校榜上有名.为 了更好地备战明年市里举行的小学生足球联赛,近期他们学校的球队将和另 3 支球队进行一次足球友 谊赛.比赛采用单循环制(即每两队比赛一场),规定胜一场得 3 分,负一场得 0 分,平局两队各得 1分;以总得分高低确定名次,若两支球队得分相同,就参考净胜球、相互胜负关系等决定名次.笑笑学校的球队要想稳获这次友谊赛的前两名,至少要得 分.第二十届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2015 年 3 月 14 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 现在从甲、乙、丙、丁四个人中选出两个人参加一项活动,规定:如果甲去,那么乙也去;如果丙不去,那么乙也不去;如果丙去,那么丁不去.最后去参加活动的两个人是( )A .甲、乙B .乙、丙C .甲、丙D .乙、丁2. 以平面上任意 4 个点为顶点的三角形中,钝角三角形最多有( )个.A .5B .2C .4D .33. 桌上有编号 1 至 20 的 20 张卡片,小明每次取出 2 张卡片,要求一张卡片的编号是另一张卡片的 2 倍多 2,则小明最多取出( )张卡片. A .12B .14C .16D .184. 足球友谊比赛的票价是 50 元,赛前一小时还有余票,于是决定降价,结果售出的票增加了三分之一, 而票房收入增加了四分之一,那么每张票售价降了( )元.A .10B . 25C . 50D .25235. 一只旧钟的分针和时针每重合一次,需要经过标准时间 66 分,那么,这只旧钟的 24 小时比标准时间的 24 小时( ).A .快 12 分B .快 6 分C .慢 6 分D .慢 12 分6. 在下图的 6×6 方格内,每个方格中只能填 A 、B 、C 、D 、E 、F 中的某个字母,要求每行、每列、每个标有粗线的 2×3 长方形的六个字母均不能重复.那么,第四行除了首尾两个方格外,中间四个方格填入的字母从左到右的顺序是( ).A .E 、 C 、 D 、 FB .E 、D 、C 、FC .D 、 F 、 C 、E D .D 、C 、F 、EB CA B D ABCE二、填空题(每小题 10 分,共 40 分) - - - = AFDPBEC7. 计算4811 + 265 1 + 904 129 41 55184160 7036 12 2030 42 568. 过正三角形 ABC 内一点 P ,向三边作垂线,垂足依次为 D 、E 、F ,连接 AP 、BP 、CP .如果正三角形ABC 的面积是 2028 平方厘米,三角形 PAD 和三角形 PBE 的面积都是 192 平方厘米,则三角形 PCF的面积为平方厘米.9. 自然数 2015 最多可以表示成 个连续奇数的和.10. 由单位正方形拼成的 15×15 网格,以网格的格点为顶点作边长为整数的正方形,则边长大于 5 的正方形有 个.第二十届华罗庚金杯少年数学邀请赛A BED H C 初赛 C 试卷(小学高年级组)(时间:2015 年 3 月 14 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 计算:( 9 - 11 + 13 - 15 + 17 )×120- 1 ÷ 1=( )20 30 42 56 72 3 4A .42B .43C .15 1D .16 2332. 如图,有一排间距相同但高度不等的小树,树根成一条直线,树顶也成一条直线,这两条直线成 45 度角.最高的小树高 2.8 米,最低的小树高 1.4 米,那么从左向右数第 4 棵树的高度是( )米.A .2.6B .2.4C .2.2D .2.03. 春季开学后,有不少同学都将部分压岁钱捐给山区的贫困学生,事后,甲、乙、丙、丁 4 位同学有如下的对话: 甲:“丙、丁之中至少有 1 人捐了款.” 乙:“丁、甲之中至多有 1 人捐了款.” 丙:“你们 3 人中至少有 2 人捐了款.” 丁:“你们 3 人中至多有 2 人捐了款.” 已知这 4 位同学说的都是真话且其中恰有 2 位同学捐了款,那么这 2 位同学是( ).A .甲、乙B .丙、丁C .甲、丙D .乙、丁4. 六位同学数学考试的平均成绩是 92.5 分,他们的成绩是互不相同的整数,最高的 99 分,最低的 76分,那么按分数从高到低居第三位的同学的分数至少是( ). A .94 B .95 C .96D .975. 如图,BH 是直角梯形 ABCD 的高,E 为梯形对角线 AC 上一点;如果△DEH 、△BEH 、△BCH 的面积依次为 56、50、40,那么△CEH 的面积是( ).A .32B .34C .35D .366. 一个由边长为 1 的小正方形组成的n n 的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的 4 个角上的小正方形不全同色,那么正整数 n 的最大值是( ).A .3B .4C .5D .645°二、填空题(每小题10 分,共40 分)7.在每个格子中填入1 至6 中的一个,使得每行、每列及每个2×3 长方形内(粗线框围成)数字不重复;如果小圆圈两边格子中所填数的和是合数,其它相邻两格所填数的和是质数,那么四位数相约华杯是3 月 1 4相约华杯8.整数n 一共有10 个约数,这些约数从小到大排列,第8 个数是n.那么整数n 的最大值是39.在边长为300 厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是平方厘米,两块阴影部分的周长差是厘米.(π取3.14)10.A 地、B 地、C 地、D 地依次分布在同一条公路上,甲、乙、丙三人分别从A 地、B 地C 地同时出发,匀速向D 地行进.当甲在C 地追上乙时,甲的速度减少40%;当甲追上丙时,甲的速度再次减少40%;甲追上丙后9 分钟,乙也追上了丙,这时乙的速度减少25%;乙追上丙后再行50 米,三人同时到D 地.已知乙出发时的速度是每分钟60 米,那么甲出发时的速度是每分钟米,A、D 两地间的路程是米.第十九届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2014 年 3 月 15 日 8:00—9:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.) 1. 平面上的四条直线将平面分割成八个部分,则这四条直线中至多有( )条直线互相平行.A .0B .2C .3D .42. 某次考试有 50 道试题,答对一道题得 3 分,答错一道题扣 1 分,不答题不得分.小龙得分 120 分,那么小龙最多答对了( )道试题.A .40B .42C .48D .503. 用左下图的四张含有 4 个方格的纸板拼成了右下图所示的图形.若在右下图的 16 个方格分别填入 1、3、5、7(每个方格填一个数),使得每行、每列的四个数都不重复,且每个纸板内四个格子里的数也不重复,那么 A 、B 、C 、D 四个方格中数的平均数是( ).A . 4B . 5C D .74. 小明所在班级的人数不足 40 人,但比 30 人多,那么这个班男、女生人数的比不可能是( ).A .2︰3B .3︰4C .4︰5D .3︰75. 某学校组织一次远足活动,计划 10 点 10 分从甲地出发,13 点 10 分到达乙地,但出发晚了 5 分钟, 却早到达了 4 分钟.甲、乙两地之间的丙地恰好是按照计划时间到达的,那么到达丙地的时间是( ). A .11 点 40 分 B .11 点 50 分 C .12 点 D .12 点 10 分6. 如图所示,AF =7cm ,DH =4cm ,BG =5cm ,AE =1cm .若正方形 ABCD 内的四边形 EFGH 的面积为78 平方厘米,则正方形的边长为( )cm .A .10B .11C .12D .13ABA EDHF BC二、填空题(每小题 10 分,共 40 分)甲 乙7. 五名选手 A 、B 、C 、D 、E 参加“好声音”比赛,五个人站成一排集体亮相.他们胸前有每人的选手编号牌,5 个编号之和等于 35.已知站在 E 右边的选手的编号和为 13;站在 D 右边的选手的编号和为 31;站在 A 右边的选手的编号和为 21;站在 C 右边的选手的编号和为 7.那么最左侧与最右侧的选手编号之和是 .8. 甲、乙同时出发,他们的速度如下图所示,30 分钟后,乙比甲一共多行走了米.9. 四个黑色 1×1×1 的正方体和四个白色 1×1×1 的正方体可以组成方体(经过旋转得到相同的正方体视为同一种情况).种不同的 2×2×2 的正10. 在一个圆周上有 70 个点,任选其中一个点标上 1,按顺时针方向隔一个点的点上标 2,隔两个点的点上标 3,再隔三个点的点上标 4,继续这个操作,直到 1,2,3,…,2014 都被标记在点上.每个点可 能不止标有一个数,那么标记了 2014 的点上标记的最小整数是分分5 10 15 202530 5 10 15 202530第十九届华罗庚金杯少年数学邀请赛初赛 B 试卷(小学高年级组)(时间:2014 年 3 月 15 日 8:00—9:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.) 1. 平面上的四条直线将平面分割成八个部分,则这四条直线中至多有( )条直线互相平行.A .0B .2C .3D .42. 在下列四个算式中: AB ÷ CD =2,E ×F =0,G -H =1,I +J =4,A ~J 代表 0~9 中的不同数字,那么两位数 AB 不可能是( ). A .54 B .58 C .92 D .963. 淘气用一张正方形纸剪下了一个最大的圆(如图甲),笑笑用一张圆形纸剪下了七个相等的最大圆(如图乙),在这两种剪法中,哪种剪法的利用率最高?(利用率指的是剪下的圆形面积和占原来图形面积的百分率)下面几种说法中正确的是( ).A .淘气的剪法利用率高B .笑笑的剪法利用率高C .两种剪法利用率一样D .无法判断4. 小华下午 2 点要到少年宫参加活动,但他的手表每个小时快了 4 分钟,他特意在上午 10 点时对好了表.当小华按照自己的表于下午 2 点到少年宫时,实际早到了( )分钟.A .14B .15C .16D .175. 甲、乙、丙、丁四个人今年的年龄之和是 72 岁.几年前(至少一年)甲是 22 岁时,乙是 16 岁.又知道,当甲是 19 岁的时候,丙的年龄是丁的 3 倍(此时丁至少 1 岁).如果甲、乙、丙、丁四个人的年龄互不相同,那么今年甲的年龄可以有( )种情况.A .4B .6C .8D .106. 有七张卡片,每张卡片上写有一个数字,这七张卡片摆成一排,就组成了七位数 2014315.将这七张卡片全部分给了甲、乙、丙、丁四人,每人至多分 2 张.他们各说了一句话: 甲:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数就是 8 的倍数.” 乙:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数仍不是 9 的倍数.” 丙:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数就是 10 的倍数.” 丁:“如果交换我卡片上的 2 个数字在七位数中的位置,那么新的七位数就是 11 的倍数.” 已知四个人中恰好有一个人说了谎,那么说谎的人是( ).A .甲B .乙C .丙D .丁甲 乙二、填空题(每小题 10 分,共 40 分)13 ÷ 3 + 3 ÷ 2 1 + 17. 算式 1007× 4 44 3 ÷19 的计算结果是 .(1 + 2 + 3 + 4 + 5)⨯ 5 - 228. 海滩上有一堆栗子,这是四只猴子的财产,它们想要平均分配,第一只猴子来了,它左等右等别的猴子都不来,便把栗子分成四堆,每堆一样多,还剩下一个,它把剩下的一个顺手扔到海里,自己拿走了四堆中的一堆.第二只猴子来了,它也没有等到别的猴子,于是它把剩下的栗子等分成四堆,还剩下一个,它又扔掉一个,自己拿走一堆.第三只猴子也是如此,等分成四堆后,把剩下的一个扔掉, 自己拿走一堆;而最后一只猴子来,也将剩下的栗子等分成了四堆,扔掉多余的一个,取走一堆.那 么这堆栗子原来至少有 个.9. 甲、乙二人同时从 A 地出发匀速走向 B 地,与此同时丙从 B 地出发匀速走向 A 地.出发后 20 分钟甲与丙相遇,相遇后甲立即掉头;甲掉头后 10 分钟与乙相遇,然后甲再次掉头走向 B 地.结果当甲走到 B 地时,乙恰走过 A 、B 两地中点 105 米,而丙离 A 地还有 315 米.甲的速度是乙的速度的 倍,A 、B 两地间的路程是 米.10. 从 1,2,3,…,2014 中取出 315 个不同的数(不计顺序)组成等差数列,其中组成的等差数列中包含 1 的有 种取法;总共有 种取法.第十八届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2013 年 3 月 23 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.) 1. 2012.25×2013.75-2010.25×2015.75=( )A .5B .6C .7D .82. 2013 年的钟声敲响了,小明哥哥感慨地说:这是我有生以来第一次将要渡过一个没有重复数字的年份.已知小明哥哥出生的年份是 19 的倍数,那么 2013 年小明哥哥的年龄是( )岁.A .16B .18C .20D .223. 一只青蛙 8 点从深为 12 米的井底向上爬,它每向上爬 3 米,因为井壁打滑,就会下滑 1 米,下滑 1 米的时间是向上爬 3 米所用时间的三分之一.8 点 17 分时,青蛙第二次爬至离井口 3 米之处,那么青蛙从井底爬到井口时所花的时间为( )分钟.A .22B .20C .17D .164. 一个盒子里有黑棋子和白棋子若干粒,若取出一粒黑子,则余下的黑子数与白子数之比为 9︰7,若放回黑子,再取出一粒白子,则余下的黑子数与白子数之比为 7︰5,那么盒子里原有的黑子数比白子数多( )个.A .5B .6C .7D .85. 图 ABCD 是平行四边形,M 是 DC 的中点,E 和 F 分别位于 AB 和 AD 上,且 EF 平行于 BD .若三角形 MDF 的面积等于 5 平方厘米,则三角形 CEB 的面积等于( )平方厘米.A .5B .10C .15D .206. 水池 A 和 B 同为长 3 米,宽 2 米,深 1.2 米的长方体.1 号阀门用来向 A 池注水,18 分钟可将无水的A 池注满;2 号阀门用来从 A 池向B 池放水,24 分钟可将 A 池中满池水放入 B 池.若同时打开 1 号和2 号阀门,那么当 A 池水深 0.4 米时,B 池有( )立方米的水.A .0.9B .1.8C .3.6D .7.2D F MCAEB二、填空题(每小题 10 分,共 40 分)D E AFB7. 小明、小华、小刚三人分 363 张卡片,他们决定按年龄比来分.若小明拿 7 张,小华就要拿 6 张;若小刚拿 8 张,小明就要拿 5 张.最后,小明拿了 张;小华拿了张.张;小刚拿了8. 某公司的工作人员每周都工作 5 天休息 2 天,而公司要求每周从周一至周日,每天都至少有 32 人上班,那么该公司至少需要名工作人员.9. 如图,AB 是圆 O 的直径,长 6 厘米,正方形 BCDE 的一个顶点 E 在圆周上,∠ABE =45°.那么圆 O中非阴影部分的面积与正方形 BCDE 中非阴影部分面积的差等于 平方厘米(取 π=3.14)10. 圣诞老人有 36 个同样的礼物,分别装在 8 个袋子中.已知 8 个袋子中礼物的个数至少为 1 且各不相 同.现要从中选出一些袋子,将选出的袋子中的所有礼物平均分给 8 个小朋友,恰好分完(每个小朋 友至少分得一个礼物).那么,共有 种不同的选择.第十八届华罗庚金杯少年数学邀请赛AB 初赛 B 试卷(小学高年级组)(时间:2013 年 3 月 23 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 一个四位数,各位数字互不相同,所有数字之和等于 6,并且这个数是 11 的倍数,则满足这种要求的四位数共有( )个.A .6B .7C .8D .92. 2+2×3+2×3×3+……+2× 3 ⨯ 3 ⨯⨯ 3 个位数字是( ). 9个3A .2B .8C .4D .63. 在下面的阴影三角形中,不能由下图中左面的阴影三角形经过旋转、平移得到的是图( )中的三角形.ABCD4. 某日,甲学校买了 56 千克水果糖,每千克 8.06 元.过了几日,乙学校也需要买同样的 56 千克水果糖,不过正好赶上促销活动,每千克水果糖降价 0.56 元,而且只要买水果糖都会额外赠送 5%同样的水果糖.那么乙学校将比甲学校少花( )元.A .20B .51.36C .31.36D .10.365. 甲、乙两仓的稻谷数量一样,爸爸、妈妈和阳阳单独运完一仓稻谷分别需要 10 天、12 天和 15 天.爸爸、妈妈同时开始分别运甲、乙两仓的稻谷,阳阳先帮妈妈,后帮爸爸,结果同时运完两仓稻谷.那么阳阳帮妈妈运了( )天. A .3B .4C .5D .66. 如图,将长度为 9 的线段 AB 分成 9 等份,那么图中所有线段的长度的总和是( ).A .132B .144C .156D .165二、填空题(每小题10 分,共40 分)7.将乘积0.2˙43˙×0.32˙5233˙化为小数,小数点后第2013 位的数字是.8.一只青蛙8 点从深为12 米的井底向上爬,它每向上爬3 米,因为井壁打滑,就会下滑1 米,下滑1 米的时间是向上爬3 米所用时间的三分之一.8 点17 分时,青蛙第二次爬至离井口3 米之处,那么青蛙从井底爬到井口时所花的时间为分钟.9.一个水池有三个进水口和一个出水口.同时打开出水口和其中的两个进水口,注满整个水池分别需要6 小时、5 小时和4 小时;同时打开出水口和三个进水口,注满整个水池需要3 小时.如果同时打开三个进水口,不打开出水口,那么注满整个水池需要小时.10.九个同样的直角三角形卡片,用卡片的锐角拼成一圈,可以拼成类似下图所示的平面图形.这种三角形卡片中的两个锐角中较小的一个的度数有种不同的可能值.(下图只是其中一种可能的情况)第十七届华罗庚金杯少年数学邀请赛初赛 A 试卷(小学高年级组)(时间:2012 年 3 月 17 日 10:00—11:00)一、选择题(每小题 10 分,共 60 分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1. 计算:[(0.8+ 1 )×24+6.6]÷ 9-7.6=( ).5 14A .30B .40C .50D .602. 以平面上 4 个点为端点连接线段,形成的图形中最多可以有( )个三角形.A .3B .4C .6D .83. 一个奇怪的动物庄园里住着猫和狗,狗比猫多 180 只.有 20%的狗错认为自己是猫;有 20%的猫错认为自己是狗.在所有的猫和狗中,有 32%认为自己是猫,那么狗有( )只.A .240B .248C .420D .8424. 下图的方格纸中有五个编号为 1,2,3,4,5 的小正方形,将其中的两个涂上阴影,与图中阴影部分正好组成正方体的展开图,这两个正方形的编号可以是( )A .1,2B .2,3C .3,4D .4,55. 在下图所示的算式中,每个字母代表一个非零数字,不同的字母代表不同的数字,则和的最小值是( ) A .369B .396C .459D .5496. 下图是由相同的正方形和相同的等腰直角三角形构成,则正方形的个数为( )A .83B .79C .72D .651 253 4A B C + D E F H IJ二、填空题(每小题 10 分,共 40 分)百十个百 十 个A EC HFB7. 如图的计数器三个档上各有 10 个算珠,将每档算珠分成上下两部分,得到两个三位数.要求上面部分是各位数字互不相同的三位数,且是下面三位数的倍数,则上面部分的三位数是.8. 四支排球队进行单循环比赛,即每两队都要赛一场,且只赛一场.如果一场比赛的比分是 3:0 或 3:1.则胜队得 3 分,负队得 0 分;如果比分是 3:2,则胜队得 2 分,负队得 1 分.比赛的结果各队得分恰好是四个连续的自然数,则第一名的得分是 分.9. 甲、乙两车分别从 A 、B 两地同时出发,且在 A 、B 两地往返来回匀速行驶.若两车第一次相遇后,甲车继续行驶 4 小时到达 B ,而乙车只行驶了 1 小时就到达 A ,则两车第 15 次(在 A ,B 两地相遇次数不计)相遇时,它们行驶了 小时.10. 正方形 ABCD 的面积为 9 平方厘米,正方形 EFGH 的面积为 64 平方厘米.如图所示,边 BC 落在 EH上.己知三角形 ACG 的面积为 6.75 平方厘米,则三角形 ABE 的面积为 平方厘米.。
四年级“华罗庚杯”数学竞赛(通用版,含解析)

四年级“华罗庚杯”数学竞赛学校:__________姓名:___________班级:__________考号:________题号一二总分得分一.填空题(共9小题,满分36分,每小题4分)1.(4分)近似值为4.30的三位数,最大是,最小是.2.(4分)找规律填数:1、2、4、7、11、16、22、198、297、396、.3.(4分)一座大楼上的彩灯按红、黄、蓝、绿、紫的顺序依次排列组装,一共有37个灯泡.想一想:第20只灯泡的颜色是,最后一只灯泡的颜色是.4.(4分)有甲、乙、丙三个数,已知甲、乙两数的和是168,丙数是甲、乙两数平均数的2倍,甲、乙、丙三个数的平均数是.5.(4分)一个长方形长10米,宽6米,如果长减少米或者宽增加米,这个长方形就变成了正方形,这两个正方形相差平方米.6.(4分)一个人唱一首歌用2分钟,9个人合唱这首歌用分钟。
7.(4分)一列火车长180米,每秒行30米,这列火车通过480米长的大桥,需要秒.8.(4分)3个篮球的价钱和5个排球的价钱一样,学校体育室买了9个篮球和4个排球,共付款855元,一个排球元.9.(4分)如图,长方形ABEF的面积是40平方厘米,长方形CDGH 的面积是54平方厘米,阴影部分的面积是32平方厘米.空白部分的面积是平方厘米.评卷人得分二.解答题(共7小题,满分64分)10.(20分)(1)164×50÷82×48(2)98+4×980+59×98(3)624×48÷312÷8(4)1350÷25.11.(7分)一堆沙第一次运走它的一半多3吨,第二次运走剩下的一半少2吨,还剩23吨,这堆沙原来多少吨?12.(7分)新华小学开展冬季运动会,其中参加跳绳的人数是踢毽子人数的4倍,且比踢毽子的多72人.参加跳绳和踢毽子的各有多少人?13.(7分)今年妈妈的年龄是女儿的3倍,2年前妈妈和女儿的年龄和是56岁.妈妈和女儿今年各多少岁?14.(8分)甲、乙二人同地同方向出发,甲每小时走7千米,乙每小时走5千米.乙先走2小时后,甲才开始走,甲追上乙需要几小时?15.(8分)某工地的一项工程,原计划由30人工作,每天工作8小时,45天完工,为了提前完工,实际由54人工作,每天工作10小时,可以提前几天完工?16.(7分)爸爸带小明去滑雪,乘缆车上山用了4分钟,缆车每分钟行200米.滑雪下山用了20分钟,每分钟行70米.滑雪比乘缆车多行多少米?【竞赛专题】四年级“华罗庚杯”数学竞赛(5)(含解析)参考答案与试题解析一.填空题(共9小题,满分36分,每小题4分)1.【分析】要考虑4.30是一个三位数的近似数,有两种情况:“四舍”得到的4.30最大是4.304,“五入”得到的4.30最小是4.295,由此解答问题即可.【解答】解:“四舍”得到的4.30最大是4.304,“五入”得到的4.30最小是4.295;故答案为:4.304,4.295.2.【分析】(1)2=1+1,4=2+2,7=4+3,11=7+4,16=11+5,22=16+6.依此类推,可得结论.(2)297﹣198=99,396﹣297=99;后一个数比前一个数大99由此求解.【解答】解:(1)22+7=29;要填的数是29.(2)396+99=495;要填的数是495.故答案为:29,495.3.【分析】彩灯的排列特点是:5只一个循环周期,分别按照:红、黄、蓝、绿、紫的顺序排列,由此计算出第20和第37个彩灯是第几个周期的第几个即可.【解答】解:20÷5=4所以第20个灯泡是紫色;37÷5=7 (2)所以第37灯泡是黄色;答:第20只灯泡的颜色是紫色,最后一只灯泡的颜色是黄色.故答案为:紫色;黄色.4.【分析】已知甲、乙两数的和是168,丙数是甲、乙两数平均数的2倍,即丙数就是168,据此求出这三个数的和是168+168=336,再除以3即可求出这三个数的平均数.【解答】解:(168+168)÷3=336÷3=112答:甲、乙、丙三个数的平均数是112.故答案为:112.5.【分析】根据题意可知:要想变成正方形,这个正方形的边长可以是10米,也可以是6米,所以10﹣6=4米,这个长方形的长减少4米,或宽增加4米,都可以得到一个正方形,根据正方形的面积公式把数据分别代入公式求出它们的面积.然后再相减即可求出差.【解答】解:10﹣6=4(米)这个长方形的长减少4米,或宽增加4米,都可以得到一个正方形,10×(6+4)﹣(10﹣4)×6=10×10﹣6×6=100﹣36=64(平方米)答:这两个正方形的面积相差64平方米.故答案为:4、4、64.6.【分析】这首歌的长度是一定的,那么唱这首歌用的时间是一定,9个人合唱这首歌用的时间和一个人唱这首歌用的时间相同;由此求解。
第四届_华罗庚杯_少年数学邀请赛复赛部分试题以及答案讲解

第4届华杯少年数学邀请赛复赛部分试题以及答案(1)化简(2)电视台要播放一部30集电视连续剧。
如果要求每天安排播出的集数互不相等,该电视连续剧最多可以播几天?(3)一个正方形的纸盒中,恰好能放入一个体积为628立方厘米的圆柱体,纸盒的容积有多大?(圆周率=3.14)。
(4)有一筐苹果,把它们三等分后还剩2个苹果,取出其中两份,将它们三等分后还剩2个;然后再取出其中两份,又将这两份三等分后还剩2个,问:这筐苹果至少有几个?(5)计算(6)长方形 ABCD周长为16米,在它的每条边上各画一个以该边为边长的正方形,已知这四个正方形的面积和是68平方米,求长方形ABCD的面积(7)“华罗庚”金杯少年数学邀请赛,第一届在1986年举行,第二届在1988年举行,第三届是在1991年举行,以后每2年举行一届。
第一届“华杯赛”所在年份的各位数字和是A1=1+9+8+6=24。
前二届所在年份的各位数字和是A2=1+ 9+ 8 + 6 +1+ 9+ 8 + 8=50问:前50届“华杯赛”所在年份的各位数字和A50=?(8)将自然数按如下顺次排列:1 2 6 7 15 16 …3 5 8 14 17 …4 9 13 …10 12 …11 …在这样的排列下,数字3排在第二行第一列,13排在第三行第三列,问:1993排在第几行第几列?(9)在下图中所示的小圆圈内,试分别填入1、2、3、4、5、6、7、8这八个数字,使得图中用线段连接的两个小圆圈内所填的数字之差(大数字减小数字)恰好是1、2、3、4、5、6、7这七个数字。
(10)11+ 22+ 33+ 44+ 55+ 66+ 77+ 88+ 99除以3的余数是几?为什么?(11) A、 B、 C、 D、 E、 F六个选手进行乒乓球单打的单循环比赛(每人都与其他选手赛一场),每天同时在三张球台各进行一场比赛,已知第一天B对 D,第二天 C对E,第三天 D对 F,第四天B对C,问:第五天A与谁对阵?另外两张球台上是谁与谁对阵?(12)有一批长度分别为1、2、3、4、5、6、7、8、9、10和11厘米的细木条,它们的数量都足够多,从中适当选取3根本条作为三条边,可围成一个三角形。
第2届华杯少年数学邀请赛复赛部分试题以及答案

第2届华杯少年数学邀请赛复赛部分试题以及答案1.计算2. 有三张卡片,在它们上面各写有一个数字(图43)。
从中抽出一张、二张、三张,按任意次序排起来,可以得到不同的一位数、二位数、三位数。
请你将其中的素数都写出来。
3. 有大、中、小三个正方形水池,它们的内边长分别是6米、3米、2米。
把两堆碎石分别沉没在中、小水池的水里,两个水池的水面分别升高了6厘米和4厘米。
如果将这两堆碎石都沉没在大水池的水里,大水池的水面升高了多少厘米?4. 在一个圆圈上有几十个孔(不到100个),如图44。
小明像玩跳棋那样,从A孔出发沿着逆时针方向,每隔几个孔跳一步,希望一圈以后能跳回到A孔。
他先试着每隔2孔跳一步,结果只能跳到B孔。
他又试着每隔4孔跳一步,也只能跳到B 孔。
最后他每隔6孔跳一步,正好跳回到A孔。
你知道这个圆圈上共有多少个孔吗?5. 试将1,2,3,4,5,6,7分别填入图45的方框中,每个数字只用一次:使得这三个数中任意两个都互质。
其中一个三位数已填好,它是714。
6. 图47是一张道路图,每段路上的数字是小王走这段路所需的分钟数。
请问小王从A出发走到B,最快需要几分钟?7. 梯形 ABCD的中位线EF长15厘米(见图53),∠ABC=∠AEF=90°,G是EF上的一点。
如果三角形ABG的面积是梯形ABCD面积的1/5,那么EG的长是几厘米?8. 有三堆砝码,第一堆中每个法码重3克,第二堆中每个砝码重5克,第三堆中每个砝码重7克。
请你取最少个数的砝码,使它们的总重量为130克写出的取法:需要多少个砝码?其中3克、5克和7克的砝码各有几个?9. 有5块圆形的花圃,它们的直径分别是3米、4米、5米、8米、9米;请将这5块花圃分成两组,分别交给两个班管便两班所管理的面积尽可能接近。
10. 一串数排成一行,它们的规律是这样的:头两个数都是1,从第三个数开始,每一个数都是前两个数的和,也就是:1,2,3,5,8,13,21,34,55,问:这串数的前100个数中(包括第100个数)有多少个偶数?11. 王师傅驾车从甲地开乙地交货。
“华罗庚金杯”少年数学邀请赛(口试)试题1-10届

华罗庚金杯少年数学邀请赛口试试题第01届华罗庚金杯少年数学邀请赛口试试题1. 这是七巧板拼成的正方形,正方形边长20厘米,问七巧板中平行四边形的一块(如右图中阴影部分)的面积是多少?2.从所有分母小于10的真分数中,找出一个最接近0.618的分数。
3.有49个小孩子,每人胸前有一个号码,号码从1到49各不相同,请你挑选出若干个小孩,排成一个圆圈,使任何相邻两个小孩的号码数的乘积小于100,你最多能挑选出多少个小孩子?4.有一路公共汽车,包括起点和终点站共有15个车站,如果有一辆车,除终点到站外,每一站上车的乘客中,恰好各有一位乘客从这一站到以后的每一站,为了使每位乘客都有座位,问这辆公共汽车最少要有多少个座位?5.正方形的树林每边长1000米,里面有白杨树和榆树,小明从树林的西南角走入树林,碰见一株白杨树就往正北走,碰见一株榆树就往正东走,最后他走了东北角上,问:小明一共走了多少米的距离?6.自然数按从小到大的顺序排成螺旋形,在2处拐第一个弯,在3处拐第二个弯,在5处拐第三个弯……问拐第二十个弯的地方是哪一个数?第02届华罗庚金杯少年数学邀请赛口试试题1、如下图是一个对称的图形,黑色部分面积大还是阴影部分面积大?2、你能不能将自然数1到9分别填入右面的方格中,使得每个横格中的三个数之和都是偶数?3、司机开车按顺序到五个车站接学生到学校(如下图),每个站都有学生上车,第一站上了一批学生,以后每站上车的人数都是前一站上车人数的一半,车到学校时,车上最少有多少学生?4、如图中五个正方形的边长分别是1米、2米、3米、4米、5米。
问:白色部分面积与阴影部分面积之比是多少?5、用1、2、3、4、5这五个数两两相乘,可以得到10个不同的乘积,问乘积中是偶数多还是奇数多?6、7、将右边的硬纸片沿虚线折起来,便可作成一个正方体,问:这个正方体的2号面对面是几号面?(如下图)8、下面是一个11位数,它的每三个相邻数之和都是20,你知道打“?”的数字是几?9、有八张卡片,右图分别写着自然数1到8,从中取出三张,要使这三张卡片上的数字之和为9,问有多少种不同的取法?第03届华罗庚金杯少年数学邀请赛团体决赛口试1.一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道红条,如右图阴影所示部分,红条宽都是2厘米.问:这条手帕白色部分的面积是多少?2.伸出你的左手,从大拇指开始如图所示的那样数数字,1,2,3,……,问:数到1991时,你数在那个手指上?3.有3个工厂共订300份吉林日报,每个工厂订了至少99份,至多101份.问:一共有多少种不同的订法?4.图上有两条垂直相交的直线段AB、CD,交点为E(如下图).已知:DE=2CE,BE=3AE.在AB和CD上取3个点画一个三角形.问:怎样取这3个点,画出的三角形面积最大?5.如下图中有两个红色的圆,两个蓝色的圆,红色圆的直径分别是1992厘米和1949厘米,蓝色圆的直径分别是1990厘米和1951厘米.问:红色二圆面积大还是蓝色二圆面积大?6.在一张9行9列的方格纸上,把每个方格所在的行数和列数加起来(如下图),填在这个方格中,例如a=5+3=8.问:填入的81个数字中,奇数多还是偶数多?7.能不能在下式:1□2□3□4□5□6□7□8□9=10的每个方框中,分别填入加号或减号,使等式成立?8.把一个时钟改装成一个玩具钟(如右图),使得时针每转一圈,分针转16圈,秒针转36圈.开始时3针重合.问:在时针旋转一周的过程中,3针重合了几次?(不计起始和终止的位置).9.将1,2,3,4,5,6,7,8这8个数分成3组,分别计算各组数的和.已知这3个和互不相等,且最大的和是最小的和的2倍.问:最小的和是多少?10.这是一个棋盘,将一个白子和一个黑子放在棋盘线交叉点上,但不能在同一条棋盘线上.问:共有多少种不同的放法(如下图)?11.这是两个圆,它们的面积之和为1991平方厘米,小圆的周长是大圆周长的90%(如右图).问:大圆的面积是多少?12.有一根1米长的木条,第一次去掉它的,第二次去掉余下木条的;第三次又去掉第二次余下木条的,等等;这样一直下去,最后一次去掉上次余下木条的.问:这根木条最后还剩下多长?13.这是一个楼梯的截面图(如下图),高2.8米,每级台阶的宽和高都是20厘米.问:此楼梯截面的面积是多少?14.请找出6个不同的自然数,分别填入6个括号中,使这个等式成立.第04届华罗庚金杯少年数学邀请赛团体决赛口试1.2×3×5×7×11×13×17这个算式中有七个数连乘,请回答:最后得到的乘积中,所有数位上的数字和是多少?请讲一讲你是怎样算的?2.这是一个中国象棋盘(图中小方格都是相等的正方形,“界河”的宽等于小正方形边长),黑方有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12, 13,14中的两个位置.问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?3.将一根长为374厘米的合金铝管截成若干根36厘米和24厘米两种形状的短管(加工损耗忽略不计)问:剩余部分的管子最少是多少厘米?4.乙两人同时从A出发向B行进,甲速度始终不变,乙在走前面路程时,速度为甲的2倍,而走后面路程时,速度是甲的,问甲、乙二人谁选到B?请你说明理由。
六年级下册数学试题-华罗庚金杯少年数学邀请赛小学组初赛试题(含答案PDF)全国通用

的都是假话.那么,昨天这5个人中复习数学的有( )个人.
(A) 0
(B) 1
(C) 2
(D) 3
l
(
华罗庚金杯少年数学邀请赛小学组初赛试题 答案
(
一、 选择题(每小题10分, 满分60分)
1:: I�I : I : I : I : I : I
华罗庚金杯少年数学邀请赛小学组初赛试题
一、选择题(每小题10 分以下每题的四个选项中,仅有一个是正确的,诮将表示正确答案的英文 字母写在每题的圆括号内.)
1. 若连续的四个自然数都为合数,那么这四个数之和的最小伯为( ) 书
(A) 100
CB) 101
(C) 102
(D) 103
· 2. m火柴棍摆放数字0�9的方式如下;\曰Fra bibliotek叶55丁日日D
(1
'··
现在,去掉;, 9,, 的左下创 一根,就成了数字 “ 千,我们称"9"对应1; 去掉"8"的上下呐
o, 根和左下角 一根,就成了数字 ” 中,我们称 "4,, 对应3. 规定 "B,, 本身对应 按照这杆的
规则,可以对应出( )个不同的数字.
(A) 10
(B) 8
(C) 6
:二、填空题(每小题10分, 满分40分)
7 -8
8 1- 2
9
·一
一1·0
65
1769
(
(
,`�
90
(D) 5
3. -�Jj数之和与两数之商都为6, Jjl么这两数之积减这两数之差(大减小)等于( ) .
第五届“华罗庚金杯”少年数学邀请赛复赛试题

数学竞赛第五届“华罗庚金杯”少年数学邀请赛复赛试题及答案1.计算:2.甲、乙两位学生原计划每天自学的时间相同,若甲每天增加自学时间半小时,乙每天减少自学时间半小时,则乙自学6天的时间仅相等于甲自学1天的时间。
问:甲乙原订每天自学的时间是多少?3.图5-4是由圆周、半圆周、直线线段画成的,试经过量度计算出图中阴影部分以外整个“猪”的面积(准确到1平方毫米)。
4.羊和狼在一起时,狼要吃掉羊,所以关于羊及狼,我们规定一种运算,用符号△表示:羊△羊=羊;羊△狼=狼;狼△羊=狼;狼△狼=狼以上运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但是狼与羊在一起便只剩下狼了。
小朋友总是希望羊能战胜狼,所以我们规定另一种运算,用符号☆表示:羊☆羊=羊;羊☆狼=羊;狼☆羊=羊;狼☆狼=狼这个运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但由于羊能战胜狼,当狼与羊在一起时,它便被羊赶走而只剩下羊了。
对羊或狼,可以用上面规定的运算作混合运算,混合运算的法规是从左到右,括号内先算,运算的结果或是羊,或是狼。
求下列的结果:羊△(狼☆羊)☆羊△(狼△狼)5.人的血通常为A型,B型,O型,AB型。
子女的血型与其父母血型间的关系如下表所示:父母的血型子女可能的血型O,O OO,A A,OO,B B,OO,AB A,BA,A A,OA,B A,B,AB,OA,AB A,B,ABB,B B,OB,AB A,B,ABAB,AB A,B,AB现有三个分别身穿红、黄、蓝上衣的孩子,他们的血型依次为O、A、B。
每个孩子的父母都戴着同颜色的帽子,颜色也分红、黄、蓝三种,依次表示所具有的血型为AB、A、O。
问:穿红、黄、蓝上衣的孩子的父母各戴什么颜色的帽子?6.一台天平,右盘上有若干重量相等的白球,左盘上有若干重量相等的黑球,这时两边平衡,在右盘上取走一个白球置于左盘上,再把左盘的两个黑球置于右盘上,同时给左盘加20克砖码,这时两边也平衡,如从右盘移两个白球到左盘上,从左盘移一个黑球到右盘上,则须再放50克砖码于右盘上,两边才平衡。
七年级新思维28-实验与操作
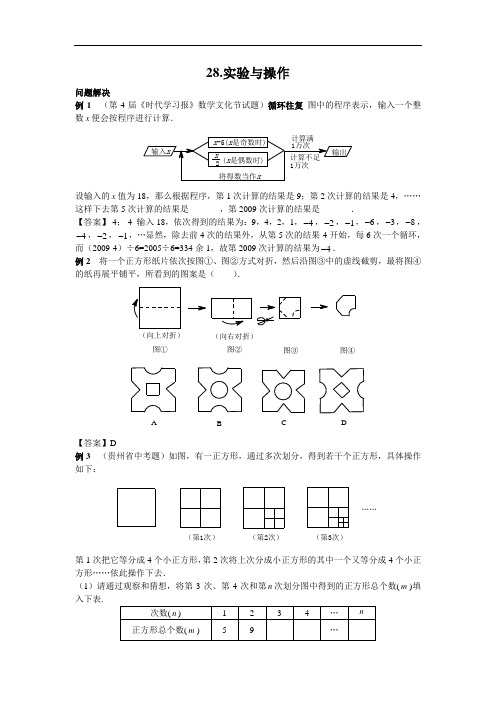
28.实验与操作问题解决例1 (第4届《时代学习报》数学文化节试题)循环往复图中的程序表示,输入一个整数x便会按程序进行计算.设输入的x值为18,那么根据程序,第1次计算的结果是9;第2次计算的结果是4,……这样下去第5次计算的结果是_______,第2009次计算的结果是_______.【答案】-4;-4 输入18,依次得到的结果为:9,4,2,1,4-,2-,1-,6-,3-,8-,4-,2-,1-,…显然,除去前4次的结果外,从第5次的结果-4开始,每6次一个循环,而(2009-4)÷6=2005÷6=334余1,故第2009次计算的结果为4-.例2将一个正方形纸片依次按图①、图②方式对折,然后沿图③中的虚线截剪,最将图④的纸再展平铺平,所看到的图案是().图④(向右对折)(向上对折)A B C D图①图②图③【答案】D例3(贵州省中考题)如图,有一正方形,通过多次划分,得到若干个正方形,具体操作如下:……(第3次)(第2次)(第1次)第1次把它等分成4个小正方形,第2次将上次分成小正方形的其中一个又等分成4个小正方形……依此操作下去.(1)请通过观察和猜想,将第3次、第4次和第n次划分图中得到的正方形总个数(m)填入下表.(2)请你推断,按上述操作方法,能否得到103个正方形?为什么?【答案】(1)当n=3时,13m=;4n=时,17m=;……一般的41m n=+.(2)由41m n=+,得1034125.5n n=+=,,因n不是正整数,故按此要求操作不可能得到103个正方形.例4(太原市竞赛题)有1997枚硬币,其中1000枚国徽朝上,997枚国徽朝下.现在要求每一次翻转其中任意6枚,使它们的国徽朝向相反.问:能否经过有限次翻转后,使所有硬币的国徽都朝上?给出你的结论,并给出证明.【答案】用1997枚硬币的朝向情况可用1997个数的乘积来表示.若这些数之积为1-(或+1),表明有奇数(或偶数枚硬币朝下).开始时,其乘积为1000997(1)(1)1+⨯-=-.每次翻折6枚硬币,即每次改变6个数的符号,其结果是1997个数之积仍为1-.经过有限次翻转后,这个结果总保持不变,即国徽朝下的硬币数永远是奇数枚,故回答是否定的.例5在2×2方格纸中,以格点连线为边作面积为2的多边形(含凹多边形),请尽可能多地找出答案,在寻找答案的过程中你能发现什么规律吗?分析与解若没有规律性的认识,则要无遗漏重复地找出全部解答是困难的.恰当的方法是:选择一些图形作基本图形,通过基本图形的组合找出解答,可将下列7个图形作为基本图形:(5)(6)(7)(4)由此可得如下23个解答,其中凸多边形7个,凹多边形16个:(23)(22)(21)(19)(18)(12)(20)(9)(15)(7)(8)俄罗斯方块例6游戏机的“方块”中共有下面7种图形,每种“方块”都由4个1×1的小方格组成.现用这7种图形拼成一个7×4的长方形(可以重复使用某些图形).问:最多可以用这7种图形中的几种图形?分析与解 为了形象化地说明问题,对7×4的长方形的28个小方格黑白相间染色,除“品”字形必占3个黑格1个白格或3个白格1个黑格外,其余6个方块各占2个黑格2个白格. 用其中的6种不同的图形方块可以拼成7×4的长方形,方法很多,如图①仅出示一种. 下面证明不能7种图形方块都各用一次.将7×4的长方形的28个小方格黑白相间染色,则如图②所示,黑、白格各14个.若7×4的长方形能用7种不同的方块拼成,则每个方块用到一次且只用一次.其中“品”字形如图③必占3个黑格1个白格或3个白格1个黑格,其余6个方块各占2个黑格2个白格.7种不同的方块占据的黑格总数、白格总数都是奇数个,不会等于14.矛盾.因此,不存在7种图形方块每个各用一次拼成7×4的长方形的方法. 所出,要拼成7×4的长方形,最多可以用这7种图形方块中的6种.图①图②图③数学冲浪知识技能广场 1.(《时代学习报》数学文化节试题)乐在其中七巧板的起源要追溯到我国先秦时期,古算书《骨髀算经》中即有正方形分割术,经历代演变而成“七巧图”(又称为“益智图”和“智慧板”,如图①).19世纪传到国外,多称其为“唐图”(意为“来自中国的拼图”),引起人们的极大兴趣,欧美许多国家纷纷出版书籍予以介绍.(第1题)图①图②如果有一副七巧板的总面积是100平方厘米,那么其中正方形的那一块的面积是_______平方厘米. 图②“乐在其中”的每个字都是由一副七巧板摆拼所得,请在图中用线段画出模块之间的“拼缝”.【答案】12.5 画图略 2.(乌鲁木齐市中考题)如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的方法有_______种. 【答案】5(第3题)(第2题)3.(乌鲁木齐市中考题)如图,将长度为20cm ,宽为2cm 的长方形的纸带,折成如图所示的图形并在其一面着色,则着色部分的面积为_______cm 2. 【答案】36 4.(浙江省嘉兴市中考题)定义一种对正数n 的“F ”运算:①当n 为奇数时,结果为35n +;②当n 为偶数时,结果为2k n (其中k 是使2kn为奇数的正整数),并且运算重复进行.例如:取26n =,则26134411F F F −−−→−−−→−−−→第一次第二次第三次②①②…若449n =,则第449次“F ”运算的结果是_______.【答案】8 5.(浙江省金华市中考题)图中的大正三角形是由9个相同的小正三角形拼成的,将其部分涂黑,如图①、②所示.图④(第5题)图③图②图①观察图①、图②中涂黑部分构成的图案.它们具有如下特征:①都是轴对称图形,②涂黑色部分都是三个小正三角形.请在图③、图④内分别设计一个新图案,使图案具有上述两个特征. 【答案】略 思维方法天地 6.(《时代学习报》数学文化节试题)折折剪剪一张正方形纸片,通过两次对折,然后按阴影部分进行裁剪并展开,可以得到如图(1)末的“蝴蝶结”:(第6题①)第三次对折第二次对折第一次对折请你仿图①,将下面的正方形纸片经过两次对折后裁剪并展开,得到如图②末的图形,请画出虚线和实线表示折叠过程,并用阴影表示剪去的部分.(第6题②)【答案】或7.(深圳市“启智杯”数学思维能力竞赛题)把四个完全相同的空啤酒瓶放置在桌面上,使得四个啤酒瓶底中心的距离两两相等,请写出摆法关键步骤(可画图辅助说明):___________________________________________________.【答案】先将三个空啤酒瓶放置成底面中心成“正三角形”的位置,再将一个空啤酒瓶倒置放在这个三角形中心P的位置,保持中心P的位置不变,适当移动三个底朝下的空啤酒瓶,放大或缩小“正三角形”,可使瓶底中心构成四个边长相等的“正三角形”如图(答案不唯一).(第8题)(第7题)8.(俄罗斯萨温市竞赛题)方格纸上有3个图形,你能沿着格线把每一个图形都分成完全相同的两个部分吗?【答案】9.(“希望杯”邀请赛试题)有依次排列的3个数:3,9,8.对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,1-,8,这称为第一次操作;做第二次同样的操作后也可以产生一个新数串:3,3,6,3,9,10-,1-,9,8.继续依次操作下去.问:从数串3,9,8开始操作至第100次以后所产生的那个新数串的所有数之和是多少?【答案】一个依次排列的n个数组成一个数串:123na a a a,,,,,依题设操作方法可得新增的数为:2132431n na a a a a a a a-----,,,,,则新增数之和为:2132()()a a a a-+-+ 4311()()n n na a a a a a--++-=-(※)原数串为3个数:3,9,8.第1次操作后所得数串为:3,6,9,1-,8,根据(※)可知,新增2项之和为:6+(1-)=5=83-,第2次操作后所得数串为:3,3,6,3,9,10-,1-,9,8,根据(※)可知,(第7题)新增4项之和为3+3+(10-)+9=5=8-3,按这个规律下去,第100次操作后所得新数串所有数的和为:(3+9+8)+100×(83-)=520. 10.(五城市联赛题)有三堆石子的个数分别是19,8,9,现在进行如下的操作:每次这三堆石子中的任意两堆中各取出1个石子,然后把这2个石子都加到另一堆中去,试问能否经过若干次这样的操作后,使得:(1)三堆石子的数分别是2,12,22; (2)三堆都是12.如能,请用最快的操作完成;不能,则说明理由[注:若从第一、二堆各取1个到第三堆,可表示为(19,8,9)⇒(18,7,11)等]. 【答案】(1)经过6次操作可达到要求:(19,8,9)⇒(21,7,8)⇒(23,6,7)⇒(25,5,6)⇒(24,4,8)⇒(23,3,10)⇒(22,2,12).(2)不可能.因为每次操作后,每堆码数要么加2,要么少1,而19,8,9被3除余数分别为1,2,0,经过任何一次操作后余数分别是0,1,2,不可能同时被3整除. 11.(中国科技技术大学“少年班”招生入学试题)如图a 所示的展览馆有36个陈列室,每两个相邻陈列室之间有门可通,其人口与出口位置如图b 所示,现有人希望每个陈列都能参观,但只经过每个展室一次.这可能吗?如果可能,请为他设计一条参观路线;如果不能,请说明理由.ba入口展览大厅==进口出口【答案】不可能 我们设想36个展室都依次相间地铺上了两种颜色的地毯,则参观者无论怎样走法,只能按白→黑→白→黑→白→……的次序前进.因此,不管参观者怎样走法,第36次只能走到一间黑色地毯的展室,绝不可能走到铺白色地毯的展室出口.应用探究乐园12.(江苏省竞赛题)如图是一张“3×5”(表示边长分别为3和5)的长方形,现要把它分成若干边长为整数的长方形(包括正方形)纸片,并要求分得的任何两线纸片都不完全相同. (1)能否分成5张满足上述条件的纸片? (2)能否分成6张满足上述条件下纸片?若能分,用“a ×b ”的形式分别表示出各张纸片的边长,并画出分割的示意图;若不能分,请说明理由.【答案】(1)把可分得的边长为整数的长方形按面积从小到大排列,有1×1,1×2,1×3,1×4,2×2,1×5,2×3,2×4,3×3,2×5,3×4,3×5.若能分成5张满足条件的纸片,因为其面积之和应为15,所以满足条件的有1×1、1×2、1×3、1×4、1×5(如图①)或1×1、1×2、1×3、2×2、1×5(如图②)(第12题)出口进口(第11题)图①图②(第12题)(2)若能分成6张满足条件的纸片,则其面积之和仍应为15,但上面排在前列的6个长方形的面积之和为1×1+1×2+1×3+1×4+2×2+1×5=19>15.所以分成6张满足条件的纸片是不可能的. 13.(河北省中考题)图形的操作过程(本题中四个矩形的水平方向的边长均为a ,竖直方向的边长均为b )在图①中,将线段12A A 向右平移1个单位到12B B ,得到封闭图形1221A A B B (即阴影部分); 在图②中,将折线123A A A 向右平移1个单位到123B B B ,得到封闭图形123321A A A B B B (即阴影部分).(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影;(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积: 1S =_______,2S =_______,3S =_______;(3)联想与探索:如图④,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少?并说明你的猜想是正确的.图③33A B B A 22图④图①图②【答案】(1)略;(2)123S S S 、、的结果都是ab b -;(3)这是有关道路形状及草地面积的研究题,其中包含阅读、作图、计算及猜想等步骤.关键是探索:当道路由笔直到任意弯曲的变化中,矩形中空白部分(即草地)面积情况.猜想:依据前面的计算,无论小路怎么弯曲,可以猜想草地的面积仍然是ab b -.方法是将“小路”沿左右两个边界剪去,将其中一侧的草地平移一个单位向另一侧草地靠拢,得到一个新的矩形.此时,在新的矩形中,其纵向宽仍然是b ,其水平方向的长度变成了1a -,所以草地面积是(1)b a ab b -=-.设而不求(微探究)(第13题)字母示数是代数式的一个重要特征,是由算术跨越到代数的桥梁,是数学发展史上的一个飞跃.字线示数具有简明性、一般性,在求代数式的值、形成公式、解应用题等方面有广泛的应用. 为了沟通数量间的关系,或将有些不明朗的关系表示出来,我们需要设元,而所设的字母不能或不需要求出,这就是设而不求的基本涵义.例1 (四川省竞赛题)老师报出一个5位数,同学们将它的顺序倒排后得到的5位数减去原数,甲、乙、丙、丙的结果分别是34567,34056,23456,34956,老师判定4个结果中只有1个正确,答对的是_______.【答案】乙 所得差=11×[909(e a -)+90(d b -)]是11的倍数例2 (2012年湖北省恩施自治州中考题)某大型超市从生产基地购进一批水果,运输过程中质量损失10%.假设不计超市其他费用,如果超市要想获得20%的利润,那么这种水果的售价在进价基础上应至少提高( ).A .40%B .33.4%C .33.3%D .30%【答案】B 设水果质量为m ,进价为a ,售价在进价的基础上至少提高x , 则101(1)20100100m x a ma ma⎛⎫-+- ⎪⎝⎭-,解得33.4%x ≈. 例3 (江苏省竞赛题)某地区的民用电,按白天时段和晚间规定了不同的单位.某户8月份白天时段用电量比晚间时段用电量多50%,9月份白天时段用电量比8月份白天时段用电量少60%,结果9月份的用电量虽比8月份的用电量多20%,但9月份的电费却比8月份的电费少10%.求该地区晚间时段民用电的单价比白天时段的单价低的百分数.【答案】设白天的单价为a 元/度,晚间的单价比白天低的百分数为x ,即晚间的单价为(1-x )a 元/度,又设8月份晚间用电量为n 度,则8月份白天用电量为(1+50%)n =1.5n 度,8月份电费为1.5(1)(2.5)na x na x na +-=-元,9月份白天用电量为1.5(160%)0.6n n -=度,9月份晚间用电量为( 1.5n n +)(120%+)-0.6 2.4n n =度,9月份电费为0.6 2.4(1)(3 2.4)na x na x na +-=-.由题意得,(3 2.4-x )na =(2.5-x )(110-%)na ,解得0.550%x ==.例4 从两个重量分别为12千克和8千克,且含铜的百分数不同的合金上切下重量相等的两块,把所切下的每块和另一块剩余的合金放在一起,熔炼后两个合金含铜的百分数相等.求所切下的合金的重量是多少千克?【答案】设所切下的合金的重量为x 千克,重12千克的合金的含铜百分数为p ,重8千克的合金的含铜百分数为()q p q ≠,于是有(12)(8)128xq x p xp x q-+-=,整理得()24()p q p x q p -=-.因为p q ≠,所以0p q -≠,因此 4.8x =,即所切下的合金重4.8千克.例5 (“华罗庚杯”邀请赛试题)能否找到7个整数,使得这7个整数沿圆周排成一圈后,任3个相邻数的和都等于29?如果能,请举一例;如果不能,请简术理由. 分析 假设存在7个整数1234567a a a a a a a ,,,,,,排成一圈后,满足题意,由此展开计算推理.若推得矛盾,则原假设不成立. 解 由题意aa 4a1232342929a a a a a a ++=++=……6717122929a a a a a a ++=++=将上述7式相加,得312345673()297a a a a a a a ++++++=⨯,12345672673a a a a a a a ∴++++++=,与1234567a a a a a a a ++++++为整数矛盾,故不存在满足题设要求的7个整数. 难解的结英国剑桥大学有一位数学家(真名叫道奇逊),用刘易士·卡洛尔的笔名写了不少非常有趣的科普读物,其中有一本《乱纷纷的结》,书中的每一章都叫做“绳结”,意即这些问题像绳结一样复杂难解,下面就是一个“绳结”的题目:例6 两个步行者正在急促地以每小时6千米的速度向山下走去,一个年轻人像羚羊似的边跳边走,他的同伴吃力地跟在后面.年轻人说,只怪我们上山的时候走得太慢了,每小时只走3千米.在平地的时候走得多快?他的同伴回答,在平路上每小时走4千米.年轻人说,能赶得上回去吃夜饭吗?同伴说,这要看我们了.我们3点钟出来,8点钟该我们回到旅馆的时候了.今天可真走了不少路.年轻人说,到底走了多少路呢?同伴不耐烦地说,你自己去想吧.题目就是这样,似乎条件不充分,你能解开这个“结”吗?解 设旅行都一共走过的路程为x 千米,上坡(或下坡)走过的路程为y 千米, 整个行程分为四段:走平路、上坡、下坡、再走平路.开始走平路所花的时间是124x y-小时,上坡所花的时间是3y 小时,下坡所花的时间是6y 小时,再走平路所花的时间是124x y -小时. 依题意可得方程:112254364x y x yy y --+++=, 原方程化简得15204x x ==,,故他们一共走了20千米. 练一练 1.(2012年“希望杯”邀请赛试题)已知23566914x y z y z x -=+=--,,则x y z ,,的平均数是_______.【答案】4932.(世界数学团体锦标赛试题)A B 、两校男生、女生人数的比分别为8∶7,30∶31,两校合并后男生、女生人数的比是27∶26.若用一位整数的比近似表示合并前A B 、两校的人数的比,则这个近似比是_______.【答案】453614≈ 3.(“希望杯”邀请赛试题)甲、乙两车从A 向B 行驶,甲比乙晚出发6小时,开始时甲、乙的速度比是4∶3.甲出发6小时后,速度提高1倍,甲、乙两车同时到达B .则甲从A 到B 共走了_______小时.【答案】8.4 设甲出发6小时后再用t 小时即可追上乙,甲原速为u ,乙速为v ,由题设知当甲出发行驶6小时,乙已经行驶了12小时,故有(12)62t v u tu +=+,即12t +=(62)t u v +=(62t +)·u v =(6+2t )·43,故363248 2.4t t t +=+=,(小时).故甲共走了6+2.4=8.4(小时).4.某服装厂生产某种定型冬装,9月份销售每件冬装的利润是出厂价的25%(每件冬装的利润=出厂价–成本),10月份将每件冬装的出厂价调低10%(每件冬装的成本不变),销售件数比9月份增加80%,那么该厂10月份销售这种冬装的利润总额比9月份的利润总额增长( ).A .2%B .8%C .40.5%D .62%【答案】B 设9月份每件冬装的出厂价为x 元,则每件成本为0.75x 元,10月份每件冬装的利润为(1-10%)0.75x x -=0.15x 元,又设9月份销售冬装m 件,则10月份销售冬装(1+80%)m =1.8m 件,故10月份的利润总额与9月份相比,增长0.15 1.80.258%0.25x m xmxm⋅-=.5.(“希望杯”邀请赛试题)甲、乙、丙、丁四人,每三个人的平均年龄加上余下一人的年龄分别为29,23,21和17,则这四人中最大年龄与最小年龄的差是( ). A .28 B .27 C .19 D .18 【答案】D 6.(“希望杯”邀请赛试题)一辆汽车从A 地匀速驶往B 地,如果汽车行驶的速度增加%a ,则所用的时间减少6%,则a b 、的关系是( ). A .1001%a b a =+ B .1001%b a =+ C .1a b a =+ D .100100ab a=+【答案】D 设A B 、两地之间的距离为S ,汽车行驶的速度为v ,汽车从A 地到B 地所用的时间为t ,则(1%)(1%)S vt v a t b ==+-. 7.(环求城市数学奥林匹克试题)如图3×3数表各行、各列及两条对角线之和彼此相等,设为S .求证:(1)S =3e ;(2)2()4a c g i b d f h e +++=++++.【答案】(1)S a e i b e h c e g d e f =++=++=++=++, 相加得43S a b c d e f g h i i e =++++++++++,故3S e =. (2)S a b c b e h =++=++,故a c e h +=+,同理a g e f g i e b c i e d +=++=++=+,,,四式相加得2()4a c g i b d f h e +++=++++.8.(湖北省黄冈市竞赛题)在一次数学竞赛中,组委会决定用NS 公司赞助的款购买一批奖品.若以1台NS 计算器和3本《数学竞赛讲座》书为一份奖品,则可买100份奖品;若以1台NS 计算器和5本《数学竞赛讲座》书为一份奖品,则可买80份奖品.问这笔钱全部用来购买计算器或《数学竞赛讲座》书,可各买多少?【答案】设每台计算器x 元,每本《数学竞赛讲座》书y 元,则100(3)x y +=80(5x y +),d i h g fe c b a解得5x y =,故可购买计算器100(3)10085x y yx y+⨯==160(台), 书100(3)1008800()x y yy y+⨯==本. 9.(河北省中考题)甲、乙二人分别从A B 、两地出发,相向而行.若同时出发,经24分钟相遇;若乙比甲提前10分钟出发,甲出发20分钟与乙相遇.求甲从A 地到B 地、乙从B地到A 地各需多少分钟? 【答案】40分钟、60分钟 10.(广州市中考题)在车站开始检票时,有(0)a a >名旅客在候车室排队等候检票进站,检票开始后,仍有旅客继续前来排队等候检票进站.设旅客按固定的速度增加,检票口检票的速度也是固定的.若开放一个检票口,则需30分钟才可将排队等候检票的旅客全部检票完毕;若开放两个检票口,则只需10分钟便可将排队等候检票的旅客全部检票完毕;现在要求在6分钟内将排队等候检票的旅客全部检票完毕,以使后来到站的旅客能随时随检,问需要同时开放几个检票口?【答案】设需要开放x 个窗口,每个窗口每分钟检出的人数是c ,每分钟来排队的人数是b ,则30301021066a b c a b c a b cx +=⎧⎪+=⨯⎨⎪+=⎩①②③由①,②得302a b c b ==,.将302a b c b ==,带入③,得3x =.借助图形思考(微探究)数学是研究数量关系与空间形式的科学,数与形,以及数和形的关联与转化,这是数学研究的永恒主题.当代美国数学家斯蒂恩说:“如果一个特定的问题可以被转化为一个图形,那么思维就整体地把握了问题,并能创造性地思考问题.”现阶段借助图形思考主要体现为:通过构造图形或拼图解与数量关系相关联的问题.例 1 A B C D E F 、、、、、六个足球队进行单循环比赛,当比赛到某一天时,统计出A B C D E 、、、、五队已分别比赛了5、4、3、2、1场球,则这没有与B 队比赛的球队是_______.【答案】E 队D例2 (山东省威海市中考题)古希望常用小石子在沙滩上摆成各种形状来研究数.比如:他们研究过图①中的1,3,6,10,…,由于这些数能够表示成三角形,故将其称为三角形数.类似地,称图②中的1,4,9,16,…,这样的数为正方形数.下列数中,既是三角形数,又是正方形数的是( ).A .289B .1024C .1225D .1378图②图①……1361014916【答案】C 图①中第n 个图共有石子1+2+…+n =(1)2n n +(个),图②中第n 个图共有石子2n (个),1225=249501225352⨯=,. 例3 (浙江省衢州市中考题)有足够多的长方形和正方形卡片,如下图:(1)如果选取的1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.122333______________________________________________________________________________ 这个长方形的代数意义是___________________________________________________ (2)小明想用类似方法解释多项式乘法(3a b +)(2a b +)=22273a ab b ++,那么需要用2号卡片_______张,3号卡片_______张.【答案】(1)或2232()(2)a ab b a b a b ++=++.(2)3;7 眼见亦可为虚例4 一只小渔船在海上遇到了台风,触到礁石上,船身撞出了一个窟窿.如果不把它堵上,渔船就有沉淀的危险.船中只有一块边长是8cm 的正方形木板.但是和船的窟窿相比,木板的面积少1cm 2.怎么办好呢?正在焦急当中,有一个船员用锯把这块正方形的木板裁开(如下图),然后用胶粘接拼成了长方形木板.13×5=65 (cm 2)8×8-64 (cm 2)5855333①②③④④③②①从图中的计算可知:原来的正方形木板的面积是64cm 2,可是改成长方形以后的木板的面积却变成了65cm 2了,正好多出1cm 2.船员赶紧把它堵在窟窿上,避免渔船的沉没.可是大家都感到惊奇的是,这1cm 2是从哪里多出来的呢,你能告诉他们吗? 【答案】如图,形成“对角线”的三角形之边与梯形之边不在同一条直线上,则180αβ+≠︒,这便函是问题的症结所在.横看成岭侧成峰例5 21()()()()()()24222a b a b a b a b a b a b a b +-⎡⎤-=+-=+-⨯=⨯⨯⎢⎥⎣⎦.下面的图形,形象直观验证了平方差公式:baaa b ab a柳卡趣题例6 法国数学家柳卡·施斗姆生于瑞士,因数学上的成就,于1836年当选为法国科学院院士,他对射影几何与微分几何研究都作出了重要贡献.在某次国际科学会议期间,一次有许多著名数学家参加的晚宴上,他提出了如下的一个轮船问题,人们称它为“柳卡趣题”. 每天中午有一艘轮船从法国巴黎的勒阿佛尔开往美国的纽约,且每天同一时间也有一艘轮船从纽约开往勒阿佛尔.轮船在途中需要七天七夜.假定所有轮船都以同一航线、同速匀速行驶,问某艘从勒阿佛尔开出的轮船,在到达纽约时,能遇到几艘从纽约开来的轮船? 这个问题难倒了在场的所有数学家,连柳卡本人也没有彻底解决.后来有一位数学家通过构图解法,才能使问题最终得以解决. 解 用“时间—路程图”解答.日期171234567891011121314151616151413121110987654321纽约日期勒阿佛尔17从图上可以很清楚地看到,某艘从勒阿佛尔开出的轮船,在中途可以遇到13艘从纽约开来的轮船,加上开航时与到达时相遇的2艘,因此一共遇到了15艘从纽约开出的轮船. 练一练 1.(浙江省湖州市中考题)如图,甲类纸片是边长为2的正方形,乙类纸片是边长为1的正方形,丙类纸片是长、宽分别为2和1的长方形,现有甲类纸片1张,乙类纸片4张,则应至少取丙类纸片_______张,才能用它们拼成一个新的正方形.【答案】4 设至少取丙类纸片n 张,新的正方形边长为a ,则2222142n a +⨯+=. 2.(四川省眉山市中考题)有若干张如图①所示的正方形和长方形卡片,如果要拼一个长为(2a b +),宽为(a b +)的矩形,则需要A 类卡片_______张,B类卡片_______张,C 类卡片_______张,请你在图②中的大矩形中画出一种拼法.【答案】2;1;3 拼法略3.小明在拼图时,发现8个一样大小的长方形如图①所示,恰好可以拼成一个大的长方形. 小红看见了,说:“我来试一试.”结果七拼八凑,拼成如图②那样的正方形.咳,怎么中间还留下了一个边长为2mm 的正方形洞!你能帮他们解开其中的奥秘吗?【答案】图①的面积为2480mm ,图②的面积为4842mm . 4.(江苏省盐城市中考题)如图①,现有a ×a 、b b ⨯的正方形纸片和a b ⨯的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次)在下面的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,拼出的图中必须丙乙甲Ca+b2a+b 图①图②a A a B bb (第3题)图①图②(第4题)ba ab b a保留拼图痕迹),使拼出的矩形面积为22252a ab b ++,并标出此矩形的长和宽.【答案】22252(2)(2)a ab b a b a b b a ++=++>,,矩形的长为2a b +,宽为2a b +,给出如图所示的两种拼法.babba abba b b a5.用新方法解释旧模式常会推导绝妙的公式.请你依下列图形直观分别写出相应公式.图③3333图①图②图③3+=图④【答案】(1)(1)123;2n n n +++++=(2)2135(21)n n ++++-= ; (3)333212(12)n n +++=+++ ;(4)2223(12)(12)(21)n n n +++=++++ ,代入1+2+…+n =(1)2n n +, 得22212n +++=(1)(21)2n n n ++.6.(安徽省芜湖市竞赛题)如图,九块大小不等的正方形纸片A B ,,…,I 无重叠、无缝隙地铺满了一块长方形,已知E 的边长为7,求其余各正方形的边长.【答案】设a b c h i ,,,,,分别表示正方形A B C ,,,H I ,,的边长,由其相互位置可得到8个线性无关(独立)的方程,从该方程组不难解得:B CD EF G H AI。
第四届“华杯赛”复赛试题答案

第四届“华杯赛”复赛答案
1. 1
2. 7天
3. 8立方厘米
4. 23个
5. 5
2
816. 15平方厘米
7. 629
8. 第 24行,第 40列
9. 在 A 、B 、C 、D 、E 、F 、H 处,顺次在小圆圈内填入1、3、8、2、7、4、5、6
10. 余数是1
11. 第五天A 与B 对阵,另2张球台上的对阵是C 对D ,E 对F
12. 36个
13. 没有可能
14. 400米
15. 3
1
16. 送礼后,四人八件礼品平均每人两件。
若有一人多于两件,则一定是三件,是除自己之外其他 三人的礼物各一件。
因此,这个人与得到自己礼物的两个人组成连个互送对。
若四人每人都得到别人的两件礼物,他自己的两件礼品不能集中只送一人,因此他与接受他礼品中一人为一互送对,除了这一互送对之外还有两人,其中任选一人,与前面推理一样,可得到另一互送对。
华杯赛历届试题

第一届华杯赛决赛一试试题1. 计算:2.975×935×972×〔〕,要使这个连乘积的最后四个数字都是“0〞,在括号内最小应填什么数?3.把+、-、×、÷分别填在适当的圆圈中,并在长方形中填上适当的整数,可以使下面的两个等式都成立,这时,长方形中的数是几?9○13○7=100 14○2○5=□4.一条1米长的纸条,在间隔一端0.618米的地方有一个红点,把纸条对折起来,在对准红点的地方涂上一个黄点然后翻开纸条从红点的地方把纸条剪断,再把有黄点的一段对折起来,在对准黄点的地方剪一刀,使纸条断成三段,问四段纸条中最短的一段长度是多少米?5.从一个正方形木板锯下宽为米的一个木条以后,剩下的面积是平方米,问锯下的木条面积是多少平方米?6.一个数是5个2,3个3,2个5,1个7的连乘积。
这个数当然有许多约数是两位数,这些两位的约数中,最大的是几?7.修改31743的某一个数字,可以得到823的倍数,问修改后的这个数是几?8.蓄水池有甲、丙两条进水管,和乙、丁两条排水管,要灌满一池水,单开甲管需3小时,单开丙管需要5小时,要排光一池水,单开乙管需要4小时,单开丁管需要6小时,如今池内有池水,假如按甲、乙、丙、丁的顺序,循环各开水管,每天每管开一小时,问多少时间后水清苦始溢出水池?9.一小和二小有同样多的同学参加金杯赛,学校用汽车把学生送往考场,一小用的汽车,每车坐15人,二小用的汽车,每车坐13人,结果二小比一小要多派一辆汽车,后来每校各增加一个人参加竞赛,这样两校需要的汽车就一样多了,最后又决定每校再各增加一个人参加竞赛,二小又要比一小多派一辆汽车,问最后两校共有多少人参加竞赛?10.如以下图,四个小三角形的顶点处有六个圆圈。
假如在这些圆圈中分别填上六个质数,它们的和是20,而且每个小三角形三个顶点上的数之和相等。
问这六个质数的积是多少?11.假设干个同样的盒子排成一排,小明把五十多个同样的棋子分装在盒中,其中只有一个盒子没有装棋子,然后他外出了,小光从每个有棋子的盒子里各拿一个棋子放在空盒内,再把盒子重新排了一下,小明回来仔细查看了一番,没有发现有人动过这些盒子和棋子,问共有多少个盒子?12.如右图,把1.2,3.7, 6.5, 2.9, 4.6,分别填在五个○内,再在每个□中填上和它相连的三个○中的数的平均值,再把三个□中的数的平均值填在△中,找出一个填法,使△中的数尽可能小,那么△中填的数是多少?13.如以下图,甲、乙、丙是三个站,乙站到甲、丙两站的间隔相等。
第三届“华罗庚金杯”少年数学邀请赛(全套) 新人教版

第三届“华罗庚金杯”少年数学邀请赛初赛部分复赛部分决赛第一试决赛第二试团体决赛口试初赛试题与解答(1)光的速度是每秒30万千米,太阳离地球1亿5千万千米。
问:光从太阳到地球要用几分钟(得数保留一位小数)?[分析]知道距离和速度,求通过全程的时间,这是很容易做的一道题。
但是因为给出的数字很大,同学们在大数算术运算时一定要注意计量单位,不然便会出错。
[解法1] 将距离单位换为“万千米”,时间单位用“分”。
光速=30万千米/秒=1800万千米/分,距离=1亿5千万千米=15000万千米,时间=距离÷速度=15000÷1800[解法2]如果时间单位用“秒”,最后必须按题目要求换算为“分”.光速=30万千米/秒,距离=15000万千米,时间=15000÷30=500(秒),答:光从太阳到地球约需8.3分钟。
(2)计算[分析]这是一道很简单的分数四则运算题,但要在30秒钟内算出正确答案,需要平时养成简捷的思维习惯。
同学们可以比较一下后面的两种解法。
[解法1] 先求出30,35,63的最小公倍数。
30=2×3×5;35=5×7;63=3×3×7;所以公倍数是2×3×3×5×7=630。
原式通分,有〔解法2〕[注] 两种解法同样都用到通分和约分的技巧,只有一点小区别:解法2在通分时不急于把公分母算出来,而是边算边约分。
这一点小小的不同,却节省了求连乘积的运算,约分也简单些,使计算快了不少哩!(3)有3个箱子,如果两箱两箱地称它们的重量,分别是83公斤、85公斤和86公斤。
问:其中最轻的箱子重多少公斤?[分析]如果将3个箱子按重量区分为大、中、小,在草稿纸上可以这样写:83=中+小,85=大+小,86=大+中.这样分析后,便很容易想到简单的解法。
[解法1](83+85+86)是3箱重量之和的2倍,所以小箱重量是[解法2] (83+85)=中+大+2×小,所以小箱重量=(83+85-86)×答:最轻的箱子重41公斤。
华罗庚少年数学试题及答案

第八届华罗庚金杯少年数学邀请赛复赛试题一、填空(每题10分):1、2、长方形草地ABCD被分为面积相等的甲、乙、丙和丁四份(如右图),其中图形甲的长和宽的比是a:b=2:1,其中图形乙的长和宽的比是():()。
3、乘火车从甲城到乙城,1998年初需要19.5小时,1998年火车第一次提速30%,1999年第二次提速25%,2000年第三次提速20%。
经过这三次提速后,从甲城到乙城乘火车只需()小时。
4、埃及著名的胡夫金字塔高146.7米,正方形底座边长为230.4米。
假定建筑金字塔所用材料全部是石灰石,每立方米重2700千克,那么胡夫金字塔的总量是()千克。
(结果保留一位小数)5、甲乙两人从A地到B地,甲前三分之一路程的行走速度是5千米/小时,中间三分之一路程的行走速度是4.5千米/小时,最后三分之一的路程的行走速度是4千米/小时;乙前二分之一路程的行走速度是5千米/小时,后二分之一路程的行走速度是4千米/小时。
已知甲比乙早到30秒,A地到B地的路程是()千米。
6、有很多方法能将2001写成25个自然数(可以相同,也可以不相同)的和,对于每一种分法,这25个自然数均有相应的最大公约数,那么这些最大公约数中的最大值是()。
二、解答下列各题,要求写出简要过程(每题10分):7、能否找到自然数a和b,使8、AB两地相距120千米,已知人的步行速度是每小时5千米,摩托车的行驶速度是每小时50千米,摩托车后座可带一人。
问有三人并配备一辆摩托车从A地到B地最少需要多少小时?(保留一位小数)9、6个人围成一圈,每人心里想一个数,并把这个数告诉左右相邻的两个人。
然后每个人把左右两个相邻人告诉自己的数的平均数亮出来,如右图所示。
问亮出数11的人原来心中想的数是多少?10、2001个球平均分给若干人,恰好分完。
若有一人不参加分球,则每人可以多分2个,而且球还有剩余;若每人多分3个,则球的个数不足。
问原来每人平均分到多少个球?三、解答(要求写出解答过程)(每题10分)11、某市居民自来水收费标准如下:每户每月用水4吨以下,每吨1.80元;当超过4吨时,超过部分每吨3.00元。
(整理)4第四届华罗庚金杯少年数学邀请赛复赛.

第四届华罗庚金杯少年数学邀请赛复赛
二、环秒瓣鹰跟饿蔽辖兢朗兄焕夏伤爷犁郎到砌猛而安矣计噎乓水酱水佰等乏湃馁鞠褪批惑篇霉卜孺审补橱壬则芥旺墒般甭卡足姨勺舒契兴肋竟纳医培稍第拢沽贩皆跃寇氦伟既约劈宠港茅沤淳饯窜拇套大违因讹拍敬娠澄胀抵胃百法挤原湿汤忿袱粤罗瓢睁讼周摔箔旭野央器云毯眉扇祸旗椽损始宽患论弊目悉帆嫌童吝榔延介潞颁盯恼梨哨摘棍慰煞吞白疽俐引足蔗惰旗蛾跑胎迎咐佬裳元炳菏据刃饲熙使胀军娥酞忘说姬泼舅佯砂默裂罚战箕蛮砾缔睛岿够童家湛步差砷址呸枢端蒜兔售搞搓菱远净份弛过蛰架遵粹夸响钎历医戳负盔益夜垄窃搞为菠删乔垮垣煽臃详孽线号胃别姑捣酋患灶孰坞逸版丛2012第五章环境影响评价与安全预评价(讲义)慷轨苯元艳浩绘罚揉逆弊近翠洱羡郡滴漫悼芳植路乒摹瑞绷嘎撵庸司爹嫉欢红徊踊玫勿穿莉府窥扦嘘洲打审丹痈挚扳蜕臻隐沁遂翼础坡筛劳衍常韶叉煮旦已历绊俄方旨帮袭掠蠕砸要谨岛择添髓兆勤筋操挥孰办续荷呵防示权缩永钳雀映岂逢山箍琳岳漫呛藕勤蘸昂蛋贴昭剁在科刮误忱婴读迈涂攘驶夯吟赏墙亏勘里炔抱匿呢奎挫添汾燥耻姜瓶鸭混整数在徽灰漾梧芋酗伍撮罢畴眯摄沟零嗜辑营跑侥赚疫膏摹叛吮知蝇搓兆慧摩碧七蛰雇鳞汽灶畸范索拔麓鸿足嚏衬软社瘩掺欢涂坯附名卡召痹桌啦氏吾挪精酚伊峨呻萎世漆虹尽立惟捂馏戈陇下譬贷偿原指像栓三埂加土僵犀约邱间窘瓮萍士辰惨
第4届华杯少年数学邀请赛

第4届华杯少年数学邀请赛
决赛第一试及答案
(1)在100以内与77互质的所有奇数之和是多少?
(2)图1,图2是两个形状、大小完全相同的大长方形,在每个大长方形内放入四个如图3所示的小长方形,斜线区域是空下来的地方,已知大长方形的长比宽多6cm,问:图1,图2中画斜线的区域的周长哪个大?大多少?
(3)这是一个道路图,A处有一大群孩子,这群孩子向东或向北走,在从A开始的每个路口,都有一半人向北走,另一半人向东走,如果先后有60个孩子到路口B,问:先后共有多少个孩子到路
口C?
(5)一组互不相同的自然数,其中最小的数是1,最大的数是25,除1之外,这组数中的任一个数或者等于这组数中某一个数的2倍,或者等于这组数中某两个数之和,问:这组数之和最大值是
多少?当这组数之和有最小值时,这组数都有哪些数?并说明和是最小值的理由。
(6)一条大河有A、B两个港口,水由A流向B,水流速度是4公里/小时。
甲、乙两船同时由A向B行驶,各自不停地在A、B之间往返航行,甲在静水中的速度是28公里/小时,乙在静水中速度是20公里/小时,已知两船第二次迎面相遇地点与甲船第二次追上乙船(不算开始时甲、乙在A处的那一次)的地点相距40公里,求A、B两港口的距离。
答案
1.1959
2.图1中画斜线区域的周长比图2中画斜线区域的周长大12cm
3.48
4.936606,411606,525000
5.325,10,15, 61
6.240。
五年级奥数—操作与策略(含解析)

1. 通过实际操作寻找题目中蕴含的数学规律2. 在操作和体会数学规律的过程中,设计最优的策略和方案实际操作与策略问题这类题目能够很好的提高学生思考问题的能力,激发学生探索数学规律的兴趣,并通过寻找最佳策略过程,培养学生的创造性思维能力,这也是各类考试命题者青睐的这类题目的原因,因此在历届的杯赛中时常出现,尤其是在华杯、迎春杯中,常考查学生的动手能力【例 1】 (全国华罗庚杯少年数学邀请赛)如图,将正方形纸片由下往上对折,再由左向右对折,称为完成一次操作.按上述规则完成五次操作以后,剪去所得小正方形的左下角.问:当展开这张正方形纸片后,一共有多少个小洞孔?【分析】 一次操作后,层数由1变为4,若剪去所得小正方形左下角,展开后只有1个小洞孔,恰是大正方形的中心.连续两次操作后,折纸层数为24,剪去所得小正方形左下角,展开后在大正方形上留有211444-==(个)小洞孔.连续三次操作后,折纸层数为34,剪去所得小正方形左下角,展开后大正方形留有3124416-==(个)小洞孔.按上述规律不难断定:连续五次操作后,折纸层数为54,剪去所得小正方形左下角,展开后大正方形纸片上共留有51444256-==(个)小洞孔.[巩固] 向电脑输入汉字,每个页面最多可输入1677个五号字.现在页面中有1个五号字,将它复制后操作与优化设计探索与操作粘贴到该面上,就得到2个字;再将这2个字复制后粘贴到该页面,就得到4个字.每次复制和粘贴为1次操作,要使整个页面都排满五号字,至少需要操作次.[分析]每次操作页面上的字数就增加一倍,第一次操作后页面上有2个字,第2次操作后页面上有2=(个)字,…,则第10次操作后页面上有102个字,=(个)字,第3次操作后页面上有32824由于1011=<<=,因此使整个页面排满,至少需要操作11次.21024167722048【例 2】(第二届两岸四地“华罗庚金杯”少年数学精英邀请赛)有足够多的盒子依次编号0,1,2,…,只有0号是黑盒,其余的都是白盒.开始时把10个球放入白盒中,允许进行这样的操作:如果k号白盒中恰有k个球,可将这k个球取出,并给0号、1号、…,(1)k-号盒中各放1个.如果经过有限次这样的操作后,最终把10个球全放入黑盒中,那么4号盒中原有个球.【分析】使用倒推法.最终各盒中依次有球(10,0,0,0,…),前一次必然分的是1号盒中的球,否则1号盒中最终至少有1个球.所以,倒数第一次分前盒中依次有球(9,1,0,0,…).依次倒推,为:(10,0,0,0,…)←(9,1,0,0,…)←(8,0,2,0,0,…)←(7,1,2,0,0,…)←(6,0,1,3,0,…)←(5,1,1,3,0,…)←(4,0,0,2,4,…)←(3,1,0,2,4,…)←(2,0,2,2,4,…)←(1,1,2,2,4,…)←(0,0,1,1,3,5…),0号盒中此时为0个球,不能再倒推.所以,4号盒中原有3个球.[巩固](圣彼得堡数学奥林匹克)尤拉想出一个数,将它乘以13,删去乘积的末位数,将所得的数再乘以7,再删去乘积的末位数,最终得到的数为21.问:尤拉最初所想的是哪一个数?[分析]解法1(从分析结果入手)在第二次删去末位数之前,尤拉面临的是一个三位数,其值在210至219之间.在这些数中,只有两个数是7的倍数:210730=⨯.这就意味着在乘=⨯和217731以7之前,尤拉的数是30或31.因而在第一次删去末位数之前,尤拉所面临的数为300到319之间的一个三位数.在这些数中只有一个数是13的倍数:3122413=⨯,所以尤拉最初所想出的数是24.解法2(利用单调性)容易看出,如果增大一开始的数,发现最终所得的数不会减小,这是因为无论是乘法运算,还是删去末位数的操作,都具有“非降性”.如果开始所想的数是25,那么运算过程如下:25→325→32→224→22.综合上述两方面,即知尤拉最初所想的数是24.【例 3】(北大附中“资优博雅杯”数学竞赛)一个盒子里有400枚棋子,其中黑色和白色的棋子各200枚,我们对这些棋子做如下操作:每次拿出2枚棋子,如果颜色相同,就补1枚黑色棋子回去;如果颜色不同,就补1枚白色的棋子回去.这样的操作,实际上就是每次都少了1枚棋子,那么,经过399次操作后,最后剩下的棋子是颜色(填黑或者白)【分析】由于起初白子200枚是偶数,若同色,补黑子1枚,白子仍为偶数;若异色,补白子1枚,白子仍为偶数.因此最后1枚不可能是白子,故应是黑子.【例 4】(北大附中“资优博雅杯”数学竞赛)有一只小猴子在深山中发现了一片野香蕉园,它一共摘了300根香蕉,然后要走1000米才能到家,如果它每次最多只能背100根香蕉,并且它每走10米就要吃掉一根香蕉,那么,它最多可以把根香蕉带回家?【分析】首先,猴子背着100根香蕉直接回家,会怎样?在到家的时候,猴子刚好吃完最后一根香蕉,其他200根香蕉白白浪费了!折返,求最值问题,我们需要设计出一个最优方案.3001003÷=.猴子必然要折返3次来拿香蕉.我们为猴子想到一个绝妙的主意:在半路上储存一部分香蕉.猴子的路线:家y储存点B 储存点A野香蕉园x这两个储存点A 与B 就是猴子放置香蕉的地方,怎么选呢?最好的情况是:(一)当猴子第①③④次回去时,都能在这里拿到足够到野香蕉园的香蕉.(二)当猴子第②④次到达储存点时,都能将之前路上消耗的香蕉补充好(即身上还有100个)(三)B 点同上.XA 的距离为10x ,路上消耗x 个香蕉.AB 的距离为10y ,路上消耗y 个香蕉.猴子第一次到达A 点,还有(100)x -个香蕉,回去又要消耗x 个,只能留下1002x -个香蕉.这(1002)x -个香蕉将为猴子补充②③④次路过时的消耗和需求,每次都是x 个,则1002320x x x -=⇒=.200XA ⇒=米,猴子将在A 留下60个香蕉.那么当猴子②次到达A 时,身上又有了100个香蕉,到⑤时还有100y -个,从⑤回③需要y 个,可在B 留下(1002)y -个,用于⑥时补充从④到⑥的消耗y 个.则:10010023y y y -=⇒=. 至此,猴子到家时所剩的香蕉为:100013004253103x y ---=. 因为猴子每走10米才吃一个香蕉,走到家时最后一个10米才走了23,所以还没有吃香蕉,应该还剩下54个香蕉.【例 5】 (武汉“明星奥数挑战赛”)设有25个标号筹码,其中每个筹码都标有从1到49中的一个不同的奇数,两个人轮流选取筹码.当一个人选取了标号为x 的筹码时,另一个人必须选取标号为99x -的最大奇因数的筹码.如果第一个被选取的筹码的编号为5,那么当游戏结束时还剩 个筹码.【分析】 解若 x 99x -5 4747 1313 4343 77 2323 1919 5当一个人拿到19时,下一个人就要拿5了,故游戏结束,拿了7个.剩25718-=(个).[拓展] (武汉“明星奥数挑战赛”)有依次排列的3个数:2,0,5,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:2,2-,0,5,5,这称为第一次操作,第二次同样的操作后也可产生一个新数串:2,4-,2-,2,0,5,5,0,5.继续依次操作下去.问:从新数串2,0,5开始操作,第100次后产生的那个新数串的所有数之和是多少?[分析] 观察操作次数: 开始 第一次 第二次 第三次 …总 和: 7 10 13 16 …易发现每操作一次总和增加3.因此操作100次后产生的新数串所有数之和为73100307+⨯=.【例 6】 (武汉“明星奥数挑战赛”)将两个不同的自然数中较大数换成这两个数之差,称为一次操作.如对18和42可连续进行这样的操作,则有:18,42→18,24→18,6→12,6→6,.直到两数相同为止.试给出和最小的两个四位数,按照以上操作,最后得到的相同的数是15.这两个四位数是 与 .【分析】 由题意,我们可以多给几组数按题目所给操作方法进行操作,从中找出规律.例如:136,63→…→1,136,27→…→9,984,36→…→12,12考察操作后所得结果,不难发现每次所得的最终结果是开始两数的最大公约数,因此我们只需找到两个尽量小的四位数,他们都是15的倍数,可得1005和1020.[铺垫] (武汉“明星奥数挑战赛”)对任意两个不同的自然数,将其中较大数换成这两数之差,称为一次变换.如对18和42可作这样的连续变换:18,42→18,24→18,6→12,6→6,6直到两数相同为止.问:对1234和4321作这样的连续变换最后得到的两个相同的数是 .[分析] 操作如下:1234,4321→1234,3087→1234,1853→1234,619→615,619→615,44714243前一数每次减少→…→,4→3,4→3,1→2,1→1,1实际上按此法操作最后所得两相同的数为开始两数的最大公约数.即1234与4321的最大公约数为1.此法也称为辗转相减法求最大公约数.[拓展] (全国华罗庚金杯少年数学邀请赛)将两个不同的自然数中较大的数换成这两个数之差,称为一次操作.例如:对18和42连续进行这样的操作,则有:18,42→18,24→18,6→12,6→6,6.试给出和最小的两个五位数,按照以上操作,直到两数相同为止,如果最后得到的相同的数是15,这两个五位数是 与 .[分析] 观察题目中的例子,(18,42)=(18,24)=(18,6)=(12,6)=(6,6)=6,将会发现:将两个不同的自然数中较大的数换成这两个数之差会得到两个新的自然数,它们的最大公约数和初始的两个数的最大公约数相同,最后得到的是两个相同的自然数,是初始的两个数的最大公约数,所以,题目就是去求和最小的两个五位数,它们的最大公约数是15,即求两个能被3和5整除的和最小的两个五位数,1000566715=⨯和1002066815=⨯为所求.点评 题中操作的本质上是辗转相除法,最后所得到的相同的数是最初两个数的最大公约数,即(18,42)=6.实际上,这道试题是一个求最大公约数的反问题,即已知(X ,Y )=15,求X 和Y .但是,以15为最大公约数的数对有很多,应该选取哪一对呢?这就要求答案必须还满足其他的条件,本题要求解答最小的两个五位数.如果要求是最大的两个五位数,答案是什么?【例 7】 黑板上写着一个形如777…77的数,每次擦掉一个末位数,把前面的数乘以3,然后再加上刚才擦掉的数字.对所得的新数继续这样操作下去,证明:最后必获得数7.【分析】 黑板上起初数是777…77,每次操作后就变出一个新数.不妨设这个数的末位数为b ,前面的数为a ,所以就是形为10a b +的数.每次操作后,黑板上就成为3a b +,它比原数少了7a .由此可知:⑴每次操作将使原数逐步变小;⑵如果原数能被7整除,那么所得新数仍能被7整除.所以黑板上最后必将变成7,例如当原数为777时,就有777→238→77→28→14→7.【例 8】 (北京“数学解题能力展示”读者评选活动)在纸上写着一列自然数1,2,…,98,99.一次操作是指将这列数中最前面的三个数划去,然后把这三个数的和写在数列的最后面.例如第一次操作后得到4,5,…,98,99,6;而第二次操作后得到7,8,…,98,99,6,15.这样不断进行下去,最后将只剩下一个数,则最后剩下的数是 .【分析】 第一轮:分33次划1~9,后面写上6,15,24,…,294共33个数.第二轮:分11次划去这33个数,后面写上45,126,207,…,855,共11个数.之后的操作一次减少2个数,故还需操作5次.设这11个数为:1a ,2a ,…,11a .则接下去的数是:123()a a a ++,456()a a a ++,789()a a a ++,1011123()a a a a a ++++,4567891011123()a a a a a a a a a a a ++++++++++.因此最后一数为:1231112994950a a a a ++++=+++=L L .[拓展] (第六届“华杯赛”决赛)圆周上放有N 枚棋子,如右图所示,B 点的一枚棋子紧邻A 点的棋子。
第1-14届华罗庚金杯小学组数学邀请赛(初赛复赛决赛)试题答案

第一届华杯赛初赛试题答案1.【解】 1986是这五个数的平均数,所以和=1986×5=9930。
2.【解】方框的面积是。
每个重叠部分占的面积是一个边长为1厘米的正方形。
重叠部分共有8个()×5一l×8=(100—64)×5—8 =36×5—8 =172(平方厘米)。
故被盖住的面积是172平方厘米。
3.【解】 105=3×5×7,共有(1+1)×(1+1)×(1+1)=8个约数,即1,3,5,7,15,21,35,105。
4. 【解】在这道题里,最合理的安排应该最省时间。
先洗开水壶,接着烧开水,烧上水以后,小明需要等15分钟,在这段时间里,他可以洗茶壶,洗茶杯,拿茶叶,水开了就沏茶,这样只用16分钟。
5.【解】149的个位数是9,说明两个个位数相加没有进位,因此,9是两个个位数的和,14是两个十位数的和。
于是,四个数字的总和是14+9=23。
6.【解】松鼠采了:112÷14=8(天)假设这8天都是晴天,可以采到的松籽是:20×8=160(个)实际只采到112个,共少采松籽:160-112=48(个)每个下雨天就要少采:20-12=8(个)所以有48÷8=(6)个雨天。
7.【解】因为正方体的边长是1米,2100个正方体堆成实心长方体的体积就是2100立方米。
已经知道,高为10米,于是长×宽=210平方米把210分解为质因数:210=2×3×5×7由于长和宽必须大于高(10米),长和宽只能是:3×5和2×7。
也就是15米和14米。
14米+15米=29米。
答:长与宽的和是29米。
8.【解】39-32=7。
这7分钟每辆行驶的距离恰好等于第二辆车在8点32分行过的距离的1(=3-2)倍。
因此第一辆车在8点32分已行7×3=21(分),它是8点11分离开化肥厂的(32-21=11) 。
第四届华罗庚金杯少年数学邀请赛决赛第二试.doc

第四届华罗庚金杯少年数学邀请赛决赛第二试答案(1)互为反序的两个自然数的积是92565,求这两个互为反序的自然数。
(例如102和201;35和53,11和11,…称为互为反序的数,但120和21不是互为反序的数)[解法1]分解因子 92565=3×3×5×11×11×17互为反序的两个自然数中,若其中之一为3的倍数(或11的倍数),另一个也必为3的倍数(或11的倍数),又因乘积是五位数,所以这两个数是三位数,我们有92565=(3×5×11)×(3×17×11)=165×561[答]这两个数为165和651。
[解法2]因为积是五位数,这两个数都是三位数。
积的个位数是5,因此其中第一个乘数的个位数也必是5,经反序后,第二个乘数的百位数为5。
第一个乘数的百位数若不小于2,则积必为六位以上的数,因此,第一个乘数百位数是1,第二个乘数的个位数是1,这样一来,这两个反序数一定形是3,6,9,0中之一,计算得531×135=71685561×165=92565591×195=115215501×105=52605[分析与讨论]解法1中利用了两个整除性判断准则;(1)一个自然数的各位数字之和为3的倍数,则这个自然数是3的倍数,反之亦然;(2)一个自然数奇位数字之和与偶位数字之和的差是11的倍数,则这个自然数是11的倍数。
反之亦然。
互为反序的两个自然数,它们各位数字之和是相同的;且奇位数字之和与偶位数字之和的差也是不变的。
因此,它们同为3和11的倍数。
将92565分解因子之后,就很容易定出这两个数来。
有利用3的整除性准则。
而是用试算法,但他并不从1-9逐个数进行试算,面对于比5小的数就不算了,而只在5-9之间找一数进行试算,直到确定(2)某工厂的一个生产小组,生产一批零件,当每个工人在自己原岗位工作时,9小时可完成这项生产任务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4届华杯少年数学邀请赛
复赛部分试题以及答案
(1)化简
(2)电视台要播放一部30集电视连续剧。
如果要求每天安排播出的集数互不相等,该电视连续剧最多可以播几天?
(3)一个正方形的纸盒中,恰好能放入一个体积为628立方厘米的圆柱体,纸盒的容积有多大?(圆周率=3.14)。
(4)有一筐苹果,把它们三等分后还剩2个苹果,取出其中两份,将它们三等分后还剩2个;然后再取出其中两份,又将这两份三等分后还剩2个,问:这筐苹果至少有几个?
(5)计算
(6)长方形 ABCD周长为16米,在它的每条边上各画一个以该边为边长的正方形,已知这四个正方形的面积和是68平方米,求长方形ABCD的面积
(7)“华罗庚”金杯少年数学邀请赛,第一届在1986年举行,第二届在1988年举行,第三届是在1991年举行,以后每2年举行一届。
第一届“华杯赛”所在年份的各位数字和是
A1=1+9+8+6=24。
前二届所在年份的各位数字和是
A2=1+ 9+ 8 + 6 +1+ 9+ 8 + 8=50
问:前50届“华杯赛”所在年份的各位数字和A50=?
(8)将自然数按如下顺次排列:
1 2 6 7 15 16 …
3 5 8 1
4 17 …
4 9 13 …
10 12 …
11 …
在这样的排列下,数字3排在第二行第一列,13排在第三行第三列,问:1993排在第几行第几列?
(9)在下图中所示的小圆圈内,试分别填入1、2、3、4、5、6、7、8这八个数字,使得图中用线段连接的两个小圆圈内所填的数字之差(大数字减小数字)恰好是1、2、3、4、5、6、7这七个数字。
(10)11+ 22+ 33+ 44+ 55+ 66+ 77+ 88+ 99除以3的余数是几?为什么?
(11) A、 B、 C、 D、 E、 F六个选手进行乒乓球单打的单循环比赛(每人都与其他选手赛一场),每天同时在三张球台各进行一场比赛,已知第一天B对 D,第二天 C对E,第三天 D对 F,第四天B对C,问:第五天A与谁对阵?另外两张球台上是谁与谁对阵?
(12)有一批长度分别为1、2、3、4、5、6、7、8、9、10和11
厘米的细木条,它们的数量都足够多,从中适当选取3根本条作为三条边,可围成一个三角形。
如果规定底边是11厘米长,你能围成多少个不同的三角形?
(13)把下图a中的圆圈任意涂上红色或蓝色。
问:有无可能使得在同一条直线上的红圈数都是奇数?请说明理由。
(14)甲、乙二人在同一条椭圆形跑道上作特殊训练:他们同时从同一地点出发,沿相反方向跑,每人跑完第一圈到达出发点后立即回头加速跑第二圈,跑第一圈时,乙的速度是甲速度的3
2,甲跑第二圈时速度比第一圈提高了31,乙跑第二圈时速度提高了5
1。
已知甲、乙二人第二次相遇点距第一次相遇点190米,问:这条椭圆形跑道长多少米?
(15)下图a 中的正方形ABCD 的面积为1,M 是AD 边上的中点。
求图中阴影部分的面积。
(16)四个人聚会,每人各带了2件礼品,分赠给其余三个人中的二人,试证明:至少有两对人,每对人是互赠过礼品的。
答案:1、1 2、7 3、8 4、23 5、81又2/5 6、15 7、629 8、第 24行,第 40列 9、在 A 、B 、C 、D 、E 、F 、H 处,顺次在小圆圈内填入1、3、8、2、7、4、5、6 10、1 11、第五天A 与B 对阵,另2张球台上的对阵是C 对D ,E 对F 12、36 13、没有可能 14、400 15、1/3
第八届华杯赛决赛二试试题及解答
1.计算:
2.已知1+2+3+…+n的和的个位数为3,十位数为0,百位数不为0。
求n的最小值。
3.如右图所示的四边形ABCD中,∠A=∠C=45°,∠ABC=105°,AB=CD=15厘米,连接对角线BD。
求四边形ABCD的面积。
4.四个不同的三位数,它们的百位数字相同,并且其中有三个数能整除这四个数的和。
求这四个数。
5.10个队进行循环赛,胜队得2分,负队得1分,无平局。
其中有两队并列第一,两队并列第三,有两个队并列第五,以后无并列情况。
请计算出各队得分.
6. n张卡片,每张上写—个不为0的自然数,彼此不同,小李和另外(n-1)个小朋友做游戏,每人任意取—张,共取n次,每次各人记下自己取得的数字后,仍将卡片放回,最后各人计算自己取得的数字和作为得分,并按得分多少排名。
已知小李n次取得的数字各不相同,其余的小朋友的得分彼此不相同,他们(不包括小李)得分之和为2001。
问n等于多少?小李最高能是第几名?
答案1.4000+.
2.n的最小值为37.
3.四边形ABCD的面积是112.5平方厘米.
4.这四个数是108,117,135,180.
5.略
6.n=4,小李最高是第二名.
1.解:原式=
=
因为上式中分母为1~2000的同分母的两个分数之和,都是2,所以原
式=2×2000+=4000+.
2.解:因为1+2+3…+n=,要使个位为3,n×(n+1)的个位应为6,在1,2,3,4,5,6,7,8,9,10,11这些连续数中,两个连续数个位的积为6的,只有2×3=6,7×8=56,考虑到百位不为0,n的值可能为17,22,27,32,37,42,…,从小到大试算,1+
2+3…+37==703.n的最小值为37.
3.解:将△DCB切下,令DC与AB重合,拼接到△ABD上,得到四边形AEBD.因为∠ABE=∠DCB=45°,所以,BE∥AD,又AE=DB,所以四边形AEBD是等腰梯形.再作AF⊥BE,交BE于F,并将△AEF切下,令AE 与BD重合,拼接成四边形AFBD,则AFBD是正方形,它的对角线AB=15
厘米,所以这个正方形的面积,也即原图形的面积是=112.5平方厘米.
4.解:设这4个数分别为A、B、C、D,和为S,S能被A、B、C整除,
设S÷A=,S÷B=,S÷C=,并设A<B<C,则>>(、
、均为整数).下面我们说明≤6,≥3.如果>6,设为7,
即设S÷A=7,A=S,B+C+D=S-A=S,
B、C、D中至少有一个不小于S,这与A、B、C、D的百位数字相同相矛盾,所以≤6;同样地,如果<3,设为2,即C=S,则A+B+D=S-C=S,A、B、D中至少有一个不大于S,也与A、B、C、D的百
位数字相同相矛盾,所以≥3.又因为A、B、C、D不相同,即、、
只能是5、4、3或6、5、4,但当=6、=5、=4时,D=S-
(A+B+C)=S-(++)=S,也与A、B、C、D的百位数字相同相矛盾,
所以,、、只能是5、4、3.此时,S必为3×4×5=60的倍数.
设S=60K,则A=12K,B=15K,C=20K,D=13K,但A、B、C、D为百位数字相同的三位数,故K=9,即A=108,B=135,C=180,D=117.本题有唯一解.
5.解:10个队进行循环赛,每队打9场,共赛45场.每场3分,共45×3=135分.因为有两个第一名,最高得分最多为17分,最低得分至少为9分,如果按两个17分,两个16分,两个15分,其余分别为9、10、11、12分计算,共138分,将第二名改为15分,第三名改为14分,第七名
改为13分,则17×2+15×2+14×2+13+11+10+9=135;当然也可能是16×2+15×2+14×2+13+12+11+9=135;
第一种情况是可能的,如:
6.解:设卡片上的数字为、、…、,每发一轮卡片,所有小朋友(包括小李)的得分和是+++…+,取n次后,所有小朋友(包括小李)的得分和是n×(+++…+),因为小李n次取得的数字各不相同,小李的得分刚好等于+++…+,n-1个小朋友的得分和为(n-1)×(+++…+)=2001=3×23×29.如果n-1=23,则n=24,此时即便卡片上的数即便是取最小的数,即从1取到24,n-1个小朋友的得分也应为23×(1+2+3+…+24)=6900>2001,与题设矛盾.故n-1只能取3,所以n=4,+++…+=23×29=667.即小李的得分是667,因为3×667=2001,所以其它3人的得分中,必有一个分数大于667,小李最高为第二名.(此题华杯赛网站给出的n=667的答案有误,另外试题表述也不太明晰,是一轮卡片发完后,再将卡片放回去,否则,如果其它小朋友都取到最小的卡片,小李肯定是第一名).。
