2015年高考真题解答题专项训练:立体几何(文科)教师版
2015年高考数学真题分类汇编:专题(10)立体几何(文科)及答案

2015年高考数学真题分类汇编 专题10 立体几何 文1.【2015高考浙江,文4】设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( )A .若l β⊥,则αβ⊥B .若αβ⊥,则l m ⊥C .若//l β,则//αβD .若//αβ,则//l m【答案】A【解析】采用排除法,选项A 中,平面与平面垂直的判定,故正确;选项B 中,当αβ⊥时,,l m 可以垂直,也可以平行,也可以异面;选项C 中,//l β时,,αβ可以相交;选项D 中,//αβ时,,l m 也可以异面.故选A.【考点定位】直线、平面的位置关系.【名师点睛】本题主要考查空间直线、平面的位置关系.解答本题时要根据空间直线、平面的位置关系,从定理、公理以及排除法等角度,对个选项的结论进行确认真假.本题属于容易题,重点考查学生的空间想象能力以及排除错误结论的能力.2.【2015高考新课标1,文6】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( )(A )14斛 (B )22斛 (C )36斛 (D )66斛【答案】B【解析】设圆锥底面半径为r ,则12384r ⨯⨯=,所以163r =,所以米堆的体积为211163()5433⨯⨯⨯⨯=3209,故堆放的米约为3209÷1.62≈22,故选B. 【考点定位】圆锥的性质与圆锥的体积公式【名师点睛】本题以《九章算术》中的问题为材料,试题背景新颖,解答本题的关键应想到米堆是14圆锥,底面周长是两个底面半径与14圆的和,根据题中的条件列出关于底面半径的方程,解出底面半径,是基础题.3.【2015高考浙江,文2】某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )A .83cmB .123cmC .3233cmD .4033cm【答案】C 【解析】由三视图可知,该几何体是一个棱长为2的正方体与一个底面边长为2,高为2的正四棱锥的组合体,故其体积为32313222233V cm =+⨯⨯=.故选C. 【考点定位】1.三视图;2.空间几何体的体积.【名师点睛】本题主要考查空间几何体的体积.解答本题时要能够根据三视图确定该几何体的结构特征,并准确利用几何体的体积计算方法计算求得体积.本题属于中等题,重点考查空间想象能力和基本的运算能力.4.【2015高考重庆,文5】某几何体的三视图如图所示,则该几何体的体积为( )(A) 123π+ (B) 136π (C) 73π (D) 52π【答案】B【解析】由三视图可知该几何体是由一个底面半径为1,高为2的圆柱,再加上一个半圆锥:其底面半径为1,高也为1,构成的一个组合体,故其体积为61311612122πππ=⨯⨯⨯+⨯⨯,故选B.【考点定位】三视图及柱体与锥体的体积.【名师点睛】本题考查三视图的概念和组合体体积的计算,采用三视图还原成直观图,再利用简单几何体的体积公式进行求解.本题属于基础题,注意运算的准确性.5.【2015高考陕西,文5】一个几何体的三视图如图所示,则该几何体的表面积为( ) A .3π B .4π C .24π+ D .34π+【答案】D【解析】由几何体的三视图可知该几何体为圆柱的截去一半,所以该几何体的表面积为21121222342πππ⨯⨯+⨯⨯⨯+⨯=+,故答案选D【考点定位】1.空间几何体的三视图;2.空间几何体的表面积.【名师点睛】1.本题考查空间几何体的三视图及几何体的表面积,意在考查考生的识图能力、空间想象能力以及技术能力;2.先根据三视图判断几何体的结构特征,再计算出几何体各个面的面积即可;3.本题属于基础题,是高考常考题型.6.【2015高考广东,文6】若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则下列命题正确的是( )A .l 至少与1l ,2l 中的一条相交B .l 与1l ,2l 都相交C .l 至多与1l ,2l 中的一条相交D .l 与1l ,2l 都不相交【答案】A【解析】若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则l 至少与1l ,2l 中的一条相交,故选A .【考点定位】空间点、线、面的位置关系.【名师点晴】本题主要考查的是空间点、线、面的位置关系,属于容易题.解题时一定要注意选项中的重要字眼“至少”、“至多”, 否则很容易出现错误.解决空间点、线、面的位置关系这类试题时一定要万分小心,除了作理论方面的推导论证外,利用特殊图形进行检验,也可作必要的合情推理.7.【2015高考浙江,文7】如图,斜线段AB 与平面α所成的角为60o ,B 为斜足,平面α上的动点P 满足30∠PAB =o ,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支【答案】C【解析】由题可知,当P 点运动时,在空间中,满足条件的AP 绕AB 旋转形成一个圆锥,用一个与圆锥高成60o 角的平面截圆锥,所得图形为椭圆.故选C.【考点定位】1.圆锥曲线的定义;2.线面位置关系.【名师点睛】本题主要考查圆锥曲线的定义以及空间线面的位置关系.解答本题时要能够根据给出的线面位置关系,通过空间想象能力,得到一个无限延展的圆锥被一个与之成60o 角的平面截得的图形是椭圆的结论.本题属于中等题,重点考查学生的空间想象能力以及对圆锥曲线的定义的理解.8.【2015高考湖北,文5】12,l l 表示空间中的两条直线,若p :12,l l 是异面直线;q :12,l l 不相交,则( )A .p 是q 的充分条件,但不是q 的必要条件B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件【答案】A .【解析】若p :12,l l 是异面直线,由异面直线的定义知,12,l l 不相交,所以命题q :12,l l 不相交成立,即p 是q 的充分条件;反过来,若q :12,l l 不相交,则12,l l 可能平行,也可能异面,所以不能推出12,l l 是异面直线,即p 不是q 的必要条件,故应选A .【考点定位】本题考查充分条件与必要条件、异面直线,属基础题.【名师点睛】以命题与命题间的充分条件与必要条件为契机,重点考查空间中直线的位置关系,其解题的关键是弄清谁是谁的充分条件谁是谁的必要条件,正确理解异面直线的定义,注意考虑问题的全面性、准确性.9、【2015高考新课标1,文11】圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r =( )(A )1 (B )2(C )4 (D )8【答案】B【解析】由正视图和俯视图知,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r ,圆柱的高为2r ,其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+=16 + 20π,解得r=2,故选B.【考点定位】简单几何体的三视图;球的表面积公式;圆柱的测面积公式【名师点睛】本题考查简单组合体的三视图的识别,是常规提,对简单组合体三三视图问题,先看俯视图确定底面的形状,根据正视图和侧视图,确定组合体的形状,再根据“长对正,宽相等,高平齐”的法则组合体中的各个量.10.【2015高考福建,文9】某几何体的三视图如图所示,则该几何体的表面积等于( )A .822+B .1122+C .1422+D .15【答案】B【解析】由三视图还原几何体,该几何体是底面为直角梯形,高为2的直四棱柱,且底面直角梯形的两底分别为12,,直角腰长为1,斜腰为2.底面积为12332⨯⨯=,侧面积为2+2+4+22=8+22, 所以该几何体的表面积为1122+,故选B .【考点定位】三视图和表面积.【名师点睛】本题考查三视图和表面积计算,关键在于根据三视图还原体,要掌握常见几何体的三视图,比如三棱柱、三棱锥、圆锥、四棱柱、四棱锥、圆锥、球、圆台以及其组合体,并且要弄明白几何体的尺寸跟三视图尺寸的关系;有时候还可以利用外部补形法,将几何体补成长方体或者正方体等常见几何体,属于中档题.11.【2015高考山东,文9】已知等腰直角三角形的直角边的长为,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )(A )错误!未找到引用源。
2015-2020年高考全国卷(文)立体几何试题(含答案)

2015-2020年全国卷立体几何试题(含答案)1.(2020年全国卷1 文3).埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A 51-B 51-C 51+D 51+2.(2020年全国卷1 文12).已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π3.(2020年全国卷1 文19).如图,D 为圆锥的顶点,O 是圆锥底面的圆心,ABC △是底面的内接正三角形,P 为DO 上一点,∠APC =90°.(1)证明:平面PAB ⊥平面PAC ;(2)设DO 23π,求三棱锥P −ABC 的体积.4.(2020年全国卷2 文11).已知ABC ∆是面积为439的等边三角形, 且其顶点都在球O 的球面上。
若球O 的表面积为π16,则O 到平面ABC 的距离为 A. 3 B. 23 C. 1 D. 23 5.(2020年全国卷2 文16).设有下列四个命题:1p :两两相交且不过同一点的三条直线必在同一平面内。
2p :过空间中任意三点有且仅有一个平面。
3p :若空间两条直线不相交,则这两条直线平行。
4p :若直线⊂l 平面α,直线⊥m 平面α,则l m ⊥。
则下述命题中所有真命题的序号是____________。
①41p p ∧②21p p ∧③32p p ∨⌝④43p p ⌝∨⌝6.(2020年全国卷2 文20).如图,已知三棱柱111C B A ABC -的底面是正三角形,侧面C C BB 11是矩形,M 、N 分别为BC 、11C B 的中点,P 为AM 上一点。
过11C B 和P 的平面交AB 于E ,交AC 于F 。
2015高考真题——立体几何解答题

如图1,在直角梯形ABCD中,AD∥BC, ∠BAD=π2,AB=BC=12AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1BCDE.(1)证明:CD⊥平面A1OC;(2)当平面A1BE⊥平面BCDE时,四棱锥A1BCDE的体积为362,求a的值.一个正方体的平面展开图及该正方体的直观图的示意图如图所示.(1) 请将字母F,G,H标记在正方体相应的顶点处(不需要说明理由);(2) 判断平面BEG与平面ACH的位置关系,并证明你的结论;(3) 证明:直线DF⊥平面BEG.如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(1)证明:平面AEC⊥平面BED;(2)若∠ABC=120°,AE⊥EC,三棱锥EACD的体积为63,求该三棱锥的侧面积.如图,三棱台DEFABC中,AB=2DE,G,H分别为AC,BC的中点.(1)求证:BD∥平面FGH;(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.如图,三棱锥P ABC 中,PA ⊥平面ABC ,PA =1,AB =1,AC =2,∠BAC =60°.(1)求三棱锥P ABC 的体积;(2)证明:在线段PC 上存在点M ,使得AC ⊥BM ,并求PMMC的值.如图,在三棱锥VABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC =2,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB;(3)求三棱锥VABC的体积.如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=25,AA1=7,BB1=27,点E C的中点.和F分别为BC和A(1)求证:EF∥平面A1B1BA;(2)求证:平面AEA1⊥平面BCB1;(3)求直线A1B1与平面BCB1所成角的大小.如图,三棱锥PABC中,平面PAC⊥平面ABC,∠ABC=π2,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.(1)证明:AB⊥平面PFE;(2)若四棱锥PDFBC的体积为7,求线段BC的长.如图,直三棱柱ABCA1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.(1)证明:平面AEF⊥平面B1BCC1;(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥FAEC的体积.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE,BD,BE.(1)证明:DE⊥平面PBC,试判断四面体EBCD是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由.(2)记阳马P-ABCD的体积为V1,四面体EBCD的体积为V2,求V1V2的值.立体几何训练11如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.(1)证明:BC∥平面PDA;(2)证明:BC⊥PD;(3)求点C到平面PDA的距离.立体几何训练12如图,在直三棱柱ABCA1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.求证:(1) DE∥平面AA1C1C;(2) BC1⊥AB1.立体几何训练13如图,在三棱柱ABCA1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.(1)证明:A1D⊥平面A1BC;(2)求直线A1B和平面BB1C1C所成的角的正弦值.立体几何训练14如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.(1)若D为线段AC的中点,求证:AC⊥平面PDO;(2)求三棱锥PABC体积的最大值;(3)若BC=2,点E在线段PB上,求CE+OE的最小值.。
2015年广东高考文科数学试题立体几何分类整理详细解答
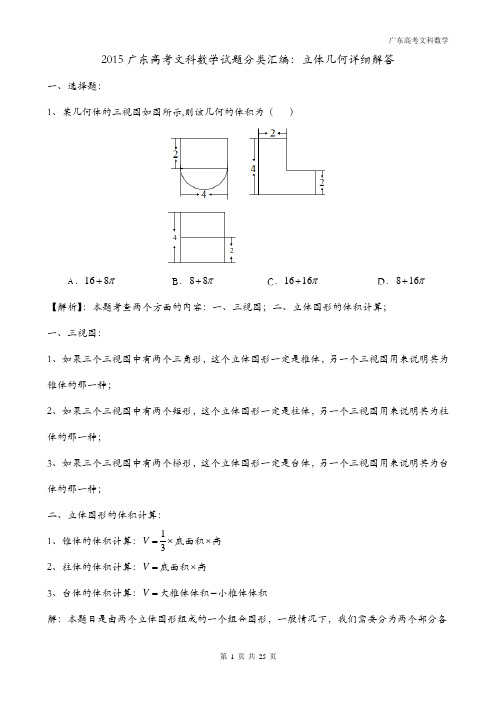
2015广东高考文科数学试题分类汇编:立体几何详细解答一、选择题:1、某几何体的三视图如图所示,则该几何的体积为( )A .168π+B .88π+C .1616π+D .816π+ 【解析】:本题考查两个方面的内容:一、三视图;二、立体图形的体积计算; 一、三视图:1、如果三个三视图中有两个三角形,这个立体图形一定是椎体,另一个三视图用来说明其为锥体的那一种;2、如果三个三视图中有两个矩形,这个立体图形一定是柱体,另一个三视图用来说明其为柱体的那一种;3、如果三个三视图中有两个梯形,这个立体图形一定是台体,另一个三视图用来说明其为台体的那一种;二、立体图形的体积计算:1、锥体的体积计算:⨯=31V 底面积⨯高2、柱体的体积计算:=V 底面积⨯高3、台体的体积计算:=V 大椎体体积-小椎体体积解:本题目是由两个立体图形组成的一个组合图形,一般情况下,我们需要分为两个部分各自处理。
上半部分:三视图为三个矩形,说明这个立体图形为四棱柱。
=V 底面积⨯高=16224=⨯⨯下半部分:三视图为两个矩形一个半圆,说明这个立体图形为圆柱的一半。
ππ842212=⨯⨯⨯=V所以:该组合立体图形的体积为π816+。
2、已知正四棱锥1111D C B A ABCD -中,AB AA 21=,则CD 与平面1BDC 所成角的正弦值等于( )A .23B .33C .23D .13【解析】本题考查线与面的夹角计算,线与面的夹角计算有两种方法: 方法一:第一步:线中两个端点一般情况下一个在平面上,一个在平面,由不在平面上的点找到在该平面上的投影点。
(该点和投影点之间的连线垂直于该平面) 第二步:连接线重在平面的端点和投影点,形成一个直角三角形。
第三步:三角形中在平面的边与该直线之间的夹角就是线与面的夹角。
第四步:在直角三角形中利用三角函数求该角的三角函数值。
如图所示:其中'PAP ∠为直线'PP 和平面α的夹角,在'PAP Rt ∆中计算'PAP ∠的三角函数值。
【数学】2015高考试题分类汇编:文科立体几何答案版

C 【解析】 如图 1- 6,由于 SC 是球的直径, 所以∠ SAC=∠ SBC= 90°,又∠ ASC=∠ BSC =45°,所以△ SAC、△ BSC 为等腰直角三角形,取 SC 中点 D ,连接 AD、BD .由此得 SC⊥
1 AD ,SC⊥BD ,即 SC⊥平面 ABD .所以 VS-ABC= VS-ABD+ VC-ABD = 3S△ABD ·SC. 由于在等腰直角三角形△ SAC 中∠ ASC= 45°, SC= 4,所以 AD = 2.同理 BD = 2.
() A . V1 比 V2 大约多一半
B. V1 比 V2 大约多两倍半 C. V1 比 V2 大约多一倍
D. V1 比 V2 大约多一倍半 D 【解析】 设球的半径为 R,则 V1=43πR3.设正方体的边长为 a,则 V2= a3.又因为 2R= 3
a,所以
4 V1 =3π
3 2a
3=
3 2
πa
′=
OD
=2,又由于
G和
G′都在线段 DA 的延长线上,所以 G 与 G′重合.
在△ GED 和△ GFD 中,由 OB
綊
1 2DE
和
OC
1 綊 2DF
,可知
B
和
C
分别是
GE 和 GF 的中点.所
以 BC 是△ GEF 的中位线,故 BC∥ EF.
3 (2) 由 OB=1, OE= 2,∠ EOB= 60°,知 S△EOB= 2 . 而△ OED 是边长为 2 的正三角形,故 S△OED= 3.
2 【解析】 ∵ EF∥平面 AB1C, EF ? 平面 ABCD ,平面 ABCD ∩平面 AB 1C=AC,
∴EF ∥AC,
又∵ E 是 AD 的中点,
2015年浙江省高考数学(文科)试题(教师版含解析)

2015年普通高等学校招生全国统一考试(浙江卷)文科数学1. 解析 {1P x x=-或}3x,所以[)34P Q =, .故选A.2. 解析 该几何体是棱长为2的正方体和底面边长为2、高为2的正四棱锥的组合体,所以3213222233V =+⨯⨯=.故选C . 3. 解析 取3a =,2b =-,所以0a b +>0ab >;反之取1a =-,2b =-,所以00ab a b >+>.故选D.4. 解析 由面面垂直判定定理知,A 正确.故选A.5. 解析 ()f x 是奇函数,排除A ,B ;当0x >, x 趋于0时,1x x-→-∞,cos 1x →,所以1cos x x x ⎛⎫-→-∞ ⎪⎝⎭.故选D. 6. 解析 解法一 特殊值:1x =,2y =,3z =,所以1a =,2b =,3c =.故选B. 解法二 利用排序不等式,最小的值是反序和.故选B.7. 解析 若30PAB ∠=,则AP 绕点A 旋转形成圆锥面,这面被平面α截得图象是椭圆.故选C.8. 解析 若t 确定,则2221a a t ++=,所以2221a a t +=-唯一确定.故选B. 9. 解析12221log log 22-==-,3222423log 3log 3log 3log 32222+=== 10. 解析 23271221a a a a a ⎧=⋅⎨+=⎩,所以()()()211112631a d a d a d a d ⎧+=++⎪⎨+=⎪⎩ , 所以1231a d ⎧=⎪⎨⎪=-⎩.11. 解析 ()1cos 21π3sin 2122242x f x x x -⎛⎫=++=-+ ⎪⎝⎭, 所以2ππ2T ==,()min 32f x =. 12. 解析 ()()61244642f f f -==+-=-⎡⎤⎣⎦, 当1x时,()()min 00f x f ==;当1x >时,()min 6f x =.综上所述,()min 6f x =.13. 解析 设1e OA =,2e OB =,由2e OB =得121cos e e 2=,,即12πe e 3=,.又12e e ⋅=⋅b b ,得12e e 0⋅-⋅=b b ,即()12e e 0⋅-=b ,故()12e e ⊥-b .过点O 作直线l AB ⊥,如图所示,因为1e 1⋅=b ,2e 1⋅=b ,据平面向量数量积的几何意义知,OC 在OA ,OB 上的投影均为1,所以12cos30OC ==故3=b .14. 解析 依题意知,240x y +-<,630x y -->,则2463x y x y +-+--=42631034x y x y x y --+--=--.令1034z x y =--,即34100x y z ++-=,且221x y +,因此圆心()00,到直线34100x y z ++-=的距离小于等于1,即1015z -,得515z ,所以z 的最大值为15,即2463x y x y +-+--的最大值为15.15. 解析 解法一 设()00Q x y ,,则12πe e 3=,OQ OF c ==,所以22200x y c +=,又2200221x y a b +=,所以()()22222220222a c b a c b x a b c--==-,所以4222002b y c x c =-=,所以2b yc =,不妨取0x =,所以QF 中点0022x c y +⎛⎫⎪⎝⎭,,代入00b y x c =, 得2bc c -=,化简得2220()b bc c b c ⎧++=⎪⎨≠⎪⎩舍去或b c =,所以2e =. 解法二 设椭圆的左焦点为1F ,依题意,1OF OQ OF ==,故112OQ FF =,且O 为1FF的中点,因此1FFQ △为Rt △,且1π2F QF ∠=,即1F Q FQ ⊥,则1F Q 所在直线斜率为 cb ,所以()0Q b ,,则1FQF △为等腰直角三角形,故b c =,2c e a ===. 16. 解析 (1) πtan tanπ1tan 4tan 2π41tan 1tan tan 4A A A AA ++⎛⎫+=== ⎪-⎝⎭-,得1tan 3A =. 2212sin 22sin cos 2tan 231sin 2cos 2sin cos cos 2tan 15213A A A A A A A A A A ⨯====+++⨯+.(2) sin 10A =,cos 10A =.由正弦定理得,sin sin a b AB =,所以b AC ==,又()sin sin sin cos cos sin 210105C A B A B A B =+=+=+=⎝⎭,所以11sin 39225ABC S ab C ==⨯⨯=△. 17. 解析 (1)由题意知{}n a 是等比数列,12a =,2q =,所以2nn a =.当2n 时,()*231111111231n n b b b b n b n -++++=-∈-N ,所以11n n n b b b n +=-,所以11n n n b b n ++=,所以12112n n b b b n n+====+,又11b =,所以n b n =.(或采用累乘法) (2)212222n n T n =⨯+⨯++⋅,所以()21212122n n n T n n +=⨯++-⨯+⋅, 所以()()()2111212122222212212n n n n n n T n n n +++--=+++-⋅=-=---,所以()1122n n T n +=-+.18. 解析 (1) 记BC 中点E ,连AE ,DE ,1A E .因为AB AC =,所以AE BC ⊥,又1A E ⊥面ABC ,AE ⊂面ABC ,所以1AE A E ⊥,又1BCA E E =,所以AE ⊥面1A BC ,又1=//AA DE ,所以1AEDA 是平行四边形,所以1//AE A D ,所以1A D ⊥面1A BC .(2)作1A F DE ⊥,垂足F ,连BF .因为1A D ⊥面1A BC ,所以1BC A D ⊥,又1BC A E ⊥,111A EA D A =,所以BC ⊥面1A DE ,又1A F ⊂面1A DE ,所以1BC A F ⊥,又DEBC E =,所以1A F ⊥面11BB C C ,所以1A BF ∠是直线1A B 和平面11BB C C 所成的角.经计算得1A D =,14A B =,1A E =11142A E A D A F DE ⋅===,所以1112sin 4A F A BF A B ∠===.19. 解析 (1)设直线AP 的方程为:()y k x t =-,联立214y x =,得2104x kx kt -+=,由直线AP 与抛物线1C 相切知,0∆=,又0k ≠,求得k t =,因为12y x t '==,所以2x t =,2y t =,所以()22A t t ,.设()00B x y ,,代入圆222(1)1C x y :,得20002x y y ,因为BP 为圆2C 的切线,所以21BP BC k k ⋅=-1==-,解得2221t y t =+,所以 0221tx t =+,所以2222211t t B t t ⎛⎫ ⎪++⎝⎭,. (2)B 到AP的距离2d ==12AB x =-=所以23111222PABS AB d t t =⋅==△. 20. 解析 (1) ()2221142a a f x x ax x ⎛⎫=+++=++ ⎪⎝⎭,对称轴2a x =-.当12a -<-,即2a >时,()()21124a g a f ab a =-=-+=-+;当112a--,即22a-时,()12a g a f ⎛⎫=-= ⎪⎝⎭;当12a ->,即2a <-时,()()2124a g a f a ==++ .综上所述,()22224122224a a a g a a a a a ⎧-+>⎪⎪⎪=-⎨⎪⎪++<-⎪⎩,, ,.(2)假设()f x 在[]11-,上的零点0x ,则2000x ax b ++=,所以[]2200001124a a b x ax x x ⎛⎫=--=-++∈- ⎪⎝⎭,,,对称轴直线02a x =-.当12a-<-,即2a >时,11a b a ---,综合221a b a +,得b ∈Φ; 当102a--<,即02a <时,214a a b--,综合221a ba +,得b ∈Φ;当012a -,即20a -时,214a ab -,综合221a b a +,得3945b--当12a->,即2a <-时,11a b a ---,综合221a b a +,得b ∈Φ.综上所述,3945b--。
2015年高考试题汇编数学文-立体几何
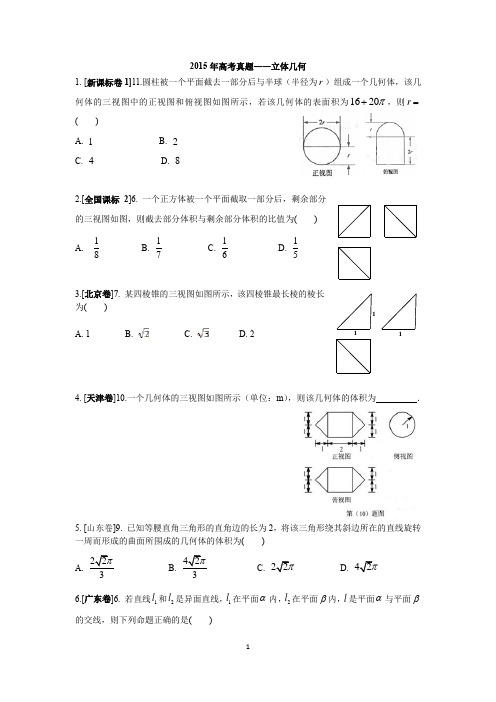
2015年高考真题――立体几何1. [新课标卷1]11.圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r =( )A. 1B. 2C. 4D. 82.[全国课标2]6. 一个正方体被一个平面截取一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( ) A.B. C. D.3.[北京卷]7. 某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( ) A. 1B.C.D. 24. [天津卷]10.一个几何体的三视图如图所示(单位:m ),则该几何体的体积为 .5. [山东卷]9. 已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.B.C.D. 6.[广东卷]6. 若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则下列命题正确的是( )81716151111A .l 至少与1l ,2l 中的一条相交B .l 与1l ,2l 都相交C .l 至多与1l ,2l 中的一条相交D .l 与1l ,2l 都不相交 7. [重庆卷]5. 某几何体的三视图如图所示,则该几何体的体积为( ) A.123π+ B. 136π C. 73π D. 52π8.[安徽卷]9. 一个四面体的三视图如图所示,则该四面体的表面积是( )A.1B.1+C.2D.9.[江苏卷]9.现有橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2、高为8的圆柱各一个. 若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为 .10.[浙江卷]2.某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )A .83cmB .123cmC .3233cm D .4033cm11.[湖南卷]10.某工作的三视图如图3所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积/原工件的体积)( )A.89πB.827πC.21)πD.21)π221112212.[陕西卷]5. 一个几何体的三视图如图所示,则该几何体的表面积为( )A.3πB. 4πC. 2π+4D. 3π+313.[湖北卷]5.12,l l 表示空间中的两条直线,若p :12,l l 是异面直线;q :12,l l 不相交,则( ) A .p 是q 的充分条件,但不是q 的必要条件 B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件14.[新课标1]18.(本小题满分12分)如图四边形ABCD 为菱形,G 为AC 与BD 交点,BE ABCD ⊥平面,(I)证明:平面AEC ⊥平面BED ;(II)若120ABC ∠=,,AE EC ⊥ 三棱锥E ACD -.15.[全国课标2]19.(本小题满分12分)如图,长方体ABCD ﹣A 1B 1C 1D 1中,AB=16,BC=10,AA 1=8,点E ,分别在A 1B 1, D 1C 1上,A 1E= D 1F=4.过点E,F 的平面α与此长方体的面相交,交线围成一个正方形. (I)在图中画出这个正方形(不必说明画法和理由) (II)求平面α把该长方体分成的两部分体积的比值.22FD C 1A 1C如图,在三棱锥E-ABC 中,平面EAB ⊥平面ABC ,三角形EAB 为等边三角形,AC ⊥ BC,且AC=BC=,O,M 分别为AB,V A 的中点.(I)求证:VB//平面MOC.(II)求证:平面MOC ⊥平面 V AB (III)求三棱锥V-ABC 的体积.17. [天津卷]17.(满分13分) 如图,已知1AA ⊥平面ABC ,11,BB AA AB=AC=3,1BC AA =,1BB =点E ,F 分别是BC ,1AC 的中点, (I )求证:EF 平面11A B BA ; (II )求证:平面1AEA ⊥平面1BCB 。
2015年高考数学(文科)真题分类汇编G单元立体几何
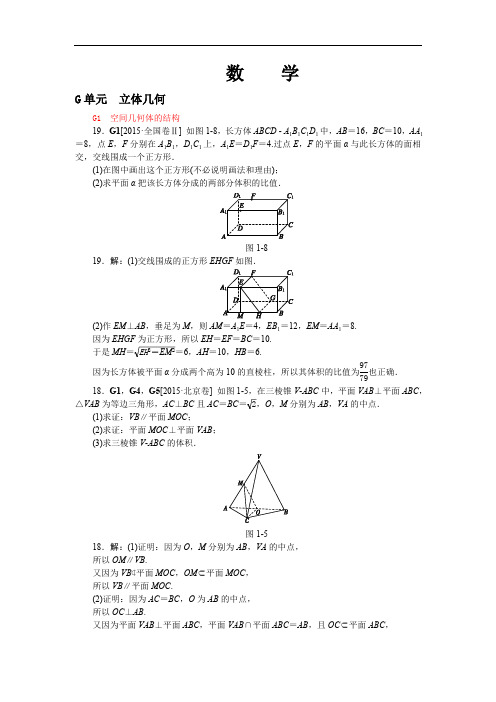
数 学G 单元 立体几何G1 空间几何体的结构19.G1[2015·全国卷Ⅱ] 如图18,长方体ABCD A 1B 1C 1D 1中,AB =16,BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由);(2)求平面α把该长方体分成的两部分体积的比值.图1819.解:(1)交线围成的正方形EHGF 如图.(2)作EM ⊥AB ,垂足为M ,则AM =A 1E =4,EB 1=12,EM =AA 1=8.因为EHGF 为正方形,所以EH =EF =BC =10.于是MH ==6,AH =10,HB =6.EH 2-EM 2因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为也正确.977918.G1,G4,G5[2015·北京卷] 如图15,在三棱锥V ABC 中,平面VAB ⊥平面ABC ,△VAB 为等边三角形,AC ⊥BC 且AC =BC =,O ,M 分别为AB ,VA 的中点.2(1)求证:VB ∥平面MOC ;(2)求证:平面MOC ⊥平面VAB ;(3)求三棱锥V ABC 的体积.图1518.解:(1)证明:因为O ,M 分别为AB ,VA 的中点,所以OM ∥VB .又因为VB ⊄平面MOC ,OM ⊂平面MOC ,所以VB ∥平面MOC .(2)证明:因为AC =BC ,O 为AB 的中点,所以OC ⊥AB .又因为平面VAB ⊥平面ABC ,平面VAB ∩平面ABC =AB ,且OC ⊂平面ABC ,所以OC ⊥平面VAB .又因为OC ⊂平面MOC ,所以平面MOC ⊥平面VAB .(3)在等腰直角三角形ACB 中,AC =BC =,2所以AB =2,OC =1.所以等边三角形VAB 的面积S △VAB =.3又因为OC ⊥平面VAB ,所以三棱锥C VAB 的体积等于OC ·S △VAB =.1333又因为三棱锥V ABC 的体积与三棱锥C VAB 的体积相等,所以三棱锥V ABC 的体积为.3318.G1、G5[2015·湖南卷] 如图14,直三棱柱ABC A 1B 1C 1的底面是边长为2的正三角形,E ,F 分别是BC ,CC 1的中点.(1)证明:平面AEF ⊥平面B 1BCC 1;(2)若直线A 1C 与平面A 1ABB 1所成的角为45°,求三棱锥F AEC 的体积.18.解:(1)证明:如图,因为三棱柱ABC A 1B 1C 1是直三棱柱,所以AE ⊥BB 1.又E 是正三角形ABC 的边BC 的中点,所以AE ⊥BC .因此AE ⊥平面B 1BCC 1.而AE ⊂平面AEF ,所以平面AEF ⊥平面B 1BCC 1.(2)设AB 的中点为D ,连接A 1D 因为△ABC 是正三角形,所以CD ⊥AB .又三棱柱ABC A 1B 1C 1是直三棱柱,所以CD ⊥AA 1.因此CD ⊥平面A 1ABB 1,于是∠CA 1D 为直线A 1C 与平面A 1ABB 1所成的角.由题设,∠CA 1D =45°,所以A 1D =CD =AB =.323在Rt △AA 1D 中,AA 1===,所以FC =AA 1=.A 1D 2-AD 23-121222故三棱锥F AEC 的体积V =S △AEC ·FC =××=.131********9.G1[2015·山东卷] 已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.B.22π342π3C .2πD .4π229.B [解析] 由条件知该直角三角形的斜边长为2,斜边上的高为,故围成的几22何体的体积为2××π×()2×=.132242π318.G1,G4,G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示.(1)请将字母F ,G ,H 标记在正方体相应的顶点处(不需说明理由);(2)判断平面BEG 与平面ACH 的位置关系,并证明你的结论;(3)证明:直线DF图1218.解:(1)点F ,G ,H 的位置如图所示.(2)平面BEG ∥平面ACH .证明如下:因为ABCD EFGH 为正方体,所以BC ∥FG ,BC =FG ,又FG ∥EH ,FG =EH ,所以BC ∥EH ,BC =EH ,于是BCHE 为平行四边形,所以BE ∥CH .又CH ⊂平面ACH ,BE ⊄平面ACH ,所以BE ∥平面ACH .同理BG ∥平面ACH .又BE ∩BG =B ,所以平面BEG ∥平面ACH .(3)证明:连接FH .因为ABCD EFGH 为正方体,所以DH ⊥平面EFGH .因为EG ⊂平面EFGH ,所以DH ⊥EG ,又EG ⊥FH ,EG ∩FH =O ,所以EG ⊥平面BFHD .又DF ⊂平面BFHD ,所以DF ⊥EG .同理DF ⊥BG .又EG ∩BG =G ,所以DF ⊥平面BEG .10.G1、G2[2015·天津卷] 一个几何体的三视图如图13所示(单位:m),则该几何体的体积为________m 3.图1310.π [解析] 根据三视图可知,该几何体是圆柱与两个圆锥的组合体,其体积V =π83×12×2+2××π×12×1=π(m 3).1383G2 空间几何体的三视图和直观图9.G2[2015·安徽卷] 一个四面体的三视图如图12所示,则该四面体的表面积是( )A .1+B .1+232C .2+D .2329.C [解析] 四面体的直观图如图所示,设O 是AC 的中点,则OP =OB =1,因此PB=,于是S △PAB =S △PBC =×()2=,S △PAC =S △ABC =×2×1=1,故四面体的表面积23423212S =2×1+2×=2+.32311.G2[2015·全国卷Ⅰ] 圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图14所示.若该几何体的表面积为16+20π,则r =( )图14A .1B .2C .4D .811.B [解析] 由三视图可知,此组合体的前半部分是一个底面半径为r ,高为2r 的半圆柱(水平放置),后半部分是一个半径为r 的半球,其中半圆柱的一个底面与半球的半个圆面重合,所以此几何体的表面积为2r ·2r +πr 2+πr 2+πr ·2r +2πr 2=4r 2+5πr 2=16+121220π,解得r =2.6.G2[2015·全国卷Ⅱ] 一个正方体被一个平面截去一部分后,剩余部分的三视图如图12,则截去部分体积与剩余部分体积的比值为( )图12A. B.1817C. D.16156.D [解析] 由剩余部分的三视图可知,正方体被截去一个三棱锥,剩余部分如图所示,设正方体的棱长为a ,则被截去的三棱锥的体积为×a 2×a =a 3,而正方体的体积为131216a 3,所以截去部分体积与剩余部分体积的比值为.157.G2[2015·北京卷] 某四棱锥的三视图如图12所示,该四棱锥最长棱的棱长为( )图12A .1 B. C. D .2237.C [解析] 根据三视图可得,此四棱锥是底面是正方形,有一条侧棱和底面垂直的四棱锥,如图所示,所以最长棱的棱长为PC ==,故选C.12+12+1239.G2[2015·福建卷] ( )图13A .8+2B .11+2 22C .14+2D .1529.B [解析] 由三视图可知,该几何体是底面为直角梯形的直四棱柱,其表面积S =(1+1+2+)×2+×(1+2)×1×2=11+2 .212210.G2、G7、K3[2015·湖南卷] 某工件的三视图如图13所示,现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)( )新工件的体积原工件的体积图13A.B.89π827πC. D.24(2-1)3π8(2-1)3π10.A [解析] 由三视图知,原工件是底面半径为1,母线长为3的圆锥.设新正方体工件的棱长为x ,借助轴截面,由三角形相似可得,=,得x =x 32-121-22x 1,故V 正=x 3=,又V 圆锥=π×12×=,故利用率为=,选223162271332-1222π316227223π89πA.5.G2[2015·陕西卷]12所示,则该几何体的表面积为( )图12A .3πB .4πC .2π+4D .3π+45.D [解析] 该几何体是底面半径为1、高为2的圆柱被其轴截面截开的半个圆柱,其表面积为×2π×1×2+2××π×12+2×2=3π+4.121214.G2,G7[2015·四川卷] 在三棱柱ABC A 1B 1C 1中,∠BAC =90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M ,N ,P 分别是棱AB ,BC ,B 1C 1的中点,则三棱锥P A 1MN 的体积是________.14. [解析] 由题意知,三棱柱的底面是直角边长为1的等腰直角三角形,棱柱的高124为1且该棱柱为直三棱柱,其底面积为,三棱锥A 1PMN 的底面积是××1,高为,故12121212三棱锥P A 1MN 的体积为××=.13121412410.G1、G2[2015·天津卷] 一个几何体的三视图如图13所示(单位:m),则该几何体的体积为________m 3.图1310.π [解析] 根据三视图可知,该几何体是圆柱与两个圆锥的组合体,其体积V =π×8312×2+2××π×12×1=π(m 3).13832.G2[2015·浙江卷] 某几何体的三视图如图11所示(单位:cm),则该几何体的体积是( )图11A .8 cm 3B .12 cm 3C. cm 3D. cm 33234032.C [解析] 该几何体为一个正方体和一个四棱锥的组合体,故所求体积为23+×2×132×2=.323G3 平面的基本性质、空间两条直线6.G3[2015·广东卷] 若直线l 1和l 2是异面直线,l 1在平面α内,l 2在平面β内,l 是平面α与平面β的交线,则下列命题正确的是( )A .l 与l 1,l 2都不相交B .l 与l 1,l 2都相交C .l 至多与l 1,l 2中的一条相交D .l 至少与l 1,l 2中的一条相交6.D [解析] 若直线l 1和l 2是异面直线,l 1在平面α内,l 2在平面β内,l 是平面α与平面β的交线,则l 至少与l 1,l 2中的一条相交,故选D.5.A2、G3[2015·湖北卷] l 1,l 2表示空间中的两条直线,若p :l 1,l 2是异面直线;q :l 1,l 2不相交,则( )A .p 是q 的充分条件,但不是q 的必要条件B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D.p既不是q的充分条件,也不是q的必要条件5.A [解析] 由l1,l2是异面直线,可得l1,l2不相交,所以p⇒q;由l1,l2不相交,可得l1,l2是异面直线或l1∥l2,所以q⇒/ p.所以p是q的充分条件,但不是q的必要条件.故选A.G4 空间中的平行关系18.G4,G5,G11[2015·广东卷] 如图13,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.(1)证明:BC∥平面PDA;(2)证明:BC⊥PD;(3)求点C到平面PDA的距离.图1318.G1,G4,G5[2015·北京卷] 如图15,在三棱锥VABC中,平面VAB⊥平面ABC,2△VAB为等边三角形,AC⊥BC且AC=BC=,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB;(3)求三棱锥VABC的体积.图1518.解:(1)证明:因为O,M分别为AB,VA的中点,所以OM∥VB.又因为VB⊄平面MOC,OM⊂平面MOC,所以VB∥平面MOC.(2)证明:因为AC=BC,O为AB的中点,所以OC⊥AB.又因为平面VAB⊥平面ABC,平面VAB∩平面ABC=AB,且OC⊂平面ABC,所以OC⊥平面VAB.又因为OC⊂平面MOC,所以平面MOC⊥平面VAB.2(3)在等腰直角三角形ACB中,AC=BC=,所以AB=2,OC=1.所以等边三角形VAB的面积S△VAB=.3又因为OC⊥平面VAB,所以三棱锥CVAB的体积等于OC ·S △VAB =.1333又因为三棱锥V ABC 的体积与三棱锥C VAB 的体积相等,所以三棱锥V ABC 的体积为.3318.G4、G5[2015·山东卷] 如图13,三棱台DEF ABC 中,AB =2DE ,G ,H 分别为AC ,BC 的中点.(1)求证:BD ∥平面FGH ;(2)若CF ⊥BC ,AB ⊥BC ,求证:平面BCD ⊥平面EGH .18.证明:(1)证法一:如图,连接DG ,CD ,设CD ∩GF =M ,连接MH .在三棱台DEF ABC 中,AB =2DE ,G 为AC 的中点,可得DF ∥GC ,DF =GC ,所以四边形DFCG 为平行四边形,则M 为CD 的中点.又H 为BC 的中点,所以HM ∥BD .又HM ⊂平面FGH ,BD ⊄平面FGH ,所以BD ∥平面FGH .证法二:在三棱台DEF ABC 中,由BC =2EF ,H 为BC 的中点,可得BH ∥EF ,BH =EF ,所以四边形HBEF 为平行四边形,可得BE ∥HF .在△ABC 中,G 为AC 的中点,H 为BC 的中点,所以GH ∥AB .又GH ∩HF =H ,AB ∩BE =B ,所以平面FGH ∥平面ABED .因为BD ⊂平面ABED ,所以BD ∥平面FGH .(2)如图,连接HE ,GE .因为G ,H 分别为AC ,BC 的中点,所以GH ∥AB .由AB ⊥BC ,得GH ⊥BC ,又H 为BC 的中点,所以EF ∥HC ,EF =HC ,因此四边形EFCH 是平行四边形,所以CF ∥HE .又CF⊥BC,所以HE⊥BC.又HE,GH⊂平面EGH,HE∩GH=H,所以BC⊥平面EGH.又BC⊂平面BCD,所以平面BCD⊥平面EGH.18.G1,G4,G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示.(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);(2)判断平面BEG与平面ACH的位置关系,并证明你的结论;(3)证明:直线DF图1218.解:(1)点F,G,H的位置如图所示.(2)平面BEG∥平面ACH.证明如下:因为ABCDEFGH为正方体,所以BC∥FG,BC=FG,又FG∥EH,FG=EH,所以BC∥EH,BC=EH,于是BCHE为平行四边形,所以BE∥CH.又CH⊂平面ACH,BE⊄平面ACH,所以BE∥平面ACH.同理BG∥平面ACH.又BE∩BG=B,所以平面BEG∥平面ACH.(3)证明:连接FH.因为ABCDEFGH为正方体,所以DH⊥平面EFGH.因为EG⊂平面EFGH,所以DH⊥EG,又EG⊥FH,EG∩FH=O,所以EG⊥平面BFHD.又DF⊂平面BFHD,所以DF⊥EG.同理DF⊥BG.又EG∩BG=G,所以DF⊥平面BEG.17.G4、G5、G11[2015·天津卷] 如图14,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC =2,AA 1=,BB 1=2,点E 和F 分别为BC 和A 1C 中点.577(1)求证:EF ∥平面A 1B 1BA ;(2)求证:平面AEA 1⊥平面BCB 1;(3)求直线A 1B 1与平面BCB 1所成角的大小.17.解:(1)证明:如图所示,连接A 1B .在△A 1BC 中,因为E 和F 分别是BC 和A 1C 的中点,所以EF ∥BA 1.又因为EF ⊄平面A A 1B 1BA .(2)证明:因为AB =AC ,E 为BC BC .因为AA 1⊥平面ABC ,BB 1∥AA 1,所以BB 1⊥平面ABC ,从而BB 1⊥AE .又因为BC ∩BB 1=B ,所以AE ⊥平面BCB 1.又因为AE ⊂平面AEA 1,所以平面AEA 1⊥平面BCB 1.(3)取BB 1的中点M 和B 1C 的中点N ,连接A 1M ,A 1N ,NE .因为N 和E 分别为B 1C 和BC的中点,所以NE ∥B 1B ,NE =B 1B ,故NE ∥A 1A ,且NE =A 1A ,所以A 1N ∥AE ,且A 1N =12AE .又因为AE ⊥平面BCB 1,所以A 1N ⊥平面BCB 1,从而∠A 1B 1N 为直线A 1B 1与平面BCB 1所成的角.在△ABC 中,可得AE =2,所以A 1N =AE =2.因为BM ∥AA 1,BM =AA 1,所以A 1M ∥AB ,A 1M =AB, 又由AB ⊥BB 1,得A 1M ⊥BB 1.在Rt △A 1MB 1中,可得A 1B 1==4.B 1M 2+A 1M 2在Rt △A 1NB 1中,sin ∠A 1B 1N ==,因此∠A 1B 1N =30°,A 1N A 1B 112所以直线A 1B 1与平面BCB 1所成的角为30°.4.G4,G5[2015·浙江卷] 设α,β是两个不同的平面,l ,m 是两条不同的直线,且l ⊂α,m ⊂β( )A .若l ⊥β,则α⊥βB .若α⊥β,则l ⊥mC .若l ∥β,则α∥βD .若α∥β,则l ∥m4.A [解析] 由两平面垂直的判定定理知,A 正确;对于B ,直线l ,m 相交、平行、异面都有可能,故不正确;对于C ,要求α内两条相交直线都平行于β,才能推出α∥β,故不正确;对于D ,l ,m 平行和异面都有可能,故不正确.16.G4、G5[2015·江苏卷] 如图12,在直三棱柱ABC A 1B 1C 1中,已知AC ⊥BC ,BC =CC 1,设AB 1的中点为D ,B 1C ∩BC 1=E .求证:(1)DE∥平面AA1C1C;(2)BC1⊥AB1.图1216.证明:(1)由题意知,E为B1C的中点,又D为AB1的中点,因此DE∥AC.又因为DE⊄平面AA1C1C,AC⊂平面AA1C1C,所以DE∥平面AA1C1C.(2)因为三棱柱ABCA1B1C1是直三棱柱,所以CC1⊥平面ABC.因为AC⊂平面ABC,所以AC⊥CC1.又因为AC⊥BC,CC1⊂平面BCC1B1,BC⊂平面BCC1B1,BC∩CC1=C,所以AC⊥平面BCC1B1.又因为BC1⊂平面BCC1B1,所以BC1⊥AC.因为BC=CC1,所以矩形BCC1B1是正方形,因此BC1⊥B1C.因为AC,B1C⊂平面B1AC,AC∩B1C=C,所以BC1⊥平面B1AC.又因为AB1⊂平面B1AC,所以BC1⊥AB1.G5 空间中的垂直关系18.G4,G5,G11[2015·广东卷] 如图13,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.(1)证明:BC∥平面PDA;(2)证明:BC⊥PD;(3)求点C到平面PDA的距离.图1320.G5、G12[2015·湖北卷] 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图14所示的阳马P ABCD 中,侧棱PD ⊥底面ABCD ,且PD =CD ,点E 是PC 的中点,连接DE ,BD ,BE .(1)证明:DE ⊥平面PBC .试判断四面体EBCD 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由.(2)记阳马P ABCD 的体积为V 1,四面体EBCD 的体积为V 2,求的值.V 1V2图1420.解:(1)证明:因为PD ⊥底面ABCD ,所以PD ⊥BC .由底面ABCD 为长方形,有BC ⊥CD ,而PD ∩CD =D ,所以BC ⊥平面PCD .又DE ⊂平面PCD ,所以BC ⊥DE .又因为PD =CD ,点E 是PC 的中点,所以DE ⊥PC .而PC ∩BC =C ,所以DE ⊥平面PBC .由BC ⊥平面PCD ,DE ⊥平面PBC ,可知四面体EBCD 的四个面都是直角三角形,即四面体EBCD 是一个鳖臑,其四个面的直角分别是∠BCD ,∠BCE ,∠DEC ,∠DEB .(2)由已知,PD 是阳马P ABCD 的高,所以V 1=S 长方形ABCD ·PD =BC ·CD ·PD ;1313由(1)知,DE 是鳖臑D BCE 的高,BC ⊥CE ,所以V 2=S △BCE ·DE =BC ·CE ·DE .1316在Rt △PDC 中,因为PD =CD ,点E 是PC 的中点,所以DE =CE =CD .22于是===4.V 1V 213BC ·CD ·PD 16BC ·CE ·DE 2CD ·PD CE ·DE18.G5[2015·全国卷Ⅰ] 如图15,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD .(1)证明:平面AEC ⊥平面BED ;(2)若∠ABC =120°,AE ⊥EC, 三棱锥E ACD 的体积为,求该三棱锥的侧面积.63图1518.解:(1)证明:因为四边形ABCD 为菱形,所以AC ⊥BD .因为BE ⊥平面ABCD ,所以AC ⊥BE ,故AC ⊥平面BED .又AC ⊂平面AEC ,所以平面AEC ⊥平面BED .(2)设AB =x ,在菱形ABCD 中,由∠ABC =120°,可得AG =GC =x ,GB =GD =.32x2因为AE ⊥EC ,所以在Rt △AEC 中,可得EG =x .32由BE ⊥平面ABCD ,知△EBG 为直角三角形,可得BE =x .22由已知得,三棱锥E ACD 的体积V E ACD =×AC ·GD ·BE =x 3=,131262463故x =2.从而可得AE =EC =ED =,6所以△EAC 的面积为3,△EAD 的面积与△ECD 的面积均为.5故三棱锥E ACD 的侧面积为3+2.518.G1,G4,G5[2015·北京卷] 如图15,在三棱锥V ABC 中,平面VAB ⊥平面ABC ,△VAB 为等边三角形,AC ⊥BC 且AC =BC =,O ,M 分别为AB ,VA 的中点.2(1)求证:VB ∥平面MOC ;(2)求证:平面MOC ⊥平面VAB ;(3)求三棱锥V ABC 的体积.图1518.解:(1)证明:因为O ,M 分别为AB ,VA 的中点,所以OM ∥VB .又因为VB ⊄平面MOC ,OM ⊂平面MOC ,所以VB ∥平面MOC .(2)证明:因为AC =BC ,O 为AB 的中点,所以OC ⊥AB .又因为平面VAB ⊥平面ABC ,平面VAB ∩平面ABC =AB ,且OC ⊂平面ABC ,所以OC ⊥平面VAB .又因为OC ⊂平面MOC ,所以平面MOC ⊥平面VAB .(3)在等腰直角三角形ACB 中,AC =BC =,2所以AB =2,OC =1.所以等边三角形VAB 的面积S △VAB =.3又因为OC ⊥平面VAB ,所以三棱锥C VAB 的体积等于OC ·S △VAB =.1333又因为三棱锥V ABC 的体积与三棱锥C VAB 的体积相等,所以三棱锥V ABC 的体积为.3320.G5、G12[2015·福建卷] 如图15,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,PO 垂直于圆O 所在的平面,且PO =OB =1.(1)若D 为线段AC 的中点,求证:AC ⊥平面PDO ;(2)求三棱锥P ABC 体积的最大值;(3)若BC =,点E 在线段PB 上,求CE +OE 的最小值.2图1520.解:方法一:(1)证明:在△AOC 中,因为OA =OC ,D 为AC 的中点,所以AC ⊥DO .又PO 垂直于圆O 所在的平面,所以PO ⊥AC .因为DO ∩PO =O ,DO ⊂平面PDO ,PO ⊂平面PDO ,所以AC ⊥平面PDO .(2)因为点C 在圆O 上,所以当CO ⊥AB 时,C 到AB 的距离最大,且最大值为1.又AB =2,所以△ABC 面积的最大值为×2×1=1.12又因为三棱锥P ABC 的高PO =1,故三棱锥P ABC 体积的最大值为×1×1=.1313(3)在△POB 中,PO =OB =1,∠POB =90°,所以PB ==.12+122同理PC =,所以PB =PC =BC .2在三棱锥P ABC 中,将侧面BCP 绕PB 旋转至平面BC ′P, 使之与平面ABP 共面,如图所示.当O ,E ,C ′共线时,CE +OE 取得最小值.又因为OP =OB ,C ′P =C ′B ,所以OC ′垂直平分PB ,即E 为PB 中点.从而OC ′=OE +EC ′=+=,22622+62亦即CE +OE 的最小值为.2+62方法二:(1)(2)同方法一.(3)在△POB 中,PO =OB =1,∠POB =90°,所以∠OPB =45°,PB ==.12+122同理PC =.2所以PB =PC =BC ,所以∠CPB =60°.在三棱锥P ABC 中,将侧面BCP 绕PB 旋转至平面BC ′P ,使之与平面ABP 共面,如图所示.当O ,E ,C ′共线时,CE +OE 取得最小值.所以在△OC ′P 中,由余弦定理得,OC ′2=1+2-2×1××cos(45°+60°)=1+2-2 ××-×=2+.22221222323从而OC ′==.2+32+62所以CE +OE 的最小值为+.226218.G1、G5[2015·湖南卷] 如图14,直三棱柱ABC A 1B 1C 1的底面是边长为2的正三角形,E ,F 分别是BC ,CC 1的中点.(1)证明:平面AEF ⊥平面B 1BCC 1;(2)若直线A 1C 与平面A 1ABB 1所成的角为45°,求三棱锥F AEC 的体积.18.解:(1)证明:如图,因为三棱柱ABC A 1B 1C 1是直三棱柱,所以AE ⊥BB 1.又E 是正三角形ABC 的边BC 的中点,所以AE ⊥BC .因此AE ⊥平面B 1BCC 1.而AE ⊂平面AEF ,所以平面AEF ⊥平面B 1BCC 1.(2)设AB 的中点为D ,连接A 1D 因为△ABC 是正三角形,所以CD ⊥AB .又三棱柱ABC A 1B 1C 1是直三棱柱,所以CD ⊥AA 1.因此CD ⊥平面A 1ABB 1,于是∠CA 1D 为直线A 1C 与平面A 1ABB 1所成的角.由题设,∠CA 1D =45°,所以A 1D =CD =AB =.323在Rt △AA 1D 中,AA 1===,所以FC =AA 1=.A 1D 2-AD 23-121222故三棱锥F AEC 的体积V =S △AEC ·FC =××=.1313322261218.G4、G5[2015·山东卷] 如图13,三棱台DEF ABC 中,AB =2DE ,G ,H 分别为AC ,BC 的中点.(1)求证:BD ∥平面FGH ;(2)若CF ⊥BC ,AB ⊥BC ,求证:平面BCD ⊥平面EGH .18.证明:(1)证法一:如图,连接DG ,CD ,设CD ∩GF =M ,连接MH .在三棱台DEF ABC 中,AB =2DE ,G 为AC 的中点,可得DF ∥GC ,DF =GC ,所以四边形DFCG 为平行四边形,则M 为CD 的中点.又H 为BC 的中点,所以HM ∥BD .又HM ⊂平面FGH ,BD ⊄平面FGH ,所以BD ∥平面FGH .证法二:在三棱台DEF ABC 中,由BC =2EF ,H 为BC 的中点,可得BH ∥EF ,BH =EF ,所以四边形HBEF 为平行四边形,可得BE ∥HF .在△ABC 中,G 为AC 的中点,H 为BC 的中点,所以GH ∥AB .又GH ∩HF =H ,AB ∩BE =B ,所以平面FGH ∥平面ABED .因为BD ⊂平面ABED ,所以BD ∥平面FGH .(2)如图,连接HE ,GE .因为G ,H 分别为AC ,BC 的中点,所以GH ∥AB .由AB ⊥BC ,得GH ⊥BC ,又H 为BC 的中点,所以EF ∥HC ,EF =HC ,因此四边形EFCH 是平行四边形,所以CF ∥HE .又CF ⊥BC ,所以HE ⊥BC .又HE ,GH ⊂平面EGH ,HE ∩GH =H ,所以BC ⊥平面EGH .又BC ⊂平面BCD ,所以平面BCD ⊥平面EGH .18.G5[2015·陕西卷] 如图15(1),在直角梯形ABCD 中,AD ∥BC ,∠BAD =,AB =π2BC =AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到图(2)中△A 1BE12的位置,得到四棱锥A 1 BCDE .(1)证明:CD ⊥平面A 1OC ;(2)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1 BCDE 的体积为36,求a 的值.2图1518.解:(1)证明:在图(1)中,因为AB =BC =AD =a ,E 是AD 的中点,12∠BAD =,所以BE ⊥AC ,π2即在图(2)中,BE ⊥A 1O ,BE ⊥OC ,从而BE ⊥平面A 1OC .又CD ∥BE ,所以CD ⊥平面A 1OC .(2)由已知,平面A 1BE ⊥平面BCDE ,且平面A 1BE ∩平面BCDE =BE ,又由(1)知,A 1O ⊥BE ,所以A 1O ⊥平面BCDE ,即A 1O 是四棱锥A 1 BCDE 的高.由图(1)知,A 1O =AB =a ,平行四边形BCDE 的面积S =BC ·AB =a 2.2222从而四棱锥A 1 BCDE 的体积V =×S ×A 1O =×a 2×a =a 3.13132226由a 3=36,得a =6.26218.G1,G4,G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示.(1)请将字母F ,G ,H 标记在正方体相应的顶点处(不需说明理由);(2)判断平面BEG 与平面ACH 的位置关系,并证明你的结论;(3)证明:直线DF图1218.解:(1)点F ,G ,H 的位置如图所示.(2)平面BEG ∥平面ACH .证明如下:因为ABCD EFGH 为正方体,所以BC ∥FG ,BC =FG ,又FG ∥EH ,FG =EH ,所以BC ∥EH ,BC =EH ,于是BCHE 为平行四边形,所以BE ∥CH .又CH ⊂平面ACH ,BE ⊄平面ACH ,所以BE ∥平面ACH .同理BG ∥平面ACH .又BE ∩BG =B ,所以平面BEG ∥平面ACH .(3)证明:连接FH .因为ABCD EFGH 为正方体,所以DH ⊥平面EFGH .因为EG ⊂平面EFGH ,所以DH ⊥EG ,又EG ⊥FH ,EG ∩FH =O ,所以EG ⊥平面BFHD .又DF ⊂平面BFHD ,所以DF ⊥EG .同理DF ⊥BG .又EG ∩BG =G ,所以DF ⊥平面BEG .17.G4、G5、G11[2015·天津卷] 如图14,已知AA 1⊥平面ABC ,BB 1∥AA 1,AB =AC =3,BC =2,AA 1=,BB 1=2,点E 和F 分别为BC 和A 1C 中点.577(1)求证:EF ∥平面A 1B 1BA ;(2)求证:平面AEA 1⊥平面BCB 1;(3)求直线A 1B 1与平面BCB 1所成角的大小.17.解:(1)证明:如图所示,连接A 1B .在△A 1BC 中,因为E 和F 分别是BC 和A 1C 的中点,所以EF ∥BA 1.又因为EF ⊄平面A A 1B 1BA .(2)证明:因为AB =AC ,E 为BC BC .因为AA 1⊥平面ABC ,BB 1∥AA 1,所以BB 1⊥平面ABC ,从而BB 1⊥AE .又因为BC ∩BB 1=B ,所以AE ⊥平面BCB 1.又因为AE ⊂平面AEA 1,所以平面AEA 1⊥平面BCB 1.(3)取BB 1的中点M 和B 1C 的中点N ,连接A 1M ,A 1N ,NE .因为N 和E 分别为B 1C 和BC的中点,所以NE ∥B 1B ,NE =B 1B ,故NE ∥A 1A ,且NE =A 1A ,所以A 1N ∥AE ,且A 1N =12AE .又因为AE ⊥平面BCB 1,所以A 1N ⊥平面BCB 1,从而∠A 1B 1N 为直线A 1B 1与平面BCB 1所成的角.在△ABC 中,可得AE =2,所以A 1N =AE =2.因为BM ∥AA 1,BM =AA 1,所以A 1M ∥AB ,A 1M =AB, 又由AB ⊥BB 1,得A 1M ⊥BB 1.在Rt △A 1MB 1中,可得A 1B 1==4.B 1M 2+A 1M 2在Rt △A 1NB 1中,sin ∠A 1B 1N ==,因此∠A 1B 1N =30°,A 1N A 1B 112所以直线A 1B 1与平面BCB 1所成的角为30°.4.G4,G5[2015·浙江卷] 设α,β是两个不同的平面,l ,m 是两条不同的直线,且l ⊂α,m ⊂β( )A .若l ⊥β,则α⊥βB .若α⊥β,则l ⊥mC .若l ∥β,则α∥βD .若α∥β,则l ∥m4.A [解析] 由两平面垂直的判定定理知,A 正确;对于B ,直线l ,m 相交、平行、异面都有可能,故不正确;对于C ,要求α内两条相交直线都平行于β,才能推出α∥β,故不正确;对于D ,l ,m 平行和异面都有可能,故不正确.18.G5,G11[2015·浙江卷] 如图14,在三棱柱ABC A 1B 1C 1中,∠BAC =90°,AB =AC =2,A 1A =4,A 1在底面ABC 的射影为BC 的中点,D 是B 1C 1的中点.(1)证明:A 1D ⊥平面A 1BC ;(2)求直线A 1B 和平面BB 1C 1C 所成的角的正弦值.图1418.解:(1)证明:设E 为BC 的中点,连接DE .由题意得A 1E ⊥平面ABC ,所以A 1E ⊥AE .因为AB =AC ,所以AE ⊥BC .故AE ⊥平面A 1BC .由D ,E 分别为B 1C 1,BC 的中点,得DE ∥B 1B 且DE =B 1B ,从而DE ∥A 1A 且DE =A 1A ,所以四边形AA 1DE 为平行四边形.于是A 1D ∥AE .又因为AE ⊥平面A 1BC ,所以A 1D ⊥平面A 1BC .(2)作A 1F ⊥DE ,垂足为F ,连接BF .因为A 1E ⊥平面ABC ,所以BC ⊥A 1E .因为BC ⊥AE ,所以BC ⊥平面AA 1DE .所以BC ⊥A 1F ,所以A 1F ⊥平面BB 1C 1C .所以∠A 1BF 为直线A 1B 和平面BB 1C 1C 所成的角.由AB =AC =2,∠CAB =90°,得EA =EB =.2由A 1E ⊥平面ABC ,得A 1A =A 1B =4,A 1E =.14由DE =BB 1=4,DA 1=EA =,∠DA 1E =90°,得A 1F =.272所以sin ∠A 1BF ==.A 1F A 1B 7820.G5、G7[2015·重庆卷] 如图14,三棱锥P ABC 中,平面PAC ⊥平面ABC ,∠ABC =,点D ,E 在线段AC 上,且AD =DE =EC =2,PD =PC =4,点F 在线段AB 上,且π2EF ∥BC .(1)证明:AB ⊥平面PFE ;(2)若四棱锥P DFBC 的体积为7,求线段BC 的长.图1420.解:(1)证明:由DE =EC ,PD =PC 知,E 为等腰三角形PDC 中DC 边的中点,故PE ⊥AC .又平面PAC ⊥平面ABC ,平面PAC ∩平面ABC =AC ,PE ⊂平面PAC ,PE ⊥AC ,所以PE ⊥平面ABC ,从而PE ⊥AB .因为∠ABC =,EF ∥BC ,故AB ⊥EF .π2从而AB 与平面PFE 内两条相交直线PE ,EF 都垂直,所以AB ⊥平面PFE .(2)设BC =x ,则在直角三角形ABC 中,AB ==,AC 2-BC 236-x 2从而S △ABC =AB ·BC =x .121236-x 2由EF ∥BC 知,==,△AFE ∽△ABC ,故=2=,即S △AFE =S △ABC .AF AB AE AC 23S △AFE S △ABC 234949由AD =AE ,得S △AFD =S △AFE =×S △ABC =S △ABC =x ,12121249291936-x 2从而四边形DFBC 的面积为S 四边形DFBC =S △ABC -S △AFD =x -x =x1236-x 21936-x 2718.36-x 2由(1)知,PE ⊥平面ABC ,所以PE 为四棱锥P DFBC 的高.在直角三角形PEC 中,PE ===2.PC 2-EC 242-223所以V 四棱锥P DFBC =·S 四边形DFBC ·PE =×x ·2=7,131371836-x 23故得x 4-36x 2+243=0,解得x 2=9或x 2=27,由于x >0,可得x =3或x =3.3所以BC =3或BC =3.3G6 多面体与球G7 棱柱与棱锥10.G2、G7、K3[2015·湖南卷] 某工件的三视图如图13所示,现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)( )新工件的体积原工件的体积图13A.B.89π827πC.D.24(2-1)3π8(2-1)3π10.A [解析] 由三视图知,原工件是底面半径为1,母线长为3的圆锥.设新正方体工件的棱长为x ,借助轴截面,由三角形相似可得,=,得x =x 32-121-22x1,故V 正=x 3=,又V 圆锥=π×12×=,故利用率为=,选223162271332-1222π316227223π89πA.14.G2,G7[2015·四川卷] 在三棱柱ABC A 1B 1C 1中,∠BAC =90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M ,N ,P 分别是棱AB ,BC ,B 1C 1的中点,则三棱锥P A 1MN 的体积是________.14. [解析] 由题意知,三棱柱的底面是直角边长为1的等腰直角三角形,棱柱的高124为1且该棱柱为直三棱柱,其底面积为,三棱锥A 1PMN 的底面积是××1,高为,故12121212三棱锥P A1MN 的体积为××=.1312141245.G2、G7、G8[2015·重庆卷] 某几何体的三视图如图12所示,则该几何体的体积为( )图12A.+2πB.1313π6C. D.7π35π25.B [解析] 由三视图知,该几何体为一个圆柱与一个半圆锥的组合体,其中圆柱的底面半径为1、高为2,半圆锥的底面半径为1、高为1,所以该几何体的体积V =××π×131212×1+π×12×2=.13π620.G5、G7[2015·重庆卷] 如图14,三棱锥P ABC 中,平面PAC ⊥平面ABC ,∠ABC =,点D ,E 在线段AC 上,且AD =DE =EC =2,PD =PC =4,点F 在线段AB 上,且π2EF ∥BC .(1)证明:AB ⊥平面PFE ;(2)若四棱锥P DFBC 的体积为7,求线段BC 的长.图1420.解:(1)证明:由DE =EC ,PD =PC 知,E 为等腰三角形PDC 中DC 边的中点,故PE ⊥AC .又平面PAC ⊥平面ABC ,平面PAC ∩平面ABC =AC ,PE ⊂平面PAC ,PE ⊥AC ,所以PE ⊥平面ABC ,从而PE ⊥AB .因为∠ABC =,EF ∥BC ,故AB ⊥EF .π2从而AB 与平面PFE 内两条相交直线PE ,EF 都垂直,所以AB ⊥平面PFE .(2)设BC =x ,则在直角三角形ABC 中,AB ==,AC 2-BC 236-x 2从而S △ABC =AB ·BC =x .121236-x 2由EF ∥BC 知,==,△AFE ∽△ABC ,故=2=,即S △AFE =S △ABC .AF AB AE AC 23S △AFE S △ABC 234949由AD =AE ,得S △AFD =S △AFE =×S △ABC =S △ABC =x ,12121249291936-x 2从而四边形DFBC 的面积为S 四边形DFBC =S △ABC -S △AFD =x -x =x1236-x 21936-x 2718.36-x 2由(1)知,PE ⊥平面ABC ,所以PE 为四棱锥P DFBC 的高.在直角三角形PEC 中,PE ===2.PC 2-EC 242-223所以V 四棱锥P DFBC =·S 四边形DFBC ·PE =×x ·2=7,131371836-x 23故得x 4-36x 2+243=0,解得x 2=9或x 2=27,由于x >0,可得x =3或x =3.3所以BC =3或BC =3.39.G7[2015·江苏卷] 现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为________.9. [解析] 设新的底面半径为r ,则π×52×4+π×22×8=πr 2×4+πr 2×8 ,71313即πr 2=π+32π,解得r =.28310037G8 多面体与球5.G2、G7、G8[2015·重庆卷] 某几何体的三视图如图12所示,则该几何体的体积为( )图12A.+2πB.1313π6C.D.7π35π25.B [解析] 由三视图知,该几何体为一个圆柱与一个半圆锥的组合体,其中圆柱的底面半径为1、高为2,半圆锥的底面半径为1、高为1,所以该几何体的体积V =××π×131212×1+π×12×2=.13π610.G8[2015·全国卷Ⅱ] 已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点.若三棱锥O ABC 体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π10.C [解析] 因为V 三棱锥O ABC =V 三棱锥C OAB ,所以三棱锥O ABC 体积的最大值即三棱锥C OAB 体积的最大值,所以当C 到平面OAB 的距离最大时,即CO ⊥平面OAB 时,体积最大,设球的半径为r ,则V 三棱锥O ABC =V 三棱锥C OAB =r 3=36,所以r =6,则球O16的表面积S =4πr 2=144π.图12A.+2πB.1313π6C.D.7π35π2G9 空间向量及运算G10 空间向量解决线面位置关系G11 空间角与距离的求法17.G4、G5、G11[2015·天津卷] 如图14,已知AA 1⊥平面ABC ,BB 1∥AA 1,AB =AC =3,BC =2,AA 1=,BB 1=2,点E 和F 分别为BC 和A 1C 中点.577(1)求证:EF ∥平面A 1B 1BA ;(2)求证:平面AEA 1⊥平面BCB 1;(3)求直线A 1B 1与平面BCB 117.解:(1)证明:如图所示,连接A 1B .在△A 1BC 中,因为E 和F 分别是BC 和A 1C 的中点,所以EF ∥BA 1.又因为EF ⊄平面A A 1B 1BA .(2)证明:因为AB =AC ,E 为BC BC .因为AA 1⊥平面ABC ,BB 1∥AA 1,所以BB 1⊥平面ABC ,从而BB 1⊥AE .又因为BC ∩BB 1=B ,所以AE ⊥平面BCB 1.又因为AE ⊂平面AEA 1,所以平面AEA 1⊥平面BCB 1.(3)取BB 1的中点M 和B 1C 的中点N ,连接A 1M ,A 1N ,NE .因为N 和E 分别为B 1C 和BC的中点,所以NE ∥B 1B ,NE =B 1B ,故NE ∥A 1A ,且NE =A 1A ,所以A 1N ∥AE ,且A 1N =12AE .又因为AE ⊥平面BCB 1,所以A 1N ⊥平面BCB 1,从而∠A 1B 1N 为直线A 1B 1与平面BCB 1所成的角.在△ABC 中,可得AE =2,所以A 1N =AE =2.因为BM ∥AA 1,BM =AA 1,所以A 1M ∥AB ,A 1M =AB, 又由AB ⊥BB 1,得A 1M ⊥BB 1.在Rt △A 1MB 1中,可得A 1B 1==4.B 1M 2+A 1M 2在Rt △A 1NB 1中,sin ∠A 1B 1N ==,因此∠A 1B 1N =30°,A 1N A 1B 112所以直线A 1B 1与平面BCB 1所成的角为30°.18.G5,G11[2015·浙江卷] 如图14,在三棱柱ABC A 1B 1C 1中,∠BAC =90°,AB =AC =2,A 1A =4,A 1在底面ABC 的射影为BC 的中点,D 是B 1C 1的中点.(1)证明:A 1D ⊥平面A 1BC ;(2)求直线A 1B 和平面BB 1C 1C 所成的角的正弦值.图1418.解:(1)证明:设E 为BC 的中点,连接DE .由题意得A 1E ⊥平面ABC ,所以A 1E ⊥AE .因为AB =AC ,所以AE ⊥BC .故AE ⊥平面A 1BC .由D ,E 分别为B 1C 1,BC 的中点,得DE ∥B 1B 且DE =B 1B ,从而DE ∥A 1A 且DE =A 1A ,所以四边形AA 1DE 为平行四边形.于是A 1D ∥AE .又因为AE ⊥平面A 1BC ,所以A 1D ⊥平面A 1BC .(2)作A 1F ⊥DE ,垂足为F ,连接BF .因为A 1E ⊥平面ABC ,所以BC ⊥A 1E .因为BC ⊥AE ,所以BC ⊥平面AA 1DE .所以BC ⊥A 1F ,所以A 1F ⊥平面BB 1C 1C .所以∠A 1BF 为直线A 1B 和平面BB 1C 1C 所成的角.由AB =AC =2,∠CAB =90°,得EA =EB =.2由A 1E ⊥平面ABC ,得A 1A =A 1B =4,A 1E =.14由DE =BB 1=4,DA 1=EA =,∠DA 1E =90°,得A 1F =.272所以sin ∠A 1BF ==.A 1F A 1B 7818.G4,G5,G11[2015·广东卷] 如图13,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC =4,AB =6,BC =3.(1)证明:BC ∥平面PDA ;(2)证明:BC ⊥PD ;(3)求点C 到平面PDA 的距离.图13图1422.G11、G12[2015·江苏卷] 如图16,在四棱锥P ABCD 中,已知PA ⊥平面ABCD ,且四边形ABCD 为直角梯形,∠ABC =∠BAD =,PA =AD =2,AB =BC =1.π2(1)求平面PAB 与平面PCD 所成二面角的余弦值;(2)点Q 是线段BP 上的动点,当直线CQ 与DP 所成的角最小时,求线段BQ 的长.图1622.解:以{,,}为正交基底建立如图所示的空间直角坐标系A xyz ,则各点的AB → AD → AP →坐标为B (1,0,0),C (1,1,0),D (0,2,0),P (0,0,2).(1)因为AD ⊥平面PAB ,所以是平面PAB 的一个法向量,=(0,2,0).AD → AD →因为=(1,1,-2),=(0,2,-2),PC → PD →设平面PCD 的一个法向量为m =(x ,y ,z ),所以m ·=0,m ·=0,PC → PD →即令y =1,解得z =1,x =1,{x +y -2z =0,2y -2z =0.)所以m =(1,1,1)是平面PCD 的一个法向量.。
高三数学专项训练:立体几何解答题(三)(文科)

中,CA CB =,1AB AA =,160BAA Ð=。
(Ⅰ)证明:1AB A C ^;(Ⅱ)若2AB CB ==,16A C =高三数学专项训练:立体几何解答题(三)(文科)1.如图,在.如图,在四棱锥四棱锥A-BCDE 中,侧面∆ADE 是等边三角形,底面BCDE 是等腰是等腰梯形梯形,且CD ∥BE,DE=2BE,DE=2,,CD=4,60CDE Ð=° ,M 是DE 的中点,F 是AC 的中点,且AC=4AC=4,,求证:(1)平面ADE ADE⊥平面⊥平面BCD;BCD;(2)FB (2)FB∥平面∥平面ADE. ADE.2.(本小题满分12分)如图,分)如图,三棱柱三棱柱111ABC A B C -,求三棱柱111ABC A B C -的体积。
45..如图,三棱锥P ABC -中,90ABC °Ð=,PA ABC ^底面(Ⅰ)求证:PAC PBC ^平面平面;(Ⅱ)若AC BC PA ==,M 是PB 的中点,求AM 3.如图,在.如图,在四棱锥四棱锥P -ABCD 中,中,PD PD PD⊥⊥平面ABCD ABCD,,AB AB∥∥DC DC,已知,已知BD BD==2AD 2AD==2PD 2PD==8,AB =2DC 2DC==(Ⅰ)设M 是PC 上一点,证明:平面MBD MBD⊥平面⊥平面PAD PAD;;(Ⅱ)若M 是PC 的中点,求棱锥P -DMB 的体积.4与平面PBC 所成角的所成角的正切正切值5中,CB DA 、是梯形的高,2AE BF ==,22AB =,现将梯形沿CB DA 、折起,使//EF AB ,且2E F A B =如图所示,已知M N P 、、(1)求证://MN6^PA 底面ABCD ,F E ,分别是PB AC ,的中点的中点. . .PFEDC B A(1)求证://EF 平面PCD ;(2)求证:平面^PBD 平面PAC ;(3)若AB PA =,求PD 与平面PAC 所成的角的大小所成的角的大小. . ..如图,在等腰.如图,在等腰梯形梯形CDEF ,得一简单,得一简单组合组合体ABCDEF 分别为,,AF BD EF 的中点平面BCF ;(2)求证:AP ^平面DAE ..如图,.如图,四棱锥四棱锥ABCD P -的底面ABCD 为正方形,7中,2AB BC =,点M 在边CD 上,点F 在边AB 上,且DF AM^,垂足为E ,若将ADM D 沿AM 折起,使点ABCM D -¢.(Ⅰ)求证:F D AM p ,求直线D8.如图,在四棱锥-P .如图,在.如图,在矩形矩形ABCD D 位于D ¢位置,连接B D ¢,C D ¢得四棱锥¢^;(Ⅱ)若3p =¢ÐEF D ,直线F D ¢与平面ABCM 所成角的大小为3A ¢与平面ABCM 所成角的所成角的正弦正弦值.值.ABCD 中,四边形ABCD 是菱形,PA PC =,E 为PB 的中点.(Ⅰ)求证:PD ∥平面AEC ;(Ⅱ)求证:平面AEC ^平面PBD .-的中点,E 为PA 的中点.的中点.ADO C PBEMNC C 1B 1A 1BA9.如图,在直.如图,在直三棱柱三棱柱ABC ABC--A 1B 1C 1中,点M 是A 1B 的中点,点N 是B 1C 的中点,连接MN MN(Ⅰ)证明:(Ⅰ)证明:MN//MN//MN//平面平面ABC ABC;; (Ⅱ)若AB=1AB=1,,AC=AA 1=3,BC=2BC=2,求二面角,求二面角A —A 1C —B 的余弦值的大小值的大小1010..如图,四棱锥P ABCD 的底面是直角的底面是直角梯形梯形,//AB CD ,AB AD ^,PAB D 和PADD 是两个边长为2的正三角形,4DC =,O 为BD (Ⅰ)求证:PO ^平面ABCD ;(Ⅱ)求证://OE 平面PDC ;(Ⅲ)求(Ⅲ)求直线直线CB 与平面PDC 所成角的所成角的正弦正弦值.11中,底面ABED 、090ADC Ð=,12BC CD AD ==,PA PD =,,EF .A B C -中,点D 是BC 的中点的中点..(Ⅰ)求证(Ⅰ)求证: : AD ^平面11BCC B ;(Ⅱ)求证(Ⅱ)求证: : 1A C 平面1AB D .A BCDA 1B 1C 1.在.在四棱锥四棱锥P ABCD -为直角为直角梯形梯形,//BC AD 为,AD PC 的中点.(1)求证://PA 平面BEF ;(2)求证:AD PB ^1212.如图,正.如图,正.如图,正三棱柱三棱柱111ABC13.如图,在多面体ABCDFE 中,四边形ABCD 是矩形,AB ∥EF , 902=Ð=EAB EF AB,(1)若G 点是DC )求证:BAF DAF 面面^.(3)若,2,1===AB AD AE ,平面ABCD ABFE 平面^.中点,求证:AED FG 面//.(2求的体积三棱锥AFC D -.∴,3AM DE AM ^=,∵在∆DMC 中,中,DM=1DM=1DM=1,,60CDE Ð=°,CD=4,CD=4,,∴22241241cos6013MC =+-´´×°= ,即MC=13.在∆AMC 中,222222(3)(13)4AM MC AC +=+==∴AM AM⊥⊥MC,MC,又∵,AM DE ^MC DE M = , , ∴∴AM ^平面BCD,BCD,∵AM Í平面ADE, ADE, ∴平面∴平面ADE ADE⊥平面⊥平面BCD.BCD.(2)取DC 的中点N ,连结FN,NB,FN,NB,∵F,N 分别是AC AC,,DC 的中点,∴的中点,∴FN FN FN∥∥AD,AD,由因为由因为FN Ë平面ADE,AD Í平面ADE, ADE, ∴∴FN FN∥平面∥平面ADE,ADE,∵N 是DC 的中点,∴的中点,∴BC=NC=2BC=NC=2BC=NC=2,又,又60CDE Ð=°,∴∆BCN 是等边三角形,∴是等边三角形,∴BN BN BN∥∥DE,DE, 由BN Ë平面ADE,ED Í平面ADE, ADE, ∴∴BN BN∥平面∥平面ADE,ADE,∵FN BN N = , , ∴平面∴平面ADE ADE∥平面∥平面FNB,FNB,∵FB Í平面FNB, FNB, ∴∴FB FB∥平面∥平面ADE.ADE.考点:考点:1.1. 1.直线与平面垂直的判定;直线与平面垂直的判定;直线与平面垂直的判定;2.2.2.平面一平面垂直的判定;平面一平面垂直的判定;平面一平面垂直的判定;3.3.3.直线与平面平行的判定直线与平面平行的判定直线与平面平行的判定..2.(1)取AB 的中点O ,连接1OC O 、1OA O 、1A B ,因为CA=CB CA=CB,所以,所以OC AB ^,由于AB=AA 1,∠,∠BA A BA A 1=600,所以1OA AB ^,所以AB ^平面1OAC ,因为1A C Ì平面1OAC ,所以AB AB⊥⊥A 1C ;(2)因为221A C OC =因为ABC D 为等边三角形,所以3CO =,底面积1232232S =´´=高三数学专项训练:立体几何解答题(三)(文科)参考答案1.(1)证明详见解析;(2)证明详见解析 【解析】【解析】试题分析:(1)首先根据直线与平民啊垂直的)首先根据直线与平民啊垂直的判定定理判定定理证明AM ^平面BCD,BCD,然后再根据平面垂直的判定定理证明平面ADE ADE⊥平面⊥平面BCD BCD;;(2),取DC 的中点N ,首先证FN ∥平面ADE,ADE,然后再证∴然后再证∴然后再证∴BN BN BN∥平面∥平面ADE,ADE,再根据平面与平民啊平行的判定定理证明∴平面再根据平面与平民啊平行的判定定理证明∴平面ADE ∥平面FNB,FNB,最后由面面平行的性质即可最后由面面平行的性质即可最后由面面平行的性质即可..试题解析:(1)∵∆ADE 是等边三角形,,M 是DE 的中点,的中点,,所以,所以体积体积123323V =´´=(Ⅱ)163P DMB V -=. 【解析】【解析】试题分析:试题解析:(I )证明:在ABD D 中,由于4,8,45A D B D A B ===,所以222AD BD AB +=.故AD BD ^。
专题6 立体几何(文科)解答题30题 教师版--高考数学专题训练

专题6立体几何(文科)解答题30题1.(贵州省贵阳市2023届高三上学期8月摸底考试数学(文)试题)如图,在直三棱柱111ABC A B C -中,1CA CB ==,90BCA ∠=︒,12AA =,M ,N 分别是11A B ,1A A 的中点.(1)求证:1BN C M ⊥;(2)求三棱锥1B BCN -的体积.2.(广西普通高中2023届高三摸底考试数学(文)试题)如图,多面体ABCDEF中,∠=︒,FA⊥平面ABCD,//ED FA,且22 ABCD是菱形,60ABC===.AB FA ED(1)求证:平面BDE⊥平面FAC;(2)求多面体ABCDEF的体积.))如图所示,取中点G ,连接3.(江西省五市九校协作体2023届高三第一次联考数学(文)试题)如图多面体ABCDEF 中,四边形ABCD 是菱形,60ABC ∠=︒,EA ⊥平面ABCD ,//EA BF ,22AB AE BF ===.(1)证明:平面EAC ⊥平面EFC ;(2)求点B 到平面CEF 的距离.(2)设B 到平面CEF 的距离为因为EA ⊥平面ABCD ,AC 因为//EA BF ,EA ⊥平面ABCD 且BC ⊂平面ABCD ,所以BF 因为60ABC ∠=︒,2AB =4.(新疆乌鲁木齐地区2023届高三第一次质量监测数学(文)试题)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,AD CD ⊥,AD BC ∥,且2PA AD CD ===,3BC =,E 是PD 的中点,点F 在PC 上,且2PF FC =.(1)证明:DF ∥平面PAB ;(2)求三棱锥P AEF -的体积.(2)作FG PD ⊥交PD 于点G 因为PA ⊥面ABCD ,所以PA 又AD CD ⊥,PA 与AD 交于点所以CD ⊥面PAD ,CD PD ⊥又FG PD ⊥,所以//FG CD ,所以所以PF FG PC CD =,得43FG =,因为E 为PD 中点,所以P AEF D AEF F ADE V V V ---===5.(新疆阿克苏地区柯坪湖州国庆中学2021-2022学年高二上学期期末数学试题)如图所示,已知AB ⊥平面BCD ,M ,N 分别是AC ,AD 的中点,BC CD ⊥.(1)求证://MN 平面BCD ;(2)求证:CD BM ⊥;【答案】(1)证明见解析;(2)证明见解析.【分析】1)根据中位线定理,可得//MN CD ,即可由线面平行的判定定理证明//MN 平面BCD ;(2)由已知推导出AB CD ⊥,再由CD BC ⊥,得CD ⊥平面ABC ,由此能证明CD BM ⊥;【详解】(1)M ,N 分别是AC ,AD 的中点,//MN CD ∴,MN ⊂/ 平面BCD ,且CD ⊂平面BCD ,//MN ∴平面BCD ;(2)AB ⊥Q 平面BCD ,M ,N 分别是AC ,AD 的中点,AB CD ∴⊥,BC CD ⊥ ,,AB BC B AB BC =⊂ ,平面ABC ,CD \^平面ABC ,BM ⊂ 平面ABC ,CD BM ∴⊥.6.(内蒙古乌兰浩特第一中学2022届高三全真模拟文科数学试题)如图在梯形中,//BC AD ,22AB AD BC ===,23ABC π∠=,E 为AD 中点,以BE 为折痕将ABE 折起,使点A 到达点P 的位置,连接,PD PC ,(1)证明:平面PED ⊥平面BCDE ;(2)当2PC =时,求点D 到平面PEB 的距离.因为PE PD =,F 为ED 因为平面PED ⊥平面BCDE 因为21122PF ⎛⎫=-= ⎪⎝⎭设D 到平面PEB 的距离为7.(山西省运城市2022届高三5月考前适应性测试数学(文)试题(A 卷))如图,四棱柱1111ABCD A B C D -中,底面ABCD 为平行四边形,侧面11ADD A 为矩形,22AB AD ==,160D DB ∠=︒,1BD AA =(1)证明:平面ABCD ⊥平面11BDD B ;(2)求三棱锥11D BCB -的体积.8.(黑龙江省八校2021-2022学年高三上学期期末联合考试数学(文)试题)已知直三棱柱111ABC A B C -中,AC BC =,点D 是AB 的中点.(1)求证:1BC ∥平面1C AD ;(2)若底面ABC 边长为2的正三角形,1BB =11B A DC -的体积.【答案】(1)证明见解析(2)1【分析】(1)连接1AC 交1AC 于点E ,连接DE ,由三角形中位线定理,得1DE BC ∥,进而由线面平行的判定定理即可证得结论;(2)利用等体积转化1111B A DC C A B D V V --=,依题意,高为CD ,再求底面11A B D 的面积,进而求三棱锥的体积.【详解】(1)连接1AC 交1AC 于点E ,连接DE∵四边形11AAC C 是矩形,∴E 为1AC 的中点,又∵D 是AB 的中点,∴1DE BC ∥,又∵DE ⊂平面1C AD ,1BC ⊄平面1C AD ,∴1BC ∥面1C AD .(2)∵AC BC =,D 是AB 的中点,∴AB CD ⊥,9.(青海省西宁市2022届高三二模数学(文)试题)如图,V是圆锥的顶点,O是底面圆心,AB是底面圆的一条直径,且点C是弧AB的中点,点D是AC的中点,2AB=,VA=.2(1)求圆锥的表面积;又D 是AC 的中点,所以OD AC ⊥,又VO OD O ⋂=,VO ⊂平面VOD ,OD ⊂平面VOD所以AC ⊥平面VOD ,又AC ⊂平面VAC ,所以平面VAC ⊥平面VOD .10.(河南省郑州市2023届高三第一次质量预测文科数学试题)如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AD ⊥AB ,AB DC ,2AD DC AP ===,1AB =,点E 为棱PC 的中点.(1)证明:平面PBC ⊥平面PCD ;(2)求四棱锥E ABCD -的体积;又点E 为棱PC 的中点,BE 由勾股定理得2AC AD =+∵△PAC 为直角三角形,E 111.(江西省部分学校2023届高三上学期1月联考数学(文)试题)如图,在正三棱柱111ABC A B C -中,12AA AB ==,D ,E 分别是棱BC ,1BB 的中点.(1)证明:平面1AC D ⊥平面1ACE .(2)求点1C 到平面1ACE 的距离.(2)连接1EC .因为1AA 由正三棱柱的性质可知因为ABC 是边长为2的等边三角形,所以故三棱锥11A CC E -的体积以15A E CE ==,1A E 则1ACE △的面积212S =12.(广西玉林、贵港、贺州市2023届高三联合调研考试(一模)数学(文)试题)在三棱锥-P ABC 中,底面ABC 是边长为2的等边三角形,点P 在底面ABC 上的射影为棱BC 的中点O ,且PB 与底面ABC 所成角为π3,点M 为线段PO 上一动点.(1)证明:BC AM ⊥;(2)若12PM MO =,求点M 到平面PAB 的距离.AO BC ∴⊥,点P 在底面ABC 上的投影为点PO ∴⊥平面ABC , PO BC ∴⊥,13.(广西南宁市第二中学2023届高三上学期第一次综合质检数学(文)试题)如图,D ,O 是圆柱底面的圆心,ABC 是底面圆的内接正三角形,AE 为圆柱的一条母线,P 为DO 的中点,Q 为AE 的中点,(1)若90APC ∠=︒,证明:DQ ⊥平面PBC ;(2)设2DO =,圆柱的侧面积为8π,求点B 到平面PAC 的距离.∴//,AQ PD AQ PD =,∴四边形AQDP 为平行四边形,∴//DQ PA .又∵P 在DO 上,而OD ∴O 为P 在ABC 内的投影,且ABC 是圆内接正三角形∴三棱锥-P ABC 为正三棱锥∴PAB PAC PBC △≌△≌△∴APB APC BPC ∠=∠=∠即,PA PC PA PB ⊥⊥.∵PC PB P = ,,PB PC14.(江西省吉安市2023届高三上学期1月期末质量检测数学(文)试题)如图,在四棱锥P -ABCD 中,AB CD ,12AD CD BC PA PC AB =====,BC PA ⊥.(1)证明:平面PBC ⊥平面PAC ;(2)若PB =D 到平面PBC 的距离.又BC PA ⊥,PA AC A = 所以BC ⊥平面PAC ,又BC (2)因为BC ⊥平面PAC ,由22PB =,BC PC =,得15.(江西省部分学校2023届高三下学期一轮复习验收考试(2月联考)数学(文)试题)如图,在长方体1111ABCD A B C D -中,1AB AD ==,1AA =E 在棱1DD 上,且1AE A D ⊥.(1)证明:1AE A C ⊥;(2)求三棱锥1E ACD -的体积.【答案】(1)证明见解析;)在平面11ADD A 中,由AE ⊥1AD DE AA AD =,所以12112A DE S DE AD =⋅= 16.(新疆兵团地州学校2023届高三一轮期中调研考试数学(文)试题)如图1,在等腰梯形ABCD 中,M ,N ,F 分别是AD ,AE ,BE 的中点,4AE BE BC CD ====,将ADE V 沿着DE 折起,使得点A 与点P 重合,平面PDE ⊥平面BCDE ,如图2.(1)证明:PC∥平面MNF.(2)求点C到平面MNF的距离.17.(宁夏银川市第一中学2023届高三上学期第四次月考数学(文)试题)如图1,在直角梯形ABCD 中,,90,5,2,3AB DC BAD AB AD DC ∠==== ∥,点E 在CD 上,且2DE =,将ADE V 沿AE 折起,使得平面ADE ⊥平面ABCE (如图2).(1)求点B 到平面ADE 的距离;(2)在线段BD 上是否存在点P ,使得CP 平面ADE ?若存在,求三棱锥-P ABC 的体积;若不存在,请说明理由..18.(陕西省汉中市2023届高三上学期教学质量第一次检测文科数学试题)如图,多面体ABCDEF 中,四边形ABCD 为菱形,60,ABC FA ∠=⊥ 平面,ABCD FA ED ∥,且22AB FA ED ===.(1)求证:BD FC ⊥;(2)求点A 到平面FBD 的距离.19.(内蒙古赤峰市2022届高三下学期5月模拟考试数学(文科)试题)如图,在四棱锥P ABCD -中,底面ABCD 是菱形,60PAB PAD BAD ∠=∠=∠= .(1)证明:BD ⊥平面PAC ;(2)若23AB PA ==,,求四棱锥P ABCD -的体积.解:如图,记AC 与BD 的交点为因为底面ABCD 为菱形,故又60PAB PAD BAD ∠=∠=∠=又PO AC O = ,故BD ⊥平面(2)解:因为2,3,AB PA ==∠20.(内蒙古2023届高三仿真模拟考试文科数学试题)如图,在四棱锥P ABCD -中,四边形ABCD 是直角梯形,AD AB ⊥,//AB CD ,22PB CD AB AD ===,PD =,PC DE ⊥,E 是棱PB 的中点.(1)证明:PD ⊥平面ABCD ;(2)若F 是棱AB 的中点,2AB =,求点C 到平面DEF 的距离.,AB AD=AB AD⊥,2BD∴=为棱PB中点,DE PBE∴⊥,又∴⊥平面PBC,又BC⊂平面DE在直角梯形ABCD中,取CD中点 ,DM AB=2CD AB∴=,又DM ∴四边形ABMD为正方形,BM∴∴===,又BC BM AD AB222BD DE⊂平面PBD ,,=BD DE D21.(山西省晋中市2022届高三下学期5月模拟数学(文)试题)如图,在三棱锥-P ABC中,PAB 为等腰直角三角形,112PA PB AC ===,PC ,平面PAB ⊥平面ABC .(1)求证:PA BC ⊥;(2)求三棱锥-P ABC 的体积.∴OP AB ⊥,22OP =,AB =又∵平面PAB ⊥平面ABC ,平面∴OP ⊥平面ABC .22.(山西省太原市2022届高三下学期三模文科数学试题)已知三角形PAD 是边长为2的正三角形,现将菱形ABCD 沿AD 折叠,所成二面角P AD B --的大小为120°,此时恰有PC AD ⊥.(1)求BD 的长;(2)求三棱锥-P ABC 的体积.∵PAD 是正三角形,∴PM AD ⊥,又∴,PC AD PC PM P⊥=I ∴AD ⊥平面PMC ,∴AD MC ⊥,故ACD 为等腰三角形23.(陕西省联盟学校2023届高三下学期第一次大联考文科数学试题)如图,在四棱锥P ABCD -中,底面ABCD 是长方形,22AD CD PD ===,PA 二面角P AD C--为120︒,点E 为线段PC 的中点,点F 在线段AB 上,且12AF =.(1)平面PCD ⊥平面ABCD ;(2)求棱锥C DEF -的高.824.(陕西省榆林市2023届高三上学期一模文科数学试题)如图,在四棱锥P ABCD -中,平面PAD ⊥底面,,60,ABCD AB CD DAB PA PD ∠=⊥ ∥,且2,22PA PD AB CD ====.(1)证明:AD PB ⊥;(2)求点A 到平面PBC 的距离.(2)因为AB CD ,所以∠2222BC BD CD BD CD =+-⋅由222BD BC CD =+,得BC 25.(陕西省宝鸡教育联盟2022-2023学年高三下学期教学质量检测(五)文科数学试题)如图,在三棱柱111ABC A B C -中,平面11ABB A ⊥平面ABC ,四边形11ABB A 是边长为2的菱形,ABC 为等边三角形,160A AB ∠=︒,E 为BC 的中点,D 为1CC 的中点,P为线段AC上的动点.AB平面PDE,请确定点P在线段AC上的位置;(1)若1//-的体积.(2)若点P为AC的中点,求三棱锥C PDE(2)解:如图,取AB 的中点∵四边形11ABB A 为边长为2∴12A B =,1AA B 为等边三角形,26.(山西省运城市2022届高三上学期期末数学(文)试题)如图,在四棱锥P -ABCD中,底面ABCD 是平行四边形,2APB π∠=,3ABC π∠=,PB =,24PA AD PC ===,点M 是AB 的中点,点N 是线段BC 上的动点.(1)证明:CM⊥平面PAB;(2)若点N到平面PCM BNBC的值.27.(2020届河南省许昌济源平顶山高三第二次质量检测文科数学试题)如图,四棱锥P ABCD -中,//AB CD ,33AB CD ==,2PA PD BC ===,90ABC ∠=︒,且PB PC =.(1)求证:平面PAD ⊥平面ABCD ;(2)求点D 到平面PBC 的距离.因为//AB CD ,33AB CD ==,所以四边形ABCD 为梯形,又M 、E 为AD 、BC 的中点,所以ME 为梯形的中位线,28.(青海省海东市2022-2023学年高三上学期12月第一次模拟数学(文)试题)如图,在直三棱柱111ABC A B C -中,ABC 是等边三角形,14AB AA ==,D 是棱AB 的中点.(1)证明:平面1ACD ⊥平面11ABB A .(2)求点1B 到平面1A CD 的距离.由题意可得11A B D △的面积因为ABC 是边长为4的等边三角形,且29.(河南省十所名校2022-2023学年高三阶段性测试(四)文科数学试题)如图,在四棱锥P —ABCD 中,PC BC ⊥,PA PB =,APC BPC ∠=∠.(1)证明:PC AD ⊥;(2)若AB CD,PD AD ⊥,PC =,且点C 到平面PAB AD 的长.∵PA PB =,APC BPC ∠=∠∴90PCA PCB ∠=∠=︒,即∵PC BC ⊥,AC BC = ∴PC ⊥平面ABCD ,又∵PA PB =,E 为AB 中点∴PE AB ⊥,由(1)知AC BC =,E 为∵PE CE E = ,,PE CE 30.(河南省部分重点中学2022-2023学年高三下学期2月开学联考文科数学试题)如图,在直三棱柱111ABC A B C -中,5AB AC ==,16BB BC ==,D ,E 分别是1AA 和1B C 的中点.(1)求证:平面BED ⊥平面11BCC B ;(2)求三棱锥E BCD -的体积.。
2015年三年高考数学(文)真题精编——专题10 立体几何(选择填空)

一、选择题2.【2013高考北京文第8题】如图,在正方体ABCD-AB1C1D1中,P为对角线BD1的三等分点,P到1各顶点的距离的不同取值有().A.3个B.4个C.5个D.6个【答案】B【解析】试题分析:设正方体的棱长为a.建立空间直角坐标系,如图所示.4.【2015高考北京,文7】某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A.1 B C D.2【答案】C【解析】四棱锥的直观图如图所示:由三视图可知,SC ⊥平面CD AB ,S A 是四棱锥最长的棱,SA ===,故选C .【考点定位】三视图.5. 【2014高考广东卷.文.9】若空间中四条直线两两不同的直线1l .2l .3l .4l ,满足12l l ⊥,23//l l ,34l l ⊥,则下列结论一定正确的是( )A .14l l ⊥B .14//l lC .1l .4l 既不平行也不垂直D .1l .4l 的位置关系不确定 【答案】D【解析】如下图所示,在正方体1111ABCD A B C D -中,取1AA 为2l ,1BB 为3l ,取AD 为1l ,BC 为4l ,【考点定位】本题考查空间中直线的位置关系的判定,属于中等题.6. 【2013高考广东卷.文.6】某三棱锥的三视图如图所示,则该三棱锥的体积是().A .16 B .13 C .23D .1 【答案】B【考点定位】本题考查立体几何中的三视图与体积,属于基础题9. 【2015高考广东,文6】若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则下列命题正确的是( )A .l 至少与1l ,2l 中的一条相交B .l 与1l ,2l 都相交C .l 至多与1l ,2l 中的一条相交D .l 与1l ,2l 都不相交 【答案】A【考点定位】空间点、线、面的位置关系.10. 【2013高考广东卷.文.8】设l 为直线,α,β是两个不同的平面.下列命题中正确的是().A .若l ∥α,l ∥β,则α∥βB .若l ⊥α,l ⊥β,则α∥βC .若l ⊥α,l ∥β,则α∥βD .若α⊥β,l ∥α,则l ⊥β 【答案】B【解析】如图,在正方体A 1B 1C 1D 1-ABCD 中,【考点定位】本题考查立体几何中线,面之间的平行垂直关系,属于能力题13.【 2014湖南文8】一块石材表示的几何体的三视图如图2所示,将石材切削、打磨、加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4【答案】B【考点定位】三视图 内切圆 球 三棱柱14. 【2013湖南,文7】已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积( ).A B .1 C 【答案】D【解析】如图所示,正方体ABCD -A 1B 1C 1D 1的俯视图为ABCD ,侧视图为BB 1D 1D ,故该正方体的正视图应为AA 1C 1C .又因AC .15. 【2015高考湖南,文10】某工作的三视图如图3所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积/原工件的体积)( )A 、89πB 、827πC D【答案】A【考点定位】三视图、基本不等式求最值、圆锥的内接长方体16. 【2013山东,文4】一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如下图所示,则该四棱锥侧面积和体积分别是( ).A .45,8B .45,83C .4(5+1),83D .8,8 【答案】B【解析】由正(主)视图数据可知正四棱锥的底面是边长为2的正方形,高也是2,如图:由图可知PO =2,OE =1,所以PE 22215+=, 所以V =13×4×2=83,S =1425=452⨯20. 【2014高考陕西版文第5题】将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积为( ).4A π .3B π .2C π .D π【答案】C考点:旋转体;几何体的侧面积.21. 【2015高考陕西,文5】一个几何体的三视图如图所示,则该几何体的表面积为( )A .3πB .4πC .24π+D .34π+【答案】D【解析】由几何体的三视图可知该几何体为圆柱的截去一半,所以该几何体的表面积为21121222342πππ⨯⨯+⨯⨯⨯+⨯=+,故答案选D【考点定位】1.空间几何体的三视图;2.空间几何体的表面积.24. 【2014全国2,文6】如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削的部分的体积与原来毛坯体积的比值为( ) A.2717 B.95 C.2710 D.31【答案】C【解析】由三视图还原几何体为一个小圆柱和大圆柱组成的简单组合体.其中小圆柱底面半径为2、高为4,大圆柱底面半径为3、高为2,则其体积和为22243234πππ⨯⨯+⨯⨯=,而圆柱形毛坯体积为23654ππ⨯⨯=,故切削部分体积为20π,从而切削的部分的体积与原来毛坯体积的比值为20105427ππ=. 25. 【2013课标全国Ⅱ,文9】一个四面体的顶点在空间直角坐标系O -xyz 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到的正视图可以为( ).【答案】:A【解析】:如图所示,该四面体在空间直角坐标系O -xyz 的图像为下图:则它在平面zOx 的投影即正视图为,故选A.27. 【2014全国2,文7】正三棱柱111ABC A B C -的底面边长为2,D 为BC 中点,则三棱锥11A B DC -的体积为( )(A )3 (B )32 (C )1 (DD A 1C 1AB 1BC【答案】C30. 【2013四川,文2】一个几何体的三视图如图所示,则该几何体可以是( )(A )棱柱 (B )棱台 (C )圆柱 (D )圆台31. 【2014四川,文4】某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是( )(锥体体积公式:13V Sh =,其中S 为底面面积,h 为高) A 、3B 、2CD 、1侧视图俯视图11222211【答案】D【考点定位】空间几何体的三视图和体积.35. 【2015高考新课标1,文6】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( ) (A )14斛 (B )22斛 (C )36斛 (D )66斛【答案】B【考点定位】圆锥的性质与圆锥的体积公式36. 【2014全国1,文8】如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是( )A.三棱锥B.三棱柱C.四棱锥D.四棱柱【答案】B【解析】根据三视图的法则:长对正,高平齐,宽相等.可得几何体如下图所示.38. 【2013课标全国Ⅰ,文11】某几何体的三视图如图所示,则该几何体的体积为( ).A .16+8πB .8+8πC .16+16πD .8+16π 【答案】:A【解析】:该几何体为一个半圆柱与一个长方体组成的一个组合体.V 半圆柱=12π×22×4=8π, V 长方体=4×2×2=16.所以所求体积为16+8π.故选A.40. 【2015高考新课标1,文11】圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r =( ) (A )1 (B )2(C )4 (D )8【答案】B【解析】由正视图和俯视图知,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r ,圆柱的高为2r ,其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+=16 + 20π,解得r=2,故选B. 【考点定位】简单几何体的三视图;球的表面积公式;圆柱的测面积公式41. 【2014年.浙江卷.文3】某几何体的三视图(单位:cm )如图所示,则该几何体的体积是( )A. 372cmB. 390cmC. 3108cmD. 3138cm 【答案】B 【解析】试题分析:由三视图知,原几何体是由一个长方体与一个三棱柱组成, 其体积为)(90343216433cm V =⨯⨯⨯+⨯⨯=,故选B. 考点:根据三视图还原几何体,求原几何体的体积,容易题.42. 【2014年.浙江卷.文6】设m 、n 是两条不同的直线,α、β是两个不同的平面,则( )A.若n m ⊥,α//n ,则α⊥mB.若β//m ,αβ⊥,则α⊥mC.若β⊥m ,β⊥n ,α⊥n ,则α⊥mD.若n m ⊥,β⊥n ,αβ⊥,则α⊥m【答案】C考点:空间中的线线、线面、面面的位置关系,容易题.43.【2013年.浙江卷.文4】设m,n是两条不同的直线,α,β是两个不同的平面().A.若m∥α,n∥α,则m∥nB.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β【答案】:C【解析】:A选项中直线m,n可能平行,也可能相交或异面,直线m,n的关系是任意的;B选项中,α与β也可能相交,此时直线m平行于α,β的交线;D选项中,m也可能平行于β.故选C.44.【2013年.浙江卷.文5】已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是().A.108 cm3B.100 cm3C.92 cm3D.84 cm3【答案】:B49. 【2015高考浙江,文4】设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( )A .若l β⊥,则αβ⊥B .若αβ⊥,则l m ⊥C .若//l β,则//αβD .若//αβ,则//l m 【答案】A【解析】采用排除法,选项A 中,平面与平面垂直的判定,故正确;选项B 中,当αβ⊥时,,l m 可以垂直,也可以平行,也可以异面;选项C 中,//l β时,,αβ可以相交;选项D 中,//αβ时,,l m 也可以异面.故选A.【考点定位】直线、平面的位置关系.50. 【2015高考浙江,文2】某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )A .83cmB .123cmC .3233cm D .4033cm【答案】C【考点定位】1.三视图;2.空间几何体的体积.51.【2015高考浙江,文7】如图,斜线段AB与平面α所成的角为60 ,B为斜足,平面α上的动点P∠PAB= ,则点P的轨迹是()满足30A.直线B.抛物线C.椭圆D.双曲线的一支【答案】C【解析】由题可知,当P点运动时,在空间中,满足条件的AP绕AB旋转形成一个圆锥,用一个与圆锥高成60 角的平面截圆锥,所得图形为椭圆.故选C.【考点定位】1.圆锥曲线的定义;2.线面位置关系.54.【2013高考重庆文第8题】某几何体的三视图如图所示,则该几何体的表面积为( ).A.180 B.200 C.220 D.240【答案】D【解析】试题分析:由三视图知该几何体是底面为等腰梯形的直棱柱,考点:三视图.55.【2014高考重庆文第7题】某几何体的三视图如图所示,则该几何体的体积为( )A.12B.18C.24D.30 【答案】C考点:1、空间几何体的三视图;2、空间几何体的体积.56. 【2015高考重庆,文5】某几何体的三视图如图所示,则该几何体的体积为( )(A)123π+ (B) 136π (C) 73π (D) 52π 【答案】B【解析】由三视图可知该几何体是由一个底面半径为1,高为2的圆柱,再加上一个半圆锥:其底面半径为1,高也为1,构成的一个组合体,故其体积为61311612122πππ=⨯⨯⨯+⨯⨯,故选B. 【考点定位】三视图及柱体与锥体的体积.57. 【2014,安徽文8】一个多面体的三视图如图所示,则多面体的体积是 ( )A.233 B.476C.6D.7【答案】A.考点:1.多面体的三视图与体积.59.【2015高考安徽,文9】一个四面体的三视图如图所示,则该四面体的表面积是()(A)1+(B)1+(C)2+(D)【答案】C【解析】由该几何体的三视图可知,该几何体的直观图,如下图所示:【考点定位】本题主要考查空间几何体的三视图、锥体表面积公式.61.【2014年普通高等学校招生全国统一考试湖北卷7】在如图所示的空间直角坐标系xyzO-中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为()A.①和②B.③和①C. ④和③D.④和② 【答案】D考点:空间由已知条件,在空间坐标系中作出几何体的形状,正视图与俯视图的面积,容易题.62. 【2015高考湖北,文5】12,l l 表示空间中的两条直线,若p :12,l l 是异面直线;q :12,l l 不相交,则( )A .p 是q 的充分条件,但不是q 的必要条件B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件 【答案】A .【解析】若p :12,l l 是异面直线,由异面直线的定义知,12,l l 不相交,所以命题q :12,l l 不相交成立,即p 是q 的充分条件;反过来,若q :12,l l 不相交,则12,l l 可能平行,也可能异面,所以不能推出12,l l 是异面直线,即p 不是q 的必要条件,故应选A .【考点定位】本题考查充分条件与必要条件、异面直线,属基础题.63. 【2014福建,文3】以边长为1的正方形的一边所在所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于 ( ).2..2.1A B C D ππ【答案】A 【解析】试题分析:由已知得,所得圆柱的底面半径和高均为为1,所以圆柱的侧面积为2π,选A . 考点:旋转体的侧面积.66. 【2015高考福建,文9】某几何体的三视图如图所示,则该几何体的表面积等于( )A .8+B .11+C .14+D .15 【答案】B【解析】由三视图还原几何体,该几何体是底面为直角梯形,高为2的直四棱柱,且底面直角梯形的两底分别为12,,直角腰长为1,.底面积为12332⨯⨯=,侧面积为所以该几何体的表面积为11+B . 【考点定位】三视图和表面积.二、填空题1.【2013高考北京文第10题】某四棱锥的三视图如图所示,该四棱锥的体积为__________.【答案】32. 【2014高考北京文第11题】某三棱锥的三视图如图所示,则该三棱锥的最长棱的棱长为 .俯视图侧(左)视图正(主)视图11122【答案】【解析】由三视图可知:该几何体为一条侧棱垂直底面的三棱锥,底面为边长为2的正三角形,棱锥的高为2=考点:本小题主要考查立体几何中的三视图,考查同学们的空间想象能力,考查分析问题与解决问题的能力.3. 【2014山东.文13】一个六棱锥的体积为32,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为 . 【答案】12考点:正六棱锥的几何特征,几何体的面积与体积.5. 【2013高考陕西版文第12题】某几何体的三视图如图所示,则其表.面积为__________.【答案】3π 【解析】试题分析:三视图可知该几何体为半径为1的球体的一半,所以表面积为12×4π×12+π×12=3π. 考点:三视图,容易题.6.【2013课标全国Ⅱ,文15】已知正四棱锥O -ABCD ,底面边长为,则以O 为球心,OA 为半径的球的表面积为__________.【答案】:24π【解析】:如图所示,在正四棱锥O -ABCD 中,V O -ABCD =13×S 正方形ABCD ·|OO 1|=13×2×|OO 1|9. 【2015高考四川,文14】在三棱住ABC -A 1B 1C 1中,∠BAC =90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边长为1的等腰直角三角形,设点M,N,P分别是AB,BC,B1C1的中点,则三棱锥P-A1MN的体积是______.【答案】1 24【考点定位】本题主要考查空间几何体的三视图、直观图及空间线面关系、三棱柱与三棱锥的体积等基础知识,考查空间想象能力、图形分割与转换的能力,考查基本运算能力.11.【2013课标全国Ⅰ,文15】已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为______.【答案】:9π2【解析】:如图,15. 【2013,安徽文15】如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点,,A P Q 的平面截该正方体所得的截面记为S ,则下列命题正确的是 (写出所有正确命题的编号).①当102CQ <<时,S 为四边形 ②当12CQ =时,S 为等腰梯形 ③当34CQ =时,S 与11C D 的交点R 满足113C R =④当314CQ <<时,S 为六边形⑤当1CQ =时,S 【答案】①②③⑤.(2)1CQ=,S=,⑤正确,图如下:(3)34CQ=,画图如下:113C R=,③正确;(4)314CQ<<,如图是五边形,④不正确;(5)12CQ<<,如下图,是四边形,故①正确.【考点】1.立体几何中线面位置关系;2.正方体的截面.19.【2013天津,文10】已知一个正方体的所有顶点在一个球面上.若球的体积为9π2,则正方体的棱长为__________.【解析】由题意知349ππ32V R==球,32R=.设正方体的棱长为a=2R,a.20.【2014天津,文10】一个几何体的三视图如图所示(单位:m),则该几何体的体积为3m.【答案】20.3π 【解析】试题分析:几何体为一个圆锥与一个圆柱的组合体. 圆锥的高为2,底半径为2;圆柱的高为4,底半径为1,所以体积为221202241.33V πππ=⨯⨯⨯+⨯⨯=考点:三视图21. 【2015高考天津,文10】一个几何体的三视图如图所示(单位:m ),则该几何体的体积为 3m .【答案】8π3【考点定位】本题主要考查三视图及几何体体积的计算.22. 【2013年普通高等学校招生全国统一考试湖北卷16】我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水. 天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸. 若盆中积水深九寸,则平地降雨量是 寸. (注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸) 【答案】3【解析】试题分析:由题意盆内所盛水的上底面直径为28122+=20(寸),下底面半径为6寸,高为9寸,故体积为V =13·9·(π·102+π·62+π·10·6)=588π,而盆上口面积为π·142=196π,故平地降雨量为588π196π=3(寸). 24. 【2014上海,文8】在长方体中割去两个小长方体后的几何体的三视图如图,则切割掉的两个小长方体的体积之和等于 .【答案】24【解析】由题意割去的两个小长方体的体积为2(51)324⨯-⨯=. 【考点】三视图,几何体的体积..25. 【2013上海,文10】已知圆柱Ω的母线长为l ,底面半径为r ,O 是上底面圆心,A 、B 是下底面圆周上两个不同的点,BC 是母线,如图.若直线OA 与BC 所成角的大小为6π,则lr=______.【解析】由题知,tan6r l π==⇒l r =三、解答题2.【2013高考北京文第17题】(本小题共14分)如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD =2AB,平面P AD⊥平面ABCD,P A⊥AD.E和F分别是CD和PC的中点.求证:(1)P A⊥底面ABCD;(2)BE∥平面P AD;(3)平面BEF⊥平面PCD.所以AB∥DE,且AB=DE.所以ABED为平行四边形.所以BE∥AD.又因为BE⊄平面P AD,AD⊂平面P AD,所以BE∥平面P AD.(3)因为AB⊥AD,而且ABED为平行四边形,所以BE⊥CD,AD⊥CD.由(1)知P A⊥底面ABCD,所以P A⊥CD.3. 【2014高考北京文第17题】(本小题满分14分)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面,AB BC ⊥,12AA AC ==,E 、F 分别为11A C 、BC 的中点.(1)求证:平面ABE ⊥平面11B BCC ; (2)求证:1//C F 平面ABE ; (3)求三棱锥E ABC -的体积.C 1B 1A 1FE C BA【答案】(3)【解析】试题分析:(1)由直线与平面垂直证明直线与平行的垂直;(2)证明直线与平面平行;(3)求三棱锥的体积就用体积公式.试题解析:(1)在三棱柱111ABC A B C -中,1BB ⊥底面ABC ,所以1BB ⊥AB ,又因为AB ⊥BC ,所以AB ⊥平面11B BCC ,因为AB ⊂平面ABE ,所以平面ABE ⊥平面11B BCC . (2)取AB 中点G ,连结EG ,FG ,因为E ,F 分别是11A C 、BC 的中点,所以FG ∥AC ,且FG=12AC , 因为AC ∥11A C ,且AC=11A C ,所以FG ∥1EC ,且FG=1EC ,所以四边形1FGEC 为平行四边形,所以1//C F EG ,考点:本小题主要考查直线与直线、直线与平面、平面与平面的垂直与平行的证明;考查几何体的体积的求解等基础知识,考查同学们的空间想象能力、推理论证能力、运算求解能力、逻辑推理能力,考查数形结合思想、化归与转化思想.5. 【2015高考北京,文18】(本小题满分14分)如图,在三棱锥V C -AB 中,平面V AB ⊥平面C AB ,V ∆AB 为等边三角形,C C A ⊥B 且C C A =B =,O ,M 分别为AB ,V A 的中点.(I )求证:V //B 平面C MO ; (II )求证:平面C MO ⊥平面V AB ; (III )求三棱锥V C -AB 的体积.【答案】(I )证明详见解析;(II )证明详见解析;(III .试题解析:(Ⅰ)因为,O M 分别为AB ,V A 的中点, 所以//OM VB .又因为VB ⊄平面C MO , 所以//VB 平面C MO .(Ⅲ)在等腰直角三角形ACB 中,AC BC ==所以2,1AB OC ==.所以等边三角形V AB 的面积VAB S ∆=. 又因为OC ⊥平面V AB ,所以三棱锥C V -AB 的体积等于13VAB OC S ∆⨯⨯=. 又因为三棱锥V C -AB 的体积与三棱锥C V -AB 的体积相等,所以三棱锥V C -AB . 考点:线线平行、线面平行、面面平行、线线垂直、线面垂直、面面垂直、三棱锥的体积公式.6. 【2014高考广东卷.文.18】(本小题满分13分)如图2,四边形ABCD 为矩形,PD ⊥平面ABCD ,1AB =,2BC PC ==,作如图3折叠,折痕//EF DC .其中点E .F 分别在线段PD .PC 上,沿EF 折叠后点P 在线段AD 上的点记为M ,并且MF CF ⊥.(1)证明:CF ⊥平面MDF ; (2)求三棱锥M CDE -的体积.图3图2MFEPDCBA PDCB A【答案】(1)详见解析;(2.(2)CF ⊥ 平面MDF ,CF DF ∴⊥,又易知60PCD ∠= ,30CDF ∴∠= ,从而1122CF CD ==, //EF DC ,DE CEDP CP ∴=,122=,DE ∴=,PE ∴=,12CDE S CD DE ∆∴=⋅=,MD ====,1133M CDE CDE V S MD -∆∴=⋅==. 【考点定位】本题以折叠图形为考查形式,考查直线与平面垂直的判定以及利用等体积法计算三棱锥的体积,属于中等题.8. 【2013高考广东卷.文.18】(本小题满分14分)如图(1),在边长为1的等边三角形ABC 中,D ,E 分别是AB ,AC 上的点,AD =AE ,F 是BC 的中点,AF 与DE 交于点G .将△ABF 沿AF 折起,得到如图(2)所示的三棱锥A -BCF ,其中BC .图(1) 图(2) (1)证明:DE ∥平面BCF ; (2)证明:CF ⊥平面ABF ; (3)当AD =23时,求三棱锥F -DEG 的体积V F -DEG .【答案】(1)详见解析 (2)详见解析 (3(2)证明:在等边三角形ABC 中,∵F 是BC 的中点,BC =1,∴AF ⊥CF ,BF =CF =12.∵在三棱锥A -BCF 中,BC , ∴BC 2=BF 2+CF 2.∴CF ⊥BF . ∵BF ∩AF =F ,∴CF ⊥平面ABF .(3)由(1)可知GE ∥CF ,结合(2)可得GE ⊥平面DFG .∴V F -DEG =V E -DFG =13×12·DG ·FG ·GE =1111132333⎛⨯⨯⨯⨯= ⎝【考点定位】本题考查立体几何中的线面平行,垂直和椎体体积,属于拔高题10. 【2015高考广东,文18】(本小题满分14分)如图3,三角形DC P 所在的平面与长方形CD AB 所在的平面垂直,D C 4P =P =,6AB =,C 3B =.(1)证明:C//B 平面D P A ; (2)证明:C D B ⊥P ;(3)求点C 到平面D P A 的距离.【答案】(1)证明见解析;(2)证明见解析;(3.试题解析:(1)因为四边形CD AB 是长方形,所以C//D B A ,因为C B ⊄平面D P A ,D A ⊂平面D P A ,所以C//B 平面D P A(2)因为四边形CD AB 是长方形,所以C CD B ⊥,因为平面DC P ⊥平面CD AB ,平面DC P 平面CD CD AB =,C B ⊂平面CD AB ,所以C B ⊥平面DC P ,因为D P ⊂平面DC P ,所以C D B ⊥P(3)取CD 的中点E ,连结AE 和PE ,因为D C P =P ,所以CD PE ⊥,在Rt D ∆PE 中,PE ===DC P ⊥平面CD AB ,平面DC P 平面CD CD AB =,PE ⊂平面DC P ,【考点定位】1、线面平行;2、线线垂直;3、点到平面的距离.11. 【 2014湖南文18】如图3,已知二面角MN αβ--的大小为60 ,菱形ABCD 在面β内,,A B两点在棱MN 上,60BAD ∠= ,E 是AB 的中点,DO ⊥面α,垂足为O .(1)证明:AB⊥平面ODE ;(2)求异面直线BC 与OD 所成角的余弦值.【答案】(1)详见解析 (2) 34【解析】试题解析:(1)如图,因为DO α⊥,AB α⊆,所以DO AB ⊥,连接BD ,由题可知ABD ∆是正三角形,又E 是AB 的中点,所以DE AB ⊥,而DO DE D = ,故AB ⊥平面ODE .(2)因为//BC AD ,所以BC 与OD 所成的角等于AD 与OD 所成的角,即ADO ∠是BC 与OD 所成的角,由(1)可知,AB ⊥平面ODE ,所以AB OE ⊥,又DE AB ⊥,于是DEO ∠是二面角MN αβ--的平面角,从而060DEO ∠=,不妨设2AB =,则2AD =,易知DE =,在Rt DOE ∆中,03sin 602DO DE ==,连接AO ,在Rt AOD ∆中,332cos 24DO ADO AD ∠===,所以异面直线BC 与OD 所成角的余弦值为34. 【考点定位】异面直线的夹角 二面角 线面垂直12. 【2013湖南,文17】如图,在直棱柱ABC -A 1B 1C 1中,∠BAC =90°,AB =AC,AA 1=3,D 是BC的中点,点E 在棱BB 1上运动.(1)证明:AD ⊥C 1E ;(2)当异面直线AC ,C 1E 所成的角为60°时,求三棱锥C 1-A 1B 1E 的体积.15. 【2015高考湖南,文18】(本小题满分12分)如图4,直三棱柱111ABC A B C -的底面是边长为2的正三角形,,E F 分别是1,BC CC 的中点。
2015届高考数学(文)一轮复习质量检测:5 立体几何 北师大版

测试内容:立体几何(时间:120分钟 满分:150分) 一、选择题(本大题共12小题,每小题5分,共60分.) 1.(大连期末)一几何体的三视图如图所示,已知这个几何体的体积为103,则h = ( ) A.32 B.3 C .2 3D .5 32.设m ,n 是平面α内的两条不同直线;l 1,l 2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是A .m ∥β且l 1∥αB .m ∥l 1且n ∥l 2C .m ∥β且n ∥βD .m ∥β且n ∥l 23.(郑州质检)一个几何体的三视图及其尺寸如下图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的体积是(单位:cm 3)( )A.π2B.π3C.π4 D .π4.(杭州质检)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )5.(广州高三调研)在正四棱锥V -ABCD 中,底面正方形ABCD 的边长为1,侧棱长为2,则异面直线VA 与BD 所成角的大小为( )A.π6B.π4C.π3D.π26.给定下列四个命题:其中为真命题的是( )(1)若一个平面内的两条直线与另外一个平面都平行,那么这两个平面相互平行; (2)若一个平面经过另一个平面的垂线,那么这两个平面相互垂直; (3)垂直于同一直线的两条直线相互平行;(4)若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂A .(1)和(2)B .(2)和(3)C .(3)和(4)D .(2)和(4)7.如图是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,则该几何体的体积是() A.24 B.12C.8 D.48.如图是某一几何体的三视图,则这个几何体的侧面积和体积分别是A.82+25+6,8B.22+85+6,8C.42+85+12,16D.82+45+12,169.如图所示,直线P A垂直于⊙O所在的平面,△ABC内接于⊙O,且AB为⊙O的直径,点M为线段PB的中点.现有结论:①BC⊥PC;②OM∥平面APC;③点B到平面P AC的距离等于线段BC的长.其中正确的是() A.①②B.①②③C.①D.②③10.(沈阳质检)如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是A.点H是△A1BD的垂心B.AH的延长线经过点C1C.AH垂直平面CB1D1D.直线AH和BB1所成角为45°11.(唐山模拟)把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都有接触点,则皮球的半径为()A.10 3 cm B.10 cm C.10 2 cm D.30 cm12.在正方形ABCD中,AB=4,沿对角线AC将正方形ABCD折成一个直二面角B-AC-D,则点B到直线CD的距离为() A.2 2 B.3 2 C.2 3 D.2+2 2二、填空题(本大题共4小题,每小题5分,共20分.)13.已知正三棱锥的底面边长为2,侧棱长为433,则它的体积_____.14.如图,已知△ABC和△BCD所在平面互相垂直,∠ABC=∠BCD=90°,AB=a,BC=b,CD=c,且a2+b2+c2=1,则三棱锥A-BCD的外接球的表面积为________.15.如果一个几何体的正视图、侧视图、俯视图均为如图所示的面积为2的等腰直角三角形,那么该几何体的表面积等于______.16.在三棱锥P-ABC中,三条侧棱P A,PB,PC两两互相垂直,且P A=PB=PC,M为AB的中点,则PM与平面ABC所成角的正弦值为________.三、解答题(本大题共6小题,共70分,17题10分,18~22题,每题12分.解答应写出文字说明,证明过程或演算步骤.)17.如图,在直四棱柱ABCD-A1B1C1D1中,四边形ABCD是梯形,AD∥BC,AC⊥CD,E是AA1上的一点.(1)求证:CD⊥平面ACE;(2)若平面CBE交DD1于点F,求证:EF∥AD.18.如图,在四棱锥P-ABCD中,P A⊥平面ABCD,底面ABCD为平行四边形,且AB=1,BC=2,∠ABC=π3,E,F分别为AD,BC的中点.(1)求证:EF∥平面PCD;(2)求证:AC⊥平面P AB.19.一个多面体的三视图和直观图分别如图(1)(2)所示,其中M、N分别为AB、AC的中点,G是DF上的一动点.(1)求证:GN⊥AC;(2)当FG=GD时,在棱AB上确定一点P,使得GP∥平面FMC,并给出证明.2015届高考数学(文)一轮复习质量检测:5 立体几何 北师大版测试内容:立体几何 (时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2012年大连期末)一几何体的三视图如图所示,已知这个几何体的体积为103,则h =( )A.32B. 3 C .2 3D .5 3解析:分析几何体的三视图,可知该几何体是底面为矩形的四棱锥,体积V =13×5×6×h =103,解得h = 3.答案:B2.设m ,n 是平面α内的两条不同直线;l 1,l 2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是( )A .m ∥β且l 1∥αB .m ∥l 1且n ∥l 2C .m ∥β且n ∥βD .m ∥β且n ∥l 2解析:⎭⎬⎫l 1∥m m ⊂α⇒l 1∥α,⎭⎬⎫同理l 2∥αl 1与l 2相交l 1,l 2⊂β⇒α∥β. 答案:B3.(2012年郑州质检)一个几何体的三视图及其尺寸如下图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的体积是(单位:cm 3)A.π2B.π3C.π4D .π解析:依三视图可知,该几何体是半个圆锥,且底面半径为1,高为3,故V =12×⎝ ⎛⎭⎪⎫13×Sh =12×⎝ ⎛⎭⎪⎫13×π×12×3=π2,选A.答案:A4.(2012年杭州质检)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为( )解析:由几何体的直观图可知,侧视图为一矩形(内有从左下到右上的对角线,因为该对角线看不到轮廓线,故用虚线).故选D.答案:D5.(2012年广州高三调研)在正四棱锥V -ABCD 中,底面正方形ABCD 的边长为1,侧棱长为2,则异面直线VA 与BD 所成角的大小为( )A.π6B.π4C.π3D.π2解析:取BD 的中点O ,则VO ⊥BD ,AC ⊥BD ,所以BD ⊥平面VAC ,则异面直线VA 与BD 所成角的大小为π2.答案:D6.给定下列四个命题:(1)若一个平面内的两条直线与另外一个平面都平行,那么这两个平面相互平行; (2)若一个平面经过另一个平面的垂线,那么这两个平面相互垂直; (3)垂直于同一直线的两条直线相互平行;(4)若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中为真命题的是( )A .(1)和(2)B .(2)和(3)C .(3)和(4)D .(2)和(4)解析:对于(1),两条直线必须相交,否则不能证明面面平行,错误;对于(3),垂直于同一条直线的两条直线还可能异面,错误;(2)(4)正确.所以选D.答案:D7.如图是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,则该几何体的体积是( )A .24B .12C .8D .4解析:依题意知,该几何体是从一个长方体中挖去一个三棱柱后剩下的几何体,因此其体积等于2×3×4-12×(2×3)×4=12,选B.答案:B8.如图是某一几何体的三视图,则这个几何体的侧面积和体积分别是( )A .82+25+6,8B .22+85+6,8C .42+85+12,16D .82+45+12,16解析:几何体的侧面积有四部分,左侧面面积S 1=12×2×25=25,右侧面面积S 2=12×2×42=42,后侧面面积S 3=12×6×4=12,前侧面面积S 4=12×6×25=65,所以侧面积为S =42+85+12,体积为V =13Sh =13×2×6×4=16,故选C.答案:C9.如图所示,直线P A 垂直于⊙O 所在的平面,△ABC 内接于⊙O ,且AB 为⊙O 的直径,点M 为线段PB 的中点.现有结论:①BC ⊥PC ;②OM ∥平面APC ;③点B 到平面P AC 的距离等于线段BC 的长.其中正确的是( )A .①②B .①②③C .①D .②③解析:对于①,∵P A ⊥平面ABC ,∴P A ⊥BC ,∵AB 为⊙O 的直径,∴BC ⊥AC ,∴BC ⊥平面P AC ,又PC ⊂平面P AC ,∴BC ⊥PC ;对于②,∵点M 为线段PB 的中点,∴OM ∥P A ,∵P A ⊂平面P AC ,∴OM ∥平面P AC ;对于③,由①知BC ⊥平面P AC ,∴线段BC 的长即是点B 到平面P AC 的距离,故①②③都正确.答案:B10.(2012年沈阳质检)如图,正方体AC 1的棱长为1,过点A 作平面A 1BD 的垂线,垂足为点H ,则以下命题中,错误的命题是( )A.点H是△A1BD的垂心B.AH的延长线经过点C1 C.AH垂直平面CB1D1D.直线AH和BB1所成角为45°解析:计算得AH=33,直线AH和BB1所成角为arccos33,故D项错误,选项A,B,C是正确的.答案:D11.(2012年唐山模拟)把一个皮球放入如图所示的由8根长均为20 cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都有接触点,则皮球的半径为() A.10 3 cm B.10 cmC.10 2 cm D.30 cm解析:该骨架为一个棱长为20 cm的正四棱锥,设为G-ABCD,与各棱均相切的球的球心记为O,则O在棱锥的高GT上,如图示,设球半径为R,与棱GB,CD分别交于点H,M,设OT=h,由正四棱锥性质可知,|TM|=12|BC|=10,|BT|=12|BD|=102,|GT|=|GB|2-|BT|2=102,在△OTM中,有R2=h2+102①,由△GHO∽△GTB可得|GO||GB|=|OH||BT|,即102-h20=R102②,联立①②可得R=10或R=30(舍),故选B.答案:B12.在正方形ABCD中,AB=4,沿对角线AC将正方形ABCD折成一个直二面角B-AC-D,则点B到直线CD的距离为() A.2 2 B.3 2C .2 3D .2+2 2解析:如图,取AC 中点E ,连接DE ,BE ,易知∠DEB 是二面角A -DC -B 的平面角, 由于两平面垂直,故∠DEB =π2,即平面BE ⊥平面ADC ,过点E 作EF ⊥DC 于F ,连接BF ,则DC ⊥平面BEF ,所以BF ⊥DC ,故线段BF 即为点B 到DC 的距离,由于EF =12AD =2,BE =22,故BF =22+(22)2=2 3.答案:C二、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中的横线上) 13.已知正三棱锥的底面边长为2,侧棱长为433,则它的体积为________.解析:如图,在正三棱锥P -ABC 中,由于P A =433,AO =233,在直角三角形P AO 中可得PO =2,故V P -ABC =13×34×22×2=233.答案:23314.如图,已知△ABC 和△BCD 所在平面互相垂直,∠ABC =∠BCD =90°,AB =a ,BC =b ,CD =c ,且a 2+b 2+c 2=1,则三棱锥A -BCD 的外接球的表面积为________.解析:如图所示,可将该三棱锥补体为一个长方体,该长方体的体对角线长即为AD ,由AB =a ,BC =b ,CD =c ,且a 2+b 2+c 2=1,可得该三棱锥外接球即为长方体的外接球的直径为1,其外接球的表面积为S =4π×⎝ ⎛⎭⎪⎫122=π.答案:π15.如果一个几何体的正视图、侧视图、俯视图均为如图所示的面积为2的等腰直角三角形,那么该几何体的表面积等于________.解析:由题可得几何体如图所示,其中AP ⊥PC ,PC ⊥CB ,并且AP =PC =CB =2,PB =AC =22,△PBC ,△P AC 的面积都是2;CB ⊥面P AC ,所以CB ⊥AC ,又AP ⊥面PBC ,所以AP ⊥PB ,进而可求得△P AB ,△ABC 的面积都是22,所以该几何体的表面积等于4+4 2.答案:4+4 216.在三棱锥P -ABC 中,三条侧棱P A ,PB ,PC 两两互相垂直,且P A =PB =PC ,M 为AB 的中点,则PM 与平面ABC 所成角的正弦值为________.解析:如图,将三棱锥补为正方体,由于三棱锥P -ABC 为正三棱锥,故点P 在底面ABC 的射影为其中心N ,连接MN ,则∠PMN 即为直线PM 与平面ABC 所成角,设P A =PB =PC =a ,则PM =22a ,PN =33a ,故sin ∠PMN =PN PM =63.答案:63三、解答题(本大题共6小题,共70分,17题10分,18~22题,每题12分.解答应写出文字说明,证明过程或演算步骤.)17.如图,在直四棱柱ABCD -A 1B 1C 1D 1中,四边形ABCD 是梯形,AD ∥BC ,AC ⊥CD ,E 是AA 1上的一点.(1)求证:CD ⊥平面ACE ;(2)若平面CBE 交DD 1于点F ,求证:EF ∥AD .证明:(1)因为ABCD -A 1B 1C 1D 1为直四棱柱,所以AA 1⊥平面ABCD . 因为CD ⊂平面ABCD ,所以AA 1⊥CD ,即AE ⊥CD .因为AC ⊥CD ,AE ⊂平面AEC ,AC ⊂平面AEC ,AE ∩AC =A ,所以CD ⊥平面AEC . (2)因为AD ∥BC ,AD ⊂平面ADD 1A 1,BC ⊄平面ADD 1A 1,所以BC ∥平面ADD 1A 1. 因为BC ⊂平面BCE ,平面BCE ∩平面ADD 1A 1=EF ,所以EF ∥BC . 因为AD ∥BC ,所以EF ∥AD .18.如图,在四棱锥P -ABCD 中,P A ⊥平面ABCD ,底面ABCD 为平行四边形,且AB =1,BC =2,∠ABC =π3,E ,F 分别为AD ,BC 的中点.(1)求证:EF ∥平面PCD ; (2)求证:AC ⊥平面P AB .证明:(1)如图,因为在平行四边形ABCD 中,E ,F 分别为AD ,BC 的中点,所以ED =FC ,ED ∥FC ,可得EFCD 为平行四边形,所以EF ∥CD .又因为EF ⊄平面PCD ,CD ⊂平面PCD ,所以EF ∥平面PCD . (2)因为P A ⊥平面ABCD ,AC ⊂平面ABCD ,故P A ⊥AC . 在△ABC 中,AB =1,BC =2,∠ABC =π3,由余弦定理得 AC =AB 2+BC 2-2AB ·BC ·cos ∠ABC =1+4-2×1×2cos π3= 3.故AB 2+AC 2=BC 2,所以AB ⊥AC .而P A ∩AB =A ,且AB ,P A ⊂平面P AB ,所以AC ⊥平面P AB .19.一个多面体的三视图和直观图分别如图(1)(2)所示,其中M 、N 分别为AB 、AC 的中点,G 是DF 上的一动点.(1)求证:GN ⊥AC ;(2)当FG =GD 时,在棱AB 上确定一点P ,使得GP ∥平面FMC ,并给出证明.证明:(1)如图,连接DB ,可知B ,N ,D 共线,且AC ⊥DN . 又∵FD ⊥AD ,FD ⊥CD ,AD ∩CD =D ,∴FD ⊥平面ABCD .又∵AC⊂平面ABCD,∴FD⊥AC.又∵DN∩FD=D,∴AC⊥平面FDN.又GN⊂平面FDN,∴GN⊥AC.(2)点P与点A重合时,GP∥平面FMC.证明:取FC中点H,连接GH,GA,MH.∵G是DF的中点,∴GH綊12CD.∵M是AB的中点,∴AM綊12CD.∴GH綊AM,∴四边形GHMA是平行四边形.∴GA∥MH.又∵MH⊂平面FMC,GA⊄平面FMC,∴GA∥平面FMC,即GP∥平面FMC.20.(2013年西安质检)如图,在四棱锥P-ABCD中,P A⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.(1)求证:BD⊥平面P AC;(2)若P A=PB,求PB与AC所成角的余弦值.解:证明:(1)因为四边形ABCD是菱形,所以AC⊥BD.又因为P A⊥平面ABCD,所以P A⊥BD,而P A∩AC=A,所以BD⊥平面P AC.(2)设AC∩BD=O.因为∠BAD=60°,P A=PB=2,所以BO=1,AO=CO= 3.如图,以O为坐标原点,OB为x轴正方向,OC为y轴正方向,与AP平行的方向为z 轴正方向,建立空间直角坐标系O-xyz,则点P(0,-3,2),A(0,-3,0),B(1,0,0),C (0,3,0).所以PB →=(1,3,-2),AC →=(0,23,0). 设PB 与AC 所成角为θ,则 cos θ=⎪⎪⎪⎪⎪⎪PB →·AC →|PB →|·|AC →|=622×23=64.21.(2012年长沙联考)如图,在直三棱柱ABC -A 1B 1C 1中,AC =3,BC =4,AB =5,AA 1=4,点D 是AB 的中点.(1)求证:AC ⊥BC 1;(2)求二面角D -CB 1-B 的平面角的正切值.解:(1)证明:在直三棱柱ABC -A 1B 1C 1中,底面三边长AC =3,BC =4,AB =5. 因为AC 2+BC 2=AB 2,所以AC ⊥BC .又AC ⊥C 1C ,且BC ∩C 1C =C ,所以AC ⊥平面BCC 1. 又BC 1⊂平面BCC 1,所以AC ⊥BC 1.(2)解法一:取BC 中点E ,过点D 作DF ⊥B 1C 于点F ,连接EF ,ED .因为D 是AB 中点,所以DE ∥AC ,又AC ⊥平面BB 1C 1C ,所以DE ⊥平面BB 1C 1C .又因为BC 1⊂平面BB 1C 1C ,所以B 1C ⊥DE .而DF ⊥B 1C 且DE ∩DF =D ,所以B 1C ⊥平面DEF ,EF ⊂平面DEF ,所以B 1C ⊥EF ,所以∠EFD 是二面角D -CB 1-B 的平面角.因为AC =3,BC =4,AA 1=4,所以在△DEF 中,DE ⊥EF ,DE =32,EF =2,所以tan∠EFD =DE EF =322=324.所以二面角D -CB 1-B的正切值为324.解法二:以CA ,CB ,CC 1分别为x ,y ,z 轴建立如图所示空间直角坐标系.因为AC =3,BC =4,AA 1=4,所以点A (3,0,0),B (0,4,0),C (0,0,0),D ⎝ ⎛⎭⎪⎫32,2,0,B 1(0,4,4),所以CD →=⎝ ⎛⎭⎪⎫32,2,0,CB 1→=(0,4,4). 平面CBB 1C 1的法向量n 1=(1,0,0),设平面DB 1C 的法向量n 2=(x 0,y 0,z 0),则n 1,n 2的夹角(或其补角)的大小就是二面角D -CB 1-B 的大小.则由⎩⎨⎧n 2·CD →=0,n 2·CB 1→=0,即⎩⎪⎨⎪⎧32x 0+2y 0=0,4y 0+4z 0=0.令x 0=4,则y 0=-3,z 0=3,所以n 2=(4,-3,3). cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=434,则tan 〈n 1,n 2〉=324. 因为二面角D -CB 1-B 是锐二面角,所以二面角D -CB 1-B 的正切值为324. 22.将两块全等的三角板的一对直角边拼接在一起,使得一块三角板的直角边与另一块三角板所在平面垂直,如图,AB =BC =CD =2,∠ABC =∠BCD =90°,E ,F ,G 分别为AB ,BC,AC 的中点,P 为BD 上的点.(1)当点P 为BD 的中点时,求证:BG ⊥PF ;(2)线段BD 上是否存在点P ,使得二面角B -EF -P 的大小为2π3?若存在,求出BPPD 的值;若不存在,说明理由.解:(1)证明:如图,以B 为坐标原点,以BC ,BA 所在直线为y 轴,z 轴,以过B 作DC 的平行线为x 轴,建立空间直角坐标系,则B (0,0,0),E (0,0,1),F (0,1,0),G (0,1,1),C (0,2,0),D (2,2,0), 当点P 为BD 的中点时,P (1,1,0),∴BG →=(0,1,1),FP →=(1,0,0), ∴BG →·FP →=0,∴BG ⊥PF .(2)假设线段BD 上存在点P (t ,t,0)(0≤t ≤2), 使得二面角B -EF -P 的大小为2π3, 由(1)得EF →=(0,1,-1),FP →=(t ,t -1,0). 设平面EFP 的一个法向量为n =(x ,y,1), 则⎩⎨⎧n ·EF →=0,n ·FP →=0,即⎩⎨⎧0+y -1=0,tx +(t -1)y =0,解方程组得⎩⎪⎨⎪⎧x =1-t t ,y =1,从而n =⎝ ⎛⎭⎪⎫1-t t ,1,1, 又取平面BEF 的一个法向量为m =(1,0,0), ∴cos 〈m ,n 〉=m ·n|m |·|n |=1-t3t 2-2t +1; 又二面角B -EF -P 的大小为2π3,∴〈m ,n 〉=2π3,故-12=1-t3t 2-2t +1,解得t =3±6,经检验不符合题意.故线段BD 上不存在点P ,使得二面角B -EF -P 的大小为2π3.。
高三数学专项训练:立体几何解答题(文科)(一)

(Ⅱ)求证:EF∥平面PAB;
21.
(本小题满分12分)如图,已知 平面 , 平面 , 为等边三角形, , 为 中点.
(1)求证: 平面 ;
(2)求证:平面 平面 ;
(3)求直线 与平面 所成角的正弦值.
22.如图,四棱锥P—ABCD的底面ABCD是边长为1的菱形,∠BCD﹦60°,E是CD中点,
(Ⅰ)求证: 平面 ;
(Ⅱ)求三棱锥 的体积.
11.如图,在三棱锥 中,侧面 与侧面 均为等边三角形, , 为 中点.
(Ⅰ)证明: 平面 ;
(Ⅱ)求异面直线BS与AC所成角的大小.
12.(本题满分12分)
如图,已知AB 平面ACD,DE∥AB,△ACD是正三角形, ,且F是CD的中点.
(Ⅰ)求证AF∥平面BCE;
(1)求证:B1C∥平面AC1M;
(2)求证:平面AC1M⊥平面AA1B1B.
44.(本小题满分12分)
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形, BCD=60 ,E是CD的中点,PA 底面ABCD,PA=2。
(1)证明:平面PBE 平面PAB;
(2)求PC与平面PAB所成角的余弦值.
(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积。
15.右图为一组合体,其底面 为正方形, 平面 , ,且
(Ⅰ)求证: 平面 ;
(Ⅱ)求四棱锥 的体积;
(Ⅲ)求该组合体的表面积.
16.四棱锥 中,底面 为平行四边形,侧面 底面 , 为 的中点,已知 ,
(Ⅰ)求证: ;
(Ⅱ)在 上求一点 ,使 平面 ;
(Ⅲ)求三棱锥 的体积.
17.(本小题满分12分) 在三棱柱 中,底面是边长为 的正三角形,点 在底面 上的射影 恰是 中点.
2015全国文数立体几何高考试题—老师专用(2)
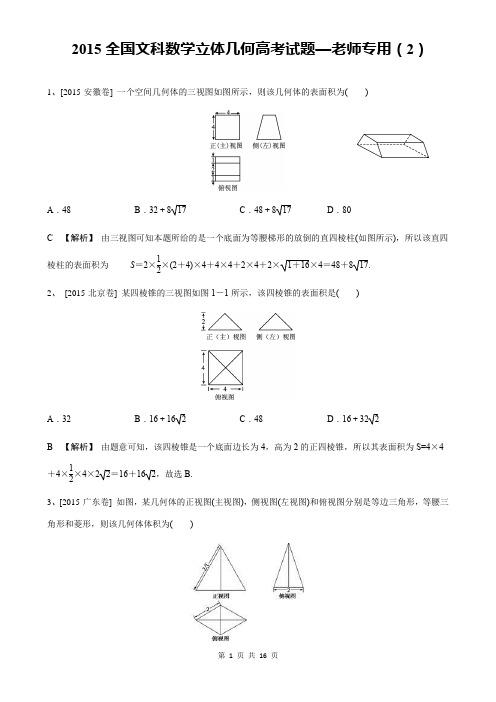
2015全国文科数学立体几何高考试题—老师专用(2)1、[2015·安徽卷]一个空间几何体的三视图如图所示,则该几何体的表面积为( )A .48B .32+817C .48+817D .80C 【解析】 由三视图可知本题所给的是一个底面为等腰梯形的放倒的直四棱柱(如图所示),所以该直四棱柱的表面积为S =2×12×(2+4)×4+4×4+2×4+2×1+16×4=48+817.2、 [2015·北京卷] 某四棱锥的三视图如图1-1所示,该四棱锥的表面积是( )A .32B .16+16 2C .48D .16+32 2B 【解析】 由题意可知,该四棱锥是一个底面边长为4,高为2的正四棱锥,所以其表面积为S=4×4+4×12×4×22=16+162,故选B.3、[2015·广东卷] 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体体积为( )A .4 3B .4C .2 3D .2C 【解析】 由三视图知该几何体为四棱锥,棱锥高h =(23)2-(3)2=3,底面为菱形,对角线长分别为23,2,所以底面积为12×23×2=23,所以V =13Sh =13×23×3=2 3.4、[2015·湖南卷] 设图是某几何体的三视图,则该几何体的体积为( )A .9π+42B .36π+18C.92π+12D.92π+18 D 【解析】 由三视图可得这个几何体是由上面是一个直径为3的球,下面是一个长、宽都为3高为2的长方体所构成的几何体,则其体积为: V =V 1+V 2=43×π×⎝⎛⎭⎫323+3×3×2=92π+18,故选D. 5、[2015·辽宁卷] 一个正三棱柱的侧棱长和底面边长相等,体积为23,它的三视图中的俯视图如图1-3所示,左视图是一个矩形,则这个矩形的面积是( )A .4B .2 3C .2D. 3B 【解析】 由俯视图知该正三棱柱的直观图为下图,其中M ,N 是中点,矩形MNC 1C 为左视图. 由于体积为23,所以设棱长为a ,则12×a 2×sin60°×a =23,解得a =2.所以CM =3,故矩形MNC 1C面积为23,故选B.6、 [2015·课标全国卷] 在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为( )D 【解析】 由正视图和俯视图知几何体的直观图是由一个半圆锥和一个三棱锥组合而成的,如图,故侧视图选D.7、[2015·陕西卷] 某几何体的三视图如图所示,则它的体积为( )A .8-2π3B .8-π3C .8-2πD.2π3A 【解析】 主视图与左视图一样是边长为2的正方形,里面有两条虚线,俯视图是边长为2的正方形与直径为2的圆相切,其直观图为棱长为2的正方体中挖掉一个底面直径为2的圆锥,故其体积为正方体的体积与圆锥的体积之差,V 正=23=8,V 锥=13πr 2h =2π3(r =1,h =2),故体积V =8-2π3,故答案为A.8、[2015·天津卷] 一个几何体的三视图如图所示(单位:m),则该几何体的体积为________ m 3.4 【解析】 根据三视图还原成直观图,可以看出,其是由两个形状一样的,底面长和宽都为1,高为2的长方体叠加而成,故其体积V =2×1×1+1×1×2=4.9、[2015·浙江卷] 若某几何体的三视图如图所示,则这个几何体的直观图可以是( )答案:B10、[2015·福建卷] 如图1-3,正方体ABCD -A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上,若EF ∥平面AB 1C ,则线段EF 的长度等于________.2 【解析】 ∵EF ∥平面AB 1C ,EF ⊂平面ABCD ,平面ABCD ∩平面AB 1C =AC ,∴EF ∥AC , 又∵E 是AD 的中点,∴F 是CD 的中点,即EF 是△ACD 的中位线,∴EF =12AC =12×22= 2.11、[2015·浙江卷] 若直线l 不平行于平面α,且l ⊄α,则( ) A .α内的所有直线与l 异面B .α内不存在与l 平行的直线 C .α内存在唯一的直线与l 平行D .α内的直线与l 都相交B 【解析】 在α内存在直线与l 相交,所以A 不正确;若α内存在直线与l 平行,又∵l ⊄α,则有l ∥α,与题设相矛盾,∴B 正确,C 不正确;在α内不过l 与α交点的直线与l 异面,D 不正确.12、[2015·广东卷] 正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有( ) A .20 B .15 C .12 D .10D 【解析】 一个下底面5个点,每个下底面的点对于5个上底面的点,满足条件的对角线有2条,所以共有5×2=10条.13、 [2015·四川卷]l 1,l 2,l 3是空间三条不同的直线,则下列命题正确的是( ) A .l 1⊥l 2,l 2⊥l 3⇒l 1∥l 3B .l 1⊥l 2,l 2∥l 3⇒l 1⊥l 3C .l 1∥l 2∥l 3⇒l 1,l 2,l 3共面D .l 1,l 2,l 3共点⇒l 1,l 2,l 3共面B 【解析】 对于A ,直线l 1与l 3可能异面;对于C ,直线l 1、l 2、l 3可能构成三棱柱三条侧棱所在直线而不共面;对于D ,直线l 1、l 2、l 3相交于同一个点时不一定共面. 所以选B.14、 [2015·湖北卷] 设球的体积为V 1,它的内接正方体的体积为V 2,下列说法中最合适的是( ) A .V 1比V 2大约多一半B .V 1比V 2大约多两倍半 C .V 1比V 2大约多一倍D .V 1比V 2大约多一倍半D 【解析】 设球的半径为R ,则V 1=43πR 3.设正方体的边长为a ,则V 2=a 3.又因为2R =3a ,所以V 1=43π⎝⎛⎭⎫32a 3=32πa 3,V 1-V 2=⎝⎛⎭⎫32π-1a 3≈1.7a 3.15、 [2015·辽宁卷] 已知球的直径SC =4,A 、B 是该球球面上的两点,AB =2,∠ASC =∠BSC =45°,则棱锥S -ABC 的体积为( ) A.33 B.233 C.433 D.533C 【解析】 如图1-6,由于SC 是球的直径,所以∠SAC =∠SBC =90°,又∠ASC =∠BSC =45°,所以△SAC 、△BSC 为等腰直角三角形,取SC 中点D ,连接AD 、BD .由此得SC ⊥AD ,SC ⊥BD ,即SC ⊥平面ABD .所以V S -ABC =V S -ABD +V C -ABD =13S △ABD ·SC .由于在等腰直角三角形△SAC 中∠ASC =45°,SC =4,所以AD =2.同理BD =2. 又AB =2,所以△ABD 为正三角形,所以V S -ABC =13S △ABD ·SC =13×12×22·sin60°×4=433,所以选C.16、 [2015·课标全国卷] 已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上,若圆锥底面面积是这个球面面积的316,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为________.13【解析】 如图,设球的半径为R ,圆锥底面半径为r ,则球面面积为4πR 2,圆锥底面面积为πr 2, 由题意πr 2=1216πR 2,所以r =32R ,所以OO 1=OA 2-O 1A 2=R 2-34R 2=12R ,所以SO 1=R +12R =32R , S 1O 1=R -12R =12R ,所以S 1O 1SO 1=R23R 2=13.17、[2015·全国卷] 已知正方体ABCD -A 1B 1C 1D 1中,E 为C 1D 1的中点,则异面直线AE 与BC 所成角的余弦值为________.23【解析】 取A 1B 1的中点F ,连EF ,则EF ∥BC ,∠AEF 是异面直线AE 与BC 所成的角,设正方体的棱长为a ,可得AE =32a ,AF =52a ,在△AEF 中,运用余弦定理得cos ∠AEF =23,即异面直线AE 与BC所成角的余弦值为23.18、[2015·安徽卷]如图,ABEDFC 为多面体,平面ABED 与平面ACFD 垂直,点O 在线段AD 上,OA =1,OD =2,△OAB ,△OAC ,△ODE ,△ODF 都是正三角形. (1)证明直线BC ∥EF ; (2)求棱锥F -OBED 的体积.【解答】(1)证明:设G 是线段DA 与EB 延长线的交点,由于△OAB 与△ODE 都是正三角形,OA =1,OD =2,所以OB 綊12DE ,OG =OD =2.同理,设G ′是线段DA 与FC 延长线的交点,有OC 綊12DF ,OG ′=OD =2,又由于G 和G ′都在线段DA 的延长线上,所以G 与G ′重合.在△GED 和△GFD 中,由OB 綊12DE 和OC 綊12DF ,可知B 和C 分别是GE 和GF 的中点.所以BC 是△GEF 的中位线,故BC ∥EF .(2)由OB =1,OE =2,∠EOB =60°,知S △EOB =32. 而△OED 是边长为2的正三角形,故S △OED = 3. 所以S OBED =S △EOB +S △OED =332. 过点F 作FQ ⊥DG ,交DG 于点Q ,由平面ABED ⊥平面ACFD 知,FQ 就是四棱锥F -OBED 的高,且FQ =3,所以V F -OBED =13FQ ·S 四边形OBED =32.19、[2015·北京卷] 如图,在四面体P ABC 中,PC ⊥AB ,P A ⊥BC ,点D ,E ,F ,G 分别是棱AP ,AC ,BC ,PB 的中点.(1)求证:DE ∥平面BCP ; (2)求证:四边形DEFG 为矩形;(3)是否存在点Q ,到四面体P ABC 六条棱的中点的距离相等?说明理由. 【解答】 (1)证明:因为D ,E 分别为AP ,AC 的中点,所以DE ∥PC .又因为DE ⊄平面BCP ,PC ⊂平面BCP , 所以DE ∥平面BCP .(2)因为D 、E 、F 、G 分别为AP 、AC 、BC 、PB 的中点, 所以DE ∥PC ∥FG , DG ∥AB ∥EF ,所以四边形DEFG 为平行四边形. 又因为PC ⊥AB , 所以DE ⊥DG ,所以平行四边形DEFG 为矩形. (3)存在点Q 满足条件,理由如下: 连接DF ,EG ,设Q 为EG 的中点.由(2)知,DF ∩EG =Q ,且QD =QE =QF =QG =12EG .分别取PC 、AB 的中点M ,N ,连接ME 、EN 、NG 、MG 、MN . 与(2)同理,可证四边形MENG 为矩形,其对角线交点为EG 的中点Q , 且QM =QN =12EG .所以Q 为满足条件的点.20、 [2015·江苏卷] 如图在四棱锥P -ABCD 中,平面P AD ⊥平面ABCD ,AB =AD ,∠BAD =60°,E 、F 分别是AP 、AD 的中点. 求证:(1)直线EF ∥平面PCD ; (2)平面BEF ⊥平面P AD .本题主要考查直线与平面、平面与平面的位置关系,考查空间想象能力和推理论证能力.【解答】 证明:(1)在△P AD 中,因为E ,F 分别为AP ,AD 的中点,所以EF ∥PD .又因为EF ⊄平面PCD ,PD ⊂平面PCD ,所以直线EF ∥平面PCD .(2)连结BD ,因为AB =AD ,∠BAD =60°,所以△ABD 为正三角形,因为F 是AD 的中点,所以BF ⊥AD . 因为平面P AD ⊥平面ABCD ,BF ⊂平面ABCD ,平面P AD ∩平面ABCD =AD ,所以BF ⊥平面P AD . 又因为BF ⊂平面BEF ,所以平面BEF ⊥平面P AD .图1-621、[2015·课标全国卷] 如图1-8,四棱锥P -ABCD 中,底面ABCD 为平行四边形,∠DAB =60°,AB =2AD ,PD ⊥底面ABCD .(1)证明:P A ⊥BD ;(2)设PD =AD =1,求棱锥D -PBC 的高.【解答】 (1)证明:因为∠DAB =60°,AB =2AD ,由余弦定理得BD =3AD , 从而BD 2+AD 2=AB 2,故BD ⊥AD . 又PD ⊥底面ABCD ,可得BD ⊥PD , 所以BD ⊥平面P AD ,故P A ⊥BD .(2)如图,作DE ⊥PB ,垂足为E . 已知PD ⊥底面ABCD ,则PD ⊥BC .由(1)知BD ⊥AD ,又BC ∥AD ,所以BC ⊥BD . 故BC ⊥平面PBD ,BC ⊥DE . 则DE ⊥平面PBC .由题设知PD =1,则BD =3,PB =2. 根据DE ·PB =PD ·BD 得DE =32. 即棱锥D -PBC 的高为32.22、 [2015·陕西卷] 如图在△ABC 中,∠ABC =45°,∠BAC =90°,AD 是BC 上的高,沿AD 把△ABD 折起,使∠BDC =90°.(1)证明:平面ADB ⊥平面BDC ;(2)若BD =1,求三棱锥D -ABC 的表面积. 【解答】 (1)∵折起前AD 是BC 边上的高, ∴当△ABD 折起后,AD ⊥DC ,AD ⊥DB . 又DB ∩DC =D . ∴AD ⊥平面BDC . ∵AD 平面ABD , ∴平面ABD ⊥平面BDC .(2)由(1)知,DA ⊥DB ,DB ⊥DC ,DC ⊥DA , DB =DA =DC =1. ∴AB =BC =CA = 2.从而S △DAB =S △DBC =S △DCA =12×1×1=12.S △ABC =12×2×2×sin60°=32.∴表面积S =12×3+32=3+32.23、[2015·江苏卷] 如图1-2,在四棱锥P -ABCD 中,平面P AD ⊥平面ABCD ,AB =AD ,∠BAD =60°,E 、F 分别是AP 、AD 的中点.求证:(1)直线EF ∥平面PCD ; (2)平面BEF ⊥平面P AD .本题主要考查直线与平面、平面与平面的位置关系,考查空间想象能力和推理论证能力.【解答】 证明:(1)在△P AD 中,因为E ,F 分别为AP ,AD 的中点,所以EF ∥PD .又因为EF ⊄平面PCD ,PD ⊂平面PCD , 所以直线EF ∥平面PCD .(2)连结BD ,因为AB =AD ,∠BAD =60°,所以△ABD 为正三角形,因为F 是AD 的中点,所以BF ⊥AD . 因为平面P AD ⊥平面ABCD ,BF ⊂平面ABCD ,平面P AD ∩平面ABCD =AD ,所以BF ⊥平面P AD . 又因为BF ⊂平面BEF ,所以平面BEF ⊥平面P AD .24、 [2015·辽宁卷] 如图1-8,四边形ABCD 为正方形,QA ⊥平面ABCD ,PD ∥QA ,QA =AB =12PD .(1)证明:PQ ⊥平面DCQ ;(2)求棱锥Q -ABCD 的体积与棱锥P -DCQ 的体积的比值. 【解答】 (1)由条件知PDAQ 为直角梯形.因为QA ⊥平面ABCD ,所以平面PDAQ ⊥平面ABCD ,交线为AD . 又四边形ABCD 为正方形,DC ⊥AD , 所以DC ⊥平面PDAQ ,可得PQ ⊥DC . 在直角梯形PDAQ 中可得DQ =PQ =22PD ,则PQ ⊥QD . 所以PQ ⊥平面DCQ . (2)设AB =a .由题设知AQ 为棱锥Q -ABCD 的高,所以棱锥Q -ABCD 的体积V 1=13a 3.由(1)知PQ 为棱锥P -DCQ 的高,而PQ =2a ,△DCQ 的面积为22a 2, 所以棱锥P -DCQ 的体积V 2=13a 3.故棱锥Q -ABCD 的体积与棱锥P -DCQ 的体积的比值为1.25、[2015·湖南卷] 如图1-5,在圆锥PO 中,已知PO =2,⊙O 的直径AB =2,点C 在AB 上,且∠CAB =30°,D 为AC 的中点.(1)证明:AC ⊥平面POD ;(2)求直线OC 和平面P AC 所成角的正弦值. 【解答】(1)因为OA =OC ,D 是AC 的中点,所以AC ⊥OD . 又PO ⊥底面⊙O ,AC ⊂底面⊙O ,所以AC ⊥PO .而OD ,PO 是平面POD 内的两条相交直线,所以AC ⊥平面POD .(2)由(1)知,AC ⊥平面POD ,又AC ⊂平面P AC ,所以平面POD ⊥平面P AC .在平面POD 中,过O 作OH ⊥PD 于H ,则OH ⊥平面P AC .连结CH ,则CH 是OC 在平面P AC 上的射影,所以∠OCH 是直线OC 和平面P AC 所成的角.在Rt △ODA 中,OD =OA ·sin30°=12. 在Rt △POD 中,OH =PO ·OD PO 2+OD 2=2×122+14=23. 在Rt △OHC 中,sin ∠OCH =OH OC =23. 故直线OC 和平面P AC 所成角的正弦值为23. 26、 [2015·福建卷] 如图四棱锥P -ABCD 中,P A ⊥底面ABCD ,AB ⊥AD ,点E 在线段AD 上,且CE ∥AB .(1)求证:CE ⊥平面P AD ;(2)若P A =AB =1,AD =3,CD =2,∠CDA =45°,求四棱锥P -ABCD 的体积.【解答】 (1)证明:因为P A ⊥平面ABCD ,CE ⊂平面ABCD ,所以P A ⊥CE .因为AB ⊥AD ,CE ∥AB ,所以CE ⊥AD .又P A ∩AD =A ,所以CE ⊥平面P AD .(2)由(1)可知CE ⊥AD .在Rt △ECD 中,DE =CD ·cos45°=1,CE =CD ·sin45°=1.又因为AB =CE =1,AB ∥CE ,所以四边形ABCE 为矩形.所以S 四边形ABCD =S 矩形ABCE +S △ECD =AB ·AE +12CE ·DE =1×2+12×1×1=52. 又P A ⊥平面ABCD ,P A =1,所以V 四棱锥P -ABCD =13S 四边形ABCD ·P A =13×52×1=56. 27、[2015·江西卷] 如图1-7,在△ABC 中,∠B =π2,AB =BC =2,P 为AB 边上一动点,PD ∥BC 交AC 于点D ,现将△PDA 沿PD 翻折至△PDA ′,使平面PDA ′⊥平面PBCD .(1)当棱锥A ′-PBCD 的体积最大时,求P A 的长;(2)若点P 为AB 的中点,E 为A ′C 的中点,求证:A ′B ⊥DE .【解答】 (1)令P A =x (0<x <2),则A ′P =PD =x ,BP =2-x .因为A ′P ⊥PD ,且平面A ′PD ⊥平面PBCD ,故A ′P ⊥平面PBCD .所以V A ′-PBCD =13Sh =16(2-x )(2+x )x =16(4x -x 3). 令f (x )=16(4x -x 3),由f ′(x )=16(4-3x 2)=0,得x =233. 当x ∈⎝⎛⎭⎫0,233时,f ′(x )>0,f (x )单调递增; 当x ∈⎝⎛⎭⎫233,2时,f ′(x )<0,f (x )单调递减, 所以,当x =233时,f (x )取得最大值,即:当V A ′-PBCD 最大时,P A =233. (2)证明:设F 为A ′B 的中点,连接PF ,FE .则有EF 綊12BC ,PD 綊12BC ,所以EF 綊PD ,四边形DEFP 为平行四边形,所以DE ∥PF ,又A ′P =PB ,所以PF ⊥A ′B ,故DE ⊥A ′B .28、 [2015·山东卷]如图1-5,在四棱台ABCD -A 1B 1C 1D 1中,D 1D ⊥平面ABCD ,底面ABCD 是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.(1)证明:AA1⊥BD;(2)证明:CC1∥平面A1BD.图1-5【解答】证明:(1)证法一:因为D1D⊥平面ABCD,且BD⊂平面ABCD,图1-6所以D1D⊥BD.又因为AB=2AD,∠BAD=60°,在△ABD中,由余弦定理得BD2=AD2+AB2-2AD·AB cos60°=3AD2.所以AD2+BD2=AB2,所以AD⊥BD.又AD∩D1D=D,所以BD⊥平面ADD1A1.又AA1⊂平面ADD1A1,所以AA1⊥BD.证法二:因为D1D⊥平面ABCD,且BD⊂平面ABCD,图1-7所以BD ⊥D 1D .取AB 的中点G ,连接DG .在△ABD 中,由AB =2AD 得AG =AD ,又∠BAD =60°,所以△ADG 为等边三角形.因此GD =GB .故∠DBG =∠GDB ,又∠AGD =60°,所以∠GDB =30°,故∠ADB =∠ADG +∠GDB =60°+30°=90°,所以BD ⊥AD .又AD ∩D 1D =D ,所以BD ⊥平面ADD 1A 1,又AA 1⊂平面ADD 1A 1,所以AA 1⊥BD .(2)连接AC ,A 1C 1.图1-8设AC ∩BD =E ,连接EA 1.因为四边形ABCD 为平行四边形,所以EC =12AC , 由棱台定义及AB =2AD =2A 1B 1知,A 1C 1∥EC 且A 1C 1=EC ,所以四边形A 1ECC 1为平行四边形.因此CC 1∥EA 1,又因为EA 1⊂平面A 1BD ,CC 1⊄平面A 1BD ,所以CC 1∥平面A 1BD .29、[2015·四川卷] 如图1-5,在直三棱柱ABC -A 1B 1C 1中,∠BAC =90°,AB =AC =AA 1=1,延长A 1C 1至点P ,使C 1P =A 1C 1,连结AP 交棱CC 1于点D .(1)求证:PB 1∥平面BDA 1;(2)求二面角A -A 1D -B 的平面角的余弦值.图1-5【解答】 解法一:(1)连结AB 1与BA 1交于点O ,连结OD .∵C 1D ∥AA 1,A 1C 1=C 1P ,∴AD =PD ,又AO =B 1O ,∴OD ∥PB 1.又OD ⊂平面BDA 1,PB 1⊄平面BDA 1,∴PB 1∥平面BDA 1.(2)过A 作AE ⊥DA 1于点E ,连结BE .∵BA ⊥CA ,BA ⊥AA 1,且AA 1∩AC =A ,∴BA ⊥平面AA 1C 1C .由三垂线定理可知BE ⊥DA 1.∴∠BEA 为二面角A -A 1D -B 的平面角.在Rt △A 1C 1D 中,A 1D =⎝⎛⎭⎫122+12=52,又S △AA 1D =12×1×1=12×52×AE ,∴AE =255.在Rt △BAE 中,BE =12+⎝⎛⎭⎫2552=355,∴cos ∠BEA =AE BE =23. 故二面角A -A 1D -B 的平面角的余弦值为23.30、[2015·天津卷] 如图在四棱锥P -ABCD 中,底面ABCD 为平行四边形,∠ADC =45°,AD =AC =1,O 为AC 的中点,PO ⊥平面ABCD ,PO =2,M 为PD 的中点.(1)证明PB ∥平面ACM ;(2)证明AD ⊥平面P AC ;(3)求直线AM 与平面ABCD 所成角的正切值.【解答】 (1)证明:连接BD ,MO .在平行四边形ABCD 中,因为O 为AC 的中点,所以O 为BD 的中点.又M 为PD 的中点,所以PB ∥MO .因为PB ⊄平面ACM ,MO ⊂平面ACM ,所以PB ∥平面ACM .(2)证明:因为∠ADC =45°,且AD =AC =1,所以∠DAC =90°,即AD ⊥AC .又PO ⊥平面ABCD ,AD ⊂平面ABCD ,所以PO ⊥AD .而AC ∩PO =O ,所以AD ⊥平面P AC .(3)取DO 中点N ,连接MN ,AN .因为M 为PD 的中点,所以MN ∥PO ,且MN =12PO =1.由PO ⊥平面ABCD ,得MN ⊥平面ABCD ,所以∠MAN 是直线AM 与平面ABCD 所成的角.在Rt △DAO 中,AD =1,AO =12,所以DO =52.从而AN =12DO =54.在Rt △ANM 中,tan ∠MAN =MN AN =154=455,即直线AM 与平面ABCD 所成角的正切值为455.。
2015年高考真题分专题复习之立体几何专题(1)

2015立体几何专题(1)(文)1.设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( )A .若l β⊥,则αβ⊥B .若αβ⊥,则l m ⊥C .若//l β,则//αβD .若//αβ,则//l m2.某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )A .83cmB .123cmC .3233cmD .4033cm 3.某几何体的三视图如图所示,则该几何体的体积为( )123π+ (B )136π (C ) 73π (D )52π 4.一个几何体的三视图如图所示,则该几何体的表面积为( )A .3πB .4πC .24π+D .34π+5.若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则下列命题正确的是( )A .l 至少与1l ,2l 中的一条相交B .l 与1l ,2l 都相交C .l 至多与1l ,2l 中的一条相交D .l 与1l ,2l 都不相交6.如图,斜线段AB 与平面α所成的角为60,B 为斜足,平面α上的动点P 满足30∠PAB =,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支7. 12,l l 表示空间中的两条直线,若p :12,l l 是异面直线;q :12,l l 不相交,则( )A .p 是q 的充分条件,但不是q 的必要条件B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件8.圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r =( )(A )1 (B )2 (C )4 (D )89.某几何体的三视图如图所示,则该几何体的表面积等于( )1112A.8+.11+.14+.1510.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) (A)3(B)3()()11.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )A.1 B.212.一个四面体的三视图如图所示,则该四面体的表面积是()(A)1(B)1+(C)2+(D)m.13.一个几何体的三视图如图所示(单位:m),则该几何体的体积为314.如图,在三棱锥V C -AB 中,平面V AB ⊥平面C AB ,V ∆AB 为等边三角形,C C A ⊥B 且C C A =B =O ,M 分别为AB ,V A 的中点.(Ⅰ)求证:V //B 平面C MO ;(Ⅱ)求证:平面C MO ⊥平面V AB ;(Ⅲ)求三棱锥V C -AB 的体积.15.如图,三角形DC P 所在的平面与长方形CD AB 所在的平面垂直,D C 4P =P =,6AB =,C 3B =.(1)证明:C//B 平面D P A ;(2)证明:C D B ⊥P ;(3)求点C 到平面D P A 的距离.16.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P ABCD -中,侧棱PD ⊥底面ABCD ,且PD CD =,点E 是PC 的中点,连接,,DE BD BE .(Ⅰ)证明:DE ⊥平面PBC .试判断四面体EBCD 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;(Ⅱ)记阳马P ABCD -的体积为1V ,四面体EBCD 的体积为2V ,求12V V 的值.17.如图,直三棱柱111ABC A B C -的底面是边长为2的正三角形,,E F 分别是1,BC CC 的中点。
2015年高考数学真题分类汇编:专题(15)几何证明选讲(文科)及答案

2015年高考数学真题分类汇编 专题15 几何证明选讲 文1.【2015高考天津,文6】如图,在圆O 中,M ,N 是弦AB 的三等分点,弦CD ,CE 分别经过点M ,N ,若CM =2,MD =4,CN =3,则线段NE 的长为( ) (A) 83 (B) 3 (C) 103 (D) 52【答案】A【解析】根据相交弦定理可得 2122,339CM MD AM MB AB AB AB ⨯=⨯=⨯= 2212,339CN NE AN NB AB AB AB ⨯=⨯=⨯= 所以8,3C M MD C M M D C N NE N E CN ⨯⨯=⨯⇒==所以选A. 【考点定位】本题主要考查圆中的相交弦定理.【名师点睛】平面几何中与圆有关的性质与定理是高考考查的热点,解题时要充分利用性质与定理求解,本部分内容中常见的命题点有:平行线分线段成比例定理;三角形的相似与性质;圆内接四边形的性质与判定;相交弦定理与切割线定理.2.【2015高考湖南,文12】在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系.若曲线C 的极坐标方程为2sin ρθ=,则曲线C 的直角坐标方程为_____.【答案】2211x y +-=()【解析】试题分析:将极坐标化为直角坐标,求解即可.曲线C 的极坐标方程为222sn sn ρθρρθ=∴=, ,它的直角坐标方程为222x y y += ,2211x y ∴+-=(). 故答案为:2211x y +-=(). 【考点定位】圆的极坐标方程【名师点睛】1.运用互化公式:222,sin ,cos x y y x ρρθρθ=+==将极坐标化为直角坐标;2.直角坐标方程与极坐标方程的互化,关键要掌握好互化公式,研究极坐标系下图形的性质,可转化直角坐标系的情境进行.3.【2015高考广东,文14】(坐标系与参数方程选做题)在平面直角坐标系x y O 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.曲线1C 的极坐标方程为()cos sin 2ρθθ+=-,曲线2C的参数方程为2x t y ⎧=⎪⎨=⎪⎩(t 为参数),则1C 与2C 交点的直角坐标为 .【答案】()2,4-【解析】曲线1C 的直角坐标方程为2x y +=-,曲线2C 的普通方程为28y x =,由228x y y x+=-⎧⎨=⎩得:24x y =⎧⎨=-⎩,所以1C 与2C 交点的直角坐标为()2,4-,所以答案应填:()2,4-. 【考点定位】1、极坐标方程化为直角坐标方程;2、参数方程化为普通方程;3、两曲线的交点.【考点定位】1、极坐标方程化为直角坐标方程;2、参数方程化为普通方程;3、两曲线的交点.【名师点晴】本题主要考查的是极坐标方程化为直角坐标方程、参数方程化为普通方程和两曲线的交点,属于容易题.解决此类问题的关键是极坐标方程或参数方程转化为平面直角坐标系方程,并把几何问题代数化.4.【2015高考广东,文15】(几何证明选讲选做题)如图1,AB 为圆O 的直径,E 为AB 的延长线上一点,过E 作圆O 的切线,切点为C ,过A 作直线C E 的垂线,垂足为D .若4AB =,C E =,则D A = .【答案】3【解析】连结C O ,则C D O ⊥E ,因为D D A ⊥E ,所以C//D O A ,所以C D O OE =A AE ,由切割线定理得:2C E =BE ⋅AE ,所以()412BE BE +=,即24120BE +BE -=,解得:2BE =或6BE =-(舍去),所以C 26D 34O ⋅AE ⨯A ===OE ,所以答案应填:3.【考点定位】1、切线的性质;2、平行线分线段成比例定理;3、切割线定理.【名师点晴】本题主要考查的是切线的性质、平行线分线段成比例定理和切割线定理,属于容易题.解题时一定要注意灵活运用圆的性质,否则很容易出现错误.凡是题目中涉及长度的,通常会使用到相似三角形、全等三角形、正弦定理、余弦定理等基础知识.【2015高考上海,文5】若线性方程组的增广矩阵为 ⎝⎛02 13 ⎪⎪⎭⎫21c c 解为⎩⎨⎧==53y x ,则=-21c c .【答案】16【解析】由题意,⎩⎨⎧==53y x 是方程组⎩⎨⎧==+2132c y c y x 的解,所以⎩⎨⎧==52121c c ,所以1652121=-=-c c .【考点定位】增广矩阵,线性方程组的解法.【名师点睛】对于增广矩阵,他是线性方程组的矩阵表现形式,最后一列是常数项,前面的几列是方程组的系数.本题虽然是容易题,按照定义,仔细计算,不出错.5.【2015高考陕西,文22】选修4-1:几何证明选讲如图,AB 切O 于点B ,直线AO 交O 于,D E 两点,,BC DE ⊥垂足为C . (I)证明:CBD DBA ∠=∠(II)若3,AD DC BC ==,求O 的直径.【答案】(I)证明略,详见解析; (II)3.所以CBD DBA ∠=∠(II)由(I)知BD 平分CBA ∠, 则3BA AD BC CD==,又BC =,从而AB =,所以4AC == 所以3AD =,由切割线定理得2AB AD AE =⋅ 即26AB AE AD==, 故3DE AE AD =-=,即O 的直径为3.【考点定位】1.几何证明;2.切割线定理.【名师点睛】(1)近几年高考对本部分的考查主要是围绕圆的性质考查考生的推理能力、逻辑思维能力,试题多是运用定理证明结论,因而圆的性质灵活运用是解题的关键;(2)在几何题目中出现求长度的问题,通常会使用到相似三角形.全等三角形.切割线定理等基础知识;(3)本题属于基础题,要求有较高分析推理能力.6.【2015高考陕西,文23】选修4-4:坐标系与参数方程在直角坐标版权法xOy 吕,直线l的参数方程为132(x t t y ⎧=+⎪⎪⎨⎪=⎪⎩为参数),以原点为极点,x 轴的正半轴为极轴建立极坐标系,C的极坐标方程为ρθ=.(I)写出C 的直角坐标方程;(II)P 为直线l 上一动点,当P 到圆心C 的距离最小时,求点P 的坐标.【答案】(I) (223x y +-=; (II) (3,0). 【解析】试题分析:(I)由ρθ=,得2sin ρθ=,从而有22x y +=,所以(223x y +-= (II)设132P t ⎛⎫+ ⎪⎝⎭,又)C ,则PC ==,故当0t =时,PC 取得最小值,此时P 点的坐标为(3,0).试题解析:(I)由ρθ=,得2sin ρθ=,从而有22x y +=所以(223x y +-=(II)设132P t ⎛⎫+ ⎪⎝⎭,又C ,则PC ==, 故当0t =时,PC 取得最小值,此时P 点的坐标为(3,0).【考点定位】1. 极坐标系与参数方程;2.点与圆的位置关系.【名师点睛】本题考查极坐标系与参数方程,解决此类问题的关键是如何正确地把极坐标方程或参数方程转化平面直角坐标系方程,并把几何问题代数化.本题属于基础题,注意运算的准确性.7. 【2015高考陕西,文24】选修4-5:不等式选讲已知关于x 的不等式x a b +<的解集为{|24}x x <<(I)求实数,a b 的值;(II)+的最大值.【答案】(I) 3,1a b =-=;(II)4.【解析】试题分析:(I)由x a b +<,得b a x b a --<<-,由题意得24b a b a --=⎧⎨-=⎩,解得3,1a b =-=;(II)=+≤4===1t =时等号成立,故min 4+=.试题解析:(I)由x a b +<,得b a x b a --<<-则24b a b a --=⎧⎨-=⎩,解得3, 1.a b =-=+=+≤4===1t=时等号成立,故min 4+=【考点定位】1.绝对值不等式;2.柯西不等式.【名师点睛】(1)零点分段法解绝对值不等式的步骤:①求零点;②划区间.去绝对值号;③分别解去掉绝对值的不等式;④取每个结果的并集,注意在分段时不要遗漏区间的端点值;(2)要注意区别不等式与方程区别;(3)用柯西不等式证明或求值事要注意两点:一是所给不等式的形式是否和柯西不等式的形式一致,若不一致,需要将所给式子变形;二是注意等号成立的条件8.【2015高考新课标1,文22】选修4-1:几何证明选讲如图AB是O直径,AC是O切线,BC交O与点E.(I)若D为AC中点,求证:DE是O切线;(II)若OA=,求ACB∠的大小.【答案】(Ⅰ)见解析(Ⅱ)60°(Ⅱ)设CE =1,AE =x ,由已知得AB =BE =,由射影定理可得,2AE CE BE =,∴2x =,解得x ACB =60°. ……10分考点:圆的切线判定与性质;圆周角定理;直角三角形射影定理【名师点睛】在解有关切线的问题时,要从以下几个方面进行思考:①见到切线,切点与圆心的连线垂直于切线;②过切点有弦,应想到弦切角定理;③若切线与一条割线相交,应想到切割线定理;④若要证明某条直线是圆的切线,则证明直线与圆的交点与圆心的连线与该直线垂直.9.【2015高考新课标1,文23】选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线1:2C x =-,圆()()222:121C x y -+-=,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系.(I )求12,C C 的极坐标方程.(II )若直线3C 的极坐标方程为()πR 4θρ=∈,设23,C C 的交点为,M N ,求2C MN ∆ 的面积.【答案】(Ⅰ)cos 2ρθ=-,22cos 4sin 40ρρθρθ--+=(Ⅱ)12 【解析】试题分析:(Ⅰ)用直角坐标方程与极坐标互化公式即可求得1C ,2C 的极坐标方程;(Ⅱ)将将=4πθ代入22cos 4sin 40ρρθρθ--+=即可求出|MN|,利用三角形面积公式即可求出2C MN 的面积.试题解析:(Ⅰ)因为cos ,sin x y ρθρθ==,∴1C 的极坐标方程为cos 2ρθ=-,2C 的极坐标方程为22cos 4sin 40ρρθρθ--+=.……5分(Ⅱ)将=4πθ代入22cos 4sin 40ρρθρθ--+=,得240ρ-+=,解得1ρ=2ρ,|MN|=1ρ-2ρ,因为2C 的半径为1,则2C MN 的面积o 11sin 452⨯=12. 考点:直角坐标方程与极坐标互化;直线与圆的位置关系【名师点睛】对直角坐标方程与极坐标方程的互化问题,要熟记互化公式,另外要注意互化时要将极坐标方程作适当转化,若是和角,常用两角和与差的三角公式展开,化为可以公式形式,有时为了出现公式形式,两边可以同乘以ρ,对直线与圆或圆与圆的位置关系,常化为直角坐标方程,再解决.10. 【2015高考新课标1,文24】(本小题满分10分)选修4-5:不等式选讲已知函数()12,0f x x x a a =+--> .(I )当1a = 时求不等式()1f x > 的解集;(II )若()f x 图像与x 轴围成的三角形面积大于6,求a 的取值范围.【答案】(Ⅰ)2{|2}3x x <<(Ⅱ)(2,+∞) 【解析】试题分析:(Ⅰ)利用零点分析法将不等式f (x )>1化为一元一次不等式组来解;(Ⅱ)将()f x 化为分段函数,求出()f x 与x 轴围成三角形的顶点坐标,即可求出三角形的面积,根据题意列出关于a 的不等式,即可解出a 的取值范围.试题解析:(Ⅰ)当a =1时,不等式f (x )>1化为|x +1|-2|x-1|>1,等价于11221x x x ≤-⎧⎨--+->⎩或111221x x x -<<⎧⎨++->⎩或11221x x x ≥⎧⎨+-+>⎩,解得223x <<, 所以不等式f (x )>1的解集为2{|2}3x x <<. ……5分 (Ⅱ)由题设可得,12,1()312,112,x a x f x x a x a x a x a --<-⎧⎪=+--≤≤⎨⎪-++>⎩,所以函数()f x 的图像与x 轴围成的三角形的三个顶点分别为21(,0)3a A -,(21,0)B a +,(,+1)C a a ,所以△ABC 的面积为22(1)3a +. 由题设得22(1)3a +>6,解得2a >. 所以a 的取值范围为(2,+∞). ……10分【考点定位】含绝对值不等式解法;分段函数;一元二次不等式解法【名师点睛】对含有两个绝对值的不等式问题,常用“零点分析法”去掉绝对值化为若干个不等式组问题,原不等式的解集是这些不等式组解集的并集;对函数多个绝对值的函数问题,常利用分类整合思想化为分段函数问题,若绝对值中未知数的系数相同,常用绝对值不等式的性质求最值,可减少计算.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年高考真题解答题专项训练:立体几何(文科)教师版1.(本题满分15分)如图,在三棱锥中,,在底面ABC的射影为BC的中点,D为的中点.(1)证明:平面;(2)求直线和平面所成的角的正弦值.【来源】2015年全国普通高等学校招生统一考试文科数学(浙江卷带解析)【答案】(1)见解析;(2)【解析】(1)利用线面垂直的定义得到线线垂直,根据线面垂直的判定证明直线与平面垂直;(2)通过添加辅助线,证明平面,以此找到直线与平面所成角的平面角,在直角三角形中通过确定边长,计算的正弦值.试题解析:(1)设为中点,由题意得平面,所以.因为,所以.所以平面.由,分别为的中点,得且,从而且,所以是平行四边形,所以.因为平面,所以平面.(2)作,垂足为,连结.因为平面,所以.因为,所以平面.所以平面.所以为直线与平面所成角的平面角.由,得由平面,得.由,得.所以考点:1.空间直线、平面垂直关系的证明;2.直线与平面所成的角.视频2.如图四边形ABCD为菱形,G为AC与BD交点,平面,(I)证明:平面平面;(II)若,三棱锥的体积为,求该三棱锥的侧面积.【来源】2015年全国普通高等学校招生统一考试文科数学(新课标Ⅰ带解析)【答案】(1)见解析(2)3+2【解析】试题分析:(Ⅰ)由四边形ABCD为菱形知AC BD,由BE平面ABCD知AC BE,由线面垂直判定定理知AC平面BED,由面面垂直的判定定理知平面平面;(Ⅱ)设AB=,通过解直角三角形将AG、GC、GB、GD用x表示出来,在AEC中,用x表示EG,在EBG中,用x表示EB,根据条件三棱锥的体积为求出x,即可求出三棱锥的侧面积.试题解析:(Ⅰ)因为四边形ABCD为菱形,所以AC BD,因为BE平面ABCD,所以AC BE,故AC平面BED.又AC平面AEC,所以平面AEC平面BED(Ⅱ)设AB=,在菱形ABCD中,由ABC=120°,可得AG=GC=,GB=GD=.因为AE EC,所以在AEC中,可得EG=.由BE平面ABCD,知EBG为直角三角形,可得BE=.由已知得,三棱锥E-ACD的体积.故=2从而可得AE=EC=ED=.所以EAC的面积为3,EAD的面积与ECD的面积均为.故三棱锥E-ACD的侧面积为.考点:线面垂直的判定与性质;面面垂直的判定;三棱锥的体积与表面积的计算;逻辑推理能力;运算求解能力视频3.如图,直三棱柱的底面是边长为2的正三角形,分别是的中点。
(1)证明:平面平面;(2)若直线与平面所成的角为,求三棱锥的体积.【来源】2015年全国普通高等学校招生统一考试文科数学(湖南卷带解析)【答案】(Ⅰ)见解析;(Ⅱ).【解析】试题分析:(1)由面面垂直的判定定理很容易得结论;(2)所求三棱锥底面积容易求得,是本题转化为求三棱锥的高,利用直线与平面所成的角为,作出线面角,进而可求得的值,则可得的长.试题解析:(1)如图,因为三棱柱是直三棱柱,所以,又是正三角形的边的中点,所以又,因此平面而平面,所以平面平面(2)设的中点为,连结,因为是正三角形,所以又三棱柱是直三棱柱,所以因此平面,于是为直线与平面所成的角,由题设,,所以在中,,所以故三棱锥的体积考点:直线与平面垂直的判定定理;直线与平面所成的角;几何体的体积.视频4.(本小题满分13分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P ABCD-中,侧棱PD⊥底面ABCD,且PD CD=,点E是PC的中点,连接,,DE BD BE.(Ⅰ)证明:DE⊥平面PBC.试判断四面体EBCD是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;(Ⅱ)记阳马P ABCD-的体积为1V,四面体EBCD的体积为2V,求12VV的值.【来源】2015年全国普通高等学校招生统一考试文科数学(湖北卷带解析)【答案】(Ⅰ)因为PD⊥底面ABCD,所以PD BC⊥.由底面ABCD为长方形,有BC CD⊥,而PD CD D⋂=,所以BC⊥平面PCD.DE⊂平面PCD,所以BC DE ⊥. 又因为P D C D =,点E 是PC 的中点,所以DE PC ⊥. 而PC BC C ⋂=,所以DE ⊥平面PBC .四面体EBCD 是一个鳖臑;(Ⅱ)124.V V = 【解析】(Ⅰ)因为PD ⊥底面ABCD ,所以PD BC ⊥. 由底面ABCD 为长方形,有BC CD ⊥,而PD CD D ⋂=,所以BC ⊥平面PCD . DE ⊂平面PCD ,所以BC DE ⊥. 又因为P D C D =,点E 是PC 的中点,所以DE PC ⊥. 而PC BC C ⋂=,所以DE ⊥平面PBC . 由BC ⊥平面PCD , DE ⊥平面PBC ,可知四面体EBCD 的四个面都是直角三角形,即四面体EBCD 是一个鳖臑,其四个面的直角分别是,,,.BCD BCE DEC DEB ∠∠∠∠(Ⅱ)由已知, PD 是阳马P ABCD -的高,所以11133ABCD V S PD BC CD PD =⋅=⋅⋅;由(Ⅰ)知, DE 是鳖臑D B C E -的高, BC CE ⊥,所以21136BCE V S DE BC CE DE ∆=⋅=⋅⋅.在Rt △PDC 中,因为PD CD =,点E 是PC 的中点,所以2DE CE ==,于是12123 4.16BC CD PD V CD PD V CE DEBC CE DE ⋅⋅⋅===⋅⋅⋅ 考点:本题考查直线与平面垂直的判定定理、直线与平面垂直的性质定理和简单几何体的体积,属中高档题.视频 5.(本小题满分14分)如图,三角形DC P 所在的平面与长方形CD AB 所在的平面垂直,D C 4P =P =,6AB =,C 3B =.(1)证明:C//B 平面D P A ;(2)证明:C D B ⊥P ;(3)求点C 到平面D P A 的距离.【来源】2015年全国普通高等学校招生统一考试文科数学(广东卷带解析)【答案】(1)证明见解析;(2)证明见解析;(3 【解析】试题分析:(1)由四边形CD AB 是长方形可证C//D B A ,进而可证C//B 平面D P A ;(2)先证C CD B ⊥,再证C B ⊥平面DC P ,进而可证C D B ⊥P ;(3)取CD 的中点E ,连结AE 和PE ,先证PE ⊥平面CD AB ,再设点C 到平面D P A 的距离为h ,利用C D CD V V -P A P-A =三棱锥三棱锥可得h 的值,进而可得点C 到平面D P A 的距离.试题解析:(1)因为四边形CD AB 是长方形,所以C//D B A ,因为C B ⊄平面D P A ,D A ⊂平面D P A ,所以C//B 平面D P A(2)因为四边形CD AB 是长方形,所以C CD B ⊥,因为平面DC P ⊥平面CD AB ,平面DC P 平面CD CD AB =,C B ⊂平面CD AB ,所以C B ⊥平面DC P ,因为D P ⊂平面DC P ,所以C D B ⊥P(3)取CD 的中点E ,连结AE 和PE ,因为D C P =P ,所以CD PE ⊥,在Rt D ∆PE ,因为平面DC P ⊥平面CD AB ,平面DC P 平面CD CD AB =,PE ⊂平面DC P ,所以PE ⊥平面CD AB ,由(2)知:C B ⊥平面DC P ,由(1)知:C//D B A ,所以D A ⊥平面DC P ,因为D P ⊂平面DC P ,所以D D A ⊥P ,设点C 到平面D P A 的距离为h ,因为C D CD V V -P A P-A =三棱锥三棱锥,,所以点C 到平面D P A 的距离是考点:1、线面平行;2、线线垂直;3、点到平面的距离.6.如图,三棱锥P-ABC 中,PA ⊥平面ABC , 1,1,2,60PA AB AC BAC ===∠=.(Ⅰ)求三棱锥P-ABC 的体积;(Ⅱ)证明:在线段PC 上存在点M ,使得AC ⊥BM ,并求PM MC的值. 【来源】2015年全国普通高等学校招生统一考试文科数学(安徽卷带解析)【答案】(Ⅱ)13 【解析】(Ⅰ)解:由题设=1, 可得. 由面 可知是三棱锥的高,又所以三棱锥的体积 (Ⅱ)证:在平面内,过点B 作,垂足为,过作交于,连接.由面知,所以.由于,故面,又面,所以. 在直角中,,从而.由,得.考点:本题主要考查锥体的体积公式、线面垂直的判定定理和其性质定理. 视频 7.如图,长方体1111ABCD A BC D -中, 116,10,8AB BC AA ===,点,E F 分别在1111,A B D C 上, 114A E D F ==,过点,E F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法与理由).(2)求平面α把该长方体分成的两部分体积的比值.【来源】2015年全国普通高等学校招生统一考试文科数学(新课标Ⅱ带解析)【答案】(Ⅰ)见试题解析(Ⅱ)97或79【解析】试题分析:(Ⅰ)分别在,AB CD 上取H,G,使10AH DG ==;长方体被平面α分成两个高为10的直棱柱,可求得其体积比值为97或79试题解析:解:(Ⅰ)交线围成的正方形EHGF 如图:(Ⅱ)作垂足为M,则18EM AA ==,,,因为E H G F是正方形,所以,于是因为长方体被平面α分成两个高为10的直棱柱,所以其体积比值为97(79也正确). 考点:本题主要考查几何体中的截面问题及几何体的体积的计算.视频8.(本题满分12分)如图, AB 是圆O 的直径,点C 是圆O 上异于,A B 的点, PO 垂直于圆O 所在的平面,且1PO =OB =.(Ⅰ)若D 为线段AC 的中点,求证C A ⊥平面D P O ;(Ⅱ)求三棱锥P ABC -体积的最大值;(Ⅲ)若BC =E 在线段PB 上,求CE OE +的最小值.【来源】2015年全国普通高等学校招生统一考试文科数学(福建卷带解析)【答案】(Ⅰ)详见解析;(Ⅱ) 13; 【解析】解法一:(Ⅰ)在C ∆AO 中,因为C OA =O , D 为C A 的中点, 所以C D A ⊥O .又PO 垂直于圆O 所在的平面,所以C PO ⊥A .因为D O ⋂PO =O ,所以C A ⊥平面D P O .(Ⅱ)因为点C 在圆O 上,所以当C O ⊥AB 时, C 到AB 的距离最大,且最大值为1.又2AB =,所以C ∆AB 面积的最大值为12112⨯⨯=. 又因为三棱锥C P -AB 的高1PO =,故三棱锥C P -AB 体积的最大值为111133⨯⨯=.(Ⅲ)在∆POB 中, 1PO =OB =, 90∠POB =,所以PB =同理C P =C C PB =P =B .在三棱锥C P -AB 中,将侧面C B P 绕PB 旋转至平面C'B P ,使之与平面ABP 共面,如图所示.当O , E , C'共线时, C E +OE 取得最小值.又因为OP =OB , C'C'P =B ,所以C'O 垂直平分PB ,即E 为PB 中点.从而C'C'O =OE +E ==亦即C E +OE解法二:(Ⅰ)、(Ⅱ)同解法一.(Ⅲ)在∆POB 中, 1PO =OB =, 90∠POB =,所以45∠OPB =, PB =C P =所以C C PB =P =B ,所以C 60∠PB =.在三棱锥C P -AB 中,将侧面C B P 绕PB 旋转至平面C'B P ,使之与平面ABP 共面,如图所示.当O , E , C'共线时, C E +OE 取得最小值.所以在C'∆O P 中,由余弦定理得: ()2C'1221cos 4560O =+-⨯+1122=+--⎭2=从而C'2O ==所以C E +OE 考点:1、直线和平面垂直的判定;2、三棱锥体积. 视频 9.如图,三棱锥P-ABC 中,平面PAC ⊥平面ABC , ∠ABC=2π,点D 、E 在线段AC 上,且AD=DE=EC=2,PD=PC=4,点F 在线段AB 上,且EF//BC .(Ⅰ)证明:AB ⊥平面PFE.(Ⅱ)若四棱锥P-DFBC 的体积为7,求线段BC 的长.【来源】2015年全国普通高等学校招生统一考试文科数学(重庆卷带解析)【答案】(1)见解析(2) BC=3或【解析】试题分析:(Ⅰ)先由已知易得PE AC ⊥,再注意平面PAC ⊥平面ABC ,且交线为AC ,由面面垂直的性质可得PE ⊥平面ABC ,再由线面垂直的性质可得到AB PE ⊥,再注意到//EF BC ,而BC AB ⊥,从而有AB EF ⊥,那么由线面垂的判定定理可得AB ⊥平面PFE ,(Ⅱ)设BC=x 则可用x 将四棱锥P DFBC -的体积表示出来,由已知其体积等于7,从而得到关于x 的一个一元方程,解此方程,再注意到0x >即可得到BC 的长. 试题解析:证明:如题(20)图.由,DE EC PD PC ==知, E 为等腰PDC ∆中DC 边的中点,故PE AC ⊥,又平面PAC ⊥平面ABC ,平面PAC ⋂平面ABC AC =, PE ⊂平面PAC ,PE AC ⊥,所以PE ⊥平面ABC ,从而PE AB ⊥. 因ABC=,,AB EF 2EF BC π∠⊥故.从而AB 与平面PFE 内两条相交直线PE , EF 都垂直, 所以AB ⊥平面PFE .(2)解:设BC=x ,则在直角ABC ∆中,从而11S AB BC=22ABC ∆=⨯由EFBC ,知23AF AE AB AC ==,得AEF ABC ∆~∆,故224S 39AEF ABC S ∆∆⎛⎫== ⎪⎝⎭,即4S 9AEF ABC S ∆∆=. 由1AD=2AE,11421S S =S S 22999AFB AFE ABC ABC ∆∆∆∆=⋅==从而四边形DFBC 的面积为DFBC 11S S -=29ABC ADF S ∆∆=718=由(1)知,PE PE ⊥平面ABC ,所以PE 为四棱锥P-DFBC 的高. 在直角PEC ∆中,==体积DFBC 117S 73318P DFBC V PE -=⋅⋅=⋅=, 故得42362430x x -+=,解得,由于0x >,可得333x x ==或.所以3BC =或BC =考点:1. 空间线面垂直关系,2. 锥体的体积,3.方程思想.视频10.(本小题满分13分)如图,已知 平面ABC,AB=AC=3,,,点E,F 分别是BC, 的中点.(Ⅰ)求证:EF ∥平面;(Ⅱ)求证:平面平面.(Ⅲ)求直线与平面所成角的大小.【来源】2015年全国普通高等学校招生统一考试文科数学(天津卷带解析)【答案】(Ⅰ)见试题解析;(Ⅱ)见试题解析;(Ⅲ).【解析】(Ⅰ)要证明EF∥平面, 只需证明且EF平面;(Ⅱ)要证明平面平面,可证明,;(Ⅲ)取中点N,连接,则就是直线与平面所成角,Rt△中,由得直线与平面所成角为.试题解析:(Ⅰ)证明:如图,连接,在△中,因为E和F分别是BC,的中点,所以,又因为EF平面, 所以EF∥平面.(Ⅱ)因为AB=AC,E为BC中点,所以,因为平面ABC,所以平面ABC,从而,又,所以平面,又因为平面,所以平面平面.(Ⅲ)取中点M和中点N,连接,因为N和E分别为,BC中点,所以,,故,,所以,,又因为平面,所以平面,从而就是直线与平面所成角,在△中,可得AE=2,所以=2,因为,所以又由,有,在Rt△中,可得,在Rt△中,因此,所以,直线与平面所成角为.考点:本题主要考查空间中线面位置关系的证明,直线与平面所成的角等基础知识,考查空间想象能力及推理论证能力.视频11.(本小题满分12分)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.(Ⅰ)请按字母F,G,H标记在正方体相应地顶点处(不需要说明理由)(Ⅱ)判断平面BEG与平面ACH的位置关系.并说明你的结论.(Ⅲ)证明:直线DF平面BEG【来源】2015年全国普通高等学校招生统一考试文科数学(四川卷带解析)【答案】见解析【解析】(Ⅰ)点F,G,H的位置如图所示(Ⅱ)平面BEG∥平面ACH.证明如下因为ABCD-EFGH为正方体,所以BC∥FG,BC=FG又FG∥EH,FG=EH,所以BC∥EH,BC=EH于是BCEH为平行四边形所以BE∥CH又CH⊂平面ACH,BE⊄平面ACH,所以BE∥平面ACH同理BG∥平面ACH又BE∩BG=B所以平面BEG∥平面ACH(Ⅲ)连接FH因为ABCD-EFGH为正方体,所以DH⊥平面EFGH因为EG⊂平面EFGH,所以DH⊥EG⊥又EG ⊥FH ,EG ∩FH =O ,所以EG ⊥平面BFHD 又DF ⊂平面BFDH ,所以DF ⊥EG 同理DF ⊥BG 又EG ∩BG =G 所以DF ⊥平面BEG.考点:本题主要考查简单空间图形的直观图、空间线面平行与垂直的判定与性质等基础知识,考查空间想象能力、推理论证能力.12.如图1,在直角梯形ABCD 中,E 是AD 的中点,O 是OC 与BE 的交点,将ABE ∆沿BE 折起到图2中1A BE ∆的位置,得到四棱锥1A BCDE -.(Ⅰ)证明:CD ⊥平面1AOC ; (Ⅱ)当平面1A BE ⊥平面BCDE 时,四棱锥1A BCDE -的体积为求a 的值. 【来源】2015年全国普通高等学校招生统一考试文科数学(陕西卷带解析) 【答案】(Ⅰ) 证明见解析,详见解析;(Ⅱ) 6a =. 【解析】试题分析:(Ⅰ) 在图1中,,E 是AD 的中点,所以四边形ABCE 是正方形,故BE AC ⊥,又在图2中,1,BE AO BE OC ⊥⊥,从而BE ⊥平面1AOC ,又//DE BC 且DE BC =,所以//CD BE ,即可证得CD ⊥平面1AOC ; (Ⅱ)由已知,平面1A BE ⊥平面BCDE ,且平面1A BE 平面BCDE BE = ,又由(Ⅰ)知,1AO BE ⊥,所以1AO ⊥平面BCDE ,即1AO 是四棱锥1A BCDE -的高,易求得平行四边形BCDE 面积2S BC AB a =⋅=,从而四棱锥1A BCDE -的为,得6a =. 试题解析:(Ⅰ)在图1中,,E 是AD 的中点所以BE AC ⊥,即在图2中,1,BE AO BE OC ⊥⊥ 从而BE ⊥平面1AOC 又//CD BE所以CD ⊥平面1AOC . (Ⅱ)由已知,平面1A BE ⊥平面BCDE , 且平面1A BE平面BCDE BE =又由(Ⅰ)知,1AO BE ⊥,所以1AO ⊥平面BCDE , 即1AO 是四棱锥1A BCDE -的高, 由图1,平行四边形BCDE 面积2S BC AB a =⋅=, 从而四棱锥1A BCDE -的为,得6a =. 考点:1.线面垂直的判定;2.面面垂直的性质定理;3.空间几何体的体积. 13.如图,三棱台DEF ABC -中, 2AB DE G H =,,分别为AC BC ,的中点.(Ⅰ)求证: //BD 平面FGH ;(Ⅱ)若CF BC AB BC ⊥⊥,,求证:平面BCD ⊥平面EGH .【来源】2015年全国普通高等学校招生统一考试文科数学(山东卷带解析) 【答案】证明见解析【解析】(Ⅰ)证法一:连接,.DG CD 设CD GF M ⋂=,连接MH ,在三棱台DEF ABC -中, 2AB DE G =,分别为AC 的中点,可得//,DF GC DF GC =,所以四边形DFCG 是平行四边形,则M 为CD 的中点,又H 是BC 的中点,所以//HM BD ,又HM ⊂平面FGH , BD ⊄平面FGH ,所以//BD 平面FGH .证法二:在三棱台DEF ABC -中,由2,BC EF H =为BC 的中点, 可得//,,BH EF BH EF =所以HBEF 为平行四边形,可得//.BE HF 在ABC ∆中, G H ,分别为AC BC ,的中点, 所以//,GH AB 又GH HF H ⋂=, 所以平面//FGH 平面ABED , 因为BD ⊂平面ABED , 所以//BD 平面FGH .(Ⅱ)证明:连接HE .因为G H ,分别为AC BC ,的中点,所以//,GH AB 由,AB BC ⊥得GH BC ⊥,又H 为BC 的中点,所以//,,EF HC EF HC =因此四边形EFCH 是平行四边形,所以//.CF HE又CF BC ⊥,所以HE BC ⊥.又,HE GH ⊂平面EGH , HE GH H ⋂=,所以BC ⊥平面EGH , 又BC ⊂平面BCD ,所以平面BCD ⊥平面.EGH 考点:1.平行关系;2.垂直关系.视频14.如图,在三棱锥 中,平面 平面 , 为等边三角形, 且 , , 分别为 , 的中点.(1)求证: 平面 ; (2)求证:平面 平面 ; (3)求三棱锥 的体积.【来源】2015年全国普通高等学校招生统一考试文科数学(北京卷带解析) 【答案】(1)见解析;(2)见解析;(3).【解析】试题分析:(Ⅰ)利用三角形的中位线得出OM ∥VB ,利用线面平行的判定定理证明VB ∥平面MOC ;(Ⅱ)证明OC ⊥平面VAB ,即可证明平面MOC ⊥平面VAB ;(Ⅲ)利用等体积法求三棱锥A-MOC 的体积即可试题解析:(Ⅰ)证明:∵O,M分别为AB,VA的中点,∴OM∥VB,∵VB平面MOC,OM平面MOC,∴VB∥平面MOC;(Ⅱ)证明:∵AC=BC,O为AB的中点,∴OC⊥AB,又∵平面VAB⊥平面ABC,平面 ∩平面VAB=AB,且OC平面ABC,∴OC⊥平面VAB,∵OC平面MOC,∴平面MOC⊥平面VAB(Ⅲ)在等腰直角三角形中,,所以.所以等边三角形的面积.又因为平面,所以三棱锥的体积等于.又因为三棱锥的体积与三棱锥的体积相等,所以三棱锥的体积为.考点:平面与平面垂直的判定;直线与平面平行的判定;用向量证明平行视频。
