全国高考文科数学立体几何综合题型汇总
高考数学立体几何题型总结

高考数学立体几何题型总结
高考数学中的立体几何题型是考生们必须要掌握的一部分,以下是一些常见的立体几何题型总结:
1. 空间图形的计算:考生需要根据已知条件计算出空间图形的表面积和体积。
2. 空间向量的运算:考生需要掌握向量的基本运算,如加减法、数乘、点积、叉积等。
3. 空间直线和平面的交点:考生需要了解两个平面或两条直线的交点的求法,以及如何计算直线和平面的交点。
4. 空间立体角的计算:考生需要了解如何计算空间立体角,通常需要用到平面向量的知识。
5. 空间几何体的判定:考生需要掌握判定空间几何体的性质,如判断平行六面体、正四面体、正方体等。
以上是高考数学中常见的立体几何题型总结,掌握这些知识点可以帮助考生在考试中更加得心应手。
- 1 -。
各个题型文科立体几何高考真题

题型一:求体积1,2019年全国统一高考数学试卷(文科)(新课标Ⅱ)如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥11E BB C C 的体积.2,2019年全国统一高考数学试卷(文科)(新课标Ⅰ)如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求点C到平面C1DE的距离.3.2017年全国普通高等学校招生统一考试文科数学(新课标1卷)如图,在四棱锥P ABCD -中,AB CD ∥,且90BAP CDP ∠=∠=︒.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,且四棱锥P ABCD -的体积为83,求该四棱锥的侧面积.题型四:折叠图形4.2019年全国统一高考数学试卷(文科)(新课标Ⅲ)图1是由矩形,ADEB Rt ABC ∆和菱形BFGC 组成的一个平面图形,其中1,2AB BE BF ===, 60FBC ∠=,将其沿,AB BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明图2中的,,,A C G D 四点共面,且平面ABC ⊥平面BCGE ;(2)求图2中的四边形ACGD 的面积.1【详解】(1)因为在长方体1111ABCD A B C D -中,11B C ⊥平面11AA B B ; BE ⊂平面11AA B B ,所以11B C BE ⊥,又1BE EC ⊥,1111B C EC C ⋂=,且1EC ⊂平面11EB C ,11B C ⊂平面11EB C ,所以BE ⊥平面11EB C ;(2)设长方体侧棱长为2a ,则1AE A E a ==,由(1)可得1EB BE ⊥;所以22211EB BE BB +=,即2212BE BB =,又3AB =,所以222122AE AB BB +=,即222184a a +=,解得3a =; 取1BB 中点F ,连结EF ,因为1AE A E =,则EF AB ∥;所以EF ⊥平面11BB C C ,所以四棱锥11E BB C C -的体积为1111111136318333E BB C C BB C C V S EF BC BB EF -=⋅=⋅⋅⋅=⨯⨯⨯=矩形.2,【详解】(1)连接ME ,1B CM ,E 分别为1BB ,BC 中点 ME ∴为1B BC ∆的中位线1//ME B C ∴且112ME B C = 又N 为1A D 中点,且11//A D B C 1//ND B C ∴且112ND B C = //ME ND ∴ ∴四边形MNDE 为平行四边形//MN DE ∴,又MN ⊄平面1C DE ,DE ⊂平面1C DE//MN ∴平面1C DE(2)在菱形ABCD 中,E 为BC 中点,所以DE BC ⊥,根据题意有3DE =,117C E =,因为棱柱为直棱柱,所以有DE ⊥平面11BCC B ,所以1DE EC ⊥,所以113172DEC S ∆=⨯⨯, 设点C 到平面1C DE 的距离为d ,根据题意有11C CDE C C DE V V --=,则有11113171343232d ⨯⨯⨯⨯=⨯⨯⨯⨯, 解得4171717d ==, 所以点C 到平面1C DE 的距离为41717. 3试题解析:(1)由已知90BAP CDP ∠=∠=︒,得AB AP ⊥,CD PD ⊥. 由于AB CD ∥,故AB PD ⊥,从而AB ⊥平面PAD .又AB 平面PAB ,所以平面PAB ⊥平面PAD .(2)在平面PAD 内作PE AD ⊥,垂足为E .由(1)知,AB ⊥面PAD ,故AB PE ⊥,可得PE ⊥平面ABCD .设AB x =,则由已知可得2AD x =,22PE x =. 故四棱锥P ABCD -的体积31133P ABCD V AB AD PE x -=⋅⋅=. 由题设得31833x =,故2x =. 从而2PA PD ==,22AD BC ==,22PB PC ==.可得四棱锥P ABCD -的侧面积为111222PA PD PA AB PD DC ⋅+⋅+⋅ 21sin606232BC +︒=+4.(1)证://AD BE ,//BF CG ,又因为E 和F 粘在一起.∴//AD CG ,A ,C ,G ,D 四点共面.又,AB BE AB BC ⊥⊥.AB ∴⊥平面BCGE ,AB ⊂平面ABC ,∴平面ABC ⊥平面BCGE ,得证.(2)取CG 的中点M ,连结,EM DM .因为//AB DE ,AB ⊥平面BCGE ,所以DE ⊥平面BCGE ,故DE CG ⊥,由已知,四边形BCGE 是菱形,且60EBC ∠=得EM CG ⊥,故CG ⊥平面DEM . 因此DM CG ⊥.在Rt DEM △中,DE=1,3EM =,故2DM =.所以四边形ACGD 的面积为4.。
高中数学立体几何大题综合归类(原卷版)

高中数学立体几何大题综合归类(原卷版)目录题型01平行:无交线型 (1)题型02平行:线面平行探索性 (3)题型03平行:面面平行探索性 (4)题型04垂直:线面垂直探索性 (5)题型05垂直:面面垂直翻折探索性 (7)题型06证明与建系:斜棱柱垂面法建系 (8)题型07证明与建系:斜棱柱垂线法建系 (10)题型08证明与建系:三棱柱投影法建系 (12)题型09证明与建系:角平分线法建系 (13)题型10二面角延长线法 (15)题型11翻折型 (16)题型12台体型 (18)高考练场..............................................................................................................................................................................19热点题型归纳题型01平行:无交线型【解题攻略】两个平面相交:1.两点确定一条直线,只需确定两平面的两个公共点即可2.由于两平面有一个公共点A ,再找一个公共点即可确定交线3.一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行,在平面内,过两平面的公共点作直线与已知直线平行,则此直线即为两平面的交线【典例1-1】如图,在平行四边形ABCD 中,60ABC ∠=︒,24==A D A B ,E 为AD 的中点,以EC 为折痕将CDE △折起,使点D 到达点P 的位置,且=10PB ,F ,G 分别为BC ,PE 的中点.(1)证明://PB 平面AFG .(2)若平面PAB 与平面PEF 的交线为l ,求直线l 与平面PBC 所成角的正弦值.【变式1-1】如图所示,在四棱柱1111ABCD A B C D -中,底面ABCD 是等腰梯形,//AB CD ,24AB CD ==,0=60BAD ∠,侧棱1DD ⊥底面ABCD 且1DD DC =.(1)指出棱1CC 与平面1ADB 的交点E 的位置(无需证明);(2)求点B 到平面1ADB 的距离.【变式1-2】如图,P 为圆锥的顶点,O 为圆锥底面的圆心,圆锥的底面直径4AB =,母线22PH =,M 是PB 的中点,四边形OBCH 为正方形.设平面POH ⋂平面PBC l =,证明://l BC ;.题型02平行:线面平行探索性【解题攻略】平行的常用构造方法①三角形中位线法;②平行四边形线法;③比例线段法.注意:平行构造主要用于:①异面直线求夹角;②平行关系的判定.【典例1-1】如图,在三棱柱111ABC A B C -中,侧面11AA C C ⊥底面ABC ,112AC A C A A ===,AB BC =,且AB BC ⊥,O 为AC 中点.(1)求证AC ⊥平面1A OB(2)在1BC 上是否存在一点E ,使得OE 平面1A AB ,若不存在,说明理由;若存在,确定点E 的位置.【变式1-1】如图,四边形ABCD 中,AB AD ⊥,//AD BC ,6AD =,24BC AB ==,E ,F 分别在BC ,AD 上,//EF AB ,现将四边形ABCD 沿EF 折起,使BE EC ⊥.(1)若1BE =,在折叠后的线段AD 上是否存在一点P ,使得//CP 平面ABEF ?若存在,求出AP PD 的值;若不存在,说明理由.(2)求三棱锥A CDF -的体积的最大值,并求出此时点F 到平面ACD 的距离.【变式1-2】如图,在直角梯形ABCD 中,AB ∥DC ,∠BAD =90°,AB =4,AD =2,DC =3,点E 在CD 上,且DE =2,将△ADE 沿AE 折起,使得平面ADE ⊥平面ABCE ,G 为AE 中点.(1)求证:DG ⊥平面ABCE ;(2)求四棱锥D -ABCE 的体积;(3)在线段BD 上是否存在点P ,使得CP ∥平面ADE ?若存在,求BP BD的值;若不存在,请说明理由.题型03平行:面面平行探索性【解题攻略】证明平行(1)线线平行:设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)线面平行:设直线l 的方向向量为v ,平面α的法向量为u ,则l ∥α或l ⊂α⇔v ⊥u .(3)面面平行:设平面α和β的法向量分别为u 1,u 2,则α∥β⇔u 1∥u 2.【典例1-1】在三棱柱111ABC A B C 中,(1)若,,,E F G H 分别是1111,,,AB AC A B AC 的中点,求证:平面1//EFA 平面BCHG .(2)若点1,D D 分别是11,AC AC 上的点,且平面1//BC D 平面11AB D ,试求AD DC 的值.【变式1-1】.在长方体1111ABCD A B C D -中,1222AB BC AA ===,P 为11A B 的中点.已知过点1 A的平面α与平面1BPC 平行,平面α与直线11,AB C D 分别相交于点M ,N ,请确定点M ,N的位置;【变式1-2】已知正方体1111ABCD A B C D -中,P 、Q 分别为对角线BD 、1CD 上的点,且123CQ BP QD PD ==.(1)求证://PQ 平面11A D DA ;(2)若R 是AB 上的点,AR AB的值为多少时,能使平面//PQR 平面11A D DA ?请给出证明.题型04垂直:线面垂直探索性【解题攻略】垂直的常见构造:①等腰三角形三线合一法;②勾股定理法;③投影法.④菱形的对角线互相垂直【典例1-1】已知正方体1111ABCD A B C D -的棱长为2,E 、F 、G 分别是1AA 、11A B 、11AD 的中点.(1)求证://EF 平面1BC D ;(2)在线段BD 上是否存在点H ,使得EH ⊥平面1BC D ?若存在,求线段BH 的长;若不存在,请说明理由;(3)求EF 到平面1BC D 的距离.【变式1-1】如图,在四棱锥S -ABCD 中,四边形ABCD 是边长为2的菱形,∠ABC =60°,△SAD 为正三角形.侧面SAD ⊥底面ABCD ,E ,F 分别为棱AD ,SB 的中点.(1)求证:AF ∥平面SEC ;(2)求证:平面ASB ⊥平面CSB ;(3)在棱SB 上是否存在一点M ,使得BD ⊥平面MAC ?若存在,求BMBS 的值;若不存在,请说明理由.【变式1-2】如图,在直三棱柱111ABC A B C -中,90ABC ∠= ,1AB BC ==,13AA =,M 为棱AC 上靠近A 的三等分点,N 为棱11AB 上靠近1A 的三等分点.(1)证明://MN 平面11BB C C ;(2)在棱1BB 上是否存在点D ,使得1C D ⊥面1B MN ?若存在,求出1B D 的大小并证明;若不存在,说明理由.题型05垂直:面面垂直翻折探索性【解题攻略】翻折1.翻折前后,在同一平平面内的点线关系不变2.翻折过程中是否存在垂直或者平行等特殊位置关系3.翻折过程中,角度是否为定值4.翻折过程中,体积是否存在变化【典例1-1】如图,在四棱锥P -ABCD 中,PA ⊥平面ABCD ,PA =AB =BC =3,AD =CD =1,∠ADC =120°,点M是AC 与BD 的交点,点N 在线段PB 上,且PN =14PB .(1)证明:MN //平面PDC ;(2)在线段BC 上是否存在一点Q ,使得平面MNQ ⊥平面PAD ,若存在,求出点Q 的位置;若不存在,请说明理由.【变式1-1】如图,在三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在,请确定G点的位置;若不存在,请说明理由.【变式1-2】如图(1),点E是直角梯形ABCD底边CD上的一点,∠ABC=90°,BC=CE=1,AB=DE =2,将DAE沿AE折起,使得D-AE-B成直二面角,连接CD和BD,如图(2).(1)求证:平面ABD 平面BCD;(2)在线段BD上确定一点F,使得CF∥平面ADE.题型06证明与建系:斜棱柱垂面法建系【解题攻略】斜棱柱垂线型建系如果存在垂线(投影型)斜棱柱,则可以直接借助垂线作为z轴建系,下底面,可以寻找或者做出一对垂线作为xy轴。
全国高考文科数学立体几何综合题型汇总

新课标立体几何常考证明题汇总ABCDE,F,G,HAB,BC,CD,DA的中点分别是边1、已知四边形是空间四边形,(1)求证:EFGH是平行四边形23,AC=2,EG=2。
求异面直线AC、BD所成的角和(2)若EGBD=、BD所成的角。
1BD?,EHEH//BD ABD?AD,E,HAB中,∵证明:在分别是的中点∴21EFGHBDFG?FG//BD,FG?FG,EHEH//是平行四边形。
同理,∴四边形∴2°(2) 90 30 °考点:证平行(利用三角形中位线),异面直线所成的角ABCD ABE BD?BCAC,AD?是、如图,已知空间四边形2,中,的中点。
?AB CDE;平面求证:(1)ABC?CDE平面。
(2)平面BC?AC??CE?AB证明:(1)?AE?BE?AD?BD??DE?AB同理,?AE?BE?CE?DE?ECDE?AB平面又∵∴CDE?AB 1)有平面2()由(AB?ABCCDE?ABC∴平面平面又∵平面,考点:线面垂直,面面垂直的判定ABCD?ABCDAA E中,的中点,是3、如图,在正方体11111AC//BDE平面求证:。
1ACOEO BD,于证明:连接交,连接OAC AA E的中点的中点,∵为为1EO AACEO//AC为三角形∴的中位线∴11EO AC BDEBDE在平面在平面内,外又1AC//BDE平面。
∴1考点:线面平行的判定AD?SBCAD?SC?ABCSA?ABC90??ACB.,面,面4、已知求证:,中∵?ACB?90?BC?AC证明:°SA?ABC?SA?BC又面?BC?SAC面?BC?ADSC?AD,SC?BC?C?AD?SBC又面考点:线面垂直的判定ABCD?ABCD OABCD对角线的交点5、已知正方体是底,. 1111ABDAC?ABD.O C∥面面;(2) 求证:(1)111111AC?BD?OAOAC,设1)连结证明:,连结(11111111DBCABCD?AACCA?是平行四边形是正方体∵111111ACAC?且∴AC∥AC 1111O?AOCACOAC,O,且O的中点,∴C又∥分别是AO1111111OAOC?是平行四边形11??CO∥AO,AODABABABDDCO?面∴CO∥面面,11111111111D?BDABC?CC?CC2()面111!1111D∵AC?BDB即CAC???BD面AC,又11111111111D??DBAC?ADAD同理可证又,111111?ABDAC?面111考点:线面平行的判定(利用平行四边形),线面垂直的判定AC?平面B'D'DBBD'?平面ACB''B'C'DABCD?A'. )(2);6、正方体中,求证:(1考点:线面垂直的判定7、正方体ABCD—ABCD中.(1)求证:平面ABD∥平面BDC;1111111 (2)若E、F分别是AA,CC的中点,求证:平面EBD∥平面FBD.1111证明:(1)由BB∥DD,得四边形BBDD是平行四边形,∴BD∥BD,111111?平面BDDC,BD ?平面BDC,B又111111∴BD ∥平面BDC.11同理AD∥平面BDC.111而AD∩BD=D,∴平面ABD∥平面BCD.111 (2)由BD∥BD,得BD∥平面EBD.取BB中点G,∴AE∥BG.111111从而得BE∥AG,同理GF∥AD.∴AG∥DF.∴BE∥DF.∴DF∥平面EBD.∴平面EBD∥平面FBD.111111考点:线面平行的判定(利用平行四边形)2AC?EF ABCDBC,E,FAD,AC?BD,的中点,8、四面体中,且分别为2?BDC?90BD?ACD平面,求证:1//ACCDGEGBC,,FGADEGF,E的中点,∴,连结的中点,∵证明:取分别为?2111//2222FGFGEF?BDFG??ACEGAC?EFG?,AC?BD,又,∴在∴中,?222 AC?CD?C90??BDCCD?ACBD?FGBD?EG,又,∴∴,即,BD?ACD∴平面考点:线面垂直的判定,三角形中位线,构造直角三角形PPABMABN?ABCPC?,CBPA?PB上的点,9、如图是是平面是所在平面外一点,,的中点,AN?3NB?APB?90AB?2?ABBC?4MNMN的长。
高考文科数学立体几何题型与方法(文科)

高考文科数学立体几何题型与方法〔文科〕一、考点回顾 1.平面〔1〕平面的基本性质:掌握三个公理与推论,会说明共点、共线、共面问题。
〔2〕证明点共线的问题,一般转化为证明这些点是某两个平面的公共点〔依据:由点在线上,线在面内,推出点在面内〕,这样,可根据公理2证明这些点都在这两个平面的公共直线上。
〔3〕证明共点问题,一般是先证明两条直线交于一点,再证明这点在第三条直线上,而这一点是两个平面的公共点,这第三条直线是这两个平面的交线。
〔4〕证共面问题一般用落入法或重合法。
〔5〕经过不在同一条直线上的三点确定一个面. 2. 空间直线.〔1〕空间直线位置分三种:相交、平行、异面. 相交直线—共面有反且有一个公共点;平行直线—共面没有公共点;异面直线—不同在任一平面内。
〔2〕异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.〔不在任何一个平面内的两条直线〕〔3〕平行公理:平行于同一条直线的两条直线互相平行.〔4〕等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,则这两个角相等推论:如果两条相交直线和另两条相交直线分别平行,则这两组直线所成锐角〔或直角〕相等.〔5〕两异面直线的距离:公垂线的长度.空间两条直线垂直的情况:相交〔共面〕垂直和异面垂直.21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. 〔l 1或l 2在这个做出的平面内不能叫l 1与l 2平行的平面〕3. 直线与平面平行、直线与平面垂直.〔1〕空间直线与平面位置分三种:相交、平行、在平面内.〔2〕直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,则这条直线和这个平面平行.〔"线线平行,线面平行"〕〔3〕直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,则这条直线和交线平行.〔"线面平行,线线平行"〕〔4〕直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直.PO A a4 若PA⊥α,a⊥AO,得a⊥PO〔三垂线定理〕,得不出α⊥PO. 因为a⊥PO,但PO不垂直OA.5 三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,则这两条直线垂直于这个平面.〔"线线垂直,线面垂直"〕直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,则另一条也垂直于这个平面.推论:如果两条直线同垂直于一个平面,则这两条直线平行.〔5〕a.垂线段和斜线段长定理:从平面外一点向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.[注]:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.〔×〕]b.射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,则这点在平面内的射影在这个角的平分线上。
立体几何(7大题型)(解析版)2024年高考数学立体几何大题突破

立体几何立体几何是高考数学的必考内容,在大题中一般分两问,第一问考查空间直线与平面的位置关系证明;第二问考查空间角、空间距离等的求解。
考题难度中等,常结合空间向量知识进行考查。
2024年高考有很大可能延续往年的出题方式。
题型一:空间异面直线夹角的求解1(2023·上海长宁·统考一模)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)求证:AO⊥CD;(2)若BD⊥DC,BD=DC,AO=BO,求异面直线BC与AD所成的角的大小.【思路分析】(1)利用面面垂直的性质、线面垂直的性质推理即得.(2)分别取AB,AC的中点M,N,利用几何法求出异面直线BC与AD所成的角.【规范解答】(1)在三棱锥A-BCD中,由AB=AD,O为BD的中点,得AO⊥BD,而平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊂平面ABD,因此AO⊥平面BCD,又CD⊂平面BCD,所以AO⊥CD.(2)分别取AB,AC的中点M,N,连接OM,ON,MN,于是MN⎳BC,OM⎳AD,则∠OMN是异面直线BC与AD所成的角或其补角,由(1)知,AO ⊥BD ,又AO =BO ,AB =AD ,则∠ADB =∠ABD =π4,于是∠BAD =π2,令AB =AD =2,则DC =BD =22,又BD ⊥DC ,则有BC =BD 2+DC 2=4,OC =DC 2+OD 2=10,又AO ⊥平面BCD ,OC ⊂平面BCD ,则AO ⊥OC ,AO =2,AC =AO 2+OC 2=23,由M ,N 分别为AB ,AC 的中点,得MN =12BC =2,OM =12AD =1,ON =12AC =3,显然MN 2=4=OM 2+ON 2,即有∠MON =π2,cos ∠OMN =OM MN =12,则∠OMN =π3,所以异面直线BC 与AD 所成的角的大小π3.1、求异面直线所成角一般步骤:(1)平移:选择适当的点,线段的中点或端点,平移异面直线中的一条或两条成为相交直线.(2)证明:证明所作的角是异面直线所成的角.(3)寻找:在立体图形中,寻找或作出含有此角的三角形,并解之.(4)取舍:因为异面直线所成角θ的取值范围是0,π2,所以所作的角为钝角时,应取它的补角作为异面直线所成的角.2、可通过多种方法平移产生,主要有三种方法:(1)直接平移法(可利用图中已有的平行线);(2)中位线平移法;(3)补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).3、异面直线所成角:若n 1 ,n 2分别为直线l 1,l 2的方向向量,θ为直线l 1,l 2的夹角,则cos θ=cos <n 1 ,n 2 > =n 1 ⋅n 2n 1 n 2.1(2023·江西萍乡·高三统考期中)如图,在正四棱台ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点.(1)证明:EF ⎳平面AB1C 1D ;(2)若AB =2A 1B 1,且正四棱台的侧面积为9,其内切球半径为22,O 为ABCD 的中心,求异面直线OB 1与CC 1所成角的余弦值.【答案】(1)证明见解析;(2)45【分析】(1)根据中位线定理,结合线面平行判定定理以及面面平行判定定理,利用面面平行的性质,可得答案;(2)根据题意,结合正四棱台的几何性质,求得各棱长,利用线线角的定义,可得答案.【解析】(1)取CC 1中点G ,连接GE ,GF ,如下图:在梯形BB 1C 1C 中,E ,G 分别为BB 1,CC 1的中点,则EG ⎳B 1C 1,同理可得FG ⎳C 1D ,因为EG ⊄平面AB 1C 1D ,B 1C 1⊂平面AB 1C 1D ,所以EG ⎳平面AB 1C 1D ,同理可得GF ⎳平面AB 1C 1D ,因为EG ∩FG =G ,EG ,FG ⊆平面EFG ,所以平面EFG ⎳平面AB 1C 1D ,又因为EF ⊆平面EFG ,所以EF ⎳平面AB 1C 1D ;(2)连接AC ,BD ,则AC ∩BD =O ,连接A 1O ,A 1C 1,B 1O ,在平面BB 1C 1C 中,作B 1N ⊥BC 交BC 于N ,在平面BB 1D 1D 中,作B 1M ⊥BD 交BD 于M ,连接MN ,如下图:因为AB =2A 1B 1,则OC =A 1C 1,且OC ⎳A 1C 1,所以A 1C 1CO 为平行四边形,则A 1O ⎳CC 1,且A 1O =CC 1,所以∠A 1OB 1为异面直线OB 1与CC 1所成角或其补角,同理可得:B 1D 1DO 为平行四边形,则B 1O =D 1D ,在正四棱台ABCD -A 1B 1C 1D 1中,易知对角面BB 1D 1D ⊥底面ABCD ,因为平面ABCD ∩平面BB 1D 1D =BD ,且B 1M ⊥BD ,B 1M ⊂平面BB 1D 1D ,所以B 1M ⊥平面ABCD ,由内切球的半径为22,则B 1M =2,在等腰梯形BB 1C 1C 中,BC =2B 1C 1且B 1N ⊥BC ,易知BN =14BC ,同理可得BM =14BD ,在△BCD 中,BN BC=BM BD =14,则MN =14CD ,设正方形ABCD 的边长为4x x >0 ,则正方形A 1B 1C 1D 1的边长为2x ,MN =x ,由正四棱台的侧面积为9,则等腰梯形BB 1C 1C 的面积S =94,因为B 1M ⊥平面ABCD ,MN ⊂平面ABCD ,所以B 1M ⊥MN ,在Rt △B 1MN ,B 1N =B 1M 2+MN 2=2+x 2,可得S =12⋅B 1N ⋅B 1C 1+BC ,则94=12×2+x 2×4x +2x ,解得x =12,所以BC =2,B 1C 1=1,BN =14BC =12,B 1N =32,则A 1B 1=1,在Rt △BB 1N 中,BB 1=B 1N 2+BN 2=102,则CC 1=DD 1=102,所以在△A 1OB 1中,则cos ∠A 1OB 1=A 1O 2+B 1O 2-A 1B 212⋅A 1O ⋅B 1O=1022+102 2-12×102×102=45,所以异面直线OB 1与CC 1所成角的余弦值为45.2(2023·辽宁丹东·统考二模)如图,平行六面体ABCD -A 1B 1C 1D 1的所有棱长都相等,平面CDD 1C 1⊥平面ABCD ,AD ⊥DC ,二面角D 1-AD -C 的大小为120°,E 为棱C 1D 1的中点.(1)证明:CD ⊥AE ;(2)点F 在棱CC 1上,AE ⎳平面BDF ,求直线AE 与DF 所成角的余弦值.【答案】(1)证明见解析;(2)37【分析】(1)根据面面垂直可得线面垂直进而得线线垂直,由二面角定义可得∠D 1DC =120°,进而根据中点得线线垂直即可求;(2)由线面平行的性质可得线线平行,由线线角的几何法可利用三角形的边角关系求解,或者建立空间直角坐标系,利用向量的夹角即可求解.【解析】(1)因为平面CDD 1C 1⊥平面ABCD ,且两平面交线为DC ,AD ⊥DC ,AD ⊂平面ABCD , 所以AD ⊥平面CDD 1C 1,所以AD ⊥D 1D ,AD ⊥DC ,∠D 1DC 是二面角D 1-AD -C 的平面角,故∠D 1DC =120°.连接DE ,E 为棱C 1D 1的中点,则DE ⊥C 1D 1,C 1D 1⎳CD ,从而DE ⊥CD .又AD ⊥CD ,DE ∩AD =D ,DE ,AD ⊂平面AED ,所以CD ⊥平面AED ,ED ⊂平面AED ,因此CD ⊥AE .(2)解法1:设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.连AC 交BD 于点O ,连接CE 交DF 于点G ,连OG .因为AE ⎳平面BDF ,AE ⊂平面AEC ,平面AEC ∩平面BDF =OG ,所以AE ∥OG ,因为O 为AC 中点,所以G 为CE 中点,故OG =12AE =72.且直线OG 与DF 所成角等于直线AE 与DF 所成角.在Rt △EDC 中,DG =12CE =72,因为OD =2,所以cos ∠OGD =722+72 2-(2)22×72×72=37.因此直线AE 与DF 所成角的余弦值为37.解法2;设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.取DC 中点为G ,连接EG 交DF 于点H ,则EG =DD 1=2.连接AG 交BD 于点I ,连HI ,因为AE ⎳平面BDF ,AE ⊂平面AGE ,平面AGE ∩平面BDF =IH ,所以AE ∥IH .HI 与DH 所成角等于直线AE 与DF 所成角.正方形ABCD 中,GI =13AG ,DI =13DB =223,所以GH =13EG ,故HI =13AE =73.在△DHG 中,GH =13EG =23,GD =1,∠EGD =60°,由余弦定理DH =1+49-1×23=73.在△DHI 中,cos ∠DHI =732+73 2-223 22×73×73=37.因此直线AE 与DF 所成角的余弦值为37.解法3:由(1)知DE ⊥平面ABCD ,以D 为坐标原点,DA为x 轴正方向,DA为2个单位长,建立如图所示的空间直角坐标系D -xyz .由(1)知DE =3,得A 2,0,0 ,B 2,2,0 ,C 0,2,0 ,E (0,0,3),C 1(0,1,3).则CC 1=(0,-1,3),DC =(0,2,0),AE =(-2,0,3),DB =(2,2,0).由CF =tCC 1 0≤t ≤1 ,得DF =DC +CF =(0,2-t ,3t ).因为AE ⎳平面BDF ,所以存在唯一的λ,μ∈R ,使得AE =λDB +μDF=λ2,2,0 +μ(0,2-t ,3t )=2λ,2λ+2μ-tμ,3μt ,故2λ=-2,2λ+2μ-tμ=0,3μt =3,解得t =23,从而DF =0,43,233 .所以直线AE 与DF 所成角的余弦值为cos AE ,DF =AE ⋅DF|AE ||DF |=37.题型二:空间直线与平面夹角的求解2(2024·安徽合肥·统考一模)如图,三棱柱ABC -A 1B 1C 1中,四边形ACC 1A 1,BCC 1B 1均为正方形,D ,E 分别是棱AB ,A 1B 1的中点,N 为C 1E 上一点.(1)证明:BN ⎳平面A 1DC ;(2)若AB =AC ,C 1E =3C 1N,求直线DN 与平面A 1DC 所成角的正弦值.【思路分析】(1)连接BE ,BC 1,DE ,则有平面BEC 1⎳平面A 1DC ,可得BN ⎳平面A 1DC ;(2)建立空间直角坐标系,利用空间向量进行计算即可.【规范解答】(1)连接BE ,BC 1,DE .因为AB ⎳A 1B 1,且AB =A 1B 1,又D ,E 分别是棱AB ,A 1B 1的中点,所以BD ⎳A 1E ,且BD =A 1E ,所以四边形BDA 1E 为平行四边形,所以A 1D ⎳EB ,又A 1D ⊂平面A 1DC ,EB ⊄平面A 1DC ,所以EB ⎳平面A 1DC ,因为DE ⎳BB 1⎳CC 1,且DE =BB 1=CC 1,所以四边形DCC 1E 为平行四边形,所以C 1E ⎳CD ,又CD ⊂平面A 1DC ,C 1E ⊄平面A 1DC ,所以C 1E ⎳平面A 1DC ,因为C 1E ∩EB =E ,C 1E ,EB ⊂平面BEC 1,所以平面BEC 1⎳平面A 1DC ,因为BN ⊂平面BEC 1,所以BN ⎳平面A 1DC .(2)四边形ACC 1A 1,BCC 1B 1均为正方形,所以CC 1⊥AC ,CC 1⊥BC ,所以CC 1⊥平面ABC .因为DE ⎳CC 1,所以DE ⊥平面ABC ,从而DE ⊥DB ,DE ⊥DC .又AB =AC ,所以△ABC 为等边三角形.因为D 是棱AB 的中点,所以CD ⊥DB ,即DB ,DC ,DE 两两垂直.以D 为原点,DB ,DC ,DE 所在直线为x ,y ,z 轴,建立如图所示的空间直角坐标系D -xyz .设AB =23,则D 0,0,0 ,E 0,0,23 ,C 0,3,0 ,C 10,3,23 ,A 1-3,0,23 ,所以DC =0,3,0 ,DA 1=-3,0,23 .设n=x ,y ,z 为平面A 1DC 的法向量,则n ⋅DC=0n ⋅DA 1 =0,即3y =0-3x +23z =0 ,可取n=2,0,1 .因为C 1E =3C 1N ,所以N 0,2,23 ,DN =0,2,23 .设直线DN 与平面A 1DC 所成角为θ,则sin θ=|cos ‹n ,DN ›|=|n ⋅DN ||n |⋅|DN |=235×4=1510,即直线DN 与平面A 1DC 所成角正弦值为1510.1、垂线法求线面角(也称直接法):(1)先确定斜线与平面,找到线面的交点B 为斜足;找线在面外的一点A ,过点A 向平面α做垂线,确定垂足O ;(2)连结斜足与垂足为斜线AB 在面α上的投影;投影BO 与斜线AB 之间的夹角为线面角;(3)把投影BO 与斜线AB 归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。
高考文科立体几何题汇总(含答案)
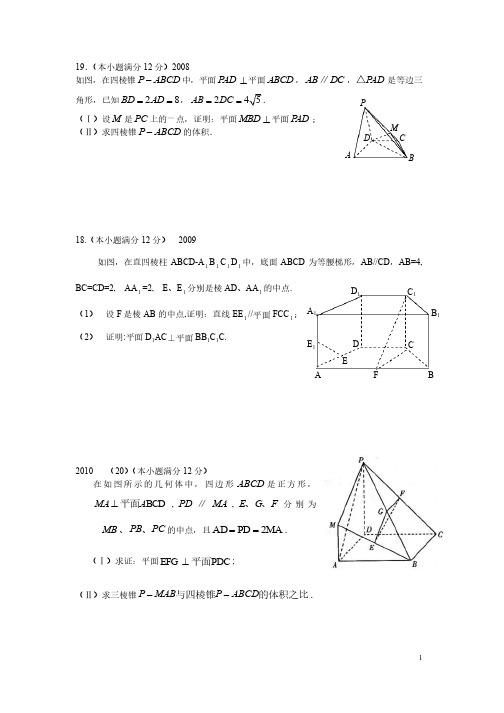
19.(本小题满分12分)2008 如图,在四棱锥P ABCD -中,平面PAD ^平面ABCD ,AB DC ∥,P AD △是等边三角形,已知28BD AD ==,245AB DC ==.(Ⅰ)设M 是PC 上的一点,证明:平面MBD ^平面PAD ; (Ⅱ)求四棱锥P ABCD -的体积.的体积.18.(本小题满分12分)分) 2009 如图,在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB//CD ,AB=4, BC=CD=2, AA 1=2, E 、E 1分别是棱AD 、AA 1的中点. (1) 设F 是棱AB 的中点,证明:直线EE 1//平面FCC 1; (2) 证明:平面D 1AC ⊥平面BB 1C 1C. 2010 (20)(本小题满分12分)分)在如图所示的几何体中,四边形ABCD 是正方形,BCD A MA 平面^,PD ∥MA ,E G F 、、分别为MB 、PC PB 、的中点,且2MA PD AD ==.(Ⅰ)求证:平面PDC EFG 平面^; (Ⅱ)求三棱锥的体积之比与四棱锥ABCD P MAB P --.A B C M P D EA B C F E 1 A 1 B 1 C 1 D 1 D 2011 19.(本小题满分12分)分)如图,在四棱台1111ABCD A B C D -中,1D D ^平面ABCD ,底面ABCD 是平行四边形,AB=2AD ,11AD=A B ,BAD=Ð60° (Ⅰ)证明:1AA BD ^;(Ⅱ)证明:11CC A BD ∥平面.2012 (19) ( (本小题满分本小题满分12分)如图,几何体E ABCD -是四棱锥,△ABD 为正三角形,,CB CD EC BD =^. (Ⅰ)求证:BE DE =;(Ⅱ)若∠120BCD =°,M 为线段AE 的中点,的中点, 求证:DM ∥平面BEC .53238545545523163 ACM PDOEA B C F 1 1 C 1 D 1 D F 1 EC 1 1 C 1 D 1 D 所以CC 1⊥AC,因为底面ABCD 为等腰梯形,AB=4, BC=2, F 是棱AB 的中点,所以CF=CB=BF ,△BCF 为正三角形,为正三角形, 60BCF Ð=°,△ACF 为等腰三角形,且30ACF Ð=°所以AC ⊥BC, 又因为BC 与CC 1都在平面BB 1C 1C 内且交于点C, 所以AC ⊥平面BB 1C 1C,而AC Ì平面D 1AC, 所以平面D 1AC ⊥平面BB 1C 1C. 2010 (20)本小题主要考查空间中的线面关系,考查线面垂直、)本小题主要考查空间中的线面关系,考查线面垂直、面面垂直的判定及几面面垂直的判定及几何体体积的计算,考查试图能力和逻辑思维能力。
高考数学立体几何题型大全总结

高考数学立体几何题型大全总结1. 三角锥的体积公式
体积公式:V=1/3∗S∗h
其中,S为底面积,h为高。
2. 三棱锥的体积公式
体积公式:V=1/3∗S∗h
其中,S为底面积,h为高。
3. 四棱锥的体积公式
体积公式:V=1/3∗S∗h
其中,S为底面积,h为高。
4. 圆锥的体积公式
体积公式:V=1/3∗π∗r2∗h
其中,r为圆锥的半径,h为圆锥的高。
5. 球的体积公式
体积公式:V=4/3∗π∗r3
其中,r为球的半径。
6. 圆柱的体积公式
体积公式:V=π∗r2∗h
其中,r为圆柱的半径,h为圆柱的高。
7. 圆台的体积公式
体积公式:V=1/3∗π∗h∗(r12+r22+r1r2)
其中,r1,r2为底面半径,h为圆台高。
8. 空间向量的共线与垂直判定公式
共线判定公式:
如果两个向量a,b共线,则有a=kb,其中k为一个实数。
垂直判定公式:
如果两个向量a,b垂直,则有a·b=0,其中“·”表示向量的数量积。
9. 空间向量的平面垂直判定公式
若向量a与平面P垂直,则a在平面P上的投影为零向量。
10. 空间向量的平面共面判定公式
若向量a和向量b在同一平面上,则a和b的向量积c在该平面内。
11. 空间中两直线相交的条件
两直线相交的条件是它们至少有一个公共点,并且既不平行也不重合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新课标立体几何常考证明题汇总1、已知四边形ABCD 是空间四边形,,,,E F G H 分别是边,,,AB BC CD DA 的中点 (1) 求证:EFGH 是平行四边形(2) 若BD=AC=2,EG=2。
求异面直线AC 、BD 所成的角和EG 、BD 所成的角。
证明:在ABD ∆中,∵,E H 分别是,AB AD 的中点∴1//,2EH BD EH BD = 同理,1//,2FG BD FG BD =∴//,EH FG EH FG =∴四边形EFGH 是平行四边形。
(2) 90° 30 °考点:证平行(利用三角形中位线),异面直线所成的角2、如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点。
求证:(1)⊥AB 平面CDE;(2)平面CDE ⊥平面ABC 。
证明:(1)BC AC CE AB AE BE =⎫⇒⊥⎬=⎭同理,AD BD DE AB AE BE =⎫⇒⊥⎬=⎭又∵CE DE E ⋂= ∴AB ⊥平面CDE (2)由(1)有AB ⊥平面CDE又∵AB ⊆平面ABC , ∴平面CDE ⊥平面ABC 考点:线面垂直,面面垂直的判定AHGFEDCB AEDBC3、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点, 求证: 1//A C 平面BDE 。
证明:连接AC 交BD 于O ,连接EO , ∵E 为1AA 的中点,O 为AC 的中点 ∴EO 为三角形1A AC 的中位线 ∴1//EO AC 又EO 在平面BDE 内,1A C 在平面BDE 外∴1//A C 平面BDE 。
考点:线面平行的判定4、已知ABC ∆中90ACB ∠=o,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC . 证明:90ACB ∠=∵° BC AC ∴⊥又SA ⊥面ABC SA BC ∴⊥ BC ∴⊥面SAC BC AD ∴⊥又,SC AD SC BC C ⊥⋂=AD ∴⊥面SBC 考点:线面垂直的判定5、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.求证:(1) C 1O ∥面11AB D ;(2)1AC ⊥面11AB D . 证明:(1)连结11A C ,设11111A CB D O ⋂=,连结1AO∵ 1111ABCD A B C D -是正方体 11A ACC ∴是平行四边形∴A 1C 1∥AC 且 11A C AC = 又1,O O 分别是11,A C AC 的中点,∴O 1C 1∥AO 且11O C AO =11AOC O ∴是平行四边形 111,C O AO AO ∴⊂∥面11AB D ,1C O ⊄面11AB D ∴C 1O ∥面11AB D(2)1CC ⊥Q 面1111A B C D 11!CC B D ∴⊥ 又1111A CB D ⊥∵, 1111B D AC C ∴⊥面 111AC B D ⊥即 同理可证11A C AD ⊥, 又1111D B AD D ⋂=∴1A C ⊥面11AB D考点:线面平行的判定(利用平行四边形),线面垂直的判定AED 1CB 1DCBASDCBAD 1ODB AC 1B 1A 1CNMPCA6、正方体''''ABCD A B C D -中,求证:(1)''AC B D DB ⊥平面;(2)''BD ACB ⊥平面.考点:线面垂直的判定7、正方体ABCD —A 1B 1C 1D 1中.(1)求证:平面A 1BD ∥平面B 1D 1C ; (2)若E 、F 分别是AA 1,CC 1的中点,求证:平面EB 1D 1∥平面FBD . 证明:(1)由B 1B ∥DD 1,得四边形BB 1D 1D 是平行四边形,∴B 1D 1∥BD , 又BD ⊄平面B 1D 1C ,B 1D 1⊂平面B 1D 1C , ∴BD ∥平面B 1D 1C .同理A 1D ∥平面B 1D 1C .而A 1D ∩BD =D ,∴平面A 1BD ∥平面B 1CD .(2)由BD ∥B 1D 1,得BD ∥平面EB 1D 1.取BB 1中点G ,∴AE ∥B 1G .从而得B 1E ∥AG ,同理GF ∥AD .∴AG ∥DF .∴B 1E ∥DF .∴DF ∥平面EB 1D 1.∴平面EB 1D 1∥平面FBD .考点:线面平行的判定(利用平行四边形)8、四面体ABCD 中,,,AC BD E F =分别为,AD BC 的中点,且22EF AC =, 90BDC ∠=o ,求证:BD ⊥平面ACD证明:取CD 的中点G ,连结,EG FG ,∵,E F 分别为,AD BC 的中点,∴EG12//AC = 12//FG BD =,又,AC BD =∴12FG AC =,∴在EFG ∆中,222212EG FG AC EF +== ∴EG FG ⊥,∴BD AC ⊥,又90BDC ∠=o,即BD CD ⊥,AC CD C ⋂= ∴BD ⊥平面ACD考点:线面垂直的判定,三角形中位线,构造直角三角形9、如图P 是ABC ∆所在平面外一点,,PA PB CB =⊥平面PAB ,M 是PC 的中点,N 是AB 上的点,3AN NB = (1)求证:MN AB ⊥;(2)当90APB ∠=o,24AB BC ==时,求MN 的长。
证明:(1)取PA 的中点Q ,连结,MQ NQ ,∵M 是PB 的中点,∴//MQ BC ,∵ CB ⊥平面PAB ,∴ MQ ⊥平面PAB ∴QN 是MN 在平面PAB 内的射影 ,取 AB 的中点D ,连结 PD ,∵,PA PB =∴PD AB ⊥,又3AN NB =,∴BN ND =A 1 AB 1C 1D 1D G EF∴//QN PD ,∴QN AB ⊥,由三垂线定理得MN AB ⊥ (2)∵90APB ∠=o,,PA PB =∴122PD AB ==,∴1QN =,∵MQ ⊥平面PAB .∴MQ NQ ⊥,且112MQ BC ==,∴2MN = 考点:三垂线定理10、如图,在正方体1111ABCD A B C D -中,E 、F 、G 分别是AB 、AD 、11C D 的中点.求证:平面1D EF ∥平面BDG .证明:∵E 、F 分别是AB 、AD 的中点,∴EF ∥BD 又EF ⊄平面BDG ,BD ⊂平面BDG ∴EF ∥平面BDG ∵1D GEB ∴四边形1D GBE 为平行四边形,1D E ∥GB又1D E ⊄平面BDG ,GB ⊂平面BDG ∴1D E ∥平面BDG1EF D E E⋂=,∴平面1D EF ∥平面BDG考点:线面平行的判定(利用三角形中位线)11、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点. (1)求证:1//A C 平面BDE ; (2)求证:平面1A AC ⊥平面BDE . 证明:(1)设AC BD O ⋂=,∵E 、O 分别是1AA 、AC 的中点,∴1A C ∥EO又1AC ⊄平面BDE ,EO ⊂平面BDE ,∴1A C ∥平面BDE (2)∵1AA ⊥平面ABCD ,BD ⊂平面ABCD ,1AA BD ⊥ 又BD AC ⊥,1AC AA A⋂=,∴BD ⊥平面1A AC ,BD ⊂平面BDE ,∴平面BDE ⊥平面1A AC考点:线面平行的判定(利用三角形中位线),面面垂直的判定12、已知ABCD 是矩形,PA ⊥平面ABCD ,2AB =,4PA AD ==,E 为BC 的中点.(1)求证:DE ⊥平面PAE ;(2)求直线DP 与平面PAE 所成的角. 证明:在ADE ∆中,222AD AE DE =+,∴AE DE ⊥ ∵PA ⊥平面ABCD ,DE ⊂平面ABCD ,∴PA DE ⊥ 又PA AE A ⋂=,∴DE ⊥平面PAE (2)DPE ∠为DP 与平面PAE 所成的角在Rt PAD ∆,42PD =,在Rt DCE ∆中,22DE =在Rt DEP ∆中,2PD DE =,∴030DPE ∠= 考点:线面垂直的判定,构造直角三角形13、如图,在四棱锥P ABCD -中,底面ABCD 是060DAB ∠=且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD 垂直于底面ABCD .(1)若G 为AD 的中点,求证:BG ⊥平面PAD ; (2)求证:AD PB ⊥;(3)求二面角A BC P --的大小. 证明:(1)ABD ∆为等边三角形且G 为AD 的中点,∴BG AD ⊥ 又平面PAD ⊥平面ABCD ,∴BG ⊥平面PAD(2)PAD 是等边三角形且G 为AD 的中点,∴AD PG ⊥ 且AD BG ⊥,PG BG G ⋂=,∴AD ⊥平面PBG ,PB ⊂平面PBG ,∴AD PB ⊥(3)由AD PB ⊥,AD ∥BC ,∴BC PB ⊥ 又BG AD ⊥,AD ∥BC ,∴BG BC ⊥ ∴PBG ∠为二面角A BC P --的平面角在Rt PBG ∆中,PG BG =,∴045PBG ∠=考点:线面垂直的判定,构造直角三角形,面面垂直的性质定理,二面角的求法(定义法)14、如图1,在正方体1111ABCD A B C D -中,M 为1CC 的中点,AC 交BD 于点O ,求证:1A O ⊥平面MBD . 证明:连结MO ,1A M ,∵DB ⊥1A A ,DB ⊥AC ,1A A AC A⋂=,∴DB ⊥平面11A ACC ,而1AO ⊂平面11A ACC ∴DB ⊥1A O . 设正方体棱长为a ,则22132A O a =,2234MO a =. 在Rt △11A C M 中,22194A M a =.∵22211A O MO A M +=,∴1AO OM ⊥. ∵OM ∩DB =O ,∴ 1A O ⊥平面MBD .考点:线面垂直的判定,运用勾股定理寻求线线垂直 15、如图2,在三棱锥A-BCD 中,BC =AC ,AD =BD ,作BE ⊥CD ,E为垂足,作AH ⊥BE 于H.求证:AH ⊥平面BCD . 证明:取AB 的中点F,连结CF ,DF . ∵AC BC =,∴CF AB ⊥.∵AD BD =,∴DF AB ⊥.又CF DF F =I ,∴AB ⊥平面CDF . ∵CD ⊂平面CDF ,∴CD AB ⊥. 又CD BE ⊥,BE AB B ⋂=, ∴CD ⊥平面ABE ,CD AH ⊥.∵AH CD ⊥,AH BE ⊥,CD BE E ⋂=, ∴ AH ⊥平面BCD . 考点:线面垂直的判定。
