第4章 正弦波振荡器(第8次课)
LC正弦波振荡器

第4章 正弦波振荡器
正弦波振荡器输出信号的频率范围是很宽的,基本上可 以分成两大类。一类是由电阻、电容元件组成的RC振荡器, 它适用于产生低频正弦波振荡信号,其振荡频率范围为几赫 兹到几十千赫兹。另一类是由集中参数LC元件组成的高频振 荡器,它的振荡频率在几十千赫兹到几十兆赫兹。如果频率 更高,进入米波、分米波范围,则由分布参数系统组成超高
(4-3)
第4章 正弦波振荡器 式(4-3)可以分为两部分, 即
AuFu=1 j=jA+j F=2n (n=0,1,2,……) (4-4) (4-5)
式(4-4)为自激振荡的振幅平衡条件, 式(4-5)为自激振荡的相 位平衡条件。 一个电路要产生自激振荡必须满足上述两个条 件。
第4章 正弦波振荡器
第4章 正弦波振荡器
4.1 概
4.1.1 振荡器的概念和用途
所谓振荡器是一种不需要外加激励信号,而能将直流电
源的能量转变为交流能量的电子设备。它与放大器最根本的 区别在于它的工作不需要外加信号的推动。
第4章 正弦波振荡器
振荡器电路是一种用途非常广泛的基本电子线路。例如,
在无线电通信、广播、电视发射系统中,高频振荡器是个核
环过程,进入到晶体管的饱和区和截止区,放大器的增益下
降,AuFu也就减小,使振荡从AuFu>1过渡到AuFu=1,振荡稳
定下来,最后达到平衡状态。
第4章 正弦波振荡器
由增幅振荡到稳幅振荡的建立过程,说明前者由起振条 件来保证,即AuFu>1,后者由晶体管特性的非线性来实现自 动限幅,而LC回路起选频作用,使振荡回路输出单一频率的 正弦信号。
式(4-2)
u A
(4-2)
u 都为 F
新版高频电子线路全部答案(高瑜翔)
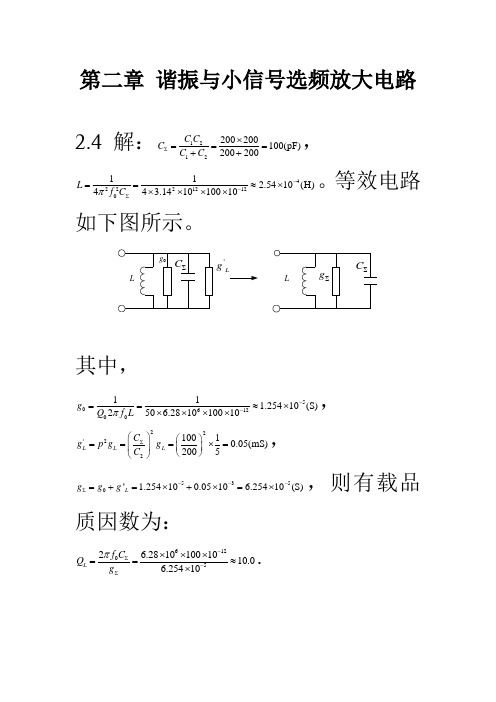
第二章 谐振与小信号选频放大电路2.4 解:1212200200100(pF)200200C C C C C ∑⨯===++, 42221212011 2.5410(H)44 3.141010010L f C π--∑==≈⨯⨯⨯⨯⨯。
等效电路如下图所示。
'Lg其中,5061200111.25410(S)250 6.281010010g Q f L π--==≈⨯⨯⨯⨯⨯,22'2210010.05(mS)2005L L L C g p g g C ∑⎛⎫⎛⎫===⨯= ⎪ ⎪⎝⎭⎝⎭,5350' 1.254100.0510 6.25410(S)L g g g ---∑=+=⨯+⨯=⨯,则有载品质因数为:612052 6.28101001010.06.25410L f C Q g π-∑-∑⨯⨯⨯==≈⨯.第三章 高频功率放大电路3.7 解:(1) 60100(W),1006040(W)0.6OC O C P P P P P η======-=-=,1008(A)12.5C CC P I V ====。
(2)'60'75(W),'''756015(W),0.8OC O C P P P P P η======-=-=。
'401525(W)C C P P -=-=。
3.8 解:集电极电流和输入电压的波形图如下所示:tt00.60.2cos 0.364,69,1.1Bz BB im U V U θθ--==≈≈0120.7A,()0.249,()0.432,()0.269,CM I αθαθαθ=≈≈≈001122()0.70.249A 0.174A,()0.70.4320.302,()0.70.2690.188C CM C m CM C m CM I I I I A A I I A Aαθαθαθ=≈⨯≈=≈⨯≈=≈⨯≈3.10 解:(1)0001(120)0.406,(120)0.536,αα≈≈000max 010C1m max 101(120)1000.40640.6(mA),(120) 1.32(120)1000.53653.6(mA)11(120)0.95 1.3262.7%22C C C c I I g I I g ααηξ=≈⨯=≈=≈⨯===⨯⨯=(2)000011(70)0.253,(70)0.436,(70) 1.73g αα≈≈≈00max 00C1m max 101(70)1000.25325.3(mA),(70)1000.43643.6(mA),11(70)0.95 1.7382.2%22C C C c I I I I g ααηξ=≈⨯==≈⨯===⨯⨯≈3.11 解:05240.256(W),651(W),83.3%6o D CC C c D o c D P P V I P P P P η==⨯==-=-===≈。
高频电子线路-第4章--习题答案
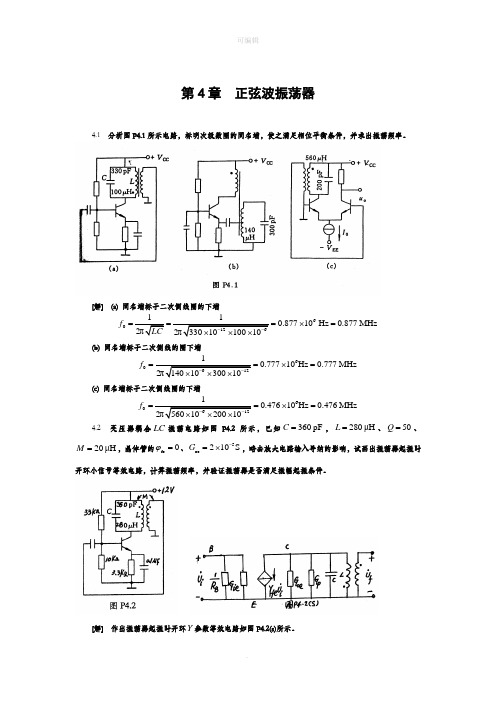
第4章 正弦波振荡器4.1 分析图P4.1所示电路,标明次级数圈的同名端,使之满足相位平衡条件,并求出振荡频率。
[解] (a) 同名端标于二次侧线圈的下端601260.87710Hz 0.877MHz 2π2π3301010010f LC--===⨯=⨯⨯⨯(b) 同名端标于二次侧线的圈下端606120.77710Hz 0.777MHz 2π1401030010f --==⨯=⨯⨯⨯(c) 同名端标于二次侧线圈的下端606120.47610Hz 0.476MHz 2π5601020010f --==⨯=⨯⨯⨯4.2 变压器耦合LC 振荡电路如图P4.2所示,已知360pF C =,280μH L =、50Q =、20μH M =,晶体管的fe 0ϕ=、5oe 210S G -=⨯,略去放大电路输入导纳的影响,试画出振荡器起振时开环小信号等效电路,计算振荡频率,并验证振荡器是否满足振幅起振条件。
[解] 作出振荡器起振时开环Y 参数等效电路如图P4.2(s)所示。
略去晶体管的寄生电容,振荡频率等于0612Hz =0.5MHz 2π2π2801036010f LC--==⨯⨯⨯略去放大电路输入导纳的影响,谐振回路的等效电导为5661121042.7μS 502π0.51028010e oe oe o G G G G S S Q Lρω--=+=+=⨯+=⨯⨯⨯⨯⨯由于三极管的静态工作点电流EQ I 为12100.712330.6mA 3.3k EQV I ⨯⎛⎫-⎪+⎝⎭==Ω所以,三极管的正向传输导纳等于/0.6/260.023S fe m EQ T Y g I U mA mV ≈===因此,放大器的谐振电压增益为o muo eiU g A G U -==而反馈系数为f oU j M M F j L LU ωω-=≈=-这样可求得振荡电路环路增益值为60.023203842.710280meg M T A F G L -====⨯ 由于T >1,故该振荡电路满足振幅起振条件。
反馈振荡器的工作原理
变压器耦合振荡器:
• 1、什么是变压器的同名端 • 同名端是指在同一交变磁通的作用下,任一时刻两个(或两个以上)绕组中都具有相
同电势极性的端头彼此互为同名端。 • 2、变压器耦合振荡器 • 变压器耦合振荡器是通过变压器的初、次级互感耦合产生反馈电压的,因此,为了满
足正反馈条件,必须正确地设置初、次级绕组的同名端
反馈振荡器的工作原理 LC正弦波振荡器 振荡器的频率和振幅稳定度 石英晶体振荡器 RC正弦波振荡器 负阻正弦波振荡器 特殊振荡现象 本章小结
4.1 反馈振荡器的工作原理
主要要求:
掌握反馈振荡器的组成和基本工作原理 理解反馈振荡器的起振条件和平衡条件, 了解其稳定条件。 掌握反馈振荡器能否振荡的判断方法。
A
.
故又得 T 1
Ui Uo Ui
4.1.2 振荡的平衡条件和起振条件
一、 振荡的平衡条件
.
..
..
T AF 1
振幅平衡条件
T AF 1
T A F 2nπ n=0,1,2…
即正反馈
相位平衡条件
振幅条件和相位条件必须同时满足。
相位平衡条件确定振荡频率;
振幅平衡条件确定振荡输出信号的幅值。
4.1.2 振荡的平衡条件和起振条件
4.1.1 反馈振荡器的组成与基本工作原理
一、 反馈振荡器的组成
放大器
Ui
Au
无外加输入信号
Uo
正弦波振荡器由放大器、
反馈网络
Uf
Fu
反馈网络和选频网络组成
二、 反馈振荡器的工作原理
放大器
Ui
Au
反馈网络
Uf
Fu
.
.
要满足 Uf Ui
Chapter_4-通信电子线路(第3版)-陈启兴-清华大学出版社

2021/3/17
6
4.2.2 起振条件和平衡条件(续)
AF A F 2nπ rad, n Z
AF 1 ----振幅平衡条件
----相位平衡条件
3. 稳定条件
(a) 平衡但不稳定
(b) 平衡且稳定
图4-3 平衡与稳定的关系示意图
A0F 1 ----振幅起振条件
----相位起振条件
其中,φA——放大器的相移;φF——反馈网络的相移; φAF——放大器和反馈网络的总相移;A0——放大器起始增 益幅值;F——反馈网络的反馈系数幅值。
2021/3/17
5
4.2.2 起振条件和平衡条件(续)
在实际工作中,只要我们判断出反馈网络属于正反馈,就 可以认为电路满足了相位起振条件。一般来说,不易判断是 否满足振幅起振条件,但总是可以调整三极管或场效应管的 静态工作点到放大区,而且可以选择具有高一些共射电流放 大倍数β或跨导gm的管子。
振荡信号的建立条件包括振荡器的起振条件、平衡条件 和稳定条件。
2 S Cb 1
Ui
+VCC T
Rb 1
+ U- o
C L1
L2
+
U -
f
VT
M
Rb2
Ce
Re
2021/3/17
放大器
选频网络
反馈网络
图4-2 互感耦合型振荡电路工作原理示意图
4
4.2.2 起振条件和平衡条件(续)
1. 起振条件
AF A F 2nπ rad, n Z
按照反馈耦合网络的不同,LC振荡器可分为互感耦合 型振荡器和三点式振荡器。
高频电子线路课后答案

说明所有习题都是我们上课布置的作业题,所有解答都是本人自己完成,其中难免有错误之处,还望大家海涵。
第2章 小信号选频放大器已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解] 90-6120.035610Hz 35.6MHz 2π2π102010f LCH F-===⨯=⨯⨯6312640.71010022.4k 22.361022.36k 201035.610Hz35.610Hz 356kH z100p HR Q Ff BW Q ρρ--===Ω=⨯Ω=Ω⨯⨯===⨯=并联谐振回路如图所示,已知:300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解] 0465kHz 2π2π390μH 300PFf LC≈==⨯0.70390μH100114k Ω300PF////100k Ω//114.k Ω//200kΩ=42k Ω42k Ω371.14k Ω390μH/300 PF/465kHz/37=12.6kHzp e s p Lee e R Q R R R R R Q BWf Q ρρ===========已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ,应在回路两端并接一个多大的电阻? [解] 6262120115105μH (2π)(2π1010)5010L H f C --===⨯=⨯⨯⨯⨯ 6030.7101066.715010f Q BW ⨯===⨯2236022*********.78.11010p oU f Q f U ••⎛⎫⎛⎫∆⨯⨯=+=+= ⎪ ⎪⨯⎝⎭⎝⎭ 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯g而471266.72.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯g 由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω并联回路如图所示,已知:360pF,C =1280μH,L ==100,Q 250μH,L = 12=/10,n N N =L 1k R =Ω。
高频电子线路正弦波振荡器.ppt
单调谐放大器
高频电子线路——第4章 正弦波振荡器
3.相位(频率)稳定条件
相位稳定条件和频率稳定条件实质上是一回事
正弦信号相位φ和频率ω的关系:
d
dt
dt
振荡器的角频率 增大导致相位不断超前 相位 的不断超前表明角频率 增大
高频电子线路——第4章 正弦波振荡器
(1)相位(频率)稳定过程
原平衡态: L (0 ) f F 0
4.1.2 起振条件
1.起振过程分析
单调谐放大器
刚通电:电路中存在很宽的频谱的电的扰动,幅值很小
通电后:
1)谐振回路的选频功能,从扰动中选出 osc 分量(osc 0)
2)放大器工作在线性放大区, |T (josc)|>1 ,形成增幅振荡
3)忽略晶体管内部相移: f =0
回路谐振: L=0
T (josc) =0,相移为零
起振 过程
平衡 状态
起振 过程
平衡 状态
输出波形:
高频电子线路——第4章 正弦波振荡器
4.1.4 稳定条件
1.平衡状态稳定分析:
(1)振荡电路中存在干扰
单调谐放大器
① 外部:电源电压、温度、湿度的变化,引起管子和回 路参数的变化。
② 内部:存在固有噪声(起振时的原始输入电压,进入平 衡后与输入电压叠加引起波动)。
单调谐放大器
外界干扰后: L (0 ) f F 0
Ub 相位超前 Ub 相位
升高
振荡回路相频特性 L 下降
L () f F 下降
L () f F 0
达到新的平衡 > 0
外界干扰消失后: L () f F 0
Ub 相位滞后 Ub 相位
降低
电工学-第四章 正弦波振荡电路

R
1 jL jC j(L 1
C
)
( R L)
.
I
L/C
R j(L 1 )
C
+ L
•
U
C
_
R
2020/4/18
24
LC并联谐振回路的选频特性
•
Z
U
•
I
L/C
R j(L
1)
C
.
I
+ L
•
U
C
_
R
•
当LC并联回路发生谐振时,端电压 U 与总电
流
•
I
同相,即阻抗Z表现为纯电阻性。
谐振频率
o
Uf
•
F
Uo
•
•
由以上知,放大电路产生自激振荡的条件是 U f U i
••
•
则
AuF
Uo
•
U
•
f
U
•
f
1
Ui Uo Ui
2020/4/18
7
自激振荡
总结出自激振荡的条件:
(1)相位平衡条件
反馈电压
•
U
f
与输入电压
•
U
i
同相位,形成正反馈
(2)幅值平衡条件
反馈电压与输入电压大小相等: U f U i
C2
uf
首先判断相位平衡条件,见瞬时极性
2020/4/18
35
RB1
RC
+
RB2
uf
+
ube
RE
UCC
+
C1
L
+
C2
CE
高频电子线路作业及答案(胡宴如 狄苏燕版)四章
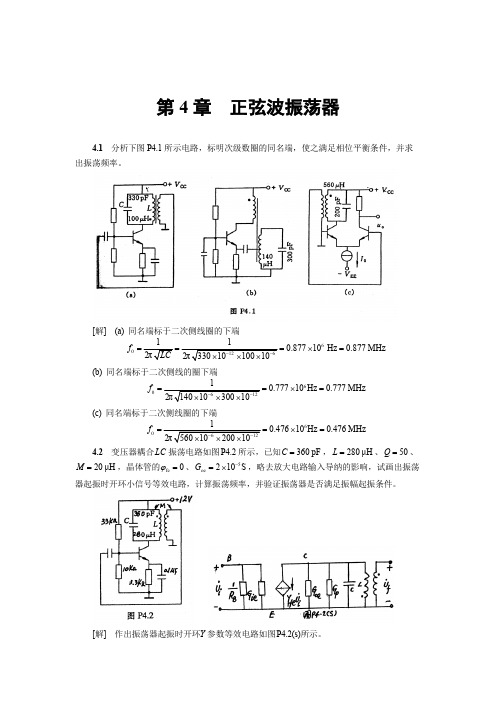
第4章 正弦波振荡器4.1 分析下图P4.1所示电路,标明次级数圈的同名端,使之满足相位平衡条件,并求出振荡频率。
[解] (a) 同名端标于二次侧线圈的下端600.87710Hz 0.877MHzf ===⨯=(b) 同名端标于二次侧线的圈下端600.77710Hz 0.777MHzf ==⨯=(c) 同名端标于二次侧线圈的下端600.47610Hz 0.476MHzf ==⨯=4.2 变压器耦合振荡电路如图P4.2所示,已知,、、LC 360pF C =280μH L =50Q =,晶体管的、,略去放大电路输入导纳的影响,试画出振荡20μH M =fe 0ϕ=5oe 210S G -=⨯器起振时开环小信号等效电路,计算振荡频率,并验证振荡器是否满足振幅起振条件。
[解] 作出振荡器起振时开环参数等效电路如图P4.2(s)所示。
Yhe b e12略去晶体管的寄生电容,振荡频率等于0Hz =0.5MHzf ==略去放大电路输入导纳的影响,谐振回路的等效电导为5661121042.7μS502π0.51028010e oe oe o G G G G S S Q L ρω--=+=+=⨯+=⨯⨯⨯⨯⨯由于三极管的静态工作点电流为EQ I 12100.712330.6mA 3.3k EQV I ⨯⎛⎫-⎪+⎝⎭==Ω所以,三极管的正向传输导纳等于/0.6/260.023Sfe m EQ T Y g I U mA mV ≈===因此,放大器的谐振电压增益为omuo eiU g A G U -==而反馈系数为f oU j M MF j L LU ωω-=≈=-这样可求得振荡电路环路增益值为60.023203842.710280m e g M T A F G L -====⨯???由于>1,故该振荡电路满足振幅起振条件。
T 4.3 试检查图P4.3所示振荡电路,指出图中错误,并加以改正。
[解] (a) 图中有如下错误:发射极直流被短路,变压器同各端标的不正确,构成负反f L 馈。
(完整版)高频电子线路课后答案(胡宴如_狄苏燕)

说明所有习题都是我们上课布置的作业题,所有解答都是本人自己完成,其中难免有错误之处,还望大家海涵。
第2章 小信号选频放大器2.1 已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解] 90-6120.035610Hz 35.6MHz 2π2π102010f LCH F-===⨯=⨯⨯6312640.71010022.4k 22.361022.36k 201035.610Hz35.610Hz 356kH z100p HR Q Ff BW Q ρρ--===Ω=⨯Ω=Ω⨯⨯===⨯=2.2 并联谐振回路如图P2.2所示,已知:300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解] 0465kHz 2π2π390μH 300PFf LC≈==⨯0.70390μH100114k Ω300PF////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω371.14k Ω390μH/300 PF/465kHz/37=12.6kHzp e s p Lee e R Q R R R R R Q BWf Q ρρ===========2.3 已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ,应在回路两端并接一个多大的电阻? [解] 6262120115105μH (2π)(2π1010)5010L H f C --===⨯=⨯⨯⨯⨯ 6030.7101066.715010f Q BW ⨯===⨯2236022*********.78.11010p oU f Q f U ••⎛⎫⎛⎫∆⨯⨯=+=+= ⎪ ⎪⨯⎝⎭⎝⎭ 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯g而471266.72.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯g 由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω2.4 并联回路如图P2.4所示,已知:360pF,C =1280μH,L ==100,Q 250μH,L = 12=/10,n N N =L 1k R =Ω。
振荡器原理

分类:
– 并联谐振型晶体振荡器:等效为电感 – 串联谐振型晶体振荡器:等效为串联谐振回路
30
4.5.1 并联谐振型晶体振荡电路
C
C
C1
E
LJ T
C2
L1
E
C
JT
L2
B
B
C-b型电路(皮尔斯电路) b-e型电路(密勒电路)
VCC C
Cq C1
C1
E
Co Lq
JT C2
C2
rq
C L RL
3、起振条件
g n GT
4、平衡条件
g n GT
40
Vf 反馈网络F
振幅平衡条件: AF 1 相位平衡条件: A F 2n (n 0,1,2,3, )
7
二、 振荡器的起振条件
1、 平均放大倍数A
Vi
Vo
放大器A
2、 起振条件
Vf 反馈网络F
振幅起振条件: AF 1 相位起振条件: A F 2n (n 0,1,2,3, )
AF越大,起振越容易,通常取F =1/2~1/8
VC C
200pF 100pF C3 C4
0.01uF
C2 200pF
L 8uH
C5 5.1pF
C1 51pF
29
4.5 石英晶体振荡器
频率稳定度可达到10-6~10-11。 石英晶体振荡器的优点:
– 石英晶体的等效谐振回路有很高的标准性; – 石英晶体的Q值可高达数百万量级; – 在串并联谐振频率之间很窄的工作频带内,具有
1 L(C3 C4 )
❖可以通过调节C4来调节输出频率 ❖频率覆盖系数为1.6~1.8
27
例1:振荡电路如图示,它是什么类型振荡器?有何优 点?计算它的振荡频率。
高频电路课后答案
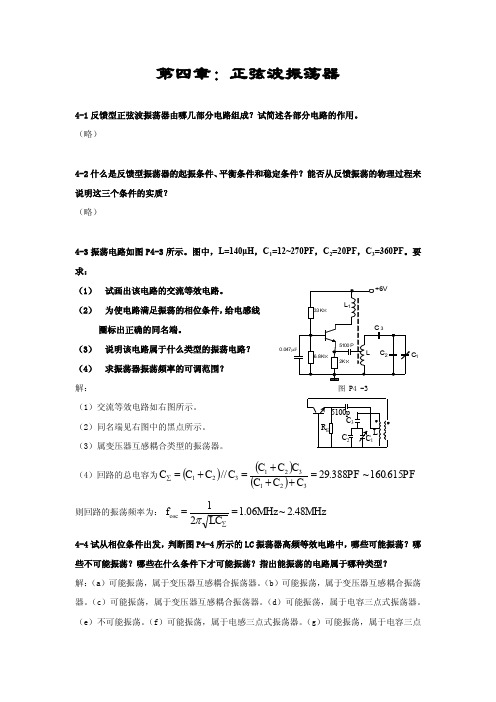
式振荡器(考虑晶体管内部的 BE 结电容) 。 (h)可能振荡,属于电感三点式振荡器,但要求 L1、C 等效为电容。(i)可能振荡,属于电容三点式振荡器,但要求 L2、C2 等效为电容,且 L1、C1 等效为电感。
C
L 1
L2 C L1 L2 L2 L1
(c)
C
(a )
(b)
C1 C1 C2
(d )
f1 f 0 f 2
4-12 10MHZ 晶体振荡器如图 P4-12 所示。图中,Ce、Cφ 视为对高频短路,LC 为高频扼流 圈。 (1) 画出交流等效电路。指出该晶振电路属于哪种类型? (2) 说明晶振器及 C、C3 在电路中的作用。 (3) 计算反馈系数 F=?求出电路能维持振荡的最小增益 AV 。
C1 // C2 C 90.71PF ~ 105.71PF
f osc
1 1.308MHz ~ 1.4123MHz 2 LC
反馈系数为: F
C1 100 0.17 。 C2 600
(3)为了保证电路起振,则要求 F A 1 即电路的增益至少为 A
1 6。 F
(3) 分析电路是否能满足振荡的相位条件。
LC
Rb1
Cb
C1
C2
Rb2
Ce LD C
Re C
L1 L2
C1 C 2 L1 L2
-1Байду номын сангаасV
图 P4 -8 题图 4. 8
解: (1)交流等效电路如右图所示。它属于电感三点式振荡器。 (2)振荡频率为:
f osc 2
1
L1 L2
f1
C1C2 C1 C2
C1 C2 L
正弦波振荡器

或者写成:
A F 1
A0F 1
A F 2n
课后思考题:在LC振荡器中,谐振回路是否等效成一个 电阻?振荡频率是否严格等于谐振回路的谐振频率?
三. 稳定条件
振荡器在工作过程中, 不可避免地要受到各种外界因素变化
的定影因响素,将如引电起源放电大压器波和动回、路温的度参变数化发、生变噪化声,干结扰果等使A。F这些变不化稳,
Uf
是反馈电压、 Ui 是输入电压、
A
是开环电压增益,
F 是反馈系数,
反馈型振荡器 正常工作的 三个条件:
一:起振条件
在接通电源瞬间, 电路中存在各种电扰动, 这些扰动均具
有很宽的频谱。 如果选频网络是由LC并联谐振回路组成,
则其中只有角频率为 谐振角频率ω0的分量才能通 过反馈产生
较大的 反馈电压 U f 。 如果在谐振频率处, U f 与原输入电
U f
j(
X
jX be be X
bc
)
U
c
X be X ce
U c
由电于路必中须U i满与足U正 c反反馈相:,所所以以UUi与f
U f
与
同相,而在共射 U c 反相
即:
X be 0 X ce
V
X1
X2
C2
C1
X3 L
(a)
V
L2
L1
X1
X2
X3 C
(b)
(a) 电容反馈振荡器; (b) 电感反馈振荡器
A 0
U c UC UCQ
Z
0
0
1)振幅平衡的稳定条件
2)相位平衡的稳定条件
第三节 反馈型LC振荡器
一 ,互感耦合振荡电路 二,电容反馈振荡电路 三,电感反馈振荡电路 电感三点式和电容三点式振荡电路的比较
第4章《高频电子线路》_(曾兴雯)_版高等教育出版社课后答案

第4章 正弦波振荡器
第一节
反馈振荡器的原理
一、反馈振荡器的原理分析
组成: (1)放大器
放大器通常是以某种选频网络(如振荡回路)作负载, 是调谐放大器。
(2)反馈网络 一般是由无源器件组成的线性网络。 正反馈: U’i(s)与Ui(s)相位相同。
5
第4章 正弦波振荡器
一、反馈振荡器的原理分析
Ui (s) Us (s) Ui(s)
若 Uo Uc
jL Uc ZL R L e 放大器的负载阻抗 所以 Ic T(j) Yf (j)ZLF(j) Yf ( j)ZL F( j) 1
9
U Uc Uo Ic c 又 K( j) Yf (j)ZL I Ui Ub c Ub 因为 jf Ic Yf ( j) Yf e 晶体管的正向转移导纳 Ub
振幅条件的图解表示
U0 U02 U01 Ub1 Ub2 Ub3 Ub
振荡开始时应为增幅振荡!
12
第4章 正弦波振荡器
四、稳定条件 1、振幅稳定条件
T U i
K U i
0
Ui UiA
0
U i U iA
U’i UiA U’’i
因此,振荡器由增幅振荡过渡到稳幅振荡,是由放
大器的非线性完成的。由于放大器的非线性,振幅稳定 条件很容易满足。
②相位平衡条件,即正反馈条件
U b jX 2 I
U c jX 1 I
X1、X2为同性质电抗元件
判断三端式振荡器能否振荡的原则:
“射同余异”
或 “源同余异”
18
第4章 正弦波振荡器
一、振荡器的组成原则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考虑晶体管输入、输出电阻时,回路有载Q会下降,
振荡频率会升高。
Zo
1
1 gie (goe gL )
LC
C1C2
2
Q1 Q2 OSC 2
0 OSC1
h
2
考必兹振荡器的振荡频率稍高于回路的振荡频率。
第4章 正弦波振荡器
4.2 LC 振荡器
4.2.2 电容反馈振荡器 (6/6)
1 2 3 2 OSC 3 考毕兹
1 > 2 > 3 3 OSC 2 哈特莱
1
1
2
2
3
3
2 OSC
3
考毕兹
321
1 3 2
第4章 正弦波振荡器
4.2 LC 振荡器
4.2.2 电容反馈振荡器 (1/6) 图(a)是一电容反馈振荡器的实际电路,图(b)是其交流 等效电路。
第4章 正弦波振荡器
4.2 LC 振荡器
4.2.4 两种改进型电容反馈振荡器 (1/5)
1.克拉泼(Clapp)振荡器
C
1
1 1
1
C3
C1 C2 C3
C3 << C1 , C3 << C2
f0
1 2π LC
2π
1 LC3
原理电路
交流通路
极间电容影响很小,且调节反馈系数时基本不影响频率。
具体化:与晶体管发射极相连的两个电抗是同性质的; 不与发射极相连的另一电抗与它们的电抗性质相反。
对晶体管:射同余异
对场效应管:源同余异
三端式振荡器的两种基本型:(1)电容反馈振荡器(考必 兹 (Colpitts) 振 荡 器 ); (2) 电 感 反 馈 振 荡 器 ( 哈 特 莱 (Hartley)振荡器).
稳定度下降
幅度下降
好 百~千兆
第4章 正弦波振荡器
4.3 振荡器的频率稳定度
4.3.1 频率稳定度的意义和表征(1/2) 振荡器的频率稳定度是指由外界条件的变化,引起振荡 器的实际工作频率偏离标称频率的程度,是振荡器的一 个很重要的指标。它又指在规定时间内,规定的温度、 湿度、电源电压等变化范围内,振荡频率的相对变化量。 频率稳定度分为绝对偏差和相对偏差。设f1为实际工作 频率,f0为标称频率,则
gie折算到放大器输出端,有
2
gie
U U
b c
gie F 2 gie
T
C1
Vf
C2 L
第4章 正弦波振荡器
4.2 LC 振荡器
4.2.2 电容反馈振荡器 (3/6)
1
F Ub C2 C1
Uc
1
C2
C1
因此,放大器总的负载电导gL为
gL F 2 gie goe gL
绝对偏差: f f1 f0
相对偏差: f f1 f
f0
f0
第4章 正弦波振荡器
4.3 振荡器的频率稳定度
4.3.1 频率稳定度的意义和表征(2/2)
频率稳定度可以分为温度稳定度和时间稳定度。按照 所规定时间的不同,频率稳定度分为:(1)长期频率稳定 度,一天以上乃至几个月内振荡频率相对变化量。主要 取决于器件老化。(2)短期频率稳定度,一天之内振荡频 率的相对变化量。主要取决于温度、电源电压等外界 因素变化。(3)秒或毫秒内振荡频率的相对变化量,由电 路内部噪声或突发性干扰引起。
哈特莱电路
考毕兹电路
克拉泼电路
西勒电路
决定频率元件 波形
L=L1+L2, C 差
L,C=C1||C2 好
L,CC3 好
L,CC3+C4 好
共发反馈系数 频率可调
L2/L1 可以
C1/C2 不方便
C1/C2
C1/C2
方便,幅度不稳 方便,幅度稳定
频率稳定度 最高振荡频率
差 十兆频率提高,
第4章 正弦波振荡器
4.2 LC 振荡器
4.2.4 两种改进型电容反馈振荡器 (2/5)
接入系数 p C C1 C3 C1
等效到CE两端的电阻
RL
p2 R0
(
C3 C1
)
2
Ro
反馈系数 F C1 C2
由以上讨论,可知:(1)由于Cce、Cbe的接入系数减小,晶 体管与谐振回路是松耦合;(2)调整C1、C2的值可以改变 反馈系数,但对谐振频率的影响很小;(3)调整C3值可以改 变系统的谐振频率,对反馈系数无影响;(4)C1、C2不能 过大,否时可能使振荡器停振;(5)克拉泼振荡器主要用
例4-1:
X
L3
C3
T C1
L1
L2
C2
(1) L1C1 > L2C2 > L3C3 (2) L1C1 L2C2 L3C3 (3) L1C1 L2C2 L3C3 (4) L1C1 L2C2 > L3C3 (5) L1C1 L2C2 L3C3 (6) L2C2 L3C3 L1C1
荡幅度就小。一般取20pF至200pF。
R'P
( C3 C1' C3
) 2 RP
C3 C1'
2
RP
f
1
2 L(C3 C4 )
C0
C1
C3
Ci
C2
C4
L
第4章 正弦波振荡器
4.2 LC 振荡器
4.2.4 两种改进型电容反馈振荡器 (5/5) 几种三端式振荡器的比较
于晶体管的基极电流İb、集电极电
流İc以及发射极电流İe, 故有
Ub jX 2 I
⑴X1与X2的电抗性质
U c jX 1 I
相同;⑵X3与X1、X2 的电抗性质相反。
X1、 X2应为同性质的电抗元件。
第4章 正弦波振荡器
4.2 LC 振荡器
4.2.1 LC振荡器的组成原则(2/5)
考毕兹电路的优点:1)振荡波形好。2)频率稳定度较 高,适当加大回路的电容量,就可以减小不稳定因素对 振荡频率的影响。3)电容三端电路的工作频率可以做得 较高,可直接利用振荡管的输出、输入电容作为回路振 荡电容。工作频率可做到几十MHz到几百MHz。缺点: 调整C1或C2改变振荡频率时,反馈系数改变。但只要在 L两端并上一个可变电容器,令C1与C2为固定电容,则 调整频率时基本上不影响反馈系数。
第4章 正弦波振荡器
4.3 振荡器的频率稳定度
4.3.2 振荡器的稳频原理(1/3)
由振荡器的相位平衡条件,有 f L F 2n
则(令n=0): L (i F)
设回路高Q值, 振荡回路在ω0附近的幅角φL可表示为
tan L
2QL ( 0
0 )
1 2
1 LC
式中,L为回路的总电感, 由上图有: L L1 L2 2M
第4章 正弦波振荡器
4.2 LC 振荡器
4.2.3 电感反馈振荡器 (3/4) 由相位平衡条件分析, 振荡器的振荡频率表达式为
1
1 LC gie (goe gL )(L1L2 M 2 )
在计算反馈系数时不考虑gie的影响,反馈系数的大小为
F G( j) L2 M L1 M
由起振条件 Yfe RLF > 1分析,同样可得起振时的gm应满足
gm
1 gL
F
gm
gie F 2
1 goe
g L
F
>1
gm
(goe
gL )
1 F
gie F
第4章 正弦波振荡器
4.2 LC 振荡器
4.2.3 电感反馈振荡器 (4/4)
哈特莱电路的优点:1、L1、L2之间有互感,反馈较强,
容易起振;2、只要调整电容C,即可方便调节振荡频
率;3、而且C的改变基本上不影响电路的反馈系数。 缺点:1、振荡波形不好,因为反馈电压是在电感上获 得,而电感对高次谐波呈高阻抗,对高次谐波的反馈较 强,使波形失真大;2、电感反馈三端电路的振荡频率 不能太高,因为频率太高,L太小且分布参数的影响太 大。
(a)
(b)
第4章 正弦波振荡器
4.2 LC 振荡器
4.2.2 电容反馈振荡器 (2/6) 1.电路的起振分析
(1) 忽 略 晶 体 管 内 部 反 馈 影 响
(Yre=0);(2)忽略晶体管的输入、输出
电容,或将其包含在回路电容C1、C2 中;(3)忽略晶体管集电极电流ic对输入 信号ub的相移,将Yfe用跨导gm表示。 g’L表示除晶体管以外的电路中所有 电导折算到CE两端后的总电导。将
由振荡器的振幅起振条件 Yfe RLF > 1 ,可得
gmF >1 gL
gm
( g oe
gL )
1 F
gie F
第4章 正弦波振荡器
4.2 LC 振荡器
4.2.2 电容反馈振荡器 (4/6)
只要晶体管的跨导满足上式,振荡器就可以振荡。上式 右边第一项表示输出电导和负载电导对振荡的影响,F 越大越易振荡;第二项表示输入电阻对振荡的影响,gie、 F越大越不易振荡。因此考虑晶体管输入电阻对回路的 加载作用,反馈系数F并非越大越好。gm、gie、goe一定
教材P26,式2-12
因此相位平衡条件可以表示为
2QL (1 0 ) 0
tan[( f
F )]
