遗传算法Genetic Algorithm(matlab GA tool用法打印了,和实验指导书放在一起)

合集下载

matlab 遗传算法参数

Matlab 中可以使用遗传算法工具箱（Genetic Algorithm Toolbox）来实现遗传算法。

该工具箱提供了许多参数可以用于调整算法的行为。

以下是一些常用的参数：1. `PopulationSize`：种群大小，即染色体数量。

通常设置为一个相对较大的数值，以保证算法的搜索能力和多样性。

2. `MaxGenerations`：最大迭代次数。

算法将根据指定的迭代次数进行搜索，直到达到最大迭代次数或找到满足条件的解。

3. `CrossoverFraction`：交叉概率。

在每一代中，根据交叉概率对染色体进行交叉操作，以产生新的染色体。

4. `MutationFcn`：变异函数。

该函数将应用于染色体上的基因，以增加种群的多样性。

5. `Elitism`：精英策略。

该参数决定是否保留最佳个体，以避免算法陷入局部最优解。

6. `PopulationType`：种群类型。

可以选择二进制、实数或整数类型。

7. `ObjectiveFunction`：目标函数。

该函数将用于评估染色体的适应度，以确定哪些染色体更有可能产生优秀的后代。

8. `Variableargin`：变量参数。

可以将需要优化的变量作为参数传递给目标函数和变异函数。

9. `Display`：显示设置。

可以选择在算法运行过程中显示哪些信息，例如每个迭代的最佳个体、平均适应度等等。

以上是一些常用的参数，可以根据具体问题进行调整。

在Matlab 中使用遗传算法时，建议仔细阅读相关文档和示例代码，以便更好地理解算法的实现细节和如何调整参数来获得更好的结果。

遗传算法的原理及MATLAB程序实现.

1 遗传算法的原理1.1 遗传算法的基本思想遗传算法（genetic algorithms，GA）是一种基于自然选择和基因遗传学原理，借鉴了生物进化优胜劣汰的自然选择机理和生物界繁衍进化的基因重组、突变的遗传机制的全局自适应概率搜索算法。

遗传算法是从一组随机产生的初始解（种群）开始，这个种群由经过基因编码的一定数量的个体组成，每个个体实际上是染色体带有特征的实体。

染色体作为遗传物质的主要载体，其内部表现（即基因型）是某种基因组合，它决定了个体的外部表现。

因此，从一开始就需要实现从表现型到基因型的映射，即编码工作。

初始种群产生后，按照优胜劣汰的原理，逐代演化产生出越来越好的近似解。

在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。

这个过程将导致种群像自然进化一样，后代种群比前代更加适应环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。

计算开始时，将实际问题的变量进行编码形成染色体，随机产生一定数目的个体，即种群，并计算每个个体的适应度值，然后通过终止条件判断该初始解是否是最优解，若是则停止计算输出结果，若不是则通过遗传算子操作产生新的一代种群，回到计算群体中每个个体的适应度值的部分，然后转到终止条件判断。

这一过程循环执行，直到满足优化准则，最终产生问题的最优解。

图1-1给出了遗传算法的基本过程。

1.2 遗传算法的特点1.2.1 遗传算法的优点遗传算法具有十分强的鲁棒性，比起传统优化方法，遗传算法有如下优点：1. 遗传算法以控制变量的编码作为运算对象。

传统的优化算法往往直接利用控制变量的实际值的本身来进行优化运算，但遗传算法不是直接以控制变量的值，而是以控制变量的特定形式的编码为运算对象。

这种对控制变量的编码处理方式，可以模仿自然界中生物的遗传和进化等机理，也使得我们可以方便地处理各种变量和应用遗传操作算子。

2. 遗传算法具有内在的本质并行性。

用MATLAB实现遗传算法程序

用MATLAB实现遗传算法程序一、本文概述遗传算法（Genetic Algorithms，GA）是一种模拟自然界生物进化过程的优化搜索算法，它通过模拟自然选择和遗传学机制，如选择、交叉、变异等，来寻找问题的最优解。

由于其全局搜索能力强、鲁棒性好以及易于实现并行化等优点，遗传算法在多个领域得到了广泛的应用，包括函数优化、机器学习、神经网络训练、组合优化等。

本文旨在介绍如何使用MATLAB实现遗传算法程序。

MATLAB作为一种强大的数学计算和编程工具，具有直观易用的图形界面和丰富的函数库，非常适合用于遗传算法的实现。

我们将从基本的遗传算法原理出发，逐步介绍如何在MATLAB中编写遗传算法程序，包括如何定义问题、编码、初始化种群、选择操作、交叉操作和变异操作等。

通过本文的学习，读者将能够掌握遗传算法的基本原理和MATLAB编程技巧，学会如何使用MATLAB实现遗传算法程序，并能够在实际问题中应用遗传算法求解最优解。

二、遗传算法基础遗传算法（Genetic Algorithm，GA）是一种模拟自然选择和遗传学机制的优化搜索算法。

它借鉴了生物进化中的遗传、交叉、变异等机制，通过模拟这些自然过程来寻找问题的最优解。

遗传算法的核心思想是将问题的解表示为“染色体”，即一组编码，然后通过模拟自然选择、交叉和变异等过程，逐步迭代搜索出最优解。

在遗传算法中，通常将问题的解表示为一个二进制字符串，每个字符串代表一个个体（Individual）。

每个个体都有一定的适应度（Fitness），适应度越高的个体在下一代中生存下来的概率越大。

通过选择（Selection）、交叉（Crossover）和变异（Mutation）等操作，生成新一代的个体，并重复这一过程，直到找到满足条件的最优解或达到预定的迭代次数。

选择操作是根据个体的适应度，选择出适应度较高的个体作为父母，参与下一代的生成。

常见的选择算法有轮盘赌选择（Roulette Wheel Selection）、锦标赛选择（Tournament Selection）等。

Matlab遗传算法工具箱简介

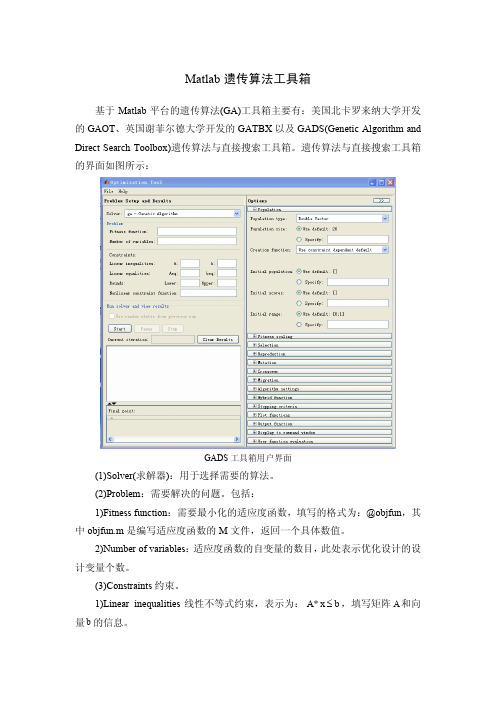
GADS 工具箱用户界面
(1)Solver(求解器)：用于选择需要的算法。 (2)Problem：需要解决的问题。包括： 1)Fitness function：需要最小化的适应度函数，填写的格式为：@objfun，其中 objfun.m 是编写适应度函数的 M 文件，返回一个具体数值。 2)Number of variables：适应度函数的自变量的数目，此处表示优化设计的设计变量个数。 (3)Constraints 约束。 1)Linear inequalities 线性不等式约束，表示为： A * x b ，填写矩阵 A 和向量 b 的信息。
2)Linear equalities 线性等式约束，表示为： Aeq * x beq ，填写矩阵 Aeq 和向量 beq 的信息。 3)Bounds：填写独立变量的取值范围。在 Lower 中填写变量的取值下界， Upper 中填写变量的取值上界，均以向量形式表示。 4)Nonlinear constraint function 非线性约束函数，编写非线性约束函数的 M 文件 nonlcon.m，则在此处填写@nonlcon。 (4)Run solver and view results 运行求解器并观察结果。点击 Start 即可开始运行。Current iteration 中将显示当前运行的代数。Final point 栏中显示最优解对应的变量的取值。 (5)Option 部分是遗传算法参数的设定。 1)Population 种群参数设定。 Population type 种群类型，设定适应度函数的输入数据类型。工具箱提供了两种输入类型：双精度、串位，用户还可以编写 M 文件自定义输入数据的类型。 Population size 种群规模，定义每一代种群的个体数量。种群规模越大，遗传算法的运行速度越慢。 Creation function 创建函数，用于创建初始种群。 Initial population 初始种群，如果不指定初始种群，则系统将运用创建函数创建初始种群。 Initial scores 初始得分，如果此处没有定义初始得分，则系统应用适应度函数来计算初始得分。 Initial range 初始范围，用于指定初始种群中的各变量的上下限。初始范围用一个矩阵表示，该矩阵行数为 2，列数为变量的个数。其中第一行描述初始种群中变量的取值下限，第二行描述初始种群中变量的取值上限。 2)Fitness scaling 适应度测量，包括：Rank 排序尺度变换、Proportional 比例尺度变换、Top 顶级尺度变换、Shift linear 线性转换尺度变换以及 Custom 用户自定义。 3)Selection 选择，工具箱提供了以下几种选择函数：Stochastic uniform 随机 Remainder 剩余、 Uniform 均匀分布、 Roulette 轮盘赌选择、 Tournament 均匀分布、锦标赛选项、Custom 用户自定义。 4)Reproduction 再生参数，需设定可生存到下一代的精英个数 Elite count，以及下一代由交叉产生的部分所占比例 Crossover fraction。

matlab遗传算法工具箱导出数据的方法 -回复

matlab遗传算法工具箱导出数据的方法-回复如何使用MATLAB遗传算法工具箱导出数据MATLAB是一种广泛使用的数值计算和数据可视化软件，其遗传算法工具箱（Genetic Algorithm Toolbox）是一款强大的用于解决优化问题的工具。

在使用遗传算法工具箱时，可能会遇到需要导出数据的情况。

本文将详细介绍如何使用MATLAB遗传算法工具箱导出数据，并提供一步一步的操作指南。

第一步：加载遗传算法工具箱首先，打开MATLAB软件并加载遗传算法工具箱。

在命令窗口输入"ga"命令，即可加载遗传算法工具箱。

第二步：定义适应度函数在使用遗传算法工具箱前，需要定义一个适应度函数。

适应度函数用于度量个体对问题的适应程度，其中最佳适应程度对应最优解。

在定义适应度函数时，可以根据特定问题的要求进行自定义。

第三步：设置遗传算法参数在使用遗传算法工具箱之前，还需要设置一些遗传算法的参数。

这些参数包括种群数量、迭代次数、交叉概率、变异概率等。

根据具体问题的要求，选择合适的参数值。

第四步：运行遗传算法在完成适应度函数和参数设置后，就可以运行遗传算法了。

在命令窗口输入"ga"命令，并将适应度函数和参数作为输入参数传递给该命令。

第五步：导出数据使用遗传算法工具箱进行优化后，可能需要将优化结果导出。

下面介绍几种常用的导出数据的方法。

方法一：使用内置函数MATLAB提供了一些内置函数用于导出数据，其中比较常用的是"save"和"xlswrite"函数。

1. 使用"save"函数"save"函数用于保存变量和工作空间中的数据。

通过在命令窗口输入"save"命令，再将需要保存的变量名作为参数传递给该命令，即可将变量保存为.mat文件。

例如，要将名为"result"的变量保存为.mat文件，可以使用以下命令：save('result.mat', 'result')2. 使用"xlswrite"函数"xlswrite"函数用于将数据写入Excel文件。

Matlab遗传算法优化工具箱GAOT的研究与应用

M a tl ab遗传算法优化工具箱(GAO T)的研究与应用3周正武1,丁同梅1,2,田毅红2,3,王晓峰2,4(1.广东省技师学院,广东博罗　516100; 2.天津大学机械工程学院,天津　300072;3.承德技师学院,河北承德　067400;4.郑州职业技术学院,河南郑州　450121)摘　要:介绍遗传算法的基本原理和Matlab的遗传算法优化工具箱(G AOT),分析了优化工具函数。

探讨Matlab遗传算法工具箱在参数优化和非线性规划中的应用。

通过优化实例,说明遗传算法是一种具有良好的全局寻优性能的优化方法。

用Matlab语言及Matlab语言编制的优化工具箱进行优化设计具有语言简单、函数丰富、用法比较灵活、编程效率高等特点。

关键词:遗传算法;Matlab工具箱;优化中图分类号:T H164 文献标识码:A 文章编号:1007-4414(2006)06-0069-03The study and appli ca ti on of geneti c a lgor ith m opti m i za ti on toolbox i n M a tl abZhou Zheng-wu1,D ing T ong-mei1,2,Tian Yi-hong2,3,W ang Xiao-feng2,4(1.College of high-grade technician,B oluo Guangdong　516100,China;2.College of m echanical and engineering,Tianjin university,Tianjin　300072,China;3.Chengde college of high-grade technician,Chengde Hebei　067400,China;4.Zhengzhou vocational college of technology,Zhengzhou Henan　450121,China)Abstract:The paper intr oduces genetic algorith m(G A)and Matlab genetic algorith m op ti m izati on t oolbox and analyses the op ti m izati on t oolbox functi on.The functi on op ti m izati on p r oble m of para meter op ti m izati on and nonlinear has been given t o de monstrate that genetic algorith m is a better gl obal op ti m izati on method.The op ti m izati on design in M atlab and Matlab op ti m i2 zati on t oolbox have si m p le language、abundant functi ons、flexible method and high p r ogramm ing efficiency.Key words:genetic agolrith m;matlab t oolbox;op ti m izati on 遗传算法(G A)是一类借鉴生物界自然选择和遗传原理的随机优化搜索算法。

matlab工具箱遗传算法使用方法

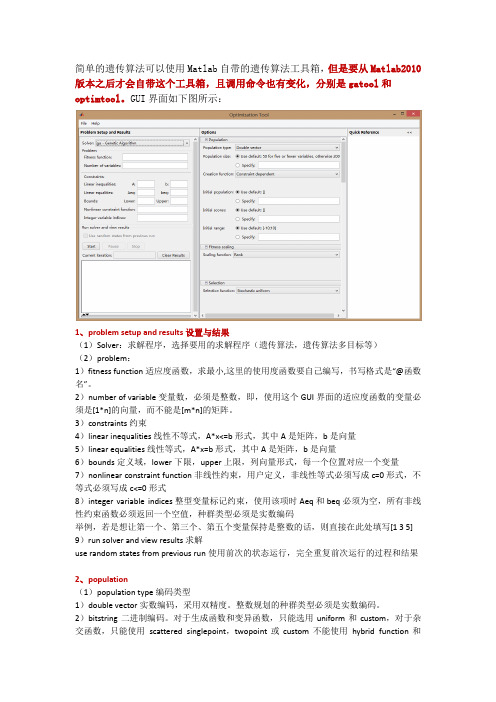
简单的遗传算法可以使用Matlab自带的遗传算法工具箱，但是要从Matlab2010版本之后才会自带这个工具箱，且调用命令也有变化，分别是gatool和optimtool。

GUI界面如下图所示：1、problem setup and results设置与结果（1）Solver：求解程序，选择要用的求解程序（遗传算法，遗传算法多目标等）（2）problem：1）fitness function适应度函数，求最小,这里的使用度函数要自己编写，书写格式是“@函数名”。

2）number of variable变量数，必须是整数，即，使用这个GUI界面的适应度函数的变量必须是[1*n]的向量，而不能是[m*n]的矩阵。

3）constraints约束4）linear inequalities线性不等式，A*x<=b形式，其中A是矩阵，b是向量5）linear equalities线性等式，A*x=b形式，其中A是矩阵，b是向量6）bounds定义域，lower下限，upper上限，列向量形式，每一个位置对应一个变量7）nonlinear constraint function非线性约束，用户定义，非线性等式必须写成c=0形式，不等式必须写成c<=0形式8）integer variable indices整型变量标记约束，使用该项时Aeq和beq必须为空，所有非线性约束函数必须返回一个空值，种群类型必须是实数编码举例，若是想让第一个、第三个、第五个变量保持是整数的话，则直接在此处填写[1 3 5] 9）run solver and view results求解use random states from previous run使用前次的状态运行，完全重复前次运行的过程和结果2、population（1）population type编码类型1）double vector实数编码，采用双精度。

整数规划的种群类型必须是实数编码。

优化算法之遗传算法（GeneticAlgorithm,GA）

优化算法之遗传算法（GeneticAlgorithm,GA）⽬录概述遗传算法（Genetic Algorithm, GA）起源于对⽣物系统所进⾏的计算机模拟研究。

它是模仿⾃然界⽣物进化机制发展起来的随机全局搜索和优化⽅法，借鉴了达尔⽂的进化论和孟德尔的遗传学说。

其本质是⼀种⾼效、并⾏、全局搜索的⽅法，能在搜索过程中⾃动获取和积累有关搜索空间的知识，并⾃适应地控制搜索过程以求得最佳解。

相关术语基因型(genotype)：性状染⾊体的内部表现；表现型(phenotype)：染⾊体决定的性状的外部表现，或者说，根据基因型形成的个体的外部表现；个体（individual）：指染⾊体带有特征的实体；种群（population）：个体的集合，该集合内个体数称为种群的⼤⼩编码(coding)：DNA中遗传信息在⼀个长链上按⼀定的模式排列。

遗传编码可看作从表现型到基因型的映射。

解码(decoding)：基因型到表现型的映射。

交叉(crossover)：两个染⾊体的某⼀相同位置处DNA被切断，前后两串分别交叉组合形成两个新的染⾊体。

也称基因重组或杂交；变异(mutation)：复制时可能（很⼩的概率）产⽣某些复制差错，变异产⽣新的染⾊体，表现出新的性状。

进化(evolution)：种群逐渐适应⽣存环境，品质不断得到改良。

⽣物的进化是以种群的形式进⾏的。

适应度(fitness)：度量某个物种对于⽣存环境的适应程度。

选择(selection)：以⼀定的概率从种群中选择若⼲个个体。

⼀般，选择过程是⼀种基于适应度的优胜劣汰的过程。

复制(reproduction)：细胞分裂时，遗传物质DNA通过复制⽽转移到新产⽣的细胞中，新细胞就继承了旧细胞的基因。

遗传算法的实现过程遗传算法的实现过程实际上就像⾃然界的进化过程那样。

⾸先寻找⼀种对问题潜在解进⾏“数字化”编码的⽅案，（建⽴表现型和基因型的映射关系）。

然后⽤随机数初始化⼀个种群（那么第⼀批袋⿏就被随意地分散在⼭脉上），种群⾥⾯的个体就是这些数字化的编码。

基于Matlab遗传算法工具箱的优化计算实现

基于Matlab遗传算法工具箱的优化计算实现一、概述随着科技的发展和社会的进步，优化问题在众多领域，如工程设计、经济管理、生物科学、交通运输等中扮演着越来越重要的角色。

优化计算的目标是在给定的约束条件下，寻找一组变量，使得某个或某些目标函数达到最优。

许多优化问题具有高度的复杂性，传统的数学方法往往难以有效求解。

寻求新的、高效的优化算法成为了科研人员的重要任务。

遗传算法（Genetic Algorithm, GA）是一种模拟自然选择和遗传学机制的搜索算法，通过模拟自然界的进化过程，寻找问题的最优解。

自20世纪70年代初由美国密歇根大学的John Holland教授提出以来，遗传算法因其全局搜索能力强、鲁棒性好、易于与其他算法结合等优点，被广泛应用于各种优化问题中。

1. 遗传算法简介遗传算法（Genetic Algorithm, GA）是一种模拟自然选择和遗传学机制的优化搜索算法。

该算法起源于对生物进化过程中遗传机制的研究，通过模拟自然选择和遗传过程中的交叉、突变等操作，在搜索空间内寻找最优解。

自20世纪70年代初由John Holland教授提出以来，遗传算法已在多个领域取得了广泛的应用，包括函数优化、机器学习、模式识别、自适应控制等。

遗传算法的基本思想是将问题的解表示为“染色体”，这些染色体在算法中通过选择、交叉和突变等操作进行演化。

选择操作模仿了自然选择中“适者生存”的原则，根据适应度函数对染色体进行筛选交叉操作则模拟了生物进化中的基因重组过程，通过交换染色体中的部分基因，生成新的个体突变操作则是对染色体中的基因进行小概率的随机改变，以维持种群的多样性。

在遗传算法中，种群初始化是算法的起点，通过随机生成一组初始解作为初始种群。

根据适应度函数对种群中的个体进行评估，选择出适应度较高的个体进行交叉和突变操作，生成新的种群。

这个过程不断迭代进行，直到满足终止条件（如达到最大迭代次数或找到满足精度要求的最优解）为止。

遗传算法（GeneticAlgorithm,GA）及MATLAB实现

遗传算法（GeneticAlgorithm,GA）及MATLAB实现遗传算法概述：• 遗传算法（Genetic Algorithm，GA）是⼀种进化算法，其基本原理是仿效⽣物界中的“物竞天择、适者⽣存”的演化法则，它最初由美国Michigan⼤学的J. Holland教授于1967年提出。

• 遗传算法是从代表问题可能潜在的解集的⼀个种群（population）开始的，⽽⼀个种群则由经过基因（gene）编码的⼀定数⽬的个体(individual)组成。

因此，第⼀步需要实现从表现型到基因型的映射即编码⼯作。

初代种群产⽣之后，按照适者⽣存和优胜劣汰的原理，逐代（generation）演化产⽣出越来越好的近似解，在每⼀代，根据问题域中个体的适应度（fitness）⼤⼩选择个体，并借助于⾃然遗传学的遗传算⼦（genetic operators）进⾏组合交叉和变异，产⽣出代表新的解集的种群。

这个过程将导致种群像⾃然进化⼀样，后⽣代种群⽐前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。

• 遗传算法有三个基本操作：选择（Selection）、交叉（Crossover）和变异（Mutation）。

• （1）选择。

选择的⽬的是为了从当前群体中选出优良的个体，使它们有机会作为⽗代为下⼀代繁衍⼦孙。

根据各个个体的适应度值，按照⼀定的规则或⽅法从上⼀代群体中选择出⼀些优良的个体遗传到下⼀代种群中。

选择的依据是适应性强的个体为下⼀代贡献⼀个或多个后代的概率⼤。

• （2）交叉。

通过交叉操作可以得到新⼀代个体，新个体组合了⽗辈个体的特性。

将群体中的各个个体随机搭配成对，对每⼀个个体，以交叉概率交换它们之间的部分染⾊体。

• （3）变异。

对种群中的每⼀个个体，以变异概率改变某⼀个或多个基因座上的基因值为其他的等位基因。

同⽣物界中⼀样，变异发⽣的概率很低，变异为新个体的产⽣提供了机会。

遗传算法的基本步骤：1)编码：GA在进⾏搜索之前先将解空间的解数据表⽰成遗传空间的基因型串结构数据，这些串结构数据的丌同组合便构成了丌同的点。

matlab遗传算法离散值

matlab遗传算法离散值
在MATLAB中，遗传算法（Genetic Algorithm，GA）可以用于解决离散值优化问题。

离散值优化问题是指变量的取值范围是离散的，而不是连续的。

下面我将从几个角度来解释如何在MATLAB中使用遗传算法来解决离散值优化问题。

首先，要使用MATLAB中的遗传算法来解决离散值优化问题，你需要定义适应度函数。

适应度函数的作用是根据给定的解（即染色体）计算其适应度值，这个值用来衡量解的优劣。

在离散值优化问题中，适应度函数的设计十分重要，它需要能够正确地评估离散解的质量。

其次，你需要定义变量的取值范围。

在离散值优化问题中，变量的取值范围是离散的，比如整数或者一组离散的选项。

在MATLAB 中，可以使用`gaoptimset`函数来定义变量的取值范围，以确保遗传算法搜索的解是合法的。

另外，遗传算法中的交叉和变异操作也需要针对离散值进行适当的设计。

在MATLAB中，可以使用`ga`函数来调用遗传算法求解离散值优化问题，并通过设置相应的参数来指定离散值变量的处理方
式。

最后，需要注意的是，离散值优化问题的求解可能会受到问题规模的限制。

对于大规模的离散值优化问题，遗传算法的求解效率可能会受到影响，因此需要合理设计算法参数和适应度函数，以提高求解效率。

综上所述，要在MATLAB中使用遗传算法求解离散值优化问题，需要合理设计适应度函数、定义变量取值范围、处理离散值的交叉和变异操作，并注意求解效率的问题。

希望这些信息能够帮助你更好地理解如何在MATLAB中应用遗传算法求解离散值优化问题。

GADS--matlab遗传算法工具箱使用总结

GADS--Matlab遗传算法工具箱使用总结e-mail:978299005@一、GADS简介与启动MATLAB是矩阵实验室（Matrix Laboratory）的简称，是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分。

遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。

在Matlab平台上主要有三个遗传算法（GA）的工具箱，分别是：GAOT，美国北卡罗来纳大学开发；GATBX，英国谢菲尔德大学开发；GADS，Matlab7以后的版本中自带的。

GATBX可以包含GAOT，而GADS显然年代又近了一些。

这里主要讲的是GADS。

GADS（Genetic Algorithm and Direct Search Toolbox）遗传算法与直接搜索工具箱。

可以在命令行中直接使用，在M文件的程序中调用ga函数，或在GUI 界面中使用它来解决实际问题。

在不同的Matlab版本中启动方法稍有区别。

以笔者的Matlab 2010b为例，启动有两种方法：1、在Matlab命令行中输入optimtool回车，在出现的对话框左上角找到Solver，选择ga- Genetic Algorithm即可。

2、Matlab界面中单击左下角Start,选择toolboxes,选择其中的optimization再点击optimization tool即可打开对话框，然后如1中，选择ga即可。

二、GADS的具体使用【1】先介绍ga函数的格式。

Ga函数可以在命令行中直接使用。

在命令行中键入命令type ga可以打印出ga函数的代码。

键入help ga，就打印出ga函数的帮助提示。

以下是help ga的输出：GA Constrained optimization using genetic algorithm.GA attempts to solve problems of the form:min F(X) subject to: A*X <= B, Aeq*X = Beq (linear constraints)X C(X) <= 0, Ceq(X) = 0 (nonlinear constraints)LB <= X <= ubX = GA(FITNESSFCN,NVARS) finds a local unconstrained minimum X to theFITNESSFCN using GA. NVARS is the dimension (number of designvariables) of the FITNESSFCN. FITNESSFCN accepts a vector X of size1-by-NVARS, and returns a scalar evaluated at X.X = GA(FITNESSFCN,NVARS,A,b) finds a local minimum X to the functionFITNESSFCN, subject to the linear inequalities A*X <= B. Linearconstraints are not satisfied when the PopulationType option is set to'bitString' or 'custom'. See the documentation for details.X = GA(FITNESSFCN,NVARS,A,b,Aeq,beq) finds a local minimum X to thefunction FITNESSFCN, subject to the linear equalities Aeq*X = beq aswell as A*X <= B. (Set A=[] and B=[] if no inequalities exist.) Linearconstraints are not satisfied when the PopulationType option is set to'bitString' or 'custom'. See the documentation for details.X = GA(FITNESSFCN,NVARS,A,b,Aeq,beq,lb,ub) defines a set of lower andupper bounds on the design variables, X, so that a solution is found inthe range lb <= X <= ub. Use empty matrices for lb and ub if no boundsexist. Set lb(i) = -Inf if X(i) is unbounded below; set ub(i) = Inf ifX(i) is unbounded above. Linear constraints are not satisfied when thePopulationType option is set to 'bitString' or 'custom'. See thedocumentation for details.X = GA(FITNESSFCN,NVARS,A,b,Aeq,beq,lb,ub,NONLCON) subjects theminimization to the constraints defined in NONLCON. The functionNONLCON accepts X and returns the vectors C and Ceq, representing thenonlinear inequalities and equalities respectively. GA minimizesFITNESSFCN such that C(X)<=0 and Ceq(X)=0. (Set lb=[] and/or ub=[] ifno bounds exist.) Nonlinear constraints are not satisfied when thePopulationType option is set to 'bitString' or 'custom'. See thedocumentation for details.X = GA(FITNESSFCN,NVARS,A,b,Aeq,beq,lb,ub,NONLCON,options) minimizeswith the default optimization parameters replaced by values in thestructure OPTIONS. OPTIONS can be created with the GAOPTIMSET function.See GAOPTIMSET for details.X = GA(PROBLEM) finds the minimum for PROBLEM. PROBLEM is a structurethat has the following fields:fitnessfcn: <Fitness function>nvars: <Number of design variables>Aineq: <A matrix for inequality constraints>bineq: <b vector for inequality constraints>Aeq: <Aeq matrix for equality constraints>beq: <beq vector for equality constraints>lb: <Lower bound on X>ub: <Upper bound on X>nonlcon: <nonlinear constraint function>options: <Options structure created with GAOPTIMSET>rngstate: <State of the random number generator>[X,FVAL] = GA(FITNESSFCN, ...) returns FVAL, the value of the fitnessfunction FITNESSFCN at the solution X.[X,FVAL,EXITFLAG] = GA(FITNESSFCN, ...) returns EXITFLAG whichdescribes the exit condition of GA. Possible values of EXITFLAG and thecorresponding exit conditions are1 Average change in value of the fitness function overoptions.StallGenLimit generations less than options.TolFun andconstraint violation less than options.TolCon.3 The value of the fitness function did not change inoptions.StallGenLimit generations and constraint violation lessthan options.TolCon.4 Magnitude of step smaller than machine precision and constraintviolation less than options.TolCon. This exit condition appliesonly to nonlinear constraints.5 Fitness limit reached and constraint violation less thanoptions.TolCon.0 Maximum number of generations exceeded.-1 Optimization terminated by the output or plot function.-2 No feasible point found.-4 Stall time limit exceeded.-5 Time limit exceeded.[X,FVAL,EXITFLAG,OUTPUT] = GA(FITNESSFCN, ...) returns astructure OUTPUT with the following information:rngstate: <State of the random number generator before GA started>generations: <Total generations, excluding HybridFcn iterations>funccount: <Total function evaluations>maxconstraint: <Maximum constraint violation>, if anymessage: <GA termination message>[X,FVAL,EXITFLAG,OUTPUT,POPULATION] = GA(FITNESSFCN, ...) returns thefinal POPULATION at termination.[X,FVAL,EXITFLAG,OUTPUT,POPULATION,SCORES] = GA(FITNESSFCN, ...) returnsthe SCORES of the final POPULATION.Example:Unconstrained minimization of 'rastriginsfcn' fitness function ofnumberOfVariables = 2x = ga(@rastriginsfcn,2)Display plotting functions while GA minimizesoptions = gaoptimset('PlotFcns',...{@gaplotbestf,@gaplotbestindiv,@gaplotexpectation,@gaplotstopping});[x,fval,exitflag,output] = ga(@rastriginsfcn,2,[],[],[],[],[],[],[],options)An example with inequality constraints and lower boundsA = [1 1; -1 2; 2 1]; b = [2; 2; 3]; lb = zeros(2,1);% Use mutation function which can handle constraintsoptions = gaoptimset('MutationFcn',@mutationadaptfeasible);[x,fval,exitflag] = ga(@lincontest6,2,A,b,[],[],lb,[],[],options);FITNESSFCN can also be an anonymous function:x = ga(@(x) 3*sin(x(1))+exp(x(2)),2)If FITNESSFCN or NONLCON are parameterized, you can use anonymousfunctions to capture the problem-dependent parameters. Suppose you wantto minimize the fitness given in the function myfit, subject to thenonlinear constraint myconstr, where these two functions areparameterized by their second argument a1 and a2, respectively. Heremyfit and myconstr are MATLAB file functions such asfunction f = myfit(x,a1)f = exp(x(1))*(4*x(1)^2 + 2*x(2)^2 + 4*x(1)*x(2) + 2*x(2) + a1);andfunction [c,ceq] = myconstr(x,a2)c = [1.5 + x(1)*x(2) - x(1) - x(2);-x(1)*x(2) - a2];% No nonlinear equality constraints:ceq = [];To optimize for specific values of a1 and a2, first assign the valuesto these two parameters. Then create two one-argument anonymousfunctions that capture the values of a1 and a2, and call myfit andmyconstr with two arguments. Finally, pass these anonymous functions toGA:a1 = 1; a2 = 10; % define parameters first% Mutation function for constrained minimizationoptions = gaoptimset('MutationFcn',@mutationadaptfeasible);x = ga(@(x)myfit(x,a1),2,[],[],[],[],[],[],@(x)myconstr(x,a2),options)解释如下：ga函数最完整的格式是[X,FVAL,EXITFLAG,OUTPUT,POPULATION,SCORES]= GA(FITNESSFCN,NVARS,A,b,Aeq,beq,lb,ub,NONLCON,options)。

matlab遗传算法ga工具箱调用gpu运算

matlab遗传算法ga工具箱调用gpu运算1. 引言1.1 背景介绍在传统的遗传算法中，遗传算法能够有效地解决一些复杂的优化问题。

随着问题规模的增大和复杂度的提高，传统的遗传算法在计算效率上显得有些力不从心。

为了提高遗传算法的计算速度和效率，研究者们开始探索将图形处理器（GPU）应用于遗传算法中，以加速计算过程。

GPU是一种高度并行化的处理器，适合处理大规模的并行计算任务。

相比于传统的中央处理器（CPU），GPU具有更多的处理单元和更快的计算速度。

通过利用GPU的并行计算能力，可以显著加速遗传算法的计算过程，从而提高算法的效率和性能。

在MATLAB中，有专门的遗传算法GA工具箱，可以方便地实现遗传算法。

结合GPU加速计算的技术，可以进一步提高遗传算法在复杂优化问题上的求解能力。

本文将介绍如何使用MATLAB遗传算法GA工具箱调用GPU进行计算，并通过实验设计和结果分析来验证其优化效果。

通过本文的研究，可以更好地了解遗传算法在GPU加速计算下的应用和优化效果，为未来的研究提供参考。

1.2 研究目的研究目的是为了探讨在遗传算法中利用GPU加速运算的优势和应用。

由于遗传算法是一种基于群体搜索的优化算法，通常需要进行大量的迭代计算以找到最优解。

而传统的CPU计算在处理大规模问题时往往效率较低，因此利用GPU进行并行计算能够显著提高算法的运行速度和效率。

通过调用MATLAB遗传算法GA工具箱，并结合GPU加速运算，可以加快算法的收敛速度，提高搜索效率，同时也能够处理更复杂的优化问题。

研究的目的是为了验证在实际应用中，利用GPU进行计算对遗传算法的性能和效果的提升程度，并进一步分析其在不同类型问题上的适用性和优势。

通过本研究的实验设计与结果分析，可以对比传统CPU计算和GPU加速计算的效果差异，评价加速计算技术在遗传算法中的实际应用效果，为进一步优化遗传算法的设计和改进提供参考依据。

2. 正文2.1 GPU加速在遗传算法中的应用遗传算法是一种通过模拟自然选择与遗传机制来搜索最优解的优化算法，然而遗传算法在处理复杂问题时往往需要大量的计算资源来进行演化计算，而传统的CPU计算速度往往难以满足需求。

matlab遗传算法ga工具箱调用gpu运算

matlab遗传算法ga工具箱调用gpu运算全文共四篇示例，供读者参考第一篇示例：Matlab是一个强大的科学计算工具，而遗传算法（Genetic Algorithm，GA）被广泛应用于优化问题的求解。

在大规模优化问题中，GA的求解速度往往是一个瓶颈，为了加速GA的求解过程，可以利用GPU进行并行计算。

在Matlab中，可以通过GPU进行加速的工具箱，称为Parallel Computing Toolbox。

本文将介绍如何利用Matlab的Parallel Computing Toolbox和GA工具箱结合起来，实现GPU加速GA的求解过程。

我们需要在Matlab中安装Parallel Computing Toolbox和GA 工具箱。

在安装完成后，就可以开始编写适用于GPU加速的GA程序了。

在编写程序时，需要注意以下几点：1. 设定GA参数：一般来说，可以设置GA的种群大小、迭代次数、交叉概率、变异概率等参数。

这些参数的设定将直接影响到GA的求解效果和速度。

2. 定义适应度函数：在GA中，适应度函数决定了个体的适应程度，从而影响被选择的几率。

在编写适用于GPU加速的适应度函数时，要注意将计算过程向量化，以便GPU并行计算。

3. 设置GPU运算环境：在Matlab中，可以通过parallel.gpu.GPUDevice函数获取当前可用的GPU设备列表，并选择一个合适的设备进行计算。

在进行GPU计算时，需要将待处理的数据转换为GPU数组，以便GPU并行计算。

4. 调用GA函数并启用GPU加速：在进行GA求解过程中，可以通过设置options参数启用GPU加速。

在调用GA函数时，可以通过设定eParallel参数为true，来启用GPU加速。

下面，我们来看一个简单的例子，演示如何利用Parallel Computing Toolbox和GA工具箱结合GPU加速GA的求解过程。

假设我们要求解一个简单的函数f(x) = x^2 + 5，在区间[-10, 10]内的最小值。

使用MATLAB遗传算法工具实例详细

使用MATLAB遗传算法工具实例详细最新发布的MATLAB Release 14已经包含了一个专门设计的遗传算法与直接搜索工具箱（Genetic Algorithm and Direct Search Toolbox，GADS）。

使用遗传算法与直接搜索工具箱，可以扩展MATLAB 及其优化工具箱在处理优化问题方面的能力，可以处理传统的优化技术难以解决的问题，包括那些难以定义或不便于数学建模的问题，可以解决目标函数较复杂的问题，比如目标函数不连续、或具有高度非线性、随机性以及目标函数没有导数的情况。

本章节首先介绍这个遗传算法与直接搜索工具箱，其余各节分别介绍该工具箱中的遗传算法工具及其使用方法。

遗传算法与直接搜索工具箱概述本节介绍MATLAB的GADS（遗传算法与直接搜索）工具箱的特点、图形用户界面及运行要求，解释如何编写待优化函数的M文件，且通过举例加以阐明。

8.1.1 工具箱的特点GADS工具箱是一系列函数的集合，它们扩展了优化工具箱和MATLAB数值计算环境的性能。

遗传算法与直接搜索工具箱包含了要使用遗传算法和直接搜索算法来求解优化问题的一些例程。

这些算法使我们能够求解那些标准优化工具箱范围之外的各种优化问题。

所有工具箱函数都是MATLAB的M文件，这些文件由实现特定优化算法的MATLAB语句所写成。

使用语句type function_name就可以看到这些函数的MATLAB代码。

我们也可以通过编写自己的M文件来实现来扩展遗传算法和直接搜索工具箱的性能，也可以将该工具箱与MATLAB的其他工具箱或Simulink结合使用，来求解优化问题。

工具箱函数可以通过图形界面或MATLAB命令行来访问，它们是用MATLAB语言编写的，对用户开放，因此可以查看算法、修改源代码或生成用户函数。

遗传算法与直接搜索工具箱可以帮助我们求解那些不易用传统方法解决的问题，譬如表查找问题等。

遗传算法与直接搜索工具箱有一个精心设计的图形用户界面，可以帮助我们直观、方便、快速地求解最优化问题。

Matlab遗传算法工具箱的应用

文章编号：1006-1576（2005）06-0115-02Matlab遗传算法工具箱的应用曾日波（江西财经大学电子学院，江西南昌 330013）摘要：Matlab遗传算法（GA）优化工具箱是基于基本操作及终止条件、二进制和十进制相互转换等操作的综合函数库。

其实现步骤包括：通过输入及输出函数求出遗传算法主函数、初始种群的生成函数，采用选择、交叉、变异操作求得基本遗传操作函数。

以函数仿真为例，对该函数优化和GA改进，只需改写函数m文件形式即可。

关键词：遗传算法；Matlab；遗传算法工具箱；仿真中图分类号：TP391.9 文献标识码：AApplication of Genetic Algorithm Toolbox Based on MatlabZENG Ri-bo(College of Finance and Economics Electronics, Jiangxi University, Nanchang 330013, China) Abstract: The optimization toolbox of Matlab genetic algorithm (GA) is a excellent generalized function library is to bases on basic operation and terminate term, the inter-conversion between binary system and ten system the system etc. Its step includes: the main function of GA and the creation functions of initial population was calculated through inputting and outputting functions, and the basic functions of genetic operation was computed by choosing, interlacing, and aberrance functions to realize the system. Take the function simulation as an example, the optimization of function and improvement of GA were achieved by modification the file format of m function.Keywords: Genetic algorithm; Matlab; Optimization toolbox; Simulation1 引言遗传算法（GA：Genetic Algorithm）是对生物进化过程进行的数学方式仿真。

matlab工具箱遗传算法使用方法

简单的遗传算法可以使用Matlab自带的遗传算法工具箱，但是要从Matlab2010版本之后才会自带这个工具箱，且调用命令也有变化，分别是gatool和optimtool。

2）number of variable变量数，必须是整数，即，使用这个GUI界面的适应度函数的变量必须是[1*n]的向量，而不能是[m*n]的矩阵。

整数规划的种群类型必须是实数编码。

遗传算法Genetic Algorithm(matlab GA tool用法打印了,和实验指导书放在一起)

matlab 遗传算法 参数

遗传算法的原理及MATLAB程序实现.

用MATLAB实现遗传算法程序

Matlab遗传算法工具箱简介

matlab遗传算法工具箱导出数据的方法 -回复

Matlab遗传算法优化工具箱GAOT的研究与应用

matlab工具箱遗传算法使用方法

优化算法之遗传算法（GeneticAlgorithm,GA）

基于Matlab遗传算法工具箱的优化计算实现

遗传算法（GeneticAlgorithm,GA）及MATLAB实现

matlab遗传算法离散值

GADS--matlab遗传算法工具箱使用总结

matlab遗传算法ga工具箱调用gpu运算

matlab遗传算法ga工具箱调用gpu运算

使用MATLAB遗传算法工具实例详细

Matlab遗传算法工具箱的应用

matlab工具箱遗传算法使用方法

matlab 遗传算法参数