关于混淆矩阵
关于混淆矩阵
关于混淆矩阵混淆矩阵是用来反映某一个分类模型的分类结果的,其中行代表的是真实的类,列代表的是模型的分类。
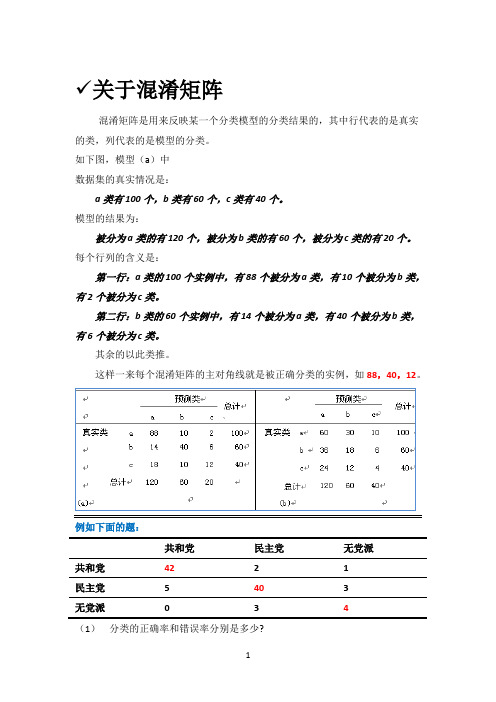
如下图,模型(a)中数据集的真实情况是:a类有100个,b类有60个,c类有40个。
模型的结果为:被分为a类的有120个,被分为b类的有60个,被分为c类的有20个。
每个行列的含义是:第一行:a类的100个实例中,有88个被分为a类,有10个被分为b类,有2个被分为c类。
第二行:b类的60个实例中,有14个被分为a类,有40个被分为b类,有6个被分为c类。
其余的以此类推。
这样一来每个混淆矩阵的主对角线就是被正确分类的实例,如88,40,12。
例如下面的题:共和党民主党无党派共和党4221民主党540 3无党派03 4(1)分类的正确率和错误率分别是多少?正确率:(42+40+4)/(42+2+1+5+40+3+0+3+4)=86 / 100 = 86%错误率:1-86%=14%(2)参议院中分别有几名民主党、几名共和党,几名无党派议员?民主:5+40+3=48共和:42+2+1=45无党:0+3+4=7(3)有几名共和党人士被分类到民主党?有几名无党派人士被分类到共和党?2个(第“共和党”行第“民主党”列)。
0个(第“无党派”行第“共和党”列)。
关于lift值lift值的应用:举例来说,如果一个公司对某一个群体进行发传单宣传。
假设有10000人,其中响应(做出回应)的人有1000人,现在构造一个模型,这个模型的执行结果是,选出来4000人,这4000人中有800人是响应(做出回应)的。
这样:最初的比例是:1000 / 10000 = 0.1模型计算后的比例为:800 / 4000 = 0.5那么lift值为:lift = 0.5 / 0.1 = 5Lift值是衡量模型好坏的一个指标,其含义是人群响应比提高的倍数。
例如下面的题:考虑下面混淆矩阵,分别计算模型X与模型Y的Lift,比较哪个模型更好?为什么?模型X计算接受计算拒绝模型Y计算接受计算拒绝接受4654接受4555拒绝22457655拒绝19557945思考方向:Lift的值是“模型计算后的响应比例”和“计算前的响应比例”的比值,所以只要计算前后的响应比例就可以了。
理解混淆矩阵

理解混淆矩阵混淆矩阵是描述分类器/分类模型的性能的表。
它包含有关分类器完成的实际和预测分类的信息,此信息用于评估分类器的性能。
请注意,混淆矩阵仅用于分类任务,因此不能用于回归模型或其他非分类模型。
在我们继续之前,让我们看看一些术语。
▪分类器:分类器基本上是一种算法,它使用从训练数据中获得的“知识”来将输入数据映射到特定类别或类别。
分类器是二元分类器或多类/多分类/多标签/多输出分类器。
▪训练和测试数据:在构建分类模型/分类器时,数据集被分成训练数据和具有相关标签的测试数据。
标签是预期的输出,它是数据所属的类别或类别。
▪实际分类:这是数据的预期输出(标签)。
▪预测分类:这是分类器为特定输入数据提供的输出。
一个例子:假设我们已经建立了一个分类器来将汽车的输入图像分类为轿车或者不是轿车,我们在数据集中有一个标记为非轿车的图像,但分类模型归类为轿车。
在这种情况下,实际分类是非轿车,而预测分类是轿车。
混淆矩阵的类型有两种类型的混淆矩阵:▪2级混淆矩阵▪多级混淆矩阵2级混淆矩阵顾名思义,2类是一个描述二元分类模型性能的混淆矩阵。
我之前描述的轿车分类器的2级矩阵可以这样显示:在此可视化中,我们有两个已概述的部分。
我们有预测的分类部分,其中包含每个类的两个子部分和实际的分类部分,每个部分有两个子部分。
如果这是您第一次看到混淆矩阵,我知道您必须想知道表中的所有变量代表什么。
实际上它很简单,我会尽可能简单地解释,但在我这样做之前,知道这些变量代表了许多预测是很重要的。
变量a变量a属于Actual和Predicted分类部分中的Non-sedan 子部分。
这意味着一个预测所做的正确分类的非轿车[作为非轿车]的图像。
变量b变量b属于实际分类部分中的非轿车子部分和预测分类部分中的轿车子部分。
这意味着进行了b预测,将非轿车的图像错误地分类为轿车。
变量c变量ç落在下的轿车在次节实际分类段和下的非轿车在小节预测分类部分。
关于混淆矩阵的一些知识?

关于混淆矩阵的一些知识?1.引言1.1 概述在机器学习和模式识别领域,混淆矩阵是一种常用的评估分类模型性能的工具。
它是通过将预测结果与真实标签进行对比而创建的一个二维表格。
混淆矩阵以分类模型的预测结果和真实标签为基准,将样本分为四个不同的类别:真正例(True Positive, TP)、假正例(False Positive, FP)、真反例(True Negative, TN)和假反例(False Negative, FN)。
其中,"真"和"假"表示模型的预测结果是否与真实情况相符,"正例"和"反例"表示样本的真实标签。
通过将预测结果和真实标签的组合进行统计,我们可以得到一个具有四个不同分类的表格。
在混淆矩阵中,TP表示分类模型正确地将正例样本分类为正例,FP 表示分类模型错误地将反例样本分类为正例,TN表示分类模型正确地将反例样本分类为反例,FN表示分类模型错误地将正例样本分类为反例。
这四个指标可以帮助我们全面了解分类模型的性能。
混淆矩阵在很多实际应用中都有广泛的应用。
例如,在医学诊断中,混淆矩阵可以用来评估模型对患者是否患有某种疾病的预测准确性;在垃圾邮件过滤中,混淆矩阵可以用来判断模型对正常邮件和垃圾邮件的分类情况。
尽管混淆矩阵在评估分类模型性能中提供了很多有用的信息,但也存在一些局限性。
例如,混淆矩阵无法直接反映分类模型的准确率和召回率,需要通过进一步的计算得到。
此外,在处理样本不平衡的情况下,混淆矩阵可能导致评估结果偏向于占多数的类别。
总之,混淆矩阵作为评估分类模型性能的重要工具,可以帮助我们全面了解模型的分类结果。
然而,我们也需要注意混淆矩阵的局限性,以便更加准确地评估模型的性能。
接下来,我们将详细介绍混淆矩阵的定义和解释,并探讨其在不同应用场景下的应用。
1.2文章结构文章结构部分的内容:在本篇文章中,我们将对混淆矩阵进行详细的探讨和解释。
python的混淆矩阵

python的混淆矩阵混淆矩阵是在机器学习领域中用于评估分类模型性能的一种表格。
它以矩阵的形式展示了分类模型在预测过程中真实类别与预测类别之间的对应关系。
在Python中,我们可以使用多种库来计算和可视化混淆矩阵,包括scikit-learn和matplotlib。
首先,我们可以使用scikit-learn库来计算混淆矩阵。
假设我们有真实类别为y_true,预测类别为y_pred的数据,我们可以使用以下代码来计算混淆矩阵:python.from sklearn.metrics import confusion_matrix.import numpy as np.y_true = np.array([1, 0, 1, 1, 0, 1])。
y_pred = np.array([0, 0, 1, 1, 0, 1])。
cm = confusion_matrix(y_true, y_pred)。
print(cm)。
上述代码将打印出计算得到的混淆矩阵。
混淆矩阵的行表示真实类别,列表示预测类别,因此对角线上的元素表示被正确预测的样本数,非对角线上的元素表示被错误预测的样本数。
接下来,我们可以使用matplotlib库来可视化混淆矩阵。
我们可以使用以下代码来绘制混淆矩阵的热力图:python.import matplotlib.pyplot as plt.import seaborn as sns.sns.heatmap(cm, annot=True, fmt="d")。
plt.xlabel('Predicted')。
plt.ylabel('Actual')。
plt.show()。
上述代码将绘制出混淆矩阵的热力图,其中矩阵的每个单元格中的数字表示对应类别的样本数,颜色的深浅表示样本数的多少。
除了计算和可视化混淆矩阵外,我们还可以从多个角度来解释混淆矩阵。
例如,我们可以计算精确度、召回率、F1分数等指标来更全面地评估分类模型的性能。
python 逻辑回归 混淆矩阵

python 逻辑回归混淆矩阵摘要:一、逻辑回归简介1.逻辑回归的定义2.逻辑回归的作用二、混淆矩阵1.混淆矩阵的概念2.混淆矩阵的组成部分3.混淆矩阵的重要性三、逻辑回归与混淆矩阵的关系1.混淆矩阵在逻辑回归中的应用2.逻辑回归结果的解读四、总结1.逻辑回归和混淆矩阵的联系2.在实际应用中应注意的问题正文:一、逻辑回归简介逻辑回归是一种常见的机器学习算法,主要用来进行二分类问题。
它的核心思想是利用逻辑函数(sigmoid 函数)将输入数据映射到输出结果,通过最小化损失函数来调整模型参数,从而达到分类的目的。
二、混淆矩阵1.混淆矩阵的概念混淆矩阵(Confusion Matrix)是在分类问题中,对模型预测结果的统计分析工具。
它是一个二维矩阵,用于表示真实类别与预测类别之间的对应关系。
2.混淆矩阵的组成部分混淆矩阵通常由四个元素组成:真正例(True Positive,TP)、假正例(False Positive,FP)、真反例(True Negative,TN)和假反例(False Negative,FN)。
3.混淆矩阵的重要性混淆矩阵可以帮助我们了解模型的预测性能,包括准确率、精确率、召回率和F1 值等指标。
通过对混淆矩阵的分析,我们可以发现模型的优点和不足,从而进行相应的优化。
三、逻辑回归与混淆矩阵的关系1.混淆矩阵在逻辑回归中的应用在逻辑回归中,混淆矩阵用于评估模型的分类效果。
我们可以通过计算混淆矩阵中的各个指标,来衡量模型的性能。
2.逻辑回归结果的解读根据混淆矩阵的结果,我们可以解读模型的预测效果。
例如,如果模型在某一类别的预测中,假正例较多,说明模型对该类别的区分度不高,需要调整模型参数以提高分类效果。
四、总结1.逻辑回归和混淆矩阵的联系逻辑回归是一种用于解决分类问题的机器学习算法,而混淆矩阵是评估分类模型效果的一种工具。
在逻辑回归中,我们可以通过混淆矩阵来分析模型的性能,发现模型的不足,并进行优化。
混淆矩阵的概念

混淆矩阵的概念嘿,朋友们!今天咱来聊聊混淆矩阵这个有意思的玩意儿。
你说混淆矩阵像不像一个神奇的魔法盒子呀?它里面装着好多关于分类结果的秘密呢!比如说,你在分辨苹果和橘子的时候,有时候可能会搞混,把苹果当成橘子,或者把橘子当成苹果。
这就好像混淆矩阵里的那些数字,它们在告诉你到底有多少次搞对了,又有多少次弄错啦。
咱可以把混淆矩阵想象成一个棋盘,上面的格子就代表着不同的情况。
比如说,有一个格子里的数字特别大,那就说明在这种情况下出错的次数可不少呢!这就好比你玩跳棋,老是跳进同一个错误的洞里,是不是很搞笑呀?再比如说,我们要判断一个人是好人还是坏人。
如果混淆矩阵里表示把好人当成坏人的数字很大,那可就糟糕啦,这不是冤枉好人嘛!反过来,如果把坏人当成好人的数字很大,那也不行呀,这不是放跑坏人了嘛!这就好像警察抓小偷,要是老是抓错人或者放走坏人,那可怎么行呢!混淆矩阵还能帮我们看出哪些情况是最容易搞混的。
就像你去超市买东西,有些东西长得特别像,你就容易拿错。
那在混淆矩阵里,这些容易搞混的情况对应的数字就会比较大呀。
那我们就得特别注意这些地方,想想办法怎么才能减少错误呢。
而且哦,混淆矩阵可不只是在简单的分类问题里有用呢!在好多领域都能派上大用场。
比如说医学上判断病情,要是把没病的人误诊成有病,或者把有病的人误诊成没病,那后果可不堪设想呀!这时候混淆矩阵就能帮医生们更好地了解诊断的准确性。
你想想看,要是没有混淆矩阵,我们怎么知道自己的判断到底准不准确呢?那不就像闭着眼睛走路一样,容易摔跟头嘛!有了它,我们就能清楚地看到自己的长处和短处,然后努力改进,让自己变得更厉害呀!总之呢,混淆矩阵就像是我们的小助手,帮助我们更好地理解和分析分类结果。
它虽然看起来有点复杂,但只要我们用心去理解,就会发现它其实很有趣呢!它能让我们在面对各种分类问题时更加有把握,不再像无头苍蝇一样乱撞啦!所以呀,可别小看了这个小小的混淆矩阵哦!原创不易,请尊重原创,谢谢!。
多分类混淆矩阵和准确率的关系

多分类混淆矩阵和准确率的关系在机器学习和数据科学领域,多分类混淆矩阵和准确率是两个重要的概念,它们之间存在着密切的关系。
准确率是评估分类模型表现的重要指标之一,它反映了分类器正确分类的比例。
而多分类混淆矩阵则提供了更加详细和全面的分类器性能评估信息,包括各类别的分类准确率、错误率、召回率和精确率等指标。
本文将深入探讨多分类混淆矩阵和准确率之间的关系,以及它们在机器学习任务中的实际应用。
首先,我们需要了解多分类混淆矩阵是什么。
在多分类问题中,混淆矩阵是一个N×N的矩阵,其中N表示类别的个数。
混淆矩阵的行代表真实类别,列代表预测类别,矩阵的每个元素表示真实类别为行索引对应类别、预测类别为列索引对应类别的样本数量。
通过观察混淆矩阵,我们可以了解到分类器在每个类别上的表现情况,进而评估分类器的整体性能。
准确率是我们最常用的评估指标之一,它定义为分类器正确分类的样本数量与总样本数量的比值。
在二分类问题中,准确率可以简单地表示为:\[Accuracy = \frac{TP + TN}{TP + TN + FP + FN}\]其中TP(True Positive)表示真正的正例,TN(True Negative)表示真正的负例,FP(False Positive)表示假正例,FN(False Negative)表示假负例。
然而,在多分类问题中,准确率的计算并不那么直观。
这时候,我们就需要借助多分类混淆矩阵来计算准确率。
多分类问题中的准确率计算通常采用微平均和宏平均两种方式。
微平均准确率是将每个类别的真正例、假正例、假负例和真负例的数量累加起来,然后计算总体的准确率。
宏平均准确率则是计算每个类别的准确率,然后求其算术平均值。
这两种方式的优缺点各有不同,选择哪种方式取决于具体的分类问题和评估需求。
多分类混淆矩阵和准确率之间的关系在于,准确率是通过混淆矩阵的信息计算得出的。
在计算微平均和宏平均准确率时,我们需要借助混淆矩阵中的真正例、假正例、假负例和真负例的数量。
多分类混淆矩阵和准确率的关系

多分类混淆矩阵和准确率的关系在机器学习领域,混淆矩阵是评估分类算法性能的重要工具之一。
它展示了模型在不同类别上的预测结果,帮助我们了解算法的准确性、精确性、召回率等关键指标。
而在多分类问题中,混淆矩阵的分析更加复杂,需要考虑多个类别之间的互相影响和误差传递。
因此,多分类混淆矩阵和准确率之间的关系就显得尤为重要。
首先,我们来简单回顾一下混淆矩阵的基本概念。
混淆矩阵是一个N×N的矩阵,其中N代表类别的数量。
在混淆矩阵中,行表示实际类别,列表示预测类别,每个元素代表在具体类别下的样本数量。
通过观察混淆矩阵,我们可以计算出准确率、精确率、召回率等评估指标,帮助我们全面了解模型的性能表现。
对于二分类问题,混淆矩阵的形式相对简单,只有四个元素:真正例(True Positive, TP)、假正例(False Positive, FP)、真负例(True Negative, TN)和假负例(False Negative, FN)。
在此基础上,我们可以计算出准确率(Accuracy)、精确率(Precision)和召回率(Recall)等指标,了解模型在不同类别下的表现情况。
然而,在多分类问题中,混淆矩阵的形式变得更加复杂。
除了计算单个类别的准确率、精确率和召回率外,我们还需要考虑多个类别之间的混淆情况。
在这种情况下,准确率的计算变得更加困难,需要综合考虑多个类别的预测结果。
具体而言,准确率的计算公式为所有正确分类的样本数除以总样本数,即准确率=(TP1 + TP2 + ... + TPn)/ Total。
在多分类问题中,准确率不再只是简单地反映模型的整体预测正确性,还需要考虑到多个类别之间的判别能力。
如果某一类别的样本数量远远超过其他类别,那么单单考虑准确率可能会存在偏差。
因此,我们需要结合其他评估指标如精确率、召回率等来全面评估模型性能。
除了准确率外,我们还可以通过绘制混淆矩阵的热图来直观地展示模型在不同类别下的预测情况。
多分类混淆矩阵和准确率的关系

多分类混淆矩阵和准确率的关系在机器学习领域,多分类混淆矩阵和准确率是两个非常重要的概念。
多分类混淆矩阵是用来评估分类模型在多个类别上的性能表现的一种工具,而准确率则是评估模型在整体上的预测准确性。
这两个概念之间存在着密切的关系,准确率的计算就是基于多分类混淆矩阵来进行的。
多分类混淆矩阵是一个二维矩阵,其中的行表示真实标签的类别,列表示模型预测的类别。
对角线上的元素表示模型正确分类的样本数量,而非对角线上的元素则表示模型错误分类的样本数量。
通过观察多分类混淆矩阵,我们可以了解模型在每个类别上的表现如何,进而进行更加深入的分析和改进。
在实际应用中,我们往往会通过计算准确率来评估模型的整体性能。
准确率是模型正确分类的样本数量与总样本数量之比,是评估分类模型优劣的一种重要指标。
然而,准确率并不能完全反映模型在不同类别上的表现,因此需要结合多分类混淆矩阵来进行综合评估。
准确率虽然是一个简单直观的指标,但在处理不均衡数据集和多类别分类问题时,可能会存在一定的局限性。
在不均衡数据集中,某些类别的样本数量较少,导致模型对这些类别的预测性能下降,进而影响整体准确率的计算结果。
此时,多分类混淆矩阵可以更加清晰地展现模型在每个类别上的表现,帮助我们更准确地评估模型的性能。
另外,对于多类别分类问题,准确率也可能存在一定的局限性。
在某些情况下,模型可能会出现“混淆”的情况,即将某些类别误判为其他类别,导致准确率下降。
通过多分类混淆矩阵,我们可以清晰地了解模型在每个类别上的混淆情况,从而有针对性地改进模型,提高分类准确性。
除了准确率之外,还有一些其他指标可以用来评估多分类模型的性能,如精确率、召回率、F1值等。
这些指标通常是基于多分类混淆矩阵计算得出的,可以更全面地评估模型在不同情况下的表现。
通过综合考虑这些指标,我们可以更加准确地评估模型的性能,为进一步的优化提供指导。
在实际应用中,我们通常会结合多分类混淆矩阵和准确率等指标进行模型评估。
混淆矩阵 对统计结果的应用

混淆矩阵对统计结果的应用
混淆矩阵是机器学习中一个常用的评估模型性能的工具,在统计学中也有广泛的应用。
它通过将预测结果和真实结果之间的差异可视化为一个矩阵,帮助我们了解模型在不同类别上的表现情况。
混淆矩阵的应用包括:
1. 评估分类模型性能:混淆矩阵可以计算出各种性能指标,如准确率、召回率、F1得分等,帮助我们了解模型在各个类别上的预测效果。
通过观察混淆矩阵可以判断哪些类别容易被误分类、哪些类别预测效果较好。
2. 优化分类模型:通过观察混淆矩阵,我们可以进一步分析模型在不同类别上的误差模式,从而改善模型的表现。
例如,如果模型在某个类别上的误差较大,我们可以尝试增加该类别的样本量、改变特征工程等来改善模型对该类别的预测效果。
3. 多类别分类任务的评估:对于多类别分类任务,混淆矩阵可以帮助我们了解模型在各个类别上的预测情况,判断不同类别之间的混淆程度。
通过观察混淆矩阵,我们可以得出哪些类别容易被误分类为其他类别,从而指导我们对模型进行改进。
4. 异常检测:混淆矩阵可以帮助我们判断模型对异常样本的识别情况。
异常样本通常在混淆矩阵中呈现较高的假阳性或假阴性率,通过观察混淆矩阵,我们可以确定模型对异常样本的检测能力,从而进行后续处理或调整模型。
综上所述,混淆矩阵可用于评估模型性能、优化模型、多类别分类任务的评估以及异常检测等多个方面,在统计学和机器学习领域都具有重要的应用价值。
关于混淆矩阵

关于混淆矩阵混淆矩阵是用来反映某一个分类模型的分类结果的,其中行代表的是真实的类,列代表的是模型的分类。
如下图,模型(a)中数据集的真实情况是:a类有100个,b类有60个,c类有40个。
模型的结果为:被分为a类的有120个,被分为b类的有60个,被分为c类的有20个。
每个行列的含义是:第一行:a类的100个实例中,有88个被分为a类,有10个被分为b类,有2个被分为c类。
第二行:b类的60个实例中,有14个被分为a类,有40个被分为b类,有6个被分为c类。
其余的以此类推。
这样一来每个混淆矩阵的主对角线就是被正确分类的实例,如88,40,12。
例如下面的题:共和党民主党无党派共和党4221民主党540 3无党派03 4(1)分类的正确率和错误率分别是多少?正确率:(42+40+4)/(42+2+1+5+40+3+0+3+4)=86 / 100 = 86%错误率:1-86%=14%(2)参议院中分别有几名民主党、几名共和党,几名无党派议员?民主:5+40+3=48共和:42+2+1=45无党:0+3+4=7(3)有几名共和党人士被分类到民主党?有几名无党派人士被分类到共和党?2个(第“共和党”行第“民主党”列)。
0个(第“无党派”行第“共和党”列)。
关于lift值lift值的应用:举例来说,如果一个公司对某一个群体进行发传单宣传。
假设有10000人,其中响应(做出回应)的人有1000人,现在构造一个模型,这个模型的执行结果是,选出来4000人,这4000人中有800人是响应(做出回应)的。
这样:最初的比例是:1000 / 10000 = 0.1模型计算后的比例为:800 / 4000 = 0.5那么lift值为:lift = 0.5 / 0.1 = 5Lift值是衡量模型好坏的一个指标,其含义是人群响应比提高的倍数。
例如下面的题:考虑下面混淆矩阵,分别计算模型X与模型Y的Lift,比较哪个模型更好?为什么?模型X计算接受计算拒绝模型Y计算接受计算拒绝接受4654接受4555拒绝22457655拒绝19557945思考方向:Lift的值是“模型计算后的响应比例”和“计算前的响应比例”的比值,所以只要计算前后的响应比例就可以了。
混淆矩阵以及各种评估模型

混淆矩阵以及各种评估模型让混淆矩阵不再混淆混淆矩阵是⽤于总结分类算法性能的技术。
如果每个类中的样本数量不等,或者数据集中有两个以上的类,则仅⽤分类准确率作为评判标准的话可能会产⽣误导。
计算混淆矩阵可以让我们更好地了解分类模型的表现情况以及它所犯的错误的类型。
阅读这篇⽂章后你会了解到:混淆矩阵是什么以及为什么需要使⽤混淆矩阵;如何⾃⼰由脚本构造两种类别的分类问题的混淆矩阵;如何在Python中创建混淆矩阵。
1.分类准确率及其局限性分类准确率是预测正确的样本数与总样本数的⽐值即:分类准确率 = 预测正确的样本数 / 总样本数错误率即:错误率 = 1 - 分类准确率分类准确率看上去是⼀个不错的评判标准,但在实际当中往往却存在着⼀些问题。
其主要问题在于它隐藏了我们需要的细节,从⽽阻碍我们更好地理解分类模型的性能。
有两个最常见的例⼦:1. 当我们的数据有2个以上的类时,如3个或更多类,我们可以得到80%的分类准确率,但是我们却不知道是否所有的类别都被预测得同样好,或者说模型是否忽略了⼀个或两个类;1. 当我们的每个类中的样本数并不接近时,我们可以达到90%或更⾼的准确率,但如果每100个记录中有90个记录属于⼀个类别,则这不是⼀个好分数,我们可以通过始终预测最常见的类值来达到此分数。
如90个样本都属于类别1,则我们的模型只需要预测所有的样本都属于类别1,便可以达到90%或更⾼的准确率。
分类准确率可以隐藏诊断模型性能所需的详细信息,但幸运的是,我们可以通过混淆矩阵来进⼀步区分这些细节。
2.什么是混淆矩阵混淆矩阵是对分类问题的预测结果的总结。
使⽤计数值汇总正确和不正确预测的数量,并按每个类进⾏细分,这是混淆矩阵的关键所在。
混淆矩阵显⽰了分类模型的在进⾏预测时会对哪⼀部分产⽣混淆。
它不仅可以让您了解分类模型所犯的错误,更重要的是可以了解哪些错误类型正在发⽣。
正是这种对结果的分解克服了仅使⽤分类准确率所带来的局限性。
【分类模型评判指标一】混淆矩阵(ConfusionMatrix)

【分类模型评判指标⼀】混淆矩阵(ConfusionMatrix)转⾃:略有改动,仅供个⼈学习使⽤简介混淆矩阵是ROC曲线绘制的基础,同时它也是衡量分类型模型准确度中最基本,最直观,计算最简单的⽅法。
⼀句话解释版本:混淆矩阵就是分别统计分类模型归错类,归对类的观测值个数,然后把结果放在⼀个表⾥展⽰出来。
这个表就是混淆矩阵。
数据分析与挖掘体系位置混淆矩阵是评判模型结果的指标,属于模型评估的⼀部分。
此外,混淆矩阵多⽤于判断分类器(Classifier)的优劣,适⽤于分类型的数据模型,如分类树(Classification Tree)、逻辑回归(Logistic Regression)、线性判别分析(Linear Discriminant Analysis)等⽅法。
在分类型模型评判的指标中,常见的⽅法有如下三种:混淆矩阵(也称误差矩阵,Confusion Matrix)ROC曲线AUC⾯积本⽂主要介绍第⼀种⽅法,即混淆矩阵,也称误差矩阵。
此⽅法在整个数据分析与挖掘体系中的位置如下图所⽰。
混淆矩阵的定义混淆矩阵(Confusion Matrix),它的本质远没有它的名字听上去那么拉风。
矩阵,可以理解为就是⼀张表格,混淆矩阵其实就是⼀张表格⽽已。
以分类模型中最简单的⼆分类为例,对于这种问题,我们的模型最终需要判断样本的结果是0还是1,或者说是positive还是negative。
我们通过样本的采集,能够直接知道真实情况下,哪些数据结果是positive,哪些结果是negative。
同时,我们通过⽤样本数据跑出分类型模型的结果,也可以知道模型认为这些数据哪些是positive,哪些是negative。
因此,我们就能得到这样四个基础指标,我称他们是⼀级指标(最底层的):真实值是positive,模型认为是positive的数量(True Positive=TP)真实值是positive,模型认为是negative的数量(False Negative=FN):这就是统计学上的第⼀类错误(Type I Error)真实值是negative,模型认为是positive的数量(False Positive=FP):这就是统计学上的第⼆类错误(Type II Error)真实值是negative,模型认为是negative的数量(True Negative=TN)将这四个指标⼀起呈现在表格中,就能得到如下这样⼀个矩阵,我们称它为混淆矩阵(Confusion Matrix):混淆矩阵的指标预测性分类模型,肯定是希望越准越好。
多 阶混淆矩阵

多阶混淆矩阵混淆矩阵是机器学习中一种常用的评估分类模型性能的工具,它可以用来衡量模型对不同类别样本的分类准确性。
在二分类问题中,混淆矩阵通常由四个元素组成:真正例(True Positive, TP)、真反例(True Negative, TN)、假正例(False Positive, FP)和假反例(False Negative, FN)。
然而,在实际应用中,很多问题不仅仅涉及到两个类别的分类,而是多个类别之间的分类。
为了解决这个问题,多阶混淆矩阵被引入。
多阶混淆矩阵是对多类问题中模型性能进行评估的一种扩展。
它的核心思想是将每个类别都看作是一个二分类问题中的一个类别,然后计算出混淆矩阵。
通过对每个类别的混淆矩阵进行求和,得到最终的多阶混淆矩阵。
多阶混淆矩阵的形式如下:类别A 类别B 类别C类别A TP FP FN类别B FN TP FP类别C FP FN TP在多阶混淆矩阵中,每个元素(i, j)表示模型将类别i样本预测为类别j的个数。
对角线上的元素表示模型的正确分类情况,非对角线上的元素表示模型的错误分类情况。
根据多阶混淆矩阵,可以计算出各种评估指标来度量模型的性能。
常用的指标包括准确率(Accuracy)、召回率(Recall)、精确率(Precision)和F1值等。
•准确率是指模型正确分类样本数占总样本数的比例,可以通过计算TP、TN 和总样本数的比值得到。
•召回率是指模型正确预测的正例样本数占所有正例样本数的比例,可以通过计算 TP 和 TP、FN 的和的比值得到。
•精确率是指模型预测为正例的样本中,真正为正例的样本数占所有预测为正例的样本数的比例,可以通过计算 TP 和 TP、FP 的和的比值得到。
•F1值是综合考虑了精确率和召回率的指标,可以通过计算 2 * (精确率 * 召回率) / (精确率 + 召回率) 得到。
多阶混淆矩阵和相应的评估指标为我们提供了一种全面而准确地评估模型性能的方法,能够帮助我们了解模型在各个类别上的分类情况,并且可以根据评估结果进行模型调整和改进。
多分类问题的混淆矩阵

多分类问题的混淆矩阵在机器学习中,多分类问题是指需要对数据进行分类,同时存在三个及以上类别的问题。
多分类问题可以使用混淆矩阵来评估分类质量。
混淆矩阵是一个方阵,其中行代表实际类别、列代表预测类别,在每个单元格中表示预测为该类别的实例数量。
在本文中,我们将介绍多分类问题的混淆矩阵及其用例。
在二分类问题中,混淆矩阵是一个二乘二的矩阵,其中有四个重要的值:真阳性(True Positive,TP)、假阳性(False Positive,FP)、真阴性(True Negative,TN)、假阴性(False Negative,FN)。
一个实例要么被正确分类为阳性(Positive,P),要么被错误分类为否定(Negative,N)。
P或N是真阳性或真阴性的组合,而FP 或FN是没有正确分类的组合。
在多分类问题中,每个类别都有自己的TP、FP、TN、FN值,因此混淆矩阵会有更多的值。
让我们以一个具体的示例来说明多分类问题的混淆矩阵。
假设我们正在对花进行分类,有三个类别:红花、黄花和白花。
我们已经输入了100个实例,用算法将它们分为三个类别。
下表是混淆矩阵:| | 红花 | 黄花 | 白花 | | :------: | :--: | :--: | :--: | | 真实值 | 25 | 10| 5 | | 红花预测 | 20 | 5 | 0 | | 黄花预测 | 4 | 15 | 1 | | 白花预测| 1 | 0 | 39 |在这个例子中,我们真正地将25个花分类为红花(真实值),将20个花预测为红花(红花预测)。
但我们也将10个黄花和5个白花不正确地分类为红花(假阳性)。
同样,我们只正确地将5个花分类为黄花(真正值),但将4个红花、15个黄花和1个白花错误地分类为黄花。
我们将一个红色和39个白色的花正确地分类为白色。
然而,我们没有正确地分类黄色和白色的花(假阴性)。
根据混淆矩阵,我们可以计算某些评估指标。
多 阶混淆矩阵

多阶混淆矩阵混淆矩阵是机器学习领域中一种常见的工具,用于评估分类模型的性能。
它通过对模型的预测结果与实际标签进行统计,将分类结果以矩阵的形式呈现。
在实际应用中,我们经常遇到需要判断多个类别的分类问题,这时就需要用到多阶混淆矩阵。
多阶混淆矩阵,也称为多类别混淆矩阵,是一种能同时展示多个类别分类性能的矩阵。
与二分类中的混淆矩阵不同,多阶混淆矩阵的行和列表示的是真实类别和预测类别,因此矩阵的行数和列数相等。
矩阵中的每个元素表示的是模型将真实类别预测为对应预测类别的样本数量。
为了更好地理解多阶混淆矩阵,我们可以通过一个例子来说明。
假设我们有一个多类别的图像分类问题,我们需要将图像分为苹果、橙子和香蕉三个类别。
我们使用某个分类模型对一批图像进行分类,得到了如下的多阶混淆矩阵:苹果橙子香蕉苹果 10 2 0在这个混淆矩阵中,我们可以看到模型将10个苹果正确地预测为苹果,将8个橙子正确地预测为橙子,将9个香蕉正确地预测为香蕉。
但也有一些错误的预测,比如模型将2个苹果错误地预测为橙子,将3个橙子错误地预测为香蕉,将1个香蕉错误地预测为橙子。
通过多阶混淆矩阵,我们可以进一步计算出一些评估指标来衡量分类模型的性能。
常用的评估指标包括准确率、召回率和F1值等。
准确率指的是模型正确预测的样本数占总样本数的比例,召回率指的是模型正确预测的样本数占某一类别的总样本数的比例,F1值是准确率和召回率的调和均值。
在多阶混淆矩阵中,准确率可以通过计算对角线元素的和除以矩阵的总和得到,召回率可以通过计算每个类别对应行的元素之和除以该行的总和得到。
而F1值则是准确率和召回率的调和均值,用于综合反映模型的性能。
除了基本的评估指标外,多阶混淆矩阵还可以帮助我们分析模型的错误分类情况。
通过观察混淆矩阵中的非对角元素,我们可以发现哪些类别容易被错误地分类,从而对模型进行改进。
比如在上述例子中,模型将苹果预测为橙子的错误较多,可能意味着模型对这两个类别的区分能力较差,我们可以考虑增加更多的训练样本或优化模型结构来改进分类性能。
二进制混淆矩阵模型

二进制混淆矩阵模型
【实用版】
目录
1.二进制混淆矩阵模型的概念
2.二进制混淆矩阵模型的应用
3.二进制混淆矩阵模型的优点和缺点
4.二进制混淆矩阵模型的实例
正文
二进制混淆矩阵模型是一种用于分类问题的机器学习模型,它通过混淆矩阵来评估模型的性能。
混淆矩阵是一个二维矩阵,矩阵的行表示真实的类别,列表示预测的类别。
混淆矩阵模型可以用于二分类问题,例如预测一个人是否患有心脏病。
二进制混淆矩阵模型的应用非常广泛,它可以用于评估任何分类模型的性能。
例如,在预测一个人是否患有心脏病的问题中,混淆矩阵可以显示模型预测为患有心脏病的概率和实际患有心脏病的概率。
这可以帮助医生更好地了解模型的性能,并决定是否使用该模型进行预测。
二进制混淆矩阵模型的优点在于它可以直观地评估模型的性能,并且可以提供有关模型准确性的详细信息。
缺点在于它只能用于二分类问题,对于多分类问题,需要使用多维混淆矩阵来评估模型的性能。
一个实例是预测一个人是否患有心脏病。
在这个问题中,混淆矩阵可以显示模型预测为患有心脏病的概率和实际患有心脏病的概率。
另一个实例是预测一张图片是否包含猫。
第1页共1页。
模型指标混淆矩阵,accuracy,precision,recall,prc,auc

模型指标混淆矩阵,accuracy,precision,recall,prc,auc ⼀、混淆矩阵T和F代表是否预测正确,P和N代表预测为正还是负这个图⽚我们见过太多次了,但其实要搞清楚我们的y值中的1定义是什么,这样就不会搞错TP、FP、FN、TN的顺序,⽐如说下⾯的混淆矩阵:[[198985 29][ 73 277]]y(真实).value_counts():0: 1990141: 350y(测试).value_counts()0 :1990581 : 306我们就会先⼊为主认为第⼀个就是TP,但其实277才是我们的TP,所以⾸要任务是要搞清楚我们的Y值等于1是属于哪⼀类,弄清楚这些,下⾯的就容易搞清楚了⼆、模型评估指标⾸先来看下这个图⽚1.准确率(accuracy):分类正确的样本占总样本个数的⽐例使⽤上⾯的例⼦就是:(198985+277)/(198985+29+73+277)=0.9994883730262234值得注意的是,这个指标在数据极度倾斜的时候是没有任意意义的,⽐如说好坏⽤户是100:1,全部预测为好⽤户,那么准确率就是100/101=0.99009900990099012.精确度(precision):预测是1类的且真实情况也是1类/预测是1类的使⽤上⾯的例⼦就是:277/306=0.9052287581699346在数据倾斜的时候,⽐如说好坏⽤户是100:1,全部预测为好⽤户,那么精确度是0,说明还是有点⽤处的简单来说就是叫你找出坏⼈,你确实找出⼀帮⼈,你找出这帮⼈中真正是坏⼈的⽐例,着重的是你捉到的这批⼈,不要冤枉太多好⼈precision是相对你⾃⼰的模型预测⽽⾔:true positive /retrieved set。
假设你的模型⼀共预测了100个正例,⽽其中80个是对的正例,那么你的precision就是80%。
我们可以把precision也理解为,当你的模型作出⼀个新的预测时,它的confidence score 是多少,或者它做的这个预测是对的的可能性是多少⼀般来说呢,鱼与熊掌不可兼得。
混淆矩阵解读

混淆矩阵解读混淆矩阵(Confusion Matrix)是机器学习中一种重要的评估模型性能的工具,尤其在分类问题上广泛应用。
本文旨在对混淆矩阵进行解读,并探讨其在实际应用中的意义和用途。
一、什么是混淆矩阵混淆矩阵是一个二维表格,用于描述分类模型在预测分类时的性能。
它总共有四个分类结果,分别是真正例(True Positive,TP)、真反例(True Negative,TN)、假正例(False Positive,FP)和假反例(False Negative,FN)。
具体可以用下面的表格表示:类别1 类别2类别1 TP FN类别2 FP TN其中,类别1和类别2分别表示所研究的分类问题的两个类别。
TP表示真正例,即分类器将正例正确分类为正例的数量;TN表示真反例,即分类器将反例正确分类为反例的数量;FP表示假正例,即分类器将反例错误地分类为正例的数量;FN表示假反例,即分类器将正例错误地分类为反例的数量。
二、解读混淆矩阵通过混淆矩阵,我们可以进一步计算出一些与模型性能相关的指标,以便更全面地评估分类模型的表现。
1. 准确率(Accuracy)准确率是最直观的指标,用来衡量分类器正确分类的样本在总样本中所占的比例。
计算公式为:准确率 = (TP + TN) / (TP + TN + FP + FN)2. 精确率(Precision)精确率是用来衡量分类器在预测为正例的样本中,真正为正例的比例。
计算公式为:精确率 = TP / (TP + FP)3. 召回率(Recall)召回率是用来衡量分类器在所有真正为正例的样本中,预测为正例的比例。
计算公式为:召回率 = TP / (TP + FN)4. F1值(F1-score)F1值是综合考虑了精确率和召回率的指标,常用于评价分类器性能的均衡性。
计算公式为:F1值 = 2 * (精确率 * 召回率) / (精确率 + 召回率)三、混淆矩阵的应用混淆矩阵不仅可以用于评估分类模型的性能,还可以帮助我们理解分类器在不同类别上的表现,并找出其潜在的问题所在。
多分类混淆矩阵计算

多分类混淆矩阵计算在计算多分类混淆矩阵之前,我们首先需要了解混淆矩阵是如何构建的。
混淆矩阵的行表示实际的类别,列表示预测的类别。
每个元素(i,j)表示实际类别为i,预测类别为j的样本数量。
下面我们将具体说明多分类混淆矩阵的计算过程:假设我们有n个类别,使用一个大小为nxn的矩阵来表示混淆矩阵。
首先,我们需要将模型的预测结果与实际结果进行比较,并统计每个类别的数量。
1.初始化一个大小为nxn的矩阵,所有元素初始化为0。
2.对于每个样本,将实际类别放在混淆矩阵的行下标为真实类别,列下标为预测类别的位置;统计每个类别的个数。
3.统计每个类别的预测正确数量:-对于每个类别i,将混淆矩阵的第i行的所有元素相加,得到类别i 的预测正确数量。
4.统计每个类别的预测错误数量:-对于每个类别i,将混淆矩阵的第i列的所有元素相加,得到类别i 的预测错误数量。
5.统计总体预测正确的数量:-对于每个类别i,将混淆矩阵的第i行的第i列元素加上总体预测正确的数量。
6.统计总体预测错误的数量:-对于每个类别i,将混淆矩阵的第i行的所有元素相加,去除混淆矩阵的第i列的第i行元素,得到总体预测错误的数量。
计算混淆矩阵后,我们可以使用多个评估指标来量化模型性能,例如准确率、召回率、F1值等。
-准确率:表示正确预测的样本数量与总体样本数量的比例。
计算公式为:准确率=(总体预测正确的数量)/(总体预测正确的数量+总体预测错误的数量)。
-召回率:表示正确预测为其中一类别的样本数量与该类别实际样本数量的比例。
计算公式为:召回率=类别i的预测正确数量/类别i的实际样本数量。
-F1值:综合考虑了准确率和召回率,是一个综合评估指标。
计算公式为:F1值=2*(准确率*召回率)/(准确率+召回率)。
除了上述指标,还可以计算每个类别的精确度和召回率,以更全面地评估模型性能。
-类别i的精确度:表示预测为类别i的样本数量与实际为类别i的样本数量的比例。
计算公式为:类别i的精确度=类别i的预测正确数量/类别i的预测为类别i的数量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
错分为类3
雷达卫星是载有合成孔径雷达(SAR)的对地观测遥感卫星的统称。
尽管迄今为止,已在一些发射的卫星上携有SAR,如Seasat SAR, Almaz SAR, JERS-1 SAR, ERS-1/2 SAR, 与它们搭载在同一遥感平台上还装载着其他传感器。
而1995年11月发射的加拿大雷达卫星(Radarsat)则是一个兼顾商用及科学试验用途的雷达系统,其主要探测目标为海冰,同时还考虑到陆地成像,以便应用于农业、地质等领域。
该系统有5种波束工作模式,即:(1)标准波束模式,入射角20°~49°,成像宽度100公里,距离及方位分辨率为25米x28米;(2)宽辐射波束,入射角20°~40°,成像宽度及空间分辨率分别为150公里和28米x35米;(3)高分辨率波束,三种参数依此为37°~48°,45公里及10米x10米;(4)扫描雷达波束,该模式具有对全球快速成像能力,成像宽度大(300公里或500公里),分辨率较低(50米x50米或100米x100米),
入射角为20°~49°;(5)试验波束,该模式最大特点为入射角大,且变化幅度小49°~59°,成像宽度及分辨率分别为75公里及28米x 30米。
与其他星载SAR系统比较,Radarsat SAR有以下三个特点:(1)具有45公里,75公里,100公里,150公里,300公里和500公里的不同辐射宽度成像能力;(2)分别为11.6MHz,17.3MHz, 30.0 MHz雷达带宽的选择性操作使距离分辨率可调;(3)较强的数据处理能力。
SAR的全天候、全天时及能穿透一些地物的成像特点,显示出它与光学遥感器相比的优越性。
雷达遥感数据也在多学科领域中得到了广泛的应用。
星载雷达在90年代得到了迅猛的发展,特别是发展了极化雷达和干涉雷达技术。
在航天飞机成像雷达SIR-A、SIR-B和SIR-C/X-SAR成功地完成单波段、单极化和多波段、多极化成像飞行之后,正在计划于1999年9月开展航天飞机雷达地形测图(SRTM)飞行。
在雷达卫星1号基础上,加拿大在2001年发射的雷达卫星2号雷达将具有全极化测量能力;欧空局也将在1999年11月发射的Envisat-1卫星上装载ASAR,有同极化和交叉极化两种极化模式;2002年将发射的LightSAR 将为L波段多极化及具有干涉测量、扫描模式的实用化成像雷达。
同年计划发射的日本ALOS/PALSAR亦为多极化、多工作模式雷达系统。
我国也将在未来的几年内,发射自行研制的L波段雷达卫星。
由此可见, 国际上星载雷达正在向新的方向发展,它们将为数字地球的发展提供丰富的数据源。
地面上各种物体由于组成物质的分子、原子性质和结构规模不同,因而各种地物对不同波长的电磁波的反射、发射及透射本领也有差异。
这种无物体反射、发射及透射电磁波的本领随入射波的改变而改变的特性,称为地物的波普特性。
