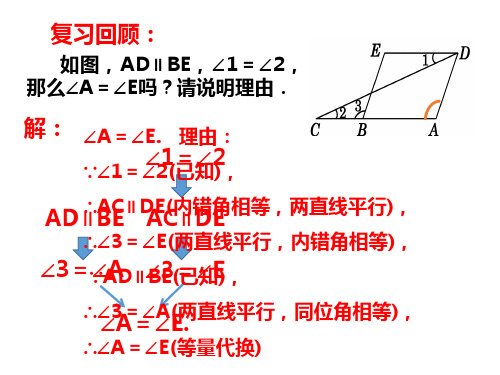
《图形的平移(2)》公开课教学PPT课件
合集下载
《图形的平移第2课时》示范公开课教学PPT课件【北师大版八年级数学下册】

北师大版·统编教材八年级数学下册
第三章 图形的平移与旋转
3.1 图形的平移 第2课时
一、 学习目标
在直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方向平移 后图形的顶点坐标,并知道对应顶点坐标之间的关系。
二、 情境导入
图3—6中的鱼是将坐标为(0,0)(5,4)
(3,0)(5,1)(5,-1)(3,0)(4,-2)
再见
新“鱼”与原来的“鱼”相比,形状和大小都没发生改变,只是 沿x轴向右平移了3个单位长度.若纵坐标保持不变,横坐标分别减2,则 形状和大小都没改变,只是沿x轴向左平移了2个单位长度.
三、 探究新知
(2)将图3—6中的“鱼”的每个“顶点”的横坐标保持不变,纵 坐标分别加3,所得到的新“鱼”与原来的“鱼”相比有什么变化?如 果横坐标保持不变,纵坐标分别减2呢?
四、 课堂练习
(2)将四边形 A3B3C3 D3 各顶点的横坐标不变,纵坐标分别减4, 得到四边形 A4B4C4 D4 ,它与四边形 A3B3C3 D3 相比有什么变化?
答:四边形 A4B4C4 D4是由四边形 A3B3C3 D3向下平移4个单位长度得到 的.
五、 课堂小结
归纳总结如下: 一般地,在平面直角坐标系中,将点(x,y)向右(或左)平移a 个单位长度,可以得到对应点的坐标是(x+a,y)或(x-a,y); 将点(x,y)向上(或下)平移b个单位长度,可以得到对应点的 坐标是(x,y+b)或(x,y-b).
如果将图3—6中的“鱼”向上平移3个单位长度,那么平移前后的 两条鱼中,对应的坐标之间有什么关系?
平移前后相对比,对应点的横坐标不变,纵坐标分别增加了3.
如果将图3—6中的“鱼”向下平移2个单位长度呢? 平移前后相对比,对应点的横坐标不变,纵坐标分别减小了2.
第三章 图形的平移与旋转
3.1 图形的平移 第2课时
一、 学习目标
在直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方向平移 后图形的顶点坐标,并知道对应顶点坐标之间的关系。
二、 情境导入
图3—6中的鱼是将坐标为(0,0)(5,4)
(3,0)(5,1)(5,-1)(3,0)(4,-2)
再见
新“鱼”与原来的“鱼”相比,形状和大小都没发生改变,只是 沿x轴向右平移了3个单位长度.若纵坐标保持不变,横坐标分别减2,则 形状和大小都没改变,只是沿x轴向左平移了2个单位长度.
三、 探究新知
(2)将图3—6中的“鱼”的每个“顶点”的横坐标保持不变,纵 坐标分别加3,所得到的新“鱼”与原来的“鱼”相比有什么变化?如 果横坐标保持不变,纵坐标分别减2呢?
四、 课堂练习
(2)将四边形 A3B3C3 D3 各顶点的横坐标不变,纵坐标分别减4, 得到四边形 A4B4C4 D4 ,它与四边形 A3B3C3 D3 相比有什么变化?
答:四边形 A4B4C4 D4是由四边形 A3B3C3 D3向下平移4个单位长度得到 的.
五、 课堂小结
归纳总结如下: 一般地,在平面直角坐标系中,将点(x,y)向右(或左)平移a 个单位长度,可以得到对应点的坐标是(x+a,y)或(x-a,y); 将点(x,y)向上(或下)平移b个单位长度,可以得到对应点的 坐标是(x,y+b)或(x,y-b).
如果将图3—6中的“鱼”向上平移3个单位长度,那么平移前后的 两条鱼中,对应的坐标之间有什么关系?
平移前后相对比,对应点的横坐标不变,纵坐标分别增加了3.
如果将图3—6中的“鱼”向下平移2个单位长度呢? 平移前后相对比,对应点的横坐标不变,纵坐标分别减小了2.
图形的平移(第2课时)同步课件

y
8
则坐标变化为:
7
6
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
5
(x,y-2) (0,-2) (5,2) (3,-2) (5,-1) (5,-3) (3,-2) (4,-4) (0,-2)
4
3 2
原图形被向下平移2个单位
1
-1 0 1 2 3 4 5 6 7 8 9 x -1 -2 -3 -4
A
A1 (5, 1)
12345 x
-4
-5
-6
归纳总结
你能总结出点(x,y) 的平移规律吗?
向右平移m个单位 对应点为(x+m,y)
那我们可以记为 “左减右加”
向左平移m个单位 对应点为(x-m,y)
学以致用
将点A(-2,3)向左平移3个单位长度,得到对应点坐标是(-5,3)。 将点A(5,-4)向右平移2个单位长度,得到对应点坐标是(7,-4)。
北师大版数学八年级下册
3.1 图形的平移 (第二课时)
学习目标
知识目标
在同一直角坐标系中, 感受图形上点的坐标变 化与图形的平移之间的 关系。
技能目标
经历图形的平移与图形 坐标的变化之间关系的 探索过程,发展学生的 形象思维和数形结合的 意识。
素养目标
通过对照新旧图形对应 点坐标的变化,培养学 生的视察、分析、归纳 的能力,从而获得分析 问题、解决问题的能力。
③. (x,y) (x,y-2)
④.(x,y) (x+2,y)
向下平移2个单位长度
向右平移2个单位长度
学以致用
如图,在平面直角坐标系中,平移△ABC后,点A的对应点A′的坐标为(-
8
则坐标变化为:
7
6
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
5
(x,y-2) (0,-2) (5,2) (3,-2) (5,-1) (5,-3) (3,-2) (4,-4) (0,-2)
4
3 2
原图形被向下平移2个单位
1
-1 0 1 2 3 4 5 6 7 8 9 x -1 -2 -3 -4
A
A1 (5, 1)
12345 x
-4
-5
-6
归纳总结
你能总结出点(x,y) 的平移规律吗?
向右平移m个单位 对应点为(x+m,y)
那我们可以记为 “左减右加”
向左平移m个单位 对应点为(x-m,y)
学以致用
将点A(-2,3)向左平移3个单位长度,得到对应点坐标是(-5,3)。 将点A(5,-4)向右平移2个单位长度,得到对应点坐标是(7,-4)。
北师大版数学八年级下册
3.1 图形的平移 (第二课时)
学习目标
知识目标
在同一直角坐标系中, 感受图形上点的坐标变 化与图形的平移之间的 关系。
技能目标
经历图形的平移与图形 坐标的变化之间关系的 探索过程,发展学生的 形象思维和数形结合的 意识。
素养目标
通过对照新旧图形对应 点坐标的变化,培养学 生的视察、分析、归纳 的能力,从而获得分析 问题、解决问题的能力。
③. (x,y) (x,y-2)
④.(x,y) (x+2,y)
向下平移2个单位长度
向右平移2个单位长度
学以致用
如图,在平面直角坐标系中,平移△ABC后,点A的对应点A′的坐标为(-
7.6《图形的平移》ppt课件(共25张PPT)
C
F
M
M
A
BD
E
B
C B'
C'
A
A'
A
BC A'
B' C'
平移的性质:
(1)连接对应点的线段平行(或在同一条 直线上) 且相等 ( 2)对应线段平行且相等,对应角相等。
例 如图,(1)将△ABC平移到△A'B'C'的位置,
连接各对对应点,并指出相等的线段和相等的角.
解:△A′B′C′即为所求。
1、图形的平移是由移动的方向和距离决定的。
2、图形上各点沿同一方向移动相同的距离。
3、平移不改变图形的大小与形状,它只改变图形 在平面中的位置。
★ 如图,ΔABC 是ΔDEF 经过平移得到的,请用虚线把 图中各对对应点连接起来,并指出相等的线段和相 等的角,然后请指出图中(包括新画的)所有的互相 平行的线段,并概括平移的特性.
分析:我们把右边的草地向左平移1米,那么草地的面 积就是新的长方形的面积.
解:长草部分的 面积为:
(21-1)×15
=300(平方米)
下面3个图形的周长是否相等?请简单说说理由.
3
3
4
4
3 4
作业
1.P57 课后练习1、2 2.课后习题A组B组.
AB与A1B1是对应线段
B
C
∠A和∠A1叫做对应角
你能说出其它的对应点,对应点的连线,
对应线段、对应角吗?它们有什么关系?
考考你:
√ 下列现象中,属于平移的是:
(1)火车在笔直的铁轨上行驶 (2)冷水受热过程中小气泡上升变成大气泡
√ (3)人随电梯上升
(4)钟摆的摆动
【优质课PPT】【名师推荐】部编小学获奖课件五年级数学上册《图形的平移(二)》PPT课件(优质课)

返 回
小试身手:移一移,画一画。
• 在小字本格子中,先画一个自己喜欢的图形, 再将它向下平移4格,最后向右平移6格。
返 回
请你欣赏:
通过平移的方法可以创造花边和喜欢的连续图样。
返 回
学 生 的 创 造 力
返 回
4、想一想,如何通过平移使图(1)变成(2)。
(1)
(2)
①② ③④
返 回
4、想一想,如何通过平移使图(1)变成(2)。
返 回
3、按要求画一画
• (1)将平行四边向右平移4格。 • (2)将梯形先向上平移4格,再向左平移3格。
返 回
3、按要求画一画
• (1)将平行四边向右平移4格。 • (2)将梯形先向上平移4格,再向左平移3格。
返 回
小试身手:移一移,画一画。
• 在小字本格子中,先画一个自己喜欢的图形, 再将它向下平移4格,最后向出概念的内涵与外延。 “含有未知数”与“等式”是方程意义的两点最重要的内涵。“含有未知数”也是方程区别于其他等式的关键特征。在第1页的两道例题里,学生陆续写出了等式,也写出了不等式;写出了不含未知数的等式,也写出了含有未知数的等式。这些都为教学方程的意义提供了鲜明的感知材料。教材首先告诉学生: 像x+50=150、2x=200这样含有未知数的等式叫做方程,让他们理解x+50=150、2x=200的共同特点是“含有未知数”,也是“等式”。这时,如果让学生对两道例题里写出的50+50=100、x+50>100和x+50<200不能称为方程的原因作出合理的解释,那么学生对方程是等式的理解会更深刻。教材接着安排讨论“等式和方程有什么关系”,并通过“练一练”第1题让学生先找出等式,再找出方
五年级数学上册
小试身手:移一移,画一画。
• 在小字本格子中,先画一个自己喜欢的图形, 再将它向下平移4格,最后向右平移6格。
返 回
请你欣赏:
通过平移的方法可以创造花边和喜欢的连续图样。
返 回
学 生 的 创 造 力
返 回
4、想一想,如何通过平移使图(1)变成(2)。
(1)
(2)
①② ③④
返 回
4、想一想,如何通过平移使图(1)变成(2)。
返 回
3、按要求画一画
• (1)将平行四边向右平移4格。 • (2)将梯形先向上平移4格,再向左平移3格。
返 回
3、按要求画一画
• (1)将平行四边向右平移4格。 • (2)将梯形先向上平移4格,再向左平移3格。
返 回
小试身手:移一移,画一画。
• 在小字本格子中,先画一个自己喜欢的图形, 再将它向下平移4格,最后向出概念的内涵与外延。 “含有未知数”与“等式”是方程意义的两点最重要的内涵。“含有未知数”也是方程区别于其他等式的关键特征。在第1页的两道例题里,学生陆续写出了等式,也写出了不等式;写出了不含未知数的等式,也写出了含有未知数的等式。这些都为教学方程的意义提供了鲜明的感知材料。教材首先告诉学生: 像x+50=150、2x=200这样含有未知数的等式叫做方程,让他们理解x+50=150、2x=200的共同特点是“含有未知数”,也是“等式”。这时,如果让学生对两道例题里写出的50+50=100、x+50>100和x+50<200不能称为方程的原因作出合理的解释,那么学生对方程是等式的理解会更深刻。教材接着安排讨论“等式和方程有什么关系”,并通过“练一练”第1题让学生先找出等式,再找出方
五年级数学上册
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
00 54 5 0 10 4
4 -2 9 -2
新知讲解
画一画:图中的“鱼”是将坐标为(0,0) ,(5,4), (3,0), (5,1), (5,-1) ,(3,0) ,(4,-2), (0,0)的点用线段依次连接而成的.将这条 “鱼”向右平移5个单位长度.
(3)你发现对应点的坐标之间 有什么关系?
你发现平移前 后对应点的坐标之
思考2:如果将原来的“鱼”向上平移3个单间位有长什度么呢变?化吗?
00 03
54 57
4 -2 41
原来的点(x,y)
现在的点( x,y+3)
橫坐标保持不变,纵坐标加3.
新知讲解
你发现平移前 后对应点的坐标之
思考3:如果将原来的“鱼”向下平移2个单间位有长什度么呢变?化吗?
(1)点F的坐标;(2)△EOF的面积.
解:(2)∵A(-10,0),AB=4,D为AB的中点,
∴B(-6,0),AD=BD=2.
图形的平移
数学 北师大版 八年级下
新知导入
1、什么是平移? 在平面内,将一个图形沿某个方向移动一定的距离,这样的
图形运动称为平移. 2、说一说平移的性质?
(1)一个图形和它经过平移所得的图形中,对应点所连的 线段平行(或在同一直线上)且相等;对应线段平行(或在同一直线 上)且相等,对应角相等.
(2)平移不改变图形的形状和大小.
(1)点F的坐标;(2)△EOF的面积. 解:(1)∴∵|Sy△CA|B=C=7.12 AB·|yC|=14,AB=4,
∵点C在第二象限,
∴yC=7. ∵△ABC沿x轴平移得到△DEF,点F在y轴上,
∴F (0,7)
拓展提高
如图,在平面直角坐标系中,点A,B在x轴上,且A(-10,0), AB=4,△ABC的面积为14.将△ABC沿x轴平移得到△DEF,当点D为AB 的中点时,点F恰好在y轴上.求:
新知讲解
坐标与平移
点(x, y)向右(左)平移a(a>0)个单位⇔平移后的坐标为 (x±a, y) 点(x, y)向上(下)平移a(a>0)个单位⇔平移后的坐标为 (x, y±a)
课堂练习
1 .如图,在平面直角坐标系中,平移△ABC后,点A的对 应点A′的坐标为(-3,-2),则点B的对应点B′的坐标为( C )
(1)画出平移后的新“鱼”.
新知讲解
画一画:图中的“鱼”是将坐标为(0,0) ,(5,4), (3,0), (5,1), (5,-1) ,(3,0) ,(4,-2), (0,0)的点用线段依次连接而成的.将这条 “鱼”向右平移5个单位长度.
(2)在图中尽量多选取几组对 应点,并将它们的坐标填入下表:
原来的“鱼”向上平移3个单位 得到这条新“鱼”
如果横坐标保持不变,纵坐标分 别减2呢?
原来的“鱼”向下平移2个单位 得到这条新“鱼”
新知讲解
点的坐标的变化与平移规律
(1)将点(x,y)的纵坐标保持不变,横坐标加(或减去) a(a>0) ,可以得到这个点向右(或左)平移a个单位长度;
(2)将点(x,y)的横坐标保持不变,纵坐标加(或减去) a(a>0) ,可以得到这个点向上(或下)平移a个单位长度.
注意:横坐标发生变化则左右平移; 纵坐标发生变化则上下平移.
新知讲解
练习2:若一个四边形上的其中一点P在平移的过程中,坐标 变化为P(x,y) →P′(x-6,y),则该四边形的平移情况是( A )
A.向左平移6个单位长度 B.向右平移6个单位长度 C.向上平移6个单位长度 D.向下平移6个单位长度
注意:左右平移横坐标发生变化; 上下平移纵坐标发生变化.
新知讲解
练习1:如图,△ABO的顶点A的坐标是(-1,2),将△ABO沿x 轴向左平移3个单位长度后,点A的对应点的坐标是_(-___4_,__2__)_.
新知讲解
做一做:将图中“鱼”的每个“顶点”的纵坐标保持不变,横 坐标分别减3,再将得到的点用线段依次连接起来,从而画出一条新 “鱼”,这条新“鱼”与原来的“鱼”相比有什么变化?
00 0 -2
54 52
4 -2 4 -4
原来的点(x,y)
现在的点( x,y-2)
橫坐标保持不变,纵坐标减2.
新知讲解
平移与点的坐标的变化规律
(1)将点(x,y)向右(或左)平移a个单位长度,可以得到 对应点的坐标是(x+a ,y) 或(x-a ,y) ;
(2)将点(x,y)向上(或下)平移b个单位长度,可以得到 对应点的坐标是(x,y + b)或(x,y-b).
原来的“鱼”向左平移3个单位 得到这条新“鱼”
如果纵坐标保持不变,横坐标分 别加2呢?
原来的“鱼”向右平移2个单位 得到这条新“鱼”
新知讲解
做一做:将图中“鱼”的每个“顶点”的横坐标保持不变,纵 坐标分别加3,再将得到的点用线段依次连接起来,从而画出一条新 “鱼”,这条新“鱼”与原来的“鱼”相比有什么变化?
A.(2,1) B.(2,2) C.(1,0) D.(1,3)
课堂练习
2.如图,与图①中的三角形相比,图②中的三角形发生的 变化是( A )
A.向左平移了3个单位长度 B.向右平移了3个单位长度 C.向上平移了3个单位长度 D.向下平移了3个单位长度
拓展提高
如图,在平面直角坐标系中,点A,B在x轴上,且A(-10,0), AB=4,△ABC的面积为14.将△ABC沿x轴平移得到△DEF,当点D为AB 的中点时,点F恰好在y轴上.求:
新知讲解
对应点的坐标
试一试:将点A(-2,-3)向右平移5个之单间位有长什度么,变得化到吗点?A1,
在图上标出它的坐标.
A(-2,-3)
+5
不 变
A1 ( 3 ,-3)
将坐标为(0,0) ,(5,4), (3,0), (5,1), (5,-1) ,(3,0) ,(4,-2), (0,0)的点用线段依次连接而成的.将这条 “鱼”向右平移5个单位长度.
原来的点(x,y)
现在的点( x+5,y)
纵坐标保持不变,横坐标加5.
新知讲解
你发现平移前 后对应点的坐标之
思考1:如果将原来的“鱼”向左平移4个单间位有长什度么呢变?化吗?
00 -4 0
54 14
4 -2 0 -2
原来的点(x,y)
现在的点( x -4,y)
纵坐标保持不变,横坐标减4.
新知讲解
