有关初中圆的定理

圆的定理初中

圆的定理初中
在初中数学中，有一些与圆有关的定理，其中最基本和常见的是：
1. 圆的直径定理：圆的直径是圆上最长的线段，且直径的两个端点都在圆上。

圆的直径等于其半径的两倍。

也就是说，如果一个圆的半径为r，那么它的直径就是2r。

2. 圆的半径定理：圆上任意一点到圆心的距离等于圆的半径。

这个定理表明，无论圆上的点在哪里，只要与圆心连线的长度等于圆的半径r，那么这个点就位于圆上。

3. 圆的圆周定理：圆的周长（也称为圆周）等于圆的直径与π（圆周率）的乘积，即C = 2πr，其中C代表圆的周长，r代表半径。

4. 圆的面积定理：圆的面积等于π（圆周率）与半径的平方的乘积的一半，即A = πr^2，其中A代表圆的面积，r代表半径。

这些基本的圆定理是初中数学中关于圆的重要概念，它们为解决与圆有关的各种几何问题提供了基础。

在学习圆相关的内容时，这些定理通常是学生首要掌握的知识点。

初三《圆》知识点及定理

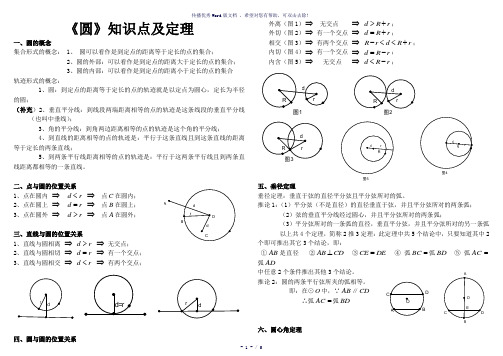
《圆》知识点及定理一、圆的概念集合形式的概念： 1、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

二、点与圆的位置关系1、点在圆内⇒d r<⇒点C在圆内；2、点在圆上⇒d r=⇒点B在圆上；3、点在圆外⇒d r>⇒点A在圆外；三、直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一个交点；3、直线与圆相交⇒d r<⇒有两个交点；四、圆与圆的位置关系外离（图1）⇒无交点⇒d R r>+；外切（图2）⇒有一个交点⇒d R r=+；相交（图3）⇒有两个交点⇒R r d R r-<<+；内切（图4）⇒有一个交点⇒d R r=-；内含（图5）⇒无交点⇒d R r<-；五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB是直径②AB CD⊥③CE DE=④弧BC=弧BD⑤弧AC=弧AD中任意2个条件推出其他3个结论。

圆的性质及相关定理

圆的性质及相关定理圆是几何学中的一个基本概念，是由平面上所有距离等于定值的点构成的图形。

在这篇文章中，我们将探讨圆的性质及相关定理，帮助读者更好地理解和应用圆的知识。

一、圆的基本性质1. 圆心和半径：每个圆都有一个圆心和一个半径。

圆心是圆上所有点的中心位置，通常用字母O表示。

半径是从圆心到圆上的任意点的距离，通常用字母r表示。

2. 直径：直径是通过圆心的任意两点间的线段。

直径的长度等于半径的两倍。

3. 弧：圆上两点之间的弧是连接这两点的圆上的一部分。

圆上的弧可以根据其长度分为弧长和弧度。

4. 弦：弦是连接圆上任意两点的线段。

直径是最长的弦。

5. 弧度和角度：弧度是一个与圆的半径相关的度量单位，用符号rad表示。

角度是以度为单位的度量，用符号°表示。

二、圆的定理1. 切线定理：从圆外一点引一条切线，切线与半径的连线垂直。

2. 切线与弦定理：切线和弦的交点处的角等于从该点到弦的两个割线所夹的弧对应的角。

3. 弧中角定理：在同一个圆上，弧所对的圆心角相等，而弧所对的弦所夹的角则相等。

4. 圆心角定理：在同一个圆上，圆心角是其所对弧的两倍。

5. 弧长定理：同样大小的圆心角所对应的弧长相等。

6. 切割圆定理：如果有两个弧相交于圆心，它们所对的圆心角互补（和为180°）。

三、应用示例1. 计算圆的面积：圆的面积公式为A = πr²，其中A表示面积，π是一个近似值，约等于3.14，r为半径。

2. 计算圆的周长：圆的周长公式为C = 2πr，其中C表示周长，π是一个近似值，约等于3.14，r为半径。

3. 判断点是否在圆内：计算点到圆心的距离，如果小于半径，则点在圆内。

4. 判断两个圆是否相交：计算两个圆心之间的距离，如果小于两个半径之和，则两个圆相交。

总结：本文介绍了圆的基本性质和相关定理。

通过学习圆的性质，我们可以更好地理解和应用圆的知识，解决与圆相关的几何问题。

希望本文对读者有所帮助，并在几何学学习中起到指导作用。

1．圆是以圆心为对称中心的中心对称图形；围绕圆心旋转任意一个角度α，都能够与原来的重合．2．顶点在圆心的角叫做圆心角．圆心到弦的距离叫做弦心距．圆幂定理（相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理）切线长定理垂径定理圆周角定理弦切角定理四圆定理3．在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等．4．在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等．5．把整个圆周等分成360份，每一份弧是1°的弧．圆心角的度数和它所对的弧的度数相等．6.圆是中心对称图形，即圆绕其对称中心(圆心)旋转180°后能够与原来图形重合，这一性质不难理解．圆和其他中心对称图形不同，它还具有旋转不变性，即围绕圆心旋转任意一个角度，都能够与原来的图形重合．7.垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧8.（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧9.圆的两条平行弦所夹的弧相等10.(1)一条弧所对的圆周角等于它所对的圆心角的一半.(2)同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等.(3)半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径.(4)如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形.11.(1)圆是轴对称图形，经过圆心的每一条直线都是它的对称轴.(2)垂直于弦的直径平分这条弦，并且平分弦所对的两条弧.(3)平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧.(4)弦的垂直平分线经过圆心，并且平分弦所对的两条弦.(5)平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧.(6)圆的两条平行弦所夹的弧度数相等.12.圆是轴对称图形，经过圆心的每一条直线都是它的对称轴．垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．13.平分弦(不是直径)的直径垂直与弦,并且平分弦所对的两条弧.14.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距也相等.15.在同圆或等圆中,相等的弦所对的弧相等,所对的圆心角相等,所对的弦的弦心距也相等.16.同一个弧有无数个相对的圆周角.17.弧的比等于弧所对的圆心角的比.18.圆的内接四边形的对角互补或相等.19.不在同一条直线上的三个点能确定一个圆.20.直径是圆中最长的弦.21.一条弦把一个圆分成一个优弧和一个劣弧。

关于圆的公式定理

关于圆的公式定理圆是数学中一个非常重要的几何形状，具有许多有用的定理和公式。

在此，我们将深入探讨关于圆的定理和公式，并了解它们在实际生活中的应用。

首先，让我们来了解一些基本的定义。

圆是指由一条完全相同距离中心点的点组成的闭合曲线。

圆上的每个点到中心的距离称为半径，我们用字母r表示。

圆的周长称为圆周长，用C表示。

圆的面积称为圆面积，用A表示。

那么，我们来看一下圆的一些重要定理和公式。

1. 圆的直径定理（Diameter Theorem）：直径是通过圆心的线段，并且是圆周长的两倍。

也就是说，d = 2r，其中d是直径长度。

这个定理在实际生活中有很多应用。

例如，在建筑领域，我们常常使用直径来计算门或窗户的宽度，确保它们能够完美地安装在开口上。

2. 圆周长公式（Circumference Formula）：圆周长等于直径乘以π（pi），即C = 2πr或C = πd。

圆周长公式非常有用，因为它可以帮助我们计算任何给定半径的圆的周长。

我们可以使用这个公式来确定绕行园艺装饰圆形花坛所需的木质栅栏的长度。

3. 圆面积公式（Area Formula）：圆的面积等于半径的平方乘以π（pi），即A = πr²。

圆面积公式在解决各种实际问题时非常有用。

例如，在制作饼或蛋糕时，我们可以使用这个公式来计算需要的面团或面糊的总量。

除了这些基本定理和公式之外，还有一些其他有用的圆的性质和应用。

4. 弧长公式（Arc Length Formula）：弧长可以通过半径和圆心角的关系来计算。

如果我们知道圆心角的度数为θ（以弧度表示），那么弧长等于θ乘以半径的长度。

弧长公式在地理学、导航和航空导航中经常被使用。

例如，在航空导航中，我们可以使用这个公式来计算一架飞机在特定角度上行驶的距离。

5. 弧度公式（Radian Formula）：弧度是一种介于0和2π之间的度量单位。

弧度可以通过将圆周长除以半径来计算。

弧度在物理学中非常常见，并且与角速度、圆周率等概念紧密相连。

关于圆的几个定理

关于圆的几个定理1. 四点共圆1.1定义：若四边形ABCD 的四点同时共于一圆上，则称A ，B ，C ，D 四点共圆基本性质：若凸四边形ABCD 是圆内接四边形，则其对角互补1.2定义：若存在一点O 使OA=OB=OC=OD ，则A ，B ，C ，D 四点共圆2.若干定理圆幂定理是圆的相交弦定理、切割线定理、割线定理、切线长定理的统一形式。

相交弦定理：P 是圆内任一点，过P 作圆的两弦AB ，CD ，则PA PB PC PD •=•（切）割线定理：P 是圆外任意一点，过P 任作圆的两割（切）线PAB ，PCD ，则PA PB PC PD •=•圆幂定理：P 是圆O 所在平面上任意一点（可以在圆内，圆上，圆外），过点P 任作一直线交圆O 于A ，B 两点（A ，B 两点可以重合，也可以之一和P 重合），圆O 半径为r ，则有：22||PA PB PO r •=-圆内接四边形判定方法相交弦定理逆定理：如果四边形ABCD 的对角线AC ，BD 交于点P ，且满足 PA PC PB PD •=•，则四边形ABCD 有一外接圆切割线定理逆定理：如果凸四边形ABCD 一双对边AB 与DC 交于点P且满足PA PC PB PD •=•，则四边形ABCD 有一外接圆射影定理：RTΔABC 中，BC 是斜边，AD 是斜边上的高,则222(1)(2)(3)AD BD CDAB BD BCAC CD BC =•=•=•Miquel 定理：ΔABC 中，X ，Y ，Z 分别是直线AB ，BC ，AC 上的点，则 ,,共于一点AXZ BXY CYZ O这样的点O 称为X ，Y ，Z 对于ΔABC 的Miquel 点Simson 定理P是ΔABC外接圆上一点，过点P作PD垂直BC，PE垂直于AB，同理PF则D，E，F是共线的三点直线DEF称为点P关于ΔABC的Simson线Carnot定理：通过ΔABC外接圆上的一点P，引与三边BC，CA，AB分别成同向等角（即∠=∠=∠PDB PEC PFB）的直线PD，PE，PF与三边或其所在直线的交点分别为D，E，F则D，E，F是共线的三点AB CD AD BC AC BD Ptolemy定理:若四边形ABCD是圆内接四边形，则•+•=•Chapple 定理：设R 是ΔABC 的外接圆半径，r 是内切圆半径,d 是这两圆的圆心距，则222=-d R Rr（注：文档可能无法思考全面，请浏览后下载，供参考。

圆的有关定理

01．切线长定理：
从圆外一点引圆的两条切线，它们的切线长相等，
圆心和这一点的连线平分两条切线的夹角。
02．圆的外切四边形的两组对边的和相等。
03．垂径定理：
垂直于弦的直径平分这条弦并且平分弦所对的两条弧
推论1①平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧
②弦的垂直平分线经过圆心，并且平分弦所对的两条弧
推论:从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等:PA∙PB＝PC∙PD
射影定理
③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧
推论2①圆的两条平行弦所夹的弧相等。
04．切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线
05．切线的性质定理：圆的切线垂直于经过切点的半径
推论1：经过圆心且垂直于切线的直线必经过切点
推论2：经过切点且垂直于切线的直线必经过圆心
07．弦切角定理：弦切角等于它所夹的弧对的圆周角
推论：如果两个弦切角所夹的弧相等，那么这两个交点分成的两条线段长的积相等
推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项
PA∙PB＝PC∙PD
09．切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。PC2＝PA∙PB

初中数学圆常用定理

初中数学圆常用定理
圆常用定理是我们初中数学学习中的重要知识点之一。

在学习圆的相关内容时，圆常用定理可以帮助我们更好地解决一些实际问题，也为我们日后的学习打下了重要的基础。

圆常用定理总共有三个，分别是：切线定理、弦切定理、弦长定理。

切线定理指出：在圆的切点处，切线与半径垂直。

也就是说，若以 $O$ 为圆心，$P$ 为切点，则 $\angle OPA=90^{\circ}$。

利用切线定理，我们可以解决一些与圆相关的实际问题，比如计算弧长、面积等。

弦切定理指出：若有一条与圆相交的弦 $AB$ 和一条切线 $CD$，则 $\angle ACD=\angle CBD$。

也就是说，弦切定理可以帮助我们找到两个相交角度相等的角。

弦长定理指出：若有一条与圆相交的弦 $AB$，则 $AB$ 的长度等于它所对应的两条弓长之和的一半。

也就是说，我们可以通过弦长定理计算出任意一条弦的长度。

总的来说，圆常用定理虽然简单，但却是圆的基础定理，是我们后续学习更深层次的圆的知识的前提。

因此，我们应该重视这些定理的学习，努力掌握它们的应用方法，从而更好地解决数学问题。

初中圆的十八个定理

初中圆的十八个定理1、圆心角定理：在同圆或等圆中，相等的圆心角所对弧相等，所对的弦相等，所对的弦的弦心距相等。

2、圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

3、垂径定理：垂直弦的直径平分该弦，并且平分这条弦所对的两条弧。

4、切线的判定定理：经过半径的外端并且垂直于该半径的直线是圆的切线。

5、切线长定理：从圆外一点引圆的两条切线，他们的切线长相等，这一点与圆心的连线平分这两条切线的夹角。

6、公切线长定理：如果两圆有两条外公切线或两条内公切线，那么这两条外公切线长相等，两条内公切线长也相等。

如果他们相交，那么交点一定在两圆的连心线上。

7、相交弦定理：圆内两条弦相交，被交点分成的两条线段长的乘积相等。

8、切割线定理：从圆外一点向圆引一条切线和一条割线，则切线长是这点到割线与圆的两个交点的两条线段长。

9、割线长定理：从圆外一点向圆引两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。

10、切线的性质定理：圆的切线垂直于经过切点的半径。

11、弦切角定理：弦切角等于它所夹的弧对的圆周角。

12、定理：相交两圆的连心线垂直平分两圆的公共弦。

13、定理：把圆分成n（n≥3），依次连结各分点所得的多边形是这个圆的内接正n边形；经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形。

14、定理：任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆。

15、定理：任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆。

16、定理：正n边形的半径和边心距把正n边形分成2n 个全等的直角三角形17、定理：圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角。

18、(d是圆心距，R、r是半径)①两圆外离d>R+r；②两圆外切d=R+r；③两圆相交R-r<dr；④两圆内切d=R-r （R>r）；⑤两圆内含dr。

有关初中圆的定理

1．圆是以圆心为对称中心的中心对称图形；围绕圆心旋转任意一个角度α，都能够与原来的重合．2．顶点在圆心的角叫做圆心角．圆心到弦的距离叫做弦心距．圆幂定理（相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理）切线长定理垂径定理圆周角定理弦切角定理四圆定理3．在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等．4．在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等．5．把整个圆周等分成360份，每一份弧是1°的弧．圆心角的度数和它所对的弧的度数相等．6.圆是中心对称图形，即圆绕其对称中心(圆心)旋转180°后能够与原来图形重合，这一性质不难理解．圆和其他中心对称图形不同，它还具有旋转不变性，即围绕圆心旋转任意一个角度，都能够与原来的图形重合．7.垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧8.（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧9.圆的两条平行弦所夹的弧相等10.(1)一条弧所对的圆周角等于它所对的圆心角的一半.(2)同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等.(3)半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径.(4)如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形.11.(1)圆是轴对称图形，经过圆心的每一条直线都是它的对称轴.(2)垂直于弦的直径平分这条弦，并且平分弦所对的两条弧.(3)平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧.(4)弦的垂直平分线经过圆心，并且平分弦所对的两条弦.(5)平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧.(6)圆的两条平行弦所夹的弧度数相等.12.圆是轴对称图形，经过圆心的每一条直线都是它的对称轴．垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．13.平分弦(不是直径)的直径垂直与弦,并且平分弦所对的两条弧.14.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距也相等.15.在同圆或等圆中,相等的弦所对的弧相等,所对的圆心角相等,所对的弦的弦心距也相等.16.同一个弧有无数个相对的圆周角.17.弧的比等于弧所对的圆心角的比.18.圆的内接四边形的对角互补或相等.19.不在同一条直线上的三个点能确定一个圆.20.直径是圆中最长的弦.21.一条弦把一个圆分成一个优弧和一个劣弧。

有关初中圆的定理[精选.]

1．圆是以圆心为对称中心的中心对称图形；围绕圆心旋转任意一个角度α，都能够与原来的重合．2．顶点在圆心的角叫做圆心角．圆心到弦的距离叫做弦心距．圆幂定理（相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理）切线长定理垂径定理圆周角定理弦切角定理四圆定理3．在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等．4．在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等．5．把整个圆周等分成360份，每一份弧是1°的弧．圆心角的度数和它所对的弧的度数相等．6.圆是中心对称图形，即圆绕其对称中心(圆心)旋转180°后能够与原来图形重合，这一性质不难理解．圆和其他中心对称图形不同，它还具有旋转不变性，即围绕圆心旋转任意一个角度，都能够与原来的图形重合．7.垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧8.（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧9.圆的两条平行弦所夹的弧相等10.(1)一条弧所对的圆周角等于它所对的圆心角的一半.(2)同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等.(3)半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径.(4)如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形.11.(1)圆是轴对称图形，经过圆心的每一条直线都是它的对称轴.(2)垂直于弦的直径平分这条弦，并且平分弦所对的两条弧.(3)平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧.(4)弦的垂直平分线经过圆心，并且平分弦所对的两条弦.(5)平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧.(6)圆的两条平行弦所夹的弧度数相等.12.圆是轴对称图形，经过圆心的每一条直线都是它的对称轴．垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．13.平分弦(不是直径)的直径垂直与弦,并且平分弦所对的两条弧.14.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距也相等.15.在同圆或等圆中,相等的弦所对的弧相等,所对的圆心角相等,所对的弦的弦心距也相等.16.同一个弧有无数个相对的圆周角.17.弧的比等于弧所对的圆心角的比.18.圆的内接四边形的对角互补或相等.19.不在同一条直线上的三个点能确定一个圆.20.直径是圆中最长的弦.21.一条弦把一个圆分成一个优弧和一个劣弧最新文件仅供参考已改成word文本。

初中圆的定理和公式汇总

4圆是定点的距离等于定长的点的集合5圆的内部可以看作是圆心的距离小于半径的点的集合6圆的外部可以看作是圆心的距离大于半径的点的集合7同圆或等圆的半径相等8到定点的距离等于定长的点的轨迹，是以定点为圆心，定长为半径的圆9定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等10推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等11定理圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角12 ①直线L和⊙O相交d＜r②直线L和⊙O相切d=r③直线L和⊙O相离d＞r13切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线14切线的性质定理圆的切线垂直于经过切点的半径15推论1 经过圆心且垂直于切线的直线必经过切点16推论2 经过切点且垂直于切线的直线必经过圆心17切线长定理从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角18圆的外切四边形的两组对边的和相等19弦切角定理弦切角等于它所夹的弧对的圆周角20推论如果两个弦切角所夹的弧相等，那么这两个弦切角也相等30相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等31推论如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项32切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项33推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等34如果两个圆相切，那么切点一定在连心线上35 ①两圆外离d＞R+r ②两圆外切d=R+r③两圆相交R-r＜d＜R+r(R＞r)④两圆内切d=R-r(R＞r) ⑤两圆内含d＜R-r(R＞r)36定理相交两圆的连心线垂直平分两圆的公共弦37 定理把圆分成n(n≥3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形38定理任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆39 正n边形的每个内角都等于（n-2）×180°／n40定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形41正n边形的面积Sn=pnrn／2 p表示正n边形的周长42正三角形面积√3a／4 a表示边长43如果在一个顶点周围有k个正n边形的角，由于这些角的和应为360°，因此k×(n-2)180°／n=360°化为（n-2）(k-2)=444弧长计算公式：L=n兀R／18045扇形面积公式：S扇形=n兀R^2／360=LR／246内公切线长= d-(R-r) 外公切线长= d-(R+r)47定理一条弧所对的圆周角等于它所对的圆心角的一半48推论1 同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等49推论2 半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径50正弦定理a/sinA=b/sinB=c/sinC=2R 注：其中R 表示三角形的外接圆半径51余弦定理b2=a2+c2-2accosB 注：角B是边a和边c的夹角52圆的标准方程(x-a)2+(y-b)2=r2 注：（a,b）是圆心坐标53圆的一般方程x2+y2+Dx+Ey+F=0 注：D2+E2-4F>054弧长公式l=a*r a是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r。

初中数学定理大全：圆

初中数学定理大全：圆 101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹，是以定点为圆心，定长为半径的圆106和线段两个端点的距离相等的点的轨迹，是着条线段的垂直平分线107到角的两边距离相等的点的轨迹，是这个角的平分线108到两条平行线距离相等的点的轨迹，是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三点确定一个圆。

110垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111推论1 ①平分弦〔不是直径〕的直径垂直于弦，并且平分弦所对的两条弧②弦的垂直平分线经过圆心，并且平分弦所对的两条弧③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧112推论2 圆的两条平行弦所夹的弧相等113圆是以圆心为对称中心的中心对称图形114定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等115推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116定理一条弧所对的圆周角等于它所对的圆心角的一半117推论1 同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等118推论2 半圆〔或直径〕所对的圆周角是直角；90°的圆周角所对的弦是直径119推论3 如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形120定理圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角121①直线L和⊙O相交d＜r②直线L和⊙O相切d=r③直线L和⊙O相离d＞r122切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123切线的性质定理圆的切线垂直于经过切点的半径124推论1 经过圆心且垂直于切线的直线必经过切点125推论2 经过切点且垂直于切线的直线必经过圆心126切线长定理从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角127圆的外切四边形的两组对边的和相等128弦切角定理弦切角等于它所夹的弧对的圆周角129推论如果两个弦切角所夹的弧相等，那么这两个弦切角也相等130相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等131推论如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项132切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项133推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等134如果两个圆相切，那么切点一定在连心线上135①两圆外离d＞R+r ②两圆外切d=R+r③两圆相交R-r＜d＜R+r(R＞r)④两圆内切d=R-r(R＞r) ⑤两圆内含d＜R-r(R＞r)136定理相交两圆的连心线垂直平分两圆的公共弦137定理把圆分成n(n≥3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138定理任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆139正n边形的每个内角都等于〔n-2〕×180°／n140定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141正n边形的面积Sn=pnrn／2 p表示正n边形的周长142正三角形面积√3a／4 a表示边长143如果在一个顶点周围有k个正n边形的角，由于这些角的和应为360°，因此k×(n-2)180°／n=360°化为〔n-2〕(k-2)=4 144弧长计算公式：L=n兀R／180145扇形面积公式：S扇形=n兀R^2／360=LR／2146内公切线长= d-(R-r) 外公切线长= d-(R+r)。

初中数学定理大全：圆

初中数学定理大全：圆 101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹，是以定点为圆心，定长为半径的圆106和已知线段两个端点的距离相等的点的轨迹，是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹，是这个角的平分线108到两条平行线距离相等的点的轨迹，是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三点确定一个圆。

110垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111推论1 ①平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧②弦的垂直平分线经过圆心，并且平分弦所对的两条弧③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧112推论2 圆的两条平行弦所夹的弧相等113圆是以圆心为对称中心的中心对称图形114定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等115推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116定理一条弧所对的圆周角等于它所对的圆心角的一半117推论1 同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等118推论2 半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径119推论3 如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形120定理圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角121①直线L和⊙O相交d＜r②直线L和⊙O相切d=r③直线L和⊙O相离d＞r122切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123切线的性质定理圆的切线垂直于经过切点的半径124推论1 经过圆心且垂直于切线的直线必经过切点125推论2 经过切点且垂直于切线的直线必经过圆心126切线长定理从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角127圆的外切四边形的两组对边的和相等128弦切角定理弦切角等于它所夹的弧对的圆周角129推论如果两个弦切角所夹的弧相等，那么这两个弦切角也相等130相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等131推论如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项132切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项133推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等134如果两个圆相切，那么切点一定在连心线上135①两圆外离d＞R+r ②两圆外切d=R+r③两圆相交R-r＜d＜R+r(R＞r)④两圆内切d=R-r(R＞r) ⑤两圆内含d＜R-r(R＞r)136定理相交两圆的连心线垂直平分两圆的公共弦137定理把圆分成n(n≥3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138定理任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆139正n边形的每个内角都等于（n-2）×180°／n140定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141正n边形的面积Sn=pnrn／2 p表示正n边形的周长142正三角形面积√3a／4 a表示边长143如果在一个顶点周围有k个正n边形的角，由于这些角的和应为360°，因此k×(n-2)180°／n=360°化为（n-2）(k-2)=4144弧长计算公式：L=n兀R／180145扇形面积公式：S扇形=n兀R^2／360=LR／2146内公切线长= d-(R-r) 外公切线长= d-(R+r)。