中国石油大学(华东)油层物理课后题答案
中国石油大学(华东)《油层物理》综合复习资料参考答案

《油层物理》综合复习资料参考答案一、填空题1.高温;高压;天然气;2.减小;增加;3.薄片法 筛析法 沉降法4.少;多;多;5.动力; 阻力;6.重碳酸钠;硫酸钠;氯化钙;氯化镁;7.温度 压力 原油和天然气组成8.基底胶结 孔隙胶结 接触胶结 基底胶结 9.正向燃烧;逆(反)向燃烧;湿式燃烧;10.饱和蒸汽压 临界点 11.小12.对应温度 对应压力 压缩因子 13. 主要的驱油能量14.宽 ])/[(g P h o w cR ρρ-= 15.孔隙度 渗透率 饱和度 16.亨利二、名词解释1.砂岩的粒度组成:构成砂岩的各种大小不同的颗粒的相对含量,以质量百分数表示。
2.地层油的等温压缩系数:在等温条件下,地层油的体积随压力的变化率。
3.润湿:液体在分子力作用下沿固体表面的流散现象。
4.平衡常数:在一定温度和压力下,系统中气液两相达到热力学平衡时,某一组分在气相和液相中的分配比例。
5.贾敏效应:液珠或气泡通过孔喉时产生的附加阻力。
6.两相体积系数:当油藏压力低于泡点压力时,地层油和其释放的气体的总体积与它在地面脱气后的体积之比。
7.压缩因子:一定温度和压力条件下,一定质量的实际气体所占有的体积与相同条件下理想气体占有的体积之比。
8.溶解气油比:在某一温度和压力下,单位体积地面油中溶解天然气的标准体积。
9.相渗透率:当岩石孔隙中饱和两种或两种以上的流体时,岩石让其中一种流体通过的能力。
10.波及系数:注入工作剂在油层中的波及程度。
或工作剂驱扫过的油藏体积占整个油藏体积的百分数。
11.润湿反转:岩石表面由于性质发生变化,使得润湿性发生变化的现象。
12.天然气的等温压缩系数:在等温条件下,天然气的体积随压力的变化率。
13.驱替过程:非湿相驱替湿相的过程。
14.吸附:溶质在相界面和相内部浓度不同的现象。
15.相对渗透率:当岩石孔隙中饱和两种或两种以上的流体时,某一相流体的有效渗透率与绝对渗透率的比值。
中国石油大学(华东)油层物理课后题问题详解

简要说明为什么油水过渡带比油气过渡带宽?为什么油越稠,油水过渡带越 宽?答:过渡带的高度取决于最细的毛细管中的油(或水)柱的上升高度。
由于油藏中的油气界面张力受温度、压力和油中溶解气的影响,油气界面张力很 小,故毛管力很小,油气过渡带高度就很小。
因为油水界面张力大于油气界 面张力,故油水过渡带的毛管力比油气过渡带的大,而且水油的密度差小于 油的密度,所以油水过渡带比油气过渡带宽,且油越稠,水油密度差越小, 油水过渡带越宽 四、简答题1、简要说明油水过渡带含水饱和度的变化规律,并说明为什么油越稠油水过渡带越宽? 由于地层中孔隙毛管的直径大小是不一样的,因此油水界面不是平面,而是一个过渡带。
从地层底层到顶层,油水的分布一般为:纯水区——油水过渡区——纯油区。
由下而上,含水饱和度逐渐降低。
由式:,在PcR 一定时,油水的密度差越小,油水的过渡带将越宽。
油越稠,油水密度 差越小,所以油越稠,油水过渡带越宽。
来源于骄者拽鹏 习题11.将气体混合物的质量组成换算为物质的量的组成。
气体混合物的质量组成如下:%404-CH ,%1062-H C ,%1583-H C ,%25104-H C ,%10105-H C 。
解:按照理想气体计算:2.已知液体混合物的质量组成:%.55%,35%,1012510483---H C H C H C 将此液体混合物的质量组成换算为物质的量的组成。
解:3.已知地面条件下天然气各组分的体积组成:%23.964-CH ,%85.162-H C ,%83.083-H C ,%41.0104-H C , %50.02-CO ,%18.02-S H 。
若地层压力为15MPa ,地层温度为50C O 。
求该天然气的以下参数:(1)视相对分子质量;(2)相对密度;(3)压缩因子;(4)地下密度;(5)体积系数;(6)等温压缩系数;(7)粘度;(8)若日产气为104m 3,求其地下体积。
解:(1)视相对分子质量836.16)(==∑i i g M y M(2)相对密度58055202983616..M M ag g ===γ (3)压缩因子244.3624.415===c r p p p 648.102.19627350=+==c r T T T3.2441.6480.84(4)地下密度)(=)(3/95.11127350008314.084.0836.1615m kg ZRT pM V m g g +⨯⨯⨯===ρ (5)体积系数)/(10255.6202735027315101325.084.0333m m T T p p Z p nRT pZnRTV V B sc sc scsc gscgf g 标-⨯=++⨯⨯=⋅⋅===(6)等温压缩系数3.2441.6480.52[])(==1068.0648.1624.452.0-⨯⋅⋅=MPa T P T C C rc rgrg(7)粘度16.836500.01171.41.6483.244[])(01638.00117.04.1/11s mPa g g g g ⋅=⨯=⨯=μμμμ(8)若日产气为104m 3,求其地下体积。
大学物理课后习题详解(第一章)中国石油大学

习 题 一1-1 一质点在平面xOy 内运动,运动方程为t x 2=,2219t y -= (SI ).(1)求质点的运动轨道;(2)求s 1=t 和s 2=t 时刻质点的位置矢量;(3)求s 1=t 和s 2=t 时刻质点的瞬时速度和瞬时加速度;(4)在什么时刻,质点的位置矢量和速度矢量垂直?这时x 、y 分量各为多少?(5)在什么时刻,质点离原点最近?最近距离为多大?[解] 质点的运动方程t x 2=,2219t y -= (1)消去参数t ,得轨道方程为:22119x y -= ()0≥x(2)把s 1=t 代入运动方程,得j i j i r 172+=+=y x把s 2=t 代入运动方程,得()j i j i r 1142219222+=⨯-+⨯=(3)由速度、加速度定义式,有4/d d ,0/d d 4/d d ,2/d d y y x x y x -====-====t v a t v a t t y v t x v所以,t 时刻质点的速度和加速度分别为=v j i j i t v v 42y x -=+j j i a 4y x -=+=a a所以,s 1=t 时,j i v 42-=,j a 4-=s 2=t 时,j i v 82-=,j a 4-= (4)当质点的位置矢量和速度矢量垂直时,有0=⋅v r即 ()[][]04221922=-⋅-+j i j i t t t 整理,得 093=-t t解得 01=t ; 32=t ;33-=t (舍去)m 19,0,s 011===y x t 时 m 1,m 6,s 322===y x t 时(5)任一时刻t 质点离原点的距离()()()222222192tt yx t r -+=+=令0d d =tr 可得 3=t所以,s 3=t 时,质点离原点最近 () 6.08m 3=r1-2 一粒子按规律59323+--=t t t x 沿x 轴运动,试分别求出该粒子沿x 轴正向运动;沿x 轴负向运动;加速运动;减速运动的时间间隔.[解] 由运动方程59323+--=t t t x 可得 质点的速度 ()()133963d d 2+-=--==t t t t tx v (1)粒子的加速度 ()16d d -==t tv a(2) 由式(1)可看出 当3s >t 时,0>v ,粒子沿x 轴正向运动;当3s <t 时,0<v ,粒子沿x 轴负向运动.由式(2)可看出 当1s >t 时,0>a ,粒子的加速度沿x 轴正方向;当1s <t 时,0<a ,粒子的加速度沿x 轴负方向. 因为粒子的加速度与速度同方向时,粒子加速运动,反向时,减速运动,所以,当s 3>t 或1s 0<<t 间隔内粒子加速运动,在3s 1s <<t 间隔内里粒子减速运动.1-3 一质点的运动学方程为2t x =,()21-=t y (S1).试求: (1)质点的轨迹方程;(2)在2=t s 时,质点的速度和加速度.[解] (1) 由质点的运动方程 2t x = (1)()21-=t y (2)消去参数t ,可得质点的轨迹方程 ()21-=x y(2) 由(1)、(2)对时间t 求一阶导数和二阶导数可得任一时刻质点的速度和加速度 t tx v 2d d x ==()12d d y -==t ty v所以 ()j i j i v 122y x -+=+=t t v v (3)2d d 22x ==tx a 2d d22y ==tya所以 j i a 22+= (4) 把2s =t 代入式(3)、(4),可得该时刻质点的速度和加速度.j i v 24+= j i a 22+=1-4 质点的运动学方程为t A x ωsin =,t B y ωcos =,其中 A 、B 、ω为正常数,质点的轨道为一椭圆.试证明质点的加速度矢量恒指向椭圆的中心.[证明] 由质点的运动方程 t A x ωs i n= (1) t B y ωc o s = (2)对时间t 求二阶导数,得质点的加速度 t A t x a ωωs i n d d 222x -==t B tya ωωcos d d222y -==所以加速度矢量为 ()r j i a 22c o s s i n ωωωω-=+-=t B t A可得加速度矢量恒指向原点——椭圆中心.1-5 质点的运动学方程为()j i r 222t t -+= (SI ),试求:(1)质点的轨道方程;(2)2s =t 时质点的速度和加速度.[解] (1) 由质点的运动方程,可得tx 2= 22t y -=消去参数t ,可得轨道方程2412x y -=(2) 由速度、加速度定义式,有j i r v t t 22d /d -==j r a 2d /d 22-==t将2s =t 代入上两式,得j i v 42-= j a 2-=1-6 已知质点的运动学方程为t r x ωcos =,t r y ωsin =,ct z =,其中r 、ω、c 均为常量.试求:(1)质点作什么运动?(2)其速度和加速度? (3)运动学方程的矢量式.[解] (1) 质点的运动方程 t r x ωc o s= (1) t r y ωsin = (2)ct z = (3)由(1)、(2)消去参数t 得 222r y x =+此方程表示以原点为圆心以r 为半径的圆,即质点的轨迹在xoy 平面上的投影为圆. 由式(2)可以看出,质点以速率c 沿z 轴匀速运动.综上可知,质点绕z 轴作螺旋线运动.(2) 由式(1)、(2)、(3)两边对时间t 求导数可得质点的速度tr tx v ωωsin d d x -==t r ty v ωωcos d d y ==c tz v ==d d z所以 k j i k j i v c t r t r v v v ++-=++=ωωωωc o s s i nz y x 由式(1)、(2)、(3)两边对时间求二阶导数,可得质点的加速度t r tx a x ωωcos d d 222-==t r ty a y ωωsin d d 222-==0z =a所以 j i k j i a t r t r a a a ωωωωs i n c o s22z y x --=++= (3) 由式(1)、(2)、(3)得运动方程的矢量式k j i k j i r ct t r t r z y x ++=++=ωωsin cos1-7 湖中一小船,岸边的人用跨过高处的定滑轮的绳子拉船靠岸(如图所示).当收绳速度为0v 时,试问:(1)船的运动速度u 比v 大还是小?(2)若常量=v .船能否作匀速运动?如果不能,其加速度为何值?[解] (1) 由图知222h s L +=两边对t 求导数,并注意到h 为常数,得 ts stL Ld d 2d d 2=又 ts u t L v d d ,d d -=-=所以 su Lv = (1) 即1>=s L vu因此船的速率u 大于收绳速率v .(2) 将(1)式两边对t 求导,并考虑到v 是常量tu sts utL vd d d d d d +=所以 sa v u =-22 即 ()32222sv h sv ua =-=1-8 质点沿x 轴运动,已知228t v +=,当8=t s 时,质点在原点左边52m 处(向右为x 轴正向).试求:(1)质点的加速度和运动学方程;(2)初速度和初位置;(3)分析质点的运动性质.[解] (1) 质点的加速度 t t v a 4/d d ==又 t x v /d d = 所以 t v x d d =对上式两边积分,并考虑到初始条件得()⎰⎰⎰+==-ttxt t t v x 82852d 28d d所以 3.4573283-+=t t x因而质点的运动学方程为 33283.457t t x ++-=(2) 将0=t 代入速度表达式和运动学方程,得m/s 802820=⨯+=vm 3.457032083.45730-=⨯+⨯+-=x(3) 质点沿x 轴正方向作变加速直线运动,初速度为8m/s ,初位置为3.457-m.1-9 一物体沿x 轴运动,其加速度与位置的关系为x a 62+=.物体在0=x 处的速度为s m 10,求物体的速度与位置的关系.[解] 根据链式法则 xv vtx x v tv a d d d d d d d d ===()x x x a v v d 62d d +==对上式两边积分并考虑到初始条件,得 ()⎰⎰+=xvx x v v 010d 62d故物体的速度与位置的关系为100462++=x x v s m1-10 一质点在平面内运动,其加速度j i a y x a a +=,且x a ,y a 为常量.(1)求t -v 和t -r 的表达式;(2)证明质点的轨迹为一抛物线.0=t 时,0r r =,0v v =.[解] 由 td d v a =得 t d a v =两边积分得⎰⎰=tvt 0d 0a v v因x a ,y a 为常量,所以a 是常矢量,上式变为t a v v =-0 即 t a v v +=0由 td d r v =得 ()t t t d d d 0a v v r +==两边积分,并考虑到0v 和a 是常矢量,()⎰⎰+=tr t t 00d d 0a v r r即 20021t t a v r r ++=(2) 为了证明过程简单起见,按如下方式选取坐标系,使一个坐标轴(如y 轴)与a平行,并使质点在0=t 时刻位于0r .这样 00x t v x x += (1)00221y t v at y y ++=(2)联立 (1)~(2)式,消去参数t 得()()00x0y 0202x021y x x v v x x v a y +-+-=此即为轨道方程,它为一条抛物线.1-11 在重力和空气阻力的作用下,某物体下落的加速度为Bv g a -=,g 为重力加速度,B 为与物体的质量、形状及介质有关的常数.设0=t 时物体的初速度为零.(1)试求物体的速度随时间变化的关系式;(2)当加速度为零时的速度(称为收尾速度)值为多大?[解] (1) 由tv a d d =得t Bvg v d d =-两边分别积分,得⎰⎰=-t v t Bvg v 0d d所以,物体的速率随时间变化的关系为:()Bte Bg v --=1(2) 当0=a 时 有 0=-=Bv g a (或以∞=t 代入)由此得收尾速率 Bg v =1-12 一质点由静止开始作直线运动,初始加速度为a ,此后随t 均匀增加,经时间τ后,加速度变为2a ,经τ2后,加速度变为3a ,…….求经时间τn 后,该质点的加速度和所走过的距离.[解] 由题意可设质点的加速度与时间t 的关系为kt a a +=t (k 为常数)由 a k a a 2τ=+=τ得τak =所以 a t t aa a ⎪⎭⎫ ⎝⎛+=+=ττ1t 故当τn t =时,质点的加速度 ()a n a 1n τ+=由tv a d d =得t a v d d =对上式两边积分得⎰⎰⎪⎭⎫ ⎝⎛+=tvt a t v 00d 1d τ 所以 22t aat v τ+=又 tx v d d = t v x d d =对上式两边积分⎰⎰⎪⎭⎫ ⎝⎛+=ττn st t a at x 020d 2d 经过时间τn 后,质点所走过的距离()2232361621τττa n nt a at s n +=⎪⎭⎫ ⎝⎛+=1-13 一物体悬挂于弹簧上沿竖直方向作谐振动,其加速ky a -=,k 为常数,y 是离开平衡位置的坐标值.设0y 处物体的速度为0v ,试求速度v 与y 的函数关系.[解] 根据链式法则 yv vty y v tv a d d d d d d d d ===y a v v d d =对上式两边积分⎰⎰⎰-==y y yy v y ky y a v v 000d d d v即 ()()2022022121y y k v v--=-故速度v 与y 的函数关系为()220202yy k v v -+=1-14 一艘正以速率0v 匀速行驶的舰艇,在发动机关闭之后匀减速行驶.其加速度的大小与速度的平方成正比,即2kv a -=, k 为正常数.试求舰艇在关闭发动机后行驶了x 距离时速度的大小.[解] 根据链式法则 xv vtx x v tv a d d d d d d d d ===v av x d d =对上式两边积分⎰⎰⎰-==vvvvxkvv v av x 0d d d 0化简得ln1v vkx -=所以kxev v -=0l-15 一粒子沿抛物线轨道2x y =运动,且知s m 3x =v .试求粒子在m 32=x 处的速度和加速度.[解] 由粒子的轨道方程 2x y = 对时间t 求导数 x y 2d d 2d d xv tx xty v ===(1)再对时间t 求导数,并考虑到x v 是恒量2x y 2d d v tv a ==(2)把m 32=x 代入式(1)得m 43322y =⨯⨯=v 所以,粒子在m 32=x 处的速度为s m 543222x 2x =+=+=v v v与x 轴正方向之间的夹角85334arctanarctanxy '===v v θ由式(2)得粒子在m 32=x 处的加速度为22s m 1832=⨯=a加速度方向沿y 轴的正方向.1-16 一质点沿半径为0.10m 的圆周运动,其角位置342t +=θ.(1)在2s =t 时,它的法向加速度和切向加速度各是多少?(2)切向加速度的大小恰是总加速度大小的一半时,θ值为多少?(3)何时切向加速度与法向加速度大小相等?[解] 质点的角速度 212d d t t==θω质点的线速度 222.11210.0t t R v =⨯==ω 质点的法向加速度n a ,切向加速度t a 为()4222n 4.1410.012t tR a =⨯==ω (1)t tv a 4.2d d t ==(2)(1)把2s =t 代入(1)式和(2)式,得此时2t 224n m/s8.424.2m/s 103.224.14=⨯=⨯=⨯=a a(2)质点的总加速度1364.262t 2n +=+=t t a a a由 a a 21t =得 1364.25.04.26+⨯=t t t解得 0.66s =t 所以 r a d 15.3423=+=t θ (3)当t n a a =即t t 4.24.144=时有 0.55s =t1-17 火车在曲率半径R =400m 的圆弧轨道上行驶.已知火车的切向加速度2.0t =a 2s m ,求火车的瞬时速率为s m 10时的法向加速度和加速度.[解] 火车的法向加速度 222n sm 25.040010===Rva方向指向曲率中心 火车的总加速度 2222t 2n s m 32.02.025.0=+=+=a a a设加速度a 与速度v 之间的夹角为θ,则025134.512.025.0arctanarctantn '====a a θ1-18 为了转播电视而发射的地球同步卫星在赤道上空的圆轨道上运动,周期等于地球的自转周期24h =T .求卫星离开地面的高度和卫星的速率(距地球中心r 处的重力加速度2e ⎪⎭⎫⎝⎛=r R g a ,e R 是地球的半径.)[解] 设同步卫星距地球的中心为r ,速率为v ,则Tr v π2=(1)2e 2⎪⎭⎫⎝⎛==r R g a r v(2) 解(2)式可得()()m 1022.443600241063788.947322233222e ⨯=⨯⨯⨯⨯==ππT gR r代入(1)式可得s m 1007.33600241022.42237⨯=⨯⨯==ππTr v所以,卫星距地面的高度m 1058.31063781022.4737e ⨯=⨯-⨯=-=R r h1-19 若登月舱在登上月球之前绕月球以半径e 31R r = (e R 为地球半径)作圆周运动,并且已知这时月球对登月舱的引力加速度g a 121=.试计算登月舱的速率和飞行一周所需要的时间.[解] 设登月舱的速率为v ,周期为T ,则a rv=2即g R v1213e2=(1)v Tr =π2 即v TR =32e π (2)解(1)式可得s m 1032.1106378368.93633e ⨯=⨯⨯==R g v代入(2)式可得s 1001.1368.931063782363243e⨯=⨯==ππg R T1-20 如图所示,一卷扬机自静止开始作匀加速运动,绞索上一点起初在A 处经3s 到达鼓轮的B 处,然后作圆周运动.已知0.45m =AB ,鼓轮半径0.5m =R ,求该点经过点C 时,其速度和加速度的大小和方向.[解] 设A 点的切向加速度为t a ,经过B 点时的速率为B v ,法向加速度为n a由A 到B 过程:2t 21t a AB =(1)t a v t B = (2)在B 点: R a R v //t B B ==βω, (3)由B 到C 过程:πβωω22B 2C =- (4)在C 点: R v C C ω= (5) 联立以上五式,得m 64.05.035.045.0435.045.02422222C C =⨯⨯⨯+⎪⎭⎫⎝⎛⨯⨯=+⎪⎭⎫⎝⎛==ππωR Rt AB Rt AB R v 方向沿切向Rv a 2C n =2t 2tAB a =22222n2ts m 83.05.064.0345.02=⎪⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛⨯=+=a a a 28330.4520.50.64arctanarctan22nt '=⨯==a a θ1-21 在一个转动的齿轮上,一个齿尖P 沿半径为R 的圆周运动,其路程随时间的变化规律为2021bt t v s +=,其中0v 和b 都是正常量.求t 时刻齿尖P 的速度及加速度的大小.[解] 设时刻t 齿尖P 的速率为v ,切向加速度t a ,法向加速度n a ,则Rbt v Rva b t va bt v t s v 202n t 0)(d d d d +====+==所以,t 时刻齿尖P 的加速度为24022n 2t )(Rbt v b a a a ++=+=1-22 一物体作斜抛运动,抛射角为α,初速度为0v ,轨迹为一抛物线(如图所示).试分别求抛物线顶点A 及下落点B 处的曲率半径.[解] 物体在A 点的速度设为A v ,法向加速度为nA a ,曲率半径为A ρ,由题图显然有αcos 0A v v = (1) nA a =g (2) A n A2Aa v =ρ (3)联立上述三式得 gv αρ220A c o s =物体在B 点的速度设为B v ,法向加速度为nB a ,曲率半径为B ρ,由题图显然有0B v v = (4) αcos nB g a = (5) nB B2Ba v =ρ (6)联立上述三式得 αρc o s 2B g v =1-23 一物体作如图所示的抛体运动,测得轨道的点A 处,速度的大小为v ,其方向与水平线的夹角为030,求点A 的切向加速度和该处的曲率半径.[解] 设A 点处物体的切向加速度为t a ,法向加速度为n a ,曲率半径为ρ,则 n t a a g +=由图知 g g a 5.030sin 0t -=-=2/330cos 0n g g a ==又 n 2a v=ρ所以 gv g va v3322/322n2===ρ1-24 一门火炮在原点处以仰角0130=θ、初速10v m 100=发射一枚炮弹.另有一门位于600=x m 处的火炮同时以初速8020=v s m 发射另一枚炮弹,其仰角2θ为何值时,可望能与第一枚炮弹在空中相碰? 相碰时间和位置如何(忽略空气阻力的影响)?[解] 设经过时间t 后,炮弹1、炮弹2的坐标分别为()11,y x 、()22,y x ,则 对炮弹1 t v x 1101cos θ= 2110121sin gt t v y -=θ对炮弹2 t v x x 22002cos θ+= 2220221sin gt t v y -=θ当炮弹1、炮弹2相碰时 21x x = 21y y =即 t v x t v 2200110cos cos θθ+= (1)2220211021sin 21sin gt t v gt t v -=-θθ (2)解(2)式可得 625.030sin 80100sin sin 0120102=⨯==θθv v (3)所以 02682.38625.0arcsin ==θ 由(1)式可得 s 48.2682.38cos 8030cos 10060cos cos 02201100=⨯-⨯=-=θθv v x t相遇时的坐标设为(x ,y ),则m 77.21448.230cos 100cos 011021=⨯⨯====t v x x x θm 86.9348.28.92148.230sin 10021sin 2211021=⨯⨯-⨯⨯=-===gtt v y y y θ1-25 河宽为d ,靠河岸处水流速度变为零,从岸边到中流,河水的流速与离开岸的距离成正比地增大,到中流处为0v .某人以相对水流不变的速率v 垂直水流方向驶船渡河,求船在达到中流之前的轨迹方程.[解] 取图示坐标系ky v =x已知 2d y =时,0x v v =代入上式得 d v k 02=所以 y dv v 0x 2=(1)又 v v =y积分得 vt y = (2) 代入(1)式得 vt d v v 0x 2=积分得 20vt d v x = (3)由(2)、(3)消去t 得 20y vdv x =1-26 如图所示,一航空母舰正以s m 17的速度向东行驶,一架直升飞机准备降落在舰的甲板上.海上有s m 12的北风吹着.若舰上的海员看到直升飞机以s m 5的速度垂直下降,求直升飞机相对海水及相对空气的速度?[解] 已知 k v 5-=机对舰 j v 17=舰对海 i v 12=气对海 故 ()s m 175j k v v v +-=+=舰对海机对舰机对海()m 51712k j i v v v -+-=+=海对气机对海机对气习题 1-26 图。
中国石油大学(华东)__大学物理课后习题答案

ax
az 0
d2 x r 2 cost 2 dt
ay
d2 y r 2 s i n t 2 dt
7-2
所以
a ax i a y j az k r 2 costi r 2 sin tj
(3) 由式(1) 、 (2) 、 (3)得运动方程的矢量式 r xi yj zk r costi r sin tj ctk 1-8 质点沿 x 轴运动,已知 v 8 2t 2 ,当 t 8 s 时,质点在原点左边 52m 处(向右为 x 轴正向) .试求: (1)质点的加速度和运动学方程; (2)初速度和初位置; (3)分析质点的 运动性质. [解] (1) 质点的加速度 a d v /d t 4t 又 v d x /d t 所以 d x vdt 对上式两边积分,并考虑到初始条件得
vx dx r sin t dt
dy r cost dt dz vz c dt vy
所以
v vx i v y j vz k r sin ti r costj ck
由式(1) 、 (2) 、 (3)两边对时间求二阶导数,可得质点的加速度
所以, t 时刻齿尖 P 的加速度为
2 a a t2 an b2
(v0 bt) 4 R2
1-17 火车在曲率半径 R=400m 的圆弧轨道上行驶. 已知火车的切向加速度 a t 0.2 m s 2 , 求火车的瞬时速率为 10 m s 时的法向加速度和加速度. [解] 火车的法向加速度 火车的总加速度
y x2
7-4
对时间 t 求导数
vy
dy dx 2x 2 xvx dt dt
(1)
中国石油大学(华东)大学物理2-1第八章习题答案

习题 88-1.选择题1.一定量的理想气体,分别经历习题8-1(1)(a) 图所示的abc 过程(图中虚线ac 为等温线)和习题8-1(1)(b) 图所示的def 过程(图中虚线df 为绝热线),试判断这两过程是吸热还是放热( )(A) abc 过程吸热,def 过程放热 (B) abc 过程放热,def 过程吸热 (C) abc 过程def 过程都吸热 (D) abc 过程def 过程都放热2.如习题8-1(2) 图所示,一定量的理想气体从体积V 1膨胀到体积V 2分别经历的过程是:A-B 等压过程;A-C 等温过程; A-D 绝热过程。
其中,吸热最多的过程( )(A) A-B (B) A-C(C) A-D(D) 既是A-B ,也是A-C ,两者一样多3.用公式E =νC V ,m T (式中C V ,m 为定容摩尔热容量,ν为气体的物质的量)计算理想气体内能增量时,此式( )(A) 只适用于准静态的等容过程 (B) 只适用于一切等容过程(C) 只适用于一切准静态过程 (D) 适用于一切始末态为平衡态的过程4.要使高温热源的温度T 1升高ΔT ,或使低温热源的温度T 2降低同样的ΔT 值,这两种方法分别可使卡诺循环的效率升高Δ1和Δ2。
两者相比有( )(A) Δ1>Δ2 (B) Δ1<Δ2(C) Δ1= Δ2 (D) 无法确定哪个大 5. 理想气体卡诺循环过程的两条绝热线下的面积大小(如习题8-1(5)图中阴影所示)分别为S 1和S 2,则两者的大小关系是( )(A) S 1 > S 2 (B) S 1 = S 2 (C) S 1 < S 2 (D) 无法确定 6. 热力学第一定律表明( )(A) 系统对外做的功不可能大于系统从外界吸收的热量 (B) 系统内能的增量等于系统从外界吸收的热量(C) 不可能存在这样的循环过程,在此循环过程中,外界对系统做的功不等于系统传给外界的热量 (D) 热机的效率不可能等于1 7. 根据热力学第二定律可知( )(A) 功可以全部转换为热,但热不能全部转换为功(B) 热可以从高温物体传到低温物体,但不能从低温物体传到高温物体 (C) 不可逆过程就是不能向相反方向进行的过程 (D) 一切宏观的自发过程都是不可逆的 8.不可逆过程是( ) (A) 不能反向进行的过程(B) 系统不能回复到初始状态的过程 (C) 有摩擦存在的过程或者非准静态过程 (D) 外界有变化的过程习题8-1(1)图习题8-1(2)图习题8-1(5)图9. 关于热功转换和热量传递过程,有下列叙述: (1) 功可以完全变为热量,热量不可以完全变为功 (2) 一切热机的效率都只能小于1 (3) 热量不能从低温物体向高温物体传递 (4) 热量从高温物体向低温物体的传递是不可逆的 以上这些叙述中正确的是( ) (A) 只有(2),(4)正确 (B) 只有(2),(3),(4)正确 (C) 只有(1),(3),(4)正确 (D) 全部正确 8-2.填空题1.一定量的理想气体处于热动平衡状态时,此热力学系统的不随时间变化的三个宏观量是 ,而随时间变化的微观是 。
油层物理习题册答案
数)
∴可得:Ppr=P/Ppc=20/4.66=4.3 Tpr=T/
Tpc=(273+75)/216=1.6
查压缩因子图版得:Z=0.84
Bg= ×20]=0.004929
ZTP0/(T0P)=0.84×(273+75)×0.1/[(273+20)
∴Ng=V地下/Bg=105×104/0.004929=2。13×108(m3)
2.根据某一地层油样的高压物性实验,作出如图所示的溶解度曲线。
求: (1)原始溶解油气比; (2)原油的饱和压力; (3)当油层压力降到10MPa时,从
油中分离出的游离气有多少?
解:由图可知:(1)Rsi=100 (标准米3/米3) (2)Pb=20 MPa (3) P=10MPa时,Rs=60(标准米3/米3)
因而,析出 △Rs=100-60=40 (标准米3/米3) 3.有一油藏,原始地层压力为20MPa,地层温度为75 ℃,饱和压力为 18MPa,原始溶解油气比为120标 ,当P=15MPa时,
=115标
,Bo=1.25,已知天然气比重为0.70,求压力为15MPa时的两相体积系 数。
解:由该天然气的比重ɣ=0.70查天然气比重与临界参数关系图得视临界
二.判断题。√×√√√× 1.地层油单相体积系数总是大于1的。
(√) 2.地层油单相体积系数在饱和压力时是最小的。
(×) 3.地层油粘度在饱和压力时是最小的。
(√) 4.在低于饱和压力下,随着压力下降地层油也将释放出弹性能量。
( √) 5.当压力等于饱和压力时,石油两相体积系数大于单相体积系数。 (√ ) 6.地层水矿化度愈大,则地层水压缩系数愈大。 (×)
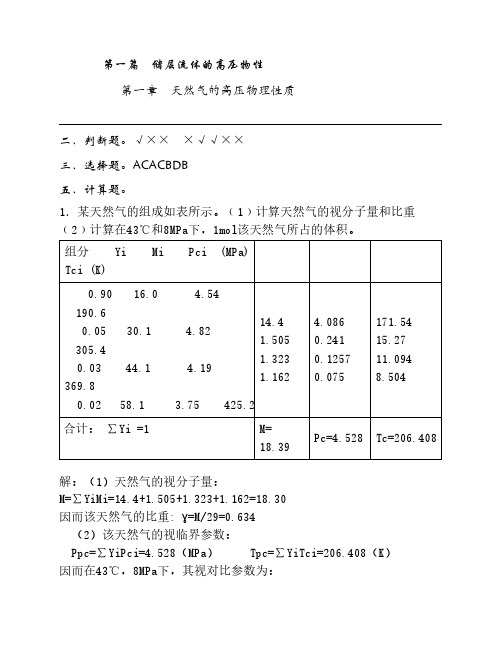
合计: ∑Yi =1
油层物理习题(答案)

目录第一篇储层流体的高压物性 (3)第一章天然气的高压物理性质 (3)一、名词解释。
(3)二.判断题。
√×××√√×× (3)三.选择题。
ACACBDB (4)四.问答题。
(4)五.计算题。
(5)第二章油气藏烃类的相态和汽液平衡 (9)一、名词解释。
(9)二.判断题。
√√×√×√√××√ (9)三.选择题。
CDAC (9)四.问答题。
(10)五.计算题。
(11)第三章油气的溶解与分离 (13)一、名词解释。
(13)二.判断题。
√××√√× (13)三.选择题。
AADCBB (13)四.问答题。
(14)五.计算题。
(15)第四章储层流体的高压物性 (19)一、名词解释。
(19)二.判断题。
√×√√√× (19)三.选择题。
CCBBC DDDDCD (19)四.问答题。
(21)五.计算题。
(22)第二篇储层岩石的物理性质 (26)第一章砂岩的物理性质 (26)一、名词解释。
(26)二.判断题。
√√×√××× (27)三.选择题。
BDBACC (27)四.问答题。
(28)五.计算题。
(29)第二章储层岩石的孔隙性 (29)一、名词解释。
(29)二.判断题。
×××√√ (30)三.选择题。
ACAB (30)四.问答题。
(31)五.计算题。
(32)第三章储层岩石的渗透性 (34)一、名词解释。
(34)二.判断题。
×√√××√×√×√ (34)三.选择题。
DBCBCBC (35)四.问答题。
(35)五.计算题。
(36)第四章储层流体饱和度 (38)一、名词解释。
(38)二.判断题。
√×√ (38)12三.选择题。
油层物理习题(答案)

目录第一篇储层流体的高压物性 (3)第一章天然气的高压物理性质 (3)一、名词解释。
(3)二.判断题。
√×××√√×× (3)三.选择题。
ACACBDB (4)四.问答题。
(4)五.计算题。
(5)第二章油气藏烃类的相态和汽液平衡 (9)一、名词解释。
(9)二.判断题。
√√×√×√√××√ (9)三.选择题。
CDAC (9)四.问答题。
(10)五.计算题。
(11)第三章油气的溶解与分离 (13)一、名词解释。
(13)二.判断题。
√××√√× (13)三.选择题。
AADCBB (13)四.问答题。
(14)五.计算题。
(15)第四章储层流体的高压物性 (19)一、名词解释。
(19)二.判断题。
√×√√√× (19)三.选择题。
CCBBC DDDDCD (19)四.问答题。
(21)五.计算题。
(22)第二篇储层岩石的物理性质 (26)第一章砂岩的物理性质 (26)一、名词解释。
(26)二.判断题。
√√×√××× (27)三.选择题。
BDBACC (27)四.问答题。
(28)五.计算题。
(29)第二章储层岩石的孔隙性 (29)一、名词解释。
(29)二.判断题。
×××√√ (30)三.选择题。
ACAB (30)四.问答题。
(31)五.计算题。
(32)第三章储层岩石的渗透性 (34)一、名词解释。
(34)二.判断题。
×√√××√×√×√ (34)三.选择题。
DBCBCBC (35)四.问答题。
(35)五.计算题。
(36)第四章储层流体饱和度 (38)一、名词解释。
(38)二.判断题。
√×√ (38)12三.选择题。
中国石油大学(华东)油层物理课后题答案

来源于骄者拽鹏 习题11.将气体混合物的质量组成换算为物质的量的组成。
气体混合物的质量组成如下:%404-CH ,%1062-H C ,%1583-H C ,%25104-H C ,%10105-H C 。
解:按照理想气体计算:2.已知液体混合物的质量组成:%.55%,35%,1012510483---H C H C H C 将此液体混合物的质量组成换算为物质的量的组成。
解:3.已知地面条件下天然气各组分的体积组成:%23.964-CH ,%85.162-H C ,%83.083-H C ,%41.0104-H C , %50.02-CO ,%18.02-S H 。
若地层压力为15MPa ,地层温度为50C O 。
求该天然气的以下参数:(1)视相对分子质量;(2)相对密度;(3)压缩因子;(4)地下密度;(5)体积系数;(6)等温压缩系数;(7)粘度;(8)若日产气为104m 3,求其地下体积。
解:(1)视相对分子质量836.16)(==∑i i g M y M(2)相对密度58055202983616..M M ag g ===γ (3)压缩因子 244.3624.415===c r p p p 648.102.19627350=+==c r T T T(4)地下密度)(=)(3/95.11127350008314.084.0836.1615m kg ZRT pM V m g g +⨯⨯⨯===ρ(5)体积系数)/(10255.6202735027315101325.084.0333m m T T p p Z p nRT pZnRTV V B sc sc scsc gscgf g 标-⨯=++⨯⨯=⋅⋅===(6)等温压缩系数3.2441.6480.52[])(==1068.0648.1624.452.0-⨯⋅⋅=MPa T P T C C rc rgrg(7)粘度16.836500.01171.41.6483.244[])(01638.00117.04.1/11s mPa g g g g ⋅=⨯=⨯=μμμμ(8)若日产气为104m 3,求其地下体积。
大学物理课后习题详解(第九章)中国石油大学

习 题 九9-1 一系统由图示的状态a 经acb 到达状态b ,系统吸收了320J 热量,系统对外作功126J . (1)若adb 过程系统对外作功 42J ,问有多少热量传入系统? (2)当系统由b 沿曲线ba 返回状态a ,外界对系统作功84 J ,试问系统是吸热还是放热? 热量是多少? [解] 由热力学第一定律A E Q +∆=得 A Q E -=∆ 在acb 过程中,E E E ∆=-a b J 19412632011=-=-=A Q在adb 过程中,内能变化量与acb 过程相同 因此 J 2364219422=+=+∆=A E Q 在ba 过程中J 2788419433b a 3-=--=+∆-=+-=A E A E E Q由于热量为负值,所以本过程中系统放热.9-2 2mol 氮气由温度为 300K ,压强为510013.1⨯Pa (1atm )的初态等温地压缩到 510026.2⨯Pa (2atm ).求气体放出的热量. [解] 在等温过程中气体吸收的热量等于气体对外做的功,所以J 1046.321ln30031.82ln321T ⨯-=⨯⨯⨯===p p RT A Q ν即气体放热为J 1046.33⨯.9-3 一定质量的理想气体的内能E 随体积的变化关系为E - V图上的一条过原点的直线,如图所示.试证此直线表示等压过程.[证明] 设此直线斜率为k ,则此直线方程为kV E = 又E 随温度的关系变化式为 T k T C MM E '=⋅=v m o l所以 T k kV '= 因此 C kk T V ='=(C 为恒量)又由理想气体的状态方程知,C T pV'= (C '为恒量)所以 p 为恒量,即此过程为等压过程.9-4 2mol 氧气由状态1变化到状态2所经历的过程如图所示:(1)沿l →m →2路径.(2)1→2直线.试分别求出两过程中氧气对外作的功、吸收的热量及内能的变化.[解] (1) 在1→m →2这一过程中,做功的大小为该曲线下的面积,氧气对外做负功.()()J 1010.81010013.11050204352121⨯-=⨯⨯⨯-⨯-=--=-V V p A由气体的内能公式T C E V ν=和理想气体的状态方程RT pV ν=得pV i RR i pVRpVC RpVC E 22VV====νν对于氧气5=i ,所以其内能的变化为 ()()J 1027.11010013.15051020252543511221⨯-=⨯⨯⨯⨯-⨯⨯=-=∆-V p V p E此过程吸收的热量为 J 1037.91010.81027.1444111⨯-=⨯-⨯-=+∆=A E Q (2)在从1→2过程中,由图知氧气对外作功为()()()()J 1007.51010013.11050520212143521122⨯-=⨯⨯⨯-⨯+⨯-=-+-=-V V p p A内能的变化 J 1027.1412⨯-=∆=∆E E吸收的热量 J 1034.61007.51027.1444222⨯-=⨯-⨯-=+∆=A E Q9-5 10mol 单原子理想气体在压缩过程中外界对它作功209J ,其温度上升1K ,试求:(1)气体吸收的热量与内能的增量.(2) 此过程中气体的摩尔热容量.[解] (1) 内能的增量为 J 65.124131.82310V =⨯⨯⨯=∆=∆T C E ν气体吸收的热量 J 35.8420965.124-=-=+∆=A E Q (2) 由气体摩尔热容量知 ())K mol J 44.835.841011⋅-=-⨯=∆=TQC ν9-6 将压强为1atm ,体积为33m 101-⨯的氧气(25V R C =)从0℃加热到100℃.试分别求在等体(积)过程和等压过程中各需吸收多少热量.[解] 由理想气体状态方程 RT pV ν= 00RT V p RTpV ==ν在等容过程中吸收的热量为 J 77.9210027310110013.1252535000V V =⨯⨯⨯⨯⨯=∆=∆=-T R RT V p T C Q ν在等压过程中吸收的热量为J 88.12977.92575727V p p =⨯==∆=∆=Q T R T C Q νν9-7 已知氩气的定体(积)比热为)K kg J 314V ⋅=c ,若将氩气看作理想气体,求氩原子的质量.(定体(积)摩尔热容V mol V c M C =).[解] 由定容摩尔热容量的定义知 R R i C 232V ==因此 VVV m o l 23c Rc C M==氩原子的质量为 kg 1059.63141002.631.823232623V A Amol-⨯=⨯⨯⨯===c N RN Mm9-8 为测定气体的γ(V p C C =)值有时用下列方法:一定量的气体的初始温度、体积和压强为0T 、0V 和0p ,用一根电炉丝对它缓慢加热.两次加热的电流强度和时间相同,第一次保持体积0V 不变,而温度和压强变为1T 和1p .第二次保持压强0p 不变,而温度和体积变为2T 和1V .试证明 ()()001001p V V V p p --=γ[证明] 两次加热气体吸收的热量相同,等容过程吸收的热量为()01V 1T T C Q -=ν 等压过程吸收的热量为 ()02p 2T T C Q -=ν 由 21Q Q =可得 ()()02p 01V T T C T T C -=-νν所以 0201Vp T T T T C C --==γ由理想气体状态方程 000RT V p ν= 101RT V p ν= 210RT V p ν= 因此 00101V R p p T T ν-=- 00102p RV V T T ν-=-所以得到 ()()001001p V V V p p --=γ9-9 已知1mol 固体的状态方程为bp aT v v ++=0,内能apT cT E +=,式中0v 、a 、b 、c 均为常量,求该固体的p C 、V C .[解] 由热力学第一定律可得 V p E A E Q d d d d d +=+= (1) 由已知条件可得 p b T a V d d d += (2) T ap p aT T c E d d d d ++= (3)将(2)、(3)代入(1)得 ()p b T a p T ap p aT T c Q d d d d d d ++++= (4) 在等压过程中,0d =p所以 ()T ap c Q d 2d += 因此 ap c TQ C 2d d p +==在等容过程中 0d =V代入(2)式得 0d d =+p b T a 因此 T ba p d d -=代入(4)式得Tb T a apc T b a b T a p T ap T b a aT T c Qd d d d d d d 2⎪⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-+++⎪⎭⎫ ⎝⎛-+= 所以 bT a ap c TQ C 2V d d -+==9-10 已知范德瓦尔斯气体的内能0V E Va T C E +-=.其中V C 、a 、0E 为常数,试证明其绝热过程方程为()常数=-VC R b V T[证明] 范德瓦尔斯气体的状态方程为 ()RT b V V a p =-⎪⎭⎫⎝⎛+2 (1) 又由已知条件可得 V Va T C E d d d 2V += (2)绝热过程 0d =Q ,由热力学第一定律得 V p A E d d d -=-= (3) 由(2)、(3)式可得 V p V Va T C d d d 2V -=+ (4)由 (1)式可得 2Va bV RT p --=(5)将(5)代入(4)式有 V bV RT V Va V Va T C d d d d 22V --=+整理得 V bV T RTC d 1d V --=积分得()常数=-+b V T RC ln ln V即 ()常数=-RCVT b V这就是范德瓦尔斯气体的绝热过程方程.9-11 如图所示是氮气循环过程,求:(1)一次循环气体对外作的功;(2)循环效率. [解] (1) 一次循环过程气体对外作功的大小为闭合曲线所包围的面积,由图知,其包围的面积为1()()1412V V p p S --= ()()J 100.2101015510335⨯=⨯⨯-⨯-=-该循环对外作功为正,所以 J 100.23⨯=A(2) 该循环过程中,从1→2,2→3为吸收热量过程 1→2为等容过程,吸收热量为()()112212V 125V p V p T T C Q -=-=ν()J 1025.110101511025335⨯=⨯⨯⨯-⨯⨯=-2→3为等压过程,吸收热量为 ()()223323p 227V p V p T T C Q -=-=ν()J 104.1101011051027435⨯=⨯⨯⨯-⨯⨯=-因此吸收的总热量为 J 10525.1421⨯=+=Q Q Q 该循环的效率为 %1.13%10010525.1100.243=⨯⨯⨯==Q A η9-12 一理想气体的循环过程如图所示,其中ca 为绝热过程,点 a 的状态参量为()11,V T ,点b 的状态参量为()22,V T ,理想气体的热容比为γ,求(1)气体在ab 、bc 过程中与外界是否有热交换? 数量是多少?(2)点c 的状态参量;(3)循环的效率.[解] (1) ab 过程是等温过程,系统吸收热量为121T lnV V RT A Q ν==因12V V >,故该过程是吸热过程.bc 过程是等容过程,系统吸收热量为 ()2c V V T T C Q -=ν 因 c T <2T ,故该过程是放热过程. (2) 从图上可看到 2c V V =又 ac 为绝热过程,故根据绝热方程 112111c1c T VV T VV T --⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=γγ又有 γγ11c c V p V p =得到 121211121211c -⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛=γγγννV V V RT V RT V V V V p p(3) ()()[]()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⋅-=--=--=-=--12121V 12111212V 121C 2V TV ln 11ln1ln11V V V V RC V V RT T V V T C V V RT T T C Q Q γγννη9-13 图中闭合曲线为一理想气体的循环过程曲线,其中ab 、cd 为绝热线,bc 为等体(积)线,da 为等压线,试证明其效率为bc ad T T T T ---=γη1式中a T 、b T 、c T 、d T 分别为a 、b 、c 、d 各状态的温度,V p C C =γ.[证明] da 为放热过程,其放出的热量为()a d p 2T T C Q -=νbc 为吸热过程,其吸收的热量为 ()b c V 1T T C Q -=ν 所以其效率为 ()()bc ad b c V a d p 12111T T T T T T C T T C Q Q ---=---=-=γννη9-14 如图所示,AB 、DC 为绝热线,COA 是等温线. 已知系统在COA 过程中放热J 100,OAB 的面积是J 30,ODC 的面积为 J 70,试问在BOD 过程中系统是吸热还是放热?热量是多少?[解] 因COA 是等温线,COA 过程中J 100CA CA -==Q A 又因AB 、DC 为绝热线,AB AB A E -=∆ DC DC A E -=∆ OAB 过程系统作负功,ODC 过程系统作正功,整个循环过程系统作功 3070CA DC BD AB -=+++A A A ABOD 过程中系统吸热A C BD DC AB BD BD 140140E E E E E E A Q -+=∆+∆+∆+=∆+=由于COA 是等温过程,过程中系统内能变化为零,即 0A C =-E E 因此BOD 过程中系统吸热 J 140=Q9-15 一制冷机进行如图所示的循环过程,其中ab 、cd 分别是温度为1T 、2T 的等温线,bc 、da 为等压过程,设工作物质为理想气体.证明这制冷机制冷系数为:12121ln22p p i T T T ++-=ω[证明] ab 为等温过程,吸收热量为12111lnp p RT A Q ν==cd 为等温过程,其放出的热量大小为12222lnp p RT A Q ν==bc 为等压过程,吸收的热量为 ()12p 3T T C Q -=ν da 为等压过程,放出的热量大小为 ()12p 4T T C Q -=ν所以致冷系数 ()()12121314231ln22p p i T T T Q Q Q Q Q Q Q Q Q AQ ++-=+-++=-==吸放吸吸ω9-16 mol 1单原子理想气体,初态压强为1p ,体积为1V ,经等温膨胀使体积增加一倍,然后保持压强不变,使其压缩到原来的体积,最后保持体积不变,使其回到初态. (1)试在V p -图上画出过程曲线;(2)求在整个过程中内能的改变,系统对外作的净功、从外界吸收的净热量以及循环效率.[解] (1) 过程曲线(2) 系统经过循环又回到初态,所以其内能改变量0=∆E a →b 为等温过程,系统对外作正功2ln ln11121V p V V RT A ==νa2p 1p 2V 1V OVb →c 为等压过程,系统对外作负功,其数值大小为()()122111222V V V V p V V p A -=-=过程中总功 ()1112211112119.02ln V p V V V V p V p A A A =--=-=系统从外界吸收的净热量 1119.0V p A Q == a →b 过程吸热为 2ln 1111V p A Q ==c →a 过程中吸收的热量为 ()c a V 2T T C Q -=ν()V p V V V p p V p p 112111121432323=⎪⎪⎭⎫ ⎝⎛-=-=所以 %2.13432ln 19.011111121=+=+=V p V p V p Q Q A η9-17 一可逆卡诺热机低温热源的温度为27℃,热机效率为 40%,它的高温热源的温度是多少? 今欲将热机效率提高到50%,若低温热源保持不变,则高温热源的温度应增加多少度?[解] 可逆卡诺循环的效率为121T T -=η所以 K 5004.01300121=-=-=ηT T若 %50='η,则 K 6005.01300121=-='-='ηT T所以 K 10050060011=-=-'=∆T T T9-18 有一卡诺热机,用29kg 空气为工作物质,高温热源和低温热源的温度分别为C 27o 和C 73-o ,求此热机的效率.若在等温膨胀过程中工作物质的体积增大到2.718倍,则此热机每一循环所作的功是多少?[解] 此热机的效率为 %3.333002001112=-=-=T T η在等温膨胀过程中,吸收的热量为J 1049.2718.2ln 30031.8291029ln631211⨯=⨯⨯⨯⨯==V V RT Q ν又 1Q A =η所以 J 103.81049.231561⨯=⨯⨯==Q A η9-19 在高温热源为127℃、低温热源为27℃之间工作的卡诺热机,一次循环对外作净功为8000J ,今维持低温热源温度不变,提高高温热源的温度,使其一次循环对外做功10000J ,若两次循环该热机都工作在相同的两条绝热线之间,试求: (1)后一卡诺循环的效率.(2)后一卡诺循环的高温热源的温度.[解] (1) 设前一卡诺循环从高温热源吸收热量为1Q ,则有11Q A =η又 414003001112=-=-=T T η所以 J 320004800011=⨯==ηA Q 后一卡诺循环从高温热源吸收热量为J 34000800010000320001211=-+=-+='A A Q Q所以第二个卡诺循环的效率为 %4.29%100340001000012=⨯='='Q A η(2) 第二个卡诺循环的高温热源温度为 K 425294.01300121=-='-='ηT T9-20 一台家用冰箱,放在气温为300K 的房间内,做一盘C 13-o 的冰需从冷冻室取走J 1009.25⨯的热量.设冰箱为理想卡诺制冷机. (1)求做一盘冰所需要的功;(2)若此冰箱能以s J 1009.22⨯的速率取走热量,求所要求的电功率是多少瓦? (3)做一盘冰需时若干?[解] (1) 致冷系数为 2122T T T A Q -==ω因此 ()()J 1022.32602603001009.2452212⨯=-⨯⨯=-=T T T Q A(2) 取走制一盘冰的热量所需要的时间为 s 101009.21009.2325=⨯⨯=t所以电功率为 W 2.32101022.334=⨯==tA P(3) 做一盘冰所需要的时间为 s 103.9-21 绝热容器中间有一无摩擦、绝热的可动活塞,如图所示,活塞两侧各有mol ν的理想气体,5.1=γ,其初态均为0p 、0V 、0T .现将一通电线圈置入左侧气体中,对气体缓慢加热,左侧气体吸热膨胀推动活塞向右移,使右侧气体压强增加为0375.3p ,求; (1)左侧气体作了多少功?(2)右侧气体的终态温度是多少?(3)左侧气体的终态温度是多少? (4)左侧气体吸收了多少热量?[解] (1) 右侧气体所发生的过程为绝热过程.它对外所做的功的负值就是左侧气体所作的功.所以左侧气体作功为 12200---='-=γV p V p A A又对右侧气体: γγγ202200375.3V p V p V p == 因此 γ102375.3V V =所以 000000122001375.3375.31V p V p V p V p V p A =--=---=γγγ(2) 对右侧气体,由绝热方程知 ()γγγγ----=210010375.3T p T p得到 00325.1375.3T T T ===(3) 左侧气体末态体积为 γ1002001375.32V V V V V V -=-+=得到 00000010011125.525.212375.3375.312375.3T T T V p V V p RV p T =⎪⎭⎫ ⎝⎛-⨯=⎪⎭⎫⎝⎛-==γν(4) 左侧气体吸收热量()()0000V 01V 1125.5V p T T C A T T C A E Q +-=+-=+∆=νν由 000RT V p ν= 知 RV p T ν000=又由 5.1VV Vp =+==C R C C C γ, 得到 R C 2V =所以 00000015.925.42V p V p RV p R Q =+⨯⨯⨯=νν9-22 如图所示,在刚性绝热容器中有一可无摩擦移动而且不漏气的导热隔板,将容器分为A 、B 两部分,各盛有1mol 的He 气和2O 气.初态He 、2O 的温度各为K 300A =T ,K 600B =T ;压强均为atm 1.求:(1)整个系统达到平衡时的温度T 、压强p (氧气可视为刚性理想气体); (2)He气和2O 气各自熵的变化,系统的熵变.[解] (1) 因中间是导热隔板,过程中两部分气体热量变化和作功的数值都相等,所以内能变化量的数值也相等,且由于初温度不同而末温度相同所以一正一负.因此 ()()T T C T T C '-=-'B VB B A VA A νν解得 K 5.487536005300325232523BA VBVA BVB A VA =+⨯+⨯=++=++='RR RT RT C C T C T C T因平衡时温度、压强都相等,且都是1mol ,所以体积也相等.()A B A A B B B A AA BA B A45021212p RT T p R p RT p RT V V V V =+=⎪⎪⎭⎫ ⎝⎛+=+='='νν 根据理想气体状态方程得到压强为atm 08.114505.478450A =⨯=⋅'=''='p T V T R p ν(2) He 气熵变⎰⎰⎰⎰''+=+==∆T T V V VVR TTC TVp E TQ S AAAd d d d d A VA A He He He ννK J 42.93002600300ln31.83005.487ln31.8232lnln23ABA A=⨯+⨯+⨯⨯=++'=T T T R T T R氧气熵变⎰⎰⎰⎰''+=+==∆T T V V VVR TTC TVp E TQ S BBB222d d d d d B VB B O O O ννK J 70.66002600300ln31.86005.487ln31.8252lnln25-=⨯+⨯+⨯⨯=++'=BBA BT T T R T T R系统的熵变 K J 72.270.642.92O He =-=∆+∆=∆S S S9-23 已知在0℃1mol 的冰溶化为0℃的水需要吸收热量 6000 J ,求: (1)在0℃条件下这些冰化为水时的熵变;(2)0℃时这些水的微观状态数与冰的微观状态数的比. [解] (1) 温度不变时,熵变为 K J 0.222736000d 1d 0====∆⎰⎰Q T TQ S(2) 根据玻尔兹曼熵公式 冰冰Ω=ln k S 水水Ω=ln k S冰水冰水冰水ΩΩ=Ω-Ω=-=∆lnln ln k k k S S S根据(1)结果,得2423106.11038.10.22⨯⨯∆===ΩΩ-ee ekS 冰水9-24 把2mol 的氧从40℃冷却到0℃,若(1)等体(积)冷却;(2)等压冷却.分别求其熵变是多少?[解] 在等容压缩过程中 T C Q d d V ν= 因此 K J 68.5313273ln252d d d 273313VV -=⨯====∆⎰⎰⎰R TT C TTC TQ S νν在等压冷却过程中, T C Q d d p ν=K J 95.7313273ln272d d d 273313pp -=⨯====∆⎰⎰⎰R TT C TTC TQ S νν9-25 取1mol 理想气体,按如图所示的两种过程由状态A 到达状态C . (1)由A 经等温过程到达状态 C ;(2)由A 经等体(积)过程到达状态B ,再经等压过程到达状态C . 按上述两种过程计算该系统的熵变A C S S -.已知A C 2V V =,A C 21p p =.[解] (1) 根据理想气体状态方程得 RV p RV p T A A AA A ==ν因此等温过程中熵变为⎰⎰⎰⎰====∆V VRTT T Vp T QTQS C Ad 1d d d AAAν2ln lnd AC AA CAR V V R VV T RT V V ===⎰(2) A →C 与A →B →C 两过程初末状态相同,熵是状态函数,只与初末位置有关,因此两过程熵变相同等于2ln R .或:根据理想气体状态方程得 A A BB B 211V p RRV p T ⋅==νA →B →C 过程熵变等于A →B 等容过程和B →C 等压过程中熵变的和⎰⎰⎰⎰+=+=+=∆CBB ACBB ATTC TTC TQ TQ S S S d d d d p V 21νν2ln 2ln 2ln p V R C C =+-=。
大学物理下课后题答案12章中国石油大学(华东)

12章习题参考答案12-1答案:1-5 DBADC 6-10 CDDAD 11-15 DDDAB 12-2 1、E R 221π 2、Sq 022ε3、略4、3028Rqdεπ,方向为从O 点指向缺口中心点5、aq 08πε-12-3真空中一长为L 的均匀带电细直杆,总电量为q ,试求在直杆延长线上到杆的一端距离为d 的点P 的电场强度。
[解] 建立如图所示的坐标系Ox ,在距O 点为x 处取电荷元x Lqx q d d d ==λ,它在P 点产生的电场强度为()()x x d L Lq x d L qrq E d 41d 414d d 202020-+=-+==πεπεπε则整个带电直导线在P 点产生的电场强度为()d L d q x x d L Lq E L+=-+=⎰2041d 41πεπε故 ()i d L d qE+=04πε12-4用绝缘细线弯成的半圆环,半径为R ,其上均匀地带有正电荷Q ,试求圆心处点O 的电场强度。
[解] 建立坐标系如图,在半圆环上取微元d l ,θd d R l =,则 l RQq d d π=, q d 在O 点的场强 20204d 4d d R lR Q R q E πεππε== 从对称性分析,y 方向的场强相互抵消,只存在x 方向的场强Ed Oxxq d d λ=θεπθθεπθd 4sin d sin 4sin d d 202302x RQ l RQ E E =⋅=⋅= 2020202x x 2d 4sin d R QR Q E E επθεπθπ===⎰⎰i R Q E o 222επ=12-5一半径为R 的无限长半圆柱面形薄筒,均匀带电,单位长度上的带电量为λ,试求圆柱面轴线上一点的电场强度E 。
[解] 建立坐标系如图,在无限长半圆柱面形薄筒上取l d 的窄条,l d 对应的无限长直线单位长度所带的电量为θπλθπλd d d ==R R q 它在轴线O 产生的场强的大小为RR qE 0202d 2d d επθλπε==因对称性y d E 成对抵消。
油层物理学答案

油层物理学答案【篇一:油层物理课后习题答案】合物的质量组成换算为物质的量的组成。
气体混合物的质量组成如下:ch4?40%,c2h6?10%,c3h8?15%,c4h10?25%,c5h10?10%。
解:按照理想气体计算:2.已知液体混合物的质量组成:c3h8?10%,c4h10?35%,c5h12?55%.将此液体混合物的质量组成换算为物质的量的组成。
解:3.已知地面条件下天然气各组分的体积组成:ch4?96.23%,c2h6?1.85%,c3h8?0.83%,c4h10?0.41%, co2?0.50%,h2s?0.18%。
若地层压力为15mpa,地层温度为50oc。
求该天然气的以下参数:(1)视相对分子质量;(2)相对密度;(3)压缩因子;(4)地下密度;(5)体积系数;(6)等温压缩系数;(7)粘度;(8)若日产气为104m3,求其地下体积。
解:(1)视相对分子质量mg??(yimi)?16.836(2)相对密度gmgma16.8360.580552 29(3)压缩因子 pr?p15t50?273??3.244 tr1.648 pc4.624tc196.02(4)地下密度mpmg15?16.836?g=111.95(kg/m3)vzrt0.84?0.008314?(50?273)(5)体积系数vgfvgscznrtpt0.101325273?50pz?sc0.84?6.255?10?3(m3/标m3)nrtscptsc15273?20pscbg?(6)等温压缩系数1.6480.523.244cg?cgrtrpc?tr=0.52=0.068(mpa?1)4.624?1.648(7)粘度0.01175016.8361.6481.43.244gg/g1g11.40.01170.01638(mpas)(8)若日产气为104m3,求其地下体积。
vgf?bgvgsc?6.255?10?3?104?62.55(m3)4.知常压下天然气各组分的体积组成:ch4?87.0%,c2h6?4.0%,c3h8?1.0%,c4h10?0.5%, n2?7.5%。
2大学物理课后习题详解(第二章)中国石油大学

2-1 质量为m 的子弹以速率0v 水平射入沙土中,设子弹所受阻力与速度反向,大小与速度成正比,比例系数为k ,忽略子弹的重力,求:(1)子弹射入沙土后,速度大小随时间的变化关系; (2)子弹射入沙土的最大深度。
[解] 设任意时刻子弹的速度为v ,子弹进入沙土的最大深度为s ,由题意知,子弹所受的阻力 f = - kv(1) 由牛顿第二定律 tv m ma f d d ==即 tv m kv d d ==-所以t mk vv d d -= 对等式两边积分⎰⎰-=tvvt mkvv 0d d 0得 t mk v v -=0ln因此 tmk ev v -=0(2) 由牛顿第二定律 xv mvtx x v mt vm ma f d d d d d d d d ====即 xv mv kv d d =-所以 v x mk d d =-对上式两边积分 ⎰⎰=-0d d v sv x m k得到 0v s m k -=-即 kmv s 0=2-2 质量为m 的小球,在水中受到的浮力为F ,当它从静止开始沉降时,受到水的粘滞阻力为f =kv (k 为常数)。
若从沉降开始计时,试证明小球在水中竖直沉降的速率v 与时间的关系为⎪⎪⎭⎫ ⎝⎛--=-m kt e kF mg v 1 [证明] 任意时刻t 小球的受力如图所示,取向下为y 轴的正方向,开始沉降处为坐标原点。
由牛顿第二定律得tv mma f F mg d d ==--即 tv mma kv F mg d d ==-- 习题2-2图整理得mt kvF mg v d d =--对上式两边积分⎰⎰=--tvm tkvF mg v 00d d得 mkt Fmg kv F mg -=---ln即 ⎪⎪⎭⎫ ⎝⎛--=-m kt e kF mg v 12-3 跳伞运动员与装备的质量共为m ,从伞塔上跳出后立即张伞,受空气的阻力与速率的平方成正比,即2kv F =。
求跳伞员的运动速率v 随时间t 变化的规律和极限速率T v 。
油层物理最新习题 有答案 第二章

4.6 第二章油层物理选择题2-1石油是()。
A.单质物质;B.化合物;C.混合物;D.不能确定答案为C。
2-2 对于单组分烃,在相同温度下,若C原子数愈少,则其饱和蒸汽压愈(),其挥发性愈()。
A.大,强B.大,弱C.小,强D.小,弱答案为A2-3 对于双组分烃体系,若较重组分含量愈高,则相图位置愈();临界点位置愈偏()。
A.高左;B.低,左;C.高,左;D.低,右答案为D2-4 多级脱气过程,各相组成将()发生变化,体系组成将()发生变化。
A.要,要;B.要,不C.不,要;D.不,不。
答案为A2-5 一次脱气与多级脱气相比,前者的分离气密度较(),前者的脱气油密度较()。
A.大,大;B.大,小;C.小,大;D.小,小答案为A2-6 单组分气体的溶解度与压力(),其溶解系数与压力()。
A.有关,有关;B.有关,无关;C.无关,有关;D.无关,无关。
答案为B2-7 就其在相同条件下的溶解能力而言,CO2、N2、CH4三者的强弱顺序为:A.CO2>N2>CH4; B.N2>CH4>CO2 C.CH4>CO2>N2 D.CO2>CH4>N2答案为D2-8 若在某平衡条件下,乙烷的平衡常数为2,此时其在液相中的摩尔分数为20%,则其在气相中的摩尔分数为()。
A.10%B.80%C.40%D.20%答案为C2-9 理想气体的压缩系数仅与()有关。
A.压力;B.温度;C.体积D.组成答案为A2-10 在相同温度下,随压力增加,天然气的压缩因子在低压区间将(),在高压区间将()。
A.上升,上升;B.上升,下降;C.下降,上升;D.下降,下降。
答案为C2-11 天然气的体积系数恒()1,地层油的体积系数恒()1。
A.大于,大于;B.大于,小于;C.小于,大于;D.小于,小于。
答案为C2-12 天然气的压缩系数将随压力增加而(),随温度增加而()。
A.上升,下降;B.下降;上升C.上升,上升D.下降,下降答案为B2-13 形成天然气水化物的有利条件是()。
油层物理课后习题答案

第一章 储层岩石的物理特性24、下图1-1为两岩样的粒度组成累积分布曲线,请画出与之对应的粒度组成分布曲线,标明坐标并对曲线加以定性分析。
图1-1 两岩样的粒度组成累积分布曲线答:粒度组成分布曲线表示了各种粒径的颗粒所占的百分数,可用它来确定任一粒级在岩石中的含量。
曲线尖峰越高,说明该岩石以某一粒径颗粒为主,即岩石粒度组成越均匀;曲线尖峰越靠右,说明岩石颗粒越粗。
一般储油砂岩颗粒的大小均在1~之间。
粒度组成累积分布曲线也能较直观地表示出岩石粒度组成的均匀程度。
上升段直线越陡,则说明岩石越均匀。
该曲线最大的用处是可以根据曲线上的一些特征点来求得不同粒度属性的粒度参数,进而可定量描述岩石粒度组成的均匀性。
曲线A 基本成直线型,说明每种直径的颗粒相互持平,岩石颗粒分布不均匀;曲线B 上升段直线叫陡,则可看出曲线B 所代表的岩石颗粒分布较均匀。
30、孔隙度的一般变化范围是多少常用测定孔隙度的方法有哪些影响孔隙度大小的因素有哪些答:1)根据我国各油气田的统计资料,实际储油气层储集岩的孔隙度范围大致为:致密砂岩孔隙度自<1%~10%;致密碳酸盐岩孔隙度自<1%~5%;中等砂岩孔隙度自10%~20%;中等碳酸盐岩孔隙度自5%~10%;好的砂岩孔隙度自20%~35%;好的碳酸盐岩孔隙度自10%~20%。
3)岩石孔隙度的测定方法有实验室内直接测定法和以各种测井方法为基础的间接测定法两类。
间接测定法影响因素多,误差较大。
实验室内通过常规岩心分析法可以较精确地测定岩心的孔隙度。
4)对于一般的碎屑岩 (如砂岩),由于它是由母岩经破碎、搬运、胶结和压实而成,因此碎屑颗粒的矿物成分、排列方式、分选程度、胶结物类型和数量以及成岩后的压实作用(即埋深)就成为影响这类岩石孔隙度的主要因素。
44、试推导含有束缚水的油藏的综合弹性系效计算式)(w w o o f C S C S C C ++=*φ其中:*C ——地层综合弹性压缩系数;fC ——岩石的压缩系效; oC ——原油压缩系效; wC ——地层水压缩系效;oS 、wiS ——分别表示含油饱和度和束缚水饱和度。
【DOC】-中国石油大学华东2007-2008学年第一学期《油层物理》(试题)(答案详解)

中国石油大学华东2007-2008学年第一学期《油层物理》(试题)(答案详解)2007-2008学年第一学期《油层物理》试卷(闭卷)专业班级姓名学号开课系室石油工程学院油藏工程系考试日期2007年12月题号得分阅卷人一二三四总分一、填空题(每空0.5分,共15分)1.常用的岩石的粒度组成的分析方法有:薄片法、筛析法和沉降法,其中沉降法用来分析粒经小于40μm的颗粒。
2.储层流体包括、、。
3.一般来说,岩石的亲水性越强,束缚水饱和度越大(越大、越小、不变);岩石中泥质含量越高,束缚水饱和度越大(越大、越小、不变)。
4.低压下天然气的粘度随轻组分含量的增加而增加,随温度的升高而增加。
5.地层油的粘度随原油中轻组分含量的增加而减小,随地层温度的增加而减小,当地层压力大于地层油饱和压力时随地层压力的减小而减小,当地层压力小于地层油饱和压力时随地层压力的减小而增加。
6.在储集岩石中,不同类型的胶结物具有不同的特性,泥质胶结物的特性是遇水膨胀;灰质胶结物的特性是遇酸反应;硫酸盐胶结物的特性是高温脱水。
7.随着油藏的开发,油藏压力降低,这会导致岩石孔隙度变小(变大、变小、不变),岩石渗透率变小(变大、变小、不变)。
8.在等径球形颗粒模型中,岩石颗粒越大,岩石孔隙度不变,岩石比面越小,岩石的绝对渗透率越大。
9.与多级分离相比,接触脱气的特点是分离出的气量较多,轻质油组分较多,得到的地面油量较少。
10.在亲水岩石中,水驱油(水驱油、油驱水)过程是吸吮过程,油驱水(水驱油、油驱水)过程是驱替过程;毛管力是水驱油的动力(动力、阻力),润湿角越大,越不利于(有利于、不利于)水驱油。
评分标准:每空0.5分,共15分。
二、名词解释(每题2分,共16分)1、天然气的体积系数:在地面标准状态下(20°C,0.101MPa)单位体积天然气在地层条件下的体积。
共4页第1页2、比面:单位体积岩石的总表面积。
3、润湿:液体在分子力的作用下在固体表面的流散现象。
中国石油大学物理答案9章习题解答.docx

习题99-3. 一轻弹簧在60N 的拉力下伸长30cm 。
现把质量为4kg 物体悬挂在该弹簧的下端,并 使之静止,再把物体向下拉10cm,然后释放并开始计吋。
求:(1)物体的振动方程;(2)物 体在平衡位置上方5cm 时弹簧対物体的拉力;(3)物体从笫一次越过平衡位置时刻起,到它 运动到上方5cm 处所需要的最短时间。
[解](1)取平衡位置为坐标原点,竖直向下为正方向,建立坐标系=200N/m A = 0.1m设振动方程为O ・l = O ・lcos0 0 = 0(2)设此时弹簧对物体作用力为凡则(3)设第一次越过平衡位置时刻为则第一次运动到上方5cm 处时刻为匚,则一 0.05 = 0.1 cos (7.07r 2) t 2 = 2刃(3 x 7.07)故所需最短时间为:△f =為—心=0.074s9-4. 一质量为M 的物体在光滑水平面上作谐振动,振幅12cm,在距平衡位置6cm 处, 速度为24cm-s'1,求:⑴ 周期T ; (2)速度为12cm ・s"时的位移。
[解]⑴ 设振动方程为x = Acos@f+ 0)cm 以 A = 12cm 、x = 6cm 、v = 24cm • s"1 代入,得:6 = 12cos(er + 0) 24 = -1269 sin (cot + cp)利用 sin 2(twt + ^) + cos 2(ax +(p)=\ 则因而有F = 200x(0.2-0.05)= 30N0 = 0」cos (7.07f Jr, =0.5龙/7・0730x1 O'2k 200解得:0 =-龙/4 A= 10.6cm故振动方程为:x = 10.6 cos(10z 一 ^/4)cm解得473 co- -------⑵以v = 24cm-s _l 代入,得:解得: 所以故2+(24、 11<-1269>12 = -12tysin (69/ + ^) = -16^/3 sin (69/ + °) sin{cot + 切= cos 伽 + 卩)=土乎卜 ±10.8cm兀=12 cos (0f + 切=12 x ±9-5. 一谐振动的振动曲线如图9-5所示,[解]设振动方程为 x = A cos {a )t + °)根据振动曲线可画出旋转矢量图由图可得:0) = —^- =Ar故振动方程为%=,0COSl?9-6. 一质点沿x 轴作简谐振动,其角频率^10 rad s'',试分别写出以下两种初始状态的 振动方程:(1)其初始位移兀o=7.5 cm,初始速度心二75.0 cm s'1;⑵ 其初始位移也=7.5 cm, 初速度 v 0=-75.0cm-s _l o[解]设振动方程为兀=4cos(10/ + 0)7.5 = Acos0 75 = -lO4sin0T 巫co71 +39-7. 一轻弹簧在60 N 的拉力作用下可伸长30cm,现将一物体悬挂在弹簧的下端并在它 上面放一小物体,它们的总质量为4kg 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
来源于骄者拽鹏 习题11.将气体混合物的质量组成换算为物质的量的组成。
气体混合物的质量组成如下:%404-CH ,%1062-H C ,%1583-H C ,%25104-H C ,%10105-H C 。
解:按照理想气体计算:2.已知液体混合物的质量组成:%.55%,35%,1012510483---H C H C H C 将此液体混合物的质量组成换算为物质的量的组成。
解:3.已知地面条件下天然气各组分的体积组成:%23.964-CH ,%85.162-H C ,%83.083-H C ,%41.0104-H C , %50.02-CO ,%18.02-S H 。
若地层压力为15MPa ,地层温度为50C O 。
求该天然气的以下参数:(1)视相对分子质量;(2)相对密度;(3)压缩因子;(4)地下密度;(5)体积系数;(6)等温压缩系数;(7)粘度;(8)若日产气为104m 3,求其地下体积。
解:(1)视相对分子质量836.16)(==∑i i g M y M(2)相对密度58055202983616..M M ag g ===γ(3)压缩因子 244.3624.415===c r p p p 648.102.19627350=+==c r T T T(4)地下密度)(=)(3/95.11127350008314.084.0836.1615m kg ZRT pM V m g g +⨯⨯⨯===ρ(5)体积系数)/(10255.6202735027315101325.084.0333m m T T p p Z p nRT pZnRTV V B sc sc scsc gscgf g 标-⨯=++⨯⨯=⋅⋅===(6)等温压缩系数3.2441.6480.52[])(==1068.0648.1624.452.0-⨯⋅⋅=MPa T P T C C rc rgrg(7)粘度16.836500.01171.41.6483.244[])(01638.00117.04.1/11s mPa g g g g ⋅=⨯=⨯=μμμμ(8)若日产气为104m 3,求其地下体积。
)(55.621010255.6343m V B V gsc g gf =⨯⨯==-4.知常压下天然气各组分的体积组成:%0.874-CH ,%0.462-H C ,%0.183-H C ,%5.0104-H C , %5.72-N 。
若相对密度为0.88,地层压力为15MPa ,地层温度为38C O ,求天然气的压缩因子。
255.3608.415==ch P γ 565.172.19827338=+=rcH T查图得0.805CH Z =222(1)0.805(17.5%) 1.0367.5%0.822g CH N N N Z Z Y Z Y ∴=-+=⨯-+⨯=5.某天然气在温度为93.33C O 、压力为14.06MPa 时,视临界温度和视临界压力分别为225.19K 和5.538MPa ,在该天然气中,S H 2的摩尔分数为18.41%,2CO 的摩尔分数为1.64%,试计算含S H 2和2CO 的天然气压缩因子。
6.求相对密度为0.743,地层压力为13.6MPa ,地层温度为93.3C O 时天然气的压缩因子。
7.在压力为10MPa ,温度为40C O 的砂岩地层中储藏有天然气,其物质的量的组成为:%,7.7%,3.6%,0.10%,0.6%,0.7012510483624-----H C H C H C H C CH 设岩层孔隙度为20%,气体饱和度为80%,求13m 岩层体积中的天然气量(标3m ) 解:c 2.2534.43940273 1.244251.64c P P T T T γγ===+===①33g 0.101325(27340)0.5870.00635(/)10(27320)sc sc P TZ B m m PT ⨯+⨯===⨯+标gs 120%80%25.20()o g V V S B φ∴==⨯⨯=3地下标m②4g 2733.45810tB ZP-+=⨯⋅ 8.有一含气层(湿气),其地层压力为20MPa ,地层温度为75C O ,气体的相对密度为0.70,该气层的地下含气体积为3910m ,求该气层的储量。
5.10210.68950.7 4.61945132.2222116.66670.7213.8889204.32954.6194575273 1.627213.8889c c P T P T γγ=-⨯==+⨯===+==查0.835z =44752733.45810 3.458100.8350.00502420g T B Z P --+=⨯⨯⋅=⨯⨯⨯= 911100.005024 1.9910(m )gs g V V B ∴===⨯3标9.天然气的相对密度为0.70,地层温度为99C O ,地层压力为15.64MPa ,计算气体的体积系数。
10.某一地层气体在65.55C O 时,压缩因子Z 随压力P 的变化情况和表1.0所示。
表1.1试绘出Z 和P 的关系曲线,并用图解法确定压力分别为7,15及28MPa 处的斜率,然后再求出在这些压力下的气体压缩系数。
11.已知某气井深4554m ,地层压力为54.141MPa ,地面平均温度为17.0C O ,地温梯度为0.02C O /m ,天然气的压缩因子为1.148,相对密度为0.574(干气),求天然气的地下密度。
45540.0217.0108.08t =⨯+=(℃)0.57428.9716.464g g g g a aM r M r M M =⇒==⨯=g/mol3484.4g g g a g g g MgPV ZRT MaM M P r M PV ZRT ZRTPZT ργρ=⇒===⇒=12.已知某气井地层压力为53.752MPa ,地层温度为105.58C O ,根据天然气分析知,相对密度为0.57,临界压力为4.762MPa ,临界温度为192.3C O ,求天然气的地下密度。
13.气体组成如表1.2所示。
表1.2若地层压力为136MPa ,地层温度为99C O ,求气体的粘度。
14.试估算某一凝析气藏气在49.2MPa 和104.44C O 下的粘度。
已知这一气体的相对密度为0.90,并含有摩尔分数为2%的2N ,4%的2CO 和6%的S H 2。
15.天然气的相对密度为0.743,地层压力为13.6MPa ,地层温度为93.3C O ,求天然气的绝对粘度和运动粘度。
16.某油田气的组成如表1.3所示。
表1.3若油层温度为32C O ,油层压力为8.3MPa 。
(1)求气体的压缩因子; (2)求气体的体积系数;(3)若油井日产气100003m (标准状态),它在地下所占的体积为多少? (4)计算该气体的压缩系数; (5)计算该气体的粘度。
(1)8.3 1.8094.5880.8232273 1.477206.44r P Z T γ⎫==⎪⎪⇒=⎬+⎪==⎪⎭(2)42733.45810tBg ZP-+=⨯ (3)40.010*******.2g g os V B V -=⨯=⨯=(m 3) (4)由P γ、T γ查[]gr C T P γγ⨯-图, 得0.142gr g C C →=[]()g gr C C T P T γγγ=⨯111[()]111[0.0625]4.5881.8090.820.14g c ZC P P Z P γγ∂=-∂=+⨯= (5)11(0.01258()n ngi i i i x x mPa s μμ====∑∑由P γ、T γ查得,1 1.251.250.12580.0157()g g g mPa s μμμ==⨯=⋅17.有一凝析气藏。
有其流体的高压物性分析得到压力-温度关系如图1.1所示,图中A 点代表气藏压力及密度。
试分析:(1)此气藏在开采过程中的相态变化;(2)为了减少凝析油的损失,可采取什么措施?为什么?18.根据某油田所取油样的高压物性试验,得到如图1.2所示的压力—温度关系图,油藏的压力及温度如A 点所示,试说明此油藏的类型,并分析开采过程中的变化情况。
19.原始气体组成列表于表 1.4中,以致原始地层压力i p =26.78MPa ,地层温度T =346.68K 。
计算地层温度下(收敛压力CV P =35.0MPa ,由其他资料得+7C 的临界温度为596.9K )。
表1.4地层温度不同压力下的平衡常数20.某油井产物的i n 值和20C O 下的平衡常数见表1.5。
表1.5试计算一次脱气分离出来的液量,并对分出液量进行对比。
(已知脱气温度:20C O ;一次脱气压力:0.1MPa ;多级脱气时,一、二、三、四级脱气压力分别为5.0,3.0,1.0,0.1 MPa 。
)21.某地油层样品,在地层条件下原始体积为3103cm ,当地温降到15.5C O ,压力降到大气压时,液体体积减少到2043cm ,并析出218⨯1033cm 气体,计算天然气在原油中的溶解度。
解:)/(10085.1)(4.2215.1527329310218333osgs 33o g gs m m V V Rs m T T V V 标标⨯===+⨯⨯=⨯=22.在饱和压力下,13m 密度为8763/m kg 的原油中溶解相对密度为0.75的天然气1383m ,在饱和压力下体积系数为1.42,求饱和压力下原油的密度。
解:油的质量:876kg/m 331m ⨯=876kg气的质量:kgV M m M M g g g g ga g ag 72.12413875.0205.1/kg 90375.01075.0205.1205.175.033g =⨯⨯===⨯⨯=∴====ρρρρργ饱和条件下油密度3/7.70442.1172.100072.124876m kg B V V M o sc gfgf gf =⨯=+==ρ23.某断块地层压力为22.55 MPa ,地层温度为72C O ,泡点压力为21.84MPa ,油气分析数据表1.6和表1.7,求当地层压力分别为21.0MPa 及20.0MPa 时的两相体积系数。
表1.6地层油的分析数据(泡点压力为21.84MPa )g γ24.某一地层油在原始压力P i =18.5MPa 时的体积为103cm ;当地层压力降到14MPa 时,释放出的13.43cm 的气体后,油的体积为8.73cm ;原油在地面脱气后剩下的体积为7.83cm ,试求原始压力下油的体积系数、14MPa 时油的单相及两相体积系数。
解:(1))(282.18.71033m m B oi ==(2),14MPa P = )(115.18.77.833m m B o ==)(833.28.74.137.833m m B t =+=25.由某一地层油样的高压物理性质试验,得出如图1.3所示的溶解度曲线。
